Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
SCHMIDT, KLAUS
and
VERSHIK, ANATOLY
2009.
Algebraic Polymorphisms– ERRATUM.
Ergodic Theory and Dynamical Systems,
Vol. 29,
Issue. 4,
p.
1369.
Cuntz, Joachim
and
Vershik, Anatoly
2013.
C*-Algebras Associated with Endomorphisms and Polymorphisms of Compact Abelian Groups.
Communications in Mathematical Physics,
Vol. 321,
Issue. 1,
p.
157.
Бухштабер, Виктор Матвеевич
Buchstaber, Victor Matveevich
Гордин, Михаил Иосифович
Gordin, Mikhail Iosifovich
Ибрагимов, Ильдар Абдуллович
Ibragimov, Il'dar Abdullovich
Кайманович, Вадим А
Kaimanovich, Vadim A
Кириллов, Александр Александрович
Kirillov, Aleksandr Aleksandrovich
Лодкин, Андрей Александрович
Lodkin, Andrei Aleksandrovich
Новиков, Сергей Петрович
Novikov, Sergei Petrovich
Окуньков, Андрей Юрьевич
Okounkov, Andrei Yur'evich
Ольшанский, Григорий Иосифович
Olshanskii, Grigorii Iosifovich
Петров, Федор Владимирович
Petrov, Fedor Vladimirovich
Синай, Яков Григорьевич
Sinai, Yakov Grigor'evich
Фаддеев, Людвиг Дмитриевич
Faddeev, Lyudvig Dmitrievich
Фомин, Сергей Владимирович
Fomin, Sergei Vladimirovich
Цилевич, Наталия Владимировна
Tsilevich, Natalia Vladimirovna
Якубович, Юрий Владимирович
and
Yakubovich, Yurii Vladimirovich
2014.
Анатолий Моисеевич Вершик (к восьмидесятилетию со дня рождения).
Успехи математических наук,
Vol. 69,
Issue. 1(415),
p.
173.
Arzumanian, V.
Grigoryan, S.
and
Kuznetsova, A.
2014.
Operator algebras associated with multi-valued mappings.
Lobachevskii Journal of Mathematics,
Vol. 35,
Issue. 2,
p.
51.
Arzumanian, V.
and
Grigoryan, S.
2018.
Functional Description of C*-Algebras Associated with Group Graded Systems.
Lobachevskii Journal of Mathematics,
Vol. 39,
Issue. 9,
p.
1300.
Jorgensen, Palle E.T.
and
Pearse, Erin P.J.
2019.
Continuum versus discrete networks, graph Laplacians, and reproducing kernel Hilbert spaces.
Journal of Mathematical Analysis and Applications,
Vol. 469,
Issue. 2,
p.
765.
Neretin, Yu. A.
2021.
Polyhomomorphisms of locally compact groups.
Sbornik: Mathematics,
Vol. 212,
Issue. 2,
p.
185.
Neretin, Yurii Aleksandrovich
2021.
Полигомоморфизмы локально компактных групп.
Математический сборник,
Vol. 212,
Issue. 2,
p.
53.
Uchida, Miki
Takei, Takahiro
Kumada, Nobuhiro
Tsutsui, Hideyuki
Azuma, Kazuki
and
Toyama, Takashi
2022.
Low temperature synthesis of aluminum nitride from anhydrous aluminum chloride-organic amine complex.
Journal of the Ceramic Society of Japan,
Vol. 130,
Issue. 8,
p.
707.
Jorgensen, Palle
and
Tian, James
2024.
Recent Developments in Fractal Geometry and Dynamical Systems.
Vol. 797,
Issue. ,
p.
37.
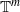 if and only if the associated rational matrix lies in
if and only if the associated rational matrix lies in 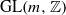 . We characterize toral polymorphisms which are factors of toral automorphisms.
. We characterize toral polymorphisms which are factors of toral automorphisms.