INTRODUCTION
The past 60 years have been a fruitful period for egalitarian political philosophy and social science. This period is long enough to include John Harsanyi's (Reference Harsanyi1953, Reference Harsanyi1955) contributions to the formulation of the veil of ignorance and utilitarianism, John Rawls's (Reference Rawls1971) transformative approach to the theory of distributive justice, Amartya Sen's (Reference Sen and McMurrin1980) amendments to Rawls involving the notions of functioning and capability, and Ronald Dworkin's (Reference Dworkin1981) resource egalitarian proposal. Dworkin, in particular, exploited a distinction that was only implicitly dealt with by Rawls, that there is a cut, perhaps partially obscure, between those characteristics of a person's environment, genetic and social, for which he should not be held responsible, and those for which he should be. Dworkin defined the cut as separating a person's resources from his preferences, a cut which G.A. Cohen (Reference Cohen1989) later criticized as being misplaced, because a person's preferences are in part endogenously determined by his environment, and hence he cannot be consistently held responsible for all aspects of his choices.
At the philosophical level, Dworkin's contribution changed the nature of the discussion in egalitarian theory, because it introduced, as key for that theory, personal responsibility, which had, generally speaking, been important only for right-wing political philosophy. Dworkin, moreover, went further than most philosophers: he proposed an economic allocation rule to implement his conception of resource egalitarianism, and this invited economists into the discussion. In a word, Dworkin proposed a thought experiment involving a thin veil of ignorance (thin, compared with the Rawlsian veil); behind the veil lived souls who represented persons in the world, who knew their person's preferences – over risk in particular – but not the resources their persons would enjoy. Resources, importantly, include alienable ones, like wealth, but also inalienable ones, like talents and birth families. Dworkin ran an insurance market among these souls, who were each equally financed to purchase insurance against their persons’ being born unlucky in resources. Presumably rational souls would purchase insurance to compensate their person, should she be born unlucky in resources. Thus, the thin veil allowed the souls to know just what Dworkin had deemed persons to be responsible for (their preferences) but not know their resources (whose distribution was, to use the Rawlsian phrase, morally arbitrary). It was an ingenious device for computing a non-morally-arbitrary distribution of resources – for at the equilibrium in the insurance market, the society (consisting of souls whose preferences matched those in actual society) would have determined a distribution of resources consonant with their preferences, and from a starting position of wealth equality (wealth, that is, in the currency that was used behind the veil). Presumably, a soul would buy insurance not only to pay out to his person, should that person be born poor, but also should she be born untalented or handicapped. Thus the distribution of alienable resources would adjust so as to compensate persons for the distribution of inalienable ones.
Unfortunately, it turns out that the insurance mechanism does not always work the way Dworkin hypothesized it would. This was initially noticed by Roemer (Reference Roemer1985); the latest form of that critique of the Dworkin insurance mechanism is available in Moreno-Ternero and Roemer (Reference Moreno-Ternero and Roemer2008). In brief, a rational decision maker (here, a soul) might transfer resources to his person in ‘good’ states (when his person was born talented) and allow his person to be relatively poorly resourced in ‘bad’ states, because the payoff to possessing wealth in good states might more than balance the paucity of wealth in bad states. This could happen even if all souls were risk averse. Consequently, although Dworkin's philosophical idea was attractive, it was not properly implemented by his hypothetical insurance scheme. Indeed, one was left with the choice of either rejecting the insurance scheme as an attractive allocation rule, or retaining it, and rejecting the fundamental tenet of resource egalitarianism, that persons should be compensated for poor resource endowments.
Further philosophical contributions were made by Cohen (Reference Cohen1989) and Richard Arneson (Reference Arneson1989), who argued that, rather than equalizing resources, the right way to implement Dworkin's responsibility-sensitive intuitions was to equalize ‘opportunities for welfare’. Cohen (Reference Cohen1989) advocated a related ‘access to advantage’. Inspired by these amendments, Roemer (Reference Roemer1993, Reference Roemer1998) proposed an algorithm for equalizing opportunities which did not rely upon a veil-of-ignorance thought experiment.
Roemer's approach, however, was only one possible rectification of Dworkin's insurance proposal, and other authors, most notably Marc Fleurbaey and Francois Maniquet, developed an alternative approach to the compensation/responsibility dyad, also not relying on the veil of ignorance. This work has been recently codified and extended in Fleurbaey (Reference Fleurbaey2008). The present paper offers some reflections on the contrasts between Roemer's approach and that of Fleurbaey and Maniquet.
Before proceeding, it is worthwhile to comment on the fact that Harsanyi, Rawls and Dworkin all relied on veil-of-ignorance thought experiments (although, strangely, Dworkin (Reference Dworkin1981) denied doing so), while Cohen, Arneson, Roemer, Fleurbaey and Maniquet do not. My own view is that the Rawlsian project – of deriving equality from impartiality and rationality – is unrealizable. It is even impossible to derive equality from impartiality, rationality and risk aversion. Something more is required, like solidarity, reciprocity (as in Kolm Reference Kolm2008) or community (as in Cohen Reference Cohen2009). As the veil of ignorance is a device for insuring impartiality, it does not suffice to determine egalitarian outcomes (see Roemer Reference Roemer2002), unless some degree of solidarity or community is postulated to motivate the souls cogitating behind it. But if that degree of solidarity is assumed, who needs the veil of ignorance or original position? One can proceed more directly to an egalitarian conclusion.
Thus, egalitarians might be deflated, because Rawls's hope, of deriving an egalitarian political philosophy from almost nothing (that is, impartiality and the moral arbitrariness of the birth lottery) fails. We are left with a more modest agenda, of arguing for equality conditional upon humans’ caring about each other, that is, having solidaristic preferences or values. We might further argue with non-egalitarians either that people should care about each other or that they do, but we cannot maintain, so I believe, that totally self-interested, risk averse agents would advocate equality in the appropriate environment for rational reflection.
In the next section, I describe some simple economic environments which I'll use to formulate the economic approaches to equality of opportunity, or in Fleurbaey's (Reference Fleurbaey2008) language, responsibility-sensitive egalitarianism. In the sections after that, I will propose a generalization of Roemer's (Reference Roemer1998) algorithm, and then describe Fleurbaey's egalitarian-equivalent allocation rule. I will offer some reflections upon the philosophical differences in the approaches along the way.
1. ECONOMIC ENVIRONMENTS
We have a society whose members’ welfare is described by a function v(x, e, j), where x is consumption of a resource, e is effort and j is the person's type. The type summarizes all aspects of the person's social and biological environment that influence his behaviour and realization of the outcome, for which society deems him to be not responsible. Effort is a measure of the chosen actions the individual takes, which influence the outcome in a positive way: thus v is an increasing function of x and e. In particular, v must be distinguished from the subjective utility function that represents a person's preference order, which is normally construed to be decreasing in effort. It is incorrect to say, however, that a person is (fully) responsible for his effort. For the distributions of effort will generally be different in different types, and the characteristics of those distributions are therefore an aspect of the type – a circumstance. An individual is only partially responsible for his effort: to wit, I say he is responsible for his rank on the distribution of effort of his type. Denote the set of types by J = {1, 2, . . ., J}. The fraction of type j individuals in the society is fj.
Consider, first, the pure resource allocation problem. There is an amount of a good, ![]() per capita, to be distributed among the individuals. A feasible allocation is a distribution of this resource to the population as a function of their types and their effort. Denote such an allocation by X. In general the distributions of effort in the types are themselves functions of the allocation of the resource: thus, we denote the distribution of effort in type j if the allocation is X by Gj(e; X). The effort expended by an individual of type j who sits at rank y ∈ [0, 1] of the distribution of effort of his type is denoted (Gj)−1(y; X). Because y, not e, is the ethically relevant quantity in our theory, we will denote an allocation as
per capita, to be distributed among the individuals. A feasible allocation is a distribution of this resource to the population as a function of their types and their effort. Denote such an allocation by X. In general the distributions of effort in the types are themselves functions of the allocation of the resource: thus, we denote the distribution of effort in type j if the allocation is X by Gj(e; X). The effort expended by an individual of type j who sits at rank y ∈ [0, 1] of the distribution of effort of his type is denoted (Gj)−1(y; X). Because y, not e, is the ethically relevant quantity in our theory, we will denote an allocation as
Thus, a feasible allocation satisfies:
Let me reiterate the important point, which develops a statement made in the Introduction, that we measure effort by the rank of a person's effort on the effort distribution of his type, rather than by his absolute effort. I pointed out that Cohen criticized Dworkin for holding persons entirely responsible for their preferences (unless, Dworkin said, these preferences were compulsions or addictions), because preferences are in part determined by one's environment. For example, think of ‘years of school attendance’ as a measure of effort, where the objective of interest is ‘wage earning capacity’. The distribution of effort in a type is a characteristic of the type, not of any individual within it, and as such, if a person is not to be held responsible for his type, he should not be responsible for characteristics of his type's distribution of effort. Now one major reason that a person of disadvantaged circumstances may choose to drop out of secondary school is that that behaviour is frequent in his type – in other words, it is because he belongs to a type with an effort distribution that has a low mean. He should not be held responsible for that low mean, and so we require a measure of effort which sterilizes out the size of the mean. The obvious choice is to measure a person's effort not by the years of school he attended but by the rank of his years of school attended in the distribution of years of school attended of his type. That is the purpose of the formalism above.
To simplify and make concrete the discussion, I will study a special case, which satisfies:
Assumption A
A1. The distributions Gj(e) are independent of X.
A2. v(x, e, j)=xaebKj, for some a, b ∈ (0, 1).
Assumption A1 is important and restrictive, for it says that the distributions of effort are not influenced by the state's policy – and, hopefully, that is not true in reality, because we would like state policy to influence effort. However, for the purposes of the present paper, the simplifying assumption is acceptable. Assumption A2 posits a simple form for the interaction of effort and resources.
We may write the welfareFootnote 1 of an individual at an allocation X = {xj(.)|j=1, . . ., J; y ∈ [0, 1]} as
Note that there are two conduits through which a person's type affects his outcome: the direct effect, through the third argument of v (i.e. Kj), and the indirect effect, through the second argument of v (i.e. the effect on the distribution of effort). Empirically, as will be noted below in section 7, the indirect effect is often very important, and so for policy purposes, it is important to use a notation which helps us to remember this.
Here are several examples. v measures a worker's wage at age 30, x is the amount of public resource per annum devoted to his education as a child, e is the amount of education he acquires, and j summarizes the effect of his family background on both the years of education he acquires and perhaps, through other channels, on his wage. It is well known that individuals from poorly educated parents in general acquire less education than individuals from highly educated parents. Thus, the family background (j) affects the distribution of effort, as well as having a direct effect on the development of the child.Footnote 2 A second example: v is health status, e is lifestyle quality, j is family background and x is medical resources. Here, I believe the model is too simple: I would rather say that circumstances and effort determine education, education and another effort determine lifestyle, and lifestyle and medical resources determine health. Thus, there are two loci at which effort enters.Footnote 3 A third example: ‘individuals’ are countries, v is GDP per capita, j summarizes the level of development and other physical characteristics and endowments of the country, e is the quality of governance in the country's institutions and x is a level of international aid.Footnote 4
Note that in these three applications, v is not a utility function that represents an individual's subjective preference order. In economics, we model education as being costly (a disutility) for the individual, and good governance in a country requires costly effort by politicians and bureaucrats. But, by hypothesis, effort here enters positively into the realization of the outcome. In most of the applications that interest me, v measures some outcome that is objective and observable about individuals, and the function v is not a representation of their subjective preferences. This reflects my intention that the theory be useful for policy makers. The Ministry of Health is interested in maximizing some distribution of life expectancy or quality-years of life, not subjective utility (e.g. it will try to discourage smoking, even though individuals may derive subjective pleasure from smoking); the Ministry of Education is interested in producing students who are well-educated, not happy students; and international lending institutions are interested in maximizing GDP per capita in countries, not the subjective utility of the country's politicians.
The standard economic hypothesis is that the choice of effort by the individual reflects the maximization of some subjective preference order. But that assumption is not necessary for the approach I propose: my approach takes as data not preference orders of individuals, but observed distributions of effort and circumstances. I contend that the theory, as I present it, does not require those who wish to use it to accept the rational-choice explanation of effort. Now it is certainly possible to take a more restrictive approach, which derives effort as the result of the maximization of a person's preference order over goods and effort, in which effort is costly. In this case, one would begin not with the objective functions v, but rather utility functions u, in which differential effort was due to a varying cost parameter in utility functions representing the psychic cost of effort expenditure to the individual. Effort would decrease utility in that formulation, and a person would be held responsible for the rank of his idiosyncratic cost parameter in the distribution of that cost parameter in his type. Although I will take this approach in the tax problem that I describe later in this section, I generally eschew it, as a less desirable and more restrictive approach than the one based on the outcome functions v.
This posture also reflects my preference to apply the theory to problems where outcomes are observable, for I believe that in all policy applications, planners will be concerned to deliver equity (here, equal opportunity) with respect to the achievement of a particular objective, which is the concern of their ministry.Footnote 5
That having been said, let me now describe a second economic environment, one designed for treating the optimal tax problem. In this case, I will begin, as students of optimal taxation do, with subjective preferences. Let the preferences of an agent over consumption (x) and years of education (s) be given by ![]() , some γ ∈ ℜ++. Call γ the agent's degree of ambition. There is a set of types J = {1, 2, . . ., J} and the distribution function of γ in type j is Gj. The frequency of type j in the population is fj. The wage a person earns is w=βs, some β > 0. The policy space is the set of affine tax policies, (t,b), where a person's after-tax consumption will be (1 − t)w+b. The tax policies are budget-balanced, so the per capita demogrant (or transfer) b is equal to per capita tax revenues.
, some γ ∈ ℜ++. Call γ the agent's degree of ambition. There is a set of types J = {1, 2, . . ., J} and the distribution function of γ in type j is Gj. The frequency of type j in the population is fj. The wage a person earns is w=βs, some β > 0. The policy space is the set of affine tax policies, (t,b), where a person's after-tax consumption will be (1 − t)w+b. The tax policies are budget-balanced, so the per capita demogrant (or transfer) b is equal to per capita tax revenues.
Facing a tax policy (t,b), the individual chooses a level of education, the solution of
which is s(t, γ)=(1 − t)βγ. It follows that per capita tax revenues, and b, are given by:
where ![]() is the average degree of ambition in the population.
is the average degree of ambition in the population.
We take people to be in part responsible for their degrees of ambition. As indicated, I define the degree of responsibility of an individual as the rank at which his degree of ambition lies, on the distribution of degrees of ambition of his type; that is, it is y where γ=(Gj)−1(y). Therefore we may write the utility of an individual as a function of the policy t and effort as:
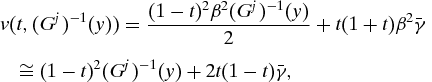
where at the end I have taken a ratio-scale transformation of v (that is, I have transformed it by the multiplicative factor 2/β2). Note that, while effort (s) enters negatively into utility, the effort rank (y) enters positively into the indirect utility v. The less ‘costly’ a person views effort (the larger his γ), the higher his eventual welfare v. However, recall that v is not the preference order over income and effort that directs a person's choices: that is summarized by u. A person is not free to choose his cost parameter – that is something that we view him as responsible for, although we do not provide the reason why we do. In this sense, the classical economic approach, of beginning with preferences, is a sort of Procrustean bed into which we can force the theory of equal opportunity, but it is not as natural, so I think, as beginning with the data of observed effort, circumstances and outcomes. Tradition requires, however, that in the optimal tax problem, we take the preference-based approach.
Finally, I remark that, like almost all the literature to date, I here ignore dynamic issues with regard to implementing equality of opportunity. Presumably, if an equal-opportunity policy succeeds, it will change the distribution of types in the next generation. A policy maker should be sensitive to this issue, and therefore be concerned with the long-run consequences of policy. Burak Ünveren and I (2012) have recently studied this problem, but I will not review that work here.
2. A GENERALIZATION OF THE EQUALITY-OF-OPPORTUNITY APPROACH
I next summarize the theory of equal opportunity, as expounded in Roemer (Reference Roemer1998). The ethical premise is that an individual is not responsible for his type, but is responsible for the rank of the distribution of effort at which he sits, within his type. The resource allocation is intended to compensate individuals for their disadvantageous circumstances, while allowing those who expended higher degrees of effort to benefit vis-à-vis others. Let us call the second feature rewards-to-effort.
I define the following function, associated with an allocation X = {xj(y)|j ∈ {1, . . ., J}, y ∈ [0, 1]}:
The difference between the welfares of individuals at the same value of y, but in different types, is ethically unjustifiable, according to the theory. In choosing an allocation, we desire to eliminate these differences. This is what Fleurbaey (Reference Fleurbaey2008) calls the compensation principle. On the other hand, it is perfectly all right if those who expend higher effort should do better. After Fleurbaey (Reference Fleurbaey2008), this is called the rewards-to-effort principle.
The compensation principle says we should make the function θ as ‘large’ as possible – thus, maximizing the welfare that the individuals who are the worst-off across types at any degree of effort achieve – while rewards-to-effort says that θ should be an increasing (or non-decreasing) function. There is, however, no unique way to make precise the idea that θ should be as large as possible. I proceed as follows. Let ![]() be the set of non-negative, weakly increasing functions on the unit interval. Let
be the set of non-negative, weakly increasing functions on the unit interval. Let ![]() be an increasing operator on Θ, that is, θ ≥ θ′ ⇒ Γ(θ) > Γ(θ′), where θ ≥ θ′ means that θ dominates θ′ and is strictly greater on a set of positive measure. Then we can write the general equal-opportunity program as:
be an increasing operator on Θ, that is, θ ≥ θ′ ⇒ Γ(θ) > Γ(θ′), where θ ≥ θ′ means that θ dominates θ′ and is strictly greater on a set of positive measure. Then we can write the general equal-opportunity program as:
![\[
\begin{array}{*{20}l}
{\max\, \Gamma (\theta )} \\
{{\rm subject}\,\,{\rm to}} \\
{(\forall y,j)v(x^j (y),(G^j )^{ - 1} (y),j) \ge \theta (y)\quad (GEOp)} \\
{\bar x \ge \sum {f_j \displaystyle\int {x^j (y)dy} } } \\
{\theta \in \Theta } \\
\end{array}
\]](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160202064828955-0409:S0266267112000156_eqnU3.gif?pub-status=live)
The point to be chosen is (θ, X). Notice that if Γ is a concave operator on Θ and v is concave in x, then (GEOp) is a concave program, and can be solved with standard methods.Footnote 6
In this article, I will often take Γ to be a member of the family:

with the convention that Γ0(θ) = ∫log (θ(y))dy.Footnote 7 Γρ is a concave operator for all ρ ∈ (−∞, 1]. Notice that if ρ = 1, we can write (GEOp) as:
![\[
\begin{array}{*{20}l}
{\max \displaystyle\int {\mathop {\min }\limits_j \tilde{v}^j (y;X)dy} } \\
{{\rm subject}\,{\rm to}} \\
{\bar x \ge \displaystyle\sum {f_j } \int {x^j (y)dy} } \\
{\theta ( \cdot ;X) \in \Theta } \\
\end{array}({\rm EOp})\]](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160202064828955-0409:S0266267112000156_eqnU4.gif?pub-status=live)
where we define ![]() . Program (EOp) is what I have defined previously (Roemer Reference Roemer1996, Reference Roemer1998) as the equal-opportunity program. The objective of (EOp) is what Fleurbaey (Reference Fleurbaey2008) calls ‘the mean of mins’, and program (EOp) is an instance of what he calls utilitarian reward.
. Program (EOp) is what I have defined previously (Roemer Reference Roemer1996, Reference Roemer1998) as the equal-opportunity program. The objective of (EOp) is what Fleurbaey (Reference Fleurbaey2008) calls ‘the mean of mins’, and program (EOp) is an instance of what he calls utilitarian reward.
We can summarize (GEOp) verbally. We associate the following value to a feasible allocation X. Compute the distributions of welfare for each type at X. The function ![]() (see its definition in eqn. 2.3) gives the welfare of those in type j, at the yth degree of effort, at the allocation X. Graph these functions for each j. The lower envelope of these functions is the function θ(·; X) associated with this allocation. We measure the ‘size’ of θ using the mapping Γ. The program says: choose the feasible allocation X that makes the associated function θ as large as possible. The function θ gives us the welfare of the worst-off individuals at each degree of effort y, across types. Our concern is to maximize the welfare of these worst-off individuals – but since there is a whole interval of them, we need to maximize some function of their welfares. That is the role of Γ.
(see its definition in eqn. 2.3) gives the welfare of those in type j, at the yth degree of effort, at the allocation X. Graph these functions for each j. The lower envelope of these functions is the function θ(·; X) associated with this allocation. We measure the ‘size’ of θ using the mapping Γ. The program says: choose the feasible allocation X that makes the associated function θ as large as possible. The function θ gives us the welfare of the worst-off individuals at each degree of effort y, across types. Our concern is to maximize the welfare of these worst-off individuals – but since there is a whole interval of them, we need to maximize some function of their welfares. That is the role of Γ.
This presentation shows that it is the function θ, induced by an allocation, which is of normative interest, and the objective of (EOp) emerges as a natural choice, because our aim is to make θ as large as possible. Of course, the family of evaluation functions {Γρ} is a natural one. Decreasing the value of ρ will flatten out the optimal function θ in (GEOp). As ρ approaches negative infinity, the objective of (GEOp) approaches ![]() , which would be the ‘extremist’ maximin objective, where individuals are taken to be not responsible for either their effort or their circumstances.Footnote 8
, which would be the ‘extremist’ maximin objective, where individuals are taken to be not responsible for either their effort or their circumstances.Footnote 8
The solution of (GEOp) under Assumption A is given by:
Proposition 1. Assume A. Let Γ = Γρ, some −∞ < ρ ≤ 1.
Then the optimal solution to (GEOp) satisfies:
a. θ (y)

b. xj(y) = θ(y)1/a(Kj(Gj)−1(y)b)− 1/a,
where ‘∝’ means ‘is proportional to.’
(Proofs are given in the appendix.)
Because there are no incentive effects on effort induced by the allocation due to assumption A1, it is obvious that at the solution, the (j,y) constraints in (GEOp) are all binding: that is, at every y, welfare is equalized across j. Notice that θ is strictly increasing, assuming that the distributions of effort are strictly increasing functions, since ρa − 1<0 for all values of ρ ∈ (−∞, 1].
We say that:
Definition. Type j strongly dominates type i if Kj > Ki and Gj FOSDFootnote 9Gi.
Strong domination is a feature of many applications. Indeed, if the types are completely ordered by strong dominance, we can say that the society is stratified with respect to the kind of welfare measured by v.
Notice that xj(y) in Proposition 1 is the product of two terms: the first, θ(y), is increasing in y, while the second term, in the special case that the environment is stratified, is decreasing in j, assuming that the most disadvantaged type is type 1. Thus, the first term implements the rewards-to-effort principle, while the second implements the compensation principle.
We now turn to a second problem that is often more appropriate on these environments. It is often, perhaps usually, not desirable to allow allocations X which are predicated on y as well as j. Consider the following example of the allocation of medical resources. There are two social classes, the Rich and the Poor, who suffer from various diseases: the Poor are susceptible to cancer and tuberculosis, while the Rich suffer only from cancer. In all cases, an unhealthy lifestyle increases the probability of the disease. Here, a general allocation policy would prescribe how much to spend on the treatment of disease d in a person of type j whose lifestyle quality was y. But we do not want medical personnel to be compelled to triage patients on the basis of what their lifestyles have been. So the policy should be at most predicated on d and j. In fact, I would argue that, in this case, we want the policy to be predicated only on the disease – not even on the type. That is, ‘horizontal equity’, a desirable feature in this problem, means that anyone with a given disease should be given the same treatment! The equal-opportunity program – which cannot be formulated as a special case of the problem in this section – will allocate medical expenditures to cancer and tuberculosis across the society so as to compensate the Poor. (Thus, relatively more will be spent on TB vis-à-vis cancer, than would be spent with a utilitarian objective.) A person's effort (lifestyle) will be positively related to his expected health outcome, although policy will not explicitly treat people differently as a function of their lifestyles. (For detailed discussion of this example, see Roemer Reference Roemer2007.)
Often it is the case that predicating the policy on effort violates other social values that we hold – including values of privacy. In the health example, we do not want to compromise the relationship between health providers and patients by forcing the former to triage the latter based upon their lifestyles. Therefore, it is important to study the pure allocation problem when the policies can only be predicated on types: that is, a policy is a vector (x 1, . . ., xJ) such that everyone in type j receives xj. Philosophers, in criticizing the theory of equal opportunity, sometime make the mistake of assuming that policy must be predicated on effort – so that (in the health case) we would spend fewer medical resources on those with unhealthy lifestyles (see, for instance, Anderson Reference Anderson1999). But this is a fallacy. If we believe that ‘horizontal equity’ is important – and in this case, we do, for at least the reason I have given – then we can define the domain of policies to require it. Thus, if we do not want to discriminate in treatment against those who have expended low effort, we define problem as:
![\[
\begin{array}{*{20}l}
{\max \Gamma (\theta )} \\
{{\rm subject}\,{\rm to}} \\
{(\forall y,j)\,v(x^j ,(G^j )^{ - 1} (y),j) \ge \theta (y)\;\quad (GEOp2)} \\
{\bar x \ge \displaystyle\sum {f_j x_j } } \\
{\theta \in \Theta } \\
\end{array}\]](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160202064828955-0409:S0266267112000156_eqnU5.gif?pub-status=live)
where Γ = Γρ, some ρ ∈ (−∞, 1].
Notice that, in (GEOp2), we restrict the policy to being constant for each type – that is, it requires horizontal equity within a type with respect to different effort levels.
Although the policy space is much simpler in (GEOp2) than in the problem (GEOp), the solution is more complicated to describe. This is because it is generally impossible to achieve the result that the (j,y) constraints in (GEOp2) are all binding. In the solution of the problem (GEOp), the welfare profiles within types, the functions ![]() , when graphed in the
, when graphed in the ![]() plane, coincide (for all j). But in the solution of (GEOp2), this is not so: their graphs will cross each other in myriad ways. Therefore the function θ(y), at the solution, will be the lower envelope of the functions
plane, coincide (for all j). But in the solution of (GEOp2), this is not so: their graphs will cross each other in myriad ways. Therefore the function θ(y), at the solution, will be the lower envelope of the functions ![]() , which will coincide with every function
, which will coincide with every function ![]() for some values of y. (It is easy to see this must be the case. For suppose not, and some function
for some values of y. (It is easy to see this must be the case. For suppose not, and some function ![]() lies entirely above the lower envelope. Then we can increase the value of the program by taking some resource away from type j and distributing it to the other types.) A description of the solution to (GEOp2) must describe the sets in [0,1] for which each function
lies entirely above the lower envelope. Then we can increase the value of the program by taking some resource away from type j and distributing it to the other types.) A description of the solution to (GEOp2) must describe the sets in [0,1] for which each function ![]() coincides with θ, which in general can be complicated.
coincides with θ, which in general can be complicated.
We therefore present a result for a special case only.
Proposition 2. Assume A. Assume that there are two types, and type 2 strongly dominates type 1. Further assume that the function ![]() is strictly monotone increasing. Then the solution (x 1, x 2, y*) of the following three equations characterizes the solution of (GEOp2):
is strictly monotone increasing. Then the solution (x 1, x 2, y*) of the following three equations characterizes the solution of (GEOp2):
![\[
\begin{array}{*{20}l}
{\left( {\displaystyle\frac{{x_2 }}{{x_1 }}} \right)^{1 - a\rho } = \displaystyle\frac{{f_1 }}{{f_2 }}\left( {\displaystyle\frac{{K_1 }}{{K_2 }}} \right)^\rho \left( {\displaystyle\frac{{\displaystyle\int_0^{y^* } {(G^2 )^{ - 1} (y)^{\rho b} dy} }}{{\displaystyle\int_{y^* }^1 {(G^1 )^{ - 1} (y)^{\rho b} dy} }}} \right)} \\[30pt]
{\left( {\displaystyle\frac{{x_2 }}{{x_1 }}} \right)^a = \displaystyle\frac{{K_1 }}{{K_2 }}\left( {\displaystyle\frac{{(G^1 )^{ - 1} (y^* )}}{{(G^2 )^{ - 1} (y^* )}}} \right)^b } \\[10pt]
{\bar x = f_1 x_1 + f_2 x_2 .} \\
\end{array}\]](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160202064828955-0409:S0266267112000156_eqnU6.gif?pub-status=live)
The function θ(·) coincides with ![]() on the interval [0, y*] and with
on the interval [0, y*] and with ![]() on the interval [y*, 1].
on the interval [y*, 1].
It is obvious in this case that the function θ is strictly increasing at the solution. Notice it follows from the second equation in the proposition's statement that x 2<x 1. Indeed, we see that the right-hand side of this equation is the product of two terms, each of which is less than one. The first term implements compensation for the direct effect of circumstances, while the second term implements compensation for the indirect effect. Indeed, the second equation merely states that the welfare of the two types must be equal at the rank y* at which the two functions ![]() cross; so we might say that the content of the optimization is primarily expressed in the first equation of the three.
cross; so we might say that the content of the optimization is primarily expressed in the first equation of the three.
Let us note there is an asymmetry in the two principles of compensation and rewards-to-effort. With respect to compensation, we have a definitive rule: at each effort degree y, attempt to maximize the welfare of the type which is worst-off. We have no comparable, definitive instruction for implementing the rewards-to-effort principle. This corresponds to there being many possible choices for the mapping Γ. I do not believe this is a weakness in the theory – rather, it reflects the fact that there is no natural or focal answer to the question, ‘how much reward does effort deserve?’ I use ‘desert’ explicitly, for I believe the equal-opportunity ethic is predicated upon the view that those who expend (costly) effort deserve to be rewarded; more precisely, they deserve to be rewarded for the effort they voluntarily choose which is not determined by their circumstances, and this is measured by their degree of effort in comparison to efforts of others of their type (hence, their rank on the effort distribution of their type).
Fleurbaey expresses a similar point, when he writes:
Compensation for unequal circumstances cannot be the only goal of social policy; it must be supplemented by a reward principle telling us whether and how redistribution should be sensitive to responsibility characteristics as well and, eventually, how final well-being should relate to responsibility characteristics. (Fleurbaey Reference Fleurbaey2008: 20)
There is another, independent reason to allow a degree of freedom in the choice of Γ. In policy applications, the typology is always a finite partition of the set of individuals, and effort is usually measured as the residual explanandum of the objective outcome v after type has been accounted for. Now in reality, we are often unsure about what the actual set of circumstances is. Even if we take a political approach, that I have advocated, and say that circumstances are those aspects of the person's environment that the society views as ones it wishes not to hold persons responsible for, the set of circumstances may be too sparse, because society may be ignorant of some causes of behaviour which, were they understood, would have been deemed to be circumstantial. Thus, the variation in welfare outcomes within types that we observe with a given typology may not be properly described as fully due to variations in effort. This is a reason to be flexible on the choice of Γ. As we choose smaller values of ρ, Γρ reduces the rewards to effort, corresponding to a view that there may be more circumstances than we have delineated. So it may be useful to compute solutions to the programs (GEOp) and (GEOp2) for various values to ρ, and take note of the sensitivity of the optimal solution to this parameter.
Indeed, I now believe the equal-opportunity ethic treats the principles ‘compensation for disadvantage’ and ‘rewards to effort’ asymmetrically. With regard to compensation for disadvantage, the theory has an explicit ideal: render the distributions of the outcome identical across types. But with regard to rewarding effort, the ethic is vague, because we have no clear view of how much reward effort deserves. The incompleteness of equality of opportunity as an ethical doctrine takes its formal form, in the present approach, in the availability of many mappings or operators Γ that may be used to pin the policy recommendation down. My current view is that we must apply some additional principle to determine the degree of acceptable inequality due to effort – such as, after Cohen (Reference Cohen2009), the desire to foster community, which is incompatible with large degrees of inequality.
There is, of course, a long history in political philosophy of proposing theories of rewards to effort. Famously, Aristotle proposed ‘proportionality’. But that proposal is poorly defined: obviously, proportionality depends upon the units in which effort and the relevant welfare are measured. I originally (that is, in Roemer Reference Roemer1996, Reference Roemer1998) resolved the problem of rewards-to-effort with a ‘utilitarian’ principle: in case there is just one type, EOp should maximize the average welfare. This is equivalent to choosing the function Γ(θ)=∫10θ(y)dy – in other words, choose ρ = 1. (To repeat, this is how program (EOp) is a special case of program (GEOp).) Fleurbaey's (2008) solution is to say: in the case there is only one type, assign the resource equally to everyone, a principle he calls ‘liberal reward’. I have become, however, more agnostic as to what comprise the right rewards to effort, and prefer to leave the theory open on that account.
In this section, we have computed optimal policies according to the EOp view. Note, however, that we can easily apply the EOp approach to create a complete ordering over feasible allocations, for any choice of Γ. Let X and X′ be two allocations. Compute θ(·; X) and θ(·; X′), where ![]() . We say that X≳X′ ⇔ Γ(θ(·; X)) ≥ Γ(θ(·; X′)).
. We say that X≳X′ ⇔ Γ(θ(·; X)) ≥ Γ(θ(·; X′)).
I wish to remark on the measurability properties that are necessary for the approach taken here to make sense. If we use the family of evaluation operators {Γρ}, the function v must be taken to be ratio-scale measurable: that is we assume that v is specified up to a positive multiplicative constant. The solutions to the programs discussed in this section will be invariant with respect to multiplying the function v by a positive constant, but not with respect to more general transformations. I do not view the measurability restriction on welfare, however, to be a limitation of the present approach because, as I said earlier, in policy applications v is virtually always an objective measure which is indeed ratio-scale measurable. Thus life expectancy can be measured in years or months, wages can be measured per annum or per month, and GDP can be measured in dollars or yen.
3. THE REPRESENTATION OF EOP RULES
To re-state, the key function of interest is ![]() , where X is the policy domain, defined by:
, where X is the policy domain, defined by:
for any feasible allocation X = {xj(y)|j ∈ {1, . . ., J}, y ∈ [0, 1]}. An equal-opportunity rule is an increasing operator ![]() . The Γ − EOp program is:
. The Γ − EOp program is:
![\[
\begin{array}{*{20}l}
{\max \Gamma (\theta ( \cdot ;X))} \\
{s.t.X \in {\bf X}} \\
{\theta \in \Theta } \\
\end{array}({\rm GEOp})\]](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160202064828955-0409:S0266267112000156_eqnU8.gif?pub-status=live)
I now argue that the representation of an EOp rule as an increasing operator Γ on the domain Θ is, formally, virtually equivalent to the compensation principle. Exactly what does the compensation principle say? After all, it is a somewhat vague statement – that individuals should be compensated for the disadvantages inherent in their circumstances. Let (R, P, I) be an orderingFootnote 10 of the set of feasible allocations X. I take the compensation principle to be an undefined requirement on R which at least satisfies the following necessary condition:
Axiom. An ordering R on X satisfies the compensation principle only if it satisfies Dom.
Principle Dom.
A. For any two allocations X, X′ such that XPX′ there exists a set of positive measures Y⊆[0, 1], ![]() . (Notation: θX(·) ≡ θ(·; X).)
. (Notation: θX(·) ≡ θ(·; X).)
B. For any X, X′ ∈ X such that XIX′, either ![]() [which means
[which means ![]() except possibly on a set of measure zero] or there is a set of positive measure Y such that
except possibly on a set of measure zero] or there is a set of positive measure Y such that ![]() and a set of positive measure Y′ such that
and a set of positive measure Y′ such that ![]() .
.
The motivation for the axiom is seen by supposing it were not true: if the first part of Dom were violated, it would be the case that there exists X, X′ such that XPX’ but for almost all y ∈ [0, 1], ![]() . It would be strange to say that this rule satisfies the compensation principle. For clearly for every y ∈ [0, 1], X′ compensates those at effort tranche y at least as well as X does, and there are some y whom it compensates better. On the other hand, suppose part B of Dom were violated. Then R deems two allocations X and X’ to be indifferent, yet (it follows that) either
. It would be strange to say that this rule satisfies the compensation principle. For clearly for every y ∈ [0, 1], X′ compensates those at effort tranche y at least as well as X does, and there are some y whom it compensates better. On the other hand, suppose part B of Dom were violated. Then R deems two allocations X and X’ to be indifferent, yet (it follows that) either ![]() or
or ![]() . If so, why be indifferent between X and X′?
. If so, why be indifferent between X and X′?
Let Γ be an operator on the set of functions Θ. Γ trivially induces an order on Θ, which we denote R Γ, by:
Definition. An operator Γ on Θ represents an order R on X if
The question is: If an order R on X satisfies principle Dom, is it represented by an increasing order Γ on the space of functions Θ* which are induced by the allocations on the economy?
Proposition 3. Let R be an order on Xsatisfying Dom. Let Θ* = {θX(·)|X ∈ X}. Then R is represented by an increasing operator Γ on Θ*. Furthermore, if R is a continuous order, then Γ can represented by a continuous increasing operator ![]() .
.
Now consider the optimization problem: Maximize the order R on X. If R satisfies the compensation principle, then the proposition says there is an increasing operator Γ on Θ such that the solution is equivalent to:
maximize the operator Γ on Θ.
We now study the opposite direction. Suppose that we are given an increasing operator, Γ, on Θ, the set of functions derived from an environment from its feasible allocations. Given two allocations X, X′ ∈ X we define the order R by:
R is well-defined, complete, reflexive and transitive. (R is obviously well-defined, since the mapping X↦θX is well-defined.)
It is clear that if we begin with an order R on X which is represented by an operator Γ on Θ, then Γ in turn induces the order R, as here described. Thus R and Γ can legitimately be considered dual.
We have:
Theorem 1. Given a dual pair (R, Γ), the order R on Xsatisfies Dom if and only if the operator Γ on Θ is increasing.
Informally, this says that if we are interested in rules satisfying the compensation principle, and we accept the axiom DOM to capture this principle, then we can restrict ourselves to studying the various increasing operators on Θ.Footnote 11 In other words, if one disagrees with my characterization of the equal-opportunity problem as the maximization of some function of the lower envelope θ, then one must object to axiom DOM. As the latest footnote explains, there is at least one possible objection to DOM.
4. THE OPTIMAL TAX PROBLEM
We continue from equation (1.4). Let us now assume that there is one type, number 1, the most disadvantaged type, whose distribution of effort is first-order-stochastic-dominated (FOSD) by the distributions of effort of all other types. As before, we define the lower envelope function by:
where the second equality follows by FOSD. Therefore, the program (GEOp) becomes:
![\[
\begin{array}{*{20}l}
{\max \Gamma (v(t,(G^1 )^{ - 1} ( \cdot )))} \\
{{\rm subject}\,{\rm to}} \\
{{\rm 0} \le {\rm t} \le {\rm 1}} \\
\end{array}({\rm GEOp})\]](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160202064828955-0409:S0266267112000156_eqnU12.gif?pub-status=live)
We have: Proposition 4. Let Γρbe the EOp rule. Then the solution of (GEOp) is the tax policy t which solves:
If ρ = 1, the solution is
It is not possible to compute the optimal tax rate analytically for values of ρ other than one. In Figure 1, I display the optimal tax rates as a function of ρ, for the case where ![]() , and G 1 is the uniform distribution on [0, 2γ1]. As ρ approaches negative infinity, the optimal tax rate approaches one-half, which is the optimal tax rate for the worst off individual in the economy, whose effort is zero.
, and G 1 is the uniform distribution on [0, 2γ1]. As ρ approaches negative infinity, the optimal tax rate approaches one-half, which is the optimal tax rate for the worst off individual in the economy, whose effort is zero.

Figure 1. The optimal tax rate approaches 0.5 as ρ → −∞
What happens if there is only one type? It is easy to check that if ρ = 1 the optimal tax rate is zero. (Just verify that (t, ρ)=(0, 1) solves equation (4.2) in this case.) This is not a general fact, but is due to the quasi-linearity of utility. However, if ρ<1, the optimal tax rate will be positive. The explanation is – recall – that we are agnostic about the degree of reward due to effort. In the case of one type, all differences in welfare are due to effort plus the action of the competitive market which sets equilibrium wages proportional to skill. Taking an evaluation function Γρ with ρ<1 is tantamount to saying that the laissez-faire solution delivers too much inequality, that it rewards effort too much. Hence, with such a choice of ρ, the optimal tax rate will be positive, implementing some redistribution of income.
There is nothing sacrosanct about the market allocation, even in the case of one type. From an ethical viewpoint, all that can be said for the laissez-faire allocation is that (under the usual Arrow-Debreu assumptions) it is Pareto efficient. Ethically speaking, it is on a par with any other Pareto efficient allocation, and it may well be normatively sub-par with respect to some non-Pareto-efficient allocations, if we believe that redistribution away from laissez-faire is worth at least the efficiency cost. Of course, to be definitive on this question, one requires a theory of just reward to effort, which we do not possess.
As I have been harping on our not possessing a theory of the just rewards to effort, let me remind readers of the solution that many economists offer to the problem: they say that just rewards to effort are determined by the market, in the case that the original endowments are just. And so it follows that rewards to effort are equal to the value of the marginal product of one's effort (in the usual general-equilibrium model, the value marginal produce equals the wage). Indeed, this is the view that Dworkin (Reference Dworkin1981) endorses. But it is a difficult view to justify. Dworkin attempts to do so by saying that ‘. . . people should pay the price of the life they have decided to lead, measured in what others give up in order that they can do so. That was the point of the auction as a device to establish initial equality of resources’ (Dworkin Reference Dworkin1981: 294). But that claim follows for any Pareto efficient resource allocation: that is, at any Pareto efficient allocation of labour and resources there exist ‘supporting prices’ at which ‘each is paying the price of the life she has decided to lead, measured in what others give up in order that she can do so’. This fact is known as the second theorem of welfare economics. The virtue of the market is that (under the usual assumptions of no externalities, complete information, no public goods or bads, etc.) it ‘finds’ one Pareto efficient allocation with decentralized information. But it does not follow from this that the market properly measures how much compensation effort deserves.
5. FLEURBAEY'S APPROACH
A. The pure allocation problem
We assume the same economic environment as in section 1. Suppose that type 1 is strongly dominated by all other types. We study the egalitarian equivalent (EE) allocation rule, introduced in Fleurbaey (Reference Fleurbaey2008: 65).
For any two allocations X = {xj(y)} and ![]() we say that
we say that ![]() if X is weakly preferred to
if X is weakly preferred to ![]() according to the lexicographic minimum ordering. The wrinkles we must add to the usual definition – since in this case, we are comparing functions, not countable sequences – involve taking measures and derivatives. Thus, the first test in comparing
according to the lexicographic minimum ordering. The wrinkles we must add to the usual definition – since in this case, we are comparing functions, not countable sequences – involve taking measures and derivatives. Thus, the first test in comparing ![]() is to ask whether the minimum value X is greater than the minimum value of
is to ask whether the minimum value X is greater than the minimum value of ![]() . If it is, we are done; if the minimum values are the same, compare the measures of the sets on which the minimum value is attained. If they are not the same, we are done. If they are the same, then we have to look at derivatives to see which allocation increases faster. To give a precise definition of leximin for functions requires some care, but in the examples that we study here, the orderings will be obvious.
. If it is, we are done; if the minimum values are the same, compare the measures of the sets on which the minimum value is attained. If they are not the same, we are done. If they are the same, then we have to look at derivatives to see which allocation increases faster. To give a precise definition of leximin for functions requires some care, but in the examples that we study here, the orderings will be obvious.
To compare two allocations X and ![]() according to EE, we first construct two fictitious allocations,
according to EE, we first construct two fictitious allocations, ![]() , defined as follows:
, defined as follows:

and we say that ![]() iff
iff ![]() . What is the allocation
. What is the allocation ![]() ? It is the (generally infeasible) allocation which renders each individual just as well off as he is in the actual allocation X, but under the (counterfactual) condition that he were to have been a member of the most disadvantaged type, and expended the same degree of effort as he actually did. In other words, if he is in fact a member of a more advantaged type, his resource under
? It is the (generally infeasible) allocation which renders each individual just as well off as he is in the actual allocation X, but under the (counterfactual) condition that he were to have been a member of the most disadvantaged type, and expended the same degree of effort as he actually did. In other words, if he is in fact a member of a more advantaged type, his resource under ![]() will be larger than it is under X.
will be larger than it is under X. ![]() is a counterfactual allocation which compensates persons for the disadvantage inherent in their circumstances, but continues to reward them (and hold them responsible) for their effort. Consider an individual in an advantaged type, j. Then Kj > K 1 and (Gj)−1(y)>(G1)−1(y). Therefore, to achieve the welfare equality of (5.1), we must have
is a counterfactual allocation which compensates persons for the disadvantage inherent in their circumstances, but continues to reward them (and hold them responsible) for their effort. Consider an individual in an advantaged type, j. Then Kj > K 1 and (Gj)−1(y)>(G1)−1(y). Therefore, to achieve the welfare equality of (5.1), we must have ![]() .
.
Thus, the EE-optimal allocation is the X whose shadow allocation ![]() leximin-dominates all other shadow allocations. We have:
leximin-dominates all other shadow allocations. We have:
Proposition 5. Assume A. In the EE-optimal allocation:
![\[
x_{EE}^j (y) \propto \left( {\frac{{((G^1 )^{ - 1} (y)^b }}{{K_j ((G^j )^{ - 1} (y)^b }}} \right)^{1/a} .\]](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160202064828955-0409:S0266267112000156_eqnU15.gif?pub-status=live)
An instructive way of comparing the EE solution to the GEOp solution is to compute the function θ associated with the EE solution, and then to compare it with the function θ for the GEOp solution. Let us consider the special case that Gj is uniformly distributed on the interval [0, Aj] so (Gj)−1(y)=yAj. Then we can compute from Proposition 5 that:
while from Proposition 1 we have that:
It follows that ![]() . From this we have:
. From this we have:
Corollary
A. For ρ > 0, θGEOpis steeper than θEE, thus GEOp rewards effort at a greater rate than EE;
B. For ρ < 0, θEEis steeper than θGEOp, thus EE rewards effort at a greater rate than GEOp;
C. For ρ = 0, θEE=θGEOpand the policies are identical.
Proof: Follows from observing whether the function y baρ/(1 − aρ) is increasing, decreasing or constant. ■
The coincidence of the EE and GEOp allocation rules (for ρ = 1) in part C is an artefact of the special case. In the more general case that we have been studying, EE does not coincide with Γρ for any ρ.
This raises a more general question: Is EE a special case of GEOp for some operator Γ? The answer is, perhaps surprisingly, affirmative.
To demonstrate this, it is costless to work on a more general space of environments than is specified in assumption A1, and so we do so. Let v(x, (Gj)−1(y), j) denote the outcome and define:
this makes sense because, fixing y and the type 1, v is a strictly increasing function of x and so the inverse function exists. The space of allocations is arbitrary. As usual, we define:
We have:
Theorem 2. Define ![]() . If the solution of (GEOp) is unique for Γ = ΓEE, then the associated allocation is the EE allocation.
. If the solution of (GEOp) is unique for Γ = ΓEE, then the associated allocation is the EE allocation.
The operators Γρ were defined on the domain Θ. The operator ΓEE is defined on the domain Θ × E, where E is the set of environments E = {e|v, {Gj}, {fj}}. Furthermore, ΓEE is only weakly increasing as an operator, in contrast to Γρ.
The distinction between leximin and maximin dissolves on the full space of allocations of the resource allocation problem. On other domains, this may not occur: that is, the premise of theorem 2 may be false. To cope with this, instead of the above formulation, we define an order on Θ by θ≳θ′⇔{R(θ(y), y)}leximin dominates {R(θ′(y), y)}.
This order is (strictly) increasing in θ, and we can write the (GEOp) program with the objective of maximizing ≳ on Θ. The solution is the EE allocation.
This is unsurprising. Resorting to the leximin refinement of maximin in the Fleurbaey definition of EE corresponds to not being able to characterize the EE allocation as the maximization of an operator on Θ. But we can still characterize it as the maximization of an order on Θ.
We next calculate the EE solution when we are restricted to the policy space of proposition 2, where allocations are not predicated upon effort.
Proposition 6. Assume A. Assume that Gj(0) = 0 for all j, and that
■ the functions
 for j≠1 are monotone increasing in y, and
for j≠1 are monotone increasing in y, and■ the derivatives
 exist and are positive.
exist and are positive.
Then on the policy space ![]() , the EE optimal solution is given by xj∝q −1jK −1/aj.
, the EE optimal solution is given by xj∝q −1jK −1/aj.
Next, let us calculate the EE solution in the optimal affine tax problem. There is ambiguity with regard to how to define the EE solution for the tax problem: Fleurbaey offers at least three alternative definitions (see Proposition 5.2, p. 140).
I will proceed as follows, motivated by the discussion thus far. For any tax policy, we define the lower envelope function:
If I am correct that we should view the EE rule as a special case of (GEOp), then we can observe the following: regardless of the choice of the operator Γ, we must have t ∈ [0, 1/2]. For note that θ(y; t) is a strictly decreasing function of t for t > 1/2. So, unambiguously, to make θ ‘as large as possible’ means to choose t ∈ [0, 1/2].
To compute the EE solution, we must construct a shadow policy where each individual expends the same degree of effort as at the actual policy, and receives the same utility. I propose to take the shadow policy as a tax policy of t=0 plus a transfer. Thus, for any tax policy (t, b(t)), we first compute the ‘shadow allocation’ X = {xj(y)} satisfying:
The shadow allocation renders every individual as well off as he is at the tax rate t, were he to have been a member of the most disadvantaged type, taken to be type 1, with his own effort y, but with a lump-sum compensation combined with a tax rate of zero. (Note that his utility before the compensation at a tax rate of zero would have been (G 1)−1(y).) We next choose that tax policy which produces the shadow allocation X that dominates all other such allocations according to the leximin order.Footnote 12
Proposition 7. The EE-optimal solution in the affine tax problem is given by
Note the difference/similarity between this policy and the optimal tax policy of proposition 4.
6. THE ‘MIN-OF-MEANS’ RULE
Another popular rule, originally published by Van de gaer (Reference Van de gaer1993), chooses the policy that solves:
Fleurbaey (Reference Fleurbaey2008) calls this the ‘min-of-means’ rule, because it maximizes the minimum mean welfare across types. Note that this rule commutes the ‘min’ operator and the integral operator from program (EOp).
The obvious appeal of the min-of-means rule is that it is a simple way of rendering the distribution functions of the outcome across types as ‘close’ as possible. Furthermore, it has the attraction of often being an easy rule to compute. But unfortunately, this rule does not maximize any operator Γ on the space of functions Θ. Because I believe, as argued, that responsibility-sensitive egalitarianism must comprise some theory of choosing a maximal θ, this is a demerit of the min-of-means rule.
Theorem 3. There is no operator ![]() which ‘represents’ the min-of-means rule on the domain of environments specified by assumption A.
which ‘represents’ the min-of-means rule on the domain of environments specified by assumption A.
Theorem 3 is proved by constructing an environment, with two types, and finding two allocations, call them X 1 and X 2, such that the following hold:
![\[
\begin{array}{*{20}l}
{\theta ( \cdot ;X_2 ) < \theta ( \cdot ;X_1 ),\,{\rm and}} \\[10pt]
\quad{\mathop {\mathop {\min }\limits_j \left[ {\displaystyle\int_0^1 {\tilde{v}^j (y;X_2 )dy} } \right] > \mathop {\min }\limits_j \left[ {\displaystyle\int_0^1 {\tilde{v}^j (y;X_1 )dy} } \right].} } \\
\end{array}
\]](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160202064828955-0409:S0266267112000156_eqnU24.gif?pub-status=live)
This means there can be no increasing operator on Θ whose solution is the allocation recommended by the min-of-means. The details are found in the appendix.
Despite theorem 3, there is a class of environments on which the min-of-means rule and the mean-of-mins rules coincide. This occurs, for example, in the affine-tax problem. The general feature of these environments is that, under all feasible policies, there is a particular type which is worse off than all other types at every degree of effort. It is often the case that on the set of feasible policies, this is true, and so the min-of-means rule may appear to be a good one, although from the deeper standpoint, I believe theorem 3 shows that it is inadequate.
The conditional equality rule (Fleurbaey Reference Fleurbaey2008: 61) is also not representable.Footnote 13
7. FURTHER DISCUSSION
I will review three topics:
• the importance of the effect of circumstances on effort,
• the liberal reward principle, and
• the central focus of responsibility-sensitive allocation rules.
A. The ‘indirect effect’ of circumstances on effort
Recently, A. Björklund, M. Jantti and I (Reference Björklund, Jantti and Roemer2012) have worked with a large Swedish dataset (approximately one-third of Swedish males), in which we have computed the effect of circumstances on the income of Swedish males. The circumstances are parental income, parental education, number of siblings, IQ, family type and body-mass index, and we also calculate the indirect effect of circumstances on the distribution of effort. Each of these circumstances is partitioned into three or four levels, yielding 1152 types. We have attempted to allocate the degree of inequality to the direct effect of each of the six circumstances, the indirect effect of circumstances on effort, and autonomous effort, using a Shapley-value decomposition of the Gini coefficient of income. We find that the largest relative contribution by far to the Gini in Sweden is autonomous effort (73.8%); among the circumstances, the largest contribution is from IQ (11.8%), the next largest from Parental Income (7.4%), and the third largest from the effect of circumstances on effort (3.4%). The other circumstances are each responsible for under 1% of the effect, except for Family Type, which is 1.4%.
Sweden is an egalitarian society, so we should not be surprised that it has succeeded in rendering quite small the effect of circumstances on income – even though our outcome is pre-tax income. But among circumstances, the indirect effect of circumstances on effort is significant.
For this reason, I believe that we must keep the indirect effect clearly in the picture. Dworkin was wrong, I believe, to assert that people should be held responsible for the effect of their preferences on their choices. One must ask to what extent preferences are formed as a defensive response to poorly resourced environments. To the extent that this is so, people should be compensated for their preferences.Footnote 14
B. The liberal reward principle
This principle states, according to Fleurbaey, that no more compensation should be made than is needed to rectify inequalities due to circumstances. It is characterized by the axiom that, if there is only one type, then the resource should be equally divided among individuals. (Versions of laissez-faire are required if the policy is not a division of resources.) Although this principle has a certain elegance, I hesitate to support it. In many problems to which we wish to apply responsibility-sensitive egalitarianism, outcomes are determined in part by markets. As I said earlier, the market allocation, from the ethical viewpoint, has only one thing to recommend it: under classical assumptions, it is Pareto efficient. (The market functions with decentralized information, which is surely a virtue, but I do not think this comprises an ethical argument for the market allocation rule.)
I am therefore wary of the liberal reward principle. To champion it as an aspect of freedom is incorrect, for non-interference by the state does not maximize freedom. Every property right, whether established by market trades or by legislative ruling, interferes with the freedom of many people: to presume that freedom is monotone decreasing in the degree of state intervention is to fall prey to a right-wing shibboleth. The liberal reward principle in fact states: do not amend the current property rights any more than is necessary to compensate persons for disadvantageous circumstances. But why should the current property rights be the benchmark? The point that there is no such thing as no intervention was made forcefully by the legal positivists at the beginning of the twentieth century (see Fried Reference Fried1998). The liberal reward principle recommends laissez-faire in the case of one type, and I worry that this pins down the theory in the wrong way. To return to my earlier discussion, it may recommend too much inequality.
C. The central focus of responsibility-sensitive egalitarianism
I have argued that the focus of the allocation problem should be the lower-envelope function θ(·; X). I believe this follows from the compensation principle: that equalizing opportunities requires annihilating differences in expected fortune due to differential circumstances. Focusing on the lower envelope is a ‘maximin’ approach, and it is radical or extreme, in the same sense that maximin is radical or extreme in standard social-choice theory. The ambiguity, here, concerns what it means to ‘maximize’ a function subject to the constraint that it be non-decreasing, with respect to the given policy space. Every proposal of the equal-opportunity type, I have argued, must choose a function θ which is maximal with respect to some order on Θ. The reason it is difficult to be less ambiguous than this is that we do not have an ethical theory of what comprise the proper rewards to effort. Aristotle proposed ‘proportionality’, but we know that approach is indefensible because of ambiguity with respect to the proper choice of units: there is no reason that outcomes should be proportional to efforts.
It may be useful to put this another way. Equality of opportunity, or responsibility-sensitive egalitarianism, comprises an equalizing principle, and a disequalizing principle: the former is to equalize fortunes over types, and the latter is to disequalize fortunes over efforts. Indeed, the left-wing attacks on the equal opportunity theories reviewed in this article are largely of the form that they permit too much inequality. I am sensitive to this critique, and that is why I have proposed to treat the two principles asymmetrically. I am militant on annihilating inequality due to circumstances; I am uncertain about how much inequality to allow due to differential effort.
I have said that we must impose a monotone increasing order on Θ. My claim is that a satisfactory ethical justification for such a choice needs to invoke some consideration outside the realm of equalizing opportunities. I have shown that, at least for an important family of resource-allocation problems, Fleurbaey–Maniquet's egalitarian-equivalent rule can also be formulated in this manner. It is not, however possible to find an order on Θ which the ‘mean of mins’ rule maximizes, nor one that the ‘conditional equality’ rule maximizes, and this, in my view, is a mark against these allocation rules. In particular, according to theorem 1, these rules violate axiom DOM.
APPENDIX: PROOFS OF PROPOSITIONS
Lemma For any functions θ, h ∈ Θ, define Φ(ϵ) = Γρ(θ + ϵh). Then
Proof: Evaluate the derivative from its definition, using l'Hôpital's rule. ■
Proof of Proposition 1
1. It is obvious that in the optimal solution all of the (j,y) constraints in (GEOp) will bind. And of course the budget constraint will bind. Therefore at the optimum we must have
and we may write (GEOp) as:![\[
x^j (y) = \theta (y)^{1/a} \left( {K_j^{ - 1} ((G^j )^{ - 1} (y)^{ - b} } \right)^{1/a} ,\]](data:image/gif;base64,R0lGODlhAQABAIAAAMLCwgAAACH5BAAAAAAALAAAAAABAAEAAAICRAEAOw==)
![\[
\begin{array}{*{20}l}
{\max \Gamma (\theta )} \\
{s.t.\quad \bar x \ge \displaystyle\sum\limits_1^J {f_j K_j^{ - 1/a} \int {\theta (y)^{1/a} ((G^j )^{ - 1} (y))} } ^{ - b/a} dy} \\
\end{array}.\quad ({\rm GEOP}^*)\]](data:image/gif;base64,R0lGODlhAQABAIAAAMLCwgAAACH5BAAAAAAALAAAAAABAAEAAAICRAEAOw==)
2. Let θ be a feasible point at which the constraint in (GEOp*) binds. Let θ′ be any other point in ΘI, and define h(y) = θ′(y) − θ(y). Then we may write (1 − ϵ)θ + ϵθ′ = θ + ϵh. By convexity, θ + ϵh ∈ ΘI is a feasible point for (GEOp*), for ϵ ∈ [0, 1].
3. Define the ‘Lagrangian’ function
![\[
\Delta (\varepsilon ) = \Gamma ^\rho (\theta + \varepsilon h) + \lambda \left( {\bar x - \sum {f_j K_j^{ - 1/a} \int {(\theta (y) + \varepsilon h(y))^{1/a} ((G^j )^{ - 1} (y))^{ - b/a} dy} } } \right).\]](data:image/gif;base64,R0lGODlhAQABAIAAAMLCwgAAACH5BAAAAAAALAAAAAABAAEAAAICRAEAOw==)
Suppose we can find a value λ≥0 and a function θ such that
 for any choice of h. Since Δ is a concave function on [0, 1], it will follow that Δ is maximized at zero. In particular, this implies that Δ(0)=Γ(θ)≥Δ(1)≥Γ(θ′), and hence θ is the solution of (GEOp*).
for any choice of h. Since Δ is a concave function on [0, 1], it will follow that Δ is maximized at zero. In particular, this implies that Δ(0)=Γ(θ)≥Δ(1)≥Γ(θ′), and hence θ is the solution of (GEOp*).4. Using the Lemma, evaluate:

Regardless of what the function h is, we can render this expression equal to zero by choosing:
But this just says that
the constant of proportionality is determined by the budget constraint. The proposition follows immediately. ■
Proof of Proposition 2
1. We conjecture a solution to (GEOp2) of the following form: for y ∈ [0, y*], the constraints (j, y) bind for j=2, and for y ∈ [y*, 1], the (j, y) constraint binds for j=1. Let (θ, x 1, x 2, y*) be defined as in the statement, and let (θ′, x′1, x′2) be any feasible solution to (GEOp2). Denote
![\[
h = \theta ' - \theta ,\Delta x_1 = x'_1 - x_1 ,\quad \Delta x_2 = x'_2 - x_2 .\]](data:image/gif;base64,R0lGODlhAQABAIAAAMLCwgAAACH5BAAAAAAALAAAAAABAAEAAAICRAEAOw==)
2. Define the Lagrangian function:
![\[
\begin{array}{l}
\Delta (\varepsilon ) = \Gamma (\theta + \varepsilon h) + \displaystyle\int_0^{y^* } {r_2 } (h)(v(x_2 + \varepsilon \Delta x_2 ,(G^2 )^{ - 1} (y),2) - (\theta (y) + \varepsilon h(y))dy \\
+\! \displaystyle\int_{y^* }^1\! {r_1 (h)(v(x_1\! + \!\varepsilon \Delta x_1 ,(G^1 )^{ - 1} (y),1) - (\theta (y) + \varepsilon h(y))dy + \lambda (\bar x\! -\! \!\displaystyle\sum {f_i } (x_i + \varepsilon \Delta x_i ).\quad\quad}
\end{array}\]](data:image/gif;base64,R0lGODlhAQABAIAAAMLCwgAAACH5BAAAAAAALAAAAAABAAEAAAICRAEAOw==)
Δ is a concave function on [0,1]. If we can produce non-negative functions {r 1, r 2} and λ≥0 and a tuple (θ, x 1, x 2, y*) such that Δ′(0)=0, then we have found a solution to (GEOp2).
3. We evaluate Δ′(0), again using the Lemma:

In this expression, the coefficient of h(y) will be zero if we define:
![\[
r_1 (y) = \Gamma ^\rho (\theta )^{1 - \rho } \theta (y)^{\rho - 1} \,{\rm for}\,y \in [y^* ,1],\]](data:image/gif;base64,R0lGODlhAQABAIAAAMLCwgAAACH5BAAAAAAALAAAAAABAAEAAAICRAEAOw==) The coefficients of Δxi for i=1, 2 will be zero if:
The coefficients of Δxi for i=1, 2 will be zero if:![\[
r_2 (y) = \Gamma ^\rho (\theta )^{1 - \rho } \theta (y)^{\rho - 1} \,{\rm for}\,y \in [0,y^* ].\]](data:image/gif;base64,R0lGODlhAQABAIAAAMLCwgAAACH5BAAAAAAALAAAAAABAAEAAAICRAEAOw==) Employing the definitions of ri(y), these last two conditions mean that
Employing the definitions of ri(y), these last two conditions mean that![\[
\begin{array}{*{20}l}
{a\displaystyle\int_{y^* }^1 {r_1 (y)\theta (y)dy = \lambda f_1 x_1 } } \\
{a\displaystyle\int_0^{y^* } {r_2 (y)\theta (y)dy = \lambda f_2 x_2 } .} \\
\end{array}\]](data:image/gif;base64,R0lGODlhAQABAIAAAMLCwgAAACH5BAAAAAAALAAAAAABAAEAAAICRAEAOw==) But by hypothesis, we have:
But by hypothesis, we have:![\[
f_i x_i \propto \int_{Y_i } {\theta (y)^\rho dy,\,{\rm where}\,Y_1 = [y^* ,1],\quad Y_2 = [0,y^* ]}\]](data:image/gif;base64,R0lGODlhAQABAIAAAMLCwgAAACH5BAAAAAAALAAAAAABAAEAAAICRAEAOw==) and so we must choose xi so that:
and so we must choose xi so that:![\[
\theta (y) = x_i^a ((G^i )^{ - 1} (y))^b K_i \,{\rm on}\,Y_i ,\]](data:image/gif;base64,R0lGODlhAQABAIAAAMLCwgAAACH5BAAAAAAALAAAAAABAAEAAAICRAEAOw==)
![\[
f_i x_i \propto \left( {x_i^a K_i } \right)^\rho \int_{Y_i } {((G^i )^{ - 1} (y))^{b\rho } dy,}\]](data:image/gif;base64,R0lGODlhAQABAIAAAMLCwgAAACH5BAAAAAAALAAAAAABAAEAAAICRAEAOw==) This formula gives us the first equation in the statement of Prop. 2. The second equation follows from the fact that the two types have the same utility at effort y*.
This formula gives us the first equation in the statement of Prop. 2. The second equation follows from the fact that the two types have the same utility at effort y*.![\[
{\rm or}\,f_i x_i^{1 - a\rho } \propto (K_i )^\rho \int_{Y_i } {((G^i )^{ - 1} (y))^{b\rho } dy.}\]](data:image/gif;base64,R0lGODlhAQABAIAAAMLCwgAAACH5BAAAAAAALAAAAAABAAEAAAICRAEAOw==)
Finally, we must verify that
with the reverse inequality holding on (y*, 1]. This immediately follows from the monotonicity hypothesis on the function![\[
v(x_2 ,(G^2 )^{ - 1} (y),2) \le v(x_1 ,(G^1 )^{ - 1} (y),1)\,{\rm on}\,[0,y^* ),\]](data:image/gif;base64,R0lGODlhAQABAIAAAMLCwgAAACH5BAAAAAAALAAAAAABAAEAAAICRAEAOw==)
 , which proves the proposition. ■
, which proves the proposition. ■
Proof of Proposition 3
1. Define the indifference classes of X induced by R to be {C α}. The meaning of ![]() is obvious: we say in this case that C α is ‘higher than’
is obvious: we say in this case that C α is ‘higher than’ ![]() . Define for any indifference class C α the set Θα = {θ|θ=θX, some X ∈ C α}.
. Define for any indifference class C α the set Θα = {θ|θ=θX, some X ∈ C α}.
2. We first note that ![]() . For suppose not, and
. For suppose not, and ![]() . Then there exists
. Then there exists ![]() such that
such that ![]() . W.l.o.g., suppose that C α is higher than
. W.l.o.g., suppose that C α is higher than ![]() . Then XPX′. It follows by Dom, part A, that
. Then XPX′. It follows by Dom, part A, that ![]() , a contradiction which proves the claim.
, a contradiction which proves the claim.
3. We now propose the following order Γ on Θ: given ![]() we say
we say ![]() . Γ is well-defined by part 2 of this proof, which says that any function θ belongs to a unique class Θα. It immediately follows that θI Γθ′⇔α=α′; so Γ is reflexive. Γ is obviously complete, and inherits transitivity from the transitivity of R.
. Γ is well-defined by part 2 of this proof, which says that any function θ belongs to a unique class Θα. It immediately follows that θI Γθ′⇔α=α′; so Γ is reflexive. Γ is obviously complete, and inherits transitivity from the transitivity of R.
4. Next we note that Γ is an increasing order. Suppose θ≥θ′ (i.e. (∀y)(θ(y)≥θ′(y)) and θ(y)>θ′(y) on a set of positive measure). Suppose to the contrary that θ′ΓRθ. Pick ![]() . Then X′RX. If X′PX, we have a contradiction to DomA; if X′IX we have a contradiction to DomB. Hence Γ is increasing.
. Then X′RX. If X′PX, we have a contradiction to DomA; if X′IX we have a contradiction to DomB. Hence Γ is increasing.
5. Now suppose that the order R is continuous on X (that is upper and lower contour sets are closed). Then R can be represented by a utility function ![]() . But this induces a utility function representing Γ in the obvious way. ■
. But this induces a utility function representing Γ in the obvious way. ■
Proof of Theorem 1
Prop. 3 is one direction of the theorem. Conversely, we wish to show that the dual preference order R to an increasing operator Γ satisfies Dom. Case 1: Given X, X′ ∈ X such that XPX′. Then ![]() . Since Γ is increasing, it cannot be that
. Since Γ is increasing, it cannot be that ![]() ; therefore, there is a non-null set Y such that y ∈ Y⇒θ(y)>θ′(y). Case 2: X, X′ ∈ X such that XIX′. Then, if
; therefore, there is a non-null set Y such that y ∈ Y⇒θ(y)>θ′(y). Case 2: X, X′ ∈ X such that XIX′. Then, if ![]() , since Γ is increasing, it follows that
, since Γ is increasing, it follows that ![]() , and so there is a non-null set Y such that
, and so there is a non-null set Y such that ![]() . The same argument holds while reversing the roles of X and X′. This proves that R satisfies Dom.
. The same argument holds while reversing the roles of X and X′. This proves that R satisfies Dom.
Proof of Proposition 4
1. As is derived in equation (3.2), and from the fact that type 1 is strictly dominated by all other types, we have:
Our problem is to choose t to maximize Γρ(θ). The function is concave in t. The first-order condition is condition (4.2) in the proposition's statement. ■
Proof of Proposition 5
1. Let xj(y) be an allocation and let
 be its shadow allocation defined in equation (4.1). Then
be its shadow allocation defined in equation (4.1). Then  . We desire to find the feasible allocation X which leximins the shadow allocation. This is achieved when
which proves the proposition. ■
. We desire to find the feasible allocation X which leximins the shadow allocation. This is achieved when
which proves the proposition. ■![\[
x^j (y)\left( {\frac{{(G^j )^{ - 1} (y)}}{{(G^1 )^{ - 1} (y)}}} \right)\left( {\frac{{K_j }}{{K_1 }}} \right)^{1/a} = {\rm constant},\]](data:image/gif;base64,R0lGODlhAQABAIAAAMLCwgAAACH5BAAAAAAALAAAAAABAAEAAAICRAEAOw==)
Proof of Theorem 2
1. Notice that
is the associated allocation that is defined for the allocation X=(xj(y)) according to the EE rule. Therefore, solving the program (GEOp) for Γ = ΓEE is equivalent to solving the following program:![\[
\hat{x}^j (y) = R^{ - 1} (v(x^j (y),(G^j )^{ - 1} (y),j),y)\]](data:image/gif;base64,R0lGODlhAQABAIAAAMLCwgAAACH5BAAAAAAALAAAAAABAAEAAAICRAEAOw==) which can be re-written:
which can be re-written:![\[
\mathop {\max }\limits_X \mathop {\min }\limits_{j,y} R(v(x^j (y),(G^j )^{ - 1} (y),j),y),\]](data:image/gif;base64,R0lGODlhAQABAIAAAMLCwgAAACH5BAAAAAAALAAAAAABAAEAAAICRAEAOw==) which in turn can be written:
which in turn can be written:![\[
\begin{array}{*{20}l}
{\max \Lambda } \\
{s.t.} \\
{(\forall j,y)\quad R(v(x^j (y),(G^j )^{ - 1} (y),y) \ge \Lambda } \\
\end{array},\]](data:image/gif;base64,R0lGODlhAQABAIAAAMLCwgAAACH5BAAAAAAALAAAAAABAAEAAAICRAEAOw==) and yet again, as:
and yet again, as:![\[
\begin{array}{*{20}l}
{\max \Lambda } \\
{s.t.} \\
{(\forall y)\,\theta (y;X) \ge v(\Lambda ,(G^1 )^{ - 1} (y),1)} \\
\end{array},\]](data:image/gif;base64,R0lGODlhAQABAIAAAMLCwgAAACH5BAAAAAAALAAAAAABAAEAAAICRAEAOw==) which is the same as:
which is the same as:![\[
\begin{array}{*{20}l}
{\max \Lambda } \\
{{\rm s}{\rm .t}{\rm .}} \\
{R(\theta (y;X),y) \ge \Lambda } \\
\end{array},\]](data:image/gif;base64,R0lGODlhAQABAIAAAMLCwgAAACH5BAAAAAAALAAAAAABAAEAAAICRAEAOw==) which proves the claim. ■
which proves the claim. ■![\[
\mathop {\max }\limits_\theta \mathop {\min }\limits_y R(\theta (y;X),y),\]](data:image/gif;base64,R0lGODlhAQABAIAAAMLCwgAAACH5BAAAAAAALAAAAAABAAEAAAICRAEAOw==)
Proof of Proposition 6
1. In this case, we leximin the shadow allocation which is
![\[
\tilde x^j (y) = x_j \left( {\frac{{(G^j )^{ - 1} (y)}}{{(G^1 )^{ - 1} (y)}}} \right)^{b/a} \left( {\frac{{K_j }}{{K_1 }}} \right)^{1/a} = x_j \psi ^j (y)\left( {\frac{{K_j }}{{K_1 }}} \right)^{1/a}.\]](data:image/gif;base64,R0lGODlhAQABAIAAAMLCwgAAACH5BAAAAAAALAAAAAABAAEAAAICRAEAOw==)
Our problem is to choose the allocation {xj} which leximins the function ![]() . Since the functions ψj are increasing, for any j, the minimum of
. Since the functions ψj are increasing, for any j, the minimum of ![]() occurs at y = 0 and j = 1. Therefore the problem is to leximin {xjψj(0)K 1/aj}. But since by hypothesis (Gj)−1(0)=0 for all j, this requires us to equalize xjqjK 1/aj. The claim follows. ■
occurs at y = 0 and j = 1. Therefore the problem is to leximin {xjψj(0)K 1/aj}. But since by hypothesis (Gj)−1(0)=0 for all j, this requires us to equalize xjqjK 1/aj. The claim follows. ■
Proof of Proposition 7
The problem is to:
which is equivalent to solving:
whose solution (as long as ![]() ) is given by
) is given by
Proof of Theorem 3
We construct an example that was described in the text after the statement of theorem 3. There are two types, each comprising one-half the population. We assume ![]() , and
, and
We shall prove the theorem ‘backwards’, by constructing the functions ![]() which have desired properties, and then deducing what the functions hi and the allocations must be.
which have desired properties, and then deducing what the functions hi and the allocations must be.
To this end, we desire to construct functions ![]() having the properties of the functions graphed in Figure 2.
having the properties of the functions graphed in Figure 2.
![\begin{array}{*{20}l}
{V^1 (y) = ay,\quad 0 \le y \le 1} \\ [8pt] {V^2 (y) = \left\{ {\begin{array}{*{20}l} {ay,\quad 0 \le y \le y_1 } \\ [8pt] {b(y - y_1 ) + ay_1 ,\quad 1 \ge y > y_1 } \\\end{array}} \right.} \\ [8pt] {{\rm with}\,a > b.} \\ [8pt] {\skew2\tilde{V}^1 (y) = \left\{ {\begin{array}{*{20}l} {cy,\quad 0 \le y \le y_1 } \\ [8pt] {a(y - y_1 ) + cy_1 ,\quad 1 \ge y > y_1 } \\\end{array}} \right.} \\ {{\rm with}\,c < a.}
\\end{array}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160202064828955-0409:S0266267112000156_eqnU100.gif?pub-status=live)

Figure 2. The counter-example in the proof of Theorem 3.
y 2 is defined as the intersection of ![]() finally,
finally,
![\[
\skew2\tilde{V}^2 (y) = \left\{ {\begin{array}{*{20}l} {dy,\quad 0 \le y \le y_3 } \\ [8pt] {dy_3 ,\quad y_3 < y \le y_2 } \\ [8pt] {e(y - y_2 ) + dy_3 ,\quad y_2 < y \le 1} \\\end{array}} \right.,
\]](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160202064828955-0409:S0266267112000156_eqnU54.gif?pub-status=live)
where y 3 is defined as the intersection of ![]() .
.
The constraints we require are d > a > c > b > e.
Allocation I is given by x 1=x 2=1. At this allocation, the outcome as a function of y should give V 1 and V 2; it immediately follows that
![\[
\begin{array}{*{20}l}
{h_1 (y) = ay} \\
{h_2 (y) = \left\{ {\begin{array}{*{20}l}
{ay,\quad 0 \le y \le y_1 } \\
{b(y - y_1 ) + ay_1 ,\quad y_1 < y \le 1} \\
\end{array}} \right.} \\
\end{array}
\]](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160202064828955-0409:S0266267112000156_eqnU55.gif?pub-status=live)
Now we must produce an allocation which generates the graphs of ![]() . By construction, we see from Figure 2 that if we do this, then θI(y)>θII(y), except at the point y 2, where these two functions are equal. Thus, if we can produce feasible allocation
. By construction, we see from Figure 2 that if we do this, then θI(y)>θII(y), except at the point y 2, where these two functions are equal. Thus, if we can produce feasible allocation ![]() which generates the functions
which generates the functions ![]() and
and
then we are done.
We must define the second allocation by: ![]()
If we can produce numbers (a, b, c, d, e, y 1, y 2, y 3) as described, such that (++) holds and
then we are done. The answer is (a, b, c, d, e, y 1, y 2, y 3, resource) = {1, 0.829763, 0.97458, 1.02134, 0.0717169, 0.497087, 0.5, 0.390259, 0.990549},
where ‘resource’ = 0.9905 is the total resource used in the second allocation. The four means are:


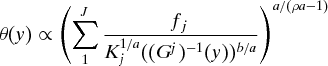
![\[
\begin{array}{*{20}l}
{\max \Gamma (\theta )} \\
{s.t.\quad \bar x \ge \displaystyle\sum\limits_1^J {f_j K_j^{ - 1/a} \int {\theta (y)^{1/a} ((G^j )^{ - 1} (y))} } ^{ - b/a} dy} \\
\end{array}.\quad ({\rm GEOP}^*)\]](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160202064828955-0409:S0266267112000156_eqnU27.gif?pub-status=live)
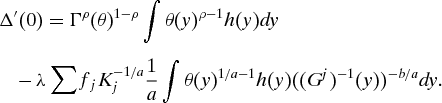
![\[
\begin{array}{l}
\Delta (\varepsilon ) = \Gamma (\theta + \varepsilon h) + \displaystyle\int_0^{y^* } {r_2 } (h)(v(x_2 + \varepsilon \Delta x_2 ,(G^2 )^{ - 1} (y),2) - (\theta (y) + \varepsilon h(y))dy \\
+\! \displaystyle\int_{y^* }^1\! {r_1 (h)(v(x_1\! + \!\varepsilon \Delta x_1 ,(G^1 )^{ - 1} (y),1) - (\theta (y) + \varepsilon h(y))dy + \lambda (\bar x\! -\! \!\displaystyle\sum {f_i } (x_i + \varepsilon \Delta x_i ).\quad\quad}
\end{array}\]](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160202064828955-0409:S0266267112000156_eqnU33.gif?pub-status=live)
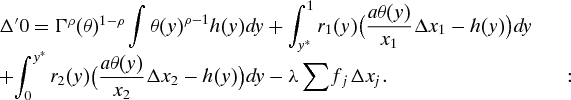
![\[
\begin{array}{*{20}l}
{a\displaystyle\int_{y^* }^1 {r_1 (y)\theta (y)dy = \lambda f_1 x_1 } } \\
{a\displaystyle\int_0^{y^* } {r_2 (y)\theta (y)dy = \lambda f_2 x_2 } .} \\
\end{array}\]](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160202064828955-0409:S0266267112000156_eqnU36.gif?pub-status=live)
![\[
x^j (y)\left( {\frac{{(G^j )^{ - 1} (y)}}{{(G^1 )^{ - 1} (y)}}} \right)\left( {\frac{{K_j }}{{K_1 }}} \right)^{1/a} = {\rm constant},\]](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160202064828955-0409:S0266267112000156_eqnU43.gif?pub-status=live)
![\[
\begin{array}{*{20}l}
{\max \Lambda } \\
{s.t.} \\
{(\forall j,y)\quad R(v(x^j (y),(G^j )^{ - 1} (y),y) \ge \Lambda } \\
\end{array},\]](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160202064828955-0409:S0266267112000156_eqnU46.gif?pub-status=live)
![\[
\begin{array}{*{20}l}
{\max \Lambda } \\
{s.t.} \\
{(\forall y)\,\theta (y;X) \ge v(\Lambda ,(G^1 )^{ - 1} (y),1)} \\
\end{array},\]](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160202064828955-0409:S0266267112000156_eqnU47.gif?pub-status=live)
![\[
\begin{array}{*{20}l}
{\max \Lambda } \\
{{\rm s}{\rm .t}{\rm .}} \\
{R(\theta (y;X),y) \ge \Lambda } \\
\end{array},\]](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160202064828955-0409:S0266267112000156_eqnU48.gif?pub-status=live)
![\[
\tilde x^j (y) = x_j \left( {\frac{{(G^j )^{ - 1} (y)}}{{(G^1 )^{ - 1} (y)}}} \right)^{b/a} \left( {\frac{{K_j }}{{K_1 }}} \right)^{1/a} = x_j \psi ^j (y)\left( {\frac{{K_j }}{{K_1 }}} \right)^{1/a}.\]](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160202064828955-0409:S0266267112000156_eqnU49a.gif?pub-status=live)


