Published online by Cambridge University Press: 23 September 2005
In this paper we analyze the effects of a very general class of time-varying variances on well-known “stationarity” tests of the I(0) null hypothesis. Our setup allows, among other things, for both single and multiple breaks in variance, smooth transition variance breaks, and (piecewise-) linear trending variances. We derive representations for the limiting distributions of the test statistics under variance breaks in the errors of I(0), I(1), and near-I(1) data generating processes, demonstrating the dependence of these representations on the precise pattern followed by the variance processes. Monte Carlo methods are used to quantify the effects of fixed and smooth transition single breaks and trending variances on the size and power properties of the tests. Finally, bootstrap versions of the tests are proposed that provide a solution to the inference problem.We are grateful to Peter Phillips, a co-editor, and two anonymous referees whose comments on an earlier draft have led to a considerable improvement in the paper.
Applied researchers have recently focused attention on the question of whether or not the variability in the shocks driving macroeconomic time series has changed over time (see, e.g., the literature review in Busetti and Taylor, 2003). The empirical evidence suggests that a decline in volatility over the past 20 years or so is a common phenomenon in many real and price variables. These findings have helped stimulate interest among econometricians in analyzing the effects of innovation variance shifts on unit root and stationarity tests. Among others, Hamori and Tokihisa (1997) and Kim, Leybourne, and Newbold (2002) have derived the implications of a single permanent variance shift in the innovations of an I(1) process on the size properties of Dickey–Fuller tests. The effect of a single variance shift on the stationarity test (KPSS test) of Kwiatkowski, Phillips, Schmidt, and Shin (1992) has been analyzed independently by Busetti and Taylor (2003) and Cavaliere (2004a), who found that the test can suffer severe size distortions when there is a late (early) positive (negative) variance shift under the null.
We analyze the effects that a very general class of permanent variance breaks has on the behavior of the KPSS stationarity test, together with those of Lo (1991) and Xiao (2001); a brief review of these tests is given in Section 3. Our unobserved components model, introduced in Section 2, generalizes that considered in, inter alia, Kwiatkowski et al. (1992) to allow for innovation processes whose variances evolve over time according to a quite general mechanism that allows, e.g., single and multiple breaks, smooth transition breaks, and trending variances. Variance nonconstancy is allowed in both the irregular component and the errors driving the level of the process. In Sections 4 and 5 we analyze the effects of time-varying variances on the large-sample behavior of these statistics under both the I(0) null and global I(1) and local alternatives. In Section 6 these effects are quantified, using Monte Carlo simulation, for the aforementioned examples.
Related but different work was carried out by Hansen (2000), who shows that the Lagrange multiplier (LM) test of Nyblom (1989) for structural change in the parameters of a linear regression model (which contains the KPSS test as a special case) underrejects the I(0) null when the marginal distribution of the regressors changes over time. Conversely, in this paper we show that where the variance of the errors changes over time the picture is quite different, with the KPSS (and other stationarity) tests both under- and overrejecting the null, but with a more pronounced tendency toward overrejecting. Similarly, whereas Hansen (2000) shows that Nyblom's test loses (size-unadjusted) power under structural changes in the marginal distribution of the regressors, for most of the cases we consider the KPSS test gains power when the errors are heteroskedastic. In Section 7 we adapt the heteroskedastic bootstrap of Hansen (2000) to the present problem and show that the bootstrap tests perform well in practice. Section 8 concludes. Sketch proofs are given in an Appendix; detailed proofs appear in Cavaliere and Taylor (2004).
We use
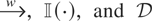
to denote weak convergence as the sample size diverges, the indicator function, and the space of cadlag processes on [0,1] endowed with the Skorohod metric, respectively, whereas x := y means that x is defined by y. Finally, as in Phillips and Sun (2001), for two processes X and Y on [0,1] we define the projections
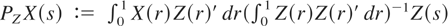
and
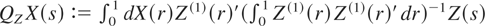
, where (1) denotes the first derivative.
Consider the unobservable components (UC) data generating process (DGP)
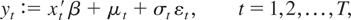
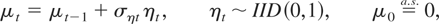
under the following set of assumptions (which are taken to hold throughout the paper, except where stated otherwise).
Assumption
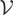
. The term {σt} satisfies σ[sT] := ω(s), where

is a nonstochastic function with a finite number of points of discontinuity; moreover, ω(·) > 0 and satisfies a (uniform) first-order Lipschitz condition except at the points of discontinuity. Similarly, except where otherwise stated, ση[sT] := ωη(s), where ωη(·) satisfies the same conditions as ω(·).
Assumption
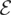
. The irregular component {εt} is a zero-mean, unit variance, strictly stationary mixing process with E|εt|p < ∞ for some p > 2 and with mixing coefficients {αm} satisfying
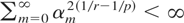
for some r ∈ (2,4], r ≤ p. The long-run variance

is strictly positive and finite. Furthermore, {εt} is independent of {ηt} at all leads and lags. As is standard, we refer to {εt} as an I(0) process.
Assumption
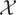
. The component xt is a p × 1 deterministic vector satisfying the condition that there exist a scaling matrix δT and a bounded piecewise-continuous function F(·) on [0,1] such that δT x[·T] → F(·) uniformly on [0,1], with

positive definite.
From (1) and (2), observe that under Assumption
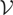
, the variance of both the irregular component, ut := σtεt, and the shocks to the level process {μt} are heteroskedastic. Consequently, {ut} is I(0) provided {σt} is constant, whereas {μt} reduces to a standard random walk if {σηt} is constant and vanishes from (1) when σηt = 0, all t. Notice that the model considered here generalizes the UC model discussed in Kwiatkowski et al. (1992) by allowing both {σt} and {σηt} to be potentially nonconstant over time.
1Busetti and Taylor (2003) consider the model discussed here under the constraint that σt = σηt. In our framework we do not require this constraint to hold.
Assumption
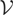
allows for a wide class of models for the variances of the errors. Models of single or multiple variance shifts satisfy Assumption

with ω(·) piecewise constant. For example, the function
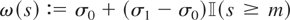
gives the single break model with a variance shift at time [mT], 0 < m < 1, analyzed by Busetti and Taylor (2003) and Cavaliere (2004a). If ω(·)2 is an affine function, then the unconditional variance of the errors displays a linear trend. Piecewise-affine functions are also permitted, allowing for variances that follow a broken trend. Moreover, smooth transition variance shifts also satisfy Assumption
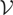
: e.g., the function

, which corresponds to a smooth (logistic) transition from σ02 to σ12. The parameter m determines the transition midpoint (for t = [mT], σt2 = 0.5(σ02 + σ12)) whereas γ > 0 controls the speed of transition (the fixed change-point model follows as a limiting case for γ → ∞).
Assumption
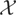
is standard and allows for a wide variety of possible forms for the deterministic component, including the pth-order trend function xt := (1,t,…,tp)′, 0 ≤ p < ∞. The broken intercept and broken intercept and trend functions considered, e.g., in Busetti and Harvey (2001) are obtained by specifying

respectively, in (1), tmj being defined as

satisfying limT→∞(m/T) = μ ∈ (0,1) (see Phillips and Xiao, 1998, p. 448).
Remark 1. If ω(·) is not constant then the irregular component, {ut}, is unconditionally heteroskedastic. Conditional heteroskedasticity is also permitted through Assumption
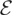
(see, e.g., Hansen, 1992b). Assumption
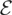
has been used extensively in the econometric literature as it allows {εt} to belong to a wide class of weakly dependent stationary processes. The strict stationarity assumption is made without loss of generality and may be weakened to allow for weak heterogeneity of the errors, as in, e.g., Phillips (1987).
Remark 2. The assumption of nonstochastic variance functions {ω(·),ωη(·)} can be easily weakened simply by assuming stochastic independence between {εt,ηt} and {σt,σηt}, given that the stochastic functionals {ω(·),ωη(·)} must have sample paths satisfying the requirements of Assumption
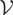
. In the stochastic variance framework, the results given in this paper hold conditionally on a given realization of {ω(·),ωη(·)}.
Kwiatkowski et al. (1992) focus on testing the I(0) null hypothesis, H0 : ση2 = 0, against the I(1) alternative hypothesis, H1 : ση2 > 0, under the ancillary assumption that σt = σ,σηt = ση, all t, so that, under H0, {yt} reduces to the I(0) process yt = xt′ β + ut, t = 1,…,T. Kwiatkowski et al. (1992) propose the test that rejects H0 for large values of the statistic
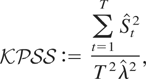
where

, the ordinary least squares (OLS) residuals from the regression of yt on xt, t = 1,…,T;
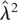
is a consistent estimator of the long-run variance of {ut} under H0 and has the form

being a bandwidth parameter and k(·) a weighting function. Kwiatkowski et al. (1992) assume
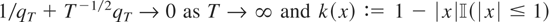
(Bartlett weights). However, because we are dealing with mixing errors (see Assumption

), throughout the paper we will require that qT and k(·) satisfy the following assumption (de Jong, 2000).
Assumption
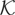
. (K1) For all
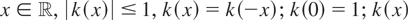
is continuous at 0 and for almost all
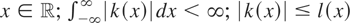
, where l(x) is a nonincreasing function such that
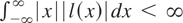
; (K2) qT ↑ ∞ as T ↑ ∞, and qT = o(Tγ), γ ≤ 1/2 − 1/r, where r is given in
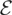
.
Assumption
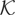
is sufficiently general for our purposes as it is satisfied by many of the most commonly employed kernels (see Hansen, 1992a; Jansson, 2002).
Remark 3. The
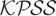
statistic maps the sequence

onto [0,1] by averaging the squared values of the sequence. Other stationarity tests can be obtained by taking different mappings. For example, the supremum of
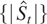
and range of
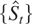
deliver, respectively, the test of Xiao (2001) and the rescaled range (RS) test of Lo (1991), which reject H0 for large values of the statistics
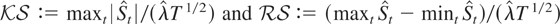
, respectively.
Under the null hypothesis considered by Kwiatkowski et al. (1992), H0 : σηt2 = ση2 = 0, all t, if {σt} is constant across the sample, it is well known that (e.g., Kwiatkowski et al., 1992, pp. 164–165)
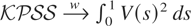
, where

, with B(·) a standard Brownian motion. For example, if xt := (1,t,…,tp−1)′, then F(s) := (1,s,…,sp−1)′ and V(·) is a pth-level Brownian bridge.
Now, assume that H0 holds but that σt is not necessarily constant over time; rather it satisfies Assumption

. Then, the asymptotic distribution of the
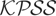
statistic assumes the form detailed in the following theorem.
THEOREM 1. Under H0 : σηt2 = ση2 = 0, all t,
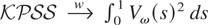
, where
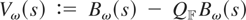
and where
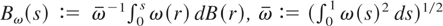
.
Consequently, with respect to the homoskedastic case, the asymptotic distribution of the

statistic has the usual structure but with B(·) replaced by Bω(·). It is only where ω(·) is constant throughout the sample that Bω(·) reduces to a standard Brownian motion and, hence, that
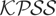
has the standard limiting distribution.
Remark 4. The process Bω(·) is a diffusion corresponding to the stochastic differential equation dBω(s) = (ω(s)/ω)dB(s) with initial condition Bω(0) = 0. Because Bω(·) has zero mean, variance
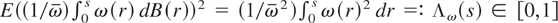
(where Λω(·) is an increasing homeomorphism on [0,1]) and has independent increments, Corollary 29.10 of Davidson (1994) implies that Bω(·) is distributed as B(Λω(·)), and therefore at time s ∈ [0,1], Bω(·) has the same distribution as the standard Brownian motion B(·) at time Λω(s) ∈ [0,1]. That is, Bω(·) is a Brownian motion under modification of the time domain (see, e.g., Revuz and Yor, 1991, p. 170).
Remark 5. Under the conditions of Theorem 1,
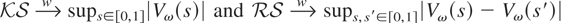
. Interestingly, in the case of no deterministic terms (i.e., xt′ β = 0), because
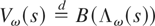
(see Remark 4), it holds that
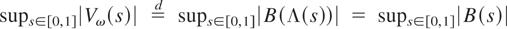
,
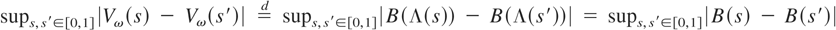
, and the asymptotic sizes of the

tests are not affected by variance changes that satisfy Assumption
. Simulation evidence reported in Cavaliere and Taylor (2004) suggests that this invariance property also holds reasonably well in small samples.
In this section we investigate the impact of time-varying variances in the irregular component in (1), and/or the error driving the level equation, (2), on both the consistency and local asymptotic power properties of the tests.
It is well known (e.g., Kwiatkowski et al., 1992, eqn. (25)) that if σηt2 = ση2 > 0, then
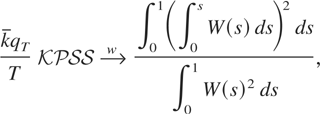
where
is a standard Brownian motion independent of B(·). Because qT /T → 0, (4) implies that

diverges to +∞ at rate Op(T/qT) under the I(1) alternative. In addition to this result, note that if the {ut} component has a time-varying variance,
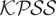
is still distributed as in (4), because as T → ∞, the I(1) component {ηt} dominates.
Now, consider the general case where σηt2 ≠ 0 but is not necessarily constant, satisfying Assumption
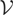
. Here the following result holds.
THEOREM 2. If σηt2 ≠ 0, all t, the weak convergence (4) holds with W(·) replaced by Wωη(·), where Wωη(s) := Bωη(s) − PF Bωη(s) with
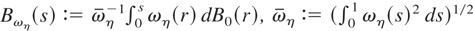
.
Consequently, as in the case of constant variances, because qT /T → 0, Theorem 2 implies that
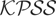
diverges to +∞ at rate Op(T/qT) under global I(1) alternatives.
Remark 6. Under the conditions of Theorem 2,

and
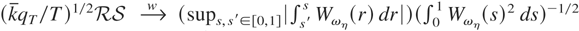
, which imply that both
also diverge to +∞, at rate Op((T/qT)1/2).
We now focus attention on the limiting behavior of the
statistic under the local alternative (see also Busetti and Taylor, 2003, p. 513):
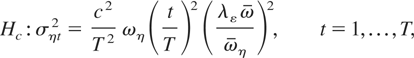
where c ≥ 0 is a noncentrality parameter and λεω/ωη > 0 is a scale factor that simplifies the representation of the asymptotic distributions. Notice that ω/ωη = 1 if σt = σηt, t = 1,…,T; i.e., if the pattern of time variation is common to the variances of the irregular component in (1) and the error driving the level in (2). Moreover, where σt = σ and σηt = ση, t = 1,…,T, Hc reduces to the local alternative considered by, inter alia, Stock (1994, p. 2799).
The following theorem details the large-sample behavior of
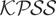
under Hc.
THEOREM 3. Under Hc of (5),

where the (independent) processes Vω(·) and Wωη(·) are as previously defined.
Remark 7. Notice from (6) that the asymptotic local power of
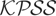
is affected by heteroskedasticity in both the irregular component and the errors driving the level process. Moreover, because the limiting processes relating to these components enter the asymptotic distribution in different forms (Wωη(·) is integrated whereas Vω(·) is not), it is anticipated that heteroskedasticity will have different effects in these two cases.
Remark 8. Under the homoskedastic condition that σt2 = σ2 and σηt2 = ση2, for all t, the local alternative simplifies to Hc : ση2 = (c2/T2)σ2λε2, and the right member of (6) reduces to
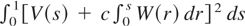
(cf. Busetti and Taylor, 2003, p. 513).
Remark 9. Under the conditions of Theorem 3,
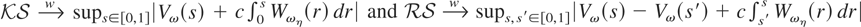
.
In this section we use Monte Carlo methods to quantify the finite-sample size and power properties of
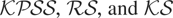
of (3) and Remark 3, for the DGP (1)–(2) with β = 0 and (εt, ηt)′ ∼ NIID(0,I2), where {σt2} and/or {σηt2} vary according to Assumption
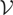
. We focus on the following three particular cases, where f (s) can be either ω(s) or ωη(s):
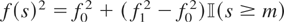
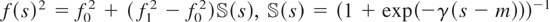

Without loss of generality, in each case we set f0 = 1 and vary the ratio d = f0 /f1 among d ∈ {0.25,4}. A positive (negative) variance shift obtains for d < 1 (d > 1). In both Cases (a) and (b) we vary the parameter m among m ∈ {0.1,0.5,0.9}. In Case (b) we report results setting the speed of transition parameter γ = 10. Under Case (c) we consider m ∈ {0.0,0.5,0.9}. For m = 0.0 the variance process follows a linear trend between f02 for s = 0 and f12 for s = 1. When m > 0 the variance is fixed at f02 up until time [mT] after which time it follows a linear trend path until s = 1 where it equals f12. Other parameter values were considered but add little to what is reported.2
Indeed, for Case (c) we also considered the generalized trend function,
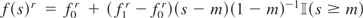
, for a range of values of r but found very little dependence on r.
We have set both {εt} and {ηt} to be serially uncorrelated Gaussian sequences as the effects we are looking to quantify are those caused by nonconstant variances rather than serial correlation. The latter are already well documented in the literature; (see, inter alia, Kwiatkowski et al., 1992, pp. 169–172). Accordingly, we use a Bartlett kernel with qT = 1. Samples of sizes T = 50 and 250 are considered; all tests were run at the nominal 5% level using critical values, obtained in the same fashion, under σt = 1 and σηt = 0, t = 1,…,T.3
All simulation experiments were conducted using the RNDN function of Gauss 3.1 over 40,000 Monte Carlo replications.
Table 1 reports empirical rejection frequencies of the
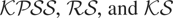
tests when σηt = 0, t = 1,…,T, and ω(s)2, 0 ≤ s ≤ 1, satisfies either Case (a), (b), or (c) with σj = fj, j = 0,1, for the range of parameter values outlined before. Results are reported for the cases where
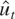
are the OLS residuals from the regression of yt on xt = 1 (a constant) or xt = (1, t)′ (a constant and linear trend), t = 1,…,T.
Empirical size of stationarity tests: Heteroskedastic errors

Consider first the results for the single break model. For early breaks (m = 0.1) the
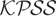
test is (over-) undersized when (d = 4) d = 0.25. For late breaks this pattern is reversed. For the constant case,
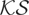
displays the largest size distortions in most cases, whereas there seems to be little to choose between the
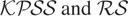
tests overall:
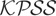
is better behaved (with only slight oversizing) than
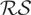
for m = 0.5, but the reverse is true for both m = 0.1 and m = 0.9. Where significant size distortions occur in the
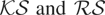
tests for the constant case, they worsen considerably for the linear trend case, especially so in the case of
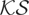
. In the trend case the
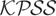
test is noticeably better behaved than the other tests, behaving similarly to the constant case. Finally, for m = 0.5 the degree of oversizing seen in each of the three tests does not vary significantly between d = 4 and d = 0.25.
The results for the smooth transition break model largely mirror those for the single break but with the distortions somewhat ameliorated. This result is perhaps not surprising given that the logistic function used in Case (b) smooths the break across the sample. Although we report results for a relatively slow transition speed, γ = 10, we computed experiments for a range of values of γ and found the differences across γ quite small with results tending toward those for the single break model as γ increased. For example, by γ = 50 these results were indistinguishable.
Turning to the results for trending variances, for m = 0 the size of the
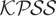
test is not substantially affected in either the constant or constant and trend cases, whereas the size distortions seen in the constant and trend cases for the
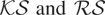
tests are roughly the same throughout for d = 4 and d = 0.25. Again the
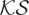
test displays the worst size distortions. For all of the tests linear trending variances seem in most cases to have a lesser impact on size than either fixed or smooth transition breaks. The patterns of size distortions for the piecewise-linear trend (m = 0.5 and m = 0.9) exaggerate (dampen) those seen in the same setting when m = 0 and d = 0.25 (d = 4).
Table 3 reports empirical rejection frequencies of the
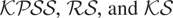
tests under a local alternative for each of Cases (a), (b) and (c). For each case, results are reported where either only {σt2} (labeled “shift in I(0) only”) or only {σηt2} (labeled “shift in I(1) only”) vary through time and for the case where both vary. The range of values for the parameters is as in Section 6.1, excepting the case where both components vary through time where {σηt2} is fixed throughout with d = 4 and m = 0.1 under Case (a), d = 4, m = 0.1, and γ = 10 under Case (b), and m = 0 and d = 4 under Case (c). In these cases, therefore, {σt2} and {σηt2} evolve according to the same function with the same parameters, whereas for the other entries in the table they evolve according to the same function but with different parameters. The local alternative considered is (5), except that we do not scale out the nuisance parameter ω/ωη.
4Recall that this was done in Theorem 3 purely to simplify the right member of (6).
Consider first Table 2, which reports benchmark results for the power of the
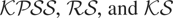
tests for the homoskedastic case, σt2 = 1, t = 1,…,T, under the local alternative Hc : σηt2 = c2/T2, t = 1,…,T, for c = 1, 5, 10, 15, 20, and 25. Observe that the
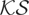
test is dominated on local power by both the
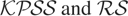
tests. The
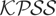
test is the locally best invariant (LBI) test in this setting, so it is no surprise that it displays the highest power in most cases. However, the

test is very competitive on power and, indeed, tends to display higher power than

for c ≥ 20.
Empirical local power of stationarity tests: Homoskedastic errors

Empirical local power of stationarity tests under heteroskedastic errors: xt = (1, t)′

Turning to the results for the heteroskedastic cases in Table 3, a number of regularities are seen. First, in each of the cases of variance shifts in the I(0), I(1), and both I(0) and I(1) components, the
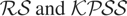
tests behave almost identically. Second, in the case of variance shifts in the I(1) component only, all three tests behave almost identically. Third, in the case where variance shifts affect both the I(0) and I(1) components, for the entries in Cases (a) and (b) for m = 0.1, d = 4 and Case (c) for m = 0.0, d = 4 (i.e., instances where precisely the same variance process applies to both the I(0) and I(1) components) the results are very similar to those seen in Table 2 for c = 10. Fourth, and as predicted by the asymptotic distribution theory (cf. Remark 7), changing variances in the I(0) and I(1) components (but not both) effect very different outcomes: negative (positive) shifts in the variance of the I(1) component result in increases (decreases) in power relative to the benchmark homoskedastic power in Table 2, whereas the converse is true for variance shifts in the I(0) component. Fifth, and in contrast to the preceding point, shifts in both the I(0) and I(1) variances tend not to inflate power beyond the homoskedastic benchmark; indeed, for single and smooth transition breaks with early positive shifts the empirical rejection frequencies of all the tests are close to the nominal level. Finally, the effects on power (relative to the homoskedastic case) of heteroskedastic variances are most pronounced for the single break case and least pronounced in the trend case (cf. Table 1).
In this section we show that the size biases caused by time-varying second moments can be corrected by properly adapting the heteroskedastic fixed regressor bootstrap of Hansen (2000) to the present framework. Interestingly, the heteroskedastic bootstrap allows us to retrieve asymptotically correct p-values even in the presence of autocorrelated errors. The rationale behind this result is that whereas the asymptotic null distribution of the
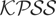
statistic is affected by the heteroskedasticity function ω(·) it is not affected by the short memory properties of the I(0) component {εt} (see Theorem 1). We outline the bootstrap procedure for the
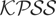
-based procedure, although the

- and
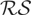
-based procedures may be bootstrapped in an entirely analogous fashion.
Let
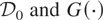
denote the limiting null distribution of
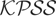
(Theorem 1) and its cumulative distribution function (c.d.f.), respectively. Let
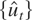
denote the residuals obtained by regressing yt on xt and let {zt}t=1T denote an independent N(0,1) sequence. The bootstrap sample is defined as
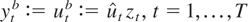
, and the bootstrap statistic is given by
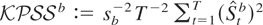
with
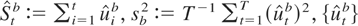
denoting the residuals obtained from the regression of ytb on xt, t = 1,…,T. The bootstrap p-value is
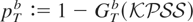
, where GTb(·) denotes the c.d.f. of
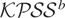
.
The usefulness of the heteroskedastic bootstrap in the present framework is given in Theorem 4, which shows (i) that the bootstrap allows us to retrieve the correct asymptotic null distribution and hence that the p-values based on
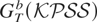
are asymptotically pivotal and (ii) that a test based on the bootstrap p-values is consistent.
THEOREM 4. (i) Under the conditions of Theorem 1,
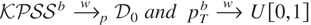
, where
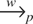
denotes weak convergence in probability (see Giné and Zinn, 1990). (ii) Under the conditions of Theorem 2,

.
In practice, GTb(·) is not known but can be approximated in the usual way through numerical simulation by generating N (conditionally) independent bootstrap statistics,
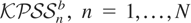
, computed as before but from

, with {{zn,t}t=1T}n=1N a doubly independent N(0,1) sequence. The simulated bootstrap p-value is then computed as
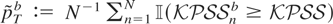
and is such that
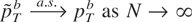
.
In Table 4 we report results for the bootstrapped KPSS testing procedure, outlined before, applied to data generated according to Case (a) of Section 6.1. The results are therefore directly comparable with those given for Case (a) in Table 1 for the
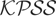
test. Results are reported only for this case because this was the form of heteroskedasticity that effected the most significant size distortions in the original tests. The reported results are for experiments run over N = 1,000 bootstrap replications. Benchmark entries for the case where the errors are homoskedastic are also reported in the column labeled “IID.”
Empirical size of bootstrap KPSS tests: Heteroskedastic errors, Case (a)

A comparison of the results in Tables 1 and 4 shows that the bootstrap performs very well in practice with empirical sizes much closer to the nominal level than for the standard
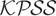
test. Some oversizing, associated with early negative and late positive variance breaks, is still seen for T = 50 but is much reduced relative to that seen for the standard

test and is largely eliminated for T = 250. The undersizing seen in the standard

test for early positive and late negative breaks is eliminated by the bootstrap. Although not reported here, qualitatively similar improvements (available on request) were seen for bootstrapped implementations of the

tests and for data generated under Cases (b) and (c).
In this paper we have analyzed the effects that time-varying second moments of a very general form have on the stationarity tests of Kwiatkowski et al. (1992), Lo (1991), and Xiao (2001). We have demonstrated that, in general, heteroskedasticity changes the limiting distributions of these stationarity test statistics under both the null and local alternatives and (for appropriately rescaled statistics) global alternatives. We have presented Monte Carlo simulation results to quantify the finite-sample effects of heteroskedasticity on the size and power properties of the three tests. Results were presented for variances displaying either a single break, a smooth transition break, or a linear/piecewise-linear trend. Bootstrap versions of the tests, adapted from the heteroskedastic bootstrap principle of Hansen (2000), were developed and shown to greatly improve the finite-sample size properties of the tests. Although not considered here, it would be interesting and reasonably straightforward to extend the results presented in this paper to the corresponding tests for the null hypothesis of cointegration of Shin (1994), inter alia.
Proof of Theorem 1. Define the partial sum

. Under Assumptions
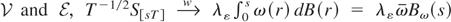
(see also Cavaliere, 2004b). Similarly,
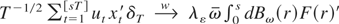
. After some algebra, the preceding results taken together with the convergence result
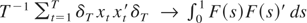
(Assumption

) allow us to conclude that

and, hence, by the continuous mapping theorem (CMT), that
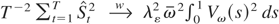
. Note that the CMT also allows us to prove that
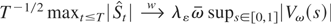
and that
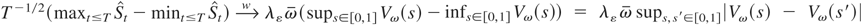
(see Remarks 3 and 5). The proof is completed by showing that
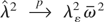
, which follows from Cavaliere (2004b, Thm. 4). █
Proof of Theorem 2. Because {σηt} satisfies Assumption

then
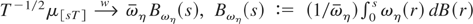
. This result also implies that
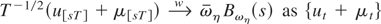
is dominated by {μt}. As in the proof of Theorem 1, it easily follows that the residuals

obey the functional central limit theorem
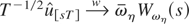
and, hence, by the CMT, the numerator of
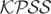
satisfies

. Finally, as in Kwiatkowski et al. (1992) one can show that for any
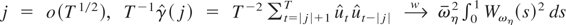
and hence that
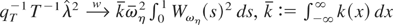
. █
Proof of Theorem 3. The proof follows directly from Theorems 1 and 2, using the CMT and the fact that, because
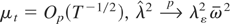
, as in Theorem 1. █
Proof of Theorem 4. (i) Conditionally on

is Gaussian with covariance kernel
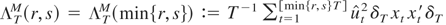
(see, e.g., Hansen, 1996). Similarly, the process
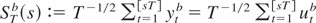
is Gaussian with covariance kernel
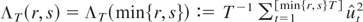
. To simplify notation, but without loss of generality, assume that xt contains a constant, i.e.,
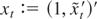
; then STb(s) = (1,0′)MTb(s), so that the asymptotic distribution of STb(·) easily follows from that of MTb(·). Now,
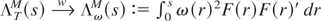
, which is a consequence of the fact that

(notice that the true value of β is zero here) is of Op(T−1/2) and the mixing properties of εt2 − E(εt2). It therefore follows that

and, by the CMT, that

. Hence,
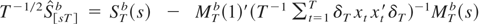
weakly converges to
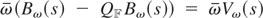
. Notice that
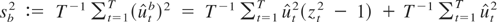
. As in Cavaliere (2004b) it is straightforward to show that
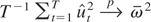
, so that

, a result that follows from a standard application of the weak law of large numbers for martingale difference sequences. The preceding results imply that

and hence that GTb(·) → G(·) uniformly in probability. The remainder of the proof is identical to the proof of Theorem 5 in Hansen (2000). (ii) Let

. Conditionally on
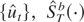
is Gaussian with zero mean and covariance kernel
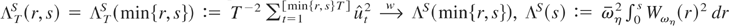
. Hence,

and by the CMT

being a standard Brownian motion, independent of Wωη(r). Using similar arguments it can be shown that

and that

being a standard Brownian motion, independent of Wωη(·) and Bz1(·). Consequently, the standardized variance estimator

satisfies
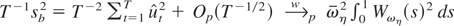
. Taken together, the preceding results imply that

weakly converges in probability to the random variable
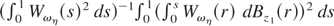
, whose c.d.f. is denoted by
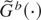
, and hence that

, uniformly. Consequently,

. Because, by Theorem 2,
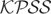
diverges at the rate qT−1T, it follows that

. █

Empirical size of stationarity tests: Heteroskedastic errors

Empirical local power of stationarity tests: Homoskedastic errors

Empirical local power of stationarity tests under heteroskedastic errors: xt = (1, t)′

Empirical size of bootstrap KPSS tests: Heteroskedastic errors, Case (a)