1. INTRODUCTION
Elliott, Rothenberg, and Stock (1996)
derive a class of point-optimal unit root tests in a time series model
with Gaussian errors. They show that, by efficiently handling intercept
and trend coefficients, their tests are generally more powerful than
the standard Dickey–Fuller tests. The present paper investigates
whether the same power improvements can be attained when using
“robust” testing methods that are designed to improve power
for non-Gaussian error distributions. I find that this improvement
occurs when the true error distribution is known or at least is known
to be symmetric. However, if one wants to be robust to thick-tailed,
possibly asymmetric, error distributions, the power improvement found
by Elliott et al. (1996) cannot be
attained.
First I consider the model with an intercept and no time trend. In
large samples the variation of a nearly integrated process dominates
the intercept of the process. Thus the intercept can be set equal to
zero when forming test statistics. The resulting point-optimal tests
dominate previously proposed robust tests (see Lucas, 1995; Herce, 1996;
Hasan and Koenker, 1997) which do not set the
intercept to zero.
However, when the error distribution is unknown and asymmetric,
setting the intercept to zero leads to a test with very bad properties.
In large samples the zero-intercept tests reject a true null hypothesis
with probability approaching one-half. The previously proposed
inefficient tests perform well under asymmetric errors. Thus there is a
trade-off between efficiently handling conditioning variables and
robustness with respect to asymmetric error distributions.
Then the model with both an intercept and a linear time trend is
considered and the form of the point-optimal test that is invariant to
the time trend is derived. In many cases it is difficult to compute the
point-optimal test, so I use Laplace's approximation to derive an
asymptotically equivalent test that is easier to calculate. I show that
tests based on the maximum likelihood estimator (MLE) and the
likelihood ratio (LR) statistic, which were previously studied by Xiao
(2001), are asymptotically admissible. When
the error distribution is known and non-Gaussian, a test based on
either of these statistics will in many cases have higher power than
the tests suggested by Elliott et al. (1996).
In the model with a time trend, an unknown asymmetric error
distribution causes the power of the point-optimal test to approach
zero in large samples. The tests based on the MLE and LR statistic have
slightly better properties—they have power approaching zero
against local alternatives, but power approaching 1 against fixed
alternatives. Thus, although asymmetric errors lead to power losses for
these two procedures, the tests do not overreject a true null and are
acceptable for both correctly and incorrectly specified errors. Monte
Carlo results suggest the power losses are substantial for the
point-optimal tests but not as bad for the MLE and LR tests.
Thus the viable unit root tests are the traditional robust tests
(which inefficiently handle intercepts and trends) and the
point-optimal Gaussian tests proposed in Elliott et al. (1996) (which are inefficient in the presence of
thick-tailed errors). In some situations the efficiency loss due to
ignoring thick-tailed errors is less than that due to inefficiently
modeling the intercept and trend. For example, the point-optimal
Gaussian test is more powerful than many traditional robust tests when
the errors are drawn from a Student's t-distribution with
five or more degrees of freedom.
Although the present paper does not specifically consider the topic,
there are similar implications for the construction of confidence
intervals for autoregressive roots close to one.1
Methods for constructing these intervals appear in Stock
(1991), Hansen (1999), and Elliott and Stock (2001).
Because many of the intervals are
based on the inversion of tests, it appears that the framework for
constructing more accurate intervals described in Elliott and Stock
(
2001) cannot be extended to non-Gaussian
models.
2. THE MODEL WITH NO TIME TREND
The observations
{yt}t=1T
come from the model
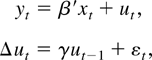
where β = (β1, β2)′ is a
two-dimensional coefficient vector and xt
= (1, t)′. I consider the model with an intercept only
(e.g., β2 = 0) and with a linear time trend (e.g., no
restrictions on β). The random errors εt
are independent and identically distributed (i.i.d.) and have
expectation zero and a finite variance. Under the unit root hypothesis,
γ = 0, and the detrended series is not stationary. I will evaluate
tests of the unit root hypothesis versus the alternatives γ < 0.
Because I am interested in inference when γ is close to one, I
adopt the local-to-zero reparameterization γ =
c/T, so the parameter space is a shrinking
neighborhood of zero as the sample size grows. Following Chan and Wei
(1987) and Phillips (1987), I take c fixed when making limiting
arguments, obtaining asymptotic power as a function of the local
alternative c.
We distinguish between the true, unknown density for ε, given
by e−f (ε), and the density
used to construct the likelihood function,
e−g(ε). The researcher chooses
g hoping that g is a reasonable approximation to
f and also hoping that the resulting tests perform well when
g ≠ f. In the model with an intercept and no time
trend,
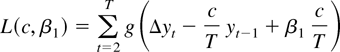
is the negative of the log-likelihood function evaluated at γ =
c/T, conditional on the first observation
y1.
Consider the classical regression model y =
α0 + α1 x + ε with
nonrandom x and i.i.d. error ε. If the true value of the
intercept α0 is zero, then regressing y on
x alone leads to a more efficient estimator of
α1 than regressing y on both x and a
constant. Now consider two estimators for c.
(1)
,
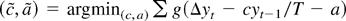
with a = −β1
c/T. These are the usual M-estimators
studied by Lucas (1995), Hoek, Lucas, and van
Dijk (1995), Herce (1996),
and Hasan and Koenker (1997).
2 Hasan and Koenker (1997) propose
rank tests instead of M-tests. Thompson (2004) notes that under the local-to-zero
reparameterization, for each rank test and error distribution there
exists a test based on
with the same asymptotic power function. Thus we will not specifically
discuss the rank tests.
(2)
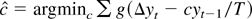
I label this statistic the “constrained” MLE.
If β1 is zero then a is zero and
should be more efficient than
.
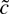
Thus a test that rejects the null for small values of
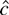
should be more powerful than a test that rejects for small
.
We include the constant a in case β1 is not
zero. However in large samples a = −β1
c/T is very close to zero no matter what the true
values for β1 and c. This suggests that
asymptotically it does not matter that we omit the constant. It turns
out that, if g equals f (the true negative
log-density of the errors), then in large samples tests based on
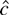
dominate tests based on
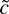
even when β1 and c are not zero.
This is the source of the power improvements in the model with no
time trend. Many existing robust unit root tests do not take advantage
of the fact that in large samples the variation in
ut dominates any fixed intercept, so
β1 can be taken equal to zero without affecting the
asymptotic distribution of
.
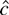
We will show that in large samples, no test dominates the test based
on
.
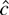
This optimality result comes from the Neyman–Pearson lemma, which
states that the most powerful test of c = 0 versus the alternative
c = c rejects for small values of L(c,
β1) − L(0, β1). In large samples,
the
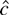
-test
is just as powerful as the Neyman–Pearson statistic for some
c. This is true even when β1 is not known.
Elliott et al. (1996) show that in a
Gaussian model with an intercept and no time trend, there is no
efficiency loss from β1 being unknown. The same is true
for nonnormal innovations. Suppose we form the Neyman–Pearson
test with an incorrect value for β1, say, 0. If
g is three times differentiable with bounded second and third
derivatives then by a Taylor series approximation,
where |εt* −
εt| ≤ |(c −
c)ut−1 /T
− cβ1 /T | and
|εt** −
εt| ≤
|cut−1 /T
|. Under regularity conditions given subsequently,
ut−1
/T1/2 is
Op(1). Therefore, because
g′′ and g′′′ are bounded, many of the terms
are asymptotically negligible:
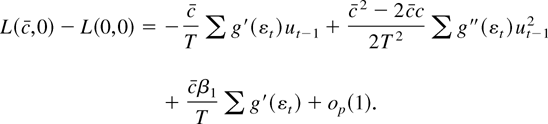
If Eg′(εt) = 0, then
,
and in large samples the test statistic does not depend on
β1. The term
Eg′(εt) will equal zero when
the errors are correctly specified, meaning that g =
f:
Thus, under correct specification of the errors, there is no
efficiency loss from β1 being unknown.
In a stationary autoregressive model, the Neyman–Pearson test
statistic typically admits an asymptotic representation in terms of a
single scalar sufficient statistic. This allows the construction of a
test that is asymptotically uniformly most powerful against all
alternatives c < 0. Here the Neyman–Pearson statistic
has an asymptotic representation that is a linear combination of the
two scalar sufficient statistics T−1
[sum ]g′(εt)ut−1
and T−2[sum ]g′′(εt)ut−12,
with weights depending on c. As Elliott, Rothenberg and
Stock (1996) have noted, this implies that there
does not exist a uniformly most powerful test, even in large samples. Each
Neyman–Pearson test is most powerful only against the point
alternative c = c. The Neyman–Pearson tests
comprise an infinite family of admissible tests, indexed by
c, no one dominating the others for all c.
Because there is no uniformly most powerful test, the goal is to find
feasible, admissible tests. Let π(c, c) denote
the asymptotic power function for the Neyman–Pearson test indexed
by c when the true value of the local autoregressive
parameter is c and the size of the test is α:
where q(c) satisfies π(0, c) =
α. Because the Neyman–Pearson test indexed by c is
asymptotically optimal against the alternative c =
c, the envelope power function Π(c) ≡
π(c, c) is the upper bound on power for all tests
against each alternative. A test is asymptotically admissible if it has
a limiting power function that is equal and tangent to the envelope
function for some c.
In the next section I show that the
-test
is asymptotically admissible whereas the
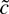
-test
is not. There are other interesting test statistics to consider: the
M-estimator t-test, which rejects for small values of
,
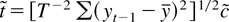
and the constrained t and LR statistics
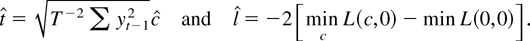
The
-tests
impose the constraint β1 = 0, so they will dominate the
M-estimator t-test.
2.1. Asymptotic Power Functions
To justify the claim that the
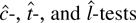
dominate the M-tests, it will prove convenient to develop asymptotic
representations for the various statistics. Consider some of the
g functions used for robust regression problems:
where the constant k is chosen by the researcher. Because
g may not be everywhere differentiable, we cannot approximate
the log-likelihood function with Taylor series expansions. Instead of
pointwise differentiability, the proofs make use of “stochastic
differentiability,” an idea described in Pollard (1985). Application of the idea requires imposition
of smoothness conditions on the error density to make up for the lack
of smoothness in the objective function.
Assumption 1. (Smoothness of the Error Density). The errors
{εt}t=1T
are i.i.d. mean zero with
E|ε1|2+δ < H
for some δ > 0. The term ε1 has a density
function f (z) that is bounded and uniformly
continuous.
The g function may have finitely many points of
nondifferentiability.
Assumption 2. (Objective Function). g(x) is convex
and strictly increasing in |x|, and
g(x) is everywhere twice differentiable except for
x in P, where P contains the D
points p1,…,
pD. There exists some finite positive
H so that |g′′(x)|
< H for x not in P. There exists some
finite positive h satisfying P ∈
[−h − δ, h + δ] for
some δ > 0, so that for all x and y in
[−h, h] we have
|g′(x)| < H and
|g(x) − g(y)|
≤ H|x − y|.
I assume that g is convex because it simplifies the proofs.
Assuming convexity allows me to extend several pointwise convergence
results to apply uniformly over the parameter space. Convexity also
greatly simplifies the demonstration of the rate of convergence of the
estimators. This extensive use of convexity is due to results in
Pollard (1991) and Hjort and Pollard (1993).
For nondifferentiable g, it is not possible to define an
approximate likelihood in terms of the derivatives g′
and g′′. We replace g′ with the
derivative-like function ψ.
DEFINITION 1. ψ(x) is equal to
g′(x) if g is differentiable at
x and ψ(x) = 0 otherwise.
If g is everywhere differentiable then g′ =
ψ. For LAD regression ψ(x) = sign(x), and
for Huber's function ψ(x) =
x1(|x| < k) +
k1(|x| ≥ k).
In standard (non–unit root) problems, the second derivative
g′′ enters the asymptotic representation though
its expectation Eg′′(ε1). We
replace Eg′′(ε1) with the
parameter
.
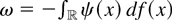
When g is everywhere twice differentiable, ω =
Eg′′(εt). For LAD
regression ω = 2f (0), and for Huber's function
ω = Pr[|x| < k] .
In large samples the power functions admit representations in terms
of functionals of Brownian motion. Define W(·) to be
standard Brownian motion and define
Wc(·) to be the
Ornstein–Uhlenbeck process
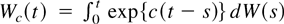
with initial condition W0(0) = 0. The asymptotic
representations make use of the parameters σε2
= Var(εt), ρ =
Corr(εt,
ψ(εt)), and
σψ2 = Var
ψ(εt) and also of the stochastic
process
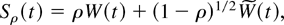
where
is standard Brownian motion, independent of W. The following theorem
is proved in Appendix A.
THEOREM 1. If Eψ(εt) = 0, and
if Assumptions 1 and 2 hold, then
Rothenberg and Stock (1997) and Xiao (2001) derive similar representations without
assuming convexity of g but do not allow for nondifferentiable
functions.
The large sample power function for the Neyman–Pearson test is
Power functions for the other tests may be obtained similarly.
Figure 1 plots envelope power functions and
asymptotic power for a variety of tests. The curves for LAD errors
(from the double exponential distribution) are given and so are
standard normal errors and Huber errors.3
The parameter k that appears in Huber's
M function is set to 1.345 for all of the figures in
this paper. At this value of k, the Huber estimate of a
location parameter from i.i.d. standard normal data has a relative
efficiency of 95% with respect to the mean. See Hampel, Ronchetti,
Rousseeuw, and Stahel (1986, p.
399).
A curve also is produced for the mixture distribution
(labeled Mixture in the figure) where a standard normal variable is
drawn with probability 0.95 and a
N(0,36) variable is drawn
with probability 0.05.
4 The log of the
density for the mixture distribution is not convex. Although this
violates the assumptions used to derive the asymptotic representations
in Appendix B, simulations not reported here suggest that the
representations are still valid.
Each curve is calculated
under the assumption of correct specification, so that
e−g is equal to the true density
e−f.
Asymptotic power curves for unit root tests in the model with no time
trend (xt = (1,0)). The curves are drawn
under the assumption of correct specification, so the g
function used to form the test statistics is equal to f, the
negative log-density of the errors. (The simulations that appear in
this paper were performed by computing stochastic integrals as the
realizations of normalized sums of 500 successive draws from a discrete
time Gaussian AR(1) process with autoregressive parameter 1 −
c/T. There are 100,000 Monte Carlo
replications.)
The power curves for nonnormal errors are all substantially higher
than the curve for normal errors. The most powerful test for Gaussian
errors achieves 50% power at c close to −7.0, and the
most powerful test for double exponential errors (corresponding to LAD
estimation under correct specification) achieves 50% power at
c close to −3.75.
Figure 1 also provides power curves for the
tests based on the constrained MLE
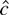
and the M-estimator
.
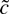
The
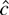
-test
is asymptotically admissible. Test power is
tangent to the power envelope when envelope power is large. The
-test
is not asymptotically admissible and is
dominated by the
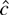
-test.
The power curve for
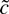
touches the envelope function only under the null (c = 0) and for
alternatives so far from zero that any sensible test would have power equal
to 1.
The M-estimator t-test is not asymptotically
admissible, whereas the constrained
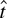
-test
is admissible. Figure 1 shows that the
constrained t-test achieves tangency to the power envelope
function at power close to 50%. The figure also shows that the
constrained
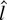
-test
is not admissible. As Rothenberg and Stock (1997)
show, straightforward manipulations of the asymptotic representations
demonstrate that rejecting for large values of
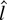
is asymptotically equivalent to rejecting for large
.
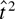
Because the tests based on
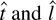
are one-sided and two-sided tests of the same one-sided hypothesis, it is not
surprising that the t-test dominates the test based on
.
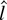
We have obtained power improvements by imposing the constraint that
the intercept estimate
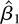
is zero. We can obtain identical results by replacing the requirement that
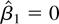
with the requirement that the estimator
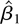
is stochastically bounded. Consider two more estimators.
(1)
,
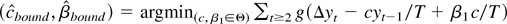
where Θ is a compact set. It is common to assume a bounded parameter
space, and this estimator imposes that assumption. The estimator
is obviously stochastically bounded, and the term
supβ1∈Θ|β1
c/T | disappears from the likelihood
function in large samples. Thus
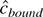
has the same limiting
distribution as
.
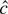
(2)
.
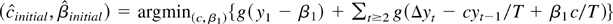
These are the MLES when we assume the initial condition u0
= 0. In an earlier draft of this paper it was shown that
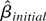
is stochastically bounded. Thus
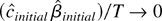
fast enough so that
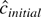
has the same distribution as
.
2.2. Failure of Robustness to Error Misspecification
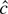
These power improvements occur as long as g, the estimating
function, is equal to f, the true negative log-density of the
errors. When g ≠ f,
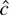
may behave poorly. Consider the classical regression model y =
α0 + α1 x + ε. If the
errors come from the double exponential distribution, ε has zero
median and the maximum likelihood estimates are the LAD estimates
.
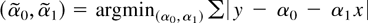
If the true value of α0 is zero, then under correct
specification we can get a better estimator for α1 by removing
α0 from the objective function:
.
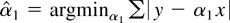
Now suppose that α0 = 0 and that ε comes from an
incorrectly specified, asymmetric error distribution with zero mean but
nonzero median. For example take ε = Z2 − 1
where Z is standard normal. It is well known that in this case
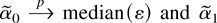
has a limiting distribution. It is also well known that the distribution of
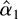
is not stochastically bounded, even if α0 = 0. Thus the
constant α0 “recenters” the incorrectly
specified errors. In the classical setting we include the constant to
protect ourselves from errors with nonzero median.
The same thing happens in the unit root problem. Herce (1996) shows that if the intercept β1 is
zero and the errors have zero median, then
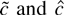
both have limiting distributions. When εt has
a nonzero median
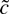
has a limiting distribution whereas
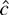
blows up. This can be
seen in Figures 2a–d. Each histogram depicts
5,000 Monte Carlo realizations of
,
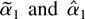
estimated from simulated data sets of 500 observations from the model with
c = 0 (so the null is true), β1 = 0 and initial
condition u0 = 0. Figures 2a and
b show that when the errors come from the zero median Student's
t-distribution with four degrees of freedom, both estimators have
limiting distributions. Figures 2c and d show
that when the errors do not have zero medians (εt
= Zt2 − 1 where
Zt are i.i.d. standard normal) the
distribution of
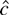
blows up. So for any fixed
critical value q, the probability of rejecting a true null
hypothesis converges to
.
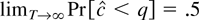
Mathematically this can be understood as failure of an identification
condition. Consider the classical regression model with no intercept:
y = α1 x + ε. If g is
differentiable, the estimator
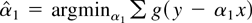
will solve the first-order condition
.
Under the usual assumptions this will deliver a consistent estimator
of α1 if the identification condition
Eg′(y − α1 x)x
= 0 holds. Because y − α1 x = ε
and x is not random, this condition is equivalent to
Eg′(ε) = 0. Thus the identification condition is that
ε has a distribution with the property that Eg′(ε)
= 0.
In our unit root problem
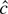
solves
,
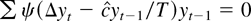
which suggests the identification condition
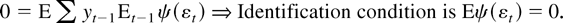
For the LAD problem ψ(εt) =
sign(εt) and the identification condition is
E sign(εt) = 0. The condition holds for LAD
only if the errors have zero medians.
What assumptions do we need to ensure that
Eψ(εt) = 0?
(1) Expression (2) demonstrates that
Eψ(εt) = 0 under correct specification
(so f = g).
(2) Eψ(εt) equals zero for the Gaussian
likelihood, no matter what the distribution of the errors. The Gaussian
likelihood has g(x) = x2/2
and ψ(x) = x, so the assumption
Eε1 = 0 insures that Eψ(ε1) =
0.
(3) Eψ(εt) equals zero when f
≠ g and both functions are symmetric around zero.
(4) When f ≠ g and f is not symmetric,
Eψ(εt) can be different from zero. For
example, for LAD estimation applied to the errors
εt =
Zt2 − 1,
Eψ(εt) = E
sign(Zt2 − 1) ≈
−.3656.
It turns out that the optimal tests are not robust to unknown,
asymmetric error distributions. To get the tests to work, we either
need to assume that we know the distribution of ε, or we need to
assume that ε comes from a symmetric distribution. Thus the
optimal tests are not robust to unknown asymmetric error distributions.
The Gaussian tests of Elliott, Rothenberg and Stock (1996) are the one exception—those tests are
valid under fairly general forms of misspecification, including asymmetric
errors.
Figure 2 depicts an example where the
optimal tests reject a true null hypothesis too often. This is
generally a problem with asymmetric errors.
Histograms of 5,000 Monte Carlo simulations of
(on the left) and
(on the right) estimated from 500 observations from the model with no trend
or intercept. The true value of c is 0. (a) and (b) Here the errors
come from the Student's t4 distribution. Because the median is zero
is more efficient and has a smaller spread around 0. (c) and (d) Here each
error is εt =
Zt2 − 1, where
Zt are i.i.d. standard normal. Because the
median is not zero,
has a limiting distribution and
blows up.
PROPOSITION 1. Suppose that g is three times differentiable
with bounded third derivatives and suppose that the errors satisfy
assumption 1. If Eψ(εt) ≠ 0 then in
large samples tests based on
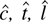
and the Neyman–Pearson statistic all reject a true null hypothesis
with probability approaching .5, no matter what the nominal size of the
test. The M-tests based on
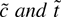
have the same limiting representations as in Theorem 1.
5 The M-tests have the same limiting
representations as in Theorem 1, with the nuisance parameters
σψ2, ρ, and ω replaced by
Var[ψ(εt − η)],
Corr[εt,
ψ(εt − η)] , and
,
where η denotes the parameter that
solves Eψ(εt − η) =
0.
M-tests are robust to asymmetric error densities. Let η
denote the parameter that solves the equation
Eψ(εt − η) = 0. So for LAD
estimation, ψ(εt − η) =
sign(εt − η), and η is the
median of the errors. The M-estimator objective function can
be rewritten
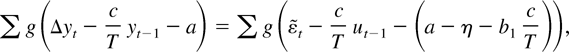
with
.
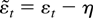
These recentered errors
satisfy
.
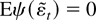
Thompson
(2004) shows that if
Eψ(εt) ≠ 0 then
in probability and
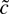
has the same limiting distribution as in Theorem 1, with a slight redefinition
of the nuisance parameters (see note 5). Thus estimation of the free parameter
a causes a power loss under correct specification but ensures
robustness against incorrect specification.
We can avoid these centering problems by assuming that
Eψ(εt) = 0. For example for LAD
estimation we could assume that the median of ε is zero and leave
the mean unspecified. The zero mean assumption is essential for nearly
integrated models because it identifies the trend. If the mean is not
zero, then the trends behave very differently under the unit root null
than for stationary alternatives. Because
ut follows the process
Δut =
γut−1 +
εt, we have
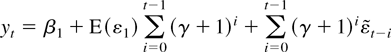
with
.
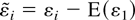
If γ = 0, then yt has both a unit root and a
nonstochastic trend. If γ < 0, then
yt is stationary with the long-run mean
.
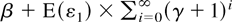
Thus the zero mean assumption is essential if
we wish to test for mean reversion around an intercept. Once we assume
zero means, adding additional centering assumptions such as zero
medians takes us closer to assuming symmetric errors.
Sketch of proof of Proposition 1.
When Eψ(εt) ≠ 0, the
Neyman–Pearson statistic is not stochastically bounded.
To understand why, notice that the statistic
T−1[sum ]ψ(εt)ut−1
appearing in the approximation to the Neyman–Pearson statistic is not
stochastically bounded. Lemma 3.1 of Phillips (1988)
implies that we must divide by T1/2 to get a limiting
distribution:
where σ2(c) =
(σεEψ(εt)/c)2[1
+ (e2c − 1)/(2c)
− 2(ec −
1)/c] . If g is three times differentiable
with bounded third derivatives, the Neyman–Pearson statistic must
also be divided by T1/2:
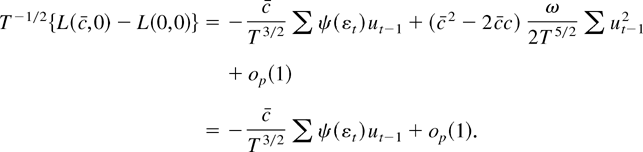
Suppose we form the Neyman–Pearson statistic and use the
critical value q(c) constructed under the
assumption that Eψ(εt) = 0. If
Eψ(εt) ≠ 0 then under the null
hypothesis the probability of rejecting is
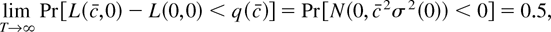
where σ2(0) = limc→0
σ2(c) =
(σεEψ(εt))2/3.
In large samples the Neyman–Pearson test rejects a true null
hypothesis 50% of the time, no matter what the nominal size of the
test.
A proof by contradiction shows that error misspecification may also
cause the constrained MLE to be stochastically unbounded. Suppose that
c = β1 = 0 and g is three times
differentiable with bounded third derivatives. If
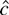
is stochastically bounded, the minimized objective function admits the
approximation
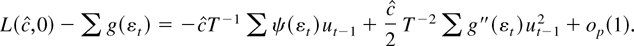
If
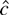
is stochastically bounded, then in large samples
must converge to the minimizer of
.
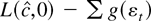
The minimizer
[T−2[sum ]g′′(εt)ut−12]−1T−1[sum ]ψ(εt)ut−1 is
not stochastically bounded, and we have our contradiction. █
2.3. Some Monte Carlo Results
A Monte Carlo study demonstrates the size distortions that occur
under incorrect specification. Table 1
presents rejection frequencies for 10 tests under various assumptions
about the true data generating process. The abbreviations in the table
are as follows.
(1) ERS—the Dickey–Fuller generalized least squares
(DF-GLS) test of Elliott et al. (1996).
This test efficiently handles the intercept for Gaussian errors but
does not use the information in thick-tailed error distributions.
(2) Adap—the adaptive test of Shin and So (1999). This test adapts to the error distribution
but does not efficiently handle the intercept.
(3)
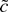
test, LAD—The Thompson (2001) version of the test based on the LAD
M-estimator.
6 The test rejects
for small values of
,
where
.
Thompson (2001) shows that
.
The test is asymptotically equivalent to the test based on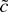
and in some cases has more accurate size. This test does not efficiently
handle the intercept.
(4)
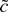
test, t3—The Thompson (2001) version of the
test based on the Student's t3 M-estimator.
(5) Trend-optimal LAD NP,
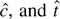
—these
tests are optimal for a double exponential likelihood. NP denotes the
Neyman–Pearson test statistic evaluated at c = −3 and
β1 = 0: L(−3,0) − L(0,0). The
three tests efficiently handle the trend and will be more powerful than the
DF-GLS test for many thick-tailed error distributions. When the errors come
from an asymmetric distribution the tests will overreject a true null
hypothesis.
(6) Trend-optimal t3 NP,
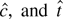
—the
optimal tests for a Student's t3 likelihood with β1 = 0.
These tests are not robust to asymmetric errors.
Rejection frequencies for selected tests in the model with no time
trend
The bold numbers in Table 1 illustrate the
size problems with asymmetric errors.
7 Critical values for first four tests are obtained using the
methods described in Elliott et al. (1996),
Shin and So (1999), and Thompson (2001). In all cases the errors are i.i.d. and no
correction is made for serial correlation. Critical values for the
trend-optimal tests are obtained by simulating from the asymptotic
distributions in Theorem 1. The representations depend on the nuisance
parameters σε, σψ, ρ, and
ω. For all four tests the nuisance parameters are estimated using
the formulas
,
where
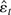
is a residual and ε and ψ are sample
averages. For the t3 estimator ω =
Eψ′(εt) is estimated by
.
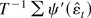
For the LAD test ω = 2f (η), which is estimated by the
usual kernel estimator of the density of
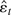
evaluated at zero:
,
where φ is the density function of a standard normal variable and
h is the bandwidth
.
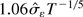
For the Neyman–Pearson test c is not estimated and there
is no residual, so we use the nuisance parameters computed for the
estimator.
All of the tests have reasonably accurate sizes for the
symmetric Student's t4 errors. However the asymmetric log normal and
chi-squared errors cause the trend-optimal tests to overreject true null hypotheses, and the problem gets worse as the sample size grows from
T = 100 to
T = 1,000. Proposition 1 predicts that as the
sample size grows the trend-optimal tests will reject a true null hypothesis
with probability approaching 0.50. The Monte Carlo results seem to confirm the
prediction, as the rejection frequencies for samples of 1,000 are close
to 0.50. The ERS, adaptive, and
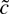
-tests
have accurate sizes for the asymmetric distributions.
The results demonstrate that the ERS test is a viable alternative to
the robust tests even when the errors are not Gaussian. The ERS test
has accurate size and good power for all four error distributions.
Somewhat surprisingly, the ERS test even has accurate size for the
infinite variance Cauchy distribution. The adaptive test works well for
the asymmetric log normal and chi-squared distributions but has poor
power for the Cauchy errors. The
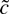
-tests
have accurate size for all four distributions. For the Cauchy errors the
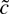
-tests
are very powerful.
3. OPTIMAL TESTS WITH A TIME TREND
If the regressors include a linear time trend,
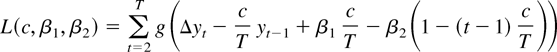
is the log-likelihood function conditional on the first observation.
Suppose we form the Neyman–Pearson statistic
L(c, β1, β2) −
L(0, β1, β2) with the unknown
coefficients replaced by the guess b =
(b1, b2)′:
In large samples the term (b1 −
β1)c/T disappears from this
expression, so the guess b1 does not matter. The
terms (b2 − β2)(1 −
(t − 1)c/T) and
(b2 − β2) do not disappear, so
unless we know the true β2 we cannot obtain the power
bound Π(c) derived in the last section. It is important to
come up with a good guess for β2.
In most situations the trend parameter β2 is unrelated
to the unit root testing problem. Following Dufour and King (1991) and Elliott, Rothenberg and Stock (1996), it is natural to restrict attention to the
family of tests that are invariant to the value of β2. By
the well-known result of Lehmann (1959, p. 249),
the most powerful invariant test of the hypothesis c = 0 versus
the alternative c = c rejects for large values of
Elliott et al. (1996) encounter a similar
integral for the Gaussian likelihood, where g(x) =
x2/2. In the Gaussian case
L(c, β1, b) is quadratic in
b, and the method of “completing the square” leads
to a closed-form solution for the integral. Because for many
non-Gaussian likelihoods it is not obvious how to solve this integral,
I approximate L(c, β1, b)
with a quadratic function of b and show that the approximate
solution is asymptotically equivalent to the exact solution. This
approach is a variant of Laplace's method (see Judd, 1998, p. 525). Laplace uses this approach to
approximate a similar integral over the double exponential
distribution.8
I thank Gary Chamberlain
for making me aware of the links between Laplace's integration
problem and this one.
The quadratic approximation is
.
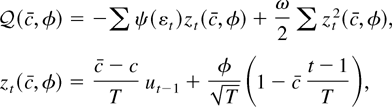
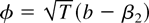
In Lemma 1 in Appendix A, it is shown that if
Eψ(εt) = 0 then
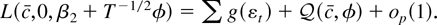
In large samples the intercept β1 disappears from the
likelihood. In the proof of Theorem 2 in Appendix A it is shown that
These integrals admit analytic solutions. Tedious algebraic
manipulations lead to the result that the log of this ratio is
asymptotically equivalent to
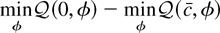
plus terms that do not depend on c. This suggests the
following theorem.
THEOREM 2. If Eψ(εt) = 0 and
Assumptions 1 and 2 hold, the most powerful invariant test is
asymptotically equivalent to the test that rejects for small values
of
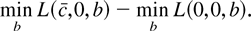
Let πτ(c, c) denote the
limiting power function for the best invariant test indexed by
c when the true value of the locally autoregressive
parameter is c:
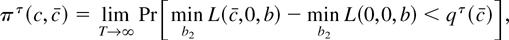
where qτ(c) satisfies
πτ(0, c) = α. The most powerful
invariant test against the alternative c has power equal to
Πτ(c) ≡
πτ(c, c), the envelope power
function.
Consider two estimators for c.
(1)
,
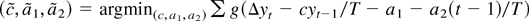
with a1 = β2 − β1
c/T and a2 =
−cβ2. These are the usual M-estimators
studied by Lucas (1995), Thompson (2004), and Hasan and Koenker (1997) (see note 2).
(2)
.
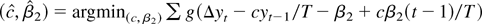
This estimator is suggested by Xiao (2001).
In large samples β1 c/T is close
to zero. This implies that the three parameters c,
a1, and a2 can be written as
just two, because limT→∞
ca1 = −a2. Under correct
specification of the errors,
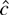
exploits the parameter restriction and a test that rejects for small
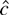
dominates one that rejects for small
.
In fact, the test based on
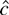
is asymptotically admissible, because its
limiting power function touches the power envelope
Πτ. The test based on
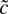
is not asymptotically admissible.
Another interesting test is the t-test based on the
M-estimator, which rejects for small values of
,
where
is the residual from a least squares regression of
yt−1 on (1,
t/T). This test is not asymptotically admissible
and is dominated by the constrained t- and LR tests, which
reject for small values of
3.1. Asymptotic Power Functions
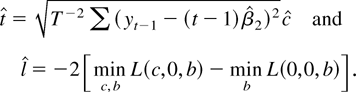
To derive the power functions of the various test statistics, it will
prove useful to provide a limiting representation for the objective
function. By Lemma 3.1 of Phillips (1988),
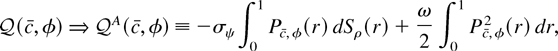
where Pc, φ(r) =
σε(c −
c)Wc(r) + φ(1
− cr) is a stochastic process. The following
theorem is proved in Appendix A.
THEOREM 3. If Eψ(εt) = 0 and
Assumptions 1 and 2 hold, then
Appendix B provides a closed-form expression for
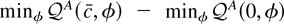
in
terms of stochastic integrals. Because
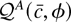
is a nonlinear
function of c and φ, the asymptotic representation for
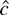
does not admit an analytic solution in terms of
random integrals. Appendix B provides a method for simulating from the
asymptotic distribution of
.
Figure 3 plots the limiting power functions
for the various tests in the model with a time trend. The curves are
lower than the corresponding power envelopes for the model with an
intercept only. Power rises as the tails of the error distribution
become thicker; for Gaussian errors 50% power is achieved at
−12.5, and for double exponential errors 50% power is achieved at
about −6.0.
Asymptotic power curves for unit root tests in the model with a time
trend (xt = (1, t)). The curves
are drawn under the assumption of correct specification, so the
g function used to form the test statistics is equal to the
negative log-density of the errors f. (The simulations that
appear in this paper were performed by computing stochastic integrals
as the realizations of normalized sums of 500 successive draws from a
discrete time Gaussian AR(1) process with autoregressive parameter 1
− c/T. There are 100,000 Monte Carlo
replications.)
Figure 3 shows that the constrained
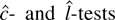
-tests
are asymptotically admissible. Careful examination of the figure leads to
the conclusion that the constrained
-statistic
is not asymptotically admissible. Neither M-test is
asymptotically admissible. The
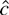
-test
is point optimal when power is high, and the
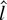
-test
is point optimal when power is close to one-half. Rothenberg (1984) describes similar results; he notes that in
standard (non–unit root) models with no nuisance parameters,
second-order asymptotic theory predicts that estimator-based tests are
optimal when power is high and LR tests are optimal when power is close
to 50%.
3.2. Failure of Robustness to Error Misspecification
The analysis in the previous section was carried out under the
assumption of correct specification, so g = f where
g is the function used to form the likelihood function and
e−f is the density of
εt. As discussed in Section 2.2, correct
specification insures that the centering condition
Eψ(εt) = 0 holds. If g ≠
f then Eψ(εt) may not equal
zero. When Eψ(εt) ≠ 0 the test
statistics can behave badly.
PROPOSITION 2. Suppose that g is three times differentiable
with bounded third derivatives and suppose that the errors satisfy
Assumption 1. If Eψ(εt) ≠ 0 then
(1) Under the local alternative
.
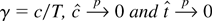
Here
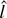
is Op(1) but does
not have the distribution given in Theorem 3. Therefore power against
any local alternative approaches zero.
(2) Under the fixed alternative
.
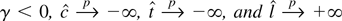
Power against any fixed alternative
approaches 1.
(3) If g′′(x) >
B > 0 for all x, then under both local and fixed
alternatives the best invariant test statistic
,
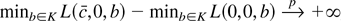
where K is a compact set. Power against any fixed or local alternative
approaches zero.
(4) The M-tests based on
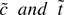
have the same limiting distributions as in
Theorem 3.
9 The M-tests have the
same limiting representations as in Theorem 3, with the nuisance
parameters redefined as in note 5.
Because the critical values for
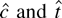
are always negative, tests that reject for small
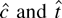
will have size converging to zero and power against any local
alternative also converging to zero. The
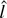
-test
has power equal to size for any local alternative, and its actual size will
not match its nominal size, even in large samples. Because the critical values
for the best invariant test are also negative, the best invariant test has
size and power approaching zero against both fixed and local
alternatives. The M-tests are robust to asymmetric errors. No
matter what the error distribution, the M-tests have power
against local alternatives and are consistent against fixed
alternatives.
Thus none of the trend-optimal tests have power against local
alternatives, but all except the best invariant test have power
approaching 1 against fixed alternatives. In a large sample with a
local alternative, the
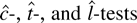
-tests
will be dominated by the robust M-tests. Furthermore, only the
M-tests are useful for forming confidence intervals for the
local parameter c, because that requires inverting a sequence
of tests, each with power against local alternatives (for the Gaussian
case, see Elliott and Stock, 2001).
On the other hand, the
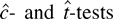
have many desirable properties even when ψ(εt)
≠ 0: in large samples they reject a true null hypothesis with probability
less than any desired size, and they reject a fixed alternative γ < 0
with probability approaching 1. Although the
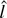
-test
may get the size wrong, because the statistic is stochastically bounded both
under the null and alternatives, the size distortions may be small. The
magnitude of those distortions is evaluated by Monte Carlo in Section
3.3.
To understand the proposition, recall that the M-estimators
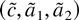
minimize the objective function
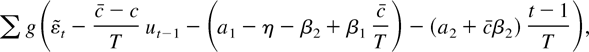
where
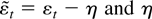
denotes the parameter that solves Eψ(εt −
η) = 0. If the condition Eψ(εt) = 0
fails to hold then
,
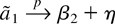
and the “recentered” errors
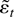
satisfy
.
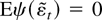
Thus
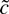
has the same limiting distribution as in Theorem 3, with a slight redefinition
of the nuisance parameters (see note 5). This result is shown by Thompson
(2004), and it implies that statement 4 of the
proposition will hold. Because there is no free “recentering”
parameter in the objective function for
,
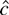
the parameter on the time trend accomplishes the recentering. If
,
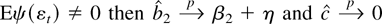
no matter what the local alternative c.
Sketch of proof of Proposition 2.
To establish statement 1 of the proposition, consider the model with the
local alternative γ = c/T. Define φ =
(φ1, φ2)′ =
(T1/2c,T1/2(b2 − β2 − η))′ and
mt =
T−1/2(−η(t −
1)/T,1)′. The likelihood function is
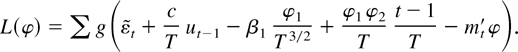
A Taylor series expansion, combined with the usual asymptotic
arguments (see Phillips, 1988, Lemma 3.1),
implies that
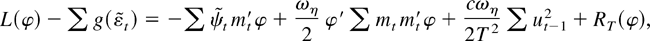
where
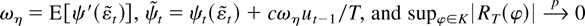
for any compact set K. By the same argument used to prove Lemma 2,
φ is stochastically bounded. Therefore, by the argmax continuous mapping
theorem of Wellner (1996, p. 286),
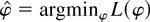
converges in probability to the minimizer of the approximating quadratic
function, so
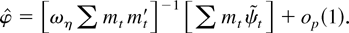
Here [sum ] mt
mt′ converges in probability to a
nonrandom matrix, and
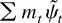
converges to a vector of mean zero Gaussian random variables. In large
samples
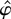
has a mean zero Gaussian distribution, which implies that
.
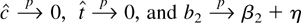
The distribution of
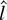
is obtained by substituting
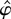
back into the likelihood function. Under the local alternative γ =
c/T, we obtain
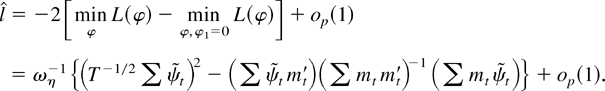
This is an Op(1) variable, but the
limiting distribution differs from the one in Theorem 1.
Statement 2 of the proposition says that the
-tests
are consistent against any fixed alternative γ < 0. The likelihood
function evaluated at (γ, b) may be written
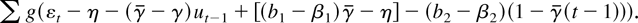
Because ut−1 is stationary under
the fixed alternative, is it straightforward to show using Taylor
series–based arguments that
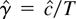
is consistent for γ.
Therefore
,
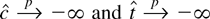
and an argument based on a Taylor series expansion demonstrates that
.
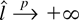
The proofs are omitted to save space.
To show statement 3 of the proposition, define the parameter
ηγ that satisfies
Eψ(εt +
γut−1 −
ηγ) = 0. For fixed γ < 0,
εt +
γut−1 is a stationary random
variable, and the expectation exists. By a Taylor series expansion,
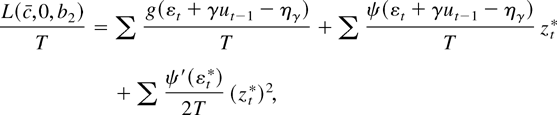
where zt* =
−cut−1
/T − β1 c/T +
ηγ − (b2 −
β2)(1 − c((t −
1))/T) and
|εt* +
γut−1 −
ηγ| ≤
|zt*|. If
b2 ∈ K then many of the terms are
asymptotically negligible. We get the approximation
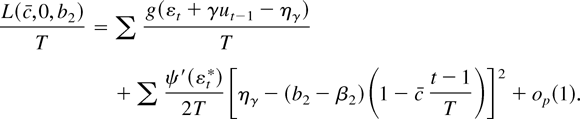
If c = 0 this expression is minimized at
b2 = β2 + ηγ, so
minb∈K
T−1L(0,0, b) =
T−1[sum ]g(εt +
γut−1 −
ηγ) + op(1). If
c ≠ 0, then because g′′(x)
≥ B we have
Therefore
T−1{minb∈K
L(c,0, b2) −
minb∈K L(c,0,
b2)} ≥
(24)−2Bηγ2
c2 + op(1), and the
best invariant test converges to +∞ under any fixed alternative.
Using the same arguments it is also possible to show that the best
invariant test converges to +∞ under any local value γ =
c/T (including the null c = 0). The
proof is omitted to save space. █
3.3. Some Monte Carlo Results
Table 2 presents rejection frequencies for
various tests in the model with a time trend. The tests are the trend
versions of the tests that appeared in Table
1, except that the
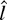
-test
appears in Table 2 in place of the
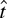
-test.
This substitution was made because the
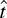
-test
is not asymptotically admissible in the model with a time trend.
10 As was the case for Table
1, the
tests are the Thompson (2001) versions of the
tests. In the model with a time trend the test rejects for small values
of
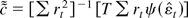
, where rt is the residual from a least
squares regression of yt−1 on (1,
t) and
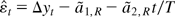
with
.
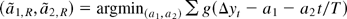
Thompson (2001) shows that
.
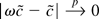
Rejection frequencies for selected tests in the model with a time
trend
The power losses from using the trend-optimal
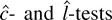
-tests
are small for samples of 100 observations but get larger for samples of 1,000.
For the asymmetric log normal and chi-squared error distributions, power
against the local alternative c = −10 declines as sample size
grows. Power against the fixed alternative γ = −0.1 increases with
sample size. This can be seen by comparing the results for the samples
with (T, c) = (100,−10) against the samples
with (T, c) = (1,000,−100). In each case
γ = −0.1. These results are consistent with Proposition 2,
which states that power against c = −10 converges to
zero as the sample grows and power against γ = −0.1 converges
to 1.
In the samples of 1,000 observations, asymmetric errors cause the NP
test to have low power against both the fixed and local alternatives.
This is consistent with Proposition 2, which predicts that power
against both kinds of alternatives converges to zero as the sample size
grows.
No test dominates the others. The ERS test performs poorly for the
Cauchy, log normal, and chi-squared errors. The adaptive test does well
for the asymmetric distributions but has very low power with Cauchy
errors. The
-tests
perform well for all the error distributions and sample sizes but are
generally dominated by the trend-optimal
-tests
for samples of 100.
APPENDIX A: PROOFS
In this Appendix we prove Theorems 1–3. Throughout the Appendix
it will prove useful to make use of the normalized likelihood
.
The remainder term RT(c,
b1, φ) is defined to be the difference between
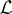
and its quadratic approximation
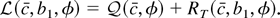
Preliminary Lemmas
LEMMA 1. Let K denote a compact set. If
Eψ(εt) = 0, and if Assumptions 1 and 2
hold, then
.
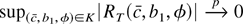
We will show that
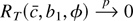
pointwise in (c, b1, φ). If
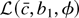
were a convex function of (c, b1, φ) then
pointwise convergence would imply uniform convergence over compact sets
(this is shown in Hjort and Pollard, 1993,
Lemma 1). However, even though g(x) is convex in
x,
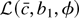
is not a convex function of (c, b1, φ)
because g(εt +
(b1 −
β1)c/T −
zt(c, φ)) is a nonlinear
function of the parameters.
A reparameterization allows us to restore the link between pointwise
and uniform convergence. Let wt =
T−1/2(T−1/2,T−1/2ut−1,1,(t
− 1)/T)′ and θ = (θ1,
θ2, θ3, θ4)′ =
(c(β1 − b1),
c − c,
φ,−φc)′. We have the reparameterized
objective function and remainder term
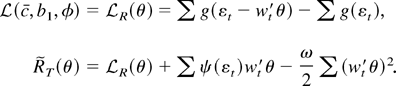
Because g is convex and εt −
wt′θ is a linear function of
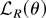
is a convex function of θ. Therefore if
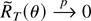
pointwise in θ then the convergence is uniform for θ in a compact
set. The relationship between the original remainder term and the
reparameterized remainder is
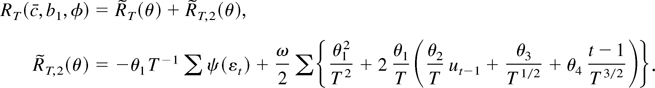
The equality holds as long as θ satisfies the constraint
θ4 = −θ3(θ2 +
c). For any compact set
,
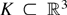
let
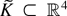
denote a compact set large enough so that if {θ1,
θ2, θ3} ∈ K then
.
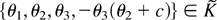
We now have a bound for the remainder RT:
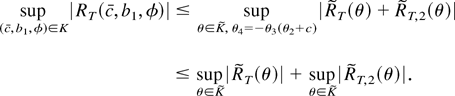
It is straightforward to show that
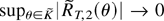
in probability for any compact set
.
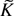
So to prove the theorem it is enough to show that
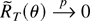
pointwise in θ. The pointwise convergence of
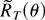
was proved in Lemma 1 of Thompson (2004).
█
LEMMA 2. In the model with a time trend, define
and
.
If Eψ(εt) = 0, and if Assumptions
1 and 2 hold, then
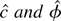
are both stochastically bounded.
If
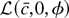
were convex in the parameters the argument in Section 3 of Pollard (1991) could be used to show that the estimators
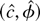
are stochastically bounded. However, even though g(x) is
convex in
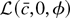
is not a convex function of (c, φ) because
g(εt − β1
c/T −
zt(c, φ)) is a nonlinear
function of the parameters. We will pursue a related method of
proof.
A reparameterization allows us to apply the arguments of Pollard
(1991) to this problem. Define θ =
(c − c, φ + β1
c/T, −φc)′,
wt =
T−1/2(T−1/2ut−1,
1, (t − 1)/T)′, and
Note that this reparameterization differs from the reparameterization
in Lemma 1 because here we take b1 = 0. For some
k > 0, define the compact set K = {(c,
φ) : |c − c| <
k, |φ +
T−1/2β1
c| < k}. For any (c, φ)
∉ K, the corresponding θ vector is equal to
vr where v is a vector with unit length and
r is a scalar with r > k. Because
g is convex and εt −
wt′θ is a linear function of
θ,
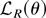
is a convex function of θ. So k = (1 − λ)0 +
λr for λ = k/r, and by the convexity of
,
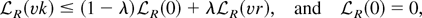
which implies that
.
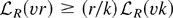
In the proof of Lemma 1 it was found that the approximation
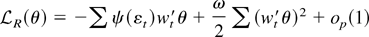
will hold uniformly over θ in a compact set. So for fixed
k,
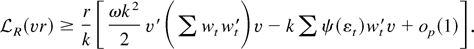
By Lemma 3.1 of Phillips
(1988),[sum ]wt
wt′ converges in distribution to a
positive definite matrix with diagonal elements bounded away from zero
with probability one. Therefore there exists ε > 0 so that
inf∥v∥=1
v′([sum ]wt
wt′)v > ε. So
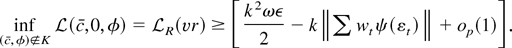
Because
∥[sum ]wtψ(εt)∥
is stochastically bounded (see Phillips, 1988, Lemma
3.1), we can choose k large enough so that
k2ωε/2 −
k∥[sum ]wtψ(εt)∥
> ε with probability arbitrarily close to 1. We have that in
large samples,
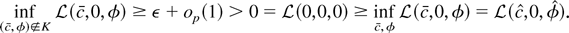
So in large samples the estimators
must be contained in K. Thus
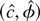
are stochastically bounded, and the theorem is proved. █
Proofs of Theorems
Proof of Theorem 1. Notice that
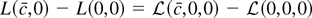
and that
.
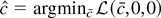
By Lemma 1,
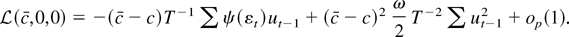
The asymptotic representation for L(c,0) −
L(0,0) follows from the following weak convergence result,
which was proved by Phillips (1988, see Lemma
3.1):
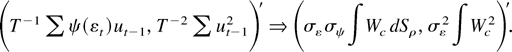
Because g is convex,
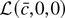
is convex in c. By slightly modifying the argument in Section 3 of
Pollard (1991), it can be shown that the
convexity of
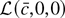
implies that
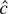
converges weakly to the minimizer of the quadratic approximation
,
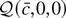
so
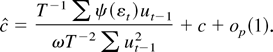
Therefore
,
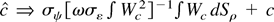
and the distribution of
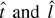
follows similarly. The representations for
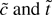
are provided in Theorem 1 of Thompson (2004).
█
Proof of Theorem 2. To prove the theorem it is sufficient to show
that
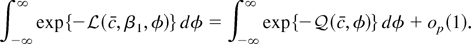
To see that this is indeed sufficient, notice that the best invariant
test rejects for large values of
where the last equality follows from the change of variables
.
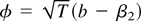
The discussion in Section 3 indicates that if the
approximation in (A.1) holds, then the best invariant test is
asymptotically equivalent to rejecting for small values of
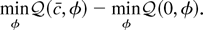
This is asymptotically equivalent to minb
L(c,0, b) − minb
L(0,0, b). To see this, notice that
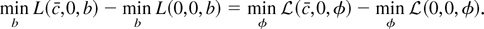
The convexity of g implies that for fixed c,
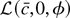
is convex in φ. By slightly modifying the method in Section 3 of Pollard
(1991), one can use the convexity to show that
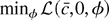
is asymptotically equal to
,
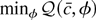
the quadratic approximation given in Lemma 1. So in large samples
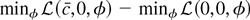
is equivalent to the statistic in (A.2). Thus verifying the condition in (A.1)
is sufficient to prove the theorem.
To verify (A.1) it will prove convenient to break the integral into
two parts. For any positive k,
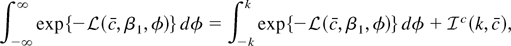
with
.
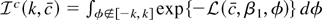
For any fixed k, Lemma 1 implies that
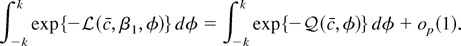
The integral on the right-hand side admits an analytic solution.
Using that analytic solution it is straightforward to show that for all
ε > 0 we can pick k large enough so that
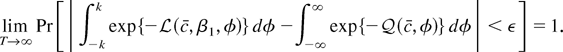
It remains to show that
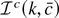
is asymptotically negligible. Because
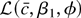
is convex in φ (for fixed c), then if φ > k
then k = (1 − λ)0 + λφ and
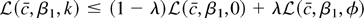
with λ = k/φ. Therefore
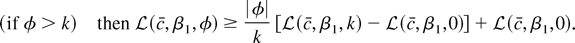
Similarly,
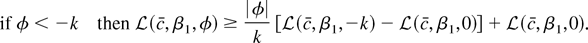
By Lemma 1, for fixed k we have
By the usual asymptotic arguments,
limT→∞
T−1[sum ](1 − c(t −
1)/T)2 = c2/3 −
c + 1 ≥ ¼, and the other terms are
Op(1). So if |φ| >
k then
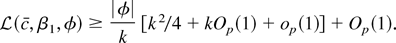
Plugging this bound into the integral, we obtain
Thus, for any ε > 0, we can choose k large enough so that
.
Thus the condition in (A.1) holds, and the theorem is proved. █
Proof of Theorem 3. In the proof of Theorem 2, we showed that
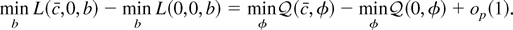
Lemma 3.1 of Phillips (1988) implies that
.
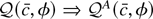
Lemma 3.1 of Phillips (1988) also implies that
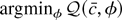
is stochastically bounded, and
by the argmax continuous mapping theorem of Wellner (1996, p. 286). We have derived the limiting representation
for the best invariant test.
The argmax continuous mapping theorem also provides the limiting
result for
.
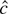
Notice that
.
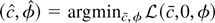
Because by Lemma 2
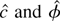
are stochastically bounded,
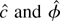
converge weakly to
.
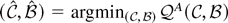
The limiting distributions of
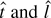
follow from a similar argument.
Limiting representations for
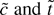
are provided in Theorem 1 of Thompson (2004).
█
APPENDIX B: SIMULATING THE ASYMPTOTIC
DISTRIBUTIONS
Theorem 3 provides asymptotic representations for various test
statistics in the model with a time trend. In this Appendix we describe
how to simulate from those distributions.
The best invariant test converges to
.
This is equal to
Simulating from this distribution is straightforward.
The normalized MLEs
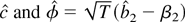
converge weakly to the random variables
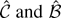
that minimize the stochastic objective function
.
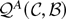
I was unable to derive a simple expression for
.
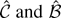
Instead the variables are expressed implicitly as solutions to the
minimization problem. Rewrite the objective function:
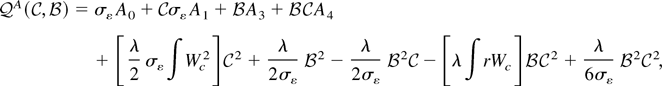
where λ = ωσε
/σψ and
The expression
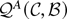
has at least one minimum. Take the derivatives of the function with
respect to
:
The values of
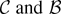
that minimize
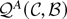
set the partial derivatives to zero. Solve
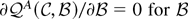
to obtain
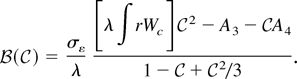
Substitute the solution for
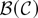
into the equation
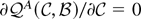
to show that
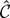
is the root of a fifth-order polynomial:
Notice that because A0, A1,
A3, and A4 depend on ρ and
λ and on no other nuisance parameters, the distribution of
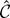
depends only on ρ and λ.
There is no known closed-form solution for the root of a general
fifth-order polynomial. Simulation was done from the asymptotic
distribution for
by the following method. Simulate a draw from the joint distribution of the
five coefficients of the polynomial. Use a software package (Matlab version
5.3 was used here) to numerically calculate the roots of the resulting
polynomial. The real root
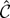
that maximizes
is the simulated draw from the asymptotic distribution of
.
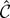
The corresponding draw from the asymptotic distribution of the
t-statistic is
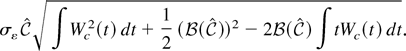
The stochastic integrals were computed as the realizations of
normalized sums of 500 successive draws from a discrete time Gaussian
AR(1) process with autoregressive parameter 1 −
c/500.
The simulation procedure was repeated 100,000 times for each value of
λ, ρ, and c. The asymptotic critical value for a size
100α% test that rejects for small
was calculated as the 100,000αth element of the vector of sorted draws
for
.
The power of the test at the alternative c was calculated as the
proportion of draws below the critical value. A similar procedure was used
to calculate the critical value and power of the test based on the
t-statistic.
