Published online by Cambridge University Press: 22 August 2005
This paper develops optimal tests for model selection between two nested models in the presence of underlying parameter instability. These are joint tests for both parameter instability and a null hypothesis on a subset of the parameters. They modify the existing tests for parameter instability to allow the parameter vector to be unknown. These test statistics are useful if one is interested in testing a null hypothesis on some parameters but is worried about the possibility that the parameters may be time varying. The paper provides the asymptotic distributions of this class of test statistics and their critical values for some interesting cases.I thank M. Watson for the idea of this paper and for numerous discussions, suggestions, comments, and teaching. I am grateful to T. Clark, G. Chow, R. Gallant, F. Sowell, N. Swanson, E. Tamer, and A. Tarozzi and also to the co-editor and two referees and to seminar participants at the University of Virginia, ECARES Université Libre de Brussels, the 2001 Triangle Econometrics Conference, the 2002 NBER Summer Institute, the 2003 Summer Meetings of the Econometric Society, and the 2003 EC2 Conference for comments. Financial support from IFS Summer Research, Princeton University, is gratefully acknowledged. All mistakes are mine.
This paper develops optimal tests for model selection between two nested models in the presence of underlying parameter instability in the data. The model selection procedure considered in this paper is hypothesis testing; in fact, when the competing models are nested, the problem of testing which model is best among the two is to test the significance of additional variables that are present only under the largest model. The tests proposed in this paper thus jointly test for both parameter instability and a null hypothesis on a subset of the parameters.
The main contribution of this paper is to address simultaneously the two problems of testing parameter instability and model selection among nested models. It is argued that tests for model selection fail to detect parameter instability and that tests for parameter instability are not designed to choose between nested models. If the goal is to jointly test parameter stability and select a model, then it is possible to identify a class of optimal tests. The optimal tests modify existing tests for parameter instability to allow them to reject the incorrect model. This is achieved by imposing, rather than estimating, the parameters of interest under the null, thus making the statistic not invariant to shifts in these parameters.
The tests presented in this paper are useful in situations in which one is interested not only in whether the explanatory variables proposed by some economic model are statistically significant in explaining the observed data, but also in whether this relationship is stable over time. For example, these tests would be useful if one is interested in testing whether inflation or exchange rates are random walks but is also worried about the possibility that parameters may be varying over time (see Clark and McCracken, 2005; Rossi, 2005).
The strand of research closest to this paper is that concerning tests for parameter instability, in particular the works by Chow (1960), Quandt (1960), Ploberger and Krämer (1990, 1992), Andrews (1993), Andrews and Ploberger (1994), Sowell (1996), Ghysels and Hall (1990), Ghysels, Guay, and Hall (1998), and Elliott and Müller (2003). However, these tests are designed to detect parameter instability only, whereas this paper is also concerned about testing hypotheses on the parameter vector and, hence, treats it as unknown.
An alternative way to deal with model selection issues in the presence of parameter instability is to do a two-stage procedure: first test whether there is parameter instability; then test which model, among the competing ones, is the best description of the data. In some special cases analyzed in this paper, that is, for the special weighting distributions over the local alternatives analyzed in Section 3, the test statistics in the two stages are asymptotically independent. In this case, it is easy to fix the size in each stage of the procedure so that the two-stage procedure will have an overall correct size asymptotically. However, this result is not true for general weighting distributions. In addition, two-stage tests have advantages and disadvantages. The advantage is that if we reject we know which part of the alternative we reject; the disadvantage is that the test will not have the optimal weighted average power for alternatives that are equally likely.
The paper is organized as follows. Section 2 derives the optimal tests for testing the joint hypothesis of parameter stability and model selection and provides their asymptotic distribution. Section 3 discusses special tests and reports their asymptotic critical values, and Section 4 compares their asymptotic local powers. Section 5 concludes. Proofs of the results are in Appendix A, whereas Appendix B contains the tables of asymptotic critical values.
To gain some intuition about the results in this paper, consider a simple example where the data generating process (DGP) is as follows and the time of the break is known:
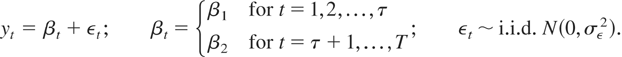
If the researcher is interested in testing whether the parameter βt is constant over time and equal to a specific value β0, a possible test statistic would be

where

are the sample averages of yt in the two subsamples. By adding and subtracting the full sample average

inside the square of the first addend on the numerator, (2) can be rewritten as

where

Thus, the test is decomposed in two components: the one on the left is a test on β, and the one on the right is the standard Chow test for structural break. Hence, the test achieves power in detecting deviations from β0 by adding to the traditional test for structural break a component that is variant to constant shifts in the mean. The asymptotic distribution of the test can easily be found in this case because the two components are independent.1
In fact, the standard Chow test can be rewritten as a Wald test:
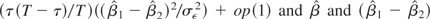
are independent. To see why, note that
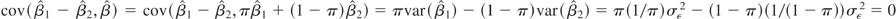
.
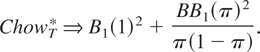
Thus, the first component, which makes the test powerful in detecting constant shifts in the mean, adds a chi-square component to the limiting distribution of a standard Chow test for parameter instability. This example provides an easy and intuitive explanation of the asymptotic distribution of the tests considered in this paper.
This section describes the class of models considered in this paper and the assumptions under which the results are valid. The parametric model applies to a stationary and ergodic time series process.
Assumption 1. For each T, the sequence {xt,T}t=1T consists of the first T elements of an r-dimensional stationary and ergodic process. The parameter space Θ is a compact subset of Rk. For notational simplicity, xt will be used to denote xt,T.
The class of local alternatives allows both for structural changes and for nonlinear hypotheses on the parameters.
Assumption 2 (Local alternatives). The local alternatives (HAT) are specified as

where g(γ,π,s), for s ∈ [0,1], is a k-dimensional step function, γ ∈ Ri, π ∈ (0,1)j denotes the times of the structural changes as fractions of the sample size (j being the number of such breaks), a(θ*) = 0 is a possibly nonlinear restriction that identifies the true parameter value under the null hypothesis when there is no structural change, and a denotes its local alternative.
Hence, the parameter θ is unknown and possibly time-varying. The class of estimators considered here are extremum estimators that minimize the objective function QT(θ), which depends on both the data and the sample size. The focus will be on the restricted estimator
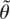
:
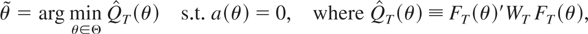
where
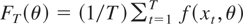
is the sample analogue of E(f (xt,θ)), the moment condition that is equal to zero at the true parameter value, and E(.) is the expected value function. The moment condition is such that f : Rr × Rk → Rm and WT is a (sequence of) positive semidefinite matrices. Note that our framework allows for both exactly and overidentified generalized method of moments (GMM).
The next assumptions are sufficient to ensure consistency and identification of the estimator (see Sowell, 1996, p. 1100; see also Andrews, 1993).2
The assumptions used in this paper are stronger than necessary, and the results are expected to hold if the assumptions are relaxed as in Andrews (1993). I thank G. Elliott and U. Muller for pointing this out.
Assumption 3 (Identification). limT→∞ E [f (x,θ)] = 0 only if θ = θ*.
Assumption 4 (Smoothness and boundedness). (i) θ* ∈ interior(Θ); (ii) f (x,θ) is continuously partially differentiable in a neighborhood ϒ of θ*, ∀θ ∈ Θ; (iii) the functions f (x,θ) and ∇θ f (x,θ) ≡ (∂/∂θ) f (x,θ) are measurable functions of x ∀θ ∈ Θ and E [∥ f (x,θ*)∥2] is finite; (iv) E [f (xt,θ*)] = 0,E [f (xt,θ*)′f (xt,θ*)] < ∞, and supθ∈Θ∥ f (xt,θ)∥ < ∞ ∀t = 1,…,T and T = 1,2,…; each element of f (xt,θt,T) is uniformly square integrable ∀t = 1,…,T and T = 1,2,…; (v) M = limT→∞ E [∇θ f (x,θ*)] ∈ Rm×k has full column rank, where ∇θ f (x,θ*) = (∂/∂θ) f (x,θ)|θ=θ* and M′WT M is nonsingular; (vi) {xt} is strong mixing with strong mixing coefficients {α(n)1−2/β} < ∞ with β > 2, and the individual elements of f (xt,θt,T) have finite absolute moments E [| f(i)(xt,θt,T)|β] for i = 1,…,m.
Assumption 5 (Constraints). a(θ) is continuously partially differentiable in a neighborhood ϒ of θ*, ∀θ ∈ Θ; A ≡ ∇θ a(θ*) ∈ Rr×k has rank r ≤ k.
Assumption 6 (Efficiency in the class of GMM estimators). The asymptotic variance of the GMM estimator is efficient in the class of GMM estimators:

.
When the alternative hypothesis of interest is either HAT(1) or HAT(2) then optimal tests are available. In the former case, an optimal test when the break date is known is the Chow (1960) test, and when the break date is unknown, a class of tests with optimal weighted average power is that of Andrews and Ploberger (1994); although Andrews' Sup-LR test (see Andrews, 1993) is not a member of that class, Andrews and Ploberger, 1993, show its asymptotic admissibility against alternatives that are sufficiently distant from the null hypothesis). In case the alternative is HAT(2) only, the likelihood ratio test (and the asymptotically equivalent Wald and Lagrange multiplier [LM] tests) is asymptotically locally most powerful among all invariant tests, and, hence, it is optimal (see Engle, 1984).
However, when both hypotheses are of interest then considering separately tests for parameter instability and likelihood ratio tests is not sufficient anymore. This paper identifies a class of tests that are optimal, in the sense of having the highest asymptotic local power function for some specified alternatives. This class of tests is discussed in Section 2.3.
We are interested in constructing a LM test statistic for testing jointly alternatives HAT(1) and HAT(2). The test builds on partial sums of the form
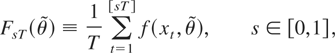
where the partial sums are evaluated at the restricted estimator vector,
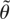
. When Assumptions 1–6 are satisfied, the asymptotic distribution of the partial sums of sample moments under the null and the alternative hypotheses is stated in Results 1 and 2, which follow. For notational convenience, let M ≡ Σ−1/2M ∈ Rm×k and partition it as M = (Mβ, Mδ). Also, let ⇒ denote weak convergence to the relevant stochastic process and

denote convergence in probability.
RESULT 1 (Distribution under the alternative hypothesis). If Assumptions 1–6 are satisfied, then

where Bm(·) is an m-dimensional standard Brownian motion, D′ ≡ D−1A′ ×(AD−1A′)−1, D ≡ M′M, H ≡ Ik − D−1/2A′(AD−1A′)−1AD−1/2, Ik is a k-dimensional identity matrix, H ≡ MD−1/2HD−1/2M′, and both H and H are idempotent with rank equal to (k − r).
See Appendix A for proofs. Result 2 shows the asymptotic distribution of the standardized moment condition under the null hypothesis that there is no parameter instability in any of the coefficients and that a subset of parameters satisfies some restriction condition as follows.
Assumption 7 (Null hypothesis). Under the null hypothesis (H0):

where θ* satisfies a(θ*) = 0.
RESULT 2. (Distribution under the null hypothesis). If Assumptions 1 and 3–7 are satisfied then
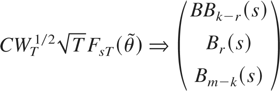
for an orthonormal matrix C such that
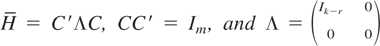
. Here BBk−r(s) is a (k − r)-dimensional Brownian bridge and [Br(s)′,Bm−k(s)′]′ is an (m − k + r)-dimensional vector Brownian motion. The Brownian motions and the Brownian bridges are independent.
Note that, under the null hypothesis, the asymptotic distribution of the standardized partial sum of moment conditions is composed by both Brownian bridges and Brownian motions. The (k − r)-dimensional Brownian bridge component derives from the parameters that are not specified under the null. In fact, this component is a partial sum of mean zero moment conditions, where the zero mean is obtained by estimating the drift.3
For example, when the process is univariate and such that yt = β0 + εt, εt ∼ i.i.d. N(0,1), β0 = 0 (as in the introductory example at the beginning of the paper) then the partial sum of moments is

and the origin of the Brownian bridge is evident. If there were no restrictions under the null hypothesis, then the asymptotic distribution of
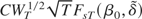
would be (BBq(s)′ Bm−q(s)′)′, which is the Sowell (1996) result. When there are restrictions on a subset of p parameters under the null hypothesis, these will show up as p-Brownian motions, in addition to the previous components. These are Brownian motions because they are the limiting distribution of a partial sum of mean zero moment conditions, where the zero mean is obtained by imposing, rather than estimating, the drift. In the previous example, in this case the partial sum of moments is

and the origin of the Brownian motion is clear. The Bm−q(s) component corresponds to the overidentified moment restrictions.
The alternative hypothesis will add drift components to the moment conditions, as Result 1 shows. In particular, the drift components originate both from deviations from the parameter stability hypothesis and from deviations from the specified null hypothesis on the value of the parameters. For the local alternatives considered in this paper, the normalized partial sum of the sample moments evaluated under the null hypothesis converges to a stochastic process denoted by Z(s). Under the local alternative, Z(s) satisfies the following stochastic differential equation:
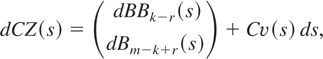
where

. Under the null hypothesis, the same expression holds with v(s) = 0. To get some insight, rearrange (7):
4The result follows because MD−1/2HD1/2 = MD−1/2HD−1/2M′M = HM, HMD′ = 0 and (I − H)MD′ = MD′, which can be verified by direct calculations.

so that

where C(1) and C(2) are, respectively, the first (k − r) and the last (m − k + r) rows of C. Thus, the null hypothesis puts restrictions on both the Brownian motions and the Brownian bridge components. In fact, it is a joint hypothesis on parameter instability (affecting the Brownian bridge component) and on the parameters (affecting the Brownian motion component). This differs from the Sowell (1996) case (see the discussion following his eqn. (3), p. 1091), where the alternative only places restrictions over Brownian bridges. However, Sowell (1996) derived optimal tests in terms of the Radon–Nikodym derivative of the measure implied by the null hypothesis for both the Brownian motion and the Brownian bridge components (see the proof of his Thm. 3), so we can apply a similar argument. Thus, the test with the greatest weighted average power, according to some weighting functions R(η,π) (on η for every π) and J(π) (on π), rejects the joint null hypothesis of no structural break and a(θ*) = 0 if
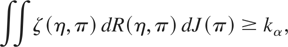
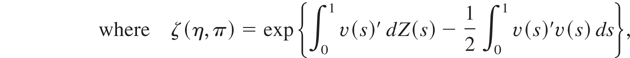
η ≡ [a,γ′]′ ∈ R2p×1, and kα is defined so that the test has size α.
I consider only two-sided alternatives here; one may generalize the argument to one-sided alternatives.
The leading case of the class of alternatives for structural break is that of alternatives that are linear in the parameters, that is,
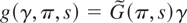
. In the case of a single structural break,
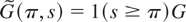
, where 1(s ≥ π) is the indicator function, equal to one if s ≥ π and zero otherwise, and G is a (k × p) matrix identifying the p-dimensional vector of time-varying parameters, say, G = [Ip 0q×p]. Let us define

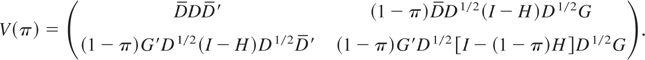
The optimal test statistic described by (11) becomes ∫∫ exp{η′A(π) − ½η′V(π)η} dR(η,π) dJ(π). As in Sowell (1996), different choices of the weighting function R(η,π) lead to different test statistics. The weighting function considered here is an (r + p)-dimensional multivariate normal distribution with zero mean and covariance U(π). When the time of the break is not known and we are interested in the test statistic that gives equal weight to alternatives that are equally difficult to detect when π is known, so that U(π)−1 = (1/c)V(π), then the test statistic in (11) becomes ∫Π(exp{½(c/(1 + c))Φ*(π)}) dJ(π) where Π is the support of J(π) and ΦT*(π) = A(π)′V(π)−1A(π). The latter is a Wald test for the fixed and known π scenario. The test statistic can be estimated as
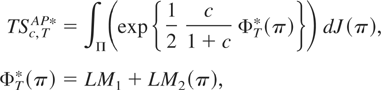
where

if ft(.) are independent and identically distributed (i.i.d.); otherwise

is estimated with a Newey–West heteroskedasticity and autocorrelation consistent (HAC) estimator. The limiting distribution of this test statistic under the null hypothesis is described in the following proposition.
PROPOSITION 1. Let Assumptions 1–6 hold. The test statistic for testing a(θ*) = 0 against HAT(1) and HAT(2) with the greatest average power according to the weighting function R(η,π) ∼ N(0,cV(π)−1), for V(π) defined in (14), is the test statistic defined in (15). Its asymptotic distribution under the null hypothesis is
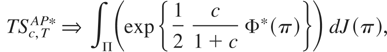

Proposition 1 shows that TSc,TAP* is a weighted average of LM tests. As noted previously, the difference between the asymptotic distribution of the tests defined in this paper and that of the test for structural break only is that the latter does not have the Br(1)′Br(1) component. This component arises from testing restrictions on θ over the whole sample. In fact, it corresponds to a centered chi-square with r degrees of freedom, the usual limiting distribution of the Wald test statistic for testing hypotheses on a parameter vector. Appendix A shows that both the tests for structural break and the classical tests obtain as special cases of (24).
Although this paper is mainly concerned about testing a null hypothesis on the parameters in the presence of possible parameter instability, instabilities may also affect other aspects of the model, namely, the overidentifying restrictions (OIRs). Hall and Sen (1999) and Sowell (1996) show that the population moment conditions can be decomposed into two orthogonal components: identifying restrictions—the part used in estimation—and overidentifying restrictions—the part unused in estimation. Hall and Sen (1999) propose tests for the structural stability of the OIRs. Their approach turns out to be useful to discriminate between situations in which the instability is confined to the parameters alone and those in which the instability permeates other aspects of the model. In what follows, we examine the relationship between the tests proposed by Hall and Sen (1999) and those proposed in the present paper, and we show that the Hall and Sen (1999) results do carry over to the tests proposed in this paper.
The tests proposed by Hall and Sen (1999) are as follows:

where

. Hall and Sen (1999) find that their test statistics are asymptotically independent of tests for parameter instability. They also show that their tests have no local power against parameter variation and tests for parameter variation have no local power against instability in the OIRs. This latter result follows from the fact that the components of OT(π) are orthogonal to the components of LM2(π). In fact, they show that

(see Hall and Sen, 1999, eqn. (A.4); Andrews, 1991, p. 848, for the more general case of subsets of parameters), where [otimes ] denotes the Kronecker product. Thus, the rescaled moment conditions in OT(π) become

and it is clear that they are orthogonal to LM2(π), which instead builds on M (see equation (16)), as M′(I − M(M′M)−1M′) = 0.
Note that all of the preceding results still hold in our framework. Also, note that the components in LM1 are orthogonal to the components of OT(π) too, as LM1, like LM2(π), builds on M. Thus, the results in Hall and Sen (1999) do carry over to the test statistics QLRT*, Mean-WaldT*, and Exp-WaldT*. More details are provided in Section 4.
From now until the end of this section, we specialize the preceding findings to situations in which the researcher is interested in testing hypotheses on a subset of the parameters. This is discussed in the following corollary.
COROLLARY 1 (Null hypotheses on subsets of parameters). Let the parameter vector θ ∈ Rk be partitioned as θ = [β′,δ′]′, where β ∈ Rp and δ ∈ Rq. Let Assumptions 1 and 3–6 hold. Let Assumption 2 be replaced by Assumption 2′:
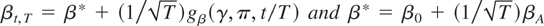
. It follows that


We will finally consider special cases of TSc,TAP* that have been considered in the literature for tests for structural break only. Each of these special cases has greatest weighted average power against particular forms of parameter instability. We will analyze the form that the optimal test proposed in this paper assumes for these particular forms of parameter instability.
Let βt = β1(π) for t = 1,2,…,[Tπ] and βt = β2(π) for t = [Tπ] + 1,…,T, where [·] denotes the greatest integer function. Also, to simplify notation, let

. Let

be the unrestricted GMM estimator under the hypothesis that there is a break at the fraction [Tπ] of the sample and let

be the constrained estimator. Thus, the Wald test for a fixed and known π can be estimated as either
6For completeness, let us mention that the LM statistic can also be obtained as

where

is a consistent estimator of
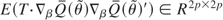
. However, the LM formula provided in the main text is easier to calculate.
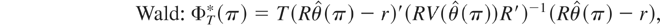
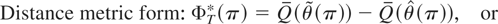
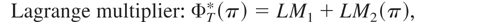
where notation is in Table 1. The table assumes that ft(.) consists of mean zero uncorrelated random variables. When ft(.) consists of mean zero but serially correlated random variables then consistent estimation of
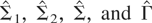
requires a HAC estimator (e.g., see Newey and West, 1987). Note that (22) is particularly easy to calculate. It is simply the sum of the two LM tests to test HAT(1) and HAT(2) separately. Then, Proposition 2 follows.
Notation related to equations (20), (21), and (22)

PROPOSITION 2. Let Assumptions 1, 2′, and 3–6 hold. The test statistic for testing β = β* against

with the greatest average power according to the weighting function R(η,π) ∼ N(0,cV(π)−1), for V(π) defined in (14) with either (20), (21), or (22). Its asymptotic distribution under the null hypothesis is
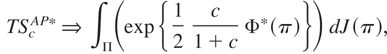

As special cases, we have
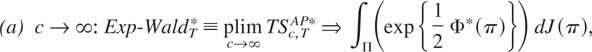
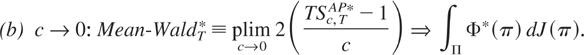
The special cases that correspond to extreme values of the parameter c are similar to those in Andrews and Ploberger (see also Andrews, Lee, and Ploberger, 1996). When c → ∞ (c → 0), more weight is assigned to alternatives about parameter instability further from (closer to) the null hypothesis.
A test statistic commonly considered in the literature of structural breaks is the Quandt likelihood ratio (QLR) test statistic (or Sup-LR test), which is the supremum (over all possible break dates) of the Chow statistic designed for these alternatives for a fixed break date. Andrews (1993) derived its asymptotic distribution. The modified QLR test statistic for the alternatives specified in this paper can be obtained by letting c/(1 + c) → ∞ in (17), which gives
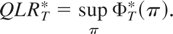
The limiting distribution of (27) under the null hypothesis is given in the following proposition.
PROPOSITION 3. Let Assumptions 1, 2′, and 3–6 hold. The test statistic for testing β = β* against
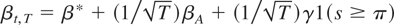
with the greatest average power according to the weighting function R(η,π) ∼ N(0,cV(π)−1), for V(π) defined in (14) and c such that c/(1 + c) → ∞, is (27), whose asymptotic distribution under the null hypothesis is
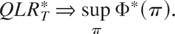
Another test for parameter instability is that considered by Nyblom (1989) and Nyblom and Mäkeläinen (1983). These authors derive the locally most powerful invariant (to translations and scale transformations) test for constancy of the parameter process against the alternative that the parameters follow a random walk process:7
The notation is the same as in Nyblom and Mäkeläinen (1983);
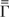
is a known matrix and σe2 is a scalar. See also King (1980), King and Hillier (1985), and Stock and Watson (1998).
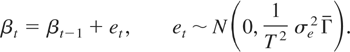
The modified Nyblom test statistic for testing whether βt is equal to β0 is
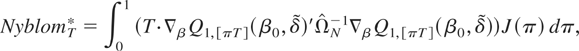
where
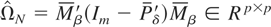
and the gradient of the objective function is defined as
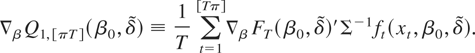
Note that (30) is a generalization of the locally best invariant test statistic proposed by Nabeya and Tanaka (1988) for the case in which β is known and equal to β0. The test proposed in this paper is more general than that of Nabeya and Tanaka, as estimation is not restricted to the ordinary least squares case and β can be a vector. Appendix A shows that the asymptotic distribution of the modified Nyblom statistic under the null hypothesis is as follows.
PROPOSITION 4. Let Assumptions 1, 2′, and 3–6 hold. The test statistic for testing β = β0 against

with the greatest average power according to the weighting function R(η,π) ∼ N(0,cV(π)−1), for V(π) defined in (14), is (30). Its asymptotic distribution under the null hypothesis is
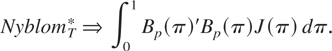
Tables B1, B2, B3, and B4 in Appendix B report critical values for the optimal tests for J(π) uniformly distributed on [0.15, 0.85].8
Trimming values are required. See Andrews (1993).
The local power properties of the optimal tests derived previously can be compared with those of tests for parameter instability only and those of tests for a(θ*) = 0 only. The comparison can be made both theoretically and by Monte Carlo simulations.
Let us first consider the theoretical local power properties of the various tests. To facilitate a comparison with the tests existing in the literature, we focus on the tests discussed in the second part of Section 3, and, for brevity, we analyze only (25).
9A similar analysis applies to the optimal mean Wald, QLR, and Nyblom tests.
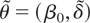
. From (22) and (25), and using the notation in Table 1, we have that
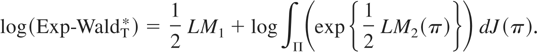
Appendix A shows that

See also Appendix A for more details. Note that
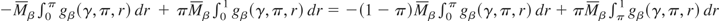
.
To verify these insights, we perform some Monte Carlo simulations. A variety of DGPs is considered, paying particular attention to situations where the standard tests fail to detect the alternative hypothesis. For simplicity, only a univariate model is considered:
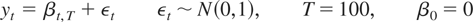
The likelihood ratio LR1 tests whether the parameter equals β0, whereas parameter instability tests check whether βt,T is constant; optimal tests jointly test the two hypotheses. The parameter instability tests (TVP) considered here are the Andrews and Ploberger exponential Wald tests (Exp-WaldT), the Nyblom test (NyblomT), and the Quandt likelihood ratio (QLRT). The optimal tests are Exp-WaldT*, QLRT*, and NyblomT* defined in Section 3. The nominal size is 5%.
We consider the following DGPs.11
Note that different Monte Carlo experiments could be designed in which all models are possibly (dynamically) misspecified, as in Corradi and Swanson (2005). This setup would not be the one for which the optimal tests proposed in this paper are designed, so it is not investigated.
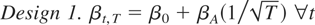
Figure 1a shows the asymptotic local power of the tests as a function of βA. It shows that when the parameter is not time-varying, the likelihood ratio LR1 is the most powerful test, according to the Neyman and Pearson lemma. The test designed to detect structural break, Exp-WaldT, has a flat power function around the size of the test, whereas the Exp-WaldT* test is almost as powerful as the LR1 test.

Asymptotic power functions of 5% tests for Designs 1–4.
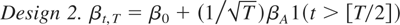
Design 2 involves a single break in the data. This particular alternative is both a deviation of the parameter vector from the null hypothesis and a structural break, so all the tests (the most powerful likelihood ratio test, LR*,12
LR* is the likelihood ratio test for testing β2 = β0 conditional on knowing that β1 = β0 (see the example at the beginning of Section 2).

Figure 1c shows that, in this design, the shift in the parameter vector is not detected by a simple likelihood ratio (LR1) because the statistic on which it is based (the average of the observations) is invariant to it; in fact, notwithstanding the structural break, the average over the whole sample is asymptotically equal to β0. Although the TVP test is the most powerful, the optimal test is powerful too.
Design 4. βt = β0 + βt−1 + ut, where ut ∼ N(0,σu2/T2) is independent from εt and σu2 ≥ 0
The asymptotic local power functions for this design are depicted in Figure 1d as functions of the parameter σu2 ≥ 0. When σu2 = 0 then βt is constant, whereas when σu2 ≠ 0 then βt is a random walk with no drift. The test designed for this hypothesis is the Nyblom test; the LR1 test is also powerful. The reason is that LR1 is detecting deviations from the null hypothesis by comparing the sample average with the null hypothesis and the sample average is not a consistent estimate of the true parameter value. Note that the optimal Nyblom test is powerful too.
The results of the simulations suggest the following conclusions. First, the tests that maintain some power across all the designs considered here are the optimal tests. For all the other tests there is at least one design (a particular direction away from the null hypothesis) in which the power is flat around the size of the test. Hence, they are not “robust” across designs, whereas the optimal tests are. Second, let us consider a two-stage testing procedure, where the first stage tests whether there is a structural break (by using either QLRT or Exp-WaldT) and the second stage, conditionally on the first stage, tests hypotheses on the parameters (by using the LR1 test). Let the tests be labeled “Seq.QLR” and “Seq.Exp-Wald,” respectively. In the special cases considered in Section 3 (obtained with particular weighting matrices), the two stages of the test are asymptotically independent. By choosing a size equal to
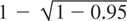
, the joint significance level will be the desired nominal level, 0.95. Figure 2 shows that there is no clear ranking between the sequential tests and the optimal tests. The power ranking will depend on the direction of the alternative hypothesis. However, by construction, the optimal tests will have the greatest average local power. Two-stage independent tests have advantages and disadvantages. The advantages are that if we reject we know which part of the alternative we reject and that the first-stage test could be used if the researcher is unsure about which elements of the parameter vector are subject to instability. The disadvantage is that they will not have the optimal weighted average power for alternatives that are equally likely; in other words, if we want tests that are invariant to nonsingular linear transformations of the hypothesis, we cannot construct the test as formed by two independent components, as two-stage tests are not invariant to these transformations.

Comparison of asymptotic power functions of 5% selected optimal tests with the naive sequential test (across different designs).
Finally, to investigate the properties of the Hall and Sen (1999) test for OIRs, we consider the following experiment.
Design 5. This design introduces instability in the OIRs. We introduce one OIR by using the following set of moment conditions: ft = (εt,zt*εt)′ where zt* is an instrument such that zt* = zt + εt(βA·1(t ≤ ½T) − βA·1(t > ½T)) and zt ∼ N(0,1) is independent of εt. Note that when βA = 0 then the OIR is valid and stable; on the other hand, it becomes unstable when βA ≠ 0. Figure 3 compares the power functions of the Exp-WaldT, the Exp-WaldT*, and the Exp-OT tests for this design (see Figure 3d). To explore the properties of the Exp-OT test in the presence of parameter instability or constant shifts in the parameters, the figure also compares these tests in Designs 1–3 (where all the tests in Figure 3 now build on the two-dimensional moment condition). Figure 3 clearly shows that the Exp-WaldT, Exp-WaldT*, and Exp-OT tests have power only against deviations from their specific null hypotheses. In particular, the Exp-WaldT and Exp-WaldT* do not have power against instabilities in the OIRs, and the Exp-OT test does not have power against parameter instability or against the joint hypotheses considered in this paper, (HAT(1)) and (HAT(2)).

Comparison of asymptotic power functions of 5% selected optimal, TVP, and OIRs tests (across different designs).
This paper shows that there exists a class of locally most powerful tests for testing the joint hypothesis of model selection between two nested models and parameter stability. This paper introduces this class of tests, states the assumptions under which they are valid, and works out their asymptotic distributions. It also derives some special cases that apply for specific forms of parameter instability. These tests are easy to calculate, and this paper reports their (asymptotic) critical values. Joint tests such as the ones developed in this paper could also be adapted to the case of multiple breaks, along the lines of Bai and Perron (1998) and Elliott and Müller (2003). We leave this issue for future research.
Proof of Result 1. To simplify notation, let
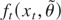
be denoted as
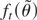
and θt,T be denoted by θt. The restricted estimator
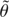
satisfies the following first-order conditions for minimizing the Lagrangian Q(θ) + a(θ)′λ, where λ is the (r × 1) vector of LMs:
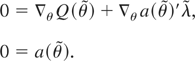
Take a mean value expansion of

around θ*:
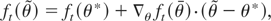
where θ is a intermediate point (in euclidean distance) between

, and by consistency of
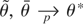
. Summing (A.2) from t = 1 to [sT] gives
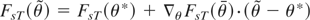
, which, evaluated at s = 1 and premultiplied by

, gives
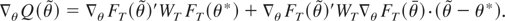
Another mean value expansion of
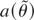
around θ* gives
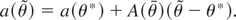
Thus, combining (A.1), (A.3), and (A.4) and

:
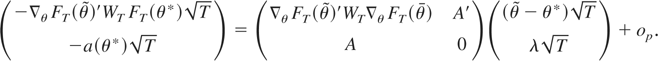
Define D ≡ M′M, A ≡ A(θ*), P ≡ D−1/2A′(AD−1A′)−1AD−1/2, and H ≡ I − P. Solving (A.5) for
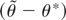
gives
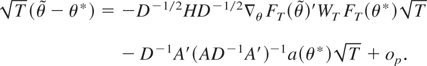
By substituting (A.6) in (A.2), summing from t = 1 to [sT], and premultiplying by
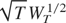
, we have

Next, a mean value expansion of FsT(θ*) around θt implies
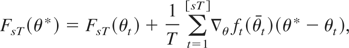
where θt is an intermediate point between θt and θ*. Substituting (A.8) in (A.7), we have

Letting T → ∞, we have

By substituting the preceding expressions in (A.9), we have

where H ≡ MD−1/2HD−1/2M′, which proves Result 1. █
Proof of Result 2. To prove Result 2, note that under the null hypothesis a = 0 and g(.) = 0 so that only the first two components on the right-hand side of (A.10) are relevant. Note also that H is a projection matrix with rank (k − r) so that H = C′ΛC, where
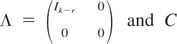
is an orthonormal matrix such that CC′ = Im. Thus C[Bm(s) − sHBm(1)] = CBm(s) − sΛCBm(1), which has the same distribution as Bm(s) − sΛBm(1) = (BBk−r(s)′,Bm−(k−r)(s)′)′, because C is orthonormal. Hence, Result 2 follows. █
Proof of Corollary 1. Let

. Also, let the restrictions be linear restrictions on subsets of the parameters, so that A = [Ip×p [vellip] 0p×q]. Let Mθ = [Mβ [vellip] Mδ], Pδ ≡ Mδ(Mδ′Mδ)Mδ′. Corollary 1 follows from (A.10) by using the following results (a)–(e). (Results (a)–(d) follow from direct calculation. Details are provided in an Appendix available upon request.)
(a) H = Pδ
(b) MD−1/2HD1/2 = Pδ M
(c) MD−1A′(AD−1A′)−1 = (I − Pδ)Mβ
(d)
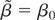
(e) g(.) = [gβ(.) 0q×p] █
Proof of (13) and (14). Let Assumption 2 hold and let the class of alternatives be linear in the parameters:

. Thus v(s), defined following (9), becomes
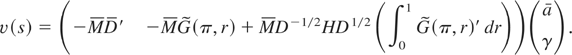
Let η ≡ (a,γ′)′ and define a(s) to be such that v(s)′ = η′a(s), that is:
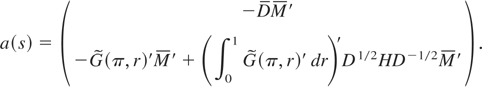
The term A(π) is defined as

, and V(π) is defined as

. When there is only one break, and
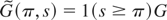
, then direct calculations show that

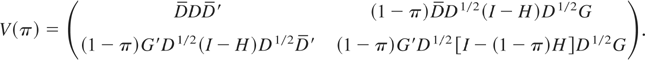
█
Proof of Propositions 1–3. When the weighting function is an (r + p)-dimensional multivariate normal distribution with zero mean and covariance U(π) then in this case, and for two-sided alternatives, the optimal tests in (11) simplify to (by completing the square and integrating out the parameter vector)

When U(π)−1 = (1/c)V(π) then (up to a constant factor that does not matter)
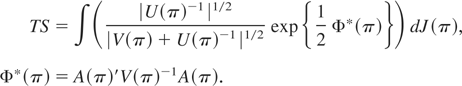
By using (A.12) and standard formulas for the inverse of a partitioned matrix,
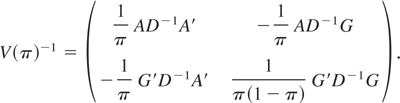
By combining (A.15) with (A.11) and (A.14), one finds that

where C1 ≡ (AD−1A′)−1AD−1M′ has dimension (r × m) and C2 ≡ G′M′ has dimension (p × m). Notice that C1(I − H) = C1 so that C1 Z(1) = C1 Bm(1). Thus, Zr(1) ≡ (C1 C1′)−1/2C1 Z(1) is an r-vector of independent standard normals and {Zp(π) − πZp(1)} ≡ (C2 C2′)−1/2C2{Z(π) − πZ(1)} is a p-vector of independent Brownian bridges because {(C1 C1′)−1/2C1}{(C1 C1′)−1/2C1}′ = Ip (same for C2). Hence:
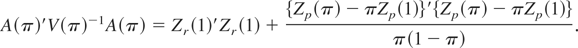
Thus, under the null hypothesis:
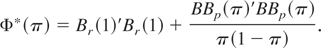
Proposition 1 thus follows from Result 1 and the continuous mapping theorem, and Propositions 2 and 3 follow directly from Proposition 1, Corollary 1, and the results in Andrews and Ploberger (1994). █
Asymptotic Local Power. Under the alternative hypothesis, and using (10):

and substituting these into (A.16):

where
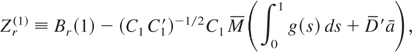

Note that when A = [Ip 0p×q] = G, g(.) = [Ip 0q×p]gβ(.), then r = p, C1 ≡ Mβ′(I − Pδ) (see (c) in the proof of Corollary 1) and C2 ≡ Mβ′; note also that Mβ′(I − Pδ)Mβ = ∇ββQ − ∇βδQ(∇δδQ)−1∇δβQ. In addition, note that when π is fixed and a = 0, which is the case examined by Chow (1960) for testing the existence of structural breaks only, only [I [vellip] 0]A(π) and [I [vellip] 0]V(π)[I′ [vellip] 0′]′ are relevant so that the test becomes Φ(π) ⇒ BBp(π)′BBp(π)/π(1 − π), which is the result of Andrews (1993) (see also Sowell, 1996). Notice also that when π = 1, which is the case without structural break, the result is the classical test statistic for tests on a subset of p parameters: Bp(1)′Bp(1) ∼ χ(p)2 because BBp(1) = 0 and Bp(1) is a p-dimensional multivariate standard normal distribution.
The proof that (20), (21), and (22) are asymptotically equivalent under both the null hypothesis and the local alternatives follows from applying results similar to those in Andrews (1993) and Newey and McFadden (1994). █
Proof of Proposition 4. The (modified) Nyblom test statistic for testing both parameter instability and that the parameter vector is equal to some value β0 was defined as
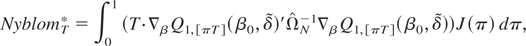
where
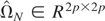
is a consistent estimate of the asymptotic variance of
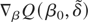
and the gradient function is defined as
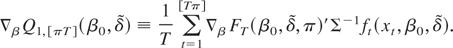
Notice that
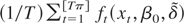
is the first component of

, so that one would expect the asymptotics to be driven by B(π). In fact, let

be estimated on observations 1,2,…,T and take a mean value expansion to obtain

where

has the following asymptotic distribution:

Hence, (A.23) is such that

Notice that, like the (modified) Andrews and Ploberger case for c → 0, this statistic is a special case of (A.13); in fact, the NyblomT* and the modified Mean-WaldT* statistics simply use two different weighting matrices. Notice that in the structural break case only, the test statistic is constructed on the basis of the first component of
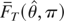
and the estimation of β transforms the Brownian motion in (A.24) into a Brownian bridge, thus originating the Nyblom test statistic:
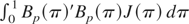
. █
Tables B1, B2, B3, and B4 report critical values for the optimal tests and the QLRT* test considered in Section 3. The significance levels considered in the tables are 10%, 5%, 2.5%, and 1%. The critical values are obtained by simulating the asymptotic distributions described in Section 3. The number of Monte Carlo replications is 5,000. (The trimming values considered are only 15% and 85% of the available sample, and the grid of points is quite sparse; basically each observation is a point in the grid.)
Asymptotic critical values of the Exp-Wald* statistic

Asymptotic critical values of the Mean-Wald* statistic

Asymptotic critical values of the QLR* statistic

Asymptotic critical values of the Nyblom* statistic


Notation related to equations (20), (21), and (22)

Asymptotic power functions of 5% tests for Designs 1–4.

Comparison of asymptotic power functions of 5% selected optimal tests with the naive sequential test (across different designs).

Comparison of asymptotic power functions of 5% selected optimal, TVP, and OIRs tests (across different designs).

Asymptotic critical values of the Exp-Wald* statistic

Asymptotic critical values of the Mean-Wald* statistic

Asymptotic critical values of the QLR* statistic

Asymptotic critical values of the Nyblom* statistic