1. INTRODUCTION
Fully modified vector autoregression (FM-VAR) was designed by
Phillips (1995) to allow for robust
statistical inference on an unrestricted vector autoregression (VAR)
without any need to examine whether the data are stationary or possibly
contain unit roots and cointegration. To allow one to ignore the number
of unit roots and their location (i.e., the cointegrating relations),
the FM-VAR estimator treats all variables as potential unit root
processes and accordingly corrects the ordinary least squares (OLS)
estimator for any harmful correlation effects and for the endogeneity
of the regressors that may arise from cointegrating relations between
these variables. All these corrections are performed by using
nonparametric kernel estimators in the manner originally developed by
Phillips and Hansen (1990). Phillips (1995) shows that whether the data are stationary or
contain unit roots and cointegration these corrections yield convenient
asymptotic estimation theory and related Wald tests on levels VARs have
limiting distributions that are bounded above by the χ2
distribution with degrees of freedom equal to the number of
restrictions. Therefore, conventional critical values can be applied to
obtain valid (but conservative) asymptotic tests of hypothesis on the
coefficients of a VAR.1
The usefulness of
the FM-VAR approach has been recently discussed and promoted by
Freeman, Houser, Kellstedt, and Williams (1998) and Quintos (1998).
On the other hand, Elliott (1998) shows
that a set of commonly used procedures that are designed for testing
hypotheses on cointegrating parameters and that require pretesting for
cointegrating rank tend to suffer from size distortions when some roots
are large but not exactly equal to one. His message is that these
techniques can easily fail to produce valid inference when some
individual variables are inferred to be exact unit root processes
although they are in fact generated by highly autocorrelated processes
with roots slightly less than unity. Although Elliott (1998) shows that the problem arises in testing
procedures for normalized cointegrating vectors based on the full
information maximum likelihood estimator or an asymptotically
equivalent estimator, his analysis does not deal with the FM-VAR
approach. Given the promises of the FM-VAR method, especially that it
does not require knowledge of the location and number of unit roots,
one could easily believe that it could overcome the problem introduced
by Elliott (1998).
However, this paper proves that although the FM-VAR testing procedure
requires neither pretesting for cointegrating rank nor explicitly
imposing unit root and cointegration restrictions in its formulations
it is basically faced with the same problem as the testing procedures
studied by Elliott (1998). With local to unit
root parametrization and related asymptotic theory, we demonstrate that
the FM-VAR estimator has second-order bias effects if some roots are
nearly one. The bias effects are present in coefficient estimates of
local to unit root variables, and therefore Wald tests based on the
FM-VAR estimator have the potential to be severely size distorted in
the same way as the tests based on the methods studied by Elliott
(1998). This is shown analytically, and a
comparison to the result of Elliott (1998) is
provided. A simulation study is reported showing that although the size
distortions of the FM-VAR testing procedure can be smaller in magnitude
than those of the procedures covered by Elliott (1998), they can often be unsatisfactorily high. In
addition, we show that with the FM-VAR estimator near unit roots become
estimated as exact unit roots with a convergence speed faster than the
order of the sample size. Tests based on estimates of this kind are not
generally valid if the investigated hypothesis happens to identify the
corresponding direction of the parameter space. The only part of the
parameter space where the FM-VAR estimator works properly involves
coefficients related to those variables or directions of the process
where the standard stationary asymptotics provide a good
approximation.
2. SETUP AND RESULTS
The analysis is carried out in terms of the first-order
n-vector autoregression
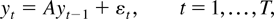
where εt is
iid(0,Σεε) with
Σεε positive definite and with finite
fourth-order cumulants. The initial values in y0
can be any random variables, including constants, whose distribution is
independent of T. Although model (1) is a special case of the
one studied by Phillips (1995), it suffices
for our purposes and allows us to make our general point on the FM-VAR
method that can be extended to any higher order VARs that possibly
include a constant and a linear time trend.
Suppose our primary interest is in testing an economic hypothesis
that can be expressed as linear restrictions on A such that
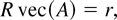
where R and r are known (q ×
n2) matrix of rank q and
q-dimensional vector, respectively. If the system contains
unit roots, then standard test statistics for this hypothesis such as a
Wald statistic based on OLS estimation of (1) generally do not have
standard asymptotic distributions, such as a χ2
distribution. This result arises from the fact that the sample
covariance of the nonstationary linear combinations of the components
of yt−1 and the error of the system
does not converge to zero, but rather, it converges weakly to a
nonstandard distribution consisting of functionals of components of a
vector Brownian motion. The associated distribution is mislocated or
shifted away from the true parameter value, and this fact generally
distorts hypothesis tests based on the OLS estimates (for a detailed
discussion, see, e.g., Phillips, 1995).
There are different ways to try to overcome the inferential problems
caused by the possible presence of unit roots in a VAR. One alternative
is to employ an error correction representation of VAR (see, e.g.,
Johansen, 1991), on which equivalent
restrictions to those on the original VAR model can be formulated.
However, this approach requires pretesting for cointegrating rank,
which is known to induce size distortions and pretest bias in many
cases (cf. Elliott, 1998). In contrast, the
FM-VAR procedure of Phillips (1995) attempts
to obtain robust statistical inference on a levels VAR without the need
to pretest the data concerning unit roots and cointegration.
To set up the formulas of the FM-VAR estimator and test statistic,
respectively, we define the following generic notation. For any pair of
covariance stationary series {at} and
{bt} the long-run covariance matrix
,
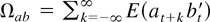
and the one-sided long-run covariance matrix
.
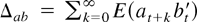
Correspondingly, kernel estimators of these matrices are defined by
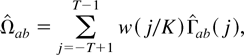
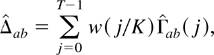
where w(·) is a kernel function with a lag truncation
or bandwidth parameter K and
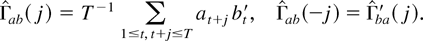
Often, the series at and
bt in (5) have to be replaced by
appropriate estimators, in which case the subscripts are modified
accordingly. The following assumptions are from Phillips (1995).
Assumption KL (Kernel Condition). The kernel function w(·):
R → [−1,1] is a twice continuously
differentiable even function with
(a) w(0) = 1, w′(0) = 0,
w′′(0) ≠ 0, and either
(b) w(x) = 0, |x| ≥ 1, with
lim|x|→1 1
w(x)/(1 − |x|)2
= constant, or
(b′) w(x) =
O(x−2), as
|x| → ∞.
Assumption BW (Bandwidth Expansion Rate). The bandwidth parameter
K in the kernel estimates (3) and (4) has an expansion rate of the
form K =
Oe(Tk) for
some k ∈ (¼,2/3), where the expansion rate
order symbol Oe is defined in Phillips
(1995, p. 1032).
Now, applying formula (43) of Phillips (1995) the
FM-VAR estimator of A in (1) is given by
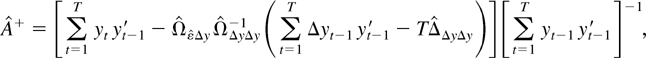
where the subscripts
in the estimated long-run covariance matrices refer to the residual series
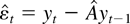
from an OLS estimation of (1) and the series
Δyt−1, respectively. The
corrections associated with the kernel estimators in (6) are designed
to remove any harmful correlations between the nonstationary directions
of the regressors and the errors of the model while preserving the
standard asymptotic theory for the stationary part of the parameter
space (for details of the argument, see Phillips,
1995). The FM-VAR-based Wald test statistic to test for the
restrictions given in (2) is
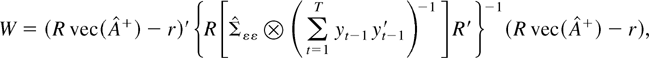
where
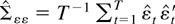
is the OLS estimator of Σεε from model (1).
The asymptotic theory for the estimator and the test statistic in (6)
and (7), respectively, can be found from Theorems 5.7 and 6.1 of
Phillips (1995). To get an idea how these
theories should be modified when some of the roots in the model are
close to but not exactly equal to one, suppose that A has the
simple form
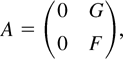
where G is an r × (n −
r) matrix and F is an (n − r)
× (n − r) matrix. Partitioning
yt =
(y1t′,y2t′)′
conformably with A the model (1) may be written as
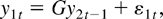
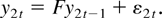
In particular, we now assume that F = I +
T−1C, where C is a fixed
diagonal matrix. If all diagonal elements in C are zeros,
y2t is a vector random walk and the model
(1) has n − r (exact) unit roots. In this case
the model reduces to the leading example used by Phillips (1995) to illustrate and motivate the FM-VAR
approach. However, if a diagonal element is negative, say, then the
corresponding variable in y2t is mean
reverting and the system has a root that is only local to one. Using
this parametrization we obtain asymptotic results that provide more
accurate approximations than those obtained assuming a fixed parameter
(F) when the underlying process for
y2t is slowly mean reverting and the
sample size is moderate (cf. Elliott, 1998).
The following theorem establishes the limiting behavior of the FM-VAR
estimator when the diagonal elements in C may be nonzero. Note
that the error covariance matrix assumes the partition
Σεε =
[Σij], (i,j = 1,2)
conformably with that of yt (or
εt).
THEOREM 1. Let
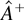
be an FM-VAR estimator for model (1) where A is given by (8) with
F = I + T−1C; and
define e1 =
[Ir 0r×(n−r)],
e2 =
[0(n−r)×r In−r],
β′ =
[Ir −G],
and β⊥′ =
[G′ In−r].
Then, under Assumptions KL and BW, as T → ∞,
where
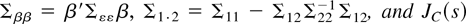
is an Ornstein–Uhlenbeck process generated by the multivariate
stochastic differential equation
dJC(s) =
CJC(s) ds +
dW2(s), JC(0)
= 0, where W2(s) denotes an (n
− r)-vector standard Brownian motion defined on
[0,1] that is given by the weak limit of the partial sum
.
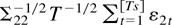
Furthermore, W1·2(s) is an
r-vector standard Brownian motion independent of
W2(s).
Part (a) of Theorem 1 gives the asymptotic behavior of the FM-VAR
estimator to the stationary directions in the same way as part
(a′) of Theorem 5.7 of Phillips (1995).
We notice that the value of C makes no difference to these
directions, and thus, the coefficients of the “clearly”
stationary variables in the model are estimated with the same limiting
theory whether the parameter F is close to or equal to a unit
root (identity) matrix.
Part (b1) of Theorem 1 gives the asymptotic properties of the FM-VAR
estimator of the parameter G in (9). It shows that the
Brownian motion that is present in the distribution when
y2t has only exact unit roots is replaced
by an Ornstein–Uhlenbeck process when some of the roots are just
local to unity. This, of course, reflects the asymptotic properties of
the local to unit root parametrization. More important, the result of
part (b1) of Theorem 1 shows that a small deviation from an exact unit
root can result in a second-order bias term,
,
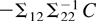
in the limiting distribution of the FM-VAR estimator. In general, this
term disappears only when there is no simultaneity in the model, i.e.,
when Σ12 = 0. Note also that the bias effect is
especially present in the estimator of the cointegrating coefficient
for which the FM-VAR estimator is efficient in the same way as
conventional cointegrating parameter estimators (cf. Phillips, 1995). This observation is closely
related to Theorem 1 of Elliott (1998) and
indicates that near unit roots distort the FM-VAR estimator especially
in that part of the parameter space where the estimator behaves
optimally when these roots are exactly one. Furthermore, it can be seen
that the bias effects appear only for those coefficients that are on
variables with near unit roots, whereas parameters on variables with
exact unit roots are unaffected by the presence of near unit roots in
the system—this same observation holds for the conventional
cointegration estimators also (see Elliott,
1998).
Part (b2) of Theorem 1 shows that with the FM-VAR method near unit
roots become estimated as exact unit roots with convergence speed that
is faster than the order of the sample size.2
Yamada and Toda (1998, pp.
62–63) note that this holds for exact unit roots.
This
result is in contrast with the analysis of Phillips (
1995), which indicates that such
“hyperconsistent” rates of convergence can only occur when
the system has a full set of unit roots (this would be
n unit
roots in the present model). However, Theorem 1 shows that this can
happen even more generally and that estimates converge to exact unit
roots even when the true roots are just nearly ones. Note that the
result holds whether the system errors are contemporaneously correlated
or not.
The result of part (b2) of Theorem 1 has severe implications for
FM-VAR testing. First, it is clear that FM-VAR hypothesis tests
involving estimates of this kind are not valid in the usual sense of a
test, because their limit distributions are degenerate under the null
hypothesis F = I, say.3
Here we refer to the Wald test statistic defined in the
usual way such as the one in (7).
This problem would be
relevant if the FM-VAR method were used to test for the cointegrating
rank, which is effectively a test for the number of unit roots in the
system. Second, such tests would have no asymptotic power against
alternatives within the
T−1 neighborhood of
unity. This would be a weakness in the case of a cointegration test,
because conventional tests for the cointegrating rank have power
against such local alternatives (see, e.g.,
Saikkonen and Lütkepohl, 1999). These remarks
indicate that the endogeneity corrections tend to invalidate any
statistical inference on (near) unit root coefficients in a VAR.
The focus of the rest of this section is on showing how FM-VAR
hypothesis testing may be distorted by the local to unit root bias
effects of part (b1) of Theorem 1. Suppose the Wald test statistic in
(7) is applied to test a linear restriction on the coefficients of
y2t in the first r equations of
the model (1) when A has the structure given in (8). We then
have the following result.
COROLLARY 1. Suppose A has the form given in (8) and let
WG be an FM-VAR-based Wald test statistic
from (1) for the hypothesis R vec(A) = r, where r is a
q-dimensional vector and R is a q × n2 matrix of
rank q
(q ≤ r(n − r)) imposing
restrictions on G only. Define a matrix
RG such that R =
RG(e1 [otimes ]
e2). Then, as T → ∞,
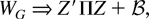
with
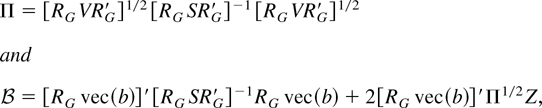
where
,
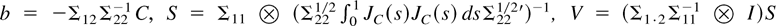
and Z is a q-vector of independent normal variables with mean zero and
variance unity. Furthermore, Z is independent of
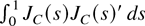
in (12).
If C = 0 in Corollary 1 we have
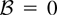
in (12) and
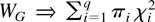
where χi2 are independent
χ2 variates and the weights πi
are the eigenvalues of the matrix
[RGVRG′][RG
SRG′]−1. This
result would be identical to one implied by Theorem 6.1 of Phillips
(1995) when F = I. Note that
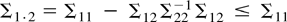
implies Π ≤ I and, thus, the weights
πi satisfy 0 < πi ≤ 1.
Therefore, the FM-VAR test is bounded above by the usual
χq2 distribution when F =
I. As this same distribution is used to obtain critical values for
the test, it is clear that the FM-VAR test is asymptotically conservative.
Note that in an “exact stationarity” case, i.e., if F
were fixed with the corresponding characteristic roots outside the unit root
circle, the test statistic WG would be
asymptotically χq2 distributed (cf.
Phillips, 1995, Theorem 6.1).
The most interesting result of Corollary 1 is that when F =
I + T−1C with nonzero
diagonal elements in C, then if there is simultaneity in the
model, i.e., Σ12 ≠ 0, the FM-VAR Wald test has a bias
term given by
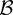
in (12). The first and second terms in
,
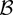
respectively, characterize the mean and variance of the
bias, which both depend upon Σ and C. The mean term is
always nonnegative, and, thus, a deviation from an exact unit root
tends to increase the size of the test. When Σ12 is
nonzero, this effect is absent only from hypothesis tests that do not
impose restrictions on coefficients of near unit root variables (cases
where RG vec(b) = 0). This latter
observation is similar to one obtained for the conventional
cointegrating parameter estimators and indicates that tests of
hypotheses imposing restrictions only on coefficients of variables with
exact unit roots are unaffected by the presence of near unit roots in
the model (the “partially misspecified” case in Elliott, 1998).
To further illustrate the result of Corollary 1 and to see how it
relates to that of Elliott (1998) we consider
a simple example. We assume that y1t and
y2t are scalars (i.e., n =
r = 1) and that we are testing for the hypothesis that the
variable y2t has no Granger-causal effect
on y1t (i.e., G = 0). Then from
Corollary 1 we see that the corresponding FM-VAR-based Wald test
statistic, Wg, say, has the limit
theory
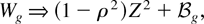
with
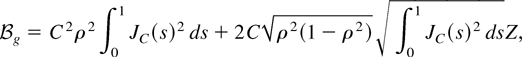
where
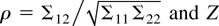
is a normal variate with mean zero and variance unity. Now, let
Wg* denote a Wald test statistic for
this same restriction that has been computed by applying the full
information maximum likelihood estimator of G assuming
y2t is generated by a unit root process.
From the corollary of Elliott (1998),
Wg* would then have the limiting
distribution
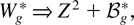
where
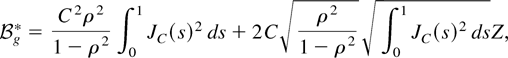
with ρ and Z just as in (14). We notice that the bias
term
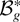
in (16) is larger than
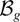
in (14) and tends to infinity as ρ goes to one. However, this difference
between the two distributions is just a reflection of the fact that the FM-VAR
test is asymptotically conservative in our data generating process. The
magnitude of this difference can be evaluated through simulations.
Table 1 gives simulated approximations to
the rejection probabilities Pr(Wg >
3.84) and Pr(Wg* > 3.84), where
Wg and Wg*
are given in (13) and (15), respectively, and 3.84 is the 5% critical
value based on the χ12-distribution. The
results are in line with our theoretical findings, and we observe that
the asymptotic size of the FM-VAR test is clearly unsatisfactory with
moderate values of ρ although it is not as high as the size of the
testing procedures covered by Elliott (1998).
Although this example indicates that the conservative nature of the
FM-VAR test can help to reduce size distortions from a near unit root
in some situations, it must be kept in mind that this property comes
with the price of lower power to reject false null hypotheses. It can
be seen theoretically that if Wg in (13)
were size adjusted by dividing with (1 − ρ2), then
the FM-VAR test would have size distortions as large as in the methods
studied by Elliott (1998).
Asymptotic rejection ratesa
Table 2 examines small sample properties of
the actual FM-VAR test for the hypothesis G = 0 in (1) when
the sample size T is 200, and the data are generated by
equations (9) and (10) with G = 0, Σ11 =
Σ22 = 1, y0 = 0, and with various
values of ρ = Σ12 and C, respectively. In
these simulations the FM-VAR estimator is computed by using the Parzen
kernel function, and in accordance with Assumption BW, we have chosen
to experiment values of the bandwidth parameter K that are the
closest integers to T0.26,
T0.36, T0.46,
T0.56, and T0.66, respectively.
The actual values of K are indicated in the table. The results
of Table 2 are clearly in line with those of
Table 1, although the choice of the bandwidth
parameter seems to play a role in these results. However, this is not
much of a surprise because Yamada and Toda (1997) have recently demonstrated by using another
simulation setup that the size performance of the FM-VAR test can be
highly dependent upon the choice of the value of the bandwidth
parameter even with relatively large sample sizes. Therefore, our
simulation results confirm our theoretical findings and indicate that
FM-VAR hypothesis testing can suffer from potentially severe size
distortions when some roots are almost but not exactly equal to one.
Rejection rates of the FM-VAR test with sample size T =
200a
3. CONCLUSION
This paper examined the robustness of hypothesis testing based on the
FM-VAR estimator when some of the roots of a VAR are large but less
than one in absolute value. It was shown that the FM-VAR test can
produce severe size distortions when the hypothesis imposes
restrictions on variables with near unit roots. As this problem occurs
in the particular part of the parameter space where the FM-VAR
estimator is efficient in the same way as conventional cointegrating
parameter estimators, this finding corresponds with that of Elliott
(1998) and confirms that estimation and
testing procedures that are somehow based on an assumption about exact
unit roots and that are trying to treat these optimally tend to fail
when there is just a slight deviation from this assumption. In
addition, we showed that with the FM-VAR method near unit roots become
estimated as exact unit roots with convergence speed that is faster
than the order of the sample size. Also this result implies problems
for FM-VAR hypothesis testing, as such “hyperconsistent”
estimates tend to give rise to degenerate limit distributions under the
null hypothesis. The only part of the parameter space where the FM-VAR
estimator is robust involves coefficients related to those variables or
directions of the process where the standard stationary asymptotics
provide a good approximation. Therefore, overall, our analysis
indicates that the FM-VAR method can easily produce invalid inference
if some variables in the system are considerably highly
autocorrelated.
As far as possible solutions to the problem studied here are
concerned, there is currently only one alternative for FM-VAR that does
not require prior knowledge of the number of (near) unit roots and
their location in a VAR. This is the lag augmentation procedure of Toda
and Yamamoto (1995). Although this method can
provide valid inference on coefficients of a levels VAR with near unit
roots it has the disadvantage of being inefficient because of its
ultimate intention to overfit the model. It also suffers from
difficulties arising from uncertainties in finding sufficiently high
lag order.
APPENDIX
Proof of Theorem 1. Let
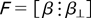
and write
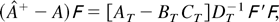
where
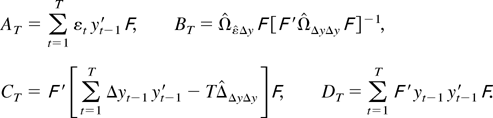
We first derive asymptotic results for
AT, BT,
CT, and DT
and then subsequently apply these to prove the main theorem. From (9)
and (10) we can derive the following notation for later use:
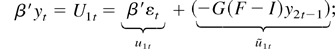
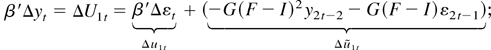
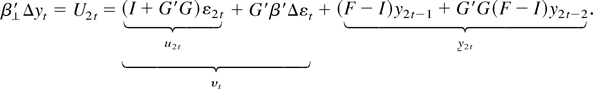
Consider AT. Using F −
I = T−1C and well-known
limiting results we obtain
where Σββ =
β′Σεε β, and
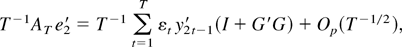
with
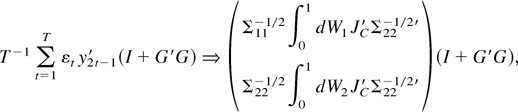
where W1 ≡
W1(s) and W2 ≡
W2(s) are standard vector Brownian motions
on [0,1] that are given by the weak limits of the partial sums
,
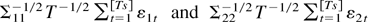
respectively, whereas JC ≡
JC(s) is an
Ornstein–Uhlenbeck process defined by the multivariate stochastic
differential equation dJC(s) =
CJC(s) ds +
dW2(s), JC(0)
= 0.
Consider BT and
CT and use (A.2)–(A.5) to write
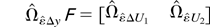
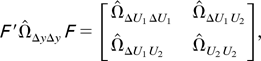
where the subscripts ΔU1 and
U2 refer to the series
ΔU1t−1 and
U2t−1, respectively. Similarly, write
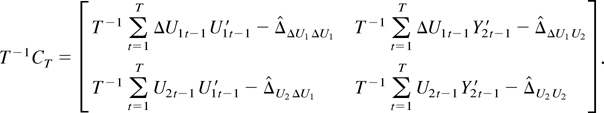
Lemma 1, which follows, summarizes the asymptotic properties of each
of the elements in (A.9)–(A.11) similarly to Lemma 8.1 of
Phillips (1995) for the C = 0 case.
In the proof of Lemma 1 we work as in the proofs of Phillips (1995) only with long-run covariance matrix
estimates that satisfy part (b) of Assumption KL (for additional
comments that apply here also, see Phillips, 1995, pp. 1057–1058).
LEMMA 1. Under Assumptions KL and BW, the following hold:
The error terms of
Op((KT)−1/2)
that appear in parts (b), (d), (g), and (h) are sharp.
Proof. Part (a): Use (A.3) to write
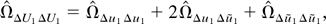
where the first term corresponds to
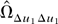
in part (a) of Lemma 8.1 in Phillips (1995, p.
1058). Thus part (a) follows from Phillips (1995)
provided that the two last terms in (A.12) are at most
op(K−2). First,
use (A.3) to write
where
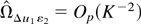
by part (b) of Lemma 8.1 in Phillips (1995).
Second, the first term on the right-hand side of (A.13) is
op(T−2),
because
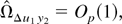
which can be proved by using similar lines to those in equation (P14)
in the proof of part (c) of Lemma 8.1 in Phillips (1995, p. 1064). An important part of these
derivations is the following intermediate result:
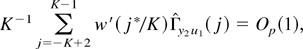
where j* ∈ [j − 1,j]
is defined for each j. This result follows from arguments
given in the proof of Theorem 3.1 of Phillips (1991, pp. 432–433) in the same way as the
respective result in Phillips (1995, p.
1065). (Note that in the proof of Theorem 3.1 of Phillips, 1991, similar [intermediate] convergence
results [as, e.g., Phillips, 1991, p.
433, the first result] can be proved when an exact unit root
process is replaced by a local to unit root one.)
Next, use the definition of
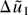
in (A.3) to write
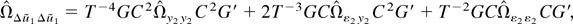
where the first term is
op(T−2),
because
where the last equality follows from Assumption BW. Using the same
argument as that in (A.15) we can show that the second term in (A.16)
is op(T−2),
whereas the last term in (A.16) is
Op(T−2), because
.
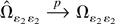
Thus,
,
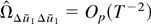
and part (a) follows.
Part (b): Use (A.3) and (A.5) to write
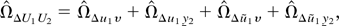
where the first term is an analog to the term
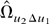
in the second result of part (b) of Lemma 8.1 in Phillips (1995). Now, the result of part (b) follows from Phillips
(1995) provided that the three last terms in (A.18)
are at most Op(T−1).
This is easily seen by applying similar arguments to those in the proof of
part (a).
Part (c): The proof is similar to those of parts (a) and (b)
and thus is omitted here.
Part (d): Use (A.3) to decompose
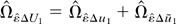
and use similar algebra to that in (P13) in Phillips (1995, p. 1064) to obtain
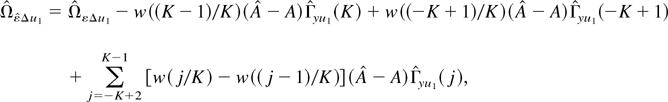
where the subscript y denotes the series
yt−1. The first term in (A.20) is
analogous to
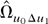
in the first result of part (b) of Lemma 8.1 in Phillips (1995) and delivers the first three terms on the
right-hand side of part (d). Thus, it remains to be shown that the rest
of the terms in (A.20) and
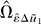
in (A.19) are at most
Op(T−1). These
results can be derived with similar arguments to those in the proofs of
parts (a) and (b) and by applying similar lines to those in equations
(P13) and (P14) in Phillips (1995, p. 1064);
details are omitted here.
Part (e): The proof is similar to that of part (d) and hence
is omitted here.
Part (f): Use the definition of
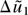
in (A.3) to write
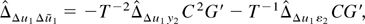
where
,
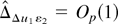
by similar arguments to those used right after (A.20) and the ones used in
(A.15), whereas
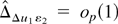
by arguments given in the proof of Lemma 8.1 in Phillips (1995). Therefore,
.
Furthermore, similar derivations to those for (A.16) imply
.
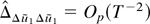
These lines together with well-known limiting arguments yield
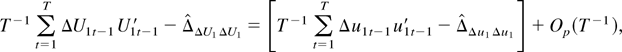
where the term in the square brackets is
Op(K2) (see Phillips,
1995, Lemma 8.1, part (e)). Thus, part (f)
follows.
Part (g): In the same way as in the proof of part (f) we can
deduce that
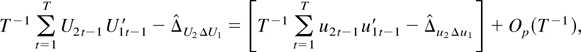
where the term in the square brackets has similar limit theory as in
part (f) of Lemma 8.1 of Phillips (1995), and
thus, part (g) follows.
Part (h): As in the proofs of parts (f) and (g) we have
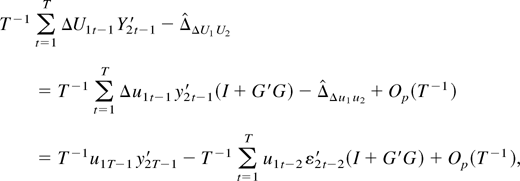
where the last line corresponds to equation (P18) in the proof of
part (g) of Lemma 8.1 of Phillips (1995), and
thus, part (h) follows from Phillips (1995,
p. 1067).
Part (i): Use (A.4) and (A.5) to write
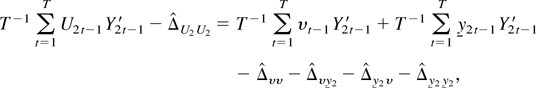
where
Furthermore, applying well-known limiting arguments we get
where the last equality follows from the definition of
Δυυ. Now, as
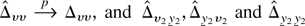
are op(1) by similar arguments to those used
in the proof of part (f), we obtain part (i). █
It follows from Lemma 1 that we can apply analogous lines to those in
Phillips (1995, p. 1065) to obtain
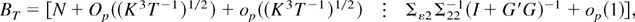
where N is a fixed nonzero matrix and
Σε2 =
(Σ12′ Σ22)′.
Combining (A.23) and parts (f)–(i) of Lemma 1 yields
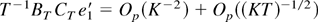
and
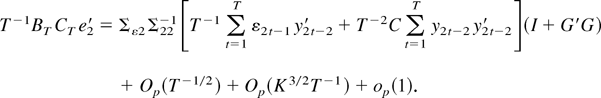
From Assumption BW we have
Op(K−2T1/2)
+ Op(K−1/2)
= op(1) (cf. Phillips, 1995, Discussion 8.5.(i)), and thus, (A.24) and
(A.25) combined with well-known limiting arguments imply
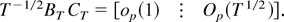
Next applying the formula of the partitioned inverse we get
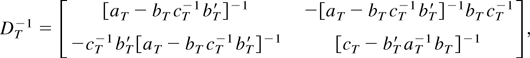
where, by well-known limiting arguments,
Using these results it is seen that
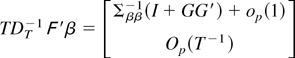
and
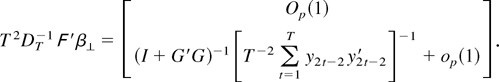
We are ready to complete the proof of Theorem 1. For part (a)
normalize the first column in (A.1) by
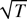
to get
where the last equation follows from (A.26) and (A.27). Thus, for
part (a) it remains to combine the results in (A.6)–(A.8) with
the one in (A.27).
For part (b1) use (A.6)–(A.8) and (A.24)–(A.28) to see that
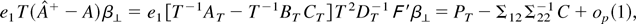
where
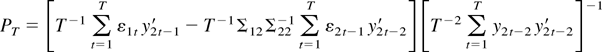
converges weakly to
where ≡ denotes equality in distribution and
is a standard Brownian motion independent of W2.
For part (b2) note that
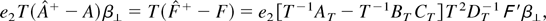
where
.
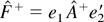
It is then straightforward to apply (A.6)–(A.8) and (A.24)–(A.28)
to show that
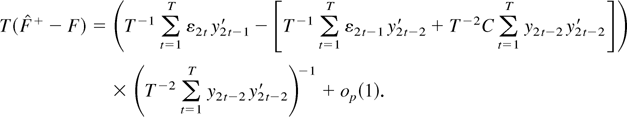
Given F = I +
T−1C we see that C cancels
out from both sides of (A.29) and thus it can be written as
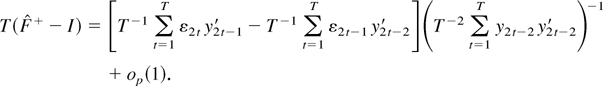
This shows why
converges to an identity matrix and why we have added C on the
left-hand side of part (b2) of Theorem 1. It remains to observe that the
difference between the two sums in the square brackets in (A.30) is just
T−1ε2T
y2,T−1′ −
T−1ε20
y2,−1′ =
op(1), whereas the inverse in (A.30) is
Op(1). █
Proof of Corollary 1. Because the hypothesis imposes restrictions
on G only, there indeed exists a q ×
(n(n − r)) matrix
RG such that R vec(A) =
RG(e1 [otimes ]
e2) vec(A) =
RG vec(G) = r.
Therefore, letting
and using the fact that RG
vec(G) = r under the null hypothesis we can write
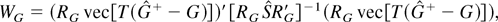
where
,
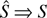
by similar arguments to those used in the proof of Theorem 1, and because
.
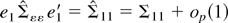
Next, because W1·2(s) and
W2(s) are vectors of independent standard
Brownian motions,
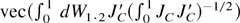
is equal in distribution to
N(0,Ir(n−r))
(e.g., Park and Phillips, 1988). Thus it
follows directly from part (b1) of Theorem 1 that
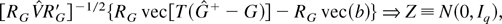
where
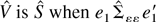
when
is replaced by Σ1·2. Taken together (A.31) and (A.32)
show the result in (11), whereas the independence statement holds because
Z in (A.32) and JC are jointly
normal and uncorrelated. █
