Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-02-11T00:32:37.862Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON THE PAPER BY H.J. BIERENS: “COMPLEX UNIT ROOTS AND BUSINESS CYCLES: ARE THEY REAL?”

Published online by Cambridge University Press:  08 June 2004

Ignacio Díaz-Emparanza
Ignacio Díaz-Emparanza
Affiliation:
Universidad del País Vasco–Euskal Herriko Unibertsitatea
Rights & Permissions [Opens in a new window]

Abstract

This note discusses the concept of aliasing and its use in the paper by H.J. Bierens (2001, Econometric Theory 17, 962–983), in the framework of a second-order autoregression with complex unit roots. The condition on the range of the angular frequency φ is extended to φ ∈ (0,2π) − {π}.Financial support from UPV-EHU research project 9/UPV-00038.321-13503/2001, Basque Government project PI9970 and Ministerio de ciencia y tecnología BEC2003-02028 is gratefully acknowledged.

Type
MISCELLANEA
Information
Econometric Theory , Volume 20 , Issue 3 , June 2004 , pp. 636 - 637
Copyright
© 2004 Cambridge University Press

Bierens (2001) studies the asymptotic properties of autoregressive moving average (ARMA) processes with complex-conjugate unit roots in the autoregressive (AR) lag polynomial and derives a nonparametric test of the complex unit root hypothesis against the stationarity hypothesis based on the standardized periodogram. The article is really a valuable work, and what I want to point out here is only a marginal note that does not affect the main results of the paper. In Section 2.1, Bierens presents the structure of an AR(2) process with complex roots. I do not agree with the interpretation of the aliasing problem in the second paragraph of Section 2.1.

The process being considered is (1): yt = 2 cos(φ)yt−1 − yt−2 + μ + ut where ut is i.i.d.(0,σ2), μ is a constant, and φ ∈ (0, π). It is assumed that yt is observable for t = 1,…,n. As mentioned in the paper, the AR lag polynomial Φ(L) = 1 − 2 cos(φ)L + L2 has two roots on the complex unit circle, exp(iφ) = cos(φ) + i sin(φ) and its complex-conjugate exp(−iφ) = cos(φ) − i sin(φ) (assuming sin(φ) ≠ 0). In the paragraph mentioned, the author says:

Note that (1) generates a persistent cycle of 2π/φ periods. If φ ∈ (π,2π), the cycle length is less than two periods. Such short cycles are unlikely to occur in macroeconomic time series, and if they occur, they are difficult, if not impossible, to distinguish from random variation. This is the reason for only considering the case φ ∈ (0,π).

If we had continuous data, each root would imply a different cycle. So, in this case we would have a cycle of 2π/φ periods (caused by the root cos(φ) + i sin(φ)) and another cycle (its alias) of 2π/(2π − φ) periods.

1

This is because the root exp(−iφ) = cos(φ) − i sin(φ) may be expressed in an equivalent form as exp[i(2π − φ)] = cos(2π − φ) + i sin(2π − φ).

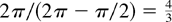
For example, if φ = π/2, we have a cycle of 2π/(π/2) = 4 periods and another cycle of

periods. But both cycles imply the same cyclical behavior in a time series observed at discrete points (for a detailed explanation of this problem, see, e.g., Hamilton, 1994, p. 161). When we work with time series data, normally we only have the values of the variables observed at discrete points, and we do not know what the structure of our variables would be if they could be observed continuously. We do not have such information, and so we cannot decide if the relevant cycle for our variable is the one of period 2π/φ or the one of period 2π/(2π − φ). This is the problem, and this is why the only solution we have is to consider both cycles together because we cannot determine, based on discrete time series data, which is the relevant frequency for our variables.

So, what happens in Bierens's paper with frequencies φ ∈ (π,2π)? They are also being considered in his analysis, given that we may define φ′ = 2π − φ, then φ′ ∈ (0,π) and

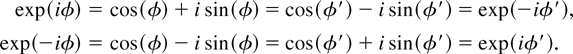
Frequencies φ ∈ (π,2π) are already included in Bierens's analysis through the root exp(−iφ). So, condition φ ∈ (0,π) may be relaxed to φ ∈ (0,2π) − {π}, and the aforementioned paragraph of Section 2.1 might (or should) be written:

Note that (1) generates two persistent cycles of 2π/φ and 2π/(2π − φ) periods. The cycle length corresponding to one of the roots—exp(−iφ) if φ ∈ (0,π) and exp(iφ) if φ ∈ (π,2π)—is less than two periods. Such short cycles are unlikely to occur in macroeconomic time series, but they are impossible to distinguish from their alias2

The alias is the cycle corresponding to root exp(iφ) if φ ∈ (0,π) and exp(−iφ) if φ ∈ (π,2π).

based only on the observed discrete data. This is the reason for working with the two cycles together.

References

REFERENCES

Bierens, H.J. (2001) Complex unit roots and business cycles: Are they real? Econometric Theory 17, 962–983.Google Scholar
Hamilton, J. (1994) Time Series Analysis. Princeton University Press.