1. INTRODUCTION
A standard tool in the asymptotic theory of integrated processes and
elsewhere is a functional central limit theorem. Typically, a
real-valued stochastic process
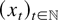
is considered such that
n−1/2x[rn],
0 ≤ r ≤ 1, converges weakly to
σW(r) (in the space D[0,1] of
cadlag functions), where W(.) represents Brownian motion and
[x] denotes the integer part of x.
Frequently, then the asymptotic behavior of a functional of the form
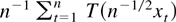
is of interest. Such functionals arise in the construction of test
statistics or in the theory of nonlinear estimation with integrated
processes (Park and Phillips, 2001). For
continuous real-valued functions T on
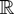
an argument based on the continuous mapping theorem shows that
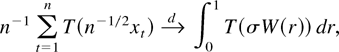
where
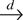
signifies convergence in distribution; for convenience we include a formal
statement and a proof in Appendix A; cf. Lemma A.1 and its proof. For an
important subclass (cf. Park and Phillips, 1999,
Assumption 2.1) of the class of all processes satisfying a functional central
limit theorem, Theorem 3.2 in Park and Phillips (1999) shows that property (1.1) actually holds for a class
of functions T wider than the class of continuous functions.
Functions in that class are dubbed “regular” in Park and Phillips
(1999). Apart from continuous functions, this class
contains, e.g., locally bounded monotone functions and piecewise
continuous functions.
1 The last claim is
true if one adopts a definition of piecewise continuity such that the
l.h.s. and r.h.s. limits exist and are finite at each point of
discontinuity.
However, it does not contain, e.g., every
bounded (measurable) function. Furthermore, it also does not include
(locally) unbounded functions such as
T(
x) =
log|
x| or
T(
x) =
|
x|
α for −1 < α <
0 (cf. Park and Phillips,
1999, Remark
3.3(c)). [For functions of this latter kind, Theorem 3.4 of Park
and Phillips (
1999) presents a modified
version of (1.1) with a suitably “clipped” approximation
Tn replacing
T on the l.h.s. of
(1.1) under stronger conditions on the process
xt; cf. Assumption 2.2 in Park and
Phillips,
1999. However, this theorem does
not establish property (1.1) itself. We also note that the proof of
this theorem, if not the theorem itself, seems to be in error.
2 A function T can be constructed that
satisfies all the conditions of Theorem 3.4 in Park and Phillips (1999) but does not satisfy
cnT(cn)
→ 0 as claimed in the proof of that theorem. It seems that to
salvage that theorem a condition such as T(x) =
o(|x|−1) for
x → 0, x ≠ 0, needs to be
added.
] In a recent paper, de Jong (
2002) establishes property (1.1) for a class of
functions different from the class of “regular” functions
appearing in Theorem 3.2 of Park and Phillips (
1999) but covering functions such as
T(
x) = log|
x| and
T(
x) = |
x|
α for
−1 < α < 0. Roughly speaking, de Jong (
2002) allows
T to have finitely many
“poles” and requires
T to be continuous and
monotone between poles; furthermore he requires
T to be
locally integrable.
3 For T to be
defined as a real-valued function on all of
,
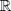
de Jong (2002) assigns the value zero to
T at the pole locations. The results in the present paper do not
rely on this (arbitrary) assignment and also work for functions that assume
the values ∞ or −∞; cf. Remarks 2.1 and 2.5. (The
arguments in these remarks also show that an assignment such as the one
in de Jong, 2002, is in fact inconsequential
under the assumptions on the process made in that paper.)
De
Jong's class neither contains all bounded (measurable) functions
nor all “regular” functions in the sense of Park and
Phillips. He establishes his result for processes satisfying (the
stronger) Assumption 2.2 of Park and Phillips (
1999).
In the present paper we establish the result (1.1) under the minimal
condition that T is locally integrable (in the Lebesgue
sense). In contrast to Park and Phillips (1999) and de Jong (2002)
we thus are able to avoid any regularity condition on
T save the unavoidable local integrability condition. Note
that any “regular” function in the sense of Park and
Phillips (1999) is locally bounded and thus
is a fortiori locally integrable (cf. also Park and Phillips, 1999, Remark 3.3(a)). Thus, apart from covering a
wider class of functions T than in Park and Phillips (1999) or de Jong (2002),
our results also have the advantage of relieving one from the
nontrivial burden of verifying regularity conditions as is necessary
when using the results of Park and Phillips or de Jong. We first prove
result (1.1) under high-level assumptions on the process
xt in Section 2. In Section 3 we provide
sufficient conditions on the process xt
that imply these high-level assumptions, and we obtain corresponding
corollaries. It turns out that one of these corollaries (Corollary 3.3)
contains the result in de Jong (2002) as a
special case in that it covers a much wider class of functions
T (e.g., functions with infinitely many “poles,”
or functions that are neither piecewise monotone nor piecewise
continuous) and at the same time imposes weaker conditions on
xt. Corollary 3.3, in fact, applies to any
locally integrable function T that satisfies a certain growth
condition at the origin. Corollary 3.2 moreover shows that this growth
condition can be dispensed with if a rather mild condition on
xt, namely, that the innovations driving
xt have a bounded density, is added.
Corollary 3.2 thus only imposes the minimal condition of local
integrability on T. Both of these corollaries cover classes of
functions much wider than the class of “regular” functions
considered in Theorem 3.2 of Park and Phillips (1999). Although the conditions on
xt maintained by these corollaries are
somewhat stronger than the corresponding conditions in Theorem 3.2 of
Park and Phillips (1999), we believe that the
extra conditions on xt in these
corollaries are a small price to pay for the ability to cover much
larger function classes. It should furthermore be noted that the
assumptions on xt in Corollary 3.3 are
strictly weaker than the assumptions on xt
employed in Theorem 3.4 of Park and Phillips (1999), thus showing that the “clipping”
device of that theorem can be avoided altogether. Section 4 concludes
the main body of the paper and discusses some generalizations of the
results in Sections 2 and 3. All proofs are relegated to the
Appendixes.
After this paper had been written, the book by Borodin and Ibragimov
(1995) came to my attention. In this
important work results of the form (1.1) and also many other related
results are established for the case when the process
xt is a random walk with increments that
are independent and identically distributed (i.i.d.) and belong to the
domain of attraction of a stable law. Their results always assume more
in terms of the function T than we do in the present paper.
(For example, one of the results in Borodin and Ibragimov, 1995, is for locally Riemann integrable functions,
which constitute a much smaller class than the class of locally
Lebesgue integrable functions. In particular, locally Riemann
integrable functions are necessarily locally bounded, thus ruling out
functions with poles.) Contrary to Park and Phillips (1999), de Jong (2002),
and the present paper, Borodin and Ibragimov (1995) do not provide results for the case where the
increments of xt are dependent (e.g.,
follow a linear process). However, it should be noted that the results
in Borodin and Ibragimov (1995) are more
general along another dimension, namely, that the limiting behavior of
xt need not be given by Brownian motion
but may be given by some stable process. A recent paper by Jeganathan
(2002) takes up this issue and extends it to
the case of dependent increments.
2. WEAK CONVERGENCE OF NONLINEAR
FUNCTIONALS
Let
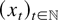
be a stochastic process with values in
.
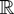
We shall make use of the following assumptions.
Assumption 2.1. The process
n−1/2x[rn],
0 ≤ r ≤ 1, converges weakly to
σW(r), where W(.) is Brownian motion on
[0,1] and
,
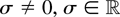
holds. (As a convention, x[rn] is set
equal to zero for r < n−1.)
4 If, instead,
x[rn] is set equal to an
arbitrary random variable x* for r <
n−1, which is defined on the probability
space supporting (xt), an equivalent
assumption is obtained. More generally, Assumption 2.1 is unaffected by
any modification made to finitely many elements of
(xt).
As usual, it is understood that W(0) = 0 a.s. and that
W(.) has continuous sample paths a.s. Furthermore, weak
convergence in the preceding assumption is understood w.r.t. the
Skorohod topology on the space D[0,1].
Assumption 2.2. For every
the distribution of
t−1/2xt
possesses a density, ht, say, w.r.t.
Lebesgue measure on
.
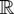
The densities ht are uniformly bounded,
i.e.,
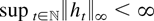
holds, where ∥.∥∞ denotes the sup-norm.
In light of the fact that the distribution of
t−1/2xt
converges to a normal distribution under Assumption 2.1, the conditions
imposed by Assumption 2.2 have some intuitive appeal; in particular, if
a local central limit theorem holds (cf. Ibragimov and Linnik, 1971, Theorem 4.3.1), then
∥ht∥∞ is
automatically uniformly bounded (at least from some index onward).
Sufficient conditions for Assumptions 2.1 and 2.2 will be discussed in
the next section.
Let T be a real-valued Borel-measurable function on
.
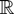
We say that T is locally integrable if and
only if
5 The integral in expression (2.2)
is to be understood in the sense of Lebesgue.
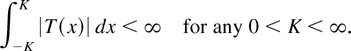
Condition (2.2) is certainly satisfied if T is locally
bounded (i.e.,
sup|x|≤K|T(x)|
< ∞ for any 0 < K < ∞) but is much less
restrictive because it allows also for many locally unbounded functions
such as, e.g., T(x) = log|x|
and T(x) =
|x|α, −1 < α <
0.
6 Condition (2.2) is of course also
satisfied if T is only essentially locally bounded (i.e., if
ess-sup|x|≤K|T(x)|
< ∞ for any 0 < K < ∞, where ess-sup
denotes the essential supremum w.r.t. Lebesgue measure).
(For
T in these latter two examples [or in similar cases]
to be a proper real-valued function defined on
all of
,
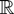
a real number has to be specified as the value of T
at x = 0; if one desires to set T(0) = −∞
or T(0) = ∞, respectively, T becomes a function
with values in the extended real line; cf. Remarks 2.1 and 2.5, which
follow.)
The following theorem establishes the main weak convergence result
for locally integrable functions. It is remarkable in that it does not
impose any regularity conditions on T beyond (2.2). Its
generalization to the case of functions with values in the extended
real line is given in Remark 2.1, which follows.
THEOREM 2.1. Suppose Assumptions 2.1 and 2.2 hold and
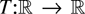
is locally integrable. Then
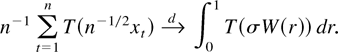
We note that the integral in (2.3) exists a.s. and is finite a.s. if
and only if T is locally integrable (see Karatzas and Shreve,
1991, Ch. 3, Proposition 6.27 and Problem
6.29; cf. also Park and Phillips, 1999,
Remark 3.3 (a)).7
The integral over the
positive part T+(σW(r)) and
also the integral over the negative part
T−(σW(r)) exist a.s.
for every Borel-measurable T, because almost every sample path
of W(.) is continuous. The argument in the proof of Theorem
2.1 then also establishes a.s. finiteness of both these integrals under
local integrability.
(In this sense the local integrability
condition is an unavoidable requirement.)
We note for later use that the integral in (2.3) can equivalently be
expressed in terms of local time. That is,
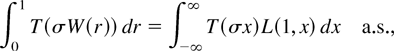
where L(t, x) denotes Brownian local time
(cf. Chung and Williams, 1990, Corollary
7.4).
Remark 2.1. (Extended Real Functions)
(a) Theorem 2.1 also holds if T is a Borel-measurable
function from
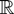
to the extended real line
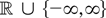
that is locally integrable (e.g., if T(x) =
log|x| for x ≠ 0 and =−∞ for
x = 0 or if T(x) =
|x|α for x ≠ 0 and = ∞
for x = 0, −1 < α < 0). To see this, first note that
we may change T into a locally integrable real-valued
function T* by modifying T only on a set of Lebesgue measure
zero. Because the distribution of xt is
absolutely continuous by Assumption 2.2,
coincides with
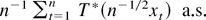
and, in particular, is a.s. well defined. It hence suffices to
show that the integral
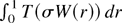
is well defined a.s. and coincides a.s. with
.
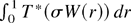
For this it is enough to show that for almost every path of Brownian motion
the set D = {r ∈ [0,1]: T
(σW(r)) ≠
T*(σW(r))} is a Lebesgue null
set: Let A denote the Lebesgue null set
.
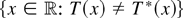
Then 1D(r) =
1A(σW(r)) and hence
.
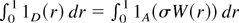
Corollary 7.4 in Chung and Williams (1990)
gives
where L(t, x) denotes local
time and where the last equality follows because A is a
Lebesgue null set and σ ≠ 0. This establishes the claim.
(b) Similar reasoning as in (a) shows that equation (2.4) also
holds for locally integrable functions
.
Remark 2.2. If T is a function from
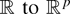
(or to
(
)
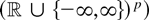
with each component being locally integrable, then Theorem 2.1 continues to
hold (where the r.h.s. of (2.3) is defined componentwise). This follows from
Theorem 2.1 (and Remark 2.1) combined with the Cramér–Wold
device.
Remark 2.3.
(a) If xt satisfies the convergence
condition in Assumption 2.1 and if Assumption 2.2 holds, then
necessarily σ ≠ 0 holds as is easily seen.
(b) If xt satisfies the convergence
condition in Assumption 2.1, but with σ = 0, and if T is
continuous, then (2.3) continues to hold by Lemma A.1. However, this is
not necessarily true for arbitrary locally integrable (even
“regular”) T as the following example shows.
8 Of course, it is trivially true for any
real-valued T if, e.g., xt = 0
with probability one for all
.
Let
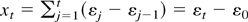
where the random variables εt are i.i.d.
standard normal. Then the convergence condition in Assumption 2.1 is
satisfied with σ = 0. Let T(x) =
1(−∞,0)(x) and note that T is
locally integrable and is even “regular” in the sense of
Park and Phillips (1999). The l.h.s. of (2.3)
is now equal to
,
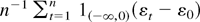
which converges a.s. to
E(1(−∞,0)(εt
− ε0)|ε0) =
Φ(ε0), which is positive (Φ denoting the
standard normal cumulative distribution function [c.d.f.]).
The r.h.s. of (2.3), however, is equal to T(0) = 0, because
σ = 0.
Theorem 2.1 is in fact a special case of a more general result that
makes use of a weaker version of Assumption 2.2.
Assumption 2.2*. There exists
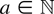
such that for every t ≥ a the distribution of
t−1/2xt
possesses a density, ht, say, w.r.t.
Lebesgue measure on
.
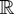
Furthermore,
supt≥a∥ht∥∞
< ∞ holds.
Assumption 2.2* does not restrict the distribution of
xt,1 ≤ t < a, at
all. Of course, under any assumption implying existence and boundedness
of ht for 1 ≤ t <
a, Assumption 2.2* becomes equivalent to Assumption 2.2. As
with Theorem 2.1, Theorem 2.2 is formulated for real-valued functions.
Its generalization to the case of extended real functions is given in
Remark 2.5, which follows.
THEOREM 2.2. Suppose Assumptions 2.1 and 2.2* hold and
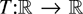
is locally integrable. Then
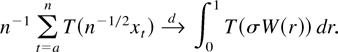
If, additionally,
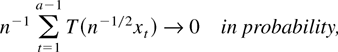
then (2.3) also holds. (In case a = 1 we use the convention
that the sum in (2.6) is zero.)
Of course, Theorem 2.1 is a special case of Theorem 2.2 (with
a = 1). It is not difficult to see that existence and
boundedness of ht for 1 ≤ t
< a is a sufficient condition for (2.6) when T is
locally integrable.9
To see this note that
for every t, 1 ≤ t < a, (and
M > 0) we have
by local integrability of
T.
However, under this condition on
ht Assumptions 2.2 and 2.2* coincide.
Theorem 2.2 is therefore useful as an alternative to Theorem 2.1 in
situations where existence and uniform boundedness of the densities
ht can only be established from a certain
index onward (cf. Section 3) and where (2.6) can be verified from some
source other than boundedness of
ht for 1
≤
t <
a. For example, if
T is bounded
in a neighborhood of
x = 0 (a fortiori if
T is
continuous at
x = 0), condition (2.6) immediately follows
regardless of the distribution of
xt, 1
≤
t <
a.
10 Although (2.6) is true for such functions T, we
stress that (2.6) is in general not true without further
conditions even for locally integrable T.
More
general sufficient conditions are given in the following
proposition.
PROPOSITION 2.3. For Borel-measurable
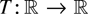
consider the following conditions:
(i) T(x) =
o(|x|−2) for
x → 0, x ≠ 0.
(ii) T is Lebesgue-integrable in a neighborhood of
x = 0, |T(x)| is increasing
on (−ε,0) and decreasing on (0, ε) for
some ε > 0.
(iii) T is Lebesgue-integrable in a neighborhood of
x = 0, |T(x)| is increasing on
(−ε,0) and bounded on (0, ε) for some
ε > 0.
(iv) T is Lebesgue-integrable in a neighborhood of
x = 0, |T(x)| is bounded on
(−ε,0) and decreasing on (0, ε) for some
ε > 0.
(v) T is bounded on (−ε,0) and
also on (0, ε) for some ε > 0.
Then each of conditions (ii)–(v) implies (i), which in turn
implies (2.6).11
In fact, each one of
(ii)–(v) even implies T(x) =
o(|x|−1) for x
→ 0, x ≠ 0.
Simple corollaries to Theorem 2.2 that immediately follow from the
preceding discussion are given next. In the important case where
xt has an absolutely continuous
distribution for all t, the conditions in these corollaries
can be weakened somewhat; see Remark 2.4, which follows.
COROLLARY 2.4. Suppose Assumptions 2.1 and 2.2* hold and
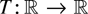
is locally integrable. If T satisfies T(x) =
o(|x|−2) for
x → 0, x ≠ 0, then the weak convergence
result (2.3) holds.
COROLLARY 2.5. Suppose Assumptions 2.1 and 2.2* hold and
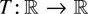
is locally bounded (and Borel-measurable). Then the weak convergence
result (2.3) holds.
As already noted, the “regularity” conditions on
T in Park and Phillips (1999) and de
Jong (2002), respectively, imply local
integrability. Furthermore, their respective “regularity”
conditions imply condition (i) in Proposition 2.3.12
Observe that any function “regular” in the
sense of Park and Phillips (1999) is locally
bounded and thus satisfies (v) of Proposition 2.3. Furthermore, any
function “regular” in the sense of de Jong (2002) satisfies at least one of (ii)–(v) in
Proposition 2.3 as is easily seen.
Hence, these
“regularity” conditions also imply (2.6). Thus the
“regularity” conditions in Park and Phillips (
1999) and also in de Jong (
2002) are stronger than the conditions imposed on
T in Theorems 2.1 and 2.2 and Corollary 2.4; cf. also Example
3.2 in Section 3.
Remark 2.4. Suppose
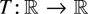
is Borel-measurable and suppose that each xt,
1 ≤ t < a, has a (possibly unbounded) density. Then
(2.6) already follows if condition (i) in Proposition 2.3 holds only outside
of a set of Lebesgue measure zero.
13 To see
this, note that after suitably modifying T on a set of Lebesgue
measure zero, condition (i) in Proposition 2.3 is satisfied for the modified
function and that this modification changes the sum in (2.6) at most on a set
of probability zero as a result of the assumption on
xt, 1 ≤ t < a.
Consequently, given the above assumption on
xt,
Corollary 2.4 already holds under this weaker form of condition (i). We also
note that this weaker form of condition (i) is satisfied if, e.g.,
T
is essentially bounded in (−ε,0) ∪ (0, ε) for a suitable
ε > 0.
14 More generally, if modifying
T on a set of Lebesgue measure zero results in a function that
satisfies one of conditions (ii)–(v) of Proposition 2.3, then
condition (i) holds outside a set of Lebesgue measure zero.
In
particular, given the above assumption on
xt, Corollary 2.5 then holds even for
essentially locally bounded
T.
Remark 2.5. (Extended Real Functions).
(a) Similarly as in Remark 2.1, the first claim in Theorem 2.2
also holds for locally integrable functions T from
the second claim also holds provided that the expression in (2.6) is
well defined (at least on a sequence of sets Ωn
with P(Ωn) → 1 as n →
∞).
15 That is, there exists a
sequence of sets Ωn with
P(Ωn) → 1 as n →
∞ such that
T(n−1/2xt(ω))
= ∞ and
T(n−1/2xs(ω))
= −∞ do not hold simultaneously for ω ∈
Ωn and some 1 ≤ s < a,
1 ≤ t < a.
This is, e.g., the case if
each
xt, 1 ≤
t <
a, has a (possibly unbounded) density. As another example, the
expression in (2.6) is also always well defined, regardless of the
distribution of
xt, 1 ≤
t <
a, if
T takes its values only in
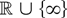
(or in
).
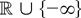
(b) Suppose the function T in Proposition 2.3 takes now
values in
).
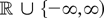
16 As a point of interest we note that for real-valued
T condition (v) is in fact equivalent to boundedness of
T on (−ε, ε), but this is not necessarily
so if T takes its values in
.
Then again each of the conditions
(ii)–(v) implies (i). (Note that under any of the conditions
(i)–(v) the function
T is in fact real-valued on
(−ε, ε)[setmn ]{0} for a suitable ε > 0.)
Furthermore, condition (i) continues to imply (2.6) if
T(0) is
finite or if none of the distributions of
xt, 1 ≤
t <
a, has
positive point mass at
x = 0. In particular, Corollary 2.4
continues to hold for
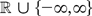
if additionally T(0) is finite or if
none of the distributions of xt, 1 ≤
t < a, has positive point mass at x =
0.
(c) Remark 2.4 continues to hold for functions T :
.
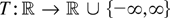
In particular, Corollary 2.4 also holds for
already under the weaker form of condition (i), provided each
xt, 1 ≤
t < a, has a (possibly unbounded) density.
Similarly, Corollary 2.5 already holds for essentially locally bounded
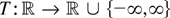
under the same provision for xt, 1 ≤
t < a. (If
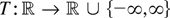
is locally bounded, we are back to the
case of real-valued T, and hence Corollary 2.5 directly
applies without any further provision on
xt, 1 ≤ t <
a.)
Remark 2.6. Suppose
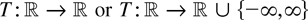
is essentially locally bounded and suppose that Assumptions 2.1 and 2.2*
hold. Then certainly (2.5) holds (even T locally integrable
would suffice). We stress, however, that (2.3) need not follow in
general without further assumptions. Remarks 2.4 and 2.5(c) provide
such additional conditions. Alternatively, it follows from the
preceding discussion that (2.3) also holds if we additionally assume
that condition (i) in Proposition 2.3 holds, and that T(0) is
finite or none of the distributions of xt,
1 ≤ t < a, has positive point mass at
x = 0.
Remark 2.7. Similarly as in Remark 2.2, Theorem 2.2 continues to hold
for functions T with values in
.
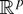
For functions T with values in (
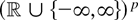
the same is also true for the first claim in Theorem 2.2, and it is true for
the second claim provided (2.6) is well defined for any linear combination
α′T. A corresponding remark applies to Corollaries
2.4 and 2.5, Remark 2.4, and their extensions discussed in Remark 2.5.
3. SUFFICIENT CONDITIONS AND COROLLARIES
In this section we discuss the important special case when
xt is an integrated process, which is the
case exclusively considered in Park and Phillips (1999) and de Jong (2002).
Assume that for n ≥ 1 the process
xn takes the form
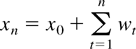
with x0 being independent of the process
(wt)t≥1 and with
wt given by
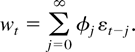
Here (εj) are i.i.d.,
E(εj) = 0,
Eεj2 < ∞,
.
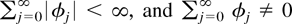
Without loss of generality we shall set the variance of
εj equal to one. Furthermore, it is assumed that
εj has a density, say, q. The preceding
assumptions will be kept throughout Section 3 and will be referred to as the
maintained assumptions of Section 3.
3.1. Sufficient Conditions for Assumptions 2.2 and
2.2*
To begin with, note that xn can be
represented as
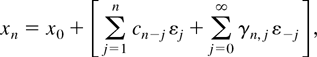
where
.
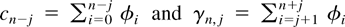
It immediately follows that
n−1/2xn has
a density for every n ≥ 1 (cf. Lukacs, 1970, Theorem 3.3.2, and observe that the term in
brackets in (3.3) cannot be identically zero because
).
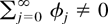
To motivate the sufficient conditions for Assumptions 2.2 and 2.2*
given in Lemma 3.1, which follows, we start with a preparatory and
informal discussion. It is easy to see that any distribution given by a
convolution has a bounded density if at least one factor in the
convolution has a bounded density. Consequently, the density
hn of
n−1/2xn is
guaranteed to be bounded (for every fixed n ≥ 1) if the
(common) density q of εj is bounded.
We note that a sufficient condition for boundedness of q is
that ψ, the characteristic function of
εj, is absolutely integrable (Lukacs, 1970, Theorem 3.2.2). However, the density
hn can be bounded even if the density
q is unbounded. To see how this can happen, consider for the
moment the special case where xn is a
random walk, i.e., where wt =
εt and where x0 = 0 (for
simplicity). Because
n−1/2xn is
then the sum of n i.i.d. random variables, its density
hn is the (scaled) n-fold
convolution of q itself. Now, for example, if q has a
pole, it can happen that this pole is “smoothed” out by the
convolution operation, resulting in a bounded density
hn. Related to this observation is the
fact that in cases where the characteristic function ψ(s)
of εj is not absolutely integrable, the
characteristic function of
n−1/2xn can
be integrable (implying that hn is
bounded) from some n onward, because it is the nth
power of ψ (evaluated at
n−1/2s) and because
|ψ| ≤ 1 holds. It follows that absolute
integrability of a power of ψ will imply (individual) boundedness
of hn, at least from a certain n
onward, and thus will be a central condition in the following. As it
turns out, this central condition implies not only individual
boundedness of hn (from a certain
n onward) but also uniform boundedness (from a
certain n onward). Returning to the case of general
xn as in (3.1), we note that (depending on
the behavior of the coefficients φj) often
hn is in fact a convolution of much more
than n factors of the form q (sometimes even of
infinitely many factors). Not too surprisingly, in this case the
previously mentioned central condition on ψ will automatically
deliver individual boundedness of hn for
every n ≥ 1.
With ψ denoting the characteristic function of
εj, we shall therefore consider the following
integrability condition:
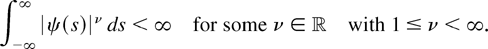
Recall that (3.4) with ν = 1 implies boundedness of q
and that (3.4) becomes less stringent as ν increases. In
particular, characteristic functions corresponding to unbounded
densities can satisfy (3.4) with ν > 1; cf. Remark 3.1(b), which
follows. We mention here that a simple sufficient condition for (3.4)
is |ψ(s)| =
O(s−η) as s →
∞ for some η > ν−1. In particular,
if |ψ(s)| =
O(s−η) for some η > 0,
then (3.4) holds for some ν ≥ 1. The latter condition with
“O” strengthened to “o” is
used in Park and Phillips (1999) and de Jong
(2002); see Section 3.3 for more
discussion.
The following lemma provides sufficient conditions for Assumptions
2.2 and 2.2* and is inspired by Section 4.3 of Ibragimov and Linnik
(1971). Part (i) of the lemma improves upon
Lemma 1 in de Jong (2002). Recall that
hn denotes the density of
n−1/2xn.
LEMMA 3.1. Suppose condition (3.4) holds. Then the following
statements are true.
(i) There exist
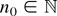
and a real number C such that for n ≥
n0
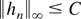
holds; i.e., Assumption 2.2* is satisfied.
(ii) If, for every n ≥ 1, at least ν
coefficients of the innovations εj,
−∞ < j ≤ n, in (3.3) are nonzero, then (3.5)
holds for n ≥ n0 = 1.17
Lemma B.2 in fact shows that if at least ν
coefficients of εj, −∞ <
j ≤ n, in (3.3) are nonzero for a given
n, then
∥hn∥∞ is finite
for this n.
(iii) If ν = 1, then (3.5) holds for n ≥
n0 = 1. That is, Assumption 2.2 is
satisfied.
(The constants C in (i)–(iii) and also the index
n0 depend only on ψ and the coefficients
φj.)
The more difficult part in the proof of the preceding lemma is to
establish Assumption 2.2*, i.e., the uniform boundedness of the
densities hn from a certain index
n0 onward. Once Assumption 2.2* is known to hold,
Assumption 2.2 then follows under any condition that implies
(individual) boundedness of hn for every
n (in fact for every n, 1 ≤ n <
a, suffices). Parts (ii) and (iii) provide such conditions.
The basic observation here is that whenever (3.4) holds and the
distribution of xn is the convolution of
not less than ν terms of the form q (not counting the
factor corresponding to x0), then
∥hn∥∞ is finite
(cf. Lemma B.2 in Appendix B). The additional assumptions in parts (ii)
and (iii) precisely imply this for the distribution of
xn. As already mentioned, boundedness of
q, i.e.,
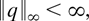
implies that
∥hn∥∞ is finite
for every n ≥ 1. Thus (3.6) is an alternative condition
under which Assumptions 2.2 and 2.2* are equivalent. (We note that
(3.4) with ν = 1 implies (3.6); cf. Lukacs, 1970, Theorem 3.2.2.)18
Together with Lemma 3.1(i) this provides an alternative
proof of part (iii) of Lemma 3.1.
Note that the conditions in Lemma 3.1(i) and (ii) allow the density
q of εj to be unbounded, whereas the
conditions for part (iii) imply boundedness of q.
Remark 3.1.
(a) The assumption in part (ii) is certainly satisfied if the
coefficients
φj are all positive (negative).
(b) The additional assumption in part (ii) cannot be removed.
Consider the example where wt =
εt −
εt−1 +
εt−2 and
α1/2εt + α is
gamma-distributed with shape parameter α satisfying 1/3
< α < ½ and scale parameter 1 and where
x0 = 0 (for simplicity). Then
x2 = ε2 +
ε−1 whereas xn for
n ≠ 2 is always the sum of at least three
εj's. Consequently, the density of
x2 (being a shifted and scaled version of a
gamma(2α,1)-distribution) has a pole, whereas the density of
xn, n ≠ 2 (being a shifted and
scaled version of a gamma(β,1)-distribution with β ≥ 3α
> 1) is bounded. Note that the characteristic function
ψ(s) of εj satisfies
|ψ(s)| = (1 +
α−1s2)−α/2
and thus ψ satisfies (3.4) for ν > 1/α > 2 but
not for ν ≤ 1/α.
3.2. Sufficient Conditions for Assumption 2.1
Sufficient conditions for Assumption 2.1 abound in the literature.
For the sake of comparability with Park and Phillips (1999) and de Jong (2002)
we shall use the condition
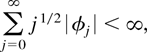
which is also used in Park and Phillips (1999) (cf. their Assumption 2.1). A stronger
summability condition is used in Assumption 2.2 of Park and Phillips
(1999) and also in de Jong (2002). It is well known that—under the
maintained assumptions of Section 3—condition (3.7) implies our
Assumption 2.1 with
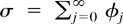
(cf., e.g., Phillips and Solo, 1992, Theorem 3.4
and Remarks 2.2(ii) and 3.5(i)).
3.3. Corollaries and Comparison with Park and Phillips
(1999) and de Jong (2002)
The following corollary collects some of the results that can be
obtained by combining Theorem 2.1 with the sufficient conditions
discussed in Sections 3.1 and 3.2.
COROLLARY 3.2. Suppose the process xt
satisfies the maintained assumptions of Section 3 and (3.4) and (3.7)
hold. Let
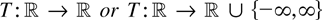
be locally integrable. Then
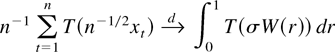
holds with
,
provided the densities
ht are (individually) bounded for every
t ≥ 1.
19 In fact, boundedness
of ht for 1 ≤ t <
n0 suffices, where n0 is as in
Lemma 3.1(i).
(i) The density of q of εj
is bounded; i.e., (3.6) holds.
(ii) The characteristic function ψ of
εj is integrable; i.e., (3.4) holds with ν = 1.
(iii) φj > 0 for all
j ≥ 0 or φj < 0 for all
j ≥ 0.
The preceding corollary gives conditions that imply the desired
convergence result for all locally integrable functions. The
next corollary operates under weaker conditions on the process
xt at the expense of imposing a mild
growth condition on the function T.
COROLLARY 3.3. Suppose the process xt
satisfies the maintained assumptions of Section 3 and (3.4) and (3.7)
hold. Let
be locally integrable. Then
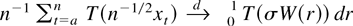
with
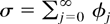
holds for some a ≥
1.
20 Namely, for a ≥
n0; cf. Lemma 3.1(i).
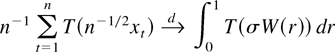
holds, provided T(x) =
o(|x|−2) for x → 0, x ≠ 0, except possibly on a set of
Lebesgue measure zero. This latter condition is satisfied if any of the
conditions (ii)–(v) of Proposition 2.3 hold.21
For a minor generalization of this implication see Remark
2.4 and note 14.
A simple special case of Corollary 3.3 is the following result.
COROLLARY 3.4. Suppose the process xt
satisfies the maintained assumptions of Section 3 and (3.4) and (3.7)
hold. Let
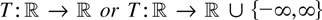
be essentially locally bounded (and Borel-measurable). Then
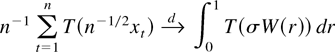
holds with
.
Corollary 3.2 is based on Theorem 2.1 and hence on Assumption 2.2,
whereas Corollary 3.3 derives from Theorem 2.2 and Assumption 2.2*. As
already noted, Assumption 2.2 differs from Assumption 2.2* only in that
it additionally requires the first few densities
ht to be (individually) bounded. As a
consequence, the requirements on the process
xt in Corollary 3.2 are only marginally
stronger than in Corollary 3.3; e.g., adding condition (3.6), i.e.,
that the density q of εj is bounded,
suffices. The advantage of Corollary 3.2 thus is that it does not
impose any regularity condition on the function T but delivers
the desired convergence result for any locally integrable
function T (at a small cost in terms of additional conditions
on xt).
It is easy to see that Corollary 3.3 contains the convergence result
in de Jong (2002) as a special case: First,
de Jong uses stronger assumptions on the process
xt (namely, the stronger summability condition
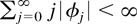
existence of moments of εj of order higher
than 2, and the stronger condition |ψ(s)| =
o(s−η) for some η > 0
on the characteristic function ψ). Second, the class of functions
considered in Corollary 3.3 is much wider than the class considered in
de Jong (2002) as the discussion subsequent
to Corollary 2.5 has shown.
Comparing Corollary 3.3 with Theorem 3.2 in Park and Phillips (1999), we observe that Corollary 3.3 (and a
fortiori Corollary 3.2) allows for a much wider class of functions than
Theorem 3.2 in Park and Phillips (1999). In
particular, Corollary 3.3 not only covers any (essentially) locally
bounded function (cf. Corollary 3.4) but also allows for locally
unbounded functions and extended real-valued functions. (Recall that
any function that is “regular” in the sense of Park and
Phillips, 1999, is locally bounded.) With
respect to the conditions imposed on the process
xt, note that Corollary 3.3 makes use of
the same assumptions as used in Theorem 3.2 in Park and Phillips (1999) plus the additional condition (3.4) and the
assumption that the innovations εj possess an
absolutely continuous distribution. (Comparing Corollary 3.2 with
Theorem 3.2 in Park and Phillips (1999) we
see that a further mild condition such as, e.g., boundedness of the
density of εj has been added.) This seems to
be a modest price to pay for the ability to cover much larger classes
of functions. Finally, we also point out that the conditions on
xt in Corollary 3.3 are strictly weaker
than the assumptions underlying Theorem 3.4 in Park and Phillips (1999) (cf. Park and Phillips, 1999, Assumption 2.2), which provides a weak
convergence result for “clipped” versions of certain
locally unbounded functions T. This shows that the
“clipping” device of that theorem can be avoided
altogether. (Recall from Section 1 that the proof of this theorem seems
to be in error; cf. also note 2.)
We illustrate the corollaries with some examples.
Example 3.1
Suppose the process xt satisfies the
assumptions of Corollary 3.3. Let T1(x) =
log|x| and T2(x) =
|x|α with −1 < α
< 0, where T1(0) and T2(0)
are set to an arbitrary element of
.
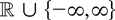
It is easy to see that both functions are locally integrable and satisfy
T1(x) =
o(|x|−2) and
T2(x) =
o(|x|−2) for
x → 0, x ≠ 0. Corollary 3.3 then implies
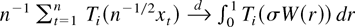
for i = 1,2 with
.
The functions in the preceding example do not satisfy the
“regularity” conditions for Theorem 3.2 in Park and
Phillips (1999) but do satisfy the
“regularity” conditions of de Jong (2002). The following example is covered neither by
the results in Park and Phillips (1999)
(because the functions are not locally bounded) nor by the results in
de Jong (2002) (because the functions are not
piecewise monotone).
Example 3.2
Suppose the process xt satisfies the
assumptions of Corollary 3.3. Let T3(x) =
(log|x|)sin(x−1) and
T4(x) =
|x|αsin(x−1)
with −1 < α < 0, where T3(0) and
T4(0) are set to an arbitrary element of
.
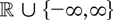
Again both functions are locally
integrable and satisfy T3(x) =
o(|x|−2) and
T4(x) =
o(|x|−2) for
x → 0, x ≠ 0. Corollary 3.3 then implies
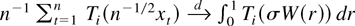
for i = 3,4 with
.
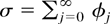
In fact, Corollary 3.3 applies as well to the functions
T5(x) =
(log|x|)S(x) and
T6(x) =
|x|αS(x) with
−1 < α < 0, where T5(0) and
T6(0) are set to an arbitrary element of
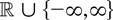
and where S is an arbitrary (essentially) local bounded
Borel-measurable function.
4. EXTENSIONS
The results in Section 3 allow for dependence in the increments of
the process xt as they are modeled as a
linear process. It is quite natural to ask to what extent the results
in Section 3 can be generalized to other dependence structures such as
mixing, near epoch dependence, and so on. Observe that the results in
Section 2 are of a generic nature in that they rely only on Assumptions
2.1 and 2.2 (or 2.2*), which do not specify a particular dependence
structure. Because functional central limit theorems as expressed in
Assumption 2.1 are widely available for various dependence structures,
including those mentioned previously, the question reduces to whether
or not Assumption 2.2 (or 2.2*) holds for such dependence structures.
In particular, the validity of a local central limit theorem would
imply Assumption 2.2*. Not much seems to be available in the literature
in that regard.
A key feature of the results in this paper is that the random
variables t−1/2xt
have to have uniformly bounded densities (at least from some index onward).
In view of local central limit theorems this appears to be a quite
natural condition. Whether or not this condition can be relaxed while
retaining the validity of the convergence result for all locally
integrable functions, I do not know. Of course, relaxation is certainly
possible if the convergence result is to be established only for a
smaller class of functions T (e.g., Assumption 2.2 or 2.2* can
be completely dropped for continuous T).
Suppose the convergence result (2.3) holds for a function H
and suppose the function T satisfies
T(λx) = g(λ)H(x)
for all λ > 0 and all
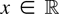
with a suitable function g (e.g., T is homogenous of degree
α and H = T). Then (2.3) applied to H can be
rewritten as
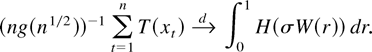
Now, if T does not satisfy a decomposition as before but
does so approximately in a suitable sense, relation (4.1) can still be
established. This then provides convergence results for nonlinear
functions of unnormalized integrated processes. Section 5 of Park and
Phillips (1999) carries through this program
under the assumption that the function H appearing in the
approximation is “regular” in their sense. De Jong and Wang
(2002) obtain analogous results when H
satisfies the “regularity” conditions of de Jong (2002). Based on the results of the present paper,
both of these results can be extended to the situation where the
function H in the approximation is locally integrable but does
not satisfy the regularity conditions in Park and Phillips (1999) or de Jong (2002).
APPENDIX A: PROOFS FOR SECTION 2
LEMMA A.1. Suppose
is continuous and Assumption 2.1 holds with the requirement σ ≠ 0
omitted. Then (1.1) holds.
Proof. Define
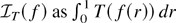
for every f ∈ D[0,1]. Because each
f ∈ D[0,1] is bounded and
measurable (Billingsley, 1968, p. 110) and
because T is continuous,
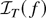
is well defined and finite. Observe that (1.1) can be rewritten as
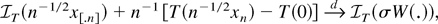
where the second term on the l.h.s. is op(1)
because T is continuous and
n−1/2xn
converges in distribution. It hence suffices to establish that
converges to
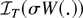
in distribution. Suppose now that fk ∈
D[0,1] converges to f ∈
C[0,1] (the subset of all continuous functions on
[0,1]) w.r.t. the Skorohod topology. Then this convergence is
in fact uniform (Billingsley, 1968, p. 112).
In particular, it follows that fk and
f are uniformly bounded (w.r.t. r ∈
[0,1] and k ≥ 1) by a finite positive constant,
say, M. Because T restricted to
[−M, M] is uniformly continuous, it
follows that T(fk(r))
converges to T(f (r)) uniformly on
[0,1]. Thus,
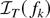
converges to
.
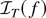
It follows that the set of continuity points of
contains C[0,1] . Because almost every sample path
of Brownian motion is an element of C[0,1] , it
follows that the set of continuity points of
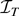
is a set of measure one under the
measure induced by σW(.). Applying the continuous mapping
theorem in its extended form (e.g., Billingsley, 1968, Theorem 5.1) then establishes (1.1). █
LEMMA A.2. Let
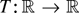
be a locally integrable function. For
every ε > 0 there exists a continuous function
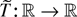
such that
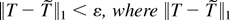
denotes
.
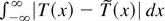
Proof. For any
define Tm(x) =
T(x)1[m,
m+1)(x). Because T is locally
integrable, the function Tm is certainly
Lebesgue-integrable over [m, m+1] . Hence,
there exists a continuous function
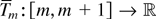
such that
(cf. Bauer, 1978, (43.6) and (44.2)). Extend
Tm to a function on all of
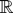
by setting Tm(x) = 0 for
x ∉ [m, m + 1] . Obviously
then ∥Tm −
Tm∥1 <
(ε/3)2−|m|−1
holds. Note that Tm is continuous on
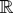
except possibly at x = m and x =
m + 1. For 0 < η < ½ let
gm, η denote the
“trapezoidal” function given by gm,
η(x) = 1 for m + η ≤ x
≤ m + 1 − η, gm,
η(x) = 0 for x ≤ m and for
x ≥ m + 1 and that linearly interpolates between
x = m and x = m + η and also
between x = m + 1 − η and x =
m + 1. Then the function Tm
gm, η is continuous on all of
and vanishes outside of (m, m + 1). By
choosing η(m) small enough (depending on T and
ε) we obtain ∥Tm −
Tm gm,
η(m)∥1 <
(ε/3)2−|m|−1.
Define
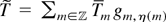
and note that
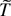
is continuous on
.
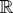
Since clearly
holds, we arrive at
.
█
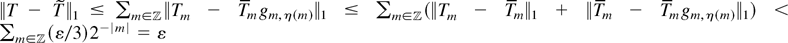
Proof of Theorem 2.1. The idea of the proof is to use Lemma A.2 to
reduce the case of locally integrable T to the case of
continuous T and then to appeal to Lemma A.1, which in turn
rests on the continuous mapping theorem.
Step 1. Let ε > 0 and let
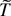
be the continuous function guaranteed by Lemma A.2. Then for all n
≥ 1 we have
Step 2. Let ε > 0 and let
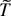
be as in step 1. Observing that
is locally integrable we may apply Corollary 7.4 in Chung and Williams
(1990) to obtain
For the last equality in (A.2) we have used Fubini's theorem.
This is justified because the functions involved are nonnegative and
because L(1, x) is a measurable stochastic process.
(That is, the map (ω, x) → L(1,
x)(ω) is measurable w.r.t. the product σ-field
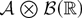
where
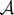
is the σ-field on the probability space supporting
is the Borel-σ-field on
.
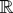
This is true because L has continuous sample paths; cf. Chung and
Williams, 1990, p. 146; Karatzas and Shreve, 1991, Remark 1.14.) Now, for every
,
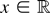
the local time L(1, x) has a distribution that has point
mass 2Φ(|x|) − 1 at the origin and
otherwise has a density given by k(y) =
(2/π)1/2 exp[−0.5(y +
|x|)2] for y > 0 and
k(y) = 0 else (cf. Borodin and Salminen, 1996, p. 127, eq. (1.3.4)). Consequently,
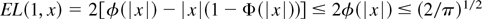
for all
,
and hence the r.h.s. of (A.2) is not less than
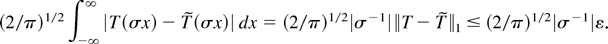
Step 3. It follows from steps 1 and 2 that for every η > 0 we
can find a continuous function
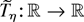
such that
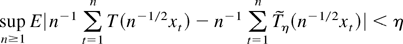
and
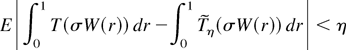
hold. By Lemma A.1 we have
Relations (A.4)–(A.6) establish the result (2.3) by a standard
argument (cf. Anderson, 1971, Theorem 7.7.1).
█
Proof of Theorem 2.2. The proof of (2.5) is identical to the proof
of Theorem 2.1 apart from mainly notational differences. (For step 3
observe that because of continuity of
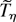
the first a − 1 terms in (A.6) are
op(1) and hence can be omitted.) The second claim
then follows from (2.5) and (2.6). █
Proof of Proposition 2.3. That (ii) implies (i) is seen as
follows. Because of the monotonicity property we have for 0 < x
< ε the inequality
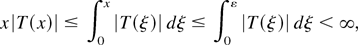
the final integral being finite because of integrability in a
neighborhood of zero. Hence,
x|T(x)| → 0 for
x → 0, x > 0. A similar argument for
−ε < x < 0 then shows that
T(x) =
o(|x|−1) and hence is
o(|x|−2) for
x → 0 and x ≠ 0. The implication (v) ⇒
(i) is trivial. The implications (iii) ⇒ (i) and (iv) ⇒ (i)
follow by combining the arguments for the proofs of (ii) ⇒ (i) and
(v) ⇒ (i). It remains to prove (i) ⇒ (2.6), and for this it
suffices to show that
n−1T(n−1/2xt)
→ 0 as n → ∞ for any given t and any
value of xt. If
xt = 0, this follows trivially, because
T(0) is a real number. Otherwise, we obtain
n−1T(n−1/2xt)
= xt−2o(1) =
o(1) as n → ∞. █
APPENDIX B: PROOFS FOR SECTION 3
LEMMA B.1. Let ψ be the characteristic function of a
distribution with mean zero and variance 1. Then there exists Δ, 0
< Δ < 1, such that |ψ(s)| ≤
exp(−s2/8) holds for −Δ
≤ s ≤ Δ.
Proof. Theorem 2.3.3 in Lukacs (1970)
implies that ψ(s) = 1 −
s2/2 + ζ(s) where
ζ(s) = o(s2) as s
→ 0 and ζ(0) = 0. Hence, there exists Δ′, 0 <
Δ′ < 1, such that |ζ(s)| ≤
s2/4 for −Δ′ ≤ s
≤ Δ′. It follows that |ψ(s)|
≤ |1 − s2/2| +
|ζ(s)| ≤ 1 −
s2/2 + s2/4 = 1 −
s2/4 for −Δ′ ≤ s
≤ Δ′. Since ψ(0) = 1 and ψ is continuous, it
follows that there exists Δ″, 0 <
Δ″ ≤ Δ′, such that
|ψ(s)| > 0 holds for
−Δ″ ≤ s ≤
Δ″. Hence, log|ψ(s)|
is well defined on −Δ″ ≤ s
≤ Δ″ and satisfies
log|ψ(s)| ≤ log(1 −
s2/4) on that interval. A Taylor series
expansion of log(1 + x) around x = 0 then shows that
for −Δ″ ≤ s ≤ Δ″
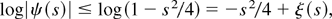
where ξ(s) = o(s2) for
s → 0 and ξ(0) = 0. Choosing Δ, 0 < Δ ≤
Δ″ < 1, small enough we obtain |ξ(s)|
≤ s2/8 for −Δ ≤ s ≤ Δ.
This implies log|ψ(s)| ≤
−s2/8 for −Δ ≤ s
≤ Δ. █
We note that a more careful choice of constant in the preceding proof
establishes that for any 0 < δ < ½ there exists a
Δ = Δ(δ) as in the lemma such that
|ψ(s)| ≤
exp(−δs2) holds for −Δ ≤
s ≤ Δ.
Proof of Lemma 3.1. It follows from Theorem 3.2.2. of Lukacs
(1970) that
∥hn∥∞ ≤
(2π)−1∥Ψn∥1
provided the latter is finite, where Ψn
denotes the characteristic function of
n−1/2xn and
∥.∥1 denotes the L1-norm w.r.t.
Lebesgue measure on
.
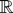
It hence suffices to bound
∥Ψn∥1.
(i) Note that x0 is independent of the term in
brackets in the representation (3.3) and that both sums in the brackets
are independent of each other. Hence,
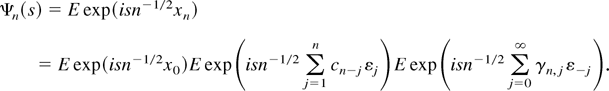
Consequently,
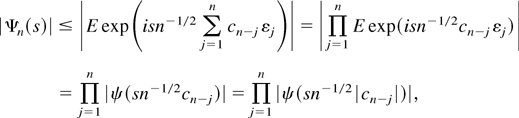
the final equality following from |ψ(−s)|
= |ψ(s)|.
Now,
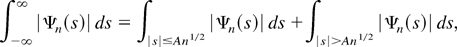
for every A > 0. Performing the substitution s →
sn−1/2 and using (B.1), the first integral on
the r.h.s. of (B.2) can be bounded by
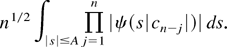
Choose A = (2|c|)−1Δ
> 0, where Δ is as in Lemma B.1 and where
,
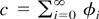
which is nonzero by assumption. Note that the coefficients
ck converge to c. Hence there is a
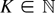
such that |c|/2 ≤
|ck| ≤
2|c| whenever k ≥ K.
Because every characteristic function is bounded by one in absolute
value, and because −A ≤ s ≤ A
implies −Δ ≤
s|cn−j|
≤ Δ for n − j ≥ K, the
expression in (B.3) for n > K is in view of Lemma
B.1 bounded by
Because (B.3) for 1 ≤ n ≤ K is clearly bounded by
2An1/2 ≤
|c|−1ΔK1/2,
the expression in (B.3) is bounded by C1 =
max((32π)1/2(K + 1)1/2,
ΔK1/2)/|c| <
∞ for all n ≥ 1.
To deal with the second term on the r.h.s. of (B.2), perform the same
substitution as before and use (B.1) to obtain
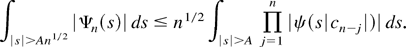
With K as defined after (B.3), we can then
for n > K bound (B.4) by
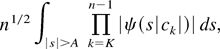
because |ψ(.)| ≤ 1. Applying
Hölder's inequality successively n −
K times, (B.5) can for n ≥ K + ν be
bounded by
Because A|c|/2 = Δ/4 > 0
and ψ is the characteristic function of an absolutely continuous
distribution, the supremum in (B.6) is less than one. In view of (3.4),
the r.h.s. of (B.6) is therefore bounded by a finite constant for n
≥ K + ν. This completes the proof of part (i).
(ii) In view of part (i) it suffices to show that
∥Ψn∥1 < ∞ holds
for 1 ≤ n < K + ν. Note that
.
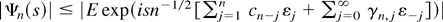
The
result then follows from Lemma B.2, which is given subsequently.
(iii) This follows from part (ii), observing that the maintained assumption
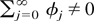
implies that at least one coefficient in the representation (3.3) is nonzero
for every n ≥ 1. █
LEMMA B.2. Suppose
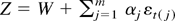
with αj ≠ 0 for 1 ≤ j ≤
m and W is independent of
.
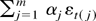
Then
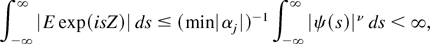
provided (3.4) with ν ≤ m holds.
Proof. Observe that
.
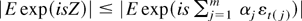
Hence
where the second inequality follows from Hölder's
inequality. █
Proof of Corollary 3.2. This follows from Theorem 2.1, Remark 2.1,
and the discussion in Sections 3.1 and 3.2, in particular, Lemma 3.1
and Remark 3.1. █
Proof of Corollary 3.3. This follows from Theorem 2.2, Proposition
2.3, Remarks 2.4 and 2.5 (note that each
xt has an absolutely continuous
distribution), and the discussion in Sections 3.1 and 3.2, in
particular, Lemma 3.1. █
