Published online by Cambridge University Press: 01 December 2004
This paper proposes a new class of estimators of the long-run average
relationship in nonstationary panel time series. The estimators are
based on the long-run average variance estimate using bandwidth equal
to T. The new estimators include the pooled least squares
estimator and the fixed effects estimator as special cases. It is shown
that the new estimators are consistent and asymptotically normal under
both the sequential limit, wherein T → ∞ followed
by n → ∞, and the joint limit where
T,n → ∞ simultaneously. The rate condition
for the joint limit to hold is relaxed to
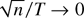 ,
which is less restrictive than the rate condition n/T
→ 0, as imposed by Phillips and Moon (1999, Econometrica 67, 1057–1111).
By exponentiating existing kernels, this paper introduces a new
approach to generating kernels and shows that these exponentiated
kernels can deliver more efficient estimates of the long-run average
coefficient.I am grateful to Bruce Hansen,
Peter Phillips, Zhijie Xiao, and three anonymous referees for constructive
comments and suggestions. All errors are mine alone.
,
which is less restrictive than the rate condition n/T
→ 0, as imposed by Phillips and Moon (1999, Econometrica 67, 1057–1111).
By exponentiating existing kernels, this paper introduces a new
approach to generating kernels and shows that these exponentiated
kernels can deliver more efficient estimates of the long-run average
coefficient.I am grateful to Bruce Hansen,
Peter Phillips, Zhijie Xiao, and three anonymous referees for constructive
comments and suggestions. All errors are mine alone.
Nonstationary panel data with large cross section (n) and time series dimension (T) have attracted much attention in recent years (e.g., Pedroni, 1995; Kao, 1999; Phillips and Moon, 1999). Financial and macroeconomic panel data sets that cover many firms, regions, or countries over a relatively long time period are familiar examples. Such panels have been used to study growth and convergence, the Feldstein–Horioka puzzle, and purchasing power parity, among other subjects. Phillips and Moon (2000) and Baltagi and Kao (2000) provide recent surveys of this rapidly growing research area. When both n and T are large, we can allow the parameters in the data generating process to be different across different individuals, which is not possible in traditional panels. Such a panel data structure also enables us to define an interesting long-run average relationship for both panel spurious models and panel cointegration models. Phillips and Moon (1999) show that both the pooled least squares (PLS) regression and the fixed effects (FE) regression provide consistent estimates of this long-run average relationship.
In this paper, we propose a new class of estimators of the long-run average relationship. Our estimators are motivated from the definition of the long-run average relationship. As shown by Phillips and Moon (1999), the long-run average relationship can be parametrized in terms of the matrix regression coefficient derived from the cross-sectional average of the long-run variance (LRV) matrices. A natural way to estimate this coefficient is to first estimate the LRV matrices directly and then use these matrices to construct an estimate of the coefficient. This leads to our LRV-based estimators of the long-run average relationship. In this paper, we use kernel estimators of the LRV matrices (e.g., White, 1980; Newey and West, 1987; Andrews, 1991; Hansen, 1992; de Jong and Davidson, 2000). The new estimator thus depends on the kernel used to construct the LRV matrices.
We show that the new estimator converges to the long-run average relationship under the sequential limit, in which T → ∞ followed by n → ∞. To develop a joint limit theory, in which T and n go to infinity simultaneously, we need to exercise some control over the relative rate that T and n diverge to infinity. The rate condition is required to eliminate the effect of the bias. For example, Phillips and Moon (1999) impose the rate condition n/T → 0 to establish the joint limit of the PLS and FE estimators. This rate condition is likely to hold when n is moderate and T is large. However, in many financial panels, the number of firms (n) is either of the same magnitude as the time series dimension (T) or far greater. To relax the rate condition, we need an LRV estimator that achieves the greatest bias reduction. It turns out that the kernel LRV estimator with the bandwidth equal to the time series dimension fits our purpose. We show that the bias of this particular estimator is of order O(1/T), which is the best obtainable rate in the nonparametric estimation of the LRV matrix. On the other hand, the variance of this estimator does not vanish. Therefore, such an estimator is necessarily inconsistent, reflecting the usual bias-variance trade-off.
Using a kernel LRV estimator with full bandwidth (the bandwidth is set equal to the time series dimension), we show that the new estimator is consistent and asymptotically normal as n and T go to infinity simultaneously such that

. This rate condition is obviously less restrictive than the rate condition n/T → 0. The so-derived joint limit theory therefore allows for a possibly wide cross section relative to the time series dimension.
We show that the PLS and FE estimators are special cases of the LRV-based estimator. These two estimators implicitly use kernel LRV estimates with full bandwidth. The underlying kernels are K(s,t) = 1 − max(s,t) and K(s,t) = min(s,t) − st, respectively. As a consequence, our joint limit theory is also applicable to these two estimators. Hence, our work reveals that the rate condition n/T → 0 is only sufficient but not necessary for the joint limit theory and that it can be weakened to
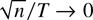
.
The new estimator is consistent under both the sequential limit and the joint limit, even though the LRV estimator is inconsistent. The reason is that the LRV estimator is proportional to the true LRV matrix up to an additive noise term. If the noise is assumed to be independent, then by averaging across independent individuals, we can recover a matrix that is proportional to the long-run average variance matrix. The consistency of the new estimator follows from the fact that it is not affected by the proportional factor.
We find that the new estimators with exponentiated kernels are more efficient than the PLS and FE estimators. The exponentiated kernels are obtained by taking powers of the popular Bartlett and Parzen kernels. In fact, the asymptotic variance of the new estimator can be made as small as possible by choosing a large exponent. This is not surprising as a larger exponent leads to LRV estimates with less variability. Variance reduction usually comes at the cost of bias inflation. We show that the bias inflation is small when T is large. In addition, for exponentiated Parzen kernels, the bias inflation occurs only to the second dominating bias term but not to the first dominating bias term. Therefore, the bias inflation is likely to factor in only when T is too small.
The kernel LRV estimator with full bandwidth has been used in hypothesis testing by Kiefer and Vogelsang (2002a, 2002b). Our paper provides another instance in which the kernel LRV estimator with full bandwidth is useful. Other papers that investigate the new LRV estimator include Jansson (2004), Sun (2004), and Phillips, Sun, and Jin (2003a, 2003b). In particular, the latter two papers consider consistent LRV estimation using exponentiated kernels.
The use of the LRV matrix to estimate the long-run average relationship has been explored by Makela (2002). He follows the traditional approach to construct the LVR matrix. His estimator therefore depends on the truncation lag and is not fully operational. In contrast, our estimator, like the PLS and FE estimators, does not involve the choice of any additional parameter and seems to be appealing to empirical analysts.
The rest of the paper is organized as follows. Section 2 describes the basic model, lays out the assumptions, and introduces the new estimator. Section 3 establishes the asymptotic properties of the kernel LRV estimator when the bandwidth is equal to the sample size. Section 4 considers the spurious panel model and investigates the asymptotic properties of the LRV-based estimator. Section 5 extends the results to the cointegration case. Section 6 concludes. Proofs are collected in the Appendix.
Throughout the paper, vec(·) is the column-by-column vectorization function, tr(·) is the trace function, and [otimes ] is the tensor (or Kronecker) product. The term Kmm denotes the m2 × m2 commutation matrix that transforms vec(A) into vec(A′), i.e.,
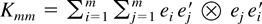
, where ei is the unit vector (e.g., Magnus and Neudecker, 1979). For a matrix A = (aij), ∥A∥ is the euclidean norm (tr(A′A))1/2, and |A| is the matrix (|aij|). A < ∞ means all the elements of matrix A are finite. The symbol ⇒ signifies weak convergence, := is definitional equivalence, and ≡ signifies equivalence in distribution. For a matrix Zn, Zn ⇒ N(0,Σ) means vec(Zn) ⇒ N(0,Σ). The term M is a generic constant.
This section introduces notation, specifies the data generating process, and defines the estimator and relates it to the existing ones.
The model we consider is the same as that in Phillips and Moon (1999). For completeness, we briefly describe the data generating process. The panel data model is based on the vector integrated process
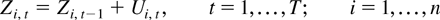
with common initialization Zi,0 = 0 for all i. The zero initialization is maintained for simplicity. All the results in the paper hold if we assume
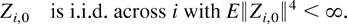
We partitioned the m-vectors Zi,t and Ui,t into my and mx components (m = mx + my) as Zi,t′ = (Yi,t′,Xi,t′) and Ui,t′ = (Uyi,t′,Uxi,t′). The error term Ui,t is assumed to be generated by the random coefficient linear process
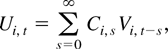
where (i) {Ci,t} is a double sequence of m × m random matrices across i and t; (ii) the m-vectors Vi,t are independent and identically distributed (i.i.d.) across i and t with EVi,t = 0, EVi,tVi,t′ = Im, and EVa,i,t4 = v4 for all i and t, where Va,i,t is the ath element of Vi,t. (iii) Ci,s and Vj,t are independent for all i,j,s,t.
Let Ca,i,s be the ath element of vec(Ci,s) and σkas = ECa,i,sk. We make two further assumptions on the random coefficients.
Assumption 1 (Random coefficient condition). Ci,s is i.i.d. across i for all s.
Assumption 2 (Summability condition).
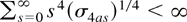
.
Assumptions 1 and 2 are the same as Assumptions 1(i) and 2(ii) of Phillips and Moon (1999). Note that their Assumptions 1(ii) and 2(i) are both implied by their Assumption 2(ii), so there is no need to state their Assumptions 1(ii) and 2(i) here. Assumption 1 and the assumption that Vi,t is i.i.d. imply cross sectional independence, an assumption that may be restrictive for some economic applications. However, because of the lack of natural ordering, there is no completely satisfactory and general way of modeling cross-sectional dependence, although some important progress has been made (see Conley, 1999; Phillips and Sul, 2003; Andrews, 2003). In this paper, we follow the large panel data literature and maintain the assumption of cross-sectional independence.
Let
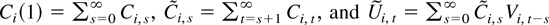
. Under Assumptions 1 and 2, we can prove the following lemma, which ensures the integrability of the terms that appear frequently in our development.
LEMMA 1. Let Assumptions 1 and 2 hold; then

Under Assumptions 1 and 2, the processes Ui,t admit the following Beveridge-Nelson decomposition almost surely:
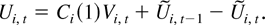
Using this decomposition and following Phillips and Solo (1992), we can prove that
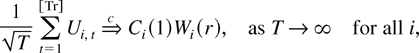
where Wi(r) is a standard Brownian motion with

signifies the weak convergence conditional on
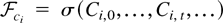
, the sigma field generated by the sequence {Ci,t}t=0∞.
To give a rigorous definition of the preceding conditional weak convergence, we expand the probability space in such a way that the partial sum process
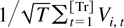
can be represented almost surely and up to a negligible error in terms of a Brownian motion Wi(r) that is defined on the same probability space. Such an expansion can be justified using the Hungarian construction (e.g., Shorack and Weller, 1986). We will proceed as if the probability space has been expanded in the rest of the paper. Let
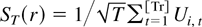
; then a formal definition of the conditional weak convergence in (2.5) is that
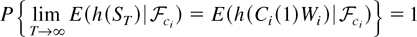
for all continuous and bounded functionals on D[0,1].
Let Ωi be the LRV matrix of Zi,t conditional on
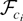
. It is well known that Ωi is proportional to the conditional spectral density matrix fUiUi(λ) of Ui,t evaluated at the origin, i.e., Ωi = 2πfUiUi(0). Partitioning Ωi conformably, we have
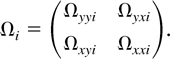
By Lemma 1(c), Ωi is integrable and
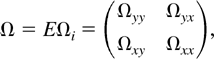
which is called the long-run average variance matrix of Zi,t. Following a classical regression approach, we can analogously define a long-run regression coefficient between Y and X by β = ΩyxΩxx−1. For more discussion on this analogy, see Phillips and Moon (2000).
To construct an estimate of β, we first estimate Ωi as follows:
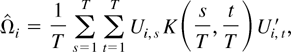
where Ui,t = Zi,t − Zi,t−1, K(·,·) is a kernel function. When K(x,y) depends only on x − y, i.e., K(x,y) is translation invariant, we write K(x,y) = k(x − y). In this case,

reduces to
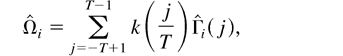
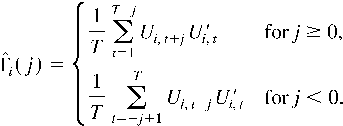
From the preceding formulation, it is clear that
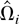
is the usual kernel LRV estimator using the full bandwidth. It should be noted that translation invariant kernels are commonly used in the estimation of the LRV matrix. We consider the kernels other than the translation invariant ones to include some existing estimators of the long-run average relationship as special cases. This will be made clear in Section 2.3.
Based on the previous estimate, we can estimate Ω by
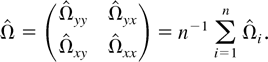
The long-run average relationship parameter β can then be estimated by
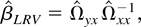
which is called the LRV-based estimator.
Note that the LRV-based estimator
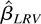
depends on the observations Zi,t only through their first-order difference. Therefore, when the model contains individual effects such that
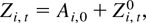
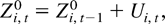
where Zi,00 = 0 and Ui,t follows the linear process defined in (2.3), the LRV-based estimator
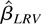
can be computed exactly the same as before. In other words, the LRV-based estimator is robust to the presence of the individual effects.
Phillips and Moon (1999) show that both PLS and FE estimators are consistent and asymptotically normal. In this section, we examine the relationships between the LRV-based estimator and the PLS and FE estimators.
The PLS estimator is
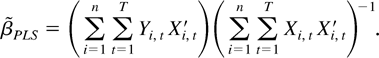
Some simple algebraic manipulations show that

where
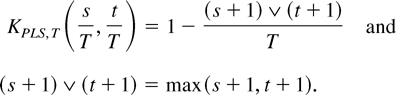
Hence, the PLS estimator is a special case of the LRV-based estimator. Note that the kernel for the PLS estimator depends on T. If we replace KPLS,T(s,t) by KPLS(s,t) = 1 − (s ∨ t), then we get an asymptotically equivalent estimator

. In view of (2.9), we see that
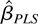
is an LRV-based estimator with kernel K(s,t) = 1 − (s ∨ t).
We now consider the FE estimator, namely,
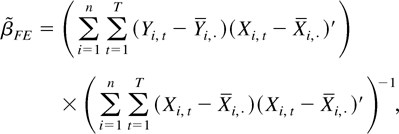
where

. Again, some algebraic manipulations yield

where
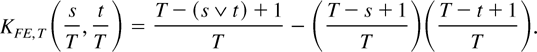
The kernel function KFE,T(s,t) depends on T. As before, we can replace KFE,T(s,t) by KFE(s,t) = min(s,t) − st to obtain an estimator
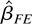
that is asymptotically equivalent to
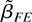
. The resulting estimator
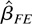
is an LRV-based estimator with kernel K(s,t) = min(s,t) − st.
In summary, the existing estimators or their asymptotically equivalent forms are special cases of the LRV-based estimator. The underlying LRV estimators use kernels that are not translation invariant. This sharply contrasts with the usual LRV estimators where translation invariant kernels are commonly used.
The properties of

evidently depend on those of the LRV matrix estimator
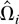
. In this section, we consider the asymptotic properties of
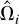
. We first examine the bias and variance of
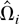
for fixed T and then establish its asymptotic distribution.
The bias of
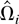
depends on the smoothness of fUiUi(λ) at zero and the properties of the kernel function. Following Parzen (1957), Hannan (1970), and Andrews (1991), we define
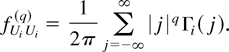
The smoothness of the spectral density at zero is indexed by q, for which fUiUi(q) is finite almost surely. The larger is q such that fUiUi(q) < ∞ a.s., the smoother is the spectral density at zero.
The following lemma establishes the smoothness of the spectral density at λ = 0.
LEMMA 2. Let Assumptions 1 and 2 hold; then
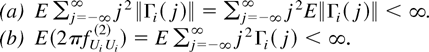
When K(s,t) = k(s − t), the bias of Ωi depends on the smoothness of k(x) at zero. To define the degree of smoothness, we let
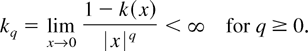
The largest q for which kq is finite is defined to be the Parzen characteristic exponent q*. The smoother is k(x) at zero, the larger is q*. The values of q* for various kernels can be found in Andrews (1991).
To investigate the asymptotic properties of

, we assume the kernel function K(s,t) satisfies the following conditions.
Assumption 3 (Kernel conditions).
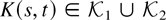
where

and
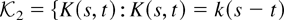
with k(0) = 1 and

Note that the two kernels in
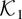
are positive semidefinite. When K(s,t) = 1 − (s ∨ t),
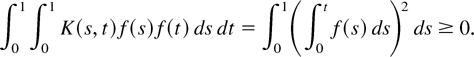
When K(s,t) = min(s,t) − st,
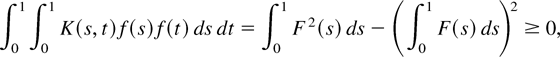
where
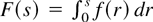
. Therefore, the kernels satisfying Assumption 3 are positive semidefinite. As shown by Newey and West (1987) and Andrews (1991), the positive semidefiniteness guarantees the positive semidefiniteness of
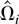
.
We proceed to investigate the bias and variance of
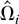
. The following two lemmas establish the limiting behaviors of the bias and variance of

as T → ∞.
LEMMA 3. Let Assumptions 1–3 hold. Define

.
(a) If K(s,t) is translation invariant with q* = 1, then
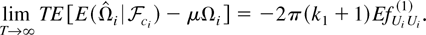
(b) If K(s,t) is translation invariant with q* ≥ 2, then
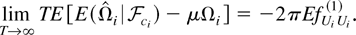
(c) If

, then
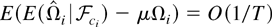
.
Remarks.
(i) When K(s,t) is translation invariant, K(s,s) = 1, so μ = 1. In this case, Lemma 3(a) and (b) show that
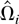
is centered around a matrix that is equal to the true LRV matrix up to a small additive error. The error has a finite expectation and is independent across i. As a consequence, the average LRV matrix can be estimated by averaging
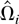
over i = 1,2,…,n. When
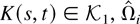
, scaled by
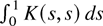
, is equal to the true variance matrix plus a noise term. The average LRV matrix can be estimated by averaging
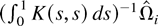
over i = 1,2,…,n.
(ii) For the conventional LRV estimator with a truncation parameter ST, the bias is of order O(1/STq*) under the assumption that ST /T + STq*/T + 1/ST → 0 (e.g., Hannan, 1970; Andrews, 1991). The bias of the conventional estimator is thus of a larger order than the estimator without truncation. This is not surprising as truncation is used in the conventional estimator to reduce the variance at the cost of the bias inflation.
(iii) When K(s,t) is translation invariant, the dominating bias term depends on the kernel through k1 if q* = 1. In contrast, when q* ≥ 2, the dominating bias term does not depend on the kernel. From the proof of the lemma, we see that when q* = 2, the next dominating bias term is −2πT−2k2 EfUiUi(2). Therefore, when q* ≥ 2, the kernels exert their bias effects only through high-order terms. This has profound implications for the asymptotic bias of

considered in Section 4.2.
LEMMA 4. Let Assumptions 1–3 hold. Then we have
(a)
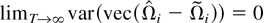
, where
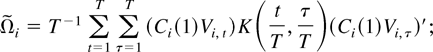
(b)

, where

Remarks.
(i) Lemma 4(b) gives the expression for the unconditional variance. It is easy to see from the proof in the Appendix that the conditional variance has a limit given by
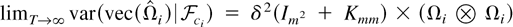
almost surely. Therefore, the magnitude of the asymptotic variance depends on δ2. This suggests using the kernel that has the smallest δ2 value when the variance of
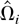
is the main concern.
(ii) Lemma 4(b) calculates the limit of the finite-sample variance of
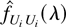
when λ = 0. Following the same procedure and using a frequency domain BN decomposition, we can calculate the limit of the finite-sample variance of
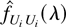
for other values of λ when the full bandwidth is used in smoothing. This extension may be needed to investigate seasonally integrated processes. This extension is straightforward but tedious and is beyond the scope of this paper.
LEMMA 5. Let Assumptions 1–3 hold. Then

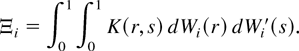
Remarks.
(i) When K(s,t) is translation invariant, μ = 1. In this case, Lemma 5 shows that

is asymptotically unbiased, even though it is inconsistent. For other kernels,

is asymptotically proportional to the true LRV matrix. We will show that the consistency of
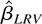
inherits from this asymptotic proportionality.
(ii) Kiefer and Vogelsang (2002a, 2002b) establish asymptotic results similar to Lemma 5(a) under different assumptions. Specifically, they assume the kernels are continuously differentiable to the second order. As a consequence, they have to treat the Bartlett kernel separately. They obtain different representations of the asymptotic distributions for these two cases. The unified representation in Lemma 5 is very valuable. It helps us shorten the proof and enables us to prove the asymptotic properties of

in a coherent way.
(iii) When

, the limiting distribution in Lemma 5(a) is the same as that obtained by using (2.5) and the continuous mapping theorem.
This section considers the case where the two component random vectors Yi,t and Xi,t of Zi,t have no cointegrating relation for any i. This case is characterized by the following assumption.
Assumption 4 (Rank condition). rank(Ωi) = m almost surely for all i = 1,…,n.
Define βi = Ωyxi(Ωxxi)−1. Assumption 4 implies that
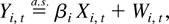
where Wi,t is a unit root process and the long-run covariance between Xi,t and Wi,t is zero, i.e.,
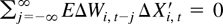
. Our interest lies in the long-run average coefficient β = EΩyxi(EΩxxi)−1, which is in general different from the “average long-run coefficient” defined by Eβi. For more discussion on this, see Phillips and Moon (1999).
Before investigating the asymptotic properties of the LRV-based estimate, we first define some notation. The sequential approach adopted in the paper is to fix n and allow T to pass to infinity, giving an intermediate limit, then by letting n pass to infinity subsequently to obtain the sequential limit. As in Phillips and Moon (1999), we write the sequential limit of this type as (T,n → ∞)seq. The joint approach adopted in the paper allows both indexes, n and T, to pass to infinity simultaneously. We write the joint limit of this type as (T,n → ∞).
The following theorem establishes the consistency of
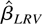
as either (T,n → ∞)seq or (T,n → ∞).
THEOREM 6. Let Assumptions 1–4 hold; then
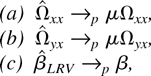
as either (T,n → ∞)seq or (T,n → ∞).
Remark.

is consistent even though

is inconsistent. This is not surprising as

equals μΩi plus a noise term. Although the noise in the time series estimation is strong, we can weaken the strong effect of noise by averaging across independent individuals. This is reflected in Theorem 6(a) and (b), which show that

are respective consistent estimates of Ωxx and Ωyx up to a multiplicative scalar.
Now we proceed to investigate the asymptotic distribution of
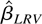
. We consider the sequential asymptotics first and then extend the result to the joint asymptotics. To get a definite joint limit, we need to control the relative rate of expansion of the two indexes. Write
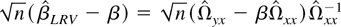
. Theorem 6 describes the asymptotic behavior of
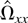
under the sequential and joint limits. Under Assumption 4, Ωxx has full rank, which implies that
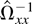
converge to μ−1Ωxx−1. Therefore, it suffices to consider the limiting distribution of

.
Under the sequential limit, we first let T → ∞ for fixed n. The intermediate limit is
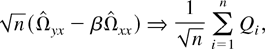
where
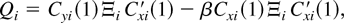
Cyi(1) is the my × m matrix consisting of the first my rows of Ci(1), and Cxi(1) is the mx × m matrix consisting of the last mx rows of Ci(1). In view of Lemma 5, the mean of the summand is
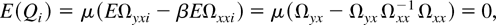
and the covariance matrix Θ is E vec(Qi)vec(Qi)′. An explicit expression for Θ is established in the following lemma.
LEMMA 7. Let Assumptions 1–4 hold. Then Θ is equal to

where Kmy mx is the my mx × my mx commutation matrix.
The sequence of random matrices Cyi(1)Ξi Cxi′(1) − βCxi(1)Ξi Cxi′(1) is i.i.d. (0,Θ) across i. From the multivariate Linderberg–Levy theorem, we then get, as n → ∞,
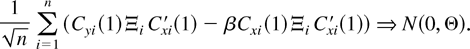
Combining (4.4) with the limit lim

, we establish the sequential limit in the following theorem.
THEOREM 8. Let Assumptions 1–4 hold. Then, as (T,n → ∞)seq,
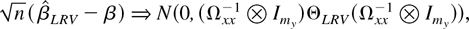
where ΘLRV is

We now show that the limiting distribution continues to hold in the joint asymptotics as (T,n → ∞). Write

as
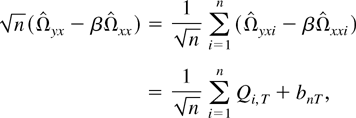
where
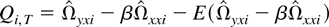
and
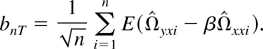
Because of Lemma 3, the term bnT vanishes under the sequential limit. However, under the joint limit, we need to exercise some control over the relative expansion rate of (T,n) so that bnT vanishes as (T,n → ∞). When this occurs, the term
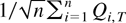
will deliver the asymptotic distribution as (T,n → ∞).
Using Lemma 3, we have
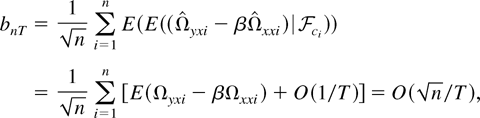
because the O(·) terms in the summand are independent across i. Therefore, to eliminate the asymptotic bias, we need to assume the two indexes pass to infinity in such a way that
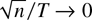
. Under this condition, we can prove the following theorem, which provides the asymptotic distribution under the joint limit.
THEOREM 9. Let Assumptions 1–4 hold. Then, as (T,n → ∞) such that
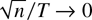
,
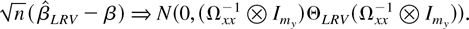
Remarks.
(i) For the PLS estimator, K(r,s) = 1 − (r ∨ s). Therefore,
. Hence, the PLS estimator satisfies, under both the sequential and joint limits,

with

The preceding limiting distribution is identical to that obtained by Phillips and Moon (1999).
(ii) For the FE estimator, K(s,t) = min(s,t) − st. In this case, it is easy to see that

. So

. Hence

has the limiting distribution given in (4.12) and (4.13) but with

replaced by

. Once again, the asymptotic result is consistent with Phillips and Moon (1999).
(iii) The efficiency of
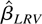
depends only on μ−2δ2. The smaller μ−2δ2 is, the more efficient the estimator is. This is because the sum of the last two terms in (4.6) is
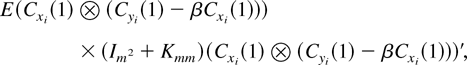
which is positive semidefinite. Therefore,
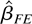
is more efficient than
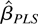
. But
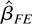
is less efficient than
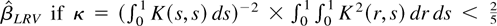
. In Section 4.2, we consider a class of new kernels that have smaller κ values.
If we assume that Ci,t are the same across individuals, then Ωi = Ω and βi = β for some β and all i. In this case, Ωyxi − βΩxxi = 0. As a consequence, ΘLRV reduces to
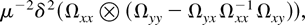
and we obtain the following corollary.
COROLLARY 10. Let Assumptions 1–4 hold. If Ci,t =a.s Ct where Ct is an m × m nonrandom matrix for all t, then, as (T,n → ∞)seq, or as (T,n → ∞) with

,
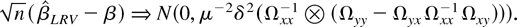
Remarks.
(i) The corollary generalizes a result of Kao (1999). He considers the homogeneous spurious regression and shows that under the sequential limit, the FE estimator satisfies (4.14) with
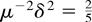
.
(ii) Note that the matrix Ωxx−1 [otimes ] (Ωyy − ΩyxΩxx−1Ωxy) is positive semidefinite. Therefore, the efficiency of
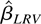
depends only on μ−2δ2 regardless of whether Ci,t is heterogeneous or not.
In this section, we exponentiate some commonly used kernels and investigate the asymptotic properties of the LRV-based estimators that these exponentiated kernels deliver.
We first consider the sharp kernels defined by k(x) = kBartρ(x), where kBart(·) is the Bartlett kernel and
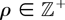
. These kernels, as so defined, exhibit a sharp peak at the origin. Sharp kernels are positive semidefinite, as they are equal to the products of the positive semidefinite kernels. To see this, we may use equation (A.11) in the Appendix and represent the Bartlett kernel by
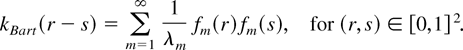
Then
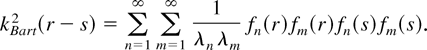
So, for any function g(x) ∈ L2[0,1], we have
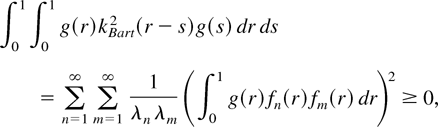
which implies that kBart2(r − s) is indeed positive semidefinite. Iterating the previous procedure leads to the positive semidefiniteness of kBartρ(r − s) for any
.
For sharp kernels, the Parzen characteristic exponent is q* = 1 and k1 = ρ. The value of κ is κ = 1/(ρ + 1). Therefore, κ is a decreasing function of the exponent ρ. In principle, we can choose ρ to make κ as small as possible. However, the finite-sample performance can be hurt when ρ is too large for a moderate time series dimension. This is because the bias of
increases as ρ increases, as shown by Lemma 3. In fact, when
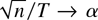
, the asymptotic distribution of
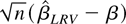
under the joint limit is
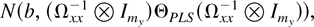
where b = −2πα(ρ + 1)(Ωxx−1 [otimes ] Imy)vec(EfUyiUxi(1) − βEfUxiUxi(1)). Therefore, the squared asymptotic bias b′b is increasing in ρ while the asymptotic variance is decreasing in ρ. This observation implies that there exists an optimal ρ that minimizes the mean squared errors. The optimal ρ depends on the ratio α and the average spectral density of Ui. We can estimate the optimal ρ along the lines of Andrews (1991), but we do not pursue this analysis in the present paper.
Next, we consider the steep kernels defined by k(x) = (kPR(x))ρ where kPR(x) is the Parzen kernel. These kernels decay to zero as x approaches one. The speed of decay depends on ρ. The larger ρ is, the faster the decay and the steeper the kernel. Steep kernels are positive semidefinite because the Parzen kernel is positive semidefinite. The difference between the sharp kernels and the steep kernels is that the former are not differentiable at the origin whereas the latter are. For steep kernels, the Parzen characteristic exponent is q* = 2 and k2 = 6ρ. The value of κ can be calculated using numerical integration. They are given in Table 1 for ρ = 1,…,6. Obviously, κ decreases as ρ increases. This is expected because (kPR(x))ρ1 ≤ (kPR(x))ρ2 if ρ1 ≥ ρ2. Therefore, the steep kernel can deliver an LRV-based estimator
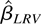
that is more efficient than
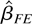
, as long as the exponent is greater than 1 (see Table 1).
The values of κ for some kernels

When the steep kernel is employed, the dominating bias of
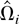
is independent of the exponent. If (n,T → ∞) such that

, then the asymptotic distribution of

is
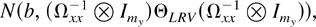
where b = −2πα(Ωxx−1 [otimes ] Imy)vec(EfUyiUxi(1) − βEfUxiUxi(1)). This limiting distribution seems to imply that we can choose ρ to make κ as small as possible without inflating the asymptotic bias. This is true in large samples. But in finite samples, a large κ may lead to a poor performance. The reason is that the second dominating bias term in
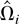
is T−22πk2 EfUiUi(2), which depends on k2. As a consequence, the asymptotic bias of
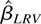
under the joint limit is
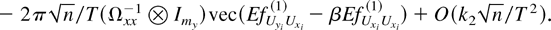
The O(·) term vanishes when (n,T → ∞) such that
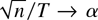
. But in finite samples, the O(·) term may have an adverse effect on the performance of
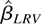
. Nevertheless, the effect is expected to be small, especially when T is large.
Finally, we may take powers of the kernels in
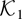
and obtain more efficient estimates. Although Assumption 3 does not cover exponentiated kernels of this sort. Theorems 8 and 9 go through without modification.
Table 1 summarizes the values of κ for different exponentiated kernels. The table clearly shows that for a given “mother” kernel, the value of κ decreases as the exponent increases. Recall that the smaller κ is, the more efficient the LRV-based estimator is. We can thus conclude that a larger exponent (ρ) gives rise to a more efficient estimator.
This section assumes that the variables in Zi,t are cointegrated. As discussed in Engle and Granger (1987), the long-run covariance matrix is singular in this case. We consider the case where the cointegration relationships are different for different individuals.
Following Phillips and Moon (1999), we strengthen the summability condition and impose additional conditions.
Assumption 5 (Summability conditions′).
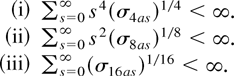
Assumption 6 (Rank conditions′). rank(Ωi) = rank(Ωxxi) = mx and rank(Ωyyi) = my almost surely for all i = 1,…,n.
Assumption 7 (Tail conditions). The random matrix Ωxxi has continuous density function f with
(i) f (Ω) = O(exp{tr(−cΩ)}) for some c > 0 when tr(Ω) → ∞.
(ii) f (Ω) = O((det(Ω)γ)) from some γ > 7 when det(Ω) → ∞.
Note that Assumption 5 is stronger than Assumption 2. Therefore, under Assumptions 1, 3, and 5, all results in Section 3 continue to hold. Let αi = (Imy,−βi), where βi = ΩyxiΩxxi−1. Assumption 6 implies that αi Ci(1)Cyi′(1) = 0. As a consequence, αi Ci(1) = 0, i.e., Cyi(1) = βi Cxi(1). Define Ei,t = αi Zi,t = Yi,t − βi Xi,t. Then, using αi Ci(1) = 0, we have
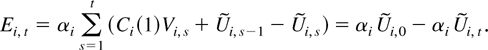
Therefore, Assumption 6 implies the existence of the following panel cointegration relationship with probability one:
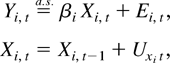
where
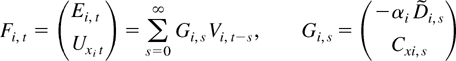
and
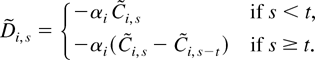
Let
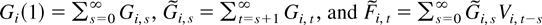
. As shown by Phillips and Moon (1999), Assumptions 5 and 7 ensure that quantities analogous to those in Lemma 1 are bounded. Specifically,
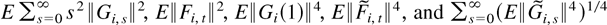
are all bounded.
Using the long-run covariance matrix, we can estimate the individual cointegration relationship by
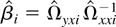
. It follows from Lemma 5 that

As a consequence,

, which implies that
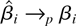
. This is because βi is a constant conditional on
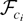
.
The following theorem establishes the rate of convergence of
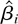
. Before stating the theorem, we define Lipschitz continuity. A function

is Lipschitz continuous if there exists a constant M > 0 such that ∥ f (x) − f (y)∥ ≤ M∥x − y∥ for all x and y in Γ. It is easy to see that the kernels satisfying Assumption 3 are Lipschitz continuous.
LEMMA 11. Let Assumptions 5–7 hold. Assume that the kernel function K(·,·) is symmetric and Lipschitz continuous. Then

Remarks.
(i) The lemma shows that
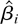
is not only consistent but also converges to the true value at the rate of
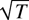
or T. This result is particularly interesting. Although both

are inconsistent, the linear combination
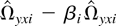
is consistent, reflecting the singularity of the long-run covariance matrix Ωi. In fact, the proof of the lemma shows that
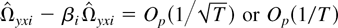
, depending on the kernel used.
(ii) The kernel K(·,·) may be called a “tied down” kernel if K(1,s) = K(r,1) = 0 for any r and s. Because both kernels in

are tied down kernels,
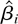
converges to β at the rate of T if

. This is of course a well-known result. Lemma 11(a) has more implications. Given any kernel function K(r,s), we can construct a new kernel K*(r,s) = K(r,s) − K(1,s) − K(r,1) + K(1,1) such that K*(1,s) = K*(r,1) = 0 for any r and s. The new kernel is then able to deliver an estimator that is superconsistent.
(iii) For translation invariance kernels, K(1,r) = k(1 − r) ≠ 0 in general. So the estimator that they deliver is only
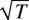
-consistent. The difference in the rate of convergence arises because the dominated terms are different for different types of kernels.
We now investigate the asymptotic distribution of

in the heterogeneous panel cointegration model. We first consider the sequential limit of

. The intermediate limit for large T is the same as that given by (4.2). More explicitly,
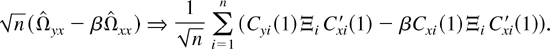
Following exactly the same arguments, we can show that the summands are i.i.d. (0,Θ). Invoking the multivariate Linderberg–Levy theorem and using the consistency of

, we have, as (T,n → ∞)seq,
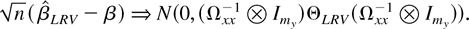
The next theorem shows that the asymptotic distribution is applicable to the case of joint limit. The proof of the theorem follows steps similar to that of Theorem 9 and is omitted.
THEOREM 12. Suppose Assumptions 1–3 and 6 hold. Then, as (T,n → ∞)seq, or as (T,n → ∞) with
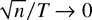
,

Remarks.
(i) Note that Assumption 7 is not needed for the theorem to hold. The strong summability conditions in Assumption 5 are also not necessary. The asymptotic distribution not only has precisely the same form as in the spurious regression case but also holds under the same conditions. However, Assumptions 5 and 7 are required for Lemma 11, as it relies on the panel BN decomposition of the error term Ei,t.
(ii) Because the limiting distribution is the same as that in Theorem 9, the remarks given there and the efficiency analyses presented in Section 4.2 remain valid. Therefore, in the presence of heterogeneity, the LRV-based estimator is more efficient than the PLS and FE estimators if exponentiated kernels are used.
(iii) The asymptotic theory developed previously allows us to test hypotheses about the long-run average coefficient β. To test the null hypothesis H0 : ψ(β) = 0, where ψ(·) is a p-vector of smooth function on a subset
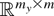
such that ∂ψ/∂β′ has full rank p (≤ my mx), we construct the Wald statistic:
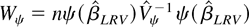
, where
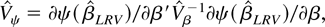
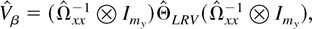
and
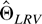
is the sample analogue of (4.6). Some simple manipulations show that this test statistic converges to a χp2 random variable under both the sequential and joint limits.
In this paper, we have proposed an LRV-based estimator of the long-run average relationship. Our estimator includes the pooled least squares and fixed effects estimators as special cases. We show that the LRV-based estimator is consistent and asymptotically normal under both the sequential limit and the joint limit. The joint limit is derived under the rate condition
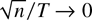
, which is less restrictive than the rate condition n/T → 0, as required by Phillips and Moon (1999). A central result is that, using exponentiated kernels introduced in this paper, the LRV-based estimator is asymptotically more efficient than the existing ones.
It should be pointed out that we have not considered the homogeneous panel cointegration model. When the long-run relations are the same across individuals, the LRV-based estimator may have a slower rate of convergence than the PLS and FE estimators. We have shown that, when translation invariant kernels are used,

is only
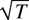
-consistent. Because of the slower rate of convergence, we expect that the LRV-based estimator converges at the rate of

in homogeneous panel cointegration models. The
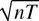
rate is slower than the
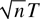
rate that is attained by the PLS and FE estimators. However, the
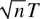
rate can be restored if “tied down” kernels are used. The efficiency of the LRV-based estimator with other tied down kernels is an open question.
This paper can be extended in several directions. First, the power parameter ρ for the sharp and steep kernels is fixed in the paper. We may extend the results to the case that ρ grows to infinity at a suitable rate with N and T along the lines of Phillips et al. (2003a, 2003b). Second, the LRV-based estimator can be employed in implementing residual-based tests for cointegration in panel data. Following the lines of Kao (1999), we can use the LRV-based estimator to construct the residuals and test for unit roots in the residuals. Because the LRV-based estimator is more efficient than the FE estimator employed by Kao (1999), the test using the LRV-based residuals may have better power properties. Finally, we generate the new kernels by exponentiating existing ones. An alternative approach to generating kernels is to start from a mother kernel k and consider the class {kb(s,t)} = {k(b−1r,b−1s) : b ∈ (0,1]} (Kiefer and Vogelsang, 2003). For this approach, Theorems 8, 9, and 12 go through but with μ and δ2 defined by
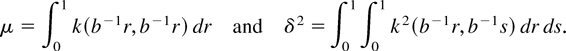
With the preceding extension, we may analyze the efficiency of the LRV-based estimators for different values of b.
Parts (a)–(d) are the same as Lemma 1 of Phillips and Moon (1999). It remains to prove part (e). From Lemma 9(a) of Phillips and Moon (1999), for any ρ ≥ 1 and any p × q matrix A = (aij), we have
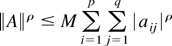
for some constant M. Therefore, to evaluate the order of
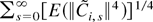
, it suffices to consider

. By the generalized Minkowski inequality and the Cauchy inequality, we have, for some constant M,

where the last line follows from Assumption 2. This completes the proof of the lemma. █
Because part (b) follows from part (a), it suffices to prove part (a). Write
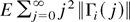
as

Therefore,

is bounded by

where the last line follows from (A.1) and Assumption 2. This completes the proof of part (a). █
We first consider the case that K(s,t) is translation invariant, i.e., K(s,t) = k(s − t). The proof follows closely those of Parzen (1957) and Hannan (1970). We decompose
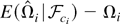
into three terms as follows:

We consider the expectations of the three terms in turn. First, for q = min(q*,2), EΩi1e is

The last inequality follows because (k(j/T) − 1)| j/T |−q converges boundedly to kq for each fixed j.
Second, EΩi2e is
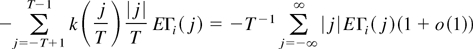
using Lemma 2.
Finally, ∥EΩi3e∥ is bounded by
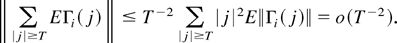
Let Ωie = (Ωi1e + Ωi2e + Ωi3e); then we have shown that, when q* = 1, limT→∞ TEΩie = −2π(k1 + 1)EfUiUi(1), and when q* ≥ 2, limT→∞ TEΩie = −2πEfUiUi(1).
Next, we consider the case that
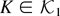
. Some algebraic manipulations show that

When K(s,t) = 1 − (s ∨ t),

Combining the preceding calculation with the steps for the translation invariant case, we can get

. Similarly, we can show that when K(s,t) = min(s,t) − st,

and

.
The proof of the theorem is completed by noting that
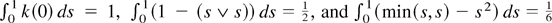
. █
Plugging the BN decomposition.
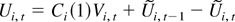
into
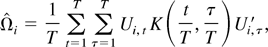
we get
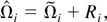
where Ri = Ri1 + Ri2 + Ri3 with

We proceed to show that E tr(vec(Ri1)vec(Ri1)′) = o(1). It is easy to see that Ri1 is

But E tr(vec(Ri1(1))vec(Ri1(1))′) is

where the first equality follows from the fact that for m × 1 vectors A and B, vec(AB′) = B [otimes ] A, and the third equality follows from the rule that (A [otimes ] B)(C [otimes ] D) = AC [otimes ] BD. In view of the fact that tr(C [otimes ] D) = tr(C)tr(D), we write E tr(vec(Ri1(1))vec(Ri1(1))′) as

where the last two equalities follow from Lemma 1(c) and (d) and the boundedness of K(·,·).
The proofs of E tr(vec(Ri1(2))vec(Ri1(2))′) = op(1) and E tr(vec(Ri1(3))vec(Ri1(3))′) = op(1) are rather lengthy. They are given in Sun (2003). The details are omitted here.
Given that E tr(vec(Ri1(k))vec(Ri1(k)))′, k = 1,2,3, we have E tr(vec(Ri1)vec(Ri1)′) = o(1). As a consequence, we also have E tr(vec(Ri2)vec(Ri2)′) = o(1). Similarly, we can prove E tr(vec(Ri3)vec(Ri3)′) = o(1). Again, details are omitted.
From part (a), we deduce immediately that
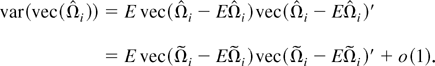
Note that E

equals

and
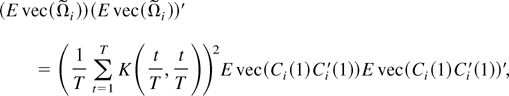
so
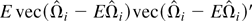
is

Letting T → ∞ completes the proof. █
Proof Lemma 5.
Lemma 3 has shown that

. To establish the asymptotic distribution of

, we only need to consider

. Because the kernels are assumed to be continuous and positive semidefinite, it follows from Mercer's theorem that K(r,s) can be represented as
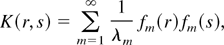
where λm > 0 are the eigenvalues of the kernel and fm(x) are the corresponding eigenfunctions, i.e.,

, and the right-hand side converges uniformly over (r,s) ∈ [0,1] × [0,1]. In fact, for the two kernels in

, we have
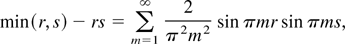
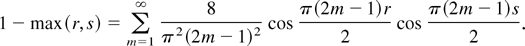
For kernels in

, we have the Fourier series representation:
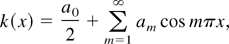
where

, and the right side of (A.14) converges uniformly over x ∈ [−1,1]. It follows from the preceding representation that for any r,s ∈ [0,1],
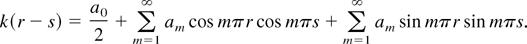
Hence, under Assumption 3, the kernels can be represented by (A.11) with smooth eigenfunctions.
Using (A.11), we have, for any T,

Therefore,
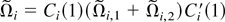
where
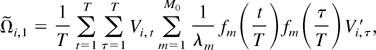
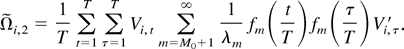
It is easy to see that, for a fixed M0,

The preceding weak convergence result follows from integration and summation by parts and the continuous mapping theorem. Note that the integral
is well defined because fm(·) is of bounded variation.
Following the same argument as in (A.10), we have, as M0 → ∞,
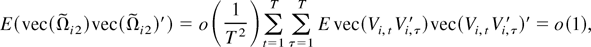
which implies that
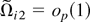
for any T as M0 → ∞. Combining the previous results (e.g., Nabeya and Tanaka, 1988), we obtain
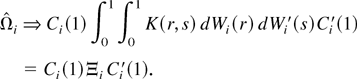
The mean of any off-diagonal element of Ξi is obviously zero. It suffices to consider the means of the diagonal elements. They are
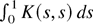
. So
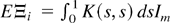
. As a consequence
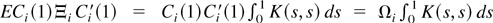
. █
Proof of Theorem 6. By Assumption 3, Ωxxi is positive definite almost surely, and c′Ωxxi c > 0 for any c ≠ 0 in
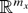
. Thus Ec′Ωxxi c = c′Ωxx c > 0, which implies that Ωxx is positive definite. Hence Ωxx−1 exists, and part (c) follows from parts (a) and (b). It remains to prove parts (a) and (b). We first consider the joint probability limits. To prove
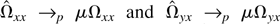
as (T,n → ∞), it is sufficient to show that
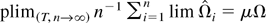
. Note that

where Ωie = Ωi1e + Ωi2e + Ωi3e and Ωike, k = 1,2,3 are defined in the proof of Lemma 3. We can write

as
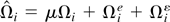
, where Ωie is i.i.d. across i with EΩie = O(1/T) and Ωiε is i.i.d. across i with EΩiε = 0. Therefore,

by the law of large numbers. The last line holds because Ωi and Ωiε do not depend on T. In this case, the joint limits as (T,n → ∞) reduce to the limits as n → ∞. It remains to show that
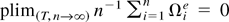
. To save space, we only present the proof for

. A sufficient condition is that

. Using Lemma 2, we have

as (T,n → ∞). By the Markov inequality, we get
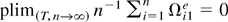
, which completes the proof of the joint limits.
Next, we consider the sequential probability limits. By Lemma 5(a) of Phillips and Moon (1999), it suffices to show that, for fixed n, the probability limit

exists. But the latter is true by Lemma 4(b). █
Proof of Lemma 7. Note that

and E(vec(Ξi)vec(Ξi)′) can be written as
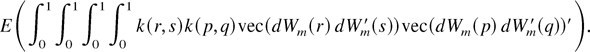
Some calculations show that E(vec(dWm(r) dWm′(s))vec(dWm(p) dWm′(q))) is
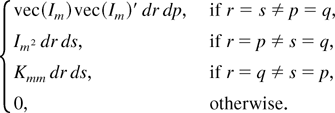
Using the preceding result, we have
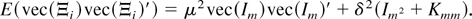
Consequently,

Here we have used the identity that

(see Magnus and Neudecker, 1979, Theorem 3.1, part (viii)). █
Proof of Theorem 9. Under the joint limit, we have shown

as

. To prove the theorem, it suffices to show that

under the joint limit. Note that Qi,T are i.i.d. random matrices across i with zero mean and covariance matrix ΘT = E vec(Qi,T)vec(Qi,T)′. To calculate ΘT, let
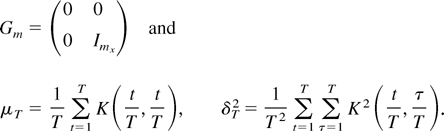
Then, by Lemma 4(b), ΘT is

A few more calculations give us

So {Qi,T}i is an i.i.d. sequence with mean zero and covariance matrix ΘT.
Next we apply Theorem 3 of Phillips and Moon (1999) with Ci = Imy mx to establish

. Conditions (i), (ii), and (iv) of the theorem are obviously satisfied in view of the facts that Ci = Imy mx and ΘT → Θ as T → ∞. To prove the uniform integrability of ∥Qi,T∥, we use Theorem 3.6 of Billingsley (1999). Put in our context, the theorem states that if ∥Qi,T∥ ⇒ ∥Qi∥ and E∥Qi,T∥ → E∥Qi∥, then ∥Qi,T∥ is uniformly integrable. Note that, using the continuous mapping theorem, we have, as T → ∞,

Therefore, ∥Qi,T∥ is uniformly integrable. We invoke Theorem 3 of Phillips and Moon (1999) to complete the proof. █
Proof of Lemma 11. Note that
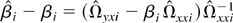
. We first consider the stochastic order of

. By definition,

where the last equality follows from summation by parts.
Therefore, when K(1,r) = K(s,1) = 0 for any r and s,
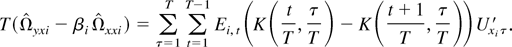
Following the same steps as the proof of Lemma 4(a), we can prove that

provided that K(·,·) is Lipschitz continuous. As a consequence, we get
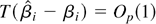
.
When

equals
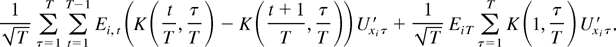
In view of (A.27), the first term is op(1). The second term is Op(1) because
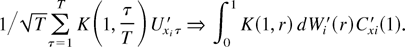
Hence
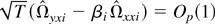
, which implies that
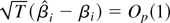
. █

The values of κ for some kernels