Published online by Cambridge University Press: 10 February 2004
This paper uses the concept of dual likelihood to develop some higher order asymptotic theory for the empirical likelihood ratio test for parameters defined implicitly by a set of estimating equations. The resulting theory is likelihood based in the sense that it relies on methods developed for ordinary parametric likelihood models to obtain valid Edgeworth expansions for the maximum dual likelihood estimator and for the dual/empirical likelihood ratio statistic. In particular, the theory relies on certain Bartlett-type identities that can be used to produce a simple proof of the existence of a Bartlett correction for the dual/empirical likelihood ratio. The paper also shows that a bootstrap version of the dual/empirical likelihood ratio achieves the same higher order accuracy as the Bartlett-corrected dual/empirical likelihood ratio.This paper is based on Chapter 2 of my Ph.D. dissertation at the University of Southampton. Partial financial support under E.S.R.C. grant R00429634019 is gratefully acknowledged. I thank my supervisor, Grant Hillier, for many stimulating conversations and Peter Phillips, Andrew Chesher, and Jan Podivisnky for some useful suggestions. In addition, I am very grateful to the co-editor Donald Andrews and two referees for many valuable comments that have improved noticeably the original draft. All remaining errors are my own responsibility.
Empirical likelihood (EL) is introduced by Owen (1988) as a way of extending parametric methods of inference to certain nonparametric situations. In the simplest situation, one is interested in obtaining a confidence region for the mean of the unknown distribution of a sample of independent and identically distributed (i.i.d.) observations. Without specifying a parametric form for the unknown distribution, Owen (1988, 1990) shows that under very weak conditions the EL ratio function can be used to construct confidence regions for the mean using an asymptotic χ2 calibration. EL confidence regions have a data-determined shape (i.e., they tend to be more concentrated in places where the density of the parameters estimator is greatest), and they are not necessarily ellipsoidal, as in the case of confidence regions based on the normal approximation. Furthermore, they are Bartlett-correctable (DiCiccio, Hall, and Romano, 1991), so that the actual coverage error differs from the nominal by a term of order O(n−2). These attractive properties have motivated various researchers to extend the EL method to more general statistical models. See the monograph of Owen (2001) for an excellent account of recent developments and applications of EL.
In this paper we consider EL inference for the class of statistical models where the parameters are defined implicitly through a set of estimating equations. This class of models is particularly relevant in econometrics, because most maximum and quasi-maximum likelihood, nonlinear least squares, and M estimators are defined through estimating equations. We shall refer to this set of estimating equations as generalized scores (GS).
The main objective of the paper is to develop some higher order asymptotic theory for the EL ratio (ELR) test of a simple hypothesis about the parameters defined by GS. The approach we follow exploits an important connection relating EL to dual likelihood (DL) (Mykland, 1995): in the case of independent observations, the ELR statistic coincides with the DL ratio (DLR) statistic. The importance of this connection stems from the fact that the DL concept is introduced by Mykland (1995) as a device for using likelihood methods in the context of martingale inference. Thus, in the special case of independent observations, the connection between DL and EL implies the possibility of using likelihood methods in the context of EL inference. This is very convenient because we can then rely on techniques developed for ordinary parametric likelihood models and can use the classical methods of Bhattacharya and Ghosh (1978), Chandra and Ghosh (1979, 1980), and Hill and Davies (1968) to derive rigorously results on the higher order properties of the ELR statistic.
The results obtained in the paper extend and/or complement results of Owen (1988, 1991), DiCiccio and Romano (1989), DiCiccio et al. (1991), Chen (1993, 1994), Mykland (1995), and others. The new results are the following: first, we prove the validity of the Edgeworth expansion for the maximum DL estimator and for the ELR statistic under a sequence of local alternatives. The latter extends to the multiparameter case and to the third order Mykland's asymptotic analysis (1995, Sect. 7) of the alternative hypothesis induced by the DL. Incidentally, we note here that, with the exception of Chen (1994) and Lazar and Mykland (1998), much of the research on the higher order properties of the ELR statistic has been focused on its accuracy rather than on its power. The Edgeworth expansion for the ELR under a sequence of local alternatives derived in the paper fills this gap, because it can be used to approximate the power of the ELR test for particular values of the local alternatives.
Second, we show that, under the null hypothesis, the ELR statistic for the parameters defined by GS admits always a Bartlett correction. This result in itself is not new in the sense that the Bartlett correction factor obtained in the paper coincides in practice1
Our calculations support Keith Baggerly's conjecture, as reported in the Errata section of Owen's empirical likelihood Web page: http://www-stat.stanford.edu/∼owen/empirical, that there is a mistake in the formula of DiCiccio et al. (1991, p. 1056) of the Bartlett correction. Specifically the term t2 should be 0, whereas the term t1 should be 1/3. With this correction, the formula of DiCiccio (1991) coincides with the one obtained in this paper (cf. (15)) in the case of GS.
Third, we provide asymptotic justification for a bootstrap version of the ELR statistic originally proposed by Owen (1988) as a “hybrid” method in which EL confidence regions for the parameters of interest are based on the bootstrap distribution of the ELR rather than the asymptotic χ2 calibration. We show that the bootstrap approximates the distribution of the ELR to an order o(n−1) except if the observed sample is contained in a set of probability o(n−1), and we also show that the ELR with bootstrap calibration accomplishes the Bartlett correction automatically; i.e., the ELR with bootstrap critical values has the same level of accuracy as the Bartlett-corrected one. The same phenomenon was noted by Beran (1988, p. 694) in the case of parametric bootstrap likelihood ratio tests.
Finally, we prove in the Appendix a general theorem on the density of generalized noncentral quadratic forms, which is of its own independent interest, because it can be used to calculate formal Edgeworth expansions of asymptotic χ2 test statistics admitting a stochastic expansion under a sequence of local alternatives.
The results in the paper are useful to obtain ELR tests that have a desirable higher order accuracy property. The bootstrap version of the ELR is particularly useful because the bootstrap calibration is likely to be more accurate than the Bartlett-corrected χ2 calibration. Monte Carlo simulations (see, e.g., Corcoran, Davison, and Spady, 1995; Baggerly, 1998; and Tables 1 and 2 in Section 4 of this paper) seem to suggest in fact that the χ2 calibration itself is not very reasonable, implying that the practical usefulness of the Bartlett correction is limited.
Nonlinear regression models

Robust regression model

The results of the paper can be applied to test simple hypotheses for parameters defined in practice by any GS: e.g., they can be applied to the ELR test for generalized linear models considered by Kolaczyk (1994) and to the ELR test for generalized projection pursuit models considered by Owen (1992). Other examples include ELR tests for “moment” models similar to those considered (albeit in the more general context of weakly dependent observations) by Burnside and Eichenbaum (1996), and for nonlinear and robust regression models; the latter are considered in Section 4 of this paper.
On the other hand, the results of this paper do not cover the case of composite hypothesis. When nuisance parameters are present (even in the form of overidentifying restrictions), it is not clear from DL arguments what the higher order behavior of the ELR statistic should be, because the Bartlett-type identities do not hold for the nuisance parameters. This is the principal way in which dual (and hence empirical) likelihood shows different behavior from an ordinary parametric likelihood, and this implies that the profile ELR test obtained by maximizing out the nuisance parameters is in general not Bartlett-correctable (Lazar and Mykland, 1999). Whether it is possible to obtain higher order refinements to the distribution of profile ELRs is an open question that is relevant to econometrics, because the latter is typically characterized by (possibly overidentified) models with many nuisance parameters. One possibility is to adjust the critical values rather than the test statistics themselves using generalized Cornish–Fisher expansions (Hill and Davies, 1968). The calculations involved in such expansions are however notoriously difficult: computerized algebra or possibly a suitable bootstrap procedure might be very useful in this respect; see the discussion at the end of Corollary 7 in Section 3.
The remainder of the paper is organized as follows. The next section reviews briefly EL inference for GS, emphasizing its DL interpretation. Section 3 contains the main results of the paper. Section 4 considers two examples that illustrate the theory and reports the results of some Monte Carlo simulations used to assess the effectiveness of the Bartlett correction and bootstrap calibration in finite samples. Section 5 contains some concluding remarks and indications for future research. All the proofs are contained in the Appendix.
Throughout the rest of the paper we follow tensor notation and indicate arrays by their elements. Thus, for any index 1 ≤ rj ≤ q (j = 1,2,…,k), ar is an

-valued vector, ars is an
-valued matrix, etc. We also follow the summation convention; i.e., for any two repeated indices, their sum is understood. Finally the sum [sum ] and product [prod ] operators are intended, unless otherwise stated, as
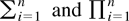
.
Suppose that the observations (zi)i=1n are i.i.d.
-valued random vectors from an unknown distribution F. Let
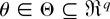
be an unknown parameter vector associated with F and E denote the expectation operator with respect to F. We assume that the information about F and θ is available in the form

for some specified value θ0 of θ, with the GS

-valued vector of known functionally independent functions, satisfying the following standard regularity conditions.
GS1. (i) E [fr(z,θ)] = 0 for a unique θ0 ∈ int{Θ}, (ii) fr(z,θ) is continuous at θ0 with probability 1, (iii) E [∂fr(z,θ0)/∂θs] is of full column rank q, (iv) E [fr(z,θ0) fs(z,θ0)] is positive definite.
The EL approach to inference for the parameter θ defined by the constraint (1) is based on the profile ELR function
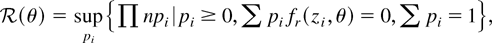
where pi = Pr(z = zi), which shows that EL inference may be interpreted as parametric likelihood inference using a data-determined multinomial distribution supported on the observations. Assume that

where ch{·} denote convex hull of the points fr(zi,θ), and suppose that we are interested in testing the hypothesis H0 : θ = θ0. A Lagrange multiplier argument shows (Owen, 1990) that the unique solution of (2) evaluated at θ = θ0 is given by pi = [n(1 + λrfr(zi,θ0))]−1, where λr = λr(θ0) is an
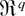
-valued vector of Lagrange multipliers determined by [sum ]fr(zi,θ0)/(1 + λrfr(zi,θ0)) = 0. Simple algebra shows that the log ELR test
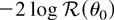
for the null hypothesis H0 : θ = θ0 is given by
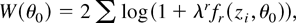
and Owen (1990) proves that, under GS1(iv) and EL,
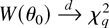
—similarly, confidence regions for θ may be obtained as the set of points θ such that W(θ) ≤ cα, where cα = Pr(χq2 ≤ cα) = 1 − α.
Suppose now that, for a fixed θ0, λ is regarded as a free-varying vector of unknown parameters and consider the following statistic:
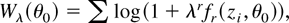
where the subscript λ is used to emphasize that (4) now depends on the unknown parameter λ. In the case of independent observations, Wλ(θ0) coincides with the logarithm of the DL Mykland (1995); the latter corresponds to the product integral of λrfr(zi,θ0) and can be viewed as a likelihood function for the parameter λ because, as long as fr(zi,θ0) is bounded and λ is contained in a neighborhood of 0,
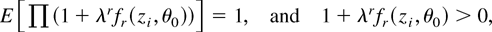
for small λ. A standard optimization argument shows that the ELR test of θ = θ0 defined in (3) is then equivalent to a DL ratio (DLR) test on the dual hypothesis H0 : λ = 0, i.e.,
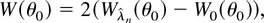
where W0(θ0) = Wλ(θ0)|λ=0 and
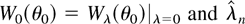
is the maximum DL estimator solution of the first-order conditions ∂Wλ(θ0)/∂λr = 0; we shall call the maximum DL estimator DLE.
As mentioned in the introduction, the equivalence between the ELR test of θ = θ0 and the DLR test of λ = 0 is crucial in the paper because it implies the possibility of analyzing the higher order properties of the ELR statistic using likelihood methods on the dual parameter λ instead. To elaborate further, let us introduce some additional notation: for k = (k1,…,kl) ∈ (Z+)l write

; let ∂kWλ(·) = ∂kWλ(·)/∂λr1…∂λrk and Γτ = Γ(0,τ) be an open sphere centered around 0 with radius τ > 0. Assume that for all λ ∈ Γτ
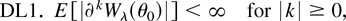
where the inequality should be interpreted componentwise. For |k| = 0, DL1 is a sufficient condition for showing the existence and consistency of the DLE
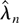
solution of ∂Wλ(θ0) = 0. To see this, notice that the
-valued matrix E [∂2Wλ(θ0)] is negative definite as long as 1 + λrfr(zi,θ0) ≥ 1/n (which is implied by the fact that under EL the set Sλ = {λr : 1 + λrfr(zi,θ0) ≥ 1/n} is closed convex and bounded). Therefore, by the implicit function theorem there exists a neighborhood Γτ where ∂Wλ(θ0) = 0 have a unique solution. Moreover, E [Wλ(θ0)] is uniquely maximized at λ = 0, and
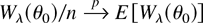
for all λ ∈ Γτ. Thus, given the strict concavity of Wλ(θ0) in Γτ, it follows by standard consistency results for concave objective functions (e.g., Theorem 2.7 of Newey and McFadden, 1994) that

.
For |k| ≥ 1, DL1 is a sufficient condition for interchanging the differential and integral operators in the equation ∂kE {exp[Wλ(θ0)] − 1} = 0; the latter can then be used to produce a new set of regularity conditions known in ordinary parametric likelihood theory as Bartlett identities (Bartlett, 1953). The resulting Bartlett-type identities relate linear combinations of expectations of DL derivatives and can be summarized concisely as
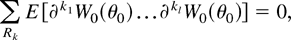
where ∂kjW0(·) = ∂kjWλ(·)|λ=0(j = 1,…,l) and the sum is over all partitions k1|k2|…|kl of the set of indices Rk. In practice (5) can be used as in parametric likelihood inference to simplify some of the expressions arising in the calculations of the higher order cumulants of the DLR statistic (see (A.20) in the Appendix), leading to the general result (13) about the Bartlett-correctability property of the DLR (whence of the ELR).
This section contains the main results of the paper. Section 3.1 derives valid Edgeworth expansions for the DLE and the ELR under both a sequence of local alternatives and the null hypothesis. Section 3.2 discusses how to estimate in practice the Bartlett correction, and Section 3.3 shows how the bootstrap and EL can be combined to produce highly accurate inference for the parameters defined by GS.
Let us introduce some additional notation and assumptions. Let ∥·∥ denote the Euclidean norm; assume that for all λ ∈ Γτ and some α,β ∈ Z+

where, for
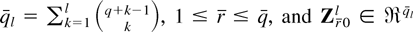
denote the vector containing all the different DL derivatives up to lth order evaluated at λr = 0. Conditions DL2 and DL3 are sufficient for proving the validity of Edgeworth expansions; notice that DL2 is satisfied if E∥ f (z,θ0)∥αβ < ∞.
Let

denote the formal Edgeworth expansion (Bhattacharya and Ghosh, 1978, eq. (1.14)) of the distribution of
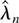
, where φq,κrs(·) denote the q-dimensional normal density with mean 0 and covariance κrs = E [fr(z,θ0) fs(z,θ0)] . The following theorem shows that the DLE admits a valid Edgeworth expansion in the sense of Bhattacharya and Ghosh (1978).
THEOREM 1. Assume that GS1, EL, and DL2 with α = 4, β = 3 hold. Then, for some constant C > 0,
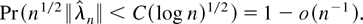
Furthermore, assume that the Cramér condition DL3 holds with l = 3. Then,
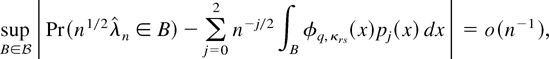
where
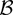
is the class of Borel subsets in
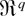
satisfying
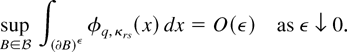
Before obtaining an Edgeworth expansion for the ELR under a sequence of local alternatives, we first discuss what type of local alternatives is consistent with the DL approach to EL inference. A simple modification of the argument of Mykland (1995, pp. 410–411) shows that the sequence of local alternatives induced by the DL is of the form
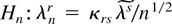
for some finite nonrandom vector

. This type of local alternatives assumes implicitly that the DL under the alternative hypothesis belongs to the same parametric subfamily specified under the null hypothesis (i.e., the product integral of λrfr(zi,θ0)), ruling out effectively the possibility of considering local alternatives where both λ and θ are allowed to depend on a sequence of local alternatives. This type of local analysis is introduced by Chesher and Smith (1997) as a generalization of the standard likelihood based local analysis (see, e.g., Peers, 1971) and requires the specification of an augmented local alternative of the form Hna : φn = [θn λn], where θn = θ0 + θ/n1/2 and λn = λ(θ/n1/2) = λ/n1/2 for some finite nonrandom vector θ. This general framework, however, might break down the DL construction for it requires the consideration of alternatives that might not necessarily lie in the (log)DL subfamily defined in (4). Bearing this in mind, it should be clear why the only sequence of local alternatives for the ELR consistent with the DL construction takes the form
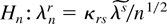
.
For simplicity we reparameterize Hn as
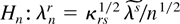
where κrs1/2 is the square root of the symmetric positive definite matrix κrs, and we define the scaled arrays (moments)
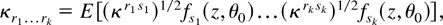
so that κrs = δrs—the Kronecker delta, i.e., δrr = 1, δrs = 0 for r ≠ s. Let Gq,τ(·) denote the distribution function of a noncentral chi square random variable with q degrees of freedom and noncentrality parameter τ. The following theorem shows that the ELR test under a sequence of local alternatives Hn admits a valid Edgeworth expansion in the sense of Chandra and Ghosh (1980).
THEOREM 2. Suppose that the assumptions of Theorem 1 hold. Then, uniformly in c ∈ [c0,∞) for some c0 ≥ 0 (c0 = 0 if r > 1),
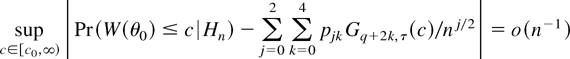
uniformly over compact subsets of
, where
and

where
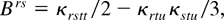
and, e.g.,
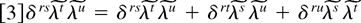
is the sum over the three different ways to partition a set of four indices into two subsets of two indices each.
The preceding expansion is useful for two reasons: first, it can be used to compute the approximate local power function of the test H0 : λ = 0 versus alternatives of the form
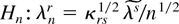
(i.e., Pr(W(θ0) > cα|Hn) where cα = Pr(χq2 ≥ cα) = α). Second, it can be used to obtain a valid Edgeworth expansion of the ELR statistic under H0 with remainder of order o(n−1). To improve the latter to the order O(n−2) we need to strengthen DL2 and DL3 as in the following corollary; let gq(·) denote the density of a chi square random variable with q degrees of freedom and let B = Brr.
COROLLARY 3. Assume that GS1, EL, and DL2 with α = 6 and β = 5 and DL3 with l = 4 hold. Then, for some c0 ≥ 0
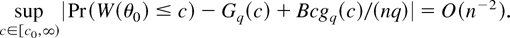
Let WB(θ0) = W(θ0)/(1 + B/(nq)) and cα = Pr(χq2 ≥ cα) = α. Then
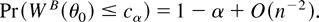
Expansion (12) shows clearly that the Bartlett factor B is the main error term for the ELR statistic; moreover because B enters linearly in the expansion it is clear that scaling W(θ0) by the same factor improves the coverage error to the order O(n−2), as in (13). This remarkable property of the ELR statistic is a direct consequence of the connection relating dual and empirical likelihood in the case of independent observations: because the ELR can be interpreted as a DLR for λ, and a DLR inherits properties of an ordinary parametric likelihood ratio statistic via the Bartlett-type identities (5), it is perhaps not surprising that the ELR shares the Bartlett-correctability property of an ordinary likelihood ratio statistic. In particular, as shown in the proof of Theorem 2 in the Appendix, the Bartlett-type identities (5) imply that, for DL2 with α = 5 and β = 4 and DL3 with l = 3, the signed square root Wr(θ0) of the ELR (i.e., an
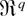
-valued random vector such that Wr(θ0)Wr(θ0) = W(θ0) + Op(n−3/2)) is asymptotically
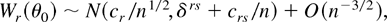
where cr and cr,s are constants defined as kr2 and kr,s3 (with
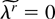
) in (A.20) in the Appendix. This result was originally proved by DiCiccio and Romano (1989), using a different technique involving some lengthy algebra, and shows that Wr(θ0) can be mean and variance corrected so that the resulting adjusted statistic is N(0,δrs) + O(n−3/2), as is typically the case for the signed square root of ordinary parametric likelihood ratios. The existence of a Bartlett correction for the ELR then follows from this result combined with an Edgeworth expansion argument. The latter shows in fact that the density of Wr(θ0)Wr(θ0) + Op(n−3/2) is proportional to exp(−x2/2)(x2)q/2−1[1 + ψ(x2)/n] + O(n−2) where ψ(x2) is a linear function in x2, so that scaling W(θ0) by a factor 1 + B/(nq) with B = cr cr + crr eliminates the coefficient of n−1 in the expansion of WB(θ0) yielding (13).
The Bartlett correction for GS
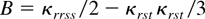
depends on the third and fourth multivariate moments of fr(z,θ0). The computation of the moments involved in the threefold summation in (15) takes O(nq3) computing time, so unless q is very large the computational cost of the Bartlett correction is not very high. Recall that B is based on the scaled moments κr1…rk = E [(κr1 s1)1/2fs1(z,θ0)…(κrk sk)1/2fsk(z,θ0)] and suppose that
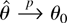
; then a simple estimator of (15) can be based on

where
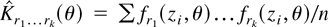
. The following theorem shows that
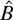
is consistent for (15) and that replacing B with
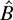
in Corollary 3 does not alter the order of magnitude of the approximation error (13). Let
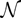
denote a neighborhood of θ0 and make the following assumption.

THEOREM 4. Assume that GS2 holds. Then,
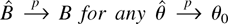
. Furthermore, suppose that the assumptions of Corollary 3 hold and that

. Then, for some c0 ≥ 0
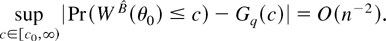
Remark. The assumption of i.i.d. sampling can be relaxed by considering (zin)i≤n,n≥1 as a triangular array of
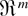
-valued random vectors as in Owen (1991); i.e., for each n, fr(z1n,θ),…,fr(znn,θ) are independent but not identically distributed
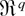
valued random vectors. The results presented in Sections 3.1 and 3.2 are still valid by replacing some of the previous regularity conditions with the following uniform (in n) version.
GS1. (i) E [fr(zin,θ0)] = 0 for a unique θ0 ∈ Θ for all n, (ii) lim infn→∞ ζn /n > 0, where ζn is the smallest eigenvalue of [sum ] E [fr(zin,θ0) fs(zin,θ0)],
GS2.
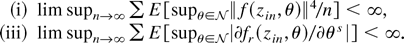
EL. Pr(0 ∈ ch{fr(z1n,θ0),…,fr(znn,θ0)}) = 1 as n → ∞,
DL2.

DL3. lim supn→∞ sup∥t∥≥δ|E [exp(ıtrZnr 0l)]| < 1 for all δ > 0 and some l ∈ Z+,
where Wnλ(·) and Znr 0l are, respectively, the log DL defined in (4) and the
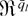
-valued vector of DL derivatives evaluated at λ = 0 for the triangular array fr(zin,θ0) n ≥ 1. In particular GS1, GS2(i), EL, and DL2(iii) with β = 3 and Znr 0l = Znr 0 for l = 1 imply Theorem 2 of Owen (1991), whereas DL2(i)–(ii) and DL3 imply that we can use Theorem 20.6 of Bhattacharya and Rao (1976) together with Theorem 3.2 and Remarks 3.3 and 3.4 in Skovgaard (1981) to justify the validity of the Edgeworth expansions in Theorems 1 and 2. The results shown in Section 3.3, which follows, are also valid by replacing BDL with uniform versions similar to those just shown.
In this section we consider the higher order properties of bootstrap dual/EL inference. Let χn* = (z1*,…,zn*) denote a bootstrap sample, i.e., a resample drawn independently and uniformly from the observed sample χn with the property that Pr(zi* = zj|χn) = 1/n for 1 ≤ i,j ≤ n, and let fr(zi*,θ0) denote the corresponding bootstrap GS.
We first consider bootstrapping the DLE
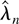
. Let
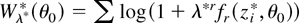
denote the bootstrap (log) DL where, in analogy to Section 2, the dual parameter λ*r is free-varying. The bootstrap DLE (BDLE)
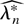
solves 0 = ∂Wλ**(θ0)/∂λr. Assume that for some α,β ∈ Z+ and γ > 0
BDL.

and let Pr* denote the bootstrap probability conditional on χn. The following theorem establishes the higher order equivalence between the original and BDLE.
THEOREM 5. Assume that GS1, EL, and BDL with α = 6, β = 3, and some γ > 0 hold. Then, for some constant C > 0

except if χn is contained in a set with probability o(n−1). Furthermore, assume that the Cramér condition DL3 holds with l = 3. Then, for every class
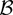
of Borel subsets in
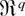
satisfying (8)
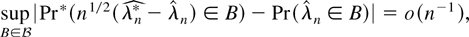
except if χn is contained in a set of probability o(n−1).
Notice that another way to express (18) (and analogously (19) and also (21), which follows) is
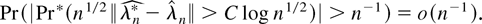
We now consider bootstrapping the ELR. It is important to note that the validity of the bootstrap in the context of EL inference depends crucially on the validity of the bootstrap moment condition E*[fr(zi*,θ)] = 0 at θ = θ0, where E* is the bootstrap expectation under Pr*. A straightforward method to achieve this is to consider the centered bootstrap GS fr*(zi,θ) = fr(zi*,θ) − E*[fr(zi*,θ0)] , which mimics the original GS as defined in (1) because by construction the bootstrap moment condition E*[fr*(zi,θ0)] = 0. Alternatively, we can consider the so-called biased bootstrap GS fr(zi[dagger],θ), where the zi[dagger]'s are resamples drawn independently from the original sample χn with the property that Pr(zi[dagger] = zj|χn) = pj for 1 ≤ i,j ≤ n, and the pjs are the estimated EL probabilities. This resampling procedure was proposed, originally in 1992, by Brown and Newey (2001) in the context of bootstrapping for generalized method of moments (GMM); the term biased used here is borrowed from Hall and Presnell (1999). Notice that fr(zi[dagger],θ) does not need to be centered, because by definition E[dagger][fr(zi[dagger],θ0)] = 0 where E[dagger] is the expectation under Pr[dagger]. Thus both methods lead to unbiased (conditional on χn) bootstrap GS at θ = θ0. The latter fact is the key to the validity of bootstrap ELR because it implies that the distribution of the bootstrap ELR (BELR) resembles the null distribution of the original ELR regardless of whether the null hypothesis is true or not. More important, at least in the context of this paper, the results of Brown and Newey (2001) (see also Horowitz, 2001) imply that biased bootstrap leads to the same theoretical improvements to the finite-sample distribution of the ELR statistic as those obtained using the standard (uniform) bootstrap (cf. Corollary 7). Bearing this in mind, in the remaining part of this section we consider bootstrap EL inference based on the centered bootstrap GS fr*(zi,θ).
An immediate consequence of centering is that the bootstrap equivalent of assumption EL holds, i.e.,
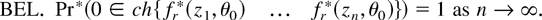
The latter implies that the bootstrap analogue of the profile ELR function defined in (2),
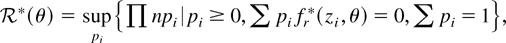
admits a unique solution at θ = θ0 and that such a solution can be obtained by the same Lagrangian argument of Section 2. Let
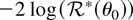
denote the resulting log BELR. Solving (20) and calculating
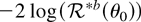
for b = 1,…,B bootstrap samples χn* yields an estimator of the distribution of the ELR that can be used to form critical values for test statistics (and/or confidence regions) in the usual way.
As in Section 2, the BELR
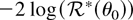
can be interpreted as a bootstrap DLR test for the dual parameter λ*r, i.e.,

where
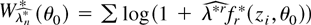
is the bootstrap DL based on the centered bootstrap GS fr*(zi,θ0), W0*(θ0) is the “restricted” bootstrap DL evaluated at λ* = 0, and
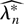
is the BDLE that solves 0 = ∂Wλ**(θ0)/∂λr using centered bootstrap GS fr*(zi,θ0). Note that because of the centering
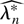
converges (in bootstrap probability) to 0 and not to the DLE

as in Theorem 5. Because W0*(θ0) = 0, let

; the following theorem shows that the BELR statistic approximates the distribution of the ELR statistic under the null hypothesis up to the order o(n−1).
THEOREM 6. Suppose that the assumptions of Theorem 2 with α = 6 hold. Then for some c0 ≥ 0
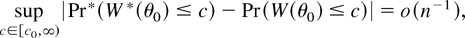
except if χn is contained in a set with probability o(n−1).
Notice that the moment assumption of Theorem 6 (which is slightly stronger than the one assumed in Theorem 2) is necessary to ensure that the BELR test is accurate up to o(n−1); i.e., the BELR test has rejection probabilities that are correct up to the same order. To see this note that (21) is equivalent to
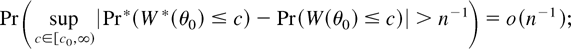
thus using the same arguments as Andrews (2002, pp. 149–150), it follows that for cα* = inf{c ∈ [c0,∞) : Pr*(W*(θ0) ≥ c) ≥ α}
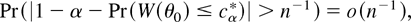
which implies that, for large n, |1 − α − Pr(W(θ0) ≤ cα*)| ≤ n−1, or equivalently
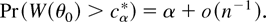
Thus, with the bootstrap calibration the level of ELR test is correct through the order O(n−1). In contrast, as shown in Theorem 2, the ELR test with χ2 calibration is accurate up to O(n−1). On the other hand, using a slightly refined argument based on generalized Cornish–Fisher expansions (Hill and Davies, 1968), the approximation error in (22) can be improved to O(n−2), as next corollary shows.
COROLLARY 7. Suppose that the assumptions of Corollary 3 with α = 8 hold. Then,
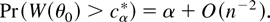
Corollary 7 shows that bootstrapping the ELR delivers the same type of higher order accurate inference implied by the existence of a Bartlett correction. The same phenomenon was noted by Beran (1988) in the context of bootstrap likelihood ratio inference. Unless dim[f (z,θ)] is very large, it is clear that the Bartlett-corrected ELR is computationally more convenient than the BELR. On the other hand, as already mentioned in the Introduction and further illustrated in Section 4 by some simulations, it seems that the BELR has better finite-sample accuracy than the Bartlett-corrected ELR. Moreover, the higher order refinements delivered by the bootstrap approach to ELR inference do not depend in general on Bartlett-type identities. This should be important when considering the ELR statistic with nuisance parameters. To see why, let η be a finite-dimensional vector of nuisance parameters and
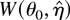
denote the resulting profile ELR (PELR) where
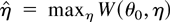
. As shown by Lazar and Mykland (1999) the fact that the Bartlett-type identities (5) do not hold for η implies that in general
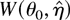
is not Bartlett-correctable. Suppose however that
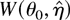
admits a valid asymptotic expansion in the sense of Chandra and Ghosh (1979) and that
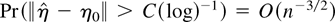
. Then, at least theoretically, generalized Cornish–Fisher expansions can be brought to bear to show that
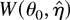
with adjusted critical values is accurate to an order O(n−2), independent of whether the Bartlett-type identities hold or not. Furthermore, using arguments similar to those used in the proofs of Theorem 6 and Corollary 7 in the Appendix it might be possible to obtain higher order refinements to the distribution of the PELR using critical values based on the bootstrap PELR
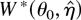
.
In this section, we illustrate the theory developed in the paper by considering EL inference for two classes of widely used econometric models that, as far as we know, have not been considered previously in the literature on EL. The finite-sample effectiveness of the two proposed methods to improve the accuracy of the ELR (i.e., Bartlett correction and bootstrap critical values) is illustrated by a small Monte Carlo study.
We consider nonlinear regression models y = g(xr,θ0r) + ε for a given (differentiable) parametric function g(·) and E(ε|xr) = 0. Following Newey (1990), the GS is given by
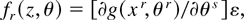
which corresponds to an IV based estimating function. Notice that as long as the regression function is correctly specified, we do not need to model explicitly the (conditional) variance σ2(x) of ε; clearly if we knew the functional form of σ2(x) we could use an IV based GS with instruments equal to ∂g(xr,θr)/∂θs and σ2(x)−1 to gain efficiency, but we stress here our view of the EL method as a technique to improve the accuracy of inference.
For this class of models the bootstrap calibration is based on the resamples (xir*,yi*), and the centered bootstrap GS is
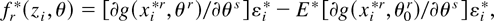
where εi* = yi* − g(xi*r,θ0r).
In the Monte Carlo study, we specify g(·) as exp(θ1 + θ2x) with x ∼ N(0,1) and ε ∼ N(0,1) or ∼t(5) or χ42 − 4. The values of θ1 and θ2 are both set equal to 1. Table 1 reports the finite-sample sizes of the ELR test (3), of the Bartlett-corrected ELR with the estimated Bartlett correction (16), and of the ELR with bootstrap critical values (23) of the null hypothesis H0 : [θ1 θ2] = [1 1] at 0.10, 0.05, and 0.01 nominal size. The results are based on 5,000 replications, and the bootstrap critical values are calculated from 1,000 bootstrap replications.
We consider robust regression models with fixed regressors xir that are assumed to satisfy max1≤i≤n∥xir∥ = O(1). The GS in this case is given by
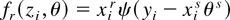
for the psi function
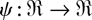
satisfying E [ψ(yi − xirθ0r)] = 0. For this model, the centered bootstrap GS is
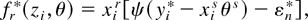
where yi* = xirθ0r + εi* is the bootstrap pseudo-observation, εi* is the bootstrap sample drawn from εi = yi − xirθ0r, and εn* = E*[ψ(εi*)] .
Following Huber (1973), we specify the psi function ψ(·) as
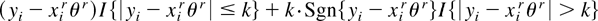
with the constant k = 1.4, the scale parameter σ2 = 1, and Sgn{·} denoting the sign function.
Table 2 reports some Monte Carlo results for a simple two covariates design with an intercept and a single fixed regressor xi generated as an equally spaced grid of numbers between −1 and 1 and points at −3 and 3, so that we have a rather substantial leverage effect. As with the previous example, the error ε is specified to be N(0,1) or t(5), or χ42 − 4, and the two parameters θ1 and θ2 are set equal to 1. Table 2 reports the finite-sample sizes of the ELR test (3), of the Bartlett-corrected ELR with estimated Bartlett correction (16), and of the ELR with bootstrap critical values (23) of the null hypothesis H0 : [θ1 θ2] = [1 1] at 0.10, 0.05, and 0.01 nominal size. The results are based on 5,000 replications, and the bootstrap critical values are calculated from 1,000 bootstrap replications.
Bearing in mind that the scale of the simulation study is small, the results of Tables 1 and 2 seem to indicate the following. First, with the exception of the nonlinear regression case with N(0,1) errors, the ELR test is characterized by a noticeable size distortion, although the distortion tends to diminish when the sample size increases. Not surprisingly, the size distortion is more severe for the skewed χ42 − 4 errors. Second, in the case of errors from a symmetric distribution, both the Bartlett correction and the bootstrap reduce the finite-sample size distortion of the ELR, although some size distortion is still present, especially at the 0.01 nominal level. On the other hand, for skewed errors the effectiveness of the Bartlett correction is reduced considerably. Finally, the ELR with bootstrap calibration has smaller size distortion than the ELR with a Bartlett-corrected χ2 calibration. The first point supports the findings of Corcoran et al. (1995) and Baggerly (1998) about the relative poor quality of the χ2 approximation to the distribution of the ELR statistic. The second point depends clearly on the form of the Bartlett correction (15), which implies that nonzero skewness typically reduces the magnitude of the Bartlett correction itself. The last point is related to the first one and should not therefore come as a surprise: the effectiveness of the Bartlett correction depends crucially on the quality of the χ2 approximation. Thus for data sets for which the latter is not reasonable there should be significant gains by using the bootstrap.
To conclude this section, it is worth mentioning that the EL framework can easily incorporate additional information, most noticeably information about the second moment. For example, the conditional variance σ2(x) of the innovations ε in Example I can be parameterized by a known function h(xr,ηa) that depends on an additional
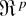
-valued vector of parameters ηa—which may include θr also—and, similarly, in Example II one can introduce an estimating equation for the scale parameter σ2.
In this paper we have developed some higher order asymptotic theory for the ELR test for parameters defined implicitly by GS. By exploiting the connection between empirical and dual likelihood we have obtained valid Edgeworth expansions for the distribution of the DLE and of the ELR. The latter is used to (i) derive an explicit expression of the third-order power function of the ELR under a sequence of local alternatives, (ii) justify rigorously the existence of a Bartlett correction for the ELR, and (iii) show that the “hybrid” bootstrap procedure suggested by Owen (1988) yields the same type of higher order accurate inference implied by the existence of a Bartlett correction for the ELR. The derivation of (i) and (ii) relies on a set of Bartlett-type identities that, apart from simplifying as in parametric likelihood inference some calculations, provide a simple explanation of the Bartlett-correctability phenomenon in the context of EL inference for GS.
The application of bootstrap methods in the context of EL inference seems very promising and suggests some directions for future research. First, ELRs with bootstrap calibration appear to have better finite-sample size properties than ELRs with a Bartlett-corrected χ2 calibration. This is certainly true in the Monte Carlo study reported in the paper; however, more simulation studies are required to support this conclusion in full generality.
Second, bootstrap methods might be used to deliver higher order refinements to the distribution of ELRs when nuisance parameters are present. We have conjectured that this might be the case as long as we can obtain Cornish–Fisher expansions for the critical values of the resulting profiled ELRs. This possibility is certainly of interest and is left for future research.
Finally, bootstrap methods can be used in the context of weakly dependent processes. Kitamura (1997) shows that it is possible to obtain higher order refinements to the distribution of the ELR statistic for smooth functions of means of α-mixing processes, using blockwise resampling techniques similar to those used in the bootstrap literature. The same methods could be used in the context of GS for time series models.
A Theorem on the Density of Generalized Noncentral Quadratic Forms and Its Application to Hermite Polynomials. The following theorem derives a general formula useful to express the density of generalized noncentral quadratic forms (i.e., of scalar random variables obtained by contracting nonzero mean normal random vectors over multidimensional arrays of constants) in terms of finite linear combinations of noncentral chi square random variables. The formula can be applied to obtain asymptotic expansions for test statistics under a sequence of local alternatives starting from the Edgeworth expansion of their corresponding signed square root, rather than from their approximate moment generating function.
Let φq,γ(·) denote the q-dimensional normal density with mean γ and identity covariance matrix and let gq,τ(·) denote the density of a noncentral chi square random variate with q degrees of freedom and noncentrality parameter τ < ∞.
THEOREM 8. Let wRk = wr1…wrk where each wrj ∼ φq,γ(w) (j = 1,2,…,k), bRk = br1…rk an
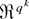
-valued array of constants not depending on n, tr an
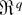
-valued vector of auxiliary variables, and ∂k(·) = ∂k(·)/∂tr1…∂trk. Consider the function
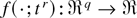
and make the following assumptions.
GQF1.
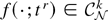
, the space of k times continuously differentiable functions on an open set
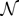
of tr = 0,
GQF2.
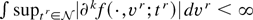
where the
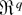
-valued vector vr is defined subsequently. Then, for any arbitrary noncentral k form wRkbRk, the following holds:
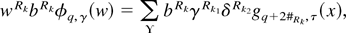
where
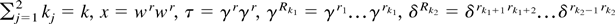
, the symbol #Rk denotes the number of different indices in the set Rk, and the sum is over ϒ = {ν2,…,νk}—the number of ways of partitioning a set of Rk indices into νj subsets containing j indices (j = 2,…,k) such that the resulting homogeneous polynomial in γRk1 is even or odd according to the number of indices in the set Rk.
Proof. We use the transformation from
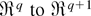
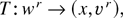
where x = wrwr, vr = wr/(wsws)1/2 and the following identity:
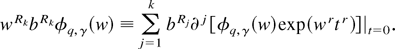
Using T, the density for x is obtained by integrating out the vector vr ∈ V1,q (i.e., over the unit sphere vrvr = 1 in
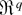
), i.e.,
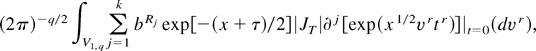
where |JT| = xq/2−1/2 is the Jacobian of the transformation T and (dvr) denotes the unnormalized Haar measure on the Stiefel manifold V1,q. Upon normalizing the Haar measure on V1,q by the constant 2πq/2/Γ(q/2) and interchanging differentiation and integration in (A.2), which is permissible under GQF2 for f (·,vr; tr) = exp(x1/2vrtr), we can then use Theorem 7.4.1 in Muirhead (1982) to obtain
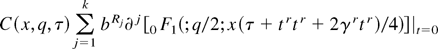
with
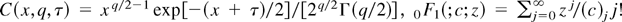
, and (c)j = Γ(c + j)/Γ(c). Differentiating (A.3) and evaluating the resulting derivatives at t = 0 yields a polynomial in x of degree at most k with coefficients given by
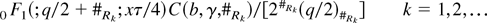
The constant C(b,γ,#Rk) in (A.4) is itself an even or odd polynomial in γRk1 with coefficients obtained by contracting accordingly the components of γRk1, δRk2, and bRk. Elementary symmetry considerations show that the number of such contractions can be found using standard combinatorial results on partitions reported, e.g., in Abramowitz and Stegun (1970, Table 24.2, p. 831). Combining (A.3) and (A.4), because gq,τ(x) = exp[−(x + τ)/2]xq/2−10 F1(;q/2; xτ/4)/2q/2Γ(q/2), (A.1) follows immediately. █
For generalized quadratic forms up to k = 6 (corresponding to the terms appearing in third-order Edgeworth expansions), (A.1) yields

from which the generalized quadratic forms bRkhRk (1 ≤ k ≤ 6) based on the multivariate Hermite polynomial hRk = hr1…rk = (−1)k∂kφq,γ(w)/∂wr1…∂wrk have densities

where ∇kgq,τ(·) is the kth-difference operator applied to the density gq,τ(·), i.e.,
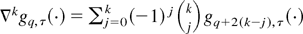
.
Proofs. Let C denote a generic positive constant not depending on n that may vary from one (in)equality to another. For simplicity of notation let W(θ0) = W and Wλ(θ0) = Wλ.
Proof of Theorem 1. We first establish (6). Let λRk = λr1…λrk; a Taylor expansion of the DL first-order condition 0 = ∂Wλ about 0 gives, for any λr ∈ Γτ,

where Rn(λ) ≤ C∥λr∥3max|k|=4 sup∥λ−λ∥≤τ|∂kWλ|/n. By DL2 for some Cε < ∞ and all ε > 0

where the first inequality follows by a moderate deviations result of Bhattacharya and Rao (1976, Corollary 17.12), the second by Rosenthal and Markov inequality, and the third by combining the second equality with the triangle inequality. Let Sn denote the union of the sets in (A.7); clearly Pr(Sn) = o(n−1), so that on the set Snc we can write (A.6) as λr = gn(λr) where gn(·) is a continuous function from
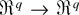
satisfying ∥gn(u)∥ ≤ Cn−1/2(log n)1/2 for all ∥u∥ ≤ Cn−1/2(log n)1/2. Application of Brower's fixed point theorem as in Theorem 2.1 of Bhattacharya and Ghosh (1978) and the concavity of Wλ show that there exists a unique sequence λnr such that Pr(∥λnr∥ < Cn−1/2(log n)1/2) ≥ 1 − Cn−1(log n)−2, whence (6). To derive the Edgeworth expansion (7), we first derive a stochastic expansion for
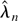
. For notational convenience let
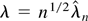
; define the following Op(1) random arrays:
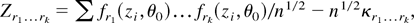
where κr1…rk = E [fr1(z,θ0)… frk(z,θ0)], and let
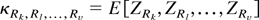
denote the vth-order (mixed) cumulant of ZRj = Zr1…rj.
Combining (A.7) and (A.8) yields
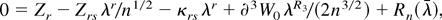
for ∥λ∥ ≤ ∥λ∥, where Pr(∥Rn(λ)∥ > Cn−2(log n)5/2) = o(n−1). Because λr = κrsZs + ζ1nr, where Pr(∥ζ1nr∥ > Cn−1/2(log n)) = o(n−1), and
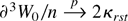
by the weak law of large numbers, (A.10) can be written as

where Pr(∥ζ2nr∥ > Cn−1(log n)3/2) = o(n−1). Upon substituting this last stochastic expansion into (A.10), because
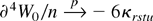
, we obtain the stochastic expansion

where Zr = κrsZs and Pr(∥ζ3nr∥ > Cn−3/2(log n)2) = o(n−1). To derive the Edgeworth expansion of λr on
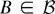
(the class of all Borel subsets of
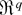
), notice that λr is a function of the three random arrays Zr, Zrs, and Zrst and recall that Zr3 is the
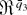
-valued vector containing all the different DL derivatives under H0 up to third order. Let γZr3(B) denote the (signed) measure corresponding to the characteristic function of Zr3 for
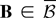
(the class of all Borel subsets of
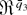
) and consider the following continuous transformation: Ur = χ(Zr3), where
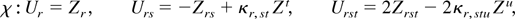
and κr,st and κr,stu are defined in (A.9). Let r1,…,rk denote indices each with
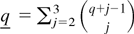
components, E(UrUs) = Σrs, E(UrUs) = Σrs = κrs, E(UrUs) = Σrs, κr1…rk = CUM(Ur1,…,Urk), the kth-order multivariate cumulant of Ur, and hr1…rk(u) = (−1)k(∂k/∂Ur1…∂Urk)φq, Σrs(Ur). Given the continuity of (A.12) and the independence of Ur from Urs and Urst we have that, for Zr3 ∈ χ−1(B), γUr(B) = γZr3 [χ−1(B)] is given by

Consider the following continuous transformation: Xr = ψ(Ur),
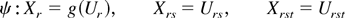
for

where Ur = κrsUs, κrst = κrr′κss′κtt′κr′s′t′, and κrstu = κrr′κss′κtt′κuu′κr′s′t′u′. By (A.7) there exists a C > 0 such that on the set SnU = {U : ∥Ur∥ < C(log n)1/2} the transformation ψ of (A.14) is a C∞ diffeomorphism on SnU onto its image. Set
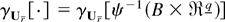
; clearly
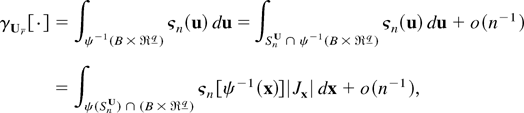
where |Jx| is the Jacobian of the transformation (A.14). Because
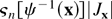
can be expressed as

for some polynomials qj(·), we can integrate Xr out, obtaining
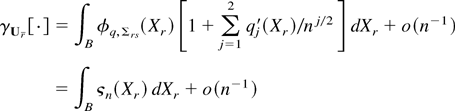
for some polynomials qj′(·). Thus by (A.15) we have that for λnr ∈ Bε with ε = Cn−3/2(log n)2
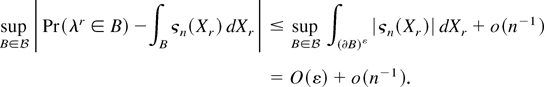
It remains to show that the density
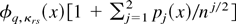
of the formal two-terms Edgeworth expansion of the DLE λr obtained by the delta method coincides with
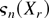
. Because λr is a maximum likelihood type estimator, its cumulants of order bigger than 4 are o(n−1), whence
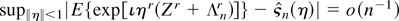
, where
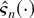
is the Fourier transform of
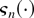
defined in (A.15). By Cauchy's estimates for derivatives of analytic functions (Bhattacharya and Rao, 1976, Lemma 9.2), we then have that all the derivatives of
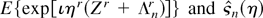
differ by o(n−1) at η = 0, implying that the two expansions are identical. █
Proof of Theorem 2. A Taylor expansion of W about the DLE λr and (A.7) show that on the same set Snc of Theorem 1 W = λrλs(∂2Wλ)pn(Zr1…rk,λr) + ζ4n, where pn(·) is a quartic polynomial in λr and the random variable ζ4n is such that Pr(|ζ4n| > Cn−3/2(log n)5/2) = o(n−1). By a further Taylor expansion of W about the normalized deviation n1/2ηr = ηr = (λr − λnr) and the second inequality in (A.7), we have that on Snc with Pr(Snc) = 1 − o(n−1) W admits the following stochastic expansion,

uniformly over compact subsets of
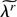
. Define the scaled arrays
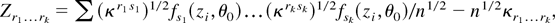
where κr1…rk = E [(κr1 s1)1/2fs1(z,θ0)…(κrk sk)1/2fsk(z,θ0)] . Substituting the stochastic expansion λr − λnr = Zr + Λnr + op(n−1) (where Λnr is as in (A.11)) in (A.16), some algebra shows that the stochastic expansion for the ELR statistic W under a sequence of local alternatives has signed square root Wr (i.e., WrWr + op(n−1) = W) given by

To prove (10), we first show that Wr admits a valid Edgeworth expansion in the sense of Bhattacharya and Ghosh (1978). Because Wr is a function of the first three DL derivatives, let γZr3(B) denote the measure corresponding to the characteristic function of the vector Zr3 (as in the proof of Theorem 1) and consider the same continuous transformation defined in (A.12), Ur = χ(Zr3) where
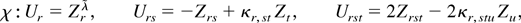
and
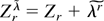
. Clearly (A.18) implies that γUr(B) = γZr3 [χ−1(B)] can be expressed using the same Edgeworth measure as in (A.13), the only difference being that the normal distribution appearing in the leading term has now nonzero mean
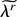
. Proceeding now as in the proof of Theorem 1, define Xr = ψ(Ur)
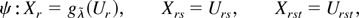
where

On the set SnU = {U : ∥Ur∥ < C(log n)1/2}, the transformation ψ defined in (A.19) is a C∞ diffeomorphism on SnU onto its image. Then, as in the proof of Theorem 1, the measure
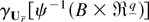
corresponding to the characteristic function of the inverse transformation of (A.19) can be expressed as in (A.15) for some polynomials qj′′(·) whose degree is even or odd according to j. Integrating out Xr, the joint expansion for Ur is then reduced to that of
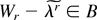
. It remains to calculate the formal Edgeworth expansion of

. Using the delta method, some algebra shows that the approximate cumulants for Wr are
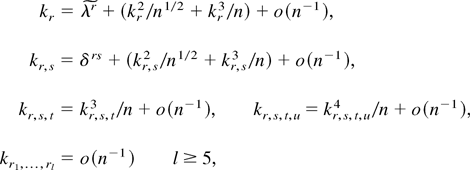
where kr = E(Wr), kr,s = Cov(Wr,Ws), etc., with

Applying now the Bartlett-type identities (5) to (A.20), it is straightforward to verify that κr,s,t − [3]κr,st + 2κrst = 0 and kr,s,t,u4 = 0. Thus, as in the conclusion of Theorem 1, for the class
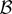
of Borel subsets in
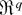
satisfying (8), the formal Edgeworth expansion of
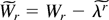
,
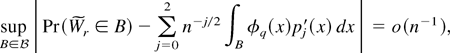
is valid in the sense of Bhattacharya and Ghosh (1978). The validity of expansion (10) follows by verifying that the conditions (a)–(c) of a theorem in Chandra and Ghosh (1980, p. 173) that we will denote as Theorem CG hold. By (A.17),
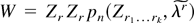
for 1 ≤ |k| ≤ 3 and pn(·) is a polynomial; therefore condition (a) of Theorem CG holds—in particular As (iv) (see p. 172) holds on the same set Snc of Theorem 1. Condition (b) of Theorem CG is a Cramér condition as assumed in DL3, whereas condition (c) of Theorem CG holds by the validity of (A.21). Expansion (10) is therefore valid in the sense of Chandra and Ghosh (1980). It remains to calculate the polynomials pjk in (10). By (A.21) and the linear transformation
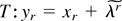
, we have that on Sc = {yr : yr yr ≤ c} for any c ∈ [c0,∞) with c0 ≥ 0

where ∂k = ∂k(·)/∂yr1…∂yrk and the cumulants krj, kr,sj (j = 2,3), and kr,s,t3 are defined in (A.20). Integrating (A.22) and using (A.5) yields
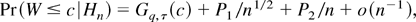
where

with
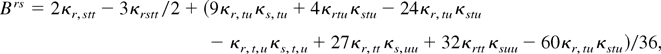
from which (10) and (11) follow after some algebra, noting that κr,stt = κrstt and κr,st = κrst. █
Proof of Corollary 3. By (essentially) the same arguments of Theorem 2, it is possible to show that, except on a set Sn with Pr(Sn) = o(n−2), Wr admits a stochastic expansion that depends on the first four DL derivatives Zr4 and that there exists a transformation ψ′ similar to the one given in (A.19) such that the measure corresponding to the characteristic function of (ψ′)−1 can be expressed as the product of a multivariate normal and some polynomials qj′′′(·)/nj/2 for j = 1,…,4. Then, the same integration argument giving (A.15) in the proof of Theorem 1 shows that Wr has a valid Edgeworth expansion up to o(n−2) whose coefficients cannot be written down explicitly. Thus, using the moment condition and Cauchy's estimates for derivatives of analytic functions (Bhattacharya and Rao, 1976, Lemma 9.2) it is possible to show that this expansion agrees with the formal four-terms Edgeworth expansion
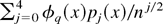
, i.e., for the class
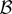
of Borel subsets in
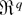
satisfying (8), the following expression,
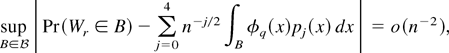
is a valid Edgeworth expansion in the sense of Bhattacharya and Ghosh (1978). Thus to show (12) it suffices to calculate
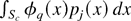
for j = 1,…,4, where Sc is a sphere in
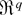
with radius c1/2 for some c ∈ [c0,∞). Integrating over the sphere Sc, using (A.5) (with γ = 0) and the standard argument based on the oddness/evenness property of the Hermite polynomials appearing in the Edgeworth expansion of W (Barndorff-Nielsen and Hall, 1988), gives the following Edgeworth expansion,
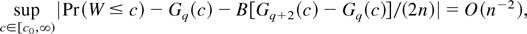
whose validity in the sense of Chandra and Ghosh (1979) follows, using the same arguments of Theorem 2, by the validity of (A.24). Let ∇Gq(·) = Gq+2(·) − Gq(·); noting that ∇Gq(·) = −2gq+2(·) and gq+2(c)/gq(c) = c/q, (12) follows immediately from (A.25). To prove (13) notice that by a Taylor expansion
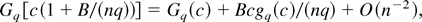
whence inserting (A.26) in (12) yields
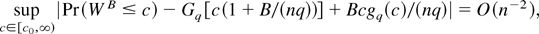
from which (13) follows. █
Proof of Theorem 4. We first show that
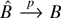
for any
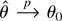
. Let fRk(z,θ) = fr1(z,θ)… frk(z,θ) and notice that by GS1(ii) fRk(z,θ) is continuous at θ0 with probability 1 (w.p.1) for k = 2,3,4; the consistency of
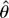
implies that there exists a δn → 0 such that
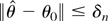
. Let Δf (θ) = sup∥θ−θ0∥≤δn| fRk(z,θ) − fRk(z,θ0)|; continuity of fRk(z,θ) at θ0 shows that Δf (θ) → 0 with probability 1. The dominance condition GS2(i) implies that
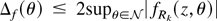
whence by dominated convergence E [Δf (θ)] → 0. By Markov inequality Pr(|[sum ]Δfi(θ)/n| > ε) ≤ E [Δf (θ)]/ε → 0 for all ε > 0. By the weak law of large numbers
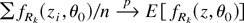
; moreover

Therefore, the triangle inequality implies that

. The consistency of
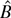
follows then by the continuity of tensor multiplication and matrix inversion. To establish (17) we use the following mean value expansion:
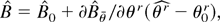
where
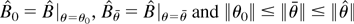
. Because by the weak law of large numbers
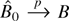
, it suffices to show that
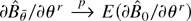
. This follows by the same argument used to establish
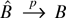
. Because by GS2(ii) the derivative ∂fRk(z,θ)/∂θr is continuous at θ0, it follows that Δ∂f (θ) = sup∥θ−θ0∥≤δn|∂fRk(z,θ)/∂θr − ∂fRk(z,θ0)/∂θr| → 0 (w.p.1), so that by GS2(iii),
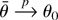
, and the triangle inequality we have that
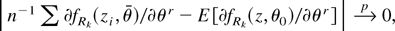
i.e., n−1 [sum ] ∂fRk(zi,θ)/∂θ = Op(1). By the n1/2 consistency of
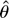
, the stochastic expansion (A.27) shows that
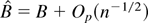
, whence by the delta method
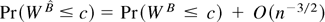
. The conclusion of the theorem follows by the oddness/evenness property of the Hermite polynomials as in Corollary 3. █
Let χn denote the observed sample. In what follows we write Pr(χn) = o(n−1) to denote the event “the observed sample χn is contained in a set of probability o(n−1).”
Proof of Theorem 5. We first show (18). Recall that ∂kWλ** = [sum ] fr1(zi*,θ0)… frk(zi*,θ0)/(1 + λ*rfr(zi*,θ0))k and that the BDLE
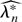
solves 0 = ∂Wλ**(θ0). By (A.7) and Markov inequality we have that for all ε > 0
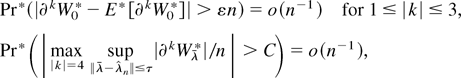
except if Pr(χn) = o(n−1). The triangle and Markov inequalities show that |E*(∂kW0*)| ≤ |E*(∂kW0*) − E(∂kW0)| + |E(∂kW0)| and Pr(|E*(∂kW0*) − E(∂kW0)| > ε) = o(n−1), implying that for 2 ≤ |k| ≤ 3 except if Pr(χn) = o(n−1)

Furthermore the moderate deviations estimates of Bhattacharya and Rao (1976, Corollary 17.12) show that for α = 6
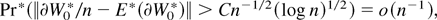
except if Pr(χn) = o(n−1). Let Sn* denote the union of sets where (A.28)–(A.30) hold, and consider a Taylor expansion of 0 = ∂Wλ**(θ0)/n about the DLE
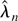
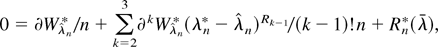
where

. A further mean value expansion of each of the
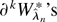
in (A.31) about 0, the uniform moment condition BDL(i) and (ii), and (A.28)–(A.30) show that outside the set Sn* with bootstrap probability Pr*(Sn*) = o(n−1), we can rewrite (A.31) as
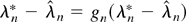
where the continuous function

satisfies ∥gn(u)∥ ≤ Cn−1/2(log n)1/2 for all ∥u∥ ≤ Cn−1/2(log n)1/2. Thus as in the proof of Theorem 1, Brower's fixed point theorem implies that there exists a sequence of random vectors
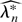
such that
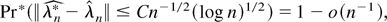
except if Pr(χn) = o(n−1). To prove (19) we follow the same arguments of Theorem 1. First, by repeated application of (A.28)–(A.30) it is possible to show that, except if
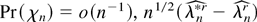
has the following stochastic expansion:
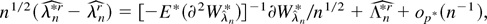
where

is an
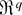
-valued function of the BDL derivatives (and their expectations) evaluated at
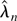
whose norm is Op*(n−1(log n)3/2) except if Pr(χn) = o(n−1) (i.e.,
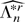
is the bootstrap analogue of Λnr given in (A.11)). Next by Lemma 2 of Babu and Singh (1984) the characteristic function of
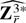
satisfies with probability 1
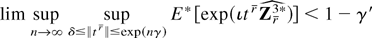
for some positive constants δ,γ,γ′, where
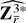
is the
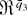
-valued vector containing all the different BDL derivatives (up to third order) evaluated at
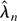
. Thus, as in Theorem 1, it is possible to show that except if Pr(χn) = o(n−1) for every class
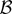
of Borel subsets in
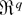
satisfying
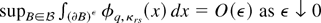
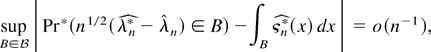
where
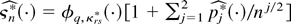
is the density of the empirical Edgeworth expansion obtained by replacing the population moments with their bootstrap analogue. Thus (19) follows if for all ε > 0
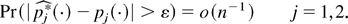
Because each bootstrap moment can be expressed as
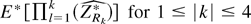
, and

where ZiRl is the ith component of the
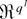
-valued array of DL derivatives evaluated at an arbitrary λ ∈ Γτ, (A.33) follows by verifying that for 1 ≤ |k| ≤ 4
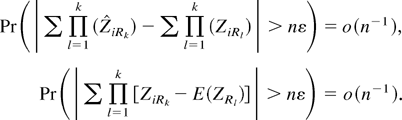
The first limit follows by a mean value expansion about 0. To see this notice that by the second equality in (A.7), we have

so that by the triangle inequality
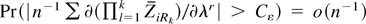
for some Cε < ∞, where
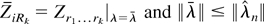
. Moreover by (6) and Markov inequality
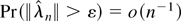
whence
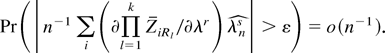
The second limit in (A.34) follows by Rosenthal and Markov inequality. █
Proof of Theorem 6. Let Zr1…rk* = [sum ] fr1(zi*,θ0)… fr1(zi*,θ0) and κr1…rk* = E*(Zr1…rk*/n) and notice that ∂kW0* = (−1)k−1(k − 1)(Zr1…rk* − κr1…rk*), where W0* = Wλ**|λ*=0 is the “restricted” BDL evaluated at 0. As in Theorem 5 we have that, except if Pr(χn) = o(n−1), for 1 ≤ |k| ≤ 3
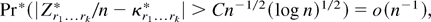
whereas by Markov inequality |κr1…rk* − κr1…rk| = op(n−1), so that
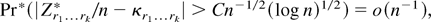
except if Pr(χn) = o(n−1). A Taylor expansion of W* about 0 gives
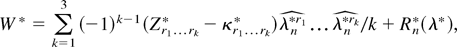
where
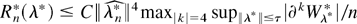
. As in Theorem 5 it is possible to show that
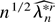
admits a stochastic expansion of the form
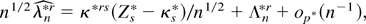
where κ*rs is the matrix inverse of κrs* and Λn*r is as in (A.32). Repeated applications of (A.35) show that
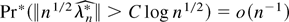
except if Pr(χn) = o(n−1), and thus by triangle inequality it follows that
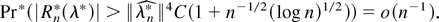
Substituting (A.37) into (A.36) shows that, except if Pr(χn) = o(n−1), the BELR admits the following stochastic expansion:
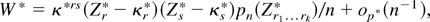
where pn(·) is a polynomial in Zr1…rk* with coefficients depending on κr1…rk*. Let Zr*c = Zr* − κr*; as in Theorem 2, we can obtain the signed square root decomposition of W* = κ*rsWr*Ws* + op*(n−1) with

which shows that, except if Pr(χn) = o(n−1), Wr* is a function of the first three BDL derivatives outside a set Sn* with bootstrap probability Pr*(Sn*) = o(n−1). Thus, by the same arguments of Theorem 5 it can be shown that Wr* admits a valid Edgeworth expansion in the sense of Bhattacharya and Ghosh (1978) except if Pr(χn) = o(n−1). Therefore following the same steps of Theorem 2 it can be shown that, except if Pr(χn) = o(n−1), W* admits the following valid (in the sense of Chandra and Ghosh, 1979) Edgeworth expansion

where B* = κrstu*κ*rsκ*tu/2 − κrtv*κsuw*κ*rsκ*tuκ*vw/3 is the bootstrap Bartlett correction, i.e., (16) at θ = θ0. By (A.34) we have
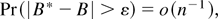
and thus combining (A.38), (A.39), and (A.25) yields

except if Pr(χn) = o(n−1). █
Proof of Corollary 7. As in the proof of Corollary 3 it is possible to show that the BELR admits a valid Edgeworth expansion up to o(n−2) except if Pr(χn) = o(n−2). Thus by the results of Corollary 3, Theorem 6, and the generalized Cornish–Fisher expansion formula of Hill and Davies (1968) it follows that the asymptotic expansions for the α point of W and W* are
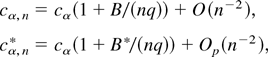
respectively, where cα = Pr(χq2 ≥ cα) = α. Therefore using the delta method, a Taylor expansion, and the Edgeworth expansion of W, we have
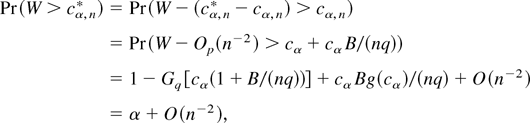
which shows that effectively the BELR accomplishes the Bartlett correction automatically. █

Nonlinear regression models

Robust regression model