Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-02-11T09:59:15.318Z Has data issue: false hasContentIssue false
  • English
  • Français

CONSISTENCY OF ASYMMETRIC KERNEL DENSITY ESTIMATORS AND SMOOTHED HISTOGRAMS WITH APPLICATION TO INCOME DATA

Published online by Cambridge University Press:  31 March 2005

Taoufik Bouezmarni  and
Olivier Scaillet
Taoufik Bouezmarni
Affiliation:
Institute of Statistics, Université Catholique de Louvain
Olivier Scaillet
Affiliation:
HEC Genève, Université de Genève and FAME
Rights & Permissions [Opens in a new window]

Abstract

We consider asymmetric kernel density estimators and smoothed histograms when the unknown probability density function f is defined on [0,+∞). Uniform weak consistency on each compact set in [0,+∞) is proved for these estimators when f is continuous on its support. Weak convergence in L1 is also established. We further prove that the asymmetric kernel density estimator and the smoothed histogram converge in probability to infinity at x = 0 when the density is unbounded at x = 0. Monte Carlo results and an empirical study of the shape of a highly skewed income distribution based on a large microdata set are finally provided.We thank O. Linton and the three referees for constructive criticism and M.P. Feser and J. Litchfield for kindly providing the Brazilian data. We are grateful to I. Gijbels, J.M. Rolin, and I. Van Keilegom for their stimulating remarks and to participants at the workshop on statistical modeling (UCL 2002), LAMES (Sao Paulo 2002), L1 Norm conference (Neuchatel 2002), Geneva econometrics seminar, and KUL econometrics seminar for their comments. Part of this research was done when the second author was visiting THEMA and IRES. The first, resp. second, author gratefully acknowledges financial support from the “Projet d'Actions de Recherche Concertées” grant 98/03-217, and from the IAP research network grant P5/24 of the Belgian state, resp. the Swiss National Science Foundation through the National Centre of Competence in Research: Financial Valuation and Risk Management (NCCR-FINRISK).

Type
Research Article
Information
Econometric Theory , Volume 21 , Issue 2 , April 2005 , pp. 390 - 412
Copyright
© 2005 Cambridge University Press

1. INTRODUCTION

The most popular nonparametric estimator of an unknown probability density function f is the standard kernel estimator. Its consistency is well documented when the support of the underlying density is unbounded. In the case of a bounded support we know that there exists a boundary bias (see, e.g., the estimation of Figure 3 in Section 5). This problem is due to the use of a fixed kernel that assigns weight outside the support when smoothing is carried out near the boundary. It is further known that the expected value of the standard kernel density estimator at x = 0 converges to the half value of the underlying density when f is twice continuously differentiable on its support [0,+∞). To solve this problem many remedies have already been suggested (see, e.g., Rice, 1984; Schuster, 1985; Müller, 1991; Marron and Ruppert, 1994; Jones, 1993; Jones and Foster, 1996). They include use of particular kernels or bandwidths.

Recently, Chen (2000) has proposed a gamma kernel estimator, and Scaillet (2004) has introduced inverse Gaussian (IG) and reciprocal inverse Gaussian (RIG) estimators for densities defined on [0,+∞). These estimators are based on asymmetric kernels that have flexible form and location on the nonnegative real line. The kernel shapes are allowed to vary according to the position of the data points, thus changing the degree of smoothing in a natural way, and their support matches the support of the probability density function to be estimated. The gamma, IG, and RIG kernel density estimators are simple to implement, free of boundary bias, and always nonnegative, and they achieve the optimal rate of convergence for the mean integrated squared error (MISE) within the class of nonnegative kernel density estimators. Furthermore, their variance reduces as the position where the smoothing is made moves away from the boundary. This is an advantage in estimating densities that have sparse areas because more data points can be pooled to smooth in areas with fewer observations. As pointed out by Cowell (2000), “Empirical income distributions typically have long tails with sparse data.” Hence it is expected that such estimators should perform well in practice on income data (this will be confirmed by our empirical results in Section 7). Note that, when the densities are defined on a compact support, similar estimators based on the asymmetric beta kernel have been proposed by Chen (1999) (for regression curve estimation, see also Brown and Chen, 1999; Chen, 2002) and have been applied in credit risk management by Renault and Scaillet (2003) to estimate the probability density function of recovery rates when corporate bonds default.

Although we concentrate in the sequel on the empirics of income distributions, the estimators considered in this paper are also relevant for applied work in insurance and finance. For example, Aït-Sahalia (1996a, 1996b) develops an estimation and specification testing procedure for diffusion models of the short-term interest rate. In this framework, the nonparametric estimation of the stationary distribution of the interest rate process plays a key role. Our results are also potentially important for estimation and specification testing of the baseline hazard function in autoregressive conditional duration (ACD) models. In this literature parametric models like the Burr and generalized gamma distribution are popular specifications for the baseline hazard. We refer to Engle (2000) for an overview and to Fernandes and Grammig (2000) for exploitation of asymmetric kernels in financial duration analysis. In insurance, a good understanding of the size of a single claim is of most importance. Loss distributions describe the probability distribution of a payment to the insured. Traditional methods in the actuarial literature use parametric specifications to model single claims. The most popular specifications are the lognormal, Weibull, and Pareto distributions (Klugman, Panjer, and Willmot, 1998). It is, however, unlikely that something as complex as the generating process of insurance claims can be described by just a few parameters. An incorrect parametric specification may lead to an inadequate measurement of the risk contained in the insurance portfolio and consequently to a mispricing of insurance contracts. Nonparametric density estimation is useful there also (see Bolancé, Guillen, and Nielsen, 2003, for a review; and Hagmann and Scaillet, 2003, for use of asymmetric kernels in that area). Clearly the standard kernel estimator is again not appropriate in these contexts, because it does not take into account that the underlying variables, interest rates, durations, and losses, are nonnegative.

In this paper we first analyze convergence of the asymmetric kernel density estimators for the class of density functions with support [0,+∞). Then we examine convergence of the smoothed histograms proposed by Gawronski and Stadtmüller (1980, 1981), which are also free of boundary bias and achieve the same rate of convergence.

The paper is organized as follows. In Section 2, we outline the framework and present both estimators, namely, the asymmetric kernel density estimator and the smoothed histogram. Particular examples are developed. Uniform weak consistency on each compact set in [0,+∞) is proved for both estimators in Section 3. The L1 convergence of the two estimators is established in Section 4. In Section 5, the density function f is assumed to be unbounded at x = 0, and we analyze the weak convergence of the two estimators to infinity at x = 0. To our best knowledge it is the first attempt at providing a consistent estimator for such a density (see, however, Marron and Ruppert, 1994; Bouezmarni and Rolin, 2002, 2003, but for densities defined on [0,1]). Relative consistency is also studied. Section 6 provides Monte Carlo results concerning the finite sample properties of the estimators for various distributions and parameter values. An empirical illustration on a large microdata set is provided in Section 7. We examine the shape of the Brazilian income distribution, which is notoriously known to be highly skewed with an accumulation of observed points near the zero boundary. In addition, a data-driven procedure based on the L1 distance (Hall and Wand, 1988) is discussed to select the bandwidth in practical situations. Section 8 contains some concluding remarks. An Appendix gathers the proofs. Finally, let us remark that secondary results have been deleted from the main text to save space. They are fully available in Bouezmarni and Scaillet (2003).

2. ASYMMETRIC KERNEL DENSITY ESTIMATORS AND SMOOTHED HISTOGRAMS

Let X1,…,Xn be a random sample from a probability distribution F with an unknown density function f. The most popular nonparametric estimator for the unknown probability density function f is the standard kernel estimator

where the kernel

is a symmetric density function and h is a smoothing parameter, called the bandwidth. When the density is defined on [0,+∞) the boundary bias of the standard kernel estimator is due to weight allocation by the fixed symmetric kernel outside the support when the estimation of density is made near the boundary. To overcome the problem a simple idea is to use a flexible kernel, which never assigns weight outside the support of the density function. This is the idea behind the first estimator considered in this paper, namely, the asymmetric kernel density estimator

where b is the bandwidth and the asymmetric kernel K is either a gamma density KG with parameters (x/b + 1,b), an IG density KIG with parameters (x,1/b), or a RIG density KRIG with parameters (1/(x − b),1/b). These densities correpond to

Note that these asymmetric kernels do not take the form κ(x − t,b) where κ is an asymmetric function (instead of a symmetric one) and thus do not belong to the class studied by Abadir and Lawford (2004).

The estimator

based on the gamma kernel was proposed by Chen (2000), whereas the IG and RIG kernel density estimators were proposed by Scaillet (2004). Figure 1 plots the shapes of the gamma, IG, and RIG kernels for some selected values of x and b = 0.2. It can be noticed that KG(t; x/b + 1,b) for x = 0 is decreasing for t > 0 and becomes unbounded at t = 0 when b shrinks to zero. This feature of the gamma kernel will be instrumental for convergence when the density is unbounded at x = 0 (see Section 5). Let us also remark that the asymmetric kernel density estimator is a particular case of the generalized kernel density estimator (Foldes and Revesz, 1974; Walter and Blum, 1979).

Shape of the gamma, IG, and RIG kernels K(x,b) for b = 0.2.

The second estimator considered in this paper is another particular case of the generalized kernel density estimator and is inspired by a well-known approximation theorem for continuous distribution (Feller, 1971, p. 219). It was developed by Gawronski and Stadtmüller (1980, 1981) and is called a smoothed histogram. It is defined by

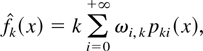
where the weights ωi,k are random. These weights are given by

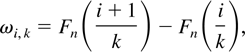
where Fn is the empirical distribution function, the integer k is the smoothing parameter, and pki(.) is based on use of either a family of lattice distribution or integrals of continuous distributions and satisfies Gawronski and Stadtmüller's conditions (for further details, see Gawronski and Stadtmüller, 1980, 1981).

Example 1

pki(x) corresponds to a Poisson distribution function with parameter kx, namely,

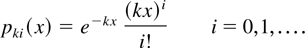
For this choice the smoothed histogram

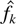
can be viewed as a random weighted sum (mixture) of Poisson mass functions or alternatively as a random weighted sum (mixture) of gamma density functions

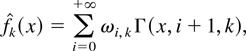
where Γ is the gamma density function

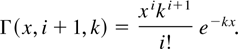
Figure 2 shows the different shapes of the gamma densities Γ(x,i + 1,k) = kpki(x) in the mixture for k = 3, and i = 0,1,2,3. Let us point out the decreasing shape of the gamma density for i = 0 and its unboundedness at x = 0 when k goes to infinity. We will come back to this characteristic in Section 5.

Shape of the gamma densities Γ(x,i + 1,k) with k = 3 and i = 0,1,2,3.

Example 2

where K(t; x,1/k) is either the IG kernel or the RIG kernel defined in (3) and (4) with a bandwidth equal to 1/k.

Gawronski and Stadtmüller (1980, 1981) found that smoothed histograms are free of boundary bias and that their rate of convergence for the MISE is O(n−4/5) for f in C2([0,+∞)). Using the Hadamard product technique, Stadtmüller (1983) proved the uniform consistency in probability for the estimators when the density function f is continuous and bounded on [0,+∞). We provide a simpler proof of this type of convergence in this paper.

3. UNIFORM WEAK CONVERGENCE OF ASYMMETRIC KERNEL DENSITY ESTIMATORS AND SMOOTHED HISTOGRAMS

In this section, we show that both estimators have the same asymptotic behavior. More precisely, we prove the uniform weak convergence on each compact set I in [0,+∞) of the asymmetric kernel estimator

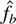
and the smoothed histogram

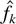
under some conditions on the smoothing parameter. To get our convergence results, we rely mainly on a large deviation device. Note further that the proofs differ completely from the proofs in the symmetric case. Here we cannot use the symmetry of the kernel and a usual change of variable, which both play a central role in deriving results for standard kernels.

The conditions on the bandwidth are as follows.

Condition 1 (Asymmetric kernel density estimator).

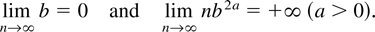
Condition 2 (Smoothed histogram).

The main result for the asymmetric kernel density estimator in this section is its uniform weak consistency under Condition 1.

THEOREM 3.1. (Uniform weak consistency of

). Let f be a continuous and bounded probability density function on [0,+∞),

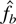
the asymmetric kernel density estimator, and I a compact set in [0,+∞). Then

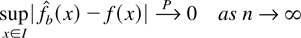
under Condition 1 with a = 1 for the gamma kernel and

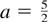
for the IG and RIG kernels.

Remark 1. We have the same result as that of Theorem 3.1 for a density estimator based on a general kernel k(t; x,b) under the following conditions, where a is a strictly positive number:

Note that we can also prove the uniform strong consistency on each compact set of the asymmetric kernel density estimator under a stronger set of conditions on the bandwidth b (see Bouezmarni and Scaillet, 2003, Corollary 3.1).

Similar results hold for smoothed histograms, namely, the following theorem.

THEOREM 3.2. (Uniform weak consistency of

). Let f be a continuous and bounded probability density function on [0,+∞),

the smoothed histogram, and I a compact set in [0,+∞). Then

under Condition 2.

Again uniform strong consistency on each compact set of the smoothed histogram can be obtained under a stronger set of conditions on the smoothing parameter k (see Bouezmarni and Scaillet, 2003, Corollary 3.2).

4. WEAK CONVERGENCE IN L1 OF ASYMMETRIC KERNEL DENSITY ESTIMATORS AND SMOOTHED HISTOGRAMS

The excellent monograph of Devroye and Gyorfi (1985) contains numerous results for the standard kernel density estimator in the L1 case (for SNP density estimators, see Fenton and Gallant, 1996). In particular many equivalences (types of convergence, conditions on bandwidth, etc.) are shown to hold. They advocate the L1 approach for three main reasons. First, it is a natural metric on the space of density functions. Second, it is proportional to the total variation metric. Finally, it is invariant under monotone transformations. Note that Hall and Wand (1988) (see also the proposal of Devroye and Lugosi, 1996; and the survey in Devroye, 1997) have proposed an algorithm that permits minimization of the L1 distance for different estimators, such as the standard kernel density estimator and the histogram. We investigate application of this type of algorithm later in the paper.

Hereafter we prove the consistency in L1 of the asymmetric kernel density estimator and the smoothed histogram.

THEOREM 4.1 (Weak consistency in L1 of

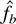
). Let f be a probability density function on

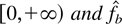
the asymmetric kernel density estimator. Then

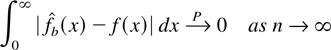
under Condition 1 with a = 1 for the gamma kernel and

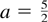
for the IG and RIG kernels.

THEOREM 4.2 (Weak consistency in L1 of

). Let f be a probability density function on [0,+∞) and

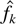
the smoothed histogram. Then

under Condition 2.

Let us remark that, if f is assumed to be twice continuously differentiable, Chen (2000) and Scaillet (2004) derive the rate of convergence of the MISE for asymmetric kernel density estimators.

Similar results are available in Stadtmüller (1983) for the smoothed histogram. Their pointwise results can also be easily used to build confidence intervals. In L1, the rate of convergence of the mean integrated absolute error remains an open question. We leave this task for future research (for the symmetric case where a complicated use of the slow convergence theorem is required, see Devroye and Gyorfi, 1985).

5. ESTIMATION OF UNBOUNDED DENSITIES AT x = 0

As already mentioned the standard kernel density estimator suffers from a boundary bias for the class of density functions defined on [0,+∞). Until now all previous methods aimed at removing this boundary bias have been developed under the assumption of a bounded density at x = 0. For such a class of density functions, we have just proved the convergence properties of asymmetric kernel density estimators and smoothed histograms. In this section, we consider a density function f defined on [0,+∞) and unbounded at x = 0. This obviously should induce a clustering of observations near the boundary. As shown in Figure 3 behaviors of the standard kernel density estimator and the true density can be dramatically different. This illustrative estimation has been performed on n = 200 data drawn from a gamma density Γ(λ,α) with α = 0.7 and λ = 2. We have used here a Gaussian kernel with a bandwidth minimizing the MISE. As far as we know only two methods have been shown to accommodate the case of an unbounded density: the complicated P and PD algorithms developed by Marron and Ruppert (1994) and the Bernstein polynomial and beta kernel estimators (Bouezmarni and Rolin, 2002, 2003). However the latter estimators do not apply here because they are designed for density functions defined on [0,1] (the P, resp. PD, algorithm further requires the presence of poles at both boundaries, resp. one boundary).

True density Γ(0.7, 2) together with its gamma kernel, smoothed histogram, standard kernel, and log-transformed kernel estimates, each based on 200 observations.

Coming back to Figure 3 we may observe that the gamma kernel density estimator and the smoothed histogram based on the Poisson distribution exhibit the same behavior at the boundary point and interior points as the true gamma density function Γ(0.7,2). In fact these two estimators satisfy the additional sufficient conditions needed to get weak convergence of the asymmetric kernel density estimator and smoothed histogram to infinity at x = 0.

THEOREM 5.1. Let f be a probability density function on [0,+∞), unbounded at

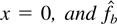
the asymmetric kernel density estimator. Under Condition 1 we have

if

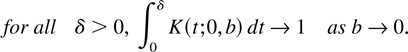
The additional condition in the preceding theorem can be checked for the asymmetric kernel density estimator based on the gamma kernel. Indeed we have for

.

Hence the gamma kernel density estimator gives almost all weight to the boundary point when the bandwidth converges to zero. This is due to the particular behavior of the gamma kernel at x = 0. The two other asymmetric kernels do not share this behavior and will not be suitable for estimation of unbounded densities. The second gamma kernel of Chen (2000), namely, KG(t;ρb(x),b) with ρb(x) = x/b if x ≥ 2b and ρb(x) = (¼)(x/b)2 + 1 if x ∈ [0,2b), also satisfies the additional condition of Theorem 5.1. As already mentioned in Chen (2000), we cannot use KG(t;(x/b),b) on the whole support because that kernel is unbounded on (0,b) and not defined at x = 0.

Let us now examine the case of smoothed histograms.

THEOREM 5.2. Let f be a probability density function on [0,+∞), unbounded at x = 0, and

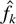
the smoothed histogram. Under Condition 2, we have

if

When pki(x) corresponds to a Poisson distribution, we have pk0(0) = 1, for all k, and the additional condition of the last theorem is fulfilled.

This means that the smoothed histogram based on the Poisson distribution gives a large weight to the boundary point. The convergence result should not come as a surprise in view of the particular behavior of kpki(x) at i = 0 (cf. Section 2).

We may also get relative convergence results in the same spirit as the result in Marron and Ruppert (1994). Note that these results hold trivially in the bounded case.

THEOREM 5.3. Let f be a density function in C1(0,+∞), unbounded at

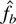
the asymmetric kernel density estimator. Then

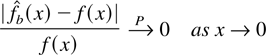
under the following conditions:

THEOREM 5.4. Let f be a density function in C1(0,+∞), unbounded at x = 0, and

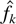
be the smoothed histogram. Then

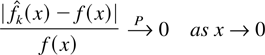
under the following conditions:

6. MONTE CARLO RESULTS

This section gathers some simulation results about the finite sample properties of the gamma kernel estimator and the smoothed histogram based on the Poisson distribution. We compare their properties with those of the Gaussian kernel estimator and a log-transformed Gaussian kernel estimator (transformation kernel density estimator based on the Gaussian kernel and the logarithmic mapping). We consider 10 test densities with a left end boundary. The group of densities contains bounded and unbounded densities with either a single mode or two modes:

Densities (e) and (i) correspond to the unbounded cases, whereas densities (i) and (j) correspond to the bimodal cases.

The study is based on 100 simulations for each density. For each simulation the bandwidth minimizing the L1 norm among a grid of values is chosen. Throughout we have a sample size of n = 200. Global performance is assessed in terms of the mean and variance of

on the 100 simulations. Tables 1 and 2 list results. They show that the gamma kernel estimator is always dominated by the smoothed histogram in terms of the mean of

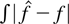
. Similar results also hold for the median (see Bouezmarni and Scaillet, 2003). The variance for the smoothed histogram is smaller for the first five densities and larger for the last five. When the shape is lognormal (density (a)) or close to (density (h)), the log-transformed kernel estimator performs better than the smoothed histogram and the gamma kernel estimator in terms of the mean. The variance in the log-transformed case is smaller for distributions (f), (g), and (i) when compared to the smoothed histogram and gamma kernel estimates. It is also smaller for distributions (b) and (c) with regard to gamma kernel estimates.

Mean of on 100 simulations

Variance of on 100 simulations

7. AN APPLICATION TO INCOME DATA

The empirical illustration concerns the analysis of the income distribution for Brazil in 1981. The estimation is performed on a comprehensive microdata set (n = 101, 864) already used in a study of the dynamics of income inequality by Cowell, Ferreira, and Litchfield (1998). These authors were interested in these data because of the importance of Brazil as a major world economy (ninth largest GDP) and the presence of a strong inequality in terms of percentage shares of income accruing to the richest and to the poorest of its population. This strong inequality is in fact revealed by the abnormal skewness of the income distribution (see Table 3 for the descriptive statistics). Income should be understood as gross monthly household income per capita denominated in 1981 cruzeiros, where the income receiver is the individual. Because lots of data are located near the boundary it would not be surprising that the true density is unbounded at the boundary.

Descriptive statistics of the Brazilian income distribution in 1981

Figure 4 compares the results of alternative estimation approaches. Figure 4a plots the gamma kernel estimator and the smoothed histogram based on the Poisson distribution together with a pseudo-maximum-likelihood estimate under a parametric assumption of a gamma distribution.

(a) The gamma kernel, smoothed histogram, and pseudo-maximum-likelihood estimates and (b) the standard kernel and log-transformed kernel estimates for the Brazilian income distribution in 1981.

The smoothing parameters b and k have been chosen according to a bandwidth selection method inspired by the proposal of Hall and Wand (1988), which leads to an asymptotically optimal window in the sense of minimizing the L1 distance. For the gamma kernel density estimator it consists in setting b* = n−2/5(u*)4, where u* is that value of u that minimizes

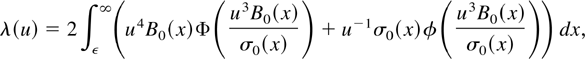
where ε is a small strictly positive number,

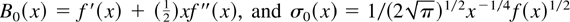
, whereas φ and Φ denote the normal density and distribution functions, respectively. The boundary value ε is set to avoid any problems coming from potential undefined derivatives at zero when performing numerical integration. We have taken ε = 10−15 in the simulation results presented here. The same procedure applies to the smoothed histogram based on the Poisson distribution by taking k* = (b*)−1 with B0(x) = (½)(f′(x) + xf′′(x)). Unknown quantities in criterion (7) have been computed from the fitted gamma distribution.

Estimated values for the gamma distribution are 0.9233, resp. 13,156, for the shape, resp. scale, parameter with standard deviation 1.59E-007, resp. 44.64. It is worth emphasizing that the estimate of the shape parameter yields an unbounded density at x = 0. The smoothing parameter values b* and k* based on this L1 reference density method with a parametric assumption of a gamma distribution (for further discussion in the context of standard kernel density estimators, see Devroye, 1997) are found to be b* = 0.02915 and k* = 33.

To check whether the chosen L1 reference density method is a satisfactory bandwidth selection procedure in practice, we have applied it on 10 simulated samples from the distribution (e) (unbounded gamma distribution) of Section 6. Table 4 shows that the values of the data-driven bandwidth are akin to the values of the optimal bandwidth, which entails similar performance in terms of

.

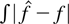
L1 errors for the gamma kernel density estimator and the smoothed histogram under optimal and data-driven bandwidths

Finally, Figure 4b plots standard nonparametric estimates performed with a Gaussian kernel on the raw data and log-transformed data (transformation kernel density estimator based on the logarithmic mapping). Bandwidth values are selected here by an L1 reference density method with a parametric assumption of a normal distribution for the raw data or the log-transformed data. This corresponds to taking

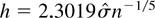
, where

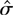
denotes the empirical standard deviation of the raw data or the log-transformed data. The difference between the two parts of the figure is striking and illustrates the practical relevance of the asymmetric kernel density estimator and of the smoothed histogram.

8. CONCLUDING REMARKS

We have studied consistency of two types of density estimators when the density function is defined on [0,+∞). These are the asymmetric kernel density estimator and the smoothed histogram. Simulation results show that they both have good finite sample properties and are able to avoid boundary bias existing in standard kernel density estimation. We think that they should be of some help in monitoring the evolution of the shape of density functions and that they should therefore be useful in applied work involving such nonparametric techniques (for example, see Härdle and Linton, 1994; Pagan and Ullah, 1999). This point has already been illustrated through a nonparametric estimation of the income distribution from a Brazilian microdata set. Nonparametric hazard rate estimation should be another important area of application (for a convincing use in goodness-of-fit testing procedures for duration models, see Fernandes and Grammig, 2000). Finally let us remark that the estimators examined in this paper may also be relevant for estimating a density that is known to exhibit symmetry with respect to a discontinuity point. For example, the product of two independent standard normal random variables has a density that is infinite at the origin and that can be represented by use of some hypergeometric functions (for several examples arising in econometrics, see Abadir and Paruolo, 1997; Abadir, 1999; Abadir and Rockinger, 2003). One may then suggest estimating the density on the absolute value of the observed data for points located on the nonnegative part of the real line and reflecting the estimated values for the points located on the negative part.

APPENDIX

Without loss of generality, we suppose that I = [η1,η2], 0 < η1 < η2, and x ∈ I.

Proof of Theorem 3.1. We begin with the usual inequality:

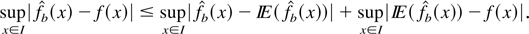
Because the second term is nonstochastic and converges to zero (see Bouezmarni and Scaillet, 2003, Proposition 3.1), we only need to prove that

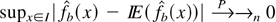
as n tends to infinity. For all x,

where C is a constant, a = 1 for the gamma kernel, and

for the IG and RIG kernels. In fact, we have for the gamma kernel

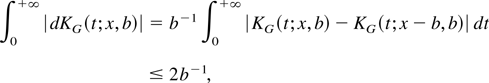
and it can be found that

. Now, applying the result in Massart (1990) on the Dvoretzky, Kiefer, and Wolfowitz (1956) inequality, we obtain

Proof of Theorem 3.2. It is clear that

For the nonstochastic term (see Bouezmarni and Scaillet, 2003, Proposition 3.2), there exists an integer n0(ε) such that

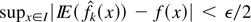
, for all n > n0(ε). Then, for all n > n0(ε),

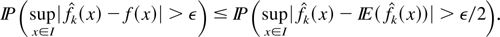
But we have for x ∈ I

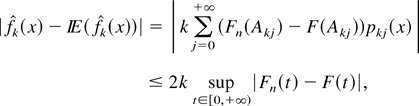
where Akj = (j/k,(j + 1)/k] j = 0,…. Hence the version of the inequality of Dvoretzky et al. (1956) given in Massart (1990) yields

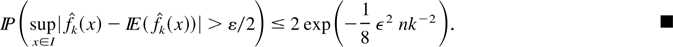
Proof of Theorem 4.1. From the convergence in L1 of the bias (see Bouezmarni and Scaillet, 2003, Proposition 4.1), it is sufficient to prove that

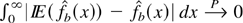
, as n → ∞. We have

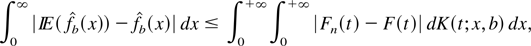
but ∫∫|dK(t; x,b)|dx = O(b−a), where a = 1 for the gamma kernel and

for the IG and RIG kernels. Then

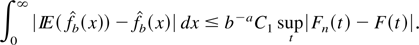
We finally get

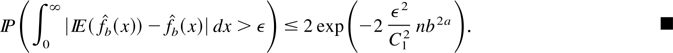
Proof of Theorem 4.2. From the convergence in L1 of the bias (see Bouezmarni and Scaillet, 2003, Proposition 4.2), it is sufficient to prove that

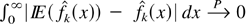
, as n → ∞. First, from the proof of Theorem 3.2 we know that

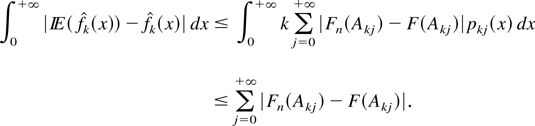
Second, from Devroye and Gyorfi (1985), we deduce that the last term converges in probability under Condition 2. █

Proof of Theorem 5.1. From the proof of Theorem 3.1, we have

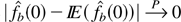
as nb2a becomes large, i.e.,

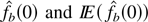
have the same asymptotic behavior as nb2a → ∞. Now we prove that

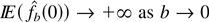
, i.e., for A > 0 there exists η > 0 such that

for all b < η. In fact, f (t) → +∞, as t → 0, and thus for A > 0 there exists δ(A) > 0 such that f (t) > 2A for all 0 < t < δ. Now

. If we suppose that for all

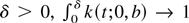
, as b → 0, we get

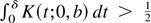
, for all b < η. Then, for A > 0 there exists η such that

, for all b < η, which leads to the stated result. █

Proof of Theorem 5.2. First, we show that

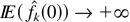
, as k → ∞, i.e., for A > 0, there exists k0 such that

, for all k ≥ k0. In fact, because f (t) → +∞, as t → 0, we have f (t) > 2A, for all k ≥ k1. Now if pk0(0) → 1, as k → +∞, we have pk0(0) > ½, for all k ≥ k2. Therefore,

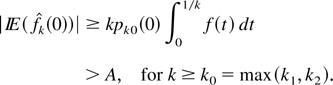
From the proof of Theorem 3.2, we know that

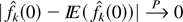
, as nk−2 → +∞, which completes the proof. █

Proof of Theorem 5.3. On one hand, we have

We get

and finally

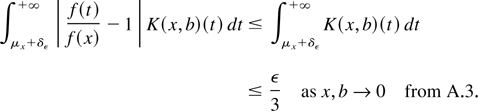
Hence we deduce

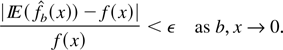
On the other hand, we have

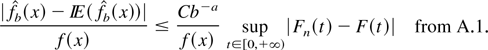
Now, from Massart (1990), we obtain

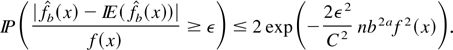
Equations (A.1) and (A.2) yield the stated result. █

Proof of Theorem 5.4. Let δ be a small positive number. We have

We get

whereas

Besides as in the proof of Theorem 3.2, we have

References

REFERENCES

Abadir, K. (1999) An introduction to hypergeometric functions for economists. Econometric Reviews 18, 287–330.Google Scholar
Abadir, K. & S. Lawford (2004) Optimal asymmetric kernels. Economics Letters 83, 61–68.Google Scholar
Abadir, K. & P. Paruolo (1997) Two mixed normal densities from cointegration analysis. Econometrica 65, 671–680.Google Scholar
Abadir, K. & M. Rockinger (2003) Density functionals with an option-pricing application. Econometric Theory 19, 778–811.Google Scholar
Aït-Sahalia, Y. (1996a) Nonparametric pricing of interest rate derivative securities. Econometrica 64, 527–560.Google Scholar
Aït-Sahalia, Y. (1996b) Continuous-time models of the spot interest rate. Review of Financial Studies 9, 385–426.Google Scholar
Bolancé, C., M. Guillen, & J.P. Nielsen (2003) Kernel density estimation of actuarial loss functions. Insurance: Mathematics and Economics 32, 3–18.Google Scholar
Bouezmarni, T. & J.M. Rolin (2002) Bernstein Estimator for Unbounded Density Function. Mimeo, Institut de Statistique, Université Catholique de Louvain.
Bouezmarni, T. & J.M. Rolin (2003) Consistency of beta kernel density function estimator. Canadian Journal of Statistics 31, 89–98.Google Scholar
Bouezmarni, T. & O. Scaillet (2003) Consistency of Asymmetric Kernel Density Estimators and Smoothed Histograms with Application to Income Data. DP 0306, Institut de Statistique, Université Catholique de Louvain.
Brown, B. & S.X. Chen (1999) Beta-Bernstein smoothing for regression curves with compact support. Scandinavian Journal of Statistics 26, 47–59.Google Scholar
Chen, S.X. (1999) A beta kernel estimator for density functions. Computational Statistics and Data Analysis 31, 131–145.Google Scholar
Chen, S.X. (2000) Probability density functions estimation using gamma kernels. Annals of the Institute of Statistical Mathematics 52, 471–480.Google Scholar
Chen, S.X. (2002) Local linear smoothers using asymmetric kernels. Annals of the Institute of Statistical Mathematics 54, 312–323.Google Scholar
Cowell, F. (2000) Measurement of inequality. In A. Atkinson & F. Bourguignon (eds.), Handbook of Income Distribution, pp. 87–166. North Holland.
Cowell, F., F. Ferreira, & J. Litchfield (1998) Income distribution in Brazil 1981–1990: Parametric and non-parametric approaches. Journal of Income Distribution 8, 63–76.Google Scholar
Devroye, L. (1997) Universal smoothing factor selection in density estimation: Theory and practice. Test 6, 223–320.Google Scholar
Devroye, L. & L. Gyorfi (1985) Nonparametric Density Estimation: The L1 View. Wiley.
Devroye, L. & G. Lugosi (1996) A universally acceptable smoothing factor for kernel density estimates. Annals of Statistics 24, 2499–2512.Google Scholar
Dvoretzky, A., J. Kiefer, & J. Wolfowitz (1956) Asymptotic minimax character of the sample distribution function and of the classical multinomial estimator. Annals of Mathematical Statistics 1, 444–453.Google Scholar
Engle, R. (2000) The econometrics of ultra-high frequency data. Econometrica 68, 1–22.Google Scholar
Feller, W. (1971) An Introduction to Probability Theory and Its Applications, vol. 2. Wiley.
Fenton, V. & R. Gallant (1996) Convergence rates of SNP density estimators. Econometrica 64, 719–727.Google Scholar
Fernandes, M. & J. Grammig (2000) Nonparametric specification tests for conditional duration models. Journal of Econometrics (forthcoming).Google Scholar
Foldes, A. & P. Revesz (1974) A general method for density estimation. Scientiarum Mathematicarun Hungarica 7, 90–94.Google Scholar
Gawronski, N. & U. Stadtmüller (1980) On density estimation by means of Poisson's distribution. Scandinavian Journal of Statistics 7, 90–94.Google Scholar
Gawronski, N. & U. Stadtmüller (1981) Smoothing histograms by means of lattice and continuous distributions. Metrika 28, 155–164.Google Scholar
Hagmann, M. & O. Scaillet (2003) Local multiplicative bias correction for asymmetric kernel density estimators. DP 91, FAME, Switzerland.
Härdle, W. & O. Linton (1994) Applied nonparametric methods. In R. Engle & D. McFadden (eds.), Handbook of Econometrics, vol. 4, pp. 2295–2339. North-Holland.
Hall, P. & M. Wand (1988) Minimizing L1 distance in nonparametric density estimation. Journal of Multivariate Analysis 26, 59–88.Google Scholar
Jones, M. (1993) Simple boundary correction for kernel density estimation. Statistics and Computing 3, 135–146.Google Scholar
Jones, M. & P. Foster (1996) A simple nonnegative boundary correction method for kernel density estimation. Statistica Sinica 6, 1005–1013.Google Scholar
Klugman, S., H. Panjer, & G. Willmot (1998) Loss Models: From Data to Decisions. Wiley.
Marron, J.S. & D. Ruppert (1994) Transformations to reduce boundary bias in kernel density estimation. Journal of the Royal Statistical Society, Series B 56, 653–671.Google Scholar
Massart, P. (1990) The tight constant in Dvoretzky-Kiefer-Wolfowitz inequality. Annals of Probability 18, 1269–1283.Google Scholar
Müller, H. (1991) Smooth optimum kernel estimators near endpoints. Biometrika 78, 521–530.Google Scholar
Pagan, A. & A. Ullah (1999) Nonparametric Econometrics. Cambridge University Press.
Renault, O. & O. Scaillet (2003) On the way to recovery: A nonparametric bias free estimation of recovery rate densities. Journal of Banking and Finance (forthcoming).Google Scholar
Rice, J. (1984) Boundary modification for kernel regression. Communications in Statistics—Theory and Methods 13, 893–900.Google Scholar
Scaillet, O. (2004) Density estimation using inverse and reciprocal inverse gaussian kernels. Journal of Nonparametric Statistics 16, 217–226.Google Scholar
Schuster, E. (1985) Incorporating support constraints into nonparametric estimators of densities. Communications in Statistics—Theory and Methods 14, 1123–1136.Google Scholar
Stadtmüller, U. (1983) Asymptotic distribution of smoothed histograms. Metrika 30, 145–158.Google Scholar
Walter, G. & J. Blum (1979) Probability density estimation using delta sequences. Annals of Statistics 7, 328–340.Google Scholar
Figure 0

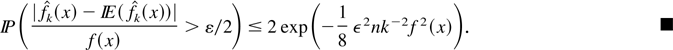
Shape of the gamma, IG, and RIG kernels K(x,b) for b = 0.2.

Figure 1

Shape of the gamma densities Γ(x,i + 1,k) with k = 3 and i = 0,1,2,3.

Figure 2

True density Γ(0.7, 2) together with its gamma kernel, smoothed histogram, standard kernel, and log-transformed kernel estimates, each based on 200 observations.

Figure 3

Mean of on 100 simulations

Figure 4

Variance of on 100 simulations

Figure 5

Descriptive statistics of the Brazilian income distribution in 1981

Figure 6

(a) The gamma kernel, smoothed histogram, and pseudo-maximum-likelihood estimates and (b) the standard kernel and log-transformed kernel estimates for the Brazilian income distribution in 1981.

Figure 7

L1 errors for the gamma kernel density estimator and the smoothed histogram under optimal and data-driven bandwidths