1. INTRODUCTION
It is often perceived that economic agents may show different
behavior depending on which regions some economic variables belong in,
though it seems hard to find explicit economic theory supporting such
behavior. For example, investors and households may make different
decisions regarding their investments and savings, respectively, when
interest rates are rising rapidly than when they are stable. Another
possible example is that employees under recession may behave
differently than under boom. Econometricians and statisticians have
developed several methods to study such behavior empirically, which
include, among others, switching regression (cf. Goldfeld and Quandt, 1973), threshold
autoregression (cf. Tong, 1983), and smooth
transition regression (cf. Granger and
Teräsvirta, 1993; Teräsvirta,
1998).
In this paper, we focus on the smooth transition regression (STR)
model. As argued in Granger and Teräsvirta (1993), the STR model is useful in explaining the
aggregate-level economy because the economy is likely to show smooth
transition if each economic agent switches sharply at different times.
Asymptotic theory for the STR model involving only stationary variables
can be inferred from standard theory in nonlinear econometrics (e.g.,
Newey and McFadden, 1994; Pötscher and Prucha, 1997). The reader is also
referred to Franses and van Dijk (2000) and
van Dijk, Teräsvirta, and Franses (2002)
for detailed discussions on the STR model.
However, general asymptotic theory for the STR model with
I(1) variables has not been developed yet. Recent work by Park
and Phillips (1999, 2001) provides methods for studying nonstationary
and nonlinear time series, but it seems difficult to apply these
methods in our context. One of the reasons for this is that we adopt a
more general assumption than martingale difference errors as in their
work. In addition, Chang and Park (1998)
study the STR model by using the methods of Park and Phillips (1999, 2001). However,
their model adopts martingale difference errors, and it seems that
their conventional asymptotics does not identify threshold parameters
(ci's in Section 2 of the current
paper).
Therefore, this paper studies asymptotic theory of the nonlinear
least squares (NLLS) estimator for the STR model with I(1)
regressors and I(0) errors. This model will be called the
cointegrating STR model in this paper. As in most cointegration models,
the regressors and errors are assumed to be dependent both serially and
contemporaneously. Because using the usual asymptotic scheme of sending
sample sizes to infinity seems to be difficult in the case of the
cointegrating STR model, we will use the triangular array asymptotics.
The triangular array asymptotics has been used, among others, in
Andrews and McDermott (1995) for nonlinear
econometric models with deterministically trending variables.
The asymptotic distribution of the NLLS estimator for the
cointegrating STR model involves a bias under the regressor-error
dependence, which implies that the NLLS estimator is inefficient and
unsuitable for use in hypothesis testing. Therefore, we propose a
Gauss–Newton type estimator that uses the NLLS estimator as an
initial estimator and is based on nonlinear regressions augmented by
leads and lags. Linear cointegrating regressions augmented by leads and
lags are studied in Saikkonen (1991),
Phillips and Loretan (1991), and Stock and
Watson (1993). The Gauss–Newton
estimator eliminates the bias and has a mixture normal distribution in
the limit, which implies that it is efficient and that standard
hypothesis tests can be performed by using the estimator.
Because the triangular array asymptotic methods have not often been
used in econometrics, one may rightfully question the finite-sample
properties of the tests and estimators using the methods. Therefore, we
report some simulation results, which indicate that the results
obtained from the triangular array asymptotics provide reasonable
approximations for the finite-sample properties of the estimators and
tests when sample sizes are moderately large.
The cointegrating STR regression model is applied to the Korean and
Indonesian data from the Asian currency crisis of 1997. The estimation
results partially support the interest Laffer curve hypothesis, which
states that higher interest rates may depreciate a currency when
interest rates are too high because excessively high interest rates may
increase the default risk by increasing the borrowing cost of
corporations, by depressing the economy and by weakening the banking
system of an economy (cf. Goldfajn and Baig,
1998). But overall the effects of interest rate on spot rate are
shown to be quite negligible in both nations. Considering the
ineffectiveness of high interest rates in stabilizing exchange rates
and the high economic cost associated with keeping high interest rates,
the appropriateness of tight monetary policy during the Asian currency
crisis should come into question.
The STR model has been used for some economic applications. The
applications are Teräsvirta and Anderson (1992) for modeling business cycle asymmetries;
Granger, Teräsvirta, and Anderson (1993)
for forecasting gross national product; Sarno (1999) and Lütkepohl, Teräsvirta, and
Wolters (1999) for money demand functions;
Michael, Nobay, and Peel (1997) and Taylor,
Peel, and Sarno (2001) for real exchange
rates; and Jansen and Teräsvirta (1996)
for consumption. Besides these, Luukkonen, Saikkonen, and
Teräsvirta (1988) consider testing
linearity against the smooth transition autoregression model.
The rest of the paper is organized as follows. Section 2 introduces
the model and basic assumptions. Section 3 studies asymptotic
properties of the NLLS and Gauss–Newton efficient estimators.
Section 4 reports some simulation results. Section 5 applies the STR
model to the data from the Asian currency crisis. Section 6 contains
further remarks. The Appendixes include auxiliary results and the
proofs of theorems.
A few words on our notation: all limits are taken as T
→ ∞. Weak convergence is denoted as ⇒. For symmetric
matrices the inequality A > B (A ≥
B) means that the difference A − B is
positive definite (semidefinite). For an arbitrary matrix A,
∥A∥ =
[tr(A′A)]1/2.
2. THE MODEL AND ASSUMPTIONS
Consider the cointegrating STR
where xjt is the jth component
of the I(1) vector xt (p
× 1), ut is a zero-mean stationary
error term, θ =
[c1′…cl′
γ′]′, and
g(xt;θ) is a smooth
real-valued transition function of the process
xt and the parameter vector θ.1
Although model (1) assumes that all the
regressors have a nonlinear effect on the regressand, our theoretical
results can readily be modified to the case where the nonlinearity only
appears in some of the regressors. In addition, our setup does not
allow for the possibility that different transition functions are used
for different regressors. But it would not be difficult to extend our
results to that case also. To simplify exposition, we have preferred to
work with a single transition function.
Moreover, μ,
ν, α
j, and δ
j are
scalar parameters.
The STR model (1) has been used to describe economic relations that
change smoothly depending on the location of some economic variables.
In model (1), the relationship between xt
and yt may change depending on where
xt is located relative to parameters
c1,…,cl.
Parameter γ in model (1) determines the smoothness of transition in
the economic relations. The reader is referred to Granger and
Teräsvirta (1993) for more discussions
on the STR model, although these authors do not explicitly consider the
case of I(1) processes.
We discuss some examples of model (1) by using the following
simplified version of model (1) where nonlinearity appears only in the
first regressor:
Example 1:
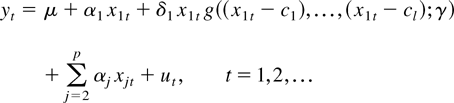
Here the transition function is a logistic function that makes the
regression coefficient for x1t vary
smoothly between α1 and α1 +
δ1. When the value of the regressor
x1t is sufficiently far below the value of
the parameter c the regression coefficient takes a value close
to α1, and when the value of the regressor
x1t increases and exceeds the value of the
parameter c the value of the regression coefficient changes
and approaches α1 + δ1.
Example 2:
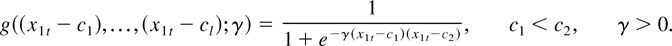
This transition function can be used when one wants to allow for the
possibility that the regression coefficient changes twice. When
|x1t| is large, the function
takes a value close to 1 so that the coefficient for
x1t approaches α1 +
δ1. But when x1t is
approximately between c1 and
c2, the function takes a value close to zero, which
makes the coefficient for x1t approach
α1. Instead of function (4), one may also use a linear
combination of two logistic functions.
When γ → ∞, functions (3) and (4) approach the
indicator functions 1{x1t ≥
c} and 1{c1 ≤
x1t ≤ c2},
respectively, and model (2) becomes close to a threshold regression
model. Then the change in the regression coefficient of
x1t is abrupt and not gradual as assumed
in (2). Our results do not apply to threshold models because the
transition function is not allowed to be discontinuous. Otherwise our
treatment is fairly general and applies to any sufficiently
well-behaved transition function.
We shall now discuss assumptions required for model (1). As already
mentioned, we make the following assumption.
Assumption 1.
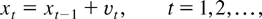
where vt is a zero-mean stationary
process and the initial value x0 may be any random
variable with the property
E∥x0∥4 < ∞.
Moreover, it will be convenient to assume that the (p +
1)-dimensional process wt =
[ut
vt′]′ satisfies the
following assumption employed by Hansen (1992) in a somewhat weaker form.
Assumption 2. For some r > 4, wt =
[ut
vt′]′ is a stationary,
zero-mean, strong mixing sequence with mixing coefficients of size
−4r/(r − 4) and
E∥wt∥r
< ∞.
Assumption 2 is fairly general and covers a variety of weakly
dependent processes. It also permits the cointegrated system defined by
(1) and (5) to have nonlinear short-run dynamics, which is convenient
because our cointegrating regression is nonlinear.
Choosing the real number p in Corollary 14.3 of Davidson
(1994) as 2r/(r + 2),
we find that Assumption 2 implies that the serial covariances of the
process wt at lag |
j| are of size −2. Thus, we have the summability
condition
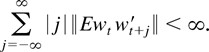
This implies that the process wt has a
continuous spectral density matrix
fww(λ) that we assume satisfies the
following assumption.
Assumption 3. The spectral density matrix
fww(λ) is bounded away from zero or that
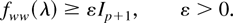
Assumption 3 specialized to the case λ = 0 implies that the
components of the I(1) process xt
are not cointegrated. In addition, it is required for the estimation
theory of Section 2 that (7) also holds for other values of λ.
Conformably to the partition of the process
wt, we write
fww(λ) =
[fab(λ)] where
a,b ∈ {u,v}.
Assumption 2 also implies the multivariate invariance principle
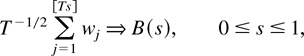
where B(s) is a Brownian motion with covariance
matrix Ω = 2πfww(0) (see Hansen,
1992, proof of Theorem 3.1). We partition
B(s) =
[Bu(s)
Bv(s)′]′ and
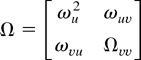
conformably with the partition of the process
wt.
As for the transition function g(x;θ), we make
the following assumption.
Assumption 4.
(i) The parameter space Θ of θ is a compact subset of an
Euclidean space.
(ii) g(x;θ) is three times continuously
differentiable on
where Θ* is an open set containing Θ.
This assumption may not be the weakest possible, but it is satisfied
by the most commonly used transition functions and simplifies
exposition. Thus, we shall not try to weaken it. The compactness of the
parameter space Θ is a standard assumption in nonlinear
regression, but no such assumption is needed for other parameters.
3. ESTIMATION PROCEDURES
The cointegrating regression (1) assumes serial and contemporaneous
correlation between the I(1) regressor
xt and the error term
ut. Adverse consequences of this on linear
least squares estimation are well known, and various modifications have
therefore been devised. In this paper, we extend the leads and lags
procedure of Saikkonen (1991) to the STR
model discussed in the previous section. Because there are some
theoretical difficulties with a direct extension of this procedure, we
will first consider the NLLS estimation that can be utilized to develop
a Gauss–Newton type leads and lags estimation.
3.1. Triangular Array Asymptotics
Before embarking on the subject of NLLS estimation, we will explain
the motivation for the employed asymptotic methods in this section.
There are two types of asymptotics that can be considered in nonlinear
regressions with I(1) regressors. One is the usual
asymptotics, and the other is the so-called triangular array
asymptotics in which the actual sample size is fixed at
T0, say, and the model is imbedded in a sequence of
models depending on a sample size T that tends to infinity.
The imbedding is obtained by replacing the I(1) regressor by
(T0
/T)1/2xt. This
makes the regressand dependent on T and, when T =
T0, the original model is obtained. Thus, if
T0 is large, the triangular array asymptotics can
be expected to give reasonable approximations for finite-sample
distributions of estimators and test statistics. The triangular array
asymptotics is also used in Andrews and McDermott (1995) for nonlinear econometric models with
deterministically trending variables. Related references can also be
found in Andrews and McDermott (1995).
We will use the triangular array asymptotics for our cointegrating
model, because we expect it to provide quite reasonable approximations
for estimators and test statistics and because some parameters cannot
be identified when the usual asymptotics is used. The identification
issue can be explained intuitively by using a special case of model
(1)—the model in Example 1. When the model in Example 1 is
applied, a typical situation is that the observations can be divided
into three groups with each group containing a reasonably large
proportion of the data. In the first and third group the values of the
regression coefficient for x1t are
essentially α1 and α1 +
δ1, respectively, whereas the second group contains part
of the sample where the value of the regression coefficient changes
between these two values. Because x1t is
an I(1) process, the use of conventional asymptotics means
that the variation of x1t increases so
that the proportion of observations in the first and third groups
increases and that in the second group decreases. Eventually the
proportion of observations in the second group becomes negligible. This
suggests that these parameters are unidentifiable in the limit, because
only observations in the second group provide information about the
parameters γ and c. This can also be seen by noting that,
for T large,
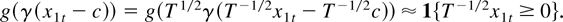
Thus, asymptotically the parameters γ and c vanish from
the model and become unidentifiable. This discussion implies that the
use of conventional asymptotics leads to a situation that is very
different from what happens in the sample where a reasonably large
proportion of observations belongs to the second group.
However, the triangular array asymptotics takes the second group and,
therefore, the parameters γ and c into account. Recall
that g(·;θ) is the logistic function. Basing the
asymptotic analysis on g(γ((T0
/T)1/2x1t
− c)) =
g(T−1/2γ(T01/2x1t
− T1/2c)) instead of
g(γ(x1t − c))
means that the slope of the logistic function is assumed to decrease so
that the proportion of observations in the three groups remains
essentially the same even though the variation of
x1t increases. In this respect the
situation for the triangular array asymptotics remains the same as for
the sample. It also makes sense that parameter c has to be of
order O(T1/2), because, due to the
increasing variation of x1t, a nonzero
value of c could otherwise be indistinguishable from zero.
Finally, note that when g(γ((T0
/T)1/2x1t
− c)) is used in asymptotic analysis the process
x1t is standardized in such a way that it
remains bounded in probability. In this context a possible
interpretation is that when T tends to infinity observations
of the standardized version of the series
x1t are obtained denser and denser within
its observed range in the sample, and thereby the proportion of
observations in each of the three groups remains essentially the same,
which makes information about parameters γ and c retained
even asymptotically.
Although the preceding discussion gives a reasonable motivation for
using the triangular array asymptotics, it would be imprudent to claim
that the triangular array asymptotics would always work well. For
instance, we already noted that problems may occur if the value of the
parameter γ in model (2) with specification (3) is large so that
the model is close to a threshold model.
3.2. NLLS Estimation
This section considers the triangular array asymptotics of the NLLS
estimator for model (1). To use the triangular array asymptotics, we
imbed model (1) in a sequence of models
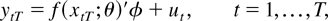
where xtT = (T0
/T)1/2xt,
f (xtT;θ) =
[1 g(xtT;θ)
xtT′
g(xtT;θ)xtT′]′
and φ =
[μ ν α′ δ′]′ with α =
[α1…αp]′
and δ =
[δ1…δp]′.2
In practice we always choose T =
T0, so that the transformation
xtT is not required. The transformation is
made only to facilitate the development of asymptotic
analysis.
In what follows we set ϑ = [θ′
φ′]′ and let ϑ0 =
[θ0′ φ0′]′
stand for the true value of ϑ. The NLLS estimator of parameter
ϑ0 is obtained by minimizing the function
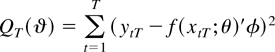
with respect to ϑ.
The assumptions made so far do not ensure that a minimum of function
(10) exists, even asymptotically. To be able to introduce further
assumptions, we first use the multivariate invariance principle (8) to
conclude that
.
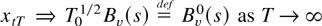
This fact and a standard application of the continuous mapping theorem
show that, for every θ ∈ Θ,
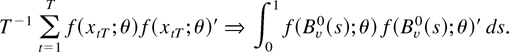
An assumption that together with our previous assumptions ensures
that the function QT(ϑ) has a
minimum for T large enough is as follows.
Assumption 5. For some ε > 0,
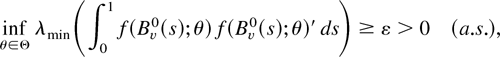
where λmin(·) signifies the smallest eigenvalue
of a square matrix.
Assumption 5 guarantees that, with probability approaching one, a
minimum of the function QT(ϑ)
exists as shown in Appendix B.
3 See Lemma
5 in Appendix A and the proof of Theorem 1 in Appendix B.
Because we are interested in asymptotic results, we may as usual assume
that a minimum exists for all values of
T and is attained at
.
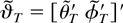
In addition to Assumption 5, the following assumption is needed for
the consistency of the least squares estimator
.
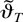
Assumption 6. For some s ∈ [0,1] and all
(θ,φ) ≠ (θ0,φ0),
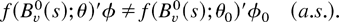
This is an identification condition that ensures that the parameters
θ and φ can be separated in the product f
(xtT;θ)′φ. Taken together,
Assumptions 5 and 6 ensure the identifiability of the parameter vector
ϑ.
The identification conditions (11) and (12) depend on the sample
paths of the Brownian motion
Bv0(s) and are
therefore different from the identification conditions used by Chang
and Park (1998), Chang, Park, and Phillips
(1999), and Park and Phillips (2001). However, conditions (11) and (12) are still
fairly easy to use. For instance, it can be checked by the conditions
that model (2) with specification (3) is identified when
δ1 ≠ 0 and γ > 0.
It may also be argued that it makes sense to use identification
conditions that depend on the sample paths of the Brownian motion
Bv0(s) when the
triangular array asymptotics is used. Indeed, in applications of model
(2) with specification (3), one can typically divide the observations
into three groups in such a way that a fair amount of observations
belongs to each group and, when the triangular array asymptotics is
used, this state of affairs prevails even asymptotically. Thus, because
xtT ⇒
Bv0(s), the triangular
array asymptotics in a sense conditions on such sample paths of
Bv0(s) for which the
shape of the function
g(γ(Bv0(s)
− c)) is similar to what is observed in the sample.
Because of this “conditioning,” it seems quite reasonable
to use identification conditions that depend on the sample paths of the
Brownian motion Bv0(s)
and ensure identifiability when the specified nonlinearity is related
to the sample paths of
Bv0(s) in the same way
as to the observed realizations of xtT
within the sample. This means, for instance, that in the case of model
(2) with specification (3) we are not interested in identification in
cases where sample paths of
Bv0(s) are such that
the function
g(γ(Bv0(s)
− c)) is effectively constant and identifiability is
very weak although it is still achieved when δ1 ≠ 0
and γ > 0. This point could be made even stronger by replacing
the logistic function by a piecewise continuous analog so that for some
realizations of Bv0(s)
the function
g(γ(Bv0(s)
− c)) would actually be constant and identifiability
would fail. Clearly, such cases would be of no interest if
g(γ(xtT − c))
is highly nonlinear within the sample.
The following theorem shows the existence and consistency of the
least squares estimator
.
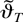
THEOREM 1. Suppose that Assumptions 1–6 hold. Then, a
NLLS estimator
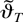
exists with probability approaching one and is consistent.
Theorem 1 shows the existence and consistency of the least squares
estimator
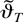
when the triangular array asymptotics is used. The following theorem shows
the limiting distribution of the estimator
.
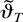
For this theorem we need an additional assumption.
Assumption 7.
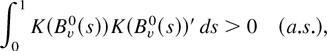
where
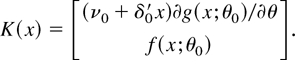
THEOREM 2. Suppose that Assumptions 1–7 hold and that
θ0 is an interior point of Θ. Then,
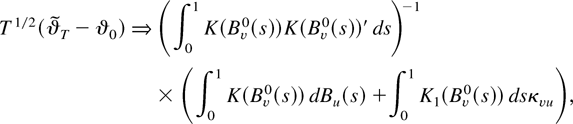
where
.
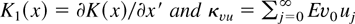
The limiting distribution given in Theorem 2 depends on nuisance
parameters in a complicated way that renders the NLLS estimator
inefficient and, in general, makes it unsuitable for hypothesis
testing. This difficulty is removed in a special case where the
processes vt and
ut are totally uncorrelated, because then
the limiting distribution becomes mixed normal as can be easily
checked.
In its general form, Theorem 2 shows that the NLLS estimator is
consistent of order
Op(T−1/2).
This will be used to obtain an efficient two-step estimator based on
the leads and lags modification. The reason why the order of
consistency differs from
Op(T−1) obtained
in previous linear cases is that we employ the triangular array
asymptotics in which the regressand is made bounded.
3.3. Efficient Estimation
This section considers efficient estimation of model (1) by using a
leads and lags regression. As in Saikkonen (1991), we can express the error term
ut as
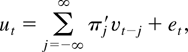
where et is a zero-mean stationary
process such that Eet
vt−j′ = 0 for all
j = 0,±1,…, and
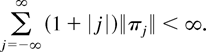
That this summability condition holds follows from condition (6) and
Theorem 3.8.3 in Brillinger (1975).
Expressions for the spectral density function and long-run variance of
the process et can be obtained from the
well-known formulas fee(λ) =
fuu(λ) −
fuv(λ)
fvv−1(λ)
fvu(λ) and
ωe2 =
ωu2 −
ωuvΩvv−1ωvu,
respectively.
Using equations (5) and (14), we can write the cointegrating
regression (1) as
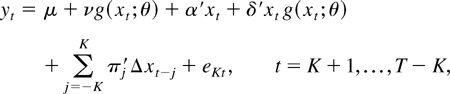
where Δ signifies the difference operator and
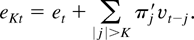
To eliminate errors caused by truncating the infinite sum in (14) we
have to consider asymptotics in which the integer K tends to
infinity with T. The condition K =
o(T3) used in the linear case by Saikkonen
(1991) can also be used here.
Because we continue with the same triangular array asymptotics as in
the previous section, we imbed model (16) in a sequence of models
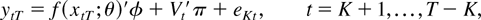
where Vt =
[Δxt−K′…Δxt+K′]′
and π =
[π−K′…πK′]′.
Combining the regressors as
q(xtT;θ) = [f
(xtT;θ)′
Vt′]′ we can write this model
more compactly as
where β =
[φ′ π′]′.
Instead of proper nonlinear least squares estimators of the
parameters in (18) we shall consider two-step estimators based on the
NLLS estimator of the previous section. These estimators are defined
by
where
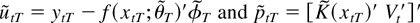
with
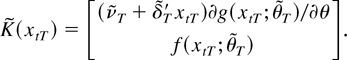
The latter term on the right-hand side of (19) is obviously the least
squares estimator obtained from a regression of
.
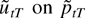
The estimator defined in (19) will be called the Gauss–Newton
estimator.
To see the motivation of the Gauss–Newton estimator, subtract
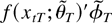
from both sides of (17) and apply the mean value approximation
to the
right-hand side. Thus, after linearization, we get the auxiliary regression
model
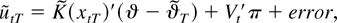
which in conjunction with standard least squares theory gives
estimator (19).
The following theorem describes asymptotic properties of the
estimators
.
The limiting distribution of the estimator
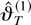
requires a standardization by the square root of T −
2K, the effective number of observations in the regression of
.
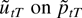
For convenience, we denote N = T − 2K.
THEOREM 3. Suppose that the assumptions of Theorem 2 hold and
that K → ∞ in such a way that
K3/T → 0 and
T1/2 [sum ]|
j|>K∥πj∥
→ 0. Then,
The independence of the Brownian motions
Be(s) and
Bv(s) implies that the limiting
distribution in Theorem 3 is mixed normal. Furthermore, we can conclude
from Saikkonen (1991) that the Gauss–Newton
estimator
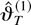
is asymptotically more efficient than the least squares estimator
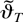
in general. In the same way as in Saikkonen (1991),
we have also here been forced to supplement the previously mentioned condition
K = o(T3) by an additional condition
that implies that the integer K may not increase too slowly.
Theorem 3 indicates that we can estimate
ωe2 consistently (see, e.g., Andrews, 1991) by using the residuals from the
regression model (16) with estimator (19). Thus, conventional tests
like Wald and t-tests can be constructed in a straightforward
manner and shown to have standard distributions in the limit.
4. SIMULATION
Implications of the theoretical results in Section 3 can be
summarized as follows. (i) The NLLS and Gauss–Newton estimators
are consistent. (ii) In large samples, the Gauss–Newton estimator
eliminates the bias in the limiting distribution of the NLLS estimator
and is more efficient than the NLLS estimator. (iii) The
t-test based on the Gauss–Newton estimator follows a
standard normal distribution in the limit. Because these results are
based on the triangular array asymptotics where the sample size of the
embedding model goes to infinity, it may not seem quite obvious whether
these results hold when the sample size T0 is
large. Therefore, this section examines the aforementioned results by
using simulation.
Data were generated by
Larger ω implies that the regressors and errors are more
correlated both serially and contemporaneously. We plotted a typical,
simulated data set with ω = 0.5 in Figure
1. It shows that the relation between the regressor and
regressand gradually changes as the value of the regressor becomes
closer to 5.
Data under smooth transition (T = 150, δ = 1, c
= 5).
Unreported simulation results indicate that it is difficult to
estimate parameter γ accurately by the NLLS method unless either
sample sizes are very large or parameter c is located close to
the median of {xt}, and the results also
indicate that other parameter estimates are quite adversely affected by
poor estimates of γ. No doubt, the occasional poor performance of
the NLLS estimator for unknown γ is neither related to the use of
triangular array asymptotics nor due to the presence of I(1)
variables. It may also occur when a given STR model involves only
I(0) variables for which standard asymptotics can be used.
Because the purpose of this section is to check the implications of the
triangular array asymptotics, we do not want our simulation results to
be affected by outliers produced by poor estimates of parameter γ.
Therefore, we assume that the value of the transition parameter γ
is known to be 1. Also, {xt} were
generated such that c is located in between the 15th and 85th
percentiles of {xt}. The purpose of this
scheme is the same as that of fixing the value of γ. When
c is near endpoints of the sample, extremely poor estimates of
parameter c are sometimes produced, which affects other
parameter estimates to the extent that evaluating their finite-sample
performance at different sample sizes becomes meaningless.
The estimators considered are the NLLS, one-step Gauss–Newton,
and two-step Gauss–Newton estimators.4
The one-step Gauss–Newton and two-step
Gauss–Newton estimators use the NLLS and one-step
Gauss–Newton estimators as initial estimators,
respectively.
The values of the leads and lags parameter for
the Gauss–Newton estimators were set at
K = 1,2,3.
Table 1 reports the empirical biases and root mean
squared errors (RMSEs) of the estimators at sample sizes 150 and
300.
5 We do not report the results for the
estimators of μ, because these are not the main concern in most
applications.
The numbers of replications at
T0 = 150 and
T0 = 300 were
5,000 and 3,000, respectively. As for the method of minimization, the
Polak–Ribiere conjugate gradient method
6 It was found that quasi-Newton methods tend to give more
outliers. The maximum number of iterations for optimization was set at
100,000.
was used. The results in
Table
1 can be summarized as follows.
- As sample size T0 grows, the RMSEs of all the
estimators decrease, which may be interpreted as evidence for
consistency.
- The Gauss–Newton estimators reduce the magnitudes of bias and
RMSE substantially in relation to the NLLS estimator as predicted by
Theorem 3.
- As the regressors and errors are more correlated both serially and
contemporaneously, the two-step Gauss–Newton estimator tends to
improve on the one-step Gauss–Newton estimator in terms of RMSE.
But the two-step Gauss–Newton estimator is sometimes more biased
than the one-step Gauss–Newton estimator, though the degree of
the biases for both the estimators is quite mild.
- The choice of the parameter K does not seem to affect the
results significantly.
- The nonlinear parameter c is subject to higher RMSE than
other linear parameters, which may reflect the computational
difficulties associated with estimating the nonlinear
parameter.
Biases and root mean squared errors
Table 2 reports empirical sizes of the
t-ratios using the Gauss–Newton estimators under the null
hypotheses α = 1, δ = 1, and c = 5. Nominal sizes were
chosen to be 5% and 10%, and the same experimental format as for Table 1 was used. The results in Table 2 can be summarized as follows.
- The t-ratios reject more often than they should in part
(a). But increasing the sample size T0 to 300
improves the performance of the t-ratios.7
Increasing the sample size to 500 further improves the
empirical size of the t-ratio, though the results are not
reported here.
- When there are fewer serial and contemporaneous correlations
between the regressors and errors at T0 = 300,
empirical sizes get closer to the corresponding nominal sizes. But this
is not noticeable at T0 = 150.
- The one-step and two-step Gauss–Newton estimators show
similar performance.
- Choosing K = 1 and K = 2 at
T0 = 150 and T0 = 300,
respectively, tends to provide the best results.
Empirical sizes of the T-ratios
In summary, the simulation results in Tables 1 and 2 seem to confirm
that the results from the triangular array asymptotics in Section 2 can
provide reasonable approximations for the finite-sample properties of
the estimators and tests when the sample size is moderately large.
5. AN EMPIRICAL EXAMPLE
One of the substantial controversies regarding the Asian currency
crisis of 1997 has been whether tight monetary policy was effective in
stabilizing foreign exchange rates during and in the aftermath of the
crisis. See Goldfajn and Baig (1998),
Kaminsky and Schmukler (1998), Ghosh and
Phillips (1998), Kraay (1998), Dekle, Hsiao, and Wang (1999), Park, Wang, and Chung (1999), and Choi and Park (2000) for empirical results regarding this issue.
In fact, tight monetary policy constituted an essential part of the IMF
rescue package for Asian countries, because it has conventionally been
believed that higher interest rates reduce capital outflows by raising
the cost of currency speculation and induce capital inflows by making
domestic assets more attractive in the short run and also that they
improve current account balance by reducing domestic absorption in the
long run.
However, as discussed in Goldfajn and Baig (1998), higher interest rates may depreciate a
currency when interest rates are too high because excessively high
interest rates may increase the default risk by increasing the
borrowing cost of corporations, by depressing the economy and by
weakening the banking system of an economy.8
In addition, Feldstein (1998),
Furman and Stiglitz (1998), and Radelet and
Sachs (1998a, 1998b), among others, argue that tight monetary
policy in Asia either was ineffective in stabilizing exchange rates or
may have even exacerbated the situation.
This hypothesis may
be called the “interest Laffer curve” hypothesis because
the effects of interest rates on spot exchange rates are hypothesized
to depend on the levels of the interest rates. This section employs the
model and asymptotic theory developed in previous sections to study the
interest Laffer curve hypothesis and reports the magnitudes of interest
elasticity of the spot rate for Korea and Indonesia during the Asian
currency crisis.
The uncovered interest rate parity relation predicts that log spot
rate is related to the difference of domestic and foreign interest
rates and log expected future spot rate.9
The uncovered interest rate parity relation is written as 1
+ it = (1 +
it*)St+1e/St,
where it and
it* denote the domestic and the foreign
interest rates at date t, respectively, and
St and
St+1e denote the spot
exchange rate at date t and the expected future spot exchange
rate at date t + 1, respectively. Taking logs of both sides of
the interest parity relation yields ln(St)
= ln(1 + it*) − ln(1 +
it) +
ln(St+1e) ≈
it* −
it +
ln(St+1e).
Though the relation predicted by the interest rate parity condition is
approximately linear, it indicates that the difference of the domestic
and foreign interest rates and the log expected future spot rate may be
considered as major variables explaining the spot rate. This
consideration leads us to employ the difference of the domestic and
foreign interest rates and the log expected future spot rate as
regressors in our nonlinear regression. But because the expected future
spot rate is not observable, forward exchange rate can be used as its
substitute. One may wonder at this point why we did not invoke the
covered interest parity relation from the beginning. However, in Korea,
there has been no well-developed forward exchange market. Without such
a market, it would be nonsensical to consider the covered interest
parity relation.
More specifically, the STR model we use in this section is
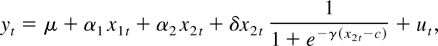
where yt and
x1t are the spot and forward rates,
respectively, and x2t is the difference
between the domestic and foreign interest rates (i.e.,
it −
it*). Because we are interested only in
the nonlinear relation between the spot rate and the interest rate
differential, the transition function includes only the interest rate
differential. Equation (21) signifies that the relation between the
spot rate and the interest rate differential changes when the latter is
well above the level c unless γ is zero. Thus, the model
is appropriate for studying the relation between the spot rate and the
interest rate differential, which may change depending on the level of
the interest rate differential.
The spot exchange rate data that we use are daily nominal exchange
rates of Korea and Indonesia vis-à-vis the U.S. dollar. For
forward exchange rates, 1-month maturity data are used. For Korea, we
use the forward exchange rate from the nondeliverable forward (NDF)
market.10
The NDFs are nondeliverable
forwards traded in the offshore market. Unlike the onshore forward
exchange rates, which have been influenced by direct regulation and
heavy intervention of the Korean government, we believe that the NDF
rates better reflect expectations of market participants.
For
Indonesia, we use data from their onshore forward exchange markets.
11 Because Indonesia had already liberalized
domestic foreign exchange markets, the Indonesian rupiah was not traded
in the NDF market.
For domestic interest rates, we use the
overnight call rates of each country. Because the overnight call rates
are the main monetary policy instruments of each country, they seem to
best reflect monetary policy stances of each country and could be
regarded as exogenous policy variables. The U.S. federal funds rate is
used as the foreign interest rate.
The whole sample covers the 19-month periods
4/1/1997–10/30/1998 for Korea and
1/3/1997–7/24/1998 for Indonesia. The sample
period for each country begins at about 6 to 7 months before the
eruption of its own currency crisis. The sample sizes for Korea and
Indonesia are 386 and 406, respectively. Figures 2 and 3 plot the Korean
and Indonesian data. These figures demonstrate the volatility
of the data during the sampling period.
Interest rate differential and spot rate (Korea).
Interest rate differential and spot rate (Indonesia).
The Dickey–Fuller-GLSμ test of Elliott, Rothenberg,
and Stock (1996) and the LM test of Choi (1994) were applied to the spot and forward rates
and the interest differentials for both Korea and Indonesia. The
results support the presence of a unit root at conventional levels, and
hence the theoretical results in previous sections are relevant here.
Truly, the interest differentials should be I(0) under normal
circumstances. Otherwise, there are unrealistically many arbitrage
opportunities. But during the currency crisis period, the test results
indicate that they look like I(1) at least in Korea and
Indonesia. Probably, market participants during the period did not
perceive the diverging interest differentials as arbitrage
opportunities in the light of the huge risks involved.
The results of the one-step and two-step Gauss–Newton
estimation of model (21) are reported in Table
3.12
Prior to estimating the STR
model, it is proper to perform linearity tests. But the linearity tests
for models with I(1) variables are not yet available, so we
bypass the stage of hypothesis testing.
The
Polak–Ribiere conjugate gradient method was used for initial
estimation as in Section 4. The results for Korea in
Table 3 show that the forward rate and interest
rate differential are significant at conventional levels excepting a
couple of cases.
13 Needless to say, this
statement assumes that the given nonlinear model represents the true
data generating process.
For the parameters inducing
nonlinearity, conventional hypothesis testing is difficult.
14 We thank Bruce Hansen for pointing out this
problem.
When δ = 0,
c and γ are not
identified. In addition, when γ = 0, δ and
c are not
identified. Thus, conventional testing procedures cannot be used for
δ and γ. Testing the null hypotheses δ = 0 and γ = 0 is
equivalent to testing the null of linearity. The standard errors for
the parameter γ are relatively high, which indicates the difficulty
of estimating the parameter. The location parameter
c is
estimated to lie between 13.80 and 16.43 depending on the choice of the
leads and lags parameter
K and the estimation method.
15 These results are based on the assumptions
that the error term in equation (21) is I(0) and that
regressors are not cointegrated. Formal tests for cointegration for the
STR model are not yet available. But fitting the AR(1) regression for
the residuals from equation (21) using the parameter values in the
first row of Table 3, we obtained AR(1)
coefficient estimate 0.557 and corresponding standard error 0.043.
Similar results were obtained for other parameter values. Thus, it
seems unlikely that the residuals are I(1). In addition, we
tested for cointegration between the future rates and interest
differentials but found no evidence of cointegration.
Gauss–Newton estimation results
For Indonesia, nonlinear effects of the interest differentials seem
to be weak relative to Korea, though coefficients for the forward rate
and the interest differential (α1 and α2)
are significant at conventional levels. The estimates of the location
parameter c are similar in magnitudes to those for Korea,
though Indonesia experienced much higher interest rates than Korea
during the period of currency crisis.16
Indonesia's maximum call rate during the sample
period was 91.5%, and the average was 29.4%. But the maximum and
average for Korea were 35% and 15.6%, respectively.
The results in Table 3 indicate that the
future rates are quite important in explaining the spot rates given the
magnitudes of the coefficient estimates. But the coefficient estimates
for the terms involving the interest differentials are close to zero.
To visualize the nonlinear effects of the interest differentials, we
draw the interest differential elasticity of spot rate in Figures 4 and 5 by assuming that
the estimation results in Table 3 (using the
one-step estimation method with K = 1) represent the true
relation.17
Ignoring the error term in
equation (21) and assuming that the parameter estimates are the true
parameter values, the elasticity was calculated by using the formula
∂yt/(1/x2t)∂x2t
= ∂yt/∂
ln(x2t) . Here the partial derivative is
multiplied by x2t, because log was taken
for the spot rate but not for the interest differential.
Interest elasticity of spot rate (Korea).
Interest elasticity of spot rate (Indonesia).
Figures 4 and 5
show that when the interest differentials take values lower than
approximately 11% and 12% for Korea and Indonesia, respectively, the
conventional wisdom that increasing interest rate helps stabilize spot
rate seems to be supported. But when the interest differentials take
higher values up to approximately 28% and 16% for Korea and Indonesia,
respectively, the elasticities become positive, which implies that
increasing interest rate has negative effects on stabilizing spot rate.
When the interest differentials are above 28% and 16% for Korea and
Indonesia, respectively, the elasticities become negative again.
Figures 4 and 5
partially support the interest Laffer curve hypothesis. But they also
indicate that tight monetary policy is effective, though very weakly,
when interest rates are very high. Notwithstanding this remark, we
conclude from the magnitudes of the elasticities shown in Figures 4 and 5 that the effects
of interest rate on the spot rate are negligible in either
direction.18
Choi and Park (2000) also report that interest differential did
not cause spot rate in both the short and long runs during the Asian
currency crisis.
For example, when the interest differential
is 30% for Korea, the elasticity is only −0.007. This implies
that raising the interest differential from 30% to 33% (i.e., a 10%
increase) has the effect of appreciating the Korean currency by only
0.07%. Considering the fact that the currency was depreciated by
approximately 30% on the average during the sampling period, such a
meager effect is certainly unsatisfactory to the Korean economy. This
is more so when one considers the negative effects of an interest rate
increase of such magnitude on the corporations and banking system of
the economy.
6. FURTHER REMARKS
We have analyzed and applied the cointegrated STR model in this
paper. However, there are a couple of topics that deserve our attention
but were not studied in this paper. First, methods for testing
linearity in the presence of I(1) variables are not yet
available but are useful for empirical analyses. Because nonlinear
models are flexible, they may give a good in-sample fit even when the
true model is linear. Thus, testing linearity prior to nonlinear model
fitting is important. Second, testing for cointegration for the STR
model should precede estimation, but relevant methods are not yet
available. We hope that these topics can be studied in the future by
the authors and other researchers.
APPENDIX A: AUXILIARY LEMMAS
We shall first prove some auxiliary results that may also have
applications elsewhere. Recall the notation N = T
− 2K and note that a (possibly) matrix-valued function
h(x) defined on
is said to be locally bounded if ∥h(x)∥ is bounded
on compact subsets of
.
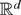
LEMMA 1. Let h(x) be a locally bounded,
vector-valued function defined on
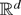
(d < ∞) and let {εt,
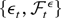
be a square integrable martingale difference sequence such that
supt
E∥εt∥2 <
∞. Let ζtT(1) (d
× 1) and ζtT(2) (t
= 1,…,T) be random vectors defined on the same
probability space as εt. Assume that
max1≤t≤T∥ζtT(1)∥
= Op(1) and
supt,T
E∥ζtT(2)∥ <
∞. Then,
when ζtT(1) is measurable
with respect to the σ-algebra
.
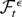
The third result also holds with
ζtT(1) replaced by
ζt+j−1,T(1).
Proof. To prove the first assertion, let ε > 0 and use
the assumption
max1≤t≤T∥ζtT(1)∥
= Op(1) to choose m > 0 such
that
P{max1≤t≤T∥ζtT(1)∥
> m} < ε for all T large. Next, use the
assumption that h(x) is locally bounded to conclude
that Hm =
sup∥x∥≤m∥h(x)∥
is finite. Then, the desired result follows because for all T
large
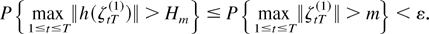
The second result is an immediate consequence of the first result and
the moment condition imposed on
ζtT(2). To prove the third
assertion, first note that an application of the triangular inequality
yields
Now, let ε > 0 and define m and
Hm in the same way as in the proof of (i).
Then, for every M > 0 and T large
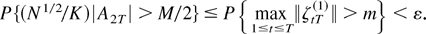
As for A1T, use the assumptions that
is a square integrable martingale difference sequence and that
ζtT(1) is measurable with respect to
the σ-algebra
to obtain
Hence,
P{(N1/2/K)|A1T|
> M/2} ≤ 2CHm
/M by Markov's inequality, and we can conclude that
for every M and T large
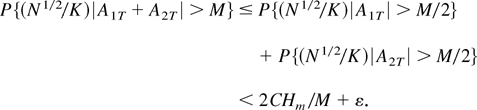
For M > 2CHm /ε
the last expression is smaller than 2ε, which proves the stated
result. A similar proof shows the final assertion. █
Note that the first two results of Lemma 1 obviously hold when
h(x) and
ζt+j,T(2) are
matrix-valued and that the third result improves Lemma A.4(c) of Park
and Phillips (2001) by relaxing the
exponentially boundedness assumption used therein to local
boundedness.
The first two results of Lemma 1 can be applied with the process
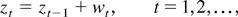
where wt is as in Assumption 2 and
z0 may be any random vector such that
E∥z0∥4 < ∞. In
this case ζtT(1) =
ztT =
T−1/2zt and
max1≤t≤T∥ztT∥
= Op(1) is an immediate consequence of the
invariance principle (8). This definition of
ztT will be assumed in subsequent lemmas.
The proofs of these lemmas make use of the fact that, as a result of
Assumption 2, we can write
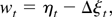
where
with Et the conditional expectation
operator with respect to the σ-algebra
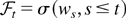
(cf. Hansen, 1992). Because
{ηt,
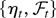
is a stationary martingale difference sequence equation (A.2) is analogous
to the so-called Beveridge–Nelson decomposition, which has been
used extensively in asymptotic analysis of linear processes (see, e.g.,
Phillips and Solo, 1992). Therefore, we shall
refer to equation (A.2) as the Beveridge–Nelson decomposition
also in the present context. In our applications of the third result of
Lemma 1 the martingale difference sequence εt
will be ηt. For these applications, and also
for other subsequent derivations, it is worth noting that the
(stationary) processes ηt and
ξt have finite moments of order 4 (see Hansen,
1992, the proof of Theorem 3.1).
LEMMA 2. Let h(x;θ) be a (possibly)
vector-valued continuously differentiable function defined on
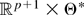
where Θ* is an open set in an Euclidean space. Suppose
that ∂h(x;θ)/∂x is also
continuously differentiable and let Θ ⊂ Θ* be a compact
set containing the point θ0 in its interior.
Then, as K2/T → 0,
where
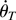
is a random vector such that
.
Proof. We shall first prove the latter assertion and then note
how the first one can be obtained from the employed arguments. Without loss of
generality, assume that h(x;θ) is real-valued and use
the Beveridge–Nelson decomposition (A.2) in conjunction with the
triangular inequality to obtain
First, consider
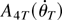
and use partial summation to obtain
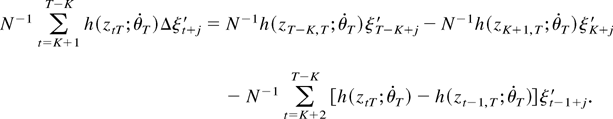
Hence, using the triangular inequality we find that
Because
supθ∈Θ∥h(x;θ)∥
is locally bounded, the first two terms on the right-hand side are
easily seen to be of order
Op(K/N). For the
third term we can use a standard mean value expansion to get
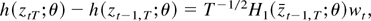
where H1(x;θ) =
∂h(x;θ)/∂x′ and
∥zt−1,T −
ztT∥ ≤
∥zt−1,T −
ztT∥ =
T−1/2∥wt∥.
Thus, we can write
Here the latter inequality is justified by the triangular inequality
whereas the equality follows from Lemma 1(ii) because
supθ∈Θ∥H1(x;θ)∥
is locally bounded,
max1≤t≤T∥zt−1,T∥
= Op(1), and
E∥wtξt−1+j′∥
is a finite constant. For later purposes we note that we actually
showed that A4T(θ) =
Op(K/N1/2)
holds uniformly in θ ∈ Θ.
Next, consider
.
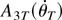
Because θ0 is an interior point of Θ and
,
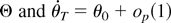
we can use the mean value expansion
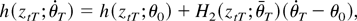
where
.
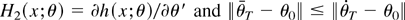
Thus, using the triangular inequality one obtains
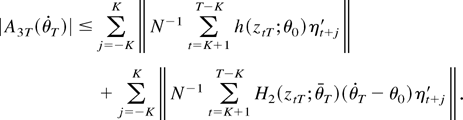
The first term on the right-hand side is
A3T(θ0), and the second
term can be bounded by
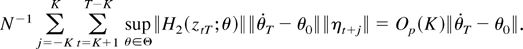
Here the equality is again obtained from Lemma 1(ii) because
supθ∈Θ∥H2(x;θ)∥
is locally bounded,
max1≤t≤T∥ztT∥
= Op(1), and
E∥ηt+j∥ is constant.
Thus, to complete the proof, we have to show that
A3T(θ0) =
Op(K/N1/2).
By the definition of
A3T(θ0),
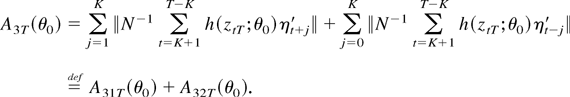
Lemma 1(iii) implies that
A31T(θ0) =
Op(K/N1/2),
so we need to show that the same holds true for
A32T(θ0). To this end, use
the Beveridge–Nelson decomposition (A.2) and the definition of
ztT to give
where
.
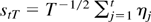
Thus, a mean value expansion yields
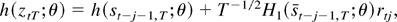
where
.
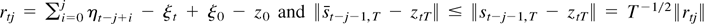
This identity and the triangular inequality imply
Here the equality is obtained from Lemma 1(iii), which obviously
applies despite the differences in subscripts. Next note that, because
the function H1(x;θ) is continuously
differentiable by assumption and because
∥st−j−1,T
−
st−j−1,T∥
≤
2T−1/2∥rtj∥,
we have
∥H1(st−j−1,T;θ0)
−
H1(st−j−1,T;θ0)∥
≤
T−1/2H1T(θ0)∥rtj∥
where H1T(θ0) is
determined by the partial derivatives of the function
H1(x;θ0) and, by Lemma
1(i), H1T(θ0) =
Op(1). Combing these facts with the
preceding upper bound of
|A32T(θ0)|
it is straightforward to show that
Consider the second term on the right-hand side. By the
Cauchy–Schwarz inequality,
E∥rtj∥2∥ηt−j∥
≤
(E∥rtj∥4E∥ηt−j∥2)1/2
≤ c1(j + 1) where
c1 is a finite constant. To justify the latter
inequality here, observe that, for some finite constants
c2, c3, and
c4,
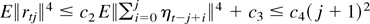
where the inequalities can be obtained from the definitions and Theorem
3.7.8(i) of Stout (1974). Thus,
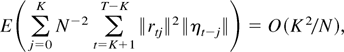
and, because H1T(θ0) =
Op(1), it follows that the second term on
the right-hand side of (A.4) is of order
Op(K/N1/2).
To complete the proof of the first assertion, we still need to show
that the first term on the right-hand side of (A.4) is of order
Op(K/N1/2).
It suffices to replace rjt in turn by each
of the four components in its definition. Thus, consider the
quantity
Arguments similar to those used for
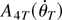
in (A.3) show that the first term on the right-hand side is of order
Op(K/N1/2).
These arguments also apply when the last three terms in the definition
of rtj are considered. Thus, we only need
to show that the latter term in the last expression is of order
Op(K/N1/2).
Using the triangular inequality, one obtains
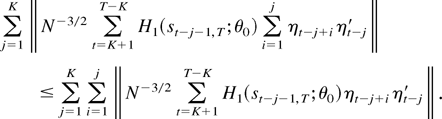
To show that the last quantity is of order
Op(K/N1/2),
we can make use of a similar truncation argument as in the proof of
Lemma 1(iii) and replace the function
H1(x;θ0) by
1{∥x∥ ≤
m}H1(x;θ0) with
an appropriately chosen real number m. Thus, because
H1(x;θ0) is locally
bounded 1{∥x∥ ≤
m}H1(x;θ0) is
bounded. To simplify notation we proceed by assuming that the function
H1(x;θ0) itself is
bounded. Assuming this shows that for i ≥ 1
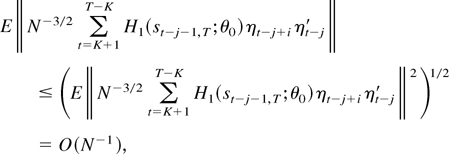
where the equality follows because the terms in the preceding sum are
uncorrelated with bounded second moments. Thus, the right-hand side of
(A.5) is of order
Op(K2/N),
which proves the desired result and completes the proof of the second
assertion.
To prove the first assertion, notice that we need to show that
A3T(θ) and
A4T(θ) are of order
Op(K/N1/2)
for every fixed θ. For A4T(θ) we
showed that this holds even uniformly in θ. As for
A3T(θ), it suffices to consider
A31T(θ) and
A32T(θ) separately. In the preceding
proof we showed that
A31T(θ0) and
A32T(θ0) are of order
Op(K/N1/2),
and an inspection of the proof reveals that θ0 can be
replaced by any θ ∈ Θ without changing the result. This
completes the proof of Lemma 2. █
It would be useful to be able to show that the pointwise result of
Lemma 2(i) also holds uniformly in θ, but we have been unable to
obtain this extension. The following result is not difficult to obtain,
however.
LEMMA 3. Suppose the assumptions of Lemma 2 hold and let
RT =
[R−KT′…RKT′]′
be a (possibly) stochastic matrix such that each
RjT has p + 1 rows and, for some
finite constant c, ∥RT∥
≤ c (a.s.). Then,
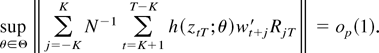
Proof. Without loss of generality assume that c = 1 and
that h(x;θ) is real-valued. Because
∥RjT∥ ≤ 1 for all j,
we have for every fixed θ ∈ Θ
where the equality is due to Lemma 2(i). Thus, the problem is to
strengthen this pointwise convergence in probability to uniform
convergence in probability. Because Θ is a compact set it suffices
to show that the quantity whose norm is taken is stochastically
equicontinuous (see, e.g., Davidson, 1994, p.
337). To this end, let θ1 and θ2 be
arbitrary points of Θ and consider the quantity
where the inequality follows from the Cauchy–Schwarz
inequality. For the difference in the last expression we can use the
mean value expansion
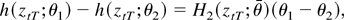
where H2(x;θ) =
∂h(x;θ)/∂θ′ and
∥θ − θ1∥ ≤
∥θ1 − θ2∥. Thus,
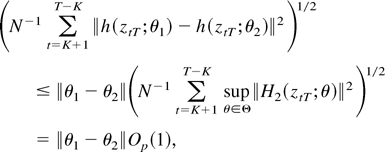
where the equality is justified by Lemma 1(i) because
supθ∈Θ∥H2(x;θ)∥2
is locally bounded and
max1≤t≤T∥ztT∥
= Op(1). Hence, the desired stochastic
equicontinuity follows in a straightforward manner from (A.6) if we
show that the latter factor in the last expression therein is of order
Op(1). To see this, define the matrix
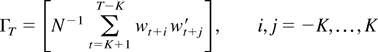
and let λmax(·) denote the largest eigenvalue
of the indicated matrix. With these definitions we have
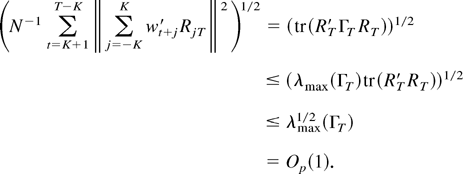
Here the last relation is a straightforward consequence of the fact
that the spectral density matrix of the process
wt is bounded, and the preceding one
follows from the assumption ∥RT∥
≤ 1 (a.s.). Thus, the proof is complete. █
The results of Lemmas 2 and 3 also hold with a fixed value of
K. In that case RjT in Lemma 3
may be replaced by an identity matrix, as can easily be checked from
the given proofs.
In the following lemma we use the notation
C(Θ)a×b to signify the
space of all continuous functions from the compact set
endowed with the uniform metric. In
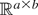
the usual euclidean metric is assumed.
LEMMA 4. Let H(x,θ) (a ×
b) be a matrix-valued continuous function defined on
.
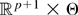
Then, if K/T → 0
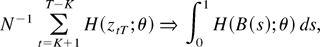
where the convergence holds in the function space
C(Θ)a×b.
Proof. Because ztT ⇒
B(s) by (8) the proof can be obtained in the same way as
the first result in Theorem 3.1 of Park and Phillips (2001). █
Lemma 4 can be used to prove the following lemma.
LEMMA 5. Let f (x;θ), θ ∈ Θ,
and xtT be as in Section 3.2. Then there
exists an ε > 0 such that with probability approaching
one
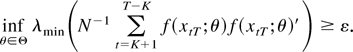
Proof. The stated result follows from condition (11), Lemma 4,
and the continuity of eigenvalues and the infimum function. █
LEMMA 6. Let h(x) be a vector-valued twice
continuously differentiable function defined on
.
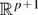
Then,
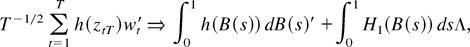
where
.
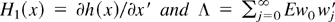
Moreover, this weak convergence holds jointly with that
in (8).
Proof. Using the Beveridge–Nelson decomposition (A.2),
one obtains
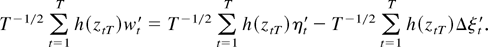
First, consider the latter term on the right-hand side. By partial
summation,
where the latter equality is an immediate consequence of the
assumptions. Thus, a standard mean value expansion and the fact
ΔztT =
T−1/2wt
yield
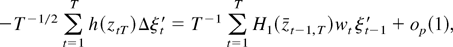
where the notation is as before so that
H1(zt−1,T)
signifies a matrix each row of which is evaluated at a possibly
different intermediate point in the line segment between
ztT and
zt−1,T. Because the
function H1(x) is continuously
differentiable by assumption, we have
∥H1(zt−1,T)
− H1(ztT)∥
≤
T−1/2H1T∥wt∥
where H1T is determined by the second
partial derivatives of the function h(x) and, as a
straightforward consequence of Lemma 1(i),
H1T =
Op(1). Hence, because
E∥wt∥∥wtξt−1′∥
is a finite constant, we can write
where the latter equality follows from the Beveridge–Nelson
decomposition (A.2). Theorems 3.2 and 3.3 of Hansen (1992) imply that replacing
wtξt′ in the
first term of the last expression by its expectation causes an error of
order op(1). To see that a similar
replacement can be done in the second term of the last expression,
observe that, by Assumption 2 and the mixing inequality in Davidson
(1994, p. 211),
wt wt′
− Ewt
wt′ is a stationary
L1-mixingale. Hence, the desired result follows
from Theorem 3.3 of Hansen (1992). As a whole
we can thus conclude that
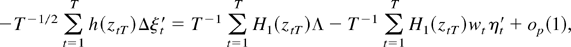
where the result
Ewtξt′ +
Ewt wt′
= Λ is a simple consequence of the definition of the matrix Λ
and the process ξt (cf. Hansen, 1992, proof of Theorem 4.1).
Now consider the first term on the right-hand side of (A.7) and use
the same mean value expansion as before to write
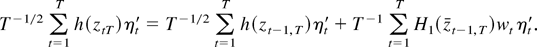
In the same way as previously, we can also here replace
H1(zt−1,T)
by H1(ztT) and combine
equations (A.8) and (A.9) with (A.7). This gives
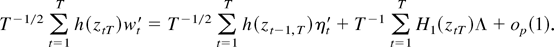
To complete the proof, notice that ηt is a
stationary square integrable martingale difference sequence and that an
invariance principle holds jointly for the processes
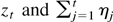
(see Hansen, 1992, proof of Theorem 3.1). Hence,
the stated result is obtained from Theorem 2.1 of Hansen (1992). █
APPENDIX B: PROOFS OF MAIN RESULTS
Proof of Theorem 1. We shall first demonstrate the existence of
the estimators
.
For any fixed value of θ, the least squares estimator of φ,
denoted by
,
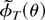
exists and is unique with probability approaching one. This is an immediate
consequence of the definition of the estimator
and Lemma 5. Thus, we have
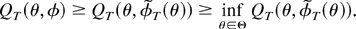
It is straightforward to check that, when the estimator
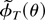
exists and is unique,
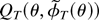
is a continuous function of θ so that, by the assumed compactness
of the parameter space Θ, there exists
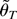
such that
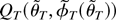
equals the preceding infimum. Thus,
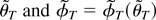
are the desired least squares estimators.
The next step is to show that
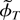
is bounded in probability. To this end, notice that
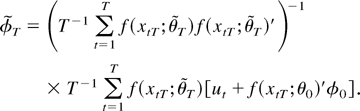
Lemma 5 implies that the largest eigenvalue of the inverse on the
right-hand side is of order Op(1). Thus,
we have to show that the latter factor on the right-hand side is of
order Op(1). To see this, note that the
assumptions imply that supθ∈Θ∥ f
(x;θ)∥ is locally bounded. Therefore, by Lemma 1(i)
we have
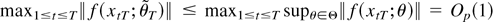
and similarly with
replaced by θ0.
Hence, it follows that
.
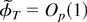
Moreover, because
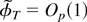
holds trivially by the compactness
of the parameter space Θ, we have
,
which means that the sequence of estimators
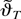
is tight.
To prove the consistency of the estimators
,
use the definitions to write
Because
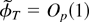
the latter equality follows from Lemma 3 with K = 0. Now suppose that
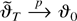
does not hold. Then, by the tightness of the sequence
,
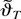
we can find a subsequence
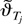
that converges weakly to ϑ* =
[θ*′ φ*′]′,
say, and ϑ* ≠ ϑ0 with a positive
probability (see Billingsley, 1968, Theorem
6.1). Thus, we can conclude that
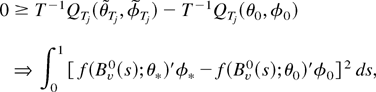
where the weak convergence is justified by Lemma 4 and Lemma A.2 of
Saikkonen (2001). (The latter lemma requires
that the relevant quantities converge jointly, which can be guaranteed
by redefining the subsequence if necessary.) When ϑ*
≠ ϑ0 it follows from condition (12) that the
difference in the weak limit in the preceding expression is nonzero for
some value of s and, by continuity, in an open interval. Thus,
the last expression is positive with a positive probability. This gives
a contradiction, so we must have ϑ* =
ϑ0. This completes the proof. █
Proof of Theorem 2. For simplicity, denote
h(xtT;ϑ) = f
(xtT;θ)′φ so that
.
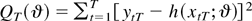
Because θ0 is assumed to be an interior point of
Θ, the consistency of the estimator
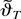
justifies the mean value expansion
where the notation is as before so that
∂2QT(ϑT)/∂ϑ∂ϑ′
signifies a matrix each row of which is evaluated at a possibly
different intermediate point in the line segment between
.
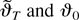
The partial derivatives can be expressed as
Next, note that
Because the function f (x;θ) is three times
continuously differentiable by assumption, it follows from the
consistency of the estimator
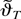
and Lemma 2(ii) with K = 0 that the first term on the
right-hand side is of order op(1). It can
be seen that the same is true for the second term by taking a mean
value expansion of the difference in the brackets and using the local
boundedness of the resulting summands in conjunction with Lemma 1(i)
and the consistency of the estimator
.
Thus, we can write
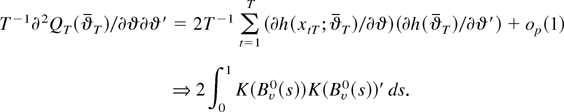
Here the weak convergence can be justified by using the consistency
of the estimator
,
Lemma 4, and Lemma A.2 of Saikkonen (2001). The
expression of the limit follows from the definitions.
To complete the proof, use Lemma 6 and the definitions to conclude that
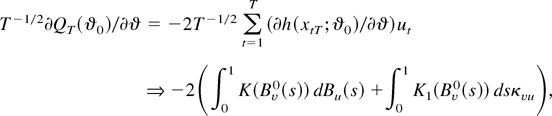
where the weak convergence holds jointly with that in (B.2). Thus,
because the weak limit in (B.2) is positive definite (a.s.) by
assumption the result of the theorem is an immediate consequence of
(B.1)–(B.3) and the continuous mapping theorem. █
Proof of Theorem 3. Denote again f
(xtT;θ)φ =
h(xtT;ϑ) and conclude from
the definitions that
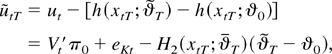
where
.
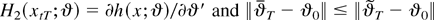
For simplicity, denote
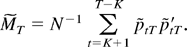
Then,
The latter equality is obtained by replacing
H2(xtT;ϑT)
in the second expression by
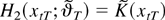
and observing that
.
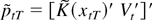
We shall show next that
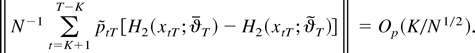
To this end, notice that, because the function
H2(x;θ) is continuously
differentiable by assumption, a mean value expansion and an application
of Lemma 1(i) show that
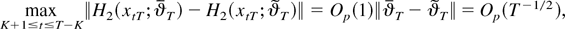
where the latter equality is due to the
T1/2-consistency of the estimator
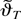
obtained from Theorem 2. Thus, because
,
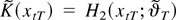
the local boundedness of
supθ∈Θ∥H2(x;ϑ)∥
and Lemma 1(i) similarly yield
.
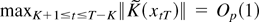
Hence, (B.5) holds with
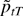
replaced by
,
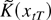
and we need to show that it also holds with
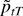
replaced by Vt. This can be seen by observing
that
where the last relation follows from Lemma 2(ii) and the
T1/2-consistency of the estimator
.
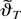
Thus, we have established (B.5).
The next step is to observe that
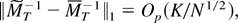
where, denoting λmax(A) as the largest
eigenvalue of matrix A, ∥A∥1 =
(λmax(A′A))1/2
and
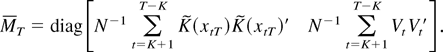
To see this, first note that
again by Lemma 2(ii) and the T1/2-consistency
of the estimator
.
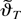
This and the well-known fact ∥·∥1 ≤
∥·∥ imply that
,
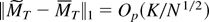
and we need to show that a similar result holds for the corresponding
inverses. By Lemma A.2 of Saikkonen and Lütkepohl (1996), this holds true if
∥MT−1∥1
= Op(1) or if
.
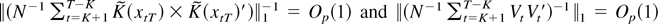
The former requirement can be obtained from condition (13), the consistency
of the estimator
,
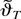
Lemma 5, and Lemma A.2 of Saikkonen (2001)
whereas the latter can be deduced from Lemmas A2–A4 of Saikkonen (1991). Because the assumptions used in Saikkonen
(1991) were slightly different from the
present ones we note that these lemmas, and also Lemmas A5 and A6 of
that paper, can also be proved under the present assumptions. For
Lemmas A3 and A5 the previous proofs apply, whereas Lemma A2 and,
consequently, Lemmas A4 and A6 can be proved by using Lemma 2(i) of
this paper and the fact that, for some finite constant C
independent of j = −K,…,K,
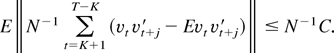
This follows from Assumption 2 and Lemma 6.19 of White (1984). For later purposes we also note that the
preceding discussion implies that
.
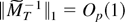
Next, note that
.
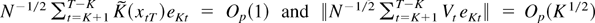
The former result will become evident subsequently, whereas the latter is
obtained from Lemmas A5 and A6 of Saikkonen (1991). Because
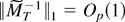
we can use (B.5), (B.6), and the
T1/2-consistency of the estimator
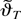
to conclude from (B.4) that
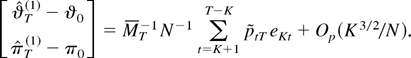
Because K3/2/N1/2
→ 0 by assumption this implies that
Here the last equality follows from results obtained in the Appendix
of Saikkonen (1991) and already used earlier.
To show that the limiting distribution of
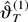
is as stated in the theorem and thereby to complete the proof, first note
that the arguments used for (B.2) in the proof of Theorem 2 show that the
inverse on the right-hand side of (B.7) converges weakly to the inverse
in the theorem. Thus, we need to consider
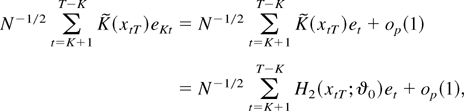
where the equalities can be justified as follows. First, recall that
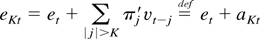
and note that
E∥aKt∥2 =
op(T−1) for all
t, as shown in the proof of Lemma A5 of Saikkonen (1991). Thus, the first equality in (B.8) follows
because
,
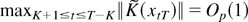
as already noted. To justify the second equality, recall that
,
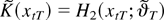
take a mean value expansion of
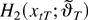
about ϑ0, and use the
T1/2-consistency of the estimator
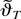
in conjunction with Lemma 3 with K = 0.
To complete the proof we have to show that the first term in the last
expression of (B.8) converges weakly to the stochastic integral in the
theorem and that this holds jointly with the weak convergence of the
inverse on the right-hand side of (B.7). If the process
[vt′
et′]′
fulfilled the conditions of Assumption 2 this would follow from Lemma
6, but, because the process et is not
guaranteed to be strong mixing, this reasoning does not apply directly.
However, using L to denote the usual lag operator we may write
et =
a(L)′wt where
.
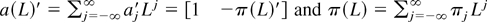
In view of the summability condition (15) and Lemma 6 we can use Theorem
4.2 of Saikkonen (1993) and obtain the needed weak
convergence results. The assumptions required to apply this theorem are
straightforward consequences of Assumption 2, which, in addition to the
summability condition (6) and the invariance principle (8), also
implies that the first and second sample moments of
wt are consistent estimators of their
theoretical counterparts. This completes the proof. █
