Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-02-05T22:49:01.404Z Has data issue: false hasContentIssue false
  • English
  • Français

ASYMPTOTIC INFERENCE FOR NONSTATIONARY GARCH

Published online by Cambridge University Press:  01 December 2004

Søren Tolver Jensen  and
Anders Rahbek
Søren Tolver Jensen
Affiliation:
University of Copenhagen
Anders Rahbek
Affiliation:
University of Copenhagen
Rights & Permissions [Opens in a new window]

Abstract

Consistency and asymptotic normality are established for the highly applied quasi-maximum likelihood estimator in the GARCH(1,1) model. Contrary to existing literature we allow the parameters to be in the region where no stationary version of the process exists. This has the important implication that the likelihood-based estimator for the GARCH parameters is consistent and asymptotically normal in the entire parameter region including both stationary and explosive behavior. In particular, there is no “knife edge result like the unit root case” as hypothesized in Lumsdaine (1996, Econometrica 64, 575–596).Anders Rahbek is grateful for support from the Danish Social Sciences Research Council, the Centre for Analytical Finance (CAF), and the EU network DYNSTOCH. Both authors thank the two anonymous referees and the editor for highly valuable and detailed comments that have, we believe, led to a much improved version of the paper, both in terms of the econometric theory and of the presentation.

Type
Research Article
Information
Econometric Theory , Volume 20 , Issue 6 , December 2004 , pp. 1203 - 1226
Copyright
© 2004 Cambridge University Press

1. INTRODUCTION

This paper considers the asymptotic behavior of the likelihood-based estimators in the generalized autoregressive conditional heteroskedastic (GARCH) model or better the “workhorse of the industry” (Lee and Hansen, 1994). The GARCH(1,1) or simply the GARCH model is given by

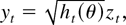
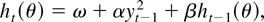
with t = 1,…,T and zt an independent and identically distributed (i.i.d.) (0,1) sequence. As to initial values the analysis is conditional on the observed value y0, whereas the unobserved variance, h0(θ), is parametrized by γ, h0(θ) = γ. The parameter θ of the GARCH model is therefore

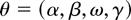
with α,β,ω, and γ all positive. Denote henceforth the positive true parameter values by θ0 = (α0,β0,ω0,γ0).

The GARCH model was introduced by Bollerslev (1986), extending the autoregressive conditional heteroskedastic (ARCH) model of Engle (1982). Asymptotic inference for the ARCH and GARCH type models has been studied in, e.g., Kristensen and Rahbek (2002), Lee and Hansen (1994), Lumsdaine (1996), and Weiss (1986). Common to these is the assumption that the (G)ARCH process yt is suitably ergodic or stationary such that appropriate laws of large numbers apply. Moreover the generic assumption for asymptotic normality is that the squared error process, zt2, has a finite (conditional) variance, κ = V(zt2) = E(zt2 − 1) < ∞. In the case of i.i.d. innovations zt the results in Lee and Hansen (1994) establish asymptotic normality essentially under the assumption that

This condition is necessary and sufficient for stationarity of the GARCH process as argued in Nelson (1990) and Bougerol and Picard (1992). Recall that the assumption in (4) is implied by the well-known sufficient condition α0 + β0 ≤ 1, which includes the much studied case of integrated GARCH where α0 + β0 = 1.

Our contribution is to relax this and work under the following assumption, which permits explosive and nonstationary behavior of the GARCH process.

Assumption 1. Assume that with zt i.i.d.(0,1), the true parameters satisfy

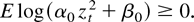
Clearly this extends the parameter region for which asymptotic normality holds. Our results show that whether or not the parameters are such that the process is ergodic, integrated, or even explosive, asymptotic normality of the likelihood-based estimators applies. Thus there is no “knife edge result like the unit root case” when entering the parameter region in Assumption 1 as hypothesized in Lumsdaine (1996, p. 580). Indeed our results imply, in particular, that requirements for existence of moments and stationarity for the GARCH process can be ignored when reporting, e.g., standard deviations and test statistics involving the likelihood-based estimators here, which until now has caused concern in the literature on GARCH inference. To this end unreported simulations indicate that in fact the convergence of the estimators to the Gaussian distribution is faster in the explosive case than in the stationary. Note that Jensen and Rahbek (2004) relax the condition about stability of the yt process in the ARCH(1) model, where β = 0, and allow the ARCH process to be nonstationary and to have no moments. The added complexity here due to the parameter β and hence lagged variance, ht−1(θ), in (2) implies that results regarding inference require different types of arguments when compared to the ARCH model. This is also noted by Lee and Hansen (1994, p. 35) for the stationary case, where it is emphasized that inference with respect to β is the most difficult.

The paper is structured as follows. Section 2 presents the two main theorems of the paper. Theorem 1 establishes asymptotic normality when the parameter that parametrizes the initial unobserved variance h0(θ) = γ is set equal to the true value, γ = γ0, and, furthermore, the scale parameter equals its true value, ω = ω0. Theorem 2 shows that the asymptotics hold independently of this choice, that is, independently of the initial values. Sections 3 and 4 establish the proofs of Theorems 1 and 2, respectively.

2. MAIN THEOREMS

As in Lee and Hansen (1994) and most of the literature, we consider the likelihood estimators based on minimization of

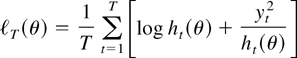
with ht(θ) defined in (2). Throughout this is referred to as the (quasi-)likelihood function, and likewise the first and second derivatives are referred to as the score and observed information, respectively. Note that it is the true log-likelihood function (multiplied by minus two) if zt is indeed Gaussian. Our first main result is the following.

THEOREM 1. With (ω,γ) fixed at their true values, (ω0,γ0), consider the model given by the (quasi-)likelihood function

as given by (6). Assume that at the true parameter θ0 = (α0,β0,ω0,γ0), yt given by (1) satisfies Assumption 1 such that no stationary version exists. Assume further that for the i.i.d.(0,1) process zt, V(zt2) = κ < ∞.

Under these assumptions there exists a fixed open neighborhood U = U(α0,β0) of (α0,β0) such that with probability tending to one as

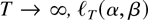
has a unique minimum point

in U. Furthermore,

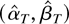
is consistent and asymptotically Gaussian,

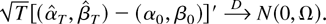
Here Ω > 0 and is given by Ω = κΣ−1, with μi = E(β0 /(α0 zt2 + β0))i, i = 1,2, and

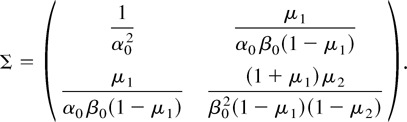
Remark 1. The covariance matrix Ω in Theorem 1 provides a lower bound for the implicitly given variance in the stationary and ergodic case analyzed in Lee and Hansen (1994, Theorem 3). This follows by the fact that the information matrix provides an upper bound as seen by the proof of Lemma 6 in Section 3.3, which applies the inequalities in Lemma 4. These inequalities hold independently of whether the process yt is stationary or not. Similarly for the two-dimensional information discussed in Section 3.5.

Remark 2. Note that if zt is Gaussian explicit expressions for μ1 and μ2 can be computed for the covariance matrix in Theorem 1.

Next, we state the result that the values of h0(θ) = γ and ω (and also the initial value y0) are asymptotically negligible. In particular,

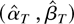
is a minimum point in U of

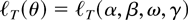
for any arbitrary values of ω and γ.

THEOREM 2. Assume that E log(α0 zt2 + β0) > 0. Then the results in Theorem 1 hold for any arbitrary values of γ > 0 and ω > 0.

Theorem 2 states that (α,β) can be estimated consistently by taking any arbitrary values of ω and γ and that the asymptotic distribution of the estimator does not depend on the arbitrary values of ω and γ. After the parameter (α,β) has been (consistently) estimated, one may estimate (ω,γ), but the estimator would not be consistent, and hence there is no need to reestimate the parameter (α,β).

Remark 3. Note that the results in Theorem 2 exclude the boundary case in Assumption 1 of E log(α0 zt2 + β0) = 0. We do not know whether there exists a consistent estimator for ω or if the asymptotic distribution of

does not depend on ω in this case.

3. PROOF OF THEOREM 1

The proof of Theorem 1 is based on applying Lemma 1, which follows. Note that conditions (A.1)–(A.3) are similar to conditions stated in the literature on asymptotic likelihood-based inference (see, e.g., Lehmann, 1999; Basawa, Feigin, and Heyde, 1976). The difference is that (A.1)–(A.3) explicitly exploit the fact that (the negative) log-likelihood function is three times continuously differentiable in the parameter. Furthermore, Lemma 1 establishes uniqueness (convexity) in addition to existence of the consistent and asymptotically Gaussian estimator.

LEMMA 1. Consider

, which is a function of the observations X1,…,XT and the parameter

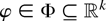
. Introduce furthermore φ0, which is an interior point of Φ. Assume that

is three times continuously differentiable in φ and that

where N(φ0) is a neighborhood of

. Then there exists a fixed open neighborhood U(φ0) ⊆ N(φ0) of φ0 such that

The proof of Lemma 1 is given in the Appendix.

Next, with

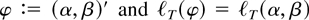
defined in Theorem 1, the results in Theorem 1 follow by establishing conditions (A.1)–(A.3) in Lemma 1. For exposition only we initially focus on the GARCH parameter β in Sections 3.1–3.4. The first-, second-, and third-order derivatives of the likelihood function with respect to β are given in Section 3.1. Upon some initial results in Section 3.1, the behavior of the score and observed information evaluated at the true value, θ = θ0, are studied in Section 3.3. In Section 3.4 it is shown that the third derivative is uniformly bounded by a suitably integrable majorant. The derivations concerning the ARCH parameter α are simple when compared with the ones with respect to β and are outlined in Section 3.5. It is also there that the asymptotic results for the joint parameter (α,β) are given. Note finally that (A.1)–(A.3) hold by Lemmas 5, 6, and 10 in Sections 3.3 and 3.4, together with the comments in Section 3.5. It follows that ΩS = κΣ in (A.1) (see Lemma 5 and (38)), whereas in (A.2), ΩI = Σ (see Lemma 6 and (39)). Finally, Σ is given by (40).

3.1. Variation with Respect to β

In this section we derive the first-, second-, and third-order derivatives of the likelihood function with respect to β.

The likelihood function is given by (6) in terms of θ, and it follows that

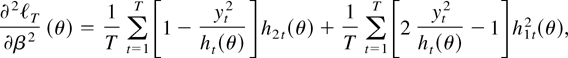
Here, applying simple recursions,

3.2. Some Initial Results

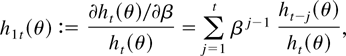
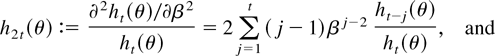
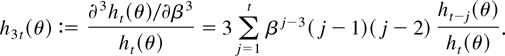
For the asymptotic likelihood analysis in the following discussion the first and the second derivatives of the likelihood function are evaluated at the true value θ0, and we introduce therefore the notation

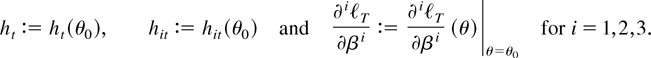
Underlying parts of the asymptotics is first of all the following observation from Nelson (1990, Theorem 2).

LEMMA 2. Under Assumption 1, as t → ∞,

Next, to study the asymptotics of the central quantities h1t, h2t, and h3t in (11)–(13) it is useful to introduce the stationary processes uit(·) for i = 1,…,4 defined in terms of the i.i.d. innovations zt. Note that the processes and their properties are well defined for the entire parameter region. In particular, Assumption 1 is not required in the lemma.

LEMMA 3. Define the processes

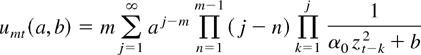
for m = 1,…,4 and with the notational convention that

. For all p ≥ 1 and m = 1,…,4, umt := umt(β0,β0) is ergodic and

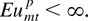
Furthermore, for each p ≥ 1 there exist βL and βU with βL < β0 < βU such that umt(β0,βL) and umt(βU,β0) are ergodic and

Proof of Lemma 3. Without loss of generality consider the case of m = 2. Define

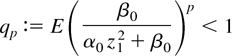
as zt is nondegenerate. Using Minkowski's inequality, (16) follows by

Next, consider, say, u2t(β0,βL):

Then as before, E [u2t(β0,βL)]p < ∞, provided

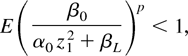
which is the case for some βL < β0 (as the innovations zt are nondegenerate). Likewise for u2t(βU,β0), which ends the proof. █

Next, we show how the hit and uit are related.

LEMMA 4. Consider h1t and h2t defined by (11) and (12), respectively, with the notational convention in (14). Then for i = 1,2,

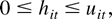
where the uit are defined in Lemma 3. Furthermore, under Assumption 1, for i = 1,2, then as t → ∞,

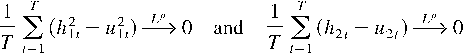
for all p ≥ 1.

It is important that the inequality in (19) holds independently of Assumption 1.

Proof of Lemma 4. From the recursions in (11) note that

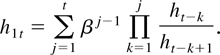
Next, use that

to establish the desired inequality,

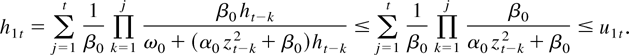
Likewise,

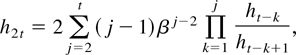
which shows (19).

Turn to h1t again. By (23) and Lemma 2, then as t → ∞,

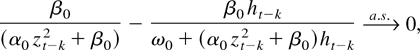
and therefore

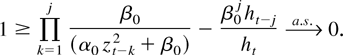
By dominated convergence also L1 convergence holds in (25). Now let t0 < t be arbitrary and consider

With t0 fixed, then as t → ∞ the first term equals zero by the just established L1 convergence. The second term equals (1/β0)(q1t0+1/(1 − q1)) with q1 defined in (18). As t0 was arbitrary, the second term then tends to zero as t0 → ∞ because q1 < 1. Hence E(u1t − h1t) tends to zero as t → ∞. Next, note that

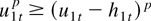
implies that the latter is uniformly integrable because the distribution of u1t does not depend on t. The just established L1 convergence implies convergence in probability of (u1t − h1t)p and hence by the uniform integrability,

Likewise for u2t and h2t, which establishes (20). Finally, the claimed Lp convergence in (21) follows by

which tends to zero as E(u1t − h1t)2p in particular tends to zero. This ends the proof of Lemma 4. █

3.3. Asymptotics of the Score and Observed Information

This section establishes asymptotic normality of the score and convergence of the observed information in probability under the true value, θ0. As noted, the idea is, asymptotically, to replace the hit terms with the corresponding uit terms in the expressions (8) and (9), respectively; see also Lemma 4.

Consider first the score.

LEMMA 5. Under Assumption 1 the score given by (8) evaluated at θ = θ0 is asymptotically Gaussian,

where u1t is given by (15) and μi = E(β0 /(α0 zt2 + β0))i, i = 1,2.

Proof of Lemma 5. Evaluated at θ = θ0 the score is given by

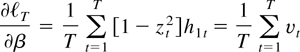
such that

. Applying the central limit theorem for martingale differences in Brown (1971), consider first

in probability (and L1) as T → ∞, using Lemma 4 and the ergodic theorem. Turning to the Lindeberg condition, as h1t ≤ u1t,

for all δ as T → ∞ because u1t (and also zt2) is stationary and has finite second-order moments. █

Next we establish the asymptotic limit of the observed information.

LEMMA 6. Under Assumption 1 the observed information given by (9) evaluated at θ = θ0 converges in probability,

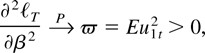
where

is given in Lemma 5.

Proof of Lemma 6. For θ = θ0 the observed information is given by

The last two terms on the right-hand side converge by the ergodic theorem to E [2zt2 − 1]Eu1t2 = Eu1t2 using the independence of uit and zt. As E|1 − zt2| and E|2zt2 − 1| are finite constants, Lemma 4 implies that the first two terms on the right-hand side converge in (L1 and hence) probability to zero. █

Remark 4. Note that the arguments for the score and information in Lemmas 5 and 6 carry over to the stationary case by using the ergodic theorem for the observed information as in Lee and Hansen (1994) and Lumsdaine (1996).

3.4. Third Derivative of the Likelihood Function

In this section the third derivative of the likelihood function is shown to be uniformly bounded in a neighborhood around the true value θ0.

Introduce lower and upper values for each parameter in θ, αL < α0 < αU, βL < β0 < βU, ωL < ω0 < ωU, and γL < γ0 < γU, and, in terms of these, the neighborhood N(θ0) around the true value θ0 defined as

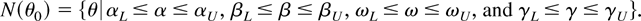
The next lemma establishes that the individual terms of the third derivative

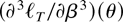
in (10) are uniformly bounded in the neighborhood N(θ0) by the corresponding terms as a function of β alone. With

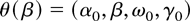
introduce the notation ht(β) and hit(β) for ht(θ(β)) and hit(θ(β)), respectively, with i = 1,2,3. Then the following lemma holds.

LEMMA 7. With N(θ0) defined in (26), then for any t,s

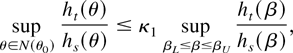
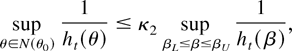
and, furthermore,

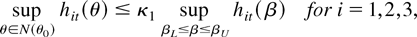
where the constants κi are given by,

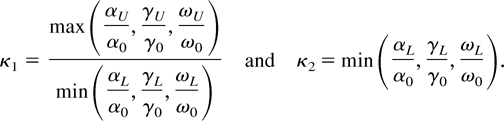
Proof of Lemma 7. Note that with h0 = γ then by simple recursion,

Hence,

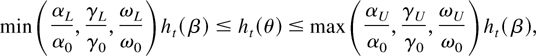
which implies (28) and (29). Next, (30) follows by applying (28) to the definition of hit(θ) in (11)–(13). █

To establish bounds for ht(β) and hit(β) in Lemma 9 we start with two fundamental identities concerning ht and ht(β).

LEMMA 8.

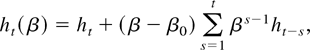
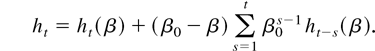
Proof of Lemma 8. Rewriting the equations for ht(β) and ht gives

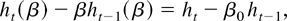
and the results follow immediately by noting that h0 = h0(β)(= γ0). █

Next turn to Lemma 9, which holds independently of Assumption 1.

LEMMA 9. With βL < β0 < βU,

where the uit(·) are defined in (15).

Proof of Lemma 9. Consider first ht /ht(θ). For β0 ≤ β < βU, using (32)

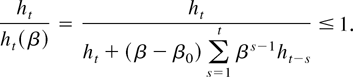
For the case of βL < β ≤ β0, use (33) to see that

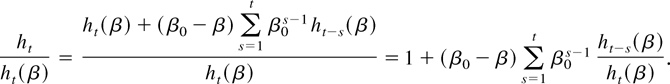
Then, similar to the proof of Lemma 4,

because ht−k /ht−k(β) ≥ 1 for β ≤ β0. Inserting, it follows that

where the right-hand side is independent of β. This establishes the inequality in (i). The inequalities (ii)–(iv) hold by identical arguments, and we give the proof only for (iv), which is the most complicated of these. By definition,

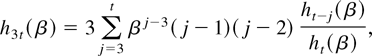
and the inequality for βL < β ≤ β0 holds by (34). Next, for β0 ≤ β < βU, ht = ht(θ0) ≤ ht(β), and using this in addition to (32) gives

where the last inequality follows as in (34). This shows (iv) and completes the proof of Lemma 9. █

We are now in a position to address the third derivative of the likelihood function,

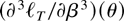
, as given by (10). We show that, independently of Assumption 1, it is uniformly bounded in a region around the true value β0.

LEMMA 10. There exists a neighborhood N(θ0) given by (26) for which

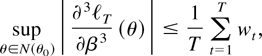
where wt is stationary and has finite moment, Ewt = M < ∞. Furthermore,

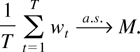
Proof of Lemma 10. Noting that by definition yt2/ht(θ) = zt2(ht /ht(θ)), the expression for

in (10) implies that

Lemma 7 implies that

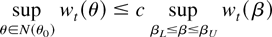
with c a constant. By Lemma 9, the quantities hit(β), i = 1,…,3, and ht /ht(β) are bounded by functions that by Lemma 3 have any desired moments. Hence, supβL≤β≤βU wt(β) ≤ wt as desired. The convergence in (36) follows by the ergodic theorem, which ends the proof of Lemma 10. █

3.5. Introducing α

The arguments with respect to α, and hence the joint variation in terms of both α and β, are completely analogous to the ones in Sections 3.1–3.4, and we emphasize only the important steps. Simple computations lead to

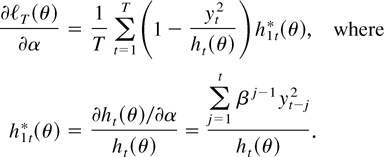
Hence

which as in Lemma 3 leads to the definition of the ergodic process,

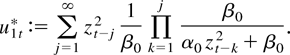
As in the proofs of Lemmas 4–6 it follows that

and

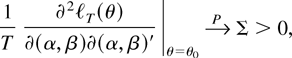
where κ = V(zt2) and

We note the surprisingly simple relationship,

which implies

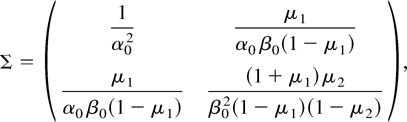
where μi = E(β0 /(α0 zt2 + β0))i, i = 1,2.

Finally, straightforward differentiation shows that inequalities completely analogous to (35) in Lemma 10 hold for the third derivatives

.

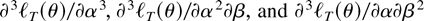
Remark 5. Note that the nonstationary condition in Assumption 1 is not needed to establish these bounds (see also Lemma 10), and hence the uniform bounds can be applied in the stationary case also. Furthermore, the bounds of the third derivatives establish inequalities of the form,

, where N(θ0) denotes a neighborhood of the true parameter values, θ0 (see also the condition (A.3) in Lemma 1). Observe that the proofs in Lee and Hansen (1994, p. 51, l.13–14 from below, regarding stochastic equicontinuity) and Lumsdaine (1996, p. 594) apply, we believe, different insufficient inequalities of the form,

.

4. PROOF OF THEOREM 2

We address here the asymptotic independence of the initial values of (ω,γ).

Recall that in the proof of Theorem 1, Lemma 1 was applied with φ := (α,β)′ and

defined in Theorem 1. If there is an extra parameter ω, say, in the likelihood function as in Theorem 2, it follows that the results are unchanged in Theorem 1 provided the conditions in Lemma 13 in Section 4.2 are fulfilled. To see this note first that in the proof of Lemma 1 in the Appendix,

can be replaced by

on the right-hand side of equation (A.2) using (44) in Lemma 13. Likewise in equation (A.2),

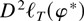
can be replaced by

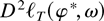
using (45) in Lemma 13. In equation (A.3), on the left-hand side,

can be replaced by

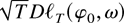
using (44) in Lemma 13, and on the right-hand side,

can be replaced by

using (45) in Lemma 13.

The derivations that follow are given in detail for ω, whereas for the case of γ we provide one lemma and note that the proof follows as in the ω case but is simpler. For presentational purposes we focus on the variation with respect to β in addition to ω and γ, respectively, which as in the proof of Theorem 1 in Section 3 is without loss of generality. To emphasize which parameters vary the following notation is adopted:

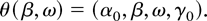
Similarly θ(β,γ) = (α0,β,ω0,γ); see also (27). We further emphasize the dependence on, e.g., ω by adopting the notation

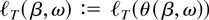
for the likelihood function and also for other functions previously defined.

Section 4.1 states an initial general lemma that is useful in the derivations. Section 4.2 addresses ω and Section 4.3 γ.

4.1. An Initial Lemma

The following lemma addresses the average of products of stochastic processes.

LEMMA 11. Let (Xt)t=1,2,… and (Yt)t=1,2,… be stochastic processes on

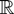
for which

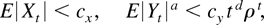
where cx, cy, a, and d are positive constants and |ρ| < 1. Then with δ > 0 and as T → ∞,

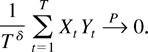
Proof of Lemma 11. We establish Ls convergence for s = a/(1 + a) < 1. First, as s < 1,

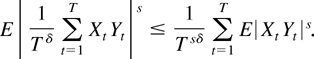
Next, with p = 1 + a > 1 and q = p/(p − 1) > 1 apply Hölder's inequality to get that this is bounded by

which tends to zero as T → ∞ and where

. █

4.2. The Role of the Scale Parameter ω

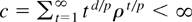
Initially we provide upper bounds for the terms appearing in the score and observed information in (8) and (9). To this end we need the following proposition.

PROPOSITION 1. Assume that Assumption 1 holds with strict inequality and with β0 < 1. Then, for some p > 0,

Proof of Proposition 1. Set vt = α0 zt2 + β0 and note that vt ≥ β0. Define the function fp(v) = (v−p − 1)/p = (exp(−p log v) − 1)/p → −log v as p → 0. Note that on A1 = [β0,1](= [empty ] if β0 > 1), 0 ≤ fp(v) ≤ (1/β0 − 1) for 0 ≤ p ≤ 1, whereas on A2 = (1,∞), −fp(v) ≥ 0 and increasing in p as p → 0. Finally, Efp(vt) = E [fp(vt)1A1(vt)] − E [−fp(vt)1A2(vt)] , which by dominated and monotone convergence respectively, converge to E [−log vt1A1(vt)] − E [log vt1A2(vt)] = −E log vt, which is negative by Assumption 1. Hence for p small enough the result holds. █

Next consider individual terms appearing in the likelihood function in (6) and also terms of the score and observed information in (8) and (9) and their variation with respect to ω.

LEMMA 12. Assume that Assumption 1 holds with strict inequality. Then for any ω > 0, there exist βL < β0 < βU such that

Here, with i = 1, 2, and 3,

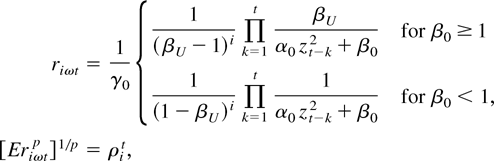
where ρi < 1 and p > 1 for β0 ≥ 1, whereas p > 0 for β0 < 1.

Proof of Lemma 12. We give only the proof for i = 1 as the other cases follow analogously. Note that

and hence

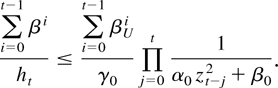
Consider first the case of β0 ≥ 1, which implies βU > 1 and in particular,

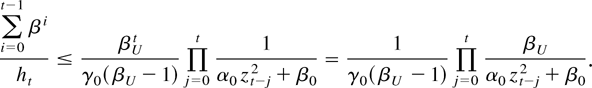
This function has exponentially decreasing absolute pth-order moment, p ≥ 1, provided

which is the case for some βU > β0; see Lemma 3.

Next turn to the case of β0 < 1. In this case, without loss of generality, it can be assumed that βU < 1, and we find

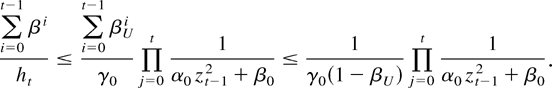
Applying Proposition 1 finishes the proof of Lemma 12. █

Next, turn to the main lemma.

LEMMA 13. Assume that Assumption 1 holds with strict inequality. Then for any arbitrary ω > 0, there exist βL and βU, βL < β0 < βU, such that

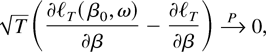
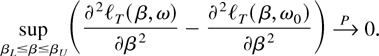
Proof of Lemma 13. Given the arbitrary value ωarb(= ω) > 0, define ωL = min(ω0,ωarb) and ωU = max(ω0,ωarb). By Taylor expansions, (44) and (45) follow by showing that

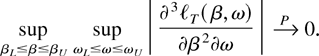
Simple computations give

Likewise,

All the preceding terms are bounded as they are all of a form that can be expressed in the form described in Lemma 11: a typical term in (48) and (49) is given by

By Lemma 12, supβL≤β≤βU supωL≤ω≤ωU|(∂ht(β,ω)/∂ω)/ht| has exponentially decreasing moments, and this factor plays the role of Yt in Lemma 11. Using Lemmas 7 and 9, the remaining three factors are bounded by variables, which by Lemma 3 have finite moments of any desired order. Hence the product of these variables plays the role of Xt in Lemma 11. This ends the proof of Theorem 2 regarding the role of ω. █

4.3. The Role of the Initial Value h0(θ) = γ

As mentioned, the proof, although simpler, follows exactly the outline of the proof of the independence on the scale parameter ω given in Section 4.2. Recall that to emphasize the dependence on γ, we adopt the notation

for the likelihood function and other functions. To establish the results in Lemma 13 with ω replaced by γ we need only the following lemma, which corresponds to Lemma 12.

LEMMA 14. Under Assumption 1, for any γ > 0 there exist βL and βU, βL < β0 < βU such that

with

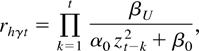
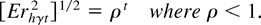
Proof of Lemma 14. The results follow as in the proof of Lemma 12 for the case of β0 > 1. █

APPENDIX: PROOF OF LEMMA 1

Note first that by condition (A.3) in Lemma 1, it follows that for any vectors

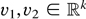
, and any φ ∈ N(φ0),

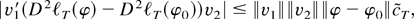
where

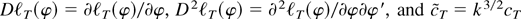
. To see this, note that the left-hand side of expression (A.1) is | f (1) − f (0)| = |∂f (λ*)/∂λ| for some 0 ≤ λ* ≤ 1, where

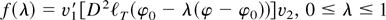
. By Taylor's formula and condition (A.3) in Lemma 1,

Next, by definition the continuous function

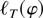
attains its minimum in any compact neighborhood K(φ0,r) = {φ| ∥φ − φ0∥ ≤ r} ⊆ N(φ0) of φ0. With vφ = (φ − φ0), and φ* on the line from φ to φ0, Taylor's formula gives

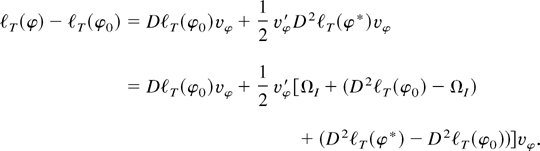
Denote by ρT and ρ, ρ > 0, the smallest eigenvalues of

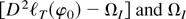
, respectively. Note that

by condition (A.2) in Lemma 1 and the fact that the smallest eigenvalue of a k × k symmetric matrix

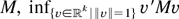
, is continuous in M. Then conditions (A.1) and (A.3) in Lemma 1, with

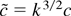
, and equation (A.2) imply that

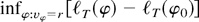
is greater than or equal to

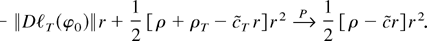
Therefore, if

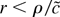
, the probability that

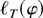
attains its minimum on the boundary of K(φ0,r) tends to zero. Next, for

, rewriting

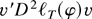
as in equation (A.2),

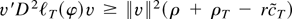
, which tends in probability to

. Hence, if

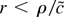
the probability that

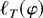
is strongly convex in the interior of K(φ0,r) tends to one, and therefore it has at most one stationary point. This establishes condition (B.1) in Lemma 1: if

, there is with a probability tending to one exactly one solution

to the likelihood equation in the interior U(φ0) = int K(φ0,r). It is the unique minimum point of

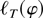
in U(φ0) and, as it is a stationary point, it solves

.

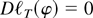
By the same argument, for any δ, 0 < δ < r there is with a probability tending to one a solution to the likelihood equation in K(φ0,δ). As

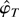
is the unique solution to the likelihood equation in K(φ0,r), it must therefore be in K(φ0,δ) with a probability tending to one. Hence we have proved that

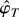
is consistent. That is, for any 0 < δ < r, the probability that

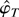
is a unique solution to

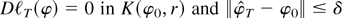
tends to one, which establishes (B.2).

That

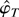
is asymptotically Gaussian follows from condition (A.1) in Lemma 1 and by Taylor's formula for the functions

:

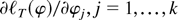
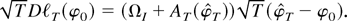
Here the elements in the matrix

are of the form

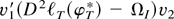
with v1,v2 unit vectors in

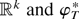
a point on the line from

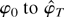
. Note that φT* depends on the first vector v1. Next, by expression (A.1),

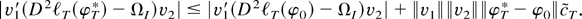
Because

it follows from condition (A.2) in Lemma 1 that the right-hand side tends in probability to zero. Hence

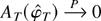
, and condition (B.3) follows by expression (A.3) using condition (A.1) in Lemma 1. █

References

REFERENCES

Basawa, I.V., P.D. Feigin, & C.C. Heyde (1976) Asymptotic properties of maximum likelihood estimators for stochastic processes. Sankya Series A 38, 259–270.Google Scholar
Bollerslev, T. (1986) Generalized autoregressive conditional heteroscedasticity. Journal of Econometrics 31, 307–327.Google Scholar
Bougerol, P. & N. Picard (1992) Stationarity of GARCH processes and of some nonnegative time series. Journal of Econometrics 52, 115–127.Google Scholar
Brown, B.M. (1971) Martingale central limit theorems. Annals of Mathematical Statistics 42, 59–66.Google Scholar
Engle, R.F. (1982) Autoregressive conditional heteroscedasticity with estimates of United Kingdom inflation. Econometrica 50, 987–1007.Google Scholar
Jensen, S.T. & A. Rahbek (2004) Non-stationary and no-moments asymptotics for the ARCH(1) model. Econometrica 72, 641–646.Google Scholar
Kristensen, D. & A. Rahbek (2002) Asymptotics of the QMLE for a Class of ARCH(q) models. Preprint 10, Department of Applied Mathematics and Statistics, University of Copenhagen.
Lee, S.-W. & B. Hansen (1994) Asymptotic theory for the GARCH(1,1) quasi-maximum likelihood estimator. Econometric Theory 10, 29–53.Google Scholar
Lehmann, E.L. (1999) Elements of Large-Sample Theory. Springer-Verlag.
Lumsdaine, R. (1996) Consistency and asymptotic normality of the quasi-maximum likelihood estimator in IGARCH(1,1) and covariance stationary GARCH(1,1) models. Econometrica 64, 575–596.Google Scholar
Nelson, D.B. (1990) Stationarity and persistence in the GARCH(1,1) model. Econometric Theory 6, 318–334.Google Scholar
Weiss, A. (1986) Asymptotic theory for ARCH models. Econometric Theory 2, 107–131.Google Scholar