Published online by Cambridge University Press: 01 August 2004
In this paper we derive representations for the limiting distributions of the regression-based seasonal unit root test statistics of Hylleberg, Engle, Granger, and Yoo (1990, Journal of Econometrics 44, 215–238) and Beaulieu and Miron (1993, Journal of Econometrics 55, 305–328), inter alia, when the underlying process displays near seasonal integration. Our results generalize those presented in previous studies by allowing for an arbitrary seasonal periodicity (including the nonseasonal case), a wide range of possible assumptions on the initial conditions, a range of (seasonal) deterministic mean effects, and finite autoregressive behavior in the driving shocks. We use these representations to simulate the asymptotic local power functions of the seasonal unit root tests, demonstrating a significant dependence on serial correlation nuisance parameters in the case of the pairs of t-statistics, but not the associated F-statistic, for unit roots at the seasonal harmonic frequencies. Monte Carlo simulation results are presented that suggest that the local limiting distribution theory provides a good approximation to the finite-sample behavior of the statistics. Our results lend further weight to the advice of previous authors that inference on the unit root hypothesis at the seasonal harmonic frequencies should be based on the F-statistic, rather than on the associated pairs of t-ratios.We are grateful to Bruce Hansen and two anonymous referees for their helpful comments and suggestions on earlier versions of this paper.
In a recent paper Rodrigues (2001) presents representations for the limiting distributions of the quarterly seasonal unit root test statistics of Hylleberg, Engle, Granger, and Yoo (1990) when the characteristic roots of the underlying seasonal process are local to unity. In deriving his results, Rodrigues (2001) assumes that the data are generated by a mean-zero near seasonally integrated process with zero starting values, whose driving shocks form an independent and identically distributed (i.i.d.) sequence.
In this paper we generalize the work of Rodrigues (2001) in four separate directions. First, we allow for any given seasonal aspect, S, say, so that our results extend those of Rodrigues (2001) for S = 4 to, inter alia, monthly (S = 12), daily trading (S = 5), biannual (S = 2), bimonthly (S = 6), and, indeed, nonseasonal (S = 1) data. Second, under the near seasonally integrated model, and following the work of Canjels and Watson (1997) and Phillips and Lee (1996), we allow for a wide spectrum of initial conditions ranging from asymptotically negligible initial conditions to the so-called unconditional case where the starting values of the process are of the same stochastic order as the subsequent data points. Third, following Smith and Taylor (1998, 1999a, 1999b) and Nabeya (2001a), we allow for (seasonal) deterministic mean effects in the process, ranging from a zero mean to seasonal intercepts and seasonal trends. Fourth, we allow for finite autoregressive (AR) behavior in the driving shocks. The final generalization also allows us to expand upon the recent work of Burridge and Taylor (2001), who derive representations for the limiting null distributions of the quarterly (S = 4) HEGY (Hylleberg, Engle, Granger, and Yoo) tests when the shocks follow a finite AR process.
The paper is organized as follows. In Section 2 we outline the seasonal framework, defining the hypotheses of interest and the regression-based, or so-called HEGY, approach to seasonal unit root testing, where one tests the null hypothesis of unit root behavior against the stable alternative at each of the zero and seasonal frequencies. In Section 3 we provide our main result, detailing the limiting distributions of the seasonal unit root test statistics under the near-integrated seasonal model. These representations are related to previous results in the literature, where relevant. In particular, the asymptotic local power functions of the t-tests (defined subsequently) for unit roots at the zero and Nyquist (S even) frequencies are shown to coincide with that of the conventional augmented Dickey–Fuller (ADF) unit root test. A key result that we demonstrate is that the limiting distributions of the t-statistics for testing a unit root at the zero and Nyquist frequencies are invariant to the serial correlation nuisance parameters in the shocks, as are the F-statistics for testing the null hypothesis of a complex pair of unit roots at each of the seasonal harmonic frequencies, but that the pairs of t-statistics for complex unit roots are not invariant to these nuisance parameters. Our results for the harmonic seasonal frequencies build upon the work of Burridge and Taylor (2001), who demonstrate this result under the seasonal unit root null for the particular case of S = 4. In Section 4 we simulate the asymptotic local power functions of the seasonal unit root tests, highlighting the relative performance of the t- and F-statistics in both serially correlated and serially uncorrelated cases and quantifying the degree of power loss seen when (seasonal) intercepts and (seasonal) time trends are included in the test regression. Finite sample simulations are also provided that suggest that the local limiting distribution theory provides a good approximation to the small sample behavior of the statistics. Section 5 concludes. A mathematical Appendix contains the proof of our main result.
Following Hylleberg et al. (1990), Beaulieu and Miron (1993), Smith and Taylor (1998, 1999a), and Nabeya (2001a), inter alia, consider the scalar process {xSn+s}, observed with seasonal periodicity S, written as the sum of a purely deterministic component, μSn+s, and a purely stochastic process, vSn+s, namely,
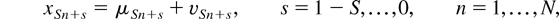
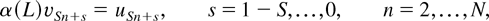
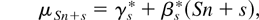
where

in (2.2) is an Sth-order autoregressive (AR(S)) polynomial in the conventional lag (backshift) operator, LkxSn+s ≡ xSn+s−k, k = 0,1,…. The driving shocks {uSn+s} of (2.2) are assumed to follow an AR(p), 0 ≤ p < ∞ process, namely, φ(L)uSn+s = εSn+s, the roots of
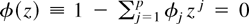
all lying outside the unit circle, |z| = 1, with εSn+s ∼ i.i.d.(0,σ2), with finite fourth moments. Exact assumptions on the initial conditions vS+s, s = 1 − S,…,0, are delayed until later. In what follows we use the notation T ≡ SN to denote the total sample size.
The specification (2.1)–(2.3) allows for the presence of deterministic mean effects in {xSn+s} through μSn+s. For the purposes of this paper, we follow Smith and Taylor (1999a) and consider the following six cases of interest.
Case 1. No intercept, no trend: γs* = 0, βs* = 0, s = 1 − S,…,0.
Case 2. Constant intercept, no trend: γs* = γ, βs* = 0, s = 1 − S,…,0.
Case 3. Seasonal intercepts, no trend: βs* = 0, s = 1 − S,…,0.
Case 4. Constant intercept, constant trend: γs* = γ, βs* = β, s = 1 − S,…,0.
Case 5. Seasonal intercepts, constant trend: βs* = β, s = 1 − S,…,0.
Case 6. Seasonal intercepts, seasonal trends: as in (2.3) with γs* and βs* unrestricted.
In this paper we are concerned with the behavior of tests for seasonal unit roots in the AR(S) polynomial, α(L), against near seasonally integrated alternatives; that is, the null hypothesis of interest is
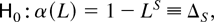
whereas, following Tanaka (1996, pp. 355–356), Rodrigues (2001), and Nabeya (2000, 2001b), inter alia, the near seasonally integrated alternative we consider is of the form
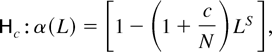
where c is a fixed nonpositive constant. Notice that
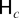
reduces to
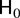
for c = 0.
Under
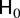
of (2.4) the data generating process (DGP) (2.1)–(2.3) of {xSn+s} is that of a seasonally integrated process (with or without drifts according to the form of μSn+s), admitting unit roots at both the zero frequency, ω0 ≡ 0, and at each of the seasonal spectral frequencies, ωk ≡ 2πk/S, k = 1,…,[S/2] , [·] denoting the integer part of its argument. Under
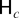
of (2.5) the process {xSn+s} is locally stable at each of the zero and seasonal frequencies if c < 0. Although we constrain c to be nonpositive, all of the analysis that follows also holds for positive c, in which case the process is locally explosive.
Denoting
, we may factorize the polynomial α(L) under
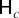
of (2.5) as
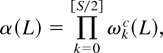
where the lag polynomial
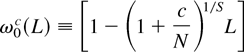
corresponds to the zero frequency ω0 ≡ 0 and the lag polynomial ωkc(L) corresponds to the harmonic seasonal frequencies (ωk,2π − ωk) and is defined by
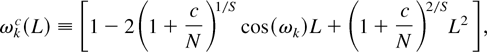
k = 1,…,S*, where S* ≡ (S/2) − 1 (if S is even) or [S/2] (if S is odd), together with
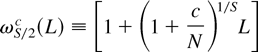
corresponding to the Nyquist frequency ωS/2 ≡ π, when S is even. Moreover, as demonstrated in Rodrigues (2001) for the case of S = 4, taking a Taylor series expansion about one on each of the factors of (2.6) allows α(L) of (2.2) to be written as

Consequently,
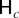
of (2.5) is correspondingly partitioned as
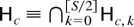
, where the hypothesis
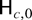
corresponds to a local to unit root at the zero frequency ω0 = 0, whereas
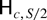
yields a local to unit root at the Nyquist frequency ωS/2 = π, where S is even. A pair of complex conjugate local to unit roots at the harmonic seasonal frequencies (ωk,2π − ωk) is obtained under
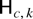
, k = 1,…,S* (see also Gregoir, 2001). Notice therefore that the particular local alternative,
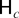
of (2.5), that we have considered imposes a common noncentrality parameter, c, on each of the zero and seasonal frequencies. However, as we see subsequently, this involves no loss of generality.
Following Hylleberg et al. (1990) and Smith and Taylor (1999a), inter alia, the regression-based approach to testing for seasonal unit roots in α(L) consists of two stages. First, one obtains the ordinary least squares (OLS) demeaned series
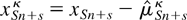
, where
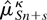
is the fitted value from the OLS regression of xSn+s on the intercept and trend variables relevant to each of Cases 1–6, κ ∈ {1,…,6} indicating the case of interest. Notice that for Case 1,
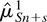
will be zero, and hence xSn+s1 = xSn+s, by definition. In what follows we assume that μSn+s is not estimated under an overly restrictive case, such that the resulting unit root tests will be exact invariant to the parameters characterizing the mean function μSn+s (see Burridge and Taylor, 2004).
Following Smith and Taylor (1999a, equation (4.17), p. 9), we then linearize α(L) in (2.2) around the seasonal unit roots exp(± i2πk/S), k = 0,…,[S/2] , to obtain the auxiliary regression equation
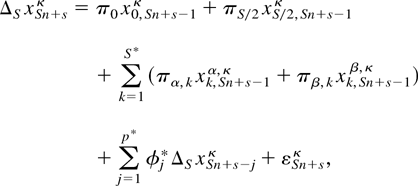
which may be estimated along Sn + s = p* + S + 1,…,T, p* ≥ p, omitting the term πS/2 xS/2,Sn+s−1κ if S is odd, and where corresponding to the zero and seasonal frequencies ωk = 2πk/S, k = 0,…,[S/2],

k = 1,…,S*, together with ΔS xSn+sκ ≡ xSn+sκ − xS(n−1)+sκ. For the case of quarterly data, S = 4, the relevant transformations are x0,Sn+sκ ≡ (1 + L + L2 + L3)xSn+sκ, x2,Sn+sκ ≡ −(1 − L + L2 − L3)xSn+sκ, x1,Sn+sα,κ ≡ −L(1 − L2)xSn+sκ, and x1,Sn+sβ,κ ≡ −(1 − L2)xSn+sκ.
It is the elements of π ≡ (π0,πS/2,π1,α,….,πS*,β)′, omitting πS/2 where S is odd, from (2.11) that are of focal interest. From the characterization theorem of Smith and Taylor (1999a, p. 7), the following expressions for the elements of π, omitting that for πS/2 where S is odd, obtain. This result is proved in the accompanying working paper, Rodrigues and Taylor (2003).
PROPOSITION 2.1. The elements of the parameter vector π from the test regression (2.11), when the DGP is (2.1)–(2.3) under
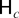
of (2.5), are given by
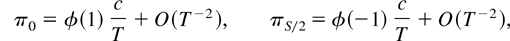
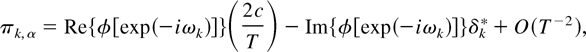
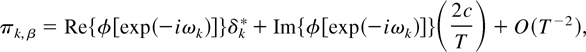
where δk* ≡ [1/sin(ωk)][((1 + 2c/T)1/2 − 1)2 cos(ωk)], k = 1,…,S*.
Remark 2.1. It follows immediately from (2.13) that Tπ0 = φ(1)c + o(1) and TπS/2 = φ(−1)c + o(1) (S even). Similarly, from (2.14) and (2.15), Tπk,α = 2c Re{φ(exp(−iωk))} + o(1), and Tπk,β = 2c Im{φ[exp(−iωk)]} + o(1), k = 1,…,S*, where we have used the result that limN→∞[T/sin(ωk)]{[(1 + (2c/T) + O(T−2))1/2 − 1]2 cos(ωk)} = 0, k = 1,…,S*.
Remark 2.2. Suppose that, instead of using a single noncentrality parameter c in (2.6), we used a set of frequency-specific noncentrality parameters (which may or may not be equal), that is,
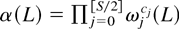
, where the ωjcj(L) are as defined in (2.7)–(2.9) but replacing c by cj, j = 0,…,[S/2] . Then the results in Proposition 2.1 remain valid on replacing c in (2.13)–(2.15) by the appropriate noncentrality parameter cj, j = 0,…,[S/2] . This result is proved in Rodrigues and Taylor (2003).
Noting that for c = 0 the expansion in (2.10) is exact,
1That is,
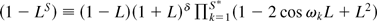
, where δ = 1(0) if S is even (odd).
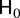
of (2.4), π = 0, regardless of the lag parameters characterizing φ(z). Under
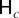
of (2.5) with c < 0 and T finite, it can be shown from Proposition 2.1 that π0, πS/2 (S even) and πk,α, k = 1,…,S*, are negative, regardless of φ(z), whereas the πk,β, k = 1,…,S*, can either be zero or nonzero, depending on the form of φ(z). Consequently, to test
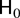
of (2.4) against the alternative of stationarity at one or more of the zero and seasonal frequencies, Hylleberg et al. (1990) and Smith and Taylor (1999a), inter alia, have suggested using standard regression t- and F-statistics from (2.11).
Specifically, tests for the presence or otherwise of a unit root at the zero and Nyquist (S even) frequencies are conventional lower tailed regression t-tests, denoted t0 and tS/2, for the exclusion of x0,Sn+s−1κ and xS/2,Sn+s−1κ, respectively, from (2.11). Similarly, the hypothesis of a pair of complex unit roots at the kth harmonic seasonal frequency may be tested by the lower tailed tkα and two-tailed tkβ regression t-tests from (2.11) for the exclusion of xk,Sn+s−1α,κ and xk,Sn+s−1β,κ, respectively, or by the regression F-test, denoted Fk, for the exclusion of both xk,Sn+s−1α,κ and xk,Sn+s−1β,κ from (2.11), k = 1,…,S*. Ghysels, Lee, and Noh (1994), Taylor (1998), and Smith and Taylor (1998, 1999a) also consider the joint frequency regression
-tests from (2.11), F1…[S/2], for the exclusion of xS/2,Sn+s−1κ (S even) and {xk,Sn+s−1α,κ,xk,Sn+s−1β,κ}k=1S*, and F0…[S/2], for the exclusion of x0,Sn+s−1κ, xS/2,Sn+s−1κ (S even) and {xk,Sn+s−1α,κ,xk,Sn+s−1β,κ}k=1S*. The former tests the null hypothesis of unit roots at all of the seasonal frequencies, whereas the latter tests the overall null,
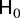
.
Various percentiles from approximations to the finite sample null distributions of the preceding t- and F-statistics for certain choices of the seasonal aspect S, obtained by Monte Carlo simulation, assuming that {uSn+s} ∼ IN(0,1), appear in the literature; see, inter alia, Hylleberg et al. (1990, Tables 1a and 1b, pp. 226–277), Smith and Taylor (1998, Tables 1a and 1b, p. 276), Beaulieu and Miron (1993, Table A.1, pp. 325–326) and Ghysels et al. (1994, Tables C.1 and C.2, pp. 440–441). Asymptotic critical values are also provided in Beaulieu and Miron (1993, Table A.1, pp. 325–326) and Taylor (1998, Tables I and II, pp. 356–357).
In this section we derive representations for the limiting distributions of the OLS seasonal unit root statistics computed from the test regression (2.11) for each of Cases 1–6 of (2.3), under the near seasonally integrated alternative,
of (2.5).
In what follows, what we assume about the initial conditions vS+s, s = 1 − S,…,0, is important. One possibility, following Elliott, Rothenberg, and Stock (1996), is to assume that the starting values satisfy T−1/2vS+s →p 0, s = 1 − S,…,0. One particular example of this is the so-called conditional case where vS+s = uS+s, s = 1 − S,…,0, so that the initial observation in each of the S seasons, xS+s, has variance equal to that of the shocks. In contrast, Pantula, Gonzalez-Farias, and Fuller (1994) argue that “there are a modest number of situations” (p. 459) where one might reasonably assume that the conditional case applies. For macroeconomic data in particular, the conditional assumption seems untenable. Pantula et al. (1994) suggest instead the unconditional case, where the initial conditions obey the same data generating process as the rest of the process. Within our near seasonally integrated model we can contain both the conditional and unconditional cases within a more general framework by making the following assumption, which is the seasonal generalization of Assumption 3 of Canjels and Watson (1997, p. 185; see also Phillips and Lee, 1996).
Assumption 3.1. The initial conditions satisfy
, where λ ≥ 0 and m ∈ {0,1,…,m*}, m* finite. As noted in Canjels and Watson (1997), the unconditional case obtains taking the limit as λN → ∞. The conditional case obtains for λ = m = 0.
In the results given in Theorem 3.1, which follows, we will use the superscript ξ to indicate which of Cases 1–6 of μSn+s of (2.3) hold. For the zero frequency ω0 tests: Case 1: ξ = 0; Cases 2 and 3: ξ = 1; Cases 4–6: ξ = 2. For the seasonal frequency ωk tests, k = 1,…,[S/2] : Cases 1, 2, and 4: ξ = 0; Cases 3 and 5: ξ = 1; Case 6: ξ = 2. For example, substituting ξ = 0 into the expression given in (3.1), which follows, for t0 gives the limiting representation for the t0 statistic under Case 1 (no deterministics) of μSn+s, whereas ξ = 1 gives the limiting representation under Case 2 (nonseasonal intercept, no trend) and Case 3 (seasonal intercepts, no trend). Similarly, substituting ξ = 2 into (3.2) and (3.3) gives the limiting representations for the tkα and tkβ statistics, respectively, under Case 6 (seasonal intercepts and seasonal trends) of μSn+s.
We now state our main theorem. Some remarks follow.
THEOREM 3.1. Let the process {xSn+s} be generated by (2.1)–(2.3) and let the (unique) polynomial ψ(z) be defined such that ψ(z)φ(z) ≡ 1. Then, under
of (2.5) and Assumption 3.1, and denoting weak convergence of the associated probability measures by ⇒,


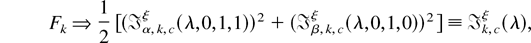
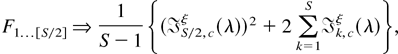
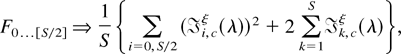
omitting
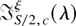
in (3.5) and (3.6) where S is odd. In (3.1), i = 0,S/2 if S is even and i = 0 if S is odd, whereas k = 1,…S* in (3.2)–(3.4). The nomenclature ξ is as defined following Assumption 3.1, ak ≡ Im{ψ[exp(iωk)]}, ak* ≡ Im{φ[exp(−iωk)]}, bk ≡ Re{ψ[exp(iωk)]}, bk* ≡ Re{φ[exp(−iωk)]}. Finally, the independent limiting processes Ji,cξ(r,λ), i = 0,S/2, and Jα,k,cξ(r,λ) and Jβ,k,cξ(r,λ), k = 1,…,S*, are as defined in Definition A.1 of the Appendix.
Remark 3.1. Setting c = 0 and S = 4, the representations provided in Theorem 3.1 reduce to the limiting null representations provided in Burridge and Taylor (2001). Theorem 3.1 therefore generalizes the results of Burridge and Taylor to an arbitrary seasonal aspect, S, and to the near seasonally integrated case, c ≠ 0. For c = 0 and φ(z) = 1, the representations in Theorem 3.1 also reduce to those given in Smith and Taylor (1999a) and Nabeya (2001a). Moreover, notice that the representations in (3.1)–(3.6) for c = 0 do not depend on the initial conditions vS+s, s = 1 − S,…,0, provided ξ > 0. Indeed, for each of Cases 3, 5, and 6 of μSn+s of (2.3), the statistics also yield exact similar tests (for detailed discussion on this point, see Smith and Taylor 1998, 1999a).
Remark 3.2. The representations given in Theorem 3.1 delineate the asymptotic local power functions of the seasonal unit root tests from (2.11) in all cases indexed by a common noncentrality parameter c. Numerical tabulations of certain of these functions are given in Section 4, which allow us to investigate the relative power properties of the tests and also to quantify the degree of power loss incurred when (seasonal) intercepts and (seasonal) time trends are included in the test regression. Notice also, for example, from the results in Theorem 3.1 that the asymptotic local power functions of the seasonal frequency tS/2 (S even), tkα, tkβ and Fk, k = 1,…,S*, and F1…[S/2] tests are not affected by including a nonseasonal intercept or time trend in (2.11) but are affected by the inclusion of seasonal intercepts and seasonal trends. Similarly, the asymptotic local power function of the t0 test is not affected by the inclusion of seasonal intercepts (trends) vis-à-vis the case where a nonseasonal intercept (trend) is included in (2.11). The asymptotic local power function of the F0…[S/2] test is, however, clearly affected by both seasonal and nonseasonal intercepts and time trends.
Remark 3.3. In practice, we would probably want to permit the noncentrality parameter to vary across the seasonal frequencies ωk ≡ 2πk/S, k = 0,…,[S/2] , as in Remark 2.2. Just as argued in Rodrigues (2001, p. 80), the asymptotic orthogonality result stated in Remark A.1 of the Appendix ensures that the representations given in Theorem 3.1 remain appropriate in such cases on substituting c for ck ≤ 0, k = 0,…,[S/2] , in (3.1) and (3.2), respectively, throughout and appropriately redefining Assumption 3.1.
Remark 3.4. From (3.1)–(3.6), it is seen that the limiting distributions of the t0, tS/2 (S even), Fk, k = 1,…,S*, F1…[S/2], and F0…[S/2] statistics do not depend on the serial correlation nuisance parameters {φi}i=1p under
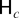
of (2.5), whereas those of the harmonic frequency t-statistics tkα and tkβ, k = 1,…S*, do, in general. We investigate this dependence for the case of an AR(1) error process in Section 4. An obvious exception occurs when φ(z) is expressible as φ(zS), that is, φ(z) is a purely seasonal polynomial. In this case the limiting distributions of the tkα and tkβ statistics in (3.2) and (3.3) are invariant to the parameters characterizing φ(z), k = 1,…S*. Other exceptions can occur at specific frequencies. For example, if S is an integer multiple of four, then the limiting distributions of the tS/4α and tS/4β statistics, corresponding to the harmonic frequency pair (π/2,3π/2), will be invariant to the parameters of φ(z), provided φ(z) is expressible as φ(z2). Notice that in the serially uncorrelated case, φ(z) = 1, ak = 0, k = 1,…,S*, and bk = 1, k = 0,…,[S/2] . For the special case of S = 4, c = 0, and λ = 0, these results reproduce those proved in Burridge and Taylor (2001).
Remark 3.5. It can be seen from (3.1) of Theorem 3.1 that for a given value of ξ, t0 and tS/2 have identical limiting representations, and hence asymptotic local power functions, under
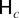
of (2.5). These limiting distributions are also seen to be independent, by virtue of the independence of J0,cξ(r,λ) and JS/2,cξ(r,λ), ξ ∈ {0,1,2}. For c = 0 and ξ = 1,2, these coincide with the corresponding limiting null representations for the augmented Dickey–Fuller (ADF) t-statistic provided in Theorem 10.1.3, p. 561, and Theorem 10.1.6, pp. 567–568, of Fuller (1996), respectively. For ξ = 0 the representations obtained for λ = 0 coincide with the representation given in Corollary 10.1.1.5 of Fuller (1996, p. 554), noting that Fuller imposes zero starting values on his analysis. For c < 0 and ξ = 2 they replicate the representation given in Canjels and Watson (1997, Footnote 13, p. 192) for the asymptotic power function of the conventional ADF test. For λ = 0 the representation in (3.1) replicates those given for the ADF test in, inter alia, Chan and Wei (1987), Nabeya and Tanaka (1990), Perron (1989), Phillips (1987), and Elliott et al. (1996), with graphs of the associated asymptotic power function for ξ = 0,1,2 provided in Figures 1, 2, and 3, respectively, of Elliott et al. (1996, pp. 822–824).
Remark 3.6. Representations (3.2)–(3.5) of Theorem 3.1 demonstrate that, under
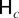
of (2.5), the tkα and tlα, k ≠ l, and tkβ and tlβ, k ≠ l, k,l = 1,…,S*, statistics are asymptotically mutually independent and are also asymptotically independent of t0 and tS/2; the F-statistics Fk, k = 1,…,S*, possess mutually independent and identical limiting representations and are asymptotically independent of the t0 and tS/2 statistics; and the F-statistic F1…[S/2] is asymptotically independent of the zero frequency t0 statistic.
Remark 3.7. The limiting representation in (3.2) for c = λ = 0 can be shown to coincide with that of the limiting null distribution of the t-statistic of Dickey, Hasza, and Fuller (1984) for the case of a biannual (S = 2) seasonal process. Moreover, for c ≤ 0, the stated representation in (3.2) for the tkα statistic when λ = 0, ak = 0 and bk = 1, k = 1,…,S*, reduces to that provided by Chan (1989, Theorem 1, p. 282) and Perron (1992, Theorem 2, p. 127) for ξ = 0 and Tanaka (1996, pp. 355–362) and Nabeya (2000, 2001b) for ξ = 0,1,2 for the limiting distribution of the Dickey et al. (1984) statistic for S = 2.
In Figures 1a–c we graph the asymptotic local power functions of the tkα, tkβ, and Fk tests for unit roots at the seasonal harmonic frequencies ωk, k ∈ {1,…,S*}, for φ(z) = 1. Figures 2a and b graph the corresponding results for the tS/4α and tS/4β tests, respectively, for unit roots at the harmonic frequency pair (π/2,3π/2) in cases where S is an integer multiple of four, when φ(z) = 1 − φ1 L, a first-order autoregression. We report results for φ1 = {0.5,0.9,0.95,0.99}.2
We need only consider positive values of φ1 because the asymptotic local power functions in this case are easily shown to be invariant to the sign of φ1. Moreover, there is no need to report results for FS/4 because its asymptotic local power function is invariant to φ1, as demonstrated in Theorem 3.1.

Asymptotic local power functions of harmonic unit root tests: (a) φ(L) = 1, ξ = 0; (b) φ(L) = 1, ξ = 1; (c) φ(L) = 1, ξ = 2.

Asymptotic local power functions of (a) tS/4α: φ(L) = 1 − φ1 L, ξ = 1; and (b) tS/4β: φ(L) = 1 − φ1 L, ξ = 1.
In the case of Figures 1a–c these functions are reported for ξ = {0,1,2}, whereas for Figures 2a and b only results for ξ = 1 are reported, these displaying the same qualitative features with respect to φ1 as were seen for ξ = 0 and ξ = 2.3
The unreported results may be obtained from the authors on request.
Consider first Figures 1a–c. A number of interesting features are apparent from these asymptotic local power functions. First, the power loss from using the Fk rather than tkα statistics in testing for unit roots at the seasonal harmonic frequencies is not too large. The biggest differences are seen in the case of ξ = 0. However, this case is arguably of no practical interest because the resulting unit root tests will neither be similar with respect to the starting values of the process nor be invariant to the seasonal intercepts, γs*, s = 1 − S,…,0, of (2.3) (for details, see Smith and Taylor, 1998, 1999a; Burridge and Taylor, 2004). For ξ = 1 the difference between the power functions of the two tests is relatively small and is further reduced for ξ = 2. Figures 1a–c also highlight the fact that the tkβ tests do not display power in the case of φ(z) = 1; indeed, it is straightforward to show from (3.3) that tkβ →p 0 as c → −∞ in this case.
Figures 1a–c also show the power loss in the tkα and Fk tests when deterministic components are included in (2.11). As has also been observed by Elliott et al. (1996, p. 823) for the asymptotic local power functions of the ADF test, the power loss incurred when moving from ξ = 0 to ξ = 1 is somewhat larger than that when moving from ξ = 1 to ξ = 2 for both the tkα and Fk tests.
Turning to Figures 2a and b one observes a strong dependence of the asymptotic local power functions of the harmonic frequency t-tests on the AR parameter, φ1. From Figure 2a it is seen that for c = 0, the tS/4α test is undersized, the more so as φ1 increases toward unity. For a given value of c, this undersizing is translated into large reductions in power relative to φ1 = 0. Indeed, comparing Figures 2a and 1b it is seen that the FS/4 test is considerably more powerful than the tS/4α test when φ ≠ 0. A similar but reversed pattern is seen in the tS/4β test, where considerable oversizing is seen for c = 0, with test size approaching 20% in many cases,4
For ξ = 2, empirical test size rises to around 40% in these cases.
We now use Monte Carlo simulation methods to investigate the finite sample local power properties of the t0, t1α, t1β, F1, and t2 tests from (2.11) for the case of quarterly data, S = 4, when the true DGP for {x4n+s} is the near seasonally integrated AR model:
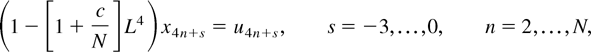
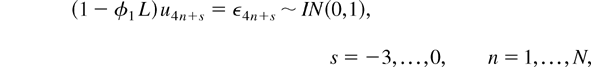
with u4k+s = 0, s = −3,…,0, k ≤ 0, for the conditional case, x4+s = u4+s, s = −3,…,0.5
We also ran our experiments under the unconditional case. The results in this case were little different from those reported.
Empirical power of quarterly unit root tests (nominal 0.05 level)

Empirical size and power of quarterly unit root tests (nominal 0.05 level)

We focus on the sample sizes N = 25, 50, 100 and on Case 3 of (2.11), where ξ = 1 for all reported tests. All tests were run at the nominal 0.05 level using finite sample critical values. These were computed using data generated according to (4.1) and (4.2) with c = φ1 = 0 and were based on 60,000 Monte Carlo replications of the statistics from (2.11), for each of the sample sizes considered.6
For this reason the results for c = 0 are omitted from Table 1.
As N is increased the reported quantities appear to be converging rapidly toward the corresponding asymptotic power levels as might be expected. As an example, for c = −7 the asymptotic local power of the t1α and F1 tests is 0.202 and 0.174, respectively, both of which are very close indeed to the local power of these tests for N = 100 given in Table 1. Mirroring the asymptotic local power results in Figure 1b we also see from Table 1 that for φ1 = 0 (the only case where the t1α statistic is correctly sized) only relatively small losses in power are incurred from using the F1 rather than the t1α test.
A general feature of the results reported in Table 1 for φ1 = 0 is that for all of the tests the finite sample powers for a given value of c approach the limiting value for that value of c from above, as has also been noted by Tanaka (1996, p. 351) for the ADF test. In Table 2 this general pattern is reversed in the case of the t0 test, which displays a relatively strong finite sample dependence on φ1. This behavior is to be expected given that positive values of φ1 will imply spectral mass at frequency zero. Indeed, in the case of φ1 = 0.9 there are cases where this yields the dominant root at frequency zero. This occurs for (c,N) = (−9,25), (−13,25), (−17,25), (−21,25), and (−21,50). The results for the t2 and F1 tests in Table 2 are very similar to those reported in Table 1, showing very little finite sample dependence on φ1. The results for the t1α and t1β tests show a clear dependence on φ1 with the finite sample results approaching the limiting values for those values of φ1 and c.
In practice it is therefore quite clear from these results that proper inference cannot be based on the tkα and tkβ tests, their size properties under autocorrelated errors being unknown, even asymptotically. The fact that the asymptotic local power functions of the Fk tests are invariant to the parameters of φ(z) and that the Fk tests display only small power losses relative to the tkα test when φ(z) = 1, and are otherwise more powerful, makes the case in favor of the use of the Fk tests overwhelming.
In this paper we have derived representations for the limiting distributions of regression-based seasonal unit root test statistics when the characteristic roots of the underlying seasonal process are local to unity. We derived our results for the case of a process observed for any given seasonal periodicity, S, under very general assumptions on the initial values of the process, for test regressions that included either no deterministic variables or variables that ranged from a nonseasonal intercept to seasonal intercepts and seasonal trends, and for driving shocks that followed a stationary AR(p) process.
Our results have built upon and generalized, in various directions, earlier representations provided in Rodrigues (2001), Burridge and Taylor (2001), Smith and Taylor (1999a), and Nabeya (2001a). In our key result we have demonstrated that the limiting distributions of the t0 and tS/2 statistics for testing for a unit root at the zero and Nyquist (S even) frequencies, respectively, under near seasonal integration coincide with that of the conventional ADF statistic and are invariant to the serial correlation nuisance parameters in the shocks. This invariance property has also been shown to hold for the Fk statistics for testing the null hypothesis of a complex pair of unit roots at the seasonal harmonic frequencies, k = 1,…,S*, but not for the corresponding tkα and tkβ statistics, whose asymptotic distributions under near seasonal integration are not, in general, invariant to these nuisance parameters. Our findings confirmed the recommendations of earlier authors against the use of the tkα and tkβ statistics for practical data analysis in favor of the Fk statistics; see, inter alia, Burridge and Taylor (2001) and Smith and Taylor (1999a).
Proof of Theorem 3.1. In what follows we simplify the exposition by setting γs* = βs* = 0, s = 1 − S,…,0, in (2.3). Before proving our main theorem, we need to set up some notation and establish some preparatory lemmas.
Under
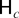
of (2.5) and Assumption 3.1 it follows from (2.1)–(2.3) that
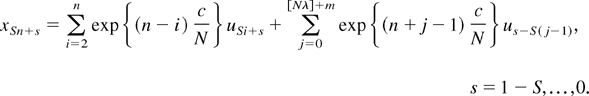
Defining the annualized processes

we may write
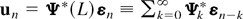
, where the sequence of S × S matrices {Ψk*}k=0∞ are as defined in the Appendix of Burridge and Taylor (2001). Notice that the sequence {kΨk*} is absolutely summable by virtue of the stationarity of {uSn+s} (cf. Burridge and Taylor, 2001). Moreover,
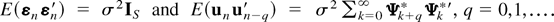
.
LEMMA A.1. Let {xSn+s} be generated by (2.1)–(2.3) under
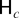
of (2.5) and Assumption 3.1. Defining the annualized process Xnκ ≡ [xS(n−1)+1κ,xS(n−1)+2κ,…,xSnκ]′, then as N → ∞,
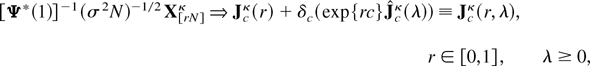
where [Ψ*(1)]−1 is the inverse of the matrix Ψ*(1) and δc is a scalar indicator variable such that δc = 1 if c ≠ 0 or if c = 0 and κ = 1,2,4, and δc = 0 otherwise. In (A.2),
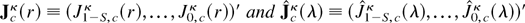
are mutually independent S-vectors each with independent elements such that Jcκ(r,λ) ≡ (J1−S,cκ(r,λ),…,J0,cκ(r,λ))′, where
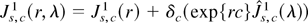
, with
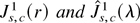
independent Ornstein–Uhlenbeck (OU) processes, s = 1 − S,…,0, and
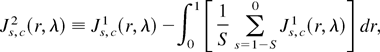
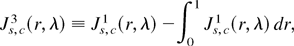
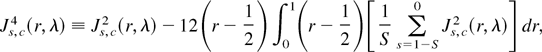
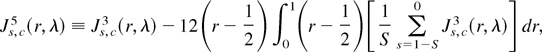
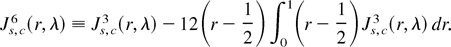
Proof. The proof follows from a straightforward extension of results proved in Rodrigues (2001), using the multivariate invariance principle of Phillips (1988, p. 1026), coupled with (A.1) of Canjels and Watson (1997, p. 197) and applications of the continuous mapping theorem (CMT). █
LEMMA A.2. Under the conditions of Lemma A.1 and as N → ∞,
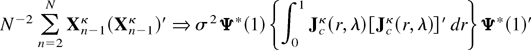
and
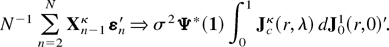
Proof. The proof follows from Lemma A.1 and applications of the CMT. █
We next define the mutually orthogonal S × 1 selection vectors,
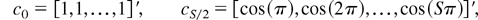
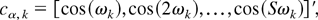
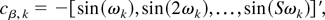
omitting cS/2 if S is odd. In the analysis that follows we will require the following definition, which makes use of the preceding selection vectors.
DEFINITION A.1. For each of Cases 1–6 and r ∈ [0,1], we define J0,cξ(r,λ), JS/2,cξ(r,λ) (S even), Jα,k,cξ(r,λ), and Jβ,k,cξ(r,λ), k = 1,…,S*, for ξ = 0,1,2, as follows:

These are straightforwardly seen to be mutually independent because they are mutually orthogonal transformations of the OU-based functionals from (A.2). Moreover, it is straightforwardly seen that for λ = 0 these are independent standard, demeaned, and demeaned and detrended OU processes for ξ = 0, ξ = 1, and ξ = 2, respectively.
Noting that the selection vectors defined in (A-10)–(A.12) are precisely those used to define the transformed level variables in (2.12), it is straightforward but tedious to show that the following relations hold, omitting (A.14) where S is odd:
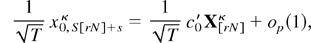
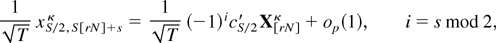
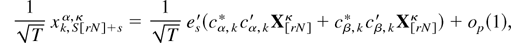
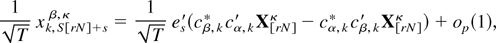
s = 1 − S,…,0, and where {es}s=1−S0 are a collection of S-dimensional selection vectors whose (S + s)th element is unity and all other elements are equal to zero, cα,k* = [cos(ωk),cos(0),…,cos((2 − S)ωk)]′, and cβ,k* = [sin(ωk),sin(0),…,sin((2 − S)ωk)]′.
In Lemma A.3, which follows, we will make use of the following identities: ci′Ψ*(1) ≡ bi ci′, where i = 0,S/2 if S is even and i = 0 otherwise, cα,k′Ψ*(1) ≡ ak cβ,k′ + bk cα,k′, and cβ,k′Ψ*(1) ≡ −ak cα,k′ + bk cβ,k′, k = 1,…,S*, where b0 ≡ ψ(1), bS/2 ≡ ψ(−1) (S even), ak ≡ Im[ψ(exp(iωk))] , and bk ≡ Re[ψ(exp(iωk))] , with ψ(z) as defined in Theorem 3.1.
LEMMA A.3. Under the conditions of Lemma A.1 and as N → ∞, and letting [ell ] ≡ S + p* + 1,

Proof. The proofs of parts (i) and (iii) follow straightforwardly from (A.13), (A.14), (A.8), (A.9), and the CMT (for full details, see Rodrigues and Taylor, 2003). █
(ii) From (A.15) and (A.16) it is straightforward to show that
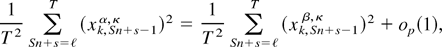
so we need only establish results for
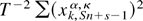
in what follows. From (A.15),
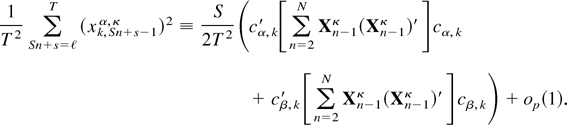
It then follows from (A.8), the orthogonality of cα,k and cβ,k, and the CMT that

(iv) From (A.15) we obtain that
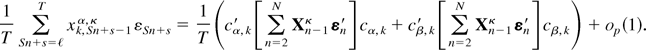
It then follows from (A.9) and applications of the CMT that

from which the stated result follows immediately.
(v) From (A.16) we obtain that
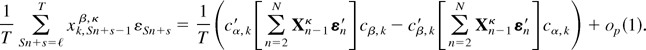
Again, from (A.9) and applications of the CMT it follows that

from which the stated result follows immediately. █
Now we move to the proof of our main result. Consider the appropriately scaled OLS estimator of π from (2.11),
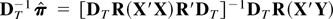
, where DT = T−1IS, R = [IS : 0S×p*] , X is the (T − p* − S) × (S + p*) matrix,

omitting the second column if S is odd, and Y = [ΔS xp*+S+1κ, ΔS xp*+S+2κ,…,ΔS xTκ]′.
Remark A.1. Using results from Jeganathan (1991) it is straightforward to show that the off-diagonal elements of DTR(X′X)R′DT are all of op(1). Moreover, notice that we may consider
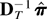
directly, because the matrix DT*(X′X)DT*, where DT* is a diagonal (S + p*) × (S + p*) matrix whose first S leading diagonal elements are T−1 and whose remaining p* leading diagonal elements are T−1/2, is block diagonal between its upper (S × S) and lower (p* × p*) blocks.
The following proposition, whose proof is given in Rodrigues and Taylor (2003), gives a convenient form for the OLS t0, tS/2 (S even), tkα and tkβ, k = 1,…,S*, statistics from (2.11), where
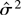
is used to denote the usual OLS estimator of σ2 from (2.11), and [ell ] ≡ S + p* + 1.
PROPOSITION A.1. The OLS t-statistics from (2.11) can be written as
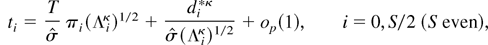
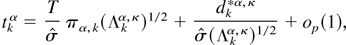
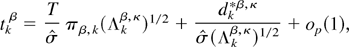
k = 1,…S*, where
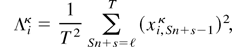
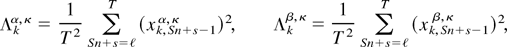
and
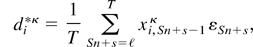
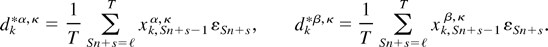
The results stated for the t-statistics in (3.1)–(3.3) then follow directly from Proposition 2.1, Proposition A.1, Lemma A.3, and applications of the CMT.
Turning to the Fk-statistics, k = 1,…,S*, observe from the asymptotic orthogonality result (see Remark A.1) that Fk = ½[(tkα)2 + (tkβ)2] + op(1). It therefore follows from (3.2) and (3.3) and the CMT that, as N → ∞, on grouping terms, that

where ak* and bk* are as defined in Theorem 3.1. Because φ(z) and, hence, ψ(z) are power series functions in z, it is trivial to show that the following identities hold: (ak*2 + bk*2)(ak2 + bk2) ≡ 1, bk* ak − ak*bk ≡ 0, and bk*bk + ak* ak ≡ 1. Substituting these identities into (A.24), the stated result follows immediately. The stated results for the F1,…,[S/2] and F0,…,[S/2] statistics then follow directly using the asymptotic orthogonality result; cf. Remark A.1. █

Asymptotic local power functions of harmonic unit root tests: (a) φ(L) = 1, ξ = 0; (b) φ(L) = 1, ξ = 1; (c) φ(L) = 1, ξ = 2.

Asymptotic local power functions of (a) tS/4α: φ(L) = 1 − φ1 L, ξ = 1; and (b) tS/4β: φ(L) = 1 − φ1 L, ξ = 1.

Empirical power of quarterly unit root tests (nominal 0.05 level)

Empirical size and power of quarterly unit root tests (nominal 0.05 level)