Published online by Cambridge University Press: 01 October 2004
The constant conditional correlation general autoregressive conditional heteroskedasticity (GARCH) model is among the most commonly applied multivariate GARCH models and serves as a benchmark against which other models can be compared. In this paper we consider an extension to this model and examine its fourth-moment structure. The extension, first defined by Jeantheau (1998, Econometric Theory 14, 70–86), is motivated by the result found and discussed in this paper that the squared observations from the extended model have a rich autocorrelation structure. This means that already the first-order model is capable of reproducing a whole variety of autocorrelation structures observed in financial return series. These autocorrelations are derived for the first- and the second-order constant conditional correlation GARCH model. The usefulness of the theoretical results of the paper is demonstrated by reconsidering an empirical example that appeared in the original paper on the constant conditional correlation GARCH model.This research has been supported by the Swedish Research Council of Humanities and Social Sciences and the Tore Browaldh's Foundation. A part of this work was carried out while the second author was visiting the School of Finance and Economics, University of Technology, Sydney, whose kind hospitality is gratefully acknowledged. The paper has been presented at the Econometric Society European Meeting, Venice, August 2002. We thank participants for comments and two anonymous referees for their remarks. Any errors and shortcomings in the paper remain our own responsibility.
Univariate models for conditional heteroskedasticity have long been popular in financial econometrics and volatility forecasting, and a large number of applications have been published using general autoregressive conditional heteroskedasticity (GARCH) models. The probability structure of univariate GARCH(p,q) models has recently been under study. Conditions of the existence of moments and, in particular, the fourth-moment structure of these models have been derived (see, e.g., He and Teräsvirta, 1999a, 1999b; Karanasos, 1999). These results are important as they help the user to find out how well the GARCH model and its extensions are capable of characterizing stylized facts typical of many high-frequency financial time series. For general results on the existence of moments in volatility models, see Carrasco and Chen (2002) and Lanne and Saikkonen (2002).
GARCH models have been generalized to the vector case, but the number of applications has remained rather limited compared to univariate models. Multivariate GARCH models are surveyed in Bollerslev, Engle, and Nelson (1994) and Gouriéroux (1997, Ch. 6); see also Palm (1996) for a short review. As yet relatively little is known about the moment structure of these models. Engle and Kroner (1995) derive a necessary and sufficient condition for weak stationarity of vector GARCH models, but results for higher order moments do not seem to exist in the literature. Our starting point is one of the frequently applied multivariate GARCH models, the so-called constant conditional correlation generalized autoregressive heteroskedasticity (CCC-GARCH) model of Bollerslev (1990). Bollerslev's model is in turn a generalization of the constant conditional correlation ARCH model that appears in Cecchetti, Cumby, and Figlewski (1988). In this paper we consider an extended version of the CCC-GARCH model. We derive a sufficient condition for the existence of the fourth moments for this model and, most important, its complete fourth-moment structure. Because of rather involved calculations we restrict our considerations to the second-order CCC-GARCH model. As most of the applications seem to rely on first-order models, this does not appear to be a serious restriction. Two other papers containing results on fourth moments of multivariate GARCH models, Hafner (2003) and Karanasos (2003), should be mentioned here. These papers contain rather general fourth-moment expressions that are not directly applicable to the rather specific problem considered in this paper.
Our model is an extension to the original CCC-GARCH model as defined in Jeantheau (1998); see also Ling and McAleer (2003). In particular, we show that the squared observations of the extended first-order CCC-GARCH model can already have a remarkably rich correlation structure able to cover many shapes of autocorrelation functions that have been observed in practice. This motivates the extension of the standard CCC-GARCH model. In particular, the autocorrelations of individual processes do not necessarily decay monotonically from the first lag onward. By comparison, the autocorrelations of squared observations in the standard CCC-GARCH(1,1) model still have the same properties as they do in the univariate GARCH(1,1) model. This includes the exponential decay of the autocorrelations of squared observations from the first lag for all variables in the model. Using an empirical example in Bollerslev (1990) we demonstrate how the use of the correlation structure of the CCC-GARCH(1,1) model worked out in this paper helps one to enrich the interpretation of the estimated models.
The plan of the paper is as follows. The extended CCC-GARCH model is defined in Section 2. Sections 3 and 4 contain the main results on the fourth-moment structure of this model. Section 5 briefly takes up a special case, a bivariate first-order model. Section 6 contains an empirical example, and the conclusions can be found in Section 7. The proofs of results appear in the Appendix.
Following Jeantheau (1998), consider the following vector stochastic process:


where Dt = diag{h1t,…,hMt} and hit is the conditional standard deviation of εit, i = 1,…,M. Furthermore, the stochastic vector zt = (z1t,…,zMt)′ is independent and identically distributed (i.i.d.) with mean 0 and positive definite covariance matrix R = [ρij] such that ρii = 1 and ρij ≠ 0, i,j = 1,…,M. The main diagonal elements of R are restricted to unity for identification reasons; compare this with the univariate case, in which customarily

. Furthermore, ht = (h1t,…,hMt)′ is an M × 1 vector of conditional standard deviations of εt. Let

where ht(2) = (h1t2,…,hMt2)′ and Zt = diag{z1t,…,zMt}. Define the vector GARCH(p,q) process
where a0 is an M × 1 vector with positive elements and Ai, i = 1,…,q, and Bj, j = 1,…,p, are M × M matrices such that each element of ht(2) is positive for every t. Note that (4) defines the diagonal elements of Dt. From (2) it follows that

where

is the σ-field generated by all the available information up through time t − 1.
Remark 1. A sufficient condition for ht(2) > 0 for all t is that all elements in a0 be positive and all elements in Ai and Bj for each i and j be nonnegative. (Note that all vector and matrix inequality signs in this paper represent element-by-element inequality.) From Nelson and Cao (1992) we conjecture that this condition is not necessary, at least not if p > 1 or q > 1 or both. It follows from zt ∼ iid(0,R) that

is positive definite.
Remark 2. The vector GARCH process defined by equations (2)–(6) is a multivariate GARCH model with constant conditional correlations. The CCC-GARCH model of Bollerslev (1990) is obtained by assuming that Ai, Bj, i = 1,…,q, and j = 1,…,p are diagonal matrices. In particular, setting Bj = 0, j = 1,…,p, yields the constant conditional correlation ARCH model introduced in Cecchetti et al. (1988).
In this section we consider the vector GARCH(2,2) model defined in (2)–(6) and set Cit = [ci,jlt] = AiZt2 + Bi, i = 1,2. Note that {Cit} is a sequence of i.i.d. random matrices such that Cit is independent of ht(2). By (3) we may rewrite (4) as

Let

, where [otimes ] denotes the Kronecker product of two matrices. Let λ(Γ) denote the modulus of the largest eigenvalue of Γ. We can now state the following result.
THEOREM 1. The vector GARCH(2,2) process defined in (2) and (3) and (7) is weakly and strictly stationary if

Proof. Apply Proposition 3.1 of Jeantheau (1998) to {εt} defined in (2) and (3) and (7). █
Remark 3. Bollerslev and Engle (1993) and Engle and Kroner (1995) derived a necessary and sufficient condition for weak stationarity of a vector GARCH(p,q) model without the assumption of the constant conditional correlation. Condition (8) is a special case of their result. When it holds, the unconditional variances of the elements of εt in the vector GARCH(2,2) model (2) and (3) and (7) are
We are now ready to state our result concerning the fourth-order unconditional moment matrix of model (2) and (3) with (7). Let vec(A) be a vector in which the columns of the M × M matrix A are stacked one underneath the other. Then vec(A′) = KMM vec(A), where KMM is the M2 × M2 commutation matrix (see, e.g., Magnus, 1988, pp. 35–37). We have the following theorem.
THEOREM 2. Consider the vector GARCH(2,2) model (2) and (3) and (7). Assume that condition (8) holds and

exists. Then the fourth-order moment matrix

of {εt} exists if
where
Under (10),

Proof. See the Appendix.
Remark 4. Figure 1 helps to compare the largest absolute eigenvalues in condition (10) and the one of Ling and McAleer (2003) for the existence of the fourth-order unconditional moments in CCC-GARCH(2,2) models. The graphs are obtained by fixing values of all parameters of the model but b2,11 and letting b2,11 increase from 0.2. The moduli of the largest eigenvalues of matrix Γ in CCC-GARCH(2,2) models are monotonically increasing functions of the parameter b2,11. The solid curve is for λ(Γ), where Γ is defined in (10), whereas the dashed-dotted one is the counterpart of the solid one with

defined in Theorem 2.2 of Ling and McAleer (2003). It is seen that these two curves have an intersection exactly at λ(Γ) = 1 (dashed line). Similar graphs can be obtained for any other parameter combination, and it appears that those two conditions, although they look different, always give the same answer. The advantage of condition (10) is that it can be used in deriving the fourth-moment matrix of εt.

Moduli of the largest eigenvalues of matrices Γ for a CCC-GARCH(2,2) model as a function of parameter b2,11 when (a) Γ is defined by condition (10) (solid curve) and (b) is defined in Theorem 2.2 of Ling and McAleer (2003) (dashed-dotted curve). The parameters of the model are a1,11 = 0.06, a1,12 = 0.08, a1,21 = 0.1, a1,22 = 0.12, a2,11 = 0.07, a2,12 = 0.1, a2,21 = 0.08, a2,22 = 0.12, b1,11 = 0.05, b1,12 = 0.08, b1,21 = 0.11, b1,22 = 0.2, b2,12 = 0.09, b2,21 = 0.1, and b2,22 = 0.12, and the nondiagonal element of the correlation matrix of the standard normal error process {zt} equals 0.2.
Remark 5. Setting M = 1 in (10) and (11) yields the condition for the existence of the fourth-order moment for the univariate GARCH(2,2) model

where

, and

, and the expression for the fourth unconditional moment of ε1t:

Both are derived in He and Teräsvirta (1999a). The necessary and sufficient conditions for finite fourth-order moments of GARCH(2,1) and GARCH(1,2) models of Bollerslev (1986) are nested in (12). The result illustrated in Figure 1 also holds for the univariate GARCH(2,2) model: the left-hand side of (12) and the corresponding eigenvalue in Theorem (2.1) of Ling and McAleer (2002) intersect at λ(Γ) = 1.1
This requires, however, that in Theorem 2.1 of Ling and McAleer (2002), λ(Γ) is redefined to be the largest eigenvalue of Γ instead of being the smallest eigenvalue.
The proof of the necessary condition for the existence of the fourth moment of the GARCH(p,q) model in He and Teräsvirta (1999a) is complete. It is important to note that the authors begin by representing the recursion formula for the squared conditional variance function ht2 such that it has a bilinear form (see pp. 835–836). The advantage of this form is obvious from formula (A.21). The authors show that under some conditions,
implies λ(Γ) < 1, where a = (a1,…,ap*)′, b = (b1,…,bp*)′ for ai > 0, bi ≥ 0 (i = 1,…,p*) and b ≠ 0, and Γs = [γij(s)] , which is a positive (p* × p*) matrix (γij(s) > 0 for any s ≥ 2), and Γ is well defined. To see that the necessary condition λ(Γ) < 1 holds for (A.21), set

. That is, for any given ε > 0, there exists an integer N > 0 such that

for any k > N. It follows from the positiveness of a and Γi and nonnegativeness of b that for any i,j = 1,…,p* and ε and N given previously,

, which implies that

converges as k approaches infinity. This shows that the necessary condition λ(Γ) < 1 in Lemma 4 of He and Teräsvirta (1999a) holds. Ling and McAleer (2002, note 1) argue that this result is proved by concluding that

follows from

. This is not the case.
Next we consider the relationship between the distributions of εt and zt through their fourth-moment structure. For this purpose, let

and define the multivariate “rescaled fourth-moment matrix” of {εt} in (2)–(4) as

The jth diagonal element of K is the kurtosis of εjt, j = 1,…,M.
COROLLARY 1. Assume that ΓZ[otimes ]Z exists and (10) holds for the vector GARCH(2,2) model (2) and (3) and (7). Then

where the inequality sign refers to element-by-element inequality and K(zt) is the “rescaled fourth-moment matrix” of {zt}.
Inequality (13) follows from Jensen's inequality. To illustrate, if zt has a multivariate normal distribution, the unconditional distribution of εt is leptokurtic in the sense of (13).
The cross-moment matrix ΓCi[otimes ]Cj, i ≠ j, is required in the considerations if the vector model is of higher order than one. Expressions in Theorem 2 simplify for the vector GARCH(1,1) model. This is seen from the following result.
COROLLARY 2. Let the assumptions of Theorem 2 hold and assume C2t = 0 in (7). Then the fourth-order moment matrix

of {εt} for the vector GARCH(1,1) model (2) and (3) and (7) exists if

Under (14),
In this section we shall derive the multidimensional correlation function of {εt(2)} for our vector GARCH(2,2) process. Let

as before and

. Furthermore, let DM = diag{γ111/2(0),…,γMM1/2(0)}. To fix notation, write the nth-order autocorrelation matrix of {εt(2)} for the vector GARCH(2,2) process as

for n ≥ 1.
The ith diagonal element, rii(n), i = 1,…,M, of RM(n) in (16), is the nth autocorrelation of the squared observations for the ith component {εit}, whereas rij(n), i,j = 1,…,M, i ≠ j, the off-diagonal elements of RM(n), represent the cross-correlations between εit2 and εjt−n2.
To obtain RM(n), we must find an expression for

. This can be done by applying (7) to εt(2) recursively up to the nth step and further applying Theorem 2 to

. The final result appears in the following theorem.
THEOREM 3. Assume that ΓZ[otimes ]Z and μ2 in (9) exist and condition (10) holds for the vector GARCH(2,2) model (2) and (3) and (7). Then the nth-order autocorrelation matrix RM(n) of {εt(2)} has the stacked form

where
such that for n = 1,2,


Furthermore, for n ≥ 3,

with

In (19),

and

.
Proof. See the Appendix.
If the assumptions of Theorem 3 are satisfied and the first two autocorrelation matrices RM(1) and RM(2) are known we can compute the nth autocorrelation matrix RM(n) recursively through equations (17)–(23). The autocorrelation structure simplifies for the first-order model. We state this result in the following corollary.
COROLLARY 3. Assume that the assumptions of Theorem 3 hold and C2t = 0 in (7). Then the vectors (19)–(21) in the definition of the autocorrelation matrix RM(n) of {εt(2)} for the CCC-GARCH(1,1) model (2) and (3) and (7) are
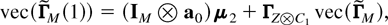
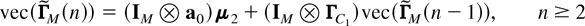
with
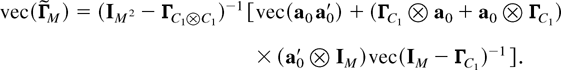
A number of theoretical properties of the autocorrelation matrix {RM(n)}, n = 1,2,…, for the first-order model, obtained through Corollary 3, are listed here:
1. RM(n) → 0 as n → ∞.
It follows from Corollary 3 that we can write
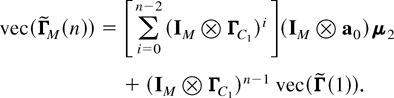
Under condition (10),

. This implies

2. The autocorrelation matrices RM(n) satisfy the Yule–Walker equations.
Suppose that

is known so that vec(RM(1)) is known (see (17) and (18)). It follows from equation (25) that vec(RM(n)), for any n ≥ 2, can be solved by RM(1) and (IM [otimes ] ΓC1) through

In particular,

3. The first-order auto- and cross-correlations rij(1) for i,j = 1,…,M, in RM(1) are positive if the positivity restrictions a0i > 0, al,ij and bl,ij ≥ 0, i,j = 1,…,M, l = 1,…,max{p,q}, mentioned in Section 2, are satisfied.
4. The decay rate of RM(n) as a function of n depends on the eigenvalues of (IM [otimes ] ΓC1). When M = 2 the autocorrelations in R2(n) will exhibit a mixture of decaying exponential decay, because (IM [otimes ] ΓC1) only has real roots. When M ≥ 3 the autocorrelations display a mixture of exponential decay if there exists a dominant real root in (IM [otimes ] ΓC1) and dampening sinusoidal behavior if the moduli of the complex conjugate pairs of eigenvalues are sufficiently large. An example of the latter case is depicted in Figure 2. When M = 1, the decay rate of the autocorrelation function of the squared observations for the univariate GARCH(1,1) model is exactly

. In this case the decay is exponential as r(n) = γc1n−1r(1), n ≥ 2. This property also holds when M > 1 and A1 and B1 are diagonal matrices as in Bollerslev (1990). Thus our extension of the CCC-GARCH model allows a considerably richer autocorrelation structure than the original CCC-GARCH model.

Auto- and cross-correlations of squared observations of a three-dimensional extended CCC-GARCH(1,1) process, lags 1–8. Here ΓC has a pair of complex conjugate eigenvalues with modulus = 0.432 and a real root = 0.858. The parameter values are a01 = 0.1, a02 = 0.2, a03 = 0.25, a11 = 0.05, a12 = 0.25, a13 = 0.06, a21 = 0.07, a22 = 0.08, a23 = 0.25, a31 = 0.25, a32 = 0.08, a33 = 0.08, b11 = 0.05, b12 = 0.4, b13 = 0.05, b21 = 0.05, b22 = 0.07, b23 = 0.3, b31 = 0.25, b32 = 0.08, and b33 = 0.08. The correlation matrix of the standard normal error process {zt} has the following nondiagonal elements: ρ12 = 0.2, ρ13 = 0.3, and ρ23 = 0.23.
To illustrate the general correlation results we consider the bivariate GARCH(1,1) process (2) and (3) and (7). The correlation matrix of {εt(2)} for this process is obtained as a special case of Corollary 3.
COROLLARY 4. Let M = 2, C2t = 0, and c1,12t = c1,21t = 0 in (7). Furthermore, let ΓC1 = [γij] where

for i,j = 1,2, ΓC1[otimes ]C1 = [γij,kl] where

for i,j,k,l = 1,2, and, finally, ΓZ[otimes ]C1 = [γzi c1,jk] where γzi cjk = E(zit2 c1,jkt), for i,j,k = 1,2. Assume that z = (z1t,z2t)′ ∼ NID(0,R) and, furthermore, that condition (10) holds for the bivariate GARCH(1,1) model (2) and (3) with (7). Then R2(n) = [rij(n)] in (17) for i,j = 1,2 has the simplified form

According to Corollary 4, the elements in R2(n), n ≥ 1, decay exponentially. The autocorrelations r11(n) and cross-correlations r12(n), n ≥ 1, have the decay rate γ11, whereas r21(n) and r22(n) also have a common decay rate γ22. The exponential decay rates generalize to the case M > 2 and are a characteristic feature of the standard CCC-GARCH model.
The purpose of this section is to illustrate practical usefulness of our theoretical results. Bollerslev (1990) fitted two CCC-GARCH models with nonzero constant conditional correlations to a set of five weekly exchange rate return series. His purpose was to analyze the dynamic behavior of these returns before the introduction of the European monetary system (EMS) and thereafter. The pre-EMS period ran from July 1973 to the second week of March 1979 (299 observations) and the second, the EMS period, from the third week of March 1979 to the second week of August 1985 (333 observations). The estimated constant correlations from the pre-EMS and EMS models appear in Table 1. The parameter estimates are not reproduced and can be found in Tables 1 and 2 of Bollerslev (1990). The exchange rates that are rates against the U.S. dollar are indexed as follows: 1 = DM (the Deutschmark), 2 = FF (the French franc), 3 = IL (the Italian lira), 4 = SF (the Swiss franc), and 5 = BP (the British pound). Bollerslev concluded, among other things, that the conditional correlations are significantly higher for the EMS period than for the period preceding it.
The estimated constant correlations , i,j = DM, FF, IL, SF, BP, from the two estimated CCC-GARCH models (EMS period and pre-EMS period) of Bollerslev (1990)

Auto- and cross-correlations rij(n),i,j = DM, FF, IL, SF, BP, n = 1, 2, 5, 10, are computed from the two estimated CCC-GARCH models (EMS period and pre-EMS period) of Bollerslev (1990)

Using plug-in auto- and cross-correlation estimates based on the definitions of the true quantities derived in the previous sections we are able to complete Bollerslev's analysis. However, in the pre-EMS model,

, so that the IL process does not have a finite variance. As this would invalidate our small example, we shrink the estimate of a33 to 0.287 to satisfy the fourth-moment existence condition for the pre-EMS system. Estimated auto- and cross-correlations of the squared observations from the two models after this adjustment can be found in Table 2. The individual autocorrelations are relatively high and persistent for FF and SF and, of course, very high and persistent for IL (the adjusted

remains just below unity). On the other hand, they are low for DM. It may also be noted that most cross-correlations are negligible.
This can be compared with the results from the model for the EMS period. The autocorrelation structure of DM is practically unaffected by EMS. But then, the three rates with previously large autocorrelations of squared returns are now much more weakly autocorrelated than before. The autocorrelations in the BP not included in the EMS increase slightly. Thus, although the conditional correlations between the returns of EMS currencies increase as a result of the EMS, the autocorrelations of squared returns decrease. The anchor currency of the monetary system, DM, constitutes an exception. On the other hand, cross-correlations appear where none were observed before the EMS: note the ones between DM and IL and FF and IL. It seems that in the EMS period, the changes in the volatility of DM and FF have dynamic effects on the volatility of IL. This may not be unexpected as these currencies belong to the EMS during the observation period. Finally, about the only nonnegligible pre-EMS cross-correlations, the ones between BP and DM, practically vanish in the EMS period. As BP has not been a part of the EMS during the observation period, this may not be an unexpected result either.
These results should be viewed with caution because one parameter estimate was adjusted to allow the estimated pre-EMS process to have finite unconditional fourth moments. Besides, the uncertainty in the parameter estimates is not accounted for in the discussion. We emphasize, however, that the main purpose of this example is to demonstrate practical uses of the theoretical results of the paper. The example shows that the fourth-moment results are useful already in the case of the standard first-order CCC-GARCH model, and the same can be said about more general situations also.
In this work we have derived the fourth-moment structure for a constant-correlation GARCH model that contains as a special case the CCC-GARCH model of Bollerslev (1990). We demonstrate the fact that already the first-order version of this model is capable of characterizing processes with rather general autocorrelation structures. This extended model could then be a viable alternative to the standard CCC-GARCH model.
Despite the appealing theoretical properties of the extended model, more work is needed to find out how useful the model is in practice. Wong, Li, and Ling (2002) can be seen as a first step in this direction. In their application, the nondiagonal parameters in the coefficient matrices of the model appear to be nonzero. Whether or not the extended model reduces the need for time-varying correlations—another extension of the basic CCC-GARCH model (see Engle, 2002; Tse and Tsui, 2002)—remains a question for further work.
Let

be an indicator function defined for nonnegative integers i such that

LEMMA 1. Let k ≥ 1. For the vector GARCH(2,2) model (2) and (3) and (7), vec(C2,t−2ht−2(2)ht−1(2)′C1,t−1′) can be expressed in terms of ht−i(2), vec(ht−j(2)ht−j(2)′), and vec(ht−i(2)ht−j(2)′) as follows:

Proof. Applying (7) to ht−1(2) in ht−2(2)ht−1(2)′ yields

Applying (7) to ht−2(2) in ht−2(2)ht−3(2)′ on the right-hand side of (A.2) and continuing the iteration until the kth step gives (A.1). █
LEMMA 2. Assume that ΓZ[otimes ]Z exists and condition (8) holds for {εt} defined in (2) and (3) and (7). Then

where

Proof.

is a sequence of i.i.d. random matrices. This and the fact that

for any j lead to limk→∞ St−k = 0 almost surely when the assumptions of the lemma hold. Then

On the other hand, as {εt} is strictly stationary we can assume that sequence {εt} started at a finite value in the infinite past. Then (A.3) holds. █
Proof of Theorem 2. From (7) we have

Noting that (C1,t−1 [otimes ] C2,t−2)vec(ht−2(2)ht−1(2)′) = vec(C2,t−2ht−2(2)ht−1(2)′C1,t−1′) and applying Lemmas 1 and 2 yields, after rewriting (A.4), that

almost surely. In (A.5), Φ(L) (M2 × M2) and Θ(L) (M2 × M) are infinite-order matrix polynomials in the lag operator L such that

. In particular,

for k = 2,3,…, and

for k = 2,3,….
Under conditions (8) and (10), [Φ(L)]−1 exists. Let

. Define

For the definition, see, for example, Tong (1990, pp. 137–138). Thus, vec(ht(2)ht(2)′) in (A.5) has a representation
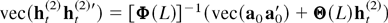
almost surely.
Because {Cit}, i = 1,2, is a sequence of i.i.d random matrices and λ(ΓC1 + ΓC2) < 1, it follows that

Condition (10) implies that

is finite and that

is invertible. Similarly,

Thus, the matrix sequences of

are absolutely summable. It follows from (A.7) and (A.8) and condition (8) that {vec(ht(2)ht(2)′)} in (A.6) is finite almost surely.
Assume that

have no common eigenvalues. It follows from (A.7) and (A.8) that vec(ht(2)ht(2)′) in (A.6) has a fourth-order weakly stationary solution and that

is finite. Under condition (10), taking expectations on both sides of (A.5) gives

Now,

, which concludes the proof of equation (11). █
LEMMA 3. Assume that ΓZ[otimes ]Z exists and condition (10) holds for the vector GARCH(2,2) model (2) and (3) and (7). Then

Proof. Equation (A.9) follows from Lemma 1 and Theorem 2. █
LEMMA 4. Assume that ΓZ[otimes ]Z exists and condition (10) holds for the vector GARCH(2,2) model (2) and (3) and (7). Let k ≥ 3. Then
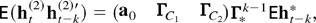
where

Proof. Rewrite (7) as
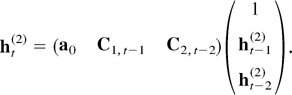
Applying equation (7) to ht−1(2) on the right-hand side of (A.11) and continuing the iteration until the kth step yields

where

Note that

for i ≠ j. Left-multiplying (A.12) by ht−k(2)′ and taking expectations yields (A.10). █
Proof of Theorem 3. We prove Theorem 3 by induction for n.
(i) We shall show that (17)–(21) hold for n = 3.
First we show that (17)–(19) hold for n = 1. Consider

Taking expectations on both sides of (A.13) and expressing them in vec form yields

Set

. Rewriting (A.14) using these definitions and applying Theorem 2 and Lemma 3 yields

Thus, (17)–(19) hold for n = 1.
Similarly, for n = 2,

so that (17)–(20) are valid for n = 2.
We shall now show that (21) holds for n = 3. We have

Applying (A.15) and (A.16) to (A.17) gives

(ii) Assume that (17)–(21) hold for all n ≤ k. We shall show that they hold for n = k + 1. From this assumption one obtains

On the other hand, using Lemma 4 one obtains

Applying (A.15) and (A.16) to the right-hand side of (A.19) gives
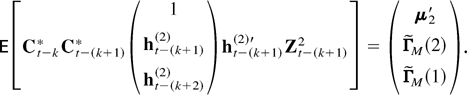
It follows from (A.18) and (A.20) that

Applying (A.20) to (A.21) and rewriting it in the vec form completes the proof of equation (21) when n = k + 1. █

Moduli of the largest eigenvalues of matrices Γ for a CCC-GARCH(2,2) model as a function of parameter b2,11 when (a) Γ is defined by condition (10) (solid curve) and (b) is defined in Theorem 2.2 of Ling and McAleer (2003) (dashed-dotted curve). The parameters of the model are a1,11 = 0.06, a1,12 = 0.08, a1,21 = 0.1, a1,22 = 0.12, a2,11 = 0.07, a2,12 = 0.1, a2,21 = 0.08, a2,22 = 0.12, b1,11 = 0.05, b1,12 = 0.08, b1,21 = 0.11, b1,22 = 0.2, b2,12 = 0.09, b2,21 = 0.1, and b2,22 = 0.12, and the nondiagonal element of the correlation matrix of the standard normal error process {zt} equals 0.2.

Auto- and cross-correlations of squared observations of a three-dimensional extended CCC-GARCH(1,1) process, lags 1–8. Here ΓC has a pair of complex conjugate eigenvalues with modulus = 0.432 and a real root = 0.858. The parameter values are a01 = 0.1, a02 = 0.2, a03 = 0.25, a11 = 0.05, a12 = 0.25, a13 = 0.06, a21 = 0.07, a22 = 0.08, a23 = 0.25, a31 = 0.25, a32 = 0.08, a33 = 0.08, b11 = 0.05, b12 = 0.4, b13 = 0.05, b21 = 0.05, b22 = 0.07, b23 = 0.3, b31 = 0.25, b32 = 0.08, and b33 = 0.08. The correlation matrix of the standard normal error process {zt} has the following nondiagonal elements: ρ12 = 0.2, ρ13 = 0.3, and ρ23 = 0.23.

The estimated constant correlations , i,j = DM, FF, IL, SF, BP, from the two estimated CCC-GARCH models (EMS period and pre-EMS period) of Bollerslev (1990)

Auto- and cross-correlations rij(n),i,j = DM, FF, IL, SF, BP, n = 1, 2, 5, 10, are computed from the two estimated CCC-GARCH models (EMS period and pre-EMS period) of Bollerslev (1990)