Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-02-11T11:56:50.665Z Has data issue: false hasContentIssue false
  • English
  • Français

04.2.2. Characterizations of Hermitian Projectors

Published online by Cambridge University Press:  11 June 2004

Geert Dhaene  and
Luc Lauwers
Geert Dhaene
Affiliation:
Center for Economic Studies, K.U. Leuven, Belgium
Luc Lauwers
Affiliation:
Center for Economic Studies, K.U. Leuven, Belgium
Rights & Permissions [Opens in a new window]

Extract

Let P in 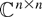be a projector with P+ its Moore–Penrose inverse and PH its conjugate transpose. Werner (2002) provides a list of equivalent conditions for P to be Hermitian.

Type
PROBLEMS AND SOLUTIONS
Information
Econometric Theory , Volume 20 , Issue 2 , April 2004 , pp. 427
Copyright
© 2004 Cambridge University Press

Let P in

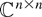
be a projector with P+ its Moore–Penrose inverse and PH its conjugate transpose. Werner (2002) provides a list of equivalent conditions for P to be Hermitian: (i) P = PPHP, (ii) P+P+ = P+, (iii) P+ = P, and (iv) P+ = PH. Extend this list and show that also condition (a) (resp. (b)) is sufficient and necessary for a projector P to be Hermitian:

(a) the composition PHP is a projector,

(b) the composition PPH is a projector.

References

REFERENCE

Werner, H.J. (2002) Partial isometry and idempotent matrices. Solution 28-7.5. IMAGE, The Bulletin of the International Linear Algebra Society 29, 31–32.Google Scholar