(a) The “if” part is easy to prove. If x_i ∼ N(μ_i,σ_i²) for i = 1,2, then their independence simplifies the moment generating function (m.g.f.) of y to

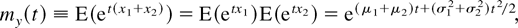
so that y ∼ N(μ₁ + μ₂,σ₁² + σ₂²).

The “only if” part is less obvious. We will assume that y ∼ N(0,1), without loss of generality (the usual extension to μ + σy applies). Then, the characteristic function (c.f.) of y is

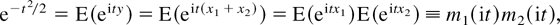
by independence of x₁ from x₂. Note that, for t real-valued,

so we have e^−t2/2 ≤ |m₁(it)| or equivalently −2 log|m₁(it)| ≤ t². Because the m.g.f. of x₁ exists, all the derivatives of m₁(it) are finite at t = 0 and log|m₁(it)| has a Taylor-series representation as a polynomial in t. From the previous inequality, the maximal power of this polynomial is 2. As a result, m₁(t) = exp(α₁ t + α₂ t²) for suitably chosen constants α₁ and α₂ (recall that m₁(0) is set to 1, by definition). This establishes normality for x₁ and, by symmetry of the argument, for x₂ too.

Cramér's (1936) deconvolution theorem is actually more general than is stated in part (a), because it does not presume the existence of m.g.f.s for x₁ and x₂, at the cost of a further complication of the proof. In our proof, we have used (without needing to resort to the language of complex analysis) the fact that the existence of the m.g.f. implies that it is analytic (satisfies the Cauchy–Riemann equations) and is thus differentiable infinitely many times in an open neighborhood of t = 0 in the complex plane. On the other hand, if one did not assume the existence of m.g.f.s, then one would require some theorem from complex function theory. One such requisite would be the “principle of isolated zeros” or “uniqueness theorem for analytic functions.” Another alternative requisite would be “Hadamard's factorization theorem,” used in Loève (1977, p. 284).

(b) For n < ∞, Cramér's deconvolution theorem (see part (a)) can be used n − 1 times to tell us that x ∼ N(μ,σ²/n) decomposes into the sum of n independent normals, so that var(x) = Σ is a diagonal matrix satisfying tr(Σ) = nσ². However, the theorem does not imply that the components of the decomposition have identical variances and means, and we need to derive these two results, respectively.

Define the idempotent matrix A = (a_ij) := I_n − ıı′/n. Then, because x′(σ⁻²A)x ∼ χ²(n − 1), we have A = σ⁻²AΣA. The fact that A is idempotent implies that ADA = O, where

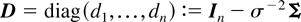
with

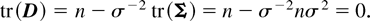
The diagonal elements of ADA are given by

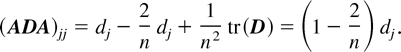
For n ≥ 3, the equation ADA = O thus gives d_j = 0 for j = 1,…,n, and hence Σ = σ²I_n.

To obtain the mean, we note that the noncentrality parameter of x′(σ⁻²A)x is given by μ′Σ^−1/2(σ⁻²A)Σ^−1/2μ. Because our quadratic form has a central χ²-distribution and Σ = σ²I_n, we obtain Aμ = 0 and hence

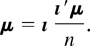
Then, E(x) = μı follows by

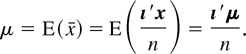
(c) When n = 2,

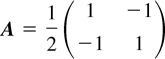
and

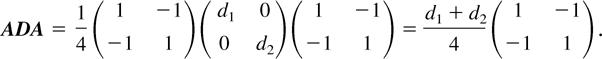
Equating the latter to zero, as in (2), provides no further information on the variance of the two normal components of x, beyond what was already known from (1). In this case, result (b) does not hold.

As a counterexample, let

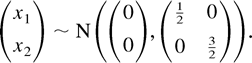
Then, it is still the case that x ∼ N(0,½) and

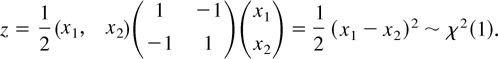
Notice, however, that cov(x₁ + x₂, x₁ − x₂) = var(x₁) − var(x₂) ≠ 0, so that x is not independent of z. We will now show that assuming independence of x from z makes the statement in (b) hold for n = 2 also.

Independence of the linear form ı′x/n from the quadratic form x′Ax/σ² occurs if and only if AΣı = 0. For n = 2, setting

equal to zero ensures that σ₁² = σ₂².

A variation on part (c) is proved by a different approach in Zinger (1958, Theorem 6). There, independence of x from z is assumed but not the normality of x. In fact, for 2 ≤ n < ∞, normality of x is obtained there as a result of one of two alternative assumptions on the components of x being pairwise identically distributed or being decomposable further as independent and identically distributed (i.i.d.) variates.