Following the detonation of an improvised nuclear device, populations evacuating through areas contaminated by fallout will be exposed to ionizing radiation. Although the gamma radiation dose to these populations during evacuation has been thoroughly studied, beta radiation dose to the skin has been largely ignored.Reference Buddemeier, Valentine and Millage 1 - Reference Brandt and Yoshimura 3 Beta radiation dose to the skin can be large from either direct skin contamination or groundshine, possibly exceeding midline dose by 3 to 66 times during the first 48 hours postdetonation.Reference Barss and Weitz 4 The large dose to the skin poses a risk of cutaneous radiation injury (CRI), caused by death of sensitive cells in the basal layer of the skin.Reference Barss and Weitz 4 - Reference Blackmar 7 The symptoms typical of CRI include erythema (reddening of the skin), dry desquamation (peeling), and moist desquamation (oozing skin).Reference Archambeau, Pezner and Wasserman 6 , 8 , Reference Evans, Moeller and Cooper 9 More severe injuries can be caused as well, including ulcers that do not heal or necrosis, but these require doses to deeper skin tissues than the basal layer.Reference Hopewell 10
CRI has not been studied extensively in the past in evacuation scenarios because of the relatively large ED50 for CRI (dose that causes CRI in 50% of the population). The ED50 for dry and moist desquamation are 14 and 20 Gy to the skin, respectively, well above the 3 Gy to the red bone marrow required to reach the ED50 for hematopoietic injury.Reference Archambeau, Pezner and Wasserman 6 , 8 , Reference Strom 11 However, the focus on hematopoietic injury neglects doses to other parts of the body which may experience much larger doses, particularly the skin. Because beta radiation dose from groundshine and skin contamination can be many times larger than the dose to the red bone marrow from combined gamma and beta radiation, CRI may still occur in evacuating populations without lethal hematopoietic injury. Although erythema can also be caused by radiation exposure to the skin, this work focuses on desquamation due to the potential loss of the protective skin barrier. Moist desquamation alone may warrant a medical response due to infection risk, but, if CRI occurs concurrently with hematopoietic injury, this infection risk could be compounded by reduced white blood cell counts.
Determining the dose from fallout contamination is complicated by fallout fractionation. Fallout fractionation is the process by which volatile chain elements (radionuclides with condensation points less than 1400°C) are separated from refractory chain elements (radionuclides with condensation points greater than 1400°C) both geographically and physically.Reference Mamuro, Yoshikawa and Maki 12 , Reference Freiling, Kay and Sanderson 13 Radioactive fallout forms when superheated fission products mix with the soil and debris entrained in the mushroom cloud. The bulk material—ie, concrete, soil, weapon debris, and other detritus—will begin condensing at approximately 1400°C.Reference Freiling, Kay and Sanderson 13 Refractory chain radionuclides which condense at higher temperatures will either condense onto larger particles which did not fully vaporize or form nucleation points for the condensation of bulk material. These early-formed particles generally have refractory chain radionuclides distributed throughout their volume and tend to be larger.Reference Glasstone and Dolan 14 By contrast, volatile chain radionuclides with lower condensation points take longer to condense and, when they do, they tend to condense onto the surface of fallout particles.Reference Glasstone and Dolan 14 As smaller particles remain aloft longer, the lower the condensation point of the radionuclide and the longer it takes to condense, the more likely the volatile radionuclide will be found only on smaller particles. The separation of refractory and volatile radionuclides in fallout alters the gamma and beta radiation energy spectra, resulting in slight changes to skin dose with depth. Fallout fractionation was included in this study by assuming contamination occurred just outside the physical damage zones.
Estimating the probability and severity of CRI injuries is complicated by a variable dose rate and beta energy spectrum, both of which vary with time and alter the dose profile to tissues underlying the basal layer. This paper discusses an adaptation of the biological effective dose (BED) for CRI and MCNP modeling of depth of dose across the body. Given knowledge of a specific individual’s contamination—including time of contamination, time from contamination to decontamination, path through contaminated areas, clothing worn, etc—the methods presented herein allow improved estimation of the risk of CRI to the individual with lower computational complexity.
METHODS
General Modeling Assumptions
While the overall method presented below for both dose rate effectiveness and depth of dose can be applied to any contamination scenario, this paper assumes the exposure was received from fallout from a 10 kt, pure fission nuclear weapon. Fallout exposure from both direct contamination of skin or clothing and groundshine are considered and calculated separately. Only fission products were considered—because of the enormous situational dependence of activation products on both the specific weapon’s design and the surrounding environment at the time of detonation, the inclusion of activation products can only be done on a specific-scenario level. Prompt radiation from the detonation of the weapon was not included in this analysis.
Dose Rate Effectiveness Factor
As skin is a fast-healing tissue, with a cell repair half-time of only 1.1 to 1.3 hours, dose rate becomes a critical variable in determining the extent of injury.Reference Turesson and Thames 5 Omitting healing of irradiated tissue in the modeling would lead to overestimation of radiation injury in the affected population, particularly for doses received at varying dose rates over long periods of time. Evacuation through contaminated areas following an improvised nuclear device detonation could take hours depending on the evacuation route chosen, and evacuating populations could be exposed to fluctuating dose rates.Reference Brandt and Yoshimura 2 , Reference Brandt and Yoshimura 3 Fallout trapped against skin or on clothing may remain until the individual decontaminates, as was seen in previous fallout contamination incidents.Reference Canard 15 , Reference Gottlober, Steinert and Weiss 16
CRI, radiation dose, and the healing of skin tissues are well studied in the medical fields.Reference Turesson and Thames 5 , Reference Barendsen 17 - Reference Koenig, Wolff and Mettler 21 Radiotherapy, fluoroscopy, and other radiation treatments or diagnostics are specially designed to spare skin tissue and avoid injury. Unfortunately, the calculation of CRI risk becomes increasingly complicated when the dose rate is not constant. Further, as injury in the most sensitive layer of the skin (ie, the basal layer) is avoided, medical knowledge of injury thresholds in deeper tissues is incomplete.
In the medical field, risk of injury is estimated using the BED calculation, which accounts for fractionation and/or protraction of radiation dose. The general form of the equation is shown in Equation 1.Reference Brenner, Hlatky and Hahnfeldt 18 , Reference Fowler 22 , Reference Brenner 23 The Lea-Catcheside protraction factor, G, accounts for noninstantaneous doses and is shown in Equation 2.Reference Brenner, Hlatky and Hahnfeldt 18 , Reference Brenner 23 Tissues, especially rapidly repairing tissues such as the skin, repair radiation damage while the dose is ongoing. Thus, the effective dose saturates based on the dose rate. The Lea-Catcheside equation, however, contains a nested integral that becomes computationally complex for exposures with variable dose rates.
The general form of the BED equationReference Brenner, Hlatky and Hahnfeldt 18 , Reference Fowler 22 , Reference Brenner 23 is
$$BED{\equals}nd{\rm }\left( {{\rm }1{\plus}{{G{\times}d} \over {{\raise0.7ex\hbox{$\alpha $} \!\mathord{\left/ {\vphantom {\alpha \beta }}\right.\kern-\nulldelimiterspace}\!\lower0.7ex\hbox{$\beta $}}}}{\rm }} \right),$$
where
n=the number of irradiation fractions,
d=the dose per fraction (Gy-eq),
G=Lea-Catcheside Protraction Factor, aka effect of tissue repair (tissue specific),
α=linear dose response parameter [Gy−1], and
β=quadratic dose respond parameter [Gy−2].
The Lea-Catcheside protraction factorReference Brenner, Hlatky and Hahnfeldt 18 , Reference Brenner 23 is
$$G\left( {t,T} \right){\equals}{2 \over {D^{2} }}\mathop {\int \limits_0^T} R(t){\times}\left( {\mathop \int \limits_0^t R\left( w \right)e^{{{\minus}\mu _{i} \left( {t{\minus}w} \right)}} dw} \right)dt,$$
where
D=total dose received between 0 and T received by the tissue of interest (Gy),
T=total time period individual is irradiated (h),
R(t)=dose rate in at time t (or time w) (Gy h−1), and
µ=tissue repair constant (tissue specific) (h−1).
The National Council on Radiation Protection and Measurements (NCRP) has recommended a different equation for calculation of acute radiation syndrome. 8 , Reference Evans, Moeller and Cooper 9 This hazard equation, shown in Equations 3 and 4, still includes an integral but can be broken into a series summation. Adjusting the equation in this fashion allows a variable dose rate to be approximated as a series of constant-dose periods. There are published values for some parameters for CRI but there are no published estimates of θ 1 , the dose rate effectiveness factor, for CRI. 8
The NCRP hazard functions 8 , Reference Evans, Moeller and Cooper 9 for acute radiation syndrome is
$$P\left( {T,S} \right){\equals}1{\minus}e^{{H_{{T,S}} \left( t \right)}} ,\,{\rm and}$$
$$H_{{T,S}} \left( t \right){\equals}\ln \left( 2 \right)\left[ {\mathop {\int \limits_0^t} {{\dot{D}_{T} \left( t \right)} \over {\theta _{{T,S}}^{\infty} {\plus}\theta _{{T,S}}^{1} \dot{D}_{T}^{{{\minus}1}} \left( t \right)}}dt} \right]^{{V_{{T,S}} }} \,for\,\dot{D}_{T} \left( t \right){\rm }{\times}t\,\gt\,TD_{{T,S}} ,$$
where
P(T,S)=probability of specific syndrome S and tissue T,
H T,S (t)=hazard function of syndrome S in tissue T,
t=time (h),
$\dot{D}_{T} (t)$
=dose rate to tissue T at time t (Gy-eq h−1),
$\theta _{{T,S}}^{\infty} $
=dose rate that causes the syndrome in 50% of the population at an infinite dose rate (Gy-eq),
$\theta _{{T,S}}^{1} $
=dose rate effectiveness parameter [(Gy-eq)2 h−1],
V T,S =shaping parameter for a given syndrome S and tissue T, and
TDT,S =threshold dose for a given syndrome S and tissue T (Gy-eq).
In order to adapt the hazard function to the BED, the probability of injury versus dose for dry or moist desquamation was calculated using the BED equation for dose protractions varying between 0 hours (immediate, acute dose) and 24 hours. A nonlinear, least squares regression method was used to determine the best fit of the hazard function to the BED-estimated risk for all doses and dose rates between the BED-predicted ED5 and ED95. For this calculation, the only parameter that was fit was the dose rate effectiveness factor, θ 1 . The region of fit was limited because fits below the threshold for injury (ED5) or above the ED95 would provide no additional information while biasing the fit to match extremely high or extremely low doses, in which outcome does not change significantly with dose. Instead, by limiting the fit to the ED5 to ED95 region, the fit is focused on the region in which a change in dose makes the greatest difference in outcome. Parameters used in the regression for both the BED equation and the hazard function are shown in Table 1.
Table 1 Modeling parameters for least-squares fit of the hazard function to the biological effective dose equation.Reference Turesson and Thames 5 , Reference Archambeau, Pezner and Wasserman 6 , 8
Depth of Dose
Depth of dose is important to modeling as deeper tissues that do not receive large doses will not experience radiation injury. The beta dose profile versus depth from either groundshine or direct skin contamination was modeled using MCNP5. 24 The basic model form, shown in Figure 1, was based on the same model framework as were previous models of fallout injury to the skin.Reference Barss and Weitz 4 The model was run using the skin layer thicknesses of the upper arm, where data on the thickness of skin layers are the most robust, using thin, medium, and thick skin layer thicknesses (Table 2).Reference Tingart, Apreleva and von Stechow 25 - 28 Other areas of the body see much greater variation of subcutaneous fat layer thicknesses, especially the skin around the abdomen, or subcutaneous muscle layers.Reference Kim, Lim and Lee 29
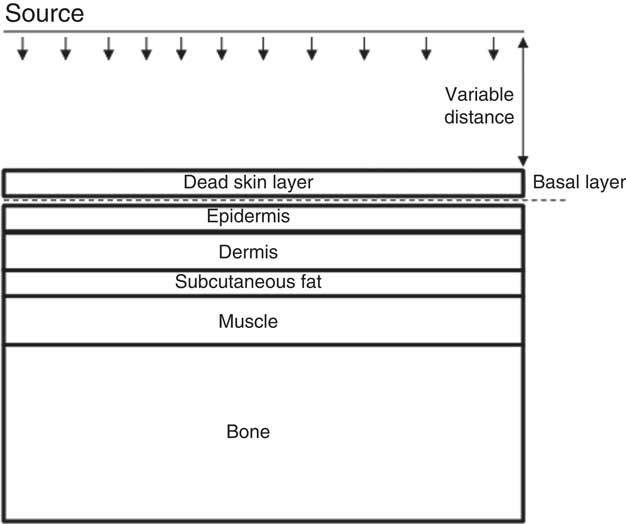
Figure 1 Basic form of the MCNP5 model, showing the different skin layers modeled.
Table 2 Modeled thicknesses of the various skin layers on the upper arm. Dead skin and basal layer thickness were not varied in this work.Reference Tingart, Apreleva and von Stechow 25 - 28
Dose to the skin from fallout has been examined previously, particularly dose to the basal layer. The present work originally came out of an examination of the methodology used by the Defense Threat Reduction Agency in their ED04 report regarding skin dose to soldiers caused by fallout from atmospheric nuclear tests. 30 Other codes exist to model dose to the skin, including VARSKIN, but are primarily designed for regulatory compliance. VARSKIN in particular was designed to measure dose from dermal contamination and hot particles with respect to a contiguous 10-cm2 area of skin at a depth of 0.007 cm up to the dose limit of 0.5 Gy.Reference Hamby, Mangini and Caffrey 31 As this work focuses on acute radiation injury to tissue including but not limited to the basal skin layer at potentially extreme doses (>10 Gy in some cases, far exceeding regulatory limits), MCNP5 was used instead.
The beta energy spectra from fallout was estimated using the fractionated fallout composition for fallout just outside the damage zones of a 10 kt pure-fission detonation.Reference Monterial and Vincent 32 This composition was compiled for a series of time points of interest and the beta spectra were calculated using beta energy spectra data for each radionuclide from the International Commission on Radiation Protection. 33 Due to the sensitive nature of fallout energy spectra, the composition and spectrum data are not shown (may be available upon request, at the discretion of the government sponsor). As beta energy also varies with distance between the source and skin, the relative dose to layers from groundshine was modeled at several different time points and distances. The spectral effects of shielding by clothing were also included in the analysis. The time and distance combinations modeled are reported in Table 3. Groundshine was examined only in the 1- and 2-hour cases because these times are when dose from groundshine is expected to be large enough to threaten CRI in addition to other acute radiation injury.
Table 3 Times postdetonation and distance between contamination source and the surface of the skin when modeling depth of radiation dose from beta radiation from fallout. A distance of 0 cm represents direct skin contamination. Distances greater than 0 cm represent exposure to groundshine.
RESULTS AND DISCUSSION
Dose Rate Effectiveness Factor
The dose rate effectiveness factors estimated were 25.5 (Gy-eq)2 h−1 for dry desquamation and 74.5 (Gy-eq)2 h−1 for moist desquamation. Both values are exceptionally high, most likely due to the extremely rapid repair of cells in the basal layer. Figure 2 shows a comparison of fit between the NCRP hazard function and the BED equation for a 2-hour protracted dose at a constant dose rate. The fit between the two equations is close, but not perfect. The NCRP equation produces a slightly steeper probit function resulting in underestimation of injury risk at low doses and an overestimation at high doses. The hazard function, however, allows for easier inclusion of CRI in complex models.
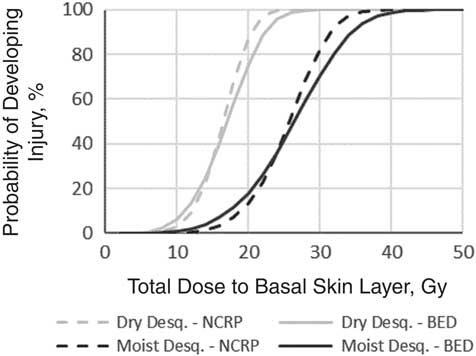
Figure 2 Probability of developing dry or moist desquamation (Desq.) following a 2-hour protracted dose at a constant dose rate. Data were estimated using both the biologically equivalent dose (BED) equation and the National Council on Radiation Protection and Measurements (NCRP) hazard function.
The difference in model outcomes between the BED model and the best-fit hazard function model is dependent on the dose distribution in the afflicted population. For a population whose individual doses are uniformly distributed between 0 and 50 Gy-eq to the basal layer, the best-fit hazard function model would overestimate the number of cutaneous injuries. If the population’s doses were skewed lower, or if the upper limit was closer to 20 or 25 Gy-eq, the best-fit model would likely underestimate injuries. Given the wide range of possible ratios of basal layer dose to whole body dose, it is not immediately clear how the dose to the evacuating population would be distributed, even assuming that no evacuating individual received a radiation dose greater than 8 or 10 Gy to the whole body.
Depth of Burn
In the MCNP5 model, the skin layers beneath the basal layer received very little dose relative to the basal layer (Figure 3 and Table 4). Underlying muscle and fat received almost no dose, and the dermis received less than 1% of the basal layer dose. Increased distance between the source and the skin changed the absolute dose of each layer but did not significantly affect the ratios (data not shown). As the dermis is one of the primary target tissues for necrosis, necrosis is unlikely in survivors except those with the most extreme doses. To achieve a dose of 25 Gy to the dermis, the ED50 for necrosis, the basal layer would need to receive a dose of approximately 1938 Gy. Further, as the dose to the basal layer can be up to 66 times greater than the whole body dose, a dose of 25 Gy to the dermis from groundshine would correspond to a whole body dose of at least 29 Gy.Reference Barss and Weitz 4 At these doses, necrosis would not develop as the individual would die from radiation-induced hematopoietic, gastrointestinal, and cerebrovascular complications before the onset of necrosis. Even if the injury was due entirely to the direct skin contamination, the injury to the upper layers of the skin would be astronomical, causing erythema and desquamation long before necrosis.
Figure 3 Relative dose of underlying skin layers to that of the basal skin layer over time for the medium thickness case at a distance of 0 cm (direct skin contamination). Changes in relative doses are driven by the changes in beta energy spectra from fallout.
Table 4 Average relative dose of underlying skin layers to that of the basal skin layer for direct skin contamination by fallout
The combination of acute skin injury without radiation-induced necrosis is not unexpected given the thicknesses of the tissues involved and the relatively low energy and penetration power of beta radiation. This outcome is in stark contrast to necrosis seen following radiotherapy, wherein radiation treatment is intentionally designed to penetrate to deeper tissues and resulting in larger doses to muscle, bone, and tendons. Historical exposures to fallout have similarly seen acute skin injury without necrosis. For example, the Marshallese Islanders on Rongelap, who suffered protracted skin contamination by fallout particles, experienced epilation, skin lesions, and hematopoietic effects (from gamma injury to red bone marrow), but no necrosis.Reference Canard 15 Workers and cleanup crews working at the Chernobyl nuclear power plant experienced a wide range of cutaneous radiation injury without any necrosis.Reference Gottlober, Steinert and Weiss 16 Although the chemical composition and isotopes present at a nuclear power plant are different than those from nuclear weapon fallout, the lack of necrosis or more severe injuries beyond nonhealing ulcers suggests that radiation injury is still limited to the upper layers of skin.Reference Gottlober, Steinert and Weiss 16 It is still possible that necrosis may occur in these populations due to secondary injury or infection if initial radiation injuries are not treated. Moist desquamation, for example, destroys the natural skin barrier and leads to high risk of infection.Reference Koenig, Wolff and Mettler 21 Infection could, in turn, lead to necrosis if left untreated.
CONCLUSIONS
These results provide a framework for better estimating CRI from protracted exposure to fallout. The basal layer of the skin heals quickly for both dry and moist desquamation, meaning inclusion of dose rate is critical to developing accurate models. If moist desquamation develops over large areas of the body, it can be life-threatening. 8 Radiation-induced necrosis and more severe injury, on the other hand, are extremely unlikely. These injuries may still occur as a result of secondary infection following moist desquamation.
The results of this study can be used in combination with blast and evacuation models to estimate the number and severity of injuries and the amount and type of medical countermeasures that would be necessary to treat CRI following an improvised nuclear device detonation in a domestic US city.
Acknowledgements
This work was supported by Contract No. HHS01002011000221 from the Biomedical Advanced Research and Development Authority (BARDA). The contents are sole the responsibility of the authors and do not necessarily represent the official views of BARDA, the Assistant Secretary for Preparedness and Response, the Department of Health and Human Services, or the United States Government.
