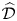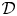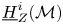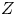1. Introduction
Let ![]() $K$ be a complete discrete valuation field of characteristic zero with valuation ring
$K$ be a complete discrete valuation field of characteristic zero with valuation ring ![]() $R$ and uniformizer
$R$ and uniformizer ![]() $\pi \in R$. We allow both the case of mixed characteristic (e.g. finite field extensions of the
$\pi \in R$. We allow both the case of mixed characteristic (e.g. finite field extensions of the ![]() $p$-adic numbers
$p$-adic numbers ![]() $\mathbb {Q}_p$) and equal characteristic (e.g.
$\mathbb {Q}_p$) and equal characteristic (e.g. ![]() $\mathbb {C}((t))$).
$\mathbb {C}((t))$).
In [Reference Ardakov and WadsleyAW19], the first and third authors introduced the sheaf ![]() $\widehat {\mathcal {D}}_X$ of analytic (infinite-order) differential operators on a smooth rigid analytic
$\widehat {\mathcal {D}}_X$ of analytic (infinite-order) differential operators on a smooth rigid analytic ![]() $K$-space
$K$-space ![]() $X$. It was shown in [Reference Ardakov and WadsleyAW19] and in greater generality in [Reference BodeBod19a] that sections over affinoids are Fréchet–Stein algebras as defined by Schneider and Teitelbaum [Reference Schneider and TeitelbaumST03], which suggests the notion of coadmissibility as the natural analogue of coherence in this setting. We denote the category of coadmissible
$X$. It was shown in [Reference Ardakov and WadsleyAW19] and in greater generality in [Reference BodeBod19a] that sections over affinoids are Fréchet–Stein algebras as defined by Schneider and Teitelbaum [Reference Schneider and TeitelbaumST03], which suggests the notion of coadmissibility as the natural analogue of coherence in this setting. We denote the category of coadmissible ![]() $\widehat {\mathcal {D}}_X$-modules by
$\widehat {\mathcal {D}}_X$-modules by ![]() $\mathcal {C}_X$.
$\mathcal {C}_X$.
In the classical theory of ![]() $\mathcal {D}$-modules (on a smooth complex algebraic variety
$\mathcal {D}$-modules (on a smooth complex algebraic variety ![]() $X$, say), one is often particularly interested in those modules which are holonomic. There are various equivalent ways to define these, one of which is as follows. One can introduce a dimension function
$X$, say), one is often particularly interested in those modules which are holonomic. There are various equivalent ways to define these, one of which is as follows. One can introduce a dimension function ![]() $d$ for coherent
$d$ for coherent ![]() $\mathcal {D}$-modules, either as the dimension of the support of the associated characteristic variety, or in terms of homological algebra by interpreting the homological grade of a module as its codimension. One then shows that any non-zero coherent
$\mathcal {D}$-modules, either as the dimension of the support of the associated characteristic variety, or in terms of homological algebra by interpreting the homological grade of a module as its codimension. One then shows that any non-zero coherent ![]() $\mathcal {D}_X$-module
$\mathcal {D}_X$-module ![]() $\mathcal {M}$ on a smooth, equidimensional variety
$\mathcal {M}$ on a smooth, equidimensional variety ![]() $X$ satisfies
$X$ satisfies
which is known as Bernstein's inequality. A coherent ![]() $\mathcal {D}_X$-module
$\mathcal {D}_X$-module ![]() $\mathcal {M}$ is said to be holonomic if
$\mathcal {M}$ is said to be holonomic if ![]() $d(\mathcal {M})\leq \dim X$, that is,
$d(\mathcal {M})\leq \dim X$, that is, ![]() $\mathcal {M}$ is either zero or of minimal dimension.
$\mathcal {M}$ is either zero or of minimal dimension.
Equivalently, holonomic ![]() $\mathcal {D}_X$-modules can be characterized as those coherent
$\mathcal {D}_X$-modules can be characterized as those coherent ![]() $\mathcal {D}_X$-modules
$\mathcal {D}_X$-modules ![]() $\mathcal {M}$ satisfying either of the following equivalent properties:
$\mathcal {M}$ satisfying either of the following equivalent properties:
(*) for every point
 $i: x\to X$ and any
$i: x\to X$ and any  $j\in \mathbb {Z}$, the cohomology
$j\in \mathbb {Z}$, the cohomology  $\mathrm {H}^{j}(i^{+}\mathcal {M})$ is a finite-dimensional vector space over
$\mathrm {H}^{j}(i^{+}\mathcal {M})$ is a finite-dimensional vector space over  $\mathbb {C}$, where
$\mathbb {C}$, where  $i^{+}$ denotes the derived inverse image of
$i^{+}$ denotes the derived inverse image of  $\mathcal {D}$-modules (see [Reference Hotta, Takeuchi and TanisakiHTT08, Theorem 3.3.1]);
$\mathcal {D}$-modules (see [Reference Hotta, Takeuchi and TanisakiHTT08, Theorem 3.3.1]);(**) for any smooth morphism
 $f: X'\to X$ and any divisor
$f: X'\to X$ and any divisor  $Z$ of
$Z$ of  $X'$, the local cohomology sheaves
$X'$, the local cohomology sheaves  $\underline {H}^{i}_Z(f^{*}\mathcal {M})$ are coherent
$\underline {H}^{i}_Z(f^{*}\mathcal {M})$ are coherent  $\mathcal {D}_{X'}$-modules for any
$\mathcal {D}_{X'}$-modules for any  $i\geq 0$ (see property
$i\geq 0$ (see property  $(**)$ in the introduction of [Reference CaroCar04]).
$(**)$ in the introduction of [Reference CaroCar04]).
The category of holonomic ![]() $\mathcal {D}_X$-modules plays a crucial role in many parts of algebraic geometry, algebraic analysis and geometric representation theory. It contains all integrable connections on
$\mathcal {D}_X$-modules plays a crucial role in many parts of algebraic geometry, algebraic analysis and geometric representation theory. It contains all integrable connections on ![]() $X$, and each holonomic module has finite length. Moreover, the notion of holonomicity is stable under pullback, pushforward, tensor product and the duality functor, which takes the form
$X$, and each holonomic module has finite length. Moreover, the notion of holonomicity is stable under pullback, pushforward, tensor product and the duality functor, which takes the form
for any holonomic ![]() $\mathcal {D}_X$-module
$\mathcal {D}_X$-module ![]() $\mathcal {M}$.
$\mathcal {M}$.
Moreover, the Riemann–Hilbert correspondence asserts an equivalence of categories between holonomic modules with regular singularities and the category of perverse sheaves.
In this paper, we begin the study of a subcategory of ![]() $\mathcal {C}_X$ analogous to the category of holonomic
$\mathcal {C}_X$ analogous to the category of holonomic ![]() $\mathcal {D}$-modules. While there is currently no satisfactory theory of characteristic varieties for coadmissible
$\mathcal {D}$-modules. While there is currently no satisfactory theory of characteristic varieties for coadmissible ![]() $\widehat {\mathcal {D}}$-modules, we can adopt the homological viewpoint by slightly generalizing the dimension theory for Fréchet–Stein algebras given in [Reference Schneider and TeitelbaumST03], where results were given for Fréchet–Stein algebras defined by Banach algebras which are Auslander regular with universally bounded global dimension. We relax this condition by allowing Banach algebras which are Auslander–Gorenstein with universally bounded self-injective dimension. This allows us to define the dimension of a coadmissible
$\widehat {\mathcal {D}}$-modules, we can adopt the homological viewpoint by slightly generalizing the dimension theory for Fréchet–Stein algebras given in [Reference Schneider and TeitelbaumST03], where results were given for Fréchet–Stein algebras defined by Banach algebras which are Auslander regular with universally bounded global dimension. We relax this condition by allowing Banach algebras which are Auslander–Gorenstein with universally bounded self-injective dimension. This allows us to define the dimension of a coadmissible ![]() $\widehat {\mathcal {D}}_X$-module. We then prove the corresponding Bernstein inequality.
$\widehat {\mathcal {D}}_X$-module. We then prove the corresponding Bernstein inequality.
Theorem A. Let ![]() $X$ be a smooth affinoid
$X$ be a smooth affinoid ![]() $K$-space such that
$K$-space such that ![]() $\mathcal {T}(X)$ is a free
$\mathcal {T}(X)$ is a free ![]() $\mathcal {O}(X)$-module.
$\mathcal {O}(X)$-module.
(i) There is a Fréchet–Stein structure
 $\widehat {\mathcal {D}}(X)\cong \varprojlim A_n$, where each
$\widehat {\mathcal {D}}(X)\cong \varprojlim A_n$, where each  $A_n$ is Auslander–Gorenstein with self-injective dimension bounded by
$A_n$ is Auslander–Gorenstein with self-injective dimension bounded by  $2\dim X$.
$2\dim X$.(ii) If
 $M$ is a non-zero coadmissible
$M$ is a non-zero coadmissible  $\widehat {\mathcal {D}}(X)$-module then
where
$\widehat {\mathcal {D}}(X)$-module then
where \[ d(M)\geq \dim X, \]
\[ d(M)\geq \dim X, \] $d(M)=2\dim X-j(M)$ for
$d(M)=2\dim X-j(M)$ for  $j(M)$ the homological grade of
$j(M)$ the homological grade of  $M$.
$M$.
We also note that Mebkhout and Narvaez-Macarro have already discussed dimensions of modules over the sheaf ![]() $\mathcal {D}$ of algebraic (i.e. finite-order) differential operators on a rigid analytic space in [Reference Mebkhout and Narvaez-MacarroMN91], and we show that the two theories are compatible in the obvious way. This rests on the following theorem.
$\mathcal {D}$ of algebraic (i.e. finite-order) differential operators on a rigid analytic space in [Reference Mebkhout and Narvaez-MacarroMN91], and we show that the two theories are compatible in the obvious way. This rests on the following theorem.
Theorem B. Let ![]() $X$ be a smooth affinoid
$X$ be a smooth affinoid ![]() $K$-space. Then
$K$-space. Then ![]() $\widehat {\mathcal {D}}(X)$ is a faithfully flat
$\widehat {\mathcal {D}}(X)$ is a faithfully flat ![]() $\mathcal {D}(X)$-module.
$\mathcal {D}(X)$-module.
We call a coadmissible ![]() $\widehat {\mathcal {D}}$-module
$\widehat {\mathcal {D}}$-module ![]() $\mathcal {M}$ on
$\mathcal {M}$ on ![]() $X$ which satisfies
$X$ which satisfies ![]() $d(\mathcal {M})\leq \dim X$ weakly holonomic. This choice of nomenclature reflects the fact that the category of weakly holonomic modules still contains some pathologies which do not appear in the algebraic theory: we present examples of weakly holonomic modules which are not of finite length and have infinite-dimensional fibres. In particular, the natural analogues of
$d(\mathcal {M})\leq \dim X$ weakly holonomic. This choice of nomenclature reflects the fact that the category of weakly holonomic modules still contains some pathologies which do not appear in the algebraic theory: we present examples of weakly holonomic modules which are not of finite length and have infinite-dimensional fibres. In particular, the natural analogues of ![]() $(*)$ and
$(*)$ and ![]() $(**)$ do not provide equivalent characterizations of weak holonomicity.
$(**)$ do not provide equivalent characterizations of weak holonomicity.
In [Reference Bitoun and BodeBB21], Bitoun and the second author already gave an example of an integrable connection on the punctured unit disc such that its direct image on the disc is not even coadmissible, so weakly holonomic ![]() $\widehat {\mathcal {D}}$-modules are not stable under pushforward either.
$\widehat {\mathcal {D}}$-modules are not stable under pushforward either.
Nonetheless, we also produce some positive results. One can define a duality functor as in the classical setting and show that this gives an involution of the category of weakly holonomic modules. We also show that the ![]() $\widehat {\mathcal {D}}$-module analogue of Kashiwara's equivalence given in [Reference Ardakov and WadsleyAW18] respects weak holonomicity. Concerning the question of pushforwards along open embeddings, we prove the following result.
$\widehat {\mathcal {D}}$-module analogue of Kashiwara's equivalence given in [Reference Ardakov and WadsleyAW18] respects weak holonomicity. Concerning the question of pushforwards along open embeddings, we prove the following result.
Theorem C. Let ![]() $j: U\to X$ be a Zariski open embedding of smooth rigid analytic
$j: U\to X$ be a Zariski open embedding of smooth rigid analytic ![]() $K$-spaces and let
$K$-spaces and let ![]() $\mathcal {M}$ be an integrable connection on
$\mathcal {M}$ be an integrable connection on ![]() $X$. Then
$X$. Then ![]() $\mathrm {R}^{i}j_*(\mathcal {M}|_U)$ is a coadmissible, weakly holonomic
$\mathrm {R}^{i}j_*(\mathcal {M}|_U)$ is a coadmissible, weakly holonomic ![]() $\widehat {\mathcal {D}}_X$-module for any
$\widehat {\mathcal {D}}_X$-module for any ![]() $i\geq 0$.
$i\geq 0$.
By ‘Zariski open embedding’, we mean that ![]() $U$ is an admissible open subspace of
$U$ is an admissible open subspace of ![]() $X$ whose complement is a closed analytic subset of
$X$ whose complement is a closed analytic subset of ![]() $X$.
$X$.
The proof of Theorem C relies on the rigid analytic analogue of Hironaka's resolution of embedded singularities as developed by Temkin [Reference TemkinTem18].
As a corollary, we obtain that the local cohomology sheaves ![]() $\underline {H}^{i}_Z(\mathcal {M})$ are also coadmissible, weakly holonomic
$\underline {H}^{i}_Z(\mathcal {M})$ are also coadmissible, weakly holonomic ![]() $\widehat {\mathcal {D}}_X$-modules, where
$\widehat {\mathcal {D}}_X$-modules, where ![]() $Z$ is any closed analytic subset of
$Z$ is any closed analytic subset of ![]() $X$.
$X$.
In this way, we verify that any integrable connection ![]() $\mathcal {M}$ on
$\mathcal {M}$ on ![]() $X$ satisfies the following natural analogue of
$X$ satisfies the following natural analogue of ![]() $(**)$:
$(**)$:
(**′) for any smooth morphism
 $f: X'\to X$ and any divisor
$f: X'\to X$ and any divisor  $Z$ of
$Z$ of  $X'$, the local cohomology sheaves
$X'$, the local cohomology sheaves  $\underline {H}^{i}_Z(f^{*}\mathcal {M})$ are coadmissible for any
$\underline {H}^{i}_Z(f^{*}\mathcal {M})$ are coadmissible for any  $i\geq 0$.
$i\geq 0$.
We mention at this point that Caro has taken property ![]() $(**)$ as the point of departure for his development of the study of overcoherent arithmetic
$(**)$ as the point of departure for his development of the study of overcoherent arithmetic ![]() $\mathscr {D}$-modules [Reference CaroCar04]. It would be very interesting to investigate whether
$\mathscr {D}$-modules [Reference CaroCar04]. It would be very interesting to investigate whether ![]() $(**')$ (maybe together with some analogue of Caro's overholonomicity condition [Reference CaroCar09]) yields a sufficiently rich subcategory of weakly holonomic
$(**')$ (maybe together with some analogue of Caro's overholonomicity condition [Reference CaroCar09]) yields a sufficiently rich subcategory of weakly holonomic ![]() $\widehat {\mathcal {D}}$-modules which has better finiteness and stability properties.
$\widehat {\mathcal {D}}$-modules which has better finiteness and stability properties.
We hope that these results bring us closer to the formulation of a theoretical framework which allows for a ![]() $p$-adic Riemann–Hilbert correspondence for
$p$-adic Riemann–Hilbert correspondence for ![]() $\widehat {\mathcal {D}}_X$-modules, generalizing results by Liu and Zhu [Reference Liu and ZhuLZ17] for (a suitable category of) integrable connections and (de Rham) local systems.
$\widehat {\mathcal {D}}_X$-modules, generalizing results by Liu and Zhu [Reference Liu and ZhuLZ17] for (a suitable category of) integrable connections and (de Rham) local systems.
Structure of the paper
In § 2 we recall some of the results and terminology from [Reference Ardakov and WadsleyAW19].
In § 4 we show that the sections ![]() $\widehat {\mathcal {D}}(X)$ over a smooth affinoid
$\widehat {\mathcal {D}}(X)$ over a smooth affinoid ![]() $X$ are of the form as claimed in Theorem A(i). In § 5 we slightly generalize the dimension theory from [Reference Schneider and TeitelbaumST03] to algebras of this form.
$X$ are of the form as claimed in Theorem A(i). In § 5 we slightly generalize the dimension theory from [Reference Schneider and TeitelbaumST03] to algebras of this form.
In § 6 we prove Bernstein's inequality, Theorem A(ii).
In § 7 we show some basic properties of the category of weakly holonomic ![]() $\widehat {\mathcal {D}}$-modules. Among other things, we prove that every integrable connection is weakly holonomic, and discuss the duality functor.
$\widehat {\mathcal {D}}$-modules. Among other things, we prove that every integrable connection is weakly holonomic, and discuss the duality functor.
In § 8 we present examples which have no analogue in the classical theory: there exist weakly holonomic ![]() $\widehat {\mathcal {D}}$-modules which do not have finite length and have fibres of infinite dimension. We also briefly recall the results from [Reference Bitoun and BodeBB21], which is concerned with the extension of meromorphic connections to coadmissible
$\widehat {\mathcal {D}}$-modules which do not have finite length and have fibres of infinite dimension. We also briefly recall the results from [Reference Bitoun and BodeBB21], which is concerned with the extension of meromorphic connections to coadmissible ![]() $\widehat {\mathcal {D}}$-modules. Crucially, it also gives an example of an integrable connection whose direct image is not coadmissible.
$\widehat {\mathcal {D}}$-modules. Crucially, it also gives an example of an integrable connection whose direct image is not coadmissible.
In §§ 9 and 10 we prove Theorem C by first considering the case where the complement of ![]() $U$ is the analytification of a strict normal crossing divisor and then reducing to that case by invoking Temkin's resolution of embedded singularities [Reference TemkinTem18] and the results in [Reference BodeBod19b].
$U$ is the analytification of a strict normal crossing divisor and then reducing to that case by invoking Temkin's resolution of embedded singularities [Reference TemkinTem18] and the results in [Reference BodeBod19b].
Convention
All our rigid analytic spaces will be quasi-separated.
Throughout, smooth rigid analytic spaces will be assumed to be equidimensional for simplicity. Arguing on each connected component separately, analogues of all our results can be formulated for arbitrary smooth spaces in a straightforward manner.
Notation
Given an ![]() $R$-module
$R$-module ![]() $M$, we denote by
$M$, we denote by ![]() $\widehat {M}$ its
$\widehat {M}$ its ![]() $\pi$-adic completion and abbreviate
$\pi$-adic completion and abbreviate ![]() $\widehat {M}\otimes _R K$ to
$\widehat {M}\otimes _R K$ to ![]() $\widehat {M_K}$.
$\widehat {M_K}$.
2. Basic theory of  $\widehat {\mathcal {D}}$-modules
$\widehat {\mathcal {D}}$-modules
We recall some definitions and results from [Reference Ardakov and WadsleyAW19].
2.1 Fréchet completed enveloping algebras
Let ![]() $k$ be a commutative base ring and
$k$ be a commutative base ring and ![]() $A$ a commutative
$A$ a commutative ![]() $k$-algebra.
$k$-algebra.
A Lie–Rinehart algebra (or ![]() $(k, A)$-Lie algebra) is an
$(k, A)$-Lie algebra) is an ![]() $A$-module
$A$-module ![]() $L$ equipped with a
$L$ equipped with a ![]() $k$-bilinear Lie bracket and an
$k$-bilinear Lie bracket and an ![]() $A$-linear Lie algebra homomorphism, called the anchor map,
$A$-linear Lie algebra homomorphism, called the anchor map,
such that ![]() $[x, ay]=a[x, y]+\rho (x)(a)y$ for any
$[x, ay]=a[x, y]+\rho (x)(a)y$ for any ![]() $a\in A$,
$a\in A$, ![]() $x, y\in L$.
$x, y\in L$.
We say that ![]() $L$ is smooth if it is coherent and projective as an
$L$ is smooth if it is coherent and projective as an ![]() $A$-module.
$A$-module.
For any ![]() $(k, A)$-Lie algebra
$(k, A)$-Lie algebra ![]() $L$, one can form the enveloping algebra
$L$, one can form the enveloping algebra ![]() $U_A(L)$ as in [Reference RinehartRin63, § 2]. Similarly to the construction of the universal enveloping algebra of a Lie algebra, this can be obtained as a quotient of the tensor algebra
$U_A(L)$ as in [Reference RinehartRin63, § 2]. Similarly to the construction of the universal enveloping algebra of a Lie algebra, this can be obtained as a quotient of the tensor algebra ![]() $T_k(A\oplus L)$ by suitable relations, such that (see [Reference Ardakov and WadsleyAW19, § 2.1])
$T_k(A\oplus L)$ by suitable relations, such that (see [Reference Ardakov and WadsleyAW19, § 2.1]) ![]() $U_A(L)$ is an associative
$U_A(L)$ is an associative ![]() $k$-algebra, equipped with canonical morphisms
$k$-algebra, equipped with canonical morphisms
of ![]() $k$-algebras and
$k$-algebras and ![]() $k$-Lie algebras respectively, satisfying the following universal property. If
$k$-Lie algebras respectively, satisfying the following universal property. If ![]() $S$ is a
$S$ is a ![]() $k$-algebra with
$k$-algebra with ![]() $j_A:A\to S$ a
$j_A:A\to S$ a ![]() $k$-algebra homomorphism and
$k$-algebra homomorphism and ![]() $j_L:L\to S$ a
$j_L:L\to S$ a ![]() $k$-Lie algebra homomorphism such that
$k$-Lie algebra homomorphism such that
for all ![]() $a\in A$,
$a\in A$, ![]() $x\in L$, then there exists a unique
$x\in L$, then there exists a unique ![]() $k$-algebra homomorphism
$k$-algebra homomorphism ![]() $\phi : U_A(L)\to S$ such that
$\phi : U_A(L)\to S$ such that ![]() $\phi \circ i_A=j_A$ and
$\phi \circ i_A=j_A$ and ![]() $\phi \circ i_L=j_L$.
$\phi \circ i_L=j_L$.
Therefore, if ![]() $M$ is an
$M$ is an ![]() $A$-module, taking for
$A$-module, taking for ![]() $j_A$ the action map
$j_A$ the action map ![]() $\sigma : A\to \mathrm {End}_k(M)$ shows that to extend the
$\sigma : A\to \mathrm {End}_k(M)$ shows that to extend the ![]() $A$-module structure on
$A$-module structure on ![]() $M$ to a
$M$ to a ![]() $U_A(L)$-module structure is equivalent to giving a
$U_A(L)$-module structure is equivalent to giving a ![]() $k$-linear Lie algebra action
$k$-linear Lie algebra action ![]() $j_L: L\to \mathrm {End}_k(M)$ of
$j_L: L\to \mathrm {End}_k(M)$ of ![]() $L$ on
$L$ on ![]() $M$ such that
$M$ such that
for all ![]() $a\in A$,
$a\in A$, ![]() $x\in L$,
$x\in L$, ![]() $m\in M$ (see, for example, [Reference RinehartRin63, p. 197]).
$m\in M$ (see, for example, [Reference RinehartRin63, p. 197]).
If ![]() $A$ is an affinoid
$A$ is an affinoid ![]() $K$-algebra, we say that an
$K$-algebra, we say that an ![]() $R$-subalgebra
$R$-subalgebra ![]() $\mathcal {A}\subset A$ is an affine formal model if
$\mathcal {A}\subset A$ is an affine formal model if ![]() $\mathcal {A}\otimes _R K=A$ and
$\mathcal {A}\otimes _R K=A$ and ![]() $\mathcal {A}$ is a topologically finitely presented
$\mathcal {A}$ is a topologically finitely presented ![]() $R$-algebra.
$R$-algebra.
Let ![]() $A$ be an affinoid
$A$ be an affinoid ![]() $K$-algebra with affine formal model
$K$-algebra with affine formal model ![]() $\mathcal {A}$. A finitely generated
$\mathcal {A}$. A finitely generated ![]() $\mathcal {A}$-submodule
$\mathcal {A}$-submodule ![]() $\mathcal {L}$ of a
$\mathcal {L}$ of a ![]() $(K, A)$-Lie algebra
$(K, A)$-Lie algebra ![]() $L$ is called an
$L$ is called an ![]() $\mathcal {A}$-Lie lattice if
$\mathcal {A}$-Lie lattice if ![]() $\mathcal {L}\otimes _R K=L$,
$\mathcal {L}\otimes _R K=L$, ![]() $\mathcal {L}$ is closed under the Lie bracket and
$\mathcal {L}$ is closed under the Lie bracket and ![]() $\rho (x)(a)\in \mathcal {A}$ for any
$\rho (x)(a)\in \mathcal {A}$ for any ![]() $x\in \mathcal {L}$,
$x\in \mathcal {L}$, ![]() $a\in \mathcal {A}$. In particular,
$a\in \mathcal {A}$. In particular, ![]() $\mathcal {L}$ is naturally an
$\mathcal {L}$ is naturally an ![]() $(R, \mathcal {A})$-Lie algebra. We note that if
$(R, \mathcal {A})$-Lie algebra. We note that if ![]() $\mathcal {L}$ is an
$\mathcal {L}$ is an ![]() $\mathcal {A}$-Lie lattice, so is
$\mathcal {A}$-Lie lattice, so is ![]() $\pi ^{n}\mathcal {L}$ for any
$\pi ^{n}\mathcal {L}$ for any ![]() $n\geq 0$.
$n\geq 0$.
We say that ![]() $L$ admits a smooth Lie lattice if there exists an affine formal model
$L$ admits a smooth Lie lattice if there exists an affine formal model ![]() $\mathcal {A}$ such that
$\mathcal {A}$ such that ![]() $L$ contains a
$L$ contains a ![]() $\mathcal {A}$-Lie lattice
$\mathcal {A}$-Lie lattice ![]() $\mathcal {L}$ which is smooth when regarded as an
$\mathcal {L}$ which is smooth when regarded as an ![]() $(R, \mathcal {A})$-Lie algebra.
$(R, \mathcal {A})$-Lie algebra.
Definition [Reference Ardakov and WadsleyAW19, § 6.2]
Let ![]() $A$ be an affinoid
$A$ be an affinoid ![]() $K$-algebra with affine formal model
$K$-algebra with affine formal model ![]() $\mathcal {A}$, and let
$\mathcal {A}$, and let ![]() $L$ be a coherent
$L$ be a coherent ![]() $(K, A)$-Lie algebra with
$(K, A)$-Lie algebra with ![]() $\mathcal {A}$-Lie lattice
$\mathcal {A}$-Lie lattice ![]() $\mathcal {L}$. The Fréchet completed enveloping algebra
$\mathcal {L}$. The Fréchet completed enveloping algebra ![]() $\widehat {U_A(L)}$ is defined to be
$\widehat {U_A(L)}$ is defined to be
It was shown in [Reference Ardakov and WadsleyAW19, § 6.2] that this does not depend on the choice of affine formal model and Lie lattice.
The key property of ![]() $\widehat {U(L)}$ is that it is a Fréchet–Stein algebra in the sense of [Reference Schneider and TeitelbaumST03] whenever
$\widehat {U(L)}$ is that it is a Fréchet–Stein algebra in the sense of [Reference Schneider and TeitelbaumST03] whenever ![]() $L$ is smooth.
$L$ is smooth.
Definition [Reference Schneider and TeitelbaumST03, § 3]
A ![]() $K$-Fréchet algebra
$K$-Fréchet algebra ![]() $U$ is called (left, right, two-sided) Fréchet–Stein if it is isomorphic to a countable inverse limit
$U$ is called (left, right, two-sided) Fréchet–Stein if it is isomorphic to a countable inverse limit ![]() $\varprojlim U_n$ for (left, right, two-sided) Noetherian
$\varprojlim U_n$ for (left, right, two-sided) Noetherian ![]() $K$-Banach algebras
$K$-Banach algebras ![]() $U_n$ whose connecting maps are flat (on the right, on the left, on both sides) with dense images.
$U_n$ whose connecting maps are flat (on the right, on the left, on both sides) with dense images.
A left ![]() $U$-module
$U$-module ![]() $M$ is called coadmissible if
$M$ is called coadmissible if ![]() $M\cong \varprojlim M_n$, where
$M\cong \varprojlim M_n$, where ![]() $M_n$ is a finitely generated
$M_n$ is a finitely generated ![]() $U_n$-module such that the natural morphism
$U_n$-module such that the natural morphism ![]() $U_n\otimes _{U_{n+1}}M_{n+1}\to M_n$ is an isomorphism for each
$U_n\otimes _{U_{n+1}}M_{n+1}\to M_n$ is an isomorphism for each ![]() $n$.
$n$.
For a given Fréchet–Stein algebra ![]() $U$, we denote the category of coadmissible left
$U$, we denote the category of coadmissible left ![]() $U$-modules by
$U$-modules by ![]() $\mathcal {C}_U$.
$\mathcal {C}_U$.
Theorem [Reference BodeBod19a, Theorem 3.5]
Let ![]() $A$ be an affinoid
$A$ be an affinoid ![]() $K$-algebra and let
$K$-algebra and let ![]() $L$ be a smooth
$L$ be a smooth ![]() $(K, A)$-Lie algebra. Then
$(K, A)$-Lie algebra. Then ![]() $\widehat {U_A(L)}$ is a two-sided Fréchet–Stein algebra.
$\widehat {U_A(L)}$ is a two-sided Fréchet–Stein algebra.
2.2 Lie algebroids and Fréchet completions
Let ![]() $X$ be a rigid analytic
$X$ be a rigid analytic ![]() $K$-variety. Recall from [Reference Bosch, Güntzer and RemmertBGR84, § 9.1.4] the strong G-topology
$K$-variety. Recall from [Reference Bosch, Güntzer and RemmertBGR84, § 9.1.4] the strong G-topology ![]() $X_{\operatorname {rig}}$ consisting of admissible open subsets of
$X_{\operatorname {rig}}$ consisting of admissible open subsets of ![]() $X$ and admissible coverings. We now discuss the sheafification of the notion of Lie–Rinehart algebra, where the role of
$X$ and admissible coverings. We now discuss the sheafification of the notion of Lie–Rinehart algebra, where the role of ![]() $\mathrm {Der}_k(A)$ is played by the tangent sheaf
$\mathrm {Der}_k(A)$ is played by the tangent sheaf ![]() $\mathcal {T}_X$.
$\mathcal {T}_X$.
Definition A Lie algebroid on a rigid analytic ![]() $K$-space
$K$-space ![]() $X$ is a pair
$X$ is a pair ![]() $(\rho , \mathscr {L})$ where
$(\rho , \mathscr {L})$ where
(i)
 $\mathscr {L}$ is a locally free sheaf of
$\mathscr {L}$ is a locally free sheaf of  $\mathcal {O}_X$-modules of finite rank on
$\mathcal {O}_X$-modules of finite rank on  $X_{\operatorname {rig}}$,
$X_{\operatorname {rig}}$,(ii)
 $\mathscr {L}$ is a sheaf of
$\mathscr {L}$ is a sheaf of  $K$-Lie algebras, and
$K$-Lie algebras, and(iii)
 $\rho : \mathscr {L}\to \mathcal {T}_X$ is an
$\rho : \mathscr {L}\to \mathcal {T}_X$ is an  $\mathcal {O}_X$-linear map of sheaves of Lie algebras such that
for any
$\mathcal {O}_X$-linear map of sheaves of Lie algebras such that
for any \[ [x, ay]=a[x, y]+\rho(x)(a)y \]
\[ [x, ay]=a[x, y]+\rho(x)(a)y \] $a\in \mathcal {O}_X$,
$a\in \mathcal {O}_X$,  $x, y\in \mathscr {L}$.
$x, y\in \mathscr {L}$.
Given a Lie algebroid ![]() $\mathscr {L}$, there exists a unique sheaf
$\mathscr {L}$, there exists a unique sheaf ![]() $\widehat {\mathscr {U}(\mathscr {L})}$ on
$\widehat {\mathscr {U}(\mathscr {L})}$ on ![]() $X_{\operatorname {rig}}$ such that on each admissible open affinoid subspace
$X_{\operatorname {rig}}$ such that on each admissible open affinoid subspace ![]() $Y\subseteq X$, we have
$Y\subseteq X$, we have
with the obvious restriction maps to smaller affinoid subdomains (see [Reference Ardakov and WadsleyAW19, Theorem 9.3] and the remark after [Reference BodeBod19a, Theorem 4.9]).
If ![]() $X$ is a smooth rigid analytic
$X$ is a smooth rigid analytic ![]() $K$-space, then its tangent sheaf
$K$-space, then its tangent sheaf ![]() $\mathcal {T}_X$ (together with
$\mathcal {T}_X$ (together with ![]() $\rho =\operatorname {id}$) is a Lie algebroid, and we write
$\rho =\operatorname {id}$) is a Lie algebroid, and we write ![]() $\widehat {\mathcal {D}}_X=\widehat {\mathscr {U}(\mathcal {T}_X)}$.
$\widehat {\mathcal {D}}_X=\widehat {\mathscr {U}(\mathcal {T}_X)}$.
2.3 Localization and coadmissible modules
Given a Lie algebroid ![]() $\mathscr {L}$ on an affinoid
$\mathscr {L}$ on an affinoid ![]() $K$-space
$K$-space ![]() $X$, write
$X$, write ![]() $\widehat {\mathscr {U}}=\widehat {\mathscr {U}(\mathscr {L})}$. We can localize coadmissible modules over the Fréchet–Stein algebra
$\widehat {\mathscr {U}}=\widehat {\mathscr {U}(\mathscr {L})}$. We can localize coadmissible modules over the Fréchet–Stein algebra ![]() $\widehat {\mathscr {U}}(X)$ as follows (see [Reference Ardakov and WadsleyAW19, § 8.2]). For any admissible open affinoid subspace
$\widehat {\mathscr {U}}(X)$ as follows (see [Reference Ardakov and WadsleyAW19, § 8.2]). For any admissible open affinoid subspace ![]() $Y$ of
$Y$ of ![]() $X$, the functor
$X$, the functor
sends coadmissible ![]() $\widehat {\mathscr {U}}(X)$-modules to coadmissible
$\widehat {\mathscr {U}}(X)$-modules to coadmissible ![]() $\widehat {\mathscr {U}}(Y)$-modules, where each term is equipped with its canonical Fréchet topology (it was shown in [Reference Bitoun and BodeBB21, Corollary A.6] that the completed tensor product
$\widehat {\mathscr {U}}(Y)$-modules, where each term is equipped with its canonical Fréchet topology (it was shown in [Reference Bitoun and BodeBB21, Corollary A.6] that the completed tensor product ![]() $\widehat {\otimes }$ agrees with the operation
$\widehat {\otimes }$ agrees with the operation ![]() $\widehat {\otimes }$ defined in [Reference Ardakov and WadsleyAW19, § 7.3]).
$\widehat {\otimes }$ defined in [Reference Ardakov and WadsleyAW19, § 7.3]).
This gives rise [Reference Ardakov and WadsleyAW19, Theorem 8.2, Theorem 9.5] to a fully faithful exact functor
and we call its essential image ![]() $\mathcal {C}_{\widehat {\mathscr {U}}}$, the category of coadmissible
$\mathcal {C}_{\widehat {\mathscr {U}}}$, the category of coadmissible ![]() $\widehat {\mathscr {U}}$-modules.
$\widehat {\mathscr {U}}$-modules.
Definition [Reference Ardakov and WadsleyAW19, Definition 9.4]
If ![]() $X$ is an arbitrary rigid analytic
$X$ is an arbitrary rigid analytic ![]() $K$-space and
$K$-space and ![]() $\mathscr {L}$ is a Lie algebroid on
$\mathscr {L}$ is a Lie algebroid on ![]() $X$, we say that a sheaf of
$X$, we say that a sheaf of ![]() $\widehat {\mathscr {U}(\mathscr {L})}$-modules
$\widehat {\mathscr {U}(\mathscr {L})}$-modules ![]() $\mathcal {M}$ on
$\mathcal {M}$ on ![]() $X_{\operatorname {rig}}$ is coadmissible if there exists an admissible covering
$X_{\operatorname {rig}}$ is coadmissible if there exists an admissible covering ![]() $(U_i)$ of
$(U_i)$ of ![]() $X$ by affinoids such that for each
$X$ by affinoids such that for each ![]() $i$,
$i$, ![]() $\mathcal {M}|_{U_i}\cong \operatorname {Loc} M_i$ for some coadmissible
$\mathcal {M}|_{U_i}\cong \operatorname {Loc} M_i$ for some coadmissible ![]() $\widehat {\mathscr {U}(\mathscr {L})}(U_i)$-module
$\widehat {\mathscr {U}(\mathscr {L})}(U_i)$-module ![]() $M_i$.
$M_i$.
If ![]() $X$ is smooth, we shorten
$X$ is smooth, we shorten ![]() $\mathcal {C}_{\widehat {\mathcal {D}}_X}$ to
$\mathcal {C}_{\widehat {\mathcal {D}}_X}$ to ![]() $\mathcal {C}_X$.
$\mathcal {C}_X$.
3. Faithfully flat completions of deformable algebras
3.1 Statement of the theorem and preliminaries
Recall that a positively filtered ![]() $R$-algebra
$R$-algebra ![]() $U$ is called deformable if
$U$ is called deformable if ![]() $\operatorname {gr} U$ is flat over
$\operatorname {gr} U$ is flat over ![]() $R$. We define its
$R$. We define its ![]() $n$th deformation to be the subring
$n$th deformation to be the subring
Let ![]() $U$ be a deformable
$U$ be a deformable ![]() $R$-algebra such that
$R$-algebra such that ![]() $\operatorname {gr} U$ is a commutative Noetherian
$\operatorname {gr} U$ is a commutative Noetherian ![]() $R$-algebra and
$R$-algebra and ![]() $F_0U$ is
$F_0U$ is ![]() $\pi$-adically separated.
$\pi$-adically separated.
Note that these assumptions make ![]() $F_0U$ a commutative Noetherian
$F_0U$ a commutative Noetherian ![]() $R$-algebra, as it is a quotient of
$R$-algebra, as it is a quotient of ![]() $\operatorname {gr} U$. Moreover,
$\operatorname {gr} U$. Moreover, ![]() $F_iU$ is a finitely generated
$F_iU$ is a finitely generated ![]() $F_0U$-module by [Reference Ardakov and WadsleyAW19, Lemma 6.5]
$F_0U$-module by [Reference Ardakov and WadsleyAW19, Lemma 6.5]
For example, the properties above are satisfied if ![]() $U=U_{\mathcal {A}}(\mathcal {L})$ is the enveloping algebra of a smooth
$U=U_{\mathcal {A}}(\mathcal {L})$ is the enveloping algebra of a smooth ![]() $(R, \mathcal {A})$-Lie algebra
$(R, \mathcal {A})$-Lie algebra ![]() $\mathcal {L}$ over an affine formal model
$\mathcal {L}$ over an affine formal model ![]() $\mathcal {A}$ of some affinoid
$\mathcal {A}$ of some affinoid ![]() $K$-algebra
$K$-algebra ![]() $A$.
$A$.
It was shown in [Reference Ardakov and WadsleyAW19, Theorem 6.7] that ![]() $\widehat {{U}_K}=\varprojlim \widehat {{U}_{n,K}}$ is a two-sided Fréchet–Stein algebra.
$\widehat {{U}_K}=\varprojlim \widehat {{U}_{n,K}}$ is a two-sided Fréchet–Stein algebra.
In this section we prove Theorem B from the introduction by proving the corresponding result for deformable algebras.
Theorem Let ![]() $U$ be a deformable
$U$ be a deformable ![]() $R$-algebra such that
$R$-algebra such that ![]() $\operatorname {gr} U$ is a commutative Noetherian
$\operatorname {gr} U$ is a commutative Noetherian ![]() $R$-algebra and
$R$-algebra and ![]() $F_0U$ is
$F_0U$ is ![]() $\pi$-adically separated. Then the natural morphism
$\pi$-adically separated. Then the natural morphism ![]() $U_K\to \widehat {{U}_K}$ is faithfully flat.
$U_K\to \widehat {{U}_K}$ is faithfully flat.
By ‘faithfully flat’ we mean that ![]() $\widehat {{U}_K}$ a faithfully flat
$\widehat {{U}_K}$ a faithfully flat ![]() $U_K$-module both on the left and on the right. We present the proof for the right module structure; the analogous statement for the left module structure can be shown mutatis mutandis.
$U_K$-module both on the left and on the right. We present the proof for the right module structure; the analogous statement for the left module structure can be shown mutatis mutandis.
We note that this result already appears in [Reference Schmidt and StrauchSS16, Proposition 3.6] under slightly modified assumptions, but we do not follow the last step in the proof and would like to put forward this alternative argument.
Note that flatness follows by the same argument as in [Reference BodeBod19a, Lemma 4.14], so it remains to show faithfulness.
Suppose that ![]() $N$ is a simple
$N$ is a simple ![]() $U_K$-module. We wish to show that
$U_K$-module. We wish to show that ![]() $\widehat {{U}_K}\otimes _{U_K}N\neq 0$, so it suffices to find some
$\widehat {{U}_K}\otimes _{U_K}N\neq 0$, so it suffices to find some ![]() $n$ such that
$n$ such that ![]() $\widehat {{U}_{n,K}}\otimes _{U_K}N\neq 0$.
$\widehat {{U}_{n,K}}\otimes _{U_K}N\neq 0$.
Let ![]() $M$ be a finitely generated
$M$ be a finitely generated ![]() $U$-submodule of
$U$-submodule of ![]() $N$ such that
$N$ such that ![]() $N=M_K$, and equip
$N=M_K$, and equip ![]() $M$ with a good filtration
$M$ with a good filtration ![]() $F_\bullet M$ (pick a finite generating set
$F_\bullet M$ (pick a finite generating set ![]() $m_1, \ldots , m_r$ and set
$m_1, \ldots , m_r$ and set ![]() $F_iM=\sum _{j=1}^{r} F_iUm_j$). We can now form the finitely generated
$F_iM=\sum _{j=1}^{r} F_iUm_j$). We can now form the finitely generated ![]() $U_n$-module
$U_n$-module
This is equipped with the filtration
 \[ F_jM_n=\sum_{i=0}^{j} \pi^{in}F_iM, \]
\[ F_jM_n=\sum_{i=0}^{j} \pi^{in}F_iM, \]
making it a filtered ![]() $U_n$-module.
$U_n$-module.
Clearly ![]() $M_n\otimes _R K=N$. Moreover,
$M_n\otimes _R K=N$. Moreover, ![]() $F_jM_n\subseteq F_jM$ is a finitely generated
$F_jM_n\subseteq F_jM$ is a finitely generated ![]() $F_0U$-module for any
$F_0U$-module for any ![]() $j, n\geq 0$, as
$j, n\geq 0$, as ![]() $F_0U$ is Noetherian.
$F_0U$ is Noetherian.
Recall that [Reference Ardakov and WadsleyAW13, Lemma 3.5] provides us with an isomorphism ![]() $\xi _n: \operatorname {gr} U\to \operatorname {gr} U_n$ given by multiplication by
$\xi _n: \operatorname {gr} U\to \operatorname {gr} U_n$ given by multiplication by ![]() $\pi ^{nj}$ on the
$\pi ^{nj}$ on the ![]() $j$th graded piece. The lemma below discusses an analogous morphism for modules.
$j$th graded piece. The lemma below discusses an analogous morphism for modules.
Lemma There exists a graded ![]() $R$-linear morphism
$R$-linear morphism ![]() $\mu _n: \operatorname {gr} M\to \operatorname {gr} M_n$ such that
$\mu _n: \operatorname {gr} M\to \operatorname {gr} M_n$ such that
(i)
 $\mu _n(m+F_{j-1}M)=\pi ^{nj}m+F_{j-1}M_n$ for all
$\mu _n(m+F_{j-1}M)=\pi ^{nj}m+F_{j-1}M_n$ for all  $m\in F_jM$,
$m\in F_jM$,(ii)
 $\mu _n(u \cdot m)=\xi _n(u)\cdot \mu _n(m)$ for all
$\mu _n(u \cdot m)=\xi _n(u)\cdot \mu _n(m)$ for all  $u\in \operatorname {gr} U$,
$u\in \operatorname {gr} U$,  $m\in \operatorname {gr} M$,
$m\in \operatorname {gr} M$,(iii)
 $\mu _n$ is surjective,
$\mu _n$ is surjective,(iv)
 $\ker (\mu _n|_{\operatorname {gr}_j M})=(\operatorname {gr}_j M)[\pi ^{nj}]$.
$\ker (\mu _n|_{\operatorname {gr}_j M})=(\operatorname {gr}_j M)[\pi ^{nj}]$.
Proof. It is immediate from the definition of the filtrations that (i) gives a well-defined ![]() $R$-linear graded morphism
$R$-linear graded morphism ![]() $\mu _n$ satisfying (ii).
$\mu _n$ satisfying (ii).
For (iii), note that ![]() $\pi ^{nj}F_jM+F_{j-1}M_n=F_jM_n$ for any
$\pi ^{nj}F_jM+F_{j-1}M_n=F_jM_n$ for any ![]() $j\geq 0$, so that
$j\geq 0$, so that ![]() $\mu _n(\operatorname {gr}_j M)=\operatorname {gr}_jM_n$.
$\mu _n(\operatorname {gr}_j M)=\operatorname {gr}_jM_n$.
For (iv), let ![]() $m\in F_jM$ with the property that
$m\in F_jM$ with the property that ![]() $\bar {m}\in \operatorname {gr}_j M$ is annihilated by
$\bar {m}\in \operatorname {gr}_j M$ is annihilated by ![]() $\mu _n$. This means that
$\mu _n$. This means that ![]() $\pi ^{nj}m\in F_{j-1}M_n=\sum _{i=0}^{j-1}\pi ^{in}F_iM\subseteq F_{j-1}M$. So
$\pi ^{nj}m\in F_{j-1}M_n=\sum _{i=0}^{j-1}\pi ^{in}F_iM\subseteq F_{j-1}M$. So ![]() $\pi ^{nj}\bar {m}=0$, that is,
$\pi ^{nj}\bar {m}=0$, that is, ![]() $\bar {m}\in (\operatorname {gr}_j M)[\pi ^{nj}]$. The reverse inclusion is clear.
$\bar {m}\in (\operatorname {gr}_j M)[\pi ^{nj}]$. The reverse inclusion is clear.
Corollary Suppose that ![]() $\pi ^{n}$ annihilates the
$\pi ^{n}$ annihilates the ![]() $\pi$-torsion of
$\pi$-torsion of ![]() $\operatorname {gr} M$. Then
$\operatorname {gr} M$. Then ![]() $\operatorname {gr} M_n$ is
$\operatorname {gr} M_n$ is ![]() $\pi$-torsionfree.
$\pi$-torsionfree.
Proof. Let ![]() $\bar {x}\in \operatorname {gr}_jM_n$ satisfy
$\bar {x}\in \operatorname {gr}_jM_n$ satisfy ![]() $\pi \bar {x}=0$. If
$\pi \bar {x}=0$. If ![]() $j\geq 1$, then surjectivity of
$j\geq 1$, then surjectivity of ![]() $\mu _n$ (Lemma 3.1(iii)) implies that there exists
$\mu _n$ (Lemma 3.1(iii)) implies that there exists ![]() $\bar {y}\in \operatorname {gr}_jM$ such that
$\bar {y}\in \operatorname {gr}_jM$ such that ![]() $\mu _n(\bar {y})=\bar {x}$, and hence
$\mu _n(\bar {y})=\bar {x}$, and hence
Therefore ![]() $\bar {y}\in \operatorname {gr} M$ is
$\bar {y}\in \operatorname {gr} M$ is ![]() $\pi$-torsion by Lemma 3.1(iv), implying that
$\pi$-torsion by Lemma 3.1(iv), implying that ![]() $\pi ^{n} \bar {y}=0$ by assumption. As
$\pi ^{n} \bar {y}=0$ by assumption. As ![]() $j\geq 1$, it follows that
$j\geq 1$, it follows that ![]() $\bar {x}=\pi ^{nj}\bar {y}=0$ as well.
$\bar {x}=\pi ^{nj}\bar {y}=0$ as well.
As ![]() $\operatorname {gr}_0 M_n=F_0 M$ is also
$\operatorname {gr}_0 M_n=F_0 M$ is also ![]() $\pi$-torsionfree, we have
$\pi$-torsionfree, we have ![]() $(\operatorname {gr} M_n)[\pi ]=\oplus _j (\operatorname {gr}_j M_n)[\pi ]=0$, as required.
$(\operatorname {gr} M_n)[\pi ]=\oplus _j (\operatorname {gr}_j M_n)[\pi ]=0$, as required.
Since ![]() $\operatorname {gr} M$ is finitely generated over the Noetherian ring
$\operatorname {gr} M$ is finitely generated over the Noetherian ring ![]() $\operatorname {gr} U$, it follows from the corollary that
$\operatorname {gr} U$, it follows from the corollary that ![]() $\operatorname {gr} M_n$ is
$\operatorname {gr} M_n$ is ![]() $\pi$-torsionfree for sufficiently large
$\pi$-torsionfree for sufficiently large ![]() $n$.
$n$.
3.2 Torsionfree deformations and the proof of Theorem 3.1
Lemma Suppose that ![]() $\operatorname {gr} M_n$ is
$\operatorname {gr} M_n$ is ![]() $\pi$-torsionfree. Then
$\pi$-torsionfree. Then ![]() $N$ is
$N$ is ![]() $(1+\pi U_n)$-torsionfree.
$(1+\pi U_n)$-torsionfree.
Proof. Let ![]() $S_n=1+\pi U_n$. Equipping
$S_n=1+\pi U_n$. Equipping ![]() $U$ with its
$U$ with its ![]() $\pi$-adic filtration, it follows from [Reference LiLi96, Corollary 2.2] that
$\pi$-adic filtration, it follows from [Reference LiLi96, Corollary 2.2] that ![]() $S_n$ is an Ore set in
$S_n$ is an Ore set in ![]() $U$ and hence in
$U$ and hence in ![]() $U_K$. In particular, the set of
$U_K$. In particular, the set of ![]() $S_n$-torsion elements in
$S_n$-torsion elements in ![]() $N$ is a
$N$ is a ![]() $U_K$-submodule of
$U_K$-submodule of ![]() $N$, and by simplicity is either
$N$, and by simplicity is either ![]() $0$ or
$0$ or ![]() $N$ itself. Assume therefore that
$N$ itself. Assume therefore that ![]() $N$ and hence
$N$ and hence ![]() $M_n$ is
$M_n$ is ![]() $S_n$-torsion.
$S_n$-torsion.
We now claim that ![]() $F_jM_n=\pi F_jM_n$ for any
$F_jM_n=\pi F_jM_n$ for any ![]() $j\geq 0$. Once we have proved the claim, finite generation of
$j\geq 0$. Once we have proved the claim, finite generation of ![]() $F_jM_n$ over the Noetherian
$F_jM_n$ over the Noetherian ![]() $\pi$-adically complete ring
$\pi$-adically complete ring ![]() $F_0U$ forces
$F_0U$ forces ![]() $F_jM_n=0$ by [Reference Atiyah and MacdonaldAM69, Corollary 10.19], so
$F_jM_n=0$ by [Reference Atiyah and MacdonaldAM69, Corollary 10.19], so ![]() $M_n=0$, which provides us with the desired contradiction, as
$M_n=0$, which provides us with the desired contradiction, as ![]() $M_n\otimes _R K=N\neq 0$.
$M_n\otimes _R K=N\neq 0$.
Let ![]() $m\in F_jM_n$. As
$m\in F_jM_n$. As ![]() $M_n$ is
$M_n$ is ![]() $S_n$-torsion, there exists
$S_n$-torsion, there exists ![]() $u\in U_n$ such that
$u\in U_n$ such that ![]() $(1-\pi u)m=0$, so
$(1-\pi u)m=0$, so ![]() $m=\pi um$.
$m=\pi um$.
Since ![]() $\operatorname {gr} M_n$ is
$\operatorname {gr} M_n$ is ![]() $\pi$-torsionfree, the same is true for
$\pi$-torsionfree, the same is true for ![]() $F_iM_n/F_{i-1}M_n$ for each
$F_iM_n/F_{i-1}M_n$ for each ![]() $i$, and thus
$i$, and thus ![]() $M_n/F_jM_n$ is also
$M_n/F_jM_n$ is also ![]() $\pi$-torsionfree. In particular,
$\pi$-torsionfree. In particular, ![]() $\pi um\in F_jM_n$ implies
$\pi um\in F_jM_n$ implies ![]() $um\in F_jM_n$ and thus
$um\in F_jM_n$ and thus ![]() $m\in \pi F_jM_n$, as required.
$m\in \pi F_jM_n$, as required.
Proof of Theorem 3.1 By the remark after Corollary 3.1 and by Lemma 3.2, there exists ![]() $t$ such that
$t$ such that ![]() $N$ is
$N$ is ![]() $S_n$-torsionfree for any
$S_n$-torsionfree for any ![]() $n\geq t$. Then
$n\geq t$. Then ![]() $\widehat {M_n}\neq 0$ by [Reference Atiyah and MacdonaldAM69, Theorem 10.17]. As
$\widehat {M_n}\neq 0$ by [Reference Atiyah and MacdonaldAM69, Theorem 10.17]. As ![]() $M_n$ is
$M_n$ is ![]() $\pi$-torsionfree, so is
$\pi$-torsionfree, so is ![]() $\widehat {M_n}\cong \widehat {U_n}\otimes _{U_n}M_n$, and hence
$\widehat {M_n}\cong \widehat {U_n}\otimes _{U_n}M_n$, and hence ![]() $\widehat {M_n}\otimes _R K\cong \widehat {{U}_{n,K}}\otimes _{U_K}N\neq 0$ for any
$\widehat {M_n}\otimes _R K\cong \widehat {{U}_{n,K}}\otimes _{U_K}N\neq 0$ for any ![]() $n\geq t$. Therefore
$n\geq t$. Therefore ![]() $\widehat {{U}_K}\otimes _{U_K}N\neq 0$, as required.
$\widehat {{U}_K}\otimes _{U_K}N\neq 0$, as required.
Corollary Let ![]() $A$ be an affinoid
$A$ be an affinoid ![]() $K$-algebra and let
$K$-algebra and let ![]() $L$ be a smooth
$L$ be a smooth ![]() $(K, A)$-Lie algebra. Then
$(K, A)$-Lie algebra. Then ![]() $U_A(L)\to \widehat {U_A(L)}$ is faithfully flat.
$U_A(L)\to \widehat {U_A(L)}$ is faithfully flat.
Proof. Flatness was already proven in [Reference BodeBod19a, Lemma 4.14], so it suffices to show faithfulness.
If ![]() $L$ admits a smooth Lie lattice, this follows directly from Theorem 3.1. In the general case, note that there exists a finite affinoid covering
$L$ admits a smooth Lie lattice, this follows directly from Theorem 3.1. In the general case, note that there exists a finite affinoid covering ![]() $(\operatorname {Sp} A_i)$ of
$(\operatorname {Sp} A_i)$ of ![]() $\operatorname {Sp} A$ such that
$\operatorname {Sp} A$ such that ![]() $A_i\otimes _A L$ is free (and in particular admits a smooth Lie lattice) for each
$A_i\otimes _A L$ is free (and in particular admits a smooth Lie lattice) for each ![]() $i$. We thus obtain the commutative diagram
$i$. We thus obtain the commutative diagram

where the left vertical arrow is faithfully flat due to the isomorphism ![]() $U(A_i\otimes _A L)\cong A_i\otimes _A U_A(L)$ (see [Reference Ardakov and WadsleyAW19, Proposition 2.3]). Theorem 3.1 thus implies that
$U(A_i\otimes _A L)\cong A_i\otimes _A U_A(L)$ (see [Reference Ardakov and WadsleyAW19, Proposition 2.3]). Theorem 3.1 thus implies that ![]() $\oplus \widehat {U(A_i\otimes _A L)}$ is faithfully flat over
$\oplus \widehat {U(A_i\otimes _A L)}$ is faithfully flat over ![]() $U_A(L)$: if
$U_A(L)$: if ![]() $N$ is a non-zero
$N$ is a non-zero ![]() $U(L)$-module, then there exists some
$U(L)$-module, then there exists some ![]() $i$ such that
$i$ such that ![]() ${U(A_i\otimes L)\otimes _{U(L)} N\neq 0}$, and hence
${U(A_i\otimes L)\otimes _{U(L)} N\neq 0}$, and hence ![]() $\widehat {U(A_i\otimes L)}\otimes _{U(L)} N\neq 0$. Therefore, if
$\widehat {U(A_i\otimes L)}\otimes _{U(L)} N\neq 0$. Therefore, if ![]() $N$ is a
$N$ is a ![]() $U(L)$-module such that
$U(L)$-module such that ![]() $\widehat {U(L)}\otimes N=0$, it follows from
$\widehat {U(L)}\otimes N=0$, it follows from ![]() $\oplus \widehat {U(A_i\otimes L)}\otimes _{U(L)}N=0$ that
$\oplus \widehat {U(A_i\otimes L)}\otimes _{U(L)}N=0$ that ![]() $N=0$.
$N=0$.
If ![]() $A$ is a smooth affinoid
$A$ is a smooth affinoid ![]() $K$-algebra and
$K$-algebra and ![]() $L=\mathcal {T}(\operatorname {Sp} A)$, this now proves Theorem B from the introduction.
$L=\mathcal {T}(\operatorname {Sp} A)$, this now proves Theorem B from the introduction.
4. Auslander–Gorenstein rings and completed enveloping algebras
4.1 Faithfully flat descent
Definition Let ![]() $A$ be a ring.
$A$ be a ring.
(i) The grade of an
 $A$-module
$A$-module  $M$ is
and
$M$ is
and \[ j(M)=\min\{i: \operatorname{Ext}^{i}_A(M, A)\neq 0\}, \]
\[ j(M)=\min\{i: \operatorname{Ext}^{i}_A(M, A)\neq 0\}, \] $\infty$ if no such
$\infty$ if no such  $i$ exists.
$i$ exists.(ii) We say that
 $A$ satisfies the Auslander condition if for every Noetherian
$A$ satisfies the Auslander condition if for every Noetherian  $A$-module
$A$-module  $M$ and any
$M$ and any  $i\geq 0$, we have
$i\geq 0$, we have  $j(N)\geq i$ whenever
$j(N)\geq i$ whenever  $N$ is a (right) submodule of
$N$ is a (right) submodule of  $\operatorname {Ext}^{i}_A(M, A)$.
$\operatorname {Ext}^{i}_A(M, A)$.(iii) A two-sided Noetherian ring is called Gorenstein if it has finite left and right self-injective dimension.
(iv) A two-sided Noetherian ring is called Auslander–Gorenstein if it satisfies the Auslander condition and has finite left and right self-injective dimension.
The proof of the following straightforward lemma can be pieced together from the literature (see, for example, [Reference Levasseur and StaffordLS06, Theorem 3.3] and [Reference Bezrukavnikov, Braverman and PositelskiiBBP02, Theorem 1.2]), but as far as we know it has never been written down in this generality in a single place.
Lemma If ![]() $S\to S'$ is a faithfully flat homomorphism of rings with
$S\to S'$ is a faithfully flat homomorphism of rings with ![]() $S'$ Auslander–Gorenstein then
$S'$ Auslander–Gorenstein then ![]() $S$ is also Auslander–Gorenstein. Moreover, the dimension of
$S$ is also Auslander–Gorenstein. Moreover, the dimension of ![]() $S$ is bounded above by the dimension of
$S$ is bounded above by the dimension of ![]() $S'$.
$S'$.
Proof. First we show that ![]() $S$ is left Noetherian. Suppose that
$S$ is left Noetherian. Suppose that ![]() $(I_n)$ is an ascending chain of left ideals in
$(I_n)$ is an ascending chain of left ideals in ![]() $S$. For each
$S$. For each ![]() $n\in \mathbb {N}$ let
$n\in \mathbb {N}$ let ![]() $J_n$ be the image of
$J_n$ be the image of ![]() $S'\otimes _S I_n\to S'$ so that
$S'\otimes _S I_n\to S'$ so that ![]() $(J_n)$ is an ascending chain of left ideals in
$(J_n)$ is an ascending chain of left ideals in ![]() $S'$. Since
$S'$. Since ![]() $S'$ is left Noetherian the chain
$S'$ is left Noetherian the chain ![]() $J_n$ must terminate. Because
$J_n$ must terminate. Because ![]() $S\to S'$ is faithfully flat
$S\to S'$ is faithfully flat ![]() $J_n/J_{n-1}\cong S'\otimes _S I_n/I_{n-1}\neq 0$ whenever
$J_n/J_{n-1}\cong S'\otimes _S I_n/I_{n-1}\neq 0$ whenever ![]() $I_n/I_{n-1}\neq 0$. Thus the chain
$I_n/I_{n-1}\neq 0$. Thus the chain ![]() $I_n$ must terminate.
$I_n$ must terminate.
By symmetry (or by considering the opposite rings) ![]() $S$ is also right Noetherian.
$S$ is also right Noetherian.
Next we show that ![]() $S$ satisfies the Auslander condition. Let
$S$ satisfies the Auslander condition. Let ![]() $N$ be a right
$N$ be a right ![]() $S$-submodule of
$S$-submodule of ![]() $\operatorname {Ext}^{i}_S(M, S)$ for some finitely generated left
$\operatorname {Ext}^{i}_S(M, S)$ for some finitely generated left ![]() $S$-module
$S$-module ![]() $M$, and let
$M$, and let ![]() $j< i$. Since
$j< i$. Since ![]() $S\to S'$ is flat there is an isomorphism
$S\to S'$ is flat there is an isomorphism ![]() $S'\otimes _S \operatorname {Ext}_S^{j}(N,S)\cong \operatorname {Ext}_{S'}^{j}(N\otimes _S S',S')$. The latter is zero since
$S'\otimes _S \operatorname {Ext}_S^{j}(N,S)\cong \operatorname {Ext}_{S'}^{j}(N\otimes _S S',S')$. The latter is zero since ![]() $S'$ satisfies the Auslander condition and
$S'$ satisfies the Auslander condition and ![]() $N\otimes _S S'$ is isomorphic to a submodule of
$N\otimes _S S'$ is isomorphic to a submodule of ![]() $\operatorname {Ext}_S^{i}(M,S)\otimes _S S'\cong \operatorname {Ext}_{S'}^{i}(S'\otimes _S M,S')$ by the flatness of
$\operatorname {Ext}_S^{i}(M,S)\otimes _S S'\cong \operatorname {Ext}_{S'}^{i}(S'\otimes _S M,S')$ by the flatness of ![]() $S\to S'$ again. Since
$S\to S'$ again. Since ![]() $S\to S'$ is faithfully flat we may deduce that
$S\to S'$ is faithfully flat we may deduce that ![]() $\operatorname {Ext}_S^{j}(N,S)=0$ as required.
$\operatorname {Ext}_S^{j}(N,S)=0$ as required.
Finally, suppose that ![]() $d=\mathrm {injdim}_{S'} S'$. For each cyclic
$d=\mathrm {injdim}_{S'} S'$. For each cyclic ![]() $S$-module
$S$-module ![]() $M$ we can compute
$M$ we can compute ![]() $\operatorname {Ext}^{d+1}(M,S)\otimes _S S'\cong \operatorname {Ext}^{d+1}(S'\otimes _S M,S')=0$. Since
$\operatorname {Ext}^{d+1}(M,S)\otimes _S S'\cong \operatorname {Ext}^{d+1}(S'\otimes _S M,S')=0$. Since ![]() $S\to S'$ is faithfully flat we can deduce
$S\to S'$ is faithfully flat we can deduce ![]() $\operatorname {Ext}^{d+1}(M,S)=0$ and so, using [Reference JansJan64, p. 55], that
$\operatorname {Ext}^{d+1}(M,S)=0$ and so, using [Reference JansJan64, p. 55], that ![]() $\mathrm {injdim}_S S\leq d$.
$\mathrm {injdim}_S S\leq d$.
4.2 Smooth affinoids and Gorenstein formal models
Recall that Raynaud's theorem [Reference Bosch and LütkebohmertBL93, Theorem 4.1] establishes an equivalence of categories ![]() $\mathcal {X}\mapsto \mathcal {X}_{\mathrm {rig}}$ between the category of quasi-compact admissible formal
$\mathcal {X}\mapsto \mathcal {X}_{\mathrm {rig}}$ between the category of quasi-compact admissible formal ![]() $R$-schemes localized by admissible formal blowing-ups, and the category of quasi-compact rigid analytic spaces over
$R$-schemes localized by admissible formal blowing-ups, and the category of quasi-compact rigid analytic spaces over ![]() $K$. (Recall that all our rigid analytic spaces are assumed to be quasi-separated.)
$K$. (Recall that all our rigid analytic spaces are assumed to be quasi-separated.)
Proposition Suppose that ![]() $X$ is a smooth quasi-compact rigid analytic space over
$X$ is a smooth quasi-compact rigid analytic space over ![]() $K$. Given any quasi-compact formal model
$K$. Given any quasi-compact formal model ![]() $\mathcal {X}$ of
$\mathcal {X}$ of ![]() $X$ over
$X$ over ![]() $R$, there is an admissible formal blowing-up
$R$, there is an admissible formal blowing-up ![]() $\mathcal {X}^{{\dagger} }\to \mathcal {X}$ of formal
$\mathcal {X}^{{\dagger} }\to \mathcal {X}$ of formal ![]() $R$-schemes with
$R$-schemes with ![]() $\mathcal {X}^{{\dagger} }$ Gorenstein.
$\mathcal {X}^{{\dagger} }$ Gorenstein.
Proof. By [Reference HartlHar03, Theorem 1.4] there is a finite separable field extension ![]() $K'$ of
$K'$ of ![]() $K$ with ring of integers
$K$ with ring of integers ![]() $R'$, a quasi-compact strictly semi-stable formal
$R'$, a quasi-compact strictly semi-stable formal ![]() $R'$-scheme
$R'$-scheme ![]() $\mathcal {X}'$, and a composition of morphisms of quasi-compact admissible formal
$\mathcal {X}'$, and a composition of morphisms of quasi-compact admissible formal ![]() $R$-schemes
$R$-schemes ![]() $\mathcal {X}'\to \mathcal {X}^{{\dagger} }\to \mathcal {X}$ such that
$\mathcal {X}'\to \mathcal {X}^{{\dagger} }\to \mathcal {X}$ such that ![]() $\mathcal {X}^{{\dagger} } \to \mathcal {X}$ is an admissible formal blowing-up and
$\mathcal {X}^{{\dagger} } \to \mathcal {X}$ is an admissible formal blowing-up and ![]() $\mathcal {X}'\to \mathcal {X}^{{\dagger} }$ is flat and surjective. Since being Gorenstein is a local condition and
$\mathcal {X}'\to \mathcal {X}^{{\dagger} }$ is flat and surjective. Since being Gorenstein is a local condition and ![]() $\mathcal {X}'\to \mathcal {X}^{{\dagger} }$ is faithfully flat it suffices by Lemma 4.1 to show that
$\mathcal {X}'\to \mathcal {X}^{{\dagger} }$ is faithfully flat it suffices by Lemma 4.1 to show that ![]() $\mathcal {X}'$ is Gorenstein. But
$\mathcal {X}'$ is Gorenstein. But ![]() $\mathcal {X}'$ is a regular scheme [Reference HartlHar03, Remark 1.1.1] and so Gorenstein.
$\mathcal {X}'$ is a regular scheme [Reference HartlHar03, Remark 1.1.1] and so Gorenstein.
4.3 Completed enveloping algebras over Gorenstein algebras
Lemma Suppose that ![]() $A$ is a commutative Gorenstein
$A$ is a commutative Gorenstein ![]() $k$-algebra for some commutative ring
$k$-algebra for some commutative ring ![]() $k$, and
$k$, and ![]() $L$ is a smooth
$L$ is a smooth ![]() $(k,A)$-Lie algebra of rank
$(k,A)$-Lie algebra of rank ![]() $r$. Then
$r$. Then ![]() $U(L)$ is Auslander–Gorenstein of dimension at most
$U(L)$ is Auslander–Gorenstein of dimension at most ![]() $\dim A+r$.
$\dim A+r$.
Proof. By [Reference RinehartRin63, Theorem 3.1] there is a positive filtration on ![]() $U(L)$ such that
$U(L)$ such that ![]() $\operatorname {gr} U(L)\cong \operatorname {Sym}(L)$ is commutative. By [Reference LevasseurLev85, Théorème 4.4, Remarque 4.5] it thus suffices to show that
$\operatorname {gr} U(L)\cong \operatorname {Sym}(L)$ is commutative. By [Reference LevasseurLev85, Théorème 4.4, Remarque 4.5] it thus suffices to show that ![]() $\operatorname {Sym}(L)$ is Auslander–Gorenstein of dimension at most
$\operatorname {Sym}(L)$ is Auslander–Gorenstein of dimension at most ![]() $\dim A+r$.
$\dim A+r$.
Since ![]() $L$ is a finitely generated projective
$L$ is a finitely generated projective ![]() $(k,A)$-module there is a cover of
$(k,A)$-module there is a cover of ![]() $\operatorname {Spec}(A)$ by basic open subsets
$\operatorname {Spec}(A)$ by basic open subsets ![]() $D(f_1),\ldots ,D(f_m)$ such that
$D(f_1),\ldots ,D(f_m)$ such that ![]() $A_{f_i}\otimes _A L$ is a free
$A_{f_i}\otimes _A L$ is a free ![]() $A_{f_i}$-module of rank
$A_{f_i}$-module of rank ![]() $r$ for each
$r$ for each ![]() $i=1,\ldots ,m$. Since
$i=1,\ldots ,m$. Since ![]() $\operatorname {Sym}(L)\to \oplus _{i=1}^{m}\operatorname {Sym}(A_{f_i}\otimes _A L)$ is faithfully flat we can use Lemma 4.1 to reduce to the case that
$\operatorname {Sym}(L)\to \oplus _{i=1}^{m}\operatorname {Sym}(A_{f_i}\otimes _A L)$ is faithfully flat we can use Lemma 4.1 to reduce to the case that ![]() $L$ is free over
$L$ is free over ![]() $A$, that is,
$A$, that is, ![]() $\operatorname {Sym}(L)$ is isomorphic to a polynomial ring
$\operatorname {Sym}(L)$ is isomorphic to a polynomial ring ![]() $A[t_1,\ldots ,t_r]$. Thus we are done by [Reference Watanabe, Ishikawa, Tachibana and OtsukaWITO69, Corollary 1].
$A[t_1,\ldots ,t_r]$. Thus we are done by [Reference Watanabe, Ishikawa, Tachibana and OtsukaWITO69, Corollary 1].
Theorem Suppose that ![]() $A$ is a smooth
$A$ is a smooth ![]() $K$-affinoid algebra over
$K$-affinoid algebra over ![]() $K$ with affine formal model
$K$ with affine formal model ![]() $\mathcal {A}$ and that
$\mathcal {A}$ and that ![]() $\mathcal {L}$ is a smooth
$\mathcal {L}$ is a smooth ![]() $(R,\mathcal {A})$-Lie algebra of rank
$(R,\mathcal {A})$-Lie algebra of rank ![]() $r$. There is an integer
$r$. There is an integer ![]() $m\geq 0$ such that
$m\geq 0$ such that ![]() $\widehat {U(\pi ^{n}\mathcal {L})_K}$ is Auslander–Gorenstein of dimension at most
$\widehat {U(\pi ^{n}\mathcal {L})_K}$ is Auslander–Gorenstein of dimension at most ![]() $\dim A+r$ for each
$\dim A+r$ for each ![]() $n\geq m$.
$n\geq m$.
Proof. First we establish the result when ![]() $\mathcal {A}$ is Gorenstein with
$\mathcal {A}$ is Gorenstein with ![]() $m=0$. In this case it follows from the lemma that
$m=0$. In this case it follows from the lemma that ![]() $U(\mathcal {L})$ is Auslander–Gorenstein of dimension at most
$U(\mathcal {L})$ is Auslander–Gorenstein of dimension at most ![]() $\dim \mathcal {A}+r=\dim A+1+r$. Thus
$\dim \mathcal {A}+r=\dim A+1+r$. Thus ![]() $U(\mathcal {L})/\pi U(\mathcal {L})$ is Auslander–Gorenstein of dimension at most
$U(\mathcal {L})/\pi U(\mathcal {L})$ is Auslander–Gorenstein of dimension at most ![]() $\dim A+r$ by [Reference Ajitabh, Smith and ZhangASZ99, Propositions 1.3 and 2.1].
$\dim A+r$ by [Reference Ajitabh, Smith and ZhangASZ99, Propositions 1.3 and 2.1].
Now ![]() $\widehat {U(\pi ^{n}\mathcal {L})_K}$ is a complete doubly filtered
$\widehat {U(\pi ^{n}\mathcal {L})_K}$ is a complete doubly filtered ![]() $K$-algebra and
$K$-algebra and
by [Reference Ardakov and WadsleyAW13, Lemma 3.7]. Thus ![]() $\widehat {U(\pi ^{n}\mathcal {L})_K}$ is Auslander–Gorenstein of dimension at most
$\widehat {U(\pi ^{n}\mathcal {L})_K}$ is Auslander–Gorenstein of dimension at most ![]() $\dim A+r$ by [Reference BjorkBjo89, Theorem 3.9].
$\dim A+r$ by [Reference BjorkBjo89, Theorem 3.9].
In the general case Proposition 4.2 shows that there is an admissible formal blowing-up ![]() $\mathcal {X}\to \operatorname {Spf}(\mathcal {A})$ over
$\mathcal {X}\to \operatorname {Spf}(\mathcal {A})$ over ![]() $R$ with
$R$ with ![]() $\mathcal {X}$ Gorenstein. Let
$\mathcal {X}$ Gorenstein. Let ![]() $\{\operatorname {Spf}(\mathcal {A}_i)\}$ be an affine cover of
$\{\operatorname {Spf}(\mathcal {A}_i)\}$ be an affine cover of ![]() $\mathcal {X}$. By [Reference Ardakov and WadsleyAW19, Proposition 7.6] and the proof of [Reference Ardakov and WadsleyAW19, Lemma 7.6(b)] there is a positive integer
$\mathcal {X}$. By [Reference Ardakov and WadsleyAW19, Proposition 7.6] and the proof of [Reference Ardakov and WadsleyAW19, Lemma 7.6(b)] there is a positive integer ![]() $m$ such that each
$m$ such that each ![]() $\mathcal {A}_i$ is
$\mathcal {A}_i$ is ![]() $\mathcal {L}$-stable and each
$\mathcal {L}$-stable and each ![]() $(\operatorname {Spf} \mathcal {A}_i)_{\mathrm {rig}}$ is a
$(\operatorname {Spf} \mathcal {A}_i)_{\mathrm {rig}}$ is a ![]() $\pi ^{n}\mathcal {L}$-accessible subdomain of
$\pi ^{n}\mathcal {L}$-accessible subdomain of ![]() $X$ for each
$X$ for each ![]() $n\geq m$. Thus each natural map
$n\geq m$. Thus each natural map
with ![]() $n\geq m$ is faithfully flat by [Reference Ardakov and WadsleyAW19, Theorem 4.9(b)]. The result now follows from Lemma 4.1 and the case
$n\geq m$ is faithfully flat by [Reference Ardakov and WadsleyAW19, Theorem 4.9(b)]. The result now follows from Lemma 4.1 and the case ![]() $\mathcal {A}$ is Gorenstein.
$\mathcal {A}$ is Gorenstein.
This proves Theorem A(i).
5. Dimension theory for coadmissible modules
5.1 Review
We slightly generalize the exposition of [Reference Schneider and TeitelbaumST03, § 8] which introduced a dimension theory for Fréchet–Stein algebras with the property that each member of the defining family of Banach algebras is Auslander regular of global dimension bounded by a universal constant; we relax this last condition to Auslander–Gorenstein with self-injective dimension bounded by a universal constant.
We suppose throughout this section that ![]() $U=\varprojlim U_n$ is a two-sided Fréchet–Stein algebra.
$U=\varprojlim U_n$ is a two-sided Fréchet–Stein algebra.
Lemma [Reference Schneider and TeitelbaumST03, Lemma 8.4]
For any coadmissible left ![]() $U$-module
$U$-module ![]() $M$ and any integer
$M$ and any integer ![]() $l\ge 0$ the
$l\ge 0$ the ![]() $U$-module
$U$-module ![]() $\operatorname {Ext}^{l}_U(M,U)$ is coadmissible with
$\operatorname {Ext}^{l}_U(M,U)$ is coadmissible with
for any ![]() $n\in \mathbb {N}$.
$n\in \mathbb {N}$.
Definition We say that ![]() $U$ is coadmissibly Auslander–Gorenstein (or c-Auslander–Gorenstein) of dimension at most
$U$ is coadmissibly Auslander–Gorenstein (or c-Auslander–Gorenstein) of dimension at most ![]() $d$ if
$d$ if ![]() $d$ is a non-negative integer such that there exists a presentation
$d$ is a non-negative integer such that there exists a presentation ![]() $U\cong \varprojlim U_n$ of
$U\cong \varprojlim U_n$ of ![]() $U$ as a Fréchet–Stein algebra with each
$U$ as a Fréchet–Stein algebra with each ![]() $U_n$ being Auslander–Gorenstein of self-injective dimension at most
$U_n$ being Auslander–Gorenstein of self-injective dimension at most ![]() $d$.
$d$.
It follows easily from the lemma that if ![]() $U$ is c-Auslander–Gorenstein of dimension at most
$U$ is c-Auslander–Gorenstein of dimension at most ![]() $d$ then every coadmissible
$d$ then every coadmissible ![]() $U$-module
$U$-module ![]() $M$ satisfies Auslander's condition; that is, for every integer
$M$ satisfies Auslander's condition; that is, for every integer ![]() $l\ge 0$ every coadmissible submodule
$l\ge 0$ every coadmissible submodule ![]() $N$ of
$N$ of ![]() $\operatorname {Ext}^{l}_U(M,U)$ has grade at least
$\operatorname {Ext}^{l}_U(M,U)$ has grade at least ![]() $l$. It is also an easy consequence that every (non-zero) coadmissible
$l$. It is also an easy consequence that every (non-zero) coadmissible ![]() $U$-module has grade at most
$U$-module has grade at most ![]() $d$.
$d$.
If ![]() $A$ is a smooth
$A$ is a smooth ![]() $K$-affinoid algebra and
$K$-affinoid algebra and ![]() $L$ is a
$L$ is a ![]() $(K,A)$-Lie algebra that admits a smooth lattice of rank
$(K,A)$-Lie algebra that admits a smooth lattice of rank ![]() $r$ then
$r$ then ![]() $\widehat {U(L)}$ is c-Auslander–Gorenstein of dimension at most
$\widehat {U(L)}$ is c-Auslander–Gorenstein of dimension at most ![]() $\dim A+r$ by Theorem 4.3. In particular, if
$\dim A+r$ by Theorem 4.3. In particular, if ![]() $\operatorname {Der}_K(A)$ admits a smooth lattice then
$\operatorname {Der}_K(A)$ admits a smooth lattice then ![]() $\widehat {\mathcal {D}}(\operatorname {Sp} A)$ is c-Auslander–Gorenstein of dimension at most
$\widehat {\mathcal {D}}(\operatorname {Sp} A)$ is c-Auslander–Gorenstein of dimension at most ![]() $2\dim A$.
$2\dim A$.
Definition Suppose that ![]() $A$ is a smooth
$A$ is a smooth ![]() $K$-affinoid algebra and
$K$-affinoid algebra and ![]() $L$ is a
$L$ is a ![]() $(K,A)$-Lie algebra that admits a smooth lattice of rank
$(K,A)$-Lie algebra that admits a smooth lattice of rank ![]() $r$. Writing
$r$. Writing ![]() $U$ for
$U$ for ![]() $\widehat {U(L)}$, the dimension of a (non-zero) coadmissible
$\widehat {U(L)}$, the dimension of a (non-zero) coadmissible ![]() $U$-module
$U$-module ![]() $M$ is defined by
$M$ is defined by
We will sometimes suppress the subscript ![]() $U$ and simply write
$U$ and simply write ![]() $d(M)$ if this will not cause confusion.
$d(M)$ if this will not cause confusion.
5.2 Left–right comparison
Let ![]() $A$ be an affinoid
$A$ be an affinoid ![]() $K$-algebra and let
$K$-algebra and let ![]() $L$ be a
$L$ be a ![]() $(K, A)$-Lie algebra that admits a smooth Lie lattice of rank
$(K, A)$-Lie algebra that admits a smooth Lie lattice of rank ![]() $r$. Recall [Reference Ardakov and WadsleyAW18, Theorem 3.4] that there is an equivalence of categories between coadmissible left
$r$. Recall [Reference Ardakov and WadsleyAW18, Theorem 3.4] that there is an equivalence of categories between coadmissible left ![]() $\widehat {U(L)}$-modules and coadmissible right
$\widehat {U(L)}$-modules and coadmissible right ![]() $\widehat {U(L)}$-modules, given by
$\widehat {U(L)}$-modules, given by ![]() $\Omega _L\otimes _A-$ and
$\Omega _L\otimes _A-$ and ![]() $\operatorname {Hom}_A(\Omega _L, -)$, where
$\operatorname {Hom}_A(\Omega _L, -)$, where
Lemma For each coadmissible left ![]() $\widehat {U(L)}$-module
$\widehat {U(L)}$-module ![]() $M$ there is a natural isomorphism
$M$ there is a natural isomorphism
In particular, ![]() $d(M)=d(\Omega _L\otimes _A M)$.
$d(M)=d(\Omega _L\otimes _A M)$.
Proof. As ![]() $\Omega _L$ is a projective
$\Omega _L$ is a projective ![]() $A$-module, the left-hand side is the
$A$-module, the left-hand side is the ![]() $j$th cohomology of
$j$th cohomology of ![]() $\mathrm {R}\operatorname {Hom}_{\widehat {U(L)}}(\Omega _L\otimes ^{\mathbb {L}}_AM, \widehat {U(L)})$, while the right-hand side is the
$\mathrm {R}\operatorname {Hom}_{\widehat {U(L)}}(\Omega _L\otimes ^{\mathbb {L}}_AM, \widehat {U(L)})$, while the right-hand side is the ![]() $j$th cohomology of
$j$th cohomology of ![]() $\mathrm {R}\operatorname {Hom}_A(\Omega _L, \mathrm {R}\operatorname {Hom}_{\widehat {U(L)}}(M, \widehat {U(L)})$. The natural isomorphism thus follows directly from the derived tensor-Hom adjunction [Reference Kashiwara and SchapiraKS06, Theorem 18.6.4(vii)].
$\mathrm {R}\operatorname {Hom}_A(\Omega _L, \mathrm {R}\operatorname {Hom}_{\widehat {U(L)}}(M, \widehat {U(L)})$. The natural isomorphism thus follows directly from the derived tensor-Hom adjunction [Reference Kashiwara and SchapiraKS06, Theorem 18.6.4(vii)].
Because ![]() $\Omega _L$ is an invertible
$\Omega _L$ is an invertible ![]() $A$-module,
$A$-module,
for each ![]() $j\geq 0$, and hence
$j\geq 0$, and hence ![]() $d(M)=d(\Omega _L\otimes _A M)$.
$d(M)=d(\Omega _L\otimes _A M)$.
5.3 Dimension theory for  ${\widehat {\mathscr {U}(\mathscr {L})}}$
${\widehat {\mathscr {U}(\mathscr {L})}}$
Let ![]() $\mathscr {L}$ be a Lie algebroid on a smooth, equidimensional rigid
$\mathscr {L}$ be a Lie algebroid on a smooth, equidimensional rigid ![]() $K$-analytic space
$K$-analytic space ![]() $X$. Let
$X$. Let ![]() $X_w(\mathscr {L})$ denote the set of affinoid subspaces
$X_w(\mathscr {L})$ denote the set of affinoid subspaces ![]() $Y$ of
$Y$ of ![]() $X$ such that
$X$ such that ![]() $\mathscr {L}(Y)$ admits a smooth Lie lattice. By [Reference Ardakov and WadsleyAW19, Lemma 9.3],
$\mathscr {L}(Y)$ admits a smooth Lie lattice. By [Reference Ardakov and WadsleyAW19, Lemma 9.3], ![]() $X_w(\mathscr {L})$ is a basis for the topology on
$X_w(\mathscr {L})$ is a basis for the topology on ![]() $X$, that is, every admissible open in
$X$, that is, every admissible open in ![]() $X$ has an admissible cover by objects in
$X$ has an admissible cover by objects in ![]() $X_w(\mathscr {L})$.
$X_w(\mathscr {L})$.
Proposition For each ![]() $t\geq 0$ there is a functor
$t\geq 0$ there is a functor ![]() $\operatorname {\mathscr {E}\!\mathit {xt}}^{t}_{\widehat {\mathscr {U}(\mathscr {L})}}(-, \widehat {\mathscr {U}(\mathscr {L})})$ from coadmissible left
$\operatorname {\mathscr {E}\!\mathit {xt}}^{t}_{\widehat {\mathscr {U}(\mathscr {L})}}(-, \widehat {\mathscr {U}(\mathscr {L})})$ from coadmissible left ![]() $\widehat {\mathscr {U}(\mathscr {L})}$-modules on
$\widehat {\mathscr {U}(\mathscr {L})}$-modules on ![]() $X$ to coadmissible right
$X$ to coadmissible right ![]() $\widehat {\mathscr {U}(\mathscr {L})}$-modules on
$\widehat {\mathscr {U}(\mathscr {L})}$-modules on ![]() $X$ such that
$X$ such that
for each coadmissible left ![]() $\widehat {\mathscr {U}(\mathscr {L})}$-module
$\widehat {\mathscr {U}(\mathscr {L})}$-module ![]() $\mathcal {M}$ and each
$\mathcal {M}$ and each ![]() $Y\in X_w(\mathscr {L})$.
$Y\in X_w(\mathscr {L})$.
Proof. Let ![]() $\mathcal {M}$ be a coadmissible
$\mathcal {M}$ be a coadmissible ![]() $\widehat {\mathscr {U}(\mathscr {L})}$-module and suppose that
$\widehat {\mathscr {U}(\mathscr {L})}$-module and suppose that ![]() $Z\subset Y$ are in
$Z\subset Y$ are in ![]() $X_w(\mathscr {L})$. Let
$X_w(\mathscr {L})$. Let ![]() $\mathcal {A}$ be an affine formal model in
$\mathcal {A}$ be an affine formal model in ![]() $\mathcal {O}(Y)$ such that
$\mathcal {O}(Y)$ such that ![]() $\mathscr {L}(Y)$ admits a smooth Lie lattice
$\mathscr {L}(Y)$ admits a smooth Lie lattice ![]() $\mathcal {L}$. By replacing
$\mathcal {L}$. By replacing ![]() $\mathcal {L}$ by
$\mathcal {L}$ by ![]() $\pi ^{m}\mathcal {L}$ for some positive integer
$\pi ^{m}\mathcal {L}$ for some positive integer ![]() $m$, we may assume that
$m$, we may assume that ![]() $Z$ is
$Z$ is ![]() $\pi ^{n}\mathcal {L}$-accessible for all
$\pi ^{n}\mathcal {L}$-accessible for all ![]() $n\geq 0$ (see [Reference Ardakov and WadsleyAW19, Proposition 7.6]).
$n\geq 0$ (see [Reference Ardakov and WadsleyAW19, Proposition 7.6]).
Let ![]() $\mathcal {B}$ be an affine formal model in
$\mathcal {B}$ be an affine formal model in ![]() $\mathcal {O}(Z)$ such that
$\mathcal {O}(Z)$ such that ![]() $\mathcal {B}\otimes _{\mathcal {A}}\mathcal {L}$ is a
$\mathcal {B}\otimes _{\mathcal {A}}\mathcal {L}$ is a ![]() $\mathcal {B}$-Lie lattice in
$\mathcal {B}$-Lie lattice in ![]() $\mathscr {L}(Z)=B\otimes _A\mathscr {L}(Y)$.
$\mathscr {L}(Z)=B\otimes _A\mathscr {L}(Y)$.
For each ![]() $n\geq 0$, let
$n\geq 0$, let ![]() $U_n$ and
$U_n$ and ![]() $V_n$ denote the
$V_n$ denote the ![]() $K$-Banach algebras
$K$-Banach algebras ![]() $\widehat {U(\pi ^{n}\mathcal {L})_K}$ and
$\widehat {U(\pi ^{n}\mathcal {L})_K}$ and ![]() $\widehat {U(\mathcal {B}\otimes \pi ^{n}\mathcal {L})_K}$ respectively and let
$\widehat {U(\mathcal {B}\otimes \pi ^{n}\mathcal {L})_K}$ respectively and let ![]() $U:=\varprojlim U_n=\widehat {U(\mathscr {L}(Y))}$ and
$U:=\varprojlim U_n=\widehat {U(\mathscr {L}(Y))}$ and ![]() $V:=\varprojlim V_n=\widehat {U(\mathscr {L}(Z))}$. Now, using [Reference Ardakov and WadsleyAW19, Theorem 9.4], we see that
$V:=\varprojlim V_n=\widehat {U(\mathscr {L}(Z))}$. Now, using [Reference Ardakov and WadsleyAW19, Theorem 9.4], we see that ![]() $M_n(Y):=U_n\otimes _{U}\mathcal {M}(Y)$ is a finitely generated left
$M_n(Y):=U_n\otimes _{U}\mathcal {M}(Y)$ is a finitely generated left ![]() $U_n$-module,
$U_n$-module, ![]() $M_n(Z):=V_n\otimes _{V}\mathcal {M}(Z)$ is a finitely generated left
$M_n(Z):=V_n\otimes _{V}\mathcal {M}(Z)$ is a finitely generated left ![]() $V_n$-module and
$V_n$-module and ![]() $M_n(Z)\cong V_n\otimes _{U_n}M_n(Y)$. Moreover, by [Reference Ardakov and WadsleyAW19, Theorem 4.8],
$M_n(Z)\cong V_n\otimes _{U_n}M_n(Y)$. Moreover, by [Reference Ardakov and WadsleyAW19, Theorem 4.8], ![]() $U_n\to V_n$ is flat on both sides for all positive integers
$U_n\to V_n$ is flat on both sides for all positive integers ![]() $n$. Thus
$n$. Thus ![]() $\operatorname {Ext}^{t}_{V_n}(M_n(Z),V_n)\cong \operatorname {Ext}^{t}_{U_n}(M_n(Y),U_n)\otimes _{U_n}V_n$ for each
$\operatorname {Ext}^{t}_{V_n}(M_n(Z),V_n)\cong \operatorname {Ext}^{t}_{U_n}(M_n(Y),U_n)\otimes _{U_n}V_n$ for each ![]() $t\geq 0$.
$t\geq 0$.
By Lemma 5.1, ![]() $\operatorname {Ext}^{t}_{U}(\mathcal {M}(Y),U)$ is a coadmissible right
$\operatorname {Ext}^{t}_{U}(\mathcal {M}(Y),U)$ is a coadmissible right ![]() $U$-module such that
$U$-module such that
and ![]() $\operatorname {Ext}^{t}_{V}(\mathcal {M}(Z),V)$ is a coadmissible
$\operatorname {Ext}^{t}_{V}(\mathcal {M}(Z),V)$ is a coadmissible ![]() $V$-module with
$V$-module with ![]() $\operatorname {Ext}^{t}_{V}(\mathcal {M}(Z),V)\otimes _{V}V_n\cong \operatorname {Ext}^{t}_{V_n}(M_n(Z),V_n)$. Thus we can compute
$\operatorname {Ext}^{t}_{V}(\mathcal {M}(Z),V)\otimes _{V}V_n\cong \operatorname {Ext}^{t}_{V_n}(M_n(Z),V_n)$. Thus we can compute
 \begin{align*} \operatorname{Ext}^{t}_V(\mathcal{M}(Z),V)\otimes V_n & \cong \operatorname{Ext}^{t}_{V_n}(M_n(Z),V_n)\\ & \cong \operatorname{Ext}^{t}_{U_n}(M_n(Y),U_n)\otimes_{U_n}V_n\\ & \cong \operatorname{Ext}^{t}_U(\mathcal{M}(Y),U)\otimes_U V_n. \end{align*}
\begin{align*} \operatorname{Ext}^{t}_V(\mathcal{M}(Z),V)\otimes V_n & \cong \operatorname{Ext}^{t}_{V_n}(M_n(Z),V_n)\\ & \cong \operatorname{Ext}^{t}_{U_n}(M_n(Y),U_n)\otimes_{U_n}V_n\\ & \cong \operatorname{Ext}^{t}_U(\mathcal{M}(Y),U)\otimes_U V_n. \end{align*}
Now we see that ![]() $\operatorname {Ext}^{t}_V(\mathcal {M}(Z),V)\cong \operatorname {Ext}^{t}_U(\mathcal {M}(Y),U) {\widehat{\otimes}}_U V$ by (the proof of) [Reference Ardakov and WadsleyAW19, Lemma 7.3]. It follows, using [Reference Ardakov and WadsleyAW19, Theorem 8.2, Theorem 8.4], that the presheaf on
$\operatorname {Ext}^{t}_V(\mathcal {M}(Z),V)\cong \operatorname {Ext}^{t}_U(\mathcal {M}(Y),U) {\widehat{\otimes}}_U V$ by (the proof of) [Reference Ardakov and WadsleyAW19, Lemma 7.3]. It follows, using [Reference Ardakov and WadsleyAW19, Theorem 8.2, Theorem 8.4], that the presheaf on ![]() $Y_w$ that sends
$Y_w$ that sends ![]() $Z\in Y_w$ to
$Z\in Y_w$ to ![]() $\operatorname {Ext}^{t}_{\widehat {U(\mathscr {L}(Z))}}(\mathcal {M}(Z),\widehat {U(\mathscr {L}(Z))})$ is a coadmissible sheaf of
$\operatorname {Ext}^{t}_{\widehat {U(\mathscr {L}(Z))}}(\mathcal {M}(Z),\widehat {U(\mathscr {L}(Z))})$ is a coadmissible sheaf of ![]() $\widehat {\mathscr {U}(\mathscr {L})}$-modules on
$\widehat {\mathscr {U}(\mathscr {L})}$-modules on ![]() $Y_w$. Applying [Reference Ardakov and WadsleyAW19, Theorem 9.1, Theorem 9.4] completes the proof of the proposition.
$Y_w$. Applying [Reference Ardakov and WadsleyAW19, Theorem 9.1, Theorem 9.4] completes the proof of the proposition.
The analogous statement for coadmissible right modules can be proven using the same argument.
Definition Suppose that ![]() $\mathcal {U}$ is an admissible cover of
$\mathcal {U}$ is an admissible cover of ![]() $X$ by affinoid subspaces in
$X$ by affinoid subspaces in ![]() $X_w(\mathscr {L})$. For each (non-zero) coadmissible
$X_w(\mathscr {L})$. For each (non-zero) coadmissible ![]() $\widehat {\mathscr {U}(\mathscr {L})}$-module
$\widehat {\mathscr {U}(\mathscr {L})}$-module ![]() $\mathcal {M}$ we define the dimension of
$\mathcal {M}$ we define the dimension of ![]() $\mathcal {M}$ with respect to
$\mathcal {M}$ with respect to ![]() $\mathcal {U}$ by
$\mathcal {U}$ by
Lemma Suppose that ![]() $\mathcal {U}$ and
$\mathcal {U}$ and ![]() $\mathcal {V}$ are two admissible covers of
$\mathcal {V}$ are two admissible covers of ![]() $X$ by affinoid subspaces in
$X$ by affinoid subspaces in ![]() $X_w(\mathscr {L})$. Then
$X_w(\mathscr {L})$. Then ![]() $d_\mathcal {U}(\mathcal {M})= d_{\mathcal {V}}(\mathcal {M})$.
$d_\mathcal {U}(\mathcal {M})= d_{\mathcal {V}}(\mathcal {M})$.
Proof. Since ![]() $X$ is quasi-separated, for any pair
$X$ is quasi-separated, for any pair ![]() $Y\in \mathcal {U}$ and
$Y\in \mathcal {U}$ and ![]() $Z\in \mathcal {V}$ that does not intersect trivially we can cover
$Z\in \mathcal {V}$ that does not intersect trivially we can cover ![]() $Y\cap Z$ by a finite set of affinoid subspaces in
$Y\cap Z$ by a finite set of affinoid subspaces in ![]() $X_{w}(\mathcal {L})$. Thus we may reduce to the case that
$X_{w}(\mathcal {L})$. Thus we may reduce to the case that ![]() $\mathcal {V}$ is a refinement of
$\mathcal {V}$ is a refinement of ![]() $\mathcal {U}$ and every element of
$\mathcal {U}$ and every element of ![]() $\mathcal {U}$ has an admissible cover by elements of
$\mathcal {U}$ has an admissible cover by elements of ![]() $\mathcal {V}$.
$\mathcal {V}$.
Now suppose ![]() $Y\in \mathcal {U}$ is covered by
$Y\in \mathcal {U}$ is covered by ![]() $Z_1,\ldots ,Z_k\in \mathcal {V}$. Then by the proposition
$Z_1,\ldots ,Z_k\in \mathcal {V}$. Then by the proposition ![]() $\operatorname {\mathscr {E}\!\mathit {xt}}_{\widehat {\mathscr {U}(\mathscr {L}|_Y)}}^{j}(\mathcal {M}|_Y, \widehat {\mathscr {U}(\mathscr {L}|_Y)})$ is a coadmissible
$\operatorname {\mathscr {E}\!\mathit {xt}}_{\widehat {\mathscr {U}(\mathscr {L}|_Y)}}^{j}(\mathcal {M}|_Y, \widehat {\mathscr {U}(\mathscr {L}|_Y)})$ is a coadmissible ![]() $\widehat {\mathscr {U}(\mathscr {L}|_Y)}$-module for each
$\widehat {\mathscr {U}(\mathscr {L}|_Y)}$-module for each ![]() $j\geq 0$. Since
$j\geq 0$. Since ![]() $\widehat {U(\mathscr {L}(Y))} \to \oplus _{i=1}^{k} \widehat {U(\mathscr {L}(Z_i))}$ is c-faithfully flat by [Reference Ardakov and WadsleyAW19, Theorem 7.7(b)] it follows that
$\widehat {U(\mathscr {L}(Y))} \to \oplus _{i=1}^{k} \widehat {U(\mathscr {L}(Z_i))}$ is c-faithfully flat by [Reference Ardakov and WadsleyAW19, Theorem 7.7(b)] it follows that ![]() $j(\mathcal {M}(Y))=\inf \{j(\mathcal {M}(Z_i))\mid \mathcal {M}(Z_i)\neq 0\}$.
$j(\mathcal {M}(Y))=\inf \{j(\mathcal {M}(Z_i))\mid \mathcal {M}(Z_i)\neq 0\}$.
As ![]() $\dim Y=\dim Z_i$ for each
$\dim Y=\dim Z_i$ for each ![]() $i$ by equidimensionality, the result follows.
$i$ by equidimensionality, the result follows.
It follows that we may define the dimension of ![]() $\mathcal {M}$ by
$\mathcal {M}$ by ![]() $d(\mathcal {M})=d_{\mathcal {U}}(\mathcal {M})$ for any choice
$d(\mathcal {M})=d_{\mathcal {U}}(\mathcal {M})$ for any choice ![]() $\mathcal {U}$ of admissible cover of
$\mathcal {U}$ of admissible cover of ![]() $X$ by affinoid subspaces in
$X$ by affinoid subspaces in ![]() $X_w(\mathscr {L})$.
$X_w(\mathscr {L})$.
6. Bernstein's inequality
6.1 Dimension and pushforward along a closed embedding
Let ![]() $\iota : Y\to X$ be a closed embedding of smooth rigid analytic
$\iota : Y\to X$ be a closed embedding of smooth rigid analytic ![]() $K$-spaces. In [Reference Ardakov and WadsleyAW18], the first and the third author produced a functor
$K$-spaces. In [Reference Ardakov and WadsleyAW18], the first and the third author produced a functor
The construction of ![]() $\iota _+$ rests on the case when
$\iota _+$ rests on the case when ![]() $\iota : Y=\operatorname {Sp} A/I\to \operatorname {Sp} A=X$ and
$\iota : Y=\operatorname {Sp} A/I\to \operatorname {Sp} A=X$ and ![]() $L=\mathcal {T}(X)$ admits an
$L=\mathcal {T}(X)$ admits an ![]() $I$-standard basis, that is, there exist an
$I$-standard basis, that is, there exist an ![]() $A$-basis
$A$-basis ![]() $\{x_1, \dots , x_d\}$ for
$\{x_1, \dots , x_d\}$ for ![]() $L$ and a generating set
$L$ and a generating set ![]() $\{f_1, \dots , f_r\}$ for
$\{f_1, \dots , f_r\}$ for ![]() $I$ with
$I$ with ![]() $r\leq d$ such that
$r\leq d$ such that ![]() $x_i\cdot f_j=\delta _{ij}$ for any
$x_i\cdot f_j=\delta _{ij}$ for any ![]() $1\leq i\leq d$,
$1\leq i\leq d$, ![]() $1\leq j\leq r$.
$1\leq j\leq r$.
Any closed embedding of smooth rigid analytic ![]() $K$-varieties is locally of this form by [Reference Ardakov and WadsleyAW18, Theorem 6.2], and we have
$K$-varieties is locally of this form by [Reference Ardakov and WadsleyAW18, Theorem 6.2], and we have
for any coadmissible right ![]() $\widehat {\mathcal {D}}_Y$-module
$\widehat {\mathcal {D}}_Y$-module ![]() $\mathcal {M}$ – the corresponding functor for left modules is obtained via side-changing operations.
$\mathcal {M}$ – the corresponding functor for left modules is obtained via side-changing operations.
We refer to [Reference Ardakov and WadsleyAW18] for details.
We will now show that ![]() $\iota _+$ respects our dimension function in a natural way, allowing us to reduce many statements about modules on smooth affinoid spaces to the corresponding statements on polydiscs.
$\iota _+$ respects our dimension function in a natural way, allowing us to reduce many statements about modules on smooth affinoid spaces to the corresponding statements on polydiscs.
Lemma Suppose that ![]() $A$ is a smooth affinoid
$A$ is a smooth affinoid ![]() $K$-algebra with affine formal model
$K$-algebra with affine formal model ![]() $\mathcal {A}$, and
$\mathcal {A}$, and ![]() $\mathcal {L}$ is a smooth
$\mathcal {L}$ is a smooth ![]() $(R, \mathcal {A})$-Lie algebra. Let
$(R, \mathcal {A})$-Lie algebra. Let ![]() $f\in \mathcal {A}$ such that
$f\in \mathcal {A}$ such that ![]() $\mathcal {L}\cdot f=\mathcal {A}$, and write
$\mathcal {L}\cdot f=\mathcal {A}$, and write ![]() $\mathcal {C}=C_{\mathcal {L}}(f)=\{x\in \mathcal {L}: x\cdot f=0\}$. Let
$\mathcal {C}=C_{\mathcal {L}}(f)=\{x\in \mathcal {L}: x\cdot f=0\}$. Let ![]() $I=(fA)\cap \mathcal {A}$.
$I=(fA)\cap \mathcal {A}$.
(i)
 $B:=A/fA$ is a smooth affinoid algebra with affine formal model
$B:=A/fA$ is a smooth affinoid algebra with affine formal model  $\mathcal {B}:=\mathcal {A}/I$, and
$\mathcal {B}:=\mathcal {A}/I$, and  $\mathcal {C}/I$ is a smooth
$\mathcal {C}/I$ is a smooth  $(R, \mathcal {B})$-Lie algebra.
$(R, \mathcal {B})$-Lie algebra.(ii) If
 $\operatorname {Sp} A$ is connected, then
$\operatorname {Sp} A$ is connected, then  $f$ is a regular central element in
$f$ is a regular central element in  $\widehat {U_{\mathcal {A}}(\mathcal {C})_K}$.
$\widehat {U_{\mathcal {A}}(\mathcal {C})_K}$.
Proof. By assumption, there exists ![]() $x\in \mathcal {L}$ such that
$x\in \mathcal {L}$ such that ![]() $x\cdot f=1$. Applying the anchor map, we also have
$x\cdot f=1$. Applying the anchor map, we also have ![]() $\partial \in \mathrm {Der}_K(A)$ such that
$\partial \in \mathrm {Der}_K(A)$ such that ![]() $\partial \cdot f=1$, and by [Reference Ardakov and WadsleyAW18, Lemma 4.1],
$\partial \cdot f=1$, and by [Reference Ardakov and WadsleyAW18, Lemma 4.1],
where ![]() $C=\{\xi \in \mathrm {Der}(A): \xi \cdot f=0\}$. In particular, it follows from smoothness that
$C=\{\xi \in \mathrm {Der}(A): \xi \cdot f=0\}$. In particular, it follows from smoothness that ![]() $C$ is a projective
$C$ is a projective ![]() $A$-module.
$A$-module.
By the second fundamental exact sequence [Reference Bosch, Lütkebohmert and RaynaudBLR95, Proposition 1.2], we have
which is projective, so ![]() $B$ is smooth. Moreover,
$B$ is smooth. Moreover, ![]() $\mathcal {B}$ is easily seen to be an affine formal model.
$\mathcal {B}$ is easily seen to be an affine formal model.
In the same vein, applying [Reference Ardakov and WadsleyAW18, Lemma 4.1] to ![]() $\mathcal {L}$ yields
$\mathcal {L}$ yields
so ![]() $\mathcal {C}$ is projective over
$\mathcal {C}$ is projective over ![]() $\mathcal {A}$, and the
$\mathcal {A}$, and the ![]() $(R, \mathcal {B})$-Lie algebra
$(R, \mathcal {B})$-Lie algebra ![]() $\mathcal {C}/I$ is also a projective
$\mathcal {C}/I$ is also a projective ![]() $\mathcal {B}$-module.
$\mathcal {B}$-module.
For (ii), note that ![]() $f$ is central in
$f$ is central in ![]() $\widehat {U(\mathcal {C})_K}$ by definition of
$\widehat {U(\mathcal {C})_K}$ by definition of ![]() $\mathcal {C}$. So it suffices to show that
$\mathcal {C}$. So it suffices to show that ![]() $f\cdot P\neq 0$ for any non-zero
$f\cdot P\neq 0$ for any non-zero ![]() $P\in \widehat {U(\mathcal {C})_K}$. In particular, this only depends on the
$P\in \widehat {U(\mathcal {C})_K}$. In particular, this only depends on the ![]() $A$-module structure of
$A$-module structure of ![]() $\widehat {U(\mathcal {C})_K}$. But it follows from [Reference RinehartRin63, Theorem 3.1] that
$\widehat {U(\mathcal {C})_K}$. But it follows from [Reference RinehartRin63, Theorem 3.1] that
as ![]() $A$-modules. Since
$A$-modules. Since ![]() $\mathcal {C}$ is a projective finitely generated
$\mathcal {C}$ is a projective finitely generated ![]() $\mathcal {A}$-module, it is a direct summand of a free
$\mathcal {A}$-module, it is a direct summand of a free ![]() $\mathcal {A}$-module of finite rank,
$\mathcal {A}$-module of finite rank, ![]() $\mathcal {L}'$. By functoriality,
$\mathcal {L}'$. By functoriality, ![]() $\widehat {\operatorname {Sym} \mathcal {C}_K}$ embeds into
$\widehat {\operatorname {Sym} \mathcal {C}_K}$ embeds into ![]() $\widehat {\operatorname {Sym} \mathcal {L}_K'}$, so we are done if we can show that
$\widehat {\operatorname {Sym} \mathcal {L}_K'}$, so we are done if we can show that ![]() $f$ is regular in
$f$ is regular in ![]() $A$.
$A$.
To show that ![]() $f$ is regular in
$f$ is regular in ![]() $A$, consider the annihilators
$A$, consider the annihilators
By Noetherianity of ![]() $A$, this chain of ideals stabilizes, so that
$A$, this chain of ideals stabilizes, so that
for some integer ![]() $r$.
$r$.
As ![]() $X=\operatorname {Sp} A$ is smooth, we can consider the Fréchet–Stein algebra
$X=\operatorname {Sp} A$ is smooth, we can consider the Fréchet–Stein algebra ![]() $D=\widehat {\mathcal {D}}(X)$. We claim that
$D=\widehat {\mathcal {D}}(X)$. We claim that ![]() $\operatorname {Ann}_A(f^{r})$ is a
$\operatorname {Ann}_A(f^{r})$ is a ![]() $D$-submodule of
$D$-submodule of ![]() $A$, from which
$A$, from which ![]() $\operatorname {Ann}(f)\subseteq \operatorname {Ann}(f^{r})=\{0\}$ follows because of [Reference Ardakov and WadsleyAW18, Proposition 7.4] (note that
$\operatorname {Ann}(f)\subseteq \operatorname {Ann}(f^{r})=\{0\}$ follows because of [Reference Ardakov and WadsleyAW18, Proposition 7.4] (note that ![]() $\operatorname {Ann}(f^{r})\neq A$ as
$\operatorname {Ann}(f^{r})\neq A$ as ![]() $f^{r}\neq 0$ by reducedness of
$f^{r}\neq 0$ by reducedness of ![]() $\operatorname {Sp} A$).
$\operatorname {Sp} A$).
If ![]() $a\in \operatorname {Ann}(f^{r})$ and
$a\in \operatorname {Ann}(f^{r})$ and ![]() $\xi \in \mathrm {Der}(A)$, then
$\xi \in \mathrm {Der}(A)$, then
so that ![]() $\xi (a)\in \operatorname {Ann}(f^{r+1})=\operatorname {Ann}(f^{r})$. By [Reference Ardakov and WadsleyAW18, Theorem 7.3], it follows that
$\xi (a)\in \operatorname {Ann}(f^{r+1})=\operatorname {Ann}(f^{r})$. By [Reference Ardakov and WadsleyAW18, Theorem 7.3], it follows that ![]() $\operatorname {Ann}(f^{r})$ is a
$\operatorname {Ann}(f^{r})$ is a ![]() $D$-submodule of
$D$-submodule of ![]() $A$, as required.
$A$, as required.
Proposition Suppose that ![]() $A$ is a smooth, connected affinoid algebra with affine formal model
$A$ is a smooth, connected affinoid algebra with affine formal model ![]() $\mathcal {A}$ and
$\mathcal {A}$ and ![]() $\mathcal {L}$ is a smooth
$\mathcal {L}$ is a smooth ![]() $(R,\mathcal {A})$-Lie algebra. Let
$(R,\mathcal {A})$-Lie algebra. Let ![]() $F=\{f_1,\ldots ,f_r\}$ be a subset of
$F=\{f_1,\ldots ,f_r\}$ be a subset of ![]() $A$ such that
$A$ such that ![]() ${\mathcal {L}\cdot (f_1,\ldots ,f_r)=\mathcal {A}^{r}}$ and write
${\mathcal {L}\cdot (f_1,\ldots ,f_r)=\mathcal {A}^{r}}$ and write ![]() $\mathcal {C}=C_\mathcal {L}(F)=\{x\in \mathcal {L}: x\cdot f=0 \ \forall f\in F\}$. If
$\mathcal {C}=C_\mathcal {L}(F)=\{x\in \mathcal {L}: x\cdot f=0 \ \forall f\in F\}$. If ![]() $M$ is a finitely generated
$M$ is a finitely generated ![]() $\widehat {U(\mathcal {C})_K}/(F)$-module then
$\widehat {U(\mathcal {C})_K}/(F)$-module then
Proof. We first introduce some notation. For ![]() $i=0, \dots , r$, write
$i=0, \dots , r$, write ![]() $A_i=A/(f_1, \dots , f_i)$,
$A_i=A/(f_1, \dots , f_i)$, ![]() $I_i=(\sum _{j=1}^{i} f_jA)\cap \mathcal {A}$ and
$I_i=(\sum _{j=1}^{i} f_jA)\cap \mathcal {A}$ and ![]() $\mathcal {A}_i=\mathcal {A}/I_i$. Let
$\mathcal {A}_i=\mathcal {A}/I_i$. Let ![]() $\mathcal {C}_i=C_{\mathcal {L}}(\{f_1, \dots , f_i\})$ and let
$\mathcal {C}_i=C_{\mathcal {L}}(\{f_1, \dots , f_i\})$ and let ![]() $\mathcal {L}_i=\mathcal {C}_i/I_i$. By applying the preceding lemma repeatedly, each
$\mathcal {L}_i=\mathcal {C}_i/I_i$. By applying the preceding lemma repeatedly, each ![]() $A_i$ is smooth, with affine formal model
$A_i$ is smooth, with affine formal model ![]() $\mathcal {A}_i$, and
$\mathcal {A}_i$, and ![]() $\mathcal {L}_i$ is a smooth
$\mathcal {L}_i$ is a smooth ![]() $(R, \mathcal {A}_i)$-Lie algebra. Note also that
$(R, \mathcal {A}_i)$-Lie algebra. Note also that ![]() $\mathcal {L}_0=\mathcal {L}$ and
$\mathcal {L}_0=\mathcal {L}$ and ![]() $\mathcal {L}_r=\mathcal {C}/(F)$.
$\mathcal {L}_r=\mathcal {C}/(F)$.
In fact, [Reference Ardakov and WadsleyAW18, Lemma 4.1] gives an explicit description of ![]() $\mathcal {L}_i$: if
$\mathcal {L}_i$: if ![]() $x_1, \dots , x_r\in \mathcal {L}$ such that
$x_1, \dots , x_r\in \mathcal {L}$ such that ![]() $x_if_j=\delta _{ij}$, then
$x_if_j=\delta _{ij}$, then
 \[ \mathcal{L}_i=\mathop{\bigoplus}\limits_{j=i+1}^{r} \mathcal{A}_ix_j\oplus \mathcal{C}/I_i. \]
\[ \mathcal{L}_i=\mathop{\bigoplus}\limits_{j=i+1}^{r} \mathcal{A}_ix_j\oplus \mathcal{C}/I_i. \]In particular, note that the natural map
is an isomorphism for ![]() $i=1, \dots , r$, and
$i=1, \dots , r$, and ![]() $\widehat {U(\mathcal {C})_K}/(F)\cong \widehat {U(\mathcal {L}_r)_K}\cong \widehat {U(C_{\mathcal {L}_{r-1}}(f_r))_K}/(f_r)$.
$\widehat {U(\mathcal {C})_K}/(F)\cong \widehat {U(\mathcal {L}_r)_K}\cong \widehat {U(C_{\mathcal {L}_{r-1}}(f_r))_K}/(f_r)$.
It thus suffices to prove the following claim. If ![]() $M$ is finitely generated
$M$ is finitely generated ![]() $\widehat {U(\mathcal {L}_i)_K}$-module then
$\widehat {U(\mathcal {L}_i)_K}$-module then
Write ![]() $U=\widehat {U(C_{\mathcal {L}_{i-1}}(f_i))_K}$,
$U=\widehat {U(C_{\mathcal {L}_{i-1}}(f_i))_K}$, ![]() $V=\widehat {U(\mathcal {L}_{i-1})_K}$. Since, by [Reference Ardakov and WadsleyAW18, Corollary 4.3],
$V=\widehat {U(\mathcal {L}_{i-1})_K}$. Since, by [Reference Ardakov and WadsleyAW18, Corollary 4.3], ![]() $U\to V$ is faithfully flat and
$U\to V$ is faithfully flat and ![]() $\operatorname {Ext}^{j}_{U}(M,U)\otimes _UV\cong \operatorname {Ext}^{j}_V(V\otimes _U M, V)$, we see that
$\operatorname {Ext}^{j}_{U}(M,U)\otimes _UV\cong \operatorname {Ext}^{j}_V(V\otimes _U M, V)$, we see that ![]() $j_U(M)=j_V(V\otimes _UM)$. Thus it suffices to show that
$j_U(M)=j_V(V\otimes _UM)$. Thus it suffices to show that ![]() $j_U(M)=j_{U/(f_i)}(M)+1$. By the preceding lemma,
$j_U(M)=j_{U/(f_i)}(M)+1$. By the preceding lemma, ![]() $f_i$ is a regular central element in
$f_i$ is a regular central element in ![]() $U$, so we can apply [Reference Ajitabh, Smith and ZhangASZ99, Lemma 1.1] to conclude the proof.
$U$, so we can apply [Reference Ajitabh, Smith and ZhangASZ99, Lemma 1.1] to conclude the proof.
Corollary Suppose that ![]() $I$ is an ideal in the smooth, connected affinoid
$I$ is an ideal in the smooth, connected affinoid ![]() $K$-algebra
$K$-algebra ![]() $A$ and let
$A$ and let ![]() $L$ be a
$L$ be a ![]() $(K,A)$-Lie algebra which admits an
$(K,A)$-Lie algebra which admits an ![]() $I$-standard basis. Write
$I$-standard basis. Write ![]() $L_Y$ for the
$L_Y$ for the ![]() $(K,A/I)$-Lie algebra
$(K,A/I)$-Lie algebra ![]() $N_L(I)/IL$. If
$N_L(I)/IL$. If ![]() $M$ is a (non-zero) coadmissible
$M$ is a (non-zero) coadmissible ![]() $\widehat {U(L_Y)}$-module then
$\widehat {U(L_Y)}$-module then ![]() $d_{\widehat {U(L)}}(\iota _+M)= d_{\widehat {U(L_Y)}}(M)+ \dim A - \dim A/I$.
$d_{\widehat {U(L)}}(\iota _+M)= d_{\widehat {U(L_Y)}}(M)+ \dim A - \dim A/I$.
Proof. By Lemma 5.2, we can consider the case where ![]() $M$ is a right coadmissible module. Let
$M$ is a right coadmissible module. Let ![]() $\{x_1, \dots , x_d\}$ be an
$\{x_1, \dots , x_d\}$ be an ![]() $I$-standard basis and let
$I$-standard basis and let ![]() $F=\{f_1, \dots , f_r\}\subset A$ be the corresponding generating set. Rescaling the
$F=\{f_1, \dots , f_r\}\subset A$ be the corresponding generating set. Rescaling the ![]() $x_i$ and
$x_i$ and ![]() $f_j$ if necessary, we can assume that there exists an affine formal model
$f_j$ if necessary, we can assume that there exists an affine formal model ![]() $\mathcal {A}$ of
$\mathcal {A}$ of ![]() $A$ such that
$A$ such that ![]() $\mathcal {L}:=\sum \mathcal {A} x_i$ is a free Lie lattice in
$\mathcal {L}:=\sum \mathcal {A} x_i$ is a free Lie lattice in ![]() $L$.
$L$.
Write ![]() $U_n=\widehat {U(\pi ^{n}\mathcal {L})_K}$. Recall that [Reference Ardakov and WadsleyAW18, Lemma 5.8] provides an isomorphism of Fréchet–Stein algebras
$U_n=\widehat {U(\pi ^{n}\mathcal {L})_K}$. Recall that [Reference Ardakov and WadsleyAW18, Lemma 5.8] provides an isomorphism of Fréchet–Stein algebras
Denote ![]() $\widehat {U(C_{\pi ^{n}\mathcal {L}}(F))_K}$ by
$\widehat {U(C_{\pi ^{n}\mathcal {L}}(F))_K}$ by ![]() $V_n$, so
$V_n$, so ![]() $\widehat {U(L_Y)}\cong \varprojlim V_n/(F)$ exhibits
$\widehat {U(L_Y)}\cong \varprojlim V_n/(F)$ exhibits ![]() $\widehat {U(L_Y)}$ as a Fréchet–Stein algebra.
$\widehat {U(L_Y)}$ as a Fréchet–Stein algebra.
Now
 \[ j_{\widehat{U(L)}}(\iota_+M)=j_{U_n}\bigg(\iota_+M\underset{\widehat{U(L)}}{\otimes} U_n\bigg) \]
\[ j_{\widehat{U(L)}}(\iota_+M)=j_{U_n}\bigg(\iota_+M\underset{\widehat{U(L)}}{\otimes} U_n\bigg) \]
for sufficiently large ![]() $n$ by Lemma 5.1, and by definition of
$n$ by Lemma 5.1, and by definition of ![]() $\iota _+$,
$\iota _+$,
 \[ \iota_+M\underset{\widehat{U(L)}}{\bigotimes} U_n\cong M\underset{\widehat{U(L_Y)}}{\bigotimes} \frac{V_n}{(F)}\underset{V_n/(F)}{\bigotimes}\frac{U_n}{IU_n}. \]
\[ \iota_+M\underset{\widehat{U(L)}}{\bigotimes} U_n\cong M\underset{\widehat{U(L_Y)}}{\bigotimes} \frac{V_n}{(F)}\underset{V_n/(F)}{\bigotimes}\frac{U_n}{IU_n}. \]Therefore Proposition 6.1 implies that
Since ![]() $\dim A-\dim A/I=r$, it follows that for sufficiently large
$\dim A-\dim A/I=r$, it follows that for sufficiently large ![]() $n$,
$n$,
 \begin{align*} {d_{\widehat{U(L)}}}(\iota_+M)&=2\dim A-j_{U_n}\big(\iota_+M\otimes U_n\big)\\ & =2\dim A-j_{V_n/(F)}(M\otimes V_n/(F))-r\\ & = 2r +(2\dim A/I-{j_{\widehat{U(L_Y)}}}(M))-r\\ &={d_{\widehat{U(L_Y)}}}(M)+r \end{align*}
\begin{align*} {d_{\widehat{U(L)}}}(\iota_+M)&=2\dim A-j_{U_n}\big(\iota_+M\otimes U_n\big)\\ & =2\dim A-j_{V_n/(F)}(M\otimes V_n/(F))-r\\ & = 2r +(2\dim A/I-{j_{\widehat{U(L_Y)}}}(M))-r\\ &={d_{\widehat{U(L_Y)}}}(M)+r \end{align*}as required.
Theorem Suppose that ![]() $\iota \colon Y\to X$ is a closed embedding of smooth, equidimensional
$\iota \colon Y\to X$ is a closed embedding of smooth, equidimensional ![]() $K$-affinoid spaces. Then for every non-zero coadmissible
$K$-affinoid spaces. Then for every non-zero coadmissible ![]() $\widehat {\mathcal {D}}_Y$-module
$\widehat {\mathcal {D}}_Y$-module ![]() $\mathcal {M}$ the dimension of
$\mathcal {M}$ the dimension of ![]() $\iota _+\mathcal {M}$ is given by
$\iota _+\mathcal {M}$ is given by
Proof. By [Reference Ardakov and WadsleyAW18, Theorem 6.2], there exists an affinoid covering ![]() $(X_i)$ of
$(X_i)$ of ![]() $X$, with
$X$, with ![]() $X_i=\operatorname {Sp} A_i$ connected such that the
$X_i=\operatorname {Sp} A_i$ connected such that the ![]() $(K, A_i)$-Lie algebra
$(K, A_i)$-Lie algebra ![]() $L_i=\mathcal {T}(X_i)$ admits an
$L_i=\mathcal {T}(X_i)$ admits an ![]() $I_i$-standard basis, where
$I_i$-standard basis, where ![]() $I_i\subset A_i$ is the vanishing ideal of
$I_i\subset A_i$ is the vanishing ideal of ![]() $Y\cap X_i$ – the conditions in the reference are satisfied by smoothness of
$Y\cap X_i$ – the conditions in the reference are satisfied by smoothness of ![]() $Y$. Moreover,
$Y$. Moreover, ![]() $\mathcal {T}_Y(Y\cap X_i)\cong N_{L_i}(I_i)/I_iL_i$ by dualizing [Reference Bosch, Lütkebohmert and RaynaudBLR95, Proposition 1.2]. Hence the claim follows from Corollary 6.1.
$\mathcal {T}_Y(Y\cap X_i)\cong N_{L_i}(I_i)/I_iL_i$ by dualizing [Reference Bosch, Lütkebohmert and RaynaudBLR95, Proposition 1.2]. Hence the claim follows from Corollary 6.1.
6.2 Proof of Bernstein's inequality
Proposition Let ![]() $X=\operatorname {Sp} K\langle x_1,\ldots , x_d\rangle$ be a polydisc. Each non-zero coadmissible
$X=\operatorname {Sp} K\langle x_1,\ldots , x_d\rangle$ be a polydisc. Each non-zero coadmissible ![]() $\widehat {\mathcal {D}}_X$-module has dimension at least
$\widehat {\mathcal {D}}_X$-module has dimension at least ![]() $d$.
$d$.
Proof. Let ![]() $\mathcal {L}$ be the
$\mathcal {L}$ be the ![]() $\mathcal {R}\langle x_1,\ldots , x_d\rangle$-submodule of
$\mathcal {R}\langle x_1,\ldots , x_d\rangle$-submodule of ![]() $\operatorname {Der}_K(K\langle x_1,\ldots ,x_d\rangle )$ spanned by
$\operatorname {Der}_K(K\langle x_1,\ldots ,x_d\rangle )$ spanned by ![]() $\{\partial _1,\ldots ,\partial _d\}$. Then
$\{\partial _1,\ldots ,\partial _d\}$. Then ![]() $\mathcal {L}$ is a smooth Lie lattice in
$\mathcal {L}$ is a smooth Lie lattice in ![]() $\mathcal {T}(X)$ and write
$\mathcal {T}(X)$ and write ![]() $D_n=\widehat {U(\pi ^{n}\mathcal {L})_K}$ and
$D_n=\widehat {U(\pi ^{n}\mathcal {L})_K}$ and ![]() $D=\widehat {\mathcal {D}}(X)$. Then
$D=\widehat {\mathcal {D}}(X)$. Then ![]() $D=\varprojlim D_n$ is a presentation of
$D=\varprojlim D_n$ is a presentation of ![]() $D$ as a Fréchet–Stein algebra.
$D$ as a Fréchet–Stein algebra.
Let ![]() $\mathcal {M}$ be a coadmissible
$\mathcal {M}$ be a coadmissible ![]() $\widehat {\mathcal {D}}_X$-module and write
$\widehat {\mathcal {D}}_X$-module and write ![]() $M:=\mathcal {M}(X)$, a coadmissible
$M:=\mathcal {M}(X)$, a coadmissible ![]() $D$-module, and
$D$-module, and ![]() $M_n=D_n\otimes _D M$. Since
$M_n=D_n\otimes _D M$. Since ![]() $X\in X_w(\mathcal {T}(X))$ it suffices to show that
$X\in X_w(\mathcal {T}(X))$ it suffices to show that ![]() $j_D(M)\leq d$. Since
$j_D(M)\leq d$. Since ![]() $\operatorname {Ext}^{j}_{D}(M,D)\otimes _{D}D_n \cong \operatorname {Ext}^{j}_{D_n}(M_n,D_n)$ by Lemma 5.1 it suffices to show that
$\operatorname {Ext}^{j}_{D}(M,D)\otimes _{D}D_n \cong \operatorname {Ext}^{j}_{D_n}(M_n,D_n)$ by Lemma 5.1 it suffices to show that ![]() $j_{D_n}(M_n)\leq d$ whenever
$j_{D_n}(M_n)\leq d$ whenever ![]() $M_n\neq 0$. This follows from [Reference Ardakov and WadsleyAW13, Corollary 7.4, Theorem 3.3].
$M_n\neq 0$. This follows from [Reference Ardakov and WadsleyAW13, Corollary 7.4, Theorem 3.3].
Theorem Suppose that ![]() $X$ is a smooth rigid analytic space over
$X$ is a smooth rigid analytic space over ![]() $K$. Then every non-zero coadmissible
$K$. Then every non-zero coadmissible ![]() $\widehat {\mathcal {D}}_X$-module has dimension at least
$\widehat {\mathcal {D}}_X$-module has dimension at least ![]() $\dim X$.
$\dim X$.
Proof. Let ![]() $\mathcal {M}$ be a non-zero coadmissible
$\mathcal {M}$ be a non-zero coadmissible ![]() $\widehat {\mathcal {D}}_X$-module. Since
$\widehat {\mathcal {D}}_X$-module. Since ![]() $\dim \mathcal {M}$ is defined locally we may assume that
$\dim \mathcal {M}$ is defined locally we may assume that ![]() $X$ is affinoid and
$X$ is affinoid and ![]() $\mathcal {T}(X)$ admits a smooth Lie lattice. Now every
$\mathcal {T}(X)$ admits a smooth Lie lattice. Now every ![]() $K$-affinoid can be viewed as a closed analytic subset of a polydisc
$K$-affinoid can be viewed as a closed analytic subset of a polydisc ![]() $Y=\operatorname {Sp} K\langle x_1,\ldots ,x_N\rangle$ for
$Y=\operatorname {Sp} K\langle x_1,\ldots ,x_N\rangle$ for ![]() $N$ sufficiently large. Let
$N$ sufficiently large. Let ![]() $\iota \colon X\to Y$ denote the closed embedding. By Theorem 6.1,
$\iota \colon X\to Y$ denote the closed embedding. By Theorem 6.1, ![]() $d(\iota _+\mathcal {M})= d(\mathcal {M})+ N -\dim X$. Thus it suffices to show that
$d(\iota _+\mathcal {M})= d(\mathcal {M})+ N -\dim X$. Thus it suffices to show that ![]() $d(\iota _+\mathcal {M})\geq N$, and the result follows from the proposition.
$d(\iota _+\mathcal {M})\geq N$, and the result follows from the proposition.
This finishes the proof of Theorem A(ii).
7. Weakly holonomic  $\widehat {\mathcal {D}}$-modules
$\widehat {\mathcal {D}}$-modules
7.1 Definition and basic properties
Definition A coadmissible ![]() $\widehat {\mathcal {D}}_X$-module
$\widehat {\mathcal {D}}_X$-module ![]() $\mathcal {M}$ on a smooth rigid analytic
$\mathcal {M}$ on a smooth rigid analytic ![]() $K$-variety
$K$-variety ![]() $X$ (assumed equidimensional by convention) is called weakly holonomic if
$X$ (assumed equidimensional by convention) is called weakly holonomic if ![]() $d( \mathcal {M})\leq \dim X$.
$d( \mathcal {M})\leq \dim X$.
We remind the reader of our convention stated at the end of the introduction: ![]() $X$ is always assumed to be equidimensional. For a non-connected smooth rigid analytic space whose components are of varying dimension, we can define the notion of weak holonomicity by imposing the inequality above on each connected component.
$X$ is always assumed to be equidimensional. For a non-connected smooth rigid analytic space whose components are of varying dimension, we can define the notion of weak holonomicity by imposing the inequality above on each connected component.
We denote the full subcategory of ![]() $\mathcal {C}_X$ consisting of weakly holonomic
$\mathcal {C}_X$ consisting of weakly holonomic ![]() $\widehat {\mathcal {D}}_X$-modules by
$\widehat {\mathcal {D}}_X$-modules by ![]() $\mathcal {C}^{\mathrm {wh}}_X$.
$\mathcal {C}^{\mathrm {wh}}_X$.
Proposition Let
be a short exact sequence of coadmissible ![]() $\widehat {\mathcal {D}}_X$-modules. Then
$\widehat {\mathcal {D}}_X$-modules. Then ![]() $\mathcal {M}_2$ is weakly holonomic if and only if both
$\mathcal {M}_2$ is weakly holonomic if and only if both ![]() $\mathcal {M}_1$ and
$\mathcal {M}_1$ and ![]() $\mathcal {M}_3$ are weakly holonomic.
$\mathcal {M}_3$ are weakly holonomic.
Proof. As the dimension can be calculated locally, we can assume that ![]() $X=\operatorname {Sp} A$ is a smooth, connected affinoid
$X=\operatorname {Sp} A$ is a smooth, connected affinoid ![]() $K$-space with
$K$-space with ![]() $\mathcal {T}(X)$ admitting a smooth Lie lattice. Choosing an affine formal model
$\mathcal {T}(X)$ admitting a smooth Lie lattice. Choosing an affine formal model ![]() $\mathcal {A}$ and a smooth
$\mathcal {A}$ and a smooth ![]() $(R, \mathcal {A})$-Lie lattice
$(R, \mathcal {A})$-Lie lattice ![]() $\mathcal {L}$ in
$\mathcal {L}$ in ![]() $\mathcal {T}(X)$, we can write
$\mathcal {T}(X)$, we can write ![]() $\widehat {\mathcal {D}}(X)=\varprojlim \widehat {U_{\mathcal {A}}(\pi ^{n}\mathcal {L})}_K$, where
$\widehat {\mathcal {D}}(X)=\varprojlim \widehat {U_{\mathcal {A}}(\pi ^{n}\mathcal {L})}_K$, where ![]() $\widehat {U_{\mathcal {A}}(\pi ^{n}\mathcal {L})}_K$ is Auslander–Gorenstein of dimension at most
$\widehat {U_{\mathcal {A}}(\pi ^{n}\mathcal {L})}_K$ is Auslander–Gorenstein of dimension at most ![]() $2 \dim A$ for sufficiently large
$2 \dim A$ for sufficiently large ![]() $n$ by Theorem 4.3. As before, we abbreviate
$n$ by Theorem 4.3. As before, we abbreviate ![]() $D=\widehat {\mathcal {D}}(X)$ and
$D=\widehat {\mathcal {D}}(X)$ and ![]() $D_n=\widehat {U(\pi ^{n}\mathcal {L})_K}$.
$D_n=\widehat {U(\pi ^{n}\mathcal {L})_K}$.
If ![]() $0\to M_1\to M_2\to M_3\to 0$ is a short exact sequence of coadmissible
$0\to M_1\to M_2\to M_3\to 0$ is a short exact sequence of coadmissible ![]() $D$-modules, there exists an integer
$D$-modules, there exists an integer ![]() $m$ such that
$m$ such that
by Lemma 5.1, so the result follows from [Reference LevasseurLev92, Proposition 4.5(ii)] applied to
which is exact by flatness of ![]() $D_n$ over
$D_n$ over ![]() $D$.
$D$.
It follows immediately from the above that ![]() $\mathcal {C}^{\mathrm {wh}}_X$ is an abelian subcategory of
$\mathcal {C}^{\mathrm {wh}}_X$ is an abelian subcategory of ![]() $\mathcal {C}_X$.
$\mathcal {C}_X$.
Lemma Let ![]() $\iota : Y\to X$ be a closed embedding of smooth rigid analytic
$\iota : Y\to X$ be a closed embedding of smooth rigid analytic ![]() $K$-varieties. Then Kashiwara's equivalence [Reference Ardakov and WadsleyAW18, Theorem A] restricts to an equivalence between
$K$-varieties. Then Kashiwara's equivalence [Reference Ardakov and WadsleyAW18, Theorem A] restricts to an equivalence between ![]() $\mathcal {C}^{\mathrm {wh}}_Y$ and the category of weakly holonomic
$\mathcal {C}^{\mathrm {wh}}_Y$ and the category of weakly holonomic ![]() $\widehat {\mathcal {D}}_X$-modules supported on
$\widehat {\mathcal {D}}_X$-modules supported on ![]() $Y$.
$Y$.
Proof. This is a direct consequence of Lemma 6.1.
7.2 Extensions
Let ![]() $X$ be a smooth rigid analytic
$X$ be a smooth rigid analytic ![]() $K$-variety and let
$K$-variety and let ![]() $\mathcal {D}_X$ denote the sheaf of algebraic (i.e. finite-order) differential operators on
$\mathcal {D}_X$ denote the sheaf of algebraic (i.e. finite-order) differential operators on ![]() $X$. In [Reference Mebkhout and Narvaez-MacarroMN91], Mebkhout and Narvaez-Macarro developed a dimension theory on the category
$X$. In [Reference Mebkhout and Narvaez-MacarroMN91], Mebkhout and Narvaez-Macarro developed a dimension theory on the category ![]() $\mathrm {coh}(\mathcal {D}_X)$ of coherent
$\mathrm {coh}(\mathcal {D}_X)$ of coherent ![]() $\mathcal {D}_X$-modules by setting
$\mathcal {D}_X$-modules by setting ![]() $d(\operatorname {Loc} M)=2\dim X-j_{\mathcal {D}(X)}(M)$ whenever
$d(\operatorname {Loc} M)=2\dim X-j_{\mathcal {D}(X)}(M)$ whenever ![]() $M$ is a finitely generated
$M$ is a finitely generated ![]() $\mathcal {D}(X)$-module on a smooth affinoid
$\mathcal {D}(X)$-module on a smooth affinoid ![]() $K$-variety
$K$-variety ![]() $X$ with free tangent sheaf. They also prove a version of Bernstein's inequality and define modules of minimal dimension as the analogue of holonomicity.
$X$ with free tangent sheaf. They also prove a version of Bernstein's inequality and define modules of minimal dimension as the analogue of holonomicity.
Recall from [Reference BodeBod19a, Lemma 4.14] that there is an exact extension functor
 \begin{gather*} E_X: \ \mathrm{coh}(\mathcal{D}_X)\to \mathcal{C}_X\\ \mathcal{M}\mapsto\widehat{\mathcal{D}}_X\otimes_{\mathcal{D}_X} \mathcal{M}. \end{gather*}
\begin{gather*} E_X: \ \mathrm{coh}(\mathcal{D}_X)\to \mathcal{C}_X\\ \mathcal{M}\mapsto\widehat{\mathcal{D}}_X\otimes_{\mathcal{D}_X} \mathcal{M}. \end{gather*}
It follows from Theorem 3.1 that ![]() $E_X$ is also faithful.
$E_X$ is also faithful.
Proposition Let ![]() $\mathcal {M}$ be a coherent
$\mathcal {M}$ be a coherent ![]() $\mathcal {D}$-module on a smooth, equidimensional rigid analytic
$\mathcal {D}$-module on a smooth, equidimensional rigid analytic ![]() $K$-space
$K$-space ![]() $X$. Then
$X$. Then
In particular, ![]() $E_X$ sends modules of minimal dimension to weakly holonomic
$E_X$ sends modules of minimal dimension to weakly holonomic ![]() $\widehat {\mathcal {D}}$-modules.
$\widehat {\mathcal {D}}$-modules.
Proof. Without loss of generality, ![]() $X=\operatorname {Sp} A$ is a smooth affinoid with free tangent sheaf. Write
$X=\operatorname {Sp} A$ is a smooth affinoid with free tangent sheaf. Write ![]() $D=\mathcal {D}(X)$ and
$D=\mathcal {D}(X)$ and ![]() $\widehat {D}=\widehat {\mathcal {D}}(X)$. If
$\widehat {D}=\widehat {\mathcal {D}}(X)$. If ![]() $M$ is a finitely generated
$M$ is a finitely generated ![]() $D$-module, then faithful flatness of
$D$-module, then faithful flatness of ![]() $\widehat {D}$ over
$\widehat {D}$ over ![]() $D$ (Theorem 3.1) implies that for any
$D$ (Theorem 3.1) implies that for any ![]() $j$,
$j$,
In particular, ![]() $j_D(M)=j_{\widehat {D}}(\widehat {D}\otimes _D M)$, and the result follows.
$j_D(M)=j_{\widehat {D}}(\widehat {D}\otimes _D M)$, and the result follows.
Corollary Let ![]() $\mathcal {M}$ be an integrable connection on a smooth rigid analytic
$\mathcal {M}$ be an integrable connection on a smooth rigid analytic ![]() $K$-space
$K$-space ![]() $X$. Then
$X$. Then ![]() $\mathcal {M}$ is a weakly holonomic
$\mathcal {M}$ is a weakly holonomic ![]() $\widehat {\mathcal {D}}_X$-module.
$\widehat {\mathcal {D}}_X$-module.
Proof. Any integrable connection is a coherent ![]() $\mathcal {D}_X$-module of minimal dimension, so we are done by applying [Reference Ardakov and WadsleyAW18, Proposition 6.2].
$\mathcal {D}_X$-module of minimal dimension, so we are done by applying [Reference Ardakov and WadsleyAW18, Proposition 6.2].
7.3 Duality
Lemma Let ![]() $X$ be a smooth rigid analytic
$X$ be a smooth rigid analytic ![]() $K$-space of dimension
$K$-space of dimension ![]() $d$. The functor
$d$. The functor
sends weakly holonomic ![]() $\widehat {\mathcal {D}}_X$-modules to weakly holonomic
$\widehat {\mathcal {D}}_X$-modules to weakly holonomic ![]() $\widehat {\mathcal {D}}_X$-modules.
$\widehat {\mathcal {D}}_X$-modules.
Proof. As ![]() $X$ is equidimensional, we can assume that
$X$ is equidimensional, we can assume that ![]() $X$ is affinoid, with
$X$ is affinoid, with ![]() $\mathcal {T}(X)$ admitting a smooth Lie lattice. Let
$\mathcal {T}(X)$ admitting a smooth Lie lattice. Let ![]() $\mathcal {M}=\operatorname {Loc} M$ be a non-zero weakly holonomic
$\mathcal {M}=\operatorname {Loc} M$ be a non-zero weakly holonomic ![]() $\widehat {\mathcal {D}}_X$-module, so that
$\widehat {\mathcal {D}}_X$-module, so that ![]() $j(M)=d$.
$j(M)=d$.
By Auslander's condition, ![]() $\operatorname {Ext}^{d}(M, \widehat {\mathcal {D}}(X))$ has grade
$\operatorname {Ext}^{d}(M, \widehat {\mathcal {D}}(X))$ has grade ![]() $\geq d$ as a right
$\geq d$ as a right ![]() $\widehat {\mathcal {D}}_X(X)$-module. Thus Proposition 5.3 implies that
$\widehat {\mathcal {D}}_X(X)$-module. Thus Proposition 5.3 implies that
is a coadmissible right ![]() $\widehat {\mathcal {D}}_X$-module of dimension
$\widehat {\mathcal {D}}_X$-module of dimension ![]() $d$, and the result follows from Lemma 5.2.
$d$, and the result follows from Lemma 5.2.
Similarly, Auslander's condition in conjunction with Bernstein's inequality forces ![]() $\operatorname {\mathscr {E}\!\mathit {xt}}^{i}(\mathcal {M}, \widehat {\mathcal {D}})=0$ for any
$\operatorname {\mathscr {E}\!\mathit {xt}}^{i}(\mathcal {M}, \widehat {\mathcal {D}})=0$ for any ![]() $\mathcal {M}\in \mathcal {C}^{\mathrm {wh}}_X$,
$\mathcal {M}\in \mathcal {C}^{\mathrm {wh}}_X$, ![]() $i\neq d$.
$i\neq d$.
We define the duality functor ![]() $\mathbb {D}$ on
$\mathbb {D}$ on ![]() $\mathcal {C}^{\mathrm {wh}}_X$ by
$\mathcal {C}^{\mathrm {wh}}_X$ by ![]() $\mathbb {D}=\operatorname {\mathscr {H}\!\mathit {om}}_{\mathcal {O}}(\Omega _X, \operatorname {\mathscr {E}\!\mathit {xt}}^{d}_{\widehat {\mathcal {D}}_X}(-, \widehat {\mathcal {D}}_X))$.
$\mathbb {D}=\operatorname {\mathscr {H}\!\mathit {om}}_{\mathcal {O}}(\Omega _X, \operatorname {\mathscr {E}\!\mathit {xt}}^{d}_{\widehat {\mathcal {D}}_X}(-, \widehat {\mathcal {D}}_X))$.
Proposition There is a natural isomorphism of functors ![]() $\mathbb {D}^{2}\cong \operatorname {id}$.
$\mathbb {D}^{2}\cong \operatorname {id}$.
Proof. Let ![]() $X$ be a smooth affinoid of dimension
$X$ be a smooth affinoid of dimension ![]() $d$ with
$d$ with ![]() $\mathcal {T}(X)$ admitting a smooth Lie lattice
$\mathcal {T}(X)$ admitting a smooth Lie lattice ![]() $\mathcal {L}$. Write
$\mathcal {L}$. Write ![]() $D=\widehat {\mathcal {D}}(X)$ and
$D=\widehat {\mathcal {D}}(X)$ and ![]() $D_n=\widehat {U(\pi ^{n}\mathcal {L})_K}$, so that
$D_n=\widehat {U(\pi ^{n}\mathcal {L})_K}$, so that ![]() $D=\varprojlim D_n$. By Theorem 4.3, we can assume that
$D=\varprojlim D_n$. By Theorem 4.3, we can assume that ![]() $D_n$ is Auslander–Gorenstein of dimension at most
$D_n$ is Auslander–Gorenstein of dimension at most ![]() $2d$ for each
$2d$ for each ![]() $n\geq 0$.
$n\geq 0$.
Let ![]() $M$ be a coadmissible
$M$ be a coadmissible ![]() $D$-module of grade
$D$-module of grade ![]() $d$. By Lemma 5.2 and [Reference Ardakov and WadsleyAW18, Theorem 3.4], we have
$d$. By Lemma 5.2 and [Reference Ardakov and WadsleyAW18, Theorem 3.4], we have
and now
 \begin{align*} \operatorname{Ext}^{d}(\operatorname{Ext}^{d}(M, D), D)&\cong\varprojlim \big(D_n\otimes_D \operatorname{Ext}^{d}_D(\operatorname{Ext}^{d}_D(M, D), D)\big)\\ & \cong \varprojlim \operatorname{Ext}^{d}_{D_n}(\operatorname{Ext}^{d}_D(M, D)\otimes_D D_n, D_n)\\ & \cong \varprojlim \operatorname{Ext}^{d}_{D_n}(\operatorname{Ext}^{d}_{D_n}(D_n\otimes_D M, D_n), D_n) \end{align*}
\begin{align*} \operatorname{Ext}^{d}(\operatorname{Ext}^{d}(M, D), D)&\cong\varprojlim \big(D_n\otimes_D \operatorname{Ext}^{d}_D(\operatorname{Ext}^{d}_D(M, D), D)\big)\\ & \cong \varprojlim \operatorname{Ext}^{d}_{D_n}(\operatorname{Ext}^{d}_D(M, D)\otimes_D D_n, D_n)\\ & \cong \varprojlim \operatorname{Ext}^{d}_{D_n}(\operatorname{Ext}^{d}_{D_n}(D_n\otimes_D M, D_n), D_n) \end{align*}by repeatedly applying Lemma 5.1.
Note that ![]() $\operatorname {Ext}^{i}_{D_n}(D_n\otimes _D M, D_n)=0$ for any
$\operatorname {Ext}^{i}_{D_n}(D_n\otimes _D M, D_n)=0$ for any ![]() $i\neq d$ by Lemma 5.1, so
$i\neq d$ by Lemma 5.1, so
by [Reference IwanagaIwa97, Theorem 4],Footnote 1 and hence
by coadmissibility of ![]() $M$.
$M$.
Thus ![]() $\mathbb {D}^{2}(\operatorname {Loc} M)\cong \operatorname {Loc} M$ as required.
$\mathbb {D}^{2}(\operatorname {Loc} M)\cong \operatorname {Loc} M$ as required.
8. Examples
8.1 Infinite length and infinite-dimensional fibres
We present an example of a weakly holonomic ![]() $\widehat {\mathcal {D}}$-module on the unit disc which is not of finite length and has infinite-dimensional fibres.
$\widehat {\mathcal {D}}$-module on the unit disc which is not of finite length and has infinite-dimensional fibres.
Let ![]() $\theta _n(t)=\prod _{m=0}^{n} (1-\pi ^{m}t)$, and consider the power series
$\theta _n(t)=\prod _{m=0}^{n} (1-\pi ^{m}t)$, and consider the power series
 \[ \theta(t)=\lim_{n\to \infty} \theta_n(t)=\prod_{m=0}^{\infty}(1-\pi^{m}t). \]
\[ \theta(t)=\lim_{n\to \infty} \theta_n(t)=\prod_{m=0}^{\infty}(1-\pi^{m}t). \]
Note that ![]() $\theta (t)\in \widehat {K[t]}=\varprojlim K\langle \pi ^{n}t \rangle$. We also note that for any
$\theta (t)\in \widehat {K[t]}=\varprojlim K\langle \pi ^{n}t \rangle$. We also note that for any ![]() $n\geq 0$,
$n\geq 0$, ![]() $(1-\pi ^{m}t)$ is a unit in
$(1-\pi ^{m}t)$ is a unit in ![]() $K\langle \pi ^{n}t\rangle$ for any
$K\langle \pi ^{n}t\rangle$ for any ![]() $m>n$. Thus
$m>n$. Thus ![]() $\theta (t)=u_n\theta _n(t)$, where
$\theta (t)=u_n\theta _n(t)$, where ![]() $u_n$ is a unit in
$u_n$ is a unit in ![]() $K\langle \pi ^{n}t\rangle$.
$K\langle \pi ^{n}t\rangle$.
Let ![]() $X=\operatorname {Sp} K\langle x\rangle$ be the unit disc over
$X=\operatorname {Sp} K\langle x\rangle$ be the unit disc over ![]() $K$, and write
$K$, and write ![]() $\partial \in \mathcal {T}(X)$ for the derivation
$\partial \in \mathcal {T}(X)$ for the derivation ![]() ${d}/{d} x$. Let
${d}/{d} x$. Let ![]() $D=\widehat {\mathcal {D}}(X)$ and set
$D=\widehat {\mathcal {D}}(X)$ and set
This is a coadmissible ![]() $\widehat {\mathcal {D}}(X)$-module, as it is finitely presented.
$\widehat {\mathcal {D}}(X)$-module, as it is finitely presented.
Let ![]() $\mathcal {A}=R\langle x\rangle$,
$\mathcal {A}=R\langle x\rangle$, ![]() $\mathcal {L}=\mathcal {A}\cdot \partial \subset \mathcal {T}(X)$, and let
$\mathcal {L}=\mathcal {A}\cdot \partial \subset \mathcal {T}(X)$, and let ![]() $D_n=\widehat {U_{\mathcal {A}}(\pi ^{n}\mathcal {L})}_K$. By the considerations above,
$D_n=\widehat {U_{\mathcal {A}}(\pi ^{n}\mathcal {L})}_K$. By the considerations above,
which is finitely generated over ![]() $K\langle x\rangle$. In particular,
$K\langle x\rangle$. In particular, ![]() $d(M)=1$.
$d(M)=1$.
But now note that for every ![]() $n\geq 0$,
$n\geq 0$, ![]() $M$ surjects onto
$M$ surjects onto ![]() $D/D\theta _n(\partial )$, which is a direct sum of
$D/D\theta _n(\partial )$, which is a direct sum of ![]() $n+1$ integrable connections of rank
$n+1$ integrable connections of rank ![]() $1$. In particular,
$1$. In particular, ![]() $M$ cannot be of finite length as a
$M$ cannot be of finite length as a ![]() $D$-module.
$D$-module.
By the same argument, the fibre at zero ![]() $M/xM$ cannot be a finite-dimensional
$M/xM$ cannot be a finite-dimensional ![]() $K$-vector space. In particular, weakly holonomic
$K$-vector space. In particular, weakly holonomic ![]() $\widehat {\mathcal {D}}$-modules need not have finite-dimensional fibres, and weak holonomicity is generally not stable under pullback.
$\widehat {\mathcal {D}}$-modules need not have finite-dimensional fibres, and weak holonomicity is generally not stable under pullback.
8.2 Pushforward along an open embedding
We now recall from [Reference Bitoun and BodeBB21] that weak holonomicity is generally not stable under pushforward either.
For this, recall from [Reference KedlayaKed10, Definition 13.1.1] that the type of ![]() $\lambda \in K$ is the radius of convergence of the formal power series
$\lambda \in K$ is the radius of convergence of the formal power series
 \[ \sum_{i\geq 0, i\neq \lambda} \frac{x^{i}}{\lambda-i}. \]
\[ \sum_{i\geq 0, i\neq \lambda} \frac{x^{i}}{\lambda-i}. \]
Let ![]() $X=\operatorname {Sp} A$ be an affinoid
$X=\operatorname {Sp} A$ be an affinoid ![]() $K$-space with free tangent sheaf, let
$K$-space with free tangent sheaf, let ![]() $f\in A$ be non-constant and consider
$f\in A$ be non-constant and consider ![]() $j: U= \{f\neq 0\}\to X$. We call a left
$j: U= \{f\neq 0\}\to X$. We call a left ![]() $\mathcal {D}(X)[f^{-1}]$-module
$\mathcal {D}(X)[f^{-1}]$-module ![]() $N$ a meromorphic connection on
$N$ a meromorphic connection on ![]() $X$ with singularities along
$X$ with singularities along ![]() $Z=X\setminus U$ if
$Z=X\setminus U$ if ![]() $N$ is free of finite rank over
$N$ is free of finite rank over ![]() $A[f^{-1}]$.
$A[f^{-1}]$.
Given ![]() $m\in N$, consider the ideal
$m\in N$, consider the ideal ![]() $I(m)\subseteq K[s]$ consisting of all polynomials
$I(m)\subseteq K[s]$ consisting of all polynomials ![]() $b(s)$ such that there exists some
$b(s)$ such that there exists some ![]() $P(s)\in \mathcal {D}(X)[s]$ satisfying
$P(s)\in \mathcal {D}(X)[s]$ satisfying
By [Reference Mebkhout and Narvaez-MacarroMN91, Théorème 3.1.1], ![]() $I(m)$ is non-zero, and we call its monic generator the
$I(m)$ is non-zero, and we call its monic generator the ![]() $b$-function of
$b$-function of ![]() $m$.
$m$.
Theorem [Reference Bitoun and BodeBB21, Theorems 1.2, 1.3]
(i) Let
 $N$ be a meromorphic connection on
$N$ be a meromorphic connection on  $X$ with singularities along
$X$ with singularities along  $Z$. Suppose that
$Z$. Suppose that  $N$ is generated as an
$N$ is generated as an  $A[f^{-1}]$-module by
$A[f^{-1}]$-module by  $m_1, \dots , m_r$ such that all the roots of the associated
$m_1, \dots , m_r$ such that all the roots of the associated  $b$-functions
$b$-functions  $b_1, \dots , b_r$ in an algebraic closure of
$b_1, \dots , b_r$ in an algebraic closure of  $K$ are of positive type. Then
$K$ are of positive type. Then  $N$ localizes to an integrable connection
$N$ localizes to an integrable connection  $\mathcal {M}$ on
$\mathcal {M}$ on  $U$ such that
$U$ such that  $j_*\mathcal {M}\in \mathcal {C}_X$.
$j_*\mathcal {M}\in \mathcal {C}_X$.(ii) Let
 $X=\operatorname {Sp} K\langle x\rangle$ and
$X=\operatorname {Sp} K\langle x\rangle$ and  $j: U\to X$ for
$j: U\to X$ for  $U=X\setminus \{0\}$. Set
$U=X\setminus \{0\}$. Set  $\mathcal {M}_{\lambda }=\mathcal {O}_Ux^{\lambda }$ for
$\mathcal {M}_{\lambda }=\mathcal {O}_Ux^{\lambda }$ for  $\lambda \in K$. Then
$\lambda \in K$. Then  $j_*\mathcal {M}_{\lambda }\in \mathcal {C}_X$ if and only if
$j_*\mathcal {M}_{\lambda }\in \mathcal {C}_X$ if and only if  $\lambda$ is of positive type. In particular, there exist integrable connections
$\lambda$ is of positive type. In particular, there exist integrable connections  $\mathcal {M}$ on
$\mathcal {M}$ on  $U$ such that
$U$ such that  $j_*\mathcal {M}$ is not coadmissible.
$j_*\mathcal {M}$ is not coadmissible.
9. Zariski open embeddings: The case of an algebraic snc divisor
Let ![]() $j: U\to X$ be an embedding of a Zariski open subspace
$j: U\to X$ be an embedding of a Zariski open subspace ![]() $U$ in a smooth rigid analytic
$U$ in a smooth rigid analytic ![]() $K$-space
$K$-space ![]() $X$. We show that, at least in the case of the structure sheaf, pathologies as in Theorem 8.2(ii) do not occur.
$X$. We show that, at least in the case of the structure sheaf, pathologies as in Theorem 8.2(ii) do not occur.
As the question is local, we can (and will) assume from now on that ![]() $X$ is a smooth affinoid with free tangent sheaf. We will first consider the case where
$X$ is a smooth affinoid with free tangent sheaf. We will first consider the case where ![]() $Z=X\setminus U$ is the analytification of a strict normal crossing divisor. In § 10 we will reduce the general case to this set-up by passing to a suitable resolution of singularities.
$Z=X\setminus U$ is the analytification of a strict normal crossing divisor. In § 10 we will reduce the general case to this set-up by passing to a suitable resolution of singularities.
9.1 Relative analytification
We recall some results from [Reference SchoutensSch99] regarding relative analytification. This was already considered by Köpf in [Reference KopfKop74], but we have decided to refer to a source that is more readily available.
Let ![]() $A$ be an affinoid
$A$ be an affinoid ![]() $K$-algebra. An
$K$-algebra. An ![]() $A$-scheme will mean for us throughout a scheme of finite type over
$A$-scheme will mean for us throughout a scheme of finite type over ![]() $\operatorname {Spec} A$.
$\operatorname {Spec} A$.
The paper [Reference SchoutensSch99] yields a relative analytification functor ![]() $\mathbf {X}\mapsto \mathbf {X}^{\mathrm {an}/A}$ from
$\mathbf {X}\mapsto \mathbf {X}^{\mathrm {an}/A}$ from ![]() $A$-schemes to rigid analytic
$A$-schemes to rigid analytic ![]() $K$-varieties. The construction of
$K$-varieties. The construction of ![]() $\mathbf {X}^{\mathrm {an}/A}$ is a straightforward generalization of the analytification procedure for
$\mathbf {X}^{\mathrm {an}/A}$ is a straightforward generalization of the analytification procedure for ![]() $A=K$.
$A=K$.
There is a natural morphism
of locally ![]() $G$-ringed spaces, satisfying the usual universal property: any morphism
$G$-ringed spaces, satisfying the usual universal property: any morphism ![]() $Y\to \mathbf {X}$ of locally
$Y\to \mathbf {X}$ of locally ![]() $G$-ringed spaces, where
$G$-ringed spaces, where ![]() $Y$ is a rigid analytic
$Y$ is a rigid analytic ![]() $K$-variety, factors uniquely through
$K$-variety, factors uniquely through ![]() $\eta _{\mathbf {X}}$ [Reference SchoutensSch99, Definition 1.1.1].
$\eta _{\mathbf {X}}$ [Reference SchoutensSch99, Definition 1.1.1].
Proposition Let ![]() $A$ and
$A$ and ![]() $B$ be affinoid
$B$ be affinoid ![]() $K$-algebras.
$K$-algebras.
(i) If
 $\mathbf {X}$ is both an
$\mathbf {X}$ is both an  $A$-scheme and a
$A$-scheme and a  $B$-scheme, then the analytification of
$B$-scheme, then the analytification of  $\mathbf {X}$ relative to
$\mathbf {X}$ relative to  $A$ is isomorphic to the analytification of
$A$ is isomorphic to the analytification of  $\mathbf {X}$ relative to
$\mathbf {X}$ relative to  $B$. In particular, we can speak of ‘the’ analytification of
$B$. In particular, we can speak of ‘the’ analytification of  $\mathbf {X}$ and write
$\mathbf {X}$ and write  $\mathbf {X}^{\mathrm{an}}$ instead of
$\mathbf {X}^{\mathrm{an}}$ instead of  $\mathbf {X}^{\mathrm {an}/A}$.
$\mathbf {X}^{\mathrm {an}/A}$.(ii) The analytification of
 $\operatorname {Spec} A$ is
$\operatorname {Spec} A$ is  $\operatorname {Sp} A$.
$\operatorname {Sp} A$.(iii) If
 $\mathbf {Z}$ is a closed subscheme of an
$\mathbf {Z}$ is a closed subscheme of an  $A$-scheme
$A$-scheme  $\mathbf {X}$ given by the vanishing ideal
$\mathbf {X}$ given by the vanishing ideal  $\mathcal {I}$, then
$\mathcal {I}$, then  $Z:=\eta ^{-1}(\mathbf {Z})$ is the closed analytic subset of
$Z:=\eta ^{-1}(\mathbf {Z})$ is the closed analytic subset of  $\mathbf {X}^{\mathrm {an}}$ defined by
$\mathbf {X}^{\mathrm {an}}$ defined by  $\eta ^{*}\mathcal {I}$. Moreover,
$\eta ^{*}\mathcal {I}$. Moreover,  $Z\cong \mathbf {Z}^{\mathrm {an}}$.
$Z\cong \mathbf {Z}^{\mathrm {an}}$.(iv) If
 $\mathbf {Y}$ is an open subscheme of an
$\mathbf {Y}$ is an open subscheme of an  $A$-scheme
$A$-scheme  $\mathbf {X}$, then
$\mathbf {X}$, then  $\mathbf {Y}^{\mathrm {an}}$ can be identified with
$\mathbf {Y}^{\mathrm {an}}$ can be identified with  $\eta ^{-1}(\mathbf {Y})$, a Zariski open subspace of
$\eta ^{-1}(\mathbf {Y})$, a Zariski open subspace of  $\mathbf {X}^{\mathrm {an}}$.
$\mathbf {X}^{\mathrm {an}}$.(v) If
 $\mathbf {X}_i$,
$\mathbf {X}_i$,  $\mathbf {X}$ are
$\mathbf {X}$ are  $A$-schemes such that the
$A$-schemes such that the  $\mathbf {X}_i$ form a covering of
$\mathbf {X}_i$ form a covering of  $\mathbf {X}$, then the
$\mathbf {X}$, then the  $\mathbf {X}_i^{\mathrm {an}}$ form an admissible covering of
$\mathbf {X}_i^{\mathrm {an}}$ form an admissible covering of  $\mathbf {X}^{\mathrm {an}}$.
$\mathbf {X}^{\mathrm {an}}$.(vi) If
 $\mathbf {X}\to \mathbf {S}, \mathbf {Y}\to \mathbf {S}$ are morphisms of
$\mathbf {X}\to \mathbf {S}, \mathbf {Y}\to \mathbf {S}$ are morphisms of  $A$-schemes, then
$A$-schemes, then  $(\mathbf {X}\times _{\mathbf {S}}\mathbf {Y})^{\mathrm {an}}\cong \mathbf {X}^{\mathrm {an}}\times _{\mathbf {S}^{\mathrm {an}}}\mathbf {Y}^{\mathrm {an}}$.
$(\mathbf {X}\times _{\mathbf {S}}\mathbf {Y})^{\mathrm {an}}\cong \mathbf {X}^{\mathrm {an}}\times _{\mathbf {S}^{\mathrm {an}}}\mathbf {Y}^{\mathrm {an}}$.
Proof. (i) is clear from the universal property, (ii) is [Reference SchoutensSch99, Example 1.3.2(1)]. (iii) is [Reference SchoutensSch99, Corollary 2.1.3]. Concerning (iv), it follows easily from the universal property that ![]() $\mathbf {Y}^{\mathrm {an}}\cong \eta ^{-1}(\mathbf {Y})$, which is an admissible open subspace of
$\mathbf {Y}^{\mathrm {an}}\cong \eta ^{-1}(\mathbf {Y})$, which is an admissible open subspace of ![]() $\mathbf {X}^{\mathrm {an}}$ by continuity of
$\mathbf {X}^{\mathrm {an}}$ by continuity of ![]() $\eta$. By (iii), it is then even Zariski open. (v) is a consequence of (iv) and the fact that
$\eta$. By (iii), it is then even Zariski open. (v) is a consequence of (iv) and the fact that ![]() $\eta$ is a morphism of locally
$\eta$ is a morphism of locally ![]() $G$-ringed spaces. (vi) follows again from the universal property.
$G$-ringed spaces. (vi) follows again from the universal property.
9.2 Algebraic snc divisors
Definition A closed subscheme ![]() $\mathbf {Z}$ of a locally Noetherian regular scheme
$\mathbf {Z}$ of a locally Noetherian regular scheme ![]() $\mathbf {X}$ is called a strict normal crossing (snc) divisor if:
$\mathbf {X}$ is called a strict normal crossing (snc) divisor if:
(i)
 $\mathbf {Z}$ is defined as the vanishing of an invertible ideal sheaf
$\mathbf {Z}$ is defined as the vanishing of an invertible ideal sheaf  $\mathcal {I}$;
$\mathcal {I}$;(ii) for each
 $x\in \mathbf {Z}$, there exists a regular set of local parameters
$x\in \mathbf {Z}$, there exists a regular set of local parameters  $x_1, \dots , x_d\in \mathcal {O}_{\mathbf {X}, x}$ such that the ideal
$x_1, \dots , x_d\in \mathcal {O}_{\mathbf {X}, x}$ such that the ideal  $\mathcal {I}_x\subseteq \mathcal {O}_{\mathbf {X}, x}$ is generated by
$\mathcal {I}_x\subseteq \mathcal {O}_{\mathbf {X}, x}$ is generated by  $\prod _{i=1}^{r} x_i$ for some
$\prod _{i=1}^{r} x_i$ for some  $1\leq r\leq d$.
$1\leq r\leq d$.
A closed analytic subset ![]() $Z$ of a rigid analytic
$Z$ of a rigid analytic ![]() $K$-variety
$K$-variety ![]() $X$ is called an algebraic snc divisor if there exist an affinoid
$X$ is called an algebraic snc divisor if there exist an affinoid ![]() $K$-algebra
$K$-algebra ![]() $B$, a regular scheme
$B$, a regular scheme ![]() $\mathbf {X}$ that is also a
$\mathbf {X}$ that is also a ![]() $B$-scheme with
$B$-scheme with ![]() $\mathbf {X}^{\mathrm {an}}\cong X$, and an snc divisor
$\mathbf {X}^{\mathrm {an}}\cong X$, and an snc divisor ![]() $\mathbf {Z}$ of
$\mathbf {Z}$ of ![]() $\mathbf {X}$ such that
$\mathbf {X}$ such that ![]() $\mathbf {Z}^{\mathrm {an}}=Z$ as in Proposition 9.1(iii).
$\mathbf {Z}^{\mathrm {an}}=Z$ as in Proposition 9.1(iii).
We now wish to lift the snc condition from the stalk level to a condition on the level of admissible coverings.
Note that if ![]() $X=\operatorname {Sp} A$ is a smooth affinoid, then
$X=\operatorname {Sp} A$ is a smooth affinoid, then ![]() $\mathbf {X}=\operatorname {Spec} A$ is a Noetherian regular scheme by [Reference Bosch, Güntzer and RemmertBGR84, Proposition 7.3.2/8].
$\mathbf {X}=\operatorname {Spec} A$ is a Noetherian regular scheme by [Reference Bosch, Güntzer and RemmertBGR84, Proposition 7.3.2/8].
Lemma Let ![]() $X=\operatorname {Sp} A$ be a smooth affinoid
$X=\operatorname {Sp} A$ be a smooth affinoid ![]() $K$-space, and let
$K$-space, and let ![]() $\mathbf {Z}\subseteq \operatorname {Spec} A=\mathbf {X}$ be an snc divisor. Then there exists an admissible covering of
$\mathbf {Z}\subseteq \operatorname {Spec} A=\mathbf {X}$ be an snc divisor. Then there exists an admissible covering of ![]() $X$ by affinoid subdomains
$X$ by affinoid subdomains ![]() $X_i=\operatorname {Sp} A_i$ with the following property: for each
$X_i=\operatorname {Sp} A_i$ with the following property: for each ![]() $i$ with
$i$ with ![]() $\mathbf {Z}^{\mathrm {an}}\cap X_i\neq \emptyset$, there exist
$\mathbf {Z}^{\mathrm {an}}\cap X_i\neq \emptyset$, there exist ![]() $x_{i1}, \dots , x_{id}\in A_i$ such that
$x_{i1}, \dots , x_{id}\in A_i$ such that
(i) the elements
 ${d} x_{i1}, \ldots , {d} x_{id}$ form a free generating set of
${d} x_{i1}, \ldots , {d} x_{id}$ form a free generating set of  $\Omega ^{1}(X_i)$, and
$\Omega ^{1}(X_i)$, and(ii) the subvariety
 $\mathbf {Z}^{\mathrm {an}}\cap X_i$ is given as the vanishing set of
$\mathbf {Z}^{\mathrm {an}}\cap X_i$ is given as the vanishing set of  $\prod _{j=1}^{r} x_{ij}$ for some
$\prod _{j=1}^{r} x_{ij}$ for some  $1\leq r\leq d$.
$1\leq r\leq d$.
Proof. Without loss of generality, we can assume that ![]() $X$ (and hence
$X$ (and hence ![]() $\mathbf {X}$) is connected.
$\mathbf {X}$) is connected.
Let ![]() $x\in \mathbf {Z}$ be a closed point in
$x\in \mathbf {Z}$ be a closed point in ![]() $\operatorname {Spec} A$, and let
$\operatorname {Spec} A$, and let ![]() $x_1, \dots , x_d\in \mathcal {O}_{\mathbf {X}, x}$ be a regular set of local parameters as in Definition 9.2. By definition, there exists some Zariski open affine subscheme
$x_1, \dots , x_d\in \mathcal {O}_{\mathbf {X}, x}$ be a regular set of local parameters as in Definition 9.2. By definition, there exists some Zariski open affine subscheme ![]() $U_x=\operatorname {Spec} B(x)\subset \mathbf {X}$ containing
$U_x=\operatorname {Spec} B(x)\subset \mathbf {X}$ containing ![]() $x$ such that
$x$ such that ![]() $x_1, \dots , x_d$ are defined on
$x_1, \dots , x_d$ are defined on ![]() $U_x$, and
$U_x$, and ![]() $\mathbf {Z}\cap U_x=\{\prod _{j=1}^{r} x_j=0\}$.
$\mathbf {Z}\cap U_x=\{\prod _{j=1}^{r} x_j=0\}$.
By smoothness, ![]() $\Omega ^{1}(X)$ is a finitely generated projective
$\Omega ^{1}(X)$ is a finitely generated projective ![]() $A$-module, so there exists
$A$-module, so there exists ![]() ${f_1, \dots , f_n\in A}$ such that
${f_1, \dots , f_n\in A}$ such that
is a free ![]() $A_{f_k}$-module for each
$A_{f_k}$-module for each ![]() $k$, with free generating set
$k$, with free generating set ![]() $s_{k1}, \dots , s_{kd}$.
$s_{k1}, \dots , s_{kd}$.
Fix ![]() $k$ such that
$k$ such that ![]() $x\in \operatorname {Spec} A_{f_k}$. Then
$x\in \operatorname {Spec} A_{f_k}$. Then ![]() $B(x)_{f_k}\otimes _A \Omega ^{1}(X)$ is freely generated by
$B(x)_{f_k}\otimes _A \Omega ^{1}(X)$ is freely generated by ![]() $s_{k1}, \dots , s_{kd}$, so there exist
$s_{k1}, \dots , s_{kd}$, so there exist ![]() $M=(m_{ij})\in \mathrm {Mat}_{d\times d}(B(x)_{f_k})$ such that
$M=(m_{ij})\in \mathrm {Mat}_{d\times d}(B(x)_{f_k})$ such that
As ![]() $x\in \mathbf {X}$ is closed, it corresponds to a unique point in
$x\in \mathbf {X}$ is closed, it corresponds to a unique point in ![]() $X=\operatorname {Sp} A$, which we also denote by
$X=\operatorname {Sp} A$, which we also denote by ![]() $x$. As the
$x$. As the ![]() $x_i$ form a regular system of local parameters in
$x_i$ form a regular system of local parameters in ![]() $\mathcal {O}_{\mathbf {X}, x}$, they also define a regular system of local parameters in the local ring
$\mathcal {O}_{\mathbf {X}, x}$, they also define a regular system of local parameters in the local ring ![]() $\mathcal {O}_{X, x}$ by [Reference BoschBos14, Propositions 4.1/1, 4.1/2], so that
$\mathcal {O}_{X, x}$ by [Reference BoschBos14, Propositions 4.1/1, 4.1/2], so that ![]() $\{{d} x_i\}$ form a free generating set in
$\{{d} x_i\}$ form a free generating set in ![]() $\Omega ^{1}_{X, x}=\mathcal {O}_{X, x}\otimes _A \Omega ^{1}(X)$. Thus
$\Omega ^{1}_{X, x}=\mathcal {O}_{X, x}\otimes _A \Omega ^{1}(X)$. Thus ![]() $M$ becomes invertible as a matrix over
$M$ becomes invertible as a matrix over ![]() $\mathcal {O}_{X, x}$ and hence over
$\mathcal {O}_{X, x}$ and hence over ![]() $\mathcal {O}_{\mathbf {X}, x}$, as
$\mathcal {O}_{\mathbf {X}, x}$, as ![]() $\mathcal {O}_{\mathbf {X}, x}\to \mathcal {O}_{X, x}$ is injective by [Reference BoschBos14, Proposition 4.1/2]. Therefore
$\mathcal {O}_{\mathbf {X}, x}\to \mathcal {O}_{X, x}$ is injective by [Reference BoschBos14, Proposition 4.1/2]. Therefore ![]() $x$ is contained in a Zariski open affine subscheme
$x$ is contained in a Zariski open affine subscheme ![]() $\operatorname {Spec} C(x)$ of
$\operatorname {Spec} C(x)$ of ![]() $\mathbf {X}$ with the property that:
$\mathbf {X}$ with the property that:
(i)
 $x_1, \dots , x_d\in C(x)$, and
$x_1, \dots , x_d\in C(x)$, and  ${d} x_i$ form a free generating set of
${d} x_i$ form a free generating set of  $C(x)\otimes _A \Omega ^{1}(X)$;
$C(x)\otimes _A \Omega ^{1}(X)$;(ii)
 $\mathbf {Z}\cap \operatorname {Spec} C(x)=\{\prod _{j=1}^{r} x_j=0\}$ for some
$\mathbf {Z}\cap \operatorname {Spec} C(x)=\{\prod _{j=1}^{r} x_j=0\}$ for some  $1\leq r\leq d$.
$1\leq r\leq d$.
As the ![]() $\operatorname {Spec} C(x)$ for varying
$\operatorname {Spec} C(x)$ for varying ![]() $x\in \mathbf {Z}$ together with
$x\in \mathbf {Z}$ together with ![]() $\mathbf {X}\setminus \mathbf {Z}$ forms a Zariski covering of
$\mathbf {X}\setminus \mathbf {Z}$ forms a Zariski covering of ![]() $\mathbf {X}$, it follows from Proposition 9.1(v) that their analytifications form an admissible covering of
$\mathbf {X}$, it follows from Proposition 9.1(v) that their analytifications form an admissible covering of ![]() $X$, and any refinement of this covering by affinoid subdomains has the desired property.
$X$, and any refinement of this covering by affinoid subdomains has the desired property.
Proposition Let ![]() $Z$ be an algebraic snc divisor of a smooth rigid analytic
$Z$ be an algebraic snc divisor of a smooth rigid analytic ![]() $K$-variety
$K$-variety ![]() $X$. Then there exists an admissible covering of
$X$. Then there exists an admissible covering of ![]() $X$ by affinoids
$X$ by affinoids ![]() $X_i=\operatorname {Sp} A_i$ with the following property: for each
$X_i=\operatorname {Sp} A_i$ with the following property: for each ![]() $i$ with
$i$ with ![]() $Z\cap X_i\neq \emptyset$, there exist
$Z\cap X_i\neq \emptyset$, there exist ![]() $x_{i1}, \dots , x_{id}\in A_i$ such that
$x_{i1}, \dots , x_{id}\in A_i$ such that
(i) the elements
 ${d} x_{i1}, \ldots , {d} x_{id}$ form a free generating set of
${d} x_{i1}, \ldots , {d} x_{id}$ form a free generating set of  $\Omega ^{1}(X_i)$, and
$\Omega ^{1}(X_i)$, and(ii) the subvariety
 $Z\cap X_i$ is given as the vanishing set of
$Z\cap X_i$ is given as the vanishing set of  $\prod _{j=1}^{r} x_{ij}$ for some
$\prod _{j=1}^{r} x_{ij}$ for some  $1\leq r\leq d$.
$1\leq r\leq d$.
Proof. By the above lemma, it is sufficient to show that ![]() $X$ admits an admissible covering by affinoid subspaces
$X$ admits an admissible covering by affinoid subspaces ![]() $Y_i=\operatorname {Sp} B_i$ such that
$Y_i=\operatorname {Sp} B_i$ such that ![]() $Z\cap Y_i$ is obtained as the analytification of an snc divisor on
$Z\cap Y_i$ is obtained as the analytification of an snc divisor on ![]() $\operatorname {Spec} B_i$.
$\operatorname {Spec} B_i$.
Let ![]() $B$ be an affinoid
$B$ be an affinoid ![]() $K$-algebra,
$K$-algebra, ![]() $\mathbf {X}$ a
$\mathbf {X}$ a ![]() $B$-scheme with snc divisor
$B$-scheme with snc divisor ![]() $\mathbf {Z}$ such that
$\mathbf {Z}$ such that ![]() $\mathbf {X}^{\mathrm {an}}\cong X$,
$\mathbf {X}^{\mathrm {an}}\cong X$, ![]() $\mathbf {Z}^{\mathrm {an}}\cong Z$. Let
$\mathbf {Z}^{\mathrm {an}}\cong Z$. Let ![]() $(\mathbf {U}_i)$ be an affine covering of
$(\mathbf {U}_i)$ be an affine covering of ![]() $\mathbf {X}$ such that
$\mathbf {X}$ such that ![]() $\mathbf {Z}\cap \mathbf {U}_i$ is given by the vanishing of a single element
$\mathbf {Z}\cap \mathbf {U}_i$ is given by the vanishing of a single element ![]() $f_i\in B_i$, where
$f_i\in B_i$, where ![]() $\mathbf {U}_i=\operatorname {Spec} B_i$.
$\mathbf {U}_i=\operatorname {Spec} B_i$.
By Proposition 9.1(v), ![]() $(\mathbf {U}_i^{\mathrm {an}})_i$ is an admissible covering of
$(\mathbf {U}_i^{\mathrm {an}})_i$ is an admissible covering of ![]() $X$. Recall from [Reference SchoutensSch99, Construction 1.2.1] that the analytification
$X$. Recall from [Reference SchoutensSch99, Construction 1.2.1] that the analytification ![]() $\mathbf {U}_i^{\mathrm {an}}$ is constructed as the union of
$\mathbf {U}_i^{\mathrm {an}}$ is constructed as the union of ![]() $\operatorname {Sp} B_{i, n}$ for various Banach completions
$\operatorname {Sp} B_{i, n}$ for various Banach completions ![]() $B_{i, n}$ of
$B_{i, n}$ of ![]() $B_i$. Thus by definition,
$B_i$. Thus by definition, ![]() $(\operatorname {Sp} B_{i, n})_{i, n}$ is also an admissible covering of
$(\operatorname {Sp} B_{i, n})_{i, n}$ is also an admissible covering of ![]() $X$.
$X$.
There are natural morphisms of schemes
Now ![]() $\operatorname {Spec} B_{i, n}$ is a regular Noetherian scheme by [Reference Bosch, Güntzer and RemmertBGR84, Proposition 7.3.2/8]. Let
$\operatorname {Spec} B_{i, n}$ is a regular Noetherian scheme by [Reference Bosch, Güntzer and RemmertBGR84, Proposition 7.3.2/8]. Let ![]() $\mathbf {Z}_{i, n}$ denote the vanishing set of
$\mathbf {Z}_{i, n}$ denote the vanishing set of ![]() $\phi _{i, n}^{\sharp }(f_i)\in B_{i, n}$. Then
$\phi _{i, n}^{\sharp }(f_i)\in B_{i, n}$. Then ![]() $\mathbf {Z}_{i, n}$ is an snc divisor, as for any
$\mathbf {Z}_{i, n}$ is an snc divisor, as for any ![]() $x\in \mathbf {Z}_{i, n}$, a regular set of local parameters in
$x\in \mathbf {Z}_{i, n}$, a regular set of local parameters in ![]() $\mathcal {O}_{\mathbf {U}_i,\phi _{i, n}(x)}$ gives a regular set of local parameters of
$\mathcal {O}_{\mathbf {U}_i,\phi _{i, n}(x)}$ gives a regular set of local parameters of ![]() $\mathcal {O}_{\operatorname {Spec} B_{i, n}, x}$ by [Reference SchoutensSch99, Claim 1.2.6].
$\mathcal {O}_{\operatorname {Spec} B_{i, n}, x}$ by [Reference SchoutensSch99, Claim 1.2.6].
Since ![]() $\mathbf {Z}_{i, n}^{\mathrm {an}}=\{f_i=0\}\subset \operatorname {Sp} B_{i, n}$ by Proposition 9.1(iii), it follows that
$\mathbf {Z}_{i, n}^{\mathrm {an}}=\{f_i=0\}\subset \operatorname {Sp} B_{i, n}$ by Proposition 9.1(iii), it follows that ![]() $\mathbf {Z}_{i, n}^{\mathrm {an}}=\mathbf {Z}^{\mathrm {an}}\cap \operatorname {Sp} B_{i, n}=Z\cap \operatorname {Sp} B_{i, n}$, as required.
$\mathbf {Z}_{i, n}^{\mathrm {an}}=\mathbf {Z}^{\mathrm {an}}\cap \operatorname {Sp} B_{i, n}=Z\cap \operatorname {Sp} B_{i, n}$, as required.
9.3 Extending across algebraic snc divisors
Proposition Let ![]() $X$ be a smooth rigid analytic
$X$ be a smooth rigid analytic ![]() $K$-variety. Let
$K$-variety. Let ![]() $Z$ be an algebraic snc divisor on
$Z$ be an algebraic snc divisor on ![]() $X$, and let
$X$, and let ![]() $j: U\to X$ be its complement. Then
$j: U\to X$ be its complement. Then ![]() $j_*(\mathcal {M}|_U)$ is a coadmissible
$j_*(\mathcal {M}|_U)$ is a coadmissible ![]() $\widehat{\mathcal {D}}_X$-module for any integrable connection
$\widehat{\mathcal {D}}_X$-module for any integrable connection ![]() $\mathcal {M}$ on
$\mathcal {M}$ on ![]() $X$.
$X$.
Proof. By Proposition 9.2, we can assume that ![]() $X\cong \operatorname {Sp} A$ is a smooth affinoid with free tangent sheaf, and also that there exist elements
$X\cong \operatorname {Sp} A$ is a smooth affinoid with free tangent sheaf, and also that there exist elements ![]() $x_1, \dots , x_d\in A$ such that
$x_1, \dots , x_d\in A$ such that ![]() $\{{d} x_i\}$ form a free generating set in
$\{{d} x_i\}$ form a free generating set in ![]() $\Omega ^{1}_X$ and
$\Omega ^{1}_X$ and ![]() $Z=\{\prod _{i=1}^{r} x_i=0\}$ for some
$Z=\{\prod _{i=1}^{r} x_i=0\}$ for some ![]() $1\leq r\leq d$.
$1\leq r\leq d$.
We denote by ![]() $\{\partial _i\}$ the derivations forming the basis in
$\{\partial _i\}$ the derivations forming the basis in ![]() $\mathcal {T}(X)$ dual to
$\mathcal {T}(X)$ dual to ![]() $\{{d} x_i\}$, so that
$\{{d} x_i\}$, so that
for all ![]() $i, j$. We write
$i, j$. We write ![]() $f=\prod _{i=1}^{r} x_i$.
$f=\prod _{i=1}^{r} x_i$.
Let ![]() $M=\mathcal {M}(X)$, which we can assume to be a free
$M=\mathcal {M}(X)$, which we can assume to be a free ![]() $A$-module of finite rank, and let
$A$-module of finite rank, and let ![]() $m\in M$. We will now show that all roots of the
$m\in M$. We will now show that all roots of the ![]() $b$-function of
$b$-function of ![]() $m$, viewed as an element in
$m$, viewed as an element in ![]() $M[f^{-1}]$, are integers, so that we can apply Theorem 8.2(i).
$M[f^{-1}]$, are integers, so that we can apply Theorem 8.2(i).
We write ![]() $\partial _i^{[k]}= {\partial _i^{k}}/{k!}$ for any non-negative integer
$\partial _i^{[k]}= {\partial _i^{k}}/{k!}$ for any non-negative integer ![]() $k$. By Noetherianity, there exists some natural number
$k$. By Noetherianity, there exists some natural number ![]() $n$ such that
$n$ such that ![]() $\partial _i^{[n]}\cdot m$ is contained in the
$\partial _i^{[n]}\cdot m$ is contained in the ![]() $A$-submodule generated by
$A$-submodule generated by ![]() $m, \partial _i \cdot m, \dots , \partial _i^{[n-1]}\cdot m$, so that there exists a monic polynomial
$m, \partial _i \cdot m, \dots , \partial _i^{[n-1]}\cdot m$, so that there exists a monic polynomial ![]() $\sum a_{i, j}x^{j}\in A[x]$ of degree
$\sum a_{i, j}x^{j}\in A[x]$ of degree ![]() $n$ satisfying
$n$ satisfying
 \[ \sum_{j=0}^{n} a_{i, j}\partial_i^{[j]}\cdot m=0. \]
\[ \sum_{j=0}^{n} a_{i, j}\partial_i^{[j]}\cdot m=0. \]
Now in ![]() $\mathcal {D}(X)[f^{-1}]$, one obtains as usual (see, for example, [Reference BerthelotBer96, Equation (2.0.2)])
$\mathcal {D}(X)[f^{-1}]$, one obtains as usual (see, for example, [Reference BerthelotBer96, Equation (2.0.2)])
 \begin{align*} \partial_i^{[j]}f^{s}&=\sum_{k=0}^{j} \partial_i^{[j-k]}(f^{s})\partial_i^{[k]} \\ &=\sum_{k=0}^{j} \bigg(\!\!\!\begin{array}{c}{s}\\ {j-k}\end{array}\!\!\!\bigg) x_i^{k-j} f^{s} \partial_i^{[k]} \ \forall s\in \mathbb{Z}, \end{align*}
\begin{align*} \partial_i^{[j]}f^{s}&=\sum_{k=0}^{j} \partial_i^{[j-k]}(f^{s})\partial_i^{[k]} \\ &=\sum_{k=0}^{j} \bigg(\!\!\!\begin{array}{c}{s}\\ {j-k}\end{array}\!\!\!\bigg) x_i^{k-j} f^{s} \partial_i^{[k]} \ \forall s\in \mathbb{Z}, \end{align*}
which can be verified by straightforward induction on ![]() $j$.
$j$.
By writing ![]() $m=f^{s}f^{-s} m$, we thus have in
$m=f^{s}f^{-s} m$, we thus have in ![]() $M[f^{-1}]$ the following equations for any integer
$M[f^{-1}]$ the following equations for any integer ![]() $s$:
$s$:
 \begin{align*} 0&= x_i^{n-1}f^{{-}s}\sum_{j=0}^{n} a_{i, j}\partial_i^{[j]}\cdot m\\ &= \sum_{j=0}^{n} x_i^{n-j} a_{i, j} \big( x_i^{j-1} f^{{-}s} \partial_i^{[j]}\cdot m\big)\\ &= \sum_{j=0}^{n} x_i^{n-j}a_{i, j} \bigg(\sum_{k=0}^{j} \bigg(\!\!\!\begin{array}{c}{s}\\ {j-k}\end{array}\!\!\!\bigg)x_i^{k-1} \partial_i^{[k]}\cdot f^{{-}s}m\bigg)\\ &= \sum_{k=0}^{n} \sum_{j=k}^{n} \bigg(\!\!\!\begin{array}{c}{s}\\ {j-k}\end{array}\!\!\!\bigg)x_i^{n-j+k-1} a_{i, j} \partial_i^{[k]}\cdot f^{{-}s}m. \end{align*}
\begin{align*} 0&= x_i^{n-1}f^{{-}s}\sum_{j=0}^{n} a_{i, j}\partial_i^{[j]}\cdot m\\ &= \sum_{j=0}^{n} x_i^{n-j} a_{i, j} \big( x_i^{j-1} f^{{-}s} \partial_i^{[j]}\cdot m\big)\\ &= \sum_{j=0}^{n} x_i^{n-j}a_{i, j} \bigg(\sum_{k=0}^{j} \bigg(\!\!\!\begin{array}{c}{s}\\ {j-k}\end{array}\!\!\!\bigg)x_i^{k-1} \partial_i^{[k]}\cdot f^{{-}s}m\bigg)\\ &= \sum_{k=0}^{n} \sum_{j=k}^{n} \bigg(\!\!\!\begin{array}{c}{s}\\ {j-k}\end{array}\!\!\!\bigg)x_i^{n-j+k-1} a_{i, j} \partial_i^{[k]}\cdot f^{{-}s}m. \end{align*}
As ![]() $a_{i, n}=1$, we obtain
$a_{i, n}=1$, we obtain
where ![]() $\sum '$ denotes the sum over all pairs
$\sum '$ denotes the sum over all pairs ![]() $(j, k)$,
$(j, k)$, ![]() $0\leq k\leq j\leq n$,
$0\leq k\leq j\leq n$, ![]() $(j, k)\neq (n, 0)$.
$(j, k)\neq (n, 0)$.
Setting ![]() $P_i(s)=-\sum ' \binom {s}{j-k}x_i^{n-j+k-1}a_{i, j} \partial _i^{[k]}\in \mathcal {D}(X)[s]$, we note that
$P_i(s)=-\sum ' \binom {s}{j-k}x_i^{n-j+k-1}a_{i, j} \partial _i^{[k]}\in \mathcal {D}(X)[s]$, we note that ![]() $P_i(s)$ is contained in the subring
$P_i(s)$ is contained in the subring ![]() $A[\partial _i, s]$ and hence commutes with
$A[\partial _i, s]$ and hence commutes with ![]() $x_j$ for any
$x_j$ for any ![]() $j\neq i$. We thus conclude from the above that
$j\neq i$. We thus conclude from the above that
for any ![]() $1\leq i\leq r$, and by induction
$1\leq i\leq r$, and by induction
 \[ \bigg(\prod_{i=1}^{r} P_i(s)\bigg)\cdot f^{{-}s}m=\bigg(\!\!\!\begin{array}{c}{s}\\ {n}\end{array}\!\!\!\bigg)^{r} f^{{-}s-1}m. \]
\[ \bigg(\prod_{i=1}^{r} P_i(s)\bigg)\cdot f^{{-}s}m=\bigg(\!\!\!\begin{array}{c}{s}\\ {n}\end{array}\!\!\!\bigg)^{r} f^{{-}s-1}m. \]
In particular, ![]() $\binom {s}{n}^{r}\in I(m)$. Thus the
$\binom {s}{n}^{r}\in I(m)$. Thus the ![]() $b$-function of
$b$-function of ![]() $m$ is a factor of
$m$ is a factor of ![]() $\binom {s}{n}^{r}$, and all its roots are integers. As integers are of positive type by [Reference KedlayaKed10, Proposition 13.1.5], applying Theorem 8.2(i) proves the result.
$\binom {s}{n}^{r}$, and all its roots are integers. As integers are of positive type by [Reference KedlayaKed10, Proposition 13.1.5], applying Theorem 8.2(i) proves the result.
10. Zariski open embeddings: The general case
10.1 Cohomology on hyperplane complements
We introduce the following notation: if ![]() $X=\operatorname {Sp} A$ and
$X=\operatorname {Sp} A$ and ![]() $f\in A$ is non-constant, we denote by
$f\in A$ is non-constant, we denote by ![]() $X_f$ the admissible open subspace given by the non-vanishing of
$X_f$ the admissible open subspace given by the non-vanishing of ![]() $f$. Note that
$f$. Note that ![]() $\mathcal {O}(X_f)\neq A_f$, but rather
$\mathcal {O}(X_f)\neq A_f$, but rather
The following is a partial generalization of [Reference KiehlKie67, Satz 2.4.2].
Proposition Let ![]() $X=\operatorname {Sp} A$ be smooth and let
$X=\operatorname {Sp} A$ be smooth and let ![]() $f\in A$ be non-constant. If
$f\in A$ be non-constant. If ![]() $\mathcal {M}$ is a coadmissible
$\mathcal {M}$ is a coadmissible ![]() $\widehat {\mathcal {D}}$-module on
$\widehat {\mathcal {D}}$-module on ![]() $X_f$ then
$X_f$ then ![]() $\mathrm {H}^{i}(X_f, \mathcal {M})=0$ for every
$\mathrm {H}^{i}(X_f, \mathcal {M})=0$ for every ![]() $i>0$.
$i>0$.
Proof. Let ![]() $\mathcal {A}\subset A$ be an affine formal model and let
$\mathcal {A}\subset A$ be an affine formal model and let ![]() $\mathcal {L}\subset \mathcal {T}(X)$ be an
$\mathcal {L}\subset \mathcal {T}(X)$ be an ![]() $\mathcal {A}$-Lie lattice. Then after rescaling
$\mathcal {A}$-Lie lattice. Then after rescaling ![]() $f$ if necessary, we can assume without loss of generality that
$f$ if necessary, we can assume without loss of generality that ![]() $f\in \mathcal {A}$, so that
$f\in \mathcal {A}$, so that ![]() $U_m:=X(\pi ^{m}f^{-1})$ is
$U_m:=X(\pi ^{m}f^{-1})$ is ![]() $\pi ^{n}\mathcal {L}$-accessible for any
$\pi ^{n}\mathcal {L}$-accessible for any ![]() $n\geq m$.
$n\geq m$.
We write ![]() $D=\widehat {\mathcal {D}}(X_f)$,
$D=\widehat {\mathcal {D}}(X_f)$, ![]() $D_n=\widehat {U(\mathcal {L}_n)_K}$, where
$D_n=\widehat {U(\mathcal {L}_n)_K}$, where ![]() $\mathcal {L}_n$ is the image of
$\mathcal {L}_n$ is the image of ![]() $\mathcal {A}\langle \pi ^{n}f^{-1}\rangle \otimes _{\mathcal {A}} \pi ^{n}\mathcal {L}$ inside
$\mathcal {A}\langle \pi ^{n}f^{-1}\rangle \otimes _{\mathcal {A}} \pi ^{n}\mathcal {L}$ inside ![]() $\mathcal {T}(U_n)$. Let
$\mathcal {T}(U_n)$. Let ![]() $\mathcal {D}_n$ be the sheaf of algebras on the site of
$\mathcal {D}_n$ be the sheaf of algebras on the site of ![]() $\mathcal {L}_n$-admissible subspaces of
$\mathcal {L}_n$-admissible subspaces of ![]() $U_n$ associated to
$U_n$ associated to
As the maps ![]() $D_{n+1}\to \mathcal {D}_{n+1}(U_n)\to D_n$ are flat by [Reference BodeBod19a, Theorem 4.10] and [Reference Ardakov and WadsleyAW19, Theorem 6.6],
$D_{n+1}\to \mathcal {D}_{n+1}(U_n)\to D_n$ are flat by [Reference BodeBod19a, Theorem 4.10] and [Reference Ardakov and WadsleyAW19, Theorem 6.6], ![]() $D=\varprojlim D_n$ exhibits
$D=\varprojlim D_n$ exhibits ![]() $D$ as a Fréchet–Stein algebra, and if
$D$ as a Fréchet–Stein algebra, and if ![]() $\mathcal {M}$ is a coadmissible
$\mathcal {M}$ is a coadmissible ![]() $\widehat {\mathcal {D}}_{X_f}$-module then
$\widehat {\mathcal {D}}_{X_f}$-module then ![]() $\mathcal {M}(X_f)=\varprojlim M_n$ for
$\mathcal {M}(X_f)=\varprojlim M_n$ for ![]() $M_n=D_n\otimes _{\widehat {\mathcal {D}}(U_n)}\mathcal {M}(U_n)$ makes
$M_n=D_n\otimes _{\widehat {\mathcal {D}}(U_n)}\mathcal {M}(U_n)$ makes ![]() $\mathcal {M}(X_f)$ a coadmissible
$\mathcal {M}(X_f)$ a coadmissible ![]() $D$-module.
$D$-module.
Let ![]() $\mathcal {M}_n$ be the sheaf
$\mathcal {M}_n$ be the sheaf ![]() $\operatorname {Loc} M_n$ on the site of
$\operatorname {Loc} M_n$ on the site of ![]() $\mathcal {L}_n$-admissible subspaces of
$\mathcal {L}_n$-admissible subspaces of ![]() $U_n$, a coherent
$U_n$, a coherent ![]() $\mathcal {D}_n$-module (see [Reference Ardakov and WadsleyAW19, § 5.1]). Let
$\mathcal {D}_n$-module (see [Reference Ardakov and WadsleyAW19, § 5.1]). Let ![]() $\mathfrak {U}=(U_i)$ and let
$\mathfrak {U}=(U_i)$ and let ![]() $\mathfrak {U}_n=\{U_1, \dots , U_n\}$. Note that by [Reference Ardakov and WadsleyAW19, Proposition 9.5],
$\mathfrak {U}_n=\{U_1, \dots , U_n\}$. Note that by [Reference Ardakov and WadsleyAW19, Proposition 9.5],
for any ![]() $i$.
$i$.
Consider the complexes ![]() $C(n)^{\bullet }=\check {C}^{\bullet }(\mathfrak {U}_n, \mathcal {M}_n)$ with natural morphisms of complexes
$C(n)^{\bullet }=\check {C}^{\bullet }(\mathfrak {U}_n, \mathcal {M}_n)$ with natural morphisms of complexes ![]() $C(n+1)^{\bullet }\to C(n)^{\bullet }$ induced by restriction. By [Reference BodeBod19a, Theorem 4.16],
$C(n+1)^{\bullet }\to C(n)^{\bullet }$ induced by restriction. By [Reference BodeBod19a, Theorem 4.16],
and ![]() $\check {\mathrm {H}}^{0}(\mathfrak {U}_{n+1}, \mathcal {M}_{n+1})=M_{n+1}\to \check {\mathrm {H}}^{0}(\mathfrak {U}_n, \mathcal {M}_n)=M_n$ is a continuous morphism of Banach spaces with dense image for each
$\check {\mathrm {H}}^{0}(\mathfrak {U}_{n+1}, \mathcal {M}_{n+1})=M_{n+1}\to \check {\mathrm {H}}^{0}(\mathfrak {U}_n, \mathcal {M}_n)=M_n$ is a continuous morphism of Banach spaces with dense image for each ![]() $n$ by [Reference Schneider and TeitelbaumST03, § 3, Theorem A].
$n$ by [Reference Schneider and TeitelbaumST03, § 3, Theorem A].
Thus by [Reference GrothendieckEGA3, Proposition 13.2.3, Remarques 13.2.4],
for each ![]() $i$.
$i$.
It hence remains to show that ![]() $\varprojlim C(n)^{\bullet }\cong \check {C}^{\bullet }(\mathfrak {U}, \mathcal {M})$. But
$\varprojlim C(n)^{\bullet }\cong \check {C}^{\bullet }(\mathfrak {U}, \mathcal {M})$. But
 \[ \varprojlim_n C(n)^{{\bullet}}=\varprojlim_{\substack{m, n\\m\geq n}} \check{C}^{{\bullet}}(\mathfrak{U}_n, \mathcal{M}_m)\cong \varprojlim_n \check{C}^{{\bullet}}(\mathfrak{U}_n, \mathcal{M})\cong \check{C}^{{\bullet}}(\mathfrak{U}, \mathcal{M}), \]
\[ \varprojlim_n C(n)^{{\bullet}}=\varprojlim_{\substack{m, n\\m\geq n}} \check{C}^{{\bullet}}(\mathfrak{U}_n, \mathcal{M}_m)\cong \varprojlim_n \check{C}^{{\bullet}}(\mathfrak{U}_n, \mathcal{M})\cong \check{C}^{{\bullet}}(\mathfrak{U}, \mathcal{M}), \]as required.
Corollary Let ![]() $X$ be a smooth affinoid
$X$ be a smooth affinoid ![]() $K$-space and let
$K$-space and let ![]() $j:U\to X$ be a Zariski open embedding. Let
$j:U\to X$ be a Zariski open embedding. Let ![]() $\mathfrak {U}=(U_i)$ be an admissible covering of
$\mathfrak {U}=(U_i)$ be an admissible covering of ![]() $U$ with the following property: for each
$U$ with the following property: for each ![]() $i$, there exists a smooth morphism of affinoids
$i$, there exists a smooth morphism of affinoids ![]() $V_i=\operatorname {Sp} A_i\to X$ fitting into a commutative diagram
$V_i=\operatorname {Sp} A_i\to X$ fitting into a commutative diagram

which identifies ![]() $U_i$ with
$U_i$ with ![]() $(V_i)_{f_i}$ for some non-constant
$(V_i)_{f_i}$ for some non-constant ![]() $f_i\in A_i$.
$f_i\in A_i$.
If ![]() $\mathcal {M}$ is a coadmissible
$\mathcal {M}$ is a coadmissible ![]() $\widehat {\mathcal {D}}$-module on
$\widehat {\mathcal {D}}$-module on ![]() $U$ then
$U$ then ![]() $\mathrm {R}^{i}j_*\mathcal {M}(X)\cong \check {\mathrm {H}}^{i}(\mathfrak {U}, \mathcal {M})$ for any
$\mathrm {R}^{i}j_*\mathcal {M}(X)\cong \check {\mathrm {H}}^{i}(\mathfrak {U}, \mathcal {M})$ for any ![]() $i\geq 0$.
$i\geq 0$.
Proof. Note that ![]() $V_{i_1}\times _X \dots \times _X V_{i_r}$ is a smooth affinoid such that
$V_{i_1}\times _X \dots \times _X V_{i_r}$ is a smooth affinoid such that ![]() $U_{i_1}\cap \dots \cap U_{i_r}$ can be identified with
$U_{i_1}\cap \dots \cap U_{i_r}$ can be identified with ![]() $(V_{i_1}\times _X \dots \times _X V_{i_r})_{f_{i_1}\dots f_{i_r}}$, so it follows from the Proposition that for
$(V_{i_1}\times _X \dots \times _X V_{i_r})_{f_{i_1}\dots f_{i_r}}$, so it follows from the Proposition that for ![]() $i\geq 1$,
$i\geq 1$,
for any ![]() $i_1, \dots , i_r$. Thus the result follows from [Sta18, Tag 03F7].
$i_1, \dots , i_r$. Thus the result follows from [Sta18, Tag 03F7].
10.2 Completed tensor products and sections of  $\widehat {\mathcal {D}}$
$\widehat {\mathcal {D}}$
In this subsection we use some basic results from [Reference Bitoun and BodeBB21] about completed tensor products to describe sections of ![]() $\widehat {\mathcal {D}}$ over Zariski open subspaces.
$\widehat {\mathcal {D}}$ over Zariski open subspaces.
Lemma Let ![]() $X=\operatorname {Sp} A$ be an affinoid
$X=\operatorname {Sp} A$ be an affinoid ![]() $K$-space with free tangent sheaf. Then the functor
$K$-space with free tangent sheaf. Then the functor ![]() $-\widehat {\otimes }_A \widehat {\mathcal {D}}(X)$ is strict exact on Fréchet
$-\widehat {\otimes }_A \widehat {\mathcal {D}}(X)$ is strict exact on Fréchet ![]() $A$-modules.
$A$-modules.
Proof. As a left ![]() $A$-module,
$A$-module, ![]() $\widehat {\mathcal {D}}(X)$ is isomorphic to
$\widehat {\mathcal {D}}(X)$ is isomorphic to ![]() $\mathcal {O}(X\times \mathbb {A}^{d, \mathrm {an}})$, where
$\mathcal {O}(X\times \mathbb {A}^{d, \mathrm {an}})$, where ![]() $d$ is the rank of
$d$ is the rank of ![]() $\mathcal {T}_X$. The result now follows from [Reference KisinKis99, Propositions 1.2.2 and 1.2.6(2)].
$\mathcal {T}_X$. The result now follows from [Reference KisinKis99, Propositions 1.2.2 and 1.2.6(2)].
Proposition Let ![]() $X=\operatorname {Sp} A$ be an affinoid
$X=\operatorname {Sp} A$ be an affinoid ![]() $K$-space with free tangent sheaf, and let
$K$-space with free tangent sheaf, and let ![]() $U$ be a Zariski open subspace. Then the natural morphism
$U$ be a Zariski open subspace. Then the natural morphism
is an isomorphism of locally convex ![]() $\mathcal {O}(U)$-modules.
$\mathcal {O}(U)$-modules.
Proof. First let ![]() $U=X_f$ for some
$U=X_f$ for some ![]() $f\in A$. Let
$f\in A$. Let ![]() $\mathcal {A}$ be an affine formal model, and let
$\mathcal {A}$ be an affine formal model, and let ![]() $\mathcal {L}$ be an
$\mathcal {L}$ be an ![]() $\mathcal {A}$-Lie lattice in
$\mathcal {A}$-Lie lattice in ![]() $\mathcal {T}(X)$. Then [Reference Ardakov and WadsleyAW19, § 3.3, Theorem 3.5] gives rise to sheaves of
$\mathcal {T}(X)$. Then [Reference Ardakov and WadsleyAW19, § 3.3, Theorem 3.5] gives rise to sheaves of ![]() $K$-algebras
$K$-algebras ![]() $\mathcal {D}_n$ on the site of
$\mathcal {D}_n$ on the site of ![]() $\pi ^{n}\mathcal {L}$-admissible affinoid subdomains of
$\pi ^{n}\mathcal {L}$-admissible affinoid subdomains of ![]() $X$ such that for any
$X$ such that for any ![]() $\pi ^{n}\mathcal {L}$-admissible affinoid subdomain
$\pi ^{n}\mathcal {L}$-admissible affinoid subdomain ![]() $Y=\operatorname {Sp} B\subset X$, we have
$Y=\operatorname {Sp} B\subset X$, we have ![]() $\widehat {\mathcal {D}}(Y)\cong \varprojlim _{m\geq n} \mathcal {D}_m(Y)$ and
$\widehat {\mathcal {D}}(Y)\cong \varprojlim _{m\geq n} \mathcal {D}_m(Y)$ and ![]() $\mathcal {D}_n(Y)\cong B\widehat {\otimes }_A \mathcal {D}_n(X)$. Without loss of generality,
$\mathcal {D}_n(Y)\cong B\widehat {\otimes }_A \mathcal {D}_n(X)$. Without loss of generality, ![]() $f\in \mathcal {A}$, so that
$f\in \mathcal {A}$, so that ![]() $U_n:=X(\pi ^{n}f^{-1})$ is
$U_n:=X(\pi ^{n}f^{-1})$ is ![]() $\pi ^{n}\mathcal {L}$-admissible. Now
$\pi ^{n}\mathcal {L}$-admissible. Now
so that the result follows from [Reference Bitoun and BodeBB21, Lemma A.2(iv)].
If ![]() $U$ is the complement of
$U$ is the complement of ![]() $V(f_1, \dots , f_r)$, we consider the Čech complex
$V(f_1, \dots , f_r)$, we consider the Čech complex ![]() $\check {C}^{\bullet }((X_{f_i}), \mathcal {O})$. Applying
$\check {C}^{\bullet }((X_{f_i}), \mathcal {O})$. Applying ![]() $-\widehat {\otimes }_A \widehat {\mathcal {D}}(X)$ and invoking the lemma then finishes the proof in general.
$-\widehat {\otimes }_A \widehat {\mathcal {D}}(X)$ and invoking the lemma then finishes the proof in general.
We also emphasize that by [Reference Bitoun and BodeBB21, Corollary A.6] the coadmissible tensor product ![]() $\widehat {\otimes }$ defined in [Reference Ardakov and WadsleyAW19, § 7.3] agrees with the completed tensor product
$\widehat {\otimes }$ defined in [Reference Ardakov and WadsleyAW19, § 7.3] agrees with the completed tensor product ![]() $\widehat {\otimes }$ with respect to the canonical Fréchet structures on coadmissible modules.
$\widehat {\otimes }$ with respect to the canonical Fréchet structures on coadmissible modules.
10.3 An algebraic analogue
In order to make the arguments below more accessible, we recall in some detail the following basic property of coherent ![]() $\mathcal {D}$-modules on algebraic varieties.
$\mathcal {D}$-modules on algebraic varieties.
Proposition Let ![]() $k$ be an algebraically closed field of characteristic zero, and consider a diagram
$k$ be an algebraically closed field of characteristic zero, and consider a diagram

of smooth algebraic varieties over ![]() $k$, where
$k$, where ![]() $j$ and
$j$ and ![]() $j'$ are open embeddings,
$j'$ are open embeddings, ![]() $\iota$ is a closed embedding, and
$\iota$ is a closed embedding, and ![]() $\mathrm {pr}$ is the natural projection. Assume further that
$\mathrm {pr}$ is the natural projection. Assume further that ![]() $j'$ is affine.
$j'$ is affine.
If ![]() $\mathcal {M}$ is a coherent
$\mathcal {M}$ is a coherent ![]() $\mathcal {D}_U$-module such that
$\mathcal {D}_U$-module such that ![]() $j'_*\mathcal {M}$ is a coherent
$j'_*\mathcal {M}$ is a coherent ![]() $\mathcal {D}_{X'}$-module, then
$\mathcal {D}_{X'}$-module, then ![]() $\mathrm {R}^{i}j_*\mathcal {M}$ is a coherent
$\mathrm {R}^{i}j_*\mathcal {M}$ is a coherent ![]() $\mathcal {D}_X$-module for every
$\mathcal {D}_X$-module for every ![]() $i\geq 0$.
$i\geq 0$.
Proof. For any morphism ![]() $f: Y'\to Y$ of smooth algebraic varieties over
$f: Y'\to Y$ of smooth algebraic varieties over ![]() $k$, one can define [Reference Hotta, Takeuchi and TanisakiHTT08, p. 40] the
$k$, one can define [Reference Hotta, Takeuchi and TanisakiHTT08, p. 40] the ![]() $\mathcal {D}$-module pushforward functor
$\mathcal {D}$-module pushforward functor
For right modules, this takes the form
where ![]() $\mathcal {D}_{Y'\to Y}$ is the transfer bimodule
$\mathcal {D}_{Y'\to Y}$ is the transfer bimodule ![]() $f^{*}\mathcal {D}_Y$. For left modules, we compose the above with suitable side-changing operations.
$f^{*}\mathcal {D}_Y$. For left modules, we compose the above with suitable side-changing operations.
By [Reference Hotta, Takeuchi and TanisakiHTT08, Proposition 1.5.21, Example 1.5.22] and the assumption on ![]() $j'$, we have
$j'$, we have
Write ![]() $P=\mathbb {P}^{n}\times X$.
$P=\mathbb {P}^{n}\times X$.
Now ![]() $\iota _+$ preserves coherence by Kashiwara's equivalence [Reference Hotta, Takeuchi and TanisakiHTT08, Theorem 1.6.1], and
$\iota _+$ preserves coherence by Kashiwara's equivalence [Reference Hotta, Takeuchi and TanisakiHTT08, Theorem 1.6.1], and ![]() $\mathrm {pr}_+$ sends
$\mathrm {pr}_+$ sends ![]() $\mathrm {D}^{b}_c(\mathcal {D}_P)$ to
$\mathrm {D}^{b}_c(\mathcal {D}_P)$ to ![]() $\mathrm {D}^{b}_c(\mathcal {D}_X)$ by [Reference Hotta, Takeuchi and TanisakiHTT08, Theorem 2.5.1]. This immediately proves the proposition.
$\mathrm {D}^{b}_c(\mathcal {D}_X)$ by [Reference Hotta, Takeuchi and TanisakiHTT08, Theorem 2.5.1]. This immediately proves the proposition.
More explicitly, if ![]() $\mathcal {M}$ is a coherent right
$\mathcal {M}$ is a coherent right ![]() $\mathcal {D}_U$-module, we can write
$\mathcal {D}_U$-module, we can write
where ![]() $\mathcal {D}_{P\to X}$ is the
$\mathcal {D}_{P\to X}$ is the ![]() $(\mathcal {D}_P, \mathrm {pr}^{-1}\mathcal {D}_X)$-bimodule
$(\mathcal {D}_P, \mathrm {pr}^{-1}\mathcal {D}_X)$-bimodule ![]() $\mathrm {pr}^{*}\mathcal {D}_X=\mathscr {U}_{\mathcal {O}_P}(\mathrm {pr}^{*}\mathcal {T}_X)$, the enveloping sheaf of the Lie algebroid
$\mathrm {pr}^{*}\mathcal {D}_X=\mathscr {U}_{\mathcal {O}_P}(\mathrm {pr}^{*}\mathcal {T}_X)$, the enveloping sheaf of the Lie algebroid ![]() $\mathrm {pr}^{*}\mathcal {T}_X$.
$\mathrm {pr}^{*}\mathcal {T}_X$.
To prove the general case of Theorem C, we will use an embedded resolution of singularities ![]() $(X', U)\to (X, U)$ to reduce to the case of an algebraic snc divisor, and an analogue of the above proposition in order to descend from
$(X', U)\to (X, U)$ to reduce to the case of an algebraic snc divisor, and an analogue of the above proposition in order to descend from ![]() $X'$ to
$X'$ to ![]() $X$ again. While a theory of general
$X$ again. While a theory of general ![]() $\widehat {\mathcal {D}}$-module pushforwards has not been established yet, it turns out that we can make all computations explicitly in our situation.
$\widehat {\mathcal {D}}$-module pushforwards has not been established yet, it turns out that we can make all computations explicitly in our situation.
10.4 Pushforward of the structure sheaf on a Zariski open subspace
Let ![]() $j: U\to X$ be an arbitrary Zariski open embedding of smooth rigid analytic
$j: U\to X$ be an arbitrary Zariski open embedding of smooth rigid analytic ![]() $K$-spaces. As always, we can assume that
$K$-spaces. As always, we can assume that ![]() $X=\operatorname {Sp} A$ is affinoid with free tangent sheaf.
$X=\operatorname {Sp} A$ is affinoid with free tangent sheaf.
Writing ![]() $Z=\operatorname {Sp} B$ for the complement of
$Z=\operatorname {Sp} B$ for the complement of ![]() $U$ with its reduced subvariety structure, we obtain a closed embedding
$U$ with its reduced subvariety structure, we obtain a closed embedding ![]() $\operatorname {Spec} B\to \operatorname {Spec} A$ of schemes over
$\operatorname {Spec} B\to \operatorname {Spec} A$ of schemes over ![]() $\mathbb {Q}$. We recall the following result from [Reference TemkinTem18].
$\mathbb {Q}$. We recall the following result from [Reference TemkinTem18].
Theorem [Reference TemkinTem18, Theorem 1.1.11]
Let ![]() $\mathbf {X}$ be a quasi-excellent Noetherian scheme over
$\mathbf {X}$ be a quasi-excellent Noetherian scheme over ![]() $\mathbb {Q}$, and let
$\mathbb {Q}$, and let ![]() $\mathbf {Z}$ be a closed subscheme of
$\mathbf {Z}$ be a closed subscheme of ![]() $\mathbf {X}$. Then there exist a regular scheme
$\mathbf {X}$. Then there exist a regular scheme ![]() $\mathbf {X}'$ and a morphism of schemes
$\mathbf {X}'$ and a morphism of schemes ![]() $\rho : \mathbf {X}'\to \mathbf {X}$ which is a sequence of blow-ups with centres contained in
$\rho : \mathbf {X}'\to \mathbf {X}$ which is a sequence of blow-ups with centres contained in ![]() $\mathbf {Z}\cup \mathbf {X}_{\mathrm {sing}}$ such that
$\mathbf {Z}\cup \mathbf {X}_{\mathrm {sing}}$ such that ![]() $\mathbf {Z}\times _{\mathbf {X}} \mathbf {X}'$ is an snc divisor in
$\mathbf {Z}\times _{\mathbf {X}} \mathbf {X}'$ is an snc divisor in ![]() $\mathbf {X}'$.
$\mathbf {X}'$.
Let ![]() $\mathbf {X}=\operatorname {Spec} A$,
$\mathbf {X}=\operatorname {Spec} A$, ![]() $\mathbf {Z}=\operatorname {Spec} B$. By [Reference Berger, Kiehl, Kunz and NastoldBKKN67, Satz 3.3.3],
$\mathbf {Z}=\operatorname {Spec} B$. By [Reference Berger, Kiehl, Kunz and NastoldBKKN67, Satz 3.3.3], ![]() $\mathbf {X}$ is an excellent Noetherian scheme, so we can apply Theorem 10.4. As
$\mathbf {X}$ is an excellent Noetherian scheme, so we can apply Theorem 10.4. As ![]() $\mathbf {X}$ is also regular by [Reference Bosch, Güntzer and RemmertBGR84, Proposition 7.3.2/8], the centres of the blow-ups in the theorem are contained in
$\mathbf {X}$ is also regular by [Reference Bosch, Güntzer and RemmertBGR84, Proposition 7.3.2/8], the centres of the blow-ups in the theorem are contained in ![]() $\mathbf {Z}$. In particular, the theorem provides us with a morphism
$\mathbf {Z}$. In particular, the theorem provides us with a morphism ![]() $\rho : \mathbf {X}'\to \mathbf {X}$ which is an isomorphism away from
$\rho : \mathbf {X}'\to \mathbf {X}$ which is an isomorphism away from ![]() $\mathbf {Z}$, so that we have the following commutative diagram:
$\mathbf {Z}$, so that we have the following commutative diagram:

where ![]() $j:\mathbf {U}\to \mathbf {X}$ is the complement of
$j:\mathbf {U}\to \mathbf {X}$ is the complement of ![]() $\mathbf {Z}$ inside
$\mathbf {Z}$ inside ![]() $\mathbf {X}$, and
$\mathbf {X}$, and ![]() $j'$ realizes
$j'$ realizes ![]() $\mathbf {U}$ as the complement of an snc divisor in
$\mathbf {U}$ as the complement of an snc divisor in ![]() $\mathbf {X}'$. Finally, we note that
$\mathbf {X}'$. Finally, we note that ![]() $\rho$ is projective, as it is a sequence of blow-ups, so that we obtain a factorization of
$\rho$ is projective, as it is a sequence of blow-ups, so that we obtain a factorization of ![]() $\rho$ as a closed immersion and a projection:
$\rho$ as a closed immersion and a projection:

By construction, all schemes in this diagram are ![]() $A$-schemes, and applying analytification, we obtain the commutative diagram of rigid analytic
$A$-schemes, and applying analytification, we obtain the commutative diagram of rigid analytic ![]() $K$-spaces
$K$-spaces

where:
(i)
 $j$ and
$j$ and  $j'$ are Zariski open embeddings by Proposition 9.1(iv), and
$j'$ are Zariski open embeddings by Proposition 9.1(iv), and  $(\mathbf {U})^{\mathrm {an}}=(\mathbf {X}\setminus \mathbf {Z})^{\mathrm {an}}=X\setminus Z=U$ by Proposition 9.1(iii);
$(\mathbf {U})^{\mathrm {an}}=(\mathbf {X}\setminus \mathbf {Z})^{\mathrm {an}}=X\setminus Z=U$ by Proposition 9.1(iii);(ii)
 $X'=\mathbf {X}'^{\mathrm {an}}$ is a smooth rigid analytic
$X'=\mathbf {X}'^{\mathrm {an}}$ is a smooth rigid analytic  $K$-space by [Reference SchoutensSch99, Corollary 1.3.5] and [Reference Bosch, Lütkebohmert and RaynaudBLR95, Lemma 2.8];
$K$-space by [Reference SchoutensSch99, Corollary 1.3.5] and [Reference Bosch, Lütkebohmert and RaynaudBLR95, Lemma 2.8];(iii)
 $X'\setminus U$ is an algebraic snc divisor in
$X'\setminus U$ is an algebraic snc divisor in  $\mathbf {X}'$ by construction;
$\mathbf {X}'$ by construction;(iv)
 $\iota$ is a closed immersion of rigid analytic spaces by Proposition 9.1(iii);
$\iota$ is a closed immersion of rigid analytic spaces by Proposition 9.1(iii);(v)
 $(\mathbb {P}^{n}\times \mathbf {X})^{\mathrm {an}}\cong \mathbb {P}^{n, \mathrm {an}}\times (\mathbf {X})^{\mathrm {an}}=\mathbb {P}^{n, \mathrm {an}}\times X$ by Proposition 9.1(ii) and (vi).
$(\mathbb {P}^{n}\times \mathbf {X})^{\mathrm {an}}\cong \mathbb {P}^{n, \mathrm {an}}\times (\mathbf {X})^{\mathrm {an}}=\mathbb {P}^{n, \mathrm {an}}\times X$ by Proposition 9.1(ii) and (vi).
We are now in a position to discuss the rigid analytic analogue of Proposition 10.3.
Proposition Let ![]() $\mathcal {M}$ be a coadmissible
$\mathcal {M}$ be a coadmissible ![]() $\widehat {\mathcal {D}}$-module on
$\widehat {\mathcal {D}}$-module on ![]() $U$. If
$U$. If ![]() $j'_*\mathcal {M}$ is a coadmissible
$j'_*\mathcal {M}$ is a coadmissible ![]() $\widehat {\mathcal {D}}_{X'}$-module, then
$\widehat {\mathcal {D}}_{X'}$-module, then ![]() $\mathrm {R}^{i}j_*\mathcal {M}$ is a coadmissible
$\mathrm {R}^{i}j_*\mathcal {M}$ is a coadmissible ![]() $\widehat {\mathcal {D}}_X$-module for every
$\widehat {\mathcal {D}}_X$-module for every ![]() $i\geq 0$.
$i\geq 0$.
Proof. We prove the proposition for right coadmissible ![]() $\widehat {\mathcal {D}}$-modules. The left module analogue follows by applying the side-changing operators.
$\widehat {\mathcal {D}}$-modules. The left module analogue follows by applying the side-changing operators.
We write ![]() $P=\mathbb {P}^{n, \mathrm {an}}\times X$. By [Reference Ardakov and WadsleyAW18, § 5.4], there exists a right coadmissible
$P=\mathbb {P}^{n, \mathrm {an}}\times X$. By [Reference Ardakov and WadsleyAW18, § 5.4], there exists a right coadmissible ![]() $\widehat {\mathcal {D}}_P$-module
$\widehat {\mathcal {D}}_P$-module ![]() $\iota _+(j'_*\mathcal {M})$ such that the following holds: for each admissible open affinoid
$\iota _+(j'_*\mathcal {M})$ such that the following holds: for each admissible open affinoid ![]() $V$ of
$V$ of ![]() $P$ with the property that
$P$ with the property that ![]() $X'\cap V$ has a free tangent sheaf, we have
$X'\cap V$ has a free tangent sheaf, we have
We now note that ![]() $\mathrm {pr}^{*}\mathcal {T}_X$ is a Lie algebroid on
$\mathrm {pr}^{*}\mathcal {T}_X$ is a Lie algebroid on ![]() $P$ which is free as an
$P$ which is free as an ![]() $\mathcal {O}_P$-module, and is naturally a direct summand of
$\mathcal {O}_P$-module, and is naturally a direct summand of ![]() $\mathcal {T}_P$. This makes
$\mathcal {T}_P$. This makes
a ![]() $(\widehat {\mathcal {D}}_P, \mathrm {pr}^{-1}\widehat {\mathcal {D}}_X)$-bimodule.
$(\widehat {\mathcal {D}}_P, \mathrm {pr}^{-1}\widehat {\mathcal {D}}_X)$-bimodule.
We can thus form the right coadmissible ![]() $\widehat {\mathscr {U}(\mathrm {pr}^{*}\mathcal {T}_X)}$-module
$\widehat {\mathscr {U}(\mathrm {pr}^{*}\mathcal {T}_X)}$-module
By [Reference BodeBod19b, Theorem 6.11], ![]() $\mathrm {R}^{i}\mathrm {pr}_*\mathcal {N}$ is coadmissible over
$\mathrm {R}^{i}\mathrm {pr}_*\mathcal {N}$ is coadmissible over ![]() $\mathrm {pr}_*\widehat {\mathscr {U}(\mathrm {pr}^{*}\mathcal {T}_X)}\cong \widehat {\mathcal {D}}_X$ for every
$\mathrm {pr}_*\widehat {\mathscr {U}(\mathrm {pr}^{*}\mathcal {T}_X)}\cong \widehat {\mathcal {D}}_X$ for every ![]() $i\geq 0$. We now show that
$i\geq 0$. We now show that ![]() $\mathrm {R}^{i}\mathrm {pr}_*\mathcal {N}$ is naturally isomorphic to
$\mathrm {R}^{i}\mathrm {pr}_*\mathcal {N}$ is naturally isomorphic to ![]() $\mathrm {R}^{i}j_*\mathcal {M}$.
$\mathrm {R}^{i}j_*\mathcal {M}$.
Let ![]() $\mathfrak {V}=(V_i)$ be a finite affinoid covering of
$\mathfrak {V}=(V_i)$ be a finite affinoid covering of ![]() $P$ where
$P$ where ![]() $V_i=W_i\times Y_i$,
$V_i=W_i\times Y_i$, ![]() $W_i$ an admissible open affinoid subspace of
$W_i$ an admissible open affinoid subspace of ![]() $\mathbb {P}^{n, \mathrm {an}}$,
$\mathbb {P}^{n, \mathrm {an}}$, ![]() $Y_i$ an affinoid subdomain of
$Y_i$ an affinoid subdomain of ![]() $X$, and
$X$, and ![]() $X'\cap V_i$ has a free tangent sheaf. Moreover, refining this covering, we can assume that the complement of
$X'\cap V_i$ has a free tangent sheaf. Moreover, refining this covering, we can assume that the complement of ![]() $U\cap V_i$ inside
$U\cap V_i$ inside ![]() $X'\cap V_i$ is cut out by a single equation for each
$X'\cap V_i$ is cut out by a single equation for each ![]() $i$.
$i$.
By comparing the Čech complex ![]() $\check {C}^{\bullet }(\mathfrak {V}, \mathcal {N})$ to
$\check {C}^{\bullet }(\mathfrak {V}, \mathcal {N})$ to ![]() $\check {C}^{\bullet }(U\cap \mathfrak {V}, \mathcal {M})$ and invoking Corollary 10.1, it suffices to show that we have natural isomorphisms
$\check {C}^{\bullet }(U\cap \mathfrak {V}, \mathcal {M})$ and invoking Corollary 10.1, it suffices to show that we have natural isomorphisms
where ![]() $V$ is any intersection of the
$V$ is any intersection of the ![]() $V_i$.
$V_i$.
Let ![]() $W$ be an admissible open affinoid subspace of
$W$ be an admissible open affinoid subspace of ![]() $\mathbb {P}^{n, \mathrm {an}}$,
$\mathbb {P}^{n, \mathrm {an}}$, ![]() $Y=\operatorname {Sp} C$ an affinoid subdomain of
$Y=\operatorname {Sp} C$ an affinoid subdomain of ![]() $X$ such that
$X$ such that ![]() $X'\cap (W\times Y)$ has a free tangent sheaf, and write
$X'\cap (W\times Y)$ has a free tangent sheaf, and write ![]() $V=W\times Y$.
$V=W\times Y$.
Now
and this is isomorphic to
By associativity of the completed tensor product [Reference Bitoun and BodeBB21, Lemma A.3], this can be simplified to
which in turn can be written as
since ![]() $\widehat {\mathcal {D}}(U\cap V)\cong \mathcal {O}(U\cap V)\underset {\mathcal {O}(X'\cap V)}{\widehat {\otimes }}\widehat {\mathcal {D}}_{X'}(X'\cap V)$ by Proposition 10.2.
$\widehat {\mathcal {D}}(U\cap V)\cong \mathcal {O}(U\cap V)\underset {\mathcal {O}(X'\cap V)}{\widehat {\otimes }}\widehat {\mathcal {D}}_{X'}(X'\cap V)$ by Proposition 10.2.
We thus obtain
 \begin{align*} \mathcal{N}(V)&\cong\mathcal{M}(U\cap V)\underset{\widehat{\mathcal{D}}_U(U\cap V)}{\widehat{\otimes}}\Big(\mathcal{O}(U\cap V)\underset{C}{\widehat{\otimes}} \widehat{\mathcal{D}}_X(Y)\Big)\\ &\cong \mathcal{M}(U\cap V)\underset{\widehat{\mathcal{D}}(U\cap V)}{\widehat{\otimes}} \Big(\mathcal{O}(U\cap V)\underset{\mathcal{O}(U\cap Y)}{\widehat{\otimes}}(\mathcal{O}(U\cap Y)\underset{C}{\widehat{\otimes}} \widehat{\mathcal{D}}(Y)) \Big)\\ &\cong \mathcal{M}(U\cap V)\underset{\widehat{\mathcal{D}}(U\cap V)}{\widehat{\otimes}} \Big(\mathcal{O}(U\cap V)\underset{\mathcal{O}(U\cap Y)}{\widehat{\otimes}} \widehat{\mathcal{D}}(U\cap Y) \Big)\\ & \cong \mathcal{M}(U\cap V)\underset{\widehat{\mathcal{D}}(U\cap V)}{\widehat{\otimes}} \widehat{\mathcal{D}}(U\cap V)\\ & \cong\mathcal{M}(U\cap V), \end{align*}
\begin{align*} \mathcal{N}(V)&\cong\mathcal{M}(U\cap V)\underset{\widehat{\mathcal{D}}_U(U\cap V)}{\widehat{\otimes}}\Big(\mathcal{O}(U\cap V)\underset{C}{\widehat{\otimes}} \widehat{\mathcal{D}}_X(Y)\Big)\\ &\cong \mathcal{M}(U\cap V)\underset{\widehat{\mathcal{D}}(U\cap V)}{\widehat{\otimes}} \Big(\mathcal{O}(U\cap V)\underset{\mathcal{O}(U\cap Y)}{\widehat{\otimes}}(\mathcal{O}(U\cap Y)\underset{C}{\widehat{\otimes}} \widehat{\mathcal{D}}(Y)) \Big)\\ &\cong \mathcal{M}(U\cap V)\underset{\widehat{\mathcal{D}}(U\cap V)}{\widehat{\otimes}} \Big(\mathcal{O}(U\cap V)\underset{\mathcal{O}(U\cap Y)}{\widehat{\otimes}} \widehat{\mathcal{D}}(U\cap Y) \Big)\\ & \cong \mathcal{M}(U\cap V)\underset{\widehat{\mathcal{D}}(U\cap V)}{\widehat{\otimes}} \widehat{\mathcal{D}}(U\cap V)\\ & \cong\mathcal{M}(U\cap V), \end{align*}by once more invoking Proposition 10.2, and by [Reference Bitoun and BodeBB21, Proposition 2.11(ii)].
Corollary Let ![]() $j:U\to X$ be a Zariski open embedding of smooth rigid analytic
$j:U\to X$ be a Zariski open embedding of smooth rigid analytic ![]() $K$-spaces, and let
$K$-spaces, and let ![]() $\mathcal {M}$ be an integrable connection on
$\mathcal {M}$ be an integrable connection on ![]() $X$. Then
$X$. Then ![]() $\mathrm {R}^{i}j_*(\mathcal {M}|_U)$ is a coadmissible
$\mathrm {R}^{i}j_*(\mathcal {M}|_U)$ is a coadmissible ![]() $\widehat {\mathcal {D}_X}$-module for every
$\widehat {\mathcal {D}_X}$-module for every ![]() $i\geq 0$.
$i\geq 0$.
10.5 Weak holonomicity
Lemma Let ![]() $X=\operatorname {Sp} A$ be a smooth affinoid
$X=\operatorname {Sp} A$ be a smooth affinoid ![]() $K$-space, and let
$K$-space, and let ![]() $U=X_f$ for
$U=X_f$ for ![]() $f\in A$ non-constant. Let
$f\in A$ non-constant. Let ![]() $\mathcal {M}$ be an integrable connection on
$\mathcal {M}$ be an integrable connection on ![]() $X$. Then
$X$. Then ![]() $j_*(\mathcal {M}|_U)$ is a weakly holonomic
$j_*(\mathcal {M}|_U)$ is a weakly holonomic ![]() $\widehat {\mathcal {D}}_X$-module, where
$\widehat {\mathcal {D}}_X$-module, where ![]() $j: U \to X$ is the natural embedding.
$j: U \to X$ is the natural embedding.
Proof. Without loss of generality, we can assume that ![]() $\mathcal {T}_X$ is free as an
$\mathcal {T}_X$ is free as an ![]() $\mathcal {O}_X$-module. By Corollary 10.4,
$\mathcal {O}_X$-module. By Corollary 10.4, ![]() $j_*(\mathcal {M}|_U)$ is a coadmissible
$j_*(\mathcal {M}|_U)$ is a coadmissible ![]() $\widehat {\mathcal {D}_X}$-module, and it remains to show that the dimension of
$\widehat {\mathcal {D}_X}$-module, and it remains to show that the dimension of ![]() $\mathcal {M}(U)$ as a
$\mathcal {M}(U)$ as a ![]() $\widehat {\mathcal {D}}_X(X)$-module is
$\widehat {\mathcal {D}}_X(X)$-module is ![]() $\dim X$. We write
$\dim X$. We write ![]() $M=\mathcal {M}(X)$.
$M=\mathcal {M}(X)$.
By [Reference Mebkhout and Narvaez-MacarroMN91, Théorème 3.2.1], ![]() $M[f^{-1}]$ is a
$M[f^{-1}]$ is a ![]() $\mathcal {D}(X)$-module of minimal dimension, so that
$\mathcal {D}(X)$-module of minimal dimension, so that
by Proposition 7.2. But by [Reference Bitoun and BodeBB21, Proposition 2.14], the natural morphism
is a surjection of coadmissible ![]() $\widehat {\mathcal {D}}(X)$-modules, so
$\widehat {\mathcal {D}}(X)$-modules, so ![]() $d_{\widehat {\mathcal {D}}(X)}(\mathcal {M}(U))=\dim X$ by Proposition 7.1.
$d_{\widehat {\mathcal {D}}(X)}(\mathcal {M}(U))=\dim X$ by Proposition 7.1.
We can now give a proof of Theorem C.
Theorem Let ![]() $j: U\to X$ be a Zariski open embedding of smooth rigid analytic
$j: U\to X$ be a Zariski open embedding of smooth rigid analytic ![]() $K$-spaces, and let
$K$-spaces, and let ![]() $\mathcal {M}$ be an integrable connection on
$\mathcal {M}$ be an integrable connection on ![]() $X$. Then
$X$. Then ![]() $\mathrm {R}^{i}j_*(\mathcal {M}|_U)$ is a coadmissible, weakly holonomic
$\mathrm {R}^{i}j_*(\mathcal {M}|_U)$ is a coadmissible, weakly holonomic ![]() $\widehat {\mathcal {D}}_X$-module for each
$\widehat {\mathcal {D}}_X$-module for each ![]() $i\geq 0$.
$i\geq 0$.
Proof. Without loss of generality, ![]() $X=\operatorname {Sp} A$ is affinoid with free tangent sheaf. There are finitely many elements
$X=\operatorname {Sp} A$ is affinoid with free tangent sheaf. There are finitely many elements ![]() $f_1, \dots , f_r\in A$ such that
$f_1, \dots , f_r\in A$ such that ![]() $U=X\setminus V(f_1, \dots , f_r)$. Note that the
$U=X\setminus V(f_1, \dots , f_r)$. Note that the ![]() $X_{f_i}$ form an admissible covering of
$X_{f_i}$ form an admissible covering of ![]() $U$, which we denote by
$U$, which we denote by ![]() $\mathfrak {V}$.
$\mathfrak {V}$.
By Corollary 10.1, ![]() $\mathrm {R}^{i}j_*(\mathcal {M}|_U)(X)\cong \check {\mathrm {H}}^{i}(\mathfrak {V}, \mathcal {M}|_U)$. By Lemma 10.5,
$\mathrm {R}^{i}j_*(\mathcal {M}|_U)(X)\cong \check {\mathrm {H}}^{i}(\mathfrak {V}, \mathcal {M}|_U)$. By Lemma 10.5, ![]() $\check {C}^{\bullet }(\mathfrak {V}, \mathcal {M}|_U)$ is a complex of coadmissible
$\check {C}^{\bullet }(\mathfrak {V}, \mathcal {M}|_U)$ is a complex of coadmissible ![]() $\widehat {\mathcal {D}}_X(X)$-modules of minimal dimension, so
$\widehat {\mathcal {D}}_X(X)$-modules of minimal dimension, so ![]() $\mathrm {R}^{i}j_*(\mathcal {M}|_U)(X)$ is a coadmissible
$\mathrm {R}^{i}j_*(\mathcal {M}|_U)(X)$ is a coadmissible ![]() $\widehat {\mathcal {D}}_X(X)$-module of minimal dimension by Proposition 7.1.
$\widehat {\mathcal {D}}_X(X)$-module of minimal dimension by Proposition 7.1.
10.6 Local cohomology
Let ![]() $X$ be a smooth rigid analytic
$X$ be a smooth rigid analytic ![]() $K$-space and let
$K$-space and let ![]() $Z$ be a closed analytic subset. The local cohomology sheaf functor
$Z$ be a closed analytic subset. The local cohomology sheaf functor ![]() $\underline {H}^{i}_Z(-)$ is then, as usual, the
$\underline {H}^{i}_Z(-)$ is then, as usual, the ![]() $i$th derived functor of
$i$th derived functor of ![]() $\underline {H}^{0}_Z(-)$, which assigns to a coherent
$\underline {H}^{0}_Z(-)$, which assigns to a coherent ![]() $\mathcal {O}_X$-module its maximal subsheaf with support in
$\mathcal {O}_X$-module its maximal subsheaf with support in ![]() $Z$ (see [Reference KisinKis99, Definition 2.1.3]).
$Z$ (see [Reference KisinKis99, Definition 2.1.3]).
Theorem Let ![]() $Z$ be a closed analytic subset of a smooth rigid analytic
$Z$ be a closed analytic subset of a smooth rigid analytic ![]() $K$-space
$K$-space ![]() $X$. Let
$X$. Let ![]() $\mathcal {M}$ be an integrable connection on
$\mathcal {M}$ be an integrable connection on ![]() $X$. Then
$X$. Then ![]() $\underline {H}^{i}_Z(\mathcal {M})$ is a coadmissible, weakly holonomic
$\underline {H}^{i}_Z(\mathcal {M})$ is a coadmissible, weakly holonomic ![]() $\widehat {\mathcal {D}}_X$-module for each
$\widehat {\mathcal {D}}_X$-module for each ![]() $i\geq 0$.
$i\geq 0$.
Proof. Suppose that ![]() $X$ is affinoid with free tangent sheaf. Let
$X$ is affinoid with free tangent sheaf. Let ![]() $j:U\to X$ be the complement of
$j:U\to X$ be the complement of ![]() $Z$. As in [Reference KisinKis99, Proposition 2.1.4], we can consider the exact sequence
$Z$. As in [Reference KisinKis99, Proposition 2.1.4], we can consider the exact sequence
as well as the isomorphism ![]() $\underline {H}^{i}_Z(\mathcal {M})\cong \mathrm {R}^{i-1}j_*(\mathcal {M}|_U)$ for any
$\underline {H}^{i}_Z(\mathcal {M})\cong \mathrm {R}^{i-1}j_*(\mathcal {M}|_U)$ for any ![]() $i\geq 2$. Thus the result follows immediately from Theorem 10.5 for
$i\geq 2$. Thus the result follows immediately from Theorem 10.5 for ![]() $i\geq 2$, and from the fact that
$i\geq 2$, and from the fact that ![]() $\mathcal {C}_X^{\mathrm {wh}}$ is an abelian category for
$\mathcal {C}_X^{\mathrm {wh}}$ is an abelian category for ![]() $i=0, 1$.
$i=0, 1$.