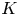1. Introduction
1.1
This paper is about power operations.

1.2 Overview
A power operation is an enhanced version of a ![]() $p$th-power, or more generally
$p$th-power, or more generally ![]() $n$th-power, map. One of the most famous examples is Steenrod's operations [Reference Steenrod and EpsteinSE62], a cornerstone of algebraic topology. We will give an account of Steenrod's construction in the language of derived categories. To be precise, we produce a categorical version of the ‘total external Steenrod operation’. When we look at what this construction does to the constant sheaf and compose with a diagonal restriction functor, we recover the Steenrod cohomology operations; when instead we focus attention on the dualizing complex of an
$n$th-power, map. One of the most famous examples is Steenrod's operations [Reference Steenrod and EpsteinSE62], a cornerstone of algebraic topology. We will give an account of Steenrod's construction in the language of derived categories. To be precise, we produce a categorical version of the ‘total external Steenrod operation’. When we look at what this construction does to the constant sheaf and compose with a diagonal restriction functor, we recover the Steenrod cohomology operations; when instead we focus attention on the dualizing complex of an ![]() $E_2$-group and compose with a pushforward along the multiplication, we recover Kudo–Araki–Dyer–Lashof operations [Reference Kudo and ArakiKA56, Reference Dyer and LashofDL62]. However, the new context in which we put these old ideas allows us to make new observations about them, including a fundamental relationship between Steenrod operations and the Artin–Schreier morphism, and one between Kudo–Araki–Dyer–Lashof operations and the concept of Frobenius constancy, proving the Frobenius constancy of all quantum Coulomb branches [Reference Braverman, Finkelberg and NakajimaBFN16] in the process. We use a version of this construction adapted to perverse sheaves to provide a geometric description of the functor which corresponds under geometric Satake [Reference Mirković and VilonenMV07] to the Frobenius twist functor from the theory of algebraic groups, and give a conjectural description of the compatibility between these structures and the (unproven at the time of writing) ‘derived geometric Satake’ (see [Reference Bezrukavnikov and FinkelbergBF08] for the characteristic
$E_2$-group and compose with a pushforward along the multiplication, we recover Kudo–Araki–Dyer–Lashof operations [Reference Kudo and ArakiKA56, Reference Dyer and LashofDL62]. However, the new context in which we put these old ideas allows us to make new observations about them, including a fundamental relationship between Steenrod operations and the Artin–Schreier morphism, and one between Kudo–Araki–Dyer–Lashof operations and the concept of Frobenius constancy, proving the Frobenius constancy of all quantum Coulomb branches [Reference Braverman, Finkelberg and NakajimaBFN16] in the process. We use a version of this construction adapted to perverse sheaves to provide a geometric description of the functor which corresponds under geometric Satake [Reference Mirković and VilonenMV07] to the Frobenius twist functor from the theory of algebraic groups, and give a conjectural description of the compatibility between these structures and the (unproven at the time of writing) ‘derived geometric Satake’ (see [Reference Bezrukavnikov and FinkelbergBF08] for the characteristic ![]() $0$ case), through the newly proposed ‘Frobenius character twist’. A key geometric input is our extension of the theory of Beilinson–Drinfeld Grassmannians [Reference Beĭlinson and DrinfeldBD91] which in particular yields a generalization of the ‘global convolution diagram’ to the case of the variety of triples [Reference Braverman, Finkelberg and NakajimaBFN16].
$0$ case), through the newly proposed ‘Frobenius character twist’. A key geometric input is our extension of the theory of Beilinson–Drinfeld Grassmannians [Reference Beĭlinson and DrinfeldBD91] which in particular yields a generalization of the ‘global convolution diagram’ to the case of the variety of triples [Reference Braverman, Finkelberg and NakajimaBFN16].
A reader who knows about equivariant constructible derived categories on complex algebraic varieties will be able to understand these constructions even if they do not know any homotopy theory. Perhaps this is an advantage.
1.3
In § 2, we will give an account of Steenrod's construction in the language of derived categories. In these terms, the construction itself is very simple, and it yields not only Steenrod's cohomology operations but also operations in Borel–Moore homology, which are related to the Kudo–Araki–Dyer–Lashof operations.
1.4
In § 3, we will introduce a different type of power operation, due to Bezrukavnikov and Kaledin [Reference Bezrukavnikov and KaledinBK08], which is an important tool in non-commutative algebraic geometry. Such a power operation is known as a Frobenius-constant quantization. Essentially, a Frobenius-constant quantization of a commutative algebra ![]() $A$ over
$A$ over ![]() $\mathbb {F}_{\rm p}$ is a one-parameter flat deformation
$\mathbb {F}_{\rm p}$ is a one-parameter flat deformation ![]() $A_\hbar$ of
$A_\hbar$ of ![]() $A$ in associative algebras which has a large center; see § 3.1 for a precise definition which also justifies regarding such a thing as a power operation. The main example is the Weyl algebra
$A$ in associative algebras which has a large center; see § 3.1 for a precise definition which also justifies regarding such a thing as a power operation. The main example is the Weyl algebra
which contains ![]() $x^p$,
$x^p$, ![]() $\partial ^p$ in its center.
$\partial ^p$ in its center.
1.5
We will then illustrate a general method to apply Steenrod's construction to produce Frobenius-constant quantizations.
Remark 1.1 The method is on the fundamental level purely homotopical, and is known to the author to apply to any ![]() $S^1$-framed
$S^1$-framed ![]() $E_3$-ring spectrum over
$E_3$-ring spectrum over ![]() $\mathbb {F}_p$. For example, it can be used in conjunction with ideas of derived algebraic geometry to explain the famous result that the algebra of differential operators on a smooth variety of characteristic
$\mathbb {F}_p$. For example, it can be used in conjunction with ideas of derived algebraic geometry to explain the famous result that the algebra of differential operators on a smooth variety of characteristic ![]() $p$ is a Frobenius-constant quantization of the ring of functions on its cotangent bundle. This appears on the surface to be of a very different flavor than the main thrust of the present paper, which is primarily concerned with mod
$p$ is a Frobenius-constant quantization of the ring of functions on its cotangent bundle. This appears on the surface to be of a very different flavor than the main thrust of the present paper, which is primarily concerned with mod ![]() $p$ homology rings on complex algebraic varieties. As previously mentioned, in this paper we take a point of view practically devoid of homotopy theory. I hope that homotopy theorists will be able to read between the lines!
$p$ homology rings on complex algebraic varieties. As previously mentioned, in this paper we take a point of view practically devoid of homotopy theory. I hope that homotopy theorists will be able to read between the lines!
The example which we use to illustrate the method is the quantum Coulomb branch of Braverman, Finkelberg and Nakajima [Reference Braverman, Finkelberg and NakajimaBFN16], or rather, its natural characteristic ![]() $p$ version. That is, we prove the following theorem.
$p$ version. That is, we prove the following theorem.
Theorem 1.2 For any complex reductive algebraic group ![]() $G$, and finite-dimensional representation
$G$, and finite-dimensional representation ![]() $\boldsymbol {N}$ of
$\boldsymbol {N}$ of ![]() $G$, and any odd prime
$G$, and any odd prime ![]() $p$, the corresponding mod
$p$, the corresponding mod ![]() $p$ quantum Coulomb branch is a Frobenius-constant quantization.
$p$ quantum Coulomb branch is a Frobenius-constant quantization.
The Coulomb branch is the ![]() $G$-equivariant mod
$G$-equivariant mod ![]() $p$ Borel–Moore homology of a certain complex algebraic space
$p$ Borel–Moore homology of a certain complex algebraic space ![]() $\mathcal {R}$ related to the affine Grassmannian
$\mathcal {R}$ related to the affine Grassmannian ![]() $Gr$ of
$Gr$ of ![]() $G$. The space
$G$. The space ![]() $\mathcal {R}$ is equipped with a ‘loop-rotation’
$\mathcal {R}$ is equipped with a ‘loop-rotation’ ![]() $\mathbb {C}^*$-action, and the quantum Coulomb branch is obtained by switching on loop-rotation equivariance; the deformation parameter
$\mathbb {C}^*$-action, and the quantum Coulomb branch is obtained by switching on loop-rotation equivariance; the deformation parameter ![]() $\hbar$ enters as the
$\hbar$ enters as the ![]() $\mathbb {C}^*$-equivariant cohomology of a point. The key geometric insight behind Theorem 1.2 is that, following ideas of Beilinson and Drinfeld [Reference Beĭlinson and DrinfeldBD91], one may deform the space
$\mathbb {C}^*$-equivariant cohomology of a point. The key geometric insight behind Theorem 1.2 is that, following ideas of Beilinson and Drinfeld [Reference Beĭlinson and DrinfeldBD91], one may deform the space ![]() $\mathcal {R}$ into to
$\mathcal {R}$ into to ![]() $\mathcal {R}^p$, in such a way that the action of
$\mathcal {R}^p$, in such a way that the action of ![]() $C_p$ (the cyclic group of order
$C_p$ (the cyclic group of order ![]() $p$) on
$p$) on ![]() $\mathcal {R}$, which applies the loop rotation by
$\mathcal {R}$, which applies the loop rotation by ![]() $p$th roots of unity, is deformed to the
$p$th roots of unity, is deformed to the ![]() $C_p$ action on
$C_p$ action on ![]() $\mathcal {R}^p$, which permutes the factors cyclically.
$\mathcal {R}^p$, which permutes the factors cyclically.
Example 1.3 Recall that the affine Grassmannian ![]() $Gr$ of the complex reductive group
$Gr$ of the complex reductive group ![]() $G$ is an algebraization of the space
$G$ is an algebraization of the space ![]() $\Omega ^{\mathrm {pol}} K$ of based polynomial loops in a fixed compact form
$\Omega ^{\mathrm {pol}} K$ of based polynomial loops in a fixed compact form ![]() $K$ of
$K$ of ![]() $G$; this is homotopy equivalent to the space
$G$; this is homotopy equivalent to the space ![]() $\Omega K$ of all based loops in
$\Omega K$ of all based loops in ![]() $K$. The
$K$. The ![]() $S^1$-action on
$S^1$-action on ![]() $\Omega K$ given by rotating loops and then renormalizing (by dividing on the right, say, by the value at
$\Omega K$ given by rotating loops and then renormalizing (by dividing on the right, say, by the value at ![]() $1\in K$) corresponds to the loop-rotation action of
$1\in K$) corresponds to the loop-rotation action of ![]() $\mathbb {C}^*$ on
$\mathbb {C}^*$ on ![]() $Gr$. We give a heuristic explanation, in terms of
$Gr$. We give a heuristic explanation, in terms of ![]() $\Omega K$ and its ‘renormalized loop-rotation’ action, of the key geometric insight mentioned above, in the case
$\Omega K$ and its ‘renormalized loop-rotation’ action, of the key geometric insight mentioned above, in the case ![]() $\mathcal {R} = Gr$.
$\mathcal {R} = Gr$.
Recall first that ![]() $\Omega K$ has a (strict) group structure given by pointwise multiplication of loops (using the group structure of
$\Omega K$ has a (strict) group structure given by pointwise multiplication of loops (using the group structure of ![]() $K$), and this is reflected in the existence of a convolution diagram for
$K$), and this is reflected in the existence of a convolution diagram for ![]() $Gr$. Next, recall that
$Gr$. Next, recall that ![]() $\Omega K$ has a (homotopy) group structure given by concatenation of based loops, and this is reflected in the existence of the Beilinson–Drinfeld affine Grassmannian, which is a deformation of
$\Omega K$ has a (homotopy) group structure given by concatenation of based loops, and this is reflected in the existence of the Beilinson–Drinfeld affine Grassmannian, which is a deformation of ![]() $Gr$ into
$Gr$ into ![]() $Gr^2$. Moreover, these two group structures of
$Gr^2$. Moreover, these two group structures of ![]() $\Omega K$ commute (up to homotopy) and are part of an
$\Omega K$ commute (up to homotopy) and are part of an ![]() $S^1$-family of group structures. This is reflected in the existence of a ‘global convolution diagram’ linking the convolution diagram and the Beilinson–Drinfeld Grassmannian. Thus we have a kind of dictionary between some homotopy-theoretical structures and some algebraic structures. The algebraic structures are not strict algebraizations of their topological counterparts (at least in any obvious sense), but we shall say that they correspond under the ‘algebraization paradigm’ (for want of a better term).
$S^1$-family of group structures. This is reflected in the existence of a ‘global convolution diagram’ linking the convolution diagram and the Beilinson–Drinfeld Grassmannian. Thus we have a kind of dictionary between some homotopy-theoretical structures and some algebraic structures. The algebraic structures are not strict algebraizations of their topological counterparts (at least in any obvious sense), but we shall say that they correspond under the ‘algebraization paradigm’ (for want of a better term).
Now, consider the map
which speeds up each loop by a factor of ![]() $p$ and then concatenates the results. Observe that the action of
$p$ and then concatenates the results. Observe that the action of ![]() $C_p$ on the left by cyclic permutation of the factors is compatible under this map by the ‘renormalized loop-rotation’ action of
$C_p$ on the left by cyclic permutation of the factors is compatible under this map by the ‘renormalized loop-rotation’ action of ![]() $C_p$ as a subgroup of
$C_p$ as a subgroup of ![]() $S^1$ on the right. Our ‘key geometric insight’ is essentially what corresponds to this under the algebraization paradigm.
$S^1$ on the right. Our ‘key geometric insight’ is essentially what corresponds to this under the algebraization paradigm.
Remark 1.4 We will never again use the notation ![]() $C_p$, since every finite cyclic group considered will be given as a subgroup of
$C_p$, since every finite cyclic group considered will be given as a subgroup of ![]() $\mathbb {C}^*$. We will use the notation
$\mathbb {C}^*$. We will use the notation ![]() $\mu _p$ instead. Given an algebraic space
$\mu _p$ instead. Given an algebraic space ![]() $X$ and a finite set
$X$ and a finite set ![]() $S$, we will write
$S$, we will write ![]() $X^S$ for
$X^S$ for ![]() $\operatorname {Hom}(S, X)$, that is, the product of
$\operatorname {Hom}(S, X)$, that is, the product of ![]() $X$ with itself
$X$ with itself ![]() $|S|$ times with factors being labeled by the elements of
$|S|$ times with factors being labeled by the elements of ![]() $S$. Bringing these together, be warned that the expression
$S$. Bringing these together, be warned that the expression ![]() $X^{\mu _p}$ denotes the
$X^{\mu _p}$ denotes the ![]() $p$-fold product of
$p$-fold product of ![]() $X$ with itself labeled by the elements of
$X$ with itself labeled by the elements of ![]() $\mu _p$, and does not denote the fixed points of some action of
$\mu _p$, and does not denote the fixed points of some action of ![]() $\mu _p$ on
$\mu _p$ on ![]() $X$.
$X$.
1.6
This is already quite a broad class of examples: for instance, partially spherical rational Cherednik algebras; see [Reference Braverman, Etingof and FinkelbergBEF20, Reference WebsterWeb19]. It is expected that the same underlying geometry will lead to the discovery of large centers of related algebras. In fact, in § 4 we indicate how the same underlying geometry shows that the ![]() $K$-theoretic version of integral quantum Coulomb branch, which is itself a
$K$-theoretic version of integral quantum Coulomb branch, which is itself a ![]() $q$-deformation of the
$q$-deformation of the ![]() $K$-theoretic version of the Coulomb branch, admits a large center when
$K$-theoretic version of the Coulomb branch, admits a large center when ![]() $q$ is evaluated at any complex root of unity (not necessarily of prime order). Essentially the only difference with the homological case is to replace Steenrod's construction with a so-called ‘Adams construction’ which is to Adams operations as Steenrod's construction is to Steenrod's operations.
$q$ is evaluated at any complex root of unity (not necessarily of prime order). Essentially the only difference with the homological case is to replace Steenrod's construction with a so-called ‘Adams construction’ which is to Adams operations as Steenrod's construction is to Steenrod's operations.
Question 1.5 Is it possible to develop the theory of equivariant elliptic Borel–Moore homology far enough to deduce the analogous ‘large center’ statements for the elliptic analogues of the Coulomb branch?
1.7
In the final section, we investigate the meaning of our constructions on the level of the constructible derived category. We are especially interested in understanding what our constructions correspond to in terms of representations of the Langlands dual group ![]() $G^\vee _{\mathbb {F}_{\rm p}}$ over
$G^\vee _{\mathbb {F}_{\rm p}}$ over ![]() $\mathbb {F}_{\rm p}$.
$\mathbb {F}_{\rm p}$.
Conjecture 1.6 (i) For sufficiently large ![]() $p$, there are monoidal equivalences (‘derived geometric Satake with coefficients modulo
$p$, there are monoidal equivalences (‘derived geometric Satake with coefficients modulo ![]() $p$’; see [Reference Bezrukavnikov and FinkelbergBF08] for the version with complex coefficients):
$p$’; see [Reference Bezrukavnikov and FinkelbergBF08] for the version with complex coefficients):
 \begin{gather*} D^b_{G(\mathcal{O})}(Gr, \mathbb{F}_{\rm p}) \cong Coh^{fr}_{ G^\vee_{\mathbb{F}_{\rm p}} }(\operatorname{Sym}( \mathfrak{g}^{{\vee}}_{\mathbb{F}_{\rm p}}[{-}2]) ),\\ D^b_{G(\mathcal{O})\,\rtimes\, \mathbb{C}^*}(Gr, \mathbb{F}_{\rm p}) \cong Coh^{fr}_{ G^\vee_{\mathbb{F}_{\rm p}} }( \mathcal{U}_\hbar (\mathfrak{g}^{{\vee}}_{\mathbb{F}_{\rm p}}[{-}2]) ). \end{gather*}
\begin{gather*} D^b_{G(\mathcal{O})}(Gr, \mathbb{F}_{\rm p}) \cong Coh^{fr}_{ G^\vee_{\mathbb{F}_{\rm p}} }(\operatorname{Sym}( \mathfrak{g}^{{\vee}}_{\mathbb{F}_{\rm p}}[{-}2]) ),\\ D^b_{G(\mathcal{O})\,\rtimes\, \mathbb{C}^*}(Gr, \mathbb{F}_{\rm p}) \cong Coh^{fr}_{ G^\vee_{\mathbb{F}_{\rm p}} }( \mathcal{U}_\hbar (\mathfrak{g}^{{\vee}}_{\mathbb{F}_{\rm p}}[{-}2]) ). \end{gather*}
Here the left-hand categories denote the equivariant constructible derived categories with coefficients in ![]() $\mathbb {F}_{\rm p}$ in the sense of Bernstein and Lunts [Reference Bernstein and LuntsBL06]. As for the right-hand side,
$\mathbb {F}_{\rm p}$ in the sense of Bernstein and Lunts [Reference Bernstein and LuntsBL06]. As for the right-hand side, ![]() $\mathfrak {g}^{\vee }_{\mathbb {F}_{\rm p}}[-2]$ denotes the Lie algebra of
$\mathfrak {g}^{\vee }_{\mathbb {F}_{\rm p}}[-2]$ denotes the Lie algebra of ![]() $G^{\vee }_{\mathbb {F}_{\rm p}}$ placed in cohomological degree
$G^{\vee }_{\mathbb {F}_{\rm p}}$ placed in cohomological degree ![]() $2$,
$2$, ![]() $\operatorname {Sym}(\mathfrak {g}^{\vee }_{\mathbb {F}_{\rm p}}[-2])$ denotes its symmetric algebra (considered as a commutative differential graded (dg) algebra with trivial differential) and
$\operatorname {Sym}(\mathfrak {g}^{\vee }_{\mathbb {F}_{\rm p}}[-2])$ denotes its symmetric algebra (considered as a commutative differential graded (dg) algebra with trivial differential) and ![]() $\mathcal {U}_\hbar (\mathfrak {g}^{\vee }_{\mathbb {F}_{\rm p}}[-2] )$ denotes its canonical (Poincaré–Birkhoff–Witt) one-parameter deformation to a non-commutative dg-algebra with
$\mathcal {U}_\hbar (\mathfrak {g}^{\vee }_{\mathbb {F}_{\rm p}}[-2] )$ denotes its canonical (Poincaré–Birkhoff–Witt) one-parameter deformation to a non-commutative dg-algebra with ![]() $\hbar$ in cohomological degree
$\hbar$ in cohomological degree ![]() $2$ (also with trivial differential). The expression
$2$ (also with trivial differential). The expression ![]() $Coh^{fr}_{ G^\vee _{\mathbb {F}_{\rm p}} }(*)$ denotes the full triangulated subcategory of the (derived) category of
$Coh^{fr}_{ G^\vee _{\mathbb {F}_{\rm p}} }(*)$ denotes the full triangulated subcategory of the (derived) category of ![]() $G^\vee _{\mathbb {F}_{\rm p}}$-equivariant dg-modules generated by the objects which are free over the
$G^\vee _{\mathbb {F}_{\rm p}}$-equivariant dg-modules generated by the objects which are free over the ![]() $G^\vee _{\mathbb {F}_{\rm p}}$-equivariant dg-algebra
$G^\vee _{\mathbb {F}_{\rm p}}$-equivariant dg-algebra ![]() $(*)$.
$(*)$.
(ii) (Paraphrasing), our geometric construction, when reinterpreted on the level of equivariant constructible derived categories, yields a triangulated functor
which corresponds under the above equivalences to the functor
which is the composition of the external Steenrod/Tate power functor
followed by the restriction of equivariance along the Frobenius map
followed by the base change along the ![]() $G^\vee _{\mathbb {F}_{\rm p}}$-equivariant central flat algebra extension
$G^\vee _{\mathbb {F}_{\rm p}}$-equivariant central flat algebra extension
In particular, for a representation ![]() $V$ of
$V$ of ![]() $G^\vee _{\mathbb {F}_{\rm p}}$, this functor sends the free object
$G^\vee _{\mathbb {F}_{\rm p}}$, this functor sends the free object
to the free object
Here ![]() $V^{(1)}$ denotes the Frobenius twist of
$V^{(1)}$ denotes the Frobenius twist of ![]() $V$, that is, the
$V$, that is, the ![]() $G^\vee _{\mathbb {F}_{\rm p}}$-representation obtained from
$G^\vee _{\mathbb {F}_{\rm p}}$-representation obtained from ![]() $V$ by pulling back along the Frobenius map. It is therefore reasonable to regard our functor as the correct ‘Frobenius twist’ functor in this context (indeed we do not believe there to be any alternative). We call this functor the ‘Frobenius character twist’, since its source and target are in some sense categories of character sheaves.
$V$ by pulling back along the Frobenius map. It is therefore reasonable to regard our functor as the correct ‘Frobenius twist’ functor in this context (indeed we do not believe there to be any alternative). We call this functor the ‘Frobenius character twist’, since its source and target are in some sense categories of character sheaves.
(iii) The Frobenius character twist is a central monoidal functor, that is, it admits a monoidal lift through the monoidal center of its target. This is not really conjectural: it is provably true of both our geometrically constructed functor and the Frobenius character twist, and the compatibility of the two lifts would surely follow from any proof of the earlier parts of the conjecture.
Although the above picture is conjectural (mainly because we cannot prove derived geometric Satake with coefficients modulo ![]() $p$), we can prove an underived version. Namely, we give a geometric description of the functor
$p$), we can prove an underived version. Namely, we give a geometric description of the functor
which corresponds to the Frobenius twist functor under the underived geometric Satake equivalence [Reference Mirković and VilonenMV07]
The construction is as follows. Consider the ![]() $\mu _p$-equivariant deformation
$\mu _p$-equivariant deformation ![]() $Gr_{(p)}$ of
$Gr_{(p)}$ of ![]() $Gr$ (with loop rotation) to
$Gr$ (with loop rotation) to ![]() $Gr^p$ (with cyclic permutation). Given a spherical perverse sheaf
$Gr^p$ (with cyclic permutation). Given a spherical perverse sheaf ![]() $\mathcal {F}\in Perv_{\mathrm {sph}}(Gr,\mathbb {F}_{\rm p})$, one may view its
$\mathcal {F}\in Perv_{\mathrm {sph}}(Gr,\mathbb {F}_{\rm p})$, one may view its ![]() $p$th external power as a spherical perverse sheaf on
$p$th external power as a spherical perverse sheaf on ![]() $Gr_{(p)}|_{\mathbb {A}^1-\{0\}}$ and take the IC sheaf of the result:
$Gr_{(p)}|_{\mathbb {A}^1-\{0\}}$ and take the IC sheaf of the result:
Let ![]() $i:Gr\to Gr_{(p)}$ denote the inclusion of the zero fiber of the deformation. Then we have a Thom map
$i:Gr\to Gr_{(p)}$ denote the inclusion of the zero fiber of the deformation. Then we have a Thom map ![]() $i^*[-1]\to i^![1]$, and this gives us a map of perverse sheaves
$i^*[-1]\to i^![1]$, and this gives us a map of perverse sheaves
Let ![]() $Fr(\mathcal {F})$ denote the image of the above Thom map.
$Fr(\mathcal {F})$ denote the image of the above Thom map.
Theorem 1.7 ![]() $Fr$ is the required functor. That is, if
$Fr$ is the required functor. That is, if
denotes the Frobenius twist functor, then we have an equivalence
where ![]() $S$ is the geometric Satake equivalence.
$S$ is the geometric Satake equivalence.
This appears as Theorem 5.1 in the text.
1.8 Background required to read this paper.
(i) Homotopy theory. As previously mentioned, no homotopy theory (besides the basics of homology and cohomology) is required to read this paper, despite the fact that its arguments are actually quite relevant to homotopy theory. Familiarity with Steenrod operations may help, but on the other hand may not because our approach is somewhat non-traditional and can be confusing to homotopy theorists. In any case that aspect of this paper is self-contained.
(ii) Algebraic geometry. We will use heavily S. Raskin's theory of placid ind-schemes [Reference RaskinRas15]. This is a beautiful theory describing a certain class of infinite-dimensional algebro-geometric objects (placid ind-schemes) which can be handled, via some categorical bookkeeping, in essentially the same way as finite-type schemes. It does not rely on any algebraic geometry deeper than a basic understanding of the functorial approach based on the Yoneda embedding and fundamental concepts such as flatness and smoothness, and nor does the present paper. We will try to explain enough of the material of [Reference RaskinRas15] ourselves that the reader need not constantly refer to it (it is nonetheless highly recommended reading).
All the algebro-geometric objects we consider will be defined over ![]() $\mathbb {C}$, and although we will use the Yoneda embedding to define them and reason about them, we will always think of them as complex analytic spaces when considering their invariants (homology, sheaf categories etc.). No understanding of stacks is required, even though much of the geometry can be interpreted in terms of quotient stacks.
$\mathbb {C}$, and although we will use the Yoneda embedding to define them and reason about them, we will always think of them as complex analytic spaces when considering their invariants (homology, sheaf categories etc.). No understanding of stacks is required, even though much of the geometry can be interpreted in terms of quotient stacks.
(iii) Sheaf theory. We use Bernstein and Lunts’ theory of equivariant constructible derived categories [Reference Bernstein and LuntsBL06] in order to build invariants out of our complex geometric objects. In particular, this involves forgetting about their algebro-geometric nature and replacing them by their sets of ![]() $\mathbb {C}$-points with the analytic topology. The primary alternative is to stay in the world of algebraic geometry and use the étale topology. Although using the étale topology has some well-known advantages (e.g. the theory of weights), we do not need them in the present work and so prefer to stick to the (in our opinion) conceptually easier analytic topology framework. The reader who is more comfortable with the étale topology most likely has no difficulty translating our results in those terms. Section 5 also uses the theory of perverse sheaves; cf. [Reference Deligne, Beĭlinson and BernsteinDBB83].
$\mathbb {C}$-points with the analytic topology. The primary alternative is to stay in the world of algebraic geometry and use the étale topology. Although using the étale topology has some well-known advantages (e.g. the theory of weights), we do not need them in the present work and so prefer to stick to the (in our opinion) conceptually easier analytic topology framework. The reader who is more comfortable with the étale topology most likely has no difficulty translating our results in those terms. Section 5 also uses the theory of perverse sheaves; cf. [Reference Deligne, Beĭlinson and BernsteinDBB83].
The reader who is not familiar with either theory of constructible derived categories but knows a little more homotopy theory may still be able to understand everything apart from § 5 which is explicitly about Bernstein and Lunts’ category. For, apart from in that section, we are only really using the constructible derived category as a mechanism for producing structures on Borel–Moore homology, and for this there are purely homotopical means. To be precise, although we describe operations on the level of the constructible derived category, ultimately we restrict attention to their effect on a single object, the dualizing complex ![]() $\omega$; and even then we only really care about its global sections complex
$\omega$; and even then we only really care about its global sections complex ![]() $\Gamma (X, \omega )$, which is (by definition) just the Borel–Moore complex of
$\Gamma (X, \omega )$, which is (by definition) just the Borel–Moore complex of ![]() $X$, that is, the reduced singular complex of the one-point compactification of
$X$, that is, the reduced singular complex of the one-point compactification of ![]() $X$ (denoted
$X$ (denoted ![]() $\mathbb {F}_{\rm p}\wedge \bar {X}$). If
$\mathbb {F}_{\rm p}\wedge \bar {X}$). If ![]() $X$ is equipped with the action of a group
$X$ is equipped with the action of a group ![]() $G$, then so is
$G$, then so is ![]() $\mathbb {F}_{\rm p}\wedge \bar {X}$, and the notation
$\mathbb {F}_{\rm p}\wedge \bar {X}$, and the notation
will refer to the ![]() $-n$th homotopy groups of the
$-n$th homotopy groups of the ![]() $G$-homotopy invariants of
$G$-homotopy invariants of ![]() $\mathbb {F}_{\rm p}\wedge \bar {X}$. If the reader bears this in mind, they should be able to translate enough of what is phrased in terms of constructible derived categories to fully understand the main result about the (quantum) Coulomb branch.
$\mathbb {F}_{\rm p}\wedge \bar {X}$. If the reader bears this in mind, they should be able to translate enough of what is phrased in terms of constructible derived categories to fully understand the main result about the (quantum) Coulomb branch.
(iv) Representation theory. The definition of the Coulomb branch (originally found in [Reference Braverman, Finkelberg and NakajimaBFN16]) takes as input a complex reductive algebraic group plus a finite-dimensional representation, but one does not really need to know to this theory well to understand the definition and the other arguments. The constructions of [Reference Mirković and VilonenMV07, Reference Braverman, Finkelberg and NakajimaBFN16, Reference Braverman, Finkelberg and NakajimaBFN17] are used throughout the paper but are explained in reasonable detail here so, while helpful, are not necessary reading, except for § 5 where Mirković and Vilonen's geometric Satake equivalence [Reference Mirković and VilonenMV07] is essential.
2. Steenrod's construction
2.1 Overview
Let ![]() $p$ be an odd prime number, and let
$p$ be an odd prime number, and let ![]() $\mu _p$ be the group of complex
$\mu _p$ be the group of complex ![]() $p$th roots of unity. Let
$p$th roots of unity. Let ![]() $R$ be a commutative ring. Let
$R$ be a commutative ring. Let ![]() $k$ be a field of characteristic
$k$ be a field of characteristic ![]() $p$, and let
$p$, and let ![]() $F:k\to k$ be the Frobenius map. Let
$F:k\to k$ be the Frobenius map. Let ![]() $X$ be a topological space and let
$X$ be a topological space and let ![]() $D^+(X,R)$ denote the bounded-below derived category of sheaves of
$D^+(X,R)$ denote the bounded-below derived category of sheaves of ![]() $k$-modules on
$k$-modules on ![]() $X$. We write
$X$. We write ![]() $X^{\mu _p}$ for
$X^{\mu _p}$ for ![]() $\operatorname {Map}(\mu _p,X)$. Following Steenrod [Reference Steenrod and EpsteinSE62], we construct a functor
$\operatorname {Map}(\mu _p,X)$. Following Steenrod [Reference Steenrod and EpsteinSE62], we construct a functor
where ![]() $D^+_{\mu _p}(X^{\mu _p},R)$ denotes the bounded-below
$D^+_{\mu _p}(X^{\mu _p},R)$ denotes the bounded-below ![]() $\mu _p$-equivariant derived category of sheaves of
$\mu _p$-equivariant derived category of sheaves of ![]() $R$-modules on
$R$-modules on ![]() $X^{\mu _p}$. This functor is not linear or triangulated, but nonetheless if we take
$X^{\mu _p}$. This functor is not linear or triangulated, but nonetheless if we take ![]() $R=k$, compose with restriction to the diagonal and apply to morphisms between shifted constant sheaves we obtain linear maps
$R=k$, compose with restriction to the diagonal and apply to morphisms between shifted constant sheaves we obtain linear maps
for each ![]() $n\geq 0$. Recall that
$n\geq 0$. Recall that ![]() $H^*({\rm B}\mu _{\rm p},k)=k[a,\hbar ]$ is the super-polynomial algebra in one variable
$H^*({\rm B}\mu _{\rm p},k)=k[a,\hbar ]$ is the super-polynomial algebra in one variable ![]() $a$ of degree
$a$ of degree ![]() $1$ and one variable
$1$ and one variable ![]() $\hbar$ of degree
$\hbar$ of degree ![]() $2$. Here
$2$. Here ![]() $\hbar$ is the first Chern class of the tautological complex line bundle on
$\hbar$ is the first Chern class of the tautological complex line bundle on ![]() ${\rm B}\mu _{\rm p}$ arising from the embedding
${\rm B}\mu _{\rm p}$ arising from the embedding ![]() $\mu _p\subset \mathbb {C}^*$.
$\mu _p\subset \mathbb {C}^*$.
The direct sum of the maps of (2.1) is not in the most naive sense an algebra homomorphism. This fact led Steenrod to introduce certain correction factors which make it so; his famous cohomology operations are then defined to be the coefficients of the resulting algebra homomorphism in the monomial basis of ![]() $k[a,\hbar ]$. However, the sum of maps of (2.1) does give a homomorphism of super-graded algebras
$k[a,\hbar ]$. However, the sum of maps of (2.1) does give a homomorphism of super-graded algebras
where ![]() $H^*(X,k)^{(1)}$ denotes the Frobenius twist of
$H^*(X,k)^{(1)}$ denotes the Frobenius twist of ![]() $H^*(X,k)$. Naively one might think that this is just the
$H^*(X,k)$. Naively one might think that this is just the ![]() $p$-dilation of
$p$-dilation of ![]() $F^*H^*(X,k)$. This is wrong: rather, the natural and correct definition of the Frobenius twist of an algebra
$F^*H^*(X,k)$. This is wrong: rather, the natural and correct definition of the Frobenius twist of an algebra ![]() $A$ in any symmetric monoidal category over
$A$ in any symmetric monoidal category over ![]() $k$ is as the Tate cohomology
$k$ is as the Tate cohomology
where the symmetric monoidal structure endows ![]() $A^{\otimes\, \mu _p}$ with the structure of
$A^{\otimes\, \mu _p}$ with the structure of ![]() $\mu _p$-equivariant algebra. In the case of the super-graded
$\mu _p$-equivariant algebra. In the case of the super-graded ![]() $k$-algebra
$k$-algebra ![]() $H^*(X,k)$, the underlying super-graded
$H^*(X,k)$, the underlying super-graded ![]() $k$-module of this construction is the same as the
$k$-module of this construction is the same as the ![]() $p$-dilation of
$p$-dilation of ![]() $F^*H^*(X,k)$, but the multiplication differs by a sign (at least when
$F^*H^*(X,k)$, but the multiplication differs by a sign (at least when ![]() $p\equiv 3\text { mod 4}$), removal of which is part of the purpose of Steenrod's correction factors.
$p\equiv 3\text { mod 4}$), removal of which is part of the purpose of Steenrod's correction factors.
We prefer therefore to use Steenrod's operations in their raw form, that is, without the correction factors and packaged as in (2.2). This has the advantage of revealing the following fundamental connection between Steenrod's operations and the Artin–Schreier map, which is obscured by the correction factors.
Fact 2.1 (i) Let ![]() $X=BT$ for some complex torus
$X=BT$ for some complex torus ![]() $T$. Then the Picard group of
$T$. Then the Picard group of ![]() $X$ is canonically isomorphic to the character lattice
$X$ is canonically isomorphic to the character lattice ![]() $\mathbb {X}^\bullet (T)$ of
$\mathbb {X}^\bullet (T)$ of ![]() $T$, and the cohomology ring is the polynomial algebra
$T$, and the cohomology ring is the polynomial algebra
with ![]() $\mathbb {X}^\bullet (T)$ in degree
$\mathbb {X}^\bullet (T)$ in degree ![]() $2$. This is equal to the ring
$2$. This is equal to the ring ![]() $\mathcal {O}(\mathfrak {t}_{\mathbb {Z}})$ of polynomial functions on the canonical
$\mathcal {O}(\mathfrak {t}_{\mathbb {Z}})$ of polynomial functions on the canonical ![]() $\mathbb {Z}$-form of the scheme
$\mathbb {Z}$-form of the scheme ![]() $\mathfrak {t}=\operatorname {Lie}(T)$. Likewise we have
$\mathfrak {t}=\operatorname {Lie}(T)$. Likewise we have
where ![]() $\mathfrak {t}_{k}$ denotes the canonical
$\mathfrak {t}_{k}$ denotes the canonical ![]() $k$-form of
$k$-form of ![]() $\mathfrak {t}$.
$\mathfrak {t}$.
(ii) Under this identification, the map of (2.2) factors as
where ![]() $AS_\hbar$ corresponds, on the level of
$AS_\hbar$ corresponds, on the level of ![]() $\bar {k}$-points, to the
$\bar {k}$-points, to the ![]() $\bar {k}^\times$-equivariant family, parameterized by
$\bar {k}^\times$-equivariant family, parameterized by ![]() $\hbar \in \bar {k}$, of additive maps of free
$\hbar \in \bar {k}$, of additive maps of free ![]() $\bar {k}$-modules
$\bar {k}$-modules
 \[ \begin{matrix} \bar{k}\otimes\mathfrak{t}_{k} & \to & \bar{k}^{(1)}\otimes\mathfrak{t}_{k}\\ \displaystyle\sum_ix_i\otimes v_i & \mapsto & \displaystyle\sum_i(x_i^p-\hbar^{p-1}x_i)\otimes v_i \end{matrix} \]
\[ \begin{matrix} \bar{k}\otimes\mathfrak{t}_{k} & \to & \bar{k}^{(1)}\otimes\mathfrak{t}_{k}\\ \displaystyle\sum_ix_i\otimes v_i & \mapsto & \displaystyle\sum_i(x_i^p-\hbar^{p-1}x_i)\otimes v_i \end{matrix} \]
for a basis ![]() $\{v_i\}$ of
$\{v_i\}$ of ![]() $\mathfrak {t}_{\mathbb {F}_{\rm p}}$. This family interpolates between the usual Artin–Schreier map for
$\mathfrak {t}_{\mathbb {F}_{\rm p}}$. This family interpolates between the usual Artin–Schreier map for ![]() $\hbar =1$ and the Frobenius map for
$\hbar =1$ and the Frobenius map for ![]() $\hbar =0$.
$\hbar =0$.
Proof. (i) This is a standard fact which boils down to the calculation
the free algebra on the degree ![]() $2$ cochain
$2$ cochain ![]() $v^*=[\mathbb {C}\mathbb {P}^1]^*$ dual to the degree
$v^*=[\mathbb {C}\mathbb {P}^1]^*$ dual to the degree ![]() $2$ chain represented by the embedded
$2$ chain represented by the embedded ![]() $\mathbb {C}\mathbb {P}^1$. An isomorphism
$\mathbb {C}\mathbb {P}^1$. An isomorphism ![]() $T= (\mathbb {C}^*)^d$ gives an isomorphism
$T= (\mathbb {C}^*)^d$ gives an isomorphism
for any commutative ring ![]() $R$, and we will fix one for ease of exposition.
$R$, and we will fix one for ease of exposition.
(ii) This is just saying that the map of (2.2), when applied to ![]() $X = BT$, sends each generator
$X = BT$, sends each generator ![]() $v_i^*$ to
$v_i^*$ to ![]() $(v_i^*)^p-\hbar ^{p-1}v_i^*$. Since we have not actually defined the map (2.2) yet, we postpone the proof until § 2.8. However, notice that since
$(v_i^*)^p-\hbar ^{p-1}v_i^*$. Since we have not actually defined the map (2.2) yet, we postpone the proof until § 2.8. However, notice that since ![]() $v_i^*$ has degree
$v_i^*$ has degree ![]() $2$ the expected image
$2$ the expected image
is exactly the generating function of the Steenrod powers of ![]() $v_i^*$ (with placeholder variable
$v_i^*$ (with placeholder variable ![]() $\hbar$), up to some sign in the coefficients. Therefore the result will follow from a careful study of Steenrod's normalization factors (or rather, what happens if we don't use them!).
$\hbar$), up to some sign in the coefficients. Therefore the result will follow from a careful study of Steenrod's normalization factors (or rather, what happens if we don't use them!).
Remark 2.2 The appearance of ![]() $AS_\hbar$ in the topological setting was the first indication that Steenrod's construction might be related to the theory of Frobenius-constant quantizations, where
$AS_\hbar$ in the topological setting was the first indication that Steenrod's construction might be related to the theory of Frobenius-constant quantizations, where ![]() $AS_\hbar$ plays a central role; see Fact 3.2.
$AS_\hbar$ plays a central role; see Fact 3.2.
2.2 Steenrod's construction
Recall that ![]() $p$ is an odd prime,
$p$ is an odd prime, ![]() $\mu _p$ is the group of complex
$\mu _p$ is the group of complex ![]() $p$th roots of unity,
$p$th roots of unity, ![]() $R$ is a commutative ring,
$R$ is a commutative ring, ![]() $k$ is a field of characteristic
$k$ is a field of characteristic ![]() $p$ and
$p$ and ![]() $X$ is a topological space. We denote by
$X$ is a topological space. We denote by ![]() $C^+(X,R)$ (respectively,
$C^+(X,R)$ (respectively, ![]() $D^+(X,R)$) the category of bounded-below cochain complexes of sheaves of
$D^+(X,R)$) the category of bounded-below cochain complexes of sheaves of ![]() $R$-modules on
$R$-modules on ![]() $X$ (respectively, the corresponding bounded-below derived category). Recall that the latter is obtained from the former by inverting quasi-isomorphisms (this is important to us, and does not hold in the unbounded case). If
$X$ (respectively, the corresponding bounded-below derived category). Recall that the latter is obtained from the former by inverting quasi-isomorphisms (this is important to us, and does not hold in the unbounded case). If ![]() $Y$ is a topological space with an action of
$Y$ is a topological space with an action of ![]() $\mu _p$, we denote by
$\mu _p$, we denote by ![]() $C^+_{\mu _p}(Y,R)$,
$C^+_{\mu _p}(Y,R)$, ![]() $D^+_{\mu _p}(Y,R)$ the corresponding
$D^+_{\mu _p}(Y,R)$ the corresponding ![]() $\mu _p$-equivariant categories. Since
$\mu _p$-equivariant categories. Since ![]() $\mu _p$ is a finite group, these are the same as the (bounded-below) cochain, derived categories of
$\mu _p$ is a finite group, these are the same as the (bounded-below) cochain, derived categories of ![]() $\mu _p$-equivariant sheaves of
$\mu _p$-equivariant sheaves of ![]() $R$-modules on
$R$-modules on ![]() $Y$.
$Y$.
Consider the functor of ![]() $p$th external tensor power
$p$th external tensor power
It sends quasi-isomorphisms to quasi-isomorphisms, and so descends to a (non-triangulated) functor
by the universal property of derived categories. Notice that the cochain-level functor factors as
To make this explicit, we first choose an isomorphism
the result will be independent of this choice. Write ![]() $\sigma$ for the generator of
$\sigma$ for the generator of ![]() $\mu _p$ corresponding to
$\mu _p$ corresponding to ![]() $1$ under the isomorphism. Then, for a complex
$1$ under the isomorphism. Then, for a complex ![]() $A^\bullet$, we give the complex
$A^\bullet$, we give the complex ![]() $(A^\bullet )^{\boxtimes p}$ with degree
$(A^\bullet )^{\boxtimes p}$ with degree ![]() $n$ term
$n$ term
the ![]() $\mu _p$-equivariant structure by letting the generator
$\mu _p$-equivariant structure by letting the generator ![]() $\sigma$ act in degree
$\sigma$ act in degree ![]() $n$ by the direct sum of the canonical isomorphisms of sheaves
$n$ by the direct sum of the canonical isomorphisms of sheaves
each twisted by the sign ![]() $(-1)^{i_1(n-i_1)}$. The sign twist is the natural (Koszul) choice which makes the action of
$(-1)^{i_1(n-i_1)}$. The sign twist is the natural (Koszul) choice which makes the action of ![]() $\mu _p$ commute with the differential. Moreover, given a chain map
$\mu _p$ commute with the differential. Moreover, given a chain map ![]() $f:A^\bullet \to B^\bullet$,
$f:A^\bullet \to B^\bullet$, ![]() $f^{\boxtimes p}$ is automatically a
$f^{\boxtimes p}$ is automatically a ![]() $\mu _p$-equivariant chain map. Since the functor
$\mu _p$-equivariant chain map. Since the functor ![]() $C^b_{\mu _p}(X^{\mu _p},R)\to C^b(X^{\mu _p},R)$ reflects quasi-isomorphisms, it follows immediately that
$C^b_{\mu _p}(X^{\mu _p},R)\to C^b(X^{\mu _p},R)$ reflects quasi-isomorphisms, it follows immediately that ![]() $St_C$ descends to a functor
$St_C$ descends to a functor ![]() $St_D$ as below:
$St_D$ as below:
Writing ![]() $\Sigma$ for the suspension functor, we have
$\Sigma$ for the suspension functor, we have ![]() $St_D\Sigma \cong \Sigma ^pSt_D$. Also,
$St_D\Sigma \cong \Sigma ^pSt_D$. Also, ![]() $St_D$ is not triangulated, nor additive, nor even linear. To control the failure of linearity, and for future reference, we now introduce the following special element of
$St_D$ is not triangulated, nor additive, nor even linear. To control the failure of linearity, and for future reference, we now introduce the following special element of ![]() $R[\mu _p]$.
$R[\mu _p]$.
Definition 2.3 The norm element ![]() $N\in R[\mu _p]$ is given by
$N\in R[\mu _p]$ is given by
Observe that, given two objects ![]() $A, B$ of
$A, B$ of ![]() $D^+_{\mu _p}(X, R)$, we have an action of
$D^+_{\mu _p}(X, R)$, we have an action of ![]() $\mu _p$ on
$\mu _p$ on
where by definition, ![]() $x\in \mu _p$ sends the non-equivariant morphism
$x\in \mu _p$ sends the non-equivariant morphism ![]() $f$ to
$f$ to ![]() $xfx^{-1}$. The following two propositions control the failure of linearity.
$xfx^{-1}$. The following two propositions control the failure of linearity.
Proposition 2.4 Suppose given two parallel morphisms ![]() $f,g:A^\bullet \to B^\bullet$ in
$f,g:A^\bullet \to B^\bullet$ in ![]() $D^+(X,R)$. Then the morphism
$D^+(X,R)$. Then the morphism
is an induced map. That is, there exists some non-equivariant map
such that the equivariant map
is equal to ![]() $St_D(f+g)-St_D(f)-St_D(g)$.
$St_D(f+g)-St_D(f)-St_D(g)$.
Proof. The maps ![]() $f, g, h$ appearing in the statement are morphisms of derived categories. Let us right away replace
$f, g, h$ appearing in the statement are morphisms of derived categories. Let us right away replace ![]() $A^\bullet ,B^\bullet$ by quasi-isomorphic complexes so that
$A^\bullet ,B^\bullet$ by quasi-isomorphic complexes so that ![]() $f,g$ may be realized as genuine maps of complexes. Let
$f,g$ may be realized as genuine maps of complexes. Let ![]() $\underline {f},\underline {g}$ denote the constant functions
$\underline {f},\underline {g}$ denote the constant functions ![]() $\mu _p\to \{f,g\}$ with respective values
$\mu _p\to \{f,g\}$ with respective values ![]() $f,g$. Then
$f,g$. Then ![]() $\mu _p$ acts freely on
$\mu _p$ acts freely on ![]() $\{f,g\}^{\mu _p}-\{\underline {f},\underline {g}\}$; choose a set
$\{f,g\}^{\mu _p}-\{\underline {f},\underline {g}\}$; choose a set ![]() $\{h_1,\ldots ,h_d\}$ of orbit representatives
$\{h_1,\ldots ,h_d\}$ of orbit representatives ![]() $(d=(2^p-2)/p)$. Then each
$(d=(2^p-2)/p)$. Then each ![]() $h_i$ determines a non-equivariant map
$h_i$ determines a non-equivariant map ![]() $(A^\bullet )^{\boxtimes \,\mu _p}\to (B^\bullet )^{\boxtimes \,\mu _p}$, hence so does their sum
$(A^\bullet )^{\boxtimes \,\mu _p}\to (B^\bullet )^{\boxtimes \,\mu _p}$, hence so does their sum ![]() $h$. Then we have
$h$. Then we have
where, by definition, ![]() $xhx^{-1}$ is the composition
$xhx^{-1}$ is the composition
where the two isomorphisms are given by the equivariant structures.
Let ![]() $Fr: R\to R$ denote the
$Fr: R\to R$ denote the ![]() $p$th-power morphism of commutative monoids (using the multiplication on
$p$th-power morphism of commutative monoids (using the multiplication on ![]() $R$ and forgetting the addition).
$R$ and forgetting the addition).
Proposition 2.5 ![]() $St_D$ is Frobenius-multiplicative with respect to the action of the multiplicative monoid
$St_D$ is Frobenius-multiplicative with respect to the action of the multiplicative monoid ![]() $R$ on hom-sets. That is,
$R$ on hom-sets. That is, ![]() $St_D$ determines a functor
$St_D$ determines a functor
which respects multiplication by ![]() $R$. Here the category on the left is obtained from
$R$. Here the category on the left is obtained from ![]() $D^b(X,R)$ by regarding each hom-set as a set with an action of the multiplicative monoid
$D^b(X,R)$ by regarding each hom-set as a set with an action of the multiplicative monoid ![]() $R$ and inducing along the
$R$ and inducing along the ![]() $p$th-power map of monoids
$p$th-power map of monoids ![]() $R\to R$.
$R\to R$.
Proof. Clear.
Note that ![]() $\operatorname {Ind}_R^RD^b(X,R)$ is not an additive category in general. However, suppose that
$\operatorname {Ind}_R^RD^b(X,R)$ is not an additive category in general. However, suppose that ![]() $R=k$ and
$R=k$ and ![]() $k$ is perfect. In that case, the Frobenius map of monoids is actually a map of rings
$k$ is perfect. In that case, the Frobenius map of monoids is actually a map of rings ![]() $F$, and is, moreover, bijective. Write
$F$, and is, moreover, bijective. Write ![]() $M:k\operatorname {-mod}\to k\operatorname {-set}$ for the forgetful functor, where
$M:k\operatorname {-mod}\to k\operatorname {-set}$ for the forgetful functor, where ![]() $k\operatorname {-set}$ denotes the category of sets with action of the multiplicative monoid
$k\operatorname {-set}$ denotes the category of sets with action of the multiplicative monoid ![]() $k$. We have the following lemma.
$k$. We have the following lemma.
Lemma 2.6 Suppose that ![]() $k$ is a perfect field of characteristic
$k$ is a perfect field of characteristic ![]() $p$. Then we have
$p$. Then we have
Proof. Indeed, in that case both ![]() $F^*$ and
$F^*$ and ![]() $\operatorname {Ind}_k^k$ are equivalent to the functor of restriction along the inverse of Frobenius.
$\operatorname {Ind}_k^k$ are equivalent to the functor of restriction along the inverse of Frobenius.
It follows that if ![]() $k$ is a perfect field of characteristic
$k$ is a perfect field of characteristic ![]() $p$, we have produced a
$p$, we have produced a ![]() $k$-multiplicative functor
$k$-multiplicative functor
Since the source ![]() $F^*D^+(X,k)$ is triangulated, we find this statement somewhat nicer than the version for general
$F^*D^+(X,k)$ is triangulated, we find this statement somewhat nicer than the version for general ![]() $R$. However, the functor
$R$. However, the functor ![]() $St_D$ itself is still not linear, triangulated etc.
$St_D$ itself is still not linear, triangulated etc.
2.3 Localization
The category ![]() $D^+_{\mu _p}(X^{\mu _p},R)$ is enriched, in a triangulated sense, over
$D^+_{\mu _p}(X^{\mu _p},R)$ is enriched, in a triangulated sense, over ![]() $H^*_{\mu _p}(X^{\mu _p},R)$. That is, the monoidal structure of
$H^*_{\mu _p}(X^{\mu _p},R)$. That is, the monoidal structure of ![]() $D^+_{\mu _p}(X^{\mu _p},R)$ gives maps of
$D^+_{\mu _p}(X^{\mu _p},R)$ gives maps of ![]() $R$-modules
$R$-modules
for each ![]() $n\geq 0$, whose sum is a map of algebras. In particular,
$n\geq 0$, whose sum is a map of algebras. In particular, ![]() $D^+_{\mu _p}(X^{\mu _p},R)$ is enriched in the same sense over
$D^+_{\mu _p}(X^{\mu _p},R)$ is enriched in the same sense over
Here ![]() $\hbar$ is the first Chern class of the tautological line bundle on
$\hbar$ is the first Chern class of the tautological line bundle on ![]() ${\rm B}\mu _{\rm p}$ corresponding to the embedding
${\rm B}\mu _{\rm p}$ corresponding to the embedding ![]() $\mu _p\to \mathbb {C}^*$. In particular, this super-commutative ring receives a map from
$\mu _p\to \mathbb {C}^*$. In particular, this super-commutative ring receives a map from ![]() $R\otimes _{\mathbb {Z}}^L\mathbb {Z}[\hbar ] = R[\hbar ]$ so that
$R\otimes _{\mathbb {Z}}^L\mathbb {Z}[\hbar ] = R[\hbar ]$ so that ![]() $D^+_{\mu _p}(X^{\mu _p},R)$ is enriched over
$D^+_{\mu _p}(X^{\mu _p},R)$ is enriched over ![]() $R[\hbar ]$. Thus we may consider the 2-periodic
$R[\hbar ]$. Thus we may consider the 2-periodic ![]() $R$-linear triangulated category
$R$-linear triangulated category ![]() $D^+_{\mu _p}(X^{\mu _p},R)[\hbar ^{-1}]$, which is enriched over
$D^+_{\mu _p}(X^{\mu _p},R)[\hbar ^{-1}]$, which is enriched over
The degree ![]() $0$ component of this ring is
$0$ component of this ring is ![]() $R/p$, and the natural map from
$R/p$, and the natural map from ![]() $R$ to here is the modular reduction map. In particular, there is a Frobenius map of rings
$R$ to here is the modular reduction map. In particular, there is a Frobenius map of rings
In this way, it makes sense to ask whether a functor from a triangulated category enriched over ![]() $R$ to one enriched over
$R$ to one enriched over ![]() $R\otimes _{\mathbb {Z}}^L \mathbb {F}_{\rm p}[\hbar ^{\pm 1}]$ is Frobenius-linear.
$R\otimes _{\mathbb {Z}}^L \mathbb {F}_{\rm p}[\hbar ^{\pm 1}]$ is Frobenius-linear.
Proposition 2.7 The composition
is exact, Frobenius-linear and preserves direct sums.
Proof. First, we prove that ![]() $St_D'$ preserves direct sums. Let
$St_D'$ preserves direct sums. Let ![]() $A^\bullet$,
$A^\bullet$, ![]() $B^\bullet$ be complexes in
$B^\bullet$ be complexes in ![]() $D^+(X,R)$. We argue as in the proof of Proposition 2.4 that we have
$D^+(X,R)$. We argue as in the proof of Proposition 2.4 that we have
for some complex ![]() $C^\bullet$ in
$C^\bullet$ in ![]() $D^b(X^{\mu _p},R)$. Here
$D^b(X^{\mu _p},R)$. Here ![]() $\operatorname {Ind}_1^{\mu _p}$ is the averaging functor
$\operatorname {Ind}_1^{\mu _p}$ is the averaging functor
bi-adjoint to the restriction functor ![]() $\operatorname {Res}_1^{\mu _p}$. Therefore, it suffices to prove that the composition
$\operatorname {Res}_1^{\mu _p}$. Therefore, it suffices to prove that the composition
is isomorphic to ![]() $0$. This follows by adjunction from the fact that
$0$. This follows by adjunction from the fact that ![]() $Res_1^{\mu _p}(\hbar )=0$.
$Res_1^{\mu _p}(\hbar )=0$.
Next, we prove Frobenius-linearity. By Proposition 2.5, it suffices to prove that ![]() $St_D'$ respects addition of parallel morphisms. By Proposition 2.4, it is enough to see that the image of an induced morphism in
$St_D'$ respects addition of parallel morphisms. By Proposition 2.4, it is enough to see that the image of an induced morphism in ![]() $D^+_{\mu _p}(X^{\mu _p},R)$ in the localized category
$D^+_{\mu _p}(X^{\mu _p},R)$ in the localized category ![]() $D^+_{\mu _p}(X^{\mu _p},R)[\hbar ^{-1}]$ is
$D^+_{\mu _p}(X^{\mu _p},R)[\hbar ^{-1}]$ is ![]() $0$. This we have shown in the previous paragraph.
$0$. This we have shown in the previous paragraph.
Finally, we prove exactness. First we must specify an exact structure, that is, an isomorphism ![]() $e:\Sigma St_D'\cong St_D'\Sigma$, which makes the image under
$e:\Sigma St_D'\cong St_D'\Sigma$, which makes the image under ![]() $St_D'$ of any triangle a triangle. Note that since
$St_D'$ of any triangle a triangle. Note that since ![]() $p$ is odd, there is a morphism in
$p$ is odd, there is a morphism in ![]() $D^+_{\mu _p}(X^{\mu _p},R)$ of functors
$D^+_{\mu _p}(X^{\mu _p},R)$ of functors ![]() $\hbar ^{(p-1)/2}:\Sigma \xrightarrow {}\Sigma ^p$ which becomes an isomorphism when
$\hbar ^{(p-1)/2}:\Sigma \xrightarrow {}\Sigma ^p$ which becomes an isomorphism when ![]() $\hbar$ is inverted. Already on the level of complexes we have a canonical isomorphism
$\hbar$ is inverted. Already on the level of complexes we have a canonical isomorphism ![]() $\Sigma ^pSt_C\cong St_C\Sigma$. The exact structure is taken to be the composition
$\Sigma ^pSt_C\cong St_C\Sigma$. The exact structure is taken to be the composition
This is indeed an isomorphism since the localized category is enriched over ![]() $\mathbb {F}_{\rm p}$. The reason for the factor
$\mathbb {F}_{\rm p}$. The reason for the factor ![]() $((p-1)/2)!$ will be explained shortly. Thus, given a triangle
$((p-1)/2)!$ will be explained shortly. Thus, given a triangle
in ![]() $D^+(X,R)$, we have a triangle
$D^+(X,R)$, we have a triangle

in ![]() $D^+_{\mu _p}(X^{\mu _p},R)[\hbar ^{-1}]$. We must show that this is exact whenever the original triangle is. Since any exact triangle in a derived category is isomorphic to a semi-split one, we may assume that
$D^+_{\mu _p}(X^{\mu _p},R)[\hbar ^{-1}]$. We must show that this is exact whenever the original triangle is. Since any exact triangle in a derived category is isomorphic to a semi-split one, we may assume that ![]() $f$ is a chain map and
$f$ is a chain map and ![]() $C^\bullet$ is the usual mapping cone satisfying
$C^\bullet$ is the usual mapping cone satisfying
with differential
So we have
 \[ St_C(C^\bullet) = \bigg(\bigoplus_{i_1+\cdots+ i_p={\bullet}}(A^{i_1+1}\oplus B^{i_1})\boxtimes\cdots\boxtimes(A^{i_p+1}\oplus B^{i_p}) \bigg)^\bullet \]
\[ St_C(C^\bullet) = \bigg(\bigoplus_{i_1+\cdots+ i_p={\bullet}}(A^{i_1+1}\oplus B^{i_1})\boxtimes\cdots\boxtimes(A^{i_p+1}\oplus B^{i_p}) \bigg)^\bullet \]
with some differential (whose precise form is not important). This complex has a ![]() $(p+1)$-step equivariant increasing filtration
$(p+1)$-step equivariant increasing filtration
where ![]() $F_iSt_C(C^\bullet )$ consists of the subcomplex of
$F_iSt_C(C^\bullet )$ consists of the subcomplex of ![]() $St_C(C^\bullet )$ in which at most
$St_C(C^\bullet )$ in which at most ![]() $i$ summands
$i$ summands ![]() $A^?$ are taken in the expansion of the external tensor product. The inclusion of the zeroth piece of this filtration is equal to
$A^?$ are taken in the expansion of the external tensor product. The inclusion of the zeroth piece of this filtration is equal to ![]() $St_C(g)$, while the quotient map
$St_C(g)$, while the quotient map
is equal to ![]() $St_C(h)$. Furthermore, arguing as in Proposition 2.4, we see that
$St_C(h)$. Furthermore, arguing as in Proposition 2.4, we see that ![]() $F_iSt_C(C^\bullet )/F_{i-1}St_C(C^\bullet )$ is an induced complex for each
$F_iSt_C(C^\bullet )/F_{i-1}St_C(C^\bullet )$ is an induced complex for each ![]() $1\leq i\leq p-1$. Therefore, the map
$1\leq i\leq p-1$. Therefore, the map
becomes an isomorphism in ![]() $D^b_{\mu _p}(X^{\mu _p},R)[\hbar ^{-1}]$. Consider now the commutative diagram
$D^b_{\mu _p}(X^{\mu _p},R)[\hbar ^{-1}]$. Consider now the commutative diagram

of equivariant chain complexes. Here ![]() $\alpha ,\beta$ are the usual chain maps which make the image of the top row in
$\alpha ,\beta$ are the usual chain maps which make the image of the top row in ![]() $D^+_{\mu _p}(X,R)$ an exact triangle,
$D^+_{\mu _p}(X,R)$ an exact triangle, ![]() $\gamma$ is the quotient map, whose image in
$\gamma$ is the quotient map, whose image in ![]() $D^+_{\mu _p}(X,R)[\hbar ^{-1}]$ is an isomorphism, and
$D^+_{\mu _p}(X,R)[\hbar ^{-1}]$ is an isomorphism, and ![]() $St_C\Sigma$ has been identified with
$St_C\Sigma$ has been identified with ![]() $\Sigma ^pSt_C$. Comparing with the definition of the triangle obtained by applying
$\Sigma ^pSt_C$. Comparing with the definition of the triangle obtained by applying ![]() $St_D'$ to
$St_D'$ to ![]() $B^\bullet \xrightarrow {g}C^\bullet \xrightarrow {h}\Sigma A^\bullet \xrightarrow {-\Sigma f}\Sigma B^\bullet$, we see that it is enough to prove that the diagram
$B^\bullet \xrightarrow {g}C^\bullet \xrightarrow {h}\Sigma A^\bullet \xrightarrow {-\Sigma f}\Sigma B^\bullet$, we see that it is enough to prove that the diagram
 \[ \begin{array}{ccl} St_D(C^\bullet)/St_D(B^\bullet) & \xrightarrow{~~~~~~~~~~~\beta~~~~~~~~~~~} & \Sigma St_D(B^\bullet)\hfill\\ \Big\downarrow{\gamma} & & \Big\downarrow{{((p-1)/2)!\hbar^{(p-1)/2}}} \\ \Sigma^pSt_D(A^\bullet) & \xrightarrow{~~~~~~-\Sigma^pSt_D(f)~~~~~~} & \Sigma^pSt_D(B^\bullet)\hfill\\ \end{array} \]
\[ \begin{array}{ccl} St_D(C^\bullet)/St_D(B^\bullet) & \xrightarrow{~~~~~~~~~~~\beta~~~~~~~~~~~} & \Sigma St_D(B^\bullet)\hfill\\ \Big\downarrow{\gamma} & & \Big\downarrow{{((p-1)/2)!\hbar^{(p-1)/2}}} \\ \Sigma^pSt_D(A^\bullet) & \xrightarrow{~~~~~~-\Sigma^pSt_D(f)~~~~~~} & \Sigma^pSt_D(B^\bullet)\hfill\\ \end{array} \]
commutes in ![]() $D^+_{\mu _p}(X,R)[\hbar ^{-1}]$. Here we have written
$D^+_{\mu _p}(X,R)[\hbar ^{-1}]$. Here we have written ![]() $\beta ,\gamma$ for their own images in
$\beta ,\gamma$ for their own images in ![]() $D^+_{\mu _p}(X,R)$. Let
$D^+_{\mu _p}(X,R)$. Let ![]() $D^\bullet$ be the cocone of
$D^\bullet$ be the cocone of ![]() $A^\bullet \xrightarrow {{\rm id}}A^\bullet$, so that
$A^\bullet \xrightarrow {{\rm id}}A^\bullet$, so that ![]() $f$ induces a map
$f$ induces a map ![]() $D^\bullet \to C^\bullet$. We have a commutative diagram
$D^\bullet \to C^\bullet$. We have a commutative diagram
 \[ \begin{matrix} St_C(D^\bullet)/St_C(A^\bullet) & \xrightarrow{\epsilon} & \Sigma St_C(A^\bullet)\\ \Big\downarrow{\delta} & & \Big\downarrow{\Sigma St_C(f)} \\ St_C(C^\bullet)/St_C(B^\bullet) & \xrightarrow{\beta} & \Sigma St_C(B^\bullet)\\ \end{matrix} \]
\[ \begin{matrix} St_C(D^\bullet)/St_C(A^\bullet) & \xrightarrow{\epsilon} & \Sigma St_C(A^\bullet)\\ \Big\downarrow{\delta} & & \Big\downarrow{\Sigma St_C(f)} \\ St_C(C^\bullet)/St_C(B^\bullet) & \xrightarrow{\beta} & \Sigma St_C(B^\bullet)\\ \end{matrix} \]
where ![]() $\epsilon$ is the standard boundary map, and the vertical arrows are induced by
$\epsilon$ is the standard boundary map, and the vertical arrows are induced by ![]() $f$ (no signs necessary). Now
$f$ (no signs necessary). Now ![]() $\gamma \delta$ becomes an isomorphism in
$\gamma \delta$ becomes an isomorphism in ![]() $D^b_{\mu _p}(X^{\mu _p},R)$ for the same reason that
$D^b_{\mu _p}(X^{\mu _p},R)$ for the same reason that ![]() $\gamma$ does; therefore so does
$\gamma$ does; therefore so does ![]() $\delta$. So it is enough to show that the composition of these two diagrams is commutative. By functoriality of
$\delta$. So it is enough to show that the composition of these two diagrams is commutative. By functoriality of ![]() $\hbar$, the resulting composition equals
$\hbar$, the resulting composition equals
 \[ \begin{array}{ccl} St_D(D^\bullet)/St_D(A^\bullet) & \xrightarrow{\epsilon} & \Sigma St_D(A^\bullet)\hfill\\ \Big\downarrow{\gamma\delta} & & \Big\downarrow{\Sigma^p St_D(f)\circ{((p-1)/2)!\hbar^{(p-1)/2}}} \\ \Sigma^pSt_D(A^\bullet) & \xrightarrow{~~~~~~-\Sigma^pSt_D(f)~~~~~~} & \Sigma^pSt_D(B^\bullet)\hfill\\ \end{array} \]
\[ \begin{array}{ccl} St_D(D^\bullet)/St_D(A^\bullet) & \xrightarrow{\epsilon} & \Sigma St_D(A^\bullet)\hfill\\ \Big\downarrow{\gamma\delta} & & \Big\downarrow{\Sigma^p St_D(f)\circ{((p-1)/2)!\hbar^{(p-1)/2}}} \\ \Sigma^pSt_D(A^\bullet) & \xrightarrow{~~~~~~-\Sigma^pSt_D(f)~~~~~~} & \Sigma^pSt_D(B^\bullet)\hfill\\ \end{array} \]Let
be the equivariant resolution of the trivial ![]() $R[\mu _p]$-module supported in degrees
$R[\mu _p]$-module supported in degrees ![]() $(1-p),\ldots ,0$. Here
$(1-p),\ldots ,0$. Here ![]() $N$ is the norm element as defined in Definition 2.3. We have the standard chain maps
$N$ is the norm element as defined in Definition 2.3. We have the standard chain maps ![]() $\mathfrak {p}\to R$, which is an isomorphism in the equivariant derived category, and
$\mathfrak {p}\to R$, which is an isomorphism in the equivariant derived category, and ![]() $\mathfrak {p}\to \Sigma ^{p-1}R$, which equals
$\mathfrak {p}\to \Sigma ^{p-1}R$, which equals ![]() $\hbar ^{(p-1)/2}$ by definition. Now
$\hbar ^{(p-1)/2}$ by definition. Now ![]() $\epsilon$ is a chain map, which is an isomorphism in the equivariant derived category but not in the equivariant complex category. However, there is a chain map
$\epsilon$ is a chain map, which is an isomorphism in the equivariant derived category but not in the equivariant complex category. However, there is a chain map
such that ![]() $\epsilon \zeta$ is induced by the standard chain map
$\epsilon \zeta$ is induced by the standard chain map ![]() $\mathfrak {p}\to R$ (i.e. counit in degree
$\mathfrak {p}\to R$ (i.e. counit in degree ![]() $0$). To see this, it is enough to do the case
$0$). To see this, it is enough to do the case ![]() $A^\bullet =R$ and then tensor on the right with
$A^\bullet =R$ and then tensor on the right with ![]() $St_C(A^\bullet )$. In that case, we are looking for an equivariant chain map from the complex
$St_C(A^\bullet )$. In that case, we are looking for an equivariant chain map from the complex
supported in degrees ![]() $-p,\ldots ,-1$ to the complex
$-p,\ldots ,-1$ to the complex ![]() $E^\bullet$ satisfying
$E^\bullet$ satisfying
 \[ E^i=\bigoplus_{\substack{S\subset [p]\\ |S|={-}i}}R_S \]
\[ E^i=\bigoplus_{\substack{S\subset [p]\\ |S|={-}i}}R_S \]
where ![]() $R_S$ is a copy of
$R_S$ is a copy of ![]() $R$, and with differential sending
$R$, and with differential sending ![]() $R_S$ to
$R_S$ to ![]() $\bigoplus _{s\in S}R_{S-\{s\}}$ by
$\bigoplus _{s\in S}R_{S-\{s\}}$ by ![]() $(1,-1,1,\ldots )$. Let us write
$(1,-1,1,\ldots )$. Let us write ![]() $1_S$ for the canonical generator of
$1_S$ for the canonical generator of ![]() $R_S$. One example of such a map is the map which sends the element
$R_S$. One example of such a map is the map which sends the element ![]() $1$ in the degree
$1$ in the degree ![]() $-(2i+1)$ copy of
$-(2i+1)$ copy of ![]() $R[\mu _p]$ to the term
$R[\mu _p]$ to the term
 \[{-}i!\sum_{\substack{T\subset \{2,\ldots,p\}\\ |T|=2i\\ \text{even block lengths }}} 1_{\{1\}\cup T} \]
\[{-}i!\sum_{\substack{T\subset \{2,\ldots,p\}\\ |T|=2i\\ \text{even block lengths }}} 1_{\{1\}\cup T} \]
and sends the element ![]() $1$ in the degree
$1$ in the degree ![]() $-(2i+2)$ copy of
$-(2i+2)$ copy of ![]() $R[\mu _p]$ to the term
$R[\mu _p]$ to the term
 \[{-}i!\sum_{\substack{T\subset \{3,\ldots,p\}\\ |T|=2i\\ \text{even block lengths}}}1_{\{1\}\cup\{2\}\cup T}. \]
\[{-}i!\sum_{\substack{T\subset \{3,\ldots,p\}\\ |T|=2i\\ \text{even block lengths}}}1_{\{1\}\cup\{2\}\cup T}. \]
The sign is chosen so that ![]() $\epsilon \zeta$ is induced by the standard chain map
$\epsilon \zeta$ is induced by the standard chain map ![]() $\mathfrak {p}\to R$. We compute
$\mathfrak {p}\to R$. We compute
Therefore, the two paths ![]() $St_D(D^\bullet )/St_D(A^\bullet )\to \Sigma ^pSt_D(B^\bullet )$ in this composed diagram are equalized by
$St_D(D^\bullet )/St_D(A^\bullet )\to \Sigma ^pSt_D(B^\bullet )$ in this composed diagram are equalized by ![]() $\zeta$. Since
$\zeta$. Since ![]() $\zeta$ is an isomorphism in
$\zeta$ is an isomorphism in ![]() $D^+_{\mu _p}(X^{\mu _p},R)[\hbar ^{-1}]$, they coincide in the localized category as required.
$D^+_{\mu _p}(X^{\mu _p},R)[\hbar ^{-1}]$, they coincide in the localized category as required.
Corollary 2.8 Suppose ![]() $R=k$ is a field of characteristic
$R=k$ is a field of characteristic ![]() $p$. Then we have a triangulated
$p$. Then we have a triangulated ![]() $k$-linear functor
$k$-linear functor
2.4 Six functors
We shall henceforth restrict ourselves to the geometric context of [Reference Bernstein and LuntsBL06]. Thus from now on every topological space ![]() $X$ will be the Borel quotient
$X$ will be the Borel quotient ![]() $EG\frac {\times }{G}Y$ of a complex algebraic variety
$EG\frac {\times }{G}Y$ of a complex algebraic variety ![]() $Y$ by the action of some affine algebraic group
$Y$ by the action of some affine algebraic group ![]() $G$, every coefficient ring
$G$, every coefficient ring ![]() $R$ will be a Noetherian ring of finite homological dimension, and we will restrict attention to the full subcategory
$R$ will be a Noetherian ring of finite homological dimension, and we will restrict attention to the full subcategory
spanned by those objects which descend from ![]() $Y$.
$Y$.
For the rest of this paper, we will cut down our scope even further (perhaps unnecessarily) to the constructible equivariant derived category
This is the full subcategory of ![]() $D^+_G(Y, R)$ spanned by those complexes
$D^+_G(Y, R)$ spanned by those complexes ![]() $\mathcal {F}$ which have only finitely many non-zero cohomology sheaves, and all of them are algebraically constructible, that is, locally constant along every stratum of some algebraic stratification of
$\mathcal {F}$ which have only finitely many non-zero cohomology sheaves, and all of them are algebraically constructible, that is, locally constant along every stratum of some algebraic stratification of ![]() $Y$ (depending on
$Y$ (depending on ![]() $\mathcal {F}$).
$\mathcal {F}$).
The constructions of the previous section preserve constructibility, so we have a Steenrod construction
Recall that we have the deep ‘six-functor formalism’ for constructible derived categories; see Bernstein and Lunts [Reference Bernstein and LuntsBL06]. We assume that the reader is familiar with this material, but remind him/her of the standard notation: for a ![]() $G$-equivariant algebraic map
$G$-equivariant algebraic map ![]() $f:Y\to Y'$, we have the adjoint pairs of exact functors
$f:Y\to Y'$, we have the adjoint pairs of exact functors
 \begin{gather*} {f^*\negmedspace: D^b_{c,G}(Y',R)\rightleftarrows D^b_{c,G}(Y,R):\negmedspace f_*},\\ {f_!\negmedspace: D^b_{c,G}(Y,R)\rightleftarrows D^b_{c,G}(Y',R):\negmedspace f^!} \end{gather*}
\begin{gather*} {f^*\negmedspace: D^b_{c,G}(Y',R)\rightleftarrows D^b_{c,G}(Y,R):\negmedspace f_*},\\ {f_!\negmedspace: D^b_{c,G}(Y,R)\rightleftarrows D^b_{c,G}(Y',R):\negmedspace f^!} \end{gather*}and also a pair of bi-exact bifunctors
 \begin{gather*} (-)\otimes(-):D^b_{c,G}(Y,R)\times D^b_{c,G}(Y,R)\to D^b_{c,G}(Y,R),\\ \mathcal{H}om(-,-):D^b_{c,G}(Y,R)^{op}\times D^b_{c,G}(Y,R)\to D^b_{c,G}(Y,R) \end{gather*}
\begin{gather*} (-)\otimes(-):D^b_{c,G}(Y,R)\times D^b_{c,G}(Y,R)\to D^b_{c,G}(Y,R),\\ \mathcal{H}om(-,-):D^b_{c,G}(Y,R)^{op}\times D^b_{c,G}(Y,R)\to D^b_{c,G}(Y,R) \end{gather*}
related by a tensor-hom adjunction. There is also a Verdier duality functor ![]() $\mathbb {D}$, and an exceptional tensor product
$\mathbb {D}$, and an exceptional tensor product ![]() $\otimes ^!$, which can be written in terms of the other functors, as can the external tensor product
$\otimes ^!$, which can be written in terms of the other functors, as can the external tensor product ![]() $\boxtimes$. We call the collection of all of these functors the six plus functors. Notice that
$\boxtimes$. We call the collection of all of these functors the six plus functors. Notice that ![]() ${G^{\mu _p}\rtimes\,\mu _p}$ is also an affine algebraic group, so the six-functor formalism exists for the target category of
${G^{\mu _p}\rtimes\,\mu _p}$ is also an affine algebraic group, so the six-functor formalism exists for the target category of ![]() $St_D$. Also if
$St_D$. Also if ![]() $f:Y\to Y'$ is
$f:Y\to Y'$ is ![]() $G$-equivariant then
$G$-equivariant then ![]() $f^{\mu _p}:Y^{\mu _p}\to (Y')^{\mu _p}$ is
$f^{\mu _p}:Y^{\mu _p}\to (Y')^{\mu _p}$ is ![]() $G^{\mu _p}\rtimes\, \mu _p$-equivariant. The following fact is essentially a consequence of the same fact for
$G^{\mu _p}\rtimes\, \mu _p$-equivariant. The following fact is essentially a consequence of the same fact for ![]() $^{\boxtimes p}$:
$^{\boxtimes p}$:
Proposition 2.9 Steenrod's construction is compatible with the six-functor formalism. That is, we have canonical isomorphisms
 \begin{align*} (f^{\mu_p})^*St_D & \cong St_Df^* ,\\ (f^{\mu_p})_*St_D & \cong St_Df_* ,\\ (f^{\mu_p})_!St_D & \cong St_Df_! ,\\ (f^{\mu_p})^!St_D & \cong St_Df^! ,\\ St_D(-)\otimes St_D(-) & \cong St_D(-{\otimes}{-}) ,\\ St_D(-)\otimes^! St_D(-) & \cong St_D(-{\otimes}^! -) ,\\ St_D(-)\boxtimes St_D(-) & \cong St_D(-\boxtimes -) ,\\ \mathcal{H}om(St_D(-),St_D(-)) & \cong St_D\mathcal{H}om(-,-) \end{align*}
\begin{align*} (f^{\mu_p})^*St_D & \cong St_Df^* ,\\ (f^{\mu_p})_*St_D & \cong St_Df_* ,\\ (f^{\mu_p})_!St_D & \cong St_Df_! ,\\ (f^{\mu_p})^!St_D & \cong St_Df^! ,\\ St_D(-)\otimes St_D(-) & \cong St_D(-{\otimes}{-}) ,\\ St_D(-)\otimes^! St_D(-) & \cong St_D(-{\otimes}^! -) ,\\ St_D(-)\boxtimes St_D(-) & \cong St_D(-\boxtimes -) ,\\ \mathcal{H}om(St_D(-),St_D(-)) & \cong St_D\mathcal{H}om(-,-) \end{align*}commuting with any and all adjunction morphisms of the six-functor formalism.
We have the same compatibilities with functors ![]() $St_D'$.
$St_D'$.
Remark 2.10 The four functors ![]() $f^*$,
$f^*$, ![]() $f_*$,
$f_*$, ![]() $f_!$,
$f_!$, ![]() $f^!$ and the three tensor product functors may all be extended to the bounded-below equivariant derived category, and are also compatible with
$f^!$ and the three tensor product functors may all be extended to the bounded-below equivariant derived category, and are also compatible with ![]() $St_D$ there, in the same way. However, the internal hom (and its special case, Verdier duality) do not make sense there, so we prefer to confine ourselves to the constructible case going forward.
$St_D$ there, in the same way. However, the internal hom (and its special case, Verdier duality) do not make sense there, so we prefer to confine ourselves to the constructible case going forward.
Proof. That the claim for ![]() $St_D'$ follows from the claim for
$St_D'$ follows from the claim for ![]() $St_D$, is a direct consequence of the
$St_D$, is a direct consequence of the ![]() $H^*_{\mu _p}(*)$-linearity of the six functors in the
$H^*_{\mu _p}(*)$-linearity of the six functors in the ![]() $\mu _p$-equivariant context. So let us focus on
$\mu _p$-equivariant context. So let us focus on ![]() $St_D$. It is known (cf. [Reference Bernstein and LuntsBL06]) that the six functors intertwine with external tensor product, so it is just a matter of showing that the
$St_D$. It is known (cf. [Reference Bernstein and LuntsBL06]) that the six functors intertwine with external tensor product, so it is just a matter of showing that the ![]() $\mu _p$-equivariant structures are carried along. This is easy for
$\mu _p$-equivariant structures are carried along. This is easy for ![]() $f^*$: it is defined on the cochain level, and strictly intertwines with
$f^*$: it is defined on the cochain level, and strictly intertwines with ![]() $St_C$ on that level (no homotopy involved). It follows by adjointness that we have a canonical map
$St_C$ on that level (no homotopy involved). It follows by adjointness that we have a canonical map
which is an isomorphism upon forgetting equivariance, hence itself an isomorphism.
We may argue similarly for ![]() $f_!$,
$f_!$, ![]() $f^!$. Indeed, the thrust of the argument for
$f^!$. Indeed, the thrust of the argument for ![]() $f^*$ was to lift both
$f^*$ was to lift both ![]() $f^*$ and
$f^*$ and ![]() $St_D$ to the concrete model of bounded-below cochain complexes and observe strict intertwining there. There is an alternative concrete model which works just as well for the purposes of defining
$St_D$ to the concrete model of bounded-below cochain complexes and observe strict intertwining there. There is an alternative concrete model which works just as well for the purposes of defining ![]() $St_D$, namely the category of bounded-below cochain complexes of soft sheaves. But
$St_D$, namely the category of bounded-below cochain complexes of soft sheaves. But ![]() $f_!$ is defined on the level of the soft model, and the intertwining holds strictly there. We deduce the desired claim for
$f_!$ is defined on the level of the soft model, and the intertwining holds strictly there. We deduce the desired claim for ![]() $f^!$ in the same way we deduced it for
$f^!$ in the same way we deduced it for ![]() $f_*$ from
$f_*$ from ![]() $f^*$.
$f^*$.
The canonical isomorphism
is a tautological consequence of the cochain-level construction of ![]() $St_D$, and intertwining for the other two tensors follows by composing with
$St_D$, and intertwining for the other two tensors follows by composing with ![]() $*$- and
$*$- and ![]() $!$- restriction along the diagonal. Finally, the canonical isomorphism
$!$- restriction along the diagonal. Finally, the canonical isomorphism
can be deduced using the hom-tensor adjunction.
Corollary 2.11 Let ![]() $R$ denote the constant sheaf and
$R$ denote the constant sheaf and ![]() $\omega _R$ denote the dualizing complex (see [Reference Chriss and GinzburgCG97] for details and evidence of its ubiquity in geometric representation theory). We have canonical isomorphisms
$\omega _R$ denote the dualizing complex (see [Reference Chriss and GinzburgCG97] for details and evidence of its ubiquity in geometric representation theory). We have canonical isomorphisms
and
Proof. The result is easy over the point ![]() $*$: we have
$*$: we have ![]() $\omega _R\cong R$ and the construction of
$\omega _R\cong R$ and the construction of ![]() $St_D$ is degenerate. For general
$St_D$ is degenerate. For general ![]() $Y$, apply the intertwining relation between
$Y$, apply the intertwining relation between ![]() $St_D$ and
$St_D$ and ![]() $f^*$,
$f^*$, ![]() $f^!$ where
$f^!$ where ![]() $f$ is the constant map
$f$ is the constant map ![]() $Y\to *$.
$Y\to *$.
2.5 Tate's construction
Note that the object ![]() $St_D(\Sigma ^nR)$ is canonically isomorphic to
$St_D(\Sigma ^nR)$ is canonically isomorphic to ![]() $\Sigma ^{pn}R$ with its trivial
$\Sigma ^{pn}R$ with its trivial ![]() $\mu _p$-equivariant structure. Here
$\mu _p$-equivariant structure. Here ![]() $R$ is the constant sheaf. Since a degree
$R$ is the constant sheaf. Since a degree ![]() $n$ cohomology class is just a morphism
$n$ cohomology class is just a morphism ![]() $R\to \Sigma ^nR$ in
$R\to \Sigma ^nR$ in ![]() $D^b(X,R)$, we thus obtain a Frobenius-multiplicative map of multiplicative
$D^b(X,R)$, we thus obtain a Frobenius-multiplicative map of multiplicative ![]() $R$-sets:
$R$-sets:
This map is not Frobenius-linear, but as in Proposition 2.4, its deviation from additivity is by a class induced from ![]() $H^{pn}(X^{\mu _p},R)$. To see how these maps interact with multiplication, we make the following definition.
$H^{pn}(X^{\mu _p},R)$. To see how these maps interact with multiplication, we make the following definition.
Definition 2.12 Let ![]() $(\mathcal {C},*,\mathbb{1},e,a,s)$ be a symmetric monoidal abelian category enriched over some commutative ring
$(\mathcal {C},*,\mathbb{1},e,a,s)$ be a symmetric monoidal abelian category enriched over some commutative ring ![]() $R$, that is,
$R$, that is, ![]() $\mathcal {C}$ is an abelian category,
$\mathcal {C}$ is an abelian category, ![]() $*$ is a bi-exact
$*$ is a bi-exact ![]() $R$-linear functor
$R$-linear functor ![]() $\mathcal {C}\times \mathcal {C}\to \mathcal {C}$,
$\mathcal {C}\times \mathcal {C}\to \mathcal {C}$, ![]() $\mathbb {1}$ is an object of
$\mathbb {1}$ is an object of ![]() $\mathcal {C}$,
$\mathcal {C}$, ![]() $e$ is a pair of equivalences
$e$ is a pair of equivalences ![]() $\mathbb {1}*{\rm id}\cong {\rm id}\cong {\rm id}*\mathbb {1}$,
$\mathbb {1}*{\rm id}\cong {\rm id}\cong {\rm id}*\mathbb {1}$, ![]() $a$ is an associativity constraint for
$a$ is an associativity constraint for ![]() $*$ and
$*$ and ![]() $s$ is a commutativity constraint for
$s$ is a commutativity constraint for ![]() $*$, satisfying natural compatibilities. Let
$*$, satisfying natural compatibilities. Let ![]() $A$ be an object of
$A$ be an object of ![]() $\mathcal {C}$. Then
$\mathcal {C}$. Then ![]() $s$ determines an action of
$s$ determines an action of ![]() $\mu _p$ on
$\mu _p$ on ![]() $A^{*\,\mu _p}$, and we define
$A^{*\,\mu _p}$, and we define
Here ![]() $N$ is the norm element defined in Definition 2.3. This is the so-called Tate construction; see [Reference Cartan and EilenbergCE99] for more details. For a morphism
$N$ is the norm element defined in Definition 2.3. This is the so-called Tate construction; see [Reference Cartan and EilenbergCE99] for more details. For a morphism ![]() $f:A\to B$ the morphism
$f:A\to B$ the morphism ![]() $f^{*\,\mu _p}:A^{*\,\mu _p}\to B^{*\,\mu _p}$ is
$f^{*\,\mu _p}:A^{*\,\mu _p}\to B^{*\,\mu _p}$ is ![]() $\mu _p$-equivariant and so induces a morphism
$\mu _p$-equivariant and so induces a morphism ![]() $A^{(1)}\to B^{(1)}$, so that
$A^{(1)}\to B^{(1)}$, so that ![]() $(-)^{(1)}$ becomes a functor.
$(-)^{(1)}$ becomes a functor.
Lemma 2.13 ![]() $(-)^{(1)}$ is additive over
$(-)^{(1)}$ is additive over ![]() $\mathbb {Z}$.
$\mathbb {Z}$.
Proof. We essentially rehash the proof of Propositions 2.4 and 2.7. First we show that ![]() $(-)^{(1)}$ is linear over
$(-)^{(1)}$ is linear over ![]() $\mathbb {Z}$. Suppose
$\mathbb {Z}$. Suppose ![]() $f,g:A\to B$ are two parallel morphisms in
$f,g:A\to B$ are two parallel morphisms in ![]() $\mathcal {C}$. Let
$\mathcal {C}$. Let ![]() $\underline {f},\underline {g}$ denote the constant functions
$\underline {f},\underline {g}$ denote the constant functions ![]() $\mu _p\to \{f,g\}$ with respective values
$\mu _p\to \{f,g\}$ with respective values ![]() $f,g$. Then
$f,g$. Then ![]() $\mu _p$ acts freely on
$\mu _p$ acts freely on ![]() $\{f,g\}^{\mu _p}-\{\underline {f},\underline {g}\}$; choose a set
$\{f,g\}^{\mu _p}-\{\underline {f},\underline {g}\}$; choose a set ![]() $\{h_1,\ldots ,h_n\}$ of orbit representatives (
$\{h_1,\ldots ,h_n\}$ of orbit representatives (![]() $n=(2^p-2)/p$). Then each
$n=(2^p-2)/p$). Then each ![]() $h_i$ determines a non-equivariant map
$h_i$ determines a non-equivariant map ![]() $A^{*\,\mu _p}\to B^{*\,\mu _p}$, and we have
$A^{*\,\mu _p}\to B^{*\,\mu _p}$, and we have
 \[ (f+g)^{*\,\mu_p}-f^{*\,\mu_p}-g^{*\,\mu_p}=\sum_{x\in\mu_p}\sum_{i=1}^n xh_ix^{{-}1}. \]
\[ (f+g)^{*\,\mu_p}-f^{*\,\mu_p}-g^{*\,\mu_p}=\sum_{x\in\mu_p}\sum_{i=1}^n xh_ix^{{-}1}. \]
Restricting to ![]() $\ker _{A^{*\,\mu _p}}(1-\sigma )$, this becomes
$\ker _{A^{*\,\mu _p}}(1-\sigma )$, this becomes
 \[ ((f+g)^{*\,\mu_p}-f^{*\,\mu_p}-g^{*\,\mu_p})_{\ker_{A^{*\,\mu_p}}(1-\sigma)}=\sum_{x\in\mu_p}\sum_{i=1}^n xh_i=N\sum_{i=1}^n h_i \]
\[ ((f+g)^{*\,\mu_p}-f^{*\,\mu_p}-g^{*\,\mu_p})_{\ker_{A^{*\,\mu_p}}(1-\sigma)}=\sum_{x\in\mu_p}\sum_{i=1}^n xh_i=N\sum_{i=1}^n h_i \]
which factors through ![]() $\operatorname {im}_{B^{*\,\mu _p}}(N)$ as required.
$\operatorname {im}_{B^{*\,\mu _p}}(N)$ as required.
Next we show that ![]() $(-)^{(1)}$ preserves direct sums. Let
$(-)^{(1)}$ preserves direct sums. Let ![]() $\underline {A},\underline {B}$ denote the constant functions
$\underline {A},\underline {B}$ denote the constant functions ![]() $\mu _p\to \{A,B\}$ with respective values
$\mu _p\to \{A,B\}$ with respective values ![]() $A,B$. Then
$A,B$. Then ![]() $\mu _p$ acts freely on
$\mu _p$ acts freely on ![]() $\{A,B\}^{\mu _p}-\{\underline {A},\underline {B}\}$; choose a set
$\{A,B\}^{\mu _p}-\{\underline {A},\underline {B}\}$; choose a set ![]() $\{C_1,\ldots ,C_n\}$ of orbit representatives. Then each
$\{C_1,\ldots ,C_n\}$ of orbit representatives. Then each ![]() $C_i$ determines an object of
$C_i$ determines an object of ![]() $\mathcal {C}$, and as a
$\mathcal {C}$, and as a ![]() $\mu _p$-module in
$\mu _p$-module in ![]() $\mathcal {C}$ we have
$\mathcal {C}$ we have
The result then follows from the fact that ![]() $\hat {H}^0_{\mu _p}(k[\mu _p])=0$ in
$\hat {H}^0_{\mu _p}(k[\mu _p])=0$ in ![]() $R\operatorname {-mod}$.
$R\operatorname {-mod}$.
Let ![]() $\operatorname {SVect}_k$ denote the symmetric monoidal category of
$\operatorname {SVect}_k$ denote the symmetric monoidal category of ![]() $\mathbb {Z}/2$-super-graded
$\mathbb {Z}/2$-super-graded ![]() $k$-vector spaces.
$k$-vector spaces.
Lemma 2.14 Suppose that ![]() $R=k$ is a field of characteristic
$R=k$ is a field of characteristic ![]() $p$ and that
$p$ and that ![]() $\mathcal {C}$ admits a super-fiber functor
$\mathcal {C}$ admits a super-fiber functor ![]() $\mathcal {C}\to \operatorname {SVect}_k$. Then
$\mathcal {C}\to \operatorname {SVect}_k$. Then ![]() $(-)^{(1)}$ is exact, monoidal and Frobenius-linear over
$(-)^{(1)}$ is exact, monoidal and Frobenius-linear over ![]() $k$. In the case
$k$. In the case ![]() $\mathcal {C}=\operatorname {SVect}_k$,
$\mathcal {C}=\operatorname {SVect}_k$, ![]() $(-)^{(1)}$ is equivalent to the functor
$(-)^{(1)}$ is equivalent to the functor ![]() $k\otimes _F$(-) which tensors the
$k\otimes _F$(-) which tensors the ![]() $k$-linear structure along the Frobenius map
$k$-linear structure along the Frobenius map ![]() $F:k\to k$.
$F:k\to k$.
Proof. Since Tate's construction commutes with the fiber functor, it is enough to take ![]() $\mathcal {C}= \operatorname {SVect}_k$, where it is a simple calculation using bases.
$\mathcal {C}= \operatorname {SVect}_k$, where it is a simple calculation using bases.
Now suppose that ![]() $A,B$ are objects of
$A,B$ are objects of ![]() $\mathcal {C}$. We have a
$\mathcal {C}$. We have a ![]() $\mu _p$-equivariant isomorphism
$\mu _p$-equivariant isomorphism ![]() $(A*B)^{*\,\mu _p}\cong (A^{*\,\mu _p}*B^{*\,\mu _p})$. We have also the natural inclusions
$(A*B)^{*\,\mu _p}\cong (A^{*\,\mu _p}*B^{*\,\mu _p})$. We have also the natural inclusions
 \begin{gather*} \ker_{A^{*\,\mu_p}}(1-\sigma)*\ker_{B^{*\,\mu_p}}(1-\sigma)\to \ker_{A^{*\,\mu_p}*B^{*\,\mu_p}}(1-\sigma),\\ \operatorname{im}_{A^{*\,\mu_p}}(N)*\ker_{B^{*\,\mu_p}}(1-\sigma)\to \operatorname{im}_{A^{*\,\mu_p}*B^{*\,\mu_p}}(N),\\ \ker_{A^{*\,\mu_p}}(1-\sigma)*\operatorname{im}_{A^{*\,\mu_p}}(N)\to \operatorname{im}_{A^{*\,\mu_p}*B^{*\,\mu_p}}(N) \end{gather*}
\begin{gather*} \ker_{A^{*\,\mu_p}}(1-\sigma)*\ker_{B^{*\,\mu_p}}(1-\sigma)\to \ker_{A^{*\,\mu_p}*B^{*\,\mu_p}}(1-\sigma),\\ \operatorname{im}_{A^{*\,\mu_p}}(N)*\ker_{B^{*\,\mu_p}}(1-\sigma)\to \operatorname{im}_{A^{*\,\mu_p}*B^{*\,\mu_p}}(N),\\ \ker_{A^{*\,\mu_p}}(1-\sigma)*\operatorname{im}_{A^{*\,\mu_p}}(N)\to \operatorname{im}_{A^{*\,\mu_p}*B^{*\,\mu_p}}(N) \end{gather*}
which induce a map ![]() $A^{(1)}*B^{(1)}\to (A*B)^{(1)}$. Suppose that
$A^{(1)}*B^{(1)}\to (A*B)^{(1)}$. Suppose that ![]() $(A,\mathbb {1}_A,m_A)$ is a unital ring in
$(A,\mathbb {1}_A,m_A)$ is a unital ring in ![]() $\mathcal {C}$. Then
$\mathcal {C}$. Then ![]() $A^{(1)}$ still has a multiplication
$A^{(1)}$ still has a multiplication
Also, there is a canonical isomorphism ![]() $\ker _{\mathbb {1}^{*\,\mu _p}}(1-\sigma )\cong \mathbb {1}$, hence a canonical surjection
$\ker _{\mathbb {1}^{*\,\mu _p}}(1-\sigma )\cong \mathbb {1}$, hence a canonical surjection ![]() $\mathbb {1}\to \mathbb {1}^{(1)}$ which determines a map
$\mathbb {1}\to \mathbb {1}^{(1)}$ which determines a map
One may check that this makes ![]() $A^{(1)}$ into a ring, and, moreover, that
$A^{(1)}$ into a ring, and, moreover, that ![]() $A^{(1)}$ is associative or commutative if
$A^{(1)}$ is associative or commutative if ![]() $A$ is. The following lemma explains how this looks in the main example.
$A$ is. The following lemma explains how this looks in the main example.
Lemma 2.15 Suppose ![]() $A=\bigoplus _{i\in \mathbb {Z}/2}A_i$ is a unital ring in
$A=\bigoplus _{i\in \mathbb {Z}/2}A_i$ is a unital ring in ![]() $\mathcal {C}=\operatorname {SVect}_k$. Then the ring structure on
$\mathcal {C}=\operatorname {SVect}_k$. Then the ring structure on ![]() $A^{(1)}$ corresponds under the identification
$A^{(1)}$ corresponds under the identification ![]() $A^{(1)}=k\otimes _FA$ to the ring structure with unit
$A^{(1)}=k\otimes _FA$ to the ring structure with unit ![]() $1\otimes _F\mathbb {1}_A$ and multiplication
$1\otimes _F\mathbb {1}_A$ and multiplication
for ![]() $a\in A_i,a'\in A_j$ and
$a\in A_i,a'\in A_j$ and ![]() $r,r'\in k$.
$r,r'\in k$.
Proof. The isomorphism of ![]() $k\otimes _FA_{i}$ with
$k\otimes _FA_{i}$ with ![]() $(A^{(1)})_{i}$ sends the element
$(A^{(1)})_{i}$ sends the element ![]() $r\otimes a$ to the class of
$r\otimes a$ to the class of ![]() ${r}.\underbrace {a\otimes \cdots \otimes a}_ {p\ {\rm times}}$. The natural map
${r}.\underbrace {a\otimes \cdots \otimes a}_ {p\ {\rm times}}$. The natural map
sends the class of ![]() $\underbrace {a\otimes \cdots \otimes a}_ {p\text { times}}\otimes \underbrace {a'\otimes \cdots \otimes a'}_ {p\text { times}}$ to the class of
$\underbrace {a\otimes \cdots \otimes a}_ {p\text { times}}\otimes \underbrace {a'\otimes \cdots \otimes a'}_ {p\text { times}}$ to the class of  $(-1)^{ij{\binom {p}{2}}}\underbrace {(a\otimes a')\otimes \cdots \otimes (a\otimes a')}_ {p\text { times}}$, since it entails permuting the
$(-1)^{ij{\binom {p}{2}}}\underbrace {(a\otimes a')\otimes \cdots \otimes (a\otimes a')}_ {p\text { times}}$, since it entails permuting the ![]() $x$th copy of
$x$th copy of ![]() $A_i$ with the
$A_i$ with the ![]() $y$th copy of
$y$th copy of ![]() $A_j$ for every
$A_j$ for every ![]() $p\geq x>y\geq 1$.
$p\geq x>y\geq 1$.
Arguing the same way, we have the following proposition.
Proposition 2.16 Let ![]() $A$ be a Hopf algebra in
$A$ be a Hopf algebra in ![]() $\operatorname {SVect}_k$. Then
$\operatorname {SVect}_k$. Then ![]() $A^{(1)}$ is naturally a Hopf algebra in
$A^{(1)}$ is naturally a Hopf algebra in ![]() $\operatorname {SVect}_k$. It has multiplication and unit given as in Lemma 2.15, comultiplication given by
$\operatorname {SVect}_k$. It has multiplication and unit given as in Lemma 2.15, comultiplication given by
counit given by ![]() $\epsilon _ {A^{(1)}}(r\otimes a) = r(\epsilon _A(a))^p$ and antipode given by
$\epsilon _ {A^{(1)}}(r\otimes a) = r(\epsilon _A(a))^p$ and antipode given by ![]() $S_ {A^{(1)}}(r\otimes a) = r\otimes S_A(a)$. Moreover, the functor
$S_ {A^{(1)}}(r\otimes a) = r\otimes S_A(a)$. Moreover, the functor ![]() $(-)^{(1)}$ on
$(-)^{(1)}$ on ![]() $\operatorname {SVect}_k$ upgrades to functor
$\operatorname {SVect}_k$ upgrades to functor
For an ![]() $A$-comodule
$A$-comodule ![]() $M$, the
$M$, the ![]() $A^{(1)}$-comodule structure on
$A^{(1)}$-comodule structure on ![]() $M^{(1)}$ is given by
$M^{(1)}$ is given by
Example 2.17 Suppose ![]() $\mathcal {O}$ is a commutative Hopf algebra in
$\mathcal {O}$ is a commutative Hopf algebra in ![]() $\operatorname {SVect}_k$. Then the monoidal category
$\operatorname {SVect}_k$. Then the monoidal category ![]() $\mathcal {C}$ of
$\mathcal {C}$ of ![]() $\mathcal {O}$-comodules is symmetric. Taking
$\mathcal {O}$-comodules is symmetric. Taking ![]() $p$th powers gives a (Frobenius) map of Hopf algebras
$p$th powers gives a (Frobenius) map of Hopf algebras ![]() $F_ {\mathcal {O}}:\mathcal {O}^{(1)}\to \mathcal {O}$. Then Tate's construction on
$F_ {\mathcal {O}}:\mathcal {O}^{(1)}\to \mathcal {O}$. Then Tate's construction on ![]() $\mathcal {C}$ factors as
$\mathcal {C}$ factors as
For instance, we could take ![]() $\mathcal {O}$ to be the ring of functions
$\mathcal {O}$ to be the ring of functions ![]() $\mathcal {O}(\mathbb {G}_m)$ on the multiplicative group
$\mathcal {O}(\mathbb {G}_m)$ on the multiplicative group ![]() $\mathbb {G}_m$ over
$\mathbb {G}_m$ over ![]() $k$, concentrated in degree
$k$, concentrated in degree ![]() $0\in \mathbb {Z}/2$. Then
$0\in \mathbb {Z}/2$. Then ![]() $\mathcal {O}(\mathbb {G}_m)\operatorname {-comod}$ contains as a full subcategory over
$\mathcal {O}(\mathbb {G}_m)\operatorname {-comod}$ contains as a full subcategory over ![]() $\operatorname {SVect}_k$ the category of
$\operatorname {SVect}_k$ the category of ![]() $\mathbb {Z}$-super-graded vector spaces, and Tate's construction there is isomorphic to the functor which applies
$\mathbb {Z}$-super-graded vector spaces, and Tate's construction there is isomorphic to the functor which applies ![]() $k\otimes _F(-)$ and multiplies degrees by
$k\otimes _F(-)$ and multiplies degrees by ![]() $p$.
$p$.
Recall we have the Frobenius-multiplicative maps of multiplicative ![]() $k$-sets
$k$-sets
We view cohomology rings as commutative ring objects of ![]() $\mathbb {Z}$-super-graded vector spaces; in particular, we can apply functor
$\mathbb {Z}$-super-graded vector spaces; in particular, we can apply functor ![]() $(-)^{(1)}$ to them. By Lemma 2.6, if
$(-)^{(1)}$ to them. By Lemma 2.6, if ![]() $k$ is perfect then it gives a map of
$k$ is perfect then it gives a map of ![]() $\mathbb {Z}$-super-graded
$\mathbb {Z}$-super-graded ![]() $k$-sets
$k$-sets
The following fact is immediate from the constructions.
Proposition 2.18 ![]() $St_ {\mathrm {ex}}$ respects the multiplicative
$St_ {\mathrm {ex}}$ respects the multiplicative ![]() $k$-monoidal structures.
$k$-monoidal structures.
Remark 2.19 If ![]() $k$ is not perfect, then the map
$k$ is not perfect, then the map ![]() $H^*(X,k)\to H^{*}_ {\mu _p}(X^{\mu _p},k)$ of
$H^*(X,k)\to H^{*}_ {\mu _p}(X^{\mu _p},k)$ of ![]() $\mathbb {Z}/2$-super-graded sets respects the multiplicative monoidal structures up to the sign change of Lemma 2.15. There is presumably an appropriate nonlinear version of Tate's construction which would allow us to say that we really have a certain
$\mathbb {Z}/2$-super-graded sets respects the multiplicative monoidal structures up to the sign change of Lemma 2.15. There is presumably an appropriate nonlinear version of Tate's construction which would allow us to say that we really have a certain ![]() $\mathbb {Z}$-super-graded
$\mathbb {Z}$-super-graded ![]() $k$-monoid
$k$-monoid ![]() $H^*(X,k)^{(1)}_ {nl}$ and a map of monoids
$H^*(X,k)^{(1)}_ {nl}$ and a map of monoids ![]() $H^*(X,k)^{(1)}_ {nl}\to H^{*}_ {\mu _p}(X^{\mu _p},k)$, but we prefer for simplicity not to do so.
$H^*(X,k)^{(1)}_ {nl}\to H^{*}_ {\mu _p}(X^{\mu _p},k)$, but we prefer for simplicity not to do so.
2.6 Borel–Moore homology
We return to the setting of § 2.4. By Corollary 2.11, we have a canonical isomorphism
Here the ![]() $\omega$ on the left-hand side denotes the
$\omega$ on the left-hand side denotes the ![]() $G$-equivariant dualizing complex on
$G$-equivariant dualizing complex on ![]() $Y$ with coefficients in
$Y$ with coefficients in ![]() $R$, while the
$R$, while the ![]() $\omega$ on the left-hand side denotes the
$\omega$ on the left-hand side denotes the ![]() $G^{\mu _p}\rtimes\, \mu _p$-equivariant dualizing complex on
$G^{\mu _p}\rtimes\, \mu _p$-equivariant dualizing complex on ![]() $Y^{\mu _p}$ with coefficients in
$Y^{\mu _p}$ with coefficients in ![]() $R$. By definition, the
$R$. By definition, the ![]() $G$-equivariant Borel–Moore homology of
$G$-equivariant Borel–Moore homology of ![]() $Y$ is
$Y$ is
See § 3.10 for more about this. Altogether ![]() $H_n^{\mathrm {BM},G}(Y,R)$ form a
$H_n^{\mathrm {BM},G}(Y,R)$ form a ![]() $\mathbb {Z}$-super-graded
$\mathbb {Z}$-super-graded ![]() $H^*_G(Y,R)$-module; in particular, it is a module for
$H^*_G(Y,R)$-module; in particular, it is a module for ![]() $H^*_G(*,R)$. By functoriality we have the nonlinear maps
$H^*_G(*,R)$. By functoriality we have the nonlinear maps
This is a map of ![]() $St^H$-monoids. Its discrepancy from additivity it averaged from
$St^H$-monoids. Its discrepancy from additivity it averaged from ![]() $H_ {pn}^{\mathrm {BM},G^{\mu _p}}(Y^{\mu _p},R)$. If
$H_ {pn}^{\mathrm {BM},G^{\mu _p}}(Y^{\mu _p},R)$. If ![]() $R$ is a perfect field
$R$ is a perfect field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p$, we can say that we have a nonlinear graded map of
$p$, we can say that we have a nonlinear graded map of ![]() $St_ {\mathrm {ex}}$-monoids:
$St_ {\mathrm {ex}}$-monoids:
2.7 Steenrod operations
For simplicity let us assume ![]() $k$ to be perfect from now on. Let us compose
$k$ to be perfect from now on. Let us compose ![]() $St_ {\mathrm {ex}}$ with the restriction map to the diagonal:
$St_ {\mathrm {ex}}$ with the restriction map to the diagonal:
This is again a map of multiplicative ![]() $k$-monoids. Tautologically we have
$k$-monoids. Tautologically we have ![]() $St_ {\mathrm {in}}(x)=x^p\text { mod }(a,\hbar )$. Also
$St_ {\mathrm {in}}(x)=x^p\text { mod }(a,\hbar )$. Also ![]() $St_ {\mathrm {in}}$ is compatible with pullback maps in cohomology in the natural way. Since induction commutes with restriction, the difference between
$St_ {\mathrm {in}}$ is compatible with pullback maps in cohomology in the natural way. Since induction commutes with restriction, the difference between ![]() $St_ {\mathrm {in}}(x+y)$ and
$St_ {\mathrm {in}}(x+y)$ and ![]() $St_ {\mathrm {in}}(x)+St_ {\mathrm {in}}(y)$ is induced from a cohomology class
$St_ {\mathrm {in}}(x)+St_ {\mathrm {in}}(y)$ is induced from a cohomology class ![]() $z\in H^\bullet (X;k)$. Since
$z\in H^\bullet (X;k)$. Since ![]() $\mu _p$ acts trivially on
$\mu _p$ acts trivially on ![]() $X$, that means that it is equal to
$X$, that means that it is equal to ![]() $pz=0$, so
$pz=0$, so ![]() $St_ {\mathrm {in}}$ is linear. That is, we have a map of super-commutative
$St_ {\mathrm {in}}$ is linear. That is, we have a map of super-commutative ![]() $k$-algebras
$k$-algebras
Remark 2.20 The coefficients of ![]() $\hbar ^m,a\hbar ^m$ in
$\hbar ^m,a\hbar ^m$ in ![]() $St_ {\mathrm {in}}$ are not the Steenrod operations. More precisely, they are the Steenrod operations only up to some non-zero scalars. Even more precisely, let
$St_ {\mathrm {in}}$ are not the Steenrod operations. More precisely, they are the Steenrod operations only up to some non-zero scalars. Even more precisely, let ![]() $x\in H^n(X,k)$ and let
$x\in H^n(X,k)$ and let ![]() $p=2q+1$. Consider
$p=2q+1$. Consider
where ![]() $x$ is viewed as a degree
$x$ is viewed as a degree ![]() $pn$ element of
$pn$ element of ![]() $H^*(X,k)^{(1)}$. The coefficient of
$H^*(X,k)^{(1)}$. The coefficient of ![]() $\hbar ^m$ in this expression vanishes unless
$\hbar ^m$ in this expression vanishes unless ![]() $m=\frac {1}{2}(p-1)(n-2s)$ for some
$m=\frac {1}{2}(p-1)(n-2s)$ for some ![]() $s$ such that
$s$ such that ![]() $2s\leq n$, in which case that coefficient is equal to
$2s\leq n$, in which case that coefficient is equal to ![]() $(-1)^sP^s(x)$ where
$(-1)^sP^s(x)$ where ![]() $P^s$ is the
$P^s$ is the ![]() $s$th Steenrod operation. Similarly, the coefficient of
$s$th Steenrod operation. Similarly, the coefficient of ![]() $a\hbar ^m$ in that expression vanishes unless
$a\hbar ^m$ in that expression vanishes unless ![]() $m=\frac {1}{2}(p-1)(n-2s)-1$ for some
$m=\frac {1}{2}(p-1)(n-2s)-1$ for some ![]() $s$ such that
$s$ such that ![]() $2s\leq n$, in which case that coefficient is equal to
$2s\leq n$, in which case that coefficient is equal to ![]() $(-1)^{s+1}\beta P^s(x)$ where
$(-1)^{s+1}\beta P^s(x)$ where ![]() $\beta$ is the Bockstein operation. A careful comparison of
$\beta$ is the Bockstein operation. A careful comparison of ![]() $St_ {\mathrm {in}}$ with the sum of Steenrod operations as defined in [Reference Steenrod and EpsteinSE62] shows the constructions are indeed identical except that N. Steenrod deliberately inserted exactly these invertible ‘correction factors’. For him, as far as we can tell, the purpose was to ensure that
$St_ {\mathrm {in}}$ with the sum of Steenrod operations as defined in [Reference Steenrod and EpsteinSE62] shows the constructions are indeed identical except that N. Steenrod deliberately inserted exactly these invertible ‘correction factors’. For him, as far as we can tell, the purpose was to ensure that
(i)
 $P^0={\rm id}$, and
$P^0={\rm id}$, and(ii) the total Steenrod,
 $\sum _ {s=0}^{\infty }P^s$, is a ring endomorphism of
$\sum _ {s=0}^{\infty }P^s$, is a ring endomorphism of  $H^*(X)$.
$H^*(X)$.
On the one hand, from the perspective of the results of this paper, these two constraints are pure obfuscation; the latter denies the reality that the natural source of the algebra homomorphism is the Tate construction ![]() $H^*(X)^{(1)}$ rather than
$H^*(X)^{(1)}$ rather than ![]() $H^*(X)$, while the former masks the resemblance (not a coincidence!) to the Artin–Schreier morphism. On the other hand, from the perspective of the author, it is rather fortunate as the core innovation of this work would surely have been discovered sooner otherwise.
$H^*(X)$, while the former masks the resemblance (not a coincidence!) to the Artin–Schreier morphism. On the other hand, from the perspective of the author, it is rather fortunate as the core innovation of this work would surely have been discovered sooner otherwise.
2.8 Artin–Schreier
We indicate how the Artin–Schreier map comes naturally out of the above considerations. First note that if ![]() $n$ is even then the number
$n$ is even then the number
boils down to ![]() $(-1)^{n/2}$. It is a standard fact that on a degree
$(-1)^{n/2}$. It is a standard fact that on a degree ![]() $2$ class
$2$ class ![]() $x$ we have
$x$ we have ![]() $P^0(x)=x,P^1(x)=x^p$, and higher powers vanish. Therefore
$P^0(x)=x,P^1(x)=x^p$, and higher powers vanish. Therefore
Let ![]() $X=BT$ for some compact torus
$X=BT$ for some compact torus ![]() $T$. Since its cohomology is supported in even degrees, the Bockstein operator acts as zero and
$T$. Since its cohomology is supported in even degrees, the Bockstein operator acts as zero and ![]() $St_ {\mathrm {in}}$, on the level of
$St_ {\mathrm {in}}$, on the level of ![]() $k$-cohomology, is exactly the
$k$-cohomology, is exactly the ![]() $\hbar$-Artin–Schreier map
$\hbar$-Artin–Schreier map
as defined in Fact 2.1.
Recall that if ![]() $G$ is a compact Lie group with maximal torus
$G$ is a compact Lie group with maximal torus ![]() $T$, and
$T$, and ![]() $p$ is large enough with respect to the Weyl group of
$p$ is large enough with respect to the Weyl group of ![]() $G$, then the projection
$G$, then the projection ![]() $BT\to BG$ induces an inclusion
$BT\to BG$ induces an inclusion
which is identified with
The ![]() $\hbar$-Artin–Schreier map induces a map on subspaces
$\hbar$-Artin–Schreier map induces a map on subspaces
which is also important in the theory of Frobenius-constant quantization. The point is that this map is also induced by ![]() $St_ {\mathrm {in}}$, since it is compatible with pullbacks.
$St_ {\mathrm {in}}$, since it is compatible with pullbacks.
It is entertaining to show more directly how ![]() $AS_\hbar$ arises, without relying on any outside facts about Steenrod operations. We can reduce to the rank
$AS_\hbar$ arises, without relying on any outside facts about Steenrod operations. We can reduce to the rank ![]() $1$ case
$1$ case ![]() $T=S^1$. Let
$T=S^1$. Let ![]() $b$ denote the degree
$b$ denote the degree ![]() $2$ generator (first Chern class of tautological line bundle) of
$2$ generator (first Chern class of tautological line bundle) of ![]() $BS^1$; we need to show that
$BS^1$; we need to show that ![]() $St_ {\mathrm {in}}(b)=b^p-\hbar ^{p-1}b$. Let
$St_ {\mathrm {in}}(b)=b^p-\hbar ^{p-1}b$. Let ![]() $C_p\subset S^1$ denote the cyclic group of order
$C_p\subset S^1$ denote the cyclic group of order ![]() $p$, considered as distinct from
$p$, considered as distinct from ![]() $\mu _p$. Consider the projection
$\mu _p$. Consider the projection
It induces an injective map
in cohomology, where ![]() $s$ is a degree
$s$ is a degree ![]() $1$ generator. By functoriality it is enough to prove the equality when
$1$ generator. By functoriality it is enough to prove the equality when ![]() $b$ is regarded as a cohomology class of
$b$ is regarded as a cohomology class of ![]() $BC_p$. Note that amongst degree
$BC_p$. Note that amongst degree ![]() $2p$ elements of
$2p$ elements of ![]() $k[b,\hbar ]$, the desired element
$k[b,\hbar ]$, the desired element ![]() $b^p-\hbar ^{p-1}b$ is the unique one which gives
$b^p-\hbar ^{p-1}b$ is the unique one which gives ![]() $0$ when we set
$0$ when we set ![]() $b$ to any multiple in
$b$ to any multiple in ![]() $\mathbb {F}_{\rm p}$ of
$\mathbb {F}_{\rm p}$ of ![]() $\hbar$, and gives
$\hbar$, and gives ![]() $b^p$ when we set
$b^p$ when we set ![]() $\hbar =0$. The latter statement is automatic, so we have to check the former. So fix some
$\hbar =0$. The latter statement is automatic, so we have to check the former. So fix some ![]() $t\in \mathbb {F}_{\rm p}$. Having chosen an isomorphism
$t\in \mathbb {F}_{\rm p}$. Having chosen an isomorphism ![]() $\mu _p\cong C_p$,
$\mu _p\cong C_p$, ![]() $t$ determines a group homomorphism
$t$ determines a group homomorphism ![]() $\mu _p\to C_p$.
$\mu _p\to C_p$.
The constant sheaf ![]() $\Sigma ^nk$ of
$\Sigma ^nk$ of ![]() $BC_p$ is contained in the full subcategory
$BC_p$ is contained in the full subcategory
Our coefficients are ![]() $k$, which we drop from the notation. It is easier for our purpose to work in
$k$, which we drop from the notation. It is easier for our purpose to work in ![]() $D^b(k[C_p]\operatorname {-mod})$. Compatible with the functor
$D^b(k[C_p]\operatorname {-mod})$. Compatible with the functor ![]() $St_D$ out of
$St_D$ out of ![]() $D(BC_p)$ we have the functor
$D(BC_p)$ we have the functor
This is then composed with the diagonal restriction
By definition ![]() $St_ {\mathrm {in}}(b)$ is given by applying that composition to the morphism
$St_ {\mathrm {in}}(b)$ is given by applying that composition to the morphism ![]() $k\xrightarrow {b}k[2]$, where
$k\xrightarrow {b}k[2]$, where ![]() $k$ is the trivial
$k$ is the trivial ![]() $C_p$-module. We want further to set
$C_p$-module. We want further to set ![]() $b=t\hbar$; this corresponds to restricting along the map
$b=t\hbar$; this corresponds to restricting along the map
Write
for the corresponding restriction map. We need to show that ![]() $({\rm id}\times t)^*\circ \Delta ^*\circ St(b)=0$. But actually there is an isomorphism of functors
$({\rm id}\times t)^*\circ \Delta ^*\circ St(b)=0$. But actually there is an isomorphism of functors
where ![]() $i^*$ is the forgetful functor
$i^*$ is the forgetful functor ![]() $D^b(k[C_p]\operatorname {-mod})=D_ {C_p}(*)\to D(*)$. Indeed, for an object
$D^b(k[C_p]\operatorname {-mod})=D_ {C_p}(*)\to D(*)$. Indeed, for an object ![]() $A^\bullet$ of
$A^\bullet$ of ![]() $D^b(k[C_p]\operatorname {-mod})$, the underlying complex of both functors is
$D^b(k[C_p]\operatorname {-mod})$, the underlying complex of both functors is ![]() $(A^\bullet )^{\otimes\, \mu _p}$, and the automorphism which sends each summand
$(A^\bullet )^{\otimes\, \mu _p}$, and the automorphism which sends each summand
to itself by ![]() $1\otimes \sigma ^t\otimes \sigma ^{2t}\otimes \cdots \otimes \sigma ^{(p-1)t}$ intertwines the two actions of
$1\otimes \sigma ^t\otimes \sigma ^{2t}\otimes \cdots \otimes \sigma ^{(p-1)t}$ intertwines the two actions of ![]() $\mu _p$. Here
$\mu _p$. Here ![]() $\sigma$ is some generator of
$\sigma$ is some generator of ![]() $\mu _p$. But the functor
$\mu _p$. But the functor ![]() $St\circ i^*$ kills
$St\circ i^*$ kills ![]() $b$, since
$b$, since ![]() $i^*$ does.
$i^*$ does.
3. Coulomb branch
3.1 Prelude: Frobenius-constant quantizations
Let ![]() $k$ be a field of characteristic
$k$ be a field of characteristic ![]() $p$ and let
$p$ and let ![]() $\mathcal {C}$ be a symmetric monoidal category over
$\mathcal {C}$ be a symmetric monoidal category over ![]() $k$. The reader may assume that
$k$. The reader may assume that ![]() $\mathcal {C}$ is the category of comodules of some commutative Hopf algebra in
$\mathcal {C}$ is the category of comodules of some commutative Hopf algebra in ![]() $\operatorname {SVect}_k$. Let
$\operatorname {SVect}_k$. Let ![]() $A$ be a commutative (and associative) algebra in
$A$ be a commutative (and associative) algebra in ![]() $\mathcal {C}$. Let
$\mathcal {C}$. Let
be the Frobenius map. Let ![]() $Q$ be an augmented commutative algebra in
$Q$ be an augmented commutative algebra in ![]() $\mathcal {C}$ with augmentation
$\mathcal {C}$ with augmentation ![]() $\epsilon :Q\to k$. Following [Reference Bezrukavnikov and KaledinBK08], we make the following definition.
$\epsilon :Q\to k$. Following [Reference Bezrukavnikov and KaledinBK08], we make the following definition.
Definition 3.1
(i) A
 $Q$-quantization of
$Q$-quantization of  $A$ is a flat associative
$A$ is a flat associative  $Q$-algebra
$Q$-algebra  $A_Q$ in
$A_Q$ in  $\mathcal {C}$ such that
$\mathcal {C}$ such that  $A_Q\otimes _Qk=A$.
$A_Q\otimes _Qk=A$.(ii) A Frobenius-constant
 $Q$-quantization of
$Q$-quantization of  $A$ is a
$A$ is a  $Q$-quantization
$Q$-quantization  $A_Q$ of
$A_Q$ of  $A$ together with a map
of algebras which lifts the Frobenius map, that is, such that
$A$ together with a map
of algebras which lifts the Frobenius map, that is, such that \[ F_Q:A^{(1)}\to Z(A_Q) \]
\[ F_Q:A^{(1)}\to Z(A_Q) \] $\epsilon \circ F_Q\equiv F$. Here
$\epsilon \circ F_Q\equiv F$. Here  $Z(A_Q)$ denotes the center of
$Z(A_Q)$ denotes the center of  $A_Q$.
$A_Q$.
The main example for us is as follow. We take ![]() $K$ to be some
$K$ to be some ![]() $\mathbb {G}_m$-equivariant algebraic group in
$\mathbb {G}_m$-equivariant algebraic group in ![]() $\operatorname {Vect}_k$, and view
$\operatorname {Vect}_k$, and view ![]() $\mathcal {O}:=\mathcal {O}(K\rtimes \mathbb {G}_m)$ as a Hopf algebra in
$\mathcal {O}:=\mathcal {O}(K\rtimes \mathbb {G}_m)$ as a Hopf algebra in ![]() $\operatorname {SVect}_k$ concentrated in degree
$\operatorname {SVect}_k$ concentrated in degree ![]() $0$. We take
$0$. We take ![]() $\mathcal {C}=\mathcal {O}\operatorname {-comod}$. Let
$\mathcal {C}=\mathcal {O}\operatorname {-comod}$. Let ![]() $\hbar$ be a basis vector of the one-dimensional representation of
$\hbar$ be a basis vector of the one-dimensional representation of ![]() $K\rtimes \mathbb {G}_m$ in which
$K\rtimes \mathbb {G}_m$ in which ![]() $K$ acts trivially and
$K$ acts trivially and ![]() $\mathbb {G}_m$ acts with weight
$\mathbb {G}_m$ acts with weight ![]() $2$. Let
$2$. Let ![]() $Q=k[\hbar ]$. In this case, we will call a
$Q=k[\hbar ]$. In this case, we will call a ![]() $Q$-quantization simply an
$Q$-quantization simply an ![]() $\hbar$-quantization, or just a quantization if the meaning is clear.
$\hbar$-quantization, or just a quantization if the meaning is clear.
Fact 3.2 (i) Let ![]() $X$ be a smooth affine algebraic variety over
$X$ be a smooth affine algebraic variety over ![]() $k$. Then the ring of asymptotic crystalline differential operators,
$k$. Then the ring of asymptotic crystalline differential operators, ![]() $\mathcal {D}_\hbar (X)$, is a canonical
$\mathcal {D}_\hbar (X)$, is a canonical ![]() $\hbar$-quantization of
$\hbar$-quantization of ![]() $\mathcal {O}(T^*X)$. Here
$\mathcal {O}(T^*X)$. Here ![]() $\mathbb {G}_m$ acts trivially on
$\mathbb {G}_m$ acts trivially on ![]() $\mathcal {O}(X)$ and on vector field with weight
$\mathcal {O}(X)$ and on vector field with weight ![]() $2$. Let
$2$. Let ![]() $\partial$ be a vector field on
$\partial$ be a vector field on ![]() $X$. Then
$X$. Then ![]() $\partial ^p$ acts as a derivation on
$\partial ^p$ acts as a derivation on ![]() $\mathcal {O}(X)$, so that
$\mathcal {O}(X)$, so that ![]() $\partial ^p-\partial ^{[p]}$ annihilates
$\partial ^p-\partial ^{[p]}$ annihilates ![]() $\mathcal {O}(X)$ for a unique vector field
$\mathcal {O}(X)$ for a unique vector field ![]() $\partial ^{[p]}$. Then
$\partial ^{[p]}$. Then ![]() $\mathcal {D}_\hbar (X)$ has a canonical Frobenius-constant structure determined by
$\mathcal {D}_\hbar (X)$ has a canonical Frobenius-constant structure determined by
(ii) Let ![]() $J$ be a smooth algebraic group over
$J$ be a smooth algebraic group over ![]() $k$. Then
$k$. Then ![]() $F_\hbar$ as above is
$F_\hbar$ as above is ![]() $K=J\times J$-equivariant (induced by left and right regular actions). In particular, if we take invariants for the left factor, we obtain a Frobenius-constant structure for the quantization
$K=J\times J$-equivariant (induced by left and right regular actions). In particular, if we take invariants for the left factor, we obtain a Frobenius-constant structure for the quantization ![]() $\mathcal {U}_\hbar (J)$ of
$\mathcal {U}_\hbar (J)$ of ![]() $\mathcal {O}(\operatorname {Lie}(J)^*)$.
$\mathcal {O}(\operatorname {Lie}(J)^*)$.
(iii) Let ![]() $T$ be a complex torus and let
$T$ be a complex torus and let ![]() $T^\vee$ be the Langlands dual split torus over
$T^\vee$ be the Langlands dual split torus over ![]() $k$, that is,
$k$, that is,
where ![]() $\mathbb {X}_\bullet (T)$ is the cocharacter lattice of
$\mathbb {X}_\bullet (T)$ is the cocharacter lattice of ![]() $T$ and
$T$ and ![]() $k[\mathbb {X}_\bullet (T)]$ is its group algebra. We have canonical identifications
$k[\mathbb {X}_\bullet (T)]$ is its group algebra. We have canonical identifications
If we take ![]() $\operatorname {Spec}$ of the Frobenius-constant structure we recover the
$\operatorname {Spec}$ of the Frobenius-constant structure we recover the ![]() $\hbar$-Artin–Schreier map
$\hbar$-Artin–Schreier map
of Fact 2.1.
Remark 3.3 If a commutative algebra and its quantization contain in a natural way ![]() $H^*_G(*,k)$ for some complex reductive group
$H^*_G(*,k)$ for some complex reductive group ![]() $G$ with maximal torus
$G$ with maximal torus ![]() $T$, then when searching for a Frobenius-constant structure it is natural to look for one which is compatible with the
$T$, then when searching for a Frobenius-constant structure it is natural to look for one which is compatible with the ![]() $\hbar$-Artin–Schreier map.
$\hbar$-Artin–Schreier map.
3.2 Interlude
The next eight subsections are intended to be a self-contained description of an extension of the theory of Beilinson–Drinfeld Grassmannians, an amazing invention first described in the canonical [Reference Beĭlinson and DrinfeldBD91]. Our extension required a little more geometric machinery than was present in [Reference Beĭlinson and DrinfeldBD91], but we were fortunately able to find what was required in Raskin's excellently concise paper [Reference RaskinRas15] on placid ind-schemes. This was actually originally written with ![]() $\mathcal {D}$-modules in mind, but the underlying geometry is the same. These eight subsections are also intended to be a self-contained account of the necessary details of [Reference RaskinRas15], and we have attempted to present things in a slightly more geometric and less categorical way, but highly recommend reading the paper. We have tried to make it clear in the text what is new and what is essentially to be found in [Reference Beĭlinson and DrinfeldBD91] and [Reference RaskinRas15]. What follows is an overview.
$\mathcal {D}$-modules in mind, but the underlying geometry is the same. These eight subsections are also intended to be a self-contained account of the necessary details of [Reference RaskinRas15], and we have attempted to present things in a slightly more geometric and less categorical way, but highly recommend reading the paper. We have tried to make it clear in the text what is new and what is essentially to be found in [Reference Beĭlinson and DrinfeldBD91] and [Reference RaskinRas15]. What follows is an overview.
We give the following very brief and incomplete overview of the purpose of Beilinson–Drinfeld Grassmannians.
(i) If
 $G$ is a complex algebraic group, its affine Grassmannian
$G$ is a complex algebraic group, its affine Grassmannian  $Gr_1$ is the algebro-geometric incarnation of the
$Gr_1$ is the algebro-geometric incarnation of the  $E_2$-group
$E_2$-group  $\Omega ^1K$ of based loops in a compact form
$\Omega ^1K$ of based loops in a compact form  $K$ of
$K$ of  $G$.
$G$.(ii)
 $Gr_1$ comes naturally equipped with a ‘convolution diagram’ which is the algebro-geometric incarnation of the pointwise multiplication structure on
$Gr_1$ comes naturally equipped with a ‘convolution diagram’ which is the algebro-geometric incarnation of the pointwise multiplication structure on  $\Omega ^1K$.
$\Omega ^1K$.(iii) The Beilinson–Drinfeld Grassmannian
 $Gr_2$ of
$Gr_2$ of  $G$ is both a deformation of
$G$ is both a deformation of  $Gr_1$ and the algebro-geometric incarnation of the loop-concatenation structure on
$Gr_1$ and the algebro-geometric incarnation of the loop-concatenation structure on  $\Omega ^1K$.
$\Omega ^1K$.(iv) The Beilinson–Drinfeld Grassmannian fits inside a deformation of the aforementioned ‘convolution diagram’, called the ‘global convolution diagram’ (see [Reference Beĭlinson and DrinfeldBD91, Reference Mirković and VilonenMV07]), which is the algebro-geometric incarnation of the Eckmann–Hilton argument.
Now we review in similar terms what we do that is new. (i) We construct a ‘global convolution diagram’ in the context of the ‘variety of triples’ (which is the geometric basis of the quantum Coulomb branch; see [Reference Braverman, Finkelberg and NakajimaBFN16]). This construction is also summarized in the appendix to [Reference Braverman, Finkelberg and NakajimaBFN17]. The Beilinson–Drinfeld Grassmannian was already constructed in this wider context in [Reference Braverman, Finkelberg and NakajimaBFN16], but the global convolution diagram (and hence the Eckmann–Hilton argument) had proved elusive.
(ii) We construct a geometric analogue of the Kudo–Araki–Dyer–Lashof operations, in the same way that the Beilinson–Drinfeld Grassmannian itself is a geometric analogue of the loop-concatenation structure of loop groups. We do this for the variety of triples,but it is new even for the ordinary Grassmannian.
(iii) We produce a gadget that is to our geometric analogue of the Kudo–Araki–Dyer–Lashof operations as the global convolution diagram is to the Beilinson–Drinfeld Grassmannian (for the variety of triples as well as the basic Grassmannian case). This provides the geometric incarnation of a principle which is similar in spirit to the Eckmann–Hilton argument, but hitherto unknown, namely, that any ![]() $S^1$-framed
$S^1$-framed ![]() $E_3$-algebra over
$E_3$-algebra over ![]() $\mathbb {F}_{\rm p}$ defines a Frobenius-constant quantization (to be elucidated in a forthcoming work; the topological insight is that one can move a ball past – or rather, through – a donut in an
$\mathbb {F}_{\rm p}$ defines a Frobenius-constant quantization (to be elucidated in a forthcoming work; the topological insight is that one can move a ball past – or rather, through – a donut in an ![]() $S^1$-equivariant way).
$S^1$-equivariant way).
3.3 Formal neighborhoods
Let ![]() $X$ be a smooth complex curve and let
$X$ be a smooth complex curve and let ![]() $S$ be a finite set. Given a commutative ring
$S$ be a finite set. Given a commutative ring ![]() $R$ and an
$R$ and an ![]() $R$-point
$R$-point ![]() $x$ of
$x$ of ![]() $X^S$, we denote the coordinates of
$X^S$, we denote the coordinates of ![]() $x$ by
$x$ by ![]() $x_s$ (
$x_s$ (![]() $s\in S$), write
$s\in S$), write ![]() $\Gamma (x_s)$ for the graph of
$\Gamma (x_s)$ for the graph of ![]() $x_s$ in
$x_s$ in ![]() $X_R$ and write
$X_R$ and write ![]() $I(x_s)$ for its ideal. We write
$I(x_s)$ for its ideal. We write ![]() $\Delta _ {S}(x)$ for the formal neighborhood of the union of the graphs of
$\Delta _ {S}(x)$ for the formal neighborhood of the union of the graphs of ![]() $x_s$ (
$x_s$ (![]() $s\in S$). That is,
$s\in S$). That is, ![]() $\Delta _S(x)$ is the direct limit in affine schemes over
$\Delta _S(x)$ is the direct limit in affine schemes over ![]() $X$:
$X$:
where
Given a subset ![]() $S'\subset S$ and an
$S'\subset S$ and an ![]() $R$-point
$R$-point ![]() $x$ of
$x$ of ![]() $X^S$, we will write
$X^S$, we will write
for the ![]() $S'$-punctured formal neighborhood, that is, the complement of the union of the graphs of
$S'$-punctured formal neighborhood, that is, the complement of the union of the graphs of ![]() $x_s$ (
$x_s$ (![]() $s\in S'$) in
$s\in S'$) in ![]() $\Delta _S(x)$. As a sheaf of algebras on
$\Delta _S(x)$. As a sheaf of algebras on ![]() $\Delta _S(x)$,
$\Delta _S(x)$, ![]() $\mathcal {O}(\Delta _S^{S'}(x))$ has an exhaustive increasing filtration:
$\mathcal {O}(\Delta _S^{S'}(x))$ has an exhaustive increasing filtration:
Suppose we have ![]() $S''\subset S'\subset S$ and
$S''\subset S'\subset S$ and ![]() $x\in X^S(R)$. The inclusion
$x\in X^S(R)$. The inclusion ![]() $S'\subset S$ defines a projection
$S'\subset S$ defines a projection ![]() $f:X^S\to X^{S'}$, and we will occasionally write
$f:X^S\to X^{S'}$, and we will occasionally write
for ![]() $\Delta _ {S'}^{S''}(f(x))$. We have a closed embedding
$\Delta _ {S'}^{S''}(f(x))$. We have a closed embedding ![]() $\Delta _ {S'}^{S''}(x)\to \Delta _S^{S''}(x)$. Note, however, that this is in a sense non-uniform in
$\Delta _ {S'}^{S''}(x)\to \Delta _S^{S''}(x)$. Note, however, that this is in a sense non-uniform in ![]() $x$: for instance, if for every
$x$: for instance, if for every ![]() $s\in S$ there exists an
$s\in S$ there exists an ![]() $s'\in S'$ such that
$s'\in S'$ such that ![]() $x_s=x_ {s'}$, then the embedding is an isomorphism; and conversely. This is essentially the fact underlying Beilinson and Drinfeld's ‘fusion’ Grassmannian [Reference Beĭlinson and DrinfeldBD91]. We will make more of this when we discuss co-placid morphisms; see Example 3.15.
$x_s=x_ {s'}$, then the embedding is an isomorphism; and conversely. This is essentially the fact underlying Beilinson and Drinfeld's ‘fusion’ Grassmannian [Reference Beĭlinson and DrinfeldBD91]. We will make more of this when we discuss co-placid morphisms; see Example 3.15.
For notational simplicity, we frequently remove commas and braces from ![]() $S$,
$S$, ![]() $S'$, and also drop the part
$S'$, and also drop the part ![]() $(x)$, when it is clear which point we refer to. So, for example, the expression
$(x)$, when it is clear which point we refer to. So, for example, the expression
becomes
Remark 3.4 Exponential objects such as ![]() $X^{\Delta _S^{S'}}$ will form the building blocks of our geometric objects. This is not really a new idea. For example,
$X^{\Delta _S^{S'}}$ will form the building blocks of our geometric objects. This is not really a new idea. For example, ![]() $G^{\Delta _S^{\varnothing }}$ is the ‘global group’ of [Reference Beĭlinson and DrinfeldBD91]; moreover, it acts on
$G^{\Delta _S^{\varnothing }}$ is the ‘global group’ of [Reference Beĭlinson and DrinfeldBD91]; moreover, it acts on ![]() $G^{\Delta _S^S}$ and the quotient is the Beilinson–Drinfeld Grassmannian of degree
$G^{\Delta _S^S}$ and the quotient is the Beilinson–Drinfeld Grassmannian of degree ![]() $|S|$. However, the idea to let
$|S|$. However, the idea to let ![]() $S'$ lie somewhere between
$S'$ lie somewhere between ![]() $\varnothing$ and
$\varnothing$ and ![]() $S$ does seem to be new, and is the essential insight in constructing the global convolution diagram for the variety of triples.
$S$ does seem to be new, and is the essential insight in constructing the global convolution diagram for the variety of triples.
3.4 Global groups; pro-smoothness
Now fix an affine algebraic group ![]() $G$ over
$G$ over ![]() $\mathbb {C}$. Consider the following functor from commutative rings to groups over
$\mathbb {C}$. Consider the following functor from commutative rings to groups over ![]() $X^S$:
$X^S$:
Then ![]() $G_ {S}$ is represented by the limit of an inverse system of smooth affine group schemes over
$G_ {S}$ is represented by the limit of an inverse system of smooth affine group schemes over ![]() $X^S$,
$X^S$,
such that each transition morphism is a smooth homomorphism. Here ![]() $G_ {S,i}$ may be taken to represent the functor
$G_ {S,i}$ may be taken to represent the functor
Later, the notation ![]() $G_ {S,i}$ may represent a piece of some other cofiltered system presenting
$G_ {S,i}$ may represent a piece of some other cofiltered system presenting ![]() $G_S$; we will refer to the specific group above as
$G_S$; we will refer to the specific group above as ![]() $\operatorname {Map}(\Delta _ {S,i},G)$. The fact that each transition morphism is smooth is directly verified using the valuative criterion. Indeed, let
$\operatorname {Map}(\Delta _ {S,i},G)$. The fact that each transition morphism is smooth is directly verified using the valuative criterion. Indeed, let ![]() $\operatorname {Spec}(\tilde {R})$ be a square-zero thickening of
$\operatorname {Spec}(\tilde {R})$ be a square-zero thickening of ![]() $\operatorname {Spec}(R)$. A commutative diagram
$\operatorname {Spec}(R)$. A commutative diagram
 \[ \begin{matrix}\operatorname{Spec}(R) & \to & G_{S,i+1}\\ \downarrow & & \downarrow\\ \operatorname{Spec}(\tilde{R}) & \to & G_{S,i}\end{matrix} \]
\[ \begin{matrix}\operatorname{Spec}(R) & \to & G_{S,i+1}\\ \downarrow & & \downarrow\\ \operatorname{Spec}(\tilde{R}) & \to & G_{S,i}\end{matrix} \]
is the same thing as a point ![]() $\tilde {x}\in X^S(\tilde {R})$, with residue
$\tilde {x}\in X^S(\tilde {R})$, with residue ![]() $x\in X^S(R)$, and a commutative diagram
$x\in X^S(R)$, and a commutative diagram
 \[ \begin{matrix}\Delta_{S,i}(x) & \to & \Delta_{S,i+1}(x)\\ \downarrow & & \downarrow\\ \Delta_{S,i}(\tilde{x}) & \to & G.\end{matrix} \]
\[ \begin{matrix}\Delta_{S,i}(x) & \to & \Delta_{S,i+1}(x)\\ \downarrow & & \downarrow\\ \Delta_{S,i}(\tilde{x}) & \to & G.\end{matrix} \]
This determines a morphism ![]() $P\to G$ where
$P\to G$ where ![]() $P$ is the appropriate pushout in affine schemes. Since
$P$ is the appropriate pushout in affine schemes. Since ![]() $\Delta _ {S,i}(x)$ is equal to the intersection of
$\Delta _ {S,i}(x)$ is equal to the intersection of ![]() $\Delta _ {S,i+1}(x)$ with
$\Delta _ {S,i+1}(x)$ with ![]() $\Delta _ {S,i}(\tilde {x})$ inside
$\Delta _ {S,i}(\tilde {x})$ inside ![]() $\Delta _ {S,i+1}(\tilde {x})$, and
$\Delta _ {S,i+1}(\tilde {x})$, and ![]() $\Delta _ {S,i+1}(\tilde {x})$ is a square-zero thickening of
$\Delta _ {S,i+1}(\tilde {x})$ is a square-zero thickening of ![]() $\Delta _ {S,i+1}({x})$, it follows that
$\Delta _ {S,i+1}({x})$, it follows that ![]() $\Delta _ {S,i+1}(\tilde {x})$ is a square-zero thickening of
$\Delta _ {S,i+1}(\tilde {x})$ is a square-zero thickening of ![]() $P$. Therefore since
$P$. Therefore since ![]() $G$ is smooth we can extend
$G$ is smooth we can extend ![]() $P\to G$ to
$P\to G$ to ![]() $\Delta _ {S,i+1}(\tilde {x})\to G$, as required. Note that
$\Delta _ {S,i+1}(\tilde {x})\to G$, as required. Note that ![]() $G_ {S,0}=X^S$ so, in particular, each
$G_ {S,0}=X^S$ so, in particular, each ![]() $G_ {S,i}$ is smooth over
$G_ {S,i}$ is smooth over ![]() $X^S$.
$X^S$.
Now fix ![]() $x\in X^S(\mathbb {C})$. It partitions
$x\in X^S(\mathbb {C})$. It partitions ![]() $S$ into subsets
$S$ into subsets ![]() $S_1,\ldots , S_n$ according to coincidence amongst the coordinates. Write
$S_1,\ldots , S_n$ according to coincidence amongst the coordinates. Write ![]() $y_m$ for the coordinate
$y_m$ for the coordinate ![]() $x_s$ for any
$x_s$ for any ![]() $s\in S_m$, and
$s\in S_m$, and ![]() $z_m$ for the
$z_m$ for the ![]() $\mathbb {C}$-point of
$\mathbb {C}$-point of ![]() $X^{S_m}$ with coordinates
$X^{S_m}$ with coordinates ![]() $y_m$. We have
$y_m$. We have
Therefore we have
The smooth transition map ![]() $G_ {\{m\},(i+1)|S_m|}\times _ {X^{\{m\}}}\{y_m\}\to G_ {\{m\},i|S_m|}\times _ {X^{\{m\}}}\{y_m\}$ is surjective for all
$G_ {\{m\},(i+1)|S_m|}\times _ {X^{\{m\}}}\{y_m\}\to G_ {\{m\},i|S_m|}\times _ {X^{\{m\}}}\{y_m\}$ is surjective for all ![]() $i\geq 0$ and has a unipotent kernel for all
$i\geq 0$ and has a unipotent kernel for all ![]() $i\geq 1$. It follows that
$i\geq 1$. It follows that ![]() $G_ {S,i+1}\to G_ {S,i}$ has the same property. Thus
$G_ {S,i+1}\to G_ {S,i}$ has the same property. Thus ![]() $G_S$ is a prosaic affine group scheme over
$G_S$ is a prosaic affine group scheme over ![]() $X^S$ in the following sense.
$X^S$ in the following sense.
Definition 3.5
(i) A scheme
 $T$ over
$T$ over  $B$ is said to be pro-smooth over
$B$ is said to be pro-smooth over  $B$ if it can be written as the limit of an inverse system of schemes
$B$ if it can be written as the limit of an inverse system of schemes  $T_i$ smooth over
$T_i$ smooth over  $B$ and with smooth transition morphisms. If
$B$ and with smooth transition morphisms. If  $T$ is pro-smooth then it is formally smooth (in particular, flat) over
$T$ is pro-smooth then it is formally smooth (in particular, flat) over  $T$.
$T$.(ii) An affine groupoid scheme
 $\mathcal {G}$ over
$\mathcal {G}$ over  $B$ is pro-smooth over
$B$ is pro-smooth over  $B$ if it can be written as the limit of an inverse system of affine groupoid schemes
$B$ if it can be written as the limit of an inverse system of affine groupoid schemes  $\mathcal {G}_i$ over
$\mathcal {G}_i$ over  $B$ whose structure maps to
$B$ whose structure maps to  $B$ are both smooth, and which has smooth transition homomorphisms.
$B$ are both smooth, and which has smooth transition homomorphisms.(iii) The scheme T (respectively, affine groupoid scheme
 $\mathcal {G}$) over B is said to be a pro-smooth cover if it is pro-smooth and the transition (respectively, transition and structure) morphisms of (i) (respectively, (ii)) are coverings (in addition to being smooth).
$\mathcal {G}$) over B is said to be a pro-smooth cover if it is pro-smooth and the transition (respectively, transition and structure) morphisms of (i) (respectively, (ii)) are coverings (in addition to being smooth).(iv) Let the affine groupoid scheme
 $\mathcal {G}=\lim _ {i\in \mathbb {Z}_{\geq 0}^{op}}\mathcal {G}_i$ over
$\mathcal {G}=\lim _ {i\in \mathbb {Z}_{\geq 0}^{op}}\mathcal {G}_i$ over  $B$ be a pro-smooth cover. Then each
$B$ be a pro-smooth cover. Then each  $\mathcal {G}_i$ is the fpqc quotient over
$\mathcal {G}_i$ is the fpqc quotient over  $B$ of
$B$ of  $\mathcal {G}$ by some pro-smooth affine subgroup
$\mathcal {G}$ by some pro-smooth affine subgroup  $K_i$. We say that
$K_i$. We say that  $\mathcal {G}$ is prosaic if the
$\mathcal {G}$ is prosaic if the  $K_i$ can be chosen to be also pro-unipotent.
$K_i$ can be chosen to be also pro-unipotent.(v) Let
 $\mathcal {G}$ be an affine group scheme over the same base
$\mathcal {G}$ be an affine group scheme over the same base  $B$. Then
$B$. Then  $\mathcal {G}$ is said to be pro-smooth, a pro-smooth cover, prosaic over
$\mathcal {G}$ is said to be pro-smooth, a pro-smooth cover, prosaic over  $B$ if it is so when regarded as a groupoid.
$B$ if it is so when regarded as a groupoid.
From now on, ‘groupoid’ will mean ‘affine pro-smooth covering groupoid’, unless it is clear from the context that this is not the case. All examples of groupoids will actually be prosaic.
Remark 3.6 Recall the construction of ![]() $G_S$. If the affine algebraic group
$G_S$. If the affine algebraic group ![]() $G$ is replaced by an arbitrary smooth affine variety
$G$ is replaced by an arbitrary smooth affine variety ![]() $T$ over
$T$ over ![]() $\mathbb {C}$, we get a pro-smooth affine variety
$\mathbb {C}$, we get a pro-smooth affine variety ![]() $T_S$ over
$T_S$ over ![]() $X^S$ in exactly the same way.
$X^S$ in exactly the same way.
3.5 Beilinson–Drinfeld Grassmannians; reasonableness
We also consider the functor
Then ![]() $G_ {S}^{S'}$ is represented by an ind-affine ind-scheme, formally smooth over
$G_ {S}^{S'}$ is represented by an ind-affine ind-scheme, formally smooth over ![]() $X^S$. It is a group in ind-schemes over
$X^S$. It is a group in ind-schemes over ![]() $X^S$, but not an inductive limit of group schemes. It is a reasonable ind-scheme in the following sense (taken from [Reference DrinfeldDri06]).
$X^S$, but not an inductive limit of group schemes. It is a reasonable ind-scheme in the following sense (taken from [Reference DrinfeldDri06]).
Definition 3.7
(i) An ind-scheme
 $T$ is reasonable if it admits a reasonable presentation, that is, an expression
where
$T$ is reasonable if it admits a reasonable presentation, that is, an expression
where \[ T=\mathop {\rm colim }\limits_{\mathrel{\mathop{\kern0pt\longrightarrow}\limits_{j\in\mathcal{J}}} } T^j \]
\[ T=\mathop {\rm colim }\limits_{\mathrel{\mathop{\kern0pt\longrightarrow}\limits_{j\in\mathcal{J}}} } T^j \] $\mathcal {J}$ is some (countable) filtered indexing category, and the transition morphisms in the filtered system of schemes
$\mathcal {J}$ is some (countable) filtered indexing category, and the transition morphisms in the filtered system of schemes  $(T^j)_ {j\in \mathcal {J}}$ are all finitely presented (f.p.) closed embeddings (that is, they have finitely generated ideal sheaves). Note that any two reasonable presentations admit a common refinement, so that the category of reasonable presentations of
$(T^j)_ {j\in \mathcal {J}}$ are all finitely presented (f.p.) closed embeddings (that is, they have finitely generated ideal sheaves). Note that any two reasonable presentations admit a common refinement, so that the category of reasonable presentations of  $T$ is filtered.
$T$ is filtered.(ii) A closed subscheme of a reasonable ind-scheme
 $T$ is reasonable if it is a term in some reasonable presentation of
$T$ is reasonable if it is a term in some reasonable presentation of  $T$.
$T$.(iii) A morphism
 $U\to T$ of reasonable ind-schemes is co-reasonable if for some (equivalently, any) reasonable presentation
$U\to T$ of reasonable ind-schemes is co-reasonable if for some (equivalently, any) reasonable presentation  $T=\underrightarrow {\rm colim }_ {j\in \mathcal {J}}T^j$ of
$T=\underrightarrow {\rm colim }_ {j\in \mathcal {J}}T^j$ of  $T$, the presentation
$T$, the presentation  $U=\underrightarrow {\rm colim }_ {j\in \mathcal {J}}U\times _TT^j$ of
$U=\underrightarrow {\rm colim }_ {j\in \mathcal {J}}U\times _TT^j$ of  $U$ as an ind-scheme is reasonable. Warning: this is not a relative version of reasonableness for ind-schemes.
$U$ as an ind-scheme is reasonable. Warning: this is not a relative version of reasonableness for ind-schemes.
Example 3.8 (i) Let ![]() $T$ be a reasonable ind-scheme and let
$T$ be a reasonable ind-scheme and let ![]() $U\to T$ be either ind-f.p. or an ind-flat cover. Then
$U\to T$ be either ind-f.p. or an ind-flat cover. Then ![]() $U\to T$ is co-reasonable.
$U\to T$ is co-reasonable.
(ii) In the case of ![]() $G_S^{S'}$, one reasonable presentation is given as follows. Fix a finite set
$G_S^{S'}$, one reasonable presentation is given as follows. Fix a finite set ![]() $\{a_1,\ldots ,a_n\}$ of generators of
$\{a_1,\ldots ,a_n\}$ of generators of ![]() $\mathcal {O}(G)$. Then set
$\mathcal {O}(G)$. Then set ![]() $\mathcal {J}=\mathbb {Z}_ {\geq 0}$ and set
$\mathcal {J}=\mathbb {Z}_ {\geq 0}$ and set ![]() $G_S^{S',j}$ to be the closed subscheme of
$G_S^{S',j}$ to be the closed subscheme of ![]() $G_S^{S'}$ which on the level of
$G_S^{S'}$ which on the level of ![]() $R$-points is given by
$R$-points is given by
Here we have taken ![]() $G_S^{S',0}=G_S$. The left- and right-regular actions of the subgroup
$G_S^{S',0}=G_S$. The left- and right-regular actions of the subgroup ![]() $G_S$ preserve the inductive structure, meaning that each
$G_S$ preserve the inductive structure, meaning that each ![]() $G_S^{S',j}$ has a free action on both sides by
$G_S^{S',j}$ has a free action on both sides by ![]() $G_S$ over
$G_S$ over ![]() $X^S$, even though it is not itself a group. Moreover, the fpqc quotient
$X^S$, even though it is not itself a group. Moreover, the fpqc quotient ![]() $G_S^{S',j}/G_S$ is of finite type over
$G_S^{S',j}/G_S$ is of finite type over ![]() $X^S$, and flat, although generally quite singular. The result is that the fpqc quotient
$X^S$, and flat, although generally quite singular. The result is that the fpqc quotient
has the structure of ind-finite-type ind-flat ind-scheme over ![]() $X^S$. In particular, it is reasonable, and
$X^S$. In particular, it is reasonable, and ![]() $G_S^{S'}\to G_S$ is an ind-flat cover and thus co-reasonable.
$G_S^{S'}\to G_S$ is an ind-flat cover and thus co-reasonable.
On ![]() $R$-points, we may identify
$R$-points, we may identify
 \[ G_S^{S'}/G_S(R) = \left\{(x,\mathcal{E},f) \,\left|\, \begin{aligned} &x\in X^S(R)\hfill\\ &\mathcal{E}\text{ a principal }G\text{-bundle over }\Delta_S(x)\hfill\\ &f\text{ a trivialization of }\mathcal{E}\text{ over }\Delta_S^{S'}(x)\hfill\end{aligned} \right.\right\}/{\sim}. \]
\[ G_S^{S'}/G_S(R) = \left\{(x,\mathcal{E},f) \,\left|\, \begin{aligned} &x\in X^S(R)\hfill\\ &\mathcal{E}\text{ a principal }G\text{-bundle over }\Delta_S(x)\hfill\\ &f\text{ a trivialization of }\mathcal{E}\text{ over }\Delta_S^{S'}(x)\hfill\end{aligned} \right.\right\}/{\sim}. \]
Here the symbol ‘![]() $/\sim$’ means ‘taken up to isomorphism’, that is, we identify two
$/\sim$’ means ‘taken up to isomorphism’, that is, we identify two ![]() $R$-points
$R$-points
if ![]() $x=x'$ and there exists an isomorphism of
$x=x'$ and there exists an isomorphism of ![]() $\mathcal {E}$ with
$\mathcal {E}$ with ![]() $\mathcal {E}'$ which intertwines
$\mathcal {E}'$ which intertwines ![]() $f,f'$. Such an isomorphism is unique if it exists. The following fact is due to [Reference Beĭlinson and DrinfeldBD91].
$f,f'$. Such an isomorphism is unique if it exists. The following fact is due to [Reference Beĭlinson and DrinfeldBD91].
Lemma 3.9
(i)
 $G_S^{S'}/G_S$ is ind-projective over
$G_S^{S'}/G_S$ is ind-projective over  $X^S$ if and only if
$X^S$ if and only if  $G$ is reductive.
$G$ is reductive.(ii)
 $G_S^{S'}/G_S$ is ind-reduced if and only if
$G_S^{S'}/G_S$ is ind-reduced if and only if  $G$ has no non-trivial characters.
$G$ has no non-trivial characters.
Remark 3.10 Ultimately we are concerned only with the analytifications of these ind-schemes, so point (ii) appears merely for interest's sake. But point (i) is crucial for the definition of convolution in Borel–Moore homology.
We may reidentify the ![]() $R$-points of
$R$-points of ![]() $G_S^{S'}$ in a way more compatible with the above identification of
$G_S^{S'}$ in a way more compatible with the above identification of ![]() $G_S^{S'}/G_S(R)$:
$G_S^{S'}/G_S(R)$:
 \[ G_S^{S'}(R) = \left\{(x,\mathcal{E},f,g) \,\left|\, \begin{aligned} &x\in X^S(R)\hfill\\ &\mathcal{E}\text{ a principal }G\text{-bundle over }\Delta_S(x)\hfill\\ &f\text{ a trivialization of }\mathcal{E}\text{ over }\Delta_S^{S'}(x)\hfill\\ &g\text{ a trivialization of }\mathcal{E}\text{ over }\Delta_S(x)\end{aligned} \right.\right\}/{\sim}. \]
\[ G_S^{S'}(R) = \left\{(x,\mathcal{E},f,g) \,\left|\, \begin{aligned} &x\in X^S(R)\hfill\\ &\mathcal{E}\text{ a principal }G\text{-bundle over }\Delta_S(x)\hfill\\ &f\text{ a trivialization of }\mathcal{E}\text{ over }\Delta_S^{S'}(x)\hfill\\ &g\text{ a trivialization of }\mathcal{E}\text{ over }\Delta_S(x)\end{aligned} \right.\right\}/{\sim}. \]
Notice that the inclusion ![]() $S'\subset S$ induces a closed embedding
$S'\subset S$ induces a closed embedding ![]() $\Delta _ {S'}^{S''}\to \Delta _S^{S''}$ for any
$\Delta _ {S'}^{S''}\to \Delta _S^{S''}$ for any ![]() $S''\subset S'$. This in turn induces restriction homomorphisms
$S''\subset S'$. This in turn induces restriction homomorphisms
These maps are co-reasonable. One readily checks by looking at points that the induced maps
are isomorphisms. In particular, we have ![]() $G_S^{S''}/G_S\xrightarrow {\sim } X^S\times _ {S''}G_ {S''}^{S''}/G_ {S''}$.
$G_S^{S''}/G_S\xrightarrow {\sim } X^S\times _ {S''}G_ {S''}^{S''}/G_ {S''}$.
Remark 3.11 ![]() $G_ {S}^{S}/G_S$ is known as the Beilinson–Drinfeld Grassmannian
$G_ {S}^{S}/G_S$ is known as the Beilinson–Drinfeld Grassmannian ![]() $Gr_S$ (on
$Gr_S$ (on ![]() $|S|$ points). In particular, the fibers of
$|S|$ points). In particular, the fibers of ![]() $G_S^{S'}/G_S$ over
$G_S^{S'}/G_S$ over ![]() $X^S$ are products of copies of the ordinary affine Grassmannian
$X^S$ are products of copies of the ordinary affine Grassmannian ![]() $Gr_G$ of
$Gr_G$ of ![]() $G$.
$G$.
3.6 Jet bundles; placidity
We will use the following notion, due to Raskin [Reference RaskinRas15].
Definition 3.12
(i) A scheme
 $T$ is called placid if it admits a placid presentation, that is, an expression
for some filtered (countable) indexing category
$T$ is called placid if it admits a placid presentation, that is, an expression
for some filtered (countable) indexing category \[ T = \mathop {\lim }\limits_{\mathrel{\mathop{\kern0pt\longleftarrow}\limits_{i\in\mathcal{I}^{op}}}}(T_i) \]
\[ T = \mathop {\lim }\limits_{\mathrel{\mathop{\kern0pt\longleftarrow}\limits_{i\in\mathcal{I}^{op}}}}(T_i) \] $\mathcal {I}$, such that each
$\mathcal {I}$, such that each  $T_i$ is of finite type over
$T_i$ is of finite type over  $\mathbb {C}$ and each transition morphism
$\mathbb {C}$ and each transition morphism  $T_i\to T_ {i'}$ is a smooth affine covering. We will denote this placid presentation by
$T_i\to T_ {i'}$ is a smooth affine covering. We will denote this placid presentation by  $T_ {\mathcal {I}}$.
$T_ {\mathcal {I}}$.(ii) An ind-scheme
 $T$ is called placid if it admits a placid presentation, that is, an expression
Here
$T$ is called placid if it admits a placid presentation, that is, an expression
Here \[ T = \mathop {\rm colim }\limits_{\mathrel{\mathop{\kern0pt\longrightarrow}\limits_{j\in\mathcal{J}}} } \mathop {\lim }\limits_{\mathrel{\mathop{\kern0pt\longleftarrow}\limits_{i\in (\mathcal{I}^j)^{op}}} }(T^j_i). \]
\[ T = \mathop {\rm colim }\limits_{\mathrel{\mathop{\kern0pt\longrightarrow}\limits_{j\in\mathcal{J}}} } \mathop {\lim }\limits_{\mathrel{\mathop{\kern0pt\longleftarrow}\limits_{i\in (\mathcal{I}^j)^{op}}} }(T^j_i). \] $\mathcal {J},\mathcal {I}^j$ are filtered (countable) indexing categories,
$\mathcal {J},\mathcal {I}^j$ are filtered (countable) indexing categories,  $T^j_ {\mathcal {I}^j}$ is a placid presentation of its limit scheme
$T^j_ {\mathcal {I}^j}$ is a placid presentation of its limit scheme  $T^j:=\underleftarrow {\lim } _ {i\in (\mathcal {I}^j)^{op}}(T^j_i)$, and the transition morphisms
$T^j:=\underleftarrow {\lim } _ {i\in (\mathcal {I}^j)^{op}}(T^j_i)$, and the transition morphisms  $T^j\to T^{j'}$ are ind-f.p. closed embeddings.
$T^j\to T^{j'}$ are ind-f.p. closed embeddings.
Remark 3.13 (i) If the placid ind-scheme ![]() $T$ maps to some base
$T$ maps to some base ![]() $B$ of finite type over
$B$ of finite type over ![]() $\mathbb {C}$, then the placid presentation may be taken over
$\mathbb {C}$, then the placid presentation may be taken over ![]() $B$.
$B$.
(ii) Let ![]() $T$ be a placid ind-scheme and let
$T$ be a placid ind-scheme and let ![]() $T=\underrightarrow {\rm colim } _ {j\in \mathcal {J}}(T_j)$ be a reasonable presentation of
$T=\underrightarrow {\rm colim } _ {j\in \mathcal {J}}(T_j)$ be a reasonable presentation of ![]() $T$. Then each
$T$. Then each ![]() $T_j$ is a placid scheme, so that this reasonable presentation can be extended to a placid presentation.
$T_j$ is a placid scheme, so that this reasonable presentation can be extended to a placid presentation.
(iii) Any two placid presentations of the placid ind-scheme ![]() $T$ admit a common refinement (which is again a placid presentation). Thus the collection of placid presentations of
$T$ admit a common refinement (which is again a placid presentation). Thus the collection of placid presentations of ![]() $T$ forms a filtered category
$T$ forms a filtered category ![]() $\mathcal {P}(T)$.
$\mathcal {P}(T)$.
(iv) Suppose that ![]() $T$ is a placid ind-scheme and
$T$ is a placid ind-scheme and ![]() $U$ is an ind-scheme with an ind-f.p. map
$U$ is an ind-scheme with an ind-f.p. map ![]() $f:U\to T$. Then
$f:U\to T$. Then ![]() $U$ is automatically placid. The short explanation is ‘by Noetherian approximation’. We spell it out: given any reasonable presentation
$U$ is automatically placid. The short explanation is ‘by Noetherian approximation’. We spell it out: given any reasonable presentation
of ![]() $T$, we set
$T$, we set ![]() $U_j:=U\times _TT_j$ and obtain the reasonable presentation
$U_j:=U\times _TT_j$ and obtain the reasonable presentation
of ![]() $U$. Then, given any placid presentation
$U$. Then, given any placid presentation
of ![]() $T^j$, there exists some index
$T^j$, there exists some index ![]() $a$ of
$a$ of ![]() $\mathcal {I}^j$ such that there is a
$\mathcal {I}^j$ such that there is a ![]() $T^j_a$-scheme
$T^j_a$-scheme ![]() $U^j_a$ fitting into a Cartesian diagram
$U^j_a$ fitting into a Cartesian diagram
 \[ \begin{matrix}U^j & \to & T^j\\ \downarrow & & \downarrow\\ U^j_a & \to & T^j_a . \end{matrix}\]
\[ \begin{matrix}U^j & \to & T^j\\ \downarrow & & \downarrow\\ U^j_a & \to & T^j_a . \end{matrix}\]
Moreover, since ![]() $T^j\to T^j_a$ is a covering, the choice of
$T^j\to T^j_a$ is a covering, the choice of ![]() $T^j_a$-scheme
$T^j_a$-scheme ![]() $U^j_a$ is unique. Thus if we replace
$U^j_a$ is unique. Thus if we replace ![]() $\mathcal {I}^j$ by its final subcategory based at
$\mathcal {I}^j$ by its final subcategory based at ![]() $a$, we can present
$a$, we can present ![]() $U^j\to T^j$ as the limit of a cofiltered system of f.p. morphisms
$U^j\to T^j$ as the limit of a cofiltered system of f.p. morphisms
such that for each ![]() $i\to i'$ in
$i\to i'$ in ![]() $\mathcal {I}$, the square
$\mathcal {I}$, the square
 \[ \begin{matrix} U^j_{i'} & \to & T^j_{i'}\\ \downarrow & & \downarrow\\ U^j_i & \to & T^j_i\end{matrix} \]
\[ \begin{matrix} U^j_{i'} & \to & T^j_{i'}\\ \downarrow & & \downarrow\\ U^j_i & \to & T^j_i\end{matrix} \]is Cartesian. Placid presentations of this form will be called Cartesian.
(v)The product (over ![]() $B$) of placid ind-schemes is placid.
$B$) of placid ind-schemes is placid.
(vi) Consider placid presentations
of ![]() $T$ with the property that
$T$ with the property that ![]() $T^j_i$ is formed out of
$T^j_i$ is formed out of ![]() $T^{j'}_i$ as in point (iv) whenever
$T^{j'}_i$ as in point (iv) whenever ![]() $i\geq j'\geq j$. We call such placid presentations neat. This is possibly a technically useless notion. But every placid presentation admits a refinement which is neat up to replacing the indexing categories
$i\geq j'\geq j$. We call such placid presentations neat. This is possibly a technically useless notion. But every placid presentation admits a refinement which is neat up to replacing the indexing categories ![]() $\mathcal {J},\mathcal {I}^j$ by final subcategories. Thus many constructions on placid ind-schemes can be phrased in terms of neat presentations.
$\mathcal {J},\mathcal {I}^j$ by final subcategories. Thus many constructions on placid ind-schemes can be phrased in terms of neat presentations.
Note that for any morphism ![]() $f:U\to T$ of placid schemes and any placid presentations
$f:U\to T$ of placid schemes and any placid presentations ![]() $U=\underleftarrow {\lim } _ {i\mathcal {I}_U^{op}}U_i$,
$U=\underleftarrow {\lim } _ {i\mathcal {I}_U^{op}}U_i$, ![]() $T=\underleftarrow {\lim } _ {i\mathcal {I}_T^{op}}T_i$, for any
$T=\underleftarrow {\lim } _ {i\mathcal {I}_T^{op}}T_i$, for any ![]() $i\in \mathcal {I}_T$ there exist
$i\in \mathcal {I}_T$ there exist ![]() $i'\in \mathcal {I}_U$ and a unique map
$i'\in \mathcal {I}_U$ and a unique map ![]() $U_ {i'}\to T_i$ making the square
$U_ {i'}\to T_i$ making the square
 \[ \begin{matrix}U & \to & T\\ \downarrow & & \downarrow\\ U_{i'} & \to & T_i\end{matrix} \]
\[ \begin{matrix}U & \to & T\\ \downarrow & & \downarrow\\ U_{i'} & \to & T_i\end{matrix} \]
commutative. Thus, by changing the indexing sets appropriately we can choose placid presentations of ![]() $U$,
$U$, ![]() $T$ with a common indexing set
$T$ with a common indexing set ![]() $\mathcal {I}$ and write
$\mathcal {I}$ and write ![]() $f=\underleftarrow {\lim } _ {i\in \mathcal {I}}(U_i\to T_i)$. Such a presentation will be called compatible. This notion extends immediately to morphisms of placid ind-schemes. A Cartesian presentation is a compatible presentation in which all appropriate squares are Cartesian. If
$f=\underleftarrow {\lim } _ {i\in \mathcal {I}}(U_i\to T_i)$. Such a presentation will be called compatible. This notion extends immediately to morphisms of placid ind-schemes. A Cartesian presentation is a compatible presentation in which all appropriate squares are Cartesian. If ![]() $\mathcal {G}$ is an affine groupoid scheme over some base
$\mathcal {G}$ is an affine groupoid scheme over some base ![]() $B$ of finite type over
$B$ of finite type over ![]() $\mathbb {C}$ and
$\mathbb {C}$ and ![]() $f$ is
$f$ is ![]() $\mathcal {G}$-equivariant (over
$\mathcal {G}$-equivariant (over ![]() $B$), then we can find a
$B$), then we can find a ![]() $\mathcal {G}$-equivariant compatible presentation. If in addition
$\mathcal {G}$-equivariant compatible presentation. If in addition ![]() $f$ is f.p. so that it admits a Cartesian presentation, then this can also be chosen to be
$f$ is f.p. so that it admits a Cartesian presentation, then this can also be chosen to be ![]() $\mathcal {G}$-equivariant.
$\mathcal {G}$-equivariant.
Definition 3.14
(i) A morphism
 $f:U\to T$ between placid schemes is called co-placid if for some (equivalently, every) pair of placid presentations
$f:U\to T$ between placid schemes is called co-placid if for some (equivalently, every) pair of placid presentations  $U_ {\mathcal {I}_U}$,
$U_ {\mathcal {I}_U}$,  $T_ {\mathcal {I}_T}$ of
$T_ {\mathcal {I}_T}$ of  $U$,
$U$,  $T$ and for every index
$T$ and for every index  $i\in \mathcal {I}_T$, then for some (equivalently, every) index
$i\in \mathcal {I}_T$, then for some (equivalently, every) index  $i'\in \mathcal {I}_U$ such that we have a commutative square
the morphism
$i'\in \mathcal {I}_U$ such that we have a commutative square
the morphism \[ \begin{matrix}U & \xrightarrow{f} & T\\ \downarrow & & \downarrow\\ U_{i'} & \xrightarrow{f'} & T_i,\end{matrix} \]
\[ \begin{matrix}U & \xrightarrow{f} & T\\ \downarrow & & \downarrow\\ U_{i'} & \xrightarrow{f'} & T_i,\end{matrix} \] $f'$ is a smooth covering.
$f'$ is a smooth covering.(ii) A morphism
 $f:U\to T$ between placid ind-schemes is called co-placid if it is co-reasonable and for some (equivalently, every) reasonable presentation
$f:U\to T$ between placid ind-schemes is called co-placid if it is co-reasonable and for some (equivalently, every) reasonable presentation  $T=\underrightarrow {\rm colim } _ {j\in \mathcal {J}}T^j$ of
$T=\underrightarrow {\rm colim } _ {j\in \mathcal {J}}T^j$ of  $T$, the map of placid schemes
$T$, the map of placid schemes  $U\times _ {T}T^j\to T^j$ is co-placid.
$U\times _ {T}T^j\to T^j$ is co-placid.
The notion of a co-placid morphism has been defined previously in the literature: see [Reference RaskinRas15], where they are called simply ‘placid’. As noted in [Reference RaskinRas15], it is not a relative version of placidity for ind-schemes. This is the reason for the present renaming.
Example 3.15 (i) Let ![]() $T$ be a placid ind-scheme. Let
$T$ be a placid ind-scheme. Let ![]() $U\to T$ be either ind-smooth or an ind-pro-smooth cover. Then it is co-placid.
$U\to T$ be either ind-smooth or an ind-pro-smooth cover. Then it is co-placid.
(ii) ![]() $G_S^{S'}$ is a placid ind-scheme, and the fpqc quotient map
$G_S^{S'}$ is a placid ind-scheme, and the fpqc quotient map
is an ind-pro-smooth ind-affine affine cover of a placid (indeed, ind-finite type) ind-scheme, so is co-placid.
(iii) Given ![]() $S''\subset S'\subset S$, the morphism
$S''\subset S'\subset S$, the morphism
is co-placid. Indeed, consider ![]() $G_ {S,i}:=\operatorname {Map}(\Delta _ {S,i},G)$. We have
$G_ {S,i}:=\operatorname {Map}(\Delta _ {S,i},G)$. We have ![]() $G_S=\underleftarrow {\lim } _ {i\in \mathbb {Z}_{\geq 0}}G_ {S,i}$ and
$G_S=\underleftarrow {\lim } _ {i\in \mathbb {Z}_{\geq 0}}G_ {S,i}$ and ![]() $X^S\times _ {X^{S'}}G_ {S'}=\underleftarrow {\lim } _ {i\in \mathbb {Z}_{\geq 0}}X^S\times _ {X^{S'}}G_ {S,i}$ and the morphism
$X^S\times _ {X^{S'}}G_ {S'}=\underleftarrow {\lim } _ {i\in \mathbb {Z}_{\geq 0}}X^S\times _ {X^{S'}}G_ {S,i}$ and the morphism
induced by the closed embeddings ![]() $\Delta _ {S',i}(x)\subset \Delta _ {S,i}(x)$ for any
$\Delta _ {S',i}(x)\subset \Delta _ {S,i}(x)$ for any ![]() $x\in X^S(R)$. This is a smooth covering, by the same argument of § 3.4 for the prosaicness of
$x\in X^S(R)$. This is a smooth covering, by the same argument of § 3.4 for the prosaicness of ![]() $G_S$. This shows that
$G_S$. This shows that
is co-placid. To conclude, note that the morphism ![]() $f$ is an ind-locally trivial
$f$ is an ind-locally trivial ![]() $g$-bundle over the ind-finite type ind-scheme
$g$-bundle over the ind-finite type ind-scheme ![]() $G_S^{S''}/G_S=X^S\times _ {X^{S'}}G_ {S'}^{S''}/G_ {S'}$.
$G_S^{S''}/G_S=X^S\times _ {X^{S'}}G_ {S'}^{S''}/G_ {S'}$.
Warning 3.16 Morphism ![]() $g$ is not a pro-smooth cover, and
$g$ is not a pro-smooth cover, and ![]() $f$ is not an ind-pro-smooth cover. It is tempting to imagine that it is the quotient map by some group scheme
$f$ is not an ind-pro-smooth cover. It is tempting to imagine that it is the quotient map by some group scheme ![]() $\ker (G_S\to X^S\times _ {X^{S'}}G_ {S'})$, but there is no such group scheme. To see this, fix some section
$\ker (G_S\to X^S\times _ {X^{S'}}G_ {S'})$, but there is no such group scheme. To see this, fix some section ![]() $S\to S'$ and consider the corresponding ‘multi-diagonal’ embedding
$S\to S'$ and consider the corresponding ‘multi-diagonal’ embedding ![]() $X^{S'}\to X^S$. Then
$X^{S'}\to X^S$. Then ![]() $g$ is an isomorphism over
$g$ is an isomorphism over ![]() $X^{S'}$. However, over a generic point of
$X^{S'}$. However, over a generic point of ![]() $X^S$,
$X^S$, ![]() $g$ is a non-trivial projection from
$g$ is a non-trivial projection from ![]() $G(\mathcal {O})^S\to G(\mathcal {O})^{S'}$; see § 3.9 for the notation.
$G(\mathcal {O})^S\to G(\mathcal {O})^{S'}$; see § 3.9 for the notation.
(iv) Fix a representation ![]() $N$ of
$N$ of ![]() $G$ of dimension
$G$ of dimension ![]() $d$. Let
$d$. Let ![]() $\boldsymbol {N}:=\operatorname {Spec}(\operatorname {Sym}(N^*))$ be the corresponding
$\boldsymbol {N}:=\operatorname {Spec}(\operatorname {Sym}(N^*))$ be the corresponding ![]() $G$-module, that is, vector space in the category of schemes over
$G$-module, that is, vector space in the category of schemes over ![]() $\mathbb {C}$ with
$\mathbb {C}$ with ![]() $G$-action. Then
$G$-action. Then ![]() $\boldsymbol {N}_S$ is a
$\boldsymbol {N}_S$ is a ![]() $G_S$-module; indeed, each
$G_S$-module; indeed, each ![]() $\operatorname {Map}(\Delta _ {S,i},\boldsymbol {N})$ is a
$\operatorname {Map}(\Delta _ {S,i},\boldsymbol {N})$ is a ![]() $\operatorname {Map}(\Delta _ {S,i},G)$-module and the transition maps are
$\operatorname {Map}(\Delta _ {S,i},G)$-module and the transition maps are ![]() $G_S$-equivariant. We have the placid ind-scheme
$G_S$-equivariant. We have the placid ind-scheme
This is an ind-pro-smooth covering of its fpqc quotient (relative to ![]() $X^S$) ind-scheme
$X^S$) ind-scheme
This is an infinite-dimensional vector bundle over ![]() $G_S^{S'}/G_S$. On the level of
$G_S^{S'}/G_S$. On the level of ![]() $R$-points we identify
$R$-points we identify
 \[ \mathcal{T}_S^{S'}(R)=\left\{(x,\mathcal{E},f,\tilde{v}) \,\left|\, \begin{aligned} &x\in X^S(R)\hfill\\ &\mathcal{E}\text{ a principal }G\text{-bundle over }\Delta_S(x)\hfill\\ &f\text{ a trivialization of }\mathcal{E}\text{ over }\Delta_S^{S'}(x)\hfill\\ &\tilde{v}\text{ an }\boldsymbol{N}\text{-section of }\mathcal{E}\hfill\end{aligned} \right.\right\}/{\sim}. \]
\[ \mathcal{T}_S^{S'}(R)=\left\{(x,\mathcal{E},f,\tilde{v}) \,\left|\, \begin{aligned} &x\in X^S(R)\hfill\\ &\mathcal{E}\text{ a principal }G\text{-bundle over }\Delta_S(x)\hfill\\ &f\text{ a trivialization of }\mathcal{E}\text{ over }\Delta_S^{S'}(x)\hfill\\ &\tilde{v}\text{ an }\boldsymbol{N}\text{-section of }\mathcal{E}\hfill\end{aligned} \right.\right\}/{\sim}. \]
Here by ‘an ![]() $\boldsymbol {N}$-section of
$\boldsymbol {N}$-section of ![]() $\mathcal {E}$’ we mean a section of the associated
$\mathcal {E}$’ we mean a section of the associated ![]() $\boldsymbol {N}$-bundle. Of course
$\boldsymbol {N}$-bundle. Of course ![]() $\mathcal {T}_S^{S'}$ is the inverse limit of vector bundles over
$\mathcal {T}_S^{S'}$ is the inverse limit of vector bundles over ![]() $G_S^{S'}/G_S$,
$G_S^{S'}/G_S$,
where ![]() $\mathcal {T}_ {S,i}^{S'}$ is the associated bundle of
$\mathcal {T}_ {S,i}^{S'}$ is the associated bundle of ![]() $\boldsymbol {N}_ {S,i}$, a vector bundle of rank
$\boldsymbol {N}_ {S,i}$, a vector bundle of rank ![]() $di|S|$. In particular,
$di|S|$. In particular, ![]() $\mathcal {T}_S^{S'}$ is a placid ind-scheme, with
$\mathcal {T}_S^{S'}$ is a placid ind-scheme, with ![]() $\mathcal {T}_S^{S',j}$ being the infinite-dimensional vector bundle
$\mathcal {T}_S^{S',j}$ being the infinite-dimensional vector bundle ![]() $\mathcal {T}_S^{S'}|_ {G_S^{S',j}/G_S}$ over
$\mathcal {T}_S^{S'}|_ {G_S^{S',j}/G_S}$ over ![]() $G_S^{S',j}/G_S$. We identify the
$G_S^{S',j}/G_S$. We identify the ![]() $R$-points of
$R$-points of ![]() $\widetilde {\mathcal {T}}_S^{S'}$ compatibly as follows:
$\widetilde {\mathcal {T}}_S^{S'}$ compatibly as follows:
 \[ \widetilde{\mathcal{T}}_S^{S'}(R)=\left\{(x,\mathcal{E},f,g,\tilde{v}) \,\left|\, \begin{aligned} &x\in X^S(R)\hfill\\ &\mathcal{E}\text{ a principal }G\text{-bundle over }\Delta_S(x)\hfill\\ &f\text{ a trivialization of }\mathcal{E}\text{ over }\Delta_S^{S'}(x)\hfill\\ &g\text{ a trivialization of }\mathcal{E}\text{ over }\Delta_S(x)\hfill\\ &\tilde{v}\text{ an }\boldsymbol{N}\text{-section of }\mathcal{E}\hfill\end{aligned}\right.\right\}/{\sim}.\]
\[ \widetilde{\mathcal{T}}_S^{S'}(R)=\left\{(x,\mathcal{E},f,g,\tilde{v}) \,\left|\, \begin{aligned} &x\in X^S(R)\hfill\\ &\mathcal{E}\text{ a principal }G\text{-bundle over }\Delta_S(x)\hfill\\ &f\text{ a trivialization of }\mathcal{E}\text{ over }\Delta_S^{S'}(x)\hfill\\ &g\text{ a trivialization of }\mathcal{E}\text{ over }\Delta_S(x)\hfill\\ &\tilde{v}\text{ an }\boldsymbol{N}\text{-section of }\mathcal{E}\hfill\end{aligned}\right.\right\}/{\sim}.\] (v) ![]() $\boldsymbol {N}_S^{S'}$ is a
$\boldsymbol {N}_S^{S'}$ is a ![]() $G_S^{S'}$-module (in ind-schemes). Therefore multiplication gives a map between the placid ind-schemes
$G_S^{S'}$-module (in ind-schemes). Therefore multiplication gives a map between the placid ind-schemes
We define ![]() $\mathcal {R}_S^{S'}$ to be the fiber product
$\mathcal {R}_S^{S'}$ to be the fiber product
This is an ind-scheme over ![]() $G_S^{S'}/G_S$, with
$G_S^{S'}/G_S$, with ![]() $\mathcal {R}_S^{S',j}:=\mathcal {T}_S^{S',j}\times _ {\boldsymbol {N}_S^{S'}}\boldsymbol {N}_S = \mathcal {R}_S^{S'}|_ {G_S^{S',j}/G_S}$. Moreover,
$\mathcal {R}_S^{S',j}:=\mathcal {T}_S^{S',j}\times _ {\boldsymbol {N}_S^{S'}}\boldsymbol {N}_S = \mathcal {R}_S^{S'}|_ {G_S^{S',j}/G_S}$. Moreover, ![]() $\mathcal {R}_S^{S'}$ is a vector space over
$\mathcal {R}_S^{S'}$ is a vector space over ![]() $G_S^{S'}/G_S$, but unlike
$G_S^{S'}/G_S$, but unlike ![]() $\mathcal {T}_S^{S'}$ it is not a vector bundle because the fibers jump. Furthermore,
$\mathcal {T}_S^{S'}$ it is not a vector bundle because the fibers jump. Furthermore, ![]() $\mathcal {R}_S^{S',j}$ contains
$\mathcal {R}_S^{S',j}$ contains ![]() $\ker (\mathcal {T}_ {S}^{S',j}\to \mathcal {T}_ {S,i}^{S',j})$ for
$\ker (\mathcal {T}_ {S}^{S',j}\to \mathcal {T}_ {S,i}^{S',j})$ for ![]() $i$ large enough (depending on
$i$ large enough (depending on ![]() $j$), that is, we have a diagram
$j$), that is, we have a diagram
of vector spaces over ![]() $G_S^{S',j}/G_S$. Therefore
$G_S^{S',j}/G_S$. Therefore ![]() $\mathcal {R}_S^{S'}$ is placid: we may take
$\mathcal {R}_S^{S'}$ is placid: we may take ![]() $\mathcal {R}_ {S,i}^{S',j}$ to be the image in
$\mathcal {R}_ {S,i}^{S',j}$ to be the image in ![]() $\mathcal {T}_ {S,i}^{S',j}$ of
$\mathcal {T}_ {S,i}^{S',j}$ of ![]() $\mathcal {R}_ {S}^{S',j}$, for
$\mathcal {R}_ {S}^{S',j}$, for ![]() $i$ large enough. Also,
$i$ large enough. Also, ![]() $\mathcal {R}_S^{S'}$ is of ind-finite codimension in
$\mathcal {R}_S^{S'}$ is of ind-finite codimension in ![]() $\mathcal {T}_S^{S'}$, that is, it is an ind-f.p. closed sub-ind-scheme. On the level of
$\mathcal {T}_S^{S'}$, that is, it is an ind-f.p. closed sub-ind-scheme. On the level of ![]() $R$-points, we have
$R$-points, we have
 \[ \mathcal{R}_S^{S'}(R)=\left\{(x,\mathcal{E},f,{v}) \,\left|\, \begin{aligned} &x\in X^S(R)\hfill\\ &\mathcal{E}\text{ a principal }G\text{-bundle over }\Delta_S(x)\hfill\\ &f\text{ a trivialization of }\mathcal{E}\text{ over }\Delta_S^{S'}(x)\hfill\\ &{v}\text{ an }\boldsymbol{N}\text{-section of }\mathcal{E}\text{ such that }f(v)\text{ extends to }\Delta_S(x)\hfill\end{aligned}\right.\right\}/{\sim}.\]
\[ \mathcal{R}_S^{S'}(R)=\left\{(x,\mathcal{E},f,{v}) \,\left|\, \begin{aligned} &x\in X^S(R)\hfill\\ &\mathcal{E}\text{ a principal }G\text{-bundle over }\Delta_S(x)\hfill\\ &f\text{ a trivialization of }\mathcal{E}\text{ over }\Delta_S^{S'}(x)\hfill\\ &{v}\text{ an }\boldsymbol{N}\text{-section of }\mathcal{E}\text{ such that }f(v)\text{ extends to }\Delta_S(x)\hfill\end{aligned}\right.\right\}/{\sim}.\]
Here ![]() $f(v)$ is a section of the trivial
$f(v)$ is a section of the trivial ![]() $\boldsymbol {N}$-bundle on
$\boldsymbol {N}$-bundle on ![]() $\Delta _S^{S'}(x)$, and we require that it extends to a section of the trivial
$\Delta _S^{S'}(x)$, and we require that it extends to a section of the trivial ![]() $\boldsymbol {N}$-bundle over
$\boldsymbol {N}$-bundle over ![]() $\Delta _S(x)$. Such an extension is unique if it exists. We denote the preimage of
$\Delta _S(x)$. Such an extension is unique if it exists. We denote the preimage of ![]() $\mathcal {R}_S^{S'}$ in
$\mathcal {R}_S^{S'}$ in ![]() $\widetilde {\mathcal {T}}_S^{S'}$ as
$\widetilde {\mathcal {T}}_S^{S'}$ as ![]() $\widetilde {\mathcal {R}}_S^{S'}$. It is an ind-f.p. closed sub-ind-scheme of
$\widetilde {\mathcal {R}}_S^{S'}$. It is an ind-f.p. closed sub-ind-scheme of ![]() $\widetilde {\mathcal {T}}_S^{S'}$, an ind-pro-smooth cover of
$\widetilde {\mathcal {T}}_S^{S'}$, an ind-pro-smooth cover of ![]() $\mathcal {R}_S^{S'}$, its fpqc quotient (locally on
$\mathcal {R}_S^{S'}$, its fpqc quotient (locally on ![]() $X^S$) by
$X^S$) by ![]() $G_S$, and on
$G_S$, and on ![]() $R$-points we identify
$R$-points we identify
 \[ \widetilde{\mathcal{R}}_S^{S'}(R)=\left\{(x,\mathcal{E},f,g,{v}) \,\left|\, \begin{aligned} &x\in X^S(R)\hfill\\ &\mathcal{E}\text{ a principal }G\text{-bundle over }\Delta_S(x)\hfill\\ &f\text{ a trivialization of }\mathcal{E}\text{ over }\Delta_S^{S'}(x)\hfill\\ &g\text{ a trivialization of }\mathcal{E}\text{ over }\Delta_S(x)\hfill\\ &{v}\text{ a section of the trivial }\boldsymbol{N}\text{-bundle on }\Delta_S(x)\\ &\quad \text{such that }fg^{{-}1}(v)\text{ extends to }\Delta_S(x)\hfill\end{aligned}\right.\right\}/{\sim}.\]
\[ \widetilde{\mathcal{R}}_S^{S'}(R)=\left\{(x,\mathcal{E},f,g,{v}) \,\left|\, \begin{aligned} &x\in X^S(R)\hfill\\ &\mathcal{E}\text{ a principal }G\text{-bundle over }\Delta_S(x)\hfill\\ &f\text{ a trivialization of }\mathcal{E}\text{ over }\Delta_S^{S'}(x)\hfill\\ &g\text{ a trivialization of }\mathcal{E}\text{ over }\Delta_S(x)\hfill\\ &{v}\text{ a section of the trivial }\boldsymbol{N}\text{-bundle on }\Delta_S(x)\\ &\quad \text{such that }fg^{{-}1}(v)\text{ extends to }\Delta_S(x)\hfill\end{aligned}\right.\right\}/{\sim}.\] (vi) The product (over ![]() $B$) of co-placid maps is co-placid.
$B$) of co-placid maps is co-placid.
Remark 3.17 (i) Suppose ![]() $X=\mathbb {G}_a$ with parameter
$X=\mathbb {G}_a$ with parameter ![]() $t$. Then
$t$. Then ![]() $I(x_s)$ is trivialized by
$I(x_s)$ is trivialized by ![]() $t - t_ {x_s}$. There is an isomorphism from
$t - t_ {x_s}$. There is an isomorphism from ![]() $\mathcal {T}_S^{S'}$ to the kernel of the covering
$\mathcal {T}_S^{S'}$ to the kernel of the covering ![]() $\mathcal {T}_S^{S'}\to \mathcal {T}_ {S,i}^{S'}$, given on
$\mathcal {T}_S^{S'}\to \mathcal {T}_ {S,i}^{S'}$, given on ![]() $R$-points by
$R$-points by
We call this isomorphism the fiberwise shift map of ![]() $\mathcal {T}$.
$\mathcal {T}$.
(ii) The placid ind-scheme ![]() $T=G_S^{S'}/G_S,\mathcal {T}_S^{S'},\mathcal {R}_S^{S'}$ is special in that one may take the smooth affine covering maps
$T=G_S^{S'}/G_S,\mathcal {T}_S^{S'},\mathcal {R}_S^{S'}$ is special in that one may take the smooth affine covering maps ![]() $T^j_i\to T^j_ {i'}$ to be vector bundles. But placidity seems to be the more flexible definition; for instance, I do not know if point (iii) of Remark 3.13 holds if we replace ‘placid’ by ‘special’.
$T^j_i\to T^j_ {i'}$ to be vector bundles. But placidity seems to be the more flexible definition; for instance, I do not know if point (iii) of Remark 3.13 holds if we replace ‘placid’ by ‘special’.
3.7 Equivariance
(i) Note that ![]() $G_S^{S'}/G_S,\mathcal {T}_S^{S'},\mathcal {R}_S^{S'}$ are all acted on by
$G_S^{S'}/G_S,\mathcal {T}_S^{S'},\mathcal {R}_S^{S'}$ are all acted on by ![]() $G_S$, and the various maps between them are
$G_S$, and the various maps between them are ![]() $G_S$-equivariant. In fact, each ‘approximation’
$G_S$-equivariant. In fact, each ‘approximation’ ![]() $G_S^{S',j}/G_S$,
$G_S^{S',j}/G_S$, ![]() $\mathcal {T}^j_i$,
$\mathcal {T}^j_i$, ![]() $\mathcal {R}^j_i$ is acted on by some quotient
$\mathcal {R}^j_i$ is acted on by some quotient ![]() $G_ {S,i'}$ of
$G_ {S,i'}$ of ![]() $G_S$, and the transition morphisms are all
$G_S$, and the transition morphisms are all ![]() $G_S$-equivariant.
$G_S$-equivariant.
(ii) Suppose that ![]() $X=\mathbb {G}_a$. Then we have the action of
$X=\mathbb {G}_a$. Then we have the action of ![]() $\mathbb {G}_m$ on
$\mathbb {G}_m$ on ![]() $X$ by multiplication. It also acts diagonally on
$X$ by multiplication. It also acts diagonally on ![]() $X^S$. Therefore we may consider
$X^S$. Therefore we may consider ![]() $\mathbb {C}^*\times X^S$ as a smooth groupoid over
$\mathbb {C}^*\times X^S$ as a smooth groupoid over ![]() $X^S$. The group
$X^S$. The group ![]() $G_S^{S'}$ over
$G_S^{S'}$ over ![]() $X^S$ is
$X^S$ is ![]() $\mathbb {C}^*\times X^S$-equivariant, so we may form the semidirect product
$\mathbb {C}^*\times X^S$-equivariant, so we may form the semidirect product
a placid affine groupoid ind-scheme over ![]() $X^S$. The special case,
$X^S$. The special case, ![]() $G_S\rtimes\, \mathbb {C}^*$, is a prosaic affine groupoid scheme over
$G_S\rtimes\, \mathbb {C}^*$, is a prosaic affine groupoid scheme over ![]() $X^S$. Then the
$X^S$. Then the ![]() $G_S$-equivariant structures of
$G_S$-equivariant structures of ![]() $G_S^{S'}/G_S,\mathcal {T}_S^{S'},\mathcal {R}_S^{S'}$ and their above approximations upgrade to
$G_S^{S'}/G_S,\mathcal {T}_S^{S'},\mathcal {R}_S^{S'}$ and their above approximations upgrade to ![]() $G_S\rtimes\, \mathbb {C}^*$-equivariant structures (over
$G_S\rtimes\, \mathbb {C}^*$-equivariant structures (over ![]() $X^S$). Again all morphisms, transition or otherwise, of the previous subsection are
$X^S$). Again all morphisms, transition or otherwise, of the previous subsection are ![]() $G_S\rtimes\, \mathbb {C}^*$-equivariant.
$G_S\rtimes\, \mathbb {C}^*$-equivariant.
Remark 3.18 (i) Let ![]() $T$ be a placid ind-scheme over some base
$T$ be a placid ind-scheme over some base ![]() $B$ and
$B$ and ![]() $\mathcal {G}$ be a groupoid scheme over
$\mathcal {G}$ be a groupoid scheme over ![]() $B$ which acts on
$B$ which acts on ![]() $T$. Then we can always choose a
$T$. Then we can always choose a ![]() $\mathcal {G}$-equivariant placid presentation of
$\mathcal {G}$-equivariant placid presentation of ![]() $T$, simply by ‘smoothing out’ any placid presentation by the action of
$T$, simply by ‘smoothing out’ any placid presentation by the action of ![]() $\mathcal {G}$. The category
$\mathcal {G}$. The category ![]() $\mathcal {P}_ {\mathcal {G}}(T)$ of
$\mathcal {P}_ {\mathcal {G}}(T)$ of ![]() $\mathcal {G}$-equivariant placid presentations of
$\mathcal {G}$-equivariant placid presentations of ![]() $T$ is filtered.
$T$ is filtered.
(ii) Now suppose that ![]() $T$ is special. I do not know whether we can choose the special presentation of
$T$ is special. I do not know whether we can choose the special presentation of ![]() $T$ to be
$T$ to be ![]() $\mathcal {G}$-equivariant. However, if
$\mathcal {G}$-equivariant. However, if ![]() $T$ is special by virtue of being a placid vector space over some intermediate
$T$ is special by virtue of being a placid vector space over some intermediate ![]() $\mathcal {G}$-equivariant ind-scheme
$\mathcal {G}$-equivariant ind-scheme ![]() $U$ of ind-finite type,
$U$ of ind-finite type, ![]() $T\to U\to B$, and
$T\to U\to B$, and ![]() $\mathcal {G}$ acts linearly, then we can do it. This is what happens for
$\mathcal {G}$ acts linearly, then we can do it. This is what happens for ![]() $G_S^{S'},\mathcal {T}_S^{S'},\mathcal {R}_S^{S'}$. In the latter two cases, we can take
$G_S^{S'},\mathcal {T}_S^{S'},\mathcal {R}_S^{S'}$. In the latter two cases, we can take ![]() $U=G_S^{S'}/G_S$. In the former case, we can take
$U=G_S^{S'}/G_S$. In the former case, we can take ![]() $U$ to be the quotient of
$U$ to be the quotient of ![]() $G_S^{S'}$ by the kernel of the surjection
$G_S^{S'}$ by the kernel of the surjection ![]() $G_S\to \operatorname {Map}(\Delta _ {S,1},G)$.
$G_S\to \operatorname {Map}(\Delta _ {S,1},G)$.
3.8 Dimension theories
The following definitions can be found in [Reference RaskinRas15], and essentially in the earlier work [Reference DrinfeldDri06], and probably in many other texts.
Definition 3.19 (i) Let ![]() $T$ be a placid scheme, with a placid presentation
$T$ be a placid scheme, with a placid presentation ![]() $T=\underleftarrow {\lim } _ {i\in (\mathcal {I})^{op}}(T_i)$. A dimension theory on
$T=\underleftarrow {\lim } _ {i\in (\mathcal {I})^{op}}(T_i)$. A dimension theory on ![]() $T_ {\mathcal {I}}$ is a function
$T_ {\mathcal {I}}$ is a function ![]() $d:\mathcal {I}\to \mathbb {Z}$, whose value on
$d:\mathcal {I}\to \mathbb {Z}$, whose value on ![]() $i\in \mathcal {I}$ will be written
$i\in \mathcal {I}$ will be written ![]() $d(T_i)$, satisfying the condition
$d(T_i)$, satisfying the condition
whenever ![]() $i\to i'$ in
$i\to i'$ in ![]() $\mathcal {I}$. The set of dimension theories on
$\mathcal {I}$. The set of dimension theories on ![]() $T_ {\mathcal {I}}$ is denoted
$T_ {\mathcal {I}}$ is denoted
(ii) Take a placid presentation ![]() $T=\underleftarrow {\lim } _ {i\in (\mathcal {I})^{op}}(T_i)$ of the scheme
$T=\underleftarrow {\lim } _ {i\in (\mathcal {I})^{op}}(T_i)$ of the scheme ![]() $T$ and a finer placid presentation
$T$ and a finer placid presentation ![]() $T=\underleftarrow {\lim } _ {i_1\in (\mathcal {I}_1)^{op}}(T_ {i_1})$,
$T=\underleftarrow {\lim } _ {i_1\in (\mathcal {I}_1)^{op}}(T_ {i_1})$, ![]() $\mathcal {I}\subset \mathcal {I}_1$. We may extend a dimension theory
$\mathcal {I}\subset \mathcal {I}_1$. We may extend a dimension theory ![]() $d$ on
$d$ on ![]() $T_ {\mathcal {I}}$ to a unique dimension theory, denoted
$T_ {\mathcal {I}}$ to a unique dimension theory, denoted ![]() $d$, on
$d$, on ![]() $T_ {\mathcal {I}_1}$ by setting
$T_ {\mathcal {I}_1}$ by setting
for any ![]() $i'\in \mathcal {I}$ such that
$i'\in \mathcal {I}$ such that ![]() $i_1\to i'$ in
$i_1\to i'$ in ![]() $\mathcal {I}_1$. We have thus constructed a filtered system
$\mathcal {I}_1$. We have thus constructed a filtered system
indexed by the filtered category ![]() $\mathcal {P}$ of placid presentations of
$\mathcal {P}$ of placid presentations of ![]() $T$.
$T$.
(iii) A dimension theory on ![]() $T$ is an element of the colimit of the above filtered system. The set of dimension theories on
$T$ is an element of the colimit of the above filtered system. The set of dimension theories on ![]() $T_ {\mathcal {I}}$ is denoted
$T_ {\mathcal {I}}$ is denoted
Now let ![]() $f:U\to T$ be an f.p. map of placid schemes and choose Cartesian placid presentations indexed by
$f:U\to T$ be an f.p. map of placid schemes and choose Cartesian placid presentations indexed by ![]() $\mathcal {I}$ as in Remark 3.13. In this presentation, a dimension theory
$\mathcal {I}$ as in Remark 3.13. In this presentation, a dimension theory ![]() $d$ on
$d$ on ![]() $T_ {\mathcal {I}}$ defines one on
$T_ {\mathcal {I}}$ defines one on ![]() $U_ {\mathcal {I}}$, denoted
$U_ {\mathcal {I}}$, denoted ![]() $f^*d$ and given by the formula
$f^*d$ and given by the formula
That is, we have a map ![]() $\operatorname {dimth}(T_ {\mathcal {I}})\to \operatorname {dimth}(U_ {\mathcal {I}})$. The composition of this with the map
$\operatorname {dimth}(T_ {\mathcal {I}})\to \operatorname {dimth}(U_ {\mathcal {I}})$. The composition of this with the map ![]() $\operatorname {dimth}(U_ {\mathcal {I}})\to \operatorname {dimth}(U)$ factors through the map
$\operatorname {dimth}(U_ {\mathcal {I}})\to \operatorname {dimth}(U)$ factors through the map ![]() $\operatorname {dimth}(T_ {\mathcal {I}})\to \operatorname {dimth}(T)$, yielding a map
$\operatorname {dimth}(T_ {\mathcal {I}})\to \operatorname {dimth}(T)$, yielding a map
independent of any choices of presentation. If context prevents confusion, we may denote ![]() $f^*d$ by
$f^*d$ by ![]() $d$.
$d$.
Similarly, suppose ![]() $f:U\to T$ is a co-placid map of placid schemes and fix a compatible presentation
$f:U\to T$ is a co-placid map of placid schemes and fix a compatible presentation ![]() $f=\underleftarrow {\lim } _ {i\in \mathcal {I}^{op}}(U_i\to T_i)$. The dimension theory
$f=\underleftarrow {\lim } _ {i\in \mathcal {I}^{op}}(U_i\to T_i)$. The dimension theory ![]() $d$ on
$d$ on ![]() $T_ {\mathcal {I}}$ defines one on
$T_ {\mathcal {I}}$ defines one on ![]() $U_ {\mathcal {I}}$, denoted
$U_ {\mathcal {I}}$, denoted ![]() $f^!d$ and given by the formula
$f^!d$ and given by the formula
This procedure again determines a map
independent of any choices of presentation.
Definition 3.20 (i) Let ![]() $T$ be a placid ind-scheme. Fix a reasonable presentation
$T$ be a placid ind-scheme. Fix a reasonable presentation
We write this as ![]() $T^{\mathcal {J}}$. A dimension theory on
$T^{\mathcal {J}}$. A dimension theory on ![]() $T$ is an element of the limit of the cofiltered system
$T$ is an element of the limit of the cofiltered system
with transition morphisms given by the ![]() $*$-pullback. For different reasonable presentations these limits are canonically isomorphic.
$*$-pullback. For different reasonable presentations these limits are canonically isomorphic.
(ii) Given an ind-f.p. map ![]() $f:U\to T$ of placid ind-schemes, we get a map
$f:U\to T$ of placid ind-schemes, we get a map
determined by the condition that the square
 \[ \begin{matrix} \operatorname{dimth}(T) & \xrightarrow{f^*} & \operatorname{dimth}(U)\\ \downarrow & & \downarrow\\ \operatorname{dimth}(T_j) & \xrightarrow{(f^j)^*} & \operatorname{dimth}(U\times_TT_j)\end{matrix} \]
\[ \begin{matrix} \operatorname{dimth}(T) & \xrightarrow{f^*} & \operatorname{dimth}(U)\\ \downarrow & & \downarrow\\ \operatorname{dimth}(T_j) & \xrightarrow{(f^j)^*} & \operatorname{dimth}(U\times_TT_j)\end{matrix} \]
commutes for every reasonable closed subscheme ![]() $T_j$ of
$T_j$ of ![]() $T$.
$T$.
(iii) Given a co-placid map ![]() $f:U\to T$ of placid ind-schemes, we get a map
$f:U\to T$ of placid ind-schemes, we get a map
determined by the condition that the square
 \[ \begin{matrix} \operatorname{dimth}(T) & \xrightarrow{f^!} & \operatorname{dimth}(U)\\ \downarrow & & \downarrow\\ \operatorname{dimth}(T_j) & \xrightarrow{(f^j)^!} & \operatorname{dimth}(U\times_TT_j)\end{matrix} \]
\[ \begin{matrix} \operatorname{dimth}(T) & \xrightarrow{f^!} & \operatorname{dimth}(U)\\ \downarrow & & \downarrow\\ \operatorname{dimth}(T_j) & \xrightarrow{(f^j)^!} & \operatorname{dimth}(U\times_TT_j)\end{matrix} \]
commutes for every reasonable closed subscheme ![]() $T_j$ of
$T_j$ of ![]() $T$.
$T$.
(iv) Given placid ind-schemes ![]() $U$,
$U$, ![]() $T$ over
$T$ over ![]() $B$, we get a map
$B$, we get a map
Indeed, if ![]() $U=\underrightarrow {\rm colim } _ {j\in \mathcal {J}_U} \underleftarrow {\lim }_ {i\in (\mathcal {I}_U^j)^{op}}U_i^j$,
$U=\underrightarrow {\rm colim } _ {j\in \mathcal {J}_U} \underleftarrow {\lim }_ {i\in (\mathcal {I}_U^j)^{op}}U_i^j$, ![]() $T=\underrightarrow {\rm colim } _ {j\in \mathcal {J}_T} \underleftarrow {\lim }_ {i\in (\mathcal {I}_T^j)^{op}}T_i^j$ are placid presentations over
$T=\underrightarrow {\rm colim } _ {j\in \mathcal {J}_T} \underleftarrow {\lim }_ {i\in (\mathcal {I}_T^j)^{op}}T_i^j$ are placid presentations over ![]() $B$ and
$B$ and ![]() $d_U$,
$d_U$, ![]() $d_T$ are dimension theories on
$d_T$ are dimension theories on ![]() $U$,
$U$, ![]() $T$ then
$T$ then
is a placid presentation and we define
If ![]() $f:U\times _BT\to U\times B$ is the ind-f.p. closed embedding, then we have
$f:U\times _BT\to U\times B$ is the ind-f.p. closed embedding, then we have ![]() $(-)+_B(-)=f^*((-)+_ {\operatorname {Spec}{C}}(-))$. We will usually write
$(-)+_B(-)=f^*((-)+_ {\operatorname {Spec}{C}}(-))$. We will usually write ![]() $(-)+_B(-)$ simply as
$(-)+_B(-)$ simply as ![]() $(-)+(-)$.
$(-)+(-)$.
Remark 3.21 (i) The set of dimension theories on a connected placid ind-scheme ![]() $T$ is a
$T$ is a ![]() $\mathbb {Z}$-torsor. Thus the set of dimension theories on a general placid ind-scheme
$\mathbb {Z}$-torsor. Thus the set of dimension theories on a general placid ind-scheme ![]() $T$ is a
$T$ is a ![]() $\mathbb {Z}^{\pi _0(T)}$-torsor. For an ind-f.p. (respectively, co-placid) map
$\mathbb {Z}^{\pi _0(T)}$-torsor. For an ind-f.p. (respectively, co-placid) map ![]() $f:U\to T$ of placid ind-schemes,
$f:U\to T$ of placid ind-schemes, ![]() $f^*$ (respectively,
$f^*$ (respectively, ![]() $f^!$) is a map of
$f^!$) is a map of ![]() $\mathbb {Z}^{\pi _0(T)}$-sets.
$\mathbb {Z}^{\pi _0(T)}$-sets.
(ii) In fact, there is a sheaf (in an appropriate sense) of ![]() $\mathbb {Z}$-torsors on any placid ind-scheme
$\mathbb {Z}$-torsors on any placid ind-scheme ![]() $T$ whose set of global sections equals the set of dimension theories on
$T$ whose set of global sections equals the set of dimension theories on ![]() $T$. We do not need to consider it since in every example of this paper, this sheaf is trivial.
$T$. We do not need to consider it since in every example of this paper, this sheaf is trivial.
Example 3.22 (i) Recall that ![]() $\mathcal {T}_S^{S'}$ is an infinite-dimensional vector bundle over
$\mathcal {T}_S^{S'}$ is an infinite-dimensional vector bundle over ![]() $G_S^{S'}/G_S$, with ‘approximations’
$G_S^{S'}/G_S$, with ‘approximations’ ![]() $\mathcal {T}_ {S,i}^{S',j}$ for
$\mathcal {T}_ {S,i}^{S',j}$ for ![]() $j\in \mathbb {Z}_ {\geq 0}$ and
$j\in \mathbb {Z}_ {\geq 0}$ and ![]() $i\in \mathbb {Z}_ {\geq ?}$ for some positive integer
$i\in \mathbb {Z}_ {\geq ?}$ for some positive integer ![]() $?$ depending on
$?$ depending on ![]() $j$ (see Example 3.15). The approximation
$j$ (see Example 3.15). The approximation ![]() $\mathcal {T}_ {S,i}^{S',j}$ is a vector bundle over
$\mathcal {T}_ {S,i}^{S',j}$ is a vector bundle over ![]() $G_S^{S',j}/G_S$ of rank
$G_S^{S',j}/G_S$ of rank ![]() $di|S|$. Thus
$di|S|$. Thus ![]() $f:\mathcal {T}_S^{S'}\to G_S^{S'}/G_S$ is co-placid, and since
$f:\mathcal {T}_S^{S'}\to G_S^{S'}/G_S$ is co-placid, and since ![]() $G_S^{S'}/G_S$ is ind-finite type it has a dimension theory
$G_S^{S'}/G_S$ is ind-finite type it has a dimension theory ![]() $d_0$ with constant value
$d_0$ with constant value ![]() $0$. We will denote the dimension theory
$0$. We will denote the dimension theory ![]() $f^!d_0$ on
$f^!d_0$ on ![]() $\mathcal {T}_S^{S'}$ by
$\mathcal {T}_S^{S'}$ by ![]() $\operatorname {rank}(\mathcal {T}_S^{S'})$. We have
$\operatorname {rank}(\mathcal {T}_S^{S'})$. We have
It would perhaps be safer to call this ![]() $\operatorname {rank}_ {G_S^{S'}/G_S}(\mathcal {T}_S^{S'})$, but the notation becomes too unwieldy. The reader should bear this in mind.
$\operatorname {rank}_ {G_S^{S'}/G_S}(\mathcal {T}_S^{S'})$, but the notation becomes too unwieldy. The reader should bear this in mind.
(ii) Let ![]() $f: \mathcal {R}_S^{S'}\to \mathcal {T}_S^{S'}$ be the defining ind-f.p. closed embedding. Then we have the dimension theory
$f: \mathcal {R}_S^{S'}\to \mathcal {T}_S^{S'}$ be the defining ind-f.p. closed embedding. Then we have the dimension theory ![]() $f^*\operatorname {rank}(\mathcal {T}_S^{S'})$ on
$f^*\operatorname {rank}(\mathcal {T}_S^{S'})$ on ![]() $\mathcal {R}_S^{S'}$. We will call this simply
$\mathcal {R}_S^{S'}$. We will call this simply ![]() $\operatorname {rank}(\mathcal {T}_S^{S'})$.
$\operatorname {rank}(\mathcal {T}_S^{S'})$.
(iii) We also have the dimension theory on ![]() $\widetilde {\mathcal {T}}_S^{S'}$ obtained as the
$\widetilde {\mathcal {T}}_S^{S'}$ obtained as the ![]() $!$-pullback of
$!$-pullback of ![]() $\operatorname {rank}(\mathcal {T}_S^{S'})$ (or of
$\operatorname {rank}(\mathcal {T}_S^{S'})$ (or of ![]() $d_0$ directly). Its
$d_0$ directly). Its ![]() $*$-pullback to
$*$-pullback to ![]() $\tilde {R}_S^{S'}$ coincides with the
$\tilde {R}_S^{S'}$ coincides with the ![]() $!$-pullback of the dimension theory
$!$-pullback of the dimension theory ![]() $\operatorname {rank}(\mathcal {T}_S^{S'})$ on
$\operatorname {rank}(\mathcal {T}_S^{S'})$ on ![]() $\mathcal {R}_S^{S'}$. These dimension theories on
$\mathcal {R}_S^{S'}$. These dimension theories on ![]() $\widetilde {\mathcal {T}}_S^{S'}$,
$\widetilde {\mathcal {T}}_S^{S'}$, ![]() $\widetilde {\mathcal {R}}_S^{S'}$ will both be denoted
$\widetilde {\mathcal {R}}_S^{S'}$ will both be denoted ![]() $\operatorname {rank}(\widetilde {\mathcal {T}}_S^{S'})$.
$\operatorname {rank}(\widetilde {\mathcal {T}}_S^{S'})$.
(iv) We will denote the ![]() $!$-pullback to
$!$-pullback to ![]() $G_S^{S'}$ of the constantly
$G_S^{S'}$ of the constantly ![]() $0$ dimension theory on
$0$ dimension theory on ![]() $G_S^{S'}/G_S$ by
$G_S^{S'}/G_S$ by ![]() $\operatorname {rank}(G_S^{S'})$. It satisfies
$\operatorname {rank}(G_S^{S'})$. It satisfies
3.9 Notational remark
We will use the same notational simplification for ![]() $G_S^{S'}$,
$G_S^{S'}$, ![]() $\mathcal {T}_S^{S'}$,
$\mathcal {T}_S^{S'}$, ![]() $\mathcal {R}_S^{S'}$,
$\mathcal {R}_S^{S'}$, ![]() $\widetilde {\mathcal {T}}_S^{S'}$,
$\widetilde {\mathcal {T}}_S^{S'}$, ![]() $\widetilde {\mathcal {R}}_S^{S'}$ as for formal neighborhoods: for instance,
$\widetilde {\mathcal {R}}_S^{S'}$ as for formal neighborhoods: for instance,
may be written as
Fix a ![]() $\mathbb {C}$-point
$\mathbb {C}$-point ![]() $x\in X$ and a local parameter
$x\in X$ and a local parameter ![]() $t$ at
$t$ at ![]() $x$. This determines isomorphisms
$x$. This determines isomorphisms ![]() $\Delta _1(x)=\operatorname {Spec}(\mathcal {O})$,
$\Delta _1(x)=\operatorname {Spec}(\mathcal {O})$, ![]() $\Delta _1^1(x)=\operatorname {Spec}(\mathcal {K})$ where
$\Delta _1^1(x)=\operatorname {Spec}(\mathcal {K})$ where ![]() $\mathcal {O}=\mathbb {C}[[t]]$,
$\mathcal {O}=\mathbb {C}[[t]]$, ![]() $\mathcal {K}=\mathbb {C}((t))$. The groups of
$\mathcal {K}=\mathbb {C}((t))$. The groups of ![]() $\mathbb {C}$-points of
$\mathbb {C}$-points of ![]() $(G_1)_x$,
$(G_1)_x$, ![]() $(G_1^1)_x$ are put in isomorphism with
$(G_1^1)_x$ are put in isomorphism with ![]() $G(\mathcal {O})$,
$G(\mathcal {O})$, ![]() $G(\mathcal {K})$. Note that since
$G(\mathcal {K})$. Note that since ![]() $G_1$ is pro-smooth over
$G_1$ is pro-smooth over ![]() $X$, we have
$X$, we have
We will write informally
 \begin{align*} (G_1)_x&=G(\mathcal{O}),\\ (G_1^1)_x&=G(\mathcal{K}),\\ (G_1^1/G_1)_x&=Gr_G. \end{align*}
\begin{align*} (G_1)_x&=G(\mathcal{O}),\\ (G_1^1)_x&=G(\mathcal{K}),\\ (G_1^1/G_1)_x&=Gr_G. \end{align*}
We will write ![]() $(\mathcal {T}_1^1)_x$,
$(\mathcal {T}_1^1)_x$, ![]() $(\mathcal {R}_1^1)_x$ as
$(\mathcal {R}_1^1)_x$ as ![]() $\mathcal {T},\mathcal {R}$. Since these are ind-f.p. sub-ind-schemes of
$\mathcal {T},\mathcal {R}$. Since these are ind-f.p. sub-ind-schemes of ![]() $\mathcal {T}_1^1$, they have dimension theories given by pulling back
$\mathcal {T}_1^1$, they have dimension theories given by pulling back ![]() $\operatorname {rank}(\mathcal {T}_1^1)$. We will write the resulting dimension theories both as
$\operatorname {rank}(\mathcal {T}_1^1)$. We will write the resulting dimension theories both as ![]() $\operatorname {rank}(\mathcal {T})$. These dimension theories correspond to the
$\operatorname {rank}(\mathcal {T})$. These dimension theories correspond to the ![]() $\dim \boldsymbol {N}(\mathcal {O})$ of [Reference Braverman, Finkelberg and NakajimaBFN16] (although dimension theories are not explicitly used in [Reference Braverman, Finkelberg and NakajimaBFN16]).
$\dim \boldsymbol {N}(\mathcal {O})$ of [Reference Braverman, Finkelberg and NakajimaBFN16] (although dimension theories are not explicitly used in [Reference Braverman, Finkelberg and NakajimaBFN16]).
3.10 Borel–Moore homology
Rather than recall the general formalism of equivariant constructible derived categories on placid ind-schemes (see [Reference RaskinRas15]), we content ourselves with the following definition.
Definition 3.23 (i) Let ![]() $R$ be a commutative ring. Let
$R$ be a commutative ring. Let ![]() $T$ be a scheme of finite type over the base
$T$ be a scheme of finite type over the base ![]() $B$ of finite type over
$B$ of finite type over ![]() $\mathbb {C}$ with an action of the affine algebraic groupoid
$\mathbb {C}$ with an action of the affine algebraic groupoid ![]() $\mathcal {G}$ over
$\mathcal {G}$ over ![]() $B$. Then
$B$. Then ![]() $T^{an}$ has a
$T^{an}$ has a ![]() $\mathcal {G}^{an}$-equivariant constant sheaf
$\mathcal {G}^{an}$-equivariant constant sheaf ![]() $R$ and dualizing complex
$R$ and dualizing complex ![]() $\omega$ with coefficients in
$\omega$ with coefficients in ![]() $R$, and we will write
$R$, and we will write
 \begin{gather*} H^{n}_{\mathcal{G}}(T,R):= H^n_{\mathcal{G}^{an}}(T^{an},R) = \operatorname{Hom}_{D^b_{\mathcal{G}^{an}}(T^{an})}(R,\Sigma^nR),\\ H_{n}^{\mathrm{BM},\mathcal{G}}(T,R):= H^n_{\mathcal{G}^{an}}(T^{an},\omega) = \operatorname{Hom}_{D^b_{\mathcal{G}^{an}}(T^{an})}(R,\Sigma^n\omega). \end{gather*}
\begin{gather*} H^{n}_{\mathcal{G}}(T,R):= H^n_{\mathcal{G}^{an}}(T^{an},R) = \operatorname{Hom}_{D^b_{\mathcal{G}^{an}}(T^{an})}(R,\Sigma^nR),\\ H_{n}^{\mathrm{BM},\mathcal{G}}(T,R):= H^n_{\mathcal{G}^{an}}(T^{an},\omega) = \operatorname{Hom}_{D^b_{\mathcal{G}^{an}}(T^{an})}(R,\Sigma^n\omega). \end{gather*} (ii) Now suppose that ![]() $\mathcal {G}$ is an affine groupoid scheme over
$\mathcal {G}$ is an affine groupoid scheme over ![]() $B$. We may write
$B$. We may write ![]() $\mathcal {G}$ as the limit of its fpqc quotient affine algebraic groupoids
$\mathcal {G}$ as the limit of its fpqc quotient affine algebraic groupoids ![]() $(\mathcal {G}_i)_ {i\in \mathcal {I}^{op}}$. We may assume that action of
$(\mathcal {G}_i)_ {i\in \mathcal {I}^{op}}$. We may assume that action of ![]() $\mathcal {G}$ on
$\mathcal {G}$ on ![]() $T$ factors through each
$T$ factors through each ![]() $\mathcal {G}_i$. We set
$\mathcal {G}_i$. We set
and
Here we have used the fact that for any ![]() $i\to i'$ in
$i\to i'$ in ![]() $\mathcal {I}$, the
$\mathcal {I}$, the ![]() $\mathcal {G}_ {i'}$-equivariant complexes obtained from the
$\mathcal {G}_ {i'}$-equivariant complexes obtained from the ![]() $\mathcal {G}_i$-equivariant constant sheaf (respectively, dualizing complex) are canonically isomorphic to their
$\mathcal {G}_i$-equivariant constant sheaf (respectively, dualizing complex) are canonically isomorphic to their ![]() $\mathcal {G}_ {i'}$-equivariant counterparts. Thus these restriction functors determine the maps of equivariant cohomology (respectively, Borel–Moore homology) which we take colimits over.
$\mathcal {G}_ {i'}$-equivariant counterparts. Thus these restriction functors determine the maps of equivariant cohomology (respectively, Borel–Moore homology) which we take colimits over.
(iii) Let ![]() $T$ be a placid scheme over some base
$T$ be a placid scheme over some base ![]() $B$ of finite type over
$B$ of finite type over ![]() $\mathbb {C}$ and let
$\mathbb {C}$ and let ![]() $\mathcal {G}$ be an affine algebraic groupoid over
$\mathcal {G}$ be an affine algebraic groupoid over ![]() $B$ which acts on
$B$ which acts on ![]() $T$. Let
$T$. Let ![]() $d$ be a dimension theory on
$d$ be a dimension theory on ![]() $T$. Then the
$T$. Then the ![]() $2d$-shifted
$2d$-shifted ![]() $\mathcal {G}$-equivariant Borel–Moore homology of
$\mathcal {G}$-equivariant Borel–Moore homology of ![]() $T$,
$T$, ![]() $H_ {*-2d}^{\mathrm {BM},\mathcal {G}}(T,R)$, is defined as follows. Let
$H_ {*-2d}^{\mathrm {BM},\mathcal {G}}(T,R)$, is defined as follows. Let ![]() $T = \underleftarrow {\lim }_ {i\in (\mathcal {I})^{op}}(T_i)$ be a
$T = \underleftarrow {\lim }_ {i\in (\mathcal {I})^{op}}(T_i)$ be a ![]() $\mathcal {G}$-equivariant placid presentation of
$\mathcal {G}$-equivariant placid presentation of ![]() $T$. Observe that pullback defines a graded map of
$T$. Observe that pullback defines a graded map of ![]() $R$-modules
$R$-modules
whenever ![]() $i\to i'$ in
$i\to i'$ in ![]() $\mathcal {I}$, since
$\mathcal {I}$, since ![]() $T_ {i'}\to T_i$ is a (
$T_ {i'}\to T_i$ is a (![]() $d(T_ {i'})-d(T_i)$)-dimensional smooth covering. We then set
$d(T_ {i'})-d(T_i)$)-dimensional smooth covering. We then set
For different choices of placid presentation, we get canonically isomorphic answers, which justifies the definition.
(iv) Let ![]() $f:T^0\to T^1$ be a
$f:T^0\to T^1$ be a ![]() $\mathcal {G}$-equivariant ind-f.p. embedding of placid ind-schemes over
$\mathcal {G}$-equivariant ind-f.p. embedding of placid ind-schemes over ![]() $B$. Let
$B$. Let ![]() $d$ be a dimension theory on
$d$ be a dimension theory on ![]() $T^1$. Then there is a pushforward map
$T^1$. Then there is a pushforward map
defined by choosing Cartesian placid presentations of ![]() $T^0,T^1$ indexed by
$T^0,T^1$ indexed by ![]() $\mathcal {I}$ and observing that for each
$\mathcal {I}$ and observing that for each ![]() $i\in \mathcal {I}$ the diagram
$i\in \mathcal {I}$ the diagram
 \[ \begin{matrix} H_{*-2d(T_{i'}^0)}^{\mathrm{BM},\mathcal{G}}(T_{i'}^0,R) & \xrightarrow{f_*} & H_{*-2d(T_{i'}^1)}^{\mathrm{BM},\mathcal{G}}(T_{i'}^1,R) & \\ \uparrow & & \uparrow \\ H_{*-2d(T_{i}^0)} ^{\mathrm{BM},\mathcal{G}}(T_{i}^0,R) & \xrightarrow{f_*} & H_{*-2d(T_{i}^0)}^{\mathrm{BM},\mathcal{G}}(T_{i}^1,R) & \end{matrix} \]
\[ \begin{matrix} H_{*-2d(T_{i'}^0)}^{\mathrm{BM},\mathcal{G}}(T_{i'}^0,R) & \xrightarrow{f_*} & H_{*-2d(T_{i'}^1)}^{\mathrm{BM},\mathcal{G}}(T_{i'}^1,R) & \\ \uparrow & & \uparrow \\ H_{*-2d(T_{i}^0)} ^{\mathrm{BM},\mathcal{G}}(T_{i}^0,R) & \xrightarrow{f_*} & H_{*-2d(T_{i}^0)}^{\mathrm{BM},\mathcal{G}}(T_{i}^1,R) & \end{matrix} \]
commutes. Here the horizontal maps are pushforwards maps along the closed embeddings ![]() $T_i^0\to T_i^1$, while the vertical maps are the pullback maps of point (1). The resulting map is independent of any choices we have made.
$T_i^0\to T_i^1$, while the vertical maps are the pullback maps of point (1). The resulting map is independent of any choices we have made.
(v) Now let ![]() $T$ be a placid ind-scheme over some base
$T$ be a placid ind-scheme over some base ![]() $B$ of finite type over
$B$ of finite type over ![]() $\mathbb {C}$ and let
$\mathbb {C}$ and let ![]() $\mathcal {G}$ be an affine algebraic groupoid over
$\mathcal {G}$ be an affine algebraic groupoid over ![]() $B$ which acts on
$B$ which acts on ![]() $T$. Let
$T$. Let ![]() $d$ be a dimension theory on
$d$ be a dimension theory on ![]() $T$. Then we set
$T$. Then we set
using the pushforward maps of point (ii) of this definition, for any choice ![]() $T = \underrightarrow {\rm colim } _ {j\in \mathcal {J}}(T^j)$ of
$T = \underrightarrow {\rm colim } _ {j\in \mathcal {J}}(T^j)$ of ![]() $\mathcal {G}$-equivariant reasonable presentation of
$\mathcal {G}$-equivariant reasonable presentation of ![]() $T$. For different presentations we get canonically isomorphic colimits. Here we have written
$T$. For different presentations we get canonically isomorphic colimits. Here we have written ![]() $d$ for the unique dimension theory on
$d$ for the unique dimension theory on ![]() $T^j$ compatible with the dimension
$T^j$ compatible with the dimension ![]() $d$ on
$d$ on ![]() $T$.
$T$.
Remark 3.24 (i) Since ![]() $\mathcal {G}$ is a pro-smooth covering groupoid, its action on any finite-type approximation
$\mathcal {G}$ is a pro-smooth covering groupoid, its action on any finite-type approximation ![]() $T_i^j$ to the placid ind-scheme factors through the quotient
$T_i^j$ to the placid ind-scheme factors through the quotient ![]() $\mathcal {H}$ by some (pro-smooth covering) subgroup. We then have
$\mathcal {H}$ by some (pro-smooth covering) subgroup. We then have
(ii) If, moreover, ![]() $\mathcal {G}$ is prosaic, then we can choose the subgroup in question to be also pro-unipotent, in which case we have
$\mathcal {G}$ is prosaic, then we can choose the subgroup in question to be also pro-unipotent, in which case we have ![]() $H^*_ {\mathcal {G}}(B,R)\cong {H^*_ {\mathcal {H}}(B,R)}$ so that
$H^*_ {\mathcal {G}}(B,R)\cong {H^*_ {\mathcal {H}}(B,R)}$ so that
(iii) It may even happen that we can choose a section ![]() $\mathcal {H}\to \mathcal {G}$. Take, for example,
$\mathcal {H}\to \mathcal {G}$. Take, for example, ![]() $X=\mathbb {G}_a$,
$X=\mathbb {G}_a$, ![]() $\mathcal {G}=G_ {1}\rtimes\, \mathbb {C}^*$,
$\mathcal {G}=G_ {1}\rtimes\, \mathbb {C}^*$, ![]() $\mathcal {H}=G\times \mathbb {C}^*\times X$ where
$\mathcal {H}=G\times \mathbb {C}^*\times X$ where ![]() $G$ embeds in
$G$ embeds in ![]() $G_ {1}$ as the subgroup of constant functions. In this case,
$G_ {1}$ as the subgroup of constant functions. In this case, ![]() $\mathcal {H}$ acts on all of
$\mathcal {H}$ acts on all of ![]() $T$, and we have
$T$, and we have
Though it may give a psychological advantage since ![]() $\mathcal {H}$ is an actual smooth algebraic groupoid, this reduction is usually technically unhelpful.
$\mathcal {H}$ is an actual smooth algebraic groupoid, this reduction is usually technically unhelpful.
The following procedures in ordinary equivariant Borel–Moore homology are also defined in the world of placid ind-schemes. Fix a ![]() $\mathcal {G}$-equivariant placid ind-scheme
$\mathcal {G}$-equivariant placid ind-scheme ![]() $T$ over
$T$ over ![]() $B$ (of finite type over
$B$ (of finite type over ![]() $\mathbb {C}$) and a dimension theory
$\mathbb {C}$) and a dimension theory ![]() $d$ on
$d$ on ![]() $T$.
$T$.
(i) Change of groupoid base. Suppose that we have some finite-type ![]() $\mathcal {G}$-space
$\mathcal {G}$-space ![]() $A$ over
$A$ over ![]() $B$. Then there exists a semi-direct groupoid scheme
$B$. Then there exists a semi-direct groupoid scheme ![]() $\mathcal {G}\ltimes _BA$, affine pro-smooth over
$\mathcal {G}\ltimes _BA$, affine pro-smooth over ![]() $A$. Suppose that
$A$. Suppose that ![]() $T\to B$ factors through
$T\to B$ factors through ![]() $A$. Then
$A$. Then ![]() $T$ is also
$T$ is also ![]() $\mathcal {G}\ltimes _BA$-equivariant (over
$\mathcal {G}\ltimes _BA$-equivariant (over ![]() $A$) and we have a canonical isomorphism
$A$) and we have a canonical isomorphism
(ii) Open restriction. Let ![]() $A\subset B$ be a
$A\subset B$ be a ![]() $\mathcal {G}$-equivariant open subscheme and let
$\mathcal {G}$-equivariant open subscheme and let ![]() $j:T|_A\to T$ be the
$j:T|_A\to T$ be the ![]() $\mathcal {G}$-equivariant ind-f.p. ind-open embedding of placid ind-schemes over
$\mathcal {G}$-equivariant ind-f.p. ind-open embedding of placid ind-schemes over ![]() $A$. The restriction to
$A$. The restriction to ![]() $A$ of a
$A$ of a ![]() $\mathcal {G}$-equivariant placid presentation of
$\mathcal {G}$-equivariant placid presentation of ![]() $T$ is a
$T$ is a ![]() $\mathcal {G}|_A$-equivariant placid presentation of
$\mathcal {G}|_A$-equivariant placid presentation of ![]() $T|_A$, and, applying the ordinary open restriction in Borel–Moore homology, one obtains a map
$T|_A$, and, applying the ordinary open restriction in Borel–Moore homology, one obtains a map
One usually goes on to compose this map with the isomorphism
(iii) Proper pushforward. Let ![]() $f:U\to T$ be a
$f:U\to T$ be a ![]() $\mathcal {G}$-equivariant ind-proper (in particular, ind-f.p.) map of placid ind-schemes over
$\mathcal {G}$-equivariant ind-proper (in particular, ind-f.p.) map of placid ind-schemes over ![]() $B$. By choosing a
$B$. By choosing a ![]() $\mathcal {G}$-equivariant Cartesian placid presentation and applying the ordinary proper pushforward in Borel–Moore homology, one obtains a map
$\mathcal {G}$-equivariant Cartesian placid presentation and applying the ordinary proper pushforward in Borel–Moore homology, one obtains a map
(iv) Restriction of equivariance. Let ![]() $\mathcal {H}\to \mathcal {G}$ be a morphism of groupoid schemes over
$\mathcal {H}\to \mathcal {G}$ be a morphism of groupoid schemes over ![]() $B$. Then we have ‘restriction of equivariance’ maps
$B$. Then we have ‘restriction of equivariance’ maps
(v) Co-placid restriction. Let ![]() $f:U\to T$ be a
$f:U\to T$ be a ![]() $\mathcal {G}$-equivariant co-placid map of placid ind-schemes over
$\mathcal {G}$-equivariant co-placid map of placid ind-schemes over ![]() $B$. By choosing a
$B$. By choosing a ![]() $\mathcal {G}$-equivariant compatible presentation of
$\mathcal {G}$-equivariant compatible presentation of ![]() $f$ and applying the ordinary smooth pullback in Borel–Moore homology, one obtains a map
$f$ and applying the ordinary smooth pullback in Borel–Moore homology, one obtains a map
(vi) Restriction with supports. Let ![]() $p:T'\to U'$ be a
$p:T'\to U'$ be a ![]() $\mathcal {G}$-equivariant co-placid map of placid ind-schemes over
$\mathcal {G}$-equivariant co-placid map of placid ind-schemes over ![]() $B$, and let
$B$, and let ![]() $f':U'\to T'$ be a
$f':U'\to T'$ be a ![]() $\mathcal {G}$-equivariant section of
$\mathcal {G}$-equivariant section of ![]() $p$. Let
$p$. Let ![]() $g:T\to T'$ be ind-f.p. and let
$g:T\to T'$ be ind-f.p. and let ![]() $U=T\times _ {T'}U'$, so that we have a Cartesian square
$U=T\times _ {T'}U'$, so that we have a Cartesian square
 \[ \begin{matrix}U & \xrightarrow{f} & T\\ \downarrow{g'} & & \downarrow{g}\\ U' & \xrightarrow{f'} & T'\end{matrix} \]
\[ \begin{matrix}U & \xrightarrow{f} & T\\ \downarrow{g'} & & \downarrow{g}\\ U' & \xrightarrow{f'} & T'\end{matrix} \]
Suppose we have a dimension theory ![]() $d'$ on
$d'$ on ![]() $U'$ such that
$U'$ such that ![]() $g^*p^!d'=d$, and set
$g^*p^!d'=d$, and set ![]() $d^g:=(g')^*d'$. We can choose a
$d^g:=(g')^*d'$. We can choose a ![]() $\mathcal {G}$-equivariant compatible presentation of this Cartesian square, that is, write it as
$\mathcal {G}$-equivariant compatible presentation of this Cartesian square, that is, write it as
 \[ \mathop {\rm colim }\limits_{\mathrel{\mathop{\kern0pt\longrightarrow}\limits_{j\in\mathcal{J}}} } \mathop {\lim }\limits_{\mathrel{\mathop{\kern0pt\longleftarrow}\limits_{i\in\mathcal{I}^j}} } \left(\begin{matrix}U_i^j & \xrightarrow{f_i^j} & T_i^j\\ \downarrow{} & & \downarrow{}\\ (U')_i^j & \xrightarrow{(f')_i^j} & (T')_i^j\end{matrix}\right) \]
\[ \mathop {\rm colim }\limits_{\mathrel{\mathop{\kern0pt\longrightarrow}\limits_{j\in\mathcal{J}}} } \mathop {\lim }\limits_{\mathrel{\mathop{\kern0pt\longleftarrow}\limits_{i\in\mathcal{I}^j}} } \left(\begin{matrix}U_i^j & \xrightarrow{f_i^j} & T_i^j\\ \downarrow{} & & \downarrow{}\\ (U')_i^j & \xrightarrow{(f')_i^j} & (T')_i^j\end{matrix}\right) \]
such that the induced presentations of the vertical morphisms ![]() $U\to U'$,
$U\to U'$, ![]() $T\to T'$ are Cartesian, and such that there exists a
$T\to T'$ are Cartesian, and such that there exists a ![]() $\mathcal {G}$-equivariant presentation
$\mathcal {G}$-equivariant presentation ![]() $\underrightarrow {\rm colim } _ {j\in \mathcal {J}} \underleftarrow {\lim }_ {i\in \mathcal {I}^j}((T')_i^j\xrightarrow {p_i^j}(U')_i^j)$ of
$\underrightarrow {\rm colim } _ {j\in \mathcal {J}} \underleftarrow {\lim }_ {i\in \mathcal {I}^j}((T')_i^j\xrightarrow {p_i^j}(U')_i^j)$ of ![]() $p$. Then
$p$. Then ![]() $p_i^j$ is a smooth covering and
$p_i^j$ is a smooth covering and ![]() $(f')_i^j$ is its section, and we have a ‘restriction with supports’ morphism
$(f')_i^j$ is its section, and we have a ‘restriction with supports’ morphism ![]() $(f_i^j)^!:H_*^{\mathrm {BM},\mathcal {G}}(T_i^j,R)\to H_ {*-2\dim (p_i^j)}^{\mathrm {BM},\mathcal {G}}(U_i^j,R)$, which assembles to give a morphism
$(f_i^j)^!:H_*^{\mathrm {BM},\mathcal {G}}(T_i^j,R)\to H_ {*-2\dim (p_i^j)}^{\mathrm {BM},\mathcal {G}}(U_i^j,R)$, which assembles to give a morphism
(vii) Averaging. Suppose that ![]() $\mathcal {H}\subset \mathcal {G}$ is a normal subgroup over
$\mathcal {H}\subset \mathcal {G}$ is a normal subgroup over ![]() $B$ of finite index. Then we have the averaging maps
$B$ of finite index. Then we have the averaging maps
(viii) Specialization. Suppose now that ![]() $B=\mathbb {G}_a$ and
$B=\mathbb {G}_a$ and ![]() $\mathcal {G}$ is a group scheme over
$\mathcal {G}$ is a group scheme over ![]() $B=\mathbb {G}_a$. We have the closed subscheme
$B=\mathbb {G}_a$. We have the closed subscheme ![]() $i:\{0\}\to \mathbb {G}_a$, and the complementary open subscheme
$i:\{0\}\to \mathbb {G}_a$, and the complementary open subscheme ![]() $j:\mathbb {G}_m\to \mathbb {G}_a$. Let us write
$j:\mathbb {G}_m\to \mathbb {G}_a$. Let us write ![]() $T^*,\mathcal {G}^*$ for the restrictions to
$T^*,\mathcal {G}^*$ for the restrictions to ![]() $\mathbb {G}_m$ and
$\mathbb {G}_m$ and ![]() $T|_0,\mathcal {G}|_0$ for the restrictions to
$T|_0,\mathcal {G}|_0$ for the restrictions to ![]() $\{0\}$. Choose a
$\{0\}$. Choose a ![]() $\mathcal {G}$-equivariant placid presentation
$\mathcal {G}$-equivariant placid presentation
of ![]() $T$ over
$T$ over ![]() $\mathbb {G}_a$. Then by restriction we obtain a
$\mathbb {G}_a$. Then by restriction we obtain a ![]() $\mathcal {G}^*$-equivariant placid presentation
$\mathcal {G}^*$-equivariant placid presentation
of ![]() $T^*$ over
$T^*$ over ![]() $\mathbb {G}_a$ and a
$\mathbb {G}_a$ and a ![]() $\mathcal {G}|_0$-equivariant placid presentation
$\mathcal {G}|_0$-equivariant placid presentation
of ![]() $T|_0$ over
$T|_0$ over ![]() $\{0\}$, both of which are Cartesian with the original placid presentation. Since
$\{0\}$, both of which are Cartesian with the original placid presentation. Since ![]() $\mathcal {G}$ is pro-smooth covering, we have specialization maps
$\mathcal {G}$ is pro-smooth covering, we have specialization maps
which are compatible, so yield
We will write ![]() $d^*:=j^*d$,
$d^*:=j^*d$, ![]() $d|_0:=i^*d$.
$d|_0:=i^*d$.
(ix) Steenrod's construction. Let ![]() $\mathcal {G}$ be an affine algebraic group and
$\mathcal {G}$ be an affine algebraic group and ![]() $B=*$ (we will not need the relative situation). Write
$B=*$ (we will not need the relative situation). Write ![]() $pd$ for the dimension theory
$pd$ for the dimension theory ![]() $\underbrace {d+\cdots +d}_ {p \text{times}}$ on the
$\underbrace {d+\cdots +d}_ {p \text{times}}$ on the ![]() $\mathcal {G}^{\mu _p}\rtimes\, \mu _p$-equivariant placid ind-scheme
$\mathcal {G}^{\mu _p}\rtimes\, \mu _p$-equivariant placid ind-scheme ![]() $T^{\mu _p}$. We have nonlinear maps
$T^{\mu _p}$. We have nonlinear maps
which are monoidal with respect to the map ![]() $St^H:H^n_ {\mathcal {G}}(*,R)\to H^{pn}_ {\mathcal {G}^{\mu _p}\rtimes\, \mu _p}(*,R)$ and whose discrepancy from additivity is averaged from
$St^H:H^n_ {\mathcal {G}}(*,R)\to H^{pn}_ {\mathcal {G}^{\mu _p}\rtimes\, \mu _p}(*,R)$ and whose discrepancy from additivity is averaged from ![]() $H_ {pn-2pd}^{\mathrm {BM},\mathcal {G}^{\mu _p}}(T^{\mu _p},R)$. If
$H_ {pn-2pd}^{\mathrm {BM},\mathcal {G}^{\mu _p}}(T^{\mu _p},R)$. If ![]() $R$ is a perfect field
$R$ is a perfect field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p$, we have the nonlinear graded
$p$, we have the nonlinear graded ![]() $St_ {\mathrm {ex}}$-monoidal maps
$St_ {\mathrm {ex}}$-monoidal maps
The following facts carry over from the ordinary case.
(i) Descent.
(a) Suppose that
 $\mathcal {H}$ is a normal (pro-smooth covering) subgroup of
$\mathcal {H}$ is a normal (pro-smooth covering) subgroup of  $\mathcal {G}$ over
$\mathcal {G}$ over  $B$, and that the fpqc quotient group
$B$, and that the fpqc quotient group  $\mathcal {G}/\mathcal {H}$ exists as a pro-smooth covering group over
$\mathcal {G}/\mathcal {H}$ exists as a pro-smooth covering group over  $B$. The main example here is
$B$. The main example here is  $\mathcal {G}=\mathcal {H}\times _B\mathcal {L}$ for pro-smooth covering groups
$\mathcal {G}=\mathcal {H}\times _B\mathcal {L}$ for pro-smooth covering groups  $\mathcal {H}$,
$\mathcal {H}$,  $\mathcal {L}$ over
$\mathcal {L}$ over  $B$. Suppose that
$B$. Suppose that  $\mathcal {H}$ acts freely on
$\mathcal {H}$ acts freely on  $T$, so that, in particular, the fpqc quotient (relative to
$T$, so that, in particular, the fpqc quotient (relative to  $B$)
$B$)  $T/\mathcal {H}$ exists as a
$T/\mathcal {H}$ exists as a  $\mathcal {G}/\mathcal {H}$-equivariant placid ind-scheme over
$\mathcal {G}/\mathcal {H}$-equivariant placid ind-scheme over  $B$. So the quotient map
$B$. So the quotient map  $f:T\to T/\mathcal {H}$ is
$f:T\to T/\mathcal {H}$ is  $\mathcal {G}$-equivariant and co-placid. Suppose that there exists a dimension theory
$\mathcal {G}$-equivariant and co-placid. Suppose that there exists a dimension theory  $d'$ on
$d'$ on  $T/\mathcal {H}$ satisfying
$T/\mathcal {H}$ satisfying  $f^!d'=d$. Then the composition
is an isomorphism.
$f^!d'=d$. Then the composition
is an isomorphism. \[ H_{*-2d'}^{\mathrm{BM},\mathcal{G}/\mathcal{H}}(T/\mathcal{H},R)\xrightarrow{\text{}}H_{*-2d'}^{\mathrm{BM},\mathcal{G}}(T/\mathcal{H},R) \xrightarrow{f^!}H_{*-2d}^{\mathrm{BM},\mathcal{G}}(T,R) \]
\[ H_{*-2d'}^{\mathrm{BM},\mathcal{G}/\mathcal{H}}(T/\mathcal{H},R)\xrightarrow{\text{}}H_{*-2d'}^{\mathrm{BM},\mathcal{G}}(T/\mathcal{H},R) \xrightarrow{f^!}H_{*-2d}^{\mathrm{BM},\mathcal{G}}(T,R) \](b) Suppose that
 $Q$ is an algebraic group acting regularly on
$Q$ is an algebraic group acting regularly on  $B$ in the sense that the stabilizer groupoid
$B$ in the sense that the stabilizer groupoid  $Q_B:=B\times _B(Q\ltimes B)$ is smooth over
$Q_B:=B\times _B(Q\ltimes B)$ is smooth over  $B$, and
$B$, and  $\mathcal {L}$ is a
$\mathcal {L}$ is a  $Q$-equivariant pro-smooth covering group over
$Q$-equivariant pro-smooth covering group over  $B$. Set
$B$. Set  $\mathcal {G}=\mathcal {L}\rtimes Q$. Thus the maximal subgroup
$\mathcal {G}=\mathcal {L}\rtimes Q$. Thus the maximal subgroup  $\mathcal {H}=\mathcal {L}\rtimes _BQ_B$ is a pro-smooth covering group over
$\mathcal {H}=\mathcal {L}\rtimes _BQ_B$ is a pro-smooth covering group over  $B$, and the quotient groupoid
$B$, and the quotient groupoid  $P:=\mathcal {G}/\mathcal {H}=(Q\ltimes B)/Q_B$ is smooth over
$P:=\mathcal {G}/\mathcal {H}=(Q\ltimes B)/Q_B$ is smooth over  $B$. Let
$B$. Let  $A=B/P$,
$A=B/P$,  $\pi :B\to A$. Suppose that we are given a slice
$\pi :B\to A$. Suppose that we are given a slice  $i:A\subset B$. Consider the placid
$i:A\subset B$. Consider the placid  $\mathcal {G}\times _B\pi ^*(\mathcal {H}|_A)$-equivariant ind-scheme
On the one hand, the normal subgroup
$\mathcal {G}\times _B\pi ^*(\mathcal {H}|_A)$-equivariant ind-scheme
On the one hand, the normal subgroup \[ \mathcal{G}|_A\times_AT|_A. \]
\[ \mathcal{G}|_A\times_AT|_A. \] $\pi ^*(\mathcal {H}|_A)$ acts freely and the quotient is
$\pi ^*(\mathcal {H}|_A)$ acts freely and the quotient is  $T$, giving
where
$T$, giving
where \[ H_{*-2d}^{\mathrm{BM},\mathcal{G}}(T,R)\xrightarrow{\sim} H_{*-2d'}^{\mathrm{BM},\mathcal{G} \, \times_A \,\mathcal{H}|_A}(\mathcal{G}|_A\times_AT|_A,R) \]
\[ H_{*-2d}^{\mathrm{BM},\mathcal{G}}(T,R)\xrightarrow{\sim} H_{*-2d'}^{\mathrm{BM},\mathcal{G} \, \times_A \,\mathcal{H}|_A}(\mathcal{G}|_A\times_AT|_A,R) \] $d'$ is the
$d'$ is the  $!$-pullback of
$!$-pullback of  $d$. On the other hand, the normal subgroup
$d$. On the other hand, the normal subgroup  $\mathcal {L}$ acts freely, and the quotient is
$\mathcal {L}$ acts freely, and the quotient is  $Q\times T|_A$ with its residual action of
$Q\times T|_A$ with its residual action of  $(Q\ltimes B)\times _B\pi ^*(\mathcal {H}|_A) = (Q\times \mathcal {H}|_A)\ltimes _AB$, where
$(Q\ltimes B)\times _B\pi ^*(\mathcal {H}|_A) = (Q\times \mathcal {H}|_A)\ltimes _AB$, where  $\mathcal {H}|_A$ acts trivially on
$\mathcal {H}|_A$ acts trivially on  $B$ over
$B$ over  $A$. Thus we have the isomorphisms
if
$A$. Thus we have the isomorphisms
if \[ \begin{matrix} H_{*-2d''}^{\mathrm{BM},\mathcal{H}|_A}(T|_A,R) & \xrightarrow{\sim} & H_{*-2d''-2\dim Q}^{Q\times \mathcal{H}|_A}(Q\times T|_A,R)\\ & & \downarrow{~}\\ H_{*-2d'}^{\mathrm{BM},\mathcal{G}\,\times_A\, \mathcal{H}|_A}(\mathcal{G}|_A\times_AT|_A,R) & \xleftarrow{\sim} & H_{*-2d''-2\dim Q}^{(Q\times \mathcal{H}|_A)\ltimes_AB}(Q\times T|_A,R)\\ \end{matrix} \]
\[ \begin{matrix} H_{*-2d''}^{\mathrm{BM},\mathcal{H}|_A}(T|_A,R) & \xrightarrow{\sim} & H_{*-2d''-2\dim Q}^{Q\times \mathcal{H}|_A}(Q\times T|_A,R)\\ & & \downarrow{~}\\ H_{*-2d'}^{\mathrm{BM},\mathcal{G}\,\times_A\, \mathcal{H}|_A}(\mathcal{G}|_A\times_AT|_A,R) & \xleftarrow{\sim} & H_{*-2d''-2\dim Q}^{(Q\times \mathcal{H}|_A)\ltimes_AB}(Q\times T|_A,R)\\ \end{matrix} \] $d''$ is a dimension theory whose
$d''$ is a dimension theory whose  $!$-pullback along
$!$-pullback along  $\mathcal {G}|_A\times _AT|_A\to Q\times T|_A\to T|_A$ equals
$\mathcal {G}|_A\times _AT|_A\to Q\times T|_A\to T|_A$ equals  $d'$. Thus we obtain an isomorphism
$d'$. Thus we obtain an isomorphism
 \[ H_{*-2d''}^{\mathrm{BM},\mathcal{H}|_A}(T|_A,R)\xrightarrow{\sim} H_{*-2d}^{\mathrm{BM},\mathcal{G}}(T,R). \]
\[ H_{*-2d''}^{\mathrm{BM},\mathcal{H}|_A}(T|_A,R)\xrightarrow{\sim} H_{*-2d}^{\mathrm{BM},\mathcal{G}}(T,R). \]
(ii) Compatibilities. These various maps between Borel–Moore homology groups all commute with each other, whenever this makes sense. Consider the following examples.
(a) If
 $f:U\to T$ (resp.
$f:U\to T$ (resp.  $p: V\to T$) is an ind-proper (resp. co-placid)
$p: V\to T$) is an ind-proper (resp. co-placid)  $\mathcal {G}$-equivariant map, so that we have a
$\mathcal {G}$-equivariant map, so that we have a  $\mathcal {G}$-equivariant Cartesian square
then we have
$\mathcal {G}$-equivariant Cartesian square
then we have \[ \begin{matrix}W & \xrightarrow{f'} & V\\ \downarrow{p'} & & \downarrow{p}\\ U & \xrightarrow{f} & T\end{matrix} \]
\[ \begin{matrix}W & \xrightarrow{f'} & V\\ \downarrow{p'} & & \downarrow{p}\\ U & \xrightarrow{f} & T\end{matrix} \] $p^!f_*=f'_*(p')^!$.
$p^!f_*=f'_*(p')^!$.(b) Specialization commutes with proper pushforward, restriction of equivariance, co-placid restriction and averaging. To spell this out in the most complicated case, take a ‘restriction with supports framework’ as in (vi) above with
 $B=\mathbb {G}_a$ and
$B=\mathbb {G}_a$ and  $\mathcal {G}$ a group. We may restrict all the data over
$\mathcal {G}$ a group. We may restrict all the data over  $\{0\}$ or over
$\{0\}$ or over  $\mathbb {G}_a-\{0\}$, and obtain again ‘restriction with supports frameworks’. We therefore obtain a square
which is commutative.
$\mathbb {G}_a-\{0\}$, and obtain again ‘restriction with supports frameworks’. We therefore obtain a square
which is commutative. \[ \begin{matrix} H_{*-2d^*}^{\mathrm{BM},\mathcal{G}^*}(T^*,R) & \xrightarrow{s_T} & H_{*-2d|_0}^{\mathrm{BM},\mathcal{G}|_0}(T|_0,R)\\ \downarrow{^{(f|_{\mathbb{G}_a-\{0\}})^!}} & & \downarrow{^{(f|_{\{0\}})^!}}\\ H_{*-2(d^g)^*}^{\mathrm{BM},\mathcal{G}^*}(U^*,R) & \xrightarrow{s_U} & H_{*-2(d^g)|_0}^{\mathrm{BM},\mathcal{G}|_0}(U|_0,R) \end{matrix} \]
\[ \begin{matrix} H_{*-2d^*}^{\mathrm{BM},\mathcal{G}^*}(T^*,R) & \xrightarrow{s_T} & H_{*-2d|_0}^{\mathrm{BM},\mathcal{G}|_0}(T|_0,R)\\ \downarrow{^{(f|_{\mathbb{G}_a-\{0\}})^!}} & & \downarrow{^{(f|_{\{0\}})^!}}\\ H_{*-2(d^g)^*}^{\mathrm{BM},\mathcal{G}^*}(U^*,R) & \xrightarrow{s_U} & H_{*-2(d^g)|_0}^{\mathrm{BM},\mathcal{G}|_0}(U|_0,R) \end{matrix} \](c) Averaging commutes with change of groupoid base, open restriction, proper pushforward, co-placid restriction. It also commutes with restriction of equivariance in the following sense. If
 $\mathcal {H}\subset \mathcal {G}$ is of finite index over
$\mathcal {H}\subset \mathcal {G}$ is of finite index over  $B$ and
$B$ and  $\mathcal {G}'\to \mathcal {G}$ is a map, the fiber product
$\mathcal {G}'\to \mathcal {G}$ is a map, the fiber product  $\mathcal {H}\times _ {\mathcal {G}}\mathcal {G}'$ is of finite index in
$\mathcal {H}\times _ {\mathcal {G}}\mathcal {G}'$ is of finite index in  $\mathcal {G}'$, and the two possible maps from the
$\mathcal {G}'$, and the two possible maps from the  $\mathcal {H}$-equivariant Borel–Moore homology to the
$\mathcal {H}$-equivariant Borel–Moore homology to the  $\mathcal {G}'$-equivariant homology coincide. For some reason, we have steadfastly avoided using quotient stacks. If we had used them, this would be an example of proper base change.
$\mathcal {G}'$-equivariant homology coincide. For some reason, we have steadfastly avoided using quotient stacks. If we had used them, this would be an example of proper base change.
3.11 The branch
We assume from now on that ![]() $X=\mathbb {G}_a$ with global parameter
$X=\mathbb {G}_a$ with global parameter ![]() $t$. Thus the
$t$. Thus the ![]() $0$-fibers
$0$-fibers ![]() $G(\mathcal {O})$ of
$G(\mathcal {O})$ of ![]() $G_1$,
$G_1$, ![]() $\mathcal {R}$ of
$\mathcal {R}$ of ![]() $\mathcal {R}_1^1$, etc., have actions of
$\mathcal {R}_1^1$, etc., have actions of ![]() $\mathbb {C}^*$. We assume also that
$\mathbb {C}^*$. We assume also that ![]() $G$ is reductive, so that
$G$ is reductive, so that ![]() $G_S^{S'}/G_S$ is ind-projective over
$G_S^{S'}/G_S$ is ind-projective over ![]() $X^S$. We recall the definitions of [Reference Braverman, Finkelberg and NakajimaBFN16] with respect to our notation.
$X^S$. We recall the definitions of [Reference Braverman, Finkelberg and NakajimaBFN16] with respect to our notation.
Definition 3.25
(i) The Coulomb branch (over
 $R$) is the graded
$R$) is the graded  $H^*_ {G(\mathcal {O})}(*,R)$-module
$H^*_ {G(\mathcal {O})}(*,R)$-module
 \[ A^*:=H_{*-2\operatorname{rank}(\mathcal{T})}^{\mathrm{BM},G(\mathcal{O})}(\mathcal{R},R). \]
\[ A^*:=H_{*-2\operatorname{rank}(\mathcal{T})}^{\mathrm{BM},G(\mathcal{O})}(\mathcal{R},R). \](ii) The quantum Coulomb branch (over
 $R$) is the graded
$R$) is the graded  $H^*_ {G(\mathcal {O})\rtimes\, \mathbb {C}^*}(*,R)=H^*_ {G(\mathcal {O})}(*,R)[\hbar ]$-module
Here
$H^*_ {G(\mathcal {O})\rtimes\, \mathbb {C}^*}(*,R)=H^*_ {G(\mathcal {O})}(*,R)[\hbar ]$-module
Here \[ A_\hbar^*:=H_{*-2\operatorname{rank}(\mathcal{T})}^{\mathrm{BM},G(\mathcal{O})\rtimes\,\mathbb{C}^*}(\mathcal{R},R). \]
\[ A_\hbar^*:=H_{*-2\operatorname{rank}(\mathcal{T})}^{\mathrm{BM},G(\mathcal{O})\rtimes\,\mathbb{C}^*}(\mathcal{R},R). \] $\hbar$ has degree
$\hbar$ has degree  $2$.
$2$.(iii) We will often write
 $A^*,A_\hbar ^*$ as simply
$A^*,A_\hbar ^*$ as simply  $A,A_\hbar$.
$A,A_\hbar$.
Lemma 3.26 ![]() $A^*$,
$A^*$, ![]() $A_\hbar ^*$ are evenly graded and free over
$A_\hbar ^*$ are evenly graded and free over ![]() $H^*_ {G(\mathcal {O})}(*,R)$,
$H^*_ {G(\mathcal {O})}(*,R)$, ![]() $H^*_ {G(\mathcal {O})}(*,R)[\hbar ]$. We have a canonical isomorphism
$H^*_ {G(\mathcal {O})}(*,R)[\hbar ]$. We have a canonical isomorphism ![]() $A_\hbar ^*/\hbar \cong A_\hbar$.
$A_\hbar ^*/\hbar \cong A_\hbar$.
Proof. The proof in [Reference Braverman, Finkelberg and NakajimaBFN16] in the case ![]() $R=\mathbb {C}$ works for any
$R=\mathbb {C}$ works for any ![]() $R$. The essential point is that the equivariant parameters are in even degrees, and an equivariant placid presentation may be chosen such that each ‘approximation’ has a complex cell decomposition.
$R$. The essential point is that the equivariant parameters are in even degrees, and an equivariant placid presentation may be chosen such that each ‘approximation’ has a complex cell decomposition.
We will also consider ![]() $\mathcal {A}^*: = H_ {*-2\operatorname {rank}(\mathcal {T})}^{\mathrm {BM},G(\mathcal {O})\rtimes\, \mu _p}(\mathcal {R},R)$. The same proof shows that the natural map
$\mathcal {A}^*: = H_ {*-2\operatorname {rank}(\mathcal {T})}^{\mathrm {BM},G(\mathcal {O})\rtimes\, \mu _p}(\mathcal {R},R)$. The same proof shows that the natural map
is an isomorphism. In particular, in the case ![]() $R=\mathbb {F}_{\rm p}$ we have
$R=\mathbb {F}_{\rm p}$ we have ![]() $\mathcal {A}^*=A^*_\hbar [a]$. We have an averaging map
$\mathcal {A}^*=A^*_\hbar [a]$. We have an averaging map ![]() $A^*\to \mathcal {A}^*$, which after identifying
$A^*\to \mathcal {A}^*$, which after identifying ![]() $A^*=R\otimes _ {R[\hbar ]}A^*_\hbar$,
$A^*=R\otimes _ {R[\hbar ]}A^*_\hbar$, ![]() $\mathcal {A}^*=H^*_ {\mu _p}(*,R)\otimes _ {R[\hbar ]}A^*_\hbar$ is induced by the averaging map of
$\mathcal {A}^*=H^*_ {\mu _p}(*,R)\otimes _ {R[\hbar ]}A^*_\hbar$ is induced by the averaging map of ![]() $R[\hbar ]$-modules
$R[\hbar ]$-modules ![]() $R\to H^*_ {\mu }(*,R)$. This is the map which multiplies by
$R\to H^*_ {\mu }(*,R)$. This is the map which multiplies by ![]() $p$ in degree
$p$ in degree ![]() $0$. Therefore in the case
$0$. Therefore in the case ![]() $R=\mathbb {F}_{\rm p}$, the averaging map equals
$R=\mathbb {F}_{\rm p}$, the averaging map equals ![]() $0$.
$0$.
Remark 3.27 (i) In [Reference Braverman, Finkelberg and NakajimaBFN16] ![]() $A^*,A_\hbar ^*$ are given ring structures by a form of convolution in Borel–Moore homology;
$A^*,A_\hbar ^*$ are given ring structures by a form of convolution in Borel–Moore homology; ![]() $\mathcal {A}^*$ is also a ring in the same way. They show that
$\mathcal {A}^*$ is also a ring in the same way. They show that ![]() $A^*$ is commutative and
$A^*$ is commutative and ![]() $A_\hbar ^*$ is an
$A_\hbar ^*$ is an ![]() $\hbar$-quantization of
$\hbar$-quantization of ![]() $A^*$. We will recall the construction in the course of the proof of our main theorem. The idea (due originally to Beilinson and Drinfeld [Reference Beĭlinson and DrinfeldBD91]) is to express the multiplication in
$A^*$. We will recall the construction in the course of the proof of our main theorem. The idea (due originally to Beilinson and Drinfeld [Reference Beĭlinson and DrinfeldBD91]) is to express the multiplication in ![]() $A^*$ by a manifestly commutative specialization map.
$A^*$ by a manifestly commutative specialization map.
(ii) Recall that ![]() $\mathcal {T}$ is the fpqc quotient
$\mathcal {T}$ is the fpqc quotient ![]() $G(\mathcal {K})\frac {\times }{^{G(\mathcal {O})}} \boldsymbol {N}(\mathcal {O})$ of the placid ind-scheme
$G(\mathcal {K})\frac {\times }{^{G(\mathcal {O})}} \boldsymbol {N}(\mathcal {O})$ of the placid ind-scheme ![]() $\tilde {T}:=G(\mathcal {K})\times \boldsymbol {N}(\mathcal {O})$. Both are ind-pro-smooth covers of (in fact, ind-pro-smooth ind-fiber bundles over)
$\tilde {T}:=G(\mathcal {K})\times \boldsymbol {N}(\mathcal {O})$. Both are ind-pro-smooth covers of (in fact, ind-pro-smooth ind-fiber bundles over) ![]() $Gr_G$, and have respective dimension theories
$Gr_G$, and have respective dimension theories ![]() $\operatorname {rank}(\mathcal {T})$,
$\operatorname {rank}(\mathcal {T})$, ![]() $\operatorname {rank}(\widetilde {\mathcal {T}})$ given by their ranks over
$\operatorname {rank}(\widetilde {\mathcal {T}})$ given by their ranks over ![]() $Gr_G$. Let us denote by
$Gr_G$. Let us denote by ![]() $\widetilde {\mathcal {R}}$ the corresponding
$\widetilde {\mathcal {R}}$ the corresponding ![]() $G(\mathcal {O})$-bundle over
$G(\mathcal {O})$-bundle over ![]() $\mathcal {R}$; it has a compatible dimension theory
$\mathcal {R}$; it has a compatible dimension theory ![]() $\operatorname {rank}(\widetilde {\mathcal {T}})$. By descent, we have the isomorphism
$\operatorname {rank}(\widetilde {\mathcal {T}})$. By descent, we have the isomorphism
and similarly for ![]() $A^*$. This shows that
$A^*$. This shows that ![]() $A^*,A_\hbar ^*$ have two module structures over
$A^*,A_\hbar ^*$ have two module structures over ![]() $H^*_ {G(\mathcal {O})}(*,R)$. In fact, these module structures coincide with the left- and right-multiplication by a subalgebra
$H^*_ {G(\mathcal {O})}(*,R)$. In fact, these module structures coincide with the left- and right-multiplication by a subalgebra ![]() $H^*_ {G(\mathcal {O})}(*,R)\subset A^*,A^*_\hbar$. Since
$H^*_ {G(\mathcal {O})}(*,R)\subset A^*,A^*_\hbar$. Since ![]() $A^*$ is commutative, these two module structures coincide everywhere. However,
$A^*$ is commutative, these two module structures coincide everywhere. However, ![]() $H^*_ {G(\mathcal {O})}(*,R)$ is not in the center of
$H^*_ {G(\mathcal {O})}(*,R)$ is not in the center of ![]() $A^*_\hbar$, so these two module structures are different there.
$A^*_\hbar$, so these two module structures are different there.
3.12 The ‘large center’ map
We will set ![]() $R=\mathbb {F}_{\rm p}$ from now on. The rest of this section is devoted to the proof (and explanation) of the following theorem.
$R=\mathbb {F}_{\rm p}$ from now on. The rest of this section is devoted to the proof (and explanation) of the following theorem.
Theorem 3.28 ![]() $A_\hbar$ is a Frobenius-constant quantization of
$A_\hbar$ is a Frobenius-constant quantization of ![]() $A$.
$A$.
We will construct the requisite map ![]() $F_\hbar$ using Steenrod's construction and a specialization map. First we introduce some new notation. We will fix
$F_\hbar$ using Steenrod's construction and a specialization map. First we introduce some new notation. We will fix ![]() $X=\mathbb {G}_a$, with parameter
$X=\mathbb {G}_a$, with parameter ![]() $t$. We will use another base curve
$t$. We will use another base curve ![]() $Y=\mathbb {G}_a$ with parameter
$Y=\mathbb {G}_a$ with parameter ![]() $t^p$. We have
$t^p$. We have ![]() $Y=X//\mu _p$, where
$Y=X//\mu _p$, where ![]() $\mu _p\subset \mathbb {C}^*$ acts on
$\mu _p\subset \mathbb {C}^*$ acts on ![]() $X$ through the character
$X$ through the character ![]() $\chi$ given by restricting the weight
$\chi$ given by restricting the weight ![]() $1$ action of
$1$ action of ![]() $\mathbb {C}^*$. Let
$\mathbb {C}^*$. Let ![]() $\pi :X\to Y$ be the quotient map; under the identifications
$\pi :X\to Y$ be the quotient map; under the identifications ![]() $X=\mathbb {G}_a=Y$,
$X=\mathbb {G}_a=Y$, ![]() $\pi$ is the
$\pi$ is the ![]() $p$th-power map, and is
$p$th-power map, and is ![]() $\mathbb {C}^*$-equivariant when
$\mathbb {C}^*$-equivariant when ![]() $\mathbb {C}^*$ acts on
$\mathbb {C}^*$ acts on ![]() $Y$ with weight
$Y$ with weight ![]() $p$. For
$p$. For ![]() $y\in Y^S(R)$, we will use
$y\in Y^S(R)$, we will use ![]() $t^p$ to identify the coordinates
$t^p$ to identify the coordinates ![]() $y_s$ with elements of
$y_s$ with elements of ![]() $R$. Then, for
$R$. Then, for ![]() $y\in Y^S(R)$, we have the affine scheme
$y\in Y^S(R)$, we have the affine scheme
Now ![]() $\chi$ determines a ‘twisted-diagonal’ embedding
$\chi$ determines a ‘twisted-diagonal’ embedding ![]() $X\subset X^{\mu _p}$ as the
$X\subset X^{\mu _p}$ as the ![]() $\chi$-eigenline for the cyclic action of
$\chi$-eigenline for the cyclic action of ![]() $\mu _p$. Let
$\mu _p$. Let ![]() $\alpha$ be one of the symbols
$\alpha$ be one of the symbols ![]() $G$,
$G$, ![]() $\boldsymbol {N}$,
$\boldsymbol {N}$, ![]() $\mathcal {T}$,
$\mathcal {T}$, ![]() $\mathcal {R}$,
$\mathcal {R}$, ![]() $\widetilde {\mathcal {T}}$,
$\widetilde {\mathcal {T}}$, ![]() $\widetilde {\mathcal {R}}$. Then we will set
$\widetilde {\mathcal {R}}$. Then we will set
 \begin{gather*} \alpha_{(p)}:=\alpha_{\mu_p}/{/}_{\chi}\mu_p,\\ \alpha_{(p)}^{(p)}:=\alpha_{\mu_p}^{\mu_p}/{/}_{\chi}\mu_p. \end{gather*}
\begin{gather*} \alpha_{(p)}:=\alpha_{\mu_p}/{/}_{\chi}\mu_p,\\ \alpha_{(p)}^{(p)}:=\alpha_{\mu_p}^{\mu_p}/{/}_{\chi}\mu_p. \end{gather*}
Here the symbol ‘![]() $//_ {\chi }\mu _p$’ means ‘restrict along the twisted-diagonal then take categorical quotient by
$//_ {\chi }\mu _p$’ means ‘restrict along the twisted-diagonal then take categorical quotient by ![]() $\mu _p$’. The action of
$\mu _p$’. The action of ![]() $\mu _p$ in question is the one that does not involve loop rotation, that is, that which scales
$\mu _p$ in question is the one that does not involve loop rotation, that is, that which scales ![]() $x\in X(R)$ but does not change any of the data
$x\in X(R)$ but does not change any of the data ![]() $\mathcal {E},f,v$ etc. These are all placid ind-schemes over
$\mathcal {E},f,v$ etc. These are all placid ind-schemes over ![]() $Y$, and behave in essentially the same way as their earlier counterparts:
$Y$, and behave in essentially the same way as their earlier counterparts: ![]() $G_ {(p)}$ is an affine pro-smooth covering group scheme over
$G_ {(p)}$ is an affine pro-smooth covering group scheme over ![]() $Y$,
$Y$, ![]() $Gr_ {(p)}:=G_ {(p)}^{(p)}/G_ {(p)}$ is an ind-projective ind-scheme over
$Gr_ {(p)}:=G_ {(p)}^{(p)}/G_ {(p)}$ is an ind-projective ind-scheme over ![]() $Y$,
$Y$, ![]() $\mathcal {T}_ {(p)}^{(p)}$ is an infinite-dimensional vector bundle over
$\mathcal {T}_ {(p)}^{(p)}$ is an infinite-dimensional vector bundle over ![]() $Gr_ {(p)}$,
$Gr_ {(p)}$, ![]() $\mathcal {R}_ {(p)}^{(p)}$ is its sub-vector space of ind-finite codimension over
$\mathcal {R}_ {(p)}^{(p)}$ is its sub-vector space of ind-finite codimension over ![]() $Gr_ {(p)}$. They are all
$Gr_ {(p)}$. They are all ![]() $G_ {(p)}\rtimes\, \mathbb {C}^*$-equivariant. They also have chosen dimension theories, denoted
$G_ {(p)}\rtimes\, \mathbb {C}^*$-equivariant. They also have chosen dimension theories, denoted ![]() $\operatorname {rank}(G_ {(p)}^{(p)})$,
$\operatorname {rank}(G_ {(p)}^{(p)})$, ![]() $\operatorname {rank}(\mathcal {T}_ {(p)}^{(p)})$,
$\operatorname {rank}(\mathcal {T}_ {(p)}^{(p)})$, ![]() $\operatorname {rank}(\widetilde {\mathcal {T}_ {(p)}^{(p)}})$ etc., which are compatible with each other in the same way as for the
$\operatorname {rank}(\widetilde {\mathcal {T}_ {(p)}^{(p)}})$ etc., which are compatible with each other in the same way as for the ![]() $\alpha _S^{S'}$, and compatible with the dimension theories on
$\alpha _S^{S'}$, and compatible with the dimension theories on ![]() $\alpha _ {\mu _p}^{\mu _p}$ in the natural way. That is, the
$\alpha _ {\mu _p}^{\mu _p}$ in the natural way. That is, the ![]() $*$- (or
$*$- (or ![]() $!$-)pullback along the
$!$-)pullback along the ![]() $\mu _p$-fppf quotient map of the chosen dimension theory on
$\mu _p$-fppf quotient map of the chosen dimension theory on ![]() $\alpha _ {(p)}^{(p)}$ coincides with the
$\alpha _ {(p)}^{(p)}$ coincides with the ![]() $*$-pullback along the ind-f.p. closed embedding
$*$-pullback along the ind-f.p. closed embedding ![]() $X\times _ {X^{\mu _p}}\alpha _ {\mu _p}^{\mu _p} \to \alpha _ {\mu _p}^{\mu _p}$ of the chosen dimension theory on
$X\times _ {X^{\mu _p}}\alpha _ {\mu _p}^{\mu _p} \to \alpha _ {\mu _p}^{\mu _p}$ of the chosen dimension theory on ![]() $\alpha _ {\mu _p}^{\mu _p}$. Unlike
$\alpha _ {\mu _p}^{\mu _p}$. Unlike ![]() $\alpha _S^{S'}$ which is globally trivial over the coincidence-free open subset of
$\alpha _S^{S'}$ which is globally trivial over the coincidence-free open subset of ![]() $X^S$, these spaces
$X^S$, these spaces ![]() $\alpha _ {(p)}$,
$\alpha _ {(p)}$, ![]() $\alpha _ {(p)}^{(p)}$ are only locally trivial away from
$\alpha _ {(p)}^{(p)}$ are only locally trivial away from ![]() $\{0\}$. On the level of
$\{0\}$. On the level of ![]() $R$-points, they admit similar interpretations to
$R$-points, they admit similar interpretations to ![]() $\alpha _S^{S'}$, only involving
$\alpha _S^{S'}$, only involving ![]() $\pi ^*\Delta _1(y)$,
$\pi ^*\Delta _1(y)$, ![]() $\pi ^*\Delta _1^1(y)$. For example, we have
$\pi ^*\Delta _1^1(y)$. For example, we have
 \[ {\mathcal{R}}_{(p)}^{(p)}(R):=\left\{(y,\mathcal{E},f,v) \,\left|\, \begin{aligned} &y\in Y(R)\hfill\\ &\mathcal{E}\text{ a principal }G\text{-bundle over }\pi^*\Delta_1(y)\hfill\\ &f\text{ a trivialization of }\mathcal{E}\text{ over }\pi^*\Delta_1^{1}(y)\hfill\\ &{v}\text{ an }\boldsymbol{N}\text{-section of }\mathcal{E}\text{ such that }f(v)\text{ extends to }\pi^*\Delta_1(y)\hfill\end{aligned}\right.\right\}/{\sim}. \]
\[ {\mathcal{R}}_{(p)}^{(p)}(R):=\left\{(y,\mathcal{E},f,v) \,\left|\, \begin{aligned} &y\in Y(R)\hfill\\ &\mathcal{E}\text{ a principal }G\text{-bundle over }\pi^*\Delta_1(y)\hfill\\ &f\text{ a trivialization of }\mathcal{E}\text{ over }\pi^*\Delta_1^{1}(y)\hfill\\ &{v}\text{ an }\boldsymbol{N}\text{-section of }\mathcal{E}\text{ such that }f(v)\text{ extends to }\pi^*\Delta_1(y)\hfill\end{aligned}\right.\right\}/{\sim}. \]
The fiber of this space over ![]() $\{0\}$ is a copy of
$\{0\}$ is a copy of ![]() $\mathcal {R}$, while the fibers over
$\mathcal {R}$, while the fibers over ![]() $Y-\{0\}:=Y^*$ are copies of
$Y-\{0\}:=Y^*$ are copies of ![]() $\mathcal {R}^p$. Another example is
$\mathcal {R}^p$. Another example is
The action of ![]() $G_ {(p)}\rtimes\, \mathbb {C}^*$ on
$G_ {(p)}\rtimes\, \mathbb {C}^*$ on ![]() $\mathcal {R}_ {(p)}^{(p)}$ is given as
$\mathcal {R}_ {(p)}^{(p)}$ is given as
where for ![]() $z\in R^\times$,
$z\in R^\times$, ![]() $z_*$ denotes the pushforward along the multiplication-by-
$z_*$ denotes the pushforward along the multiplication-by-![]() $z$ endomorphism of
$z$ endomorphism of ![]() $X_R$,
$X_R$, ![]() $t\mapsto zt$, which transforms
$t\mapsto zt$, which transforms ![]() $\pi ^*\Delta _ {1}(y)$ into
$\pi ^*\Delta _ {1}(y)$ into ![]() $\pi ^*\Delta _ {1}(z^py)$. The key new feature is that
$\pi ^*\Delta _ {1}(z^py)$. The key new feature is that ![]() $G_ {(p)}\rtimes\, \mu _p$ is a subgroup of
$G_ {(p)}\rtimes\, \mu _p$ is a subgroup of ![]() $G_ {(p)}\rtimes\, \mathbb {C}^*$. In fact,
$G_ {(p)}\rtimes\, \mathbb {C}^*$. In fact, ![]() $G_ {(p)}\rtimes\, \mu _p$ is one component of the maximal subgroup of
$G_ {(p)}\rtimes\, \mu _p$ is one component of the maximal subgroup of ![]() $G_ {(p)}\rtimes\, \mathbb {C}^*$, the other being
$G_ {(p)}\rtimes\, \mathbb {C}^*$, the other being ![]() $\{0\}\times \mathbb {C}^*$. Contrast with
$\{0\}\times \mathbb {C}^*$. Contrast with ![]() $G_S\rtimes\, \mathbb {C}^*$, whose maximal subgroup is
$G_S\rtimes\, \mathbb {C}^*$, whose maximal subgroup is ![]() $G_S\cup (\{0\}\times \mathbb {C}^*)$.
$G_S\cup (\{0\}\times \mathbb {C}^*)$.
Note that the ![]() $0$-fiber of
$0$-fiber of ![]() is identified with
is identified with ![]() (
(![]() $\mathbb {C}^*$ acting in the usual way, that is, with weight
$\mathbb {C}^*$ acting in the usual way, that is, with weight ![]() $1$ on
$1$ on ![]() $t\in \mathcal {O}$). Meanwhile, the
$t\in \mathcal {O}$). Meanwhile, the ![]() $1$-fiber of
$1$-fiber of ![]() is identified with
is identified with ![]() , where now
, where now ![]() $\mu _p$ acts in the usual cyclic way of § 2 (without any loop rotation). The latter identification comes from the defining identification of
$\mu _p$ acts in the usual cyclic way of § 2 (without any loop rotation). The latter identification comes from the defining identification of ![]() $\pi ^*\{1\}$ with
$\pi ^*\{1\}$ with ![]() $\mu _p$.
$\mu _p$.
Warning 3.29 The notation ![]() $\mathcal {R}^{\mu _p}$ means
$\mathcal {R}^{\mu _p}$ means ![]() $\operatorname {Map}(\mu _p,\mathcal {R})$. This
$\operatorname {Map}(\mu _p,\mathcal {R})$. This ![]() $\mu _p$ superscript is not to be confused with the
$\mu _p$ superscript is not to be confused with the ![]() $\mu _p$ superscript in
$\mu _p$ superscript in ![]() $\mathcal {R}_ {\mu _p}^{\mu _p}$, where it indicates a set of allowed poles as in
$\mathcal {R}_ {\mu _p}^{\mu _p}$, where it indicates a set of allowed poles as in ![]() $\mathcal {R}_S^{S'}$.
$\mathcal {R}_S^{S'}$.
Consider the following composition ![]() $F'_\hbar : A^n\to \mathcal {A}^{pn}$.
$F'_\hbar : A^n\to \mathcal {A}^{pn}$.

For degree reasons it factors through the inclusion ![]() $A^*_\hbar \subset A^*_\hbar [a]=\mathcal {A}^*$. We may form the graded
$A^*_\hbar \subset A^*_\hbar [a]=\mathcal {A}^*$. We may form the graded ![]() $H^*_ {G(\mathcal {O})}(*,\mathbb {F}_{\rm p})^{(1)}$-module
$H^*_ {G(\mathcal {O})}(*,\mathbb {F}_{\rm p})^{(1)}$-module ![]() $(A^*)^{(1)}$, and we have a map of
$(A^*)^{(1)}$, and we have a map of ![]() $\mathbb {Z}$-graded multiplicative
$\mathbb {Z}$-graded multiplicative ![]() $\mathbb {F}_{\rm p}$-sets
$\mathbb {F}_{\rm p}$-sets
3.13 Linearity
We have the following proposition.
Proposition 3.30 ![]() $F_\hbar$ is
$F_\hbar$ is ![]() $St_ {\mathrm {in}}$-linear. That is, it is linear and transports multiplication by
$St_ {\mathrm {in}}$-linear. That is, it is linear and transports multiplication by ![]() $r\in H^m_ {G(\mathcal {O})}(*,\mathbb {F}_{\rm p})$ to multiplication by
$r\in H^m_ {G(\mathcal {O})}(*,\mathbb {F}_{\rm p})$ to multiplication by ![]() $St_ {\mathrm {in}}(r)\in H^{pm}_ {G(\mathcal {O})\rtimes\, \mathbb {C}^*}(*,\mathbb {F}_{\rm p})\subset H^{pm}_ {G(\mathcal {O})\rtimes\, \mathbb {C}^*}(*,\mathbb {F}_{\rm p}).$
$St_ {\mathrm {in}}(r)\in H^{pm}_ {G(\mathcal {O})\rtimes\, \mathbb {C}^*}(*,\mathbb {F}_{\rm p})\subset H^{pm}_ {G(\mathcal {O})\rtimes\, \mathbb {C}^*}(*,\mathbb {F}_{\rm p}).$
Proof. First we show that ![]() $F_\hbar$ is
$F_\hbar$ is ![]() $St_ {\mathrm {in}}$-multiplicative. Recall that restriction of equivariance commutes with specialization. We have a closed embedding from the
$St_ {\mathrm {in}}$-multiplicative. Recall that restriction of equivariance commutes with specialization. We have a closed embedding from the ![]() $Y$-version of
$Y$-version of ![]() $G_ {\{1\}}$ to
$G_ {\{1\}}$ to ![]() $G_ {(p)}$ determined by the formula
$G_ {(p)}$ determined by the formula
Over ![]() $0$, this is identified with the embedding
$0$, this is identified with the embedding ![]() $G(\mathcal {O})\to G(\mathcal {O})$,
$G(\mathcal {O})\to G(\mathcal {O})$, ![]() $t\mapsto t$. Over
$t\mapsto t$. Over ![]() $1$ this is identified with the diagonal embedding
$1$ this is identified with the diagonal embedding ![]() $G(\mathcal {O})\to G(\mathcal {O})^{\mu _p}$. Since the restriction of equivariance along the former embedding,
$G(\mathcal {O})\to G(\mathcal {O})^{\mu _p}$. Since the restriction of equivariance along the former embedding,
is an isomorphism, it follows that the map ![]() $H_ {*-2-2p\operatorname {rank}(\mathcal {T}_{(p)}^{(p)})^*}^{\mathrm {BM},G_ {(p)}^*\rtimes\, \mu _p}((\mathcal {R}_ {(p)}^{(p)})^*,\mathbb {F}_{\rm p})\to \mathcal {A}^{*}$ factors as
$H_ {*-2-2p\operatorname {rank}(\mathcal {T}_{(p)}^{(p)})^*}^{\mathrm {BM},G_ {(p)}^*\rtimes\, \mu _p}((\mathcal {R}_ {(p)}^{(p)})^*,\mathbb {F}_{\rm p})\to \mathcal {A}^{*}$ factors as
Since ![]() $G_ {\{1\}}\rtimes\, \mu _p$ is a constant group over
$G_ {\{1\}}\rtimes\, \mu _p$ is a constant group over ![]() $Y$ with fibers
$Y$ with fibers ![]() $G(\mathcal {O})\rtimes\, \mu _p$, the latter specialization map is
$G(\mathcal {O})\rtimes\, \mu _p$, the latter specialization map is ![]() $H^*_ {G(\mathcal {O})\rtimes\, \mu _p}(*,\mathbb {F}_{\rm p})$-linear. Certainly the descent isomorphism (b) and the restriction of equivariance from
$H^*_ {G(\mathcal {O})\rtimes\, \mu _p}(*,\mathbb {F}_{\rm p})$-linear. Certainly the descent isomorphism (b) and the restriction of equivariance from ![]() $\mathbb {C}^*$ to
$\mathbb {C}^*$ to ![]() $\mu _p$ in the diagram defining
$\mu _p$ in the diagram defining ![]() $F'_\hbar$ commute with restriction of equivariance from
$F'_\hbar$ commute with restriction of equivariance from ![]() $G_ {(p)}$ to
$G_ {(p)}$ to ![]() $G_ {\{1\}}$. It follows that
$G_ {\{1\}}$. It follows that ![]() $F_\hbar$ is
$F_\hbar$ is ![]() $St_ {\mathrm {in}}$-multiplicative, by definition of
$St_ {\mathrm {in}}$-multiplicative, by definition of ![]() $St_ {\mathrm {in}}$.
$St_ {\mathrm {in}}$.
Now we show linearity. Averaging (over ![]() $\mu _p$) commutes with the descent isomorphism (b) and restriction of equivariance in that we have the following commutative diagram.
$\mu _p$) commutes with the descent isomorphism (b) and restriction of equivariance in that we have the following commutative diagram.

Here for the second two averaging maps we have identified ![]() $H_ {pn-2-2\operatorname {rank}(\mathcal {T}_{(p)}^{(p)})^*}^{\mathrm {BM},G_ {(p)}^*\rtimes ?}((\mathcal {R}_ {(p)}^{(p)})^*,\mathbb {F}_{\rm p})$ with
$H_ {pn-2-2\operatorname {rank}(\mathcal {T}_{(p)}^{(p)})^*}^{\mathrm {BM},G_ {(p)}^*\rtimes ?}((\mathcal {R}_ {(p)}^{(p)})^*,\mathbb {F}_{\rm p})$ with ![]() $H_ {pn-2-2\pi ^*\operatorname {rank}(\mathcal {T}_{(p)}^{(p)})^*}^{\mathrm {BM},(\pi ^*G_ {(p)}^*)\rtimes (?\times \mu _p)}(\pi ^*(\mathcal {R}_ {(p)}^{(p)})^*,\mathbb {F}_{\rm p})$ for
$H_ {pn-2-2\pi ^*\operatorname {rank}(\mathcal {T}_{(p)}^{(p)})^*}^{\mathrm {BM},(\pi ^*G_ {(p)}^*)\rtimes (?\times \mu _p)}(\pi ^*(\mathcal {R}_ {(p)}^{(p)})^*,\mathbb {F}_{\rm p})$ for ![]() $?=\mathbb {C}^*$,
$?=\mathbb {C}^*$,![]() $\mu _p$.
$\mu _p$.
Since averaging commutes also with specialization, it follows that the discrepancy from additivity lies in the image of the averaging map ![]() $A^*\to \mathcal {A}^*$. But this map is equal to
$A^*\to \mathcal {A}^*$. But this map is equal to ![]() $0$.
$0$.
3.14 Centrality
We have the following proposition.
Proposition 3.31 ![]() $F_\hbar$ maps into the center of
$F_\hbar$ maps into the center of ![]() $A^*_\hbar$.
$A^*_\hbar$.
Proof. The idea is to adapt the proof of commutativity of ![]() $A^*$ given in the Appendix to [Reference Braverman, Finkelberg and NakajimaBFN17] to the present setup. That proof is itself an adaptation of the construction, using Beilinson–Drinfeld Grassmannians, of the commutativity constraint on the Satake category; see [Reference Mirković and VilonenMV07]. Consider the following diagram.
$A^*$ given in the Appendix to [Reference Braverman, Finkelberg and NakajimaBFN17] to the present setup. That proof is itself an adaptation of the construction, using Beilinson–Drinfeld Grassmannians, of the commutativity constraint on the Satake category; see [Reference Mirković and VilonenMV07]. Consider the following diagram.

Let ![]() $\alpha$ be as before, that is, any of the symbols
$\alpha$ be as before, that is, any of the symbols ![]() $G$,
$G$, ![]() $\boldsymbol {N}$,
$\boldsymbol {N}$, ![]() $\mathcal {T}$,
$\mathcal {T}$, ![]() $\mathcal {R}$,
$\mathcal {R}$, ![]() $\widetilde {\mathcal {T}}$,
$\widetilde {\mathcal {T}}$, ![]() $\widetilde {\mathcal {R}}$. We set
$\widetilde {\mathcal {R}}$. We set
Here the fiber product is taken using the map ![]() $X\to X^{\mu _p\cup \{0\}}$ given by the product of the ‘twisted-diagonal’ embedding
$X\to X^{\mu _p\cup \{0\}}$ given by the product of the ‘twisted-diagonal’ embedding ![]() $X\to X^{\mu _p}$ determined
$X\to X^{\mu _p}$ determined ![]() $\chi$ and the inclusion of
$\chi$ and the inclusion of ![]() $\{0\}$ in
$\{0\}$ in ![]() $\mathbb {G}_a$ under the identification
$\mathbb {G}_a$ under the identification ![]() $X^{\mu _p\cup \{0\}}=X^{\mu _p}\times X^{\{0\}}=X^{\mu _p}\times \mathbb {G}_a$. The action of
$X^{\mu _p\cup \{0\}}=X^{\mu _p}\times X^{\{0\}}=X^{\mu _p}\times \mathbb {G}_a$. The action of ![]() $\mu _p$ is again the one which does not involve any loop rotation. Removing the superscript
$\mu _p$ is again the one which does not involve any loop rotation. Removing the superscript ![]() $(p)$ (respectively,
$(p)$ (respectively, ![]() $0$,
$0$, ![]() $(p)0$) from
$(p)0$) from ![]() $\alpha _ {(p)0}^{(p)0}$ corresponds to removing the superscript
$\alpha _ {(p)0}^{(p)0}$ corresponds to removing the superscript ![]() $\mu _p\cup$ (respectively,
$\mu _p\cup$ (respectively, ![]() $\cup \{0\}$,
$\cup \{0\}$, ![]() $\mu _p\cup \{0\}$) from
$\mu _p\cup \{0\}$) from ![]() $\alpha _ {\mu _p\cup \{0\}}^{\mu _p\cup \{0\}}$ in its defining equation. We may write the spaces of the ‘left path’ as follows:
$\alpha _ {\mu _p\cup \{0\}}^{\mu _p\cup \{0\}}$ in its defining equation. We may write the spaces of the ‘left path’ as follows:
 \begin{align}\mathcal{R}_{(p)}^{(p)}\times \mathcal{R}(R)&=\left\{ \begin{matrix} (y,\mathcal{E},f,v,\hfill\\ \hfill\mathcal{E}_0,f_0,v_0)\end{matrix} \,\left|\, \begin{aligned} &y\in Y(R)\hfill\\ &\mathcal{E}\text{ a principal }G\text{-bundle over }\pi^*\Delta_1(y)\hfill\\ &f\text{ a trivialization of }\mathcal{E}\text{ over }\pi^*\Delta_1^{1}(y)\hfill\\ &{v}\text{ an }\boldsymbol{N}\text{-section of }\mathcal{E}\text{ such that }f(v)\text{ extends}\hfill\\ &\quad\text{to }\pi^*\Delta_1(y)\hfill\\ &\mathcal{E}_0\text{ a principal }G\text{-bundle over }\Delta_1(\{0\})\hfill\\ &f_0\text{ a trivialization of }\mathcal{E}_0\text{ over }\Delta_1^1(\{0\})\hfill\\ &{v_0}\text{ an }\boldsymbol{N}\text{-section of }\mathcal{E}_0\text{ such that }f_0(v_0)\text{ extends}\hfill\\ &\quad\text{to }\Delta_1(\{0\})\hfill \end{aligned}\right.\right\}/{\sim}, \nonumber\end{align}
\begin{align}\mathcal{R}_{(p)}^{(p)}\times \mathcal{R}(R)&=\left\{ \begin{matrix} (y,\mathcal{E},f,v,\hfill\\ \hfill\mathcal{E}_0,f_0,v_0)\end{matrix} \,\left|\, \begin{aligned} &y\in Y(R)\hfill\\ &\mathcal{E}\text{ a principal }G\text{-bundle over }\pi^*\Delta_1(y)\hfill\\ &f\text{ a trivialization of }\mathcal{E}\text{ over }\pi^*\Delta_1^{1}(y)\hfill\\ &{v}\text{ an }\boldsymbol{N}\text{-section of }\mathcal{E}\text{ such that }f(v)\text{ extends}\hfill\\ &\quad\text{to }\pi^*\Delta_1(y)\hfill\\ &\mathcal{E}_0\text{ a principal }G\text{-bundle over }\Delta_1(\{0\})\hfill\\ &f_0\text{ a trivialization of }\mathcal{E}_0\text{ over }\Delta_1^1(\{0\})\hfill\\ &{v_0}\text{ an }\boldsymbol{N}\text{-section of }\mathcal{E}_0\text{ such that }f_0(v_0)\text{ extends}\hfill\\ &\quad\text{to }\Delta_1(\{0\})\hfill \end{aligned}\right.\right\}/{\sim}, \nonumber\end{align} \begin{align}{\mathcal{R}}_{(p)0}^{(p)}\times_{Y} \mathcal{R}_{(p)0}^{0}(R)&=\left\{ \begin{matrix}(y,\mathcal{E},f,v,\hfill\\ \hfill\mathcal{E}_0,f_0,v_0)\end{matrix} \,\left|\, \begin{aligned} &y\in Y(R)\hfill\\ &\mathcal{E}\text{ a principal }G\text{-bundle over }\pi^*\Delta_1(y)\cup\Delta_1(\{0\})\hfill\\ &f\text{ a trivialization of }\mathcal{E}\text{ over }\pi^*\Delta_1^{1}(y)\cup\Delta_1(\{0\})\hfill\\ &{v}\text{ an }\boldsymbol{N}\text{-section of }\mathcal{E}\text{ such that }f(v)\text{ extends}\hfill\\ &\quad\text{to }\pi^*\Delta_1(y)\cup\Delta_1(\{0\})\hfill\\ &\mathcal{E}_0\text{ a principal }G\text{-bundle over }\pi^*\Delta_1(y)\cup\Delta_1(\{0\})\hfill\\ &f_0\text{ a trivialization of }\mathcal{E}_0\text{ over }\pi^*\Delta_1(y)\cup\Delta_1^1(\{0\})\hfill\\ &{v_0}\text{ an }\boldsymbol{N}\text{-section of }\mathcal{E}_0\text{ such that }f_0(v_0)\text{ extends}\hfill\\ &\quad \text{to }\pi^*\Delta_1(y)\cup\Delta_1(\{0\})\hfill \end{aligned}\right.\right\}/{\sim}, \nonumber\end{align}
\begin{align}{\mathcal{R}}_{(p)0}^{(p)}\times_{Y} \mathcal{R}_{(p)0}^{0}(R)&=\left\{ \begin{matrix}(y,\mathcal{E},f,v,\hfill\\ \hfill\mathcal{E}_0,f_0,v_0)\end{matrix} \,\left|\, \begin{aligned} &y\in Y(R)\hfill\\ &\mathcal{E}\text{ a principal }G\text{-bundle over }\pi^*\Delta_1(y)\cup\Delta_1(\{0\})\hfill\\ &f\text{ a trivialization of }\mathcal{E}\text{ over }\pi^*\Delta_1^{1}(y)\cup\Delta_1(\{0\})\hfill\\ &{v}\text{ an }\boldsymbol{N}\text{-section of }\mathcal{E}\text{ such that }f(v)\text{ extends}\hfill\\ &\quad\text{to }\pi^*\Delta_1(y)\cup\Delta_1(\{0\})\hfill\\ &\mathcal{E}_0\text{ a principal }G\text{-bundle over }\pi^*\Delta_1(y)\cup\Delta_1(\{0\})\hfill\\ &f_0\text{ a trivialization of }\mathcal{E}_0\text{ over }\pi^*\Delta_1(y)\cup\Delta_1^1(\{0\})\hfill\\ &{v_0}\text{ an }\boldsymbol{N}\text{-section of }\mathcal{E}_0\text{ such that }f_0(v_0)\text{ extends}\hfill\\ &\quad \text{to }\pi^*\Delta_1(y)\cup\Delta_1(\{0\})\hfill \end{aligned}\right.\right\}/{\sim}, \nonumber\end{align} \begin{align}\widetilde{\mathcal{R}}_{(p)0}^{(p)}\times_{\boldsymbol{N}_{(p)0}} \mathcal{R}_{(p)0}^{0}(R)&=\left\{ \begin{matrix}(y,\mathcal{E},f,\hfill \\ g,v,\mathcal{E}_0,\hfill\\ \hfill f_0,v_0)\end{matrix} \,\left|\, \begin{aligned} &y\in Y(R)\hfill\\ &\mathcal{E}\text{ a principal }G\text{-bundle over }\pi^*\Delta_1(y)\cup\Delta_1(\{0\})\hfill\\ &f\text{ a trivialization of }\mathcal{E}\text{ over }\pi^*\Delta_1^{1}(y)\cup\Delta_1(\{0\})\hfill\\ &g\text{ a trivialization of }\mathcal{E}\text{ over }\pi^*\Delta_1(y)\cup\Delta_1(\{0\})\hfill\\ &{v}\text{ an }\boldsymbol{N}\text{-section of }\mathcal{E}\text{ such that }f(v)\text{ extends}\hfill\\ &\quad \text{to }\pi^*\Delta_1(y)\cup\Delta_1(\{0\})\hfill\\ &\mathcal{E}_0\text{ a principal }G\text{-bundle over }\pi^*\Delta_1(y)\cup\Delta_1(\{0\})\hfill\\ &f_0\text{ a trivialization of }\mathcal{E}_0\text{ over }\pi^*\Delta_1(y)\cup\Delta_1^1(\{0\})\hfill\\ &{v_0}\text{ an }\boldsymbol{N}\text{-section of }\mathcal{E}_0\text{ such that }f_0(v_0)=g(v)\hfill \end{aligned}\right.\right\}/{\sim}, \nonumber\end{align}
\begin{align}\widetilde{\mathcal{R}}_{(p)0}^{(p)}\times_{\boldsymbol{N}_{(p)0}} \mathcal{R}_{(p)0}^{0}(R)&=\left\{ \begin{matrix}(y,\mathcal{E},f,\hfill \\ g,v,\mathcal{E}_0,\hfill\\ \hfill f_0,v_0)\end{matrix} \,\left|\, \begin{aligned} &y\in Y(R)\hfill\\ &\mathcal{E}\text{ a principal }G\text{-bundle over }\pi^*\Delta_1(y)\cup\Delta_1(\{0\})\hfill\\ &f\text{ a trivialization of }\mathcal{E}\text{ over }\pi^*\Delta_1^{1}(y)\cup\Delta_1(\{0\})\hfill\\ &g\text{ a trivialization of }\mathcal{E}\text{ over }\pi^*\Delta_1(y)\cup\Delta_1(\{0\})\hfill\\ &{v}\text{ an }\boldsymbol{N}\text{-section of }\mathcal{E}\text{ such that }f(v)\text{ extends}\hfill\\ &\quad \text{to }\pi^*\Delta_1(y)\cup\Delta_1(\{0\})\hfill\\ &\mathcal{E}_0\text{ a principal }G\text{-bundle over }\pi^*\Delta_1(y)\cup\Delta_1(\{0\})\hfill\\ &f_0\text{ a trivialization of }\mathcal{E}_0\text{ over }\pi^*\Delta_1(y)\cup\Delta_1^1(\{0\})\hfill\\ &{v_0}\text{ an }\boldsymbol{N}\text{-section of }\mathcal{E}_0\text{ such that }f_0(v_0)=g(v)\hfill \end{aligned}\right.\right\}/{\sim}, \nonumber\end{align} \begin{align}\widetilde{\mathcal{R}}_{(p)0}^{(p)} \frac{\times_{\boldsymbol{N}_{(p)0}}}{^{G_{(p)0}}} {\mathcal{R}}_{(p)0}^{0}(R)=\left\{ \begin{matrix}(y,\mathcal{E},f,v,\hfill \\ \hfill\mathcal{E}_0,h_0,v_0)\end{matrix} \,\left|\, \begin{aligned} &y\in Y(R)\hfill\\ &\mathcal{E}\text{ a principal }G\text{-bundle over }\pi^*\Delta_1(y)\cup\Delta_1(\{0\})\hfill\\ &f\text{ a trivialization of }\mathcal{E}\text{ over }\pi^*\Delta_1^{1}(y)\cup\Delta_1(\{0\})\hfill\\ &{v}\text{ an }\boldsymbol{N}\text{-section of }\mathcal{E}\text{ such that }f(v)\text{ extends}\hfill\\ &\quad \text{to }\pi^*\Delta_1(y)\cup\Delta_1(\{0\})\hfill\\ &\mathcal{E}_0\text{ a principal }G\text{-bundle over }\pi^*\Delta_1(y)\cup\Delta_1(\{0\})\hfill\\ &h_0\text{ an isomorphism of }\mathcal{E}_0\text{ with }\mathcal{E}\hfill\\ &\quad \text{over }\pi^*\Delta_1(y)\cup\Delta_1^1(\{0\})\hfill\\ &{v_0}\text{ an }\boldsymbol{N}\text{-section of }\mathcal{E}_0\text{ such that }h_0(v_0)=v\hfill \end{aligned}\right.\right\}/{\sim}\nonumber \end{align}
\begin{align}\widetilde{\mathcal{R}}_{(p)0}^{(p)} \frac{\times_{\boldsymbol{N}_{(p)0}}}{^{G_{(p)0}}} {\mathcal{R}}_{(p)0}^{0}(R)=\left\{ \begin{matrix}(y,\mathcal{E},f,v,\hfill \\ \hfill\mathcal{E}_0,h_0,v_0)\end{matrix} \,\left|\, \begin{aligned} &y\in Y(R)\hfill\\ &\mathcal{E}\text{ a principal }G\text{-bundle over }\pi^*\Delta_1(y)\cup\Delta_1(\{0\})\hfill\\ &f\text{ a trivialization of }\mathcal{E}\text{ over }\pi^*\Delta_1^{1}(y)\cup\Delta_1(\{0\})\hfill\\ &{v}\text{ an }\boldsymbol{N}\text{-section of }\mathcal{E}\text{ such that }f(v)\text{ extends}\hfill\\ &\quad \text{to }\pi^*\Delta_1(y)\cup\Delta_1(\{0\})\hfill\\ &\mathcal{E}_0\text{ a principal }G\text{-bundle over }\pi^*\Delta_1(y)\cup\Delta_1(\{0\})\hfill\\ &h_0\text{ an isomorphism of }\mathcal{E}_0\text{ with }\mathcal{E}\hfill\\ &\quad \text{over }\pi^*\Delta_1(y)\cup\Delta_1^1(\{0\})\hfill\\ &{v_0}\text{ an }\boldsymbol{N}\text{-section of }\mathcal{E}_0\text{ such that }h_0(v_0)=v\hfill \end{aligned}\right.\right\}/{\sim}\nonumber \end{align}and
 \[ \mathcal{R}_{(p)0}^{(p)0}(R)=\left\{(y,\mathcal{F},e,w) \,\left|\, \begin{aligned} &y\in Y(R)\hfill\\ &\mathcal{F}\text{ a principal }G\text{-bundle over }\pi^*\Delta_1(y)\cup\Delta_1(\{0\})\hfill\\ &e\text{ a trivialization of }\mathcal{F}\text{ over }\pi^*\Delta_1^{1}(y)\cup\Delta_1^1(\{0\})\hfill\\ &{w}\text{ an }\boldsymbol{N}\text{-section of }\mathcal{F}\text{ such that }e(w)\text{ extends}\hfill\\ &\quad \text{to }\pi^*\Delta_1(y)\cup\Delta_1(\{0\})\hfill\end{aligned}\right.\right\}/{\sim}. \]
\[ \mathcal{R}_{(p)0}^{(p)0}(R)=\left\{(y,\mathcal{F},e,w) \,\left|\, \begin{aligned} &y\in Y(R)\hfill\\ &\mathcal{F}\text{ a principal }G\text{-bundle over }\pi^*\Delta_1(y)\cup\Delta_1(\{0\})\hfill\\ &e\text{ a trivialization of }\mathcal{F}\text{ over }\pi^*\Delta_1^{1}(y)\cup\Delta_1^1(\{0\})\hfill\\ &{w}\text{ an }\boldsymbol{N}\text{-section of }\mathcal{F}\text{ such that }e(w)\text{ extends}\hfill\\ &\quad \text{to }\pi^*\Delta_1(y)\cup\Delta_1(\{0\})\hfill\end{aligned}\right.\right\}/{\sim}. \]
Here the ![]() $\{0\}$ of
$\{0\}$ of ![]() $\Delta _1^?(\{0\})$ denotes the fixed
$\Delta _1^?(\{0\})$ denotes the fixed ![]() $R$-point
$R$-point ![]() $\{0\}$ of
$\{0\}$ of ![]() $X$. By definition,
$X$. By definition, ![]() $\beta$ is the product of the co-placid map
$\beta$ is the product of the co-placid map ![]() $\mathcal {R}_ {(p)0}^{(p)}\to \mathcal {R}_ {(p)}^{(p)}$ induced by the embedding
$\mathcal {R}_ {(p)0}^{(p)}\to \mathcal {R}_ {(p)}^{(p)}$ induced by the embedding ![]() $\pi ^*\Delta _ {1}^{1}(y)\to \pi ^*\Delta _ {1}^{1}(y)\cup \Delta _1(\{0\})$, and the co-placid map
$\pi ^*\Delta _ {1}^{1}(y)\to \pi ^*\Delta _ {1}^{1}(y)\cup \Delta _1(\{0\})$, and the co-placid map ![]() $\mathcal {R}_ {(p)0}^{0}\to Y\times \mathcal {R}$ induced by the embedding
$\mathcal {R}_ {(p)0}^{0}\to Y\times \mathcal {R}$ induced by the embedding ![]() $\Delta _ {1}^{1}(\{0\})\to \pi ^*\Delta _ {1}(y)\cup \Delta ^1_1(\{0\})$. The map
$\Delta _ {1}^{1}(\{0\})\to \pi ^*\Delta _ {1}(y)\cup \Delta ^1_1(\{0\})$. The map ![]() $\gamma _l$ factors as
$\gamma _l$ factors as
where ![]() $v_l$ is a
$v_l$ is a ![]() $G_ {(p)0}$-torsor and
$G_ {(p)0}$-torsor and ![]() $u_l$ fits into a ‘restriction with supports framework’: a Cartesian diagram
$u_l$ fits into a ‘restriction with supports framework’: a Cartesian diagram
 \[ \begin{matrix} \widetilde{\mathcal{R}}_{(p)0}^{(p)}\times_{\boldsymbol{N}_{(p)0}} \mathcal{R}_{(p)0}^{0} & \xrightarrow{u_l} & \widetilde{\mathcal{R}}_{(p)0}^{(p)}\times_{Y} \mathcal{R}_{(p)0}^{0}\\ \downarrow & & \downarrow\\ \widetilde{\mathcal{T}}_{(p)0}^{(p)}\times_{\boldsymbol{N}_{(p)0}} \mathcal{R}_{(p)0}^{0} & \xrightarrow{u'_l} & \widetilde{\mathcal{T}}_{(p)0}^{(p)}\times_{Y} \mathcal{R}_{(p)0}^{0}\\ \end{matrix} \]
\[ \begin{matrix} \widetilde{\mathcal{R}}_{(p)0}^{(p)}\times_{\boldsymbol{N}_{(p)0}} \mathcal{R}_{(p)0}^{0} & \xrightarrow{u_l} & \widetilde{\mathcal{R}}_{(p)0}^{(p)}\times_{Y} \mathcal{R}_{(p)0}^{0}\\ \downarrow & & \downarrow\\ \widetilde{\mathcal{T}}_{(p)0}^{(p)}\times_{\boldsymbol{N}_{(p)0}} \mathcal{R}_{(p)0}^{0} & \xrightarrow{u'_l} & \widetilde{\mathcal{T}}_{(p)0}^{(p)}\times_{Y} \mathcal{R}_{(p)0}^{0}\\ \end{matrix} \]
such that ![]() $u_l'$ is a section of a vector bundle map
$u_l'$ is a section of a vector bundle map
and whose vertical arrows are ind-f.p closed embeddings. The map ![]() $\delta _l$ is a
$\delta _l$ is a ![]() $G_ {(p)0}$-torsor, defined by
$G_ {(p)0}$-torsor, defined by
The map ![]() $\epsilon _l$ is ind-proper, defined by
$\epsilon _l$ is ind-proper, defined by
This describes the ‘left path’. The ‘right path’ exactly mirrors it and has all the same properties: just exchange superscripts ![]() $\mu _p$,
$\mu _p$, ![]() $0$, and on the level of points exchange
$0$, and on the level of points exchange ![]() $\mathcal {E}$ with
$\mathcal {E}$ with ![]() $\mathcal {E}_0$,
$\mathcal {E}_0$, ![]() $f$ with
$f$ with ![]() $f_0$,
$f_0$, ![]() $v$ with
$v$ with ![]() $v_0$,
$v_0$, ![]() $g$ with
$g$ with ![]() $g_0$,
$g_0$, ![]() $h$ with
$h$ with ![]() $h_0$, etc. We have labeled our data
$h_0$, etc. We have labeled our data ![]() $\mathcal {F}$,
$\mathcal {F}$, ![]() $e$,
$e$, ![]() $w$ in
$w$ in ![]() $\mathcal {R}_ {(p)0}^{(p)0}$ because in the ‘left path’ we have
$\mathcal {R}_ {(p)0}^{(p)0}$ because in the ‘left path’ we have ![]() $(\mathcal {F},e,w)=(\mathcal {E}_0,fg^{-1}f_0,v_0)$ while in the ‘right path’ we have
$(\mathcal {F},e,w)=(\mathcal {E}_0,fg^{-1}f_0,v_0)$ while in the ‘right path’ we have ![]() $(\mathcal {F},e,w)=(\mathcal {E},f_0g_0^{-1}f,v)$. If we restrict our diagram to
$(\mathcal {F},e,w)=(\mathcal {E},f_0g_0^{-1}f,v)$. If we restrict our diagram to ![]() $Y^*$, then the subscripts
$Y^*$, then the subscripts ![]() $(p)$,
$(p)$, ![]() $0$ ‘split apart’, and the result is rather degenerate. That is, it coincides with the restriction to
$0$ ‘split apart’, and the result is rather degenerate. That is, it coincides with the restriction to ![]() $Y^*$ of
$Y^*$ of

Here the maps from the fourth row to the top are the obvious projection maps, while the maps from the fourth row to the bottom are the obvious action maps. If instead we restrict our diagram to ![]() $\{0\}\subset Y$, the subscripts
$\{0\}\subset Y$, the subscripts ![]() $(p)$,
$(p)$, ![]() $0$ ‘fuse’ and the result is again degenerate: we get
$0$ ‘fuse’ and the result is again degenerate: we get

We leave it to the reader to write out the appropriate equivariant structures implicit in the following chain of maps, and to check that the quoted dimension theories are appropriately compatible:

Here we have dropped the homological coefficients ‘![]() $\mathbb {F}_{\rm p}$’ for brevity. This is called the ‘homological left path over
$\mathbb {F}_{\rm p}$’ for brevity. This is called the ‘homological left path over ![]() $Y$’. Similarly, there is a ‘homological right path over
$Y$’. Similarly, there is a ‘homological right path over ![]() $Y$’. Moreover, we have versions of both ‘homological paths’ for the restrictions of our original diagram to
$Y$’. Moreover, we have versions of both ‘homological paths’ for the restrictions of our original diagram to ![]() $Y^*$,
$Y^*$, ![]() $\{0\}$, and specialization map of paths
$\{0\}$, and specialization map of paths
since every step of both paths is compatible with specialization. One the one hand, both ‘homological paths over ![]() $Y^*$’ give as their composition the identity map
$Y^*$’ give as their composition the identity map
On the other hand, the ‘left homological path over ![]() $\{0\}$’ gives as its composition the multiplication map (indeed, this is the definition of convolution from [Reference Braverman, Finkelberg and NakajimaBFN16])
$\{0\}$’ gives as its composition the multiplication map (indeed, this is the definition of convolution from [Reference Braverman, Finkelberg and NakajimaBFN16])
while the ‘right homological path over ![]() $\{0\}$’ gives as its composition the twisted multiplication map
$\{0\}$’ gives as its composition the twisted multiplication map
It follows that in fact the image of the specialization map
is in the center of ![]() $A^*_\hbar [a]$. By its very definition,
$A^*_\hbar [a]$. By its very definition, ![]() $F_\hbar$ factors through this map.
$F_\hbar$ factors through this map.
3.15 Completion of the proof
(i) ![]() $F_\hbar$ is multiplicative. The proof is essentially the same as the proof of centrality, but instead of keeping one copy of
$F_\hbar$ is multiplicative. The proof is essentially the same as the proof of centrality, but instead of keeping one copy of ![]() $\mathcal {R}$ fixed and allowing the other to deform to
$\mathcal {R}$ fixed and allowing the other to deform to ![]() $\mathcal {R}^{\mu _p}$ with its cyclic
$\mathcal {R}^{\mu _p}$ with its cyclic ![]() $\mu _p$-action, we allow both copies of
$\mu _p$-action, we allow both copies of ![]() $\mathcal {R}$ to deform in that way. In fact it is easier because we only need one ‘path’. We will content ourselves with drawing the defining diagram; the conscientious reader can plug in the method of specialization:
$\mathcal {R}$ to deform in that way. In fact it is easier because we only need one ‘path’. We will content ourselves with drawing the defining diagram; the conscientious reader can plug in the method of specialization:
(ii) ![]() $F_\hbar$ sends
$F_\hbar$ sends ![]() $1$ to
$1$ to ![]() $1$. Note that
$1$. Note that ![]() $1\in A^*$ is the fundamental class of the fiber
$1\in A^*$ is the fundamental class of the fiber ![]() $\boldsymbol {N}(\mathcal {O})$ of
$\boldsymbol {N}(\mathcal {O})$ of ![]() $\mathcal {R}$ over the base point of
$\mathcal {R}$ over the base point of ![]() $Gr$. Certainly Steenrod's construction sends this to the fundamental class of the fiber
$Gr$. Certainly Steenrod's construction sends this to the fundamental class of the fiber ![]() $\boldsymbol {N}(\mathcal {O})^{\mu _p}$ of
$\boldsymbol {N}(\mathcal {O})^{\mu _p}$ of ![]() $\mathcal {R}^{\mu _p}$ over the base point of
$\mathcal {R}^{\mu _p}$ over the base point of ![]() $Gr^{\mu _p}$, and this is sent by the ‘descent isomorphism (b)’ construction to the fundamental class of the fiber
$Gr^{\mu _p}$, and this is sent by the ‘descent isomorphism (b)’ construction to the fundamental class of the fiber ![]() $\boldsymbol {N}_ {(p)}^*$ of
$\boldsymbol {N}_ {(p)}^*$ of ![]() $(\mathcal {R}_ {(p)}^{(p)})^*$ over the base section of
$(\mathcal {R}_ {(p)}^{(p)})^*$ over the base section of ![]() $Gr_ {(p)}^*$. But this section extends to a base section of
$Gr_ {(p)}^*$. But this section extends to a base section of ![]() $Gr_ {(p)}$, namely, the trivial
$Gr_ {(p)}$, namely, the trivial ![]() $G$-bundle with the trivial trivialization. The fiber of
$G$-bundle with the trivial trivialization. The fiber of ![]() $\mathcal {R}_ {(p)}^{(p)}$ over this section is
$\mathcal {R}_ {(p)}^{(p)}$ over this section is ![]() $\boldsymbol {N}_ {(p)}$. Since this is a vector bundle over
$\boldsymbol {N}_ {(p)}$. Since this is a vector bundle over ![]() $Y$, specialization sends its fundamental class to the fundamental class of its
$Y$, specialization sends its fundamental class to the fundamental class of its ![]() $0$-fiber
$0$-fiber ![]() $\boldsymbol {N}(\mathcal {O})$, as required.
$\boldsymbol {N}(\mathcal {O})$, as required.
(iii) ![]() $F_\hbar \text { mod }\hbar$ is the Frobenius map. This is essentially clear from the construction. It amounts to showing that the specialization (over
$F_\hbar \text { mod }\hbar$ is the Frobenius map. This is essentially clear from the construction. It amounts to showing that the specialization (over ![]() $Y$) of the class
$Y$) of the class ![]() $b$ in
$b$ in
obtained by applying Steenrod's construction to ![]() $a\in (A^*)^{(1)}$, then applying descent isomorphism (b) and then restricting all the way to
$a\in (A^*)^{(1)}$, then applying descent isomorphism (b) and then restricting all the way to ![]() $G_ {(p)}$-equivariance, equals
$G_ {(p)}$-equivariance, equals ![]() $x^p$ (recall diagram (3.1)). But by a general property of specialization, it is equal to the specialization over
$x^p$ (recall diagram (3.1)). But by a general property of specialization, it is equal to the specialization over ![]() $X$ of the class
$X$ of the class ![]() $\pi ^*(b)$ in
$\pi ^*(b)$ in
Under the identifications ![]() $\pi ^*(\mathcal {R}_ {(p)}^{(p)})^*=\mathcal {R}^{\mu _p}\times Y^*$,
$\pi ^*(\mathcal {R}_ {(p)}^{(p)})^*=\mathcal {R}^{\mu _p}\times Y^*$, ![]() $\pi ^*G_ {(p)}^*=G(\mathcal {O})^{\mu _p}\times Y^*$,
$\pi ^*G_ {(p)}^*=G(\mathcal {O})^{\mu _p}\times Y^*$, ![]() $\pi ^*(b)$ is just the pullback of
$\pi ^*(b)$ is just the pullback of ![]() $a^{\boxtimes p}$ along the projection away from
$a^{\boxtimes p}$ along the projection away from ![]() $Y^*$. Thus it is enough to prove the more general statement that for
$Y^*$. Thus it is enough to prove the more general statement that for ![]() $a_1,\ldots ,a_p\in A^*$, the convolution product
$a_1,\ldots ,a_p\in A^*$, the convolution product ![]() $a_1\ldots a_p$ is equal to the specialization in
$a_1\ldots a_p$ is equal to the specialization in ![]() $\pi ^*\mathcal {R}_ {(p)}^{(p)}$ of
$\pi ^*\mathcal {R}_ {(p)}^{(p)}$ of ![]() $a_1\boxtimes \cdots \boxtimes a_p$. That is achieved by choosing an enumeration
$a_1\boxtimes \cdots \boxtimes a_p$. That is achieved by choosing an enumeration ![]() $\mu _p=\{1,\ldots ,p\}$ and considering the restriction along the ‘twisted-diagonal’ embedding
$\mu _p=\{1,\ldots ,p\}$ and considering the restriction along the ‘twisted-diagonal’ embedding ![]() $X\to X^{\mu _p}$ of the global convolution diagram (see the Appendix to [Reference Braverman, Finkelberg and NakajimaBFN17]):
$X\to X^{\mu _p}$ of the global convolution diagram (see the Appendix to [Reference Braverman, Finkelberg and NakajimaBFN17]):

3.16 Closing remarks
(i) There is a closed embedding
 \begin{align*} \begin{array}{ccc}\mathcal{R}_1^1&\to &\mathcal{R}_{(p)}^{(p)}\\ (y,\mathcal{E},f,v)&\mapsto &(y,\pi^*\mathcal{E},\pi^*f,\pi^*v) \end{array}\end{align*}
\begin{align*} \begin{array}{ccc}\mathcal{R}_1^1&\to &\mathcal{R}_{(p)}^{(p)}\\ (y,\mathcal{E},f,v)&\mapsto &(y,\pi^*\mathcal{E},\pi^*f,\pi^*v) \end{array}\end{align*}
and similarly compatible closed embeddings ![]() $\alpha _1^1\to \alpha _ {(p)}^{(p)}$ for any symbol
$\alpha _1^1\to \alpha _ {(p)}^{(p)}$ for any symbol ![]() $\alpha$ (see § 3.12). We also have the compatible closed embeddings of groups
$\alpha$ (see § 3.12). We also have the compatible closed embeddings of groups ![]() $G_1\to G_ {(p)}$,
$G_1\to G_ {(p)}$, ![]() $\boldsymbol {N}_1\to \boldsymbol {N}_ {(p)}$. In fact we have already used one of these to prove linearity of
$\boldsymbol {N}_1\to \boldsymbol {N}_ {(p)}$. In fact we have already used one of these to prove linearity of ![]() $F_\hbar$ in § 3.13.
$F_\hbar$ in § 3.13.
(ii) For large ![]() $p$, the
$p$, the ![]() $\boldsymbol {N}=0$ version of
$\boldsymbol {N}=0$ version of ![]() $A_\hbar$ has a name: it is the quantum Toda lattice, denoted
$A_\hbar$ has a name: it is the quantum Toda lattice, denoted ![]() $Toda_\hbar$ and given as the two-sided quantum Hamiltonian reduction
$Toda_\hbar$ and given as the two-sided quantum Hamiltonian reduction ![]() $N^\vee _\psi \backslash \backslash \mathcal {D}_\hbar (G^\vee )//_\psi$ of the Rees algebra of crystalline differential operators,
$N^\vee _\psi \backslash \backslash \mathcal {D}_\hbar (G^\vee )//_\psi$ of the Rees algebra of crystalline differential operators, ![]() $\mathcal {D}_\hbar (G^\vee )$, of the Langlands dual group
$\mathcal {D}_\hbar (G^\vee )$, of the Langlands dual group ![]() $G^\vee$ over
$G^\vee$ over ![]() $\mathbb {F}_{\rm p}$, with respect to a regular character
$\mathbb {F}_{\rm p}$, with respect to a regular character ![]() $\psi$ of a maximal unipotent
$\psi$ of a maximal unipotent ![]() $N^\vee \subset G^\vee$. As a quantum Hamiltonian reduction of a ring of differential operators, it has a canonical Frobenius-constant structure. It follows from a torus localization argument that this Frobenius-constant structure coincides with the one we have produced in this paper. The ind-f.p. closed embedding
$N^\vee \subset G^\vee$. As a quantum Hamiltonian reduction of a ring of differential operators, it has a canonical Frobenius-constant structure. It follows from a torus localization argument that this Frobenius-constant structure coincides with the one we have produced in this paper. The ind-f.p. closed embedding ![]() $\mathcal {R}\to \mathcal {T}$ induces a pushforward map of
$\mathcal {R}\to \mathcal {T}$ induces a pushforward map of ![]() $H^*_ {G\times \mathbb {C}^*}(*,\mathbb {F}_{\rm p})$-algebras
$H^*_ {G\times \mathbb {C}^*}(*,\mathbb {F}_{\rm p})$-algebras
For all ![]() $p$, this map is compatible with the Frobenius-constant structure. For large
$p$, this map is compatible with the Frobenius-constant structure. For large ![]() $p$ this map is an embedding. So for large
$p$ this map is an embedding. So for large ![]() $p$, Theorem 3.28 can be understood as saying that the subalgebra
$p$, Theorem 3.28 can be understood as saying that the subalgebra ![]() $A^*_\hbar$ of the quantum Toda lattice contains the image of
$A^*_\hbar$ of the quantum Toda lattice contains the image of ![]() $A^*\subset Toda:=Toda_\hbar /\hbar$ under the canonical Frobenius-constancy map
$A^*\subset Toda:=Toda_\hbar /\hbar$ under the canonical Frobenius-constancy map ![]() $Toda^{(1)}\to Toda_\hbar$.
$Toda^{(1)}\to Toda_\hbar$.
(iii) An example. Let ![]() $G=\mathbb {C}^*$,
$G=\mathbb {C}^*$, ![]() $\boldsymbol {N}=\mathbb {C}_ {-r}$,
$\boldsymbol {N}=\mathbb {C}_ {-r}$, ![]() $r\geq 0$. Then on
$r\geq 0$. Then on ![]() $\mathbb {C}$-points we identify:
$\mathbb {C}$-points we identify:
(a)
 $Gr=\mathbb {Z}$;
$Gr=\mathbb {Z}$;(b)
 $\mathcal {T}=\mathbb {Z}\times \mathbb {C}_ {-r}[[t]]$;
$\mathcal {T}=\mathbb {Z}\times \mathbb {C}_ {-r}[[t]]$;(c)
 $\mathcal {R}= \mathbb {Z}_ {\leq 0}\times \mathbb {C}_ {-r}[[t]]\cup \{1\}\times t^{r}\mathbb {C}_ {-r}[[t]]\cup \{2\}\times t^{2r}\mathbb {C}_ {-r}[[t]]\cup \ldots .$
$\mathcal {R}= \mathbb {Z}_ {\leq 0}\times \mathbb {C}_ {-r}[[t]]\cup \{1\}\times t^{r}\mathbb {C}_ {-r}[[t]]\cup \{2\}\times t^{2r}\mathbb {C}_ {-r}[[t]]\cup \ldots .$
For ![]() $\boldsymbol {N}=0$,
$\boldsymbol {N}=0$, ![]() $A_\hbar$ is the Weyl algebra
$A_\hbar$ is the Weyl algebra ![]() $\mathbb {F}_{\rm p}[\hbar ]\langle x^{\pm },\partial \rangle /([\partial ,x]=\hbar )$. The equivariant Borel–Moore homology of a point
$\mathbb {F}_{\rm p}[\hbar ]\langle x^{\pm },\partial \rangle /([\partial ,x]=\hbar )$. The equivariant Borel–Moore homology of a point ![]() $n\in \mathbb {Z}$ is identified with
$n\in \mathbb {Z}$ is identified with ![]() $\mathbb {F}_{\rm p}[\hbar ,x\partial ].x^n$. It is a direct calculation that
$\mathbb {F}_{\rm p}[\hbar ,x\partial ].x^n$. It is a direct calculation that ![]() $F_\hbar$ is the map
$F_\hbar$ is the map
 \begin{align*} \begin{array}{ccl} x^{(1)} &\mapsto &x^p,\hfill\\ y^{(1)} &\mapsto &\partial^p,\hfill\\ (xy)^{(1)}&\mapsto &\displaystyle x^p\partial^p=\prod_{i=0}^{p-1}(x\partial-i\hbar) =(x\partial)^p-\hbar^{p-1}x\partial=AS_\hbar(x\partial). \end{array} \end{align*}
\begin{align*} \begin{array}{ccl} x^{(1)} &\mapsto &x^p,\hfill\\ y^{(1)} &\mapsto &\partial^p,\hfill\\ (xy)^{(1)}&\mapsto &\displaystyle x^p\partial^p=\prod_{i=0}^{p-1}(x\partial-i\hbar) =(x\partial)^p-\hbar^{p-1}x\partial=AS_\hbar(x\partial). \end{array} \end{align*}
Here ![]() $y=\partial \text { mod }\hbar$. For
$y=\partial \text { mod }\hbar$. For ![]() $\boldsymbol {N}=\mathbb {C}_{-r}$ with
$\boldsymbol {N}=\mathbb {C}_{-r}$ with ![]() $r\geq 0$,
$r\geq 0$, ![]() $A_\hbar$ is the reduction modulo
$A_\hbar$ is the reduction modulo ![]() $p$ of the subalgebra of the integral Weyl algebra
$p$ of the subalgebra of the integral Weyl algebra ![]() $\mathbb {Z}[\hbar ]\langle x^{\pm },\partial \rangle /([\partial ,x]=\hbar )$ with
$\mathbb {Z}[\hbar ]\langle x^{\pm },\partial \rangle /([\partial ,x]=\hbar )$ with ![]() $\mathbb {F}_{\rm p}[\hbar ,x\partial ]$-basis
$\mathbb {F}_{\rm p}[\hbar ,x\partial ]$-basis
 \[ \ldots x^{{-}2},x^{{-}1},1, \bigg(\prod_{i=1}^{r}(rx\partial-i\hbar)\bigg)x, \bigg(\prod_{i=1}^{2r}(rx\partial-i\hbar)\bigg)x^{2},\ldots. \]
\[ \ldots x^{{-}2},x^{{-}1},1, \bigg(\prod_{i=1}^{r}(rx\partial-i\hbar)\bigg)x, \bigg(\prod_{i=1}^{2r}(rx\partial-i\hbar)\bigg)x^{2},\ldots. \]
It satisfies ![]() $(\prod _{i=1}^{nr}(rx\partial -i\hbar )x^n)(\prod _{i=1}^{mr}(rx\partial -i\hbar )x^m) =\prod _{i=1}^{(m+n)r}(rx\partial -i\hbar )x^{m+n}$. Note that this is a subalgebra of the mod
$(\prod _{i=1}^{nr}(rx\partial -i\hbar )x^n)(\prod _{i=1}^{mr}(rx\partial -i\hbar )x^m) =\prod _{i=1}^{(m+n)r}(rx\partial -i\hbar )x^{m+n}$. Note that this is a subalgebra of the mod ![]() $p$ Weyl algebra if and only if
$p$ Weyl algebra if and only if ![]() $p$ does not divide
$p$ does not divide ![]() $r$. It is again a direct computation that
$r$. It is again a direct computation that ![]() $F_\hbar$ is the map
$F_\hbar$ is the map

It is an interesting exercise to check that these are really central (of course their images in the mod ![]() $p$ Weyl algebra are).
$p$ Weyl algebra are).
(iv) For large ![]() $p$ one can prove the centrality and multiplicativity of the map
$p$ one can prove the centrality and multiplicativity of the map ![]() $F_\hbar$, constructed in § 3.12, via torus localization in conjunction with the above example. But Theorem 3.28 is true for all odd primes
$F_\hbar$, constructed in § 3.12, via torus localization in conjunction with the above example. But Theorem 3.28 is true for all odd primes ![]() $p$. In fact, the same construction works for
$p$. In fact, the same construction works for ![]() $p=2$ but one has to be a little careful to account for the fact that
$p=2$ but one has to be a little careful to account for the fact that ![]() $a^2=\hbar$ in that case.
$a^2=\hbar$ in that case.
(v) Suppose that the action of ![]() $G$ on
$G$ on ![]() $N$ extends to an action of a normalizing supergroup
$N$ extends to an action of a normalizing supergroup ![]() $\tilde {G}$ of
$\tilde {G}$ of ![]() $G$. Then the same proof shows that the corresponding flavor deformation is also a Frobenius-constant quantization.
$G$. Then the same proof shows that the corresponding flavor deformation is also a Frobenius-constant quantization.
(vi) In [Reference Braverman, Finkelberg and NakajimaBFN17], an algebra ind-object ![]() $\Omega _\hbar$ of the Satake category
$\Omega _\hbar$ of the Satake category ![]() $D^b_{G(\mathcal {O})\rtimes\, \mathbb {C}^*}(Gr,\mathbb {C})$ is constructed; its cohomology algebra is the quantum Coulomb branch. The commutativity of the Coulomb branch corresponds to commutativity of the image algebra
$D^b_{G(\mathcal {O})\rtimes\, \mathbb {C}^*}(Gr,\mathbb {C})$ is constructed; its cohomology algebra is the quantum Coulomb branch. The commutativity of the Coulomb branch corresponds to commutativity of the image algebra ![]() $\Omega$ of
$\Omega$ of ![]() $\Omega _\hbar$ in
$\Omega _\hbar$ in ![]() $D^b_{G(\mathcal {O})}(Gr,\mathbb {C})$. It is also possible, by essentially the same method given in the Appendix to [Reference Braverman, Finkelberg and NakajimaBFN17], to tell the same story with
$D^b_{G(\mathcal {O})}(Gr,\mathbb {C})$. It is also possible, by essentially the same method given in the Appendix to [Reference Braverman, Finkelberg and NakajimaBFN17], to tell the same story with ![]() $\mathbb {F}_{\rm p}$ coefficients.
$\mathbb {F}_{\rm p}$ coefficients.
4.  $K$-theoretic version
$K$-theoretic version
4.1  $K$-theory and
$K$-theory and  $K$-homology
$K$-homology
Let ![]() $X$ be a scheme over some base
$X$ be a scheme over some base ![]() $B$ over
$B$ over ![]() $\mathbb {C}$ and let
$\mathbb {C}$ and let ![]() $\mathcal {G}$ be an (affine, pro-smooth) groupoid scheme over
$\mathcal {G}$ be an (affine, pro-smooth) groupoid scheme over ![]() $B$ acting on
$B$ acting on ![]() $X$. We have the
$X$. We have the ![]() $\mathcal {G}$-equivariant
$\mathcal {G}$-equivariant ![]() $K$-homology of
$K$-homology of ![]() $X$,
$X$,
which is by definition the Grothendieck group of ![]() $D^b_{\mathcal {G}}\operatorname {Coh}(X)$, the
$D^b_{\mathcal {G}}\operatorname {Coh}(X)$, the ![]() $\mathcal {G}$-equivariant derived category of complexes of sheaves on
$\mathcal {G}$-equivariant derived category of complexes of sheaves on ![]() $X$ with bounded, coherent cohomology sheaves. We have also the
$X$ with bounded, coherent cohomology sheaves. We have also the ![]() $\mathcal {G}$-equivariant
$\mathcal {G}$-equivariant ![]() $K$-theory of
$K$-theory of ![]() $X$,
$X$,
which is by definition the Grothendieck group of the full subcategory ![]() $\operatorname {Perf}_{\mathcal {G}}(X)$ of
$\operatorname {Perf}_{\mathcal {G}}(X)$ of ![]() $D^b_{\mathcal {G}}\operatorname {Coh}(X)$ consisting of perfect complexes. We recall some basic facts (see [Reference Chriss and GinzburgCG97]).
$D^b_{\mathcal {G}}\operatorname {Coh}(X)$ consisting of perfect complexes. We recall some basic facts (see [Reference Chriss and GinzburgCG97]).
(i) ![]() $K_{\mathcal {G}}(X)$ forms a ring, since
$K_{\mathcal {G}}(X)$ forms a ring, since ![]() $\operatorname {Perf}_{\mathcal {G}}(X)$ is monoidal. The unit element is given by the class of the structure sheaf.
$\operatorname {Perf}_{\mathcal {G}}(X)$ is monoidal. The unit element is given by the class of the structure sheaf.
(ii) ![]() $K^{\mathcal {G}}(X)$ is a module over
$K^{\mathcal {G}}(X)$ is a module over ![]() $K_{\mathcal {G}}(X)$, since
$K_{\mathcal {G}}(X)$, since ![]() $D^b_{\mathcal {G}}\operatorname {Coh}(X)$ is a module category over
$D^b_{\mathcal {G}}\operatorname {Coh}(X)$ is a module category over ![]() $\operatorname {Perf}_{\mathcal {G}}(X)$. Under suitable conditions, for instance, if
$\operatorname {Perf}_{\mathcal {G}}(X)$. Under suitable conditions, for instance, if ![]() $X$ is smooth and
$X$ is smooth and ![]() $\mathcal {G}$ is a connected linear algebraic group, every equivariant coherent sheaf has a bounded equivariant resolution by vector bundles, so that the defining functor
$\mathcal {G}$ is a connected linear algebraic group, every equivariant coherent sheaf has a bounded equivariant resolution by vector bundles, so that the defining functor ![]() $\operatorname {Perf}_{\mathcal {G}}(X)\to D^b_{\mathcal {G}}(X)$ is an equivalence, and in particular the map from
$\operatorname {Perf}_{\mathcal {G}}(X)\to D^b_{\mathcal {G}}(X)$ is an equivalence, and in particular the map from ![]() $K_{\mathcal {G}}(X)$ to
$K_{\mathcal {G}}(X)$ to ![]() $K^{\mathcal {G}}(X)$ is an isomorphism. But this will certainly not be the case in most of our examples.
$K^{\mathcal {G}}(X)$ is an isomorphism. But this will certainly not be the case in most of our examples.
(iii) Let ![]() $f:X\to Y$ be a
$f:X\to Y$ be a ![]() $\mathcal {G}$-equivariant map of schemes over
$\mathcal {G}$-equivariant map of schemes over ![]() $B$. We have a monoidal pullback map
$B$. We have a monoidal pullback map
hence the ring map ![]() $f^*:K_{\mathcal {G}}(Y)\to K_{\mathcal {G}}(X)$. If the derived functor
$f^*:K_{\mathcal {G}}(Y)\to K_{\mathcal {G}}(X)$. If the derived functor ![]() $f^*:D^b_{\mathcal {G}}\operatorname {QCoh}(Y)\to D^b_{\mathcal {G}}\operatorname {QCoh}(X)$ sends
$f^*:D^b_{\mathcal {G}}\operatorname {QCoh}(Y)\to D^b_{\mathcal {G}}\operatorname {QCoh}(X)$ sends ![]() $D^b_{\mathcal {G}}\operatorname {Coh}(Y)$ to
$D^b_{\mathcal {G}}\operatorname {Coh}(Y)$ to ![]() $D^b_{\mathcal {G}}\operatorname {Coh}(X)$ (e.g. if
$D^b_{\mathcal {G}}\operatorname {Coh}(X)$ (e.g. if ![]() $f$ may be flat or is a regular closed embedding), then we also get a map
$f$ may be flat or is a regular closed embedding), then we also get a map
of ![]() $K_{\mathcal {G}}(Y)$-modules.
$K_{\mathcal {G}}(Y)$-modules.
(iv) If instead the derived functor ![]() $f_*:D^+_{\mathcal {G}}\operatorname {Sh}(X)\to D^+_{\mathcal {G}}\operatorname {Sh}(Y)$ sends
$f_*:D^+_{\mathcal {G}}\operatorname {Sh}(X)\to D^+_{\mathcal {G}}\operatorname {Sh}(Y)$ sends ![]() $D^b_{\mathcal {G}}\operatorname {Coh}(X)$ to
$D^b_{\mathcal {G}}\operatorname {Coh}(X)$ to ![]() $D^b_{\mathcal {G}}\operatorname {Coh}(Y)$ (e.g., if
$D^b_{\mathcal {G}}\operatorname {Coh}(Y)$ (e.g., if ![]() $f$ is proper and
$f$ is proper and ![]() $Y$ is of finite type), then we have a map
$Y$ is of finite type), then we have a map
of ![]() $K_{\mathcal {G}}(Y)$-modules.
$K_{\mathcal {G}}(Y)$-modules.
(v) There is also a version of specialization in equivariant ![]() $K$-homology, due to [Reference Vezzosi and VistoliVV03]. Let
$K$-homology, due to [Reference Vezzosi and VistoliVV03]. Let ![]() $f:X\to B\times \mathbb {G}_a$ be a
$f:X\to B\times \mathbb {G}_a$ be a ![]() $\mathcal {G}$-equivariant map, where the factor
$\mathcal {G}$-equivariant map, where the factor ![]() $\mathbb {G}_a$ is a ‘multiplicity space’ ignored by the action of
$\mathbb {G}_a$ is a ‘multiplicity space’ ignored by the action of ![]() $\mathcal {G}$. Let
$\mathcal {G}$. Let ![]() $i:X_0\to X$ denote the inclusion of the fiber of
$i:X_0\to X$ denote the inclusion of the fiber of ![]() $B\times \{0\}$, and
$B\times \{0\}$, and ![]() $j:X^o\to X$ denote the inclusion of the complement. Assume that
$j:X^o\to X$ denote the inclusion of the complement. Assume that ![]() $i$ is a regular embedding. Then the map
$i$ is a regular embedding. Then the map ![]() $i^*i_*$ on
$i^*i_*$ on ![]() $K$-homology vanishes, and so we get a map
$K$-homology vanishes, and so we get a map
Note that the restriction map ![]() $j^*:K^{\mathcal {G}}(X)\to K^{\mathcal {G}}(X^o)$ has kernel
$j^*:K^{\mathcal {G}}(X)\to K^{\mathcal {G}}(X^o)$ has kernel ![]() $i_*K^{\mathcal {G}}(X_0)$, so we get an injection
$i_*K^{\mathcal {G}}(X_0)$, so we get an injection ![]() $K^{\mathcal {G}}(X)/i_*K^{\mathcal {G}}(X_0)\to K^{\mathcal {G}}(X^o)$. Assume that this injection is also a surjection (e.g. if
$K^{\mathcal {G}}(X)/i_*K^{\mathcal {G}}(X_0)\to K^{\mathcal {G}}(X^o)$. Assume that this injection is also a surjection (e.g. if ![]() $X$ is quasi-projective). Then we have obtained a map
$X$ is quasi-projective). Then we have obtained a map
which is the promised specialization map.
(vi) There is also a version of restriction with supports. Suppose ![]() $f:X\to Y$ is a
$f:X\to Y$ is a ![]() $\mathcal {G}$-equivariant regular closed embedding, and
$\mathcal {G}$-equivariant regular closed embedding, and ![]() $g:Z\to Y$ is an arbitrary
$g:Z\to Y$ is an arbitrary ![]() $G$-equivariant map. Then
$G$-equivariant map. Then ![]() $f_*\mathcal {O}_X$ is isomorphic to an object of
$f_*\mathcal {O}_X$ is isomorphic to an object of ![]() $\operatorname {Perf}_{\mathcal {G}}(Y)$, so that
$\operatorname {Perf}_{\mathcal {G}}(Y)$, so that ![]() $g^*f_*\mathcal {O}_X$ is isomorphic to an object of
$g^*f_*\mathcal {O}_X$ is isomorphic to an object of ![]() $\operatorname {Perf}_{\mathcal {G}}(Z)$. Moreover, this perfect complex is set-theoretically supported on
$\operatorname {Perf}_{\mathcal {G}}(Z)$. Moreover, this perfect complex is set-theoretically supported on ![]() $W:=X\times _YZ$, that is, its restriction to the complement of
$W:=X\times _YZ$, that is, its restriction to the complement of ![]() $W$ in
$W$ in ![]() $Z$ is isomorphic to
$Z$ is isomorphic to ![]() $0$. Thus tensoring with
$0$. Thus tensoring with ![]() $g^*f_*\mathcal {O}_X$ gives an exact functor:
$g^*f_*\mathcal {O}_X$ gives an exact functor:
The right-hand side is the full subcategory of ![]() $D^b_{\mathcal {G}}\operatorname {Coh}(Z)$ consisting of complexes set-theoretically supported on
$D^b_{\mathcal {G}}\operatorname {Coh}(Z)$ consisting of complexes set-theoretically supported on ![]() $W$; the pushforward functor
$W$; the pushforward functor ![]() $D^b_{\mathcal {G}}\operatorname {Coh}(W)\to D^b_{\mathcal {G}}\operatorname {Coh}(Z)$ factors through this category. Since the embedding
$D^b_{\mathcal {G}}\operatorname {Coh}(W)\to D^b_{\mathcal {G}}\operatorname {Coh}(Z)$ factors through this category. Since the embedding ![]() $W\to Z$ is f.p., being the base change of the f.p. embedding
$W\to Z$ is f.p., being the base change of the f.p. embedding ![]() $X\to Y$, the resulting functor
$X\to Y$, the resulting functor ![]() $D^b_{\mathcal {G}}\operatorname {Coh}(W)\to D^b_{\mathcal {G}}\operatorname {Coh}(Z)_W$ induces an isomorphism in
$D^b_{\mathcal {G}}\operatorname {Coh}(W)\to D^b_{\mathcal {G}}\operatorname {Coh}(Z)_W$ induces an isomorphism in ![]() $K$-homology:
$K$-homology:
Thus, we have produced a map
which is the promised restriction with supports.
(vii) Change of groupoid base, restriction of equivariance, and averaging work exactly as for equivariant Borel–Moore homology; see § 3.10.
The same compatibilities which were used in the previous section to extend the analogous procedures in equivariant Borel–Moore homology to the case of ind-schemes hold just as well for equivariant ![]() $K$-homology. Thus we are able to define the
$K$-homology. Thus we are able to define the ![]() $K$-theoretic versions of the Coulomb branch and the quantum Coulomb branch by using precisely the same underlying geometry: we have rings (under convolution)
$K$-theoretic versions of the Coulomb branch and the quantum Coulomb branch by using precisely the same underlying geometry: we have rings (under convolution)
and
which receive ring maps from respectively
and
Here ![]() $R(G)$ is the (integral) representation ring of
$R(G)$ is the (integral) representation ring of ![]() $G$. For a maximal torus
$G$. For a maximal torus ![]() $T$ of
$T$ of ![]() $G$, we have
$G$, we have ![]() $R(G)=\mathbb {Z}[\mathbb {X}^\bullet (T)]^W$ where
$R(G)=\mathbb {Z}[\mathbb {X}^\bullet (T)]^W$ where ![]() $W$ is the Weyl group. Moreover, the various compatibilities between specialization and the other procedures hold here as in the case of Borel–Moore homology (see § 3.10), so that the ring structure on
$W$ is the Weyl group. Moreover, the various compatibilities between specialization and the other procedures hold here as in the case of Borel–Moore homology (see § 3.10), so that the ring structure on ![]() $KA$ may also be defined using specialization on the appropriate Beilinson–Drinfeld Grassmannian, and is commutative. Also,
$KA$ may also be defined using specialization on the appropriate Beilinson–Drinfeld Grassmannian, and is commutative. Also, ![]() $KA$ is free over
$KA$ is free over ![]() $R(G)$,
$R(G)$, ![]() $KA_q$ is free over
$KA_q$ is free over ![]() $R(G)[q,q^{-1}]$ with respect to both left and right multiplication,
$R(G)[q,q^{-1}]$ with respect to both left and right multiplication, ![]() $q$ is in the center
$q$ is in the center ![]() $Z(KA_q)$ of
$Z(KA_q)$ of ![]() $KA_q$, and
$KA_q$, and ![]() $KA=KA_1:=KA_q|_{q=1}$. We will show the following theorem.
$KA=KA_1:=KA_q|_{q=1}$. We will show the following theorem.
Theorem 4.1 Fix a positive integer ![]() $n$ and a primitive
$n$ and a primitive ![]() $n$th root of unity
$n$th root of unity ![]() $\zeta$. Then there is an injective map of algebras
$\zeta$. Then there is an injective map of algebras
Here ![]() $KA_\zeta :=KA_q/\Phi _n(q)$ where
$KA_\zeta :=KA_q/\Phi _n(q)$ where ![]() $\Phi _n$ is the
$\Phi _n$ is the ![]() $n$th cyclotomic polynomial. Equivalently, since
$n$th cyclotomic polynomial. Equivalently, since ![]() $KA_q$ is free over
$KA_q$ is free over ![]() $\mathbb {Z}[q,q^{-1}]$, this is the same as the subalgebra
$\mathbb {Z}[q,q^{-1}]$, this is the same as the subalgebra ![]() $1\otimes KA_q$ of
$1\otimes KA_q$ of ![]() $\mathbb {C}_\zeta \otimes _{\mathbb {Z}[q,q^{-1}]}KA_q$, where
$\mathbb {C}_\zeta \otimes _{\mathbb {Z}[q,q^{-1}]}KA_q$, where ![]() $\mathbb {C}_\zeta$ is the
$\mathbb {C}_\zeta$ is the ![]() $\mathbb {Z}[q,q^{-1}]$-algebra whose underlying ring is
$\mathbb {Z}[q,q^{-1}]$-algebra whose underlying ring is ![]() $\mathbb {C}$ and in which
$\mathbb {C}$ and in which ![]() $q$ acts as
$q$ acts as ![]() $\zeta$.
$\zeta$.
The proof is essentially the same as for the quantum Coulomb branch, except for the following observation.
Remark 4.2 We must generalize from ![]() $\mathcal {R}^{\mu _p}$,
$\mathcal {R}^{\mu _p}$, ![]() $\mathcal {R}_{(p)}^{(p)}$ etc. to
$\mathcal {R}_{(p)}^{(p)}$ etc. to ![]() $\mathcal {R}^{\mu _n}$,
$\mathcal {R}^{\mu _n}$, ![]() $\mathcal {R}_{(n)}^{(n)}$, which are defined exactly as before by replacing any instance of
$\mathcal {R}_{(n)}^{(n)}$, which are defined exactly as before by replacing any instance of ![]() $p$ with
$p$ with ![]() $n$. Indeed, we never used that
$n$. Indeed, we never used that ![]() $p$ was prime in any of our previous constructions, nor in any of our proofs except for questions of linearity. So, for instance, it is true that we have maps from the mod
$p$ was prime in any of our previous constructions, nor in any of our proofs except for questions of linearity. So, for instance, it is true that we have maps from the mod ![]() $n$ rings
$n$ rings
which lift the ![]() $n$th power map
$n$th power map ![]() $A^*\to A^*$; to linearize these maps, we have to kill all non-unit factors of
$A^*\to A^*$; to linearize these maps, we have to kill all non-unit factors of ![]() $n$. If
$n$. If ![]() $n$ is not a prime power, this means we have to kill everything, so we do not obtain an interesting linear map. If
$n$ is not a prime power, this means we have to kill everything, so we do not obtain an interesting linear map. If ![]() $n=p^d$ is a prime power, it amounts to killing
$n=p^d$ is a prime power, it amounts to killing ![]() $p$, and the resulting map
$p$, and the resulting map ![]() $F_{\hbar ;p^d}\text { mod }p$ is the composition of
$F_{\hbar ;p^d}\text { mod }p$ is the composition of ![]() $F_{\hbar ;p}$ with the
$F_{\hbar ;p}$ with the ![]() $(d-1)$th power of the Frobenius endomorphism of
$(d-1)$th power of the Frobenius endomorphism of ![]() $A\text { mod }p$, so gives nothing new. However, the map of Theorem 4.1 is a linear map between algebras free over
$A\text { mod }p$, so gives nothing new. However, the map of Theorem 4.1 is a linear map between algebras free over ![]() $\mathbb {Z}$, and is something genuinely different for all
$\mathbb {Z}$, and is something genuinely different for all ![]() $q$.
$q$.
4.2 Adams operations
Let ![]() $X$,
$X$, ![]() $B$,
$B$, ![]() $\mathcal {G}$ be as in the previous subsection, and
$\mathcal {G}$ be as in the previous subsection, and ![]() $n$ be a positive integer. We have a monoidal (nonlinear) functor
$n$ be a positive integer. We have a monoidal (nonlinear) functor
whose composition with the functor ![]() $D^b_{\mathcal {G}^{\mu _n}\rtimes\,\mu _n}Coh(X^{\mu _n})\to D^b_{\mathcal {G}^{\mu _n}}Coh(X^{\mu _n})$ which forgets the
$D^b_{\mathcal {G}^{\mu _n}\rtimes\,\mu _n}Coh(X^{\mu _n})\to D^b_{\mathcal {G}^{\mu _n}}Coh(X^{\mu _n})$ which forgets the ![]() $\mu _n$-equivariant structure coincides with the
$\mu _n$-equivariant structure coincides with the ![]() $n$th external tensor power functor. The construction is exactly the same as Steenrod's construction of § 2.2, except we work with coherent complexes rather than constructible ones (and with
$n$th external tensor power functor. The construction is exactly the same as Steenrod's construction of § 2.2, except we work with coherent complexes rather than constructible ones (and with ![]() $n$ rather than
$n$ rather than ![]() $p$). Proposition 2.4 also holds in this situation with the sole caveat that by ‘is an induced map’ we mean ‘is a sum of maps induced from various proper subgroups of
$p$). Proposition 2.4 also holds in this situation with the sole caveat that by ‘is an induced map’ we mean ‘is a sum of maps induced from various proper subgroups of ![]() $\mu _n$’ (rather than only from the trivial subgroup). The analogous fact holds also for objects, so we get linear maps
$\mu _n$’ (rather than only from the trivial subgroup). The analogous fact holds also for objects, so we get linear maps
where ![]() $I$ is the subgroup of
$I$ is the subgroup of ![]() $K^{\mathcal {G}^{\mu _n}\rtimes\,\mu _n}(X^{\mu _n})$ spanned by all classes of
$K^{\mathcal {G}^{\mu _n}\rtimes\,\mu _n}(X^{\mu _n})$ spanned by all classes of ![]() $\mathcal {G}^{\mu _n}\rtimes\,\mu _n$-equivariant complexes induced from
$\mathcal {G}^{\mu _n}\rtimes\,\mu _n$-equivariant complexes induced from ![]() $\mathcal {G}^{\mu _n}\rtimes \Gamma$-equivariant complexes, for some proper subgroup
$\mathcal {G}^{\mu _n}\rtimes \Gamma$-equivariant complexes, for some proper subgroup ![]() $\Gamma$ of
$\Gamma$ of ![]() $\mu _n$. Furthermore, the functor
$\mu _n$. Furthermore, the functor ![]() $St$ preserves perfectness: we have
$St$ preserves perfectness: we have
and thus linear maps
where ![]() $J$ is the subgroup of
$J$ is the subgroup of ![]() $K_{\mathcal {G}^{\mu _n}\rtimes\,\mu _n}(X^{\mu _n})$ spanned by all classes of
$K_{\mathcal {G}^{\mu _n}\rtimes\,\mu _n}(X^{\mu _n})$ spanned by all classes of ![]() $\mathcal {G}^{\mu _n}\rtimes\,\mu _n$-equivariant complexes induced from
$\mathcal {G}^{\mu _n}\rtimes\,\mu _n$-equivariant complexes induced from ![]() $\mathcal {G}^{\mu _n}\rtimes \Gamma$-equivariant perfect complexes, for some proper subgroup
$\mathcal {G}^{\mu _n}\rtimes \Gamma$-equivariant perfect complexes, for some proper subgroup ![]() $\Gamma$ of
$\Gamma$ of ![]() $\mu _n$. In fact,
$\mu _n$. In fact, ![]() $J$ is an ideal (by the projection formula),
$J$ is an ideal (by the projection formula), ![]() $I$ is a
$I$ is a ![]() $J$-stable submodule for the same reason,
$J$-stable submodule for the same reason, ![]() $Ad_n$ is a map of rings, and
$Ad_n$ is a map of rings, and ![]() $Ad^n$ is a map of
$Ad^n$ is a map of ![]() $Ad_n$-modules.
$Ad_n$-modules.
Remark 4.3 (True Adams operations) Induction commutes with restriction, so we have a ring map
Here ![]() $J'$ is the subgroup of
$J'$ is the subgroup of ![]() $K_{\mathcal {G}\times \mu _n}(X)=K_{\mathcal {G}}(X)[q,q^{-1}]/(q^n-1)$ spanned by induced classes. This equals the ideal generated by the elements
$K_{\mathcal {G}\times \mu _n}(X)=K_{\mathcal {G}}(X)[q,q^{-1}]/(q^n-1)$ spanned by induced classes. This equals the ideal generated by the elements ![]() $\sum _{j=1}^dq^{nj/d}$ for all
$\sum _{j=1}^dq^{nj/d}$ for all ![]() $d>1$ dividing
$d>1$ dividing ![]() $n$; and the lowest common factor of these is
$n$; and the lowest common factor of these is ![]() $\Phi _n(q)$. By the splitting principle, the image of this map is contained in
$\Phi _n(q)$. By the splitting principle, the image of this map is contained in
The resulting ring endomorphism of ![]() $K_{\mathcal {G}}(X)$ is the
$K_{\mathcal {G}}(X)$ is the ![]() $n$th Adams operation. The relevant example for us is with
$n$th Adams operation. The relevant example for us is with ![]() $\mathcal {G}=G(\mathcal {O})$,
$\mathcal {G}=G(\mathcal {O})$, ![]() $X=*$. Fix a maximal torus
$X=*$. Fix a maximal torus ![]() $T$ of
$T$ of ![]() $G$; then the
$G$; then the ![]() $n$th Adams operation is identified with the ring map
$n$th Adams operation is identified with the ring map
which sends a ![]() $W$-invariant sum
$W$-invariant sum ![]() $\sum _i\chi _i$ of characters
$\sum _i\chi _i$ of characters ![]() $\chi _i$ to the
$\chi _i$ to the ![]() $W$-invariant sum
$W$-invariant sum ![]() $\sum _i\chi _i^n$.
$\sum _i\chi _i^n$.
4.3 Proof of Theorem 4.1
The map in question is constructed as in (3.1), as the composition

where:
(i)
 $I$ is the ideal of
$I$ is the ideal of  $K^{G(\mathcal {O})^{\mu _n}\rtimes\,\mu _n}(\mathcal {R}^{\mu _n})$ spanned by all classes induced from
$K^{G(\mathcal {O})^{\mu _n}\rtimes\,\mu _n}(\mathcal {R}^{\mu _n})$ spanned by all classes induced from  $K^{G(\mathcal {O})^{\mu _{n}}\rtimes\,\mu _{n/d}}(\mathcal {R}^{\mu _n})$, for some
$K^{G(\mathcal {O})^{\mu _{n}}\rtimes\,\mu _{n/d}}(\mathcal {R}^{\mu _n})$, for some  $d>1$ dividing
$d>1$ dividing  $n$.
$n$.(ii)
 $I'$ is the ideal of
$I'$ is the ideal of  $K^{G_{(n)}^*\rtimes\, \mathbb {C}^*}((\mathcal {R}_{(n)}^{(n)})^*)$ corresponding to
$K^{G_{(n)}^*\rtimes\, \mathbb {C}^*}((\mathcal {R}_{(n)}^{(n)})^*)$ corresponding to  $I$ under the descent isomorphism. It is equal to the ideal spanned by all classes pushed forward from
$I$ under the descent isomorphism. It is equal to the ideal spanned by all classes pushed forward from  $K^{\mathbb {C}\times _{\mathbb {C}}G_{(n)}^*\rtimes\, \mathbb {C}^*}((\mathbb {C}\times _{\mathbb {C}}\mathcal {R}_{(n)}^{(n)})^*)$, for some non-trivial
$K^{\mathbb {C}\times _{\mathbb {C}}G_{(n)}^*\rtimes\, \mathbb {C}^*}((\mathbb {C}\times _{\mathbb {C}}\mathcal {R}_{(n)}^{(n)})^*)$, for some non-trivial  $\mathbb {C}^*$-equivariant cover
$\mathbb {C}^*$-equivariant cover  $\mathbb {C}\to \mathbb {C}$. Recall that in this situation, the base copy of
$\mathbb {C}\to \mathbb {C}$. Recall that in this situation, the base copy of  $\mathbb {C}$ has the action of
$\mathbb {C}$ has the action of  $\mathbb {C}^*$ of weight
$\mathbb {C}^*$ of weight  $n$, so a
$n$, so a  $\mathbb {C}^*$-equivariant non-trivial cover
$\mathbb {C}^*$-equivariant non-trivial cover  $\mathbb {C}\to \mathbb {C}$ is the
$\mathbb {C}\to \mathbb {C}$ is the  $d$th-power map for some
$d$th-power map for some  $d>1$ dividing
$d>1$ dividing  $n$.
$n$.(iii)
 $I''$ is the image of
$I''$ is the image of  $I'$ under restriction. It is the ideal of
$I'$ under restriction. It is the ideal of  $K^{G_{(n)}^*\rtimes\,\mu _n}((\mathcal {R}_{(n)}^{(n)})^*)$ spanned by all classes pushed forward from
for some non-trivial
$K^{G_{(n)}^*\rtimes\,\mu _n}((\mathcal {R}_{(n)}^{(n)})^*)$ spanned by all classes pushed forward from
for some non-trivial \[ K^{\mathbb{C}\times_{\mathbb{C}}G_{(n)}^*\rtimes\,\mu_n}((\mathbb{C}\times_{\mathbb{C}}\mathcal{R}_{(n)}^{(n)})^*) \]
\[ K^{\mathbb{C}\times_{\mathbb{C}}G_{(n)}^*\rtimes\,\mu_n}((\mathbb{C}\times_{\mathbb{C}}\mathcal{R}_{(n)}^{(n)})^*) \] $\mathbb {C}^*$-equivariant cover
$\mathbb {C}^*$-equivariant cover  $\mathbb {C}\to \mathbb {C}$. Note that for the degree
$\mathbb {C}\to \mathbb {C}$. Note that for the degree  $d$ equivariant cover we have
$d$ equivariant cover we have  $K^{\mathbb {C}\times _{\mathbb {C}}G_{(n)}^*\rtimes\,\mu _n}((\mathbb {C}\times _{\mathbb {C}}\mathcal {R}_{(n)}^{(n)})^*) = K^{G_{(n)}^*\rtimes\,\mu _{n/d}}((\mathcal {R}_{(n)}^{(n)})^*)$, and pushing forward along
$K^{\mathbb {C}\times _{\mathbb {C}}G_{(n)}^*\rtimes\,\mu _n}((\mathbb {C}\times _{\mathbb {C}}\mathcal {R}_{(n)}^{(n)})^*) = K^{G_{(n)}^*\rtimes\,\mu _{n/d}}((\mathcal {R}_{(n)}^{(n)})^*)$, and pushing forward along  $\mathbb {C}\to \mathbb {C}$ corresponds to inducing from
$\mathbb {C}\to \mathbb {C}$ corresponds to inducing from  $\mu _{n/d}$-equivariance to
$\mu _{n/d}$-equivariance to  $\mu _n$-equivariance.
$\mu _n$-equivariance.(iv)
 $I'''$ is the image of
$I'''$ is the image of  $I''$ under specialization. Using the second description of
$I''$ under specialization. Using the second description of  $I''$ given above, we see that this is the ideal of
$I''$ given above, we see that this is the ideal of  $K^{G(\mathcal {O})\rtimes\,\mu _n}(\mathcal {R})$ spanned by all classes induced from
$K^{G(\mathcal {O})\rtimes\,\mu _n}(\mathcal {R})$ spanned by all classes induced from  $K^{G(\mathcal {O})\rtimes\,\mu _{n/d}}(\mathcal {R})$ for some
$K^{G(\mathcal {O})\rtimes\,\mu _{n/d}}(\mathcal {R})$ for some  $d>1$ dividing
$d>1$ dividing  $n$.
$n$.
Now on the one hand, by the projection formula we see that the composition
coincides with multiplication by the class ![]() $\sum _{j=1}^dq^{nj/d}$. On the other hand, it is a consequence of the ‘cellularity’ of
$\sum _{j=1}^dq^{nj/d}$. On the other hand, it is a consequence of the ‘cellularity’ of ![]() $\mathcal {R}$ that the restriction of equivariance
$\mathcal {R}$ that the restriction of equivariance ![]() $K^{G(\mathcal {O})\rtimes\,\mu _{n}}(\mathcal {R})\to K^{G(\mathcal {O})\rtimes\,\mu _{n/d}}(\mathcal {R})$ is surjective; so the ideal
$K^{G(\mathcal {O})\rtimes\,\mu _{n}}(\mathcal {R})\to K^{G(\mathcal {O})\rtimes\,\mu _{n/d}}(\mathcal {R})$ is surjective; so the ideal ![]() $I'''$ coincides with the ideal generated by the sums
$I'''$ coincides with the ideal generated by the sums ![]() $\sum _{j=1}^dq^{nj/d}$, whose lowest common factor is
$\sum _{j=1}^dq^{nj/d}$, whose lowest common factor is ![]() $\Phi _n(q)$. For the same reason, the restriction
$\Phi _n(q)$. For the same reason, the restriction
is also surjective, and realizes ![]() $K^{G(\mathcal {O})\rtimes\,\mu _{n}}(\mathcal {R})\cong K^{G(\mathcal {O})\rtimes\, \mathbb {C}^*}(\mathcal {R})/(q^n-1)$. Therefore we have produced the map
$K^{G(\mathcal {O})\rtimes\,\mu _{n}}(\mathcal {R})\cong K^{G(\mathcal {O})\rtimes\, \mathbb {C}^*}(\mathcal {R})/(q^n-1)$. Therefore we have produced the map
This map is linear by construction. The proof that it is a map of ![]() $Ad_n$-algebras, and lands in the center, is just as for the Borel–Moore homology.
$Ad_n$-algebras, and lands in the center, is just as for the Borel–Moore homology.
Example 4.4 We return to the situation of the example in § 3.16, Example (iii). We have ![]() $R(G)=\mathbb {Z}[y,y^{-1}]$ and, for
$R(G)=\mathbb {Z}[y,y^{-1}]$ and, for ![]() $\boldsymbol {N}=0$,
$\boldsymbol {N}=0$, ![]() $KA_q$ is the
$KA_q$ is the ![]() $\mathbb {Z}[y,y^{-1},q,q^{-1}]$-algebra
$\mathbb {Z}[y,y^{-1},q,q^{-1}]$-algebra
For ![]() $\boldsymbol {N}=\mathbb {C}_{-r}$,
$\boldsymbol {N}=\mathbb {C}_{-r}$, ![]() $r\geq 0$,
$r\geq 0$, ![]() $KA_q$ is given instead by the subalgebra with basis
$KA_q$ is given instead by the subalgebra with basis
 \[ \ldots,x^{{-}2},x^{{-}1},1,\bigg(\prod_{i=0}^{r-1}(1-y^r/q^i)\bigg)x, \bigg(\prod_{i=0}^{2r-1}(1-y^r/q^i)\bigg)x^2,\ldots \]
\[ \ldots,x^{{-}2},x^{{-}1},1,\bigg(\prod_{i=0}^{r-1}(1-y^r/q^i)\bigg)x, \bigg(\prod_{i=0}^{2r-1}(1-y^r/q^i)\bigg)x^2,\ldots \]
as a left (or right) ![]() $\mathbb {Z}[y,y^{-1},q,q^{-1}]$-module. The map of Theorem 4.1 sends
$\mathbb {Z}[y,y^{-1},q,q^{-1}]$-module. The map of Theorem 4.1 sends
which are central when ![]() $q^n=1$, in particular when
$q^n=1$, in particular when ![]() $q=\zeta$ is a primitive
$q=\zeta$ is a primitive ![]() $n$th root of unity. It sends
$n$th root of unity. It sends ![]() $(1-y^r)^rx$ to
$(1-y^r)^rx$ to
 \[ (1-y^{nr})^rx^n = \bigg(\prod_{i=0}^{n-1}(1-y^r/\zeta^i)^r\bigg)x^n = \bigg(\prod_{i=0}^{nr-1}(1-y^r/\zeta^i)\bigg)x^n, \]
\[ (1-y^{nr})^rx^n = \bigg(\prod_{i=0}^{n-1}(1-y^r/\zeta^i)^r\bigg)x^n = \bigg(\prod_{i=0}^{nr-1}(1-y^r/\zeta^i)\bigg)x^n, \]which is indeed an element of the appropriate subalgebra.
5. The Frobenius twist
In this short section we use the previous considerations to give a geometric construction of the Frobenius twist functor. First recall the notation of § 3.12: we have an ind-projective flat complex ind-scheme
over ![]() $\mathbb {A}^1$, which is the moduli space of triples
$\mathbb {A}^1$, which is the moduli space of triples ![]() $(y,\mathcal {E},f)$ where
$(y,\mathcal {E},f)$ where ![]() $y\in \mathbb {A}^1$,
$y\in \mathbb {A}^1$, ![]() $\mathcal {E}$ is a principal
$\mathcal {E}$ is a principal ![]() $G$-bundle on the formal neighborhood of the set
$G$-bundle on the formal neighborhood of the set ![]() $\pi ^{-1}\{y\}$ of
$\pi ^{-1}\{y\}$ of ![]() $p$th roots of
$p$th roots of ![]() $y$, and
$y$, and ![]() $f$ is a trivialization of
$f$ is a trivialization of ![]() $\mathcal {E}$ away from
$\mathcal {E}$ away from ![]() $\pi ^{-1}\{y\}$. There is a pro-smooth algebraic group
$\pi ^{-1}\{y\}$. There is a pro-smooth algebraic group
over ![]() $\mathbb {A}^1$, which is the moduli space of pairs
$\mathbb {A}^1$, which is the moduli space of pairs ![]() $(y,g)$ where
$(y,g)$ where ![]() $y\in \mathbb {A}^1$ and
$y\in \mathbb {A}^1$ and ![]() $g$ is a map from the formal neighborhood on
$g$ is a map from the formal neighborhood on ![]() $\pi ^{-1}\{y\}$ to
$\pi ^{-1}\{y\}$ to ![]() $G$, and
$G$, and ![]() $G_{(p)}$ acts on
$G_{(p)}$ acts on ![]() $Gr_{(p)}$ by changing the trivialization
$Gr_{(p)}$ by changing the trivialization ![]() $f$. The group
$f$. The group ![]() $\mathbb {C}^*$ acts on
$\mathbb {C}^*$ acts on ![]() $Gr_{(p)}$ by
$Gr_{(p)}$ by
and on ![]() $G_{(p)}$ (as a group) by
$G_{(p)}$ (as a group) by
Thus we have an action of the pro-smooth algebraic groupoid ![]() $G_{(p)}\rtimes\, \mathbb {C}^*$ over
$G_{(p)}\rtimes\, \mathbb {C}^*$ over ![]() $\mathbb {C}^*$ on
$\mathbb {C}^*$ on ![]() $Gr_{(p)}$. Now we have an equivalence
$Gr_{(p)}$. Now we have an equivalence
where by the bounded derived category of an ind-scheme we mean simply the 2-colimit of the bounded derived categories of its closed subschemes. Thus by applying the Steenrod functor ![]() $St_D$ we have a functor
$St_D$ we have a functor
Now note that ![]() $St_D'$ is exact for the perverse t-structure, up to a homological shift of degree
$St_D'$ is exact for the perverse t-structure, up to a homological shift of degree ![]() $1$. Thus we consider the shifted functor
$1$. Thus we consider the shifted functor
We will compose this functor with the ![]() $IC$ functor, and so get
$IC$ functor, and so get
Now let ![]() $i:Gr\to Gr_{(p)}$ denote the embedding of the fiber at
$i:Gr\to Gr_{(p)}$ denote the embedding of the fiber at ![]() $0$. There is a ‘Thom homomorphism’
$0$. There is a ‘Thom homomorphism’
so called because in the case where ![]() $i$ is the section of a smooth fibration,
$i$ is the section of a smooth fibration, ![]() $Th$ is an isomorphism on the constant sheaf, and the consequence in cohomology is the Thom isomorphism theorem. But
$Th$ is an isomorphism on the constant sheaf, and the consequence in cohomology is the Thom isomorphism theorem. But ![]() $i^*[-1]$,
$i^*[-1]$, ![]() $i^![1]$ send
$i^![1]$ send ![]() $IC$ sheaves to perverse sheaves, and so we may take the image of
$IC$ sheaves to perverse sheaves, and so we may take the image of ![]() $Th$.
$Th$.
Theorem 5.1 The functor
corresponds under geometric Satake to the Frobenius twist. In particular, it is linear in spite of the nonlinearity of ![]() $F$.
$F$.
Proof. Since we are working with perverse sheaves, we are free to work non-equivariantly, and we will do so for the entire proof; in particular, the functor ![]() $St_D'$ secretly means the composition of usual
$St_D'$ secretly means the composition of usual ![]() $St_D'$ with the functor which forgets the equivariance. Let us put ourselves in the general situation of a variety
$St_D'$ with the functor which forgets the equivariance. Let us put ourselves in the general situation of a variety ![]() $X$ with a proper map
$X$ with a proper map ![]() $f:X\to \mathbb {A}^1$. We recall some general facts; see [Reference Grothendieck, Raynaud and RimSGA7, Reference BeĭlinsonBeĭ87] for detailed discussions.
$f:X\to \mathbb {A}^1$. We recall some general facts; see [Reference Grothendieck, Raynaud and RimSGA7, Reference BeĭlinsonBeĭ87] for detailed discussions.
(i) The Thom homomorphism factors as
Here ![]() $\psi =\psi _f$ is the nearby cycles functor, the map
$\psi =\psi _f$ is the nearby cycles functor, the map ![]() $i^*[-1]\to \psi$ is the adjunction map, and the map
$i^*[-1]\to \psi$ is the adjunction map, and the map ![]() $\psi \to i^![1]$ comes from the defining map by self-duality of
$\psi \to i^![1]$ comes from the defining map by self-duality of ![]() $\psi$. Recall that
$\psi$. Recall that ![]() $\psi$ is perverse t-exact, and that it is equipped with a monodromy automorphism
$\psi$ is perverse t-exact, and that it is equipped with a monodromy automorphism ![]() $T=T_{f}$. Now let
$T=T_{f}$. Now let ![]() $\mathcal {F}$ be a perverse sheaf on
$\mathcal {F}$ be a perverse sheaf on ![]() $X|_{\mathbb {A}^1-\{0\}}$. Then
$X|_{\mathbb {A}^1-\{0\}}$. Then ![]() $i^*IC(\mathcal {F})[-1]$ and
$i^*IC(\mathcal {F})[-1]$ and ![]() $i^!IC(\mathcal {F})[1]$ are also perverse, and indeed we have
$i^!IC(\mathcal {F})[1]$ are also perverse, and indeed we have
 \begin{align*} i^*IC(\mathcal{F})[{-}1]\cong \psi(\mathcal{F})^T,\\ i^!IC(\mathcal{F})[1]\cong \psi(\mathcal{F})_T, \end{align*}
\begin{align*} i^*IC(\mathcal{F})[{-}1]\cong \psi(\mathcal{F})^T,\\ i^!IC(\mathcal{F})[1]\cong \psi(\mathcal{F})_T, \end{align*}and the Thom homomorphism is simply the natural map.
(ii) Let ![]() $\pi :\mathbb {A}^1\to \mathbb {A}^1$ be the
$\pi :\mathbb {A}^1\to \mathbb {A}^1$ be the ![]() $p$th power map. Then we consider
$p$th power map. Then we consider ![]() $\pi ^*X:= \mathbb {A}^1\times _{\mathbb {A}^1}X$ as mapping to the copy of
$\pi ^*X:= \mathbb {A}^1\times _{\mathbb {A}^1}X$ as mapping to the copy of ![]() $\mathbb {A}^1$ which is the source of
$\mathbb {A}^1$ which is the source of ![]() $\pi$, via the morphism
$\pi$, via the morphism ![]() $\pi ^*f$. Then we have a canonical isomorphism
$\pi ^*f$. Then we have a canonical isomorphism
The same is true with ![]() $p$ replaced by an arbitrary integer.
$p$ replaced by an arbitrary integer.
Now let us write ![]() $S$ for the geometric Satake equivalence. Then it suffices to identify
$S$ for the geometric Satake equivalence. Then it suffices to identify ![]() $\psi \circ St_D'\circ S(V)$ with
$\psi \circ St_D'\circ S(V)$ with ![]() $S(V^{\otimes p})$, and
$S(V^{\otimes p})$, and ![]() $T$ with its usual cyclic automorphism of order
$T$ with its usual cyclic automorphism of order ![]() $p$. The identification of
$p$. The identification of ![]() $\psi \circ St_D'\circ S(V)$ with
$\psi \circ St_D'\circ S(V)$ with ![]() $S(V^{\otimes p})$ is essentially by definition after applying point (ii) above. Finally, let
$S(V^{\otimes p})$ is essentially by definition after applying point (ii) above. Finally, let ![]() $H$ denote the global (non-equivariant) cohomology functor
$H$ denote the global (non-equivariant) cohomology functor ![]() $Perv_{G(\mathcal {O})}(Gr,\mathbb {F}_p)\to \textit{Vect}$. By the geometric Satake equivalence, it suffices to show that the action of
$Perv_{G(\mathcal {O})}(Gr,\mathbb {F}_p)\to \textit{Vect}$. By the geometric Satake equivalence, it suffices to show that the action of ![]() $T$ on
$T$ on ![]() $H(\psi \circ St_D'\circ S(V))\cong V^{\otimes p}$ is by the usual cyclic automorphism of order
$H(\psi \circ St_D'\circ S(V))\cong V^{\otimes p}$ is by the usual cyclic automorphism of order ![]() $p$. Since nearby cycles (and associated monodromy) commute with proper pushforward, it suffices to show it for
$p$. Since nearby cycles (and associated monodromy) commute with proper pushforward, it suffices to show it for
where ![]() $f:Gr_{(p)}|_{\mathbb {A}^1-\{0\}}\to \mathbb {A}^1-\{0\}$ is the structure map. But
$f:Gr_{(p)}|_{\mathbb {A}^1-\{0\}}\to \mathbb {A}^1-\{0\}$ is the structure map. But ![]() $f_*$ commutes with
$f_*$ commutes with ![]() $St_D'$, so we need to show it for
$St_D'$, so we need to show it for
The result now follows from the definition of ![]() $St_D'$ and the (tautological) fact that for a local system
$St_D'$ and the (tautological) fact that for a local system ![]() $\mathcal {L}$ on
$\mathcal {L}$ on ![]() $\mathbb {C}^*$ with fiber (say, at
$\mathbb {C}^*$ with fiber (say, at ![]() $1$)
$1$) ![]() $V$ and monodromy
$V$ and monodromy ![]() $T$, we have
$T$, we have
The proof is complete.
Remark 5.2 In fact, it is possible to show that the composition of ![]() $St_D'$ with
$St_D'$ with
may be equipped with a central structure for the convolution monoidal structures. That is, we can give ![]() $\psi '\circ St_D'$ a monoidal structure, and can give an isomorphism
$\psi '\circ St_D'$ a monoidal structure, and can give an isomorphism
as functors
which is compatible with this monoidal structure. It will also be compatible with the commutativity constraint for the convolution monoidal structure on ![]() $D^b_{G(\mathcal {O})}(Gr,\mathbb {F}_p)$ constructed in [Reference Mirković and VilonenMV07] (using similar considerations).
$D^b_{G(\mathcal {O})}(Gr,\mathbb {F}_p)$ constructed in [Reference Mirković and VilonenMV07] (using similar considerations).
This functor has the advantage of making sense on the entire derived category, not just for perverse sheaves. However, it has the disadvantages of being nonlinear and involving a loss of equivariance from ![]() $\mathbb {C}^*$ to
$\mathbb {C}^*$ to ![]() $\mu _p$. The former disadvantage can be forcibly removed by inverting
$\mu _p$. The former disadvantage can be forcibly removed by inverting ![]() $\hbar$; we are left with a central monoidal triangulated functor
$\hbar$; we are left with a central monoidal triangulated functor
which is compatible with the Artin–Schreier map on the level of equivariant parameters. It also corresponds to the Frobenius twist functor for perverse sheaves, in the sense that when applied to a perverse sheaf, it yields the image of our functor ![]() $im(Th)\circ IC\circ F$ under the operation of demoting equivariance from
$im(Th)\circ IC\circ F$ under the operation of demoting equivariance from ![]() $\mathbb {C}^*$ to
$\mathbb {C}^*$ to ![]() $\mu _p$ and inverting
$\mu _p$ and inverting ![]() $\hbar$. Indeed, in our analysis of
$\hbar$. Indeed, in our analysis of ![]() $im(Th)\circ IC\circ F$ we saw that it differs from
$im(Th)\circ IC\circ F$ we saw that it differs from ![]() $\psi '\circ St'_D$ only by
$\psi '\circ St'_D$ only by ![]() $\mu _p$-induced objects, which are killed off by inverting
$\mu _p$-induced objects, which are killed off by inverting ![]() $\hbar$.
$\hbar$.
In Conjecture 1.6, we attempt to describe this functor in terms of representations of the Langlands dual group and the ![]() $p$-center of its universal enveloping algebra. Our conjecture is predicated on a characteristic
$p$-center of its universal enveloping algebra. Our conjecture is predicated on a characteristic ![]() $p$ version of the derived geometric Satake theorem of [Reference Bezrukavnikov and FinkelbergBF08], which at the time of writing is unproven. Therefore we do not prove it here. Additionally, we foresee a complication arising from the loss of equivariance from
$p$ version of the derived geometric Satake theorem of [Reference Bezrukavnikov and FinkelbergBF08], which at the time of writing is unproven. Therefore we do not prove it here. Additionally, we foresee a complication arising from the loss of equivariance from ![]() $\mathbb {C}^*$ to
$\mathbb {C}^*$ to ![]() $\mu _p$. We hope very much that it will prove possible to remove this, but do not yet know how to go about it.
$\mu _p$. We hope very much that it will prove possible to remove this, but do not yet know how to go about it.
Acknowledgements
I wish to thank many people for their interest, help and encouragement, even if they are not aware of it, including D. Ben-Zvi, A. Braverman, P. Etingof, V. Ginzburg, I. Loseu, D. Vogan. Special thanks go to D. Nadler and V. Drinfeld for inviting me to speak about this project at their seminars, causing a dramatic improvement in my productivity levels; to G. Williamson for raising the question, ‘What is the representation-theoretic meaning of the Steenrod algebra action on mod-![]() $p$ cohomology?’ which this project is an attempt to answer; to my adviser R. Bezrukavnikov for eternal patience and support; and to J. Louveau, whom this is for.
$p$ cohomology?’ which this project is an attempt to answer; to my adviser R. Bezrukavnikov for eternal patience and support; and to J. Louveau, whom this is for.
Thanks also to the anonymous referee for their helpful suggestions.