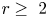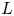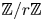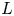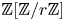1. Introduction
The construction of Khovanov homology in [Reference KhovanovKho00] was the first in a family of link homology theories categorifying quantum invariants of links in ![]() $\mathbb {R}^3$. To a planar diagram
$\mathbb {R}^3$. To a planar diagram ![]() $D$ of an oriented link
$D$ of an oriented link ![]() $L$ in
$L$ in ![]() $\mathbb {R}^3$ it associates a chain complex
$\mathbb {R}^3$ it associates a chain complex ![]() $CKh(D)$ of graded modules. The homotopy class of
$CKh(D)$ of graded modules. The homotopy class of ![]() $CKh(D)$ is an invariant of the link, and the graded Euler characteristic of
$CKh(D)$ is an invariant of the link, and the graded Euler characteristic of ![]() $CKh(D)$ is the Jones polynomial of
$CKh(D)$ is the Jones polynomial of ![]() $L$. Applications of Khovanov homology have been widely studied, and its functoriality properties with respect to surface cobordisms in
$L$. Applications of Khovanov homology have been widely studied, and its functoriality properties with respect to surface cobordisms in ![]() $4$-space are a particularly important aspect of the theory.
$4$-space are a particularly important aspect of the theory.
Using the framework of the Cohen–Jones–Segal construction [Reference Cohen, Jones and SegalCJS95], Lipshitz and Sarkar constructed in [Reference Lipshitz and SarkarLS14a] a stable homotopy refinement of Khovanov homology. (An alternative construction was proposed by Hu, Kriz and Kriz in [Reference Hu, Kriz and KrizHKK16].) This theory assigns to a link ![]() $L$ in
$L$ in ![]() $\mathbb {R}^3$ a suspension spectrum
$\mathbb {R}^3$ a suspension spectrum ![]() $\mathcal {X}_{Kh}(L)$ whose cohomology is the Khovanov homology of
$\mathcal {X}_{Kh}(L)$ whose cohomology is the Khovanov homology of ![]() $L$. The stable homotopy type carries additional information about the link, not seen at the level of Khovanov homology; specifically, it induces an action of the Steenrod algebra. Another construction of
$L$. The stable homotopy type carries additional information about the link, not seen at the level of Khovanov homology; specifically, it induces an action of the Steenrod algebra. Another construction of ![]() $\mathcal {X}_{Kh}(L)$, using the Burnside category, was given by Lawson, Lipshitz and Sarkar in [Reference Lawson, Lipshitz and SarkarLLS20]. Its analogue for the odd Khovanov homology was introduced in [Reference Sarkar, Scaduto and StoffregenSSS20] and extensions to tangles were developed in [Reference Lawson, Lipshitz and SarkarLLS17b, Reference Lawson, Lipshitz and SarkarLLS19]. Some proposals for defining a stable homotopy refinement of Khovanov–Rozansky
$\mathcal {X}_{Kh}(L)$, using the Burnside category, was given by Lawson, Lipshitz and Sarkar in [Reference Lawson, Lipshitz and SarkarLLS20]. Its analogue for the odd Khovanov homology was introduced in [Reference Sarkar, Scaduto and StoffregenSSS20] and extensions to tangles were developed in [Reference Lawson, Lipshitz and SarkarLLS17b, Reference Lawson, Lipshitz and SarkarLLS19]. Some proposals for defining a stable homotopy refinement of Khovanov–Rozansky ![]() $\mathfrak {sl}_N$ homology for
$\mathfrak {sl}_N$ homology for ![]() $N\geq 3$ have been outlined in [Reference Hu, Kriz and SombergHKS19, Reference Jones, Lobb and SchützJLS19, Reference KitchlooKit19].
$N\geq 3$ have been outlined in [Reference Hu, Kriz and SombergHKS19, Reference Jones, Lobb and SchützJLS19, Reference KitchlooKit19].
1.1 Annular homology theories
This paper concerns annular links, that is, links in the thickened annulus ![]() $\mathbb {A}\times I$, where
$\mathbb {A}\times I$, where ![]() $\mathbb {A}=S^1\times [0,1]$. Given a link
$\mathbb {A}=S^1\times [0,1]$. Given a link ![]() $L$ in
$L$ in ![]() $\mathbb {A}\times I$, consider its projection
$\mathbb {A}\times I$, consider its projection ![]() $D$ onto the first factor
$D$ onto the first factor ![]() $\mathbb {A}$. Following constructions by Asaeda, Przytycki and Sikora [Reference Asaeda, Przytycki and SikoraAPS04], Bar-Natan [Reference Bar-NatanBar05], and Roberts [Reference RobertsRob13], the triply graded annular Khovanov homology
$\mathbb {A}$. Following constructions by Asaeda, Przytycki and Sikora [Reference Asaeda, Przytycki and SikoraAPS04], Bar-Natan [Reference Bar-NatanBar05], and Roberts [Reference RobertsRob13], the triply graded annular Khovanov homology ![]() $Kh_{\mathbb {A}}(L)$ (sometimes called sutured annular Khovanov homology) may be obtained from the usual Khovanov chain complex [Reference KhovanovKho00] of
$Kh_{\mathbb {A}}(L)$ (sometimes called sutured annular Khovanov homology) may be obtained from the usual Khovanov chain complex [Reference KhovanovKho00] of ![]() $D$, viewed as a diagram in
$D$, viewed as a diagram in ![]() ${\mathbb {R}}^2$ by including
${\mathbb {R}}^2$ by including ![]() $\mathbb {A}\subset {\mathbb {R}}^2$, and then taking the annular degree zero part of the differential. Alternatively,
$\mathbb {A}\subset {\mathbb {R}}^2$, and then taking the annular degree zero part of the differential. Alternatively, ![]() $Kh_{\mathbb {A}}(L)$ may be obtained by applying a certain topological quantum field theory (TQFT) to the Bar-Natan category
$Kh_{\mathbb {A}}(L)$ may be obtained by applying a certain topological quantum field theory (TQFT) to the Bar-Natan category ![]() ${\mathcal {BN}}(\mathbb {A})$ of the annulus. It was shown by Grigsby, Licata and Wehrli [Reference Grigsby, Licata and WehrliGLW18] that this homology carries an action of
${\mathcal {BN}}(\mathbb {A})$ of the annulus. It was shown by Grigsby, Licata and Wehrli [Reference Grigsby, Licata and WehrliGLW18] that this homology carries an action of ![]() $\mathfrak {sl}_2$.
$\mathfrak {sl}_2$.
The quantum annular homology ![]() $Kh_{\mathbb {A}_\mathfrak {q}}(L)$, introduced by Beliakova, Putyra and Wehrli in [Reference Beliakova, Putyra and WehrliBPW19], is a far-reaching extension. Consider a ring
$Kh_{\mathbb {A}_\mathfrak {q}}(L)$, introduced by Beliakova, Putyra and Wehrli in [Reference Beliakova, Putyra and WehrliBPW19], is a far-reaching extension. Consider a ring ![]() $\Bbbk$ and a fixed unit
$\Bbbk$ and a fixed unit ![]() $\mathfrak {q}\in \Bbbk$. Following the notation of [Reference Beliakova, Putyra and WehrliBPW19], we note that there are two units
$\mathfrak {q}\in \Bbbk$. Following the notation of [Reference Beliakova, Putyra and WehrliBPW19], we note that there are two units ![]() $q$ in the theory. One corresponds to the usual
$q$ in the theory. One corresponds to the usual ![]() $q$-grading and the second one is the unit
$q$-grading and the second one is the unit ![]() $\mathfrak {q}\in \Bbbk$; we distinguish them by using different fonts. In a sense
$\mathfrak {q}\in \Bbbk$; we distinguish them by using different fonts. In a sense ![]() $\mathfrak {q}$ may be thought of as a deformation parameter, explaining the term ‘quantum homology’.
$\mathfrak {q}$ may be thought of as a deformation parameter, explaining the term ‘quantum homology’.
A rough outline of the construction of ![]() $Kh_{\mathbb {A}_\mathfrak {q}}(L)$ is as follows (see § 2.2 for a more detailed description). Given an annular link diagram
$Kh_{\mathbb {A}_\mathfrak {q}}(L)$ is as follows (see § 2.2 for a more detailed description). Given an annular link diagram ![]() $D\subset \mathbb {A}=S^1\times I$, we cut it along a seam
$D\subset \mathbb {A}=S^1\times I$, we cut it along a seam ![]() $\{*\}\times I$ to obtain an
$\{*\}\times I$ to obtain an ![]() $(n,n)$-tangle
$(n,n)$-tangle ![]() $D^\textrm {cut}$. A construction of Chen and Khovanov [Reference Chen and KhovanovCK14] then yields graded platform algebras
$D^\textrm {cut}$. A construction of Chen and Khovanov [Reference Chen and KhovanovCK14] then yields graded platform algebras ![]() $A^n$ and a functor
$A^n$ and a functor ![]() $\mathcal {F}^{}_{CK} : \mathcal {BN}(n,m) \to \text {gBimod}(A^n, A^m),$ where
$\mathcal {F}^{}_{CK} : \mathcal {BN}(n,m) \to \text {gBimod}(A^n, A^m),$ where ![]() $\mathcal {BN}(n,m)$ is the Bar-Natan category of the rectangle with marked points, and
$\mathcal {BN}(n,m)$ is the Bar-Natan category of the rectangle with marked points, and ![]() $\text {gBimod}(A^n, A^m)$ is the category of graded
$\text {gBimod}(A^n, A^m)$ is the category of graded ![]() $(A^n, A^m)$-bimodules. In [Reference Beliakova, Putyra and WehrliBPW19], the authors introduced quantum Hochschild homology, denoted
$(A^n, A^m)$-bimodules. In [Reference Beliakova, Putyra and WehrliBPW19], the authors introduced quantum Hochschild homology, denoted ![]() $qHH$, a deformation of the usual Hochschild homology of bimodules. The link homology theory is then defined using the quantum annular TQFT
$qHH$, a deformation of the usual Hochschild homology of bimodules. The link homology theory is then defined using the quantum annular TQFT ![]() $\mathcal {F}_{\mathbb {A}_{\mathfrak {q}}}$:
$\mathcal {F}_{\mathbb {A}_{\mathfrak {q}}}$:
The functorial extension to surfaces in ![]() $\mathbb {A}\times I\times I$ relies on the theory of (twisted) horizontal traces of bicategories. Quantum annular homology has a number of interesting properties [Reference Beliakova, Putyra and WehrliBPW19].
$\mathbb {A}\times I\times I$ relies on the theory of (twisted) horizontal traces of bicategories. Quantum annular homology has a number of interesting properties [Reference Beliakova, Putyra and WehrliBPW19].
(i) The homology
 $Kh_{\mathbb {A}_\mathfrak {q}}(L)$ in general depends on the choice of
$Kh_{\mathbb {A}_\mathfrak {q}}(L)$ in general depends on the choice of  $\mathfrak {q}$; for example, different roots of unity
$\mathfrak {q}$; for example, different roots of unity  $\mathfrak {q}\in \mathbb {C}$ may give non-isomorphic theories.
$\mathfrak {q}\in \mathbb {C}$ may give non-isomorphic theories.(ii)
 $Kh_{\mathbb {A}_\mathfrak {q}}(L)$ carries an action of
$Kh_{\mathbb {A}_\mathfrak {q}}(L)$ carries an action of  $U_{\mathfrak {q}}(\mathfrak {sl}_2)$.
$U_{\mathfrak {q}}(\mathfrak {sl}_2)$.(iii) Let
 $\Sigma$ be a closed surface in
$\Sigma$ be a closed surface in  $S^1\times {\mathbb {R}}^3$. Denoting by
$S^1\times {\mathbb {R}}^3$. Denoting by  $L$ the link
$L$ the link  ${\Sigma }\cap ( * \times {\mathbb {R}}^3)$,
${\Sigma }\cap ( * \times {\mathbb {R}}^3)$,  $\Sigma ^\textrm {cut}$ gives a cobordism from
$\Sigma ^\textrm {cut}$ gives a cobordism from  $L$ to itself in
$L$ to itself in  $I\times {\mathbb {R}}^3$. The evaluation of
$I\times {\mathbb {R}}^3$. The evaluation of  $Kh_{\mathbb {A}_\mathfrak {q}}(\Sigma )$ equals the graded Lefschetz trace of
$Kh_{\mathbb {A}_\mathfrak {q}}(\Sigma )$ equals the graded Lefschetz trace of  ${\Sigma }_* : Kh(L)\longrightarrow Kh(L)$, the endomorphism of the Khovanov homology of
${\Sigma }_* : Kh(L)\longrightarrow Kh(L)$, the endomorphism of the Khovanov homology of  $L$ induced by
$L$ induced by  $\Sigma ^\textrm {cut}$. In particular,
$\Sigma ^\textrm {cut}$. In particular,  $Kh_{\mathbb {A}_\mathfrak {q}}(S^1 \times L)$ coincides with the Jones polynomial of
$Kh_{\mathbb {A}_\mathfrak {q}}(S^1 \times L)$ coincides with the Jones polynomial of  $L$.
$L$.
1.2 Spectra for annular links
A stable homotopy refinement ![]() ${\mathcal {X}}_{\mathbb {A}}(L)$ of the annular Khovanov homology may be defined along the lines of [Reference Lipshitz and SarkarLS14a, Reference Lawson, Lipshitz and SarkarLLS20]. A different approach was used by Lawson, Lipshitz and Sarkar in [Reference Lawson, Lipshitz and SarkarLLS19]: they constructed a stable homotopy refinement of Chen–Khovanov algebras, giving rise to an alternative construction of
${\mathcal {X}}_{\mathbb {A}}(L)$ of the annular Khovanov homology may be defined along the lines of [Reference Lipshitz and SarkarLS14a, Reference Lawson, Lipshitz and SarkarLLS20]. A different approach was used by Lawson, Lipshitz and Sarkar in [Reference Lawson, Lipshitz and SarkarLLS19]: they constructed a stable homotopy refinement of Chen–Khovanov algebras, giving rise to an alternative construction of ![]() ${\mathcal {X}}_{\mathbb {A}}(L)$ as the topological Hochschild homology of the resulting ring spectrum.
${\mathcal {X}}_{\mathbb {A}}(L)$ as the topological Hochschild homology of the resulting ring spectrum.
The main result of this paper is a construction of a stable homotopy refinement of quantum annular homology. We work over the Laurent polynomial ring ![]() $\Bbbk :=\mathbb {Z}[\mathfrak {q},\mathfrak {q}^{-1}]$ and tensor the resulting theory with
$\Bbbk :=\mathbb {Z}[\mathfrak {q},\mathfrak {q}^{-1}]$ and tensor the resulting theory with ![]() $\Bbbk _r:=\mathbb {Z}[\mathfrak {q},\mathfrak {q}^{-1}]/(\mathfrak {q}^r-1)$, where
$\Bbbk _r:=\mathbb {Z}[\mathfrak {q},\mathfrak {q}^{-1}]/(\mathfrak {q}^r-1)$, where ![]() $r\geq 2$.
$r\geq 2$.
Theorem 1.1 Let ![]() $L$ be an oriented link in the thickened annulus
$L$ be an oriented link in the thickened annulus ![]() $\mathbb {A}\times I$. Then, for each
$\mathbb {A}\times I$. Then, for each ![]() $r\geq 2$, there exists a naive
$r\geq 2$, there exists a naive ![]() ${\mathbb {Z}}/r{\mathbb {Z}}$-equivariant spectrum
${\mathbb {Z}}/r{\mathbb {Z}}$-equivariant spectrum ![]() ${\mathcal {X}}^r_{\mathbb {A}_\mathfrak {q}}(L)$ which is well defined up to equivariant homotopy equivalence and whose cohomology is isomorphic to the quantum annular homology
${\mathcal {X}}^r_{\mathbb {A}_\mathfrak {q}}(L)$ which is well defined up to equivariant homotopy equivalence and whose cohomology is isomorphic to the quantum annular homology ![]() $Kh_{\mathbb {A}_\mathfrak {q}}(L)$, as modules over
$Kh_{\mathbb {A}_\mathfrak {q}}(L)$, as modules over ![]() $\mathbb {Z}[{\mathbb {Z}}/r{\mathbb {Z}}]$.
$\mathbb {Z}[{\mathbb {Z}}/r{\mathbb {Z}}]$.
A key point in the construction ![]() ${\mathcal {X}}^r_{\mathbb {A}_\mathfrak {q}}(L)$ is the interpretation of
${\mathcal {X}}^r_{\mathbb {A}_\mathfrak {q}}(L)$ is the interpretation of ![]() $\mathfrak {q}$ as a generator of the cyclic group
$\mathfrak {q}$ as a generator of the cyclic group ![]() ${\mathbb {Z}}/r{\mathbb {Z}}$. The proof then proceeds by building in § 4 the quantum annular Burnside functor: a strictly unitary lax
${\mathbb {Z}}/r{\mathbb {Z}}$. The proof then proceeds by building in § 4 the quantum annular Burnside functor: a strictly unitary lax ![]() $2$-functor to a suitably defined equivariant Burnside category, and then constructing in § 5 an equivariant version of spatial refinement, building on the approaches of [Reference Lawson, Lipshitz and SarkarLLS20, Reference Sarkar, Scaduto and StoffregenSSS20]. The definition of
$2$-functor to a suitably defined equivariant Burnside category, and then constructing in § 5 an equivariant version of spatial refinement, building on the approaches of [Reference Lawson, Lipshitz and SarkarLLS20, Reference Sarkar, Scaduto and StoffregenSSS20]. The definition of ![]() $\mathcal {X}^r_{\mathbb {A}_\mathfrak {q}}(D)$ is given for link diagrams
$\mathcal {X}^r_{\mathbb {A}_\mathfrak {q}}(D)$ is given for link diagrams ![]() $D$ in Definition 5.2 in § 5.5; the proof of invariance with respect to all choices involved (including choice of diagram) is presented there via Theorems 5.10 and 5.11.
$D$ in Definition 5.2 in § 5.5; the proof of invariance with respect to all choices involved (including choice of diagram) is presented there via Theorems 5.10 and 5.11.
Part of our construction involves a concrete description of generators and of the differential, starting from the quantum Hochschild homology definition [Reference Beliakova, Putyra and WehrliBPW19] of the quantum annular TQFT ![]() $\mathcal {F}_{\mathbb {A}_{\mathfrak {q}}}(D)$ in (1.1); this may be of independent interest to the reader interested in computational aspects of the theory. In fact, there is an important distinction between (annular) Khovanov homology and the quantum annular homology
$\mathcal {F}_{\mathbb {A}_{\mathfrak {q}}}(D)$ in (1.1); this may be of independent interest to the reader interested in computational aspects of the theory. In fact, there is an important distinction between (annular) Khovanov homology and the quantum annular homology ![]() $Kh_{\mathbb {A}_\mathfrak {q}}(L)$. In the setting of Khovanov homology, each resolution of the link diagram has a preferred collection of generators, and this is a crucial feature used in constructions of stable homotopy refinements in [Reference Lipshitz and SarkarLS14a, Reference Lawson, Lipshitz and SarkarLLS20]. On the other hand, in the context of quantum annular homology, generators are well defined only up to a multiple of a power of
$Kh_{\mathbb {A}_\mathfrak {q}}(L)$. In the setting of Khovanov homology, each resolution of the link diagram has a preferred collection of generators, and this is a crucial feature used in constructions of stable homotopy refinements in [Reference Lipshitz and SarkarLS14a, Reference Lawson, Lipshitz and SarkarLLS20]. On the other hand, in the context of quantum annular homology, generators are well defined only up to a multiple of a power of ![]() $\mathfrak {q}$. The proof of Theorem 1.1 involves a careful analysis of this indeterminacy and its relation to the group action on the spectrum. Moreover, the differential depends in a non-trivial way on the combinatorics of a given curve configuration in the annulus. A detailed analysis of the saddle maps defining the differential, using the definition in terms of the quantum annular TQFT
$\mathfrak {q}$. The proof of Theorem 1.1 involves a careful analysis of this indeterminacy and its relation to the group action on the spectrum. Moreover, the differential depends in a non-trivial way on the combinatorics of a given curve configuration in the annulus. A detailed analysis of the saddle maps defining the differential, using the definition in terms of the quantum annular TQFT ![]() $\mathcal {F}_{\mathbb {A}_{\mathfrak {q}}}$, is given in § 2.4. For
$\mathcal {F}_{\mathbb {A}_{\mathfrak {q}}}$, is given in § 2.4. For ![]() $r>2$, the powers of
$r>2$, the powers of ![]() $\mathfrak {q}$ appearing in the differential affect the construction of the Burnside functor, similar to how the signs appearing in odd Khovanov homology affect the analysis in [Reference Sarkar, Scaduto and StoffregenSSS20].
$\mathfrak {q}$ appearing in the differential affect the construction of the Burnside functor, similar to how the signs appearing in odd Khovanov homology affect the analysis in [Reference Sarkar, Scaduto and StoffregenSSS20].
The proof of the following result is presented in § 7.
Theorem 1.2 The quotient of ![]() ${\mathcal {X}}^r_{\mathbb {A}_\mathfrak {q}}(L)$ under the action of
${\mathcal {X}}^r_{\mathbb {A}_\mathfrak {q}}(L)$ under the action of ![]() ${\mathbb {Z}}/r{\mathbb {Z}}$ recovers
${\mathbb {Z}}/r{\mathbb {Z}}$ recovers ![]() ${\mathcal {X}}_{\mathbb {A}}(L)$, the stable homotopy refinement of the classical annular Khovanov homology of
${\mathcal {X}}_{\mathbb {A}}(L)$, the stable homotopy refinement of the classical annular Khovanov homology of ![]() $L$.
$L$.
It is important to note that no group action is assumed to be present on the link ![]() $L\subset \mathbb {A}\times I$, so the context for our work is different from that in [Reference Borodzik, Politarczyk and SilveroBPS18, Reference MusytMus19, Reference Stoffregen and ZhangSZ18]. Therefore,
$L\subset \mathbb {A}\times I$, so the context for our work is different from that in [Reference Borodzik, Politarczyk and SilveroBPS18, Reference MusytMus19, Reference Stoffregen and ZhangSZ18]. Therefore, ![]() ${\mathcal {X}}^r_{\mathbb {A}_\mathfrak {q}}(L)$ may be thought of as an ‘equivariant refinement’ of
${\mathcal {X}}^r_{\mathbb {A}_\mathfrak {q}}(L)$ may be thought of as an ‘equivariant refinement’ of ![]() ${\mathcal {X}}_{\mathbb {A}}(L)$, a structure that is not apparent in other constructions of the annular spectrum
${\mathcal {X}}_{\mathbb {A}}(L)$, a structure that is not apparent in other constructions of the annular spectrum ![]() ${\mathcal {X}}_{\mathbb {A}}(L)$.
${\mathcal {X}}_{\mathbb {A}}(L)$.
1.3 Properties and questions
It is an interesting question to what extent properties of the quantum annular homology theory ![]() $Kh_{\mathbb {A}_\mathfrak {q}}(L)$ can be lifted to the level of spectra. In Theorem 6.1, we prove that a generically embedded cobordism
$Kh_{\mathbb {A}_\mathfrak {q}}(L)$ can be lifted to the level of spectra. In Theorem 6.1, we prove that a generically embedded cobordism ![]() $W\subset \mathbb {A}\times I\times [0,1]$ between two annular links
$W\subset \mathbb {A}\times I\times [0,1]$ between two annular links ![]() $L_0$ and
$L_0$ and ![]() $L_1$ gives rise to a map
$L_1$ gives rise to a map
which induces the map on quantum annular Khovanov homology over the ring ![]() $\Bbbk _r$, defined in [Reference Beliakova, Putyra and WehrliBPW19]. As usual, the construction proceeds by decomposing
$\Bbbk _r$, defined in [Reference Beliakova, Putyra and WehrliBPW19]. As usual, the construction proceeds by decomposing ![]() $W$ into elementary cobordisms, whose annular projections correspond to Reidemeister moves and Morse surgeries. However, in the case of quantum annular homology, additional complexity arises from isotopies of the link diagram across the seam of the annulus. The map on quantum homology induced by cobordisms in four dimensions in [Reference Beliakova, Putyra and WehrliBPW19] relies on the theory of horizontal traces and quantum Hochschild homology. To define maps on spectra, we need to introduce chain maps by specifying their values on chosen generators. A detailed discussion of these chain maps, as well as verification that they match the maps defined by the TQFT
$W$ into elementary cobordisms, whose annular projections correspond to Reidemeister moves and Morse surgeries. However, in the case of quantum annular homology, additional complexity arises from isotopies of the link diagram across the seam of the annulus. The map on quantum homology induced by cobordisms in four dimensions in [Reference Beliakova, Putyra and WehrliBPW19] relies on the theory of horizontal traces and quantum Hochschild homology. To define maps on spectra, we need to introduce chain maps by specifying their values on chosen generators. A detailed discussion of these chain maps, as well as verification that they match the maps defined by the TQFT ![]() $\mathcal {F}_{\mathbb {A}_{\mathfrak {q}}}$, are given in the proof of Theorem 6.1 and in the appendix.
$\mathcal {F}_{\mathbb {A}_{\mathfrak {q}}}$, are given in the proof of Theorem 6.1 and in the appendix.
We are now in a position to formulate a spectrum-level analogue of property (iii) in § 1.1.
Theorem 1.3 Let ![]() $L$ be a link in the 3-ball
$L$ be a link in the 3-ball ![]() $B^3$ and consider the surface
$B^3$ and consider the surface ![]() $\widehat {W}=S^1\times L$ in
$\widehat {W}=S^1\times L$ in ![]() $\mathbb {A}\times D^2\cong S^1\times B^3$. Let
$\mathbb {A}\times D^2\cong S^1\times B^3$. Let ![]() $W$ denote a copy of
$W$ denote a copy of ![]() $\widehat {W}$ perturbed to be generic, viewed as a cobordism from
$\widehat {W}$ perturbed to be generic, viewed as a cobordism from ![]() $\varnothing$ to itself. Then the map
$\varnothing$ to itself. Then the map
induces the map on quantum annular homology ![]() $(\varphi _W^r)^*: \Bbbk _r\longrightarrow \Bbbk _r$ which is given by multiplication by the Jones polynomial of
$(\varphi _W^r)^*: \Bbbk _r\longrightarrow \Bbbk _r$ which is given by multiplication by the Jones polynomial of ![]() $L$, considered as an element of
$L$, considered as an element of ![]() $\Bbbk _r$, up to a sign and an overall power of
$\Bbbk _r$, up to a sign and an overall power of ![]() $\mathfrak {q}$.
$\mathfrak {q}$.
Here the spectrum ![]() $\mathcal {X}_{\mathbb {A}_\mathfrak {q}}(\varnothing )$ associated to the empty set is the wedge sum of
$\mathcal {X}_{\mathbb {A}_\mathfrak {q}}(\varnothing )$ associated to the empty set is the wedge sum of ![]() $r$ copies of the sphere spectrum, with cohomology isomorphic to
$r$ copies of the sphere spectrum, with cohomology isomorphic to ![]() $\Bbbk _r$. For brevity the theorem is stated for product surfaces
$\Bbbk _r$. For brevity the theorem is stated for product surfaces ![]() $S^1\times L$; the graded Lefschetz trace statement for more general closed surfaces holds as well. See Corollary 6.4 and remarks following it for further details.
$S^1\times L$; the graded Lefschetz trace statement for more general closed surfaces holds as well. See Corollary 6.4 and remarks following it for further details.
An important feature of stable homotopy refinement, not available on the level of link homology, is the action of Steenrod algebra. We do not address this aspect of the theory in the present paper; we plan to analyze the equivariant aspect of Steenrod operations on the spectra ![]() ${\mathcal {X}}^r_{\mathbb {A}_\mathfrak {q}}(L)$ in a future work.
${\mathcal {X}}^r_{\mathbb {A}_\mathfrak {q}}(L)$ in a future work.
Recall property (ii) in § 1.1, stating that ![]() $Kh_{\mathbb {A}_\mathfrak {q}}$ carries an action of
$Kh_{\mathbb {A}_\mathfrak {q}}$ carries an action of ![]() $U_{\mathfrak {q}}(\mathfrak {sl}_2)$; see [Reference Beliakova, Putyra and WehrliBPW19, Theorem B] and § 8 below for a more detailed discussion.
$U_{\mathfrak {q}}(\mathfrak {sl}_2)$; see [Reference Beliakova, Putyra and WehrliBPW19, Theorem B] and § 8 below for a more detailed discussion.
Conjecture 1.4 The action of ![]() $U_{\mathfrak {q}}(\mathfrak {sl}_2)$ on quantum annular homology
$U_{\mathfrak {q}}(\mathfrak {sl}_2)$ on quantum annular homology ![]() $Kh_{\mathbb {A}_\mathfrak {q}}(L)$ can be lifted to an action on
$Kh_{\mathbb {A}_\mathfrak {q}}(L)$ can be lifted to an action on ![]() ${\mathcal {X}}^r_{\mathbb {A}_\mathfrak {q}}(L)$.
${\mathcal {X}}^r_{\mathbb {A}_\mathfrak {q}}(L)$.
In § 8, we show that the invertible generator ![]() $K$ of
$K$ of ![]() $U_{\mathfrak {q}}(\mathfrak {sl}_2)$ admits a lift to an equivariant automorphism of
$U_{\mathfrak {q}}(\mathfrak {sl}_2)$ admits a lift to an equivariant automorphism of ![]() $\mathcal {X}^r_{\mathbb {A}_\mathfrak {q}}(L)$, but lifting the other generators and the relations between them is outside the scope of this paper. See the discussion at the end of § 8 for more comments on this matter.
$\mathcal {X}^r_{\mathbb {A}_\mathfrak {q}}(L)$, but lifting the other generators and the relations between them is outside the scope of this paper. See the discussion at the end of § 8 for more comments on this matter.
We conclude the introduction with another question. As discussed above, recently Lawson, Lipshitz and Sarkar gave a reformulation [Reference Lawson, Lipshitz and SarkarLLS19] of the annular Khovanov spectrum ![]() ${\mathcal {X}}_{\mathbb {A}}(L)$ as the topological Hochschild homology of their stable homotopy refinement of Chen–Khovanov algebras. Our construction of the spectra
${\mathcal {X}}_{\mathbb {A}}(L)$ as the topological Hochschild homology of their stable homotopy refinement of Chen–Khovanov algebras. Our construction of the spectra ![]() ${\mathcal {X}}^r_{\mathbb {A}_\mathfrak {q}}(L)$ is based on the definition of the quantum annular homology
${\mathcal {X}}^r_{\mathbb {A}_\mathfrak {q}}(L)$ is based on the definition of the quantum annular homology ![]() $Kh_{\mathbb {A}_\mathfrak {q}}(L)$ in [Reference Beliakova, Putyra and WehrliBPW19] using quantum Hochschild homology of bimodules. It is an interesting question whether there is a formulation of
$Kh_{\mathbb {A}_\mathfrak {q}}(L)$ in [Reference Beliakova, Putyra and WehrliBPW19] using quantum Hochschild homology of bimodules. It is an interesting question whether there is a formulation of ![]() ${\mathcal {X}}^r_{\mathbb {A}_\mathfrak {q}}(L)$ using some twisted or equivariant version of topological Hochschild homology of the ring spectra associated in [Reference Lawson, Lipshitz and SarkarLLS19] to Chen–Khovanov algebras.
${\mathcal {X}}^r_{\mathbb {A}_\mathfrak {q}}(L)$ using some twisted or equivariant version of topological Hochschild homology of the ring spectra associated in [Reference Lawson, Lipshitz and SarkarLLS19] to Chen–Khovanov algebras.
2. The quantum annular TQFT
2.1 Classical annular Khovanov homology
This section reviews the construction of sutured annular Khovanov homology [Reference Asaeda, Przytycki and SikoraAPS04, Reference Bar-NatanBar05, Reference RobertsRob13]. We will refer to it as classical annular homology, to distinguish it from the quantum version discussed in § 2.2. Let ![]() $I:= [0,1]$ denote the unit interval; we fix the notation
$I:= [0,1]$ denote the unit interval; we fix the notation ![]() $\mathbb {A}$ for the annulus
$\mathbb {A}$ for the annulus ![]() $S^1\times I$. An annular link is a link in the thickened annulus
$S^1\times I$. An annular link is a link in the thickened annulus ![]() $\mathbb {A}\times I$, and its diagram is a projection onto the first factor of
$\mathbb {A}\times I$, and its diagram is a projection onto the first factor of ![]() $\mathbb {A} \times I$. Link diagrams are disjoint from the boundary of
$\mathbb {A} \times I$. Link diagrams are disjoint from the boundary of ![]() $\mathbb {A}$. Identifying
$\mathbb {A}$. Identifying ![]() $S^1\times (0,1)$ with
$S^1\times (0,1)$ with ![]() $\mathbb {R}^2$ minus a point, we represent the annulus by simply indicating the deleted point using the symbol
$\mathbb {R}^2$ minus a point, we represent the annulus by simply indicating the deleted point using the symbol ![]() $\times$. Figure 1 illustrates an example of a link diagram.
$\times$. Figure 1 illustrates an example of a link diagram.

Figure 1. An annular link diagram.
Let ![]() $\mathcal {BN}(\mathbb {A})$ denote the Bar-Natan category of the annulus [Reference Bar-NatanBar05]. Its objects are formal
$\mathcal {BN}(\mathbb {A})$ denote the Bar-Natan category of the annulus [Reference Bar-NatanBar05]. Its objects are formal ![]() $\mathbb {Z}$-linear combinations of formally graded collections of simple closed curves in
$\mathbb {Z}$-linear combinations of formally graded collections of simple closed curves in ![]() $\mathbb {A}$. Morphisms are matrices whose entries are formal
$\mathbb {A}$. Morphisms are matrices whose entries are formal ![]() $\mathbb {Z}$-linear combinations of dotted cobordisms embedded in
$\mathbb {Z}$-linear combinations of dotted cobordisms embedded in ![]() $\mathbb {A}\times I$, modulo isotopy relative to the boundary, subject to the Bar-Natan relations, Figure 2.
$\mathbb {A}\times I$, modulo isotopy relative to the boundary, subject to the Bar-Natan relations, Figure 2.

Figure 2. Bar-Natan relations.
Let ![]() $D$ be a diagram for an oriented annular link
$D$ be a diagram for an oriented annular link ![]() $L$. We briefly review the construction of the chain complex
$L$. We briefly review the construction of the chain complex ![]() $[[D]]$; a complete treatment can be found in [Reference Bar-NatanBar05]. To begin, one first forms the cube of resolutions as follows. Label the crossings of the diagram by
$[[D]]$; a complete treatment can be found in [Reference Bar-NatanBar05]. To begin, one first forms the cube of resolutions as follows. Label the crossings of the diagram by ![]() $1,\ldots , n$. Every crossing may be resolved in two ways, called the 0-smoothing and the 1-smoothing, as in (
$1,\ldots , n$. Every crossing may be resolved in two ways, called the 0-smoothing and the 1-smoothing, as in (
). For each ![]() $u = (u_1,\ldots , u_n)\in \{0,1\}^n$, perform the
$u = (u_1,\ldots , u_n)\in \{0,1\}^n$, perform the ![]() $u_i$-smoothing at the
$u_i$-smoothing at the ![]() $i$th crossing. The resulting diagram is a collection of disjoint simple closed curves in
$i$th crossing. The resulting diagram is a collection of disjoint simple closed curves in ![]() $\mathbb {A}$, which we denote
$\mathbb {A}$, which we denote ![]() $D_u$. Thinking of elements of
$D_u$. Thinking of elements of ![]() $\{0,1\}^n$ as vertices of an
$\{0,1\}^n$ as vertices of an ![]() $n$-dimensional cube, decorate the vertex
$n$-dimensional cube, decorate the vertex ![]() $u$ by the smoothing
$u$ by the smoothing ![]() $D_u$.
$D_u$.

Let ![]() $v=(v_1,\ldots , v_n)$ and
$v=(v_1,\ldots , v_n)$ and ![]() $u=(u_1,\ldots , u_n)$ be vertices which differ only in the
$u=(u_1,\ldots , u_n)$ be vertices which differ only in the ![]() $i$th entry, where
$i$th entry, where ![]() $v_i = 0$ and
$v_i = 0$ and ![]() $u_i=1$. Then the diagrams
$u_i=1$. Then the diagrams ![]() $D_v$ and
$D_v$ and ![]() $D_u$ are the same outside of a small disk around the
$D_u$ are the same outside of a small disk around the ![]() $i$th crossing. There is a cobordism from
$i$th crossing. There is a cobordism from ![]() $D_v$ to
$D_v$ to ![]() $D_u$, which is the obvious saddle near the
$D_u$, which is the obvious saddle near the ![]() $i$th crossing and the identity (product cobordism) elsewhere. We will call this the saddle cobordism from
$i$th crossing and the identity (product cobordism) elsewhere. We will call this the saddle cobordism from ![]() $D_v$ to
$D_v$ to ![]() $D_u$ and denote it by
$D_u$ and denote it by ![]() $d_{v,u}$. Decorate each edge of the
$d_{v,u}$. Decorate each edge of the ![]() $n$-dimensional cube by these saddle cobordisms. We now have a commutative cube in the category
$n$-dimensional cube by these saddle cobordisms. We now have a commutative cube in the category ![]() $\mathcal {BN}(\mathbb {A})$. There is a way to assign
$\mathcal {BN}(\mathbb {A})$. There is a way to assign ![]() $s_{u,v} \in \{0,1\}$ to each edge so that multiplying the edge map
$s_{u,v} \in \{0,1\}$ to each edge so that multiplying the edge map ![]() $d_{v,u}$ by
$d_{v,u}$ by ![]() $(-1)^{s_{v,u}}$ results in an anti-commutative cube (see [Reference Bar-NatanBar05, § 2.7]; see also [Reference Lipshitz and SarkarLS14a, Definition 4.5]).
$(-1)^{s_{v,u}}$ results in an anti-commutative cube (see [Reference Bar-NatanBar05, § 2.7]; see also [Reference Lipshitz and SarkarLS14a, Definition 4.5]).
For ![]() $u=(u_1,\ldots , u_n) \in \{0,1\}^n$, let
$u=(u_1,\ldots , u_n) \in \{0,1\}^n$, let ![]() $\vert u \vert = \sum _i u_i$. Now form the chain complex
$\vert u \vert = \sum _i u_i$. Now form the chain complex ![]() $[[D]]$ by setting
$[[D]]$ by setting
where ![]() $n_-$ and
$n_-$ and ![]() $n_+$ are the numbers of negative and positive crossings in
$n_+$ are the numbers of negative and positive crossings in ![]() $D$, and the brackets
$D$, and the brackets ![]() $\{-\}$ denote the formal grading shift in
$\{-\}$ denote the formal grading shift in ![]() $\mathcal {BN}(\mathbb {A})$. The differential is given on each summand by the edge map
$\mathcal {BN}(\mathbb {A})$. The differential is given on each summand by the edge map ![]() $(-1)^{s_{v,u}}d_{v,u}$. Anti-commutativity of the cube ensures that
$(-1)^{s_{v,u}}d_{v,u}$. Anti-commutativity of the cube ensures that ![]() $[[D]]$ is a complex.
$[[D]]$ is a complex.
Theorem 2.1 [Reference Bar-NatanBar05, Theorem 1]
If diagrams ![]() $D$ and
$D$ and ![]() $D'$ are related by a Reidemeister move, then
$D'$ are related by a Reidemeister move, then ![]() $[[D]]$ and
$[[D]]$ and ![]() $[[D']]$ are chain homotopy equivalent.
$[[D']]$ are chain homotopy equivalent.
To obtain classical annular Khovanov homology, one applies the annular TQFT
defined as follows. Let ![]() $V_\mathbb {Z}$ and
$V_\mathbb {Z}$ and ![]() $W_\mathbb {Z}$ be free rank two
$W_\mathbb {Z}$ be free rank two ![]() $\mathbb {Z}$-modules with bases
$\mathbb {Z}$-modules with bases ![]() $v_-, v_+$ and
$v_-, v_+$ and ![]() $w_-, w_+$, respectively. Equip each with two gradings, the quantum grading
$w_-, w_+$, respectively. Equip each with two gradings, the quantum grading ![]() $\text {qdeg}$ and the annular grading
$\text {qdeg}$ and the annular grading ![]() $\text {adeg}$, defined on generators by
$\text {adeg}$, defined on generators by
We follow the grading convention of [Reference Beliakova, Putyra and WehrliBPW19]; note that the quantum grading on ![]() $V$ is different than the quantum grading appearing elsewhere in the literature; see Remark 2.3.
$V$ is different than the quantum grading appearing elsewhere in the literature; see Remark 2.3.
There are two types of simple closed curves in ![]() $\mathbb {A}$; essential curves and trivial curves which bound disks in
$\mathbb {A}$; essential curves and trivial curves which bound disks in ![]() $\mathbb {A}$. The functor
$\mathbb {A}$. The functor ![]() $\mathcal {F}_\mathbb {A}$ assigns
$\mathcal {F}_\mathbb {A}$ assigns ![]() $V_\mathbb {Z}$ to each essential circle and
$V_\mathbb {Z}$ to each essential circle and ![]() $W_\mathbb {Z}$ to each trivial circle. Then for
$W_\mathbb {Z}$ to each trivial circle. Then for ![]() $\mathcal {C}\subset \mathbb {A}$ a collection of disjoint simple closed curves with
$\mathcal {C}\subset \mathbb {A}$ a collection of disjoint simple closed curves with ![]() $e$ essential and
$e$ essential and ![]() $t$ trivial circles, the free abelian group
$t$ trivial circles, the free abelian group ![]() $\mathcal {F}_\mathbb {A}(\mathcal {C}) =$
$\mathcal {F}_\mathbb {A}(\mathcal {C}) =$ ![]() $\otimes ^e V_\mathbb {Z} \otimes ^t W_\mathbb {Z}$ (where the tensor product is taken over
$\otimes ^e V_\mathbb {Z} \otimes ^t W_\mathbb {Z}$ (where the tensor product is taken over ![]() $\mathbb {Z}$) has a standard basis consisting of a label of
$\mathbb {Z}$) has a standard basis consisting of a label of ![]() $v_-$ or
$v_-$ or ![]() $v_+$ on each essential circle, and
$v_+$ on each essential circle, and ![]() $w_-$ or
$w_-$ or ![]() $w_+$ on each trivial one. Following the conventions in [Reference Beliakova, Putyra and WehrliBPW19], a generator of
$w_+$ on each trivial one. Following the conventions in [Reference Beliakova, Putyra and WehrliBPW19], a generator of ![]() $\mathcal {C}$ will be represented as a choice of counterclockwise or clockwise orientations on each essential circle, corresponding to
$\mathcal {C}$ will be represented as a choice of counterclockwise or clockwise orientations on each essential circle, corresponding to ![]() $v_+$ and
$v_+$ and ![]() $v_-$, respectively, and either a dot or no dot on each trivial circle, corresponding to
$v_-$, respectively, and either a dot or no dot on each trivial circle, corresponding to ![]() $w_-$ and
$w_-$ and ![]() $w_+$. We will often switch between the diagrammatic and algebraic representations of generators, Figure 3.
$w_+$. We will often switch between the diagrammatic and algebraic representations of generators, Figure 3.

Figure 3. Diagrammatic representation of generators.
To define ![]() $\mathcal {F}_\mathbb {A}$ on a cobordism, it is enough to consider cups, caps, and saddles. To a cup,
$\mathcal {F}_\mathbb {A}$ on a cobordism, it is enough to consider cups, caps, and saddles. To a cup, ![]() $\mathcal {F}_\mathbb {A}$ assigns the unit
$\mathcal {F}_\mathbb {A}$ assigns the unit ![]() $\varepsilon : \mathbb {Z} \to W_\mathbb {Z}$ defined by
$\varepsilon : \mathbb {Z} \to W_\mathbb {Z}$ defined by ![]() $\varepsilon (1) = w_+$. To a cap,
$\varepsilon (1) = w_+$. To a cap, ![]() $\mathcal {F}_\mathbb {A}$ assigns the counit
$\mathcal {F}_\mathbb {A}$ assigns the counit ![]() $\eta : W_\mathbb {Z} \to \mathbb {Z}$ defined by
$\eta : W_\mathbb {Z} \to \mathbb {Z}$ defined by
A saddle is assigned one of the six maps shown in Figure 4, depending on whether it is a merge or a split and the types of curves involved.
Definition 2.1 If ![]() $D$ is a diagram for an annular link
$D$ is a diagram for an annular link ![]() $L$, define the annular Khovanov complex of
$L$, define the annular Khovanov complex of ![]() $D$ to be
$D$ to be
it is an invariant of ![]() $L$ up to chain homotopy equivalence.
$L$ up to chain homotopy equivalence.

Figure 4. Surgery formulas in classical annular Khovanov homology. The table lists topological types of surgeries and corresponding maps on generators.
Remark 2.2 Some of these formulas have an interpretation in terms of relations on cobordisms, as follows. Let ![]() $\mathcal {BBN}(\mathbb {A})$ [Reference Beliakova, Putyra and WehrliBPW19] denote the quotient of
$\mathcal {BBN}(\mathbb {A})$ [Reference Beliakova, Putyra and WehrliBPW19] denote the quotient of ![]() $\mathcal {BN}(\mathbb {A})$ by Boerner's relation, introduced in [Reference BoernerBoe08], which says that any cobordism carrying a dot and an essential curve is set to
$\mathcal {BN}(\mathbb {A})$ by Boerner's relation, introduced in [Reference BoernerBoe08], which says that any cobordism carrying a dot and an essential curve is set to ![]() $0$ (see Figure 5).
$0$ (see Figure 5).

Figure 5. Boerner's relation.
Algebraically, a dot on a cobordism corresponds to multiplication with ![]() $w_-$. Then, for a trivial circle
$w_-$. Then, for a trivial circle ![]() $C$, the standard generator
$C$, the standard generator ![]() $w_+$ (respectively
$w_+$ (respectively ![]() $w_-$) of
$w_-$) of ![]() $\mathcal {F}_\mathbb {A}(C) = W_\mathbb {Z}$ is the image of
$\mathcal {F}_\mathbb {A}(C) = W_\mathbb {Z}$ is the image of ![]() $1\in \mathbb {Z}$ under the undotted (respectively dotted) cup cobordism from
$1\in \mathbb {Z}$ under the undotted (respectively dotted) cup cobordism from ![]() $\varnothing$ to
$\varnothing$ to ![]() $C$. The surgery formulas of Figure 4 then imply that
$C$. The surgery formulas of Figure 4 then imply that ![]() $\mathcal {F}_\mathbb {A}$ factors through
$\mathcal {F}_\mathbb {A}$ factors through ![]() $\mathcal {BBN}(\mathbb {A})$. Algebraically, Boerner's relation can be seen as enforcing the equations
$\mathcal {BBN}(\mathbb {A})$. Algebraically, Boerner's relation can be seen as enforcing the equations ![]() $w_-\cdot v_- = w_- \cdot v_+ = 0$.
$w_-\cdot v_- = w_- \cdot v_+ = 0$.
Remark 2.3 To relate this to other constructions and grading conventions present in the literature (cf. [Reference RobertsRob13, § 3] and [Reference Grigsby, Licata and WehrliGLW18, § 3.1]), the annular chain complex may also be formed as follows. We may disregard the annular structure and view the resolutions ![]() $D_u$ in the cube
$D_u$ in the cube ![]() $[[D]]$ as lying in the plane. Then we may apply the usual Khovanov TQFT
$[[D]]$ as lying in the plane. Then we may apply the usual Khovanov TQFT ![]() $\mathcal {F}_{Kh}$ to the cube, obtaining the Khovanov chain complex
$\mathcal {F}_{Kh}$ to the cube, obtaining the Khovanov chain complex ![]() $CKh(D)$. Every circle
$CKh(D)$. Every circle ![]() $C$ is assigned a free
$C$ is assigned a free ![]() $\mathbb {Z}$-module
$\mathbb {Z}$-module ![]() $U$ generated by
$U$ generated by ![]() $u_+$ and
$u_+$ and ![]() $u_-$. The module
$u_-$. The module ![]() $U$ carries an internal grading
$U$ carries an internal grading ![]() $\deg _U$, with
$\deg _U$, with ![]() $\deg _U(u_\pm ) = \pm {1}$. Curves in the annulus carry an additional grading,
$\deg _U(u_\pm ) = \pm {1}$. Curves in the annulus carry an additional grading, ![]() $\text {adeg}$, with
$\text {adeg}$, with ![]() $\text {adeg}(u_{\pm })$ equal to
$\text {adeg}(u_{\pm })$ equal to ![]() $\pm {1}$ if
$\pm {1}$ if ![]() $C$ is essential and
$C$ is essential and ![]() $0$ if
$0$ if ![]() $C$ is trivial. The Khovanov differential
$C$ is trivial. The Khovanov differential ![]() $d^{Kh}$ splits as
$d^{Kh}$ splits as ![]() $d^{Kh} = d^\mathbb {A} + d'$, where
$d^{Kh} = d^\mathbb {A} + d'$, where ![]() $d^\mathbb {A}$ preserves the annular grading and is precisely the map in Figure 4, while
$d^\mathbb {A}$ preserves the annular grading and is precisely the map in Figure 4, while ![]() $d'$ lowers the annular grading. Thus, the annular grading induces a filtration on the Khovanov complex
$d'$ lowers the annular grading. Thus, the annular grading induces a filtration on the Khovanov complex ![]() $CKh(D)$. Taking the annual degree zero part of the differential and defining
$CKh(D)$. Taking the annual degree zero part of the differential and defining ![]() $\text {q deg}$ to be the difference between the degree
$\text {q deg}$ to be the difference between the degree ![]() $\deg _U$ and
$\deg _U$ and ![]() $\text {adeg}$ yields precisely the classical annular chain complex
$\text {adeg}$ yields precisely the classical annular chain complex ![]() $CKh_\mathbb {A}(D)$. The gradings
$CKh_\mathbb {A}(D)$. The gradings ![]() $\deg _U$,
$\deg _U$, ![]() $\text {q deg}$, and
$\text {q deg}$, and ![]() $\text {adeg}$ are denoted
$\text {adeg}$ are denoted ![]() $j$,
$j$, ![]() $j'$, and
$j'$, and ![]() $k$ in [Reference Grigsby, Licata and WehrliGLW18], respectively.
$k$ in [Reference Grigsby, Licata and WehrliGLW18], respectively.
2.2 Overview of quantum annular homology
This section outlines the construction of the Beliakova–Putyra–Wehrli quantum annular link homology [Reference Beliakova, Putyra and WehrliBPW19]. The theory is built over a commutative ring ![]() $\Bbbk$ and a unit
$\Bbbk$ and a unit ![]() $\mathfrak {q}\in \Bbbk$. We set
$\mathfrak {q}\in \Bbbk$. We set ![]() $\Bbbk :=\mathbb {Z}[\mathfrak {q},\mathfrak {q}^{-1}]$; the distinguished unit
$\Bbbk :=\mathbb {Z}[\mathfrak {q},\mathfrak {q}^{-1}]$; the distinguished unit ![]() $\mathfrak {q}\in \Bbbk$ is the same
$\mathfrak {q}\in \Bbbk$ is the same ![]() $\mathfrak {q}$ appearing in
$\mathfrak {q}$ appearing in ![]() $\mathbb {Z}[\mathfrak {q},\mathfrak {q}^{-1}]$. The main object is the quantum annular TQFT
$\mathbb {Z}[\mathfrak {q},\mathfrak {q}^{-1}]$. The main object is the quantum annular TQFT
where ![]() $\text {Mod}(\Bbbk )$ is the category of graded
$\text {Mod}(\Bbbk )$ is the category of graded ![]() $\Bbbk$-modules and
$\Bbbk$-modules and ![]() $\mathcal {BN}_{\mathfrak {q}}(\mathbb {A})$ is a certain deformation of the Bar-Natan category of the annulus. We will give a brief overview of the functor
$\mathcal {BN}_{\mathfrak {q}}(\mathbb {A})$ is a certain deformation of the Bar-Natan category of the annulus. We will give a brief overview of the functor ![]() $\mathcal {F}_{\mathbb {A}_\mathfrak {q}}$ and state a main theorem [Reference Beliakova, Putyra and WehrliBPW19, Theorem 6.3].
$\mathcal {F}_{\mathbb {A}_\mathfrak {q}}$ and state a main theorem [Reference Beliakova, Putyra and WehrliBPW19, Theorem 6.3].
Remark 2.4 As mentioned above, we work over the Laurent polynomial ring ![]() $\Bbbk$ throughout this section. We will tensor the resulting theory with
$\Bbbk$ throughout this section. We will tensor the resulting theory with ![]() $\Bbbk _r:= \Bbbk /(\mathfrak {q}^r-1)$ to construct the quantum annular Burnside functor in § 4.
$\Bbbk _r:= \Bbbk /(\mathfrak {q}^r-1)$ to construct the quantum annular Burnside functor in § 4.
Let ![]() $\mathcal {BN}(n,m)$ denote the Bar-Natan category of the rectangle with
$\mathcal {BN}(n,m)$ denote the Bar-Natan category of the rectangle with ![]() $n$ points on the bottom and
$n$ points on the bottom and ![]() $m$ on the top. Its objects are formal direct sums of formally graded planar tangles in
$m$ on the top. Its objects are formal direct sums of formally graded planar tangles in ![]() $I^2$ with
$I^2$ with ![]() $n$ endpoints on
$n$ endpoints on ![]() $I \times \{0\}$ and
$I \times \{0\}$ and ![]() $m$ endpoints on
$m$ endpoints on ![]() $I \times \{1\}$, cf. Figure 6. Such a tangle will be called a planar
$I \times \{1\}$, cf. Figure 6. Such a tangle will be called a planar ![]() $(n,m)$-tangle. Morphisms in
$(n,m)$-tangle. Morphisms in ![]() $\mathcal {BN}(n,m)$ are matrices whose entries are formal
$\mathcal {BN}(n,m)$ are matrices whose entries are formal ![]() $\Bbbk$-linear combinations of embedded dotted cobordisms in
$\Bbbk$-linear combinations of embedded dotted cobordisms in ![]() $I^3$ between planar
$I^3$ between planar ![]() $(n,m)$-tangles, subject to the Bar-Natan relations (see Figure 2).
$(n,m)$-tangles, subject to the Bar-Natan relations (see Figure 2).

Figure 6. A planar ![]() $(3,1)$-tangle.
$(3,1)$-tangle.
A seam of ![]() $\mathbb {A}=S^1\times I$, denoted
$\mathbb {A}=S^1\times I$, denoted ![]() $\mu$, is an interval
$\mu$, is an interval ![]() $\{*\}\times I$. In our representation of the interior of the annulus as
$\{*\}\times I$. In our representation of the interior of the annulus as ![]() $\mathbb {R}^2\smallsetminus \times$, we will fix the seam as the positive
$\mathbb {R}^2\smallsetminus \times$, we will fix the seam as the positive ![]() $x$-axis, ending on the left in
$x$-axis, ending on the left in ![]() $\times$. See Figure 8 for an example.
$\times$. See Figure 8 for an example.
The quantum Bar-Natan category of the annulus, denoted ![]() $\mathcal {BN}_{\mathfrak {q}}(\mathbb {A})$, is a deformation of
$\mathcal {BN}_{\mathfrak {q}}(\mathbb {A})$, is a deformation of ![]() $\mathcal {BN}(\mathbb {A}$). The objects of
$\mathcal {BN}(\mathbb {A}$). The objects of ![]() $\mathcal {BN}_{\mathfrak {q}}(\mathbb {A})$ are nearly the same as those of
$\mathcal {BN}_{\mathfrak {q}}(\mathbb {A})$ are nearly the same as those of ![]() $\mathcal {BN}(\mathbb {A})$, with the slight modification that curves in
$\mathcal {BN}(\mathbb {A})$, with the slight modification that curves in ![]() $\mathbb {A}$ must be transverse to
$\mathbb {A}$ must be transverse to ![]() $\mu$. Morphisms in
$\mu$. Morphisms in ![]() $\mathcal {BN}_{\mathfrak {q}}(\mathbb {A})$ are also similar to those in
$\mathcal {BN}_{\mathfrak {q}}(\mathbb {A})$ are also similar to those in ![]() $\mathcal {BN}(\mathbb {A})$. In
$\mathcal {BN}(\mathbb {A})$. In ![]() $\mathcal {BN}_{\mathfrak {q}}(\mathbb {A})$, isotopic cobordisms are identified if the isotopy fixes the membrane
$\mathcal {BN}_{\mathfrak {q}}(\mathbb {A})$, isotopic cobordisms are identified if the isotopy fixes the membrane ![]() $\mu \times I \subset \mathbb {A}\times I$. Otherwise, the cobordisms are scaled according to the degree of the part of the cobordism that passes through the membrane during the isotopy, accounting also for the co-orientation of the membrane induced by the standard orientation of the core circle of
$\mu \times I \subset \mathbb {A}\times I$. Otherwise, the cobordisms are scaled according to the degree of the part of the cobordism that passes through the membrane during the isotopy, accounting also for the co-orientation of the membrane induced by the standard orientation of the core circle of ![]() $\mathbb {A}$. These will be referred to as trace moves. The relations are depicted in Figure 7; for details, see [Reference Beliakova, Putyra and WehrliBPW19, § 6.2].
$\mathbb {A}$. These will be referred to as trace moves. The relations are depicted in Figure 7; for details, see [Reference Beliakova, Putyra and WehrliBPW19, § 6.2].

Figure 7. Relations in ![]() $\mathcal {BN}_{\mathfrak {q}}(\mathbb {A})$.
$\mathcal {BN}_{\mathfrak {q}}(\mathbb {A})$.
The Bar-Natan relations (Figure 2) are imposed, where the local pictures are understood to be disjoint from the membrane.
By general position, if two annular cobordisms are isotopic, then they are related by a sequence of trace moves and isotopies fixing the membrane. Therefore, if two cobordisms ![]() $S, S'\subset \mathbb {A}\times I$ are isotopic, then
$S, S'\subset \mathbb {A}\times I$ are isotopic, then ![]() $S = \mathfrak {q}^k S'$ as morphisms in
$S = \mathfrak {q}^k S'$ as morphisms in ![]() $\mathcal {BN}_{\mathfrak {q}}(\mathbb {A})$ for some
$\mathcal {BN}_{\mathfrak {q}}(\mathbb {A})$ for some ![]() $k\in \mathbb {Z}$. (See also [Reference Beliakova, Putyra and WehrliBPW19, Proposition 6.2].)
$k\in \mathbb {Z}$. (See also [Reference Beliakova, Putyra and WehrliBPW19, Proposition 6.2].)
A configuration ![]() $\mathcal {C}$ is a collection of disjoint simple closed curves in
$\mathcal {C}$ is a collection of disjoint simple closed curves in ![]() $\mathbb {A}$ which are transverse to
$\mathbb {A}$ which are transverse to ![]() $\mu$. Note that an object of
$\mu$. Note that an object of ![]() $\mathcal {BN}_{\mathfrak {q}}(\mathbb {A})$ is a formal direct sum of formally graded configurations. Given a configuration
$\mathcal {BN}_{\mathfrak {q}}(\mathbb {A})$ is a formal direct sum of formally graded configurations. Given a configuration ![]() $\mathcal {C}$ which intersects
$\mathcal {C}$ which intersects ![]() $\mu$ in
$\mu$ in ![]() $n$ points, we can cut along
$n$ points, we can cut along ![]() $\mu$ to obtain a planar
$\mu$ to obtain a planar ![]() $(n,n)$-tangle
$(n,n)$-tangle ![]() $\mathcal {C}^\textrm {cut}$. See Figure 8 for an example. A construction of Chen and Khovanov [Reference Chen and KhovanovCK14] yields graded
$\mathcal {C}^\textrm {cut}$. See Figure 8 for an example. A construction of Chen and Khovanov [Reference Chen and KhovanovCK14] yields graded ![]() $\Bbbk$-algebras
$\Bbbk$-algebras ![]() $A^k$ for each
$A^k$ for each ![]() $k\geq 0$ and a functor
$k\geq 0$ and a functor
where ![]() $\text {gBimod}(A^n, A^m)$ is the category of graded
$\text {gBimod}(A^n, A^m)$ is the category of graded ![]() $(A^n, A^m)$-bimodules. Let
$(A^n, A^m)$-bimodules. Let ![]() $\mathbb {I}^n$ denote the planar tangle consisting of
$\mathbb {I}^n$ denote the planar tangle consisting of ![]() $n$ vertical strands. Then, by definition of
$n$ vertical strands. Then, by definition of ![]() $\mathcal {F}_{CK}$, we have
$\mathcal {F}_{CK}$, we have ![]() $\mathcal {F}_{CK}(\mathbb {I}^n) = A^n$.
$\mathcal {F}_{CK}(\mathbb {I}^n) = A^n$.

Figure 8. Cutting open a configuration ![]() $\mathcal {C}$ along
$\mathcal {C}$ along ![]() $\mu$ to obtain a
$\mu$ to obtain a ![]() $(3,3)$-tangle
$(3,3)$-tangle ![]() $\mathcal {C}^\textrm {cut}$.
$\mathcal {C}^\textrm {cut}$.
The quantum Hochschild homology, denoted ![]() $qHH$ and defined in [Reference Beliakova, Putyra and WehrliBPW19, § 3.8.5], is a deformation of the usual Hochschild homology of bimodules. It takes as input a graded
$qHH$ and defined in [Reference Beliakova, Putyra and WehrliBPW19, § 3.8.5], is a deformation of the usual Hochschild homology of bimodules. It takes as input a graded ![]() $\Bbbk$-algebra
$\Bbbk$-algebra ![]() $B$ and a graded
$B$ and a graded ![]() $(B,B)$-bimodule
$(B,B)$-bimodule ![]() $M$. The output
$M$. The output ![]() $qHH(B,M) = {\bigoplus} _{i\geq 0} qHH_i(B,M)$ is a
$qHH(B,M) = {\bigoplus} _{i\geq 0} qHH_i(B,M)$ is a ![]() $\Bbbk$-module. Due to [Reference Beliakova, Putyra and WehrliBPW19, Proposition 6.6] (stating that
$\Bbbk$-module. Due to [Reference Beliakova, Putyra and WehrliBPW19, Proposition 6.6] (stating that ![]() $qHH_i(\mathcal {F}_{CK}(\mathcal {C}^\textrm {cut})) = 0$ for
$qHH_i(\mathcal {F}_{CK}(\mathcal {C}^\textrm {cut})) = 0$ for ![]() $i>0$), we will mostly be interested in
$i>0$), we will mostly be interested in ![]() $qHH_0$. It follows immediately from the definition of
$qHH_0$. It follows immediately from the definition of ![]() $qHH$ that
$qHH$ that
where ![]() $\vert b \vert$ denotes the degree of
$\vert b \vert$ denotes the degree of ![]() $b$.
$b$.
We are now ready to define ![]() $\mathcal {F}_{\mathbb {A}_{\mathfrak {q}}}$ on objects. Let
$\mathcal {F}_{\mathbb {A}_{\mathfrak {q}}}$ on objects. Let ![]() $\mathcal {C}$ be a configuration which intersects
$\mathcal {C}$ be a configuration which intersects ![]() $\mu$ in
$\mu$ in ![]() $n$ points. Using the Chen–Khovanov functor, form the
$n$ points. Using the Chen–Khovanov functor, form the ![]() $(A^n, A^n$)-bimodule
$(A^n, A^n$)-bimodule ![]() $\mathcal {F}_{CK}(\mathcal {C}^\textrm {cut})$. The quantum annular TQFT
$\mathcal {F}_{CK}(\mathcal {C}^\textrm {cut})$. The quantum annular TQFT ![]() $\mathcal {F}_{\mathbb {A}_{\mathfrak {q}}}$ is then defined on objects by
$\mathcal {F}_{\mathbb {A}_{\mathfrak {q}}}$ is then defined on objects by
By [Reference Beliakova, Putyra and WehrliBPW19, Proposition 6.6], we have ![]() $qHH_i(\mathcal {F}_{CK}(\mathcal {C}^\textrm {cut})) = 0$ for
$qHH_i(\mathcal {F}_{CK}(\mathcal {C}^\textrm {cut})) = 0$ for ![]() $i>0$. Suppose that
$i>0$. Suppose that ![]() $\mathcal {C}$ consists of
$\mathcal {C}$ consists of ![]() $n$ essential curves each intersecting the seam once. Then
$n$ essential curves each intersecting the seam once. Then ![]() $\mathcal {C}^\textrm {cut} = \mathbb {I}^n$, so
$\mathcal {C}^\textrm {cut} = \mathbb {I}^n$, so
Let ![]() $A^n_0 \subset A^n$ denote the subalgebra consisting of elements of degree
$A^n_0 \subset A^n$ denote the subalgebra consisting of elements of degree ![]() $0$. By [Reference Beliakova, Putyra and WehrliBPW19, Proposition 6.6], the inclusion
$0$. By [Reference Beliakova, Putyra and WehrliBPW19, Proposition 6.6], the inclusion ![]() $A^n_0 \hookrightarrow A^n$ induces an isomorphism
$A^n_0 \hookrightarrow A^n$ induces an isomorphism ![]() $qHH_0(A^n_0, A^n_0) \cong qHH_0(A^n, A^n)$. Moreover,
$qHH_0(A^n_0, A^n_0) \cong qHH_0(A^n, A^n)$. Moreover, ![]() $A^n_0$ is freely generated over
$A^n_0$ is freely generated over ![]() $\Bbbk$ by
$\Bbbk$ by ![]() $2^n$ elements
$2^n$ elements ![]() $x_1,\ldots , x_{2^n}$, which are the primitive idempotents of [Reference Beliakova, Putyra and WehrliBPW19, § 5.5]. They are in bijection with the cup diagrams and satisfy
$x_1,\ldots , x_{2^n}$, which are the primitive idempotents of [Reference Beliakova, Putyra and WehrliBPW19, § 5.5]. They are in bijection with the cup diagrams and satisfy ![]() $x_ix_j =\delta _{ij} x_i$. It follows from (2.4) that
$x_ix_j =\delta _{ij} x_i$. It follows from (2.4) that
Every configuration ![]() $\mathcal {C}$ is isomorphic in
$\mathcal {C}$ is isomorphic in ![]() $\mathcal {BN}_{\mathfrak {q}}(\mathbb {A})$ to a configuration
$\mathcal {BN}_{\mathfrak {q}}(\mathbb {A})$ to a configuration ![]() $\mathcal {C}^\circ$ in which every curve intersects the seam at most once. If
$\mathcal {C}^\circ$ in which every curve intersects the seam at most once. If ![]() $\mathcal {C}$ has
$\mathcal {C}$ has ![]() $e$ essential and
$e$ essential and ![]() $t$ trivial circles, then, by delooping, one obtains
$t$ trivial circles, then, by delooping, one obtains
We have so far only explained what ![]() $\mathcal {F}_{\mathbb {A}_{\mathfrak {q}}}$ does on objects. The full construction of
$\mathcal {F}_{\mathbb {A}_{\mathfrak {q}}}$ does on objects. The full construction of ![]() $\mathcal {F}_{\mathbb {A}_{\mathfrak {q}}}$ in [Reference Beliakova, Putyra and WehrliBPW19] follows from a more general theory of (twisted) horizontal traces of bicategories, which we will not describe. The definition of
$\mathcal {F}_{\mathbb {A}_{\mathfrak {q}}}$ in [Reference Beliakova, Putyra and WehrliBPW19] follows from a more general theory of (twisted) horizontal traces of bicategories, which we will not describe. The definition of ![]() $\mathcal {F}_{\mathbb {A}_{\mathfrak {q}}}$ on morphisms follows from this general theory. The rest of this subsection describes the set-up for [Reference Beliakova, Putyra and WehrliBPW19, Theorem 6.3], which is stated as our Theorem 2.5, and which is the main computational tool.
$\mathcal {F}_{\mathbb {A}_{\mathfrak {q}}}$ on morphisms follows from this general theory. The rest of this subsection describes the set-up for [Reference Beliakova, Putyra and WehrliBPW19, Theorem 6.3], which is stated as our Theorem 2.5, and which is the main computational tool.
Let ![]() $\mathcal {BBN}_{\mathfrak {q}}(\mathbb {A})$ denote the quotient of
$\mathcal {BBN}_{\mathfrak {q}}(\mathbb {A})$ denote the quotient of ![]() $\mathcal {BN}_{\mathfrak {q}}(\mathbb {A})$ by Boerner's relation; see Figure 5. The functor
$\mathcal {BN}_{\mathfrak {q}}(\mathbb {A})$ by Boerner's relation; see Figure 5. The functor ![]() $\mathcal {F}_{\mathbb {A}_{\mathfrak {q}}}$ factors through
$\mathcal {F}_{\mathbb {A}_{\mathfrak {q}}}$ factors through ![]() $\mathcal {BBN}_{\mathfrak {q}}(\mathbb {A})$. Given a diagram
$\mathcal {BBN}_{\mathfrak {q}}(\mathbb {A})$. Given a diagram ![]() $D$ for an annular link
$D$ for an annular link ![]() $L$ such that
$L$ such that ![]() $D$ is transverse to
$D$ is transverse to ![]() $\mu$ and the crossings are disjoint from
$\mu$ and the crossings are disjoint from ![]() $\mu$, we form the cube of resolutions
$\mu$, we form the cube of resolutions ![]() $[[D]]$ in the usual manner and view the result as a chain complex over the quantized category
$[[D]]$ in the usual manner and view the result as a chain complex over the quantized category ![]() $\mathcal {BBN}_{\mathfrak {q}}(\mathbb {A})$.
$\mathcal {BBN}_{\mathfrak {q}}(\mathbb {A})$.
Definition 2.2 If ![]() $D$ is a diagram for an annular link
$D$ is a diagram for an annular link ![]() $L$ which is transverse to the seam, define the quantum annular Khovanov complex of
$L$ which is transverse to the seam, define the quantum annular Khovanov complex of ![]() $D$ to be
$D$ to be
The chain complex ![]() $CKh_{\mathbb {A}_\mathfrak {q}}(D)$ is an invariant of
$CKh_{\mathbb {A}_\mathfrak {q}}(D)$ is an invariant of ![]() $L$ up to chain homotopy equivalence by [Reference Beliakova, Putyra and WehrliBPW19, Proposition 6.8].
$L$ up to chain homotopy equivalence by [Reference Beliakova, Putyra and WehrliBPW19, Proposition 6.8].
Let ![]() $TL$ denote the additive closure of the formally graded Temperley–Lieb category [Reference Beliakova, Putyra and WehrliBPW19, Appendix A.1]. Its objects are formal direct sums of formally graded finite collections of points on a line, and morphisms are
$TL$ denote the additive closure of the formally graded Temperley–Lieb category [Reference Beliakova, Putyra and WehrliBPW19, Appendix A.1]. Its objects are formal direct sums of formally graded finite collections of points on a line, and morphisms are ![]() $\Bbbk$-linear combinations of planar tangles between the points, modulo planar isotopy and the local relation that a circle is set to
$\Bbbk$-linear combinations of planar tangles between the points, modulo planar isotopy and the local relation that a circle is set to ![]() $\mathfrak {q}+\mathfrak {q}^{-1}$. Composition is given by stacking planar tangles; see Figure 9 for an example. There is a functor
$\mathfrak {q}+\mathfrak {q}^{-1}$. Composition is given by stacking planar tangles; see Figure 9 for an example. There is a functor ![]() $S^1\times (-) : TL \to \mathcal {BN}_{\mathfrak {q}}(\mathbb {A})$, which sends a collection of
$S^1\times (-) : TL \to \mathcal {BN}_{\mathfrak {q}}(\mathbb {A})$, which sends a collection of ![]() $n$ points to
$n$ points to ![]() $n$ essential circles in
$n$ essential circles in ![]() $\mathbb {A}$, each intersecting
$\mathbb {A}$, each intersecting ![]() $\mu$ once, and sends a planar tangle
$\mu$ once, and sends a planar tangle ![]() $T$ to the cobordism
$T$ to the cobordism ![]() $S^1\times T$. The relations in
$S^1\times T$. The relations in ![]() $\mathcal {BN}_{\mathfrak {q}}(\mathbb {A})$ (see Figure 7) imply that a torus wrapping once around the annulus evaluates to
$\mathcal {BN}_{\mathfrak {q}}(\mathbb {A})$ (see Figure 7) imply that a torus wrapping once around the annulus evaluates to ![]() $\mathfrak {q}+\mathfrak {q}^{-1}$, so that
$\mathfrak {q}+\mathfrak {q}^{-1}$, so that ![]() $S^1 \times (-)$ is well defined.
$S^1 \times (-)$ is well defined.

Figure 9. Composition and relations in ![]() $TL$.
$TL$.
Let ![]() $\text {gRep}(U_{\mathfrak {q}}(\mathfrak {sl}_2))$ denote the category of graded representations of
$\text {gRep}(U_{\mathfrak {q}}(\mathfrak {sl}_2))$ denote the category of graded representations of ![]() $U_{\mathfrak {q}}(\mathfrak {sl}_2)$. We follow the conventions established in [Reference Beliakova, Putyra and WehrliBPW19, Appendix A.1] concerning
$U_{\mathfrak {q}}(\mathfrak {sl}_2)$. We follow the conventions established in [Reference Beliakova, Putyra and WehrliBPW19, Appendix A.1] concerning ![]() $U_{\mathfrak {q}}(\mathfrak {sl}_2)$; also see § 8 of this paper. There is another functor
$U_{\mathfrak {q}}(\mathfrak {sl}_2)$; also see § 8 of this paper. There is another functor ![]() $\mathcal {F}_{TL} : TL \to \text {gRep}(U_{\mathfrak {q}}(\mathfrak {sl}_2))$, defined as follows. Let
$\mathcal {F}_{TL} : TL \to \text {gRep}(U_{\mathfrak {q}}(\mathfrak {sl}_2))$, defined as follows. Let ![]() $V_1 = \langle v_{-1}, v_1 \rangle$ be the fundamental representation of
$V_1 = \langle v_{-1}, v_1 \rangle$ be the fundamental representation of ![]() $U_{\mathfrak {q}}(\mathfrak {sl}_2)$ and
$U_{\mathfrak {q}}(\mathfrak {sl}_2)$ and ![]() $V_1^* = \langle v_{-1}^* , v_1^* \rangle$ its dual. Let
$V_1^* = \langle v_{-1}^* , v_1^* \rangle$ its dual. Let ![]() $V$ be free over
$V$ be free over ![]() $\Bbbk$ with basis
$\Bbbk$ with basis ![]() $\{v_+, v_-\}$. Consider two
$\{v_+, v_-\}$. Consider two ![]() $\Bbbk$-linear isomorphisms
$\Bbbk$-linear isomorphisms ![]() $\alpha : V_1 \to V$ and
$\alpha : V_1 \to V$ and ![]() $\beta : V_1^*\to V$ defined by
$\beta : V_1^*\to V$ defined by
These equip ![]() $V$ with two actions of
$V$ with two actions of ![]() $U_{\mathfrak {q}}(\mathfrak {sl}_2)$, which are detailed in [Reference Beliakova, Putyra and WehrliBPW19, Appendix A.1]. Note that
$U_{\mathfrak {q}}(\mathfrak {sl}_2)$, which are detailed in [Reference Beliakova, Putyra and WehrliBPW19, Appendix A.1]. Note that ![]() $\beta ^{-1}\circ \alpha : V_1 \to V_1^*$ is not
$\beta ^{-1}\circ \alpha : V_1 \to V_1^*$ is not ![]() $U_{\mathfrak {q}}(\mathfrak {sl}_2)$-linear, even though
$U_{\mathfrak {q}}(\mathfrak {sl}_2)$-linear, even though ![]() $V_1$ and
$V_1$ and ![]() $V_1^*$ are isomorphic as
$V_1^*$ are isomorphic as ![]() $U_{\mathfrak {q}}(\mathfrak {sl}_2)$-modules.
$U_{\mathfrak {q}}(\mathfrak {sl}_2)$-modules.
The functor ![]() $\mathcal {F}_{TL}$ assigns
$\mathcal {F}_{TL}$ assigns ![]() $V^{\otimes n}$ to a collection of
$V^{\otimes n}$ to a collection of ![]() $n$ points. Since
$n$ points. Since ![]() $\beta ^{-1}\alpha$ is not
$\beta ^{-1}\alpha$ is not ![]() $U_{\mathfrak {q}}(\mathfrak {sl}_2)$-linear, there is an ambiguity in specifying the
$U_{\mathfrak {q}}(\mathfrak {sl}_2)$-linear, there is an ambiguity in specifying the ![]() $U_{\mathfrak {q}}(\mathfrak {sl}_2)$-module structure on
$U_{\mathfrak {q}}(\mathfrak {sl}_2)$-module structure on ![]() $V^{\otimes n}$. The convention is that the
$V^{\otimes n}$. The convention is that the ![]() $m$th point is assigned
$m$th point is assigned ![]() $V_1$ if
$V_1$ if ![]() $m$ is odd and
$m$ is odd and ![]() $V_1^*$ if
$V_1^*$ if ![]() $m$ is even, so that the module assigned to
$m$ is even, so that the module assigned to ![]() $n$ points is given the
$n$ points is given the ![]() $U_{\mathfrak {q}}(\mathfrak {sl}_2)$-action according to the identification
$U_{\mathfrak {q}}(\mathfrak {sl}_2)$-action according to the identification
To define the value of ![]() $\mathcal {F}_{TL}$ on any planar tangle, it suffices to specify its value on caps and cups. For a cap
$\mathcal {F}_{TL}$ on any planar tangle, it suffices to specify its value on caps and cups. For a cap ![]() $\cap$,
$\cap$, ![]() $\mathcal {F}_{TL}$ assigns the evaluation map
$\mathcal {F}_{TL}$ assigns the evaluation map ![]() $ev : V\otimes V \to \Bbbk$, defined by
$ev : V\otimes V \to \Bbbk$, defined by
On a cup ![]() $\cup$,
$\cup$, ![]() $\mathcal {F}_{TL}$ assigns the coevaluation
$\mathcal {F}_{TL}$ assigns the coevaluation ![]() $coev: \Bbbk \to V\otimes V$, defined by
$coev: \Bbbk \to V\otimes V$, defined by
The evaluation map is always identified with either ![]() $V_1 \otimes V_1^* \to \Bbbk$ or
$V_1 \otimes V_1^* \to \Bbbk$ or ![]() $V_1^*\otimes V_1 \to \Bbbk$, and the coevaluation is identified with either
$V_1^*\otimes V_1 \to \Bbbk$, and the coevaluation is identified with either ![]() $\Bbbk \to V_1 \otimes V_1^*$ or
$\Bbbk \to V_1 \otimes V_1^*$ or ![]() $\Bbbk \to V_1^* \otimes V_1$. With these identifications, the cap and cup are assigned
$\Bbbk \to V_1^* \otimes V_1$. With these identifications, the cap and cup are assigned ![]() $U_{\mathfrak {q}}(\mathfrak {sl}_2)$-linear maps by
$U_{\mathfrak {q}}(\mathfrak {sl}_2)$-linear maps by ![]() $\mathcal {F}_{TL}$.
$\mathcal {F}_{TL}$.
We have now explained the functors ![]() $\mathcal {F}_{TL} : TL\to \text {gRep}(U_{\mathfrak {q}}(\mathfrak {sl}_2))$ and
$\mathcal {F}_{TL} : TL\to \text {gRep}(U_{\mathfrak {q}}(\mathfrak {sl}_2))$ and ![]() $S^1\times (-): TL\to \mathcal {BN}_\mathfrak {q}(\mathbb {A})$. To compare
$S^1\times (-): TL\to \mathcal {BN}_\mathfrak {q}(\mathbb {A})$. To compare ![]() $\mathcal {F}_{TL}$ with the composition
$\mathcal {F}_{TL}$ with the composition ![]() $\mathcal {F}_{\mathbb {A}_\mathfrak {q}}\circ S^1\times (-)$ in the statement of Theorem 2.5, the value of
$\mathcal {F}_{\mathbb {A}_\mathfrak {q}}\circ S^1\times (-)$ in the statement of Theorem 2.5, the value of ![]() $\mathcal {F}_{\mathbb {A}_\mathfrak {q}}$ on
$\mathcal {F}_{\mathbb {A}_\mathfrak {q}}$ on ![]() $n$ essential circles intersecting the seam once needs to be given a
$n$ essential circles intersecting the seam once needs to be given a ![]() $U_{\mathfrak {q}}(\mathfrak {sl}_2)$-module structure. Recall that the Chen–Khovanov functor assigns the
$U_{\mathfrak {q}}(\mathfrak {sl}_2)$-module structure. Recall that the Chen–Khovanov functor assigns the ![]() $\Bbbk$-algebra
$\Bbbk$-algebra ![]() $A^n$ to the planar tangle
$A^n$ to the planar tangle ![]() $\mathbb {I}^n$ consisting of
$\mathbb {I}^n$ consisting of ![]() $n$ vertical strands. There is a distinguished
$n$ vertical strands. There is a distinguished ![]() $\Bbbk$-linear isomorphism
$\Bbbk$-linear isomorphism
which we now describe. Recall that the inclusion ![]() $A^n_0 \hookrightarrow A_n$ induces an isomorphism on
$A^n_0 \hookrightarrow A_n$ induces an isomorphism on ![]() $qHH_0$, and that
$qHH_0$, and that ![]() $qHH_0(A^n, A^n_0)$ has a distinguished
$qHH_0(A^n, A^n_0)$ has a distinguished ![]() $\Bbbk$-basis
$\Bbbk$-basis ![]() $\{x_1,\ldots , x_{2^n}\}$ corresponding to cup diagrams. Chen and Khovanov in [Reference Chen and KhovanovCK14, § 6] assigned to each
$\{x_1,\ldots , x_{2^n}\}$ corresponding to cup diagrams. Chen and Khovanov in [Reference Chen and KhovanovCK14, § 6] assigned to each ![]() $x_i$ an element
$x_i$ an element ![]() $p_i\in V^{\otimes n}$ such that the collection
$p_i\in V^{\otimes n}$ such that the collection ![]() $\{p_i\}$ forms a basis of
$\{p_i\}$ forms a basis of ![]() $V^{\otimes n}$. The isomorphism (2.5) is obtained by composing
$V^{\otimes n}$. The isomorphism (2.5) is obtained by composing ![]() $qHH_0(A^n, A^n) \cong qHH_0(A^n, A^n_0)$ with the assignment
$qHH_0(A^n, A^n) \cong qHH_0(A^n, A^n_0)$ with the assignment ![]() $x_i\mapsto p_i$.
$x_i\mapsto p_i$.
Theorem 2.5 [Reference Beliakova, Putyra and WehrliBPW19, Theorem 6.3]
There is a commuting diagram

with the horizontal functor an equivalence of categories.
This theorem will play an important role in determining the values of the differential on generators in the next section.
2.3 Fixing generators
In the construction of Khovanov homotopy types in [Reference Lipshitz and SarkarLS14a] and [Reference Sarkar, Scaduto and StoffregenSSS20] it is important to have a fixed set of generators for each configuration. Due to the definition of ![]() $\mathcal {F}_{\mathbb {A}_\mathfrak {q}}$, the situation is more complicated in quantum annular homology. In this subsection, we explain how to fix generators for a general configuration.
$\mathcal {F}_{\mathbb {A}_\mathfrak {q}}$, the situation is more complicated in quantum annular homology. In this subsection, we explain how to fix generators for a general configuration.
We will say that a configuration ![]() $\mathcal {C}$ is standard if every component intersects the seam in at most one point. Every configuration
$\mathcal {C}$ is standard if every component intersects the seam in at most one point. Every configuration ![]() $\mathcal {C}$ is isotopic in
$\mathcal {C}$ is isotopic in ![]() $\mathbb {A}$ to a standard configuration, denoted
$\mathbb {A}$ to a standard configuration, denoted ![]() $\mathcal {C}^\circ$, which is unique up to planar isotopy of the cut-open planar tangle. Next we explain in detail how Theorem 2.5 gives a canonical choice of generators for
$\mathcal {C}^\circ$, which is unique up to planar isotopy of the cut-open planar tangle. Next we explain in detail how Theorem 2.5 gives a canonical choice of generators for ![]() $\mathcal {F}_{\mathbb {A}_{\mathfrak {q}}}(\mathcal {C})$ when
$\mathcal {F}_{\mathbb {A}_{\mathfrak {q}}}(\mathcal {C})$ when ![]() $\mathcal {C}$ is standard.
$\mathcal {C}$ is standard.
For a configuration ![]() $\mathcal {C}$, we will write
$\mathcal {C}$, we will write ![]() $\mathcal {C}_\textrm {E}$ to denote the essential circles in
$\mathcal {C}_\textrm {E}$ to denote the essential circles in ![]() $\mathcal {C}$ and
$\mathcal {C}$ and ![]() $\mathcal {C}_\textrm {T}$ to denote the trivial circles. Figure 10 illustrates these conventions.
$\mathcal {C}_\textrm {T}$ to denote the trivial circles. Figure 10 illustrates these conventions.

Figure 10. (a) A configuration ![]() $\mathcal {C}$, (b) its standard form
$\mathcal {C}$, (b) its standard form ![]() $\mathcal {C}^\circ$, (c)
$\mathcal {C}^\circ$, (c) ![]() $\mathcal {C}_\textrm {E}$, and (d)
$\mathcal {C}_\textrm {E}$, and (d) ![]() $\mathcal {C}_\textrm {T}$.
$\mathcal {C}_\textrm {T}$.
For a cobordism ![]() $S\subset \mathbb {A} \times I$, let
$S\subset \mathbb {A} \times I$, let ![]() $\bar {S}$ denote its reflection in the
$\bar {S}$ denote its reflection in the ![]() $I$ coordinate. For a configuration
$I$ coordinate. For a configuration ![]() $\mathcal {C}$, we will often suppress the notation
$\mathcal {C}$, we will often suppress the notation ![]() $\mathcal {F}_{\mathbb {A}_{\mathfrak {q}}}(\mathcal {C})$ when it is clear from context; that is,
$\mathcal {F}_{\mathbb {A}_{\mathfrak {q}}}(\mathcal {C})$ when it is clear from context; that is, ![]() $x\in \mathcal {C}$ means
$x\in \mathcal {C}$ means ![]() $x\in \mathcal {F}_{\mathbb {A}_{\mathfrak {q}}}(\mathcal {C})$. Likewise, for a cobordism
$x\in \mathcal {F}_{\mathbb {A}_{\mathfrak {q}}}(\mathcal {C})$. Likewise, for a cobordism ![]() $S:\mathcal {C}\to \mathcal {C}'$, we will often write
$S:\mathcal {C}\to \mathcal {C}'$, we will often write ![]() $S(x)$ to mean
$S(x)$ to mean ![]() $\mathcal {F}_{\mathbb {A}_\mathfrak {q}}(S)(x)$, where
$\mathcal {F}_{\mathbb {A}_\mathfrak {q}}(S)(x)$, where ![]() $\mathcal {F}_{\mathbb {A}_\mathfrak {q}}(S): \mathcal {F}_{\mathbb {A}_{\mathfrak {q}}}(\mathcal {C}) \to \mathcal {F}_{\mathbb {A}_{\mathfrak {q}}}(\mathcal {C}')$ is the induced map. For cobordisms
$\mathcal {F}_{\mathbb {A}_\mathfrak {q}}(S): \mathcal {F}_{\mathbb {A}_{\mathfrak {q}}}(\mathcal {C}) \to \mathcal {F}_{\mathbb {A}_{\mathfrak {q}}}(\mathcal {C}')$ is the induced map. For cobordisms ![]() $\mathcal {C} \xrightarrow {S_1} \mathcal {C}'$ and
$\mathcal {C} \xrightarrow {S_1} \mathcal {C}'$ and ![]() $\mathcal {C}' \xrightarrow {S_2} \mathcal {C}''$, we will write
$\mathcal {C}' \xrightarrow {S_2} \mathcal {C}''$, we will write ![]() $S_2S_1$ to denote their composition.
$S_2S_1$ to denote their composition.
Suppose that ![]() $C\subset \mathbb {A}$ is a trivial circle and set
$C\subset \mathbb {A}$ is a trivial circle and set ![]() $n=\vert C \cap \mu \vert$. The circle
$n=\vert C \cap \mu \vert$. The circle ![]() $C$ bounds an embedded disk
$C$ bounds an embedded disk ![]() $D\subset \mathbb {A}$, and we may push the interior of
$D\subset \mathbb {A}$, and we may push the interior of ![]() $D$ down in the
$D$ down in the ![]() $I$ coordinate to obtain a cobordism
$I$ coordinate to obtain a cobordism ![]() $\Sigma \subset \mathbb {A}\times I$ from the empty set to
$\Sigma \subset \mathbb {A}\times I$ from the empty set to ![]() $C$ which intersects the membrane in exactly
$C$ which intersects the membrane in exactly ![]() $n/2$ arcs. We refer to
$n/2$ arcs. We refer to ![]() $\Sigma$ as the cup cobordism on
$\Sigma$ as the cup cobordism on ![]() $C$. Similarly, we may pull
$C$. Similarly, we may pull ![]() $D$ up in the
$D$ up in the ![]() $I$ coordinate to obtain the cap cobordism on C, which is simply
$I$ coordinate to obtain the cap cobordism on C, which is simply ![]() $\bar {\Sigma }$.
$\bar {\Sigma }$.
Let ![]() $W$ denote the
$W$ denote the ![]() $\Bbbk$-module assigned by
$\Bbbk$-module assigned by ![]() $\mathcal {F}_{\mathbb {A}_{\mathfrak {q}}}$ to a trivial circle
$\mathcal {F}_{\mathbb {A}_{\mathfrak {q}}}$ to a trivial circle ![]() $C$ which is disjoint from the seam. The module
$C$ which is disjoint from the seam. The module ![]() $W = \langle w_-, w_+\rangle$ is free of rank
$W = \langle w_-, w_+\rangle$ is free of rank ![]() $2$. The standard generator
$2$. The standard generator ![]() $w_+$ (respectively
$w_+$ (respectively ![]() $w_-$) is the image of
$w_-$) is the image of ![]() $1\in \Bbbk$ under the undotted (respectively dotted) cup cobordism on
$1\in \Bbbk$ under the undotted (respectively dotted) cup cobordism on ![]() $C$. Therefore, we will often identify
$C$. Therefore, we will often identify ![]() $w_\pm$ with these cup cobordisms. Diagrammatically, we will signify that a trivial circle
$w_\pm$ with these cup cobordisms. Diagrammatically, we will signify that a trivial circle ![]() $C$ in
$C$ in ![]() $\mathcal {C}$ is labelled by
$\mathcal {C}$ is labelled by ![]() $w_-$ by drawing a dot on
$w_-$ by drawing a dot on ![]() $C$, as in Figure 3.
$C$, as in Figure 3.
Suppose that ![]() $\mathcal {C}$ is a standard configuration with
$\mathcal {C}$ is a standard configuration with ![]() $e$ essential circles and
$e$ essential circles and ![]() $t$ trivial circles. Order the trivial circles in some way, and order the essential circles from the innermost to the outermost. The exact ordering of the trivial circles is irrelevant, but it is important to order the essential circles in this way in light of Theorem 2.5 and the asymmetry of the evaluation and coevaluation maps. We have that
$t$ trivial circles. Order the trivial circles in some way, and order the essential circles from the innermost to the outermost. The exact ordering of the trivial circles is irrelevant, but it is important to order the essential circles in this way in light of Theorem 2.5 and the asymmetry of the evaluation and coevaluation maps. We have that
where the tensor products above are understood to be over ![]() $\Bbbk$, and the identification of the value of
$\Bbbk$, and the identification of the value of ![]() $\mathcal {F}_{\mathbb {A}_\mathfrak {q}}$ on
$\mathcal {F}_{\mathbb {A}_\mathfrak {q}}$ on ![]() $e$ standard essential circles with
$e$ standard essential circles with ![]() $V^{\otimes e}$ is the isomorphism from (2.5). The modules
$V^{\otimes e}$ is the isomorphism from (2.5). The modules ![]() $V$ and
$V$ and ![]() $W$ are each bigraded, carrying a quantum grading
$W$ are each bigraded, carrying a quantum grading ![]() $\text {q deg}$ and an annular grading
$\text {q deg}$ and an annular grading ![]() $\text {adeg}$. The degrees of generators are as in (2.2) and (2.3). Algebraically, we will write a standard generator as
$\text {adeg}$. The degrees of generators are as in (2.2) and (2.3). Algebraically, we will write a standard generator as
where each ![]() $a_i, b_j \in \{-, +\}$, the
$a_i, b_j \in \{-, +\}$, the ![]() $v_{a_i}$ label the essential circles, and the
$v_{a_i}$ label the essential circles, and the ![]() $w_{b_j}$ label the trivial circles. We will often shorten the notation to
$w_{b_j}$ label the trivial circles. We will often shorten the notation to ![]() $v_\mathcal {I} \otimes w_\mathcal {J}$, where
$v_\mathcal {I} \otimes w_\mathcal {J}$, where ![]() $\mathcal {I}$ is a sequence of
$\mathcal {I}$ is a sequence of ![]() $\pm$ labelling the essential circles and
$\pm$ labelling the essential circles and ![]() $\mathcal {J}$ is a sequence of
$\mathcal {J}$ is a sequence of ![]() $\pm$ labelling the trivial ones. Note also that each standard generator
$\pm$ labelling the trivial ones. Note also that each standard generator ![]() $x = v_\mathcal {I} \otimes w_\mathcal {J} \in \mathcal {C}$ of a standard configuration
$x = v_\mathcal {I} \otimes w_\mathcal {J} \in \mathcal {C}$ of a standard configuration ![]() $\mathcal {C}$ is the image of
$\mathcal {C}$ is the image of ![]() $v_\mathcal {I}$ under the cobordism
$v_\mathcal {I}$ under the cobordism
which is the identity on ![]() $\mathcal {C}_\textrm {E}$ and a cup cobordism on each trivial circle, with some cups possibly carrying dots as specified by the labels
$\mathcal {C}_\textrm {E}$ and a cup cobordism on each trivial circle, with some cups possibly carrying dots as specified by the labels ![]() $\mathcal {J}$. Diagrammatically, we will use the same convention as in Figure 3.
$\mathcal {J}$. Diagrammatically, we will use the same convention as in Figure 3.
The following lemma concerns general (not necessarily standard) configurations; the argument is similar to the proof of [Reference Beliakova, Putyra and WehrliBPW19, Lemma 6.4].
Lemma 2.6 Let ![]() $\mathcal {C}, \mathcal {C}' \subset \mathbb {A}$ be two isotopic configurations. Let
$\mathcal {C}, \mathcal {C}' \subset \mathbb {A}$ be two isotopic configurations. Let ![]() $\phi$ be an isotopy from
$\phi$ be an isotopy from ![]() $\mathcal {C}$ to
$\mathcal {C}$ to ![]() $\mathcal {C}'$, and denote by
$\mathcal {C}'$, and denote by ![]() $S:\mathcal {C}\to \mathcal {C}'$ the cylindrical cobordism in
$S:\mathcal {C}\to \mathcal {C}'$ the cylindrical cobordism in ![]() $\mathbb {A}\times I$ formed by
$\mathbb {A}\times I$ formed by ![]() $\phi$. Then
$\phi$. Then ![]() $S$ is an isomorphism in
$S$ is an isomorphism in ![]() $\mathcal {BN}_{\mathfrak {q}}(\mathbb {A})$, with
$\mathcal {BN}_{\mathfrak {q}}(\mathbb {A})$, with ![]() $S^{-1} = \mathfrak {q}^k \bar {S}$ for some
$S^{-1} = \mathfrak {q}^k \bar {S}$ for some ![]() $k\in \mathbb {Z}$.
$k\in \mathbb {Z}$.
Proof. Isotopic cobordisms are equal in ![]() $\mathcal {BN}_{\mathfrak {q}}(\mathbb {A})$ if the isotopy between them fixes the membrane. We may therefore assume that the isotopy
$\mathcal {BN}_{\mathfrak {q}}(\mathbb {A})$ if the isotopy between them fixes the membrane. We may therefore assume that the isotopy ![]() $\phi$ is a sequence of the local moves in Figure 11, denoted
$\phi$ is a sequence of the local moves in Figure 11, denoted ![]() $P, P^{-1}, N,$ and
$P, P^{-1}, N,$ and ![]() $N^{-1}$.
$N^{-1}$.

Figure 11. The moves ![]() $P, P^{-1}, N, N^{-1}$.
$P, P^{-1}, N, N^{-1}$.
Let ![]() $p$ denote the number of moves of type
$p$ denote the number of moves of type ![]() $P$ or
$P$ or ![]() $P^{-1}$, let
$P^{-1}$, let ![]() $n$ denote the number of moves of type
$n$ denote the number of moves of type ![]() $N$ or
$N$ or ![]() $N^{-1}$, and set
$N^{-1}$, and set ![]() $k=n-p$. It follows from the relations in Figure 7 that
$k=n-p$. It follows from the relations in Figure 7 that
Lemma 2.7 Let ![]() $\mathcal {C}$ be a standard configuration. Let
$\mathcal {C}$ be a standard configuration. Let ![]() $\phi$ be a component-preserving isotopy from
$\phi$ be a component-preserving isotopy from ![]() $\mathcal {C}$ to itself, with corresponding cobordism
$\mathcal {C}$ to itself, with corresponding cobordism ![]() $S: \mathcal {C} \to \mathcal {C}$. For any standard generator
$S: \mathcal {C} \to \mathcal {C}$. For any standard generator ![]() $x\in \mathcal {C}$,
$x\in \mathcal {C}$, ![]() $\mathfrak {q}^k S(x) = x$ for some
$\mathfrak {q}^k S(x) = x$ for some ![]() $k\in \mathbb {Z}$.
$k\in \mathbb {Z}$.
Proof. As discussed earlier, a standard generator ![]() $x= v_\mathcal {I} \otimes w_\mathcal {J} \in \mathcal {C}$ is the image of
$x= v_\mathcal {I} \otimes w_\mathcal {J} \in \mathcal {C}$ is the image of ![]() $v_\mathcal {I}$ under a cobordism
$v_\mathcal {I}$ under a cobordism
which is the identity on ![]() $\mathcal {C}_\textrm {E}$ and a cup cobordism on all circles in
$\mathcal {C}_\textrm {E}$ and a cup cobordism on all circles in ![]() $\mathcal {C}_\textrm {T}$, with some cups possibly carrying dots as specified by
$\mathcal {C}_\textrm {T}$, with some cups possibly carrying dots as specified by ![]() $\mathcal {J}$. Every component of the cobordism
$\mathcal {J}$. Every component of the cobordism ![]() $S \Sigma _\mathcal {J}$ is either an undotted annulus between essential circles or a possibly dotted disk with trivial boundary. Each disk can be isotoped to a cup cobordism on its trivial boundary circle at the cost of multiplying by a power of
$S \Sigma _\mathcal {J}$ is either an undotted annulus between essential circles or a possibly dotted disk with trivial boundary. Each disk can be isotoped to a cup cobordism on its trivial boundary circle at the cost of multiplying by a power of ![]() $\mathfrak {q}$. Then, at the cost of introducing further powers of
$\mathfrak {q}$. Then, at the cost of introducing further powers of ![]() $\mathfrak {q}$, the remaining annuli may be isotoped to the identity cobordism on
$\mathfrak {q}$, the remaining annuli may be isotoped to the identity cobordism on ![]() $\mathcal {C}_\textrm {E}$ while fixing each cup cobordism. This yields
$\mathcal {C}_\textrm {E}$ while fixing each cup cobordism. This yields ![]() $\mathfrak {q}^k S\Sigma _\mathcal {J} = \Sigma _\mathcal {J}$ for some
$\mathfrak {q}^k S\Sigma _\mathcal {J} = \Sigma _\mathcal {J}$ for some ![]() $k\in \mathbb {Z}$, so
$k\in \mathbb {Z}$, so ![]() $\mathfrak {q}^k S(x) = \mathfrak {q}^k S \Sigma _\mathcal {J}(v_\mathcal {I}) = \Sigma _\mathcal {J}(v_\mathcal {I}) = x$.
$\mathfrak {q}^k S(x) = \mathfrak {q}^k S \Sigma _\mathcal {J}(v_\mathcal {I}) = \Sigma _\mathcal {J}(v_\mathcal {I}) = x$.
Lemma 2.8 Let ![]() $\mathcal {C}$ be a configuration and let
$\mathcal {C}$ be a configuration and let ![]() $\phi _1$,
$\phi _1$, ![]() $\phi _2$ be two isotopies from
$\phi _2$ be two isotopies from ![]() $\mathcal {C}^\circ$ to
$\mathcal {C}^\circ$ to ![]() $\mathcal {C}$ that induce the same correspondence between components. Denote the corresponding cobordisms by
$\mathcal {C}$ that induce the same correspondence between components. Denote the corresponding cobordisms by ![]() $S_1, S_2: \mathcal {C}^\circ \to \mathcal {C}$. If
$S_1, S_2: \mathcal {C}^\circ \to \mathcal {C}$. If ![]() $x\in \mathcal {C}^\circ$ is a standard generator, then
$x\in \mathcal {C}^\circ$ is a standard generator, then ![]() $S_1(x) = \mathfrak {q}^k S_2(x)$ for some
$S_1(x) = \mathfrak {q}^k S_2(x)$ for some ![]() $k\in \mathbb {Z}$.
$k\in \mathbb {Z}$.
Proof. Consider the component-preserving cobordism ![]() $\overline {S_1}S_2: \mathcal {C}^\circ \to \mathcal {C}^\circ$, which is formed by the isotopy
$\overline {S_1}S_2: \mathcal {C}^\circ \to \mathcal {C}^\circ$, which is formed by the isotopy ![]() $\phi _1^{-1} \phi$. By Lemma 2.7, we have
$\phi _1^{-1} \phi$. By Lemma 2.7, we have ![]() $\mathfrak {q}^m \overline {S_1}S_2 (x) = x$ for some
$\mathfrak {q}^m \overline {S_1}S_2 (x) = x$ for some ![]() $m\in \mathbb {Z}$. By Lemma 2.6, we know that
$m\in \mathbb {Z}$. By Lemma 2.6, we know that ![]() $\mathfrak {q}^\ell \overline {S_1} S_1 = \text {id}_{\mathcal {C}}$ for some
$\mathfrak {q}^\ell \overline {S_1} S_1 = \text {id}_{\mathcal {C}}$ for some ![]() $\ell \in \mathbb {Z}$. Then
$\ell \in \mathbb {Z}$. Then
and we obtain
Remark 2.9 Given ![]() $S_1, S_2$ as in Lemma 2.8, in general the power
$S_1, S_2$ as in Lemma 2.8, in general the power ![]() $k$ of
$k$ of ![]() $\mathfrak {q}$ depends on the generator
$\mathfrak {q}$ depends on the generator ![]() $x\in \mathcal {C}^\circ$.
$x\in \mathcal {C}^\circ$.
So far the discussion concerned only generators of standard configurations. Next we consider generators for arbitrary configurations.
Definition 2.3 Fix a configuration ![]() $\mathcal {C}$ and an isotopy from
$\mathcal {C}$ and an isotopy from ![]() $\mathcal {C}^\circ$ to
$\mathcal {C}^\circ$ to ![]() $\mathcal {C}$. Let
$\mathcal {C}$. Let ![]() $S$ denote the resulting cobordism
$S$ denote the resulting cobordism ![]() $\mathcal {C}^\circ \to \mathcal {C}$. The generators of
$\mathcal {C}^\circ \to \mathcal {C}$. The generators of ![]() $\mathcal {F}_{\mathbb {A}_{\mathfrak {q}}}(\mathcal {C})$ corresponding to the cobordism
$\mathcal {F}_{\mathbb {A}_{\mathfrak {q}}}(\mathcal {C})$ corresponding to the cobordism ![]() $S$ are the images of the standard generators of
$S$ are the images of the standard generators of ![]() $\mathcal {C}^\circ$ under
$\mathcal {C}^\circ$ under ![]() $S$. We will also write generators of
$S$. We will also write generators of ![]() $\mathcal {C}$ as
$\mathcal {C}$ as ![]() $v_\mathcal {I} \otimes w_\mathcal {J}$, which is to be understood as the image of the corresponding standard generator of
$v_\mathcal {I} \otimes w_\mathcal {J}$, which is to be understood as the image of the corresponding standard generator of ![]() $\mathcal {C}^\circ$. Note that this image
$\mathcal {C}^\circ$. Note that this image ![]() $v_\mathcal {I}\otimes w_\mathcal {J}$ depends on the choice of isotopy
$v_\mathcal {I}\otimes w_\mathcal {J}$ depends on the choice of isotopy ![]() $\mathcal {C}^\circ \to \mathcal {C}$, which we suppress from the notation.
$\mathcal {C}^\circ \to \mathcal {C}$, which we suppress from the notation.
By Lemma 2.8, these generators of ![]() $\mathcal {C}$ are well defined up to multiplication by a (non-uniform, according to Remark 2.9) power of
$\mathcal {C}$ are well defined up to multiplication by a (non-uniform, according to Remark 2.9) power of ![]() $\mathfrak {q}$, and also a possible re-ordering of the trivial circles in
$\mathfrak {q}$, and also a possible re-ordering of the trivial circles in ![]() $\mathcal {C}^\circ$ which corresponds to a permutation of the indexing set
$\mathcal {C}^\circ$ which corresponds to a permutation of the indexing set ![]() $\mathcal {J}$. We assume throughout that there is a fixed isotopy
$\mathcal {J}$. We assume throughout that there is a fixed isotopy ![]() $\mathcal {C}^\circ \to \mathcal {C}$, which will often not be named. Likewise, an unnamed cobordism
$\mathcal {C}^\circ \to \mathcal {C}$, which will often not be named. Likewise, an unnamed cobordism ![]() $\mathcal {C}\to \mathcal {C}^\circ$ denotes the inverse of
$\mathcal {C}\to \mathcal {C}^\circ$ denotes the inverse of ![]() $\mathcal {C}^\circ \to \mathcal {C}$.
$\mathcal {C}^\circ \to \mathcal {C}$.
As discussed earlier, a standard generator ![]() $x\in \mathcal {C}^\circ$ is the image of the corresponding standard generator of
$x\in \mathcal {C}^\circ$ is the image of the corresponding standard generator of ![]() $\mathcal {C}^\circ _\textrm {E}$ under a cobordism
$\mathcal {C}^\circ _\textrm {E}$ under a cobordism ![]() $\Sigma _\mathcal {J} : \mathcal {C}^\circ _\textrm {E} \to \mathcal {C}^\circ$, where
$\Sigma _\mathcal {J} : \mathcal {C}^\circ _\textrm {E} \to \mathcal {C}^\circ$, where ![]() $\Sigma _\mathcal {J}$ is the identity on
$\Sigma _\mathcal {J}$ is the identity on ![]() $\mathcal {C}^\circ _\textrm {E}$ and a cup cobordism on each circle in
$\mathcal {C}^\circ _\textrm {E}$ and a cup cobordism on each circle in ![]() $\mathcal {C}^\circ _\textrm {T}$, with some cups possibly carrying dots. Up to a power of
$\mathcal {C}^\circ _\textrm {T}$, with some cups possibly carrying dots. Up to a power of ![]() $\mathfrak {q}$, the cobordism
$\mathfrak {q}$, the cobordism ![]() $S\Sigma _\mathcal {J}$ represents a cobordism which traces out an isotopy
$S\Sigma _\mathcal {J}$ represents a cobordism which traces out an isotopy ![]() $\mathcal {C}^\circ _\textrm {E} \to \mathcal {C}_\textrm {E}$ and is a cup cobordism on each circle in
$\mathcal {C}^\circ _\textrm {E} \to \mathcal {C}_\textrm {E}$ and is a cup cobordism on each circle in ![]() $\mathcal {C}_\textrm {T}$. Then each standard generator of
$\mathcal {C}_\textrm {T}$. Then each standard generator of ![]() $\mathcal {C}$ can also be realized as the image of a cup cobordism on each trivial circle and an isotopy on the essential circles.
$\mathcal {C}$ can also be realized as the image of a cup cobordism on each trivial circle and an isotopy on the essential circles.
Note also that we do not make any assumptions about how these isotopies are picked for different configurations within a single cube of resolutions.
2.4 Computation of the saddle maps
In this subsection, we compute saddle maps in quantum annular homology using the relations in ![]() $\mathcal {BBN}_\mathfrak {q}(\mathbb {A})$ and Theorem 2.5. These results will be used in the formulation of the quantum annular Burnside functor in § 4.
$\mathcal {BBN}_\mathfrak {q}(\mathbb {A})$ and Theorem 2.5. These results will be used in the formulation of the quantum annular Burnside functor in § 4.
We start with several examples; the general case is treated in Proposition 2.16. Saddle maps for various types of configurations (where intersections with the seam are minimal) are summarized in Figure 12. In the first two examples the calculation relies on the Boerner relation and relations satisfied by cobordisms in the Bar-Natan category. Specifically, one uses the neck-cutting relation and delooping; cf. [Reference Beliakova, Putyra and WehrliBPW19, Proposition 5.3]. (Note that delooping makes sense only for trivial, and not for essential, circles in the annulus.)

Figure 12. Surgery formulas in quantum annular Khovanov homology for curves with minimal intersections with the seam.
To analyze our saddle maps, we will use the language of surgery arcs, as in [Reference Lipshitz and SarkarLS14a, § 2]. For a configuration ![]() $\mathcal {C}$, a surgery arc is an interval embedded in
$\mathcal {C}$, a surgery arc is an interval embedded in ![]() $\mathbb {A}$ whose endpoints lie on
$\mathbb {A}$ whose endpoints lie on ![]() $\mathcal {C}$ and whose interior is disjoint from
$\mathcal {C}$ and whose interior is disjoint from ![]() $\mathcal {C}$. In the construction of quantum annular homology, link diagrams are assumed transverse to
$\mathcal {C}$. In the construction of quantum annular homology, link diagrams are assumed transverse to ![]() $\mu$ and all crossings are away from
$\mu$ and all crossings are away from ![]() $\mu$. In light of this, we will assume that surgery arcs are disjoint from the seam. For a configuration
$\mu$. In light of this, we will assume that surgery arcs are disjoint from the seam. For a configuration ![]() $\mathcal {C}$ with a surgery arc, let
$\mathcal {C}$ with a surgery arc, let ![]() $s(\mathcal {C})$ denote the configuration obtained by surgery on the arc. There is a saddle cobordism
$s(\mathcal {C})$ denote the configuration obtained by surgery on the arc. There is a saddle cobordism ![]() $\mathcal {C}\to s(\mathcal {C})$, which is well defined in
$\mathcal {C}\to s(\mathcal {C})$, which is well defined in ![]() $\mathcal {BN}_{\mathfrak {q}}(\mathbb {A})$. In terms of the cube of resolutions of a link diagram, a surgery arc may be placed at a
$\mathcal {BN}_{\mathfrak {q}}(\mathbb {A})$. In terms of the cube of resolutions of a link diagram, a surgery arc may be placed at a ![]() $0$-smoothing to indicate that there will be a saddle cobordism at that smoothing.
$0$-smoothing to indicate that there will be a saddle cobordism at that smoothing.
Example 2.10 For the saddle

between standard configurations, we have the following formulas:

Algebraically, this is written as
These can be deduced from Boerner's relation (Figure 5) and the fact that the two standard generators of a trivial circle are picked out by an undotted cup and a once-dotted cup.
Example 2.11 For the saddle

we have the formulas

which, algebraically, can be written as
This can be deduced by cutting the neck along the trivial circle, which splits off as a result of the saddle, and then applying Boerner's relation.
The next two examples are also discussed in [Reference Beliakova, Putyra and WehrliBPW19, § 6.4].
Example 2.12 Let ![]() $S$ denote the following saddle:
$S$ denote the following saddle:

Let ![]() $C$ denote the trivial circle on the right-hand side above. Since
$C$ denote the trivial circle on the right-hand side above. Since ![]() $C$ is not standard, we need to pick an isotopy to specify its generators. For the sake of calculation, we pick the following isotopy:
$C$ is not standard, we need to pick an isotopy to specify its generators. For the sake of calculation, we pick the following isotopy:

which specifies generators, represented diagrammatically, as

These generators are the images of ![]() $1\in \Bbbk$ under the undotted and dotted cup cobordisms on
$1\in \Bbbk$ under the undotted and dotted cup cobordisms on ![]() $C$, respectively. Since the cup cobordism on
$C$, respectively. Since the cup cobordism on ![]() $C$ intersects the membrane, the placement of the dot is relevant, and the diagram shows where the dot is placed.
$C$ intersects the membrane, the placement of the dot is relevant, and the diagram shows where the dot is placed.
Now let ![]() $\Sigma$ denote the undotted cap cobordism on
$\Sigma$ denote the undotted cap cobordism on ![]() $C$, and let
$C$, and let ![]() $\Sigma '$ denote the dotted cap cobordism on
$\Sigma '$ denote the dotted cap cobordism on ![]() $C$, with the dot placed as in the generator
$C$, with the dot placed as in the generator ![]() $w_-$. Using the relations in
$w_-$. Using the relations in ![]() $\mathcal {BN}_{\mathfrak {q}}(\mathbb {A})$, we obtain
$\mathcal {BN}_{\mathfrak {q}}(\mathbb {A})$, we obtain
 \begin{align*} &\ \, \Sigma(w_+) = 0, \qquad \ \Sigma(w_-) = \mathfrak{q}^{{-}1}, \\ & \ \Sigma'(w_+) = \mathfrak{q}^{{-}1}, \quad \Sigma'(w_-) = 0.\hphantom{00} \end{align*}
\begin{align*} &\ \, \Sigma(w_+) = 0, \qquad \ \Sigma(w_-) = \mathfrak{q}^{{-}1}, \\ & \ \Sigma'(w_+) = \mathfrak{q}^{{-}1}, \quad \Sigma'(w_-) = 0.\hphantom{00} \end{align*}
Composing with the saddle ![]() $S$, observe that
$S$, observe that ![]() $\Sigma S = S^1\times \cap$ in
$\Sigma S = S^1\times \cap$ in ![]() $\mathcal {BBN}_\mathfrak {q}(\mathbb {A})$, and that
$\mathcal {BBN}_\mathfrak {q}(\mathbb {A})$, and that ![]() $\Sigma 'S = 0$ by Boerner's relation. We are now in a position to write down formulas for
$\Sigma 'S = 0$ by Boerner's relation. We are now in a position to write down formulas for ![]() $S$. For example, we may write
$S$. For example, we may write
for some ![]() $\alpha , \beta \in \Bbbk$. Applying
$\alpha , \beta \in \Bbbk$. Applying ![]() $\Sigma$ to the above equality, we obtain
$\Sigma$ to the above equality, we obtain
Theorem 2.5 tells us that ![]() $\Sigma S(v_+ \otimes v_-) = ev(v_+ \otimes v_-) = \mathfrak {q}$, so that
$\Sigma S(v_+ \otimes v_-) = ev(v_+ \otimes v_-) = \mathfrak {q}$, so that ![]() $\beta = \mathfrak {q}^2$. By applying
$\beta = \mathfrak {q}^2$. By applying ![]() $\Sigma '$ to both sides of 2.7, we obtain
$\Sigma '$ to both sides of 2.7, we obtain ![]() $\alpha = 0$. A similar argument for the remaining generators yields the full table of formulas for
$\alpha = 0$. A similar argument for the remaining generators yields the full table of formulas for ![]() $S$:
$S$:

Equivalently,
 \begin{align*} S(v_+\otimes v_-) & = \mathfrak{q}^2 w_-, \quad S(v_+\otimes v_+) = 0, \\ S(v_-\otimes v_+) & = \mathfrak{q} w_-, \quad\ S(v_-\otimes v_-) = 0. \end{align*}
\begin{align*} S(v_+\otimes v_-) & = \mathfrak{q}^2 w_-, \quad S(v_+\otimes v_+) = 0, \\ S(v_-\otimes v_+) & = \mathfrak{q} w_-, \quad\ S(v_-\otimes v_-) = 0. \end{align*}Example 2.13 Let ![]() $S$ denote the following saddle:
$S$ denote the following saddle:

Pick generators ![]() $w_+$ and
$w_+$ and ![]() $w_-$ for the left-hand trivial circle
$w_-$ for the left-hand trivial circle ![]() $C$ as in Example 2.12. Let
$C$ as in Example 2.12. Let ![]() $\Sigma$ and
$\Sigma$ and ![]() $\Sigma '$ be the undotted and dotted cups on
$\Sigma '$ be the undotted and dotted cups on ![]() $C$, so that
$C$, so that ![]() $w_+ = \Sigma (1)$ and
$w_+ = \Sigma (1)$ and ![]() $w_- = \Sigma '(1)$. Observe that
$w_- = \Sigma '(1)$. Observe that ![]() $S \Sigma ' = 0$ by Boerner's relation, so
$S \Sigma ' = 0$ by Boerner's relation, so
Finally, note that ![]() $S \Sigma = S^1 \times \cup$. By Theorem 2.5, we obtain
$S \Sigma = S^1 \times \cup$. By Theorem 2.5, we obtain
Diagrammatically, the formulas for ![]() $S$ are
$S$ are

Saddle maps for various topological types of configurations, including the result of calculations in Examples 2.10–2.13, are summarized in Figure 12. The next example illustrates a calculation of the saddle map in a case of higher multiplicity of intersections between the configuration and the seam.
Example 2.14 Here is a slightly more involved version of Example 2.12. Consider the configurations ![]() $\mathcal {C}_1$ and
$\mathcal {C}_1$ and ![]() $\mathcal {C}_2$, and the saddle
$\mathcal {C}_2$, and the saddle ![]() $S: \mathcal {C}_1 \to \mathcal {C}_2$ as shown in Figure 13.
$S: \mathcal {C}_1 \to \mathcal {C}_2$ as shown in Figure 13.

Figure 13. The saddle ![]() $S\colon {\mathcal C}_1\to {\mathcal C}_2$ in Example 2.14.
$S\colon {\mathcal C}_1\to {\mathcal C}_2$ in Example 2.14.
Fix generators for ![]() $\mathcal {C}_1$ and
$\mathcal {C}_1$ and ![]() $\mathcal {C}_2$ using the isotopies
$\mathcal {C}_2$ using the isotopies ![]() $S_1$ and
$S_1$ and ![]() $S_2$ depicted in Figures 14 and 15. Since generators of
$S_2$ depicted in Figures 14 and 15. Since generators of ![]() $\mathcal {C}_2$ are the images of the standard generators of
$\mathcal {C}_2$ are the images of the standard generators of ![]() $\mathcal {C}_2^\circ$ under the isomorphism
$\mathcal {C}_2^\circ$ under the isomorphism ![]() $S_2: \mathcal {C}_2^\circ \to \mathcal {C}_2$, it suffices to write down formulas for the composition
$S_2: \mathcal {C}_2^\circ \to \mathcal {C}_2$, it suffices to write down formulas for the composition
Note that ![]() $S_2^{-1} = \mathfrak {q}^3\overline{S_2}$ (see Lemma 2.6). Let
$S_2^{-1} = \mathfrak {q}^3\overline{S_2}$ (see Lemma 2.6). Let ![]() $\Phi$ denote the composition (2.8).
$\Phi$ denote the composition (2.8).

Figure 14. An isotopy ![]() $S_1: \mathcal {C}_1^\circ \to \mathcal {C}_1$.
$S_1: \mathcal {C}_1^\circ \to \mathcal {C}_1$.

Figure 15. An isotopy ![]() $S_2: \mathcal {C}_2^\circ \to \mathcal {C}_2$.
$S_2: \mathcal {C}_2^\circ \to \mathcal {C}_2$.
Let ![]() $\Sigma$ and
$\Sigma$ and ![]() $\Sigma '$ be the undotted and dotted cap cobordisms, respectively, on the trivial circle
$\Sigma '$ be the undotted and dotted cap cobordisms, respectively, on the trivial circle ![]() $\mathcal {C}_2^\circ$. Note that
$\mathcal {C}_2^\circ$. Note that ![]() $\Sigma '\Phi = 0$ by Boerner's relation. Applying a trace move from Figure 7 to the part of the cobordism depicted in (
$\Sigma '\Phi = 0$ by Boerner's relation. Applying a trace move from Figure 7 to the part of the cobordism depicted in (
), we see that
is equal to ![]() $\mathfrak {q}^{-1}(S^1\times \cap )$, so that
$\mathfrak {q}^{-1}(S^1\times \cap )$, so that
Arguing as in Example 2.12, we obtain
 \begin{align*} & S(v_+\otimes v_-) = \mathfrak{q}^3w_-, \quad S(v_+\otimes v_+) = 0, \\ & S(v_-\otimes v_+) = \mathfrak{q}^2 w_-, \quad S(v_-\otimes v_-) = 0. \end{align*}
\begin{align*} & S(v_+\otimes v_-) = \mathfrak{q}^3w_-, \quad S(v_+\otimes v_+) = 0, \\ & S(v_-\otimes v_+) = \mathfrak{q}^2 w_-, \quad S(v_-\otimes v_-) = 0. \end{align*}
Remark 2.15 Here is a slightly different way to finish the computation in Example 2.14, which will be used in Proposition 2.16. In the morphism ![]() $\Phi : \mathcal {C}_1^\circ \to \mathcal {C}_2^\circ$, we may cut the neck along a small push-off of the trivial circle
$\Phi : \mathcal {C}_1^\circ \to \mathcal {C}_2^\circ$, we may cut the neck along a small push-off of the trivial circle ![]() $\mathcal {C}_2^\circ$ to write
$\mathcal {C}_2^\circ$ to write ![]() $\Phi$ as a sum of two dotted cobordisms. One of the summands is
$\Phi$ as a sum of two dotted cobordisms. One of the summands is ![]() $0$ by Boerner's relation, and the other is isotopic to a disjoint union of
$0$ by Boerner's relation, and the other is isotopic to a disjoint union of
and a dotted cup cobordism on ![]() $\mathcal {C}_2^\circ$, which is denoted
$\mathcal {C}_2^\circ$, which is denoted ![]() $\overline {\Sigma '}$ using the notation of Example 2.14. Then, using the trace relations in
$\overline {\Sigma '}$ using the notation of Example 2.14. Then, using the trace relations in ![]() $\mathcal {BN}_{\mathfrak {q}}(\mathbb {A})$, we see that
$\mathcal {BN}_{\mathfrak {q}}(\mathbb {A})$, we see that
and the formulas in Example 2.14 follow.
Example 2.14 shows that there is considerable complexity in computing the saddle map when curves have multiple intersections with the seam. The next proposition extends Examples 2.12–2.14 to the case of arbitrary configurations. It will be important for the analysis in § 2.5. Recall the numbering of circles discussed in the paragraph preceding (2.6).
Proposition 2.16 Let ![]() $\mathcal {C}$ be a configuration with a surgery arc
$\mathcal {C}$ be a configuration with a surgery arc ![]() $A$. Let
$A$. Let ![]() $S: \mathcal {C} \to s(\mathcal {C})$ denote the saddle.
$S: \mathcal {C} \to s(\mathcal {C})$ denote the saddle.
(1) Suppose that both endpoints of ![]() $A$ are on a trivial circle
$A$ are on a trivial circle ![]() $C$, and that surgery along
$C$, and that surgery along ![]() $A$ splits
$A$ splits ![]() $C$ into two essential circles. Assume that
$C$ into two essential circles. Assume that ![]() $C$ is first in the ordering on trivial circles of
$C$ is first in the ordering on trivial circles of ![]() $\mathcal {C}$, and it splits into the
$\mathcal {C}$, and it splits into the ![]() $i$th and
$i$th and ![]() $(i+1)$th essential circles in
$(i+1)$th essential circles in ![]() $s(\mathcal {C})$. Let
$s(\mathcal {C})$. Let ![]() $x= v_{\mathcal {I}'} \otimes v_{\mathcal {I}''} \otimes w_+ \otimes w_\mathcal {J}$ be a generator of
$x= v_{\mathcal {I}'} \otimes v_{\mathcal {I}''} \otimes w_+ \otimes w_\mathcal {J}$ be a generator of ![]() $\mathcal {C}$ in which
$\mathcal {C}$ in which ![]() $C$ is undotted, where
$C$ is undotted, where ![]() $\mathcal {I}'$ labels the first
$\mathcal {I}'$ labels the first ![]() $i-1$ essential circles. Then
$i-1$ essential circles. Then
for some ![]() $a\in \mathbb {Z}$.
$a\in \mathbb {Z}$.
(2) Suppose that the endpoints of ![]() $A$ are on the
$A$ are on the ![]() $i$th and
$i$th and ![]() $(i+1)$th essential circles of
$(i+1)$th essential circles of ![]() $\mathcal {C}$. Consider the generators
$\mathcal {C}$. Consider the generators
of ![]() $\mathcal {C}$, where
$\mathcal {C}$, where ![]() $\mathcal {I}'$ labels the first
$\mathcal {I}'$ labels the first ![]() $i-1$ essential circles. Then
$i-1$ essential circles. Then
 \begin{align*} S(y_1) &= \mathfrak{q}^{b+1} v_{\mathcal{I}'} \otimes v_{\mathcal{I}''} \otimes w_-\otimes w_\mathcal{J}, \\ S(y_2) &= \mathfrak{q}^b v_{\mathcal{I}'} \otimes v_{\mathcal{I}''} \otimes w_-\otimes w_\mathcal{J} \end{align*}
\begin{align*} S(y_1) &= \mathfrak{q}^{b+1} v_{\mathcal{I}'} \otimes v_{\mathcal{I}''} \otimes w_-\otimes w_\mathcal{J}, \\ S(y_2) &= \mathfrak{q}^b v_{\mathcal{I}'} \otimes v_{\mathcal{I}''} \otimes w_-\otimes w_\mathcal{J} \end{align*}
for some ![]() $b\in \mathbb {Z}$.
$b\in \mathbb {Z}$.
Proof. For both ![]() $(1)$ and
$(1)$ and ![]() $(2)$, it is enough to show that the result holds after applying
$(2)$, it is enough to show that the result holds after applying ![]() $s(\mathcal {C}) \to s(\mathcal {C})^\circ$.
$s(\mathcal {C}) \to s(\mathcal {C})^\circ$.
(1). The generator ![]() $x$ is the image of
$x$ is the image of ![]() $v_{\mathcal {I}'}\otimes v_{\mathcal {I}''}$ under the composition
$v_{\mathcal {I}'}\otimes v_{\mathcal {I}''}$ under the composition ![]() $\mathcal {C}_\textrm {E}^\circ \xrightarrow {\Sigma _\mathcal {J}} \mathcal {C}^\circ \to \mathcal {C}$, where
$\mathcal {C}_\textrm {E}^\circ \xrightarrow {\Sigma _\mathcal {J}} \mathcal {C}^\circ \to \mathcal {C}$, where ![]() $\Sigma _\mathcal {J}$ is a cup cobordism on trivial circles in
$\Sigma _\mathcal {J}$ is a cup cobordism on trivial circles in ![]() $\mathcal {C}^\circ$, with the cups dotted according to
$\mathcal {C}^\circ$, with the cups dotted according to ![]() $\mathcal {J}$. Note that the cup on
$\mathcal {J}$. Note that the cup on ![]() $C$ is undotted. Let
$C$ is undotted. Let ![]() $\Psi$ denote the composition
$\Psi$ denote the composition
The cobordism ![]() $\Psi$ is isotopic to a disjoint union of
$\Psi$ is isotopic to a disjoint union of
and cup cobordisms on each trivial circle in ![]() $s(\mathcal {C})^\circ$, with dots placed according to
$s(\mathcal {C})^\circ$, with dots placed according to ![]() $\mathcal {J}$. By Theorem 2.5, the cobordism
$\mathcal {J}$. By Theorem 2.5, the cobordism ![]() $(*)$ induces the map
$(*)$ induces the map
and the result follows.
(2). The generators ![]() $y_1$ and
$y_1$ and ![]() $y_2$ are the images of
$y_2$ are the images of ![]() $v_{\mathcal {I}'} \otimes v_+ \otimes v_-\otimes v_{\mathcal {I}''}$ and
$v_{\mathcal {I}'} \otimes v_+ \otimes v_-\otimes v_{\mathcal {I}''}$ and ![]() $v_{\mathcal {I}'} \otimes v_- \otimes v_+ \otimes v_{\mathcal {I}''}$, respectively, under
$v_{\mathcal {I}'} \otimes v_- \otimes v_+ \otimes v_{\mathcal {I}''}$, respectively, under
where ![]() $\Sigma _\mathcal {J}$ is a cup cobordism on trivial circles with dots placed according to
$\Sigma _\mathcal {J}$ is a cup cobordism on trivial circles with dots placed according to ![]() $\mathcal {J}$. Let
$\mathcal {J}$. Let ![]() $\Phi$ denote the composition
$\Phi$ denote the composition
Let ![]() $C\in s(\mathcal {C})$ denote the trivial circle obtained by surgery along
$C\in s(\mathcal {C})$ denote the trivial circle obtained by surgery along ![]() $A$ and let
$A$ and let ![]() $C'\in s(\mathcal {C})^\circ$ denote the corresponding circle. In the cobordism
$C'\in s(\mathcal {C})^\circ$ denote the corresponding circle. In the cobordism ![]() $\Phi$, we may cut the neck along
$\Phi$, we may cut the neck along ![]() $C'$ to write
$C'$ to write ![]() $\Phi$ as a sum of two cobordisms. One of the summands is
$\Phi$ as a sum of two cobordisms. One of the summands is ![]() $0$ by Boerner's relation, and the other is isotopic to the disjoint union of
$0$ by Boerner's relation, and the other is isotopic to the disjoint union of
and cup cobordisms on each trivial circle. Observe also that the cup cobordism on ![]() $C'$ is dotted. Finally, Theorem 2.5 says that the cobordism
$C'$ is dotted. Finally, Theorem 2.5 says that the cobordism ![]() $(**)$ induces the map
$(**)$ induces the map
and the result follows.
We end this subsection with a discussion about recovering classical annular homology. Consider the map ![]() $\Bbbk \to \mathbb {Z}$ which is the identity on
$\Bbbk \to \mathbb {Z}$ which is the identity on ![]() $\mathbb {Z} \subset \Bbbk$ and sends
$\mathbb {Z} \subset \Bbbk$ and sends ![]() $\mathfrak {q}$ to
$\mathfrak {q}$ to ![]() $1$. It induces a functor
$1$. It induces a functor ![]() $(-) \otimes _{\Bbbk } \mathbb {Z} : \text {Mod}(\Bbbk ) \to \text {Mod}(\mathbb {Z})$. Thus, one can consider the composition
$(-) \otimes _{\Bbbk } \mathbb {Z} : \text {Mod}(\Bbbk ) \to \text {Mod}(\mathbb {Z})$. Thus, one can consider the composition
which we denote ![]() $\mathcal {F}_{\mathbb {A}_{\mathfrak {q}}} \otimes _{\Bbbk } \mathbb {Z}$. Tensoring with
$\mathcal {F}_{\mathbb {A}_{\mathfrak {q}}} \otimes _{\Bbbk } \mathbb {Z}$. Tensoring with ![]() $\mathbb {Z}$ forgets the action of
$\mathbb {Z}$ forgets the action of ![]() $\mathfrak {q}$, in the sense that isotopic cobordisms induce equal maps under
$\mathfrak {q}$, in the sense that isotopic cobordisms induce equal maps under ![]() $\mathcal {F}_{\mathbb {A}_{\mathfrak {q}}} \otimes _{\Bbbk } \mathbb {Z}$ even when the isotopy is not required to fix the seam. Let
$\mathcal {F}_{\mathbb {A}_{\mathfrak {q}}} \otimes _{\Bbbk } \mathbb {Z}$ even when the isotopy is not required to fix the seam. Let ![]() $\mathcal {C}$ be a configuration with
$\mathcal {C}$ be a configuration with ![]() $e$ essential and
$e$ essential and ![]() $t$ trivial circles. By Lemma 2.8, there is a canonical isomorphism
$t$ trivial circles. By Lemma 2.8, there is a canonical isomorphism
obtained by picking an isotopy ![]() $\mathcal {C}^\circ \to \mathcal {C}$. It is implicit in [Reference Beliakova, Putyra and WehrliBPW19] that
$\mathcal {C}^\circ \to \mathcal {C}$. It is implicit in [Reference Beliakova, Putyra and WehrliBPW19] that ![]() $\mathcal {F}_{\mathbb {A}_{\mathfrak {q}}} \otimes _{\Bbbk } \mathbb {Z}$ is the classical annular functor
$\mathcal {F}_{\mathbb {A}_{\mathfrak {q}}} \otimes _{\Bbbk } \mathbb {Z}$ is the classical annular functor ![]() $\mathcal {F}_\mathbb {A}$; indeed, this is straightforward to check using the relations in
$\mathcal {F}_\mathbb {A}$; indeed, this is straightforward to check using the relations in ![]() $\mathcal {BBN}_\mathfrak {q}(\mathbb {A})$ and Theorem 2.5 as in the proof of Proposition 2.16.
$\mathcal {BBN}_\mathfrak {q}(\mathbb {A})$ and Theorem 2.5 as in the proof of Proposition 2.16.
Lemma 2.17 Let ![]() $\mathcal {C}$ be a configuration with a single surgery arc and let
$\mathcal {C}$ be a configuration with a single surgery arc and let ![]() $S: \mathcal {C} \to s(\mathcal {C})$ denote the saddle. Let
$S: \mathcal {C} \to s(\mathcal {C})$ denote the saddle. Let ![]() $x\in \mathcal {C}$ be a generator. Then
$x\in \mathcal {C}$ be a generator. Then
where the sum is over generators of ![]() $s(\mathcal {C})$ and each
$s(\mathcal {C})$ and each ![]() $\varepsilon _y$ is either
$\varepsilon _y$ is either ![]() $0$ or a power of
$0$ or a power of ![]() $\mathfrak {q}$. Moreover,
$\mathfrak {q}$. Moreover, ![]() $\varepsilon _y \neq 0$ if and only if
$\varepsilon _y \neq 0$ if and only if ![]() $y$ appears in
$y$ appears in ![]() $\mathcal {F}_{\mathbb {A}}(S)(x)$, where
$\mathcal {F}_{\mathbb {A}}(S)(x)$, where ![]() $\mathcal {F}_\mathbb {A}$ is the classical (unquantized) annular TQFT.
$\mathcal {F}_\mathbb {A}$ is the classical (unquantized) annular TQFT.
Proof. There are six types of saddles to check, corresponding to merges and splits between various combinations of essential and trivial circles as in Figure 4. The first part of the lemma was verified for two of these types of saddles in Proposition 2.16. It is straightforward to verify the lemma for the other four using similar arguments. The second part follows from the discussion preceding the lemma.
2.5 Ladybug configurations
In this subsection, we analyze the ladybug configuration (see [Reference Lipshitz and SarkarLS14a, Definition 5.6]; see also [Reference Lipshitz and SarkarLS14a, Figure 5.1]). Examining ladybug configurations is crucial in the construction of Khovanov homotopy types in various contexts. We start with a discussion of ladybug configurations in classical annular homology. We will then examine a particular type of ladybug configuration in quantum annular homology, and we will indicate how the analysis differs from that in classical annular homology.
We recall the notion of a ladybug configuration. A circle ![]() $C\subset \mathbb {A}$ with two surgery arcs forms a ladybug configuration if the endpoints of the two arcs alternate around
$C\subset \mathbb {A}$ with two surgery arcs forms a ladybug configuration if the endpoints of the two arcs alternate around ![]() $C$. We will say that a configuration
$C$. We will say that a configuration ![]() $\mathcal {C}$ with surgery arcs has a ladybug configuration if a circle
$\mathcal {C}$ with surgery arcs has a ladybug configuration if a circle ![]() $C$ in
$C$ in ![]() $\mathcal {C}$ and two of the surgery arcs form a ladybug configuration.
$\mathcal {C}$ and two of the surgery arcs form a ladybug configuration.
First, consider ladybug configurations in classical annular homology. Let ![]() $C\subset \mathbb {A}$ be a circle carrying two surgery arcs
$C\subset \mathbb {A}$ be a circle carrying two surgery arcs ![]() $A_1$ and
$A_1$ and ![]() $A_2$ which form a ladybug configuration. Figure 16 illustrates the three possibilities in the annulus.
$A_2$ which form a ladybug configuration. Figure 16 illustrates the three possibilities in the annulus.

Figure 16. Three ladybug configurations in the annulus.
For ![]() $i=1,2$, let
$i=1,2$, let ![]() $\mathcal {C}_i$ denote the configuration obtained by performing surgery along
$\mathcal {C}_i$ denote the configuration obtained by performing surgery along ![]() $A_i$, and let
$A_i$, and let ![]() $d_i : \mathcal {F}_\mathbb {A}(C) \to \mathcal {F}_\mathbb {A}(\mathcal {C}_i)$ denote the maps assigned to the saddles in classical annular Khovanov homology. Let
$d_i : \mathcal {F}_\mathbb {A}(C) \to \mathcal {F}_\mathbb {A}(\mathcal {C}_i)$ denote the maps assigned to the saddles in classical annular Khovanov homology. Let ![]() $\mathcal {C}'$ denote the final configuration, obtained by performing surgery on
$\mathcal {C}'$ denote the final configuration, obtained by performing surgery on ![]() $C$ along both
$C$ along both ![]() $A_1$ and
$A_1$ and ![]() $A_2$. When
$A_2$. When ![]() $C$ is essential, as in Figure 16(a), composing two saddle maps yields
$C$ is essential, as in Figure 16(a), composing two saddle maps yields ![]() $0$ (see the formulas in Figure 4). Now consider the cases where
$0$ (see the formulas in Figure 4). Now consider the cases where ![]() $C$ is trivial, as in Figure 16(b) and 16(c). The dotted generator
$C$ is trivial, as in Figure 16(b) and 16(c). The dotted generator ![]() $w_-$ is sent to
$w_-$ is sent to ![]() $0$ by the composition of two saddle maps. On the other hand, the two summands appearing in each of
$0$ by the composition of two saddle maps. On the other hand, the two summands appearing in each of ![]() $d_1(w_+)$ and
$d_1(w_+)$ and ![]() $d_2(w_+)$ are mapped to the same element in the final configuration
$d_2(w_+)$ are mapped to the same element in the final configuration ![]() $\mathcal {C}'$. The case of Figure 16(c) is illustrated in Figure 17.
$\mathcal {C}'$. The case of Figure 16(c) is illustrated in Figure 17.

Figure 17. The analysis in the case of Figure 16(c).
When constructing stable homotopy refinements in this framework, it is important to have a bijection between these intermediate generators which appear in ![]() $d_1(w_+)$ and
$d_1(w_+)$ and ![]() $d_2(w_+)$, such that these bijections are coherent, in an appropriate sense, within higher dimensional cubes (cf. § 3.2 below). The bijections are the ladybug matchings defined in [Reference Lipshitz and SarkarLS14a, § 5.4].
$d_2(w_+)$, such that these bijections are coherent, in an appropriate sense, within higher dimensional cubes (cf. § 3.2 below). The bijections are the ladybug matchings defined in [Reference Lipshitz and SarkarLS14a, § 5.4].
In the case of Figure 16(b), the annulus and seam play no role, and the ladybug matching from [Reference Lipshitz and SarkarLS14a] can be used without significant alteration for both classical and quantum annular homology. The remainder of this subsection examines the ladybug configuration of the type in Figure 16(c) in quantum annular homology.
Let ![]() $\mathcal {C}$ be a configuration with two surgery arcs
$\mathcal {C}$ be a configuration with two surgery arcs ![]() $A_\textrm {T}$ and
$A_\textrm {T}$ and ![]() $A_\textrm {E}$, both having endpoints on a trivial circle
$A_\textrm {E}$, both having endpoints on a trivial circle ![]() $C$ in
$C$ in ![]() $\mathcal {C}$. Suppose also that surgery along
$\mathcal {C}$. Suppose also that surgery along ![]() $A_\textrm {T}$ splits
$A_\textrm {T}$ splits ![]() $C$ into two trivial circles and surgery along
$C$ into two trivial circles and surgery along ![]() $A_\textrm {E}$ splits
$A_\textrm {E}$ splits ![]() $C$ into two essential circles; cf. Figure 18. Let
$C$ into two essential circles; cf. Figure 18. Let ![]() $s_\textrm {T}(\mathcal {C})$ and
$s_\textrm {T}(\mathcal {C})$ and ![]() $s_\textrm {E}(\mathcal {C})$ denote the configurations obtained by surgery along
$s_\textrm {E}(\mathcal {C})$ denote the configurations obtained by surgery along ![]() $A_\textrm {T}$ and
$A_\textrm {T}$ and ![]() $A_\textrm {E}$, respectively. Let
$A_\textrm {E}$, respectively. Let ![]() $\mathcal {C}'$ denote the final configuration, obtained by surgery along both arcs. Let
$\mathcal {C}'$ denote the final configuration, obtained by surgery along both arcs. Let ![]() $C'\in \mathcal {C}'$ denote the circle obtained by both surgeries. We have the following commutative square.
$C'\in \mathcal {C}'$ denote the circle obtained by both surgeries. We have the following commutative square.

Figure 18 exhibits the specific instance of this set-up corresponding directly to Figure 16(c), but there are many such cases depending on how ![]() $C$ intersects the seam. As usual, we will not distinguish between cobordisms and their induced maps. We assume that
$C$ intersects the seam. As usual, we will not distinguish between cobordisms and their induced maps. We assume that ![]() $C$ occurs first in the ordering on trivial circles in
$C$ occurs first in the ordering on trivial circles in ![]() $\mathcal {C}$. Surgery along
$\mathcal {C}$. Surgery along ![]() $A_\textrm {T}$ splits
$A_\textrm {T}$ splits ![]() $C$ into two trivial circles in
$C$ into two trivial circles in ![]() $s_\textrm {T}(\mathcal {C})$, which we assume are the first two trivial circles in
$s_\textrm {T}(\mathcal {C})$, which we assume are the first two trivial circles in ![]() $s_\textrm {T}(\mathcal {C})$. Finally, we order these first two circles as follows. Orient the arc
$s_\textrm {T}(\mathcal {C})$. Finally, we order these first two circles as follows. Orient the arc ![]() $A_\textrm {T}$ such that it points from the outer essential circle in
$A_\textrm {T}$ such that it points from the outer essential circle in ![]() $s_\textrm {E}(\mathcal {C})$ to the inner one. Declare that the first circle
$s_\textrm {E}(\mathcal {C})$ to the inner one. Declare that the first circle ![]() $C_1$ is to the left of
$C_1$ is to the left of ![]() $A_\textrm {T}$ and the second
$A_\textrm {T}$ and the second ![]() $C_2$ is to the right of
$C_2$ is to the right of ![]() $A_\textrm {T}$. Our ordering convention is illustrated in Figure 19.
$A_\textrm {T}$. Our ordering convention is illustrated in Figure 19.

Figure 18. Further analysis in the case of Figure 16(c).

Figure 19. Ordering convention on ![]() $C_1$ and
$C_1$ and ![]() $C_2$.
$C_2$.
Let ![]() $x= v_\mathcal {I} \otimes w_+ \otimes w_\mathcal {J} \in \mathcal {C}$ be a generator in which
$x= v_\mathcal {I} \otimes w_+ \otimes w_\mathcal {J} \in \mathcal {C}$ be a generator in which ![]() $C$ is undotted. By Lemma 2.17, we obtain
$C$ is undotted. By Lemma 2.17, we obtain
for some ![]() $k,\ell \in \mathbb {Z}$.
$k,\ell \in \mathbb {Z}$.
The following corollary implies that, in fact, in the quantum annular setting, there is no need for a ladybug matching for this ladybug configuration because intermediate generators are mapped to different elements in the final configuration.
Corollary 2.18 With the above notation,
for some ![]() $m\in \mathbb {Z}$. Moreover, one of
$m\in \mathbb {Z}$. Moreover, one of ![]() $m_{\rm T}(\mathfrak {q}^k v_\mathcal {I} \otimes w_-\otimes w_+ \otimes w_\mathcal {J})$ or
$m_{\rm T}(\mathfrak {q}^k v_\mathcal {I} \otimes w_-\otimes w_+ \otimes w_\mathcal {J})$ or ![]() $m_{\rm T}(\mathfrak {q}^\ell v_\mathcal {I} \otimes w_+ \otimes w_- \otimes w_\mathcal {J})$ is equal to
$m_{\rm T}(\mathfrak {q}^\ell v_\mathcal {I} \otimes w_+ \otimes w_- \otimes w_\mathcal {J})$ is equal to ![]() $\mathfrak {q}^m v_\mathcal {I} \otimes w_-\otimes w_\mathcal {J}$ and the other is equal to
$\mathfrak {q}^m v_\mathcal {I} \otimes w_-\otimes w_\mathcal {J}$ and the other is equal to ![]() $\mathfrak {q}^{m+2} v_\mathcal {I} \otimes w_-\otimes w_\mathcal {J}$.
$\mathfrak {q}^{m+2} v_\mathcal {I} \otimes w_-\otimes w_\mathcal {J}$.
Proof. In the case when the whole configuration ![]() ${\mathcal {C}}$ consists of just the curve
${\mathcal {C}}$ consists of just the curve ![]() $C$ intersecting the seam in two points as in Figure 18, the first statement can be easily checked using the formulas in Figure 12. (Also see Figure 22 below.) In full generality it follows from Proposition 2.16. The second statement follows from the commutativity of the square (2.10).
$C$ intersecting the seam in two points as in Figure 18, the first statement can be easily checked using the formulas in Figure 12. (Also see Figure 22 below.) In full generality it follows from Proposition 2.16. The second statement follows from the commutativity of the square (2.10).
Remark 2.19 Note that generators for each configuration depend, up to a power of ![]() $\mathfrak {q}$, on a choice of a cobordism: see Definition 2.3 and discussion following it. The powers
$\mathfrak {q}$, on a choice of a cobordism: see Definition 2.3 and discussion following it. The powers ![]() $k, \ell$, and
$k, \ell$, and ![]() $m$ above are determined by the cobordisms chosen for the different configurations.
$m$ above are determined by the cobordisms chosen for the different configurations.
It will be important for § 7 to know which of ![]() $m_\textrm {T}(\mathfrak {q}^k v_\mathcal {I} \otimes w_-\otimes w_+ \otimes w_\mathcal {J})$ or
$m_\textrm {T}(\mathfrak {q}^k v_\mathcal {I} \otimes w_-\otimes w_+ \otimes w_\mathcal {J})$ or ![]() $m_\textrm {T}(\mathfrak {q}^\ell v_\mathcal {I} \otimes w_+ \otimes w_- \otimes w_\mathcal {J})$ is equal to
$m_\textrm {T}(\mathfrak {q}^\ell v_\mathcal {I} \otimes w_+ \otimes w_- \otimes w_\mathcal {J})$ is equal to ![]() $\mathfrak {q}^m v_\mathcal {I} \otimes w_-\otimes w_\mathcal {J}$. This is addressed in the following proposition.
$\mathfrak {q}^m v_\mathcal {I} \otimes w_-\otimes w_\mathcal {J}$. This is addressed in the following proposition.
Proposition 2.20 With the above notation,
 \begin{align*} m_{\rm T}(\mathfrak{q}^k v_\mathcal{I} \otimes w_-\otimes w_+\otimes w_\mathcal{J}) &=\mathfrak{q}^m v_\mathcal{I} \otimes w_-\otimes w_\mathcal{J},\\ m_{\rm T}(\mathfrak{q}^\ell v_\mathcal{I} \otimes w_+\otimes w_-\otimes w_\mathcal{J}) &= \mathfrak{q}^{m+2} v_\mathcal{I} \otimes w_-\otimes w_\mathcal{J}. \end{align*}
\begin{align*} m_{\rm T}(\mathfrak{q}^k v_\mathcal{I} \otimes w_-\otimes w_+\otimes w_\mathcal{J}) &=\mathfrak{q}^m v_\mathcal{I} \otimes w_-\otimes w_\mathcal{J},\\ m_{\rm T}(\mathfrak{q}^\ell v_\mathcal{I} \otimes w_+\otimes w_-\otimes w_\mathcal{J}) &= \mathfrak{q}^{m+2} v_\mathcal{I} \otimes w_-\otimes w_\mathcal{J}. \end{align*}Proof. The generator ![]() $x = v_\mathcal {I} \otimes w_+ \otimes w_\mathcal {J}$ is the image of
$x = v_\mathcal {I} \otimes w_+ \otimes w_\mathcal {J}$ is the image of ![]() $v_\mathcal {I}$ under
$v_\mathcal {I}$ under ![]() $\mathcal {C}^\circ _\textrm {E} \xrightarrow {\Sigma _\mathcal {J}} \mathcal {C}^\circ \xrightarrow {S} \mathcal {C}$. Here
$\mathcal {C}^\circ _\textrm {E} \xrightarrow {\Sigma _\mathcal {J}} \mathcal {C}^\circ \xrightarrow {S} \mathcal {C}$. Here ![]() $\Sigma _\mathcal {J}$ is the usual identity cobordism on the essential part together with an undotted cup corresponding to
$\Sigma _\mathcal {J}$ is the usual identity cobordism on the essential part together with an undotted cup corresponding to ![]() $w_+$ on
$w_+$ on ![]() $C$ and various other cups dotted according to
$C$ and various other cups dotted according to ![]() $\mathcal {J}$, while
$\mathcal {J}$, while ![]() $S$ is some chosen cobordism from the standard
$S$ is some chosen cobordism from the standard ![]() $\mathcal {C}^\circ$ to
$\mathcal {C}^\circ$ to ![]() $\mathcal {C}$. Isotope the resulting disk in
$\mathcal {C}$. Isotope the resulting disk in ![]() $S\Sigma _\mathcal {J}$ bounding
$S\Sigma _\mathcal {J}$ bounding ![]() $C$ to a cup cobordism on
$C$ to a cup cobordism on ![]() $C$ to obtain a new cobordism
$C$ to obtain a new cobordism ![]() $\Sigma ' : \mathcal {C}^\circ _\textrm {E} \to \mathcal {C}$, so that
$\Sigma ' : \mathcal {C}^\circ _\textrm {E} \to \mathcal {C}$, so that ![]() $S\Sigma _\mathcal {J} =\mathfrak {q}^c \Sigma '$ for some
$S\Sigma _\mathcal {J} =\mathfrak {q}^c \Sigma '$ for some ![]() $c\in \mathbb {Z}$.
$c\in \mathbb {Z}$.
Since ![]() $C$ is trivial, it bounds a disk
$C$ is trivial, it bounds a disk ![]() $D$ in the annulus. Note that
$D$ in the annulus. Note that ![]() $A_\textrm {T}$ lies inside
$A_\textrm {T}$ lies inside ![]() $D$, so we may push it into the cup cobordism on
$D$, so we may push it into the cup cobordism on ![]() $C$ in
$C$ in ![]() $\Sigma '$ to obtain an arc
$\Sigma '$ to obtain an arc ![]() $A$. We may also pull
$A$. We may also pull ![]() $A_\textrm {T}$ onto the saddle
$A_\textrm {T}$ onto the saddle ![]() $\Delta _\textrm {T}$ to obtain another arc
$\Delta _\textrm {T}$ to obtain another arc ![]() $A'$. Performing neck cutting on the circle
$A'$. Performing neck cutting on the circle ![]() $A\cup A'$ on
$A\cup A'$ on ![]() $S\Sigma '$ yields
$S\Sigma '$ yields
where ![]() $S_1$ and
$S_1$ and ![]() $S_2$ are labelled such that
$S_2$ are labelled such that ![]() $S_1$ is dotted on
$S_1$ is dotted on ![]() $C_1$ and
$C_1$ and ![]() $S_2$ is dotted on
$S_2$ is dotted on ![]() $C_2$. Figure 20 illustrates the local picture near
$C_2$. Figure 20 illustrates the local picture near ![]() $A_\textrm {T}$; the surgery arc
$A_\textrm {T}$; the surgery arc ![]() $A_\textrm {T}$ is decorated by an arrowhead. From this we obtain
$A_\textrm {T}$ is decorated by an arrowhead. From this we obtain
and it follows that
 \begin{align*} \mathfrak{q}^cS_1(v_\mathcal{I}) &= \mathfrak{q}^k v_\mathcal{I} \otimes w_-\otimes w_+\otimes w_\mathcal{J},\\ \mathfrak{q}^cS_2(v_\mathcal{I}) &= \mathfrak{q}^\ell v_\mathcal{I} \otimes w_+\otimes w_-\otimes w_\mathcal{J}. \end{align*}
\begin{align*} \mathfrak{q}^cS_1(v_\mathcal{I}) &= \mathfrak{q}^k v_\mathcal{I} \otimes w_-\otimes w_+\otimes w_\mathcal{J},\\ \mathfrak{q}^cS_2(v_\mathcal{I}) &= \mathfrak{q}^\ell v_\mathcal{I} \otimes w_+\otimes w_-\otimes w_\mathcal{J}. \end{align*}
Figure 20. Neck cutting in the proof of Proposition 2.20.
The relation

implies that ![]() $\mathfrak {q}^d m_\textrm {T}S_1 = m_\textrm {T}S_2$ for some
$\mathfrak {q}^d m_\textrm {T}S_1 = m_\textrm {T}S_2$ for some ![]() $d\in \mathbb {Z}$. To compute
$d\in \mathbb {Z}$. To compute ![]() $\mathfrak {q}^d$, we need to move the dot on
$\mathfrak {q}^d$, we need to move the dot on ![]() $S_2$ along
$S_2$ along ![]() $C'$ until it is in the same position as the dot on
$C'$ until it is in the same position as the dot on ![]() $S_1$, and count (with sign) the number of times the dot intersects the membrane during this process. This is the same as the signed intersection between the seam and one of the essential circles in
$S_1$, and count (with sign) the number of times the dot intersects the membrane during this process. This is the same as the signed intersection between the seam and one of the essential circles in ![]() $s_\textrm {E}(\mathcal {C})$ obtained by surgery on
$s_\textrm {E}(\mathcal {C})$ obtained by surgery on ![]() $C$. The situation is depicted below in (
$C$. The situation is depicted below in (
); we need to move the dot on the right-hand diagram along the circle, without intersecting the surgery arc, to the other side of the arc.

Our convention of ordering ![]() $C_1$ and
$C_1$ and ![]() $C_2$ (see Figure 19) guarantees that the dot is moved counterclockwise along an essential circle in
$C_2$ (see Figure 19) guarantees that the dot is moved counterclockwise along an essential circle in ![]() $s_\textrm {E}(\mathcal {C})$, so that
$s_\textrm {E}(\mathcal {C})$, so that ![]() $m_\textrm {T}S_2= \mathfrak {q}^2 m_\textrm {T}S_1$. Finally, this implies that
$m_\textrm {T}S_2= \mathfrak {q}^2 m_\textrm {T}S_1$. Finally, this implies that
and the result follows.
There is always either a ‘right’ or a ‘left’ choice which is made at the very beginning of defining the ladybug matching (see [Reference Lipshitz and SarkarLS14a, § 5.4]). Consider the classical annular differential for the ladybug configuration of Figure 17. The ladybug matching made with the left choice identifies the circles in the middle smoothings as shown in Figure 21(a). Then the ladybug matching pairs up the intermediate generators appearing in ![]() $\Delta _\textrm {T}(w_+)$ and
$\Delta _\textrm {T}(w_+)$ and ![]() $\Delta _\textrm {E}(w_+)$ as shown in Figure 21(b).
$\Delta _\textrm {E}(w_+)$ as shown in Figure 21(b).

Figure 21. The left choice in the ladybug matching.
Now consider the quantum annular surgery formulas for the same configuration (Figure 18), which are detailed in Figure 22. We see that the intermediate generators get paired up as in (
2.12):

Algebraically, the matching is
where the ordering on trivial circles follows the convention illustrated in Figure 19. After forgetting powers of ![]() $\mathfrak {q}$, the matching in (
$\mathfrak {q}$, the matching in (
) is consistent with the matching in Figure 21. Our remaining goal in this section is to show that the matching forced by powers of ![]() $\mathfrak {q}$ agrees with the ladybug matching made with the left pair, as stated in Proposition 2.21.
$\mathfrak {q}$ agrees with the ladybug matching made with the left pair, as stated in Proposition 2.21.

Figure 22. Note that the term with coefficient ![]() ${\mathfrak {q}}^2$ on bottom right matches the term directly above it, because dragging the dot across the seam amounts to multiplication by
${\mathfrak {q}}^2$ on bottom right matches the term directly above it, because dragging the dot across the seam amounts to multiplication by ![]() ${\mathfrak {q}}^2$.
${\mathfrak {q}}^2$.
We will use the notation and conventions established in this section. By Proposition 2.16(1), we can write
for some ![]() $a\in \mathbb {Z}$. Proposition 2.16(2), Corollary 2.18, and Proposition 2.20 imply that in the quantum setting, the pairing on intermediate generators is forced to be
$a\in \mathbb {Z}$. Proposition 2.16(2), Corollary 2.18, and Proposition 2.20 imply that in the quantum setting, the pairing on intermediate generators is forced to be
 \begin{equation} \begin{gathered} \mathfrak{q}^\ell v_\mathcal{I} \otimes w_+\otimes w_-\otimes w_\mathcal{J} \longleftrightarrow \mathfrak{q}^a v_{\mathcal{I}'} \otimes v_+\otimes v_-\otimes v_{\mathcal{I}''}\otimes w_\mathcal{J}, \\ \mathfrak{q}^k v_\mathcal{I} \otimes w_-\otimes w_+\otimes w_\mathcal{J} \longleftrightarrow \mathfrak{q}^{a-1} v_{\mathcal{I}'} \otimes v_-\otimes v_+\otimes v_{\mathcal{I}''}\otimes w_\mathcal{J}. \end{gathered} \end{equation}
\begin{equation} \begin{gathered} \mathfrak{q}^\ell v_\mathcal{I} \otimes w_+\otimes w_-\otimes w_\mathcal{J} \longleftrightarrow \mathfrak{q}^a v_{\mathcal{I}'} \otimes v_+\otimes v_-\otimes v_{\mathcal{I}''}\otimes w_\mathcal{J}, \\ \mathfrak{q}^k v_\mathcal{I} \otimes w_-\otimes w_+\otimes w_\mathcal{J} \longleftrightarrow \mathfrak{q}^{a-1} v_{\mathcal{I}'} \otimes v_-\otimes v_+\otimes v_{\mathcal{I}''}\otimes w_\mathcal{J}. \end{gathered} \end{equation}Proposition 2.21 Given a ladybug configuration ![]() $(C, A_{\rm T}, A_{\rm E})$ of the type described in the paragraph preceding (2.10), the matching in (2.13) is the same as the ladybug matching made with the left pair.
$(C, A_{\rm T}, A_{\rm E})$ of the type described in the paragraph preceding (2.10), the matching in (2.13) is the same as the ladybug matching made with the left pair.
Proof. Looking at the surgery arc ![]() $A_\textrm {T}$, the left choice makes the following identification on circles in
$A_\textrm {T}$, the left choice makes the following identification on circles in ![]() $s_\textrm {E}(\mathcal {C})$ and
$s_\textrm {E}(\mathcal {C})$ and ![]() $s_\textrm {T}(\mathcal {C})$:
$s_\textrm {T}(\mathcal {C})$:

Therefore, the ladybug matching makes the following identification on generators:

Comparing with our ordering convention on the circles in ![]() $s_\textrm {T}(\mathcal {C})$ in Figure 19 demonstrates that this is consistent with (2.13).
$s_\textrm {T}(\mathcal {C})$ in Figure 19 demonstrates that this is consistent with (2.13).
3. Burnside categories and functors
Following the general strategy of [Reference Lawson, Lipshitz and SarkarLLS20], the first step towards lifting a Khovanov homology theory to a spectrum is to build a Burnside functor from the cube category ![]() $\underline {2}^n$ [Reference Lawson, Lipshitz and SarkarLLS20, § 2.1] to the Burnside category
$\underline {2}^n$ [Reference Lawson, Lipshitz and SarkarLLS20, § 2.1] to the Burnside category ![]() $\mathscr {B}$ [Reference Lawson, Lipshitz and SarkarLLS20, § 4.1] which encodes the information underlying the chain complex in a higher categorical manner, beyond the data of chain groups and differentials. In this section, we review the general framework of such categories and functors along with their equivariant versions, before turning to the specific case of quantum annular Khovanov homology in § 4. In particular, a strategy for constructing natural isomorphisms of Burnside functors, outlined in § 3.6, will be used in follow-up sections.
$\mathscr {B}$ [Reference Lawson, Lipshitz and SarkarLLS20, § 4.1] which encodes the information underlying the chain complex in a higher categorical manner, beyond the data of chain groups and differentials. In this section, we review the general framework of such categories and functors along with their equivariant versions, before turning to the specific case of quantum annular Khovanov homology in § 4. In particular, a strategy for constructing natural isomorphisms of Burnside functors, outlined in § 3.6, will be used in follow-up sections.
3.1 The cube category
We first recall the cube category ![]() $\underline {2}^n$ from [Reference Lawson, Lipshitz and SarkarLLS20, § 2.1]. The objects of
$\underline {2}^n$ from [Reference Lawson, Lipshitz and SarkarLLS20, § 2.1]. The objects of ![]() $\underline {2}^n$ are the elements of
$\underline {2}^n$ are the elements of ![]() $\{0,1\}^n$, thought of as vertices of the
$\{0,1\}^n$, thought of as vertices of the ![]() $n$-dimensional cube
$n$-dimensional cube ![]() $I^n$. There is a natural partial order on
$I^n$. There is a natural partial order on ![]() $\{0,1\}^n$: for vertices
$\{0,1\}^n$: for vertices ![]() $u=(u_1,\ldots , u_n)$ and
$u=(u_1,\ldots , u_n)$ and ![]() $v=(v_1, \ldots , v_n)$ in
$v=(v_1, \ldots , v_n)$ in ![]() $\{0,1\}^n$, write
$\{0,1\}^n$, write ![]() $u\geq v$ if each
$u\geq v$ if each ![]() $u_i \geq v_i$. The set of morphisms
$u_i \geq v_i$. The set of morphisms ![]() $\text {Hom}_{\underline {2}^n}(u,v)$ is defined to be empty unless
$\text {Hom}_{\underline {2}^n}(u,v)$ is defined to be empty unless ![]() $u\geq v$, in which case
$u\geq v$, in which case ![]() $\text {Hom}_{\underline {2}^n}(u,v)$ consists of a single element, denoted
$\text {Hom}_{\underline {2}^n}(u,v)$ consists of a single element, denoted ![]() $\varphi _{u,v}$. Therefore, for
$\varphi _{u,v}$. Therefore, for ![]() $u\geq w$, we have
$u\geq w$, we have ![]() $\varphi _{u,w} = \varphi _{v,w} \circ \varphi _{u,v}$ for any
$\varphi _{u,w} = \varphi _{v,w} \circ \varphi _{u,v}$ for any ![]() $v$ such that
$v$ such that ![]() $u\geq v \geq w$. We note that the edges in
$u\geq v \geq w$. We note that the edges in ![]() $\underline {2}^n$ point in the opposite direction of those in the cube of resolutions of a link diagram.
$\underline {2}^n$ point in the opposite direction of those in the cube of resolutions of a link diagram.
For a vertex ![]() $u=(u_1,\ldots , u_n)$, define
$u=(u_1,\ldots , u_n)$, define ![]() $\vert {u} \vert := \sum _i u_i$. Write
$\vert {u} \vert := \sum _i u_i$. Write ![]() $u\geq _k v$ if
$u\geq _k v$ if ![]() $u \geq v$ and
$u \geq v$ and ![]() $\vert {u} \vert - \vert {v} \vert = k$. In particular,
$\vert {u} \vert - \vert {v} \vert = k$. In particular, ![]() $u \geq _1 v$ means there is an edge from
$u \geq _1 v$ means there is an edge from ![]() $u$ to
$u$ to ![]() $v$ in the cube
$v$ in the cube ![]() $I^n$. Vertices
$I^n$. Vertices ![]() $u,v$ with
$u,v$ with ![]() $u\geq _k v$ specify a
$u\geq _k v$ specify a ![]() $k$-dimensional subcube, which is the full subcategory of
$k$-dimensional subcube, which is the full subcategory of ![]() $\underline {2}^n$ with objects consisting of all vertices
$\underline {2}^n$ with objects consisting of all vertices ![]() $w$ satisfying
$w$ satisfying ![]() $u\geq w \geq v$.
$u\geq w \geq v$.
3.2 Burnside categories and functors
This section discusses the Burnside category, ![]() $\mathscr {B}$, and Burnside functors, following [Reference Lawson, Lipshitz and SarkarLLS20, § 4.1].
$\mathscr {B}$, and Burnside functors, following [Reference Lawson, Lipshitz and SarkarLLS20, § 4.1].
For sets ![]() $X$ and
$X$ and ![]() $Y$, a correspondence from
$Y$, a correspondence from ![]() $X$ to
$X$ to ![]() $Y$ is a triple
$Y$ is a triple ![]() $(A,s,t)$, where
$(A,s,t)$, where ![]() $A$ is a set and
$A$ is a set and ![]() $s:A\to X$,
$s:A\to X$, ![]() $t: A\to Y$ are functions, called the source map and target map, respectively. We will often denote a correspondence by
$t: A\to Y$ are functions, called the source map and target map, respectively. We will often denote a correspondence by ![]() $X \xleftarrow {s} A \xrightarrow {t} Y$ or simply
$X \xleftarrow {s} A \xrightarrow {t} Y$ or simply ![]() $X \leftarrow A \to Y$. Given correspondences
$X \leftarrow A \to Y$. Given correspondences ![]() $X \xleftarrow {s_A} A \xrightarrow {t_A} Y$ and
$X \xleftarrow {s_A} A \xrightarrow {t_A} Y$ and ![]() $Y \xleftarrow {s_B} B \xrightarrow {t_B} Z$, their composition
$Y \xleftarrow {s_B} B \xrightarrow {t_B} Z$, their composition ![]() $(B, s_B, t_B) \circ (A, s_A, t_A)$ is the correspondence
$(B, s_B, t_B) \circ (A, s_A, t_A)$ is the correspondence ![]() $(C, s, t)$ from
$(C, s, t)$ from ![]() $X$ to
$X$ to ![]() $Z$ obtained as the fiber product
$Z$ obtained as the fiber product
with the source and target maps
The composition can be summarized by the fiber product diagram

A morphism from a correspondence ![]() $X \xleftarrow {s_A} A \xrightarrow {t_A} Y$ to a correspondence
$X \xleftarrow {s_A} A \xrightarrow {t_A} Y$ to a correspondence ![]() $X \xleftarrow {s_B} B \xrightarrow {t_B} Y$ is a bijection
$X \xleftarrow {s_B} B \xrightarrow {t_B} Y$ is a bijection ![]() $f:A\to B$ which commutes with the source and target maps. That is,
$f:A\to B$ which commutes with the source and target maps. That is, ![]() $f$ is a bijection fitting into the following commutative diagram.
$f$ is a bijection fitting into the following commutative diagram.

The collection of sets, correspondences between them, and morphisms of correspondences forms a bicategory in the language of [Reference Beliakova, Putyra and WehrliBPW19] or, equivalently, a weak ![]() $2$-category in the language of [Reference Lawson, Lipshitz and SarkarLLS20]. The objects are sets,
$2$-category in the language of [Reference Lawson, Lipshitz and SarkarLLS20]. The objects are sets, ![]() $1$-morphisms are correspondences, and
$1$-morphisms are correspondences, and ![]() $2$-morphisms are morphisms of correspondences. We will use the terms bicategory and weak
$2$-morphisms are morphisms of correspondences. We will use the terms bicategory and weak ![]() $2$-category interchangeably. A quick reference for the notion of bicategories is [Reference Beliakova, Putyra and WehrliBPW19, Appendix A.4].
$2$-category interchangeably. A quick reference for the notion of bicategories is [Reference Beliakova, Putyra and WehrliBPW19, Appendix A.4].
The identity ![]() $1$-morphism of a set
$1$-morphism of a set ![]() $X$ is the identity correspondence
$X$ is the identity correspondence
Given correspondences ![]() $X \xleftarrow {s_A} A \xrightarrow {t_A} Y$ and
$X \xleftarrow {s_A} A \xrightarrow {t_A} Y$ and ![]() $Z \xleftarrow {s_B} B \xrightarrow {t_B} X$, the compositions
$Z \xleftarrow {s_B} B \xrightarrow {t_B} X$, the compositions ![]() $(A, s_A, t_A) \circ (X, \text {id}_X, \text {id}_X)$ and
$(A, s_A, t_A) \circ (X, \text {id}_X, \text {id}_X)$ and ![]() $(X, \text {id}_X, \text {id}_X) \circ (B, s_B, t_B)$ are not equal to
$(X, \text {id}_X, \text {id}_X) \circ (B, s_B, t_B)$ are not equal to ![]() $(A, s_A, t_A)$ and
$(A, s_A, t_A)$ and ![]() $(B, s_B, t_B)$, but there are natural
$(B, s_B, t_B)$, but there are natural ![]() $2$-morphisms
$2$-morphisms
Similarly, composition of correspondences is not strictly associative, but is associative up to natural isomorphism. This is the sense in which we have only a weak 2-category, as opposed to a strict 2-category.
The Burnside category, denoted ![]() $\mathscr {B}$, is the sub-bicategory of the above consisting of finite sets and finite correspondences. Even though
$\mathscr {B}$, is the sub-bicategory of the above consisting of finite sets and finite correspondences. Even though ![]() $\mathscr {B}$ is a bicategory, it will always be referred to as a category.
$\mathscr {B}$ is a bicategory, it will always be referred to as a category.
The construction of Khovanov homotopy types in [Reference Lawson, Lipshitz and SarkarLLS20] and [Reference Sarkar, Scaduto and StoffregenSSS20] utilizes functors ![]() $F: \underline {2}^n \to \mathscr {B}$, which we explain here. First, make
$F: \underline {2}^n \to \mathscr {B}$, which we explain here. First, make ![]() $\underline {2}^n$ into a (strict)
$\underline {2}^n$ into a (strict) ![]() $2$-category by introducing only identity
$2$-category by introducing only identity ![]() $2$-morphisms. There is a notion of a lax 2-functor between
$2$-morphisms. There is a notion of a lax 2-functor between ![]() $2$-categories, and also of a strictly unitary lax 2-functor. The complete definitions, consisting of a slew of data and various natural morphisms, can be found in [Reference Lawson, Lipshitz and SarkarLLS20, Definitions 4.2 and 4.3]. We will only be interested in the notion of a Burnside functor, which is a strictly unitary lax 2-functor
$2$-categories, and also of a strictly unitary lax 2-functor. The complete definitions, consisting of a slew of data and various natural morphisms, can be found in [Reference Lawson, Lipshitz and SarkarLLS20, Definitions 4.2 and 4.3]. We will only be interested in the notion of a Burnside functor, which is a strictly unitary lax 2-functor ![]() $F: \underline {2}^n \to \mathscr {B}$. Lemma 3.1 specifies the data needed to define a Burnside functor uniquely up to natural isomorphism (see § 3.5 for the definition of natural isomorphisms).
$F: \underline {2}^n \to \mathscr {B}$. Lemma 3.1 specifies the data needed to define a Burnside functor uniquely up to natural isomorphism (see § 3.5 for the definition of natural isomorphisms).
Lemma 3.1 ([Reference Lawson, Lipshitz and SarkarLLS20, Lemma 4.5], [Reference Lawson, Lipshitz and SarkarLLS17a, Proposition 4.3])
Consider the following data.
• A finite set
 $F(u)$ for each vertex
$F(u)$ for each vertex  $u\in \underline {2}^n$.
$u\in \underline {2}^n$.• A finite correspondence
 $F(\varphi _{u,v})$ from
$F(\varphi _{u,v})$ from  $F(u)$ to
$F(u)$ to  $F(v)$ for each pair of vertices
$F(v)$ for each pair of vertices  $u,v\in \underline {2}^n$ with
$u,v\in \underline {2}^n$ with  $u\geq _1 v$.
$u\geq _1 v$.• A
 $2$-morphism
for each two-dimensional face of
$2$-morphism
for each two-dimensional face of \[ F_{u,v,v',w} : F(\varphi_{v,w}) \circ F(\varphi_{u,v}) \to F(\varphi_{v',w}) \circ F(\varphi_{u,v'}) \]
\[ F_{u,v,v',w} : F(\varphi_{v,w}) \circ F(\varphi_{u,v}) \to F(\varphi_{v',w}) \circ F(\varphi_{u,v'}) \] $\underline {2}^n$ with vertices
$\underline {2}^n$ with vertices  $u,v,v',w$ satisfying
$u,v,v',w$ satisfying  $u\geq _1 v, v' \geq _1 w$.
$u\geq _1 v, v' \geq _1 w$.
Suppose also that the above data satisfies the following conditions.
(1)
 $F_{u,v,v',w}^{-1} = F_{u,v',v,w}$.
$F_{u,v,v',w}^{-1} = F_{u,v',v,w}$.(2) For every three-dimensional subcube of
 $\underline {2}^n$ as in Figure 23(a), the hexagon of Figure 23(b) commutes.
$\underline {2}^n$ as in Figure 23(a), the hexagon of Figure 23(b) commutes.
Then the data can be extended to a strictly unitary lax ![]() $2$-functor
$2$-functor ![]() $F:\underline {2}^n \to \mathscr {B}$, which is unique up to natural isomorphism.
$F:\underline {2}^n \to \mathscr {B}$, which is unique up to natural isomorphism.

Figure 23. (a) Three-dimensional cube and (b) the hexagon relation.
The hexagon of Figure 23(b) comes from two ways of traversing the faces of the three-dimensional cube, starting from the correspondence ![]() $F(\varphi _{w,z}) \circ F(\varphi _{v,w}) \circ F(\varphi _{u,v})$ and ending at
$F(\varphi _{w,z}) \circ F(\varphi _{v,w}) \circ F(\varphi _{u,v})$ and ending at ![]() $F(\varphi _{w',z}) \circ F(\varphi _{v'',w'})\circ F(\varphi _{u,v''})$. The top half of the hexagon comes from traversing the faces as in Figure 24(a) and the bottom half comes from traversing the faces as in Figure 24(b). Lemma 3.1 states that the hexagon relation is enough to guarantee that the functor is coherent on all higher dimensional cubes as well.
$F(\varphi _{w',z}) \circ F(\varphi _{v'',w'})\circ F(\varphi _{u,v''})$. The top half of the hexagon comes from traversing the faces as in Figure 24(a) and the bottom half comes from traversing the faces as in Figure 24(b). Lemma 3.1 states that the hexagon relation is enough to guarantee that the functor is coherent on all higher dimensional cubes as well.
Remark 3.2 We end this subsection with some comments about verifying the hexagon relation which will be useful in proving Theorem 4.2. Suppose that we have ![]() $2$-morphisms
$2$-morphisms ![]() $F_{u,v,v',w}$ for each square face
$F_{u,v,v',w}$ for each square face ![]() $u\geq _1 v,v' \geq _1 w$ of
$u\geq _1 v,v' \geq _1 w$ of ![]() $\underline {2}^n$, which satisfy
$\underline {2}^n$, which satisfy ![]() $F_{u,v,v',w}^{-1} = F_{u,v',v,w}$ as in condition (1) of Lemma 3.1. Then verifying the hexagon relation is equivalent to the following. Start at the correspondence
$F_{u,v,v',w}^{-1} = F_{u,v',v,w}$ as in condition (1) of Lemma 3.1. Then verifying the hexagon relation is equivalent to the following. Start at the correspondence ![]() $F(\varphi _{w,z}) \circ F(\varphi _{v,w}) \circ F(\varphi _{u,v})$ and traverse the six faces of the cube using the
$F(\varphi _{w,z}) \circ F(\varphi _{v,w}) \circ F(\varphi _{u,v})$ and traverse the six faces of the cube using the ![]() $2$-morphisms; i.e. first move across the three faces as shown in Figure 24(a) and then move across the remaining three faces as in Figure 24(b), except in the reverse order. Composing these six
$2$-morphisms; i.e. first move across the three faces as shown in Figure 24(a) and then move across the remaining three faces as in Figure 24(b), except in the reverse order. Composing these six ![]() $2$-morphisms yields a
$2$-morphisms yields a ![]() $2$-morphism
$2$-morphism
Verifying commutativity of the hexagon of Lemma 3.1 is equivalent to verifying that ![]() $\Phi _{u,v,w,z}$ is the identity. Moreover, for each three-dimensional subcube of
$\Phi _{u,v,w,z}$ is the identity. Moreover, for each three-dimensional subcube of ![]() $\underline {2}^n$, it suffices to verify that
$\underline {2}^n$, it suffices to verify that ![]() $\Phi _{u,v,w,z}=\text {id}$ for just one tuple of vertices
$\Phi _{u,v,w,z}=\text {id}$ for just one tuple of vertices ![]() $u\geq _1 v \geq _1 w \geq _1 z$ within the subcube.
$u\geq _1 v \geq _1 w \geq _1 z$ within the subcube.

Figure 24. Illustration of the hexagon relation in Remark 3.2.
Furthermore, such verifications are immediate under certain circumstances, which we now describe. Let ![]() $A$ denote the correspondence
$A$ denote the correspondence ![]() $F(\varphi _{w,z}) \circ F(\varphi _{v,w}) \circ F(\varphi _{u,v})$, and let
$F(\varphi _{w,z}) \circ F(\varphi _{v,w}) \circ F(\varphi _{u,v})$, and let ![]() $s: A\to F(u)$,
$s: A\to F(u)$, ![]() $t: A\to F(z)$ denote the source and target maps, respectively. Suppose that for every
$t: A\to F(z)$ denote the source and target maps, respectively. Suppose that for every ![]() $x\in F(u)$ and
$x\in F(u)$ and ![]() $y\in F(z)$,
$y\in F(z)$, ![]() $s^{-1}(x) \cap t^{-1}(y)$ is either empty or has one element. Let
$s^{-1}(x) \cap t^{-1}(y)$ is either empty or has one element. Let ![]() $a\in A$ and let
$a\in A$ and let ![]() $a' = \Phi _{u,v,w,z}(a)$. Since
$a' = \Phi _{u,v,w,z}(a)$. Since ![]() $\Phi _{u,v,w,z}(a)$ is a
$\Phi _{u,v,w,z}(a)$ is a ![]() $2$-morphism, we have
$2$-morphism, we have ![]() $s(a') = s(a)$ and
$s(a') = s(a)$ and ![]() $t(a') = t(a)$. Then
$t(a') = t(a)$. Then ![]() $a'=a$, so the hexagon relation is satisfied for this three-dimensional subcube. In this situation, we will say that this three-dimensional cube is simple.
$a'=a$, so the hexagon relation is satisfied for this three-dimensional subcube. In this situation, we will say that this three-dimensional cube is simple.
3.3 The equivariant Burnside category
Let ![]() $G$ be a finite group. The
$G$ be a finite group. The ![]() $G$-equivariant Burnside category, denoted
$G$-equivariant Burnside category, denoted ![]() $\mathscr {B}_G$, is an equivariant analogue of
$\mathscr {B}_G$, is an equivariant analogue of ![]() $\mathscr {B}$. Objects of
$\mathscr {B}$. Objects of ![]() $\mathscr {B}_G$ are finite free
$\mathscr {B}_G$ are finite free ![]() $G$-sets. A
$G$-sets. A ![]() $1$-morphism from
$1$-morphism from ![]() $X$ to
$X$ to ![]() $Y$ is a triple
$Y$ is a triple ![]() $(A, s, t)$, where
$(A, s, t)$, where ![]() $A$ is another finite free
$A$ is another finite free ![]() $G$-set, and
$G$-set, and ![]() $s : A\to X$,
$s : A\to X$, ![]() $t : A\to Y$ are
$t : A\to Y$ are ![]() $G$-equivariant maps. We will call such a triple
$G$-equivariant maps. We will call such a triple ![]() $(A,s,t$) an equivariant correspondence. Given equivariant correspondences
$(A,s,t$) an equivariant correspondence. Given equivariant correspondences ![]() $X\xleftarrow {s_A} A \xrightarrow {t_A} Y$ and
$X\xleftarrow {s_A} A \xrightarrow {t_A} Y$ and ![]() $Y \xleftarrow {s_B} B \xrightarrow {t_B} Z$, the composition
$Y \xleftarrow {s_B} B \xrightarrow {t_B} Z$, the composition ![]() $(B, s_B, t_B) \circ (A, s_A, t_A)$ is the same as in
$(B, s_B, t_B) \circ (A, s_A, t_A)$ is the same as in ![]() $\mathscr {B}$. The
$\mathscr {B}$. The ![]() $G$-action on
$G$-action on ![]() $B\times _Y A$ is inherited from the diagonal
$B\times _Y A$ is inherited from the diagonal ![]() $G$-action on
$G$-action on ![]() $B\times A$; that is,
$B\times A$; that is, ![]() $g(b,a) = (gb,ga)$. The additional requirement on
$g(b,a) = (gb,ga)$. The additional requirement on ![]() $2$-morphisms between correspondences is that they be
$2$-morphisms between correspondences is that they be ![]() $G$-equivariant.
$G$-equivariant.
The equivariant Burnside category is discussed in [Reference Sarkar, Scaduto and StoffregenSSS20, § 3.3] in the case ![]() $G= \mathbb {Z}_2$. Lemma 3.2 in [Reference Sarkar, Scaduto and StoffregenSSS20] (our Lemma 3.1) gives sufficient conditions for defining a functor
$G= \mathbb {Z}_2$. Lemma 3.2 in [Reference Sarkar, Scaduto and StoffregenSSS20] (our Lemma 3.1) gives sufficient conditions for defining a functor ![]() $F:\underline {2}^n \to \mathscr {B}_{\mathbb {Z}_2}$, and the same conditions clearly work for general
$F:\underline {2}^n \to \mathscr {B}_{\mathbb {Z}_2}$, and the same conditions clearly work for general ![]() $G$. The modification to the data of Lemma 3.1 is that all sets should be finite free
$G$. The modification to the data of Lemma 3.1 is that all sets should be finite free ![]() $G$-sets and all set maps should be equivariant. Note that if
$G$-sets and all set maps should be equivariant. Note that if ![]() $G=\{1\}$, then
$G=\{1\}$, then ![]() $\mathscr {B}_{\{1\}} = \mathscr {B}$, so everything stated about
$\mathscr {B}_{\{1\}} = \mathscr {B}$, so everything stated about ![]() $\mathscr {B}_G$ in the following sections holds just as well for
$\mathscr {B}_G$ in the following sections holds just as well for ![]() $\mathscr {B}$.
$\mathscr {B}$.
We will later be interested in the quotient functor ![]() $(-)/G : \mathscr {B}_G\to \mathscr {B}$, which simply takes the quotient of all sets and set maps. Explicitly, the quotient functor sends a
$(-)/G : \mathscr {B}_G\to \mathscr {B}$, which simply takes the quotient of all sets and set maps. Explicitly, the quotient functor sends a ![]() $G$-set
$G$-set ![]() $X$ to the set of orbits
$X$ to the set of orbits ![]() $X/G = X/(x\sim gx)$. For
$X/G = X/(x\sim gx)$. For ![]() $G$-sets
$G$-sets ![]() $X$ and
$X$ and ![]() $Y$ and an equivariant map
$Y$ and an equivariant map ![]() $f:X\to Y$, there is an induced map
$f:X\to Y$, there is an induced map ![]() $f/G : X/G \to Y/G$, given by
$f/G : X/G \to Y/G$, given by ![]() $(f/G)([x]) = [f(x)]$. The quotient functor sends an equivariant correspondence
$(f/G)([x]) = [f(x)]$. The quotient functor sends an equivariant correspondence ![]() $X\xleftarrow {s} A \xrightarrow {t} Y$ to the correspondence
$X\xleftarrow {s} A \xrightarrow {t} Y$ to the correspondence ![]() $X/G \xleftarrow {s/G} A/G \xrightarrow {t/G} Y/G$. Likewise, a
$X/G \xleftarrow {s/G} A/G \xrightarrow {t/G} Y/G$. Likewise, a ![]() $2$-morphism
$2$-morphism ![]() $f:A\to B$ is assigned:
$f:A\to B$ is assigned: ![]() $f/G: A/G \to B/G$.
$f/G: A/G \to B/G$.
3.4 Totalizations of Burnside functors
Associated to any Burnside functor ![]() $\underline {2}^n \to \mathscr {B}_G$ is a chain complex, called the totalization (see [Reference Lawson, Lipshitz and SarkarLLS17a, Definition 5.1] and [Reference Sarkar, Scaduto and StoffregenSSS20, § 3.6]). For a set
$\underline {2}^n \to \mathscr {B}_G$ is a chain complex, called the totalization (see [Reference Lawson, Lipshitz and SarkarLLS17a, Definition 5.1] and [Reference Sarkar, Scaduto and StoffregenSSS20, § 3.6]). For a set ![]() $X$, let
$X$, let ![]() $\mathcal {A}(X)$ denote the free abelian group generated by
$\mathcal {A}(X)$ denote the free abelian group generated by ![]() $X$. Let
$X$. Let ![]() $X \xleftarrow {s} A \xrightarrow {t} Y$ be an equivariant correspondence. Define a map
$X \xleftarrow {s} A \xrightarrow {t} Y$ be an equivariant correspondence. Define a map ![]() $\mathcal {A}(A) : \mathcal {A}(X) \to \mathcal {A}(Y)$ by
$\mathcal {A}(A) : \mathcal {A}(X) \to \mathcal {A}(Y)$ by
Let ![]() $F:\underline {2}^n \to \mathscr {B}_G$ be a Burnside functor. For
$F:\underline {2}^n \to \mathscr {B}_G$ be a Burnside functor. For ![]() $u\geq v$, let
$u\geq v$, let ![]() $A_{u,v}$ denote the correspondence assigned by
$A_{u,v}$ denote the correspondence assigned by ![]() $F$ to the morphism
$F$ to the morphism ![]() $\varphi _{u,v} : u \to v$. The complex
$\varphi _{u,v} : u \to v$. The complex ![]() $\text {Tot}(F)$ is defined by
$\text {Tot}(F)$ is defined by
with the term ![]() $\mathcal {A}(F(u))$ in homological degree
$\mathcal {A}(F(u))$ in homological degree ![]() $\vert {u} \vert$. The differential
$\vert {u} \vert$. The differential
is given on summands by maps ![]() $\partial _{u,v} : \mathcal {A}(F(u)) \to \mathcal {A}(F(v))$, for
$\partial _{u,v} : \mathcal {A}(F(u)) \to \mathcal {A}(F(v))$, for ![]() $\vert {u} \vert = i$,
$\vert {u} \vert = i$, ![]() $\vert {v} \vert = i+1$, defined as
$\vert {v} \vert = i+1$, defined as
The sign assignment ![]() $s_{u,v}$ ensures that
$s_{u,v}$ ensures that ![]() $\partial ^2=0$ (see [Reference Bar-NatanBar05, § 2.7]; see also [Reference Lipshitz and SarkarLS14a, Definition 4.5] for a discussion of
$\partial ^2=0$ (see [Reference Bar-NatanBar05, § 2.7]; see also [Reference Lipshitz and SarkarLS14a, Definition 4.5] for a discussion of ![]() $s_{u,v}$).
$s_{u,v}$).
If ![]() $X$ is a
$X$ is a ![]() $G$-set, then
$G$-set, then ![]() $\mathcal {A}(X)$ is naturally a
$\mathcal {A}(X)$ is naturally a ![]() $\mathbb {Z}[G]$-module. Moreover, if
$\mathbb {Z}[G]$-module. Moreover, if ![]() $X \xleftarrow {s} A \xrightarrow {t} Y$ is an equivariant correspondence, then the map
$X \xleftarrow {s} A \xrightarrow {t} Y$ is an equivariant correspondence, then the map ![]() $\mathcal {A}(A)$ is
$\mathcal {A}(A)$ is ![]() $\mathbb {Z}[G]$-linear. Thus, if
$\mathbb {Z}[G]$-linear. Thus, if ![]() $F$ is an equivariant Burnside functor taking values in
$F$ is an equivariant Burnside functor taking values in ![]() $\mathscr {B}_G$, then
$\mathscr {B}_G$, then ![]() $\text {Tot}(F)$ is a complex of
$\text {Tot}(F)$ is a complex of ![]() $\mathbb {Z}[G]$-modules.
$\mathbb {Z}[G]$-modules.
3.5 Natural transformations of Burnside functors
There is a canonical identification ![]() $\underline {2}^{n+1} = \underline {2} \times \underline {2}^n$. A natural transformation
$\underline {2}^{n+1} = \underline {2} \times \underline {2}^n$. A natural transformation ![]() $\eta : F_1\to F_0$ of Burnside functors
$\eta : F_1\to F_0$ of Burnside functors ![]() $F_1, F_0: \underline {2}^n \to \mathscr {B}_G$ is a functor
$F_1, F_0: \underline {2}^n \to \mathscr {B}_G$ is a functor ![]() $\eta :\underline {2}^{n+1} \to \mathscr {B}_G$ such that the restriction of
$\eta :\underline {2}^{n+1} \to \mathscr {B}_G$ such that the restriction of ![]() $\eta$ to
$\eta$ to ![]() $\{i\} \times \underline {2}^n$ is equal to
$\{i\} \times \underline {2}^n$ is equal to ![]() $F_i$.
$F_i$.
In the context of natural transformations, we will think of ![]() $\underline {2}^{n+1} = \underline {2} \times \underline {2}^n$ as two ‘horizontal’ copies of
$\underline {2}^{n+1} = \underline {2} \times \underline {2}^n$ as two ‘horizontal’ copies of ![]() $\underline {2}^n$ with vertical edges connecting them, pointing downwards. The top copy of
$\underline {2}^n$ with vertical edges connecting them, pointing downwards. The top copy of ![]() $\underline {2}^n$ corresponds to
$\underline {2}^n$ corresponds to ![]() $\{1\} \times \underline {2}^n \subset \underline {2} \times \underline {2}^n$ and likewise the bottom copy corresponds to
$\{1\} \times \underline {2}^n \subset \underline {2} \times \underline {2}^n$ and likewise the bottom copy corresponds to ![]() $\{0\}\times \underline {2}^n \subset \underline {2}\times \underline {2}^n$. Recall that for
$\{0\}\times \underline {2}^n \subset \underline {2}\times \underline {2}^n$. Recall that for ![]() $u\geq v$,
$u\geq v$, ![]() $\varphi _{u,v}$ denotes the unique element in
$\varphi _{u,v}$ denotes the unique element in ![]() $\text {Hom}_{\underline {2}^n}(u,v)$. We distinguish two types of morphisms in
$\text {Hom}_{\underline {2}^n}(u,v)$. We distinguish two types of morphisms in ![]() $\underline {2} \times \underline {2}^n$. First, for each
$\underline {2} \times \underline {2}^n$. First, for each ![]() $u\in \underline {2}^n$, there is a morphism
$u\in \underline {2}^n$, there is a morphism
We denote this edge by ![]() $e_u$ and think of it as a vertical arrow
$e_u$ and think of it as a vertical arrow
The second type consists of morphisms in ![]() $\underline {2}\times \underline {2}^n$ of the form
$\underline {2}\times \underline {2}^n$ of the form
where ![]() $i \in \{0,1\}$ and
$i \in \{0,1\}$ and ![]() $u,v\in \underline {2}^n$ with
$u,v\in \underline {2}^n$ with ![]() $u\geq v$. We will denote these morphisms by
$u\geq v$. We will denote these morphisms by ![]() $\varphi ^i_{u,v}$, and think of them as living in the ‘horizontal’ cube
$\varphi ^i_{u,v}$, and think of them as living in the ‘horizontal’ cube ![]() $\{i\} \times \underline {2}^n$.
$\{i\} \times \underline {2}^n$.
With these conventions, the diagram

lives in the horizontal cube ![]() $\{i\}\times \underline {2}^n$ and the diagram
$\{i\}\times \underline {2}^n$ and the diagram

is between the horizontal cubes. In the context of natural transformations, we will often not label some or all of the edges, with the understanding that the above conventions (
3.2) and (
3.3) are followed. To define a natural transformation ![]() $\eta :F_1\to F_0$, one needs to specify a correspondence
$\eta :F_1\to F_0$, one needs to specify a correspondence ![]() $\eta (e_u)$ for each vertical edge
$\eta (e_u)$ for each vertical edge ![]() $e_u$, a
$e_u$, a ![]() $2$-morphism
$2$-morphism ![]() $\eta _{u,v} : \eta (e_v) \circ \eta (\varphi ^1_{u,v}) \to \eta (\varphi ^0_{u,v}) \circ \eta (e_u)$ for each vertical face as in (
$\eta _{u,v} : \eta (e_v) \circ \eta (\varphi ^1_{u,v}) \to \eta (\varphi ^0_{u,v}) \circ \eta (e_u)$ for each vertical face as in (
), and verify that the hexagon of Lemma 3.1 commutes.
Given a natural transformation ![]() $\eta : F_1\to F_0$, there is an induced map
$\eta : F_1\to F_0$, there is an induced map ![]() $\text {Tot}(\eta ) : \text {Tot}(F_1) \to \text {Tot}(F_0)$. The map
$\text {Tot}(\eta ) : \text {Tot}(F_1) \to \text {Tot}(F_0)$. The map ![]() $\text {Tot}(\eta )$ is defined on each summand by
$\text {Tot}(\eta )$ is defined on each summand by ![]() $\mathcal {A}(\eta (e_u)): \mathcal {A}(F_1(u)) \to \mathcal {A}(F_0(u))$.
$\mathcal {A}(\eta (e_u)): \mathcal {A}(F_1(u)) \to \mathcal {A}(F_0(u))$.
3.6 A strategy for constructing natural isomorphisms
Given Burnside functors ![]() $F_1, F_0 : \underline {2}^n \to \mathscr {B}_G$, a natural isomorphism from
$F_1, F_0 : \underline {2}^n \to \mathscr {B}_G$, a natural isomorphism from ![]() $F_1$ to
$F_1$ to ![]() $F_0$ is a natural transformation
$F_0$ is a natural transformation ![]() $\eta : F_1\to F_0$ such that
$\eta : F_1\to F_0$ such that ![]() $\eta (e_u) : F_1(u) \to F_0(u)$ is an isomorphism in
$\eta (e_u) : F_1(u) \to F_0(u)$ is an isomorphism in ![]() $\mathscr {B}_G$ for each vertex
$\mathscr {B}_G$ for each vertex ![]() $u$. We will have several occasions to show that two Burnside functors are isomorphic (Propositions 4.3, 4.4, and 7.1). The general strategy is the same in all these cases, so we outline it here.
$u$. We will have several occasions to show that two Burnside functors are isomorphic (Propositions 4.3, 4.4, and 7.1). The general strategy is the same in all these cases, so we outline it here.
Note that a correspondence ![]() $X \xleftarrow {s} A \xrightarrow {t} Y$, thought of as a morphism in
$X \xleftarrow {s} A \xrightarrow {t} Y$, thought of as a morphism in ![]() $\mathscr {B}_G$, is an isomorphism if and only if
$\mathscr {B}_G$, is an isomorphism if and only if ![]() $s$ and
$s$ and ![]() $t$ are bijective. In particular, given an equivariant bijection
$t$ are bijective. In particular, given an equivariant bijection ![]() $t: X\to Y$, the correspondence
$t: X\to Y$, the correspondence ![]() $X \xleftarrow {\text {id}} X \xrightarrow {t} Y$ is an isomorphism in
$X \xleftarrow {\text {id}} X \xrightarrow {t} Y$ is an isomorphism in ![]() $\mathscr {B}_G$, with inverse
$\mathscr {B}_G$, with inverse ![]() $Y \xleftarrow {t} X \xrightarrow {\text {id}} X$ (up to a canonical identification of a set with the diagonal in its cartesian square).
$Y \xleftarrow {t} X \xrightarrow {\text {id}} X$ (up to a canonical identification of a set with the diagonal in its cartesian square).
Suppose that we are given two functors ![]() $F_1, F_0 : \underline {2}^n \to \mathscr {B}_G$ and equivariant bijections
$F_1, F_0 : \underline {2}^n \to \mathscr {B}_G$ and equivariant bijections ![]() $\psi _{u}: F_1(u) \to F_0(u)$ for each vertex
$\psi _{u}: F_1(u) \to F_0(u)$ for each vertex ![]() $u \in \underline {2}^n$. For
$u \in \underline {2}^n$. For ![]() $u\geq _1 v$, let
$u\geq _1 v$, let
be the correspondence assigned to the edge ![]() $\varphi _{u,v}:u\to v$ by
$\varphi _{u,v}:u\to v$ by ![]() $F_i$ for
$F_i$ for ![]() $i=0,1$. Suppose also that for each
$i=0,1$. Suppose also that for each ![]() $u\geq _1 v$, the following conditions hold.
$u\geq _1 v$, the following conditions hold.
(NI 1)
 $A^i_{u,v} \subset F_i(u) \times F_i(v)$, and the
$A^i_{u,v} \subset F_i(u) \times F_i(v)$, and the  $G$-action on
$G$-action on  $A^i_{u,v}$ is inherited from the diagonal
$A^i_{u,v}$ is inherited from the diagonal  $G$-action on
$G$-action on  $F_i(u)\times F_i(v)$ (i.e.
$F_i(u)\times F_i(v)$ (i.e.  $g(x,y) = (g x, g y)$ for
$g(x,y) = (g x, g y)$ for  $g\in G$,
$g\in G$,  $(x,y) \in F_i(u) \times F_i(v)$).
$(x,y) \in F_i(u) \times F_i(v)$).(NI 2) The map
 $F_1(u) \times F_1(v) \xrightarrow {\psi _u\times \psi _v} F_0(u) \times F_0(v)$ restricts to a bijection
$F_1(u) \times F_1(v) \xrightarrow {\psi _u\times \psi _v} F_0(u) \times F_0(v)$ restricts to a bijection  $A^1_{u,v} \to A^0_{u,v}$, denoted
$A^1_{u,v} \to A^0_{u,v}$, denoted  $\psi _{u,v}$.
$\psi _{u,v}$.(NI 3) The source and target maps,
 $s^i_{u,v}$ and
$s^i_{u,v}$ and  $t^i_{u,v}$, are restrictions of the projections
$t^i_{u,v}$, are restrictions of the projections  $F_i(u) \twoheadleftarrow F_i(u)\times F_i(v) \twoheadrightarrow F_i(v)$.
$F_i(u) \twoheadleftarrow F_i(u)\times F_i(v) \twoheadrightarrow F_i(v)$.
In this situation, we have a systematic method for building a natural isomorphism ![]() $\eta : F_1 \to F_0$ using Lemma 3.1 as follows. Define
$\eta : F_1 \to F_0$ using Lemma 3.1 as follows. Define ![]() $\eta$ on objects by
$\eta$ on objects by
for ![]() $i\in \{0,1\}$ and
$i\in \{0,1\}$ and ![]() $u\in \{0,1\}^n$. We then define
$u\in \{0,1\}^n$. We then define ![]() $\eta$ on each vertical edge
$\eta$ on each vertical edge ![]() $e_u : (1,u) \to (0,u)$ by
$e_u : (1,u) \to (0,u)$ by
That is, the underlying set of the correspondence ![]() $\eta (e_u)$ is simply
$\eta (e_u)$ is simply ![]() $F_1(u)$, the source map is the identity, and the target map is the given equivariant bijection
$F_1(u)$, the source map is the identity, and the target map is the given equivariant bijection ![]() $\psi _{u}$.
$\psi _{u}$.
We have now specified ![]() $\eta$ on objects and edges. It remains to define the
$\eta$ on objects and edges. It remains to define the ![]() $2$-morphisms for each square face of
$2$-morphisms for each square face of ![]() $\underline {2}^{n+1}$. Since
$\underline {2}^{n+1}$. Since ![]() $\eta$ must restrict to
$\eta$ must restrict to ![]() $F_i$ on
$F_i$ on ![]() $\{i\}\times \underline {2}^n$, we need only to specify a
$\{i\}\times \underline {2}^n$, we need only to specify a ![]() $2$-morphism
$2$-morphism
corresponding to the vertical square faces (3.3) of ![]() $\underline {2}\times \underline {2}^n$.
$\underline {2}\times \underline {2}^n$.
The situation is illustrated in Figure 25. Note that every element of ![]() $F_1(v) \times _{F_1(v)} A^1_{u,v}$ is of the form
$F_1(v) \times _{F_1(v)} A^1_{u,v}$ is of the form ![]() $(y,x,y)$, where
$(y,x,y)$, where ![]() $(x,y) \in A^1_{u,v} \subset F_1(u) \times F_1(v)$. Likewise, an element of
$(x,y) \in A^1_{u,v} \subset F_1(u) \times F_1(v)$. Likewise, an element of ![]() $A^0_{u,v} \times _{F_0(u)} F_1(u)$ is of the form
$A^0_{u,v} \times _{F_0(u)} F_1(u)$ is of the form ![]() $(a,b, \psi _u^{-1}(a))$, where
$(a,b, \psi _u^{-1}(a))$, where ![]() $(a,b) \in A^0_{u,v} \subset F_0(u) \times F_0(v)$. Condition (NI 1) ensures that the bijections
$(a,b) \in A^0_{u,v} \subset F_0(u) \times F_0(v)$. Condition (NI 1) ensures that the bijections
 \begin{align*} \ \ F_1(v) \times_{F_1(v)} A^1_{u,v} &\to A^1_{u,v}, \quad \, \ A^0_{u,v} \to A^0_{u,v} \times_{F_0(u)} F_1(u),\\ (y,x,y) & \mapsto (x,y), \quad (a,b) \mapsto (a,b, \psi_u^{{-}1}(a))\hphantom{0000} \end{align*}
\begin{align*} \ \ F_1(v) \times_{F_1(v)} A^1_{u,v} &\to A^1_{u,v}, \quad \, \ A^0_{u,v} \to A^0_{u,v} \times_{F_0(u)} F_1(u),\\ (y,x,y) & \mapsto (x,y), \quad (a,b) \mapsto (a,b, \psi_u^{{-}1}(a))\hphantom{0000} \end{align*}are equivariant. Then the composition
is given by ![]() $(y,x,y) \mapsto (\psi _u(x), \psi _v(y), x)$, and condition (NI 2) guarantees that it is also an equivariant bijection. Moreover, condition (NI 3) ensures that this composition commutes with the source and target maps. Therefore, we may define the
$(y,x,y) \mapsto (\psi _u(x), \psi _v(y), x)$, and condition (NI 2) guarantees that it is also an equivariant bijection. Moreover, condition (NI 3) ensures that this composition commutes with the source and target maps. Therefore, we may define the ![]() $2$-morphism
$2$-morphism ![]() $\eta _{u,v}$ to be the composition (3.4).
$\eta _{u,v}$ to be the composition (3.4).

Figure 25. We draw the square diagram required for building our natural isomorphism ![]() $\eta :F_1\rightarrow F_0$. The correspondences are indicated along each edge together with their source and target maps, drawn as curved arrows. Specific elements are also indicated, showing how the 2-morphism
$\eta :F_1\rightarrow F_0$. The correspondences are indicated along each edge together with their source and target maps, drawn as curved arrows. Specific elements are also indicated, showing how the 2-morphism ![]() $\eta _{u,v}$ (indicated by the double arrow) should be defined such that the entire diagram is consistent.
$\eta _{u,v}$ (indicated by the double arrow) should be defined such that the entire diagram is consistent.
To extend ![]() $\eta$ to a natural transformation, one still needs to check the hexagon relation of Lemma 3.1. We need only to verify commutativity of the hexagon coming from a three-dimensional cube of the form
$\eta$ to a natural transformation, one still needs to check the hexagon relation of Lemma 3.1. We need only to verify commutativity of the hexagon coming from a three-dimensional cube of the form

Let
be the ![]() $2$-morphism assigned by the functor
$2$-morphism assigned by the functor ![]() $F_i$ corresponding to the horizontal square face
$F_i$ corresponding to the horizontal square face

of ![]() $\underline {2}\times \underline {2}^n$. In this situation, checking that the hexagon of Lemma 3.1 commutes comes down to verifying commutativity of the diagram in (
$\underline {2}\times \underline {2}^n$. In this situation, checking that the hexagon of Lemma 3.1 commutes comes down to verifying commutativity of the diagram in (
) below.

If the diagram (
3.5) commutes, then ![]() $\eta$ extends to a natural transformation
$\eta$ extends to a natural transformation ![]() $\eta : F_1 \to F_0$. Moreover, since each
$\eta : F_1 \to F_0$. Moreover, since each ![]() $\eta (e_u) : F_1(u) \to F_0(u)$ is an isomorphism in
$\eta (e_u) : F_1(u) \to F_0(u)$ is an isomorphism in ![]() $\mathscr {B}_G$, the natural transformation
$\mathscr {B}_G$, the natural transformation ![]() $\eta$ is a natural isomorphism of Burnside functors.
$\eta$ is a natural isomorphism of Burnside functors.
4. The quantum annular Burnside functor
In this section, we construct the quantum annular Burnside functor corresponding to an annular link diagram ![]() $D$. Before giving the outline of the section, we emphasize one small but important caveat. In the quantum annular theory over the base ring
$D$. Before giving the outline of the section, we emphasize one small but important caveat. In the quantum annular theory over the base ring ![]() $\Bbbk =\mathbb {Z}[\mathfrak {q}, \mathfrak {q}^{-1}]$, every configuration is assigned a module which has infinite rank over
$\Bbbk =\mathbb {Z}[\mathfrak {q}, \mathfrak {q}^{-1}]$, every configuration is assigned a module which has infinite rank over ![]() $\mathbb {Z}$, with generators of the form
$\mathbb {Z}$, with generators of the form ![]() $\mathfrak {q}^k x$ for
$\mathfrak {q}^k x$ for ![]() $k\in \mathbb {Z}$. In our set-up, this would correspond to assigning an infinite set to each vertex in the cube of resolutions. This would require considering spaces of infinitely many boxes in § 5, and also of CW-complexes with a
$k\in \mathbb {Z}$. In our set-up, this would correspond to assigning an infinite set to each vertex in the cube of resolutions. This would require considering spaces of infinitely many boxes in § 5, and also of CW-complexes with a ![]() $\mathbb {Z}$-action. Although we believe that such a version of the theory could be worked out, in the present paper we stay in the context of finite cyclic group actions. This is motivated in part by the fact that a substantial part of equivariant homotopy theory is formulated for compact group actions. To this end, we make the following modification to the quantum annular complex.
$\mathbb {Z}$-action. Although we believe that such a version of the theory could be worked out, in the present paper we stay in the context of finite cyclic group actions. This is motivated in part by the fact that a substantial part of equivariant homotopy theory is formulated for compact group actions. To this end, we make the following modification to the quantum annular complex.
For ![]() $r> 0$, set
$r> 0$, set ![]() $\Bbbk _r: = \Bbbk /(\mathfrak {q}^r-1)$. Let
$\Bbbk _r: = \Bbbk /(\mathfrak {q}^r-1)$. Let ![]() $\mathcal {F}^r_{\mathbb {A}_{\mathfrak {q}}}$ denote the composition
$\mathcal {F}^r_{\mathbb {A}_{\mathfrak {q}}}$ denote the composition
We can define a modified quantum annular homology by applying ![]() $\mathcal {F}^r_{\mathbb {A}_{\mathfrak {q}}}$ to each vertex in the cube of resolutions of an annular link diagram
$\mathcal {F}^r_{\mathbb {A}_{\mathfrak {q}}}$ to each vertex in the cube of resolutions of an annular link diagram ![]() $D$. The result is the same as applying
$D$. The result is the same as applying ![]() $(-)\otimes _\Bbbk \Bbbk _r$ to the quantum annular chain complex
$(-)\otimes _\Bbbk \Bbbk _r$ to the quantum annular chain complex ![]() $CKh_{\mathbb {A}_{\mathfrak {q}}}(D)$. Every vertex is assigned a free
$CKh_{\mathbb {A}_{\mathfrak {q}}}(D)$. Every vertex is assigned a free ![]() $\Bbbk _r$-module, and the formulas in § 2 remain true, modulo the relation
$\Bbbk _r$-module, and the formulas in § 2 remain true, modulo the relation ![]() $\mathfrak {q}^r=1$.
$\mathfrak {q}^r=1$.
With this modification in place, we proceed as follows. Given an annular link diagram ![]() $D$ with
$D$ with ![]() $n$ crossings, we will define the quantum annular Burnside functor
$n$ crossings, we will define the quantum annular Burnside functor ![]() $F_\mathfrak {q} : \underline {2}^n \to \mathscr {B}_G$, where
$F_\mathfrak {q} : \underline {2}^n \to \mathscr {B}_G$, where
is the finite cyclic group of order ![]() $r$ with distinguished generator
$r$ with distinguished generator ![]() $\mathfrak {q}$. Note that there is a natural ring isomorphism
$\mathfrak {q}$. Note that there is a natural ring isomorphism ![]() $\mathbb {Z}[G] \cong \Bbbk _r$, so that it is possible to compare the cellular cohomology of the stable homotopy type, which is a
$\mathbb {Z}[G] \cong \Bbbk _r$, so that it is possible to compare the cellular cohomology of the stable homotopy type, which is a ![]() $\mathbb {Z}[G]$-module, with the modified quantum annular homology, which is a
$\mathbb {Z}[G]$-module, with the modified quantum annular homology, which is a ![]() $\Bbbk _r$-module. The dependence on
$\Bbbk _r$-module. The dependence on ![]() $r$ will be omitted from the group
$r$ will be omitted from the group ![]() $G$ and the Burnside functor
$G$ and the Burnside functor ![]() $F_\mathfrak {q}$ in order to simplify the notation.
$F_\mathfrak {q}$ in order to simplify the notation.
Because we want the totalization ![]() $\text {Tot}(F_{\mathfrak {q}})$ to recover the quantum annular complex
$\text {Tot}(F_{\mathfrak {q}})$ to recover the quantum annular complex
we already know what ![]() $F_{\mathfrak {q}}$ should assign to vertices and edges of
$F_{\mathfrak {q}}$ should assign to vertices and edges of ![]() $\underline {2}^n$. The subtlety here is that generators are defined only up to a power of
$\underline {2}^n$. The subtlety here is that generators are defined only up to a power of ![]() $\mathfrak {q}$, and the formulas for the differential non-trivially depend on the configuration, so the full extent of the analysis in §§ 2.3, 2.4 is used here. Once
$\mathfrak {q}$, and the formulas for the differential non-trivially depend on the configuration, so the full extent of the analysis in §§ 2.3, 2.4 is used here. Once ![]() $F_\mathfrak {q}$ is determined on vertices and edges, it remains to assign specific bijections to the (identity) 2-morphisms in
$F_\mathfrak {q}$ is determined on vertices and edges, it remains to assign specific bijections to the (identity) 2-morphisms in ![]() $\underline {2}^n$ and check the hexagon relation of Lemma 3.1. This will be done in § 4.1 for the case
$\underline {2}^n$ and check the hexagon relation of Lemma 3.1. This will be done in § 4.1 for the case ![]() $r>2$; this restriction is to guarantee that
$r>2$; this restriction is to guarantee that ![]() $\mathfrak {q}^2\neq 1$, allowing the use of Corollary 2.18 to simplify the analysis. We will show in Proposition 4.3 that the Burnside functor
$\mathfrak {q}^2\neq 1$, allowing the use of Corollary 2.18 to simplify the analysis. We will show in Proposition 4.3 that the Burnside functor ![]() $F_\mathfrak {q}$ is independent of the choice of generators for each vertex, and in § 4.2 we will show that planar isotopies of the link diagram induce natural isomorphisms of the corresponding Burnside functors. Finally, in § 4.3, we will address the cases
$F_\mathfrak {q}$ is independent of the choice of generators for each vertex, and in § 4.2 we will show that planar isotopies of the link diagram induce natural isomorphisms of the corresponding Burnside functors. Finally, in § 4.3, we will address the cases ![]() $r=1,2$.
$r=1,2$.
4.1 The quantum annular Burnside functor for a link diagram
Let ![]() $D$ be a diagram for an annular link with
$D$ be a diagram for an annular link with ![]() $n$ crossings, which are assumed to be disjoint from the seam. For each
$n$ crossings, which are assumed to be disjoint from the seam. For each ![]() $u\in \{0,1\}^n$, let
$u\in \{0,1\}^n$, let ![]() $D_u$ denote the smoothing of
$D_u$ denote the smoothing of ![]() $D$ corresponding to
$D$ corresponding to ![]() $u$. Fix
$u$. Fix ![]() $r>2$ and set
$r>2$ and set ![]() $G= \langle \mathfrak {q} \mid \mathfrak {q}^r=1\rangle$. We will specify the data of the quantum annular Burnside functor
$G= \langle \mathfrak {q} \mid \mathfrak {q}^r=1\rangle$. We will specify the data of the quantum annular Burnside functor ![]() $F_{\mathfrak {q}}: \underline {2}^n \to \mathscr {B}_G$.
$F_{\mathfrak {q}}: \underline {2}^n \to \mathscr {B}_G$.
For each vertex ![]() $u\in \{0,1\}^n$, pick a set of generators
$u\in \{0,1\}^n$, pick a set of generators ![]() $\Gamma (u)$ of
$\Gamma (u)$ of ![]() $D_u$, following § 2.3. Define
$D_u$, following § 2.3. Define ![]() $F_{\mathfrak {q}}$ on vertices by
$F_{\mathfrak {q}}$ on vertices by
The ![]() $G$-action on
$G$-action on ![]() $F_{\mathfrak {q}}(u)$ is on the first factor:
$F_{\mathfrak {q}}(u)$ is on the first factor: ![]() $\mathfrak {q}^k \cdot (\mathfrak {q}^\ell , x) = (\mathfrak {q}^{k+\ell },x)$.
$\mathfrak {q}^k \cdot (\mathfrak {q}^\ell , x) = (\mathfrak {q}^{k+\ell },x)$.
We will write an element of ![]() $F_{\mathfrak {q}}(u)$ as
$F_{\mathfrak {q}}(u)$ as ![]() $\mathfrak {q}^kx$ instead of
$\mathfrak {q}^kx$ instead of ![]() $(\mathfrak {q}^k, x)$.
$(\mathfrak {q}^k, x)$.
For ![]() $u\geq _1 v$, let
$u\geq _1 v$, let ![]() $d_{v,u}$ denote the map assigned to the edge
$d_{v,u}$ denote the map assigned to the edge ![]() $v\to u$ by the modified quantum annular functor
$v\to u$ by the modified quantum annular functor ![]() $\mathcal {F}_{\mathbb {A}_\mathfrak {q}}^r$. Recall from Lemma 2.17 that for each
$\mathcal {F}_{\mathbb {A}_\mathfrak {q}}^r$. Recall from Lemma 2.17 that for each ![]() $x\in \Gamma (v)$,
$x\in \Gamma (v)$,
where each ![]() $\varepsilon _y$ is either
$\varepsilon _y$ is either ![]() $0$ or
$0$ or ![]() $\mathfrak {q}^k$ for some
$\mathfrak {q}^k$ for some ![]() $k\in \mathbb {Z}$. We will say that
$k\in \mathbb {Z}$. We will say that ![]() $\mathfrak {q}^k y$ appears in
$\mathfrak {q}^k y$ appears in ![]() $d_{v,u}(\mathfrak {q}^\ell x)$ if in the equation
$d_{v,u}(\mathfrak {q}^\ell x)$ if in the equation
the coefficient ![]() $\varepsilon _y$ is equal to
$\varepsilon _y$ is equal to ![]() $\mathfrak {q}^k$. For
$\mathfrak {q}^k$. For ![]() $u\geq _1 v$, define the correspondence
$u\geq _1 v$, define the correspondence ![]() $A_{u,v} \subset F_{\mathfrak {q}}(u) \times F_{\mathfrak {q}}(v)$ from
$A_{u,v} \subset F_{\mathfrak {q}}(u) \times F_{\mathfrak {q}}(v)$ from ![]() $F_{\mathfrak {q}}(u)$ to
$F_{\mathfrak {q}}(u)$ to ![]() $F_{\mathfrak {q}}(v)$ by
$F_{\mathfrak {q}}(v)$ by
The source and target maps of ![]() $A_{u,v}$ are the projections to
$A_{u,v}$ are the projections to ![]() $F_{\mathfrak {q}}(u)$ and
$F_{\mathfrak {q}}(u)$ and ![]() $F_{\mathfrak {q}}(v)$, respectively. Note that
$F_{\mathfrak {q}}(v)$, respectively. Note that ![]() $A_{u,v}$ is a sub
$A_{u,v}$ is a sub ![]() $G$-set of
$G$-set of ![]() $F_{\mathfrak {q}}(u)\times F_{\mathfrak {q}}(v)$ since
$F_{\mathfrak {q}}(u)\times F_{\mathfrak {q}}(v)$ since ![]() $d_{v,u}(\mathfrak {q} x) = \mathfrak {q} d_{v,u}(x)$.
$d_{v,u}(\mathfrak {q} x) = \mathfrak {q} d_{v,u}(x)$.
We will show that the above data extends to a Burnside functor ![]() $F_q : \underline {2}^n \to \mathscr {B}_G$. The following lemma will be useful in our analysis of the hexagon relation.
$F_q : \underline {2}^n \to \mathscr {B}_G$. The following lemma will be useful in our analysis of the hexagon relation.
Lemma 4.1 Let ![]() $\mathcal {C}$ be a configuration with three surgery arcs
$\mathcal {C}$ be a configuration with three surgery arcs ![]() $A_1$,
$A_1$, ![]() $A_2$, and
$A_2$, and ![]() $A_3$. Let
$A_3$. Let ![]() $\mathcal {C}'$ denote the circles in
$\mathcal {C}'$ denote the circles in ![]() $\mathcal {C}$ containing the endpoints of the surgery arcs. Assume that there is a circle
$\mathcal {C}$ containing the endpoints of the surgery arcs. Assume that there is a circle ![]() $C$ in
$C$ in ![]() $\mathcal {C}'$ such that
$\mathcal {C}'$ such that ![]() $C\cup A_1 \cup A_2$ forms a ladybug configuration. Then one of the following holds.
$C\cup A_1 \cup A_2$ forms a ladybug configuration. Then one of the following holds.
(1) The diagram
 $\mathcal {C}'\cup A_1 \cup A_2 \cup A_3$ is trivial in the annulus; i.e.
$\mathcal {C}'\cup A_1 \cup A_2 \cup A_3$ is trivial in the annulus; i.e.  $\mathcal {C}'$ and the three surgery arcs lie in a disk in
$\mathcal {C}'$ and the three surgery arcs lie in a disk in  $\mathbb {A}$.
$\mathbb {A}$.(2) The composition of three edge maps is
 $0$.
$0$.(3) The three-dimensional cube is simple (see the discussion in Remark 3.2).
(4)
 $C\cup A_1 \cup A_2$ is trivial in the annulus and disjoint from
$C\cup A_1 \cup A_2$ is trivial in the annulus and disjoint from  $A_3$.
$A_3$.
Proof. If ![]() $C$ is essential in the annulus, then (2) follows from the neck-cutting and Boerner's relations (see Figures 2 and 5). We may therefore assume that
$C$ is essential in the annulus, then (2) follows from the neck-cutting and Boerner's relations (see Figures 2 and 5). We may therefore assume that ![]() $C$ is trivial. Let
$C$ is trivial. Let ![]() $C'$ denote the (necessarily trivial) circle obtained by performing surgery along both
$C'$ denote the (necessarily trivial) circle obtained by performing surgery along both ![]() $A_1$ and
$A_1$ and ![]() $A_2$. Note that the result of composing the two saddle maps corresponding to
$A_2$. Note that the result of composing the two saddle maps corresponding to ![]() $A_1$ and
$A_1$ and ![]() $A_2$ will send any generator of
$A_2$ will send any generator of ![]() $\mathcal {C}$ in which
$\mathcal {C}$ in which ![]() $C$ is undotted to a sum of elements in which
$C$ is undotted to a sum of elements in which ![]() $C'$ is dotted, and will send any generator which is dotted on
$C'$ is dotted, and will send any generator which is dotted on ![]() $C$ to
$C$ to ![]() $0$. It therefore suffices to consider the effect of surgery along
$0$. It therefore suffices to consider the effect of surgery along ![]() $A_3$ on a dotted
$A_3$ on a dotted ![]() $C'$.
$C'$.
First, assume that ![]() $C \cup A_1 \cup A_2$ is trivial but
$C \cup A_1 \cup A_2$ is trivial but ![]() $\mathcal {C}'\cup A_1 \cup A_2 \cup A_3$ is not. There are several cases to consider. If neither endpoint of
$\mathcal {C}'\cup A_1 \cup A_2 \cup A_3$ is not. There are several cases to consider. If neither endpoint of ![]() $A_3$ is on
$A_3$ is on ![]() $C$, then (4) holds. If precisely one endpoint of
$C$, then (4) holds. If precisely one endpoint of ![]() $A_3$ is on
$A_3$ is on ![]() $C$, then the other endpoint must be on another circle
$C$, then the other endpoint must be on another circle ![]() $\bar {C}$, as in Figure 26(a). In this situation, Boerner's relation implies that (2) holds. Finally, suppose that both endpoints of
$\bar {C}$, as in Figure 26(a). In this situation, Boerner's relation implies that (2) holds. Finally, suppose that both endpoints of ![]() $A_3$ are on
$A_3$ are on ![]() $C$, as in Figure 26(b). Then surgery along
$C$, as in Figure 26(b). Then surgery along ![]() $A_3$ must split
$A_3$ must split ![]() $C'$ into two essential circles. In this situation, (2) holds again, since a dotted trivial circle splitting into two essential circles is sent to
$C'$ into two essential circles. In this situation, (2) holds again, since a dotted trivial circle splitting into two essential circles is sent to ![]() $0$.
$0$.

Figure 26. The two cases where ![]() $C\cup A_1 \cup A_2$ is trivial. Note that these are only schematic depictions, since the interaction of the curves with the seam could be complicated.
$C\cup A_1 \cup A_2$ is trivial. Note that these are only schematic depictions, since the interaction of the curves with the seam could be complicated.
Now suppose that the diagram ![]() $C\cup A_1 \cup A_2$ is non-trivial. Then we are in the situation of § 2.5 (see Figure 18, for example), where Corollary 2.18 shows that we have a sum of terms
$C\cup A_1 \cup A_2$ is non-trivial. Then we are in the situation of § 2.5 (see Figure 18, for example), where Corollary 2.18 shows that we have a sum of terms ![]() $y+\mathfrak {q}^2 y$ in which
$y+\mathfrak {q}^2 y$ in which ![]() $C'$ is dotted. If surgery along
$C'$ is dotted. If surgery along ![]() $A_3$ either splits off a trivial circle from
$A_3$ either splits off a trivial circle from ![]() $C'$ or merges
$C'$ or merges ![]() $C'$ with another trivial circle, then (3) holds since the two terms retain distinct powers of
$C'$ with another trivial circle, then (3) holds since the two terms retain distinct powers of ![]() $\mathfrak {q}$ (see Figure 12). If surgery along
$\mathfrak {q}$ (see Figure 12). If surgery along ![]() $A_3$ splits
$A_3$ splits ![]() $C'$ into two essential circles or merges
$C'$ into two essential circles or merges ![]() $C'$ with an essential circle, then (2) holds as above.
$C'$ with an essential circle, then (2) holds as above.
Theorem 4.2 There is a functor ![]() $F_{\mathfrak {q}}: \underline {2}^n \to \mathscr {B}_G$ which extends the data (4.2) and (4.3).
$F_{\mathfrak {q}}: \underline {2}^n \to \mathscr {B}_G$ which extends the data (4.2) and (4.3).
Proof. Following Lemma 3.1, it remains to define the ![]() $2$-morphisms
$2$-morphisms
for each square face of ![]() $\underline {2}^n$ with vertices
$\underline {2}^n$ with vertices ![]() $u \geq _1 v,v'\geq _1 w$, and to verify the hexagon relation.
$u \geq _1 v,v'\geq _1 w$, and to verify the hexagon relation.
For all cases except the ladybug configuration, the ![]() $2$-morphism
$2$-morphism ![]() $\phi _{u,v,v',w}$ is uniquely determined by the property that it commutes with the source and target maps. Therefore, we need to consider only the ladybug configurations. Assume that a circle
$\phi _{u,v,v',w}$ is uniquely determined by the property that it commutes with the source and target maps. Therefore, we need to consider only the ladybug configurations. Assume that a circle ![]() $C$ in
$C$ in ![]() $D_w$ carries two surgery arcs as in the ladybug configuration. We distinguish three cases, as in Figure 16.
$D_w$ carries two surgery arcs as in the ladybug configuration. We distinguish three cases, as in Figure 16.
(a)
 $C$ is essential.
$C$ is essential.(b)
 $C$ is trivial and surgery along both arcs results in trivial circles.
$C$ is trivial and surgery along both arcs results in trivial circles.(c)
 $C$ is trivial, surgery along one arc produces two trivial circles, and surgery along the other arc produces two essential circles.
$C$ is trivial, surgery along one arc produces two trivial circles, and surgery along the other arc produces two essential circles.
For (a), the composition of two edge maps is ![]() $0$. Therefore,
$0$. Therefore,
and there is no ![]() $2$-morphism to specify. For (b), we rely on the ladybug matching made with the left pair (see [Reference Lipshitz and SarkarLS14a, § 5.4]). Finally, for (c), note that generators dotted on
$2$-morphism to specify. For (b), we rely on the ladybug matching made with the left pair (see [Reference Lipshitz and SarkarLS14a, § 5.4]). Finally, for (c), note that generators dotted on ![]() $C$ are sent to
$C$ are sent to ![]() $0$ by the composition of two edges. For generators undotted on
$0$ by the composition of two edges. For generators undotted on ![]() $C$, Corollary 2.18 implies that
$C$, Corollary 2.18 implies that ![]() $\phi _{u,v,v',w}$ is uniquely determined by the property that it commutes with the source and target maps.
$\phi _{u,v,v',w}$ is uniquely determined by the property that it commutes with the source and target maps.
It remains to verify the hexagon relation. Let ![]() $\mathcal {C}$ denote a configuration with three surgery arcs. We may assume that two of the three surgery arcs form a ladybug configuration, since otherwise the three-dimensional cube is simple. Then the analysis consists of the four cases in Lemma 4.1. In case (1), the verification reduces to classical Khovanov homology (see, for example, [Reference Lawson, Lipshitz and SarkarLLS17a, Proposition 6.1]). For case (2), the composition of three correspondences coming from any three edge maps is empty, so there is nothing to check. Similarly, in case (3), the hexagon relation follows from the discussion in Remark 3.2. Finally, case (4) is straightforward to check by hand since the disjoint arc
$\mathcal {C}$ denote a configuration with three surgery arcs. We may assume that two of the three surgery arcs form a ladybug configuration, since otherwise the three-dimensional cube is simple. Then the analysis consists of the four cases in Lemma 4.1. In case (1), the verification reduces to classical Khovanov homology (see, for example, [Reference Lawson, Lipshitz and SarkarLLS17a, Proposition 6.1]). For case (2), the composition of three correspondences coming from any three edge maps is empty, so there is nothing to check. Similarly, in case (3), the hexagon relation follows from the discussion in Remark 3.2. Finally, case (4) is straightforward to check by hand since the disjoint arc ![]() $A_3$ cannot interfere with the classical Khovanov ladybug matching used on
$A_3$ cannot interfere with the classical Khovanov ladybug matching used on ![]() $C\cup A_1 \cup A_2$.
$C\cup A_1 \cup A_2$.
Proposition 4.3 Up to natural isomorphism, ![]() $F_{\mathfrak {q}}$ is independent of the choices of generators
$F_{\mathfrak {q}}$ is independent of the choices of generators ![]() $\Gamma (u)$.
$\Gamma (u)$.
Proof. For each ![]() $u\in \{0,1\}^n$, let
$u\in \{0,1\}^n$, let ![]() $\Gamma (u)$,
$\Gamma (u)$, ![]() $\Gamma '(u)$ be two sets of generators of
$\Gamma '(u)$ be two sets of generators of ![]() $D_u$, obtained by picking different isotopies
$D_u$, obtained by picking different isotopies ![]() $S,S'$ from standard configurations
$S,S'$ from standard configurations ![]() $D_u^\circ ,{D_u^\circ }'$ to
$D_u^\circ ,{D_u^\circ }'$ to ![]() $D_u$. The natural isomorphism is straightforward to construct when
$D_u$. The natural isomorphism is straightforward to construct when ![]() $S' = S S''$, where
$S' = S S''$, where ![]() $S'' : {D_u^\circ }' \to D_u^\circ$ is a planar isotopy of standard configurations, similar to the usual re-indexing of circles in Khovanov homology under planar isotopy of a link diagram. Thus, it is enough to consider the case when
$S'' : {D_u^\circ }' \to D_u^\circ$ is a planar isotopy of standard configurations, similar to the usual re-indexing of circles in Khovanov homology under planar isotopy of a link diagram. Thus, it is enough to consider the case when ![]() ${D_u^\circ }'=D_u^\circ$ and
${D_u^\circ }'=D_u^\circ$ and ![]() $S,S':D_u^\circ \rightarrow D_u$ induce the same correspondence on components.
$S,S':D_u^\circ \rightarrow D_u$ induce the same correspondence on components.
Let ![]() $F_{\mathfrak {q}}, F_{\mathfrak {q}}' :\underline {2}^n\to \mathscr {B}_G$ denote the corresponding functors, and let
$F_{\mathfrak {q}}, F_{\mathfrak {q}}' :\underline {2}^n\to \mathscr {B}_G$ denote the corresponding functors, and let ![]() $A_{u,v}$,
$A_{u,v}$, ![]() $A'_{u,v}$ denote the correspondences assigned to edges by
$A'_{u,v}$ denote the correspondences assigned to edges by ![]() $F_{\mathfrak {q}}$ and
$F_{\mathfrak {q}}$ and ![]() $F_{\mathfrak {q}}'$, respectively. We will use the strategy of § 3.6 to build a natural isomorphism
$F_{\mathfrak {q}}'$, respectively. We will use the strategy of § 3.6 to build a natural isomorphism ![]() $F_\mathfrak {q} \to F_\mathfrak {q}'$.
$F_\mathfrak {q} \to F_\mathfrak {q}'$.
There is a clear bijection ![]() $\Gamma (u) \to \Gamma '(u)$, denoted
$\Gamma (u) \to \Gamma '(u)$, denoted ![]() $x\mapsto x'$. Lemma 2.8 says that for any
$x\mapsto x'$. Lemma 2.8 says that for any ![]() $x\in \Gamma (u)$, there exists
$x\in \Gamma (u)$, there exists ![]() $m_x\in \mathbb {Z}$ such that
$m_x\in \mathbb {Z}$ such that ![]() $x=\mathfrak {q}^{m_x} x'$. Consider the equivariant bijection
$x=\mathfrak {q}^{m_x} x'$. Consider the equivariant bijection ![]() $\psi _{u}: F_{\mathfrak {q}}(u) \to F_{\mathfrak {q}}'(u)$ defined by
$\psi _{u}: F_{\mathfrak {q}}(u) \to F_{\mathfrak {q}}'(u)$ defined by ![]() $\psi _u(\mathfrak {q}^k x) =\mathfrak {q}^{k+ m_x}x'$. Observe that conditions (NI 1) and (NI 3) in § 3.6 hold by definition of
$\psi _u(\mathfrak {q}^k x) =\mathfrak {q}^{k+ m_x}x'$. Observe that conditions (NI 1) and (NI 3) in § 3.6 hold by definition of ![]() $F_\mathfrak {q}$ and
$F_\mathfrak {q}$ and ![]() $F_\mathfrak {q} '$. Condition (NI 2) holds since
$F_\mathfrak {q} '$. Condition (NI 2) holds since ![]() $x= \mathfrak {q}^{m_x} x'$. To complete the proof, observe that the diagram (3.5) commutes, since the vertical maps act on generators by multiplication by powers of
$x= \mathfrak {q}^{m_x} x'$. To complete the proof, observe that the diagram (3.5) commutes, since the vertical maps act on generators by multiplication by powers of ![]() $\mathfrak {q}$ and thus do not interfere with the ladybug matchings.
$\mathfrak {q}$ and thus do not interfere with the ladybug matchings.
4.2 Isotoping the link diagram
In this section, we show that a planar isotopy of link diagrams induces a natural isomorphism between the corresponding quantum annular Burnside functors. Elementary isotopies away from the seam are trivial, but isotopies which involve intersections with the seam need to be handled more carefully. These results will also be used to show Reidemeister invariance for the stable homotopy type in § 5.5.
Proposition 4.4 Let ![]() $D$ be a link diagram with
$D$ be a link diagram with ![]() $n$ crossings and let
$n$ crossings and let ![]() $D'$ be a link diagram obtained from
$D'$ be a link diagram obtained from ![]() $D$ by one of the following moves.
$D$ by one of the following moves.
(1) Moving an arc (as in the
 $P^{\pm {1}}$ and
$P^{\pm {1}}$ and  $N^{\pm {1}}$ moves of Figure 11) across the seam.
$N^{\pm {1}}$ moves of Figure 11) across the seam.(2) Moving a crossing across the seam (see diagram (4.4)).
Let ![]() $F_{\mathfrak {q}}$ and
$F_{\mathfrak {q}}$ and ![]() $F_{\mathfrak {q}}'$ be Burnside functors for
$F_{\mathfrak {q}}'$ be Burnside functors for ![]() $D$ and
$D$ and ![]() $D'$, respectively. Then
$D'$, respectively. Then ![]() $F_{\mathfrak {q}}$ is naturally isomorphic to
$F_{\mathfrak {q}}$ is naturally isomorphic to ![]() $F_{\mathfrak {q}}'$.
$F_{\mathfrak {q}}'$.
Proof. We will again follow the strategy of § 3.6. By Proposition 4.3, we are free to choose generators for each configuration ![]() $D_u$ using any isotopy
$D_u$ using any isotopy ![]() $D_u^\circ \to D_u$, and likewise for
$D_u^\circ \to D_u$, and likewise for ![]() $D_u'$. For each
$D_u'$. For each ![]() $u\in \underline {2}^n$, let
$u\in \underline {2}^n$, let ![]() $S_u: D_u^\circ \to D_u$ be the cobordism formed by a fixed choice of isotopy from
$S_u: D_u^\circ \to D_u$ be the cobordism formed by a fixed choice of isotopy from ![]() $D_u^\circ$ to
$D_u^\circ$ to ![]() $D_u$. There is also an obvious isotopy
$D_u$. There is also an obvious isotopy ![]() $R_u : D_u\to D'_u$, corresponding to the moves in the statement of the proposition. Since
$R_u : D_u\to D'_u$, corresponding to the moves in the statement of the proposition. Since ![]() $D_u^\circ = D_u'^\circ$, we can choose generators for
$D_u^\circ = D_u'^\circ$, we can choose generators for ![]() $D_u'$ using the cobordism
$D_u'$ using the cobordism ![]() $R_uS_u$. For
$R_uS_u$. For ![]() $u,v\in \underline {2}^n$ with
$u,v\in \underline {2}^n$ with ![]() $u\geq _1 v$, let
$u\geq _1 v$, let ![]() $d_{v,u}$ and
$d_{v,u}$ and ![]() $d'_{v,u}$ denote the maps assigned to the edge
$d'_{v,u}$ denote the maps assigned to the edge ![]() $v\to u$ in
$v\to u$ in ![]() $[[D]]$ and
$[[D]]$ and ![]() $[[D']]$, respectively.
$[[D']]$, respectively.
Suppose that we are in the situation (1). We have equivariant bijections ![]() $\psi _u: F_{\mathfrak {q}}(u) \to F_{\mathfrak {q}}'(u)$ for each
$\psi _u: F_{\mathfrak {q}}(u) \to F_{\mathfrak {q}}'(u)$ for each ![]() $u$, given by
$u$, given by ![]() $\psi _v(\mathfrak {q}^k x) = \mathfrak {q}^k R_u(x)$ (as usual, we do not distinguish between a cobordism and its induced map). Conditions (NI 1) and (NI 3) are satisfied by definition. For each
$\psi _v(\mathfrak {q}^k x) = \mathfrak {q}^k R_u(x)$ (as usual, we do not distinguish between a cobordism and its induced map). Conditions (NI 1) and (NI 3) are satisfied by definition. For each ![]() $u,v\in \underline {2}^n$ with
$u,v\in \underline {2}^n$ with ![]() $u\geq _1 v$, we have
$u\geq _1 v$, we have
It follows that, for ![]() $\mathfrak {q}^k y \in F_\mathfrak {q}(u)$ and
$\mathfrak {q}^k y \in F_\mathfrak {q}(u)$ and ![]() $\mathfrak {q}^\ell x\in F_\mathfrak {q}(v)$,
$\mathfrak {q}^\ell x\in F_\mathfrak {q}(v)$, ![]() $\mathfrak {q}^k y \text { appears in } d_{v,u}(\mathfrak {q}^\ell x)$ if and only if
$\mathfrak {q}^k y \text { appears in } d_{v,u}(\mathfrak {q}^\ell x)$ if and only if ![]() $\mathfrak {q}^k R_u(y)$ appears in
$\mathfrak {q}^k R_u(y)$ appears in ![]() $d'_{v,u}(\mathfrak {q}^k R_v(x))$. Therefore, condition (NI 2) is satisfied as well. Observe that the diagram (3.5) commutes since we do not interfere with any potential ladybug matchings.
$d'_{v,u}(\mathfrak {q}^k R_v(x))$. Therefore, condition (NI 2) is satisfied as well. Observe that the diagram (3.5) commutes since we do not interfere with any potential ladybug matchings.
For case ![]() $(2)$, the maps
$(2)$, the maps ![]() $\psi _{u}$ need to be modified slightly in order to satisfy (NI 2). We illustrate one case in detail. Suppose that
$\psi _{u}$ need to be modified slightly in order to satisfy (NI 2). We illustrate one case in detail. Suppose that ![]() $D$ and
$D$ and ![]() $D'$ are as shown in (
$D'$ are as shown in (
). Assume also that the crossing shown is first in the ordering of crossings.

Let ![]() $u\in \underline {2}^n$. If
$u\in \underline {2}^n$. If ![]() $u_1=0$, define
$u_1=0$, define ![]() $\psi _u : F_\mathfrak {q}(u) \to F_\mathfrak {q}'(u)$ as in case (1). If
$\psi _u : F_\mathfrak {q}(u) \to F_\mathfrak {q}'(u)$ as in case (1). If ![]() $u_1=1$, then define
$u_1=1$, then define ![]() $\psi _u$ by
$\psi _u$ by
We will now verify that condition (NI 2) holds for this choice of equivariant bijections ![]() $\{\psi _u\}_{u\in \underline {2}^n}$. Let
$\{\psi _u\}_{u\in \underline {2}^n}$. Let ![]() $u,v\in \underline {2}^n$ with
$u,v\in \underline {2}^n$ with ![]() $u\geq _1 v$. If
$u\geq _1 v$. If ![]() $u_1=v_1$, then the edge maps
$u_1=v_1$, then the edge maps ![]() $d_{v,u}$ and
$d_{v,u}$ and ![]() $d'_{v,u}$ are induced by changing the smoothing at a crossing away from the one shown in (
$d'_{v,u}$ are induced by changing the smoothing at a crossing away from the one shown in (
). As in case (1) above, we have
so condition (NI 2) holds. Suppose now that ![]() $u_1=1$ and
$u_1=1$ and ![]() $v_1=0$. Then
$v_1=0$. Then
where the factor of ![]() $\mathfrak {q}$ comes from moving a saddle across the membrane (see Figure 7). The situation is depicted in the (non-commutative) diagram (
$\mathfrak {q}$ comes from moving a saddle across the membrane (see Figure 7). The situation is depicted in the (non-commutative) diagram (
).

Let ![]() $\mathfrak {q}^k y\in F_\mathfrak {q}(u)$ and
$\mathfrak {q}^k y\in F_\mathfrak {q}(u)$ and ![]() $\mathfrak {q}^\ell x\in F_\mathfrak {q}(v)$. It follows from (4.5) that
$\mathfrak {q}^\ell x\in F_\mathfrak {q}(v)$. It follows from (4.5) that ![]() $\mathfrak {q}^k y$ appears in
$\mathfrak {q}^k y$ appears in ![]() $d_{v,u}(\mathfrak {q}^\ell x)$ if and only if
$d_{v,u}(\mathfrak {q}^\ell x)$ if and only if ![]() $\mathfrak {q}^{k+1} R_u(y)$ appears in
$\mathfrak {q}^{k+1} R_u(y)$ appears in ![]() $d'_{v,u}(\mathfrak {q}^\ell R_v(x))$. Therefore, condition (NI 2) is satisfied. Again, the hexagon relation is satisfied because the
$d'_{v,u}(\mathfrak {q}^\ell R_v(x))$. Therefore, condition (NI 2) is satisfied. Again, the hexagon relation is satisfied because the ![]() $2$-morphisms do not interfere with the ladybug matching.
$2$-morphisms do not interfere with the ladybug matching.
4.3 The cases  $r=1,2$ and the classical annular homotopy type
$r=1,2$ and the classical annular homotopy type
Our proof of Theorem 4.2 relies on ![]() $r>2$. In this section, we address the cases
$r>2$. In this section, we address the cases ![]() $r=1,2$ in that order.
$r=1,2$ in that order.
Let ![]() $D$ be a diagram for an annular link with
$D$ be a diagram for an annular link with ![]() $n$ crossings. When
$n$ crossings. When ![]() $r=1$, the modified quantum annular chain complex
$r=1$, the modified quantum annular chain complex
is just the classical annular chain complex ![]() $CKh_\mathbb {A}(D)$ (see the discussion preceding Lemma 2.17). We sketch how to define the annular Burnside functor, denoted
$CKh_\mathbb {A}(D)$ (see the discussion preceding Lemma 2.17). We sketch how to define the annular Burnside functor, denoted ![]() $F_1$, for the classical annular Khovanov chain complex below. An alternative construction, using Hochschild homology of Chen–Khovanov spectra for tangles, was recently introduced in [Reference Lawson, Lipshitz and SarkarLLS19].
$F_1$, for the classical annular Khovanov chain complex below. An alternative construction, using Hochschild homology of Chen–Khovanov spectra for tangles, was recently introduced in [Reference Lawson, Lipshitz and SarkarLLS19].
Let ![]() $F_{Kh} : \underline {2}^n \to \mathscr {B}$ denote the usual Khovanov Burnside functor (see [Reference Lawson, Lipshitz and SarkarLLS20, Example 4.21] and also [Reference Lawson, Lipshitz and SarkarLLS17a, § 6]), where the ladybug matching is made with the left pair. For
$F_{Kh} : \underline {2}^n \to \mathscr {B}$ denote the usual Khovanov Burnside functor (see [Reference Lawson, Lipshitz and SarkarLLS20, Example 4.21] and also [Reference Lawson, Lipshitz and SarkarLLS17a, § 6]), where the ladybug matching is made with the left pair. For ![]() $u\geq _1 v$, let
$u\geq _1 v$, let
denote the classical annular differential and let ![]() $d^{Kh}_{v,u}$ denote the usual Khovanov differential. We have that
$d^{Kh}_{v,u}$ denote the usual Khovanov differential. We have that ![]() $d^{Kh}_{v,u} = d^\mathbb {A}_{v,u} + d'_{v,u}$ (see the discussion in Remark 2.3).
$d^{Kh}_{v,u} = d^\mathbb {A}_{v,u} + d'_{v,u}$ (see the discussion in Remark 2.3).
Recall from § 2.1 that annular Khovanov generators may be taken to be the usual Khovanov generators (where the annular link diagram is considered as a planar diagram under the inclusion ![]() $\mathbb {A}\subset \mathbb {R}^2$), so set
$\mathbb {A}\subset \mathbb {R}^2$), so set ![]() $F_1(u) = F_{Kh}(u)$ for each
$F_1(u) = F_{Kh}(u)$ for each ![]() $u\in \underline {2}^n$. For
$u\in \underline {2}^n$. For ![]() $u\geq _1 v$, let
$u\geq _1 v$, let ![]() $A^{Kh}_{u,v}$ denote the correspondence assigned by
$A^{Kh}_{u,v}$ denote the correspondence assigned by ![]() $F_{Kh}$ to the edge
$F_{Kh}$ to the edge ![]() $\varphi _{u,v} :u\to v$. Define the correspondence
$\varphi _{u,v} :u\to v$. Define the correspondence ![]() $A^{\mathbb {A}}_{u,v}$ from
$A^{\mathbb {A}}_{u,v}$ from ![]() $F_1(u)$ to
$F_1(u)$ to ![]() $F_1(v)$ by
$F_1(v)$ by
with the obvious source and target maps, and set ![]() $F_1(\varphi _{u,v}) = A^{\mathbb {A}}_{u,v}$. Note that
$F_1(\varphi _{u,v}) = A^{\mathbb {A}}_{u,v}$. Note that ![]() $A^{\mathbb {A}}_{u,v} \subset A^{Kh}_{u,v}$.
$A^{\mathbb {A}}_{u,v} \subset A^{Kh}_{u,v}$.
Let ![]() $\phi ^{Kh}_{u,v,v',w}$ be the
$\phi ^{Kh}_{u,v,v',w}$ be the ![]() $2$-morphism assigned by
$2$-morphism assigned by ![]() $F_{Kh}$ to the square face with vertices
$F_{Kh}$ to the square face with vertices ![]() $u \geq _1 v, v' \geq _1 w$. One can check that
$u \geq _1 v, v' \geq _1 w$. One can check that ![]() $\phi ^{Kh}_{u,v,v',w}$ restricts to
$\phi ^{Kh}_{u,v,v',w}$ restricts to
Taking ![]() $\phi ^\mathbb {A}_{u,v,v',w}$ to be the
$\phi ^\mathbb {A}_{u,v,v',w}$ to be the ![]() $2$-morphisms assigned to square faces by
$2$-morphisms assigned to square faces by ![]() $F_1$, the conditions of Lemma 3.1 are satisfied as a consequence of the construction of
$F_1$, the conditions of Lemma 3.1 are satisfied as a consequence of the construction of ![]() $F_{Kh}$.
$F_{Kh}$.
When ![]() $r=2$, Lemma 4.1 and the ensuing analysis in case (c) of the proof of Theorem 4.2 do not hold, since
$r=2$, Lemma 4.1 and the ensuing analysis in case (c) of the proof of Theorem 4.2 do not hold, since ![]() $\mathfrak {q}^2=1$. Instead, we rely on the ladybug matching made with the left pair to define the
$\mathfrak {q}^2=1$. Instead, we rely on the ladybug matching made with the left pair to define the ![]() $2$-morphism in case (c) of Theorem 4.2. Let us verify the hexagon relation, using the formulation in Remark 3.2. Start with an element
$2$-morphism in case (c) of Theorem 4.2. Let us verify the hexagon relation, using the formulation in Remark 3.2. Start with an element ![]() $x=(\mathfrak {q}^i a, \mathfrak {q}^j b , \mathfrak {q}^k c, \mathfrak {q}^\ell d)$ in the correspondence obtained as the composition of correspondences for three consecutive edge maps. Going around the six faces of the cube, the
$x=(\mathfrak {q}^i a, \mathfrak {q}^j b , \mathfrak {q}^k c, \mathfrak {q}^\ell d)$ in the correspondence obtained as the composition of correspondences for three consecutive edge maps. Going around the six faces of the cube, the ![]() $2$-morphisms send
$2$-morphisms send ![]() $x$ to an element
$x$ to an element ![]() $x' = (\mathfrak {q}^i a, \mathfrak {q}^{j'} b' , \mathfrak {q}^{k'} c', \mathfrak {q}^\ell d)$ in the same correspondence. It follows from the classical annular case, where powers of
$x' = (\mathfrak {q}^i a, \mathfrak {q}^{j'} b' , \mathfrak {q}^{k'} c', \mathfrak {q}^\ell d)$ in the same correspondence. It follows from the classical annular case, where powers of ![]() $\mathfrak {q}$ are disregarded, that labels on the circles in the generators
$\mathfrak {q}$ are disregarded, that labels on the circles in the generators ![]() $b$ and
$b$ and ![]() $c$ match the labels on the circles in the generators
$c$ match the labels on the circles in the generators ![]() $b'$ and
$b'$ and ![]() $c'$, respectively. Then
$c'$, respectively. Then ![]() $b=b'$ and, since both
$b=b'$ and, since both ![]() $\mathfrak {q}^j b$ and
$\mathfrak {q}^j b$ and ![]() $\mathfrak {q}^{j'} b' = \mathfrak {q}^{j'} b$ appear in the image of
$\mathfrak {q}^{j'} b' = \mathfrak {q}^{j'} b$ appear in the image of ![]() $\mathfrak {q}^i a$ under a saddle map, Lemma 2.17 implies that
$\mathfrak {q}^i a$ under a saddle map, Lemma 2.17 implies that ![]() $\mathfrak {q}^j =\mathfrak {q}^{j'}$. Likewise,
$\mathfrak {q}^j =\mathfrak {q}^{j'}$. Likewise, ![]() $\mathfrak {q}^k c= \mathfrak {q}^{k'} c'$ and we conclude that the hexagon relation is satisfied.
$\mathfrak {q}^k c= \mathfrak {q}^{k'} c'$ and we conclude that the hexagon relation is satisfied.
5. From Burnside functors to stable homotopy types
This section describes a general framework for obtaining a spectrum from a Burnside functor. This general construction is then applied to the case of the quantum annular Burnside functor, establishing the main result of the paper, Theorem 1.1. In more detail in § 5.1 we recall box maps and their required properties for the non-equivariant case as in [Reference Lawson, Lipshitz and SarkarLLS20, § 5]. Then, in § 5.2, we discuss ![]() $G$-equivariant box maps via a slight generalization of the ideas established in [Reference Sarkar, Scaduto and StoffregenSSS20], ensuring that the required properties are still satisfied. Sections 5.3 and 5.4 describe how to use box maps to pass from an equivariant Burnside functor
$G$-equivariant box maps via a slight generalization of the ideas established in [Reference Sarkar, Scaduto and StoffregenSSS20], ensuring that the required properties are still satisfied. Sections 5.3 and 5.4 describe how to use box maps to pass from an equivariant Burnside functor ![]() $F$ to a
$F$ to a ![]() $G$-CW complex realizing
$G$-CW complex realizing ![]() $F$, following [Reference Sarkar, Scaduto and StoffregenSSS20, § 4], by taking the homotopy colimit (see [Reference VogtVog73]) of an appropriate diagram. Finally, in § 5.5, we apply this theory to the quantum annular Burnside functor of § 4.1 to define the equivariant spectrum
$F$, following [Reference Sarkar, Scaduto and StoffregenSSS20, § 4], by taking the homotopy colimit (see [Reference VogtVog73]) of an appropriate diagram. Finally, in § 5.5, we apply this theory to the quantum annular Burnside functor of § 4.1 to define the equivariant spectrum ![]() $\mathcal {X}_{\mathbb {A}_\mathfrak {q}}^r(L)$ and check that it is well defined, proving Theorem 1.1.
$\mathcal {X}_{\mathbb {A}_\mathfrak {q}}^r(L)$ and check that it is well defined, proving Theorem 1.1.
We emphasize some differences and similarities between this paper and others appearing in the literature. There is no group action on the links considered in this paper, so our box maps and homotopy coherent refinements are different from those in [Reference Borodzik, Politarczyk and SilveroBPS18, Reference MusytMus19, Reference Stoffregen and ZhangSZ18]. Functors ![]() $\underline {2}^n \to \mathscr {B}_{\mathbb {Z}/2\mathbb {Z}}$ are considered in [Reference Sarkar, Scaduto and StoffregenSSS20], and there the authors introduced actions of
$\underline {2}^n \to \mathscr {B}_{\mathbb {Z}/2\mathbb {Z}}$ are considered in [Reference Sarkar, Scaduto and StoffregenSSS20], and there the authors introduced actions of ![]() $\mathbb {Z}/2\mathbb {Z}$ and
$\mathbb {Z}/2\mathbb {Z}$ and ![]() $\mathbb {Z}/2 \mathbb {Z} \times \mathbb {Z}/ 2 \mathbb {Z}$, which involve an internal action on boxes. We are interested in an external
$\mathbb {Z}/2 \mathbb {Z} \times \mathbb {Z}/ 2 \mathbb {Z}$, which involve an internal action on boxes. We are interested in an external ![]() $G$-action which permutes the boxes, so our work is different in this respect.
$G$-action which permutes the boxes, so our work is different in this respect.
5.1 Box maps
We begin by reviewing a key part of the non-equivariant case allowing us to set some notation following [Reference Lawson, Lipshitz and SarkarLLS20, § 5.1].
A ![]() $k$-dimensional box is
$k$-dimensional box is ![]() $\prod _{i=1}^k [a_i, b_i] \subset \mathbb {R}^k$. For two
$\prod _{i=1}^k [a_i, b_i] \subset \mathbb {R}^k$. For two ![]() $k$-dimensional boxes
$k$-dimensional boxes ![]() $B$ and
$B$ and ![]() $B'$, there is a canonical homeomorphism
$B'$, there is a canonical homeomorphism ![]() $B\xrightarrow {\sim } B'$, obtained by scaling and translating the ambient space
$B\xrightarrow {\sim } B'$, obtained by scaling and translating the ambient space ![]() $\mathbb {R}^k$. Fix an identification
$\mathbb {R}^k$. Fix an identification ![]() $S^k = [0,1]^k/\partial ([0,1]^k)$, so that for any
$S^k = [0,1]^k/\partial ([0,1]^k)$, so that for any ![]() $k$-dimensional box
$k$-dimensional box ![]() $B$,
$B$, ![]() $B/\partial B$ is canonically identified with
$B/\partial B$ is canonically identified with ![]() $S^k$.
$S^k$.
Suppose that we have a correspondence ![]() $X\xleftarrow {s} A \xrightarrow {t} Y$. Pick disjoint
$X\xleftarrow {s} A \xrightarrow {t} Y$. Pick disjoint ![]() $k$-dimensional boxes
$k$-dimensional boxes ![]() $\{B_x\}_{x\in X}$. Following [Reference Lawson, Lipshitz and SarkarLLS20], let
$\{B_x\}_{x\in X}$. Following [Reference Lawson, Lipshitz and SarkarLLS20], let
denote the space of all collections ![]() $\{B_a\}_{a\in A}$ of disjoint
$\{B_a\}_{a\in A}$ of disjoint ![]() $k$-dimensional boxes such that
$k$-dimensional boxes such that ![]() $B_a\subset B_{s(a)}$. A point
$B_a\subset B_{s(a)}$. A point ![]() $e=\{B_a\} \in E(\{B_x\},s)$ determines a map
$e=\{B_a\} \in E(\{B_x\},s)$ determines a map
defined as follows. On each wedge summand, ![]() $\Phi (e,A)$ is the composition
$\Phi (e,A)$ is the composition
 \begin{equation} S^k_x = B_x/\partial B_x \to B_x \bigg/ \bigg( B_x\setminus \bigcup_{a\in s^{{-}1}(x)} B_a^{\text{int}} \bigg) = \bigvee_{a\in s^{{-}1}(x)} B_a/\partial B_a \xrightarrow{t} \bigvee_{y\in Y}S^k_y, \end{equation}
\begin{equation} S^k_x = B_x/\partial B_x \to B_x \bigg/ \bigg( B_x\setminus \bigcup_{a\in s^{{-}1}(x)} B_a^{\text{int}} \bigg) = \bigvee_{a\in s^{{-}1}(x)} B_a/\partial B_a \xrightarrow{t} \bigvee_{y\in Y}S^k_y, \end{equation}
where the first map is a quotient and the last map sends the sphere ![]() $B_a/\partial B_a$ to
$B_a/\partial B_a$ to ![]() $B_{t(a)}/ \partial B_{t(a)} = S^k_{t(a)}$ via the canonical homeomorphism
$B_{t(a)}/ \partial B_{t(a)} = S^k_{t(a)}$ via the canonical homeomorphism ![]() $B_a\cong B_{t(a)}$. A map of this form is said to refine the correspondence
$B_a\cong B_{t(a)}$. A map of this form is said to refine the correspondence ![]() $X \xleftarrow {s} A \xrightarrow {t} Y$.
$X \xleftarrow {s} A \xrightarrow {t} Y$.
Suppose that we have correspondences ![]() $X \xleftarrow {s_A} A \xrightarrow {t_A} Y$ and
$X \xleftarrow {s_A} A \xrightarrow {t_A} Y$ and ![]() $Y\xleftarrow {s_B} B \xrightarrow {t_B} Z$ with boxes
$Y\xleftarrow {s_B} B \xrightarrow {t_B} Z$ with boxes ![]() $\{B_x\}_{x\in X}$ and
$\{B_x\}_{x\in X}$ and ![]() $\{B_y\}_{y\in Y}$. Given
$\{B_y\}_{y\in Y}$. Given ![]() $e\in E(\{B_x\}_{x\in X},s_A)$ and
$e\in E(\{B_x\}_{x\in X},s_A)$ and ![]() $e'\in E(\{B_y\}_{y\in Y},s_B)$, we can consider the preimage of the boxes in
$e'\in E(\{B_y\}_{y\in Y},s_B)$, we can consider the preimage of the boxes in ![]() $e'$ under the map
$e'$ under the map ![]() $\Phi (e,A)$. An important point in the proof of existence and uniqueness of spatial refinements is that
$\Phi (e,A)$. An important point in the proof of existence and uniqueness of spatial refinements is that ![]() $\Phi (e,A)^{-1}(e')$ is a collection of little boxes in
$\Phi (e,A)^{-1}(e')$ is a collection of little boxes in ![]() $\{B_x\}_{x\in X}$ labelled by the composition
$\{B_x\}_{x\in X}$ labelled by the composition ![]() $C:=B\times _Y A$; that is,
$C:=B\times _Y A$; that is,
where ![]() $s_C: C \to X$ is the source map of the composition. See Figure 27 for an explanation of this.
$s_C: C \to X$ is the source map of the composition. See Figure 27 for an explanation of this.

Figure 27. Fix two collections of sub-boxes ![]() $e\in E(\{B_x\}_{x\in X}, s_A)$,
$e\in E(\{B_x\}_{x\in X}, s_A)$, ![]() $e'\in E(\{B_y\}_{y\in Y}, s_B)$, and an element
$e'\in E(\{B_y\}_{y\in Y}, s_B)$, and an element ![]() $(b,a)$ in the composition correspondence
$(b,a)$ in the composition correspondence ![]() $C=B\times _Y A$. Then by definition
$C=B\times _Y A$. Then by definition ![]() $e'$ gives us a box
$e'$ gives us a box ![]() $B_b\subset S^k_y$ (in black on the right) where
$B_b\subset S^k_y$ (in black on the right) where ![]() $y=s_B(b)=t_A(a)$ and
$y=s_B(b)=t_A(a)$ and ![]() $e$ gives us a box
$e$ gives us a box ![]() $B_a\subset S^k_x$ where
$B_a\subset S^k_x$ where ![]() $x=s_A(a)$ (in gray on the left). The maps in the figure are those appearing in (5.2), composing to give
$x=s_A(a)$ (in gray on the left). The maps in the figure are those appearing in (5.2), composing to give ![]() $\Phi (e,A)$. If we pull back the box
$\Phi (e,A)$. If we pull back the box ![]() $B_b$ under this map (restricted to
$B_b$ under this map (restricted to ![]() $S^k_x$), we obtain a smaller sub-box
$S^k_x$), we obtain a smaller sub-box ![]() $B_{(b,a)}\subset B_a \subset S^k_x$ for any such pair
$B_{(b,a)}\subset B_a \subset S^k_x$ for any such pair ![]() $(b,a)\in C$. Taking the collection of such boxes and preimages together, we see that
$(b,a)\in C$. Taking the collection of such boxes and preimages together, we see that ![]() $\Phi (e,A)^{-1}(e') \in E(\{B_x\}_{x\in X}, s_C)$.
$\Phi (e,A)^{-1}(e') \in E(\{B_x\}_{x\in X}, s_C)$.
5.2 Equivariant box maps
Throughout this section, we will continue to use ![]() $G$ to denote a finite cyclic group, but all of the statements below generalize to more general finite groups acting freely on finite sets.
$G$ to denote a finite cyclic group, but all of the statements below generalize to more general finite groups acting freely on finite sets.
Suppose that a correspondence ![]() $X \xleftarrow {s} A \xrightarrow {t} Y$ consists of
$X \xleftarrow {s} A \xrightarrow {t} Y$ consists of ![]() $G$-sets and equivariant maps. Then in particular the spaces
$G$-sets and equivariant maps. Then in particular the spaces ![]() ${\bigvee} _{x\in X} S^k_x$ and
${\bigvee} _{x\in X} S^k_x$ and ![]() ${\bigvee} _{y\in Y} S^k_y$ inherit a
${\bigvee} _{y\in Y} S^k_y$ inherit a ![]() $G$-action via the canonical homeomorphism
$G$-action via the canonical homeomorphism ![]() $B_x\cong B_{gx}$. In terms of the wedge summands, this
$B_x\cong B_{gx}$. In terms of the wedge summands, this ![]() $G$-action permutes the copies of
$G$-action permutes the copies of ![]() $S^k$. However, to obtain a
$S^k$. However, to obtain a ![]() $G$-equivariant refinement
$G$-equivariant refinement ![]() ${\bigvee} _{x\in X} S^k_x \rightarrow {\bigvee} _{y\in Y} S^k_y$, a second condition needs to be imposed on the sub-boxes
${\bigvee} _{x\in X} S^k_x \rightarrow {\bigvee} _{y\in Y} S^k_y$, a second condition needs to be imposed on the sub-boxes ![]() $\{B_a\} \in E(\{B_x\},s)$.
$\{B_a\} \in E(\{B_x\},s)$.
Let
denote the subset of ![]() $E(\{B_x\},s)$ consisting of the little boxes
$E(\{B_x\},s)$ consisting of the little boxes ![]() $\{B_a\}$ satisfying the following property: for each
$\{B_a\}$ satisfying the following property: for each ![]() $g\in G$,
$g\in G$, ![]() $x\in X$, and
$x\in X$, and ![]() $a\in s^{-1}(x)$, the canonical homeomorphism
$a\in s^{-1}(x)$, the canonical homeomorphism ![]() $B_x \to B_{gx}$ restricts to a homeomorphism
$B_x \to B_{gx}$ restricts to a homeomorphism ![]() $B_a \to B_{ga}$. With this condition in place, the restricted homeomorphism
$B_a \to B_{ga}$. With this condition in place, the restricted homeomorphism ![]() $B_a \to B_{ga}$ is also the canonical one. In particular, if we identify all boxes
$B_a \to B_{ga}$ is also the canonical one. In particular, if we identify all boxes ![]() $B_{gx}$ canonically with
$B_{gx}$ canonically with ![]() $[0,1]^k$, then the sub-boxes
$[0,1]^k$, then the sub-boxes ![]() $B_{ga}\subset B_{gx}$ for various
$B_{ga}\subset B_{gx}$ for various ![]() $g$ all have the same image in
$g$ all have the same image in ![]() $[0,1]^k$.
$[0,1]^k$.
Lemma 5.1 Let ![]() $X\xleftarrow {s} A \xrightarrow {t} B$ be an equivariant correspondence. If
$X\xleftarrow {s} A \xrightarrow {t} B$ be an equivariant correspondence. If ![]() $e\in E_G(\{B_x\},s)$, then the induced box map
$e\in E_G(\{B_x\},s)$, then the induced box map ![]() $\Phi (e,A)$ is
$\Phi (e,A)$ is ![]() $G$-equivariant.
$G$-equivariant.
Proof. Let ![]() $g\in G$ and
$g\in G$ and ![]() $x\in X$. We need to verify commutativity of the diagram
$x\in X$. We need to verify commutativity of the diagram

where the horizontal maps are those of (5.2) and the vertical maps are induced by canonical homeomorphisms between boxes. The left-hand square commutes since ![]() $e\in E_G(\{B_x\},s)$, and the right-hand square commutes because all the maps there are induced by canonical homeomorphisms of boxes.
$e\in E_G(\{B_x\},s)$, and the right-hand square commutes because all the maps there are induced by canonical homeomorphisms of boxes.
In the construction of stable homotopy refinements, it is crucial that the space of little boxes is highly connected and that boxes pull back to boxes. The remainder of this subsection is devoted to verifying these properties for ![]() $E_G(\{B_x\},s)$. For the following statement, recall the notation for the quotient functor, introduced in the last paragraph of § 3.3.
$E_G(\{B_x\},s)$. For the following statement, recall the notation for the quotient functor, introduced in the last paragraph of § 3.3.
Lemma 5.2 Let ![]() $X \xleftarrow {s} A \xrightarrow {t} Y$ be a correspondence of
$X \xleftarrow {s} A \xrightarrow {t} Y$ be a correspondence of ![]() $G$-sets and equivariant maps between them. Then we have the following homeomorphism of spaces of sub-boxes:
$G$-sets and equivariant maps between them. Then we have the following homeomorphism of spaces of sub-boxes:
Proof. For a fixed ![]() $x\in X$, a subcollection of little boxes
$x\in X$, a subcollection of little boxes ![]() $\{B_a\}_{a\in s^{-1}(x)}$ in
$\{B_a\}_{a\in s^{-1}(x)}$ in ![]() $B_x$ determines the little boxes
$B_x$ determines the little boxes ![]() $\{B_c\}_{c\in s^{-1}(gx)}$ in
$\{B_c\}_{c\in s^{-1}(gx)}$ in ![]() $B_{gx}$ for all
$B_{gx}$ for all ![]() $g\in G$. Explicitly, for each
$g\in G$. Explicitly, for each ![]() $a\in s^{-1}(x)$ and
$a\in s^{-1}(x)$ and ![]() $g\in G$,
$g\in G$, ![]() $B_{ga} \subset B_{gx}$ is the image of
$B_{ga} \subset B_{gx}$ is the image of ![]() $B_a$ under the canonical homeomorphism
$B_a$ under the canonical homeomorphism ![]() $B_x\to B_{gx}$ and, since
$B_x\to B_{gx}$ and, since ![]() $s$ is a
$s$ is a ![]() $G$-equivariant map,
$G$-equivariant map, ![]() $c\in s^{-1}(gx)$ if and only if
$c\in s^{-1}(gx)$ if and only if ![]() $c=ga$ for some
$c=ga$ for some ![]() $a\in s^{-1}(x)$.
$a\in s^{-1}(x)$.
Thus, a collection of equivariant boxes in ![]() $E_G(\{B_x\},s)$ is equivalent to a (non-equivariant) choice of boxes in each
$E_G(\{B_x\},s)$ is equivalent to a (non-equivariant) choice of boxes in each ![]() $G$-orbit of
$G$-orbit of ![]() $X$ for each
$X$ for each ![]() $G$-orbit of
$G$-orbit of ![]() $A$, which is the meaning of
$A$, which is the meaning of ![]() $E(\{B_{[x]}\}_{[x] \in X/G}, s/G)$.
$E(\{B_{[x]}\}_{[x] \in X/G}, s/G)$.
Corollary 5.3 ![]() $E_G(\{B_x\},s)$ is
$E_G(\{B_x\},s)$ is ![]() $(k-2)$-connected.
$(k-2)$-connected.
Proof. This follows from Lemma 5.2 together with the connectivity for spaces of (non-equivariant) sub-boxes shown in [Reference Lawson, Lipshitz and SarkarLLS20, Lemma 5.18].
Lemma 5.4 Let ![]() $X\xleftarrow {s_A} A \xrightarrow {t_A} Y$ and
$X\xleftarrow {s_A} A \xrightarrow {t_A} Y$ and ![]() $Y \xleftarrow {s_B} B \xrightarrow {t_B} Z$ be equivariant correspondences. Let
$Y \xleftarrow {s_B} B \xrightarrow {t_B} Z$ be equivariant correspondences. Let ![]() $\{B_x\}_{x\in X}$ and
$\{B_x\}_{x\in X}$ and ![]() $\{B_y\}_{y\in Y}$ be collections of
$\{B_y\}_{y\in Y}$ be collections of ![]() $k$-dimensional boxes, and let
$k$-dimensional boxes, and let ![]() $e\in E_G(\{B_x\}, s_A)$,
$e\in E_G(\{B_x\}, s_A)$, ![]() $e'\in E_G(\{B_y\}, s_B)$. Then
$e'\in E_G(\{B_y\}, s_B)$. Then ![]() $\Phi (e,A)^{-1}(e') \in E_G(\{B_x\}_{x\in X}, s_C)$.
$\Phi (e,A)^{-1}(e') \in E_G(\{B_x\}_{x\in X}, s_C)$.
Proof. Fix ![]() $g\in G$. Let
$g\in G$. Let ![]() $B_{(b,a)} \in \Phi (e,A)^{-1}(e')$ and set
$B_{(b,a)} \in \Phi (e,A)^{-1}(e')$ and set ![]() $y=s_B(b)$ and
$y=s_B(b)$ and ![]() $x=s_A(a)$ as in Figure 27. We need to show that the canonical homeomorphism
$x=s_A(a)$ as in Figure 27. We need to show that the canonical homeomorphism ![]() $B_x\to B_{gx}$ sends
$B_x\to B_{gx}$ sends ![]() $B_{(b,a)}$ to
$B_{(b,a)}$ to ![]() $B_{(gb,ga)}$. By construction,
$B_{(gb,ga)}$. By construction, ![]() $\Phi (e,A)(B_{(b,a)}) = B_b$. Since
$\Phi (e,A)(B_{(b,a)}) = B_b$. Since ![]() $e\in E_G(\{B_x\}_{x\in X},s_A)$, we also know that
$e\in E_G(\{B_x\}_{x\in X},s_A)$, we also know that ![]() $g B_b = B_{gb}$. Recall from Lemma 5.1 that
$g B_b = B_{gb}$. Recall from Lemma 5.1 that ![]() $\Phi (e,A)$ is
$\Phi (e,A)$ is ![]() $G$-equivariant. These facts yield
$G$-equivariant. These facts yield
Since ![]() $e'\in E_G(\{B_y\}_{y\in Y},s_B)$ and
$e'\in E_G(\{B_y\}_{y\in Y},s_B)$ and ![]() $B_{(b,a)} \subset B_a$, we have that
$B_{(b,a)} \subset B_a$, we have that ![]() $g B_{(b,a)} \subset g B_a = B_{ga}$. Then
$g B_{(b,a)} \subset g B_a = B_{ga}$. Then ![]() $g B_{(b,a)}$ is a box contained in
$g B_{(b,a)}$ is a box contained in ![]() $B_{ga}$, which is sent to
$B_{ga}$, which is sent to ![]() $B_{gb}$ by
$B_{gb}$ by ![]() $\Phi (e,A)$. It follows that
$\Phi (e,A)$. It follows that ![]() $g B_{(b,a)} = B_{(gb,ga)}$, which completes the proof.
$g B_{(b,a)} = B_{(gb,ga)}$, which completes the proof.
5.3 From Burnside functors to spatial refinements
In this section, we describe how to use box maps to transform a Burnside functor ![]() $F:\mathscr {C}\rightarrow \mathscr {B}_G$ into a certain homotopy coherent diagram of spaces, called a spatial refinement of
$F:\mathscr {C}\rightarrow \mathscr {B}_G$ into a certain homotopy coherent diagram of spaces, called a spatial refinement of ![]() $F$, in an equivariant manner.
$F$, in an equivariant manner.
Let ![]() $\text {Top}_*^G$ denote the category of based
$\text {Top}_*^G$ denote the category of based ![]() $G$-spaces. We refer the reader to [Reference Sarkar, Scaduto and StoffregenSSS20, § 4.2] for the definition and discussion of homotopy coherent diagrams and homotopy colimits in the equivariant setting, parallel to the non-equivariant treatment in [Reference Lawson, Lipshitz and SarkarLLS20, § 4.2]. The following is an equivariant analogue of [Reference Lawson, Lipshitz and SarkarLLS20, Definition 5.21 and Proposition 5.22] (and extends [Reference Sarkar, Scaduto and StoffregenSSS20, Definition 4.11 and Proposition 4.12] from
$G$-spaces. We refer the reader to [Reference Sarkar, Scaduto and StoffregenSSS20, § 4.2] for the definition and discussion of homotopy coherent diagrams and homotopy colimits in the equivariant setting, parallel to the non-equivariant treatment in [Reference Lawson, Lipshitz and SarkarLLS20, § 4.2]. The following is an equivariant analogue of [Reference Lawson, Lipshitz and SarkarLLS20, Definition 5.21 and Proposition 5.22] (and extends [Reference Sarkar, Scaduto and StoffregenSSS20, Definition 4.11 and Proposition 4.12] from ![]() $\mathbb {Z}/2\mathbb {Z}$ to general finite groups
$\mathbb {Z}/2\mathbb {Z}$ to general finite groups ![]() $G$).
$G$).
Definition 5.1 Fix a small category ![]() $\mathscr {C}$ and a strictly unitary lax 2-functor
$\mathscr {C}$ and a strictly unitary lax 2-functor ![]() $F:\mathscr {C} \to \mathscr {B}_G$. A
$F:\mathscr {C} \to \mathscr {B}_G$. A ![]() $k$-dimensional spatial refinement of
$k$-dimensional spatial refinement of ![]() $F$ is a homotopy coherent diagram
$F$ is a homotopy coherent diagram ![]() $\widetilde {F}_k:\mathscr {C} \to {Top}^G_*$ satisfying:
$\widetilde {F}_k:\mathscr {C} \to {Top}^G_*$ satisfying:
(1) for any
 $u\in \mathscr {C}$,
$u\in \mathscr {C}$,  $\widetilde {F}_k(u) = {\bigvee} _{x\in F(u)} S^k$;
$\widetilde {F}_k(u) = {\bigvee} _{x\in F(u)} S^k$;(2) for any sequence
 $u_0 \xrightarrow {f_1} \cdots \xrightarrow {f_m} u_m$ of morphisms in
$u_0 \xrightarrow {f_1} \cdots \xrightarrow {f_m} u_m$ of morphisms in  $\mathscr {C}$ and
$\mathscr {C}$ and  $t\in I^{m-1}$, the map
is a box map which refines the correspondence
$t\in I^{m-1}$, the map
is a box map which refines the correspondence \[ \widetilde{F}_k(f_m,\ldots, f_1)(t) : \bigvee_{x\in F(u_0)} S^k \to \bigvee_{y\in F(u_m)} S^k \]
\[ \widetilde{F}_k(f_m,\ldots, f_1)(t) : \bigvee_{x\in F(u_0)} S^k \to \bigvee_{y\in F(u_m)} S^k \] $F(f_m \circ \cdots \circ f_1)$. Note that, by assumption, the diagram lands in
$F(f_m \circ \cdots \circ f_1)$. Note that, by assumption, the diagram lands in  ${Top}^G_*$, so that the map in
${Top}^G_*$, so that the map in  $(2)$ is also
$(2)$ is also  $G$-equivariant.
$G$-equivariant.
Proposition 5.5 Let ![]() $\mathscr {C}$ be a small category in which every sequence of composable non-identity morphisms has length at most
$\mathscr {C}$ be a small category in which every sequence of composable non-identity morphisms has length at most ![]() $n$, and let
$n$, and let ![]() $F:\mathscr {C} \to \mathscr {B}_G$ be a strictly unitary lax 2-functor.
$F:\mathscr {C} \to \mathscr {B}_G$ be a strictly unitary lax 2-functor.
(1) If
 $k\geq n$, there is a
$k\geq n$, there is a  $k$-dimensional spatial refinement of
$k$-dimensional spatial refinement of  $F$.
$F$.(2) If
 $k\geq n+1$, then any two
$k\geq n+1$, then any two  $k$-dimensional spatial refinements of
$k$-dimensional spatial refinements of  $F$ are equivariantly weakly equivalent (see [Reference Sarkar, Scaduto and StoffregenSSS20, § 4.2] for a detailed discussion of weak equivalences between spatial refinements).
$F$ are equivariantly weakly equivalent (see [Reference Sarkar, Scaduto and StoffregenSSS20, § 4.2] for a detailed discussion of weak equivalences between spatial refinements).(3) If
 $\widetilde {F}_k$ is a
$\widetilde {F}_k$ is a  $k$-dimensional spatial refinement of
$k$-dimensional spatial refinement of  $F$, then the (reduced) suspension of each
$F$, then the (reduced) suspension of each  $\widetilde {F}_k(u)$ and of each
$\widetilde {F}_k(u)$ and of each  $\widetilde {F}_k(f_m,\ldots , f_1)(t)$ gives a
$\widetilde {F}_k(f_m,\ldots , f_1)(t)$ gives a  $(k+1)$-dimensional spatial refinement of
$(k+1)$-dimensional spatial refinement of  $F$.
$F$.
Proof. This is completely parallel to the proofs of [Reference Lawson, Lipshitz and SarkarLLS20, Proposition 5.22] and [Reference Sarkar, Scaduto and StoffregenSSS20, Proposition 4.12]. The modification is that the maps
should land in ![]() $E_G(\{B_x\}, s_{f_m\circ \cdots \circ f_1})$, which is still highly connected by Corollary 5.3. We have also verified that equivariant boxes pull back to equivariant boxes in Lemma 5.4. Note that suspension respects the group action, which permutes spheres.
$E_G(\{B_x\}, s_{f_m\circ \cdots \circ f_1})$, which is still highly connected by Corollary 5.3. We have also verified that equivariant boxes pull back to equivariant boxes in Lemma 5.4. Note that suspension respects the group action, which permutes spheres.
5.4 From spatial refinements to realizations
In this section, we discuss how to pass from a ![]() $G$-equivariant homotopy coherent spatial refinement
$G$-equivariant homotopy coherent spatial refinement ![]() $\tilde {F}_k$ to a realization
$\tilde {F}_k$ to a realization ![]() $\lVert {F_k}\rVert \in \text {Top}_*^G$. We also recall some of the cellular properties of such
$\lVert {F_k}\rVert \in \text {Top}_*^G$. We also recall some of the cellular properties of such ![]() $\lVert {F_k}\rVert$ and the induced maps between them.
$\lVert {F_k}\rVert$ and the induced maps between them.
Following [Reference Lawson, Lipshitz and SarkarLLS20, Definition 5.1], we begin by defining a slight enlargement of the cube category ![]() $\underline {2}^n$, denoted
$\underline {2}^n$, denoted ![]() $\underline {2}^n_+$. The objects of
$\underline {2}^n_+$. The objects of ![]() $\underline {2}^n_+$ are
$\underline {2}^n_+$ are ![]() $\text {ob}(\underline {2}^n) \cup \{*\}$; that is,
$\text {ob}(\underline {2}^n) \cup \{*\}$; that is, ![]() $\underline {2}^n_+$ has an extra object added. Set
$\underline {2}^n_+$ has an extra object added. Set ![]() $\text {Hom}_{\underline {2}^n_+}(u,v) = \text {Hom}_{\underline {2}^n}(u,v)$ if
$\text {Hom}_{\underline {2}^n_+}(u,v) = \text {Hom}_{\underline {2}^n}(u,v)$ if ![]() $u,v\in \underline {2}^n$. Otherwise, for
$u,v\in \underline {2}^n$. Otherwise, for ![]() $u\in \underline {2}^n\setminus \{0\}$, set
$u\in \underline {2}^n\setminus \{0\}$, set ![]() $\text {Hom}_{\underline {2}^n_+}(u,*)$ to consist of a single morphism. Finally, set
$\text {Hom}_{\underline {2}^n_+}(u,*)$ to consist of a single morphism. Finally, set ![]() $\text {Hom}_{\underline {2}^n_+}(0,*) = \text {Hom}_{\underline {2}^n_+}(*,0) = \text {Hom}_{\underline {2}^n_+}(*,u) = \varnothing$.
$\text {Hom}_{\underline {2}^n_+}(0,*) = \text {Hom}_{\underline {2}^n_+}(*,0) = \text {Hom}_{\underline {2}^n_+}(*,u) = \varnothing$.
Let ![]() $F:\underline {2}^n \to \mathscr {B}_G$ be a Burnside functor and let
$F:\underline {2}^n \to \mathscr {B}_G$ be a Burnside functor and let ![]() $\widetilde {F}_k : \underline {2}^n \to \text {Top}_*^G$ be a
$\widetilde {F}_k : \underline {2}^n \to \text {Top}_*^G$ be a ![]() $k$-dimensional spatial refinement of
$k$-dimensional spatial refinement of ![]() $F$. Extend
$F$. Extend ![]() $\widetilde {F}_k$ to a homotopy coherent diagram
$\widetilde {F}_k$ to a homotopy coherent diagram ![]() $\widetilde {F}_k^+ : \underline {2}^n_+ \to \text {Top}_*^G$ by setting
$\widetilde {F}_k^+ : \underline {2}^n_+ \to \text {Top}_*^G$ by setting ![]() $\widetilde {F}_k^+(*)$ to be a single point. Following [Reference Sarkar, Scaduto and StoffregenSSS20, Definition 4.9], define the space
$\widetilde {F}_k^+(*)$ to be a single point. Following [Reference Sarkar, Scaduto and StoffregenSSS20, Definition 4.9], define the space
called a realization of ![]() $F$. Since the homotopy coherent diagram
$F$. Since the homotopy coherent diagram ![]() $\widetilde {F}_k$ takes values in
$\widetilde {F}_k$ takes values in ![]() $\text {Top}_*^G$, the space
$\text {Top}_*^G$, the space ![]() $\lVert {F}\rVert _k$ is again a based
$\lVert {F}\rVert _k$ is again a based ![]() $G$-space.
$G$-space.
There is a cell structure on ![]() $\lVert {F}\rVert _k$, called the coarse cell structure in § 4.4 of [Reference Sarkar, Scaduto and StoffregenSSS20], with the cells of
$\lVert {F}\rVert _k$, called the coarse cell structure in § 4.4 of [Reference Sarkar, Scaduto and StoffregenSSS20], with the cells of ![]() $\lVert {F}\rVert _k$ in bijection with
$\lVert {F}\rVert _k$ in bijection with ![]() $\coprod _{u\in \underline {2}^n} F(u)$. This cell structure is described in [Reference Lawson, Lipshitz and SarkarLLS20, § 6].
$\coprod _{u\in \underline {2}^n} F(u)$. This cell structure is described in [Reference Lawson, Lipshitz and SarkarLLS20, § 6].
Lemma 5.6 With the above notation:
(1) the
 $G$-action on
$G$-action on  $\lVert {F}\rVert _k$ is cellular, and the bijection
is
$\lVert {F}\rVert _k$ is cellular, and the bijection
is \[ \{{\rm Cells\ of\ }\lVert{F}\rVert_k\} \longleftrightarrow \coprod_{u\in \underline{2}^n} F(u) \]
\[ \{{\rm Cells\ of\ }\lVert{F}\rVert_k\} \longleftrightarrow \coprod_{u\in \underline{2}^n} F(u) \] $G$-equivariant;
$G$-equivariant;(2) the
 $G$-action on
$G$-action on  $\lVert {F}\rVert _k$ is free away from the basepoint;
$\lVert {F}\rVert _k$ is free away from the basepoint;(3) the weak equivalences of Proposition 5.5 induce equivariant homotopy equivalences on realizations. Thus,
 $\lVert {F_k}\rVert$ is well defined and
$\lVert {F_k}\rVert$ is well defined and  $\Sigma \lVert {F}\rVert _k \simeq \lVert {F}\rVert _{k+1}$.
$\Sigma \lVert {F}\rVert _k \simeq \lVert {F}\rVert _{k+1}$.
Proof. Statement (1) follows from inspecting the cell decomposition in [Reference Lawson, Lipshitz and SarkarLLS20, Proposition 6.1] (see also the discussion in [Reference Sarkar, Scaduto and StoffregenSSS20, § 4.4]). Statement (2) follows from (1) and the fact that ![]() $G$ acts freely on the set
$G$ acts freely on the set ![]() $\coprod _{u\in \underline {2}^n} F(u)$.
$\coprod _{u\in \underline {2}^n} F(u)$.
For (3), we first note that (1) and (2) imply that our realizations are ![]() $G$-CW complexes (the action of
$G$-CW complexes (the action of ![]() $G$ is cellular and its fixed set is the basepoint, which is trivially a subcomplex). Then, as described in [Reference Sarkar, Scaduto and StoffregenSSS20, § 4.5], equivariant weak equivalences of homotopy coherent diagrams induce equivariant weak equivalences on their homotopy colimits (which can be taken to be cellular), which induce equivariant homotopy equivalences for large enough
$G$ is cellular and its fixed set is the basepoint, which is trivially a subcomplex). Then, as described in [Reference Sarkar, Scaduto and StoffregenSSS20, § 4.5], equivariant weak equivalences of homotopy coherent diagrams induce equivariant weak equivalences on their homotopy colimits (which can be taken to be cellular), which induce equivariant homotopy equivalences for large enough ![]() $k$ by the equivariant Whitehead theorem.
$k$ by the equivariant Whitehead theorem.
Now recall from § 3.4 that the totalization ![]() $\text {Tot}(F)$ of an equivariant Burnside functor
$\text {Tot}(F)$ of an equivariant Burnside functor ![]() $F :\underline {2}^n \to \mathscr {B}_G$ is a complex of
$F :\underline {2}^n \to \mathscr {B}_G$ is a complex of ![]() $\mathbb {Z}[G]$-modules, and that any natural transformation
$\mathbb {Z}[G]$-modules, and that any natural transformation ![]() $\eta : F_1 \to F_0$ between two such functors induces a chain map over
$\eta : F_1 \to F_0$ between two such functors induces a chain map over ![]() $\mathbb {Z}[G]$,
$\mathbb {Z}[G]$, ![]() $\text {Tot}(\eta ): \text {Tot}(F_1) \to \text {Tot}(F_0)$. Also recall [Reference Sarkar, Scaduto and StoffregenSSS20, Lemma 4.15], which in particular says that if
$\text {Tot}(\eta ): \text {Tot}(F_1) \to \text {Tot}(F_0)$. Also recall [Reference Sarkar, Scaduto and StoffregenSSS20, Lemma 4.15], which in particular says that if ![]() $F_1, F_0 : \underline {2}^n \to \mathscr {B}$ are Burnside functors and
$F_1, F_0 : \underline {2}^n \to \mathscr {B}$ are Burnside functors and ![]() $\eta :F_1\to F_0$ is a natural transformation, then there is an induced map
$\eta :F_1\to F_0$ is a natural transformation, then there is an induced map ![]() $\eta : \lVert {F_1}\rVert _k \to \lVert {F_0}\rVert _k$ for any realization. We state [Reference Sarkar, Scaduto and StoffregenSSS20, Proposition 4.16] below relating these notions, where the notation
$\eta : \lVert {F_1}\rVert _k \to \lVert {F_0}\rVert _k$ for any realization. We state [Reference Sarkar, Scaduto and StoffregenSSS20, Proposition 4.16] below relating these notions, where the notation ![]() $[k]$ denotes a homological shift by
$[k]$ denotes a homological shift by ![]() $k$ (that is,
$k$ (that is, ![]() $C^i[k] := C^{i-k}$).
$C^i[k] := C^{i-k}$).
Proposition 5.7 [Reference Sarkar, Scaduto and StoffregenSSS20, Proposition 4.16]
If ![]() $F : \underline {2}^n \to \mathscr {B}$, then its reduced shifted cellular chain complex
$F : \underline {2}^n \to \mathscr {B}$, then its reduced shifted cellular chain complex ![]() $\widetilde {C}^{cell}_*(\lVert {F}\rVert _k)[-k]$ is isomorphic to
$\widetilde {C}^{cell}_*(\lVert {F}\rVert _k)[-k]$ is isomorphic to ![]() ${\rm Tot}(F)$, with the cells mapping to the corresponding generators. If
${\rm Tot}(F)$, with the cells mapping to the corresponding generators. If ![]() $\eta : F_1\to F_0$ is a natural transformation of Burnside functors, then the map
$\eta : F_1\to F_0$ is a natural transformation of Burnside functors, then the map ![]() $\lVert {F_1}\rVert _k \to \lVert {F_0}\rVert _k$ is cellular, and the induced cellular chain map agrees with
$\lVert {F_1}\rVert _k \to \lVert {F_0}\rVert _k$ is cellular, and the induced cellular chain map agrees with ![]() ${\rm Tot}(\eta)$.
${\rm Tot}(\eta)$.
When ![]() $F$ takes values in
$F$ takes values in ![]() $\mathscr {B}_G$, the above discussion shows that
$\mathscr {B}_G$, the above discussion shows that ![]() $\widetilde {C}_{*}^{cell}(\lVert {F}\rVert _k)[-k]$ is a
$\widetilde {C}_{*}^{cell}(\lVert {F}\rVert _k)[-k]$ is a ![]() $\mathbb {Z}[G]$-module, and the isomorphism
$\mathbb {Z}[G]$-module, and the isomorphism
of Proposition 5.7 is an isomorphism of complexes of ![]() $\mathbb {Z}[G]$-modules (see [Reference Sarkar, Scaduto and StoffregenSSS20, Proposition 4.23]). Likewise, a natural transformation
$\mathbb {Z}[G]$-modules (see [Reference Sarkar, Scaduto and StoffregenSSS20, Proposition 4.23]). Likewise, a natural transformation ![]() $\eta$ between two equivariant Burnside functors induces an equivariant cellular map on their realizations that recovers
$\eta$ between two equivariant Burnside functors induces an equivariant cellular map on their realizations that recovers ![]() $\text {Tot}(\eta )$ on the chain complex level.
$\text {Tot}(\eta )$ on the chain complex level.
Lemma 5.8 [Reference Sarkar, Scaduto and StoffregenSSS20, Lemma 4.17]
Let ![]() $F_1, F_0: \underline {2}^n \to \mathscr {B}_G$ be equivariant Burnside functors and let
$F_1, F_0: \underline {2}^n \to \mathscr {B}_G$ be equivariant Burnside functors and let ![]() $\lVert {F_1}\rVert _k$,
$\lVert {F_1}\rVert _k$, ![]() $\lVert {F_0}\rVert _k$ be
$\lVert {F_0}\rVert _k$ be ![]() $k$-dimensional spatial refinements. If
$k$-dimensional spatial refinements. If ![]() $\eta : F_1\to F_0$ is a natural transformation such that the induced map
$\eta : F_1\to F_0$ is a natural transformation such that the induced map ![]() ${\rm Tot}(\eta ) : {\rm Tot}(F_1) \to {\rm Tot}(F_0)$ is a chain homotopy equivalence, then the induced map
${\rm Tot}(\eta ) : {\rm Tot}(F_1) \to {\rm Tot}(F_0)$ is a chain homotopy equivalence, then the induced map ![]() $\eta :\lVert {F_1}\rVert _k \to \lVert {F_0}\rVert _k$ is an equivariant homotopy equivalence.
$\eta :\lVert {F_1}\rVert _k \to \lVert {F_0}\rVert _k$ is an equivariant homotopy equivalence.
Proof. The argument is the same as in [Reference Sarkar, Scaduto and StoffregenSSS20, Lemma 4.17]. The previous discussion shows that the induced map on spaces ![]() $\eta :\lVert {F_1}\rVert _k \to \lVert {F_0}\rVert _k$ is
$\eta :\lVert {F_1}\rVert _k \to \lVert {F_0}\rVert _k$ is ![]() $G$-equivariant and cellular. We may take
$G$-equivariant and cellular. We may take ![]() $k$ big enough, so that the realizations are simply connected. Note that the
$k$ big enough, so that the realizations are simply connected. Note that the ![]() $G$-action on the realization is free away from the basepoint. Since
$G$-action on the realization is free away from the basepoint. Since ![]() $\text {Tot}(\eta )$ is a
$\text {Tot}(\eta )$ is a ![]() $\mathbb {Z}[G]$-linear isomorphism on homology, the equivariant Whitehead theorem implies that
$\mathbb {Z}[G]$-linear isomorphism on homology, the equivariant Whitehead theorem implies that ![]() $\eta :\lVert {F_1}\rVert _k \to \lVert {F_0}\rVert _k$ is an equivariant homotopy equivalence.
$\eta :\lVert {F_1}\rVert _k \to \lVert {F_0}\rVert _k$ is an equivariant homotopy equivalence.
Remark 5.9 Although the discussion in [Reference Sarkar, Scaduto and StoffregenSSS20, § 4.4] actually makes use of spatial refinements out of the category ![]() $(\underline {2}_+)^n$ rather than
$(\underline {2}_+)^n$ rather than ![]() $\underline {2}^n_+$, the cellular structures described on the realizations there induce equivalent cellular structures on our realizations via a simple quotient within each cell. This is implicit in their reference to [Reference Lawson, Lipshitz and SarkarLLS20, § 6] which builds the coarse structure for realizations using
$\underline {2}^n_+$, the cellular structures described on the realizations there induce equivalent cellular structures on our realizations via a simple quotient within each cell. This is implicit in their reference to [Reference Lawson, Lipshitz and SarkarLLS20, § 6] which builds the coarse structure for realizations using ![]() $\underline {2}^n_+$ as we do here; the alternative use of
$\underline {2}^n_+$ as we do here; the alternative use of ![]() $(\underline {2}_+)^n$ in [Reference Lawson, Lipshitz and SarkarLLS20] is denoted by
$(\underline {2}_+)^n$ in [Reference Lawson, Lipshitz and SarkarLLS20] is denoted by ![]() $\underline {2}_{\dagger} ^n$ there.
$\underline {2}_{\dagger} ^n$ there.
5.5 The quantum annular spectrum  $\mathcal {X}_{\mathbb {A}_\mathfrak {q}}^r(L)$
$\mathcal {X}_{\mathbb {A}_\mathfrak {q}}^r(L)$
Finally, we turn to defining our quantum annular spectrum and proving Theorem 1.1. Let ![]() $D$ be a diagram for an annular link with
$D$ be a diagram for an annular link with ![]() $n_-$ negative crossings, and fix
$n_-$ negative crossings, and fix ![]() $G=\mathbb {Z}/r\mathbb {Z}$ for some
$G=\mathbb {Z}/r\mathbb {Z}$ for some ![]() $r\geq 2$. Let
$r\geq 2$. Let ![]() $F_\mathfrak {q} : \underline {2}^n\to \mathscr {B}_G$ be a quantum annular Burnside functor for
$F_\mathfrak {q} : \underline {2}^n\to \mathscr {B}_G$ be a quantum annular Burnside functor for ![]() $D$ as provided by Theorem 4.2. Let
$D$ as provided by Theorem 4.2. Let ![]() $\widetilde {F}_{\mathfrak {q},k}^+ : \underline {2}^n_+ \to \text {Top}_*^G$ be a
$\widetilde {F}_{\mathfrak {q},k}^+ : \underline {2}^n_+ \to \text {Top}_*^G$ be a ![]() $k$-dimensional spatial refinement extended to the enlarged cube category
$k$-dimensional spatial refinement extended to the enlarged cube category ![]() $\underline {2}^n_+$, as described in § 5.3 and the beginning of § 5.4. Let
$\underline {2}^n_+$, as described in § 5.3 and the beginning of § 5.4. Let ![]() $\lVert {F_\mathfrak {q}}\rVert _k$ be the realization, as defined in (5.3).
$\lVert {F_\mathfrak {q}}\rVert _k$ be the realization, as defined in (5.3).
Definition 5.2 Define the quantum annular Khovanov spectrum ![]() $\mathcal {X}_{\mathbb {A}_\mathfrak {q}}^r(D)$ to be the suspension spectrum of
$\mathcal {X}_{\mathbb {A}_\mathfrak {q}}^r(D)$ to be the suspension spectrum of ![]() $\lVert {F_\mathfrak {q}}\rVert _k$, desuspended
$\lVert {F_\mathfrak {q}}\rVert _k$, desuspended ![]() $k+n_-$ times; that is,
$k+n_-$ times; that is,
By dualizing the isomorphism in Proposition 5.7, we obtain the following isomorphism of ![]() $\mathbb {Z}[G]$-modules:
$\mathbb {Z}[G]$-modules:
Theorem 5.10 For a fixed annular link diagram ![]() $D$ and
$D$ and ![]() $r\geq 2$, the naive
$r\geq 2$, the naive ![]() $G$-spectrum
$G$-spectrum ![]() $\mathcal {X}_{\mathbb {A}_\mathfrak {q}}^r(D)$ is well defined; that is, different choices during the construction yield equivariantly stably homotopy equivalent spectra.
$\mathcal {X}_{\mathbb {A}_\mathfrak {q}}^r(D)$ is well defined; that is, different choices during the construction yield equivariantly stably homotopy equivalent spectra.
Proof. The construction of ![]() $\mathcal {X}^r_{\mathbb {A}_\mathfrak {q}}(D)$ requires a choice of generators at each vertex of the cube to build
$\mathcal {X}^r_{\mathbb {A}_\mathfrak {q}}(D)$ requires a choice of generators at each vertex of the cube to build ![]() $F_\mathfrak {q}$, together with a choice of spatial refinement of
$F_\mathfrak {q}$, together with a choice of spatial refinement of ![]() $F_\mathfrak {q}$. Any two choices of generators give naturally isomorphic Burnside functors (see Proposition 4.3), which in turn yield equivariantly stably homotopy equivalent spectra by Lemma 5.8. Meanwhile, any two spatial refinements yield homotopy equivalent realizations by Lemma 5.6 (so long as
$F_\mathfrak {q}$. Any two choices of generators give naturally isomorphic Burnside functors (see Proposition 4.3), which in turn yield equivariantly stably homotopy equivalent spectra by Lemma 5.8. Meanwhile, any two spatial refinements yield homotopy equivalent realizations by Lemma 5.6 (so long as ![]() $k$ is large enough) and thus equivariantly stably homotopy equivalent spectra.
$k$ is large enough) and thus equivariantly stably homotopy equivalent spectra.
Finally, we address the independence of choice of diagram with the following theorem.
Theorem 5.11 Let ![]() $D$ and
$D$ and ![]() $D'$ be two annular link diagrams for the same annular link
$D'$ be two annular link diagrams for the same annular link ![]() $L\subset \mathbb {A}\times I$. Then
$L\subset \mathbb {A}\times I$. Then ![]() $\mathcal {X}_{\mathbb {A}_\mathfrak {q}}^r(D)$ is equivariantly stably homotopy equivalent to
$\mathcal {X}_{\mathbb {A}_\mathfrak {q}}^r(D)$ is equivariantly stably homotopy equivalent to ![]() $\mathcal {X}_{\mathbb {A}_\mathfrak {q}}^r(D')$ and as such we may use the notation
$\mathcal {X}_{\mathbb {A}_\mathfrak {q}}^r(D')$ and as such we may use the notation ![]() $\mathcal {X}_{\mathbb {A}_\mathfrak {q}}^r(L)$ to denote the quantum annular
$\mathcal {X}_{\mathbb {A}_\mathfrak {q}}^r(L)$ to denote the quantum annular ![]() $G$-equivariant stable homotopy type of
$G$-equivariant stable homotopy type of ![]() $L$.
$L$.
Proof. The diagrams ![]() $D$ and
$D$ and ![]() $D'$ are connected by a series of moves corresponding either to the annular isotopies of § 4.2 or Reidemeister moves. Isotopies were shown to induce natural isomorphisms of Burnside functors (Proposition 4.4), which therefore induce equivariant stable equivalences by Lemma 5.8.
$D'$ are connected by a series of moves corresponding either to the annular isotopies of § 4.2 or Reidemeister moves. Isotopies were shown to induce natural isomorphisms of Burnside functors (Proposition 4.4), which therefore induce equivariant stable equivalences by Lemma 5.8.
With such planar equivalences available, we can assume that any Reidemeister move takes place in a disk disjoint from the seam ![]() $\mu$. Such moves then induce homotopy equivalences in precisely the same fashion as they do for the classical Khovanov homotopy type [Reference Lipshitz and SarkarLS14a, § 6]. That is to say, any Reidemeister move corresponds to finding subfaces of the relevant cube corresponding to acyclic subcomplexes (or quotient complexes) in the totalization. (These subfaces are referred to as upwards- and downwards-closed subcategories in the original treatment of [Reference Lipshitz and SarkarLS14a].) The complements of these acyclic faces can then be included into the large cube; the inclusion induces a map on stable homotopy types that gives an isomorphism on homology, and therefore is a stable equivalence by Whitehead's theorem. All of this continues to hold in the equivariant setting so long as the group
$\mu$. Such moves then induce homotopy equivalences in precisely the same fashion as they do for the classical Khovanov homotopy type [Reference Lipshitz and SarkarLS14a, § 6]. That is to say, any Reidemeister move corresponds to finding subfaces of the relevant cube corresponding to acyclic subcomplexes (or quotient complexes) in the totalization. (These subfaces are referred to as upwards- and downwards-closed subcategories in the original treatment of [Reference Lipshitz and SarkarLS14a].) The complements of these acyclic faces can then be included into the large cube; the inclusion induces a map on stable homotopy types that gives an isomorphism on homology, and therefore is a stable equivalence by Whitehead's theorem. All of this continues to hold in the equivariant setting so long as the group ![]() $G$ is finite – face inclusions induce equivariant maps by definition.
$G$ is finite – face inclusions induce equivariant maps by definition.
As in [Reference Lawson, Lipshitz and SarkarLLS20, § 4.7] and [Reference Sarkar, Scaduto and StoffregenSSS20, § 3.9], we also have a splitting of the functor ![]() $F_\mathfrak {q}$ into a coproduct over the two gradings
$F_\mathfrak {q}$ into a coproduct over the two gradings ![]() $\text {qdeg}$ and
$\text {qdeg}$ and ![]() $\text {adeg}$ (see (2.2) and (2.3)). Thus, the spectrum also splits as a wedge sum
$\text {adeg}$ (see (2.2) and (2.3)). Thus, the spectrum also splits as a wedge sum
where ![]() $j$ corresponds to
$j$ corresponds to ![]() $\text {qdeg}$ and
$\text {qdeg}$ and ![]() $k$ corresponds to
$k$ corresponds to ![]() $\text {adeg}$. As in [Reference Lipshitz and SarkarLS14a, Theorem 1.1] (see also [Reference Lawson, Lipshitz and SarkarLLS17a, Theorem 1]), Theorems 5.10 and 5.11 respect this splitting, as does (5.4) as indicated below:
$\text {adeg}$. As in [Reference Lipshitz and SarkarLS14a, Theorem 1.1] (see also [Reference Lawson, Lipshitz and SarkarLLS17a, Theorem 1]), Theorems 5.10 and 5.11 respect this splitting, as does (5.4) as indicated below:
We end this section with some remarks about the spectrum ![]() $\mathcal {X}_{\mathbb {A}_\mathfrak {q}}^r(L)$. Although the construction above was aimed at building a naive
$\mathcal {X}_{\mathbb {A}_\mathfrak {q}}^r(L)$. Although the construction above was aimed at building a naive ![]() $G$-spectrum, one could also construct a genuine
$G$-spectrum, one could also construct a genuine ![]() $G$-spectrum in a similar manner by applying the functor
$G$-spectrum in a similar manner by applying the functor ![]() $\Sigma _G^\infty$, rather than
$\Sigma _G^\infty$, rather than ![]() $\Sigma ^\infty$, to the realization
$\Sigma ^\infty$, to the realization ![]() $\lVert {F_\mathfrak {q}}\rVert _k$. This functor produces genuine
$\lVert {F_\mathfrak {q}}\rVert _k$. This functor produces genuine ![]() $G$-spectra using smash products with all
$G$-spectra using smash products with all ![]() $G$-representation spheres, rather than using only spheres with trivial
$G$-representation spheres, rather than using only spheres with trivial ![]() $G$-action as
$G$-action as ![]() $\Sigma ^\infty$ does.
$\Sigma ^\infty$ does.
We also note that, in general, ![]() $G$ acts on
$G$ acts on ![]() $\mathcal {X}_{\mathbb {A}_\mathfrak {q}}^r(L)$ in a non-trivial way. Precisely,
$\mathcal {X}_{\mathbb {A}_\mathfrak {q}}^r(L)$ in a non-trivial way. Precisely, ![]() $\mathcal {X}_{\mathbb {A}_\mathfrak {q}}^r(L)$ does not decompose into a wedge product which is simply permuted by
$\mathcal {X}_{\mathbb {A}_\mathfrak {q}}^r(L)$ does not decompose into a wedge product which is simply permuted by ![]() $G$. This is already evident on homology due to the calculation in [Reference Beliakova, Putyra and WehrliBPW19, Proposition 6.9] for the annular closure of
$G$. This is already evident on homology due to the calculation in [Reference Beliakova, Putyra and WehrliBPW19, Proposition 6.9] for the annular closure of ![]() $(2,n)$ torus links. For an appropriate
$(2,n)$ torus links. For an appropriate ![]() $n$, homological degree
$n$, homological degree ![]() $i$, and
$i$, and ![]() $q$-degree
$q$-degree ![]() $j$, the quantum annular homology is of the form
$j$, the quantum annular homology is of the form ![]() $Kh_{\mathbb {A}_\mathfrak {q}}^{i,j}(T_{2,n}) = \Bbbk _r/(\mathfrak {q}^2+1)$.
$Kh_{\mathbb {A}_\mathfrak {q}}^{i,j}(T_{2,n}) = \Bbbk _r/(\mathfrak {q}^2+1)$.
6. Maps on spectra induced by annular link cobordisms
In [Reference Lipshitz and SarkarLS14b, § 3], the authors showed that an embedded cobordism ![]() $W\subset S^3\times [0,1]$ between two links
$W\subset S^3\times [0,1]$ between two links ![]() $L_0\subset S^3\times \{0\}$ and
$L_0\subset S^3\times \{0\}$ and ![]() $L_1\subset S^3\times \{1\}$ induces a map on spectra
$L_1\subset S^3\times \{1\}$ induces a map on spectra
such that the induced map on cohomology
recovers the corresponding link cobordism maps ![]() $W_*$ in Khovanov homology as studied in [Reference KhovanovKho00, Reference JacobssonJac04, Reference Bar-NatanBar05]. The map
$W_*$ in Khovanov homology as studied in [Reference KhovanovKho00, Reference JacobssonJac04, Reference Bar-NatanBar05]. The map ![]() $\varphi _W$ is constructed by first decomposing
$\varphi _W$ is constructed by first decomposing ![]() $W$ into elementary cobordisms whose planar projections correspond to either Reidemeister moves or Morse moves (births/cups, saddles, or deaths/caps) and assigning maps to each elementary cobordism. A generically embedded
$W$ into elementary cobordisms whose planar projections correspond to either Reidemeister moves or Morse moves (births/cups, saddles, or deaths/caps) and assigning maps to each elementary cobordism. A generically embedded ![]() $W$ determines such a decomposition. It is conjectured in [Reference Lipshitz and SarkarLS14b] that isotopic cobordisms induce stably homotopic maps, but this conjecture has not yet been verified.
$W$ determines such a decomposition. It is conjectured in [Reference Lipshitz and SarkarLS14b] that isotopic cobordisms induce stably homotopic maps, but this conjecture has not yet been verified.
Now consider a cobordism ![]() $W\subset (\mathbb {A}\times I)\times [0,1]$ between two annular links
$W\subset (\mathbb {A}\times I)\times [0,1]$ between two annular links ![]() $L_0\subset \mathbb {A}\times I \times \{0\}$ and
$L_0\subset \mathbb {A}\times I \times \{0\}$ and ![]() $L_1\subset \mathbb {A}\times I \times \{1\}$ that is transverse to the three-dimensional membrane
$L_1\subset \mathbb {A}\times I \times \{1\}$ that is transverse to the three-dimensional membrane ![]() $\mu \times I \times [0,1]$. In [Reference Beliakova, Putyra and WehrliBPW19], the authors showed that there is an induced map
$\mu \times I \times [0,1]$. In [Reference Beliakova, Putyra and WehrliBPW19], the authors showed that there is an induced map
on the quantum annular homology, defined using the general theory of twisted horizontal traces and shadows established in [Reference Beliakova, Putyra and WehrliBPW19, § 3], as well as the functoriality of Chen–Khovanov bimodules under tangle cobordisms [Reference Chen and KhovanovCK14, Proposition 6]. The map induced by ![]() $W$ on the chain complex level can be determined by the sequence of maps given in [Reference Beliakova, Putyra and WehrliBPW19, (7.2)]. In the appendix we compute
$W$ on the chain complex level can be determined by the sequence of maps given in [Reference Beliakova, Putyra and WehrliBPW19, (7.2)]. In the appendix we compute ![]() $W_*$ explicitly for certain elementary cobordisms; this computation is used in the proof of Theorem 6.1 below.
$W_*$ explicitly for certain elementary cobordisms; this computation is used in the proof of Theorem 6.1 below.
We note that an isotopy of ![]() $W$ can alter
$W$ can alter ![]() $W_*$ by a sign change and a power of
$W_*$ by a sign change and a power of ![]() $\mathfrak {q}$ by [Reference Beliakova, Putyra and WehrliBPW19, Theorem B]; the sign ambiguity is inherited from the similar statement in the usual Khovanov homology (see [Reference JacobssonJac04] and [Reference Bar-NatanBar05]), while the power of
$\mathfrak {q}$ by [Reference Beliakova, Putyra and WehrliBPW19, Theorem B]; the sign ambiguity is inherited from the similar statement in the usual Khovanov homology (see [Reference JacobssonJac04] and [Reference Bar-NatanBar05]), while the power of ![]() $\mathfrak {q}$ comes from the ability to isotope parts of
$\mathfrak {q}$ comes from the ability to isotope parts of ![]() $W$ through the membrane. If one instead demands that isotopies fix the membrane, then
$W$ through the membrane. If one instead demands that isotopies fix the membrane, then ![]() $W_*$ is well defined up to a sign.
$W_*$ is well defined up to a sign.
Theorem 6.1 Fix ![]() $r\in \mathbb {N}$. A generically embedded cobordism
$r\in \mathbb {N}$. A generically embedded cobordism ![]() $W\subset \mathbb {A}\times I\times [0,1]$ between two annular links
$W\subset \mathbb {A}\times I\times [0,1]$ between two annular links ![]() $L_0$ and
$L_0$ and ![]() $L_1$ induces a map
$L_1$ induces a map
whose induced map on cohomology
equals the map ![]() $W_*$ on quantum annular Khovanov homology over the ring
$W_*$ on quantum annular Khovanov homology over the ring ![]() $\Bbbk _r$.
$\Bbbk _r$.
Remark 6.2 We stress that Theorem 6.1 assigns a map to cobordisms ![]() $W$ that come with a particular decomposition into a sequence of elementary cobordisms in the thickened annulus with membrane. The map
$W$ that come with a particular decomposition into a sequence of elementary cobordisms in the thickened annulus with membrane. The map ![]() $\varphi ^r_W$ is not known to be an invariant of
$\varphi ^r_W$ is not known to be an invariant of ![]() $W$, even up to a factor of
$W$, even up to a factor of ![]() $\pm \mathfrak {q}^k$. But see Remark 6.3 below.
$\pm \mathfrak {q}^k$. But see Remark 6.3 below.
Proof of Theorem 6.1 A generic annular cobordism determines a sequence of elementary cobordisms (called elementary string interactions in [Reference Bar-NatanBar05, Reference Grigsby, Licata and WehrliGLW18]), which are either Reidemeister moves or Morse moves. When accounting for the presence of the membrane ![]() $\mu \times I \times [0,1]$, there are certain additional elementary isotopies of a link through the seam which must be considered: we have the
$\mu \times I \times [0,1]$, there are certain additional elementary isotopies of a link through the seam which must be considered: we have the ![]() $P$ and
$P$ and ![]() $N$ moves of Figure 11, as well as pushing a crossing through the seam, as in (4.4). Meanwhile, the genericity of
$N$ moves of Figure 11, as well as pushing a crossing through the seam, as in (4.4). Meanwhile, the genericity of ![]() $W$ here implies that all Reidemeister moves and Morse moves occur away from the seam.
$W$ here implies that all Reidemeister moves and Morse moves occur away from the seam.
For all elementary isotopies of the link, we already have stable homotopy equivalences via Theorem 5.11. As in the case for ![]() $S^3$, we wish to use the inverses of these maps. It is clear that such inverses induce the maps
$S^3$, we wish to use the inverses of these maps. It is clear that such inverses induce the maps ![]() $W_\bullet$ described in the appendix and so, according to Lemma A.1, any such map will recover its corresponding
$W_\bullet$ described in the appendix and so, according to Lemma A.1, any such map will recover its corresponding ![]() $W_*$ up to some power of
$W_*$ up to some power of ![]() $\mathfrak {q}$. We may thus compose any such stable homotopy equivalence with some iterate of the group action on
$\mathfrak {q}$. We may thus compose any such stable homotopy equivalence with some iterate of the group action on ![]() $\mathcal {X}_{\mathbb {A}_\mathfrak {q}}^r(L_0)$ to define
$\mathcal {X}_{\mathbb {A}_\mathfrak {q}}^r(L_0)$ to define ![]() $\varphi _W^r$ which induces precisely
$\varphi _W^r$ which induces precisely ![]() $W_*$.
$W_*$.
Meanwhile, Morse moves induce natural transformations of Burnside functors in the same manner as they do in ![]() $S^3$: births induce correspondences which involve a
$S^3$: births induce correspondences which involve a ![]() $w_+$ label on the new (trivial, disjoint from the seam) circle; deaths induce correspondences which place a
$w_+$ label on the new (trivial, disjoint from the seam) circle; deaths induce correspondences which place a ![]() $w_-$ label on the dying (trivial, disjoint from the seam) circle; and saddles utilize the higher dimensional cube which would be built if the diagram had a crossing placed at the point of the saddle. Carrying out these constructions equivariantly does not present any new issues, leading to constructions of maps
$w_-$ label on the dying (trivial, disjoint from the seam) circle; and saddles utilize the higher dimensional cube which would be built if the diagram had a crossing placed at the point of the saddle. Carrying out these constructions equivariantly does not present any new issues, leading to constructions of maps ![]() $\varphi _W^r$ via Proposition 5.7 which again induce the maps
$\varphi _W^r$ via Proposition 5.7 which again induce the maps ![]() $W_\bullet$ of the appendix. For these moves (Type II in Lemma A.1) we have
$W_\bullet$ of the appendix. For these moves (Type II in Lemma A.1) we have ![]() $W_*=W_\bullet$, concluding the proof of the theorem.
$W_*=W_\bullet$, concluding the proof of the theorem.
Remark 6.3 Let ![]() $W,W'$ be two isotopic annular link cobordisms with corresponding maps on spectra
$W,W'$ be two isotopic annular link cobordisms with corresponding maps on spectra ![]() $\varphi ^r_W,\varphi ^r_{W'}$ via Theorem 6.1. Let
$\varphi ^r_W,\varphi ^r_{W'}$ via Theorem 6.1. Let ![]() $\tau _\mathfrak {q}$ denote the map on spectra determined by the action of the distinguished generator of the group
$\tau _\mathfrak {q}$ denote the map on spectra determined by the action of the distinguished generator of the group ![]() $G=\mathbb {Z}/r\mathbb {Z}$. Then it is reasonable to conjecture that there exists some
$G=\mathbb {Z}/r\mathbb {Z}$. Then it is reasonable to conjecture that there exists some ![]() $m\in \mathbb {Z}$ such that the maps
$m\in \mathbb {Z}$ such that the maps ![]() $\varphi ^r_W$ and
$\varphi ^r_W$ and ![]() $\tau _\mathfrak {q}^m \circ \varphi _{W'}^r$ are stably homotopic.
$\tau _\mathfrak {q}^m \circ \varphi _{W'}^r$ are stably homotopic.
This is based on the similar conjecture in [Reference Lipshitz and SarkarLS14b] for cobordisms in ![]() $S^3$. Notice that the composition with the map
$S^3$. Notice that the composition with the map ![]() $\tau _\mathfrak {q}^m$ recovers the ambiguity in the power of
$\tau _\mathfrak {q}^m$ recovers the ambiguity in the power of ![]() $\mathfrak {q}$ which is known to exist for the corresponding maps on the quantum annular homology.
$\mathfrak {q}$ which is known to exist for the corresponding maps on the quantum annular homology.
Let ![]() $\mathbb {S}$ denote the sphere spectrum and define
$\mathbb {S}$ denote the sphere spectrum and define
where ![]() $G$ acts by permuting the wedge summands as usual. Then we have the following corollary for closed surfaces in
$G$ acts by permuting the wedge summands as usual. Then we have the following corollary for closed surfaces in ![]() $\mathbb {A}\times D^2$ formed by sweeping out a link in the
$\mathbb {A}\times D^2$ formed by sweeping out a link in the ![]() $S^1$ direction.
$S^1$ direction.
Corollary 6.4 Let ![]() $L$ be a link in the 3-ball
$L$ be a link in the 3-ball ![]() $B^3$, and consider the surface
$B^3$, and consider the surface ![]() $\widehat {W}=S^1\times L$ in
$\widehat {W}=S^1\times L$ in ![]() $\mathbb {A}\times D^2\cong S^1\times B^3$. Let
$\mathbb {A}\times D^2\cong S^1\times B^3$. Let ![]() $W$ denote a copy of
$W$ denote a copy of ![]() $\widehat {W}$ perturbed to be generic, viewed as a cobordism from
$\widehat {W}$ perturbed to be generic, viewed as a cobordism from ![]() $\varnothing$ to itself. Then the map
$\varnothing$ to itself. Then the map
induces the map on quantum annular homology
which is given by multiplication by the Jones polynomial of ![]() $L$, considered as an element of
$L$, considered as an element of ![]() $\Bbbk _r$, up to a sign and a power of
$\Bbbk _r$, up to a sign and a power of ![]() $\mathfrak {q}$ (where the standard basis of the groups
$\mathfrak {q}$ (where the standard basis of the groups ![]() $\Bbbk _r\cong {\bigoplus} _G \mathbb {Z}$ is written as
$\Bbbk _r\cong {\bigoplus} _G \mathbb {Z}$ is written as ![]() $\{1,\mathfrak {q},\ldots , \mathfrak {q}^{r-1}\}$).
$\{1,\mathfrak {q},\ldots , \mathfrak {q}^{r-1}\}$).
Remark 6.5 In order to make sense of assigning a wedge of sphere spectra to the empty diagram ![]() $\varnothing$ in terms of Burnside functors, we assign to
$\varnothing$ in terms of Burnside functors, we assign to ![]() $\varnothing$ the functor
$\varnothing$ the functor ![]() $F_\mathfrak {q} : \underline {2}^0=\{0\} \to \mathscr {B}_G$ defined by setting
$F_\mathfrak {q} : \underline {2}^0=\{0\} \to \mathscr {B}_G$ defined by setting ![]() $F_\mathfrak {q}({0}) := G \times \{1\}$, where
$F_\mathfrak {q}({0}) := G \times \{1\}$, where ![]() $1\in \mathcal {F}_{\mathbb {A}_\mathfrak {q}}(\varnothing ) \otimes _\Bbbk \Bbbk _r = \Bbbk _r$ is the chosen generator. The spatial refinement is then a wedge of
$1\in \mathcal {F}_{\mathbb {A}_\mathfrak {q}}(\varnothing ) \otimes _\Bbbk \Bbbk _r = \Bbbk _r$ is the chosen generator. The spatial refinement is then a wedge of ![]() $r$ spheres with no box maps, and in the homotopy colimit there is nothing to identify except the basepoint of
$r$ spheres with no box maps, and in the homotopy colimit there is nothing to identify except the basepoint of ![]() ${\bigvee} _G S^k$ with the new basepoint in
${\bigvee} _G S^k$ with the new basepoint in ![]() $\underline {2}^0_+$. Thus, the final space is just a wedge of
$\underline {2}^0_+$. Thus, the final space is just a wedge of ![]() $r$ spheres with the natural action, desuspended
$r$ spheres with the natural action, desuspended ![]() $k$ times, and its reduced cohomology is isomorphic to
$k$ times, and its reduced cohomology is isomorphic to ![]() $\Bbbk _r$ as a
$\Bbbk _r$ as a ![]() $\Bbbk _r$-module.
$\Bbbk _r$-module.
Proof of Corollary 6.4 Theorem 6.1 implies that ![]() $(\varphi _W^r)^* = W_*$ and, by [Reference Beliakova, Putyra and WehrliBPW19, Proposition 6.8], we also have
$(\varphi _W^r)^* = W_*$ and, by [Reference Beliakova, Putyra and WehrliBPW19, Proposition 6.8], we also have ![]() $W_* = \pm \mathfrak {q}^k \widehat {W}_*$ for some
$W_* = \pm \mathfrak {q}^k \widehat {W}_*$ for some ![]() $k\in \mathbb {Z}$. Finally, [Reference Beliakova, Putyra and WehrliBPW19, Theorem D] states that
$k\in \mathbb {Z}$. Finally, [Reference Beliakova, Putyra and WehrliBPW19, Theorem D] states that ![]() $\widehat {W}_*$ is multiplication by the Jones polynomial of
$\widehat {W}_*$ is multiplication by the Jones polynomial of ![]() $L$. In fact, the more general statement about Lefschetz traces in [Reference Beliakova, Putyra and WehrliBPW19, Theorem D] also applies here.
$L$. In fact, the more general statement about Lefschetz traces in [Reference Beliakova, Putyra and WehrliBPW19, Theorem D] also applies here.
7. Taking the quotient
Our goal in this section is to prove Theorem 1.2, stating that the quotient ![]() $\mathcal {X}_{\mathbb {A}_\mathfrak {q}}^r(D)/G$ of the quantum annular homotopy type is stably homotopy equivalent to the classical annular homotopy type
$\mathcal {X}_{\mathbb {A}_\mathfrak {q}}^r(D)/G$ of the quantum annular homotopy type is stably homotopy equivalent to the classical annular homotopy type ![]() $\mathcal {X}_\mathbb {A}(D)$. This is accomplished in two stages.
$\mathcal {X}_\mathbb {A}(D)$. This is accomplished in two stages.
First, we show that the quotient of ![]() $F_\mathfrak {q}$ is naturally isomorphic to the classical annular Burnside functor
$F_\mathfrak {q}$ is naturally isomorphic to the classical annular Burnside functor ![]() $F_1$ defined in § 4.3. This will follow from Proposition 2.21, which establishes that the matching forced by powers of
$F_1$ defined in § 4.3. This will follow from Proposition 2.21, which establishes that the matching forced by powers of ![]() $\mathfrak {q}$ in the quantum theory agrees with the ladybug matching made with the left pair in the classical theory.
$\mathfrak {q}$ in the quantum theory agrees with the ladybug matching made with the left pair in the classical theory.
Next we show that taking the quotient of a spatial refinement for ![]() $F_q$ yields a spatial refinement for
$F_q$ yields a spatial refinement for ![]() $F_1$. The result will then follow from the property that homotopy colimits commute with taking quotients.
$F_1$. The result will then follow from the property that homotopy colimits commute with taking quotients.
Let ![]() $D$ be a diagram for an annular link with
$D$ be a diagram for an annular link with ![]() $n$ crossings. Let
$n$ crossings. Let ![]() $F_1 : \underline {2}^n\to \mathscr {B}$ denote the classical annular Khovanov Burnside functor, where the ladybug matching is made with the left choice. Recall the quotient functor
$F_1 : \underline {2}^n\to \mathscr {B}$ denote the classical annular Khovanov Burnside functor, where the ladybug matching is made with the left choice. Recall the quotient functor ![]() $(-)/G : \mathscr {B}_G \to \mathscr {B}$ from § 3.3. We can compose
$(-)/G : \mathscr {B}_G \to \mathscr {B}$ from § 3.3. We can compose ![]() $F_\mathfrak {q}: \underline {2}^n \to \mathscr {B}_G$ with the quotient functor to obtain a Burnside functor
$F_\mathfrak {q}: \underline {2}^n \to \mathscr {B}_G$ with the quotient functor to obtain a Burnside functor ![]() $F_\mathfrak {q}/G : \underline {2}^n \to \mathscr {B}$. We will also use
$F_\mathfrak {q}/G : \underline {2}^n \to \mathscr {B}$. We will also use ![]() $(-)/G: \text {Top}_*^G \to \text {Top}_*$ to denote the quotient functor on
$(-)/G: \text {Top}_*^G \to \text {Top}_*$ to denote the quotient functor on ![]() $G$-spaces. It will be clear from context which functor is used.
$G$-spaces. It will be clear from context which functor is used.
Proposition 7.1 The functors ![]() $F_{\mathfrak {q}}/G :\underline {2}^n \to \mathscr {B}$ and
$F_{\mathfrak {q}}/G :\underline {2}^n \to \mathscr {B}$ and ![]() $F_1: \underline {2}^n\to \mathscr {B}$ are naturally isomorphic.
$F_1: \underline {2}^n\to \mathscr {B}$ are naturally isomorphic.
Proof. We will use the strategy of § 3.6 to build a natural isomorphism ![]() $\eta : F_\mathfrak {q}/G \to F_1$. For
$\eta : F_\mathfrak {q}/G \to F_1$. For ![]() $u\in \underline {2}^n$, there is a natural identification
$u\in \underline {2}^n$, there is a natural identification
Let ![]() $\psi _u : F_\mathfrak {q}(u)/G \to F_1(u)$ be the above bijection. For
$\psi _u : F_\mathfrak {q}(u)/G \to F_1(u)$ be the above bijection. For ![]() $u\geq _1 v$, let
$u\geq _1 v$, let ![]() $A_{u,v}$ denote the correspondence assigned by
$A_{u,v}$ denote the correspondence assigned by ![]() $F_q$ to the edge
$F_q$ to the edge ![]() $u\to v$, and let
$u\to v$, and let ![]() $A'_{u,v}$ denote the correspondence assigned by
$A'_{u,v}$ denote the correspondence assigned by ![]() $F_1$. There is an injection
$F_1$. There is an injection
given by ![]() $[\mathfrak {q}^k y, \mathfrak {q}^\ell x] \mapsto ([x],[y])$. We will identify
$[\mathfrak {q}^k y, \mathfrak {q}^\ell x] \mapsto ([x],[y])$. We will identify ![]() $A_{u,v}/G$ with its image in
$A_{u,v}/G$ with its image in ![]() $F_\mathfrak {q}(u)/G \times F_\mathfrak {q}(v)/G$. By Lemma 2.17, the map
$F_\mathfrak {q}(u)/G \times F_\mathfrak {q}(v)/G$. By Lemma 2.17, the map
restricts to a bijection
Thus, conditions (NI 1), (NI 2), and (NI 3) of § 3.6 are satisfied. It remains to verify that the diagram (3.5) commutes. Recall that we have used the ladybug matching made with the left pair for both ![]() $F_\mathfrak {q}$ and
$F_\mathfrak {q}$ and ![]() $F_1$. Then commutativity of (3.5) follows from Proposition 2.21.
$F_1$. Then commutativity of (3.5) follows from Proposition 2.21.
Note that any homotopy coherent diagram in ![]() $\text {Top}^G_*$ can be composed with the quotient functor
$\text {Top}^G_*$ can be composed with the quotient functor ![]() $(-)/G:\text {Top}^G_*\rightarrow \text {Top}_*$ to give a homotopy coherent diagram in
$(-)/G:\text {Top}^G_*\rightarrow \text {Top}_*$ to give a homotopy coherent diagram in ![]() $\text {Top}_*$ as in [Reference Sarkar, Scaduto and StoffregenSSS20, § 4.2].
$\text {Top}_*$ as in [Reference Sarkar, Scaduto and StoffregenSSS20, § 4.2].
Proposition 7.2 Let ![]() $\widetilde {F_{\mathfrak {q}}} :\underline {2}^n \to {\rm Top}_*^G$ be a
$\widetilde {F_{\mathfrak {q}}} :\underline {2}^n \to {\rm Top}_*^G$ be a ![]() $d$-dimensional spatial refinement of
$d$-dimensional spatial refinement of ![]() $F_{\mathfrak {q}}$. Then the homotopy coherent diagram
$F_{\mathfrak {q}}$. Then the homotopy coherent diagram ![]() $\widetilde {F_{\mathfrak {q}}}/G$, obtained by applying
$\widetilde {F_{\mathfrak {q}}}/G$, obtained by applying ![]() $(-)/G$ to each
$(-)/G$ to each ![]() $\widetilde {F_{\mathfrak {q}}}(v)$ and each
$\widetilde {F_{\mathfrak {q}}}(v)$ and each ![]() $\widetilde {F_{\mathfrak {q}}}(f_m,\ldots , f_1)$, is a
$\widetilde {F_{\mathfrak {q}}}(f_m,\ldots , f_1)$, is a ![]() $d$-dimensional spatial refinement of
$d$-dimensional spatial refinement of ![]() $F_{\mathfrak {q}}/G$.
$F_{\mathfrak {q}}/G$.
Proof. On a vertex ![]() $u\in \underline {2}^n$, since
$u\in \underline {2}^n$, since ![]() $F_{\mathfrak {q}}(u)=G\times F_1(u)$, it is again clear that the quotient
$F_{\mathfrak {q}}(u)=G\times F_1(u)$, it is again clear that the quotient
 \[ (\widetilde{F_{\mathfrak{q}}}/G)(u) = \widetilde{F_{\mathfrak{q}}}(u)/G = \bigg(\bigvee_{\mathfrak{q}^k x\in F_{\mathfrak{q}}(u)} S^d \bigg)\bigg/G \]
\[ (\widetilde{F_{\mathfrak{q}}}/G)(u) = \widetilde{F_{\mathfrak{q}}}(u)/G = \bigg(\bigvee_{\mathfrak{q}^k x\in F_{\mathfrak{q}}(u)} S^d \bigg)\bigg/G \]is canonically identified with
 \[ \widetilde{F_{\mathfrak{q}}/G}(u)=\bigvee_{x\in F_{\mathfrak{q}}(u)/G} S^d. \]
\[ \widetilde{F_{\mathfrak{q}}/G}(u)=\bigvee_{x\in F_{\mathfrak{q}}(u)/G} S^d. \]
The key point is to recognize that, for any correspondence ![]() $A=F_{\mathfrak {q}}(f)$ assigned to some morphism
$A=F_{\mathfrak {q}}(f)$ assigned to some morphism ![]() $f:u\rightarrow v$ in
$f:u\rightarrow v$ in ![]() $\underline {2}^n$ (with source and target maps
$\underline {2}^n$ (with source and target maps ![]() $s$ and
$s$ and ![]() $t$, respectively), the quotient of a box map refining
$t$, respectively), the quotient of a box map refining ![]() $A$ is itself a box map which refines the quotient of
$A$ is itself a box map which refines the quotient of ![]() $A$. That is to say, given a choice of equivariant little boxes
$A$. That is to say, given a choice of equivariant little boxes
which induces a map
 \[ \bigg(\bigvee_{\mathfrak{q}^k x\in F_{\mathfrak{q}}(u)} S^d \bigg) \xrightarrow{\Phi(e,A)} \bigg(\bigvee_{\mathfrak{q}^\ell y\in F_{\mathfrak{q}}(v)} S^d \bigg), \]
\[ \bigg(\bigvee_{\mathfrak{q}^k x\in F_{\mathfrak{q}}(u)} S^d \bigg) \xrightarrow{\Phi(e,A)} \bigg(\bigvee_{\mathfrak{q}^\ell y\in F_{\mathfrak{q}}(v)} S^d \bigg), \]
the image of the boxes ![]() $e$ in the quotient gives a new collection of little boxes
$e$ in the quotient gives a new collection of little boxes
such that the following diagram commutes.

Note that the group is simply permuting equivalent boxes, and recall that all correspondences coming from edges of the cube are subsets of the products of their source and target. Furthermore, all boxes remain distinct after taking the quotient. Thus, the quotient boxes ![]() $e/G$ fit into the commuting diagram as required, and the homotopy coherent diagram
$e/G$ fit into the commuting diagram as required, and the homotopy coherent diagram ![]() $\widetilde {F}_\mathfrak {q}/G$ can be identified with a spatial refinement of
$\widetilde {F}_\mathfrak {q}/G$ can be identified with a spatial refinement of ![]() $F_\mathfrak {q}/G$.
$F_\mathfrak {q}/G$.
Recall the enlarged cube category ![]() $\underline {2}^n_+$ from § 5.4. Any homotopy coherent diagram
$\underline {2}^n_+$ from § 5.4. Any homotopy coherent diagram ![]() $D: \underline {2}^n \to \text {Top}_*$ (respectively
$D: \underline {2}^n \to \text {Top}_*$ (respectively ![]() $D: \underline {2}^n \to \text {Top}_*^G$) can be extended to
$D: \underline {2}^n \to \text {Top}_*^G$) can be extended to ![]() $D^+ : \underline {2}^n_+ \to \text {Top}_*$ (respectively
$D^+ : \underline {2}^n_+ \to \text {Top}_*$ (respectively ![]() $D^+ : \underline {2}^n_+ \to \text {Top}_*^G$) by setting
$D^+ : \underline {2}^n_+ \to \text {Top}_*^G$) by setting ![]() $D^+(*)$ to be a single point space. Take
$D^+(*)$ to be a single point space. Take ![]() $k$-dimensional spatial refinements of
$k$-dimensional spatial refinements of ![]() $F_{\mathfrak {q}}$,
$F_{\mathfrak {q}}$, ![]() $F_1$, and
$F_1$, and ![]() $F_{\mathfrak {q}}/G$, denoted
$F_{\mathfrak {q}}/G$, denoted ![]() $\widetilde {F_{\mathfrak {q}}}$,
$\widetilde {F_{\mathfrak {q}}}$, ![]() $\widetilde {F_1}$, and
$\widetilde {F_1}$, and ![]() $\widetilde {F_{\mathfrak {q}}/G}$, respectively (suppressing the subscript
$\widetilde {F_{\mathfrak {q}}/G}$, respectively (suppressing the subscript ![]() $k$). Extend each of them to diagrams
$k$). Extend each of them to diagrams ![]() $\widetilde {F_{\mathfrak {q}}}^+$,
$\widetilde {F_{\mathfrak {q}}}^+$, ![]() $\widetilde {F_1}^+$, and
$\widetilde {F_1}^+$, and ![]() $\widetilde {F_{\mathfrak {q}}/G}^+$ out of
$\widetilde {F_{\mathfrak {q}}/G}^+$ out of ![]() $\underline {2}^n_+$, and take the corresponding homotopy colimits
$\underline {2}^n_+$, and take the corresponding homotopy colimits ![]() $\lVert F_{\mathfrak {q}}\rVert _k$,
$\lVert F_{\mathfrak {q}}\rVert _k$, ![]() $\lVert F_1\rVert _k$, and
$\lVert F_1\rVert _k$, and ![]() $\lVert F_{\mathfrak {q}}/G \rVert _k$. We also have the homotopy coherent diagram
$\lVert F_{\mathfrak {q}}/G \rVert _k$. We also have the homotopy coherent diagram ![]() $\widetilde {F_{\mathfrak {q}}}/G$; its two extensions
$\widetilde {F_{\mathfrak {q}}}/G$; its two extensions ![]() $\widetilde {F_{\mathfrak {q}}}^+ /G$ and
$\widetilde {F_{\mathfrak {q}}}^+ /G$ and ![]() $(\widetilde {F_{\mathfrak {q}}}/G)^+$ are equal.
$(\widetilde {F_{\mathfrak {q}}}/G)^+$ are equal.
Corollary 7.3 ![]() $\lVert F_1 \rVert _k \simeq (\lVert F_{\mathfrak {q}} \rVert _k) /G$.
$\lVert F_1 \rVert _k \simeq (\lVert F_{\mathfrak {q}} \rVert _k) /G$.
Proof. By Proposition 7.1, Proposition 5.5, and Lemma 5.8, there is a homotopy equivalence ![]() $\lVert F_1 \rVert _k \simeq \lVert F_{\mathfrak {q}}/G \rVert _k$. By Propositions 7.2 and 5.5, there is also a homotopy equivalence
$\lVert F_1 \rVert _k \simeq \lVert F_{\mathfrak {q}}/G \rVert _k$. By Propositions 7.2 and 5.5, there is also a homotopy equivalence ![]() $\lVert F_{\mathfrak {q}}/G \rVert _k \simeq \text {hocolim} (\widetilde {F_{\mathfrak {q}}}/G)^+$. Since
$\lVert F_{\mathfrak {q}}/G \rVert _k \simeq \text {hocolim} (\widetilde {F_{\mathfrak {q}}}/G)^+$. Since ![]() $(\widetilde {F_{\mathfrak {q}}}/G)^+ = \widetilde {F_{\mathfrak {q}}}^+/G$, we obtain
$(\widetilde {F_{\mathfrak {q}}}/G)^+ = \widetilde {F_{\mathfrak {q}}}^+/G$, we obtain
Finally, homotopy colimits commute with the quotient functor ![]() $(-)/G$. This is clear from the definition of homotopy colimit, but is also stated explicitly as property (ho-4) in [Reference Sarkar, Scaduto and StoffregenSSS20, § 4.2]. Therefore,
$(-)/G$. This is clear from the definition of homotopy colimit, but is also stated explicitly as property (ho-4) in [Reference Sarkar, Scaduto and StoffregenSSS20, § 4.2]. Therefore,
Remark 7.4 The techniques in this section can also be used to show that, for any subgroup ![]() $\mathbb {Z}/s\mathbb {Z}$ of
$\mathbb {Z}/s\mathbb {Z}$ of ![]() $\mathbb {Z}/r\mathbb {Z}$, the quotient
$\mathbb {Z}/r\mathbb {Z}$, the quotient ![]() $\mathcal {X}^r_{\mathbb {A}_\mathfrak {q}}(D) / (\mathbb {Z}/s\mathbb {Z})$ recovers the naive spectrum
$\mathcal {X}^r_{\mathbb {A}_\mathfrak {q}}(D) / (\mathbb {Z}/s\mathbb {Z})$ recovers the naive spectrum ![]() $\mathcal {X}^{r/s}_{\mathbb {A}_\mathfrak {q}}(D)$.
$\mathcal {X}^{r/s}_{\mathbb {A}_\mathfrak {q}}(D)$.
8. Towards lifting the  $U_{\mathfrak {q}}(\mathfrak {sl}_2)$ action
$U_{\mathfrak {q}}(\mathfrak {sl}_2)$ action
This section concerns Conjecture 1.4 on lifting the ![]() $U_{\mathfrak {q}}(\mathfrak {sl}_2)$ action on quantum annular homology, constructed in [Reference Beliakova, Putyra and WehrliBPW19, Theorem D], to the level of spectra. We start by briefly summarizing the relevant background material; see [Reference Beliakova, Putyra and WehrliBPW19, Appendix A.1] for more details. Let
$U_{\mathfrak {q}}(\mathfrak {sl}_2)$ action on quantum annular homology, constructed in [Reference Beliakova, Putyra and WehrliBPW19, Theorem D], to the level of spectra. We start by briefly summarizing the relevant background material; see [Reference Beliakova, Putyra and WehrliBPW19, Appendix A.1] for more details. Let ![]() $U_{\mathfrak {q}}(\mathfrak {sl}_2)$ be the
$U_{\mathfrak {q}}(\mathfrak {sl}_2)$ be the ![]() $\Bbbk$-algebra generated by
$\Bbbk$-algebra generated by ![]() $E,F,K,$ and
$E,F,K,$ and ![]() $K^{-1}$ subject to the relations
$K^{-1}$ subject to the relations
 \begin{equation} \begin{split} & KE = \mathfrak{q}^2 EK, \\ & KF = \mathfrak{q}^{{-}2} FK, \end{split} \quad \begin{split} & KK^{{-}1} = 1 = K^{{-}1}K, \\ & K-K^{{-}1} = (\mathfrak{q}-\mathfrak{q}^{{-}1})(EF - FE). \end{split} \end{equation}
\begin{equation} \begin{split} & KE = \mathfrak{q}^2 EK, \\ & KF = \mathfrak{q}^{{-}2} FK, \end{split} \quad \begin{split} & KK^{{-}1} = 1 = K^{{-}1}K, \\ & K-K^{{-}1} = (\mathfrak{q}-\mathfrak{q}^{{-}1})(EF - FE). \end{split} \end{equation}
Let ![]() $\mathcal {C}$ be a configuration consisting of
$\mathcal {C}$ be a configuration consisting of ![]() $e$ essential circles and
$e$ essential circles and ![]() $t$ trivial circles, with corresponding standard configuration
$t$ trivial circles, with corresponding standard configuration ![]() $\mathcal {C}^\circ$. Recall from § 2.2 that
$\mathcal {C}^\circ$. Recall from § 2.2 that ![]() $\mathcal {F}_{\mathbb {A}_\mathfrak {q}}(\mathcal {C}^\circ ) \cong V^{\otimes e} \otimes W^{\otimes t}$ carries an action of
$\mathcal {F}_{\mathbb {A}_\mathfrak {q}}(\mathcal {C}^\circ ) \cong V^{\otimes e} \otimes W^{\otimes t}$ carries an action of ![]() $U_{\mathfrak {q}}(\mathfrak {sl}_2)$ via an identification
$U_{\mathfrak {q}}(\mathfrak {sl}_2)$ via an identification
where ![]() $V_1$ is the fundamental representation of
$V_1$ is the fundamental representation of ![]() $U_{\mathfrak {q}}(\mathfrak {sl}_2)$ and
$U_{\mathfrak {q}}(\mathfrak {sl}_2)$ and ![]() $W$ is the trivial two-dimensional representation. Fix an isotopy from
$W$ is the trivial two-dimensional representation. Fix an isotopy from ![]() $\mathcal {C}^\circ$ to
$\mathcal {C}^\circ$ to ![]() $\mathcal {C}$. Then
$\mathcal {C}$. Then ![]() $\mathcal {F}_{\mathbb {A}_\mathfrak {q}}(\mathcal {C})$ inherits a
$\mathcal {F}_{\mathbb {A}_\mathfrak {q}}(\mathcal {C})$ inherits a ![]() $U_{\mathfrak {q}}(\mathfrak {sl}_2)$-action via the isomorphism
$U_{\mathfrak {q}}(\mathfrak {sl}_2)$-action via the isomorphism ![]() $\mathcal {F}_{\mathbb {A}_\mathfrak {q}}(\mathcal {C}^\circ ) \cong \mathcal {F}_{\mathbb {A}_\mathfrak {q}}(\mathcal {C})$.
$\mathcal {F}_{\mathbb {A}_\mathfrak {q}}(\mathcal {C}^\circ ) \cong \mathcal {F}_{\mathbb {A}_\mathfrak {q}}(\mathcal {C})$.
The stable homotopy type in this paper is constructed for the modified quantum annular functor ![]() $\mathcal {F}_{\mathbb {A}_\mathfrak {q}}^r$; see the discussion in the beginning of § 4. In what follows we will also denote by
$\mathcal {F}_{\mathbb {A}_\mathfrak {q}}^r$; see the discussion in the beginning of § 4. In what follows we will also denote by ![]() $U_{\mathfrak {q}}(\mathfrak {sl}_2)$ the result of applying
$U_{\mathfrak {q}}(\mathfrak {sl}_2)$ the result of applying ![]() $(-)\otimes _\Bbbk \Bbbk _r$ to the algebra defined above. It has the same generators and relations, with the additional relation that
$(-)\otimes _\Bbbk \Bbbk _r$ to the algebra defined above. It has the same generators and relations, with the additional relation that ![]() $\mathfrak {q}^r=1$.
$\mathfrak {q}^r=1$.
Let ![]() $F_1,F_0 : \underline {2}^n \to \mathscr {B}_G$ be Burnside functors. Recall from Proposition 5.7 (and the discussion following it) that a natural transformation
$F_1,F_0 : \underline {2}^n \to \mathscr {B}_G$ be Burnside functors. Recall from Proposition 5.7 (and the discussion following it) that a natural transformation ![]() $\eta : F_1\to F_0$ induces a cellular map
$\eta : F_1\to F_0$ induces a cellular map ![]() $\lVert {F_1}\rVert _k \to \lVert {F_0}\rVert _k$ which agrees with the map
$\lVert {F_1}\rVert _k \to \lVert {F_0}\rVert _k$ which agrees with the map ![]() $\text {Tot}(\eta ): \text {Tot}(F_1) \to \text {Tot}(F_0)$.
$\text {Tot}(\eta ): \text {Tot}(F_1) \to \text {Tot}(F_0)$.
Each of ![]() $E, F, K$, and
$E, F, K$, and ![]() $K^{-1}$ can be viewed as
$K^{-1}$ can be viewed as ![]() $\Bbbk$-linear endomorphisms of
$\Bbbk$-linear endomorphisms of ![]() $\mathcal {F}_{\mathbb {A}_\mathfrak {q}}^r(\mathcal {C})$. It is natural to ask whether the generators
$\mathcal {F}_{\mathbb {A}_\mathfrak {q}}^r(\mathcal {C})$. It is natural to ask whether the generators ![]() $E, F, K^{\pm {1}}$ lift to natural endomorphisms of the quantum Burnside functor
$E, F, K^{\pm {1}}$ lift to natural endomorphisms of the quantum Burnside functor ![]() $F_\mathfrak {q}$ constructed in § 4. Let
$F_\mathfrak {q}$ constructed in § 4. Let ![]() $J$ denote one of
$J$ denote one of ![]() $E, F, K$, or
$E, F, K$, or ![]() $K^{-1}$. For a generator
$K^{-1}$. For a generator ![]() $x\in F_{\mathbb {A}_\mathfrak {q}}(\mathcal {C})$,
$x\in F_{\mathbb {A}_\mathfrak {q}}(\mathcal {C})$,
where the sum is over generators and each ![]() $\varepsilon _y$ is either
$\varepsilon _y$ is either ![]() $0$ or of the form
$0$ or of the form ![]() $\pm \mathfrak {q}^k$. Note that the appearance of negatively signed coefficients in odd Khovanov homology was dealt with by using signed correspondences [Reference Sarkar, Scaduto and StoffregenSSS20, § 3.2] and signed box maps [Reference Sarkar, Scaduto and StoffregenSSS20, § 4.1].
$\pm \mathfrak {q}^k$. Note that the appearance of negatively signed coefficients in odd Khovanov homology was dealt with by using signed correspondences [Reference Sarkar, Scaduto and StoffregenSSS20, § 3.2] and signed box maps [Reference Sarkar, Scaduto and StoffregenSSS20, § 4.1].
Let ![]() $D$ be a diagram for an annular link with
$D$ be a diagram for an annular link with ![]() $n$ crossings, and fix a corresponding Burnside functor
$n$ crossings, and fix a corresponding Burnside functor ![]() $F_\mathfrak {q}:\underline {2}^n\to \mathscr {B}_G$ for
$F_\mathfrak {q}:\underline {2}^n\to \mathscr {B}_G$ for ![]() $D$. For
$D$. For ![]() $u\in \underline {2}^n$, one can define the signed correspondence
$u\in \underline {2}^n$, one can define the signed correspondence
from ![]() $F_\mathfrak {q}(u)$ to
$F_\mathfrak {q}(u)$ to ![]() $F_\mathfrak {q}(u)$, with the obvious source and target maps. The sign map
$F_\mathfrak {q}(u)$, with the obvious source and target maps. The sign map ![]() $\sigma : J_u \to \mathbb {Z}_2 = \{-1,1\}$ returns the sign of
$\sigma : J_u \to \mathbb {Z}_2 = \{-1,1\}$ returns the sign of ![]() $\mathfrak {q}^k y$. Such a correspondence
$\mathfrak {q}^k y$. Such a correspondence ![]() $J_u$ is equivariant since
$J_u$ is equivariant since ![]() $J$ is
$J$ is ![]() $\Bbbk$-linear. In the case when
$\Bbbk$-linear. In the case when ![]() $J=K^{\pm 1}$, the signs are not needed and we have the following lifts.
$J=K^{\pm 1}$, the signs are not needed and we have the following lifts.
Proposition 8.1 Let ![]() $D$ be a diagram for an annular link with
$D$ be a diagram for an annular link with ![]() $n$ crossings, and let
$n$ crossings, and let ![]() $F_\mathfrak {q}:\underline {2}^n\to \mathscr {B}_G$ be a Burnside functor for
$F_\mathfrak {q}:\underline {2}^n\to \mathscr {B}_G$ be a Burnside functor for ![]() $D$. Then there is a natural isomorphism
$D$. Then there is a natural isomorphism ![]() $\mathcal {K}^{\pm {1}}: F_\mathfrak {q} \to F_\mathfrak {q}$ which extends the correspondences
$\mathcal {K}^{\pm {1}}: F_\mathfrak {q} \to F_\mathfrak {q}$ which extends the correspondences ![]() $K_u^{\pm {1}}$ of (8.2).
$K_u^{\pm {1}}$ of (8.2).
Proof. We will use the strategy of § 3.6. For each ![]() $u\in \underline {2}^n$, we define the required equivariant bijection
$u\in \underline {2}^n$, we define the required equivariant bijection ![]() $\psi ^\pm _u: F_\mathfrak {q}(u)\to F_\mathfrak {q}(u)$ by
$\psi ^\pm _u: F_\mathfrak {q}(u)\to F_\mathfrak {q}(u)$ by
for all generators ![]() $x\in D_u$. Now let
$x\in D_u$. Now let ![]() $u\geq _1 v$. The conditions (NI 1) and (NI 3) of § 3.6 have already been checked on correspondences assigned to edges
$u\geq _1 v$. The conditions (NI 1) and (NI 3) of § 3.6 have already been checked on correspondences assigned to edges ![]() $\varphi _{u,v}:u\to v$ by
$\varphi _{u,v}:u\to v$ by ![]() $F_\mathfrak {q}$. In order to check condition (NI 2), we let
$F_\mathfrak {q}$. In order to check condition (NI 2), we let ![]() $\mathfrak {q}^k y \in F_\mathfrak {q}(u)$,
$\mathfrak {q}^k y \in F_\mathfrak {q}(u)$, ![]() $\mathfrak {q}^\ell x \in F_\mathfrak {q}(v)$ be elements such that
$\mathfrak {q}^\ell x \in F_\mathfrak {q}(v)$ be elements such that ![]() $\mathfrak {q}^k y$ appears in
$\mathfrak {q}^k y$ appears in ![]() $d_{v,u} (q^\ell x)$. Since
$d_{v,u} (q^\ell x)$. Since ![]() $d_{v,u}$ preserves annular degree, we have
$d_{v,u}$ preserves annular degree, we have ![]() $\text {adeg}(x) = \text {adeg}(y)$, so
$\text {adeg}(x) = \text {adeg}(y)$, so ![]() $\mathfrak {q}^{k\mp \text {adeg}(y)}y$ appears in
$\mathfrak {q}^{k\mp \text {adeg}(y)}y$ appears in ![]() $d_{v,u} ( \mathfrak {q}^{\ell -\mp \text {adeg}(x)} x)$. This implies condition (NI 2).
$d_{v,u} ( \mathfrak {q}^{\ell -\mp \text {adeg}(x)} x)$. This implies condition (NI 2).
Thus, we can build a natural transformation ![]() $\eta ^\pm$ as in § 3.6; the diagram 3.5 commutes, since
$\eta ^\pm$ as in § 3.6; the diagram 3.5 commutes, since ![]() $\psi _u$ simply multiplies generators by powers of
$\psi _u$ simply multiplies generators by powers of ![]() $\mathfrak {q}$. Finally, note that
$\mathfrak {q}$. Finally, note that ![]() $K^{\pm {1}}x = \mathfrak {q}^{\pm \text {adeg}(x)} x$, so
$K^{\pm {1}}x = \mathfrak {q}^{\pm \text {adeg}(x)} x$, so
is naturally identified with ![]() $\eta ^\pm (e_u)$ via
$\eta ^\pm (e_u)$ via ![]() $(\mathfrak {q}^k x, \mathfrak {q}^{k\mp \text {adeg}(x)} x)\mapsto \mathfrak {q}^k x$.
$(\mathfrak {q}^k x, \mathfrak {q}^{k\mp \text {adeg}(x)} x)\mapsto \mathfrak {q}^k x$.
We note that when ![]() $J=E$ or
$J=E$ or ![]() $J=F$, this overall strategy does not produce such a lift. Consider the saddle
$J=F$, this overall strategy does not produce such a lift. Consider the saddle ![]() $S$ from Example 2.13, thought of as the cube of resolutions for a link diagram with one crossing. Let
$S$ from Example 2.13, thought of as the cube of resolutions for a link diagram with one crossing. Let ![]() $u=1$ and
$u=1$ and ![]() $v = 0$ denote the vertices of the cube
$v = 0$ denote the vertices of the cube ![]() $\underline {2}$, and let
$\underline {2}$, and let ![]() $d : \mathcal {F}_{\mathbb {A}_\mathfrak {q}}^r(D_v) \to \mathcal {F}_{\mathbb {A}_\mathfrak {q}}^r(D_u)$ denote the differential. Let
$d : \mathcal {F}_{\mathbb {A}_\mathfrak {q}}^r(D_v) \to \mathcal {F}_{\mathbb {A}_\mathfrak {q}}^r(D_u)$ denote the differential. Let ![]() $A$ denote the correspondence
$A$ denote the correspondence ![]() $F_\mathfrak {q}(\varphi _{u,v})$ from
$F_\mathfrak {q}(\varphi _{u,v})$ from ![]() $F_\mathfrak {q}(u)$ to
$F_\mathfrak {q}(u)$ to ![]() $F_\mathfrak {q}(v)$ assigned by the Burnside functor
$F_\mathfrak {q}(v)$ assigned by the Burnside functor ![]() $F_\mathfrak {q}$.
$F_\mathfrak {q}$.

The surgery formulas are
and actions of ![]() $E$ and
$E$ and ![]() $F$ are given by
$F$ are given by
The correspondence ![]() $J_v\times _{F_\mathfrak {q}(v)} A$ is empty, whereas the correspondence
$J_v\times _{F_\mathfrak {q}(v)} A$ is empty, whereas the correspondence ![]() $A\times _{F_\mathfrak {q}(u)} J_u$ is non-empty, containing two oppositely signed elements.
$A\times _{F_\mathfrak {q}(u)} J_u$ is non-empty, containing two oppositely signed elements.
Remark 8.2 It may be possible to overcome these difficulties using a suitably refined ![]() $G$-equivariant Burnside category. In the event that one has natural transformations lifting each of the
$G$-equivariant Burnside category. In the event that one has natural transformations lifting each of the ![]() $E,F$, and
$E,F$, and ![]() $K$ maps, one might also ask for some notion of a lift of the relations (8.1), perhaps in terms of the cones on the corresponding maps of spectra. The authors hope to continue investigating these topics in the future.
$K$ maps, one might also ask for some notion of a lift of the relations (8.1), perhaps in terms of the cones on the corresponding maps of spectra. The authors hope to continue investigating these topics in the future.
Acknowledgments
We would like to thank Nick Kuhn, Krzysztof Putyra, and Sucharit Sarkar for helpful conversations. We are also grateful to Matt Stoffregen for discussions and for his comments on an earlier version of the paper.
Appendix. Elementary cobordisms
Here we compare two ways of constructing a map on quantum annular chain complexes for certain elementary annular link cobordisms ![]() $W$. On the one hand,
$W$. On the one hand, ![]() $W$ induces a chain map
$W$ induces a chain map ![]() $W_*$ as defined in [Reference Beliakova, Putyra and WehrliBPW19, (7.2)]. On the other hand, for each type of elementary annular link cobordism
$W_*$ as defined in [Reference Beliakova, Putyra and WehrliBPW19, (7.2)]. On the other hand, for each type of elementary annular link cobordism ![]() $W$, we can define a second map
$W$, we can define a second map ![]() $W_\bullet$ tailored towards the maps on spectra corresponding to our constructions in this paper (mainly those in §§ 2.4 and 4.2). Our goal will be to show that these two maps
$W_\bullet$ tailored towards the maps on spectra corresponding to our constructions in this paper (mainly those in §§ 2.4 and 4.2). Our goal will be to show that these two maps ![]() $W_*,W_\bullet$ differ at most by some power of
$W_*,W_\bullet$ differ at most by some power of ![]() $\mathfrak {q}$ in all cases.
$\mathfrak {q}$ in all cases.
We begin by describing the general construction of the map ![]() $W_*$. Let
$W_*$. Let ![]() $W\subset \mathbb {A}\times I \times [0,1]$ be a cobordism between annular links
$W\subset \mathbb {A}\times I \times [0,1]$ be a cobordism between annular links ![]() $L$ and
$L$ and ![]() $L'$ which intersect the membrane in
$L'$ which intersect the membrane in ![]() $k$ and
$k$ and ![]() $\ell$ points, respectively, and let
$\ell$ points, respectively, and let ![]() $T$,
$T$, ![]() $T'$ denote the tangles obtained by cutting
$T'$ denote the tangles obtained by cutting ![]() $L$ and
$L$ and ![]() $L'$ along the membrane. Then
$L'$ along the membrane. Then ![]() $W$ intersects the three-dimensional membrane
$W$ intersects the three-dimensional membrane ![]() $\mu \times I \times [0,1]$ in a
$\mu \times I \times [0,1]$ in a ![]() $(k,\ell )$-tangle
$(k,\ell )$-tangle ![]() $P$. As in [Reference Beliakova, Putyra and WehrliBPW19, § 7.1], we represent
$P$. As in [Reference Beliakova, Putyra and WehrliBPW19, § 7.1], we represent ![]() $W$ by a tangle cobordism
$W$ by a tangle cobordism ![]() $\widetilde {W}: PT \to T' P$:
$\widetilde {W}: PT \to T' P$:

The chain map ![]() $W_* : CKh_{\mathbb {A}_\mathfrak {q}}(L) \to CKh_{\mathbb {A}_\mathfrak {q}}(L')$ is then given in each homological grading and quantum grading by the formula (7.2) in [Reference Beliakova, Putyra and WehrliBPW19].
$W_* : CKh_{\mathbb {A}_\mathfrak {q}}(L) \to CKh_{\mathbb {A}_\mathfrak {q}}(L')$ is then given in each homological grading and quantum grading by the formula (7.2) in [Reference Beliakova, Putyra and WehrliBPW19].
To describe the map ![]() $W_\bullet$, we distinguish four types of elementary cobordisms.
$W_\bullet$, we distinguish four types of elementary cobordisms.
I. Reidemeister moves away from the seam.
II. Morse moves away from the seam.
III. Moving an arc across the seam as in the
 $P^{\pm {1}}$ and
$P^{\pm {1}}$ and  $N^{\pm {1}}$ moves of Figure 11.
$N^{\pm {1}}$ moves of Figure 11.IV. Moving a crossing through the seam as in Figure A.1.

Figure A.1. Moving a crossing through the seam.
For Type I moves, we define ![]() $W_\bullet$ as in [Reference KhovanovKho00] and [Reference Bar-NatanBar05]; that is, a Reidemeister move is assigned its chain homotopy equivalence.
$W_\bullet$ as in [Reference KhovanovKho00] and [Reference Bar-NatanBar05]; that is, a Reidemeister move is assigned its chain homotopy equivalence.
For the remaining types of moves, let ![]() $D$ and
$D$ and ![]() $D'$ denote the diagrams for
$D'$ denote the diagrams for ![]() $L$ and
$L$ and ![]() $L'$ differing locally as indicated by the elementary cobordism
$L'$ differing locally as indicated by the elementary cobordism ![]() $W$, and let
$W$, and let ![]() $n$ be the number of crossings. For each
$n$ be the number of crossings. For each ![]() $u\in \{0,1\}^n$,
$u\in \{0,1\}^n$, ![]() $W$ induces an annular cobordism
$W$ induces an annular cobordism ![]() $R_u : D_u \to D'_u$ in
$R_u : D_u \to D'_u$ in ![]() $\mathbb {A}\times [0,1]$. The quantum annular TQFT
$\mathbb {A}\times [0,1]$. The quantum annular TQFT ![]() $\mathcal {F}_{\mathbb {A}_\mathfrak {q}}$ assigns a map to this cobordism; after tensoring with
$\mathcal {F}_{\mathbb {A}_\mathfrak {q}}$ assigns a map to this cobordism; after tensoring with ![]() $\Bbbk _r$, we write this as
$\Bbbk _r$, we write this as
If we pick out generators for ![]() $\mathcal {F}_{\mathbb {A}_\mathfrak {q}}^r(D_u)$ and
$\mathcal {F}_{\mathbb {A}_\mathfrak {q}}^r(D_u)$ and ![]() $\mathcal {F}_{\mathbb {A}_\mathfrak {q}}^r(D_u')$ via cobordisms from standard configurations as in § 2.3, then the image of these generators under this map can be computed by composing cobordisms. We will use shifted copies of this map to define the components
$\mathcal {F}_{\mathbb {A}_\mathfrak {q}}^r(D_u')$ via cobordisms from standard configurations as in § 2.3, then the image of these generators under this map can be computed by composing cobordisms. We will use shifted copies of this map to define the components ![]() $W_{\bullet u} : \mathcal {F}^r_{\mathbb {A}_\mathfrak {q}}(D_u) \to \mathcal {F}^r_{\mathbb {A}_\mathfrak {q}}(D'_u)$ of
$W_{\bullet u} : \mathcal {F}^r_{\mathbb {A}_\mathfrak {q}}(D_u) \to \mathcal {F}^r_{\mathbb {A}_\mathfrak {q}}(D'_u)$ of ![]() $W_\bullet$ on each smoothing individually. Note that this is precisely how the natural isomorphisms of the quantum annular Burnside functors are determined in § 4.2 (although there we omitted the functor
$W_\bullet$ on each smoothing individually. Note that this is precisely how the natural isomorphisms of the quantum annular Burnside functors are determined in § 4.2 (although there we omitted the functor ![]() $\mathcal {F}_{\mathbb {A}_\mathfrak {q}}^r$ from the notation).
$\mathcal {F}_{\mathbb {A}_\mathfrak {q}}^r$ from the notation).
If ![]() $W$ is of Type II or III, we define
$W$ is of Type II or III, we define ![]() $W_{\bullet u}$ on each smoothing to be
$W_{\bullet u}$ on each smoothing to be ![]() $\mathcal {F}_{\mathbb {A}_\mathfrak {q}}^r(R_u)$. Notice that for Type II moves, this is equivalent to defining
$\mathcal {F}_{\mathbb {A}_\mathfrak {q}}^r(R_u)$. Notice that for Type II moves, this is equivalent to defining ![]() $W_\bullet$ as in [Reference KhovanovKho00] and [Reference Bar-NatanBar05] where Morse moves are assigned the unit, saddle map, or counit on each smoothing, corresponding to
$W_\bullet$ as in [Reference KhovanovKho00] and [Reference Bar-NatanBar05] where Morse moves are assigned the unit, saddle map, or counit on each smoothing, corresponding to ![]() $0$-handle,
$0$-handle, ![]() $1$-handle, and
$1$-handle, and ![]() $2$-handle attachments, respectively.
$2$-handle attachments, respectively.
Finally, if ![]() $W$ is of Type IV, then there are four cases to consider depending on the type of crossing and the direction of movement across the seam.In all of these cases, we will define
$W$ is of Type IV, then there are four cases to consider depending on the type of crossing and the direction of movement across the seam.In all of these cases, we will define
for some power ![]() $a\in \mathbb {Z}$ which is determined by the resolution of the crossing near the seam. If the smoothing corresponding to
$a\in \mathbb {Z}$ which is determined by the resolution of the crossing near the seam. If the smoothing corresponding to ![]() $u$ resolves this crossing into two parallel lines each intersecting
$u$ resolves this crossing into two parallel lines each intersecting ![]() $\mu$ once, we set
$\mu$ once, we set ![]() $a:=0$ in the formula (A.2) for
$a:=0$ in the formula (A.2) for ![]() $W_{\bullet u}$, so that
$W_{\bullet u}$, so that ![]() $W_{\bullet u}=\mathcal {F}_{\mathbb {A}_\mathfrak {q}}^r(R_u)$ once again. Note that
$W_{\bullet u}=\mathcal {F}_{\mathbb {A}_\mathfrak {q}}^r(R_u)$ once again. Note that ![]() $R_u$ is just the identity cobordism in this case, so
$R_u$ is just the identity cobordism in this case, so ![]() $W_{\bullet u}$ is the identity map. Otherwise, we set
$W_{\bullet u}$ is the identity map. Otherwise, we set ![]() $a:=1$ for the moves
$a:=1$ for the moves ![]() $(a)$ and
$(a)$ and ![]() $(d)$, and
$(d)$, and ![]() $a:=-1$ for the moves
$a:=-1$ for the moves ![]() $(b)$ and
$(b)$ and ![]() $(c)$.
$(c)$.
Note that in all cases, ![]() $W_\bullet$ is a chain map; for Type I and II moves this follows from the definitions, while for Type III and IV moves this follows from the trace relations in Figure 7. Note also that, for Type III and IV moves, the maps
$W_\bullet$ is a chain map; for Type I and II moves this follows from the definitions, while for Type III and IV moves this follows from the trace relations in Figure 7. Note also that, for Type III and IV moves, the maps ![]() $W_\bullet$ defined here are precisely the totalizations of the natural isomorphisms built in Proposition 4.4.
$W_\bullet$ defined here are precisely the totalizations of the natural isomorphisms built in Proposition 4.4.
Lemma A.1 Let ![]() $L$ and
$L$ and ![]() $L'$ be annular links and let
$L'$ be annular links and let ![]() $W: L \to L'$ be an elementary cobordism.
$W: L \to L'$ be an elementary cobordism.
(1) If
 $W$ is of Type I, II, or III, then
$W$ is of Type I, II, or III, then  $W_* = W_\bullet$.
$W_* = W_\bullet$.(2) If
 $W$ is Type IV, then
$W$ is Type IV, then  $W_* = \mathfrak {q}^m W_\bullet$ for some
$W_* = \mathfrak {q}^m W_\bullet$ for some  $m$ which depends only on the sign of the crossing involved in the move.
$m$ which depends only on the sign of the crossing involved in the move.
Proof. Throughout the proof, we will use ![]() $C(-)$ to denote the Chen–Khovanov complex of bimodules, which is denoted by
$C(-)$ to denote the Chen–Khovanov complex of bimodules, which is denoted by ![]() $C_{CK}(-)$ in [Reference Beliakova, Putyra and WehrliBPW19, § 5.5].
$C_{CK}(-)$ in [Reference Beliakova, Putyra and WehrliBPW19, § 5.5].
The first thing to notice is that, in any case where the intersection tangle ![]() $P=W\cap \mu \times I \times [0,1]$ has no crossings, the formula [Reference Beliakova, Putyra and WehrliBPW19, (7.2)] for
$P=W\cap \mu \times I \times [0,1]$ has no crossings, the formula [Reference Beliakova, Putyra and WehrliBPW19, (7.2)] for ![]() $W_*$ simplifies drastically. There is no summation over indices
$W_*$ simplifies drastically. There is no summation over indices ![]() $i'$ since
$i'$ since ![]() $C(P)$ has only one term. In all such cases (which include Type I, II, and III here), one shows that
$C(P)$ has only one term. In all such cases (which include Type I, II, and III here), one shows that ![]() $W_*$ is equal to
$W_*$ is equal to ![]() $W_\bullet$ by direct comparison.
$W_\bullet$ by direct comparison.
Finally, for elementary cobordisms ![]() $W$ of Type IV, we focus on the case (a) from Figure A.1. Observe that the tangle
$W$ of Type IV, we focus on the case (a) from Figure A.1. Observe that the tangle ![]() $P$ in this case has a single crossing, that
$P$ in this case has a single crossing, that ![]() $T$ and
$T$ and ![]() $T'$ can be written as
$T'$ can be written as ![]() $T = T''P$ and
$T = T''P$ and ![]() $T' = PT''$, and that
$T' = PT''$, and that ![]() $\widetilde {W}: PT \to T'P$ is the identity cobordism. All of this is illustrated in Figure A.2.
$\widetilde {W}: PT \to T'P$ is the identity cobordism. All of this is illustrated in Figure A.2.

Figure A.2. Proof of Lemma A.1 for elementary cobordisms of Type IV.
Using ![]() $\otimes$ to denote the tensor product over the relevant Chen–Khovanov arc algebra, the map
$\otimes$ to denote the tensor product over the relevant Chen–Khovanov arc algebra, the map ![]() $\widetilde {W}_*: C^i(T) \otimes C^{i'}(P) \to C^{i'}(P) \otimes C^{i}(T')$ is the identity on the summand
$\widetilde {W}_*: C^i(T) \otimes C^{i'}(P) \to C^{i'}(P) \otimes C^{i}(T')$ is the identity on the summand ![]() $C^{i'}(P) \otimes C^{i-i'}(T'') \otimes C^{i'}(P)$ which appears in both
$C^{i'}(P) \otimes C^{i-i'}(T'') \otimes C^{i'}(P)$ which appears in both ![]() $C^i(T) \otimes C^{i'}(P)$ and
$C^i(T) \otimes C^{i'}(P)$ and ![]() $C^{i'}(P) \otimes C^{i}(T')$, and
$C^{i'}(P) \otimes C^{i}(T')$, and ![]() $\widetilde {W}_*$ is
$\widetilde {W}_*$ is ![]() $0$ on the other summands. In particular, there is no need for summing over various
$0$ on the other summands. In particular, there is no need for summing over various ![]() $i'$ in the formula [Reference Beliakova, Putyra and WehrliBPW19, (7.2)] for
$i'$ in the formula [Reference Beliakova, Putyra and WehrliBPW19, (7.2)] for ![]() $W_*$, and the only possible difference between
$W_*$, and the only possible difference between ![]() $W_*$ and
$W_*$ and ![]() $W_\bullet$ acting on any given generator is in the use of the third map
$W_\bullet$ acting on any given generator is in the use of the third map ![]() $\theta$ in [Reference Beliakova, Putyra and WehrliBPW19, (7.2)] which permutes the tensor factors and multiplies generators
$\theta$ in [Reference Beliakova, Putyra and WehrliBPW19, (7.2)] which permutes the tensor factors and multiplies generators ![]() $x\otimes y \otimes \alpha$ by a power of
$x\otimes y \otimes \alpha$ by a power of ![]() $\mathfrak {q}$ according to the grading of
$\mathfrak {q}$ according to the grading of ![]() $x$ as defined in [Reference Beliakova, Putyra and WehrliBPW19, § 5.5].
$x$ as defined in [Reference Beliakova, Putyra and WehrliBPW19, § 5.5].
To analyze this potential difference, let ![]() $P_0,P_1$ denote the 0- and 1-resolutions of
$P_0,P_1$ denote the 0- and 1-resolutions of ![]() $P$. When constructing
$P$. When constructing ![]() $W_\bullet$ on each resolution, we view
$W_\bullet$ on each resolution, we view ![]() $x$ as living in either
$x$ as living in either ![]() $\mathcal {F}_{CK}(P_0)$ or
$\mathcal {F}_{CK}(P_0)$ or ![]() $\mathcal {F}_{CK}(P_1)$. If
$\mathcal {F}_{CK}(P_1)$. If ![]() $x\in \mathcal {F}_{CK}(P_1)$, there is an extra factor of
$x\in \mathcal {F}_{CK}(P_1)$, there is an extra factor of ![]() $\mathfrak {q}^1$ in our map (recall that we are considering case (a) amongst the Type IV moves; see the paragraph following (A.2)). However, in the definition of
$\mathfrak {q}^1$ in our map (recall that we are considering case (a) amongst the Type IV moves; see the paragraph following (A.2)). However, in the definition of ![]() $W_*$, we view
$W_*$, we view ![]() $x$ as living in
$x$ as living in
where the grading shift ![]() $m$ depends on the sign of the crossing. And so the map
$m$ depends on the sign of the crossing. And so the map ![]() $\theta$ multiplies generators by an extra overall factor of
$\theta$ multiplies generators by an extra overall factor of ![]() $\mathfrak {q}^m$ when defining
$\mathfrak {q}^m$ when defining ![]() $W_*$ as compared to how it would act when defining
$W_*$ as compared to how it would act when defining ![]() $W_\bullet$, as desired.
$W_\bullet$, as desired.
The proof for case ![]() $(c)$ of Figure A.1 is similar. For the cases
$(c)$ of Figure A.1 is similar. For the cases ![]() $(b)$ and
$(b)$ and ![]() $(d)$, note that the map
$(d)$, note that the map ![]() $W_\bullet$ is precisely the inverse of the map defined in
$W_\bullet$ is precisely the inverse of the map defined in ![]() $(a)$ and
$(a)$ and ![]() $(c)$, respectively. Moreover, the cobordisms
$(c)$, respectively. Moreover, the cobordisms ![]() $W$ of moves
$W$ of moves ![]() $(b)$ and
$(b)$ and ![]() $(d)$ are inverses (in the category
$(d)$ are inverses (in the category ![]() $Links_\mathfrak {q}(\mathbb {A})$; see [Reference Beliakova, Putyra and WehrliBPW19, Proposition 6.8]) to the cobordisms of
$Links_\mathfrak {q}(\mathbb {A})$; see [Reference Beliakova, Putyra and WehrliBPW19, Proposition 6.8]) to the cobordisms of ![]() $(a)$ and
$(a)$ and ![]() $(c)$, respectively. This completes the proof.
$(c)$, respectively. This completes the proof.