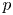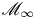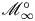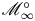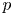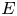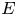1. Main theorem
Let ![]() $p$ be a prime number. Rapoport–Zink spaces [Reference Rapoport and ZinkRZ96] are deformation spaces of
$p$ be a prime number. Rapoport–Zink spaces [Reference Rapoport and ZinkRZ96] are deformation spaces of ![]() $p$-divisible groups equipped with some extra structure. This article concerns the geometry of Rapoport–Zink spaces of EL type (endomorphisms
$p$-divisible groups equipped with some extra structure. This article concerns the geometry of Rapoport–Zink spaces of EL type (endomorphisms ![]() $+$ level structure). In particular we consider the infinite-level spaces
$+$ level structure). In particular we consider the infinite-level spaces ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty }$, which are preperfectoid spaces [Reference Scholze and WeinsteinSW13]. An example is the space
${{\mathscr M}}_{{{\mathcal {D}}},\infty }$, which are preperfectoid spaces [Reference Scholze and WeinsteinSW13]. An example is the space ![]() ${{\mathscr M}}_{H,\infty }$, where
${{\mathscr M}}_{H,\infty }$, where ![]() $H/\overline {{{\mathbf {F}}}}_p$ is a
$H/\overline {{{\mathbf {F}}}}_p$ is a ![]() $p$-divisible group of height
$p$-divisible group of height ![]() $n$. The points of
$n$. The points of ![]() ${{\mathscr M}}_{H,\infty }$ over a nonarchimedean field
${{\mathscr M}}_{H,\infty }$ over a nonarchimedean field ![]() $K$ containing
$K$ containing ![]() $W(\overline {{{\mathbf {F}}}}_p)$ are in correspondence with isogeny classes of
$W(\overline {{{\mathbf {F}}}}_p)$ are in correspondence with isogeny classes of ![]() $p$-divisible groups
$p$-divisible groups ![]() $G/\mathcal {O}_K$ equipped with a quasi-isogeny
$G/\mathcal {O}_K$ equipped with a quasi-isogeny ![]() $G\otimes _{\mathcal {O}_K} \mathcal {O}_K/p \to H\otimes _{\overline {{{\mathbf {F}}}}_p} \mathcal {O}_K/p$ and an isomorphism
$G\otimes _{\mathcal {O}_K} \mathcal {O}_K/p \to H\otimes _{\overline {{{\mathbf {F}}}}_p} \mathcal {O}_K/p$ and an isomorphism ![]() $\mathbf {Q}_p^{n}\cong VG$ (where
$\mathbf {Q}_p^{n}\cong VG$ (where ![]() $VG$ is the rational Tate module).
$VG$ is the rational Tate module).
The infinite-level space ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty }$ appears as the limit of finite-level spaces, each of which is a smooth rigid-analytic space. We would like to investigate the question of smoothness for the space
${{\mathscr M}}_{{{\mathcal {D}}},\infty }$ appears as the limit of finite-level spaces, each of which is a smooth rigid-analytic space. We would like to investigate the question of smoothness for the space ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty }$ itself, which is quite a different matter. We need the notion of cohomological smoothness [Reference ScholzeSch17], which makes sense for general morphisms of analytic adic spaces, and which is reviewed in § 4. Roughly speaking, an adic space is cohomologically smooth over
${{\mathscr M}}_{{{\mathcal {D}}},\infty }$ itself, which is quite a different matter. We need the notion of cohomological smoothness [Reference ScholzeSch17], which makes sense for general morphisms of analytic adic spaces, and which is reviewed in § 4. Roughly speaking, an adic space is cohomologically smooth over ![]() $C$ (where
$C$ (where ![]() $C/\mathbf {Q}_p$ is complete and algebraically closed) if it satisfies local Verdier duality. In particular, if
$C/\mathbf {Q}_p$ is complete and algebraically closed) if it satisfies local Verdier duality. In particular, if ![]() $U$ is a quasi-compact adic space which is cohomologically smooth over
$U$ is a quasi-compact adic space which is cohomologically smooth over ![]() $\operatorname {Spa} (C,\mathcal {O}_C)$, then the cohomology group
$\operatorname {Spa} (C,\mathcal {O}_C)$, then the cohomology group ![]() $H^{i}(U,{{\mathbf {F}}}_\ell )$ is finite for all
$H^{i}(U,{{\mathbf {F}}}_\ell )$ is finite for all ![]() $i$ and all primes
$i$ and all primes ![]() $\ell \neq p$.
$\ell \neq p$.
Our main theorem shows that each connected component of the geometric fiber of ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty }$ has a dense open subset which is cohomologically smooth.
${{\mathscr M}}_{{{\mathcal {D}}},\infty }$ has a dense open subset which is cohomologically smooth.
Theorem 1.0.1 Let ![]() ${{\mathcal {D}}}$ be a basic EL datum (cf. § 2). Let
${{\mathcal {D}}}$ be a basic EL datum (cf. § 2). Let ![]() $C$ be a complete algebraically closed extension of the field of scalars of
$C$ be a complete algebraically closed extension of the field of scalars of ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty }$, and let
${{\mathscr M}}_{{{\mathcal {D}}},\infty }$, and let ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\circ }$ be a connected component of the base change
${{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\circ }$ be a connected component of the base change ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty ,C}$. Let
${{\mathscr M}}_{{{\mathcal {D}}},\infty ,C}$. Let ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\circ ,\operatorname {non-sp}}\subset {{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\circ }$ be the nonspecial locus (cf. § 3.5), corresponding to
${{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\circ ,\operatorname {non-sp}}\subset {{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\circ }$ be the nonspecial locus (cf. § 3.5), corresponding to ![]() $p$-divisible groups without extra endomorphisms. Then
$p$-divisible groups without extra endomorphisms. Then ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\circ ,\operatorname {non-sp}}$ is cohomologically smooth over
${{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\circ ,\operatorname {non-sp}}$ is cohomologically smooth over ![]() $C$.
$C$.
We remark that outside of trivial cases, ![]() $\pi _0({{\mathscr M}}_{{{\mathcal {D}}},\infty ,C})$ has no isolated points, which implies that no open subset of
$\pi _0({{\mathscr M}}_{{{\mathcal {D}}},\infty ,C})$ has no isolated points, which implies that no open subset of ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty ,C}$ can be cohomologically smooth. (Indeed, the
${{\mathscr M}}_{{{\mathcal {D}}},\infty ,C}$ can be cohomologically smooth. (Indeed, the ![]() $H^{0}$ of any quasi-compact open fails to be finitely generated.) Therefore it really is necessary to work with individual connected components of the geometric fiber of
$H^{0}$ of any quasi-compact open fails to be finitely generated.) Therefore it really is necessary to work with individual connected components of the geometric fiber of ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty }$.
${{\mathscr M}}_{{{\mathcal {D}}},\infty }$.
Theorem 1.0.1 is an application of the perfectoid version of the Jacobian criterion for smoothness, due to Fargues and Scholze [Reference Fargues and ScholzeFS]; cf. Theorem 4.2.1. The latter theorem involves the Fargues–Fontaine curve ![]() $X_C$ (reviewed in § 3). It asserts that a functor
$X_C$ (reviewed in § 3). It asserts that a functor ![]() ${{\mathscr M}}$ on perfectoid spaces over
${{\mathscr M}}$ on perfectoid spaces over ![]() $\operatorname {Spa}(C,\mathcal {O}_C)$ is cohomologically smooth, when
$\operatorname {Spa}(C,\mathcal {O}_C)$ is cohomologically smooth, when ![]() ${{\mathscr M}}$ can be interpreted as global sections of a smooth morphism
${{\mathscr M}}$ can be interpreted as global sections of a smooth morphism ![]() $Z\to X_C$, subject to a certain condition on the tangent bundle
$Z\to X_C$, subject to a certain condition on the tangent bundle ![]() $\operatorname {Tan}_{Z/X_C}$.
$\operatorname {Tan}_{Z/X_C}$.
In our application to Rapoport–Zink spaces, we construct a smooth morphism ![]() $Z\to X_C$, whose moduli space of global sections is isomorphic to
$Z\to X_C$, whose moduli space of global sections is isomorphic to ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\circ }$ (Lemma 5.2.1). Next, we show that a geometric point
${{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\circ }$ (Lemma 5.2.1). Next, we show that a geometric point ![]() $x \in {{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\circ }(C)$ lies in
$x \in {{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\circ }(C)$ lies in ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\circ ,\textrm {non-sp}}(C)$ if and only if the corresponding section
${{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\circ ,\textrm {non-sp}}(C)$ if and only if the corresponding section ![]() $s \colon X_C \rightarrow Z$ satisfies the condition that all slopes of the vector bundle
$s \colon X_C \rightarrow Z$ satisfies the condition that all slopes of the vector bundle ![]() $s^{\ast }\operatorname {Tan}_{Z/X_C}$ on
$s^{\ast }\operatorname {Tan}_{Z/X_C}$ on ![]() $X_C$ are positive (Theorem 5.5.1). This is exactly the condition on
$X_C$ are positive (Theorem 5.5.1). This is exactly the condition on ![]() $\operatorname {Tan}_{Z/X_C}$ required by Theorem 4.2.1, so we can conclude that
$\operatorname {Tan}_{Z/X_C}$ required by Theorem 4.2.1, so we can conclude that ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\circ }$ is cohomologically smooth.
${{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\circ }$ is cohomologically smooth.
The geometry of Rapoport–Zink spaces is related to the geometry of Shimura varieties. As an example, consider the tower of classical modular curves ![]() $X(p^{\infty })$, considered as rigid spaces over
$X(p^{\infty })$, considered as rigid spaces over ![]() $C$. There is a perfectoid space
$C$. There is a perfectoid space ![]() $X(p^{\infty })$ over
$X(p^{\infty })$ over ![]() $C$ for which
$C$ for which ![]() $X(p^{\infty })\sim \varprojlim _n X(p^{n})$, and a Hodge–Tate period map
$X(p^{\infty })\sim \varprojlim _n X(p^{n})$, and a Hodge–Tate period map ![]() $\pi _{HT}\colon X(p^{\infty })\to {{\mathbf {P}}}^{1}_C$ [Reference ScholzeSch15], which is
$\pi _{HT}\colon X(p^{\infty })\to {{\mathbf {P}}}^{1}_C$ [Reference ScholzeSch15], which is ![]() $\operatorname {GL}_2(\mathbf {Q}_p)$-equivariant. Let
$\operatorname {GL}_2(\mathbf {Q}_p)$-equivariant. Let ![]() $X(p^{\infty })^{\circ }\subset X(p^{\infty })$ be a connected component.
$X(p^{\infty })^{\circ }\subset X(p^{\infty })$ be a connected component.
Corollary 1.0.2 The following are equivalent for a ![]() $C$-point
$C$-point ![]() $x$ of
$x$ of ![]() $X(p^{\infty })^{\circ }$.
$X(p^{\infty })^{\circ }$.
(i) The point
 $x$ corresponds to an elliptic curve
$x$ corresponds to an elliptic curve  $E$, such that the
$E$, such that the  $p$-divisible group
$p$-divisible group  $E[p^{\infty }]$ has
$E[p^{\infty }]$ has  $\operatorname {End} E[p^{\infty }]=\mathbf {Z}_p$.
$\operatorname {End} E[p^{\infty }]=\mathbf {Z}_p$.(ii) The stabilizer of
 $\pi _{HT}(x)$ in
$\pi _{HT}(x)$ in  $\operatorname {PGL}_2(\mathbf {Q}_p)$ is trivial.
$\operatorname {PGL}_2(\mathbf {Q}_p)$ is trivial.(iii) There is a neighborhood of
 $x$ in
$x$ in  $X(p^{\infty })^{\circ }$ which is cohomologically smooth over
$X(p^{\infty })^{\circ }$ which is cohomologically smooth over  $C$.
$C$.
2. Review of Rapoport–Zink spaces at infinite level
2.1 The infinite-level Rapoport–Zink space  ${{\mathscr M}}_{H,\infty }$
${{\mathscr M}}_{H,\infty }$
Let ![]() $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic ![]() $p$, and let
$p$, and let ![]() $H$ be a
$H$ be a ![]() $p$-divisible group of height
$p$-divisible group of height ![]() $n$ and dimension
$n$ and dimension ![]() $d$ over
$d$ over ![]() $k$. We review here the definition of the infinite-level Rapoport–Zink space associated with
$k$. We review here the definition of the infinite-level Rapoport–Zink space associated with ![]() $H$.
$H$.
First there is the formal scheme ![]() ${{\mathscr M}}_H$ over
${{\mathscr M}}_H$ over ![]() $\operatorname {Spf} W(k)$ parametrizing deformations of
$\operatorname {Spf} W(k)$ parametrizing deformations of ![]() $H$ up to isogeny, as in [Reference Rapoport and ZinkRZ96]. For a
$H$ up to isogeny, as in [Reference Rapoport and ZinkRZ96]. For a ![]() $W(k)$-algebra
$W(k)$-algebra ![]() $R$ in which
$R$ in which ![]() $p$ is nilpotent,
$p$ is nilpotent, ![]() ${{\mathscr M}}_H(R)$ is the set of isomorphism classes of pairs
${{\mathscr M}}_H(R)$ is the set of isomorphism classes of pairs ![]() $(G,\rho )$, where
$(G,\rho )$, where ![]() $G/R$ is a
$G/R$ is a ![]() $p$-divisible group and
$p$-divisible group and ![]() $\rho \colon H\otimes _k R/p \to G\otimes _R R/p$ is a quasi-isogeny.
$\rho \colon H\otimes _k R/p \to G\otimes _R R/p$ is a quasi-isogeny.
The formal scheme ![]() ${{\mathscr M}}_H$ locally admits a finitely generated ideal of definition. Therefore it makes sense to pass to its adic space
${{\mathscr M}}_H$ locally admits a finitely generated ideal of definition. Therefore it makes sense to pass to its adic space ![]() ${{\mathscr M}}_H^{\operatorname{ad}}$, which has generic fiber
${{\mathscr M}}_H^{\operatorname{ad}}$, which has generic fiber ![]() $({{\mathscr M}}_H^{\operatorname{ad}})_\eta$, a rigid-analytic space over
$({{\mathscr M}}_H^{\operatorname{ad}})_\eta$, a rigid-analytic space over ![]() $\operatorname {Spa}(W(k)[1/p],W(k))$. Then
$\operatorname {Spa}(W(k)[1/p],W(k))$. Then ![]() $({{\mathscr M}}_H^{\operatorname{ad}})_{\eta }$ has the following moduli interpretation: it is the sheafification of the functor assigning to a complete affinoid
$({{\mathscr M}}_H^{\operatorname{ad}})_{\eta }$ has the following moduli interpretation: it is the sheafification of the functor assigning to a complete affinoid ![]() $(W(k)[1/p],W(k))$-algebra
$(W(k)[1/p],W(k))$-algebra ![]() $(R,R^{+})$ the set of pairs
$(R,R^{+})$ the set of pairs ![]() $(G,\rho )$, where
$(G,\rho )$, where ![]() $G$ is a
$G$ is a ![]() $p$-divisible group defined over an open and bounded subring
$p$-divisible group defined over an open and bounded subring ![]() $R_0\subset R^{+}$, and
$R_0\subset R^{+}$, and ![]() $\rho \colon H\otimes _k R_0/p\to G\otimes _{R_0} R_0/p$ is a quasi-isogeny. There is an action of
$\rho \colon H\otimes _k R_0/p\to G\otimes _{R_0} R_0/p$ is a quasi-isogeny. There is an action of ![]() $\operatorname {Aut} H$ on
$\operatorname {Aut} H$ on ![]() ${{\mathscr M}}_H^{\operatorname{ad}}$ obtained by composition with
${{\mathscr M}}_H^{\operatorname{ad}}$ obtained by composition with ![]() $\rho$.
$\rho$.
Given such a pair ![]() $(G,\rho )$, Grothendieck–Messing theory produces a surjection
$(G,\rho )$, Grothendieck–Messing theory produces a surjection ![]() $M(H)\otimes _{W(k)} R \to \operatorname {Lie} G[1/p]$ of locally free
$M(H)\otimes _{W(k)} R \to \operatorname {Lie} G[1/p]$ of locally free ![]() $R$-modules, where
$R$-modules, where ![]() $M(H)$ is the covariant Dieudonné module. There is a Grothendieck–Messing period map
$M(H)$ is the covariant Dieudonné module. There is a Grothendieck–Messing period map ![]() $\pi _{GM}\colon ({{\mathscr M}}_H^{\operatorname{ad}})_{\eta }\to {{\mathcal {F}}}\ell$, where
$\pi _{GM}\colon ({{\mathscr M}}_H^{\operatorname{ad}})_{\eta }\to {{\mathcal {F}}}\ell$, where ![]() ${{\mathcal {F}}}\ell$ is the rigid-analytic space parametrizing rank
${{\mathcal {F}}}\ell$ is the rigid-analytic space parametrizing rank ![]() $d$ locally free quotients of
$d$ locally free quotients of ![]() $M(H)[1/p]$. The morphism
$M(H)[1/p]$. The morphism ![]() $\pi _{GM}$ is equivariant for the action of
$\pi _{GM}$ is equivariant for the action of ![]() $\operatorname {Aut} H$. It has open image
$\operatorname {Aut} H$. It has open image ![]() ${{\mathcal {F}}}\ell ^{a}$ (the admissible locus).
${{\mathcal {F}}}\ell ^{a}$ (the admissible locus).
We obtain a tower of rigid-analytic spaces over ![]() $({{\mathscr M}}_H^{\operatorname{ad}})_{\eta }$ by adding level structures. For a complete affinoid
$({{\mathscr M}}_H^{\operatorname{ad}})_{\eta }$ by adding level structures. For a complete affinoid ![]() $(W(k)[1/p],W(k))$-algebra
$(W(k)[1/p],W(k))$-algebra ![]() $(R,R^{+})$, and an element of
$(R,R^{+})$, and an element of ![]() $({{\mathscr M}}_H^{\operatorname{ad}})_{\eta }(R,R^{+})$ represented locally on
$({{\mathscr M}}_H^{\operatorname{ad}})_{\eta }(R,R^{+})$ represented locally on ![]() $\operatorname {Spa}(R,R^{+})$ by a pair
$\operatorname {Spa}(R,R^{+})$ by a pair ![]() $(G,\rho )$ as above, we have the Tate module
$(G,\rho )$ as above, we have the Tate module ![]() $TG=\varprojlim _m G[p^{m}]$, considered as an adic space over
$TG=\varprojlim _m G[p^{m}]$, considered as an adic space over ![]() $\operatorname {Spa}(R,R^{+})$ with the structure of a
$\operatorname {Spa}(R,R^{+})$ with the structure of a ![]() $\mathbf {Z}_p$-module [Reference Scholze and WeinsteinSW13, (3.3)]. Finite-level spaces
$\mathbf {Z}_p$-module [Reference Scholze and WeinsteinSW13, (3.3)]. Finite-level spaces ![]() ${{\mathscr M}}_{H,m}$ are obtained by trivializing the
${{\mathscr M}}_{H,m}$ are obtained by trivializing the ![]() $G[p^{m}]$; these are finite étale covers of
$G[p^{m}]$; these are finite étale covers of ![]() $({{\mathscr M}}_H^{\operatorname{ad}})_{\eta }$. The infinite-level space is obtained by trivializing all of
$({{\mathscr M}}_H^{\operatorname{ad}})_{\eta }$. The infinite-level space is obtained by trivializing all of ![]() $TG$ at once, as in the following definition.
$TG$ at once, as in the following definition.
Definition 2.1.1 [SW13, Definition 6.3.3] Let ![]() ${{\mathscr M}}_{H,\infty }$ be the functor which sends a complete affinoid
${{\mathscr M}}_{H,\infty }$ be the functor which sends a complete affinoid ![]() $(W(k)[1/p],W(k))$-algebra
$(W(k)[1/p],W(k))$-algebra ![]() $(R,R^{+})$ to the set of triples
$(R,R^{+})$ to the set of triples ![]() $(G,\rho ,\alpha )$, where
$(G,\rho ,\alpha )$, where ![]() $(G,\rho )$ is an element of
$(G,\rho )$ is an element of ![]() $({{\mathscr M}}_H)^{\operatorname{ad}}_{\eta }(R,R^{+})$, and
$({{\mathscr M}}_H)^{\operatorname{ad}}_{\eta }(R,R^{+})$, and ![]() $\alpha \colon \mathbf {Z}_p^{n} \to TG$ is a
$\alpha \colon \mathbf {Z}_p^{n} \to TG$ is a ![]() $\mathbf {Z}_p$-linear map which is an isomorphism pointwise on
$\mathbf {Z}_p$-linear map which is an isomorphism pointwise on ![]() $\operatorname {Spa}(R,R^{+})$.
$\operatorname {Spa}(R,R^{+})$.
There is an equivalent definition in terms of isogeny classes of triples ![]() $(G,\rho ,\alpha )$, where this time
$(G,\rho ,\alpha )$, where this time ![]() $\alpha \colon \mathbf {Q}_p^{n}\to VG$ is a trivialization of the rational Tate module. Using this definition, it becomes clear that
$\alpha \colon \mathbf {Q}_p^{n}\to VG$ is a trivialization of the rational Tate module. Using this definition, it becomes clear that ![]() ${{\mathscr M}}_{H,\infty }$ admits an action of the product
${{\mathscr M}}_{H,\infty }$ admits an action of the product ![]() $\operatorname {GL}_n(\mathbf {Q}_p)\times \operatorname {Aut}^{0} H$, where
$\operatorname {GL}_n(\mathbf {Q}_p)\times \operatorname {Aut}^{0} H$, where ![]() $\operatorname {Aut}^{0}$ means automorphisms in the isogeny category. Then the period map
$\operatorname {Aut}^{0}$ means automorphisms in the isogeny category. Then the period map ![]() $\pi _{GM}\colon {{\mathscr M}}_{H,\infty }\to {{\mathcal {F}}}\ell$ is equivariant for
$\pi _{GM}\colon {{\mathscr M}}_{H,\infty }\to {{\mathcal {F}}}\ell$ is equivariant for ![]() $\operatorname {GL}_n(\mathbf {Q}_p)\times \operatorname {Aut}^{0} H$, where
$\operatorname {GL}_n(\mathbf {Q}_p)\times \operatorname {Aut}^{0} H$, where ![]() $\operatorname {GL}_n(\mathbf {Q}_p)$ acts trivially on
$\operatorname {GL}_n(\mathbf {Q}_p)$ acts trivially on ![]() ${{\mathcal {F}}}\ell$.
${{\mathcal {F}}}\ell$.
We remark that ![]() ${{\mathscr M}}_{H,\infty }\sim \varprojlim _m {{\mathscr M}}_{H,m}$ in the sense of [Reference Scholze and WeinsteinSW13, Definition 2.4.1].
${{\mathscr M}}_{H,\infty }\sim \varprojlim _m {{\mathscr M}}_{H,m}$ in the sense of [Reference Scholze and WeinsteinSW13, Definition 2.4.1].
One of the main theorems of [Reference Scholze and WeinsteinSW13] is the following.
Theorem 2.1.2 The adic space ![]() ${{\mathscr M}}_{H,\infty }$ is a preperfectoid space.
${{\mathscr M}}_{H,\infty }$ is a preperfectoid space.
This means that for any perfectoid field ![]() $K$ containing
$K$ containing ![]() $W(k)$, the base change
$W(k)$, the base change ![]() ${{\mathscr M}}_{H,\infty }\times _{\operatorname {Spa}(W(k)[1/p],W(k))} \operatorname {Spa}(K,\mathcal {O}_K)$ becomes perfectoid after
${{\mathscr M}}_{H,\infty }\times _{\operatorname {Spa}(W(k)[1/p],W(k))} \operatorname {Spa}(K,\mathcal {O}_K)$ becomes perfectoid after ![]() $p$-adically completing.
$p$-adically completing.
We sketch here the proof of Theorem 2.1.2. Consider the ‘universal cover’ ![]() $\tilde {H}=\varprojlim _p H$ as a sheaf of
$\tilde {H}=\varprojlim _p H$ as a sheaf of ![]() $\mathbf {Q}_p$-vector spaces on the category of
$\mathbf {Q}_p$-vector spaces on the category of ![]() $k$-algebras. This has a canonical lift to the category of
$k$-algebras. This has a canonical lift to the category of ![]() $W(k)$-algebras [Reference Scholze and WeinsteinSW13, Proposition 3.1.3(ii)], which we continue to call
$W(k)$-algebras [Reference Scholze and WeinsteinSW13, Proposition 3.1.3(ii)], which we continue to call ![]() $\tilde {H}$. The adic generic fiber
$\tilde {H}$. The adic generic fiber ![]() $\tilde {H}^{\operatorname{ad}}_{\eta }$ is a preperfectoid space, as can be checked ‘by hand’: it is a product of the
$\tilde {H}^{\operatorname{ad}}_{\eta }$ is a preperfectoid space, as can be checked ‘by hand’: it is a product of the ![]() $d$-dimensional preperfectoid open ball
$d$-dimensional preperfectoid open ball ![]() $(\operatorname {Spa} W(k) [\kern-1pt[ {T_1^{1/p^{\infty }},\ldots ,T_d^{1/p^{\infty }}} ]\kern-1pt])_{\eta }$ by the constant adic space
$(\operatorname {Spa} W(k) [\kern-1pt[ {T_1^{1/p^{\infty }},\ldots ,T_d^{1/p^{\infty }}} ]\kern-1pt])_{\eta }$ by the constant adic space ![]() $VH^{\mathop e\limits^{{\prime}}t}$, where
$VH^{\mathop e\limits^{{\prime}}t}$, where ![]() $H^{\mathop e\limits{{\prime}}t}$ is the étale part of
$H^{\mathop e\limits{{\prime}}t}$ is the étale part of ![]() $H$. Given a triple
$H$. Given a triple ![]() $(G,\rho ,\alpha )$ representing an element of
$(G,\rho ,\alpha )$ representing an element of ![]() ${{\mathscr M}}_{H,\infty }(R,R^{+})$, the quasi-isogeny
${{\mathscr M}}_{H,\infty }(R,R^{+})$, the quasi-isogeny ![]() $\rho$ induces an isomorphism
$\rho$ induces an isomorphism ![]() $\tilde {H}^{\operatorname{ad}}_{\eta }\times _{\operatorname {Spa}(W(k)[1/p],W(k))} \operatorname {Spa}(R,R^{+})\to \tilde {G}^{\operatorname{ad}}_{\eta }$; composing this with
$\tilde {H}^{\operatorname{ad}}_{\eta }\times _{\operatorname {Spa}(W(k)[1/p],W(k))} \operatorname {Spa}(R,R^{+})\to \tilde {G}^{\operatorname{ad}}_{\eta }$; composing this with ![]() $\alpha$ gives a morphism
$\alpha$ gives a morphism ![]() $\mathbf {Q}_p^{n}\to \tilde {H}^{\operatorname{ad}}_{\eta }(R,R^{+})$. We have therefore described a morphism
$\mathbf {Q}_p^{n}\to \tilde {H}^{\operatorname{ad}}_{\eta }(R,R^{+})$. We have therefore described a morphism ![]() ${{\mathscr M}}_{H,\infty } \to (\tilde {H}^{\operatorname{ad}}_{\eta })^{n}$.
${{\mathscr M}}_{H,\infty } \to (\tilde {H}^{\operatorname{ad}}_{\eta })^{n}$.
Theorem 2.1.2 follows from the fact that the morphism ![]() ${{\mathscr M}}_{H,\infty }\to (\tilde {H}^{\operatorname{ad}})_{\eta }^{n}$ presents
${{\mathscr M}}_{H,\infty }\to (\tilde {H}^{\operatorname{ad}})_{\eta }^{n}$ presents ![]() ${{\mathscr M}}_{H,\infty }$ as an open subset of a Zariski closed subset of
${{\mathscr M}}_{H,\infty }$ as an open subset of a Zariski closed subset of ![]() $(\tilde {H}^{\operatorname{ad}})_{\eta }^{n}$. We conclude this subsection by spelling out how this is done. We have a quasi-logarithm map
$(\tilde {H}^{\operatorname{ad}})_{\eta }^{n}$. We conclude this subsection by spelling out how this is done. We have a quasi-logarithm map ![]() $\operatorname {qlog}_H\colon \tilde {H}^{\operatorname{ad}}_{\eta } \to M(H)[1/p] \otimes _{W(k)[1/p]} {{\mathbf {G}}}_a$ [Reference Scholze and WeinsteinSW13, Definition 3.2.3], a
$\operatorname {qlog}_H\colon \tilde {H}^{\operatorname{ad}}_{\eta } \to M(H)[1/p] \otimes _{W(k)[1/p]} {{\mathbf {G}}}_a$ [Reference Scholze and WeinsteinSW13, Definition 3.2.3], a ![]() $\mathbf {Q}_p$-linear morphism of adic spaces over
$\mathbf {Q}_p$-linear morphism of adic spaces over ![]() $\operatorname {Spa}(W(k)[1/p],W(k))$.
$\operatorname {Spa}(W(k)[1/p],W(k))$.
Now suppose ![]() $(G,\rho )$ is a deformation of
$(G,\rho )$ is a deformation of ![]() $H$ to
$H$ to ![]() $(R,R^{+})$. The logarithm map on
$(R,R^{+})$. The logarithm map on ![]() $G$ fits into an exact sequence of
$G$ fits into an exact sequence of ![]() $\mathbf {Z}_p$-modules:
$\mathbf {Z}_p$-modules:
After taking projective limits along multiplication-by-![]() $p$, this turns into an exact sequence of
$p$, this turns into an exact sequence of ![]() $\mathbf {Q}_p$-vector spaces,
$\mathbf {Q}_p$-vector spaces,
On the other hand, we have a commutative diagram.

The lower horizontal map ![]() $M(H)\otimes _{W(k)} R\to \operatorname {Lie} G[1/p]$ is the quotient by the
$M(H)\otimes _{W(k)} R\to \operatorname {Lie} G[1/p]$ is the quotient by the ![]() $R$-submodule of
$R$-submodule of ![]() $M(H)\otimes _{W(k)} R$ generated by the image of
$M(H)\otimes _{W(k)} R$ generated by the image of ![]() $VG(R,R^{+}) \to \tilde {G}_{\eta }^{\operatorname{ad}}(R,R^{+})\cong \tilde {H}_{\eta }^{\operatorname{ad}}(R,R^{+})\to M(H)\otimes _{W(k)} R$.
$VG(R,R^{+}) \to \tilde {G}_{\eta }^{\operatorname{ad}}(R,R^{+})\cong \tilde {H}_{\eta }^{\operatorname{ad}}(R,R^{+})\to M(H)\otimes _{W(k)} R$.
Now suppose we have a point of ![]() ${{\mathscr M}}_{H,\infty }(R,R^{+})$ represented by a triple
${{\mathscr M}}_{H,\infty }(R,R^{+})$ represented by a triple ![]() $(G,\rho ,\alpha )$. Then we have a
$(G,\rho ,\alpha )$. Then we have a ![]() $\mathbf {Q}_p$-linear map
$\mathbf {Q}_p$-linear map ![]() $\mathbf {Q}_p^{n}\to \tilde {H}_{\eta }^{\operatorname{ad}}(R,R^{+})\to M(H)\otimes _{W(k)} R$. The cokernel of its
$\mathbf {Q}_p^{n}\to \tilde {H}_{\eta }^{\operatorname{ad}}(R,R^{+})\to M(H)\otimes _{W(k)} R$. The cokernel of its ![]() $R$-extension
$R$-extension ![]() $R^{n}\to M(H)\otimes _{W(k)} R$ is a projective
$R^{n}\to M(H)\otimes _{W(k)} R$ is a projective ![]() $R$-module of rank
$R$-module of rank ![]() $d$, namely
$d$, namely ![]() $\operatorname {Lie} G[1/p]$. This condition on the cokernel allows us to formulate an alternate description of
$\operatorname {Lie} G[1/p]$. This condition on the cokernel allows us to formulate an alternate description of ![]() ${{\mathscr M}}_{H,\infty }$ which is independent of deformations.
${{\mathscr M}}_{H,\infty }$ which is independent of deformations.
Proposition 2.1.3 The adic space ![]() ${{\mathscr M}}_{H,\infty }$ is isomorphic to the functor which assigns to a complete affinoid
${{\mathscr M}}_{H,\infty }$ is isomorphic to the functor which assigns to a complete affinoid ![]() $(W(k)[1/p],W(k))$-algebra
$(W(k)[1/p],W(k))$-algebra ![]() $(R,R^{+})$ the set of
$(R,R^{+})$ the set of ![]() $n$-tuples
$n$-tuples ![]() $(s_1,\ldots ,s_n)\in \tilde {H}^{\operatorname{ad}}_{\eta }(R,R^{+})^{n}$ such that the following conditions are satisfied.
$(s_1,\ldots ,s_n)\in \tilde {H}^{\operatorname{ad}}_{\eta }(R,R^{+})^{n}$ such that the following conditions are satisfied.
(i) The quotient of
 $M(H)\otimes _{W(k)} R$ by the
$M(H)\otimes _{W(k)} R$ by the  $R$-span of the
$R$-span of the  $\operatorname {qlog}(s_i)$ is a projective
$\operatorname {qlog}(s_i)$ is a projective  $R$-module
$R$-module  $W$ of rank
$W$ of rank  $d$.
$d$.(ii) For all geometric points
 $\operatorname {Spa}(C,\mathcal {O}_C)\to \operatorname {Spa}(R,R^{+})$, the sequence
is exact.
$\operatorname {Spa}(C,\mathcal {O}_C)\to \operatorname {Spa}(R,R^{+})$, the sequence
is exact. \[ 0 \to \mathbf{Q}_p^{n}\stackrel{(s_1,\ldots,s_n)}{\to} \tilde{H}^{\operatorname{ad}}_{\eta}(C,\mathcal{O}_C)\to W\otimes_R C \to 0 \]
\[ 0 \to \mathbf{Q}_p^{n}\stackrel{(s_1,\ldots,s_n)}{\to} \tilde{H}^{\operatorname{ad}}_{\eta}(C,\mathcal{O}_C)\to W\otimes_R C \to 0 \]
2.2 Infinite-level Rapoport–Zink spaces of EL type
This article treats the more general class of Rapoport–Zink spaces of EL type. We review these here.
Definition 2.2.1 Let ![]() $k$ be an algebraically closed field of characteristic
$k$ be an algebraically closed field of characteristic ![]() $p$. A rational EL datum is a quadruple
$p$. A rational EL datum is a quadruple ![]() ${{\mathcal {D}}}=(B,V, H,\mu )$, where:
${{\mathcal {D}}}=(B,V, H,\mu )$, where:
–
 $B$ is a semisimple
$B$ is a semisimple  $\mathbf {Q}_p$-algebra;
$\mathbf {Q}_p$-algebra;–
 $V$ is a finite
$V$ is a finite  $B$-module;
$B$-module;–
 $H$ is an object of the isogeny category of
$H$ is an object of the isogeny category of  $p$-divisible groups over
$p$-divisible groups over  $k$, equipped with an action
$k$, equipped with an action  $B\to \operatorname {End} H$;
$B\to \operatorname {End} H$;–
 $\mu$ is a conjugacy class of
$\mu$ is a conjugacy class of  $\overline {\mathbf {Q}}_p$-rational cocharacters
$\overline {\mathbf {Q}}_p$-rational cocharacters  $\mathbf {G}_m\to {{\mathbf {G}}}$, where
$\mathbf {G}_m\to {{\mathbf {G}}}$, where  ${{\mathbf {G}}}/\mathbf {Q}_p$ is the algebraic group
${{\mathbf {G}}}/\mathbf {Q}_p$ is the algebraic group  $\operatorname {GL}_B(V)$.
$\operatorname {GL}_B(V)$.
These are subject to the following conditions.
– If
 $M(H)$ is the (rational) Dieudonné module of
$M(H)$ is the (rational) Dieudonné module of  $H$, then there exists an isomorphism
$H$, then there exists an isomorphism  $M(H)\cong V\otimes _{\mathbf {Q}_p} W(k)[1/p]$ of
$M(H)\cong V\otimes _{\mathbf {Q}_p} W(k)[1/p]$ of  $B\otimes _{\mathbf {Q}_p} W(k)[1/p]$-modules. In particular
$B\otimes _{\mathbf {Q}_p} W(k)[1/p]$-modules. In particular  $\dim V=\operatorname {ht} H$.
$\dim V=\operatorname {ht} H$.– In the weight decomposition of
 $V\otimes _{\mathbf {Q}_p} \overline {\mathbf {Q}}_p\cong \bigoplus _{i\in \mathbf {Z}} V_i$ determined by
$V\otimes _{\mathbf {Q}_p} \overline {\mathbf {Q}}_p\cong \bigoplus _{i\in \mathbf {Z}} V_i$ determined by  $\mu$, only weights 0 and 1 appear, and
$\mu$, only weights 0 and 1 appear, and  $\dim V_0=\dim H$.
$\dim V_0=\dim H$.
The reflex field ![]() $E$ of
$E$ of ![]() ${{\mathcal {D}}}$ is the field of definition of the conjugacy class
${{\mathcal {D}}}$ is the field of definition of the conjugacy class ![]() $\mu$. We remark that the weight filtration (but not necessarily the weight decomposition) of
$\mu$. We remark that the weight filtration (but not necessarily the weight decomposition) of ![]() $V\otimes _{\mathbf {Q}_p}\overline {\mathbf {Q}}_p$ may be descended to
$V\otimes _{\mathbf {Q}_p}\overline {\mathbf {Q}}_p$ may be descended to ![]() $E$, and so we will be viewing
$E$, and so we will be viewing ![]() $V_0$ and
$V_0$ and ![]() $V_1$ as
$V_1$ as ![]() $B\otimes _{\mathbf {Q}_p} E$-modules.
$B\otimes _{\mathbf {Q}_p} E$-modules.
The infinite-level Rapoport–Zink space ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty }$ is defined in [Reference Scholze and WeinsteinSW13] in terms of moduli of deformations of the
${{\mathscr M}}_{{{\mathcal {D}}},\infty }$ is defined in [Reference Scholze and WeinsteinSW13] in terms of moduli of deformations of the ![]() $p$-divisible group
$p$-divisible group ![]() $H$ along with its
$H$ along with its ![]() $B$-action. It admits an alternate description along the lines of Proposition 2.1.3.
$B$-action. It admits an alternate description along the lines of Proposition 2.1.3.
Proposition 2.2.2 [SW13, Theorem 6.5.4] Let ![]() ${{\mathcal {D}}}=(B,V,H,\mu )$ be a rational EL datum. Let
${{\mathcal {D}}}=(B,V,H,\mu )$ be a rational EL datum. Let ![]() $\breve {E}=E\cdot W(k)$. Then
$\breve {E}=E\cdot W(k)$. Then ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty }$ is isomorphic to the functor which inputs a complete affinoid
${{\mathscr M}}_{{{\mathcal {D}}},\infty }$ is isomorphic to the functor which inputs a complete affinoid ![]() $(\breve {E},\mathcal {O}_{\breve {E}})$-algebra
$(\breve {E},\mathcal {O}_{\breve {E}})$-algebra ![]() $(R,R^{+})$ and outputs the set of
$(R,R^{+})$ and outputs the set of ![]() $B$-linear maps
$B$-linear maps
subject to the following conditions.
– Let
 $W$ be the quotient
Then
$W$ be the quotient
Then \[ V\otimes_{\mathbf{Q}_p} R\stackrel{\operatorname{qlog}_H\circ s}{\longrightarrow} M(H)\otimes_{W(k)} R \to W \to 0. \]
\[ V\otimes_{\mathbf{Q}_p} R\stackrel{\operatorname{qlog}_H\circ s}{\longrightarrow} M(H)\otimes_{W(k)} R \to W \to 0. \] $W$ is a finite projective
$W$ is a finite projective  $R$-module, which locally on
$R$-module, which locally on  $R$ is isomorphic to
$R$ is isomorphic to  $V_0\otimes _{E} R$ as a
$V_0\otimes _{E} R$ as a  $B\otimes _{\mathbf {Q}_p} R$-module.
$B\otimes _{\mathbf {Q}_p} R$-module.– For any geometric point
 $x=\operatorname {Spa}(C,\mathcal {O}_C)\to \operatorname {Spa}(R,R^{+})$, the sequence of
$x=\operatorname {Spa}(C,\mathcal {O}_C)\to \operatorname {Spa}(R,R^{+})$, the sequence of  $B$-modules
is exact.
$B$-modules
is exact. \[ 0\to V \to \tilde{H}(\mathcal{O}_C) \to W\otimes_R C \to 0 \]
\[ 0\to V \to \tilde{H}(\mathcal{O}_C) \to W\otimes_R C \to 0 \]
If ![]() ${{\mathcal {D}}} = (\mathbf {Q}_p, \mathbf {Q}_p^{n}, H, \mu )$, where
${{\mathcal {D}}} = (\mathbf {Q}_p, \mathbf {Q}_p^{n}, H, \mu )$, where ![]() $H$ has height
$H$ has height ![]() $n$ and dimension
$n$ and dimension ![]() $d$ and
$d$ and ![]() $\mu (t)=(t^{\oplus d},1^{\oplus (n-d)})$, then
$\mu (t)=(t^{\oplus d},1^{\oplus (n-d)})$, then ![]() $E=\mathbf {Q}_p$ and
$E=\mathbf {Q}_p$ and ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty } = {{\mathscr M}}_{H,\infty }$.
${{\mathscr M}}_{{{\mathcal {D}}},\infty } = {{\mathscr M}}_{H,\infty }$.
In general, we call ![]() $\breve E$ the field of scalars of
$\breve E$ the field of scalars of ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty }$, and for a complete algebraically closed extension
${{\mathscr M}}_{{{\mathcal {D}}},\infty }$, and for a complete algebraically closed extension ![]() $C$ of
$C$ of ![]() $\breve E$, we write
$\breve E$, we write ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty ,C} = {{\mathscr M}}_{{{\mathcal {D}}},\infty } \times _{\operatorname {Spa}(\breve E,\mathcal {O}_{\breve E})} \operatorname {Spa}(C,\mathcal {O}_C)$ for the corresponding geometric fiber of
${{\mathscr M}}_{{{\mathcal {D}}},\infty ,C} = {{\mathscr M}}_{{{\mathcal {D}}},\infty } \times _{\operatorname {Spa}(\breve E,\mathcal {O}_{\breve E})} \operatorname {Spa}(C,\mathcal {O}_C)$ for the corresponding geometric fiber of ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty }$.
${{\mathscr M}}_{{{\mathcal {D}}},\infty }$.
The space ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty }$ admits an action by the product group
${{\mathscr M}}_{{{\mathcal {D}}},\infty }$ admits an action by the product group ![]() ${{\mathbf {G}}}(\mathbf {Q}_p)\times J(\mathbf {Q}_p)$, where
${{\mathbf {G}}}(\mathbf {Q}_p)\times J(\mathbf {Q}_p)$, where ![]() $J/\mathbf {Q}_p$ is the algebraic group
$J/\mathbf {Q}_p$ is the algebraic group ![]() $\operatorname {Aut}_B^{\circ }(H)$. A pair
$\operatorname {Aut}_B^{\circ }(H)$. A pair ![]() $(\alpha ,\alpha ')\in {{\mathbf {G}}}(\mathbf {Q}_p)\times J(\mathbf {Q}_p)$ sends
$(\alpha ,\alpha ')\in {{\mathbf {G}}}(\mathbf {Q}_p)\times J(\mathbf {Q}_p)$ sends ![]() $s$ to
$s$ to ![]() $\alpha '\circ s\circ \alpha ^{-1}$.
$\alpha '\circ s\circ \alpha ^{-1}$.
There is once again a Grothendieck–Messing period map ![]() $\pi _{GM}\colon {{\mathscr M}}_{{{\mathcal {D}}},\infty }\to {{\mathcal {F}}}\ell _\mu$ onto the rigid-analytic variety whose
$\pi _{GM}\colon {{\mathscr M}}_{{{\mathcal {D}}},\infty }\to {{\mathcal {F}}}\ell _\mu$ onto the rigid-analytic variety whose ![]() $(R,R^{+})$-points parametrize
$(R,R^{+})$-points parametrize ![]() $B\otimes _{\mathbf {Q}_p} R$-module quotients of
$B\otimes _{\mathbf {Q}_p} R$-module quotients of ![]() $M(H)\otimes _{W(k)} R$ which are projective over
$M(H)\otimes _{W(k)} R$ which are projective over ![]() $R$, and which are of type
$R$, and which are of type ![]() $\mu$ in the sense that they are (locally on
$\mu$ in the sense that they are (locally on ![]() $R$) isomorphic to
$R$) isomorphic to ![]() $V_0\otimes _E R$. The morphism
$V_0\otimes _E R$. The morphism ![]() $\pi _{GM}$ sends an
$\pi _{GM}$ sends an ![]() $(R,R^{+})$-point of
$(R,R^{+})$-point of ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty }$ to the quotient
${{\mathscr M}}_{{{\mathcal {D}}},\infty }$ to the quotient ![]() $W$ of
$W$ of ![]() $M(H)\otimes _{W(k)} R$ as above. It is equivariant for the action of
$M(H)\otimes _{W(k)} R$ as above. It is equivariant for the action of ![]() ${{\mathbf {G}}}(\mathbf {Q}_p)\times J(\mathbf {Q}_p)$, where
${{\mathbf {G}}}(\mathbf {Q}_p)\times J(\mathbf {Q}_p)$, where ![]() ${{\mathbf {G}}}(\mathbf {Q}_p)$ acts trivially on
${{\mathbf {G}}}(\mathbf {Q}_p)$ acts trivially on ![]() ${{\mathcal {F}}}\ell _\mu$. In terms of deformations of the
${{\mathcal {F}}}\ell _\mu$. In terms of deformations of the ![]() $p$-divisible group
$p$-divisible group ![]() $H$, the period map
$H$, the period map ![]() $\pi _{GM}$ sends a deformation
$\pi _{GM}$ sends a deformation ![]() $G$ to
$G$ to ![]() $\operatorname {Lie} G$.
$\operatorname {Lie} G$.
There is also a Hodge–Tate period map ![]() $\pi _{HT}\colon {{\mathscr M}}_{{{\mathcal {D}}},\infty }\to {{\mathcal {F}}}\ell _{\mu }'$, where
$\pi _{HT}\colon {{\mathscr M}}_{{{\mathcal {D}}},\infty }\to {{\mathcal {F}}}\ell _{\mu }'$, where ![]() ${{\mathcal {F}}}\ell _\mu '(R,R^{+})$ parametrizes
${{\mathcal {F}}}\ell _\mu '(R,R^{+})$ parametrizes ![]() $B\otimes _{\mathbf {Q}_p} R$-module quotients of
$B\otimes _{\mathbf {Q}_p} R$-module quotients of ![]() $V\otimes _{\mathbf {Q}_p} R$ which are projective over
$V\otimes _{\mathbf {Q}_p} R$ which are projective over ![]() $R$, and which are (locally on
$R$, and which are (locally on ![]() $R$) isomorphic to
$R$) isomorphic to ![]() $V_1\otimes _E R$. The morphism
$V_1\otimes _E R$. The morphism ![]() $\pi _{HT}$ sends an
$\pi _{HT}$ sends an ![]() $(R,R^{+})$-point of
$(R,R^{+})$-point of ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty }$ to the image of
${{\mathscr M}}_{{{\mathcal {D}}},\infty }$ to the image of ![]() $V\otimes _{\mathbf {Q}_p} R\to M(H)\otimes _{W(k)} R$. It is equivariant for the action of
$V\otimes _{\mathbf {Q}_p} R\to M(H)\otimes _{W(k)} R$. It is equivariant for the action of ![]() ${{\mathbf {G}}}(\mathbf {Q}_p)\times J(\mathbf {Q}_p)$, where this time
${{\mathbf {G}}}(\mathbf {Q}_p)\times J(\mathbf {Q}_p)$, where this time ![]() $J(\mathbf {Q}_p)$ acts trivially on
$J(\mathbf {Q}_p)$ acts trivially on ![]() ${{\mathcal {F}}}\ell _\mu '(R,R^{+})$. In terms of deformations of the
${{\mathcal {F}}}\ell _\mu '(R,R^{+})$. In terms of deformations of the ![]() $p$-divisible group
$p$-divisible group ![]() $H$, the period map
$H$, the period map ![]() $\pi _{HT}$ sends a deformation
$\pi _{HT}$ sends a deformation ![]() $G$ to
$G$ to ![]() $(\operatorname {Lie} G^{\vee })^{\vee }$.
$(\operatorname {Lie} G^{\vee })^{\vee }$.
3. The Fargues–Fontaine curve
3.1 Review of the curve
We briefly review here some constructions and results from [Reference Fargues and FontaineFF18]. First we review the absolute curve, and then we cover the version of the curve which works in families.
Fix a perfectoid field ![]() $F$ of characteristic
$F$ of characteristic ![]() $p$, with
$p$, with ![]() $F^{\circ }\subset F$ its ring of integral elements. Let
$F^{\circ }\subset F$ its ring of integral elements. Let ![]() $\varpi \in F^{\circ }$ be a pseudo-uniformizer for
$\varpi \in F^{\circ }$ be a pseudo-uniformizer for ![]() $F$, and let
$F$, and let ![]() $k$ be the residue field of
$k$ be the residue field of ![]() $F$. Let
$F$. Let ![]() $W(F^{\circ })$ be the ring of Witt vectors, which we equip with the
$W(F^{\circ })$ be the ring of Witt vectors, which we equip with the ![]() $(p,[\varpi ])$-adic topology. Let
$(p,[\varpi ])$-adic topology. Let ![]() ${{\mathcal {Y}}}_F=\operatorname {Spa}(W(F^{\circ }),W(F^{\circ }))\backslash \{ {\left \lvert {p[\varpi ]} \right \rvert =0} \}$. Then
${{\mathcal {Y}}}_F=\operatorname {Spa}(W(F^{\circ }),W(F^{\circ }))\backslash \{ {\left \lvert {p[\varpi ]} \right \rvert =0} \}$. Then ![]() ${{\mathcal {Y}}}_F$ is an analytic adic space over
${{\mathcal {Y}}}_F$ is an analytic adic space over ![]() $\mathbf {Q}_p$. The Frobenius automorphism of
$\mathbf {Q}_p$. The Frobenius automorphism of ![]() $F$ induces an automorphism
$F$ induces an automorphism ![]() $\phi$ of
$\phi$ of ![]() ${{\mathcal {Y}}}_F$. Let
${{\mathcal {Y}}}_F$. Let ![]() $B_F=H^{0}({{\mathcal {Y}}}_F,\mathcal {O}_{{{\mathcal {Y}}}_F})$, a
$B_F=H^{0}({{\mathcal {Y}}}_F,\mathcal {O}_{{{\mathcal {Y}}}_F})$, a ![]() $\mathbf {Q}_p$-algebra endowed with an action of
$\mathbf {Q}_p$-algebra endowed with an action of ![]() $\phi$. Let
$\phi$. Let ![]() $P_F$ be the graded ring
$P_F$ be the graded ring ![]() $P_F=\bigoplus _{n\geq 0} B_F^{\phi =p^{n}}$. Finally, the Fargues–Fontaine curve is
$P_F=\bigoplus _{n\geq 0} B_F^{\phi =p^{n}}$. Finally, the Fargues–Fontaine curve is ![]() $X_F=\operatorname {Proj} P_F$. It is shown in [Reference Fargues and FontaineFF18] that
$X_F=\operatorname {Proj} P_F$. It is shown in [Reference Fargues and FontaineFF18] that ![]() $X_F$ is the union of spectra of Dedekind rings, which justifies the use of the word ‘curve’ to describe
$X_F$ is the union of spectra of Dedekind rings, which justifies the use of the word ‘curve’ to describe ![]() $X_F$. Note however that there is no ‘structure morphism’
$X_F$. Note however that there is no ‘structure morphism’ ![]() $X_F\to \operatorname {Spec} F$.
$X_F\to \operatorname {Spec} F$.
If ![]() $x\in X_F$ is a closed point, then the residue field of
$x\in X_F$ is a closed point, then the residue field of ![]() $x$ is a perfectoid field
$x$ is a perfectoid field ![]() $F_x$ containing
$F_x$ containing ![]() $\mathbf {Q}_p$ which comes equipped with an inclusion
$\mathbf {Q}_p$ which comes equipped with an inclusion ![]() $i\colon F\hookrightarrow F_x^{\flat }$, which presents
$i\colon F\hookrightarrow F_x^{\flat }$, which presents ![]() $F_x^{\flat }$ as a finite extension of
$F_x^{\flat }$ as a finite extension of ![]() $F$. Such a pair
$F$. Such a pair ![]() $(F_x,i)$ is called an untilt of
$(F_x,i)$ is called an untilt of ![]() $F$. Then
$F$. Then ![]() $x\mapsto (F_x,i)$ is a bijection between closed points of
$x\mapsto (F_x,i)$ is a bijection between closed points of ![]() $X_F$ and isomorphism classes of untilts of
$X_F$ and isomorphism classes of untilts of ![]() $F$, modulo the action of Frobenius on
$F$, modulo the action of Frobenius on ![]() $i$. Thus if
$i$. Thus if ![]() $F=E^{\flat }$ is the tilt of a given perfectoid field
$F=E^{\flat }$ is the tilt of a given perfectoid field ![]() $E/\mathbf {Q}_p$, then
$E/\mathbf {Q}_p$, then ![]() $X_{E^{\flat }}$ has a canonical closed point
$X_{E^{\flat }}$ has a canonical closed point ![]() $\infty$, corresponding to the untilt
$\infty$, corresponding to the untilt ![]() $E$ of
$E$ of ![]() $E^{\flat }$.
$E^{\flat }$.
An important result in [Reference Fargues and FontaineFF18] is the classification of vector bundles on ![]() $X_F$. (By a vector bundle on
$X_F$. (By a vector bundle on ![]() $X_F$ we are referring to a locally free
$X_F$ we are referring to a locally free ![]() $\mathcal {O}_{X_F}$-module
$\mathcal {O}_{X_F}$-module ![]() ${{\mathcal {E}}}$ of finite rank. We will use the notation
${{\mathcal {E}}}$ of finite rank. We will use the notation ![]() $V({{\mathcal {E}}})$ to mean the corresponding geometric vector bundle over
$V({{\mathcal {E}}})$ to mean the corresponding geometric vector bundle over ![]() $X_F$, whose sections correspond to sections of
$X_F$, whose sections correspond to sections of ![]() ${{\mathcal {E}}}$.) Recall that an isocrystal over
${{\mathcal {E}}}$.) Recall that an isocrystal over ![]() $k$ is a finite-dimensional vector space
$k$ is a finite-dimensional vector space ![]() $N$ over
$N$ over ![]() $W(k)[1/p]$ together with a Frobenius semilinear automorphism
$W(k)[1/p]$ together with a Frobenius semilinear automorphism ![]() $\phi$ of
$\phi$ of ![]() $N$. Given
$N$. Given ![]() $N$, we have the graded
$N$, we have the graded ![]() $P_F$-module
$P_F$-module ![]() $\bigoplus _{n\geq 0} (N\otimes _{W(k)[1/p]} B_F)^{\phi =p^{n}}$, which corresponds to a vector bundle
$\bigoplus _{n\geq 0} (N\otimes _{W(k)[1/p]} B_F)^{\phi =p^{n}}$, which corresponds to a vector bundle ![]() ${{\mathcal {E}}}_F(N)$ on
${{\mathcal {E}}}_F(N)$ on ![]() $X_F$. Then the Harder–Narasimhan slopes of
$X_F$. Then the Harder–Narasimhan slopes of ![]() ${{\mathcal {E}}}_F(N)$ are negative to those of
${{\mathcal {E}}}_F(N)$ are negative to those of ![]() $N$. If
$N$. If ![]() $F$ is algebraically closed, then every vector bundle on
$F$ is algebraically closed, then every vector bundle on ![]() $X_F$ is isomorphic to
$X_F$ is isomorphic to ![]() ${{\mathcal {E}}}_F(N)$ for some
${{\mathcal {E}}}_F(N)$ for some ![]() $N$.
$N$.
It is straightforward to ‘relativize’ the above constructions. If ![]() $S=\operatorname {Spa}(R,R^{+})$ is an affinoid perfectoid space over
$S=\operatorname {Spa}(R,R^{+})$ is an affinoid perfectoid space over ![]() $k$, one can construct the adic space
$k$, one can construct the adic space ![]() ${{\mathcal {Y}}}_S$, the ring
${{\mathcal {Y}}}_S$, the ring ![]() $B_S$, the scheme
$B_S$, the scheme ![]() $X_S$, and the vector bundles
$X_S$, and the vector bundles ![]() ${{\mathcal {E}}}_S(N)$ as above. Frobenius-equivalences classes of untilts of
${{\mathcal {E}}}_S(N)$ as above. Frobenius-equivalences classes of untilts of ![]() $S$ correspond to effective Cartier divisors of
$S$ correspond to effective Cartier divisors of ![]() $X_S$ of degree 1.
$X_S$ of degree 1.
In our applications, we will start with an affinoid perfectoid space ![]() $S$ over
$S$ over ![]() $\mathbf {Q}_p$. We will write
$\mathbf {Q}_p$. We will write ![]() $X_S=X_{S^{\flat }}$, and we will use
$X_S=X_{S^{\flat }}$, and we will use ![]() $\infty$ to refer to the canonical Cartier divisor of
$\infty$ to refer to the canonical Cartier divisor of ![]() $X_{S}$ corresponding to the untilt
$X_{S}$ corresponding to the untilt ![]() $S$ of
$S$ of ![]() $S^{\flat }$. Thus if
$S^{\flat }$. Thus if ![]() $N$ is an isocrystal over
$N$ is an isocrystal over ![]() $k$, and
$k$, and ![]() $S=\operatorname {Spa}(R,R^{+})$ is an affinoid perfectoid space over
$S=\operatorname {Spa}(R,R^{+})$ is an affinoid perfectoid space over ![]() $W(k)[1/p]$, then the fiber of
$W(k)[1/p]$, then the fiber of ![]() ${{\mathcal {E}}}_{S}(N)$ over
${{\mathcal {E}}}_{S}(N)$ over ![]() $\infty$ is
$\infty$ is ![]() $N\otimes _{W(k)[1/p]} R$.
$N\otimes _{W(k)[1/p]} R$.
Let ![]() $S = \operatorname {Spa}(R,R^{+})$ be as above and let
$S = \operatorname {Spa}(R,R^{+})$ be as above and let ![]() $\infty$ be the corresponding Cartier divisor. We denote the completion of the ring of functions on
$\infty$ be the corresponding Cartier divisor. We denote the completion of the ring of functions on ![]() $\mathcal {Y}_S$ along
$\mathcal {Y}_S$ along ![]() $\infty$ by
$\infty$ by ![]() $B_{\operatorname {dR}}^{+}(R)$. It comes equipped with a surjective homomorphism
$B_{\operatorname {dR}}^{+}(R)$. It comes equipped with a surjective homomorphism ![]() $\theta \colon B_{\operatorname {dR}}^{+}(R) \rightarrow R$, whose kernel is a principal ideal
$\theta \colon B_{\operatorname {dR}}^{+}(R) \rightarrow R$, whose kernel is a principal ideal ![]() $\ker (\theta ) = (\xi )$.
$\ker (\theta ) = (\xi )$.
3.2 Relation to  $p$-divisible groups
$p$-divisible groups
Here we recall the relationships between ![]() $p$-divisible groups and global sections of vector bundles on the Fargues–Fontaine curve. Let us fix a perfect field
$p$-divisible groups and global sections of vector bundles on the Fargues–Fontaine curve. Let us fix a perfect field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p$, and write
$p$, and write ![]() $\operatorname {Perf}_{W(k)[1/p]}$ for the category of perfectoid spaces over
$\operatorname {Perf}_{W(k)[1/p]}$ for the category of perfectoid spaces over ![]() $W(k)[1/p]$. Given a
$W(k)[1/p]$. Given a ![]() $p$-divisible group
$p$-divisible group ![]() $H$ over
$H$ over ![]() $k$ with covariant isocrystal
$k$ with covariant isocrystal ![]() $N$, if
$N$, if ![]() $H$ has slopes
$H$ has slopes ![]() $s_1,\ldots ,s_k \in \mathbb {Q}$, then
$s_1,\ldots ,s_k \in \mathbb {Q}$, then ![]() $N$ has the slopes
$N$ has the slopes ![]() $1-s_1, \ldots ,1-s_k$. For an object
$1-s_1, \ldots ,1-s_k$. For an object ![]() $S$ in
$S$ in ![]() $\operatorname {Perf}_{W(k)[1/p]}$ we define the vector bundle
$\operatorname {Perf}_{W(k)[1/p]}$ we define the vector bundle ![]() ${{\mathcal {E}}}_S(H)$ on
${{\mathcal {E}}}_S(H)$ on ![]() $X_S$ by
$X_S$ by
Under this normalization, the Harder–Narasimhan slopes of ![]() ${{\mathcal {E}}}_S(H)$ are (pointwise on
${{\mathcal {E}}}_S(H)$ are (pointwise on ![]() $S$) the same as the slopes of
$S$) the same as the slopes of ![]() $H$.
$H$.
Let us write ![]() $H^{0}({{\mathcal {E}}}(H))$ for the sheafification of the functor on
$H^{0}({{\mathcal {E}}}(H))$ for the sheafification of the functor on ![]() $\operatorname {Perf}_{W(k)[1/p]}$, which sends
$\operatorname {Perf}_{W(k)[1/p]}$, which sends ![]() $S$ to
$S$ to ![]() $H^{0}(X_S,{{\mathcal {E}}}_S(H))$.
$H^{0}(X_S,{{\mathcal {E}}}_S(H))$.
Proposition 3.2.1 Let ![]() $H$ be a
$H$ be a ![]() $p$-divisible group over a perfect field
$p$-divisible group over a perfect field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p$, with isocrystal
$p$, with isocrystal ![]() $N$. There is an isomorphism
$N$. There is an isomorphism ![]() $\tilde {H}^{\operatorname{ad}}_{\eta }\cong H^{0}({{\mathcal {E}}}(H))$ of sheaves on
$\tilde {H}^{\operatorname{ad}}_{\eta }\cong H^{0}({{\mathcal {E}}}(H))$ of sheaves on ![]() $\operatorname {Perf}_{W(k)[1/p]}$ making the following diagram commute,
$\operatorname {Perf}_{W(k)[1/p]}$ making the following diagram commute,

where the morphism ![]() $H^{0}({{\mathcal {E}}}(H))\to N\otimes _{W(k)[1/p]} {{\mathbf {G}}}_a$ sends a global section of
$H^{0}({{\mathcal {E}}}(H))\to N\otimes _{W(k)[1/p]} {{\mathbf {G}}}_a$ sends a global section of ![]() ${{\mathcal {E}}}(H)$ to its fiber at
${{\mathcal {E}}}(H)$ to its fiber at ![]() $\infty$.
$\infty$.
Proof. Let ![]() $S=\operatorname {Spa}(R,R^{+})$ be an affinoid perfectoid space over
$S=\operatorname {Spa}(R,R^{+})$ be an affinoid perfectoid space over ![]() $W(k)[1/p]$. Then
$W(k)[1/p]$. Then ![]() $\tilde {H}^{\operatorname{ad}}_{\eta }(R,R^{+})\cong \tilde {H}(R^{\circ })\cong \tilde {H}(R^{\circ }/p)$. Observe that
$\tilde {H}^{\operatorname{ad}}_{\eta }(R,R^{+})\cong \tilde {H}(R^{\circ })\cong \tilde {H}(R^{\circ }/p)$. Observe that ![]() $\tilde {H}(R^{\circ }/p)=\operatorname {Hom}_{R^{\circ }/p}(\mathbf {Q}_p/\mathbf {Z}_p,H)[1/p]$, where the Hom is taken in the category of
$\tilde {H}(R^{\circ }/p)=\operatorname {Hom}_{R^{\circ }/p}(\mathbf {Q}_p/\mathbf {Z}_p,H)[1/p]$, where the Hom is taken in the category of ![]() $p$-divisible groups over
$p$-divisible groups over ![]() $R^{\circ }/p$. Recall the crystalline Dieudonné functor
$R^{\circ }/p$. Recall the crystalline Dieudonné functor ![]() $G\mapsto M(G)$ from
$G\mapsto M(G)$ from ![]() $p$-divisible groups to Dieudonné crystals [Reference MessingMes72]. Since the base ring
$p$-divisible groups to Dieudonné crystals [Reference MessingMes72]. Since the base ring ![]() $R^{\circ }/p$ is semiperfect, the latter category is equivalent to the category of finite projective modules over Fontaine's period ring
$R^{\circ }/p$ is semiperfect, the latter category is equivalent to the category of finite projective modules over Fontaine's period ring ![]() $A_\textrm {cris}(R^{\circ }/p)=A_\textrm {cris}(R^{\circ })$, equipped with Frobenius and Verschiebung.
$A_\textrm {cris}(R^{\circ }/p)=A_\textrm {cris}(R^{\circ })$, equipped with Frobenius and Verschiebung.
Now we apply [Reference Scholze and WeinsteinSW13, Theorem A]: since ![]() $R^{\circ }/p$ is f-semiperfect, the crystalline Dieudonné functor is fully faithful up to isogeny. Thus
$R^{\circ }/p$ is f-semiperfect, the crystalline Dieudonné functor is fully faithful up to isogeny. Thus
where the latter Hom is in the category of modules over ![]() $A_\textrm {cris}(R^{\circ })$ equipped with Frobenius. Recall that
$A_\textrm {cris}(R^{\circ })$ equipped with Frobenius. Recall that ![]() $B_\textrm {cris}^{+}(R^{\circ })=A_\textrm {cris}(R^{\circ })[1/p]$. Since
$B_\textrm {cris}^{+}(R^{\circ })=A_\textrm {cris}(R^{\circ })[1/p]$. Since ![]() $H$ arises via base change from
$H$ arises via base change from ![]() $k$, we have
$k$, we have ![]() $M(H)[1/p]=B_\textrm {cris}^{+}(R^{\circ }) \otimes _{W(k)[1/p]} N$. For its part,
$M(H)[1/p]=B_\textrm {cris}^{+}(R^{\circ }) \otimes _{W(k)[1/p]} N$. For its part, ![]() $M(\mathbf {Q}_p/\mathbf {Z}_p)[1/p]=B_\textrm {cris}^{+}(R^{\circ })e$, for a basis element
$M(\mathbf {Q}_p/\mathbf {Z}_p)[1/p]=B_\textrm {cris}^{+}(R^{\circ })e$, for a basis element ![]() $e$ on which Frobenius acts as
$e$ on which Frobenius acts as ![]() $p$. Therefore
$p$. Therefore
On the Fargues–Fontaine curve side, we have by definition ![]() $H^{0}(X_S,{{\mathcal {E}}}_S(H))=(B_S\otimes _{W(k)[1/p]} N)^{\phi =p}$. The isomorphism between
$H^{0}(X_S,{{\mathcal {E}}}_S(H))=(B_S\otimes _{W(k)[1/p]} N)^{\phi =p}$. The isomorphism between ![]() $(B_S\otimes _{W(k)[1/p]} N)^{\phi =p}$ and
$(B_S\otimes _{W(k)[1/p]} N)^{\phi =p}$ and ![]() $(B_\textrm {cris}^{+}(R^{\circ }) \otimes _{W(k)[1/p]} N )^{\phi =p}$ is discussed in [Reference Le BrasLB18, Remarque 6.6].
$(B_\textrm {cris}^{+}(R^{\circ }) \otimes _{W(k)[1/p]} N )^{\phi =p}$ is discussed in [Reference Le BrasLB18, Remarque 6.6].
The commutativity of the diagram in the proposition is [Reference Scholze and WeinsteinSW13, Proposition 5.1.6(ii)], at least in the case that ![]() $S$ is a geometric point, but this suffices to prove the general case.
$S$ is a geometric point, but this suffices to prove the general case.
With Proposition 3.2.1 we can reinterpret the infinite-level Rapoport Zink spaces as moduli spaces of modifications of vector bundles on the Fargues–Fontaine curve. First we do this for ![]() ${{\mathscr M}}_{H,\infty }$. In the following, we consider
${{\mathscr M}}_{H,\infty }$. In the following, we consider ![]() ${{\mathscr M}}_{H,\infty }$ as a sheaf on the category of perfectoid spaces over
${{\mathscr M}}_{H,\infty }$ as a sheaf on the category of perfectoid spaces over ![]() $W(k)[1/p]$.
$W(k)[1/p]$.
Proposition 3.2.2 Let ![]() $H$ be a
$H$ be a ![]() $p$-divisible group of height
$p$-divisible group of height ![]() $n$ and dimension
$n$ and dimension ![]() $d$ over a perfect field
$d$ over a perfect field ![]() $k$. Let
$k$. Let ![]() $N$ be the associated isocrystal over
$N$ be the associated isocrystal over ![]() $k$. Then
$k$. Then ![]() ${{\mathscr M}}_{H,\infty }$ is isomorphic to the functor which inputs an affinoid perfectoid space
${{\mathscr M}}_{H,\infty }$ is isomorphic to the functor which inputs an affinoid perfectoid space ![]() $S=\operatorname {Spa}(R,R^{+})$ over
$S=\operatorname {Spa}(R,R^{+})$ over ![]() $W(k)[1/p]$ and outputs the set of exact sequences
$W(k)[1/p]$ and outputs the set of exact sequences
where ![]() $i_\infty \colon \operatorname {Spec} R\to X_S$ is the inclusion, and
$i_\infty \colon \operatorname {Spec} R\to X_S$ is the inclusion, and ![]() $W$ is a projective
$W$ is a projective ![]() $\mathcal {O}_S$-module quotient of
$\mathcal {O}_S$-module quotient of ![]() $N\otimes _{W(k)[1/p]} \mathcal {O}_S$ of rank
$N\otimes _{W(k)[1/p]} \mathcal {O}_S$ of rank ![]() $d$.
$d$.
Proof. We briefly describe this isomorphism on the level of points over ![]() $S=\operatorname {Spa}(R,R^{+})$. Suppose that we are given a point of
$S=\operatorname {Spa}(R,R^{+})$. Suppose that we are given a point of ![]() ${{\mathscr M}}_{H,\infty }(S)$, corresponding to a
${{\mathscr M}}_{H,\infty }(S)$, corresponding to a ![]() $p$-divisible group
$p$-divisible group ![]() $G$ over
$G$ over ![]() $R^{\circ }$, together with a quasi-isogeny
$R^{\circ }$, together with a quasi-isogeny ![]() $\iota \colon H\otimes _{k} R^{\circ }/p \to G\otimes _{R^{\circ }} R^{\circ }/p$ and an isomorphism
$\iota \colon H\otimes _{k} R^{\circ }/p \to G\otimes _{R^{\circ }} R^{\circ }/p$ and an isomorphism ![]() $\alpha \colon \mathbf {Q}_p^{n}\to VG$ of sheaves of
$\alpha \colon \mathbf {Q}_p^{n}\to VG$ of sheaves of ![]() $\mathbf {Q}_p$-vector spaces on
$\mathbf {Q}_p$-vector spaces on ![]() $S$. The logarithm map on
$S$. The logarithm map on ![]() $G$ fits into an exact sequence of sheaves of
$G$ fits into an exact sequence of sheaves of ![]() $\mathbf {Z}_p$-modules on
$\mathbf {Z}_p$-modules on ![]() $S$,
$S$,
After taking projective limits along multiplication-by-![]() $p$, this turns into an exact sequence of sheaves of
$p$, this turns into an exact sequence of sheaves of ![]() $\mathbf {Q}_p$-vector spaces on
$\mathbf {Q}_p$-vector spaces on ![]() $S$,
$S$,
The quasi-isogeny induces an isomorphism ![]() $\tilde {H}_{\eta }^{\operatorname{ad}} \times _{\operatorname {Spa} W(k)[1/p]} S \cong \tilde {G}_{\eta }^{\operatorname{ad}}$; composing this with the level structure gives an injective map
$\tilde {H}_{\eta }^{\operatorname{ad}} \times _{\operatorname {Spa} W(k)[1/p]} S \cong \tilde {G}_{\eta }^{\operatorname{ad}}$; composing this with the level structure gives an injective map ![]() $\mathbf {Q}_p^{n}\to \tilde {H}^{\operatorname{ad}}_{\eta }(S)$, whose cokernel
$\mathbf {Q}_p^{n}\to \tilde {H}^{\operatorname{ad}}_{\eta }(S)$, whose cokernel ![]() $W$ is isomorphic to the projective
$W$ is isomorphic to the projective ![]() $R$-module
$R$-module ![]() $\operatorname {Lie} G$ of rank
$\operatorname {Lie} G$ of rank ![]() $d$. In light of Theorem 3.2.1, the map
$d$. In light of Theorem 3.2.1, the map ![]() $\mathbf {Q}_p^{n}\to \tilde {H}^{\operatorname{ad}}_{\eta }(S)$ corresponds to an
$\mathbf {Q}_p^{n}\to \tilde {H}^{\operatorname{ad}}_{\eta }(S)$ corresponds to an ![]() $\mathcal {O}_{X_{S}}$-linear map
$\mathcal {O}_{X_{S}}$-linear map ![]() $s\colon \mathcal {O}_{X_S}^{n}\to {{\mathcal {E}}}_S(H)$, which fits into the exact sequence in (3.2.1).
$s\colon \mathcal {O}_{X_S}^{n}\to {{\mathcal {E}}}_S(H)$, which fits into the exact sequence in (3.2.1).
Similarly, we have a description of ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty }$ in terms of modifications.
${{\mathscr M}}_{{{\mathcal {D}}},\infty }$ in terms of modifications.
Proposition 3.2.3 Let ![]() ${{\mathcal {D}}}=(B,V,H,\mu )$ be a rational EL datum. Then
${{\mathcal {D}}}=(B,V,H,\mu )$ be a rational EL datum. Then ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty }$ is isomorphic to the functor which inputs an affinoid perfectoid space
${{\mathscr M}}_{{{\mathcal {D}}},\infty }$ is isomorphic to the functor which inputs an affinoid perfectoid space ![]() $S$ over
$S$ over ![]() $\breve {E}$ and outputs the set of exact sequences of
$\breve {E}$ and outputs the set of exact sequences of ![]() $B \otimes _{\mathbf {Q}_p} \mathcal {O}_{X_S}$-modules
$B \otimes _{\mathbf {Q}_p} \mathcal {O}_{X_S}$-modules
where ![]() $W$ is a finite projective
$W$ is a finite projective ![]() $\mathcal {O}_S$-module, which is locally isomorphic to
$\mathcal {O}_S$-module, which is locally isomorphic to ![]() $V_0\otimes _{\mathbf {Q}_p} \mathcal {O}_S$ as a
$V_0\otimes _{\mathbf {Q}_p} \mathcal {O}_S$ as a ![]() $B\otimes _{\mathbf {Q}_p} \mathcal {O}_S$-module (using notation from Definition 2.2.1).
$B\otimes _{\mathbf {Q}_p} \mathcal {O}_S$-module (using notation from Definition 2.2.1).
3.3 The determinant morphism, and connected components
If we are given a rational EL datum ![]() ${{\mathcal {D}}}$, there is a determinant morphism
${{\mathcal {D}}}$, there is a determinant morphism ![]() $\det \colon {{\mathscr M}}_{{{\mathcal {D}}},\infty }\to {{\mathscr M}}_{\det {{\mathcal {D}}},\infty }$, which we review below. For an algebraically closed perfectoid field
$\det \colon {{\mathscr M}}_{{{\mathcal {D}}},\infty }\to {{\mathscr M}}_{\det {{\mathcal {D}}},\infty }$, which we review below. For an algebraically closed perfectoid field ![]() $C$ containing
$C$ containing ![]() $W(k)[1/p]$, the base change
$W(k)[1/p]$, the base change ![]() ${{\mathscr M}}_{\det {{\mathcal {D}}},\infty ,C}$ is a locally profinite set of copies of
${{\mathscr M}}_{\det {{\mathcal {D}}},\infty ,C}$ is a locally profinite set of copies of ![]() $\operatorname {Spa} C$. For a point
$\operatorname {Spa} C$. For a point ![]() $\tau \in {{\mathscr M}}_{\det {{\mathcal {D}}},\infty }(C)$, let
$\tau \in {{\mathscr M}}_{\det {{\mathcal {D}}},\infty }(C)$, let ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\tau }$ be the fiber of
${{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\tau }$ be the fiber of ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty }\to {{\mathscr M}}_{\det {{\mathcal {D}}},\infty }$ over
${{\mathscr M}}_{{{\mathcal {D}}},\infty }\to {{\mathscr M}}_{\det {{\mathcal {D}}},\infty }$ over ![]() $\tau$. We will prove in § 5 that each
$\tau$. We will prove in § 5 that each ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\tau ,\operatorname {non-sp}}$ is cohomologically smooth if
${{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\tau ,\operatorname {non-sp}}$ is cohomologically smooth if ![]() ${{\mathcal {D}}}$ is basic. This implies that
${{\mathcal {D}}}$ is basic. This implies that ![]() $\pi _0({{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\tau ,\operatorname {non-sp}})$ is discrete, so that cohomogical smoothness of
$\pi _0({{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\tau ,\operatorname {non-sp}})$ is discrete, so that cohomogical smoothness of ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\tau ,\operatorname {non-sp}}$ is inherited by each of its connected components. This is Theorem 1.0.1. In certain cases (for example Lubin–Tate space) it is known that
${{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\tau ,\operatorname {non-sp}}$ is inherited by each of its connected components. This is Theorem 1.0.1. In certain cases (for example Lubin–Tate space) it is known that ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\tau }$ is already connected [Reference ChenChe14].
${{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\tau }$ is already connected [Reference ChenChe14].
We first review the determinant morphism for the space ![]() ${{\mathscr M}}_{H,\infty }$, where
${{\mathscr M}}_{H,\infty }$, where ![]() $H$ is a
$H$ is a ![]() $p$-divisible group of height
$p$-divisible group of height ![]() $n$ and dimension
$n$ and dimension ![]() $d$ over a perfect field
$d$ over a perfect field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p$. Let
$p$. Let ![]() $\breve {E}=W(k)[1/p]$. For a perfectoid space
$\breve {E}=W(k)[1/p]$. For a perfectoid space ![]() $S=\operatorname {Spa}(R,R^{+})$ over
$S=\operatorname {Spa}(R,R^{+})$ over ![]() $\breve {E}$, we have the vector bundle
$\breve {E}$, we have the vector bundle ![]() ${{\mathcal {E}}}_S(H)$ and its determinant
${{\mathcal {E}}}_S(H)$ and its determinant ![]() $\det {{\mathcal {E}}}_S(H)$, a line bundle of degree
$\det {{\mathcal {E}}}_S(H)$, a line bundle of degree ![]() $d$. (This does not correspond to a
$d$. (This does not correspond to a ![]() $p$-divisible group ‘
$p$-divisible group ‘![]() $\det H$’ unless
$\det H$’ unless ![]() $d\leq 1$.) We define
$d\leq 1$.) We define ![]() ${{\mathscr M}}_{\det H,\infty }(S)$ to be the set of morphisms
${{\mathscr M}}_{\det H,\infty }(S)$ to be the set of morphisms ![]() $s\colon \mathcal {O}_{X_S}\to \det {{\mathcal {E}}}_S(H)$, such that the cokernel of
$s\colon \mathcal {O}_{X_S}\to \det {{\mathcal {E}}}_S(H)$, such that the cokernel of ![]() $s$ is a projective
$s$ is a projective ![]() $B_{\operatorname {dR}}^{+}(R)/(\xi )^{d}$-module of rank 1, where
$B_{\operatorname {dR}}^{+}(R)/(\xi )^{d}$-module of rank 1, where ![]() $(\xi )$ is the kernel of
$(\xi )$ is the kernel of ![]() $B_{\operatorname {dR}}^{+}(R)\to R$. The morphism
$B_{\operatorname {dR}}^{+}(R)\to R$. The morphism ![]() $\det \colon {{\mathscr M}}_{H,\infty }\to {{\mathscr M}}_{\det H,\infty }$ is simply
$\det \colon {{\mathscr M}}_{H,\infty }\to {{\mathscr M}}_{\det H,\infty }$ is simply ![]() $s\mapsto \det s$.
$s\mapsto \det s$.
Regarding the structure of ![]() ${{\mathscr M}}_{\det H,\infty }$: we claim that for an algebraically closed perfectoid field
${{\mathscr M}}_{\det H,\infty }$: we claim that for an algebraically closed perfectoid field ![]() $C/\breve {E}$, the set
$C/\breve {E}$, the set ![]() ${{\mathscr M}}_{\det H,\infty }(C)$ is a
${{\mathscr M}}_{\det H,\infty }(C)$ is a ![]() $\mathbf {Q}_p^{\times }$-torsor. Indeed, since the vector bundle
$\mathbf {Q}_p^{\times }$-torsor. Indeed, since the vector bundle ![]() ${{\mathcal {E}}}_C(H)$ has degree
${{\mathcal {E}}}_C(H)$ has degree ![]() $d$, so does the line bundle
$d$, so does the line bundle ![]() $\det {{\mathcal {E}}}_C(H)$, so that
$\det {{\mathcal {E}}}_C(H)$, so that ![]() $\det {{\mathcal {E}}}_C(H)\cong \mathcal {O}_{X_C}(d)$. A
$\det {{\mathcal {E}}}_C(H)\cong \mathcal {O}_{X_C}(d)$. A ![]() $C$-point of
$C$-point of ![]() ${{\mathscr M}}_{\det H,\infty }$ is therefore a global section of
${{\mathscr M}}_{\det H,\infty }$ is therefore a global section of ![]() $\mathcal {O}_{X_C}(d)$ with a zero of order
$\mathcal {O}_{X_C}(d)$ with a zero of order ![]() $d$ at
$d$ at ![]() $\infty$. In other words, it is a nonzero element of
$\infty$. In other words, it is a nonzero element of ![]() $\operatorname {Fil}^{0}B_C^{\phi =p^{d}}\cong \mathbf {Q}_p(d)$.
$\operatorname {Fil}^{0}B_C^{\phi =p^{d}}\cong \mathbf {Q}_p(d)$.
For the general case, let ![]() ${{\mathcal {D}}}=(B,V,H,\mu )$ be a rational EL datum. Let
${{\mathcal {D}}}=(B,V,H,\mu )$ be a rational EL datum. Let ![]() $F=Z(B)$ be the center of
$F=Z(B)$ be the center of ![]() $B$. Then
$B$. Then ![]() $F$ is a semisimple commutative
$F$ is a semisimple commutative ![]() $\mathbf {Q}_p$-algebra; i.e., it is a product of fields. The idea is now to construct the determinant datum
$\mathbf {Q}_p$-algebra; i.e., it is a product of fields. The idea is now to construct the determinant datum ![]() $\det {{\mathcal {D}}}=(F,\det _F V,\det _F H,\det _F\circ \mu )$, noting once again that there may not be a
$\det {{\mathcal {D}}}=(F,\det _F V,\det _F H,\det _F\circ \mu )$, noting once again that there may not be a ![]() $p$-divisible group ‘
$p$-divisible group ‘![]() $\det _F H$’. The determinant
$\det _F H$’. The determinant ![]() $\det _F V$ is a free
$\det _F V$ is a free ![]() $F$-module of rank 1. For a perfectoid space
$F$-module of rank 1. For a perfectoid space ![]() $S=\operatorname {Spa}(R,R^{+})$ over
$S=\operatorname {Spa}(R,R^{+})$ over ![]() $\breve {E}$, we have the
$\breve {E}$, we have the ![]() $F\otimes _{\mathbf {Q}_p}{{\mathcal {O}}}_{X_S}$-module
$F\otimes _{\mathbf {Q}_p}{{\mathcal {O}}}_{X_S}$-module ![]() ${{\mathcal {E}}}_S(H)$ and its determinant
${{\mathcal {E}}}_S(H)$ and its determinant ![]() $\det _F {{\mathcal {E}}}_S(H)$; the latter is a locally free
$\det _F {{\mathcal {E}}}_S(H)$; the latter is a locally free ![]() $F\otimes _{\mathbf {Q}_p}{{\mathcal {O}}}_{X_S}$-module of rank 1. Let
$F\otimes _{\mathbf {Q}_p}{{\mathcal {O}}}_{X_S}$-module of rank 1. Let ![]() $d$ be the degree of
$d$ be the degree of ![]() $\det _F{{\mathcal {E}}}_S(H)$, considered as a function on
$\det _F{{\mathcal {E}}}_S(H)$, considered as a function on ![]() $\operatorname {Spec} F$. We define
$\operatorname {Spec} F$. We define ![]() ${{\mathscr M}}_{\det {{\mathcal {D}}},\infty }(S)$ to be the set of
${{\mathscr M}}_{\det {{\mathcal {D}}},\infty }(S)$ to be the set of ![]() $F$-linear morphisms
$F$-linear morphisms ![]() $s\colon \det _F V\otimes _{\mathbf {Q}_p}\mathcal {O}_{X_S} \to \det _F {{\mathcal {E}}}_S(H)$, such that the cokernel of
$s\colon \det _F V\otimes _{\mathbf {Q}_p}\mathcal {O}_{X_S} \to \det _F {{\mathcal {E}}}_S(H)$, such that the cokernel of ![]() $s$ is (locally on
$s$ is (locally on ![]() $\operatorname {Spec} F$) a projective
$\operatorname {Spec} F$) a projective ![]() $B_{\operatorname {dR}}^{+}(R)/(\xi )^{d}$-module of rank 1. (We remark here that the
$B_{\operatorname {dR}}^{+}(R)/(\xi )^{d}$-module of rank 1. (We remark here that the ![]() $\det _F$ in
$\det _F$ in ![]() $\det _F\circ \mu$ means the morphism from
$\det _F\circ \mu$ means the morphism from ![]() ${{\mathbf {G}}}=\operatorname {Aut}_B(V)$ to
${{\mathbf {G}}}=\operatorname {Aut}_B(V)$ to ![]() ${{\mathbf {G}}}^{\text {ab}}=\operatorname {Aut}_F(\det _F V)=\mathop { \rm Res}_{F/\mathbf {Q}_p}{{\mathbf {G}}}_m$. If
${{\mathbf {G}}}^{\text {ab}}=\operatorname {Aut}_F(\det _F V)=\mathop { \rm Res}_{F/\mathbf {Q}_p}{{\mathbf {G}}}_m$. If ![]() $\det _F \mu$ is a minuscule cocharacter, meaning that it is a vector of only 0s and 1s in the character group
$\det _F \mu$ is a minuscule cocharacter, meaning that it is a vector of only 0s and 1s in the character group ![]() $X_*({{\mathbf {G}}}^{\text {ab}})\cong \mathbf {Z}^{[F:\mathbf {Q}_p]})$, then
$X_*({{\mathbf {G}}}^{\text {ab}})\cong \mathbf {Z}^{[F:\mathbf {Q}_p]})$, then ![]() $\det {{\mathcal {D}}}$ is an honest rational EL datum.) The morphism
$\det {{\mathcal {D}}}$ is an honest rational EL datum.) The morphism ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty }\to {{\mathscr M}}_{\det {{\mathcal {D}}},\infty }$ sends a
${{\mathscr M}}_{{{\mathcal {D}}},\infty }\to {{\mathscr M}}_{\det {{\mathcal {D}}},\infty }$ sends a ![]() $B\otimes _{\mathbf {Q}_p}\mathcal {O}_{X_S}$-linear map
$B\otimes _{\mathbf {Q}_p}\mathcal {O}_{X_S}$-linear map ![]() $s\colon V\otimes _{\mathbf {Q}_p} \mathcal {O}_{X_S} \to {{\mathcal {E}}}_S(H)$ to the
$s\colon V\otimes _{\mathbf {Q}_p} \mathcal {O}_{X_S} \to {{\mathcal {E}}}_S(H)$ to the ![]() $F\otimes _{\mathbf {Q}_p}\mathcal {O}_{X_S}$-linear map
$F\otimes _{\mathbf {Q}_p}\mathcal {O}_{X_S}$-linear map ![]() $\det s\colon \det _F V\otimes _{\mathbf {Q}_p}\mathcal {O}_{X_S} \to \det _F {{\mathcal {E}}}_S(H)$.
$\det s\colon \det _F V\otimes _{\mathbf {Q}_p}\mathcal {O}_{X_S} \to \det _F {{\mathcal {E}}}_S(H)$.
An argument similar to the above shows that for an algebraically closed perfectoid field ![]() $C/\breve {E}$, the set
$C/\breve {E}$, the set ![]() ${{\mathscr M}}_{\det {{\mathcal {D}}},\infty }(C)$ is an
${{\mathscr M}}_{\det {{\mathcal {D}}},\infty }(C)$ is an ![]() $F^{\times }$-torsor, equal to the set of
$F^{\times }$-torsor, equal to the set of ![]() $F$-bases for
$F$-bases for ![]() $F(d)$. Here the Tate twist is interpreted (locally on
$F(d)$. Here the Tate twist is interpreted (locally on ![]() $\operatorname {Spec} F$) as the
$\operatorname {Spec} F$) as the ![]() $d$th tensor power of the rational Tate module of the Lubin–Tate module for
$d$th tensor power of the rational Tate module of the Lubin–Tate module for ![]() $F$.
$F$.
3.4 Basic Rapoport–Zink spaces
The main theorem of this article concerns basic Rapoport–Zink spaces, so we recall some facts about these here.
Let ![]() $H$ be a
$H$ be a ![]() $p$-divisible group over a perfect field
$p$-divisible group over a perfect field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p$. The space
$p$. The space ![]() ${{\mathcal {M}}}_{H,\infty }$ is said to be basic when the
${{\mathcal {M}}}_{H,\infty }$ is said to be basic when the ![]() $p$-divisible group
$p$-divisible group ![]() $H$ (or rather, its Dieudonné module
$H$ (or rather, its Dieudonné module ![]() $M(H)$) is isoclinic. This is equivalent to saying that the natural map
$M(H)$) is isoclinic. This is equivalent to saying that the natural map
is an isomorphism, where on the right the endomorphisms are not required to commute with Frobenius.
More generally we have a notion of basicness for a rational EL datum ![]() $(B,H,V,\mu )$, referring to the following equivalent conditions.
$(B,H,V,\mu )$, referring to the following equivalent conditions.
– The
 ${{\mathbf {G}}}$-isocrystal (
${{\mathbf {G}}}$-isocrystal ( ${{\mathbf {G}}}=\operatorname {Aut}_B V$) associated to
${{\mathbf {G}}}=\operatorname {Aut}_B V$) associated to  $H$ is basic in the sense of Kottwitz [Reference KottwitzKot85].
$H$ is basic in the sense of Kottwitz [Reference KottwitzKot85].– The natural map
is an isomorphism. \[ \operatorname{End}^{\circ}_B(H) \otimes_{\mathbf{Q}_p} W(k)[1/p] \to \operatorname{End}_{B\otimes_{\mathbf{Q}_p} W(k)[1/p]} M(H)[1/p] \]
\[ \operatorname{End}^{\circ}_B(H) \otimes_{\mathbf{Q}_p} W(k)[1/p] \to \operatorname{End}_{B\otimes_{\mathbf{Q}_p} W(k)[1/p]} M(H)[1/p] \]– Considered as an algebraic group over
 $\mathbf {Q}_p$, the automorphism group
$\mathbf {Q}_p$, the automorphism group  $J=\operatorname {Aut}^{\circ }_B H$ is an inner form of
$J=\operatorname {Aut}^{\circ }_B H$ is an inner form of  ${{\mathbf {G}}}$.
${{\mathbf {G}}}$.– Let
 $D'=\operatorname {End}^{\circ }_B H$. For any algebraically closed perfectoid field
$D'=\operatorname {End}^{\circ }_B H$. For any algebraically closed perfectoid field  $C$ containing
$C$ containing  $W(k)$, the map
is an isomorphism.
$W(k)$, the map
is an isomorphism. \[ D'\otimes_{\mathbf{Q}_p} \mathcal{O}_{X_C} \to \operatorname{\mathscr{E}{\mathcal{nd}}\,}_{(B\otimes_{\mathbf{Q}_p} \mathcal{O}_{X_C})} {{\mathcal{E}}}_C(H) \]
\[ D'\otimes_{\mathbf{Q}_p} \mathcal{O}_{X_C} \to \operatorname{\mathscr{E}{\mathcal{nd}}\,}_{(B\otimes_{\mathbf{Q}_p} \mathcal{O}_{X_C})} {{\mathcal{E}}}_C(H) \]
In brief, the duality theorem from [Reference Scholze and WeinsteinSW13] says the following. Given a basic EL datum ![]() ${{\mathcal {D}}}$, there is a dual datum
${{\mathcal {D}}}$, there is a dual datum ![]() $\check {{{\mathcal {D}}}}$, for which the roles of the groups
$\check {{{\mathcal {D}}}}$, for which the roles of the groups ![]() ${{\mathbf {G}}}$ and
${{\mathbf {G}}}$ and ![]() $J$ are reversed. There is a
$J$ are reversed. There is a ![]() ${{\mathbf {G}}}(\mathbf {Q}_p)\times J(\mathbf {Q}_p)$-equivariant isomorphism
${{\mathbf {G}}}(\mathbf {Q}_p)\times J(\mathbf {Q}_p)$-equivariant isomorphism ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty }\cong {{\mathscr M}}_{\check {{{\mathcal {D}}}},\infty }$ which exchanges the roles of
${{\mathscr M}}_{{{\mathcal {D}}},\infty }\cong {{\mathscr M}}_{\check {{{\mathcal {D}}}},\infty }$ which exchanges the roles of ![]() $\pi _{GM}$ and
$\pi _{GM}$ and ![]() $\pi _{HT}$.
$\pi _{HT}$.
3.5 The special locus
Let ![]() ${{\mathcal {D}}}=(B,V,H,\mu )$ be a basic rational EL datum relative to a perfect field
${{\mathcal {D}}}=(B,V,H,\mu )$ be a basic rational EL datum relative to a perfect field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p$, with reflex field
$p$, with reflex field ![]() $E$. Let
$E$. Let ![]() $F$ be the center of
$F$ be the center of ![]() $B$. Define
$B$. Define ![]() $F$-algebras
$F$-algebras ![]() $D$ and
$D$ and ![]() $D'$ by
$D'$ by
Finally, let ![]() ${{\mathbf {G}}}=\operatorname {Aut}_B V$ and
${{\mathbf {G}}}=\operatorname {Aut}_B V$ and ![]() $J=\operatorname {Aut}_B H$, considered as algebraic groups over
$J=\operatorname {Aut}_B H$, considered as algebraic groups over ![]() $\mathbf {Q}_p$. Then
$\mathbf {Q}_p$. Then ![]() ${{\mathbf {G}}}$ and
${{\mathbf {G}}}$ and ![]() $J$ both contain
$J$ both contain ![]() $\mathop { \rm Res}_{F/\mathbf {Q}_p}{{\mathbf {G}}}_m$.
$\mathop { \rm Res}_{F/\mathbf {Q}_p}{{\mathbf {G}}}_m$.
Let ![]() $C$ be an algebraically closed perfectoid field containing
$C$ be an algebraically closed perfectoid field containing ![]() $\breve {E}$, and let
$\breve {E}$, and let ![]() $x\in {{\mathscr M}}_{{{\mathcal {D}}},\infty }(C)$. Then
$x\in {{\mathscr M}}_{{{\mathcal {D}}},\infty }(C)$. Then ![]() $x$ corresponds to a
$x$ corresponds to a ![]() $p$-divisible group
$p$-divisible group ![]() $G$ over
$G$ over ![]() $\mathcal {O}_C$ with endomorphisms by
$\mathcal {O}_C$ with endomorphisms by ![]() $B$, and also it corresponds to a
$B$, and also it corresponds to a ![]() $B\otimes _{\mathbf {Q}_p}\mathcal {O}_{X_C}$-linear map
$B\otimes _{\mathbf {Q}_p}\mathcal {O}_{X_C}$-linear map ![]() $s\colon V\otimes _{\mathbf {Q}_p}\mathcal {O}_X\to {{\mathcal {E}}}_C(N)$ as in Proposition 3.2.3. Define
$s\colon V\otimes _{\mathbf {Q}_p}\mathcal {O}_X\to {{\mathcal {E}}}_C(N)$ as in Proposition 3.2.3. Define ![]() $A_x=\operatorname {End}_B G$ (endomorphisms in the isogeny category). Then
$A_x=\operatorname {End}_B G$ (endomorphisms in the isogeny category). Then ![]() $A_x$ is a semisimple
$A_x$ is a semisimple ![]() $F$-algebra. In light of Proposition 3.2.3, an element of
$F$-algebra. In light of Proposition 3.2.3, an element of ![]() $A_x$ is a pair
$A_x$ is a pair ![]() $(\alpha ,\alpha ')$, where
$(\alpha ,\alpha ')$, where ![]() $\alpha \in \operatorname {End}_{B\otimes _{\mathbf {Q}_p}\mathcal {O}_{X_C}} V\otimes \mathcal {O}_{X_C}=\operatorname {End}_B V=D$ and
$\alpha \in \operatorname {End}_{B\otimes _{\mathbf {Q}_p}\mathcal {O}_{X_C}} V\otimes \mathcal {O}_{X_C}=\operatorname {End}_B V=D$ and ![]() $\alpha '\in \operatorname {End}_{B\otimes _{\mathbf {Q}_p} \mathcal {O}_{X_C}} {{\mathscr E}}_C(H)=D'$ (the last equality is due to basicness), such that
$\alpha '\in \operatorname {End}_{B\otimes _{\mathbf {Q}_p} \mathcal {O}_{X_C}} {{\mathscr E}}_C(H)=D'$ (the last equality is due to basicness), such that ![]() $s\circ \alpha =\alpha '\circ s$. Thus we have
$s\circ \alpha =\alpha '\circ s$. Thus we have
Lemma 3.5.1 The following are equivalent.
(i) The
 $F$-algebra
$F$-algebra  $A_x$ strictly contains
$A_x$ strictly contains  $F$.
$F$.(ii) The stabilizer of
 $\pi _{GM}(x)\in \mathcal {F}\ell _\mu (C)$ in
$\pi _{GM}(x)\in \mathcal {F}\ell _\mu (C)$ in  $J(\mathbf {Q}_p)$ strictly contains
$J(\mathbf {Q}_p)$ strictly contains  $F^{\times }$.
$F^{\times }$.(iii) The stabilizer of
 $\pi _{HT}(x)\in \mathcal {F}\ell _\mu '(C)$ in
$\pi _{HT}(x)\in \mathcal {F}\ell _\mu '(C)$ in  ${{\mathbf {G}}}(\mathbf {Q}_p)$ strictly contains
${{\mathbf {G}}}(\mathbf {Q}_p)$ strictly contains  $F^{\times }$.
$F^{\times }$.
Proof. As in Proposition 3.2.3, let ![]() $s \colon V\otimes _{\mathbf {Q}_p} \mathcal {O}_{X_S} \stackrel {s}{\to } {{\mathcal {E}}}_S(H)$ be the modification corresponding to
$s \colon V\otimes _{\mathbf {Q}_p} \mathcal {O}_{X_S} \stackrel {s}{\to } {{\mathcal {E}}}_S(H)$ be the modification corresponding to ![]() $x$.
$x$.
Note that the condition (1) is equivalent to the existence of an invertible element ![]() $(\alpha ,\alpha ') \in A_x$ not contained in (the diagonally embedded)
$(\alpha ,\alpha ') \in A_x$ not contained in (the diagonally embedded) ![]() $F$. Also note that if one of
$F$. Also note that if one of ![]() $\alpha ,\alpha '$ lies in
$\alpha ,\alpha '$ lies in ![]() $F$, then so does the other, in which case they are equal.
$F$, then so does the other, in which case they are equal.
Suppose ![]() $(\alpha ,\alpha ')\in A_x$ is invertible. The point
$(\alpha ,\alpha ')\in A_x$ is invertible. The point ![]() $\pi _{GM}(x)\in {{\mathcal {F}}}\ell _\mu$ corresponds to the cokernel of the fiber of
$\pi _{GM}(x)\in {{\mathcal {F}}}\ell _\mu$ corresponds to the cokernel of the fiber of ![]() $s$ at
$s$ at ![]() $\infty$. Since
$\infty$. Since ![]() $\alpha '\circ s=s\circ \alpha$, the cokernels of
$\alpha '\circ s=s\circ \alpha$, the cokernels of ![]() $\alpha '\circ s$ and
$\alpha '\circ s$ and ![]() $s$ are the same, which means exactly that
$s$ are the same, which means exactly that ![]() $\alpha '\in J(\mathbf {Q}_p)$ stabilizes
$\alpha '\in J(\mathbf {Q}_p)$ stabilizes ![]() $\pi _{GM}(x)$. Thus (1) implies (2). Conversely, if there exists
$\pi _{GM}(x)$. Thus (1) implies (2). Conversely, if there exists ![]() $\alpha '\in J(\mathbf {Q}_p)\backslash F^{\times }$ which stabilizes
$\alpha '\in J(\mathbf {Q}_p)\backslash F^{\times }$ which stabilizes ![]() $\pi _{GM}(x)$, it means that the
$\pi _{GM}(x)$, it means that the ![]() $B\otimes _{\mathbf {Q}_p}\mathcal {O}_{X_C}$-linear maps
$B\otimes _{\mathbf {Q}_p}\mathcal {O}_{X_C}$-linear maps ![]() $s$ and
$s$ and ![]() $\alpha '\circ s$ have the same cokernel, and therefore there exists
$\alpha '\circ s$ have the same cokernel, and therefore there exists ![]() $\alpha \in \operatorname {End}_{B\otimes _{\mathbf {Q}_p}\mathcal {O}_{X_C}} V\otimes _{\mathbf {Q}_p} \mathcal {O}_{X_C}=D$ such that
$\alpha \in \operatorname {End}_{B\otimes _{\mathbf {Q}_p}\mathcal {O}_{X_C}} V\otimes _{\mathbf {Q}_p} \mathcal {O}_{X_C}=D$ such that ![]() $s\circ \alpha = \alpha '\circ s$, and then
$s\circ \alpha = \alpha '\circ s$, and then ![]() $(\alpha ,\alpha ')\in A_x\backslash F^{\times }$. This shows that (2) implies (1).
$(\alpha ,\alpha ')\in A_x\backslash F^{\times }$. This shows that (2) implies (1).
The equivalence between (1) and (3) is proved similarly.
Definition 3.5.2 The special locus in ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty }$ is the subset
${{\mathscr M}}_{{{\mathcal {D}}},\infty }$ is the subset ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\operatorname {sp}}$ defined by the condition
${{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\operatorname {sp}}$ defined by the condition ![]() $A_x\neq F$. The nonspecial locus
$A_x\neq F$. The nonspecial locus ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\operatorname {non-sp}}$ is the complement of the special locus.
${{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\operatorname {non-sp}}$ is the complement of the special locus.
The special locus is built out of ‘smaller’ Rapoport–Zink spaces, in the following sense. Let ![]() $A$ be a semisimple
$A$ be a semisimple ![]() $F$-algebra, equipped with two
$F$-algebra, equipped with two ![]() $F$-embeddings
$F$-embeddings ![]() $A\to D$ and
$A\to D$ and ![]() $A\to D'$, so that
$A\to D'$, so that ![]() $A\otimes _F B$ acts on
$A\otimes _F B$ acts on ![]() $V$ and
$V$ and ![]() $H$. Also assume that a cocharacter in the conjugacy class
$H$. Also assume that a cocharacter in the conjugacy class ![]() $\mu$ factors through a cocharacter
$\mu$ factors through a cocharacter ![]() $\mu _0\colon {{\mathbf {G}}}_m\to \operatorname {Aut}_{A\otimes _F B} V$. Let
$\mu _0\colon {{\mathbf {G}}}_m\to \operatorname {Aut}_{A\otimes _F B} V$. Let ![]() ${{\mathcal {D}}}_0=(A\otimes _F B,V,H,\mu _0)$. Then there is an evident morphism
${{\mathcal {D}}}_0=(A\otimes _F B,V,H,\mu _0)$. Then there is an evident morphism ![]() ${{\mathscr M}}_{{{\mathcal {D}}}_0,\infty }\to {{\mathscr M}}_{{{\mathcal {D}}},\infty }$. The special locus
${{\mathscr M}}_{{{\mathcal {D}}}_0,\infty }\to {{\mathscr M}}_{{{\mathcal {D}}},\infty }$. The special locus ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\operatorname {sp}}$ is the union of the images of all the
${{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\operatorname {sp}}$ is the union of the images of all the ![]() ${{\mathscr M}}_{{{\mathcal {D}}}_0,\infty }$, as
${{\mathscr M}}_{{{\mathcal {D}}}_0,\infty }$, as ![]() $A$ ranges through all semisimple
$A$ ranges through all semisimple ![]() $F$-subalgebras of
$F$-subalgebras of ![]() $D\times D'$ strictly containing
$D\times D'$ strictly containing ![]() $F$.
$F$.
4. Cohomological smoothness
Let ![]() $\operatorname {Perf}$ be the category of perfectoid spaces in characteristic
$\operatorname {Perf}$ be the category of perfectoid spaces in characteristic ![]() $p$, with its pro-étale topology [Reference ScholzeSch17, Definition 8.1]. For a prime
$p$, with its pro-étale topology [Reference ScholzeSch17, Definition 8.1]. For a prime ![]() $\ell \neq p$, there is a notion of
$\ell \neq p$, there is a notion of ![]() $\ell$-cohomological smoothness [Reference ScholzeSch17, Definition 23.8]. We only need the notion for morphisms
$\ell$-cohomological smoothness [Reference ScholzeSch17, Definition 23.8]. We only need the notion for morphisms ![]() $f\colon Y'\to Y$ between sheaves on
$f\colon Y'\to Y$ between sheaves on ![]() $\operatorname {Perf}$ which are separated and representable in locally spatial diamonds. If such an
$\operatorname {Perf}$ which are separated and representable in locally spatial diamonds. If such an ![]() $f$ is
$f$ is ![]() $\ell$-cohomologically smooth, and
$\ell$-cohomologically smooth, and ![]() $\Lambda$ is an
$\Lambda$ is an ![]() $\ell$-power torsion ring, then the relative dualizing complex
$\ell$-power torsion ring, then the relative dualizing complex ![]() $Rf^{!}\Lambda$ is an invertible object in
$Rf^{!}\Lambda$ is an invertible object in ![]() $D_{\mathop e\limits{{\prime}}t}(Y',\Lambda )$ (thus, it is v-locally isomorphic to
$D_{\mathop e\limits{{\prime}}t}(Y',\Lambda )$ (thus, it is v-locally isomorphic to ![]() $\Lambda [n]$ for some
$\Lambda [n]$ for some ![]() $n\in {{\mathbf {Z}}}$), and the natural transformation
$n\in {{\mathbf {Z}}}$), and the natural transformation ![]() $Rf^{!}\Lambda \otimes f^{*}\to Rf^{!}$ of functors
$Rf^{!}\Lambda \otimes f^{*}\to Rf^{!}$ of functors ![]() $D_{\mathop e\limits{{\prime}}t}(Y,\Lambda )\to D_{\mathop e\limits{{\prime}}t}(Y',\Lambda )$ is an equivalence [Reference ScholzeSch17, Proposition 23.12]. In particular, if
$D_{\mathop e\limits{{\prime}}t}(Y,\Lambda )\to D_{\mathop e\limits{{\prime}}t}(Y',\Lambda )$ is an equivalence [Reference ScholzeSch17, Proposition 23.12]. In particular, if ![]() $f$ is projection onto a point, and
$f$ is projection onto a point, and ![]() $Rf^{!}\Lambda \cong \Lambda [n]$, one derives a statement of Poincaré duality for
$Rf^{!}\Lambda \cong \Lambda [n]$, one derives a statement of Poincaré duality for ![]() $Y'$:
$Y'$:
We will say that ![]() $f$ is cohomologically smooth if it is
$f$ is cohomologically smooth if it is ![]() $\ell$-cohomologically smooth for all
$\ell$-cohomologically smooth for all ![]() $\ell \neq p$. As an example, if
$\ell \neq p$. As an example, if ![]() $f\colon Y'\to Y$ is a separated smooth morphism of rigid-analytic spaces over
$f\colon Y'\to Y$ is a separated smooth morphism of rigid-analytic spaces over ![]() $\mathbf {Q}_p$, then the associated morphism of diamonds
$\mathbf {Q}_p$, then the associated morphism of diamonds ![]() $f^{\diamond }\colon (Y')^{\diamond }\to Y^{\diamond }$ is cohomologically smooth [Reference ScholzeSch17, Proposition 24.3]. There are other examples where
$f^{\diamond }\colon (Y')^{\diamond }\to Y^{\diamond }$ is cohomologically smooth [Reference ScholzeSch17, Proposition 24.3]. There are other examples where ![]() $f$ does not arise from a finite-type map of adic spaces. For instance, if
$f$ does not arise from a finite-type map of adic spaces. For instance, if ![]() $\tilde {B}_C=\operatorname {Spa} C \langle T^{1/p^{\infty }} \rangle$ is the perfectoid closed ball over an algebraically closed perfectoid field
$\tilde {B}_C=\operatorname {Spa} C \langle T^{1/p^{\infty }} \rangle$ is the perfectoid closed ball over an algebraically closed perfectoid field ![]() $C$, then
$C$, then ![]() $\tilde {B}_C$ is cohomologically smooth over
$\tilde {B}_C$ is cohomologically smooth over ![]() $C$.
$C$.
If ![]() $Y$ is a perfectoid space over an algebraically closed perfectoid field
$Y$ is a perfectoid space over an algebraically closed perfectoid field ![]() $C$, it seems quite difficult to detect whether
$C$, it seems quite difficult to detect whether ![]() $Y$ is cohomologically smooth over
$Y$ is cohomologically smooth over ![]() $C$. We will review in § 4.2 a ‘Jacobian criterion’ from [Reference Fargues and ScholzeFS] which applies to certain kinds of
$C$. We will review in § 4.2 a ‘Jacobian criterion’ from [Reference Fargues and ScholzeFS] which applies to certain kinds of ![]() $Y$. But first we give a classical analogue of this criterion in the context of schemes.
$Y$. But first we give a classical analogue of this criterion in the context of schemes.
4.1 The Jacobian criterion: classical setting
Proposition 4.1.1 Let ![]() $X$ be a smooth projective curve over an algebraically closed field
$X$ be a smooth projective curve over an algebraically closed field ![]() $k$. Let
$k$. Let ![]() $Z\to X$ be a smooth morphism. Define
$Z\to X$ be a smooth morphism. Define ![]() ${{\mathscr M}}_Z$ to be the functor which inputs a
${{\mathscr M}}_Z$ to be the functor which inputs a ![]() $k$-scheme
$k$-scheme ![]() $T$ and outputs the set of sections of
$T$ and outputs the set of sections of ![]() $Z\to X$ over
$Z\to X$ over ![]() $X_T$, that is, the set of morphisms
$X_T$, that is, the set of morphisms ![]() $s$ making
$s$ making

commute, subject to the condition that, fiberwise on ![]() $T$, the vector bundle
$T$, the vector bundle ![]() $s^{*}\operatorname {Tan}_{Z/X}$ has vanishing
$s^{*}\operatorname {Tan}_{Z/X}$ has vanishing ![]() $H^{1}$. Then
$H^{1}$. Then ![]() ${{\mathscr M}}_Z \to \operatorname {Spec} k$ is formally smooth.
${{\mathscr M}}_Z \to \operatorname {Spec} k$ is formally smooth.
Here ![]() $\operatorname {Tan}_{Z/X}$ is the tangent bundle, equal to the
$\operatorname {Tan}_{Z/X}$ is the tangent bundle, equal to the ![]() $\mathcal {O}_Z$-linear dual of the sheaf of differentials
$\mathcal {O}_Z$-linear dual of the sheaf of differentials ![]() $\Omega _{Z/X}$, which is locally free of finite rank. Let
$\Omega _{Z/X}$, which is locally free of finite rank. Let ![]() $\pi \colon X\times _k T \to T$ be the projection. For
$\pi \colon X\times _k T \to T$ be the projection. For ![]() $t\in T$, let
$t\in T$, let ![]() $X_t$ be the fiber of
$X_t$ be the fiber of ![]() $\pi$ over
$\pi$ over ![]() $t$, and let
$t$, and let ![]() $s_t\colon X_t\to Z$ be the restriction of
$s_t\colon X_t\to Z$ be the restriction of ![]() $s$ to
$s$ to ![]() $X_t$. By proper base change, the fiber of
$X_t$. By proper base change, the fiber of ![]() $R^{1}\pi _*s^{*}\operatorname {Tan}_{Z/X}$ at
$R^{1}\pi _*s^{*}\operatorname {Tan}_{Z/X}$ at ![]() $t\in T$ is
$t\in T$ is ![]() $H^{1}(X_t,s_t^{*}\operatorname {Tan}_{Z/X})$. The condition about the vanishing of
$H^{1}(X_t,s_t^{*}\operatorname {Tan}_{Z/X})$. The condition about the vanishing of ![]() $H^{1}$ in the proposition is equivalent to
$H^{1}$ in the proposition is equivalent to ![]() $H^{1}(X_t,s_t^{*}\operatorname {Tan}_{Z/X})=0$ for each
$H^{1}(X_t,s_t^{*}\operatorname {Tan}_{Z/X})=0$ for each ![]() $t\in T$. By Nakayama's lemma, this condition is equivalent to
$t\in T$. By Nakayama's lemma, this condition is equivalent to ![]() $R^{1}\pi _*s^{*}\operatorname {Tan}_{Z/X}=0$.
$R^{1}\pi _*s^{*}\operatorname {Tan}_{Z/X}=0$.
Proof. Suppose we are given a commutative diagram,

where ![]() $T_0\to T$ is a first-order thickening of affine schemes; thus
$T_0\to T$ is a first-order thickening of affine schemes; thus ![]() $T_0$ is the vanishing locus of a square-zero ideal sheaf
$T_0$ is the vanishing locus of a square-zero ideal sheaf ![]() $I\subset \mathcal {O}_T$. Note that
$I\subset \mathcal {O}_T$. Note that ![]() $I$ becomes an
$I$ becomes an ![]() $\mathcal {O}_{T_0}$-module.
$\mathcal {O}_{T_0}$-module.
The morphism ![]() $T_0\to {{\mathscr M}}_Z$ in (4.1.1) corresponds to a section of
$T_0\to {{\mathscr M}}_Z$ in (4.1.1) corresponds to a section of ![]() $Z\to X$ over
$Z\to X$ over ![]() $T_0$. Thus there is a solid diagram.
$T_0$. Thus there is a solid diagram.

We claim that there exists a dotted arrow making the diagram commute. Since ![]() $Z\to X$ is smooth, it is formally smooth, and therefore this arrow exists Zariski-locally on
$Z\to X$ is smooth, it is formally smooth, and therefore this arrow exists Zariski-locally on ![]() $X$. Let
$X$. Let ![]() $\pi \colon X\times _k T\to T$ and
$\pi \colon X\times _k T\to T$ and ![]() $\pi _0\colon X\times _k T_0\to T_0$ be the projections. Then
$\pi _0\colon X\times _k T_0\to T_0$ be the projections. Then ![]() $X\times _k T_0$ is the vanishing locus of the ideal sheaf
$X\times _k T_0$ is the vanishing locus of the ideal sheaf ![]() $\pi ^{*}I\subset \mathcal {O}_{X\times _k T}$. Note that sheaves of sets on
$\pi ^{*}I\subset \mathcal {O}_{X\times _k T}$. Note that sheaves of sets on ![]() $X\times _k T$ are equivalent to sheaves of sets on
$X\times _k T$ are equivalent to sheaves of sets on ![]() $X\times _k T_0$; under this equivalence,
$X\times _k T_0$; under this equivalence, ![]() $\pi ^{*}I$ and
$\pi ^{*}I$ and ![]() $\pi _0^{*}I$ correspond. By [Sta14, Remark 36.9.6], the set of such morphisms form a (Zariski) sheaf of sets on
$\pi _0^{*}I$ correspond. By [Sta14, Remark 36.9.6], the set of such morphisms form a (Zariski) sheaf of sets on ![]() $X\times _k T$, which when viewed as a sheaf on
$X\times _k T$, which when viewed as a sheaf on ![]() $X\times _k T_0$ is a torsor for
$X\times _k T_0$ is a torsor for
This torsor corresponds to class in
This ![]() $H^{1}$ is the limit of a spectral sequence with terms
$H^{1}$ is the limit of a spectral sequence with terms
But since ![]() $T_0$ is affine and
$T_0$ is affine and ![]() $R^{q}\pi _{0*}(s_0^{*}\operatorname {Tan}_{Z/X}\otimes \ \pi _0^{*}I)$ is quasi-coherent, the above terms vanish for all
$R^{q}\pi _{0*}(s_0^{*}\operatorname {Tan}_{Z/X}\otimes \ \pi _0^{*}I)$ is quasi-coherent, the above terms vanish for all ![]() $p>0$, and therefore
$p>0$, and therefore
Since ![]() $s_0^{*}\operatorname {Tan}_{Z/X}$ is locally free, we have
$s_0^{*}\operatorname {Tan}_{Z/X}$ is locally free, we have ![]() $s_0^{*}\operatorname {Tan}_{Z/X}\otimes \ \pi _0^{*}I \cong s_0^{*}\operatorname {Tan}_{Z/X}\otimes ^{{{\mathbf {L}}}} \ \pi _{0*}I$, and we may apply the projection formula [Sta14, Lemma 35.21.1] to obtain
$s_0^{*}\operatorname {Tan}_{Z/X}\otimes \ \pi _0^{*}I \cong s_0^{*}\operatorname {Tan}_{Z/X}\otimes ^{{{\mathbf {L}}}} \ \pi _{0*}I$, and we may apply the projection formula [Sta14, Lemma 35.21.1] to obtain
Now we apply the hypothesis about vanishing of ![]() $H^{1}$, which implies that
$H^{1}$, which implies that ![]() $R\pi _{0*}s_0^{*}\operatorname {Tan}_{Z/X}$ is quasi-isomorphic to the locally free sheaf
$R\pi _{0*}s_0^{*}\operatorname {Tan}_{Z/X}$ is quasi-isomorphic to the locally free sheaf ![]() $\pi _{0*}s_0^{*}\operatorname {Tan}_{Z/X}$ in degree 0. Therefore the complex displayed above has
$\pi _{0*}s_0^{*}\operatorname {Tan}_{Z/X}$ in degree 0. Therefore the complex displayed above has ![]() $H^{1}=0$.
$H^{1}=0$.
Thus our torsor is trivial, and so a morphism ![]() $s\colon X\times _k T\to Z$ exists filling in (4.1.2). The final thing to check is that
$s\colon X\times _k T\to Z$ exists filling in (4.1.2). The final thing to check is that ![]() $s$ corresponds to a morphism
$s$ corresponds to a morphism ![]() $T\to {{\mathscr M}}_Z$, i.e., that it satisfies the fiberwise
$T\to {{\mathscr M}}_Z$, i.e., that it satisfies the fiberwise ![]() $H^{1}=0$ condition. But this is automatic, since
$H^{1}=0$ condition. But this is automatic, since ![]() $T_0$ and
$T_0$ and ![]() $T$ have the same schematic points.
$T$ have the same schematic points.
In the setup of Proposition 4.1.1, let ![]() $s\colon X \times _k {{\mathscr M}}_Z \to Z$ be the universal section. That is, the pull-back of
$s\colon X \times _k {{\mathscr M}}_Z \to Z$ be the universal section. That is, the pull-back of ![]() $s$ along a morphism
$s$ along a morphism ![]() $T \to {{\mathscr M}}_Z$ is the section
$T \to {{\mathscr M}}_Z$ is the section ![]() $X\times _k T\to Z$ to which this morphism corresponds. Let
$X\times _k T\to Z$ to which this morphism corresponds. Let ![]() $\pi \colon X\times _k {{\mathscr M}}_Z\to {{\mathscr M}}_Z$ be the projection. By Proposition 4.1.1
$\pi \colon X\times _k {{\mathscr M}}_Z\to {{\mathscr M}}_Z$ be the projection. By Proposition 4.1.1 ![]() ${{\mathscr M}}_Z\to \operatorname {Spec} k$ is formally smooth. There is an isomorphism
${{\mathscr M}}_Z\to \operatorname {Spec} k$ is formally smooth. There is an isomorphism
Indeed, the proof of Proposition 4.1.1 shows that ![]() $\pi _*s^{*}\operatorname {Tan}_{Z/X}$ has the same universal property with respect to first order deformations as
$\pi _*s^{*}\operatorname {Tan}_{Z/X}$ has the same universal property with respect to first order deformations as ![]() $\operatorname {Tan}_{{{\mathscr M}}_Z/\operatorname {Spec} k}$.
$\operatorname {Tan}_{{{\mathscr M}}_Z/\operatorname {Spec} k}$.
The following example is of similar spirit as our main application of the perfectoid Jacobian criterion below.
Example 4.1.2 Let ![]() $X = {{\mathbf {P}}}^{1}$ over the algebraically closed field
$X = {{\mathbf {P}}}^{1}$ over the algebraically closed field ![]() $k$. For
$k$. For ![]() $d \in {{\mathbf {Z}}}$, let
$d \in {{\mathbf {Z}}}$, let
be the geometric vector bundle over ![]() $X$ whose global sections are
$X$ whose global sections are ![]() $\Gamma (X,{{\mathcal {O}}}(d))$. Fix integers
$\Gamma (X,{{\mathcal {O}}}(d))$. Fix integers ![]() $n,d, \delta > 0$ and let
$n,d, \delta > 0$ and let ![]() $P$ be a homogeneous polynomial over
$P$ be a homogeneous polynomial over ![]() $k$ of degree
$k$ of degree ![]() $\delta$ in
$\delta$ in ![]() $n$ variables. Then
$n$ variables. Then ![]() $P$ defines a morphism
$P$ defines a morphism ![]() $P \colon \prod _{i=1}^{n} V_d \rightarrow V_{d\delta }$, by sending sections
$P \colon \prod _{i=1}^{n} V_d \rightarrow V_{d\delta }$, by sending sections ![]() $(s_i)_{i=1}^{n}$ of
$(s_i)_{i=1}^{n}$ of ![]() $V_d$ to the section
$V_d$ to the section ![]() $P(s_1,\ldots ,s_n)$ of
$P(s_1,\ldots ,s_n)$ of ![]() $V_{d\delta }$. Fix a global section
$V_{d\delta }$. Fix a global section ![]() $f \colon X \rightarrow V_{d\delta }$ to the projection morphism and consider the pull-back of
$f \colon X \rightarrow V_{d\delta }$ to the projection morphism and consider the pull-back of ![]() $P$ along
$P$ along ![]() $f$.
$f$.

Moreover, let ![]() $Z$ be the smooth locus of
$Z$ be the smooth locus of ![]() $P^{-1}(f)$ over
$P^{-1}(f)$ over ![]() $X$. It is an open subset. The derivatives
$X$. It is an open subset. The derivatives ![]() ${\partial P}/{\partial x_i}$ of
${\partial P}/{\partial x_i}$ of ![]() $P$ are homogeneous polynomials of degree
$P$ are homogeneous polynomials of degree ![]() $\delta - 1$ in
$\delta - 1$ in ![]() $n$ variables, hence can be regarded as functions
$n$ variables, hence can be regarded as functions ![]() $\prod _{i=1}^{n} V_d \rightarrow V_{d(\delta - 1)}$. A point
$\prod _{i=1}^{n} V_d \rightarrow V_{d(\delta - 1)}$. A point ![]() $y \in P^{-1}(f)$ lies in
$y \in P^{-1}(f)$ lies in ![]() $Z$ if and only if
$Z$ if and only if ![]() $({\partial P}/{\partial x_i})(y)$,
$({\partial P}/{\partial x_i})(y)$, ![]() $i=1,\ldots ,n$ are not all zero. We wish to apply Proposition 4.1.1 to
$i=1,\ldots ,n$ are not all zero. We wish to apply Proposition 4.1.1 to ![]() $Z/X$. Let
$Z/X$. Let ![]() ${{\mathscr M}}'_Z$ denote the space of global sections of
${{\mathscr M}}'_Z$ denote the space of global sections of ![]() $Z$ over
$Z$ over ![]() $X$, that is for a
$X$, that is for a ![]() $k$-scheme
$k$-scheme ![]() $T$,
$T$, ![]() ${{\mathscr M}}_Z'(T)$ is the set of morphisms
${{\mathscr M}}_Z'(T)$ is the set of morphisms ![]() $s \colon X \times _k T \rightarrow Z$ as in the proposition (without any further conditions). A
$s \colon X \times _k T \rightarrow Z$ as in the proposition (without any further conditions). A ![]() $k$-point
$k$-point ![]() $g \in {{\mathscr M}}'_Z(k)$ corresponds to a section
$g \in {{\mathscr M}}'_Z(k)$ corresponds to a section ![]() $g \colon X \rightarrow \prod _{i=1}^{n} V_d$, satisfying
$g \colon X \rightarrow \prod _{i=1}^{n} V_d$, satisfying ![]() $P \circ g = f$. In general, for a (geometric) vector bundle
$P \circ g = f$. In general, for a (geometric) vector bundle ![]() $V$ on
$V$ on ![]() $X$ with corresponding locally free
$X$ with corresponding locally free ![]() ${{\mathcal {O}}}_X$-module
${{\mathcal {O}}}_X$-module ![]() ${{\mathscr E}}$, the pull-back of the tangent space
${{\mathscr E}}$, the pull-back of the tangent space ![]() $\mathrm {Tan}_{V/X}$ along a section
$\mathrm {Tan}_{V/X}$ along a section ![]() $s \colon X \rightarrow V$ is canonically isomorphic to
$s \colon X \rightarrow V$ is canonically isomorphic to ![]() ${{\mathscr E}}$. Hence in our situation (using that
${{\mathscr E}}$. Hence in our situation (using that ![]() $Z \subseteq P^{-1}(f)$ is open) the tangent space
$Z \subseteq P^{-1}(f)$ is open) the tangent space ![]() $g^{\ast } \mathrm {Tan}_{Z/X}$ can be computed from the short exact sequence,
$g^{\ast } \mathrm {Tan}_{Z/X}$ can be computed from the short exact sequence,
 \[ 0 \rightarrow g^{\ast} \mathrm{Tan}_{Z/X} \rightarrow \bigoplus_{i=1}^{n} {{\mathcal{O}}}(d) \stackrel{D_g P}{\longrightarrow} {{\mathcal{O}}}(d\delta) \rightarrow 0, \]
\[ 0 \rightarrow g^{\ast} \mathrm{Tan}_{Z/X} \rightarrow \bigoplus_{i=1}^{n} {{\mathcal{O}}}(d) \stackrel{D_g P}{\longrightarrow} {{\mathcal{O}}}(d\delta) \rightarrow 0, \]
where ![]() $D_g P$ is the derivative of
$D_g P$ is the derivative of ![]() $P$ at
$P$ at ![]() $g$. It is the
$g$. It is the ![]() ${{\mathcal {O}}}_X$-linear map given by
${{\mathcal {O}}}_X$-linear map given by ![]() $(t_i)_{i=1}^{n} \mapsto \sum _{i = 1}^{n} ({\partial P}/{\partial x_i})(g)t_i$ (note that
$(t_i)_{i=1}^{n} \mapsto \sum _{i = 1}^{n} ({\partial P}/{\partial x_i})(g)t_i$ (note that ![]() $({\partial P}/{\partial x_i})(g)$ are global sections of
$({\partial P}/{\partial x_i})(g)$ are global sections of ![]() ${{\mathcal {O}}}(d(\delta - 1))$). Note that
${{\mathcal {O}}}(d(\delta - 1))$). Note that ![]() $D_g P$ is surjective: by Nakayama, it suffices to check this fiberwise, where it is true by the condition defining
$D_g P$ is surjective: by Nakayama, it suffices to check this fiberwise, where it is true by the condition defining ![]() $Z$.
$Z$.
The space ![]() ${{\mathscr M}}_Z$ is the subfunctor of
${{\mathscr M}}_Z$ is the subfunctor of ![]() ${{\mathscr M}}'_Z$ consisting of all
${{\mathscr M}}'_Z$ consisting of all ![]() $g$ such that (fiberwise)
$g$ such that (fiberwise) ![]() $g^{\ast }\mathrm {Tan}_{Z/X} = \mathrm {ker}(D_g P)$ has vanishing
$g^{\ast }\mathrm {Tan}_{Z/X} = \mathrm {ker}(D_g P)$ has vanishing ![]() $H^{1}$. Writing
$H^{1}$. Writing ![]() $\mathrm {ker}(D_g P) = \bigoplus _{i=1}^{r} {{\mathcal {O}}}(m_i)$ (
$\mathrm {ker}(D_g P) = \bigoplus _{i=1}^{r} {{\mathcal {O}}}(m_i)$ (![]() $m_i \in {{\mathbf {Z}}}$), this is equivalent to
$m_i \in {{\mathbf {Z}}}$), this is equivalent to ![]() $m_i \geq -1$. By the Proposition 4.1.1 we conclude that
$m_i \geq -1$. By the Proposition 4.1.1 we conclude that ![]() ${{\mathscr M}}_Z$ is formally smooth over
${{\mathscr M}}_Z$ is formally smooth over ![]() $k$.
$k$.
Consider now a numerical example. Let ![]() $n = 3$,
$n = 3$, ![]() $d = 1$ and
$d = 1$ and ![]() $\delta = 4$ and let
$\delta = 4$ and let ![]() $g \in {{\mathscr M}}'_Z(k)$. Then
$g \in {{\mathscr M}}'_Z(k)$. Then ![]() $D_g P \in \mathrm {Hom}_{{{\mathcal {O}}}_X}({{\mathcal {O}}}(1)^{\oplus 3}, {{\mathcal {O}}}(4)) = \Gamma (X,{{\mathcal {O}}}(3)^{\oplus 3})$, a
$D_g P \in \mathrm {Hom}_{{{\mathcal {O}}}_X}({{\mathcal {O}}}(1)^{\oplus 3}, {{\mathcal {O}}}(4)) = \Gamma (X,{{\mathcal {O}}}(3)^{\oplus 3})$, a ![]() $12$-dimensional
$12$-dimensional ![]() $k$-vector space, and moreover,
$k$-vector space, and moreover, ![]() $D_g P$ lies in the open subspace of surjective maps. We have the short exact sequence of
$D_g P$ lies in the open subspace of surjective maps. We have the short exact sequence of ![]() ${{\mathcal {O}}}_X$-modules
${{\mathcal {O}}}_X$-modules
This shows that ![]() $g^{\ast } \mathrm {Tan}_{Z/X}$ has rank
$g^{\ast } \mathrm {Tan}_{Z/X}$ has rank ![]() $2$ and degree
$2$ and degree ![]() $-1$. Moreover, being a subbundle of
$-1$. Moreover, being a subbundle of ![]() ${{\mathcal {O}}}(1)^{\oplus 3}$ it only can have slopes less than or equal to
${{\mathcal {O}}}(1)^{\oplus 3}$ it only can have slopes less than or equal to ![]() $1$. There are only two options, either
$1$. There are only two options, either ![]() $g^{\ast } \mathrm {Tan}_{Z/X} \cong {{\mathcal {O}}}(-1) \oplus {{\mathcal {O}}}$ or
$g^{\ast } \mathrm {Tan}_{Z/X} \cong {{\mathcal {O}}}(-1) \oplus {{\mathcal {O}}}$ or ![]() $g^{\ast } \mathrm {Tan}_{Z/X} \cong {{\mathcal {O}}}(-2) \oplus {{\mathcal {O}}}(1)$. The point
$g^{\ast } \mathrm {Tan}_{Z/X} \cong {{\mathcal {O}}}(-2) \oplus {{\mathcal {O}}}(1)$. The point ![]() $g$ lies in
$g$ lies in ![]() ${{\mathscr M}}_Z$ if and only if the first option occurs for
${{\mathscr M}}_Z$ if and only if the first option occurs for ![]() $g$. Which option occurs can be seen from the long exact cohomology sequence associated to (4.1.3):
$g$. Which option occurs can be seen from the long exact cohomology sequence associated to (4.1.3):
 \[ 0 \rightarrow \Gamma(X, g^{\ast} \mathrm{Tan}_{Z/X}) \rightarrow \underbrace{\Gamma(X, {{\mathcal{O}}}(1))^{\oplus 3}}_{\text{6-dim'l}} \stackrel{\Gamma(D_g P)}{\longrightarrow} \underbrace{\Gamma(X, {{\mathcal{O}}}(4))}_{\text{5-dim'l}} \rightarrow {\textrm{H}}^{1}(X, g^{\ast} \mathrm{Tan}_{Z/X}) \rightarrow 0 . \]
\[ 0 \rightarrow \Gamma(X, g^{\ast} \mathrm{Tan}_{Z/X}) \rightarrow \underbrace{\Gamma(X, {{\mathcal{O}}}(1))^{\oplus 3}}_{\text{6-dim'l}} \stackrel{\Gamma(D_g P)}{\longrightarrow} \underbrace{\Gamma(X, {{\mathcal{O}}}(4))}_{\text{5-dim'l}} \rightarrow {\textrm{H}}^{1}(X, g^{\ast} \mathrm{Tan}_{Z/X}) \rightarrow 0 . \]
It is clear that ![]() $\Gamma (X, g^{\ast } \mathrm {Tan}_{Z/X})$ is
$\Gamma (X, g^{\ast } \mathrm {Tan}_{Z/X})$ is ![]() $1$-dimensional if and only if
$1$-dimensional if and only if ![]() $g^{\ast } \mathrm {Tan}_{Z/X} \cong {{\mathcal {O}}}(-1) \oplus {{\mathcal {O}}}$ and
$g^{\ast } \mathrm {Tan}_{Z/X} \cong {{\mathcal {O}}}(-1) \oplus {{\mathcal {O}}}$ and ![]() $2$-dimensional otherwise. The first option is generic, i.e.,
$2$-dimensional otherwise. The first option is generic, i.e., ![]() ${{\mathscr M}}_Z$ is an open subscheme of
${{\mathscr M}}_Z$ is an open subscheme of ![]() ${{\mathscr M}}'_Z$.
${{\mathscr M}}'_Z$.
4.2 The Jacobian criterion: perfectoid setting
We present here the perfectoid version of Proposition 4.1.1
Theorem 4.2.1 (Fargues and Scholze [FS]) Let ![]() $S=\operatorname {Spa}(R,R^{+})$ be an affinoid perfectoid space in characteristic
$S=\operatorname {Spa}(R,R^{+})$ be an affinoid perfectoid space in characteristic ![]() $p$. Let
$p$. Let ![]() $Z\to X_S$ be a smooth morphism of schemes. Let
$Z\to X_S$ be a smooth morphism of schemes. Let ![]() ${{\mathscr M}}_Z^{>0}$ be the functor which inputs a perfectoid space
${{\mathscr M}}_Z^{>0}$ be the functor which inputs a perfectoid space ![]() $T\to S$ and outputs the set of sections of
$T\to S$ and outputs the set of sections of ![]() $Z\to X_S$ over
$Z\to X_S$ over ![]() $T$, that is, the set of morphisms
$T$, that is, the set of morphisms ![]() $s$ making
$s$ making

commute, subject to the condition that, fiberwise on ![]() $T$, all Harder–Narasimhan slopes of the vector bundle
$T$, all Harder–Narasimhan slopes of the vector bundle ![]() $s^{*}\operatorname {Tan}_{Z/X_S}$ are positive. Then
$s^{*}\operatorname {Tan}_{Z/X_S}$ are positive. Then ![]() ${{\mathscr M}}_Z^{>0}\to S$ is a cohomologically smooth morphism of locally spatial diamonds.
${{\mathscr M}}_Z^{>0}\to S$ is a cohomologically smooth morphism of locally spatial diamonds.
Example 4.2.2 Let ![]() $S=\eta =\operatorname {Spa}(C,\mathcal {O}_C)$, where
$S=\eta =\operatorname {Spa}(C,\mathcal {O}_C)$, where ![]() $C$ is an algebraically closed perfectoid field of characteristic
$C$ is an algebraically closed perfectoid field of characteristic ![]() $0$, and let
$0$, and let ![]() $Z={{\mathbf {V}}}({{\mathcal {E}}}_S(H))\to X_S$ be the geometric vector bundle attached to
$Z={{\mathbf {V}}}({{\mathcal {E}}}_S(H))\to X_S$ be the geometric vector bundle attached to ![]() ${{\mathcal {E}}}_S(H)$, where
${{\mathcal {E}}}_S(H)$, where ![]() $H$ is a
$H$ is a ![]() $p$-divisible group over the residue field of
$p$-divisible group over the residue field of ![]() $C$. Then
$C$. Then ![]() ${{\mathscr M}}_Z=H^{0}({{\mathcal {E}}}_S(H))$ is isomorphic to
${{\mathscr M}}_Z=H^{0}({{\mathcal {E}}}_S(H))$ is isomorphic to ![]() $\tilde {H}_\eta ^{\operatorname{ad}}$ by Proposition 3.2.1. Let
$\tilde {H}_\eta ^{\operatorname{ad}}$ by Proposition 3.2.1. Let ![]() $s\colon X_{{{\mathscr M}}_Z}\to Z$ be the universal morphism; then
$s\colon X_{{{\mathscr M}}_Z}\to Z$ be the universal morphism; then ![]() $s^{*}\operatorname {Tan}_{Z/X_S}$ is the constant Banach–Colmez space associated to
$s^{*}\operatorname {Tan}_{Z/X_S}$ is the constant Banach–Colmez space associated to ![]() $H$ (i.e., the pull-back of
$H$ (i.e., the pull-back of ![]() ${{\mathcal {E}}}_S(H)$ along
${{\mathcal {E}}}_S(H)$ along ![]() $X_{{{\mathscr M}}_Z} \rightarrow X_S$). This has vanishing
$X_{{{\mathscr M}}_Z} \rightarrow X_S$). This has vanishing ![]() $H^{1}$ if and only if
$H^{1}$ if and only if ![]() $H$ has no étale part. This is true if and only if
$H$ has no étale part. This is true if and only if ![]() ${{\mathscr M}}_Z^{>0}$ is isomorphic to a perfectoid open ball. The perfectoid open ball is cohomologically smooth, in accord with Theorem 4.2.1. In contrast, if the étale quotient
${{\mathscr M}}_Z^{>0}$ is isomorphic to a perfectoid open ball. The perfectoid open ball is cohomologically smooth, in accord with Theorem 4.2.1. In contrast, if the étale quotient ![]() $H^{\mathop e\limits{{\prime}}t}$ has height
$H^{\mathop e\limits{{\prime}}t}$ has height ![]() $d > 0$, then
$d > 0$, then ![]() $\pi _0(\tilde {H}_{\eta }^{\operatorname{ad}})\cong \mathbf {Q}_p^{d}$ implies that
$\pi _0(\tilde {H}_{\eta }^{\operatorname{ad}})\cong \mathbf {Q}_p^{d}$ implies that ![]() $\tilde {H}_{\eta }^{\operatorname{ad}}$ is not cohomologically smooth.
$\tilde {H}_{\eta }^{\operatorname{ad}}$ is not cohomologically smooth.
In the setup of Theorem 4.2.1, suppose that ![]() $x= \operatorname {Spa}(C,\mathcal {O}_C)\to S$ is a geometric point, and that
$x= \operatorname {Spa}(C,\mathcal {O}_C)\to S$ is a geometric point, and that ![]() $x\to {{\mathscr M}}_Z^{>0}$ is an
$x\to {{\mathscr M}}_Z^{>0}$ is an ![]() $S$-morphism, corresponding to a section
$S$-morphism, corresponding to a section ![]() $s\colon X_C\to Z$. Then
$s\colon X_C\to Z$. Then ![]() $s^{*}\operatorname {Tan}_{Z/X_S}$ is a vector bundle on
$s^{*}\operatorname {Tan}_{Z/X_S}$ is a vector bundle on ![]() $X_C$. In light of the discussion in the previous section, we are tempted to interpret
$X_C$. In light of the discussion in the previous section, we are tempted to interpret ![]() $H^{0}(X_C,s^{*}\operatorname {Tan}_{Z/X_S})$ as the ‘tangent space of
$H^{0}(X_C,s^{*}\operatorname {Tan}_{Z/X_S})$ as the ‘tangent space of ![]() ${{\mathscr M}}_Z^{>0}\to S$ at
${{\mathscr M}}_Z^{>0}\to S$ at ![]() $x$’. At points
$x$’. At points ![]() $x$ where
$x$ where ![]() $s^{*}\operatorname {Tan}_{Z/X_S}$ has only positive Harder–Narasimhan slopes, this tangent space is a perfectoid open ball.
$s^{*}\operatorname {Tan}_{Z/X_S}$ has only positive Harder–Narasimhan slopes, this tangent space is a perfectoid open ball.
5. Proof of the main theorem
5.1 Dilatations and modifications
As preparation for the proof of Theorem 1.0.1, we review the notion of a dilatation of a scheme at a locally closed subscheme [Reference Bosch, Lütkebohmert and RaynaudBLR90, § 3.2].
Throughout this subsection, we fix some data. Let ![]() $X$ be a curve, meaning that
$X$ be a curve, meaning that ![]() $X$ is a scheme which is locally the spectrum of a Dedekind ring. Let
$X$ is a scheme which is locally the spectrum of a Dedekind ring. Let ![]() $\infty \in X$ be a closed point with residue field
$\infty \in X$ be a closed point with residue field ![]() $C$. Let
$C$. Let ![]() $i_\infty \colon \operatorname {Spec} C \to X$ be the embedding, and let
$i_\infty \colon \operatorname {Spec} C \to X$ be the embedding, and let ![]() $\xi \in \mathcal {O}_{X,\infty }$ be a local uniformizer at
$\xi \in \mathcal {O}_{X,\infty }$ be a local uniformizer at ![]() $\infty$.
$\infty$.
Proposition 5.1.1 Let ![]() $V\to X$ be a morphism of finite type, and let
$V\to X$ be a morphism of finite type, and let ![]() $Y\subset V_\infty$ be a locally closed subscheme of the fiber of
$Y\subset V_\infty$ be a locally closed subscheme of the fiber of ![]() $V$ at
$V$ at ![]() $\infty$.
$\infty$.
There exists a morphism of ![]() $X$-schemes
$X$-schemes ![]() $V'\to V$ which is universal for the following property:
$V'\to V$ which is universal for the following property: ![]() $V'\to X$ is flat at
$V'\to X$ is flat at ![]() $\infty$, and
$\infty$, and ![]() $V_\infty '\to V_\infty$ factors through
$V_\infty '\to V_\infty$ factors through ![]() $Y\subset V_\infty$.
$Y\subset V_\infty$.
The ![]() $X$-scheme
$X$-scheme ![]() $V'$ is the dilatation of
$V'$ is the dilatation of ![]() $V$ at
$V$ at ![]() $Y$. We review here its construction.
$Y$. We review here its construction.
First suppose that ![]() $Y\subset V_\infty$ is closed. Let
$Y\subset V_\infty$ is closed. Let ![]() ${{\mathscr I}}\subset \mathcal {O}_V$ be the ideal sheaf which cuts out
${{\mathscr I}}\subset \mathcal {O}_V$ be the ideal sheaf which cuts out ![]() $Y$. Let
$Y$. Let ![]() $B\to V$ be the blow-up of
$B\to V$ be the blow-up of ![]() $V$ along
$V$ along ![]() $Y$. Then
$Y$. Then ![]() ${{\mathscr I}}\cdot \mathcal {O}_B$ is a locally principal ideal sheaf. The dilatation
${{\mathscr I}}\cdot \mathcal {O}_B$ is a locally principal ideal sheaf. The dilatation ![]() $V'$ of
$V'$ of ![]() $V$ at
$V$ at ![]() $Y$ is the open subscheme of
$Y$ is the open subscheme of ![]() $B$ obtained by imposing the condition that the ideal
$B$ obtained by imposing the condition that the ideal ![]() $({{\mathscr I}}\cdot \mathcal {O}_B)_x\subset \mathcal {O}_{B,x}$ is generated by
$({{\mathscr I}}\cdot \mathcal {O}_B)_x\subset \mathcal {O}_{B,x}$ is generated by ![]() $\xi$ at all
$\xi$ at all ![]() $x\in B$ lying over
$x\in B$ lying over ![]() $\infty$.
$\infty$.
We give here an explicit local description of the dilatation ![]() $V'$. Let
$V'$. Let ![]() $\operatorname {Spec} A$ be an affine neighborhood of
$\operatorname {Spec} A$ be an affine neighborhood of ![]() $\infty$, such that
$\infty$, such that ![]() $\xi \in A$, and let
$\xi \in A$, and let ![]() $\operatorname {Spec} R\subset V$ be an open subset lying over
$\operatorname {Spec} R\subset V$ be an open subset lying over ![]() $\operatorname {Spec} A$. Let
$\operatorname {Spec} A$. Let ![]() $I=(f_1,\ldots ,f_n)$ be the restriction of
$I=(f_1,\ldots ,f_n)$ be the restriction of ![]() ${{\mathscr I}}$ to
${{\mathscr I}}$ to ![]() $\operatorname {Spec} R$, so that
$\operatorname {Spec} R$, so that ![]() $I$ cuts out
$I$ cuts out ![]() $Y\cap \operatorname {Spec} A$. Then the restriction of
$Y\cap \operatorname {Spec} A$. Then the restriction of ![]() $V'\to V$ to
$V'\to V$ to ![]() $\operatorname {Spec} R$ is
$\operatorname {Spec} R$ is ![]() $\operatorname {Spec} R'$, where
$\operatorname {Spec} R'$, where
Now suppose ![]() $Y\subset V_\infty$ is only locally closed, so that
$Y\subset V_\infty$ is only locally closed, so that ![]() $Y$ is open in its closure
$Y$ is open in its closure ![]() $\overline {Y}$. Then the dilatation of
$\overline {Y}$. Then the dilatation of ![]() $V$ at
$V$ at ![]() $Y$ is the dilatation of
$Y$ is the dilatation of ![]() $V\backslash (\overline {Y}\backslash Y)$ at
$V\backslash (\overline {Y}\backslash Y)$ at ![]() $Y$.
$Y$.
Note that a dilatation ![]() $V'\to V$ is an isomorphism away from
$V'\to V$ is an isomorphism away from ![]() $\infty$, and that it is affine.
$\infty$, and that it is affine.
Example 5.1.2 Let
be an exact sequence of ![]() $\mathcal {O}_X$-modules, where
$\mathcal {O}_X$-modules, where ![]() ${{\mathcal {E}}}$ (and thus
${{\mathcal {E}}}$ (and thus ![]() ${{\mathcal {E}}}'$) is locally free, and
${{\mathcal {E}}}'$) is locally free, and ![]() $W$ is a
$W$ is a ![]() $C$-vector space. (This is an elementary modification of the vector bundle
$C$-vector space. (This is an elementary modification of the vector bundle ![]() ${{\mathcal {E}}}$.) Let
${{\mathcal {E}}}$.) Let ![]() $K=\ker ({{\mathcal {E}}}_\infty \to W)$.
$K=\ker ({{\mathcal {E}}}_\infty \to W)$.
Let ![]() ${{\mathbf {V}}}({{\mathcal {E}}})\to X$ be the geometric vector bundle corresponding to
${{\mathbf {V}}}({{\mathcal {E}}})\to X$ be the geometric vector bundle corresponding to ![]() ${{\mathcal {E}}}$. Similarly, we have
${{\mathcal {E}}}$. Similarly, we have ![]() ${{\mathbf {V}}}({{\mathcal {E}}}')\to X$, and an
${{\mathbf {V}}}({{\mathcal {E}}}')\to X$, and an ![]() $X$-morphism
$X$-morphism ![]() ${{\mathbf {V}}}({{\mathcal {E}}}')\to {{\mathbf {V}}}({{\mathcal {E}}})$. Let
${{\mathbf {V}}}({{\mathcal {E}}}')\to {{\mathbf {V}}}({{\mathcal {E}}})$. Let ![]() ${{\mathbf {V}}}(K)\subset {{\mathbf {V}}}({{\mathcal {E}}})_\infty$ be the affine space associated to
${{\mathbf {V}}}(K)\subset {{\mathbf {V}}}({{\mathcal {E}}})_\infty$ be the affine space associated to ![]() $K\subset {{\mathcal {E}}}_\infty$. We claim that
$K\subset {{\mathcal {E}}}_\infty$. We claim that ![]() ${{\mathbf {V}}}({{\mathcal {E}}}')$ is isomorphic to the dilatation
${{\mathbf {V}}}({{\mathcal {E}}}')$ is isomorphic to the dilatation ![]() ${{\mathbf {V}}}({{\mathcal {E}}})'$ of
${{\mathbf {V}}}({{\mathcal {E}}})'$ of ![]() ${{\mathbf {V}}}({{\mathcal {E}}})$ at
${{\mathbf {V}}}({{\mathcal {E}}})$ at ![]() ${{\mathbf {V}}}(K)$. Indeed, by the universal property of dilatations, there is a morphism
${{\mathbf {V}}}(K)$. Indeed, by the universal property of dilatations, there is a morphism ![]() ${{\mathbf {V}}}({{\mathcal {E}}}')\to {{\mathbf {V}}}({{\mathcal {E}}})'$, which is an isomorphism away from
${{\mathbf {V}}}({{\mathcal {E}}}')\to {{\mathbf {V}}}({{\mathcal {E}}})'$, which is an isomorphism away from ![]() $\infty$.
$\infty$.
To see that ![]() ${{\mathbf {V}}}({{\mathcal {E}}}')\to {{\mathbf {V}}}({{\mathcal {E}}})'$ is an isomorphism, it suffices to work over
${{\mathbf {V}}}({{\mathcal {E}}}')\to {{\mathbf {V}}}({{\mathcal {E}}})'$ is an isomorphism, it suffices to work over ![]() $\mathcal {O}_{X,\infty }$. Over this base, we may give a basis
$\mathcal {O}_{X,\infty }$. Over this base, we may give a basis ![]() $f_1,\ldots ,f_n$ of global sections of
$f_1,\ldots ,f_n$ of global sections of ![]() ${{\mathcal {E}}}$, with
${{\mathcal {E}}}$, with ![]() $f_1,\ldots ,f_k$ lifting a basis for
$f_1,\ldots ,f_k$ lifting a basis for ![]() $K\subset {{\mathcal {E}}}_\infty$. Then the localization of
$K\subset {{\mathcal {E}}}_\infty$. Then the localization of ![]() ${{\mathbf {V}}}({{\mathcal {E}}})'\to {{\mathbf {V}}}({{\mathcal {E}}})$ at
${{\mathbf {V}}}({{\mathcal {E}}})'\to {{\mathbf {V}}}({{\mathcal {E}}})$ at ![]() $\infty$ is isomorphic to
$\infty$ is isomorphic to
This agrees with the localization of ![]() ${{\mathbf {V}}}({{\mathcal {E}}}')\to {{\mathbf {V}}}({{\mathcal {E}}})$ at
${{\mathbf {V}}}({{\mathcal {E}}}')\to {{\mathbf {V}}}({{\mathcal {E}}})$ at ![]() $\infty$.
$\infty$.
Lemma 5.1.3 Let ![]() $V\to X$ be a smooth morphism, let
$V\to X$ be a smooth morphism, let ![]() $Y\subset V_\infty$ be a smooth locally closed subscheme, and let
$Y\subset V_\infty$ be a smooth locally closed subscheme, and let ![]() $\pi \colon V'\to V$ be the dilatation of
$\pi \colon V'\to V$ be the dilatation of ![]() $V$ at
$V$ at ![]() $Y$. Then
$Y$. Then ![]() $V'\to X$ is smooth, and
$V'\to X$ is smooth, and ![]() $\operatorname {Tan}_{V'/X}$ lies in an exact sequence of
$\operatorname {Tan}_{V'/X}$ lies in an exact sequence of ![]() $\mathcal {O}_{V'}$-modules
$\mathcal {O}_{V'}$-modules
where ![]() $N_{Y/V_\infty }$ is the normal bundle of
$N_{Y/V_\infty }$ is the normal bundle of ![]() $Y\subset V_\infty$, and
$Y\subset V_\infty$, and ![]() $j\colon Y\to V$ is the inclusion.
$j\colon Y\to V$ is the inclusion.
Finally, let ![]() $T\to X$ be a morphism which is flat at
$T\to X$ be a morphism which is flat at ![]() $\infty$, and let
$\infty$, and let ![]() $s\colon T\to V$ be a morphism of
$s\colon T\to V$ be a morphism of ![]() $X$-schemes, such that
$X$-schemes, such that ![]() $s_\infty$ factors through
$s_\infty$ factors through ![]() $Y$. By the universal property of dilatations,
$Y$. By the universal property of dilatations, ![]() $s$ factors through a morphism
$s$ factors through a morphism ![]() $s'\colon T\to V'$. Then we have an exact sequence of
$s'\colon T\to V'$. Then we have an exact sequence of ![]() $\mathcal {O}_V$-modules
$\mathcal {O}_V$-modules
Proof. One reduces to the case that ![]() $Y$ is closed in
$Y$ is closed in ![]() $V_\infty$. The smoothness of
$V_\infty$. The smoothness of ![]() $V'\to X$ is [Reference Bosch, Lütkebohmert and RaynaudBLR90, § 3.2, Proposition 3]. We turn to the exact sequence (5.1.1). The morphism
$V'\to X$ is [Reference Bosch, Lütkebohmert and RaynaudBLR90, § 3.2, Proposition 3]. We turn to the exact sequence (5.1.1). The morphism ![]() $\operatorname {Tan}_{V'/X}\to \pi ^{*}\operatorname {Tan}_{V/X}$ comes from functoriality of the tangent bundle. To construct the morphism
$\operatorname {Tan}_{V'/X}\to \pi ^{*}\operatorname {Tan}_{V/X}$ comes from functoriality of the tangent bundle. To construct the morphism ![]() $\pi ^{*}\operatorname {Tan}_{V/X}\to \pi ^{*}j_*N_{Y/V_\infty }$, we consider the diagram
$\pi ^{*}\operatorname {Tan}_{V/X}\to \pi ^{*}j_*N_{Y/V_\infty }$, we consider the diagram

in which the outer rectangle is cartesian. For its part, the normal bundle ![]() $N_{Y/V_\infty }$ sits in an exact sequence of
$N_{Y/V_\infty }$ sits in an exact sequence of ![]() $\mathcal {O}_Y$-modules
$\mathcal {O}_Y$-modules
The composite
 \begin{align*} i_{V'}^{*}\pi^{*}\operatorname{Tan}_{V/X} & = \pi_\infty^{*} i_V^{*} \operatorname{Tan}_{V/X}\\ &\cong \pi_\infty^{*} \operatorname{Tan}_{V_\infty/C} \\ &=(\pi_\infty')^{*} i_Y^{*} \operatorname{Tan}_{V/C} \\ &\to (\pi_\infty')^{*} N_{Y/V_\infty} \end{align*}
\begin{align*} i_{V'}^{*}\pi^{*}\operatorname{Tan}_{V/X} & = \pi_\infty^{*} i_V^{*} \operatorname{Tan}_{V/X}\\ &\cong \pi_\infty^{*} \operatorname{Tan}_{V_\infty/C} \\ &=(\pi_\infty')^{*} i_Y^{*} \operatorname{Tan}_{V/C} \\ &\to (\pi_\infty')^{*} N_{Y/V_\infty} \end{align*}induces by adjunction a morphism
where the last step is justified because ![]() $j$ is a closed immersion.
$j$ is a closed immersion.
We check that (5.1.1) is exact using our explicit description of ![]() $V'$. The sequence is clearly exact away from the preimage of
$V'$. The sequence is clearly exact away from the preimage of ![]() $Y$ in
$Y$ in ![]() $V'$, since on the complement of this locus, the morphism
$V'$, since on the complement of this locus, the morphism ![]() $\pi$ is an isomorphism, and
$\pi$ is an isomorphism, and ![]() $\pi ^{*}j_*=0$. Therefore we let
$\pi ^{*}j_*=0$. Therefore we let ![]() $y\in Y$ and check exactness after localization at
$y\in Y$ and check exactness after localization at ![]() $y$. Let
$y$. Let ![]() ${{\mathcal {I}}}\subset \mathcal {O}_V$ be the ideal sheaf which cuts out
${{\mathcal {I}}}\subset \mathcal {O}_V$ be the ideal sheaf which cuts out ![]() $Y$, and let
$Y$, and let ![]() $I\subset \mathcal {O}_{V,y}$ be the localization of
$I\subset \mathcal {O}_{V,y}$ be the localization of ![]() ${{\mathcal {I}}}$ at
${{\mathcal {I}}}$ at ![]() $y$. Then
$y$. Then ![]() $\mathcal {O}_{V_\infty ,y}=\mathcal {O}_{V,y}/\xi$. Since
$\mathcal {O}_{V_\infty ,y}=\mathcal {O}_{V,y}/\xi$. Since ![]() $Y\subset V_\infty$ are both smooth at
$Y\subset V_\infty$ are both smooth at ![]() $y$, we can find a system of local coordinates
$y$, we can find a system of local coordinates ![]() $\overline {f}_1,\ldots ,\overline {f}_n\in \mathcal {O}_{V_\infty ,y}$ (meaning that the differentials
$\overline {f}_1,\ldots ,\overline {f}_n\in \mathcal {O}_{V_\infty ,y}$ (meaning that the differentials ![]() $d\overline {f}_i$ form a basis for
$d\overline {f}_i$ form a basis for ![]() $\Omega ^{1}_{V_{\infty }/C,y}$), such that
$\Omega ^{1}_{V_{\infty }/C,y}$), such that ![]() $\overline {f}_{k+1},\ldots ,\overline {f}_n$ generate
$\overline {f}_{k+1},\ldots ,\overline {f}_n$ generate ![]() $I/\xi$. If
$I/\xi$. If ![]() $\partial /\partial \overline {f}_i$ are the dual basis, then the stalk of
$\partial /\partial \overline {f}_i$ are the dual basis, then the stalk of ![]() $N_{Y/V_\infty }$ at
$N_{Y/V_\infty }$ at ![]() $y$ is the free
$y$ is the free ![]() $\mathcal {O}_{Y,y}$-module with basis
$\mathcal {O}_{Y,y}$-module with basis ![]() $\partial /\partial \overline {f}_{k+1},\ldots ,\partial /\partial \overline {f}_n$.
$\partial /\partial \overline {f}_{k+1},\ldots ,\partial /\partial \overline {f}_n$.
Choose lifts ![]() $f_i\in \mathcal {O}_{V,y}$ of the
$f_i\in \mathcal {O}_{V,y}$ of the ![]() $\overline {f}_i$. Then
$\overline {f}_i$. Then ![]() $I$ is generated by
$I$ is generated by ![]() $\xi ,f_k,\ldots ,f_n$. The localization of
$\xi ,f_k,\ldots ,f_n$. The localization of ![]() $V'\to V$ over
$V'\to V$ over ![]() $y$ is
$y$ is ![]() $\operatorname {Spec} \mathcal {O}_{V',y}$, where
$\operatorname {Spec} \mathcal {O}_{V',y}$, where ![]() $\mathcal {O}_{V',y}=\mathcal {O}_{V,y}[g_{k+1},\ldots ,g_n]/(\xi \text {-torsion})$, where
$\mathcal {O}_{V',y}=\mathcal {O}_{V,y}[g_{k+1},\ldots ,g_n]/(\xi \text {-torsion})$, where ![]() $\xi g_i=f_i$ for
$\xi g_i=f_i$ for ![]() $i=k+1,\ldots ,n$. Then the stalk of
$i=k+1,\ldots ,n$. Then the stalk of ![]() $\operatorname {Tan}_{V'/X}$ at
$\operatorname {Tan}_{V'/X}$ at ![]() $y$ is the free
$y$ is the free ![]() $\mathcal {O}_{V',y}$-module with basis
$\mathcal {O}_{V',y}$-module with basis ![]() $\partial /\partial f_1,\ldots ,\partial /\partial f_k,\partial /\partial g_{k+1},\ldots ,\partial /\partial g_n$, whereas the stalk of
$\partial /\partial f_1,\ldots ,\partial /\partial f_k,\partial /\partial g_{k+1},\ldots ,\partial /\partial g_n$, whereas the stalk of ![]() $\pi ^{*}\operatorname {Tan}_{V/X}$ at
$\pi ^{*}\operatorname {Tan}_{V/X}$ at ![]() $y$ is the free
$y$ is the free ![]() $\mathcal {O}_{V',y}$-module with basis
$\mathcal {O}_{V',y}$-module with basis ![]() $\partial /\partial f_1,\ldots ,\partial / \partial f_n$. The quotient between these stalks is evidently the free module over
$\partial /\partial f_1,\ldots ,\partial / \partial f_n$. The quotient between these stalks is evidently the free module over ![]() $\mathcal {O}_{V',y}/\xi$ with basis
$\mathcal {O}_{V',y}/\xi$ with basis ![]() $\partial /\partial f_{k+1},\ldots ,\partial /\partial f_n$, and this agrees with the stalk of
$\partial /\partial f_{k+1},\ldots ,\partial /\partial f_n$, and this agrees with the stalk of ![]() $\pi ^{*}j_*N_{Y/V_\infty }$.
$\pi ^{*}j_*N_{Y/V_\infty }$.
Given a morphism of ![]() $X$-schemes
$X$-schemes ![]() $s\colon T\to V$ as in the lemma, we apply
$s\colon T\to V$ as in the lemma, we apply ![]() $(s')^{*}$ to (5.1.1); this is exact because
$(s')^{*}$ to (5.1.1); this is exact because ![]() $s'$ is flat. The term on the right is
$s'$ is flat. The term on the right is ![]() $s^{*}j_*N_{Y/V_\infty }\cong i_{T_\infty *}s_\infty ^{*} N_{Y/V_\infty }$ (once again, this is valid because
$s^{*}j_*N_{Y/V_\infty }\cong i_{T_\infty *}s_\infty ^{*} N_{Y/V_\infty }$ (once again, this is valid because ![]() $j$ is a closed immersion).
$j$ is a closed immersion).
5.2 The space  ${{\mathscr M}}_{H,\infty }$ as global sections of a scheme over
${{\mathscr M}}_{H,\infty }$ as global sections of a scheme over  $X_C$
$X_C$
We will prove Theorem 1.0.1 for the Rapoport–Zink spaces of the form ![]() ${{\mathscr M}}_{H,\infty }$ before proceeding to the general case. Let
${{\mathscr M}}_{H,\infty }$ before proceeding to the general case. Let ![]() $H$ be a
$H$ be a ![]() $p$-divisible group of height
$p$-divisible group of height ![]() $n$ and dimension
$n$ and dimension ![]() $d$ over a perfect field
$d$ over a perfect field ![]() $k$. In this context,
$k$. In this context, ![]() $\breve {E}=W(k)[1/p]$. Let
$\breve {E}=W(k)[1/p]$. Let ![]() ${{\mathcal {E}}}={{\mathcal {E}}}_C(H)$. Throughout, we will be interpreting
${{\mathcal {E}}}={{\mathcal {E}}}_C(H)$. Throughout, we will be interpreting ![]() ${{\mathscr M}}_{H,\infty }$ as a functor on
${{\mathscr M}}_{H,\infty }$ as a functor on ![]() $\operatorname {Perf}_{\breve {E}}$ as in Proposition 3.2.2.
$\operatorname {Perf}_{\breve {E}}$ as in Proposition 3.2.2.
We have a determinant morphism ![]() $\det \colon {{\mathscr M}}_{H,\infty }\to {{\mathscr M}}_{\det H, \infty }$. Let
$\det \colon {{\mathscr M}}_{H,\infty }\to {{\mathscr M}}_{\det H, \infty }$. Let ![]() $\tau \in {{\mathscr M}}_{\det H,\infty }(C)$ be a geometric point of
$\tau \in {{\mathscr M}}_{\det H,\infty }(C)$ be a geometric point of ![]() ${{\mathscr M}}_{\det H, \infty }$. This point corresponds to a section
${{\mathscr M}}_{\det H, \infty }$. This point corresponds to a section ![]() $\tau$ of
$\tau$ of ![]() ${{\mathbf {V}}}(\det {{\mathcal {E}}})\to X_C$, which we also call
${{\mathbf {V}}}(\det {{\mathcal {E}}})\to X_C$, which we also call ![]() $\tau$. Let
$\tau$. Let ![]() ${{\mathscr M}}_{H,\infty }^{\tau }$ be the fiber of
${{\mathscr M}}_{H,\infty }^{\tau }$ be the fiber of ![]() $\det$ over
$\det$ over ![]() $\tau$.
$\tau$.
Our first order of business is to express ![]() ${{\mathscr M}}_{H,\infty }^{\tau }$ as the space of global sections of a smooth morphism
${{\mathscr M}}_{H,\infty }^{\tau }$ as the space of global sections of a smooth morphism ![]() $Z\to X_C$, defined as follows. We have the geometric vector bundle
$Z\to X_C$, defined as follows. We have the geometric vector bundle ![]() ${{\mathbf {V}}}({{\mathcal {E}}}^{n})\to X$, whose global sections parametrize morphisms
${{\mathbf {V}}}({{\mathcal {E}}}^{n})\to X$, whose global sections parametrize morphisms ![]() $s\colon \mathcal {O}_{X_C}^{n}\to {{\mathcal {E}}}$. Let
$s\colon \mathcal {O}_{X_C}^{n}\to {{\mathcal {E}}}$. Let ![]() $U_{n-d}$ be the locally closed subscheme of the fiber of
$U_{n-d}$ be the locally closed subscheme of the fiber of ![]() ${{\mathbf {V}}}({{\mathcal {E}}}^{n})$ over
${{\mathbf {V}}}({{\mathcal {E}}}^{n})$ over ![]() $\infty$, which parametrizes all morphisms of rank
$\infty$, which parametrizes all morphisms of rank ![]() $n-d$. We consider the dilatation
$n-d$. We consider the dilatation ![]() ${{\mathbf {V}}}({{\mathcal {E}}}^{n})^{\operatorname {rk}_\infty = n-d} \rightarrow {{\mathbf {V}}}({{\mathcal {E}}}^{n})$ of
${{\mathbf {V}}}({{\mathcal {E}}}^{n})^{\operatorname {rk}_\infty = n-d} \rightarrow {{\mathbf {V}}}({{\mathcal {E}}}^{n})$ of ![]() ${{\mathbf {V}}}({{\mathcal {E}}}^{n})$ along
${{\mathbf {V}}}({{\mathcal {E}}}^{n})$ along ![]() $U_{n-d}$. For any flat
$U_{n-d}$. For any flat ![]() $X_C$-scheme
$X_C$-scheme ![]() $T$,
$T$, ![]() ${{\mathbf {V}}}({{\mathcal {E}}}^{n})^{\operatorname {rk}_\infty = n-d}(T)$ is the set of all
${{\mathbf {V}}}({{\mathcal {E}}}^{n})^{\operatorname {rk}_\infty = n-d}(T)$ is the set of all ![]() $s \colon {{\mathcal {O}}}_T^{n} \rightarrow {{\mathcal {E}}}_T$ such that
$s \colon {{\mathcal {O}}}_T^{n} \rightarrow {{\mathcal {E}}}_T$ such that ![]() $\textrm {cok}(s) \otimes C$ is projective
$\textrm {cok}(s) \otimes C$ is projective ![]() ${{\mathcal {O}}}_T \otimes C$-module of rank
${{\mathcal {O}}}_T \otimes C$-module of rank ![]() $d$. Define
$d$. Define ![]() $Z$ as the following cartesian product.
$Z$ as the following cartesian product.

Lemma 5.2.1 Let ![]() ${{\mathscr M}}_Z$ be the functor which inputs a perfectoid space
${{\mathscr M}}_Z$ be the functor which inputs a perfectoid space ![]() $T/C$ and outputs the set of sections of
$T/C$ and outputs the set of sections of ![]() $Z\to X_C$ over
$Z\to X_C$ over ![]() $X_T$. Then
$X_T$. Then ![]() ${{\mathscr M}}_Z$ is isomorphic to
${{\mathscr M}}_Z$ is isomorphic to ![]() ${{\mathscr M}}_{H,\infty }^{\tau }$.
${{\mathscr M}}_{H,\infty }^{\tau }$.
Proof. Let ![]() $T=\operatorname {Spa}(R,R^{+})$ be an affinoid perfectoid space over
$T=\operatorname {Spa}(R,R^{+})$ be an affinoid perfectoid space over ![]() $C$. The morphism
$C$. The morphism ![]() $X_T\to X_C$ is flat. (This can be checked locally:
$X_T\to X_C$ is flat. (This can be checked locally: ![]() $B_{\operatorname {dR}}^{+}(R)$ is torsion-free over the discrete valuation ring
$B_{\operatorname {dR}}^{+}(R)$ is torsion-free over the discrete valuation ring ![]() $B_{\operatorname {dR}}^{+}(C)$, and so it is flat.) By the description in (5.2.1), an
$B_{\operatorname {dR}}^{+}(C)$, and so it is flat.) By the description in (5.2.1), an ![]() $X_T$-point of
$X_T$-point of ![]() ${{\mathscr M}}_Z$ corresponds to a morphism
${{\mathscr M}}_Z$ corresponds to a morphism ![]() $\sigma \colon \mathcal {O}_{X_T}^{n}\to {{\mathcal {E}}}_T(H)$ which has the following properties.
$\sigma \colon \mathcal {O}_{X_T}^{n}\to {{\mathcal {E}}}_T(H)$ which has the following properties.
(1) The cokernel of
 $\sigma _\infty$ is a projective
$\sigma _\infty$ is a projective  $R$-module quotient of
$R$-module quotient of  ${{\mathcal {E}}}_T(H)_\infty$ of rank
${{\mathcal {E}}}_T(H)_\infty$ of rank  $d$.
$d$.(2) The determinant of
 $\sigma$ equals
$\sigma$ equals  $\tau$.
$\tau$.
On the other hand, by Proposition 3.2.2, ![]() ${{\mathscr M}}_{H,\infty }(T)$ is the set of morphisms
${{\mathscr M}}_{H,\infty }(T)$ is the set of morphisms ![]() $\sigma \colon \mathcal {O}_{X_T}^{n}\to {{\mathcal {E}}}_T(H)$ satisfying the following.
$\sigma \colon \mathcal {O}_{X_T}^{n}\to {{\mathcal {E}}}_T(H)$ satisfying the following.
(
 $1'$) The cokernel of
$1'$) The cokernel of  $\sigma$ is
$\sigma$ is  $i_{\infty *} W$, for a projective
$i_{\infty *} W$, for a projective  $R$-module quotient
$R$-module quotient  $W$ of
$W$ of  ${{\mathcal {E}}}_T(H)_\infty$ of rank
${{\mathcal {E}}}_T(H)_\infty$ of rank  $d$.
$d$.(
 $2$) The determinant of
$2$) The determinant of  $\sigma$ equals
$\sigma$ equals  $\tau$.
$\tau$.
We claim the two sets of conditions are equivalent for a morphism ![]() $\sigma \colon \mathcal {O}_{X_T}^{n}\to {{\mathcal {E}}}_T(H)$. Clearly (
$\sigma \colon \mathcal {O}_{X_T}^{n}\to {{\mathcal {E}}}_T(H)$. Clearly (![]() $1'$) implies (1), so that (
$1'$) implies (1), so that (![]() $1'$) and (
$1'$) and (![]() $2$) together imply (1) and (2) together. Conversely, suppose (1) and (2) hold. Since
$2$) together imply (1) and (2) together. Conversely, suppose (1) and (2) hold. Since ![]() $\tau$ represents a point of
$\tau$ represents a point of ![]() ${{\mathscr M}}_{\det H,\infty }$, it is an isomorphism outside of
${{\mathscr M}}_{\det H,\infty }$, it is an isomorphism outside of ![]() $\infty$, and therefore so is
$\infty$, and therefore so is ![]() $\sigma$. This means that
$\sigma$. This means that ![]() $\operatorname {cok} \sigma$ is supported at
$\operatorname {cok} \sigma$ is supported at ![]() $\infty$. Thus
$\infty$. Thus ![]() $\operatorname {cok} \sigma$ is a
$\operatorname {cok} \sigma$ is a ![]() $B_{\operatorname {dR}}^{+}(R)$-module. For degree reasons, the length of
$B_{\operatorname {dR}}^{+}(R)$-module. For degree reasons, the length of ![]() $(\operatorname {cok} \sigma )\otimes _{B_{\operatorname {dR}}^{+}(R)} B_{\operatorname {dR}}^{+}(C')$ has length
$(\operatorname {cok} \sigma )\otimes _{B_{\operatorname {dR}}^{+}(R)} B_{\operatorname {dR}}^{+}(C')$ has length ![]() $d$ for every geometric point
$d$ for every geometric point ![]() $\operatorname {Spa}(C',(C')^{+})\to T$. Whereas condition (1) says that
$\operatorname {Spa}(C',(C')^{+})\to T$. Whereas condition (1) says that ![]() $(\operatorname {cok} \sigma )\otimes _{B_{\operatorname {dR}}^{+}(R)} R$ is a projective
$(\operatorname {cok} \sigma )\otimes _{B_{\operatorname {dR}}^{+}(R)} R$ is a projective ![]() $R$-module of rank
$R$-module of rank ![]() $d$. This shows that
$d$. This shows that ![]() $(\operatorname {cok} \sigma )$ is already a projective
$(\operatorname {cok} \sigma )$ is already a projective ![]() $R$-module of rank
$R$-module of rank ![]() $d$, which is condition (
$d$, which is condition (![]() $1'$).
$1'$).
Lemma 5.2.2 The morphism ![]() $Z\to X_C$ is smooth.
$Z\to X_C$ is smooth.
Proof. Let ![]() $\infty '\in X_C$ be a closed point, with residue field
$\infty '\in X_C$ be a closed point, with residue field ![]() $C'$. It suffices to show that the stalk of
$C'$. It suffices to show that the stalk of ![]() $Z$ at
$Z$ at ![]() $\infty '$ is smooth over
$\infty '$ is smooth over ![]() $\operatorname {Spec} B_{\operatorname {dR}}^{+}(C')$.
$\operatorname {Spec} B_{\operatorname {dR}}^{+}(C')$.
If ![]() $\infty '\neq \infty$, then this stalk is isomorphic to the variety
$\infty '\neq \infty$, then this stalk is isomorphic to the variety ![]() $({{\mathbf {A}}}^{n^{2}})^{\det = \tau }$ consisting of
$({{\mathbf {A}}}^{n^{2}})^{\det = \tau }$ consisting of ![]() $n\times n$ matrices with fixed determinant
$n\times n$ matrices with fixed determinant ![]() $\tau$. Since
$\tau$. Since ![]() $\tau$ is invertible in
$\tau$ is invertible in ![]() $B_{\operatorname {dR}}^{+}(C')$, this variety is smooth.
$B_{\operatorname {dR}}^{+}(C')$, this variety is smooth.
Now suppose ![]() $\infty '=\infty$. Let
$\infty '=\infty$. Let ![]() $\xi$ be a generator for the kernel of
$\xi$ be a generator for the kernel of ![]() $B_{\operatorname {dR}}^{+}(C)\to C$. Then the stalk of
$B_{\operatorname {dR}}^{+}(C)\to C$. Then the stalk of ![]() $Z$ at
$Z$ at ![]() $\infty$ is isomorphic to the flat
$\infty$ is isomorphic to the flat ![]() $B_{\operatorname {dR}}^{+}(C)$-scheme
$B_{\operatorname {dR}}^{+}(C)$-scheme ![]() $Y$, whose
$Y$, whose ![]() $T$-points for a flat
$T$-points for a flat ![]() $B_{\operatorname {dR}}^{+}(C)$-scheme
$B_{\operatorname {dR}}^{+}(C)$-scheme ![]() $T$ are
$T$ are ![]() $n\times n$ matrices with coefficients in
$n\times n$ matrices with coefficients in ![]() $\Gamma (T,\mathcal {O}_T)$, which are rank
$\Gamma (T,\mathcal {O}_T)$, which are rank ![]() $n-d$ modulo
$n-d$ modulo ![]() $\xi$, and which have fixed determinant
$\xi$, and which have fixed determinant ![]() $\tau$ (which must equal
$\tau$ (which must equal ![]() $u\xi ^{d}$ for a unit
$u\xi ^{d}$ for a unit ![]() $u\in B_{\operatorname {dR}}^{+}(C)$). Consider the open subset
$u\in B_{\operatorname {dR}}^{+}(C)$). Consider the open subset ![]() $Y_0\subset Y$ consisting of matrices
$Y_0\subset Y$ consisting of matrices ![]() $M$ where the first
$M$ where the first ![]() $(n-d)$ columns have rank
$(n-d)$ columns have rank ![]() $(n-d)$. Then the final
$(n-d)$. Then the final ![]() $d$ columns of
$d$ columns of ![]() $M$ are congruent modulo
$M$ are congruent modulo ![]() $\xi$ to a linear combination of the first
$\xi$ to a linear combination of the first ![]() $(n-d)$ columns. After row reduction operations only depending on those first
$(n-d)$ columns. After row reduction operations only depending on those first ![]() $(n-d)$ columns,
$(n-d)$ columns, ![]() $M$ becomes
$M$ becomes
with ![]() $\det Q=w$ for a unit
$\det Q=w$ for a unit ![]() $w\in B_{\operatorname {dR}}^{+}(C)$ which only depends on the first
$w\in B_{\operatorname {dR}}^{+}(C)$ which only depends on the first ![]() $(n-d)$ columns of
$(n-d)$ columns of ![]() $M$. We therefore have a fibration
$M$. We therefore have a fibration ![]() $Y_0\to {{\mathbf {A}}}^{n(n-d)}$, namely projection onto the first
$Y_0\to {{\mathbf {A}}}^{n(n-d)}$, namely projection onto the first ![]() $(n-d)$ columns, whose fibers are
$(n-d)$ columns, whose fibers are ![]() ${{\mathbf {A}}}^{d(n-d)} \times ({{\mathbf {A}}}^{d^{2}})^{\det = w}$, which is smooth. Therefore
${{\mathbf {A}}}^{d(n-d)} \times ({{\mathbf {A}}}^{d^{2}})^{\det = w}$, which is smooth. Therefore ![]() $Y_0$ is smooth. The variety
$Y_0$ is smooth. The variety ![]() $Y$ is covered by opens isomorphic to
$Y$ is covered by opens isomorphic to ![]() $Y_0$, and so it is smooth.
$Y_0$, and so it is smooth.
We intend to apply Theorem 4.2.1 to the morphism ![]() $Z\to X$, and so we need some preparations regarding the relative tangent space of
$Z\to X$, and so we need some preparations regarding the relative tangent space of ![]() ${{\mathbf {V}}}({{\mathcal {E}}}^{n})^{\operatorname {rk}_\infty = n-d}\to X_C$.
${{\mathbf {V}}}({{\mathcal {E}}}^{n})^{\operatorname {rk}_\infty = n-d}\to X_C$.
5.3 A linear algebra lemma
Let ![]() $f\colon V'\to V$ be a rank
$f\colon V'\to V$ be a rank ![]() $r$ linear map between
$r$ linear map between ![]() $n$-dimensional vector spaces over a field
$n$-dimensional vector spaces over a field ![]() $C$. Thus there is an exact sequence
$C$. Thus there is an exact sequence
with ![]() $\dim W=\dim W'=n-r$.
$\dim W=\dim W'=n-r$.
Consider the minor map ![]() $\Lambda \colon \operatorname {Hom}(V',V)\to \operatorname {Hom}(\bigwedge ^{r+1}V',\bigwedge ^{r+1}V)$ given by
$\Lambda \colon \operatorname {Hom}(V',V)\to \operatorname {Hom}(\bigwedge ^{r+1}V',\bigwedge ^{r+1}V)$ given by ![]() $\sigma \mapsto \bigwedge ^{r+1} \sigma$. This is a polynomial map, whose derivative at
$\sigma \mapsto \bigwedge ^{r+1} \sigma$. This is a polynomial map, whose derivative at ![]() $f$ is a linear map
$f$ is a linear map
 \[ D_f\Lambda\colon \operatorname{Hom}(V',V) \to \operatorname{Hom} \biggl (\bigwedge^{r+1}V',\bigwedge^{r+1} V \biggr ). \]
\[ D_f\Lambda\colon \operatorname{Hom}(V',V) \to \operatorname{Hom} \biggl (\bigwedge^{r+1}V',\bigwedge^{r+1} V \biggr ). \]Explicitly, this map is
 \begin{equation} D_f\Lambda(\sigma)(v_1\wedge\cdots \wedge v_{r+1}) = \sum_{i=1}^{r+1} f(v_1)\wedge f(v_2)\wedge \cdots \wedge \sigma(v_i) \wedge \cdots \wedge f(v_{r+1}). \end{equation}
\begin{equation} D_f\Lambda(\sigma)(v_1\wedge\cdots \wedge v_{r+1}) = \sum_{i=1}^{r+1} f(v_1)\wedge f(v_2)\wedge \cdots \wedge \sigma(v_i) \wedge \cdots \wedge f(v_{r+1}). \end{equation}Lemma 5.3.1 Let
be the kernel of the map ![]() $\sigma \mapsto q\circ (\sigma \vert _{W'})$. Then
$\sigma \mapsto q\circ (\sigma \vert _{W'})$. Then ![]() $\ker D_f\Lambda = K$.
$\ker D_f\Lambda = K$.
Proof. Suppose ![]() $\sigma \in K$. Since
$\sigma \in K$. Since ![]() $f$ has rank
$f$ has rank ![]() $r$, the exterior power
$r$, the exterior power ![]() $\bigwedge ^{r+1} V'$ is spanned over
$\bigwedge ^{r+1} V'$ is spanned over ![]() $C$ by elements of the form
$C$ by elements of the form ![]() $v_1\wedge \cdots \wedge v_{r+1}$, where
$v_1\wedge \cdots \wedge v_{r+1}$, where ![]() $v_{r+1}\in \ker f = W'$. Since
$v_{r+1}\in \ker f = W'$. Since ![]() $f(v_{r+1})=0$, the sum in (5.3.1) reduces to
$f(v_{r+1})=0$, the sum in (5.3.1) reduces to
Since ![]() $\sigma \in K$ and
$\sigma \in K$ and ![]() $v_{r+1}\in W'$ we have
$v_{r+1}\in W'$ we have ![]() $\sigma (v_{r+1})\in \ker q=f(V')$, which means that
$\sigma (v_{r+1})\in \ker q=f(V')$, which means that
Thus ![]() $\sigma \in \ker D_f\Lambda$.
$\sigma \in \ker D_f\Lambda$.
Now suppose ![]() $\sigma \in \ker D_f\Lambda$. Let
$\sigma \in \ker D_f\Lambda$. Let ![]() $w\in W'$. We wish to show that
$w\in W'$. We wish to show that ![]() $\sigma (w)\in f(V')$. Let
$\sigma (w)\in f(V')$. Let ![]() $v_1,\ldots ,v_r\in V'$ be vectors for which
$v_1,\ldots ,v_r\in V'$ be vectors for which ![]() $f(v_1),\ldots ,f(v_r)$ is a basis for
$f(v_1),\ldots ,f(v_r)$ is a basis for ![]() $f(V')$. Since
$f(V')$. Since ![]() $\sigma \in \ker D_f\Lambda$, we have
$\sigma \in \ker D_f\Lambda$, we have ![]() $D_f\Lambda (\sigma )(v_1\wedge \cdots \wedge v_r\wedge w)=0$. On the other hand,
$D_f\Lambda (\sigma )(v_1\wedge \cdots \wedge v_r\wedge w)=0$. On the other hand,
because all other terms in the sum in (5.3.1) are 0, owing to ![]() $f(w)=0$. Since the wedge product above is 0, and the
$f(w)=0$. Since the wedge product above is 0, and the ![]() $f(v_i)$ are a basis for
$f(v_i)$ are a basis for ![]() $f(V')$, we must have
$f(V')$, we must have ![]() $\sigma (w)\in f(V')$. Thus
$\sigma (w)\in f(V')$. Thus ![]() $\sigma \in K$.
$\sigma \in K$.
We interpret Lemma 5.3.1 as the calculation of a certain normal bundle. Let ![]() $Y={{\mathbf {V}}}(\operatorname {Hom}(V',V))$ be the affine space over
$Y={{\mathbf {V}}}(\operatorname {Hom}(V',V))$ be the affine space over ![]() $C$ representing morphisms
$C$ representing morphisms ![]() $V'\to V$ over a
$V'\to V$ over a ![]() $C$-scheme, and let
$C$-scheme, and let ![]() $j\colon Y^{\operatorname {rk} =r}\to Y$ be the locally closed subscheme representing morphisms which are everywhere of rank
$j\colon Y^{\operatorname {rk} =r}\to Y$ be the locally closed subscheme representing morphisms which are everywhere of rank ![]() $r$. Thus,
$r$. Thus, ![]() $Y^{\operatorname {rk} = r}$ is an open subset of the fiber over 0 of (the geometric version of) the minor map
$Y^{\operatorname {rk} = r}$ is an open subset of the fiber over 0 of (the geometric version of) the minor map ![]() $\Lambda$. It is well known that
$\Lambda$. It is well known that ![]() $Y^{\operatorname {rk} = r}/C$ is smooth of codimension
$Y^{\operatorname {rk} = r}/C$ is smooth of codimension ![]() $(n-r)^{2}$ in
$(n-r)^{2}$ in ![]() $Y/C$, and so the normal bundle
$Y/C$, and so the normal bundle ![]() $N_{Y^{\operatorname {rk}= r}/Y}$ is locally free of this rank.
$N_{Y^{\operatorname {rk}= r}/Y}$ is locally free of this rank.
We have a universal morphism of ![]() $\mathcal {O}_{Y^{\operatorname {rk}=r}}$-modules
$\mathcal {O}_{Y^{\operatorname {rk}=r}}$-modules ![]() $\sigma \colon \mathcal {O}_{Y^{\operatorname {rk} = r}}\otimes _C V'\to \mathcal {O}_{Y^{\operatorname {rk} = r}}\otimes _C V$. Let
$\sigma \colon \mathcal {O}_{Y^{\operatorname {rk} = r}}\otimes _C V'\to \mathcal {O}_{Y^{\operatorname {rk} = r}}\otimes _C V$. Let ![]() ${{\mathcal {W}}}'=\ker \sigma$ and
${{\mathcal {W}}}'=\ker \sigma$ and ![]() ${{\mathcal {W}}}=\operatorname {cok} \sigma$, so that
${{\mathcal {W}}}=\operatorname {cok} \sigma$, so that ![]() ${{\mathcal {W}}}'$ and
${{\mathcal {W}}}'$ and ![]() ${{\mathcal {W}}}$ are locally free
${{\mathcal {W}}}$ are locally free ![]() $\mathcal {O}_{Y^{\operatorname {rk} = r}}$-modules of rank
$\mathcal {O}_{Y^{\operatorname {rk} = r}}$-modules of rank ![]() $n-r$. We also have the
$n-r$. We also have the ![]() $\mathcal {O}_{Y^{\operatorname {rk} = r}}$-linear morphism
$\mathcal {O}_{Y^{\operatorname {rk} = r}}$-linear morphism ![]() $D\Lambda \colon \mathcal {O}_{Y^{\operatorname {rk}=r}} \otimes _C \operatorname {Hom}(V',V) \rightarrow \mathcal {O}_{Y^{\operatorname {rk}=r}} \otimes _C \operatorname {Hom}(\Lambda ^{r+1}V',\Lambda ^{r+1}V)$, whose kernel is precisely
$D\Lambda \colon \mathcal {O}_{Y^{\operatorname {rk}=r}} \otimes _C \operatorname {Hom}(V',V) \rightarrow \mathcal {O}_{Y^{\operatorname {rk}=r}} \otimes _C \operatorname {Hom}(\Lambda ^{r+1}V',\Lambda ^{r+1}V)$, whose kernel is precisely ![]() $\operatorname {Tan}_{Y^{\operatorname {rk}=r}/C}$. The geometric interpretation of Lemma 5.3.1 is a commutative diagram with short exact rows.
$\operatorname {Tan}_{Y^{\operatorname {rk}=r}/C}$. The geometric interpretation of Lemma 5.3.1 is a commutative diagram with short exact rows.

5.4 Moduli of morphisms of vector bundles with fixed rank at  $\infty$
$\infty$
We return to the setup of § 5.1. We have a curve ![]() $X$ and a closed point
$X$ and a closed point ![]() $\infty \in X$, with inclusion map
$\infty \in X$, with inclusion map ![]() $i_\infty$ and residue field
$i_\infty$ and residue field ![]() $C$.
$C$.
Let ![]() ${{\mathcal {E}}}$ and
${{\mathcal {E}}}$ and ![]() ${{\mathcal {E}}}'$ be rank
${{\mathcal {E}}}'$ be rank ![]() $n$ vector bundles over
$n$ vector bundles over ![]() $X$, with fibers
$X$, with fibers ![]() $V={{\mathcal {E}}}_\infty$ and
$V={{\mathcal {E}}}_\infty$ and ![]() $V'={{\mathcal {E}}}'_\infty$. We have the geometric vector bundle
$V'={{\mathcal {E}}}'_\infty$. We have the geometric vector bundle ![]() ${{\mathbf {V}}}(\operatorname {\mathscr {H} {\mathcal{om}}\,}({{\mathcal {E}}}',{{\mathcal {E}}}))\to X$. If
${{\mathbf {V}}}(\operatorname {\mathscr {H} {\mathcal{om}}\,}({{\mathcal {E}}}',{{\mathcal {E}}}))\to X$. If ![]() $f\colon T\to X$ is a morphism, then
$f\colon T\to X$ is a morphism, then ![]() $T$-points of
$T$-points of ![]() ${{\mathbf {V}}}(\operatorname {\mathscr {H}{\mathcal{om}}\,}({{\mathcal {E}}}',{{\mathcal {E}}}))$ classify
${{\mathbf {V}}}(\operatorname {\mathscr {H}{\mathcal{om}}\,}({{\mathcal {E}}}',{{\mathcal {E}}}))$ classify ![]() $\mathcal {O}_T$-linear maps
$\mathcal {O}_T$-linear maps ![]() $f^{*}{{\mathcal {E}}}'\to f^{*}{{\mathcal {E}}}$.
$f^{*}{{\mathcal {E}}}'\to f^{*}{{\mathcal {E}}}$.
Let ![]() ${{\mathbf {V}}}(\operatorname {\mathscr {H}{\mathcal{om}}\,}({{\mathcal {E}}}',{{\mathcal {E}}}))^{\operatorname {rk}_\infty = r}$ be the dilatation of
${{\mathbf {V}}}(\operatorname {\mathscr {H}{\mathcal{om}}\,}({{\mathcal {E}}}',{{\mathcal {E}}}))^{\operatorname {rk}_\infty = r}$ be the dilatation of ![]() ${{\mathbf {V}}}(\operatorname {\mathscr {H}{\mathcal{om}}\,}({{\mathcal {E}}}',{{\mathcal {E}}}))$ at the locally closed subscheme
${{\mathbf {V}}}(\operatorname {\mathscr {H}{\mathcal{om}}\,}({{\mathcal {E}}}',{{\mathcal {E}}}))$ at the locally closed subscheme ![]() ${{\mathbf {V}}}(\operatorname {Hom}(V',V))^{\operatorname {rk} =r}$ of the fiber
${{\mathbf {V}}}(\operatorname {Hom}(V',V))^{\operatorname {rk} =r}$ of the fiber ![]() ${{\mathbf {V}}}(\operatorname {\mathscr {H}{\mathcal{om}}\,}({{\mathcal {E}}}',{{\mathcal {E}}}))_\infty ={{\mathbf {V}}}(\operatorname {Hom}(V',V))$. This has the following property, for a flat morphism
${{\mathbf {V}}}(\operatorname {\mathscr {H}{\mathcal{om}}\,}({{\mathcal {E}}}',{{\mathcal {E}}}))_\infty ={{\mathbf {V}}}(\operatorname {Hom}(V',V))$. This has the following property, for a flat morphism ![]() $f\colon T\to X$: the
$f\colon T\to X$: the ![]() $X$-morphisms
$X$-morphisms ![]() $s\colon T\to {{\mathbf {V}}}(\operatorname {\mathscr {H}{\mathcal{om}}\,}({{\mathcal {E}}}',{{\mathcal {E}}}))^{\operatorname {rk}_\infty = r}$ parametrize those
$s\colon T\to {{\mathbf {V}}}(\operatorname {\mathscr {H}{\mathcal{om}}\,}({{\mathcal {E}}}',{{\mathcal {E}}}))^{\operatorname {rk}_\infty = r}$ parametrize those ![]() $\mathcal {O}_T$-linear maps
$\mathcal {O}_T$-linear maps ![]() $\sigma \colon f^{*}{{\mathcal {E}}}'\to f^{*}{{\mathcal {E}}}$, for which the fiber
$\sigma \colon f^{*}{{\mathcal {E}}}'\to f^{*}{{\mathcal {E}}}$, for which the fiber ![]() $\sigma _\infty \colon f_\infty ^{*}V'\to f_\infty ^{*}V$ has rank
$\sigma _\infty \colon f_\infty ^{*}V'\to f_\infty ^{*}V$ has rank ![]() $r$ everywhere on
$r$ everywhere on ![]() $T_\infty$.
$T_\infty$.
Given a morphism ![]() $s$ as above, corresponding to a morphism
$s$ as above, corresponding to a morphism ![]() $\sigma \colon f^{*}{{\mathcal {E}}}'\to f^{*}{{\mathcal {E}}}$, we let
$\sigma \colon f^{*}{{\mathcal {E}}}'\to f^{*}{{\mathcal {E}}}$, we let ![]() ${{\mathcal {W}}}'$ and
${{\mathcal {W}}}'$ and ![]() ${{\mathcal {W}}}$ denote the kernel and cokernel of
${{\mathcal {W}}}$ denote the kernel and cokernel of ![]() $\sigma _\infty$. Then
$\sigma _\infty$. Then ![]() ${{\mathcal {W}}}'$ and
${{\mathcal {W}}}'$ and ![]() ${{\mathcal {W}}}$ are locally free
${{\mathcal {W}}}$ are locally free ![]() $\mathcal {O}_{T_\infty }$-modules of rank
$\mathcal {O}_{T_\infty }$-modules of rank ![]() $r$. Let
$r$. Let ![]() $i_{T_\infty }\colon T_\infty \to T$ denote the pull-back of
$i_{T_\infty }\colon T_\infty \to T$ denote the pull-back of ![]() $i_\infty$ through
$i_\infty$ through ![]() $f$.
$f$.
We intend to use Lemma 5.1.3 to compute ![]() $s^{*}\operatorname {Tan}_{{{\mathbf {V}}}(\operatorname {\mathscr {H}{\mathcal{om}}\,}({{\mathcal {E}}}',{{\mathcal {E}}}))^{\operatorname {rk}_\infty =r}/X}$. The tangent bundle
$s^{*}\operatorname {Tan}_{{{\mathbf {V}}}(\operatorname {\mathscr {H}{\mathcal{om}}\,}({{\mathcal {E}}}',{{\mathcal {E}}}))^{\operatorname {rk}_\infty =r}/X}$. The tangent bundle ![]() $\operatorname {Tan}_{{{\mathbf {V}}}(\operatorname {\mathscr {H}{\mathcal{om}}\,}({{\mathcal {E}}}',{{\mathcal {E}}}))/X}$ is isomorphic to the pull-back
$\operatorname {Tan}_{{{\mathbf {V}}}(\operatorname {\mathscr {H}{\mathcal{om}}\,}({{\mathcal {E}}}',{{\mathcal {E}}}))/X}$ is isomorphic to the pull-back ![]() $f^{*}\operatorname {\mathscr {H}{\mathcal{om}}\,}({{\mathcal {E}}}',{{\mathcal {E}}})$. Also, we have identified the normal bundle
$f^{*}\operatorname {\mathscr {H}{\mathcal{om}}\,}({{\mathcal {E}}}',{{\mathcal {E}}})$. Also, we have identified the normal bundle ![]() $N_{{{\mathbf {V}}}(\operatorname {Hom}(V',V))^{\operatorname {rk} =r}/{{\mathbf {V}}}(\operatorname {Hom}(V',V)}$ in (5.3.2). So when we apply the lemma to this situation, we obtain an exact sequence of
$N_{{{\mathbf {V}}}(\operatorname {Hom}(V',V))^{\operatorname {rk} =r}/{{\mathbf {V}}}(\operatorname {Hom}(V',V)}$ in (5.3.2). So when we apply the lemma to this situation, we obtain an exact sequence of ![]() $\mathcal {O}_T$-modules
$\mathcal {O}_T$-modules
where the third arrow is adjoint to the map
which sends ![]() $\sigma \in \operatorname {\mathscr {H}{\mathcal{om}}\,}(f_\infty ^{*}V',f_\infty ^{*}V)$ to the composite
$\sigma \in \operatorname {\mathscr {H}{\mathcal{om}}\,}(f_\infty ^{*}V',f_\infty ^{*}V)$ to the composite
The short exact sequence in (5.4.1) identifies the ![]() $\mathcal {O}_T$-module
$\mathcal {O}_T$-module ![]() $s^{*}\mathrm {Tan}_{{{\mathbf {V}}}(\operatorname {\mathscr {H}{\mathcal{om}}\,}({{\mathcal {E}}}',{{\mathcal {E}}}))^{\operatorname {rk}_\infty = r}/X}$ as a modification of
$s^{*}\mathrm {Tan}_{{{\mathbf {V}}}(\operatorname {\mathscr {H}{\mathcal{om}}\,}({{\mathcal {E}}}',{{\mathcal {E}}}))^{\operatorname {rk}_\infty = r}/X}$ as a modification of ![]() $f^{*}\operatorname {\mathscr {H}{\mathcal{om}}\,}({{\mathcal {E}}}',{{\mathcal {E}}})$ at the divisor
$f^{*}\operatorname {\mathscr {H}{\mathcal{om}}\,}({{\mathcal {E}}}',{{\mathcal {E}}})$ at the divisor ![]() $T_\infty$. We can say a little more in the case that
$T_\infty$. We can say a little more in the case that ![]() $\sigma$ itself is a modification. Let us assume that
$\sigma$ itself is a modification. Let us assume that ![]() $\sigma$ fits into an exact sequence
$\sigma$ fits into an exact sequence
Dualizing gives another exact sequence
Then
 \begin{align*} s^{*}\mathrm{Tan}_{{{\mathbf{V}}}(\operatorname{\mathscr{H}{\mathcal{om}}\,}({{\mathcal{E}}}',{{\mathcal{E}}}))^{\operatorname{rk}_\infty= r}/X} &= \ker[ f^{\ast}\operatorname{\mathscr{H}{\mathcal{om}}\,}({{\mathcal{E}}}',{{\mathcal{E}}}) \to i_{T_\infty*}\operatorname{\mathscr{H}{\mathcal{om}}\,}({{\mathcal{W}}}',{{\mathcal{W}}}) ]\\ &\cong \ker(\alpha\otimes \alpha') . \end{align*}
\begin{align*} s^{*}\mathrm{Tan}_{{{\mathbf{V}}}(\operatorname{\mathscr{H}{\mathcal{om}}\,}({{\mathcal{E}}}',{{\mathcal{E}}}))^{\operatorname{rk}_\infty= r}/X} &= \ker[ f^{\ast}\operatorname{\mathscr{H}{\mathcal{om}}\,}({{\mathcal{E}}}',{{\mathcal{E}}}) \to i_{T_\infty*}\operatorname{\mathscr{H}{\mathcal{om}}\,}({{\mathcal{W}}}',{{\mathcal{W}}}) ]\\ &\cong \ker(\alpha\otimes \alpha') . \end{align*}
The kernel of ![]() $\alpha \otimes \alpha '$ can be computed in terms of
$\alpha \otimes \alpha '$ can be computed in terms of ![]() $\ker \alpha =f^{\ast }{{\mathcal {E}}}'$ and
$\ker \alpha =f^{\ast }{{\mathcal {E}}}'$ and ![]() $\ker \alpha '=f^{\ast }({{\mathcal {E}}}^{\vee })$, see Lemma 5.4.1 below. It sits in a diagram.
$\ker \alpha '=f^{\ast }({{\mathcal {E}}}^{\vee })$, see Lemma 5.4.1 below. It sits in a diagram.

Lemma 5.4.1 Let ![]() ${{\mathcal {A}}}$ be an abelian
${{\mathcal {A}}}$ be an abelian ![]() $\otimes$-category. Let
$\otimes$-category. Let
be two exact sequences in ![]() ${{\mathcal {A}}}$, with
${{\mathcal {A}}}$, with ![]() $A,A',K,K'$ projective. The homology of the complex
$A,A',K,K'$ projective. The homology of the complex
is given by ![]() $H_2=0$,
$H_2=0$, ![]() $H_1\cong \operatorname {Tor}_1(B,B')$, and
$H_1\cong \operatorname {Tor}_1(B,B')$, and ![]() $H_0\cong B\otimes B'$. Thus,
$H_0\cong B\otimes B'$. Thus, ![]() $K''=\ker (f\otimes f'\colon A\otimes A' \to B\otimes B')$ appears in a diagram
$K''=\ker (f\otimes f'\colon A\otimes A' \to B\otimes B')$ appears in a diagram

where both sequences are exact.
Proof. Let ![]() $C_{\bullet }$ be the complex
$C_{\bullet }$ be the complex ![]() $K\to A$, and let
$K\to A$, and let ![]() $C'_{\bullet }$ be the complex
$C'_{\bullet }$ be the complex ![]() $K'\to A'$. Since
$K'\to A'$. Since ![]() $C'_{\bullet }$ is a projective resolution of
$C'_{\bullet }$ is a projective resolution of ![]() $B'$, we have a Tor spectral sequence [Sta14, Tag 061Z]
$B'$, we have a Tor spectral sequence [Sta14, Tag 061Z]
We have ![]() $E^{2}_{0,0}=B\otimes B'$ and
$E^{2}_{0,0}=B\otimes B'$ and ![]() $E^{2}_{0,1}=\operatorname {Tor}_1(B,B')$, and
$E^{2}_{0,1}=\operatorname {Tor}_1(B,B')$, and ![]() $E^{2}_{i,j}=0$ for all other
$E^{2}_{i,j}=0$ for all other ![]() $(i,j)$. Therefore
$(i,j)$. Therefore ![]() $H_0(C_{\bullet } \otimes C'_{\bullet }) \cong B\otimes B'$ and
$H_0(C_{\bullet } \otimes C'_{\bullet }) \cong B\otimes B'$ and ![]() $H_1(C_{\bullet } \otimes C'_{\bullet }) \cong \operatorname {Tor}_1(B,B')$, which is the lemma.
$H_1(C_{\bullet } \otimes C'_{\bullet }) \cong \operatorname {Tor}_1(B,B')$, which is the lemma.
5.5 A tangent space calculation
We return to the setup of § 5.2. Thus we have fixed a ![]() $p$-divisible group
$p$-divisible group ![]() $H$ over a perfect field
$H$ over a perfect field ![]() $k$, and an algebraically closed perfectoid field
$k$, and an algebraically closed perfectoid field ![]() $C$ containing
$C$ containing ![]() $W(k)[1/p]$. But now we specialize to the case that
$W(k)[1/p]$. But now we specialize to the case that ![]() $H$ is isoclinic. Therefore
$H$ is isoclinic. Therefore ![]() $D=\operatorname {End} H$ (up to isogeny) is a central simple
$D=\operatorname {End} H$ (up to isogeny) is a central simple ![]() $\mathbf {Q}_p$-algebra. Let
$\mathbf {Q}_p$-algebra. Let ![]() ${{\mathcal {E}}}={{\mathcal {E}}}_C(H)$; we have
${{\mathcal {E}}}={{\mathcal {E}}}_C(H)$; we have ![]() $\operatorname {\mathscr {H}{\mathcal{om}}\,}({{\mathcal {E}}},{{\mathcal {E}}})\cong D\otimes _{\mathbf {Q}_p} \mathcal {O}_{X_C}$.
$\operatorname {\mathscr {H}{\mathcal{om}}\,}({{\mathcal {E}}},{{\mathcal {E}}})\cong D\otimes _{\mathbf {Q}_p} \mathcal {O}_{X_C}$.
Recall the scheme ![]() $Z\to X_C$, defined as a fiber product in (5.2.1). Let
$Z\to X_C$, defined as a fiber product in (5.2.1). Let ![]() $s\colon X_C\to Z$ be a section. This corresponds to a morphism
$s\colon X_C\to Z$ be a section. This corresponds to a morphism ![]() $\sigma \colon \mathcal {O}_{X_C}^{n}\to {{\mathcal {E}}}$. Let
$\sigma \colon \mathcal {O}_{X_C}^{n}\to {{\mathcal {E}}}$. Let ![]() $W'$ and
$W'$ and ![]() $W$ be the cokernel of
$W$ be the cokernel of ![]() $\sigma _\infty$; these are
$\sigma _\infty$; these are ![]() $C$-vector spaces.
$C$-vector spaces.
We are interested in the vector bundle ![]() $s^{*}\mathrm {Tan}_{Z/X_C}$. This is the kernel of the derivative of the determinant map:
$s^{*}\mathrm {Tan}_{Z/X_C}$. This is the kernel of the derivative of the determinant map:
We apply (5.4.2) to give a description of ![]() $s^{*}\mathrm {Tan}_{{{\mathbf {V}}}({{\mathcal {E}}}^{n})^{\operatorname {rk}_\infty = n-d}/X_C}$. We get a diagram of
$s^{*}\mathrm {Tan}_{{{\mathbf {V}}}({{\mathcal {E}}}^{n})^{\operatorname {rk}_\infty = n-d}/X_C}$. We get a diagram of ![]() $\mathcal {O}_{X_C}$-modules.
$\mathcal {O}_{X_C}$-modules.

On the other hand, the horizontal exact sequence fits into a diagram.

The arrow labeled ![]() ${\textrm {tr}}$ is induced from the
${\textrm {tr}}$ is induced from the ![]() $\mathbf {Q}_p$-linear map
$\mathbf {Q}_p$-linear map ![]() $M_n(\mathbf {Q}_p)\times D\to \mathbf {Q}_p$ carrying
$M_n(\mathbf {Q}_p)\times D\to \mathbf {Q}_p$ carrying ![]() $(\alpha ',\alpha )$ to
$(\alpha ',\alpha )$ to ![]() ${\textrm {tr}}(\alpha ')-{\textrm {tr}}(\alpha )$ (reduced trace on
${\textrm {tr}}(\alpha ')-{\textrm {tr}}(\alpha )$ (reduced trace on ![]() $D$). The commutativity of the lower right square boils down to the identity, valid for sections
$D$). The commutativity of the lower right square boils down to the identity, valid for sections ![]() $s_1,\ldots ,s_n\in H^{0}(X_C,{{\mathcal {E}}})$ and
$s_1,\ldots ,s_n\in H^{0}(X_C,{{\mathcal {E}}})$ and ![]() $\alpha \in D$:
$\alpha \in D$:
(There is a similar identity for ![]() $\alpha '\in M_n(\mathbf {Q}_p)$.) Because the arrow labeled
$\alpha '\in M_n(\mathbf {Q}_p)$.) Because the arrow labeled ![]() $\tau$ is injective, we can combine (5.5.1) and (5.5.2) to arrive at a description of
$\tau$ is injective, we can combine (5.5.1) and (5.5.2) to arrive at a description of ![]() $s^{*}\operatorname {Tan}_{Z/X_C}$.
$s^{*}\operatorname {Tan}_{Z/X_C}$.

We pass to duals to obtain the following.

The dotted arrow is induced from the map ![]() $(M_n(\mathbf {Q}_p)\times D)\otimes _{\mathbf {Q}_p} \mathcal {O}_{X_C}\to {{\mathcal {E}}}^{n}$ sending
$(M_n(\mathbf {Q}_p)\times D)\otimes _{\mathbf {Q}_p} \mathcal {O}_{X_C}\to {{\mathcal {E}}}^{n}$ sending ![]() $(\alpha ',\alpha )\otimes 1$ to
$(\alpha ',\alpha )\otimes 1$ to ![]() $\alpha \circ \sigma - \sigma \circ \alpha '$.
$\alpha \circ \sigma - \sigma \circ \alpha '$.
Theorem 5.5.1 If ![]() $s$ is a section to
$s$ is a section to ![]() $Z \rightarrow X_C$ corresponding, under the isomorphism of Lemma 5.2.1, to a point
$Z \rightarrow X_C$ corresponding, under the isomorphism of Lemma 5.2.1, to a point ![]() $x \in {{\mathcal {M}}}_{H,\infty }^{\tau }(C)$, then the following are equivalent.
$x \in {{\mathcal {M}}}_{H,\infty }^{\tau }(C)$, then the following are equivalent.
(i) The vector bundle
 $s^{*}\mathrm {Tan}_{Z/X_C}$ has a Harder–Narasimhan slope which is less than or equal to
$s^{*}\mathrm {Tan}_{Z/X_C}$ has a Harder–Narasimhan slope which is less than or equal to  $0$.
$0$.(ii) The point
 $x$ lies in the special locus
$x$ lies in the special locus  ${{\mathscr M}}_{H,\infty }^{\tau ,\operatorname {sp}}$.
${{\mathscr M}}_{H,\infty }^{\tau ,\operatorname {sp}}$.
Proof. Let ![]() $\sigma \colon \mathcal {O}_{X_C}^{n}\to {{\mathcal {E}}}$ denote the homomorphism corresponding to
$\sigma \colon \mathcal {O}_{X_C}^{n}\to {{\mathcal {E}}}$ denote the homomorphism corresponding to ![]() $x$. Condition (1) is true if and only if
$x$. Condition (1) is true if and only if ![]() $H^{0}(X_C,s^{*}\mathrm {Tan}_{Z/X_C}^{\vee })\neq 0$. We now take
$H^{0}(X_C,s^{*}\mathrm {Tan}_{Z/X_C}^{\vee })\neq 0$. We now take ![]() $H^{0}$ of (5.5.4), noting that
$H^{0}$ of (5.5.4), noting that ![]() $H^{0}(X_C,{{\mathcal {F}}}^{\vee })\to H^{0}(X_C,{{\mathcal {E}}}^{n})$ is injective. We find that
$H^{0}(X_C,{{\mathcal {F}}}^{\vee })\to H^{0}(X_C,{{\mathcal {E}}}^{n})$ is injective. We find that
 \begin{align*} H^{0}(X_C,s^{*}\mathrm{Tan}_{Z/X_C}^{\vee})&\cong \{(\alpha',\alpha)\in M_n(\mathbf{Q}_p)\times D \mid \alpha\circ \sigma=\sigma\circ \alpha'\}/\mathbf{Q}_p \\ &= A_x/\mathbf{Q}_p. \end{align*}
\begin{align*} H^{0}(X_C,s^{*}\mathrm{Tan}_{Z/X_C}^{\vee})&\cong \{(\alpha',\alpha)\in M_n(\mathbf{Q}_p)\times D \mid \alpha\circ \sigma=\sigma\circ \alpha'\}/\mathbf{Q}_p \\ &= A_x/\mathbf{Q}_p. \end{align*}
This is nonzero exactly when ![]() $x$ lies in the special locus.
$x$ lies in the special locus.
Combining Theorem 5.5.1 with the criterion for cohomological smoothness in Theorem 4.2.1 proves Theorem 1.0.1 for the space ![]() ${{\mathscr M}}_{H,\infty }$.
${{\mathscr M}}_{H,\infty }$.
Naturally we wonder whether it is possible to give a complete description of ![]() $s^{*}\operatorname {Tan}_{Z/X_C}$, as this is the ‘tangent space’ of
$s^{*}\operatorname {Tan}_{Z/X_C}$, as this is the ‘tangent space’ of ![]() ${{\mathscr M}}_{H,\infty }^{\tau }$ at the point
${{\mathscr M}}_{H,\infty }^{\tau }$ at the point ![]() $x$. Note that
$x$. Note that ![]() $s^{*}\operatorname {Tan}_{Z/X_C}$ can only have nonnegative slopes, since it is a quotient of a trivial bundle. Therefore Theorem 5.5.1 says that 0 appears as a slope of
$s^{*}\operatorname {Tan}_{Z/X_C}$ can only have nonnegative slopes, since it is a quotient of a trivial bundle. Therefore Theorem 5.5.1 says that 0 appears as a slope of ![]() $s^{*}\operatorname {Tan}_{Z/X_C}$ if and only if
$s^{*}\operatorname {Tan}_{Z/X_C}$ if and only if ![]() $s$ corresponds to a special point of
$s$ corresponds to a special point of ![]() ${{\mathscr M}}_{H,\infty }^{\tau }$.
${{\mathscr M}}_{H,\infty }^{\tau }$.
Example 5.5.2 Consider the case that ![]() $H$ has dimension 1 and height
$H$ has dimension 1 and height ![]() $n$, so that
$n$, so that ![]() ${{\mathscr M}}_{H,\infty }$ is an infinite-level Lubin–Tate space. Suppose that
${{\mathscr M}}_{H,\infty }$ is an infinite-level Lubin–Tate space. Suppose that ![]() $x\in {{\mathscr M}}_{H,\infty }(C)$ corresponds to a section
$x\in {{\mathscr M}}_{H,\infty }(C)$ corresponds to a section ![]() $s\colon X_C\to Z$. Then
$s\colon X_C\to Z$. Then ![]() $s^{*}\operatorname {Tan}_{Z/X_C}$ is a vector bundle of rank
$s^{*}\operatorname {Tan}_{Z/X_C}$ is a vector bundle of rank ![]() $n^{2}-1$ and degree
$n^{2}-1$ and degree ![]() $n-1$, with slopes lying in
$n-1$, with slopes lying in ![]() $[0,1/n]$; this already limits the possibilities for the slopes to a finite list.
$[0,1/n]$; this already limits the possibilities for the slopes to a finite list.
If ![]() $n=2$ there are only two possibilities for the slopes appearing in
$n=2$ there are only two possibilities for the slopes appearing in ![]() $s^{*}\operatorname {Tan}_{Z/X_C}$:
$s^{*}\operatorname {Tan}_{Z/X_C}$: ![]() $\{ {1/3} \}$ and
$\{ {1/3} \}$ and ![]() $\{ {0,1/2} \}$. These correspond exactly to the nonspecial and special loci, respectively.
$\{ {0,1/2} \}$. These correspond exactly to the nonspecial and special loci, respectively.
If ![]() $n=3$, there are a priori five possibilities for the slopes appearing in
$n=3$, there are a priori five possibilities for the slopes appearing in ![]() $s^{*}\operatorname {Tan}_{Z/X_C}$:
$s^{*}\operatorname {Tan}_{Z/X_C}$: ![]() $\{ {1/4,1/4} \}$,
$\{ {1/4,1/4} \}$, ![]() $\{ {1/3,1/5} \}$,
$\{ {1/3,1/5} \}$, ![]() $\{ {1/3,1/3,0,0} \}$,
$\{ {1/3,1/3,0,0} \}$, ![]() $\{ {2/7,0} \}$, and
$\{ {2/7,0} \}$, and ![]() $\{ {1/3,1/4,0} \}$. But in fact the final two cases cannot occur: if 0 appears as a slope, then
$\{ {1/3,1/4,0} \}$. But in fact the final two cases cannot occur: if 0 appears as a slope, then ![]() $x$ lies in the special locus, so that
$x$ lies in the special locus, so that ![]() $A_x\neq \mathbf {Q}_p$. But as
$A_x\neq \mathbf {Q}_p$. But as ![]() $A_x$ is isomorphic to a subalgebra of
$A_x$ is isomorphic to a subalgebra of ![]() $\operatorname {End}^{\circ } H$, the division algebra of invariant 1/3, it must be the case that
$\operatorname {End}^{\circ } H$, the division algebra of invariant 1/3, it must be the case that ![]() $\dim _{\mathbf {Q}_p} A_x = 3$, which forces 0 to appear as a slope with multiplicity
$\dim _{\mathbf {Q}_p} A_x = 3$, which forces 0 to appear as a slope with multiplicity ![]() $\dim _{\mathbf {Q}_p} A_x/\mathbf {Q}_p = 2$. On the nonspecial locus, we suspect that the generic (semistable) case
$\dim _{\mathbf {Q}_p} A_x/\mathbf {Q}_p = 2$. On the nonspecial locus, we suspect that the generic (semistable) case ![]() $\{ {1/4,1/4} \}$ always occurs, as otherwise there would be some unexpected stratification of
$\{ {1/4,1/4} \}$ always occurs, as otherwise there would be some unexpected stratification of ![]() ${{\mathscr M}}_{H,\infty }^{\circ ,\operatorname {non-sp}}$. But currently we do not know how to rule out the case
${{\mathscr M}}_{H,\infty }^{\circ ,\operatorname {non-sp}}$. But currently we do not know how to rule out the case ![]() $\{ {1/3,1/5} \}$.
$\{ {1/3,1/5} \}$.
5.6 The general case
Let ![]() ${{\mathcal {D}}} = (B,V,H,\mu )$ be a rational EL datum over
${{\mathcal {D}}} = (B,V,H,\mu )$ be a rational EL datum over ![]() $k$, with reflex field
$k$, with reflex field ![]() $E$. Let
$E$. Let ![]() $F$ be the center of
$F$ be the center of ![]() $B$. As in § 3.5, let
$B$. As in § 3.5, let ![]() $D=\operatorname {End}_{B} V$ and
$D=\operatorname {End}_{B} V$ and ![]() $D'=\operatorname {End}_{B} H$, so that
$D'=\operatorname {End}_{B} H$, so that ![]() $D$ and
$D$ and ![]() $D'$ are both
$D'$ are both ![]() $F$-algebras.
$F$-algebras.
Let ![]() $C$ be a perfectoid field containing
$C$ be a perfectoid field containing ![]() $\breve {E}$, and let
$\breve {E}$, and let ![]() $\tau \in {{\mathscr M}}_{\det {{\mathcal {D}}},\infty }(C)$. Let
$\tau \in {{\mathscr M}}_{\det {{\mathcal {D}}},\infty }(C)$. Let ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\tau }$ be the fiber of the determinant map over
${{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\tau }$ be the fiber of the determinant map over ![]() $\tau$. We will sketch the proof that
$\tau$. We will sketch the proof that ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\tau }\to \operatorname {Spa} C$ is cohomologically smooth. It is along the same lines as the proof for
${{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\tau }\to \operatorname {Spa} C$ is cohomologically smooth. It is along the same lines as the proof for ![]() ${{\mathscr M}}_{H,\infty }$, but with some extra linear algebra added.
${{\mathscr M}}_{H,\infty }$, but with some extra linear algebra added.
The space ![]() ${{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\tau }$ may be expressed as the space of global sections of a smooth morphism
${{\mathscr M}}_{{{\mathcal {D}}},\infty }^{\tau }$ may be expressed as the space of global sections of a smooth morphism ![]() $Z\to X_C$, defined as follows. We have the geometric vector bundle
$Z\to X_C$, defined as follows. We have the geometric vector bundle ![]() ${{\mathbf {V}}}(\operatorname {\mathscr {H}{\mathcal{om}}\,}_B(V\otimes _{\mathbf {Q}_p}\mathcal {O}_X, {{\mathcal {E}}}_C(H)))$. In its fiber over
${{\mathbf {V}}}(\operatorname {\mathscr {H}{\mathcal{om}}\,}_B(V\otimes _{\mathbf {Q}_p}\mathcal {O}_X, {{\mathcal {E}}}_C(H)))$. In its fiber over ![]() $\infty$, we have the locally closed subscheme whose
$\infty$, we have the locally closed subscheme whose ![]() $R$-points for a
$R$-points for a ![]() $C$-algebra
$C$-algebra ![]() $R$ are morphisms, whose cokernel is as a
$R$ are morphisms, whose cokernel is as a ![]() $B\otimes _{{{\mathbf {Q}}}_p} R$-module isomorphic to
$B\otimes _{{{\mathbf {Q}}}_p} R$-module isomorphic to ![]() $V_0 \otimes _{\breve E} R$, where
$V_0 \otimes _{\breve E} R$, where ![]() $V_0$ is the weight 0 subspace of
$V_0$ is the weight 0 subspace of ![]() $V\otimes _{\mathbf {Q}_p} \breve {E}$ determined by
$V\otimes _{\mathbf {Q}_p} \breve {E}$ determined by ![]() $\mu$. We then have the dilatation
$\mu$. We then have the dilatation ![]() ${{\mathbf {V}}}(\operatorname {\mathscr {H}{\mathcal{om}}\,}_B(V\otimes _{\mathbf {Q}_p}\mathcal {O}_{X_C}, {{\mathcal {E}}}_C(H)))^{\mu }$ of
${{\mathbf {V}}}(\operatorname {\mathscr {H}{\mathcal{om}}\,}_B(V\otimes _{\mathbf {Q}_p}\mathcal {O}_{X_C}, {{\mathcal {E}}}_C(H)))^{\mu }$ of ![]() ${{\mathbf {V}}}(\operatorname {\mathscr {H}{\mathcal{om}}\,}_B(V\otimes _{\mathbf {Q}_p}\mathcal {O}_X, {{\mathcal {E}}}_C(H)))$ at this locally closed subscheme. Its points over
${{\mathbf {V}}}(\operatorname {\mathscr {H}{\mathcal{om}}\,}_B(V\otimes _{\mathbf {Q}_p}\mathcal {O}_X, {{\mathcal {E}}}_C(H)))$ at this locally closed subscheme. Its points over ![]() $S=\operatorname {Spa}(R,R^{+})$ parametrize
$S=\operatorname {Spa}(R,R^{+})$ parametrize ![]() $B$-linear morphisms
$B$-linear morphisms ![]() $s\colon V\otimes _{\mathbf {Q}_p} \mathcal {O}_{X_S}\to {{\mathcal {E}}}_S(H)$, such that (locally on
$s\colon V\otimes _{\mathbf {Q}_p} \mathcal {O}_{X_S}\to {{\mathcal {E}}}_S(H)$, such that (locally on ![]() $S$) the cokernel of the fiber
$S$) the cokernel of the fiber ![]() $s_\infty$ is isomorphic as a
$s_\infty$ is isomorphic as a ![]() $(B\otimes _{\mathbf {Q}_p} R)$-module to
$(B\otimes _{\mathbf {Q}_p} R)$-module to ![]() $V_0\otimes _{\breve {E}} R$. Finally, the morphism
$V_0\otimes _{\breve {E}} R$. Finally, the morphism ![]() $Z\to X_C$ is defined by the following cartesian diagram.
$Z\to X_C$ is defined by the following cartesian diagram.

Let ![]() $x\in {{\mathscr M}}_{{{\mathcal {D}}},\infty }(C)$ correspond to a
$x\in {{\mathscr M}}_{{{\mathcal {D}}},\infty }(C)$ correspond to a ![]() $B$-linear morphism
$B$-linear morphism ![]() $s\colon V\otimes _{\mathbf {Q}_p} \mathcal {O}_{X_C} \to {{\mathcal {E}}}_C(H)$ and a section of
$s\colon V\otimes _{\mathbf {Q}_p} \mathcal {O}_{X_C} \to {{\mathcal {E}}}_C(H)$ and a section of ![]() $Z\to X_C$ which we also call
$Z\to X_C$ which we also call ![]() $s$. Define
$s$. Define ![]() $B\otimes _{\mathbf {Q}_p} C$-modules
$B\otimes _{\mathbf {Q}_p} C$-modules ![]() $W'$ and
$W'$ and ![]() $W$ by
$W$ by
The analogue of (5.5.4) is a diagram which computes the dual of ![]() $s^{*}\operatorname {Tan}_{Z/X_C}$.
$s^{*}\operatorname {Tan}_{Z/X_C}$.

This time, the dotted arrow is induced from the map ![]() $(D'\times D)\otimes _{\mathbf {Q}_p} \mathcal {O}_{X_C}\to \operatorname {\mathscr {H}{\mathcal{om}}\,}(V\otimes _{\mathbf {Q}_p} \mathcal {O}_{X_C},{{\mathcal {E}}}_C(H))$ sending
$(D'\times D)\otimes _{\mathbf {Q}_p} \mathcal {O}_{X_C}\to \operatorname {\mathscr {H}{\mathcal{om}}\,}(V\otimes _{\mathbf {Q}_p} \mathcal {O}_{X_C},{{\mathcal {E}}}_C(H))$ sending ![]() $(\alpha ',\alpha )\otimes 1$ to
$(\alpha ',\alpha )\otimes 1$ to ![]() $\alpha \circ s- s\circ \alpha '$. Taking
$\alpha \circ s- s\circ \alpha '$. Taking ![]() $H^{0}$ in (
$H^{0}$ in (
) shows that ![]() $H^{0}(X_C,s^{*}\operatorname {Tan}_{Z/X_C}^{\vee }) = A_x / F$, and this is nonzero exactly when
$H^{0}(X_C,s^{*}\operatorname {Tan}_{Z/X_C}^{\vee }) = A_x / F$, and this is nonzero exactly when ![]() $x$ lies in the special locus.
$x$ lies in the special locus.
5.7 Proof of Corollary 1.0.2
We conclude with a discussion of the infinite-level modular curve ![]() $X(p^{\infty })$. Recall from [Reference ScholzeSch15] the following facts about the Hodge–Tate period map
$X(p^{\infty })$. Recall from [Reference ScholzeSch15] the following facts about the Hodge–Tate period map ![]() $\pi _{HT}\colon X(p^{\infty })\to {{\mathbf {P}}}^{1}$. The ordinary locus in
$\pi _{HT}\colon X(p^{\infty })\to {{\mathbf {P}}}^{1}$. The ordinary locus in ![]() $X(p^{\infty })$ is sent to
$X(p^{\infty })$ is sent to ![]() ${{\mathbf {P}}}^{1}(\mathbf {Q}_p)$. The supersingular locus is isomorphic to finitely many copies of
${{\mathbf {P}}}^{1}(\mathbf {Q}_p)$. The supersingular locus is isomorphic to finitely many copies of ![]() ${{\mathscr M}}_{H,\infty ,C}$, where
${{\mathscr M}}_{H,\infty ,C}$, where ![]() $H$ is a connected
$H$ is a connected ![]() $p$-divisible group of height 2 and dimension 1 over the residue field of
$p$-divisible group of height 2 and dimension 1 over the residue field of ![]() $C$; the restriction of
$C$; the restriction of ![]() $\pi _{HT}$ to this locus agrees with the
$\pi _{HT}$ to this locus agrees with the ![]() $\pi _{HT}$ we had already defined on each
$\pi _{HT}$ we had already defined on each ![]() ${{\mathscr M}}_{H,\infty ,C}$.
${{\mathscr M}}_{H,\infty ,C}$.
We claim that the following are equivalent for a ![]() $C$-point
$C$-point ![]() $x$ of
$x$ of ![]() $X(p^{\infty })^{\circ }$.
$X(p^{\infty })^{\circ }$.
(i) The point
 $x$ corresponds to an elliptic curve
$x$ corresponds to an elliptic curve  $E/\mathcal {O}_C$, such that the
$E/\mathcal {O}_C$, such that the  $p$-divisible group
$p$-divisible group  $E[p^{\infty }]$ has
$E[p^{\infty }]$ has  $\operatorname {End} E[p^{\infty }]=\mathbf {Z}_p$.
$\operatorname {End} E[p^{\infty }]=\mathbf {Z}_p$.(ii) The stabilizer of
 $\pi _{HT}(x)$ in
$\pi _{HT}(x)$ in  $\operatorname {PGL}_2(\mathbf {Q}_p)$ is trivial.
$\operatorname {PGL}_2(\mathbf {Q}_p)$ is trivial.(iii) There is a neighborhood of
 $x$ in
$x$ in  $X(p^{\infty })^{\circ }$ which is cohomologically smooth over
$X(p^{\infty })^{\circ }$ which is cohomologically smooth over  $C$.
$C$.
First we discuss the equivalence of (1) and (2). If ![]() $E$ is ordinary, then
$E$ is ordinary, then ![]() $E[p^{\infty }]\cong \mathbf {Q}_p/\mathbf {Z}_p \times \mu _{p^{\infty }}$ certainly has endomorphism ring larger than
$E[p^{\infty }]\cong \mathbf {Q}_p/\mathbf {Z}_p \times \mu _{p^{\infty }}$ certainly has endomorphism ring larger than ![]() $\mathbf {Z}_p$, so that (1) is false. Meanwhile, the stabilizer of
$\mathbf {Z}_p$, so that (1) is false. Meanwhile, the stabilizer of ![]() $\pi _{HT}(x)$ in
$\pi _{HT}(x)$ in ![]() $\operatorname {PGL}_2(\mathbf {Q}_p)$ is a Borel subgroup, so that (2) is false as well. The equivalence between (1) and (2) in the supersingular case is a special case of the equivalence discussed in § 3.5.
$\operatorname {PGL}_2(\mathbf {Q}_p)$ is a Borel subgroup, so that (2) is false as well. The equivalence between (1) and (2) in the supersingular case is a special case of the equivalence discussed in § 3.5.
Theorem 1.0.1 tells us that ![]() ${{\mathscr M}}_{H,\infty }^{\circ ,\operatorname {non-sp}}$ is cohomologically smooth, which implies that shows that (2) implies (3). We therefore are left with showing that if (2) is false for a point
${{\mathscr M}}_{H,\infty }^{\circ ,\operatorname {non-sp}}$ is cohomologically smooth, which implies that shows that (2) implies (3). We therefore are left with showing that if (2) is false for a point ![]() $x\in X(p^{\infty })^{\circ }$, then no neighborhood of
$x\in X(p^{\infty })^{\circ }$, then no neighborhood of ![]() $x$ is cohomologically smooth.
$x$ is cohomologically smooth.
First suppose that ![]() $x$ lies in the ordinary locus. This locus is fibered over
$x$ lies in the ordinary locus. This locus is fibered over ![]() ${{\mathbf {P}}}^{1}(\mathbf {Q}_p)$. Suppose
${{\mathbf {P}}}^{1}(\mathbf {Q}_p)$. Suppose ![]() $U$ is a sufficiently small neighborhood of
$U$ is a sufficiently small neighborhood of ![]() $x$. Then
$x$. Then ![]() $U$ is contained in the ordinary locus, and so
$U$ is contained in the ordinary locus, and so ![]() $\pi _0(U)$ is nondiscrete. This implies that
$\pi _0(U)$ is nondiscrete. This implies that ![]() $H^{0}(U,{{\mathbf {F}}}_\ell )$ is infinite, and so
$H^{0}(U,{{\mathbf {F}}}_\ell )$ is infinite, and so ![]() $U$ cannot be cohomologically smooth.
$U$ cannot be cohomologically smooth.
Now suppose that ![]() $x$ lies in the supersingular locus, and that
$x$ lies in the supersingular locus, and that ![]() $\pi _{HT}(x)$ has nontrivial stabilizer in
$\pi _{HT}(x)$ has nontrivial stabilizer in ![]() $\operatorname {PGL}_2(\mathbf {Q}_p)$. We can identify
$\operatorname {PGL}_2(\mathbf {Q}_p)$. We can identify ![]() $x$ with a point in
$x$ with a point in ![]() ${{\mathscr M}}_{H,\infty }^{\circ ,\operatorname {sp}}(C)$. We intend to show that every neighborhood of
${{\mathscr M}}_{H,\infty }^{\circ ,\operatorname {sp}}(C)$. We intend to show that every neighborhood of ![]() $x$ in
$x$ in ![]() ${{\mathscr M}}_{H,\infty }^{\circ }$ fails to be cohomologically smooth.
${{\mathscr M}}_{H,\infty }^{\circ }$ fails to be cohomologically smooth.
Not knowing a direct method, we appeal to the calculations in [Reference WeinsteinWei16], which constructed semistable formal models for each ![]() ${{\mathscr M}}_{H,m}^{\circ }$. The main result we need is Theorem 5.1.2, which uses the term ‘CM points’ for what we have called special points. There exists a decreasing basis of neighborhoods
${{\mathscr M}}_{H,m}^{\circ }$. The main result we need is Theorem 5.1.2, which uses the term ‘CM points’ for what we have called special points. There exists a decreasing basis of neighborhoods ![]() $Z_{x,0}\supset Z_{x,1}\supset \cdots$ of
$Z_{x,0}\supset Z_{x,1}\supset \cdots$ of ![]() $x$ in
$x$ in ![]() ${{\mathscr M}}_{H,\infty }^{\circ }$. For each affinoid
${{\mathscr M}}_{H,\infty }^{\circ }$. For each affinoid ![]() $Z=\operatorname {Spa}(R,R^{+})$, let
$Z=\operatorname {Spa}(R,R^{+})$, let ![]() $\overline {Z}=\operatorname {Spec} R^{+}\otimes _{\mathcal {O}_C} \kappa$, where
$\overline {Z}=\operatorname {Spec} R^{+}\otimes _{\mathcal {O}_C} \kappa$, where ![]() $\kappa$ is the residue field of
$\kappa$ is the residue field of ![]() $C$. For each
$C$. For each ![]() $m\geq 0$, there exists a nonconstant morphism
$m\geq 0$, there exists a nonconstant morphism ![]() $\overline {Z}_{x,m}\to C_{x,m}$, where
$\overline {Z}_{x,m}\to C_{x,m}$, where ![]() $C_{x,m}$ is an explicit nonsingular affine curve over
$C_{x,m}$ is an explicit nonsingular affine curve over ![]() $\kappa$. This morphism is equivariant for the action of the stabilizer of
$\kappa$. This morphism is equivariant for the action of the stabilizer of ![]() $Z_{x,m}$ in
$Z_{x,m}$ in ![]() $\operatorname {SL}_2(\mathbf {Q}_p)$. For infinitely many
$\operatorname {SL}_2(\mathbf {Q}_p)$. For infinitely many ![]() $m$, the completion
$m$, the completion ![]() $C_{x,m}^\textrm {{cl}}$ of
$C_{x,m}^\textrm {{cl}}$ of ![]() $C_{x,m}$ is a projective curve with positive genus.
$C_{x,m}$ is a projective curve with positive genus.
Let ![]() $U\subset {{\mathscr M}}_{H,\infty }^{\circ }$ be an affinoid neighborhood of
$U\subset {{\mathscr M}}_{H,\infty }^{\circ }$ be an affinoid neighborhood of ![]() $x$. Then there exists
$x$. Then there exists ![]() $N\geq 0$ such that
$N\geq 0$ such that ![]() $Z_{x,m}\subset U$ for all
$Z_{x,m}\subset U$ for all ![]() $m\geq N$. Let
$m\geq N$. Let ![]() $K\subset \operatorname {SL}_2(\mathbf {Q}_p)$ be a compact open subgroup which stabilizes
$K\subset \operatorname {SL}_2(\mathbf {Q}_p)$ be a compact open subgroup which stabilizes ![]() $U$, so that
$U$, so that ![]() $U/K$ is an affinoid subset of the rigid-analytic curve
$U/K$ is an affinoid subset of the rigid-analytic curve ![]() ${{\mathscr M}}_{H,\infty }^{\circ }/K$. For each
${{\mathscr M}}_{H,\infty }^{\circ }/K$. For each ![]() $m\geq N$, let
$m\geq N$, let ![]() $K_m\subset K$ be the stabilizer of
$K_m\subset K$ be the stabilizer of ![]() $Z_{x,m}$, so that
$Z_{x,m}$, so that ![]() $K_m$ acts on
$K_m$ acts on ![]() $C_{x,m}$.
$C_{x,m}$.
There exists an integral model of ![]() $U/K$ whose special fiber contains as a component the completion of each
$U/K$ whose special fiber contains as a component the completion of each ![]() $\overline {Z}_{x,m}/K_m$ which has positive genus. Since there is a nonconstant morphism
$\overline {Z}_{x,m}/K_m$ which has positive genus. Since there is a nonconstant morphism ![]() $\overline {Z}_{x,m}/K_m\to C_{x,m}/K_m$, we must have
$\overline {Z}_{x,m}/K_m\to C_{x,m}/K_m$, we must have
Now we take a limit as ![]() $K$ shrinks. Since
$K$ shrinks. Since ![]() $U\sim \varprojlim U/K$, we have
$U\sim \varprojlim U/K$, we have ![]() $H^{1}(U,{{\mathbf {F}}}_\ell )\cong \varinjlim H^{1}(U/K,{{\mathbf {F}}}_\ell )$. Also, for each
$H^{1}(U,{{\mathbf {F}}}_\ell )\cong \varinjlim H^{1}(U/K,{{\mathbf {F}}}_\ell )$. Also, for each ![]() $m$, the action of
$m$, the action of ![]() $K_m$ on
$K_m$ on ![]() $C_{x,m}$ is trivial for all sufficiently small
$C_{x,m}$ is trivial for all sufficiently small ![]() $K$. Therefore
$K$. Therefore
This shows that ![]() $U$ is not cohomologically smooth.
$U$ is not cohomologically smooth.
Acknowledgements
The authors want to thank Peter Scholze for his help and his interest in their work. Also they thank Andreas Mihatsch for pointing out a mistake in a previous version of the manuscript. The first named author was supported by Peter Scholze's Leibniz Preis. The second author was supported by NSF Grant No. DMS-1440140 while in residence at the Mathematical Sciences Research Institute in Berkeley, California.