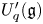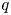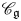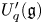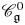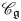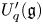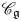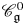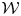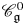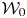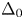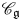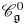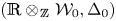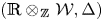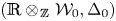1. Introduction
Let ![]() $q$ be an indeterminate and let
$q$ be an indeterminate and let ![]() $U_q'({\mathfrak {g}})$ be a quantum affine algebra. The category
$U_q'({\mathfrak {g}})$ be a quantum affine algebra. The category ![]() $\mathscr {C}_{\mathfrak {g}}$ of finite-dimensional integrable
$\mathscr {C}_{\mathfrak {g}}$ of finite-dimensional integrable ![]() $U_q'({\mathfrak {g}})$-modules has a rich structure. For example, the category
$U_q'({\mathfrak {g}})$-modules has a rich structure. For example, the category ![]() $\mathscr {C}_{\mathfrak {g}}$ is not semi-simple and has a rigid monoidal category structure. Because of its rich structure, it has been studied actively in various research areas of mathematics and physics (see [Reference Akasaka and KashiwaraAK97, Reference Chari and PressleyCP94, Reference Frenkel and ReshetikhinFR99, Reference KashiwaraKas02, Reference NakajimaNak01] for examples).
$\mathscr {C}_{\mathfrak {g}}$ is not semi-simple and has a rigid monoidal category structure. Because of its rich structure, it has been studied actively in various research areas of mathematics and physics (see [Reference Akasaka and KashiwaraAK97, Reference Chari and PressleyCP94, Reference Frenkel and ReshetikhinFR99, Reference KashiwaraKas02, Reference NakajimaNak01] for examples).
The category ![]() $\mathscr {C}_{\mathfrak {g}}$ has been studied from the viewpoint of cluster algebras. Suppose that
$\mathscr {C}_{\mathfrak {g}}$ has been studied from the viewpoint of cluster algebras. Suppose that ![]() ${\mathfrak {g}}$ is of simply laced affine ADE type. In [Reference Hernandez and LeclercHL10], Hernandez and Leclerc defined the full subcategory
${\mathfrak {g}}$ is of simply laced affine ADE type. In [Reference Hernandez and LeclercHL10], Hernandez and Leclerc defined the full subcategory ![]() $\mathscr {C}_{\mathfrak {g}}^0$ of
$\mathscr {C}_{\mathfrak {g}}^0$ of ![]() $\mathscr {C}_{\mathfrak {g}}$ such that all simple subquotients of its objects are obtained via simple subquotients of tensor products of certain fundamental representations. They then introduced certain monoidal subcategories
$\mathscr {C}_{\mathfrak {g}}$ such that all simple subquotients of its objects are obtained via simple subquotients of tensor products of certain fundamental representations. They then introduced certain monoidal subcategories ![]() $\mathscr {C}_\ell$ (
$\mathscr {C}_\ell$ (![]() $\ell \in \mathbb {\mspace {1mu}Z\mspace {1mu}}_{>0 }$) and studied their Grothendieck rings using cluster algebras. As any simple module in
$\ell \in \mathbb {\mspace {1mu}Z\mspace {1mu}}_{>0 }$) and studied their Grothendieck rings using cluster algebras. As any simple module in ![]() $\mathscr {C}_{\mathfrak {g}}$ can be obtained from a tensor product of suitable parameter shifts of simple modules in
$\mathscr {C}_{\mathfrak {g}}$ can be obtained from a tensor product of suitable parameter shifts of simple modules in ![]() $\mathscr {C}_{\mathfrak {g}}^0$, the category
$\mathscr {C}_{\mathfrak {g}}^0$, the category ![]() $\mathscr {C}_{\mathfrak {g}}^0$ has an essential position in
$\mathscr {C}_{\mathfrak {g}}^0$ has an essential position in ![]() $\mathscr {C}_{\mathfrak {g}}$. Note that an algorithm for computing
$\mathscr {C}_{\mathfrak {g}}$. Note that an algorithm for computing ![]() $q$-characters of Kirillov–Reshetikhin modules for any untwisted quantum affine algebras was described in [Reference Hernandez and LeclercHL16], by studying the cluster algebra structure of the Grothendieck ring of the subcategory
$q$-characters of Kirillov–Reshetikhin modules for any untwisted quantum affine algebras was described in [Reference Hernandez and LeclercHL16], by studying the cluster algebra structure of the Grothendieck ring of the subcategory ![]() $\mathscr {C}_{\mathfrak {g}}^-$ of
$\mathscr {C}_{\mathfrak {g}}^-$ of ![]() $\mathscr {C}_{\mathfrak {g}}^0$. On the other hand, Hernandez and Leclerc introduced another abelian monoidal subcategory
$\mathscr {C}_{\mathfrak {g}}^0$. On the other hand, Hernandez and Leclerc introduced another abelian monoidal subcategory ![]() ${\mathscr {C}_{\mathfrak {g}}^{Q}}$ which categorifies the coordinate ring
${\mathscr {C}_{\mathfrak {g}}^{Q}}$ which categorifies the coordinate ring ![]() $\mathbb {C}[N]$ of the unipotent group associated with the finite-dimensional simple Lie algebra
$\mathbb {C}[N]$ of the unipotent group associated with the finite-dimensional simple Lie algebra ![]() ${\mathfrak {g}}_0$ inside
${\mathfrak {g}}_0$ inside ![]() ${\mathfrak {g}}$ [Reference Hernandez and LeclercHL15]. For each Dynkin quiver
${\mathfrak {g}}$ [Reference Hernandez and LeclercHL15]. For each Dynkin quiver ![]() $Q$, they defined an abelian subcategory
$Q$, they defined an abelian subcategory ![]() ${\mathscr {C}_{\mathfrak {g}}^{Q}}$ of
${\mathscr {C}_{\mathfrak {g}}^{Q}}$ of ![]() $\mathscr {C}_{\mathfrak {g}}^0$ which contains some fundamental representations parameterized by the coordinates of vertices of the Auslander–Reiten quiver of
$\mathscr {C}_{\mathfrak {g}}^0$ which contains some fundamental representations parameterized by the coordinates of vertices of the Auslander–Reiten quiver of ![]() $Q$, and proved that
$Q$, and proved that ![]() ${\mathscr {C}_{\mathfrak {g}}^{Q}}$ is stable under taking tensor products and that its complexified Grothendieck ring
${\mathscr {C}_{\mathfrak {g}}^{Q}}$ is stable under taking tensor products and that its complexified Grothendieck ring ![]() $\mathbb {C} \otimes _\mathbb {\mspace {1mu}Z\mspace {1mu}} K({\mathscr {C}_{\mathfrak {g}}^{Q}})$ is isomorphic to the coordinate ring
$\mathbb {C} \otimes _\mathbb {\mspace {1mu}Z\mspace {1mu}} K({\mathscr {C}_{\mathfrak {g}}^{Q}})$ is isomorphic to the coordinate ring ![]() $\mathbb {C}[N]$. Moreover, under this isomorphism, the set of isomorphism classes of simple modules in
$\mathbb {C}[N]$. Moreover, under this isomorphism, the set of isomorphism classes of simple modules in ![]() ${\mathscr {C}_{\mathfrak {g}}^{Q}}$ corresponds to the upper global basis of
${\mathscr {C}_{\mathfrak {g}}^{Q}}$ corresponds to the upper global basis of ![]() $\mathbb {C}[N]$.
$\mathbb {C}[N]$.
The notion of the categories ![]() $\mathscr {C}_{\mathfrak {g}}^0$ and
$\mathscr {C}_{\mathfrak {g}}^0$ and ![]() ${\mathscr {C}_{\mathfrak {g}}^{Q}}$ has been extended to all untwisted and twisted quantum affine algebras [Reference Kang, Kashiwara, Kim and OhKKKO16, Reference Kashiwara and OhKO19, Reference Oh and ScrimshawOS19a, Reference Oh and SuhOS19b]. Let
${\mathscr {C}_{\mathfrak {g}}^{Q}}$ has been extended to all untwisted and twisted quantum affine algebras [Reference Kang, Kashiwara, Kim and OhKKKO16, Reference Kashiwara and OhKO19, Reference Oh and ScrimshawOS19a, Reference Oh and SuhOS19b]. Let ![]() ${\sigma ({\mathfrak {g}})} \mathbin {:=} I_0 \times \mathbf {k}^\times / \sim,$ where the equivalence relation is given by
${\sigma ({\mathfrak {g}})} \mathbin {:=} I_0 \times \mathbf {k}^\times / \sim,$ where the equivalence relation is given by ![]() $(i,x) \sim (j,y)$ if and only if
$(i,x) \sim (j,y)$ if and only if ![]() $V(\varpi _i)_x \simeq V(\varpi _j)_y$. The set
$V(\varpi _i)_x \simeq V(\varpi _j)_y$. The set ![]() ${\sigma ({\mathfrak {g}})}$ has a quiver structure determined by the pole of R-matrices between tensor products of fundamental representations
${\sigma ({\mathfrak {g}})}$ has a quiver structure determined by the pole of R-matrices between tensor products of fundamental representations ![]() $V(\varpi _i)_x$ (
$V(\varpi _i)_x$ (![]() $(i,x)\in {\sigma ({\mathfrak {g}})}$). Let
$(i,x)\in {\sigma ({\mathfrak {g}})}$). Let ![]() ${\sigma _0({\mathfrak {g}})}$ be a connected component of
${\sigma _0({\mathfrak {g}})}$ be a connected component of ![]() ${\sigma ({\mathfrak {g}})}$. Then the category
${\sigma ({\mathfrak {g}})}$. Then the category ![]() $\mathscr {C}_{\mathfrak {g}}^0$ is defined to be the smallest full subcategory of
$\mathscr {C}_{\mathfrak {g}}^0$ is defined to be the smallest full subcategory of ![]() $\mathscr {C}_{\mathfrak {g}}$ that has the following properties:
$\mathscr {C}_{\mathfrak {g}}$ that has the following properties:
(a)
 $\mathscr {C}_{\mathfrak {g}}^0$ contains
$\mathscr {C}_{\mathfrak {g}}^0$ contains  $V(\varpi _i)_x$ for all
$V(\varpi _i)_x$ for all  $(i,x) \in {\sigma _0({\mathfrak {g}})}$;
$(i,x) \in {\sigma _0({\mathfrak {g}})}$;(b)
 $\mathscr {C}_{\mathfrak {g}}^0$ is stable by taking subquotients, extensions and tensor products.
$\mathscr {C}_{\mathfrak {g}}^0$ is stable by taking subquotients, extensions and tensor products.
The subcategory ![]() ${\mathscr {C}_{\mathfrak {g}}^{Q}}$ was introduced in [Reference Kang, Kashiwara, Kim and OhKKKO16] for twisted affine type
${\mathscr {C}_{\mathfrak {g}}^{Q}}$ was introduced in [Reference Kang, Kashiwara, Kim and OhKKKO16] for twisted affine type ![]() $A^{(2)}$ and
$A^{(2)}$ and ![]() $D^{(2)}$, in [Reference Kashiwara and OhKO19] for untwisted affine types
$D^{(2)}$, in [Reference Kashiwara and OhKO19] for untwisted affine types ![]() $B^{(1)}$ and
$B^{(1)}$ and ![]() $C^{(1)}$, and in [Reference Oh and ScrimshawOS19a, Reference Oh and SuhOS19b] for exceptional affine type. For a Dynkin quiver
$C^{(1)}$, and in [Reference Oh and ScrimshawOS19a, Reference Oh and SuhOS19b] for exceptional affine type. For a Dynkin quiver ![]() $Q$ of a certain type with additional data, a finite subset
$Q$ of a certain type with additional data, a finite subset ![]() ${\sigma _Q({\mathfrak {g}})}$ of
${\sigma _Q({\mathfrak {g}})}$ of ![]() ${\sigma _0({\mathfrak {g}})}$ was determined. Then the category
${\sigma _0({\mathfrak {g}})}$ was determined. Then the category ![]() ${\mathscr {C}_{\mathfrak {g}}^{Q}}$ is defined to be the smallest full subcategory of
${\mathscr {C}_{\mathfrak {g}}^{Q}}$ is defined to be the smallest full subcategory of ![]() $\mathscr {C}_{\mathfrak {g}}^0$ for which the following hold:
$\mathscr {C}_{\mathfrak {g}}^0$ for which the following hold:
(a)
 ${\mathscr {C}_{\mathfrak {g}}^{Q}}$ contains
${\mathscr {C}_{\mathfrak {g}}^{Q}}$ contains  $\mathbf {1}$ and
$\mathbf {1}$ and  $V(\varpi _i)_x$ for all
$V(\varpi _i)_x$ for all  $(i,x) \in {\sigma _Q({\mathfrak {g}})}$;
$(i,x) \in {\sigma _Q({\mathfrak {g}})}$;(b)
 ${\mathscr {C}_{\mathfrak {g}}^{Q}}$ is stable by taking subquotients, extensions and tensor products
${\mathscr {C}_{\mathfrak {g}}^{Q}}$ is stable by taking subquotients, extensions and tensor products
(see §§ 2.3 and 2.4 for more details).
We can summarize the results of this paper as follows:
(i) we associate a simply laced root system to each quantum affine algebra
 $U_q'({\mathfrak {g}})$ in a natural way;
$U_q'({\mathfrak {g}})$ in a natural way;(ii) we give the block decomposition of
 $\mathscr {C}_{\mathfrak {g}}$ parameterized by a lattice
$\mathscr {C}_{\mathfrak {g}}$ parameterized by a lattice  $\mathcal {W}$ associated with the root system.
$\mathcal {W}$ associated with the root system.
Let ![]() $U_q'({\mathfrak {g}})$ be a quantum affine algebra of arbitrary type. We first consider certain subgroups
$U_q'({\mathfrak {g}})$ be a quantum affine algebra of arbitrary type. We first consider certain subgroups ![]() $\mathcal {W}$ and
$\mathcal {W}$ and ![]() $\mathcal {W} _0$ of the abelian group
$\mathcal {W} _0$ of the abelian group ![]() $\operatorname {Hom}({\sigma ({\mathfrak {g}})}, \mathbb {\mspace {1mu}Z\mspace {1mu}})$ arising from simple modules of
$\operatorname {Hom}({\sigma ({\mathfrak {g}})}, \mathbb {\mspace {1mu}Z\mspace {1mu}})$ arising from simple modules of ![]() $\mathscr {C}_{\mathfrak {g}}$ and
$\mathscr {C}_{\mathfrak {g}}$ and ![]() $\mathscr {C}_{\mathfrak {g}}^0$, respectively (see (4.2)). The subgroups
$\mathscr {C}_{\mathfrak {g}}^0$, respectively (see (4.2)). The subgroups ![]() $\mathcal {W}$ and
$\mathcal {W}$ and ![]() $\mathcal {W} _0$ have subsets
$\mathcal {W} _0$ have subsets ![]() $\Delta$ and
$\Delta$ and ![]() $\Delta _0$ determined by the fundamental representations in
$\Delta _0$ determined by the fundamental representations in ![]() $\mathscr {C}_{\mathfrak {g}}$ and
$\mathscr {C}_{\mathfrak {g}}$ and ![]() $\mathscr {C}_{\mathfrak {g}}^0$, respectively. Let
$\mathscr {C}_{\mathfrak {g}}^0$, respectively. Let ![]() $\mathcal {E} \mathbin {:=} \mathbb {R} \otimes _\mathbb {\mspace {1mu}Z\mspace {1mu}} \mathcal {W}$ and
$\mathcal {E} \mathbin {:=} \mathbb {R} \otimes _\mathbb {\mspace {1mu}Z\mspace {1mu}} \mathcal {W}$ and ![]() $\mathcal {E} _0 \mathbin {:=} \mathbb {R} \otimes _\mathbb {\mspace {1mu}Z\mspace {1mu}} \mathcal {W} _0$. Let
$\mathcal {E} _0 \mathbin {:=} \mathbb {R} \otimes _\mathbb {\mspace {1mu}Z\mspace {1mu}} \mathcal {W} _0$. Let ![]() ${{\mathfrak {g}}_{\mathrm {fin}}}$ be the simply laced finite-type Lie algebra corresponding to the affine type of
${{\mathfrak {g}}_{\mathrm {fin}}}$ be the simply laced finite-type Lie algebra corresponding to the affine type of ![]() ${\mathfrak {g}}$ in table (4.5). When
${\mathfrak {g}}$ in table (4.5). When ![]() ${\mathfrak {g}}$ is of untwisted affine type ADE,
${\mathfrak {g}}$ is of untwisted affine type ADE, ![]() ${{\mathfrak {g}}_{\mathrm {fin}}}$ coincides with
${{\mathfrak {g}}_{\mathrm {fin}}}$ coincides with ![]() ${\mathfrak {g}}_0$. We prove that the pair
${\mathfrak {g}}_0$. We prove that the pair ![]() $( \mathcal {E} _0, \Delta _0)$ is the irreducible root system of the Lie algebra
$( \mathcal {E} _0, \Delta _0)$ is the irreducible root system of the Lie algebra ![]() ${{\mathfrak {g}}_{\mathrm {fin}}}$ and the pair
${{\mathfrak {g}}_{\mathrm {fin}}}$ and the pair ![]() $( \mathcal {E} , \Delta )$ is isomorphic to the direct sum of infinite copies of
$( \mathcal {E} , \Delta )$ is isomorphic to the direct sum of infinite copies of ![]() $( \mathcal {E} _0, \Delta _0)$ as a root system (see Theorem 4.6 and Corollary 4.7). Interestingly enough, the quantum affine algebra
$( \mathcal {E} _0, \Delta _0)$ as a root system (see Theorem 4.6 and Corollary 4.7). Interestingly enough, the quantum affine algebra ![]() $U_q'({\mathfrak {g}})$ and its Langlands dual
$U_q'({\mathfrak {g}})$ and its Langlands dual ![]() $U_q'(^{L}{\mathfrak {g}})$, whose Cartan matrix is the transpose of that of
$U_q'(^{L}{\mathfrak {g}})$, whose Cartan matrix is the transpose of that of ![]() ${\mathfrak {g}}$, yield the same simply laced root system. This coincidence can also be viewed in terms of the mysterious duality between
${\mathfrak {g}}$, yield the same simply laced root system. This coincidence can also be viewed in terms of the mysterious duality between ![]() $U_q'({\mathfrak {g}})$ and its Langlands dual
$U_q'({\mathfrak {g}})$ and its Langlands dual ![]() $U_q'(^{L}{\mathfrak {g}})$ (see [Reference Frenkel and HernandezFH11a, Reference Frenkel and HernandezFH11b, Reference Frenkel and ReshetikhinFR98]). We conjecture that the categories of representations of two quantum affine algebras are equivalent if and only if their associated root systems are the same. From this viewpoint, the simply laced finite-type root system plays the role of an invariant for the representation categories of quantum affine algebras. For each simply laced finite-type root system, the corresponding untwisted quantum affine algebra, the one of twisted type (if it exists) and its Langland dual have the same categorical structure.
$U_q'(^{L}{\mathfrak {g}})$ (see [Reference Frenkel and HernandezFH11a, Reference Frenkel and HernandezFH11b, Reference Frenkel and ReshetikhinFR98]). We conjecture that the categories of representations of two quantum affine algebras are equivalent if and only if their associated root systems are the same. From this viewpoint, the simply laced finite-type root system plays the role of an invariant for the representation categories of quantum affine algebras. For each simply laced finite-type root system, the corresponding untwisted quantum affine algebra, the one of twisted type (if it exists) and its Langland dual have the same categorical structure.
We then show that there exist direct decompositions of ![]() $\mathscr {C}_{\mathfrak {g}}$ and
$\mathscr {C}_{\mathfrak {g}}$ and ![]() $\mathscr {C}_{\mathfrak {g}}^0$ parameterized by elements of
$\mathscr {C}_{\mathfrak {g}}^0$ parameterized by elements of ![]() $\mathcal {W}$ and
$\mathcal {W}$ and ![]() $\mathcal {W} _0$, respectively (Theorem 5.10), and we prove that each direct summand of the decompositions is a block (Theorem 5.14). This approach covers all untwisted and twisted quantum affine algebras in a uniform way and provides a transparent explanation of how the blocks of
$\mathcal {W} _0$, respectively (Theorem 5.10), and we prove that each direct summand of the decompositions is a block (Theorem 5.14). This approach covers all untwisted and twisted quantum affine algebras in a uniform way and provides a transparent explanation of how the blocks of ![]() $\mathscr {C}_{\mathfrak {g}}^0$ exist from the perspective of the root system
$\mathscr {C}_{\mathfrak {g}}^0$ exist from the perspective of the root system ![]() $( \mathcal {E} _0, \Delta _0)$ and the category
$( \mathcal {E} _0, \Delta _0)$ and the category ![]() ${\mathscr {C}_{\mathfrak {g}}^{Q}}$.
${\mathscr {C}_{\mathfrak {g}}^{Q}}$.
When ![]() ${\mathfrak {g}}$ is of untwisted type, the block decomposition was studied in [Reference Chari and MouraCM05, Reference Etingof and MouraEM03, Reference Jakelić and MouraJM11]. Etingof and Moura [Reference Etingof and MouraEM03] found the block decomposition of
${\mathfrak {g}}$ is of untwisted type, the block decomposition was studied in [Reference Chari and MouraCM05, Reference Etingof and MouraEM03, Reference Jakelić and MouraJM11]. Etingof and Moura [Reference Etingof and MouraEM03] found the block decomposition of ![]() $\mathscr {C}_{\mathfrak {g}}$ whose blocks are parameterized by the elliptic central characters under the condition
$\mathscr {C}_{\mathfrak {g}}$ whose blocks are parameterized by the elliptic central characters under the condition ![]() $|q|<1$. Later, Chari and Moura [Reference Chari and MouraCM05] gave a different description of the block decomposition of
$|q|<1$. Later, Chari and Moura [Reference Chari and MouraCM05] gave a different description of the block decomposition of ![]() $\mathscr {C}_{\mathfrak {g}}$ by using the quotient group
$\mathscr {C}_{\mathfrak {g}}$ by using the quotient group ![]() $\mathscr {P}_q / \mathscr {Q}_q$ of the
$\mathscr {P}_q / \mathscr {Q}_q$ of the ![]() $\ell$-weight lattice
$\ell$-weight lattice ![]() $\mathscr {P}_q$ by the
$\mathscr {P}_q$ by the ![]() $\ell$-root lattice
$\ell$-root lattice ![]() $\mathscr {Q}_q$. In the case of the quantum affine algebra
$\mathscr {Q}_q$. In the case of the quantum affine algebra ![]() $U_\xi ({{\mathfrak {g}}})$ at roots of unity, its block decomposition was studied in [Reference Jakelić and MouraJM11]. For affine Kac–Moody algebras, the block decomposition of the category of finite-dimensional modules was studied in [Reference Chari and MouraCM04, Reference SenesiSen10]. Note that the block decomposition for affine Kac–Moody algebras does not explain blocks for quantum affine algebras
$U_\xi ({{\mathfrak {g}}})$ at roots of unity, its block decomposition was studied in [Reference Jakelić and MouraJM11]. For affine Kac–Moody algebras, the block decomposition of the category of finite-dimensional modules was studied in [Reference Chari and MouraCM04, Reference SenesiSen10]. Note that the block decomposition for affine Kac–Moody algebras does not explain blocks for quantum affine algebras ![]() $U'_q({\mathfrak {g}})$. We remark that in the untwisted-type case, the quotient group
$U'_q({\mathfrak {g}})$. We remark that in the untwisted-type case, the quotient group ![]() $\mathscr {P}_q / \mathscr {Q}_q$ given in [Reference Chari and MouraCM05] (and also the result of [Reference Etingof and MouraEM03]) provides another group presentation of
$\mathscr {P}_q / \mathscr {Q}_q$ given in [Reference Chari and MouraCM05] (and also the result of [Reference Etingof and MouraEM03]) provides another group presentation of ![]() $\mathcal {W}$ (see Remark 5.16).
$\mathcal {W}$ (see Remark 5.16).
The main tools used to prove our results are the new invariants ![]() $\Lambda$,
$\Lambda$, ![]() $\Lambda ^\infty$ and
$\Lambda ^\infty$ and ![]() $\operatorname {\mathfrak {d}}$ for a pair of modules in
$\operatorname {\mathfrak {d}}$ for a pair of modules in ![]() $\mathscr {C}_{\mathfrak {g}}$ introduced in [Reference Kashiwara, Kim, Oh and ParkKKOP20]. For non-zero modules
$\mathscr {C}_{\mathfrak {g}}$ introduced in [Reference Kashiwara, Kim, Oh and ParkKKOP20]. For non-zero modules ![]() $M$ and
$M$ and ![]() $N$ in
$N$ in ![]() $\mathscr {C}_{\mathfrak {g}}$ such that
$\mathscr {C}_{\mathfrak {g}}$ such that ![]() $R^{\mspace {1mu}\mathrm {univ}}_{M,N_z}$ is rationally renormalizable, the integers
$R^{\mspace {1mu}\mathrm {univ}}_{M,N_z}$ is rationally renormalizable, the integers ![]() $\Lambda (M,N)$,
$\Lambda (M,N)$, ![]() $\Lambda ^\infty (M,N)$ and
$\Lambda ^\infty (M,N)$ and ![]() $\operatorname {\mathfrak {d}}(M,N)$ are defined by using the renormalizing coefficient
$\operatorname {\mathfrak {d}}(M,N)$ are defined by using the renormalizing coefficient ![]() $c_{M,N}(z)$ (see § 3 for details). These invariants are quantum affine algebra analogues of the invariants (with the same notation) for pairs of graded modules over quiver Hecke algebras arising from the grading of R-matrices. The new invariants play similar roles in the representation theory of quantum affine algebras to those for quiver Hecke algebras.
$c_{M,N}(z)$ (see § 3 for details). These invariants are quantum affine algebra analogues of the invariants (with the same notation) for pairs of graded modules over quiver Hecke algebras arising from the grading of R-matrices. The new invariants play similar roles in the representation theory of quantum affine algebras to those for quiver Hecke algebras.
Let us explain our results more precisely. Let ![]() $U_q'({\mathfrak {g}})$ be a quantum affine algebra of arbitrary type. For
$U_q'({\mathfrak {g}})$ be a quantum affine algebra of arbitrary type. For ![]() $M \in \mathscr {C}_{\mathfrak {g}}$ such that the universal R-matrix
$M \in \mathscr {C}_{\mathfrak {g}}$ such that the universal R-matrix ![]() $R^{\mspace {1mu}\mathrm {univ}}_{M, V(\varpi _i)_z}$ is rationally renormalizable for any
$R^{\mspace {1mu}\mathrm {univ}}_{M, V(\varpi _i)_z}$ is rationally renormalizable for any ![]() $i\in I_0$, we define
$i\in I_0$, we define ![]() $\mathsf {E} (M) \in \operatorname {Hom}({\sigma ({\mathfrak {g}})}, \mathbb {\mspace {1mu}Z\mspace {1mu}})$ by
$\mathsf {E} (M) \in \operatorname {Hom}({\sigma ({\mathfrak {g}})}, \mathbb {\mspace {1mu}Z\mspace {1mu}})$ by
and investigate its properties (Lemma 4.1). For ![]() $(i,a) \in {\sigma ({\mathfrak {g}})}$, we set
$(i,a) \in {\sigma ({\mathfrak {g}})}$, we set
and
 \begin{alignat*}{4} \mathcal{W} & \mathbin{:=} \{ \mathsf{E} (M) \mid M \text{ is simple in } \mathscr{C}_{\mathfrak{g}}\}, & \quad \Delta & \mathbin{:=} \{ \mathsf{s} _{i,a} \mid (i,a) \in {\sigma({\mathfrak{g}})} \} \subset \mathcal{W} , \\ \mathcal{W} _0 & \mathbin{:=} \{ \mathsf{E} (M) \mid M \text{ is simple in } \mathscr{C}_{\mathfrak{g}}^0 \}, & \quad \Delta_0 & \mathbin{:=} \{ \mathsf{s} _{i,a} \mid (i,a) \in {\sigma_0({\mathfrak{g}})} \} \subset \mathcal{W} _0. \end{alignat*}
\begin{alignat*}{4} \mathcal{W} & \mathbin{:=} \{ \mathsf{E} (M) \mid M \text{ is simple in } \mathscr{C}_{\mathfrak{g}}\}, & \quad \Delta & \mathbin{:=} \{ \mathsf{s} _{i,a} \mid (i,a) \in {\sigma({\mathfrak{g}})} \} \subset \mathcal{W} , \\ \mathcal{W} _0 & \mathbin{:=} \{ \mathsf{E} (M) \mid M \text{ is simple in } \mathscr{C}_{\mathfrak{g}}^0 \}, & \quad \Delta_0 & \mathbin{:=} \{ \mathsf{s} _{i,a} \mid (i,a) \in {\sigma_0({\mathfrak{g}})} \} \subset \mathcal{W} _0. \end{alignat*}
Then ![]() $\mathcal {W}$ and
$\mathcal {W}$ and ![]() $\mathcal {W} _0$ are abelian subgroups of
$\mathcal {W} _0$ are abelian subgroups of ![]() $\operatorname {Hom}({\sigma ({\mathfrak {g}})}, \mathbb {\mspace {1mu}Z\mspace {1mu}})$. Moreover, we see in Lemma 4.2 that there exists a unique symmetric bilinear form
$\operatorname {Hom}({\sigma ({\mathfrak {g}})}, \mathbb {\mspace {1mu}Z\mspace {1mu}})$. Moreover, we see in Lemma 4.2 that there exists a unique symmetric bilinear form ![]() $(-,-)$ on
$(-,-)$ on ![]() $\mathcal {W}$ such that
$\mathcal {W}$ such that ![]() $( \mathsf {E} (M), \mathsf {E} (N) ) = - \Lambda ^\infty (M,N)$ for any simple modules
$( \mathsf {E} (M), \mathsf {E} (N) ) = - \Lambda ^\infty (M,N)$ for any simple modules ![]() $M,N \in \mathscr {C}_{\mathfrak {g}}$; it induces a symmetric bilinear form on
$M,N \in \mathscr {C}_{\mathfrak {g}}$; it induces a symmetric bilinear form on ![]() $\mathcal {E}$. Then we prove that the pair
$\mathcal {E}$. Then we prove that the pair ![]() $( \mathcal {E} _0, \Delta _0)$ is an irreducible root system of the simply laced finite type given in (4.5) (Theorem 4.6) and that the pair
$( \mathcal {E} _0, \Delta _0)$ is an irreducible root system of the simply laced finite type given in (4.5) (Theorem 4.6) and that the pair ![]() $( \mathcal {E} , \Delta )$ is isomorphic to the direct sum of infinite copies of
$( \mathcal {E} , \Delta )$ is isomorphic to the direct sum of infinite copies of ![]() $( \mathcal {E} _0, \Delta _0)$ as a root system (Corollary 4.7). Furthermore, the bilinear form
$( \mathcal {E} _0, \Delta _0)$ as a root system (Corollary 4.7). Furthermore, the bilinear form ![]() $(-,-)$ is invariant under the Weyl group action. Theorem 4.6 is proved in § 6 via a case-by-case approach, using the explicit descriptions of
$(-,-)$ is invariant under the Weyl group action. Theorem 4.6 is proved in § 6 via a case-by-case approach, using the explicit descriptions of ![]() ${\sigma _Q({\mathfrak {g}})}$ for
${\sigma _Q({\mathfrak {g}})}$ for ![]() ${\mathscr {C}_{\mathfrak {g}}^{Q}}$ given in § 2.4 and the denominator formulas in Appendix A.
${\mathscr {C}_{\mathfrak {g}}^{Q}}$ given in § 2.4 and the denominator formulas in Appendix A.
We then consider the block decompositions of ![]() $\mathscr {C}_{\mathfrak {g}}$ and
$\mathscr {C}_{\mathfrak {g}}$ and ![]() $\mathscr {C}_g^0$. For
$\mathscr {C}_g^0$. For ![]() $\alpha \in \mathcal {W}$, let
$\alpha \in \mathcal {W}$, let ![]() $\mathscr {C}_{{\mathfrak {g}}, \alpha }$ be the full subcategory of
$\mathscr {C}_{{\mathfrak {g}}, \alpha }$ be the full subcategory of ![]() $\mathscr {C}_{\mathfrak {g}}$ consisting of objects
$\mathscr {C}_{\mathfrak {g}}$ consisting of objects ![]() $X$ such that
$X$ such that ![]() $\mathsf {E} (S)=\alpha$ for any simple subquotient
$\mathsf {E} (S)=\alpha$ for any simple subquotient ![]() $S$ of
$S$ of ![]() $X$. We show that there exist the direct decompositions
$X$. We show that there exist the direct decompositions
by proving that ![]() $\operatorname {Ext}^1_{U_q'({\mathfrak {g}})}(M,N)=0$ for
$\operatorname {Ext}^1_{U_q'({\mathfrak {g}})}(M,N)=0$ for ![]() $M \in \mathscr {C}_{{\mathfrak {g}}, \alpha }$ and
$M \in \mathscr {C}_{{\mathfrak {g}}, \alpha }$ and ![]() $N \in \mathscr {C}_{{\mathfrak {g}}, \beta }$ with
$N \in \mathscr {C}_{{\mathfrak {g}}, \beta }$ with ![]() $\alpha \ne \beta$ (Theorem 5.10). We set
$\alpha \ne \beta$ (Theorem 5.10). We set ![]() $\mathcal {P} \mathbin {:=} \bigoplus _{(i,a) \in {\sigma ({\mathfrak {g}})}} \mathbb {\mspace {1mu}Z\mspace {1mu}} \mathsf {e}_{(i,a)}$ and
$\mathcal {P} \mathbin {:=} \bigoplus _{(i,a) \in {\sigma ({\mathfrak {g}})}} \mathbb {\mspace {1mu}Z\mspace {1mu}} \mathsf {e}_{(i,a)}$ and ![]() $\mathcal {P}_0 \mathbin {:=} \bigoplus _{(i,a) \in {\sigma _0({\mathfrak {g}})}} \mathbb {\mspace {1mu}Z\mspace {1mu}} \mathsf {e}_{(i,a)}$, where
$\mathcal {P}_0 \mathbin {:=} \bigoplus _{(i,a) \in {\sigma _0({\mathfrak {g}})}} \mathbb {\mspace {1mu}Z\mspace {1mu}} \mathsf {e}_{(i,a)}$, where ![]() $\mathsf {e}_{(i,a)}$ is a symbol. Then we define a group homomorphism
$\mathsf {e}_{(i,a)}$ is a symbol. Then we define a group homomorphism ![]() $p\colon \mathcal {P} \twoheadrightarrow \mathcal {W}$ by
$p\colon \mathcal {P} \twoheadrightarrow \mathcal {W}$ by ![]() $p( \mathsf {e}_{(i,a)} )= \mathsf {s} _{i,a}$ and set
$p( \mathsf {e}_{(i,a)} )= \mathsf {s} _{i,a}$ and set ![]() $p_0 \mathbin {:=} p|_{\mathcal {P}_0}\colon \mathcal {P}_0 \twoheadrightarrow \mathcal {W} _0.$ It turns out that the kernel
$p_0 \mathbin {:=} p|_{\mathcal {P}_0}\colon \mathcal {P}_0 \twoheadrightarrow \mathcal {W} _0.$ It turns out that the kernel ![]() $\ker p_0$ coincides with the subgroup
$\ker p_0$ coincides with the subgroup ![]() $\mathcal {Q}_0$ of
$\mathcal {Q}_0$ of ![]() $\mathcal {P}_0$ generated by elements of the form
$\mathcal {P}_0$ generated by elements of the form ![]() $\sum _{k=1}^m \mathsf {e}_{(i_k,a_k)}$ (
$\sum _{k=1}^m \mathsf {e}_{(i_k,a_k)}$ (![]() $(i_k,a_k) \in {\sigma _0({\mathfrak {g}})}$) such that the trivial module
$(i_k,a_k) \in {\sigma _0({\mathfrak {g}})}$) such that the trivial module ![]() $\mathbf {1}$ appears in
$\mathbf {1}$ appears in ![]() $V(i_1)_{a_1} \otimes \cdots \otimes V(i_m)_{a_m}$ as a simple subquotient (Lemma 5.13). We then prove that
$V(i_1)_{a_1} \otimes \cdots \otimes V(i_m)_{a_m}$ as a simple subquotient (Lemma 5.13). We then prove that ![]() $\mathscr {C}_{{\mathfrak {g}}, \alpha }$ is a block for any
$\mathscr {C}_{{\mathfrak {g}}, \alpha }$ is a block for any ![]() $\alpha \in \mathcal {W}$ (Theorem 5.14), which implies that the above decompositions are block decompositions of
$\alpha \in \mathcal {W}$ (Theorem 5.14), which implies that the above decompositions are block decompositions of ![]() $\mathscr {C}_{\mathfrak {g}}$ and
$\mathscr {C}_{\mathfrak {g}}$ and ![]() $\mathscr {C}_{\mathfrak {g}}^0$.
$\mathscr {C}_{\mathfrak {g}}^0$.
This paper is organized as follows. In § 2, we give the necessary background on quantum affine algebras, R-matrices, and the categories ![]() $\mathscr {C}_{\mathfrak {g}}$ and
$\mathscr {C}_{\mathfrak {g}}$ and ![]() ${\mathscr {C}_{\mathfrak {g}}^{Q}}$. In § 3, we review the new invariants introduced in [Reference Kashiwara, Kim, Oh and ParkKKOP20]. In § 4, we investigate properties of
${\mathscr {C}_{\mathfrak {g}}^{Q}}$. In § 3, we review the new invariants introduced in [Reference Kashiwara, Kim, Oh and ParkKKOP20]. In § 4, we investigate properties of ![]() $\mathcal {W}$,
$\mathcal {W}$, ![]() $\Delta$ and
$\Delta$ and ![]() $\mathsf {s} _{i,a}$ and state the main theorem for the root systems
$\mathsf {s} _{i,a}$ and state the main theorem for the root systems ![]() $( \mathcal {E} _0, \Delta _0)$ and
$( \mathcal {E} _0, \Delta _0)$ and ![]() $( \mathcal {E} , \Delta )$. In § 5, we prove the block decompositions of
$( \mathcal {E} , \Delta )$. In § 5, we prove the block decompositions of ![]() $\mathscr {C}_{\mathfrak {g}}$ and
$\mathscr {C}_{\mathfrak {g}}$ and ![]() $\mathscr {C}_{\mathfrak {g}}^0$. Section 6 is devoted to a case-by-case proof of Theorem 4.6.
$\mathscr {C}_{\mathfrak {g}}^0$. Section 6 is devoted to a case-by-case proof of Theorem 4.6.
2. Preliminaries
Convention
(i) For a statement
 $P$,
$P$,  $\delta (P)$ is
$\delta (P)$ is  $1$ or
$1$ or  $0$ according to whether
$0$ according to whether  $P$ is true or not.
$P$ is true or not.(ii) For an element
 $a$ in a field
$a$ in a field  $\mathbf {k}$ and
$\mathbf {k}$ and  $f(z)\in \mathbf {k}(z)$, we denote by
$f(z)\in \mathbf {k}(z)$, we denote by  $\mspace {1mu}\mathrm {zero}\mspace {1mu}_{z=a}f(z)$ the order of zero of
$\mspace {1mu}\mathrm {zero}\mspace {1mu}_{z=a}f(z)$ the order of zero of  $f(z)$ at
$f(z)$ at  $z=a$.
$z=a$.
2.1 Quantum affine algebras
The quintuple ![]() $( \mathsf {A}, \mathsf {P}, \Pi, \mathsf {P}^\vee, \Pi ^\vee )$ is called an affine Cartan datum if it consists of the following components:
$( \mathsf {A}, \mathsf {P}, \Pi, \mathsf {P}^\vee, \Pi ^\vee )$ is called an affine Cartan datum if it consists of the following components:
(i) an affine Cartan matrix
 $\mathsf {A}=(a_{ij})_{i,j\in I}$ with a finite index set
$\mathsf {A}=(a_{ij})_{i,j\in I}$ with a finite index set  $I$;
$I$;(ii) a free abelian group
 $\mathsf {P}$ of rank
$\mathsf {P}$ of rank  $|I|+1$, called the weight lattice;
$|I|+1$, called the weight lattice;(iii) a set
 $\Pi =\{\alpha _i \in \mathsf {P} \mid i \in I\}$, whose elements are called simple roots;
$\Pi =\{\alpha _i \in \mathsf {P} \mid i \in I\}$, whose elements are called simple roots;(iv) the group
 $\mathsf {P}^\vee \mathbin {:=} \operatorname {Hom}_\mathbb {\mspace {1mu}Z\mspace {1mu}}(\mathsf {P},\mathbb {\mspace {1mu}Z\mspace {1mu}})$, called the coweight lattice;
$\mathsf {P}^\vee \mathbin {:=} \operatorname {Hom}_\mathbb {\mspace {1mu}Z\mspace {1mu}}(\mathsf {P},\mathbb {\mspace {1mu}Z\mspace {1mu}})$, called the coweight lattice;(v) a set
 $\Pi ^\vee =\{h_i \mid i \in I\} \subset \mathsf {P}^\vee$, whose elements are simple coroots;
$\Pi ^\vee =\{h_i \mid i \in I\} \subset \mathsf {P}^\vee$, whose elements are simple coroots;
and if it satisfies the following properties:
(a)
 $\langle h_i, \alpha _j \rangle = a_{i,j}$ for any
$\langle h_i, \alpha _j \rangle = a_{i,j}$ for any  $i,j\in I$;
$i,j\in I$;(b) for any
 $i\in I$, there exists
$i\in I$, there exists  $\Lambda _i\in \mathsf {P}$ such that
$\Lambda _i\in \mathsf {P}$ such that  $\langle {h_j,\Lambda _i}\rangle =\delta (i=j)$ for any
$\langle {h_j,\Lambda _i}\rangle =\delta (i=j)$ for any  $j\in I$;
$j\in I$;(c)
 $\Pi$ is linearly independent.
$\Pi$ is linearly independent.
Let ![]() ${\mathfrak {g}}$ be the affine Kac–Moody algebra associated with
${\mathfrak {g}}$ be the affine Kac–Moody algebra associated with ![]() $(\mathsf {A},\mathsf {P},\Pi,\mathsf {P}^\vee,\Pi ^\vee )$. We set
$(\mathsf {A},\mathsf {P},\Pi,\mathsf {P}^\vee,\Pi ^\vee )$. We set ![]() $\mathsf {Q} \mathbin {:=} \bigoplus _{i \in I}\mathbb {\mspace {1mu}Z\mspace {1mu}}\alpha _i \subset \mathsf {P}$, which is called the root lattice, and
$\mathsf {Q} \mathbin {:=} \bigoplus _{i \in I}\mathbb {\mspace {1mu}Z\mspace {1mu}}\alpha _i \subset \mathsf {P}$, which is called the root lattice, and ![]() $\mathsf {Q}^+ \mathbin {:=} \sum _{i \in I}\mathbb {\mspace {1mu}Z\mspace {1mu}}_{\geqslant 0}\alpha _i\subset \mathsf {Q}$. For
$\mathsf {Q}^+ \mathbin {:=} \sum _{i \in I}\mathbb {\mspace {1mu}Z\mspace {1mu}}_{\geqslant 0}\alpha _i\subset \mathsf {Q}$. For ![]() $\beta = \sum _{i\in I} b_i \alpha _i \in \mathsf {Q}^+$, we write
$\beta = \sum _{i\in I} b_i \alpha _i \in \mathsf {Q}^+$, we write ![]() $|\beta | = \sum _{i\in I} b_i$. We denote by
$|\beta | = \sum _{i\in I} b_i$. We denote by ![]() $\delta \in \mathsf {Q}$ the imaginary root and by
$\delta \in \mathsf {Q}$ the imaginary root and by ![]() $c \in \mathsf {Q}^\vee$ the central element. Note that the positive imaginary root
$c \in \mathsf {Q}^\vee$ the central element. Note that the positive imaginary root ![]() $\Delta _+^{\rm im}$ is equal to
$\Delta _+^{\rm im}$ is equal to ![]() $\mathbb {\mspace {1mu}Z\mspace {1mu}}_{>0}\, \delta$ and the center of
$\mathbb {\mspace {1mu}Z\mspace {1mu}}_{>0}\, \delta$ and the center of ![]() ${\mathfrak {g}}$ is generated by
${\mathfrak {g}}$ is generated by ![]() $c$. We write
$c$. We write ![]() $\mathsf {P}_{\mathrm {cl}\mspace {1mu}} \mathbin {:=} \mathsf {P} / (\mathsf {P}\cap \mathbb {Q} \delta )$, which is called the classical weight lattice, and take
$\mathsf {P}_{\mathrm {cl}\mspace {1mu}} \mathbin {:=} \mathsf {P} / (\mathsf {P}\cap \mathbb {Q} \delta )$, which is called the classical weight lattice, and take ![]() $\rho \in \mathsf {P}$ (respectively
$\rho \in \mathsf {P}$ (respectively ![]() $\rho ^\vee \in \mathsf {P}^\vee$) such that
$\rho ^\vee \in \mathsf {P}^\vee$) such that ![]() $\langle h_i,\rho \rangle =1$ (respectively
$\langle h_i,\rho \rangle =1$ (respectively ![]() $\langle \rho ^\vee,\alpha _i\rangle =1$) for any
$\langle \rho ^\vee,\alpha _i\rangle =1$) for any ![]() $i \in I$. There exists a
$i \in I$. There exists a ![]() $\mathbb {Q}$-valued non-degenerate symmetric bilinear form
$\mathbb {Q}$-valued non-degenerate symmetric bilinear form ![]() $( \ , \ )$ on
$( \ , \ )$ on ![]() $\mathsf {P}$ satisfying
$\mathsf {P}$ satisfying
for any ![]() $i \in I$ and
$i \in I$ and ![]() $\lambda \in \mathsf {P}$. We write
$\lambda \in \mathsf {P}$. We write ![]() $\mathsf {W} \mathbin {:=} \langle s_i \mid i \in I \rangle \subset \textrm {Aut}(\mathsf {P})$ for the Weyl group of
$\mathsf {W} \mathbin {:=} \langle s_i \mid i \in I \rangle \subset \textrm {Aut}(\mathsf {P})$ for the Weyl group of ![]() $\mathsf {A}$, where
$\mathsf {A}$, where ![]() $s_i (\lambda ) \mathbin {:=} \lambda - \langle h_i,\lambda \rangle \alpha _i$ for
$s_i (\lambda ) \mathbin {:=} \lambda - \langle h_i,\lambda \rangle \alpha _i$ for ![]() $\lambda \in \mathsf {P}$. We will use the standard convention in [Reference KacKac90] of choosing
$\lambda \in \mathsf {P}$. We will use the standard convention in [Reference KacKac90] of choosing ![]() $0\in I$ except for type
$0\in I$ except for type ![]() $A^{(2)}_{2n}$, in which case we take the longest simple root to be
$A^{(2)}_{2n}$, in which case we take the longest simple root to be ![]() $\alpha _0$, and for types
$\alpha _0$, and for types ![]() $B_2^{(1)}$,
$B_2^{(1)}$, ![]() $A_3^{(2)}$ and
$A_3^{(2)}$ and ![]() $E_k^{(1)}$ (
$E_k^{(1)}$ (![]() $k=6,7,8$), in which cases we take the following Dynkin diagrams.
$k=6,7,8$), in which cases we take the following Dynkin diagrams.

Note that ![]() $B^{(1)}_2$ and
$B^{(1)}_2$ and ![]() $A^{(2)}_3$ in (
$A^{(2)}_3$ in (
) are denoted by ![]() $C_2^{(1)}$ and
$C_2^{(1)}$ and ![]() $D_3^{(2)}$, respectively, in [Reference KacKac90].
$D_3^{(2)}$, respectively, in [Reference KacKac90].
Let ![]() ${\mathfrak {g}}_0$ be the subalgebra of
${\mathfrak {g}}_0$ be the subalgebra of ![]() ${\mathfrak {g}}$ generated by the Chevalley generators
${\mathfrak {g}}$ generated by the Chevalley generators ![]() $e_i$,
$e_i$, ![]() $f_i$ and
$f_i$ and ![]() $h_i$ for
$h_i$ for ![]() $i \in I_0 \mathbin {:=} I \setminus \{ 0 \}$, and let
$i \in I_0 \mathbin {:=} I \setminus \{ 0 \}$, and let ![]() $\mathsf {W}_0$ be the subgroup of
$\mathsf {W}_0$ be the subgroup of ![]() $\mathsf {W}$ generated by
$\mathsf {W}$ generated by ![]() $s_i$ for
$s_i$ for ![]() $i \in I_0$. Note that
$i \in I_0$. Note that ![]() ${\mathfrak {g}}_0$ is a finite-dimensional simple Lie algebra and
${\mathfrak {g}}_0$ is a finite-dimensional simple Lie algebra and ![]() $\mathsf {W}_0$ contains the longest element
$\mathsf {W}_0$ contains the longest element ![]() $w_0$.
$w_0$.
Let ![]() $q$ be an indeterminate and
$q$ be an indeterminate and ![]() ${{\mathbf {k}}}$ the algebraic closure of the subfield
${{\mathbf {k}}}$ the algebraic closure of the subfield ![]() $\mathbb {C}(q)$ in the algebraically closed field
$\mathbb {C}(q)$ in the algebraically closed field ![]() $\hat {\mathbf {k}}\mathbin {:=}\bigcup _{m >0}\mathbb {C}((q^{1/m}))$. For
$\hat {\mathbf {k}}\mathbin {:=}\bigcup _{m >0}\mathbb {C}((q^{1/m}))$. For ![]() $m,n \in \mathbb {\mspace {1mu}Z\mspace {1mu}}_{\geqslant 0}$ and
$m,n \in \mathbb {\mspace {1mu}Z\mspace {1mu}}_{\geqslant 0}$ and ![]() $i\in I$, we define
$i\in I$, we define ![]() $q_i = q^{(\alpha _i,\alpha _i)/2}$ and
$q_i = q^{(\alpha _i,\alpha _i)/2}$ and
 \[ [n]_i =\frac{ q^n_{i} - q^{{-}n}_{i} }{ q_{i} - q^{{-}1}_{i} }, \quad [n]_i! = \prod^{n}_{k=1} [k]_i , \quad \Big[\begin{matrix}m \\ n\\ \end{matrix} \Big]_i= \frac{ [m]_i! }{[m-n]_i! [n]_i! }. \]
\[ [n]_i =\frac{ q^n_{i} - q^{{-}n}_{i} }{ q_{i} - q^{{-}1}_{i} }, \quad [n]_i! = \prod^{n}_{k=1} [k]_i , \quad \Big[\begin{matrix}m \\ n\\ \end{matrix} \Big]_i= \frac{ [m]_i! }{[m-n]_i! [n]_i! }. \] Let ![]() $d$ be the smallest positive integer such that
$d$ be the smallest positive integer such that ![]() $d ({(\alpha _i, \alpha _i)}/{2})\in \mathbb {\mspace {1mu}Z\mspace {1mu}}$ for all
$d ({(\alpha _i, \alpha _i)}/{2})\in \mathbb {\mspace {1mu}Z\mspace {1mu}}$ for all ![]() $i\in I$.
$i\in I$.
Definition 2.1 The quantum affine algebra ![]() $U_q({\mathfrak {g}})$ associated with an affine Cartan datum
$U_q({\mathfrak {g}})$ associated with an affine Cartan datum ![]() $(\mathsf {A},\mathsf {P},\Pi,\mathsf {P}^\vee,\Pi ^\vee )$ is the associative algebra over
$(\mathsf {A},\mathsf {P},\Pi,\mathsf {P}^\vee,\Pi ^\vee )$ is the associative algebra over ![]() ${{\mathbf {k}}}$ with
${{\mathbf {k}}}$ with ![]() $1$ generated by
$1$ generated by ![]() $e_i,f_i$
$e_i,f_i$ ![]() $(i \in I)$ and
$(i \in I)$ and ![]() $q^{h}$
$q^{h}$ ![]() $(h \in d^{-1} \mathsf {P}^{\vee })$ which satisfies the following relations:
$(h \in d^{-1} \mathsf {P}^{\vee })$ which satisfies the following relations:
(i)
 $q^0=1$ and
$q^0=1$ and  $q^{h} q^{h'}=q^{h+h'}$ for
$q^{h} q^{h'}=q^{h+h'}$ for  $h,h' \in d^{-1} \mathsf {P}^{\vee }$;
$h,h' \in d^{-1} \mathsf {P}^{\vee }$;(ii)
 $q^{h}e_i q^{-h}= q^{\langle h, \alpha _i \rangle } e_i$ and
$q^{h}e_i q^{-h}= q^{\langle h, \alpha _i \rangle } e_i$ and  $q^{h}f_i q^{-h} = q^{-\langle h, \alpha _i \rangle }f_i$ for
$q^{h}f_i q^{-h} = q^{-\langle h, \alpha _i \rangle }f_i$ for  $h \in d^{-1}\mathsf {P}^{\vee }$ and
$h \in d^{-1}\mathsf {P}^{\vee }$ and  $i \in I$;
$i \in I$;(iii)
 $e_if_j - f_je_i = \delta _{ij} (({K_i -K^{-1}_i})/({q_i- q^{-1}_i })), \text { where } K_i=q_i^{ h_i}$;
$e_if_j - f_je_i = \delta _{ij} (({K_i -K^{-1}_i})/({q_i- q^{-1}_i })), \text { where } K_i=q_i^{ h_i}$;(iv)
 $\sum ^{1-a_{ij}}_{k=0} (-1)^ke^{(1-a_{ij}-k)}_i e_j e^{(k)}_i = \sum ^{1-a_{ij}}_{k=0} (-1)^k f^{(1-a_{ij}-k)}_i f_jf^{(k)}_i=0 \text { for } i \ne j$;
$\sum ^{1-a_{ij}}_{k=0} (-1)^ke^{(1-a_{ij}-k)}_i e_j e^{(k)}_i = \sum ^{1-a_{ij}}_{k=0} (-1)^k f^{(1-a_{ij}-k)}_i f_jf^{(k)}_i=0 \text { for } i \ne j$;
here ![]() $e_i^{(k)}=e_i^k/[k]_i!$ and
$e_i^{(k)}=e_i^k/[k]_i!$ and ![]() $f_i^{(k)}=f_i^k/[k]_i!$.
$f_i^{(k)}=f_i^k/[k]_i!$.
Let us denote by ![]() $U_q'({\mathfrak {g}})$ the
$U_q'({\mathfrak {g}})$ the ![]() $\mathbf {k}$-subalgebra of
$\mathbf {k}$-subalgebra of ![]() $U_q({\mathfrak {g}})$ generated by
$U_q({\mathfrak {g}})$ generated by ![]() $e_i,f_i$ and
$e_i,f_i$ and ![]() $K^{\pm 1}_i$
$K^{\pm 1}_i$ ![]() $(i \in I)$. The coproduct
$(i \in I)$. The coproduct ![]() $\Delta$ of
$\Delta$ of ![]() $U_q'({\mathfrak {g}})$ is given by
$U_q'({\mathfrak {g}})$ is given by
and the bar involution ![]() $\bar{}$ of
$\bar{}$ of ![]() $U_q'({\mathfrak {g}})$ is defined as
$U_q'({\mathfrak {g}})$ is defined as
Let ![]() $\mathscr {C}_{\mathfrak {g}}$ be the category of finite-dimensional integrable
$\mathscr {C}_{\mathfrak {g}}$ be the category of finite-dimensional integrable ![]() $U_q'({\mathfrak {g}})$-modules, i.e. finite-dimensional modules
$U_q'({\mathfrak {g}})$-modules, i.e. finite-dimensional modules ![]() $M$ with a weight decomposition
$M$ with a weight decomposition
Note that the trivial module ![]() $\mathbf {1}$ is contained in
$\mathbf {1}$ is contained in ![]() $\mathscr {C}_{\mathfrak {g}}$ and the tensor product
$\mathscr {C}_{\mathfrak {g}}$ and the tensor product ![]() $\otimes$ gives a monoidal category structure on
$\otimes$ gives a monoidal category structure on ![]() $\mathscr {C}_{\mathfrak {g}}$. It is known that the Grothendieck ring
$\mathscr {C}_{\mathfrak {g}}$. It is known that the Grothendieck ring ![]() $K(\mathscr {C}_{\mathfrak {g}})$ is a commutative ring [Reference Frenkel and ReshetikhinFR99]. A simple module
$K(\mathscr {C}_{\mathfrak {g}})$ is a commutative ring [Reference Frenkel and ReshetikhinFR99]. A simple module ![]() $L$ in
$L$ in ![]() $\mathscr {C}_{\mathfrak {g}}$ contains a non-zero vector
$\mathscr {C}_{\mathfrak {g}}$ contains a non-zero vector ![]() $u \in L$ of weight
$u \in L$ of weight ![]() $\lambda \in \mathsf {P}_{\mathrm {cl}\mspace {1mu}}$ such that (i)
$\lambda \in \mathsf {P}_{\mathrm {cl}\mspace {1mu}}$ such that (i) ![]() $\langle h_i,\lambda \rangle \geqslant 0$ for all
$\langle h_i,\lambda \rangle \geqslant 0$ for all ![]() $i \in I_0$ and (ii) all the weights of
$i \in I_0$ and (ii) all the weights of ![]() $L$ are contained in
$L$ are contained in ![]() $\lambda - \sum _{i \in I_0} \mathbb {\mspace {1mu}Z\mspace {1mu}}_{\geqslant 0}\, {\mathrm {cl}\mspace {1mu}}(\alpha _i)$, where
$\lambda - \sum _{i \in I_0} \mathbb {\mspace {1mu}Z\mspace {1mu}}_{\geqslant 0}\, {\mathrm {cl}\mspace {1mu}}(\alpha _i)$, where ![]() ${\mathrm {cl}\mspace {1mu}}\colon \mathsf {P}\to \mathsf {P}_{\mathrm {cl}\mspace {1mu}}$ is the canonical projection. Such a
${\mathrm {cl}\mspace {1mu}}\colon \mathsf {P}\to \mathsf {P}_{\mathrm {cl}\mspace {1mu}}$ is the canonical projection. Such a ![]() $\lambda$ is unique, and
$\lambda$ is unique, and ![]() $u$ is unique up to a constant multiple. We call
$u$ is unique up to a constant multiple. We call ![]() $\lambda$ the dominant extremal weight of
$\lambda$ the dominant extremal weight of ![]() $L$ and
$L$ and ![]() $u$ a dominant extremal weight vector of
$u$ a dominant extremal weight vector of ![]() $L$.
$L$.
Let ![]() $\mathsf {P}_{\mathrm {cl}\mspace {1mu}}^0\mathbin {:=}\{\lambda \in \mathsf {P}_{\mathrm {cl}\mspace {1mu}}\mid \langle {c,\lambda }\rangle =0\}$. For each
$\mathsf {P}_{\mathrm {cl}\mspace {1mu}}^0\mathbin {:=}\{\lambda \in \mathsf {P}_{\mathrm {cl}\mspace {1mu}}\mid \langle {c,\lambda }\rangle =0\}$. For each ![]() $i \in I_0$ we set
$i \in I_0$ we set
where the central element ![]() $c$ is equal to
$c$ is equal to ![]() $\sum _{ i\in I} \mathsf {c}_i h_i$. Note that
$\sum _{ i\in I} \mathsf {c}_i h_i$. Note that ![]() $\mathsf {P}_{\mathrm {cl}\mspace {1mu}}^0= \bigoplus _{i\in I_0}\mathbb {\mspace {1mu}Z\mspace {1mu}}\varpi _i$. For any
$\mathsf {P}_{\mathrm {cl}\mspace {1mu}}^0= \bigoplus _{i\in I_0}\mathbb {\mspace {1mu}Z\mspace {1mu}}\varpi _i$. For any ![]() $i\in I_0$, there exists a unique simple module
$i\in I_0$, there exists a unique simple module ![]() $V(\varpi _i)$ in
$V(\varpi _i)$ in ![]() $\mathscr {C}_{\mathfrak {g}}$ satisfying certain good conditions (see [Reference KashiwaraKas02, § 5.2]), which is called the
$\mathscr {C}_{\mathfrak {g}}$ satisfying certain good conditions (see [Reference KashiwaraKas02, § 5.2]), which is called the ![]() $i$th fundamental representation. Note that the dominant extremal weight of
$i$th fundamental representation. Note that the dominant extremal weight of ![]() $V(\varpi _i)$ is
$V(\varpi _i)$ is ![]() $\varpi _i$.
$\varpi _i$.
For simple modules ![]() $M$ and
$M$ and ![]() $N$ in
$N$ in ![]() $\mathscr {C}_{\mathfrak {g}}$, we say that
$\mathscr {C}_{\mathfrak {g}}$, we say that ![]() $M$ and
$M$ and ![]() $N$ commute or
$N$ commute or ![]() $M$ commutes with
$M$ commutes with ![]() $N$ if
$N$ if ![]() $M\mathop \otimes N\simeq N\mathop \otimes M$. We say that
$M\mathop \otimes N\simeq N\mathop \otimes M$. We say that ![]() $M$ and
$M$ and ![]() $N$ strongly commute or
$N$ strongly commute or ![]() $M$ strongly commutes with
$M$ strongly commutes with ![]() $N$ if
$N$ if ![]() $M\mathop \otimes N$ is simple. Note that
$M\mathop \otimes N$ is simple. Note that ![]() $M\mathop \otimes N$ is simple if and only if
$M\mathop \otimes N$ is simple if and only if ![]() $N\mathop \otimes M$ is simple, since
$N\mathop \otimes M$ is simple, since ![]() $K(\mathscr {C}_{\mathfrak {g}})$ is a commutative ring. It is clear that if simple modules
$K(\mathscr {C}_{\mathfrak {g}})$ is a commutative ring. It is clear that if simple modules ![]() $M$ and
$M$ and ![]() $N$ strongly commute, then they commute. We say that a simple module
$N$ strongly commute, then they commute. We say that a simple module ![]() $M$ is real if
$M$ is real if ![]() $M$ strongly commutes with itself.
$M$ strongly commutes with itself.
For an integrable ![]() $U_q'({\mathfrak {g}})$-module
$U_q'({\mathfrak {g}})$-module ![]() $M$, we denote by
$M$, we denote by ![]() $M_z$ the affinization of
$M_z$ the affinization of ![]() $M$ and by
$M$ and by ![]() $z_M \colon M_z \to M_z$ the
$z_M \colon M_z \to M_z$ the ![]() $U_q'({\mathfrak {g}})$-module automorphism of weight
$U_q'({\mathfrak {g}})$-module automorphism of weight ![]() $\delta$. Note that
$\delta$. Note that ![]() $M_z \simeq \mathbf {k}[z^{\pm 1}]\otimes _{\mathbf {k}} M$ for an indeterminate
$M_z \simeq \mathbf {k}[z^{\pm 1}]\otimes _{\mathbf {k}} M$ for an indeterminate ![]() $z$ as a
$z$ as a ![]() $\mathbf {k}$-vector space. For
$\mathbf {k}$-vector space. For ![]() $x \in {{\mathbf {k}}}^\times$, we define
$x \in {{\mathbf {k}}}^\times$, we define
We call ![]() $x$ a spectral parameter. The functor
$x$ a spectral parameter. The functor ![]() $T_x$ defined by
$T_x$ defined by ![]() $T_x(M)=M_x$ is an endofunctor of
$T_x(M)=M_x$ is an endofunctor of ![]() $\mathscr {C}_{\mathfrak {g}}$ that commutes with tensor products (see [Reference KashiwaraKas02, § 4.2] for details).
$\mathscr {C}_{\mathfrak {g}}$ that commutes with tensor products (see [Reference KashiwaraKas02, § 4.2] for details).
It is known that a fundamental representation is a good module, which is a simple ![]() $U_q'({\mathfrak {g}})$-module with good properties including a bar involution, a crystal basis with simple crystal graph, and a global basis (see [Reference KashiwaraKas02] for the precise definition). We say that a
$U_q'({\mathfrak {g}})$-module with good properties including a bar involution, a crystal basis with simple crystal graph, and a global basis (see [Reference KashiwaraKas02] for the precise definition). We say that a ![]() $U_q'({\mathfrak {g}})$-module
$U_q'({\mathfrak {g}})$-module ![]() $M$ is quasi-good if
$M$ is quasi-good if
for some good module ![]() $V$ and
$V$ and ![]() $c \in \mathbf {k}^\times$. Note that any quasi-good module is a simple
$c \in \mathbf {k}^\times$. Note that any quasi-good module is a simple ![]() $U_q'({\mathfrak {g}})$-module. Moreover the tensor product
$U_q'({\mathfrak {g}})$-module. Moreover the tensor product ![]() $M^{\otimes k} \mathbin {:=} \underbrace {M \mathop \otimes \cdots \mathop \otimes M}_{k\text { times}}$ for a quasi-good module
$M^{\otimes k} \mathbin {:=} \underbrace {M \mathop \otimes \cdots \mathop \otimes M}_{k\text { times}}$ for a quasi-good module ![]() $M$ and
$M$ and ![]() $k \in \mathbb {\mspace {1mu}Z\mspace {1mu}}_{\geqslant 1}$ is again quasi-good.
$k \in \mathbb {\mspace {1mu}Z\mspace {1mu}}_{\geqslant 1}$ is again quasi-good.
For a ![]() $U_q'({\mathfrak {g}})$-module
$U_q'({\mathfrak {g}})$-module ![]() $M$, we denote by
$M$, we denote by ![]() $\bar {M}=\{ \bar {u} \mid u \in M \}$ the
$\bar {M}=\{ \bar {u} \mid u \in M \}$ the ![]() $U_q'({\mathfrak {g}})$-module defined by
$U_q'({\mathfrak {g}})$-module defined by ![]() $x \bar {u} \mathbin {:=} \overline { \bar {x} u }$ for
$x \bar {u} \mathbin {:=} \overline { \bar {x} u }$ for ![]() $x \in U_q'({\mathfrak {g}})$. Then we have
$x \in U_q'({\mathfrak {g}})$. Then we have
Note that ![]() $V(\varpi _i)$ is bar-invariant, i.e.
$V(\varpi _i)$ is bar-invariant, i.e. ![]() $\overline {V(\varpi _i)}\simeq V(\varpi _i)$ (see [Reference Akasaka and KashiwaraAK97, Appendix A]).
$\overline {V(\varpi _i)}\simeq V(\varpi _i)$ (see [Reference Akasaka and KashiwaraAK97, Appendix A]).
Let ![]() $m_i$ be a positive integer such that
$m_i$ be a positive integer such that
where ![]() $\pi _i$ is an element of
$\pi _i$ is an element of ![]() $\mathsf {P}$ such that
$\mathsf {P}$ such that ![]() ${\mathrm {cl}\mspace {1mu}}(\pi _i)=\varpi _i$. Note that
${\mathrm {cl}\mspace {1mu}}(\pi _i)=\varpi _i$. Note that ![]() $m_i=(\alpha _i,\alpha _i)/2$ in the case where
$m_i=(\alpha _i,\alpha _i)/2$ in the case where ![]() ${\mathfrak {g}}$ is the dual of an untwisted affine algebra, and
${\mathfrak {g}}$ is the dual of an untwisted affine algebra, and ![]() $m_i=1$ otherwise. Then for
$m_i=1$ otherwise. Then for ![]() $x,y\in {{\mathbf {k}}}^\times$ we have (see [Reference Akasaka and KashiwaraAK97, § 1.3])
$x,y\in {{\mathbf {k}}}^\times$ we have (see [Reference Akasaka and KashiwaraAK97, § 1.3])
We set
where the equivalence relation is given by
We denote by ![]() $[(i,a)]$ the equivalence class of
$[(i,a)]$ the equivalence class of ![]() $(i,a)$ in
$(i,a)$ in ![]() ${\sigma ({\mathfrak {g}})}$. When confusion is unlikely to arise, we simply write
${\sigma ({\mathfrak {g}})}$. When confusion is unlikely to arise, we simply write ![]() $(i,a)$ for the equivalence class
$(i,a)$ for the equivalence class ![]() $[(i,a)]$.
$[(i,a)]$.
The monoidal category ![]() $\mathscr {C}_{\mathfrak {g}}$ is rigid. For
$\mathscr {C}_{\mathfrak {g}}$ is rigid. For ![]() $M\in \mathscr {C}_{\mathfrak {g}}$, we denote by
$M\in \mathscr {C}_{\mathfrak {g}}$, we denote by ![]() ${}^*\mspace {-3mu} M$ and
${}^*\mspace {-3mu} M$ and ![]() $M^*$ the right and left duals of
$M^*$ the right and left duals of ![]() $M$, respectively. We set
$M$, respectively. We set
The integer ![]() $\langle \rho ^\vee, \delta \rangle$ is called the Coxeter number, and
$\langle \rho ^\vee, \delta \rangle$ is called the Coxeter number, and ![]() $\langle c, \rho \rangle$ is called the dual Coxeter number (see [Reference KacKac90, Ch. 6]). For the reader's convenience we list
$\langle c, \rho \rangle$ is called the dual Coxeter number (see [Reference KacKac90, Ch. 6]). For the reader's convenience we list ![]() $p^*$ for all types in the following table.
$p^*$ for all types in the following table.
 \begin{align} \small
\begin{array}{|c||c|c|c|c|c|c|c|} \hline \text{Type of
${\mathfrak{g}}$} & A_n^{(1)^{\vphantom{1}}} & B_n^{(1)} & C_n^{(1)} &
D_n^{(1)} & A_{2n}^{(2)} & A_{2n-1}^{(2)} & D_{n+1}^{(2)} \\
& (n\geqslant1) & (n\geqslant2) & (n\geqslant3) &
(n\geqslant4) & (n\geqslant1) & (n\geqslant2) &
(n\geqslant3)\\ \hline p^* & ({-}q)^{n+1^{\vphantom{1}}} & q^{2n-1} &
q^{n+1} & q^{2n-2} & -q^{2n+1} & -q^{2n} & ({-}1)^{n+1}
q^{2n} \\ \hline \hline \text{Type of ${\mathfrak{g}}$} &
E_6^{(1)} & E_7^{(1)} & E_8^{(1)^{\vphantom{1}}} & F_4^{(1)} & G_{2}^{(1)}
& E_{6}^{(2)} & D_{4}^{(3)} \\ \hline p^* & q^{12} & q^{18^{\vphantom{1}}}
& q^{30} & q^9 & q^4 & -q^{12} & q^6 \\ \hline\end{array} \end{align}
\begin{align} \small
\begin{array}{|c||c|c|c|c|c|c|c|} \hline \text{Type of
${\mathfrak{g}}$} & A_n^{(1)^{\vphantom{1}}} & B_n^{(1)} & C_n^{(1)} &
D_n^{(1)} & A_{2n}^{(2)} & A_{2n-1}^{(2)} & D_{n+1}^{(2)} \\
& (n\geqslant1) & (n\geqslant2) & (n\geqslant3) &
(n\geqslant4) & (n\geqslant1) & (n\geqslant2) &
(n\geqslant3)\\ \hline p^* & ({-}q)^{n+1^{\vphantom{1}}} & q^{2n-1} &
q^{n+1} & q^{2n-2} & -q^{2n+1} & -q^{2n} & ({-}1)^{n+1}
q^{2n} \\ \hline \hline \text{Type of ${\mathfrak{g}}$} &
E_6^{(1)} & E_7^{(1)} & E_8^{(1)^{\vphantom{1}}} & F_4^{(1)} & G_{2}^{(1)}
& E_{6}^{(2)} & D_{4}^{(3)} \\ \hline p^* & q^{12} & q^{18^{\vphantom{1}}}
& q^{30} & q^9 & q^4 & -q^{12} & q^6 \\ \hline\end{array} \end{align}
Then for any ![]() $M \in \mathscr {C}_{\mathfrak {g}}$ we have
$M \in \mathscr {C}_{\mathfrak {g}}$ we have
and for ![]() $i\in I_0$ and
$i\in I_0$ and ![]() $x\in \mathbf {k}^\times$ we have
$x\in \mathbf {k}^\times$ we have
where ![]() $i^*\in I_0$ is defined by
$i^*\in I_0$ is defined by ![]() $\alpha _{i^*}=-w_0\,\alpha _i$ (see [Reference Akasaka and KashiwaraAK97, Appendix A]). Note that the involution
$\alpha _{i^*}=-w_0\,\alpha _i$ (see [Reference Akasaka and KashiwaraAK97, Appendix A]). Note that the involution ![]() $i \mapsto i^*$ is the identity for all types except
$i \mapsto i^*$ is the identity for all types except ![]() $A_n, D_n$ and
$A_n, D_n$ and ![]() $E_6$, which are given as follows:
$E_6$, which are given as follows:
(a) (type
 $A_n$)
$A_n$)  $i^* = n+1-i$;
$i^* = n+1-i$;(b) (type
 $D_n$)
$D_n$)  $i^* = \begin {cases} n-(1-\epsilon ) & \text {if } n \hbox { is odd and } i=n-\epsilon\ (\epsilon =0,1), \\ i & \text {otherwise;} \end {cases}$
$i^* = \begin {cases} n-(1-\epsilon ) & \text {if } n \hbox { is odd and } i=n-\epsilon\ (\epsilon =0,1), \\ i & \text {otherwise;} \end {cases}$(c) (type
 $E_6$) the map
$E_6$) the map  $i \mapsto i^*$ is determined by
where the Dynkin diagram of type
$i \mapsto i^*$ is determined by
where the Dynkin diagram of type \[ i^* = \begin{cases} 6 & \text{if } i=1, \\ i & \text{if } i=2,4, \\ 5 & \text{if } i=3, \end{cases} \]
\[ i^* = \begin{cases} 6 & \text{if } i=1, \\ i & \text{if } i=2,4, \\ 5 & \text{if } i=3, \end{cases} \] $E_6$ is given in (A.3) in Appendix A.
$E_6$ is given in (A.3) in Appendix A.
2.2 R-matrices
We recall the notion of R-matrices on ![]() $U_q'({\mathfrak {g}})$-modules and their coefficients (see [Reference Drinfel'dDri86], as well as [Reference Akasaka and KashiwaraAK97, Appendices A and B] and [Reference KashiwaraKas02, § 8], for details). Choose a basis
$U_q'({\mathfrak {g}})$-modules and their coefficients (see [Reference Drinfel'dDri86], as well as [Reference Akasaka and KashiwaraAK97, Appendices A and B] and [Reference KashiwaraKas02, § 8], for details). Choose a basis ![]() $\{P_\nu \}_\nu$ of
$\{P_\nu \}_\nu$ of ![]() $U_q^+({\mathfrak {g}})$ and a basis
$U_q^+({\mathfrak {g}})$ and a basis ![]() $\{Q_\nu \}_\nu$ of
$\{Q_\nu \}_\nu$ of ![]() $U_q^-({\mathfrak {g}})$ that are dual to each other with respect to a suitable coupling between
$U_q^-({\mathfrak {g}})$ that are dual to each other with respect to a suitable coupling between ![]() $U_q^+({\mathfrak {g}})$ and
$U_q^+({\mathfrak {g}})$ and ![]() $U_q^-({\mathfrak {g}})$. For
$U_q^-({\mathfrak {g}})$. For ![]() $U_q'({\mathfrak {g}})$-modules
$U_q'({\mathfrak {g}})$-modules ![]() $M$ and
$M$ and ![]() $N$, we define
$N$, we define
so that ![]() $R^{\mspace {1mu}\mathrm {univ}}_{M,N}$ gives a
$R^{\mspace {1mu}\mathrm {univ}}_{M,N}$ gives a ![]() $U_q'({\mathfrak {g}})$-linear homomorphism
$U_q'({\mathfrak {g}})$-linear homomorphism ![]() $M\otimes N \rightarrow N\otimes M$, called the universal R-matrix, provided that the infinite sum has a meaning. As
$M\otimes N \rightarrow N\otimes M$, called the universal R-matrix, provided that the infinite sum has a meaning. As ![]() $R^{\mspace {1mu}\mathrm {univ}}_{M,N_z}$ converges in the
$R^{\mspace {1mu}\mathrm {univ}}_{M,N_z}$ converges in the ![]() $z$-adic topology for
$z$-adic topology for ![]() $M,N\in \mathscr {C}_{\mathfrak {g}}$, we have a morphism of
$M,N\in \mathscr {C}_{\mathfrak {g}}$, we have a morphism of ![]() ${{\mathbf {k}}}((z))\mathop \otimes U_q'({\mathfrak {g}})$-modules
${{\mathbf {k}}}((z))\mathop \otimes U_q'({\mathfrak {g}})$-modules
Note that ![]() $R^{\mspace {1mu}\mathrm {univ}}_{M,N_z}$ is an isomorphism.
$R^{\mspace {1mu}\mathrm {univ}}_{M,N_z}$ is an isomorphism.
Let ![]() $M$ and
$M$ and ![]() $N$ be non-zero modules in
$N$ be non-zero modules in ![]() $\mathscr {C}_{\mathfrak {g}}$. The universal R-matrix
$\mathscr {C}_{\mathfrak {g}}$. The universal R-matrix ![]() $R^{\mspace {1mu}\mathrm {univ}}_{M,N_z}$ is rationally renormalizable if there exists
$R^{\mspace {1mu}\mathrm {univ}}_{M,N_z}$ is rationally renormalizable if there exists ![]() $f(z) \in {{\mathbf {k}}}((z))^\times$ such that
$f(z) \in {{\mathbf {k}}}((z))^\times$ such that
In this case, we can choose ![]() $c_{M,N}(z) \in {{\mathbf {k}}}((z))^\times$ such that for any
$c_{M,N}(z) \in {{\mathbf {k}}}((z))^\times$ such that for any ![]() $x \in {{\mathbf {k}}}^\times$, the specialization of
$x \in {{\mathbf {k}}}^\times$, the specialization of ![]() $R^{\mspace {1mu}\mathrm {ren}}_{M,N_z} \mathbin {:=} c_{M,N}(z)R^{\mspace {1mu}\mathrm {univ}}_{M,N_z} \colon M \otimes N_z \to N_z \otimes M$ at
$R^{\mspace {1mu}\mathrm {ren}}_{M,N_z} \mathbin {:=} c_{M,N}(z)R^{\mspace {1mu}\mathrm {univ}}_{M,N_z} \colon M \otimes N_z \to N_z \otimes M$ at ![]() $z=x$,
$z=x$,
does not vanish. Note that ![]() $R^{\mspace {1mu}\mathrm {ren}}_{M,N_z}$ and
$R^{\mspace {1mu}\mathrm {ren}}_{M,N_z}$ and ![]() $c_{M,N}(z)$ are unique up to a multiple of
$c_{M,N}(z)$ are unique up to a multiple of ![]() ${\mathbf {k}[z^{\pm 1}]}^\times = \bigsqcup _{n \in \mathbb {\mspace {1mu}Z\mspace {1mu}}}{{\mathbf {k}}}^\times z^n$. We call
${\mathbf {k}[z^{\pm 1}]}^\times = \bigsqcup _{n \in \mathbb {\mspace {1mu}Z\mspace {1mu}}}{{\mathbf {k}}}^\times z^n$. We call ![]() $c_{M,N}(z)$ the renormalizing coefficient. We denote by
$c_{M,N}(z)$ the renormalizing coefficient. We denote by ![]() ${{\mathbf {r}}_{{\scriptstyle {M,N}}}}$ the specialization at
${{\mathbf {r}}_{{\scriptstyle {M,N}}}}$ the specialization at ![]() $z=1$,
$z=1$,
and call it the R-matrix. The R-matrix ![]() ${{\mathbf {r}}_ {{\scriptstyle {M,N}}}}$ is well-defined up to a constant multiple whenever
${{\mathbf {r}}_ {{\scriptstyle {M,N}}}}$ is well-defined up to a constant multiple whenever ![]() $R^{\mspace {1mu}\mathrm {univ}}_{M,N_z}$ is rationally renormalizable. By the definition,
$R^{\mspace {1mu}\mathrm {univ}}_{M,N_z}$ is rationally renormalizable. By the definition, ![]() ${{\mathbf {r}}_{{\scriptstyle {M,N}}}}$ never vanishes.
${{\mathbf {r}}_{{\scriptstyle {M,N}}}}$ never vanishes.
Suppose that ![]() $M$ and
$M$ and ![]() $N$ are simple
$N$ are simple ![]() $U_q'({\mathfrak {g}})$-modules in
$U_q'({\mathfrak {g}})$-modules in ![]() $\mathscr {C}_{\mathfrak {g}}$. Let
$\mathscr {C}_{\mathfrak {g}}$. Let ![]() $u$ and
$u$ and ![]() $v$ be dominant extremal weight vectors of
$v$ be dominant extremal weight vectors of ![]() $M$ and
$M$ and ![]() $N$, respectively. Then there exists
$N$, respectively. Then there exists ![]() $a_{M,N}(z)\in {{\mathbf {k}}}[[z]]^\times$ such that
$a_{M,N}(z)\in {{\mathbf {k}}}[[z]]^\times$ such that
Thus we have a unique ![]() ${{\mathbf {k}}}(z)\mathop \otimes U_q'({\mathfrak {g}})$-module isomorphism
${{\mathbf {k}}}(z)\mathop \otimes U_q'({\mathfrak {g}})$-module isomorphism
from ![]() ${{\mathbf {k}}}(z)\otimes _{{{\mathbf {k}}}[z^{\pm 1}]} ( M \otimes N_z)$ to
${{\mathbf {k}}}(z)\otimes _{{{\mathbf {k}}}[z^{\pm 1}]} ( M \otimes N_z)$ to ![]() ${{\mathbf {k}}}(z)\otimes _{{{\mathbf {k}}}[z^{\pm 1}]} ( N_z \otimes M )$, which satisfies
${{\mathbf {k}}}(z)\otimes _{{{\mathbf {k}}}[z^{\pm 1}]} ( N_z \otimes M )$, which satisfies
We call ![]() $a_{M,N}(z)$ the universal coefficient of
$a_{M,N}(z)$ the universal coefficient of ![]() $M$ and
$M$ and ![]() $N$, and call
$N$, and call ![]() $R^{\mathrm {norm}}_{M,N_z}$ the normalized
$R^{\mathrm {norm}}_{M,N_z}$ the normalized ![]() $R$-matrix.
$R$-matrix.
Let ![]() $d_{M,N}(z) \in {{\mathbf {k}}}[z]$ be a monic polynomial of the smallest degree such that the image of
$d_{M,N}(z) \in {{\mathbf {k}}}[z]$ be a monic polynomial of the smallest degree such that the image of ![]() $d_{M,N}(z) R^{\mathrm {norm}}_{M,N_z}(M\mathop \otimes N_z)$ is contained in
$d_{M,N}(z) R^{\mathrm {norm}}_{M,N_z}(M\mathop \otimes N_z)$ is contained in ![]() $N_z \otimes M$; we call it the denominator of
$N_z \otimes M$; we call it the denominator of ![]() $R^{\mathrm {norm}}_{M,N_z}$. Then we have
$R^{\mathrm {norm}}_{M,N_z}$. Then we have
Thus
up to a multiple of ![]() ${{\mathbf {k}}}[z^{\pm 1}]^\times$. In particular,
${{\mathbf {k}}}[z^{\pm 1}]^\times$. In particular, ![]() $R^{\mspace {1mu}\mathrm {univ}}_{M,N_z}$ is rationally renormalizable whenever
$R^{\mspace {1mu}\mathrm {univ}}_{M,N_z}$ is rationally renormalizable whenever ![]() $M$ and
$M$ and ![]() $N$ are simple.
$N$ are simple.
The denominator formulas between fundamental representations are summarized for all types in Appendix A.
The next theorem follows from the results of [Reference Akasaka and KashiwaraAK97, Reference ChariCha10, Reference KashiwaraKas02, Reference Kang, Kashiwara, Kim and OhKKKO15]. In the theorem, (ii) follows essentially from [Reference Kang, Kashiwara, Kim and OhKKKO15, Corollary 3.16] together with properties of R-matrices (see also [Reference Kashiwara, Kim, Oh and ParkKKOP20, Proposition 3.16 and Corollary 3.17]), and (i), (iii) and (iv) were conjectured in [Reference Akasaka and KashiwaraAK97, § 2] and proved in [Reference Akasaka and KashiwaraAK97, § 4] for affine types ![]() $A$ and
$A$ and ![]() $C$, in [Reference KashiwaraKas02, § 9] for general cases in terms of good modules, and in [Reference ChariCha10, §§ 4 and 6] using the braid group actions.
$C$, in [Reference KashiwaraKas02, § 9] for general cases in terms of good modules, and in [Reference ChariCha10, §§ 4 and 6] using the braid group actions.
Theorem 2.2 [Reference Akasaka and KashiwaraAK97, Reference ChariCha10, Reference KashiwaraKas02, Reference Kang, Kashiwara, Kim and OhKKKO15]
(i) For good modules
 $M$ and
$M$ and  $N$, the zeros of
$N$, the zeros of  $d_{M,N}(z)$ belong to
$d_{M,N}(z)$ belong to  $\mathbb {C}[[q^{1/m}]]q^{1/m}$ for some
$\mathbb {C}[[q^{1/m}]]q^{1/m}$ for some  $m\in \mathbb {\mspace {1mu}Z\mspace {1mu}}_{>0}$.
$m\in \mathbb {\mspace {1mu}Z\mspace {1mu}}_{>0}$.(ii) For simple modules
 $M$ and
$M$ and  $N$ such that one of them is real,
$N$ such that one of them is real,  $M_x$ and
$M_x$ and  $N_y$ strongly commute with each other if and only if
$N_y$ strongly commute with each other if and only if  $d_{M,N}(z)d_{N,M}(1/z)$ does not vanish at
$d_{M,N}(z)d_{N,M}(1/z)$ does not vanish at  $z=y/x$.
$z=y/x$.(iii) Let
 $M_k$ be a good module with a dominant extremal vector
$M_k$ be a good module with a dominant extremal vector  $u_k$ of weight
$u_k$ of weight  $\lambda _k$, and let
$\lambda _k$, and let  $a_k\in {{\mathbf {k}}}^\times$ for
$a_k\in {{\mathbf {k}}}^\times$ for  $k=1,\ldots, t$. Assume that
$k=1,\ldots, t$. Assume that  $a_j/a_i$ is not a zero of
$a_j/a_i$ is not a zero of  $d_{M_i, M_j}(z)$ for any
$d_{M_i, M_j}(z)$ for any  $1\leqslant i< j\leqslant t$. Then the following statements hold.
$1\leqslant i< j\leqslant t$. Then the following statements hold.
(a)
 $(M_1)_{a_1}\otimes \cdots \otimes (M_t)_{a_t}$ is generated by
$(M_1)_{a_1}\otimes \cdots \otimes (M_t)_{a_t}$ is generated by  $u_1\otimes \cdots \otimes u_t$.
$u_1\otimes \cdots \otimes u_t$.(b) The head of
 $(M_1)_{a_1}\otimes \cdots \otimes (M_t)_{a_t}$ is simple.
$(M_1)_{a_1}\otimes \cdots \otimes (M_t)_{a_t}$ is simple.(c) Any non-zero submodule of
 $(M_t)_{a_t}\otimes \cdots \otimes (M_1)_{a_1}$ contains the vector
$(M_t)_{a_t}\otimes \cdots \otimes (M_1)_{a_1}$ contains the vector  $u_t\otimes \cdots \otimes u_1$.
$u_t\otimes \cdots \otimes u_1$.(d) The socle of
 $(M_t)_{a_t}\otimes \cdots \otimes (M_1)_{a_1}$ is simple.
$(M_t)_{a_t}\otimes \cdots \otimes (M_1)_{a_1}$ is simple.(e) Let
 ${{\mathbf {r}}_{\mspace {-2mu}{{\scriptstyle {}}}}}\colon (M_1)_{a_1}\!\otimes\! \cdots \!\otimes\! (M_t)_{a_t} \!\to\! (M_t)_{a_t}\otimes \cdots \otimes (M_1)_{a_1}$ be the specialization of
${{\mathbf {r}}_{\mspace {-2mu}{{\scriptstyle {}}}}}\colon (M_1)_{a_1}\!\otimes\! \cdots \!\otimes\! (M_t)_{a_t} \!\to\! (M_t)_{a_t}\otimes \cdots \otimes (M_1)_{a_1}$ be the specialization of  ${{\mathbf {r}}_{\mspace {-2mu}{{\scriptstyle {M_1,\ldots, M_t}}}}}\mathbin {:=}\prod _{1\leqslant j< k\leqslant t}{{\mathbf {r}}_{\mspace {-2mu}{{\scriptstyle {M_j,M_k}}}}}$ at
${{\mathbf {r}}_{\mspace {-2mu}{{\scriptstyle {M_1,\ldots, M_t}}}}}\mathbin {:=}\prod _{1\leqslant j< k\leqslant t}{{\mathbf {r}}_{\mspace {-2mu}{{\scriptstyle {M_j,M_k}}}}}$ at  $z_k=a_k$; see (2.8). Then the image of
$z_k=a_k$; see (2.8). Then the image of  ${\mathbf {r}}$ is simple and coincides with the head of
${\mathbf {r}}$ is simple and coincides with the head of  $(M_1)_{a_1}\otimes \cdots \otimes (M_t)_{a_t}$ and also with the socle of
$(M_1)_{a_1}\otimes \cdots \otimes (M_t)_{a_t}$ and also with the socle of  $(M_t)_{a_t}\otimes \cdots \otimes (M_1)_{a_1}$.
$(M_t)_{a_t}\otimes \cdots \otimes (M_1)_{a_1}$.
(iv) For any simple integrable
 $U_q'({\mathfrak {g}})$-module
$U_q'({\mathfrak {g}})$-module  $M$, there exists a finite sequence in
$M$, there exists a finite sequence in  ${\sigma ({\mathfrak {g}})}$ (see (2.3)) such that
${\sigma ({\mathfrak {g}})}$ (see (2.3)) such that  $M$ has
$M$ has  $\sum _{k=1}^t \varpi _{i_k}$ as a dominant extremal weight and is isomorphic to a simple subquotient of
$\sum _{k=1}^t \varpi _{i_k}$ as a dominant extremal weight and is isomorphic to a simple subquotient of  $V(\varpi _{i_1})_{a_1}\mathop \otimes \cdots V(\varpi _{i_t})_{a_t}$. Moreover, such a sequence
$V(\varpi _{i_1})_{a_1}\mathop \otimes \cdots V(\varpi _{i_t})_{a_t}$. Moreover, such a sequence  $\bigl ((i_1,a_1),\ldots, (i_t,a_t)\bigr )$ is unique up to a permutation.
$\bigl ((i_1,a_1),\ldots, (i_t,a_t)\bigr )$ is unique up to a permutation.We call
 $\sum _{k=1}^t(i_k,a_k)\in \mathbb {\mspace {1mu}Z\mspace {1mu}}^{\oplus {\sigma ({\mathfrak {g}})}}$ the affine highest weight of
$\sum _{k=1}^t(i_k,a_k)\in \mathbb {\mspace {1mu}Z\mspace {1mu}}^{\oplus {\sigma ({\mathfrak {g}})}}$ the affine highest weight of  $M$.
$M$.
2.3 Hernandez–Leclerc categories
Recall ![]() ${\sigma ({\mathfrak {g}})}$ in (2.3). For
${\sigma ({\mathfrak {g}})}$ in (2.3). For ![]() $(i,x)$ and
$(i,x)$ and ![]() $(j,y) \in {\sigma ({\mathfrak {g}})}$, we put
$(j,y) \in {\sigma ({\mathfrak {g}})}$, we put ![]() $d$ arrows from
$d$ arrows from ![]() $(i,x)$ to
$(i,x)$ to ![]() $(j,y)$, where
$(j,y)$, where ![]() $d$ is the order of the zeros of
$d$ is the order of the zeros of ![]() $d_{ V(\varpi _i), V(\varpi _j) } ( z_{V(\varpi _j)} / z_{V(\varpi _i)} )$ at
$d_{ V(\varpi _i), V(\varpi _j) } ( z_{V(\varpi _j)} / z_{V(\varpi _i)} )$ at ![]() $z_{V(\varpi _j)} / z_{V(\varpi _i)} = y/x$. Then
$z_{V(\varpi _j)} / z_{V(\varpi _i)} = y/x$. Then ![]() ${\sigma ({\mathfrak {g}})}$ has a quiver structure. Note that
${\sigma ({\mathfrak {g}})}$ has a quiver structure. Note that ![]() $(i, x)$ and
$(i, x)$ and ![]() $(j,y)$ are linked in
$(j,y)$ are linked in ![]() ${\sigma ({\mathfrak {g}})}$ if and only if the tensor product
${\sigma ({\mathfrak {g}})}$ if and only if the tensor product ![]() $V(\varpi _i)_x \otimes V(\varpi _j)_y$ is reducible [Reference Akasaka and KashiwaraAK97, Corollary 2.4]. The denominator formulas are explicitly given in Appendix A.
$V(\varpi _i)_x \otimes V(\varpi _j)_y$ is reducible [Reference Akasaka and KashiwaraAK97, Corollary 2.4]. The denominator formulas are explicitly given in Appendix A.
We choose a connected component ![]() ${\sigma _0({\mathfrak {g}})}$ of
${\sigma _0({\mathfrak {g}})}$ of ![]() ${\sigma ({\mathfrak {g}})}$. Since a connected component of
${\sigma ({\mathfrak {g}})}$. Since a connected component of ![]() ${\sigma ({\mathfrak {g}})}$ is unique up to a spectral parameter shift,
${\sigma ({\mathfrak {g}})}$ is unique up to a spectral parameter shift, ![]() ${\sigma _0({\mathfrak {g}})}$ is uniquely determined up to a quiver isomorphism. We set
${\sigma _0({\mathfrak {g}})}$ is uniquely determined up to a quiver isomorphism. We set
The distance ![]() $\mathrm {d}(u,v)$ between two vertices
$\mathrm {d}(u,v)$ between two vertices ![]() $u$ and
$u$ and ![]() $v$ in a finite Dynkin diagram is the length of the path connecting them. For example,
$v$ in a finite Dynkin diagram is the length of the path connecting them. For example, ![]() $\mathrm {d}(1,4)=2$ in a Dynkin diagram of type
$\mathrm {d}(1,4)=2$ in a Dynkin diagram of type ![]() $D_4$, and
$D_4$, and ![]() $\mathrm {d}(1,3)=2$ in a Dynkin diagram of type
$\mathrm {d}(1,3)=2$ in a Dynkin diagram of type ![]() $F_4$. We denote by
$F_4$. We denote by ![]() $\mathrm {d}_\circ (i,j)$ the distance between
$\mathrm {d}_\circ (i,j)$ the distance between ![]() $i$ and
$i$ and ![]() $j$ in the Dynkin diagram of
$j$ in the Dynkin diagram of ![]() ${\mathfrak {g}}_0$. For the rest of this paper, we make the following choices of
${\mathfrak {g}}_0$. For the rest of this paper, we make the following choices of ![]() $\sigma _0({\mathfrak {g}})$ (see table (2.6) for the range of
$\sigma _0({\mathfrak {g}})$ (see table (2.6) for the range of ![]() $n$):
$n$):
 \begin{align*} &\sigma_0(X) \mathbin{:=} \{(i,({-}q)^{p}) \in I_0 \times {{\mathbf{k}}}^{{\times}} \mid p \equiv_2 \mathrm{d}_\circ(1,i) \} \quad ( X=A^{(1)}_{n}, D^{(1)}_{n}, E^{(1)}_{k} (k=6,7,8) ), \\ & \sigma_0({B_{n}^{(1)}}) \mathbin{:=} \{{ (i,({-}1)^{ n+i} q_s q^m), (n,q^m)}\mid{1\leqslant i \leqslant n-1,\: m \in \mathbb{\mspace{1mu}Z\mspace{1mu}}}\}, \\ &\sigma_0(C^{(1)}_{n}) \mathbin{:=} \{(i,({-}q_s)^{p}) \in I_0 \times {{\mathbf{k}}}^{{\times}} \mid p \equiv_2 \mathrm{d}_\circ(1,i) \}, \\ &\sigma_0(F^{(1)}_{4}) \mathbin{:=} \{(i,({-}1)^iq_s^{2p-\delta_{i,3}}) \in I_0 \times {{\mathbf{k}}}^{{\times}} \mid p \in \mathbb{\mspace{1mu}Z\mspace{1mu}} \}, \\ &\sigma_0(G^{(1)}_{2}) \mathbin{:=} \{(i,({-}q_t)^{p}) \in I_0 \times {{\mathbf{k}}}^{{\times}} \mid p \equiv_2 \mathrm{d}_\circ(2, i ) \}, \\ &\sigma_0(A^{(2)}_{2n}) \mathbin{:=} \{(i,({-}q)^{p}) \in I_0 \times {{\mathbf{k}}}^{{\times}} \mid p \in \mathbb{\mspace{1mu}Z\mspace{1mu}} \}, \\ &\sigma_0(A^{(2)}_{2n-1}) \mathbin{:=} \{( i,\pm({-}q)^{p}), ( n, ({-}q)^{r}) \mid 1 \leqslant i < n,\: p \equiv_2 i+1, \: r \equiv_2 n+1 \}, \\ & \sigma_0(D^{(2)}_{n+1}) \mathbin{:=} \{ (i, (\sqrt{-1}^{n+1-i}) ({-}q)^p), (n, \pm ({-}q)^{r}) \mid 1\leqslant i < n,\: p \equiv_2 i+1 ,\: r \equiv_2 n+1 \}, \\ & \sigma_0(E^{(2)}_{6}) \mathbin{:=} \{ (i,\pm q^r), (i', \sqrt{-1} ({-}q )^{r'}) \mid i \in \{ 1,2 \}, \: i' \in \{3,4\}, \: r \equiv_2 i+1, \: r'\equiv_2 i'+1 \}, \\ & \sigma_0(D^{(3)}_{4}) \mathbin{:=} \{ (1, q^r),(1, \omega q^r), (1, \omega^2 q^r), (2,-q^{r+1}) \mid r\equiv_2 0 \} \quad (\omega^2+\omega+1=0), \end{align*}
\begin{align*} &\sigma_0(X) \mathbin{:=} \{(i,({-}q)^{p}) \in I_0 \times {{\mathbf{k}}}^{{\times}} \mid p \equiv_2 \mathrm{d}_\circ(1,i) \} \quad ( X=A^{(1)}_{n}, D^{(1)}_{n}, E^{(1)}_{k} (k=6,7,8) ), \\ & \sigma_0({B_{n}^{(1)}}) \mathbin{:=} \{{ (i,({-}1)^{ n+i} q_s q^m), (n,q^m)}\mid{1\leqslant i \leqslant n-1,\: m \in \mathbb{\mspace{1mu}Z\mspace{1mu}}}\}, \\ &\sigma_0(C^{(1)}_{n}) \mathbin{:=} \{(i,({-}q_s)^{p}) \in I_0 \times {{\mathbf{k}}}^{{\times}} \mid p \equiv_2 \mathrm{d}_\circ(1,i) \}, \\ &\sigma_0(F^{(1)}_{4}) \mathbin{:=} \{(i,({-}1)^iq_s^{2p-\delta_{i,3}}) \in I_0 \times {{\mathbf{k}}}^{{\times}} \mid p \in \mathbb{\mspace{1mu}Z\mspace{1mu}} \}, \\ &\sigma_0(G^{(1)}_{2}) \mathbin{:=} \{(i,({-}q_t)^{p}) \in I_0 \times {{\mathbf{k}}}^{{\times}} \mid p \equiv_2 \mathrm{d}_\circ(2, i ) \}, \\ &\sigma_0(A^{(2)}_{2n}) \mathbin{:=} \{(i,({-}q)^{p}) \in I_0 \times {{\mathbf{k}}}^{{\times}} \mid p \in \mathbb{\mspace{1mu}Z\mspace{1mu}} \}, \\ &\sigma_0(A^{(2)}_{2n-1}) \mathbin{:=} \{( i,\pm({-}q)^{p}), ( n, ({-}q)^{r}) \mid 1 \leqslant i < n,\: p \equiv_2 i+1, \: r \equiv_2 n+1 \}, \\ & \sigma_0(D^{(2)}_{n+1}) \mathbin{:=} \{ (i, (\sqrt{-1}^{n+1-i}) ({-}q)^p), (n, \pm ({-}q)^{r}) \mid 1\leqslant i < n,\: p \equiv_2 i+1 ,\: r \equiv_2 n+1 \}, \\ & \sigma_0(E^{(2)}_{6}) \mathbin{:=} \{ (i,\pm q^r), (i', \sqrt{-1} ({-}q )^{r'}) \mid i \in \{ 1,2 \}, \: i' \in \{3,4\}, \: r \equiv_2 i+1, \: r'\equiv_2 i'+1 \}, \\ & \sigma_0(D^{(3)}_{4}) \mathbin{:=} \{ (1, q^r),(1, \omega q^r), (1, \omega^2 q^r), (2,-q^{r+1}) \mid r\equiv_2 0 \} \quad (\omega^2+\omega+1=0), \end{align*}
where ![]() $a \equiv _2 b$ means that
$a \equiv _2 b$ means that ![]() $a\equiv b\mspace {3mu}\mathbin {\mathrm {mod}}\mspace {1mu} 2$ (see [Reference Hernandez and LeclercHL10, § 3.7], [Reference Kang, Kashiwara, Kim and OhKKKO16, § 4.1], [Reference Kashiwara and OhKO19, § 6] and [Reference Oh and ScrimshawOS19a, § 6]). Note that in [Reference Oh and ScrimshawOS19a, § 6] the category
$a\equiv b\mspace {3mu}\mathbin {\mathrm {mod}}\mspace {1mu} 2$ (see [Reference Hernandez and LeclercHL10, § 3.7], [Reference Kang, Kashiwara, Kim and OhKKKO16, § 4.1], [Reference Kashiwara and OhKO19, § 6] and [Reference Oh and ScrimshawOS19a, § 6]). Note that in [Reference Oh and ScrimshawOS19a, § 6] the category ![]() ${\mathscr {C}_{\mathfrak {g}}^{Q}}$ and
${\mathscr {C}_{\mathfrak {g}}^{Q}}$ and ![]() ${\sigma _Q({\mathfrak {g}})}$ were dealt with only in exceptional cases, but it is easy to obtain
${\sigma _Q({\mathfrak {g}})}$ were dealt with only in exceptional cases, but it is easy to obtain ![]() ${\sigma _0({\mathfrak {g}})}$ using
${\sigma _0({\mathfrak {g}})}$ using ![]() ${\sigma _Q({\mathfrak {g}})}$. We use the notation
${\sigma _Q({\mathfrak {g}})}$. We use the notation ![]() $B_2^{(1)}$ and
$B_2^{(1)}$ and ![]() $A^{(2)}_{3}$ instead of
$A^{(2)}_{3}$ instead of ![]() $C_2^{(1)}$ and
$C_2^{(1)}$ and ![]() $D_{3}^{(2)}$, respectively. Here we use the standard convention for Dynkin diagrams in [Reference KacKac90, Ch. 4] except for
$D_{3}^{(2)}$, respectively. Here we use the standard convention for Dynkin diagrams in [Reference KacKac90, Ch. 4] except for ![]() $A^{(2)}_{2n}$,
$A^{(2)}_{2n}$, ![]() $A_3^{(2)}$,
$A_3^{(2)}$, ![]() $B_2^{(1)}$ and
$B_2^{(1)}$ and ![]() $E^{(1)}_{k}$ (
$E^{(1)}_{k}$ (![]() $k=6,7,8$), which are given in (2.1).
$k=6,7,8$), which are given in (2.1).
We define ![]() $\mathscr {C}_{\mathfrak {g}}^0$ to be the smallest full subcategory of
$\mathscr {C}_{\mathfrak {g}}^0$ to be the smallest full subcategory of ![]() $\mathscr {C}_{\mathfrak {g}}$ for which the following hold:
$\mathscr {C}_{\mathfrak {g}}$ for which the following hold:
(a)
 $\mathscr {C}_{\mathfrak {g}}^0$ contains
$\mathscr {C}_{\mathfrak {g}}^0$ contains  $V(\varpi _i)_x$ for all
$V(\varpi _i)_x$ for all  $(i,x) \in {\sigma _0({\mathfrak {g}})}$;
$(i,x) \in {\sigma _0({\mathfrak {g}})}$;(b)
 $\mathscr {C}_{\mathfrak {g}}^0$ is stable by taking subquotients, extensions and tensor products.
$\mathscr {C}_{\mathfrak {g}}^0$ is stable by taking subquotients, extensions and tensor products.
For symmetric affine types, this category was introduced in [Reference Hernandez and LeclercHL10]. Note that every simple module in ![]() $\mathscr {C}_{\mathfrak {g}}$ is isomorphic to a tensor product of certain spectral parameter shifts of some simple modules in
$\mathscr {C}_{\mathfrak {g}}$ is isomorphic to a tensor product of certain spectral parameter shifts of some simple modules in ![]() $\mathscr {C}_{\mathfrak {g}}^0$ (see [Reference Hernandez and LeclercHL10, § 3.7]).
$\mathscr {C}_{\mathfrak {g}}^0$ (see [Reference Hernandez and LeclercHL10, § 3.7]).
2.4 The categories  ${\mathscr {C}_{\mathfrak {g}}^{Q}}$
${\mathscr {C}_{\mathfrak {g}}^{Q}}$
In this subsection, we recall very briefly a certain subcategory ![]() ${\mathscr {C}_{\mathfrak {g}}^{Q}}$ of
${\mathscr {C}_{\mathfrak {g}}^{Q}}$ of ![]() $\mathscr {C}_{\mathfrak {g}}$ categorifying the coordinate ring
$\mathscr {C}_{\mathfrak {g}}$ categorifying the coordinate ring ![]() $\mathbb {C}[N]$ of the maximal unipotent group
$\mathbb {C}[N]$ of the maximal unipotent group ![]() $N$ associated with a certain simple Lie algebra.
$N$ associated with a certain simple Lie algebra.
This subcategory ![]() ${\mathscr {C}_{\mathfrak {g}}^{Q}}$ was introduced in [Reference Hernandez and LeclercHL15] for simply laced affine type ADE, in [Reference Kang, Kashiwara, Kim and OhKKKO16] for twisted affine types
${\mathscr {C}_{\mathfrak {g}}^{Q}}$ was introduced in [Reference Hernandez and LeclercHL15] for simply laced affine type ADE, in [Reference Kang, Kashiwara, Kim and OhKKKO16] for twisted affine types ![]() $A^{(2)}$ and
$A^{(2)}$ and ![]() $D^{(2)}$, in [Reference Kashiwara and OhKO19, Reference Oh and SuhOS19b] for untwisted affine types
$D^{(2)}$, in [Reference Kashiwara and OhKO19, Reference Oh and SuhOS19b] for untwisted affine types ![]() $B^{(1)}$ and
$B^{(1)}$ and ![]() $C^{(1)}$, and in [Reference Oh and ScrimshawOS19a] for exceptional affine type. The quantum affine Schur–Weyl duality functor between the finite-dimensional module category of a quiver Hecke algebra and
$C^{(1)}$, and in [Reference Oh and ScrimshawOS19a] for exceptional affine type. The quantum affine Schur–Weyl duality functor between the finite-dimensional module category of a quiver Hecke algebra and ![]() ${\mathscr {C}_{\mathfrak {g}}^{Q}}$ was also constructed in [Reference Kang, Kashiwara and KimKKK15] for untwisted affine types
${\mathscr {C}_{\mathfrak {g}}^{Q}}$ was also constructed in [Reference Kang, Kashiwara and KimKKK15] for untwisted affine types ![]() $A^{(1)}$ and
$A^{(1)}$ and ![]() $D^{(1)}$, in [Reference Kang, Kashiwara, Kim and OhKKKO16] for twisted affine types
$D^{(1)}$, in [Reference Kang, Kashiwara, Kim and OhKKKO16] for twisted affine types ![]() $A^{(2)}$ and
$A^{(2)}$ and ![]() $D^{(2)}$, in [Reference Kashiwara and OhKO19] for untwisted affine types
$D^{(2)}$, in [Reference Kashiwara and OhKO19] for untwisted affine types ![]() $B^{(1)}$ and
$B^{(1)}$ and ![]() $C^{(1)}$, in [Reference Oh and ScrimshawOS19a] for exceptional affine type, and in [Reference FujitaFuj20] for simply laced affine type ADE in a geometric manner.
$C^{(1)}$, in [Reference Oh and ScrimshawOS19a] for exceptional affine type, and in [Reference FujitaFuj20] for simply laced affine type ADE in a geometric manner.
We shall describe ![]() ${\sigma _Q({\mathfrak {g}})}$ and
${\sigma _Q({\mathfrak {g}})}$ and ![]() ${\mathscr {C}_{\mathfrak {g}}^{Q}}$ by using
${\mathscr {C}_{\mathfrak {g}}^{Q}}$ by using ![]() $Q$-data [Reference Fujita and OhFO21]. A
$Q$-data [Reference Fujita and OhFO21]. A ![]() $Q$-datum generalizes a Dynkin quiver with a height function, which provides a uniform way of describing the Hernandez–Leclerc category
$Q$-datum generalizes a Dynkin quiver with a height function, which provides a uniform way of describing the Hernandez–Leclerc category ![]() ${\mathscr {C}_{\mathfrak {g}}^{Q}}$. Our brief explanation follows [Reference Fujita and OhFO21, § 3] (see also [Reference Fujita, Hernandez, Oh and OyaFHOO21, § 4] and [Reference Kashiwara, Kim, Oh and ParkKKOP21, § 6]). Let
${\mathscr {C}_{\mathfrak {g}}^{Q}}$. Our brief explanation follows [Reference Fujita and OhFO21, § 3] (see also [Reference Fujita, Hernandez, Oh and OyaFHOO21, § 4] and [Reference Kashiwara, Kim, Oh and ParkKKOP21, § 6]). Let ![]() ${\mathfrak {g}}$ be an affine Kac–Moody algebra and let
${\mathfrak {g}}$ be an affine Kac–Moody algebra and let ![]() ${{\mathfrak {g}}_{\mathrm {fin}}}$ be the simply laced finite-type Lie algebra corresponding to the affine type of
${{\mathfrak {g}}_{\mathrm {fin}}}$ be the simply laced finite-type Lie algebra corresponding to the affine type of ![]() ${\mathfrak {g}}$ in table (4.5). Let
${\mathfrak {g}}$ in table (4.5). Let ![]() ${\mathrm {I_{fin}}}$ be the index set of
${\mathrm {I_{fin}}}$ be the index set of ![]() ${{\mathfrak {g}}_{\mathrm {fin}}}$ and let
${{\mathfrak {g}}_{\mathrm {fin}}}$ and let ![]() $\mathsf {D}_{\rm fin}$ be the Dynkin diagram for
$\mathsf {D}_{\rm fin}$ be the Dynkin diagram for ![]() ${{\mathfrak {g}}_{\mathrm {fin}}}$.
${{\mathfrak {g}}_{\mathrm {fin}}}$.
We first assume that ![]() ${\mathfrak {g}}$ is of untwisted type. We define an Dynkin diagram automorphism
${\mathfrak {g}}$ is of untwisted type. We define an Dynkin diagram automorphism ![]() $\varrho$ of
$\varrho$ of ![]() $\mathsf {D}_{\rm fin}$ as follows. For
$\mathsf {D}_{\rm fin}$ as follows. For ![]() ${\mathfrak {g}}=A_n^{(1)}, D_n^{(1)}$ or
${\mathfrak {g}}=A_n^{(1)}, D_n^{(1)}$ or ![]() $E_k^{(1)}$ type (
$E_k^{(1)}$ type (![]() $k=6,7,8$) we set
$k=6,7,8$) we set ![]() $\varrho :={\rm id}$, and for the remaining types
$\varrho :={\rm id}$, and for the remaining types ![]() $\varrho$ is defined as follows (see [Reference Fujita and OhFO21, § 3.1]).
$\varrho$ is defined as follows (see [Reference Fujita and OhFO21, § 3.1]).

Let ![]() $I_0 =\{ 1,2,\ldots, n \}$ be the index set of
$I_0 =\{ 1,2,\ldots, n \}$ be the index set of ![]() ${\mathfrak {g}}_0$. Note that
${\mathfrak {g}}_0$. Note that ![]() ${\mathrm {I_{fin}}} = I_0$ when
${\mathrm {I_{fin}}} = I_0$ when ![]() ${\mathfrak {g}}=A_n^{(1)}, D_n^{(1)}, E_k^{(1)}$ (
${\mathfrak {g}}=A_n^{(1)}, D_n^{(1)}, E_k^{(1)}$ (![]() $k=6,7,8$). Let
$k=6,7,8$). Let ![]() $\mathrm {ord}(\varrho )$ be the order of
$\mathrm {ord}(\varrho )$ be the order of ![]() $\varrho$. For
$\varrho$. For ![]() $i\in {\mathrm {I_{fin}}}$, we denote by
$i\in {\mathrm {I_{fin}}}$, we denote by ![]() $\mathrm {orb}(i)$ the orbit of
$\mathrm {orb}(i)$ the orbit of ![]() $i$ under the action
$i$ under the action ![]() $\varrho$ and set
$\varrho$ and set ![]() $\mathsf {d}_i := | \mathrm {orb}(i) |$. We identify the set of orbits of
$\mathsf {d}_i := | \mathrm {orb}(i) |$. We identify the set of orbits of ![]() ${\mathrm {I_{fin}}}$ with
${\mathrm {I_{fin}}}$ with ![]() $I_0$ by mapping
$I_0$ by mapping ![]() $\mathrm {orb}(i) \mapsto \min \{ \mathrm {orb}(i) \}$ for
$\mathrm {orb}(i) \mapsto \min \{ \mathrm {orb}(i) \}$ for ![]() ${\mathfrak {g}} \ne F_4^{(1)}$ and mapping
${\mathfrak {g}} \ne F_4^{(1)}$ and mapping ![]() $\mathrm {orb}(1) \mapsto 1$,
$\mathrm {orb}(1) \mapsto 1$, ![]() $\mathrm {orb}(3) \mapsto 2$,
$\mathrm {orb}(3) \mapsto 2$, ![]() $\mathrm {orb}(4) \mapsto 3$ and
$\mathrm {orb}(4) \mapsto 3$ and ![]() $\mathrm {orb}(2) \mapsto 4$ for
$\mathrm {orb}(2) \mapsto 4$ for ![]() ${\mathfrak {g}} = F_4^{(1)}$. We write
${\mathfrak {g}} = F_4^{(1)}$. We write ![]() $\pi \colon {\mathrm {I_{fin}}}\to I_0$ for the projection via this identification.
$\pi \colon {\mathrm {I_{fin}}}\to I_0$ for the projection via this identification.
Definition 2.3 [Reference Fujita and OhFO21, Definition 3.5]
A function ![]() $\xi \colon {\mathrm {I_{fin}}} \to \mathbb {\mspace {1mu}Z\mspace {1mu}}$ is called a height function on
$\xi \colon {\mathrm {I_{fin}}} \to \mathbb {\mspace {1mu}Z\mspace {1mu}}$ is called a height function on ![]() $(\mathsf {D}_{\rm fin}, \varrho )$ if the following two conditions are satisfied.
$(\mathsf {D}_{\rm fin}, \varrho )$ if the following two conditions are satisfied.
(i) For any
 $i, j \in {\mathrm {I_{fin}}}$ such that
$i, j \in {\mathrm {I_{fin}}}$ such that  $\mathrm {d}(i,j)=1$ and
$\mathrm {d}(i,j)=1$ and  $\mathsf {d}_i= \mathsf {d}_j$, we have
$\mathsf {d}_i= \mathsf {d}_j$, we have  $|\xi _{i} - \xi _{j}| =\mathsf {d}_i$.
$|\xi _{i} - \xi _{j}| =\mathsf {d}_i$.(ii) For any
 $i,j \in {\mathrm {I_{fin}}}$ such that
$i,j \in {\mathrm {I_{fin}}}$ such that  $\mathrm {d}(i,j)=1$ and
$\mathrm {d}(i,j)=1$ and  $1=\mathsf {d}_i < \mathsf {d}_j=\mathrm {ord}(\varrho )$, there exists a unique element
$1=\mathsf {d}_i < \mathsf {d}_j=\mathrm {ord}(\varrho )$, there exists a unique element  $j^{\circ } \in \mathrm {orb}(j)$ such that
$j^{\circ } \in \mathrm {orb}(j)$ such that  $|\xi _{i} - \xi _{j^{\circ }}| = 1$ and
$|\xi _{i} - \xi _{j^{\circ }}| = 1$ and  $\xi _{\varrho ^{k}(j^{\circ })} = \xi _{j^{\circ }} - 2k$ for any
$\xi _{\varrho ^{k}(j^{\circ })} = \xi _{j^{\circ }} - 2k$ for any  $0 \leqslant k < \mathrm {ord}(\varrho )$.
$0 \leqslant k < \mathrm {ord}(\varrho )$.
Here ![]() $\mathrm {d}(i,j)$ denotes the distance between
$\mathrm {d}(i,j)$ denotes the distance between ![]() $i$ and
$i$ and ![]() $j$ in the Dynkin diagram
$j$ in the Dynkin diagram ![]() $\mathsf {D}_{\rm fin}$. We call the triple
$\mathsf {D}_{\rm fin}$. We call the triple ![]() $Q = (\mathsf {D}_{\rm fin}, \varrho, \xi )$ a
$Q = (\mathsf {D}_{\rm fin}, \varrho, \xi )$ a ![]() $Q$-datum for
$Q$-datum for ![]() ${\mathfrak {g}}$.
${\mathfrak {g}}$.
For a ![]() $Q$-datum
$Q$-datum ![]() $Q = (\mathsf {D}_{\rm fin}, \varrho, \xi )$ associated to
$Q = (\mathsf {D}_{\rm fin}, \varrho, \xi )$ associated to ![]() ${\mathfrak {g}}$, let
${\mathfrak {g}}$, let
The generalized ![]() $\varrho$-Coxeter element
$\varrho$-Coxeter element ![]() $\tau _Q \in \mathsf {W}_{\rm fin} \rtimes \textrm {Aut} (\mathsf {D}_{\rm fin})$ associated with
$\tau _Q \in \mathsf {W}_{\rm fin} \rtimes \textrm {Aut} (\mathsf {D}_{\rm fin})$ associated with ![]() $Q$ is defined in [Reference Fujita and OhFO21, Definition 3.33] and can be understood as a generalization of a Coxeter element. Here
$Q$ is defined in [Reference Fujita and OhFO21, Definition 3.33] and can be understood as a generalization of a Coxeter element. Here ![]() $\mathsf {W}_{\rm fin}$ is the Weyl group of
$\mathsf {W}_{\rm fin}$ is the Weyl group of ![]() ${{\mathfrak {g}}_{\mathrm {fin}}}$.
${{\mathfrak {g}}_{\mathrm {fin}}}$.
For ![]() $i\in I_0$, we denote by
$i\in I_0$, we denote by ![]() $o(i)$ the corresponding orbit of
$o(i)$ the corresponding orbit of ![]() ${\mathrm {I_{fin}}}$. For each
${\mathrm {I_{fin}}}$. For each ![]() $i\in I_0$, we denote by
$i\in I_0$, we denote by ![]() $i^\circ$ the unique vertex in the orbit
$i^\circ$ the unique vertex in the orbit ![]() $o( i)$ satisfying
$o( i)$ satisfying ![]() $\xi _{i^\circ } = \max \{ \xi _j \mid j\in o(i) \}$. In this paper, we assume further that the height function
$\xi _{i^\circ } = \max \{ \xi _j \mid j\in o(i) \}$. In this paper, we assume further that the height function ![]() $\xi$ satisfies
$\xi$ satisfies
Let ![]() $\{ i_1, i_2, \ldots, i_n\}$ be a total order of
$\{ i_1, i_2, \ldots, i_n\}$ be a total order of ![]() $I_0$ satisfying
$I_0$ satisfying ![]() $\xi _{i_1^\circ } \geqslant \xi _{i_2^\circ } \geqslant \cdots \geqslant \xi _{i_n^\circ }$. Then we have
$\xi _{i_1^\circ } \geqslant \xi _{i_2^\circ } \geqslant \cdots \geqslant \xi _{i_n^\circ }$. Then we have
(see [Reference Fujita and OhFO21, § 3.6] and also [Reference Fujita, Hernandez, Oh and OyaFHOO21, Proposition 4.4] for more details).
Let ![]() ${\Delta ^+_{Q}}$ be the set of positive roots of
${\Delta ^+_{Q}}$ be the set of positive roots of ![]() ${{\mathfrak {g}}_{\mathrm {fin}}}$, and let
${{\mathfrak {g}}_{\mathrm {fin}}}$, and let ![]() $\hat {\Phi } \mathbin {:=} {\Delta ^+_{Q}} \times \mathbb {\mspace {1mu}Z\mspace {1mu}}$. For each
$\hat {\Phi } \mathbin {:=} {\Delta ^+_{Q}} \times \mathbb {\mspace {1mu}Z\mspace {1mu}}$. For each ![]() $i \in {\mathrm {I_{fin}}}$ we define
$i \in {\mathrm {I_{fin}}}$ we define
where ![]() $\Lambda _i$ is the
$\Lambda _i$ is the ![]() $i$th fundamental weight of
$i$th fundamental weight of ![]() ${{\mathfrak {g}}_{\mathrm {fin}}}$. It is shown in [Reference Hernandez and LeclercHL15, § 2.2] and [Reference Fujita and OhFO21, Theorem 3.35] that there exists a unique bijection
${{\mathfrak {g}}_{\mathrm {fin}}}$. It is shown in [Reference Hernandez and LeclercHL15, § 2.2] and [Reference Fujita and OhFO21, Theorem 3.35] that there exists a unique bijection ![]() $\psi _Q \colon \hat {I}_Q \to \hat {\Phi }$ defined inductively as follows:
$\psi _Q \colon \hat {I}_Q \to \hat {\Phi }$ defined inductively as follows:
(i)
 $\psi _Q(i,\xi _i)=(\gamma ^Q_i,0)$;
$\psi _Q(i,\xi _i)=(\gamma ^Q_i,0)$;(ii) if
 $\psi _Q(i,p)=(\beta,m)$, then define:
$\psi _Q(i,p)=(\beta,m)$, then define:
(a)
 $\psi _Q(i,p\pm 2\mathsf {d}_i) = (\tau _Q^{\mp \mathsf {d}_i} (\beta ),m)$ if
$\psi _Q(i,p\pm 2\mathsf {d}_i) = (\tau _Q^{\mp \mathsf {d}_i} (\beta ),m)$ if  $\tau _Q^{ \mp \mathsf {d}_i}(\beta ) \in {\Delta ^+_{Q}}$;
$\tau _Q^{ \mp \mathsf {d}_i}(\beta ) \in {\Delta ^+_{Q}}$;(b)
 $\psi _Q(i,p\pm 2\mathsf {d}_i) = (-\tau _Q^{\mp \mathsf {d}_i}(\beta ),m\pm 1)$ if
$\psi _Q(i,p\pm 2\mathsf {d}_i) = (-\tau _Q^{\mp \mathsf {d}_i}(\beta ),m\pm 1)$ if  $\tau _Q^{\mp \mathsf {d}_i}(\beta ) \in - {\Delta ^+_{Q}}$.
$\tau _Q^{\mp \mathsf {d}_i}(\beta ) \in - {\Delta ^+_{Q}}$.
Let ![]() $I_Q\mathbin {:=} \psi _Q^{-1}({\Delta ^+_{Q}}\times \{0\})\subset {\mathrm {I_{fin}}}\times \mathbb {\mspace {1mu}Z\mspace {1mu}}.$ Then one can describe
$I_Q\mathbin {:=} \psi _Q^{-1}({\Delta ^+_{Q}}\times \{0\})\subset {\mathrm {I_{fin}}}\times \mathbb {\mspace {1mu}Z\mspace {1mu}}.$ Then one can describe
where ![]() $\mathsf {h}^\vee$ is the dual Coxeter number of
$\mathsf {h}^\vee$ is the dual Coxeter number of ![]() ${\mathfrak {g}}_0$ (see [Reference Fujita and OhFO21, Theorem 3.35] and also [Reference Fujita, Hernandez, Oh and OyaFHOO21, Proposition 4.15]). We define
${\mathfrak {g}}_0$ (see [Reference Fujita and OhFO21, Theorem 3.35] and also [Reference Fujita, Hernandez, Oh and OyaFHOO21, Proposition 4.15]). We define
where we set ![]() ${{q}_{\mspace {1mu}{\scriptstyle {\mathrm {sh}}}}} \mathbin {:=} q^{1/\mathrm {ord}(\varrho )}$ and
${{q}_{\mspace {1mu}{\scriptstyle {\mathrm {sh}}}}} \mathbin {:=} q^{1/\mathrm {ord}(\varrho )}$ and
 \begin{align*} \zeta(i,p) := \begin{cases} (\pi(i), (-{{q}_{\mspace{1mu}{\scriptstyle{\mathrm{sh}}}}})^p) & \text{if } {\mathfrak{g}} = A^{(1)}_n, \; C_n^{(1)}, \; D^{(1)}_n, \; E_{6,7,8}^{(1)}, \; G_2^{(1)}, \\ (\pi(i), ({-}1)^{i+n}({{q}_{\mspace{1mu}{\scriptstyle{\mathrm{sh}}}}})^p) & \text{if } {\mathfrak{g}} = B_n^{(1)}, \\ (\pi(i), ({-}1)^{ \pi(i) }({{q}_{\mspace{1mu}{\scriptstyle{\mathrm{sh}}}}})^p) & \text{if } {\mathfrak{g}} = F_4^{(1)} \end{cases} \end{align*}
\begin{align*} \zeta(i,p) := \begin{cases} (\pi(i), (-{{q}_{\mspace{1mu}{\scriptstyle{\mathrm{sh}}}}})^p) & \text{if } {\mathfrak{g}} = A^{(1)}_n, \; C_n^{(1)}, \; D^{(1)}_n, \; E_{6,7,8}^{(1)}, \; G_2^{(1)}, \\ (\pi(i), ({-}1)^{i+n}({{q}_{\mspace{1mu}{\scriptstyle{\mathrm{sh}}}}})^p) & \text{if } {\mathfrak{g}} = B_n^{(1)}, \\ (\pi(i), ({-}1)^{ \pi(i) }({{q}_{\mspace{1mu}{\scriptstyle{\mathrm{sh}}}}})^p) & \text{if } {\mathfrak{g}} = F_4^{(1)} \end{cases} \end{align*}(see [Reference Fujita and OhFO21, § 5.4]). We define
by ![]() $\phi _Q( \beta ) := \zeta \circ \psi _Q^{-1} (\beta, 0)$ for
$\phi _Q( \beta ) := \zeta \circ \psi _Q^{-1} (\beta, 0)$ for ![]() $\beta \in {\Delta ^+_{Q}}$. The map
$\beta \in {\Delta ^+_{Q}}$. The map ![]() $\phi _Q$ is bijective.
$\phi _Q$ is bijective.
For the rest of this paper, we make the following choices of ![]() $Q$-data:
$Q$-data:
• for simply laced ADE type,
 $\mathrm {ord}(\varrho )=1$ and the height function
$\mathrm {ord}(\varrho )=1$ and the height function  $\xi$ is defined in Appendix A.1;
$\xi$ is defined in Appendix A.1;• for
 ${\mathfrak {g}}=B_n^{(1)}$,
${\mathfrak {g}}=B_n^{(1)}$,  $\mathrm {ord}(\varrho )=2$ and
$\mathrm {ord}(\varrho )=2$ and  ;
;• for
 ${\mathfrak {g}}=C_n^{(1)}$,
${\mathfrak {g}}=C_n^{(1)}$,  $\mathrm {ord}(\varrho )=2$ and
$\mathrm {ord}(\varrho )=2$ and  ;
;• for
 ${\mathfrak {g}}=F_4^{(1)}$,
${\mathfrak {g}}=F_4^{(1)}$,  $\mathrm {ord}(\varrho )=2$ and
$\mathrm {ord}(\varrho )=2$ and  ;
;• for
 ${\mathfrak {g}}=G_2^{(1)}$,
${\mathfrak {g}}=G_2^{(1)}$,  $\mathrm {ord}(\varrho )=3$ and
$\mathrm {ord}(\varrho )=3$ and  .
.
Here an underlined integer stands for the value of ![]() $\xi _i$ at each vertex
$\xi _i$ at each vertex ![]() $i \in \mathsf {D}_{\rm fin}$ and an arrow
$i \in \mathsf {D}_{\rm fin}$ and an arrow ![]() $i \to j$ means that
$i \to j$ means that ![]() $\xi _i>\xi _j$ and
$\xi _i>\xi _j$ and ![]() $\mathrm {d}(i,j)=1$ in the Dynkin diagram
$\mathrm {d}(i,j)=1$ in the Dynkin diagram ![]() $\mathsf {D}_{\rm fin}$. Note that our choice of
$\mathsf {D}_{\rm fin}$. Note that our choice of ![]() $Q$ satisfies (2.10). Then
$Q$ satisfies (2.10). Then ![]() $\tau _Q$ is given as follows:
$\tau _Q$ is given as follows:
• for simply laced ADE type,
 $\tau _Q$ is the same as
$\tau _Q$ is the same as  $\tau$ in Appendix A.1;
$\tau$ in Appendix A.1;• for
 ${\mathfrak {g}}=B_n^{(1)}, C_n^{(1)}$,
${\mathfrak {g}}=B_n^{(1)}, C_n^{(1)}$,  $\tau _Q = s_1 s_2 \cdots s_n \varrho$;
$\tau _Q = s_1 s_2 \cdots s_n \varrho$;• for
 ${\mathfrak {g}}=F_4^{(1)}$,
${\mathfrak {g}}=F_4^{(1)}$,  $\tau _Q = s_1 s_2 s_3 s_4 \varrho$;
$\tau _Q = s_1 s_2 s_3 s_4 \varrho$;• for
 ${\mathfrak {g}}=G_2^{(1)}$,
${\mathfrak {g}}=G_2^{(1)}$,  $\tau _Q = s_2 s_1 \varrho$.
$\tau _Q = s_2 s_1 \varrho$.
In this case the set ![]() ${\sigma _Q({\mathfrak {g}})}$ is contained in
${\sigma _Q({\mathfrak {g}})}$ is contained in ![]() ${\sigma _0({\mathfrak {g}})}$ in § 2.3 and can be written explicitly as follows (where
${\sigma _0({\mathfrak {g}})}$ in § 2.3 and can be written explicitly as follows (where ![]() $a\leqslant _2 b$ means that
$a\leqslant _2 b$ means that ![]() $a\leqslant b$ and
$a\leqslant b$ and ![]() $a\equiv b\mspace {3mu}\mathbin {\mathrm {mod}}\mspace {1mu} 2$):
$a\equiv b\mspace {3mu}\mathbin {\mathrm {mod}}\mspace {1mu} 2$):
 \begin{align*} &\sigma_Q(A^{(1)}_{n }) \mathbin{:=} \{(i,({-}q)^{k}) \in \sigma_0(A^{(1)}_{n }) \mid i-2n +1 \leqslant_2 k \leqslant_2 -i +1 \}, \\ &\sigma_Q(B^{(1)}_{n}) \mathbin{:=} \{ (i,({-}1)^{n+i}q_s^{k}), (n,q^{k'}) \in \sigma_0(B^{(1)}_{n}) \mid i < n, -2n-2i+3 \leqslant_2 k \leqslant_2 2n-2i-1, \\ &\hspace{48ex} -\!2n+2 \leqslant k' \leqslant 0 \}, \\ & \sigma_Q({C_{n}^{(1)}}) \mathbin{:=} \{ (i, ({-}q_s)^{k}) \in \sigma_0(C^{(1)}_{n}) \mid{-}\mathrm{d}_\circ(1,i)-2n \leqslant_2 k \leqslant_2 -\mathrm{d}_\circ(1,i) \} , \\ & \sigma_Q({D_{n}^{(1)}}) \mathbin{:=} \{ (i, ({-}q)^{k}) \in \sigma_0(D^{(1)}_{n}) \mid{-}\mathrm{d}_\circ(1,i)-2n+4 \leqslant_2 k \leqslant_2 -\mathrm{d}_\circ(1,i) \} , \\ & \sigma_Q({E_{6}^{(1)}}) \mathbin{:=} \{ (i,({-}q)^k) \in \sigma_0(E^{(1)}_{6}) \mid \mathrm{d}_\circ(1,i)-14 \leqslant_2 k \leqslant_2 -\mathrm{d}_\circ(1,i) + 2\delta_{i,2} \}, \\ & \sigma_Q({E_{7}^{(1)}}) \mathbin{:=} \{ (i,({-}q)^k) \in \sigma_0(E^{(1)}_{7}) \mid{-}\mathrm{d}_\circ(1,i)-16 + 2\delta_{i,2} \leqslant_2 k \leqslant_2-\mathrm{d}_\circ(1,i) + 2\delta_{i,2} \}, \\ & \sigma_Q({E_{8}^{(1)}}) \mathbin{:=} \{ (i,({-}q)^k) \in \sigma_0(E^{(1)}_{8}) \mid{-}\mathrm{d}_\circ(1,i)-28 + 2\delta_{i,2} \leqslant_2 k \leqslant_2 -\mathrm{d}_\circ(1,i) + 2\delta_{i,2} \}, \\ & \sigma_Q({F_{4}^{(1)}}) \mathbin{:=} \biggl\{ (i, ({-}1)^iq^{k}) \in \sigma_0(F^{(1)}_{4}) \biggm| \mathrm{d}_\circ(i,3)-10 + \frac{\delta_{i,3}}{2} \leqslant k \leqslant \mathrm{d}_\circ(i,3)-2 + \frac{\delta_{i,3}}{2} \biggr\}, \\ & \sigma_Q({G_{2}^{(1)}}) \mathbin{:=} \{ (i, ({-}q_t)^{k}) \in \sigma_0(G^{(1)}_{2}) \mid{-}\mathrm{d}_\circ(2,i)-10 \leqslant_2 k \leqslant_2 -\mathrm{d}_\circ(2,i) \} , \end{align*}
\begin{align*} &\sigma_Q(A^{(1)}_{n }) \mathbin{:=} \{(i,({-}q)^{k}) \in \sigma_0(A^{(1)}_{n }) \mid i-2n +1 \leqslant_2 k \leqslant_2 -i +1 \}, \\ &\sigma_Q(B^{(1)}_{n}) \mathbin{:=} \{ (i,({-}1)^{n+i}q_s^{k}), (n,q^{k'}) \in \sigma_0(B^{(1)}_{n}) \mid i < n, -2n-2i+3 \leqslant_2 k \leqslant_2 2n-2i-1, \\ &\hspace{48ex} -\!2n+2 \leqslant k' \leqslant 0 \}, \\ & \sigma_Q({C_{n}^{(1)}}) \mathbin{:=} \{ (i, ({-}q_s)^{k}) \in \sigma_0(C^{(1)}_{n}) \mid{-}\mathrm{d}_\circ(1,i)-2n \leqslant_2 k \leqslant_2 -\mathrm{d}_\circ(1,i) \} , \\ & \sigma_Q({D_{n}^{(1)}}) \mathbin{:=} \{ (i, ({-}q)^{k}) \in \sigma_0(D^{(1)}_{n}) \mid{-}\mathrm{d}_\circ(1,i)-2n+4 \leqslant_2 k \leqslant_2 -\mathrm{d}_\circ(1,i) \} , \\ & \sigma_Q({E_{6}^{(1)}}) \mathbin{:=} \{ (i,({-}q)^k) \in \sigma_0(E^{(1)}_{6}) \mid \mathrm{d}_\circ(1,i)-14 \leqslant_2 k \leqslant_2 -\mathrm{d}_\circ(1,i) + 2\delta_{i,2} \}, \\ & \sigma_Q({E_{7}^{(1)}}) \mathbin{:=} \{ (i,({-}q)^k) \in \sigma_0(E^{(1)}_{7}) \mid{-}\mathrm{d}_\circ(1,i)-16 + 2\delta_{i,2} \leqslant_2 k \leqslant_2-\mathrm{d}_\circ(1,i) + 2\delta_{i,2} \}, \\ & \sigma_Q({E_{8}^{(1)}}) \mathbin{:=} \{ (i,({-}q)^k) \in \sigma_0(E^{(1)}_{8}) \mid{-}\mathrm{d}_\circ(1,i)-28 + 2\delta_{i,2} \leqslant_2 k \leqslant_2 -\mathrm{d}_\circ(1,i) + 2\delta_{i,2} \}, \\ & \sigma_Q({F_{4}^{(1)}}) \mathbin{:=} \biggl\{ (i, ({-}1)^iq^{k}) \in \sigma_0(F^{(1)}_{4}) \biggm| \mathrm{d}_\circ(i,3)-10 + \frac{\delta_{i,3}}{2} \leqslant k \leqslant \mathrm{d}_\circ(i,3)-2 + \frac{\delta_{i,3}}{2} \biggr\}, \\ & \sigma_Q({G_{2}^{(1)}}) \mathbin{:=} \{ (i, ({-}q_t)^{k}) \in \sigma_0(G^{(1)}_{2}) \mid{-}\mathrm{d}_\circ(2,i)-10 \leqslant_2 k \leqslant_2 -\mathrm{d}_\circ(2,i) \} , \end{align*}
where ![]() $\mathrm {d}_\circ (i,j)$ denotes the distance between
$\mathrm {d}_\circ (i,j)$ denotes the distance between ![]() $i$ and
$i$ and ![]() $j$ in the Dynkin diagram of
$j$ in the Dynkin diagram of ![]() ${\mathfrak {g}}_0$.
${\mathfrak {g}}_0$.
We now assume that ![]() ${\mathfrak {g}}$ is of twisted type. Then one can define
${\mathfrak {g}}$ is of twisted type. Then one can define
 \begin{align*} &\sigma_Q(A^{(2)}_{N}) \mathbin{:=} \{(i, ({-}q)^{k} )^\star \mid (i,({-}q)^{k}) \in \sigma_Q(A^{(1)}_{N}) \} \quad (N=2n-1 \text{ or } 2n) , \\ &\sigma_Q(D^{(2)}_{n+1}) \mathbin{:=} \{(i, ({-}q)^{k})^\star\mid (i,({-}q)^{k}) \in \sigma_Q(D^{(1)}_{n+1}) \}, \\ &\sigma_Q(E^{(2)}_{6}) \mathbin{:=} \{(i,({-}q)^{k} )^\star\mid (i,({-}q)^{k}) \in \sigma_Q(E^{(1)}_{6}) \}, \\ &\sigma_Q(D^{(3)}_{4}) \mathbin{:=} \{(i,({-}q)^{k})^{{\dagger}}\mid (i,({-}q)^{k}) \in \sigma_Q(D^{(1)}_{4}) \}, \end{align*}
\begin{align*} &\sigma_Q(A^{(2)}_{N}) \mathbin{:=} \{(i, ({-}q)^{k} )^\star \mid (i,({-}q)^{k}) \in \sigma_Q(A^{(1)}_{N}) \} \quad (N=2n-1 \text{ or } 2n) , \\ &\sigma_Q(D^{(2)}_{n+1}) \mathbin{:=} \{(i, ({-}q)^{k})^\star\mid (i,({-}q)^{k}) \in \sigma_Q(D^{(1)}_{n+1}) \}, \\ &\sigma_Q(E^{(2)}_{6}) \mathbin{:=} \{(i,({-}q)^{k} )^\star\mid (i,({-}q)^{k}) \in \sigma_Q(E^{(1)}_{6}) \}, \\ &\sigma_Q(D^{(3)}_{4}) \mathbin{:=} \{(i,({-}q)^{k})^{{\dagger}}\mid (i,({-}q)^{k}) \in \sigma_Q(D^{(1)}_{4}) \}, \end{align*}
where for ![]() $(i,a) \in \sigma _0({\mathfrak {g}}^{(1)}_{N})$ we set
$(i,a) \in \sigma _0({\mathfrak {g}}^{(1)}_{N})$ we set
 \[ \begin{aligned} (i,a)^\star{=} \begin{cases} (i,a) & \text{if } \mathfrak{g}=A^{(1)}_{N}, \, i \leqslant \lfloor (N+1)/2 \rfloor \:\text{ or }\: \mathfrak{g}=E^{(1)}_{6}, \, i =1, \\ (N+1-i,({-}1)^Na) & \text{if } \mathfrak{g}=A^{(1)}_{N}, \: i > \lfloor (N+1)/2 \rfloor, \\ (i,\sqrt{-1}^{n+1-i}a) & \text{if } \mathfrak{g}=D^{(1)}_{n+1}, \: i \leqslant n-1, \\ (n,({-}1)^ia) & \text{if } \mathfrak{g}=D^{(1)}_{n+1}, \: i\in \{n,n+1\}, \\ (2,a) & \text{if } \mathfrak{g}=E^{(1)}_{6}, \: i=3, \\ (2,-a) & \text{if } \mathfrak{g}=E^{(1)}_{6}, \: i=5, \\ (1,-a) & \text{if } \mathfrak{g}=E^{(1)}_{6}, \: i=6 , \\ (3,\sqrt{-1}a) & \text{if } \mathfrak{g}=E^{(1)}_{6}, \: i=4 , \\ (4,\sqrt{-1}a) & \text{if } \mathfrak{g}=E^{(1)}_{6}, \: i=2 \end{cases} \end{aligned} \]
\[ \begin{aligned} (i,a)^\star{=} \begin{cases} (i,a) & \text{if } \mathfrak{g}=A^{(1)}_{N}, \, i \leqslant \lfloor (N+1)/2 \rfloor \:\text{ or }\: \mathfrak{g}=E^{(1)}_{6}, \, i =1, \\ (N+1-i,({-}1)^Na) & \text{if } \mathfrak{g}=A^{(1)}_{N}, \: i > \lfloor (N+1)/2 \rfloor, \\ (i,\sqrt{-1}^{n+1-i}a) & \text{if } \mathfrak{g}=D^{(1)}_{n+1}, \: i \leqslant n-1, \\ (n,({-}1)^ia) & \text{if } \mathfrak{g}=D^{(1)}_{n+1}, \: i\in \{n,n+1\}, \\ (2,a) & \text{if } \mathfrak{g}=E^{(1)}_{6}, \: i=3, \\ (2,-a) & \text{if } \mathfrak{g}=E^{(1)}_{6}, \: i=5, \\ (1,-a) & \text{if } \mathfrak{g}=E^{(1)}_{6}, \: i=6 , \\ (3,\sqrt{-1}a) & \text{if } \mathfrak{g}=E^{(1)}_{6}, \: i=4 , \\ (4,\sqrt{-1}a) & \text{if } \mathfrak{g}=E^{(1)}_{6}, \: i=2 \end{cases} \end{aligned} \]and
 \begin{align*} (i,a)^{{\dagger}}= \begin{cases} (2,a) & \text{if } i=2, \\ (1,(\delta_{i,1}+\delta_{i,3} \omega+\delta_{i,4} \omega^2)a) & \text{if } i \ne 2 \end{cases} \end{align*}
\begin{align*} (i,a)^{{\dagger}}= \begin{cases} (2,a) & \text{if } i=2, \\ (1,(\delta_{i,1}+\delta_{i,3} \omega+\delta_{i,4} \omega^2)a) & \text{if } i \ne 2 \end{cases} \end{align*}
(see [Reference Kang, Kashiwara, Kim and OhKKKO16, Proposition 4.3] and [Reference Oh and ScrimshawOS19a, Proposition 6.5] for details of ![]() $\star$ and
$\star$ and ![]() ${{\dagger}}$). The bijection
${{\dagger}}$). The bijection ![]() $\phi _Q\colon {\Delta ^+_{Q}} \mathop {\xrightarrow {\sim}}{\sigma _Q({\mathfrak {g}})}$ is defined by composing the bijection for untwisted type with the maps
$\phi _Q\colon {\Delta ^+_{Q}} \mathop {\xrightarrow {\sim}}{\sigma _Q({\mathfrak {g}})}$ is defined by composing the bijection for untwisted type with the maps ![]() $\star$ and
$\star$ and ![]() ${{\dagger}}$.
${{\dagger}}$.
Comparing the above descriptions of ![]() ${\sigma _Q({\mathfrak {g}})}$ with the descriptions of
${\sigma _Q({\mathfrak {g}})}$ with the descriptions of ![]() ${\sigma _0({\mathfrak {g}})}$ given in § 2.3, one can easily show that
${\sigma _0({\mathfrak {g}})}$ given in § 2.3, one can easily show that
 \begin{equation} \begin{aligned} & {\sigma_0({\mathfrak{g}})} = \bigsqcup_{k \in \mathbb{\mspace{1mu}Z\mspace{1mu}} } {\sigma_Q({\mathfrak{g}})} ^{*k}, \\ & {\sigma_Q({\mathfrak{g}})} ^{*k} \cap {\sigma_Q({\mathfrak{g}})} ^{*k'} = \emptyset \quad \text{for } k,k' \in \mathbb{\mspace{1mu}Z\mspace{1mu}} \text{ with } k \ne k', \end{aligned} \end{equation}
\begin{equation} \begin{aligned} & {\sigma_0({\mathfrak{g}})} = \bigsqcup_{k \in \mathbb{\mspace{1mu}Z\mspace{1mu}} } {\sigma_Q({\mathfrak{g}})} ^{*k}, \\ & {\sigma_Q({\mathfrak{g}})} ^{*k} \cap {\sigma_Q({\mathfrak{g}})} ^{*k'} = \emptyset \quad \text{for } k,k' \in \mathbb{\mspace{1mu}Z\mspace{1mu}} \text{ with } k \ne k', \end{aligned} \end{equation}
where ![]() ${\sigma _Q({\mathfrak {g}})} ^{*k} \mathbin {:=} \{ (i^{*k},(p^*)^ka) \mid (i,a) \in {\sigma _Q({\mathfrak {g}})} \}$ with
${\sigma _Q({\mathfrak {g}})} ^{*k} \mathbin {:=} \{ (i^{*k},(p^*)^ka) \mid (i,a) \in {\sigma _Q({\mathfrak {g}})} \}$ with ![]() $i^{*k} =i$ if
$i^{*k} =i$ if ![]() $k$ is even and
$k$ is even and ![]() $i^{*k} =i^*$ if
$i^{*k} =i^*$ if ![]() $k$ is odd (see [Reference Fujita and OhFO21, Proposition 5.9]). Note that
$k$ is odd (see [Reference Fujita and OhFO21, Proposition 5.9]). Note that ![]() $p^*$ is given in (2.5).
$p^*$ is given in (2.5).
Let ![]() ${\mathscr {C}_{\mathfrak {g}}^{Q}}$ be the smallest full subcategory of
${\mathscr {C}_{\mathfrak {g}}^{Q}}$ be the smallest full subcategory of ![]() $\mathscr {C}_{\mathfrak {g}}^0$ with the following properties:
$\mathscr {C}_{\mathfrak {g}}^0$ with the following properties:
(a)
 ${\mathscr {C}_{\mathfrak {g}}^{Q}}$ contains
${\mathscr {C}_{\mathfrak {g}}^{Q}}$ contains  $\mathbf {1}$ and
$\mathbf {1}$ and  $V(\varpi _i)_x$ for all
$V(\varpi _i)_x$ for all  $(i,x) \in {\sigma _Q({\mathfrak {g}})}$;
$(i,x) \in {\sigma _Q({\mathfrak {g}})}$;(b)
 ${\mathscr {C}_{\mathfrak {g}}^{Q}}$ is stable by taking subquotients, extensions and tensor products.
${\mathscr {C}_{\mathfrak {g}}^{Q}}$ is stable by taking subquotients, extensions and tensor products.
It was shown in [Reference Hernandez and LeclercHL15, Theorem 6.1], [Reference Kang, Kashiwara, Kim and OhKKKO16, Corollary 5.6], [Reference Kashiwara and OhKO19, Corollary 6.6] and [Reference Oh and ScrimshawOS19a, § 6] that the Grothendieck ring ![]() $K({\mathscr {C}_{\mathfrak {g}}^{Q}})$ of the monoidal category
$K({\mathscr {C}_{\mathfrak {g}}^{Q}})$ of the monoidal category ![]() ${\mathscr {C}_{\mathfrak {g}}^{Q}}$ is isomorphic to the coordinate ring
${\mathscr {C}_{\mathfrak {g}}^{Q}}$ is isomorphic to the coordinate ring ![]() $\mathbb {C}[N]$ of the maximal unipotent group
$\mathbb {C}[N]$ of the maximal unipotent group ![]() $N$ associated with
$N$ associated with ![]() ${{\mathfrak {g}}_{\mathrm {fin}}}$. The set
${{\mathfrak {g}}_{\mathrm {fin}}}$. The set ![]() ${\Delta ^+_{Q}}$ has a convex order
${\Delta ^+_{Q}}$ has a convex order ![]() $\prec _Q$ arising from
$\prec _Q$ arising from ![]() $Q$.
$Q$.
Let ![]() $\beta \in {\Delta ^+_{Q}}$ and write
$\beta \in {\Delta ^+_{Q}}$ and write ![]() $(i,a) = \phi _Q(\beta )$. Then set
$(i,a) = \phi _Q(\beta )$. Then set
Under the categorification, the modules ![]() $V_Q(\beta )$ correspond to the dual PBW vectors of
$V_Q(\beta )$ correspond to the dual PBW vectors of ![]() $\mathbb {C}[N]$ with respect to the convex order
$\mathbb {C}[N]$ with respect to the convex order ![]() $\prec _Q$ on
$\prec _Q$ on ![]() ${\Delta ^+_{Q}}$.
${\Delta ^+_{Q}}$.
The proposition below follows from [Reference Kang, Kashiwara and KimKKK15, § 4.3], [Reference Kang, Kashiwara, Kim and OhKKKO16, Proposition 4.9 and Theorem 5.1], [Reference Kashiwara and OhKO19, § 4.3] and [Reference Oh and ScrimshawOS19a, § 6].
Proposition 2.4 [Reference Kang, Kashiwara and KimKKK15, Reference Kang, Kashiwara, Kim and OhKKKO16, Reference Kashiwara and OhKO19, Reference Oh and ScrimshawOS19a]
For a minimal pair ![]() $(\alpha, \beta )$ of a positive root
$(\alpha, \beta )$ of a positive root ![]() $\gamma \in {\Delta ^+_{Q}}$,
$\gamma \in {\Delta ^+_{Q}}$, ![]() $V_Q(\gamma )$ is isomorphic to the head of
$V_Q(\gamma )$ is isomorphic to the head of ![]() $V_Q(\alpha ) \otimes V_Q(\beta )$. Here,
$V_Q(\alpha ) \otimes V_Q(\beta )$. Here, ![]() $(\alpha, \beta )$ is called a minimal pair of
$(\alpha, \beta )$ is called a minimal pair of ![]() $\gamma$ if
$\gamma$ if ![]() $\alpha \prec _Q \beta$,
$\alpha \prec _Q \beta$, ![]() $\gamma = \alpha +\beta$ and there exists no pair
$\gamma = \alpha +\beta$ and there exists no pair ![]() $(\alpha ', \beta ')$ such that
$(\alpha ', \beta ')$ such that ![]() $\gamma = \alpha '+\beta '$ and
$\gamma = \alpha '+\beta '$ and ![]() $\alpha \prec _Q \alpha ' \prec _Q \beta ' \prec _Q \beta$.
$\alpha \prec _Q \alpha ' \prec _Q \beta ' \prec _Q \beta$.
3. New invariants for pairs of modules
In this section, we recall several properties of the new invariants arising from R-matrices introduced in [Reference Kashiwara, Kim, Oh and ParkKKOP20].
We set
 \[ \varphi(z) \mathbin{:=} \prod_{s=0}^\infty (1-{\tilde{p}}^{s}z) =\sum_{n=0}^\infty\frac{({-}1)^n{\tilde{p}}^{n(n-1)/2}}{\prod_{k=1}^n(1-{\tilde{p}}^k)} z^n \in{{\mathbf{k}}}[[z]]\subset\hat{\mathbf{k}}[[z]], \]
\[ \varphi(z) \mathbin{:=} \prod_{s=0}^\infty (1-{\tilde{p}}^{s}z) =\sum_{n=0}^\infty\frac{({-}1)^n{\tilde{p}}^{n(n-1)/2}}{\prod_{k=1}^n(1-{\tilde{p}}^k)} z^n \in{{\mathbf{k}}}[[z]]\subset\hat{\mathbf{k}}[[z]], \]
where ![]() $\tilde {p}$ is given in (2.5). We consider the subgroup
$\tilde {p}$ is given in (2.5). We consider the subgroup ![]() $\mathcal {G}$ of
$\mathcal {G}$ of ![]() $\mathbf {k}((z))^\times$ given by
$\mathbf {k}((z))^\times$ given by
 \[ \mathcal{G} \mathbin{:=} \biggl\{ cz^m \prod_{a \in \mathbf{k}^\times} \varphi(az)^{\eta_a} \biggm| \begin{matrix} c \in \mathbf{k}^\times, \ m \in \mathbb{\mspace{1mu}Z\mspace{1mu}} , \\ \eta_a \in \mathbb{\mspace{1mu}Z\mspace{1mu}} \text{ vanishes except for finitely many $a$} \end{matrix} \biggr\}. \]
\[ \mathcal{G} \mathbin{:=} \biggl\{ cz^m \prod_{a \in \mathbf{k}^\times} \varphi(az)^{\eta_a} \biggm| \begin{matrix} c \in \mathbf{k}^\times, \ m \in \mathbb{\mspace{1mu}Z\mspace{1mu}} , \\ \eta_a \in \mathbb{\mspace{1mu}Z\mspace{1mu}} \text{ vanishes except for finitely many $a$} \end{matrix} \biggr\}. \]
Note that if ![]() $R^{\mspace {1mu}\mathrm {univ}}_{M,N_z}$ is rationally renormalizable for
$R^{\mspace {1mu}\mathrm {univ}}_{M,N_z}$ is rationally renormalizable for ![]() $M, N \in \mathscr {C}_{\mathfrak {g}}$, then the renormalizing coefficient
$M, N \in \mathscr {C}_{\mathfrak {g}}$, then the renormalizing coefficient ![]() $c_{M,N}(z)$ belongs to
$c_{M,N}(z)$ belongs to ![]() $\mathcal {G}$ (see [Reference Kashiwara, Kim, Oh and ParkKKOP20, Proposition 3.2]). In particular, for simple modules
$\mathcal {G}$ (see [Reference Kashiwara, Kim, Oh and ParkKKOP20, Proposition 3.2]). In particular, for simple modules ![]() $M$ and
$M$ and ![]() $N$ in
$N$ in ![]() $\mathscr {C}_{\mathfrak {g}}$, the universal coefficient
$\mathscr {C}_{\mathfrak {g}}$, the universal coefficient ![]() $a_{M,N}(z)$ belongs to
$a_{M,N}(z)$ belongs to ![]() $\mathcal {G}$.
$\mathcal {G}$.
For a subset ![]() $S$ of
$S$ of ![]() $\mathbb {\mspace {1mu}Z\mspace {1mu}}$, let
$\mathbb {\mspace {1mu}Z\mspace {1mu}}$, let ![]() ${\tilde {p}}^{S} \mathbin {:=} \{ {\tilde {p}}^k \mid k \in S\}$. We define the group homomorphisms
${\tilde {p}}^{S} \mathbin {:=} \{ {\tilde {p}}^k \mid k \in S\}$. We define the group homomorphisms
by
for ![]() $f(z)=cz^m \prod _{ a\in \mathbf {k}^\times } \varphi (az)^{\eta _a} \in \mathcal {G}$.
$f(z)=cz^m \prod _{ a\in \mathbf {k}^\times } \varphi (az)^{\eta _a} \in \mathcal {G}$.
Lemma 3.1 [Reference Kashiwara, Kim, Oh and ParkKKOP20, Lemma 3.4]
Let ![]() $f(z)\in \mathcal {G}$.
$f(z)\in \mathcal {G}$.
(i) If
 $f(z)\in \mathbf {k}(z)^\times$, then we have
$f(z)\in \mathbf {k}(z)^\times$, then we have  $f(z)\in \mathcal {G}$,
$f(z)\in \mathcal {G}$,
 \[ \mathrm{Deg}^\infty(f(z))=0\quad \text{and}\quad \mathrm{Deg}(f(z))=2\,\mspace{1mu}\mathrm{zero}\mspace{1mu}_{z=1}f(z). \]
\[ \mathrm{Deg}^\infty(f(z))=0\quad \text{and}\quad \mathrm{Deg}(f(z))=2\,\mspace{1mu}\mathrm{zero}\mspace{1mu}_{z=1}f(z). \](ii) If
 $g(z),h(z)\in \mathcal {G}$ satisfy
$g(z),h(z)\in \mathcal {G}$ satisfy  $g(z)/h(z)\in {\mathbf {k}[z^{\pm 1}]}$, then
$g(z)/h(z)\in {\mathbf {k}[z^{\pm 1}]}$, then  $\mathrm {Deg}(h(z))\leqslant \mathrm {Deg}(g(z))$.
$\mathrm {Deg}(h(z))\leqslant \mathrm {Deg}(g(z))$.(iii) We have that
 $\mathrm {Deg}^\infty f(z)= -\mathrm {Deg}\bigl ( f({\tilde {p}}^{n}z)\bigr )=\mathrm {Deg}\bigl ( f({\tilde {p}}^{-n}z)\bigr )$ for
$\mathrm {Deg}^\infty f(z)= -\mathrm {Deg}\bigl ( f({\tilde {p}}^{n}z)\bigr )=\mathrm {Deg}\bigl ( f({\tilde {p}}^{-n}z)\bigr )$ for  $n \gg 0$.
$n \gg 0$.(iv) If
 $\mathrm {Deg}^\infty \bigl ( f(cz)\bigr )=0$ for any
$\mathrm {Deg}^\infty \bigl ( f(cz)\bigr )=0$ for any  $c\in \mathbf {k}^\times$, then
$c\in \mathbf {k}^\times$, then  $f(z)\in \mathbf {k}(z)^\times$.
$f(z)\in \mathbf {k}(z)^\times$.
The following invariants for a pair of modules ![]() $M$ and
$M$ and ![]() $N$ in
$N$ in ![]() $\mathscr {C}_{\mathfrak {g}}$ such that
$\mathscr {C}_{\mathfrak {g}}$ such that ![]() $R^{\mspace {1mu}\mathrm {univ}}_{M,N_z}$ is rationally renormalizable were introduced in [Reference Kashiwara, Kim, Oh and ParkKKOP20] by using the homomorphisms
$R^{\mspace {1mu}\mathrm {univ}}_{M,N_z}$ is rationally renormalizable were introduced in [Reference Kashiwara, Kim, Oh and ParkKKOP20] by using the homomorphisms ![]() $\mathrm {Deg}$ and
$\mathrm {Deg}$ and ![]() $\mathrm {Deg}^\infty$.
$\mathrm {Deg}^\infty$.
Definition 3.2 For non-zero modules ![]() $M$ and
$M$ and ![]() $N$ in
$N$ in ![]() $\mathscr {C}_{\mathfrak {g}}$ such that
$\mathscr {C}_{\mathfrak {g}}$ such that ![]() $R^{\mspace {1mu}\mathrm {univ}}_{M,N_z}$ is rationally renormalizable, we define the integers
$R^{\mspace {1mu}\mathrm {univ}}_{M,N_z}$ is rationally renormalizable, we define the integers ![]() $\Lambda (M,N)$ and
$\Lambda (M,N)$ and ![]() $\Lambda ^\infty (M,N)$ by
$\Lambda ^\infty (M,N)$ by
We have ![]() $\Lambda (M,N)\equiv \Lambda ^\infty (M,N)\mspace {3mu}\mathbin {\mathrm {mod}}\mspace {1mu} 2$.
$\Lambda (M,N)\equiv \Lambda ^\infty (M,N)\mspace {3mu}\mathbin {\mathrm {mod}}\mspace {1mu} 2$.
Proposition 3.3 [Reference Kashiwara, Kim, Oh and ParkKKOP20, Lemma 3.7]
For any simple modules ![]() $M,N\in \mathscr {C}_{\mathfrak {g}}$ and
$M,N\in \mathscr {C}_{\mathfrak {g}}$ and ![]() $x \in \mathbf {k}^\times$, we have
$x \in \mathbf {k}^\times$, we have
Proposition 3.4 [Reference Kashiwara, Kim, Oh and ParkKKOP20, Lemmas 3.7 and 3.8 and Corollary 3.23]
Let ![]() $M$ and
$M$ and ![]() $N$ be simple modules in
$N$ be simple modules in ![]() $\mathscr {C}_{\mathfrak {g}}$. Then the following hold:
$\mathscr {C}_{\mathfrak {g}}$. Then the following hold:
(i)
 $\Lambda ^\infty (M,N) =-\mathrm {Deg}^\infty (a_{M,N}(z))$;
$\Lambda ^\infty (M,N) =-\mathrm {Deg}^\infty (a_{M,N}(z))$;(ii)
 $\Lambda ^\infty (M,N) = \Lambda ^\infty (N,M)$;
$\Lambda ^\infty (M,N) = \Lambda ^\infty (N,M)$;(iii)
 $\Lambda ^\infty (M,N) = - \Lambda ^\infty (M^*, N) = - \Lambda ^\infty (M,{}^*\mspace {-3mu} N)$;
$\Lambda ^\infty (M,N) = - \Lambda ^\infty (M^*, N) = - \Lambda ^\infty (M,{}^*\mspace {-3mu} N)$;(iv) in particular,
 $\Lambda ^\infty (M,N) = \Lambda ^\infty (M^*, N^*) = \Lambda ^\infty ( {}^*\mspace {-3mu} M,{}^*\mspace {-3mu} N)$.
$\Lambda ^\infty (M,N) = \Lambda ^\infty (M^*, N^*) = \Lambda ^\infty ( {}^*\mspace {-3mu} M,{}^*\mspace {-3mu} N)$.
Proposition 3.5 [Reference Kashiwara, Kim, Oh and ParkKKOP20, Lemma 3.7 and Proposition 3.18]
Let ![]() $M$ and
$M$ and ![]() $N$ be simple modules in
$N$ be simple modules in ![]() $\mathscr {C}_{\mathfrak {g}}$. Then the following hold:
$\mathscr {C}_{\mathfrak {g}}$. Then the following hold:
(i)
 $\Lambda (M,N) = \Lambda (N^*, M) = \Lambda (N,{}^*\mspace {-3mu} M)$;
$\Lambda (M,N) = \Lambda (N^*, M) = \Lambda (N,{}^*\mspace {-3mu} M)$;(ii) in particular,
 \[ \Lambda(M,N) = \Lambda(M^*, N^*) = \Lambda( {}^*\mspace{-3mu} M,{}^*\mspace{-3mu} N). \]
\[ \Lambda(M,N) = \Lambda(M^*, N^*) = \Lambda( {}^*\mspace{-3mu} M,{}^*\mspace{-3mu} N). \]
Proposition 3.6 [Reference Kashiwara, Kim, Oh and ParkKKOP20, Proposition 3.9]
Let ![]() $M$ and
$M$ and ![]() $N$ be modules in
$N$ be modules in ![]() $\mathscr {C}_{\mathfrak {g}}$, and let
$\mathscr {C}_{\mathfrak {g}}$, and let ![]() $M'$ and
$M'$ and ![]() $N'$ be non-zero subquotients of
$N'$ be non-zero subquotients of ![]() $M$ and
$M$ and ![]() $N$, respectively. Assume that
$N$, respectively. Assume that ![]() $R^{\mspace {1mu}\mathrm {univ}}_{M,N_z}$ is rationally renormalizable. Then
$R^{\mspace {1mu}\mathrm {univ}}_{M,N_z}$ is rationally renormalizable. Then ![]() $R^{\mspace {1mu}\mathrm {univ}}_{M',N'_z}$ is rationally renormalizable, and we have
$R^{\mspace {1mu}\mathrm {univ}}_{M',N'_z}$ is rationally renormalizable, and we have
Proposition 3.7 [Reference Kashiwara, Kim, Oh and ParkKKOP20, Proposition 3.11]
Let ![]() $M$,
$M$, ![]() $N$ and
$N$ and ![]() $L$ be non-zero modules in
$L$ be non-zero modules in ![]() $\mathscr {C}_{\mathfrak {g}}$, and let
$\mathscr {C}_{\mathfrak {g}}$, and let ![]() $S$ be a non-zero subquotient of
$S$ be a non-zero subquotient of ![]() $M\mathop \otimes N$.
$M\mathop \otimes N$.
(i) Assume that
 $R^{\mspace {1mu}\mathrm {univ}}_{M,L_z}$ and
$R^{\mspace {1mu}\mathrm {univ}}_{M,L_z}$ and  $R^{\mspace {1mu}\mathrm {univ}}_{N,L_z}$ are rationally renormalizable. Then
$R^{\mspace {1mu}\mathrm {univ}}_{N,L_z}$ are rationally renormalizable. Then  $R^{\mspace {1mu}\mathrm {univ}}_{S,L_z}$ is rationally renormalizable, and we have
$R^{\mspace {1mu}\mathrm {univ}}_{S,L_z}$ is rationally renormalizable, and we have
 \[ \Lambda(S,L)\leqslant \Lambda(M,L) + \Lambda(N,L) \quad\text{{and}}\quad \Lambda^\infty(S,L)=\Lambda^\infty(M,L) + \Lambda^\infty(N,L). \]
\[ \Lambda(S,L)\leqslant \Lambda(M,L) + \Lambda(N,L) \quad\text{{and}}\quad \Lambda^\infty(S,L)=\Lambda^\infty(M,L) + \Lambda^\infty(N,L). \](ii) Assume that
 $R^{\mspace {1mu}\mathrm {univ}}_{L,M_z}$ and
$R^{\mspace {1mu}\mathrm {univ}}_{L,M_z}$ and  $R^{\mspace {1mu}\mathrm {univ}}_{L,N_z}$ are rationally renormalizable. Then
$R^{\mspace {1mu}\mathrm {univ}}_{L,N_z}$ are rationally renormalizable. Then  $R^{\mspace {1mu}\mathrm {univ}}_{L,S_z}$ is rationally renormalizable, and we have
$R^{\mspace {1mu}\mathrm {univ}}_{L,S_z}$ is rationally renormalizable, and we have
 \[ \Lambda(L,S)\leqslant\Lambda(L,M) + \Lambda(L,N) \quad\text{{and}}\quad\Lambda^\infty(L,S)=\Lambda^\infty(L,M) + \Lambda^\infty(L,N). \]
\[ \Lambda(L,S)\leqslant\Lambda(L,M) + \Lambda(L,N) \quad\text{{and}}\quad\Lambda^\infty(L,S)=\Lambda^\infty(L,M) + \Lambda^\infty(L,N). \]
Corollary 3.8 [Reference Kashiwara, Kim, Oh and ParkKKOP20, Corollary 3.12]
Let ![]() $M$ and
$M$ and ![]() $N$ be simple modules in
$N$ be simple modules in ![]() $\mathscr {C}_{\mathfrak {g}}$. Suppose that
$\mathscr {C}_{\mathfrak {g}}$. Suppose that ![]() $M$ (respectively
$M$ (respectively ![]() $N$) is isomorphic to a subquotient of
$N$) is isomorphic to a subquotient of ![]() $V(\varpi _{i_1 })_{a_1} \otimes V(\varpi _{i_2 })_{a_2}\otimes \cdots \otimes V(\varpi _{i_k})_{a_k}$ (respectively
$V(\varpi _{i_1 })_{a_1} \otimes V(\varpi _{i_2 })_{a_2}\otimes \cdots \otimes V(\varpi _{i_k})_{a_k}$ (respectively ![]() $V(\varpi _{j_1 })_{b_1} \otimes V(\varpi _{j_2 })_{b_2}\otimes \cdots \otimes V(\varpi _{j_l})_{b_l}$). Then we have
$V(\varpi _{j_1 })_{b_1} \otimes V(\varpi _{j_2 })_{b_2}\otimes \cdots \otimes V(\varpi _{j_l})_{b_l}$). Then we have
For simple modules ![]() $M$ and
$M$ and ![]() $N$ in
$N$ in ![]() $\mathscr {C}_{\mathfrak {g}}$, we define
$\mathscr {C}_{\mathfrak {g}}$, we define ![]() $\operatorname {\mathfrak {d}}(M,N)$ by
$\operatorname {\mathfrak {d}}(M,N)$ by
Proposition 3.9 [Reference Kashiwara, Kim, Oh and ParkKKOP20, Proposition 3.16 and Corollary 3.19]
Let ![]() $M$ and
$M$ and ![]() $N$ be simple modules in
$N$ be simple modules in ![]() $\mathscr {C}_{\mathfrak {g}}$. Then the following hold:
$\mathscr {C}_{\mathfrak {g}}$. Then the following hold:
(i)
 $\operatorname {\mathfrak {d}}(M,N)=\mspace {1mu}\mathrm {zero}\mspace {1mu}_{z=1}\bigl ( d_{M,N}(z)d_{N,M}(z^{-1})\bigr )$;
$\operatorname {\mathfrak {d}}(M,N)=\mspace {1mu}\mathrm {zero}\mspace {1mu}_{z=1}\bigl ( d_{M,N}(z)d_{N,M}(z^{-1})\bigr )$;(ii)
 $\operatorname {\mathfrak {d}}(M,N)=\frac {1}{2}\bigl (\Lambda (M,N)+\Lambda (N,M)\bigr )$;
$\operatorname {\mathfrak {d}}(M,N)=\frac {1}{2}\bigl (\Lambda (M,N)+\Lambda (N,M)\bigr )$;(iii) in particular,
 $\operatorname {\mathfrak {d}}(M,N) = \operatorname {\mathfrak {d}}(N,M)$.
$\operatorname {\mathfrak {d}}(M,N) = \operatorname {\mathfrak {d}}(N,M)$.
Corollary 3.10 [Reference Kashiwara, Kim, Oh and ParkKKOP20, Corollaries 3.17 and 3.20]
Let ![]() $M$ and
$M$ and ![]() $N$ be simple modules in
$N$ be simple modules in ![]() $\mathscr {C}_{\mathfrak {g}}$.
$\mathscr {C}_{\mathfrak {g}}$.
(i) Suppose that one of
 $M$ and
$M$ and  $N$ is real. Then
$N$ is real. Then  $M$ and
$M$ and  $N$ strongly commute if and only if
$N$ strongly commute if and only if  $\operatorname {\mathfrak {d}}(M,N)=0$.
$\operatorname {\mathfrak {d}}(M,N)=0$.(ii) In particular, if
 $M$ is real, then
$M$ is real, then  $\Lambda (M,M)=0.$
$\Lambda (M,M)=0.$
Proposition 3.11 [Reference Kashiwara, Kim, Oh and ParkKKOP20, Proposition 3.22]
For simple modules ![]() $M$ and
$M$ and ![]() $N$ in
$N$ in ![]() $\mathscr {C}_{\mathfrak {g}}$, we have
$\mathscr {C}_{\mathfrak {g}}$, we have
 \begin{align*} \Lambda(M,N) & = \sum_{k \in \mathbb{\mspace{1mu}Z\mspace{1mu}}} ({-}1)^{k+\delta(k<0)} \operatorname{\mathfrak{d}}(M,\mathscr{D}^{k}N) , \\ \Lambda^\infty(M,N) &= \sum_{k \in \mathbb{\mspace{1mu}Z\mspace{1mu}}} ({-}1)^{k} \operatorname{\mathfrak{d}}(M,\mathscr{D}^{k}N), \end{align*}
\begin{align*} \Lambda(M,N) & = \sum_{k \in \mathbb{\mspace{1mu}Z\mspace{1mu}}} ({-}1)^{k+\delta(k<0)} \operatorname{\mathfrak{d}}(M,\mathscr{D}^{k}N) , \\ \Lambda^\infty(M,N) &= \sum_{k \in \mathbb{\mspace{1mu}Z\mspace{1mu}}} ({-}1)^{k} \operatorname{\mathfrak{d}}(M,\mathscr{D}^{k}N), \end{align*}
where ![]() $\mathscr {D}^kN$ is defined as
$\mathscr {D}^kN$ is defined as
 \[ \mathscr{D}^kN \mathbin{:=} \begin{cases} (\cdots(N^* \underbrace{ )^* \cdots )^* }_{\text{$({-}k)$ times}} & \text{if } k <0, \\ \underbrace{{}^*\mspace{-3mu} ( \cdots ( }_{\text{$k$ times}} {}^*\mspace{-3mu} N )\cdots) & \text{if } k \geqslant 0. \end{cases} \]
\[ \mathscr{D}^kN \mathbin{:=} \begin{cases} (\cdots(N^* \underbrace{ )^* \cdots )^* }_{\text{$({-}k)$ times}} & \text{if } k <0, \\ \underbrace{{}^*\mspace{-3mu} ( \cdots ( }_{\text{$k$ times}} {}^*\mspace{-3mu} N )\cdots) & \text{if } k \geqslant 0. \end{cases} \]4. Root systems associated with  $\mathscr {C}_{\mathfrak {g}}$
$\mathscr {C}_{\mathfrak {g}}$
Let ![]() $\operatorname {Hom}({\sigma ({\mathfrak {g}})}, \mathbb {\mspace {1mu}Z\mspace {1mu}})$ be the set of
$\operatorname {Hom}({\sigma ({\mathfrak {g}})}, \mathbb {\mspace {1mu}Z\mspace {1mu}})$ be the set of ![]() $\mathbb {\mspace {1mu}Z\mspace {1mu}}$-valued functions on
$\mathbb {\mspace {1mu}Z\mspace {1mu}}$-valued functions on ![]() ${\sigma ({\mathfrak {g}})}$. It is obvious that
${\sigma ({\mathfrak {g}})}$. It is obvious that ![]() $\operatorname {Hom}({\sigma ({\mathfrak {g}})}, \mathbb {\mspace {1mu}Z\mspace {1mu}})$ forms a torsion-free abelian group under addition. Let
$\operatorname {Hom}({\sigma ({\mathfrak {g}})}, \mathbb {\mspace {1mu}Z\mspace {1mu}})$ forms a torsion-free abelian group under addition. Let ![]() $M \in \mathscr {C}_{\mathfrak {g}}$ be a module such that
$M \in \mathscr {C}_{\mathfrak {g}}$ be a module such that ![]() $R^{\mspace {1mu}\mathrm {univ}}_{M, V(\varpi _i)_z}$ is rationally renormalizable for any
$R^{\mspace {1mu}\mathrm {univ}}_{M, V(\varpi _i)_z}$ is rationally renormalizable for any ![]() $i\in I_0$. Then we define
$i\in I_0$. Then we define ![]() $\mathsf {E} (M) \in \operatorname {Hom}({\sigma ({\mathfrak {g}})}, \mathbb {\mspace {1mu}Z\mspace {1mu}})$ by
$\mathsf {E} (M) \in \operatorname {Hom}({\sigma ({\mathfrak {g}})}, \mathbb {\mspace {1mu}Z\mspace {1mu}})$ by
which is well-defined by (2.4).
Lemma 4.1 Let ![]() $M$ and
$M$ and ![]() $N$ be simple modules in
$N$ be simple modules in ![]() $\mathscr {C}_{\mathfrak {g}}$.
$\mathscr {C}_{\mathfrak {g}}$.
(i) We have
 $\mathsf {E} (M) = - \mathsf {E} (M^*) = - \mathsf {E} ({}^*\mspace {-3mu} M )$.
$\mathsf {E} (M) = - \mathsf {E} (M^*) = - \mathsf {E} ({}^*\mspace {-3mu} M )$.(ii) Let
 $\{{M_k}\}_{1\leqslant k\leqslant r}$ be a sequence of simple modules. Then for any non-zero subquotient
$\{{M_k}\}_{1\leqslant k\leqslant r}$ be a sequence of simple modules. Then for any non-zero subquotient  $S$ of
$S$ of  $M_1\mathop \otimes \cdots \mathop \otimes M_r$, we have
$M_1\mathop \otimes \cdots \mathop \otimes M_r$, we have
 \[ \mathsf{E} (S) =\sum_{k=1}^r \mathsf{E} (M_k). \]
\[ \mathsf{E} (S) =\sum_{k=1}^r \mathsf{E} (M_k). \](iii)
 $\mathsf {E} (M) = \mathsf {E} (N)$ if and only if
$\mathsf {E} (M) = \mathsf {E} (N)$ if and only if  ${a_{M,V(\varpi _i)}(z) }/{a_{N,V(\varpi _i)}(z) } \in \mathbf {k}(z)^\times$ for any
${a_{M,V(\varpi _i)}(z) }/{a_{N,V(\varpi _i)}(z) } \in \mathbf {k}(z)^\times$ for any  $i\in I_0$.
$i\in I_0$.
Proof. Assertions (i) and (ii) easily follow from Propositions 3.4 and 3.7.
Let us show (iii). For ![]() $(i,a) \in {\sigma ({\mathfrak {g}})}$, the condition
$(i,a) \in {\sigma ({\mathfrak {g}})}$, the condition ![]() $\Lambda ^\infty (M, V(\varpi _i)_a) = \Lambda ^\infty (N, V(\varpi _i)_a)$ is equivalent to
$\Lambda ^\infty (M, V(\varpi _i)_a) = \Lambda ^\infty (N, V(\varpi _i)_a)$ is equivalent to
Since ![]() $\mathrm {Deg}^\infty \colon \mathcal {G} \rightarrow \mathbb {\mspace {1mu}Z\mspace {1mu}}$ is a group homomorphism, it is equivalent to
$\mathrm {Deg}^\infty \colon \mathcal {G} \rightarrow \mathbb {\mspace {1mu}Z\mspace {1mu}}$ is a group homomorphism, it is equivalent to
Then (iii) follows from Lemma 3.1(iv).
For ![]() $(i,a) \in {\sigma ({\mathfrak {g}})}$, we set
$(i,a) \in {\sigma ({\mathfrak {g}})}$, we set
and
It is obvious that ![]() $\mathcal {W} _0 \subset \mathcal {W}$ and
$\mathcal {W} _0 \subset \mathcal {W}$ and ![]() $\Delta _0 \subset \Delta$.
$\Delta _0 \subset \Delta$.
Lemma 4.2
(i) We have
 $\mathcal {W} = \sum _{(i,a) \in {\sigma ({\mathfrak {g}})}} \mathbb {\mspace {1mu}Z\mspace {1mu}} \mathsf {s} _{i,a}$ and
$\mathcal {W} = \sum _{(i,a) \in {\sigma ({\mathfrak {g}})}} \mathbb {\mspace {1mu}Z\mspace {1mu}} \mathsf {s} _{i,a}$ and  $\mathcal {W} _0 = \sum _{(i,a) \in {\sigma _0({\mathfrak {g}})}} \mathbb {\mspace {1mu}Z\mspace {1mu}} \mathsf {s} _{i,a}=\sum _{(i,a) \in {\sigma _Q({\mathfrak {g}})}} \mathbb {\mspace {1mu}Z\mspace {1mu}} \mathsf {s} _{i,a}$. In particular,
$\mathcal {W} _0 = \sum _{(i,a) \in {\sigma _0({\mathfrak {g}})}} \mathbb {\mspace {1mu}Z\mspace {1mu}} \mathsf {s} _{i,a}=\sum _{(i,a) \in {\sigma _Q({\mathfrak {g}})}} \mathbb {\mspace {1mu}Z\mspace {1mu}} \mathsf {s} _{i,a}$. In particular,  $\mathcal {W} _0$ is a finitely generated free
$\mathcal {W} _0$ is a finitely generated free  $\mathbb {\mspace {1mu}Z\mspace {1mu}}$-module.
$\mathbb {\mspace {1mu}Z\mspace {1mu}}$-module.(ii) There exists a unique symmetric bilinear form
 $(-,-)$ on
$(-,-)$ on  $\mathcal {W}$ such that
for any simple modules
$\mathcal {W}$ such that
for any simple modules \[ ( \mathsf{E} (M), \mathsf{E} (N) ) ={-} \Lambda^\infty(M,N) \]
\[ ( \mathsf{E} (M), \mathsf{E} (N) ) ={-} \Lambda^\infty(M,N) \] $M,N \in \mathscr {C}_{\mathfrak {g}}$.
$M,N \in \mathscr {C}_{\mathfrak {g}}$.
Proof. Assertion (i) follows from Theorem 2.2(iv), Lemma 4.1 and (2.12).
Let us show (ii). By Corollary 3.8, it reduces to the existence of a bilinear form ![]() $(-,-)$ on
$(-,-)$ on ![]() $\mathcal {W}$ such that
$\mathcal {W}$ such that
Therefore it is enough to show that for a sequence ![]() $\{{(i_k,a_k)}\}_{k=1,\ldots,r}$ in
$\{{(i_k,a_k)}\}_{k=1,\ldots,r}$ in ![]() ${\sigma ({\mathfrak {g}})}$ such that
${\sigma ({\mathfrak {g}})}$ such that ![]() ${\sum _{k=1}^r \mathsf {s} _{i_k,a_k}=0}$, we have
${\sum _{k=1}^r \mathsf {s} _{i_k,a_k}=0}$, we have ![]() $\sum _{k=1}^r\Lambda ^\infty \bigl ( V(\varpi _{i_k})_{a_k},V(\varpi _j)_b\bigr )=0$ for any
$\sum _{k=1}^r\Lambda ^\infty \bigl ( V(\varpi _{i_k})_{a_k},V(\varpi _j)_b\bigr )=0$ for any ![]() $(j,b)\in {\sigma ({\mathfrak {g}})}$. Let us take a simple subquotient
$(j,b)\in {\sigma ({\mathfrak {g}})}$. Let us take a simple subquotient ![]() $M$ of
$M$ of ![]() $V(\varpi _{i_1})_{a_1}\mathop \otimes \cdots \mathop \otimes V(\varpi _{i_r})_{a_r}$. Then we have
$V(\varpi _{i_1})_{a_1}\mathop \otimes \cdots \mathop \otimes V(\varpi _{i_r})_{a_r}$. Then we have ![]() $\mathsf {E} (M)= \sum _{k=1}^r \mathsf {s} _{i_k,a_k}=0$. Hence we obtain
$\mathsf {E} (M)= \sum _{k=1}^r \mathsf {s} _{i_k,a_k}=0$. Hence we obtain
 \[ \sum _{k=1}^r\Lambda^\infty\bigl( V(\varpi_{i_k})_{a_k},V(\varpi_j)_b\bigr)= \Lambda^\infty(M,V(\varpi_j)_b)={-} \mathsf{E} (M)(j,b)=0. \]
\[ \sum _{k=1}^r\Lambda^\infty\bigl( V(\varpi_{i_k})_{a_k},V(\varpi_j)_b\bigr)= \Lambda^\infty(M,V(\varpi_j)_b)={-} \mathsf{E} (M)(j,b)=0. \]Lemma 4.3 For ![]() $i\in I_0$ and
$i\in I_0$ and ![]() $a\in \mathbf {k}^\times$, we have
$a\in \mathbf {k}^\times$, we have
In particular,
Proof. The statement ![]() $\Lambda ^\infty ( V(\varpi _i), V(\varpi _{i}) ) = -2$ follows from (4.3) and Proposition 3.11.
$\Lambda ^\infty ( V(\varpi _i), V(\varpi _{i}) ) = -2$ follows from (4.3) and Proposition 3.11.
Let us show (4.3). Let ![]() $h^\vee$ be the dual Coxeter number of
$h^\vee$ be the dual Coxeter number of ![]() ${\mathfrak {g}}$, and write
${\mathfrak {g}}$, and write
The denominator formula for ![]() $d_{i,j}(z)$ is given in Appendix A. Using this formula, one can easily check that if
$d_{i,j}(z)$ is given in Appendix A. Using this formula, one can easily check that if ![]() $\epsilon q^t$ (
$\epsilon q^t$ (![]() $|\epsilon |=1$) is a zero of
$|\epsilon |=1$) is a zero of ![]() $d_{i,i}(z)$, then
$d_{i,i}(z)$, then ![]() $t$ should be between
$t$ should be between ![]() $1$ and
$1$ and ![]() $h^\vee$. Combining this with Proposition 3.9, we obtain
$h^\vee$. Combining this with Proposition 3.9, we obtain
Now we shall show that ![]() $\operatorname {\mathfrak {d}}( V(\varpi _i), \mathscr {D}^{\pm 1} V(\varpi _{ i }) )=1$.
$\operatorname {\mathfrak {d}}( V(\varpi _i), \mathscr {D}^{\pm 1} V(\varpi _{ i }) )=1$.
Case of simply laced affine ADE type. In this case, the dual Coxeter number is equal to the Coxeter number. Then from the denominator formula in Appendix A it follows that
Since ![]() $\tilde {c}_{i,j}(k) = \tilde {c}_{j,i^*}(h^\vee - k)$ for
$\tilde {c}_{i,j}(k) = \tilde {c}_{j,i^*}(h^\vee - k)$ for ![]() $1 \leqslant k \leqslant h^\vee -1$ (see [Reference FujitaFuj22, Lemma 3.7]) and
$1 \leqslant k \leqslant h^\vee -1$ (see [Reference FujitaFuj22, Lemma 3.7]) and ![]() $\tilde {c}_{i ,i}( 1)=1$ by Proposition A.1, we have
$\tilde {c}_{i ,i}( 1)=1$ by Proposition A.1, we have
Other case. In this case, we know that ![]() $i^* = i$ for any
$i^* = i$ for any ![]() $i\in I_0$. Thus we have
$i\in I_0$. Thus we have
Using (2.6) and the denominator formula in Appendix A, one can compute directly that
For ![]() $t \in \mathbf {k}^\times$,
$t \in \mathbf {k}^\times$, ![]() $(i,a) \in {\sigma ({\mathfrak {g}})}$ and
$(i,a) \in {\sigma ({\mathfrak {g}})}$ and ![]() $f \in \operatorname {Hom}({\sigma ({\mathfrak {g}})}, \mathbb {\mspace {1mu}Z\mspace {1mu}})$, we define
$f \in \operatorname {Hom}({\sigma ({\mathfrak {g}})}, \mathbb {\mspace {1mu}Z\mspace {1mu}})$, we define
Lemma 4.4
(i) For
 $(i,a) \in {\sigma ({\mathfrak {g}})}$, we have
$(i,a) \in {\sigma ({\mathfrak {g}})}$, we have  $\mathsf {s} _{i,a} = - \mathsf {s} _{i^*,a p^* } = - \mathsf {s} _{i^*,a (p^*)^{-1} }$.
$\mathsf {s} _{i,a} = - \mathsf {s} _{i^*,a p^* } = - \mathsf {s} _{i^*,a (p^*)^{-1} }$.(ii) For
 $t\in \mathbf {k}^\times$ and
$t\in \mathbf {k}^\times$ and  $(i,a) \in {\sigma ({\mathfrak {g}})}$, we have
$(i,a) \in {\sigma ({\mathfrak {g}})}$, we have  $\tau _t ( \mathsf {s} _{i,a}) = \mathsf {s} _{i,ta}$.
$\tau _t ( \mathsf {s} _{i,a}) = \mathsf {s} _{i,ta}$.
Proof. Assertion (i) follows from (2.7) and Lemma 4.1.
(ii) For ![]() $(j,b)\in {\sigma ({\mathfrak {g}})}$, we have
$(j,b)\in {\sigma ({\mathfrak {g}})}$, we have
 \begin{align*} (\tau_t ( \mathsf{s} _{i,a})) (j,b) &= ( \mathsf{s} _{i,a}) (j,t^{{-}1}b) = \Lambda^\infty( V(\varpi_i)_a, V(\varpi_j)_{t^{{-}1}b} ) = \Lambda^\infty( V(\varpi_i)_{ta}, V(\varpi_j)_{b} ) \\ & = ( \mathsf{s} _{i,ta}) (j, b), \end{align*}
\begin{align*} (\tau_t ( \mathsf{s} _{i,a})) (j,b) &= ( \mathsf{s} _{i,a}) (j,t^{{-}1}b) = \Lambda^\infty( V(\varpi_i)_a, V(\varpi_j)_{t^{{-}1}b} ) = \Lambda^\infty( V(\varpi_i)_{ta}, V(\varpi_j)_{b} ) \\ & = ( \mathsf{s} _{i,ta}) (j, b), \end{align*}where the third equality follows from Proposition 3.3. Thus, we have the desired assertion.
For ![]() $t\in \mathbf {k}^\times$,
$t\in \mathbf {k}^\times$, ![]() $A \subset {\sigma ({\mathfrak {g}})}$ and
$A \subset {\sigma ({\mathfrak {g}})}$ and ![]() $F \subset \operatorname {Hom}({\sigma ({\mathfrak {g}})}, \mathbb {\mspace {1mu}Z\mspace {1mu}})$, we set
$F \subset \operatorname {Hom}({\sigma ({\mathfrak {g}})}, \mathbb {\mspace {1mu}Z\mspace {1mu}})$, we set
We write ![]() ${\mathbf {k}_0}$ for the stabilizer subgroup of
${\mathbf {k}_0}$ for the stabilizer subgroup of ![]() ${\sigma _0({\mathfrak {g}})}$ with respect to the action of
${\sigma _0({\mathfrak {g}})}$ with respect to the action of ![]() $\mathbf {k}^\times$ on
$\mathbf {k}^\times$ on ![]() ${\sigma ({\mathfrak {g}})}$ through
${\sigma ({\mathfrak {g}})}$ through ![]() $\tau _t$, i.e.
$\tau _t$, i.e.
Proposition 4.5 The following hold:
(i)
 ${\sigma ({\mathfrak {g}})} = \bigsqcup _{a\in \mathbf {k}^\times / {\mathbf {k}_0} } \bigl ({\sigma _0({\mathfrak {g}})}\bigr )_a$;
${\sigma ({\mathfrak {g}})} = \bigsqcup _{a\in \mathbf {k}^\times / {\mathbf {k}_0} } \bigl ({\sigma _0({\mathfrak {g}})}\bigr )_a$;(ii)
 $\Delta = \bigsqcup _{a\in \mathbf {k}^\times / {\mathbf {k}_0} } (\Delta _0)_a$;
$\Delta = \bigsqcup _{a\in \mathbf {k}^\times / {\mathbf {k}_0} } (\Delta _0)_a$;(iii) for
 $k,k'\in \mathbf {k}^\times$ such that
$k,k'\in \mathbf {k}^\times$ such that  $k/k'\not \in {\mathbf {k}_0}$, we have
$k/k'\not \in {\mathbf {k}_0}$, we have  $\bigl (( \mathcal {W} _0)_k,( \mathcal {W} _0)_{k'}\bigr )=0$.
$\bigl (( \mathcal {W} _0)_k,( \mathcal {W} _0)_{k'}\bigr )=0$.
Proof. Assertion (i) follows from the fact that any connected component of ![]() ${\sigma ({\mathfrak {g}})}$ is a translation of
${\sigma ({\mathfrak {g}})}$ is a translation of ![]() ${\sigma _0({\mathfrak {g}})}$.
${\sigma _0({\mathfrak {g}})}$.
(iii) It is enough to show that for ![]() $(i,a)\in ({\sigma _0({\mathfrak {g}})})_k$ and
$(i,a)\in ({\sigma _0({\mathfrak {g}})})_k$ and ![]() $(j,b)\in ({\sigma _0({\mathfrak {g}})})_{k'}$ we have
$(j,b)\in ({\sigma _0({\mathfrak {g}})})_{k'}$ we have ![]() $( \mathsf {s} _{i,a}, \mathsf {s} _{ j,b })=0$. By the definition of
$( \mathsf {s} _{i,a}, \mathsf {s} _{ j,b })=0$. By the definition of ![]() ${\sigma _0({\mathfrak {g}})}$,
${\sigma _0({\mathfrak {g}})}$, ![]() $V(\varpi _i)_a$ and
$V(\varpi _i)_a$ and ![]() $\mathscr {D}^mV(\varpi _j)_b$ strongly commute for any
$\mathscr {D}^mV(\varpi _j)_b$ strongly commute for any ![]() $m$, which tells us that
$m$, which tells us that
by Corollary 3.10 and Proposition 3.11.
(ii) It is enough to show that
For ![]() $(i,a) \in {\sigma _0({\mathfrak {g}})}$ and
$(i,a) \in {\sigma _0({\mathfrak {g}})}$ and ![]() $(j,b) \in {\sigma _0({\mathfrak {g}})}_k$, we have
$(j,b) \in {\sigma _0({\mathfrak {g}})}_k$, we have ![]() $( \mathsf {s} _{i,a}, \mathsf {s} _{i,a})= 2$ by Lemma 4.3 and
$( \mathsf {s} _{i,a}, \mathsf {s} _{i,a})= 2$ by Lemma 4.3 and ![]() $( \mathsf {s} _{i,a}, \mathsf {s} _{j,b}) = 0$ by (iii). Thus we conclude that
$( \mathsf {s} _{i,a}, \mathsf {s} _{j,b}) = 0$ by (iii). Thus we conclude that ![]() $\mathsf {s} _{i,a} \ne \mathsf {s} _{j,b}$.
$\mathsf {s} _{i,a} \ne \mathsf {s} _{j,b}$.
We set
Then the pairing ![]() $(-,-)$ gives a symmetric bilinear form on
$(-,-)$ gives a symmetric bilinear form on ![]() $\mathcal {E}$. Theorem 4.6 below is the main theorem of this section; its proof is postponed until § 6.
$\mathcal {E}$. Theorem 4.6 below is the main theorem of this section; its proof is postponed until § 6.
Theorem 4.6
(i) The pair
 $( \mathcal {E} _0, \Delta _0)$ is an irreducible simply laced root system of type shown in the following table.
(4.5)
$( \mathcal {E} _0, \Delta _0)$ is an irreducible simply laced root system of type shown in the following table.
(4.5) \begin{align} \small
\begin{array}{|c||c|c|c|c|c|c|c|} \hline \text{Type of
${\mathfrak{g}}$} & A_n^{(1)} & B_n^{(1)} & C_n^{(1)^{\vphantom{1}}} &
D_n^{(1)} & A_{2n}^{(2)} & A_{2n-1}^{(2)} & D_{n+1}^{(2)}
\\ & (n\geqslant1) & (n\geqslant2) & (n\geqslant3) &
(n\geqslant4) & (n\geqslant1) & (n\geqslant2) &
(n\geqslant3)\\ \hline \text{Type of $( \mathcal{E} _0,
\Delta_0)$} & A_n & A_{2n-1} & D_{n+1} & D_n & A_{2n} &
A_{2n-1} & D_{n+1} \\ \hline \hline \text{Type of
${\mathfrak{g}}$} & E_6^{(1)^{\vphantom{1}}} & E_7^{(1)} & E_8^{(1)} &
F_4^{(1)} & G_{2}^{(1)} & E_{6}^{(2)} & D_{4}^{(3)} \\
\hline \text{Type of $( \mathcal{E} _0, \Delta_0)$} & E_6 &
E_{7} & E_{8} & E_6 & D_{4} & E_{6} & D_{4} \\ \hline
\end{array} \end{align}
\begin{align} \small
\begin{array}{|c||c|c|c|c|c|c|c|} \hline \text{Type of
${\mathfrak{g}}$} & A_n^{(1)} & B_n^{(1)} & C_n^{(1)^{\vphantom{1}}} &
D_n^{(1)} & A_{2n}^{(2)} & A_{2n-1}^{(2)} & D_{n+1}^{(2)}
\\ & (n\geqslant1) & (n\geqslant2) & (n\geqslant3) &
(n\geqslant4) & (n\geqslant1) & (n\geqslant2) &
(n\geqslant3)\\ \hline \text{Type of $( \mathcal{E} _0,
\Delta_0)$} & A_n & A_{2n-1} & D_{n+1} & D_n & A_{2n} &
A_{2n-1} & D_{n+1} \\ \hline \hline \text{Type of
${\mathfrak{g}}$} & E_6^{(1)^{\vphantom{1}}} & E_7^{(1)} & E_8^{(1)} &
F_4^{(1)} & G_{2}^{(1)} & E_{6}^{(2)} & D_{4}^{(3)} \\
\hline \text{Type of $( \mathcal{E} _0, \Delta_0)$} & E_6 &
E_{7} & E_{8} & E_6 & D_{4} & E_{6} & D_{4} \\ \hline
\end{array} \end{align}
(ii) The bilinear form
 $(-,-)\vert _{ \mathcal {W} _0}$ is positive definite. Moreover, it is Weyl group invariant, i.e.
$(-,-)\vert _{ \mathcal {W} _0}$ is positive definite. Moreover, it is Weyl group invariant, i.e.  $s_\alpha (\Delta _0)\subset \Delta _0$ for any
$s_\alpha (\Delta _0)\subset \Delta _0$ for any  $\alpha \in \Delta _0$. Here
$\alpha \in \Delta _0$. Here  $s_\alpha \in \operatorname {End}( \mathcal {E} _0)$ is the reflection defined by
$s_\alpha \in \operatorname {End}( \mathcal {E} _0)$ is the reflection defined by  $s_\alpha (\lambda )= \lambda -(\alpha,\lambda )\alpha$.
$s_\alpha (\lambda )= \lambda -(\alpha,\lambda )\alpha$.
The next corollary follows from Proposition 4.5 and Theorem 4.6.
Corollary 4.7
(i) We have
 $\mathcal {W} = \bigoplus _{k \in \mathbf {k}^\times / {\mathbf {k}_0} } ( \mathcal {W} _0)_k$.
$\mathcal {W} = \bigoplus _{k \in \mathbf {k}^\times / {\mathbf {k}_0} } ( \mathcal {W} _0)_k$.(ii) As a root system,
 $( ( \mathcal {E} _0)_k, (\Delta _0)_k)$ is isomorphic to
$( ( \mathcal {E} _0)_k, (\Delta _0)_k)$ is isomorphic to  $( \mathcal {E} _0, \Delta _0)$ for
$( \mathcal {E} _0, \Delta _0)$ for  $k \in \mathbf {k}^\times / {\mathbf {k}_0}$, and
$k \in \mathbf {k}^\times / {\mathbf {k}_0}$, and
 \[ ( \mathcal{E} , \Delta) = \bigsqcup_{k \in \mathbf{k}^\times{/} {\mathbf{k}_0} } ( ( \mathcal{E} _0)_k, (\Delta_0)_k). \]
\[ ( \mathcal{E} , \Delta) = \bigsqcup_{k \in \mathbf{k}^\times{/} {\mathbf{k}_0} } ( ( \mathcal{E} _0)_k, (\Delta_0)_k). \]
Proof. We know already that ![]() $\mathcal {W} = \sum _{k \in \mathbf {k}^\times / {\mathbf {k}_0} } ( \mathcal {W} _0)_k$. Since
$\mathcal {W} = \sum _{k \in \mathbf {k}^\times / {\mathbf {k}_0} } ( \mathcal {W} _0)_k$. Since ![]() $( \mathcal {W} _0)_k$ and
$( \mathcal {W} _0)_k$ and ![]() $( \mathcal {W} _0)_{k'}$ are orthogonal if
$( \mathcal {W} _0)_{k'}$ are orthogonal if ![]() $k/k'\not \in {\mathbf {k}_0}$, the non-degeneracy of
$k/k'\not \in {\mathbf {k}_0}$, the non-degeneracy of ![]() $(-,-)\vert _{ \mathcal {E} }$ implies that
$(-,-)\vert _{ \mathcal {E} }$ implies that ![]() $\mathcal {W} = \bigoplus _{k \in \mathbf {k}^\times / {\mathbf {k}_0} } ( \mathcal {W} _0)_k$.
$\mathcal {W} = \bigoplus _{k \in \mathbf {k}^\times / {\mathbf {k}_0} } ( \mathcal {W} _0)_k$.
Assertion (ii) easily follows from (i) and Theorem 4.6.
The following corollary is an immediate consequence of Theorem 4.6.
Corollary 4.8 The following hold:
(i)
 $(\lambda,\lambda )\in 2\mathbb {\mspace {1mu}Z\mspace {1mu}}_{>0}$ for any
$(\lambda,\lambda )\in 2\mathbb {\mspace {1mu}Z\mspace {1mu}}_{>0}$ for any  $\lambda \in \mathcal {W} _0\setminus \{{0}\}$;
$\lambda \in \mathcal {W} _0\setminus \{{0}\}$;(ii)
 $\Delta _0=\{{\lambda \in \mathcal {W} _0\mid (\lambda,\lambda )=2}\}$.
$\Delta _0=\{{\lambda \in \mathcal {W} _0\mid (\lambda,\lambda )=2}\}$.
Hence the root system ![]() $( \mathcal {E} _0, \Delta _0)$ is completely determined by the pair
$( \mathcal {E} _0, \Delta _0)$ is completely determined by the pair ![]() $( \mathcal {W} _0,\,(-,-)\vert _{ \mathcal {W} _0})$.
$( \mathcal {W} _0,\,(-,-)\vert _{ \mathcal {W} _0})$.
5. Block decomposition of  $\mathscr {C}_{\mathfrak {g}}$
$\mathscr {C}_{\mathfrak {g}}$
In this section, we give a block decomposition of ![]() $\mathscr {C}_{\mathfrak {g}}$ parameterized by
$\mathscr {C}_{\mathfrak {g}}$ parameterized by ![]() $\mathcal {W}$.
$\mathcal {W}$.
5.1 Blocks
We recall the notion of blocks. Let ![]() $\mathcal {C}$ be an abelian category such that any object of
$\mathcal {C}$ be an abelian category such that any object of ![]() $\mathcal {C}$ has finite length.
$\mathcal {C}$ has finite length.
Definition 5.1 A block ![]() $\mathcal {B}$ of
$\mathcal {B}$ of ![]() $\mathcal {C}$ is a full abelian subcategory with the following properties:
$\mathcal {C}$ is a full abelian subcategory with the following properties:
(i) there is a decomposition
 $\mathcal {C} = \mathcal {B} \oplus \mathcal {C}'$ for some full abelian subcategory
$\mathcal {C} = \mathcal {B} \oplus \mathcal {C}'$ for some full abelian subcategory  $\mathcal {C}'$,
$\mathcal {C}'$,(ii) there is no non-trivial decomposition
 $\mathcal {B} = \mathcal {B}' \oplus \mathcal {B}''$ with full abelian subcategories
$\mathcal {B} = \mathcal {B}' \oplus \mathcal {B}''$ with full abelian subcategories  $\mathcal {B}'$ and
$\mathcal {B}'$ and  $\mathcal {B}''$.
$\mathcal {B}''$.
The following lemma is obvious.
Lemma 5.2 Let ![]() $\mathcal {B}$ be a full subcategory of
$\mathcal {B}$ be a full subcategory of ![]() $\mathcal {C}$ satisfying condition (i) in Definition 5.1. Then
$\mathcal {C}$ satisfying condition (i) in Definition 5.1. Then ![]() $\mathcal {B}$ has the following properties:
$\mathcal {B}$ has the following properties:
(i)
 $\mathcal {B}$ is stable by taking subquotients and extensions;
$\mathcal {B}$ is stable by taking subquotients and extensions;(ii) for simple objects
 $S,S' \in \mathcal {C}$ such that
$S,S' \in \mathcal {C}$ such that  $\operatorname {Ext}^1_\mathcal {C}(S,S') \not \simeq 0$, if one of them belongs to
$\operatorname {Ext}^1_\mathcal {C}(S,S') \not \simeq 0$, if one of them belongs to  $\mathcal {B}$ then so does the other.
$\mathcal {B}$ then so does the other.
Lemma 5.3 Let ![]() $X, X' \in \mathcal {C}$. Suppose that
$X, X' \in \mathcal {C}$. Suppose that ![]() $\operatorname {Ext}^{1}_\mathcal {C}( S,S' )=0$ for any simple subquotients
$\operatorname {Ext}^{1}_\mathcal {C}( S,S' )=0$ for any simple subquotients ![]() $S$ and
$S$ and ![]() $S'$ of
$S'$ of ![]() $X$ and
$X$ and ![]() $X'$, respectively. Then we have
$X'$, respectively. Then we have ![]() $\operatorname {Ext}^{1}_\mathcal {C}( X,X' )=0$.
$\operatorname {Ext}^{1}_\mathcal {C}( X,X' )=0$.
Proof. Let ![]() $\ell$ and
$\ell$ and ![]() $\ell '$ be the lengths of
$\ell '$ be the lengths of ![]() $X$ and
$X$ and ![]() $X'$, respectively. We use induction on
$X'$, respectively. We use induction on ![]() $\ell +\ell '$. If
$\ell +\ell '$. If ![]() $X$ and
$X$ and ![]() $X'$ are simple, then the claimed result is clear by the assumption.
$X'$ are simple, then the claimed result is clear by the assumption.
Suppose that ![]() $X'$ is not simple. Then there exists an exact sequence
$X'$ is not simple. Then there exists an exact sequence ![]() $0 \rightarrow M \rightarrow X' \rightarrow N \rightarrow 0$ with a simple
$0 \rightarrow M \rightarrow X' \rightarrow N \rightarrow 0$ with a simple ![]() $M$. It in turn gives the exact sequence
$M$. It in turn gives the exact sequence
By the induction hypothesis we have ![]() $\operatorname {Ext}^1_\mathcal {C}(X, M) = \operatorname {Ext}^1_\mathcal {C}(X, N) = 0$, which tells us that
$\operatorname {Ext}^1_\mathcal {C}(X, M) = \operatorname {Ext}^1_\mathcal {C}(X, N) = 0$, which tells us that ![]() $\operatorname {Ext}^{1}_\mathcal {C}( X,X' )=0$.
$\operatorname {Ext}^{1}_\mathcal {C}( X,X' )=0$.
The case where ![]() $X$ is not simple can be proved in the same manner.
$X$ is not simple can be proved in the same manner.
Lemma 5.4 Let ![]() $\mathfrak {c}$ be the set of isomorphism classes of simple objects of
$\mathfrak {c}$ be the set of isomorphism classes of simple objects of ![]() $\mathcal {C}$, and let
$\mathcal {C}$, and let ![]() $\mathfrak {c}=\bigsqcup _{a\in A}\mathfrak {c}_a$ be a partition of
$\mathfrak {c}=\bigsqcup _{a\in A}\mathfrak {c}_a$ be a partition of ![]() $\mathfrak {c}$. We assume that
$\mathfrak {c}$. We assume that
For ![]() $a\in A$, let
$a\in A$, let ![]() $\mathcal {C}_a$ be the full subcategory of
$\mathcal {C}_a$ be the full subcategory of ![]() $\mathcal {C}$ consisting of objects
$\mathcal {C}$ consisting of objects ![]() $X$ such that any simple subquotient of
$X$ such that any simple subquotient of ![]() $X$ belongs to
$X$ belongs to ![]() $\mathfrak {c}_a$. Then
$\mathfrak {c}_a$. Then ![]() $\mathcal {C}=\bigoplus _{a\in A}\mathcal {C}_a$.
$\mathcal {C}=\bigoplus _{a\in A}\mathcal {C}_a$.
Proof. It is enough to show that any object ![]() $X$ of
$X$ of ![]() $\mathcal {C}$ has a decomposition
$\mathcal {C}$ has a decomposition ![]() $X\simeq \bigoplus _{a\in A}X_a$ with
$X\simeq \bigoplus _{a\in A}X_a$ with ![]() $X_a\in \mathcal {C}_a$. In order to prove this, we shall argue by induction on the length of
$X_a\in \mathcal {C}_a$. In order to prove this, we shall argue by induction on the length of ![]() $X$. We may assume that X is non-zero. Let us take a subobject
$X$. We may assume that X is non-zero. Let us take a subobject ![]() $Y$ of
$Y$ of ![]() $X$ such that
$X$ such that ![]() $X/Y$ is simple. Then the induction hypothesis implies that
$X/Y$ is simple. Then the induction hypothesis implies that ![]() $Y = \bigoplus _{a\in A}Y_a$ with
$Y = \bigoplus _{a\in A}Y_a$ with ![]() $Y_a\in \mathcal {C}_a$.
$Y_a\in \mathcal {C}_a$.
Take ![]() $a_0\in A$ such that
$a_0\in A$ such that ![]() $X/Y$ belongs to
$X/Y$ belongs to ![]() $\mathfrak {c}_{a_0}$. Then define
$\mathfrak {c}_{a_0}$. Then define ![]() $Z\in \mathcal {C}$ by the exact sequence
$Z\in \mathcal {C}$ by the exact sequence
Since we have an exact sequence ![]() $0\to Y_{a_0}\to Z\to X/Y\to 0$,
$0\to Y_{a_0}\to Z\to X/Y\to 0$, ![]() $Z$ belongs to
$Z$ belongs to ![]() $\mathcal {C}_{a_0}$. Then Lemma 5.3 tells us that
$\mathcal {C}_{a_0}$. Then Lemma 5.3 tells us that ![]() $\operatorname {Ext}^1(Z,\bigoplus _{a\not =a_0}Y_a )=0$. Hence the exact sequence (5.1) splits, i.e.
$\operatorname {Ext}^1(Z,\bigoplus _{a\not =a_0}Y_a )=0$. Hence the exact sequence (5.1) splits, i.e. ![]() $X \simeq Z\oplus \bigoplus _{a\not =a_0}Y_a$.
$X \simeq Z\oplus \bigoplus _{a\not =a_0}Y_a$.
Let ![]() $\approx$ be the equivalence relation on the set of isomorphism classes of simple objects of
$\approx$ be the equivalence relation on the set of isomorphism classes of simple objects of ![]() $\mathcal {C}$ generated by the relation
$\mathcal {C}$ generated by the relation ![]() $\approx '$ defined as follows: for simple objects
$\approx '$ defined as follows: for simple objects ![]() $S,S' \in \mathcal {C}$,
$S,S' \in \mathcal {C}$,
Theorem 5.5 Let ![]() $A$ be the set of
$A$ be the set of ![]() $\approx$-equivalence classes. For
$\approx$-equivalence classes. For ![]() $a\in A$, let
$a\in A$, let ![]() $\mathcal {C}_a$ be the full subcategory of
$\mathcal {C}_a$ be the full subcategory of ![]() $\mathcal {C}$ consisting of objects
$\mathcal {C}$ consisting of objects ![]() $X$ such that any simple subquotient of
$X$ such that any simple subquotient of ![]() $X$ belongs to
$X$ belongs to ![]() $a$. Then
$a$. Then ![]() $\mathcal {C}_a$ is a block, and the category
$\mathcal {C}_a$ is a block, and the category ![]() $\mathcal {C}$ has a decomposition
$\mathcal {C}$ has a decomposition ![]() $\mathcal {C} = \bigoplus _{a \in A} \mathcal {C}_a$. Moreover, any block of
$\mathcal {C} = \bigoplus _{a \in A} \mathcal {C}_a$. Moreover, any block of ![]() $\mathcal {C}$ is equal to
$\mathcal {C}$ is equal to ![]() $\mathcal {C}_a$ for some
$\mathcal {C}_a$ for some ![]() $a$.
$a$.
Proof. Lemma 5.4 implies the decomposition
Moreover, since ![]() $a$ is a
$a$ is a ![]() $\approx$-equivalence class, there is no non-trivial decomposition of
$\approx$-equivalence class, there is no non-trivial decomposition of ![]() $\mathcal {C}_a$ for any
$\mathcal {C}_a$ for any ![]() $a \in A$.
$a \in A$.
The next corollary follows directly from Theorem 5.5.
Corollary 5.6 Let ![]() $X$ be an indecomposable object of
$X$ be an indecomposable object of ![]() $\mathcal {C}$. Then
$\mathcal {C}$. Then ![]() $X$ belongs to some block. In particular, all the simple subquotients of
$X$ belongs to some block. In particular, all the simple subquotients of ![]() $X$ belong to the same block.
$X$ belong to the same block.
5.2 Direct decomposition of  $\mathscr {C}_{\mathfrak {g}}$
$\mathscr {C}_{\mathfrak {g}}$
In this subsection, we shall prove that ![]() $\mathscr {C}_{\mathfrak {g}}$ has a decomposition parameterized by elements of
$\mathscr {C}_{\mathfrak {g}}$ has a decomposition parameterized by elements of ![]() $\mathcal {W}$.
$\mathcal {W}$.
Lemma 5.7 For modules ![]() $M,N \in \mathscr {C}_{\mathfrak {g}}$, there exists an isomorphism
$M,N \in \mathscr {C}_{\mathfrak {g}}$, there exists an isomorphism
defined by ![]() $\Psi (a(z) \otimes f \otimes g ) = a(z) ( g \circ f )$ for
$\Psi (a(z) \otimes f \otimes g ) = a(z) ( g \circ f )$ for ![]() $a(z) \in \mathbf {k}[z^{\pm 1}]$,
$a(z) \in \mathbf {k}[z^{\pm 1}]$, ![]() $f \in \operatorname {Hom}_{U'_q({\mathfrak {g}})}(N, \mathbf {1})$ and
$f \in \operatorname {Hom}_{U'_q({\mathfrak {g}})}(N, \mathbf {1})$ and ![]() $g \in \operatorname {Hom}_{U'_q({\mathfrak {g}})}(\mathbf {1}, M)$.
$g \in \operatorname {Hom}_{U'_q({\mathfrak {g}})}(\mathbf {1}, M)$.
Proof. Note that ![]() $\mathbf {k}[z^{\pm 1}] \otimes \operatorname {Hom}_{U'_q({\mathfrak {g}})}( \mathbf {1}, M)\mathop {\xrightarrow {\sim}}\operatorname {Hom}_{U'_q({\mathfrak {g}})}( \mathbf {1}, M_z)$. There is a quotient
$\mathbf {k}[z^{\pm 1}] \otimes \operatorname {Hom}_{U'_q({\mathfrak {g}})}( \mathbf {1}, M)\mathop {\xrightarrow {\sim}}\operatorname {Hom}_{U'_q({\mathfrak {g}})}( \mathbf {1}, M_z)$. There is a quotient ![]() $N'$ of
$N'$ of ![]() $N$ which is a direct sum of copies of
$N$ which is a direct sum of copies of ![]() ${\bf {1}}$ and
${\bf {1}}$ and ![]() $\operatorname {Hom}(N',{\bf {1}})\mathop {\xrightarrow {\sim}}\operatorname {Hom}(N,{\bf {1}})$. Since (5.2) for
$\operatorname {Hom}(N',{\bf {1}})\mathop {\xrightarrow {\sim}}\operatorname {Hom}(N,{\bf {1}})$. Since (5.2) for ![]() $N'$ is obviously an isomorphism,
$N'$ is obviously an isomorphism, ![]() $\Psi$ is injective.
$\Psi$ is injective.
To prove that ![]() $\Psi$ is surjective, we shall decompose a given non-zero
$\Psi$ is surjective, we shall decompose a given non-zero ![]() $f\colon N \to M_z$ into
$f\colon N \to M_z$ into ![]() $N \to {\bf {1}}^{\oplus \ell } \to M_z$ for some
$N \to {\bf {1}}^{\oplus \ell } \to M_z$ for some ![]() $\ell \in \mathbb {\mspace {1mu}Z\mspace {1mu}}_{>0}$. Here
$\ell \in \mathbb {\mspace {1mu}Z\mspace {1mu}}_{>0}$. Here ![]() $\mathbf {1}^{\oplus \ell }$ is the direct sum of
$\mathbf {1}^{\oplus \ell }$ is the direct sum of ![]() $\ell$ copies of the trivial module
$\ell$ copies of the trivial module ![]() $\mathbf {1}$. Without loss of generality, we may assume that
$\mathbf {1}$. Without loss of generality, we may assume that ![]() $f$ is injective. We set
$f$ is injective. We set ![]() $\operatorname {wt}(N) \mathbin {:=} \{ \lambda \in \mathsf {P}_{\mathrm {cl}\mspace {1mu}} \mid N_\lambda \ne 0 \}$.
$\operatorname {wt}(N) \mathbin {:=} \{ \lambda \in \mathsf {P}_{\mathrm {cl}\mspace {1mu}} \mid N_\lambda \ne 0 \}$.
If ![]() $\operatorname {wt}(N) =\{0\}$, then
$\operatorname {wt}(N) =\{0\}$, then ![]() $N$ should be isomorphic to
$N$ should be isomorphic to ![]() $\mathbf {1} ^{\oplus \ell }$ for some
$\mathbf {1} ^{\oplus \ell }$ for some ![]() $\ell \in \mathbb {\mspace {1mu}Z\mspace {1mu}}_{>0}$, which is the desired result.
$\ell \in \mathbb {\mspace {1mu}Z\mspace {1mu}}_{>0}$, which is the desired result.
Now suppose that ![]() $\operatorname {wt}(N)\not =\{0\}$. We choose a non-zero weight
$\operatorname {wt}(N)\not =\{0\}$. We choose a non-zero weight ![]() $\lambda \in \operatorname {wt}(N)$.
$\lambda \in \operatorname {wt}(N)$.
Note that the ![]() $U'_q({\mathfrak {g}})$-module structure on
$U'_q({\mathfrak {g}})$-module structure on ![]() $M_z$ extends to a
$M_z$ extends to a ![]() $U_q({\mathfrak {g}})$-module structure and we have a weight decomposition
$U_q({\mathfrak {g}})$-module structure and we have a weight decomposition ![]() $M_z=\bigoplus _{\mu \in \mathsf {P}}(M_z)_\mu$. Then
$M_z=\bigoplus _{\mu \in \mathsf {P}}(M_z)_\mu$. Then
where ![]() ${\mathrm {cl}\mspace {1mu}}\colon \mathsf {P}\to \mathsf {P}_{\mathrm {cl}\mspace {1mu}}$ is the classical projection. There exist
${\mathrm {cl}\mspace {1mu}}\colon \mathsf {P}\to \mathsf {P}_{\mathrm {cl}\mspace {1mu}}$ is the classical projection. There exist ![]() $w \in \mathsf {W}$ and a non-zero integer
$w \in \mathsf {W}$ and a non-zero integer ![]() $n$ such that
$n$ such that ![]() $w( \mu ) = \mu +n\delta$ for any
$w( \mu ) = \mu +n\delta$ for any ![]() $\mu \in {\mathrm {cl}\mspace {1mu}}^{-1}(\lambda )$. We now consider the braid group action
$\mu \in {\mathrm {cl}\mspace {1mu}}^{-1}(\lambda )$. We now consider the braid group action ![]() $T_w$ defined by
$T_w$ defined by ![]() $w$ on an integral module (see [Reference LusztigLus90, Reference SaitoSai94]). Then the
$w$ on an integral module (see [Reference LusztigLus90, Reference SaitoSai94]). Then the ![]() $\mathbf {k}$-linear automorphism
$\mathbf {k}$-linear automorphism ![]() $T_w$ sends
$T_w$ sends ![]() $(M_z)_\mu$ to
$(M_z)_\mu$ to ![]() $(M_z)_{w\mu }$. The space
$(M_z)_{w\mu }$. The space ![]() $f(N_\lambda )$ is invariant under the automorphism
$f(N_\lambda )$ is invariant under the automorphism ![]() $T_w$, but any non-zero finite-dimensional subspace of
$T_w$, but any non-zero finite-dimensional subspace of ![]() $\bigoplus _{\mu \in \mathsf {P},\,{\mathrm {cl}\mspace {1mu}}(\mu )=\lambda } (M_z)_{\mu }$ cannot be invariant under
$\bigoplus _{\mu \in \mathsf {P},\,{\mathrm {cl}\mspace {1mu}}(\mu )=\lambda } (M_z)_{\mu }$ cannot be invariant under ![]() $T_w$. This is a contradiction.
$T_w$. This is a contradiction.
Proposition 5.8 For modules ![]() $M,N \in \mathscr {C}_{\mathfrak {g}}$ and a simple module
$M,N \in \mathscr {C}_{\mathfrak {g}}$ and a simple module ![]() $L \in \mathscr {C}_{\mathfrak {g}}$, we have the isomorphisms
$L \in \mathscr {C}_{\mathfrak {g}}$, we have the isomorphisms
Proof. By Lemma 5.7, we obtain that
 \begin{align*} \operatorname{Hom}_{ \mathbf{k}[z^{\pm1}] \otimes U_q'({\mathfrak{g}}) }(M\otimes L_z,N \otimes L_z) & \simeq \operatorname{Hom}_{U_q'({\mathfrak{g}}) }(N^* \otimes M , (L \otimes L^*)_z) \\ & \simeq {{\mathbf{k}}}[z^{\pm1}] \otimes \operatorname{Hom}_{U_q'({\mathfrak{g}})}(N^* \otimes M ,{\bf{1}}) \mathop\otimes \operatorname{Hom}_{U_q'({\mathfrak{g}})}({\bf{1}}, L\otimes L^*)\\ & \simeq {{\mathbf{k}}}[z^{\pm1}] \otimes \operatorname{Hom}_{U_q'({\mathfrak{g}})}(M ,N). \end{align*}
\begin{align*} \operatorname{Hom}_{ \mathbf{k}[z^{\pm1}] \otimes U_q'({\mathfrak{g}}) }(M\otimes L_z,N \otimes L_z) & \simeq \operatorname{Hom}_{U_q'({\mathfrak{g}}) }(N^* \otimes M , (L \otimes L^*)_z) \\ & \simeq {{\mathbf{k}}}[z^{\pm1}] \otimes \operatorname{Hom}_{U_q'({\mathfrak{g}})}(N^* \otimes M ,{\bf{1}}) \mathop\otimes \operatorname{Hom}_{U_q'({\mathfrak{g}})}({\bf{1}}, L\otimes L^*)\\ & \simeq {{\mathbf{k}}}[z^{\pm1}] \otimes \operatorname{Hom}_{U_q'({\mathfrak{g}})}(M ,N). \end{align*}Lemma 5.9 Let ![]() $M$ and
$M$ and ![]() $N$ be simple modules in
$N$ be simple modules in ![]() $\mathscr {C}_{\mathfrak {g}}$. If
$\mathscr {C}_{\mathfrak {g}}$. If
then we have
Proof. Let ![]() $L \in \mathscr {C}_{\mathfrak {g}}$ be a simple module such that
$L \in \mathscr {C}_{\mathfrak {g}}$ be a simple module such that ![]() ${c_{M,L}(z)}/{c_{N,L}(z)} \notin \mathbf {k}(z)$.
${c_{M,L}(z)}/{c_{N,L}(z)} \notin \mathbf {k}(z)$.
We shall prove that any exact sequence
splits. We set ![]() $\hat {L}_z \mathbin {:=} \mathbf {k}((z)) \otimes _{\mathbf {k} [z^{\pm 1}] } L_z$, where
$\hat {L}_z \mathbin {:=} \mathbf {k}((z)) \otimes _{\mathbf {k} [z^{\pm 1}] } L_z$, where ![]() $L_z$ is the affinization of
$L_z$ is the affinization of ![]() $L$. Then the following diagram commutes.
$L$. Then the following diagram commutes.

We set
It follows from
that
Therefore ![]() $R$ induces the
$R$ induces the ![]() $\mathbf {k}[z^{\pm 1}]\mathop \otimes U'_q({\mathfrak {g}})$-linear homomorphism
$\mathbf {k}[z^{\pm 1}]\mathop \otimes U'_q({\mathfrak {g}})$-linear homomorphism
We set ![]() $\mathcal {P} \mathbin {:=} {\mathbf {k}((z))}/({\mathbf {k}(z) + f(z) \mathbf {k}(z)})$. Since
$\mathcal {P} \mathbin {:=} {\mathbf {k}((z))}/({\mathbf {k}(z) + f(z) \mathbf {k}(z)})$. Since
 \begin{align*} \frac{ \mathbf{k}(z) \otimes L_z \otimes X + \hat{L}_z \otimes N}{ \mathbf{k}(z) \otimes L_z \otimes X + f(z) \mathbf{k}(z) \otimes L_z \otimes N } & \simeq \frac{\hat{L}_z \otimes N}{\mathbf{k}(z) \otimes L_z \otimes N + f(z) \mathbf{k}(z) \otimes L_z \otimes N }\\ & \simeq \mathcal{P} \otimes_{\mathbf{k}[z^{\pm1}]} L_z \otimes N, \end{align*}
\begin{align*} \frac{ \mathbf{k}(z) \otimes L_z \otimes X + \hat{L}_z \otimes N}{ \mathbf{k}(z) \otimes L_z \otimes X + f(z) \mathbf{k}(z) \otimes L_z \otimes N } & \simeq \frac{\hat{L}_z \otimes N}{\mathbf{k}(z) \otimes L_z \otimes N + f(z) \mathbf{k}(z) \otimes L_z \otimes N }\\ & \simeq \mathcal{P} \otimes_{\mathbf{k}[z^{\pm1}]} L_z \otimes N, \end{align*}
we have the homomorphism of ![]() $\mathbf {k}[z^{\pm 1}] \mathop \otimes U'_q({\mathfrak {g}})$-modules
$\mathbf {k}[z^{\pm 1}] \mathop \otimes U'_q({\mathfrak {g}})$-modules
Let us show that ![]() $\mathcal {R}$ vanishes.
$\mathcal {R}$ vanishes.
Assume that ![]() $\mathcal {R}\not =0$. Then
$\mathcal {R}\not =0$. Then
implies that ![]() $\operatorname {Hom}_{\mathbf {k}[z^{\pm 1}]\mathop \otimes U'_q({\mathfrak {g}})}(M\mathop \otimes L_z,L_z \otimes N)\not \simeq 0$.
$\operatorname {Hom}_{\mathbf {k}[z^{\pm 1}]\mathop \otimes U'_q({\mathfrak {g}})}(M\mathop \otimes L_z,L_z \otimes N)\not \simeq 0$.
Since ![]() $\mathbf {k}(z)\mathop \otimes _{\mathbf {k}[z^{\pm 1}]}(M\mathop \otimes L_z)$ and
$\mathbf {k}(z)\mathop \otimes _{\mathbf {k}[z^{\pm 1}]}(M\mathop \otimes L_z)$ and ![]() $\mathbf {k}(z)\mathop \otimes _{\mathbf {k}[z^{\pm 1}]}(L_z \otimes N)$ are simple
$\mathbf {k}(z)\mathop \otimes _{\mathbf {k}[z^{\pm 1}]}(L_z \otimes N)$ are simple ![]() $\mathbf {k}(z)\mathop \otimes U'_q({\mathfrak {g}})$-modules, they are isomorphic. Since
$\mathbf {k}(z)\mathop \otimes U'_q({\mathfrak {g}})$-modules, they are isomorphic. Since ![]() $\mathbf {k}(z)\mathop \otimes _{\mathbf {k}[z^{\pm 1}]}(L_z \otimes N)$ and
$\mathbf {k}(z)\mathop \otimes _{\mathbf {k}[z^{\pm 1}]}(L_z \otimes N)$ and ![]() $\mathbf {k}(z)\mathop \otimes _{\mathbf {k}[z^{\pm 1}]}(N\mathop \otimes L_z)$ are isomorphic, we conclude that
$\mathbf {k}(z)\mathop \otimes _{\mathbf {k}[z^{\pm 1}]}(N\mathop \otimes L_z)$ are isomorphic, we conclude that ![]() $\mathbf {k}(z)\mathop \otimes _{\mathbf {k}[z^{\pm 1}]}(M\mathop \otimes L_z)\simeq \mathbf {k}(z)\mathop \otimes _{\mathbf {k}[z^{\pm 1}]}(N\mathop \otimes L_z)$. On the other hand, Proposition 5.8 implies that
$\mathbf {k}(z)\mathop \otimes _{\mathbf {k}[z^{\pm 1}]}(M\mathop \otimes L_z)\simeq \mathbf {k}(z)\mathop \otimes _{\mathbf {k}[z^{\pm 1}]}(N\mathop \otimes L_z)$. On the other hand, Proposition 5.8 implies that
Hence ![]() $\operatorname {Hom}_{U_q'({\mathfrak {g}})}(M,N) \not =0$, and we obtain that
$\operatorname {Hom}_{U_q'({\mathfrak {g}})}(M,N) \not =0$, and we obtain that ![]() $M$ and
$M$ and ![]() $N$ are isomorphic, which is a contradiction. Therefore
$N$ are isomorphic, which is a contradiction. Therefore ![]() $\mathcal {R}=0$, which means that
$\mathcal {R}=0$, which means that
Let us consider the composition
We have
Hence ![]() $\ker (\Phi )=K\cap \bigl (\mathbf {k}(z) \otimes L_z \otimes N\bigr ) =\bigl ( f(z)\mathbf {k}(z) \otimes L_z \otimes N)\cap \bigl (\mathbf {k}(z) \otimes L_z \otimes N\bigr )$ vanishes, which means that
$\ker (\Phi )=K\cap \bigl (\mathbf {k}(z) \otimes L_z \otimes N\bigr ) =\bigl ( f(z)\mathbf {k}(z) \otimes L_z \otimes N)\cap \bigl (\mathbf {k}(z) \otimes L_z \otimes N\bigr )$ vanishes, which means that ![]() $\Phi$ is a monomorphism.
$\Phi$ is a monomorphism.
Since ![]() $\mathbf {k}(z) \otimes L_z\mathop \otimes M$ and
$\mathbf {k}(z) \otimes L_z\mathop \otimes M$ and ![]() $\mathbf {k}(z) \otimes L_z\mathop \otimes N$ are simple
$\mathbf {k}(z) \otimes L_z\mathop \otimes N$ are simple ![]() $\mathbf {k}(z)\mathop \otimes U'_q({\mathfrak {g}})$-modules,
$\mathbf {k}(z)\mathop \otimes U'_q({\mathfrak {g}})$-modules, ![]() $\mathbf {k}(z) \otimes L_z \otimes X$ has length
$\mathbf {k}(z) \otimes L_z \otimes X$ has length ![]() $2$. Similarly,
$2$. Similarly, ![]() $R\bigl (\mathbf {k}(z)\mathop \otimes (X\mathop \otimes L_z)\bigr )$ also has length
$R\bigl (\mathbf {k}(z)\mathop \otimes (X\mathop \otimes L_z)\bigr )$ also has length ![]() $2$. On the other hand,
$2$. On the other hand, ![]() $\mathbf {k}(z) \otimes L_z \otimes X + f(z) \mathbf {k}(z) \otimes L_z \otimes N$ has length no more than
$\mathbf {k}(z) \otimes L_z \otimes X + f(z) \mathbf {k}(z) \otimes L_z \otimes N$ has length no more than ![]() $3$, which implies that
$3$, which implies that ![]() $K$ does not vanish. Hence
$K$ does not vanish. Hence ![]() $\Phi$ is an isomorphism. Thus we conclude that the homomorphism
$\Phi$ is an isomorphism. Thus we conclude that the homomorphism
is surjective. Then Proposition 5.8 implies that this homomorphism is isomorphic to
Thus we conclude that ![]() $\operatorname {Hom}(M,X)\to \operatorname {Hom}(M,M)$ is surjective, that is,
$\operatorname {Hom}(M,X)\to \operatorname {Hom}(M,M)$ is surjective, that is,
splits.
For ![]() $\alpha \in \mathcal {W}$, let
$\alpha \in \mathcal {W}$, let ![]() $\mathscr {C}_{{\mathfrak {g}}, \alpha }$ be the full subcategory of
$\mathscr {C}_{{\mathfrak {g}}, \alpha }$ be the full subcategory of ![]() $\mathscr {C}_{\mathfrak {g}}$ consisting of objects
$\mathscr {C}_{\mathfrak {g}}$ consisting of objects ![]() $X$ such that
$X$ such that ![]() $\mathsf {E} (S)=\alpha$ for any simple subquotient
$\mathsf {E} (S)=\alpha$ for any simple subquotient ![]() $S$ of
$S$ of ![]() $X$.
$X$.
Theorem 5.10 There exist the decompositions
Proof. Let ![]() $\alpha, \beta \in \mathcal {W}$ with
$\alpha, \beta \in \mathcal {W}$ with ![]() $\alpha \ne \beta$. For simple modules
$\alpha \ne \beta$. For simple modules ![]() $M \in \mathscr {C}_{{\mathfrak {g}}, \alpha }$ and
$M \in \mathscr {C}_{{\mathfrak {g}}, \alpha }$ and ![]() $N \in \mathscr {C}_{{\mathfrak {g}}, \beta }$, Lemma 4.1(iii) says that
$N \in \mathscr {C}_{{\mathfrak {g}}, \beta }$, Lemma 4.1(iii) says that ![]() ${a_{M,V(\varpi _i)}(z)}/{a_{N,V(\varpi _i)}(z)} \notin \mathbf {k}(z)$ for some
${a_{M,V(\varpi _i)}(z)}/{a_{N,V(\varpi _i)}(z)} \notin \mathbf {k}(z)$ for some ![]() $i\in I_0$. Hence Lemma 5.9 implies that
$i\in I_0$. Hence Lemma 5.9 implies that ![]() $\operatorname {Ext}^1_{U_q'({\mathfrak {g}})}(M,N)=0.$ The desired result then follows from Lemma 5.4.
$\operatorname {Ext}^1_{U_q'({\mathfrak {g}})}(M,N)=0.$ The desired result then follows from Lemma 5.4.
5.3 The block  $\mathscr {C}_{{\mathfrak {g}}, \alpha }$
$\mathscr {C}_{{\mathfrak {g}}, \alpha }$
Recall the automorphism ![]() $\tau _t$ on
$\tau _t$ on ![]() ${\sigma ({\mathfrak {g}})}$ defined in (4.4). For
${\sigma ({\mathfrak {g}})}$ defined in (4.4). For ![]() $(i,a) \in {\sigma ({\mathfrak {g}})}$ we write
$(i,a) \in {\sigma ({\mathfrak {g}})}$ we write
Note that ![]() $V(\tau _t \alpha ) = V(\alpha )_t$ for
$V(\tau _t \alpha ) = V(\alpha )_t$ for ![]() $\alpha \in {\sigma ({\mathfrak {g}})}$ and
$\alpha \in {\sigma ({\mathfrak {g}})}$ and ![]() $t\in \mathbf {k}^\times$. For
$t\in \mathbf {k}^\times$. For ![]() $\alpha \in {\sigma ({\mathfrak {g}})}$, we define
$\alpha \in {\sigma ({\mathfrak {g}})}$, we define ![]() $\alpha ^* \in {\sigma ({\mathfrak {g}})}$ by
$\alpha ^* \in {\sigma ({\mathfrak {g}})}$ by
Thus we have
Lemma 5.11 Let ![]() $\alpha _1, \ldots, \alpha _k \in {\sigma ({\mathfrak {g}})}$ for
$\alpha _1, \ldots, \alpha _k \in {\sigma ({\mathfrak {g}})}$ for ![]() $k\in \mathbb {\mspace {1mu}Z\mspace {1mu}}_{>0}$. Then all the simple subquotients of
$k\in \mathbb {\mspace {1mu}Z\mspace {1mu}}_{>0}$. Then all the simple subquotients of ![]() $V(\alpha _1) \otimes V(\alpha _2) \otimes \cdots \otimes V(\alpha _k)$ are contained in the same block of
$V(\alpha _1) \otimes V(\alpha _2) \otimes \cdots \otimes V(\alpha _k)$ are contained in the same block of ![]() $\mathscr {C}_{\mathfrak {g}}$.
$\mathscr {C}_{\mathfrak {g}}$.
Proof. There exists a permutation ![]() $\sigma \in \mathfrak {S}_k$ such that the tensor product
$\sigma \in \mathfrak {S}_k$ such that the tensor product ![]() $V(\alpha _{\sigma (1)}) \otimes V(\alpha _{\sigma (2)}) \otimes \cdots \otimes V(\alpha _{\sigma (k)})$ has a simple head by Theorem 2.2, and hence it is indecomposable. Thus, all the simple subquotients of
$V(\alpha _{\sigma (1)}) \otimes V(\alpha _{\sigma (2)}) \otimes \cdots \otimes V(\alpha _{\sigma (k)})$ has a simple head by Theorem 2.2, and hence it is indecomposable. Thus, all the simple subquotients of ![]() $V(\alpha _{\sigma (1)}) \otimes V(\alpha _{\sigma (2)}) \otimes \cdots \otimes V(\alpha _{\sigma (k)})$ are contained in the same block by Corollary 5.6. Since any simple subquotient of
$V(\alpha _{\sigma (1)}) \otimes V(\alpha _{\sigma (2)}) \otimes \cdots \otimes V(\alpha _{\sigma (k)})$ are contained in the same block by Corollary 5.6. Since any simple subquotient of ![]() $V(\alpha _1) \otimes V(\alpha _2) \otimes \cdots \otimes V(\alpha _k)$ is isomorphic to some simple subquotient of
$V(\alpha _1) \otimes V(\alpha _2) \otimes \cdots \otimes V(\alpha _k)$ is isomorphic to some simple subquotient of ![]() $V(\alpha _{\sigma (1)}) \otimes V(\alpha _{\sigma (2)}) \otimes \cdots \otimes V(\alpha _{\sigma (k)})$, we obtain the desired result.
$V(\alpha _{\sigma (1)}) \otimes V(\alpha _{\sigma (2)}) \otimes \cdots \otimes V(\alpha _{\sigma (k)})$, we obtain the desired result.
We set
and
where ![]() $\mathsf {e}_\alpha$ is a symbol. Define a group homomorphism
$\mathsf {e}_\alpha$ is a symbol. Define a group homomorphism
and set
By Proposition 4.5, we have
Let ![]() $\mathcal {Q}_0$ be the subgroup of
$\mathcal {Q}_0$ be the subgroup of ![]() $\mathcal {P}_0$ generated by elements of the form
$\mathcal {P}_0$ generated by elements of the form ![]() $\sum _{k=1}^m \mathsf {e}_{\alpha _k}$ (
$\sum _{k=1}^m \mathsf {e}_{\alpha _k}$ (![]() $\alpha _k \in {\sigma _0({\mathfrak {g}})}$) such that the trivial module
$\alpha _k \in {\sigma _0({\mathfrak {g}})}$) such that the trivial module ![]() $\mathbf {1}$ appears in
$\mathbf {1}$ appears in ![]() $V(\alpha _1) \otimes V(\alpha _2) \otimes \cdots \otimes V(\alpha _{ m })$ as a simple subquotient. We then have
$V(\alpha _1) \otimes V(\alpha _2) \otimes \cdots \otimes V(\alpha _{ m })$ as a simple subquotient. We then have ![]() $p_0 ( \mathcal {Q}_0 ) = 0$.
$p_0 ( \mathcal {Q}_0 ) = 0$.
We set
Recall ![]() $\phi _Q\colon {\Delta ^+_{Q}} \mathop {\xrightarrow {\sim}}{\sigma _Q({\mathfrak {g}})}$ in (2.11). Let
$\phi _Q\colon {\Delta ^+_{Q}} \mathop {\xrightarrow {\sim}}{\sigma _Q({\mathfrak {g}})}$ in (2.11). Let ![]() ${\Pi _{Q}}\subset {\Delta ^+_{Q}}$ be the set of simple roots of the positive root system
${\Pi _{Q}}\subset {\Delta ^+_{Q}}$ be the set of simple roots of the positive root system ![]() ${\Delta ^+_{Q}}$ and
${\Delta ^+_{Q}}$ and ![]() $\mathsf {Q}_Q$ the corresponding root lattice. Hence we have
$\mathsf {Q}_Q$ the corresponding root lattice. Hence we have ![]() ${\Pi _{Q}}\subset {\Delta ^+_{Q}}\subset \mathsf {Q}_Q$.
${\Pi _{Q}}\subset {\Delta ^+_{Q}}\subset \mathsf {Q}_Q$.
In the proof of the following lemma, we do not use Theorem 4.6.
Lemma 5.12 For ![]() $\alpha \in {\sigma _0({\mathfrak {g}})}$, denote by
$\alpha \in {\sigma _0({\mathfrak {g}})}$, denote by ![]() $\bar {\mathsf {e}}_\alpha \in \mathcal {P}_0/\mathcal {Q}_0$ the image of
$\bar {\mathsf {e}}_\alpha \in \mathcal {P}_0/\mathcal {Q}_0$ the image of ![]() $\mathsf {e}_\alpha$ under the projection
$\mathsf {e}_\alpha$ under the projection ![]() $\mathcal {P}_0\to \mathcal {P}_0/\mathcal {Q}_0$.
$\mathcal {P}_0\to \mathcal {P}_0/\mathcal {Q}_0$.
(i) The map
 ${\Delta ^+_{Q}}\ni \alpha \mapsto \bar {\mathsf {e}}_{\phi _Q(\alpha )}\in \mathcal {P}_0/\mathcal {Q}_0$ extends to an additive map
${\Delta ^+_{Q}}\ni \alpha \mapsto \bar {\mathsf {e}}_{\phi _Q(\alpha )}\in \mathcal {P}_0/\mathcal {Q}_0$ extends to an additive map  $\psi '_Q\colon \mathsf {Q}_Q\to \mathcal {P}_0/\mathcal {Q}_0$.
$\psi '_Q\colon \mathsf {Q}_Q\to \mathcal {P}_0/\mathcal {Q}_0$.(ii) We have that
 $\psi '_Q$ is surjective, i.e.
$\psi '_Q$ is surjective, i.e.
 \[ \mathcal{P}_0/\mathcal{Q}_0=\sum_{\beta\in{\Pi_{Q}}}\mathbb{\mspace{1mu}Z\mspace{1mu}}\bar{\mathsf{e}}_{\phi_Q(\beta)}. \]
\[ \mathcal{P}_0/\mathcal{Q}_0=\sum_{\beta\in{\Pi_{Q}}}\mathbb{\mspace{1mu}Z\mspace{1mu}}\bar{\mathsf{e}}_{\phi_Q(\beta)}. \](iii) Let
 $\psi _Q\colon \mathsf {Q}_Q\to \mathcal {W} _0$ be the composition
$\psi _Q\colon \mathsf {Q}_Q\to \mathcal {W} _0$ be the composition  $\mathsf {Q}_Q\xrightarrow {\,{\psi '_Q}\,}\mathcal {P}_0/\mathcal {Q}_0\xrightarrow {\,{\hspace {2ex}}\,} \mathcal {W} _0$. Then
$\mathsf {Q}_Q\xrightarrow {\,{\psi '_Q}\,}\mathcal {P}_0/\mathcal {Q}_0\xrightarrow {\,{\hspace {2ex}}\,} \mathcal {W} _0$. Then
 \[ \psi_Q(\beta)= \mathsf{E} \bigl( V_Q(\beta)\bigr). \]
\[ \psi_Q(\beta)= \mathsf{E} \bigl( V_Q(\beta)\bigr). \](iv) We have that
 $\psi _Q$ is surjective, i.e.
$\psi _Q$ is surjective, i.e.  $\mathcal {W} _0=\sum _{\alpha \in \phi _Q({\Pi _{Q}})}\mathbb {\mspace {1mu}Z\mspace {1mu}} p_0( \mathsf {e}_\alpha )$.
$\mathcal {W} _0=\sum _{\alpha \in \phi _Q({\Pi _{Q}})}\mathbb {\mspace {1mu}Z\mspace {1mu}} p_0( \mathsf {e}_\alpha )$.
Proof. (i) The map ![]() ${\Pi _{Q}}\ni \alpha \mapsto \bar {\mathsf {e}}_{\phi _Q(\alpha )}\in \mathcal {P}_0/\mathcal {Q}_0$ extends to a linear map
${\Pi _{Q}}\ni \alpha \mapsto \bar {\mathsf {e}}_{\phi _Q(\alpha )}\in \mathcal {P}_0/\mathcal {Q}_0$ extends to a linear map ![]() $\psi '_Q\colon \mathsf {Q}_Q\to \mathcal {P}_0/\mathcal {Q}_0$. It is enough to show that
$\psi '_Q\colon \mathsf {Q}_Q\to \mathcal {P}_0/\mathcal {Q}_0$. It is enough to show that ![]() $\bar {\mathsf {e}}_{\phi _Q(\gamma )}=\psi '_Q(\gamma )$ for any
$\bar {\mathsf {e}}_{\phi _Q(\gamma )}=\psi '_Q(\gamma )$ for any ![]() $\gamma \in {\Delta ^+_{Q}}$. Let us show this by induction on the length of
$\gamma \in {\Delta ^+_{Q}}$. Let us show this by induction on the length of ![]() $\gamma$. If
$\gamma$. If ![]() $\gamma$ is not a simple root, take a minimal pair
$\gamma$ is not a simple root, take a minimal pair ![]() $(\beta,\beta ')$ of
$(\beta,\beta ')$ of ![]() $\gamma$ (see Proposition 2.4). Since
$\gamma$ (see Proposition 2.4). Since ![]() $V_Q(\gamma )$ appears as a composition factor of
$V_Q(\gamma )$ appears as a composition factor of ![]() $V_Q(\beta ) \otimes V_Q(\beta ')$ by Proposition 2.4, we have
$V_Q(\beta ) \otimes V_Q(\beta ')$ by Proposition 2.4, we have
Assertion (ii) follows from (i), and (iii) follows from (ii) and a surjective map ![]() $\mathcal {P}_0/\mathcal {Q}_0\twoheadrightarrow \mathcal {W} _0$.
$\mathcal {P}_0/\mathcal {Q}_0\twoheadrightarrow \mathcal {W} _0$.
In the proof of the following lemma, we use the fact that the rank of ![]() $\mathcal {W} _0$ is at least the rank of
$\mathcal {W} _0$ is at least the rank of ![]() ${\Delta ^+_{Q}}$ (stated in Theorem 4.6, whose proof is postponed to § 6; see (6.3)).
${\Delta ^+_{Q}}$ (stated in Theorem 4.6, whose proof is postponed to § 6; see (6.3)).
Lemma 5.13 We have the isomorphisms
Proof. The second isomorphism easily follows from the first isomorphism together with (5.3) and (5.4). So we need only show that ![]() $\mathcal {P}_0/\mathcal {Q}_0\twoheadrightarrow \mathcal {W} _0$ is an isomorphism.
$\mathcal {P}_0/\mathcal {Q}_0\twoheadrightarrow \mathcal {W} _0$ is an isomorphism.
Let ![]() $r$ be the rank of
$r$ be the rank of ![]() ${\Delta ^+_{Q}}$. By (6.3), the rank of
${\Delta ^+_{Q}}$. By (6.3), the rank of ![]() $\mathcal {W} _0$ is at least
$\mathcal {W} _0$ is at least ![]() $r$. Let us consider a surjective homomorphism
$r$. Let us consider a surjective homomorphism
By Lemma 5.12, ![]() $\mathcal {P}_0/\mathcal {Q}_0$ is generated by
$\mathcal {P}_0/\mathcal {Q}_0$ is generated by ![]() $r$ elements. Hence (5.5) is an isomorphism.
$r$ elements. Hence (5.5) is an isomorphism.
For ![]() $\lambda = \sum _{t=1}^k \mathsf {e}_{\alpha _t} \in \mathcal {P}^+$, we set
$\lambda = \sum _{t=1}^k \mathsf {e}_{\alpha _t} \in \mathcal {P}^+$, we set
Note that for ![]() $\lambda, \mu \in \mathcal {P}^+$, if
$\lambda, \mu \in \mathcal {P}^+$, if ![]() $\mathbf {1}$ appears in
$\mathbf {1}$ appears in ![]() $\bar {V}(\lambda )$ and
$\bar {V}(\lambda )$ and ![]() $\bar {V}(\mu )$, then
$\bar {V}(\mu )$, then ![]() $\mathbf {1}$ also appears in
$\mathbf {1}$ also appears in ![]() $\bar {V}(\lambda ) \otimes \bar {V}(\mu )$. Hence any element of
$\bar {V}(\lambda ) \otimes \bar {V}(\mu )$. Hence any element of ![]() $\mathcal {Q}$ can be written as
$\mathcal {Q}$ can be written as ![]() $\lambda - \mu$ with
$\lambda - \mu$ with ![]() $\lambda, \mu \in \mathcal {P}^+$ such that
$\lambda, \mu \in \mathcal {P}^+$ such that ![]() ${\bf {1}}$ appears in both
${\bf {1}}$ appears in both ![]() $\bar {V}(\lambda )$ and
$\bar {V}(\lambda )$ and ![]() $\bar {V}(\mu )$.
$\bar {V}(\mu )$.
Theorem 5.14 For any ![]() $\alpha \in \mathcal {W}$, the subcategory
$\alpha \in \mathcal {W}$, the subcategory ![]() $\mathscr {C}_{{\mathfrak {g}}, \alpha }$ is a block of
$\mathscr {C}_{{\mathfrak {g}}, \alpha }$ is a block of ![]() $\mathscr {C}_{\mathfrak {g}}$.
$\mathscr {C}_{\mathfrak {g}}$.
Proof. Let ![]() $\alpha \in \mathcal {W}$, and let
$\alpha \in \mathcal {W}$, and let ![]() $S$ and
$S$ and ![]() $S'$ be simple modules in
$S'$ be simple modules in ![]() $\mathscr {C}_{{\mathfrak {g}}, \alpha }$. We shall show that
$\mathscr {C}_{{\mathfrak {g}}, \alpha }$. We shall show that ![]() $S$ and
$S$ and ![]() $S'$ belong to the same block.
$S'$ belong to the same block.
Thanks to Theorem 2.2(iv), there exist ![]() $\lambda, \lambda ' \in \mathcal {P}^+$ such that
$\lambda, \lambda ' \in \mathcal {P}^+$ such that ![]() $S$ appears in
$S$ appears in ![]() $\bar {V}(\lambda )$ and
$\bar {V}(\lambda )$ and ![]() $S'$ appears in
$S'$ appears in ![]() $\bar {V}(\lambda ')$. By Lemma 5.13, we have
$\bar {V}(\lambda ')$. By Lemma 5.13, we have ![]() $\lambda - \lambda ' \in \ker p = \mathcal {Q}$. Then there exist
$\lambda - \lambda ' \in \ker p = \mathcal {Q}$. Then there exist ![]() $\mu, \mu ' \in \mathcal {P}^+$ that satisfy the following:
$\mu, \mu ' \in \mathcal {P}^+$ that satisfy the following:
•
 $\lambda - \lambda ' = \mu ' - \mu$;
$\lambda - \lambda ' = \mu ' - \mu$;•
 $\mathbf {1}$ appears in
$\mathbf {1}$ appears in  $\bar {V}(\mu )$ and
$\bar {V}(\mu )$ and  $\bar {V}(\mu ')$.
$\bar {V}(\mu ')$.
Thus the following hold:
(a)
 $\lambda + \mu = \lambda ' + \mu '$, i.e.
$\lambda + \mu = \lambda ' + \mu '$, i.e.  $\bar {V}(\lambda +\mu ) = \bar {V}(\lambda '+\mu ')$;
$\bar {V}(\lambda +\mu ) = \bar {V}(\lambda '+\mu ')$;(b)
 $S$ appears in
$S$ appears in  $\bar {V}(\lambda ) \otimes \bar {V}(\mu ) = \bar {V}(\lambda +\mu )$;
$\bar {V}(\lambda ) \otimes \bar {V}(\mu ) = \bar {V}(\lambda +\mu )$;(c)
 $S'$ appears in
$S'$ appears in  $\bar {V}(\lambda ') \otimes \bar {V}(\mu ') = \bar {V}(\lambda '+\mu ')$.
$\bar {V}(\lambda ') \otimes \bar {V}(\mu ') = \bar {V}(\lambda '+\mu ')$.
This tells us that ![]() $S$ and
$S$ and ![]() $S'$ belong to the same block by Lemma 5.11.
$S'$ belong to the same block by Lemma 5.11.
Combining Theorem 5.10 with Theorem 5.14, we have the following block decomposition.
Corollary 5.15 There exist the block decompositions
Remark 5.16 Lemma 5.13 gives a group presentation of ![]() $\mathcal {W}$ which parameterizes the block decomposition of
$\mathcal {W}$ which parameterizes the block decomposition of ![]() $\mathscr {C}_{\mathfrak {g}}$. When
$\mathscr {C}_{\mathfrak {g}}$. When ![]() ${\mathfrak {g}}$ is of untwisted type, the block decomposition of
${\mathfrak {g}}$ is of untwisted type, the block decomposition of ![]() $\mathscr {C}_{\mathfrak {g}}$ was given in [Reference Chari and MouraCM05] and [Reference Etingof and MouraEM03]. Considering [Reference Chari and MouraCM05] and [Reference Etingof and MouraEM03] in our setting, their results give another group presentation of
$\mathscr {C}_{\mathfrak {g}}$ was given in [Reference Chari and MouraCM05] and [Reference Etingof and MouraEM03]. Considering [Reference Chari and MouraCM05] and [Reference Etingof and MouraEM03] in our setting, their results give another group presentation of ![]() $\mathcal {W}$. Let us explain more precisely what this means in our setting.
$\mathcal {W}$. Let us explain more precisely what this means in our setting.
Suppose that ![]() ${\mathfrak {g}}$ is of untwisted type. We define
${\mathfrak {g}}$ is of untwisted type. We define
where
 \[ S = \begin{cases} \{1\} & \text{if ${\mathfrak{g}}$ is of type $A_n^{(1)}$, $C_n^{(1)}$ or $E_6^{(1)}$,} \\ \{n\} & \text{if ${\mathfrak{g}}$ is of type $B_n^{(1)}$ or $D_n^{(1)}$ ($n$ odd)}, \\ \{ n-1, n \} & \text{if ${\mathfrak{g}}$ is of type $D_n^{(1)}$ ($n$ even)}, \end{cases} \]
\[ S = \begin{cases} \{1\} & \text{if ${\mathfrak{g}}$ is of type $A_n^{(1)}$, $C_n^{(1)}$ or $E_6^{(1)}$,} \\ \{n\} & \text{if ${\mathfrak{g}}$ is of type $B_n^{(1)}$ or $D_n^{(1)}$ ($n$ odd)}, \\ \{ n-1, n \} & \text{if ${\mathfrak{g}}$ is of type $D_n^{(1)}$ ($n$ even)}, \end{cases} \]
and ![]() $S$ is
$S$ is ![]() $\{2\}$,
$\{2\}$, ![]() $\{4\}$,
$\{4\}$, ![]() $\{7\}$ or
$\{7\}$ or ![]() $\{8\}$ if
$\{8\}$ if ![]() ${\mathfrak {g}}$ is of type
${\mathfrak {g}}$ is of type ![]() $G_2^{(1)}$,
$G_2^{(1)}$, ![]() $F_4^{(1)}$,
$F_4^{(1)}$, ![]() $E_7^{(1)}$ or
$E_7^{(1)}$ or ![]() $E_8^{(1)}$, respectively.
$E_8^{(1)}$, respectively.
One can show that ![]() $p( \mathcal {P}_S ) = \mathcal {W}$. Thus we have the surjective homomorphism
$p( \mathcal {P}_S ) = \mathcal {W}$. Thus we have the surjective homomorphism
Then the results in [Reference Chari and MouraCM05, Proposition 4.1 and Appendix A] and [Reference Etingof and MouraEM03, Lemma 4.6 and § 6] explain that the kernel ![]() $\ker (p_S)$ is generated by the subset
$\ker (p_S)$ is generated by the subset ![]() $G$ described as follows:
$G$ described as follows:
(a) if
 ${\mathfrak {g}}$ is of type
${\mathfrak {g}}$ is of type  $A_n^{(1)}$, then
$A_n^{(1)}$, then  $G = \{ \sum _{k=0}^n \mathsf {e}_{(1, tq^{2k})} \mid t \in \mathbf {k}^\times \}$;
$G = \{ \sum _{k=0}^n \mathsf {e}_{(1, tq^{2k})} \mid t \in \mathbf {k}^\times \}$;(b) if
 ${\mathfrak {g}}$ is of type
${\mathfrak {g}}$ is of type  $B_n^{(1)}$, then
$B_n^{(1)}$, then  $G = \{ \mathsf {e}_{(n,t)} + \mathsf {e}_{(n,tq^{2n-1})} \mid t \in \mathbf {k}^\times \}$;
$G = \{ \mathsf {e}_{(n,t)} + \mathsf {e}_{(n,tq^{2n-1})} \mid t \in \mathbf {k}^\times \}$;(c) if
 ${\mathfrak {g}}$ is of type
${\mathfrak {g}}$ is of type  $C_n^{(1)}$, then
$C_n^{(1)}$, then  $G = \{ \mathsf {e}_{(1,t)} + \mathsf {e}_{(1,tq^{ n+1})} \mid t \in \mathbf {k}^\times \}$;
$G = \{ \mathsf {e}_{(1,t)} + \mathsf {e}_{(1,tq^{ n+1})} \mid t \in \mathbf {k}^\times \}$;(d) if
 ${\mathfrak {g}}$ is of type
${\mathfrak {g}}$ is of type  $D_n^{(1)}$ and
$D_n^{(1)}$ and  $n$ is odd, then
$n$ is odd, then  $G = \{ \mathsf {e}_{n,t} + \mathsf {e}_{n,tq^2} + \mathsf {e}_{n,tq^{2n-2}} + \mathsf {e}_{n,tq^{2n}} \mid t \in \mathbf {k}^\times \}$;
$G = \{ \mathsf {e}_{n,t} + \mathsf {e}_{n,tq^2} + \mathsf {e}_{n,tq^{2n-2}} + \mathsf {e}_{n,tq^{2n}} \mid t \in \mathbf {k}^\times \}$;(e) if
 ${\mathfrak {g}}$ is of type
${\mathfrak {g}}$ is of type  $D_n^{(1)}$ and
$D_n^{(1)}$ and  $n$ is even, then
$n$ is even, then  $G = \{ \mathsf {e}_{(n-1,t)} + \mathsf {e}_{(n-1,tq^2)} + \mathsf {e}_{(n,tq^{2n-2})} + \mathsf {e}_{(n,tq^{2n})}, \mathsf {e}_{(n-1,t)} + \mathsf {e}_{(n-1,tq^{2n-2})}, \mathsf {e}_{(n ,t)} + \mathsf {e}_{(n ,tq^{2n-2})} \mid t \in \mathbf {k}^\times \}$;
$G = \{ \mathsf {e}_{(n-1,t)} + \mathsf {e}_{(n-1,tq^2)} + \mathsf {e}_{(n,tq^{2n-2})} + \mathsf {e}_{(n,tq^{2n})}, \mathsf {e}_{(n-1,t)} + \mathsf {e}_{(n-1,tq^{2n-2})}, \mathsf {e}_{(n ,t)} + \mathsf {e}_{(n ,tq^{2n-2})} \mid t \in \mathbf {k}^\times \}$;(f) if
 ${\mathfrak {g}}$ is of type
${\mathfrak {g}}$ is of type  $E_6^{(1)}$, then
$E_6^{(1)}$, then  $G = \{ \mathsf {e}_{(1,t)} + \mathsf {e}_{(1,tq^{ 8})} + \mathsf {e}_{(1,tq^{ 16})} , \mathsf {e}_{(1,t)} + \mathsf {e}_{(1,tq^{ 2})} + \mathsf {e}_{(1,tq^{ 4})} + \mathsf {e}_{(1,tq^{ 12})} + \mathsf {e}_{(1,tq^{ 14})} + \mathsf {e}_{(1,tq^{ 16})} \mid t \in \mathbf {k}^\times \}$;
$G = \{ \mathsf {e}_{(1,t)} + \mathsf {e}_{(1,tq^{ 8})} + \mathsf {e}_{(1,tq^{ 16})} , \mathsf {e}_{(1,t)} + \mathsf {e}_{(1,tq^{ 2})} + \mathsf {e}_{(1,tq^{ 4})} + \mathsf {e}_{(1,tq^{ 12})} + \mathsf {e}_{(1,tq^{ 14})} + \mathsf {e}_{(1,tq^{ 16})} \mid t \in \mathbf {k}^\times \}$;(g) if
 ${\mathfrak {g}}$ is of type
${\mathfrak {g}}$ is of type  $E_7^{(1)}$, then
$E_7^{(1)}$, then  $G = \{ \mathsf {e}_{(7,t)} + \mathsf {e}_{(7,tq^{ 18})}, \mathsf {e}_{(7,t)} + \mathsf {e}_{(7,tq^{ 2})} + \mathsf {e}_{(7,tq^{ 12})} + \mathsf {e}_{(7,tq^{ 14})} + \mathsf {e}_{(7,tq^{ 24})} + \mathsf {e}_{(7,tq^{ 26})} \mid t \in \mathbf {k}^\times \}$;
$G = \{ \mathsf {e}_{(7,t)} + \mathsf {e}_{(7,tq^{ 18})}, \mathsf {e}_{(7,t)} + \mathsf {e}_{(7,tq^{ 2})} + \mathsf {e}_{(7,tq^{ 12})} + \mathsf {e}_{(7,tq^{ 14})} + \mathsf {e}_{(7,tq^{ 24})} + \mathsf {e}_{(7,tq^{ 26})} \mid t \in \mathbf {k}^\times \}$;(h) if
 ${\mathfrak {g}}$ is of type
${\mathfrak {g}}$ is of type  $E_8^{(1)}$, then
$E_8^{(1)}$, then  $G = \{ \mathsf {e}_{(8,t)} + \mathsf {e}_{(8,tq^{ 30})}, \mathsf {e}_{(8,t)} + \mathsf {e}_{(8,tq^{ 20})} + \mathsf {e}_{(8,tq^{ 40})} ,\ \mathsf {e}_{(8,t)} + \mathsf {e}_{(8,tq^{ 12})} + \mathsf {e}_{(8,tq^{ 24})} + \mathsf {e}_{(8,tq^{ 36})} + \mathsf {e}_{(8,tq^{ 48})} \mid t \in \mathbf {k}^\times \}$;
$G = \{ \mathsf {e}_{(8,t)} + \mathsf {e}_{(8,tq^{ 30})}, \mathsf {e}_{(8,t)} + \mathsf {e}_{(8,tq^{ 20})} + \mathsf {e}_{(8,tq^{ 40})} ,\ \mathsf {e}_{(8,t)} + \mathsf {e}_{(8,tq^{ 12})} + \mathsf {e}_{(8,tq^{ 24})} + \mathsf {e}_{(8,tq^{ 36})} + \mathsf {e}_{(8,tq^{ 48})} \mid t \in \mathbf {k}^\times \}$;(i) if
 ${\mathfrak {g}}$ is of type
${\mathfrak {g}}$ is of type  $F_4^{(1)}$, then
$F_4^{(1)}$, then  $G = \{ \mathsf {e}_{(4,t)} + \mathsf {e}_{(4,tq^{ 9})} , \mathsf {e}_{(4,t)} + \mathsf {e}_{(4,tq^{6})} + \mathsf {e}_{(4,tq^{ 12})} \mid t \in \mathbf {k}^\times \}$;
$G = \{ \mathsf {e}_{(4,t)} + \mathsf {e}_{(4,tq^{ 9})} , \mathsf {e}_{(4,t)} + \mathsf {e}_{(4,tq^{6})} + \mathsf {e}_{(4,tq^{ 12})} \mid t \in \mathbf {k}^\times \}$;(j) if
 ${\mathfrak {g}}$ is of type
${\mathfrak {g}}$ is of type  $G_2^{(1)}$, then
$G_2^{(1)}$, then  $G = \{\mathsf {e}_{(2,t)} + \mathsf {e}_{(2,tq^{ 4})} , \mathsf {e}_{(2,t)} + \mathsf {e}_{(2,{t(-q_t)}^{8})} + \mathsf {e}_{(2,{t(-q_t)}^{ 16}}) \mid t \in \mathbf {k}^\times \}$.
$G = \{\mathsf {e}_{(2,t)} + \mathsf {e}_{(2,tq^{ 4})} , \mathsf {e}_{(2,t)} + \mathsf {e}_{(2,{t(-q_t)}^{8})} + \mathsf {e}_{(2,{t(-q_t)}^{ 16}}) \mid t \in \mathbf {k}^\times \}$.
We remark that there are typos in the descriptions for types ![]() $E_8$ and
$E_8$ and ![]() $F_4$ in [Reference Chari and MouraCM05, Appendix A].
$F_4$ in [Reference Chari and MouraCM05, Appendix A].
6. Proof of Theorem 4.6
6.1 Strategy of the proof
We now start to prove Theorem 4.6. We shall use the same notation as in §§ 2.3 and 2.4. Recall the explicit descriptions for ![]() ${\sigma _0({\mathfrak {g}})}$ and
${\sigma _0({\mathfrak {g}})}$ and ![]() ${\sigma _Q({\mathfrak {g}})}$. Let
${\sigma _Q({\mathfrak {g}})}$. Let ![]() ${\Pi _{Q}}=\{{\alpha _i}\}_{i\in {\mathrm {I_{fin}}}}$ be the set of simple roots of
${\Pi _{Q}}=\{{\alpha _i}\}_{i\in {\mathrm {I_{fin}}}}$ be the set of simple roots of ![]() ${\Delta ^+_{Q}}$, and let
${\Delta ^+_{Q}}$, and let ![]() $\mathsf {Q}_Q$ be the root lattice of
$\mathsf {Q}_Q$ be the root lattice of ![]() ${{\mathfrak {g}}_{\mathrm {fin}}}$. Hence
${{\mathfrak {g}}_{\mathrm {fin}}}$. Hence
Then, by Lemma 5.12, we have
where ![]() $\phi _Q\colon {\Delta ^+_{Q}}\mathop {\xrightarrow {\sim}}{\sigma _Q({\mathfrak {g}})}$ is the bijection given in (2.11).
$\phi _Q\colon {\Delta ^+_{Q}}\mathop {\xrightarrow {\sim}}{\sigma _Q({\mathfrak {g}})}$ is the bijection given in (2.11).
Let ![]() ${ \mathsf {M}_Q } \mathbin {:=} ( { \mathsf {m}^Q_{i,j} } )_{i,j\in {\mathrm {I_{fin}}} }$ be the square matrix given by
${ \mathsf {M}_Q } \mathbin {:=} ( { \mathsf {m}^Q_{i,j} } )_{i,j\in {\mathrm {I_{fin}}} }$ be the square matrix given by
Thanks to Lemma 4.3, we know that
To prove Theorem 4.6, it suffices to show that ![]() ${ \mathsf {M}_Q }$ is the Cartan matrix of the finite simple Lie algebra
${ \mathsf {M}_Q }$ is the Cartan matrix of the finite simple Lie algebra ![]() ${{\mathfrak {g}}_{\mathrm {fin}}}$, i.e.
${{\mathfrak {g}}_{\mathrm {fin}}}$, i.e.
Indeed, (6.2) implies the following lemma, and Theorem 4.6 is its immediate consequence.
Lemma 6.1 Assume ( 6.2). Then the map ![]() ${\Delta ^+_{Q}}\ni \beta \mapsto \mathsf {E} \bigl ( V_Q(\beta )\bigr )\in \Delta _0\subset \mathcal {W} _0$ extends uniquely to an additive isomorphism
${\Delta ^+_{Q}}\ni \beta \mapsto \mathsf {E} \bigl ( V_Q(\beta )\bigr )\in \Delta _0\subset \mathcal {W} _0$ extends uniquely to an additive isomorphism
Moreover, it preserves the inner products of ![]() $\mathsf {Q}_Q$ and
$\mathsf {Q}_Q$ and ![]() $\mathcal {W} _0$.
$\mathcal {W} _0$.
Proof. Since the Cartan matrix is a symmetric positive-definite matrix, ![]() $\{{ \mathsf {s} _{\phi _Q(\alpha _i)}}\}_{i\in {\mathrm {I_{fin}}}}$ is linearly independent. Hence we obtain that
$\{{ \mathsf {s} _{\phi _Q(\alpha _i)}}\}_{i\in {\mathrm {I_{fin}}}}$ is linearly independent. Hence we obtain that
On the other hand, Lemma 5.12 implies that ![]() $\psi _Q\colon \mathsf {Q}_Q\to \mathcal {W} _0$ is surjective. Hence
$\psi _Q\colon \mathsf {Q}_Q\to \mathcal {W} _0$ is surjective. Hence ![]() $\psi _Q$ is an isomorphism. Moreover, (6.2) shows that
$\psi _Q$ is an isomorphism. Moreover, (6.2) shows that ![]() $\psi _Q$ preserves the inner products of
$\psi _Q$ preserves the inner products of ![]() $\mathsf {Q}_Q$ and
$\mathsf {Q}_Q$ and ![]() $\mathcal {W} _0$. The other assertions then easily follow.
$\mathcal {W} _0$. The other assertions then easily follow.
6.2 Calculation of the inner products
In this subsection, we give a type-by-type proof of (6.2).
Lemma 6.2 Suppose that ![]() ${\mathfrak {g}}$ is of affine ADE type. Let
${\mathfrak {g}}$ is of affine ADE type. Let ![]() $i,j \in I_0$.
$i,j \in I_0$.
(i) For
 $t\in \mathbb {\mspace {1mu}Z\mspace {1mu}}$, we have
where
$t\in \mathbb {\mspace {1mu}Z\mspace {1mu}}$, we have
where \[ \operatorname{\mathfrak{d}}( V(\varpi_i), V(\varpi_{j})_{ ({-}q)^t} ) = \delta( 2 \leqslant |t| \leqslant h ) \, \tilde{c}_{i,j}(|t|-1), \]
\[ \operatorname{\mathfrak{d}}( V(\varpi_i), V(\varpi_{j})_{ ({-}q)^t} ) = \delta( 2 \leqslant |t| \leqslant h ) \, \tilde{c}_{i,j}(|t|-1), \] $h$ is the Coxeter number of
$h$ is the Coxeter number of  ${\mathfrak {g}}$ and
${\mathfrak {g}}$ and  $\tilde {c}_{i,j}(k)$ is the integer defined in (A.1) in Appendix A.
$\tilde {c}_{i,j}(k)$ is the integer defined in (A.1) in Appendix A.(ii) If
 $0 < t < 2h$, then we have
and
$0 < t < 2h$, then we have
and \[ \Lambda^\infty(V(\varpi_i), V(\varpi_j)_{({-}q)^{t}} ) = \tilde{c}_{i,j}(t-1)-\tilde{c}_{i,j}(t+1) \]
\[ \Lambda^\infty(V(\varpi_i), V(\varpi_j)_{({-}q)^{t}} ) = \tilde{c}_{i,j}(t-1)-\tilde{c}_{i,j}(t+1) \] $\Lambda ^\infty (V(\varpi _i), V(\varpi _j)) = -2 \delta _{i,j}$.
$\Lambda ^\infty (V(\varpi _i), V(\varpi _j)) = -2 \delta _{i,j}$.
Proof. (i) For ![]() $i,j \in I$, we write
$i,j \in I$, we write ![]() $d_{i,j}(z) \mathbin {:=} d_{V(\varpi _i), V(\varpi _j)} (z)$. Combining Proposition 3.9 with the denominator formula
$d_{i,j}(z) \mathbin {:=} d_{V(\varpi _i), V(\varpi _j)} (z)$. Combining Proposition 3.9 with the denominator formula
 \[ d_{i,j}(z) = \prod_{k=1}^{h-1} (z - ({-}q)^{k+1})^{\tilde{c}_{i,j}(k)} \]
\[ d_{i,j}(z) = \prod_{k=1}^{h-1} (z - ({-}q)^{k+1})^{\tilde{c}_{i,j}(k)} \]given in (A.2), we compute
(ii) For ![]() $a \in \mathbb {\mspace {1mu}Z\mspace {1mu}}$, let
$a \in \mathbb {\mspace {1mu}Z\mspace {1mu}}$, let ![]() $[a]\mathbin {:=}\prod _{n=0}^\infty (1 - (-q)^{a} {\tilde {p}}^n z)$. Combining the equation (A.13) in [Reference Akasaka and KashiwaraAK97] with the denominator formula (A.2), we have
$[a]\mathbin {:=}\prod _{n=0}^\infty (1 - (-q)^{a} {\tilde {p}}^n z)$. Combining the equation (A.13) in [Reference Akasaka and KashiwaraAK97] with the denominator formula (A.2), we have
 \begin{align*} a_{i,j} (({-}q)^t z) &=\prod_{1\leqslant k \leqslant h-1} \frac{([h+k+1+t]^{\tilde{c}_{j,i^*}(k)}) ( [h-k-1+t]^{\tilde{c}_{j,i^*}(k)} )} { ([k+1+t]^{\tilde{c}_{i,j}(k)}) ([2h-k-1+t]^{\tilde{c}_{i,j}(k)}) } \\ &=\prod_{1\leqslant k \leqslant h-1} \frac{([h+k+1+t]^{-\tilde{c}_{i,j}(h+k)}) ( [h-k-1+t]^{-\tilde{c}_{i,j}(h+k)} )} { ([k+1+t]^{\tilde{c}_{i,j}(k)}) ([2h-k-1+t]^{\tilde{c}_{i,j}(k)}) } \\ &=\prod_{1\leqslant k \leqslant 2h-1} \frac{1}{ ([k+1+t]^{\tilde{c}_{i,j}(k)}) ([2h-k-1+t]^{\tilde{c}_{i,j}(k)}) } \end{align*}
\begin{align*} a_{i,j} (({-}q)^t z) &=\prod_{1\leqslant k \leqslant h-1} \frac{([h+k+1+t]^{\tilde{c}_{j,i^*}(k)}) ( [h-k-1+t]^{\tilde{c}_{j,i^*}(k)} )} { ([k+1+t]^{\tilde{c}_{i,j}(k)}) ([2h-k-1+t]^{\tilde{c}_{i,j}(k)}) } \\ &=\prod_{1\leqslant k \leqslant h-1} \frac{([h+k+1+t]^{-\tilde{c}_{i,j}(h+k)}) ( [h-k-1+t]^{-\tilde{c}_{i,j}(h+k)} )} { ([k+1+t]^{\tilde{c}_{i,j}(k)}) ([2h-k-1+t]^{\tilde{c}_{i,j}(k)}) } \\ &=\prod_{1\leqslant k \leqslant 2h-1} \frac{1}{ ([k+1+t]^{\tilde{c}_{i,j}(k)}) ([2h-k-1+t]^{\tilde{c}_{i,j}(k)}) } \end{align*}
for any ![]() $t\in \mathbb {\mspace {1mu}Z\mspace {1mu}}$, up to a constant multiple. For the second equality, we used
$t\in \mathbb {\mspace {1mu}Z\mspace {1mu}}$, up to a constant multiple. For the second equality, we used
which comes from [Reference FujitaFuj22, Lemma 3.7 (4) and (5)]. Hence we have
 \begin{align*} & \Lambda^\infty(V(\varpi_i), V(\varpi_j)_{({-}q)^{t}} ) ={-} \mathrm{Deg}^{\infty} (a_{i,j} (({-}q)^t z) )\\ &\quad =\sum_{1\leqslant k \leqslant 2h-1} \bigl(\, \tilde{c}_{i,j}(k)(\delta(k+1+t\equiv 0 \mspace{3mu}\mathbin{\mathrm{mod}}\mspace{1mu} 2h) + \delta(2h-k-1+t\equiv 0 \mspace{3mu}\mathbin{\mathrm{mod}}\mspace{1mu} 2h) ) \bigr) \\ &\quad = \tilde{c}_{ij}(2h-t-1) +\tilde{c}_{ij}(t-1) \\ &\quad ={-} \tilde{c}_{ij}( t+1) + \tilde{c}_{ij}(t-1) \end{align*}
\begin{align*} & \Lambda^\infty(V(\varpi_i), V(\varpi_j)_{({-}q)^{t}} ) ={-} \mathrm{Deg}^{\infty} (a_{i,j} (({-}q)^t z) )\\ &\quad =\sum_{1\leqslant k \leqslant 2h-1} \bigl(\, \tilde{c}_{i,j}(k)(\delta(k+1+t\equiv 0 \mspace{3mu}\mathbin{\mathrm{mod}}\mspace{1mu} 2h) + \delta(2h-k-1+t\equiv 0 \mspace{3mu}\mathbin{\mathrm{mod}}\mspace{1mu} 2h) ) \bigr) \\ &\quad = \tilde{c}_{ij}(2h-t-1) +\tilde{c}_{ij}(t-1) \\ &\quad ={-} \tilde{c}_{ij}( t+1) + \tilde{c}_{ij}(t-1) \end{align*}
for ![]() $1\leqslant t\leqslant 2h-1$. If
$1\leqslant t\leqslant 2h-1$. If ![]() $t=0$, then we have
$t=0$, then we have
as desired.
Type ![]() $A_n^{(1)}$. If
$A_n^{(1)}$. If ![]() $n=1$, then it is obvious that
$n=1$, then it is obvious that ![]() ${ \mathsf {M}_Q }$ is a Cartan matrix, so we may assume that
${ \mathsf {M}_Q }$ is a Cartan matrix, so we may assume that ![]() $n\geqslant 2$. Recall the explicit description of
$n\geqslant 2$. Recall the explicit description of ![]() ${\sigma _Q({\mathfrak {g}})}$ for type
${\sigma _Q({\mathfrak {g}})}$ for type ![]() $A_n^{(1)}$. Note that the Dynkin quiver corresponding to
$A_n^{(1)}$. Note that the Dynkin quiver corresponding to ![]() ${\sigma _Q({\mathfrak {g}})}$ is given in (A.3). In this case,
${\sigma _Q({\mathfrak {g}})}$ is given in (A.3). In this case, ![]() $h=n+1$ and
$h=n+1$ and
by [Reference Kang, Kashiwara and KimKKK15, Lemma 3.2.3]. For example, if it is of type ![]() $A_4^{(1)}$, then elements
$A_4^{(1)}$, then elements ![]() $(i,(-q)^{k})$ of
$(i,(-q)^{k})$ of ![]() ${\sigma _Q({\mathfrak {g}})}$ with the values of
${\sigma _Q({\mathfrak {g}})}$ with the values of ![]() $\phi _Q^{-1}$ can be drawn as follows.
$\phi _Q^{-1}$ can be drawn as follows.

Here ![]() $(a_1,a_2,a_3,a_4) \mathbin {:=} \sum _{k=1}^4 a_k\alpha _k \in {\Delta ^+_{Q}}$ is placed at the position
$(a_1,a_2,a_3,a_4) \mathbin {:=} \sum _{k=1}^4 a_k\alpha _k \in {\Delta ^+_{Q}}$ is placed at the position ![]() $\phi _Q( a_1, a_2, a_3, a_4 )$, and the underlined ones are simple roots. Using the formula given in Appendix A.1, one can compute that
$\phi _Q( a_1, a_2, a_3, a_4 )$, and the underlined ones are simple roots. Using the formula given in Appendix A.1, one can compute that ![]() $\tilde {c}_{1,1}(2k)=0$ and
$\tilde {c}_{1,1}(2k)=0$ and
Lemma 6.2 implies that
Therefore, for ![]() $i > j$ we have
$i > j$ we have
which tells us that ![]() ${ \mathsf {M}_Q }$ is a Cartan matrix of type
${ \mathsf {M}_Q }$ is a Cartan matrix of type ![]() $A_n$.
$A_n$.
Type ![]() $B_n^{(1)}$. Recall the explicit description of
$B_n^{(1)}$. Recall the explicit description of ![]() ${\sigma _Q({\mathfrak {g}})}$ for type
${\sigma _Q({\mathfrak {g}})}$ for type ![]() $B_n^{(1)}$ (
$B_n^{(1)}$ (![]() $n \geqslant 2$), which can be obtained from [Reference Kashiwara and OhKO19]. Note that the Dynkin diagram of
$n \geqslant 2$), which can be obtained from [Reference Kashiwara and OhKO19]. Note that the Dynkin diagram of ![]() $B_2^{(1)}$ is given in (2.1). In this case
$B_2^{(1)}$ is given in (2.1). In this case ![]() ${{\mathfrak {g}}_{\mathrm {fin}}}$ is of type
${{\mathfrak {g}}_{\mathrm {fin}}}$ is of type ![]() $A_{2n-1}$, and for
$A_{2n-1}$, and for ![]() $i\in {\mathrm {I_{fin}}}=\{{1,\ldots, 2n-1}\}$ we have
$i\in {\mathrm {I_{fin}}}=\{{1,\ldots, 2n-1}\}$ we have
 \[ \phi_Q(\alpha_i) = \begin{cases} (1, ({-}1)^{n+1} q_s^{2n+1-4i}) & \text{if } 1 \leqslant i \leqslant n-1, \\ (n, q^{ {-}2n+2 }) & \text{if } i=n, \\ (n, q^{ {-}2n+3 }) & \text{if } i=n+1, \\ (1, ({-}1)^{n+1} q_s ^{{-}6n+4i-1}) & \text{if } n+2 \leqslant i \leqslant 2n-1. \end{cases} \]
\[ \phi_Q(\alpha_i) = \begin{cases} (1, ({-}1)^{n+1} q_s^{2n+1-4i}) & \text{if } 1 \leqslant i \leqslant n-1, \\ (n, q^{ {-}2n+2 }) & \text{if } i=n, \\ (n, q^{ {-}2n+3 }) & \text{if } i=n+1, \\ (1, ({-}1)^{n+1} q_s ^{{-}6n+4i-1}) & \text{if } n+2 \leqslant i \leqslant 2n-1. \end{cases} \]
For example, if it is of type ![]() $B_3^{(1)}$, then elements of
$B_3^{(1)}$, then elements of ![]() ${\sigma _Q({\mathfrak {g}})}$ with the values of
${\sigma _Q({\mathfrak {g}})}$ with the values of ![]() $\phi _Q^{-1}$ can be drawn as follows.
$\phi _Q^{-1}$ can be drawn as follows.

Here we set ![]() $(a_1,a_2,a_3,a_4,a_5) \mathbin {:=} \sum _{k=1}^5 a_k\alpha _k \in {\Delta ^+_{Q}}$, and the underlined ones are simple roots. Combining Propositions 3.11 and 3.9 with the denominator formula given in Appendix A, we compute that
$(a_1,a_2,a_3,a_4,a_5) \mathbin {:=} \sum _{k=1}^5 a_k\alpha _k \in {\Delta ^+_{Q}}$, and the underlined ones are simple roots. Combining Propositions 3.11 and 3.9 with the denominator formula given in Appendix A, we compute that ![]() $\operatorname {\mathfrak {d}} (V_Q(\alpha _i), \mathscr {D}^k V_Q(\alpha _j) ) = 0$ for
$\operatorname {\mathfrak {d}} (V_Q(\alpha _i), \mathscr {D}^k V_Q(\alpha _j) ) = 0$ for ![]() $i\ne j$ and
$i\ne j$ and ![]() $k \ne 0$ and that
$k \ne 0$ and that
 \begin{align*} \Lambda^\infty(V(\varpi_1), V(\varpi_1)_{q^k}) &= \operatorname{\mathfrak{d}} ( V(\varpi_1), V(\varpi_1)_{q^k} ) \\ & = \delta_{k,2} \quad \text{for } k=1, 2, \ldots, 2n-4,\\ \Lambda^\infty(V(\varpi_n), V(\varpi_1)_{({-}1)^{n+1}q_s^t}) &= \operatorname{\mathfrak{d}} ( V(\varpi_n), V(\varpi_1)_{({-}1)^{n+1}q_s^t} ) \\ & = \delta_{t, 2n+1} \quad \text{for } t=2n-1, 2n+1 , \ldots, 6n-7,\\ \Lambda^\infty(V(\varpi_n), V(\varpi_n)_{q}) &= 1. \end{align*}
\begin{align*} \Lambda^\infty(V(\varpi_1), V(\varpi_1)_{q^k}) &= \operatorname{\mathfrak{d}} ( V(\varpi_1), V(\varpi_1)_{q^k} ) \\ & = \delta_{k,2} \quad \text{for } k=1, 2, \ldots, 2n-4,\\ \Lambda^\infty(V(\varpi_n), V(\varpi_1)_{({-}1)^{n+1}q_s^t}) &= \operatorname{\mathfrak{d}} ( V(\varpi_n), V(\varpi_1)_{({-}1)^{n+1}q_s^t} ) \\ & = \delta_{t, 2n+1} \quad \text{for } t=2n-1, 2n+1 , \ldots, 6n-7,\\ \Lambda^\infty(V(\varpi_n), V(\varpi_n)_{q}) &= 1. \end{align*} Therefore, for ![]() $i > j$ we obtain
$i > j$ we obtain
which tells us that ![]() ${ \mathsf {M}_Q }$ is a Cartan matrix of type
${ \mathsf {M}_Q }$ is a Cartan matrix of type ![]() $A_{2n-1}$.
$A_{2n-1}$.
Type ![]() $C_n^{(1)}$. Recall the explicit description of
$C_n^{(1)}$. Recall the explicit description of ![]() ${\sigma _Q({\mathfrak {g}})}$ for type
${\sigma _Q({\mathfrak {g}})}$ for type ![]() $C_n^{(1)}$ (
$C_n^{(1)}$ (![]() $n \geqslant 3$), which can be obtained from [Reference Kashiwara and OhKO19]. In this case
$n \geqslant 3$), which can be obtained from [Reference Kashiwara and OhKO19]. In this case ![]() ${{\mathfrak {g}}_{\mathrm {fin}}}$ is of type
${{\mathfrak {g}}_{\mathrm {fin}}}$ is of type ![]() $D_{n+1}$, and for
$D_{n+1}$, and for ![]() $1 \leqslant i \leqslant n+1$ we have
$1 \leqslant i \leqslant n+1$ we have
 \[ \phi_Q (\alpha_i) = \begin{cases} (1, ({-}q_s)^{2-2i}) & \text{if } 1 \leqslant i \leqslant n, \\ (n, ({-}q_s)^{{-}3n+1}) & \text{if } i=n+1. \end{cases} \]
\[ \phi_Q (\alpha_i) = \begin{cases} (1, ({-}q_s)^{2-2i}) & \text{if } 1 \leqslant i \leqslant n, \\ (n, ({-}q_s)^{{-}3n+1}) & \text{if } i=n+1. \end{cases} \]
For example, if it is of type ![]() $C_4^{(1)}$, then elements of
$C_4^{(1)}$, then elements of ![]() ${\sigma _Q({\mathfrak {g}})}$ with the values of
${\sigma _Q({\mathfrak {g}})}$ with the values of ![]() $\phi _Q^{-1}$ can be drawn as follows.
$\phi _Q^{-1}$ can be drawn as follows.

Here we set ![]() ${\bigl (\begin {smallmatrix}{a_5}\\[3pt]{a_1a_2a_3a_4}\end {smallmatrix}\bigr )} \mathbin {:=} \sum _{k=1}^5 a_k\alpha _k \in {\Delta ^+_{Q}}$, and the underlined ones are simple roots. Combining Propositions 3.11 and 3.9 with the denominator formula given in Appendix A, we compute that
${\bigl (\begin {smallmatrix}{a_5}\\[3pt]{a_1a_2a_3a_4}\end {smallmatrix}\bigr )} \mathbin {:=} \sum _{k=1}^5 a_k\alpha _k \in {\Delta ^+_{Q}}$, and the underlined ones are simple roots. Combining Propositions 3.11 and 3.9 with the denominator formula given in Appendix A, we compute that ![]() $\operatorname {\mathfrak {d}} (V_Q(\alpha _i), \mathscr {D}^k V_Q(\alpha _j) ) = 0$ for
$\operatorname {\mathfrak {d}} (V_Q(\alpha _i), \mathscr {D}^k V_Q(\alpha _j) ) = 0$ for ![]() $i\ne j$ and
$i\ne j$ and ![]() $k \ne 0$ and that
$k \ne 0$ and that
 \begin{align*} \Lambda^\infty(V(\varpi_1), V(\varpi_1)_{({-}q_s)^k}) & = \operatorname{\mathfrak{d}} ( V(\varpi_1), V(\varpi_1)_{({-}q_s)^k} ) \\ & = \delta_{k,2} \quad \text{for } k=2, 4, \ldots, 2n-2,\\ \Lambda^\infty(V(\varpi_n), V(\varpi_1)_{({-}q_s)^t}) & = \operatorname{\mathfrak{d}} ( V(\varpi_n), V(\varpi_1)_{({-}q_s)^t} ) \\ & = \delta_{t, n+3} \quad \text{for } t=n+1, n+3, \ldots, 3n-1. \end{align*}
\begin{align*} \Lambda^\infty(V(\varpi_1), V(\varpi_1)_{({-}q_s)^k}) & = \operatorname{\mathfrak{d}} ( V(\varpi_1), V(\varpi_1)_{({-}q_s)^k} ) \\ & = \delta_{k,2} \quad \text{for } k=2, 4, \ldots, 2n-2,\\ \Lambda^\infty(V(\varpi_n), V(\varpi_1)_{({-}q_s)^t}) & = \operatorname{\mathfrak{d}} ( V(\varpi_n), V(\varpi_1)_{({-}q_s)^t} ) \\ & = \delta_{t, n+3} \quad \text{for } t=n+1, n+3, \ldots, 3n-1. \end{align*}
Therefore, for ![]() $i > j$ we have
$i > j$ we have
 \[ { \mathsf{m}^Q_{i,j} } = \begin{cases} -1 & \text{if ($i \leqslant n$ and $i-j=1$) or $(i,j)= (n+1,n-1) $}, \\ 0 & \text{otherwise,} \end{cases} \]
\[ { \mathsf{m}^Q_{i,j} } = \begin{cases} -1 & \text{if ($i \leqslant n$ and $i-j=1$) or $(i,j)= (n+1,n-1) $}, \\ 0 & \text{otherwise,} \end{cases} \]
which says that ![]() ${ \mathsf {M}_Q }$ is a Cartan matrix of type
${ \mathsf {M}_Q }$ is a Cartan matrix of type ![]() $D_{ n+1}$.
$D_{ n+1}$.
Type ![]() $D_n^{(1)}$. Recall the explicit description of
$D_n^{(1)}$. Recall the explicit description of ![]() ${\sigma _Q({\mathfrak {g}})}$ for type
${\sigma _Q({\mathfrak {g}})}$ for type ![]() $D_n^{(1)}$ (
$D_n^{(1)}$ (![]() $n \geqslant 4$). Note that the Dynkin quiver corresponding to
$n \geqslant 4$). Note that the Dynkin quiver corresponding to ![]() ${\sigma ({\mathfrak {g}})}_Q$ is given in (A.3). In this case
${\sigma ({\mathfrak {g}})}_Q$ is given in (A.3). In this case ![]() $h=2n-2$, and for
$h=2n-2$, and for ![]() $1 \leqslant i \leqslant n$ we have
$1 \leqslant i \leqslant n$ we have
 \[ \phi_Q(\alpha_i) = \begin{cases} (1, ({-}q)^{{-}2(i-1)}) & \text{if } i \leqslant n-2, \\ (n-1, ({-}q)^{ {-}3n+6 }) & \text{if ($i = n-1$ and $n$ is even) or ($i = n$ and $n$ is odd)}, \\ (n, ({-}q)^{ {-}3n+6 }) & \text{if ($i = n $ and $n$ is even) or ($i = n-1$ and $n$ is odd)} \end{cases} \]
\[ \phi_Q(\alpha_i) = \begin{cases} (1, ({-}q)^{{-}2(i-1)}) & \text{if } i \leqslant n-2, \\ (n-1, ({-}q)^{ {-}3n+6 }) & \text{if ($i = n-1$ and $n$ is even) or ($i = n$ and $n$ is odd)}, \\ (n, ({-}q)^{ {-}3n+6 }) & \text{if ($i = n $ and $n$ is even) or ($i = n-1$ and $n$ is odd)} \end{cases} \]
by [Reference Kang, Kashiwara and KimKKK15, Lemma 3.2.3]. For example, if it is of type ![]() $D_5^{(1)}$, then elements
$D_5^{(1)}$, then elements ![]() $(i, (-q)^k)$ of
$(i, (-q)^k)$ of ![]() ${\sigma _Q({\mathfrak {g}})}$ with the values of
${\sigma _Q({\mathfrak {g}})}$ with the values of ![]() $\phi _Q^{-1}$ can be drawn as follows.
$\phi _Q^{-1}$ can be drawn as follows.

Here we set ![]() ${\bigl (\begin {smallmatrix}{a_5}\\[3pt]{a_1a_2a_3a_4}\end {smallmatrix}\bigr )} \mathbin {:=} \sum _{k=1}^5 a_k\alpha _k \in {\Delta ^+_{Q}}$, and the underlined ones are simple roots. Using the formula given in Appendix A.1, one can compute that for
${\bigl (\begin {smallmatrix}{a_5}\\[3pt]{a_1a_2a_3a_4}\end {smallmatrix}\bigr )} \mathbin {:=} \sum _{k=1}^5 a_k\alpha _k \in {\Delta ^+_{Q}}$, and the underlined ones are simple roots. Using the formula given in Appendix A.1, one can compute that for ![]() $1 \leqslant k < h$,
$1 \leqslant k < h$,
 \begin{align*} & \tilde{c}_{1,1}(k) = \delta_{k,1} + \delta_{k,2n-3}, \quad \tilde{c}_{n,1}(k)=\tilde{c}_{n-1,1}(k) = \delta_{k,n-1} , \\ & \tilde{c}_{n,n}(k) = \tilde{c}_{n-1,n-1}(k) = \delta( k\equiv 1 \mspace{3mu}\mathbin{\mathrm{mod}}\mspace{1mu} 4 ), \\ & \tilde{c}_{n,n-1}(k) = \tilde{c}_{n-1,n}(k) = \delta( k\equiv 3 \mspace{3mu}\mathbin{\mathrm{mod}}\mspace{1mu} 4 ). \end{align*}
\begin{align*} & \tilde{c}_{1,1}(k) = \delta_{k,1} + \delta_{k,2n-3}, \quad \tilde{c}_{n,1}(k)=\tilde{c}_{n-1,1}(k) = \delta_{k,n-1} , \\ & \tilde{c}_{n,n}(k) = \tilde{c}_{n-1,n-1}(k) = \delta( k\equiv 1 \mspace{3mu}\mathbin{\mathrm{mod}}\mspace{1mu} 4 ), \\ & \tilde{c}_{n,n-1}(k) = \tilde{c}_{n-1,n}(k) = \delta( k\equiv 3 \mspace{3mu}\mathbin{\mathrm{mod}}\mspace{1mu} 4 ). \end{align*}Combining this with Lemma 6.2, we compute that
 \begin{align*} \Lambda^\infty(V(\varpi_1), V(\varpi_1)_{({-}q)^{k}} ) & = \delta_{k,2} \quad \text{for $ 2 \leqslant k \leqslant h-4 $}, \\ \Lambda^\infty(V(\varpi_n), V(\varpi_1)_{({-}q)^{k}} ) & = \delta_{k,n} \quad \text{for $ n \leqslant k \leqslant 3n-6 $}, \\ \Lambda^\infty(V(\varpi_n), V(\varpi_{n-1})) & = 0. \end{align*}
\begin{align*} \Lambda^\infty(V(\varpi_1), V(\varpi_1)_{({-}q)^{k}} ) & = \delta_{k,2} \quad \text{for $ 2 \leqslant k \leqslant h-4 $}, \\ \Lambda^\infty(V(\varpi_n), V(\varpi_1)_{({-}q)^{k}} ) & = \delta_{k,n} \quad \text{for $ n \leqslant k \leqslant 3n-6 $}, \\ \Lambda^\infty(V(\varpi_n), V(\varpi_{n-1})) & = 0. \end{align*}
Therefore, for ![]() $i > j$ we have
$i > j$ we have
 \[ { \mathsf{m}^Q_{i,j} } = \begin{cases} -1 & \text{if ($i \leqslant n-1$ and $i-j=1$) or $(i,j)= (n,n-2) $}, \\ 0 & \text{otherwise,} \end{cases} \]
\[ { \mathsf{m}^Q_{i,j} } = \begin{cases} -1 & \text{if ($i \leqslant n-1$ and $i-j=1$) or $(i,j)= (n,n-2) $}, \\ 0 & \text{otherwise,} \end{cases} \]
which says that ![]() ${ \mathsf {M}_Q }$ is a Cartan matrix of type
${ \mathsf {M}_Q }$ is a Cartan matrix of type ![]() $D_n$.
$D_n$.
Type ![]() $A_{2n}^{(2)}$. Recall the explicit description of
$A_{2n}^{(2)}$. Recall the explicit description of ![]() ${\sigma _Q({\mathfrak {g}})}$ for type
${\sigma _Q({\mathfrak {g}})}$ for type ![]() $A_{2n}^{(2)}$ (
$A_{2n}^{(2)}$ (![]() $n \geqslant 1$), which can be obtained from [Reference Kang, Kashiwara, Kim and OhKKKO16]. In this case
$n \geqslant 1$), which can be obtained from [Reference Kang, Kashiwara, Kim and OhKKKO16]. In this case ![]() ${{\mathfrak {g}}_{\mathrm {fin}}}$ is of type
${{\mathfrak {g}}_{\mathrm {fin}}}$ is of type ![]() $A_{2n}$, and for
$A_{2n}$, and for ![]() $1 \leqslant i \leqslant 2n$ we have
$1 \leqslant i \leqslant 2n$ we have
For example, if it is of type ![]() $A_4^{(2)}$, then elements of
$A_4^{(2)}$, then elements of ![]() ${\sigma _Q({\mathfrak {g}})}$ with the values of
${\sigma _Q({\mathfrak {g}})}$ with the values of ![]() $\phi _Q^{-1}$ can be drawn as follows.
$\phi _Q^{-1}$ can be drawn as follows.

Here ![]() $(a_1,a_2,a_3,a_4) \mathbin {:=} \sum _{k=1}^4 a_k\alpha _k \in {\Delta ^+_{Q}}$, and the underlined ones are simple roots. It follows from Propositions 3.11 and 3.9 and the denominator formula in Appendix A that
$(a_1,a_2,a_3,a_4) \mathbin {:=} \sum _{k=1}^4 a_k\alpha _k \in {\Delta ^+_{Q}}$, and the underlined ones are simple roots. It follows from Propositions 3.11 and 3.9 and the denominator formula in Appendix A that ![]() $\operatorname {\mathfrak {d}} (V_Q(\alpha _i), \mathscr {D}^k V_Q(\alpha _j) ) = 0$ for
$\operatorname {\mathfrak {d}} (V_Q(\alpha _i), \mathscr {D}^k V_Q(\alpha _j) ) = 0$ for ![]() $i\ne j$ and
$i\ne j$ and ![]() $k \ne 0$ and that
$k \ne 0$ and that
 \begin{align*} \Lambda^\infty(V(\varpi_1), V(\varpi_1)_{({-}q)^k}) & = \operatorname{\mathfrak{d}} ( V(\varpi_1), V(\varpi_1)_{({-}q )^k} ) \\ & = \delta_{k,2} \quad \text{for } k=2, 4, \ldots, 4n-2. \end{align*}
\begin{align*} \Lambda^\infty(V(\varpi_1), V(\varpi_1)_{({-}q)^k}) & = \operatorname{\mathfrak{d}} ( V(\varpi_1), V(\varpi_1)_{({-}q )^k} ) \\ & = \delta_{k,2} \quad \text{for } k=2, 4, \ldots, 4n-2. \end{align*}
Therefore, for ![]() $i > j$ we have
$i > j$ we have
which tells us that ![]() ${ \mathsf {M}_Q }$ is a Cartan matrix of type
${ \mathsf {M}_Q }$ is a Cartan matrix of type ![]() $A_{2n}$.
$A_{2n}$.
Type ![]() $A_{2n-1}^{(2)}$. Recall the explicit description of
$A_{2n-1}^{(2)}$. Recall the explicit description of ![]() ${\sigma _Q({\mathfrak {g}})}$ for type
${\sigma _Q({\mathfrak {g}})}$ for type ![]() $A_{2n-1}^{(2)}$ (
$A_{2n-1}^{(2)}$ (![]() $n \geqslant 2$), which can be obtained from [Reference Kang, Kashiwara, Kim and OhKKKO16]. In this case
$n \geqslant 2$), which can be obtained from [Reference Kang, Kashiwara, Kim and OhKKKO16]. In this case ![]() ${{\mathfrak {g}}_{\mathrm {fin}}}$ is of type
${{\mathfrak {g}}_{\mathrm {fin}}}$ is of type ![]() $A_{2n-1}$, and for
$A_{2n-1}$, and for ![]() $1 \leqslant i \leqslant 2n-1$ we have
$1 \leqslant i \leqslant 2n-1$ we have
For example, if it is of type ![]() $A_5^{(2)}$, then elements of
$A_5^{(2)}$, then elements of ![]() ${\sigma _Q({\mathfrak {g}})}$ with the values of
${\sigma _Q({\mathfrak {g}})}$ with the values of ![]() $\phi _Q ^{-1}$ can be drawn as follows.
$\phi _Q ^{-1}$ can be drawn as follows.

Here ![]() $(a_1,a_2,a_3,a_4,a_5) \mathbin {:=} \sum _{k=1}^5 a_k\alpha _k \in {\Delta ^+_{Q}}$, and the underlined ones are simple roots. Note that
$(a_1,a_2,a_3,a_4,a_5) \mathbin {:=} \sum _{k=1}^5 a_k\alpha _k \in {\Delta ^+_{Q}}$, and the underlined ones are simple roots. Note that ![]() $V(\varpi _n)_{a} \simeq V(\varpi _n)_{-a}$. It follows from Propositions 3.11 and 3.9 and the denominator formula in Appendix A that
$V(\varpi _n)_{a} \simeq V(\varpi _n)_{-a}$. It follows from Propositions 3.11 and 3.9 and the denominator formula in Appendix A that ![]() $\operatorname {\mathfrak {d}} (V_Q(\alpha _i), \mathscr {D}^k V_Q(\alpha _j) ) = 0$ for
$\operatorname {\mathfrak {d}} (V_Q(\alpha _i), \mathscr {D}^k V_Q(\alpha _j) ) = 0$ for ![]() $i\ne j$ and
$i\ne j$ and ![]() $k \ne 0$ and that
$k \ne 0$ and that
 \begin{align*} \Lambda^\infty(V(\varpi_1), V(\varpi_1)_{({-}q)^k}) & = \operatorname{\mathfrak{d}} ( V(\varpi_1), V(\varpi_1)_{({-}q )^k} ) \\ & = \delta_{k,2} \quad \text{for } k=2, 4, \ldots, 4n-4. \end{align*}
\begin{align*} \Lambda^\infty(V(\varpi_1), V(\varpi_1)_{({-}q)^k}) & = \operatorname{\mathfrak{d}} ( V(\varpi_1), V(\varpi_1)_{({-}q )^k} ) \\ & = \delta_{k,2} \quad \text{for } k=2, 4, \ldots, 4n-4. \end{align*}Thus we obtain
which implies that ![]() ${ \mathsf {M}_Q }$ is a Cartan matrix of type
${ \mathsf {M}_Q }$ is a Cartan matrix of type ![]() $A_{2n-1}$.
$A_{2n-1}$.
Type ![]() $D_{n+1}^{(2)}$. Recall the explicit description of
$D_{n+1}^{(2)}$. Recall the explicit description of ![]() ${\sigma _Q({\mathfrak {g}})}$ for type
${\sigma _Q({\mathfrak {g}})}$ for type ![]() $D_{n+1}^{(2)}$ (
$D_{n+1}^{(2)}$ (![]() $n \geqslant 3$), which can be obtained from [Reference Kang, Kashiwara, Kim and OhKKKO16]. In this case
$n \geqslant 3$), which can be obtained from [Reference Kang, Kashiwara, Kim and OhKKKO16]. In this case ![]() ${{\mathfrak {g}}_{\mathrm {fin}}}$ is of type
${{\mathfrak {g}}_{\mathrm {fin}}}$ is of type ![]() $D_{ n+1}$, and for
$D_{ n+1}$, and for ![]() $1 \leqslant i \leqslant n+1$ we have
$1 \leqslant i \leqslant n+1$ we have
 \[ \phi_Q (\alpha_i) = \begin{cases} (1, (\sqrt{-1})^{n} ({-}q)^{{-}2(i-1)}) & \text{if } i \leqslant n-1, \\ ( n, ({-}1)^i ({-}q)^{ {-}3n+3 }) & \text{if } i=n, n+1. \end{cases} \]
\[ \phi_Q (\alpha_i) = \begin{cases} (1, (\sqrt{-1})^{n} ({-}q)^{{-}2(i-1)}) & \text{if } i \leqslant n-1, \\ ( n, ({-}1)^i ({-}q)^{ {-}3n+3 }) & \text{if } i=n, n+1. \end{cases} \]
For example, if it is of type ![]() $D_5^{(2)}$, then elements of
$D_5^{(2)}$, then elements of ![]() ${\sigma _Q({\mathfrak {g}})}$ with the values of
${\sigma _Q({\mathfrak {g}})}$ with the values of ![]() $\phi _Q^{-1}$ can be drawn as follows.
$\phi _Q^{-1}$ can be drawn as follows.

Here we set ![]() ${\bigl (\begin {smallmatrix}{a_5}\\[3pt]{a_1a_2a_3a_4}\end {smallmatrix}\bigr )} \mathbin {:=} \sum _{k=1}^5 a_k\alpha _k \in {\Delta ^+_{Q}}$, and the underlined ones are simple roots. Note that
${\bigl (\begin {smallmatrix}{a_5}\\[3pt]{a_1a_2a_3a_4}\end {smallmatrix}\bigr )} \mathbin {:=} \sum _{k=1}^5 a_k\alpha _k \in {\Delta ^+_{Q}}$, and the underlined ones are simple roots. Note that ![]() $V(\varpi _i)_{a} \simeq V(\varpi _i)_{-a}$ for
$V(\varpi _i)_{a} \simeq V(\varpi _i)_{-a}$ for ![]() $i < n$. It follows from Propositions 3.11 and 3.9 and the denominator formula in Appendix A that
$i < n$. It follows from Propositions 3.11 and 3.9 and the denominator formula in Appendix A that ![]() $\operatorname {\mathfrak {d}} (V_Q(\alpha _i), \mathscr {D}^k V_Q(\alpha _j) ) = 0$ for
$\operatorname {\mathfrak {d}} (V_Q(\alpha _i), \mathscr {D}^k V_Q(\alpha _j) ) = 0$ for ![]() $i\ne j$ and
$i\ne j$ and ![]() $k \ne 0$ and that
$k \ne 0$ and that
 \begin{align*} \Lambda^\infty(V(\varpi_1), V(\varpi_1)_{({-}q)^k}) & = \operatorname{\mathfrak{d}} ( V(\varpi_1), V(\varpi_1)_{({-}q)^k} ) \\ & = \delta_{k,2} \quad \text{for } k=2, 4, \ldots, 2n-4, \\ \Lambda^\infty(V(\varpi_n), V(\varpi_1)_{{\pm} \sqrt{-1}^{n } ({-}q)^{k}}) & = \operatorname{\mathfrak{d}} ( V(\varpi_{n }), V(\varpi_1)_{{\pm} \sqrt{-1}^{n } ({-}q)^{k}} ) \\ & = \delta_{k,n+1} \quad \text{for } k=n+1, n+3, \ldots, 3n-3,\\ \Lambda^\infty(V(\varpi_n), V(\varpi_n)_{{-}1}) & = 0, \end{align*}
\begin{align*} \Lambda^\infty(V(\varpi_1), V(\varpi_1)_{({-}q)^k}) & = \operatorname{\mathfrak{d}} ( V(\varpi_1), V(\varpi_1)_{({-}q)^k} ) \\ & = \delta_{k,2} \quad \text{for } k=2, 4, \ldots, 2n-4, \\ \Lambda^\infty(V(\varpi_n), V(\varpi_1)_{{\pm} \sqrt{-1}^{n } ({-}q)^{k}}) & = \operatorname{\mathfrak{d}} ( V(\varpi_{n }), V(\varpi_1)_{{\pm} \sqrt{-1}^{n } ({-}q)^{k}} ) \\ & = \delta_{k,n+1} \quad \text{for } k=n+1, n+3, \ldots, 3n-3,\\ \Lambda^\infty(V(\varpi_n), V(\varpi_n)_{{-}1}) & = 0, \end{align*}
which give the values of ![]() ${ \mathsf {m}^Q_{i,j} }$. Thus, one can check that the matrix
${ \mathsf {m}^Q_{i,j} }$. Thus, one can check that the matrix ![]() ${ \mathsf {M}_Q }$ is a Cartan matrix of type
${ \mathsf {M}_Q }$ is a Cartan matrix of type ![]() $D_{n+1}$.
$D_{n+1}$.
Type ![]() $E_6^{(1)}$. Recall the explicit description of
$E_6^{(1)}$. Recall the explicit description of ![]() ${\sigma _Q({\mathfrak {g}})}$ for type
${\sigma _Q({\mathfrak {g}})}$ for type ![]() $E_6^{(1)}$. The Dynkin quiver corresponding to
$E_6^{(1)}$. The Dynkin quiver corresponding to ![]() ${\sigma ({\mathfrak {g}})}_Q$ is given in (A.3). In this case,
${\sigma ({\mathfrak {g}})}_Q$ is given in (A.3). In this case, ![]() $h=12$ and elements
$h=12$ and elements ![]() $(i, (-q)^k)$ of
$(i, (-q)^k)$ of ![]() ${\sigma _Q({\mathfrak {g}})}$ with the values of
${\sigma _Q({\mathfrak {g}})}$ with the values of ![]() $\phi _Q^{-1}$ can be drawn as follows.
$\phi _Q^{-1}$ can be drawn as follows.

Here we set ![]() ${\bigl (\begin {smallmatrix}{a_1a_2a_3}\\[3pt]{a_4a_5a_6}\end {smallmatrix}\bigr )} \mathbin {:=} \sum _{i=1}^6 a_i \alpha _i \in {\Delta ^+_{Q}}$, and the underlined ones are simple roots. Using the formula given in Appendix A.1, one can compute that for
${\bigl (\begin {smallmatrix}{a_1a_2a_3}\\[3pt]{a_4a_5a_6}\end {smallmatrix}\bigr )} \mathbin {:=} \sum _{i=1}^6 a_i \alpha _i \in {\Delta ^+_{Q}}$, and the underlined ones are simple roots. Using the formula given in Appendix A.1, one can compute that for ![]() $1 \leqslant k < h$,
$1 \leqslant k < h$,
By Lemma 6.2, we compute
 \begin{align*} \Lambda^\infty(V(\varpi_1), V(\varpi_1)_{({-}q)^{k}} ) & = \delta_{k,2} + \delta_{k,8} \quad \text{for $ k=2,4,8,10,12,14 $}, \\ \Lambda^\infty(V(\varpi_1), V(\varpi_2)_{({-}q)^{k}} ) & = \delta_{k,9} \quad \text{for $ k={-}1, 1,9,11,13$}, \end{align*}
\begin{align*} \Lambda^\infty(V(\varpi_1), V(\varpi_1)_{({-}q)^{k}} ) & = \delta_{k,2} + \delta_{k,8} \quad \text{for $ k=2,4,8,10,12,14 $}, \\ \Lambda^\infty(V(\varpi_1), V(\varpi_2)_{({-}q)^{k}} ) & = \delta_{k,9} \quad \text{for $ k={-}1, 1,9,11,13$}, \end{align*}
which give the values of ![]() ${ \mathsf {m}^Q_{i,j} }$. Therefore, one can check that the matrix
${ \mathsf {m}^Q_{i,j} }$. Therefore, one can check that the matrix ![]() ${ \mathsf {M}_Q }$ is a Cartan matrix of type
${ \mathsf {M}_Q }$ is a Cartan matrix of type ![]() $E_6$.
$E_6$.
Type ![]() $E_7^{(1)}$. Recall the explicit description of
$E_7^{(1)}$. Recall the explicit description of ![]() ${\sigma _Q({\mathfrak {g}})}$ for type
${\sigma _Q({\mathfrak {g}})}$ for type ![]() $E_7^{(1)}$. The Dynkin quiver corresponding to
$E_7^{(1)}$. The Dynkin quiver corresponding to ![]() ${\sigma ({\mathfrak {g}})}_Q$ is given in (A.3). In this case,
${\sigma ({\mathfrak {g}})}_Q$ is given in (A.3). In this case, ![]() $h=18$ and elements
$h=18$ and elements ![]() $(i, (-q)^k)$ of
$(i, (-q)^k)$ of ![]() ${\sigma _Q({\mathfrak {g}})}$ with the values of
${\sigma _Q({\mathfrak {g}})}$ with the values of ![]() $\phi _Q^{-1}$ can be drawn as follows.
$\phi _Q^{-1}$ can be drawn as follows.

Here we set ![]() ${\bigl (\begin {smallmatrix}{a_1a_2a_3a_4}\\[3pt]{a_5a_6a_7}\end {smallmatrix}\bigr )} \mathbin {:=} \sum _{i=1}^7 a_i \alpha _i \in {\Delta ^+_{Q}}$, and the underlined ones are simple roots. Using the formula given in Appendix A.1, one can compute that for
${\bigl (\begin {smallmatrix}{a_1a_2a_3a_4}\\[3pt]{a_5a_6a_7}\end {smallmatrix}\bigr )} \mathbin {:=} \sum _{i=1}^7 a_i \alpha _i \in {\Delta ^+_{Q}}$, and the underlined ones are simple roots. Using the formula given in Appendix A.1, one can compute that for ![]() $1 \leqslant k < h$,
$1 \leqslant k < h$,
By Lemma 6.2, we compute
 \begin{align*} \Lambda^\infty(V(\varpi_1), V(\varpi_1)_{({-}q)^{2}} ) & = 1, \quad \Lambda^\infty(V(\varpi_1), V(\varpi_2)_{({-}q)} ) = \Lambda^\infty(V(\varpi_2), V(\varpi_1)_{({-}q)} )= 0, \\ \Lambda^\infty(V(\varpi_7), V(\varpi_1)_{({-}q)^{k}} ) & = \delta_{k,13} \quad \text{for $ k=13,15,17,19,21$}, \\ \Lambda^\infty(V(\varpi_7), V(\varpi_{2})_{{({-}q)}^k}) & = \delta_{k,14} \quad \text{for $ k=14,16,18,20$}, \\ \Lambda^\infty(V(\varpi_7), V(\varpi_{7})_{{({-}q)}^k} ) & = \delta_{k,2} \quad \text{for $ k=2,4,6$}, \end{align*}
\begin{align*} \Lambda^\infty(V(\varpi_1), V(\varpi_1)_{({-}q)^{2}} ) & = 1, \quad \Lambda^\infty(V(\varpi_1), V(\varpi_2)_{({-}q)} ) = \Lambda^\infty(V(\varpi_2), V(\varpi_1)_{({-}q)} )= 0, \\ \Lambda^\infty(V(\varpi_7), V(\varpi_1)_{({-}q)^{k}} ) & = \delta_{k,13} \quad \text{for $ k=13,15,17,19,21$}, \\ \Lambda^\infty(V(\varpi_7), V(\varpi_{2})_{{({-}q)}^k}) & = \delta_{k,14} \quad \text{for $ k=14,16,18,20$}, \\ \Lambda^\infty(V(\varpi_7), V(\varpi_{7})_{{({-}q)}^k} ) & = \delta_{k,2} \quad \text{for $ k=2,4,6$}, \end{align*}
which give the values of ![]() ${ \mathsf {m}^Q_{i,j} }$. Therefore, one can check that the matrix
${ \mathsf {m}^Q_{i,j} }$. Therefore, one can check that the matrix ![]() ${ \mathsf {M}_Q }$ is a Cartan matrix of type
${ \mathsf {M}_Q }$ is a Cartan matrix of type ![]() $E_7$.
$E_7$.
Type ![]() $E_8^{(1)}$. Recall the explicit description of
$E_8^{(1)}$. Recall the explicit description of ![]() ${\sigma _Q({\mathfrak {g}})}$ for type
${\sigma _Q({\mathfrak {g}})}$ for type ![]() $E_8^{(1)}$. The Dynkin quiver corresponding to
$E_8^{(1)}$. The Dynkin quiver corresponding to ![]() ${\sigma ({\mathfrak {g}})}_Q$ is given in (A.3). In this case,
${\sigma ({\mathfrak {g}})}_Q$ is given in (A.3). In this case, ![]() $h=30$ and elements
$h=30$ and elements ![]() $(i, (-q)^k)$ of
$(i, (-q)^k)$ of ![]() ${\sigma _Q({\mathfrak {g}})}$ with the values of
${\sigma _Q({\mathfrak {g}})}$ with the values of ![]() $\phi _Q^{-1}$ can be drawn as follows.
$\phi _Q^{-1}$ can be drawn as follows.

Here we set ![]() ${\Bigl (\begin {smallmatrix}{a_1a_2}\\ {a_3a_4}\\ {a_5a_6}\\ {a_7a_8}\end {smallmatrix}\Bigr )} \mathbin {:=} \sum _{i=1}^8 a_i \alpha _i \in {\Delta ^+_{Q}}$, and the underlined ones are simple roots. Using the formula given in Appendix A.1, one can compute that for
${\Bigl (\begin {smallmatrix}{a_1a_2}\\ {a_3a_4}\\ {a_5a_6}\\ {a_7a_8}\end {smallmatrix}\Bigr )} \mathbin {:=} \sum _{i=1}^8 a_i \alpha _i \in {\Delta ^+_{Q}}$, and the underlined ones are simple roots. Using the formula given in Appendix A.1, one can compute that for ![]() $1 \leqslant k < h$,
$1 \leqslant k < h$,
 \begin{align*} \tilde{c}_{1,1}(k) & = \delta(k=1,7,11,13,17,19,23,29), \\ \tilde{c}_{1,2}(k) & = \delta(k=4,8,10,12,14,16,18,20,22,26), \\ \tilde{c}_{8,1}(k) & = \delta(k=7,13,17,23), \\ \tilde{c}_{8,2}(k) & = \delta(k=6,10,14,16,20,24), \\ \tilde{c}_{8,8}(k) & = \delta(k=1,11,19,29). \end{align*}
\begin{align*} \tilde{c}_{1,1}(k) & = \delta(k=1,7,11,13,17,19,23,29), \\ \tilde{c}_{1,2}(k) & = \delta(k=4,8,10,12,14,16,18,20,22,26), \\ \tilde{c}_{8,1}(k) & = \delta(k=7,13,17,23), \\ \tilde{c}_{8,2}(k) & = \delta(k=6,10,14,16,20,24), \\ \tilde{c}_{8,8}(k) & = \delta(k=1,11,19,29). \end{align*}By Lemma 6.2, we compute
 \begin{align*} \Lambda^\infty(V(\varpi_1), V(\varpi_1)_{({-}q)^{2}} ) & = 1, \quad \Lambda^\infty(V(\varpi_1), V(\varpi_2)_{({-}q)} ) = \Lambda^\infty(V(\varpi_2), V(\varpi_1)_{({-}q)} )= 0, \\ \Lambda^\infty(V(\varpi_8), V(\varpi_1)_{({-}q)^{k}} ) & = \delta_{k,24} \quad \text{for $ k=24,26,28,30,32,34$}, \\ \Lambda^\infty(V(\varpi_8), V(\varpi_{2})_{({-}q)^k} ) & = \delta_{k,25} \quad \text{for $ k=25,27,29,31,33$}, \\ \Lambda^\infty(V(\varpi_8), V(\varpi_{8})_{({-}q)^k} ) & = \delta_{k,2} \quad \text{for $ k=2,4,6,8$}, \end{align*}
\begin{align*} \Lambda^\infty(V(\varpi_1), V(\varpi_1)_{({-}q)^{2}} ) & = 1, \quad \Lambda^\infty(V(\varpi_1), V(\varpi_2)_{({-}q)} ) = \Lambda^\infty(V(\varpi_2), V(\varpi_1)_{({-}q)} )= 0, \\ \Lambda^\infty(V(\varpi_8), V(\varpi_1)_{({-}q)^{k}} ) & = \delta_{k,24} \quad \text{for $ k=24,26,28,30,32,34$}, \\ \Lambda^\infty(V(\varpi_8), V(\varpi_{2})_{({-}q)^k} ) & = \delta_{k,25} \quad \text{for $ k=25,27,29,31,33$}, \\ \Lambda^\infty(V(\varpi_8), V(\varpi_{8})_{({-}q)^k} ) & = \delta_{k,2} \quad \text{for $ k=2,4,6,8$}, \end{align*}
which give the values of ![]() ${ \mathsf {m}^Q_{i,j} }$. Therefore, one can check that the matrix
${ \mathsf {m}^Q_{i,j} }$. Therefore, one can check that the matrix ![]() ${ \mathsf {M}_Q }$ is a Cartan matrix of type
${ \mathsf {M}_Q }$ is a Cartan matrix of type ![]() $E_8$.
$E_8$.
Type ![]() $F_4^{(1)}$. Recall the explicit description of
$F_4^{(1)}$. Recall the explicit description of ![]() ${\sigma _Q({\mathfrak {g}})}$ for type
${\sigma _Q({\mathfrak {g}})}$ for type ![]() $F_4^{(1)}$, which can be obtained from [Reference Oh and ScrimshawOS19a]. In this case
$F_4^{(1)}$, which can be obtained from [Reference Oh and ScrimshawOS19a]. In this case ![]() ${{\mathfrak {g}}_{\mathrm {fin}}}$ is of type
${{\mathfrak {g}}_{\mathrm {fin}}}$ is of type ![]() $E_{6}$, and elements of
$E_{6}$, and elements of ![]() ${\sigma _Q({\mathfrak {g}})}$ with the values of
${\sigma _Q({\mathfrak {g}})}$ with the values of ![]() $\phi _Q^{-1}$ can be drawn as follows.
$\phi _Q^{-1}$ can be drawn as follows.

Here we set ![]() ${\bigl (\begin {smallmatrix}{a_1a_2a_3}\\[3pt]{a_4a_5a_6}\end {smallmatrix}\bigr )} \mathbin {:=} \sum _{i=1}^6 a_i \alpha _i \in {\Delta ^+_{Q}}$, and the underlined ones are simple roots. It follows from Propositions 3.11 and 3.9 and the denominator formula in Appendix A that
${\bigl (\begin {smallmatrix}{a_1a_2a_3}\\[3pt]{a_4a_5a_6}\end {smallmatrix}\bigr )} \mathbin {:=} \sum _{i=1}^6 a_i \alpha _i \in {\Delta ^+_{Q}}$, and the underlined ones are simple roots. It follows from Propositions 3.11 and 3.9 and the denominator formula in Appendix A that ![]() $\operatorname {\mathfrak {d}} (V_Q(\alpha _i), \mathscr {D}^k V_Q(\alpha _j) ) = 0$ for
$\operatorname {\mathfrak {d}} (V_Q(\alpha _i), \mathscr {D}^k V_Q(\alpha _j) ) = 0$ for ![]() $i\ne j$ and
$i\ne j$ and ![]() $k \ne 0$ and that
$k \ne 0$ and that
 \begin{align*} \Lambda^\infty(V(\varpi_1), V(\varpi_1)_{ q_s ^k}) & = \operatorname{\mathfrak{d}} ( V(\varpi_1), V(\varpi_1)_{ q_s^k} ) = \delta_{k,4} \quad \text{for } k=2,4, \\ \Lambda^\infty(V(\varpi_3), V(\varpi_1)_{ q_s ^k}) & = \operatorname{\mathfrak{d}} ( V(\varpi_3), V(\varpi_1)_{ q_s^k} ) = \delta_{k, {15} } \quad \text{for } k= {15}, {17}, {19}, \\ \Lambda^\infty(V(\varpi_4), V(\varpi_1)_{ {-}q_s ^k}) & = \operatorname{\mathfrak{d}} ( V(\varpi_4), V(\varpi_1)_{ - q_s^k} ) \\ & = \delta_{k,14} \quad \text{for } k={-}2,0,2,12,14,16, \\ \Lambda^\infty(V(\varpi_3), V(\varpi_4)_{ - q_s^k}) & = \operatorname{\mathfrak{d}} ( V(\varpi_3), V(\varpi_4)_{- q_s^k} ) = 1 \quad \text{for } k= {3}, {17}, \\ \Lambda^\infty(V(\varpi_4), V(\varpi_4)_{ q_s^{14}}) & = \operatorname{\mathfrak{d}} ( V(\varpi_4), V(\varpi_4)_{ q_s^{14}} ) = 0, \end{align*}
\begin{align*} \Lambda^\infty(V(\varpi_1), V(\varpi_1)_{ q_s ^k}) & = \operatorname{\mathfrak{d}} ( V(\varpi_1), V(\varpi_1)_{ q_s^k} ) = \delta_{k,4} \quad \text{for } k=2,4, \\ \Lambda^\infty(V(\varpi_3), V(\varpi_1)_{ q_s ^k}) & = \operatorname{\mathfrak{d}} ( V(\varpi_3), V(\varpi_1)_{ q_s^k} ) = \delta_{k, {15} } \quad \text{for } k= {15}, {17}, {19}, \\ \Lambda^\infty(V(\varpi_4), V(\varpi_1)_{ {-}q_s ^k}) & = \operatorname{\mathfrak{d}} ( V(\varpi_4), V(\varpi_1)_{ - q_s^k} ) \\ & = \delta_{k,14} \quad \text{for } k={-}2,0,2,12,14,16, \\ \Lambda^\infty(V(\varpi_3), V(\varpi_4)_{ - q_s^k}) & = \operatorname{\mathfrak{d}} ( V(\varpi_3), V(\varpi_4)_{- q_s^k} ) = 1 \quad \text{for } k= {3}, {17}, \\ \Lambda^\infty(V(\varpi_4), V(\varpi_4)_{ q_s^{14}}) & = \operatorname{\mathfrak{d}} ( V(\varpi_4), V(\varpi_4)_{ q_s^{14}} ) = 0, \end{align*}
which give the values of ![]() ${ \mathsf {m}^Q_{i,j} }$. Thus, one can check that the matrix
${ \mathsf {m}^Q_{i,j} }$. Thus, one can check that the matrix ![]() ${ \mathsf {M}_Q }$ is a Cartan matrix of type
${ \mathsf {M}_Q }$ is a Cartan matrix of type ![]() $E_6$.
$E_6$.
Type ![]() $G_2^{(1)}$. Recall the explicit description of
$G_2^{(1)}$. Recall the explicit description of ![]() ${\sigma _Q({\mathfrak {g}})}$ for type
${\sigma _Q({\mathfrak {g}})}$ for type ![]() $G_2^{(1)}$, which can be obtained from [Reference Oh and ScrimshawOS19a]. In this case
$G_2^{(1)}$, which can be obtained from [Reference Oh and ScrimshawOS19a]. In this case ![]() ${{\mathfrak {g}}_{\mathrm {fin}}}$ is of type
${{\mathfrak {g}}_{\mathrm {fin}}}$ is of type ![]() $D_{4}$, and elements of
$D_{4}$, and elements of ![]() ${\sigma _Q({\mathfrak {g}})}$ with the values of
${\sigma _Q({\mathfrak {g}})}$ with the values of ![]() $\phi _Q^{-1}$ can be drawn as follows.
$\phi _Q^{-1}$ can be drawn as follows.

Here we set ![]() ${ \bigl (\begin {smallmatrix} a_4 \\[3pt] a_1 a_2 a_3 \end {smallmatrix}\bigr ) } \mathbin {:=} \sum _{k=1}^4 a_k\alpha _k \in {\Delta ^+_{Q}}$, and the underlined ones are simple roots. It follows from Propositions 3.11 and 3.9 and the denominator formula in Appendix A that
${ \bigl (\begin {smallmatrix} a_4 \\[3pt] a_1 a_2 a_3 \end {smallmatrix}\bigr ) } \mathbin {:=} \sum _{k=1}^4 a_k\alpha _k \in {\Delta ^+_{Q}}$, and the underlined ones are simple roots. It follows from Propositions 3.11 and 3.9 and the denominator formula in Appendix A that ![]() $\operatorname {\mathfrak {d}} (V_Q(\alpha _i), \mathscr {D}^k V_Q(\alpha _j) ) = 0$ for
$\operatorname {\mathfrak {d}} (V_Q(\alpha _i), \mathscr {D}^k V_Q(\alpha _j) ) = 0$ for ![]() $i\ne j$ and
$i\ne j$ and ![]() $k \ne 0$ and that
$k \ne 0$ and that
 \begin{align*} \Lambda^\infty(V(\varpi_1), V(\varpi_2)_{ ({-}q_t)^k}) & = \operatorname{\mathfrak{d}} ( V(\varpi_1), V(\varpi_2)_{ ({-}q_t)^k} ) = \delta_{k,11} \quad \text{for } k=3,9,11, \\ \Lambda^\infty(V(\varpi_2), V(\varpi_2)_{ ({-}q_t)^k}) & = \operatorname{\mathfrak{d}} ( V(\varpi_2), V(\varpi_2)_{ ({-}q_t)^k} ) = \delta_{k,2} + \delta_{k,8} \quad \text{for } k=2,6,8, \end{align*}
\begin{align*} \Lambda^\infty(V(\varpi_1), V(\varpi_2)_{ ({-}q_t)^k}) & = \operatorname{\mathfrak{d}} ( V(\varpi_1), V(\varpi_2)_{ ({-}q_t)^k} ) = \delta_{k,11} \quad \text{for } k=3,9,11, \\ \Lambda^\infty(V(\varpi_2), V(\varpi_2)_{ ({-}q_t)^k}) & = \operatorname{\mathfrak{d}} ( V(\varpi_2), V(\varpi_2)_{ ({-}q_t)^k} ) = \delta_{k,2} + \delta_{k,8} \quad \text{for } k=2,6,8, \end{align*}
which give the values of ![]() ${ \mathsf {m}^Q_{i,j} }$. Thus, one can check that the matrix
${ \mathsf {m}^Q_{i,j} }$. Thus, one can check that the matrix ![]() ${ \mathsf {M}_Q }$ is a Cartan matrix of type
${ \mathsf {M}_Q }$ is a Cartan matrix of type ![]() $D_4$.
$D_4$.
Type ![]() $E_6^{(2)}$. Recall the explicit description of
$E_6^{(2)}$. Recall the explicit description of ![]() ${\sigma _Q({\mathfrak {g}})}$ for type
${\sigma _Q({\mathfrak {g}})}$ for type ![]() $E_6^{(2)}$, which can be obtained from [Reference Oh and ScrimshawOS19a]. In this case
$E_6^{(2)}$, which can be obtained from [Reference Oh and ScrimshawOS19a]. In this case ![]() ${{\mathfrak {g}}_{\mathrm {fin}}}$ is of type
${{\mathfrak {g}}_{\mathrm {fin}}}$ is of type ![]() $E_{6}$, and elements of
$E_{6}$, and elements of ![]() ${\sigma _Q({\mathfrak {g}})}$ with the values of
${\sigma _Q({\mathfrak {g}})}$ with the values of ![]() $\phi _Q^{-1}$ can be drawn as follows.
$\phi _Q^{-1}$ can be drawn as follows.

Here we set ![]() ${\bigl (\begin {smallmatrix}{a_1a_2a_3}\\[3pt]{a_4a_5a_6}\end {smallmatrix}\bigr )}\mathbin {:=} \sum _{i=1}^6 a_i \alpha _i \in {\Delta ^+_{Q}}$, and the underlined ones are simple roots. Note that
${\bigl (\begin {smallmatrix}{a_1a_2a_3}\\[3pt]{a_4a_5a_6}\end {smallmatrix}\bigr )}\mathbin {:=} \sum _{i=1}^6 a_i \alpha _i \in {\Delta ^+_{Q}}$, and the underlined ones are simple roots. Note that ![]() $V(\varpi _i)_{a} \simeq V(\varpi _i)_{-a}$ for
$V(\varpi _i)_{a} \simeq V(\varpi _i)_{-a}$ for ![]() $i =3,4$. It follows from Propositions 3.11 and 3.9 and the denominator formula in Appendix A that
$i =3,4$. It follows from Propositions 3.11 and 3.9 and the denominator formula in Appendix A that ![]() $\operatorname {\mathfrak {d}} (V_Q(\alpha _i), \mathscr {D}^k V_Q(\alpha _j) ) = 0$ for
$\operatorname {\mathfrak {d}} (V_Q(\alpha _i), \mathscr {D}^k V_Q(\alpha _j) ) = 0$ for ![]() $i\ne j$ and
$i\ne j$ and ![]() $k \ne 0$ and that
$k \ne 0$ and that
 \begin{align*} \Lambda^\infty(V(\varpi_1), V(\varpi_1)_{ q ^k}) & = \operatorname{\mathfrak{d}} ( V(\varpi_1), V(\varpi_1)_{ q^k} ) = \delta_{k,2} + \delta_{k,8} \quad \text{for } k=2,4,8,10,12,14, \\ \Lambda^\infty(V(\varpi_1), V(\varpi_4)_{ \sqrt{-1}q ^k}) & = \operatorname{\mathfrak{d}} ( V(\varpi_1), V(\varpi_4)_{ \sqrt{-1} q^k} ) \\ & = \delta_{k,9} \quad \text{for } k={-}1,0,1,9,11,13, \end{align*}
\begin{align*} \Lambda^\infty(V(\varpi_1), V(\varpi_1)_{ q ^k}) & = \operatorname{\mathfrak{d}} ( V(\varpi_1), V(\varpi_1)_{ q^k} ) = \delta_{k,2} + \delta_{k,8} \quad \text{for } k=2,4,8,10,12,14, \\ \Lambda^\infty(V(\varpi_1), V(\varpi_4)_{ \sqrt{-1}q ^k}) & = \operatorname{\mathfrak{d}} ( V(\varpi_1), V(\varpi_4)_{ \sqrt{-1} q^k} ) \\ & = \delta_{k,9} \quad \text{for } k={-}1,0,1,9,11,13, \end{align*}
which give the values of ![]() ${ \mathsf {m}^Q_{i,j} }$. Thus, one can check that the matrix
${ \mathsf {m}^Q_{i,j} }$. Thus, one can check that the matrix ![]() ${ \mathsf {M}_Q }$ is a Cartan matrix of type
${ \mathsf {M}_Q }$ is a Cartan matrix of type ![]() $E_6$.
$E_6$.
Type ![]() $D_4^{(3)}$. Recall the explicit description of
$D_4^{(3)}$. Recall the explicit description of ![]() ${\sigma _Q({\mathfrak {g}})}$ for type
${\sigma _Q({\mathfrak {g}})}$ for type ![]() $D_4^{(3)}$, which can be obtained from [Reference Oh and ScrimshawOS19a]. In this case
$D_4^{(3)}$, which can be obtained from [Reference Oh and ScrimshawOS19a]. In this case ![]() ${{\mathfrak {g}}_{\mathrm {fin}}}$ is of type
${{\mathfrak {g}}_{\mathrm {fin}}}$ is of type ![]() $D_{4}$, and elements of
$D_{4}$, and elements of ![]() ${\sigma _Q({\mathfrak {g}})}$ with the values of
${\sigma _Q({\mathfrak {g}})}$ with the values of ![]() $\phi _Q^{-1}$ can be drawn as follows.
$\phi _Q^{-1}$ can be drawn as follows.

Here we set ![]() ${\bigl (\begin {smallmatrix} a_4 \\[3pt] a_1 a_2 a_3 \end {smallmatrix}\bigr ) } \mathbin {:=} \sum _{k=1}^4 a_k\alpha _k \in {\Delta ^+_{Q}}$, and the underlined ones are simple roots. Note that
${\bigl (\begin {smallmatrix} a_4 \\[3pt] a_1 a_2 a_3 \end {smallmatrix}\bigr ) } \mathbin {:=} \sum _{k=1}^4 a_k\alpha _k \in {\Delta ^+_{Q}}$, and the underlined ones are simple roots. Note that ![]() $V(\varpi _2)_{a} \simeq V(\varpi _2)_{\omega ^t a}$ for
$V(\varpi _2)_{a} \simeq V(\varpi _2)_{\omega ^t a}$ for ![]() $t=1,2$. It follows from Propositions 3.11 and 3.9 and the denominator formula in Appendix A that
$t=1,2$. It follows from Propositions 3.11 and 3.9 and the denominator formula in Appendix A that ![]() $\operatorname {\mathfrak {d}} (V_Q(\alpha _i), \mathscr {D}^k V_Q(\alpha _j) ) = 0$ for
$\operatorname {\mathfrak {d}} (V_Q(\alpha _i), \mathscr {D}^k V_Q(\alpha _j) ) = 0$ for ![]() $i\ne j$ and
$i\ne j$ and ![]() $k \ne 0$ and that
$k \ne 0$ and that
 \begin{align*} \Lambda^\infty(V(\varpi_1), V(\varpi_1)_{ \omega^t q^k}) = \begin{cases} 1 & \text{if } (t,k)= (0,2), (1,4), (2,4), \\ 0 & \text{if } (t,k)= (1,0), (2,0), (1,6), (2,6), \end{cases} \end{align*}
\begin{align*} \Lambda^\infty(V(\varpi_1), V(\varpi_1)_{ \omega^t q^k}) = \begin{cases} 1 & \text{if } (t,k)= (0,2), (1,4), (2,4), \\ 0 & \text{if } (t,k)= (1,0), (2,0), (1,6), (2,6), \end{cases} \end{align*}
which give the values of ![]() ${ \mathsf {m}^Q_{i,j} }$. Thus, one can check that the matrix
${ \mathsf {m}^Q_{i,j} }$. Thus, one can check that the matrix ![]() ${ \mathsf {M}_Q }$ is a Cartan matrix of type
${ \mathsf {M}_Q }$ is a Cartan matrix of type ![]() $D_4$.
$D_4$.
Acknowledgements
The second, third and fourth authors gratefully acknowledge the hospitality of RIMS (Kyoto University) during their visit in 2020. The authors would like to thank the anonymous referee for valuable comments and suggestions.
Appendix A. Denominator formulas
The denominator formulas were studied and computed in [Reference Akasaka and KashiwaraAK97, Reference Date and OkadoDO94, Reference FujitaFuj22, Reference Kang, Kashiwara and KimKKK15, Reference OhOh15, Reference Oh and ScrimshawOS19a]. In this appendix we present the denominator formulas for all types.
Let ![]() $q_s, q_t \in \mathbf {k}^\times$ be such that
$q_s, q_t \in \mathbf {k}^\times$ be such that ![]() $q = q_s^2= q_t^3$, and let
$q = q_s^2= q_t^3$, and let ![]() $\omega \in \mathbf {k}$ be such that
$\omega \in \mathbf {k}$ be such that ![]() $\omega ^2+\omega +1=0$. For
$\omega ^2+\omega +1=0$. For ![]() $i,j \in I$, we set
$i,j \in I$, we set
A.1 Simply laced affine ADE types
Suppose that the Cartan matrix ![]() $\mathsf {C} = (c_{i,j})_{i,j\in I_0}$ is of type
$\mathsf {C} = (c_{i,j})_{i,j\in I_0}$ is of type ![]() $A_n$,
$A_n$, ![]() $D_n$ or
$D_n$ or ![]() $E_k$ (
$E_k$ (![]() $k=6,7,8$). The quantum Cartan matrix
$k=6,7,8$). The quantum Cartan matrix ![]() $\mathsf {C}(z)= (c_{i,j}(z))_{i,j\in I_0}$ is defined by
$\mathsf {C}(z)= (c_{i,j}(z))_{i,j\in I_0}$ is defined by
We denote by ![]() $\tilde {\mathsf {C}} (z) = ( \tilde {c}_{i,j}(z) )_{i,j\in I_0}$ the inverse of
$\tilde {\mathsf {C}} (z) = ( \tilde {c}_{i,j}(z) )_{i,j\in I_0}$ the inverse of ![]() $\mathsf {C}(z)$, and write
$\mathsf {C}(z)$, and write
Then the following beautiful formula is given in [Reference FujitaFuj22, Theorem 2.10]:
 \begin{equation} d_{i,j}(z) = \prod_{k=1}^{h -1} (z - ({-}q)^{k+1})^{\tilde{c}_{i,j}(k)}, \end{equation}
\begin{equation} d_{i,j}(z) = \prod_{k=1}^{h -1} (z - ({-}q)^{k+1})^{\tilde{c}_{i,j}(k)}, \end{equation}
where ![]() $h$ is the Coxeter number. Note that the dual Coxeter number is equal to the Coxeter number in this case.
$h$ is the Coxeter number. Note that the dual Coxeter number is equal to the Coxeter number in this case.
Let ![]() ${\mathfrak {g}}_0$ be a simple Lie algebra of type ADE with index set
${\mathfrak {g}}_0$ be a simple Lie algebra of type ADE with index set ![]() $I_0$, and let
$I_0$, and let ![]() $Q$ be a Dynkin quiver of
$Q$ be a Dynkin quiver of ![]() ${\mathfrak {g}}$. Let
${\mathfrak {g}}$. Let ![]() $\xi \colon I_0 \rightarrow \mathbb {\mspace {1mu}Z\mspace {1mu}}$ be a height function such that
$\xi \colon I_0 \rightarrow \mathbb {\mspace {1mu}Z\mspace {1mu}}$ be a height function such that ![]() $\xi _j = \xi _i - 1$ for
$\xi _j = \xi _i - 1$ for ![]() $i \rightarrow j$ in
$i \rightarrow j$ in ![]() $Q$. Choose a total order > on
$Q$. Choose a total order > on ![]() $I$ such that
$I$ such that ![]() $i > j$ for
$i > j$ for ![]() $\xi _i > \xi _j$ and write
$\xi _i > \xi _j$ and write ![]() $I_0 = \{ i_1 > i_2 > \cdots > i_n \}$. We set
$I_0 = \{ i_1 > i_2 > \cdots > i_n \}$. We set ![]() $\tau \mathbin {:=} s_{i_1} \cdots s_{i_n}$, which is a Coxeter element. For
$\tau \mathbin {:=} s_{i_1} \cdots s_{i_n}$, which is a Coxeter element. For ![]() $i\in I_0$ we set
$i\in I_0$ we set ![]() $\gamma _i \mathbin {:=} \sum _{j\in B(i)} \alpha _j,$ where
$\gamma _i \mathbin {:=} \sum _{j\in B(i)} \alpha _j,$ where ![]() $B(i)$ is the subset of
$B(i)$ is the subset of ![]() $I_0$ consisting of all elements
$I_0$ consisting of all elements ![]() $j$ such that there is a path from
$j$ such that there is a path from ![]() $j$ to
$j$ to ![]() $i$ in
$i$ in ![]() $Q$. Then we have the following.
$Q$. Then we have the following.
Proposition A.1 [Reference Hernandez and LeclercHL15, Proposition 2.1]
For ![]() $i,j\in I$ and
$i,j\in I$ and ![]() $k \in \mathbb {\mspace {1mu}Z\mspace {1mu}}_{>0}$, we have
$k \in \mathbb {\mspace {1mu}Z\mspace {1mu}}_{>0}$, we have
 \begin{align*} \tilde{c}_{i,j}(k) = \begin{cases} ( \tau^{(k +\xi_i - \xi_j -1)/2} (\gamma_i), \varpi_j) & \text{if $k +\xi_i - \xi_j -1$ is even}, \\ 0 & \text{otherwise.} \end{cases} \end{align*}
\begin{align*} \tilde{c}_{i,j}(k) = \begin{cases} ( \tau^{(k +\xi_i - \xi_j -1)/2} (\gamma_i), \varpi_j) & \text{if $k +\xi_i - \xi_j -1$ is even}, \\ 0 & \text{otherwise.} \end{cases} \end{align*}In this paper, we make the following choice of Dynkin quivers:

In this case we have the following data, which allow us to compute ![]() $\tilde {c}_{i,j}(k)$ explicitly.
$\tilde {c}_{i,j}(k)$ explicitly.
(a) (Type
 $A_n$)
$A_n$)  $\tau = s_1s_2 \cdots s_n$,
$\tau = s_1s_2 \cdots s_n$,  $\xi _i =1-i$ and
$\xi _i =1-i$ and  $\gamma _i = \sum _{j=1}^i \alpha _j$.
$\gamma _i = \sum _{j=1}^i \alpha _j$.(b) (Type
 $D_n$)
$D_n$)  $\tau = s_1s_2 \cdots s_{n-1} s_n$ and
$\tau = s_1s_2 \cdots s_{n-1} s_n$ and
 \begin{align*} \xi_i = \begin{cases} 1-i & \text{if } i < n-1, \\ -n+2 & \text{if } i=n-1,n, \end{cases} \qquad \gamma_i = \begin{cases} \displaystyle \sum_{j=1}^i \alpha_j & \text{if } i < n, \\ \displaystyle \sum_{j=1}^{n-2} \alpha_j + \alpha_n & \text{if } i=n. \end{cases} \end{align*}
\begin{align*} \xi_i = \begin{cases} 1-i & \text{if } i < n-1, \\ -n+2 & \text{if } i=n-1,n, \end{cases} \qquad \gamma_i = \begin{cases} \displaystyle \sum_{j=1}^i \alpha_j & \text{if } i < n, \\ \displaystyle \sum_{j=1}^{n-2} \alpha_j + \alpha_n & \text{if } i=n. \end{cases} \end{align*}(c) (Type
 $E_n, \: n=6,7,8$)
$E_n, \: n=6,7,8$)  $\tau = s_1s_2\ldots s_n$,
$\tau = s_1s_2\ldots s_n$,  $\xi _1= 0$,
$\xi _1= 0$,  $\xi _2=-1$ and
$\xi _2=-1$ and  $\xi _k =2-k$ for
$\xi _k =2-k$ for  $k=3,4,\ldots,n$, and
$k=3,4,\ldots,n$, and  $\gamma _1 = \alpha _1$,
$\gamma _1 = \alpha _1$,  $\gamma _2 = \alpha _2$,
$\gamma _2 = \alpha _2$,  $\gamma _3 = \alpha _1+\alpha _3$ and
$\gamma _3 = \alpha _1+\alpha _3$ and  $\gamma _t = \sum _{k=1}^t \alpha _k$ for
$\gamma _t = \sum _{k=1}^t \alpha _k$ for  $t=4,\ldots,n$.
$t=4,\ldots,n$.
Indeed, in the figures of § 6.2, the root ![]() $\gamma _i$ is the rightmost one in the row labeled by
$\gamma _i$ is the rightmost one in the row labeled by ![]() $i$, and
$i$, and ![]() $\tau$ corresponds to horizontal translation by
$\tau$ corresponds to horizontal translation by ![]() $-2$. Hence one can read such values of
$-2$. Hence one can read such values of ![]() $\tilde {c}_{i,j}(k)$ easily from the figures.
$\tilde {c}_{i,j}(k)$ easily from the figures.
A.2 Other classical affine types
The denominator formulas for other classical affine types can be found in [Reference Akasaka and KashiwaraAK97, Appendix C.4] for type ![]() $C_n^{(1)}$ and in [Reference OhOh15, Appendix] for types
$C_n^{(1)}$ and in [Reference OhOh15, Appendix] for types ![]() $B_n^{(1)}$,
$B_n^{(1)}$, ![]() $D_{n+1}^{(2)}$ and
$D_{n+1}^{(2)}$ and ![]() $A_N^{(2)}$ (
$A_N^{(2)}$ (![]() $N=2n, 2n-1$).
$N=2n, 2n-1$).
(i) Type
 $B_{n}^{(1)}$ (
$B_{n}^{(1)}$ ( $n \geqslant 2$):
$n \geqslant 2$):
(a)
 $d_{k,l}(z) = \prod _{s=1}^{\min (k,l)} \bigl (z-(-q)^{|k-l|+2s}\bigr )\bigl (z+(-q)^{2n-k-l-1+2s}\bigr )$ for
$d_{k,l}(z) = \prod _{s=1}^{\min (k,l)} \bigl (z-(-q)^{|k-l|+2s}\bigr )\bigl (z+(-q)^{2n-k-l-1+2s}\bigr )$ for  $1 \leqslant k,l \leqslant n-1$;
$1 \leqslant k,l \leqslant n-1$;(b)
 $d_{k,n}(z) = \prod _{s=1}^{k}\bigl (z-(-1)^{n+k}q_s^{2n-2k-1+4s}\bigr )$ for
$d_{k,n}(z) = \prod _{s=1}^{k}\bigl (z-(-1)^{n+k}q_s^{2n-2k-1+4s}\bigr )$ for  $1 \leqslant k \leqslant n-1$;
$1 \leqslant k \leqslant n-1$;(c)
 $d_{n,n}(z)= \prod _{s=1}^{n} \bigl (z-(q_s)^{4s-2}\bigr )$.
$d_{n,n}(z)= \prod _{s=1}^{n} \bigl (z-(q_s)^{4s-2}\bigr )$.
(ii) Type
 $C_{n}^{(1)}$ (
$C_{n}^{(1)}$ ( $n \geqslant 2$):
$n \geqslant 2$):
(a)
 $d_{k,l}(z)= \prod _{s=1}^{ \min (k,l,n-k,n-l)} \bigl (z-(-q_s)^{|k-l|+2s}\bigr ) \prod _{s=1}^{ \min (k,l)} \bigl (z-(-q_s)^{2n+2-k-l+2s}\bigr )$ for
$d_{k,l}(z)= \prod _{s=1}^{ \min (k,l,n-k,n-l)} \bigl (z-(-q_s)^{|k-l|+2s}\bigr ) \prod _{s=1}^{ \min (k,l)} \bigl (z-(-q_s)^{2n+2-k-l+2s}\bigr )$ for  $1 \leqslant k,l \leqslant n$.
$1 \leqslant k,l \leqslant n$.
(iii) Type
 $A_{2n-1}^{(2)}$ (
$A_{2n-1}^{(2)}$ ( $n\geqslant 2$):
$n\geqslant 2$):
(a)
 $d_{k,l}(z)= \prod _{s=1}^{\min (k,l)} \bigl (z-(-q)^{|k-l|+2s}\bigr )\bigl (z+(-q)^{2n-k-l+2s}\bigr )$ for
$d_{k,l}(z)= \prod _{s=1}^{\min (k,l)} \bigl (z-(-q)^{|k-l|+2s}\bigr )\bigl (z+(-q)^{2n-k-l+2s}\bigr )$ for  $1 \leqslant k,l \leqslant n$.
$1 \leqslant k,l \leqslant n$.
(iv) Type
 $A_{2n}^{(2)}$ (
$A_{2n}^{(2)}$ ( $n \geqslant 1$):
$n \geqslant 1$):
(a)
 $d_{k,l}(z) = \prod _{s=1}^{\min (k,l)} \bigl (z-(-q)^{|k-l|+2s}\bigr )\bigl (z-(-q)^{2n+1-k-l+2s}\bigr )$ for
$d_{k,l}(z) = \prod _{s=1}^{\min (k,l)} \bigl (z-(-q)^{|k-l|+2s}\bigr )\bigl (z-(-q)^{2n+1-k-l+2s}\bigr )$ for  $1 \leqslant k,l \leqslant n$.
$1 \leqslant k,l \leqslant n$.
(v) Type
 $D_{n+1}^{(2)}$ (
$D_{n+1}^{(2)}$ ( $n \geqslant 3$):
$n \geqslant 3$):
(a)
 $d_{k,l}(z) = \prod _{s=1}^{\min (k,l)} \bigl (z^2 - (-q^2)^{|k-l|+2s}\bigr )\bigl (z^2 - (-q^2)^{2n-k-l+2s}\bigr )$ for
$d_{k,l}(z) = \prod _{s=1}^{\min (k,l)} \bigl (z^2 - (-q^2)^{|k-l|+2s}\bigr )\bigl (z^2 - (-q^2)^{2n-k-l+2s}\bigr )$ for  $1 \leqslant k,l \leqslant n-1$;
$1 \leqslant k,l \leqslant n-1$;(b)
 $d_{k,n}(z) = \prod _{s=1}^{k}\bigl (z^2+(-q^{2})^{n-k+2s}\bigr )$ for
$d_{k,n}(z) = \prod _{s=1}^{k}\bigl (z^2+(-q^{2})^{n-k+2s}\bigr )$ for  $1 \leqslant k \leqslant n-1$;
$1 \leqslant k \leqslant n-1$;(c)
 $d_{n,n}(z)= \prod _{s=1}^{n} \bigl (z+(-q^2)^{s}\bigr )$ for
$d_{n,n}(z)= \prod _{s=1}^{n} \bigl (z+(-q^2)^{s}\bigr )$ for  $k=l=n$.
$k=l=n$.
A.3 Other exceptional affine types
The denominator formulas for exceptional affine type can be found in [Reference Oh and ScrimshawOS19a, §§ 4 and 7].
(i) Type
 $G_2^{(1)}$:
$G_2^{(1)}$:
(a)
 $d_{1,1}(z) = (z - q_t^6) (z - q_t^{8}) (z - q_t^{10}) (z - q_t^{12})$;
$d_{1,1}(z) = (z - q_t^6) (z - q_t^{8}) (z - q_t^{10}) (z - q_t^{12})$;(b)
 $d_{1,2}(z) = (z + q_t^7) (z + q_t^{11})$;
$d_{1,2}(z) = (z + q_t^7) (z + q_t^{11})$;(c)
 $d_{2,2}(z) = (z -q_t^2) (z -q_t^{8}) (z -q_t^{12})$.
$d_{2,2}(z) = (z -q_t^2) (z -q_t^{8}) (z -q_t^{12})$.
(ii) Type
 $F_4^{(1)}$:
$F_4^{(1)}$:
(a)
 $d_{1,1}(z) = (z-q_s^4) (z-q_s^{10}) (z-q_s^{12}) (z-q_s^{18})$;
$d_{1,1}(z) = (z-q_s^4) (z-q_s^{10}) (z-q_s^{12}) (z-q_s^{18})$;(b)
 $d_{1,2}(z) = (z+q_s^{6}) (z+q_s^{8}) (z+q_s^{10}) (z+q_s^{12}) (z+q_s^{14}) (z+q_s^{16})$;
$d_{1,2}(z) = (z+q_s^{6}) (z+q_s^{8}) (z+q_s^{10}) (z+q_s^{12}) (z+q_s^{14}) (z+q_s^{16})$;(c)
 $d_{1,3}(z) = (z-q_s^{7}) (z-q_s^{9}) (z-q_s^{13}) (z-q_s^{15})$;
$d_{1,3}(z) = (z-q_s^{7}) (z-q_s^{9}) (z-q_s^{13}) (z-q_s^{15})$;(d)
 $d_{1,4}(z) = (z+q_s^{8}) (z+q_s^{14})$;
$d_{1,4}(z) = (z+q_s^{8}) (z+q_s^{14})$;(e)
 $d_{2,2}(z) = (z-q_s^{4}) (z-q_s^{6}) (z-q_s^{8})^2 (z-q_s^{10})^2 (z-q_s^{12})^2 (z-q_s^{14})^2 (z-q_s^{16}) (z-q_s^{18})$;
$d_{2,2}(z) = (z-q_s^{4}) (z-q_s^{6}) (z-q_s^{8})^2 (z-q_s^{10})^2 (z-q_s^{12})^2 (z-q_s^{14})^2 (z-q_s^{16}) (z-q_s^{18})$;(f)
 $d_{2,3}(z) = (z+q_s^{5}) (z+q_s^{7}) (z+q_s^{9}) (z+q_s^{11})^2 (z+q_s^{13}) (z+q_s^{15}) (z+q_s^{17})$;
$d_{2,3}(z) = (z+q_s^{5}) (z+q_s^{7}) (z+q_s^{9}) (z+q_s^{11})^2 (z+q_s^{13}) (z+q_s^{15}) (z+q_s^{17})$;(g)
 $d_{2,4}(z) = (z-q_s^{6}) (z-q_s^{10}) (z-q_s^{12}) (z-q_s^{16})$;
$d_{2,4}(z) = (z-q_s^{6}) (z-q_s^{10}) (z-q_s^{12}) (z-q_s^{16})$;(h)
 $d_{3,3}(z) = (z - q_s^{2}) (z - q_s^{6}) (z - q_s^{8}) (z - q_s^{10}) (z - q_s^{12})^2 (z - q_s^{16}) (z - q_s^{18})$;
$d_{3,3}(z) = (z - q_s^{2}) (z - q_s^{6}) (z - q_s^{8}) (z - q_s^{10}) (z - q_s^{12})^2 (z - q_s^{16}) (z - q_s^{18})$;(i)
 $d_{3,4}(z) = (z+q_s^{3}) (z+q_s^{7}) (z+q_s^{11}) (z+q_s^{13}) (z+q_s^{17})$;
$d_{3,4}(z) = (z+q_s^{3}) (z+q_s^{7}) (z+q_s^{11}) (z+q_s^{13}) (z+q_s^{17})$;(j)
 $d_{4,4}(z) = (z - q_s^{2}) (z - q_s^{8}) (z - q_s^{12}) (z - q_s^{18})$.
$d_{4,4}(z) = (z - q_s^{2}) (z - q_s^{8}) (z - q_s^{12}) (z - q_s^{18})$.
(iii) Type
 $D_4^{(3)}$:
$D_4^{(3)}$:
(a)
 $d_{1,1}(z) = (z-q^2) (z-q^6) (z-\omega q^4) (z - \omega ^2 q^4)$;
$d_{1,1}(z) = (z-q^2) (z-q^6) (z-\omega q^4) (z - \omega ^2 q^4)$;(b)
 $d_{1,2}(z) = (z^3 + q^9) (z^3 + q^{15})$;
$d_{1,2}(z) = (z^3 + q^9) (z^3 + q^{15})$;(c)
 $d_{2,2}(z) = (z^3-q^6) (z^3-q^{12})^{2} (z^3-q^{18})$.
$d_{2,2}(z) = (z^3-q^6) (z^3-q^{12})^{2} (z^3-q^{18})$.
(iv) Type
 $E_6^{(2)}$:
$E_6^{(2)}$:
(a)
 $d_{1,1}(z) = (z-q^{2}) (z+q^{6}) (z-q^{8}) (z+q^{12})$;
$d_{1,1}(z) = (z-q^{2}) (z+q^{6}) (z-q^{8}) (z+q^{12})$;(b)
 $d_{1,2} (z) = ( z+q^{3}) ( z-q^{5}) ( z-q^{7}) ( z+q^{7}) ( z+q^{9}) ( z-q^{11})$;
$d_{1,2} (z) = ( z+q^{3}) ( z-q^{5}) ( z-q^{7}) ( z+q^{7}) ( z+q^{9}) ( z-q^{11})$;(c)
 $d_{1,3}(z) = (z^2 + q^{8}) (z^2 + q^{12}) (z^2 + q^{16}) (z^2 + q^{20})$;
$d_{1,3}(z) = (z^2 + q^{8}) (z^2 + q^{12}) (z^2 + q^{16}) (z^2 + q^{20})$;(d)
 $d_{1,4}(z) = (z^2 + q^{10}) (z^2 + q^{18})$;
$d_{1,4}(z) = (z^2 + q^{10}) (z^2 + q^{18})$;(e)
 $d_{2,2}(z) = (z-q^{2}) (z-q^{4}) (z-q^{6}) (z-q^{8})^2 (z-q^{10}) (z+q^{4}) (z+q^{6})^2 (z+q^{8}) (z+q^{10}) (z+q^{12})$;
$d_{2,2}(z) = (z-q^{2}) (z-q^{4}) (z-q^{6}) (z-q^{8})^2 (z-q^{10}) (z+q^{4}) (z+q^{6})^2 (z+q^{8}) (z+q^{10}) (z+q^{12})$;(f)
 $d_{2,3}(z) = (z^2 + q^{6}) (z^2 + q^{10})^2 (z^2 + q^{14})^2 (z^2 + q^{18})^2 (z^2 + q^{22})$;
$d_{2,3}(z) = (z^2 + q^{6}) (z^2 + q^{10})^2 (z^2 + q^{14})^2 (z^2 + q^{18})^2 (z^2 + q^{22})$;(g)
 $d_{2,4}(z) = (z^2 + q^8) (z^2 + q^{12}) (z^2 + q^{16}) (z^2 + q^{20})$;
$d_{2,4}(z) = (z^2 + q^8) (z^2 + q^{12}) (z^2 + q^{16}) (z^2 + q^{20})$;(h)
 $d_{3,3}(z) = (z^2 - q^{4}) (z^2 - q^{8})^2 (z^2 - q^{12})^3 (z^2 - q^{16})^3 (z^2 - q^{20})^2 (z^2 - q^{24})$;
$d_{3,3}(z) = (z^2 - q^{4}) (z^2 - q^{8})^2 (z^2 - q^{12})^3 (z^2 - q^{16})^3 (z^2 - q^{20})^2 (z^2 - q^{24})$;(i)
 $d_{3,4}(z) = ( z^2 - q^{6}) ( z^2 - q^{10}) ( z^2 - q^{14})^2 ( z^2 - q^{18})^{2} ( z^2 - q^{22})$;
$d_{3,4}(z) = ( z^2 - q^{6}) ( z^2 - q^{10}) ( z^2 - q^{14})^2 ( z^2 - q^{18})^{2} ( z^2 - q^{22})$;(j)
 $d_{4,4}(z) = (z^2 - q^4) (z^2 - q^{12}) (z^2 - q^{16}) (z^2 - q^{24})$.
$d_{4,4}(z) = (z^2 - q^4) (z^2 - q^{12}) (z^2 - q^{16}) (z^2 - q^{24})$.