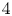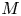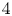1. Introduction
The Seiberg–Witten invariant is an integer-valued differential topological invariant of a 
$\operatorname {Spin}^{c}$ 
$4$-manifold, which reflects the smooth structure for various examples of 
$4$-manifolds. Nevertheless, if the 
$\operatorname {Spin}^{c}$ structure is induced from a spin structure, one may expect a sort of ‘rigidity theorem’ for the Seiberg–Witten invariant mod 
$2$. Namely, the value of the Seiberg–Witten invariant mod 
$2$ may depend only on some underlying topological structure of the smooth manifold, such as on its homotopy type. Such results have been obtained by Morgan and Szabó [Reference Morgan and SzabóMS97], Ruberman and Strle [Reference Ruberman and StrleRS00], Bauer [Reference BauerBau08] and Li [Reference LiLi06b, Reference Li and LiuLL01].
Various authors developed gauge theory not just for a single 
$4$-manifold, but for families of 
$4$-manifolds with many interesting applications, such as [Reference RubermanRub98, Reference RubermanRub99, Reference RubermanRub01, Reference Li and LiuLL01, Reference SzymikSzy10, Reference BaragliaBar19a, Reference NakamuraNak10]. In particular, for a smooth family of 
$4$-manifolds, the families Seiberg–Witten invariant has been defined as a 
${\Bbb Z}$- or 
${\Bbb Z}/2$-valued invariant.
In this paper, we study a family version of rigidity results on the 
${\Bbb Z}/2$-valued Seiberg–Witten invariant. Namely, for a given family of spin 
$4$-manifolds with some topological conditions, we consider the 
${\Bbb Z}/2$-valued families Seiberg–Witten invariant, and verify that it depends only on weaker information than is a priori expected. Roughly speaking, we verify that the 
${\Bbb Z}/2$-valued families Seiberg–Witten invariant is determined by the linearization of a family of Seiberg–Witten equations. A mechanism of this rigidity theorem also gives a family version of Furuta's 10/8-inequality [Reference FurutaFur01] in a suitable situation.
This family version of 10/8-type inequality gives us the following topological applications: we prove the existence of a non-smoothable family of 
$4$-manifolds whose fiber, base space, and the total space are smoothable as manifolds. To our knowledge, this interesting topological phenomenon has not been discussed so far. This non-smoothability result gives a new approach to detecting homotopical difference between the diffeomorphism and homeomorphism groups of 
$4$-manifolds. For example, let 
$M$ be a smooth 
$4$-manifold which is homeomorphic to 
$K3\# n S^{2} \times S^{2}$ with 
$0\leq n \leq 3$. Then it follows from our non-smoothability result that the inclusion map from the diffeomorphism group to the homeomorphism group
\[ \operatorname{Diff}(M) \hookrightarrow \operatorname{Homeo}(M) \]
is not a weak homotopy equivalence. This result has not been known even when 
$M$ is diffeomorphic to 
$K3\# n S^{2} \times S^{2}$ with 
$n>0$. As another application, we shall also detect a new series of non-smoothable topological actions on some spin 
$4$-manifolds using the family version of the 10/8-inequality.
Let us summarize the statements of our main theorems and their applications. Henceforth, all manifolds are assumed to be connected. Let 
$B$ be a closed smooth manifold, 
$M$ a closed smooth 
$4$-manifold equipped with a spin structure 
$\mathfrak {s}$ and 
$M \to X \to B$ be a fiber bundle whose structure group is 
$\operatorname {Diff}^{+}(M)$, the group of diffeomorphisms preserving orientation. Assume that 
$X$ admits a fiberwise spin structure 
$\mathfrak {s}_{X}$ whose fiber coincides with the given spin structure on 
$M$. We call it a global spin structure modeled on 
$\mathfrak {s}$ (See § 2.2). In this situation, we have two real bundles over 
$B$: 
$H^{+} \to B$ and 
${\rm ind}\, {D}$, where the fiber of 
$H^+$ is 
$H^{+}(M)$ which is a maximal-dimensional positive-definite subspace of 
$H^{2}(M;{\Bbb R})$ with respect to the intersection form, and 
${\rm ind}\, {D}$ is the virtual Dirac index bundle associated to 
$X \to B$. Note that the Dirac operator 
$D$ is 
$\operatorname {Pin}(2)$-equivariant since 
$D$ is 
${\Bbb H}$-linear. We define the 
$\operatorname {Pin}(2)$-action on 
$H^+$ via the surjective homomorphism 
$\operatorname {Pin}(2)\to \operatorname {Pin}(2)/S^1 =\{\pm 1\}$ and the multiplication by 
$\{\pm 1\}$ to real vector spaces. Then 
${\rm ind}\, {D}$ and 
$H^+$ determine an element in the 
$\operatorname {Pin}(2)$-equivariant 
$KO$-group:
\[ \alpha = \alpha(X,\mathfrak{s}_{X}) := [{\rm ind}\, {D}] - [H^{+}] \in KO_{\operatorname {Pin}(2)}(B). \]
Let 
$b_{+}(M) := \dim H^{+}(M)$.
If 
$b_{+}(M) \geq \dim {B} +2$, we can define the (mod 
$2$) families Seiberg–Witten invariant
\[ FSW^{{\Bbb Z}_2}(X,\mathfrak{s}_{X}) \in {\Bbb Z}/2 \]
of 
$(X,\mathfrak {s}_{X})$ (see § 2.2). The first main result in this paper claims that 
$FSW^{{\Bbb Z}_2}(X,\mathfrak {s}_{X})$ depends only on 
$\alpha (X,\mathfrak {s}_{X})$ which is determined by the linearization of a family of Seiberg–Witten equations.
Theorem 1.1 (Theorem 4.1)
Let 
$M_1$ and 
$M_2$ be oriented closed smooth 
$4$-manifolds with spin structures 
$\mathfrak {s}_1$ and 
$\mathfrak {s}_2$, respectively. Assume the following conditions:
•
$b_1(M_1)=b_1(M_2)=0$, $b_+(M_1)=b_+(M_2)\geq \dim B + 2$;•
$-{\operatorname {sign}(M_i)}/{4} -1-b_+(M_i)+\dim B =0$ $(i=1,2)$.
For 
$i=1,2$, let 
$X_i\to B$ be a smooth fiber bundle whose fiber is 
$M_i$ equipped with a global spin structure 
$\mathfrak {s}_{X_i}$ modeled on 
$\mathfrak {s}_i$.
If 
$\alpha (X_{1},\mathfrak {s}_{X_{1}})=\alpha (X_{2},\mathfrak {s}_{X_{2}})$ holds in 
$KO_{\operatorname {Pin}(2)}(B)$, then the equality
\[ FSW^{{\Bbb Z}_2}(X_1,\mathfrak{s}_{X_1}) = FSW^{{\Bbb Z}_2}(X_2,\mathfrak{s}_{X_2}) \]
holds.
In general, it is not easy to calculate 
$FSW^{{\Bbb Z}_2}(X,\mathfrak {s})$, since it is defined by counting the solutions to a system of nonlinear partial differential equations. Compared with 
$FSW^{{\Bbb Z}_2}(X,\mathfrak {s})$, the linearized data 
$\alpha (X,\mathfrak {s}_{X})$ is easier to handle. This allows us to obtain some interesting applications described below.
Combining the rigidity result in Theorem 1.1 with a non-vanishing theorem for a specific family of 
$4$-manifolds in [Reference Baraglia and KonnoBK20], we can obtain non-vanishing of the families Seiberg–Witten invariants for some class of families. This non-vanishing result and a family version of the argument in [Reference Furuta, Kametani and MatsueFKM01] give us a family version of 10/8-type inequality as follows. Let 
$\ell$ be the unique non-trivial real line bundle over 
$S^1$, and 
$\pi _i\colon T^n=S^1\times \cdots \times S^1\to S^1$ be the projection to the 
$i$th component. Let us define the real vector bundle 
$\xi _n$ over 
$T^n$ by
\[ \xi_n=\pi_1^*\ell\oplus\cdots\oplus \pi_n^*\ell. \]
Theorem 1.2 (Corollary 4.3)
Let 
$M$ be a 
$4$-manifold with 
$\operatorname {sign}(M)=-16$ and 
$b_1(M)=0$. Let 
$\mathfrak {s}$ be a spin structure on 
$M$ and 
$f_1,\ldots ,f_n$ be self-diffeomorphisms on 
$M$ whose supports 
$\operatorname {supp}{f}_{1}, \ldots , \operatorname {supp}{f}_{n}$ are mutually disjoint. Let 
$H^+\to T^n$ be the bundle of 
$H^+(M)$ associated to the multiple mapping torus of 
$f_{1}, \ldots , f_{n}$. Suppose that each of 
$f_1,\ldots ,f_n$ preserves 
$\mathfrak {s}$ and that there exists a non-negative integer 
$a$ such that
\[ H^+{\cong} \xi_n\oplus \underline{{\Bbb R}}^a, \]
where 
$\underline {{\Bbb R}}^a$ denotes the trivial bundle over 
$T^{n}$ with fiber 
${\Bbb R}^{a}$. Then the inequality
\begin{equation} b_+(M)\geq n+3 \end{equation}holds.
Let us make two remarks on Theorem 1.2.
Remark 1.1 Denote by 
$K3$ the underlying smooth 4-manifold of a 
$K3$ surface. Recall that 
$K3$ admits no diffeomorphisms reversing orientation of 
$H^{+}(K3)$, which was shown first by Donaldson [Reference DonaldsonDon90], and later proven also using Seiberg–Witten invariants (for example, see the proof of [Reference NicolaescuNic00, Theorem 3.3.28]). This fact follows also from the case where 
$n=1$ and 
$M=K3$ in Theorem 1.2, and therefore Theorem 1.2 can be regarded as a generalization of this fact.
Remark 1.2 One may check that inequality (1) is sharp as follows. Let us consider the 
$4$-manifold 
$M = K3\#n S^{2} \times S^{2}$. Let 
$f_{1}, \ldots , f_{n}$ be copies on 
$n S^{2} \times S^{2}$ of an orientation-preserving diffeomorphism on 
$S^{2} \times S^{2}$ which reverses orientation of 
$H^{+}(S^{2} \times S^{2})$ and has a fixed disk. Then 
$f_{1}, \ldots , f_{n}$ have mutually disjoint supports, and each of them reverses the orientation of 
$H^{+}(M)$. Moreover, the bundle 
$H^{+} \to T^{n}$ associated to the multiple mapping torus of 
$f_{1}, \ldots , f_{n}$ is isomorphic to 
$\xi _{n} \oplus \underline {{\Bbb R}}^3$. Therefore 
$M$ and 
$f_{1}, \ldots , f_{n}$ satisfy all the assumptions in Theorem 1.2. Since 
$b_{+}(M)=n+3$, this example ensures that inequality (1) is sharp.
Theorem 1.2 claims that, even when 
$H^+$ for given 
$f_{1}, \ldots , f_{n}$ is just stably equivalent to the above example, one still cannot eliminate the part corresponding to ‘
$nS^{2} \times S^{2}$.’
As applications of Theorem 1.2 and its generalization, Theorem 4.2, we shall present two non-smoothability results: non-smoothable families and non-smoothable actions. First we describe the background to our study of non-smoothable families. One of the motivations of this study is comparison between the diffeomorphism and homeomorphism groups of a given manifold. For lower-dimensional manifolds, it is known that there is no essential difference between these two groups from a homotopical point of view: for an arbitrary orientable closed manifold 
$M$ of dimension no greater than 
$3$, the inclusion
\begin{equation} \operatorname{Diff}(M) \hookrightarrow \operatorname{Homeo}(M)\end{equation}
is known to be a weak homotopy equivalence, where 
$\operatorname {Homeo}(M)$ and 
$\operatorname {Diff}(M)$ are equipped with the 
$C^{0}$-Whitney topology and the 
$C^{\infty }$-Whitney topology, respectively. (One can check this fact directly in both cases of dimension 
$1$ and of dimension 
$2$ with genus less than 
$2$. The case of dimension 
$2$ and genus greater than 
$1$ can be reduced to a consideration about the mapping class groups (see, for example, [Reference Farb and MargalitFM12]). For the three-dimensional case, see [Reference HatcherHat80].) Dimension 
$4$ is the smallest dimension in which the inclusion (2) may not be a weak homotopy equivalence.
Here we summarize known results in dimension 
$4$. First, Donaldson's result on his polynomial invariant [Reference DonaldsonDon90, § VI (i)] and Quinn's result [Reference QuinnQui86, 1.1 Theorem] imply that the natural map 
$\pi _{0}(\operatorname {Diff}(K3)) \to \pi _{0}(\operatorname {Homeo}(K3))$ is not a surjection. This follows also from a property of the Seiberg–Witten invariant (see [Reference NicolaescuNic00, Theorem 3.3.28], for example). Using Morgan and Szabó's rigidity result on the Seiberg–Witten invariant [Reference Morgan and SzabóMS97], one may also show that 
$\pi _{0}(\operatorname {Diff}(M)) \to \pi _{0}(\operatorname {Homeo}(M))$ is not a surjection also for a homotopy 
$K3$ surface 
$M$. Ruberman [Reference RubermanRub99] gave the first example of 
$4$-manifolds 
$M$ for which 
$\pi _{0}(\operatorname {Diff}(M)) \to \pi _{0}(\operatorname {Homeo}(M))$ are not injections. Ruberman's work is based on one-parameter families of Yang–Mills anti-self-dual equations, and this is the first striking application of gauge theory for families. Later, Baraglia and the second author [Reference Baraglia and KonnoBK20] generalized Ruberman's result using 
$1$-parameter families of Seiberg–Witten equations, and it was confirmed that 
$\pi _{0}(\operatorname {Diff}(M)) \to \pi _{0}(\operatorname {Homeo}(M))$ is not an injection for 
$M=n(K3 \# S^{2} \times S^{2})$ with 
$n \geq 2$ or 
$M=2n\operatorname {{\Bbb C} P}^{2} \# m(-\operatorname {{\Bbb C} P}^{2})$ with 
$n \geq 2$, 
$m \geq 10n+1$. By a totally different approach, Watanabe [Reference WatanabeWat18] showed that 
$\pi _{1}(\operatorname {Diff}(S^{4})) \to \pi _{1}(\operatorname {Homeo}(S^{4}))$ is not an injection using Kontsevich's characteristic classes for sphere bundles.
In this paper we propose a new approach to the comparison problem between 
$\operatorname {Diff}(M)$ and 
$\operatorname {Homeo}(M)$ in dimension 
$4$. Our strategy is that, developing gauge theory for families, we shall obtain a constraint on a smooth fiber bundle of a 
$4$-manifold, and detect non-smoothable topological families of smooth 
$4$-manifolds. The existence of such a family implies that 
$\operatorname {Diff}(M) \hookrightarrow \operatorname {Homeo}(M)$ is not a weak homotopy equivalence for the fiber 
$M$. Here let us clarify the meaning of ‘non-smoothable’ topological families. Let 
$M$ be an oriented topological manifold admitting a smooth structure, 
$B$ be a smooth manifold and 
$M \to X \to B$ be a fiber bundle whose structure group is in 
$\operatorname {Homeo}(M)$. We say that the bundle 
$X$ is non-smoothable as a family or 
$X$ has no smooth reduction if for any smooth structure on 
$M$ there is no reduction of the structure group of 
$X$ to 
$\operatorname {Diff}(M)$ via the inclusion 
$\operatorname {Diff}(M) \hookrightarrow \operatorname {Homeo}(M)$. Namely, we say that 
$X$ is non-smoothable as a family if there is no lift of the classifying map 
$\varphi : B \to B\operatorname {Homeo}(M)$ of 
$X$ to 
$B \operatorname {Diff}(M)$ along the natural map 
$B \operatorname {Diff}(M) \to B \operatorname {Homeo}(M)$ with respect to any smooth structure on 
$M$:
Now we can describe our non-smoothability results. Let 
$-E_{8}$ denote the (unique) closed simply connected oriented topological 4-manifold whose intersection form is the negative-definite 
$E_{8}$-lattice. For a subset 
$I=\{i_{1},\ldots ,i_{k}\} \subset \{1,2,\ldots ,m\}$ with cardinality 
$k$, denote by 
$T^{k}_{I}$ the 
$k$-torus embedded in the 
$m$-torus 
$T^{m}$ defined as the product of the 
$i_{1}, \ldots , i_{k}$th 
$S^{1}$-components. The following theorem claims that there exist non-smoothable families over the torus 
$T^{n}$ for 
$n \in \{1, \ldots ,4\}$ whose fibers are the topological (but smoothable) 
$4$-manifolds 
$2(-E_{8}) \# m S^{2}\times S^{2}$ with 
$m = n+2$. Moreover, we shall ensure that the total spaces of the families are smoothable as manifolds.
Theorem 1.3 (Theorem 5.2)
Let 
$3\leq m \leq 6$. Let 
$M$ be the topological (but smoothable) 
$4$-manifold defined by
\[ M = 2({-}E_{8}) \# m S^{2}\times S^{2}. \]
Then there exists a 
$\operatorname {Homeo}(M)$-bundle
\[ M \to X \to T^{m} \]
over the 
$m$-torus satisfying the following properties. Let 
$I=\{i_{1},\ldots ,i_{k}\}$ be an arbitrary subset of 
$\{1,2,\ldots ,m\}$ with cardinality 
$k$.
• The total space
$X$ admits a smooth manifold structure.• If
$k\leq m-3$, the restricted family
admits a reduction to\[ X|_{T^{k}_{I}} \to T^{k}_{I} \]
$\operatorname {Diff}(M)$ for some smooth structure on $M$.• If
$m-2\leq k\leq m$, the restricted family
has no reduction to\[ X|_{T^{k}_{I}} \to T^{k}_{I} \]
$\operatorname {Diff}(M)$ for any smooth structure on $M$.
Non-smoothability as families in Theorem 1.3 is detected by Theorem 4.2, which generalizes Theorem 1.2. To apply this theorem, we need to calculate the Dirac index bundle. To do this, we shall use (a variant of) the celebrated Novikov theorem on topological invariance of rational Pontryagin classes. Smoothability as manifolds is verified using Kirby–Siebenmann theory.
Remark 1.3 As noted above, for a homotopy 
$K3$ surface 
$M$, it was shown that 
$\pi _{0}(\operatorname {Diff}(M)) \to \pi _{0}(\operatorname {Homeo}(M))$ is not a surjection. Let 
$M \to X \to S^{1}$ be the mapping torus for a representative of a non-zero topological isotopy class in the cokernel of 
$\pi _{0}(\operatorname {Diff}(M)) \to \pi _{0}(\operatorname {Homeo}(M))$. Then 
$X$ is an example of a non-smoothable family. Theorem 1.3 contains this simplest example 
$M \to X \to S^{1}$. To our knowledge, non-smoothable families over higher-dimensional base spaces and the problem of smoothing of the total spaces have not been discussed so far.
From the last property of 
$X$ in Theorem 1.3, non-smoothability as a family, we immediately obtain the following corollary.
Corollary 1.1 For 
$0\leq n\leq 3$, let 
$M$ be a smooth 
$4$-manifold which is homeomorphic to 
$K3\# n S^{2} \times S^{2}$. Then the inclusion
\[ \operatorname{Diff}(M) \hookrightarrow \operatorname{Homeo}(M) \]
is not a weak homotopy equivalence.
Here are three remarks on Corollary 1.1.
Remark 1.4 The result of Corollary 1.1 in the case where 
$n=0$ follows also from the combination of Morgan and Szabó [Reference Morgan and SzabóMS97] and Quinn [Reference QuinnQui86]. However, to the best of our knowledge, the result in the case where 
$n >0$ is new even when 
$M$ is diffeomorphic to 
$K3\# n S^{2} \times S^{2}$. To see that the case where 
$n=0$ follows from [Reference Morgan and SzabóMS97, Reference QuinnQui86], consider the unique spin structure on a smooth 
$4$-manifold homeomorphic to 
$K3$. This 
$4$-manifold has non-zero Seiberg–Witten invariant for the spin structure by [Reference Morgan and SzabóMS97], and from this we can deduce that there does not exist an orientation-preserving diffeomorphism which reverses the orientation of 
$H^{+}$.
Remark 1.5 We note that there exist exotic 
$K3\#nS^{2} \times S^{2}$ not only for 
$n=0$. To see the existence of exotic 
$K3\#nS^{2} \times S^{2}$ for some positive 
$n$, we may use a result of Park and Szabó [Reference Park and SzabóPS00]. By Theorem 1.1 or Proposition 3.2 of [Reference Park and SzabóPS00], we may ensure that there exist exotic 
$K3\#2k(S^{2} \times S^{2})$ for all 
$k>0$.
Remark 1.6 By results of Wall [Reference WallWal64] and Quinn [Reference QuinnQui86], any algebraic automorphism of the intersection form of 
$K3\# nS^{2} \times S^{2}$ is realized both by a homeomorphism and a diffeomorphism for 
$n \geq 1$. Therefore we cannot find any difference between 
$\operatorname {Diff}(K3\# n S^{2} \times S^{2})$ and 
$\operatorname {Homeo}(K3\# n S^{2} \times S^{2})$ only using realizability of an automorphism on the intersection form.
Furthermore, combining Theorem 1.3 with an observation relating to results of Wall [Reference WallWal64] and Quinn [Reference QuinnQui86] (Proposition 5.1), we can also obtain information about a sort of quotient of 
$\operatorname {Homeo}(M)$ divided by 
$\operatorname {Diff}(M)$ for 
$M=K3 \# S^{2} \times S^{2}$. To be precise, since 
$\operatorname {Diff}(M)$ is not closed in 
$\operatorname {Homeo}(M)$ with respect to a natural topology such as the 
$C^{0}$-topology, we consider the homotopy quotient
As another application, on the topological 
$4$-manifold 
$2(-E_{8}) \# m S^{2}\times S^{2}$ with 
$m \geq 3$, we shall construct non-smoothable 
${\Bbb Z}^{m-2}$-actions. Note that the 
$4$-manifold 
$2(-E_{8}) \# m S^{2}\times S^{2}$ is homeomorphic to 
$K3\#(m-3)S^{2} \times S^{2}$ and hence admits a smooth structure.
Theorem 1.5 (See Theorem 5.1)
Let 
$m \geq 3$. The topological (but smoothable) 
$4$-manifold 
$M$ defined by
\[ M = 2({-}E_{8}) \# m S^{2}\times S^{2} \]
admits commuting self-homeomorphisms 
$f_{1}, \ldots , f_{m}$ satisfying the following properties. Let 
$I=\{i_{1},\ldots ,i_{k}\}$ be an arbitrary subset of 
$\{1,2,\ldots ,m\}$ with cardinality 
$k$.
• If
$k\leq m-3$, then there exists a smooth structure on $M$ such that $f_{i_{1}}, \ldots , f_{i_{k}}$ are diffeomorphisms with respect to the smooth structure.• If
$k\geq m-2$, then there exists no smooth structure on $M$ such that all $f_{i_{1}}, \ldots , f_{i_{k}}$ are diffeomorphisms with respect to the smooth structure.
Non-smoothable group actions on 
$4$-manifolds has been studied by many authors. The main tool to detect them is equivariant gauge theory, but the third author of this paper found that gauge theory for families can be also used to study non-smoothable actions in [Reference NakamuraNak10], and this direction was developed by Baraglia [Reference BaragliaBar19a]. The proof of Theorem 1.5 is based on a technique different from [Reference NakamuraNak10, Reference BaragliaBar19a], and the result itself is new. We will compare the result of Theorem 1.5 with previous research in Remark 5.1 in detail.
As a further research direction, once one can establish a Bauer–Furuta version of the gluing result in [Reference Baraglia and KonnoBK20], then we one get results on non-smoothable actions and families on any spin 
$4$-manifold with signature 
$-32$ following the same strategy of this paper. However, we are also considering developing a way to deal with more general signature and 
$b_{+}$.
A brief outline of the contents of this paper is as follows. In § 2 we shall recall some materials of the families Seiberg–Witten invariant. In § 3 we shall discuss when the tangent bundle along fibers admits a fiberwise spin structure. In § 4 we shall prove the main results in this paper, the rigidity theorem, and its consequences, such as a 
$10/8$-type inequality. In § 5 we shall give two applications, non-smoothable actions and families, of the results given in § 4. Sections 6 and 7 are devoted to proving some results needed to establish the applications in § 5. The main tool in §§ 6 and 7 is Kirby–Siebenmann theory, and arguments there may be of independent interest even outside the gauge-theoretic context. In § 6 we shall calculate the Dirac index bundle. More precisely, we shall give a few sufficient conditions for families of spin 
$4$-manifolds to have trivial index bundles. In § 7 we shall show the smoothability as manifolds of the total spaces of the non-smoothable families given in § 5.
Addendum
After the first version of this paper appeared on the arXiv, David Baraglia informed the second author about a draft of his paper [Reference BaragliaBar19b]. Adapting the construction of examples of families in this paper for his constraints on families of 
$4$-manifolds, he generalizes Corollary 1.1 of this paper as Theorem 1.8 and Corollary 1.9 of [Reference BaragliaBar19b]. We note that his way to prove these results is different from ours: to prove his Theorem 1.8 and Corollary 1.9, Baraglia used a family version of Donaldson's diagonalization theorem (corresponding to Theorems 1.1 and 1.2 in [Reference BaragliaBar19b]), while we use a family version of the 10/8-inequality to prove Corollary 1.1.
2. Families Seiberg–Witten invariant
In this section we shall recall some materials of the families Seiberg–Witten invariant. In particular, we shall recall an interpretation of the families Seiberg–Witten invariant as a kind of mapping degree in § 2.2.
2.1 Seiberg–Witten equations with $j$-action
First we recall some basics of the Seiberg–Witten equations on a spin 
$4$-manifold in the unparameterized setting. A special feature of the Seiberg–Witten equations on a spin 
$4$-manifold is that the equations have an extra symmetry, written as the ‘
$j$-action’, compared with the Seiberg–Witten equations on a general 
$\operatorname {Spin}^{c}$ 
$4$-manifold. We refer the reader to [Reference MorganMor96] for the generality of the Seiberg–Witten equations, and to [Reference FurutaFur01, Reference FurutaFur, Reference Bauer and FurutaBF04] for the monopole maps on spin 
$4$-manifolds.
Let 
$M$ be a closed Riemannian 
$4$-manifold with a spin structure 
$\mathfrak {s}$. Let 
$S=S^+\oplus S^-$ be the spinor bundle. Note that 
$S$ has a quaternionic structure; in particular, the multiplication of 
$j \in \mathbb {H}$ is defined. The 
$j$-action is anti-linear with respect to the complex structure of 
$S$. Let us abbreviate the tangent bundle 
$TM$ to 
$T$ and identify 
$T$ with the cotangent bundle 
$T^*M$ by the metric. Let 
$C(T)$ be the Clifford bundle of 
$T$. As a vector bundle, the bundle 
$C(T)$ is identified with the bundle of exterior product 
$\Lambda ^*T$. The Clifford multiplication is given by a bundle morphism
\[ \rho\colon \Lambda^*T\to\operatorname{End}_{{\Bbb R}}( S). \]
Namely, for 
$v\in \Lambda ^*T_x$, 
$\rho (v)$ is an endomorphism of 
$S_x$. Here 
$T_x$, 
$S_x$ are the fibers over 
$x$. The spinor bundle has a 
${\Bbb Z}_2$-grading 
$S=S^+\oplus S^-$, and we have also 
$\Lambda ^*T=\Lambda ^{\text {even}}T\oplus \Lambda ^{\text {odd}}T$. If 
$v$ is in 
$\Lambda ^{\text {even}}T$, 
$\rho (v)$ preserves the 
${\Bbb Z}_2$-grading of 
$S^+\oplus S^-$. If 
$v\in \Lambda ^{\text {odd}}T$, then 
$\rho (v)$ switches 
$S^+$ and 
$S^-$. Note that the Clifford multiplication 
$\rho (v)$ commutes with the 
$j$-action:
\[ \rho(v)j = j\rho(v). \]
The complexified Clifford multiplication is also defined,
\[ \rho\colon\Lambda^*T\otimes_{\Bbb R}{\Bbb C}\to\operatorname{End}_{{\Bbb C}}(S), \]
which anti-commutes with the 
$j$-action, that is, for 
$v\otimes c \in \Lambda ^*T\otimes _{\Bbb R}{\Bbb C}$, we have
\[ \rho(v\otimes c) j = j\rho(v\otimes \bar{c}). \]
The Levi-Civita connection on 
$T$ induces a spin connection 
$\nabla _0$ on 
$S$, and the spin Dirac operator
\[ D_0\colon\Gamma(S^+)\to\Gamma(S^-) \]
is defined by
\[ D_0=\sum_i\rho(e_i)(\nabla_0)_{e_i}, \]
where 
$\{e_i\}$ is a local orthonormal frame of 
$T$. Then 
$D_0$ commutes with 
$j$. Note that the spin connection 
$\nabla _0$ induces a trivial flat connection 
$A_0$ on 
$L_0=\det S^+ \cong M\times {\Bbb C}$. The 
$j$-action on 
$S^+$ induces the 
$j$-action on 
$L_0$ given by complex conjugation. Let 
$A$ be a 
$\operatorname {U}(1)$-connection on 
$L_0$. If we write 
$A$ as 
$A=A_0+a$ for an imaginary-valued 
$1$-form 
$a\in i\Omega ^1(M)$, then the 
$j$-action on 
$L_0$ induces the 
$j$-action on 
$\operatorname {U}(1)$-connections given by
\[ j\cdot A = A_0-a. \]
For a 
$\operatorname {U}(1)$-connection 
$A=A_0+a$, we have a unique 
$\operatorname {Spin}^{c}(4)$-connection 
on 
$S$ which induces the Levi-Civita connection on 
$T$ and 
$A$ on 
$L_0$. We have the Dirac operator associated with 
as follows:
\[ D_A\phi=D_0\phi+\tfrac12\rho(a)\phi. \]
In fact, 
$D_A$ is a Dirac operator on the 
$\operatorname {Spin}^{c}$ structure associated to the spin structure 
$\mathfrak {s}$. Note that 
$D_A$ is 
$j$-equivariant:
\[ D_{(j\cdot A)}(j\phi) = jD_A\phi. \]
As mentioned above, 
$\rho (v)$ for even degree 
$v$ preserves the components 
$S^\pm$. In particular, it can be seen that 
$\rho (v)$ for a self-dual 
$2$-form 
$v$ is an endomorphism of 
$S^+$, that is, 
$\rho (\Lambda _+^2T\otimes {\Bbb C})\subset \operatorname {End}_{{\Bbb C}}(S^+)$.
Proposition 2.1 [Reference MorganMor96, Lemma 4.1.1]
For 
$\phi \in \Gamma (S^+)$, define the traceless endomorphism 
$q(\phi )$ by
\[ q(\phi)=\phi\otimes\phi^*-\frac{|\phi|^2}{2}\operatorname{id}. \]
Then 
$q(\phi )$ can be identified with a section of 
$\Lambda _+^2(T)\otimes i{\Bbb R}$.
Now we can write down the Seiberg–Witten equations:
\begin{equation} \left\{\begin{array}{@{}l} D_{A}\phi=0,\\ F_{A}^{+} = q(\phi), \end{array}\right. \end{equation}
where 
$F_A^+$ is the self-dual part of the curvature of 
$A$. If we write 
$A=A_0+a$, then equations (3) are rewritten as
\[ \left\{\begin{array}{@{}l} D_{A_0}\phi+\tfrac12\rho(a)\phi=0,\\ d^+a -q(\phi) =0. \end{array}\right. \]
As we have already seen, the first equation is 
$j$-equivariant. Since we have
\[ F_{jA}=F_{A_0-a}={-}da,\quad q(j\phi)={-}q(\phi), \]
the second equation is also 
$j$-equivariant.
The gauge transformation group 
${\mathcal {G}}=\operatorname {Map}(M,\operatorname {U}(1))$ acts on the space of 
$\operatorname {U}(1)$-connections of 
$L_{0}$ and positive spinors by
\[ u(A,\phi) = (A-2u^{{-}1}du,u\phi) \]
for 
$u \in {\mathcal {G}}$. The Seiberg–Witten equations (3) are 
${\mathcal {G}}$-equivariant. The gauge action anti-commutes with the 
$j$-action:
\[ u(x)j=j\overline{u(x)}\quad\text{for }x\in M. \]
The moduli space of solutions to the Seiberg–Witten equations is the set of gauge equivalence classes of solutions:
\[ \mathcal{M}=\{\text{solutions to \eqref{eqn3}}\}/{\mathcal{G}}. \]
Roughly speaking, the Seiberg–Witten invariant is defined by ‘counting of 
$\#\mathcal {M}$’. Furthermore, the number ‘
$\#\mathcal {M}$’ can be interpreted as the ‘mapping degree’ of a map, called the monopole map, whose zero set is essentially 
$\mathcal {M}$. (The precise meaning of these will be explained in § 2.2 in a parameterized setting.)
The monopole map is defined by
\begin{equation} \begin{gathered} m\colon {\rm i}\Omega^1(M)\oplus \Gamma(S^+)\to {\rm i}(\Omega^0_*\oplus\Omega^+)(M)\oplus \Gamma(S^-),\\ m(a,\phi)= (d^*a, d^+a - q(\phi), D_{A_0}\phi+\tfrac12\rho(a)\phi), \end{gathered} \end{equation}
where 
$\Omega ^0_*(M)=\operatorname {Im}(d^*\colon \Omega ^1(M)\to \Omega ^0(M))$. The map 
$m$ is decomposed into the sum 
$m=l+c$ of the linear map 
$l=(d^*,d^+, D_{A_0})$ and the quadratic part 
$c$ given by 
$c(a,\phi )=(0,-q(\phi ),\frac 12\rho (a)\phi )$. For the purpose of carrying out a suitable analysis, we take the 
$L^2_k$-completion (
$k\geq 4$) of the domain, and the 
$L^2_{k-1}$-completion of the target, and extend 
$m$ to the completed spaces. Denote by 
$\mathcal {U}^\prime$ and 
$\mathcal {U}$ the completed domain and target, respectively. Then 
$m\colon \mathcal {U}^\prime \to \mathcal {U}$ is a smooth map between Hilbert spaces. The linear part 
$l$ is a Fredholm map of index
\[ -\frac{\operatorname{sign}(M)}4 + b_1(M) -b_+(M), \]
and 
$c$ is a nonlinear compact map.
We take the 
$L^2_{k+1}$-completion of the gauge group 
${\mathcal {G}}$. Then the 
${\mathcal {G}}$-action is smooth. The space 
$\ker (d^*\colon i\Omega ^1(M)\to i\Omega ^0(M))$ is a global slice of the 
${\mathcal {G}}$-action at 
$(0,0)$, and we have
\[ m^{{-}1}(0) = \{\text{solutions to \eqref{eqn3}}\}\cap \ker d^*. \]
The slice 
$\ker d^*$ still has a remaining gauge symmetry. Let 
$\mathrm {Harm}(M,S^1)$ be the kernel of the composition of the maps
\[ L^2_{k+1}(\operatorname{Map}(M,S^1))\overset{d}{\to}L^2_k(i\Omega(M)) \xrightarrow[]{d^*+d^+} L^2_{k-1}(i(\Omega^0\oplus\Omega^+)(M)). \]
Denote by 
$\mathrm {Harm}(M,S^1)$ the space of harmonic maps from 
$M$ to 
$S^{1}$. Then 
$m$ is 
$\mathrm {Harm}(M,S^1)$-equivariant, and we have
\[ \mathcal{M} = m^{{-}1}(0)/\mathrm{Harm}(M,S^1). \]
We also have an identification
\[ \mathrm{Harm}(M,S^1) \cong S^1\times H^1(M;{\Bbb Z}), \]
which is obtained by fixing a splitting of the exact sequence
\[ 1\to S^1\to \mathrm{Harm}(M,S^1)\to H^1(M;{\Bbb Z})\to 0. \]
The monopole map 
$m$ is also 
$j$-equivariant, when 
$j$ acts on the spaces 
$i\Omega ^*(M)$ of imaginary-valued forms by multiplication by 
$-1$. The 
$j$ action anti-commutes with the 
$\mathrm {Harm}(M,S^1)$-action in the sense that
\[ j(z,a)= (\bar{z}, -a)j \]
for 
$(z,a)\in S^1\times H^1(M;{\Bbb Z})$.
Set 
$\operatorname {Pin}(2) = \langle S^1, j\rangle$, the group generated by 
$S^{1}$ and 
$j$ in 
$\mathbb {H}$. Assuming 
$b_1(M)=0$, we have 
$\mathrm {Harm}(M,S^1) = S^1$, and 
$m$ is 
$\operatorname {Pin}(2)$-equivariant. Since 
$\mathcal {M}=m^{-1}(0)/S^1$, the 
$j$-action descends to a 
$\operatorname {Pin}(2)/S^1$-action on 
$\mathcal {M}$, where 
$\operatorname {Pin}(2)/S^1=\{\pm 1\}$.
2.2 Families Seiberg–Witten invariants
For a given family of 
$4$-manifolds, one can define a family version of the Seiberg–Witten invariant by counting the numbers of the parameterized moduli space of the Seiberg–Witten equations. This invariant can be also interpreted as the mapping degree of a finite-dimensional approximation of a family of monopole maps. In this subsection we shall recall these arguments. See, for example, [Reference BauerBau08, Reference Li and LiuLL01, Reference Bauer and FurutaBF04, Reference Baraglia and KonnoBK19, Reference SzymikSzy10] for references for this subsection.
Let 
$M$ be a closed oriented smooth 
$4$-manifold with a spin structure 
$\mathfrak {s}$, 
$B$ be a closed smooth connected manifold, and 
$\pi \colon X\to B$ be a locally trivial fiber bundle with fibers diffeomorphic to 
$M$. We assume that the structure group of 
$\pi \colon X\to B$ is in the group of orientation-preserving diffeomorphisms of 
$M$. In such a case we call 
$\pi \colon X\to B$ a smooth family of 
$M$. Let 
$T(X/B)$ be the tangent bundle along the fibers and choose a metric on 
$T(X/B)$. We shall consider the situation where 
$T(X/B)$ admits a spin structure 
$\mathfrak {s}_X$ whose restriction on each fiber is isomorphic to 
$\mathfrak {s}$. We call such a spin structure 
$\mathfrak {s}_X$ a global spin structure modeled on 
$\mathfrak {s}$. If we start with a 
$4$-manifold 
$M$ with 
$\operatorname {Spin}^{c}$ structure 
$\mathfrak {s}^c$, a global 
$\operatorname {Spin}^{c}$ structure modeled on 
$\mathfrak {s}^c$ is similarly defined.
Remark 2.1 As above, we say that a topological fiber bundle 
$X \to B$ is smooth if its structure group has been reduced to 
$\operatorname {Diff}(M)$ from 
$\operatorname {Homeo}(M)$. On the other hand, since we assumed that 
$B$ is a smooth manifold, another option of the definition of a smooth fiber bundle is a stronger one. Namely, one might assume some smoothness on the transition functions in the following sense. Let 
$\{g_{\alpha \beta } : U_{\alpha } \cap U_{\beta } \to \operatorname {Diff}(M)\}$ be the transition functions of 
$X \to B$ for some open covering 
$M={\bigcup} _{\alpha } U_{\alpha }$. We say that the transition functions are smooth if the map
\[ (U_{\alpha} \cap U_{\beta}) \times M \to M \]
given by
\[ (b,x) \mapsto g_{\alpha\beta}(b)x \]
is smooth. If the transition functions satisfy this smoothness, then the total space 
$X$ is a smooth manifold and the projection 
$X \to B$ is a smooth map. One might call 
$X \to B$ a smooth fiber bundle only in this case.
However, it is in fact shown in [Reference Müller and WockelMW09] that these two definitions of a smooth fiber bundle are equivalent to each other: if a topological fiber bundle 
$X\to B$ over a smooth manifold 
$B$ has a reduction to 
$\operatorname {Diff}(M)$, then, after replacing 
$X$ with an isomorphic bundle, we may assume that the transition functions of 
$X$ satisfy the smoothness in the above sense.
Assume that 
$b_1(M)=0$ and that a global spin structure 
$\mathfrak {s}_X$ modeled on 
$\mathfrak {s}$ is given on 
$\pi \colon X\to B$. Let 
$m\colon \mathcal {U}^\prime \to \mathcal {U}$ be the Sobolev completed monopole map given in § 2.1. Recall that 
$m$ is 
$\operatorname {Pin}(2)$-equivariant since 
$b_1(M)=0$. Once we fix a fiberwise Riemannian metric on 
$X$, we can obtain a family of monopole maps
\[ \tilde{\mu}\colon\mathcal{A}\to\mathcal{C} \]
by parameterizing the argument in § 2.1 over 
$B$. Here 
$\mathcal {A}$ and 
$\mathcal {C}$ are the Hilbert bundles over 
$B$ with fibers 
$\mathcal {U}^\prime$ and 
$\mathcal {U}$, and 
$\tilde {\mu }$ is a fiber-preserving map whose restriction on each fiber is identified with the monopole map 
$m$.
It is convenient to trivialize 
$\mathcal {C}\cong B\times \mathcal {U}$ by the Kuiper–Segal theorem [Reference KuiperKui65, Reference SegalSeg69]. Define 
$\mu \colon \mathcal {A}\to \mathcal {U}$ by the composition of 
$\tilde \mu$ with the projection 
$\mathcal {C}\cong B\times \mathcal {U}\to \mathcal {U}$. The map 
$\mu$ satisfies the following compactness property.
Proposition 2.2 (cf. [Reference Bauer and FurutaBF04])
The preimage 
$\mu ^{-1}(O)$ of a bounded set 
$O\subset \mathcal {U}$ is contained in some bounded disk bundle.
This can be verified straightforwardly by extending the argument in [Reference Bauer and FurutaBF04, Proposition 3.1] since we have assumed that 
$B$ is compact. By Proposition 2.2, the map 
$\mu$ can be extended to the map
\[ \mu^+\colon T\mathcal{A}\to S^{\mathcal{U}}, \]
where 
$T\mathcal {A}$ is the Thom space and 
$S^{\mathcal {U}}$ is the one-point completion of 
$\mathcal {U}$ obtained by collapsing.
The family 
$\pi \colon X\to B$ induces a vector bundle
\[ {\Bbb R}^{b_{+}(M)} \to H^+ \to B \]
whose fiber over 
$b\in B$ is the space 
$H^+(M_b)$ of harmonic self-dual 
$2$-forms on 
$M_b=\pi ^{-1}(b)$. We call 
$H^+$ the bundle of 
$H^+(M)$. The isomorphism class of 
$H^{+}$ is independent of the choice of fiberwise Riemannian metric on 
$X$ since the Grassmannian of maximal-dimensional positive-definite subspaces of 
$H^{2}(M;{\Bbb R})$ is contractible. We also have the index bundle 
${\rm ind}\, {D} \in KO_G(B)$ of the family of Dirac operators on the spin family 
$X\to B$. Here we assume 
$G=\operatorname {Pin}(2)$ or 
$G=S^1 \subset \operatorname {Pin}(2)$. Let 
$L\colon \mathcal {A}\to \mathcal {C}$ be the family of linear parts of 
$\mu$, which is a fiberwise linear map whose restriction on each fiber is 
$l$ in § 2.1. In § 4 we will use the element 
$\alpha \in KO_G(B)$ defined by
\[ \alpha:=[{\rm ind}\, {L}]=[{\rm ind}\, D] -[H^+] \in KO_G(B). \]
Choose a finite-dimensional trivial vector subbundle 
$F^\prime = \underline {V}=B\times V\subset \mathcal {C}$ so that 
$F^\prime$ contains the fiberwise cokernel of 
$L$, and let 
$F=L^{-1}(F^\prime )$. Then 
$\alpha = [F]-[F^\prime ]$ holds and the image of 
$F$ under 
$L$ is contained in 
$\underline {V}$. On the other hand, the image of 
$F$ under the nonlinear part 
$\mu -L$ is not necessarily contained in 
$\underline {V}$, and we shall project the image of 
$\mu$ on 
$V$. Let 
$S(V^\perp )$ be the unit sphere in the orthogonal complement 
$V^\perp$ of 
$V$. The inclusion 
$S^{V}\to S^{\mathcal {U}}\setminus S(V^\perp )$ is a deformation retract. Let 
$\rho _V$ be a retracting map. A finite-dimensional approximation of the family of monopole maps is defined by
\[ f_{V}=\rho_V\circ\mu|_{TF}\colon TF\to V. \]
By [Reference Bauer and FurutaBF04], the above construction defines a well-defined class 
$[f_V]$ in the stable cohomotopy set
\begin{equation} \{T({\rm ind}\, {D} -H^+),S^0\}^G_{\mathcal{U}} = \underset{W\subset V^\perp}{\operatorname{colim}}\big[S^W\wedge TF,S^W\wedge S^V\big]^G. \end{equation}
We call the class 
$[f_V]$ the Bauer–Furuta invariant or the stable cohomotopy Seiberg–Witten invariant of the family 
$\pi \colon X\to B$.
In the case where 
$G=S^1$, we shall define the (mod 
$2$) degree homomorphism
\[ \deg\colon \{TF,S^V\}^{S^1}_{\mathcal{U}}\to{\Bbb Z}_2 \]
below, provided that
\[ d:={-}\frac{\operatorname{sign}(M)}{4} -1-b_+(M_i)+\dim B =0. \]
The condition 
$d=0$ is equivalent to
\[ \operatorname{rank} F +\dim B -\dim V =1, \]
and therefore the preimage of 
$f_{V}$ is one-dimensional. For a finite-dimensional approximation 
$f_V$ with sufficient large 
$V$ such that (7) below holds, we let
\[ FSW^{{\Bbb Z}_2}(X,\mathfrak{s}_X) = \deg [f_V]. \]
This definition coincides with the one in [Reference Baraglia and KonnoBK19, § 2].
When 
$G=S^1$, the universe 
$\mathcal {U}$ consists of 
${\Bbb C}$ on which 
$S^1$ acts by multiplication and the trivial real one-dimensional 
$S^1$-representation 
${\Bbb R}$ as irreducible summands. In this case, the stable cohomotopy set (5) is a group. The bundle 
$F$ is an 
$S^1$-equivariant bundle with fiber 
${\Bbb C}^{x+2a}\oplus {\Bbb R}^y$ over 
$B$ and 
$V={\Bbb C}^x\oplus {\Bbb R}^{y+b}$, where 
$x$, 
$y$ are non-negative integers and
\[ a ={-}\frac{\operatorname{sign}(M)}{16},\quad b=b_+(M). \]
When 
$G=\operatorname {Pin}(2)$, the universe 
$\mathcal {U}$ consists of 
${\Bbb H}$ on which 
$\operatorname {Pin}(2)$ acts by multiplication and the real one-dimensional non-trivial 
$\operatorname {Pin}(2)$-representation 
$\widetilde {{\Bbb R}}$ as irreducible summands. In order to distinguish this universe from that in the case where 
$G=S^1$, this 
$\operatorname {Pin}(2)$-universe is henceforth denoted by 
$\mathcal {U}^\prime$. In this case, 
$F$ is a 
$\operatorname {Pin}(2)$-equivariant bundle with fiber 
${\Bbb H}^{x+a}\oplus \widetilde {{\Bbb R}}^y$ over 
$B$ and 
$V={\Bbb H}^x\oplus \widetilde {{\Bbb R}}^{y+b}$ for some non-negative integers 
$x$, 
$y$.
Suppose that
\begin{equation} b_+(M)\geq \dim B+2. \end{equation}
Let 
$Ci$ be the mapping cone of the inclusion 
$i \colon TF^{S^1}\hookrightarrow TF$ of the 
$S^1$-fixed point set. We have a long exact sequence associated with the cofiber sequence 
$TF^{S^1}\to TF\to Ci$:
\[ \{S^1\wedge TF^{S^1},S^V\}^G_{\mathcal{U}}\to \{Ci,S^V\}^G_{\mathcal{U}}\to \{TF,S^V\}^G_{\mathcal{U}}\to\{ TF^{S^1},S^V\}^G_{\mathcal{U}}. \]
Since both the first and the last terms are trivial by assumption (6), the cohomotopy invariant 
$[f_V]$ can be regarded as an element of 
$\{Ci,S^V\}^G_{\mathcal {U}}$. Following [Reference BauerBau08], we let 
$[TF,S^V]^{G}_q$ be the set of homotopy classes of maps 
$g\colon TF\to S^V$ such that 
$g|_{TF^{S^1}}=f_{V}|_{TF^{S^1}}$. Then condition (6) implies a natural bijective correspondence
\[ [TF,S^V]^{G}_q\cong [TF/TF^{S^1},S^V]^{G}. \]
Since 
$F$ is a finite-dimensional 
$\operatorname {Pin}(2)$-equivariant vector bundle over a smooth compact connected manifold 
$B$ and 
$V$ is a finite-dimensional 
$\operatorname {Pin}(2)$-representation, the Thom space 
$TF$ and 
$S^V$ can be equipped with structures of 
$\operatorname {Pin}(2)$-equivariant CW complexes. By the equivariant Freudenthal suspension theorem [Reference tom DiecktDie11, Chapter II, (2.10)], we can choose sufficiently large 
$F$, 
$V$ satisfying
\begin{equation} \{T({\rm ind}\, {D}-[H^+]), S^0\}^{G}_{\mathcal{U}}\cong [TF,S^V]^{G}_q. \end{equation} To analyze 
$[TF,S^V]^{G}_q$, it is convenient to use the equivariant obstruction theory (see the appendix). Let 
$U=(TF/S^1)\setminus N(TF^{S^1})$, where 
$N(TF^{S^1})$ is an equivariant tubular neighborhood of 
$TF^{S^1}$ in 
$TF/S^1$. Then 
$U$ is a (possibly non-orientable) manifold with boundary. Set 
$k=\dim S^V$. The condition 
$d=0$ implies that 
$\dim U=k$. Note that 
$(TF/S^1)\setminus TF^{S^1}$ is 
${\Bbb Z}_2$-equivariantly homotopic to 
$U$, where 
${\Bbb Z}_{2}=\operatorname {Pin}(2)/S^1$. Then we have the following identifications:
\begin{gather*} H^k_{S^1}(TF,TF^{S^1};\pi_kS^V)\cong H^k(TF/S^1,TF^{S^1};{\Bbb Z})\cong H^k(U,\partial U; {\Bbb Z}), \\ H^k_{\operatorname {Pin}(2)}(TF,TF^{S^1};\pi_kS^V)\cong H^k_{{\Bbb Z}_2}(TF/S^1,TF^{S^1};\pi_kS^V)\cong H^k_{{\Bbb Z}_2}(U,\partial U; \pi_kS^V), \end{gather*}
where 
$H^k_G(\cdot ,\cdot ;\pi _kS^V)$ are the Bredon cohomology groups with coefficient 
$G$-module 
$\pi _kS^V$. Let us recall the following facts.
(F1) If we choose
$\beta _0 \in [TF,S^V]^{G}_q$ for each $G=\operatorname {Pin}(2)$ and $S^1$, then the correspondence $\beta \mapsto \gamma _G(\beta ,\beta _0)$ gives a bijective correspondence between
and\[ \{ TF,S^V\}^{G}_{\mathcal{U}}\big({\cong}\,[TF,S^V]^{G}_q\big) \]
by Theorem A.2, where\[ H^k_{G}(TF,TF^{S^1};\pi_kS^V) \]
$\gamma _{G}(\beta ,\beta _0)$ is the $G$-equivariant difference obstruction class.(F2)
$H^k(U,\partial U; {\Bbb Z})$ is isomorphic to ${\Bbb Z}$ if $U$ is orientable, and ${\Bbb Z}_2$ if $U$ is non-orientable.(F3) The forgetful map
is given by multiplication by\[ \bar\varphi\colon H^k_{{\Bbb Z}_2}(U,\partial U; \pi_kS^V)\to H^k(U,\partial U; {\Bbb Z})\cong{\Bbb Z}\text{ or } {\Bbb Z}_2 \]
$2$ (Proposition A.2). In particular, $\bar {\varphi }(c) \equiv 0\ \mathrm {mod} 2$ for
\[ c\in H^k_{\operatorname {Pin}(2)}(TF,TF^{S^1};\pi_kS^V) \cong H^k_{{\Bbb Z}_2}(U,\partial U; \pi_kS^V). \]
Let 
$\beta _0$ be the unit of the stable cohomotopy group 
$\{ TF,S^V\}^{S^1}_{\mathcal {U}}$. By (F1), the correspondence 
$\beta \mapsto \gamma _{S^1}(\beta ,\beta _0)$ for 
$\beta \in \{ TF,S^V\}^{S^1}_{\mathcal {U}}$ gives a bijective correspondence between 
$\{ TF,S^V\}^{S^1}_{\mathcal {U}}$ and 
$H^k_{S^1}(TF,TF^{S^1};\pi _kS^V)$ which is identified with 
$H^k(U,\partial U; {\Bbb Z})\cong {\Bbb Z}\text { or } {\Bbb Z}_2$. Define 
$\deg \beta \in {\Bbb Z}_{2}$ by
\[ \deg\beta = \gamma_{S^1}(\beta,\beta_0)\mod 2. \]
Since the degree 
$\deg \beta$ is the mod 
$2$ difference obstruction class of maps essentially from a manifold to a sphere with same dimension, this can be interpreted as a kind of mod 2 mapping degree. We may assume 
$\beta$ is represented by a map 
$g\colon (TF/{S^1}, TF^{S^1})\to (S^V,S^{V^{S^1}})$ which is smooth on the complement of 
$TF^{S^1}$. By perturbing 
$g$, the image of 
$g|_{TF^{S^1}}$ is contained in a subspace of 
$S^{V^{S^1}}$ of codimension 
$b_+(M)-\dim B\geq 2$. A choice of a generic point 
$v\in S^{V^{S^1}}\setminus (\operatorname {Im} g|_{TF^{S^1}})$ makes the preimage 
$g^{-1}(v)$ a compact 
$0$-manifold. Then 
$\deg \beta$ is the number modulo 
$2$ of elements in 
$g^{-1}(v)$.
Remark 2.2 For a single 
$4$-manifold, the moduli space is always orientable and the 
${\Bbb Z}$-valued Seiberg–Witten invariants can be defined. On the other hand, the moduli space for a family of 
$4$-manifolds may be non-orientable. Therefore only the 
${\Bbb Z}_2$-valued invariants can be defined in general.
3. Spin families
Let 
$M$ be a closed oriented smooth 
$4$-manifold with a spin structure 
$\mathfrak {s}$, 
$B$ be a closed manifold, and 
$\pi \colon X\to B$ be a smooth family with fiber 
$M$. Let 
$T(X/B)$ be the tangent bundle along the fibers. In this subsection we shall discuss when 
$T(X/B)$ admits a global spin structure modeled on 
$\mathfrak {s}$ defined in § 2.2.
Let 
$\operatorname {Diff}(M,[\mathfrak {s}])$ be the group of orientation-preserving self-diffeomorphisms 
$f\colon M\to M$ for which the pulled-back spin structures 
$f^*\mathfrak {s}$ are isomorphic to 
$\mathfrak {s}$. The notation 
$[\mathfrak {s}]$ indicates the isomorphism class of 
$\mathfrak {s}$. When a diffeomorphism 
$f$ belongs to 
$\operatorname {Diff}(M,[\mathfrak {s}])$, we just say that 
$f$ preserves 
$\mathfrak {s}$ for the sake of simplicity , although to be precise it should be said that 
$f$ preserves 
$[\mathfrak {s}]$. Let 
$\operatorname {Aut}(M,\mathfrak {s})$ be the group of pairs 
$(f,\hat {f})$, where 
$f\in \operatorname {Diff}(M,[\mathfrak {s}])$ and 
$\hat {f}$ is an automorphism of 
$\mathfrak {s}$ covering 
$f$. Then we have an exact sequence
\begin{equation} 1\to{\mathcal{G}}(\mathfrak{s})\to\operatorname{Aut}(M,\mathfrak{s})\to\operatorname{Diff}(M,[\mathfrak{s}])\to 1, \end{equation}
where 
${\mathcal {G}}(\mathfrak {s})$ is the gauge transformation group of the spin structure 
$\mathfrak {s}$, that is, the group of automorphisms of 
$\mathfrak {s}$ covering 
$\operatorname {id}_M$. Note that 
${\mathcal {G}}(\mathfrak {s})\cong \{\pm 1\}$. Taking the classifying spaces, we obtain a fibration
\[ B{\mathcal{G}}(\mathfrak{s})\to B\operatorname{Aut}(M,\mathfrak{s})\to B\operatorname{Diff}(M,[\mathfrak{s}]). \]
The homotopy class of a map 
$\tilde {\rho }\colon B\to B\operatorname {Aut}(M,\mathfrak {s})$ corresponds to the isomorphism class of a family 
$\pi \colon X\to B$ with a global spin structure on 
$T(X/B)$ modeled on 
$\mathfrak {s}$. Suppose that a map 
$\rho \colon B\to B\operatorname {Diff}(M,[\mathfrak {s}])$ is given. Since 
$B{\mathcal {G}}(\mathfrak {s})=B{\Bbb Z}_2\cong \operatorname {{\Bbb R} P}^\infty$, there exists a sole obstruction in 
$H^2(B;{\Bbb Z}/2)$ to lifting 
$\rho$ to a map 
$\tilde {\rho }\colon B\to B\operatorname {Aut}(M,\mathfrak {s})$. Denote by 
$O(\rho )$ the obstruction class.
Suppose that we have finitely many commuting orientation-preserving self-diffeomorphisms 
$f_1,\ldots ,f_n \in \operatorname {Diff}(M,[\mathfrak {s}])$. Then we can form the multiple mapping torus
\[ X=X_{f_1,\ldots,f_n} \to T^n. \]
Let us denote also by 
$O(f_1,\ldots ,f_n)$ the obstruction 
$O(\rho )$ for such a family, where 
$\rho \colon T^n\to B\operatorname {Diff}(M,[\mathfrak {s}])$ is the classifying map.
Proposition 3.1 The obstruction class 
$O(f_1,\ldots ,f_n) \in H^2(T^n;{\Bbb Z}/2)$ is zero if and only if 
$f_1,\ldots ,f_n$ admit lifts 
$\hat {f}_1,\ldots , \hat {f}_n$ to the spin structure 
$\mathfrak {s}$ which mutually commute.
Proof. If the lifts commute, then we can obviously construct a global spin structure by patching a product spin structure on 
$M\times [0,1]^n$ by the lifts. Therefore 
$O(f_1,\ldots ,f_n) =0$.
Conversely, suppose that 
$O(f_1,\ldots ,f_n) =0$. Let 
$C$ be the CW complex with one 
$0$-cell and one 
$1$-cell which forms a circle. Let 
$C_1,\ldots ,C_n$ be copies of 
$C$. A cell structure of 
$T^n$ is given by the product of 
$C_1,\ldots ,C_n$. Then
• the
$1$-skeleton of $T^{n}$ is the wedge sum of $C_1,\ldots ,C_n$, and• there is a bijection between the set of
$2$-cells and the set of pairs $(i,j)$ with $i\neq j$. Here each pair $(i,j)$ corresponds to a unique $2$-cell $D_{ij}$ bounded by the wedge sum $C_i\vee C_j$.
A choice of lifts 
$\hat {f}_i$ for 
$f_i$ determines a global spin structure on 
$\pi^{-1}(\text{$1$-skeleton})$ by identifying the spin structures on the endpoints of the 
$1$-cells via 
$\hat {f}_i$. The class 
$O(f_1,\ldots ,f_n)$ is the obstruction to extending such a spin structure on 
$\pi^{-1}(\text{$1$-skeleton})$ to 
$\pi^{-1}(\text{$2$-skeleton})$. To extend the spin structure on 
$\pi ^{-1}(C_i\vee C_j)$ to 
$\pi ^{-1}(D_{ij})$, the monodromy 
$\hat {f}_i \hat {f}_j \hat {f}_i^{-1} \hat {f}_j^{-1}$ should be 
$1 \in \operatorname {Aut}(M,\mathfrak {s})$. This completes the proof.
Definition 3.1 Let 
$(M,\mathfrak {s})$ be a spin 
$4$-manifold. Finitely many self-diffeomorphisms 
$f_1,\ldots ,f_n$ on 
$M$ are called spin commuting when
(i)
$f_1,\ldots ,f_n$ commute with each other,(ii) each
$f_i$ preserves the orientation of $M$ and the spin structure $\mathfrak {s}$,(iii)
$O(f_1,\ldots ,f_n)=0$, or equivalently, there exist commuting lifts $\hat {f}_1\cdots \hat {f}_n$.
If spin commuting diffeomorphisms 
$f_1,\ldots ,f_n$ are given, then we can form a multiple mapping torus 
$X=X_{f_1,\ldots ,f_n}$ with fibers 
$M$ which admits a global spin structure 
$\mathfrak {s}_{X}$ modeled on 
$\mathfrak {s}$. We call 
$(X,\mathfrak {s}_{X})$ the spin mapping torus associated with the spin commuting diffeomorphisms 
$f_1,\ldots ,f_n$.
Let us give a sufficient condition for vanishing of 
$O(f_{1}, \ldots ,f_{n})$. For a self-diffeomorphism 
$f$ on 
$M$, the support of 
$f$ is defined by
\[ \operatorname{supp} f = \overline{\{x\in M\,|\, f(x)\neq x\}}, \]
and so is the support of an element of 
$\operatorname {Aut}(M,\mathfrak {s})$ similarly.
Lemma 3.1 Let 
$(M,\mathfrak {s})$ be a spin manifold, and 
$f_{1}, \ldots , f_{n}$ be commuting diffeomorphisms on 
$M$ preserving the orientation of 
$M$ and 
$\mathfrak {s}$. If 
$\operatorname {supp}{f}_{1}, \ldots , \operatorname {supp}{f}_{n}$ are mutually disjoint and 
$M \setminus \operatorname {supp}{f}_{i}$ is connected for each 
$i$, then 
$O(f_{1}, \ldots ,f_{n})=0$ holds.
Proof. Because of Proposition 3.1, it suffices to show that there exist commuting lifts 
$\hat {f}_{1},\ldots , \hat {f}_{n}$ of 
$f_{1}, \ldots , f_{n}$ to the spin structure. Recall that we have an exact sequence (8). Let 
$\tilde {f}_{1}, \ldots , \tilde {f}_{n} \in \operatorname {Aut}(M,\mathfrak {s})$ be lifts of 
$f_{1}, \ldots , f_{n}$. For each 
$i \in \{1, \ldots , n\}$, the lift 
$\tilde {f}_{i}$ lives in the (spin) gauge group outside 
$\operatorname {supp}{f}_{i}$:
\[ \tilde{f}_{i}|_{M \setminus \operatorname{supp}{f}_{i}} \in \mathcal{G}(\mathfrak{s}|_{M \setminus \operatorname{supp}{f}_{i}}) = \mathrm{Map}(M \setminus \operatorname{supp}{f}_{i}, {\Bbb Z}/2) \cong {\Bbb Z}/2 = \{\pm1\}. \]
Define a lift 
$\hat {f}_{i} \in \operatorname {Aut}(M,\mathfrak {s})$ of 
$f_{i}$ by
\[ \hat{f}_{i} = \left\{\begin{array}{@{}ll} \widetilde{f_{i}} & {\rm if}\ \tilde{f}_{i}|_{M \setminus \operatorname{supp}{f}_{i}} = 1, \\ -1 \cdot \tilde{f}_{i} & {\rm if}\ \tilde{f}_{i}|_{M \setminus \operatorname{supp}{f}_{i}} ={-}1. \end{array}\right. \]
Then 
$\hat {f}_{1},\ldots , \hat {f}_{n}$ have disjoint supports each other, and hence mutually commute.
We note that, on the other hand, the obstruction class 
$O(f_1,\ldots ,f_n)$ may be non-trivial for some example of 
$f_1,\ldots ,f_n$.
Example 3.1 An example of a multiple mapping torus 
$X\to T^n$ with non-zero 
$O(f_1,\ldots ,f_n)$ is given as follows. Let 
$M$ be 
$T^3$ equipped with the spin structure 
$\mathfrak {s}_0$ with trivial 
$\operatorname {Spin}(3)$-bundle. The two-to-one homomorphism 
$h\colon \operatorname {Spin}(3)\to \operatorname {SO}(3)$ is given by the action of 
$\operatorname {Spin}(3)=\operatorname {Sp}(1)$ on 
$\operatorname {Im} {\Bbb H}$ by conjugation. Then the multiplication by
\[ h(i) = \begin{pmatrix} 1 & 0 & 0\\ 0 & -1 & 0\\ 0 & 0 & -1 \end{pmatrix}\quad \text{and}\quad h(j) = \begin{pmatrix} -1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & -1 \end{pmatrix} \]
on 
${\Bbb R}^3$ induces a pair 
$(f_1,f_2)$ of commuting diffeomorphisms on 
$T^3$. Their lifts 
$\hat {f}_1,\hat {f}_2$ to 
$\mathfrak {s}_0$ anticommute since 
$ij=-ji$. Therefore 
$O(f_1,f_2)$ is not zero.
So far we have considered the case of diffeomorphisms, but we can also consider its topological analogue. Namely, we can consider topological spin structures as discussed in [Reference NakamuraNak10] and also discuss an obstruction 
$O(f_{1}, \ldots , f_{n})$ to the lifting problem to topological spin structures for given commuting homeomorphisms 
$f_{1}, \ldots , f_{n}$. By a parallel argument, we have a topological version of Lemma 3.1.
Lemma 3.2 Let 
$M$ be an oriented topological manifold, 
$\mathfrak {s}$ be a topological spin structure on 
$M$, and 
$f_{1}, \ldots , f_{n}$ be commuting homeomorphisms on 
$M$ preserving the orientation of 
$M$ and 
$\mathfrak {s}$. If 
$\operatorname {supp}{f}_{1}, \ldots , \operatorname {supp}{f}_{n}$ are mutually disjoint, then 
$O(f_{1}, \ldots ,f_{n})=0$ holds.
4. Main results
In this section we shall give the main results in this paper and their consequences. Theorem 4.1 is a rigidity theorem for the families Seiberg–Witten invariants on families of spin 
$4$-manifolds. Combining Theorem 4.1 with Proposition 4.1, a non-vanishing of the families Seiberg–Witten invariants shown in [Reference Baraglia and KonnoBK20] for specific families, we obtain a non-vanishing result for more general families as Corollary 4.1. Theorem 4.2 gives a constraint on 
$b_{+}$ of the fibers of families of spin 
$4$-manifolds satisfying certain conditions. This is a family analogue of Furuta's 10/8-inequality [Reference FurutaFur01].
Theorem 4.1 Let 
$B$ be a closed smooth manifold. Let 
$M_1$ and 
$M_2$ be oriented closed smooth 
$4$-manifolds with spin structures 
$\mathfrak {s}_1$ and 
$\mathfrak {s}_2$, respectively, satisfying the following:
•
$b_1(M_1)=b_1(M_2)=0$, $b_+(M_1)=b_+(M_2)\geq \dim B + 2$.•
$-{\operatorname {sign}(M_i)}/{4} -1-b_+(M_i)+\dim B =0\ (i=1,2)$.
For 
$i=1,2$, let 
$X_i\to B$ be a smooth fiber bundle with fibers 
$M_i$ equipped with a global spin structures 
$\mathfrak {s}_{X_i}$ modeled on 
$\mathfrak {s}_i$, 
${\rm ind}\, {D}_i$ be the virtual index bundle of the family of Dirac operators for 
$\mathfrak {s}_{X_i}$ and 
$H^+_i\to B$ be the bundle of 
$H^+(M_i)$ associated to 
$X_{i}$. Set 
$\alpha _i= [{\rm ind}\, {D}_i] - [H_i^+]\in KO_{\operatorname {Pin}(2)}(B)$. If 
$\alpha _1=\alpha _2$, then we have
\[ FSW^{{\Bbb Z}_2}(X_1,\mathfrak{s}_{X_1}) = FSW^{{\Bbb Z}_2}(X_2,\mathfrak{s}_{X_2}). \]
We shall use the following lemma to prove Theorem 4.1, which is fundamental in this section.
Lemma 4.1 In the setting of § 2.2, suppose that condition (6) holds. Consider the maps
where 
$\varphi$ is the forgetful map restricting 
$\operatorname {Pin}(2)$-action to 
$S^1$-action. Then the image of 
$(\deg \circ \varphi )$ is 
$\{0\}$ or 
$\{1\}$, and is determined by 
$\alpha =[F]-[\underline {V}]\in KO_{\operatorname {Pin}(2)}(B)$.
Proof. The class 
$\alpha$ determines 
$\{TF,S^V\}^{\operatorname {Pin}(2)}_{\mathcal {U}^\prime }$, 
$\{ TF,S^V\}^{S^1}_{\mathcal {U}}$, 
$\varphi$, and hence also the image of 
$(\deg \circ \varphi )$. For 
$\beta _1^\prime ,\beta _2^\prime \in \{TF,S^V\}^{\operatorname {Pin}(2)}_{\mathcal {U}^\prime }$, the additivity of difference obstruction classes implies that
\[ \deg\varphi(\beta_1^\prime)-\deg\varphi(\beta_2^\prime) = \gamma_{S^1}(\varphi(\beta_1^\prime),\beta_0)-\gamma_{S^1}(\varphi(\beta_2^\prime),\beta_0) =\gamma_{S^1}(\varphi(\beta_1^\prime),\varphi(\beta_2^\prime)). \]
Moreover, fact (F3) in § 2.2 implies that
\[ \gamma_{S^1}(\varphi(\beta_1^\prime),\varphi(\beta_2^\prime))= \bar{\varphi}(\gamma_{\operatorname {Pin}(2)}(\beta_1^\prime,\beta_2^\prime)) \underset{(2)}{\equiv}0. \]
Therefore the image of 
$(\deg \circ \varphi )$ is 
$\{0\}$ or 
$\{1\}$.
Proof Proof of Theorem 4.1
We shall use the notation of § 2.2. As explained there, it follows that a family of monopole maps for each 
$(X_i,\mathfrak {s}_{X_i})$ defines a class 
$\beta _i^\prime$ in 
$\{TF,S^V\}^{\operatorname {Pin}(2)}_{\mathcal {U}^\prime }$, where 
$F$ and 
$V$ satisfy
\[ [F] - [\underline{V}] = \alpha_1 =\alpha_2. \]
Since the families Sieberg–Witten invariants for 
$(X_i,\mathfrak {s}_{X_i})$ are given by
\[ FSW^{{\Bbb Z}_2}(X_i,\mathfrak{s}_{X_i}) = \deg\varphi(\beta_i^\prime), \]
Lemma 4.1 implies that 
$FSW^{{\Bbb Z}_2}(X_1,\mathfrak {s}_{X_1})=FSW^{{\Bbb Z}_2}(X_2,\mathfrak {s}_{X_2})$.
Remark 4.1 The idea of using that 
$\varphi$ is given as multiplication by 
$2$ has appeared in [Reference LiLi06a, Reference LiLi06b, Reference BauerBau08].
Remark 4.2 Let 
$G=\operatorname {Pin}(2)$. Since the 
$G$-action on 
$B$ is trivial, we have an isomorphism
\[ KO_G(B) \cong (KO(B)\otimes R(G;{\Bbb R})) \oplus (K(B)\otimes R(G;{\Bbb C})) \oplus (KSp(B)\otimes R(G;{\Bbb H})), \]
where 
$R(G;\mathbb {F})$ is the free abelian group generated by irreducible 
$G$-representations over the field 
$\mathbb {F}$ [Reference SegalSeg69]. In our case, 
$[{\rm ind}\, {D}]$ is in the component 
$KSp(B)\otimes R(G;{\Bbb H})$, and 
$[H^+]$ is in 
$KO(B)\otimes R(G;{\Bbb R})$. Furthermore, we may assume
\[ [{\rm ind}\, {D}] = [{\rm ind}\, {D}]_0\otimes h_1,\quad [H^+] = [H^+]_0\otimes \widetilde{{\Bbb R}}, \]
where
•
$[{\rm ind}\, {D}]_0\in KSp(B)$ is the class of the index bundle of $D$ which is regarded as a non-equivariant ${\Bbb H}$-linear operator,•
$h_1\in R(G;{\Bbb H})$ is a representation given by the multiplication by $G$ on ${\Bbb H}$,•
$[H^+]_0$ is the class of $H^+$ in $KO(B)$ and $\widetilde {{\Bbb R}}$ is the $G$-representation given by composition of the projection $G\to G/S^1=\{\pm 1\}$ with multiplication on ${\Bbb R}$.
We shall exhibit an example of families with non-zero families Seiberg–Witten invariants. Let 
$M_0= K3 \# n(S^2\times S^2)$ and 
$\mathfrak {s}_0$ be the spin structure on 
$M_0$ which is unique up to isomorphism. We construct spin commuting diffeomorphisms 
$f_1,\ldots ,f_n$ on 
$M_0$ as follows. Let 
$\varrho$ be an orientation-preserving self-diffeomorphism of 
$S^2\times S^2$ satisfying the following properties.
(i) There is a
$4$-ball $B_0$ embedded in $S^2\times S^2$ such that the restriction of $\varrho$ on a neighborhood $N(B_0)$ of $B_0$ is the identity map on $N(B_0)$.(ii)
$\varrho$ reverses orientation of $H^+(S^2\times S^2)$.
One way to get such 
$\varrho$ is as follows. Let 
$\varrho '$ be the orientation-preserving self-diffeomorphism on 
$S^{2} \times S^{2}$ given by the direct product of complex conjugation on 
$S^{2}=\mathbb {CP}^{1}$. This diffeomorphism 
$\varrho '$ acts on the intersection form by 
$(-1)$-multiplication, hence reverses the orientation of 
$H^{+}$. Obviously 
$\varrho '$ admits a fixed point, and deforming 
$\varrho '$ by isotopy near a fixed point, we can get a fixed ball rather than a fixed point. Then the deformed diffeomorphism 
$\varrho$ satisfies the desired properties.
Choose 
$n$ disjoint 
$4$-balls 
$B_1,\ldots ,B_n\subset K3$. We assume 
$M_0$ is constructed by removing 
$B_1,\ldots ,B_n$ from 
$K3$ and gluing 
$n$ copies of 
$S^2\times S^2\setminus B_0$. The construction of 
$f_i$ is as follows. Consider 
$M_0$ as the connected sum of the summand of the 
$i$th 
$S^2\times S^2$ with the remaining part 
$M_{(i)}:= K3\#(n-1)S^2\times S^2$. Define 
$f_i$ by
\[ f_i = (\varrho\text{ on the $i$th $S^2\times S^2$})\#\operatorname{id}_{M_{(i)}}.\]
Note that 
$f_{1}, \ldots , f_{n}$ obviously commute with each other. Note that 
$f_{i}$ preserves orientation of 
$M$.
Remark 4.3 Let 
$H^+_0\to T^n$ be the bundle of 
$H^+(M_0)$. Let 
$\ell$ be the unique non-trivial real line bundle over 
$S^1$ and 
$\pi _i\colon T^n=S^1\times \cdots \times S^1\to S^1$ be the projection to the 
$i$th 
$S^1$. Let
\[ \xi_n=\pi_1^*\ell\oplus\cdots\oplus \pi_n^*\ell. \]
Then 
$H^+_0\cong \xi _n\oplus \underline {{\Bbb R}}^3$.
The following calculation gives us instances of families with non-zero families Seiberg–Witten invariants.
Proposition 4.1 [Reference Baraglia and KonnoBK20]
For 
$(M_0,\mathfrak {s}_0)$ and 
$f_1,\ldots ,f_n$ as above, we have the following assertions.
(i) The set
$\{f_1,\ldots ,f_n\}$ is spin commuting. Let $(X_0,\mathfrak {s}_{X_0})$ be the associated spin mapping torus.(ii)
$[{\rm ind}\, {D}_0]=[\underline {{\Bbb H}}]\in KO_{\operatorname {Pin}(2)}(T^n)$, where ${\rm ind}\, {D}_0$ is the Dirac index bundle of $(X_0,\mathfrak {s}_{X_0})$.(iii)
$FSW^{{\Bbb Z}_2}(X_0,\mathfrak {s}_{X_0}) =1 \in {\Bbb Z}_{2} = \{0,1\}$.
Proof. Lemma 3.1 implies assertion (1). Assertion (2) will be proved by Lemma 6.1 below. To prove assertion (3), we use [Reference Baraglia and KonnoBK20, Theorem 1.1]. Let 
$N=n (S^2\times S^2)$, and assume 
$M_0=K3\# N$. Let 
$H^+_N$ be the bundle of 
$H^+(N)$. Then 
$H^+_N\cong \xi _n$. By [Reference Baraglia and KonnoBK20, Theorem 1.1],
\[ FSW^{{\Bbb Z}_2}(X_0,\mathfrak{s}_{X_0})=SW(K3,\mathfrak{s}_0|_{K3})\cdot\langle w_n(\xi_n), [T^n]\rangle = 1 \]
holds.
Combining Remark 4.3, Theorem 4.1 and Proposition 4.1, we obtain the following corollary.
Corollary 4.1 Let 
$M$ be a closed smooth spin 
$4$-manifold such that we have a ring isomorphism 
$H^*(M;{\Bbb Q})\cong H^*(M_0;{\Bbb Q})$. Suppose that we have a smooth fiber bundle 
$X \to T^{n}$ with fiber 
$M$ and with a global spin structure 
$\mathfrak {s}_{X}$ modeled on the given spin structure on 
$M$. Let 
${\rm ind}\, {D}$ be the Dirac index bundle of 
$(X,\mathfrak {s}_X)$ and 
$H^+\to T^n$ be the bundle of 
$H^+(M)$ associated to 
$X$. Suppose that 
$[{\rm ind}\, {D}]=[\underline {{\Bbb H}}]\in KO_{\operatorname {Pin}(2)}(T^n)$ and 
$H^+\cong \xi _n\oplus \underline {{\Bbb R}}^3$. Then we have
\[ FSW^{{\Bbb Z}_2}(X,\mathfrak{s}_X) = 1. \]
Remark 4.4 Morgan and Szabó [Reference Morgan and SzabóMS97] prove the rigidity theorem that every homotopy 
$K3$ surface admits a 
$\operatorname {Spin}^{c}$ structure with trivial determinant line bundle whose Seiberg–Witten invariant is congruent to 
$1$ modulo 
$2$. Corollary 4.1 can be considered as a family version of the Morgan–Szabó theorem.
The following theorem gives a family version of the 10/8-inequality for families with fiber having 
$\operatorname {sign}=-16$ and 
$b_1=0$.
Theorem 4.2 Let 
$M$ be a spin 
$4$-manifold with 
$\operatorname {sign}(M)=-16$ and 
$b_1(M)=0$. Suppose that we have a smooth fiber bundle 
$X \to T^{n}$ with fiber 
$M$ and with a global spin structure 
$\mathfrak {s}_{X}$ modeled on the given spin structure on 
$M$. Let 
${\rm ind}\, {D}$ and 
$H^+$ be as in Corollary 4.1. Suppose 
$[{\rm ind}\, {D}]=[\underline {{\Bbb H}}]$ and there exists a non-negative integer 
$a$ such that
\[ H^+{\cong} \xi_n\oplus \underline{{\Bbb R}}^a. \]
Then
\[ b_+(M)\geq n+3 \]
holds.
Proof. The proof is parallel to an argument in [Reference Furuta, Kametani and MatsueFKM01, Proposition 2]. First, it follows from the assumption on 
$H^{+}$ that 
$b_+(M)\geq n$. Suppose 
$n\leq b_+(M)< n+3$. Then we have 
$0\leq a < 3$. Let 
${\rm ind}\, {D}_0$ and 
$H_0^+$ be as in Proposition 4.1 and Remark 4.3. Choose a vector bundle 
$\xi ^\prime$ over 
$T^n$ so that
\[ -[\xi_n] = [\xi^\prime] - [\underline{{\Bbb R}}^l]\quad \text{in } KO_{S^1}(T^n). \]
Then, for some non-negative integers 
$x$, 
$y$, we have
\begin{align*} [{\rm ind}\, {D}] -[H^+] &= [\underline{{\Bbb H}}^{x+1}\oplus \underline{{\Bbb R}}^y\oplus\xi^\prime] - [\underline{{\Bbb H}}^{x}\oplus \underline{{\Bbb R}}^{y+l+a}],\\ [{\rm ind}\, {D}_0] -[H^+_0] &= [\underline{{\Bbb H}}^{x+1}\oplus \underline{{\Bbb R}}^y\oplus\xi^\prime] - [\underline{{\Bbb H}}^{x}\oplus \underline{{\Bbb R}}^{y+l+3}]. \end{align*}
Let us consider the following commutative diagram.
Here the 
$\iota _{i}$ are induced from the inclusion 
$V \hookrightarrow V\oplus {\Bbb R}^{3-a}$, and the 
$\varphi _{i}$ are the forgetful maps restricting the 
$\operatorname {Pin}(2)$-actions to 
$S^{1}$-actions. We shall compare two compositions 
$\deg \circ \varphi _{0} \circ \iota _{0}$ and 
$\deg \circ \iota _{1} \circ \varphi _{1}$ in the diagram.
Proposition 4.1 and Lemma 4.1 imply that the image of the composition 
$\deg \circ \varphi _0$ is 
$\{1\}$ and therefore the image of 
$\deg \circ \varphi _0\circ \iota _0$ is also 
$\{1\}$.
On the other hand, 
$S^V$ is 
$S^{1}$-equivariantly contractible in 
$S^{V\oplus {\Bbb R}^{3-a}}$, since we assumed that 
$a<3$ and the 
$S^{1}$-action on 
$S^{{\Bbb R}^{3-a}}$ is trivial. Therefore the image of the composition 
$\deg \circ \iota _{1} \circ \phi _{1}$ should be 
$\{0\}$. This contradicts the commutativity of the diagram.
In Lemma 6.1, we shall give a way to replace the assumption that 
$[{\rm ind}\, {D}]=[\underline {{\Bbb H}}]$ in Corollary 4.1 and Theorem 4.2 with a more geometric condition. Let us combine Lemma 6.1 with Corollary 4.1 and Theorem 4.2 here.
Corollary 4.2 Let 
$(M,\mathfrak {s})$ be an oriented closed smooth spin 
$4$-manifold with 
$H^*(M;{\Bbb Q})\cong H^*(M_0;{\Bbb Q})$ and 
$f_1,\ldots ,f_n$ be diffeomorphisms on 
$M$. Suppose that each of 
$f_{i}$ preserves 
$\mathfrak {s}$ and that 
$\operatorname {supp}{f}_{1}, \ldots , \operatorname {supp}{f}_{n}$ are mutually disjoint. Then, by Lemma 3.1, there exist lifts of 
$f_{1}, \ldots , f_{n}$ to the spin structure. Fix such lifts and form the spin mapping torus 
$(X,\mathfrak {s}_X)$. Let 
$H^+\to T^n$ be the bundle of 
$H^+(M)$ for 
$X$. Suppose that 
$H^+\cong \xi _n\oplus \underline {{\Bbb R}}^3$. Then we have
\[ FSW^{{\Bbb Z}_2}(X,\mathfrak{s}_X) = 1. \]
Proof. By Lemma 6.1, either 
${\rm ind}\, {D}$ or 
$-{\rm ind}\, {D}$ is represented by a trivial bundle, and 
${\rm ind}_{{\Bbb C}}{D}=-\operatorname {sign}(M)/8=2$ by the index theorem. Therefore the assertion of the corollary follows from Corollary 4.1.
Corollary 4.3 Let 
$(M,\mathfrak {s})$ be an oriented closed spin smooth 
$4$-manifold with 
$\operatorname {sign}(M)=-16$ and let 
$b_1(M)=0$ and 
$f_1,\ldots ,f_n$ be diffeomorphisms on 
$M$. Suppose that each of 
$f_1,\ldots ,f_n$ preserves 
$\mathfrak {s}$ and that 
$\operatorname {supp}{f}_{1}, \ldots , \operatorname {supp}{f}_{n}$ are mutually disjoint. Let 
$H^+\to T^n$ be the bundle of 
$H^+(M)$ associated with 
$f_{1}, \ldots , f_{n}$. Suppose that there exists a non-negative integer 
$a$ such that 
$H^+ \cong \xi _n\oplus \underline {{\Bbb R}}^a$. Then we have
\[ b_+(M)\geq n+3. \]
5. Applications
In this section we shall give two topological applications of our main results in the previous section. The first application is to detect non-smoothable actions on 
$4$-manifolds. The second is to detect non-smoothable families. We note that most 
$4$-manifolds 
$M$ appearing in this section have non-zero signature, and for such 
$M$, we have 
$\operatorname {Diff}^{+}(M)=\operatorname {Diff}(M)$ and 
$\operatorname {Homeo}^{+}(M) = \operatorname {Homeo}(M)$.
Let us denote by 
$-E_{8}$ the (unique) closed simply connected oriented topological 4-manifold whose intersection form is the negative-definite 
$E_{8}$-lattice [Reference FreedmanFre82, Theorem 1.7]. In Theorem 5.1, for any 
$m \geq 3$, we construct non-smoothable 
${\Bbb Z}^{m-2}$-actions on the topological 
$4$-manifold 
$2(-E_{8}) \# m S^{2}\times S^{2}$. Notice that the 
$4$-manifold 
$2(-E_{8}) \# m S^{2}\times S^{2}$ is homeomorphic to 
$K3\#(m-3)S^{2} \times S^{2}$ and hence admits a smooth structure.
Theorem 5.1 Let 
$m \geq 3$. Then the topological (but smoothable) 
$4$-manifold 
$M$ defined by
\[ M = 2({-}E_{8}) \# m S^{2}\times S^{2} \]
admits commuting self-homeomorphisms 
$f_{1}, \ldots , f_{m}$ with the following properties.
• For any distinct numbers
$i_{1},\ldots , i_{m-3} \in \{1, \ldots , m\}$, there exists a smooth structure on $M$ for which $f_{i_{1}}, \ldots , f_{i_{m-3}}$ are diffeomorphisms.• For any distinct numbers
$i_{1},\ldots , i_{m-2} \in \{1, \ldots , m\}$, there exists no smooth structure on $M$ for which all of $f_{i_{1}}, \ldots , f_{i_{m-2}}$ are diffeomorphisms.
Proof. Let us write the connected sum components of 
$mS^{2} \times S^{2}$ as
\[ mS^{2} \times S^{2} = \#_{i=1}^{m} (S^{2} \times S^{2}) = \#_{i=1}^{m} N_{i}. \]
For each 
$i \in \{1, \ldots ,m\}$, let
\[ f_{i} : N_{i} \to N_{i} \]
be an orientation-preserving self-diffeomorphism given by a copy on 
$N_{i}$ of 
$\varrho : S^{2} \times S^{2} \to S^{2} \times S^{2}$ given in § 4. Since 
$f_{i}$ has a fixed ball, we can extend 
$f_{i}$ as a self-homeomorphism onto 
$M$ by the identity map outside 
$N_{i}$. Let us write 
$f_{i} : M \to M$ also for the extended self-homeomorphism. Note that obviously 
$\operatorname {supp}{f}_{1}, \ldots , \operatorname {supp}{f}_{m}$ are mutually disjoint.
We first show that, for any distinct numbers 
$i_{1},\ldots , i_{m-3} \in \{1, \ldots , m\}$, there exists a smooth structure on 
$M$ such that 
$f_{i_{1}}, \ldots , f_{i_{m-3}}$ are diffeomorphisms with respect to the smooth structure. For simplicity of notation, let us consider the case where 
$i_{1}=1, \ldots , i_{m-3}=m-3$. First, note that Freedman's theorem (see, for example, [Reference Freedman and QuinnFQ90]) implies that there exists a homeomorphism
\[ \varphi : 2({-}E_{8}) \#_{i=m-2}^{m}N_{i} \to K3. \]
For 
$j \in \{1, \ldots , m-3\}$, denote by 
$B_{j}$ the (topologically) embedded 
$4$-ball in 
$2(-E_{8}) \#_{i=m-2}^{m}N_{i}$ which was used to define the extension of 
$f_{j} : N_{j} \to N_{j}$ onto 
$M$. Let 
$B'_{1}, \ldots , B'_{m-3} \subset K3$ be smoothly embedded disjoint 
$4$-balls. We can construct a self-homeomorphism 
$\psi$ on 
$2(-E_{8}) \#_{i=m-2}^{m}N_{i}$ which maps 
$B_{j}$ to 
$\varphi ^{-1}(B'_{j})$ for all 
$j \in \{1, \ldots , m-3\}$: by taking a suitable isotopy, we may assume each 
$\varphi ^{-1}(B'_{j})$ is contained in the interior of 
$B_{j}$. Since the boundary spheres of 
$B_{j}$ and 
$\varphi ^{-1}(B'_{j})$ are locally flatly embedded, the annulus theorem [Reference QuinnQui82] implies that 
$\overline {B_{j}\setminus \varphi ^{-1}(B'_{j})}$ is homeomorphic to 
$S^3\times I$. Then we can find an ambient isotopy which moves 
$B_{j}$ to 
$\varphi ^{-1}(B'_{j})$. We can extend the homeomorphism
\[ \varphi \circ \psi : 2({-}E_{8}) \#_{i=m-2}^{m}N_{i} \to K3 \]
to a homeomorphism
\[ \phi : M \to K3\#(m-3)S^{2} \times S^{2} \]
by forming the connected sum along 
$B_{1}, \ldots , B_{m-3}$ and 
$B'_{1}, \ldots , B'_{m-3}$ with the identity map on the 
$(m-3)$-copies of 
$S^{2} \times S^{2}$. By construction, the composition
\[ \phi \circ f_{j} \circ \phi^{{-}1} : K3\#(m-3)S^{2} \times S^{2} \to K3\#(m-3)S^{2} \times S^{2} \]
is obviously a diffeomorphism for any 
$j \in \{1, \ldots , m-3\}$. This means that 
$f_{j}$ is a diffeomorphism on 
$M$ equipped with the smooth structure of 
$K3\#(m-3)S^{2} \times S^{2}$ via 
$\phi$.
It remains to show that 
$f_{i_{1}}, \ldots , f_{i_{m-2}}$ are not smoothable at the same time for distinct numbers 
$i_{1},\ldots , i_{m-2} \in \{1, \ldots , m\}$. Set 
$n=m-2$. Assume that 
$f_{i_{1}}, \ldots , f_{i_{n}}$ are diffeomorphisms for some smooth structure on 
$M$. Let 
$H^+\to T^n$ be the bundle of 
$H^+(M)$ associated with 
$f_{i_{1}}, \ldots , f_{i_{n}}$. For each 
$k \in \{1,\ldots ,n\}$, the diffeomorphism 
$f_{i_{k}}$ reverses the orientation of 
$H^{+}$ for the 
$i_{k}$th component of 
$S^{2} \times S^{2}$ of 
$2(-E_{8}) \# m S^{2}\times S^{2}$ and 
$f_{i_{k}}$ acts trivially on 
$H^{+}$ for the remaining connected sum component. Thus we have 
$H^{+} \cong \xi _{n} \oplus \underline {{\Bbb R}}^{2}$, and therefore we can apply Corollary 4.3 to 
$f_{i_{1}}, \ldots , f_{i_{n}}$. It follows from this corollary that 
$b_{+}(M) \geq n+3 = m+1$, but obviously 
$b_{+}(M) = m$. This is a contradiction.
This completes the proof of Theorem 5.1.
Remark 5.1 Non-smoothable actions have been studied by many authors, but for groups having several generators, there is only little previous work. Here we explain such work briefly and compare it with Theorem 5.1. The third author [Reference NakamuraNak10] constructed a non-smoothable 
${\Bbb Z}^{2}$-action on the connected sum of an Enriques surface and 
$S^{2} \times S^{2}$. Kato [Reference KatoKat17] constructed non-smoothable 
$({\Bbb Z}/2)^{2}$-actions on certain spin 
$4$-manifolds with 
$|{\operatorname {sign}}| \geq 64$. Baraglia [Reference BaragliaBar19a] constructed 
${\Bbb Z}^{2}$-actions and 
$({\Bbb Z}/2)^{2}$-actions on certain non-spin 
$4$-manifolds. In these results, each of the generators of 
${\Bbb Z}^{2}$ or 
$({\Bbb Z}/2)^{2}$ can be realized as a smooth diffeomorphism for some smooth structure, so they are similar to Theorem 5.1 in this sense. However, Theorem 5.1 provides a non-smoothable 
${\Bbb Z}^{n}$-action for all 
$n \geq 2$ and the 
$4$-manifold acted on by 
${\Bbb Z}^{n}$ is different from that in all of the work explained in this remark.
Let 
$M$ be an oriented topological (but smoothable) manifold, 
$B$ be a smooth manifold, and 
$M \to X \to B$ be a fiber bundle whose structure group is 
$\operatorname {Homeo}(M)$.
We say that the bundle 
$X$ is smoothable as a family or 
$X$ has a smooth reduction, if there exists a smooth structure on 
$M$ such that there is a reduction of the structure group of 
$X$ to 
$\operatorname {Diff}(M)$ with respect to the smooth structure via the inclusion 
$\operatorname {Diff}(M) \hookrightarrow \operatorname {Homeo}(M)$. If 
$X$ is not smoothable as a family, we say that 
$X$ is non-smoothable as a family or 
$X$ has no smooth reduction.
Remark 5.2 For a topological fiber bundle 
$X \to B \times B'$, if the restriction 
$X|_{B} \to B$ is non-smoothable as a family, then so is 
$X\to B \times B'$.
In Theorem 5.2, we shall construct a non-smoothable family whose fiber is the topological 
$4$-manifold 
$2(-E_{8}) \# m S^{2}\times S^{2}$. Here we use the following notation. Set 
$[m]=\{1,2,\ldots ,m\}$. For the 
$m$-torus 
$T^{m}$ and a subset 
$I=\{i_{1},\ldots ,i_{k}\} \subset [m]$ with cardinality 
$k$, denote by 
$T^{k}_{I}$ the embedded 
$k$-torus in 
$T^{m}$ defined as the product of the 
$i_{1}$th,…, 
$i_{k}$th 
$S^{1}$-components.
Theorem 5.2 Let 
$3\leq m \leq 6$. Let 
$M$ be the topological (but smoothable) 
$4$-manifold defined by
\[ M = 2({-}E_{8}) \# m S^{2}\times S^{2}. \]
Then there exists a 
$\operatorname {Homeo}(M)$-bundle
\[ M \to X \to T^{m} \]
over the 
$m$-torus with the following properties. Let 
$I=\{i_{1},\ldots ,i_{k}\} \subset [m]$ be a subset with cardinality 
$k$.
• The total space
$X$ admits a smooth manifold structure.• If
$k\leq m-3$, the restricted family
has a reduction to\[ X|_{T^{k}_{I}} \to T^{k}_{I} \]
$\operatorname {Diff}(M)$ for some smooth structure on $M$.• If
$m-2\leq k\leq m$, the restricted family
has no reduction to\[ X|_{T^{k}_{I}} \to T^{k}_{I} \]
$\operatorname {Diff}(M)$ for any smooth structure on $M$.
Proof. Let 
$f_{1}, \ldots , f_{m}$ be the commuting self-homeomorphisms on 
$M$ constructed in the proof of Theorem 5.1. Let 
$M \to X \to T^{m}$ be the multiple mapping torus for 
$f_{1}, \ldots , f_{m}$. Then 
$X$ is a 
$\operatorname {Homeo}(M)$-bundle. Note that, because of Lemma 3.2, there exists a global topological spin structure on the bundle 
$X$.
First, smoothability of 
$X$ as a manifold will be verified in Proposition 7.1.
Second, we shall verify by contradiction that 
$X|_{T^{k}_{I}} \to T^{k}_{I}$ has no reduction to 
$\operatorname {Diff}(M)$ for any smooth structure on 
$M$ if 
$I=\{i_{1},\ldots , i_{k}\}$ with 
$k\geq m-2$. We shall show the non-smoothability for 
$m-2\leq k\leq 4$, but this is enough also for general 
$k \geq m-2$ by Remark 5.2. Assume that 
$X|_{T^{k}_{I}}$ could be smoothable as a family for some smooth structure on 
$M$. Then the global topological structure induces a global spin structure and we have the family of Dirac operators 
${\rm ind}\, {D}$ associated with 
$X|_{T^{k}_{I}}$. We shall show Lemmas 6.2 and 6.3 in § 6, and they ensure triviality 
${\rm ind}\, {D}=[\underline {{\Bbb H}}]$. Moreover, the bundle of 
$H^{+}$ associated with 
$X|_{T^{k}_{I}}$ satisfies 
$H^{+} \cong \xi _{k} \oplus \underline {{\Bbb R}}^{a}$ for 
$a=m-k$, as explained in the proof of Theorem 5.1. Therefore we can apply Theorem 4.2 to 
$X|_{T^{k}_{I}} \to T^{k}_{I}$, and the inequality 
$b_{+}(M) \geq k+3\geq m+1$ should hold, but obviously 
$b_{+}(M) = m$. This is a contradiction.
Finally, let us check that 
$X|_{T^{k}_{I}} \to T^{k}_{I}$ is smoothable as a family for 
$I=\{i_{1},\ldots , i_{k}\}$ with 
$k\leq m-3$. The restriction 
$X|_{T^{k}_{I}}$ is the multiple mapping torus of 
$f_{i_{1}}, \ldots , f_{i_{k}}$. By Theorem 5.1, there exists a smooth structure on 
$M$ such that 
$f_{i_{1}}, \ldots , f_{i_{k}}$ are diffeomorphisms. Therefore the structure group of 
$X|_{T^{k}_{I}}$ obviously reduces to 
$\operatorname {Diff}(M)$ with respect to this smooth structure.
Remark 5.3 The assertion on non-smoothability of 
$f_{i_{1}}, \ldots , f_{i_{m-2}}$ in Theorem 5.1 obviously follows from Theorem 5.2.
Remark 5.4 In the case of 
$m=3$ in Theorem 5.2, the second condition does not provide any additional information.
Remark 5.5 The non-smoothability of 
$X$ given in Theorem 5.2 in the case where 
$m=3$ follows from Morgan andSzabó [Reference Morgan and SzabóMS97] without using Theorem 5.2 as follows. The family 
$X$ in the case where 
$m=3$ is a 
$\operatorname {Homeo}(M)$-bundle 
$M \to X \to T^{k}$ with 
$k \in \{1,2,3\}$ and 
$M = 2(-E_{8}) \# 3S^{2} \times S^{2}$. This bundle is given as the multiple mapping torus for commuting homeomorphisms supported in the 
$3S^{2}\times S^{2}$-components. Assume that the family 
$X$ is smoothable as a family. Let us take a smooth structure on 
$M=2(-E_{8}) \# 3S^{2} \times S^{2}$ for which the structure group of 
$X$ has a reduction to the diffeomorphism group. Consider the unique spin structure on the smooth 
$4$-manifold. This 
$4$-manifold has non-zero Seiberg–Witten invariant for the spin structure by [Reference Morgan and SzabóMS97], and from this we can deduce that there does not exist a diffeomorphism which reverses the orientation of 
$H^{+}$. By restricting the family to 
$S^{1}$ embedded into 
$T^{k}=(S^{1})^{k}$ as the first factor, we can get a smoothable family over the circle 
$M \to X|_{S^{1}} \to S^{1}$. Since this restricted family is the mapping torus of the homeomorphism 
$f_{1}$, the smoothability of 
$X|_{S^{1}}$ implies that 
$f_{1}$ is topologically isotopic to a diffeomorphism 
$g$ on 
$M$. Since 
$f_{1}$ reverses the orientation of 
$H^{+}(M)$, so does 
$g$. This is a contradiction.
One can verify a slightly stronger result on the smoothability of 
$X|_{S^{1}}$ for any 
$S^{1}$ embedded in 
$T^{m}$ in Theorem 5.2.
Proposition 5.1 Let 
$4\leq m\leq 6$ and let 
$M \to X \to T^{m}$ be the 
$\operatorname {Homeo}(M)$-bundle given in Theorem 5.2. Then, for any homeomorphism 
$\varphi : M \to K3\#(m-3)S^{2} \times S^{2}$ and any embedding of 
$S^{1}$ to 
$T^{m}$, the structure group of 
$X|_{S^{1}}$ reduces to 
$\operatorname {Diff}(M)$, where 
$\operatorname {Diff}(M)$ is the diffeomorphism group with respect to the smooth structure on 
$M$ defined as that of 
$K3\#(m-3)S^{2} \times S^{2}$ via 
$\varphi$.
Proof. Equip 
$M$ with a smooth structure through 
$\varphi$. Take an embedding of 
$S^{1}$ into 
$T^{m}$. Note that 
$X|_{S^{1}}$ can be regarded as the mapping torus of a homeomorphism 
$g$ on 
$M$. Recall the following two classical results.
• Every algebraic automorphism of the intersection form of
$M \cong K3 \# (m-3)S^{2} \times S^{2}$ is induced from a diffeomorphism by a result of Wall [Reference WallWal64].• An algebraic automorphism of the intersection form corresponds to a topological isotopy class by a result of Quinn [Reference QuinnQui86].
Therefore there exists a diffeomorphism on 
$M$ which is topologically isotopic to 
$g$. This means that the structure group of 
$X|_{S^{1}}$ reduces to 
$\operatorname {Diff}(M)$.
Let us denote by 
the homotopy quotient:
Corollary 5.1 We have
Proof. Set 
$M=K3\# S^{2} \times S^{2}$. The case where 
$m=4$ of Theorem 5.2 and Proposition 5.1 implies that the fundamental group of the homotopy fiber of the natural map 
$B\operatorname {Diff}(M) \to B\operatorname {Homeo}(M)$ is non-trivial. To finish the proof, just recall that this homotopy fiber is homotopy equivalent to 
.
Remark 5.6 Note that the argument of the proof in Corollary 5.1 is valid also for the 
$4$-manifold as 
$Z\#S^{2} \times S^{2}$ instead of 
$K3\#S^{2} \times S^{2}$, where 
$Z$ is an exotic 
$K3$. However, we do not know of an example of 
$Z$ such that 
$Z\#S^{2} \times S^{2}$ is not diffeomorphic to 
$K3\#S^{2} \times S^{2}$.
6. Calculation of the index bundle
In this section we shall provide a few ways to give a sufficient condition for the Dirac index bundle associated with a given family of 
$4$-manifolds to be trivial. The results given in this section have been used in the previous sections.
Lemma 6.1 Let 
$M$ be a closed spin 
$4$-manifold. Let 
$f_1,\ldots ,f_n$ be spin commuting diffeomorphisms on 
$M$. If 
$\operatorname {supp}{f}_{1}, \ldots , \operatorname {supp}{f}_{n}$ are mutually disjoint, then either the spin Dirac index bundle 
${\rm ind}\, {D}$ associated with 
$f_1,\ldots ,f_n$ or 
$-{\rm ind}\, {D}$ is represented by a trivial bundle.
Proof. We shall use the excision formula of the index of families of Fredholm operators, and for the sake of it, decompose 
$M$ into 
$n$ pieces of codimension-0 submanifolds
\[ M = M_{1} \cup_{Y_{1}} \cdots \cup_{Y_{n-1}} M_{n} \]
so that 
$\operatorname {supp}{f_{i}} \subset M_{i}$ for each 
$i$ as follows. Set 
$N_{0} := M$. Let us define closed subsets 
$A_{1}, B_{1} \subset N_{0}$ by 
$A_{1} := \operatorname {supp}{f}_{1}$ and 
$B_{1} := \operatorname {supp}{f}_{2} \sqcup \cdots \sqcup \operatorname {supp}{f}_{n}$. By Urysohn's lemma, we can take a continuous function 
$\tilde {\chi }_{1} : N_{0} \to [-1,1]$ such that 
$\tilde {\chi }_{1}(A_{1}) = \{-1\}$ and 
$\tilde {\chi }_{1}(B_{1})=\{1\}$. By perturbing 
$\tilde {\chi }_{1}$, we can get a smooth function 
$\chi _{1} : N_{0} \to [-3/2, 3/2]$ such that 
$\chi _{1}(A_{1}) \subset [-3/2,-1]$ and 
$\chi _{1}(B_{1}) \subset [1,3/2]$. By Sard's theorem, for a generic point 
$\epsilon \in (-1,1)$, the inverse image 
$Y_{1} := \chi _{1}^{-1}(\epsilon )$ is a three-dimensional closed submanifold of 
$N_{0}$. Define 
$M_{1} := \chi _{1}^{-1}([-3/2,\epsilon ])$ and 
$N_{1} := \chi _{1}^{-1}([\epsilon ,3/2])$. Then we get a decomposition into codimension-
$0$ submanifolds of 
$N_{0} = M_{1} \cup _{Y_{1}} N_{1}$ along 
$Y_{1}$. Next, let us define closed subsets 
$A_{2}, B_{2} \subset N_{1}$ by 
$A_{2} := \operatorname {supp}{f}_{2} \sqcup Y_{1}$ and 
$B_{2} := \operatorname {supp}{f}_{3} \sqcup \cdots \sqcup \operatorname {supp}{f}_{n}$. By the same procedure, we can get a decomposition of 
$N_{1}$ into codimension-
$0$ submanifolds along a three-dimensional submanifold 
$Y_{2}$ of 
$\mathop {\rm {int}}{N_{2}}$: 
$N_{1} = M_{2} \cup _{Y_{2}} N_{2}$. Note that 
$Y_{1}$ is a closed 
$3$-manifold. Proceeding inductively, we can get a decomposition of 
$M$ into codimension-
$0$ submanifolds
\[ M = M_{1} \cup_{Y_{1}} \cdots \cup_{Y_{n-1}} M_{n} \]
along closed 
$3$-manifolds 
$Y_{1}, \ldots , Y_{n-1}$. By construction, each 
$\operatorname {supp}{f}_{i}$ is contained in 
$M_{i}$. Let 
$M_{i} \to X_{i} \to S^{1}$ be the mapping cylinder of 
$f_{i}$. This 
$X_{i}$ is a bundle of a smooth 
$4$-manifold with boundary. Our multiple mapping cylinder 
$M \to X \to T^{n}$ is regarded as the fiberwise sum of 
$\pi _{1}^{\ast }X_{1}, \ldots , \pi _{n}^{\ast }X_{n}$ along trivial bundles 
$Y_{1} \times T^{n} \to T^{n}, \ldots , Y_{n-1} \times T^{n} \to T^{n}$, where 
$\pi _{i} : T^{n} \to S^{1}$ is the 
$i$th projection. Denote by 
$\hat {M}_{i}$ the cylindrical 
$4$-manifold obtained by gluing 
$M_{i}$ with 
$\partial M_{i} \times [0, \infty )$. Then we can get a bundle of a cylindrical 
$4$-manifold 
$\hat {M}_{i} \to \hat {X}_{i} \to S^{1}$, and can define the family of spin Dirac operators 
$D_{i}$ on 
$\hat {X}_{i}$. Then, under suitable weighted Sobolev norms (for example, see Donaldson's book [Reference DonaldsonDon02, § 3.3.1]), we can obtain
\begin{equation} [{\rm ind}\, {D}] = [{\rm ind}\,\pi_{1}^{{\ast}} D_{1}] + \cdots + [{\rm ind}\,\pi_{n}^{{\ast}} D_{n}] \end{equation}
in 
$KO_{\operatorname {Pin}(2)}(T^{n})$ by the excision formula of the index of families.
Since 
$[{\rm ind}\, {D}_i]\in KSp(S^1)\otimes R(G;{\Bbb H})$ and 
$KSp(S^1)=KSp(pt)={\Bbb Z}$, 
${\rm ind}\,{D_{i}}$ or 
$-{\rm ind}\, D_{i}$ is represented by a trivial quaternion bundle in 
$KO_{\operatorname {Pin}(2)}(S^{1})$ (see Remark 4.2). Hence 
${\rm ind}\, {D}$ and 
$-{\rm ind}\, {D}$ are the same by (9).
Remark 6.1 Note that we cannot apply Lemma 6.1 for the proof of Theorem 5.2.
To verify non-smoothability of 
$X|_{T^k_I}$ as a family, we argue by contradiction, and for this we assume that 
$X|_{T^k_I}$ has a reduction to the diffeomorphism group with respect to some smooth structure of the fiber. However this assumption does not guarantee that 
$f_{i_1}, \ldots , f_{i_k}$ are diffeomorphisms, but just homeomorphisms.
Remark 6.2 One can deduce the assumption 
${\rm ind}\, {D}=[\underline {{\Bbb H}}]$ in Corollary 4.1 and Theorem 4.2 from the following stronger but more geometric condition, which is different from Lemma 6.1. Assume that there exists a Riemannian metric on 
$M$ which is invariant under the pull-backs of all 
$f_{1}, \ldots , f_{n}$. For example, this assumption is satisfied if all of 
$f_{1}, \ldots , f_{n}$ have finite order. Indeed, the group generated by them is finite since 
$f_{1}, \ldots , f_{n}$ mutually commute, and then we can obtain an invariant metric by taking the average of any metric by the action of this finite group. Let us derive 
${\rm ind}\, {D}=[\underline {{\Bbb H}}]$ assuming the existence of an invariant metric 
$g_{0}$ for 
$f_{1}, \ldots , f_{n}$. The metric 
$g_{0}$ gives a ‘constant’ fiberwise metric on the mapping torus for 
$f_{1}, \ldots , f_{n}$. Note that we can employ this fiberwise metric in the process of a finite-dimensional approximation of a family of Seiberg–Witten equations described in Section 2.2, since any genericity for the metric is not necessary for the finite-dimensional approximation. Then the index bundle 
${\rm ind}\, {D}$ is clearly trivial. Because of the usual index calculation, the complex rank of the fiber of 
${\rm ind}\, {D}$ is 
$|{\rm sign}(M)|/8=2$. Therefore we obtain 
${\rm ind}\, {D}=[\underline {{\Bbb H}}]$.
The index bundle is always trivial when the base space is a low-dimensional torus.
Lemma 6.2 Let 
$(M,\mathfrak {s})$ be a closed spin 
$4$-manifold. Let 
$B$ be a closed manifold and 
$X\to T^k$ be a fiber bundle with fibers 
$M$ with a global spin structure 
$\mathfrak {s}_X$ modeled on 
$\mathfrak {s}$. Let 
$[{\rm ind}\, {D}] \in KO_{\operatorname {Pin}(2)}(T^k)$ denote the class of the (virtual) index bundle of the family of spin Dirac operators associated to 
$X$. If 
$k \leq 3$, then 
$[{\rm ind}\, {D}]$ or 
$-[{\rm ind}\, {D}]$ is represented by a trivial quaternionic vector bundle.
Before proving Lemma 6.2, we need some preliminaries. By Remark 4.2, we may assume that 
$[{\rm ind}\, {D}]$ is in 
$KSp(T^n)\otimes R(\operatorname {Pin}(2);{\Bbb H})$ and can be written as
\[ [{\rm ind}\, {D}] = [{\rm ind}\, {D}]_0\otimes h_1, \]
where 
$[{\rm ind}\, {D}]_0\in KSp(T^n)$ is the class of the index bundle of 
$D$ as an non-equivariant 
${\Bbb H}$-linear operator, and 
$h_1\in R(\operatorname {Pin}(2);{\Bbb H})$ is the representation given by the multiplication of 
$\operatorname {Pin}(2)$ on 
${\Bbb H}$. Then we have the following useful decomposition of the 
$KSp$-groups of 
$T^n$.
Proposition 6.1 [Reference Furuta and KametaniFK05, Lemma 31 and Remark 32]
For integers 
$q$ and 
$p$ with 
$p\geq 0$, we have an isomorphism
\[ KSp^q(T^n\times{\Bbb R}^p)\cong \bigoplus_{S\subset[n]}KSp^q({\Bbb R}^S\times{\Bbb R}^p), \]
where 
$S$ runs through all the subsets of 
$[n]=\{1,2,\ldots ,n\}$ and 
${\Bbb R}^S$ is defined as follows. Let 
${\Bbb R}_k$ be the 
$k$th component of 
${\Bbb R}^n$. Then 
${\Bbb R}^S=\prod _{k\in S}{\Bbb R}_k$ if 
$S\neq \emptyset$, and 
${\Bbb R}^S=\{pt\}$ if 
$S=\emptyset$.
Proof. Consider the exact sequence
By using excision, the first term is identified with
\[ KSp^q((T^n,T^{n-1})\times ({\Bbb R}^p\cup\{\infty\},\{\infty\})) \cong KSp^q(T^{n-1}\times{\Bbb R}^{p+1}). \]
Then 
$j^*$ is identified with the push-forward map 
$i_{!}\colon KSp^q(T^{n-1}\times {\Bbb R}^{p+1})\to KSp^q(T^n\times {\Bbb R}^p)$ induced from an open embedding 
$i\colon {\Bbb R}\to T^1\subset T^n$. Let 
$\pi \colon T^n\times {\Bbb R}^p\to T^{n-1}\times {\Bbb R}^p$ be the projection. Then 
$\pi ^*$ gives a right-inverse of 
$h^*$. Therefore the above sequence splits. Moreover, 
$h^*$ is a surjection, and then 
$j^*$ turns out to be an injection. Thus we obtain an isomorphism
\[ i_!+\pi^*\colon KSp^q(T^{n-1}\times{\Bbb R}^{p+1})\oplus KSp^q(T^{n-1}\times{\Bbb R}^p) \overset{\cong}{\to} KSp^q(T^n\times{\Bbb R}^p). \]
By an induction on the cardinality 
$|S|$ of 
$S$, the proposition is proved.
Proof Proof of Lemma 6.2
Note that 
$KSp(pt)={\Bbb Z}$, 
$KSp({\Bbb R}^q)=0$ for 
$q=1,2,3$ (see, for example, [Reference SwitzerSwi17, Chapter 11]). If 
$k\leq 3$, Proposition 6.1 implies that
\[ KSp(T^k) \cong KSp(pt)\cong {\Bbb Z}. \]
This means that every element in 
$KSp(T^k)$ is represented by a trivial bundle and classified by its rank over 
${\Bbb H}$ if 
$k\leq 3$. Therefore 
$[{\rm ind}\, {D}]_0$, and hence 
$[{\rm ind}\, {D}]$, is represented by a trivial bundle.
The main part of this section is devoted to proving the following lemma. The argument is based on the celebrated result by Novikov that the rational Pontryagin classes are topological invariants.
Lemma 6.3 Let 
$M\to X \to T^{m}$ be the topological bundle given in the proof of Theorem 5.2. For 
$I\subset [m]$ with 
$k=|I|=4$, suppose 
$X|_{T_{I}^4}$ has a smooth reduction. Then the Dirac index bundle satisfies 
$[{\rm ind}\, {D}]=[\underline {{\Bbb H}}]$.
Before giving the proof of Lemma 6.3, let us describe a strategy for the proof and give some preliminaries. Denote 
$X|_{T_{I}^4}$ by 
$X_I$ and 
$T_I^k$ by 
$T_I$. Suppose 
$X_I$ is smoothable as a family and a smooth reduction is given. We will proceed in the following way.
• We verify that the forgetful map
$c\colon KSp(T^4)\to K(T^4)$ is injective.• Hence it suffices to prove that the image of
$[{\rm ind}\, {D}]$ under $c$ is represented by a trivial complex bundle.• Since the complex
$K$-group of the base space $T_I$ is torsion-free, it suffices to prove that $Ch({\rm ind}\, {D})$, the image of ${\rm ind}\, {D}$ under the Chern character, is in $H^0(T_I;{\Bbb Q})$.• By the index theorem for families (13), it suffices to check
$p_{1}^{2}=0$ and $p_{i}=0$ for $i \geq 2$, where $p_i$ are the rational Pontryagin classes of the tangent bundle along the fibers $T(X_I/T_I)$ of $X_I\to T_I$.
It is well known that the rational Pontryagin classes of a 
${\Bbb R}^n$-bundle depend only on its topological type. In fact, the rational Pontryagin classes can be defined not only for a vector bundle, but also for a topological 
${\Bbb R}^n$-bundle whose structure group is in the group 
$TOP_n$ of self-homeomorphisms on 
${\Bbb R}^n$ preserving the origin. Furthermore, the rational Pontryagin classes of a bundle are determined by the isomorphism classes as topological bundles, and do not depend on vector bundle structures on them. (See Rudyak [Reference RudyakRud16, Chapter 3], for example. This generalizes the Novikov's theorem.) Therefore the rational Pontryagin classes 
$p_i$ of the tangent micro-bundle along the fibers 
$\tau (X_I/T_I)$ are defined over the underlying topological 
${\Bbb R}^n$-bundle of 
$T(X_I/T_I)$ without using the smooth structure. We will prove the required properties of 
$p_i$ directly for 
$\tau (X_I/T_I)$ from the construction of the topological bundle 
$X_I$.
To proceed with the above strategy, we recall some classical objects in differential topology.
6.1 Universal Pontryagin classes
Let us recall the rational Pontryagin classes for topological 
${\Bbb R}^n$ bundles (see [Reference RudyakRud16], for example). It is known that the forgetful map 
$\alpha \colon BO\to BTOP$ induces an isomorphism of their rational cohomology groups
\[ \alpha^*\colon H^*(BTOP;{\Bbb Q})\overset{\cong}{\to} H^*(BO;{\Bbb Q}). \]
Recall that 
$H^*(BO;{\Bbb Q})$ is generated by the universal Pontryagin classes 
$p_{i}^{\rm univ}$. Then we have
\[ H^*(BTOP;{\Bbb Q}) \cong H^*(BO;{\Bbb Q}) \cong {\Bbb Q}[p_{1}^{\rm univ}, p_{2}^{\rm univ},\ldots] \]
via the identification 
$\alpha ^*$. The stable class of a topological 
${\Bbb R}^n$-bundle 
$\xi \to B$ is classified by its classifying map 
$t\colon B\to BTOP$. Define the 
$i$th rational Pontryagin class 
$p_i(\xi )$ by
\[ p_i(\xi)=t^*p_{i}^{\rm univ}. \]
6.2 Rational localization
Below we utilize the 
${\Bbb Q}$-localizations 
$BO[0]$ and 
$BTOP[0]$ of 
$BO$ and 
$BTOP$. The existence of these 
${\Bbb Q}$-localizations is guaranteed by the fact that both of 
$BO$ and 
$BTOP$ are infinite loop spaces, and hence 
$H$-spaces (see [Reference Boardman and VogtBV68, Theorems A and C]). In general an 
$H$-space is a simple space, and hence is a nilpotent space for which a 
${\Bbb Q}$-localization can be constructed (see, for example, [Reference May and PontoMP12, Corollary 1.4.5 and § 5.3]).
6.3 Tangent micro-bundle
We clarify the notion of the tangent micro-bundle along the fibers of a topological bundle 
$M\to X\overset {\pi }{\to } B$. Denote the fiber of 
$X$ over 
$b\in B$ by 
$M_b$ and define the space 
$E$ by
\[ E=\{(x,y)\in X\times X\,|\, y\in M_{\pi(x)}\}. \]
Note that 
$E$ contains the diagonal set 
$\Delta _X=\{(x,x)\,|\,x\in X\}$. The tangent micro-bundle along the fibers 
$\tau (X/B)$ of 
$M\to X{\to } B$ is defined as
where 
$\Delta$ is the diagonal map and 
$\pi _1$ is the projection to the first component. It is easy to check the following properties of 
$\tau (X/B)$.
• The sequence (11) defines a micro-bundle in Milnor's sense [Reference MilnorMil64]. (By the Kister–Mazur theorem [Reference KisterKis64], the micro-bundle determines a topological
${\Bbb R}^n$-bundle which is unique up to isomorphism.)• If the structure group of
$M\to X\to B$ is reduced to $\operatorname {Diff}(M)$ for some smooth structure on $M$, then $\tau (X/B)$ is the underlying micro-bundle of the tangent bundle along the fibers $T(X/B)$.
Lemma 6.4 Let 
$f : N \to N$ be an orientation-preserving diffeomorphism on 
$N=S^{2} \times S^{2}$. Assume that 
$f$ has a fixed embedded ball 
$B^{4} \subset N$. Let 
$N_{f} \to S^{1}$ be the mapping torus of 
$f$. Define a map
\[ \phi : (T^{k-1} \times N_{f}, T^{k} \times B^{4}) \to (BO[0],{\rm pt}) \]
as the composition of the classifying map 
$T^{k-1} \times N_{f} \to BO$ of the tangent bundle along the fibers 
$T((T^{k-1} \times N_{f})/T^{k})$ of the fiber bundle 
$T^{k-1} \times N_{f} \to T^{k}$ and the natural map 
$BO \to BO[0]$. Then 
$\phi$ is homotopic to the constant map onto 
$({\rm pt}, {\rm pt}) \subset (BO[0],{\rm pt})$.
Proof. Note that
\[ \pi_i(BO[0]) =\pi_i(BO)\otimes{\Bbb Q}= \left\{\begin{array}{@{}ll} {\Bbb Q} & i = 0\mod 4,\\ 0 & i\neq 0\mod 4. \end{array}\right. \]
Let 
$u : BO[0] \to BO[0]$ be the identity map and 
$u_{0} : BO[0] \to \{{\rm pt}\} \subset BO[0]$ be the map onto a point in 
$BO[0]$. Then the primary difference obstruction 
$\delta (u,u_{0})$ is non-zero in 
$H^{4}(BO[0];\pi _{4}(BO[0])) \cong H^{4}(BO[0];{\Bbb Q}) \cong {\Bbb Q}[p_{1}^{\rm univ}]$. Therefore there exists a non-zero number 
$r \in {\Bbb Q} \setminus \{0\}$ such that 
$r\delta (u,u_{0}) = p_{1}^{\rm univ}$.
In general, let 
$N$ be an oriented closed and simply connected 
$4$-manifold, 
$\tau : N \to BO[0]$ be the composition of the classifying map 
$N \to BO$ of the tangent bundle of 
$N$ and the natural map 
$BO \to BO[0]$, and 
$\tau _{0} : N \to \{{\rm pt}\} \to BO[0]$ be the map onto a point of 
$BO[0]$. We claim that 
$\tau$ is homotopic to 
$\tau _0$ if 
$p_1(N)=0$. Since 
$\pi _i(BO[0]) =0$ for 
$0< i<4$ and 
$H^i(N;{\Bbb Q})=0$ for 
$i>4$, the difference obstruction 
$\delta (\tau ,\tau _{0})\in H^4(N;\pi _4(BO[0]))$ is the sole obstruction to homotoping 
$\tau$ to 
$\tau _0$. Because of the naturality of the obstruction class, we have 
$p_{1}(N) = \tau ^{\ast } p_{1}^{\rm univ} = r \tau ^{\ast } \delta (u,u_{0}) = r \delta (\tau ,\tau _{0})$ in 
$H^{4}(N;{\Bbb Q})$. Therefore, if 
$p_{1}(N)=0$, we have 
$\delta (\tau ,\tau _{0})=0$, and hence 
$\tau$ is homotopic to the constant map 
$\tau _0$. In particular, if we take 
$N = S^{2} \times S^{2}$, since 
$S^{2} \times S^{2}$ has trivial signature, we have 
$p_{1}(S^{2} \times S^{2})=0$, and thus we can deduce that 
$\tau$ is homotopic to a constant map onto a point in 
$BO[0]$. Similarly, if we fix an embedded ball 
$B^{4} \subset S^{2} \times S^{2}$ and fix a trivialization of 
$T(S^{2} \times S^{2})$ over 
$B^{4}$, we can conclude that the pairwise map 
$\tau : (S^{2} \times S^{2}, B^{4}) \to (BO[0], {\rm pt} )$ is homotopic to the map onto 
$({\rm pt}, {\rm pt} ) \subset (BO[0], {\rm pt})$.
Next, let 
$f : N \to N$ be an orientation-preserving diffeomorphism on 
$N=S^{2} \times S^{2}$. Assume that 
$f$ has a fixed embedded ball 
$B^{4} \subset N$. Let 
$N_{f} \to S^{1}$ be the mapping torus of 
$f$. By the Serre spectral sequence, one can easily see that 
$H^{4}(N_{f};{\Bbb Q}) \cong H^{4}(N;{\Bbb Q})$, and 
$p_{1}(T(N_{f}/S^{1}))$ corresponds to 
$p_{1}(N)$ via this isomorphism, therefore we have 
$p_{1}(T(N_{f}/S^{1}))=0$. Using 
$T(N_{f}/S^{1})$ instead of 
$T(N)$ in the last paragraph, we can see that the composition 
$\tau _{f} : N_{f} \to BO[0]$ of the classifying map 
$N_{f} \to BO$ of 
$T(N_{f}/S^{1})$ and the natural map 
$BO \to BO[0]$ is homotopic to a constant map onto a point in 
$BO[0]$. Similarly, the map 
$\tau _{f} : (N_{f}, S^{1} \times B^{4}) \to (BO[0],{\rm pt})$ is homotopic to the constant map onto 
$({\rm pt}, {\rm pt}) \subset (BO[0],{\rm pt})$. Let 
$\phi : T^{k-1} \times N_{f} \to BO[0]$ be the composition of the classifying map of 
$T((T^{k-1} \times N_{f})/T^{k}) \to T^{k-1} \times N_{f}$ and the natural map 
$BO \to BO[0]$. Since 
$\phi = p^{\ast }\tau _{f}$, where 
$p : T^{k-1} \times N_{f} \to N_{f}$, we have that 
$\phi$ is homotopic to a constant map, and similarly 
$\phi : (T^{k-1} \times N_{f}, T^{k-1} \times S^{1} \times B^{4}) \to (BO[0],{\rm pt})$ is homotopic to the constant map onto 
$({\rm pt}, {\rm pt}) \subset (BO[0],{\rm pt})$.
To proceed the proof of Lemma 6.3, let us describe several facts about 
$K$-theory. Firstly, it is easy to see that the complex 
$K$-group of 
$T^n$ admits a direct sum decomposition
\begin{equation} K(T^n)\cong \bigoplus_{S\subset[n]}K({\Bbb R}^S). \end{equation}(The proof is parallel to that of Proposition 6.1.)
Let 
$c\colon KSp(B)\to K(B), c_S\colon KSp({\Bbb R}^S)\to K({\Bbb R}^S)$ be the forgetful maps which forget the quaternion structures.
Lemma 6.5 The forgetful map 
$c\colon KSp(T^n)\to K(T^n)$ is identified with the direct sum of the forgetful maps 
$c_S\colon KSp({\Bbb R}^S)\to K({\Bbb R}^S)$:
\[ c=\sum_{S\subset[n]} c_S. \]
Proof. The forgetful map 
$c$ builds a bridge between the exact sequence (10) and the corresponding exact sequence of the complex 
$K$-groups, which gives rise to the following commutative diagram.
Thus 
$c\colon KSp(T^n)\to K(T^n)$ is identified with the direct sum of the forgetful maps:
\[ KSp(T^{n-1}\times{\Bbb R})\oplus KSp(T^{n-1})\to K(T^{n-1}\times{\Bbb R})\oplus K(T^{n-1}) \]
via the isomorphisms 
$i_!+\pi ^*$. The lemma is proved by induction.
Proof Proof of Lemma 6.3
Suppose 
$X_I$ is smoothable as a family and a smooth reduction is given. Let 
$T(X_I/T_I) \to X_I$ be the tangent bundle along the fibers. By Proposition 6.1 and (12), we have the splittings
\begin{align*} KSp(T^4) &\cong KSp(pt)\oplus KSp({\Bbb R}^4)\cong {\Bbb Z}\oplus {\Bbb Z}, \\ K(T^4) &\cong K(pt)\oplus K({\Bbb R}^4)\cong {\Bbb Z}\oplus {\Bbb Z}. \end{align*}
Since 
$c_S\colon KSp({\Bbb R}^S)\to K({\Bbb R}^S)$ is injective if 
$S=\emptyset$ or 
$|S|=4$, Lemma 6.5 implies that the forgetful map 
$c\colon KSp(T^4)\to K(T^4)$ is injective. Therefore, in order to verify 
$[{\rm ind}\, {D}]=[\underline {{\Bbb H}}]$, it suffices to check that 
$c([{\rm ind}\, {D}])=[\underline {{\Bbb C}^2}]$.
Since 
$K(T^k)$ is torsion-free, the Chern character 
$Ch : K(T^k) \to H^{\rm even}(T^k;{\Bbb Q})$ is also injective. The index theorem for families [Reference Atiyah and SingerAS71, Theorem (5.1)] gives the equality
\begin{equation} Ch(c([{\rm ind}\, {D}])) = \int_{\rm fiber} \hat{A}(T(X_I/T_I)), \end{equation}
and the integrand is expressed by a polynomial of rational Pontryagin classes, and so belongs to 
$H^{4\ast }(T_I;{\Bbb Q})$. Denote by 
$p_{i} = p_{i}(T(X_I/T_I)) \in H^{4i}(X_I;{\Bbb Q})$ the 
$i$th rational Pontryagin classes of 
$T(X_I/T_I)$.
Once we have seen the vanishings 
$p_{1}^{2}=0$ and 
$p_{i}=0$ for 
$i \geq 2$ in 
$H^{\ast }(X_I;{\Bbb Q})$, then the 
$\hat {A}$-genus of 
$T(X_I/T_I)$ is given by 
$\hat {A}(T(X_I/T_I)) = 1 -p_{1}/24$. Then 
$Ch(c([{\rm ind}\, {D}]))$ is in 
$H^0(T_I;{\Bbb Q})={\Bbb Q}$ and actually it coincides with 
$-\operatorname {sign}(M)/8 =2$. This implies 
$c([{\rm ind}\, {D}])=[\underline {{\Bbb C}^2}]$.
Therefore it suffices to verify that 
$p_{1}^{2}=0$ and 
$p_{i}=0$ for 
$i \geq 2$. Note that 
$p_{i}=0$ holds for 
$i \geq 3$, since 
$\operatorname {rank}_{{\Bbb R}}{T(X_I/T_I)}=4$. Therefore we just need to check that 
$p_{1}^{2}=0$ and 
$p_2=0$. We shall verify such vanishings directly in the topological category from the construction of 
$X$ as follows.
Set 
$M^\prime =2(-E_8)\#(m-k)S^2\times S^2$ and 
$W = T^k \times M^\prime$. Let 
$\tau M^\prime$ and 
$\tau (W/T^k)$ be the tangent micro-bundle of 
$M'$ and that along the fibers of 
$W$, respectively. Thus we have 
$\tau (W/T^k) \cong \pi _{2}^{\ast }\tau M^\prime$, where 
$\pi _{2} : W \to M^\prime$ is the projection. Therefore it follows from degree reasoning that
\begin{equation} p_{1}(\tau(W/T^k))^{2}=0,\quad p_{i}(\tau(W/T^k))=0\quad \text{for}\ i \geq 2. \end{equation} Now decompose 
$X_I$ as
\[ X_I = \big(T^{k} \times \big(M^\prime \setminus \sqcup_{i=1}^{k} B^{4}_{i}\big) \big) \cup \bigsqcup_{i=1}^{k} \big(T^{k-1} \times \big( N_{f_{i}} \setminus S^{1} \times B^{4}_{i}\big) \big), \]
where 
$N=S^{2} \times S^{2}$ and 
$B^{4}_{i}$ are embedded balls. Let
\[ \kappa\colon X_I \to T^{k} \times M^\prime \]
be the collapsing map which collapses each 
$T^{k-1} \times ( N_{f_{i}} \setminus S^{1} \times B^{4}_{i}))$-part into 
$T^k\times \ast$. Let 
$\psi : X_I \to BTOP[0]$ be the composition of the classifying map 
$X_I \to BTOP$ of the tangent micro-bundle along the fibers 
$\tau (X_I/T_I)$ with the natural map 
$BTOP \to BTOP[0]$. Let 
$\psi ^\prime \colon T^{k} \times M^\prime \to BTOP[0]$ be the similarly defined map. By Lemma 6.4, the restriction
\[ \psi : (T^{k-1} \times N_{f_{i}}, T^{k} \times B^{4}_{i}) \to (BTOP[0], {\rm pt}) \]
is homotopic to the constant map onto 
$({\rm pt},{\rm pt}) \subset (BTOP[0],{\rm pt})$. Then the following diagram is homotopy-commutative.
Thus we have
\[ p_{i} = \psi^{{\ast}}p_{i}^{\rm univ} = \kappa^*(\psi^\prime)^*p_{i}^{\rm univ}= \kappa^*p_{i}(\tau((T^{k} \times M^\prime)/T^{k}). \]
By combining this with (14), we obtain 
$p_{1}^{2}=0$ and 
$p_{i}=0$ for 
$i \geq 2$. This completes the proof of the lemma.
Remark 6.3 One can verify 
$c([{\rm ind}\, {D}])=[\underline {{\Bbb C}^2}]$ in a more general setting. In fact, the following can be shown by an argument above: for arbitrary 
$m$, let 
$M$ and 
$f_1,\ldots ,f_m$ be as in Theorem 5.1. Let 
$M\to X\to T^m$ be the multiple mapping torus for 
$f_1,\ldots ,f_m$. If 
$X_I\to T_I$ is smoothed as a family for any 
$I\subset [m]$, then we have 
$c([{\rm ind}\, {D}])=[\underline {{\Bbb C}^2}]$.
On the other hand, for the proof of Theorem 5.2, we need 
${\rm ind}\, {D}=[\underline {{\Bbb H}}]$, but the forgetful map 
$c\colon KSp({\Bbb R}^q)\to K({\Bbb R}^q)$ is not injective if 
$q\equiv 5,6$ mod 
$8$. This is reason why the argument of the proof of Theorem 5.2 is valid only when 
$m\leq 6$, 
$k\leq 4$.
7. Smoothing of the total spaces
In this section we give a proof of the smoothability of the total spaces of the non-smoothable families in Theorem 5.2. A basic tool in this section is Kirby–Siebenmann theory [Reference Kirby and SiebenmannKS77]. We refer the reader to Rudyak's expository book [Reference RudyakRud16] or the ‘Essays’ [Reference Kirby and SiebenmannKS77].
Lemma 7.1 The topological 
$5$-manifold 
$S^{1} \times 2(-E_{8})$ admits a smooth structure.
Proof. For a topological manifold 
$W$, let us denote by 
$\Delta (W) \in H^{4}(W;{\Bbb Z}/2)$ the Kirby–Siebenmann invariant. If 
$W$ is of dimension 
$5$ and written as 
$W = S^{1} \times N$ for a simply connected and closed topological 
$4$-manifold 
$N$, we have 
$H^{4}(W;{\Bbb Z}/2) \cong H^{4}(N;{\Bbb Z}/2)$ by the Künneth theorem, and 
$\Delta (W)$ corresponds to 
$\Delta (N)$ via this isomorphism. This follows from the definition of the Kirby–Siebenmann invariant as an obstruction class (see, for example, [Reference RudyakRud16, § 3.4]). Since the Kirby–Siebenmann invariant is additive with respect to the connected sum of topological 
$4$-manifolds, we have 
$\Delta (2(-E_{8}))=0$, and thus we get 
$\Delta (S^{1} \times 2(-E_{8}))=0$. Recall that, for a closed topological manifold of dimension 
$5$, the Kirby–Siebenmann invariant is the only obstruction to the smoothability. (This follows from the celebrated theorem 
$TOP/PL \simeq K({\Bbb Z}/2,3)$ by Kirby and Siebenmann, stated in [Reference RudyakRud16, page xii], and 
$\pi _{k}(TOP/PL) = \pi _{k}(PL/DIFF)$ for 
$k <7$ [Reference Kirby and SiebenmannKS77, p. 318].) Therefore this proves that 
$S^{1} \times 2(-E_{8})$ is smoothable.
Following Schultz's survey [Reference SchultzSch], we give a smoothing result of a topological embedding of a circle into a higher-dimensional smooth manifold.
Lemma 7.2 Let 
$W$ be a smooth manifold of dimension 
$d \geq 5$, and 
$f : S^{1} \times {\Bbb R}^{d-1} \to W$ be a topological embedding, that is, a homeomorphism onto its image. Then there exists a topological isotopy
\[ \{F_{t} : S^{1} \times {\Bbb R}^{d-1} \to f(S^{1} \times {\Bbb R}^{d-1}) \subset W\}_{t \in [0,1]} \]
such that 
$F_{0} = f$ holds and 
$F_{1} : S^{1} \times {\Bbb R}^{d-1} \to W$ is a smooth embedding.
Proof. Set 
$U := f(S^{1} \times {\Bbb R}^{d-1})$. We can equip the open topological manifold 
$U$ with the smooth structure defined as the restriction of the smooth structure of 
$W$, and also with the smooth structure coming from the standard smooth structure of 
$S^{1} \times {\Bbb R}^{d-1}$ via 
$f$. By Kirby–Siebenmann theory (see [Reference Kirby and SiebenmannKS77, p. 194], and note that ‘concordant implies isotopy’ in 
$\dim \geq 5$), there is a bijection from the set of smoothing of 
$U$ up to isotopy to 
$[U,TOP/O] \cong [S^{1},TOP/O]$, which is just a single point since 
$TOP/O$ is known to be 
$2$-connected. Hence smoothing of 
$U$ is unique up to isotopy. Therefore there exist a diffeomorphism
\[ g : S^{1} \times {\Bbb R}^{d-1} \to U, \]
where 
$U$ is equipped with the restricted smooth structure of 
$W$, and a topological isotopy
\[ F_{t} : S^{1} \times {\Bbb R}^{d-1} \to U \]
such that 
$F_{0} = f$ and 
$F_{1}=g$.
The following proposition is the goal of this section.
Proposition 7.1 The total spaces 
$X$ of the non-smoothable families given in Theorem 5.2 are smoothable as manifolds.
Proof. Set 
$W = S^{1} \times 2(-E_{8})$, which admits a smooth structure by Lemma 7.1. Henceforth we fix a smooth structure on 
$W$. Fix a point 
$p \in 2(-E_{8})$ and whose disk-like neighborhood 
$B^{4} \subset 2(-E_{8})$. Then the map 
$S^{1} \to W$ given by 
$t \mapsto (t,p)$ induces a topological embedding 
$f : S^{1} \times {\Bbb R}^{4} \to W$. Note that 
$T^{n} \times (2(-E_{8}) \setminus B^{4}) = T^{n-1} \times (W \setminus S^{1} \times B^{4})$, where 
$S^{1} \times B^{4}$ is the image of 
$f$. By Lemma 7.2, 
$f$ can be deformed into a smooth embedding 
$g : S^{1} \times {\Bbb R}^{4} \to W$ via a topological isotopy. This gives a homeomorphism
\[ \varphi : X_{1} \to X_{1}', \]
where
\begin{align*} & X_{1} := (T^{n} \times 2({-}E_{8})) \setminus (T^{n-1} \times f(S^{1} \times {\Bbb R}^{4})), \\ & X_{1}' := (T^{n} \times 2({-}E_{8})) \setminus (T^{n-1} \times g(S^{1} \times {\Bbb R}^{4})). \end{align*}
Note that, although 
$X_{1}$ is just a topological manifold, 
$X_{1}'$ is a smooth manifold.
Let 
$f_{1}, \ldots , f_{m}$ be the homeomorphisms used in the construction of 
$X$ in Theorem 5.2. Recall that they act trivially on 
$2(-E_{8})$, and smoothly on 
$mS^{2} \times S^{2}$. Let 
$E \to T^{n}$ be the mapping torus of 
$m S^{2} \times S^{2}$ by commuting diffeomorphism 
$f_{1}, \ldots , f_{m}$. Let 
$D^{4}$ be a fixed ball common for all of 
$f_{1}, \ldots , f_{m}$. (If necessary, we may find such a ball by deforming 
$f_{1}, \ldots , f_{m}$ by smooth isotopy.) Then 
$X$ can be regarded as a topological manifold obtained by gluing the topological manifold 
$X_{1}$ and a smooth manifold 
$X_{2} := E \setminus (T^{n} \times D^{4})$ via a homeomorphism. Since 
$X_{1}$ is homeomorphic to a smooth manifold 
$X_{1}'$ via 
$\varphi$, the topological manifold 
$X = X_{1} \cup X_{2}$ is also homeomorphic to a smooth manifold, that is, 
$X$ is smoothable as a manifold.
Acknowledgements
The authors would like to thank Yosuke Morita for helpful conversations on Proposition 5.1. The authors also appreciate useful comments on algebraic topology by Yuli Rudyak and Daisuke Kishimoto. The authors also wish to thank Mikio Furuta for pointing out a mistake in an earlier version of this paper, and also to thank Ko Ohashi and Yukio Kametani for helpful comments and discussion. Tsuyoshi Kato was supported by JSPS Grant-in-Aid for Scientific Research (B) no. 17H02841 and JSPS Grant-in-Aid for Scientific Research on Innovative Areas (Research in a Proposed Research Area) No. 17H06461. Hokuto Konno was partially supported by JSPS KAKENHI grants 16J05569, 17H06461, 19K23412 and the Program for Leading Graduate Schools, MEXT, Japan, and further, a part of this work was done under the RIKEN Special Postdoctoral Researcher program. Nobuhiro Nakamura was supported by JSPS Grant-in-Aid for Scientific Research (C) no. 19K03506.
Appendix. Equivariant obstruction theory
In this appendix, for the reader's convenience, we summarize some basic materials of equivariant obstruction theory. See tom Dieck's book [Reference tom DiecktDie11] for details. Henceforth we denote by 
$G$ a compact Lie group.
A.1 $G$-CW complexes
A 
$G$-CW complex is a CW complex 
$X$ whose 
$n$-cells are of the forms 
$G / H_{\sigma } \times D^n$, where 
$H_{\sigma } \subset G$ are closed subgroups of 
$G$ and 
$D^{0}=\{{\rm pt}\}$. Here the characteristic map of each cell is assumed to be a 
$G$-map 
$G / H_{\sigma } \times S^{n-1} \to X^{n-1}$, where 
$X^{n-1}$ denotes the 
$(n-1)$-skeleton of 
$X$.
For a pair of 
$G$-CW complexes 
$(X,A)$, we always assume that 
$G$ acts on 
$X \backslash A$ freely. Consider the long exact sequence of homology groups over 
${\Bbb Z}$:
\[ \cdots \rightarrow H_{n+1}(X^{n+1},X^n) \xrightarrow{\partial} H_n(X^n, X^{n-1}) \rightarrow \cdots. \]
Let 
$G_0 \subset G$ be the identity component. Then 
$G/G_0$ acts on each 
$H_n(X^n, X^{n-1})$, and hence
\[ C_n(X,A):= H_n(X^n, X^{n-1}) \]
is a 
${\Bbb Z}[G/G_0]$-module. Let 
$M$ be a 
${\Bbb Z}[G/G_0]$-module. Then we have the cochain complex
\[ C_G^*(X,A):= \operatorname{Hom}_{{\Bbb Z}[G/G_0]} (C_*(X,A); M) \]
whose cohomology group 
$H_G^*(X,A;M)$ is called the Bredon cohomology.
Lemma A.1 There is a chain isomorphism
\[ C_*(X,A) \cong C_*(X/G_0, A/G_0). \]
Proof. Let 
$\phi : \sqcup _j G \times (D^n_j, S^{n-1}_j) \to (X^n, X^{n-1})$ be the characteristic maps. By excision, we have the isomorphisms
\[ \oplus_j H_n (G \times (D^n_j, S^{n-1}_j)) \cong H_n(X^n, X^{n-1}). \]
The former is isomorphic to
\[ \oplus_j H_n (G/ G_0 \times (D^n_j, S^{n-1}_j)) \cong H_n(X^n/G_0, X^{n-1}/G_0) \]
by another excision.
Corollary A.1 We have
\[ H_G^n(X,A;M) \cong H_{G/G_0}^n(X/G_0,A/G_0;M). \]
Let 
$Y$ be a path connected 
$G$-space. Assume, moreover, that 
$Y$ is 
$n$-simple in the sense that the action of 
$\pi _1(Y,y_0)$ on 
$\pi _n(Y, y_0)$ is trivial. Then we have a one-to-one correspondence between 
$\pi _n(Y,y_0)$ and 
$[S^n, Y]$, the space of free homotopy of maps. The 
$G$-action on 
$Y$ induces a homomorphism 
$G/G_0 \to \text {Aut}(\pi _n(Y))$, which gives a 
${\Bbb Z}[G/G_0]$-module structure on 
$\pi _n(Y)$.
Example A.1 Let 
$G = \operatorname {Pin}(2)$. Then 
$G_0 =S^1$ and 
$G/G_0 = {\Bbb Z}_2$. Let 
$V$ be a finite-dimensional unitary representation of 
$G$ with 
$\dim V =n$. The one-point compactification 
$S^V$ of 
$V$ naturally admits a 
$G$-action, and hence 
${\Bbb Z}_2$ acts on
\[ M := \pi_n(S^V) \cong {\Bbb Z} \]
through the quotient homomorphism 
$G \to G/G_0 = \{ \pm 1\}$.
Let 
$U$ be a manifold on which 
$G$ acts freely. We shall consider the pair 
$(X,A) =(U, \partial U)$. Define a bundle 
$l$ over 
$U/G$ with fiber 
${\Bbb Z}$ by
\[ l := U \times_G {\Bbb Z} \to U/ G. \]
Then we have isomorphisms
\[ H^n_G(U, \partial U; M) \cong H^n_{{\Bbb Z}_2} (U/G_0, \partial U/ G_0; M) \cong H^n (U/G, \partial U/ G; l). \]
A.2 $G$-equivariant obstruction class
Let 
$X, Y$ be path connected 
$G$-spaces. Assume also that 
$Y$ is 
$n$-simple.
Theorem A.1 For 
$n \geq 1$, there is an exact sequence
\[ [X^{n+1}, Y]^G \to \text{im} \big( [X^n, Y]^G \to [X^{n-1}, Y]^G \big) \xrightarrow{C^{n+1}} H^{n+1}_G(X_A; \pi_n Y). \]
A sketch of the construction of the map 
$C^{n+1}$ above is as follows. Fix 
$[h] \in [ X^n, Y]^G$. Let us consider the diagram
\[ H_{n+1}(X^{n+1}, X^n) \xleftarrow{\rho}\pi_{n+1}(X^{n+1}, X^n) \xrightarrow{\partial} \pi_n(X^n) \xrightarrow{h_*} \pi_n (Y) =[S^n, Y], \]
where 
$\rho$ is the Hurewicz homomorphism. Since 
$Y$ is 
$n$-simple, we have that 
$\ker \rho = \langle x - \alpha x \,|\, \alpha \in \pi _1(X^n)\rangle$ and that 
$h_* \circ \partial (x - \alpha x) =0$. Thus we obtain a well-defined cochain
\begin{align*} C^{n+1} (h) \in C_G^{n+1}(X,A; \pi_n(Y)) &= \operatorname{Hom}_{{\Bbb Z}[G/G_0]} (C_{n+1}(X,A); \pi_n(Y)) \\ &= \operatorname{Hom}_{{\Bbb Z}[G/G_0]} (H_{n+1}(X^{n+1},X^n); \pi_n(Y)) \end{align*}
given by 
$C^{n+1}(h) : = h_* \circ \partial \circ \rho ^{-1}$. This construction gives a map
\[ C^{n+1} : [X^n, Y]^G \to C_G^{n+1}(X,A; \pi_n(Y)), \]
which induces 
$C^{n+1}$ in Theorem A.1.
Proposition A.1 Let 
$Y$ be an 
$(n-1)$-connected and 
$n$-simple space. Then an arbitrary continuous map 
$f: A \to Y$ is extendable to a continuous map 
$\tilde {f}: X^n \to Y$. Moreover, any two such extensions are homotopic to each other relative to 
$A$.
Let 
$f: A \to Y$ be a continuous map. The primary obstruction class is given by
\[ \gamma(f) := C^{n+1}(\tilde{f}) \in H^{n+1}_G(X,A; \pi_n(Y)), \]
where 
$\tilde {f}: X^n \to Y$ is an extension. Define
\[ (X^*,A^*) := (I, \partial I) \times (X,A)= (X \times I, I \times A \cup \partial I \times X). \]
Given 
$F: I \times A \cup \partial I \times X \to Y$, let us denote 
$f_i = F|_{\{i\} \times X}$ for 
$i =0,1$. The difference obstruction class between 
$f_{0}$ and 
$f_{1}$ is defined by
\[ \gamma(f_0,f_1) := C^{n+1}(F) \in H^{n+1}_G(X^*, A^*; \pi_n(Y))\cong H^n_G(X,A; \pi_n(Y)), \]
where the last isomorphism is the suspension isomorphism.
Theorem A.2 Fix a map 
$f_\ast : X \to Y$. Let us denote
\[ [X, Y]^G_A : = \left\{G\text{-homotopy classes rel } A \text{ of } f: X \to Y \text{ with } f|_A = f_\ast|_A\right\}. \]
Then we have a one-to-one correspondence
\[ [X, Y]^G_A \leftrightarrow H^n_G(X,A; \pi_n(Y)) \]
given by 
$f \leftrightarrow \gamma (f, f_\ast )$.
A.3 The image of a forgetful map
Let 
$U$ be an 
$n$-dimensional compact (possibly non-orientable) manifold with boundary 
$\partial U \ne \emptyset$. Assume that 
${\Bbb Z}_2$ acts freely on the pair 
$(U, \partial U)$. Let 
$\pi$ be the quotient map
\[ \pi : (U, \partial U) \to (\bar{U}, \bar{\partial U}) = (U/ {\Bbb Z}_2, \partial U / {\Bbb Z}_2). \]
Consider a real 
$n$-dimensional representation 
$V$ of 
${\Bbb Z}_2$. For 
$Y = S^V$, 
${\Bbb Z}_2$ acts on 
$\pi _n(Y) \cong {\Bbb Z}$.
Proposition A.2 (cf. [Reference tom DiecktDie11, II.4])
The image of the forgetful map
\[ \varphi\colon H_{{\Bbb Z}_2}^n(U, \partial U; \pi_n(Y))\to H^n(U, \partial U; {\Bbb Z}) \]
is 
$2{\Bbb Z} \subset {\Bbb Z} \cong H^n(U, \partial U; {\Bbb Z})$ if 
$U$ is orientable, and is 
$\{0\}$ if 
$U$ is non-orientable.
Proof. Let us consider the bundle
\[ l := U \times_{{\Bbb Z}_2} \pi_n(Y) \to \bar{U}. \]
Since the 
${\Bbb Z}_2$-action on 
$(U,\partial U)$ is free, the Bredon cohomology 
$H_{{\Bbb Z}_2}^n(U, \partial U; \pi _n(Y))$ is identified with the 
$l$-coefficient cohomology 
$H^n(\bar {U}, \bar {\partial U}; l)$, and we have the following commutative diagram.
Then the conclusion follows from the next commutative diagram.
Here the right vertical map is zero since it is induced from the quotient map of the double cover 
$(U, \partial U) \to ( \bar {U}, \bar {\partial U})$.
