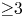1. Introduction
A powerful tool in algebraic geometry over the field of complex numbers is viewing smooth projective varieties as complex manifolds and henceforth using complex analysis to study them. An important role for that technique is played by Kähler manifolds: this is a subclass of complex manifolds large enough to contain all smooth projective algebraic varieties and small enough to be amenable to Hodge theory. In particular, for any compact Kähler manifold ![]() $X$ the Hodge-to-de Rham spectral sequence
$X$ the Hodge-to-de Rham spectral sequence ![]() $E_1^{i,j}=H^{j}(X,\Omega ^{i}_X)\Rightarrow H^{i+j}_{\mathrm {dR}}(X/{\mathbb {C}})$ degenerates at the first page and the Hodge numbers satisfy Hodge symmetry:
$E_1^{i,j}=H^{j}(X,\Omega ^{i}_X)\Rightarrow H^{i+j}_{\mathrm {dR}}(X/{\mathbb {C}})$ degenerates at the first page and the Hodge numbers satisfy Hodge symmetry: ![]() $\dim _{{\mathbb {C}}} H^{j}(X,\Omega ^{i}_X)=\dim _{{\mathbb {C}}}H^{i}(X,\Omega ^{j}_X)$.
$\dim _{{\mathbb {C}}} H^{j}(X,\Omega ^{i}_X)=\dim _{{\mathbb {C}}}H^{i}(X,\Omega ^{j}_X)$.
The situation in ![]() $p$-adic geometry is somewhat different:
$p$-adic geometry is somewhat different: ![]() $p$-adic Hodge theory has been developed for all smooth proper rigid-analytic varieties, without any ‘Kähler’ assumption. It was proven by Scholze [Reference ScholzeSch13] that for any such variety the Hodge-to-de Rham spectral sequence degenerates. There are, however, examples of smooth proper rigid-analytic varieties that fail Hodge symmetry. This might suggest that there should be a natural narrower class of rigid-analytic varieties for which Hodge symmetry does hold.
$p$-adic Hodge theory has been developed for all smooth proper rigid-analytic varieties, without any ‘Kähler’ assumption. It was proven by Scholze [Reference ScholzeSch13] that for any such variety the Hodge-to-de Rham spectral sequence degenerates. There are, however, examples of smooth proper rigid-analytic varieties that fail Hodge symmetry. This might suggest that there should be a natural narrower class of rigid-analytic varieties for which Hodge symmetry does hold.
Let ![]() $K$ be a discretely valued
$K$ be a discretely valued ![]() $p$-adic field with ring of integers
$p$-adic field with ring of integers ![]() ${\mathcal {O}}_K$ and perfect residue field
${\mathcal {O}}_K$ and perfect residue field ![]() $k$. In [Reference Hansen and LiHL20] David Hansen and Shizhang Li raised the following question (see also [Reference ScholzeSch18, Conjecture 2.4]) suggesting a candidate for this narrower class.
$k$. In [Reference Hansen and LiHL20] David Hansen and Shizhang Li raised the following question (see also [Reference ScholzeSch18, Conjecture 2.4]) suggesting a candidate for this narrower class.
Question Let ![]() $X$ be a smooth proper rigid-analytic variety over
$X$ be a smooth proper rigid-analytic variety over ![]() $K$ admitting a formal model over
$K$ admitting a formal model over ![]() ${\mathcal {O}}_K$ with projective special fiber. Is it true that
${\mathcal {O}}_K$ with projective special fiber. Is it true that ![]() $\dim _K H^{i}(X,\Omega ^{j}_{X/K})=\dim _K H^{j}(X,\Omega ^{i}_{X/K})$ for all
$\dim _K H^{i}(X,\Omega ^{j}_{X/K})=\dim _K H^{j}(X,\Omega ^{i}_{X/K})$ for all ![]() $i, j$?
$i, j$?
Hansen and Li answered this question positively for ![]() $i+j=1$ in [Reference Hansen and LiHL20, Theorem 1.2]. The main result of this text is that the answer is in general negative for
$i+j=1$ in [Reference Hansen and LiHL20, Theorem 1.2]. The main result of this text is that the answer is in general negative for ![]() $i+j\geq 3$.
$i+j\geq 3$.
Theorem (Corollary 4.4)
For every pair of positive integers ![]() $i\neq j$ with
$i\neq j$ with ![]() $i+j\geq 3$ there exists a smooth proper rigid-analytic variety
$i+j\geq 3$ there exists a smooth proper rigid-analytic variety ![]() $X$ over
$X$ over ![]() ${\mathbb {Q}}_p$ admitting a smooth formal model
${\mathbb {Q}}_p$ admitting a smooth formal model ![]() ${\mathfrak X}$ over
${\mathfrak X}$ over ![]() $\operatorname {{Spf}} {\mathbb {Z}}_p$ with projective special fiber
$\operatorname {{Spf}} {\mathbb {Z}}_p$ with projective special fiber ![]() ${\mathfrak X}_{{\mathbb {F}}_p}$ such that
${\mathfrak X}_{{\mathbb {F}}_p}$ such that
The idea behind the examples comes from the following difference between complex Hodge theory and ![]() $p$-adic Hodge theory. For any compact Kähler manifold
$p$-adic Hodge theory. For any compact Kähler manifold ![]() $X$ not only is there an equality of numbers
$X$ not only is there an equality of numbers ![]() $h^{i,j}(X)=h^{j,i}(X)$ but there is also a canonical isomorphism of
$h^{i,j}(X)=h^{j,i}(X)$ but there is also a canonical isomorphism of ![]() ${\mathbb {C}}$-vector spaces:
${\mathbb {C}}$-vector spaces:
In particular, for a finite group ![]() $G$ acting on
$G$ acting on ![]() $X$ the
$X$ the ![]() $G$-representations
$G$-representations ![]() $H^{j}(X,\Omega ^{i}_X)$ and
$H^{j}(X,\Omega ^{i}_X)$ and ![]() $H^{i}(X,\Omega ^{j}_X)$ are dual to each other.
$H^{i}(X,\Omega ^{j}_X)$ are dual to each other.
We show that the analogous statement in ![]() $p$-adic geometry fails already for abeloid varieties. We construct a formal abelian scheme
$p$-adic geometry fails already for abeloid varieties. We construct a formal abelian scheme ![]() ${\mathfrak A}$ (necessarily a non-algebraizable one) with an action of a finite group
${\mathfrak A}$ (necessarily a non-algebraizable one) with an action of a finite group ![]() $G$ of order prime to
$G$ of order prime to ![]() $p$ such that the
$p$ such that the ![]() $G$-representations on the cohomology groups
$G$-representations on the cohomology groups ![]() $H^{0}(A,\Omega ^{1}_{A})$ and
$H^{0}(A,\Omega ^{1}_{A})$ and ![]() $H^{1}(A,{\mathcal {O}})$ of the abeloid generic fiber
$H^{1}(A,{\mathcal {O}})$ of the abeloid generic fiber ![]() $A$ of
$A$ of ![]() ${\mathfrak A}$ are not dual to each other.
${\mathfrak A}$ are not dual to each other.
Moreover, for ![]() $i+j= 3$ we can arrange (Proposition 3.1) that the dimensions of G-invariants on the spaces
$i+j= 3$ we can arrange (Proposition 3.1) that the dimensions of G-invariants on the spaces ![]() $H^{i}(A,\Omega _A^{j})$ and
$H^{i}(A,\Omega _A^{j})$ and ![]() $H^{j}(A,\Omega _A^{i})$ are different (note that these
$H^{j}(A,\Omega _A^{i})$ are different (note that these ![]() $G$-representations are obtained from
$G$-representations are obtained from ![]() $H^{0}(A,\Omega ^{1}_{A})$ and
$H^{0}(A,\Omega ^{1}_{A})$ and ![]() $H^{1}(A,{\mathcal {O}})$ by taking exterior powers and tensor products). Taking the direct product with an auxiliary smooth projective formal scheme to make the
$H^{1}(A,{\mathcal {O}})$ by taking exterior powers and tensor products). Taking the direct product with an auxiliary smooth projective formal scheme to make the ![]() $G$-action free and taking the quotient by
$G$-action free and taking the quotient by ![]() $G$ gives the desired example. The examples for
$G$ gives the desired example. The examples for ![]() $i+j>3$ are obtained simply by taking the direct product with an appropriate projective scheme to move the asymmetry to higher cohomology via the Künneth formula.
$i+j>3$ are obtained simply by taking the direct product with an appropriate projective scheme to move the asymmetry to higher cohomology via the Künneth formula.
This strategy does not work for ![]() $i+j= 2$ for a good reason: any smooth proper rigid-analytic variety that admits a smooth (not necessarily with a projective special fiber) formal model satisfies Hodge symmetry on first and second cohomology.
$i+j= 2$ for a good reason: any smooth proper rigid-analytic variety that admits a smooth (not necessarily with a projective special fiber) formal model satisfies Hodge symmetry on first and second cohomology.
Proposition 1.1 (Corollary 2.2)
If a smooth proper rigid-analytic variety ![]() $X$ over
$X$ over ![]() $K$ admits a smooth formal model over
$K$ admits a smooth formal model over ![]() ${\mathcal {O}}_K$, then
${\mathcal {O}}_K$, then ![]() $\dim H^{0}(X,\Omega ^{i}_{X/K})=\dim _K H^{i}(X,{\mathcal {O}})$ for
$\dim H^{0}(X,\Omega ^{i}_{X/K})=\dim _K H^{i}(X,{\mathcal {O}})$ for ![]() $i=1,2$.
$i=1,2$.
Proposition 1.1 is a consequence of a certain self-duality of Frobenius action on the crystalline cohomology of the special fiber and weak admissibility (in the sense of filtered ![]() $\varphi$-modules) of de Rham cohomology of
$\varphi$-modules) of de Rham cohomology of ![]() $X$ coming from the crystalline comparison theorem. As mentioned above, Hansen and Li proved this statement by a different method for
$X$ coming from the crystalline comparison theorem. As mentioned above, Hansen and Li proved this statement by a different method for ![]() $i=1$ in the case of (arbitrarily singular) projective reduction. Piotr Achinger has independently obtained Proposition 1.1 in the case of smooth projective reduction by the same method, see [Reference AchingerAch20] for a treatment of a number of situations where Hodge symmetry does follow from the existence of a model with projective special fiber, including some cases when reduction is singular.
$i=1$ in the case of (arbitrarily singular) projective reduction. Piotr Achinger has independently obtained Proposition 1.1 in the case of smooth projective reduction by the same method, see [Reference AchingerAch20] for a treatment of a number of situations where Hodge symmetry does follow from the existence of a model with projective special fiber, including some cases when reduction is singular.
Notation
Let ![]() $p$ be a prime number fixed throughout the text. If
$p$ be a prime number fixed throughout the text. If ![]() $X$ is an object of any of the three types
$X$ is an object of any of the three types ![]() $\{$smooth proper rigid-analytic variety over
$\{$smooth proper rigid-analytic variety over ![]() $K$, smooth proper formal scheme over
$K$, smooth proper formal scheme over ![]() $\operatorname {{Spf}}{\mathcal {O}}_K$, smooth proper algebraic variety over an arbitrary field
$\operatorname {{Spf}}{\mathcal {O}}_K$, smooth proper algebraic variety over an arbitrary field ![]() $F\}$, denote by
$F\}$, denote by ![]() $h^{i,j}(X)$ the number
$h^{i,j}(X)$ the number ![]() $\dim _K H^{j}(X,\Omega ^{i}_{X/K}),\operatorname {{rk}}_{{\mathcal {O}}_K}H^{j}(X,\Omega ^{i}_{X/{\mathcal {O}}_K})$ or
$\dim _K H^{j}(X,\Omega ^{i}_{X/K}),\operatorname {{rk}}_{{\mathcal {O}}_K}H^{j}(X,\Omega ^{i}_{X/{\mathcal {O}}_K})$ or ![]() $\dim _F H^{j}(X,\Omega ^{i}_{X/F})$ respectively. Denote also by
$\dim _F H^{j}(X,\Omega ^{i}_{X/F})$ respectively. Denote also by ![]() $\delta ^{i,j}(X)$ the number
$\delta ^{i,j}(X)$ the number ![]() $h^{i,j}(X)-h^{j,i}(X)$ in any of the three situations. For the convenience of notation, we declare
$h^{i,j}(X)-h^{j,i}(X)$ in any of the three situations. For the convenience of notation, we declare ![]() $h^{i,j}(X)=0$ if
$h^{i,j}(X)=0$ if ![]() $i$ or
$i$ or ![]() $j$ is negative. Note that
$j$ is negative. Note that ![]() $h^{i,j}(X)=h^{i,j}({\mathfrak X})$ if
$h^{i,j}(X)=h^{i,j}({\mathfrak X})$ if ![]() $X$ is the generic fiber of a smooth proper formal scheme
$X$ is the generic fiber of a smooth proper formal scheme ![]() ${\mathfrak X}$ by Lemma 4.1. We say that an object
${\mathfrak X}$ by Lemma 4.1. We say that an object ![]() $X$ ‘satisfies Hodge symmetry in degree
$X$ ‘satisfies Hodge symmetry in degree ![]() $d$’ if
$d$’ if ![]() $h^{i,j}(X)=h^{j,i}(X)$ for all
$h^{i,j}(X)=h^{j,i}(X)$ for all ![]() $i,j$ with
$i,j$ with ![]() $i+j=d$ and
$i+j=d$ and ![]() $X$ ‘satisfies Hodge symmetry’ if it does so for all
$X$ ‘satisfies Hodge symmetry’ if it does so for all ![]() $d$.
$d$.
2. Hodge symmetry in degree  $2$
$2$
For the duration of this section let ![]() $K$ be a discretely valued field of characteristic zero with perfect residue field
$K$ be a discretely valued field of characteristic zero with perfect residue field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p$. Denote by
$p$. Denote by ![]() $K_0$ the subfield
$K_0$ the subfield ![]() $W(k)[{1}/{p}]$, and let
$W(k)[{1}/{p}]$, and let ![]() $\sigma$ be its automorphism induced by Frobenius action on
$\sigma$ be its automorphism induced by Frobenius action on ![]() $k$.
$k$.
The goal of this section is to observe that results of ![]() $p$-adic Hodge theory impose the following relation between Hodge numbers of a rigid-analytic variety with good reduction. A similar idea has been used in [Reference Fontaine and MessingFM87, I.4.4] to prove Hodge symmetry for smooth proper algebraic varieties over
$p$-adic Hodge theory impose the following relation between Hodge numbers of a rigid-analytic variety with good reduction. A similar idea has been used in [Reference Fontaine and MessingFM87, I.4.4] to prove Hodge symmetry for smooth proper algebraic varieties over ![]() $K$.
$K$.
Proposition 2.1 If ![]() ${\mathfrak X}$ is a smooth proper formal scheme over
${\mathfrak X}$ is a smooth proper formal scheme over ![]() ${\mathcal {O}}_K$, then for its generic fiber
${\mathcal {O}}_K$, then for its generic fiber ![]() $X$ and every
$X$ and every ![]() $n$ the following relation among
$n$ the following relation among ![]() $h^{i,j}:=h^{i,j}(X)$ holds:
$h^{i,j}:=h^{i,j}(X)$ holds:
Corollary 2.2 For a smooth proper formal scheme ![]() ${\mathfrak X}$ over
${\mathfrak X}$ over ![]() $\operatorname {{Spf}}{\mathcal {O}}_K$ we have the following for the generic fiber
$\operatorname {{Spf}}{\mathcal {O}}_K$ we have the following for the generic fiber ![]() $X={\mathfrak X}_K$:
$X={\mathfrak X}_K$:
(i)
 $h^{1,0}(X)=h^{0,1}(X)$ and
$h^{1,0}(X)=h^{0,1}(X)$ and  $h^{2,0}(X)=h^{0,2}(X)$;
$h^{2,0}(X)=h^{0,2}(X)$;(ii) for odd
 $n$ the Betti numbers
$n$ the Betti numbers  $\dim _{{\mathbb {Q}}_p}H^{n}_{\acute {e}t}(X_{\bar {K}},{\mathbb {Q}}_p)=\dim _{K}H^{n}_{\mathrm {dR}}(X/K)$ are even.
$\dim _{{\mathbb {Q}}_p}H^{n}_{\acute {e}t}(X_{\bar {K}},{\mathbb {Q}}_p)=\dim _{K}H^{n}_{\mathrm {dR}}(X/K)$ are even.
Proof. (i) The equality (1) takes forms ![]() $h^{1,0}=h^{0,1}$ and
$h^{1,0}=h^{0,1}$ and ![]() $h^{1,1}+2h^{2,0}=2h^{0,2}+h^{1,1}$ for
$h^{1,1}+2h^{2,0}=2h^{0,2}+h^{1,1}$ for ![]() $n=1,2$ respectively.
$n=1,2$ respectively.
(ii) The sum of the left-hand side and the right-hand side of (1) is, of course, even and is also equal to ![]() $n\cdot (h^{0,n}+h^{1,n-1}+\cdots +h^{n,0})=n\cdot \dim _{K}H^{n}_{\mathrm {dR}}(X/K)$, so
$n\cdot (h^{0,n}+h^{1,n-1}+\cdots +h^{n,0})=n\cdot \dim _{K}H^{n}_{\mathrm {dR}}(X/K)$, so ![]() $\dim _K H^{n}_{\mathrm {dR}}(X/K)$ is even for odd
$\dim _K H^{n}_{\mathrm {dR}}(X/K)$ is even for odd ![]() $n$.
$n$.
We first recall the set-up of rational ![]() $p$-adic Hodge theory. Let
$p$-adic Hodge theory. Let ![]() $\mathrm {MF}^{\varphi }_{K}$ be the category of filtered
$\mathrm {MF}^{\varphi }_{K}$ be the category of filtered ![]() $\varphi$-modules over
$\varphi$-modules over ![]() $K$ [Reference FontaineFon79]. Its objects are finite-dimensional vector spaces
$K$ [Reference FontaineFon79]. Its objects are finite-dimensional vector spaces ![]() $D$ over
$D$ over ![]() $K_0$ equipped with a semi-linear automorphism
$K_0$ equipped with a semi-linear automorphism ![]() $\varphi _D:D\to D$ and a deceasing filtration
$\varphi _D:D\to D$ and a deceasing filtration ![]() $F^{i}D_K$ on the
$F^{i}D_K$ on the ![]() $K$-vector space
$K$-vector space ![]() $D_K:=D\otimes _{K_0}K$. To every such object we can attach two integers
$D_K:=D\otimes _{K_0}K$. To every such object we can attach two integers
Here ![]() $D_{\alpha }$ is the slope
$D_{\alpha }$ is the slope ![]() $\alpha$ direct summand of the
$\alpha$ direct summand of the ![]() $\varphi$-module
$\varphi$-module ![]() $D$ under the Dieudonne–Manin decomposition and
$D$ under the Dieudonne–Manin decomposition and ![]() $\operatorname {{gr}}^{i}D_K:=F^{i}D_K/F^{i+1}D_K$ are the graded pieces of the filtration. Note that
$\operatorname {{gr}}^{i}D_K:=F^{i}D_K/F^{i+1}D_K$ are the graded pieces of the filtration. Note that ![]() $t_N$ depends only on the semi-linear endomorphism and we will also use the notation
$t_N$ depends only on the semi-linear endomorphism and we will also use the notation ![]() $t_N(D)$ for a
$t_N(D)$ for a ![]() $\varphi$-module
$\varphi$-module ![]() $D$ not equipped with a filtration. A filtered
$D$ not equipped with a filtration. A filtered ![]() $\varphi$-module
$\varphi$-module ![]() $D\in \mathrm {MF}^{\varphi }_{K}$ is called weakly admissible if
$D\in \mathrm {MF}^{\varphi }_{K}$ is called weakly admissible if ![]() $t_N(D)=t_H(D)$ and for every subobject
$t_N(D)=t_H(D)$ and for every subobject ![]() $D'\subset D$ we have
$D'\subset D$ we have ![]() $t_N(D')\geq t_H(D')$. For an integer
$t_N(D')\geq t_H(D')$. For an integer ![]() $i$ denote by
$i$ denote by ![]() $K_0(i)$ the filtered
$K_0(i)$ the filtered ![]() $\varphi$-module given by a one-dimensional vector space
$\varphi$-module given by a one-dimensional vector space ![]() $D=K_0$ with
$D=K_0$ with ![]() $\varphi _d=p^{-i}\sigma$ and the filtration defined by
$\varphi _d=p^{-i}\sigma$ and the filtration defined by ![]() $F^{-i}D_K=D_K,F^{-i+1}D_{K}=0$. For a filtered
$F^{-i}D_K=D_K,F^{-i+1}D_{K}=0$. For a filtered ![]() $\varphi$-module
$\varphi$-module ![]() $D$ define its
$D$ define its ![]() $i$-fold twist
$i$-fold twist ![]() $D(i)$ as the tensor product
$D(i)$ as the tensor product ![]() $D\otimes _{K_0}K_0(i)$, we use the same notation for twisting
$D\otimes _{K_0}K_0(i)$, we use the same notation for twisting ![]() $\varphi$-modules not equipped with a filtration.
$\varphi$-modules not equipped with a filtration.
We have the following symmetry of Frobenius slopes, due to [Reference SuhSuh12].
Lemma 2.3 (Corollary 2.2.4 in [Reference SuhSuh12])
Let ![]() $Y$ be a smooth proper variety over
$Y$ be a smooth proper variety over ![]() $k$. For the
$k$. For the ![]() $\varphi$-module
$\varphi$-module ![]() $D=H^{n}_{\mathrm {cris}}(Y/W(k))[{1}/{p}]$ we have
$D=H^{n}_{\mathrm {cris}}(Y/W(k))[{1}/{p}]$ we have ![]() $t_N(D)=n\cdot \dim _{K_0}D-t_N(D)$.
$t_N(D)=n\cdot \dim _{K_0}D-t_N(D)$.
Proof. For the convenience of the reader we recall the proof in the case when ![]() $Y$ is projective over an arbitrary perfect field or arbitrary proper defined over a finite field.
$Y$ is projective over an arbitrary perfect field or arbitrary proper defined over a finite field.
If ![]() $Y$ is projective, denote by
$Y$ is projective, denote by ![]() $L\in H^{2}_{\mathrm {cris}}(Y/W(k))$ the crystalline Chern class of an ample line bundle on
$L\in H^{2}_{\mathrm {cris}}(Y/W(k))$ the crystalline Chern class of an ample line bundle on ![]() $Y$. The hard Lefschetz theorem for crystalline cohomology ([Reference Katz and MessingKM74, Corollary 1(2)] in the case of a finite base field) shows that cup-product with
$Y$. The hard Lefschetz theorem for crystalline cohomology ([Reference Katz and MessingKM74, Corollary 1(2)] in the case of a finite base field) shows that cup-product with ![]() $L^{d-\min (n,2d-n)}$ induces an isomorphism
$L^{d-\min (n,2d-n)}$ induces an isomorphism ![]() $H^{n}_{\mathrm {cris}}(Y/W(k))[{1}/{p}](n-d)\simeq H^{2d-n}_{\mathrm {cris}}(Y/W(k))[{1}/{p}]$ of
$H^{n}_{\mathrm {cris}}(Y/W(k))[{1}/{p}](n-d)\simeq H^{2d-n}_{\mathrm {cris}}(Y/W(k))[{1}/{p}]$ of ![]() $\varphi$-modules over
$\varphi$-modules over ![]() $K_0$. On the other hand, Poincaré duality provides an isomorphism
$K_0$. On the other hand, Poincaré duality provides an isomorphism ![]() $H^{2d-n}_{\mathrm {cris}}(Y/W(k))[{1}/{p}]\simeq H^{n}_{\mathrm {cris}}(Y/W(k))^{\vee }[{1}/{p}](-d)$. Combining these isomorphisms we get
$H^{2d-n}_{\mathrm {cris}}(Y/W(k))[{1}/{p}]\simeq H^{n}_{\mathrm {cris}}(Y/W(k))^{\vee }[{1}/{p}](-d)$. Combining these isomorphisms we get ![]() $H^{n}_{\rm cris}(Y/W(k))[{1}/{p}](n)\simeq H^{n}_{\mathrm {cris}}(Y/W(k))[1/p]^{\vee }$. Since
$H^{n}_{\rm cris}(Y/W(k))[{1}/{p}](n)\simeq H^{n}_{\mathrm {cris}}(Y/W(k))[1/p]^{\vee }$. Since ![]() $t_N(D^{\vee }(-n))=-t_N(D(n))=-t_N(D)+n\cdot \dim _{K_0}D$ we get the desired equality.
$t_N(D^{\vee }(-n))=-t_N(D(n))=-t_N(D)+n\cdot \dim _{K_0}D$ we get the desired equality.
If ![]() $Y$ is not projective but is defined over a finite field
$Y$ is not projective but is defined over a finite field ![]() $k={\mathbb {F}}_{q}$ the result follows from Weil conjectures: the multiset of
$k={\mathbb {F}}_{q}$ the result follows from Weil conjectures: the multiset of ![]() $q$-power Frobenius eigenvalues consists of algebraic integers and is stable under complex conjugation. Hence, it is stable under the operation
$q$-power Frobenius eigenvalues consists of algebraic integers and is stable under complex conjugation. Hence, it is stable under the operation ![]() $\alpha \mapsto q^{n}\alpha ^{-1}=\bar {\alpha }$ so the multiset of slopes is stable under
$\alpha \mapsto q^{n}\alpha ^{-1}=\bar {\alpha }$ so the multiset of slopes is stable under ![]() $\lambda \mapsto n-\lambda$, as desired.
$\lambda \mapsto n-\lambda$, as desired.
Proof of Proposition 2.1 Consider the filtered ![]() $\varphi$-module given by
$\varphi$-module given by ![]() $D=H^{n}_{\mathrm {cris}}({\mathfrak X}_k/W(k))[{1}/{p}]$ with the Frobenius structure induced by
$D=H^{n}_{\mathrm {cris}}({\mathfrak X}_k/W(k))[{1}/{p}]$ with the Frobenius structure induced by ![]() $\mathop {Fr}:{\mathfrak X}_k \to {\mathfrak X}_k\times _{k,\sigma }k$ and the filtration on
$\mathop {Fr}:{\mathfrak X}_k \to {\mathfrak X}_k\times _{k,\sigma }k$ and the filtration on ![]() $D_K$ is given by the Hodge filtration on the de Rham cohomology of the generic fiber
$D_K$ is given by the Hodge filtration on the de Rham cohomology of the generic fiber ![]() $H^{n}_{\mathrm {dR}}(X/K)\simeq H^{n}_{\mathrm {cris}}({\mathfrak X}/W(k))\otimes _{W(k)}K=D_K$.
$H^{n}_{\mathrm {dR}}(X/K)\simeq H^{n}_{\mathrm {cris}}({\mathfrak X}/W(k))\otimes _{W(k)}K=D_K$.
By the crystalline comparison theorem proved in [Reference Bhatt, Morrow and ScholzeBMS18, Theorem 1.1(i)] for smooth proper formal schemes, the filtered ![]() $\varphi$-module
$\varphi$-module ![]() $D$ is obtained by applying the functor
$D$ is obtained by applying the functor ![]() $D_{\mathrm {cris}}$ to the
$D_{\mathrm {cris}}$ to the ![]() $p$-adic Galois representation
$p$-adic Galois representation ![]() $H^{n}_{\mathrm {et}}(X_{\bar {K}},{\mathbb {Q}}_p)$. In particular,
$H^{n}_{\mathrm {et}}(X_{\bar {K}},{\mathbb {Q}}_p)$. In particular, ![]() $D$ is weakly admissible by [Reference FontaineFon79, Proposition 4.4.5].
$D$ is weakly admissible by [Reference FontaineFon79, Proposition 4.4.5].
Hence, ![]() $t_H(D)=t_N(D)$ so by Lemma 2.3 we get
$t_H(D)=t_N(D)$ so by Lemma 2.3 we get ![]() $t_H(D)=n\cdot \dim _K H^{n}_{\mathrm {dR}}(X/K)-t_H(D)$. As
$t_H(D)=n\cdot \dim _K H^{n}_{\mathrm {dR}}(X/K)-t_H(D)$. As ![]() $t_H(D)=h^{1,{n-1}}+2h^{2,n-2}+\cdots + n\cdot h^{n,0}$ and
$t_H(D)=h^{1,{n-1}}+2h^{2,n-2}+\cdots + n\cdot h^{n,0}$ and ![]() $\dim _K H^{n}_{\mathrm {dR}}(X/K)=h^{0,n}+h^{1,n-1}+\cdots + h^{n,0}$ we get the desired equality.
$\dim _K H^{n}_{\mathrm {dR}}(X/K)=h^{0,n}+h^{1,n-1}+\cdots + h^{n,0}$ we get the desired equality.
Remark 2.4 The above proof used only that the endpoints of the Newton and Hodge polygons of ![]() $D$ coincide. The full strength of weak admissibility, however, does not put any further restrictions on the Hodge numbers. For any tuple of non-negative integers
$D$ coincide. The full strength of weak admissibility, however, does not put any further restrictions on the Hodge numbers. For any tuple of non-negative integers ![]() $h^{0,n},h^{1,n-1},\ldots , h^{n,0}$ satisfying (1) equip the vector space
$h^{0,n},h^{1,n-1},\ldots , h^{n,0}$ satisfying (1) equip the vector space ![]() $D:={\mathbb {Q}}_p^{b}$ of dimension
$D:={\mathbb {Q}}_p^{b}$ of dimension ![]() $b=h^{0,n}+h^{1,n-1}+\cdots + h^{n,0}$ with an endomorphism
$b=h^{0,n}+h^{1,n-1}+\cdots + h^{n,0}$ with an endomorphism ![]() $\varphi$ that has irreducible characteristic polynomial with all roots having valuation
$\varphi$ that has irreducible characteristic polynomial with all roots having valuation ![]() $a/b$ where
$a/b$ where ![]() $a=h^{1,n-1}+2h^{2,n-2}\cdots + n\cdot h^{n,0}$. Endowing
$a=h^{1,n-1}+2h^{2,n-2}\cdots + n\cdot h^{n,0}$. Endowing ![]() $D$ with an arbitrary filtration
$D$ with an arbitrary filtration ![]() $F^{i}D$ such that
$F^{i}D$ such that ![]() $\dim _{{\mathbb {Q}}_p}F^{i}D=h^{i,n-i}+h^{i+1,n-i-1}+\cdots +h^{n,0}$ turns
$\dim _{{\mathbb {Q}}_p}F^{i}D=h^{i,n-i}+h^{i+1,n-i-1}+\cdots +h^{n,0}$ turns ![]() $D$ into an object of
$D$ into an object of ![]() $\mathrm {MF}_{{\mathbb {Q}}_p}^{\varphi }$ with Hodge numbers
$\mathrm {MF}_{{\mathbb {Q}}_p}^{\varphi }$ with Hodge numbers ![]() $h^{i,n-i}$ which is weakly admissible just because there are no proper non-zero submodules stable under
$h^{i,n-i}$ which is weakly admissible just because there are no proper non-zero submodules stable under ![]() $\varphi$. Alternatively, we can apply [Reference Fontaine and RapoportFR05, Theorem 1] that shows the existence of a weakly admissible module over
$\varphi$. Alternatively, we can apply [Reference Fontaine and RapoportFR05, Theorem 1] that shows the existence of a weakly admissible module over ![]() $W(\bar {k})[{1}/{p}]$ with any given Newton polygon and any Hodge polygon having the same endpoints and lying below it.
$W(\bar {k})[{1}/{p}]$ with any given Newton polygon and any Hodge polygon having the same endpoints and lying below it.
3. Cyclic group acting on a formal abelian scheme
Fix once and for all a prime number ![]() $l$ satisfying the following condition:
$l$ satisfying the following condition:
This condition is equivalent to ![]() $l$ being a prime divisor of a number of the form
$l$ being a prime divisor of a number of the form ![]() $p^{2r}+1$. Denote by
$p^{2r}+1$. Denote by ![]() $k$ the finite field
$k$ the finite field ![]() ${\mathbb {F}}_{p}(\mu _l)$ obtained by adjoining to
${\mathbb {F}}_{p}(\mu _l)$ obtained by adjoining to ![]() ${\mathbb {F}}_p$ all
${\mathbb {F}}_p$ all ![]() $l$th roots of unity and by
$l$th roots of unity and by ![]() $\kappa \subset k$ the finite field
$\kappa \subset k$ the finite field ![]() $\kappa ={\mathbb {F}}_{p^{2}}$. Let
$\kappa ={\mathbb {F}}_{p^{2}}$. Let ![]() $G$ denote the cyclic group
$G$ denote the cyclic group ![]() ${\mathbb {Z}}/l$ with a chosen generator
${\mathbb {Z}}/l$ with a chosen generator ![]() $\sigma \in G$. We will denote by
$\sigma \in G$. We will denote by ![]() ${\mathbb {Z}}[\mu _l]$ the ring of integers of the cyclotomic extension
${\mathbb {Z}}[\mu _l]$ the ring of integers of the cyclotomic extension ![]() ${\mathbb {Q}}(\mu _l)$ inside a chosen algebraic closure
${\mathbb {Q}}(\mu _l)$ inside a chosen algebraic closure ![]() $\bar {\mathbb {Q}}$.
$\bar {\mathbb {Q}}$.
The goal of this section is to exploit the existence of abelian varieties over a finite field with multiplication by ![]() ${\mathbb {Z}}[\mu _l]$ such that the resulting CM type is different from those appearing over characteristic zero fields. This allows us to construct a formal abelian scheme with an action of
${\mathbb {Z}}[\mu _l]$ such that the resulting CM type is different from those appearing over characteristic zero fields. This allows us to construct a formal abelian scheme with an action of ![]() $G$ having asymmetric dimensions of invariant spaces on Hodge cohomology groups in degree
$G$ having asymmetric dimensions of invariant spaces on Hodge cohomology groups in degree ![]() $3$.
$3$.
Proposition 3.1 There exists a formal abelian scheme ![]() ${\mathfrak Z}$ with an action of
${\mathfrak Z}$ with an action of ![]() $G$ over
$G$ over ![]() $\operatorname {{Spf}} W(k')$ for some finite field
$\operatorname {{Spf}} W(k')$ for some finite field ![]() $k'$ such that
$k'$ such that
Remark 3.2 The proof also produces examples with inequalities going in the other direction, we record here this particular version for the convenience of applying it to Lemma 5.1.
We first collect the necessary facts about abelian varieties in Lemmas 3.3–3.8 and then use them together with the combinatorial Lemma 3.10 to prove the Proposition 3.1 at the end of this section. All the facts about abelian varieties used in this section are contained in [Reference Chai, Conrad and OortCCO14] (especially, cf. [Reference Chai, Conrad and OortCCO14, Example 4.1.2]). We include here the proofs in an attempt to make the exposition relatively self-contained.
Lemma 3.3 There exists an abelian variety ![]() $A$ over
$A$ over ![]() $\kappa$ of dimension
$\kappa$ of dimension ![]() $({l-1})/{2}$ equipped with an action of
$({l-1})/{2}$ equipped with an action of ![]() $G$ such that the eigenvalues of
$G$ such that the eigenvalues of ![]() $\sigma \in G$ on
$\sigma \in G$ on ![]() $H^{1}_{\mathrm {cris}}(A/W(\kappa ))\otimes _{W(\kappa )}W(k)[{1}/{p}]$ are the
$H^{1}_{\mathrm {cris}}(A/W(\kappa ))\otimes _{W(\kappa )}W(k)[{1}/{p}]$ are the ![]() $l-1$ pairwise different non-trivial roots of unity of order
$l-1$ pairwise different non-trivial roots of unity of order ![]() $l$ and the
$l$ and the ![]() $p^{2}$-Frobenius endomorphism of
$p^{2}$-Frobenius endomorphism of ![]() $A$ is given by
$A$ is given by ![]() $\sigma \circ [p]_A$.
$\sigma \circ [p]_A$.
Proof. Let ![]() $\zeta _l$ be a primitive
$\zeta _l$ be a primitive ![]() $l$th root of unity in
$l$th root of unity in ![]() $\bar {\mathbb {Q}}$. By Honda–Tate theory, there exists an abelian variety
$\bar {\mathbb {Q}}$. By Honda–Tate theory, there exists an abelian variety ![]() $A'$ (unique up to isogeny) over
$A'$ (unique up to isogeny) over ![]() $\kappa$ with eigenvalues of the
$\kappa$ with eigenvalues of the ![]() $p^{2}$-Frobenius endomorphism on first étale cohomology given by the conjugates of the Weil number
$p^{2}$-Frobenius endomorphism on first étale cohomology given by the conjugates of the Weil number ![]() $p\cdot \zeta _l$. Since
$p\cdot \zeta _l$. Since ![]() $[{\mathbb {Q}}_p(\mu _l):{\mathbb {Q}}_p]=\operatorname {{ord}}_{({\mathbb {Z}}/l)^{\times }}p$ is even we have
$[{\mathbb {Q}}_p(\mu _l):{\mathbb {Q}}_p]=\operatorname {{ord}}_{({\mathbb {Z}}/l)^{\times }}p$ is even we have ![]() $2\dim A'=[{\mathbb {Q}}(\mu _l):{\mathbb {Q}}]=l-1$ by [Reference TateTat71, Theoreme 1(ii)]. If
$2\dim A'=[{\mathbb {Q}}(\mu _l):{\mathbb {Q}}]=l-1$ by [Reference TateTat71, Theoreme 1(ii)]. If ![]() $\varphi _{A'}$ denotes the
$\varphi _{A'}$ denotes the ![]() $p^{2}$-Frobenius endomorphism of
$p^{2}$-Frobenius endomorphism of ![]() $A'$ then
$A'$ then ![]() $\varphi _{A'}^{l}$ acts by
$\varphi _{A'}^{l}$ acts by ![]() $p^{l}$ on
$p^{l}$ on ![]() $H^{1}_{\mathrm {et}}(A'_{\bar {{\mathbb {F}}}_p},{\mathbb {Z}}_t)$ (where
$H^{1}_{\mathrm {et}}(A'_{\bar {{\mathbb {F}}}_p},{\mathbb {Z}}_t)$ (where ![]() $t$ is any prime different from
$t$ is any prime different from ![]() $p$) so
$p$) so ![]() $\varphi _{A'}^{l}$ is equal to the multiplication-by-
$\varphi _{A'}^{l}$ is equal to the multiplication-by-![]() $p^{l}$ endomorphism of
$p^{l}$ endomorphism of ![]() $A'$. Hence,
$A'$. Hence, ![]() $\varphi _{A'}$ induces the action of the subalgebra
$\varphi _{A'}$ induces the action of the subalgebra ![]() ${\mathbb {Z}}[p\zeta _l]\subset {\mathbb {Z}}[\mu _l]$ on the abelian variety
${\mathbb {Z}}[p\zeta _l]\subset {\mathbb {Z}}[\mu _l]$ on the abelian variety ![]() $A'$ with
$A'$ with ![]() $p\zeta _l$ acting by
$p\zeta _l$ acting by ![]() $\varphi _{A'}$.
$\varphi _{A'}$.
[Reference Chai, Conrad and OortCCO14, Proposition 1.7.4.4] shows that the Serre's tensor product ![]() $A:={\mathbb {Z}}[\zeta _l]\otimes _{{\mathbb {Z}}[p\zeta _l]}A'$ is an abelian variety isogenous to
$A:={\mathbb {Z}}[\zeta _l]\otimes _{{\mathbb {Z}}[p\zeta _l]}A'$ is an abelian variety isogenous to ![]() $A'$ that has an action of
$A'$ that has an action of ![]() $G$ with
$G$ with ![]() $\sigma$ acting as
$\sigma$ acting as ![]() $\zeta _l$. The eigenvalues of
$\zeta _l$. The eigenvalues of ![]() $\sigma$ on
$\sigma$ on ![]() $H^{1}_{\mathrm {cris}}(A/W(\kappa ))$ are equal to the eigenvalues of
$H^{1}_{\mathrm {cris}}(A/W(\kappa ))$ are equal to the eigenvalues of ![]() $\varphi _A$ divided by
$\varphi _A$ divided by ![]() $p$ and, since characteristic polynomials of
$p$ and, since characteristic polynomials of ![]() $\varphi _A$ on crystalline and étale cohomology are equal, the eigenvalues of
$\varphi _A$ on crystalline and étale cohomology are equal, the eigenvalues of ![]() $\sigma$ are the
$\sigma$ are the ![]() $l-1$ Galois conjugates of
$l-1$ Galois conjugates of ![]() $\zeta _l$, as desired.
$\zeta _l$, as desired.
Remark 3.4 This particular construction does not require the full power of Honda–Tate theory: we can take ![]() $A'$ to be the Weil restriction of scalars
$A'$ to be the Weil restriction of scalars ![]() $\operatorname {{Res}}^{{\mathbb {F}}_{p^{2l}}}_{{\mathbb {F}}_{p^{2}}}E$ of a supersingular elliptic curve
$\operatorname {{Res}}^{{\mathbb {F}}_{p^{2l}}}_{{\mathbb {F}}_{p^{2}}}E$ of a supersingular elliptic curve ![]() $E$ defined over
$E$ defined over ![]() ${\mathbb {F}}_p$ with vanishing trace of
${\mathbb {F}}_p$ with vanishing trace of ![]() $p$-Frobenius endomorphism, cf. [Reference TateTat71, Lemme 1 in § 3].
$p$-Frobenius endomorphism, cf. [Reference TateTat71, Lemme 1 in § 3].
The map ![]() $g\mapsto g^{p}$ is an automorphism of the group
$g\mapsto g^{p}$ is an automorphism of the group ![]() $G$. For a representation
$G$. For a representation ![]() $\rho :G\to \operatorname {{Aut}}(V)$ on a module
$\rho :G\to \operatorname {{Aut}}(V)$ on a module ![]() $V$ we denote by
$V$ we denote by ![]() $V^{\tau }$ the representation on the same module in which
$V^{\tau }$ the representation on the same module in which ![]() $g\in G$ acts by
$g\in G$ acts by ![]() $\rho (g^{p})$.
$\rho (g^{p})$.
Lemma 3.5 For any ![]() $A$ as in Lemma 3.3 we have the following:
$A$ as in Lemma 3.3 we have the following:
(i) the representations
 $H^{1}(A,{\mathcal {O}})$ and
$H^{1}(A,{\mathcal {O}})$ and  $H^{0}(A,\Omega ^{1}_{A/\kappa })^{\tau }$ are isomorphic;
$H^{0}(A,\Omega ^{1}_{A/\kappa })^{\tau }$ are isomorphic;(ii)
 $A$ lifts to a formal abelian scheme
$A$ lifts to a formal abelian scheme  ${\mathfrak A}$ over
${\mathfrak A}$ over  $\operatorname {{Spf}} W(\kappa )$ together with an action of
$\operatorname {{Spf}} W(\kappa )$ together with an action of  $G$ such that the representations
$G$ such that the representations  $H^{1}({\mathfrak A},{\mathcal {O}})$ and
$H^{1}({\mathfrak A},{\mathcal {O}})$ and  $H^{0}({\mathfrak A},\Omega ^{1}_{{\mathfrak A}/W(\kappa )})^{\tau }$ are isomorphic.
$H^{0}({\mathfrak A},\Omega ^{1}_{{\mathfrak A}/W(\kappa )})^{\tau }$ are isomorphic.
Proof. (i) Denote by ![]() $A^{(1)}=A\times _{\kappa ,\mathop {Fr}}\kappa$ the Frobenius-twist of
$A^{(1)}=A\times _{\kappa ,\mathop {Fr}}\kappa$ the Frobenius-twist of ![]() $A$. For a vector space
$A$. For a vector space ![]() $W$ over
$W$ over ![]() $\kappa$ denote as well by
$\kappa$ denote as well by ![]() $W^{(1)}:=W\otimes _{\kappa ,\mathop {Fr}}\kappa$ its twist. Note that the double twist
$W^{(1)}:=W\otimes _{\kappa ,\mathop {Fr}}\kappa$ its twist. Note that the double twist ![]() $A^{(2)}:=(A^{(1)})^{(1)}$ is canonically identified with
$A^{(2)}:=(A^{(1)})^{(1)}$ is canonically identified with ![]() $A$.
$A$.
The de Rham cohomology ![]() $H^{1}_{\mathrm {dR}}(A/\kappa )$ carries the Hodge filtration
$H^{1}_{\mathrm {dR}}(A/\kappa )$ carries the Hodge filtration ![]() $H^{1}_{\mathrm {dR}}(A/\kappa )=F^{0}\supset F^{1}\supset F^{2}=0$ and the conjugate filtration
$H^{1}_{\mathrm {dR}}(A/\kappa )=F^{0}\supset F^{1}\supset F^{2}=0$ and the conjugate filtration ![]() $H^{1}_{\mathrm {dR}}(A/\kappa )=G_2\supset G_1\supset G_0=0$ satisfying
$H^{1}_{\mathrm {dR}}(A/\kappa )=G_2\supset G_1\supset G_0=0$ satisfying ![]() $F^{0}/F^{1}=H^{0}(A,\Omega ^{1}_{A/\kappa })$,
$F^{0}/F^{1}=H^{0}(A,\Omega ^{1}_{A/\kappa })$, ![]() $F^{1}/F^{2}=H^{1}(A,{\mathcal {O}})$,
$F^{1}/F^{2}=H^{1}(A,{\mathcal {O}})$, ![]() $G_2/G_1=H^{0}(A^{(1)}$,
$G_2/G_1=H^{0}(A^{(1)}$, ![]() $\Omega ^{1}_{A^{(1)}/\kappa }), G_1/G_0=H^{1}(A^{(1)},{\mathcal {O}})$, see [Reference KatzKat70, § 7]. The compositions
$\Omega ^{1}_{A^{(1)}/\kappa }), G_1/G_0=H^{1}(A^{(1)},{\mathcal {O}})$, see [Reference KatzKat70, § 7]. The compositions
and
are both induced by the relative Frobenius morphism ![]() $\mathop {Fr}_A:A\to A^{(1)}$.
$\mathop {Fr}_A:A\to A^{(1)}$.
Since ![]() $\mathop {Fr}_A^{2}$ is equal to the multiplication by
$\mathop {Fr}_A^{2}$ is equal to the multiplication by ![]() $p$ endomorphism
$p$ endomorphism ![]() $[p]_A$ up to composition with an automorphism,
$[p]_A$ up to composition with an automorphism, ![]() $\mathop {Fr}_A^{2}$ induces the zero map on
$\mathop {Fr}_A^{2}$ induces the zero map on ![]() $H^{1}_{\mathrm {dR}}(A/k)$. Equivalently,
$H^{1}_{\mathrm {dR}}(A/k)$. Equivalently, ![]() $\ker (\mathop {Fr}_A^{*}:H^{1}_{\mathrm {dR}}(A^{(1)}/\kappa )\to H^{1}_{\mathrm {dR}}(A/\kappa ))$ contains
$\ker (\mathop {Fr}_A^{*}:H^{1}_{\mathrm {dR}}(A^{(1)}/\kappa )\to H^{1}_{\mathrm {dR}}(A/\kappa ))$ contains ![]() $\operatorname {{im}}(\mathop {Fr}_A^{*}:H^{1}_{\mathrm {dR}}(A/\kappa )=H^{1}_{\mathrm {dR}}(A^{(2)}/\kappa )\to H^{1}_{\mathrm {dR}}(A^{(1)}/\kappa ))=G_1^{(1)}$. The sum of the dimensions of these two vector space is
$\operatorname {{im}}(\mathop {Fr}_A^{*}:H^{1}_{\mathrm {dR}}(A/\kappa )=H^{1}_{\mathrm {dR}}(A^{(2)}/\kappa )\to H^{1}_{\mathrm {dR}}(A^{(1)}/\kappa ))=G_1^{(1)}$. The sum of the dimensions of these two vector space is ![]() $\dim _{\kappa } H^{1}_{\mathrm {dR}}(A/\kappa )=2g$ and the dimension of the image is equal to
$\dim _{\kappa } H^{1}_{\mathrm {dR}}(A/\kappa )=2g$ and the dimension of the image is equal to ![]() $g$, so the containment is in fact equality and we get
$g$, so the containment is in fact equality and we get ![]() $G_1=F^{1}$.
$G_1=F^{1}$.
This gives a ![]() $G$-equivariant
$G$-equivariant ![]() $\kappa$-linear isomorphism
$\kappa$-linear isomorphism ![]() $H^{1}(A^{(1)},{\mathcal {O}})\simeq H^{0}(A,\Omega ^{1}_{A/\kappa })$. If
$H^{1}(A^{(1)},{\mathcal {O}})\simeq H^{0}(A,\Omega ^{1}_{A/\kappa })$. If ![]() $V$ is a representation of
$V$ is a representation of ![]() $G$ on a vector space over a field of characteristic
$G$ on a vector space over a field of characteristic ![]() $p$ then the character of Frobenius-twisted representation
$p$ then the character of Frobenius-twisted representation ![]() $V^{(1)}$ is equal to that of
$V^{(1)}$ is equal to that of ![]() $V^{\tau }$ so the first assertion of the lemma follows.
$V^{\tau }$ so the first assertion of the lemma follows.
(ii) By [Reference MessingMes72, Theorem V.1.10] the category of formal abelian schemes over ![]() $W(\kappa )$ is equivalent to the category of pairs
$W(\kappa )$ is equivalent to the category of pairs ![]() $(A_0, \widetilde {F})$ where
$(A_0, \widetilde {F})$ where ![]() $A_0$ is an abelian variety over
$A_0$ is an abelian variety over ![]() $\kappa$ and
$\kappa$ and ![]() $\widetilde {F}$ is a
$\widetilde {F}$ is a ![]() $W(\kappa )$-submodule of
$W(\kappa )$-submodule of ![]() $H^{1}_{\mathrm {cris}}(A_0/W(\kappa ))$ such that the quotient
$H^{1}_{\mathrm {cris}}(A_0/W(\kappa ))$ such that the quotient ![]() $H^{1}_{\mathrm {cris}}(A_0/W(\kappa ))/\widetilde {F}$ is torsion-free and
$H^{1}_{\mathrm {cris}}(A_0/W(\kappa ))/\widetilde {F}$ is torsion-free and ![]() $\widetilde {F}/p$ is equal to the first step of Hodge filtration
$\widetilde {F}/p$ is equal to the first step of Hodge filtration ![]() $F^{1}\subset H^{1}_{\mathrm {dR}}(A/\kappa )=H^{1}_{\rm cris}(A/W(\kappa ))/p$.
$F^{1}\subset H^{1}_{\mathrm {dR}}(A/\kappa )=H^{1}_{\rm cris}(A/W(\kappa ))/p$.
Since the eigenvalues of ![]() $\sigma$ on
$\sigma$ on ![]() $H^{1}_{\mathrm {cris}}(A/W(\kappa ))$ are pair-wise different, the same is true for the action of
$H^{1}_{\mathrm {cris}}(A/W(\kappa ))$ are pair-wise different, the same is true for the action of ![]() $\sigma$ on
$\sigma$ on ![]() $H^{1}_{\mathrm {dR}}(A/\kappa )$ so there is a unique isomorphism
$H^{1}_{\mathrm {dR}}(A/\kappa )$ so there is a unique isomorphism ![]() $H^{1}_{\mathrm {dR}}(A/\kappa )\simeq H^{0}(A,\Omega ^{1}_{A/\kappa })\oplus H^{1}(A,{\mathcal {O}})$ of
$H^{1}_{\mathrm {dR}}(A/\kappa )\simeq H^{0}(A,\Omega ^{1}_{A/\kappa })\oplus H^{1}(A,{\mathcal {O}})$ of ![]() $G$-representations splitting the Hodge filtration on
$G$-representations splitting the Hodge filtration on ![]() $H^{1}_{\mathrm {dR}}(A/\kappa )$. Since the isomorphism class of a representation of
$H^{1}_{\mathrm {dR}}(A/\kappa )$. Since the isomorphism class of a representation of ![]() $G$ on a finite free
$G$ on a finite free ![]() $W(\kappa )$-module is completely determined by its reduction modulo
$W(\kappa )$-module is completely determined by its reduction modulo ![]() $p$, there is a unique
$p$, there is a unique ![]() $G$-equivariant decomposition
$G$-equivariant decomposition ![]() $H^{1}_{\mathrm {cris}}(A/W(\kappa ))=\widetilde {F}\oplus \widetilde {F}'$ lifting the decomposition of the de Rham cohomology. The formal lift
$H^{1}_{\mathrm {cris}}(A/W(\kappa ))=\widetilde {F}\oplus \widetilde {F}'$ lifting the decomposition of the de Rham cohomology. The formal lift ![]() ${\mathfrak A}$ of
${\mathfrak A}$ of ![]() $A$ defined by
$A$ defined by ![]() $\widetilde {F}$ then comes equipped with a lift of the action of
$\widetilde {F}$ then comes equipped with a lift of the action of ![]() $G$ because
$G$ because ![]() $\widetilde {F}\subset H^{1}_{\mathrm {cris}}(A/W(\kappa ))$ is stable under
$\widetilde {F}\subset H^{1}_{\mathrm {cris}}(A/W(\kappa ))$ is stable under ![]() $G$. The assertion about the action of
$G$. The assertion about the action of ![]() $G$ on Hodge cohomology groups of
$G$ on Hodge cohomology groups of ![]() ${\mathfrak A}$ is a formal consequence of (i).
${\mathfrak A}$ is a formal consequence of (i).
The result of Lemma 3.5(i) is specific to positive characteristic: for an abelian variety ![]() $B$ with an action of
$B$ with an action of ![]() $G$ over a field
$G$ over a field ![]() $F$ of characteristic zero the representations
$F$ of characteristic zero the representations ![]() $H^{0}(B,\Omega ^{1}_{B/F})$ and
$H^{0}(B,\Omega ^{1}_{B/F})$ and ![]() $H^{1}(B,{\mathcal {O}})^{\vee }$ have to be isomorphic by the next lemma, whereas for
$H^{1}(B,{\mathcal {O}})^{\vee }$ have to be isomorphic by the next lemma, whereas for ![]() $A$ as above the representations
$A$ as above the representations ![]() $H^{0}(A,\Omega ^{1}_{A/\kappa })$ and
$H^{0}(A,\Omega ^{1}_{A/\kappa })$ and ![]() $H^{1}(A,{\mathcal {O}})^{\vee }\simeq H^{0}(A,\Omega ^{1}_{A/\kappa })^{\tau \vee }$ are self-dual and are not isomorphic to each other (in fact, any representation of
$H^{1}(A,{\mathcal {O}})^{\vee }\simeq H^{0}(A,\Omega ^{1}_{A/\kappa })^{\tau \vee }$ are self-dual and are not isomorphic to each other (in fact, any representation of ![]() $G$ on a
$G$ on a ![]() ${\mathbb {F}}_{p^{2}}$-vector space has to be self-dual because
${\mathbb {F}}_{p^{2}}$-vector space has to be self-dual because ![]() $-1=p^{2r}$ in
$-1=p^{2r}$ in ![]() $({\mathbb {Z}}/l)^{\times }$ for some
$({\mathbb {Z}}/l)^{\times }$ for some ![]() $r$ by the assumption on
$r$ by the assumption on ![]() $l$). The same is happening for the lift
$l$). The same is happening for the lift ![]() ${\mathfrak A}$, so, in particular, it has to be non-algebraizable.
${\mathfrak A}$, so, in particular, it has to be non-algebraizable.
Lemma 3.6 For an abelian variety ![]() $B$ over a field
$B$ over a field ![]() $F$ of characteristic zero equipped with an action of a finite group
$F$ of characteristic zero equipped with an action of a finite group ![]() $H$ the representations
$H$ the representations ![]() $H^{0}(B,\Omega ^{1}_{B/F})$ and
$H^{0}(B,\Omega ^{1}_{B/F})$ and ![]() $H^{1}(B,{\mathcal {O}})^{\vee }$ are isomorphic.
$H^{1}(B,{\mathcal {O}})^{\vee }$ are isomorphic.
Proof. Choose an ample line bundle ![]() $L$ on
$L$ on ![]() $B$. Then
$B$. Then ![]() $M:={\bigotimes} _{h\in H}h^{*}(L)$ is an ample line bundle inducing a
$M:={\bigotimes} _{h\in H}h^{*}(L)$ is an ample line bundle inducing a ![]() $H$-equivariant polarization
$H$-equivariant polarization ![]() $\lambda _{M}:B\to B^{\vee }$ that is separable because
$\lambda _{M}:B\to B^{\vee }$ that is separable because ![]() $\mathrm {char}\, F=0$. The induced map
$\mathrm {char}\, F=0$. The induced map ![]() $\lambda _{M}^{*}:H^{0}(B^{\vee },\Omega ^{1}_{B^{\vee }/F})\to H^{0}(B,\Omega ^{1}_{B/F})$ provides a
$\lambda _{M}^{*}:H^{0}(B^{\vee },\Omega ^{1}_{B^{\vee }/F})\to H^{0}(B,\Omega ^{1}_{B/F})$ provides a ![]() $H$-equivariant isomorphism between
$H$-equivariant isomorphism between ![]() $H^{0}(B,\Omega ^{1}_{B/F})$ and
$H^{0}(B,\Omega ^{1}_{B/F})$ and ![]() $H^{1}(B,{\mathcal {O}})^{\vee }\simeq H^{0}(B^{\vee },\Omega ^{1}_{B^{\vee }/F})$
$H^{1}(B,{\mathcal {O}})^{\vee }\simeq H^{0}(B^{\vee },\Omega ^{1}_{B^{\vee }/F})$
The abelian schemes constructed in Lemma 3.5 do not yet provide the desired ![]() ${\mathfrak Z}$ because for all
${\mathfrak Z}$ because for all ![]() $i,j$ the module
$i,j$ the module ![]() $H^{i}({\mathfrak A},\Omega ^{j}_{{\mathfrak A}/W(\kappa )})$ is the
$H^{i}({\mathfrak A},\Omega ^{j}_{{\mathfrak A}/W(\kappa )})$ is the ![]() $\tau$-twist of
$\tau$-twist of ![]() $H^{j}({\mathfrak A},\Omega ^{i}_{{\mathfrak A}/W(\kappa )})$ and, in particular, these modules have equal ranks of invariants. We will break this symmetry by taking the direct product with an appropriate algebraic abelian scheme with complex multiplication by
$H^{j}({\mathfrak A},\Omega ^{i}_{{\mathfrak A}/W(\kappa )})$ and, in particular, these modules have equal ranks of invariants. We will break this symmetry by taking the direct product with an appropriate algebraic abelian scheme with complex multiplication by ![]() ${\mathbb {Q}}(\mu _l)$.
${\mathbb {Q}}(\mu _l)$.
Recall that ![]() $k$ is an extension of
$k$ is an extension of ![]() ${\mathbb {F}}_p$ containing all
${\mathbb {F}}_p$ containing all ![]() $l$th roots of unity, so any representation of
$l$th roots of unity, so any representation of ![]() $G$ on a finite free module over
$G$ on a finite free module over ![]() $W(k)$ is isomorphic to a direct sum of characters
$W(k)$ is isomorphic to a direct sum of characters ![]() $\chi _{\zeta }$ given by sending
$\chi _{\zeta }$ given by sending ![]() $\sigma$ to a degree
$\sigma$ to a degree ![]() $l$ root of unity
$l$ root of unity ![]() $\zeta \in \mu _l\subset W(k)^{\times }$.
$\zeta \in \mu _l\subset W(k)^{\times }$.
Definition 3.7 We call a representation ![]() $U$ of
$U$ of ![]() $G$ on a finite free
$G$ on a finite free ![]() $W(k)$-module typical if it has the form
$W(k)$-module typical if it has the form ![]() ${\bigoplus} _{i=1}^{d}{\bigoplus} _{\zeta \in S_i}\chi _{\zeta }$ where each
${\bigoplus} _{i=1}^{d}{\bigoplus} _{\zeta \in S_i}\chi _{\zeta }$ where each ![]() $S_i$ is a subset of
$S_i$ is a subset of ![]() $\mu _l$ of cardinality
$\mu _l$ of cardinality ![]() $({l-1})/{2}$ such that
$({l-1})/{2}$ such that ![]() $S_i\cap S_i^{-1}=\varnothing$ and d is some number.
$S_i\cap S_i^{-1}=\varnothing$ and d is some number.
If ![]() ${\mathfrak B}$ is an algebraic abelian scheme over
${\mathfrak B}$ is an algebraic abelian scheme over ![]() $W(k)$ of dimension
$W(k)$ of dimension ![]() $({l-1})/{2}$ with a non-trivial action of
$({l-1})/{2}$ with a non-trivial action of ![]() $G$ then the representation
$G$ then the representation ![]() $H^{0}({\mathfrak B},\Omega ^{1}_{{\mathfrak B}/W(k)})$ is typical: singular cohomology
$H^{0}({\mathfrak B},\Omega ^{1}_{{\mathfrak B}/W(k)})$ is typical: singular cohomology ![]() $H^{1}({\mathfrak B}_{{\mathbb {C}}}({\mathbb {C}}),{\mathbb {Z}})$ of the base change of
$H^{1}({\mathfrak B}_{{\mathbb {C}}}({\mathbb {C}}),{\mathbb {Z}})$ of the base change of ![]() ${\mathfrak B}$ along any embedding
${\mathfrak B}$ along any embedding ![]() $W(k)\to {\mathbb {C}}$ is a free abelian group of rank
$W(k)\to {\mathbb {C}}$ is a free abelian group of rank ![]() $l-1$ with a non-trivial action of
$l-1$ with a non-trivial action of ![]() $G$. Hence, all non-trivial characters appear in
$G$. Hence, all non-trivial characters appear in ![]() $H^{1}({\mathfrak B}_{{\mathbb {C}}},{\mathbb {Z}})$ exactly once and by Lemma 3.6 these characters have to be distributed between
$H^{1}({\mathfrak B}_{{\mathbb {C}}},{\mathbb {Z}})$ exactly once and by Lemma 3.6 these characters have to be distributed between ![]() $H^{0}({\mathfrak B}_{{\mathbb {C}}},\Omega ^{1}_{{\mathfrak B}_{{\mathbb {C}}}/{\mathbb {C}}})=H^{0}({\mathfrak B},\Omega ^{1}_{{\mathfrak B}/W(k)})\otimes _{W(k)}{\mathbb {C}}$ and
$H^{0}({\mathfrak B}_{{\mathbb {C}}},\Omega ^{1}_{{\mathfrak B}_{{\mathbb {C}}}/{\mathbb {C}}})=H^{0}({\mathfrak B},\Omega ^{1}_{{\mathfrak B}/W(k)})\otimes _{W(k)}{\mathbb {C}}$ and ![]() $H^{1}({\mathfrak B}_{{\mathbb {C}}},{\mathcal {O}})$ in such a way that
$H^{1}({\mathfrak B}_{{\mathbb {C}}},{\mathcal {O}})$ in such a way that ![]() $\chi _{\zeta }$ and
$\chi _{\zeta }$ and ![]() $\chi _{\zeta ^{-1}}$ never occur in the same piece of the Hodge decomposition. The next lemma deduces from the theory of complex multiplication that every typical representation arises from an abelian scheme over the ring of integers in an unramified extension of
$\chi _{\zeta ^{-1}}$ never occur in the same piece of the Hodge decomposition. The next lemma deduces from the theory of complex multiplication that every typical representation arises from an abelian scheme over the ring of integers in an unramified extension of ![]() ${\mathbb {Q}}_p$.
${\mathbb {Q}}_p$.
Lemma 3.8 For any typical representation of ![]() $G$ on a finite free
$G$ on a finite free ![]() $W(k)$-module
$W(k)$-module ![]() $U$ there exists an abelian scheme
$U$ there exists an abelian scheme ![]() ${\mathfrak B}$ with an action of
${\mathfrak B}$ with an action of ![]() $G$ over the ring of integers
$G$ over the ring of integers ![]() ${\mathcal {O}}_L=W(k')$ of a finite unramified extension
${\mathcal {O}}_L=W(k')$ of a finite unramified extension ![]() $L=W(k')[{1}/{p}]\supset W(k)[{1}/{p}]$ such that
$L=W(k')[{1}/{p}]\supset W(k)[{1}/{p}]$ such that ![]() $H^{0}({\mathfrak B},\Omega ^{1}_{{\mathfrak B}/{\mathcal {O}}_L})\simeq U\otimes _{W(k)}{{\mathcal {O}}_L}$ and
$H^{0}({\mathfrak B},\Omega ^{1}_{{\mathfrak B}/{\mathcal {O}}_L})\simeq U\otimes _{W(k)}{{\mathcal {O}}_L}$ and ![]() $H^{1}({\mathfrak B},{\mathcal {O}})\simeq U^{\vee }\otimes _{W(k)}{\mathcal {O}}_L$ as
$H^{1}({\mathfrak B},{\mathcal {O}})\simeq U^{\vee }\otimes _{W(k)}{\mathcal {O}}_L$ as ![]() $G$-representations.
$G$-representations.
Proof. It is enough to prove the lemma for typical representations of rank ![]() $({l-1})/{2}$ because we have
$({l-1})/{2}$ because we have ![]() $H^{0}({\mathfrak B}_1\times _{{\mathcal {O}}_L}{\mathfrak B}_2,\Omega ^{1}_{{\mathfrak B}_1\times _{{\mathcal {O}}_L}{\mathfrak B}_2/{\mathcal {O}}_L})\simeq H^{0}({\mathfrak B}_1,\Omega ^{1}_{{\mathfrak B}_1/{\mathcal {O}}_L})\oplus H^{0}({\mathfrak B}_2,\Omega ^{1}_{{\mathfrak B}_2/{\mathcal {O}}_L})$ and likewise
$H^{0}({\mathfrak B}_1\times _{{\mathcal {O}}_L}{\mathfrak B}_2,\Omega ^{1}_{{\mathfrak B}_1\times _{{\mathcal {O}}_L}{\mathfrak B}_2/{\mathcal {O}}_L})\simeq H^{0}({\mathfrak B}_1,\Omega ^{1}_{{\mathfrak B}_1/{\mathcal {O}}_L})\oplus H^{0}({\mathfrak B}_2,\Omega ^{1}_{{\mathfrak B}_2/{\mathcal {O}}_L})$ and likewise ![]() $H^{1}({\mathfrak B}_1\times _{{\mathcal {O}}_L}{\mathfrak B}_2,{\mathcal {O}})\simeq H^{1}({\mathfrak B}_1,{\mathcal {O}})\oplus H^{1}({\mathfrak B}_2,{\mathcal {O}})$ for all abelian schemes
$H^{1}({\mathfrak B}_1\times _{{\mathcal {O}}_L}{\mathfrak B}_2,{\mathcal {O}})\simeq H^{1}({\mathfrak B}_1,{\mathcal {O}})\oplus H^{1}({\mathfrak B}_2,{\mathcal {O}})$ for all abelian schemes ![]() ${\mathfrak B}_1,{\mathfrak B}_2$, so the general case can be obtained by taking the products.
${\mathfrak B}_1,{\mathfrak B}_2$, so the general case can be obtained by taking the products.
Fix a non-trivial root of unity ![]() $\zeta _l\in {\mathbb {Q}}(\mu _l)$ and an embedding
$\zeta _l\in {\mathbb {Q}}(\mu _l)$ and an embedding ![]() ${\mathbb {Q}}(\mu _l)\subset W(k)[{1}/{p}]$, giving a bijection between roots of unity in
${\mathbb {Q}}(\mu _l)\subset W(k)[{1}/{p}]$, giving a bijection between roots of unity in ![]() ${\mathbb {Q}}(\mu _l)$ and
${\mathbb {Q}}(\mu _l)$ and ![]() $W(k)$. Each non-trivial root of unity
$W(k)$. Each non-trivial root of unity ![]() $\zeta \in \mu _l(W(k))$ thus defines an embedding of the cyclotomic field
$\zeta \in \mu _l(W(k))$ thus defines an embedding of the cyclotomic field ![]() $\varphi _{\zeta }:{\mathbb {Q}}(\mu _l)\to \bar {{\mathbb {Q}}}$ into the algebraic closure given by
$\varphi _{\zeta }:{\mathbb {Q}}(\mu _l)\to \bar {{\mathbb {Q}}}$ into the algebraic closure given by ![]() $\zeta _l\mapsto \zeta$.
$\zeta _l\mapsto \zeta$.
Let ![]() $U$ be a typical representation of rank
$U$ be a typical representation of rank ![]() $({l-1})/{2}$ over
$({l-1})/{2}$ over ![]() $W(k)$. We associate to
$W(k)$. We associate to ![]() $U$ the set
$U$ the set ![]() $\Phi =\{\varphi _{\zeta }|\chi _{\zeta ^{-1}}\text { appears in }U\}$ of embeddings. By the definition of typical representation
$\Phi =\{\varphi _{\zeta }|\chi _{\zeta ^{-1}}\text { appears in }U\}$ of embeddings. By the definition of typical representation ![]() $\Phi$ is a CM type of the field
$\Phi$ is a CM type of the field ![]() ${\mathbb {Q}}(\mu _l)$. Since
${\mathbb {Q}}(\mu _l)$. Since ![]() ${\mathbb {Q}}(\mu _l)$ is Galois over
${\mathbb {Q}}(\mu _l)$ is Galois over ![]() ${\mathbb {Q}}$, the reflex field of
${\mathbb {Q}}$, the reflex field of ![]() $\Phi$ is contained in
$\Phi$ is contained in ![]() ${\mathbb {Q}}(\mu _l)$. By [Reference Chai, Conrad and OortCCO14, Corollary A.4.6.5] applied with
${\mathbb {Q}}(\mu _l)$. By [Reference Chai, Conrad and OortCCO14, Corollary A.4.6.5] applied with ![]() $N=p$ (beware that the symbol ‘
$N=p$ (beware that the symbol ‘![]() $p$’ bears its own meaning in this corollary) there exists an abelian variety
$p$’ bears its own meaning in this corollary) there exists an abelian variety ![]() $B'$ with complex multiplication by
$B'$ with complex multiplication by ![]() ${\mathbb {Q}}(\mu _l)$ of type
${\mathbb {Q}}(\mu _l)$ of type ![]() $\Phi$ defined over an unramified extension
$\Phi$ defined over an unramified extension ![]() $F$ of the reflex field that has good reduction at all primes above
$F$ of the reflex field that has good reduction at all primes above ![]() $p$. Take
$p$. Take ![]() $L=F_{{\mathfrak p}}$ for some prime
$L=F_{{\mathfrak p}}$ for some prime ![]() ${\mathfrak p}\subset {\mathcal {O}}_F$ above
${\mathfrak p}\subset {\mathcal {O}}_F$ above ![]() $p$ and consider the good model
$p$ and consider the good model ![]() ${\mathfrak B}'$ of
${\mathfrak B}'$ of ![]() $B'$ over
$B'$ over ![]() ${\mathcal {O}}_L$. The isogeny action of
${\mathcal {O}}_L$. The isogeny action of ![]() ${\mathbb {Q}}(\mu _l)$ then extends onto
${\mathbb {Q}}(\mu _l)$ then extends onto ![]() ${\mathfrak B}'$. In particular, embedding
${\mathfrak B}'$. In particular, embedding ![]() $G$ into
$G$ into ![]() ${\mathbb {Q}}(\mu _l)$ via
${\mathbb {Q}}(\mu _l)$ via ![]() $\sigma \mapsto \zeta _l$ gives an action of
$\sigma \mapsto \zeta _l$ gives an action of ![]() $G$ on
$G$ on ![]() ${\mathfrak B}'$ in the isogeny category. By our choice of
${\mathfrak B}'$ in the isogeny category. By our choice of ![]() $\Phi$ the
$\Phi$ the ![]() $G$-representation
$G$-representation ![]() $H^{0}({\mathfrak B}',\Omega ^{1}_{{\mathfrak B}'/{\mathcal {O}}_L})\otimes _{{\mathcal {O}}_L}L$ is isomorphic to
$H^{0}({\mathfrak B}',\Omega ^{1}_{{\mathfrak B}'/{\mathcal {O}}_L})\otimes _{{\mathcal {O}}_L}L$ is isomorphic to ![]() $U\otimes _{W(k)}L$.
$U\otimes _{W(k)}L$.
Analogously to the proof of Lemma 3.3, Serre's tensor product construction gives an isogeny ![]() ${\mathfrak B}'\to {\mathfrak B}$ to an abelian scheme
${\mathfrak B}'\to {\mathfrak B}$ to an abelian scheme ![]() ${\mathfrak B}$ that carries a genuine action of
${\mathfrak B}$ that carries a genuine action of ![]() ${\mathbb {Z}}[\mu _l]$. In particular,
${\mathbb {Z}}[\mu _l]$. In particular, ![]() $G$ acts on
$G$ acts on ![]() ${\mathfrak B}$ such that
${\mathfrak B}$ such that ![]() $H^{0}({\mathfrak B},\Omega ^{1}_{{\mathfrak B}/{\mathcal {O}}_L})$ is isomorphic to
$H^{0}({\mathfrak B},\Omega ^{1}_{{\mathfrak B}/{\mathcal {O}}_L})$ is isomorphic to ![]() $U\otimes _{W(k)}{\mathcal {O}}_L$, as desired. To see that
$U\otimes _{W(k)}{\mathcal {O}}_L$, as desired. To see that ![]() $H^{1}({\mathfrak B},{\mathcal {O}})$ is isomorphic to
$H^{1}({\mathfrak B},{\mathcal {O}})$ is isomorphic to ![]() $U^{\vee }\otimes _{W(k)}{\mathcal {O}}_L$ it is enough to check the analogous statement for the generic fiber
$U^{\vee }\otimes _{W(k)}{\mathcal {O}}_L$ it is enough to check the analogous statement for the generic fiber ![]() ${\mathfrak B}_L$ and this is given by Lemma 3.6.
${\mathfrak B}_L$ and this is given by Lemma 3.6.
Remark 3.9 We have appealed to stronger results of [Reference Chai, Conrad and OortCCO14] to make sure that there exists ![]() ${\mathfrak B}$ defined over the ring of integers in an unramified extension of
${\mathfrak B}$ defined over the ring of integers in an unramified extension of ![]() ${\mathbb {Q}}_p$. If we did not care about the field of definition of the ultimate counterexamples to Hodge symmetry we could have applied a cruder form of CM theory given e.g. by [Reference TateTat71, Lemme 4].
${\mathbb {Q}}_p$. If we did not care about the field of definition of the ultimate counterexamples to Hodge symmetry we could have applied a cruder form of CM theory given e.g. by [Reference TateTat71, Lemme 4].
Lemma 3.10 Let ![]() $V$ be a representation of
$V$ be a representation of ![]() $G$ on a finite free
$G$ on a finite free ![]() $W(k)$-module such that
$W(k)$-module such that ![]() $V$ is isomorphic to its dual
$V$ is isomorphic to its dual ![]() $V^{\vee }$ but is not isomorphic to the twist
$V^{\vee }$ but is not isomorphic to the twist ![]() $V^{\tau }$. Then there exists a typical representation
$V^{\tau }$. Then there exists a typical representation ![]() $U$ such that
$U$ such that
Proof. Suppose on the contrary that these ranks of invariant subspaces are equal for all typical ![]() $U$. Using that
$U$. Using that ![]() $\Lambda ^{3}(V\oplus U)\simeq \Lambda ^{3} V\oplus \Lambda ^{2}V\otimes U\oplus V\otimes \Lambda ^{2} U\oplus \Lambda ^{3} U$ and the fact that twisting by an automorphism of
$\Lambda ^{3}(V\oplus U)\simeq \Lambda ^{3} V\oplus \Lambda ^{2}V\otimes U\oplus V\otimes \Lambda ^{2} U\oplus \Lambda ^{3} U$ and the fact that twisting by an automorphism of ![]() $G$ does not change the invariant submodule of a representation we get
$G$ does not change the invariant submodule of a representation we get
for all typical ![]() $U$ and any multiplicity
$U$ and any multiplicity ![]() $r$ (by definition, the class of typical representations is closed under direct sums). Since
$r$ (by definition, the class of typical representations is closed under direct sums). Since ![]() $\Lambda ^{2}(U^{\oplus r})\simeq (\Lambda ^{2}U)^{\oplus r}\oplus (U^{\otimes 2})^{\oplus \binom {r}{2}}$ both sides of the equality are quadratic polynomials in
$\Lambda ^{2}(U^{\oplus r})\simeq (\Lambda ^{2}U)^{\oplus r}\oplus (U^{\otimes 2})^{\oplus \binom {r}{2}}$ both sides of the equality are quadratic polynomials in ![]() $r$ for a fixed
$r$ for a fixed ![]() $U$, and comparing the leading coefficients we get
$U$, and comparing the leading coefficients we get
As ![]() $V$ is assumed to be self-dual this equality is equivalent to
$V$ is assumed to be self-dual this equality is equivalent to ![]() $\operatorname {{rk}}(V\otimes U^{\otimes 2})^{G}=\operatorname {{rk}}(V^{\tau }\otimes U^{\otimes 2})^{G}$. In other words, the difference of characters
$\operatorname {{rk}}(V\otimes U^{\otimes 2})^{G}=\operatorname {{rk}}(V^{\tau }\otimes U^{\otimes 2})^{G}$. In other words, the difference of characters ![]() $\chi _V-\chi _{V^{\tau }}$ is orthogonal to any character
$\chi _V-\chi _{V^{\tau }}$ is orthogonal to any character ![]() $\chi _{U^{\otimes 2}}$ for a typical
$\chi _{U^{\otimes 2}}$ for a typical ![]() $U$ with respect to the pairing
$U$ with respect to the pairing ![]() $\langle \chi _1,\chi _2\rangle :=\sum _{g\in G}\chi _1(g)\chi _2(g)$ on the character ring
$\langle \chi _1,\chi _2\rangle :=\sum _{g\in G}\chi _1(g)\chi _2(g)$ on the character ring ![]() $W(k)[G]$. Moreover, this implies that
$W(k)[G]$. Moreover, this implies that ![]() $\chi _V-\chi _{V^{\tau }}$ is orthogonal to
$\chi _V-\chi _{V^{\tau }}$ is orthogonal to ![]() $\chi _{U_1\otimes U_2}=\chi _{U_1}\cdot \chi _{U_2}$ for any two typical representations
$\chi _{U_1\otimes U_2}=\chi _{U_1}\cdot \chi _{U_2}$ for any two typical representations ![]() $U_1,U_2$ because
$U_1,U_2$ because ![]() $2\chi _{U_1\otimes U_2}=\chi _{(U_1\oplus U_2)^{\otimes 2}}-\chi _{U_1^{\otimes 2}}-\chi _{U_2^{\otimes 2}}$.
$2\chi _{U_1\otimes U_2}=\chi _{(U_1\oplus U_2)^{\otimes 2}}-\chi _{U_1^{\otimes 2}}-\chi _{U_2^{\otimes 2}}$.
If ![]() $\zeta$ is any non-trivial root of unity, then for a set
$\zeta$ is any non-trivial root of unity, then for a set ![]() $\zeta _1,\ldots ,\zeta _{({l-3})/{2}}$ of pairwise different roots such that
$\zeta _1,\ldots ,\zeta _{({l-3})/{2}}$ of pairwise different roots such that ![]() $\zeta _i\neq \zeta _j^{-1}$ and
$\zeta _i\neq \zeta _j^{-1}$ and ![]() $\zeta _i\neq \zeta ^{\pm 1}$ for all
$\zeta _i\neq \zeta ^{\pm 1}$ for all ![]() $i,j$ both representations
$i,j$ both representations ![]() $\chi _{\zeta }\oplus \chi _{\zeta _1}\oplus \cdots \oplus \chi _{\zeta _{({l-3})/{2}}}$ and
$\chi _{\zeta }\oplus \chi _{\zeta _1}\oplus \cdots \oplus \chi _{\zeta _{({l-3})/{2}}}$ and ![]() $\chi _{\zeta ^{-1}}\oplus \chi _{\zeta _1}\oplus \cdots \oplus \chi _{\zeta _{({l-3})/{2}}}$ are typical. Hence the span of characters of typical representations in
$\chi _{\zeta ^{-1}}\oplus \chi _{\zeta _1}\oplus \cdots \oplus \chi _{\zeta _{({l-3})/{2}}}$ are typical. Hence the span of characters of typical representations in ![]() $W(k)[G]$ contains all characters of the form
$W(k)[G]$ contains all characters of the form ![]() $\chi _{\zeta }-\chi _{\zeta ^{-1}}$ for a non-trivial root of unity
$\chi _{\zeta }-\chi _{\zeta ^{-1}}$ for a non-trivial root of unity ![]() $\zeta$. By linearity of the pairing,
$\zeta$. By linearity of the pairing, ![]() $\chi _V-\chi _{V^{\tau }}$ is hence also orthogonal to
$\chi _V-\chi _{V^{\tau }}$ is hence also orthogonal to ![]() $\chi ^{2}_{\zeta }+\chi ^{2}_{\zeta ^{-1}}=(\chi _{\zeta }-\chi _{\zeta ^{-1}})^{2}+2\chi _{1}$. However,
$\chi ^{2}_{\zeta }+\chi ^{2}_{\zeta ^{-1}}=(\chi _{\zeta }-\chi _{\zeta ^{-1}})^{2}+2\chi _{1}$. However, ![]() $\langle \chi _V,\chi ^{2}_{\zeta }+\chi ^{2}_{\zeta ^{-1}}\rangle =2\langle \chi _V,\chi ^{2}_{\zeta }\rangle$ by self-duality of
$\langle \chi _V,\chi ^{2}_{\zeta }+\chi ^{2}_{\zeta ^{-1}}\rangle =2\langle \chi _V,\chi ^{2}_{\zeta }\rangle$ by self-duality of ![]() $V$ and likewise for
$V$ and likewise for ![]() $V^{\tau }$ so we get a contradiction since, by assumption, there exists
$V^{\tau }$ so we get a contradiction since, by assumption, there exists ![]() $\zeta$ such that multiplicities of
$\zeta$ such that multiplicities of ![]() $\chi _{\zeta ^{-2}}$ in
$\chi _{\zeta ^{-2}}$ in ![]() $V$ and
$V$ and ![]() $V^{\tau }$ are different.
$V^{\tau }$ are different.
Proof of Proposition 3.1 Let ![]() ${\mathfrak A}$ be a formal abelian scheme with an action of
${\mathfrak A}$ be a formal abelian scheme with an action of ![]() $G$ provided by Lemma 3.5(ii). Consider the representation
$G$ provided by Lemma 3.5(ii). Consider the representation ![]() $V=H^{0}({\mathfrak A},\Omega ^{1}_{{\mathfrak A}/W(\kappa )})$. We have
$V=H^{0}({\mathfrak A},\Omega ^{1}_{{\mathfrak A}/W(\kappa )})$. We have ![]() $G$-equivariant isomorphisms
$G$-equivariant isomorphisms ![]() $V\oplus V^{\tau }\simeq H^{0}({\mathfrak A},\Omega ^{1}_{{\mathfrak A}/W(\kappa )})\oplus H^{1}({\mathfrak A},{\mathcal {O}})\simeq H^{1}_{\mathrm {dR}}({\mathfrak A}/W(\kappa ))\simeq H^{1}_{\mathrm {cris}}(A/W(\kappa ))$, so every non-trivial character
$V\oplus V^{\tau }\simeq H^{0}({\mathfrak A},\Omega ^{1}_{{\mathfrak A}/W(\kappa )})\oplus H^{1}({\mathfrak A},{\mathcal {O}})\simeq H^{1}_{\mathrm {dR}}({\mathfrak A}/W(\kappa ))\simeq H^{1}_{\mathrm {cris}}(A/W(\kappa ))$, so every non-trivial character ![]() $\chi _{\zeta }$ appears in exactly one of
$\chi _{\zeta }$ appears in exactly one of ![]() $V$ and
$V$ and ![]() $V^{\tau }$ with multiplicity one. It follows that
$V^{\tau }$ with multiplicity one. It follows that ![]() $V\simeq (V^{\tau })^{\tau }$. Since
$V\simeq (V^{\tau })^{\tau }$. Since ![]() $V^{\vee }$ is obtained from
$V^{\vee }$ is obtained from ![]() $V$ by applying the twist
$V$ by applying the twist ![]() $\tau$ an even number of times, the representation
$\tau$ an even number of times, the representation ![]() $V\otimes _{W(\kappa )}W(k)$ satisfies the assumptions of Lemma 3.10 and there exists a typical representation
$V\otimes _{W(\kappa )}W(k)$ satisfies the assumptions of Lemma 3.10 and there exists a typical representation ![]() $U$ such that non-equality (5) holds. Let
$U$ such that non-equality (5) holds. Let ![]() ${\mathfrak B}$ be an abelian scheme over
${\mathfrak B}$ be an abelian scheme over ![]() ${\mathcal {O}}_L=W(k')$ provided by Lemma 3.8 applied to
${\mathcal {O}}_L=W(k')$ provided by Lemma 3.8 applied to ![]() $U$. The product
$U$. The product ![]() ${\mathfrak Z}'={\mathcal {A}}\times _{W(k)}{\mathfrak B}$ equipped with the diagonal action then has
${\mathfrak Z}'={\mathcal {A}}\times _{W(k)}{\mathfrak B}$ equipped with the diagonal action then has ![]() $H^{0}({\mathfrak Z}',\Omega ^{1}_{{\mathfrak Z}/{\mathcal {O}}_L})\simeq (V\oplus U)\otimes _{W(k)}{{\mathcal {O}}_L}$ and
$H^{0}({\mathfrak Z}',\Omega ^{1}_{{\mathfrak Z}/{\mathcal {O}}_L})\simeq (V\oplus U)\otimes _{W(k)}{{\mathcal {O}}_L}$ and ![]() $H^{1}({\mathfrak Z}',{\mathcal {O}})\simeq (V^{\tau }\oplus U^{\vee })\otimes _{W(k)}{{\mathcal {O}}_L}$ as
$H^{1}({\mathfrak Z}',{\mathcal {O}})\simeq (V^{\tau }\oplus U^{\vee })\otimes _{W(k)}{{\mathcal {O}}_L}$ as ![]() $G$-representations.
$G$-representations.
Since ![]() $H^{0}({\mathfrak Z}',\Omega ^{3}_{{\mathfrak Z}/{\mathcal {O}}_L})\simeq \Lambda ^{3} H^{0}({\mathfrak Z}',\Omega ^{1}_{{\mathfrak Z}'/{\mathcal {O}}_L})$ and
$H^{0}({\mathfrak Z}',\Omega ^{3}_{{\mathfrak Z}/{\mathcal {O}}_L})\simeq \Lambda ^{3} H^{0}({\mathfrak Z}',\Omega ^{1}_{{\mathfrak Z}'/{\mathcal {O}}_L})$ and ![]() $H^{3}({\mathfrak Z}',{\mathcal {O}})\simeq \Lambda ^{3} H^{1}({\mathfrak Z}',{\mathcal {O}})$ we get
$H^{3}({\mathfrak Z}',{\mathcal {O}})\simeq \Lambda ^{3} H^{1}({\mathfrak Z}',{\mathcal {O}})$ we get
If ![]() $\operatorname {{rk}} H^{0}({\mathfrak Z}',\Omega ^{3}_{{\mathfrak Z}/{\mathcal {O}}_L})^{G}> \operatorname {{rk}} H^{3}({\mathfrak Z}',{\mathcal {O}})^{G}$, then
$\operatorname {{rk}} H^{0}({\mathfrak Z}',\Omega ^{3}_{{\mathfrak Z}/{\mathcal {O}}_L})^{G}> \operatorname {{rk}} H^{3}({\mathfrak Z}',{\mathcal {O}})^{G}$, then ![]() ${\mathfrak Z}={\mathfrak Z}'$ gives the desired inequality (4). If the inequality goes the other way, take
${\mathfrak Z}={\mathfrak Z}'$ gives the desired inequality (4). If the inequality goes the other way, take ![]() ${\mathfrak Z}={\mathfrak Z}'^{\vee }$ using that there are
${\mathfrak Z}={\mathfrak Z}'^{\vee }$ using that there are ![]() $G$-equivariant isomorphisms
$G$-equivariant isomorphisms ![]() $H^{0}({\mathfrak Z}'^{\vee },\Omega ^{1}_{{\mathcal {O}}_L})\simeq H^{1}({\mathfrak Z}',{\mathcal {O}})^{\vee }$ and
$H^{0}({\mathfrak Z}'^{\vee },\Omega ^{1}_{{\mathcal {O}}_L})\simeq H^{1}({\mathfrak Z}',{\mathcal {O}})^{\vee }$ and ![]() $H^{1}({\mathfrak Z}'^{\vee },{\mathcal {O}})\simeq H^{0}({\mathfrak Z}',\Omega ^{1}_{{\mathfrak Z}'/{\mathcal {O}}_L})^{\vee }$.
$H^{1}({\mathfrak Z}'^{\vee },{\mathcal {O}})\simeq H^{0}({\mathfrak Z}',\Omega ^{1}_{{\mathfrak Z}'/{\mathcal {O}}_L})^{\vee }$.
Remark 3.11 (i) The same argument works just as well to provide an abelian scheme with different ranks of invariants ![]() $\operatorname {{rk}} H^{i}({\mathfrak Z},\Omega ^{j}_{{\mathfrak Z}/W(k)})^{G}\neq \operatorname {{rk}} H^{i}({\mathfrak Z},\Omega ^{j}_{{\mathfrak Z}/W(k)})^{G}$ for any
$\operatorname {{rk}} H^{i}({\mathfrak Z},\Omega ^{j}_{{\mathfrak Z}/W(k)})^{G}\neq \operatorname {{rk}} H^{i}({\mathfrak Z},\Omega ^{j}_{{\mathfrak Z}/W(k)})^{G}$ for any ![]() $i\neq j, i+j\geq 3$. We chose to treat here only the case
$i\neq j, i+j\geq 3$. We chose to treat here only the case ![]() $(i,j)=(3,0)$ and obtain counterexamples to symmetry in higher degrees by taking products with auxiliary varieties because that simplifies the argument in the next section.
$(i,j)=(3,0)$ and obtain counterexamples to symmetry in higher degrees by taking products with auxiliary varieties because that simplifies the argument in the next section.
(ii) I am not aware of a simple way of choosing ![]() ${\mathfrak Z}$ that would work uniformly for all
${\mathfrak Z}$ that would work uniformly for all ![]() $p$. However, for any fixed
$p$. However, for any fixed ![]() $l$ everything can be made more explicit for primes
$l$ everything can be made more explicit for primes ![]() $p$ for which
$p$ for which ![]() $l$ satisfied condition (3). For instance, for
$l$ satisfied condition (3). For instance, for ![]() $p$ congruent to
$p$ congruent to ![]() $2$ or
$2$ or ![]() $3$ modulo
$3$ modulo ![]() $5$ we can take
$5$ we can take ![]() $l=5$ so that
$l=5$ so that ![]() $\dim {\mathfrak A}=2$ and
$\dim {\mathfrak A}=2$ and ![]() ${\mathfrak B}$ can also be chosen to be
${\mathfrak B}$ can also be chosen to be ![]() $2$-dimensional. In this case (for any of the particular choices of
$2$-dimensional. In this case (for any of the particular choices of ![]() ${\mathfrak A}$ and
${\mathfrak A}$ and ![]() ${\mathfrak B}$ that give non-symmetric dimensions of invariants)
${\mathfrak B}$ that give non-symmetric dimensions of invariants) ![]() $H^{3}_{\mathrm {dR}}(A\times B/L)^{G}$ is a filtered
$H^{3}_{\mathrm {dR}}(A\times B/L)^{G}$ is a filtered ![]() $\varphi$-module with Hodge numbers
$\varphi$-module with Hodge numbers ![]() $(h^{3,0},h^{2,1},h^{1,2},h^{0,3})=(0,5,2,1)$ or
$(h^{3,0},h^{2,1},h^{1,2},h^{0,3})=(0,5,2,1)$ or ![]() $(1,2,5,0)$ and single slope
$(1,2,5,0)$ and single slope ![]() ${3}/{2}$ (the slopes can be computed by the Shimura–Taniyama formula). Note that such Hodge numbers satisfy the relation (1).
${3}/{2}$ (the slopes can be computed by the Shimura–Taniyama formula). Note that such Hodge numbers satisfy the relation (1).
4. Main example
Theorem 4.1 For every pair of distinct positive integers ![]() $i\neq j$ with
$i\neq j$ with ![]() $i+j\geq 3$ there exists a smooth proper formal scheme
$i+j\geq 3$ there exists a smooth proper formal scheme ![]() ${\mathfrak X}$ over
${\mathfrak X}$ over ![]() ${\mathbb {Z}}_p$ with projective special fiber
${\mathbb {Z}}_p$ with projective special fiber ![]() ${\mathfrak X}_{{\mathbb {F}}_p}$ such that the Hodge cohomology groups
${\mathfrak X}_{{\mathbb {F}}_p}$ such that the Hodge cohomology groups ![]() $H^{i}({\mathfrak X},\Omega ^{j}_{{\mathfrak X}/{\mathbb {Z}}_p})$ and
$H^{i}({\mathfrak X},\Omega ^{j}_{{\mathfrak X}/{\mathbb {Z}}_p})$ and ![]() $H^{j}({\mathfrak X},\Omega ^{i}_{{\mathfrak X}/{\mathbb {Z}}_p})$ are free
$H^{j}({\mathfrak X},\Omega ^{i}_{{\mathfrak X}/{\mathbb {Z}}_p})$ are free ![]() ${\mathbb {Z}}_p$-modules of different rank.
${\mathbb {Z}}_p$-modules of different rank.
We first record two standard general facts from formal geometry. The main reference on rigid-analytic generic fibers of formal schemes is [Reference Bosch and LütkebohmertBL93]. Let ![]() $K$ be a discretely valued field of characteristic zero with ring of integers
$K$ be a discretely valued field of characteristic zero with ring of integers ![]() ${\mathcal {O}}_K$, maximal ideal
${\mathcal {O}}_K$, maximal ideal ![]() ${\mathfrak m}\subset {\mathcal {O}}_K$ and perfect residue field
${\mathfrak m}\subset {\mathcal {O}}_K$ and perfect residue field ![]() $k={\mathcal {O}}_K/{\mathfrak m}$ of characteristic
$k={\mathcal {O}}_K/{\mathfrak m}$ of characteristic ![]() $p$.
$p$.
Lemma 4.1 If ![]() ${\mathfrak X}$ is a smooth proper formal scheme over
${\mathfrak X}$ is a smooth proper formal scheme over ![]() $\operatorname {{Spf}}{\mathcal {O}}_K$ with generic fiber
$\operatorname {{Spf}}{\mathcal {O}}_K$ with generic fiber ![]() $X$, then there is a canonical isomorphism
$X$, then there is a canonical isomorphism ![]() $H^{i}(X,\Omega ^{j}_{X/K})\simeq H^{i}({\mathfrak X},\Omega ^{j}_{{\mathfrak X}/{\mathcal {O}}_K})[{1}/{p}]$. In particular,
$H^{i}(X,\Omega ^{j}_{X/K})\simeq H^{i}({\mathfrak X},\Omega ^{j}_{{\mathfrak X}/{\mathcal {O}}_K})[{1}/{p}]$. In particular, ![]() $h^{i,j}(X)=h^{i,j}({\mathfrak X})$.
$h^{i,j}(X)=h^{i,j}({\mathfrak X})$.
Proof. Let ![]() $({\mathfrak U}_i)_{i\in I}$ be a finite cover of
$({\mathfrak U}_i)_{i\in I}$ be a finite cover of ![]() ${\mathfrak X}$ by affine open formal subschemes. Their generic fibers
${\mathfrak X}$ by affine open formal subschemes. Their generic fibers ![]() $U_i$ induce a covering of
$U_i$ induce a covering of ![]() $X$ by affinoid subdomains. For any coherent sheaf
$X$ by affinoid subdomains. For any coherent sheaf ![]() ${\mathcal {F}}$ on
${\mathcal {F}}$ on ![]() ${\mathfrak X}$ its cohomology is computed by the Čech complex
${\mathfrak X}$ its cohomology is computed by the Čech complex ![]() ${\bigoplus} _{i\in I}{\mathcal {F}}({\mathfrak U}_i)\to {\bigoplus} _{i,j\in I}{\mathcal {F}}({\mathfrak U}_i\cap {\mathfrak U}_j)\to \cdots$. The cohomology of the sheaf
${\bigoplus} _{i\in I}{\mathcal {F}}({\mathfrak U}_i)\to {\bigoplus} _{i,j\in I}{\mathcal {F}}({\mathfrak U}_i\cap {\mathfrak U}_j)\to \cdots$. The cohomology of the sheaf ![]() $F$ on
$F$ on ![]() $X$ associated to
$X$ associated to ![]() ${\mathcal {F}}$ is computed by the Čech complex
${\mathcal {F}}$ is computed by the Čech complex ![]() ${\bigoplus} _{i\in I}F(U_i)\to {\bigoplus} _{i,j\in I}F(U_i\cap U_j)\to \cdots$ since higher cohomology of coherent sheaves on affinoids vanish. By definition,
${\bigoplus} _{i\in I}F(U_i)\to {\bigoplus} _{i,j\in I}F(U_i\cap U_j)\to \cdots$ since higher cohomology of coherent sheaves on affinoids vanish. By definition, ![]() $F(U_i)={\mathcal {F}}({\mathfrak U}_i)[{1}/{p}]$ so the Čech complex on the generic fiber is obtained from that of the formal scheme by inverting
$F(U_i)={\mathcal {F}}({\mathfrak U}_i)[{1}/{p}]$ so the Čech complex on the generic fiber is obtained from that of the formal scheme by inverting ![]() $p$ and we get the isomorphism
$p$ and we get the isomorphism ![]() $H^{i}(X,F)\simeq H^{i}({\mathfrak X},{\mathcal {F}})$ which implies the statement by using
$H^{i}(X,F)\simeq H^{i}({\mathfrak X},{\mathcal {F}})$ which implies the statement by using ![]() ${\mathcal {F}}=\Omega ^{j}_{{\mathfrak X}/{\mathcal {O}}_K}$.
${\mathcal {F}}=\Omega ^{j}_{{\mathfrak X}/{\mathcal {O}}_K}$.
Lemma 4.2 Let ![]() ${\mathfrak Y}$ be a smooth proper formal scheme over
${\mathfrak Y}$ be a smooth proper formal scheme over ![]() ${\mathcal {O}}_K$ with an action of a finite group
${\mathcal {O}}_K$ with an action of a finite group ![]() $\Gamma$ of order prime to
$\Gamma$ of order prime to ![]() $p$. If the special fiber
$p$. If the special fiber ![]() ${\mathfrak Y}_k$ is projective over
${\mathfrak Y}_k$ is projective over ![]() $k$ and the action of
$k$ and the action of ![]() $\Gamma$ on it is free there exists a quotient smooth proper formal scheme
$\Gamma$ on it is free there exists a quotient smooth proper formal scheme ![]() ${\mathfrak X}$ over
${\mathfrak X}$ over ![]() ${\mathcal {O}}_K$ with projective special fiber such that
${\mathcal {O}}_K$ with projective special fiber such that
Proof. For each ![]() $n$, the quotient
$n$, the quotient ![]() ${\mathfrak X}_n:={\mathfrak Y}_{{\mathcal {O}}_K/{\mathfrak m}^{n}}/\Gamma$ exists by [Reference GrothendieckSGA1, Expose 1, Proposition V.1.8] because admissibility of the action can be checked on the reduced subscheme which is projective in this case. The closed immersions
${\mathfrak X}_n:={\mathfrak Y}_{{\mathcal {O}}_K/{\mathfrak m}^{n}}/\Gamma$ exists by [Reference GrothendieckSGA1, Expose 1, Proposition V.1.8] because admissibility of the action can be checked on the reduced subscheme which is projective in this case. The closed immersions ![]() ${\mathfrak Y}_{{\mathcal {O}}_K/{\mathfrak m}^{n}}\to {\mathfrak Y}_{{\mathcal {O}}_K/{\mathfrak m}^{n+1}}$ induce morphisms
${\mathfrak Y}_{{\mathcal {O}}_K/{\mathfrak m}^{n}}\to {\mathfrak Y}_{{\mathcal {O}}_K/{\mathfrak m}^{n+1}}$ induce morphisms ![]() ${\mathfrak X}_n\to {\mathfrak X}_{n+1}$. Since the action is free, by [Reference GrothendieckSGA1, Corollarie V.2.4] the morphisms
${\mathfrak X}_n\to {\mathfrak X}_{n+1}$. Since the action is free, by [Reference GrothendieckSGA1, Corollarie V.2.4] the morphisms ![]() $\pi _n:{\mathfrak Y}_n\to {\mathfrak X}_n$ are étale with Galois group
$\pi _n:{\mathfrak Y}_n\to {\mathfrak X}_n$ are étale with Galois group ![]() $\Gamma$ and the canonical maps
$\Gamma$ and the canonical maps ![]() ${\mathcal {O}}_{{\mathfrak X}_n}\otimes _{{\mathbb {Z}}}{\mathbb {Z}}[\Gamma ]\to \pi _{n*}{\mathcal {O}}_{Y_n}$ are isomorphisms.
${\mathcal {O}}_{{\mathfrak X}_n}\otimes _{{\mathbb {Z}}}{\mathbb {Z}}[\Gamma ]\to \pi _{n*}{\mathcal {O}}_{Y_n}$ are isomorphisms.
Hence, the maps ![]() ${\mathfrak X}_n\to {\mathfrak X}_{n+1}$ are closed immersions inducing isomorphisms (this also follows from order of
${\mathfrak X}_n\to {\mathfrak X}_{n+1}$ are closed immersions inducing isomorphisms (this also follows from order of ![]() $\Gamma$ being invertible on
$\Gamma$ being invertible on ![]() ${\mathfrak Y}$, but is not true in general for a non-free action)
${\mathfrak Y}$, but is not true in general for a non-free action)
and the schemes ![]() ${\mathfrak X}_n$ form the desired quotient formal scheme
${\mathfrak X}_n$ form the desired quotient formal scheme ![]() ${\mathfrak X}$. If
${\mathfrak X}$. If ![]() $L$ is an ample line bundle on
$L$ is an ample line bundle on ![]() ${\mathfrak Y}_k$ then
${\mathfrak Y}_k$ then ![]() ${\bigotimes} _{\gamma \in \Gamma }\gamma ^{*}(L)$ descends to an ample line bundle on
${\bigotimes} _{\gamma \in \Gamma }\gamma ^{*}(L)$ descends to an ample line bundle on ![]() ${\mathfrak X}_k$ so
${\mathfrak X}_k$ so ![]() ${\mathfrak X}_k$ is projective over
${\mathfrak X}_k$ is projective over ![]() $k$.
$k$.
By the étaleness of the quotient map ![]() $\pi :{\mathfrak Y}\to {\mathfrak X}$ the canonical morphisms
$\pi :{\mathfrak Y}\to {\mathfrak X}$ the canonical morphisms ![]() $\Omega ^{i}_{{\mathfrak X}/{\mathcal {O}}_K}\to (\pi _*\Omega ^{i}_{{\mathfrak Y}/{\mathcal {O}}_K})^{\Gamma }$ are isomorphisms and we get a Hochschild–Serre spectral sequence with the second page
$\Omega ^{i}_{{\mathfrak X}/{\mathcal {O}}_K}\to (\pi _*\Omega ^{i}_{{\mathfrak Y}/{\mathcal {O}}_K})^{\Gamma }$ are isomorphisms and we get a Hochschild–Serre spectral sequence with the second page ![]() $E_2^{ab}=H^{a}(\Gamma , H^{b}({\mathfrak Y},\Omega ^{i}_{{\mathfrak Y}/{\mathcal {O}}_K}))$ converging to
$E_2^{ab}=H^{a}(\Gamma , H^{b}({\mathfrak Y},\Omega ^{i}_{{\mathfrak Y}/{\mathcal {O}}_K}))$ converging to ![]() $H^{a+b}({\mathfrak X},\Omega ^{i}_{{\mathfrak X}/{\mathcal {O}}_K})$. Since higher cohomology of
$H^{a+b}({\mathfrak X},\Omega ^{i}_{{\mathfrak X}/{\mathcal {O}}_K})$. Since higher cohomology of ![]() $\Gamma$ with coefficients in
$\Gamma$ with coefficients in ![]() ${\mathcal {O}}_K$-modules vanishes, we get the desired isomorphism.
${\mathcal {O}}_K$-modules vanishes, we get the desired isomorphism.
Proof of Theorem 4.1 We first treat the case of ![]() $i+j=3$, and the general case follows from the Lemma 4.3 below. Let
$i+j=3$, and the general case follows from the Lemma 4.3 below. Let ![]() ${\mathfrak Z}$ be a formal abelian scheme with an action of
${\mathfrak Z}$ be a formal abelian scheme with an action of ![]() $G$ over the ring of integers
$G$ over the ring of integers ![]() ${\mathcal {O}}_L=W(k')$ in some unramified extension
${\mathcal {O}}_L=W(k')$ in some unramified extension ![]() $L\supset {\mathbb {Q}}_p$ provided by Proposition 3.1. We would like to construct
$L\supset {\mathbb {Q}}_p$ provided by Proposition 3.1. We would like to construct ![]() ${\mathfrak X}$ by taking the quotient of
${\mathfrak X}$ by taking the quotient of ![]() ${\mathfrak Z}$ by
${\mathfrak Z}$ by ![]() $G$, but first we need to make the action free in a way that does not spoil the discrepancy between ranks of invariant submodules. By [Reference RaynaudRay79, Proposition 4.2.3] or [Reference Bhatt, Morrow and ScholzeBMS18, § 2.2] there exists a smooth projective complete intersection
$G$, but first we need to make the action free in a way that does not spoil the discrepancy between ranks of invariant submodules. By [Reference RaynaudRay79, Proposition 4.2.3] or [Reference Bhatt, Morrow and ScholzeBMS18, § 2.2] there exists a smooth projective complete intersection ![]() ${\mathfrak Y}$ of dimension
${\mathfrak Y}$ of dimension ![]() $\geq 4$ in projective space over
$\geq 4$ in projective space over ![]() ${\mathcal {O}}_L$ equipped with a free action of
${\mathcal {O}}_L$ equipped with a free action of ![]() $G$. We equip the product
$G$. We equip the product ![]() ${\mathfrak Z}\times _{{\mathcal {O}}_L}{\mathfrak Y}$ with the diagonal action of
${\mathfrak Z}\times _{{\mathcal {O}}_L}{\mathfrak Y}$ with the diagonal action of ![]() $G$ which is free because the action on the second factor is free. Note that
$G$ which is free because the action on the second factor is free. Note that ![]() $H^{i}({\mathfrak Z}\times {\mathfrak Y},{\mathcal {O}})\simeq H^{i}({\mathfrak Z},{\mathcal {O}})$ and
$H^{i}({\mathfrak Z}\times {\mathfrak Y},{\mathcal {O}})\simeq H^{i}({\mathfrak Z},{\mathcal {O}})$ and ![]() $H^{0}({\mathfrak Z}\times {\mathfrak Y},\Omega ^{i}_{{\mathfrak Z}\times {\mathfrak Y}/{\mathcal {O}}_L})\simeq H^{0}({\mathfrak Z},\Omega ^{i}_{{\mathfrak Z}/{\mathcal {O}}_L})$ for
$H^{0}({\mathfrak Z}\times {\mathfrak Y},\Omega ^{i}_{{\mathfrak Z}\times {\mathfrak Y}/{\mathcal {O}}_L})\simeq H^{0}({\mathfrak Z},\Omega ^{i}_{{\mathfrak Z}/{\mathcal {O}}_L})$ for ![]() $i\leq 3$ by Künneth formula and Lefschetz hyperplane theorem [Reference Antieau, Bhatt and MathewABM19, Proposition 5.3] applied to
$i\leq 3$ by Künneth formula and Lefschetz hyperplane theorem [Reference Antieau, Bhatt and MathewABM19, Proposition 5.3] applied to ![]() ${\mathfrak Y}$.
${\mathfrak Y}$.
First, we construct the scheme with desired property over the unramified extension ![]() ${\mathcal {O}}_L$ as the quotient
${\mathcal {O}}_L$ as the quotient ![]() ${\mathfrak X}':=({\mathfrak Z}\times {\mathfrak Y})/G$ provided by the Lemma 4.2. We have
${\mathfrak X}':=({\mathfrak Z}\times {\mathfrak Y})/G$ provided by the Lemma 4.2. We have ![]() $H^{3}({\mathfrak X}',{\mathcal {O}})=H^{3}({\mathfrak Z}\times {\mathfrak Y},{\mathcal {O}})^{G}=H^{3}({\mathfrak Z},{\mathcal {O}})^{G}$ and
$H^{3}({\mathfrak X}',{\mathcal {O}})=H^{3}({\mathfrak Z}\times {\mathfrak Y},{\mathcal {O}})^{G}=H^{3}({\mathfrak Z},{\mathcal {O}})^{G}$ and ![]() $H^{0}({\mathfrak X}',\Omega ^{3}_{{\mathfrak X}'/{\mathcal {O}}_L})^{G}=H^{0}({\mathfrak Z},\Omega ^{3}_{{\mathfrak Z}/{\mathcal {O}}_L})^{G}$. Proposition 3.1 supplied
$H^{0}({\mathfrak X}',\Omega ^{3}_{{\mathfrak X}'/{\mathcal {O}}_L})^{G}=H^{0}({\mathfrak Z},\Omega ^{3}_{{\mathfrak Z}/{\mathcal {O}}_L})^{G}$. Proposition 3.1 supplied ![]() ${\mathfrak Z}$ such that the ranks of invariant modules
${\mathfrak Z}$ such that the ranks of invariant modules ![]() $H^{3}({\mathfrak Z},{\mathcal {O}})^{G}$ and
$H^{3}({\mathfrak Z},{\mathcal {O}})^{G}$ and ![]() $H^{0}({\mathfrak Z},\Omega ^{3}_{{\mathfrak Z}/{\mathcal {O}}_L})^{G}$ are different, so
$H^{0}({\mathfrak Z},\Omega ^{3}_{{\mathfrak Z}/{\mathcal {O}}_L})^{G}$ are different, so ![]() $H^{3}({\mathfrak X}',{\mathcal {O}})$ and
$H^{3}({\mathfrak X}',{\mathcal {O}})$ and ![]() $H^{0}({\mathfrak X}',\Omega _{{\mathfrak X}'/{\mathcal {O}}_L}^{3})$ are indeed of different rank. By Proposition 2.1 we have
$H^{0}({\mathfrak X}',\Omega _{{\mathfrak X}'/{\mathcal {O}}_L}^{3})$ are indeed of different rank. By Proposition 2.1 we have ![]() $3h^{3,0}({\mathfrak X}')+h^{2,1}({\mathfrak X}')=3h^{0,3}({\mathfrak X}')+h^{1,2}({\mathfrak X}')$ so the ranks of
$3h^{3,0}({\mathfrak X}')+h^{2,1}({\mathfrak X}')=3h^{0,3}({\mathfrak X}')+h^{1,2}({\mathfrak X}')$ so the ranks of ![]() $H^{2}({\mathfrak X}',\Omega ^{1}_{{\mathfrak X}'/{\mathcal {O}}_L})$ and
$H^{2}({\mathfrak X}',\Omega ^{1}_{{\mathfrak X}'/{\mathcal {O}}_L})$ and ![]() $H^{1}({\mathfrak X}',\Omega ^{2}_{{\mathfrak X}'/{\mathcal {O}}_L})$ are forced to be different as well.
$H^{1}({\mathfrak X}',\Omega ^{2}_{{\mathfrak X}'/{\mathcal {O}}_L})$ are forced to be different as well.
Finally, the example over ![]() ${\mathbb {Z}}_p$ is obtained by Weil restriction of scalars
${\mathbb {Z}}_p$ is obtained by Weil restriction of scalars ![]() ${\mathfrak X}:=\operatorname {{Res}}^{{\mathcal {O}}_L}_{{\mathbb {Z}}_p}{\mathfrak X}'$. Since
${\mathfrak X}:=\operatorname {{Res}}^{{\mathcal {O}}_L}_{{\mathbb {Z}}_p}{\mathfrak X}'$. Since ![]() ${\mathcal {O}}_L$ is finite étale over
${\mathcal {O}}_L$ is finite étale over ![]() ${\mathbb {Z}}_p$ this is a smooth proper formal scheme over
${\mathbb {Z}}_p$ this is a smooth proper formal scheme over ![]() ${\mathbb {Z}}_p$ with projective special fiber
${\mathbb {Z}}_p$ with projective special fiber ![]() ${\mathfrak X}_{{\mathbb {F}}_p}=\operatorname {{Res}}^{k'}_{{\mathbb {F}}_p}{\mathfrak X}_{k'}$. Since
${\mathfrak X}_{{\mathbb {F}}_p}=\operatorname {{Res}}^{k'}_{{\mathbb {F}}_p}{\mathfrak X}_{k'}$. Since ![]() ${\mathfrak X}\times _{{\mathbb {Z}}_p}{\mathcal {O}}_L$ is isomorphic to
${\mathfrak X}\times _{{\mathbb {Z}}_p}{\mathcal {O}}_L$ is isomorphic to ![]() $({\mathfrak X}')^{\times d}$ where
$({\mathfrak X}')^{\times d}$ where ![]() $d$ is the degree of
$d$ is the degree of ![]() $k'$ over
$k'$ over ![]() ${\mathbb {F}}_p$, the Hodge cohomology modules of
${\mathbb {F}}_p$, the Hodge cohomology modules of ![]() ${\mathfrak X}$ are free and
${\mathfrak X}$ are free and ![]() $h^{3,0}({\mathfrak X})-h^{0,3}({\mathfrak X})=d(h^{3,0}({\mathfrak X}')-h^{0,3}({\mathfrak X}'))$ because the symmetry on cohomology of
$h^{3,0}({\mathfrak X})-h^{0,3}({\mathfrak X})=d(h^{3,0}({\mathfrak X}')-h^{0,3}({\mathfrak X}'))$ because the symmetry on cohomology of ![]() ${\mathfrak X}'$ in degrees
${\mathfrak X}'$ in degrees ![]() $1$ and
$1$ and ![]() $2$ holds by Corollary 2.2.
$2$ holds by Corollary 2.2.
Lemma 4.3 Let ![]() ${\mathfrak X}$ be a smooth proper formal scheme over
${\mathfrak X}$ be a smooth proper formal scheme over ![]() ${\mathcal {O}}_K$ such that
${\mathcal {O}}_K$ such that ![]() $h^{3,0}({\mathfrak X})\neq h^{0,3}({\mathfrak X})$. Then for any
$h^{3,0}({\mathfrak X})\neq h^{0,3}({\mathfrak X})$. Then for any ![]() $i,j\geq 0$ with
$i,j\geq 0$ with ![]() $i\neq j$ and
$i\neq j$ and ![]() $i+j>3$ there exists a smooth projective scheme
$i+j>3$ there exists a smooth projective scheme ![]() ${\mathfrak Y}$ over
${\mathfrak Y}$ over ![]() ${\mathcal {O}}_K$ such that
${\mathcal {O}}_K$ such that ![]() $h^{i,j}({\mathfrak X}\times {\mathfrak Y})\neq h^{j,i}({\mathfrak X}\times {\mathfrak Y})$.
$h^{i,j}({\mathfrak X}\times {\mathfrak Y})\neq h^{j,i}({\mathfrak X}\times {\mathfrak Y})$.
Proof Recall that for a formal scheme ![]() ${\mathfrak T}$ the number
${\mathfrak T}$ the number ![]() $\delta ^{i,j}({\mathfrak T})$ is defined as the difference
$\delta ^{i,j}({\mathfrak T})$ is defined as the difference ![]() $h^{i,j}({\mathfrak T})-h^{j,i}({\mathfrak T})$. Note that if
$h^{i,j}({\mathfrak T})-h^{j,i}({\mathfrak T})$. Note that if ![]() ${\mathfrak Y}$ satisfies Hodge symmetry then
${\mathfrak Y}$ satisfies Hodge symmetry then
 \begin{equation} \delta^{i,j}({\mathfrak T}\times{\mathfrak Y})=\displaystyle\sum_{\substack{i_1+i_2=i\\ j_1+j_2=j}}\delta^{i_1,j_1}({\mathfrak T})h^{i_2,j_2}({\mathfrak Y}). \end{equation}
\begin{equation} \delta^{i,j}({\mathfrak T}\times{\mathfrak Y})=\displaystyle\sum_{\substack{i_1+i_2=i\\ j_1+j_2=j}}\delta^{i_1,j_1}({\mathfrak T})h^{i_2,j_2}({\mathfrak Y}). \end{equation} By Proposition 2.1 we have ![]() $\delta ^{2,1}({\mathfrak X})=-3\delta ^{3,0}({\mathfrak X})$ and
$\delta ^{2,1}({\mathfrak X})=-3\delta ^{3,0}({\mathfrak X})$ and ![]() $\delta ^{1,0}({\mathfrak X})=\delta ^{2,0}({\mathfrak X})=0$. Let us assume that
$\delta ^{1,0}({\mathfrak X})=\delta ^{2,0}({\mathfrak X})=0$. Let us assume that ![]() $i>j$. For a scheme
$i>j$. For a scheme ![]() ${\mathfrak Y}$ denote by
${\mathfrak Y}$ denote by ![]() $H_{{\mathfrak Y}}(x,y):=\sum _{i,j}h^{i,j}({\mathfrak Y})x^{i}y^{j}$ its Hodge polynomial. If
$H_{{\mathfrak Y}}(x,y):=\sum _{i,j}h^{i,j}({\mathfrak Y})x^{i}y^{j}$ its Hodge polynomial. If ![]() ${\mathfrak Y}_1\subset {\mathfrak Y}_2$ is a smooth closed subscheme of codimension
${\mathfrak Y}_1\subset {\mathfrak Y}_2$ is a smooth closed subscheme of codimension ![]() $r+1$ in a smooth proper scheme, then the Hodge polynomial of the blow-up is given by
$r+1$ in a smooth proper scheme, then the Hodge polynomial of the blow-up is given by
Let ![]() ${\mathfrak T}_{d,n}$ be a smooth degree
${\mathfrak T}_{d,n}$ be a smooth degree ![]() $d$ hypersurface in
$d$ hypersurface in ![]() ${\mathbb {P}}^{n+1}_{{\mathcal {O}}_K}$ where
${\mathbb {P}}^{n+1}_{{\mathcal {O}}_K}$ where ![]() $d$ and
$d$ and ![]() $n$ are numbers that we will choose later. Construct a sequence of smooth projective schemes starting with
$n$ are numbers that we will choose later. Construct a sequence of smooth projective schemes starting with ![]() ${\mathfrak Y}_0={\mathfrak T}_{d,n}$ and for
${\mathfrak Y}_0={\mathfrak T}_{d,n}$ and for ![]() $s\geq 0$ defining the scheme
$s\geq 0$ defining the scheme ![]() ${\mathfrak Y}_{s+1}$ as the blow-up of some projective space
${\mathfrak Y}_{s+1}$ as the blow-up of some projective space ![]() ${\mathbb {P}}^{N_s}_{{\mathcal {O}}_K}$ along some embedding
${\mathbb {P}}^{N_s}_{{\mathcal {O}}_K}$ along some embedding ![]() ${\mathfrak Y}_s\subset {\mathbb {P}}^{N_s}_{{\mathcal {O}}_K}$ of codimension
${\mathfrak Y}_s\subset {\mathbb {P}}^{N_s}_{{\mathcal {O}}_K}$ of codimension ![]() $\geq 2$ (the numbers
$\geq 2$ (the numbers ![]() $N_s>\dim _{{\mathcal {O}}_K}{\mathfrak Y}_s+1$ can be chosen arbitrarily). By the above formula we have
$N_s>\dim _{{\mathcal {O}}_K}{\mathfrak Y}_s+1$ can be chosen arbitrarily). By the above formula we have ![]() $H_{{\mathfrak Y}_s}(x,y)=F(xy)+H_{{\mathfrak T}_{d,n}}(x,y)\cdot (xy)^{s}\cdot G(xy)$ where
$H_{{\mathfrak Y}_s}(x,y)=F(xy)+H_{{\mathfrak T}_{d,n}}(x,y)\cdot (xy)^{s}\cdot G(xy)$ where ![]() $F(t),G(t)\in 1+t{\mathbb {Z}}[t]$ are some polynomials.
$F(t),G(t)\in 1+t{\mathbb {Z}}[t]$ are some polynomials.
Assume first that ![]() $i> j+3$. Then take
$i> j+3$. Then take ![]() $n=i-3-j,s=j$ and consider
$n=i-3-j,s=j$ and consider ![]() ${\mathfrak Y}:={\mathfrak Y}_s$ obtained by the above inductive procedure from
${\mathfrak Y}:={\mathfrak Y}_s$ obtained by the above inductive procedure from ![]() ${\mathfrak T}_{d,n}$. We then have
${\mathfrak T}_{d,n}$. We then have ![]() $h^{i-2,j-1}({\mathfrak Y})=h^{i-1,j-2}({\mathfrak Y})=h^{i,j-3}({\mathfrak Y})=0$ and
$h^{i-2,j-1}({\mathfrak Y})=h^{i-1,j-2}({\mathfrak Y})=h^{i,j-3}({\mathfrak Y})=0$ and ![]() $h^{i-3,j}({\mathfrak Y})=h^{n,0}({\mathfrak T}_{d,n})$. This turns (6) into
$h^{i-3,j}({\mathfrak Y})=h^{n,0}({\mathfrak T}_{d,n})$. This turns (6) into
By [Reference Deligne and KatzSGA7, XI.Theoreme 1.5] the Hodge numbers ![]() $h^{a,b}({\mathfrak T}_{d,n})$ of a hypersurface are zero unless
$h^{a,b}({\mathfrak T}_{d,n})$ of a hypersurface are zero unless ![]() $a+b=n$ or
$a+b=n$ or ![]() $a=b$ and
$a=b$ and ![]() $h^{a,a}({\mathfrak T}_{d,n})=1$ for
$h^{a,a}({\mathfrak T}_{d,n})=1$ for ![]() $0\leq a\leq n, 2a\neq n$. It follows that the Hodge polynomial
$0\leq a\leq n, 2a\neq n$. It follows that the Hodge polynomial ![]() $H_{{\mathfrak Y}}(x,y)$ is congruent modulo the ideal
$H_{{\mathfrak Y}}(x,y)$ is congruent modulo the ideal ![]() $(x,y)^{n+s}$ to a polynomial of the form
$(x,y)^{n+s}$ to a polynomial of the form ![]() $K(xy)$ with coefficients not depending on the degree
$K(xy)$ with coefficients not depending on the degree ![]() $d$ of the hypersurface. In particular,
$d$ of the hypersurface. In particular, ![]() $\delta ^{i,j}({\mathfrak X}\times {\mathfrak Y})$ is the sum of
$\delta ^{i,j}({\mathfrak X}\times {\mathfrak Y})$ is the sum of ![]() $\delta ^{3,0}({\mathfrak X})\cdot h^{i-3,j}({\mathfrak Y})=\delta ^{3,0}({\mathfrak X})\cdot h^{n,0}({\mathfrak T}_{d,n})$ and a number that does not depend on
$\delta ^{3,0}({\mathfrak X})\cdot h^{i-3,j}({\mathfrak Y})=\delta ^{3,0}({\mathfrak X})\cdot h^{n,0}({\mathfrak T}_{d,n})$ and a number that does not depend on ![]() $d$. By [Reference Deligne and KatzSGA7, Corollaire 2.4] the number is
$d$. By [Reference Deligne and KatzSGA7, Corollaire 2.4] the number is ![]() $h^{n,0}({\mathfrak T}_{d,n})$ is equal to
$h^{n,0}({\mathfrak T}_{d,n})$ is equal to ![]() $\binom {d-1}{n+1}$ so for large enough
$\binom {d-1}{n+1}$ so for large enough ![]() $d$ this sum will be non-zero.
$d$ this sum will be non-zero.
If ![]() $i=j+2$, then take
$i=j+2$, then take ![]() ${\mathfrak Y}={\mathfrak Y}_s$ with
${\mathfrak Y}={\mathfrak Y}_s$ with ![]() $n=1,s=j-1$. An analogous computation gives that
$n=1,s=j-1$. An analogous computation gives that ![]() $\delta ^{i,j}({\mathfrak X}\times {\mathfrak Y})$ is the sum of a number that does not depend on
$\delta ^{i,j}({\mathfrak X}\times {\mathfrak Y})$ is the sum of a number that does not depend on ![]() $d$ and the expression
$d$ and the expression
which is non-zero for ![]() $d>2$.
$d>2$.
Finally, if ![]() $i= j+3$ or
$i= j+3$ or ![]() $i=j+1$ we will be able to move asymmetry into higher cohomology just via Tate twists. Consider the scheme
$i=j+1$ we will be able to move asymmetry into higher cohomology just via Tate twists. Consider the scheme ![]() ${\mathfrak Y}=({\mathbb {P}}^{1}_{{\mathcal {O}}_K})^{d}$ where we will again choose
${\mathfrak Y}=({\mathbb {P}}^{1}_{{\mathcal {O}}_K})^{d}$ where we will again choose ![]() $d$ at the end. We have
$d$ at the end. We have
 \[ \delta^{i,j}({\mathfrak X}\times{\mathfrak Y})=\sum_{r\leq ({i+j-3})/{2}}\delta^{i-r,j-r}({\mathfrak X})\cdot\binom{d}{r}. \]
\[ \delta^{i,j}({\mathfrak X}\times{\mathfrak Y})=\sum_{r\leq ({i+j-3})/{2}}\delta^{i-r,j-r}({\mathfrak X})\cdot\binom{d}{r}. \]
This is a polynomial in ![]() $d$ with leading coefficient
$d$ with leading coefficient ![]() $\delta ^{i-r,j-r}({\mathfrak X})$ with
$\delta ^{i-r,j-r}({\mathfrak X})$ with ![]() $r=({i+j-3})/{2}$ which is nothing but
$r=({i+j-3})/{2}$ which is nothing but ![]() $\pm \delta ^{3,0}({\mathfrak X})$ or
$\pm \delta ^{3,0}({\mathfrak X})$ or ![]() $\pm \delta ^{2,1}({\mathfrak X})$ so this expression is non-zero for a large enough value of
$\pm \delta ^{2,1}({\mathfrak X})$ so this expression is non-zero for a large enough value of ![]() $d$.
$d$.
This finishes the proof of Theorem 4.1.
Corollary 4.4 For every pair of positive numbers ![]() $i\neq j$ with
$i\neq j$ with ![]() $i+j\geq 3$ there exists a smooth proper rigid-analytic variety
$i+j\geq 3$ there exists a smooth proper rigid-analytic variety ![]() $X$ over
$X$ over ![]() ${\mathbb {Q}}_p$ admitting a smooth formal model
${\mathbb {Q}}_p$ admitting a smooth formal model ![]() ${\mathfrak X}$ over
${\mathfrak X}$ over ![]() $\operatorname {{Spf}}{\mathbb {Z}}_p$ with projective special fiber
$\operatorname {{Spf}}{\mathbb {Z}}_p$ with projective special fiber ![]() ${\mathfrak X}_{{\mathbb {F}}_p}$ such that
${\mathfrak X}_{{\mathbb {F}}_p}$ such that
5. Embellishing the main example and a question
We end by noting that the examples provided by Theorem 4.1 can be modified to avoid some of the characteristic ![]() $p$ ‘pathologies’.
$p$ ‘pathologies’.
In all of the examples constructed above the Hodge cohomology groups ![]() $H^{i}({\mathfrak X},\Omega ^{j}_{{\mathfrak X}/{\mathbb {Z}}_p})$ are free modules over
$H^{i}({\mathfrak X},\Omega ^{j}_{{\mathfrak X}/{\mathbb {Z}}_p})$ are free modules over ![]() ${\mathbb {Z}}_p$ so the Hodge numbers of the special and generic fibers of
${\mathbb {Z}}_p$ so the Hodge numbers of the special and generic fibers of ![]() ${\mathfrak X}$ coincide. In particular, the Hodge symmetry for the special fiber
${\mathfrak X}$ coincide. In particular, the Hodge symmetry for the special fiber ![]() ${\mathfrak X}_{{\mathbb {F}}_p}$ fails as well. The next lemma shows that symmetry for the generic fiber cannot be salvaged by requiring that for the special fiber: there are enough projective schemes failing symmetry for the special fiber to cancel out the asymmetry on the special fiber by taking products. We only treat here one particular pair of degrees.
${\mathfrak X}_{{\mathbb {F}}_p}$ fails as well. The next lemma shows that symmetry for the generic fiber cannot be salvaged by requiring that for the special fiber: there are enough projective schemes failing symmetry for the special fiber to cancel out the asymmetry on the special fiber by taking products. We only treat here one particular pair of degrees.
Lemma 5.1 There exists a smooth proper formal scheme ![]() ${\mathfrak X}'$ over
${\mathfrak X}'$ over ![]() $\operatorname {{Spf}}{\mathbb {Z}}_p$ with projective special fiber such that
$\operatorname {{Spf}}{\mathbb {Z}}_p$ with projective special fiber such that ![]() $h^{3,0}({\mathfrak X}')\neq h^{0,3}({\mathfrak X}')$ while
$h^{3,0}({\mathfrak X}')\neq h^{0,3}({\mathfrak X}')$ while ![]() $h^{3,0}({\mathfrak X}'_{{\mathbb {F}}_p})=h^{0,3}({\mathfrak X}'_{{\mathbb {F}}_p})$.
$h^{3,0}({\mathfrak X}'_{{\mathbb {F}}_p})=h^{0,3}({\mathfrak X}'_{{\mathbb {F}}_p})$.
Proof. The proof of Theorem 4.1 provides us with a smooth proper scheme ![]() ${\mathfrak X}$ over
${\mathfrak X}$ over ![]() ${\mathbb {Z}}_p$ with projective special fiber such that all Hodge groups
${\mathbb {Z}}_p$ with projective special fiber such that all Hodge groups ![]() $H^{i}({\mathfrak X},\Omega ^{j}_{{\mathfrak X}/{\mathbb {Z}}_p})$ are free over
$H^{i}({\mathfrak X},\Omega ^{j}_{{\mathfrak X}/{\mathbb {Z}}_p})$ are free over ![]() ${\mathbb {Z}}_p$ and
${\mathbb {Z}}_p$ and ![]() $h^{3,0}({\mathfrak X})< h^{0,3}({\mathfrak X})$ while
$h^{3,0}({\mathfrak X})< h^{0,3}({\mathfrak X})$ while ![]() $h^{1,0}({\mathfrak X})=h^{0,1}({\mathfrak X})=0$ (the Hodge numbers in degree
$h^{1,0}({\mathfrak X})=h^{0,1}({\mathfrak X})=0$ (the Hodge numbers in degree ![]() $1$ vanish because representations
$1$ vanish because representations ![]() $U,V$ used in proof of Proposition 3.1 have trivial invariants). Since Hodge cohomology modules are free, the Hodge numbers of the special fiber
$U,V$ used in proof of Proposition 3.1 have trivial invariants). Since Hodge cohomology modules are free, the Hodge numbers of the special fiber ![]() ${\mathfrak X}_{{\mathbb {F}}_p}$ are equal to those of
${\mathfrak X}_{{\mathbb {F}}_p}$ are equal to those of ![]() ${\mathfrak X}$.
${\mathfrak X}$.
We will now take the product of ![]() ${\mathfrak X}$ with an auxiliary projective scheme that will be constructed by approximating the stack
${\mathfrak X}$ with an auxiliary projective scheme that will be constructed by approximating the stack ![]() $B(\mu _p\times {\mathbb {Z}}/p)$. By [Reference Antieau, Bhatt and MathewABM19, Theorem 1.2] applied over
$B(\mu _p\times {\mathbb {Z}}/p)$. By [Reference Antieau, Bhatt and MathewABM19, Theorem 1.2] applied over ![]() ${\mathbb {Z}}_p$ to the group scheme
${\mathbb {Z}}_p$ to the group scheme ![]() $\mu _p\times {\mathbb {Z}}/p$ with
$\mu _p\times {\mathbb {Z}}/p$ with ![]() $d=3$ there exists a smooth projective scheme
$d=3$ there exists a smooth projective scheme ![]() ${\mathfrak Y}'$ such that
${\mathfrak Y}'$ such that ![]() $H^{j}({\mathfrak Y}'_{{\mathbb {F}}_p},\Omega ^{i}_{{\mathfrak Y}'_{{\mathbb {F}}_p}})=H^{j}(B(\mu _p\times {\mathbb {Z}}/p)_{{\mathbb {F}}_p},\Omega ^{i})$ and
$H^{j}({\mathfrak Y}'_{{\mathbb {F}}_p},\Omega ^{i}_{{\mathfrak Y}'_{{\mathbb {F}}_p}})=H^{j}(B(\mu _p\times {\mathbb {Z}}/p)_{{\mathbb {F}}_p},\Omega ^{i})$ and ![]() $H^{j}({\mathfrak Y}',\Omega ^{i}_{{\mathfrak Y}'/{\mathbb {Z}}_p})=H^{j}(B(\mu _p\times {\mathbb {Z}}/p)_{{\mathbb {Z}}_p},\Omega ^{i})$ for pairs
$H^{j}({\mathfrak Y}',\Omega ^{i}_{{\mathfrak Y}'/{\mathbb {Z}}_p})=H^{j}(B(\mu _p\times {\mathbb {Z}}/p)_{{\mathbb {Z}}_p},\Omega ^{i})$ for pairs ![]() $i,j$ with
$i,j$ with ![]() $i+j\geq 3$ and
$i+j\geq 3$ and ![]() $i=0$ or
$i=0$ or ![]() $j=0$. The Hodge polynomial
$j=0$. The Hodge polynomial ![]() $H_{B(\mu _p\times {\mathbb {Z}}/p)_{{\mathbb {F}}_p}}(x,y):=\sum _{i,j}h^{i,j}(B(\mu _p\times {\mathbb {Z}}/p)_{{\mathbb {F}}_p})x^{i}y^{j}$ of this stack is given by the product
$H_{B(\mu _p\times {\mathbb {Z}}/p)_{{\mathbb {F}}_p}}(x,y):=\sum _{i,j}h^{i,j}(B(\mu _p\times {\mathbb {Z}}/p)_{{\mathbb {F}}_p})x^{i}y^{j}$ of this stack is given by the product ![]() $H_{B\mu _{p,{\mathbb {F}}_p}}(x,y)H_{B({\mathbb {Z}}/p)_{{\mathbb {F}}_p}}(x,y)$. By [Reference TotaroTot18, Proposition 11.1] the first multiple
$H_{B\mu _{p,{\mathbb {F}}_p}}(x,y)H_{B({\mathbb {Z}}/p)_{{\mathbb {F}}_p}}(x,y)$. By [Reference TotaroTot18, Proposition 11.1] the first multiple ![]() $H_{B\mu _{p,{\mathbb {F}}_p}}$ is equal to
$H_{B\mu _{p,{\mathbb {F}}_p}}$ is equal to ![]() $({1+x})/({1-xy})$ and
$({1+x})/({1-xy})$ and ![]() $H_{B({\mathbb {Z}}/p)_{{\mathbb {F}}_p}}$ is equal to
$H_{B({\mathbb {Z}}/p)_{{\mathbb {F}}_p}}$ is equal to ![]() ${1}/({1-y})$ because the only non-zero Hodge cohomology groups of the classifying stack of a finite discrete group
${1}/({1-y})$ because the only non-zero Hodge cohomology groups of the classifying stack of a finite discrete group ![]() $\Gamma$ are given by group cohomology
$\Gamma$ are given by group cohomology ![]() $H^{i}(B\Gamma _{{\mathbb {F}}_p},{\mathcal {O}})\simeq H^{i}(\Gamma ,{\mathbb {F}}_p)$. Take
$H^{i}(B\Gamma _{{\mathbb {F}}_p},{\mathcal {O}})\simeq H^{i}(\Gamma ,{\mathbb {F}}_p)$. Take ![]() ${\mathfrak Y}:={\mathfrak Y}'\times {\mathfrak E}^{l}$ where
${\mathfrak Y}:={\mathfrak Y}'\times {\mathfrak E}^{l}$ where ![]() ${\mathfrak E}$ is an elliptic curve over
${\mathfrak E}$ is an elliptic curve over ![]() ${\mathbb {Z}}_p$ and
${\mathbb {Z}}_p$ and ![]() $l$ is a number that we will choose at the end.
$l$ is a number that we will choose at the end.
By the above computation, ![]() $H_{{\mathfrak Y}_{{\mathbb {F}}_p}}(x,y)$ is given by
$H_{{\mathfrak Y}_{{\mathbb {F}}_p}}(x,y)$ is given by ![]() $({1}/({1-y}))\cdot (({1+x})/({1-xy}))\cdot (1+x+y+xy)^{l}$ modulo an element of the ideal
$({1}/({1-y}))\cdot (({1+x})/({1-xy}))\cdot (1+x+y+xy)^{l}$ modulo an element of the ideal ![]() $(x^{4},xy,y^{4})$. For the purpose of computing
$(x^{4},xy,y^{4})$. For the purpose of computing ![]() $h^{3,0}(({\mathfrak X}\times {\mathfrak Y})_{{\mathbb {F}}_p})$ and
$h^{3,0}(({\mathfrak X}\times {\mathfrak Y})_{{\mathbb {F}}_p})$ and ![]() $h^{0,3}(({\mathfrak X}\times {\mathfrak Y})_{{\mathbb {F}}_p})$ we only care about this polynomial modulo
$h^{0,3}(({\mathfrak X}\times {\mathfrak Y})_{{\mathbb {F}}_p})$ we only care about this polynomial modulo ![]() $xy$ and we have
$xy$ and we have ![]() $H_{({\mathfrak X}\times {\mathfrak Y})_{{\mathbb {F}}_p}}(x,y)\equiv (1+h^{2,0}({\mathfrak X}_{{\mathbb {F}}_p})x^{2}$
$H_{({\mathfrak X}\times {\mathfrak Y})_{{\mathbb {F}}_p}}(x,y)\equiv (1+h^{2,0}({\mathfrak X}_{{\mathbb {F}}_p})x^{2}$ ![]() $+h^{3,0}({\mathfrak X}_{{\mathbb {F}}_p})x^{3}+h^{0,2}({\mathfrak X}_{{\mathbb {F}}_p})y^{2}+h^{0,3}({\mathfrak X}_{{\mathbb {F}}_p})y^{3})(1+(l+1)x+(\binom {l}{2}+l)x^{2}$
$+h^{3,0}({\mathfrak X}_{{\mathbb {F}}_p})x^{3}+h^{0,2}({\mathfrak X}_{{\mathbb {F}}_p})y^{2}+h^{0,3}({\mathfrak X}_{{\mathbb {F}}_p})y^{3})(1+(l+1)x+(\binom {l}{2}+l)x^{2}$ ![]() $+(\binom {l}{3}+\binom {l}{2})x^{3}+(l+1)y+(\binom {l}{2}+l+1)y^{2}+(\binom {l}{3}+\binom {l}{2}+l+1)y^{3})$ modulo the ideal
$+(\binom {l}{3}+\binom {l}{2})x^{3}+(l+1)y+(\binom {l}{2}+l+1)y^{2}+(\binom {l}{3}+\binom {l}{2}+l+1)y^{3})$ modulo the ideal ![]() $(x^{4},xy,y^{4})$. The Hodge numbers of the special fiber
$(x^{4},xy,y^{4})$. The Hodge numbers of the special fiber ![]() ${\mathfrak X}_{{\mathbb {F}}_p}\times {\mathfrak Y}_{{\mathbb {F}}_p}$ are thus given by
${\mathfrak X}_{{\mathbb {F}}_p}\times {\mathfrak Y}_{{\mathbb {F}}_p}$ are thus given by ![]() $h^{3,0}(({\mathfrak X}\times {\mathfrak Y})_{{\mathbb {F}}_p})=\binom {l}{3}+\binom {l}{2}+h^{3,0}({\mathfrak X}_{{\mathbb {F}}_p})+(l+1)h^{2,0}({\mathfrak X}_{{\mathbb {F}}_p})$,
$h^{3,0}(({\mathfrak X}\times {\mathfrak Y})_{{\mathbb {F}}_p})=\binom {l}{3}+\binom {l}{2}+h^{3,0}({\mathfrak X}_{{\mathbb {F}}_p})+(l+1)h^{2,0}({\mathfrak X}_{{\mathbb {F}}_p})$, ![]() $h^{0,3}(({\mathfrak X}\times {\mathfrak Y})_{{\mathbb {F}}_p})=\binom {l}{3}+\binom {l}{2}+l+1+h^{0,3}({\mathfrak X}_{{\mathbb {F}}_p})+(l+1)h^{0,2}({\mathfrak X}_{{\mathbb {F}}_p})$. Hence,
$h^{0,3}(({\mathfrak X}\times {\mathfrak Y})_{{\mathbb {F}}_p})=\binom {l}{3}+\binom {l}{2}+l+1+h^{0,3}({\mathfrak X}_{{\mathbb {F}}_p})+(l+1)h^{0,2}({\mathfrak X}_{{\mathbb {F}}_p})$. Hence, ![]() $\delta ^{3,0}(({\mathfrak X}\times {\mathfrak Y})_{{\mathbb {F}}_p})=\delta ^{3,0}({\mathfrak X}_{{\mathbb {F}}_p})+l+1$. Since
$\delta ^{3,0}(({\mathfrak X}\times {\mathfrak Y})_{{\mathbb {F}}_p})=\delta ^{3,0}({\mathfrak X}_{{\mathbb {F}}_p})+l+1$. Since ![]() $\delta ^{3,0}({\mathfrak X}_{{\mathbb {F}}_p})<0$ there exists
$\delta ^{3,0}({\mathfrak X}_{{\mathbb {F}}_p})<0$ there exists ![]() $l$ that makes this difference equal to zero.
$l$ that makes this difference equal to zero.
The product ![]() ${\mathfrak X}\times {\mathfrak Y}$ is our desired scheme
${\mathfrak X}\times {\mathfrak Y}$ is our desired scheme ![]() ${\mathfrak X}'$. Note that the Hodge numbers
${\mathfrak X}'$. Note that the Hodge numbers ![]() $h^{i,0}({\mathfrak Y}_{{\mathbb {Q}}_p})$ of the generic fiber
$h^{i,0}({\mathfrak Y}_{{\mathbb {Q}}_p})$ of the generic fiber ![]() ${\mathfrak Y}_{{\mathbb {Q}}_p}$ vanish for
${\mathfrak Y}_{{\mathbb {Q}}_p}$ vanish for ![]() $i\leq 3$ so the asymmetry
$i\leq 3$ so the asymmetry ![]() $h^{3,0}({\mathfrak X}')=h^{3,0}({\mathfrak X})\neq h^{0,3}({\mathfrak X})= h^{0,3}({\mathfrak X}')$ persists.
$h^{3,0}({\mathfrak X}')=h^{3,0}({\mathfrak X})\neq h^{0,3}({\mathfrak X})= h^{0,3}({\mathfrak X}')$ persists.
Another feature of the counterexamples to Hodge symmetry obtained by taking quotients of formal abelian schemes by finite groups is the absence on the special fiber of an ample line bundle of degree prime to ![]() $p$. Indeed, if the
$p$. Indeed, if the ![]() $d$-dimensional special fiber of
$d$-dimensional special fiber of ![]() ${\mathfrak X}$ (in the notation of the proof of Theorem 4.1) admits a line bundle
${\mathfrak X}$ (in the notation of the proof of Theorem 4.1) admits a line bundle ![]() $L$ such that
$L$ such that ![]() $L^{d}\not \equiv 0\pmod {p}$ then it induces a
$L^{d}\not \equiv 0\pmod {p}$ then it induces a ![]() $G$-equivariant ample line bundle
$G$-equivariant ample line bundle ![]() $L'$ on
$L'$ on ![]() ${\mathfrak Z}_{k'}$ with
${\mathfrak Z}_{k'}$ with ![]() $(L')^{\dim {\mathfrak Z}_{k'}}\not \equiv 0\pmod {p}$ as well (because the order of
$(L')^{\dim {\mathfrak Z}_{k'}}\not \equiv 0\pmod {p}$ as well (because the order of ![]() $G$ is prime to
$G$ is prime to ![]() $p$). It induces a separable
$p$). It induces a separable ![]() $G$-equivariant polarization and hence and isomorphism
$G$-equivariant polarization and hence and isomorphism ![]() $H^{0}({\mathfrak Z},\Omega ^{1}_{{\mathfrak Z}_k'/k'})\simeq H^{1}({\mathfrak Z}_{k'},{\mathcal {O}})^{\vee }$ of
$H^{0}({\mathfrak Z},\Omega ^{1}_{{\mathfrak Z}_k'/k'})\simeq H^{1}({\mathfrak Z}_{k'},{\mathcal {O}})^{\vee }$ of ![]() $G$-representations. Hence, for all
$G$-representations. Hence, for all ![]() $i$ and
$i$ and ![]() $j$ the representations
$j$ the representations ![]() $H^{i}({\mathfrak Z}_{k'},\Omega ^{j}_{{\mathfrak Z}_{k'}/k'})$ and
$H^{i}({\mathfrak Z}_{k'},\Omega ^{j}_{{\mathfrak Z}_{k'}/k'})$ and ![]() $H^{j}({\mathfrak Z}_{k'},\Omega ^{i}_{{\mathfrak Z}_{k'}/{k'}})$ would be dual to each other and Hodge symmetry for
$H^{j}({\mathfrak Z}_{k'},\Omega ^{i}_{{\mathfrak Z}_{k'}/{k'}})$ would be dual to each other and Hodge symmetry for ![]() ${\mathfrak X}_{k'}$ and, hence, for
${\mathfrak X}_{k'}$ and, hence, for ![]() ${\mathfrak X}$ would have to hold.
${\mathfrak X}$ would have to hold.
We note, however, that blowing up a point provides the special fiber with a prime to ![]() $p$ polarization without spoiling Hodge asymmetry.
$p$ polarization without spoiling Hodge asymmetry.
Lemma 5.2 For every pair of distinct positive integers ![]() $i,j$ with
$i,j$ with ![]() $i+j\geq 3$ there exists a smooth proper formal scheme
$i+j\geq 3$ there exists a smooth proper formal scheme ![]() ${\mathfrak X}'$ over
${\mathfrak X}'$ over ![]() ${\mathbb {Z}}_p$ such that
${\mathbb {Z}}_p$ such that ![]() $h^{i,j}({\mathfrak X}')\neq h^{j,i}({\mathfrak X}')$ and the special fiber carries an ample divisor
$h^{i,j}({\mathfrak X}')\neq h^{j,i}({\mathfrak X}')$ and the special fiber carries an ample divisor ![]() $L$ such that its top self-intersection is prime to
$L$ such that its top self-intersection is prime to ![]() $p$:
$p$: ![]() $L^{\dim ({\mathfrak X}'_{{\mathbb {F}}_p})}\not \equiv 0\pmod {p}$.
$L^{\dim ({\mathfrak X}'_{{\mathbb {F}}_p})}\not \equiv 0\pmod {p}$.
Proof. Let ![]() ${\mathfrak X}$ be a formal scheme provided by Theorem 4.1. Choose a point
${\mathfrak X}$ be a formal scheme provided by Theorem 4.1. Choose a point ![]() $x:\operatorname {{Spf}}{\mathbb {Z}}_p\to {\mathfrak X}$ (one sees easily that the proof of Theorem 4.1 can be modified to make sure that at least one point exists). Let
$x:\operatorname {{Spf}}{\mathbb {Z}}_p\to {\mathfrak X}$ (one sees easily that the proof of Theorem 4.1 can be modified to make sure that at least one point exists). Let ![]() $f:{\mathfrak X}'\to {\mathfrak X}$ be the blow-up of
$f:{\mathfrak X}'\to {\mathfrak X}$ be the blow-up of ![]() ${\mathfrak X}$ at the closed subscheme given by
${\mathfrak X}$ at the closed subscheme given by ![]() $x$. Note that
$x$. Note that ![]() $h^{i,j}({\mathfrak X}')=h^{i,j}({\mathfrak X})$ for
$h^{i,j}({\mathfrak X}')=h^{i,j}({\mathfrak X})$ for ![]() $i\neq j$.
$i\neq j$.
The special fiber ![]() ${\mathfrak X}'_{{\mathbb {F}}_p}$ is the blow-up of
${\mathfrak X}'_{{\mathbb {F}}_p}$ is the blow-up of ![]() ${\mathfrak X}_{{\mathbb {F}}_p}$ at a point; denote by
${\mathfrak X}_{{\mathbb {F}}_p}$ at a point; denote by ![]() $E\subset {\mathfrak X}'_{{\mathbb {F}}_p}$ the exceptional divisor. Let
$E\subset {\mathfrak X}'_{{\mathbb {F}}_p}$ the exceptional divisor. Let ![]() $H$ be any ample divisor on
$H$ be any ample divisor on ![]() ${\mathfrak X}'_{{\mathbb {F}}_p}$. We will find a linear combination
${\mathfrak X}'_{{\mathbb {F}}_p}$. We will find a linear combination ![]() $H+nE$ with
$H+nE$ with ![]() $n\geq 0$ such that the top self-intersection
$n\geq 0$ such that the top self-intersection ![]() $(H+nE)^{d}$ is prime to
$(H+nE)^{d}$ is prime to ![]() $p$. Since the sum of an ample divisor with an effective divisor is ample, this will provide an ample divisor with the desired property.
$p$. Since the sum of an ample divisor with an effective divisor is ample, this will provide an ample divisor with the desired property.
Suppose that ![]() $H|_E$ has degree
$H|_E$ has degree ![]() $k$ in
$k$ in ![]() $\operatorname {{Pic}}(E)={\mathbb {Z}}$. Then
$\operatorname {{Pic}}(E)={\mathbb {Z}}$. Then ![]() $H^{d-i}\cdot E^{i}=k^{d-i}\cdot (-1)^{i}$ for
$H^{d-i}\cdot E^{i}=k^{d-i}\cdot (-1)^{i}$ for ![]() $i>0$ by [Reference FultonFul98, Example 8.3.9.] and the projection formula, so
$i>0$ by [Reference FultonFul98, Example 8.3.9.] and the projection formula, so
 \begin{equation} (H+nE)^{d}=H^{d}+\sum_{i=1}^{d}\binom{d}{i}n^{i}k^{d-i}({-}1)^{i-1}=H^{d}-(k-n)^{d}+k^{d}. \end{equation}
\begin{equation} (H+nE)^{d}=H^{d}+\sum_{i=1}^{d}\binom{d}{i}n^{i}k^{d-i}({-}1)^{i-1}=H^{d}-(k-n)^{d}+k^{d}. \end{equation}
For varying ![]() $n$ the residue of
$n$ the residue of ![]() $(k-n)^{d}$ modulo
$(k-n)^{d}$ modulo ![]() $p$ takes at least two different values, so we can find
$p$ takes at least two different values, so we can find ![]() $n$ such that the expression (7) is prime to
$n$ such that the expression (7) is prime to ![]() $p$.
$p$.
Apart from satisfying Hodge symmetry, compact Kähler manifolds must have nonzero middle Hodge numbers ![]() $h^{i,i}(X)\neq 0$ for
$h^{i,i}(X)\neq 0$ for ![]() $i\leq \dim X$ because
$i\leq \dim X$ because ![]() $H^{i}(X,\Omega ^{i}_{X/{\mathbb {C}}})$ contains the non-zero
$H^{i}(X,\Omega ^{i}_{X/{\mathbb {C}}})$ contains the non-zero ![]() $i$th power of the class of a Kähler form. It would be interesting to find out whether this is the case for rigid-analytic varieties with projective reduction.
$i$th power of the class of a Kähler form. It would be interesting to find out whether this is the case for rigid-analytic varieties with projective reduction.
Question 1 Does there exist a smooth proper rigid-analytic variety ![]() $X$ of
$X$ of ![]() $\dim X>0$ admitting a formal model with projective special fiber such that
$\dim X>0$ admitting a formal model with projective special fiber such that ![]() $H^{1}(X,\Omega ^{1}_{X/K})=0$?
$H^{1}(X,\Omega ^{1}_{X/K})=0$?
Note that ![]() $X$ must have non-zero second de Rham cohomology
$X$ must have non-zero second de Rham cohomology ![]() $H^{2}_{\mathrm {dR}}(X/K)$. If
$H^{2}_{\mathrm {dR}}(X/K)$. If ![]() $X$ is algebraic projective, then a non-zero class is given by the first Chern class of an ample line bundle. If, on the contrary,
$X$ is algebraic projective, then a non-zero class is given by the first Chern class of an ample line bundle. If, on the contrary, ![]() $X$ is not projective, then no ample line bundle on the special fiber
$X$ is not projective, then no ample line bundle on the special fiber ![]() ${\mathfrak X}_k$ can lift to
${\mathfrak X}_k$ can lift to ![]() ${\mathfrak X}$. The obstruction to lifting a line bundle gives a non-zero class in second cohomology as follows. Consider the long exact sequence
${\mathfrak X}$. The obstruction to lifting a line bundle gives a non-zero class in second cohomology as follows. Consider the long exact sequence
obtained from the short exact sequence ![]() $1\to (1+{\mathfrak m}{\mathcal {O}}_{{\mathfrak X}})^{\times }\to {\mathcal {O}}_{{\mathfrak X}}^{\times }\to {\mathcal {O}}_{{\mathfrak X}_k}^{\times }\to 1$ of sheaves of abelian groups on the Zariski site of
$1\to (1+{\mathfrak m}{\mathcal {O}}_{{\mathfrak X}})^{\times }\to {\mathcal {O}}_{{\mathfrak X}}^{\times }\to {\mathcal {O}}_{{\mathfrak X}_k}^{\times }\to 1$ of sheaves of abelian groups on the Zariski site of ![]() ${\mathfrak X}$. For any ample line bundle
${\mathfrak X}$. For any ample line bundle ![]() $L\in \operatorname {{Pic}}({\mathfrak X}_k)$ the image
$L\in \operatorname {{Pic}}({\mathfrak X}_k)$ the image ![]() $\delta (L)\in H^{2}({\mathfrak X},(1+{\mathfrak m}{\mathcal {O}}_{{\mathfrak X}})^{\times })$ is non-zero and, since no power of
$\delta (L)\in H^{2}({\mathfrak X},(1+{\mathfrak m}{\mathcal {O}}_{{\mathfrak X}})^{\times })$ is non-zero and, since no power of ![]() $L$ lifts to
$L$ lifts to ![]() ${\mathfrak X}$, is a non-torsion element. Applying to
${\mathfrak X}$, is a non-torsion element. Applying to ![]() $\delta (L)$ the isomorphism given by the logarithm
$\delta (L)$ the isomorphism given by the logarithm ![]() $\log :(1+{\mathfrak m}{\mathcal {O}}_{{\mathfrak X}})^{\times }[{1}/{p}]\simeq {\mathcal {O}}_{{\mathfrak X}}[{1}/{p}]$ gives a non-zero class in
$\log :(1+{\mathfrak m}{\mathcal {O}}_{{\mathfrak X}})^{\times }[{1}/{p}]\simeq {\mathcal {O}}_{{\mathfrak X}}[{1}/{p}]$ gives a non-zero class in ![]() $H^{2}({\mathfrak X},{\mathcal {O}}_{{\mathfrak X}}[{1}/{p}])=H^{2}(X,{\mathcal {O}})$.
$H^{2}({\mathfrak X},{\mathcal {O}}_{{\mathfrak X}}[{1}/{p}])=H^{2}(X,{\mathcal {O}})$.
Acknowledgements
I am grateful to Piotr Achinger, Shizhang Li, Vadim Vologodsky, Zijian Yao and Bogdan Zavyalov for their interest and several useful discussions and to Piotr Achinger, Borys Kadets and Zhiyu Zhang for comments on the drafts of this text. I am indebted to Vasily Rogov whose talk on the work [Reference RogovRog19] motivated the examples presented here.