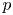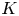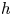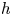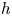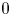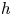1. Introduction
Recall that rational ![]() $p$-adic period morphismsFootnote 1 make it possible to describe the
$p$-adic period morphismsFootnote 1 make it possible to describe the ![]() $p$-adic étale cohomology of algebraic varieties over local fields of mixed characteristic in terms of differential forms. This is advantageous since the latter can often be computed. There are by now four main different approaches to the construction of these period morphisms:
$p$-adic étale cohomology of algebraic varieties over local fields of mixed characteristic in terms of differential forms. This is advantageous since the latter can often be computed. There are by now four main different approaches to the construction of these period morphisms:
– syntomic: Fontaine and Messing [Reference Fontaine, Messing and RibetFM87], Hyodo and Kato [Reference Hyodo and KatoHK94], Kato [Reference KatoKat94a], Tsuji [Reference TsujiTsu99a], Yamashita [Reference YamashitaYam11], Colmez and Nizioł [Reference Colmez and NiziołCN17];
– almost étale: Faltings [Reference Faltings and IgusaFal89, Reference FaltingsFal02], Scholze [Reference ScholzeSch13], Li and Pan [Reference Li and PanLP19], Diao et al. [Reference Diao, Lan, Liu and ZhuDLLZ19], Tan and Tong [Reference Tan and TongTT19], Bhatt, Morrow and Scholze [Reference Bhatt, Morrow and ScholzeBMS18, Reference Bhatt, Morrow and ScholzeBMS19], Česnavičius and Koshikawa [Reference Česnavičius and KoshikawaČK19];
– motivic: Nizioł [Reference NiziołNiz98, Reference NiziołNiz08];
–
 $h$-cohomology: Beilinson [Reference BeilinsonBei12, Reference BeilinsonBei13], Bhatt [Reference BhattBha12].
$h$-cohomology: Beilinson [Reference BeilinsonBei12, Reference BeilinsonBei13], Bhatt [Reference BhattBha12].
Each of these approaches has its advantages and it is important to be able to compare the resulting period morphisms in the case one needs to pass from one to another. Since all the above period morphisms are normalized using Chern classes we expect them to be equal.
The two theorems below are examples of the results we obtain in the paper. Let ![]() ${{\mathcal O} _K}$ be a complete discrete valuation ring with fraction field
${{\mathcal O} _K}$ be a complete discrete valuation ring with fraction field ![]() $K$ of characteristic 0 and with perfect residue field
$K$ of characteristic 0 and with perfect residue field ![]() $k$ of positive characteristic
$k$ of positive characteristic ![]() $p$. Let
$p$. Let ![]() $\pi$ be a uniformizer of
$\pi$ be a uniformizer of ![]() ${\mathcal O} _K$. Let
${\mathcal O} _K$. Let ![]() ${\mathcal O} _F$ be the ring of Witt vectors of
${\mathcal O} _F$ be the ring of Witt vectors of ![]() $k$ with fraction field
$k$ with fraction field ![]() $F$. Let
$F$. Let ![]() $X$ be a proper scheme over
$X$ be a proper scheme over ![]() ${\mathcal O} _K$ with semistable reduction and of pure relative dimension
${\mathcal O} _K$ with semistable reduction and of pure relative dimension ![]() $d$. Let
$d$. Let ![]() $i:D\hookrightarrow X$ be the horizontal divisor and set
$i:D\hookrightarrow X$ be the horizontal divisor and set ![]() $U=X\setminus D$. Equip
$U=X\setminus D$. Equip ![]() $X$ with the log-structure induced by
$X$ with the log-structure induced by ![]() $D$ and the special fiber. Denote by
$D$ and the special fiber. Denote by ![]() ${\mathcal O} _F^0$ the scheme
${\mathcal O} _F^0$ the scheme ![]() $\operatorname {Spec} ({{\mathcal O} _F})$ with the log-structure given by
$\operatorname {Spec} ({{\mathcal O} _F})$ with the log-structure given by ![]() $({\mathbf {N}}\to {{\mathcal O} _K}, 1\mapsto 0)$.
$({\mathbf {N}}\to {{\mathcal O} _K}, 1\mapsto 0)$.
The first theorem is a generalization of the ![]() $K$-theoretical uniqueness criterion for
$K$-theoretical uniqueness criterion for ![]() $p$-adic period isomorphisms from [Reference NiziołNiz09] as well as its applications.
$p$-adic period isomorphisms from [Reference NiziołNiz09] as well as its applications.
Theorem 1.1 (i) There exists a unique natural ![]() $p$-adic period isomorphism
$p$-adic period isomorphism
where ![]() $H^i_{\operatorname {HK} }(X)= H^i_{\operatorname {cr} }(X_0/{\mathcal O} _F^0)_{\mathbf {Q}}$ is the Hyodo–Kato cohomology, such that:
$H^i_{\operatorname {HK} }(X)= H^i_{\operatorname {cr} }(X_0/{\mathcal O} _F^0)_{\mathbf {Q}}$ is the Hyodo–Kato cohomology, such that:
(a)
 $\alpha _i$ is
$\alpha _i$ is  $\mathbf {B}_{\operatorname {st}}$-linear, Galois equivariant, and compatible with Frobenius;
$\mathbf {B}_{\operatorname {st}}$-linear, Galois equivariant, and compatible with Frobenius;(b)
 $\alpha _i$, extended to
$\alpha _i$, extended to  $\mathbf {B}_{\operatorname {dR} }$ via the Hyodo–Kato morphism
$\mathbf {B}_{\operatorname {dR} }$ via the Hyodo–Kato morphism  $\rho _{\pi }:H^i_{\operatorname {HK} }(X)\to H^i_{\operatorname {dR} }(X_K)$ and the morphism
$\rho _{\pi }:H^i_{\operatorname {HK} }(X)\to H^i_{\operatorname {dR} }(X_K)$ and the morphism  $\iota _{\pi }:\mathbf {B}_{\operatorname {st}}\to \mathbf {B}_{\operatorname {dR} }$, induces a filtered isomorphism
$\iota _{\pi }:\mathbf {B}_{\operatorname {st}}\to \mathbf {B}_{\operatorname {dR} }$, induces a filtered isomorphism
 \[ \alpha^{\operatorname{dR} }_i: H^i_{\operatorname{\acute{e}t} ,c}(U_{\overline{K}},{\mathbf{Q}}_p)\otimes \mathbf{B}_{\operatorname{dR} }\stackrel{\sim}{\to} H^i_{\operatorname{dR} ,c}(X_K)\otimes_{K} \mathbf{B}_{\operatorname{dR} }; \]
\[ \alpha^{\operatorname{dR} }_i: H^i_{\operatorname{\acute{e}t} ,c}(U_{\overline{K}},{\mathbf{Q}}_p)\otimes \mathbf{B}_{\operatorname{dR} }\stackrel{\sim}{\to} H^i_{\operatorname{dR} ,c}(X_K)\otimes_{K} \mathbf{B}_{\operatorname{dR} }; \](c)
 $\alpha _i$ is compatible with the étale and syntomic higher Chern classes from
$\alpha _i$ is compatible with the étale and syntomic higher Chern classes from  $p$-adic
$p$-adic  $K$-theory.
$K$-theory.
(ii) The syntomic, almost étale, and motivic semistable period morphisms for cohomology with compact support are equal.
The second theorem takes a different approach to comparing ![]() $p$-adic period morphisms. It uses
$p$-adic period morphisms. It uses ![]() $h$-topology, the Beilinson (filtered) Poincaré lemma [Reference BeilinsonBei13], and the computations from [Reference Nekovář and NiziołNN16] to formulate a simple uniqueness criterion using the fundamental exact sequence of
$h$-topology, the Beilinson (filtered) Poincaré lemma [Reference BeilinsonBei13], and the computations from [Reference Nekovář and NiziołNN16] to formulate a simple uniqueness criterion using the fundamental exact sequence of ![]() $p$-adic Hodge theory and hence, basically, the case of dimension
$p$-adic Hodge theory and hence, basically, the case of dimension ![]() $0$.
$0$.
Theorem 1.2 The syntomic, Faltings almost étale, and ![]() $h$-cohomology period morphisms lift to the Voevodsky category of motives over
$h$-cohomology period morphisms lift to the Voevodsky category of motives over ![]() $K$. They are equal. In particular, they are compatible with (mixed) products.
$K$. They are equal. In particular, they are compatible with (mixed) products.
Remark 1.3 The above theorems do not cover the ![]() $p$-adic period morphisms of Bhatt, Morrow and Scholze [Reference Bhatt, Morrow and ScholzeBMS18, Reference Bhatt, Morrow and ScholzeBMS19] and Česnavičius and Koshikawa [Reference Česnavičius and KoshikawaČK19] (which fall into the ‘almost étale’ category) but these morphisms are already known (at least the ones from [Reference Bhatt, Morrow and ScholzeBMS18, Reference Česnavičius and KoshikawaČK19]) to be the same as the syntomic period morphisms.
$p$-adic period morphisms of Bhatt, Morrow and Scholze [Reference Bhatt, Morrow and ScholzeBMS18, Reference Bhatt, Morrow and ScholzeBMS19] and Česnavičius and Koshikawa [Reference Česnavičius and KoshikawaČK19] (which fall into the ‘almost étale’ category) but these morphisms are already known (at least the ones from [Reference Bhatt, Morrow and ScholzeBMS18, Reference Česnavičius and KoshikawaČK19]) to be the same as the syntomic period morphisms.
(i) It is likely that one can use the ![]() $K$-theory criterion from Theorem 1.1 to show this fact. Some compatibilities with Chern classes were already checked in [Reference Colmez, Dospinescu and NiziołCDN19]. The
$K$-theory criterion from Theorem 1.1 to show this fact. Some compatibilities with Chern classes were already checked in [Reference Colmez, Dospinescu and NiziołCDN19]. The ![]() $h$-topology method of comparing period morphisms from Theorem 1.2 cannot be applied directly in this case because the period morphism of Bhatt, Morrow and Scholze, as of now, is not allowing horizontal divisors.
$h$-topology method of comparing period morphisms from Theorem 1.2 cannot be applied directly in this case because the period morphism of Bhatt, Morrow and Scholze, as of now, is not allowing horizontal divisors.
(ii) However, the compatibility of the period morphism from [Reference Bhatt, Morrow and ScholzeBMS18, Reference Česnavičius and KoshikawaČK19] with the other period morphisms has been already checked in the forthcoming thesis of Sally Gilles (at ENS Lyon) by a more direct method. This involves the period morphism defined in [Reference Colmez and NiziołCN17]: Gilles lifted the local definition of this morphism to the geometric setting, globalized it together with its comparison with the Fontaine–Messing period morphism, and then directly compared the resulting morphism with the period morphism from [Reference Česnavičius and KoshikawaČK19] (which is a reasonable approach since both morphisms are defined using very similar complexes).
Remark 1.4 Recently, there has been considerable interest in generalizing Faltings’ original approach to ![]() $p$-adic comparison theorems. This started with the work of Scholze [Reference ScholzeSch13] on the de Rham comparison theorem for proper smooth rigid varieties and nontrivial coefficients that extended Faltings’ proof of the algebraic de Rham comparison theorem using Scholze's powerful almost purity theorem and his proof of the finiteness of
$p$-adic comparison theorems. This started with the work of Scholze [Reference ScholzeSch13] on the de Rham comparison theorem for proper smooth rigid varieties and nontrivial coefficients that extended Faltings’ proof of the algebraic de Rham comparison theorem using Scholze's powerful almost purity theorem and his proof of the finiteness of ![]() $p$-adic étale cohomology. Recall that Faltings’ proof of the de Rham comparison theorem used the Faltings site, the Faltings Poincaré lemma, and a basic comparison theorem and worked for all smooth algebraic varieties and trivial coefficients. This was extended to nontrivial coefficients in the thesis of Tsuzuki, which was, unfortunately, never published.
$p$-adic étale cohomology. Recall that Faltings’ proof of the de Rham comparison theorem used the Faltings site, the Faltings Poincaré lemma, and a basic comparison theorem and worked for all smooth algebraic varieties and trivial coefficients. This was extended to nontrivial coefficients in the thesis of Tsuzuki, which was, unfortunately, never published.
More work followed: Li and Pan [Reference Li and PanLP19] extended Scholze's de Rham comparison for trivial coefficients to the open case (with a nice compactification), Diao et al. [Reference Diao, Lan, Liu and ZhuDLLZ19] added a treatment of nontrivial coefficients; from another angle, Tan and Tong [Reference Tan and TongTT19] extended Scholze's proof to the case of good reduction (over an unramified base) proving the crystalline conjecture in this setting.
When specialized to algebraic varieties all these constructions of ![]() $p$-adic period morphisms are modifications of the original construction of Faltings (recall that Faltings’ construction works for any smooth variety), the main one being a replacement of the Faltings site with the pro-étale site (see the discussion in [Reference Li and PanLP19, § 3]). Their equality with Faltings period morphisms is conceptually clear but, with all the modifications involved, the detailed proof of this fact is best left for the time when it is really needed (and then it can be checked in a direct, if tedious, way, or, in some cases, using our
$p$-adic period morphisms are modifications of the original construction of Faltings (recall that Faltings’ construction works for any smooth variety), the main one being a replacement of the Faltings site with the pro-étale site (see the discussion in [Reference Li and PanLP19, § 3]). Their equality with Faltings period morphisms is conceptually clear but, with all the modifications involved, the detailed proof of this fact is best left for the time when it is really needed (and then it can be checked in a direct, if tedious, way, or, in some cases, using our ![]() $K$-theory approach).
$K$-theory approach).
1.1 Proof of Theorem 1.1
To prove Theorem 1.1, we start with showing that the ![]() $K$-theoretical uniqueness criterion we had found for proper smooth schemes in [Reference NiziołNiz09] extends to finite simplicial schemes in the good reduction case and to cohomology with compact support in the semistable reduction case. Using it we show the equality of the period morphisms for cohomology with compact support defined by the syntomic and almost étale methods. Along the way we extend our definition of the motivic period morphisms from [Reference NiziołNiz98, Reference NiziołNiz08] to the above-mentioned setting. By construction, this period morphism satisfies the
$K$-theoretical uniqueness criterion we had found for proper smooth schemes in [Reference NiziołNiz09] extends to finite simplicial schemes in the good reduction case and to cohomology with compact support in the semistable reduction case. Using it we show the equality of the period morphisms for cohomology with compact support defined by the syntomic and almost étale methods. Along the way we extend our definition of the motivic period morphisms from [Reference NiziołNiz98, Reference NiziołNiz08] to the above-mentioned setting. By construction, this period morphism satisfies the ![]() $K$-theoretical uniqueness criterion and hence it is equal to the syntomic and almost étale period morphisms.
$K$-theoretical uniqueness criterion and hence it is equal to the syntomic and almost étale period morphisms.
To present the proof of Theorem 1.1 in more detail, recall the definition of the motivic period morphisms in the simpler case of good reduction (see also the survey [Reference NiziołNiz06b]). Let ![]() $X$ be a smooth proper scheme over
$X$ be a smooth proper scheme over ![]() ${\mathcal O} _K$. Using the Suslin comparison theorem between
${\mathcal O} _K$. Using the Suslin comparison theorem between ![]() $p$-adic motivic cohomology and
$p$-adic motivic cohomology and ![]() $p$-adic étale cohomology [Reference SuslinSus00], we lift étale cohomology classes of
$p$-adic étale cohomology [Reference SuslinSus00], we lift étale cohomology classes of ![]() $X_{\overline {K}}$ to
$X_{\overline {K}}$ to ![]() $p$-adic motivic cohomology classes via the étale regulator (here we use
$p$-adic motivic cohomology classes via the étale regulator (here we use ![]() $\lambda$-graded pieces of
$\lambda$-graded pieces of ![]() $p$-adic
$p$-adic ![]() $K$-theory as a substitute for
$K$-theory as a substitute for ![]() $p$-adic motivic cohomology), then we lift those to the integral model
$p$-adic motivic cohomology), then we lift those to the integral model ![]() $X_{{\mathcal O} _{\overline {K}}}$, and, finally, we project them via the syntomic regulator to the syntomic cohomology of
$X_{{\mathcal O} _{\overline {K}}}$, and, finally, we project them via the syntomic regulator to the syntomic cohomology of ![]() $X_{{\mathcal O} _{\overline {K}}}$ that maps canonically to the absolute crystalline cohomology of
$X_{{\mathcal O} _{\overline {K}}}$ that maps canonically to the absolute crystalline cohomology of ![]() $X_{{\mathcal O} _{\overline {K}}}$.
$X_{{\mathcal O} _{\overline {K}}}$.
This extends rather easily to simplicial schemes: there is no problem in defining the ![]() $p$-adic regulators and the fact that the étale regulator and the localization map from the integral model to the generic fiber are isomorphisms can be reduced to the case of schemes using the filtration of simplicial schemes by skeletons.
$p$-adic regulators and the fact that the étale regulator and the localization map from the integral model to the generic fiber are isomorphisms can be reduced to the case of schemes using the filtration of simplicial schemes by skeletons.
We have shown in [Reference NiziołNiz09] that the construction of the motivic period morphisms for proper smooth schemes implies a simple ![]() $K$-theoretical uniqueness criterion for period morphisms. This can be extended now to proper smooth finite simplicial schemes: two period morphisms are equal if and only if the induced period morphisms from étale to syntomic cohomology are equal and this is true if and only if the latter agree on the values of étale regulators from
$K$-theoretical uniqueness criterion for period morphisms. This can be extended now to proper smooth finite simplicial schemes: two period morphisms are equal if and only if the induced period morphisms from étale to syntomic cohomology are equal and this is true if and only if the latter agree on the values of étale regulators from ![]() $p$-adic
$p$-adic ![]() $K$-theory. This, in turn, would follow if the period morphisms were compatible with the étale and syntomic regulators from
$K$-theory. This, in turn, would follow if the period morphisms were compatible with the étale and syntomic regulators from ![]() $p$-adic
$p$-adic ![]() $K$-theory. For motivic period morphisms this compatibility follows from the definition; for the syntomic and almost étale period morphisms of Tsuji [Reference TsujiTsu99a] and Faltings [Reference FaltingsFal02], respectively, this can be checked on the level of the universal Chern classes and this was done in [Reference NiziołNiz09].
$K$-theory. For motivic period morphisms this compatibility follows from the definition; for the syntomic and almost étale period morphisms of Tsuji [Reference TsujiTsu99a] and Faltings [Reference FaltingsFal02], respectively, this can be checked on the level of the universal Chern classes and this was done in [Reference NiziołNiz09].
1.2 Proof of Theorem 1.2
To prove Theorem 1.2, we take a different approach to comparing ![]() $p$-adic period morphisms: we compare them with the
$p$-adic period morphisms: we compare them with the ![]() $h$-cohomology period morphism. First, we note that it is enough to compare the induced morphisms, after a change of Hyodo–Kato cohomology, from syntomic cohomology to étale cohomology (we call them syntomic period morphisms). Then we take the syntomic period morphism (in the derived category) and sheafify it in the
$h$-cohomology period morphism. First, we note that it is enough to compare the induced morphisms, after a change of Hyodo–Kato cohomology, from syntomic cohomology to étale cohomology (we call them syntomic period morphisms). Then we take the syntomic period morphism (in the derived category) and sheafify it in the ![]() $h$-topology of
$h$-topology of ![]() $X_{\overline {K}}$. This is possible because Beilinson has shown [Reference BeilinsonBei12] that de Jong augmentations allow us to exhibit a basis of
$X_{\overline {K}}$. This is possible because Beilinson has shown [Reference BeilinsonBei12] that de Jong augmentations allow us to exhibit a basis of ![]() $h$-topology that consists of proper (strictly) semistable schemes over
$h$-topology that consists of proper (strictly) semistable schemes over ![]() ${\mathcal O} _K$. We obtain a map between the
${\mathcal O} _K$. We obtain a map between the ![]() $h$-sheafification of syntomic cohomology and the
$h$-sheafification of syntomic cohomology and the ![]() $h$-sheafification of étale cohomology. Now, for
$h$-sheafification of étale cohomology. Now, for ![]() $r\geq 0$, the étale cohomology of the Tate twist
$r\geq 0$, the étale cohomology of the Tate twist ![]() $\mathbf {Z}/p^n(r)^{\prime }:=(p^aa!)^{-1}{\mathbf {Z}}/p^n(r)$, for
$\mathbf {Z}/p^n(r)^{\prime }:=(p^aa!)^{-1}{\mathbf {Z}}/p^n(r)$, for ![]() $r=(p-1)a+b,a,b\in {\mathbf {Z}}, 0\leq b < p-1$,
$r=(p-1)a+b,a,b\in {\mathbf {Z}}, 0\leq b < p-1$, ![]() $h$-sheafifies to the constant sheaf
$h$-sheafifies to the constant sheaf ![]() $\mathbf {Z}/p^n(r)^{\prime }$. Using the Beilinson filtered Poincaré lemma [Reference BeilinsonBei13], we see that the syntomic cohomology of the
$\mathbf {Z}/p^n(r)^{\prime }$. Using the Beilinson filtered Poincaré lemma [Reference BeilinsonBei13], we see that the syntomic cohomology of the ![]() $r$th twist sheafifies to the kernel of the surjective map of constant sheaves
$r$th twist sheafifies to the kernel of the surjective map of constant sheaves ![]() $F^r_p\mathbf {A}_{\operatorname {cr} } {\buildrel {1-\phi _r} \over \longrightarrow} \mathbf {A}_{\operatorname {cr} }$,
$F^r_p\mathbf {A}_{\operatorname {cr} } {\buildrel {1-\phi _r} \over \longrightarrow} \mathbf {A}_{\operatorname {cr} }$, ![]() $\phi _r$ being the divided Frobenius
$\phi _r$ being the divided Frobenius ![]() $\phi /p^r$ and
$\phi /p^r$ and ![]() $F^r_p\mathbf {A}_{\operatorname {cr} }$ the Frobenius-divisible filtration. By the fundamental exact sequence this is
$F^r_p\mathbf {A}_{\operatorname {cr} }$ the Frobenius-divisible filtration. By the fundamental exact sequence this is ![]() $\mathbf {Z}/p^n(r)^{\prime }$ and the syntomic period morphism, by functoriality, is the map that sends
$\mathbf {Z}/p^n(r)^{\prime }$ and the syntomic period morphism, by functoriality, is the map that sends ![]() $t^{\{r\}}:=t^{b}(t^{p-1}/p)^{a}$ to
$t^{\{r\}}:=t^{b}(t^{p-1}/p)^{a}$ to ![]() $1$. But, as was shown in [Reference Nekovář and NiziołNN16], this is the same map as the one induced by the
$1$. But, as was shown in [Reference Nekovář and NiziołNN16], this is the same map as the one induced by the ![]() $h$-cohomology period morphism. The argument for the almost étale period morphism is analogous.
$h$-cohomology period morphism. The argument for the almost étale period morphism is analogous.
The last claim of the theorem was proved for the Beilinson period isomorphism in [Reference Déglise and NiziołDN18] and hence it is true for the other period maps as well.
Conventions We assume all the schemes (outside of some obvious exceptions) to be locally noetherian. We work in the category of fine log-schemes. For a scheme ![]() $X$ over
$X$ over ![]() $\mathbf {Z}_p$, we will denote by
$\mathbf {Z}_p$, we will denote by ![]() $X_n$ its reduction modulo
$X_n$ its reduction modulo ![]() $p^n$.
$p^n$.
2. Preliminaries
We collect in this section basic cohomological computations, the study of the localization map in ![]() $K$-theory, and the study of the étale cycle class map. All of this is done in the context of cohomology with compact support and generalizes the computations done for the usual cohomology in [Reference NiziołNiz98, Reference NiziołNiz08].
$K$-theory, and the study of the étale cycle class map. All of this is done in the context of cohomology with compact support and generalizes the computations done for the usual cohomology in [Reference NiziołNiz98, Reference NiziołNiz08].
Let ![]() ${{\mathcal O} _K}$ be a complete discrete valuation ring with fraction field
${{\mathcal O} _K}$ be a complete discrete valuation ring with fraction field ![]() $K$ of characteristic 0 and with perfect residue field
$K$ of characteristic 0 and with perfect residue field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p$. Let
$p$. Let ![]() $W(k)={\mathcal O} _F$ be the ring of Witt vectors of
$W(k)={\mathcal O} _F$ be the ring of Witt vectors of ![]() $k$ with fraction field
$k$ with fraction field ![]() $F$. Let
$F$. Let ![]() $\overline {K}$ be an algebraic closure of
$\overline {K}$ be an algebraic closure of ![]() $K$ and let
$K$ and let ![]() $C$ be its
$C$ be its ![]() $p$-adic completion. Set
$p$-adic completion. Set ![]() $G_K=\operatorname {Gal}(\overline {K}/K)$ and let
$G_K=\operatorname {Gal}(\overline {K}/K)$ and let ![]() $\sigma$ be the absolute Frobenius on
$\sigma$ be the absolute Frobenius on ![]() $W(\overline {k})$. For an
$W(\overline {k})$. For an ![]() ${{\mathcal O} _K}$-scheme
${{\mathcal O} _K}$-scheme ![]() $X$, let
$X$, let ![]() $X_0$ denote the special fiber of
$X_0$ denote the special fiber of ![]() $X$. We will denote by
$X$. We will denote by ![]() ${{\mathcal O} _K}$,
${{\mathcal O} _K}$, ![]() ${\mathcal O} _K^{\times }$, and
${\mathcal O} _K^{\times }$, and ![]() ${\mathcal O} _K^0$ the scheme
${\mathcal O} _K^0$ the scheme ![]() $\operatorname {Spec} ({{\mathcal O} _K})$ with the trivial, canonical (i.e., associated to the closed point), and
$\operatorname {Spec} ({{\mathcal O} _K})$ with the trivial, canonical (i.e., associated to the closed point), and ![]() $({\mathbf {N}}\to {{\mathcal O} _K}, 1\mapsto 0)$ log-structure respectively. We will freely use the notation from [Reference NiziołNiz16].
$({\mathbf {N}}\to {{\mathcal O} _K}, 1\mapsto 0)$ log-structure respectively. We will freely use the notation from [Reference NiziołNiz16].
2.1 Cohomological identities
We briefly review here certain facts involving syntomic and crystalline cohomologies that we will need.
2.1.1 Rings of periods
We start with reviewing basic facts concerning the rings of periods. Consider the ring ![]() $R={\buildrel {\lim } \over \longleftarrow} {\mathcal O} _{\overline {K}}/p{\mathcal O} _{\overline {K}}$, where the maps in the projective system are the
$R={\buildrel {\lim } \over \longleftarrow} {\mathcal O} _{\overline {K}}/p{\mathcal O} _{\overline {K}}$, where the maps in the projective system are the ![]() $p$th power maps. With addition and multiplication defined coordinate-wise,
$p$th power maps. With addition and multiplication defined coordinate-wise, ![]() $R$ is a ring of characteristic
$R$ is a ring of characteristic ![]() $p$. Take its ring of Witt vectors
$p$. Take its ring of Witt vectors ![]() $W(R)$. Then
$W(R)$. Then ![]() $\mathbf {A}_{\operatorname {cr} }$ is the
$\mathbf {A}_{\operatorname {cr} }$ is the ![]() $p$-adic completion of the divided power envelope
$p$-adic completion of the divided power envelope ![]() $D_\xi (W(R))$ of the ideal
$D_\xi (W(R))$ of the ideal ![]() $\xi W(R)$ in
$\xi W(R)$ in ![]() $W(R)$. Here
$W(R)$. Here ![]() $\xi =[p^{\flat }]-p$ and, for
$\xi =[p^{\flat }]-p$ and, for ![]() $x \in R$,
$x \in R$, ![]() $[x]=[x,0,0,\ldots ] \in W(R)$ is its Teichmüller representative.
$[x]=[x,0,0,\ldots ] \in W(R)$ is its Teichmüller representative.
(1) The rings ![]() $\mathbf {B}_{\operatorname {cr} }$ and
$\mathbf {B}_{\operatorname {cr} }$ and ![]() $\mathbf {B}_{\operatorname {dR} }$. The ring
$\mathbf {B}_{\operatorname {dR} }$. The ring ![]() $\mathbf {A}_{\operatorname {cr} }$ is a topological
$\mathbf {A}_{\operatorname {cr} }$ is a topological ![]() $W(k)$-module having the following properties:
$W(k)$-module having the following properties:
(i)
 $W(\overline {k})$ is embedded as a subring of
$W(\overline {k})$ is embedded as a subring of  $\mathbf {A}_{\operatorname {cr} }$ and
$\mathbf {A}_{\operatorname {cr} }$ and  $\sigma$ extends naturally to a Frobenius
$\sigma$ extends naturally to a Frobenius  $\phi$ on
$\phi$ on  $\mathbf {A}_{\operatorname {cr} }$;
$\mathbf {A}_{\operatorname {cr} }$;(ii)
 $\mathbf {A}_{\operatorname {cr} }$ is equipped with a decreasing separated filtration
$\mathbf {A}_{\operatorname {cr} }$ is equipped with a decreasing separated filtration  $F^{n}\mathbf {A}_{\operatorname {cr} }$, where
$F^{n}\mathbf {A}_{\operatorname {cr} }$, where  $F^{n}\mathbf {A}_{\operatorname {cr} }$ is the closure of the
$F^{n}\mathbf {A}_{\operatorname {cr} }$ is the closure of the  $n$th divided power of the PD ideal of
$n$th divided power of the PD ideal of  $D_\xi (W(S))$; for
$D_\xi (W(S))$; for  $n < p$,
$n < p$,  $\phi (F^{n}\mathbf {A}_{\operatorname {cr} })\subset p^{n}\mathbf {A}_{\operatorname {cr} }$;
$\phi (F^{n}\mathbf {A}_{\operatorname {cr} })\subset p^{n}\mathbf {A}_{\operatorname {cr} }$;(iii)
 $G_K$ acts on
$G_K$ acts on  $\mathbf {A}_{\operatorname {cr} }$; the action is
$\mathbf {A}_{\operatorname {cr} }$; the action is  $W(\overline {k})$-semilinear, continuous, commutes with
$W(\overline {k})$-semilinear, continuous, commutes with  $\phi$, and preserves the filtration;
$\phi$, and preserves the filtration;(iv) there exists an element
 $t\in F^1\mathbf {A}_{\operatorname {cr} }$ such that
$t\in F^1\mathbf {A}_{\operatorname {cr} }$ such that  $\phi (t)=pt$ and
$\phi (t)=pt$ and  $G_K$ acts on
$G_K$ acts on  $t$ via the cyclotomic character: if we fix
$t$ via the cyclotomic character: if we fix  $\varepsilon \in R$, a sequence of nontrivial
$\varepsilon \in R$, a sequence of nontrivial  $p$-roots of unity, then
$p$-roots of unity, then  $t=\log ([\varepsilon ])$.
$t=\log ([\varepsilon ])$.
The rings ![]() $\mathbf {B}_{\operatorname {cr} }^+$ and
$\mathbf {B}_{\operatorname {cr} }^+$ and ![]() $\mathbf {B}_{\operatorname {cr} }$ are defined as the rings
$\mathbf {B}_{\operatorname {cr} }$ are defined as the rings ![]() $\mathbf {A}_{\operatorname {cr} }[p^{-1}]$ and
$\mathbf {A}_{\operatorname {cr} }[p^{-1}]$ and ![]() $\mathbf {A}_{\operatorname {cr} }[p^{-1},t^{-1}]$, respectively, with the induced topology, filtration, Frobenius, and the Galois action. For us, in this paper, it will be essential that the ring
$\mathbf {A}_{\operatorname {cr} }[p^{-1},t^{-1}]$, respectively, with the induced topology, filtration, Frobenius, and the Galois action. For us, in this paper, it will be essential that the ring ![]() $\mathbf {A}_{\operatorname {cr} }$ can be thought of as a cohomology of an ‘arithmetic point’, namely that
$\mathbf {A}_{\operatorname {cr} }$ can be thought of as a cohomology of an ‘arithmetic point’, namely that
where, for a scheme ![]() $Y$ over
$Y$ over ![]() $W(k)$, we set
$W(k)$, we set
The canonical morphism ![]() $\mathbf {A}_{\operatorname {cr} ,n}\to {\mathcal O} _{\overline {K}}/p^n$ is surjective. Let
$\mathbf {A}_{\operatorname {cr} ,n}\to {\mathcal O} _{\overline {K}}/p^n$ is surjective. Let ![]() $J_{\operatorname {cr} ,n}$ denote its kernel. Let
$J_{\operatorname {cr} ,n}$ denote its kernel. Let
The ring ![]() $\mathbf {B}_{\operatorname {dR} }^+$ has a discrete valuation given by powers of
$\mathbf {B}_{\operatorname {dR} }^+$ has a discrete valuation given by powers of ![]() $t$. Its quotient field is
$t$. Its quotient field is ![]() $\mathbf {B}_{\operatorname {dR} }$. We will denote by
$\mathbf {B}_{\operatorname {dR} }$. We will denote by ![]() $F^n\mathbf {B}^+_{\operatorname {dR} }$ the filtration induced on
$F^n\mathbf {B}^+_{\operatorname {dR} }$ the filtration induced on ![]() $\mathbf {B}^+_{\operatorname {dR} }$ by powers of
$\mathbf {B}^+_{\operatorname {dR} }$ by powers of ![]() $t$.
$t$.
(2) The rings ![]() $\mathbf {B}_{\operatorname {st}}$ and
$\mathbf {B}_{\operatorname {st}}$ and ![]() $\widehat {\mathbf {B}}_{\operatorname {st}}$. Let us now recall the definition of the ring
$\widehat {\mathbf {B}}_{\operatorname {st}}$. Let us now recall the definition of the ring ![]() $\mathbf {B}_{\operatorname {st}}$ [Reference FontaineFon94]. Set
$\mathbf {B}_{\operatorname {st}}$ [Reference FontaineFon94]. Set ![]() $\mathbf {B}^+_{\operatorname {st}}:=\mathbf {B}^+_{\operatorname {cr} }[u]$,
$\mathbf {B}^+_{\operatorname {st}}:=\mathbf {B}^+_{\operatorname {cr} }[u]$, ![]() $\phi (u)=pu$, and
$\phi (u)=pu$, and ![]() $Nu=-1$. Let
$Nu=-1$. Let ![]() $\pi$ be a uniformizer of
$\pi$ be a uniformizer of ![]() ${{\mathcal O} _K}$ (which we will fix in the rest of the paper). Let
${{\mathcal O} _K}$ (which we will fix in the rest of the paper). Let ![]() $\iota =\iota _{\pi }:\mathbf {B}^+_{\operatorname {st}}\hookrightarrow \mathbf {B}^+_{\operatorname {dR} }$ denote the embedding
$\iota =\iota _{\pi }:\mathbf {B}^+_{\operatorname {st}}\hookrightarrow \mathbf {B}^+_{\operatorname {dR} }$ denote the embedding ![]() $u\mapsto u_{\pi }=\log ([\pi ^{\flat }]/\pi )$. We use it to induce the Galois action on
$u\mapsto u_{\pi }=\log ([\pi ^{\flat }]/\pi )$. We use it to induce the Galois action on ![]() $\mathbf {B}^+_{\operatorname {st}}$ from the one on
$\mathbf {B}^+_{\operatorname {st}}$ from the one on ![]() $\mathbf {B}^+_{\operatorname {dR} }$. Let
$\mathbf {B}^+_{\operatorname {dR} }$. Let ![]() $\mathbf {B}_{\operatorname {st} }=\mathbf {B}_{\operatorname {cr} }[u_{\pi }]$.
$\mathbf {B}_{\operatorname {st} }=\mathbf {B}_{\operatorname {cr} }[u_{\pi }]$.
We will need the following crystalline interpretation of the ring ![]() $\mathbf {B}^+_{\operatorname {st}}$ (see [Reference KatoKat94a, Reference TsujiTsu99a]). Let
$\mathbf {B}^+_{\operatorname {st}}$ (see [Reference KatoKat94a, Reference TsujiTsu99a]). Let ![]() $R_{\pi ,n}$ denote the PD envelope of the ring
$R_{\pi ,n}$ denote the PD envelope of the ring ![]() $W_n(k)[x]$ with respect to the closed immersion
$W_n(k)[x]$ with respect to the closed immersion ![]() $W_n(k)[x]\to {{\mathcal O} _{K,n}}$,
$W_n(k)[x]\to {{\mathcal O} _{K,n}}$, ![]() $x\mapsto \pi$, equipped with the log-structure associated to
$x\mapsto \pi$, equipped with the log-structure associated to ![]() $\mathbf {N}\to R_{\pi ,n},$
$\mathbf {N}\to R_{\pi ,n},$ ![]() $1\mapsto x$. Set
$1\mapsto x$. Set ![]() $R_{\pi }:={\mathrel{\mathop{\kern0pt\longleftarrow}\limits_n^{\lim }}}R_{\pi ,n}$. Let
$R_{\pi }:={\mathrel{\mathop{\kern0pt\longleftarrow}\limits_n^{\lim }}}R_{\pi ,n}$. Let
The ring ![]() $\widehat {\mathbf {B}}^+_{\operatorname {st}}$ has a natural action of
$\widehat {\mathbf {B}}^+_{\operatorname {st}}$ has a natural action of ![]() $G_K$, Frobenius
$G_K$, Frobenius ![]() $\phi$, and a monodromy operator
$\phi$, and a monodromy operator ![]() $N$. Kato showed [Reference KatoKat94a, 3.7] that the ring
$N$. Kato showed [Reference KatoKat94a, 3.7] that the ring ![]() $\mathbf {B}^+_{\operatorname {st}}$ is canonically (and compatibly with all the structures) isomorphic to the subring of elements of
$\mathbf {B}^+_{\operatorname {st}}$ is canonically (and compatibly with all the structures) isomorphic to the subring of elements of ![]() $\widehat {\mathbf {B}}^+_{\operatorname {st}}$ annihilated by a power of the monodromy operator
$\widehat {\mathbf {B}}^+_{\operatorname {st}}$ annihilated by a power of the monodromy operator ![]() $N$. The map
$N$. The map ![]() $\iota : \mathbf {B}^+_{\operatorname {st}}\to \mathbf {B}^+_{\operatorname {dR} }$ extends naturally to a map
$\iota : \mathbf {B}^+_{\operatorname {st}}\to \mathbf {B}^+_{\operatorname {dR} }$ extends naturally to a map ![]() $\iota : \widehat {\mathbf {B}}^+_{\operatorname {st}}\to \mathbf {B}^+_{\operatorname {dR} }$.
$\iota : \widehat {\mathbf {B}}^+_{\operatorname {st}}\to \mathbf {B}^+_{\operatorname {dR} }$.
2.1.2 Syntomic cohomology
We will recall briefly the definition of syntomic cohomology. For a log-scheme ![]() $X$, we denote by
$X$, we denote by ![]() $X_{\operatorname {syn}}$ the small log-syntomic site of
$X_{\operatorname {syn}}$ the small log-syntomic site of ![]() $X$. For a log-scheme
$X$. For a log-scheme ![]() $X$ log-syntomic over
$X$ log-syntomic over ![]() $\operatorname {Spec} (W(k))$, define
$\operatorname {Spec} (W(k))$, define
where ![]() ${\mathcal O} _{X_n}$ is the structure sheaf of the absolute log-crystalline site (i.e., over
${\mathcal O} _{X_n}$ is the structure sheaf of the absolute log-crystalline site (i.e., over ![]() $W_n(k)$),
$W_n(k)$), ![]() ${\mathcal {J}}_{X_n}=\operatorname {Ker} ({\mathcal O} _{X_n/W_n(k)}\to {\mathcal O} _{X_n})$, and
${\mathcal {J}}_{X_n}=\operatorname {Ker} ({\mathcal O} _{X_n/W_n(k)}\to {\mathcal O} _{X_n})$, and ![]() ${\mathcal {J}}^{[r]}_{X_n}$ is its
${\mathcal {J}}^{[r]}_{X_n}$ is its ![]() $r$th divided power of
$r$th divided power of ![]() ${\mathcal {J}}_{X_n}$. Set
${\mathcal {J}}_{X_n}$. Set ![]() ${\mathcal {J}}^{[r]}_{X_n}={\mathcal O} _{X_n}$ if
${\mathcal {J}}^{[r]}_{X_n}={\mathcal O} _{X_n}$ if ![]() $r\leq 0$. There is a canonical, compatible with Frobenius, and functorial isomorphism
$r\leq 0$. There is a canonical, compatible with Frobenius, and functorial isomorphism
It is easy to see that ![]() $\phi ({\mathcal {J}}_n^{[r]} )\subset p^r{\mathcal O} ^{\operatorname {cr} }_n$ for
$\phi ({\mathcal {J}}_n^{[r]} )\subset p^r{\mathcal O} ^{\operatorname {cr} }_n$ for ![]() $0\leq r\leq p-1$. This fails in general and we modify
$0\leq r\leq p-1$. This fails in general and we modify ![]() ${\mathcal {J}}_n^{[r]}$:
${\mathcal {J}}_n^{[r]}$:
for some ![]() $s\geq r$. This definition is independent of
$s\geq r$. This definition is independent of ![]() $s$. We can define the divided Frobenius
$s$. We can define the divided Frobenius
Set
We will write ![]() ${\mathcal {S}}_n(r)$ for the syntomic sheaves on
${\mathcal {S}}_n(r)$ for the syntomic sheaves on ![]() $X_{m,\operatorname {syn}}$,
$X_{m,\operatorname {syn}}$, ![]() $m\geq n$, as well as on
$m\geq n$, as well as on ![]() $X_{\operatorname {syn}}$. We will also need the ‘undivided’ version of syntomic complexes of sheaves:
$X_{\operatorname {syn}}$. We will also need the ‘undivided’ version of syntomic complexes of sheaves:
The natural map ![]() ${\mathcal {S}}^{\prime }_n(r)\to {\mathcal {S}}_n(r)$ induced by the maps
${\mathcal {S}}^{\prime }_n(r)\to {\mathcal {S}}_n(r)$ induced by the maps ![]() $p^{r}: {\mathcal {J}}_n^{[r]}\to {\mathcal {J}}_n^{\langle r\rangle }$ and
$p^{r}: {\mathcal {J}}_n^{[r]}\to {\mathcal {J}}_n^{\langle r\rangle }$ and ![]() $\operatorname {Id} : {\mathcal O} ^{\operatorname {cr} }_n \to {\mathcal O} ^{\operatorname {cr} }_n$ has kernel and cokernel killed by
$\operatorname {Id} : {\mathcal O} ^{\operatorname {cr} }_n \to {\mathcal O} ^{\operatorname {cr} }_n$ has kernel and cokernel killed by ![]() $p^{r}$. We will also write
$p^{r}$. We will also write ![]() ${\mathcal {S}}_n(r)$,
${\mathcal {S}}_n(r)$, ![]() ${\mathcal {S}}^{\prime }_n(r)$ for
${\mathcal {S}}^{\prime }_n(r)$ for ![]() $\mathrm {R} \varepsilon _*{\mathcal {S}}_n(r)$,
$\mathrm {R} \varepsilon _*{\mathcal {S}}_n(r)$, ![]() $\mathrm {R} \varepsilon _*{\mathcal {S}}^{\prime }_n(r)$, respectively, where
$\mathrm {R} \varepsilon _*{\mathcal {S}}^{\prime }_n(r)$, respectively, where ![]() $\varepsilon : X_{n,\operatorname {syn}}\to X_{n,\operatorname {\acute {e}t} }$ is the canonical projection to the étale site.
$\varepsilon : X_{n,\operatorname {syn}}\to X_{n,\operatorname {\acute {e}t} }$ is the canonical projection to the étale site.
The ![]() $p$-adic syntomic cohomology of
$p$-adic syntomic cohomology of ![]() $X$ is defined as
$X$ is defined as
2.1.3 Cohomology with compact support
Let ![]() $X$ be a finite and saturated log-smooth log-scheme over
$X$ be a finite and saturated log-smooth log-scheme over ![]() ${\mathcal O} _K^{\times }$ (respectively over
${\mathcal O} _K^{\times }$ (respectively over ![]() ${{\mathcal O} _K}$). Since
${{\mathcal O} _K}$). Since ![]() $X$ is log-regular it is normal and the maximal open subset
$X$ is log-regular it is normal and the maximal open subset ![]() $U=X_{\operatorname {tr}}\subset X$, where the log-structure
$U=X_{\operatorname {tr}}\subset X$, where the log-structure ![]() $M_X$ is trivial, is dense in
$M_X$ is trivial, is dense in ![]() $X$. We have
$X$. We have ![]() $M_X={\mathcal O} _X\cap j_*{\mathcal O} _U^*$, where
$M_X={\mathcal O} _X\cap j_*{\mathcal O} _U^*$, where ![]() $j:U\hookrightarrow X$ is the open immersion. By [Reference NiziołNiz06a, Theorem 5.10], there exists a log-blow-up of
$j:U\hookrightarrow X$ is the open immersion. By [Reference NiziołNiz06a, Theorem 5.10], there exists a log-blow-up of ![]() $X$ that has Zariski log-structure and is (classically) regular.
$X$ that has Zariski log-structure and is (classically) regular.
Assume that ![]() $X$ itself has these properties. Then
$X$ itself has these properties. Then ![]() $U$ is a complement of a divisor with simple normal crossings that is a union
$U$ is a complement of a divisor with simple normal crossings that is a union ![]() $D_0\cup D$ (respectively
$D_0\cup D$ (respectively ![]() $D$) of the reduced special fiber and the horizontal part
$D$) of the reduced special fiber and the horizontal part ![]() $D$. The scheme
$D$. The scheme ![]() $X$ has generalized semistable reduction, i.e., Zariski locally on
$X$ has generalized semistable reduction, i.e., Zariski locally on ![]() $X$, there exists an étale morphism over
$X$, there exists an étale morphism over ![]() ${{\mathcal O} _K}$:
${{\mathcal O} _K}$:
for some integers ![]() $u\geq 1$ (respectively
$u\geq 1$ (respectively ![]() $u=0$),
$u=0$), ![]() $m,t\geq 0, n_i>0$. The divisor
$m,t\geq 0, n_i>0$. The divisor ![]() $D$ is the inverse image of
$D$ is the inverse image of ![]() $U_1\cdots U_m=0$. In particular, all the closed strata of
$U_1\cdots U_m=0$. In particular, all the closed strata of ![]() $D$ are log-smooth over
$D$ are log-smooth over ![]() ${\mathcal O} _K^{\times }$ and regular (respectively smooth over
${\mathcal O} _K^{\times }$ and regular (respectively smooth over ![]() ${{\mathcal O} _K}$). If all
${{\mathcal O} _K}$). If all ![]() $n_i=1$, we say that
$n_i=1$, we say that ![]() $X$ has semistable reduction.
$X$ has semistable reduction.
Take ![]() $X$ as above with semistable reduction. Recall the following definitions. The
$X$ as above with semistable reduction. Recall the following definitions. The ![]() $p$-adic étale cohomology of
$p$-adic étale cohomology of ![]() $X_{\overline {K}}$ with compact support.Footnote 2
$X_{\overline {K}}$ with compact support.Footnote 2
The de Rham cohomology of ![]() $X_K$ with compact support [Reference TsujiTsu99b, Definition 3.2]
$X_K$ with compact support [Reference TsujiTsu99b, Definition 3.2]
where ![]() ${\mathcal {I}}_{D_K}\subset j_{K*}{\mathcal O} ^*_{U_K}\cap {\mathcal O} _{X_K}$ is the ideal of
${\mathcal {I}}_{D_K}\subset j_{K*}{\mathcal O} ^*_{U_K}\cap {\mathcal O} _{X_K}$ is the ideal of ![]() ${\mathcal O} _{X_K}$ corresponding to
${\mathcal O} _{X_K}$ corresponding to ![]() $D_K$. We filter it by
$D_K$. We filter it by
The crystalline cohomology of ![]() $X_0$ over
$X_0$ over ![]() $W(k)^0$ with compact support [Reference TsujiTsu99b, Definition 5.4]
$W(k)^0$ with compact support [Reference TsujiTsu99b, Definition 5.4]
where ![]() ${\mathcal {K}}_{D_0}$ is an ideal sheaf induced by the sheaf
${\mathcal {K}}_{D_0}$ is an ideal sheaf induced by the sheaf ![]() ${\mathcal {I}}_{D_0}$ [Reference TsujiTsu99b, Lemma 5.3]. The crystalline cohomology
${\mathcal {I}}_{D_0}$ [Reference TsujiTsu99b, Lemma 5.3]. The crystalline cohomology ![]() $\mathrm {R}\Gamma _{\operatorname {cr} ,c}(X)$ is defined in a similar way. We filter it by setting
$\mathrm {R}\Gamma _{\operatorname {cr} ,c}(X)$ is defined in a similar way. We filter it by setting ![]() $F^r\mathrm {R}\Gamma _{\operatorname {cr} ,c}(X)=\mathrm {R}\Gamma _{\operatorname {cr} }(X,{\mathcal {K}}_{D_0}{\mathcal {J}}^{[r]}_X)$,
$F^r\mathrm {R}\Gamma _{\operatorname {cr} ,c}(X)=\mathrm {R}\Gamma _{\operatorname {cr} }(X,{\mathcal {K}}_{D_0}{\mathcal {J}}^{[r]}_X)$, ![]() $r\in \mathbf {Z}$. This allows us to define the syntomic cohomology with compact support
$r\in \mathbf {Z}$. This allows us to define the syntomic cohomology with compact support ![]() $\mathrm {R}\Gamma _{\operatorname {syn},c}(X,{\mathcal {S}}_n(r))$ and
$\mathrm {R}\Gamma _{\operatorname {syn},c}(X,{\mathcal {S}}_n(r))$ and ![]() $\mathrm {R}\Gamma _{\operatorname {syn},c}(X,{\mathcal {S}}^{\prime }_n(r))$.
$\mathrm {R}\Gamma _{\operatorname {syn},c}(X,{\mathcal {S}}^{\prime }_n(r))$.
The above cohomologies with compact support are special cases of cohomologies of finite simplicial schemes. Define ![]() $C(X,D):=\operatorname {cofiber}(\widetilde {D}_{{\scriptscriptstyle \bullet }}\stackrel {i_*}{\to } X)$, where
$C(X,D):=\operatorname {cofiber}(\widetilde {D}_{{\scriptscriptstyle \bullet }}\stackrel {i_*}{\to } X)$, where ![]() $\widetilde {D}_{{\scriptscriptstyle \bullet }}$ is the Čech nerve of the map
$\widetilde {D}_{{\scriptscriptstyle \bullet }}$ is the Čech nerve of the map ![]() $\coprod _i D_i\to D$,
$\coprod _i D_i\to D$, ![]() $D_i$ being an irreducible component of
$D_i$ being an irreducible component of ![]() $D$. The log-structure on the schemes in
$D$. The log-structure on the schemes in ![]() $C(X,D)$ is trivial if
$C(X,D)$ is trivial if ![]() $X$ is over
$X$ is over ![]() ${\mathcal O} _K$ and induced from the special fiber if
${\mathcal O} _K$ and induced from the special fiber if ![]() $X$ is over
$X$ is over ![]() ${\mathcal O} _K^{\times }$.
${\mathcal O} _K^{\times }$.
Lemma 2.1 Let ![]() $\mathrm {R}\Gamma (X)$ denote one of the cohomologies mentioned above. We have a natural (filtered) quasi-isomorphism
$\mathrm {R}\Gamma (X)$ denote one of the cohomologies mentioned above. We have a natural (filtered) quasi-isomorphism
It is compatible with products.Footnote 3
Proof. The étale and de Rham cases follow immediately from the following exact sequences (![]() $r\in \mathbf {Z}$):
$r\in \mathbf {Z}$):
 \begin{equation} \begin{gathered} 0\to \overline{j}_{K!}\mathbf{Q}_p\to \mathbf{Q}_{p,X_{\overline{K}}} \to\overline{ i}_{1*}\mathbf{Q}_{p,D^1_{\overline{K}}}\to \overline{i}_{2*}\mathbf{Q}_{p,D^2_{\overline{K}}}\to \cdots,\\ 0\to {\mathcal{I}}_{D_K}\Omega^{\geq r}_{X_K}\to \Omega^{\geq r}_{X_K}\to i_{1*}\Omega^{\geq r}_{D^{1}_K}\to i_{2*}\Omega^{\geq r}_{D^2_K}\to \cdots. \end{gathered} \end{equation}
\begin{equation} \begin{gathered} 0\to \overline{j}_{K!}\mathbf{Q}_p\to \mathbf{Q}_{p,X_{\overline{K}}} \to\overline{ i}_{1*}\mathbf{Q}_{p,D^1_{\overline{K}}}\to \overline{i}_{2*}\mathbf{Q}_{p,D^2_{\overline{K}}}\to \cdots,\\ 0\to {\mathcal{I}}_{D_K}\Omega^{\geq r}_{X_K}\to \Omega^{\geq r}_{X_K}\to i_{1*}\Omega^{\geq r}_{D^{1}_K}\to i_{2*}\Omega^{\geq r}_{D^2_K}\to \cdots. \end{gathered} \end{equation}
Here ![]() $D^m:=\widetilde {D}_m$ is the direct sum of the intersections of
$D^m:=\widetilde {D}_m$ is the direct sum of the intersections of ![]() $m$ irreducible components of
$m$ irreducible components of ![]() $D$. We note that
$D$. We note that ![]() $C(X,D)_{\overline {K}}\simeq C(X_{\overline {K}},D_{\overline {K}})$ even if
$C(X,D)_{\overline {K}}\simeq C(X_{\overline {K}},D_{\overline {K}})$ even if ![]() $(X,D)$ is not geometrically irreducible.
$(X,D)$ is not geometrically irreducible.
The crystalline case over ![]() $W(k)^0$ follows from a mixed characteristic analog of the second sequence. And the case over
$W(k)^0$ follows from a mixed characteristic analog of the second sequence. And the case over ![]() $W(k)$ reduces to this sequence as well. Indeed, if
$W(k)$ reduces to this sequence as well. Indeed, if ![]() ${\mathcal O} _K=W(k)$, this is clear. In general, locally, we have an embedding into such a situation. Because, by assumption, this embedding is regular, the above-mentioned sequence remains exact after tensoring with the divided power envelope and computes cohomology with compact support.
${\mathcal O} _K=W(k)$, this is clear. In general, locally, we have an embedding into such a situation. Because, by assumption, this embedding is regular, the above-mentioned sequence remains exact after tensoring with the divided power envelope and computes cohomology with compact support.
For the syntomic case, it suffices to check that the above crystalline quasi-isomorphism preserves filtrations. But this follows easily from the fact that the associated grading of the filtration on the divided power envelope is free over ![]() ${\mathcal O} _X$.
${\mathcal O} _X$.
Concerning compatibility with products, the étale, the de Rham, and the crystalline cases are immediate from the expressions (2.2). In the syntomic case, compatibility follows from the fact that syntomic cohomology is defined as a mapping fiber of (filtered) crystalline cohomology and the syntomic product is the mapping fiber product induced from the crystalline product.
2.1.4 Fontaine–Lafaille theory
The main reference for this section is [Reference Fontaine and LafailleFL82]. Assume first that ![]() ${{\mathcal O} _K}=W(k)$. For the integral crystalline theory (Fontaine–Laffaille theory), we will need the following abelian categories:
${{\mathcal O} _K}=W(k)$. For the integral crystalline theory (Fontaine–Laffaille theory), we will need the following abelian categories:
(i)
 $\mathcal {M }{\mathcal {F}}_{\rm big}({{\mathcal O} _K})$: an object is given by a
$\mathcal {M }{\mathcal {F}}_{\rm big}({{\mathcal O} _K})$: an object is given by a  $p$-torsion
$p$-torsion  ${{\mathcal O} _K}$-module
${{\mathcal O} _K}$-module  $M$ and a family of
$M$ and a family of  $p$-torsion
$p$-torsion  ${{\mathcal O} _K}$-modules
${{\mathcal O} _K}$-modules  $F^{i}M$ together with
$F^{i}M$ together with  ${{\mathcal O} _K}$-linear maps
${{\mathcal O} _K}$-linear maps  $F^{i}M\rightarrow F^{i-1}M,$
$F^{i}M\rightarrow F^{i-1}M,$  $F^{i}M\rightarrow M$, and
$F^{i}M\rightarrow M$, and  $\sigma$-semilinear maps
$\sigma$-semilinear maps  $\phi _{i} : F^{i}M\rightarrow M$ satisfying certain compatibility conditions;
$\phi _{i} : F^{i}M\rightarrow M$ satisfying certain compatibility conditions;(ii)
 ${\mathcal {M}}{\mathcal {F}} ({{\mathcal O} _K})$: the full subcategory of
${\mathcal {M}}{\mathcal {F}} ({{\mathcal O} _K})$: the full subcategory of  ${\mathcal {M}}{\mathcal {F}} _{\rm big}({{\mathcal O} _K})$ with objects: finite
${\mathcal {M}}{\mathcal {F}} _{\rm big}({{\mathcal O} _K})$ with objects: finite  ${{\mathcal O} _K}$-modules
${{\mathcal O} _K}$-modules  $M$ such that
$M$ such that  $F^{i}M=0\text { for } i\gg 0$, the maps
$F^{i}M=0\text { for } i\gg 0$, the maps  $F^{i}(M)\rightarrow M$ are injective and
$F^{i}(M)\rightarrow M$ are injective and  $\sum \text {Im}\, \phi _{i} = M$;
$\sum \text {Im}\, \phi _{i} = M$;(iii)
 ${\mathcal {M}}{\mathcal {F}} _{[a,b]}({{\mathcal O} _K})$: the full subcategory of objects
${\mathcal {M}}{\mathcal {F}} _{[a,b]}({{\mathcal O} _K})$: the full subcategory of objects  $M$ of
$M$ of  ${\mathcal {M}}{\mathcal {F}} ({{\mathcal O} _K})$ such that
${\mathcal {M}}{\mathcal {F}} ({{\mathcal O} _K})$ such that  $F^{a}M=M$ and
$F^{a}M=M$ and  $F^{b+1}M=0$.
$F^{b+1}M=0$.
Consider the category ![]() ${\mathcal {M}}{\mathcal {F}} _{[a,b]}({{\mathcal O} _K})\text { with } b-a\leq p-2$. There exists an exact and fully faithful functor
${\mathcal {M}}{\mathcal {F}} _{[a,b]}({{\mathcal O} _K})\text { with } b-a\leq p-2$. There exists an exact and fully faithful functor
where ![]() $\{-b\}$ and
$\{-b\}$ and ![]() $(-b)$ are the
$(-b)$ are the ![]() ${\mathcal {M}}{\mathcal {F}}$ and Tate twistsFootnote 4, respectively, from
${\mathcal {M}}{\mathcal {F}}$ and Tate twistsFootnote 4, respectively, from ![]() ${\mathcal {M}}{\mathcal {F}} _{[a,b]}({{\mathcal O} _K})$ to finite
${\mathcal {M}}{\mathcal {F}} _{[a,b]}({{\mathcal O} _K})$ to finite ![]() ${\mathbf {Z}}_{p}$-Galois representations. Its essential image is called the category of crystalline representations of weight between
${\mathbf {Z}}_{p}$-Galois representations. Its essential image is called the category of crystalline representations of weight between ![]() $a$ and
$a$ and ![]() $b$. This category is closed under taking tensor products and duals (assuming that we stay in the admissible range of the filtration).
$b$. This category is closed under taking tensor products and duals (assuming that we stay in the admissible range of the filtration).
The following proposition generalizes [Reference Fontaine, Messing and RibetFM87, 2.7], Faltings [Reference Faltings and IgusaFal89, 4.1], and [Reference NiziołNiz09, Lemma 2.3] from schemes to finite simplicial schemes.
Proposition 2.3 Let ![]() $X$ be a smooth and proper
$X$ be a smooth and proper ![]() $m$-truncated simplicial scheme over
$m$-truncated simplicial scheme over ![]() ${{\mathcal O} _K}=W(k)$ whose components have dimension smaller than
${{\mathcal O} _K}=W(k)$ whose components have dimension smaller than ![]() $d$. Then, for
$d$. Then, for ![]() $d\leq p-2$ or for
$d\leq p-2$ or for ![]() $i\leq p-2$, the filtered Frobenius module
$i\leq p-2$, the filtered Frobenius module ![]() $H^i_{\operatorname {cr} }(X_n)$ lies in
$H^i_{\operatorname {cr} }(X_n)$ lies in ![]() ${\mathcal {M}}{\mathcal {F}}_{[0,d]} ({{\mathcal O} _K})$ or
${\mathcal {M}}{\mathcal {F}}_{[0,d]} ({{\mathcal O} _K})$ or ![]() ${\mathcal {M}}{\mathcal {F}}_{[0,i]} ({{\mathcal O} _K})$, respectively. Moreover, then the natural morphism
${\mathcal {M}}{\mathcal {F}}_{[0,i]} ({{\mathcal O} _K})$, respectively. Moreover, then the natural morphism
is an isomorphism for ![]() $p-2\geq r\geq d$ or for
$p-2\geq r\geq d$ or for ![]() $0\leq i\leq r\leq p-2$, respectively.
$0\leq i\leq r\leq p-2$, respectively.
Here
and the maps
where ![]() $\phi$ denotes the crystalline Frobenius. The Hodge filtration is
$\phi$ denotes the crystalline Frobenius. The Hodge filtration is
since the Hodge–de Rham spectral sequence of ![]() $X_n$ degenerates: by devissage, we can reduce to
$X_n$ degenerates: by devissage, we can reduce to ![]() $n=1$ and then it follows from the results of Deligne and Illusie [Reference Deligne and IllusieDI87, Corollary 3.7].
$n=1$ and then it follows from the results of Deligne and Illusie [Reference Deligne and IllusieDI87, Corollary 3.7].
Proof. The proof of [Reference Fontaine, Messing and RibetFM87, 2.7] for schemes goes through for truncated simplicial schemes, proving the first claim of the proposition. For the second claim, we argue by induction on ![]() $m\geq 0$ such that
$m\geq 0$ such that ![]() $X\simeq \operatorname {sk} _mX$. The case of
$X\simeq \operatorname {sk} _mX$. The case of ![]() $m=0$ is treated in [Reference Fontaine, Messing and RibetFM87, 2.7]. Assume that our proposition is true for
$m=0$ is treated in [Reference Fontaine, Messing and RibetFM87, 2.7]. Assume that our proposition is true for ![]() $m-1$. To show it for
$m-1$. To show it for ![]() $m$, consider the homotopy cofiber sequence
$m$, consider the homotopy cofiber sequence
and apply the maps ![]() $\psi _n$ to it. We get the following map of sequences.
$\psi _n$ to it. We get the following map of sequences.

Here we set ![]() $H^*_{\operatorname {syn}}(Y)=H^*_{\operatorname {\acute {e}t} }(Y_{{\mathcal O} _{\overline {K}}}, {\mathcal {S}}_n(r))$,
$H^*_{\operatorname {syn}}(Y)=H^*_{\operatorname {\acute {e}t} }(Y_{{\mathcal O} _{\overline {K}}}, {\mathcal {S}}_n(r))$, ![]() ${\mathbf {L}}(H^*_{\operatorname {cr} }(Y))={\mathbf {L}}(H^*_{\operatorname {cr} }(Y_n)\{-r\})$. We also put
${\mathbf {L}}(H^*_{\operatorname {cr} }(Y))={\mathbf {L}}(H^*_{\operatorname {cr} }(Y_n)\{-r\})$. We also put
where each ![]() $s_i: X_{m-1}\to X_m$ is a degeneracy map. The top sequence is exact. So is the bottom: it is clearly exact before applying
$s_i: X_{m-1}\to X_m$ is a degeneracy map. The top sequence is exact. So is the bottom: it is clearly exact before applying ![]() ${\mathbf {L}}$ and it stays exact because the relevant categories
${\mathbf {L}}$ and it stays exact because the relevant categories ![]() ${\mathcal {M}}{\mathcal {F}}$ are closed under taking subobjects and the functor
${\mathcal {M}}{\mathcal {F}}$ are closed under taking subobjects and the functor ![]() ${\mathbf {L}}$ is exact.
${\mathbf {L}}$ is exact.
By the inductive hypothesis, we have the isomorphisms shown. It follows that the map
is an isomorphism as well. Since ![]() $H^i_{\operatorname {\acute {e}t} }(\operatorname {sk} _{m}X_{{\mathcal O} _{\overline {K}}},{\mathcal {S}}_n(r))\stackrel {\sim }{\to }H^i_{\operatorname {\acute {e}t} }(X_{{\mathcal O} _{\overline {K}}},{\mathcal {S}}_n(r))$ and
$H^i_{\operatorname {\acute {e}t} }(\operatorname {sk} _{m}X_{{\mathcal O} _{\overline {K}}},{\mathcal {S}}_n(r))\stackrel {\sim }{\to }H^i_{\operatorname {\acute {e}t} }(X_{{\mathcal O} _{\overline {K}}},{\mathcal {S}}_n(r))$ and ![]() $H^*_{\operatorname {cr} }(\operatorname {sk} _mX_n)\stackrel {\sim }{\to }H^*_{\operatorname {cr} }(X_n)$, we are done.
$H^*_{\operatorname {cr} }(\operatorname {sk} _mX_n)\stackrel {\sim }{\to }H^*_{\operatorname {cr} }(X_n)$, we are done.
The above proposition can be applied to cohomology with compact support.
Corollary 2.4 Let ![]() $X$ be a smooth and proper scheme over
$X$ be a smooth and proper scheme over ![]() ${{\mathcal O} _K}=W(k)$ with a divisor
${{\mathcal O} _K}=W(k)$ with a divisor ![]() $D$ that has relative simple normal crossings and all the closed strata smooth over
$D$ that has relative simple normal crossings and all the closed strata smooth over ![]() ${{\mathcal O} _K}$. Equip
${{\mathcal O} _K}$. Equip ![]() $X$ with the log-structure coming from
$X$ with the log-structure coming from ![]() $D$. Then, if the relative dimension
$D$. Then, if the relative dimension ![]() $d$ of
$d$ of ![]() $X$ is
$X$ is ![]() $\leq p-2$ or if
$\leq p-2$ or if ![]() $i\leq p-2$, the filtered Frobenius module
$i\leq p-2$, the filtered Frobenius module ![]() $H^i_{\operatorname {cr} }(X_n)$ lies in
$H^i_{\operatorname {cr} }(X_n)$ lies in ![]() ${\mathcal {M}}{\mathcal {F}}_{[0,d]} ({{\mathcal O} _K})$ or
${\mathcal {M}}{\mathcal {F}}_{[0,d]} ({{\mathcal O} _K})$ or ![]() ${\mathcal {M}}{\mathcal {F}}_{[0,i]} ({{\mathcal O} _K})$, respectively. Moreover, then the natural morphism
${\mathcal {M}}{\mathcal {F}}_{[0,i]} ({{\mathcal O} _K})$, respectively. Moreover, then the natural morphism
is an isomorphism for ![]() $p-2\geq r\geq d$ or for
$p-2\geq r\geq d$ or for ![]() $0\leq i\leq r\leq p-2$, respectively.
$0\leq i\leq r\leq p-2$, respectively.
2.1.5 More cohomological identities
Let ![]() ${\mathcal O} _K$ be general and let
${\mathcal O} _K$ be general and let ![]() $X$ be an
$X$ be an ![]() ${{\mathcal O} _K}$-scheme. Recall that, if
${{\mathcal O} _K}$-scheme. Recall that, if ![]() $X$ is smooth and proper, Kato and Messing [Reference Kato and MessingKM92] have constructed the following isomorphisms:
$X$ is smooth and proper, Kato and Messing [Reference Kato and MessingKM92] have constructed the following isomorphisms:
 \begin{align*} h_{\operatorname{cr}}:\ &H ^i_{\operatorname{cr} } (X_{0})_\mathbf{Q} \otimes \mathbf{B}^+_{\operatorname{cr} } \stackrel{\sim}{\to} H^i_{\operatorname{cr} }(X_{{\mathcal O}_{\overline{K}}})_{\mathbf{Q}} \quad [\text{KM92}, 1.2],\\ &H^i_{\operatorname{dR} } (X_K) \otimes \mathbf{B}^+_{\operatorname{dR} } \simeq {\mathrel{\mathop{\kern0pt\longleftarrow}\limits_N^{\lim }}}\Bigl({\mathrel{\mathop{\kern0pt\longleftarrow}\limits_n^{\lim }}} H^i_{\operatorname{cr} }(X_{{\mathcal O}_{\overline{K}},n},{\mathcal O}_{n}/J_n^{[N]})\Bigr)_{\mathbf{Q}} \quad [\text{KM92}, 1.4],\\ h_{\operatorname{dR} }:\ &F^r (H^i_{\operatorname{dR} }(X_K) \otimes \mathbf{B}^+_{\operatorname{dR} }) \stackrel{\sim}{\to} {\mathrel{\mathop{\kern0pt\longleftarrow}\limits_N^{\lim }}}\Bigl({\mathrel{\mathop{\kern0pt\longleftarrow}\limits_n^{\lim }}} H^i_{\operatorname{cr} }(X_{{\mathcal O}_{\overline{K},n}},J_n^{[r]}/J_n^{[N]})\Bigr)_{\mathbf{Q}}. \end{align*}
\begin{align*} h_{\operatorname{cr}}:\ &H ^i_{\operatorname{cr} } (X_{0})_\mathbf{Q} \otimes \mathbf{B}^+_{\operatorname{cr} } \stackrel{\sim}{\to} H^i_{\operatorname{cr} }(X_{{\mathcal O}_{\overline{K}}})_{\mathbf{Q}} \quad [\text{KM92}, 1.2],\\ &H^i_{\operatorname{dR} } (X_K) \otimes \mathbf{B}^+_{\operatorname{dR} } \simeq {\mathrel{\mathop{\kern0pt\longleftarrow}\limits_N^{\lim }}}\Bigl({\mathrel{\mathop{\kern0pt\longleftarrow}\limits_n^{\lim }}} H^i_{\operatorname{cr} }(X_{{\mathcal O}_{\overline{K}},n},{\mathcal O}_{n}/J_n^{[N]})\Bigr)_{\mathbf{Q}} \quad [\text{KM92}, 1.4],\\ h_{\operatorname{dR} }:\ &F^r (H^i_{\operatorname{dR} }(X_K) \otimes \mathbf{B}^+_{\operatorname{dR} }) \stackrel{\sim}{\to} {\mathrel{\mathop{\kern0pt\longleftarrow}\limits_N^{\lim }}}\Bigl({\mathrel{\mathop{\kern0pt\longleftarrow}\limits_n^{\lim }}} H^i_{\operatorname{cr} }(X_{{\mathcal O}_{\overline{K},n}},J_n^{[r]}/J_n^{[N]})\Bigr)_{\mathbf{Q}}. \end{align*}We will need also to know the following lemma [Reference NiziołNiz98, Lemma 2.2].
Lemma 2.5 The following two compositions of maps are equal:
 \begin{align*} \mathbf{Q} &\otimes{\mathrel{\mathop{\kern0pt\longleftarrow}\limits_n^{\lim }}} H^i_{\operatorname{\acute{e}t} }(X_{{\mathcal O}_{\overline{K}}},{\mathcal{S}}_n'(r)) \to {\mathrel{\mathop{\kern0pt\longleftarrow}\limits_N^{\lim }}}\Bigl( \mathbf{Q}\otimes{\mathrel{\mathop{\kern0pt\longleftarrow}\limits_n^{\lim }}} H^i_{\operatorname{cr} }(X_{{\mathcal O}_{\overline{K}},n},J_n^{[r]}/J_n^{[N]})\Bigr) {\buildrel { h^{-1}_{\operatorname{dR} }} \over \longrightarrow} F^r(H^i_{\operatorname{dR} }(X_K) \otimes \mathbf{B}^+_{\operatorname{dR} })\\ &\quad \to H^i_{\operatorname{dR} }(X_K) \otimes \mathbf{B}^+_{\operatorname{dR} },\\ \mathbf{Q} &\otimes{\mathrel{\mathop{\kern0pt\longleftarrow}\limits_n^{\lim }}} H^i_{\operatorname{\acute{e}t} }( X_{{\mathcal O}_{\overline{K}}},{\mathcal{S}}_n'(r)) \to \mathbf{Q}\otimes{\mathrel{\mathop{\kern0pt\longleftarrow}\limits_n^{\lim }}} H^i_{\operatorname{cr} }(X_{{\mathcal O}_{\overline{K},n}}) {\buildrel { h^{-1}_{\operatorname{cr} } } \over \longrightarrow} H ^i _{\operatorname{cr} }(X_{0})\otimes_{W(k)} \mathbf{B}^+_{\operatorname{cr} } {\buildrel { \delta} \over \longrightarrow} H^i_{\operatorname{dR} }(X_K) \otimes \mathbf{B}^+_{\operatorname{dR} }, \end{align*}
\begin{align*} \mathbf{Q} &\otimes{\mathrel{\mathop{\kern0pt\longleftarrow}\limits_n^{\lim }}} H^i_{\operatorname{\acute{e}t} }(X_{{\mathcal O}_{\overline{K}}},{\mathcal{S}}_n'(r)) \to {\mathrel{\mathop{\kern0pt\longleftarrow}\limits_N^{\lim }}}\Bigl( \mathbf{Q}\otimes{\mathrel{\mathop{\kern0pt\longleftarrow}\limits_n^{\lim }}} H^i_{\operatorname{cr} }(X_{{\mathcal O}_{\overline{K}},n},J_n^{[r]}/J_n^{[N]})\Bigr) {\buildrel { h^{-1}_{\operatorname{dR} }} \over \longrightarrow} F^r(H^i_{\operatorname{dR} }(X_K) \otimes \mathbf{B}^+_{\operatorname{dR} })\\ &\quad \to H^i_{\operatorname{dR} }(X_K) \otimes \mathbf{B}^+_{\operatorname{dR} },\\ \mathbf{Q} &\otimes{\mathrel{\mathop{\kern0pt\longleftarrow}\limits_n^{\lim }}} H^i_{\operatorname{\acute{e}t} }( X_{{\mathcal O}_{\overline{K}}},{\mathcal{S}}_n'(r)) \to \mathbf{Q}\otimes{\mathrel{\mathop{\kern0pt\longleftarrow}\limits_n^{\lim }}} H^i_{\operatorname{cr} }(X_{{\mathcal O}_{\overline{K},n}}) {\buildrel { h^{-1}_{\operatorname{cr} } } \over \longrightarrow} H ^i _{\operatorname{cr} }(X_{0})\otimes_{W(k)} \mathbf{B}^+_{\operatorname{cr} } {\buildrel { \delta} \over \longrightarrow} H^i_{\operatorname{dR} }(X_K) \otimes \mathbf{B}^+_{\operatorname{dR} }, \end{align*}
where ![]() $\delta$ is induced by the Berthelot–Ogus isomorphism [Reference Berthelot and OgusBO83, 2.2]
$\delta$ is induced by the Berthelot–Ogus isomorphism [Reference Berthelot and OgusBO83, 2.2] ![]() $H^i_{\operatorname {cr} }(X_{0})\otimes _{W(k)} K \simeq H^i_{\operatorname {dR} }(X_K)$.
$H^i_{\operatorname {cr} }(X_{0})\otimes _{W(k)} K \simeq H^i_{\operatorname {dR} }(X_K)$.
Let ![]() $X$ be any fine log-scheme which is log-smooth and proper over
$X$ be any fine log-scheme which is log-smooth and proper over ![]() ${\mathcal O} _K^{\times }$ with saturated log-structure on the generic fiber. We will need the crystalline interpretation of
${\mathcal O} _K^{\times }$ with saturated log-structure on the generic fiber. We will need the crystalline interpretation of ![]() $\mathbf {B}^+_{\operatorname {dR} }\otimes _{K} H^i_{\operatorname {dR} }(X_K)$ from [Reference KatoKat94a] (see also [Reference TsujiTsu99a, 4.7]):
$\mathbf {B}^+_{\operatorname {dR} }\otimes _{K} H^i_{\operatorname {dR} }(X_K)$ from [Reference KatoKat94a] (see also [Reference TsujiTsu99a, 4.7]):
 \begin{equation} \begin{gathered} \mathbf{B}^+_{\operatorname{dR} }\otimes _{K} H^i_{\operatorname{dR} }(X_K)\stackrel{\sim}{\to} {\mathrel{\mathop{\kern0pt\longleftarrow}\limits_s^{\lim }}} H^{i}_{\operatorname{cr} }(X_{{\mathcal O}_{\overline{K}}}/ {\mathcal O}_K^{\times },{\mathcal O}/J^{[s]})_{\mathbf{Q}}\quad [\text{Tsu99a}, 4.7.6],\\ F^r(\mathbf{B}^+_{\operatorname{dR} }\otimes _{K} H^i_{\operatorname{dR} }(X_K))\stackrel{\sim}{\to} {\mathrel{\mathop{\kern0pt\longleftarrow}\limits_{s\geq r}^{\lim }}} H^{i}_{\operatorname{cr} }(X_{{\mathcal O}_{\overline{K}}}/ {\mathcal O}_K^{\times },J^{[r]}/J^{[s]})_{\mathbf{Q}}\quad [\text{Tsu99a}, 4.7.13]. \end{gathered} \end{equation}
\begin{equation} \begin{gathered} \mathbf{B}^+_{\operatorname{dR} }\otimes _{K} H^i_{\operatorname{dR} }(X_K)\stackrel{\sim}{\to} {\mathrel{\mathop{\kern0pt\longleftarrow}\limits_s^{\lim }}} H^{i}_{\operatorname{cr} }(X_{{\mathcal O}_{\overline{K}}}/ {\mathcal O}_K^{\times },{\mathcal O}/J^{[s]})_{\mathbf{Q}}\quad [\text{Tsu99a}, 4.7.6],\\ F^r(\mathbf{B}^+_{\operatorname{dR} }\otimes _{K} H^i_{\operatorname{dR} }(X_K))\stackrel{\sim}{\to} {\mathrel{\mathop{\kern0pt\longleftarrow}\limits_{s\geq r}^{\lim }}} H^{i}_{\operatorname{cr} }(X_{{\mathcal O}_{\overline{K}}}/ {\mathcal O}_K^{\times },J^{[r]}/J^{[s]})_{\mathbf{Q}}\quad [\text{Tsu99a}, 4.7.13]. \end{gathered} \end{equation}Finally, let us recall briefly the Hyodo–Kato isomorphism. We define the Hyodo–Kato cohomology as
If the special fiber of ![]() $X$ is of Cartier type, Kato defined [Reference KatoKat94a, 4.2 and 4.5] canonical morphisms (that however depend on the choice of
$X$ is of Cartier type, Kato defined [Reference KatoKat94a, 4.2 and 4.5] canonical morphisms (that however depend on the choice of ![]() $\pi$)
$\pi$)
It can be checked (see [Reference TsujiTsu99a, 4.5.6 and 4.5.7]) that these morphisms are compatible with Galois action and the Frobenius. Moreover, Hyodo and Kato [Reference Hyodo and KatoHK94, 5.1] have constructed a canonical ![]() $K$-isomorphism
$K$-isomorphism
Hence, the composition
is functorial in ![]() $X$ and compatible with Galois action.
$X$ and compatible with Galois action.
It is easy to check that all the above extends to finite simplicial (log-)schemes ![]() $X$.
$X$.
(i) The map
 $h_{\operatorname {cr} }$ actually lifts in a functorial way to a statement in the
$h_{\operatorname {cr} }$ actually lifts in a functorial way to a statement in the  $\infty$-derived categoryFootnote 5 and hence extends to simplicial schemes. Similarly for the morphisms in (2.7).
$\infty$-derived categoryFootnote 5 and hence extends to simplicial schemes. Similarly for the morphisms in (2.7).(ii) Similarly for the Hyodo–Kato isomorphism (2.8), though here finiteness of the simplicial scheme is an important assumption one needs to make to control the denominators (for details, see [Reference TsujiTsu98, 6.3] and [Reference KisinKis02, 2.8]).
(iii) Similarly for the map
 $h_{\operatorname {dR} }$, the maps in Lemma 2.5, and the maps in (2.6), where in addition one needs to use that the Hodge–de Rham spectral sequence for
$h_{\operatorname {dR} }$, the maps in Lemma 2.5, and the maps in (2.6), where in addition one needs to use that the Hodge–de Rham spectral sequence for  $X$ degenerates (which, by passing to the complex numbers, follows from the classical Hodge theory; see [Reference DeligneDel74, 7.2.8]).
$X$ degenerates (which, by passing to the complex numbers, follows from the classical Hodge theory; see [Reference DeligneDel74, 7.2.8]).
2.1.6 A key isomorphism
Let ![]() $X$ be a proper semistable scheme over
$X$ be a proper semistable scheme over ![]() ${\mathcal O} _K$. The following lemma will be crucial in the comparison of period morphisms.
${\mathcal O} _K$. The following lemma will be crucial in the comparison of period morphisms.
Lemma 2.9 Let ![]() $r\geq i$. There exists a natural isomorphism
$r\geq i$. There exists a natural isomorphism
Proof. This is well known; see [Reference Nekovář and NiziołNN16, Corollary 3.23] and [Reference Colmez and NiziołCN17, Proposition 5.22]. We will sketch here the construction of the map for future reference; see [Reference Nekovář and NiziołNN16, Corollary 3.23] for details. Consider the following sequence of maps of homotopy limits; they are all quasi-isomorphisms. Homotopy limits are taken in the ![]() $\infty$-derived category.
$\infty$-derived category.

Here the eigenspaces are taken in the derived sense and we used the brackets ![]() $[-]$ to denote a mapping fiber. The first two maps and the last map are the canonical maps. We wrote
$[-]$ to denote a mapping fiber. The first two maps and the last map are the canonical maps. We wrote ![]() $p_{\pi }$ for the projection
$p_{\pi }$ for the projection ![]() $x\mapsto \pi$. The second map is induced by the distinguished triangle
$x\mapsto \pi$. The second map is induced by the distinguished triangle
The third map is induced by the Künneth map; we also used here the quasi-isomorphism (2.6). The fourth map is induced by the section ![]() $\iota _{\pi }: \mathrm {R}\Gamma _{\operatorname {HK} }(X)\to \mathrm {R}\Gamma _{\operatorname {cr} }(X/R_{\pi })_{\mathbf {Q}}$ of the projection
$\iota _{\pi }: \mathrm {R}\Gamma _{\operatorname {HK} }(X)\to \mathrm {R}\Gamma _{\operatorname {cr} }(X/R_{\pi })_{\mathbf {Q}}$ of the projection ![]() $x\mapsto 0$ (recall that
$x\mapsto 0$ (recall that ![]() $\rho _{\pi }=p_{\pi }\iota _{\pi }$).
$\rho _{\pi }=p_{\pi }\iota _{\pi }$).
2.2 Localization map
For (finite simplicial) schemes ![]() $X$ over
$X$ over ![]() ${{\mathcal O} _K}$ that are smooth or log-smooth and regular, the localization map
${{\mathcal O} _K}$ that are smooth or log-smooth and regular, the localization map
where ![]() $j:X_{\overline {K}}\hookrightarrow X_{{\mathcal O} _{\overline {K}}}$ is the natural open immersion, is easy to understand as the two following lemmas show. Here
$j:X_{\overline {K}}\hookrightarrow X_{{\mathcal O} _{\overline {K}}}$ is the natural open immersion, is easy to understand as the two following lemmas show. Here ![]() $K_i(-,\mathbf {Z}/n)$ is the
$K_i(-,\mathbf {Z}/n)$ is the ![]() $K$-theory with coefficients
$K$-theory with coefficients ![]() $\mathbf {Z}/n$ (see [Reference NiziołNiz16, § 4.1.1]).
$\mathbf {Z}/n$ (see [Reference NiziołNiz16, § 4.1.1]).
Lemma 2.11 Let ![]() $X$ be a finite smooth simplicial
$X$ be a finite smooth simplicial ![]() ${{\mathcal O} _K}$-scheme. For any integer
${{\mathcal O} _K}$-scheme. For any integer ![]() $n$, the localization morphism
$n$, the localization morphism
is an isomorphism.
Proof. Recall that we have proved in [Reference NiziołNiz98, Lemma 3.1] that this lemma is true if ![]() $X$ is a single smooth scheme over
$X$ is a single smooth scheme over ![]() ${{\mathcal O} _K}$. By the same method, we get the other hypercohomology spectral sequences, namely, the weight spectral sequences [Reference ThomasonTho85, 5.13 and 5.48]
${{\mathcal O} _K}$. By the same method, we get the other hypercohomology spectral sequences, namely, the weight spectral sequences [Reference ThomasonTho85, 5.13 and 5.48]
Here ![]() $K$ is the presheaf
$K$ is the presheaf ![]() ${\mathbf {Z}}\times {\mathbf {Z}}_{\infty }BGL$, where
${\mathbf {Z}}\times {\mathbf {Z}}_{\infty }BGL$, where ![]() $BGL(U)=\injlim _nBGL_n(U)$. Since the natural inclusion
$BGL(U)=\injlim _nBGL_n(U)$. Since the natural inclusion ![]() $j:X_{\overline {K}}\hookrightarrow X_{{\mathcal O} _{\overline {K}}}$ induces a localization map on the corresponding spectral sequences compatible with the localization maps on individual schemes, we get isomorphisms on the terms of the spectral sequences that induce an isomorphism on the abutments, as wanted.
$j:X_{\overline {K}}\hookrightarrow X_{{\mathcal O} _{\overline {K}}}$ induces a localization map on the corresponding spectral sequences compatible with the localization maps on individual schemes, we get isomorphisms on the terms of the spectral sequences that induce an isomorphism on the abutments, as wanted.
Let ![]() $X$ be a finite and saturated Zariski log-smooth log-scheme over
$X$ be a finite and saturated Zariski log-smooth log-scheme over ![]() ${\mathcal O} _K^{\times }$ (respectively over
${\mathcal O} _K^{\times }$ (respectively over ![]() ${{\mathcal O} _K}$) that is classically regular. The maximal open subset
${{\mathcal O} _K}$) that is classically regular. The maximal open subset ![]() $U=X_{\operatorname {tr}}\subset X$ where the log-structure
$U=X_{\operatorname {tr}}\subset X$ where the log-structure ![]() $M_X$ is trivial is dense in
$M_X$ is trivial is dense in ![]() $X$ and we have
$X$ and we have ![]() $M_X={\mathcal O} _X\cap l_*{\mathcal O} _U^*$, where
$M_X={\mathcal O} _X\cap l_*{\mathcal O} _U^*$, where ![]() $l:U\hookrightarrow X$ is the open immersion. The subset
$l:U\hookrightarrow X$ is the open immersion. The subset ![]() $U$ is a complement of a divisor with simple normal crossings that is a union
$U$ is a complement of a divisor with simple normal crossings that is a union ![]() $D_0\cup D$ (respectively
$D_0\cup D$ (respectively ![]() $D$) of the reduced special fiber and the horizontal part
$D$) of the reduced special fiber and the horizontal part ![]() $D$.
$D$.
Let ![]() $K_1$ be a finite extension of
$K_1$ be a finite extension of ![]() $K$ and let
$K$ and let ![]() ${{\mathcal O} _{K_1}}$ be its ring of integers. The log-scheme
${{\mathcal O} _{K_1}}$ be its ring of integers. The log-scheme ![]() $X_{{\mathcal O} _{K_1}}$ is in general singular but it can be desingularized by a log-blow-up, i.e., there exists a log-blow-up
$X_{{\mathcal O} _{K_1}}$ is in general singular but it can be desingularized by a log-blow-up, i.e., there exists a log-blow-up ![]() $f: Y\to X_{{\mathcal O} _{K_1}}$ that does not modify the regular locus and such that
$f: Y\to X_{{\mathcal O} _{K_1}}$ that does not modify the regular locus and such that ![]() $Y$ is a (classically) regular Zariski log-scheme. Below we will only consider log-blow-ups of
$Y$ is a (classically) regular Zariski log-scheme. Below we will only consider log-blow-ups of ![]() $X_{{\mathcal O} _{K_1}}$ that are vertical, i.e., we blow up only closed strata involving the vertical divisor
$X_{{\mathcal O} _{K_1}}$ that are vertical, i.e., we blow up only closed strata involving the vertical divisor ![]() $D_{0,{\mathcal O} _{K_1}}$. More precisely, let
$D_{0,{\mathcal O} _{K_1}}$. More precisely, let ![]() $F(X)$ be the fan of
$F(X)$ be the fan of ![]() $X$ [Reference KatoKat94b, 10] (recall that
$X$ [Reference KatoKat94b, 10] (recall that ![]() $X$ is assumed to be Zariski and regular). It is a fan over the fan
$X$ is assumed to be Zariski and regular). It is a fan over the fan ![]() $F({\mathcal O} _K^{\times })=\operatorname {Spec} ({\mathbf {N}})$,
$F({\mathcal O} _K^{\times })=\operatorname {Spec} ({\mathbf {N}})$, ![]() $\pi : F(X)\to \operatorname {Spec} ({\mathbf {N}})$. Let
$\pi : F(X)\to \operatorname {Spec} ({\mathbf {N}})$. Let ![]() $F_0(X)$ be the vertical fan of
$F_0(X)$ be the vertical fan of ![]() $F(X)$, i.e., the maximal open subfan of
$F(X)$, i.e., the maximal open subfan of ![]() $F(X)$ containing the closed fiber
$F(X)$ containing the closed fiber ![]() $\pi ^{-1}(s)$, where
$\pi ^{-1}(s)$, where ![]() $s=\{n\geq 1|n\in {\mathbf {N}}\}$ is the closed point of
$s=\{n\geq 1|n\in {\mathbf {N}}\}$ is the closed point of ![]() $\operatorname {Spec} ({\mathbf {N}})$ [Reference TsujiSai04, proof of Lemma 2.5]. We have a natural map
$\operatorname {Spec} ({\mathbf {N}})$ [Reference TsujiSai04, proof of Lemma 2.5]. We have a natural map ![]() $F(X)\to F_0(X)$.
$F(X)\to F_0(X)$.
The log-scheme ![]() $X_{{\mathcal O} _{K_1}}$ has the fan
$X_{{\mathcal O} _{K_1}}$ has the fan ![]() $F(X_{{\mathcal O} _{K_1}})=F_e(X)=F(X)\times _{\operatorname {Spec} ({\mathbf {N}})}\operatorname {Spec} ({\mathbf {N}}_e)$, where
$F(X_{{\mathcal O} _{K_1}})=F_e(X)=F(X)\times _{\operatorname {Spec} ({\mathbf {N}})}\operatorname {Spec} ({\mathbf {N}}_e)$, where ![]() $e$ denotes the ramification index of
$e$ denotes the ramification index of ![]() ${\mathcal O} _{K_1}/{{\mathcal O} _K}$. We have the natural map
${\mathcal O} _{K_1}/{{\mathcal O} _K}$. We have the natural map ![]() $F(X_{{\mathcal O} _{K_1}})\to F_{0,e}(X)$. From now on we consider only log-blow-ups
$F(X_{{\mathcal O} _{K_1}})\to F_{0,e}(X)$. From now on we consider only log-blow-ups ![]() $Y\to X_{{\mathcal O} _{K_1}}$ induced from regular subdivisions of the vertical fan
$Y\to X_{{\mathcal O} _{K_1}}$ induced from regular subdivisions of the vertical fan ![]() $F_{0,e}(X)$. In the local picture above, we consider only log-blow-ups of
$F_{0,e}(X)$. In the local picture above, we consider only log-blow-ups of ![]() $X_{{\mathcal O} _{K_1}}$ induced from log-blow-ups of the vertical part
$X_{{\mathcal O} _{K_1}}$ induced from log-blow-ups of the vertical part ![]() $X_{{\mathcal O} _{K_1}}^v$. Notice that the scheme
$X_{{\mathcal O} _{K_1}}^v$. Notice that the scheme ![]() $Y$ has generalized semistable reduction as well and the horizontal divisor
$Y$ has generalized semistable reduction as well and the horizontal divisor ![]() $D_Y$ is the preimage of
$D_Y$ is the preimage of ![]() $D_{{\mathcal O} _{K_1}}$.
$D_{{\mathcal O} _{K_1}}$.
Let ![]() ${\mathcal {X}}_{{\mathcal O} _{\overline {K}}}$ denote the projective system of such pairs
${\mathcal {X}}_{{\mathcal O} _{\overline {K}}}$ denote the projective system of such pairs ![]() $(f:Y\to Y_{{\mathcal O} _{K_1}}, {\mathcal O} _{K_1})$ (that we will sometimes just call
$(f:Y\to Y_{{\mathcal O} _{K_1}}, {\mathcal O} _{K_1})$ (that we will sometimes just call ![]() $Y$) and
$Y$) and ![]() ${\mathcal {D}}_{{\mathcal O} _{\overline {K}}}$ denote the induced projective system
${\mathcal {D}}_{{\mathcal O} _{\overline {K}}}$ denote the induced projective system ![]() $(D_Y\subset Y,f, {\mathcal O} _{K_1})$ for
$(D_Y\subset Y,f, {\mathcal O} _{K_1})$ for ![]() $(f:Y\to X_{{\mathcal O} _{K_1}},{\mathcal O} _{K_1})\in {\mathcal {X}}_{{\mathcal O} _{\overline {K}}}$. We will show that we can pass from the
$(f:Y\to X_{{\mathcal O} _{K_1}},{\mathcal O} _{K_1})\in {\mathcal {X}}_{{\mathcal O} _{\overline {K}}}$. We will show that we can pass from the ![]() $K$-theory with compact support of the generic fiber
$K$-theory with compact support of the generic fiber ![]() $X_{\overline {K}}$ to the
$X_{\overline {K}}$ to the ![]() $K$-theory with compact support of the regular model
$K$-theory with compact support of the regular model ![]() ${\mathcal {X}}_{{\mathcal O} _{\overline {K}}}$ that we define as
${\mathcal {X}}_{{\mathcal O} _{\overline {K}}}$ that we define as
Lemma 2.12 Let ![]() $j: X_{\overline {K}}\hookrightarrow {\mathcal {X}}_{{\mathcal O} _{\overline {K}}}$ be the natural open immersion. Then the restriction
$j: X_{\overline {K}}\hookrightarrow {\mathcal {X}}_{{\mathcal O} _{\overline {K}}}$ be the natural open immersion. Then the restriction
is an isomorphism and the induced map on the ![]() $\gamma$-graded pieces
$\gamma$-graded pieces
has kernel and cokernel annihilated by ![]() $M(2d,i+1,2j)$ and
$M(2d,i+1,2j)$ and ![]() $M(2d,i,2j),$ respectively. Here
$M(2d,i,2j),$ respectively. Here ![]() $F^i_{\gamma }K_j(-,{\mathbf {Z}}/p^n)$ is a
$F^i_{\gamma }K_j(-,{\mathbf {Z}}/p^n)$ is a ![]() $\gamma$-filtration (see [Reference NiziołNiz16, § 4.1.4]).
$\gamma$-filtration (see [Reference NiziołNiz16, § 4.1.4]).
Remark 2.13 The integers ![]() $M(k,m,n)$ are defined by the following procedure [Reference SouléSou82, 3.4]. Let
$M(k,m,n)$ are defined by the following procedure [Reference SouléSou82, 3.4]. Let ![]() $l$ be a positive integer, and let
$l$ be a positive integer, and let ![]() $w_l$ be the greatest common divisor of the set of integers
$w_l$ be the greatest common divisor of the set of integers ![]() $k^{N}(k^l-1)$ as
$k^{N}(k^l-1)$ as ![]() $k$ runs over the positive integers and
$k$ runs over the positive integers and ![]() $N$ is large enough with respect to
$N$ is large enough with respect to ![]() $l$. Let
$l$. Let ![]() $M(k)$ be the product of the
$M(k)$ be the product of the ![]() $w_l$ for
$w_l$ for ![]() $2l < k$. Set
$2l < k$. Set ![]() $M(k,m,n)=\prod _{2m\leq 2l\leq n+2k+1}M(2l)$. An odd prime
$M(k,m,n)=\prod _{2m\leq 2l\leq n+2k+1}M(2l)$. An odd prime ![]() $p$ divides
$p$ divides ![]() $M(d,i,j)$ if and only if
$M(d,i,j)$ if and only if ![]() $p<(j+2d+3)/2$, and divides
$p<(j+2d+3)/2$, and divides ![]() $M(l)$ if and only if
$M(l)$ if and only if ![]() $p<(l/2)+1$.
$p<(l/2)+1$.
Proof. It suffices to argue on finite levels. So, we may simply assume that we have a regular scheme ![]() $X$ over
$X$ over ![]() ${{\mathcal O} _K}$ with a divisor
${{\mathcal O} _K}$ with a divisor ![]() $D$ that has relative simple normal crossings and whose irreducible components are all regular. We need to show the above lemma just for the pair
$D$ that has relative simple normal crossings and whose irreducible components are all regular. We need to show the above lemma just for the pair ![]() $(X,D)$.
$(X,D)$.
For the first statement of the lemma, consider the following commutative diagram with the horizontal sequences exact.

It shows that it suffices to prove that the restriction map
is an isomorphism. To see that, write ![]() $D=\bigcup _{i=1}^{i=m}D_i$ as a union of irreducible components
$D=\bigcup _{i=1}^{i=m}D_i$ as a union of irreducible components ![]() $D_i$ and argue by induction on
$D_i$ and argue by induction on ![]() $m$. Recall that we have proved in [Reference NiziołNiz08, Lemma 3.5] that the above lemma is true if
$m$. Recall that we have proved in [Reference NiziołNiz08, Lemma 3.5] that the above lemma is true if ![]() $m=1$. Assume now that the above isomorphism holds for
$m=1$. Assume now that the above isomorphism holds for ![]() $m-1$. To prove it for
$m-1$. To prove it for ![]() $m$, consider the restriction map of the following long exact sequences.
$m$, consider the restriction map of the following long exact sequences.

Here we wrote ![]() $Y=D_1$,
$Y=D_1$, ![]() $D^{\prime }=\bigcup _{i=2}^{i=m}D_i$, and
$D^{\prime }=\bigcup _{i=2}^{i=m}D_i$, and ![]() $D_Y=D^{\prime }\cap Y$. By the inductive hypothesis, we have the isomorphisms shown. It follows that we have the isomorphism
$D_Y=D^{\prime }\cap Y$. By the inductive hypothesis, we have the isomorphisms shown. It follows that we have the isomorphism
as wanted.
Hence, the first statement of the lemma is true. It implies that, for ![]() $j>d+1$, the top map in the following commutative diagram is an isomorphism.
$j>d+1$, the top map in the following commutative diagram is an isomorphism.

Here ![]() $\widetilde {F}^i_{\gamma }$ refers to a modified
$\widetilde {F}^i_{\gamma }$ refers to a modified ![]() $\gamma$-filtration (see [Reference NiziołNiz16, § 4.1.4] for details). Since, by [Reference NiziołNiz16, Lemma 4.4],
$\gamma$-filtration (see [Reference NiziołNiz16, § 4.1.4] for details). Since, by [Reference NiziołNiz16, Lemma 4.4], ![]() $M(2d,i,2j)F^i_{\gamma }K^{\rm c}_j(X_{K},D_{K},{\mathbf {Z}}/p^n)\subset \widetilde {F}^i_{\gamma }K^{\rm c}_j(X_{K},D_{K},{\mathbf {Z}}/p^n)$, we get the second statement of our lemma.
$M(2d,i,2j)F^i_{\gamma }K^{\rm c}_j(X_{K},D_{K},{\mathbf {Z}}/p^n)\subset \widetilde {F}^i_{\gamma }K^{\rm c}_j(X_{K},D_{K},{\mathbf {Z}}/p^n)$, we get the second statement of our lemma.
2.3 Étale Chern classes
The following proposition shows that we can invert étale Chern classes modulo some constants.
Proposition 2.14 Let ![]() $Y$ be a smooth finite simplicial scheme over
$Y$ be a smooth finite simplicial scheme over ![]() $\overline {K}$ such that
$\overline {K}$ such that ![]() $Y\simeq \operatorname {sk} _mY$. Set
$Y\simeq \operatorname {sk} _mY$. Set ![]() $d=\max _{s\leq m}\dim Y_s$. Let
$d=\max _{s\leq m}\dim Y_s$. Let ![]() $p^n\geq 5$,
$p^n\geq 5$, ![]() $j\geq \max \{2d,2\}$,
$j\geq \max \{2d,2\}$, ![]() $j\geq 3$ for
$j\geq 3$ for ![]() $d=0$ and
$d=0$ and ![]() $p=2$, and
$p=2$, and ![]() $2i-j\geq 0$. There exists an integer
$2i-j\geq 0$. There exists an integer ![]() $D(d,m,i,j)$ depending only on
$D(d,m,i,j)$ depending only on ![]() $d$,
$d$, ![]() $m$,
$m$, ![]() $i$, and
$i$, and ![]() $j$ such that the kernel and cokernel of the Chern class map
$j$ such that the kernel and cokernel of the Chern class map
are annihilated by ![]() $D(d,m,i,j)$. Any prime
$D(d,m,i,j)$. Any prime ![]() $p> d+m+j+1$ does not divide
$p> d+m+j+1$ does not divide ![]() $D(d,m,i,j)$.
$D(d,m,i,j)$.
Remark 2.15 This proposition is a ![]() $K$-theory version of the following theorem of Suslin [Reference SuslinSus00, Reference GeisserGei10].
$K$-theory version of the following theorem of Suslin [Reference SuslinSus00, Reference GeisserGei10].
Theorem 2.16 Suslin For ![]() $Y$ a smooth scheme of dimension
$Y$ a smooth scheme of dimension ![]() $d$ over
$d$ over ![]() $\overline {K}$, the change of topology map
$\overline {K}$, the change of topology map
is an isomorphism for ![]() $i\geq d$. Here
$i\geq d$. Here ![]() $\mathbf {Z}/p^n(i)_M$ is the complex of motivic sheaves (Bloch higher Chow complex).
$\mathbf {Z}/p^n(i)_M$ is the complex of motivic sheaves (Bloch higher Chow complex).
Proof. To prove the proposition, we are going to argue by induction on ![]() $m$. The case of
$m$. The case of ![]() $m=0$ was treated in [Reference NiziołNiz08, Proposition 3.2]. We computed there that
$m=0$ was treated in [Reference NiziołNiz08, Proposition 3.2]. We computed there that
Assume that ![]() $m\geq 1$. For the inductive step, we need to filter
$m\geq 1$. For the inductive step, we need to filter ![]() $Y$ by its skeletons. We work on the site of schemes smooth over
$Y$ by its skeletons. We work on the site of schemes smooth over ![]() $\overline {K}$ equipped with the Zariski topology. Take a fibrant replacement
$\overline {K}$ equipped with the Zariski topology. Take a fibrant replacement ![]() $K\to K^f$. The pointed simplicial sets
$K\to K^f$. The pointed simplicial sets ![]() $\operatorname {Hom}(\operatorname {sk} _tY,K^f)$ form a tower of fibrations converging to
$\operatorname {Hom}(\operatorname {sk} _tY,K^f)$ form a tower of fibrations converging to ![]() $\operatorname {Hom}(Y,K^f)$ [Reference Bousfield and KanBK72, X.3.2]. Let
$\operatorname {Hom}(Y,K^f)$ [Reference Bousfield and KanBK72, X.3.2]. Let ![]() $F_t$ be the fiber over
$F_t$ be the fiber over ![]() $*$ of
$*$ of ![]() $\operatorname {Hom}(\operatorname {sk} _tY,K^f)\to \operatorname {Hom}(\operatorname {sk} _{t-1}Y,K^f)$. Then, by Bousfield and Kan [Reference Bousfield and KanBK72, Proposition X.6.3],
$\operatorname {Hom}(\operatorname {sk} _tY,K^f)\to \operatorname {Hom}(\operatorname {sk} _{t-1}Y,K^f)$. Then, by Bousfield and Kan [Reference Bousfield and KanBK72, Proposition X.6.3],
where
and ![]() $s_i:Y_{t-1}\to Y_{t}$ is a codegeneracy. In particular, the natural map
$s_i:Y_{t-1}\to Y_{t}$ is a codegeneracy. In particular, the natural map
is a weak equivalence.
For ![]() $j\geq 2$ and
$j\geq 2$ and ![]() $j+t\geq 3$, using again [Reference Bousfield and KanBK72, Proposition X.6.3], we get the long exact sequence
$j+t\geq 3$, using again [Reference Bousfield and KanBK72, Proposition X.6.3], we get the long exact sequence
Here we set
By functoriality, ![]() $\lambda$-operations act on this exact sequence and this yields a sequence of
$\lambda$-operations act on this exact sequence and this yields a sequence of ![]() $\gamma$-gradings
$\gamma$-gradings
that is exact only up to certain universal constants. More precisely, we have the following lemma.
Lemma 2.18 If the element ![]() $[x]$ at any level of the long sequence (2.17) is a cocycle, then
$[x]$ at any level of the long sequence (2.17) is a cocycle, then ![]() $C[x]$ is a coboundary for the following constant
$C[x]$ is a coboundary for the following constant ![]() $C$:
$C$:
(i) if
 $d_1([x])=0$ then
$d_1([x])=0$ then  $C=M(2i)M(2(j+t+d-i))$;
$C=M(2i)M(2(j+t+d-i))$;(ii) if
 $d_2([x])=0$ then
$d_2([x])=0$ then  $C=M(2i)M(2(j+t+d-i))$;
$C=M(2i)M(2(j+t+d-i))$;(iii) if
 $d([x])=0$ then
$d([x])=0$ then  $C=M(2i)M(2(j+t+d+1-i))$.
$C=M(2i)M(2(j+t+d+1-i))$.
Proof. First, note that ![]() $F^{j+t+1}_{\gamma }K_{j+t}(Y^{\prime }_t,\mathbf {Z}/p^n)=0$ since
$F^{j+t+1}_{\gamma }K_{j+t}(Y^{\prime }_t,\mathbf {Z}/p^n)=0$ since ![]() $K_{j+t}(Y^{\prime }_t,\mathbf {Z}/p^n)\subset K_{j+t}(Y_t,\mathbf {Z}/p^n)$ and we have [Reference NiziołNiz16, Lemma 4.3].
$K_{j+t}(Y^{\prime }_t,\mathbf {Z}/p^n)\subset K_{j+t}(Y_t,\mathbf {Z}/p^n)$ and we have [Reference NiziołNiz16, Lemma 4.3].
We will prove (i). The other cases can be proved in a similar way. Assume that ![]() $[x]\in \operatorname {gr}^i_{\gamma }K_j(\operatorname {sk} _{t}Y,\mathbf {Z}/p^n)$ and look at the sequence
$[x]\in \operatorname {gr}^i_{\gamma }K_j(\operatorname {sk} _{t}Y,\mathbf {Z}/p^n)$ and look at the sequence
Assume that ![]() $x\in F_{\gamma }^iK_j(\operatorname {sk} _{t}Y,\mathbf {Z}/p^n)$ is such that
$x\in F_{\gamma }^iK_j(\operatorname {sk} _{t}Y,\mathbf {Z}/p^n)$ is such that ![]() $d_1([x])=0$. That means that on the level of the long exact sequence (2.17),
$d_1([x])=0$. That means that on the level of the long exact sequence (2.17), ![]() $d_1(x)\in F_{\gamma }^{i+1}K_j(\operatorname {sk} _{t-1}Y,\mathbf {Z}/p^n)$. We will need certain projectors [Reference SouléSou82, 2.8]. For two natural numbers
$d_1(x)\in F_{\gamma }^{i+1}K_j(\operatorname {sk} _{t-1}Y,\mathbf {Z}/p^n)$. We will need certain projectors [Reference SouléSou82, 2.8]. For two natural numbers ![]() $a\neq b$, denote by
$a\neq b$, denote by ![]() $A_{abk}$,
$A_{abk}$, ![]() $k\geq 2$, a family of integers such that
$k\geq 2$, a family of integers such that ![]() $w_{|b-a|}=\sum _{k\geq 2}A_{abk}(k^a-k^b)$. Let
$w_{|b-a|}=\sum _{k\geq 2}A_{abk}(k^a-k^b)$. Let
Note that, for any ![]() $x\in K_j(-,{\mathbf {Z}}/p^n)$, we have
$x\in K_j(-,{\mathbf {Z}}/p^n)$, we have ![]() $\phi _a(x)\in F^a_{\gamma }K_j(-, {\mathbf {Z}}/p^n)$. Since the
$\phi _a(x)\in F^a_{\gamma }K_j(-, {\mathbf {Z}}/p^n)$. Since the ![]() $k$th Adams operation
$k$th Adams operation ![]() $\psi _k$ acts on
$\psi _k$ acts on ![]() $gr^{\rm c}_{\gamma }K_j(\operatorname {sk} _{t}Y,\mathbf {Z}/p^n)$ as
$gr^{\rm c}_{\gamma }K_j(\operatorname {sk} _{t}Y,\mathbf {Z}/p^n)$ as ![]() $k^{\rm c}$, we have
$k^{\rm c}$, we have
so ![]() $M(2(j+t+d-i))[x]=[\phi ^i_{t-1}(x)]$. Since
$M(2(j+t+d-i))[x]=[\phi ^i_{t-1}(x)]$. Since ![]() $d_1x\in F_{\gamma }^{i+1}K_j(\operatorname {sk} _{t-1}Y,\mathbf {Z}/p^n)$ and by [Reference NiziołNiz16, Lemma 4.3] the length of the
$d_1x\in F_{\gamma }^{i+1}K_j(\operatorname {sk} _{t-1}Y,\mathbf {Z}/p^n)$ and by [Reference NiziołNiz16, Lemma 4.3] the length of the ![]() $\gamma$-filtration is
$\gamma$-filtration is ![]() $j+t-1+d$, we compute that
$j+t-1+d$, we compute that ![]() $d_1(\phi ^i_{t-1}(x))=\phi ^i_{t-1}(d_1x)=0$. Hence,
$d_1(\phi ^i_{t-1}(x))=\phi ^i_{t-1}(d_1x)=0$. Hence, ![]() $M(2(j+t+d-i))[x]=[y]$ is such that
$M(2(j+t+d-i))[x]=[y]$ is such that ![]() $d_1(y)=0$ and
$d_1(y)=0$ and ![]() $y\in F_{\gamma }^iK_j(\operatorname {sk} _{t}Y,\mathbf {Z}/p^n)$.
$y\in F_{\gamma }^iK_j(\operatorname {sk} _{t}Y,\mathbf {Z}/p^n)$.
From the long exact sequence (2.17), we then get ![]() $w\in K_{j+t}(Y^{\prime }_t,\mathbf {Z}/p^n)$ such that
$w\in K_{j+t}(Y^{\prime }_t,\mathbf {Z}/p^n)$ such that ![]() $dw=y$. Consider
$dw=y$. Consider ![]() $w_1=\phi _i(w)\in F_{\gamma }^{i}K_{j+t}(Y^{\prime }_t,\mathbf {Z}/p^n)$. We have
$w_1=\phi _i(w)\in F_{\gamma }^{i}K_{j+t}(Y^{\prime }_t,\mathbf {Z}/p^n)$. We have
 \begin{align*} [d(w_1)]=[\phi_i(dw)]&=\prod_{2\leq b\leq i-1}\biggl(\sum_{k\geq 2} A_{ibk}([\psi_k(dw)]-k^{b}[dw])\biggr)\\ &=\prod_{2\leq b\leq i-1}\biggl(\sum_{k\geq 2} A_{ibk}(k^{i}-k^{b})\biggr)[dw]=M(2i)[dw]. \end{align*}
\begin{align*} [d(w_1)]=[\phi_i(dw)]&=\prod_{2\leq b\leq i-1}\biggl(\sum_{k\geq 2} A_{ibk}([\psi_k(dw)]-k^{b}[dw])\biggr)\\ &=\prod_{2\leq b\leq i-1}\biggl(\sum_{k\geq 2} A_{ibk}(k^{i}-k^{b})\biggr)[dw]=M(2i)[dw]. \end{align*}
Hence, ![]() $M(2i)M(2(j+t+d-i))[x]$ is a coboundary, as wanted.
$M(2i)M(2(j+t+d-i))[x]$ is a coboundary, as wanted.
To proceed, we will need the following two lemmas.
Lemma 2.19 For a ![]() $d$-dimensional scheme
$d$-dimensional scheme ![]() $Y$ smooth over
$Y$ smooth over ![]() $\overline {K}$, we have
$\overline {K}$, we have
Proof. This is the ![]() $K$-theory version of the mod-
$K$-theory version of the mod-![]() $p^n$ Beilinson–Soulé conjecture. Recall that we know its motivic version to be true. That is,
$p^n$ Beilinson–Soulé conjecture. Recall that we know its motivic version to be true. That is, ![]() $H^{2i-j}_{\operatorname {Zar}}(Y,{\mathbf {Z}}/p^n)=0$ for
$H^{2i-j}_{\operatorname {Zar}}(Y,{\mathbf {Z}}/p^n)=0$ for ![]() $2i-j<0$ [Reference AkhtarAkh07]. So, we just need to translate this statement into
$2i-j<0$ [Reference AkhtarAkh07]. So, we just need to translate this statement into ![]() $K$-theory. Recall that Levine [Reference LevineLev04] has constructed a Zariski Atiyah–Hirzebruch spectral sequence from motivic cohomology to
$K$-theory. Recall that Levine [Reference LevineLev04] has constructed a Zariski Atiyah–Hirzebruch spectral sequence from motivic cohomology to ![]() $K$-theory:
$K$-theory:
Here the differential ![]() $d_r: E^{s,q}_r\to E^{s+r,q+r-1}_r$. Denote by
$d_r: E^{s,q}_r\to E^{s+r,q+r-1}_r$. Denote by ![]() $F^i_{AH}$ the filtration on
$F^i_{AH}$ the filtration on ![]() $K$-theory groups defined by this spectral sequence. Levine showed [Reference LevineLev04, 13.11] that
$K$-theory groups defined by this spectral sequence. Levine showed [Reference LevineLev04, 13.11] that
By the above, the kernel of the map
is annihilated by ![]() $M(d,i+1,2j)$ and the cokernel by
$M(d,i+1,2j)$ and the cokernel by ![]() $M(d,i,2j)$. By [Reference NiziołNiz16, (4.4)], the same holds for the map
$M(d,i,2j)$. By [Reference NiziołNiz16, (4.4)], the same holds for the map
Since ![]() $F^i_{AH}/F^{i+1}_{AH}K_j(Y,{\mathbf {Z}}/p^n)$ is a subquotient of
$F^i_{AH}/F^{i+1}_{AH}K_j(Y,{\mathbf {Z}}/p^n)$ is a subquotient of ![]() $E^{2i-j,2i}_2=H^{2i-j}_{\operatorname {Zar}}(Y,{\mathbf {Z}}/p^n(i)_M)$, we are done.
$E^{2i-j,2i}_2=H^{2i-j}_{\operatorname {Zar}}(Y,{\mathbf {Z}}/p^n(i)_M)$, we are done.
Lemma 2.20 (i) For ![]() $i,j$ as in Proposition 2.14, the kernel and cokernel of the Chern class map
$i,j$ as in Proposition 2.14, the kernel and cokernel of the Chern class map
where ![]() $H^{2i-j}_{\operatorname {\acute {e}t} }(Y^{\prime }_m,\mathbf {Z}/p^n(i)) =H^{2i-j}_{\operatorname {\acute {e}t} }(Y_m,\mathbf {Z}/p^n(i))\cap \ker s_0^*\cap \cdots \cap \ker s_{m-1}^*$, are annihilated by a constant
$H^{2i-j}_{\operatorname {\acute {e}t} }(Y^{\prime }_m,\mathbf {Z}/p^n(i)) =H^{2i-j}_{\operatorname {\acute {e}t} }(Y_m,\mathbf {Z}/p^n(i))\cap \ker s_0^*\cap \cdots \cap \ker s_{m-1}^*$, are annihilated by a constant ![]() $T(d,m,i,j)$. Any prime
$T(d,m,i,j)$. Any prime ![]() $p>d+j+1$ does not divide
$p>d+j+1$ does not divide ![]() $T(d,m,i,j)$.
$T(d,m,i,j)$.
(ii) For ![]() $2i-j<0$, we have
$2i-j<0$, we have
Proof. Let us start with the first statement. For the kernel, take ![]() $x\in F^i_{\gamma }K_{j}(Y^{\prime }_m,\mathbf {Z}/p^n)$ such that
$x\in F^i_{\gamma }K_{j}(Y^{\prime }_m,\mathbf {Z}/p^n)$ such that ![]() $\overline {c}_{i,j}^{\operatorname {\acute {e}t} }(x)=0$. Then
$\overline {c}_{i,j}^{\operatorname {\acute {e}t} }(x)=0$. Then ![]() $D(d,0,i,j)x\in F^{i+1}_{\gamma }K_{j}(Y_m,\mathbf {Z}/p^n)\cap K_{j}(Y^{\prime }_m,\mathbf {Z}/p^n).$ Set
$D(d,0,i,j)x\in F^{i+1}_{\gamma }K_{j}(Y_m,\mathbf {Z}/p^n)\cap K_{j}(Y^{\prime }_m,\mathbf {Z}/p^n).$ Set ![]() $y=D(d,0,i,j)x$. We have
$y=D(d,0,i,j)x$. We have
Since, by [Reference NiziołNiz16, Lemma 4.3], ![]() $F^{j+d+1}_{\gamma }K_{j}(Y_m,\mathbf {Z}/p^n)=0$, by the inductive argument, we get
$F^{j+d+1}_{\gamma }K_{j}(Y_m,\mathbf {Z}/p^n)=0$, by the inductive argument, we get
So, the kernel is annihilated by ![]() $i!(i+1)!\cdots (j+d)!D(d,0,i,j)$.
$i!(i+1)!\cdots (j+d)!D(d,0,i,j)$.
For the cokernel, take ![]() $x\in H^{2i-j}_{\operatorname {\acute {e}t} }(Y^{\prime }_m,\mathbf {Z}/p^n(i))$. Then
$x\in H^{2i-j}_{\operatorname {\acute {e}t} }(Y^{\prime }_m,\mathbf {Z}/p^n(i))$. Then ![]() $D(d,0,i,j)x=\overline {c}_{i,j}^{\operatorname {\acute {e}t} }(y)$ for some element
$D(d,0,i,j)x=\overline {c}_{i,j}^{\operatorname {\acute {e}t} }(y)$ for some element ![]() $y$ of
$y$ of ![]() $F^i_{\gamma }K_{j}(Y_m,\mathbf {Z}/p^n)$. We need to show that some multiple of
$F^i_{\gamma }K_{j}(Y_m,\mathbf {Z}/p^n)$. We need to show that some multiple of ![]() $y$ lies in
$y$ lies in ![]() $F^i_{\gamma }K_{j}(Y^{\prime }_m,\mathbf {Z}/p^n)$. For each
$F^i_{\gamma }K_{j}(Y^{\prime }_m,\mathbf {Z}/p^n)$. For each ![]() $l$,
$l$, ![]() $0\leq l\leq m-1$, consider the following commutative diagram.
$0\leq l\leq m-1$, consider the following commutative diagram.

Since ![]() $s_l^*(x)=0$, we have
$s_l^*(x)=0$, we have ![]() $D(d,0,i,j)s_l^*(y)\in F^{i+1}_{\gamma }K_{j}(Y_{m-1},\mathbf {Z}/p^n)$. Arguing just like in the proof of Lemma 2.18, we find that
$D(d,0,i,j)s_l^*(y)\in F^{i+1}_{\gamma }K_{j}(Y_{m-1},\mathbf {Z}/p^n)$. Arguing just like in the proof of Lemma 2.18, we find that
Hence, repeating this argument for all ![]() $l$, we get
$l$, we get
As above, ![]() $i!(i+1)!\cdots (j+d)!D(d,0,i,j)^mM(2(j+d-i))^m[y]=[y^{\prime }]$,
$i!(i+1)!\cdots (j+d)!D(d,0,i,j)^mM(2(j+d-i))^m[y]=[y^{\prime }]$, ![]() $y^{\prime }\in F^i_{\gamma }K_{j}(Y^{\prime }_{m},\mathbf {Z}/p^n)$. Hence, the cokernel is annihilated by
$y^{\prime }\in F^i_{\gamma }K_{j}(Y^{\prime }_{m},\mathbf {Z}/p^n)$. Hence, the cokernel is annihilated by ![]() $i!(i+1)!\cdots (j+d)!D(d,0,i,j)^{m+1}M(2(j+d-i))^m$. Set
$i!(i+1)!\cdots (j+d)!D(d,0,i,j)^{m+1}M(2(j+d-i))^m$. Set
For the second statement, assume that ![]() $2i-j<0$ and take
$2i-j<0$ and take ![]() $x\in F^i_{\gamma }K_j(Y^{\prime }_m,{\mathbf {Z}}/p^n)$. By Lemma 2.19, we have
$x\in F^i_{\gamma }K_j(Y^{\prime }_m,{\mathbf {Z}}/p^n)$. By Lemma 2.19, we have ![]() $M(d,i+1,2j)M(d,i,2j)x\in F^{i+1}_{\gamma }K_j(Y_m,{\mathbf {Z}}/p^n)\cap K_j(Y^{\prime }_m,{\mathbf {Z}}/p^n).$ Arguing as above,
$M(d,i+1,2j)M(d,i,2j)x\in F^{i+1}_{\gamma }K_j(Y_m,{\mathbf {Z}}/p^n)\cap K_j(Y^{\prime }_m,{\mathbf {Z}}/p^n).$ Arguing as above, ![]() $i!(i+1)!\cdots (j+d)!M(d,i+1,2j)M(d,i,2j)x\in F^{i+1}_{\gamma }K_j(Y^{\prime }_m,{\mathbf {Z}}/p^n).$
$i!(i+1)!\cdots (j+d)!M(d,i+1,2j)M(d,i,2j)x\in F^{i+1}_{\gamma }K_j(Y^{\prime }_m,{\mathbf {Z}}/p^n).$
Consider now the homotopy cofiber sequence
By [Reference NiziołNiz16, Remark 5.4], the étale Chern class maps are compatible with it and we get the following commutative diagram (where we skipped the coefficients ![]() $\mathbf {Z}/p^n$ and
$\mathbf {Z}/p^n$ and ![]() $\mathbf {Z}/p^n(i)$, respectively).
$\mathbf {Z}/p^n(i)$, respectively).

Here we put ![]() $H^{*}_{\operatorname {\acute {e}t} }(Y^{\prime }_m)=H^{*}_{\operatorname {\acute {e}t} }(Y_m)\cap \ker s_0^*\cap \cdots \cap \ker s_{m-1}^*$.
$H^{*}_{\operatorname {\acute {e}t} }(Y^{\prime }_m)=H^{*}_{\operatorname {\acute {e}t} }(Y_m)\cap \ker s_0^*\cap \cdots \cap \ker s_{m-1}^*$.
Let us first look at the kernel of the map ![]() $\overline {c}_{ij}^{\operatorname {\acute {e}t} }:\operatorname {gr}^i_{\gamma }K_j(\operatorname {sk} _{m}Y,\mathbf {Z}/p^n)\to H^{2i-j}_{\operatorname {\acute {e}t} }(\operatorname {sk} _mY,\mathbf {Z}/p^n(i))$. Diagram chasing and the inductive hypothesis together with Lemmas 2.18 and 2.20 imply easily that this kernel is annihilated by
$\overline {c}_{ij}^{\operatorname {\acute {e}t} }:\operatorname {gr}^i_{\gamma }K_j(\operatorname {sk} _{m}Y,\mathbf {Z}/p^n)\to H^{2i-j}_{\operatorname {\acute {e}t} }(\operatorname {sk} _mY,\mathbf {Z}/p^n(i))$. Diagram chasing and the inductive hypothesis together with Lemmas 2.18 and 2.20 imply easily that this kernel is annihilated by
if ![]() $2i\geq j+m$; if
$2i\geq j+m$; if ![]() $2i< j+m$, we can drop the first term. Here we used the fact that the numbers
$2i< j+m$, we can drop the first term. Here we used the fact that the numbers ![]() $M(d,i+1,2j)$ and
$M(d,i+1,2j)$ and ![]() $M(d,i,2j)$ that appear in Lemma 2.19 divide
$M(d,i,2j)$ that appear in Lemma 2.19 divide ![]() $D(d,0,i,j)$.
$D(d,0,i,j)$.
By a very similar argument, we get that the cokernel of the map ![]() $\overline {c}_{ij}^{\operatorname {\acute {e}t} }:\operatorname {gr}^i_{\gamma }K_j(\operatorname {sk} _{m}Y,\mathbf {Z}/p^n)\to H^{2i-j}_{\operatorname {\acute {e}t} }(\operatorname {sk} _mY,\mathbf {Z}/p^n(i))$ is annihilated by
$\overline {c}_{ij}^{\operatorname {\acute {e}t} }:\operatorname {gr}^i_{\gamma }K_j(\operatorname {sk} _{m}Y,\mathbf {Z}/p^n)\to H^{2i-j}_{\operatorname {\acute {e}t} }(\operatorname {sk} _mY,\mathbf {Z}/p^n(i))$ is annihilated by
if ![]() $2i\geq j+m$; if
$2i\geq j+m$; if ![]() $2i=j+m-1$, we can drop the first term; if
$2i=j+m-1$, we can drop the first term; if ![]() $2i < j+m-1$, we can drop the first two terms.
$2i < j+m-1$, we can drop the first two terms.
Set
for ![]() $2i\geq j+m$; if
$2i\geq j+m$; if ![]() $2i=j+m-1$, we drop the first term; if
$2i=j+m-1$, we drop the first term; if ![]() $2i < j+m-1$, we drop the first two terms. Since an odd prime
$2i < j+m-1$, we drop the first two terms. Since an odd prime ![]() $p$ divides
$p$ divides ![]() $M(l)$ if and only if
$M(l)$ if and only if ![]() $p<(l/2)+1$ and
$p<(l/2)+1$ and ![]() $H^t_{\operatorname {\acute {e}t} }(\operatorname {sk} _mY)=0$ for
$H^t_{\operatorname {\acute {e}t} }(\operatorname {sk} _mY)=0$ for ![]() $t>2d+m+1$, we get the last statement of the proposition.
$t>2d+m+1$, we get the last statement of the proposition.
3. Comparison theorems for finite simplicial schemes via  $K$-theory
$K$-theory
We are now ready to prove comparison theorems for finite simplicial schemes using ![]() $K$-theory.
$K$-theory.
3.1 Crystalline conjecture for finite simplicial schemes
We start with the crystalline conjecture.
3.1.1 Integral crystalline conjecture
We treat first its integral version. Let ![]() $X$ be a smooth proper finite simplicial scheme over
$X$ be a smooth proper finite simplicial scheme over ![]() ${{\mathcal O} _K}$,
${{\mathcal O} _K}$, ![]() ${{\mathcal O} _K}=W(k)$. Assume that
${{\mathcal O} _K}=W(k)$. Assume that ![]() $X\simeq \operatorname {sk} _mX$ and that the dimension
$X\simeq \operatorname {sk} _mX$ and that the dimension ![]() $d\leq p-2$,
$d\leq p-2$, ![]() $d=\max _{s\leq m}\dim X_s$. We would like to construct functorial Galois-equivariant morphisms
$d=\max _{s\leq m}\dim X_s$. We would like to construct functorial Galois-equivariant morphisms
We will be able to do it under certain additional restrictions on the integers ![]() $a,b$, and
$a,b$, and ![]() $d$. Our construction is based on the following diagram.
$d$. Our construction is based on the following diagram.

Here ![]() $1\leq b < p-1$,
$1\leq b < p-1$, ![]() $2b-a\geq 3$,
$2b-a\geq 3$, ![]() $p^n\geq 5$, and
$p^n\geq 5$, and ![]() $p\neq 2$. The Chern class map
$p\neq 2$. The Chern class map
is defined as the limit over finite extensions ![]() ${\mathcal O} _K'/{{\mathcal O} _K}$ of the syntomic Chern class maps
${\mathcal O} _K'/{{\mathcal O} _K}$ of the syntomic Chern class maps
Due to [Reference NiziołNiz16, Lemma 5.3], the Chern class maps ![]() $\overline {c}_{b,2b-a}^{\operatorname {\acute {e}t} }$ and
$\overline {c}_{b,2b-a}^{\operatorname {\acute {e}t} }$ and ![]() $\overline {c}_{b,2b-a}^{\operatorname {syn}}$ factor through
$\overline {c}_{b,2b-a}^{\operatorname {syn}}$ factor through ![]() $F^{b+1}_{\gamma }$ yielding the maps in the above diagram. The restriction map
$F^{b+1}_{\gamma }$ yielding the maps in the above diagram. The restriction map
is an isomorphism by Lemma 2.11. By Proposition 2.14, the étale Chern class map
is an isomorphism if ![]() $p>d+m+2b-a+1$.
$p>d+m+2b-a+1$.
Assume now that ![]() $b\geq d$,
$b\geq d$, ![]() $2b-a\geq 3$, and
$2b-a\geq 3$, and ![]() $p-2\geq d+m+2b-a$. Define the morphisms
$p-2\geq d+m+2b-a$. Define the morphisms
as the composition ![]() $\alpha _{ab}:= \psi _n \overline {c}^{\operatorname {syn}}_{b,2b-a}(j^*)^{-1}(\overline {c}^{\operatorname {\acute {e}t} }_{b,2b-a})^{-1}$, where
$\alpha _{ab}:= \psi _n \overline {c}^{\operatorname {syn}}_{b,2b-a}(j^*)^{-1}(\overline {c}^{\operatorname {\acute {e}t} }_{b,2b-a})^{-1}$, where ![]() $\psi _n$ is the natural map
$\psi _n$ is the natural map
Note that, by Proposition 2.3, this map is an isomorphism.
The following theorem generalizes our [Reference NiziołNiz98, Theorem 4.1] from schemes to finite simplicial schemes.
Theorem 3.2 For any proper smooth finite simplicial scheme ![]() $X$ over
$X$ over ![]() ${{\mathcal O} _K}=W(k)$,
${{\mathcal O} _K}=W(k)$, ![]() $X\simeq \operatorname {sk} _mX$, the functorial Galois-equivariant morphism
$X\simeq \operatorname {sk} _mX$, the functorial Galois-equivariant morphism
is an isomorphism if the numbers ![]() $p,b,d$ are such that
$p,b,d$ are such that ![]() $b\geq 2d+3$,
$b\geq 2d+3$, ![]() $p-2\geq 2b+d+m$ for
$p-2\geq 2b+d+m$ for ![]() $d=\max _{s\leq m}\dim X_s$.
$d=\max _{s\leq m}\dim X_s$.
Remark 3.3 The original constants that appear in [Reference NiziołNiz98] are different than (worse than) the ones we have quoted here. Also there we have assumed that the scheme ![]() $X$ was projective over
$X$ was projective over ![]() ${{\mathcal O} _K}$. However, one can easily modify the proof of Theorem 4.1 from [Reference NiziołNiz98] by replacing the weak Proposition 4.1 used in [Reference NiziołNiz98] with its improved version (Proposition 3.2) from [Reference NiziołNiz08] to get the above theorem for schemes.
${{\mathcal O} _K}$. However, one can easily modify the proof of Theorem 4.1 from [Reference NiziołNiz98] by replacing the weak Proposition 4.1 used in [Reference NiziołNiz98] with its improved version (Proposition 3.2) from [Reference NiziołNiz08] to get the above theorem for schemes.
Proof. By Lemma 2.11, Proposition 2.14, and Proposition 2.3, it suffices to show that the syntomic Chern class map
is an isomorphism. Note that for ![]() $a<0$ this is an isomorphism by Lemma 2.19.
$a<0$ this is an isomorphism by Lemma 2.19.
We argue by induction on ![]() $m\geq 0$ such that
$m\geq 0$ such that ![]() $X\simeq \operatorname {sk} _mX$. The case of
$X\simeq \operatorname {sk} _mX$. The case of ![]() $m=0$ is treated by [Reference NiziołNiz98, Theorem 4.1]. Assume that our theorem is true for
$m=0$ is treated by [Reference NiziołNiz98, Theorem 4.1]. Assume that our theorem is true for ![]() $m-1$. To show it for
$m-1$. To show it for ![]() $m$, consider the homotopy cofiber sequence
$m$, consider the homotopy cofiber sequence
and apply the syntomic Chern class maps to it. We get the following map of sequences.

Here we set ![]() $K^*_{*}(Y)=\operatorname {gr}^*_{\gamma }K_{*}(Y_{{\mathcal O} _{\overline {K}}})$,
$K^*_{*}(Y)=\operatorname {gr}^*_{\gamma }K_{*}(Y_{{\mathcal O} _{\overline {K}}})$, ![]() $H^*(Y, *)=H^*_{\operatorname {\acute {e}t} }(Y_{{\mathcal O} _{\overline {K}}},{\mathcal {S}}_n(*))$, and skipped the coefficients
$H^*(Y, *)=H^*_{\operatorname {\acute {e}t} }(Y_{{\mathcal O} _{\overline {K}}},{\mathcal {S}}_n(*))$, and skipped the coefficients ![]() $\mathbf {Z}/p^n$ in
$\mathbf {Z}/p^n$ in ![]() $K$-theory. We also put
$K$-theory. We also put
where each ![]() $s_i: X_{m-1}\to X_m$ is a degeneracy map. The bottom sequence is exact. By Lemma 2.18, so is the top. By the inductive hypothesis and by the case
$s_i: X_{m-1}\to X_m$ is a degeneracy map. The bottom sequence is exact. By Lemma 2.18, so is the top. By the inductive hypothesis and by the case ![]() $m=0$ of this theorem plus Lemmas 2.20 and 2.11, we have the isomorphisms shown. It follows that the syntomic Chern class map
$m=0$ of this theorem plus Lemmas 2.20 and 2.11, we have the isomorphisms shown. It follows that the syntomic Chern class map
is an isomorphism as well. Since
we are done.
Example 3.4 Integral crystalline conjecture for cohomology with compact support. As a corollary of the above comparison theorem, we obtain a comparison theorem for cohomology with compact support. Consider a proper smooth scheme ![]() $X$ over
$X$ over ![]() ${{\mathcal O} _K}=W(k)$. Let
${{\mathcal O} _K}=W(k)$. Let ![]() $i:D\hookrightarrow X$, built from
$i:D\hookrightarrow X$, built from ![]() $m$ irreducible components that are smooth over
$m$ irreducible components that are smooth over ![]() ${{\mathcal O} _K}$, be the divisor at infinity of
${{\mathcal O} _K}$, be the divisor at infinity of ![]() $X$. Let
$X$. Let ![]() $U=X\setminus D$. Consider the simplicial scheme
$U=X\setminus D$. Consider the simplicial scheme ![]() $C(X,D):=\operatorname {cofiber}(\widetilde {D}_{{\scriptscriptstyle \bullet }}\stackrel {i_*}{\to } X)$. We have
$C(X,D):=\operatorname {cofiber}(\widetilde {D}_{{\scriptscriptstyle \bullet }}\stackrel {i_*}{\to } X)$. We have ![]() $C(X,D)\simeq \operatorname {sk} _mC(X,D)$. Equip
$C(X,D)\simeq \operatorname {sk} _mC(X,D)$. Equip ![]() $X$ with the log-structure associated to
$X$ with the log-structure associated to ![]() $D$. Applying the above constructions to
$D$. Applying the above constructions to ![]() $C(X,D)$, we obtain the basic following diagram
$C(X,D)$, we obtain the basic following diagram

and the induced period morphism
But, by Lemma 2.1,
 \begin{align*} H^{a}_{\operatorname{\acute{e}t} }(C(X_{\overline{K}},D_{\overline{K}}),\mathbf{Z}/p^n(b))&\simeq H^{a}_{\operatorname{\acute{e}t} ,c}(U_{\overline{K}},\mathbf{Z}/p^n(b)), \\ H^{a}_{\operatorname{\acute{e}t} }(C(X_{{\mathcal O}_{\overline{K}}},D_{{\mathcal O}_{\overline{K}}}),{\mathcal{S}}_n(b))&\simeq H^{a}_{\operatorname{\acute{e}t} ,c}(X_{{\mathcal O}_{\overline{K}}},{\mathcal{S}}_n(b)). \end{align*}
\begin{align*} H^{a}_{\operatorname{\acute{e}t} }(C(X_{\overline{K}},D_{\overline{K}}),\mathbf{Z}/p^n(b))&\simeq H^{a}_{\operatorname{\acute{e}t} ,c}(U_{\overline{K}},\mathbf{Z}/p^n(b)), \\ H^{a}_{\operatorname{\acute{e}t} }(C(X_{{\mathcal O}_{\overline{K}}},D_{{\mathcal O}_{\overline{K}}}),{\mathcal{S}}_n(b))&\simeq H^{a}_{\operatorname{\acute{e}t} ,c}(X_{{\mathcal O}_{\overline{K}}},{\mathcal{S}}_n(b)). \end{align*}Hence, we obtain a period morphism
that composed with the map ![]() $H^{a}_{\operatorname {\acute {e}t} ,c}(X_{{\mathcal O} _{\overline {K}}},{\mathcal {S}}_n(b)) \to \mathbf {L}(H^a_{\operatorname {cr} ,c}(X_n)\{-b\})$ yields a Galois-equivariant map
$H^{a}_{\operatorname {\acute {e}t} ,c}(X_{{\mathcal O} _{\overline {K}}},{\mathcal {S}}_n(b)) \to \mathbf {L}(H^a_{\operatorname {cr} ,c}(X_n)\{-b\})$ yields a Galois-equivariant map
We get the following corollary of Theorem 3.2.
Corollary 3.5 The Galois-equivariant morphism
is an isomorphism if the numbers ![]() $p,b,d$ are such that
$p,b,d$ are such that ![]() $b\geq 2d+3$ and
$b\geq 2d+3$ and ![]() $p-2\geq 2b+d+m$.
$p-2\geq 2b+d+m$.
3.1.2 Rational crystalline conjecture
We will treat now the rational crystalline conjecture. Let ![]() $X$ be a smooth proper finite simplicial scheme over
$X$ be a smooth proper finite simplicial scheme over ![]() ${{\mathcal O} _K}$, where the ring
${{\mathcal O} _K}$, where the ring ![]() ${{\mathcal O} _K}$ is possibly ramified over
${{\mathcal O} _K}$ is possibly ramified over ![]() $W(k)$. Assume that
$W(k)$. Assume that ![]() $X\simeq \operatorname {sk} _mX$ and set
$X\simeq \operatorname {sk} _mX$ and set ![]() $d=\max _{s\leq m}\dim X_s$. For large
$d=\max _{s\leq m}\dim X_s$. For large ![]() $b$, we will construct Galois-equivariant functorial period morphisms
$b$, we will construct Galois-equivariant functorial period morphisms
Assume that ![]() $p^n\geq 5$,
$p^n\geq 5$, ![]() $2b-a\geq \max \{2d,2\}$,
$2b-a\geq \max \{2d,2\}$, ![]() $2b-a\geq 3$ for
$2b-a\geq 3$ for ![]() $d=0$ and
$d=0$ and ![]() $p=2$, and
$p=2$, and ![]() $a\geq 0$. Nizioł [Reference NiziołNiz16, Lemma 5.3] and Lemma 2.11 give us the following diagram.
$a\geq 0$. Nizioł [Reference NiziołNiz16, Lemma 5.3] and Lemma 2.11 give us the following diagram.

Define the morphisms
as the composition
where ![]() $\psi _n$ is the natural projection
$\psi _n$ is the natural projection
Here ![]() $(\overline {c}_{b,2b-a}^{\operatorname {\acute {e}t} })^{-1}(D(d,m,b,2b-a)x)$ is any element in the preimage of
$(\overline {c}_{b,2b-a}^{\operatorname {\acute {e}t} })^{-1}(D(d,m,b,2b-a)x)$ is any element in the preimage of ![]() $D(d,m,b,2b-a)x$ (by Proposition 2.14,
$D(d,m,b,2b-a)x$ (by Proposition 2.14, ![]() $D(d,m,b,2b-a)x$ lies in the image of
$D(d,m,b,2b-a)x$ lies in the image of ![]() $\overline {c}_{b,2b-a}^{\operatorname {\acute {e}t} }$). By Proposition 2.14, any ambiguity in that definition comes from a class of
$\overline {c}_{b,2b-a}^{\operatorname {\acute {e}t} }$). By Proposition 2.14, any ambiguity in that definition comes from a class of ![]() $y$ such that
$y$ such that ![]() $D(d,m,b,2b-a)[y]=[z]$,
$D(d,m,b,2b-a)[y]=[z]$, ![]() $z\in F^{b+1}_{\gamma }K_{2b-a}(X_{\overline {K}},\mathbf {Z}/p^n)$, and this ambiguity we killed by twisting the definition of
$z\in F^{b+1}_{\gamma }K_{2b-a}(X_{\overline {K}},\mathbf {Z}/p^n)$, and this ambiguity we killed by twisting the definition of ![]() $\alpha ^n_{ab}$ by a factor of
$\alpha ^n_{ab}$ by a factor of ![]() $D(d,m,b,2b-a)$.
$D(d,m,b,2b-a)$.
Define the morphism
as the composition of ![]() $\mathbf {Q}\otimes {\mathrel{\mathop{\kern0pt\longleftarrow}\limits_n^{\lim }}} \alpha ^n_{ab}$ with the Kato–Messing isomorphism
$\mathbf {Q}\otimes {\mathrel{\mathop{\kern0pt\longleftarrow}\limits_n^{\lim }}} \alpha ^n_{ab}$ with the Kato–Messing isomorphism ![]() $h_{\operatorname {cr} }: H^a_{\operatorname {cr} }(X_{{{\mathcal O} _{\overline {K}}}})_{\mathbf {Q}}\simeq H^a_{\operatorname {cr} }(X_{0})\otimes _{W(k)} \mathbf {B}^+_{\operatorname {cr} }$ and the division by
$h_{\operatorname {cr} }: H^a_{\operatorname {cr} }(X_{{{\mathcal O} _{\overline {K}}}})_{\mathbf {Q}}\simeq H^a_{\operatorname {cr} }(X_{0})\otimes _{W(k)} \mathbf {B}^+_{\operatorname {cr} }$ and the division by ![]() $D(d,m,b,2b-a)^2$.
$D(d,m,b,2b-a)^2$.
The following theorem generalizes our [Reference NiziołNiz08, Theorem 3.8] from schemes to finite simplicial schemes.
Theorem 3.6 Let ![]() $X$ be any proper smooth finite simplicial
$X$ be any proper smooth finite simplicial ![]() ${{\mathcal O} _K}$-scheme. Assume that
${{\mathcal O} _K}$-scheme. Assume that ![]() $X\simeq \operatorname {sk} _mX$ and let
$X\simeq \operatorname {sk} _mX$ and let ![]() $d=\max _{s\leq m}\dim X_m$. Then, assuming that
$d=\max _{s\leq m}\dim X_m$. Then, assuming that ![]() $b\geq 2d+2$, the functorial Galois-equivariant morphism
$b\geq 2d+2$, the functorial Galois-equivariant morphism
is an isomorphism. Moreover, the map ![]() $\alpha _{ab}$ preserves the Frobenius, is compatible with products and Tate twists, and, after extension to
$\alpha _{ab}$ preserves the Frobenius, is compatible with products and Tate twists, and, after extension to ![]() $\mathbf {B}_{\operatorname {dR} }$, induces an isomorphism of filtrations.
$\mathbf {B}_{\operatorname {dR} }$, induces an isomorphism of filtrations.
Proof. We argue by induction on ![]() $m\geq 0$. The case
$m\geq 0$. The case ![]() $m=0$ is treated by [Reference NiziołNiz08, Theorem 3.8]. Assume that our theorem is true for
$m=0$ is treated by [Reference NiziołNiz08, Theorem 3.8]. Assume that our theorem is true for ![]() $m-1$. To show it for
$m-1$. To show it for ![]() $m$, consider the homotopy cofiber sequence
$m$, consider the homotopy cofiber sequence
and apply the period morphisms ![]() $\alpha _{*,*}$ to it. We get the following map of sequences.
$\alpha _{*,*}$ to it. We get the following map of sequences.

Here we put ![]() $H^*_{\operatorname {\acute {e}t} }(T,b)=H^{*}_{\operatorname {\acute {e}t} }(T_{\overline {K}},\mathbf {Q}_p(b))\otimes \mathbf {B}_{\operatorname {cr} }$,
$H^*_{\operatorname {\acute {e}t} }(T,b)=H^{*}_{\operatorname {\acute {e}t} }(T_{\overline {K}},\mathbf {Q}_p(b))\otimes \mathbf {B}_{\operatorname {cr} }$, ![]() $H^*_{\operatorname {cr} }(T,b)= H^{*}_{\operatorname {cr} }(T)\otimes \mathbf {B}_{\operatorname {cr} }\{-b \}$. And we defined
$H^*_{\operatorname {cr} }(T,b)= H^{*}_{\operatorname {cr} }(T)\otimes \mathbf {B}_{\operatorname {cr} }\{-b \}$. And we defined
 \begin{gather*} H^{*}_{\operatorname{\acute{e}t} }(X^{\prime}_{m},b) =H^{*}_{\operatorname{\acute{e}t} }(X_{m},b)\cap\ker s_0^*\cap\cdots\cap\ker s_{m-1}^*,\\ H^{*}_{\operatorname{cr} }(X^{\prime}_{m,0},b) =H^{*}_{\operatorname{cr} }(X_{m,0},b)\cap\ker s_0^*\cap\cdots\cap\ker s_{m-1}^*, \end{gather*}
\begin{gather*} H^{*}_{\operatorname{\acute{e}t} }(X^{\prime}_{m},b) =H^{*}_{\operatorname{\acute{e}t} }(X_{m},b)\cap\ker s_0^*\cap\cdots\cap\ker s_{m-1}^*,\\ H^{*}_{\operatorname{cr} }(X^{\prime}_{m,0},b) =H^{*}_{\operatorname{cr} }(X_{m,0},b)\cap\ker s_0^*\cap\cdots\cap\ker s_{m-1}^*, \end{gather*}
where each ![]() $s_i: X_{m-1}\to X_{m}$ is a degeneracy map. The horizontal sequences are exact by functoriality and finiteness of the étale and crystalline cohomologies. By the inductive hypothesis, we have the isomorphisms shown in the diagram. Hence, the period morphism
$s_i: X_{m-1}\to X_{m}$ is a degeneracy map. The horizontal sequences are exact by functoriality and finiteness of the étale and crystalline cohomologies. By the inductive hypothesis, we have the isomorphisms shown in the diagram. Hence, the period morphism
is an isomorphism. Since ![]() $H^a_{\operatorname {\acute {e}t} }(\operatorname {sk} _mX_{\overline {K}},\mathbf {Q}_p(b))\stackrel {\sim }{\to }H^a_{\operatorname {\acute {e}t} }(X_{\overline {K}},\mathbf {Q}_p(b))$ and
$H^a_{\operatorname {\acute {e}t} }(\operatorname {sk} _mX_{\overline {K}},\mathbf {Q}_p(b))\stackrel {\sim }{\to }H^a_{\operatorname {\acute {e}t} }(X_{\overline {K}},\mathbf {Q}_p(b))$ and ![]() $H^a_{\operatorname {cr} }(\operatorname {sk} _mX_{0})\stackrel {\sim }{\to }H^a_{\operatorname {cr} }(X_{0})$, this proves the first claim of the theorem.
$H^a_{\operatorname {cr} }(\operatorname {sk} _mX_{0})\stackrel {\sim }{\to }H^a_{\operatorname {cr} }(X_{0})$, this proves the first claim of the theorem.
We will now check that the morphism ![]() $\alpha _{ab}$ is compatible with products. This follows from the fact that the morphism
$\alpha _{ab}$ is compatible with products. This follows from the fact that the morphism ![]() $h_{\operatorname {cr} }$ is compatible with products and from the following lemma.
$h_{\operatorname {cr} }$ is compatible with products and from the following lemma.
Lemma 3.7 Let ![]() $x\in H^a(X_{\overline {K}},\mathbf {Z}/p^n(b))$,
$x\in H^a(X_{\overline {K}},\mathbf {Z}/p^n(b))$, ![]() $y\in H^{\rm c}(X_{\overline {K}},\mathbf {Z}/p^n(e))$,
$y\in H^{\rm c}(X_{\overline {K}},\mathbf {Z}/p^n(e))$, ![]() $2b-a>2$,
$2b-a>2$, ![]() $2e-c>2$, and
$2e-c>2$, and ![]() $p^n\geq 5$. Set
$p^n\geq 5$. Set ![]() $K(b,e)=-(b+e-1)!/((b-1)!(e-1)!)$. Then (assuming that all the indices are in the valid range)
$K(b,e)=-(b+e-1)!/((b-1)!(e-1)!)$. Then (assuming that all the indices are in the valid range)
 \begin{align*} &K(b,e)D(d,m,b,2b-a)^2 D(d,m,e,2e-c)^2 \alpha^n_{a+c, b+e}(x\cup y)\\ &\quad =K(b,e)D(d,m,b+e,2b+2e-a-c)^2\alpha^n_{ab}(x)\cup \alpha^n_{ce}(y). \end{align*}
\begin{align*} &K(b,e)D(d,m,b,2b-a)^2 D(d,m,e,2e-c)^2 \alpha^n_{a+c, b+e}(x\cup y)\\ &\quad =K(b,e)D(d,m,b+e,2b+2e-a-c)^2\alpha^n_{ab}(x)\cup \alpha^n_{ce}(y). \end{align*}Proof. Use the product formulas from [Reference NiziołNiz16, Lemma 5.3] and [Reference NiziołNiz16, Remark 5.4].
The claim about Tate twists follows from the following computation.
Lemma 3.8 Let ![]() $p^n\geq 5$ and
$p^n\geq 5$ and ![]() $b\geq 2d+2$. We have the following relationship between Tate twists:
$b\geq 2d+2$. We have the following relationship between Tate twists:
Proof. This follows just as in [Reference NiziołNiz08, Lemma 3.6] from Lemma 3.7 and the fact that ![]() $\overline {c}_{1,2}^{\operatorname {\acute {e}t} }(\beta _n)=\zeta _n$ and
$\overline {c}_{1,2}^{\operatorname {\acute {e}t} }(\beta _n)=\zeta _n$ and ![]() $\overline {c}_{1,2}^{\operatorname {syn}}(\tilde {\beta }_n)=t$ (see [Reference NiziołNiz98, Lemma 4.1]). Here
$\overline {c}_{1,2}^{\operatorname {syn}}(\tilde {\beta }_n)=t$ (see [Reference NiziołNiz98, Lemma 4.1]). Here ![]() $\beta _n\in K_2(\overline {K},\mathbf {Z}/p^n)$ and
$\beta _n\in K_2(\overline {K},\mathbf {Z}/p^n)$ and ![]() $\tilde {\beta }_n\in K_2({\mathcal O} _{\overline {K}},\mathbf {Z}/p^n)$ are the Bott elements associated to
$\tilde {\beta }_n\in K_2({\mathcal O} _{\overline {K}},\mathbf {Z}/p^n)$ are the Bott elements associated to ![]() $\zeta _n$.
$\zeta _n$.
Now, to prove the claim about filtrations, first we evoke Lemma 2.5 that yields compatibility of the period morphism with filtrations and then we note that it suffices to prove the analog of our claim for the associated grading, i.e., that, for ![]() $i\in \mathbf {Z}$, the induced map
$i\in \mathbf {Z}$, the induced map
is an isomorphism. But this can be proved by an analogous argument to the one we used to prove the first claim of the theorem.
Example 3.9 Rational crystalline conjecture for cohomology with compact support Again, as a special case consider a smooth proper scheme ![]() $X$ over
$X$ over ![]() ${{\mathcal O} _K}$ with a divisor
${{\mathcal O} _K}$ with a divisor ![]() $D$. We assume
$D$. We assume ![]() $D$ to have relative simple normal crossings and all the irreducible components smooth over
$D$ to have relative simple normal crossings and all the irreducible components smooth over ![]() ${{\mathcal O} _K}$. Let
${{\mathcal O} _K}$. Let ![]() $U$ denote the complement of
$U$ denote the complement of ![]() $D$ in
$D$ in ![]() $X$ and
$X$ and ![]() $d$ be the relative dimension of
$d$ be the relative dimension of ![]() $X$. Equip
$X$. Equip ![]() $X$ with the log-structure induced by
$X$ with the log-structure induced by ![]() $D$. Consider the simplicial scheme
$D$. Consider the simplicial scheme ![]() $C(X,D):=\operatorname {cofiber}(\widetilde {D}_{{\scriptscriptstyle \bullet }}\stackrel {i}{\to } X),$ where all the schemes have trivial log-structure. We have
$C(X,D):=\operatorname {cofiber}(\widetilde {D}_{{\scriptscriptstyle \bullet }}\stackrel {i}{\to } X),$ where all the schemes have trivial log-structure. We have ![]() $C(X,D)\simeq \operatorname {sk} _mC(X,D)$, where
$C(X,D)\simeq \operatorname {sk} _mC(X,D)$, where ![]() $m$ is the number of irreducible components of
$m$ is the number of irreducible components of ![]() $D$. Applying the above constructions to
$D$. Applying the above constructions to ![]() $C(X,D)$, we obtain the following basic diagram.
$C(X,D)$, we obtain the following basic diagram.

Recall that we have
From this, we get a Galois-equivariant map
and the following corollary of Theorem 3.6.
Corollary 3.10 The Galois-equivariant morphism
is an isomorphism for ![]() $b\geq 2d+2$. Moreover, the map
$b\geq 2d+2$. Moreover, the map ![]() $\alpha _{ab}$ preserves the Frobenius, is compatible with products and Tate twists, and, after extension to
$\alpha _{ab}$ preserves the Frobenius, is compatible with products and Tate twists, and, after extension to ![]() $\mathbf {B}_{\operatorname {dR} }$, induces an isomorphism of filtrations.
$\mathbf {B}_{\operatorname {dR} }$, induces an isomorphism of filtrations.
3.2 Semistable conjecture for cohomology with compact support
We will now prove a comparison theorem for cohomology with compact support in the semistable case using ![]() $K$-theory. We start with the definition of the period morphism. Let
$K$-theory. We start with the definition of the period morphism. Let ![]() $X$ be a proper scheme over
$X$ be a proper scheme over ![]() ${\mathcal O} _K$ with (strictly) semistable reduction and of pure relative dimension
${\mathcal O} _K$ with (strictly) semistable reduction and of pure relative dimension ![]() $d$. Let
$d$. Let ![]() $i:D\hookrightarrow X$ be the horizontal divisor and set
$i:D\hookrightarrow X$ be the horizontal divisor and set ![]() $U=X\setminus D$. Equip
$U=X\setminus D$. Equip ![]() $X$ with the log-structure induced by
$X$ with the log-structure induced by ![]() $D$ and the special fiber. Assume that
$D$ and the special fiber. Assume that ![]() $p^n\geq 5$ and
$p^n\geq 5$ and ![]() $b\geq 2d+2$. We will define a period morphism
$b\geq 2d+2$. We will define a period morphism
We will use the following diagram.

where ![]() $j: X_{\overline {K}}\hookrightarrow {\mathcal {X}}_{{\mathcal O} _{\overline {K}}}$ is the natural open immersion and we set
$j: X_{\overline {K}}\hookrightarrow {\mathcal {X}}_{{\mathcal O} _{\overline {K}}}$ is the natural open immersion and we set
Here the log-structure on the schemes ![]() $Y,D_Y$ is trivial.
$Y,D_Y$ is trivial.
Define
 \begin{align*} \alpha^n_{ab}(x)&:=\psi_n(\pi^*)^{-1}\varepsilon \overline{c}_{b,2b-a}^{\operatorname{syn}}M(2d,b+1,2(2b-a))(j^*)^{-1}\\ &\quad \times M(2d,b,2(2b-a))D(d,d,b,2b-a)(\overline {c}_{b,2b-a}^{\operatorname{\acute{e}t} })^{-1}(D(d,d,b,2b-a)x), \end{align*}
\begin{align*} \alpha^n_{ab}(x)&:=\psi_n(\pi^*)^{-1}\varepsilon \overline{c}_{b,2b-a}^{\operatorname{syn}}M(2d,b+1,2(2b-a))(j^*)^{-1}\\ &\quad \times M(2d,b,2(2b-a))D(d,d,b,2b-a)(\overline {c}_{b,2b-a}^{\operatorname{\acute{e}t} })^{-1}(D(d,d,b,2b-a)x), \end{align*}
where ![]() $\psi _n(\pi ^*)^{-1}\varepsilon$ is the composition
$\psi _n(\pi ^*)^{-1}\varepsilon$ is the composition
where we set
Here the log-structure on the schemes defining ![]() $C(Y,D_Y)$ is induced from the special fiber. The pullback map
$C(Y,D_Y)$ is induced from the special fiber. The pullback map
is an isomorphism by a simplicial (and easy to prove) version of [Reference NiziołNiz08, Corollary 2.4].
In the definition of ![]() $\alpha _{ab}^n(x)$, for
$\alpha _{ab}^n(x)$, for ![]() $x\in H^a_c(U_{\overline {K}},{\mathbf {Z}}/p^n(b))$, we take
$x\in H^a_c(U_{\overline {K}},{\mathbf {Z}}/p^n(b))$, we take ![]() $(\overline {c}^{\operatorname {\acute {e}t} }_{b,2b-a})^{-1}(D(d,d,b,2b-a)x)\in F^b_{\gamma }/F^{b+1}_{\gamma }K_{2b-a}^{\rm c} (X_{\overline {K}},D_{\overline {K}},{\mathbf {Z}}/p^n)$ to be any element in the preimage of
$(\overline {c}^{\operatorname {\acute {e}t} }_{b,2b-a})^{-1}(D(d,d,b,2b-a)x)\in F^b_{\gamma }/F^{b+1}_{\gamma }K_{2b-a}^{\rm c} (X_{\overline {K}},D_{\overline {K}},{\mathbf {Z}}/p^n)$ to be any element in the preimage of ![]() $D(d,d,b,2b-a)x$ (this is possible by Proposition 2.14). By Proposition 2.14, any ambiguity in that definition comes from a class of
$D(d,d,b,2b-a)x$ (this is possible by Proposition 2.14). By Proposition 2.14, any ambiguity in that definition comes from a class of ![]() $y$ such that
$y$ such that ![]() $D(d,d,b,2b-a)[y]=[z]$,
$D(d,d,b,2b-a)[y]=[z]$, ![]() $z\in F^{b+1}_{\gamma }K_{2b-a}^{\rm c}(X_{\overline {K}},D_{\overline {K}},{\mathbf {Z}}/p^n)$, and that we killed by twisting the definition of
$z\in F^{b+1}_{\gamma }K_{2b-a}^{\rm c}(X_{\overline {K}},D_{\overline {K}},{\mathbf {Z}}/p^n)$, and that we killed by twisting the definition of ![]() $\alpha ^n_{ab}$ by a factor of
$\alpha ^n_{ab}$ by a factor of ![]() $D(d,d,b,2b-a)$. Similarly, for
$D(d,d,b,2b-a)$. Similarly, for ![]() $x\in F^b_{\gamma }/F^{b+1}_{\gamma }K_{2b-a}^{\rm c}(X_{\overline {K}},D_{\overline {K}},{\mathbf {Z}}/p^n)$, we take
$x\in F^b_{\gamma }/F^{b+1}_{\gamma }K_{2b-a}^{\rm c}(X_{\overline {K}},D_{\overline {K}},{\mathbf {Z}}/p^n)$, we take ![]() $(j^*)^{-1}(M(2d,b,2(2b-a))x)$ to be any element in the preimage of
$(j^*)^{-1}(M(2d,b,2(2b-a))x)$ to be any element in the preimage of ![]() $M(2d,b,2(2b-a))x$ under
$M(2d,b,2(2b-a))x$ under ![]() $j^*$. This is possible by Lemma 2.12 and by the same lemma any ambiguity is killed by twisting the definition of
$j^*$. This is possible by Lemma 2.12 and by the same lemma any ambiguity is killed by twisting the definition of ![]() $\alpha ^n_{ab}$ by
$\alpha ^n_{ab}$ by ![]() $M(2d,b+1,2(2b-a))$.
$M(2d,b+1,2(2b-a))$.
Let ![]() $b\geq 2d+2$. We can now define the rational period morphism
$b\geq 2d+2$. We can now define the rational period morphism
as the composition of ![]() ${\mathbf {Q}}\otimes {\mathrel{\mathop{\kern0pt\longleftarrow}\limits_n^{\lim }}} \alpha ^n_{ab}$ with the map [Reference KatoKat94a, 4.2 and 4.5]
${\mathbf {Q}}\otimes {\mathrel{\mathop{\kern0pt\longleftarrow}\limits_n^{\lim }}} \alpha ^n_{ab}$ with the map [Reference KatoKat94a, 4.2 and 4.5]
and with the division by ![]() $M(2d,b+1,2(2b-a))M(2d,b,2(2b-a))D(d,d,b,2b-a)^2$.
$M(2d,b+1,2(2b-a))M(2d,b,2(2b-a))D(d,d,b,2b-a)^2$.
The morphism ![]() $\alpha _{ab}$ preserves the Frobenius, the action of
$\alpha _{ab}$ preserves the Frobenius, the action of ![]() $\operatorname {Gal}(\overline {K}/K)$, and the monodromy operator, and, after extension to
$\operatorname {Gal}(\overline {K}/K)$, and the monodromy operator, and, after extension to ![]() $\mathbf {B}_{\operatorname {dR} }$, is compatible with filtrations (use the simplicial analog of Lemma 4.8.4 from [Reference TsujiTsu99a], which can be easily shown, as in § 2.1.5, by lifting all the maps functorially to the
$\mathbf {B}_{\operatorname {dR} }$, is compatible with filtrations (use the simplicial analog of Lemma 4.8.4 from [Reference TsujiTsu99a], which can be easily shown, as in § 2.1.5, by lifting all the maps functorially to the ![]() $\infty$-derived category as was done in detail in [Reference BeilinsonBei13] and [Reference Nekovář and NiziołNN16]; see also [Reference TsujiTsu98, § 7]).
$\infty$-derived category as was done in detail in [Reference BeilinsonBei13] and [Reference Nekovář and NiziołNN16]; see also [Reference TsujiTsu98, § 7]).
We have the following generalization of our [Reference NiziołNiz08, Theorem 3.8] (where the divisor at infinity ![]() $D$ is trivial).
$D$ is trivial).
Theorem 3.11 Let ![]() $X$ be a proper scheme over
$X$ be a proper scheme over ![]() ${\mathcal O} _K$ with semistable reduction. Let
${\mathcal O} _K$ with semistable reduction. Let ![]() $D$ be the horizontal divisor, let
$D$ be the horizontal divisor, let ![]() $U=X\setminus D$, and let
$U=X\setminus D$, and let ![]() $d$ be the relative dimension of
$d$ be the relative dimension of ![]() $X$. Equip
$X$. Equip ![]() $X$ with the log-structure induced by
$X$ with the log-structure induced by ![]() $D$ and the special fiber. Then, assuming that
$D$ and the special fiber. Then, assuming that ![]() $b\geq 2d+2$, the morphism
$b\geq 2d+2$, the morphism
is an isomorphism. The map ![]() $\alpha _{ab}$ preserves the Frobenius, the action of
$\alpha _{ab}$ preserves the Frobenius, the action of ![]() $\operatorname {Gal}(\overline {K}/K)$, and the monodromy operator. It is independent of the choice of
$\operatorname {Gal}(\overline {K}/K)$, and the monodromy operator. It is independent of the choice of ![]() $\pi$ and compatible with products and Tate twists. Moreover, after extension to
$\pi$ and compatible with products and Tate twists. Moreover, after extension to ![]() $\mathbf {B}_{\operatorname {dR} }$, it induces a filtered isomorphism
$\mathbf {B}_{\operatorname {dR} }$, it induces a filtered isomorphism
Proof. Consider the finite semistable vertical simplicial log-scheme ![]() $C=C(X,D)$. The individual schemes in the simplicial scheme are equipped with the log-structure induced from the special fiber. We have
$C=C(X,D)$. The individual schemes in the simplicial scheme are equipped with the log-structure induced from the special fiber. We have ![]() $C(X,D)\simeq \operatorname {sk} _mC(X,D)$ if
$C(X,D)\simeq \operatorname {sk} _mC(X,D)$ if ![]() $D$ has
$D$ has ![]() $m$ irreducible components. We filter
$m$ irreducible components. We filter ![]() $C(X,D)$ by its skeleta
$C(X,D)$ by its skeleta ![]() $\operatorname {sk} _iC(X,D)$ and will show, by induction on
$\operatorname {sk} _iC(X,D)$ and will show, by induction on ![]() $i\geq 0$, that the period morphismFootnote 6
$i\geq 0$, that the period morphismFootnote 6
is an isomorphism. Start with ![]() $i=0$, where the statement is known. For
$i=0$, where the statement is known. For ![]() $i\geq 1$, assume that our theorem is true for
$i\geq 1$, assume that our theorem is true for ![]() $i-1$. To show it for
$i-1$. To show it for ![]() $i$, consider the homotopy cofiber sequences
$i$, consider the homotopy cofiber sequences
and apply the period morphisms ![]() $\alpha _{*,*}$ to it. We get the following map of exact sequences.
$\alpha _{*,*}$ to it. We get the following map of exact sequences.

Here we put ![]() $H^*_{\operatorname {\acute {e}t} }(T,*)=H^{*}_{\operatorname {\acute {e}t} }(T_{\overline {K}},\mathbf {Q}_p(b))\otimes \mathbf {B}_{\operatorname {st}}$,
$H^*_{\operatorname {\acute {e}t} }(T,*)=H^{*}_{\operatorname {\acute {e}t} }(T_{\overline {K}},\mathbf {Q}_p(b))\otimes \mathbf {B}_{\operatorname {st}}$, ![]() $H^*_{\operatorname {cr} }(T,b)=H^{*}_{\operatorname {cr} }(T)\otimes \mathbf {B}_{\operatorname {st}}\{-b \}$. And we defined
$H^*_{\operatorname {cr} }(T,b)=H^{*}_{\operatorname {cr} }(T)\otimes \mathbf {B}_{\operatorname {st}}\{-b \}$. And we defined
 \begin{gather*} H^{*}_{\operatorname{\acute{e}t} }(C^{\prime}_{i},b) =H^{*}_{\operatorname{\acute{e}t} }(C_i,b)\cap\ker s_0^*\cap\cdots\cap\ker s_{i-1}^*,\\ H^{*}_{\operatorname{cr} }(C^{\prime}_{i,0},b) =H^{*}_{\operatorname{cr} }(C_{i,0},b)\cap\ker s_0^*\cap\cdots\cap\ker s_{i-1}^*, \end{gather*}
\begin{gather*} H^{*}_{\operatorname{\acute{e}t} }(C^{\prime}_{i},b) =H^{*}_{\operatorname{\acute{e}t} }(C_i,b)\cap\ker s_0^*\cap\cdots\cap\ker s_{i-1}^*,\\ H^{*}_{\operatorname{cr} }(C^{\prime}_{i,0},b) =H^{*}_{\operatorname{cr} }(C_{i,0},b)\cap\ker s_0^*\cap\cdots\cap\ker s_{i-1}^*, \end{gather*}
where each ![]() $s_i: \operatorname {sk} _{i-1}C\to \operatorname {sk} _iC$ is a degeneracy map. By the inductive hypothesis, we have the isomorphisms shown in the diagram. Hence, the period morphism
$s_i: \operatorname {sk} _{i-1}C\to \operatorname {sk} _iC$ is a degeneracy map. By the inductive hypothesis, we have the isomorphisms shown in the diagram. Hence, the period morphism
is an isomorphism. Since ![]() $H^a_{\operatorname {\acute {e}t} }(\operatorname {sk} _mC_{\overline {K}},\mathbf {Q}_p(b))\stackrel {\sim }{\to }H^a_{\operatorname {\acute {e}t} }(C_{\overline {K}},\mathbf {Q}_p(b))$ and
$H^a_{\operatorname {\acute {e}t} }(\operatorname {sk} _mC_{\overline {K}},\mathbf {Q}_p(b))\stackrel {\sim }{\to }H^a_{\operatorname {\acute {e}t} }(C_{\overline {K}},\mathbf {Q}_p(b))$ and ![]() $H^a_{\operatorname {cr} }(\operatorname {sk} _mC_{0})\stackrel {\sim }{\to }H^a_{\operatorname {cr} }(C_{0})$, this proves the first claim of the theorem.
$H^a_{\operatorname {cr} }(\operatorname {sk} _mC_{0})\stackrel {\sim }{\to }H^a_{\operatorname {cr} }(C_{0})$, this proves the first claim of the theorem.
For the claim about the filtrations, we need to show that ![]() $\alpha ^{\operatorname {dR} }_{ab}$ (that is,
$\alpha ^{\operatorname {dR} }_{ab}$ (that is, ![]() $\alpha _{ab}$ extended to
$\alpha _{ab}$ extended to ![]() $\mathbf {B}_{\operatorname {dR} }$) induces an isomorphism on filtrations. Passing to the associated grading, one reduces to showing that the induced Hodge–Tate period map
$\mathbf {B}_{\operatorname {dR} }$) induces an isomorphism on filtrations. Passing to the associated grading, one reduces to showing that the induced Hodge–Tate period map
where we set
is an isomorphism. But this can be checked exactly as above.
The claim about the uniformizer can be checked as in the proof of [Reference NiziołNiz08, Theorem 3.8]. The claims about products and Tate twists can be checked as in the proof of Theorem 3.6 using analogs of Lemmas 3.7 and 3.8 (where the constants have to be modified accordingly to the definition of the maps ![]() $\alpha ^n_{ab}$).
$\alpha ^n_{ab}$).
4. Comparison of period morphisms
This section has two parts. In the first part we formulate a ![]() $K$-theoretical uniqueness criterion for
$K$-theoretical uniqueness criterion for ![]() $p$-adic period morphisms for cohomology with compact support and, using it, we prove that the period morphisms defined using the syntomic, almost étale, and motivic methods are equal. In the second part we use
$p$-adic period morphisms for cohomology with compact support and, using it, we prove that the period morphisms defined using the syntomic, almost étale, and motivic methods are equal. In the second part we use ![]() $h$-topology and the Beilinson (filtered) Poincaré lemma to formulate a simple uniqueness criterion for
$h$-topology and the Beilinson (filtered) Poincaré lemma to formulate a simple uniqueness criterion for ![]() $p$-adic period morphisms. Using it, we show that the
$p$-adic period morphisms. Using it, we show that the ![]() $p$-adic period morphisms of Faltings, Tsuji (and Yamashita), and Beilinson are the same whenever they are defined (so, in particular, for open varieties with semistable compactifications). Moreover, they are all compatible with (possibly mixed) products. This all holds up to a change of the Hyodo–Kato cohomology described in § 4.3.2.
$p$-adic period morphisms of Faltings, Tsuji (and Yamashita), and Beilinson are the same whenever they are defined (so, in particular, for open varieties with semistable compactifications). Moreover, they are all compatible with (possibly mixed) products. This all holds up to a change of the Hyodo–Kato cohomology described in § 4.3.2.
4.1 A simple uniqueness criterion
We start with a very simple uniqueness criterion.
4.1.1 The case of schemes
Recall the following formulation of the semistable conjecture of Fontaine and Jannsen.
Conjecture 4.1 Semistable conjecture Let ![]() $X$ be a proper, log-smooth, fine, and saturated
$X$ be a proper, log-smooth, fine, and saturated ![]() ${\mathcal O} _K^{\times }$-log-scheme with Cartier-type reduction. There exists a natural
${\mathcal O} _K^{\times }$-log-scheme with Cartier-type reduction. There exists a natural ![]() $\mathbf {B}_{\operatorname {st}}$-linear Galois-equivariant period isomorphism
$\mathbf {B}_{\operatorname {st}}$-linear Galois-equivariant period isomorphism
that preserves the Frobenius and the monodromy operators and, after extension to ![]() $\mathbf {B}_{\operatorname {dR} }$, induces a filtered isomorphism
$\mathbf {B}_{\operatorname {dR} }$, induces a filtered isomorphism
This conjecture was proved, possibly under additional assumptions, by Kato [Reference KatoKat94a], Tsuji [Reference TsujiTsu99a, Reference TsujiTsu03], Yamashita [Reference YamashitaYam11], Faltings [Reference FaltingsFal02], Nizioł [Reference NiziołNiz08], and Beilinson [Reference BeilinsonBei13]. It was generalized to formal schemes by Colmez and Nizioł [Reference Colmez and NiziołCN17] and by Česnavičius and Koshikawa [Reference Česnavičius and KoshikawaČK19] (who generalized the proof of the crystalline conjecture by Bhatt, Morrow and Scholze [Reference Bhatt, Morrow and ScholzeBMS18]) in the case when there is no horizontal divisor.
Let ![]() $r\geq 0$. For a period isomorphism
$r\geq 0$. For a period isomorphism ![]() $\alpha _i$ as above, we define its twist
$\alpha _i$ as above, we define its twist
as ![]() $\alpha _{i,r}:=t^r\alpha _{i}\epsilon ^{-r}$. Clearly, it is an isomorphism. It follows from Conjecture 4.1 that we can recover the étale cohomology with the Galois action from the Hyodo–Kato cohomology:
$\alpha _{i,r}:=t^r\alpha _{i}\epsilon ^{-r}$. Clearly, it is an isomorphism. It follows from Conjecture 4.1 that we can recover the étale cohomology with the Galois action from the Hyodo–Kato cohomology:
For ![]() $r\geq i$, by Lemma 2.9, the right-hand side is isomorphic to
$r\geq i$, by Lemma 2.9, the right-hand side is isomorphic to ![]() $H^i_{\operatorname {\acute {e}t} }(X_{{\mathcal O} _{\overline {K}}},{\mathcal {S}}'(r))_{\mathbf {Q}}$, i.e., there exists a natural isomorphism
$H^i_{\operatorname {\acute {e}t} }(X_{{\mathcal O} _{\overline {K}}},{\mathcal {S}}'(r))_{\mathbf {Q}}$, i.e., there exists a natural isomorphism
We will denote by
the induced isomorphism and call it the syntomic period isomorphism.
The following lemma is immediate.
Lemma 4.3 Let ![]() $r\geq i$. A period isomorphism
$r\geq i$. A period isomorphism ![]() $\alpha _{i,r}$, and hence also a period isomorphism
$\alpha _{i,r}$, and hence also a period isomorphism ![]() $\alpha _i$ satisfying Conjecture 4.1, is uniquely determined by the induced syntomic period isomorphism
$\alpha _i$ satisfying Conjecture 4.1, is uniquely determined by the induced syntomic period isomorphism ![]() $\tilde {\alpha }_{i,r}$.
$\tilde {\alpha }_{i,r}$.
4.1.2 The case of simplicial schemes
The above discussion carries over to finite simplicial schemes. That is, we assume that we have a period isomorphism ![]() $\alpha _i$ as in Conjecture 4.1 but for a finite simplicial scheme
$\alpha _i$ as in Conjecture 4.1 but for a finite simplicial scheme ![]() $X$ with components as in Conjecture 4.1. It then yields an isomorphism
$X$ with components as in Conjecture 4.1. It then yields an isomorphism ![]() $\alpha _{i,r}$ as in (4.2) for
$\alpha _{i,r}$ as in (4.2) for ![]() $i\leq r$. We will need the following analog of Lemma 2.9.
$i\leq r$. We will need the following analog of Lemma 2.9.
Lemma 4.4 Let ![]() $r\geq i$. There exists a natural isomorphism
$r\geq i$. There exists a natural isomorphism
Proof. By functoriality of all the maps involved, the proof of Lemma 2.9 yields a quasi-isomorphism
We have natural isomorphisms
 \begin{gather*} H^i((\mathrm{R}\Gamma_{\operatorname{HK} }(X)\otimes_F{\mathbf{B}}^+_{\operatorname{st}})^{N=0,\phi=p^r}) \simeq (H^i_{\operatorname{HK} }(X)\otimes_F{\mathbf{B}}^+_{\operatorname{st}})^{N=0,\phi=p^r},\\ H^i((\mathrm{R}\Gamma_{\operatorname{dR} }(X_K) \otimes_K\mathbf{B}^+_{\operatorname{dR} })/F^r) \simeq (H^i_{\operatorname{dR} }(X_K) \otimes_K\mathbf{B}^+_{\operatorname{dR} })/F^r. \end{gather*}
\begin{gather*} H^i((\mathrm{R}\Gamma_{\operatorname{HK} }(X)\otimes_F{\mathbf{B}}^+_{\operatorname{st}})^{N=0,\phi=p^r}) \simeq (H^i_{\operatorname{HK} }(X)\otimes_F{\mathbf{B}}^+_{\operatorname{st}})^{N=0,\phi=p^r},\\ H^i((\mathrm{R}\Gamma_{\operatorname{dR} }(X_K) \otimes_K\mathbf{B}^+_{\operatorname{dR} })/F^r) \simeq (H^i_{\operatorname{dR} }(X_K) \otimes_K\mathbf{B}^+_{\operatorname{dR} })/F^r. \end{gather*}
The first isomorphism holds because ![]() $H^i_{\operatorname {HK} }(X)\otimes _F{\mathbf {B}}^+_{\operatorname {st}}$ is a
$H^i_{\operatorname {HK} }(X)\otimes _F{\mathbf {B}}^+_{\operatorname {st}}$ is a ![]() $(\phi ,N)$-module (see [Reference Nekovář and NiziołNN16, proof of Corollary 3.25] for an argument) and the second one because we have a degeneration of the Hodge–de Rham spectral sequence for
$(\phi ,N)$-module (see [Reference Nekovář and NiziołNN16, proof of Corollary 3.25] for an argument) and the second one because we have a degeneration of the Hodge–de Rham spectral sequence for ![]() $X$. This yields a natural long exact sequence
$X$. This yields a natural long exact sequence
 \begin{align*} (H^{i-1}_{\operatorname{HK} }(X)\otimes_F{\mathbf{B}}^+_{\operatorname{st}})^{N=0,\phi=p^r} & {\buildrel {\rho_{\pi}\otimes\iota} \over \longrightarrow} (H^{i-1}_{\operatorname{dR} }(X_K) \otimes_K\mathbf{B}^+_{\operatorname{dR} })/F^r {\buildrel {\partial} \over \longrightarrow} H^i_{\operatorname{\acute{e}t} }(X_{{\mathcal O}_{\overline{K}}},{\mathcal{S}}'(r))_{\mathbf{Q}}\\ & \to (H^i_{\operatorname{HK} }(X)\otimes_F{\mathbf{B}}^+_{\operatorname{st}})^{N=0,\phi=p^r} {\buildrel {\rho_{\pi}\otimes\iota} \over \longrightarrow} (H^i_{\operatorname{dR} }(X_K) \otimes_K\mathbf{B}^+_{\operatorname{dR} })/F^r. \end{align*}
\begin{align*} (H^{i-1}_{\operatorname{HK} }(X)\otimes_F{\mathbf{B}}^+_{\operatorname{st}})^{N=0,\phi=p^r} & {\buildrel {\rho_{\pi}\otimes\iota} \over \longrightarrow} (H^{i-1}_{\operatorname{dR} }(X_K) \otimes_K\mathbf{B}^+_{\operatorname{dR} })/F^r {\buildrel {\partial} \over \longrightarrow} H^i_{\operatorname{\acute{e}t} }(X_{{\mathcal O}_{\overline{K}}},{\mathcal{S}}'(r))_{\mathbf{Q}}\\ & \to (H^i_{\operatorname{HK} }(X)\otimes_F{\mathbf{B}}^+_{\operatorname{st}})^{N=0,\phi=p^r} {\buildrel {\rho_{\pi}\otimes\iota} \over \longrightarrow} (H^i_{\operatorname{dR} }(X_K) \otimes_K\mathbf{B}^+_{\operatorname{dR} })/F^r. \end{align*} It suffices thus to show that, for ![]() $i\leq r$, the map
$i\leq r$, the map ![]() $\partial$ in the above exact sequence is zero. Or that the map
$\partial$ in the above exact sequence is zero. Or that the map
is surjective. But this follows from the fact that the pair ![]() $H^{i-1}_{\operatorname {HK} }(X),H^{i-1}_{\operatorname {dR} }(X_K)$ is an admissible filtered
$H^{i-1}_{\operatorname {HK} }(X),H^{i-1}_{\operatorname {dR} }(X_K)$ is an admissible filtered ![]() $(\phi ,N)$-module such that
$(\phi ,N)$-module such that ![]() $F^{r}H^{i-1}_{\operatorname {dR} }(X_K)=0$ (see [Reference Colmez and NiziołCN17, Proposition 5.20]).
$F^{r}H^{i-1}_{\operatorname {dR} }(X_K)=0$ (see [Reference Colmez and NiziołCN17, Proposition 5.20]).
As above, we will denote by
the induced isomorphism and call it the syntomic period isomorphism. Again, the following lemma is immediate.
Lemma 4.5 Let ![]() $r\geq i$. A period isomorphism
$r\geq i$. A period isomorphism ![]() $\alpha _{i,r}$, and hence also a period isomorphism
$\alpha _{i,r}$, and hence also a period isomorphism ![]() $\alpha _i$ satisfying Conjecture 4.1 for
$\alpha _i$ satisfying Conjecture 4.1 for ![]() $X$, is uniquely determined by the induced syntomic period morphism
$X$, is uniquely determined by the induced syntomic period morphism ![]() $\tilde {\alpha }_{i,r}$.
$\tilde {\alpha }_{i,r}$.
4.2 Comparison of period morphisms for cohomology with compact support
We will prove in this section that the comparison morphisms for cohomology with compact support defined using the syntomic, almost étale, and motivic methods are equal. We will use for that a motivic uniqueness criterion.
4.2.1 A  $K$-theoretical uniqueness criterion
$K$-theoretical uniqueness criterion
We will prove now a uniqueness criterion for period morphisms that generalizes the one stated in [Reference NiziołNiz09]. Let ![]() $X$ be a proper scheme over
$X$ be a proper scheme over ![]() ${\mathcal O} _K$ with semistable reduction and of pure relative dimension
${\mathcal O} _K$ with semistable reduction and of pure relative dimension ![]() $d$. Let
$d$. Let ![]() $i:D\hookrightarrow X$ be the horizontal divisor and set
$i:D\hookrightarrow X$ be the horizontal divisor and set ![]() $U=X\setminus D$. Equip
$U=X\setminus D$. Equip ![]() $X$ with the log-structure induced by
$X$ with the log-structure induced by ![]() $D$ and the special fiber.
$D$ and the special fiber.
Proposition 4.6 Let ![]() $r\geq 2d+2$. There exists a unique semistable period morphism
$r\geq 2d+2$. There exists a unique semistable period morphism
that makes the diagram from § 3.2 commute.
4.2.2 Comparison of period morphisms for cohomology with compact support
The comparison morphisms of Faltings [Reference Faltings and IgusaFal89, Reference FaltingsFal02] and Tsuji [Reference TsujiTsu99a] extend easily to finite simplicial schemes. This was done explicitly in [Reference KisinKis02, Reference TsujiTsu98]. In particular, they extend to cohomology with compact support. We will show in this section that they are equal to the period morphisms constructed in § 3. We will use for that the uniqueness criterion for period morphisms stated above. We will do the computations just for cohomology with compact support in the semistable case. The arguments in other cases are analogous.
Theorem 4.7 (i) There exists a unique natural ![]() $p$-adic period isomorphism
$p$-adic period isomorphism
such that:
(a)
 $\alpha _i$ is
$\alpha _i$ is  $\mathbf {B}_{\operatorname {st}}$-linear, Galois equivariant, and compatible with Frobenius;
$\mathbf {B}_{\operatorname {st}}$-linear, Galois equivariant, and compatible with Frobenius;(b)
 $\alpha _i$, extended to
$\alpha _i$, extended to  $\mathbf {B}_{dR}$, induces a filtered isomorphism
$\mathbf {B}_{dR}$, induces a filtered isomorphism
 \[ \alpha^{\operatorname{dR} }_i: H^i_{\operatorname{\acute{e}t} ,c}(U_{\overline{K}},{\mathbf{Q}}_p)\otimes \mathbf{B}_{\operatorname{dR} }\stackrel{\sim}{\to} H^i_{\operatorname{dR} ,c}(X_K)\otimes_{K} \mathbf{B}_{\operatorname{dR} }; \]
\[ \alpha^{\operatorname{dR} }_i: H^i_{\operatorname{\acute{e}t} ,c}(U_{\overline{K}},{\mathbf{Q}}_p)\otimes \mathbf{B}_{\operatorname{dR} }\stackrel{\sim}{\to} H^i_{\operatorname{dR} ,c}(X_K)\otimes_{K} \mathbf{B}_{\operatorname{dR} }; \](c)
 $\alpha _i$ is compatible with the étale and syntomic higher Chern classes from
$\alpha _i$ is compatible with the étale and syntomic higher Chern classes from  $p$-adic
$p$-adic  $K$-theory.
$K$-theory.
(ii) The period morphisms of Faltings, Tsuji, and Nizioł are equal.Footnote 7
Proof. The first claim follows from Proposition 4.6 and Lemma 4.5.
For the second claim, choose ![]() $r$ such that
$r$ such that ![]() $r\geq 2d+2$ and
$r\geq 2d+2$ and ![]() $r\geq i$. It suffices to show that the Faltings, Tsuji, and Nizioł period morphisms
$r\geq i$. It suffices to show that the Faltings, Tsuji, and Nizioł period morphisms ![]() $\alpha ^{F}_{i,r}$,
$\alpha ^{F}_{i,r}$, ![]() $\alpha ^{T}_{i,r}$, and
$\alpha ^{T}_{i,r}$, and ![]() $\alpha ^{N}_{i,r}$
$\alpha ^{N}_{i,r}$
and their de Rham analogs are equal. For that, apply the first claim. The needed compatibility of the period morphism with higher ![]() $p$-adic Chern classes is clear in the case of the map
$p$-adic Chern classes is clear in the case of the map ![]() $\alpha ^{N}_{i,r}$ and was proved in [Reference NiziołNiz09, Corollaries 4.14 and 5.9] for the other two maps. These corollaries are stated for proper log-schemes but their proofs carry over to the case of finite simplicial schemes (with the same properties).
$\alpha ^{N}_{i,r}$ and was proved in [Reference NiziołNiz09, Corollaries 4.14 and 5.9] for the other two maps. These corollaries are stated for proper log-schemes but their proofs carry over to the case of finite simplicial schemes (with the same properties).
4.3 Comparison of Tsuji and Beilinson period morphisms
We prove in the next two sections that the Beilinson period morphisms [Reference BeilinsonBei12, Reference BeilinsonBei13] agree with the period morphisms of Faltings and Tsuji whenever the latter are defined (and modulo a change of Hodo–Kato cohomology). Our strategy is to appeal to Lemma 4.3 and then to sheafify the syntomic morphisms induced by the latter period morphisms in the ![]() $h$-topology on the generic fiber. We identify the syntomic period morphisms on the sheaf level as certain canonical maps appearing in the fundamental exact sequence. Since we had shown in [Reference Nekovář and NiziołNN16] that the same maps are used to define the Beilinson syntomic period morphism, it follows that all the period morphisms are equal. Along the way we obtain useful properties of the Faltings and Tsuji period morphisms.
$h$-topology on the generic fiber. We identify the syntomic period morphisms on the sheaf level as certain canonical maps appearing in the fundamental exact sequence. Since we had shown in [Reference Nekovář and NiziołNN16] that the same maps are used to define the Beilinson syntomic period morphism, it follows that all the period morphisms are equal. Along the way we obtain useful properties of the Faltings and Tsuji period morphisms.
We start with comparing the period morphisms of Tsuji and Beilinson.
4.3.1 Tsuji period morphism
We will briefly discuss the period morphism used by Tsuji. Let ![]() $X$ be a log-smooth log-scheme over
$X$ be a log-smooth log-scheme over ![]() ${\mathcal O} _K^{\times }$. Recall that Fontaine and Messing, and Kato have defined natural period morphisms on the étale site of
${\mathcal O} _K^{\times }$. Recall that Fontaine and Messing, and Kato have defined natural period morphisms on the étale site of ![]() $X_0$ [Reference Fontaine, Messing and RibetFM87, Reference TsujiTsu98]
$X_0$ [Reference Fontaine, Messing and RibetFM87, Reference TsujiTsu98]
where ![]() $i:X_0\hookrightarrow X, j: X_{K,\operatorname {tr}}\hookrightarrow X$ are the natural immersions. Here we set
$i:X_0\hookrightarrow X, j: X_{K,\operatorname {tr}}\hookrightarrow X$ are the natural immersions. Here we set ![]() ${\mathbf {Z}}/p^n(r)^{\prime }:=(1/(p^aa!){\mathbf {Z}}_p(r))\otimes {\mathbf {Z}}/p^n$, where
${\mathbf {Z}}/p^n(r)^{\prime }:=(1/(p^aa!){\mathbf {Z}}_p(r))\otimes {\mathbf {Z}}/p^n$, where ![]() $a$ is the largest integer
$a$ is the largest integer ![]() $\leq r/(p-1)$. Recall that we have the fundamental exact sequence [Reference TsujiTsu99a, Theorem 1.2.4]
$\leq r/(p-1)$. Recall that we have the fundamental exact sequence [Reference TsujiTsu99a, Theorem 1.2.4]
where
for some ![]() $s\geq r$.
$s\geq r$.
The above period morphisms were used to prove the following comparison theorem.
Theorem 4.8 (Tsuji [Tsu99a, 3.3.4, Theorem 3.4.4]) (i) Let ![]() $X$ be a semistable scheme over
$X$ be a semistable scheme over ![]() ${\mathcal O} _K$ or a finite base change of such a scheme. Then, for any
${\mathcal O} _K$ or a finite base change of such a scheme. Then, for any ![]() $0\leq i\leq r$, the kernel and cokernel of the period morphism
$0\leq i\leq r$, the kernel and cokernel of the period morphism
are annihilated by ![]() $p^N$ for an integer
$p^N$ for an integer ![]() $N$ which depends only on
$N$ which depends only on ![]() $p$,
$p$, ![]() $r$, and
$r$, and ![]() $i$. Here
$i$. Here ![]() $\overline {i}$ and
$\overline {i}$ and ![]() $\overline {j}$ are extensions of
$\overline {j}$ are extensions of ![]() $i$ and
$i$ and ![]() $j$ to
$j$ to ![]() $\overline {X}:=X_{{\mathcal O} _{\overline {K}}}$.
$\overline {X}:=X_{{\mathcal O} _{\overline {K}}}$.
(ii) Assume moreover that ![]() $X$ is proper. Then, for any
$X$ is proper. Then, for any ![]() $0\leq i\leq r$, the induced morphism
$0\leq i\leq r$, the induced morphism
is an isomorphism.
For a proper semistable scheme ![]() $X$ over
$X$ over ![]() ${\mathcal O} _K$ and
${\mathcal O} _K$ and ![]() $r\geq i$, the modulo
$r\geq i$, the modulo ![]() $p^n$ and rational semistable Tsuji period morphisms are defined as
$p^n$ and rational semistable Tsuji period morphisms are defined as
 \begin{equation} \begin{gathered} \beta_{r,n}^{\rm T}: \mathrm{R}\Gamma_{\operatorname{\acute{e}t} }(X_{{\mathcal O}_{\overline{K}}},{\mathcal{S}}^{\prime}_n(r)) {\buildrel {\operatorname{can}} \over \longrightarrow} \mathrm{R}\Gamma_{\operatorname{\acute{e}t} }(X_{{\mathcal O}_{\overline{K}}},{\mathcal{S}}_n(r)) {\buildrel {\beta^{\rm T}_r} \over \longrightarrow} \mathrm{R}\Gamma_{\operatorname{\acute{e}t} }(X_{\overline{K},\operatorname{tr}},\mathbf{Z}/p^n(r)^{\prime}),\\ \beta_{r}^{\rm T}: \mathrm{R}\Gamma_{\operatorname{\acute{e}t} }(X_{{\mathcal O}_{\overline{K}}},{\mathcal{S}}^{\prime}(r))_{\mathbf{Q}} {\buildrel {\operatorname{can}} \over \longrightarrow} \mathrm{R}\Gamma_{\operatorname{\acute{e}t} }(X_{{\mathcal O}_{\overline{K}}},{\mathcal{S}}(r))_{\mathbf{Q}} {\buildrel {\beta^{\rm T}_r} \over \longrightarrow} \nonumber \mathrm{R}\Gamma_{\operatorname{\acute{e}t} }(X_{\overline{K},\operatorname{tr}},{\mathbf{Q}}_p(r))\stackrel{ p^{-r}}{\to} \mathrm{R}\Gamma_{\operatorname{\acute{e}t} }(X_{\overline{K},\operatorname{tr}},{\mathbf{Q}}_p(r)). \end{gathered} \end{equation}
\begin{equation} \begin{gathered} \beta_{r,n}^{\rm T}: \mathrm{R}\Gamma_{\operatorname{\acute{e}t} }(X_{{\mathcal O}_{\overline{K}}},{\mathcal{S}}^{\prime}_n(r)) {\buildrel {\operatorname{can}} \over \longrightarrow} \mathrm{R}\Gamma_{\operatorname{\acute{e}t} }(X_{{\mathcal O}_{\overline{K}}},{\mathcal{S}}_n(r)) {\buildrel {\beta^{\rm T}_r} \over \longrightarrow} \mathrm{R}\Gamma_{\operatorname{\acute{e}t} }(X_{\overline{K},\operatorname{tr}},\mathbf{Z}/p^n(r)^{\prime}),\\ \beta_{r}^{\rm T}: \mathrm{R}\Gamma_{\operatorname{\acute{e}t} }(X_{{\mathcal O}_{\overline{K}}},{\mathcal{S}}^{\prime}(r))_{\mathbf{Q}} {\buildrel {\operatorname{can}} \over \longrightarrow} \mathrm{R}\Gamma_{\operatorname{\acute{e}t} }(X_{{\mathcal O}_{\overline{K}}},{\mathcal{S}}(r))_{\mathbf{Q}} {\buildrel {\beta^{\rm T}_r} \over \longrightarrow} \nonumber \mathrm{R}\Gamma_{\operatorname{\acute{e}t} }(X_{\overline{K},\operatorname{tr}},{\mathbf{Q}}_p(r))\stackrel{ p^{-r}}{\to} \mathrm{R}\Gamma_{\operatorname{\acute{e}t} }(X_{\overline{K},\operatorname{tr}},{\mathbf{Q}}_p(r)). \end{gathered} \end{equation}
By Theorem 4.8, ![]() $\beta _{r}^{\rm T}$ is a quasi-isomorphism after truncation at
$\beta _{r}^{\rm T}$ is a quasi-isomorphism after truncation at ![]() $\tau _{\leq r}$.
$\tau _{\leq r}$.
The Tsuji period morphism
is defined by composing the above morphism with the map ![]() $h_{\pi }$ (and changing
$h_{\pi }$ (and changing ![]() $\widehat {\mathbf {B}}_{\operatorname {st}}$ to
$\widehat {\mathbf {B}}_{\operatorname {st}}$ to ![]() $\mathbf {B}_{\operatorname {st}}$).
$\mathbf {B}_{\operatorname {st}}$).
4.3.2 Beilinson comparison theorem
In [Reference BeilinsonBei13], Beilinson proved the following comparison theorem.
Theorem 4.10 Semistable conjecture [Bei13] Let ![]() $X$ be a proper semistable scheme over
$X$ be a proper semistable scheme over ![]() ${\mathcal O} _K$ endowed with its canonical log-structure. There exists a natural
${\mathcal O} _K$ endowed with its canonical log-structure. There exists a natural ![]() $\mathbf {B}_{\operatorname {st}}$-linear Galois-equivariant period isomorphismFootnote 8
$\mathbf {B}_{\operatorname {st}}$-linear Galois-equivariant period isomorphismFootnote 8
that preserves the Frobenius and the monodromy operators and, after extension to ![]() $\mathbf {B}_{\operatorname {dR} }$, induces a filtered isomorphism
$\mathbf {B}_{\operatorname {dR} }$, induces a filtered isomorphism
We added the subscript ![]() $h$ (for
$h$ (for ![]() $h$-topology) to underscore the different formulation from Theorem 4.1. Here
$h$-topology) to underscore the different formulation from Theorem 4.1. Here ![]() $H^{B,i}_{\operatorname {HK} }(X)$ is the Beilinson–Hyodo–Kato cohomology [Reference BeilinsonBei13, 1.16.1] and the base change to the de Rham comparison uses the Beilinson–Hyodo–Kato isomorphism
$H^{B,i}_{\operatorname {HK} }(X)$ is the Beilinson–Hyodo–Kato cohomology [Reference BeilinsonBei13, 1.16.1] and the base change to the de Rham comparison uses the Beilinson–Hyodo–Kato isomorphism
as well as the canonical map ![]() $\iota _p:\mathbf {B}_{\operatorname {st}}\to \mathbf {B}_{\operatorname {dR} }$ [Reference Nekovář and NiziołNN16, § 2.1]. A priori, these Hyodo–Kato-type constructions are not the same as the original ones (for one thing, they are independent of the choice of the uniformizer
$\iota _p:\mathbf {B}_{\operatorname {st}}\to \mathbf {B}_{\operatorname {dR} }$ [Reference Nekovář and NiziołNN16, § 2.1]. A priori, these Hyodo–Kato-type constructions are not the same as the original ones (for one thing, they are independent of the choice of the uniformizer ![]() $\pi$; in fact, they should be seen, in a sense that can be made precise, as associated to the canonical choice of
$\pi$; in fact, they should be seen, in a sense that can be made precise, as associated to the canonical choice of ![]() $p$). However, the two constructions are related by a natural quasi-isomorphism, i.e., there is a natural map
$p$). However, the two constructions are related by a natural quasi-isomorphism, i.e., there is a natural map ![]() $\kappa$ that makes the following diagram commute [Reference Nekovář and NiziołNN16, (31)].
$\kappa$ that makes the following diagram commute [Reference Nekovář and NiziołNN16, (31)].

4.3.3 Beilinson equivalence of topoi
To describe the Beilinson period morphism, we will need to work with ![]() $h$-topology on the generic fiber. Beilinson has shown that
$h$-topology on the generic fiber. Beilinson has shown that ![]() $h$-topology has a base consisting of semistable schemes. We will review his result briefly.
$h$-topology has a base consisting of semistable schemes. We will review his result briefly.
For a field ![]() $K$, let
$K$, let ![]() ${\mathcal {V}}ar_K$ denote the category of varieties over
${\mathcal {V}}ar_K$ denote the category of varieties over ![]() $K$. We will equip it with
$K$. We will equip it with ![]() $h$-topology (see [Reference BeilinsonBei12, 2.3]), i.e., the coarsest topology finer than the Zariski and proper topologies.Footnote 9 We note that the
$h$-topology (see [Reference BeilinsonBei12, 2.3]), i.e., the coarsest topology finer than the Zariski and proper topologies.Footnote 9 We note that the ![]() $h$-topology is finer than the étale topology. It is generated by the pretopology whose coverings are finite families of maps
$h$-topology is finer than the étale topology. It is generated by the pretopology whose coverings are finite families of maps ![]() $\{Y_i\to X\}$ such that
$\{Y_i\to X\}$ such that ![]() $Y:=\coprod Y_i\to X$ is a universal topological epimorphism (i.e., a subset of
$Y:=\coprod Y_i\to X$ is a universal topological epimorphism (i.e., a subset of ![]() $X$ is Zariski open if and only if its preimage in
$X$ is Zariski open if and only if its preimage in ![]() $Y$ is open). We denote by
$Y$ is open). We denote by ![]() $\mathcal {V}ar_{K,h},X_h$,
$\mathcal {V}ar_{K,h},X_h$, ![]() $X\in \mathcal {V}ar_{K}$, the corresponding
$X\in \mathcal {V}ar_{K}$, the corresponding ![]() $h$-sites.
$h$-sites.
Let ![]() $K$ be now as in § 2. An arithmetic pair over
$K$ be now as in § 2. An arithmetic pair over ![]() $K$ is an open embedding
$K$ is an open embedding ![]() $j:U\hookrightarrow \overline {U}$ with dense image of a
$j:U\hookrightarrow \overline {U}$ with dense image of a ![]() $K$-variety
$K$-variety ![]() $U$ into a reduced proper flat
$U$ into a reduced proper flat ![]() $V$-scheme
$V$-scheme ![]() $\overline {U}$. A morphism
$\overline {U}$. A morphism ![]() $(U,\overline {U})\to (T,\overline {T})$ of pairs is a map
$(U,\overline {U})\to (T,\overline {T})$ of pairs is a map ![]() $\overline {U}\to \overline {T}$ which sends
$\overline {U}\to \overline {T}$ which sends ![]() $U$ to
$U$ to ![]() $T$. In the case that the pairs represent log-regular schemes, this is the same as a map of log-schemes. For a pair
$T$. In the case that the pairs represent log-regular schemes, this is the same as a map of log-schemes. For a pair ![]() $(U,\overline {U})$, we set
$(U,\overline {U})$, we set ![]() $V_U:=\Gamma (\overline {U},{\mathcal O} _{\overline {U}})$ and
$V_U:=\Gamma (\overline {U},{\mathcal O} _{\overline {U}})$ and ![]() $K_U:=\Gamma (\overline {U}_K,{\mathcal O} _{\overline {U}})$. The ring
$K_U:=\Gamma (\overline {U}_K,{\mathcal O} _{\overline {U}})$. The ring ![]() $K_U$ is a product of several finite extensions of
$K_U$ is a product of several finite extensions of ![]() $K$ (labeled by the connected components of
$K$ (labeled by the connected components of ![]() $\overline {U}$) and, if
$\overline {U}$) and, if ![]() $\overline {U}$ is normal,
$\overline {U}$ is normal, ![]() $V_U$ is the product of the corresponding rings of integers.
$V_U$ is the product of the corresponding rings of integers.
A semistable pair over ![]() $K$ [Reference BeilinsonBei12, 2.2] is a pair of schemes
$K$ [Reference BeilinsonBei12, 2.2] is a pair of schemes ![]() $(U,\overline {U})$ over
$(U,\overline {U})$ over ![]() $(K,V)$ such that:
$(K,V)$ such that:
(i)
 $\overline {U}$ is regular and proper over
$\overline {U}$ is regular and proper over  $V$;
$V$;(ii)
 $\overline {U}\setminus U$ is a divisor with normal crossings on
$\overline {U}\setminus U$ is a divisor with normal crossings on  $\overline {U}$;
$\overline {U}$;(iii) the closed fiber
 $\overline {U}_0$ of
$\overline {U}_0$ of  $\overline {U}$ is reduced and its irreducible components are regular.
$\overline {U}$ is reduced and its irreducible components are regular.
A closed fiber is taken over the closed points of ![]() $V_U$. We will think of semistable pairs as log-schemes equipped with log-structure given by the divisor
$V_U$. We will think of semistable pairs as log-schemes equipped with log-structure given by the divisor ![]() $\overline {U}\setminus U$. The closed fiber
$\overline {U}\setminus U$. The closed fiber ![]() $\overline {U}_0$ has the induced log-structure.
$\overline {U}_0$ has the induced log-structure.
A semistable pair over ![]() $\overline {K}$ [Reference BeilinsonBei12, 2.2] is a pair of connected schemes
$\overline {K}$ [Reference BeilinsonBei12, 2.2] is a pair of connected schemes ![]() $(T,\overline {T})$ over
$(T,\overline {T})$ over ![]() $(\overline {K},\overline {V})$ such that there exist a semistable pair
$(\overline {K},\overline {V})$ such that there exist a semistable pair ![]() $(U,\overline {U})$ over
$(U,\overline {U})$ over ![]() $K$ and a
$K$ and a ![]() $\overline {K}$-point
$\overline {K}$-point ![]() $\alpha : K_U\to \overline {K}$ such that
$\alpha : K_U\to \overline {K}$ such that ![]() $(T,\overline {T})$ is isomorphic to the base change
$(T,\overline {T})$ is isomorphic to the base change ![]() $(U_{\overline {K}},\overline {U}_{\overline {V}})$. We will denote by
$(U_{\overline {K}},\overline {U}_{\overline {V}})$. We will denote by ![]() ${\mathcal {P}}_{\overline {K}}^{\rm ss}$ the category of semistable pairs over
${\mathcal {P}}_{\overline {K}}^{\rm ss}$ the category of semistable pairs over ![]() $\overline {K}$.
$\overline {K}$.
Let, for just a moment, ![]() $K$ be any field of characteristic 0. A geometric pair over
$K$ be any field of characteristic 0. A geometric pair over ![]() $K$ is a pair
$K$ is a pair ![]() $(U,\overline {U})$ of varieties over
$(U,\overline {U})$ of varieties over ![]() $K$ such that
$K$ such that ![]() $\overline {U}$ is proper and
$\overline {U}$ is proper and ![]() $U\subset \overline {U}$ is open and dense. We say that the pair
$U\subset \overline {U}$ is open and dense. We say that the pair ![]() $(U,\overline {U})$ is an nc-pair if
$(U,\overline {U})$ is an nc-pair if ![]() $\overline {U}$ is regular and
$\overline {U}$ is regular and ![]() $\overline {U}\setminus U$ is a divisor with normal crossings in
$\overline {U}\setminus U$ is a divisor with normal crossings in ![]() $\overline {U}$; it is a strict nc-pair if the irreducible components of
$\overline {U}$; it is a strict nc-pair if the irreducible components of ![]() $U\setminus \overline {U}$ are regular. A morphism of pairs
$U\setminus \overline {U}$ are regular. A morphism of pairs ![]() $f:(U_1,\overline {U}_1)\to (U,\overline {U})$ is a map
$f:(U_1,\overline {U}_1)\to (U,\overline {U})$ is a map ![]() $\overline {U}_1\to \overline {U}$ that sends
$\overline {U}_1\to \overline {U}$ that sends ![]() $U_1$ to
$U_1$ to ![]() $U$. We denote the category of nc-pairs over
$U$. We denote the category of nc-pairs over ![]() $K$ by
$K$ by ![]() ${\mathcal {P}}_K^{\rm nc}$.
${\mathcal {P}}_K^{\rm nc}$.
For the category ![]() ${\mathcal {P}}_{\overline {K}}^{\rm ss}$ mentioned above, let
${\mathcal {P}}_{\overline {K}}^{\rm ss}$ mentioned above, let ![]() $\gamma : (U,\overline {U})\to U$ denote the forgetful functor. Beilinson proved [Reference BeilinsonBei12, 2.5] that the category
$\gamma : (U,\overline {U})\to U$ denote the forgetful functor. Beilinson proved [Reference BeilinsonBei12, 2.5] that the category ![]() $({\mathcal {P}}_{\overline {K}}^{\rm ss},\gamma )$ forms a base for
$({\mathcal {P}}_{\overline {K}}^{\rm ss},\gamma )$ forms a base for ![]() $\mathcal {V}ar_{\overline {K},h}$. This implies that
$\mathcal {V}ar_{\overline {K},h}$. This implies that ![]() $\gamma$ induces an equivalence of the topoi
$\gamma$ induces an equivalence of the topoi
Similarly for the categories ![]() ${\mathcal {P}}_{K}^{\rm ss}$ and
${\mathcal {P}}_{K}^{\rm ss}$ and ![]() ${\mathcal {P}}_K^{\rm nc}$ (and the category
${\mathcal {P}}_K^{\rm nc}$ (and the category ![]() $\mathcal {V}ar_{K}$).
$\mathcal {V}ar_{K}$).
4.3.4 Definitions of cohomology sheaves
We will now recall briefly the definition of geometric syntomic cohomology, i.e., syntomic cohomology over ![]() $\overline {K}$, from [Reference Nekovář and NiziołNN16], and the related cohomologies from [Reference BeilinsonBei13].
$\overline {K}$, from [Reference Nekovář and NiziołNN16], and the related cohomologies from [Reference BeilinsonBei13].
(i) Absolute crystalline cohomology. For ![]() $(U,\overline {U})\in {\mathcal {P}}^{\rm ss}_{\overline {K}}$,
$(U,\overline {U})\in {\mathcal {P}}^{\rm ss}_{\overline {K}}$, ![]() $r\geq 0$, we have the absolute crystalline cohomology complexes and their completions
$r\geq 0$, we have the absolute crystalline cohomology complexes and their completions
 \begin{align*} \mathrm{R}\Gamma_{\operatorname{cr} }(U,\overline{U},{\mathcal{J}}^{[r]})_n&:=\mathrm{R}\Gamma_{\operatorname{cr} }(\overline{U}_{n,\operatorname{\acute{e}t} },\mathrm{R} u_*{\mathcal{J}}^{[r]}),\\ \mathrm{R}\Gamma_{\operatorname{cr} }(U,\overline{U},{\mathcal{J}}^{[r]})&:= \operatorname{holim} _n\mathrm{R}\Gamma_{\operatorname{cr} }(U,\overline{U},{\mathcal{J}}^{[r]})_n,\\ \mathrm{R}\Gamma_{\operatorname{cr} }(U,\overline{U},{\mathcal{J}}^{[r]})_\mathbf{Q}&:=\mathrm{R}\Gamma_{\operatorname{cr} }(U,\overline{U},{\mathcal{J}}^{[r]})\otimes\mathbf{Q}_p, \end{align*}
\begin{align*} \mathrm{R}\Gamma_{\operatorname{cr} }(U,\overline{U},{\mathcal{J}}^{[r]})_n&:=\mathrm{R}\Gamma_{\operatorname{cr} }(\overline{U}_{n,\operatorname{\acute{e}t} },\mathrm{R} u_*{\mathcal{J}}^{[r]}),\\ \mathrm{R}\Gamma_{\operatorname{cr} }(U,\overline{U},{\mathcal{J}}^{[r]})&:= \operatorname{holim} _n\mathrm{R}\Gamma_{\operatorname{cr} }(U,\overline{U},{\mathcal{J}}^{[r]})_n,\\ \mathrm{R}\Gamma_{\operatorname{cr} }(U,\overline{U},{\mathcal{J}}^{[r]})_\mathbf{Q}&:=\mathrm{R}\Gamma_{\operatorname{cr} }(U,\overline{U},{\mathcal{J}}^{[r]})\otimes\mathbf{Q}_p, \end{align*}
where ![]() $u: \overline {U}_{n,\operatorname {cr} }\to \overline {U}_{n,\operatorname {\acute {e}t} }$ is the natural projection. The complex
$u: \overline {U}_{n,\operatorname {cr} }\to \overline {U}_{n,\operatorname {\acute {e}t} }$ is the natural projection. The complex ![]() $\mathrm {R}\Gamma _{\operatorname {cr} }(U,\overline {U})$ is a perfect
$\mathrm {R}\Gamma _{\operatorname {cr} }(U,\overline {U})$ is a perfect ![]() $\mathbf {A}_{\operatorname {cr} }$-complex and
$\mathbf {A}_{\operatorname {cr} }$-complex and
In general, we have ![]() $\mathrm {R}\Gamma _{\operatorname {cr} }(U,\overline {U},{\mathcal {J}}^{[r]})_n\simeq \mathrm {R}\Gamma _{\operatorname {cr} }(U,\overline {U},{\mathcal {J}}^{[r]})\otimes ^{L}{\mathbf {Z}}/p^n$. Moreover, by [Reference TsujiTsu99a, 1.6.3 and 1.6.4],
$\mathrm {R}\Gamma _{\operatorname {cr} }(U,\overline {U},{\mathcal {J}}^{[r]})_n\simeq \mathrm {R}\Gamma _{\operatorname {cr} }(U,\overline {U},{\mathcal {J}}^{[r]})\otimes ^{L}{\mathbf {Z}}/p^n$. Moreover, by [Reference TsujiTsu99a, 1.6.3 and 1.6.4],
The absolute crystalline cohomology complexes are filtered ![]() $E_{\infty }$ algebras over
$E_{\infty }$ algebras over ![]() $\mathbf {A}_{\operatorname {cr} ,n}$,
$\mathbf {A}_{\operatorname {cr} ,n}$, ![]() $\mathbf {A}_{\operatorname {cr} }$, or
$\mathbf {A}_{\operatorname {cr} }$, or ![]() $\mathbf {A}_{\operatorname {cr} ,\mathbf {Q}}$, respectively. Moreover, the rational ones are filtered commutative dg algebras.
$\mathbf {A}_{\operatorname {cr} ,\mathbf {Q}}$, respectively. Moreover, the rational ones are filtered commutative dg algebras.
Let ![]() ${\mathcal {J}}^{[r]}_{\operatorname {cr} }$ and
${\mathcal {J}}^{[r]}_{\operatorname {cr} }$ and ![]() ${\mathcal {A}}_{\operatorname {cr} }$ be the
${\mathcal {A}}_{\operatorname {cr} }$ be the ![]() $h$-sheafifications on
$h$-sheafifications on ![]() $\mathcal {V}ar_{\overline {K}}$ of the presheaves sending
$\mathcal {V}ar_{\overline {K}}$ of the presheaves sending ![]() $(U,\overline {U})\in {\mathcal {P}}^{\rm ss}_{\overline {K}}$ to
$(U,\overline {U})\in {\mathcal {P}}^{\rm ss}_{\overline {K}}$ to ![]() $\mathrm {R}\Gamma _{\operatorname {cr} }(U,\overline {U},{\mathcal {J}}^{[r]})$ and
$\mathrm {R}\Gamma _{\operatorname {cr} }(U,\overline {U},{\mathcal {J}}^{[r]})$ and ![]() $\mathrm {R}\Gamma _{\operatorname {cr} }(U,\overline {U})$, respectively. Let
$\mathrm {R}\Gamma _{\operatorname {cr} }(U,\overline {U})$, respectively. Let ![]() ${\mathcal {J}}^{[r]}_{\operatorname {cr} ,n}$ and
${\mathcal {J}}^{[r]}_{\operatorname {cr} ,n}$ and ![]() ${\mathcal {A}}_{\operatorname {cr} ,n}$ denote the
${\mathcal {A}}_{\operatorname {cr} ,n}$ denote the ![]() $h$-sheafifications of the mod-
$h$-sheafifications of the mod-![]() $p^n$ versions of the respective presheaves; and let
$p^n$ versions of the respective presheaves; and let ![]() ${\mathcal {J}}^{[r]}_{\operatorname {cr} ,\mathbf {Q}}$ and
${\mathcal {J}}^{[r]}_{\operatorname {cr} ,\mathbf {Q}}$ and ![]() ${\mathcal {A}}_{\operatorname {cr} ,\mathbf {Q}}$ be the
${\mathcal {A}}_{\operatorname {cr} ,\mathbf {Q}}$ be the ![]() $h$-sheafifications of the rational versions of the same presheaves.
$h$-sheafifications of the rational versions of the same presheaves.
For ![]() $X\in \mathcal {V}ar_{\overline {K}}$, set
$X\in \mathcal {V}ar_{\overline {K}}$, set ![]() $\mathrm {R}\Gamma _{\operatorname {cr} }(X_h):=\mathrm {R}\Gamma (X_h,{\mathcal {A}}_{\operatorname {cr} })$. It is a filtered (by
$\mathrm {R}\Gamma _{\operatorname {cr} }(X_h):=\mathrm {R}\Gamma (X_h,{\mathcal {A}}_{\operatorname {cr} })$. It is a filtered (by ![]() $\mathrm {R}\Gamma (X_h,{\mathcal {J}}^{[r]}_{\operatorname {cr} })$,
$\mathrm {R}\Gamma (X_h,{\mathcal {J}}^{[r]}_{\operatorname {cr} })$, ![]() $r\geq 0$)
$r\geq 0$) ![]() $E_{\infty }$
$E_{\infty }$ ![]() $\mathbf {A}_{\operatorname {cr} }$-algebra equipped with the Frobenius action
$\mathbf {A}_{\operatorname {cr} }$-algebra equipped with the Frobenius action ![]() $\phi$. The Galois group
$\phi$. The Galois group ![]() $G_K$ acts on
$G_K$ acts on ![]() ${\mathcal {V}}ar_{\overline {K}}$ and it acts on
${\mathcal {V}}ar_{\overline {K}}$ and it acts on ![]() $X\mapsto \mathrm {R}\Gamma _{\operatorname {cr} }(X_h)$ by transport of structure. If
$X\mapsto \mathrm {R}\Gamma _{\operatorname {cr} }(X_h)$ by transport of structure. If ![]() $X$ is defined over
$X$ is defined over ![]() $K$, then
$K$, then ![]() $G_K$ acts naturally on
$G_K$ acts naturally on ![]() $\mathrm {R}\Gamma _{\operatorname {cr} }(X_h)$.
$\mathrm {R}\Gamma _{\operatorname {cr} }(X_h)$.
(ii) Geometric syntomic cohomology. For ![]() $r\geq 0$, the mod-
$r\geq 0$, the mod-![]() $p^n$, completed, and rational syntomic complexes
$p^n$, completed, and rational syntomic complexes ![]() $\mathrm {R}\Gamma _{\operatorname {syn}}(U,\overline {U},r)_n$,
$\mathrm {R}\Gamma _{\operatorname {syn}}(U,\overline {U},r)_n$, ![]() $\mathrm {R}\Gamma _{\operatorname {syn}}(U,\overline {U},r)$, and
$\mathrm {R}\Gamma _{\operatorname {syn}}(U,\overline {U},r)$, and ![]() $\mathrm {R}\Gamma _{\operatorname {syn}}(U,\overline {U},r)_\mathbf {Q}$ are defined by the formulas
$\mathrm {R}\Gamma _{\operatorname {syn}}(U,\overline {U},r)_\mathbf {Q}$ are defined by the formulas
 \begin{align*} \mathrm{R}\Gamma_{\operatorname{syn}}(U,\overline{U},r)_n& := [\mathrm{R}\Gamma_{\operatorname{cr} }(U,\overline{U},{\mathcal{J}}^{[r]})_n {\buildrel {p^r-\phi} \over \longrightarrow} \mathrm{R}\Gamma_{\operatorname{cr} }(U,\overline{U})_n)],\\ \mathrm{R}\Gamma_{\operatorname{syn}}(U,\overline{U},r)& :=\operatorname{holim} _n\mathrm{R}\Gamma_{\operatorname{syn}}(U,\overline{U},r)_n,\\ \mathrm{R}\Gamma_{\operatorname{syn}}(U,\overline{U},r)_{\mathbf{Q}}& := [\mathrm{R}\Gamma_{\operatorname{cr} }(U,\overline{U},{\mathcal{J}}^{[r]})_\mathbf{Q} {\buildrel {1-\phi_r} \over \longrightarrow} \mathrm{R}\Gamma_{\operatorname{cr} }(U,\overline{U})_\mathbf{Q})]. \end{align*}
\begin{align*} \mathrm{R}\Gamma_{\operatorname{syn}}(U,\overline{U},r)_n& := [\mathrm{R}\Gamma_{\operatorname{cr} }(U,\overline{U},{\mathcal{J}}^{[r]})_n {\buildrel {p^r-\phi} \over \longrightarrow} \mathrm{R}\Gamma_{\operatorname{cr} }(U,\overline{U})_n)],\\ \mathrm{R}\Gamma_{\operatorname{syn}}(U,\overline{U},r)& :=\operatorname{holim} _n\mathrm{R}\Gamma_{\operatorname{syn}}(U,\overline{U},r)_n,\\ \mathrm{R}\Gamma_{\operatorname{syn}}(U,\overline{U},r)_{\mathbf{Q}}& := [\mathrm{R}\Gamma_{\operatorname{cr} }(U,\overline{U},{\mathcal{J}}^{[r]})_\mathbf{Q} {\buildrel {1-\phi_r} \over \longrightarrow} \mathrm{R}\Gamma_{\operatorname{cr} }(U,\overline{U})_\mathbf{Q})]. \end{align*}
We have ![]() $\mathrm {R}\Gamma _{\operatorname {syn}}(U,\overline {U},r)_n\simeq \mathrm {R}\Gamma _{\operatorname {syn}}(U,\overline {U},r)\otimes ^{L}{\mathbf {Z}}/p^n$. Let
$\mathrm {R}\Gamma _{\operatorname {syn}}(U,\overline {U},r)_n\simeq \mathrm {R}\Gamma _{\operatorname {syn}}(U,\overline {U},r)\otimes ^{L}{\mathbf {Z}}/p^n$. Let ![]() ${\mathcal {S}}^{\prime }(r)$ be the
${\mathcal {S}}^{\prime }(r)$ be the ![]() $h$-sheafification on
$h$-sheafification on ![]() $\mathcal {V}ar_{\overline {K}}$ of the presheaf sending
$\mathcal {V}ar_{\overline {K}}$ of the presheaf sending ![]() $(U,\overline {U})\in {\mathcal {P}}^{\rm ss}_{\overline {K}}$ to
$(U,\overline {U})\in {\mathcal {P}}^{\rm ss}_{\overline {K}}$ to ![]() $\mathrm {R}\Gamma _{\operatorname {syn}}(U,\overline {U},r)$. Let
$\mathrm {R}\Gamma _{\operatorname {syn}}(U,\overline {U},r)$. Let ![]() ${\mathcal {S}}^{\prime }_n(r)$ and
${\mathcal {S}}^{\prime }_n(r)$ and ![]() ${\mathcal {S}}^{\prime }(r)_{\mathbf {Q}}$ denote the
${\mathcal {S}}^{\prime }(r)_{\mathbf {Q}}$ denote the ![]() $h$-sheafifications of the mod-
$h$-sheafifications of the mod-![]() $p^n$ and the rational versions of the same presheaf, respectively.
$p^n$ and the rational versions of the same presheaf, respectively.
For ![]() $r\geq 0$, set
$r\geq 0$, set ![]() $\mathrm {R}\Gamma _{\operatorname {syn}}(X_h,r)_n=\mathrm {R}\Gamma (X_h,{\mathcal {S}}^{\prime }_n(r))$,
$\mathrm {R}\Gamma _{\operatorname {syn}}(X_h,r)_n=\mathrm {R}\Gamma (X_h,{\mathcal {S}}^{\prime }_n(r))$, ![]() $\mathrm {R}\Gamma _{\operatorname {syn}}(X_h,r):=\mathrm {R}\Gamma (X_h,{\mathcal {S}}^{\prime }(r)_\mathbf {Q})$. We have
$\mathrm {R}\Gamma _{\operatorname {syn}}(X_h,r):=\mathrm {R}\Gamma (X_h,{\mathcal {S}}^{\prime }(r)_\mathbf {Q})$. We have
 \begin{align*} \mathrm{R}\Gamma_{\operatorname{syn}}(X_h,r)_n &\simeq [\mathrm{R}\Gamma(X_h,{\mathcal{J}}^{[r]}_{\operatorname{cr} ,n})\stackrel{p^r-\phi}{\longrightarrow}\mathrm{R}\Gamma(X_h,{\mathcal{A}}_{\operatorname{cr} ,n})],\\ \mathrm{R}\Gamma_{\operatorname{syn}}(X_h,r) &\simeq [\mathrm{R}\Gamma(X_h,{\mathcal{J}}^{[r]}_{\operatorname{cr} ,{\mathbf{Q}}})\stackrel{1-\phi_r}{\longrightarrow}\mathrm{R}\Gamma(X_h,{\mathcal{A}}_{\operatorname{cr} ,{\mathbf{Q}}})]. \end{align*}
\begin{align*} \mathrm{R}\Gamma_{\operatorname{syn}}(X_h,r)_n &\simeq [\mathrm{R}\Gamma(X_h,{\mathcal{J}}^{[r]}_{\operatorname{cr} ,n})\stackrel{p^r-\phi}{\longrightarrow}\mathrm{R}\Gamma(X_h,{\mathcal{A}}_{\operatorname{cr} ,n})],\\ \mathrm{R}\Gamma_{\operatorname{syn}}(X_h,r) &\simeq [\mathrm{R}\Gamma(X_h,{\mathcal{J}}^{[r]}_{\operatorname{cr} ,{\mathbf{Q}}})\stackrel{1-\phi_r}{\longrightarrow}\mathrm{R}\Gamma(X_h,{\mathcal{A}}_{\operatorname{cr} ,{\mathbf{Q}}})]. \end{align*}
The direct sum ![]() $\bigoplus _{r\geq 0}\mathrm {R}\Gamma _{\operatorname {syn}}(X_h,r)$ is a graded
$\bigoplus _{r\geq 0}\mathrm {R}\Gamma _{\operatorname {syn}}(X_h,r)$ is a graded ![]() $E_{\infty }$ algebra over
$E_{\infty }$ algebra over ![]() ${\mathbf {Z}}_p$.
${\mathbf {Z}}_p$.
(iii) de Rham cohomology. Consider the presheaf ![]() $(U,\overline {U})\mapsto \mathrm {R}\Gamma _{\operatorname {dR} }(U,\overline {U}):=\mathrm {R}\Gamma (\overline {U},\Omega ^{\scriptscriptstyle \bullet }_{(U,\overline {U})})$ of filtered dg
$(U,\overline {U})\mapsto \mathrm {R}\Gamma _{\operatorname {dR} }(U,\overline {U}):=\mathrm {R}\Gamma (\overline {U},\Omega ^{\scriptscriptstyle \bullet }_{(U,\overline {U})})$ of filtered dg ![]() $K$-algebras on
$K$-algebras on ![]() ${\mathcal {P}}^{\rm nc}_K$. Let
${\mathcal {P}}^{\rm nc}_K$. Let ![]() ${\mathcal {A}}_{\operatorname {dR} }$ be its
${\mathcal {A}}_{\operatorname {dR} }$ be its ![]() $h$-sheafification. It is a sheaf of filtered
$h$-sheafification. It is a sheaf of filtered ![]() $K$-algebras on
$K$-algebras on ![]() $\mathcal {V}ar_K$. For
$\mathcal {V}ar_K$. For ![]() $X\in \mathcal {V}ar_K$, we have Deligne's de Rham complex of
$X\in \mathcal {V}ar_K$, we have Deligne's de Rham complex of ![]() $X$ equipped with Deligne's Hodge filtration:
$X$ equipped with Deligne's Hodge filtration: ![]() $\mathrm {R}\Gamma _{\operatorname {dR} }(X_h):=\mathrm {R}\Gamma (X_h,{\mathcal {A}}_{\operatorname {dR} })$.
$\mathrm {R}\Gamma _{\operatorname {dR} }(X_h):=\mathrm {R}\Gamma (X_h,{\mathcal {A}}_{\operatorname {dR} })$.
(iv) Beilinson–Hyodo–Kato cohomology. Let ![]() ${\mathcal {A}}^B_{\operatorname {HK} }$ be the
${\mathcal {A}}^B_{\operatorname {HK} }$ be the ![]() $h$-sheafification of the presheaf of (arithmetic) Beilinson–Hyodo–Kato cohomology
$h$-sheafification of the presheaf of (arithmetic) Beilinson–Hyodo–Kato cohomology ![]() $(U,\overline {U})\mapsto \mathrm {R}\Gamma ^B_{\operatorname {HK} }(U,\overline {U})_{\mathbf {Q}}$ on
$(U,\overline {U})\mapsto \mathrm {R}\Gamma ^B_{\operatorname {HK} }(U,\overline {U})_{\mathbf {Q}}$ on ![]() ${\mathcal {P}}_{K}^{\rm ss}$; this is an
${\mathcal {P}}_{K}^{\rm ss}$; this is an ![]() $h$-sheaf of
$h$-sheaf of ![]() $E_{\infty }$
$E_{\infty }$ ![]() $F$-algebras on
$F$-algebras on ![]() ${\mathcal {V}}ar_{K}$ equipped with a
${\mathcal {V}}ar_{K}$ equipped with a ![]() $\phi$-action and a derivation
$\phi$-action and a derivation ![]() $N$ such that
$N$ such that ![]() $N\phi =p\phi N$. For
$N\phi =p\phi N$. For ![]() $X\in {\mathcal {V}}ar_{K}$, set
$X\in {\mathcal {V}}ar_{K}$, set ![]() $\mathrm {R}\Gamma ^B_{\operatorname {HK} }(X_h):=\mathrm {R}\Gamma (X_h,{\mathcal {A}}^B_{\operatorname {HK} })$.
$\mathrm {R}\Gamma ^B_{\operatorname {HK} }(X_h):=\mathrm {R}\Gamma (X_h,{\mathcal {A}}^B_{\operatorname {HK} })$.
Let ![]() ${\mathcal {A}}^B_{\operatorname {HK} }$ be the
${\mathcal {A}}^B_{\operatorname {HK} }$ be the ![]() $h$-sheafification of the presheaf
$h$-sheafification of the presheaf ![]() $(U,\overline {U})\mapsto \mathrm {R}\Gamma ^B_{\operatorname {HK} }(U,\overline {U})_{\mathbf {Q}}$ of (geometric) Beilinson–Hyodo–Kato cohomology on
$(U,\overline {U})\mapsto \mathrm {R}\Gamma ^B_{\operatorname {HK} }(U,\overline {U})_{\mathbf {Q}}$ of (geometric) Beilinson–Hyodo–Kato cohomology on ![]() ${\mathcal {P}}^{\rm ss}_{\overline {K}}$. This is an
${\mathcal {P}}^{\rm ss}_{\overline {K}}$. This is an ![]() $h$-sheaf of
$h$-sheaf of ![]() $E_{\infty }$
$E_{\infty }$ ![]() $F^{\rm nr}$-algebras, where
$F^{\rm nr}$-algebras, where ![]() $F^{\rm nr}$ is the maximal unramified extension of
$F^{\rm nr}$ is the maximal unramified extension of ![]() $F$, equipped with a
$F$, equipped with a ![]() $\phi$-action and locally nilpotent derivation
$\phi$-action and locally nilpotent derivation ![]() $N$ such that
$N$ such that ![]() $N\phi =p\phi N$. For
$N\phi =p\phi N$. For ![]() $X\in \mathcal {V}ar_{\overline {K}}$, set
$X\in \mathcal {V}ar_{\overline {K}}$, set ![]() $\mathrm {R}\Gamma ^B_{\operatorname {HK} }(X_h):=\mathrm {R}\Gamma (X_h,{\mathcal {A}}^B_{\operatorname {HK} }).$ We have the Beilnson–Hyodo–Kato quasi-isomorphism
$\mathrm {R}\Gamma ^B_{\operatorname {HK} }(X_h):=\mathrm {R}\Gamma (X_h,{\mathcal {A}}^B_{\operatorname {HK} }).$ We have the Beilnson–Hyodo–Kato quasi-isomorphism
(v) Comparison statements. The ![]() $h$-topology definitions of cohomology are often compatible with the original definitions.
$h$-topology definitions of cohomology are often compatible with the original definitions.
Lemma 4.11 We have the following comparison statements.
(i) For ![]() $(U,\overline {U})\in {\mathcal {P}}^{\rm nc}_L$,
$(U,\overline {U})\in {\mathcal {P}}^{\rm nc}_L$, ![]() $L=K,\overline {K}$, the canonical map
$L=K,\overline {K}$, the canonical map ![]() $\mathrm {R}\Gamma _{\operatorname {dR} }(U,\overline {U})\stackrel {\sim }{\to } \mathrm {R}\Gamma _{\operatorname {dR} }(U_h)$ is a filtered quasi-isomorphism [Reference BeilinsonBei12, 2.4].
$\mathrm {R}\Gamma _{\operatorname {dR} }(U,\overline {U})\stackrel {\sim }{\to } \mathrm {R}\Gamma _{\operatorname {dR} }(U_h)$ is a filtered quasi-isomorphism [Reference BeilinsonBei12, 2.4].
(ii) For any ![]() $(U,\overline {U})\in {\mathcal {P}}^{\rm ss}_{\overline {K}}$,
$(U,\overline {U})\in {\mathcal {P}}^{\rm ss}_{\overline {K}}$, ![]() $r\geq 0$, the canonical maps
$r\geq 0$, the canonical maps
are quasi-isomorphisms (see [Reference BeilinsonBei13, 2.4] and [Reference Nekovář and NiziołNN16, Proposition 3.21]). In particular,
(iii) For any arithmetic pair ![]() $(U,\overline {U})$ that is fine, log-smooth over
$(U,\overline {U})$ that is fine, log-smooth over ![]() ${\mathcal O} _K^{\times }$, and of Cartier type, the canonical map
${\mathcal O} _K^{\times }$, and of Cartier type, the canonical map
is a quasi-isomorphism [Reference Nekovář and NiziołNN16, Proposition 3.18].
4.3.5 Poincaré lemma
We will recall the Poincaré lemma of Beilinson [Reference BeilinsonBei13] and its syntomic cohomology version [Reference Nekovář and NiziołNN16].
Theorem 4.12 (Filtered crystalline Poincaré lemma [Bei13, 2.3], [Bha12, Theorem 10.14]) Let ![]() $r\geq 0$. The canonical map
$r\geq 0$. The canonical map ![]() $J^{[r]}_{\operatorname {cr} ,n}\to {\mathcal {J}}^{[r]}_{\operatorname {cr} ,n}$ is a quasi-isomorphism of
$J^{[r]}_{\operatorname {cr} ,n}\to {\mathcal {J}}^{[r]}_{\operatorname {cr} ,n}$ is a quasi-isomorphism of ![]() $h$-sheaves on
$h$-sheaves on ![]() ${\mathcal {V}}ar_{\overline {K}}$.
${\mathcal {V}}ar_{\overline {K}}$.
Set ![]() $S^{\prime }_n(r):=\operatorname {Cone}(J^{[r]}_{\operatorname {cr} ,n} {\buildrel {p^r-\phi } \over \longrightarrow} \mathbf {A}_{\operatorname {cr} ,n})[-1]$. There is a natural morphism of complexes
$S^{\prime }_n(r):=\operatorname {Cone}(J^{[r]}_{\operatorname {cr} ,n} {\buildrel {p^r-\phi } \over \longrightarrow} \mathbf {A}_{\operatorname {cr} ,n})[-1]$. There is a natural morphism of complexes ![]() $\tau _n: S^{\prime }_n(r)\to {\mathbf {Z}}/p^n(r)^{\prime }$ (induced by
$\tau _n: S^{\prime }_n(r)\to {\mathbf {Z}}/p^n(r)^{\prime }$ (induced by ![]() $p^r$ on
$p^r$ on ![]() $J_{\operatorname {cr} ,n}^{[r]}$ and
$J_{\operatorname {cr} ,n}^{[r]}$ and ![]() $\operatorname {Id}$ on
$\operatorname {Id}$ on ![]() $\mathbf {A}_{\operatorname {cr} ,n}$), whose kernel and cokernel are annihilated by
$\mathbf {A}_{\operatorname {cr} ,n}$), whose kernel and cokernel are annihilated by ![]() $p^r$. The filtered crystalline Poincaré lemma implies easily the following syntomic Poincaré lemma.
$p^r$. The filtered crystalline Poincaré lemma implies easily the following syntomic Poincaré lemma.
Corollary 4.13 There is a unique quasi-isomorphism ![]() $S^{\prime }_n(r)\stackrel {\sim }{\to }{\mathcal {S}}^{\prime }_n(r)$ of complexes of sheaves on
$S^{\prime }_n(r)\stackrel {\sim }{\to }{\mathcal {S}}^{\prime }_n(r)$ of complexes of sheaves on ![]() ${\mathcal {V}}ar_{\overline {K},h}$ that is compatible with the crystalline Poincaré lemma.
${\mathcal {V}}ar_{\overline {K},h}$ that is compatible with the crystalline Poincaré lemma.
Proof. We include here the simple proof from [Reference Nekovář and NiziołNN16, Corollary 4.5]. Consider the following map of distinguished triangles.

The triangles are distinguished by definition. The vertical continuous arrows are quasi-isomorphisms by the crystalline Poincaré lemma. They induce the dashed arrow that is clearly a quasi-isomorphism.
4.3.6 Beilinson period morphism
We will now recall the definition of the period morphism of Beilinson [Reference BeilinsonBei13, 3.1]. Let ![]() $X\in {\mathcal {V}}ar_{\overline {K}}$. Recall first the definition of the crystalline period morphism [Reference BeilinsonBei13]
$X\in {\mathcal {V}}ar_{\overline {K}}$. Recall first the definition of the crystalline period morphism [Reference BeilinsonBei13]
Consider the natural map ![]() $\pi _n: \mathrm {R}\Gamma _{\operatorname {cr} }(X_h)\to \mathrm {R}\Gamma (X_h,{\mathcal {A}}_{\operatorname {cr} ,n})$ and take the composition
$\pi _n: \mathrm {R}\Gamma _{\operatorname {cr} }(X_h)\to \mathrm {R}\Gamma (X_h,{\mathcal {A}}_{\operatorname {cr} ,n})$ and take the composition
Set ![]() $\beta ^{\rm B}_{\operatorname {cr} ,n}:=\rho _n^{-1}\pi _n$ and
$\beta ^{\rm B}_{\operatorname {cr} ,n}:=\rho _n^{-1}\pi _n$ and ![]() $\beta ^{\rm B}_{\operatorname {cr} }:=\operatorname {holim} _n\beta ^{\rm B}_{\operatorname {cr} ,n}$.
$\beta ^{\rm B}_{\operatorname {cr} }:=\operatorname {holim} _n\beta ^{\rm B}_{\operatorname {cr} ,n}$.
The Beilinson–Hyodo–Kato period map
is obtained by composing the map ![]() $\beta _{\operatorname {cr} , {\mathbf {Q}}}$ with the quasi-isomorphism
$\beta _{\operatorname {cr} , {\mathbf {Q}}}$ with the quasi-isomorphism
We have the induced quasi-isomorphism
and we set ![]() $\alpha ^B_h:=\beta _{\operatorname {HK} }^{-1}$.
$\alpha ^B_h:=\beta _{\operatorname {HK} }^{-1}$.
The Beilinson–de Rham period map
is obtained from the Beilinson–Hyodo–Kato period map ![]() $\beta _{\operatorname {HK} }$ using the Beilinson–Hyodo–Kato isomorphism
$\beta _{\operatorname {HK} }$ using the Beilinson–Hyodo–Kato isomorphism ![]() $\rho _{\operatorname {HK} }: \mathrm {R}\Gamma ^B_{\operatorname {HK} }(X_h)\otimes ^L_{F^{\rm nr}}\overline {K}\stackrel {\sim }{\to }\mathrm {R}\Gamma _{\operatorname {dR} }(X_h)$ and the canonical map
$\rho _{\operatorname {HK} }: \mathrm {R}\Gamma ^B_{\operatorname {HK} }(X_h)\otimes ^L_{F^{\rm nr}}\overline {K}\stackrel {\sim }{\to }\mathrm {R}\Gamma _{\operatorname {dR} }(X_h)$ and the canonical map ![]() $\iota _p: \mathbf {B}_{\operatorname {st}}\to \mathbf {B}_{\operatorname {dR} }$. We set
$\iota _p: \mathbf {B}_{\operatorname {st}}\to \mathbf {B}_{\operatorname {dR} }$. We set ![]() $\alpha ^B:=\beta _{\operatorname {dR} }^{-1}$.
$\alpha ^B:=\beta _{\operatorname {dR} }^{-1}$.
The induced syntomic period morphism
can be described in the following way. Take the natural map ![]() $\pi _n: \mathrm {R}\Gamma (X_h,{\mathcal {S}}^{\prime }(r))\to \mathrm {R}\Gamma (X_h,{\mathcal {S}}^{\prime }_n(r))$ and the zigzag
$\pi _n: \mathrm {R}\Gamma (X_h,{\mathcal {S}}^{\prime }(r))\to \mathrm {R}\Gamma (X_h,{\mathcal {S}}^{\prime }_n(r))$ and the zigzag
Set ![]() $\beta ^{\rm B}:=(\operatorname {holim} _n\beta ^{\rm B}_{n})\otimes {\mathbf {Q}}$. Then the map
$\beta ^{\rm B}:=(\operatorname {holim} _n\beta ^{\rm B}_{n})\otimes {\mathbf {Q}}$. Then the map
where ![]() $\pi :=(\operatorname {holim} _n\pi _{n})\otimes {\mathbf {Q}}$, is the induced syntomic period morphism. By [Reference Nekovář and NiziołNN16, Proposition 4.6], it is an isomorphism after truncation
$\pi :=(\operatorname {holim} _n\pi _{n})\otimes {\mathbf {Q}}$, is the induced syntomic period morphism. By [Reference Nekovář and NiziołNN16, Proposition 4.6], it is an isomorphism after truncation ![]() $\tau _{\leq r}$.
$\tau _{\leq r}$.
Remark 4.14 It is worth looking carefully at the composition
This composition is a quasi-isomorphism after truncation ![]() $\tau _{\leq r}$. Since, by Corollary 4.13, the second map is a quasi-isomorphism, it follows that the first map is a quasi-isomorphism after truncation
$\tau _{\leq r}$. Since, by Corollary 4.13, the second map is a quasi-isomorphism, it follows that the first map is a quasi-isomorphism after truncation ![]() $\tau _{\leq r}$ as well.
$\tau _{\leq r}$ as well.
4.3.7 A very simple comparison criterion
This is an analog of the criterion in Lemma 4.3 in the context of Beilinson comparison morphisms from Theorem 4.10.
Let ![]() $X$ be a semistable scheme over
$X$ be a semistable scheme over ![]() ${\mathcal O} _K$. Let
${\mathcal O} _K$. Let ![]() $r\geq 0$. For a period isomorphism
$r\geq 0$. For a period isomorphism ![]() $\alpha _{h,i}$ as in Theorem 4.10, we define its twist
$\alpha _{h,i}$ as in Theorem 4.10, we define its twist
as ![]() $\alpha _{h,i,r}:=t^r\alpha _{h,i}\epsilon ^{-r}$. Clearly, it is an isomorphism. It follows from Theorem 4.10 that we can recover the étale cohomology with the Galois action from the Beilinson–Hyodo–Kato cohomology:
$\alpha _{h,i,r}:=t^r\alpha _{h,i}\epsilon ^{-r}$. Clearly, it is an isomorphism. It follows from Theorem 4.10 that we can recover the étale cohomology with the Galois action from the Beilinson–Hyodo–Kato cohomology:
For ![]() $r\geq i$, by [Reference Nekovář and NiziołNN16, Proposition 3.25 and Corollary 3.26], the right-hand side is isomorphic to
$r\geq i$, by [Reference Nekovář and NiziołNN16, Proposition 3.25 and Corollary 3.26], the right-hand side is isomorphic to ![]() $H^i_{\operatorname {syn}}(X_{\overline {K},h},r)$, i.e., there exists a natural isomorphism
$H^i_{\operatorname {syn}}(X_{\overline {K},h},r)$, i.e., there exists a natural isomorphism
We will denote by
the induced isomorphism and call it the syntomic period isomorphism.
The following lemma is immediate.
Lemma 4.17 Let ![]() $r\geq i$. A period isomorphism
$r\geq i$. A period isomorphism ![]() $\alpha _{h,i,r}$, and hence also a period isomorphism
$\alpha _{h,i,r}$, and hence also a period isomorphism ![]() $\alpha _{h,i}$ satisfying Theorem 4.10, is uniquely determined by the induced syntomic period isomorphism
$\alpha _{h,i}$ satisfying Theorem 4.10, is uniquely determined by the induced syntomic period isomorphism ![]() $\tilde {\alpha }_{h,i,r}$.
$\tilde {\alpha }_{h,i,r}$.
4.3.8 Comparison of Tsuji and Beilinson period morphisms
Let ![]() $X\in {\mathcal {V}}ar_{\overline {K}}$. We can
$X\in {\mathcal {V}}ar_{\overline {K}}$. We can ![]() $h$-sheafify the Tsuji syntomic period morphism by setting, for
$h$-sheafify the Tsuji syntomic period morphism by setting, for ![]() $(U,\overline {U})\in {\mathcal {P}}^{\rm ss}_{\overline {K}}$,
$(U,\overline {U})\in {\mathcal {P}}^{\rm ss}_{\overline {K}}$,
from (4.9) to obtain the compatible maps of ![]() $h$-sheaves
$h$-sheaves
Taking cohomology, we get the induced compatible syntomic period morphisms
As in the case of the Beilinson period morphism, they induce a syntomic period morphism
It is a quasi-isomorphism after truncation ![]() $\tau _{\leq r}$: by Remark 4.14, the map
$\tau _{\leq r}$: by Remark 4.14, the map ![]() $\pi$ is a quasi-isomorphism after truncation
$\pi$ is a quasi-isomorphism after truncation ![]() $\tau _{\leq r}$ and, by Corollary 4.13, the map (4.19) is a
$\tau _{\leq r}$ and, by Corollary 4.13, the map (4.19) is a ![]() $p^r$-quasi-isomorphism and hence the map
$p^r$-quasi-isomorphism and hence the map ![]() $\beta^{\rm T}$ is a quasi-isomorphism after truncation
$\beta^{\rm T}$ is a quasi-isomorphism after truncation ![]() $\tau _{\leq r}$ as well.
$\tau _{\leq r}$ as well.
Theorem 4.21 Let ![]() $r\geq 0$.
$r\geq 0$.
(i) Let ![]() $X\in {\mathcal {V}}ar_{\overline {K}}$. The Tsuji and Beilinson syntomic period morphisms
$X\in {\mathcal {V}}ar_{\overline {K}}$. The Tsuji and Beilinson syntomic period morphisms
are equal.
(ii) If ![]() $X=(U,\overline {U})\in {\mathcal {P}}^{\rm ss}_K$ and is split overFootnote 10
$X=(U,\overline {U})\in {\mathcal {P}}^{\rm ss}_K$ and is split overFootnote 10 ![]() ${\mathcal O} _K$, the period isomorphisms
${\mathcal O} _K$, the period isomorphisms
 \begin{align*} {\alpha}_{h,i}^{\rm T}, {\alpha}_{h,i}^{\rm B}&: H^i_{\operatorname{\acute{e}t} }(U_{\overline{K}},{\mathbf{Q} }_p) \otimes_{{\mathbf{Q} }_p} \mathbf{B}_{\operatorname{st}} \stackrel{\sim}{\to} H^{B,i}_{\operatorname{HK} }(X)\otimes_{F} \mathbf{B}_{\operatorname{st}},\\ {\alpha}_{i}^{\rm T}, {\alpha}_{i}^{\rm B}&: H^i_{\operatorname{\acute{e}t} }(U_{\overline{K}},{\mathbf{Q} }_p) \otimes_{{\mathbf{Q} }_p} \mathbf{B}_{\operatorname{dR} } \stackrel{\sim}{\to} H^{i}_{\operatorname{dR} }(X_K)\otimes_{K} \mathbf{B}_{\operatorname{dR} }, \end{align*}
\begin{align*} {\alpha}_{h,i}^{\rm T}, {\alpha}_{h,i}^{\rm B}&: H^i_{\operatorname{\acute{e}t} }(U_{\overline{K}},{\mathbf{Q} }_p) \otimes_{{\mathbf{Q} }_p} \mathbf{B}_{\operatorname{st}} \stackrel{\sim}{\to} H^{B,i}_{\operatorname{HK} }(X)\otimes_{F} \mathbf{B}_{\operatorname{st}},\\ {\alpha}_{i}^{\rm T}, {\alpha}_{i}^{\rm B}&: H^i_{\operatorname{\acute{e}t} }(U_{\overline{K}},{\mathbf{Q} }_p) \otimes_{{\mathbf{Q} }_p} \mathbf{B}_{\operatorname{dR} } \stackrel{\sim}{\to} H^{i}_{\operatorname{dR} }(X_K)\otimes_{K} \mathbf{B}_{\operatorname{dR} }, \end{align*}
where we set ![]() ${\alpha }_{h,i}^{\rm T}:= \kappa ^{-1}{\alpha }_{i}^{\rm T}$, are equal as well.
${\alpha }_{h,i}^{\rm T}:= \kappa ^{-1}{\alpha }_{i}^{\rm T}$, are equal as well.
Proof. For the first claim, by construction of the syntomic period morphisms ![]() $\widetilde {\beta }_{h,r}^{\rm T}$ and
$\widetilde {\beta }_{h,r}^{\rm T}$ and ![]() $\widetilde {\beta }_{h,r}^{\rm B}$, it suffices to show that, for all
$\widetilde {\beta }_{h,r}^{\rm B}$, it suffices to show that, for all ![]() $n\geq 1$, the maps
$n\geq 1$, the maps
 \begin{align*} \beta_{n}^{\rm B}&: {\mathcal{S}}^{\prime}_n(r)\stackrel{\sim}{\leftarrow} S^{\prime}_n(r) {\buildrel {\tau_n} \over \longrightarrow} \mathbf{Z}/p^n(r)^{\prime},\\ \beta_{n}^{\rm T}&: {\mathcal{S}}^{\prime}_n(r) {\buildrel {\alpha^{\rm T}_r} \over \longrightarrow} \mathbf{Z}/p^n(r)^{\prime} \end{align*}
\begin{align*} \beta_{n}^{\rm B}&: {\mathcal{S}}^{\prime}_n(r)\stackrel{\sim}{\leftarrow} S^{\prime}_n(r) {\buildrel {\tau_n} \over \longrightarrow} \mathbf{Z}/p^n(r)^{\prime},\\ \beta_{n}^{\rm T}&: {\mathcal{S}}^{\prime}_n(r) {\buildrel {\alpha^{\rm T}_r} \over \longrightarrow} \mathbf{Z}/p^n(r)^{\prime} \end{align*}are equal. Or that so are the maps
 \begin{gather*} \tau_{n}: S^{\prime}_n(r)\to \mathbf{Z}/p^n(r)^{\prime},\\ S^{\prime}_n(r)\stackrel{\sim}{\to} {\mathcal{S}}^{\prime}_n(r) {\buildrel {\beta^{\rm T}_r} \over \longrightarrow} \mathbf{Z}/p^n(r)^{\prime}. \end{gather*}
\begin{gather*} \tau_{n}: S^{\prime}_n(r)\to \mathbf{Z}/p^n(r)^{\prime},\\ S^{\prime}_n(r)\stackrel{\sim}{\to} {\mathcal{S}}^{\prime}_n(r) {\buildrel {\beta^{\rm T}_r} \over \longrightarrow} \mathbf{Z}/p^n(r)^{\prime}. \end{gather*}
But this is immediate from the functoriality of ![]() $\beta ^{\rm T}_{r,n}$: for
$\beta ^{\rm T}_{r,n}$: for ![]() $(U,\overline {U})\in {\mathcal {P}}^{\rm ss}_{\overline {K}}$, the canonical map
$(U,\overline {U})\in {\mathcal {P}}^{\rm ss}_{\overline {K}}$, the canonical map ![]() $(U,\overline {U})\to (\operatorname {Spec} \overline {K}, \operatorname {Spec} {\mathcal O} _{\overline {K}})$ yields the following commutative diagram.
$(U,\overline {U})\to (\operatorname {Spec} \overline {K}, \operatorname {Spec} {\mathcal O} _{\overline {K}})$ yields the following commutative diagram.

For the second claim, let ![]() $X=(U,\overline {U})\in {\mathcal {P}}^{\rm ss}_K$ be split over
$X=(U,\overline {U})\in {\mathcal {P}}^{\rm ss}_K$ be split over ![]() ${\mathcal O} _K$. By Lemma 4.17, it suffices to show that, for
${\mathcal O} _K$. By Lemma 4.17, it suffices to show that, for ![]() $r\geq i$, the induced maps
$r\geq i$, the induced maps ![]() $\tilde {\alpha }_{h,i,r}^{\rm T}$ and
$\tilde {\alpha }_{h,i,r}^{\rm T}$ and ![]() $\tilde {\alpha }_{h,i,r}^{\rm B}$ from
$\tilde {\alpha }_{h,i,r}^{\rm B}$ from ![]() $H^i_{\operatorname {\acute {e}t} }(U_{\overline {K}},\mathbf {Q}_p(r))$ to
$H^i_{\operatorname {\acute {e}t} }(U_{\overline {K}},\mathbf {Q}_p(r))$ to ![]() $H^i_{\operatorname {syn}}(U_{\overline {K}, h}, r)$ are equal. But, by the first claim of this theorem, it suffices to prove the following lemma.
$H^i_{\operatorname {syn}}(U_{\overline {K}, h}, r)$ are equal. But, by the first claim of this theorem, it suffices to prove the following lemma.
Lemma 4.22 (i) The map ![]() $\tilde {\alpha }_{h,i,r}^{\rm B}$ is the inverse of the map
$\tilde {\alpha }_{h,i,r}^{\rm B}$ is the inverse of the map ![]() $\tilde {\beta }_{h,i,r}^{\rm B}$.
$\tilde {\beta }_{h,i,r}^{\rm B}$.
(ii) The map ![]() $\tilde {\alpha }_{h,i,r}^{\rm T}$ is the inverse of the map
$\tilde {\alpha }_{h,i,r}^{\rm T}$ is the inverse of the map ![]() $\tilde {\beta }_{h,i,r}^{\rm T}: H^i_{\operatorname {syn}}(U_{\overline {K}, h}, r)\to H^i_{\operatorname {\acute {e}t} }(U_{\overline {K}},\mathbf {Q}_p(r))$ induced by
$\tilde {\beta }_{h,i,r}^{\rm T}: H^i_{\operatorname {syn}}(U_{\overline {K}, h}, r)\to H^i_{\operatorname {\acute {e}t} }(U_{\overline {K}},\mathbf {Q}_p(r))$ induced by ![]() $\tilde {\beta }_{h,r}^{\rm T}$.
$\tilde {\beta }_{h,r}^{\rm T}$.
Proof. The first claim was shown in [Reference Nekovář and NiziołNN16, (49)]. The second claim is also basically shown in [Reference Nekovář and NiziołNN16] (which contains a detailed analysis of the Beilinson–Hyodo–Kato map and its interaction with more classical constructions). However, we could not find there the exact statement we need here so we provide an argument how the proof can be glued from statements proved already in [Reference Nekovář and NiziołNN16].
Consider the following diagram (all the maps are isomorphisms)

where we set
 \begin{align*} C(H^{B,i}_{\operatorname{HK} }(U_{\overline{K},h}),r)&:= \ker((H^{B,i}_{\operatorname{HK} }(U_{\overline{K},h})\otimes_{F^{\rm nr}}\mathbf{B}^+_{\operatorname{st}})^{N=0,\phi=p^r} {\buildrel {\rho^B\otimes\iota_p} \over \longrightarrow} (H^i_{\operatorname{dR} }(U_{\overline{K},h})\otimes_{\overline{K}}\mathbf{B}^+_{\operatorname{dR} })/F^r),\\ C(H^{i}_{\operatorname{HK} }(X),r)&:= \ker((H^{i}_{\operatorname{HK} }(X)\otimes_F\mathbf{B}^+_{\operatorname{st}})^{N=0,\phi=p^r} {\buildrel {\rho_{\pi}\otimes\iota_{\pi}} \over \longrightarrow}(H^i_{\operatorname{dR} }(X_K)\otimes_K\mathbf{B}^+_{\operatorname{dR} })/F^r),\\ H^i_{\operatorname{syn}}(X_{\overline{K}},r)&:= H^i\mathrm{R}\Gamma_{\operatorname{syn}}(X_{\overline{K}},r):=H^i\mathrm{R}\Gamma_{\operatorname{\acute{e}t} }(X_{{\mathcal O}_{\overline{K}}},{\mathcal{S}}^{\prime}(r))_{\mathbf{Q}}. \end{align*}
\begin{align*} C(H^{B,i}_{\operatorname{HK} }(U_{\overline{K},h}),r)&:= \ker((H^{B,i}_{\operatorname{HK} }(U_{\overline{K},h})\otimes_{F^{\rm nr}}\mathbf{B}^+_{\operatorname{st}})^{N=0,\phi=p^r} {\buildrel {\rho^B\otimes\iota_p} \over \longrightarrow} (H^i_{\operatorname{dR} }(U_{\overline{K},h})\otimes_{\overline{K}}\mathbf{B}^+_{\operatorname{dR} })/F^r),\\ C(H^{i}_{\operatorname{HK} }(X),r)&:= \ker((H^{i}_{\operatorname{HK} }(X)\otimes_F\mathbf{B}^+_{\operatorname{st}})^{N=0,\phi=p^r} {\buildrel {\rho_{\pi}\otimes\iota_{\pi}} \over \longrightarrow}(H^i_{\operatorname{dR} }(X_K)\otimes_K\mathbf{B}^+_{\operatorname{dR} })/F^r),\\ H^i_{\operatorname{syn}}(X_{\overline{K}},r)&:= H^i\mathrm{R}\Gamma_{\operatorname{syn}}(X_{\overline{K}},r):=H^i\mathrm{R}\Gamma_{\operatorname{\acute{e}t} }(X_{{\mathcal O}_{\overline{K}}},{\mathcal{S}}^{\prime}(r))_{\mathbf{Q}}. \end{align*}
The map ![]() $h_{i,r}$ is induced by the map
$h_{i,r}$ is induced by the map ![]() $h_r$ defined in (2.10). Since, by definition,
$h_r$ defined in (2.10). Since, by definition, ![]() $\alpha ^{\rm T}_{i,r}=h_{i,r}(\tilde {\beta }^{\rm T}_{i,r})^{-1}$ and the maps
$\alpha ^{\rm T}_{i,r}=h_{i,r}(\tilde {\beta }^{\rm T}_{i,r})^{-1}$ and the maps ![]() $\tilde {\beta }^{\rm T}_{h,i,r}$,
$\tilde {\beta }^{\rm T}_{h,i,r}$, ![]() $\tilde {\beta }^{\rm T}_{i,r}$ are compatible, a diagram chase shows that it suffices to show that the right square in the diagram commutes.
$\tilde {\beta }^{\rm T}_{i,r}$ are compatible, a diagram chase shows that it suffices to show that the right square in the diagram commutes.
This diagram can be lifted to the ![]() $\infty$-derived category, where it takes the following form:
$\infty$-derived category, where it takes the following form:

where we set
 \begin{align*} C(\mathrm{R}\Gamma^{B}_{\operatorname{HK} }(U_{\overline{K},h}),r)&:= [[\mathrm{R}\Gamma^{B}_{\operatorname{HK} }(U_{\overline{K},h})\otimes^L_{F^{\rm nr}}\mathbf{B}^+_{\operatorname{st}}]^{N=0,\phi=p^r} {\buildrel {\rho^B\otimes\iota_p} \over \longrightarrow}(\mathrm{R}\Gamma_{\operatorname{dR} }(U_{\overline{K},h})\otimes^L_{\overline{K}}\mathbf{B}^+_{\operatorname{dR} })/F^r],\\ C(\mathrm{R}\Gamma_{\operatorname{HK} }(X),r)&:= [[\mathrm{R}\Gamma_{\operatorname{HK} }(X)\otimes^L_F\mathbf{B}^+_{\operatorname{st}}]^{N=0,\phi=p^r} {\buildrel {\rho_{\pi}\otimes\iota_{\pi}} \over \longrightarrow} (\mathrm{R}\Gamma_{\operatorname{dR} }(X)\otimes^L_K\mathbf{B}^+_{\operatorname{dR} })/F^r]. \end{align*}
\begin{align*} C(\mathrm{R}\Gamma^{B}_{\operatorname{HK} }(U_{\overline{K},h}),r)&:= [[\mathrm{R}\Gamma^{B}_{\operatorname{HK} }(U_{\overline{K},h})\otimes^L_{F^{\rm nr}}\mathbf{B}^+_{\operatorname{st}}]^{N=0,\phi=p^r} {\buildrel {\rho^B\otimes\iota_p} \over \longrightarrow}(\mathrm{R}\Gamma_{\operatorname{dR} }(U_{\overline{K},h})\otimes^L_{\overline{K}}\mathbf{B}^+_{\operatorname{dR} })/F^r],\\ C(\mathrm{R}\Gamma_{\operatorname{HK} }(X),r)&:= [[\mathrm{R}\Gamma_{\operatorname{HK} }(X)\otimes^L_F\mathbf{B}^+_{\operatorname{st}}]^{N=0,\phi=p^r} {\buildrel {\rho_{\pi}\otimes\iota_{\pi}} \over \longrightarrow} (\mathrm{R}\Gamma_{\operatorname{dR} }(X)\otimes^L_K\mathbf{B}^+_{\operatorname{dR} })/F^r]. \end{align*}
Proceeding now as in the proof of [Reference Nekovář and NiziołNN16, Lemma 4.7], we reduce to proving that, possibly changing the base field ![]() $K$, the following diagram commutes for all
$K$, the following diagram commutes for all ![]() $X=(U,\overline {U})\in {\mathcal {P}}^{\rm ss}_K$ that are split over
$X=(U,\overline {U})\in {\mathcal {P}}^{\rm ss}_K$ that are split over ![]() ${\mathcal O} _K$.
${\mathcal O} _K$.

Recall that the map ![]() $h^B_r$ is defined as the following composition:
$h^B_r$ is defined as the following composition:

where we have used the quasi-isomorphism ![]() $\gamma _r: (\mathrm {R}\Gamma _{\operatorname {dR} }(X_{\overline {K}})\otimes ^L_{\overline {K}}\mathbf {B}^+_{\operatorname {dR} }) /F^r\stackrel {\sim }{\to }\mathrm {R}\Gamma _{\operatorname {cr} }(X_{{\mathcal O} _{\overline {K}}})_{\mathbf {Q}}/F^r$ and the second quasi-isomorphism in the definition of
$\gamma _r: (\mathrm {R}\Gamma _{\operatorname {dR} }(X_{\overline {K}})\otimes ^L_{\overline {K}}\mathbf {B}^+_{\operatorname {dR} }) /F^r\stackrel {\sim }{\to }\mathrm {R}\Gamma _{\operatorname {cr} }(X_{{\mathcal O} _{\overline {K}}})_{\mathbf {Q}}/F^r$ and the second quasi-isomorphism in the definition of ![]() $h^B_r$ uses the Beilinson crystalline period quasi-isomorphism
$h^B_r$ uses the Beilinson crystalline period quasi-isomorphism
(that is compatible with the action of ![]() $N$ and
$N$ and ![]() $\phi$) as well as [Reference Nekovář and NiziołNN16, Lemma 3.24] (which shows that we have the needed commutative diagrams). Recall that the map
$\phi$) as well as [Reference Nekovář and NiziołNN16, Lemma 3.24] (which shows that we have the needed commutative diagrams). Recall that the map ![]() $h_r$ is defined as the following composition:
$h_r$ is defined as the following composition:

Here the map ![]() $\gamma _{\pi }$ is defined as the composition
$\gamma _{\pi }$ is defined as the composition
The fact that the second and the third quasi-isomorphisms in the definition of the map ![]() $h_r$ are well defined follows from the last commutative diagram in the proof of [Reference Colmez, Dospinescu and NiziołCDN20, Proposition 3.48].
$h_r$ are well defined follows from the last commutative diagram in the proof of [Reference Colmez, Dospinescu and NiziołCDN20, Proposition 3.48].
Finally, recall that the map ![]() $\kappa$ can be lifted to the
$\kappa$ can be lifted to the ![]() $\infty$-derived category as well: we have the following commutative diagram (see [Reference Nekovář and NiziołNN16, (31)]).
$\infty$-derived category as well: we have the following commutative diagram (see [Reference Nekovář and NiziołNN16, (31)]).

Using this map ![]() $\kappa$ and its analogs, one can write the bottom four homotopy fibers in the definition of the map
$\kappa$ and its analogs, one can write the bottom four homotopy fibers in the definition of the map ![]() $h_{r}$ (and the maps between them) using Beilinson–Hyodo–Kato cohomology instead of the original Hyodo–Kato cohomology (this includes a change of
$h_{r}$ (and the maps between them) using Beilinson–Hyodo–Kato cohomology instead of the original Hyodo–Kato cohomology (this includes a change of ![]() $p$ to
$p$ to ![]() $\pi$). See the last large diagram in the proof of [Reference Nekovář and NiziołNN16, Lemma 4.7] for how this is done. This diagram also shows that the obtained result is isomorphic to the map
$\pi$). See the last large diagram in the proof of [Reference Nekovář and NiziołNN16, Lemma 4.7] for how this is done. This diagram also shows that the obtained result is isomorphic to the map ![]() $h^B_r$, as wanted.□
$h^B_r$, as wanted.□
4.3.9 Period morphisms for motives, I
Recall that the Beilinson period morphism lifts to the Voevodsky triangulated category of (homological) motives ![]() ${\rm DM}_{\rm gm}(K,\mathbf {Q}_p)$ [Reference Déglise and NiziołDN18, 4.15]. That is, for any Voevodsky motive
${\rm DM}_{\rm gm}(K,\mathbf {Q}_p)$ [Reference Déglise and NiziołDN18, 4.15]. That is, for any Voevodsky motive ![]() $M$, we have the Hyodo–Kato and de Rham comparison quasi-isomorphisms
$M$, we have the Hyodo–Kato and de Rham comparison quasi-isomorphisms
 \begin{gather*} \alpha^{\rm B}_{\rm pst}: \mathrm{R}\Gamma_{\operatorname{\acute{e}t} }(M)\otimes^L_{\mathbf{Q}_p}\mathbf{B}_{\operatorname{st}}\stackrel{\sim}{\to}\mathrm{R}\Gamma_{\operatorname{HK} }(M)\otimes^L_{F^{\rm nr}}\mathbf{B}_{\operatorname{st}},\\ \alpha^{\rm B}_{\operatorname{dR} }: \mathrm{R}\Gamma_{\operatorname{\acute{e}t} }(M)\otimes^L_{\mathbf{Q}_p}\mathbf{B}_{\operatorname{dR} }\stackrel{\sim}{\to}\mathrm{R}\Gamma_{\operatorname{dR} }(M)\otimes^L_{\overline{K}}\mathbf{B}_{\operatorname{dR} }. \end{gather*}
\begin{gather*} \alpha^{\rm B}_{\rm pst}: \mathrm{R}\Gamma_{\operatorname{\acute{e}t} }(M)\otimes^L_{\mathbf{Q}_p}\mathbf{B}_{\operatorname{st}}\stackrel{\sim}{\to}\mathrm{R}\Gamma_{\operatorname{HK} }(M)\otimes^L_{F^{\rm nr}}\mathbf{B}_{\operatorname{st}},\\ \alpha^{\rm B}_{\operatorname{dR} }: \mathrm{R}\Gamma_{\operatorname{\acute{e}t} }(M)\otimes^L_{\mathbf{Q}_p}\mathbf{B}_{\operatorname{dR} }\stackrel{\sim}{\to}\mathrm{R}\Gamma_{\operatorname{dR} }(M)\otimes^L_{\overline{K}}\mathbf{B}_{\operatorname{dR} }. \end{gather*}
They are compatible via the Hyodo–Kato quasi-isomorphism ![]() $\rho : \mathrm {R}\Gamma _{\operatorname {HK} }(M)\otimes ^L_{F^{\rm nr}}\overline {K}\stackrel {\sim }{\to } \mathrm {R}\Gamma _{\operatorname {dR} }(M)$ and the map
$\rho : \mathrm {R}\Gamma _{\operatorname {HK} }(M)\otimes ^L_{F^{\rm nr}}\overline {K}\stackrel {\sim }{\to } \mathrm {R}\Gamma _{\operatorname {dR} }(M)$ and the map ![]() $\iota _p:\mathbf {B}_{\operatorname {st}}\to \mathbf {B}_{\operatorname {dR} }$. The complexes
$\iota _p:\mathbf {B}_{\operatorname {st}}\to \mathbf {B}_{\operatorname {dR} }$. The complexes ![]() $\mathrm {R}\Gamma _{\operatorname {\acute {e}t} }(M)$,
$\mathrm {R}\Gamma _{\operatorname {\acute {e}t} }(M)$, ![]() $\mathrm {R}\Gamma _{\operatorname {HK} }(M)$, and
$\mathrm {R}\Gamma _{\operatorname {HK} }(M)$, and ![]() $\mathrm {R}\Gamma _{\operatorname {dR} }(M)$ are the étale, Hyodo–Kato, and de Rham realizations of
$\mathrm {R}\Gamma _{\operatorname {dR} }(M)$ are the étale, Hyodo–Kato, and de Rham realizations of ![]() $M$, respectively. All cohomologies are geometric. The comparison quasi-isomorphisms are compatible with Galois action, filtrations, monodromy, and Frobenius (when appropriate). If we apply them to the cohomological Voevodsky motive
$M$, respectively. All cohomologies are geometric. The comparison quasi-isomorphisms are compatible with Galois action, filtrations, monodromy, and Frobenius (when appropriate). If we apply them to the cohomological Voevodsky motive ![]() $M(X)^{\vee }=f_*(1_X)$ of any variety
$M(X)^{\vee }=f_*(1_X)$ of any variety ![]() $X$ over
$X$ over ![]() $K$ with structural morphism
$K$ with structural morphism ![]() $f$, we get back Beilinson period quasi-isomorphisms from § 4.3.6.
$f$, we get back Beilinson period quasi-isomorphisms from § 4.3.6.
Example 4.25 An interesting case is obtained by using the (homological) motive with compact support ![]() $M^{\rm c}(X)$ in
$M^{\rm c}(X)$ in ![]() ${\rm DM}_{\rm gm}(K,\mathbf {Q}_p)$ of Voevodsky for any
${\rm DM}_{\rm gm}(K,\mathbf {Q}_p)$ of Voevodsky for any ![]() $K$-variety
$K$-variety ![]() $X$, and its dual
$X$, and its dual ![]() $M^{\rm c}(X)^\vee =\underline {\operatorname {Hom}}(M^{\rm c}(X),\mathbf {Q}_p)$ which belongs to
$M^{\rm c}(X)^\vee =\underline {\operatorname {Hom}}(M^{\rm c}(X),\mathbf {Q}_p)$ which belongs to ![]() ${\rm DM}_{\rm gm}(K,\mathbf {Q}_p)$ as well. Since, in terms of the six-functors formalism,
${\rm DM}_{\rm gm}(K,\mathbf {Q}_p)$ as well. Since, in terms of the six-functors formalism, ![]() $M^{\rm c}(X)^\vee =f_!(1_X)$ [Reference Cisinski and DégliseCD15, Proposition 8.10],
$M^{\rm c}(X)^\vee =f_!(1_X)$ [Reference Cisinski and DégliseCD15, Proposition 8.10], ![]() $\mathrm {R}\Gamma _{\operatorname {\acute {e}t} }(M^{\rm c}(X)^\vee )$ is the étale cohomology with compact support (as defined by Grothendieck and Deligne).
$\mathrm {R}\Gamma _{\operatorname {\acute {e}t} }(M^{\rm c}(X)^\vee )$ is the étale cohomology with compact support (as defined by Grothendieck and Deligne).
Similarly for the Hyodo–Kato and de Rham cohomologies. Let ![]() $X$ be a scheme over
$X$ be a scheme over ![]() ${\mathcal O} _K$ with generalized semistable reduction as in § 2.1.3. Let
${\mathcal O} _K$ with generalized semistable reduction as in § 2.1.3. Let ![]() $D$ be its divisor at
$D$ be its divisor at ![]() $\infty$. Define the Voevodsky motive
$\infty$. Define the Voevodsky motive ![]() $M(X_K,D_K)\in {\rm DM}_{\rm gm}(K,\mathbf {Q}_p)$ as the cone
$M(X_K,D_K)\in {\rm DM}_{\rm gm}(K,\mathbf {Q}_p)$ as the cone
where ![]() $\widetilde {D}_{{\scriptscriptstyle \bullet }}$ is the Čech nerve of the map
$\widetilde {D}_{{\scriptscriptstyle \bullet }}$ is the Čech nerve of the map ![]() $\coprod _i D_i\to D$,
$\coprod _i D_i\to D$, ![]() $D_i$ being an irreducible component of
$D_i$ being an irreducible component of ![]() $D$. Hence, the dual motive
$D$. Hence, the dual motive ![]() $M(X_K,D_K)^{\vee }\in {\rm DM}_{\rm gm}(K,\mathbf {Q}_p)$ is
$M(X_K,D_K)^{\vee }\in {\rm DM}_{\rm gm}(K,\mathbf {Q}_p)$ is
Lemma 4.26 For ![]() $U:=X\setminus D$, we have
$U:=X\setminus D$, we have
Proof. This easily follows from the localization property:
and the Mayer–Vietoris property for closed coverings (a special case of cdh-descent [Reference Cisinski and DégliseCD19, 3.3.10]), which yields
Hence, by Lemma 2.1, the realization ![]() $\mathrm {R}\Gamma _{\epsilon }(M^{\rm c}(U_K)^{\vee })$,
$\mathrm {R}\Gamma _{\epsilon }(M^{\rm c}(U_K)^{\vee })$, ![]() $\epsilon =\operatorname {HK} , \operatorname {dR}$, represents the compactly supported cohomology of
$\epsilon =\operatorname {HK} , \operatorname {dR}$, represents the compactly supported cohomology of ![]() $U_K$.
$U_K$.
Similarly, the Tsuji period morphism also lifts to the Voevodsky triangulated category of (homological) motives ![]() ${\rm DM}_{\rm gm}(K,\mathbf {Q}_p)$ [Reference Déglise and NiziołDN18, 4.15]. More specifically, for
${\rm DM}_{\rm gm}(K,\mathbf {Q}_p)$ [Reference Déglise and NiziołDN18, 4.15]. More specifically, for ![]() $X\in {\mathcal {V}}ar_{\overline {K}}$, the syntomic period morphism from (4.20)
$X\in {\mathcal {V}}ar_{\overline {K}}$, the syntomic period morphism from (4.20)
extends to a syntomic period morphism
It is quasi-isomorphism after truncation ![]() $\tau _{\leq r}$. If we apply it to the cohomological Voevodsky motive
$\tau _{\leq r}$. If we apply it to the cohomological Voevodsky motive ![]() $M(U)^{\vee }=f_*(1_X)$ for any proper semistable scheme
$M(U)^{\vee }=f_*(1_X)$ for any proper semistable scheme ![]() $X$ over
$X$ over ![]() ${\mathcal O} _K$, and
${\mathcal O} _K$, and ![]() $U=X_K\setminus D_K$ with structural morphism
$U=X_K\setminus D_K$ with structural morphism ![]() $f$, we get back Fontaine–Messing period quasi-isomorphisms (modulo identifications of the cohomologies involved and their
$f$, we get back Fontaine–Messing period quasi-isomorphisms (modulo identifications of the cohomologies involved and their ![]() $h$-localizations).
$h$-localizations).
For ![]() $M\in {\rm DM}_{\rm gm}(K,\mathbf {Q}_p)$, define
$M\in {\rm DM}_{\rm gm}(K,\mathbf {Q}_p)$, define
 \begin{align*} \widetilde{\alpha}_{r}^{\rm T}&: \tau_{\leq r}\mathrm{R}\Gamma_{\operatorname{\acute{e}t} }(M,{\mathbf{Q}}_p(r))\xleftarrow[\sim]{\widetilde{\beta}_{r}^{\rm T}}\tau_{\leq r}\mathrm{R}\Gamma_{\operatorname{syn}}(M,r) {\buildrel {h_{h,r}} \over \longrightarrow} \tau_{\leq r}(\mathrm{R}\Gamma_{\operatorname{HK} }(M)\otimes^L_{F^{\rm nr}}\mathbf{B}_{\operatorname{st}}\{-r\}),\\ {\alpha}_{{\rm pst},r}^{\rm T}&: \tau_{\leq r}\mathrm{R}\Gamma_{\operatorname{\acute{e}t} }(M,{\mathbf{Q}}_p)\to\tau_{\leq r}(\mathrm{R}\Gamma_{\operatorname{HK} }(M)\otimes^L_{F^{\rm nr}}\mathbf{B}_{\operatorname{st}}),\quad {\alpha}_{{\rm pst},r}^{\rm T}:=t^{-r}\widetilde{\alpha}_{r}^{\rm T}\epsilon^r. \end{align*}
\begin{align*} \widetilde{\alpha}_{r}^{\rm T}&: \tau_{\leq r}\mathrm{R}\Gamma_{\operatorname{\acute{e}t} }(M,{\mathbf{Q}}_p(r))\xleftarrow[\sim]{\widetilde{\beta}_{r}^{\rm T}}\tau_{\leq r}\mathrm{R}\Gamma_{\operatorname{syn}}(M,r) {\buildrel {h_{h,r}} \over \longrightarrow} \tau_{\leq r}(\mathrm{R}\Gamma_{\operatorname{HK} }(M)\otimes^L_{F^{\rm nr}}\mathbf{B}_{\operatorname{st}}\{-r\}),\\ {\alpha}_{{\rm pst},r}^{\rm T}&: \tau_{\leq r}\mathrm{R}\Gamma_{\operatorname{\acute{e}t} }(M,{\mathbf{Q}}_p)\to\tau_{\leq r}(\mathrm{R}\Gamma_{\operatorname{HK} }(M)\otimes^L_{F^{\rm nr}}\mathbf{B}_{\operatorname{st}}),\quad {\alpha}_{{\rm pst},r}^{\rm T}:=t^{-r}\widetilde{\alpha}_{r}^{\rm T}\epsilon^r. \end{align*}
Here ![]() $h_{h,r}$ is the motivic lift of the
$h_{h,r}$ is the motivic lift of the ![]() $h$-sheafification of the map
$h$-sheafification of the map ![]() $h_r$ from (4.23). Write
$h_r$ from (4.23). Write
and set
This makes sense since, by [Reference TsujiTsu99a, Corollary 4.8.8], we have ![]() $t\widetilde {\alpha }_{r-1}^{\rm T}=\widetilde {\alpha }_{r}^{\rm T}\epsilon$.
$t\widetilde {\alpha }_{r-1}^{\rm T}=\widetilde {\alpha }_{r}^{\rm T}\epsilon$.
To sum up, for any Voevodsky motive ![]() $M$, we have the Hyodo–Kato and de Rham comparison quasi-isomorphisms
$M$, we have the Hyodo–Kato and de Rham comparison quasi-isomorphisms
 \begin{equation} \begin{gathered} \alpha^{\rm T}_{\rm pst}: \mathrm{R}\Gamma_{\operatorname{\acute{e}t} }(M)\otimes^L_{\mathbf{Q}_p}\mathbf{B}_{\operatorname{st}}\stackrel{\sim}{\to}\mathrm{R}\Gamma_{\operatorname{HK} }(M)\otimes^L_{F^{\rm nr}}\mathbf{B}_{\operatorname{st}},\\ \alpha^{\rm T}_{\operatorname{dR} }: \mathrm{R}\Gamma_{\operatorname{\acute{e}t} }(M)\otimes^L_{\mathbf{Q}_p}\mathbf{B}_{\operatorname{dR} }\stackrel{\sim}{\to}\mathrm{R}\Gamma_{\operatorname{dR} }(M)\otimes^L_{\overline{K}}\mathbf{B}_{\operatorname{dR} } \end{gathered} \end{equation}
\begin{equation} \begin{gathered} \alpha^{\rm T}_{\rm pst}: \mathrm{R}\Gamma_{\operatorname{\acute{e}t} }(M)\otimes^L_{\mathbf{Q}_p}\mathbf{B}_{\operatorname{st}}\stackrel{\sim}{\to}\mathrm{R}\Gamma_{\operatorname{HK} }(M)\otimes^L_{F^{\rm nr}}\mathbf{B}_{\operatorname{st}},\\ \alpha^{\rm T}_{\operatorname{dR} }: \mathrm{R}\Gamma_{\operatorname{\acute{e}t} }(M)\otimes^L_{\mathbf{Q}_p}\mathbf{B}_{\operatorname{dR} }\stackrel{\sim}{\to}\mathrm{R}\Gamma_{\operatorname{dR} }(M)\otimes^L_{\overline{K}}\mathbf{B}_{\operatorname{dR} } \end{gathered} \end{equation}
as in the case of Beilinson comparison quasi-isomorphisms. By Theorem 4.21, these comparison quasi-isomorphisms are the same as the ones of Beilinson. If we apply them to the cohomological Voevodsky motive ![]() $M(U)^{\vee }=f_*(1_X)$ for any proper semistable scheme
$M(U)^{\vee }=f_*(1_X)$ for any proper semistable scheme ![]() $X$ over
$X$ over ![]() ${\mathcal O} _K$, and
${\mathcal O} _K$, and ![]() $U=X_K\setminus D_K$ with structural morphism
$U=X_K\setminus D_K$ with structural morphism ![]() $f$, we get back Tsuji period quasi-isomorphisms after the identification of the Beilinson–Hyodo–Kato and the original Hyodo–Kato cohomologies via the map
$f$, we get back Tsuji period quasi-isomorphisms after the identification of the Beilinson–Hyodo–Kato and the original Hyodo–Kato cohomologies via the map ![]() $\kappa : \mathrm {R}\Gamma _{\operatorname {HK} }^B(X)\to \mathrm {R}\Gamma _{\operatorname {HK} }(X)$ from (4.24).
$\kappa : \mathrm {R}\Gamma _{\operatorname {HK} }^B(X)\to \mathrm {R}\Gamma _{\operatorname {HK} }(X)$ from (4.24).
Remark 4.28 In [Reference TsujiTsu03], Tsuji has shown that the Fontaine–Messing period morphism yields a comparison theorem for ![]() $U$ as above. This was done by showing compatibility of the period morphism with the Gysin sequence and thus reducing to the proper case. The period quasi-isomorphisms (4.27) imply Tsuji's result. But we know now of another way: using Banach–Colmez spaces [Reference ColmezCol02] as in [Reference Colmez and NiziołCN17] one can obtain the isomorphism (4.16), which is enough to prove that the period map is an isomorphism; in this way one avoids using Poincaré duality.
$U$ as above. This was done by showing compatibility of the period morphism with the Gysin sequence and thus reducing to the proper case. The period quasi-isomorphisms (4.27) imply Tsuji's result. But we know now of another way: using Banach–Colmez spaces [Reference ColmezCol02] as in [Reference Colmez and NiziołCN17] one can obtain the isomorphism (4.16), which is enough to prove that the period map is an isomorphism; in this way one avoids using Poincaré duality.
The map ![]() $\kappa$ and its properties extend to finite proper simplicial schemes with semistable reduction and of Cartier type, which implies that the Tsuji comparison theorem for cohomology with compact support from [Reference TsujiTsu98] agrees with the one of Beilinson (after the identification of Hyodo–Kato cohomologies). Similarly, since the comparison theorems of Yamashita for cohomology with (possibly partial) compact support can also be seen as defined using finite simplicial schemes (use the arguments of Lemma 2.1) and the Fontaine–Messing period morphisms, they are the same as those of Tsuji and Beilinson.
$\kappa$ and its properties extend to finite proper simplicial schemes with semistable reduction and of Cartier type, which implies that the Tsuji comparison theorem for cohomology with compact support from [Reference TsujiTsu98] agrees with the one of Beilinson (after the identification of Hyodo–Kato cohomologies). Similarly, since the comparison theorems of Yamashita for cohomology with (possibly partial) compact support can also be seen as defined using finite simplicial schemes (use the arguments of Lemma 2.1) and the Fontaine–Messing period morphisms, they are the same as those of Tsuji and Beilinson.
Finally, as shown in [Reference Déglise and NiziołDN18, Proposition 4.24], the Beilinson period morphisms are compatible with (possibly mixed) products. By the same argument, so are the period morphisms (4.27). It follows that so are the period morphisms of Tsuji and Yamashita (the change of the Hyodo–Kato cohomology map ![]() $\kappa$ is compatible with products: pass through the Hyodo–Kato isomorphisms, which are compatible with products, to de Rham cohomology).
$\kappa$ is compatible with products: pass through the Hyodo–Kato isomorphisms, which are compatible with products, to de Rham cohomology).
4.4 Comparison of Faltings and Beilinson period morphisms
We will compare now the Faltings and Beilinson period morphisms.
4.4.1 Faltings period morphism
We will briefly recall the definition of the period morphism of Faltings.
(i) Faltings site. Faltings’ construction of the period morphism uses an auxiliary topos, a topos of ‘sheaves of local systems’ (see [Reference Faltings and IgusaFal89, III] and [Reference FaltingsFal02, 3]), that is now known as the ‘Faltings topos’ (a term coined by Abbes and Gros [Reference Abbes and GrosAG16]). We will briefly describe it.
For a scheme ![]() $X$, let
$X$, let ![]() $X_{\operatorname {F\acute {e}t}}$ denote the topos defined by the site of finite étale morphisms
$X_{\operatorname {F\acute {e}t}}$ denote the topos defined by the site of finite étale morphisms ![]() $U\to X$ with coverings given by surjective maps. For a connected
$U\to X$ with coverings given by surjective maps. For a connected ![]() $X$ and a choice of a geometric point
$X$ and a choice of a geometric point ![]() $\overline {x}\to X$,
$\overline {x}\to X$, ![]() $X_{\operatorname {F\acute {e}t}}$ is equivalent to the topos of sets with a continuous action of the fundamental group
$X_{\operatorname {F\acute {e}t}}$ is equivalent to the topos of sets with a continuous action of the fundamental group ![]() $\pi _1(X,\overline {x})$. In particular, for an abelian sheaf
$\pi _1(X,\overline {x})$. In particular, for an abelian sheaf ![]() ${\mathcal {F}}$, the étale cohomology
${\mathcal {F}}$, the étale cohomology ![]() $H^*(X_{\operatorname {F\acute {e}t}},{\mathcal {F}})$ is isomorphic to the (continuous) group cohomology
$H^*(X_{\operatorname {F\acute {e}t}},{\mathcal {F}})$ is isomorphic to the (continuous) group cohomology ![]() $H^*(\pi _1(X,\overline {x}),{\mathcal {F}}_{\overline {x}})$. Let
$H^*(\pi _1(X,\overline {x}),{\mathcal {F}}_{\overline {x}})$. Let ![]() $X$ be noetherian. Then
$X$ be noetherian. Then ![]() $X_{\operatorname {F\acute {e}t}}$ is equivalent to the topos of étale sheaves that are inductive limits of locally constant sheaves.Footnote 11 There is a map of topoi
$X_{\operatorname {F\acute {e}t}}$ is equivalent to the topos of étale sheaves that are inductive limits of locally constant sheaves.Footnote 11 There is a map of topoi
with ![]() $\pi _*{{\mathcal {F}}}$ given by the restriction of
$\pi _*{{\mathcal {F}}}$ given by the restriction of ![]() ${\mathcal {F}}$ to finite étale schemes over
${\mathcal {F}}$ to finite étale schemes over ![]() $X$ and
$X$ and ![]() $\pi ^*({\mathcal {F}})={\mathcal {F}}$ for an ind-locally constant sheaf
$\pi ^*({\mathcal {F}})={\mathcal {F}}$ for an ind-locally constant sheaf ![]() ${\mathcal {F}}$.
${\mathcal {F}}$.
Recall the following notion.
Definition 4.29 A noetherian scheme ![]() $X$ is a
$X$ is a ![]() $K(\pi ,1)$-space if for every integer
$K(\pi ,1)$-space if for every integer ![]() $n$ invertible on
$n$ invertible on ![]() $X$ and any locally constant sheaf
$X$ and any locally constant sheaf ![]() ${\mathcal {L}}$ of
${\mathcal {L}}$ of ![]() ${\mathbf {Z}}/n$-modules, the natural map
${\mathbf {Z}}/n$-modules, the natural map ![]() ${\mathcal {L}}\to R\pi _*\pi ^*({\mathcal {L}})$ is an isomorphism.
${\mathcal {L}}\to R\pi _*\pi ^*({\mathcal {L}})$ is an isomorphism.
The following analog of a classical result of Artin [Reference Artin, Grothendieck and VerdierAGV73, Exposé XI, 4.4] on the existence of a base for the Zariski topology consisting of ![]() $K(\pi ,1)$-spaces was proved by Faltings [Reference FaltingsFal88, 2.1] in the good reduction case and by Achinger [Reference AchingerAch15, Theorem 9.5] in general.
$K(\pi ,1)$-spaces was proved by Faltings [Reference FaltingsFal88, 2.1] in the good reduction case and by Achinger [Reference AchingerAch15, Theorem 9.5] in general.
Theorem 4.30 (Faltings, Achinger) Let ![]() $X$ be a log-smooth
$X$ be a log-smooth ![]() ${\mathcal O} _K^{\times }$-log-scheme such that
${\mathcal O} _K^{\times }$-log-scheme such that ![]() $X_K$ is smooth over
$X_K$ is smooth over ![]() $K$. For every geometric point
$K$. For every geometric point ![]() $\overline {x}$ of
$\overline {x}$ of ![]() $X$,
$X$, ![]() $X_{(\overline {x})}\times _XX_{\operatorname {tr},\overline {K}}$ is a
$X_{(\overline {x})}\times _XX_{\operatorname {tr},\overline {K}}$ is a ![]() $K(\pi ,1)$-space.
$K(\pi ,1)$-space.
Let ![]() $X$ be a noetherian
$X$ be a noetherian ![]() ${\mathcal O} _K$-scheme. The Faltings topos
${\mathcal O} _K$-scheme. The Faltings topos ![]() $\widetilde {X}_{\overline {K},\operatorname {\acute {e}t} }$ is definedFootnote 12 by a site which has for objects pairs
$\widetilde {X}_{\overline {K},\operatorname {\acute {e}t} }$ is definedFootnote 12 by a site which has for objects pairs ![]() $(U,V)$, where
$(U,V)$, where ![]() $U$ is an étale
$U$ is an étale ![]() $X$-scheme and
$X$-scheme and ![]() $V\to X_{\overline {K}}$ is a finite étale morphism; morphisms are compatible pairs of maps, and coverings are pairs of surjective maps (see [Reference Abbes and GrosAG16] for details).
$V\to X_{\overline {K}}$ is a finite étale morphism; morphisms are compatible pairs of maps, and coverings are pairs of surjective maps (see [Reference Abbes and GrosAG16] for details).
There is a canonical map
from the étale topos of ![]() $X_{\overline {K}}$ to
$X_{\overline {K}}$ to ![]() $\widetilde {X}_{\overline {K},\operatorname {\acute {e}t} }$. On the level of sites, this map is given by sending
$\widetilde {X}_{\overline {K},\operatorname {\acute {e}t} }$. On the level of sites, this map is given by sending ![]() $(U,V)$ to
$(U,V)$ to ![]() $V$. If
$V$. If ![]() $X$ is a log-smooth log-scheme over
$X$ is a log-smooth log-scheme over ![]() ${\mathcal O} ^{\times }_K$ with a smooth generic fiber, it follows (see [Reference FaltingsFal02, III] and [Reference AchingerAch15, Corollary 9.6]) from Theorem 4.30 that, for a locally constant sheaf
${\mathcal O} ^{\times }_K$ with a smooth generic fiber, it follows (see [Reference FaltingsFal02, III] and [Reference AchingerAch15, Corollary 9.6]) from Theorem 4.30 that, for a locally constant sheaf ![]() ${\mathcal {L}}$ on
${\mathcal {L}}$ on ![]() $X_{\overline {K}}$, the natural map
$X_{\overline {K}}$, the natural map
is a quasi-isomorphism.
(ii) Faltings period morphism. Let ![]() $X$ be a saturated, log-smooth, and proper log-scheme over
$X$ be a saturated, log-smooth, and proper log-scheme over ![]() ${\mathcal O} ^{\times }_K$. Then, by [Reference FaltingsFal02, Corollary 3.1], we have a natural almost quasi-isomorphism
${\mathcal O} ^{\times }_K$. Then, by [Reference FaltingsFal02, Corollary 3.1], we have a natural almost quasi-isomorphism
where ![]() ${\mathcal {A}}_{\operatorname {cr} ,n}$ is a relative version of the crystalline period ring (equipped with the log-structure
${\mathcal {A}}_{\operatorname {cr} ,n}$ is a relative version of the crystalline period ring (equipped with the log-structure ![]() $({\mathbf {N}}\to {\mathcal {A}}_{\operatorname {cr} ,n},1\mapsto [\pi ^{\flat }])$). For
$({\mathbf {N}}\to {\mathcal {A}}_{\operatorname {cr} ,n},1\mapsto [\pi ^{\flat }])$). For ![]() $r\geq 0$, there is a natural morphism
$r\geq 0$, there is a natural morphism
Faltings’ main comparison result is the following theorem.
Theorem 4.32 (Faltings [Fal02, Corollary 5.4]) The almost morphism
has an inverse up to ![]() $t^{d}$ (that is, composition either way is the multiplication by
$t^{d}$ (that is, composition either way is the multiplication by ![]() $t^{d}$),
$t^{d}$), ![]() $d=\dim X_K$. It is compatible with Frobenius and filtration.
$d=\dim X_K$. It is compatible with Frobenius and filtration.
The map ![]() $R_{\pi ,n}\to \mathbf {A}_{\operatorname {cr} ,n}$ above is induced by
$R_{\pi ,n}\to \mathbf {A}_{\operatorname {cr} ,n}$ above is induced by ![]() $x\mapsto [\pi ^{\flat }]$. This is not Galois-equivariant and hence, for the period morphism
$x\mapsto [\pi ^{\flat }]$. This is not Galois-equivariant and hence, for the period morphism ![]() $\tilde {\alpha }$ to be compatible with the Galois action, this action has to be twisted (using monodromy) on the domain (see [Reference FaltingsFal02, p. 259] for details). Passing to the limit over
$\tilde {\alpha }$ to be compatible with the Galois action, this action has to be twisted (using monodromy) on the domain (see [Reference FaltingsFal02, p. 259] for details). Passing to the limit over ![]() $n$ and tensoring with
$n$ and tensoring with ![]() ${\mathbf {Q}}$ in the above yields an almost morphism
${\mathbf {Q}}$ in the above yields an almost morphism
Taking cohomology, we get an isomorphism
The Faltings period isomorphism
is defined as ![]() $\alpha _{i}^{\rm F}:=(\beta _i^{\rm F})^{-1}$,
$\alpha _{i}^{\rm F}:=(\beta _i^{\rm F})^{-1}$, ![]() $\beta _i^{\rm F}:=\widetilde {\beta }_{i}\iota _{\pi }$, where
$\beta _i^{\rm F}:=\widetilde {\beta }_{i}\iota _{\pi }$, where ![]() $\iota _{\pi }: H^i_{\operatorname {HK} }(X)\to H^i_{\operatorname {cr} }(X/R_{\pi })_{\mathbf {Q}}$ is the Hyodo–Kato section.
$\iota _{\pi }: H^i_{\operatorname {HK} }(X)\to H^i_{\operatorname {cr} }(X/R_{\pi })_{\mathbf {Q}}$ is the Hyodo–Kato section.
(iii) Faltings syntomic period morphism. Let ![]() $r\geq 0$. The definition of the map
$r\geq 0$. The definition of the map ![]() $\beta _{r,n}$ above can be generalized easily to obtain an almost map
$\beta _{r,n}$ above can be generalized easily to obtain an almost map
Here we set ![]() $\mathrm {R}\Gamma ((\widetilde {X}_{{\mathcal O} _{\overline {K}}})_{\overline {K},\operatorname {\acute {e}t} },F^r{\mathcal {A}}_{\operatorname {cr} ,n}) :=\operatorname {hocolim}_{K^{\prime }}\mathrm {R}\Gamma ((\widetilde {X}_{{\mathcal O} _{K^{\prime }}})_{\overline {K},\operatorname {\acute {e}t} },F^r{\mathcal {A}}_{\operatorname {cr} ,n})$, where the limit is over finite extensions
$\mathrm {R}\Gamma ((\widetilde {X}_{{\mathcal O} _{\overline {K}}})_{\overline {K},\operatorname {\acute {e}t} },F^r{\mathcal {A}}_{\operatorname {cr} ,n}) :=\operatorname {hocolim}_{K^{\prime }}\mathrm {R}\Gamma ((\widetilde {X}_{{\mathcal O} _{K^{\prime }}})_{\overline {K},\operatorname {\acute {e}t} },F^r{\mathcal {A}}_{\operatorname {cr} ,n})$, where the limit is over finite extensions ![]() $K^{\prime }/K$. In an analogous way we define almost mapsFootnote 13
$K^{\prime }/K$. In an analogous way we define almost mapsFootnote 13
All these maps are compatible.
Recall that we have the fundamental exact sequence
Here ![]() $F^r_p{\mathcal {A}}_{\operatorname {cr} ,n}$ denotes the Frobenius ‘divisible’ filtration and, for a sheaf
$F^r_p{\mathcal {A}}_{\operatorname {cr} ,n}$ denotes the Frobenius ‘divisible’ filtration and, for a sheaf ![]() ${\mathcal {F}}$ on
${\mathcal {F}}$ on ![]() $\widetilde {X}_{\overline {K},\operatorname {\acute {e}t} }$,
$\widetilde {X}_{\overline {K},\operatorname {\acute {e}t} }$, ![]() ${\mathcal {F}}_s$ stands for its restriction to the special fiber, i.e., to the complement of the generic fiber (the site consisting of objects with trivial special fiber). For
${\mathcal {F}}_s$ stands for its restriction to the special fiber, i.e., to the complement of the generic fiber (the site consisting of objects with trivial special fiber). For ![]() $X$ proper and
$X$ proper and ![]() ${\mathcal {F}}$ torsion, the proper base-change theorem yields that the cohomologies of
${\mathcal {F}}$ torsion, the proper base-change theorem yields that the cohomologies of ![]() ${\mathcal {F}}$ and
${\mathcal {F}}$ and ![]() ${\mathcal {F}}_s$ coincide.
${\mathcal {F}}_s$ coincide.
Using the map ![]() $\tilde {\beta }_{r,n}$ and the above sequence, we obtain a map
$\tilde {\beta }_{r,n}$ and the above sequence, we obtain a map
More precisely, we get a canonical map from ![]() $\mathrm {R}\Gamma _{\operatorname {\acute {e}t} }(X_{{\mathcal O} _{\overline {K}}},{\mathcal {S}}'_n(r))$ to the
$\mathrm {R}\Gamma _{\operatorname {\acute {e}t} }(X_{{\mathcal O} _{\overline {K}}},{\mathcal {S}}'_n(r))$ to the ![]() $\widetilde {X}_{\overline {K}}$-cohomology of the mapping fiber of
$\widetilde {X}_{\overline {K}}$-cohomology of the mapping fiber of ![]() $\phi -p^r : F^r{\mathcal {A}}_{\operatorname {cr} ,n}\to {\mathcal {A}}_{\operatorname {cr} ,n}$, which in turn maps via multiplication by
$\phi -p^r : F^r{\mathcal {A}}_{\operatorname {cr} ,n}\to {\mathcal {A}}_{\operatorname {cr} ,n}$, which in turn maps via multiplication by ![]() $p^r$ on
$p^r$ on ![]() $F^r{\mathcal {A}}_{\operatorname {cr} ,n}$ to the
$F^r{\mathcal {A}}_{\operatorname {cr} ,n}$ to the ![]() $\widetilde {X}_{\overline {K}}$-cohomology of the mapping fiber of
$\widetilde {X}_{\overline {K}}$-cohomology of the mapping fiber of ![]() $\phi _r-1: F^r_p{\mathcal {A}}_{\operatorname {cr} ,n}\to {\mathcal {A}}_{\operatorname {cr} ,n}$. But the last mapping fiber, by the fundamental exact sequence (4.33), is quasi-isomorphic to
$\phi _r-1: F^r_p{\mathcal {A}}_{\operatorname {cr} ,n}\to {\mathcal {A}}_{\operatorname {cr} ,n}$. But the last mapping fiber, by the fundamental exact sequence (4.33), is quasi-isomorphic to ![]() ${\mathbf {Z}}/p^n(r)'_s$.
${\mathbf {Z}}/p^n(r)'_s$.
Hence, the Faltings period isomorphism induces a morphism (a genuine morphism not just an almost morphism; see [Reference NiziołNiz09, § 5.1])
as the composition
The first quasi-isomorphism holds because ![]() $X$ is proper. The last quasi-isomorphism holds by (4.31). Consider now the composition (
$X$ is proper. The last quasi-isomorphism holds by (4.31). Consider now the composition (![]() $\beta ^{\rm F}_r:=(\operatorname {holim} _n\beta ^{\rm F}_{r,n})_{\mathbf {Q}}$)
$\beta ^{\rm F}_r:=(\operatorname {holim} _n\beta ^{\rm F}_{r,n})_{\mathbf {Q}}$)
For ![]() $r\geq i$, using the diagram (2.10) and the discussion in [Reference NiziołNiz09] preceding Theorem 5.8, it is easy to check that, on degree-
$r\geq i$, using the diagram (2.10) and the discussion in [Reference NiziołNiz09] preceding Theorem 5.8, it is easy to check that, on degree-![]() $i$ cohomology,
$i$ cohomology, ![]() $(\tilde {\beta }^{\rm F}_{i,r})^{-1}$ is the syntomic period morphism
$(\tilde {\beta }^{\rm F}_{i,r})^{-1}$ is the syntomic period morphism ![]() $\tilde {\alpha }^{\rm F}_{i,r}$ induced from the Faltings period morphism
$\tilde {\alpha }^{\rm F}_{i,r}$ induced from the Faltings period morphism ![]() $\alpha^{\rm F}_{i,r}$ via the procedure described in § 4.1.
$\alpha^{\rm F}_{i,r}$ via the procedure described in § 4.1.
4.4.2 Comparison of Faltings and Beilinson period morphisms
Let ![]() $X\in {\mathcal {V}}ar_{\overline {K}}$. We can
$X\in {\mathcal {V}}ar_{\overline {K}}$. We can ![]() $h$-sheafify the Faltings period morphism by setting, for
$h$-sheafify the Faltings period morphism by setting, for ![]() $(U,\overline {U})\in {\mathcal {P}}^{\rm ss}_{\overline {K}}$,
$(U,\overline {U})\in {\mathcal {P}}^{\rm ss}_{\overline {K}}$,
where the morphism ![]() $\beta ^{\rm F}_{r,n}$ is the one from (4.34), to obtain the compatible maps of
$\beta ^{\rm F}_{r,n}$ is the one from (4.34), to obtain the compatible maps of ![]() $h$-sheaves
$h$-sheaves
Taking cohomology, we get the induced compatible syntomic period morphisms
As in the case of the Beilinson period morphism, they induce a syntomic period morphism
It is a quasi-isomorphism after truncation ![]() $\tau _{\leq r}$: by Remark 4.14, the map
$\tau _{\leq r}$: by Remark 4.14, the map ![]() $\pi$ is a quasi-isomorphism after truncation
$\pi$ is a quasi-isomorphism after truncation ![]() $\tau _{\leq r}$ and, by Corollary 4.13, the map (4.35) is a
$\tau _{\leq r}$ and, by Corollary 4.13, the map (4.35) is a ![]() $p^r$-quasi-isomorphism and hence the map
$p^r$-quasi-isomorphism and hence the map ![]() $\beta ^{\rm F}$ is a quasi-isomorphism after truncation
$\beta ^{\rm F}$ is a quasi-isomorphism after truncation ![]() $\tau _{\leq r}$ as well.
$\tau _{\leq r}$ as well.
Since the Faltings syntomic period morphism ![]() ${\beta }_{r,n}^{\rm F}$ is functorial, an argument analogous to the one we used in the proof of Theorem 4.21 shows that
${\beta }_{r,n}^{\rm F}$ is functorial, an argument analogous to the one we used in the proof of Theorem 4.21 shows that ![]() $\tilde {\beta }_{h,r}^{\rm F}=\tilde {\beta }_{h,r}^{\rm B}$. We have obtained the first claim of the following theorem.
$\tilde {\beta }_{h,r}^{\rm F}=\tilde {\beta }_{h,r}^{\rm B}$. We have obtained the first claim of the following theorem.
Theorem 4.36 Let ![]() $r\geq 0$.
$r\geq 0$.
(i) Let ![]() $X\in {\mathcal {V}}ar_{\overline {K}}$. The induced Faltings and Beilinson syntomic period morphisms
$X\in {\mathcal {V}}ar_{\overline {K}}$. The induced Faltings and Beilinson syntomic period morphisms
are equal.
(ii) If ![]() $X=(U,\overline {U})\in {\mathcal {P}}^{\rm ss}_K$ and is split over
$X=(U,\overline {U})\in {\mathcal {P}}^{\rm ss}_K$ and is split over ![]() ${\mathcal O} _K$, the period morphisms
${\mathcal O} _K$, the period morphisms
 \begin{align*} {\alpha}_{h,i}^{\rm F}, {\alpha}_{h,i}^{\rm B}&: H^i_{\operatorname{\acute{e}t} }(U_{\overline{K}},{\mathbf{Q} }_p) \otimes_{{\mathbf{Q} }_p} \mathbf{B}_{\operatorname{st}} \stackrel{\sim}{\to} H^{B,i}_{\operatorname{HK} }(X)\otimes_{F} \mathbf{B}_{\operatorname{st}},\\ {\alpha}_{i}^{\rm F}, {\alpha}_{i}^{\rm B}&: H^i_{\operatorname{\acute{e}t} }(U_{\overline{K}},{\mathbf{Q} }_p) \otimes_{{\mathbf{Q} }_p} \mathbf{B}_{\operatorname{dR} } \stackrel{\sim}{\to} H^{i}_{\operatorname{dR} }(X_K)\otimes_{K} \mathbf{B}_{\operatorname{dR} } \end{align*}
\begin{align*} {\alpha}_{h,i}^{\rm F}, {\alpha}_{h,i}^{\rm B}&: H^i_{\operatorname{\acute{e}t} }(U_{\overline{K}},{\mathbf{Q} }_p) \otimes_{{\mathbf{Q} }_p} \mathbf{B}_{\operatorname{st}} \stackrel{\sim}{\to} H^{B,i}_{\operatorname{HK} }(X)\otimes_{F} \mathbf{B}_{\operatorname{st}},\\ {\alpha}_{i}^{\rm F}, {\alpha}_{i}^{\rm B}&: H^i_{\operatorname{\acute{e}t} }(U_{\overline{K}},{\mathbf{Q} }_p) \otimes_{{\mathbf{Q} }_p} \mathbf{B}_{\operatorname{dR} } \stackrel{\sim}{\to} H^{i}_{\operatorname{dR} }(X_K)\otimes_{K} \mathbf{B}_{\operatorname{dR} } \end{align*}
are equal as well. Here we set ![]() ${\alpha }_{h,i}^{\rm F}:=\kappa ^{-1}\alpha ^{\rm F}_i$.
${\alpha }_{h,i}^{\rm F}:=\kappa ^{-1}\alpha ^{\rm F}_i$.
Proof. Let ![]() $X=(U,\overline {U})\in {\mathcal {P}}^{\rm ss}_K$ be split over
$X=(U,\overline {U})\in {\mathcal {P}}^{\rm ss}_K$ be split over ![]() ${\mathcal O} _K$. By Lemma 4.17, it suffices to show that, for
${\mathcal O} _K$. By Lemma 4.17, it suffices to show that, for ![]() $r\geq i$, the induced maps
$r\geq i$, the induced maps ![]() $\tilde {\alpha }_{h,i,r}^{\rm F}$ and
$\tilde {\alpha }_{h,i,r}^{\rm F}$ and ![]() $\tilde {\alpha }_{h,i,r}^{\rm B}$ from
$\tilde {\alpha }_{h,i,r}^{\rm B}$ from ![]() $H^i_{\operatorname {\acute {e}t} }(U_{\overline {K}},\mathbf {Q}_p(r))$ to
$H^i_{\operatorname {\acute {e}t} }(U_{\overline {K}},\mathbf {Q}_p(r))$ to ![]() $H^i_{\operatorname {syn}}(U_{\overline {K}, h}, r)$ are equal. But, by Lemma 4.22, the map
$H^i_{\operatorname {syn}}(U_{\overline {K}, h}, r)$ are equal. But, by Lemma 4.22, the map ![]() $\tilde {\alpha }_{h,i,r}^{\rm B}$ is the inverse of the map
$\tilde {\alpha }_{h,i,r}^{\rm B}$ is the inverse of the map ![]() $\tilde {\beta }_{h,i,r}^{\rm B}$. Hence, by the first claim of our theorem, it suffices to prove the lemma below.
$\tilde {\beta }_{h,i,r}^{\rm B}$. Hence, by the first claim of our theorem, it suffices to prove the lemma below.
Lemma 4.37 The map ![]() $\tilde {\alpha }_{h,i,r}^{\rm F}$ is the inverse of the map
$\tilde {\alpha }_{h,i,r}^{\rm F}$ is the inverse of the map ![]() $\tilde {\beta }_{h,i,r}^{\rm F}$.
$\tilde {\beta }_{h,i,r}^{\rm F}$.
Proof. Identical to the proof of the second claim of Lemma 4.22 (recall that the main issue there was a relation between syntomic cohomology and the Hyodo–Kato and Beilinson–Hyodo–Kato cohomologies).
4.4.3 Period morphisms for motives, II
The content of § 4.3.9 goes through practically verbatim for the Faltings period morphism. We obtain that, for any Voevodsky motive ![]() $M$, we have the Hyodo–Kato and de Rham comparison quasi-isomorphisms
$M$, we have the Hyodo–Kato and de Rham comparison quasi-isomorphisms
 \begin{align*} \alpha^{\rm F}_{\rm pst}&: \mathrm{R}\Gamma_{\operatorname{\acute{e}t} }(M)\otimes^L{\mathbf{Q}_p}\,\,\mathbf{B}_{\operatorname{st}}\stackrel{\sim}{\to}\mathrm{R}\Gamma_{\operatorname{HK} }(M)\otimes^L_{F^{\rm nr}}\mathbf{B}_{\operatorname{st}},\\ \alpha^{\rm F}_{\operatorname{dR} }&: \mathrm{R}\Gamma_{\operatorname{\acute{e}t} }(M)\otimes^L_{\mathbf{Q}_p}\mathbf{B}_{\operatorname{dR} }\stackrel{\sim}{\to}\mathrm{R}\Gamma_{\operatorname{dR} }(M)\otimes^L_{\overline{K}}\mathbf{B}_{\operatorname{dR} } \end{align*}
\begin{align*} \alpha^{\rm F}_{\rm pst}&: \mathrm{R}\Gamma_{\operatorname{\acute{e}t} }(M)\otimes^L{\mathbf{Q}_p}\,\,\mathbf{B}_{\operatorname{st}}\stackrel{\sim}{\to}\mathrm{R}\Gamma_{\operatorname{HK} }(M)\otimes^L_{F^{\rm nr}}\mathbf{B}_{\operatorname{st}},\\ \alpha^{\rm F}_{\operatorname{dR} }&: \mathrm{R}\Gamma_{\operatorname{\acute{e}t} }(M)\otimes^L_{\mathbf{Q}_p}\mathbf{B}_{\operatorname{dR} }\stackrel{\sim}{\to}\mathrm{R}\Gamma_{\operatorname{dR} }(M)\otimes^L_{\overline{K}}\mathbf{B}_{\operatorname{dR} } \end{align*}
as in the case of Beilinson comparison quasi-isomorphisms. By Theorem 4.36, these comparison quasi-isomorphisms are the same as the ones of Beilinson. If we apply them to the cohomological Voevodsky motive ![]() $M(U)^{\vee }=f_*(1_X)$ for any proper semistable scheme
$M(U)^{\vee }=f_*(1_X)$ for any proper semistable scheme ![]() $X$ over
$X$ over ![]() ${\mathcal O} _K$, and
${\mathcal O} _K$, and ![]() $U=X_K\setminus D_K$ with structural morphism
$U=X_K\setminus D_K$ with structural morphism ![]() $f$, we get back Faltings period quasi-isomorphisms after the identification of the Beilinson–Hyodo–Kato and the original Hyodo–Kato cohomologies via the map
$f$, we get back Faltings period quasi-isomorphisms after the identification of the Beilinson–Hyodo–Kato and the original Hyodo–Kato cohomologies via the map ![]() $\kappa : \mathrm {R}\Gamma _{\operatorname {HK} }^B(X)\to \mathrm {R}\Gamma _{\operatorname {HK} }(X)$ from (4.24).
$\kappa : \mathrm {R}\Gamma _{\operatorname {HK} }^B(X)\to \mathrm {R}\Gamma _{\operatorname {HK} }(X)$ from (4.24).
Hence, we recover Theorem 4.7 comparing Faltings and Fontaine–Messing period morphisms for cohomology with compact support. But we also get:
(i) Faltings and Fontaine–Messing period morphisms are equal for open varieties: because they are equal to Beilinson period morphisms;
(ii) Faltings period morphisms are compatible with (mixed) products (which recovers [Reference FaltingsFal02]): use the argument for Tsuji products in § 4.3.9.
Acknowledgements
Parts of this paper were written during my visits to the Institut Henri Poincaré in Paris, the Institut de Mathématiques de Jussieu, Columbia University, and the IAS at Princeton. I would like to thank these institutions for their support, hospitality, and for the wonderful working conditions they have supplied. I thank Frederic Déglise for helpful comments related to the content of this paper and the referee for a very careful reading of the manuscript and useful comments.