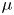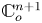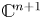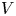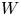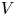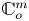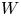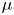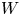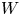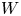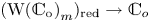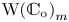1. Introduction
Before stating and discussing the main problem of this article we give some brief preliminaries and introduce the notation that is used in the article.
1.0.1 Preliminaries on  $\mu$-constant deformations
$\mu$-constant deformations
Let
be the ![]() $ {\mathbb {C}}$-algebra of analytic function germs at the origin
$ {\mathbb {C}}$-algebra of analytic function germs at the origin ![]() $o$ of
$o$ of ![]() $ {\mathbb {C}}^{n+1}$ and
$ {\mathbb {C}}^{n+1}$ and ![]() $ {\mathbb {C}}^{n+1}_{o}$ the complex-analytic germ of
$ {\mathbb {C}}^{n+1}_{o}$ the complex-analytic germ of ![]() $ {\mathbb {C}}^{n+1}$. By abuse of notation we denote by
$ {\mathbb {C}}^{n+1}$. By abuse of notation we denote by ![]() $o$ the origin of
$o$ the origin of ![]() $ {\mathbb {C}}^{n+1}_{o}$. Let
$ {\mathbb {C}}^{n+1}_{o}$. Let ![]() $V$ be a hypersurface of
$V$ be a hypersurface of ![]() $ {\mathbb {C}}^{n+1}_{o}$,
$ {\mathbb {C}}^{n+1}_{o}$, ![]() $n\geq 1$, given by an equation
$n\geq 1$, given by an equation ![]() $f(x)=0$, where
$f(x)=0$, where ![]() $f$ is irreducible in
$f$ is irreducible in ![]() $ {\mathcal {O}_{n+1}^{x}}$. Assume that
$ {\mathcal {O}_{n+1}^{x}}$. Assume that ![]() $V$ has an isolated singularity at
$V$ has an isolated singularity at ![]() $o$. One of the important topological invariants of the singularity
$o$. One of the important topological invariants of the singularity ![]() $o\in V$ is the Milnor number
$o\in V$ is the Milnor number ![]() $\mu (f)$, defined by
$\mu (f)$, defined by
where ![]() $J(f):=(\partial _1f,\ldots,\partial _{n+1}f) \subset {\mathcal {O}_{n+1}^{x}}$ is the Jacobian ideal of
$J(f):=(\partial _1f,\ldots,\partial _{n+1}f) \subset {\mathcal {O}_{n+1}^{x}}$ is the Jacobian ideal of ![]() $f$. In this article, we consider deformations of
$f$. In this article, we consider deformations of ![]() $f$ that preserve the Milnor number. Let
$f$ that preserve the Milnor number. Let ![]() $F\in {\mathbb {C}}\{x_1,\ldots,x_{n+1},s_1,\ldots,s_m\}$ be a deformation of
$F\in {\mathbb {C}}\{x_1,\ldots,x_{n+1},s_1,\ldots,s_m\}$ be a deformation of ![]() $f$:
$f$:
 \[ F(x,s):=f(x)+\sum_{i=1}^{\infty}h_i(s)g_i(x) \]
\[ F(x,s):=f(x)+\sum_{i=1}^{\infty}h_i(s)g_i(x) \]
where ![]() $h_i\in {\mathcal {O}_{m}^{s}}:= {\mathbb {C}\{s_{1},\ldots,s_{m}\}}$,
$h_i\in {\mathcal {O}_{m}^{s}}:= {\mathbb {C}\{s_{1},\ldots,s_{m}\}}$, ![]() $m\geq 1$, and
$m\geq 1$, and ![]() $g_i\in {\mathcal {O}_{n+1}^{x}}$ satisfy
$g_i\in {\mathcal {O}_{n+1}^{x}}$ satisfy
Take a sufficiently small open set ![]() $\Omega \subset {\mathbb {C}}^{m}$ containing
$\Omega \subset {\mathbb {C}}^{m}$ containing ![]() $o$, and representatives of the analytic function germs
$o$, and representatives of the analytic function germs ![]() $h_1,\ldots,h_i,\ldots$ in
$h_1,\ldots,h_i,\ldots$ in ![]() $\Omega$. By a standard abuse of notation we denote these representatives by the same letters
$\Omega$. By a standard abuse of notation we denote these representatives by the same letters ![]() $h_1,\ldots,h_l$. We use the notation
$h_1,\ldots,h_l$. We use the notation ![]() $F_{s'}(x):=F(x,s')$ when
$F_{s'}(x):=F(x,s')$ when ![]() $s'\in \Omega$ is fixed. We say that the deformation
$s'\in \Omega$ is fixed. We say that the deformation ![]() $F$ is
$F$ is ![]() $\mu$-constant if the open set
$\mu$-constant if the open set ![]() $\Omega$ can be chosen so that
$\Omega$ can be chosen so that ![]() $\mu (F_{s'})=\mu (f)$ for all
$\mu (F_{s'})=\mu (f)$ for all ![]() $s'\in \Omega$.
$s'\in \Omega$.
Let ![]() $\mathcal {E}:=\{e_1,e_2,\ldots,e_{n+1}\}\subset {\mathbb {Z}}_{\geq 0}^{n+1}$ be the standard basis of
$\mathcal {E}:=\{e_1,e_2,\ldots,e_{n+1}\}\subset {\mathbb {Z}}_{\geq 0}^{n+1}$ be the standard basis of ![]() $ {\mathbb {R}}^{n+1}$. Let
$ {\mathbb {R}}^{n+1}$. Let ![]() $g\in {\mathbb {C}}\{x_1,\ldots,x_{n+1}\}$ be a convergent power series. Write
$g\in {\mathbb {C}}\{x_1,\ldots,x_{n+1}\}$ be a convergent power series. Write
in the multi-index notation. The Newton polyhedron ![]() $\Gamma _{+}(g)$ is the convex hull of the set
$\Gamma _{+}(g)$ is the convex hull of the set ![]() $\bigcup _{\alpha \in \operatorname {Supp}(g)}(\alpha + {\mathbb {R}}_{\geq 0}^n)$, where
$\bigcup _{\alpha \in \operatorname {Supp}(g)}(\alpha + {\mathbb {R}}_{\geq 0}^n)$, where ![]() $\operatorname {Supp}(g)$ (short for ‘the support of
$\operatorname {Supp}(g)$ (short for ‘the support of ![]() $g$’) is defined by
$g$’) is defined by
The Newton boundary of ![]() $\Gamma _{+}(g)$, denoted by
$\Gamma _{+}(g)$, denoted by ![]() $\Gamma (g)$, is the union of the compact faces of
$\Gamma (g)$, is the union of the compact faces of ![]() $\Gamma _{+}(g)$. For a face
$\Gamma _{+}(g)$. For a face ![]() $\gamma$ of
$\gamma$ of ![]() $\Gamma _{+}(g)$, the polynomial
$\Gamma _{+}(g)$, the polynomial ![]() $g_{\gamma }$ is defined as follows:
$g_{\gamma }$ is defined as follows:
We say that ![]() $g$, is non-degenerate with respect to its Newton boundary (or Newton non-degenerate) if for every compact face
$g$, is non-degenerate with respect to its Newton boundary (or Newton non-degenerate) if for every compact face ![]() $\gamma$ of the Newton polyhedron
$\gamma$ of the Newton polyhedron ![]() $\Gamma _{+}(g)$ the partial derivatives
$\Gamma _{+}(g)$ the partial derivatives ![]() $\partial _{x_1}g_{\gamma },\partial _{x_2}g_{\gamma } ,\ldots,\partial _{x_{n+1}}g_{\gamma }$ have no common zeros in
$\partial _{x_1}g_{\gamma },\partial _{x_2}g_{\gamma } ,\ldots,\partial _{x_{n+1}}g_{\gamma }$ have no common zeros in ![]() $( {\mathbb {C}}^{\star })^{n+1}$.
$( {\mathbb {C}}^{\star })^{n+1}$.
We say that a deformation of ![]() $F$ of
$F$ of ![]() $f$ is non-degenerate if the neighborhood
$f$ is non-degenerate if the neighborhood ![]() $\Omega$ of
$\Omega$ of ![]() $o$ in
$o$ in ![]() $ {\mathbb {C}}^m$ can be chosen so that for all
$ {\mathbb {C}}^m$ can be chosen so that for all ![]() $s'\in \Omega$ the germ
$s'\in \Omega$ the germ ![]() $F_{s'}$ is non-degenerate with respect to its Newton boundary
$F_{s'}$ is non-degenerate with respect to its Newton boundary ![]() $\Gamma (F_{s'})$.
$\Gamma (F_{s'})$.
We rewrite the deformation ![]() $F$ in the form:
$F$ in the form:
and let ![]() $\operatorname {Supp}(F):=\{\alpha \, | \, a_{\alpha }(s)\not \equiv 0\}$. Given a sufficiently small open set
$\operatorname {Supp}(F):=\{\alpha \, | \, a_{\alpha }(s)\not \equiv 0\}$. Given a sufficiently small open set ![]() $\Omega \subset {\mathbb {C}}^m$ containing
$\Omega \subset {\mathbb {C}}^m$ containing ![]() $o$, we say that
$o$, we say that ![]() $s'\in \Omega$ is a general point of
$s'\in \Omega$ is a general point of ![]() $ {\mathbb {C}}^m_{o}$ if
$ {\mathbb {C}}^m_{o}$ if
We remark that
and that ![]() $s'$ is general if whenever
$s'$ is general if whenever ![]() $s'$ belongs to the non-empty open set
$s'$ belongs to the non-empty open set
In particular, plenty of general points ![]() $s'$ exist.
$s'$ exist.
1.0.2 Preliminaries on simultaneous embedded resolutions
Let us keep the notation from the previous section. We put ![]() $S:= {\mathbb {C}}^m_o$, and denote by
$S:= {\mathbb {C}}^m_o$, and denote by ![]() $W$ the deformation of
$W$ the deformation of ![]() $V$ given by
$V$ given by ![]() $F$. Then we have the commutative diagram
$F$. Then we have the commutative diagram

where the morphism ![]() $\varrho$ is flat. Given a sufficiently small open set
$\varrho$ is flat. Given a sufficiently small open set ![]() $\Omega \subset {\mathbb {C}}^{m}$ containing
$\Omega \subset {\mathbb {C}}^{m}$ containing ![]() $o$, by a standard abuse of notation we denote by the same letters the representatives of
$o$, by a standard abuse of notation we denote by the same letters the representatives of ![]() $\varrho$ and
$\varrho$ and ![]() $W$. (We usually use this abuse of notation for any representative of a germ). We use the notation
$W$. (We usually use this abuse of notation for any representative of a germ). We use the notation ![]() $W_{s'}:=\varrho ^{-1}(s')$,
$W_{s'}:=\varrho ^{-1}(s')$, ![]() $s'\in \Omega$.
$s'\in \Omega$.
In what follows we define what we mean by simultaneous embedded resolution of ![]() $W$. We give the general definition here, even though, as explained in Remark 1.5, the simultaneous embedded resolutions that we construct in the main theorem are of a special type.
$W$. We give the general definition here, even though, as explained in Remark 1.5, the simultaneous embedded resolutions that we construct in the main theorem are of a special type.
We consider a proper bimeromorphic morphism ![]() $\varphi :\widetilde { {\mathbb {C}}^{n+1}_o\times S}\rightarrow {\mathbb {C}}^{n+1}_o\times S$ such that
$\varphi :\widetilde { {\mathbb {C}}^{n+1}_o\times S}\rightarrow {\mathbb {C}}^{n+1}_o\times S$ such that ![]() $\widetilde { {\mathbb {C}}^{n+1}_o\times S}$ is formally smooth over
$\widetilde { {\mathbb {C}}^{n+1}_o\times S}$ is formally smooth over ![]() $S$, and we denote by
$S$, and we denote by ![]() $\widetilde {W}^{\rm s}$ and
$\widetilde {W}^{\rm s}$ and ![]() $\widetilde {W}^{\rm t}$ the strict and the total transform of
$\widetilde {W}^{\rm t}$ the strict and the total transform of ![]() $W$ in
$W$ in ![]() $\widetilde { {\mathbb {C}}^{n+1}_o\times S}$, respectively.
$\widetilde { {\mathbb {C}}^{n+1}_o\times S}$, respectively.
Denote by ![]() ${\rm Exp}(\varphi )$, the exceptional fiber of
${\rm Exp}(\varphi )$, the exceptional fiber of ![]() $\varphi$.
$\varphi$.
Definition 1.1 The morphism ![]() $\widetilde {W}^{\rm s}\rightarrow W$ is a very weak simultaneous resolution if there exists a sufficiently small open set
$\widetilde {W}^{\rm s}\rightarrow W$ is a very weak simultaneous resolution if there exists a sufficiently small open set ![]() $\Omega \subset {\mathbb {C}}^{m}$ containing
$\Omega \subset {\mathbb {C}}^{m}$ containing ![]() $o$ such that
$o$ such that ![]() $\widetilde {W}^{\rm s}_{s'}\rightarrow W_{s'}$ is a resolution of singularities for each
$\widetilde {W}^{\rm s}_{s'}\rightarrow W_{s'}$ is a resolution of singularities for each ![]() $s'\in \Omega$.
$s'\in \Omega$.
Definition 1.2 We say that ![]() $\widetilde {W}^{\rm t}$ is a normal crossing divisor relative to
$\widetilde {W}^{\rm t}$ is a normal crossing divisor relative to ![]() $S$ if
$S$ if ![]() $\widetilde {W}^{\rm t}$ is locally embedded trivial, which is to say that for each
$\widetilde {W}^{\rm t}$ is locally embedded trivial, which is to say that for each ![]() $p\in \varphi ^{-1}(o,o)$ there exist sufficiently small open sets
$p\in \varphi ^{-1}(o,o)$ there exist sufficiently small open sets ![]() $o\in \Omega \subset {\mathbb {C}}^{m}$,
$o\in \Omega \subset {\mathbb {C}}^{m}$, ![]() $o\in \Omega '\subset {\mathbb {C}}^{n+1}$,
$o\in \Omega '\subset {\mathbb {C}}^{n+1}$, ![]() $o\in \Omega ''\subset {\mathbb {C}}^{n+1}$ and a neighborhood of
$o\in \Omega ''\subset {\mathbb {C}}^{n+1}$ and a neighborhood of ![]() $p$,
$p$,
such that there exists a map ![]() $\phi$,
$\phi$,

biholomorphic onto its image, such that ![]() $\widetilde {W}^t\cap U$ is defined by the ideal
$\widetilde {W}^t\cap U$ is defined by the ideal ![]() $\phi ^{\star }\mathcal {I}$, where
$\phi ^{\star }\mathcal {I}$, where ![]() $\mathcal {I}=(y_{1}^{a_{1}}\cdots y_{n+1}^{a_{n+1}})$,
$\mathcal {I}=(y_{1}^{a_{1}}\cdots y_{n+1}^{a_{n+1}})$, ![]() $y_1,\ldots y_{n+1}$ is a coordinate system at
$y_1,\ldots y_{n+1}$ is a coordinate system at ![]() $o$ in
$o$ in ![]() $\Omega ''$, and the
$\Omega ''$, and the ![]() $a_i$ are non-negative integers.
$a_i$ are non-negative integers.
If ![]() $p\in \widetilde {W}^{\rm s}_{o}\cap \varphi ^{-1}(o,o)$, we require that
$p\in \widetilde {W}^{\rm s}_{o}\cap \varphi ^{-1}(o,o)$, we require that ![]() $a_{n+1}=1$ and that
$a_{n+1}=1$ and that ![]() $\widetilde {W}^s\cap U$ be defined by the ideal
$\widetilde {W}^s\cap U$ be defined by the ideal ![]() $\phi ^{\star }\mathcal {I}'$, where
$\phi ^{\star }\mathcal {I}'$, where ![]() $\mathcal {I}'=(y_{n+1})$.
$\mathcal {I}'=(y_{n+1})$.
Remark 1.3 Assume that ![]() $\widetilde {W}^{\rm t}$ is a normal crossing divisor relative to
$\widetilde {W}^{\rm t}$ is a normal crossing divisor relative to ![]() $S$. Then
$S$. Then ![]() $\mathcal {O}_{\widetilde {W}^{\rm t}}$ is a locally free sheaf of
$\mathcal {O}_{\widetilde {W}^{\rm t}}$ is a locally free sheaf of ![]() $ {\mathcal {O}_{m}^{s}}$-modules. In particular, the morphism
$ {\mathcal {O}_{m}^{s}}$-modules. In particular, the morphism ![]() $\widetilde {W}^{\rm t}\rightarrow S$ is flat.
$\widetilde {W}^{\rm t}\rightarrow S$ is flat.
Definition 1.4 We say ![]() $\varphi$ is a simultaneous embedded resolution if, in the above notation, the morphism
$\varphi$ is a simultaneous embedded resolution if, in the above notation, the morphism ![]() $\widetilde {W}^{\rm s}\rightarrow W$ is a very weak simultaneous resolution and
$\widetilde {W}^{\rm s}\rightarrow W$ is a very weak simultaneous resolution and ![]() $\widetilde {W}^{\rm t}$ is a normal crossing divisor relative to
$\widetilde {W}^{\rm t}$ is a normal crossing divisor relative to ![]() $S$.
$S$.
Remark 1.5 In the proof of the main result (Theorem 3.2), the construction of a simultaneous embedded resolution ![]() $\varphi$ goes as follows: first we construct an adapted toric birational proper morphism
$\varphi$ goes as follows: first we construct an adapted toric birational proper morphism ![]() $\pi :\widetilde { {\mathbb {C}}^{n+1}_{o}}\rightarrow {\mathbb {C}}^{n+1}_o$ (here
$\pi :\widetilde { {\mathbb {C}}^{n+1}_{o}}\rightarrow {\mathbb {C}}^{n+1}_o$ (here ![]() $ {\mathbb {C}}^{n+1}_o$ is endowed with the natural toric structure respecting the chosen coordinates) such that
$ {\mathbb {C}}^{n+1}_o$ is endowed with the natural toric structure respecting the chosen coordinates) such that ![]() ${\rm Exp(\varphi )}=\pi ^{-1}(o)$. Then
${\rm Exp(\varphi )}=\pi ^{-1}(o)$. Then ![]() $\varphi$ is the product morphism which is defined by
$\varphi$ is the product morphism which is defined by
Let us recall that ![]() $W$ is defined by
$W$ is defined by
 \[ F(x,s):=f(x)+\sum_{i=1}^{\infty}h_i(s)g_i(x) \]
\[ F(x,s):=f(x)+\sum_{i=1}^{\infty}h_i(s)g_i(x) \]
where ![]() $h_i\in {\mathcal {O}_{m}^{s}}$,
$h_i\in {\mathcal {O}_{m}^{s}}$, ![]() $m\geq 1$, and
$m\geq 1$, and ![]() $g_i\in {\mathcal {O}_{n+1}^{x}}$ such that
$g_i\in {\mathcal {O}_{n+1}^{x}}$ such that ![]() $h_i(o)=g_i(o)=0$.
$h_i(o)=g_i(o)=0$.
Let ![]() $\epsilon >0$ (respectively,
$\epsilon >0$ (respectively, ![]() $\epsilon '>0$) be small enough so that
$\epsilon '>0$) be small enough so that ![]() $f, g_1,\ldots,g_l$ (respectively,
$f, g_1,\ldots,g_l$ (respectively, ![]() $h_1,\ldots,h_l$) are defined in the open ball
$h_1,\ldots,h_l$) are defined in the open ball ![]() $B_{\epsilon '}(o)\subset {\mathbb {C}}^{n+1}$ (respectively,
$B_{\epsilon '}(o)\subset {\mathbb {C}}^{n+1}$ (respectively, ![]() $B_{\epsilon }(o)\subset {\mathbb {C}}^{m}$), and the singular locus of
$B_{\epsilon }(o)\subset {\mathbb {C}}^{m}$), and the singular locus of ![]() $W$ is
$W$ is ![]() $\{o\}\times B_{\epsilon }(o)$. We say that the deformation of
$\{o\}\times B_{\epsilon }(o)$. We say that the deformation of ![]() $W$ is embedded topologically trivial (in the classical literature, one often says simply that
$W$ is embedded topologically trivial (in the classical literature, one often says simply that ![]() $F$ is topologically trivial) if, in addition, there exists a homeomorphism
$F$ is topologically trivial) if, in addition, there exists a homeomorphism
such that ![]() $\xi (W)=V'\times B_{\epsilon }(o)$, where
$\xi (W)=V'\times B_{\epsilon }(o)$, where ![]() $V':=\xi (V)$, that is,
$V':=\xi (V)$, that is, ![]() $\xi$ trivializes
$\xi$ trivializes ![]() $W$.
$W$.
The following proposition relates simultaneous embedded resolutions, embedded topologically trivial deformations and ![]() $\mu$-constant deformations.
$\mu$-constant deformations.
Proposition 1.6 Let ![]() $V$ and
$V$ and ![]() $W$ be as previously. Assume that
$W$ be as previously. Assume that ![]() $W$ admits a simultaneous embedded resolution such that
$W$ admits a simultaneous embedded resolution such that ![]() ${\rm Exp}(\varphi )=\varphi ^{-1}(\{o\}\times S)$. Then:
${\rm Exp}(\varphi )=\varphi ^{-1}(\{o\}\times S)$. Then:
(i) the deformation
 $W$ is embedded topologically trivial;
$W$ is embedded topologically trivial;(ii) the deformation
 $W$ is
$W$ is  $\mu$-constant.
$\mu$-constant.
Proof. The Milnor number ![]() $\mu$ is a topological invariant, hence part (i) implies part (ii), see Theorem 1.4 of [Reference TeissierTei73]
$\mu$ is a topological invariant, hence part (i) implies part (ii), see Theorem 1.4 of [Reference TeissierTei73]
We apply Thom's first isotopy lemma (see [Reference MatherMat12, Proposition 2.11]) to a closed neighborhood ![]() $C$ (that we describe in the following) of the compact set
$C$ (that we describe in the following) of the compact set ![]() $\varphi ^{-1}(o,o)$ and to the restriction of
$\varphi ^{-1}(o,o)$ and to the restriction of ![]() $\varphi$ to
$\varphi$ to ![]() $C$.
$C$.
We begin by describing ![]() $C$ and then we show that the hypotheses of the lemma are satisfied.
$C$ and then we show that the hypotheses of the lemma are satisfied.
As ![]() $W$ admits a simultaneous embedded resolution, there exists a proper bimeromorphic morphism
$W$ admits a simultaneous embedded resolution, there exists a proper bimeromorphic morphism ![]() $\varphi :\widetilde { {\mathbb {C}}^{n+1}_o\times S}\rightarrow {\mathbb {C}}^{n+1}_o\times S$ such that
$\varphi :\widetilde { {\mathbb {C}}^{n+1}_o\times S}\rightarrow {\mathbb {C}}^{n+1}_o\times S$ such that ![]() $\widetilde { {\mathbb {C}}^{n+1}_o\times S}$ is formally smooth over
$\widetilde { {\mathbb {C}}^{n+1}_o\times S}$ is formally smooth over ![]() $S$, and
$S$, and ![]() $\widetilde {W}^t$ is a normal crossing divisor relative to
$\widetilde {W}^t$ is a normal crossing divisor relative to ![]() $S$. By Definition 1.2, we have that for each
$S$. By Definition 1.2, we have that for each ![]() $p\in \varphi ^{-1}(o,o)$ there exist sufficiently small
$p\in \varphi ^{-1}(o,o)$ there exist sufficiently small ![]() $\epsilon, \epsilon ',\epsilon ''>0$, and a map
$\epsilon, \epsilon ',\epsilon ''>0$, and a map ![]() $\phi _p$ biholomorphic onto its image
$\phi _p$ biholomorphic onto its image

that trivializes ![]() $\widetilde {W}^t\cap U_p$, where
$\widetilde {W}^t\cap U_p$, where ![]() $U_p\subset \varphi ^{-1}(B_{\epsilon '}(o)\times B_{\epsilon }(o))$ is a neighborhood of
$U_p\subset \varphi ^{-1}(B_{\epsilon '}(o)\times B_{\epsilon }(o))$ is a neighborhood of ![]() $p$. Without loss of generality, we assume that
$p$. Without loss of generality, we assume that ![]() $\phi _p$ is bijective.
$\phi _p$ is bijective.
As ![]() $\varphi ^{-1}(o,o)$ is a compact set, there exists a finite set of points
$\varphi ^{-1}(o,o)$ is a compact set, there exists a finite set of points ![]() $\{ p_1,\ldots,p_l\}\subset \varphi ^{-1}(o,o)$ such that
$\{ p_1,\ldots,p_l\}\subset \varphi ^{-1}(o,o)$ such that ![]() $\varphi ^{-1}(o,o)\subset \Omega =\bigcup _{1}^l U_{p_i}$. Moreover, we may assume that
$\varphi ^{-1}(o,o)\subset \Omega =\bigcup _{1}^l U_{p_i}$. Moreover, we may assume that ![]() $\epsilon$,
$\epsilon$, ![]() $\epsilon '$ do not depend on
$\epsilon '$ do not depend on ![]() $p_i$, that
$p_i$, that ![]() $\Omega \subset \varphi ^{-1}(B_{\epsilon '}(o)\times B_{\epsilon }(o))$, and using at most a homothetic transformation that
$\Omega \subset \varphi ^{-1}(B_{\epsilon '}(o)\times B_{\epsilon }(o))$, and using at most a homothetic transformation that ![]() $\epsilon ''$ does not depend on
$\epsilon ''$ does not depend on ![]() $p$.
$p$.
The open set ![]() $\Omega$ is an open neighborhood of
$\Omega$ is an open neighborhood of ![]() $\varphi ^{-1}(o,o)$, and there exist
$\varphi ^{-1}(o,o)$, and there exist ![]() $\epsilon _0'>0$ and
$\epsilon _0'>0$ and ![]() $\epsilon _0>0$ such that
$\epsilon _0>0$ such that ![]() $\varphi ^{-1}(B_{\epsilon '_0}(o)\times B_{\epsilon _0}(o))\subset \Omega$. Indeed, if this was not true, there would exist a sequence
$\varphi ^{-1}(B_{\epsilon '_0}(o)\times B_{\epsilon _0}(o))\subset \Omega$. Indeed, if this was not true, there would exist a sequence ![]() $x_n\in \varphi ^{-1}(B_{\epsilon '/n}(o)\times B_{\epsilon /n}(o))$ such that
$x_n\in \varphi ^{-1}(B_{\epsilon '/n}(o)\times B_{\epsilon /n}(o))$ such that ![]() $x_n\not \in \Omega$ for all
$x_n\not \in \Omega$ for all ![]() $n>0$. The morphism
$n>0$. The morphism ![]() $\varphi$ is proper, hence
$\varphi$ is proper, hence ![]() $\varphi ^{-1}(\overline {B_{\epsilon '/n}(o)}\times \overline {B_{\epsilon /n'}(o)})$ is a compact set. We may assume that the sequence
$\varphi ^{-1}(\overline {B_{\epsilon '/n}(o)}\times \overline {B_{\epsilon /n'}(o)})$ is a compact set. We may assume that the sequence ![]() $x_n$ converges to a point
$x_n$ converges to a point ![]() $q\in \varphi ^{-1}(o,o)$ (because
$q\in \varphi ^{-1}(o,o)$ (because ![]() $\varphi (x_n)$ converge to
$\varphi (x_n)$ converge to ![]() $(o,o))$. Then there exists
$(o,o))$. Then there exists ![]() $n_0\in \mathbb {N}$ such that
$n_0\in \mathbb {N}$ such that ![]() $x_n\in \Omega$ for all
$x_n\in \Omega$ for all ![]() $n\geq n_0$, which is a contradiction. Note that we can also assume that
$n\geq n_0$, which is a contradiction. Note that we can also assume that ![]() $\varphi ^{-1}(\overline {B_{\epsilon '_0}(o)}\times B_{\epsilon _0}(o))\subset \Omega$.
$\varphi ^{-1}(\overline {B_{\epsilon '_0}(o)}\times B_{\epsilon _0}(o))\subset \Omega$.
Now, it is well known that there exists ![]() $\epsilon '_1>0$ small enough such that for all
$\epsilon '_1>0$ small enough such that for all ![]() $0<\delta \leq \epsilon '_1$ the hypersurface
$0<\delta \leq \epsilon '_1$ the hypersurface ![]() $V$ intersects the
$V$ intersects the ![]() $(2n+1)$-sphere
$(2n+1)$-sphere ![]() $S_{\delta }(o):=\partial \overline {B_{\delta }(o)}$ transversally (see [Reference MilnorMil68]). There exists
$S_{\delta }(o):=\partial \overline {B_{\delta }(o)}$ transversally (see [Reference MilnorMil68]). There exists ![]() $\epsilon _1>0$ small enough so that the hypersurface
$\epsilon _1>0$ small enough so that the hypersurface ![]() $W_s$ intersects the
$W_s$ intersects the ![]() $2n+1$-sphere
$2n+1$-sphere ![]() $S_{\delta }(o)$ transversally for all
$S_{\delta }(o)$ transversally for all ![]() $s\in B_{\epsilon _1}(o)\subset {\mathbb {C}}^m$.
$s\in B_{\epsilon _1}(o)\subset {\mathbb {C}}^m$.
Without loss of generality, we assume that ![]() $\epsilon =\epsilon _0=\epsilon _1$ and
$\epsilon =\epsilon _0=\epsilon _1$ and ![]() $\epsilon '_0=\epsilon '_1$ (we can replace
$\epsilon '_0=\epsilon '_1$ (we can replace ![]() $\epsilon$ by
$\epsilon$ by ![]() $\epsilon _0$ in the definition of
$\epsilon _0$ in the definition of ![]() $\Omega$). The set
$\Omega$). The set ![]() $C:=\varphi ^{-1}(\overline {B_{\epsilon '_0}}(o)\times B_{\epsilon }(o))$ is a closed set of
$C:=\varphi ^{-1}(\overline {B_{\epsilon '_0}}(o)\times B_{\epsilon }(o))$ is a closed set of ![]() $\Omega$.
$\Omega$.
We now verify the hypotheses of Thom's first isotopy lemma.
(i) The morphisms
and \[ \varphi|_C:C\rightarrow \overline{B_{\epsilon'_0}}(o)\times B_{\epsilon}(o) \]are proper, hence so is
\[ \varphi|_C:C\rightarrow \overline{B_{\epsilon'_0}}(o)\times B_{\epsilon}(o) \]are proper, hence so is \[ pr_2:\overline{B_{\epsilon'_0}(o)}\times B_{\epsilon}(o)\rightarrow B_{\epsilon}(o) \]
\[ pr_2:\overline{B_{\epsilon'_0}(o)}\times B_{\epsilon}(o)\rightarrow B_{\epsilon}(o) \] $\psi :=pr_2\circ \varphi |_C$.
$\psi :=pr_2\circ \varphi |_C$.(ii) As each intersection of
 $(C\cap W^t)\cup \varphi ^{-1}(S_{\epsilon '_o}(o)\times B_{\epsilon }(o))$ is transverse, the set
$(C\cap W^t)\cup \varphi ^{-1}(S_{\epsilon '_o}(o)\times B_{\epsilon }(o))$ is transverse, the set  $(C\cap W^t)\cup \varphi ^{-1}(S_{\epsilon '_o}(o)\times B_{\epsilon }(o))$ induces a Whitney stratification of
$(C\cap W^t)\cup \varphi ^{-1}(S_{\epsilon '_o}(o)\times B_{\epsilon }(o))$ induces a Whitney stratification of  $C$ (obtained by first considering the complement in
$C$ (obtained by first considering the complement in  $(C\cap W^t)\cup \varphi ^{-1}(S_{\epsilon '_o}(o)\times B_{\epsilon }(o))$ and then by the natural stratification of
$(C\cap W^t)\cup \varphi ^{-1}(S_{\epsilon '_o}(o)\times B_{\epsilon }(o))$ and then by the natural stratification of  $(C\cap W^t)\cup \varphi ^{-1}(S_{\epsilon '_o}(o)\times B_{\epsilon }(o))$ which is a union of manifolds intersecting transversally). Moreover, as
$(C\cap W^t)\cup \varphi ^{-1}(S_{\epsilon '_o}(o)\times B_{\epsilon }(o))$ which is a union of manifolds intersecting transversally). Moreover, as  $\widetilde { {\mathbb {C}}^{n+1}_0\times S}$ is formally smooth over
$\widetilde { {\mathbb {C}}^{n+1}_0\times S}$ is formally smooth over  $S$, on each stratum
$S$, on each stratum  $X$ of
$X$ of  $C$ the morphism
$C$ the morphism  $\psi |_X$ is smooth.
$\psi |_X$ is smooth.(iii) Observe that, by construction, for each stratum
 $X$ of
$X$ of  $C$ and each
$C$ and each  $q\in X$ there exists a section
$q\in X$ there exists a section  $r$ of
$r$ of  $\psi$ such that
$\psi$ such that  $r(\psi |_{X}(q))=q$:
hence,
$r(\psi |_{X}(q))=q$:
hence,
 $\psi |_{X}:X\rightarrow B_{\epsilon }(o)$ is a submersive map.
$\psi |_{X}:X\rightarrow B_{\epsilon }(o)$ is a submersive map.
Let ![]() $C_o:=C\cap \psi ^{-1}(o)$ and
$C_o:=C\cap \psi ^{-1}(o)$ and ![]() $X_o:=X\cap \psi ^{-1}(o)$, where
$X_o:=X\cap \psi ^{-1}(o)$, where ![]() $X$ is a stratum of
$X$ is a stratum of ![]() $C$. Thom's first isotopy lemma assures us that there exists
$C$. Thom's first isotopy lemma assures us that there exists ![]() $\epsilon >0$ small enough and a homeomorphism
$\epsilon >0$ small enough and a homeomorphism

such that ![]() $\xi _o(X)=X_o\times {B}_{\epsilon }(o)$, see Proposition
$\xi _o(X)=X_o\times {B}_{\epsilon }(o)$, see Proposition ![]() $11.1$ and Corollary
$11.1$ and Corollary ![]() $10.3$ of [Reference MatherMat12]. Then the morphism
$10.3$ of [Reference MatherMat12]. Then the morphism ![]() $\xi _0$ trivializes simultaneously
$\xi _0$ trivializes simultaneously
We denote by ![]() $\varphi _o$ the morphism obtained by restricting
$\varphi _o$ the morphism obtained by restricting ![]() $\varphi$ to the special fiber.
$\varphi$ to the special fiber.

Consider the morphism
Then for small enough ![]() $\epsilon '_0$ and
$\epsilon '_0$ and ![]() $\epsilon$, the map
$\epsilon$, the map
is the desired trivialization.
1.0.3 On the main result of the article
Keep the notation of the previous sections. Recall that ![]() $W$ is a deformation of
$W$ is a deformation of ![]() $V$ over
$V$ over ![]() $S:= {\mathbb {C}}^m_o$ given by
$S:= {\mathbb {C}}^m_o$ given by ![]() $F$. In [Reference OkaOka89], Oka proved that if
$F$. In [Reference OkaOka89], Oka proved that if ![]() $W$ is a non-degenerate
$W$ is a non-degenerate ![]() $\mu$-constant deformation of
$\mu$-constant deformation of ![]() $V$ that induces a negligible truncation of the Newton boundary then
$V$ that induces a negligible truncation of the Newton boundary then ![]() $W$ admits a very weak simultaneous resolution. However, if the method of proof used is observed with detail, what is really proved is that
$W$ admits a very weak simultaneous resolution. However, if the method of proof used is observed with detail, what is really proved is that ![]() $W$ admits a simultaneous embedded resolution in the special case when
$W$ admits a simultaneous embedded resolution in the special case when
Intuitively one might think that the condition that ![]() $W$ admit a simultaneous embedded resolution is more restrictive than the condition that
$W$ admit a simultaneous embedded resolution is more restrictive than the condition that ![]() $W$ is a
$W$ is a ![]() $\mu$-constant deformation. However, this intuition is wrong in the case of Newton non-degenerate
$\mu$-constant deformation. However, this intuition is wrong in the case of Newton non-degenerate ![]() $\mu$-constant deformations. More precisely, in this article we prove the following result.
$\mu$-constant deformations. More precisely, in this article we prove the following result.
Theorem Assume that ![]() $W$ is a Newton non-degenerate deformation. Then the deformation
$W$ is a Newton non-degenerate deformation. Then the deformation ![]() $W$ is
$W$ is ![]() $\mu$-constant if and only if
$\mu$-constant if and only if ![]() $W$ admits a simultaneous embedded resolution.
$W$ admits a simultaneous embedded resolution.
Observe that if ![]() $W$ admits a simultaneous embedded resolution it follows directly from Proposition 1.6 that
$W$ admits a simultaneous embedded resolution it follows directly from Proposition 1.6 that ![]() $W$ is a
$W$ is a ![]() $\mu$-constant deformation. The converse of this is what needs to be proved.
$\mu$-constant deformation. The converse of this is what needs to be proved.
From this theorem and Proposition 1.6 we obtain the following corollary.
Corollary 1.7 Let ![]() $W$ be a Newton non-degenerate
$W$ be a Newton non-degenerate ![]() $\mu$-constant deformation. Then
$\mu$-constant deformation. Then ![]() $W$ is topologically trivial.
$W$ is topologically trivial.
The result of the corollary was already obtained in Theorem 1.1 of [Reference AbderrahmaneAbd16].
It was pointed out to us by the referee that Corollary 1.5 follows from the following two known statements:
(i) every small Newton-non-degenerate deformation is a pullback from a linear one (that is, a deformation of type
 $f(x) + sg(x)$);
$f(x) + sg(x)$);(ii) every
 $\mu$-constant family of isolated hypersurface singularities of type
$\mu$-constant family of isolated hypersurface singularities of type  $f(x) + sg(x)$, is topologically trivial; this is a result of Parusinki (Corollary
$f(x) + sg(x)$, is topologically trivial; this is a result of Parusinki (Corollary  $2.1$ of [Reference ParusinskiPar99]).
$2.1$ of [Reference ParusinskiPar99]).
In the general case, for ![]() $n\neq 2$ it is known that if
$n\neq 2$ it is known that if ![]() $W$ is a
$W$ is a ![]() $\mu$-constant deformation, then the deformation
$\mu$-constant deformation, then the deformation ![]() $W$ is topologically trivial (see [Reference Lê Dũng and RamanujamLDR76]). The case
$W$ is topologically trivial (see [Reference Lê Dũng and RamanujamLDR76]). The case ![]() $n=2$ is a conjecture (the Lê–Ramanujan conjecture).
$n=2$ is a conjecture (the Lê–Ramanujan conjecture).
Beyond this article, the main result here initiates a new approach to the Lê–Ramanujam conjecture. In characteristic zero every singularity can be embedded in a higher-dimensional affine space in such a way that it is Newton non-degenerate in the sense of Khovanskii or Schön (this is a possible reading of a result of Tevelev, answering a question of Teissier, see [Reference TeissierTei14], [Reference TevelevTev14] and [Reference MourtadaMou17]). Note that Schön (Newton non-degenerate in the sense of Khovanskii) is the notion that generalizes Newton non-degenerate singularities to higher codimensions, and guarantees the existence of embedded toric resolutions for singularities having this property. For example, the plane curve singularity ![]() $(\mathcal {C},o)$ embedded in
$(\mathcal {C},o)$ embedded in ![]() $ {\mathbb {C}}^{2}_{o}$ via the equation
$ {\mathbb {C}}^{2}_{o}$ via the equation ![]() $(x_2^2-x_1^3)^2-x_1^5x_2=0$ is degenerate with respect to its Newton polygon; but embedded in
$(x_2^2-x_1^3)^2-x_1^5x_2=0$ is degenerate with respect to its Newton polygon; but embedded in ![]() $ {\mathbb {C}}^{3}_{o}$ via the equations
$ {\mathbb {C}}^{3}_{o}$ via the equations ![]() $x_3-(x_2^2-x_1^3)=0$ and
$x_3-(x_2^2-x_1^3)=0$ and ![]() $x_3^2 -x_1^5x_2=0,$ it is non-degenerate in the sense of Khovanskii [Reference Bivia-AusinaBA07, Reference MourtadaMou17, Reference NguyenNgu20]. Now by [Reference NguyenNgu20] (see also [Reference Bivia-AusinaBA07]), we can compute its Milnor number using mixed Newton numbers. Then the idea is to study the monotonicity of the mixed Newton number and to prove a generalization of Theorems 2.4 and 2.25. This should allow us to generalize the main theorem of this article for an adapted embedding and then to apply part (i) of Proposition 1.6. This idea is a research project that, while not developed in the rest of this paper, we nevertheless find important to mention.
$x_3^2 -x_1^5x_2=0,$ it is non-degenerate in the sense of Khovanskii [Reference Bivia-AusinaBA07, Reference MourtadaMou17, Reference NguyenNgu20]. Now by [Reference NguyenNgu20] (see also [Reference Bivia-AusinaBA07]), we can compute its Milnor number using mixed Newton numbers. Then the idea is to study the monotonicity of the mixed Newton number and to prove a generalization of Theorems 2.4 and 2.25. This should allow us to generalize the main theorem of this article for an adapted embedding and then to apply part (i) of Proposition 1.6. This idea is a research project that, while not developed in the rest of this paper, we nevertheless find important to mention.
The theorem has an interesting implication to spaces of ![]() $m$-jets. Let
$m$-jets. Let ![]() $ {\mathbb {K}}$ be a field and
$ {\mathbb {K}}$ be a field and ![]() $Y$ a scheme over
$Y$ a scheme over ![]() $ {\mathbb {K}}$. We denote by
$ {\mathbb {K}}$. We denote by ![]() $Y\!-\!\mathcal {S}ch$ (respectively,
$Y\!-\!\mathcal {S}ch$ (respectively, ![]() $\mathcal {S}et$) the category of schemes over
$\mathcal {S}et$) the category of schemes over ![]() $Y$ (respectively, sets), and let
$Y$ (respectively, sets), and let ![]() $X$ be a
$X$ be a ![]() $Y$-scheme. It is known that the functor
$Y$-scheme. It is known that the functor ![]() $Y\!-\!\mathcal {S}ch\rightarrow \mathcal {S}et:Z\mapsto {\operatorname {Hom}}_Y(Z\times _{ {\mathbb {K}}} {\operatorname {Spec}} {\mathbb {K}}[t]/(t^{m+1}), X)$,
$Y\!-\!\mathcal {S}ch\rightarrow \mathcal {S}et:Z\mapsto {\operatorname {Hom}}_Y(Z\times _{ {\mathbb {K}}} {\operatorname {Spec}} {\mathbb {K}}[t]/(t^{m+1}), X)$, ![]() $m\geq 1$, is representable. More precisely, there exists a
$m\geq 1$, is representable. More precisely, there exists a ![]() $Y$-scheme, denoted by
$Y$-scheme, denoted by ![]() $\operatorname {X(Y)}_{m}$, such that
$\operatorname {X(Y)}_{m}$, such that ![]() $ {\operatorname {Hom}}_Y(Z\times _{ {\mathbb {K}}} {\operatorname {Spec}} {\mathbb {K}}[t]/(t^{m+1}), X)\cong {\operatorname {Hom}}_{Y}(Z,\operatorname {X(Y)}_{m})$ for all
$ {\operatorname {Hom}}_Y(Z\times _{ {\mathbb {K}}} {\operatorname {Spec}} {\mathbb {K}}[t]/(t^{m+1}), X)\cong {\operatorname {Hom}}_{Y}(Z,\operatorname {X(Y)}_{m})$ for all ![]() $Z$ in
$Z$ in ![]() $Y\!-\!\mathcal {S}ch$. The scheme
$Y\!-\!\mathcal {S}ch$. The scheme ![]() $\operatorname {X(Y)}_{m}$ is called the space of m-jets of
$\operatorname {X(Y)}_{m}$ is called the space of m-jets of ![]() $X$ relative to
$X$ relative to ![]() $Y$. For more details see [Reference VojtaVoj07] or [Reference Leyton-ÁlvarezLA18]. Let us assume that
$Y$. For more details see [Reference VojtaVoj07] or [Reference Leyton-ÁlvarezLA18]. Let us assume that ![]() $Y$ is a reduced
$Y$ is a reduced ![]() $ {\mathbb {K}}$-scheme, and let
$ {\mathbb {K}}$-scheme, and let ![]() $Z$ be a
$Z$ be a ![]() $Y$-scheme. We denote by
$Y$-scheme. We denote by ![]() $Z_{{\rm red}}$ the reduced
$Z_{{\rm red}}$ the reduced ![]() $Y$-scheme associated to
$Y$-scheme associated to ![]() $Z$.
$Z$.
Corollary 1.8 Let ![]() $S= {\mathbb {C}}_{0}$ and let
$S= {\mathbb {C}}_{0}$ and let ![]() $W$ be a non-degenerate
$W$ be a non-degenerate ![]() $\mu$-constant deformation. The structure morphism
$\mu$-constant deformation. The structure morphism ![]() $(\operatorname {W(S)}_{m})_{{\rm red}}\rightarrow S$ is flat for all
$(\operatorname {W(S)}_{m})_{{\rm red}}\rightarrow S$ is flat for all ![]() $m\geq 1$.
$m\geq 1$.
Proof. By the previous theorem ![]() $W$ admits an embedded simultaneous resolution. Hence, the corollary is an immediate consequence of Theorem
$W$ admits an embedded simultaneous resolution. Hence, the corollary is an immediate consequence of Theorem ![]() $3.4$ of [Reference Leyton-ÁlvarezLA18].
$3.4$ of [Reference Leyton-ÁlvarezLA18].
Finally, we comment on the organization of the article. In § 2 we study geometric properties of pairs of Newton polyhedra that have the same Newton number. This allows us to construct the desired simultaneous resolution. In this section, we give an affirmative answer to the conjecture presented in [Reference Brzostowski, Krasiński and WalewskaBKW19]. This result together with Theorem 2.4 (see [Reference FuruyaFur04]) is a complete solution to an Arnold problem (No. 1982-16 in his list of problems, see [Reference ArnoldArn05]) in the case of convenient Newton polyhedra. In § 3 we prove the main result of the article. Finally, in § 4 we study properties of degenerate ![]() $\mu$-constant deformations. The main result of this section is Proposition 4.2, which is a kind of analogue to the existence of a good apex (see Definition 2.21).
$\mu$-constant deformations. The main result of this section is Proposition 4.2, which is a kind of analogue to the existence of a good apex (see Definition 2.21).
2. Preliminaries on Newton polyhedra
In this section we study geometric properties of pairs of Newton polyhedra having the same Newton number, one contained in the other. In this article we study the deformations of hypersurfaces ![]() $ {\mathbb {C}}^{n+1}_{o}$, whereby the natural things would be to study polytopes in
$ {\mathbb {C}}^{n+1}_{o}$, whereby the natural things would be to study polytopes in ![]() $ {\mathbb {R}}^{n+1}$,
$ {\mathbb {R}}^{n+1}$, ![]() $n\geq 1$. Nevertheless, in order to avoid complicating the notations unnecessarily, we work with polytopes in
$n\geq 1$. Nevertheless, in order to avoid complicating the notations unnecessarily, we work with polytopes in ![]() $ {\mathbb {R}}^{n}$,
$ {\mathbb {R}}^{n}$, ![]() $n\geq 2$.
$n\geq 2$.
Given an affine subspace ![]() $H$ of
$H$ of ![]() $ {\mathbb {R}}^n$, a convex polytope in
$ {\mathbb {R}}^n$, a convex polytope in ![]() $H$ is a non-empty set
$H$ is a non-empty set ![]() $P$ given by the intersection of
$P$ given by the intersection of ![]() $H$ with a finite set of half spaces of
$H$ with a finite set of half spaces of ![]() $ {\mathbb {R}}^n$. In particular, a compact convex polytope can be seen as the convex hull of a finite set of points in
$ {\mathbb {R}}^n$. In particular, a compact convex polytope can be seen as the convex hull of a finite set of points in ![]() $ {\mathbb {R}}^n$. The dimension of a convex polytope is the dimension of the smallest affine subspace of
$ {\mathbb {R}}^n$. The dimension of a convex polytope is the dimension of the smallest affine subspace of ![]() $ {\mathbb {R}}^n$ that contains it. We say that
$ {\mathbb {R}}^n$ that contains it. We say that ![]() $P$ is a polyhedron (respectively, compact polyhedron) if
$P$ is a polyhedron (respectively, compact polyhedron) if ![]() $P$ can be decomposed into a finite union of convex (respectively, compact convex) polytopes of disjoint interiors. We will say that
$P$ can be decomposed into a finite union of convex (respectively, compact convex) polytopes of disjoint interiors. We will say that ![]() $P$ is of pure dimension
$P$ is of pure dimension ![]() $n$ if
$n$ if ![]() $P$ is a finite union of
$P$ is a finite union of ![]() $n$-dimensional convex polytopes. A hyperplane
$n$-dimensional convex polytopes. A hyperplane ![]() $K$ of
$K$ of ![]() $ {\mathbb {R}}^n$ is supporting
$ {\mathbb {R}}^n$ is supporting ![]() $P$ if one of the two closed half spaces defined by
$P$ if one of the two closed half spaces defined by ![]() $K$ contains
$K$ contains ![]() $P$. A subset
$P$. A subset ![]() $F$ of
$F$ of ![]() $P$ is called a face of
$P$ is called a face of ![]() $P$ if it is either
$P$ if it is either ![]() $\emptyset$,
$\emptyset$, ![]() $P$ itself, or the intersection of
$P$ itself, or the intersection of ![]() $P$ with a supporting hyperplane. A face
$P$ with a supporting hyperplane. A face ![]() $F$ of
$F$ of ![]() $P$ of dimension
$P$ of dimension ![]() $0\leq d \leq \dim (P)-1$ is called
$0\leq d \leq \dim (P)-1$ is called ![]() $d$-dimensional face. In the case that
$d$-dimensional face. In the case that ![]() $d$ is
$d$ is ![]() $0$ or
$0$ or ![]() $1$,
$1$, ![]() $F$ is called a vertex or edge, respectively.
$F$ is called a vertex or edge, respectively.
An ![]() $n$-dimensional simplex
$n$-dimensional simplex ![]() $\Delta$ is a compact convex polytope generated by
$\Delta$ is a compact convex polytope generated by ![]() $n+1$ points of
$n+1$ points of ![]() $ {\mathbb {R}}^n$ in general position.
$ {\mathbb {R}}^n$ in general position.
Given an ![]() $n$-dimensional compact polyhedron
$n$-dimensional compact polyhedron ![]() $P\subset {\mathbb {R}}^{n}_{\geq 0}$ , the Newton number of
$P\subset {\mathbb {R}}^{n}_{\geq 0}$ , the Newton number of ![]() $P$ is defined by
$P$ is defined by
where ![]() $V_n(P)$ is the volume of
$V_n(P)$ is the volume of ![]() $P$,
$P$, ![]() $V_{k}(P)$,
$V_{k}(P)$, ![]() $1\leq k\leq n-1$, is the sum of the
$1\leq k\leq n-1$, is the sum of the ![]() $k$-dimensional volumes of the intersection of
$k$-dimensional volumes of the intersection of ![]() $P$ with the coordinate planes of dimension
$P$ with the coordinate planes of dimension ![]() $k$, and
$k$, and ![]() $V_0(P)=1$ (respectively,
$V_0(P)=1$ (respectively, ![]() $V_0(P)=0$) if
$V_0(P)=0$) if ![]() $o\in P$ (respectively,
$o\in P$ (respectively, ![]() $o\notin P$), where
$o\notin P$), where ![]() $o$ is the origin of
$o$ is the origin of ![]() $ {\mathbb {R}}^n$. In this section, we are interested in studying the monotonicity of the Newton Number, we always consider the case when
$ {\mathbb {R}}^n$. In this section, we are interested in studying the monotonicity of the Newton Number, we always consider the case when ![]() $P$ is compact.
$P$ is compact.
Let ![]() $I\subset \{1,2,\ldots,n\}$. We define the following sets:
$I\subset \{1,2,\ldots,n\}$. We define the following sets:
Given a polyhedron ![]() $P$ in
$P$ in ![]() $ {\mathbb {R}}^n$, we write
$ {\mathbb {R}}^n$, we write ![]() $P^I:=P\cap {\mathbb {R}}^{I}$. Consider an
$P^I:=P\cap {\mathbb {R}}^{I}$. Consider an ![]() $n$-dimensional simplex
$n$-dimensional simplex ![]() $\Delta \subset {\mathbb {R}}^n_{\geq 0}$. A full supporting coordinate subspace of
$\Delta \subset {\mathbb {R}}^n_{\geq 0}$. A full supporting coordinate subspace of ![]() $\Delta$ is a coordinate subspace
$\Delta$ is a coordinate subspace ![]() $ {\mathbb {R}}^{I}\subset {\mathbb {R}}^n$ such that
$ {\mathbb {R}}^{I}\subset {\mathbb {R}}^n$ such that ![]() $\dim \Delta ^I=|I|$. In [Reference FuruyaFur04], Furuya proved that there exists a unique full-supporting coordinate subspace of
$\dim \Delta ^I=|I|$. In [Reference FuruyaFur04], Furuya proved that there exists a unique full-supporting coordinate subspace of ![]() $\Delta$ of minimal dimension. We call this subspace the minimal full-supporting coordinate subspace (m.f.-s.c.s.) of
$\Delta$ of minimal dimension. We call this subspace the minimal full-supporting coordinate subspace (m.f.-s.c.s.) of ![]() $\Delta$.
$\Delta$.
We denote by ![]() $\operatorname {Ver}(P)$ the set of vertices of
$\operatorname {Ver}(P)$ the set of vertices of ![]() $P$.
$P$.
The next result gives us a way of calculating the Newton number of certain polyhedra using projections.
Proposition 2.1 [Reference FuruyaFur04]
Let ![]() $o\notin P\subset {\mathbb {R}}^{n}_{\geq 0}$ be a compact polyhedron that is a finite union of
$o\notin P\subset {\mathbb {R}}^{n}_{\geq 0}$ be a compact polyhedron that is a finite union of ![]() $n$-simplices
$n$-simplices ![]() $\Delta _i$,
$\Delta _i$, ![]() $1\leq i\leq m$, that satisfy
$1\leq i\leq m$, that satisfy
Assume that there exists ![]() $I\subset \{1,2,\ldots,n\}$ such that
$I\subset \{1,2,\ldots,n\}$ such that ![]() $ {\mathbb {R}}^I$ is the m.f.-s.c.s. of
$ {\mathbb {R}}^I$ is the m.f.-s.c.s. of ![]() $\Delta _i$ and
$\Delta _i$ and ![]() $P^I=\Delta _{i}^{I}$ for all
$P^I=\Delta _{i}^{I}$ for all ![]() $1\leq i\leq m$. Then
$1\leq i\leq m$. Then ![]() $\nu (P)= |I|!V_{|I|}(P^I)\nu (\pi _I(P))$ where
$\nu (P)= |I|!V_{|I|}(P^I)\nu (\pi _I(P))$ where ![]() $\pi _I: {\mathbb {R}}^n\rightarrow {\mathbb {R}}_{I}$ is the projection map.
$\pi _I: {\mathbb {R}}^n\rightarrow {\mathbb {R}}_{I}$ is the projection map.
Let ![]() $\mathcal {E}:=\{e_1,e_2,\ldots,e_n\}\subset {\mathbb {Z}}_{\geq 0}^n$ be the standard basis of
$\mathcal {E}:=\{e_1,e_2,\ldots,e_n\}\subset {\mathbb {Z}}_{\geq 0}^n$ be the standard basis of ![]() $ {\mathbb {R}}^n$. Let
$ {\mathbb {R}}^n$. Let
be a polyhedron of pure dimension ![]() $n$. Consider the following conditions:
$n$. Consider the following conditions:
(i)
 $o\in P$;
$o\in P$;(ii)
 $P^J$ is homeomorphic to a
$P^J$ is homeomorphic to a  $|J|$-dimensional closed disk for each
$|J|$-dimensional closed disk for each  $J\subset \{1,\ldots,n\}$;
$J\subset \{1,\ldots,n\}$;(iii) Let
 $I\subset \{1,\ldots,n\}$ be a non-empty subset; if
$I\subset \{1,\ldots,n\}$ be a non-empty subset; if  $(\alpha _1,\ldots,\alpha _n)\in \operatorname {Ver}(P)$, then for each
$(\alpha _1,\ldots,\alpha _n)\in \operatorname {Ver}(P)$, then for each  $i\in I$ we must have either
$i\in I$ we must have either  $\alpha _i\geq 1$ or
$\alpha _i\geq 1$ or  $\alpha _i=0$ (recall that the
$\alpha _i=0$ (recall that the  $\alpha _i$ are real numbers that need not be integers).
$\alpha _i$ are real numbers that need not be integers).
We say that ![]() $P$ is pre-convenient (respectively,
$P$ is pre-convenient (respectively, ![]() $I$-convenient) if it satisfies conditions (i) and (ii) (respectively, conditions (i), (ii), and (iii)). In the case when
$I$-convenient) if it satisfies conditions (i) and (ii) (respectively, conditions (i), (ii), and (iii)). In the case when ![]() $I:=\{1,\ldots,n\}$ we simply say that
$I:=\{1,\ldots,n\}$ we simply say that ![]() $P$ is convenient instead of
$P$ is convenient instead of ![]() $I$-convenient.
$I$-convenient.
Given a closed discrete set ![]() $S\subset {\mathbb {R}}^{n}_{\geq 0} {\setminus} \{o\}$, denote by
$S\subset {\mathbb {R}}^{n}_{\geq 0} {\setminus} \{o\}$, denote by ![]() $\Gamma _{+}(S)$ the convex hull of the set
$\Gamma _{+}(S)$ the convex hull of the set ![]() $\bigcup _{\alpha \in S}(\alpha + {\mathbb {R}}_{\geq 0}^n)$. The polyhedron
$\bigcup _{\alpha \in S}(\alpha + {\mathbb {R}}_{\geq 0}^n)$. The polyhedron ![]() $\Gamma _{+}(S)$ is called the Newton polyhedron associated to
$\Gamma _{+}(S)$ is called the Newton polyhedron associated to ![]() $S$. The Newton boundary of
$S$. The Newton boundary of ![]() $\Gamma _{+}(S)$, denoted by
$\Gamma _{+}(S)$, denoted by ![]() $\Gamma (S)$, is the union of the compact faces of
$\Gamma (S)$, is the union of the compact faces of ![]() $\Gamma _{+}(S)$. Let
$\Gamma _{+}(S)$. Let ![]() $\operatorname {Ver}(S):=\operatorname {Ver}(\Gamma (S))$ denote the set of vertices of
$\operatorname {Ver}(S):=\operatorname {Ver}(\Gamma (S))$ denote the set of vertices of ![]() $\Gamma (S)$
$\Gamma (S)$
Remark 2.2 Note that when we refer to vertices of ![]() $\Gamma (S)$ we are speaking about zero-dimensional faces of
$\Gamma (S)$ we are speaking about zero-dimensional faces of ![]() $\Gamma (S)$. For example, if
$\Gamma (S)$. For example, if
then ![]() $\operatorname {Ver}(S)=\{(0,3),(2,1), (4,0)\}$.
$\operatorname {Ver}(S)=\{(0,3),(2,1), (4,0)\}$.
We say that a closed discrete set ![]() $S\subset {\mathbb {R}}^{n}_{\geq 0} {\setminus} \{o\}$ is pre-convenient (respectively,
$S\subset {\mathbb {R}}^{n}_{\geq 0} {\setminus} \{o\}$ is pre-convenient (respectively, ![]() $I$-convenient) if
$I$-convenient) if ![]() $\Gamma _{-}(S):=\overline { {\mathbb {R}}_{\geq 0}^n{\setminus} \Gamma _{+}(S)}$ is pre-convenient (respectively,
$\Gamma _{-}(S):=\overline { {\mathbb {R}}_{\geq 0}^n{\setminus} \Gamma _{+}(S)}$ is pre-convenient (respectively, ![]() $I$-convenient). The Newton number of a pre-convenient closed discrete set
$I$-convenient). The Newton number of a pre-convenient closed discrete set ![]() $S\subset {\mathbb {R}}^{n}_{\geq 0} {\setminus} \{o\}$ is
$S\subset {\mathbb {R}}^{n}_{\geq 0} {\setminus} \{o\}$ is
Note that this number can be negative. In the case when ![]() $P$ is the polyhedron
$P$ is the polyhedron ![]() $\Gamma _-(S)$ associated with a closed discrete set
$\Gamma _-(S)$ associated with a closed discrete set ![]() $S$, condition (i) holds automatically and condition (ii) can be replaced by the following:
$S$, condition (i) holds automatically and condition (ii) can be replaced by the following:
(ii′) for each
 $e\in \mathcal {E}$ there exists
$e\in \mathcal {E}$ there exists  $m>0$ such that
$m>0$ such that  $me\in \operatorname {Ver}(S)$.
$me\in \operatorname {Ver}(S)$.
Consider a convergent power series ![]() $g\in {\mathbb {C}}\{x_1,\ldots,x_n\}$:
$g\in {\mathbb {C}}\{x_1,\ldots,x_n\}$:
We define ![]() $\Gamma _{+}(g)=\Gamma _+(\operatorname {Supp}(g))$ and
$\Gamma _{+}(g)=\Gamma _+(\operatorname {Supp}(g))$ and ![]() $\Gamma (g)=\Gamma (\operatorname {Supp}(g))$. We say that
$\Gamma (g)=\Gamma (\operatorname {Supp}(g))$. We say that ![]() $g$ is a convenient power series if for all
$g$ is a convenient power series if for all ![]() $e\in \mathcal {E}$ there exists
$e\in \mathcal {E}$ there exists ![]() $m>0$ such that
$m>0$ such that ![]() $me\in \operatorname {Supp}(g)$.
$me\in \operatorname {Supp}(g)$.
Observe that the closed discrete set ![]() $\operatorname {Supp}(g)$ is convenient if and only if the power series
$\operatorname {Supp}(g)$ is convenient if and only if the power series ![]() $g$ is convenient. We use the following notation:
$g$ is convenient. We use the following notation: ![]() $\operatorname {Ver}(g):=\operatorname {Ver}(\operatorname {Supp}(g))$, and
$\operatorname {Ver}(g):=\operatorname {Ver}(\operatorname {Supp}(g))$, and ![]() $\nu (g)=\nu (\operatorname {Supp}(g))$.
$\nu (g)=\nu (\operatorname {Supp}(g))$.
Remark 2.3 Observe that in the case that ![]() $S$ is a closed discrete, pre-convenient set, there exists at least one finite subset
$S$ is a closed discrete, pre-convenient set, there exists at least one finite subset ![]() $S'\subset S$ such that
$S'\subset S$ such that ![]() $\Gamma _{+}(S')=\Gamma _{+}(S)$ (in fact, it suffices to consider
$\Gamma _{+}(S')=\Gamma _{+}(S)$ (in fact, it suffices to consider ![]() $S'=\Gamma (S)\cap S$). Nevertheless, it is more comfortable to work with
$S'=\Gamma (S)\cap S$). Nevertheless, it is more comfortable to work with ![]() $S$ than with finite choices, above all because in our proofs we eliminate or move points of
$S$ than with finite choices, above all because in our proofs we eliminate or move points of ![]() $S$.
$S$.
Theorem 2.4 [Reference FuruyaFur04]
Let ![]() $P'\subset P$ be two convenient polyhedra. We have
$P'\subset P$ be two convenient polyhedra. We have ![]() $\nu (P)-\nu (P')=\nu (\overline {P{\setminus} P'})\geq 0$, and
$\nu (P)-\nu (P')=\nu (\overline {P{\setminus} P'})\geq 0$, and ![]() $\nu (P')\geq 0$.
$\nu (P')\geq 0$.
Corollary 2.5
(i) Let
 $S$ and
$S$ and  $S'$ be two convenient closed discrete subsets of
$S'$ be two convenient closed discrete subsets of  $ {\mathbb {R}}_{\geq 0}^{n}{\setminus} \{o\}$, and assume that
$ {\mathbb {R}}_{\geq 0}^{n}{\setminus} \{o\}$, and assume that  $\Gamma _{+}(S)\subsetneq \Gamma _{+}(S')$. We have
$\Gamma _{+}(S)\subsetneq \Gamma _{+}(S')$. We have
 \[ 0\leq\nu(S)-\nu(S')=\nu(\overline{\Gamma_{-}(S){\setminus}\Gamma_{-}(S')}). \]
\[ 0\leq\nu(S)-\nu(S')=\nu(\overline{\Gamma_{-}(S){\setminus}\Gamma_{-}(S')}). \](ii) Let
 $S$,
$S$,  $S'$, and
$S'$, and  $S''$ be three convenient closed discrete subsets of
$S''$ be three convenient closed discrete subsets of  $ {\mathbb {R}}^{n}_{\geq 0}{\setminus} \{o\}$ such that their Newton polyhedra satisfy
and
$ {\mathbb {R}}^{n}_{\geq 0}{\setminus} \{o\}$ such that their Newton polyhedra satisfy
and \[ \Gamma_{+}(S)\subset \Gamma_{+}(S')\subset\Gamma_{+}(S'') \]
\[ \Gamma_{+}(S)\subset \Gamma_{+}(S')\subset\Gamma_{+}(S'') \] $\nu (S)=\nu (S'')$. Then
$\nu (S)=\nu (S'')$. Then  $\nu (S)=\nu (S')=\nu (S'')$.
$\nu (S)=\nu (S')=\nu (S'')$.
For a set ![]() $I\subset \{1,\ldots,n\}$, we write
$I\subset \{1,\ldots,n\}$, we write ![]() $I^c:=\{1,\ldots,n\}{\setminus} I$. The following result gives us a criterion for the positivity of the Newton number of certain polyhedra.
$I^c:=\{1,\ldots,n\}{\setminus} I$. The following result gives us a criterion for the positivity of the Newton number of certain polyhedra.
Proposition 2.6 Let ![]() $o\notin P$ be a pure
$o\notin P$ be a pure ![]() $n$-dimensional compact polyhedron such that there exists
$n$-dimensional compact polyhedron such that there exists ![]() $I\subset \{1,\ldots,n\}$ such that
$I\subset \{1,\ldots,n\}$ such that ![]() $\dim (P^J)<|J|$ (respectively,
$\dim (P^J)<|J|$ (respectively, ![]() $P^J$ is homeomorphic to a
$P^J$ is homeomorphic to a ![]() $|J|$-dimensional closed disk) for all
$|J|$-dimensional closed disk) for all ![]() $I\not \subset J$ (respectively,
$I\not \subset J$ (respectively, ![]() $I\subset J$). Assume that if
$I\subset J$). Assume that if
then for each ![]() $i\in I^c$ we have
$i\in I^c$ we have ![]() $\beta _i\geq 1$ or
$\beta _i\geq 1$ or ![]() $\beta _i=0$. Then there exists a sequence of sets
$\beta _i=0$. Then there exists a sequence of sets ![]() $I\subset I_1,I_2,\ldots,I_m\subset \{1,\ldots,n\}$, and of polyhedra
$I\subset I_1,I_2,\ldots,I_m\subset \{1,\ldots,n\}$, and of polyhedra ![]() $Z_{i}$,
$Z_{i}$, ![]() $1\leq i \leq m$, such that:
$1\leq i \leq m$, such that:
(i)
 $P=\bigcup _{i=1}^{m}Z_i$;
$P=\bigcup _{i=1}^{m}Z_i$;(ii)
 $\nu (P)=\sum _{i=1}^{m}\nu (Z_i)$;
$\nu (P)=\sum _{i=1}^{m}\nu (Z_i)$;(iii)
 $\nu (Z_{i})= |I_i|!V_{|I_i|}(Z_{i}^{I_{i}})\nu (\pi _{I_i}(Z_{i}))\geq 0$.
$\nu (Z_{i})= |I_i|!V_{|I_i|}(Z_{i}^{I_{i}})\nu (\pi _{I_i}(Z_{i}))\geq 0$.
In particular, ![]() $\nu (P)\geq 0$.
$\nu (P)\geq 0$.
Given ![]() $S\subset {\mathbb {R}}_{\geq }^{n}{\setminus} \{o\}$ and
$S\subset {\mathbb {R}}_{\geq }^{n}{\setminus} \{o\}$ and ![]() $R\subset {\mathbb {R}}^n_{\geq 0}$, we denote
$R\subset {\mathbb {R}}^n_{\geq 0}$, we denote ![]() $S(R):=S\cup R$.
$S(R):=S\cup R$.
Remark 2.7 Let ![]() $S$ be a closed discrete subset of
$S$ be a closed discrete subset of ![]() $ {\mathbb {R}}^{n}_{\geq 0}{\setminus} \{o\}$ and
$ {\mathbb {R}}^{n}_{\geq 0}{\setminus} \{o\}$ and ![]() $\alpha \in {\mathbb {R}}_{>}^{I}$,
$\alpha \in {\mathbb {R}}_{>}^{I}$, ![]() $I\subset \{1,\ldots,n\}$.
$I\subset \{1,\ldots,n\}$.
If ![]() $\alpha \not \in \Gamma _{+}(S)$, then
$\alpha \not \in \Gamma _{+}(S)$, then ![]() $P:=\overline {\Gamma _{+}(S(\alpha )){\setminus} \Gamma _{+}(S)}$,
$P:=\overline {\Gamma _{+}(S(\alpha )){\setminus} \Gamma _{+}(S)}$, ![]() $S(\alpha ):=S\cup \{\alpha \}$, is homeomorphic to an
$S(\alpha ):=S\cup \{\alpha \}$, is homeomorphic to an ![]() $|n|$-dimensional closed disk. Furthermore, by induction on
$|n|$-dimensional closed disk. Furthermore, by induction on ![]() $n$ we obtain that
$n$ we obtain that ![]() $\dim (P^{J})=|J|$ for all
$\dim (P^{J})=|J|$ for all ![]() $J\supset I$ if and only if
$J\supset I$ if and only if ![]() $P^J$ is topologically equivalent to a
$P^J$ is topologically equivalent to a ![]() $|J|$-dimensional closed disk. In addition, we observe that
$|J|$-dimensional closed disk. In addition, we observe that ![]() $\dim (P^{J})<|J|$ for all
$\dim (P^{J})<|J|$ for all ![]() $J\not \supset I$.
$J\not \supset I$.
Proof. The method of proof that we use is similar to the proof of Theorem ![]() $2.3$ of [Reference FuruyaFur04].
$2.3$ of [Reference FuruyaFur04].
As ![]() $P$ is a pure
$P$ is a pure ![]() $n$-dimensional compact polyhedron, there exists a finite simplicial subdivision
$n$-dimensional compact polyhedron, there exists a finite simplicial subdivision ![]() $\Sigma$ of
$\Sigma$ of ![]() $P$ such that:
$P$ such that:
(i) if
 $\Delta \in \Sigma$, then
$\Delta \in \Sigma$, then  $\dim \Delta =n$;
$\dim \Delta =n$;(ii) for all
 $\Delta \in \Sigma$,
$\Delta \in \Sigma$,  $\operatorname {Ver}(\Delta )\subset \operatorname {Ver}(P)$;
$\operatorname {Ver}(\Delta )\subset \operatorname {Ver}(P)$;(iii) given
 $\Delta, \Delta '\in \Sigma$, we have
$\Delta, \Delta '\in \Sigma$, we have  $\dim (\Delta \cap \Delta ')< n$ whenever
$\dim (\Delta \cap \Delta ')< n$ whenever  $\Delta \neq \Delta '$.
$\Delta \neq \Delta '$.
Let ![]() $\mathcal {S}$ be the set formed by all the subsets
$\mathcal {S}$ be the set formed by all the subsets ![]() $I'\subset \{1,\ldots,n\}$ such that there exists
$I'\subset \{1,\ldots,n\}$ such that there exists ![]() $\Delta \in \Sigma$ such that its m.f.-s.c.s. is
$\Delta \in \Sigma$ such that its m.f.-s.c.s. is ![]() $ {\mathbb {R}}^{I'}$.
$ {\mathbb {R}}^{I'}$.
As ![]() $\dim P^{J}<|J|$ for all
$\dim P^{J}<|J|$ for all ![]() $J\not \supset I$, we obtain that
$J\not \supset I$, we obtain that ![]() $I'\supset I$ for all
$I'\supset I$ for all ![]() $I'\in \mathcal {S}$. We define
$I'\in \mathcal {S}$. We define
Let us consider the set
Given ![]() $\sigma _i\in \Sigma ^{I'}$ , let
$\sigma _i\in \Sigma ^{I'}$ , let ![]() $C_i:=\{\Delta \in \Sigma (I') : \Delta ^I=\sigma _i\}$. Consider the closed set
$C_i:=\{\Delta \in \Sigma (I') : \Delta ^I=\sigma _i\}$. Consider the closed set
Observe that given ![]() $\alpha \in \sigma _i^{\circ }$ (where
$\alpha \in \sigma _i^{\circ }$ (where ![]() $\sigma _i^{\circ }$ is the relative interior of
$\sigma _i^{\circ }$ is the relative interior of ![]() $\sigma _i$), there exists
$\sigma _i$), there exists ![]() $\epsilon >0$ such that for each
$\epsilon >0$ such that for each ![]() $J\supset I'$, we have
$J\supset I'$, we have ![]() $B_{\epsilon }(\alpha )\cap Z_{(i,I')}^J=B_{\epsilon }(\alpha )\cap {\mathbb {R}}_{\geq 0}^J$. Indeed, as
$B_{\epsilon }(\alpha )\cap Z_{(i,I')}^J=B_{\epsilon }(\alpha )\cap {\mathbb {R}}_{\geq 0}^J$. Indeed, as ![]() $P^J$ is topologically equivalent to a
$P^J$ is topologically equivalent to a ![]() $|J|$-dimensional closed disk for all
$|J|$-dimensional closed disk for all ![]() $J\supset I'$, there exists
$J\supset I'$, there exists ![]() $\epsilon >0$ such that
$\epsilon >0$ such that ![]() $B_{\epsilon }(\alpha )\cap {\mathbb {R}}_{\geq 0}^J\subset P^J$. Making
$B_{\epsilon }(\alpha )\cap {\mathbb {R}}_{\geq 0}^J\subset P^J$. Making ![]() $\epsilon$ smaller we may assume that
$\epsilon$ smaller we may assume that ![]() $B_{\epsilon }(\alpha )\cap {\mathbb {R}}_{\geq 0}^J \subset Z_{(i,I')}^{J}$. This implies that
$B_{\epsilon }(\alpha )\cap {\mathbb {R}}_{\geq 0}^J \subset Z_{(i,I')}^{J}$. This implies that ![]() $\pi _{I'}\big (Z_{(i,I')}\big )$ is a convenient polyhedron in
$\pi _{I'}\big (Z_{(i,I')}\big )$ is a convenient polyhedron in ![]() $ {\mathbb {R}}_{I'}$ (remember that if
$ {\mathbb {R}}_{I'}$ (remember that if ![]() $(\beta _1,\ldots,\beta _n)\in \operatorname {Ver}(P)$, then for each
$(\beta _1,\ldots,\beta _n)\in \operatorname {Ver}(P)$, then for each ![]() $i\in I^c$ we have
$i\in I^c$ we have ![]() $\beta _i\geq 1$ or
$\beta _i\geq 1$ or ![]() $\beta _i=0$), from which it follows that
$\beta _i=0$), from which it follows that ![]() $\nu \big (\pi _{I'}\big (Z_{(i,I')}\big )\big )\geq 0$ (see Theorem 2.4). Now using Proposition 2.1 we obtain
$\nu \big (\pi _{I'}\big (Z_{(i,I')}\big )\big )\geq 0$ (see Theorem 2.4). Now using Proposition 2.1 we obtain ![]() $\nu \big (Z_{(i,I')}\big )= |I|!V_{|I|}(\sigma _i)\nu \big (\pi _{I'}\big (Z_{(i,I')}\big )\big )\geq 0$.
$\nu \big (Z_{(i,I')}\big )= |I|!V_{|I|}(\sigma _i)\nu \big (\pi _{I'}\big (Z_{(i,I')}\big )\big )\geq 0$.
By construction, we obtain
 \[ P=\bigcup_{I'\in \mathcal{S}}\bigcup_{i=1}^{l(I')} Z_{(i,I')} \]
\[ P=\bigcup_{I'\in \mathcal{S}}\bigcup_{i=1}^{l(I')} Z_{(i,I')} \]and
This implies that
 \[ \nu(P)=\sum_{I'\in S}\sum_{i=1}^{l(I')}\nu\big(Z_{(i,I')}\big). \]
\[ \nu(P)=\sum_{I'\in S}\sum_{i=1}^{l(I')}\nu\big(Z_{(i,I')}\big). \]Rearranging the indices, we obtain the desired subdivision.
Let ![]() $S$ and
$S$ and ![]() $S'$ be two closed discrete subsets of
$S'$ be two closed discrete subsets of ![]() $ {\mathbb {R}}_{\geq 0}^{n}{\setminus} \{o\}$ such that
$ {\mathbb {R}}_{\geq 0}^{n}{\setminus} \{o\}$ such that
We define ![]() $\operatorname {Ver}(S',S):=\operatorname {Ver}(S') {\setminus} \operatorname {Ver}(S)$. The following result tells us where the vertices
$\operatorname {Ver}(S',S):=\operatorname {Ver}(S') {\setminus} \operatorname {Ver}(S)$. The following result tells us where the vertices ![]() $\operatorname {Ver}(S',S)$ are found.
$\operatorname {Ver}(S',S)$ are found.
Proposition 2.8 Let ![]() $S$,
$S$, ![]() $S'$ be two convenient closed discrete subsets of
$S'$ be two convenient closed discrete subsets of ![]() $ {\mathbb {R}}^{n}_{\geq 0}{\setminus} \{o\}$. Suppose that
$ {\mathbb {R}}^{n}_{\geq 0}{\setminus} \{o\}$. Suppose that ![]() $\Gamma _{+}(S)\subsetneqq \Gamma _{+}(S')$ and
$\Gamma _{+}(S)\subsetneqq \Gamma _{+}(S')$ and ![]() $\nu (S)=\nu (S')$. Then
$\nu (S)=\nu (S')$. Then
Proof. Let us suppose that ![]() $\operatorname {Ver}(S',S)\not \subset ( {\mathbb {R}}^n_{\geq 0}{\setminus} {\mathbb {R}}^n_{>0})$. Let
$\operatorname {Ver}(S',S)\not \subset ( {\mathbb {R}}^n_{\geq 0}{\setminus} {\mathbb {R}}^n_{>0})$. Let
and ![]() $\alpha \in \operatorname {Ver}(S',S){\setminus} W$. Let us consider
$\alpha \in \operatorname {Ver}(S',S){\setminus} W$. Let us consider ![]() $S'':=S\cup \{\alpha \}$. As the closed discrete sets
$S'':=S\cup \{\alpha \}$. As the closed discrete sets ![]() $S$,
$S$, ![]() $S'$, and
$S'$, and ![]() $S''$ are convenient and
$S''$ are convenient and
we obtain ![]() $\nu (S'')=\nu (S)=\nu (S')$ (see Corollary 2.5). Let us prove that this is a contradiction. In effect, by definition of Newton number we have
$\nu (S'')=\nu (S)=\nu (S')$ (see Corollary 2.5). Let us prove that this is a contradiction. In effect, by definition of Newton number we have
 \begin{align*} \nu(S)&=n!V_{n} -(n-1)!V_{n-1}+\cdots (-1)^{n-1}V_1+(-1)^{n},\\ \nu(S'')&=n!V''_{n} -(n-1)!V''_{n-1}+\cdots (-1)^{n-1}V''_1+(-1)^{n}, \end{align*}
\begin{align*} \nu(S)&=n!V_{n} -(n-1)!V_{n-1}+\cdots (-1)^{n-1}V_1+(-1)^{n},\\ \nu(S'')&=n!V''_{n} -(n-1)!V''_{n-1}+\cdots (-1)^{n-1}V''_1+(-1)^{n}, \end{align*}
where ![]() $V_{k}:=V_k(\Gamma _{-}(S))$ and
$V_{k}:=V_k(\Gamma _{-}(S))$ and ![]() $V''_{k}:=V_k(\Gamma _{-}(S''))$ are the
$V''_{k}:=V_k(\Gamma _{-}(S''))$ are the ![]() ${k}$-dimensional Newton volumes of
${k}$-dimensional Newton volumes of ![]() $\Gamma _{-}(S)$ and
$\Gamma _{-}(S)$ and ![]() $\Gamma _{-}(S'')$, respectively. By construction,
$\Gamma _{-}(S'')$, respectively. By construction, ![]() $V''_{n}< V_{n}$ and
$V''_{n}< V_{n}$ and ![]() $V'_k=V_k$,
$V'_k=V_k$, ![]() $1\leq k\leq n-1$, which implies that
$1\leq k\leq n-1$, which implies that ![]() $\nu (S'')<\nu (S)$.
$\nu (S'')<\nu (S)$.
If we suppose that ![]() $\nu (S')=\nu (S)$, it is not difficult to verify that this equality is not preserved by homotheties of
$\nu (S')=\nu (S)$, it is not difficult to verify that this equality is not preserved by homotheties of ![]() $ {\mathbb {R}}_{\geq 0}^{n}$. The following result describes certain partial homotheties of
$ {\mathbb {R}}_{\geq 0}^{n}$. The following result describes certain partial homotheties of ![]() $ {\mathbb {R}}_{\geq 0}^{n}$ which preserve the equality of the Newton numbers.
$ {\mathbb {R}}_{\geq 0}^{n}$ which preserve the equality of the Newton numbers.
Let us consider ![]() $D(S,S')=\{I\subset \{1,2,\ldots,n\}:\Gamma _{-}(S)\cap {\mathbb {R}}^{I}\neq \Gamma _{-}(S')\cap {\mathbb {R}}^{I}\}$ and
$D(S,S')=\{I\subset \{1,2,\ldots,n\}:\Gamma _{-}(S)\cap {\mathbb {R}}^{I}\neq \Gamma _{-}(S')\cap {\mathbb {R}}^{I}\}$ and ![]() $I(S,S')=\bigcap _{I\in D(S,S')}I$. It may happen that
$I(S,S')=\bigcap _{I\in D(S,S')}I$. It may happen that
or
Proposition 2.9 Let ![]() $S, S'\subset {\mathbb {R}}_{\geq 0}^{n}{\setminus} \{o\}$ be two pre-convenient closed discrete sets such that
$S, S'\subset {\mathbb {R}}_{\geq 0}^{n}{\setminus} \{o\}$ be two pre-convenient closed discrete sets such that ![]() $\Gamma _{+}(S)\subset \Gamma _{+}(S')$. Suppose that
$\Gamma _{+}(S)\subset \Gamma _{+}(S')$. Suppose that ![]() $\{1,2,\ldots,k\}\subset I(S,S')$, and consider the map
$\{1,2,\ldots,k\}\subset I(S,S')$, and consider the map
Then ![]() $\nu (\varphi _{\lambda }(S'))-\nu (\varphi _{\lambda }(S))=\lambda ^k(\nu (S')-\nu (S))$.
$\nu (\varphi _{\lambda }(S'))-\nu (\varphi _{\lambda }(S))=\lambda ^k(\nu (S')-\nu (S))$.
Proof. We use the notation ![]() $V_m(S):=V_m(\Gamma _{-}(S))$. Recall that
$V_m(S):=V_m(\Gamma _{-}(S))$. Recall that
where ![]() $\operatorname {Vol}_{m}(\cdot )$ is the
$\operatorname {Vol}_{m}(\cdot )$ is the ![]() $m$-dimensional volume.
$m$-dimensional volume.
Let ![]() $J=\{1,2,\ldots,k\}$. Observe that if
$J=\{1,2,\ldots,k\}$. Observe that if ![]() $J\not \subset I$, then
$J\not \subset I$, then
which implies that ![]() $\operatorname {Vol}_{|I|}(\Gamma _{-}(\varphi _{\lambda }(S))\cap {\mathbb {R}}^{I})=\operatorname {Vol}_{|I|}(\Gamma _{-}(\varphi _{\lambda }(S'))\cap {\mathbb {R}}^{I})$. In particular, if
$\operatorname {Vol}_{|I|}(\Gamma _{-}(\varphi _{\lambda }(S))\cap {\mathbb {R}}^{I})=\operatorname {Vol}_{|I|}(\Gamma _{-}(\varphi _{\lambda }(S'))\cap {\mathbb {R}}^{I})$. In particular, if ![]() $m< k$ we have
$m< k$ we have ![]() $V_m(\varphi _{\lambda }(S))=V_m(\varphi _{\lambda }(S'))$. Let us suppose that
$V_m(\varphi _{\lambda }(S))=V_m(\varphi _{\lambda }(S'))$. Let us suppose that ![]() $m\geq k$. Then
$m\geq k$. Then
 \[ V_m(\varphi_{\lambda}(S'))-V_m(\varphi_{\lambda}(S))=\sum_{\substack{|I|=m\\ J\subset I}}(\operatorname{Vol}_{m}(\Gamma_{-}(\varphi_{\lambda}(S'))\cap {\mathbb{R}}^{I})-\operatorname{Vol}_{m}(\Gamma_{-}(\varphi_{\lambda}(S))\cap {\mathbb{R}}^{I})). \]
\[ V_m(\varphi_{\lambda}(S'))-V_m(\varphi_{\lambda}(S))=\sum_{\substack{|I|=m\\ J\subset I}}(\operatorname{Vol}_{m}(\Gamma_{-}(\varphi_{\lambda}(S'))\cap {\mathbb{R}}^{I})-\operatorname{Vol}_{m}(\Gamma_{-}(\varphi_{\lambda}(S))\cap {\mathbb{R}}^{I})). \]
From this we obtain that ![]() $V_m(\varphi _{\lambda }(S'))-V_m(\varphi _{\lambda }(S))=\lambda ^k(V_m(S')-V_m(S))$ and
$V_m(\varphi _{\lambda }(S'))-V_m(\varphi _{\lambda }(S))=\lambda ^k(V_m(S')-V_m(S))$ and ![]() $\nu (\varphi _{\lambda }(S'))-\nu (\varphi _{\lambda }(S))=\lambda ^k(\nu (S')-\nu (S))$.
$\nu (\varphi _{\lambda }(S'))-\nu (\varphi _{\lambda }(S))=\lambda ^k(\nu (S')-\nu (S))$.
The following corollary is an analogue of Proposition 2.8 in the pre-convenient case. Remember that given ![]() $S\subset {\mathbb {R}}_{\geq }^{n}{\setminus} \{o\}$ and
$S\subset {\mathbb {R}}_{\geq }^{n}{\setminus} \{o\}$ and ![]() $R\subset {\mathbb {R}}^n_{\geq 0}$, we use the notation
$R\subset {\mathbb {R}}^n_{\geq 0}$, we use the notation ![]() $S(R):=S\cup R$.
$S(R):=S\cup R$.
Corollary 2.10 Let ![]() $S\subset {\mathbb {R}}_{\geq 0}^{n}{\setminus} \{o\}$ be a pre-convenient closed discrete set, and
$S\subset {\mathbb {R}}_{\geq 0}^{n}{\setminus} \{o\}$ be a pre-convenient closed discrete set, and ![]() $\alpha \in {\mathbb {R}}^n_{>0}$, such that
$\alpha \in {\mathbb {R}}^n_{>0}$, such that ![]() $\Gamma _{+}(S)\subsetneqq \Gamma _{+}(S(\alpha ))$. Then
$\Gamma _{+}(S)\subsetneqq \Gamma _{+}(S(\alpha ))$. Then ![]() $\nu (S(\alpha ))<\nu (S)$.
$\nu (S(\alpha ))<\nu (S)$.
Proof. Observe that there exists ![]() $\lambda >0$ such that the closed discrete sets
$\lambda >0$ such that the closed discrete sets ![]() $\varphi _{\lambda }(S)$,
$\varphi _{\lambda }(S)$, ![]() $\varphi _{\lambda }(S(\alpha ))$ are convenient where
$\varphi _{\lambda }(S(\alpha ))$ are convenient where ![]() $\varphi _{\lambda }$ is the homothety consisting of multiplication by
$\varphi _{\lambda }$ is the homothety consisting of multiplication by ![]() $\lambda$. As
$\lambda$. As ![]() $I(S,S(\alpha ))=\{1,\ldots,n\}$, we have
$I(S,S(\alpha ))=\{1,\ldots,n\}$, we have
(see Proposition 2.9). By Theorem 2.4, we have ![]() $\nu (\varphi _{\lambda }(S(\alpha )))\leq \nu (\varphi _{\lambda }(S))$, hence
$\nu (\varphi _{\lambda }(S(\alpha )))\leq \nu (\varphi _{\lambda }(S))$, hence ![]() $\nu (S(\alpha ))\leq \nu (S)$. If
$\nu (S(\alpha ))\leq \nu (S)$. If
then ![]() $\nu (\varphi _{\lambda }(S))=\nu (\varphi _{\lambda }(S(\alpha ))$. This contradicts Proposition 2.8.
$\nu (\varphi _{\lambda }(S))=\nu (\varphi _{\lambda }(S(\alpha ))$. This contradicts Proposition 2.8.
Take a set ![]() $I\subset \{1,\dots,n\}$.
$I\subset \{1,\dots,n\}$.
Corollary 2.11 Let ![]() $S$,
$S$, ![]() $S'$, and
$S'$, and ![]() $S''$ be three
$S''$ be three ![]() $I^c$-convenient closed discrete sets such that
$I^c$-convenient closed discrete sets such that ![]() $\Gamma _{+}(S)\subset \Gamma _{+}(S')\subset \Gamma _{+}(S'')$. Suppose that
$\Gamma _{+}(S)\subset \Gamma _{+}(S')\subset \Gamma _{+}(S'')$. Suppose that
Then ![]() $\nu (S)\geq \nu (S')\geq \nu (S'')$.
$\nu (S)\geq \nu (S')\geq \nu (S'')$.
Proof. Without loss of generality, we may take ![]() $I=\{1,\ldots,k\}$. As
$I=\{1,\ldots,k\}$. As ![]() $S$,
$S$, ![]() $S'$, and
$S'$, and ![]() $S''$ are
$S''$ are ![]() $I^c$-convenient, there exists
$I^c$-convenient, there exists ![]() $\lambda >0$ such that after applying the map
$\lambda >0$ such that after applying the map ![]() $\varphi _{\lambda }$ given by
$\varphi _{\lambda }$ given by ![]() $\varphi _{\lambda }(x_1,\ldots,x_n)=(\lambda x_1,\ldots,\lambda x_k,x_{k+1},\ldots, x_n)$, the closed discrete sets
$\varphi _{\lambda }(x_1,\ldots,x_n)=(\lambda x_1,\ldots,\lambda x_k,x_{k+1},\ldots, x_n)$, the closed discrete sets ![]() $\varphi _{\lambda }(S)$,
$\varphi _{\lambda }(S)$, ![]() $\varphi _{\lambda }(S')$, and
$\varphi _{\lambda }(S')$, and ![]() $\varphi _{\lambda }(S'')$ are convenient.
$\varphi _{\lambda }(S'')$ are convenient.
As ![]() $I\subset I(S,S')\cap I(S',S'')$, we have
$I\subset I(S,S')\cap I(S',S'')$, we have
and
By Theorem 2.4, we obtain ![]() $0\leq \nu (S)-\nu (S')$ and
$0\leq \nu (S)-\nu (S')$ and ![]() $0\leq \nu (S')-\nu (S'')$.
$0\leq \nu (S')-\nu (S'')$.
Convention From now until the end of the paper, whenever we talk about a vertex ![]() $\gamma$ of a certain polyhedron and an edge (one-dimensional face) of this polyhedron denoted by
$\gamma$ of a certain polyhedron and an edge (one-dimensional face) of this polyhedron denoted by ![]() $E_\gamma$, it should be understood that
$E_\gamma$, it should be understood that ![]() $\gamma$ is one of the endpoints of
$\gamma$ is one of the endpoints of ![]() $E_\gamma$.
$E_\gamma$.
Given ![]() $I\subset \{1,2,\ldots,n\}$, let
$I\subset \{1,2,\ldots,n\}$, let ![]() $ {\mathbb {R}}^{I}_{>0}:=\{(x_1,x_2,\ldots,x_n)\in {\mathbb {R}}^{I}:x_i>0\ \text {if}\ i\in I\}$. Let
$ {\mathbb {R}}^{I}_{>0}:=\{(x_1,x_2,\ldots,x_n)\in {\mathbb {R}}^{I}:x_i>0\ \text {if}\ i\in I\}$. Let ![]() $S\subset {\mathbb {R}}_{\geq }^{n}{\setminus} \{0\}$ be a closed discrete set, and let
$S\subset {\mathbb {R}}_{\geq }^{n}{\setminus} \{0\}$ be a closed discrete set, and let ![]() $\alpha \in {\mathbb {R}}_{>0}^{I}$ be such that
$\alpha \in {\mathbb {R}}_{>0}^{I}$ be such that
Let ![]() $E_{\alpha }$ be an edge of
$E_{\alpha }$ be an edge of ![]() $\Gamma (S(\alpha ))$ such that
$\Gamma (S(\alpha ))$ such that ![]() $\alpha$ is one of its endpoints. Given a set
$\alpha$ is one of its endpoints. Given a set ![]() $J$ with
$J$ with
we say that ![]() $E_{\alpha }$ is
$E_{\alpha }$ is ![]() $(I,J)$-convenient if for all
$(I,J)$-convenient if for all
we have ![]() $\beta _{i}\geq 1$ for
$\beta _{i}\geq 1$ for ![]() $i\in J{\setminus} I$ and
$i\in J{\setminus} I$ and ![]() $\beta _i=0$ for
$\beta _i=0$ for ![]() $i\in J^{c}$. We say that
$i\in J^{c}$. We say that ![]() $E_{\alpha }$ is strictly
$E_{\alpha }$ is strictly ![]() $(I,J)$-convenient if
$(I,J)$-convenient if ![]() $E_{\alpha }$ is
$E_{\alpha }$ is ![]() $(I,J)$-convenient and whenever
$(I,J)$-convenient and whenever
there exists ![]() $i\in J{\setminus} I$ such that
$i\in J{\setminus} I$ such that ![]() $\beta _i>1$.
$\beta _i>1$.
Example 2.12 Let ![]() $0< a<1$,
$0< a<1$, ![]() $S:=\{(2,0), (0,2), (\frac {3}{2}(1-a), 2a)\}$, and
$S:=\{(2,0), (0,2), (\frac {3}{2}(1-a), 2a)\}$, and ![]() $\alpha := (\frac {3}{2}, 0)$. For the edge
$\alpha := (\frac {3}{2}, 0)$. For the edge ![]() $E_{\alpha }$ of
$E_{\alpha }$ of ![]() $\Gamma _{+}(S(\alpha ))$ (with endpoints
$\Gamma _{+}(S(\alpha ))$ (with endpoints ![]() $(\frac {3}{2}, 0)$ and
$(\frac {3}{2}, 0)$ and ![]() $(0,2)$), we have
$(0,2)$), we have
Then ![]() $E_{\alpha }$ is
$E_{\alpha }$ is ![]() $(\{1\}, \{1,2\})$-convenient (respectively, strictly
$(\{1\}, \{1,2\})$-convenient (respectively, strictly ![]() $(\{1\}, \{1,2\})$-convenient) if and only if
$(\{1\}, \{1,2\})$-convenient) if and only if ![]() $\frac {1}{2}\leq a <1$ (respectively,
$\frac {1}{2}\leq a <1$ (respectively, ![]() $\frac {1}{2}< a <1$).
$\frac {1}{2}< a <1$).
Example 2.13 Let ![]() $0< a<1$,
$0< a<1$, ![]() $S:=\{(1,0,0), (0,2,0), (\frac {3}{4}(1-a), 2a,0), (0,0,1)\}$, and
$S:=\{(1,0,0), (0,2,0), (\frac {3}{4}(1-a), 2a,0), (0,0,1)\}$, and ![]() $\alpha := (\frac {3}{4}, 0,0)$. For the edge
$\alpha := (\frac {3}{4}, 0,0)$. For the edge ![]() $E_{\alpha }$ of
$E_{\alpha }$ of ![]() $\Gamma _{+}(S(\alpha ))$ (with endpoints
$\Gamma _{+}(S(\alpha ))$ (with endpoints ![]() $(\frac {3}{4}, 0,0)$ and
$(\frac {3}{4}, 0,0)$ and ![]() $(0,2,0)$) we have
$(0,2,0)$) we have
Then ![]() $E_{\alpha }$ is
$E_{\alpha }$ is ![]() $(\{1\}, \{1,2\})$-convenient (respectively, strictly
$(\{1\}, \{1,2\})$-convenient (respectively, strictly ![]() $(\{1\}, \{1,2\})$-convenient) if and only if
$(\{1\}, \{1,2\})$-convenient) if and only if ![]() $\frac {1}{2}\leq a <1$ (respectively,
$\frac {1}{2}\leq a <1$ (respectively, ![]() $\frac {1}{2}< a <1$).
$\frac {1}{2}< a <1$).
The following proposition allows us to eliminate certain vertices.
Proposition 2.14 Let ![]() $S\subset {\mathbb {R}}_{\geq 0}^{n}{\setminus} \{0\}$ be an
$S\subset {\mathbb {R}}_{\geq 0}^{n}{\setminus} \{0\}$ be an ![]() $I^{c}$-convenient closed discrete set,
$I^{c}$-convenient closed discrete set, ![]() $J$ a set such that
$J$ a set such that ![]() $I\subsetneqq J\subset \{1,\ldots,n\}$, and
$I\subsetneqq J\subset \{1,\ldots,n\}$, and ![]() $\alpha \in {\mathbb {R}}^{I}_{>0}$ such that
$\alpha \in {\mathbb {R}}^{I}_{>0}$ such that
and ![]() $\nu (S(\alpha ))=\nu (S)$. Assume that at least one of the following conditions are satisfied:
$\nu (S(\alpha ))=\nu (S)$. Assume that at least one of the following conditions are satisfied:
(i)
 $\alpha '\in \overline {\Gamma _{+}(S(\alpha )){\setminus} \Gamma _{+}(S)}\cap {\mathbb {R}}^I$;
$\alpha '\in \overline {\Gamma _{+}(S(\alpha )){\setminus} \Gamma _{+}(S)}\cap {\mathbb {R}}^I$;(ii)
 $\alpha '\in \overline {\Gamma _{+}(S(\alpha )){\setminus} \Gamma _{+}(S)}\cap {\mathbb {R}}_{>0}^J$ and there exists a strictly
$\alpha '\in \overline {\Gamma _{+}(S(\alpha )){\setminus} \Gamma _{+}(S)}\cap {\mathbb {R}}_{>0}^J$ and there exists a strictly  $(I,J)$-convenient edge
$(I,J)$-convenient edge  $E_{\alpha }$ of
$E_{\alpha }$ of  $\,\Gamma (S(\alpha ))$.
$\,\Gamma (S(\alpha ))$.
Then ![]() $\nu (S(\alpha '))=\nu (S)$.
$\nu (S(\alpha '))=\nu (S)$.
Remark 2.15 In Example 2.12 we have ![]() $\nu (S)= \nu (S(\alpha ))$ if and only if
$\nu (S)= \nu (S(\alpha ))$ if and only if
In particular, if ![]() $\nu (S)= \nu (S(\alpha ))$ then there are no strictly
$\nu (S)= \nu (S(\alpha ))$ then there are no strictly ![]() $(\{1\}, \{1,2\})$-convenient edges for
$(\{1\}, \{1,2\})$-convenient edges for ![]() $\alpha$.
$\alpha$.
Observe that for each ![]() $0< a<1$, if
$0< a<1$, if ![]() $\alpha ' \in ( \Gamma _{+}(S(\alpha )){\setminus} \Gamma _{+}(S))\cap {\mathbb {R}}^2_{>0}$, then
$\alpha ' \in ( \Gamma _{+}(S(\alpha )){\setminus} \Gamma _{+}(S))\cap {\mathbb {R}}^2_{>0}$, then ![]() $\mu (S)\neq \mu (S(\alpha '))$.
$\mu (S)\neq \mu (S(\alpha '))$.
In Example 2.13 we have ![]() $\nu (S)= \nu (S(\alpha ))$ for all
$\nu (S)= \nu (S(\alpha ))$ for all ![]() $0< a<1$. Furthermore, for all
$0< a<1$. Furthermore, for all ![]() $\alpha '\in \overline {\Gamma _{+}(S(\alpha )){\setminus} \Gamma _{+}(S)}\cap {\mathbb {R}}^{\{1,2\}}$ we have
$\alpha '\in \overline {\Gamma _{+}(S(\alpha )){\setminus} \Gamma _{+}(S)}\cap {\mathbb {R}}^{\{1,2\}}$ we have ![]() $\nu (S(\alpha '))=\nu (S)$, which indicates that the hypotheses of the preceding proposition are just sufficient.
$\nu (S(\alpha '))=\nu (S)$, which indicates that the hypotheses of the preceding proposition are just sufficient.
Observe that ![]() $\overline {\Gamma _{+}(S(\alpha )){\setminus} \Gamma _{+}(S)}\cap {\mathbb {R}}^{\{1,2\}}$ is the region of the plane bounded by the triangle of the vertices
$\overline {\Gamma _{+}(S(\alpha )){\setminus} \Gamma _{+}(S)}\cap {\mathbb {R}}^{\{1,2\}}$ is the region of the plane bounded by the triangle of the vertices ![]() $(\frac {3}{4},0,0)$,
$(\frac {3}{4},0,0)$,![]() $(2,0,0)$ and
$(2,0,0)$ and ![]() $(\frac {3}{4}(1-a), 2a,0)$).
$(\frac {3}{4}(1-a), 2a,0)$).
Proof. Let us assume that ![]() $\alpha '\in \overline {\Gamma _{+}(S(\alpha )){\setminus} \Gamma _{+}(S)}\cap {\mathbb {R}}^{I}$. We may assume that
$\alpha '\in \overline {\Gamma _{+}(S(\alpha )){\setminus} \Gamma _{+}(S)}\cap {\mathbb {R}}^{I}$. We may assume that ![]() $\Gamma _{+}(S)\subsetneqq \Gamma _{+}(S(\alpha '))\subsetneqq \Gamma _{+}(S(\alpha ))$ (otherwise there is nothing to prove).
$\Gamma _{+}(S)\subsetneqq \Gamma _{+}(S(\alpha '))\subsetneqq \Gamma _{+}(S(\alpha ))$ (otherwise there is nothing to prove).
Observe that the closed discrete sets ![]() $S$,
$S$, ![]() $S(\alpha ')$, and
$S(\alpha ')$, and ![]() $S(\alpha )$ are
$S(\alpha )$ are ![]() $I^c$-convenient and
$I^c$-convenient and
Using Corollary 2.11, we obtain ![]() $\nu (S)=\nu (S(\alpha '))=\nu (S(\alpha ))$. This completes the proof in case (i).
$\nu (S)=\nu (S(\alpha '))=\nu (S(\alpha ))$. This completes the proof in case (i).
Next, assume that case (ii) holds. Consider a strictly ![]() $(I,J)$-convenient edge
$(I,J)$-convenient edge ![]() $E_{\alpha }$ of
$E_{\alpha }$ of ![]() $\Gamma (S(\alpha ))$. Let
$\Gamma (S(\alpha ))$. Let ![]() $\beta :=(\beta _1,\ldots,\beta _n)\in E_{\alpha }\cap \operatorname {Ver}(S)$. Let
$\beta :=(\beta _1,\ldots,\beta _n)\in E_{\alpha }\cap \operatorname {Ver}(S)$. Let ![]() $E'\subset E_{\alpha }$ be the line segment with endpoints
$E'\subset E_{\alpha }$ be the line segment with endpoints ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$. Without loss of generality, we may assume that
$\beta$. Without loss of generality, we may assume that ![]() $E'\cap \operatorname {Ver}(S)=\{\beta \}$. As
$E'\cap \operatorname {Ver}(S)=\{\beta \}$. As ![]() $E_{\alpha }$ is strictly
$E_{\alpha }$ is strictly ![]() $(I,J)$-convenient, there exists
$(I,J)$-convenient, there exists ![]() $i\in J{\setminus} I$ such that
$i\in J{\setminus} I$ such that ![]() $\beta _i>1$. Let
$\beta _i>1$. Let ![]() $\delta >0$ be sufficiently small so that
$\delta >0$ be sufficiently small so that ![]() $\beta _i-\delta \geq 1$ and let
$\beta _i-\delta \geq 1$ and let ![]() $\beta '\in {\mathbb {R}}_{\geq 0}^I$ be such that
$\beta '\in {\mathbb {R}}_{\geq 0}^I$ be such that ![]() $\gamma :=\beta -\delta e_i+\beta '\in \Gamma (S(\alpha ))\cap {\mathbb {R}}^J_{>0}$. Then
$\gamma :=\beta -\delta e_i+\beta '\in \Gamma (S(\alpha ))\cap {\mathbb {R}}^J_{>0}$. Then
Observe that the closed discrete sets ![]() $S$s,
$S$s, ![]() $S(\gamma )$, and
$S(\gamma )$, and ![]() $S(\alpha )$ are
$S(\alpha )$ are ![]() $I^c$-convenient and
$I^c$-convenient and
Then ![]() $\nu (S(\gamma ))=\nu (S(\alpha ))=\nu (S)$.
$\nu (S(\gamma ))=\nu (S(\alpha ))=\nu (S)$.
If ![]() $\alpha '\in \overline { \Gamma _{+}(S(\gamma )){\setminus} \Gamma _{+}(S)}\cap {\mathbb {R}}^{J}$, we have
$\alpha '\in \overline { \Gamma _{+}(S(\gamma )){\setminus} \Gamma _{+}(S)}\cap {\mathbb {R}}^{J}$, we have
The closed discrete sets ![]() $S$,
$S$, ![]() $S(\alpha ')$, and
$S(\alpha ')$, and ![]() $S(\gamma )$ are
$S(\gamma )$ are ![]() $J^{c}$-convenient and
$J^{c}$-convenient and
Then ![]() $\nu (S(\alpha '))=\nu (S(\gamma ))=\nu (S)$.
$\nu (S(\alpha '))=\nu (S(\gamma ))=\nu (S)$.
We still need to study the case ![]() $\alpha '\in (\Gamma _{+}(S(\alpha )){\setminus} \Gamma _{+}(S(\gamma )))\cap {\mathbb {R}}^J_{>0}$.
$\alpha '\in (\Gamma _{+}(S(\alpha )){\setminus} \Gamma _{+}(S(\gamma )))\cap {\mathbb {R}}^J_{>0}$.
Consider the compact set ![]() $C:=\overline {(\Gamma _{+}(S(\alpha ')){\setminus} \Gamma _{+}(S))}\cap {\mathbb {R}}^J$, and the map
$C:=\overline {(\Gamma _{+}(S(\alpha ')){\setminus} \Gamma _{+}(S))}\cap {\mathbb {R}}^J$, and the map
 \[ \nu_S:C\rightarrow {\mathbb{R}};\;\tau\mapsto \nu_S(\tau):= \nu(S(\tau))=\sum_{m=0}^{n}(-1)^{n-m}m!V_m(S(\tau)) \]
\[ \nu_S:C\rightarrow {\mathbb{R}};\;\tau\mapsto \nu_S(\tau):= \nu(S(\tau))=\sum_{m=0}^{n}(-1)^{n-m}m!V_m(S(\tau)) \]
where ![]() $V_m(S(\tau )):=V_m(\Gamma _{-}(S(\tau ))))$. The map
$V_m(S(\tau )):=V_m(\Gamma _{-}(S(\tau ))))$. The map ![]() $\nu _S$ is continuous in
$\nu _S$ is continuous in ![]() $C$. In effect, recall that
$C$. In effect, recall that ![]() $V_m(S(\tau ))=\sum _{|I'|= m}\operatorname {Vol}_{m}(\Gamma _{-}(S(\tau ))\cap {\mathbb {R}}^{I'})$. Hence,
$V_m(S(\tau ))=\sum _{|I'|= m}\operatorname {Vol}_{m}(\Gamma _{-}(S(\tau ))\cap {\mathbb {R}}^{I'})$. Hence,
where
 \[ V(\tau):= \sum_{\substack{|I'|=m\\ I'\supseteq J}}\operatorname{Vol}_{m}(\Gamma_{-}(S(\tau))\cap {\mathbb{R}}^{I'}),\quad V'(\tau):= \sum_{\substack{ |I'|=m\\ I'\not\supset J}}\operatorname{Vol}_{m}(\Gamma_{-}(S(\tau))\cap {\mathbb{R}}^{I'}). \]
\[ V(\tau):= \sum_{\substack{|I'|=m\\ I'\supseteq J}}\operatorname{Vol}_{m}(\Gamma_{-}(S(\tau))\cap {\mathbb{R}}^{I'}),\quad V'(\tau):= \sum_{\substack{ |I'|=m\\ I'\not\supset J}}\operatorname{Vol}_{m}(\Gamma_{-}(S(\tau))\cap {\mathbb{R}}^{I'}). \] The function ![]() $V: {\mathbb {R}}^J\rightarrow {\mathbb {R}};\tau \mapsto V(\tau )$ is continuous, because each summand is continuous in
$V: {\mathbb {R}}^J\rightarrow {\mathbb {R}};\tau \mapsto V(\tau )$ is continuous, because each summand is continuous in ![]() $ {\mathbb {R}}^J$. The function
$ {\mathbb {R}}^J$. The function ![]() $V':C\rightarrow {\mathbb {R}};\tau \mapsto V'(\tau )$ is constant, because
$V':C\rightarrow {\mathbb {R}};\tau \mapsto V'(\tau )$ is constant, because ![]() $\Gamma _{-}(S(\alpha '))\cap ( {\mathbb {R}}_{\geq 0}^J{\setminus} {\mathbb {R}}_{>0}^J) =\Gamma _{-}(S) \cap ( {\mathbb {R}}_{\geq 0}^J{\setminus} {\mathbb {R}}_{>0}^J)$. Then each
$\Gamma _{-}(S(\alpha '))\cap ( {\mathbb {R}}_{\geq 0}^J{\setminus} {\mathbb {R}}_{>0}^J) =\Gamma _{-}(S) \cap ( {\mathbb {R}}_{\geq 0}^J{\setminus} {\mathbb {R}}_{>0}^J)$. Then each ![]() $V_{m}(S(\tau ))$ is continuous in
$V_{m}(S(\tau ))$ is continuous in ![]() $\tau \in C$, which implies that the function
$\tau \in C$, which implies that the function ![]() $\nu _S$ is continuous in
$\nu _S$ is continuous in ![]() $C$.
$C$.
Let us assume that ![]() $\alpha '\in (\Gamma _{+}(S(\alpha )){\setminus} \Gamma _{+}(S(\gamma )))\cap {\mathbb {R}}^J_{>0}$ and
$\alpha '\in (\Gamma _{+}(S(\alpha )){\setminus} \Gamma _{+}(S(\gamma )))\cap {\mathbb {R}}^J_{>0}$ and ![]() $\alpha '\notin \Gamma (S(\alpha ))$. Let us suppose that
$\alpha '\notin \Gamma (S(\alpha ))$. Let us suppose that ![]() $\nu _S(\alpha ')=\nu (S(\alpha '))\neq \nu (S)$. Let us consider the set
$\nu _S(\alpha ')=\nu (S(\alpha '))\neq \nu (S)$. Let us consider the set ![]() $\mathcal {C}:=\{ \tau \in C:\nu _S(\tau ))=\nu _S(\alpha '))\}$. The continuity of
$\mathcal {C}:=\{ \tau \in C:\nu _S(\tau ))=\nu _S(\alpha '))\}$. The continuity of ![]() $\nu _S$ implies that
$\nu _S$ implies that ![]() $\mathcal {C}$ is compact. We define the following partial order on
$\mathcal {C}$ is compact. We define the following partial order on ![]() $\mathcal {C}$. For
$\mathcal {C}$. For ![]() $\tau,\tau '\in \mathcal {C}$ we will say that
$\tau,\tau '\in \mathcal {C}$ we will say that ![]() $\tau \leq \tau '$ if
$\tau \leq \tau '$ if ![]() $\Gamma _{+}(S(\tau '))\subset \Gamma _{+}(S(\tau ))$. Let us consider an ascending chain
$\Gamma _{+}(S(\tau '))\subset \Gamma _{+}(S(\tau ))$. Let us consider an ascending chain
We prove that this chain is bounded above in ![]() $\mathcal {C}$. Let us consider the convex closed set
$\mathcal {C}$. Let us consider the convex closed set
As ![]() $\mathcal {C}$ is compact, the sequence
$\mathcal {C}$ is compact, the sequence ![]() $\{\tau _1,\tau _2,\ldots,\tau _n,\ldots \}$ has a convergent subsequence
$\{\tau _1,\tau _2,\ldots,\tau _n,\ldots \}$ has a convergent subsequence ![]() $\{\tau _{i_1}, \tau _{i_2},\ldots,\tau _{i_n},\ldots \}$. Observe that
$\{\tau _{i_1}, \tau _{i_2},\ldots,\tau _{i_n},\ldots \}$. Observe that
where ![]() $\tau :=\lim _{n\rightarrow \infty }\tau _{i_n}\in \mathcal {C}$. By definition,
$\tau :=\lim _{n\rightarrow \infty }\tau _{i_n}\in \mathcal {C}$. By definition, ![]() $\Gamma \subset \Gamma _{+}(S(\tau ))$, and by construction for each
$\Gamma \subset \Gamma _{+}(S(\tau ))$, and by construction for each ![]() $i\geq 1$ there exists
$i\geq 1$ there exists ![]() $n\geq 1$ such that
$n\geq 1$ such that ![]() $\Gamma _{+}(S(\tau _{i_n}))\subset \Gamma _{+}(S(\tau _{i}))$. Then
$\Gamma _{+}(S(\tau _{i_n}))\subset \Gamma _{+}(S(\tau _{i}))$. Then ![]() $\Gamma =\Gamma _{+}(S(\tau ))$, which implies that
$\Gamma =\Gamma _{+}(S(\tau ))$, which implies that ![]() $\tau _i\leq \tau$ for all
$\tau _i\leq \tau$ for all ![]() $i\geq 1$. By Zorn's lemma
$i\geq 1$. By Zorn's lemma ![]() $\mathcal {C}$ contains at least one maximal element. Let
$\mathcal {C}$ contains at least one maximal element. Let ![]() $\tau \in \mathcal {C}$ be a maximal element. Recall that we consider
$\tau \in \mathcal {C}$ be a maximal element. Recall that we consider ![]() $\alpha '\notin \Gamma (S(\alpha ))$, and we made the assumption that
$\alpha '\notin \Gamma (S(\alpha ))$, and we made the assumption that ![]() $\nu (S(\alpha '))\neq \nu (S)$. Hence,
$\nu (S(\alpha '))\neq \nu (S)$. Hence, ![]() $\tau \notin (\overline { \Gamma _{+}(S(\gamma )){\setminus} \Gamma _{+}(S)})\cap {\mathbb {R}}^{J}$.
$\tau \notin (\overline { \Gamma _{+}(S(\gamma )){\setminus} \Gamma _{+}(S)})\cap {\mathbb {R}}^{J}$.
Observe that for all ![]() $\alpha ''\in \Gamma _{+}(S(\alpha ))$ we have
$\alpha ''\in \Gamma _{+}(S(\alpha ))$ we have
As the closed discrete sets ![]() $S$,
$S$, ![]() $S(\alpha '')$, and
$S(\alpha '')$, and ![]() $S(\gamma,\alpha '')$ are
$S(\gamma,\alpha '')$ are ![]() $I^{c}$-convenient and
$I^{c}$-convenient and
we obtain ![]() $\nu (S(\gamma,\alpha ''))=\nu (S(\alpha ''))=\nu (S)$.
$\nu (S(\gamma,\alpha ''))=\nu (S(\alpha ''))=\nu (S)$.
As ![]() $\tau \notin \overline {\Gamma _{+}(S(\gamma )){\setminus} \Gamma _{+}(S)}\cap {\mathbb {R}}^{J}$ and
$\tau \notin \overline {\Gamma _{+}(S(\gamma )){\setminus} \Gamma _{+}(S)}\cap {\mathbb {R}}^{J}$ and ![]() $\gamma \in \Gamma (S(\alpha ))$, there exists a relatively open subset
$\gamma \in \Gamma (S(\alpha ))$, there exists a relatively open subset ![]() $\Omega$ of the relative interior of
$\Omega$ of the relative interior of ![]() $\overline {\Gamma _{+}(S(\alpha )){\setminus} \Gamma _{+}(S)}\cap {\mathbb {R}}^{I}$ such that
$\overline {\Gamma _{+}(S(\alpha )){\setminus} \Gamma _{+}(S)}\cap {\mathbb {R}}^{I}$ such that ![]() $\tau$ belongs to the relative interior of
$\tau$ belongs to the relative interior of
for all ![]() $\alpha ''\in \Omega$. We obtain
$\alpha ''\in \Omega$. We obtain
The closed discrete sets ![]() $S(\alpha '')$,
$S(\alpha '')$, ![]() $S(\tau,\alpha '')$, and
$S(\tau,\alpha '')$, and ![]() $S(\gamma,\alpha '')$ are
$S(\gamma,\alpha '')$ are ![]() $J^{c}$-convenient, and
$J^{c}$-convenient, and
Hence, ![]() $\nu (S(\tau,\alpha ''))=\nu (S(\alpha ''))=\nu (S)$.
$\nu (S(\tau,\alpha ''))=\nu (S(\alpha ''))=\nu (S)$.
Given an edge ![]() $E_{\tau }$ of
$E_{\tau }$ of ![]() $\Gamma (S(\tau ))$ that connects
$\Gamma (S(\tau ))$ that connects ![]() $\tau$ with a vertex in
$\tau$ with a vertex in ![]() $\operatorname {Ver}(\Gamma (S))$, let
$\operatorname {Ver}(\Gamma (S))$, let ![]() $E'_{\tau }$ be the subsegment of
$E'_{\tau }$ be the subsegment of ![]() $E_{\tau }$ containing
$E_{\tau }$ containing ![]() $\tau$ such that
$\tau$ such that ![]() $|E'_{\tau }\cap \operatorname {Ver}(S)|=1$. We choose
$|E'_{\tau }\cap \operatorname {Ver}(S)|=1$. We choose ![]() $\alpha ''\in \Omega '$ such that for each edge
$\alpha ''\in \Omega '$ such that for each edge ![]() $E_{\tau }$ of
$E_{\tau }$ of ![]() $\Gamma (S(\tau ))$ connecting
$\Gamma (S(\tau ))$ connecting ![]() $\tau$ with an element of
$\tau$ with an element of ![]() $\operatorname {Ver}(\Gamma (S))$ we have
$\operatorname {Ver}(\Gamma (S))$ we have ![]() $\dim (E'_{\tau }\cap \Gamma (S(\alpha '')))=0$. In other words, no subsegment of
$\dim (E'_{\tau }\cap \Gamma (S(\alpha '')))=0$. In other words, no subsegment of ![]() $E'_{\tau }$ is contained in the Newton boundary
$E'_{\tau }$ is contained in the Newton boundary ![]() $\Gamma (S(\alpha ''))$.
$\Gamma (S(\alpha ''))$.
Let us consider the compact polyhedron ![]() $P:=\overline {\Gamma _{+}(S(\tau,\alpha '')){\setminus} \Gamma _{+}(S(\alpha ''))}$. Observe that
$P:=\overline {\Gamma _{+}(S(\tau,\alpha '')){\setminus} \Gamma _{+}(S(\alpha ''))}$. Observe that ![]() $\nu (P)=0$ (see Theorem 2.4).
$\nu (P)=0$ (see Theorem 2.4).
Given the choice of ![]() $\alpha ''$, there exists
$\alpha ''$, there exists ![]() $\tau '\in P$ such that
$\tau '\in P$ such that
and ![]() $Q_0:=\overline {(\Gamma _{+}(S(\tau )){\setminus} \Gamma _{+}(S(\tau ')))}\subset P$ (it is for achieving the last inclusion that the choice of
$Q_0:=\overline {(\Gamma _{+}(S(\tau )){\setminus} \Gamma _{+}(S(\tau ')))}\subset P$ (it is for achieving the last inclusion that the choice of ![]() $\alpha ''$ is really important).
$\alpha ''$ is really important).
Let ![]() $Q_1:=\overline {P{\setminus} Q_0}$. As
$Q_1:=\overline {P{\setminus} Q_0}$. As ![]() $\dim (Q_0^{J'}\cap Q_{1}^{J'})<|J'|$, for all
$\dim (Q_0^{J'}\cap Q_{1}^{J'})<|J'|$, for all ![]() $J'\subset \{1,\ldots,n\}$, we obtain
$J'\subset \{1,\ldots,n\}$, we obtain ![]() $\nu (P)=\nu (Q_0)+\nu (Q_1)$. The polyhedra
$\nu (P)=\nu (Q_0)+\nu (Q_1)$. The polyhedra ![]() $ {Q}_0$ and
$ {Q}_0$ and ![]() $ {Q}_1$ satisfy the hypotheses of Proposition 2.6. In effect, we have the following.
$ {Q}_1$ satisfy the hypotheses of Proposition 2.6. In effect, we have the following.
(i) By construction
 $Q_0$ and
$Q_0$ and  $Q_1$ are pure
$Q_1$ are pure  $n$-dimensional compact polyhedra and
$n$-dimensional compact polyhedra and  $o\not \in P=Q_0\cup Q_1$.
$o\not \in P=Q_0\cup Q_1$.(ii) Recall that
 $\tau \in {\mathbb {R}}^J_{>0}$. The polyhedron
$\tau \in {\mathbb {R}}^J_{>0}$. The polyhedron  $P$ satisfies
which implies
$P$ satisfies
which implies \[ \dim(P^{J'})<|J'|\quad\text{for all }J'\not \supset J, \]
\[ \dim(P^{J'})<|J'|\quad\text{for all }J'\not \supset J, \] $\dim (Q_0^{J'})<|J'|$ and
$\dim (Q_0^{J'})<|J'|$ and  $\dim (Q_1^{J'})<|J'|$ for all
$\dim (Q_1^{J'})<|J'|$ for all  $J'\not \supset J$.
$J'\not \supset J$.(iii) Now we verify that
 $Q_{0}^{J'}$ is homeomorphic to a
$Q_{0}^{J'}$ is homeomorphic to a  $|J'|$-dimensional closed disk for all
$|J'|$-dimensional closed disk for all  $J'\supset J$. As
$J'\supset J$. As  $S$ is
$S$ is  $I^c$-convenient and
$I^c$-convenient and  $\tau \in {\mathbb {R}}^J_{>0}$, we have
$\tau \in {\mathbb {R}}^J_{>0}$, we have  $\dim (Q_{0}^{J'})=|J'|$ for each
$\dim (Q_{0}^{J'})=|J'|$ for each  $J'\supset J$. By Remark 2.7 we obtain that
$J'\supset J$. By Remark 2.7 we obtain that  $Q_{0}^{J'}$ is homeomorphic to a
$Q_{0}^{J'}$ is homeomorphic to a  $|J'|$-dimensional closed disc. The proof for
$|J'|$-dimensional closed disc. The proof for  $Q_{1}^{J'}$ is analogous to the proof for
$Q_{1}^{J'}$ is analogous to the proof for  $Q_{0}^{J'}$.
$Q_{0}^{J'}$.(iv) As
 $S$ is
$S$ is  $I^c$-convenient (in particular,
$I^c$-convenient (in particular,  $J^c$-convenient), we obtain that if
$J^c$-convenient), we obtain that if  $(\beta _1,\ldots,\beta _n)\in \operatorname {Ver}(P)$, then for each
$(\beta _1,\ldots,\beta _n)\in \operatorname {Ver}(P)$, then for each  $i\in J^c$ we have
$i\in J^c$ we have  $\beta _i\geq 1$ or
$\beta _i\geq 1$ or  $\beta _i=0$. This property is inherited by
$\beta _i=0$. This property is inherited by  $Q_0$ and
$Q_0$ and  $Q_1$.
$Q_1$.
By Proposition 2.6 we have ![]() $\nu (Q_0)\geq 0$,
$\nu (Q_0)\geq 0$, ![]() $\nu (Q_1)\geq 0$. As
$\nu (Q_1)\geq 0$. As ![]() $\nu (P)=0$, we obtain
$\nu (P)=0$, we obtain ![]() $\nu (Q_0)=\nu (Q_1)\!=\! 0$. We have
$\nu (Q_0)=\nu (Q_1)\!=\! 0$. We have ![]() $\tau <\tau '\in \mathcal {C}$, which contradicts the maximality of
$\tau <\tau '\in \mathcal {C}$, which contradicts the maximality of ![]() $\tau$ in
$\tau$ in ![]() $\mathcal {C}$. As a consequence, we obtain
$\mathcal {C}$. As a consequence, we obtain ![]() $\nu (S(\alpha '))=\nu (S)$.
$\nu (S(\alpha '))=\nu (S)$.
Now let us suppose that ![]() $\alpha ' \in \Gamma (S(\alpha ))\cap {\mathbb {R}}_{>0}^J$, and let
$\alpha ' \in \Gamma (S(\alpha ))\cap {\mathbb {R}}_{>0}^J$, and let ![]() $v\in {\mathbb {R}}^J_{>0}$. For
$v\in {\mathbb {R}}^J_{>0}$. For ![]() $\epsilon >0$ small enough
$\epsilon >0$ small enough ![]() $\alpha _{\epsilon }:=\alpha '+\epsilon v$ belongs to the relative interior of
$\alpha _{\epsilon }:=\alpha '+\epsilon v$ belongs to the relative interior of ![]() $\Gamma _{+}(S(\alpha ')){\setminus} \Gamma _{+}(S)$. For the continuity of
$\Gamma _{+}(S(\alpha ')){\setminus} \Gamma _{+}(S)$. For the continuity of ![]() $\nu _S$ in
$\nu _S$ in ![]() $C:=\overline {(\Gamma _{+}(S(\alpha ')){\setminus} \Gamma _{+}(S))}\cap {\mathbb {R}}^J$ we obtain
$C:=\overline {(\Gamma _{+}(S(\alpha ')){\setminus} \Gamma _{+}(S))}\cap {\mathbb {R}}^J$ we obtain
which implies that ![]() $\nu (S(\alpha '))=\nu (S)$.
$\nu (S(\alpha '))=\nu (S)$.
Corollary 2.16 Let ![]() $I\subsetneqq J:= \{1,\ldots,n\}$. Let
$I\subsetneqq J:= \{1,\ldots,n\}$. Let ![]() $S, S'\subset {\mathbb {R}}_{\geq 0}^{n}{\setminus} \{o\}$ be two convenient closed discrete sets such that
$S, S'\subset {\mathbb {R}}_{\geq 0}^{n}{\setminus} \{o\}$ be two convenient closed discrete sets such that ![]() $\Gamma _{+}(S)\subsetneqq \Gamma _{+}(S')$ and
$\Gamma _{+}(S)\subsetneqq \Gamma _{+}(S')$ and ![]() $\nu (S)=\nu (S')$. Suppose that there exists
$\nu (S)=\nu (S')$. Suppose that there exists ![]() $\alpha \in \operatorname {Ver}(S',S)\cap {\mathbb {R}}^I_{>0}$ and an edge
$\alpha \in \operatorname {Ver}(S',S)\cap {\mathbb {R}}^I_{>0}$ and an edge ![]() $E_{\alpha }$ of
$E_{\alpha }$ of ![]() $\Gamma (S)$ that is
$\Gamma (S)$ that is ![]() $(I,J)$-convenient. Then there exists
$(I,J)$-convenient. Then there exists
such that ![]() $\beta _i=1$ for all
$\beta _i=1$ for all ![]() $i\in I^c$.
$i\in I^c$.
Proof. Let ![]() $R:= \operatorname {Ver}(S',S){\setminus} \{\alpha \}$ and
$R:= \operatorname {Ver}(S',S){\setminus} \{\alpha \}$ and ![]() $S(R)=S\cup R$. The closed discrete sets
$S(R)=S\cup R$. The closed discrete sets ![]() $S,$
$S,$ ![]() $S(R)$ and
$S(R)$ and ![]() $S'$ are convenient, and
$S'$ are convenient, and ![]() $\Gamma _{+}(S)\subset \Gamma _{+}(S(R))\subsetneqq \Gamma _{+}(S')$. Then
$\Gamma _{+}(S)\subset \Gamma _{+}(S(R))\subsetneqq \Gamma _{+}(S')$. Then
We argue by contradiction. If there is no ![]() $(\beta _1,\ldots,\beta _n)$ as in the corollary, then the edge
$(\beta _1,\ldots,\beta _n)$ as in the corollary, then the edge ![]() $E_{\alpha }$ is strictly
$E_{\alpha }$ is strictly ![]() $(I,J)$-convenient. By Proposition 2.14, for all
$(I,J)$-convenient. By Proposition 2.14, for all ![]() $\alpha '\in \overline {\Gamma _{+}(S(\alpha ){\setminus} \Gamma _{+}(S)}\cap {\mathbb {R}}_{>0}^n$ we have
$\alpha '\in \overline {\Gamma _{+}(S(\alpha ){\setminus} \Gamma _{+}(S)}\cap {\mathbb {R}}_{>0}^n$ we have
which contradicts Proposition 2.8.
The following proposition allows us to fix a special coordinate hyperplane and gives information about the edges not contained in the hyperplane that contain a vertex of interest belonging to the hyperplane.
Proposition 2.17 Let ![]() $S,S'\subset {\mathbb {R}}_{\geq 0}^{n}{\setminus} \{o\}$ be two convenient closed discrete sets such that
$S,S'\subset {\mathbb {R}}_{\geq 0}^{n}{\setminus} \{o\}$ be two convenient closed discrete sets such that ![]() $\Gamma _{+}(S)\subsetneqq \Gamma _{+}(S')$ and
$\Gamma _{+}(S)\subsetneqq \Gamma _{+}(S')$ and ![]() $\nu (S)=\nu (S')$. Let us suppose that
$\nu (S)=\nu (S')$. Let us suppose that
Then there exists ![]() $i\in I^c$ such that for all the edges
$i\in I^c$ such that for all the edges ![]() $E_{\alpha }$ of
$E_{\alpha }$ of ![]() $\Gamma (S')$ not contained in
$\Gamma (S')$ not contained in ![]() $ {\mathbb {R}}_{\{i\}}$ there exists
$ {\mathbb {R}}_{\{i\}}$ there exists ![]() $(\beta _1,\ldots,\beta _n)\in \operatorname {Ver}(S)\cap E_{\alpha }$ such that
$(\beta _1,\ldots,\beta _n)\in \operatorname {Ver}(S)\cap E_{\alpha }$ such that ![]() $\beta _i=1$.
$\beta _i=1$.
Proof. First we prove the following lemma.
Lemma 2.18 Let ![]() $S\subset {\mathbb {R}}_{\geq 0}^{n} {\setminus} \{o\}$ be an
$S\subset {\mathbb {R}}_{\geq 0}^{n} {\setminus} \{o\}$ be an ![]() $I^c$-convenient closed discrete set and
$I^c$-convenient closed discrete set and
such that ![]() $\nu (S)=\nu (S(\alpha ))$. Then there exists
$\nu (S)=\nu (S(\alpha ))$. Then there exists ![]() $i\in I^c$ such that for each edge
$i\in I^c$ such that for each edge ![]() $E_{\alpha }$ of
$E_{\alpha }$ of ![]() $\Gamma (S(\alpha ))$ not contained in
$\Gamma (S(\alpha ))$ not contained in ![]() $ {\mathbb {R}}_{\{i\}}$ there exists
$ {\mathbb {R}}_{\{i\}}$ there exists ![]() $(\beta _1,\ldots,\beta _n)\in \operatorname {Ver}(S)\cap E_{\alpha }$ such that
$(\beta _1,\ldots,\beta _n)\in \operatorname {Ver}(S)\cap E_{\alpha }$ such that ![]() $\beta _i=1$.
$\beta _i=1$.
Proof of Lemma 2.18. By Corollary 2.10, we have ![]() $|I|< n$. Let
$|I|< n$. Let ![]() $k$ be the greatest element of
$k$ be the greatest element of ![]() $\{1,\dots,n-1\}$ such that the lemma is false for some
$\{1,\dots,n-1\}$ such that the lemma is false for some ![]() $I$ with
$I$ with ![]() $|I|=k$. In other words, for all
$|I|=k$. In other words, for all ![]() $i\in I^c$ there exists an edge
$i\in I^c$ there exists an edge ![]() $E_{\alpha }$, not contained in
$E_{\alpha }$, not contained in ![]() $ {\mathbb {R}}_{\{i\}}$, such that for all
$ {\mathbb {R}}_{\{i\}}$, such that for all ![]() $(\beta _1,\ldots,\beta _n)\in \operatorname {Ver}(S)\cap E_{\alpha }$ we have
$(\beta _1,\ldots,\beta _n)\in \operatorname {Ver}(S)\cap E_{\alpha }$ we have ![]() $\beta _i>1$. Let
$\beta _i>1$. Let ![]() $J\subset \{1,\ldots,n\}$ be a set of the smallest cardinality such that
$J\subset \{1,\ldots,n\}$ be a set of the smallest cardinality such that ![]() $E_{\alpha }\subset {\mathbb {R}}^J$. Then
$E_{\alpha }\subset {\mathbb {R}}^J$. Then ![]() $E_{\alpha }$ is a strictly
$E_{\alpha }$ is a strictly ![]() $(I,J)$-convenient edge. Using Proposition 2.14 we obtain that for all
$(I,J)$-convenient edge. Using Proposition 2.14 we obtain that for all ![]() $\alpha '\in \overline {\Gamma _{+}(S(\alpha ){\setminus} \Gamma _{+}(S)}\cap {\mathbb {R}}_{>0}^J$ we have
$\alpha '\in \overline {\Gamma _{+}(S(\alpha ){\setminus} \Gamma _{+}(S)}\cap {\mathbb {R}}_{>0}^J$ we have ![]() $\nu (S(\alpha '))=\nu (S)$. Now let us choose
$\nu (S(\alpha '))=\nu (S)$. Now let us choose ![]() $\alpha '$ sufficiently close to
$\alpha '$ sufficiently close to ![]() $\alpha$ so that for each edge
$\alpha$ so that for each edge ![]() $E_{\alpha '}$ of
$E_{\alpha '}$ of ![]() $\Gamma (S(\alpha '))$, and
$\Gamma (S(\alpha '))$, and ![]() $\beta \in E_{\alpha '}\cap \operatorname {Ver}(S)$ adjacent to
$\beta \in E_{\alpha '}\cap \operatorname {Ver}(S)$ adjacent to ![]() $\alpha '$ in
$\alpha '$ in ![]() $E_{\alpha '}$, there exists an edge
$E_{\alpha '}$, there exists an edge ![]() $E_{\alpha }$ of
$E_{\alpha }$ of ![]() $\Gamma (S(\alpha ))$ such that
$\Gamma (S(\alpha ))$ such that ![]() $\beta \in E_{\alpha }$. Then the closed discrete sets
$\beta \in E_{\alpha }$. Then the closed discrete sets ![]() $S$,
$S$, ![]() $S(\alpha ')$ are
$S(\alpha ')$ are ![]() $J^c$-convenient and do not satisfy the conclusion of the lemma, which is a contradiction, because
$J^c$-convenient and do not satisfy the conclusion of the lemma, which is a contradiction, because ![]() $|J|>k$.
$|J|>k$.
The proof of the proposition is by induction on the cardinality of ![]() $\operatorname {Ver}(S',S)$. Lemma 2.18 says that the proposition is true whenever
$\operatorname {Ver}(S',S)$. Lemma 2.18 says that the proposition is true whenever ![]() $|\!\operatorname {Ver}(S',S)|=1$. Let us assume that the proposition is true for all
$|\!\operatorname {Ver}(S',S)|=1$. Let us assume that the proposition is true for all ![]() $S$,
$S$, ![]() $S'$ such that
$S'$ such that
Let ![]() $S$,
$S$, ![]() $S'$ with
$S'$ with ![]() $|\!\operatorname {Ver}(S',S)|= m\geq 2$ be such that the proposition is false. Then there exists
$|\!\operatorname {Ver}(S',S)|= m\geq 2$ be such that the proposition is false. Then there exists ![]() $\alpha \in \operatorname {Ver}(S',S)$ such that for each
$\alpha \in \operatorname {Ver}(S',S)$ such that for each ![]() $i\in I^c$ there exists an edge
$i\in I^c$ there exists an edge ![]() $E_{\alpha }$ of
$E_{\alpha }$ of ![]() $\Gamma _{+}(S')$, not contained in
$\Gamma _{+}(S')$, not contained in ![]() $ {\mathbb {R}}_{\{i\}}$, that satisfies the following condition:
$ {\mathbb {R}}_{\{i\}}$, that satisfies the following condition:
() for all
 $\beta =(\beta _1,\ldots,\beta _n)\in \operatorname {Ver}(S)\cap E_{\alpha }$ we have
$\beta =(\beta _1,\ldots,\beta _n)\in \operatorname {Ver}(S)\cap E_{\alpha }$ we have  $\beta _i>1$;
$\beta _i>1$;
note that condition ![]() $(*)$ is vacuously true if
$(*)$ is vacuously true if
Observe that for each ![]() $\alpha '\in \operatorname {Ver}(S',S){\setminus} \{\alpha \}$, we have
$\alpha '\in \operatorname {Ver}(S',S){\setminus} \{\alpha \}$, we have ![]() $|\!\operatorname {Ver}(S',S(\alpha '))|=m-1$ and, by Corollary 2.11,
$|\!\operatorname {Ver}(S',S(\alpha '))|=m-1$ and, by Corollary 2.11, ![]() $\nu (S(\alpha '))=\nu (S')$.
$\nu (S(\alpha '))=\nu (S')$.
First, let us suppose that there exists ![]() $i\in I^c$ such that (1) does not hold for the corresponding edge
$i\in I^c$ such that (1) does not hold for the corresponding edge ![]() $E_\alpha$. Let us fix
$E_\alpha$. Let us fix ![]() $\alpha '\in \operatorname {Ver}(S',S){\setminus} \{\alpha \}$. Then
$\alpha '\in \operatorname {Ver}(S',S){\setminus} \{\alpha \}$. Then ![]() $E_\alpha$ connects
$E_\alpha$ connects ![]() $\alpha$ with a vertex
$\alpha$ with a vertex ![]() $\beta$ of
$\beta$ of ![]() $S$, hence
$S$, hence ![]() $\alpha '\notin E'$, where
$\alpha '\notin E'$, where ![]() $E'\subset E_{\alpha }$ is the line segment with endpoints
$E'\subset E_{\alpha }$ is the line segment with endpoints ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$. We obtain that the polyhedra
$\beta$. We obtain that the polyhedra ![]() $\Gamma _{+}(S(\alpha '))\subsetneqq \Gamma _{+}(S')$ do not satisfy the conclusion of the Proposition, which contradicts the induction hypothesis.
$\Gamma _{+}(S(\alpha '))\subsetneqq \Gamma _{+}(S')$ do not satisfy the conclusion of the Proposition, which contradicts the induction hypothesis.
Next, let us suppose that there exists ![]() $i\in I^c$ such that (1) is satisfied for the corresponding edge
$i\in I^c$ such that (1) is satisfied for the corresponding edge ![]() $E_\alpha$. Then
$E_\alpha$. Then ![]() $|E_{\alpha }\cap \operatorname {Ver}(S',S)|=2$. Now, take
$|E_{\alpha }\cap \operatorname {Ver}(S',S)|=2$. Now, take
such that ![]() $\alpha '\neq \alpha$. If
$\alpha '\neq \alpha$. If ![]() $\alpha '_i>1$, then the Newton polyhedra
$\alpha '_i>1$, then the Newton polyhedra
do not satisfy the Proposition and (1) does not hold, which is a contradiction. Hence, ![]() $\alpha '_i=1$. Let
$\alpha '_i=1$. Let ![]() $\epsilon >0$ be such that
$\epsilon >0$ be such that
Put
Then ![]() $\Gamma _{+}(S)\subsetneqq \Gamma _{+}(S(\alpha '_{\epsilon }))) \subsetneqq \Gamma _{+}(S(R)))\subsetneqq \Gamma _{+}(S')$.
$\Gamma _{+}(S)\subsetneqq \Gamma _{+}(S(\alpha '_{\epsilon }))) \subsetneqq \Gamma _{+}(S(R)))\subsetneqq \Gamma _{+}(S')$.
The closed discrete sets ![]() $S$,
$S$, ![]() $S(\alpha '_{\epsilon })$,
$S(\alpha '_{\epsilon })$, ![]() $S(R)$, and
$S(R)$, and ![]() $S'$ are convenient. We have
$S'$ are convenient. We have
Let us assume that ![]() $\epsilon$ is small enough so that there exists an edge
$\epsilon$ is small enough so that there exists an edge ![]() $E'_{\alpha }\ni \alpha$ of
$E'_{\alpha }\ni \alpha$ of ![]() $\Gamma (S(R))$ such that
$\Gamma (S(R))$ such that ![]() $\alpha '_{\epsilon }\in E'_{\alpha }$. Then the Newton polyhedra
$\alpha '_{\epsilon }\in E'_{\alpha }$. Then the Newton polyhedra ![]() $\Gamma _{+}(S) \subsetneqq \Gamma _{+}(S(R))$ satisfy the preceding case (namely,
$\Gamma _{+}(S) \subsetneqq \Gamma _{+}(S(R))$ satisfy the preceding case (namely, ![]() $\alpha '_i>1$). This completes the proof of the proposition.
$\alpha '_i>1$). This completes the proof of the proposition.
Corollary 2.19 Assume given two convenient closed discrete sets
such that ![]() $\Gamma _{+}(S)\subsetneqq \Gamma _{+}(S')$ and
$\Gamma _{+}(S)\subsetneqq \Gamma _{+}(S')$ and ![]() $\nu (S)=\nu (S')$. Assume that
$\nu (S)=\nu (S')$. Assume that
Then, for the ![]() $i\in I^c$ of Proposition 2.17 there exists an edge
$i\in I^c$ of Proposition 2.17 there exists an edge ![]() $E_{\alpha }$ of
$E_{\alpha }$ of ![]() $\Gamma (S')$, and
$\Gamma (S')$, and ![]() $(\beta _1,\ldots,\beta _n)\in E_{\alpha }\cap \operatorname {Ver}(S)$, such that
$(\beta _1,\ldots,\beta _n)\in E_{\alpha }\cap \operatorname {Ver}(S)$, such that ![]() $\beta _j=\delta _{ij}$,
$\beta _j=\delta _{ij}$, ![]() $j\in I^c$, where
$j\in I^c$, where ![]() $\delta _{ij}$ is the Kronecker delta.
$\delta _{ij}$ is the Kronecker delta.
Proof of the corollary By Proposition 2.17 there exists ![]() $i\in I^c$ such that for all the edges
$i\in I^c$ such that for all the edges ![]() $E_{\alpha }$ of
$E_{\alpha }$ of ![]() $\Gamma (S')$, not contained in
$\Gamma (S')$, not contained in ![]() $ {\mathbb {R}}_{\{i\}}$, there exists
$ {\mathbb {R}}_{\{i\}}$, there exists
such that ![]() $\beta _i=1$. As the set
$\beta _i=1$. As the set ![]() $S$ is convenient, there exists
$S$ is convenient, there exists ![]() $m>1$ such that
$m>1$ such that ![]() $me_i\in \operatorname {Ver}(S)$. Let
$me_i\in \operatorname {Ver}(S)$. Let ![]() $J=I\cup \{i\}$. As
$J=I\cup \{i\}$. As ![]() $\alpha,me_i\in {\mathbb {R}}^J$, there exists a chain of edges of
$\alpha,me_i\in {\mathbb {R}}^J$, there exists a chain of edges of ![]() $\Gamma (S')$ connecting
$\Gamma (S')$ connecting ![]() $\alpha$ with
$\alpha$ with ![]() $me_i$, contained in
$me_i$, contained in ![]() $ {\mathbb {R}}^J$. The edge
$ {\mathbb {R}}^J$. The edge ![]() $E_\alpha$ belonging to this chain and containing
$E_\alpha$ belonging to this chain and containing ![]() $\alpha$ satisfies the conclusion of the corollary.
$\alpha$ satisfies the conclusion of the corollary.
Remark 2.20 Using the same idea as in Corollary 2.19, but using Lemma 2.18 instead of Proposition 2.17, we can prove the following fact: let ![]() $I\subsetneqq \{1,\ldots,n\}$ and let
$I\subsetneqq \{1,\ldots,n\}$ and let ![]() $S\subset {\mathbb {R}}_{\geq 0}^{n}{\setminus} \{o\}$ be an
$S\subset {\mathbb {R}}_{\geq 0}^{n}{\setminus} \{o\}$ be an ![]() $I^c$-convenient closed discrete set. Let
$I^c$-convenient closed discrete set. Let ![]() $\alpha \in {\mathbb {R}}^I_{>0}$ be such that
$\alpha \in {\mathbb {R}}^I_{>0}$ be such that ![]() $\Gamma _{+}(S)\subsetneqq \Gamma _{+}(S(\alpha ))$, and
$\Gamma _{+}(S)\subsetneqq \Gamma _{+}(S(\alpha ))$, and ![]() $\nu (S)=\nu (S')$. Then for the
$\nu (S)=\nu (S')$. Then for the ![]() $i\in I^c$ of Lemma 2.18 there exists an edge
$i\in I^c$ of Lemma 2.18 there exists an edge ![]() $E_{\alpha }$ of
$E_{\alpha }$ of ![]() $\Gamma (S(\alpha ))$, and
$\Gamma (S(\alpha ))$, and ![]() $(\beta _1,\ldots,\beta _n)\in E_{\alpha }\cap \operatorname {Ver}(S)$, such that
$(\beta _1,\ldots,\beta _n)\in E_{\alpha }\cap \operatorname {Ver}(S)$, such that ![]() $\beta _j=\delta _{ij}$,
$\beta _j=\delta _{ij}$, ![]() $j\in I^c$, where
$j\in I^c$, where ![]() $\delta _{ij}$ is the Kronecker delta.
$\delta _{ij}$ is the Kronecker delta.
The following theorem generalizes to all dimensions the main theorem of [Reference Brzostowski, Krasiński and WalewskaBKW19]. In [Reference Brzostowski, Krasiński and WalewskaBKW19] this result is conjectured.
Definition 2.21 Let ![]() $S, S'\subset {\mathbb {R}}_{\geq 0}^{n}{\setminus} \{o\}$ be two closed discrete sets such that
$S, S'\subset {\mathbb {R}}_{\geq 0}^{n}{\setminus} \{o\}$ be two closed discrete sets such that
![]() $I\subsetneqq \{1,\ldots,n\}$ and
$I\subsetneqq \{1,\ldots,n\}$ and ![]() $\alpha \in \operatorname {Ver}(S',S)\cap {\mathbb {R}}_{>0}^{I}$. We say that
$\alpha \in \operatorname {Ver}(S',S)\cap {\mathbb {R}}_{>0}^{I}$. We say that ![]() $\alpha$ has an apex if there exists
$\alpha$ has an apex if there exists ![]() $i\in I^c$ and a unique edge
$i\in I^c$ and a unique edge ![]() $E_{\alpha }$ of
$E_{\alpha }$ of ![]() $\Gamma (S')$ that contains
$\Gamma (S')$ that contains ![]() $\alpha$, and is not contained in
$\alpha$, and is not contained in ![]() $ {\mathbb {R}}_{\{i\}}$.
$ {\mathbb {R}}_{\{i\}}$.
In this case the point ![]() $\beta \in \operatorname {Ver}(S)\cap E_{\alpha }$ adjacent to
$\beta \in \operatorname {Ver}(S)\cap E_{\alpha }$ adjacent to ![]() $\alpha$ in
$\alpha$ in ![]() $E_{\alpha }$ is called the apex of
$E_{\alpha }$ is called the apex of ![]() $\alpha$. We say that an apex,
$\alpha$. We say that an apex, ![]() $\beta :=(\beta _1,\ldots,\beta _n)$, is good if
$\beta :=(\beta _1,\ldots,\beta _n)$, is good if ![]() $\beta _j=\delta _{ij}$,
$\beta _j=\delta _{ij}$, ![]() $j\in I^c$.
$j\in I^c$.
Remark 2.22 Let ![]() $S\subset {\mathbb {R}}_{\geq 0}^{n}{\setminus} \{o\}$ be a convenient closed discrete set,
$S\subset {\mathbb {R}}_{\geq 0}^{n}{\setminus} \{o\}$ be a convenient closed discrete set,
and ![]() $\alpha \in {\mathbb {R}}_{>0}^I$ such that
$\alpha \in {\mathbb {R}}_{>0}^I$ such that ![]() $\Gamma _{+}(S)\subsetneqq \Gamma _{+}(S(\alpha ))$. The condition that
$\Gamma _{+}(S)\subsetneqq \Gamma _{+}(S(\alpha ))$. The condition that ![]() $\alpha$ has a good apex
$\alpha$ has a good apex ![]() $\beta \in {\mathbb {R}}^{I\cup \{i\}}_{>0}$,
$\beta \in {\mathbb {R}}^{I\cup \{i\}}_{>0}$, ![]() $i\in I^c$, is equivalent to
$i\in I^c$, is equivalent to ![]() $P:=\overline {\Gamma _{+}(S(\alpha )){\setminus} \Gamma _{+}(S)}$ being a pyramid with apex
$P:=\overline {\Gamma _{+}(S(\alpha )){\setminus} \Gamma _{+}(S)}$ being a pyramid with apex ![]() $\beta$ and base
$\beta$ and base ![]() $P\cap {\mathbb {R}}_{\{i\}}$.
$P\cap {\mathbb {R}}_{\{i\}}$.
Example 2.23 For example, in the case of the ![]() $\mu$-constant deformation of Briançon–Speder convenient version (see [Reference Briançon and SpederBS75]),
$\mu$-constant deformation of Briançon–Speder convenient version (see [Reference Briançon and SpederBS75]),
the pyramid is formed by the base with vertices ![]() $(5,0,0)$,
$(5,0,0)$, ![]() $(0,8,0)$,
$(0,8,0)$, ![]() $\alpha =(1,6,0)$, and the good apex
$\alpha =(1,6,0)$, and the good apex ![]() $\beta =(0,7,1)$. Note that the vertices
$\beta =(0,7,1)$. Note that the vertices ![]() $(5,0,0)$,
$(5,0,0)$, ![]() $(0,7,1)$,
$(0,7,1)$, ![]() $(1,6,0)$,
$(1,6,0)$, ![]() $(0,0,15)$ are coplanar.
$(0,0,15)$ are coplanar.
Remark 2.24 The element ![]() $i\in I^{c}$ of condition (ii) of Definition 2.21 may not be unique, and the edge
$i\in I^{c}$ of condition (ii) of Definition 2.21 may not be unique, and the edge ![]() $E_{\alpha }$ is unique only for the chosen
$E_{\alpha }$ is unique only for the chosen ![]() $i$. For example, if
$i$. For example, if ![]() $S=\{(2,0,0),(0,2,0), (1,0,1), (0,1,1), (0,0,3)\}$ and
$S=\{(2,0,0),(0,2,0), (1,0,1), (0,1,1), (0,0,3)\}$ and ![]() $\alpha =(0,0,2)$, we have
$\alpha =(0,0,2)$, we have ![]() $I=\{3\}$.
$I=\{3\}$.
If ![]() $i=1$, the unique edge
$i=1$, the unique edge ![]() $E_{\alpha }$ is the segment between the point
$E_{\alpha }$ is the segment between the point ![]() $\alpha =(0,0,2)$ and the good apex
$\alpha =(0,0,2)$ and the good apex ![]() $\beta =(1,0,1)$.
$\beta =(1,0,1)$.
If ![]() $i=2$, the unique edge
$i=2$, the unique edge ![]() $E_{\alpha }$ is the segment between the point
$E_{\alpha }$ is the segment between the point ![]() $\alpha =(0,0,2)$ and the good apex
$\alpha =(0,0,2)$ and the good apex ![]() $\beta =(0,1,1)$.
$\beta =(0,1,1)$.
Theorem 2.25 Let ![]() $S, S'\subset {\mathbb {R}}_{\geq 0}^{n}{\setminus} \{o\}$ be two convenient closed discrete sets such that
$S, S'\subset {\mathbb {R}}_{\geq 0}^{n}{\setminus} \{o\}$ be two convenient closed discrete sets such that ![]() $\Gamma _{+}(S)\subsetneqq \Gamma _{+}(S')$. Then
$\Gamma _{+}(S)\subsetneqq \Gamma _{+}(S')$. Then ![]() $\nu (S)=\nu (S')$ if and only if each
$\nu (S)=\nu (S')$ if and only if each ![]() $\alpha \in \operatorname {Ver}(S',S)$ has a good apex.
$\alpha \in \operatorname {Ver}(S',S)$ has a good apex.
Proof. First we prove the following Lemma.
Lemma 2.26 Let ![]() $S\subset {\mathbb {R}}_{\geq 0}^{n}{\setminus} \{o\}$ be a closed discrete set and
$S\subset {\mathbb {R}}_{\geq 0}^{n}{\setminus} \{o\}$ be a closed discrete set and ![]() $\alpha \in {\mathbb {R}}_{>0}^I$,
$\alpha \in {\mathbb {R}}_{>0}^I$, ![]() $I\subsetneqq \{1,\ldots,n\}$, such that
$I\subsetneqq \{1,\ldots,n\}$, such that ![]() $\Gamma _{+}(S)\subsetneqq \Gamma _{+}(S(\alpha ))$, and
$\Gamma _{+}(S)\subsetneqq \Gamma _{+}(S(\alpha ))$, and ![]() $\alpha$ has a good apex. Then
$\alpha$ has a good apex. Then
Proof of Lemma 2.26 Let ![]() $\beta$ be a good apex of
$\beta$ be a good apex of ![]() $\alpha$. Let
$\alpha$. Let ![]() $i\in I^c$ be such that
$i\in I^c$ be such that ![]() $\beta \in {\mathbb {R}}_{>0}^{I\cup \{i\}}$.
$\beta \in {\mathbb {R}}_{>0}^{I\cup \{i\}}$.
Given an element ![]() $m\in \{1,\dots,n\}$ and
$m\in \{1,\dots,n\}$ and ![]() $J\subset \{1,\ldots,n\}$ such that
$J\subset \{1,\ldots,n\}$ such that ![]() $|J|=m$, we use the notation
$|J|=m$, we use the notation
As ![]() $\alpha \in {\mathbb {R}}^{I}_{>0}$, we have
$\alpha \in {\mathbb {R}}^{I}_{>0}$, we have
 \begin{align*} \nu(S(\alpha))-\nu(S)&= \sum_{m=|I|}^{n}(-1)^{m} \sum _{\substack{|J|=m\\ I\subset J}}|J|!V_{m}(\alpha,J)\\ &= \sum_{m=|I|}^{n-1}(-1)^{m}\sum_{\substack{|J|=m\\ i\notin J, I\subset J}} (|J|!V_{m}(\alpha,J)-(|J|+1)!V_{m+1}(\alpha,J\cup\{i\})). \end{align*}
\begin{align*} \nu(S(\alpha))-\nu(S)&= \sum_{m=|I|}^{n}(-1)^{m} \sum _{\substack{|J|=m\\ I\subset J}}|J|!V_{m}(\alpha,J)\\ &= \sum_{m=|I|}^{n-1}(-1)^{m}\sum_{\substack{|J|=m\\ i\notin J, I\subset J}} (|J|!V_{m}(\alpha,J)-(|J|+1)!V_{m+1}(\alpha,J\cup\{i\})). \end{align*}
As the apex of ![]() $\alpha$ is good, we obtain
$\alpha$ is good, we obtain
which implies that ![]() $\nu (S)=\nu (S(\alpha ))$.
$\nu (S)=\nu (S(\alpha ))$.
Now we prove that if each ![]() $\alpha \in \operatorname {Ver}(S',S)$ has a good apex, then
$\alpha \in \operatorname {Ver}(S',S)$ has a good apex, then
The proof is by induction on the cardinality of ![]() $\operatorname {Ver}(S',S)$. Let us assume that the implication is true for all
$\operatorname {Ver}(S',S)$. Let us assume that the implication is true for all ![]() $S$ and
$S$ and ![]() $S'$ such that
$S'$ such that ![]() $|\!\operatorname {Ver}(S',S)|< m$. To verify the implication for
$|\!\operatorname {Ver}(S',S)|< m$. To verify the implication for ![]() $|\!\operatorname {Ver}(S',S)|=m$, let
$|\!\operatorname {Ver}(S',S)|=m$, let ![]() $\alpha \in \operatorname {Ver}(S',S)$ and
$\alpha \in \operatorname {Ver}(S',S)$ and ![]() $R=\operatorname {Ver}(S',S){\setminus} \{\alpha \}$. By the induction hypothesis
$R=\operatorname {Ver}(S',S){\setminus} \{\alpha \}$. By the induction hypothesis ![]() $\nu (S(R))=\nu (S)$ and by Lemma 2.26 we have
$\nu (S(R))=\nu (S)$ and by Lemma 2.26 we have ![]() $\nu (S')=\nu (S(R))$. This proves that
$\nu (S')=\nu (S(R))$. This proves that ![]() $\nu (S')=\nu (S)$.
$\nu (S')=\nu (S)$.
To finish the proof of the theorem we need the following lemma.
Lemma 2.27 Let ![]() $S\subset {\mathbb {R}}_{\geq 0}^{n}{\setminus} \{o\}$ be a closed discrete set and let
$S\subset {\mathbb {R}}_{\geq 0}^{n}{\setminus} \{o\}$ be a closed discrete set and let ![]() $\alpha \in {\mathbb {R}}_{>0}^I$,
$\alpha \in {\mathbb {R}}_{>0}^I$, ![]() $I\subsetneqq \{1,\ldots,n\}$, be such that
$I\subsetneqq \{1,\ldots,n\}$, be such that ![]() $\Gamma _{+}(S)\subsetneqq \Gamma _{+}(S(\alpha ))$. Let us suppose that
$\Gamma _{+}(S)\subsetneqq \Gamma _{+}(S(\alpha ))$. Let us suppose that ![]() $S(\alpha )$ is
$S(\alpha )$ is ![]() $I^c$-convenient and that
$I^c$-convenient and that ![]() $\nu (S(\alpha ))=\nu (S)$. Then
$\nu (S(\alpha ))=\nu (S)$. Then ![]() $\alpha$ has a good apex.
$\alpha$ has a good apex.
Proof of Lemma 2.27 Let ![]() $i\in I^c$ be as in Remark 2.20. Then there exists
$i\in I^c$ be as in Remark 2.20. Then there exists ![]() $E_{\alpha }$ of
$E_{\alpha }$ of ![]() $\Gamma (S(\alpha ))$, and
$\Gamma (S(\alpha ))$, and ![]() $\beta :=(\beta _1,\ldots,\beta _n)\in E_{\alpha }\cap \operatorname {Ver}(S)$, such that
$\beta :=(\beta _1,\ldots,\beta _n)\in E_{\alpha }\cap \operatorname {Ver}(S)$, such that ![]() $\beta _j=\delta _{ij}$,
$\beta _j=\delta _{ij}$, ![]() $j\in I^c$. We want to prove that
$j\in I^c$. We want to prove that ![]() $\beta$ is a (necessarily good) apex of
$\beta$ is a (necessarily good) apex of ![]() $\alpha$. Let us assume that
$\alpha$. Let us assume that ![]() $\beta$ is not an apex of
$\beta$ is not an apex of ![]() $\alpha$, aiming for contradiction. Then there exits another edge
$\alpha$, aiming for contradiction. Then there exits another edge ![]() $\alpha \in E'_{\alpha }$ de
$\alpha \in E'_{\alpha }$ de ![]() $\Gamma (S(\alpha ))$, and
$\Gamma (S(\alpha ))$, and ![]() $\beta ':=(\beta '_1,\ldots,\beta '_n)\in E'_{\alpha }\cap \operatorname {Ver}(S)$ adjacent to
$\beta ':=(\beta '_1,\ldots,\beta '_n)\in E'_{\alpha }\cap \operatorname {Ver}(S)$ adjacent to ![]() $\alpha$ in
$\alpha$ in ![]() $E'_{\alpha }$ such that
$E'_{\alpha }$ such that ![]() $\beta '_i=1$.
$\beta '_i=1$.
Let us consider ![]() $\beta '_{\epsilon }:= \beta '+\epsilon e_i$, and the closed discrete set
$\beta '_{\epsilon }:= \beta '+\epsilon e_i$, and the closed discrete set ![]() $S^{\epsilon }=(S{\setminus} \{\beta '\})\cup \{\beta '_{\epsilon }\}$,
$S^{\epsilon }=(S{\setminus} \{\beta '\})\cup \{\beta '_{\epsilon }\}$, ![]() $\epsilon > 0$. Let us assume that
$\epsilon > 0$. Let us assume that ![]() $\epsilon$ is small enough so that:
$\epsilon$ is small enough so that:
(i)
 $\operatorname {Ver}(S^{\epsilon })=(\operatorname {Ver}(S){\setminus} \{\beta '\})\cup \{\beta '_{\epsilon }\}$;
$\operatorname {Ver}(S^{\epsilon })=(\operatorname {Ver}(S){\setminus} \{\beta '\})\cup \{\beta '_{\epsilon }\}$;(ii) there exists an edge
 $E_{\alpha }^{\epsilon }$ of
$E_{\alpha }^{\epsilon }$ of  $\Gamma (S^{\epsilon }(\alpha ))$ such that
$\Gamma (S^{\epsilon }(\alpha ))$ such that  $\beta _{\epsilon }\in E_{\alpha }^{\epsilon }\cap \operatorname {Ver}(S^{\epsilon })$ is adjacent to
$\beta _{\epsilon }\in E_{\alpha }^{\epsilon }\cap \operatorname {Ver}(S^{\epsilon })$ is adjacent to  $\alpha$ in
$\alpha$ in  $E_{\alpha }^{\epsilon }$.
$E_{\alpha }^{\epsilon }$.
Let ![]() $P^{\epsilon }=\overline {(\Gamma _{+}(S^{\epsilon }(\alpha ){\setminus} \Gamma _{+}(S^{\epsilon }))}$. Let
$P^{\epsilon }=\overline {(\Gamma _{+}(S^{\epsilon }(\alpha ){\setminus} \Gamma _{+}(S^{\epsilon }))}$. Let ![]() $Q_{0}$ be the convex hull of the set
$Q_{0}$ be the convex hull of the set
(observe that ![]() $Q_0$ does not depend on
$Q_0$ does not depend on ![]() $\epsilon$) and
$\epsilon$) and ![]() $Q^{\epsilon }_1:=\overline {P^{\epsilon }{\setminus} Q_0}$. Recall that
$Q^{\epsilon }_1:=\overline {P^{\epsilon }{\setminus} Q_0}$. Recall that ![]() $\beta$ satisfies
$\beta$ satisfies ![]() $\beta _j=\delta _{ij}$,
$\beta _j=\delta _{ij}$, ![]() $j\in I^c$. Then, using the same idea as in the proof of Lemma 2.26 we obtain
$j\in I^c$. Then, using the same idea as in the proof of Lemma 2.26 we obtain ![]() $\nu (Q_0)=0$. As
$\nu (Q_0)=0$. As ![]() $\dim (Q_{0}^{J}\cap (Q^{\epsilon }_1)^{J} )<|J|$ for all
$\dim (Q_{0}^{J}\cap (Q^{\epsilon }_1)^{J} )<|J|$ for all ![]() $J\subset \{1,\ldots,n\}$, we have
$J\subset \{1,\ldots,n\}$, we have
As ![]() $S^{\epsilon }(\alpha )$ is
$S^{\epsilon }(\alpha )$ is ![]() $I^c$-convenient,
$I^c$-convenient, ![]() $Q^{\epsilon }_1$ satisfies the hypotheses of Proposition 2.6 (to prove this statement use the same idea as in the proof of Proposition 2.14). Let us consider the sequence
$Q^{\epsilon }_1$ satisfies the hypotheses of Proposition 2.6 (to prove this statement use the same idea as in the proof of Proposition 2.14). Let us consider the sequence
and the polyhedra ![]() $Z^{\epsilon }_{j}$,
$Z^{\epsilon }_{j}$, ![]() $1\leq j\leq m$, such that:
$1\leq j\leq m$, such that:
(i)
 $Q^{\epsilon }_1=\bigcup _{j=1}^{m}Z^{\epsilon }_{j}$;
$Q^{\epsilon }_1=\bigcup _{j=1}^{m}Z^{\epsilon }_{j}$;(ii)
 $\nu (Q^{\epsilon }_1)=\sum _{j=1}^{m}\nu (Z^{\epsilon }_{j})$;
$\nu (Q^{\epsilon }_1)=\sum _{j=1}^{m}\nu (Z^{\epsilon }_{j})$;(iii)
 $\nu (Z^{\epsilon }_{j})=|I_{j}|!V_{|I_{j}|}((Z^{\epsilon }_{j})^{I_{j}}) \nu (\pi _{I_{j}}(Z^{\epsilon }_{j}))\geq 0$;
$\nu (Z^{\epsilon }_{j})=|I_{j}|!V_{|I_{j}|}((Z^{\epsilon }_{j})^{I_{j}}) \nu (\pi _{I_{j}}(Z^{\epsilon }_{j}))\geq 0$;
(the existence of these objects is given by Proposition 2.6). For each ![]() $j$,
$j$, ![]() $1\le j\le m$, we may choose the family
$1\le j\le m$, we may choose the family ![]() $Z_j^\epsilon$ of polyhedra to vary continuously with
$Z_j^\epsilon$ of polyhedra to vary continuously with ![]() $\epsilon$. More precisely, we can choose the
$\epsilon$. More precisely, we can choose the ![]() $Z_j^\epsilon$ to satisfy the following additional condition: for each
$Z_j^\epsilon$ to satisfy the following additional condition: for each ![]() $j$,
$j$, ![]() $1\le j\le m$, either
$1\le j\le m$, either ![]() $Z_j^\epsilon =Z_j^0$ for all small
$Z_j^\epsilon =Z_j^0$ for all small ![]() $\epsilon$ or
$\epsilon$ or ![]() $\operatorname {Ver}(Z_j^\epsilon )$ differs from
$\operatorname {Ver}(Z_j^\epsilon )$ differs from ![]() $\operatorname {Ver}(Z_j^0)$ in exactly one element,
$\operatorname {Ver}(Z_j^0)$ in exactly one element, ![]() $\beta '_\epsilon \ne \beta '$, for all small
$\beta '_\epsilon \ne \beta '$, for all small ![]() $\epsilon >0$. As
$\epsilon >0$. As ![]() $i\in I_j$, we have
$i\in I_j$, we have ![]() $\pi _{I_j}( \beta '_{\epsilon })=\pi _{I_j}(\beta ')$. This implies that
$\pi _{I_j}( \beta '_{\epsilon })=\pi _{I_j}(\beta ')$. This implies that ![]() $\nu (\pi _{I_{j}}(Z^{\epsilon }_{j}))$ is independent of
$\nu (\pi _{I_{j}}(Z^{\epsilon }_{j}))$ is independent of ![]() $\epsilon$ for all
$\epsilon$ for all ![]() $1\leq {j}\leq m$. For
$1\leq {j}\leq m$. For ![]() $\epsilon =0$, we have
$\epsilon =0$, we have
Hence, ![]() $\nu (P^{\epsilon })=\nu (Q_1^{\epsilon })=0$ for
$\nu (P^{\epsilon })=\nu (Q_1^{\epsilon })=0$ for ![]() $\epsilon$ small enough. Then there exists a set
$\epsilon$ small enough. Then there exists a set ![]() $J$,
$J$, ![]() $\{i\}\cup I\subset J\subset \{1,2,\ldots,n\}$, such that the edge
$\{i\}\cup I\subset J\subset \{1,2,\ldots,n\}$, such that the edge ![]() $E^{\epsilon }_{\alpha }$ is strictly
$E^{\epsilon }_{\alpha }$ is strictly ![]() $(I,J)$-convenient. By Proposition 2.14, given
$(I,J)$-convenient. By Proposition 2.14, given ![]() $\alpha '\in \overline {\Gamma _{+}(S^{\epsilon }(\alpha )){\setminus} \Gamma _{+}(S^\epsilon )}\cap {\mathbb {R}}_{>0}^J$ we have
$\alpha '\in \overline {\Gamma _{+}(S^{\epsilon }(\alpha )){\setminus} \Gamma _{+}(S^\epsilon )}\cap {\mathbb {R}}_{>0}^J$ we have
This proves that ![]() $|I|< n-1$: indeed, if
$|I|< n-1$: indeed, if ![]() $|I|=n-1$, then
$|I|=n-1$, then ![]() $\alpha '\in {\mathbb {R}}_{>0}^n$, which contradicts Corollary 2.10.
$\alpha '\in {\mathbb {R}}_{>0}^n$, which contradicts Corollary 2.10.
Let ![]() $r$ be the largest element of
$r$ be the largest element of ![]() $\{1,\ldots,n-1\}$ such that the lemma is true for all
$\{1,\ldots,n-1\}$ such that the lemma is true for all ![]() $I$ such that
$I$ such that ![]() $|I|>r$. Now let us assume that
$|I|>r$. Now let us assume that ![]() $|I|=r$. Let us choose
$|I|=r$. Let us choose ![]() $\alpha '$ sufficiently close to
$\alpha '$ sufficiently close to ![]() $\alpha$ so that for each edge
$\alpha$ so that for each edge ![]() $E_{\alpha '}$ of
$E_{\alpha '}$ of ![]() $\Gamma (S^{\epsilon }(\alpha '))$ and
$\Gamma (S^{\epsilon }(\alpha '))$ and
adjacent to ![]() $\alpha '$ in
$\alpha '$ in ![]() $E_{\alpha '}$, there exists an edge
$E_{\alpha '}$, there exists an edge ![]() $E_{\alpha }$ of
$E_{\alpha }$ of ![]() $\Gamma (S^{\epsilon }(\alpha ))$ such that
$\Gamma (S^{\epsilon }(\alpha ))$ such that ![]() $\beta \in E_{\alpha }$. This implies that
$\beta \in E_{\alpha }$. This implies that ![]() $\alpha '$ does not have a good apex, which contradicts the choice of
$\alpha '$ does not have a good apex, which contradicts the choice of ![]() $r$, since
$r$, since ![]() $|J|>r$. This completes the proof of the lemma.
$|J|>r$. This completes the proof of the lemma.
Now we can finish the proof of the theorem. We prove that if
then each ![]() $\alpha \in \operatorname {Ver}(S',S)$ has a good apex. The proof is by induction on the cardinality of
$\alpha \in \operatorname {Ver}(S',S)$ has a good apex. The proof is by induction on the cardinality of ![]() $\operatorname {Ver}(S',S)$. Lemma 2.27 shows that the implication is true for
$\operatorname {Ver}(S',S)$. Lemma 2.27 shows that the implication is true for ![]() $|\!\operatorname {Ver}(S',S)|=1$. Let us assume that this is true for every pair
$|\!\operatorname {Ver}(S',S)|=1$. Let us assume that this is true for every pair ![]() $(S,S')$ of convenient closed discrete sets such that
$(S,S')$ of convenient closed discrete sets such that ![]() $|\!\operatorname {Ver}(S',S)|< m$. Let us prove the result for
$|\!\operatorname {Ver}(S',S)|< m$. Let us prove the result for ![]() $|\!\operatorname {Ver}(S',S)|=m$. Let
$|\!\operatorname {Ver}(S',S)|=m$. Let ![]() $\alpha \in \operatorname {Ver}(S',S)$,
$\alpha \in \operatorname {Ver}(S',S)$, ![]() $R=\operatorname {Ver}(S',S){\setminus} \{\alpha \}$ and
$R=\operatorname {Ver}(S',S){\setminus} \{\alpha \}$ and ![]() $\alpha _{\epsilon }=(1+\epsilon )\alpha$, where
$\alpha _{\epsilon }=(1+\epsilon )\alpha$, where ![]() $\epsilon >0$. Then
$\epsilon >0$. Then
By Corollary 2.5 we have ![]() $\nu (S(\alpha _{\epsilon })(R))=\nu (S(\alpha _{\epsilon }))$. Observe that
$\nu (S(\alpha _{\epsilon })(R))=\nu (S(\alpha _{\epsilon }))$. Observe that
By the induction hypothesis, each ![]() $\alpha '\in R$ has a good apex
$\alpha '\in R$ has a good apex ![]() $\beta \in \operatorname {Ver}(S(\alpha _{\epsilon }))$ for the inclusion
$\beta \in \operatorname {Ver}(S(\alpha _{\epsilon }))$ for the inclusion ![]() $\Gamma _{+}(S(\alpha _{\epsilon }))\subsetneqq \Gamma _{+}(S(\alpha _{\epsilon })(R))$ of Newton polyhedra. As all the non-zero coordinates of
$\Gamma _{+}(S(\alpha _{\epsilon }))\subsetneqq \Gamma _{+}(S(\alpha _{\epsilon })(R))$ of Newton polyhedra. As all the non-zero coordinates of ![]() $\alpha _\epsilon$ are strictly greater than one, we have
$\alpha _\epsilon$ are strictly greater than one, we have ![]() $\beta \neq \alpha _{\epsilon }$, so that
$\beta \neq \alpha _{\epsilon }$, so that ![]() $\beta \in \operatorname {Ver}(S)$. We take
$\beta \in \operatorname {Ver}(S)$. We take ![]() $\epsilon$ small enough so that for every
$\epsilon$ small enough so that for every ![]() $\alpha '\in R$ every edge
$\alpha '\in R$ every edge ![]() $E_{\alpha '}$ of
$E_{\alpha '}$ of ![]() $\Gamma (S(\alpha _{\epsilon })(R))$ that connects
$\Gamma (S(\alpha _{\epsilon })(R))$ that connects ![]() $\alpha '$ with a vertex in
$\alpha '$ with a vertex in ![]() $\operatorname {Ver}(S)$ is an edge of
$\operatorname {Ver}(S)$ is an edge of ![]() $\Gamma (S')$. Thus, every
$\Gamma (S')$. Thus, every ![]() $\alpha '\in R$ has a good apex for the inclusion
$\alpha '\in R$ has a good apex for the inclusion
of Newton polyhedra.
Now it suffices to verify that ![]() $\alpha$ has a good apex for the inclusion
$\alpha$ has a good apex for the inclusion
of Newton polyhedra. Let ![]() $\epsilon >0$ and put
$\epsilon >0$ and put ![]() $R_{\epsilon }:=\{(1+\epsilon )\alpha ': \alpha '\in R\}$. Then
$R_{\epsilon }:=\{(1+\epsilon )\alpha ': \alpha '\in R\}$. Then
By Corollary 2.5 we have ![]() $\nu (S(R_{\epsilon }))=\nu (S(R_{\epsilon })(\alpha ))=\nu (S)$. Observe that
$\nu (S(R_{\epsilon }))=\nu (S(R_{\epsilon })(\alpha ))=\nu (S)$. Observe that ![]() $\operatorname {Ver}(S(R_{\epsilon })(\alpha ), S(R_{\epsilon }))=\{\alpha \}$. By Lemma 2.27,
$\operatorname {Ver}(S(R_{\epsilon })(\alpha ), S(R_{\epsilon }))=\{\alpha \}$. By Lemma 2.27, ![]() $\alpha$ has a good apex
$\alpha$ has a good apex
As every non-zero coordinate of every element of ![]() $R_\epsilon$ is strictly greater than one, we have
$R_\epsilon$ is strictly greater than one, we have ![]() $\beta \notin R_{\epsilon }$, so that
$\beta \notin R_{\epsilon }$, so that ![]() $\beta \in \operatorname {Ver}(S)$. Take
$\beta \in \operatorname {Ver}(S)$. Take ![]() $\epsilon$ small enough so that every edge
$\epsilon$ small enough so that every edge ![]() $E_{\alpha }$ of
$E_{\alpha }$ of ![]() $\Gamma (S(R_{\epsilon })(\alpha ))$ that connects
$\Gamma (S(R_{\epsilon })(\alpha ))$ that connects ![]() $\alpha$ with a vertex in
$\alpha$ with a vertex in ![]() $\operatorname {Ver}(S)$ is an edge of
$\operatorname {Ver}(S)$ is an edge of ![]() $\Gamma (S')$. Then
$\Gamma (S')$. Then ![]() $\beta$ is a good apex of
$\beta$ is a good apex of ![]() $\alpha$ for the inclusion (2), as desired. This completes the proof of the theorem.
$\alpha$ for the inclusion (2), as desired. This completes the proof of the theorem.
We end this section by recalling a result that relates the Milnor number to the Newton number.
If the formal power series ![]() $g$ is not convenient, we can define the Newton number
$g$ is not convenient, we can define the Newton number ![]() $\nu (g)$ of
$\nu (g)$ of ![]() $g$ (
$g$ (![]() $\nu (g)$ could be
$\nu (g)$ could be ![]() $\infty$) in the following way. Let
$\infty$) in the following way. Let ![]() $\mathcal {E'}\subset \mathcal {E}$ such that there does not exist
$\mathcal {E'}\subset \mathcal {E}$ such that there does not exist ![]() $m\in {\mathbb {Z}}_{>0}$, such that
$m\in {\mathbb {Z}}_{>0}$, such that ![]() $me\in \operatorname {Ver}(g)$. We define the Newton number of
$me\in \operatorname {Ver}(g)$. We define the Newton number of ![]() $g$ as
$g$ as
where ![]() $\mathcal {E'}_m:=\{me:e\in \mathcal {E'}\}$.
$\mathcal {E'}_m:=\{me:e\in \mathcal {E'}\}$.
Theorem 2.28 [Reference KouchnirenkoKou76]
Let ![]() $h\in \mathcal {O}_{n+1}^x$. Then
$h\in \mathcal {O}_{n+1}^x$. Then ![]() $\mu ( h ) \geq \nu ( h )$. Moreover,
$\mu ( h ) \geq \nu ( h )$. Moreover, ![]() $\mu ( h ) = \nu ( h )$ if
$\mu ( h ) = \nu ( h )$ if ![]() $h$ is non-degenerate.
$h$ is non-degenerate.
Remark 2.29 Let ![]() $h\in \mathcal {O}_{n+1}^x$ be non-degenerate and convenient. Then
$h\in \mathcal {O}_{n+1}^x$ be non-degenerate and convenient. Then ![]() $\mu (h)<\infty$, which implies that
$\mu (h)<\infty$, which implies that ![]() $h$ has, at most, an isolated singularity in the origin
$h$ has, at most, an isolated singularity in the origin ![]() $o$.
$o$.
Example 2.30 Consider the following families of non-degenerate deformations:
Observe that ![]() $F^1$ is a
$F^1$ is a ![]() $\mu$-constant deformation of Briançon–Speder (convenient version), see [Reference Briançon and SpederBS75]. By virtue of Theorem 2.28 and Proposition 2.9, for each
$\mu$-constant deformation of Briançon–Speder (convenient version), see [Reference Briançon and SpederBS75]. By virtue of Theorem 2.28 and Proposition 2.9, for each ![]() $\lambda \geq 1$ the deformation
$\lambda \geq 1$ the deformation ![]() $F^{\lambda }$ is
$F^{\lambda }$ is ![]() $\mu$-constant.
$\mu$-constant.
3. Characterization of Newton non-degenerate  $\mu$-constant deformations
$\mu$-constant deformations
First, let us recall some information regarding the Newton fan and toric varieties. Given ![]() $S\subset {\mathbb {Z}}_{\geq 0}^{n+1}{\setminus} \{o\}$, consider the support function
$S\subset {\mathbb {Z}}_{\geq 0}^{n+1}{\setminus} \{o\}$, consider the support function
where ![]() $\Delta := {\mathbb {R}}^{n+1}_{\geq 0}$ is the standard cone and
$\Delta := {\mathbb {R}}^{n+1}_{\geq 0}$ is the standard cone and ![]() $\langle \cdot,\cdot \rangle$ is the standard scalar product. Let
$\langle \cdot,\cdot \rangle$ is the standard scalar product. Let ![]() $1\leq i\leq n$ and let
$1\leq i\leq n$ and let ![]() $F$ be an
$F$ be an ![]() $i$-dimensional face of the Newton polyhedron
$i$-dimensional face of the Newton polyhedron ![]() $\Gamma _{+}(S)$. The set
$\Gamma _{+}(S)$. The set ![]() $\sigma _F := \{\alpha \in \Delta : \langle \alpha, p\rangle = {\operatorname {h}}_{\Gamma _{+}(S)}(\alpha ),\; \forall p \in F \}$ is a cone, and
$\sigma _F := \{\alpha \in \Delta : \langle \alpha, p\rangle = {\operatorname {h}}_{\Gamma _{+}(S)}(\alpha ),\; \forall p \in F \}$ is a cone, and ![]() $\Gamma ^{\star }(S):=\{\sigma _F : F \text { is a face of } \Gamma _{+}(S)\}$ is a subdivision of the fan
$\Gamma ^{\star }(S):=\{\sigma _F : F \text { is a face of } \Gamma _{+}(S)\}$ is a subdivision of the fan ![]() $\Delta$ (by abuse of notation we denote by
$\Delta$ (by abuse of notation we denote by ![]() $\Delta$ the fan induced by the standard cone
$\Delta$ the fan induced by the standard cone ![]() $\Delta$). The fan
$\Delta$). The fan ![]() $\Gamma ^{\star }(S)$ is called the Newton fan of
$\Gamma ^{\star }(S)$ is called the Newton fan of ![]() $S$. Given a formal power series
$S$. Given a formal power series ![]() $g$, we define
$g$, we define ![]() $\Gamma ^{\star }(g):= \Gamma ^{\star }(\operatorname {Supp}(g))$.
$\Gamma ^{\star }(g):= \Gamma ^{\star }(\operatorname {Supp}(g))$.
Let ![]() be a strict face of the standard cone
be a strict face of the standard cone ![]() $\Delta$ and
$\Delta$ and ![]() $(\Delta ')^{\circ }$ its interior relative to
$(\Delta ')^{\circ }$ its interior relative to ![]() $\Delta '$. Observe that if there exists
$\Delta '$. Observe that if there exists ![]() $\alpha \in (\Delta ')^{\circ }$ such that
$\alpha \in (\Delta ')^{\circ }$ such that ![]() $ {\operatorname {h}}_{\Gamma _{+}(\alpha )}=0$, then
$ {\operatorname {h}}_{\Gamma _{+}(\alpha )}=0$, then ![]() $\Delta '$ is a cone of the fan
$\Delta '$ is a cone of the fan ![]() $\Gamma ^{\star }(S)$. We say that
$\Gamma ^{\star }(S)$. We say that ![]() $\Sigma$ is an admissible subdivision of
$\Sigma$ is an admissible subdivision of ![]() $\Gamma ^{\star }(S)$ if
$\Gamma ^{\star }(S)$ if ![]() $\Sigma$ is a subdivision that preserves the above property, which is to say that if there exists
$\Sigma$ is a subdivision that preserves the above property, which is to say that if there exists ![]() $\alpha \in (\Delta ')^{\circ }$ such that
$\alpha \in (\Delta ')^{\circ }$ such that ![]() $ {\operatorname {h}}_{\Gamma _{+}(S)}(\alpha )=0$, then
$ {\operatorname {h}}_{\Gamma _{+}(S)}(\alpha )=0$, then ![]() $\Delta '\in \Sigma$. In the case that the closed discrete set
$\Delta '\in \Sigma$. In the case that the closed discrete set ![]() $S$ is convenient, an admissible subdivision of
$S$ is convenient, an admissible subdivision of ![]() $\Gamma ^{\star }(S)$ is a fan where there are no subdivisions of strict faces of
$\Gamma ^{\star }(S)$ is a fan where there are no subdivisions of strict faces of ![]() $\Delta$.
$\Delta$.
Given a fan ![]() $\Sigma$, we denote by
$\Sigma$, we denote by ![]() $X_{\Sigma }$ the toric variety associated to it. Given
$X_{\Sigma }$ the toric variety associated to it. Given ![]() $\sigma \in \Sigma$, we denote by
$\sigma \in \Sigma$, we denote by ![]() $X_{\sigma }$ the open affine of
$X_{\sigma }$ the open affine of ![]() $X_{\Sigma }$ associated with the cone
$X_{\Sigma }$ associated with the cone ![]() $\sigma$. Let
$\sigma$. Let ![]() $\Sigma '$ be a subdivision of
$\Sigma '$ be a subdivision of ![]() $\Sigma$. It is known that there exists a proper, birational and equivariant morphism
$\Sigma$. It is known that there exists a proper, birational and equivariant morphism ![]() $\pi :X_{\Sigma '}\rightarrow X_{\Sigma }$, induced by the subdivision. Given
$\pi :X_{\Sigma '}\rightarrow X_{\Sigma }$, induced by the subdivision. Given ![]() $\sigma '\in \Sigma '$, we write
$\sigma '\in \Sigma '$, we write ![]() $\pi _{\sigma '}:=\pi |_{X_{\sigma '}}$.
$\pi _{\sigma '}:=\pi |_{X_{\sigma '}}$.
Now we use the notation from § 1.0.1. Let ![]() $V$ be a hypersurface of
$V$ be a hypersurface of ![]() $ {\mathbb {C}}^{n+1}_o$ having a unique isolated singularity at the point
$ {\mathbb {C}}^{n+1}_o$ having a unique isolated singularity at the point ![]() $o$. Let us assume that
$o$. Let us assume that ![]() $V$ is given by the equation
$V$ is given by the equation ![]() $f(x)=0$, where
$f(x)=0$, where ![]() $f\in {\mathcal {O}_{n+1}^{x}}$ is irreducible, and let
$f\in {\mathcal {O}_{n+1}^{x}}$ is irreducible, and let ![]() $\varrho :W\rightarrow {\mathbb {C}}^{m}_o$ be a deformation of
$\varrho :W\rightarrow {\mathbb {C}}^{m}_o$ be a deformation of ![]() $V$ given by
$V$ given by ![]() $F(x,s)\in {\mathbb {C}}\{x_1,\ldots,x_{n+1},s_1,\ldots,s_m\}$.
$F(x,s)\in {\mathbb {C}}\{x_1,\ldots,x_{n+1},s_1,\ldots,s_m\}$.
Without loss of generality we may assume that the germ of analytic function ![]() $f$ is convenient. In effect, the Milnor number
$f$ is convenient. In effect, the Milnor number ![]() $\mu (f):=\dim _{ {\mathbb {C}}} {\mathcal {O}_{n+1}^{x}}/ J(f)$ is finite. Hence, for each
$\mu (f):=\dim _{ {\mathbb {C}}} {\mathcal {O}_{n+1}^{x}}/ J(f)$ is finite. Hence, for each ![]() $e\in \mathcal {E}$ there exists
$e\in \mathcal {E}$ there exists ![]() $m \gg 0$ such that
$m \gg 0$ such that ![]() $x^{me}$ belongs to the ideal
$x^{me}$ belongs to the ideal ![]() $J(f)$. This implies that the singularities of
$J(f)$. This implies that the singularities of ![]() $f$ and of
$f$ and of ![]() $f+x^{me}$ have the same analytic type.
$f+x^{me}$ have the same analytic type.
Let ![]() $s$ be a general point of
$s$ be a general point of ![]() $ {\mathbb {C}}^m_o$, and let
$ {\mathbb {C}}^m_o$, and let ![]() $\Sigma$ be an admissible subdivision of
$\Sigma$ be an admissible subdivision of ![]() $\Gamma ^{\star }(F_s)$ (not necessarily regular). Denote by
$\Gamma ^{\star }(F_s)$ (not necessarily regular). Denote by ![]() $\pi :X_{\Sigma }\rightarrow {\mathbb {C}}^{n+1}$ the morphism given by the subdivision of
$\pi :X_{\Sigma }\rightarrow {\mathbb {C}}^{n+1}$ the morphism given by the subdivision of ![]() $\Delta$. Using the morphism
$\Delta$. Using the morphism ![]() $ {\mathbb {C}}_{o}^{n+1}\rightarrow {\mathbb {C}}^{n+1}$ we can consider the base change of
$ {\mathbb {C}}_{o}^{n+1}\rightarrow {\mathbb {C}}^{n+1}$ we can consider the base change of ![]() $\pi$ and
$\pi$ and ![]() $X_{\Sigma }$ to the base
$X_{\Sigma }$ to the base ![]() $ {\mathbb {C}}_{o}^{n+1}$. By abuse of notation we denote by
$ {\mathbb {C}}_{o}^{n+1}$. By abuse of notation we denote by ![]() $\pi : X_{\Sigma }\rightarrow {\mathbb {C}}_0^{n+1}$ the resulting morphism after the base change.
$\pi : X_{\Sigma }\rightarrow {\mathbb {C}}_0^{n+1}$ the resulting morphism after the base change.
Let us recall the following known fact. Let ![]() $V'$ be a hypersurface of
$V'$ be a hypersurface of ![]() $ {\mathbb {C}}^{n+1}_o$,
$ {\mathbb {C}}^{n+1}_o$, ![]() $n\geq 1$, having a unique isolated singularity at the point
$n\geq 1$, having a unique isolated singularity at the point ![]() $o$. Let us assume that
$o$. Let us assume that ![]() $V'$ is given by the equation
$V'$ is given by the equation ![]() $g(x)=0$, where
$g(x)=0$, where ![]() $g\in {\mathcal {O}_{n+1}^{x}}$. Let us assume that
$g\in {\mathcal {O}_{n+1}^{x}}$. Let us assume that ![]() $\Sigma$ is a regular admissible subdivision of a Newton fan
$\Sigma$ is a regular admissible subdivision of a Newton fan ![]() $\Gamma ^{\star }(g)$. If
$\Gamma ^{\star }(g)$. If ![]() $g$ is non-degenerate with respect to the Newton boundary, then the morphism
$g$ is non-degenerate with respect to the Newton boundary, then the morphism ![]() $\pi :X_{\Sigma }\rightarrow {\mathbb {C}}^{n+1}_o$ of toric varieties defines an embedded resolution of
$\pi :X_{\Sigma }\rightarrow {\mathbb {C}}^{n+1}_o$ of toric varieties defines an embedded resolution of ![]() $V'$ in a neighborhood of
$V'$ in a neighborhood of ![]() $\pi ^{-1}(o)$ (see [Reference VarchenkoVar76], [Reference OkaOka87] or [Reference IshiiIsh07]). This shows that if
$\pi ^{-1}(o)$ (see [Reference VarchenkoVar76], [Reference OkaOka87] or [Reference IshiiIsh07]). This shows that if ![]() $\Gamma _{+}(F_s)=\Gamma _{+}(f)$, where
$\Gamma _{+}(F_s)=\Gamma _{+}(f)$, where ![]() $s$ is a general point of
$s$ is a general point of ![]() $ {\mathbb {C}}^m_o$, and
$ {\mathbb {C}}^m_o$, and ![]() $F$ is a Newton non-degenerate deformation of
$F$ is a Newton non-degenerate deformation of ![]() $f$ (in particular, a
$f$ (in particular, a ![]() $\mu$-constant deformation of
$\mu$-constant deformation of ![]() $f$ by Theorem 2.28), a regular admissible resolution of the Newton fan defines a simultaneous embedded resolution of
$f$ by Theorem 2.28), a regular admissible resolution of the Newton fan defines a simultaneous embedded resolution of ![]() $W$. In view of this, for the rest of this section we assume:
$W$. In view of this, for the rest of this section we assume:
(i)
 $F(x,s)\in {\mathbb {C}}\{x_1,\ldots,x_{n+1},s_1,\ldots,s_m\}$ is a Newton non-degenerate
$F(x,s)\in {\mathbb {C}}\{x_1,\ldots,x_{n+1},s_1,\ldots,s_m\}$ is a Newton non-degenerate  $\mu$-constant deformation of
$\mu$-constant deformation of  $f$;
$f$;(ii)
 $\Gamma _{+}(F_s)\neq \Gamma _{+}(f)$. In particular,
$\Gamma _{+}(F_s)\neq \Gamma _{+}(f)$. In particular,  $\operatorname {Ver}(F_s,f):=\operatorname {Ver}(F_s) {\setminus} \operatorname {Ver}(f)\neq \emptyset$.
$\operatorname {Ver}(F_s,f):=\operatorname {Ver}(F_s) {\setminus} \operatorname {Ver}(f)\neq \emptyset$.
Let ![]() $\varphi :X_{\Sigma }\times {\mathbb {C}}^m_o\rightarrow {\mathbb {C}}^{n+1}_o\times {\mathbb {C}}^{m}_o$ be the morphism induced by
$\varphi :X_{\Sigma }\times {\mathbb {C}}^m_o\rightarrow {\mathbb {C}}^{n+1}_o\times {\mathbb {C}}^{m}_o$ be the morphism induced by ![]() $\pi$. Let
$\pi$. Let ![]() $s$ be a general point of
$s$ be a general point of ![]() $ {\mathbb {C}}^{m}_{o}$. Given
$ {\mathbb {C}}^{m}_{o}$. Given ![]() $\alpha \in \operatorname {Ver}(F_s)$ we denote by
$\alpha \in \operatorname {Ver}(F_s)$ we denote by ![]() $\sigma _{\alpha }$ the
$\sigma _{\alpha }$ the ![]() $(n+1)$-dimensional cone of
$(n+1)$-dimensional cone of ![]() $\Gamma ^{\star }(F_s)$ generated by all the non-negative normal vectors to faces of
$\Gamma ^{\star }(F_s)$ generated by all the non-negative normal vectors to faces of ![]() $\Gamma _{+}(F_s)$ which contain
$\Gamma _{+}(F_s)$ which contain ![]() $\alpha$. Denote by
$\alpha$. Denote by ![]() $\widetilde {W}^{\rm t}$ the total transform of
$\widetilde {W}^{\rm t}$ the total transform of ![]() $W$ under
$W$ under ![]() $\varphi$.
$\varphi$.
Proposition 3.1 Let ![]() $s$ be a general point of
$s$ be a general point of ![]() $ {\mathbb {C}}^m_o$, and assume that
$ {\mathbb {C}}^m_o$, and assume that
There exists an admissible subdivision, ![]() $\Sigma$, of
$\Sigma$, of ![]() $\Gamma ^{\star }(F_s)$ having the following properties.
$\Gamma ^{\star }(F_s)$ having the following properties.
(i) For each
 $\alpha \in \operatorname {Ver}(F_s,f)$, the fan
$\alpha \in \operatorname {Ver}(F_s,f)$, the fan  $\Sigma$ defines a subdivision,
$\Sigma$ defines a subdivision,  $\{\sigma _{\alpha }^1,\ldots,\sigma _{\alpha }^r\}$, regular to
$\{\sigma _{\alpha }^1,\ldots,\sigma _{\alpha }^r\}$, regular to  $\sigma _{\alpha }$.
$\sigma _{\alpha }$.(ii) For each
 $j\in \{1,\ldots,r\}$,
$j\in \{1,\ldots,r\}$,  $\widetilde {W}^t\cap (X_{\sigma _{\alpha }^j}\times {\mathbb {C}}^m_o)$ is a normal crossings divisor relative to
$\widetilde {W}^t\cap (X_{\sigma _{\alpha }^j}\times {\mathbb {C}}^m_o)$ is a normal crossings divisor relative to  $ {\mathbb {C}}^m_o$.
$ {\mathbb {C}}^m_o$.
Proof. Let us recall that ![]() $\mathcal {E}:=\{e_1,e_2,\ldots,e_{n+1}\}\subset {\mathbb {Z}}_{\geq 0}^{n+1}$ is the standard basis of
$\mathcal {E}:=\{e_1,e_2,\ldots,e_{n+1}\}\subset {\mathbb {Z}}_{\geq 0}^{n+1}$ is the standard basis of ![]() $ {\mathbb {R}}^{n+1}$. First we construct a simplicial subdivision of
$ {\mathbb {R}}^{n+1}$. First we construct a simplicial subdivision of ![]() $\Gamma ^{\star }(F_s)$. Let
$\Gamma ^{\star }(F_s)$. Let ![]() $\Gamma ^{\star }(F_s)(j)$ be the set of all the
$\Gamma ^{\star }(F_s)(j)$ be the set of all the ![]() $j$-dimensional cones of
$j$-dimensional cones of ![]() $\Gamma ^{\star }(F_s)$. Let us consider a compatible simplicial subdivision,
$\Gamma ^{\star }(F_s)$. Let us consider a compatible simplicial subdivision, ![]() $\Sigma S$, of
$\Sigma S$, of ![]() $\bigcup _{j=1}^{n}\Gamma ^{\star }(F_s)(j)$, such that if
$\bigcup _{j=1}^{n}\Gamma ^{\star }(F_s)(j)$, such that if ![]() $\sigma '$ is a simplicial
$\sigma '$ is a simplicial ![]() $j$-dimensional cone of
$j$-dimensional cone of ![]() $\Gamma ^{\star }(F_s)(j)$,
$\Gamma ^{\star }(F_s)(j)$, ![]() $1\leq j\leq n$, then
$1\leq j\leq n$, then ![]() $\sigma '\in \Sigma S$ and
$\sigma '\in \Sigma S$ and ![]() $\Sigma S(1)=\Gamma ^{\star }(F_s)(1)$, where
$\Sigma S(1)=\Gamma ^{\star }(F_s)(1)$, where ![]() $\Sigma S(1)$ is the set of all the one-dimensional cones of
$\Sigma S(1)$ is the set of all the one-dimensional cones of ![]() $\Sigma S$.
$\Sigma S$.
Let us consider the case
By Theorem 2.25, ![]() $\alpha$ has a good apex. Then there exists
$\alpha$ has a good apex. Then there exists ![]() $I\subsetneqq \{1,\ldots,n+1\}$ such that
$I\subsetneqq \{1,\ldots,n+1\}$ such that ![]() $\alpha \in {\mathbb {R}}^I_{>0}$ and
$\alpha \in {\mathbb {R}}^I_{>0}$ and ![]() $i\in I^c$ such that there exists a single edge
$i\in I^c$ such that there exists a single edge ![]() $E_{\alpha }\ni \alpha$, of
$E_{\alpha }\ni \alpha$, of ![]() $\Gamma (F_s)$ not contained in
$\Gamma (F_s)$ not contained in ![]() $ {\mathbb {R}}_{\{i\}}$. Let
$ {\mathbb {R}}_{\{i\}}$. Let ![]() $\beta =(\beta _1,\ldots,\beta _{n+1})\in \operatorname {Ver}(F_s)\cap E_{\alpha }$ be the good apex, which is to say
$\beta =(\beta _1,\ldots,\beta _{n+1})\in \operatorname {Ver}(F_s)\cap E_{\alpha }$ be the good apex, which is to say ![]() $\beta _i=\delta _{ij}$,
$\beta _i=\delta _{ij}$, ![]() $j\in I^c$.
$j\in I^c$.
Observe that ![]() $e_{i}\in \mathcal {E}$, is an extremal vector of
$e_{i}\in \mathcal {E}$, is an extremal vector of ![]() $\sigma _{\alpha }$. Let us consider the following simplicial subdivision of
$\sigma _{\alpha }$. Let us consider the following simplicial subdivision of ![]() $\sigma _{\alpha }$:
$\sigma _{\alpha }$:
where cone ![]() $\operatorname {Cone}(\{\cdot \})$ is the cone generated by
$\operatorname {Cone}(\{\cdot \})$ is the cone generated by ![]() $\{\cdot \}$. Now let us consider the case
$\{\cdot \}$. Now let us consider the case
let ![]() $\Sigma ^s(\sigma _{\alpha })$ be an arbitrary simplicial subdivision of
$\Sigma ^s(\sigma _{\alpha })$ be an arbitrary simplicial subdivision of ![]() $\sigma _{\alpha }$ that is compatible with
$\sigma _{\alpha }$ that is compatible with ![]() $\Sigma S$. Then
$\Sigma S$. Then
is a simplicial subdivision of ![]() $\Gamma ^{\star }(F_s)$. As
$\Gamma ^{\star }(F_s)$. As ![]() $F_s$ is convenient, the faces of
$F_s$ is convenient, the faces of ![]() $\sigma _{\alpha }$,
$\sigma _{\alpha }$, ![]() $\alpha \in \operatorname {Ver}(F_s)$, contained in a coordinate plane are simplicial cones, then
$\alpha \in \operatorname {Ver}(F_s)$, contained in a coordinate plane are simplicial cones, then ![]() $\Sigma ^s$ is an admissible subdivision.
$\Sigma ^s$ is an admissible subdivision.
Now we define a subdivision of ![]() $\Sigma ^s$ to obtain the sought after fan.
$\Sigma ^s$ to obtain the sought after fan.
Let ![]() $\alpha \in \operatorname {Ver}(F_s,f)$. By abuse of notation we denote for
$\alpha \in \operatorname {Ver}(F_s,f)$. By abuse of notation we denote for ![]() $\sigma _{\alpha }$ a cone in
$\sigma _{\alpha }$ a cone in ![]() $\Sigma ^s(\sigma _{\alpha })(n+1)$. Without loss of generality we can suppose
$\Sigma ^s(\sigma _{\alpha })(n+1)$. Without loss of generality we can suppose ![]() $i=n+1$, in this manner we have that
$i=n+1$, in this manner we have that ![]() $\sigma _{\alpha }=\operatorname {Cone}(e_{n+1},\tau )$ with
$\sigma _{\alpha }=\operatorname {Cone}(e_{n+1},\tau )$ with ![]() $\tau \in \Sigma S$. We denote
$\tau \in \Sigma S$. We denote ![]() $H_{0}= {\mathbb {R}}_{\{n+1\}}\cap \Gamma _{+}(F_s)$ and
$H_{0}= {\mathbb {R}}_{\{n+1\}}\cap \Gamma _{+}(F_s)$ and ![]() $H_1$,…,
$H_1$,…,![]() $H_n$ the
$H_n$ the ![]() $n$-dimensional faces of
$n$-dimensional faces of ![]() $\Gamma _{+}(F_s)$ that define
$\Gamma _{+}(F_s)$ that define ![]() $\sigma _{\alpha }$, then
$\sigma _{\alpha }$, then ![]() $\bigcap _{j=0}^{n}H_j=\{\alpha \}$. Then
$\bigcap _{j=0}^{n}H_j=\{\alpha \}$. Then ![]() $E_{\alpha }:=\bigcap _{j=1}^{n}H_j$
$E_{\alpha }:=\bigcap _{j=1}^{n}H_j$
Let ![]() $p_1,\ldots,p_n$ be non-negative normal vectors to the faces
$p_1,\ldots,p_n$ be non-negative normal vectors to the faces ![]() $H_1,\ldots,H_n$. Then
$H_1,\ldots,H_n$. Then
Now we construct a regular subdivision of ![]() $\sigma _{\alpha }$. Let us consider the cone
$\sigma _{\alpha }$. Let us consider the cone
and a regular subdivision ![]() $\operatorname {RS}(\tau )$ of
$\operatorname {RS}(\tau )$ of ![]() $\tau$ that does not subdivide regular faces of
$\tau$ that does not subdivide regular faces of ![]() $\tau$. Then
$\tau$. Then ![]() $\operatorname {RS}(\tau )$ does not subdivide faces
$\operatorname {RS}(\tau )$ does not subdivide faces ![]() . Let
. Let ![]() $\tau '\in \operatorname {RS}(\tau )$, then there exists
$\tau '\in \operatorname {RS}(\tau )$, then there exists ![]() $q_1,\ldots,q_n\in \operatorname {Cone}(p_1,\ldots,p_n)$ such that
$q_1,\ldots,q_n\in \operatorname {Cone}(p_1,\ldots,p_n)$ such that ![]() $\tau ':=\operatorname {Cone}(q_1,\ldots,q_n)$. Observe that the cones
$\tau ':=\operatorname {Cone}(q_1,\ldots,q_n)$. Observe that the cones
define a subdivision of the cone ![]() $\sigma _{\alpha }$ that can be extended to a subdivision
$\sigma _{\alpha }$ that can be extended to a subdivision ![]() $\Sigma$ of
$\Sigma$ of ![]() $\Sigma ^s$ that does not subdivide faces
$\Sigma ^s$ that does not subdivide faces ![]() , which implies that
, which implies that ![]() $\Sigma$ is admissible.
$\Sigma$ is admissible.
Now we prove that ![]() $\sigma '_{\alpha }:=\operatorname {Cone}(q_1,\ldots,q_n,e_{n+1})$ is regular. Looking at
$\sigma '_{\alpha }:=\operatorname {Cone}(q_1,\ldots,q_n,e_{n+1})$ is regular. Looking at ![]() $q_j$ as column vectors, and consider the matrix of the size
$q_j$ as column vectors, and consider the matrix of the size ![]() $(n+1)\times n$:
$(n+1)\times n$:
 \[ A:=(q_1\quad \cdots \quad q_{n}) =\Bigg(\begin{array}{ccc} q_{1\;1} & \cdots & q_{n\;1}\\ \vdots & \vdots & \\ q_{1\;n+1} & \cdots & q_{n\;n+1} \\ \end{array} \Bigg). \]
\[ A:=(q_1\quad \cdots \quad q_{n}) =\Bigg(\begin{array}{ccc} q_{1\;1} & \cdots & q_{n\;1}\\ \vdots & \vdots & \\ q_{1\;n+1} & \cdots & q_{n\;n+1} \\ \end{array} \Bigg). \] For each ![]() $j\in \{1,\ldots,n+1\}$ let
$j\in \{1,\ldots,n+1\}$ let ![]() $A_j$ be the matrix of the size
$A_j$ be the matrix of the size ![]() $n\times n$ obtained by deleting the row
$n\times n$ obtained by deleting the row ![]() $j$ of the matrix
$j$ of the matrix ![]() $A$. As
$A$. As ![]() $\tau ':=\operatorname {Cone}(q_1,\ldots,q_n)$ is regular, we have that the greatest common divisor,
$\tau ':=\operatorname {Cone}(q_1,\ldots,q_n)$ is regular, we have that the greatest common divisor, ![]() $\gcd (d_1,\ldots,d_{n+1})$, where
$\gcd (d_1,\ldots,d_{n+1})$, where
is equal to ![]() $1$. Let us suppose that the cone
$1$. Let us suppose that the cone
is not regular, then ![]() $|\det (q_1,\ldots,q_n,e_{n+1})|=d_{n+1}\geq 2$. For each
$|\det (q_1,\ldots,q_n,e_{n+1})|=d_{n+1}\geq 2$. For each ![]() $H_j$,
$H_j$, ![]() $1\leq j \leq n$ we have that
$1\leq j \leq n$ we have that ![]() $\alpha,\beta \in H_j$, then
$\alpha,\beta \in H_j$, then ![]() $\langle \alpha, p_j \rangle =\langle \beta, p_j\rangle$ for all
$\langle \alpha, p_j \rangle =\langle \beta, p_j\rangle$ for all ![]() $1\leq j \leq n$, which implies that
$1\leq j \leq n$, which implies that ![]() $\langle \alpha, q_j \rangle =\langle \beta, q_j\rangle$ for all
$\langle \alpha, q_j \rangle =\langle \beta, q_j\rangle$ for all ![]() $1\leq j \leq n$. From this we obtain that
$1\leq j \leq n$. From this we obtain that
 \[ q_{j\;n+1}=\sum_{k=1}^{n} (\alpha_k-\beta_k)q_{j k} \]
\[ q_{j\;n+1}=\sum_{k=1}^{n} (\alpha_k-\beta_k)q_{j k} \]
for all ![]() $1\leq i \leq n$ (remember that
$1\leq i \leq n$ (remember that ![]() $\beta$ is the good apex of
$\beta$ is the good apex of ![]() $\alpha$). Then
$\alpha$). Then ![]() $d_{n+1}$ divides to
$d_{n+1}$ divides to ![]() $d_j$ for all
$d_j$ for all ![]() $1\leq j\leq n$, which contradicts the fact that
$1\leq j\leq n$, which contradicts the fact that ![]() $\gcd (d_1,\ldots,d_{n+1})=1$. This implies that
$\gcd (d_1,\ldots,d_{n+1})=1$. This implies that ![]() $\sigma '_{\alpha }$ is regular.
$\sigma '_{\alpha }$ is regular.
Observe that there exist coordinates ![]() $y_1,\ldots,y_{n+1}$ of
$y_1,\ldots,y_{n+1}$ of ![]() $X_{\sigma '_{\alpha }}\cong {\mathbb {C}}^{n+1}$ (before the base change) such that the morphism
$X_{\sigma '_{\alpha }}\cong {\mathbb {C}}^{n+1}$ (before the base change) such that the morphism
is defined by
From this we obtain
Let us assume that ![]() $r=(r_1,\ldots,r_{n+1})$ is a singular point of
$r=(r_1,\ldots,r_{n+1})$ is a singular point of ![]() $\overline {F}(y,o)$. Then there exists
$\overline {F}(y,o)$. Then there exists ![]() $1\leq j \leq n$ such that
$1\leq j \leq n$ such that ![]() $r_j=0$. Without loss of generality, we can suppose that
$r_j=0$. Without loss of generality, we can suppose that ![]() $r_n=0$. We know that for each
$r_n=0$. We know that for each ![]() $\beta '\in E_{\alpha }\cap \operatorname {Ver}(f)$ we have that
$\beta '\in E_{\alpha }\cap \operatorname {Ver}(f)$ we have that ![]() $\langle \alpha, q_i \rangle =\langle \beta ', q_i\rangle$, for all
$\langle \alpha, q_i \rangle =\langle \beta ', q_i\rangle$, for all ![]() $1\leq i \leq n$, and as
$1\leq i \leq n$, and as ![]() $\alpha$ has a good apex, we obtain
$\alpha$ has a good apex, we obtain
where ![]() $\overline {y}=(y_1,\ldots,y_{n-1})$,
$\overline {y}=(y_1,\ldots,y_{n-1})$, ![]() $c_0(o)=0$, and
$c_0(o)=0$, and
If ![]() $E_{\alpha }\cap \operatorname {Ver}(f)=\{\beta \}$, then
$E_{\alpha }\cap \operatorname {Ver}(f)=\{\beta \}$, then ![]() $\overline {K}(y_{n+1},s)=c_1(s)y_{n+1}$. This shows that
$\overline {K}(y_{n+1},s)=c_1(s)y_{n+1}$. This shows that ![]() $r$ cannot be a singular point of
$r$ cannot be a singular point of ![]() $\overline {F}$. If
$\overline {F}$. If ![]() $|E_{\alpha }\cap \operatorname {Ver}(f)|>1$, then the singular point
$|E_{\alpha }\cap \operatorname {Ver}(f)|>1$, then the singular point ![]() $r=(r_1,\ldots,r_{n+1})$ satisfies
$r=(r_1,\ldots,r_{n+1})$ satisfies
This implies that ![]() $r_{n+1}\neq 0$. We prove that this is contradiction.
$r_{n+1}\neq 0$. We prove that this is contradiction.
Let ![]() $W=\operatorname {Ver}(F_s,f)\cap {\mathbb {R}}_{n+1}$ and we define
$W=\operatorname {Ver}(F_s,f)\cap {\mathbb {R}}_{n+1}$ and we define
We may assume that ![]() $F'$ is a non-degenerate deformation of
$F'$ is a non-degenerate deformation of ![]() $f$. As
$f$. As
we have ![]() $\nu (F'_s)=\nu (f)$ (see Corollary 2.5). By the definition of
$\nu (F'_s)=\nu (f)$ (see Corollary 2.5). By the definition of ![]() $F'$, the point
$F'$, the point ![]() $\alpha$ belongs to
$\alpha$ belongs to ![]() $\operatorname {Ver}(F'_s,f)=W$. We note
$\operatorname {Ver}(F'_s,f)=W$. We note ![]() $\sigma _{\alpha }$ the cone of
$\sigma _{\alpha }$ the cone of ![]() $\Gamma ^{\star }(F'_s)$ associated with
$\Gamma ^{\star }(F'_s)$ associated with ![]() $\alpha$. By construction, the cone
$\alpha$. By construction, the cone ![]() $\sigma _{\alpha }$ of
$\sigma _{\alpha }$ of ![]() $\Gamma ^{\star }(F'_s)$ is the cone
$\Gamma ^{\star }(F'_s)$ is the cone ![]() $\sigma _{\alpha }$ of
$\sigma _{\alpha }$ of ![]() $\Gamma ^{\star }(F_s)$ defined previously. Using the same regular subdivision of
$\Gamma ^{\star }(F_s)$ defined previously. Using the same regular subdivision of ![]() $\sigma _{\alpha }$ we can define a regular admissible subdivision
$\sigma _{\alpha }$ we can define a regular admissible subdivision ![]() $\Sigma '$ of the fan
$\Sigma '$ of the fan ![]() $\Gamma ^{\star }(F'_s)$.
$\Gamma ^{\star }(F'_s)$.
Let ![]() $\sigma '_{\alpha }$ be one of the two regular cones of the subdivision of
$\sigma '_{\alpha }$ be one of the two regular cones of the subdivision of ![]() $\sigma _{\alpha }$ (see
$\sigma _{\alpha }$ (see ![]() $(\star )$). As we previously obtained
$(\star )$). As we previously obtained
Then ![]() $r$ is a singular point of
$r$ is a singular point of ![]() $\overline {F}(y,o)$ if and only if
$\overline {F}(y,o)$ if and only if ![]() $r$ is a singular point of
$r$ is a singular point of ![]() $\overline {F'}(y,o)$ (in fact,
$\overline {F'}(y,o)$ (in fact, ![]() $\overline {F}(y,o)=\overline {F'}(y,o)$). We recall that
$\overline {F}(y,o)=\overline {F'}(y,o)$). We recall that ![]() $|E_{\alpha }\cap \operatorname {Ver}(f)|>1$, and that
$|E_{\alpha }\cap \operatorname {Ver}(f)|>1$, and that ![]() $E_{\alpha }$ is the only edge of
$E_{\alpha }$ is the only edge of ![]() $\Gamma _{+}(F_s)$ not contained in
$\Gamma _{+}(F_s)$ not contained in ![]() $ {\mathbb {R}}_{i}$, which contains
$ {\mathbb {R}}_{i}$, which contains ![]() $\alpha$ and its good apex. Observe that
$\alpha$ and its good apex. Observe that ![]() $E_{\alpha }$ also is the unique edge
$E_{\alpha }$ also is the unique edge ![]() $\Gamma _{+}(F'_s)$ which satisfies the previous properties. Let
$\Gamma _{+}(F'_s)$ which satisfies the previous properties. Let ![]() $\beta '\neq \alpha$ an end point of
$\beta '\neq \alpha$ an end point of ![]() $ {\operatorname {E}}_{\alpha }$, and
$ {\operatorname {E}}_{\alpha }$, and ![]() $\sigma _{\beta '}\in \Gamma ^{\star }(F_s)$ the cone associated with
$\sigma _{\beta '}\in \Gamma ^{\star }(F_s)$ the cone associated with ![]() $\beta '$. As
$\beta '$. As ![]() $|E_{\alpha }\cap \operatorname {Ver}(f)|>1$, and
$|E_{\alpha }\cap \operatorname {Ver}(f)|>1$, and ![]() $\operatorname {Ver}(F'_s,f)\subset {\mathbb {R}}_{n+1}$, we have that the cone
$\operatorname {Ver}(F'_s,f)\subset {\mathbb {R}}_{n+1}$, we have that the cone ![]() $\sigma _{\beta '}$ belongs to
$\sigma _{\beta '}$ belongs to ![]() $\Gamma ^{\star }(f)$. Then the regular subdivision
$\Gamma ^{\star }(f)$. Then the regular subdivision ![]() $\sigma ^1_{\beta '}$,…,
$\sigma ^1_{\beta '}$,…,![]() $\sigma ^t_{\beta '}$ of
$\sigma ^t_{\beta '}$ of ![]() $\sigma _{\beta '}$ defined by the regular admissible subdivision
$\sigma _{\beta '}$ defined by the regular admissible subdivision ![]() $\Sigma '$ can be extended to regular admissible subdivision
$\Sigma '$ can be extended to regular admissible subdivision ![]() $\Sigma ''$ of
$\Sigma ''$ of ![]() $\Gamma _{+}(f)$. By construction, there exists
$\Gamma _{+}(f)$. By construction, there exists ![]() $1\leq j\leq t$ such that
$1\leq j\leq t$ such that ![]() $r\in X_{\sigma ^{j}_{\beta '}}\cong {\mathbb {C}}^{n+1}$. But
$r\in X_{\sigma ^{j}_{\beta '}}\cong {\mathbb {C}}^{n+1}$. But ![]() $f$ is non-degenerate, which implies that
$f$ is non-degenerate, which implies that ![]() $\widetilde {V}^{\rm s}\cap X_{\sigma ^{i}_{\beta '}}$ is smooth, from where we obtain the sought after contradiction. This implies that
$\widetilde {V}^{\rm s}\cap X_{\sigma ^{i}_{\beta '}}$ is smooth, from where we obtain the sought after contradiction. This implies that ![]() $F(\pi _{\sigma '}(y),s)$, which is a normal crossings divisor relative to
$F(\pi _{\sigma '}(y),s)$, which is a normal crossings divisor relative to ![]() $ {\mathbb {C}}^m_o$ around
$ {\mathbb {C}}^m_o$ around ![]() $\pi ^{-1}_{\sigma '_{\alpha }}(o)\times {\mathbb {C}}^m_o$.
$\pi ^{-1}_{\sigma '_{\alpha }}(o)\times {\mathbb {C}}^m_o$.
The following theorem is the main result of this article. Let ![]() $s$ be a general point of
$s$ be a general point of ![]() $ {\mathbb {C}}^m_{o}$. We construct a regular admissible subdivision,
$ {\mathbb {C}}^m_{o}$. We construct a regular admissible subdivision, ![]() $\Sigma$, of
$\Sigma$, of ![]() $\Gamma ^{\star }(F_s)$ in the manner that
$\Gamma ^{\star }(F_s)$ in the manner that ![]() $\rho :X_{\Sigma }\times ( {\mathbb {C}}^m,o)\rightarrow {\mathbb {C}}^{n+1}_o\times {\mathbb {C}}^m_o$ is the sought after simultaneous embedded resolution. Observe that for the result commented upon previously,
$\rho :X_{\Sigma }\times ( {\mathbb {C}}^m,o)\rightarrow {\mathbb {C}}^{n+1}_o\times {\mathbb {C}}^m_o$ is the sought after simultaneous embedded resolution. Observe that for the result commented upon previously, ![]() $\pi :X_{\Sigma }\rightarrow {\mathbb {C}}^{n+1}_o$ defines an embedded resolution of
$\pi :X_{\Sigma }\rightarrow {\mathbb {C}}^{n+1}_o$ defines an embedded resolution of ![]() $W_s$.
$W_s$.
Theorem 3.2 Assume that ![]() $W$ is a Newton non-degenerate deformation. The deformation
$W$ is a Newton non-degenerate deformation. The deformation ![]() $W$ is
$W$ is ![]() $\mu$-constant if and only if
$\mu$-constant if and only if ![]() $W$ admits a simultaneous embedded resolution.
$W$ admits a simultaneous embedded resolution.
Proof. The ‘if’ part is given by Proposition 1.6. We prove ‘only if’.
By Proposition 3.1 there exists an admissible subdivision, ![]() $\Sigma$, of
$\Sigma$, of ![]() $\Gamma ^{\star }(F_s)$ (where
$\Gamma ^{\star }(F_s)$ (where ![]() $s$ is a general point of
$s$ is a general point of ![]() $ {\mathbb {C}}^{m}_{o}$) such that for each
$ {\mathbb {C}}^{m}_{o}$) such that for each ![]() $\alpha \in \operatorname {Ver}(F_s,f)$, the fan
$\alpha \in \operatorname {Ver}(F_s,f)$, the fan ![]() $\Sigma$ defines a subdivision
$\Sigma$ defines a subdivision ![]() $\sigma _{\alpha }^1,\ldots,\sigma _{\alpha }^r$, regular of
$\sigma _{\alpha }^1,\ldots,\sigma _{\alpha }^r$, regular of ![]() $\sigma _{\alpha }$, such that
$\sigma _{\alpha }$, such that ![]() $\widetilde {W}^t\cap X_{\sigma _{\alpha }^i}\times {\mathbb {C}}^m_o$ is a normal crossings divisor relative to
$\widetilde {W}^t\cap X_{\sigma _{\alpha }^i}\times {\mathbb {C}}^m_o$ is a normal crossings divisor relative to ![]() $ {\mathbb {C}}^m_o$ for
$ {\mathbb {C}}^m_o$ for ![]() $i\in \{1,\ldots,r\}$. Consider the set,
$i\in \{1,\ldots,r\}$. Consider the set, ![]() $\Sigma (j)$, of all the cones of dimension
$\Sigma (j)$, of all the cones of dimension ![]() $j$ of
$j$ of ![]() $\Sigma$. Observe that given a regular admissible subdivision of
$\Sigma$. Observe that given a regular admissible subdivision of ![]() $\Sigma (j)$, there exists a regular admissible subdivision of
$\Sigma (j)$, there exists a regular admissible subdivision of ![]() $\Sigma (j+1)$ compatible with the given subdivision. Using recurrence we have that there exists a regular admissible subdivision of
$\Sigma (j+1)$ compatible with the given subdivision. Using recurrence we have that there exists a regular admissible subdivision of ![]() $\Sigma$ that does not subdivide its regular cones. By abuse of notation we denote for
$\Sigma$ that does not subdivide its regular cones. By abuse of notation we denote for ![]() $\Sigma$ the regular admissible subdivision. To finish the proof we still need to consider
$\Sigma$ the regular admissible subdivision. To finish the proof we still need to consider ![]() $\alpha \in \operatorname {Ver}(F_s)\cap \operatorname {Ver}(f)$. Let us consider the cone
$\alpha \in \operatorname {Ver}(F_s)\cap \operatorname {Ver}(f)$. Let us consider the cone ![]() $\sigma \subset {\mathbb {R}}^{n+1}_{\geq 0}$ generated by all the non-negative normal vectors to faces of
$\sigma \subset {\mathbb {R}}^{n+1}_{\geq 0}$ generated by all the non-negative normal vectors to faces of ![]() $\Gamma _{+}(F_s)$ which contain a
$\Gamma _{+}(F_s)$ which contain a ![]() $\alpha$, and let
$\alpha$, and let ![]() $\sigma ^1,\ldots,\sigma ^r$ be the regular subdivision defined by
$\sigma ^1,\ldots,\sigma ^r$ be the regular subdivision defined by ![]() $\Sigma$. Let us suppose that
$\Sigma$. Let us suppose that ![]() $p_{1}^i,\ldots,p_{n+1}^i$ are the extremal vectors of
$p_{1}^i,\ldots,p_{n+1}^i$ are the extremal vectors of ![]() $\sigma ^i$. As
$\sigma ^i$. As ![]() $\sigma ^i$ is regular, we have that
$\sigma ^i$ is regular, we have that ![]() $X_{\sigma ^i}\cong {\mathbb {C}}^{n+1}$ (before the base change). Then we can associate the coordinates
$X_{\sigma ^i}\cong {\mathbb {C}}^{n+1}$ (before the base change). Then we can associate the coordinates ![]() $y_1,\ldots,y_{n+1}$ to
$y_1,\ldots,y_{n+1}$ to ![]() $X_{\sigma ^i}$ such that
$X_{\sigma ^i}$ such that ![]() $\pi _{\sigma ^i}:=\pi |_{X_{\sigma ^i}}$ is defined by
$\pi _{\sigma ^i}:=\pi |_{X_{\sigma ^i}}$ is defined by
where ![]() $x_j:=y_1^{p_{1j}^i}\cdots y_{n+1}^{p_{n+1\;j}^i}$,
$x_j:=y_1^{p_{1j}^i}\cdots y_{n+1}^{p_{n+1\;j}^i}$, ![]() $p_{j}^i:=(p^i_{j 1},\ldots,p^i_{j \;n+1})$,
$p_{j}^i:=(p^i_{j 1},\ldots,p^i_{j \;n+1})$, ![]() $1\leq j\leq n+1$. Then
$1\leq j\leq n+1$. Then
Let ![]() $c(s)$ be the degree zero term of
$c(s)$ be the degree zero term of ![]() $\overline {F}(y,s)$. As
$\overline {F}(y,s)$. As ![]() $\alpha \not \in \operatorname {Ver}(F_s,f)$, there exits a sufficiently small open set
$\alpha \not \in \operatorname {Ver}(F_s,f)$, there exits a sufficiently small open set ![]() $0\in \Omega \subset {\mathbb {C}}^{m}$ such that
$0\in \Omega \subset {\mathbb {C}}^{m}$ such that ![]() $c(s')\neq 0$ for all
$c(s')\neq 0$ for all ![]() $s'\in \Omega$. Moreover, for each
$s'\in \Omega$. Moreover, for each ![]() $s'\in \Omega$, we have
$s'\in \Omega$, we have ![]() $\sigma ^i\subset \sigma _{\alpha,s'}$,
$\sigma ^i\subset \sigma _{\alpha,s'}$, ![]() $1\leq i\leq r$, where
$1\leq i\leq r$, where ![]() $\sigma _{\alpha, s'}$ is the
$\sigma _{\alpha, s'}$ is the ![]() $(n+1)$-dimensional cone of
$(n+1)$-dimensional cone of ![]() $\Gamma ^{\star }(F_{s'})$ generated by all the non-negative normal vectors to faces of
$\Gamma ^{\star }(F_{s'})$ generated by all the non-negative normal vectors to faces of ![]() $\Gamma _{+}(F_{s'})$ which contain
$\Gamma _{+}(F_{s'})$ which contain ![]() $\alpha$. Observe that for each
$\alpha$. Observe that for each ![]() $s'\in \Omega$ we can extend the fan formed by the cones
$s'\in \Omega$ we can extend the fan formed by the cones ![]() $\sigma ^i$,
$\sigma ^i$, ![]() $1\leq i\leq r$, to a subdivision of the cone
$1\leq i\leq r$, to a subdivision of the cone ![]() $\sigma _{\alpha,s'} \in \Gamma ^{\star }(F_{s'})$ without subdivisions of strict faces of
$\sigma _{\alpha,s'} \in \Gamma ^{\star }(F_{s'})$ without subdivisions of strict faces of ![]() $\Delta$ (this allows us to return to the classical case of non-degenerate hypersurface for each
$\Delta$ (this allows us to return to the classical case of non-degenerate hypersurface for each ![]() $s'\in \Omega$). Then the property of non-degeneracy of
$s'\in \Omega$). Then the property of non-degeneracy of ![]() $F$ implies that
$F$ implies that ![]() $F_{s'}(\pi _{\sigma ^i}(y))$ is a normal crossings divisor for each
$F_{s'}(\pi _{\sigma ^i}(y))$ is a normal crossings divisor for each ![]() $s'\in \Omega$. This implies that
$s'\in \Omega$. This implies that ![]() $F(\pi _{\sigma ^i}(y),s)$ is a normal crossings divisor relative to
$F(\pi _{\sigma ^i}(y),s)$ is a normal crossings divisor relative to ![]() $ {\mathbb {C}}^m_o$ around
$ {\mathbb {C}}^m_o$ around ![]() $\pi ^{-1}_{\sigma ^i}(o)\times {\mathbb {C}}^m_o$.
$\pi ^{-1}_{\sigma ^i}(o)\times {\mathbb {C}}^m_o$.
4. The degenerate case
Let us recall that ![]() $V$ is a hypersurface of
$V$ is a hypersurface of ![]() $C_{o}^{n+1}$,
$C_{o}^{n+1}$, ![]() $n\geq 1$, given by
$n\geq 1$, given by ![]() $f\in {\mathcal {O}_{n+1}^{x}}$ irreducible such that
$f\in {\mathcal {O}_{n+1}^{x}}$ irreducible such that ![]() $V$ has an isolated singularity at
$V$ has an isolated singularity at ![]() $o$. Let
$o$. Let ![]() $F\in {\mathbb {C}}\{x_1,\ldots,x_{n+1},s_1,\ldots,s_m\}$ be a deformation of
$F\in {\mathbb {C}}\{x_1,\ldots,x_{n+1},s_1,\ldots,s_m\}$ be a deformation of ![]() $f\in {\mathbb {C}}\{x_1,\ldots,x_{n+1}\}$:
$f\in {\mathbb {C}}\{x_1,\ldots,x_{n+1}\}$:
 \[ F(x,s):=f(x)+\sum_{i=1}^{\infty} h_i(s)g_i(x), \]
\[ F(x,s):=f(x)+\sum_{i=1}^{\infty} h_i(s)g_i(x), \]
where ![]() $h_i\in {\mathcal {O}_{m}^{s}}:= {\mathbb {C}\{s_{1},\ldots,s_{m}\}}$,
$h_i\in {\mathcal {O}_{m}^{s}}:= {\mathbb {C}\{s_{1},\ldots,s_{m}\}}$, ![]() $m\geq 1$, and
$m\geq 1$, and ![]() $g_i\in {\mathcal {O}_{n+1}^{x}}$ such that
$g_i\in {\mathcal {O}_{n+1}^{x}}$ such that ![]() $h_i(o)=g_i(o)=0$. Consider the relative Jacobian ideal
$h_i(o)=g_i(o)=0$. Consider the relative Jacobian ideal
The following theorem gives a valuative criterion for the ![]() $\mu$-constancy of a deformation.
$\mu$-constancy of a deformation.
Theorem 4.1 [Reference GreuelGre86, Reference Lê Dũng and SaitoLDS73, Reference TeissierTei73]
The following are equivalent:
(i)
 $F$ is a
$F$ is a  $\mu$-constant deformation of
$\mu$-constant deformation of  $f$;
$f$;(ii) for all
 $i\in {1,\ldots,m}$ we have that
$i\in {1,\ldots,m}$ we have that  $\partial _{s_{i}}F\in \overline {J_x(F)}$, where
$\partial _{s_{i}}F\in \overline {J_x(F)}$, where  $\overline {J_x(F)}$ denotes the integral closure of the ideal
$\overline {J_x(F)}$ denotes the integral closure of the ideal  $J_x(F)$;
$J_x(F)$;(iii) for all analytic curve
 $\gamma :( {\mathbb {C}},o)\rightarrow ( {\mathbb {C}}^{n+1}\times {\mathbb {C}}^{m},o)$,
$\gamma :( {\mathbb {C}},o)\rightarrow ( {\mathbb {C}}^{n+1}\times {\mathbb {C}}^{m},o)$,  $\gamma (o)=o$, and for all
$\gamma (o)=o$, and for all  $i\in \{1,\ldots,m\}$ we have that
$i\in \{1,\ldots,m\}$ we have that  $ {\operatorname {Ord}}_t(\partial _{s_i}F\circ \gamma (t))> \min \{ {\operatorname {Ord}}_t(\partial _{x_j}F\circ \gamma (t))\,|\, 1\leq j\leq n+1\}$.
$ {\operatorname {Ord}}_t(\partial _{s_i}F\circ \gamma (t))> \min \{ {\operatorname {Ord}}_t(\partial _{x_j}F\circ \gamma (t))\,|\, 1\leq j\leq n+1\}$.(iv) same statement as in statement (iii) with ‘
 $>$’ replaced by ‘
$>$’ replaced by ‘ $\geq$’.
$\geq$’.
Next, we state and prove an analogue of Corollary 2.19 for deformations that do not satisfy the non-degeneracy assumption. Let ![]() $s$ be a general point of
$s$ be a general point of ![]() $ {\mathbb {C}}_{o}^m$,
$ {\mathbb {C}}_{o}^m$, ![]() $I$ a proper subset of
$I$ a proper subset of ![]() $\{1,\dots n+1\}$ and consider
$\{1,\dots n+1\}$ and consider
such that ![]() $\operatorname {Ver}(F_s,f)\cap {\mathbb {R}}^I_{>0}\neq \emptyset$. If
$\operatorname {Ver}(F_s,f)\cap {\mathbb {R}}^I_{>0}\neq \emptyset$. If ![]() $F$ is a
$F$ is a ![]() $\mu$-constant non-degenerate deformation of
$\mu$-constant non-degenerate deformation of ![]() $f$, then by virtue of Corollary 2.19 there exists
$f$, then by virtue of Corollary 2.19 there exists ![]() $i\in I^c$ such that
$i\in I^c$ such that ![]() $\beta _i=\delta _{ij}$ for
$\beta _i=\delta _{ij}$ for ![]() $j\in I^c$, which is analogous to statement (ii) of the following proposition.
$j\in I^c$, which is analogous to statement (ii) of the following proposition.
In the rest of the section, we use the following notation. Given that ![]() $J\subsetneqq \{1,\ldots,n+1\}$, we denote by
$J\subsetneqq \{1,\ldots,n+1\}$, we denote by ![]() $ {\mathbb {C}}_o^J$ the complex-analytic germs at the origin of
$ {\mathbb {C}}_o^J$ the complex-analytic germs at the origin of ![]() $ {\mathbb {C}}^J:=\{(x_1,\ldots,x_{n+1})\in {\mathbb {C}}^{n+1}:x_i=0\;\text {if}\;i\notin J\}$ and by
$ {\mathbb {C}}^J:=\{(x_1,\ldots,x_{n+1})\in {\mathbb {C}}^{n+1}:x_i=0\;\text {if}\;i\notin J\}$ and by ![]() $f_J$ (respectively,
$f_J$ (respectively, ![]() $F_J$) the natural restriction of
$F_J$) the natural restriction of ![]() $f$ (respectively,
$f$ (respectively, ![]() $F$) to
$F$) to ![]() $ {\mathbb {C}}^J_o$ (respectively,
$ {\mathbb {C}}^J_o$ (respectively, ![]() $ {\mathbb {C}}_o^J\times {\mathbb {C}}_{o}^{m}$). Let
$ {\mathbb {C}}_o^J\times {\mathbb {C}}_{o}^{m}$). Let ![]() $V_J$ be the subset of
$V_J$ be the subset of ![]() $ {\mathbb {C}}_{o}^J$ defined by the equation
$ {\mathbb {C}}_{o}^J$ defined by the equation ![]() $f_J(x)=0$.
$f_J(x)=0$.
Let ![]() $\operatorname {Supp}(F,f):=\operatorname {Supp}(F){\setminus} \operatorname {Supp}(f)$.
$\operatorname {Supp}(F,f):=\operatorname {Supp}(F){\setminus} \operatorname {Supp}(f)$.
Proposition 4.2 Fix a set ![]() $I\subsetneqq \{1,\ldots,n+1\}$. Let us assume that
$I\subsetneqq \{1,\ldots,n+1\}$. Let us assume that ![]() $F$ is a
$F$ is a ![]() $\mu$-constant deformation of
$\mu$-constant deformation of ![]() $f$, and that
$f$, and that ![]() $\operatorname {Supp}(F_s,f)\cap {\mathbb {R}}^{I}_{>0}\neq \emptyset$.
$\operatorname {Supp}(F_s,f)\cap {\mathbb {R}}^{I}_{>0}\neq \emptyset$.
Then given
at least one of the following conditions is satisfied.
(i) The restriction
 $f_J$ is reduced,
$f_J$ is reduced,  $V_J$ is a hypersurface of
$V_J$ is a hypersurface of  $ {\mathbb {C}}_{0}^J$ with an isolated singularity at
$ {\mathbb {C}}_{0}^J$ with an isolated singularity at  $o$, and
$o$, and  $F_J$ is a
$F_J$ is a  $\mu$-constant deformation of
$\mu$-constant deformation of  $f_J$.
$f_J$.(ii) There exists
 $i\in J^c$ and
$i\in J^c$ and  $\beta :=(\beta _1,\ldots,\beta _{n+1})\in \operatorname {Supp}(F)$ such that
$\beta :=(\beta _1,\ldots,\beta _{n+1})\in \operatorname {Supp}(F)$ such that  $\beta _i=\delta _{ij}$, for
$\beta _i=\delta _{ij}$, for  $j\in J^c$.
$j\in J^c$.
A difference between the degenerate and the non-degenerate cases is that the point ![]() $\beta \in \operatorname {Supp}(F_s)$ of the previous proposition need not, in general, belong to the set
$\beta \in \operatorname {Supp}(F_s)$ of the previous proposition need not, in general, belong to the set ![]() $\operatorname {Supp}(f)$.
$\operatorname {Supp}(f)$.
Example 4.3 Consider the following deformation
In [Reference AltmannAlt87] it was shown that ![]() $F$ is a
$F$ is a ![]() $\mu$-constant degenerate deformation of the non-degenerate polynomial
$\mu$-constant degenerate deformation of the non-degenerate polynomial ![]() $f(x_1,x_2,x_3):=x_1^5+x_2^6+x_3^5+x_2^3x_3^2$ . In this example, we have that
$f(x_1,x_2,x_3):=x_1^5+x_2^6+x_3^5+x_2^3x_3^2$ . In this example, we have that ![]() $\operatorname {Ver}(F_s,f):=\{(4,1,0)\}\subset {\mathbb {R}}_{>0}^{\{1,2\}}$ and
$\operatorname {Ver}(F_s,f):=\{(4,1,0)\}\subset {\mathbb {R}}_{>0}^{\{1,2\}}$ and ![]() $\beta :=(2,2,1)$. Observe that
$\beta :=(2,2,1)$. Observe that ![]() $\beta \notin \operatorname {Supp}(f)$.
$\beta \notin \operatorname {Supp}(f)$.
Proof of Proposition 4.2 There is no loss of generality in supposing that ![]() $J= \{1,\ldots,k\}$,
$J= \{1,\ldots,k\}$, ![]() $k\leq n$. We can always write
$k\leq n$. We can always write ![]() $F$ in the following manner:
$F$ in the following manner:
where ![]() $s=(s_1,\ldots,s_m)$. Observe that
$s=(s_1,\ldots,s_m)$. Observe that ![]() $F_J=G$, and let
$F_J=G$, and let ![]() $g:=f_J=G|_{s=0}$. Let us suppose that condition (ii) is not satisfied, then
$g:=f_J=G|_{s=0}$. Let us suppose that condition (ii) is not satisfied, then ![]() $G_{i}(x_1,\ldots,x_k,s)\equiv 0$ for all
$G_{i}(x_1,\ldots,x_k,s)\equiv 0$ for all ![]() $k< i\leq n+1$, then
$k< i\leq n+1$, then
Thus, we obtain that:
(i)
 $\partial _{l}F=\partial _{l}G+ \sum _{k< i\leq j}x_ix_j\partial _lG_{ij},$ for
$\partial _{l}F=\partial _{l}G+ \sum _{k< i\leq j}x_ix_j\partial _lG_{ij},$ for  $1\leq l\leq k$;
$1\leq l\leq k$;(ii)
 $\partial _{l}F=\sum _{k< i\leq l}x_iG_{il}+\sum _{l\leq j}x_jG_{lj}+\sum _{k< i\leq j}x_ix_j\partial _lG_{ij},$ for
$\partial _{l}F=\sum _{k< i\leq l}x_iG_{il}+\sum _{l\leq j}x_jG_{lj}+\sum _{k< i\leq j}x_ix_j\partial _lG_{ij},$ for  $k< l$;
$k< l$;(iii)
 $\partial _{s_{j'}}F=\partial _{s_{j'}}G+ \sum _{k< i\leq j}x_ix_j\partial _{s_{j'}}G_{ij},$ for
$\partial _{s_{j'}}F=\partial _{s_{j'}}G+ \sum _{k< i\leq j}x_ix_j\partial _{s_{j'}}G_{ij},$ for  $1\leq j'\leq m$.
$1\leq j'\leq m$.
Let us suppose that the singularity of ![]() $g(x)=G(x_1,\ldots,x_{k},0)$ is not isolated in the origin
$g(x)=G(x_1,\ldots,x_{k},0)$ is not isolated in the origin ![]() $o$, or
$o$, or ![]() $g\equiv 0$, or
$g\equiv 0$, or ![]() $g$ not reduced. Then for each open set
$g$ not reduced. Then for each open set ![]() $o\in \Omega \subset {\mathbb {C}}^{k}$ there exists
$o\in \Omega \subset {\mathbb {C}}^{k}$ there exists ![]() $(p_1,\ldots,p_{k})\in \Omega$ such that:
$(p_1,\ldots,p_{k})\in \Omega$ such that:
(a)
 $g(p_1,\ldots,p_{k})=0,$
$g(p_1,\ldots,p_{k})=0,$(b)
 $\partial _{l}g(p_1,\ldots,p_{k})=0$, for
$\partial _{l}g(p_1,\ldots,p_{k})=0$, for  $1\leq l\leq k$.
$1\leq l\leq k$.
Then ![]() $(p_1,\ldots,p_{k},0,\ldots,0)\in {\mathbb {C}}^{n+1}$ is a singularity of
$(p_1,\ldots,p_{k},0,\ldots,0)\in {\mathbb {C}}^{n+1}$ is a singularity of ![]() $f$, which is a contradiction.
$f$, which is a contradiction.
Let us suppose that ![]() $G(x_1,\ldots,x_{k},s)$ is not a
$G(x_1,\ldots,x_{k},s)$ is not a ![]() $\mu$-constant deformation of
$\mu$-constant deformation of ![]() $g$. Then by virtue of Theorem 4.1 there exists
$g$. Then by virtue of Theorem 4.1 there exists ![]() $1\leq j\leq m$, and an analytic curve
$1\leq j\leq m$, and an analytic curve
such that
Let us consider the following analytic curve:
Using (i), (ii), and statement (iii), we observe that we can choose the large enough ![]() $r_{k+1},\ldots r_{n+1}$, and the
$r_{k+1},\ldots r_{n+1}$, and the ![]() $a_{k+1}(t),\ldots a_{n+1}(t)$, which are general enough in the manner that:
$a_{k+1}(t),\ldots a_{n+1}(t)$, which are general enough in the manner that:
(i)
 $ {\operatorname {Ord}}_t \partial _{s_j}F\circ \beta (t)= {\operatorname {Ord}}_t\partial _{s_j}G\circ \gamma (t)$ for
$ {\operatorname {Ord}}_t \partial _{s_j}F\circ \beta (t)= {\operatorname {Ord}}_t\partial _{s_j}G\circ \gamma (t)$ for  $1\leq j\leq m$;
$1\leq j\leq m$;(ii)
 $ {\operatorname {Ord}}_t\partial _{i}F\circ \beta (t)= {\operatorname {Ord}}_t\partial _{i}G\circ \gamma (t)$ for
$ {\operatorname {Ord}}_t\partial _{i}F\circ \beta (t)= {\operatorname {Ord}}_t\partial _{i}G\circ \gamma (t)$ for  $1\leq i\leq k$;
$1\leq i\leq k$;(iii)
 $ {\operatorname {Ord}}_t \partial _{l}F\circ \beta (t)\geq \max _{1\leq i\leq k}\{ {\operatorname {Ord}}_t \partial _{i}F\circ \beta (t)\}$ for
$ {\operatorname {Ord}}_t \partial _{l}F\circ \beta (t)\geq \max _{1\leq i\leq k}\{ {\operatorname {Ord}}_t \partial _{i}F\circ \beta (t)\}$ for  $k< l$.
$k< l$.
This implies that
This contradicts Theorem 4.1 since ![]() $F$ defines a
$F$ defines a ![]() $\mu$-constant deformation. Then
$\mu$-constant deformation. Then ![]() $G(x_1,\ldots,x_{k},s)$ is a
$G(x_1,\ldots,x_{k},s)$ is a ![]() $\mu$-constant deformation of
$\mu$-constant deformation of ![]() $g$ or there exists at least one non-zero
$g$ or there exists at least one non-zero ![]() $G_i$.
$G_i$.
Acknowledgements
The authors would like to thank the anonymous referees for their valuable comments which helped to improve the manuscript. The first author would also to thank Rachel Rogers for her unconditional support during this time.