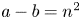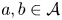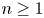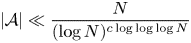1. Introduction
Sárközy [Reference SárközySár78] and Furstenberg [Reference FurstenbergFur77] independently showed that any set of integers whose difference set contains no non-zero squares must have asymptotic density zero, answering a question of Lovász. Sárközy's proof is based on the circle method, and gives the quantitative bound that if 
$\mathcal {A}\subseteq \{1,\ldots,N\}$ has no non-zero square differences, then 
$|\mathcal {A}|\le N/(\log {N})^{1/3+o(1)}$, whereas Furstenberg's result relies on ergodic theory. There have since been a variety of proofs of the qualitative result 
$|\mathcal {A}|=o(N)$; we refer the reader to the introduction of [Reference RiceRic19] for more details.
Sárközy's argument was refined by Pintz, Steiger, and Szemerédi [Reference Pintz, Steiger and SzemerédiPSS88] who improved the upper bound on the size of 
$\mathcal {A}\subseteq \{1,\ldots,N\}$ with no non-zero square differences to
\begin{equation} |\mathcal{A}|\ll \frac{N}{(\log N)^{c\log \log \log \log N}} \end{equation}
for some absolute constant 
$c>0$. (Here we use Vinogradov's notation 
$X\ll Y$ to mean that 
$X\leq CY$ for some absolute constant 
$C>0$.) One interesting feature of (1) is that it is a noticeably stronger bound than what is currently known for Roth's theorem on three-term arithmetic progressions [Reference Bloom and SisaskBS21], despite both proofs following a Fourier-analytic density increment argument.
In this paper, we improve the upper bound (1) for the size of sets of integers with no square differences.
Theorem 1 Let 
$N$ be sufficiently large. If 
$\mathcal {A}\subset \{1,\ldots,N\}$ has no solutions to 
$a-b=n^2$ with 
$a,b\in \mathcal {A}$ and 
$n\geq 1$, then
\[ \left\lvert \mathcal{A}\right\rvert\ll \frac{N}{(\log N)^{c\log \log\log N}} \]
for some absolute constant 
$c>0$.
Our proof of Theorem 1 follows a Fourier-analytic density increment argument as with previous approaches, but is actually more direct (and, we hope, simpler) than the approach of Pintz, Steiger, and Szemerédi. The key new tool in our work is an upper bound for the additive energy of sets of rationals with small denominator, which may be of independent interest. To state this, we recall that the 
$2m$-fold additive energy of a set 
$\mathcal {B}$ is given by
\[ E_{2m}(\mathcal{B}):= \lvert \{ (b_1,\ldots,b_{2m})\in \mathcal{B}^{2m} : b_1+\cdots+b_m=b_{m+1}+\cdots+b_{2m}\}\rvert. \]
We also introduce the notation
\begin{align*} \mathbb{Q}_{=q} &:= \left\{ \frac{a}{q}\in [0,1] : 1\leq a\leq q\text{ and }\gcd(a,q)=1\right\},\\ \mathbb{Q}_{\leq Q} &:= \bigcup_{1\leq q\leq Q}\mathbb{Q}_{=q}, \end{align*}
to denote the set of reduced rationals in 
$[0,1]$ with denominator precisely 
$q$, and for the set of all rationals with denominator at most 
$Q$. Our additive energy result is then the following.
Theorem 2 Let 
$Q\geq 4$ and 
$m\geq 2$. Suppose that 
$\mathcal {B}\subset \mathbb {Q}_{\leq Q}$ is such that there is 
$n\geq 1$ with 
$\left \lvert \mathcal {B}\cap \mathbb {Q}_{=q}\right \rvert \leq n$ for any 
$1\leq q\leq Q$. Then we have
\[ E_{2m}(\mathcal{B}) \leq (\log Q)^{C^m} (Qn)^m \]
for some absolute constant 
$C>0$.
We note that there is a trivial lower bound 
$E_{2m}(\mathcal {B})\ge |\mathcal {B}|^m$ from diagonal solutions where 
$b_{i}=b_{i+m}$ for 
$1\leq i\leq m$. If 
$\mathcal {B}$ contains 
$n$ rationals with denominator 
$q$ for each 
$q\in [Q/2,Q]$, then 
$|\mathcal {B}|\gg nQ$ and we see that Theorem 2 gives an upper bound of the form 
$|\mathcal {B}|^m (\log {|\mathcal {B}|})^{C^m}$, and so the contribution from the diagonal terms is comparable to the whole contribution. Thus, sets of rationals with small distinct denominators have similar additive energy estimates to dissociated sets where the only solutions to 
$b_1+\cdots +b_m=b_{m+1}+\cdots +b_{2m}$ are the diagonal ones.
Dissociated sets have been used in additive combinatorics since at least the work of Chang [Reference ChangCha02], and Theorem 2 allows one to extend Chang's ideas to sets whose large Fourier coefficients are close to rationals with small denominators, as is the situation in the Furstenberg–Sárközy problem. The original argument of Pintz, Steiger, and Szemerédi can be viewed as showing that there is a lack of additive structure in the rationals which make up the large Fourier coefficients, but Theorem 2 allows for a more efficient and direct use of this idea. Indeed, the original argument of [Reference Pintz, Steiger and SzemerédiPSS88] proves (implicitly) a lower bound for the size of the 
$m$-fold sumset, namely something of the strength of 
$\left \lvert m\mathcal {B}\right \rvert \gg _{m,\epsilon } \left \lvert \mathcal {B}\right \rvert ^{m-\epsilon }$, which follows from Theorem 2 and the simple inequality 
$|m\mathcal {B}|\geq |\mathcal {B}|^{2m}/E_{2m}(\mathcal {B})$, which is an immediate consequence of the Cauchy–Schwarz inequality. An important feature of Theorem 2 for our work is that it remains non-trivial even with 
$m$ as large as a small multiple of 
$\log \log {Q}$.
Clearly one can have sets 
$\mathcal {B}\subset \mathbb {Q}_{\leq Q}$ with very large additive energy if many elements of 
$\mathcal {B}$ have the same denominator; for example, if 
$Q$ is prime and 
$\mathcal {B}= \{ a/Q : 1\leq a< Q\}$, then 
$E_{2m}(\mathcal {B})=E_{2m}(\{1,\ldots,Q-1\})\gg _m Q^{2m-1}$. Some hypothesis restricting the size of 
$|\mathcal {B}\cap \mathbb {Q}_{=q}|\leq n$ is therefore natural for this problem.
Other results and generalizations. For comparison, the best known lower bound for the size 
$r(N)$ of the largest set 
$\mathcal {A}\subset \{1,\ldots,N\}$ with no non-zero square differences is much smaller than the upper bound in Theorem 1. Ruzsa [Reference RuzsaRuz84] gives a construction that shows, in particular, that 
$r(N) \gg N^{0.73}$. The constant in the exponent here has been slightly improved by Lewko [Reference LewkoLew15], but even whether 
$r(N)\gg N^{3/4}$ is open. We do not know where the truth lies, and it remains a fascinating open problem whether the true order of magnitude of 
$r(N)$ is 
$N^{1-o(1)}$ or 
$N^{1-c}$ for some absolute constant 
$c>0$.
For the analogous problem in the function field case, where 
$\mathbb {Z}$ is replaced by the polynomial ring 
$\mathbb {F}_q[t]$ over some finite field 
$\mathbb {F}_q$, much stronger quantitative bounds are known. Using the polynomial method, Green [Reference GreenGre17] has recently shown that if 
$\mathcal {A}\subset \mathbb {F}_q[t]_{\mathrm {deg}< n}$ contains no non-zero square differences, then
\begin{equation} \lvert \mathcal{A} \rvert \ll q^{(1-c(q))n}, \end{equation}
where 
$c(q)>0$ is some constant depending only on 
$q$. As 
$\mathbb {F}_q[t]_{\mathrm {deg}< n}$ has size 
$q^n$, this bound is analogous to a bound of the shape 
$r(N) \ll N^{1-c}$ in the integer case. The polynomial method used by Green is very different to the analytic arguments used in this paper, and depends in a fundamental way on the bounded characteristic of 
$\mathbb {F}_q[t]$.
The method of Pintz, Steiger, and Szemerédi [Reference Pintz, Steiger and SzemerédiPSS88] has been generalised to yield a similar bound for related problems. This was done for sets without differences of the form 
$n^k$ for any fixed 
$k\geq 3$ by Balog, Pelikan, Pintz, and Szemerédi [Reference Balog, Pelikan, Pintz and SzemerédiBPPS94], and then recently by Rice [Reference RiceRic19] to differences of the form 
$f(n)$ where 
$f\in \mathbb {Z}[x]$ is any intersective polynomialFootnote 1 of degree at least two. These proofs directly extend the method of [Reference Pintz, Steiger and SzemerédiPSS88], and as such it seems likely that one could combine the ideas of [Reference Balog, Pelikan, Pintz and SzemerédiBPPS94] and [Reference RiceRic19] with those in this paper to obtain a quantitative bound of strength comparable to Theorem 1 for these generalisations; we do not address these questions here.
Recent work of the second author [Reference MaynardMay20] showed that any system of polynomials simultaneously attain values with small fractional parts. There are various similarities with this work (a density increment argument enhanced by there being few solutions to linear equations involving rationals with small denominator), but there the problem was more structured which allowed for an almost optimal bound of the form 
$N^{1-c}$, whereas in this situation we are forced to consider much more arbitrary sets 
$\mathcal {A}$.
An upper bound for the additive energy of sets of well-distributed rationals similar (qualitatively) to Theorem 2 has also been applied within theoretical computer science, where it was used by Bourgain, Dilworth, Ford, Konyagin, and Kutzarova [Reference Bourgain, Dilworth, Ford, Konyagin and KutzarovaBDFKK11] to construct matrices satisfying the restricted isometry property. It follows from their Lemma 5, for example, that if 
$\mathcal {B}\subset \mathbb {Q}_{\leq Q}$ is such that for any 
$1\leq q\leq Q$ we have 
$\left \lvert \mathcal {B}\cap \mathbb {Q}_{=q}\right \rvert \leq 1$, then, for any 
$\epsilon >0$, we have 
$E_{2m}(\mathcal {B})\ll _{m,\epsilon }Q^\epsilon \left \lvert \mathcal {B}\right \rvert ^m$, where the dependence on 
$m$ and 
$\epsilon$ is unspecified. It is vital for our purposes that we explicitly control the dependence on 
$m$ and 
$\epsilon$.
2. Outline
In this section, we sketch how Theorem 2 can be used to give Theorem 1. As mentioned in the introduction, our proof is similar to the original work of Sárközy [Reference SárközySár78] (and its later refinements) in that we base our argument on a density increment argument coming out of the circle method. Our Theorem 2 allows us to show that no set 
$\mathcal {A}$ can have many large Fourier coefficients which are rationals with small distinct denominators, and this is the key which allows us to have a more efficient density increment argument than that of [Reference Pintz, Steiger and SzemerédiPSS88].
First we recall the basic setup. If 
$\mathcal {A}\subset \{1,\ldots,N\}$ has no non-zero square differences and density 
$\alpha =|\mathcal {A}|/N$, then by the circle method
\begin{align*} 0&=|\{(a_1,a_2,n):\,a_1-a_2=n^2,\,a_1,a_2\in\mathcal{A},\,1\le n\le N^{1/2}\}|\\ &=\int_0^1 |\widehat{1}_{\mathcal{A}}(\gamma)|^2\widehat{1}_{\square}(\gamma)\,{d}\gamma, \end{align*}
where 
$\widehat {1}_{\mathcal {A}}(\gamma )=\sum _{a\in \mathcal {A}}e(a\gamma )$ is the Fourier transform of the set 
$\mathcal {A}$, and similarly 
$\widehat {1}_{\square }$ is the Fourier transform of squares in 
$[1,N]$. Comparing this with the expected count of solutions in a random set of density 
$\alpha$, which is 
$\asymp \alpha ^2 N^{3/2}$, we find
\begin{equation} \int_0^1 |\widehat{g}_{\mathcal{A}}(\gamma)|^2|\widehat{1}_{\square}(\gamma)|\,{d}\gamma\gg \alpha^2 N^{3/2}, \end{equation}
where 
$g_{\mathcal {A}}=1_{\mathcal {A}}-\alpha 1_{[N]}$ is the balanced function of 
$\mathcal {A}$.
Following the standard major arc decomposition of the circle method, we then divide the unit interval 
$[0,1]$ into short intervals around rationals with small denominators. For precise details we refer to § 5. For the purpose of this heuristic discussion, the basic idea is that because we are working on an additive problem at ‘scale 
$N$’, after rescaling by a factor of 
$N$, we can replace the integration over 
$[0,1]$ with a discrete sum over the Fourier coefficients at rationals 
$a/q$ with small denominator, say 
$q\ll N$. Thus, (3) becomes
\[ \sum_{\substack{1\leq a\leq q\\ (a,q)=1\\ q\ll N}}|\widehat{g}_{\mathcal{A}}(a/q)|^2|\widehat{1}_{\square}(a/q)|\gg \alpha^2 N^{5/2}. \]
The classical major arc asymptotic and Gauss sum estimates (see § 6 for more details) imply that
\[ \lvert\widehat{1}_{\square}(a/q)\rvert\ll N^{1/2}/q^{1/2}. \]
By Parseval's identity, 
$\sum |\widehat {g}_{\mathcal {A}}(a/q)|^2\ll \alpha N^2$ and, hence, the contribution to (3) from those 
$a/q$ with 
$q\gg \alpha ^{-2}$ is negligible. By dividing the remaining range of integration according to the size of 
$q$, and applying the dyadic pigeonhole principle, we deduce that there must exist some 
$1\leq Q\ll \alpha ^{-2}$ such that
\begin{equation} \sum_{\substack{1\leq a\leq q \\ (a,q)=1\\ q\in [Q,2Q]}}\lvert\widehat{g}_{\mathcal{A}}(a/q)\rvert^2\gtrsim \alpha^2N^2Q^{1/2}, \end{equation}
where the use of 
$\gtrsim$ hides factors of 
$(\log (1/\alpha ))^{O(1)}$. In particular, there are ‘many’ rationals 
$a/q$ with 
$q\in [Q,2Q]$ for which 
$\widehat {g}_{\mathcal {A}}(a/q)$ is large. The basic density increment strategy is then to deduce that this implies that there is a large arithmetic progression, of size 
$\gg N/q\gg \alpha ^2N$, on which 
$\mathcal {A}$ has density 
$\alpha +\rho \alpha$ (for some suitable 
$\rho >0$), so this argument can then be iterated.
To explain how such an increment can be found, with a large value of 
$\rho$, it is convenient to use another application of the pigeonhole principle, after dividing into dyadic ranges according to the size of 
$\lvert \widehat {g}_{\mathcal {A}}(a/q)\rvert$, on (4). This produces some 
$\eta$ such that there are 
$\gtrsim \eta ^{-2}Q^{1/2}$ many 
$a/q$ with 
$q\in [Q,2Q]$ such that 
$\lvert \widehat {g}_{\mathcal {A}}(a/q)\rvert \gg \eta \lvert \mathcal {A} \rvert$.
We obtain a good density increment by showing that there must be many such rationals 
$a/q$ with the same denominator. More precisely, let 
$\rho$ be some parameter to be chosen later, and suppose that there are at least 
$\eta ^{-2}\rho ^2$ different rationals 
$\gamma$ with the same denominator 
$q$ where 
$|\widehat {g}_\mathcal {A}(\gamma )|\gg \eta |\mathcal {A}|$. A simple application of orthogonality then yields
\[ \sum_{b\ (\mathrm{mod}\ q)}\biggl(|\{a\in\mathcal{A}:\,a\equiv b\ (\mathrm{mod}\ q)\}|-\frac{|\mathcal{A}|}{q}\biggr)^2=\frac{1}{q}\sum_{c\ (\mathrm{mod}\ q)}\biggl|\widehat{g}_{\mathcal{A}}\biggl(\frac{c}{q}\biggr)\biggr|^2\gg \frac{\rho^2 |\mathcal{A}|^2}{q}, \]
and it is easily deduced that there must be some arithmetic progression with common difference 
$q$ on which 
$\mathcal {A}$ has relative density 
$\alpha +c\rho \alpha$, for some constant 
$c>0$, as required.
We now show that this must hold, by using the additive energy estimate of Theorem 2 to obtain a contradiction if there are 
$O(\eta ^{-2}\rho ^2)$ many such rationals with any fixed denominator. This is where our approach diverges significantly from previous works. Let 
$\mathcal {B}$ be the set of rationals 
$a/q$ with 
$|\widehat {g}_{\mathcal {A}}(a/q)|\gg \eta |\mathcal {A}|$ (so that 
$\left \lvert \mathcal {B}\right \rvert \gtrsim \eta ^{-2}Q^{1/2}$ by the above discussion). A variation of the proof of Chang's lemma shows roughly that, for any choice of 
$m\ge 1$,
\begin{equation} \eta |\mathcal{A}||\mathcal{B}|\ll \sum_{a/q\in \mathcal{B}}|\widehat{g}_{\mathcal{A}}(a/q)| \le |\mathcal{A}|^{1-1/2m}N^{1/2m}E_{2m}(\mathcal{B})^{1/2m}. \end{equation}
In particular, there cannot be a large set 
$\mathcal {B}$ with very small additive energy whilst also having the Fourier transform 
$\widehat {g}_\mathcal {A}$ of 
$\mathcal {A}$ large on all elements of 
$\mathcal {B}$. We can now apply Theorem 2 to bound 
$E_{2m}(\mathcal {B})$. Theorem 2 yields that, if there are 
$O(\eta ^{-2}\rho ^2)$ many rationals of any fixed denominator in 
$\mathcal {B}$, then (for some constant 
$C$)
\[ E_{2m}(\mathcal{B}) \ll (\log Q)^{C^m}(Q\eta^{-2}\rho^2)^m. \]
Inserting this bound into (5) and rearranging, we deduce that
\[ |\mathcal{B}|\ll \rho\eta^{-2}\alpha^{-1/2m}(\log Q)^{C^m}Q^{1/2}. \]
This contradicts the lower bound 
$|\mathcal {B}|\gtrsim \eta ^{-2}Q^{1/2}$ if
\[ \rho\approx \frac{\alpha^{1/2m}}{(\log Q)^{C^m}}. \]
Choosing 
$m=c\log \log ({1/\alpha })$ for some suitably small constant 
$c>0$, and recalling 
$Q\ll \alpha ^{-O(1)}$, this yields a contradiction with a choice of 
$\rho$ satisfying
\[ \rho\approx \exp\left( -O\left( \frac{\log{1/\alpha}}{\log\log{1/\alpha}}\right)\right). \]
In particular, the above discussion implies that there is an arithmetic progression 
$\mathcal {P}\subseteq \{1,\ldots,N\}$ with 
$|\mathcal {P}|\ge \alpha ^{O(1)}N$ on which 
$\mathcal {A}$ has density 
$\alpha (1+\rho )$. We may then iterate this statement, with 
$\mathcal {P}$ playing the role of 
$\{1,\ldots,N\}$ (there is a slight technical obstruction that we have glossed over here, namely that the common difference of 
$\mathcal {P}$ must be a square to preserve the property of having no non-zero square differences, but this is easily arranged in practice).
After iterating this procedure 
$\approx \rho ^{-1}\log (1/\alpha )$ many times, we must halt because the density of a set can never exceed 1. The only reason that our iteration must halt is because the length of the progression, say 
$N'$, becomes too short, say 
$N'\ll 1$. As we have only lost a factor of 
$\alpha ^{O(1)}$ in the length of the progression at each step, however, this means that
\[ 1 \gg \alpha^{O(\rho^{-1}(\log(1/\alpha))}N\gg \exp\left( -(\log(1/\alpha))^2\exp\left( O\left( \frac{\log{1/\alpha}}{\log\log{1/\alpha}}\right)\right)\right)N. \]
Simplifying this inequality yields 
$\log (1/\alpha )\gg (\log \log N)(\log \log \log N)$, and Theorem 1 follows.
Theorem 2 is established using a different, purely elementary, argument. Although it can be deduced from a direct combinatorial approach based on splitting according to suitable greatest common divisors we use an iterative argument which we hope is cleaner.
3. Notation
We begin by establishing the basic notation that we use. For any 
$N\geq 1$, we use 
$[N]$ to denote the set 
$\{1,\ldots,N\}$. We fix throughout our proof some large integer 
$N$ (large enough in particular such that 
$\log \log \log N\geq 4$, say). For functions 
$f:\mathbb {Z}\to \mathbb {C}$ we define the Fourier transform 
$\widehat {f}:[0,1]\to \mathbb {C}$ by
\[ \widehat{f}(\gamma) = \sum_{n\in \mathbb{Z}}f(n)e(\gamma n), \]
where 
$e(x)=e^{2\pi i x}$. We define the convolution of two functions 
$f,g:\mathbb {Z}\to \mathbb {C}$ by
\[ (f\ast g)(n)= \sum_{m\in\mathbb{Z}}f(m)g(n-m) \]
and use 
$f^{(\ast m)}(x)=(f\ast \ldots \ast f)(x)$ to denote the 
$m$-fold iterated convolution of 
$f$ (and 
$f^{(\ast 0)}:=f$). Without subscript, the notation 
$\left \lVert \gamma \right \rVert$ denotes the distance of 
$\gamma \in \mathbb {R}$ from the nearest integer, whereas 
$\left \lVert f\right \rVert _2=(\sum _{x\in \mathbb {Z}}|f(x)|^2)^{1/2}$ and 
$\left \lVert f\right \rVert _{\infty }=\sup _{x\in \mathbb {Z}}|f(x)|$ denotes the usual 
$L^2$ and 
$L^\infty$ norms.
We write 
$\tau _3(n)$ to denote the ternary divisor function 
$\sum _{abc=n}1$.
4. Addition of rational numbers and the proof of Theorem 2
In this section we prove Theorem 2. This section is essentially self-contained and can be read independently of the rest of the paper.
Theorem 2 follows quickly from the more technical Proposition 1. To state this we require some more notation. For any function 
$\omega :\mathbb {N}\to \mathbb {R}$ we define the maximal average function of 
$\omega$ by
\begin{equation} M(\omega;X):= \max_{1\leq x\leq X}\frac{1}{x}\sum_{n\leq x}\omega(n), \end{equation}and the logarithmic maximal average by
\begin{equation} M_{\mathrm{log}}(\omega;X):=\max_{2\leq x\leq X}\frac{1}{\log x}\sum_{n\leq x}\frac{\omega(n)}{n}. \end{equation}
We recall that 
$\tau _3(n)$ is the ternary divisor function 
$\sum _{abc=n}1$. Our technical bound on the additive energy is as follows.
Proposition 1 (Rationals with small denominators have small additive energy)
Let 
$m\,\geq\, 2$. Suppose that 
$\mathcal {B}\subset \mathbb {Q}_{\leq Q}$ and 
$n\geq 1$ is such that for any 
$1\leq q\leq Q$ we have 
$\left \lvert \mathcal {B}\cap \mathbb {Q}_{=q}\right \rvert \leq n$. Then we have the upper bound
\[ E_{2m}(\mathcal{B}) \leq (m\log Q M_{\mathrm{log}}(\tau_3^{2m};Q))^{O(m)}M(\tau_3^{2m-2};Q)(Qn)^m. \]
Proof Proof of Theorem 2 assuming Proposition 1
We claim that, for any 
$x\geq 3$ and 
$k\geq 0$,
\begin{equation} \sum_{n\leq x}\frac{\tau_3(n)^k}{n}\leq \prod_{p\leq x}\biggl(1-\frac{1}{p}\biggr)^{-3^k}. \end{equation}
The proof of this is elementary and standard, but textbook references do not track the explicit dependence on 
$k$, which is important for our application, and so we include a proof here. As any 
$n\leq x$ can be uniquely written as a product of prime powers at most 
$x$, and 
$\tau _3$ is multiplicative,
\[ \sum_{n\leq x}\frac{\tau_3(n)^k}{n}\leq \prod_{p\leq x}\left( 1+\frac{\tau_3(p)^k}{p}+\frac{\tau_3(p^2)^k}{p^2}+\cdots\right). \]
We also have, for any 
$0\leq z<1$,
\[ (1-z)^{-3^k}=\sum_{r\geq 0}\binom{3^k+r-1}{3^k-1}z^r. \]
To prove (8) it therefore suffices to show that 
$\tau _3(p^r)^k \leq \binom {3^k+r-1}{3^k-1}$ for all primes 
$p$ and integer 
$r\geq 0$. The divisor count 
$\tau _3(p^r)$ is the number of non-negative 
$a,b,c\geq 0$ such that 
$a+b+c=r$, which is 
$\binom {r+2}{2}$, and so it suffices to prove that, for any 
$k\geq 0$ and 
$r\geq 0$,
\[ \binom{r+2}{2}^k\leq \binom{3^k+r-1}{3^k-1}. \]
This is easily established via induction on 
$r$, because 
$\binom {3^k+r-1}{3^k-1}\geq 3^k\binom {3^k+r-2}{3^k-1}$ and 
$3\binom {r+1}{2}\geq \binom {r+2}{2}$.
Applying the bound (8), we therefore have
\[ M(\tau_3^k;X)\leq \max_{1\leq x\leq X}\sum_{n\leq x}\frac{\tau_3(n)^k}{n}\leq \prod_{p\leq X}\biggl(1-\frac{1}{p}\biggr)^{-3^k}. \]
By Mertens’ product bound (see, for example, [Reference Montgomery and VaughanMV07, Theorem 2.7]) we have 
$\prod _{p\leq X}(1-1/p)^{-1}\leq (\log X)^{O(1)}$ for all 
$X\geq 3$, whence 
$M(\tau _3^k;X) \leq (\log X)^{O(3^k)}$, and via an identical argument we also have 
$M_{\mathrm {log}}(\tau _3^k;X) \leq (\log X)^{O(3^k)}$. Therefore, Proposition 1 gives
\[ E_{2m}(\mathcal{B})\ll m^{O(m)}(\log Q)^{O(m9^m)} (Q n)^m. \]
Simplifying the exponents gives Theorem 2.
Proposition 1 will be proved via an iterative application of the following lemma. Roughly speaking, it says that if 
$\mathcal {B}\subset \mathbb {Q}_{\leq L}$ is spread evenly between different denominators, then for any sets 
$\mathcal {A},\mathcal {C}$ we have 
$\sum _{a\in \mathcal {A}}\sum _{b\in \mathcal {B}}\sum _{c\in \mathcal {C}}1_{a-b=c} \ll (\left \lvert \mathcal {A}\right \rvert \left \lvert \mathcal {B}\right \rvert \left \lvert \mathcal {C}\right \rvert )^{1/2}$. This should be compared with the trivial bound of 
$(\left \lvert \mathcal {A}\right \rvert \left \lvert \mathcal {C}\right \rvert )^{1/2}\left \lvert \mathcal {B}\right \rvert$. To attain the quantitative strength of Theorem 1 we will take care to prove an explicit weighted form of this inequality. To state this lemma precisely we make the following definition.
Definition 1 An arithmetic function 
$\omega :\mathbb {N}\to \mathbb {R}_{\ge 0}$ is sub-multiplicative if 
$\omega (ab)\leq \omega (a)\omega (b)$ for all 
$a,b\in \mathbb {N}$ and whenever 
$d\mid n$ we have 
$\omega (d)\leq \omega (n)$.
We note, in particular, that 
$\tau _3(n)$ is sub-multiplicative. To prove this, note that because 
$\tau _3$ is multiplicative it suffices to consider the case of prime powers, i.e. to show that 
$\tau _3(p^{r+s})\leq \tau _3(p^r)\tau _3(p^s)$ for any 
$r,s\geq 0$. Using the explicit formula 
$\tau _3(p^{m})=\binom {m+2}{2}$, this inequality becomes
\[ \binom{r+s+2}{2}\leq \binom{r+2}{2}\binom{s+2}{2}, \]
or, after rearranging,
\[ 2(r+s+2)(r+s+1)\leq (r+2)(r+1)(s+2)(s+1). \]
This inequality is immediate because 
$(r+2)(s+2)\geq 2r+2s+4$ and 
$(r+1)(s+1)\geq r+s+1$. The fact that 
$\tau _3(d)\leq \tau _3(n)$ whenever 
$d\mid n$ can be proved similarly, using multiplicativity to reduce to the case of prime powers, when it becomes the elementary inequality 
$\binom {r+2}{2}\leq \binom {s+2}{2}$ whenever 
$r\geq s$.
It follows immediately that 
$\tau _3(n)^k$ is also sub-multiplicative, for any 
$k\geq 0$.
Lemma 1 (Few solutions to linear equations in rationals with small denominators)
Let 
$Z\geq 1$ be an integer. Let 
$\mathcal {A}\subset \mathbb {Q}\cap (0,Z]$ and 
$\mathcal {C}\subset \mathbb {Q}$. Suppose that 
$\mathcal {B}\subset \mathbb {Q}_{\leq Q}$ is such that, for any 
$1\leq \ell \leq Q$, we have 
$\left \lvert \mathcal {B}\cap \mathbb {Q}_{=\ell }\right \rvert \leq n$. Let 
$\omega :\mathbb {N}\to \mathbb {R}_{\geq 0}$ be any sub-multiplicative function. Then
\[
\sideset{}{'}\sum_{\substack{a/k-b/\ell=c/q\\
a/k\in\mathcal{A}, \,b/\ell\in\mathcal{B},\,c/q\in
\mathcal{C}}}\omega(k)\ll \biggl( QnZ(\log{Q})
M_{\mathrm{log}}(\omega\tau_3;Q)\sideset{}{'}\sum_{c/q\in
\mathcal{C}}\omega(q)\tau_3(q)^2\sideset{}{'}\sum_{a/k\in
\mathcal{A}}\omega(k)\biggr)^{1/2}. \]
Here we use 
$\sum '$ to indicate that the fractions 
$a/k,b/\ell,c/q$ are all reduced (i.e. 
$\gcd (a,k)=\gcd (b,\ell )=\gcd (c,q)=1$).
We note that the summation on the left-hand side in Lemma 1 can also be written as 
$\sum _{x\in \mathcal {C}}(\widetilde {\omega }1_{\mathcal {A}}\ast 1_{-\mathcal {B}})(x)$, where 
$\widetilde {\omega }(a/q)=\omega (q)$ for 
$\gcd (a,q)=1$. If 
$\omega \approx 1$ and 
$|\mathcal {B}|\approx Qn$, then because 
$\tau _3$ is typically quite small the bound on the right-hand side is roughly of size 
$(\left \lvert \mathcal {A}\right \rvert \left \lvert \mathcal {B}\right \rvert \left \lvert \mathcal {C}\right \rvert )^{1/2}$.
Proof. Throughout the proof we use 
$\sum '$ to indicate that the fractions in the summation are reduced.
We claim that for any choice of parameter 
$T>0$, there is a decomposition of 
$\mathcal {A}\times \mathcal {B}$ into two sets 
$\mathcal {E}_1$ and 
$\mathcal {E}_2$ such that, if we let
\[ F_i(x):= \sideset{}{'}\sum_{(a/k,b/\ell)\in \mathcal{E}_i} \omega(k)1_{a/k-b/\ell=x}, \]
then we have
\begin{equation} \sideset{}{'}\sum_{c/q\in \mathcal{C}}F_1\biggl(\frac{c}{q}\biggr) \leq \frac{QnZ\log Q}{T}M_{\mathrm{log}}(\omega\tau_3;Q)\sideset{}{'}\sum_{c/q\in \mathcal{C}}\omega(q)\tau_3(q)^2 \end{equation}and
\begin{equation} \quad\sideset{}{'}\sum_{c/q\in \mathcal{C}}F_2\biggl(\frac{c}{q}\biggr) \leq T\sideset{}{'}\sum_{a/k\in \mathcal{A}}\omega(k). \end{equation}The lemma now follows from this claim by choosing
\[ T=\biggl( \frac {Qn Z(\log Q)
M_{\mathrm{log}}(\omega\tau_3;Q) \sum_{c/q\in
\mathcal{C}}^{'}\omega(q)\tau_3(q)^2}
{\sum_{a/k\in
\mathcal{A}}^{'}\omega(k)}\biggr)^{1/2}, \]
because
\[ \sideset{}{'}\sum_{\substack{a/k-b/\ell=c/q\\ a/k\in\mathcal{A}, \,b/\ell\in\mathcal{B},\,c/q\in \mathcal{C}}}\omega(k)= \sideset{}{'}\sum_{c/q\in \mathcal{C}}\left( F_1(c/q)+F_2(c/q)\right). \]
Thus, we are left to establish the claim by constructing the sets 
$\mathcal {E}_1$ and 
$\mathcal {E}_2$. We colour 
$\mathcal {A}\times \mathcal {B}$ by assigning 
$(a/k,b/\ell )$ the colour 
$C(a/k,b/\ell )=(d,f)\in \mathbb {Z}^2$, where
\[ d = \mathrm{gcd}(k,\ell)\quad\text{and}\quad f = \mathrm{gcd}\left( \frac{a\ell-bk}{d},d\right). \]
We then say that the colour 
$(d,f)$ is ‘popular at 
$a/k$’ if
\[ |\{ b/\ell\in \mathcal{B} : C(a/k,b/\ell)=(d,f)\}|\geq \frac{T}{\tau_3(k)}. \]
We say that a pair 
$(a/k,b/\ell )\in \mathcal {A}\times \mathcal {B}$ is ‘popular’ if its colour is popular at 
$a/k$, then let 
$\mathcal {E}_1\subset \mathcal {A}\times \mathcal {B}$ be the set of all popular pairs, and let 
$\mathcal {E}_2$ be the remaining set 
$(\mathcal {A}\times \mathcal {B})\backslash \mathcal {E}_1$.
The bound in (10) now follows easily. Indeed, it follows by construction that if 
$(a/k,b/\ell )$ is coloured 
$(d,f)$, then 
$f|d|k$, so for any fixed 
$a/k\in \mathcal {A}$ there are at most 
$\tau _3(k)$ possible different colours of pairs of the form 
$(a/k,b/\ell )$. As 
$\mathcal {E}_2$ only consists of the pairs which are not popular, for any colour 
$(d,f)$ there are at most 
$T/\tau _3(k)$ many 
$b/\ell \in \mathcal {B}$ such that 
$(a/k,b/\ell )$ receives the colour 
$(d,f)$. Thus, for any 
$a/k\in \mathcal {A}$, there are at most 
$T$ many 
$b/\ell \in \mathcal {B}$ such that 
$(a/k,b/\ell )\in \mathcal {E}_2$, and so
\[ \sideset{}{'}\sum_{ c/q\in \mathcal{C}} F_2(c/q)\leq \sideset{}{'}\sum_{a/k\in \mathcal{A}}\omega(k)\,\sideset{}{'}\sum_{b/\ell\in \mathcal{B}}1_{(a/k,b/\ell)\in \mathcal{E}_2}\leq T\sideset{}{'}\sum_{a/k\in A}\omega(k). \]
This gives (10).
It remains to establish (9). Given a choice of 
$d,f$ and 
$k$, let 
$R_{d,f,k}$ count the number of distinct possibilities for 
$a\pmod {f}$ such that the colour 
$(d,f)$ is popular at some 
$a/k\in \mathcal {A}$. We first show that, for any pair 
$(d,f)$ and 
$k$, we have
\begin{equation} R_{d,f,k}\leq \frac{Qn}{dT}\tau_3(k). \end{equation}
Let 
$\mathcal {A}_{d,f,k}\subset \mathcal {A}$ be some subset representing the 
$R_{d,f,k}$ different possibilities. That is, 
$\mathcal {A}_{d,f,k}$ is a set with the following properties.
(i) The colour
$(d,f)$ is popular at each $a/k\in \mathcal {A}_{d,f,k}$.(ii) If
$a/k,a'/k\in A_{d,f,k}$, then $a\not \equiv a'\pmod {f}$.(iii) For each
$a'/k\in \mathcal {A}$ such that $(d,f)$ is popular at $a'/k$, there is $a/k\in \mathcal {A}_{d,f,k}$ such that $a\equiv a'\pmod {f}$.(iv) We have
$R_{d,f,k}=\left \lvert \mathcal {A}_{d,f,k}\right \rvert$.
By the definition of edges being popular at 
$a/k$, we have
\[ R_{d,f,k}\frac{T}{\tau_3(k)}\leq \sideset{}{'}\sum_{a/k\in \mathcal{A}_{d,f,k}}\sideset{}{'}\sum_{\substack{b/\ell \in \mathcal{B}\\ C({a}/{k},{b}/{\ell})=(d,f)}}1. \]
The key observation is that each 
$b/\ell \in \mathcal {B}$ appears at most once in total on the right-hand side, because if 
$C(a_1/k,b/\ell )=C(a_2/k,b/\ell )=(d,f)$, then we must have
\[ \gcd(k,\ell)=d\quad\text{and}\quad\gcd\biggl(\frac{a_1\ell-b k}{d},d\biggr)=\mathrm{gcd}\biggl(\frac{a_2\ell-bk}{d},d\biggr)=f. \]
In particular, 
$a_1\ell /d\equiv a_2\ell /d\pmod {f}$. Note that, because 
$\gcd (\ell/d,k/d)=1$ and 
$\gcd (b,\ell )=1$, we have
\[ \gcd(\ell/d,f)\mid \gcd(\ell/d, a_1(\ell/d)-b(k/d))=\gcd(\ell/d,b(k/d))=\gcd(\ell/d,k/d)=1, \]
whence 
$\gcd (\ell /d,f)=1$. It follows that 
$a_1\equiv a_2\pmod {f}$ and so, by construction of 
$\mathcal {A}_{d,f,k}$, we have 
$a_1=a_2$. In particular,
\[ R_{d,f,k}\frac{T}{\tau_3(k)}\leq \sideset{}{'}\sum_{a/k\in \mathcal{A}_{d,f,k}}\sideset{}{'}\sum_{\substack{b/\ell \in \mathcal{B}\\ C ({a}/{k},{b}/{\ell})=(d,f)}}1\leq \sum_{\substack{\ell\leq Q\\ d\mid l}}\left\lvert \mathcal{B}\cap \mathbb{Q}_{=\ell}\right\rvert\leq \frac{n Q}{d}, \]
and the estimate (11) follows immediately.
We now establish (9) by bounding 
$F_1(c/q)$ for each 
$c/q$ separately. Given a choice of 
$c/q$ (with 
$\gcd (c,q)=1$) we see that if 
$a,k,b,\ell$ are such that 
$\gcd (a,k)=\gcd (b,\ell )=1$ and
\[ \frac{c}{q}=\frac{a}{k}-\frac{b}{\ell}, \]
then 
$q=\ell ' k' e$ and 
$c=(a\ell '-bk')/f$, where
\[ k'=\frac{k}{\gcd(k,\ell)},\quad \ell'=\frac{\ell}{\gcd(k,\ell)},\quad \gcd(k,\ell)=e f, \quad f=\gcd(a \ell'-b k',\gcd(k,\ell)). \]
Thus, given a choice of 
$c,k',\ell ',e,f$ with 
$k'\ell 'e=q$ and 
$1\leq f\leq Q$, there is a unique choice of 
$k=k'ef$ and 
$\ell =\ell 'ef$. Moreover, 
$a\ell '\equiv c f\ (\mathrm {mod}\ k')$, so 
$a$ is fixed modulo 
$k'$. There are at most 
$e$ choices of 
$a\ (\mathrm {mod}\ e)$ and at most 
$R_{ef,f,k'ef}$ choices of 
$a\ (\mathrm {mod}\ f)$, so at most 
$e R_{ef,f,k'ef}$ choices of 
$a\ (\mathrm {mod}\ k)$. If we then further fix the value of 
$\lceil a/k\rceil$, for which there are at most 
$Z$ choices, then we have determined 
$a$. Given such a choice of 
$a$, 
$b$ is uniquely determined because 
$b=\ell (c/q-a/k)$. It follows that
\begin{align} F_1(c/q)\leq
Z\sum_{k'\ell'e=q}\sum_{1\leq f\leq Q}\omega(k'ef)e
R_{ef,f,k'ef}. \end{align}
Using (11) and the sub-multiplicativity of 
$\omega$ and 
$\tau _3$, this is bounded above by
\[ \frac{QnZ}{T}\sum_{k'\ell'e=q}\omega(k'e)\tau_3(k'e)\sum_{1\leq f\leq Q}\frac{\omega(f)\tau_3(f)}{f} \le \frac{QnZ\log{Q}}{T}M_{\mathrm{log}}(\omega\tau_3;Q)\omega(q)\tau_3(q)^2. \]
Summing this over 
$c/q\in \mathcal {C}$ then gives (9), and so completes the proof.
We actually use a weighted version of Lemma 1, which follows immediately by a dyadic decomposition of the support of the weights.
Lemma 2 Let 
$Z\geq 1$ be an integer. Let 
$f:\mathbb {Q}_{> 0}\to \mathbb {Z}_{\ge 0}$ and 
$g:\mathbb {Q}\cap (0,Z]\to \mathbb {Z}_{\ge 0}$ be functions with finite support such that 
$\left \lVert f\right \rVert _\infty,\left \lVert g\right \rVert _\infty \leq X$. Suppose that 
$\mathcal {B}\subset \mathbb {Q}_{\leq Q}$ is such that, for any 
$1\leq \ell \leq Q$, we have 
$\left \lvert \mathcal {B}\cap \mathbb {Q}_{=\ell }\right \rvert \leq n$. Then, for any sub-multiplicative function 
$\omega :\mathbb {N}\to \mathbb {R}_{\geq 0}$,
\[ \sideset{}{'}\sum_{\substack{a/k-b/\ell=c/q\\ b/\ell\in\mathcal{B}}}\omega(k)g\biggl(\frac{a}{k}\biggr)f\biggl(\frac{c}{q}\biggr)\ll C \biggl(\sideset{}{'}\sum_{c/q}\omega(q)\tau_3(q)^2f\biggl(\frac{c}{q}\biggr)^2\biggr)^{1/2} \biggl(\sideset{}{'}\sum_{a/k}\omega(k)g\biggl(\frac{a}{k}\biggr)^2\biggr)^{1/2}, \]
where
\[ C:=(\log{X})(QnZ(\log{Q}) M_{\mathrm{log}}(\omega\tau_3;Q))^{1/2}. \]
Here we use 
$\sum '$ to indicate that the fractions 
$a/k,b/\ell,c/q$ are all reduced (i.e. 
$\gcd (a,k)=\gcd (b,\ell )=\gcd (c,q)=1$).
Proof Proof of Lemma 2
We decompose the support of 
$f$ into 
$\mathcal {C}_j$ for 
$j\geq 0$, where
\[ \mathcal{C}_j = \{ x: 2^j\leq f(x) < 2^{j+1}\}, \]
and similarly decompose the support of 
$g$ into 
$\mathcal {A}_i$. Using this decomposition we have
\[ \sideset{}{'}\sum_{\substack{a/k-b/\ell=c/q\\ b/\ell\in\mathcal{B}}}\omega(k)g\biggl(\frac{a}{k}\biggr)f\biggl(\frac{c}{q}\biggr) \ll\sum_{0\leq i,j \leq \log{X}}2^{i+j}\sideset{}{'}\sum_{\substack{a/k-b/\ell=c/q\\ a/k\in\mathcal{A}_i,\,b/\ell\in\mathcal{B},\,c/q\in\mathcal{C}_j}}\omega(k). \]
Applying Lemma 1 to each summand gives the upper bound
\[ \ll \sum_{0\leq i,j \leq \log{X}
}2^{i+j}\biggl( Q n
Z(\log{Q})M_{\mathrm{log}}(\omega\tau_3;Q)\sideset{}{'}\sum_{c/q\in
\mathcal{C}_j}\omega(q)\tau_3(q)^2\sideset{}{'}\sum_{a/k\in
\mathcal{A}_i}\omega(k)\biggr)^{1/2}. \]
Lemma 2 now follows by the Cauchy–Schwarz inequality.
The proof of Proposition 1 may now proceed via induction.
Proof Proof of Proposition 1
Again, we use 
$\sum '$ to indicate that the summation is restricted to reduced fractions. We show that, for any 
$t\geq 0$ and 
$1\le j\le m$, we have
\begin{equation} \sideset{}{'}\sum_{c/q\in\mathbb{Q}} \tau_3(q)^{2t}1_{\mathcal{B}}^{(\ast j)}(c/q)^2 \ll (m\log Q)^3(Q n M_{2t+1}) \sideset{}{'}\sum_{c/q\in\mathbb{Q}} \tau_3(q)^{2t+2}1_{\mathcal{B}}^{(\ast j-1)}(c/q)^2, \end{equation}
where we recall 
$1_{\mathcal {B}}^{(\ast m)}(x)=\sum _{x_1+\cdots +x_m=x}1_{\mathcal {B}}(x_1)\cdots 1_{\mathcal {B}}(x_m)$ is the 
$m$-fold convolution of 
$1_{\mathcal {B}}$, and where
\[ M_t := M_{\mathrm{log}}(\tau_3^{t};Q). \]
Repeatedly applying (13) 
$m-1$ times gives
\begin{align*} E_{2m}(\mathcal{B})&=\sideset{}{'}\sum_{c/q\in\mathbb{Q}} 1_{\mathcal{B}}^{(\ast m)}(c/q)^2\\ &\ll (m\log Q)^{3(m-1)}(Q n)^{m-1}(M_1\cdots M_{2m-3})\sideset{}{'}\sum_{c/q\in\mathbb{Q}} \tau_3(q)^{2m-2}1_{\mathcal{B}}(c/q)^2. \end{align*}
As 
$|\mathcal {B}\cap \mathbb {Q}_{=q}|\le n$, we have
\[ \sideset{}{'}\sum_{c/q\in\mathbb{Q}} \tau_3(q)^{2m-2}1_{\mathcal{B}}(c/q)^2\leq n\sum_{1\leq q\leq Q}\tau_3(q)^{2m-2}\leq n Q M(\tau_3^{2m-2};Q). \]
Noting that 
$M_t\le M_{2m}=M_{\mathrm {log}}(\tau _3^{2m};Q)$ for each 
$t\le 2m$, this completes the proof of Proposition 1. Thus, we are left to establish (13).
We first observe that, because 
$1_{\mathcal {B}}^{(\ast j)}(c/q)=\sum _{b/\ell \in \mathcal {B}}1_{\mathcal {B}}^{(\ast j-1)}(c/q-b/\ell )$, we have
\[ \sideset{}{'}\sum_{c/q\in\mathbb{Q}} \tau_3(q)^{2t} 1_{\mathcal{B}}^{(\ast j)}(c/q)^2=\sideset{}{'}\sum_{\substack{c/q=c'/q'+b/\ell\\ b/\ell\in\mathcal{B}}}\tau_3(q)^{2t}1_{\mathcal{B}}^{(\ast j)}(c/q)1_{\mathcal{B}}^{(\ast j-1)}(c'/q'). \]
We let 
$f(x):=1_{\mathcal {B}}^{(\ast j-1)}(x)$ and 
$g(x):=1_{\mathcal {B}}^{(\ast j)}(x)$, so that, in particular, 
$g$ is supported on 
$j\mathcal {B}$. As 
$\mathcal {B}\subset (0,1]$ we know that 
$g$ is supported on 
$(0,j]$. Furthermore, because 
$\mathcal {B}\subset \mathbb {Q}_{\le Q}$ we have 
$\left \lvert \mathcal {B}\right \rvert \leq Q^2$ so 
$\|f\|_\infty,\|g\|_\infty \leq Q^{2j}$. We now apply Lemma 2 with 
$\omega (q)=\tau _3(q)^{2t}$. This gives the upper bound
\begin{align*}
&\sideset{}{'}\sum_{c/q\in\mathbb{Q}} \tau_3(q)^{2t}
1_{\mathcal{B}}^{(\ast j)}(c/q)^2=
\sideset{}{'}\sum_{\substack{c/q=c'/q'+b/\ell\\
b/\ell\in\mathcal{B}}}\omega(q)g(c/q)f(c'/q')\\ &\qquad \ll
(m\log Q)^{3/2}(Q n M_{2t+1})^{1/2} \biggl(
\sideset{}{'}\sum_{c'/q'\in\mathbb{Q}}
\tau_3(q')^{2t+2}f\biggl(\frac{c'}{q'}\biggr)^2\biggr)^{1/2}\biggl(
\sideset{}{'}\sum_{c/q\in\mathbb{Q}}
\tau_3(q)^{2t}g\biggl(\frac{c}{q}\biggr)^2\biggr)^{1/2}.
\end{align*}
The left-hand side is 
$\sum _{c/q\in \mathbb {Q}} \tau _3(q)^{2t}g(c/q)^2$, so this rearranges to give the claimed bound (13).
5. Basic density increment
In this section, we establish a simple 
$L^2$ density increment lemma, which says that if there are many large Fourier coefficients which are close to rationals with the same denominator, then one can find a large arithmetic progression on which the set has increased density. Statements of this type are standard, and our lemma differs only cosmetically from similar statements used in [Reference Pintz, Steiger and SzemerédiPSS88] or [Reference Ruzsa and SandersRS08]. It may be helpful to bear in mind that this will be applied with some 
$q,K\ll \alpha ^{-O(1)}$ and 
$\nu \gg \alpha ^{o(1)}$ (where the 
$o(1)\to 0$ as 
$\alpha \to 0$).
We introduce the notation
\[ \mathfrak{M}\biggl(\frac{a}{q};N,K\biggr):=\{\gamma\in (0,1] : \left\lVert \gamma-a/q\right\rVert\leq K/qN\} \]
to denote the major arcs which appear in the circle method. Note that these major arcs are disjoint for distinct 
$a/q\in \mathbb {Q}_{=q}$ provided 
$K< N/2$.
Lemma 3 (Large Fourier coefficients with the same denominator give density increment)
Let 
$\nu,\alpha \in (0,1]$ and let 
$N, K,q\ge 1$ be such that 
$K< N/2$ and 
$\nu \alpha N/(K q^2)$ is sufficiently large. Let 
$\mathcal {A}\subset [N]$ be a set with no non-zero square differences and density 
$\alpha =\left \lvert \mathcal {A}\right \rvert /N$, and
\[ \sum_{{a}/{q}\in
\mathbb{Q}_{=q}}\int_{\mathfrak{M}
({a}/{q};N,K)}\left\lvert
\widehat{1_{\mathcal{A}}}(\gamma)-\alpha\widehat{1_{[N]}}(\gamma)\right\rvert^2\,\,{d}\gamma
\geq \nu\alpha \left\lvert \mathcal{A}\right\rvert.
\]
Then there exists 
$N'\gg \nu \alpha N/(K q^2)$ and a set 
$\mathcal {A}'\subset [N']$ with no non-zero square differences such that the density 
$\alpha '=|\mathcal {A}'|/N'$ satisfies
\[ \alpha'\geq (1+\nu/5)\alpha. \]
Proof. Let 
$\mathcal {P}=(q^2)\cdot [N']$ be an arithmetic progression of difference 
$q^2$ and length 
$N'$, for some 
$N'$ to be chosen later. If 
$\gamma \in \mathfrak {M}(a/q;N,K)$ for some 
$a/q$, then for any 
$1\le n'\le N'$ we have
\[ \left\lvert 1-e(\gamma q^2 n')\right\rvert\ll \left\lVert \gamma q^2 n'\right\rVert\leq\left\lVert \gamma q^2 n'-a q n'\right\rVert= q^2 n'\left\lVert \gamma-a/q\right\rVert\leq \frac{q^2 N' K}{q N}. \]
(We recall that 
$\left \lVert \cdot \right \rVert$ is the distance to the nearest integer.) In particular, we can ensure that 
$\left \lvert 1-e(\gamma q^2k)\right \rvert \leq 1/2$ provided we have
\begin{equation} N'\leq \frac{c N}{q K}\end{equation}
for some sufficiently small absolute constant 
$c>0$. Thus, if 
$\gamma \in \mathfrak {M}(a/q;N,K)$ and (14) holds,
\[ \left\lvert \widehat{1_{\mathcal{P}}}(\gamma)-N'\right\rvert\leq \sum_{1\leq n'\leq N'}\left\lvert 1-e(\gamma q^2 n')\right\rvert\leq N'/2, \]
and so 
$|\widehat {1_{\mathcal {P}}}(\gamma )|\ge N'/2$. Let 
$g=1_{\mathcal {A}}-\alpha 1_{[N]}$ be the balanced function of 
$\mathcal {A}$. It follows that (using the assumption of the lemma)
\begin{align}
\sum_{x\in\mathbb{Z}}(1_{\mathcal{P}}\ast g)(x)^2=\int_0^1
\lvert \widehat{1_{\mathcal{P}}}(\gamma)\rvert^2\left\lvert
\widehat{g}(\gamma)\right\rvert^2\,\,{d}\gamma&\ge
\frac{(N')^2}{4}\sum_{{a}/{q}\in
\mathbb{Q}_{=q}}\int_{\mathfrak{M}({a}/{q};N,K)}\left\lvert
\widehat{g}(\gamma)\right\rvert^2\,\,{d}\gamma\nonumber\\
&\ge \frac{\nu \alpha(N')^2\left\lvert
\mathcal{A}\right\rvert}{4}.
\end{align}
On the other hand, recalling that 
$g=1_{\mathcal {A}}-\alpha 1_{[N]}$, the left-hand side is equal to
\begin{equation} \left\lVert 1_{\mathcal{P}}\ast 1_{\mathcal{A}}\right\rVert_2^2-2\alpha \sum_{x\in\mathbb{Z}} (1_{\mathcal{P}}\ast 1_{\mathcal{A}})(x)\cdot(1_{\mathcal{P}}\ast 1_{[N]})(x) +\alpha^2\left\lVert 1_{\mathcal{P}}\ast 1_{[N]}\right\rVert_2^2. \end{equation}The third term of (16) trivially satisfies
\begin{equation} \alpha^2\left\lVert 1_{\mathcal{P}}\ast 1_{[N]}\right\rVert_2^2\le \alpha^2 N \left\lvert \mathcal{P}\right\rvert^2=\alpha \left\lvert \mathcal{A}\right\rvert(N')^2. \end{equation}For the second term of (16), we note that
\begin{align*} \sum_{x\in\mathbb{Z}}\left\lvert (1_{\mathcal{P}}\ast 1_{-\mathcal{P}}\ast 1_{[N]})(x)-(N')^21_{[N]}(x)\right\rvert &\leq \sum_{y\in\mathbb{Z}}(1_{\mathcal{P}}\ast1_{-\mathcal{P}})(y)\sum_{x\in\mathbb{Z}}\left\lvert 1_{[N]}(x-y)-1_{[N]}(x)\right\rvert\\ &\ll \sum_{y\in\mathbb{Z}}(1_{\mathcal{P}}\ast1_{-\mathcal{P}})(y) |y|\\ &\ll q^2(N')^3. \end{align*}
In particular,
\begin{align} \sum_{x\in\mathbb{Z}} (1_{\mathcal{P}}\ast 1_{\mathcal{A}})(x)\cdot (1_{\mathcal{P}}\ast 1_{[N]})(x) &= \sum_{y\in \mathcal{A}}1_{\mathcal{P}}\ast 1_{-\mathcal{P}}\ast 1_{[N]}(y)\nonumber\\ &=\left\lvert \mathcal{A}\right\rvert(N')^2+O(q^2(N')^3). \end{align}By substituting (17) and (18) into (16), we have
\[ \left\lVert 1_{\mathcal{P}}\ast
1_{\mathcal{A}}\right\rVert_2^2\geq
2\alpha\bigl(\left\lvert
\mathcal{A}\right\rvert(N')^2+O(q^2(N')^3)\bigr)-\alpha\left\lvert
\mathcal{A}\right\rvert(N')^2+\frac{\nu
\alpha(N')^2\left\lvert \mathcal{A}\right\rvert}{4}.
\]
Provided we have
\begin{equation} N'\leq \frac{c \nu \alpha N}{q^2}\end{equation}
for some sufficiently small constant 
$c>0$, we see that the 
$O(q^2(N')^3)$ term contributes at most 
$\nu \alpha \left \lvert \mathcal {A}\right \rvert (N')^2/100$ in total, and so
\[ \left\lVert 1_{\mathcal{P}}\ast 1_{-\mathcal{A}}\right\rVert_2^2=\left\lVert 1_{\mathcal{P}}\ast 1_{\mathcal{A}}\right\rVert_2^2\geq \biggl(1+\frac{\nu}{5}\biggr)\alpha \left\lvert \mathcal{A}\right\rvert(N')^2. \]
As 
$\left \lVert 1_{\mathcal {P}}\ast 1_{-\mathcal {A}}\right \rVert _1=N'\left \lvert \mathcal {A}\right \rvert$ there exists some 
$x\in \mathbb {Z}$ such that
\[ \left\lvert (q^2\cdot [N'])\cap (\mathcal{A}+x)\right\rvert=1_{\mathcal{P}}\ast 1_{-\mathcal{A}}(x)\geq \biggl(1+\frac{\nu}{5}\biggr)\alpha N'. \]
Therefore, if we set
\[ \mathcal{A}' := \frac{1}{q^2}\cdot ((q^2\cdot [N'])\cap (\mathcal{A}+x)), \]
then 
$\mathcal {A}'\subset [N']$, 
$\mathcal {A}'$ has density 
$\alpha '\ge (1+\nu /5)\alpha$ and 
$\mathcal {A}'$ has no non-zero square differences because any non-zero square difference in 
$\mathcal {A}'$ would create one in 
$q^2\cdot \mathcal {A}'$ and, hence, one in 
$\mathcal {A}+x$, and, hence, one in 
$\mathcal {A}$, which is a contradiction. This therefore gives the result with 
$N'=\lfloor c\nu \alpha N/(K q^2)\rfloor$ for a suitably small absolute constant 
$c>0$ (because this choice satisfies (14) and (19) and 
$N'\gg \nu \alpha N/(K q^2)$).
6. Large Fourier coefficients at rationals with small denominators
In this section, we show how to find many rationals with small denominator in the large spectrum of 
$\mathcal {A}$ (that is, the set of frequencies with large Fourier coefficient). This follows standard lines, combining the circle method with classical bounds for Weyl sums.
Lemma 4 (Bounds for exponential sums over squares)
Let 
$1\le a \le q$ with 
$\gcd (a,q)=1$ and
\begin{align*} \mathfrak{M}\biggl(\frac{a}{q};N,K\biggr)&:=\{\gamma\in (0,1] : \left\lVert \gamma-a/q\right\rVert\leq K/qN\},\\ W(n) &:= \begin{cases} \dfrac{2m}{N^{1/2}}, & \text{if }n=m^2\leq N,\\ 0, & \text{otherwise.}\end{cases} \end{align*}
Then we have the following bounds.
(i) For all
$\beta \in \mathbb {R}$ we have
\[ \lvert \widehat{W}(a/q+\beta)\rvert\ll \frac{N^{1/2}}{q^{1/2}}+(q\log q)^{1/2}(1+\left\lvert \beta\right\rvert N). \]
(ii) If
$Kq\log q\ll N$ and $K^3\log q\ll qN$, then
\[
\int_{\mathfrak{M}({a}/{q};N,K)}\lvert
\widehat{W}(\gamma)\rvert^2\,\,{d}\gamma \ll \frac{1}{q}.
\]
Proof. This is standard. By [Reference Pintz, Steiger and SzemerédiPSS88, Equation (8)] (which is a consequence of partial summation and the standard bound for incomplete Gauss sums 
$\sum _{n\leq X}e(an^2/q)\ll (q\log q)^{1/2}$ for 
$X\leq q$) we have
\[ \widehat{W}(a/q+\beta) =
\frac{S(a;q)}{q} \widehat{W}(\beta)+O\bigl((q\log
q)^{1/2}(1+\left\lvert \beta\right\rvert N)\bigr),
\]
where 
$S(a;q):=\sum _{1\leq n\leq q}e(an^2/q)$ is the complete Gauss sum. The classical estimate 
$S(a;q)\ll q^{1/2}$ for 
$\gcd (a,q)=1$ now gives bound (i). Using this estimate again, we find
\[ \int_{\mathfrak{M}({a}/{q};N,K)}\lvert \widehat{W}(\gamma)\rvert^2\,\,{d}\gamma \ll \frac{1}{q}\int_{0}^{K/qN}\lvert \widehat{W}(\beta)\rvert^2\,\,{d} \beta + \frac{K\log q}{N}+(q\log q)N^2\int_0^{K/qN}\beta^2\,\,{d} \beta. \]
The second and third summands contribute
\[ \ll \frac{K\log q}{N}+(q \log q)N^2\frac{K^3}{q^3N^3}\ll \frac{K\log q}{N}+ \frac{K^3\log q}{q^2N}\ll \frac{1}{q} \]
by our assumptions on 
$q$ and 
$K$. By [Reference Pintz, Steiger and SzemerédiPSS88, equation (10)] and the trivial bound, if 
$\beta \leq N^{-7/8}$, then
\[ \lvert \widehat{W}(\beta)\rvert\ll \min\biggl(N^{1/2},\frac{\beta^{-1}}{N^{1/2}}\biggr). \]
(Note that this bound is slightly better than what one gets with the unweighted sum, but could be improved further with more smoothing.) This gives
\[ \frac{1}{q}\int_{0}^{K/qN}\lvert \widehat{W}(\beta)\rvert^2\,\,{d} \beta\ll \frac{1}{q}+\frac{1}{qN}\int_{1/N}^{K/qN}\beta^{-2}\,\,{d}\beta\ll \frac{1}{q}, \]
as required.
Lemma 5 Suppose 
$N$ is sufficiently large. Let 
$\mathcal {A}\subset [N]$ be a set of density 
$\alpha =\left \lvert \mathcal {A}\right \rvert /N\ge N^{-1/8}$ with no non-zero square differences. Then there exist quantities 
$B,Q,K$ with 
$\alpha ^{O(1)}\ll B\ll \alpha ^{-O(1)}$ and 
$1\leq Q,K \leq \alpha ^{-7}$, and a set 
$\mathcal {B}\subset \mathbb {Q}_{\leq Q}$ such that:
(i) for each
$a/q\in \mathcal {B}$ there exists $\gamma _{a/q}\in (0,1]$ with $\left \lVert \gamma _{a/q}-a/q\right \rVert \ll \alpha ^{-O(1)}/N$ and
\[ \sum_{{a}/{q}\in \mathcal{B}}\lvert \widehat{1_{\mathcal{A}}}(\gamma_{a/q})\rvert\gg B\frac{\left\lvert \mathcal{A}\right\rvert Q^{1/2}}{\log(1/\alpha)^{2}}; \]
(ii) for each
$a/q\in \mathcal {B}$ we have, if $g=1_{\mathcal {A}}-\alpha 1_{[N]}$,
\[ \int_{\mathfrak{M}({a}/{q};N,K)}\lvert \widehat{g}(\gamma)\rvert^2\,\,{d}\gamma\gg \frac{\alpha \left\lvert \mathcal{A}\right\rvert}{B^2}. \]
Proof. We first note that, by the estimate of [Reference SárközySár78], say, we may assume that 
$\alpha \ll 1/(\log N)^{1/4}$ because 
$\mathcal {A}$ has no non-zero square differences. (This is not essential to the method, but allows for cleaner bounds in the final statements.) Let
\[ W(n) := \begin{cases}
\dfrac{2m}{N^{1/2}} & \text{if }n=m^2\leq N,\\ 0
& \text{otherwise.}\end{cases} \]
By orthogonality and the fact that 
$\mathcal {A}$ has no non-zero square differences, we have
\begin{align*} \int_0^1\widehat{1_{\mathcal{A}}}(\gamma)\overline{\widehat{1_{\mathcal{A}}}(\gamma)}\widehat{W}(\gamma)\,\,{d}\gamma &=\sum_{a,b\in \mathcal{A}}\sum_{1\leq n\leq N^{1/2}}W(n^2)\int_0^1 e(\gamma(a-b+n^2))\,\,{d}\gamma\\ &=\sum_{a,b\in \mathcal{A}}\sum_{1\leq n\leq N^{1/2}} W(n^2)1_{b-a=n^2}\\ &= 0. \end{align*}
Suppose first that 
$\left \lvert \mathcal {A}\cap (N/2,N]\right \rvert \geq \left \lvert \mathcal {A}\right \rvert /2$. In this case, if we let 
$g=1_{\mathcal {A}}-\alpha 1_{[N]}$, then
\begin{align*} \int_0^1\widehat{g}(\gamma)\overline{\widehat{1_{\mathcal{A}}}(\gamma)}\widehat{W}(\gamma)\,\,{d}\gamma &=-\alpha \sum_{a\in A}\sum_{1\leq y\leq N}\sum_{1\leq n\leq N^{1/2}}W(n^2)\int_0^1 e(\gamma(y-a+n^2))\,\,{d}\gamma\\ &=-\alpha\sum_{a\in A}\sum_{1\leq n\leq N^{1/2}}W(n^2)1_{1\leq a-n^2\leq N}\\ &\leq -\tfrac{1}{8}\alpha \left\lvert \mathcal{A}\right\rvert N^{1/2}, \end{align*}
say, because certainly all 
$a\in \mathcal {A}\cap (N/2,N]$ and 
$n\leq (N/2)^{1/2}$ will satisfy 
$1\leq a-n^2\leq N$. If 
$\left \lvert \mathcal {A}\cap [1,N/2]\right \rvert \geq \left \lvert \mathcal {A}\right \rvert /2$, then arguing similarly, we have
\[ \int_0^1\overline{\widehat{g}(\gamma)}\widehat{1_{\mathcal{A}}}(\gamma)\widehat{W}(\gamma)\,\,{d}\gamma \leq -\tfrac{1}{8}\alpha\left\lvert \mathcal{A}\right\rvert N^{1/2}. \]
Thus, in either case, we have
\begin{equation} \int_0^1\lvert \widehat{g}(\gamma)\widehat{1_{\mathcal{A}}}(\gamma)\widehat{W}(\gamma)\rvert\,\,{d}\gamma \geq \tfrac{1}{8}\alpha\left\lvert \mathcal{A}\right\rvert N^{1/2}. \end{equation}
By Dirichlet's theorem on Diophantine approximation, given any choice of 
$1\leq K\leq N$, every 
$\gamma \in [0,1]$ satisfies 
$\left \lVert \gamma -a/q\right \rVert < K/(N q)$ for some 
$1\leq q\leq N/K$ and 
$1\leq a\leq q$ with 
$\gcd (a,q)=1$. If this holds for some 
$q>K$ and 
$K\leq N^{1/2}$, say, then by Lemma 4,
\[ \lvert \widehat{W}(\gamma)\rvert\ll \left( \frac{N(\log N)}{K}\right)^{1/2}. \]
If we choose
\begin{equation} K:=\lceil C\alpha^{-2}\log N\rceil \end{equation}
for some suitably large absolute constant 
$C>0$, then we see that 
$\lvert \widehat {W}(\gamma )\rvert \leq \alpha N^{1/2}/32$ for such 
$\gamma$. (Note that the assumption 
$\alpha \ll (\log N)^{-1/4}$ implies that 
$K\leq \alpha ^{-7}$, assuming that 
$N$ is sufficiently large.) The contribution to (20) from these 
$\gamma$ is thus at most
\begin{align} \frac{\alpha N^{1/2}}{32}\int_0^1\lvert \widehat{g}(\gamma)\widehat{1_{\mathcal{A}}}(\gamma)\rvert\,\,{d}\gamma &\leq \frac{\alpha N^{1/2}}{32}\biggl(\int_0^1\lvert \widehat{1_{\mathcal{A}}}(\gamma)\rvert^2\,\,{d}\gamma+\int_0^1\left\lvert \alpha\widehat{1_{[N]}}(\gamma)\widehat{1_{\mathcal{A}}}(\gamma)\right\rvert\,\,{d}\gamma\biggr)\nonumber\\ &\leq \frac{ \alpha\left\lvert \mathcal{A}\right\rvert N^{1/2}}{16}. \end{align}
(Here we used the triangle inequality in the first line, and the Cauchy–Schwarz inequality and Parseval's identity in the second.) We recall that for 
$\gcd (a,q)=1$
\[ \mathfrak{M}(a/q)=\mathfrak{M}(a/q;N,K) := \{ \gamma\in (0,1] : \left\lVert \gamma-a/q\right\rVert\leq K/q N\}, \]
and note that with our choice 
$K=\lceil C\alpha ^{-2}\log N\rceil$ these sets are disjoint for 
$q\le K$ and 
$\gcd (a,q)=1$ because 
$\alpha \ge N^{-1/3}$ and 
$N$ is sufficiently large. Therefore, combining (20) and (22), we find
\begin{equation} \sum_{{a}/{q}\in \mathbb{Q}_{\leq K}}\int_{\mathfrak{M}({a}/{q})}\lvert \widehat{g}(\gamma)\widehat{1_{\mathcal{A}}}(\gamma)\widehat{W}(\gamma)\rvert\,\,{d}\gamma\geq \frac{\alpha \left\lvert \mathcal{A}\right\rvert N^{1/2}}{16}. \end{equation}By the Cauchy–Schwarz inequality and Lemma 4, we have
\begin{align*} \int_{\mathfrak{M}({a}/{q})}&\lvert \widehat{g}(\gamma)\widehat{1_{\mathcal{A}}}(\gamma)\widehat{W}(\gamma)\rvert\,\,{d}\gamma\\ &\ll \biggl(\int_{\mathfrak{M}({a}/{q})} \left\lvert \widehat{g}(\gamma)\right\rvert^2\,\,{d} \gamma\biggr)^{1/2}\biggl(\int_{\mathfrak{M}({a}/{q})} \left\lvert \widehat{W}(\gamma)\right\rvert^2\,\,{d} \gamma\biggr)^{1/2}\sup_{\gamma\in\mathfrak{M}({a}/{q})}\left\lvert \widehat{1_{\mathcal{A}}}(\gamma)\right\rvert\\ &\ll\frac{1}{q^{1/2}}\biggl(\int_{\mathfrak{M}({a}/{q})} \left\lvert \widehat{g}(\gamma)\right\rvert^2\,\,{d} \gamma\biggr)^{1/2}\sup_{\gamma\in\mathfrak{M}({a}/{q})}\left\lvert \widehat{1_{\mathcal{A}}}(\gamma)\right\rvert. \end{align*}
Therefore,
\begin{equation} \sum_{{a}/{q}\in \mathbb{Q}_{\leq K}}\frac{1}{q^{1/2}}\biggl(\int_{\mathfrak{M}({a}/{q})}\lvert \widehat{g}(\gamma)\rvert^2\,\,{d}\gamma\biggr)^{1/2}\biggl(\sup_{\gamma\in \mathfrak{M}({a}/{q})}\left\lvert \widehat{1_{\mathcal{A}}}(\gamma)\right\rvert\biggr)\gg \alpha \left\lvert \mathcal{A}\right\rvert N^{1/2}. \end{equation}
Let 
$\Gamma _1$ be the set of 
$a/q\in \mathbb {Q}_{\le K}$ for which
\begin{equation} \int_{\mathfrak{M}({a}/{q})}\lvert \widehat{g}(\gamma)\rvert^2\,\,{d}\gamma\le \frac{N}{K^5}. \end{equation}
As 
$|\Gamma _1|\le |\mathbb {Q}_{\le K}|\le K^2$ and 
$|\widehat {1_{\mathcal {A}}}(\gamma )|\le |\mathcal {A}|$, the contribution to (24) from 
$\gamma \in \Gamma _1$ is
\[ \ll \sum_{{a}/{q}\in \mathbb{Q}_{\leq K}} \frac{1}{q^{1/2}}\cdot \frac{N^{1/2}}{K^{5/2}} \cdot |\mathcal{A}| \ll \frac{\alpha \left\lvert \mathcal{A}\right\rvert N^{1/2} }{(\log{N})^{1/2}}. \]
Thus, we may restrict our attention to the set 
$\Gamma _2=\mathbb {Q}_{\le K}\backslash \Gamma _1$ of 
$a/q\in \mathbb {Q}_{\le K}$ for which (25) does not hold. Indeed, we have
\begin{equation} \sum_{{a}/{q}\in\Gamma_2}\frac{1}{q^{1/2}}\biggl(\int_{\mathfrak{M}({a}/{q})}\lvert \widehat{g}(\gamma)\rvert^2\,\,{d}\gamma\biggr)^{1/2}\biggl(\sup_{\gamma\in \mathfrak{M}({a}/{q})}\left\lvert \widehat{1_{\mathcal{A}}}(\gamma)\right\rvert\biggr)\gg \alpha \left\lvert \mathcal{A}\right\rvert N^{1/2}. \end{equation}
As 
$\lvert \widehat {g}(\gamma )\rvert \le 2\left \lvert \mathcal {A}\right \rvert \le 2N$ and 
$\mathrm {meas}(\mathfrak {M}(a/q))\ll K/N$, we see that for any 
$\gamma \in \mathbb {Q}_{\le K}$
\[ \biggl(\int_{\mathfrak{M}({a}/{q})}\lvert \widehat{g}(\gamma)\rvert^2\,\,{d}\gamma\biggr)^{1/2}\ll K^{1/2}N^{1/2}, \]
and so, comparing with (25), for 
$\gamma \in \Gamma _2$ we have
\[ K^{1/2}N^{1/2}\ll \biggl(\int_{\mathfrak{M}({a}/{q})}\lvert \widehat{g}(\gamma)\rvert^2\,\,{d}\gamma\biggr)^{1/2}\le K^{-5/2}N^{1/2}. \]
Therefore, by dyadic pigeonholing, there are some quantities 
$B,Q$ with 
$\alpha K^{-1/2}\ll B\ll \alpha K^{5/2}$ and 
$1\le Q\le K$, together with a set 
$\mathcal {B}\subset \Gamma _2$, such that:
(i) if
$a/q\in \mathcal {B}$ with $\gcd (a,q)=1$, then $q\in [Q,2Q]$;(ii) for all
$\gamma \in \mathcal {B}$ we have
\[ \frac{\alpha N^{1/2}}{B}\leq \biggl(\int_{\mathfrak{M}({a}/{q})}\lvert \widehat{g}(\gamma)\rvert^2\,\,{d}\gamma\biggr)^{1/2}\leq \frac{2 \alpha N^{1/2}}{B}; \]
(iii) we have
\[ \sum_{{a}/{q}\in\mathcal{B}}\frac{1}{q^{1/2}}\biggl(\int_{\mathfrak{M}({a}/{q})}\lvert \widehat{g}(\gamma)\rvert^2\,\,{d}\gamma\biggr)^{1/2}\biggl(\sup_{\gamma\in \mathfrak{M}({a}/{q})}\left\lvert \widehat{1_{\mathcal{A}}}(\gamma)\right\rvert\biggr)\gg \frac{\alpha \left\lvert \mathcal{A}\right\rvert N^{1/2}}{(\log{K})^2}. \]
Recalling that 
$K\ll \alpha ^{-O(1)}$ (because we are assuming that 
$\alpha \le 1/(\log {N})^{1/4}$), and letting 
$\gamma _{a/q}$ be the point in 
$\mathfrak {M}(a/q)$ where 
$|\widehat {1_{\mathcal {A}}}(\gamma )|$ attains its maximum, we see that this gives the result.
Combining Lemma 5 with Lemma 3 gives the following result.
Lemma 6 Let 
$N$ be sufficiently large, and suppose that 
$\nu \geq N^{-1/2}$. Let 
$\mathcal {A}\subset [N]$ be a set of density 
$\alpha =\left \lvert \mathcal {A}\right \rvert /N$ with no non-zero square differences. Then at least one of the following holds.
(i) (
$\mathcal {A}$ is sparse) We have $\log (1/\alpha )\gg \log N$.(ii) (There is a density increment) There is some
$N'\gg \nu \alpha ^{O(1)}N$ and $\mathcal {A}'\subset [N']$ with no non-zero square differences, which has density
\[ \alpha'\geq (1+\nu/5)\alpha. \]
(iii) (There are many large Fourier coefficients close to rationals of different denominators) There are
$B,Q\ll \alpha ^{-O(1)}$ and a set $\mathcal {B}\subset \mathbb {Q}_{\leq Q}$ such that both of the following hold:
(a) for each
$a/q\in \mathcal {B}$ there exists $\gamma _{a/q}\in (0,1]$ such that $\left \lVert \gamma _{a/q}-a/q\right \rVert \ll \alpha ^{-O(1)}/N$ and
\[ \sum_{{a}/{q}\in \mathcal{B}}\lvert \widehat{1_{\mathcal{A}}}(\gamma_{a/q})\rvert\gg \frac{B\left\lvert \mathcal{A}\right\rvert Q^{1/2}}{\log(1/\alpha)^{O(1)}}; \]
(b) for every
$1\leq q\leq Q$ we have
\[ \left\lvert \mathcal{B}\cap \mathbb{Q}_{=q}\right\rvert\ll \nu B^2. \]
Proof. Assume that neither part (i) nor (ii) hold, so we wish to establish part (iii). Let 
$C_1,C_2>0$ be two absolute constants to be determined later. As part (ii) does not hold, by Lemma 3, we have that, for any 
$q\leq 2\alpha ^{-7}$ and 
$K\leq \alpha ^{-7}$,
\[ \sum_{{a}/{q}\in
\mathbb{Q}_{=q}}\int_{\mathfrak{M}({a}/{q}:N,K)}|\widehat{g}(\gamma)|^2\,\,{d}\gamma
\leq \nu\alpha \left\lvert \mathcal{A}\right\rvert.
\]
(Note that we may assume that 
$\nu \alpha N/Kq^2\geq N^{1/4}$, say, or otherwise 
$\alpha \geq N^{-1/60}$ and we are in case (i). In particular, for 
$N$ sufficiently large, the conditions of Lemma 3 are satisfied.)
By Lemma 5 there are 
$B,Q,K$ satisfying 
$B\ll \alpha ^{-O(1)}$ and 
$Q,K\leq \alpha ^{-7}$ and 
$\mathcal {B}\subset \mathbb {Q}_{\leq Q}$ such that for all 
$a/q\in \mathcal {B}$ there exists 
$\gamma _{a/q}$ such that 
$\| \gamma _{a/q}-a/q\|\ll \alpha ^{-O(1)}/N$ and
\[ \sum_{{a}/{q}\in \mathcal{B}}\lvert \widehat{1_{\mathcal{A}}}(\gamma_{a/q})\rvert\gg B\frac{\left\lvert \mathcal{A}\right\rvert Q^{1/2}}{\log(1/\alpha)^{O(1)}}, \]
and for all 
$a/q\in \mathcal {B}$
\[
\int_{\mathfrak{M}({a}/{q};N,K)}\lvert
\widehat{g}(\gamma)\rvert^2\,\,{d}\gamma\gg \frac{\alpha
\left\lvert \mathcal{A}\right\rvert}{B^2}. \]
Summing this second inequality over 
$a/q\in \mathcal {B}\cap \mathbb {Q}_{=q}$ we see that
\[ \frac{\alpha \left\lvert
\mathcal{A}\right\rvert}{B^2}|\mathcal{B}\cap\mathbb{Q}_{=q}|\ll
\sum_{{a}/{q}\in \mathcal{B}\cap\mathbb{Q}_{=q}}
\int_{\mathfrak{M}({a}/{q};N,K)}\lvert
\widehat{g}(\gamma)\rvert^2\,\,{d}\gamma\leq \nu\alpha
\left\lvert \mathcal{A}\right\rvert. \]
Thus, 
$|\mathcal {B}\cap \mathbb {Q}_{=q}|\ll \nu B^2$, as required.
7. Refined density increment and proof of Theorem 1
We now show that there cannot be a large set of rationals with distinct denominators each of which has a large Fourier coefficient. This relies on Theorem 2 which shows that there is a lack of additive structure amongst such rationals, and a variant of Chang's lemma [Reference ChangCha02] (or its predecessors such as the Montgomery–Halász method [Reference MontgomeryMon69]) which shows that any large set of frequencies with large Fourier coefficients must have some additive structure, and is the key way in which our argument differs from previous approaches. Ultimately this will show that for a suitable choice of parameter 
$\nu$, the third possibility in Lemma 6 cannot occur, and Lemma 6 can be refined to give a density increment. An iterative application of this density increment then proves our main result, Theorem 1.
Lemma 7 (Variant of Chang's lemma)
Let 
$\mathcal {A}\subset [N]$ be a set of density 
$\alpha =\left \lvert \mathcal {A}\right \rvert /N$ and let 
$\mathcal {B}\subset (0,1]$. Then, for each 
$m\ge 1$,
\[ \sum_{b\in\mathcal{B}}|\widehat{1_{\mathcal{A}}}(b)|\ll |\mathcal{A}|\alpha^{-1/2m}E_{2m}(\mathcal{B};1/2N)^{1/2m}, \]
where the approximate additive energy 
$E_{2m}(\mathcal {C};\delta )$ is given by
\[ E_{2m}(\mathcal{C};\delta):=|\{b_1,\ldots,b_{2m}\in\mathcal{C}:\,\|b_1+\cdots+b_m-b_{m+1}\ldots-b_{2m}\|\le \delta\}| \]
(where we recall that 
$\|\cdot \|$ denotes the distance to the nearest integer).
Proof. Let 
$\theta _b\in \mathbb {R}$ be a phase such that 
$e(\theta _b)\widehat {1_{\mathcal {A}}}(b)=|\widehat {1_{\mathcal {A}}}(b)|\in \mathbb {R}_{\geq 0}$. Then, by Hölder's inequality, we have
\begin{align} \sum_{b\in\mathcal{B}}|\widehat{1_{\mathcal{A}}}(b)|&= \sum_{b\in\mathcal{B}}e(\theta_b)\sum_{a\in\mathcal{A}}e(ab)\nonumber\\ &\le \biggl(\sum_{a\in\mathcal{A}}1\biggr)^{1-1/2m}\biggl(\sum_{a\in\mathcal{A}}\biggl|\sum_{b\in B}e(\theta_b+b a)\biggr|^{2m}\biggr)^{1/2m}. \end{align}
Let 
$\psi (t):=\sin (\pi t)^2/(\pi t)^2$ so that 
$\widehat {\psi }(\xi )=\int _{-\infty }^{\infty }\psi (t)e^{-2\pi i \xi t}\,\,{d} t$ satisfies 
$\widehat {\psi }(\xi )=1-|\xi |$ for 
$|\xi |\le 1$ and 
$\widehat {\psi }(\xi )=0$ for 
$|\xi |>1$. As 
$\psi (t)\ge 0$ and 
$\psi (t)\ge 4/\pi ^2\ge 1/3$ on 
$[0,1/2]$ we see that
\begin{align*}
\sum_{a\in\mathcal{A}}\biggl|\sum_{b\in
B}e(\theta_b+ba)\biggr|^{2m}&\le
3\sum_{n\in\mathbb{Z}}\psi\biggl(\frac{n}{2N}\biggr)\biggl|\sum_{b\in
B}e(\theta_b+bn)\biggr|^{2m}\\ &\le
3\sum_{b_1,\ldots,b_{2m}\in\mathcal{B}}\biggl|\sum_{n\in\mathbb{Z}}\psi\biggl(\frac{n}{2N}\biggr)e\bigl(n(b_1+\cdots+b_m-b_{m+1}\cdots
-b_{2m})\bigr)\biggr|. \end{align*}
Applying Poisson summation to the inner sum, and recalling that 
$\hat {\psi }$ is supported on 
$[-1,1]$, we see that this is equal to
\begin{align*}& 6\sum_{b_1,\ldots,b_{2m}\in\mathcal{B}}N\biggl|\sum_{h\in \mathbb{Z}}\hat{\psi}\bigl(2N(b_1+\cdots+b_m-b_{m+1}\cdots-b_{2m}-h)\bigr)\biggr| \\ & \qquad \ll N|\{b_1,\ldots,b_{2m}\in\mathcal{B}:\,\|b_1+\cdots+b_m-b_{m+1}\cdots-b_{2m}\|\le 1/2N\}|. \end{align*}Substituting this into (27) and rearranging then gives the result.
Lemma 8 Let 
$N$ be sufficiently large, and let 
$\mathcal {A}\subset [N]$ be a set of density 
$\alpha =\left \lvert \mathcal {A}\right \rvert /N$ with no non-zero square differences. There exists an absolute constant 
$c>0$ such that if
\begin{align*} \nu = \exp\left( -c \frac{\log(1/\alpha)}{\log\log(1/\alpha)}\right), \end{align*}
then either:
(i)
$\log (1/\alpha ) \gg \log N/\log \log N$; or(ii) there are
$N'\gg \alpha ^{O(1)}N$ and $\mathcal {A}'\subset [N']$ with no non-zero square differences, which has density
\[ \alpha'\geq (1+\nu/5)\alpha. \]
Proof. As before, we may assume that 
$\log N \ll \alpha ^{-O(1)}$, by the result of [Reference SárközySár78]. We assume that cases (i) and (ii) do not hold, and hope to arrive at a contradiction, for a suitable choice of 
$\nu$.
Note that we may assume that 
$\nu \geq N^{-1/2}$, or otherwise we are in case (i). Therefore, we are able to apply Lemma 6, of which we must be in the third case because otherwise case (i) or (ii) would hold. Thus, there are 
$B,Q\ll \alpha ^{-O(1)}$ and a set 
$\mathcal {B}\subset \mathbb {Q}_{\leq Q}$ such that for each 
$a/q\in \mathcal {B}$ there exists 
$\gamma _{a/q}=a/q+O(\alpha ^{-O(1)}/N)$ satisfying
\[ \sum_{{a}/{q}\in \mathcal{B}}\lvert \widehat{1_{\mathcal{A}}}(\gamma_{a/q})\rvert\gg \frac{B\left\lvert \mathcal{A}\right\rvert Q^{1/2}}{\log(1/\alpha)^{O(1)}}, \]
and for every 
$1\leq q\leq Q$ we have 
$\left \lvert \mathcal {B}\cap \mathbb {Q}_{=q}\right \rvert \leq \nu B^2$. By the pigeonhole principle, there must exist some 
$\mathcal {B}'\subset \mathcal {B}$ which is contained in an interval of width at most 
$1/8m$ such that
\[ \sum_{{a}/{q}\in \mathcal{B}'}\lvert \widehat{1_{\mathcal{A}}}(\gamma_{a/q})\rvert\gg \frac{B\left\lvert \mathcal{A}\right\rvert Q^{1/2}}{m\log(1/\alpha)^{O(1)}}. \]
Let 
$m\geq 2$ be some integer to be chosen later, and let 
$\Gamma :=\{\gamma _b:\,b\in \mathcal {B}'\}$. Note that the assumption that 
$\left \lVert \gamma _b-b\right \rVert \ll \alpha ^{-O(1)}/N$, together with the fact that 
$\mathcal {B}\subset \mathbb {Q}_{\leq \alpha ^{-O(1)}}$, implies that these 
$\gamma _b$ are distinct for distinct 
$b\in \mathcal {B}'$, or otherwise we are in case (i). We now apply Lemma 7, which shows that
\[ \frac{B \left\lvert \mathcal{A}\right\rvert Q^{1/2}}{m\log(1/\alpha)^{O(1)}}\ll \left\lvert \mathcal{A}\right\rvert\alpha^{-1/2m}E_{2m}(\Gamma;1/2N)^{1/2m}. \]
As 
$\mathcal {B}'$ is contained in an interval of width at most 
$1/8m$ we know that 
$b_1+\cdots -b_{2m}\in [-1/4,1/4]$. In particular, because 
$\left \lvert \gamma _b-b\right \rvert \ll \alpha ^{-O(1)}/N$ for 
$b\in \mathcal {B}$, provided 
$m\alpha ^{-O(1)}< cN$ for some sufficiently small 
$c>0$, we have 
$\gamma _{b_1}+\cdots -\gamma _{b_{2m}}\in (-1/2,1/2)$, and so
\[ E_{2m}(\Gamma;1/2N) = \lvert \{ b_1,\ldots,b_{2m}\in \mathcal{B}' : \lvert \gamma_{b_1}+\cdots-\gamma_{b_{2m}}\rvert \leq 1/2N\}\rvert. \]
Furthermore, because 
$\mathcal {B}\subset \mathbb {Q}_{\le Q}$, 
$b_1+\cdots -b_{2m}$ is always a rational of denominator at most 
$Q^{2m}$ for 
$b_1,\ldots,b_{2m}\in \mathcal {B}$. Therefore, if 
$b_1+\cdots -b_{2m}$ is not zero, then it is at least 
$Q^{-2m}$ in absolute value. As before, because 
$\left \lvert \gamma _b-b\right \rvert \ll \alpha ^{-O(1)}/N$, provided 
$m Q^{O(m)}\alpha ^{-O(1)}< cN$ for some small constant 
$c>0$, it follows that for any 
$\gamma _{b_1},\ldots,\gamma _{b_{2m}}\in \Gamma$ either 
$\left \lvert \gamma _{b_1}+\cdots -\gamma _{b_{2m}}\right \rvert \ge Q^{-2m}/2$ or 
$b_1+\cdots -b_{2m}=0$. Therefore, provided 
$m Q^{O(m)}\alpha ^{-O(1)}< cN$ for sufficiently small 
$c>0$, the approximate additive energy 
$E_{2m}(\Gamma ;1/N)$ actually only counts the times when the corresponding sum of rationals is zero, so
\[ E_{2m}(\Gamma;1/2N)=E_{2m}(\mathcal{B}'). \]
Recalling that 
$Q\ll \alpha ^{-O(1)}$, we have shown that either 
$\alpha ^{-O(m)}\gg N$ or
\begin{equation} E_{2m}(\mathcal{B}') \gg \alpha \left( \frac{B Q^{1/2}}{m\log(1/\alpha)^{O(1)}}\right)^{2m}.\end{equation}
We impose the condition 
$m\ll \log \log (1/\alpha )$, so that 
$\alpha ^{-O(m)}=o(N)$ (or otherwise we are in case (i)), so we have (28). We now apply Theorem 2 to bound 
$E_{2m}(\mathcal {B}')$ from above, which shows that for some absolute constant 
$C>0$ we have
\begin{equation} m^{O(m)}(\log Q)^{C^m}(C\nu B^2 Q)^{m}\gg \alpha \left( \frac{ B Q^{1/2}}{\log(1/\alpha)^{O(1)}}\right)^{2m}. \end{equation}
Here we used the assumption that 
$|\mathcal {B}'\cap \mathbb {Q}_{=q}|\le \lvert \mathcal {B}\cap \mathbb {Q}_{=q}\rvert \ll \nu B^2$ for all 
$q$, as ensured by the conclusion of Lemma 6.
The key feature of this bound is that the powers of 
$B$ and 
$Q$ exactly cancel and, in particular, the lower bound on 
$\nu$ in terms of 
$\alpha$ is only of order 
$\alpha ^{-O(1/m)}\log (1/\alpha )^{O(1)}$. We derive a contradiction from this bound with a suitable choice of 
$\nu$, thereby proving the lemma. First note that we can rewrite (29) as
\[ \nu \gg \frac{\alpha^{1/m}}{m^{O(1)}\log(1/\alpha)^{O(1)}}\exp\left( -C^m\frac{\log \log Q}{m}\right). \]
As 
$Q\ll \alpha ^{-O(1)}$, if we choose 
$m=\lceil c'\log \log (1/\alpha )\rceil$, for some sufficiently small constant 
$c'>0$, then this gives
\[ \nu \gg \exp\left( -O\left( \frac{\log(1/\alpha)}{\log\log(1/\alpha)}\right)\right), \]
which gives a contradiction for a suitable choice of the constant 
$c$ in our definition of 
$\nu$. This completes the proof.
We may now finish the proof of our main theorem with an iterative application of Lemma 8.
Proof Proof of Theorem 1
Suppose that 
$\mathcal {A}\subset [N]$ has density 
$\alpha =\left \lvert \mathcal {A}\right \rvert /N$ and has no non-zero square differences. We wish to show that
\[ \log(1/\alpha) \gg (\log\log N)(\log\log\log N). \]
Let
\[ \nu := \exp\left( -c \frac{\log(1/\alpha)}{\log\log(1/\alpha)}\right) \]
be as in Lemma 8. If 
$\log (1/\alpha ) \gg \log N/\log \log N$, then we are done. Otherwise, by Lemma 8, there are 
$N'\geq \alpha ^{O(1)}N$ and 
$\mathcal {A}'\subset [N']$ which has no non-zero square differences, with density
\[ \alpha' \geq (1+\nu/5)\alpha. \]
Repeatedly applying Lemma 8, we obtain some sequence 
$N_1,\ldots,N_t$ of integers and associated sets 
$\mathcal {A}_t\subset [N_t]$ such that:
(i) each set
$\mathcal {A}_t$ has no non-zero square differences;(ii)
$\mathcal {A}_t\subset [N_t]$ has density $\alpha _t=|\mathcal {A}_t|/N_t \geq (1+\nu /5)^t\alpha$;(iii) we have
$N_t \geq \alpha ^{O(t)}N$.
This process can only terminate if 
$N_t< N^{1/2}$, because otherwise all conditions of Lemma 8 remain satisfied. However, the density of any set can never exceed 
$1$, so we must have 
$\alpha (1+\nu /20)^t\le \alpha _t\le 1$, which implies that
\[ t\ll \nu^{-1}\log(1/\alpha). \]
Therefore,
\[ N^{1/2}>N_t\ge \alpha^{O(t)}N\gg
N\exp\bigl(-O\bigl(\nu^{-1}\log(1/\alpha)^2\bigr)\bigr).
\]
Thus,
\[ \log N \ll \nu^{-1}(\log 1/\alpha)^2. \]
Recalling that 
$\log (1/\nu )\ll \log (1/\alpha )/\log \log (1/\alpha )$, taking logarithms of both sides and rearranging yields
\[ \frac{\log(1/\alpha)}{\log\log(1/\alpha)}\gg \log\log{N}. \]
This implies 
$\log (1/\alpha )\gg (\log \log {N})(\log \log \log {N})$, which gives the result.
Acknowledgements
T.B. would like to thank Julia Wolf for many helpful discussions regarding the original proof of Pintz, Steiger, and Szemerédi (of which the first chapter of [Reference WolfWol08] is an excellent exposition), and would also like to thank Alex Rice for pointing out an error in an earlier draft of this paper. J.M. would like to thank Ben Green for introducing him to this question.
Both authors would like to thank the anonymous referee for a careful reading of the paper and several helpful suggestions.
