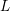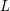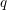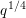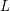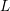1 Introduction
1.1 A reciprocity formula
A landmark result in the theory of  $L$-functions, because of both its structural beauty and its applications, is Motohashi’s identity for the fourth moment of the Riemann zeta function [Reference MotohashiMot97, Theorem 4.2]: if
$L$-functions, because of both its structural beauty and its applications, is Motohashi’s identity for the fourth moment of the Riemann zeta function [Reference MotohashiMot97, Theorem 4.2]: if  $F$ is a sufficiently nice test function, then
$F$ is a sufficiently nice test function, then
 $$\begin{eqnarray}\int _{\mathbb{R}}|\unicode[STIX]{x1D701}(1/2+it)|^{4}F(t)\,dt\end{eqnarray}$$
$$\begin{eqnarray}\int _{\mathbb{R}}|\unicode[STIX]{x1D701}(1/2+it)|^{4}F(t)\,dt\end{eqnarray}$$is equal to an explicit main term plus a cubic moment of the shape
 $$\begin{eqnarray}\mathop{\sum }_{j}L(1/2,\unicode[STIX]{x1D713}_{j})^{3}\check{F}(t_{j})+\text{similar holomorphic and Eisenstein contribution},\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{j}L(1/2,\unicode[STIX]{x1D713}_{j})^{3}\check{F}(t_{j})+\text{similar holomorphic and Eisenstein contribution},\end{eqnarray}$$ where the sum runs over Maaß forms  $\unicode[STIX]{x1D713}_{j}$ with spectral parameter
$\unicode[STIX]{x1D713}_{j}$ with spectral parameter  $t_{j}$ for the group
$t_{j}$ for the group  $\text{SL}_{2}(\mathbb{Z})$ and
$\text{SL}_{2}(\mathbb{Z})$ and $\check{F}$ is a certain integral transform of
$\check{F}$ is a certain integral transform of  $F$ given explicitly in terms of hypergeometric functions. This is an important instance of a formula between two different families of
$F$ given explicitly in terms of hypergeometric functions. This is an important instance of a formula between two different families of  $L$-functions that may be regarded as a ‘reciprocity formula’. Choosing the test function
$L$-functions that may be regarded as a ‘reciprocity formula’. Choosing the test function  $F$ appropriately, it can be used, for instance, to prove sharp upper bounds for the fourth moment of the Riemann zeta function on the critical line in short intervals
$F$ appropriately, it can be used, for instance, to prove sharp upper bounds for the fourth moment of the Riemann zeta function on the critical line in short intervals  $t\in [T,T+T^{2/3}]$. Motohashi’s formula can also be inverted to some extent; Ivić [Reference IvićIvi01] used this to obtain Weyl-type subconvexity bounds for the
$t\in [T,T+T^{2/3}]$. Motohashi’s formula can also be inverted to some extent; Ivić [Reference IvićIvi01] used this to obtain Weyl-type subconvexity bounds for the  $L$-values
$L$-values  $L(1/2,\unicode[STIX]{x1D713}_{j})$.
$L(1/2,\unicode[STIX]{x1D713}_{j})$.
Motohashi’s proof starts by opening the four zeta values as Dirichlet series and integrating over  $t$, which, after a change of variables, gives a Dirichlet series containing a shifted convolution problem
$t$, which, after a change of variables, gives a Dirichlet series containing a shifted convolution problem
 $$\begin{eqnarray}\unicode[STIX]{x1D70F}(n)\unicode[STIX]{x1D70F}(n+h).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}(n)\unicode[STIX]{x1D70F}(n+h).\end{eqnarray}$$A spectral decomposition then yields the spectral cubic moment.
A very different strategy was suggested by Michel and Venkatesh [Reference Michel and VenkateshMV10, §4.5]: we interpret (1.1) as a second moment of  $L$-functions associated with an Eisenstein series
$L$-functions associated with an Eisenstein series  $E$ and choose
$E$ and choose  $F$ as the corresponding local
$F$ as the corresponding local  $L$-factors at infinity. Denoting the completed
$L$-factors at infinity. Denoting the completed  $L$-functions by
$L$-functions by  $\unicode[STIX]{x1D6EC}(s,E)$, we have by Hecke’s integral representation and Parseval’s theorem (ignoring convergence)
$\unicode[STIX]{x1D6EC}(s,E)$, we have by Hecke’s integral representation and Parseval’s theorem (ignoring convergence)
 $$\begin{eqnarray}\int _{\mathbb{R}}|\unicode[STIX]{x1D6EC}(1/2+it,E)|^{2}\,dt\approx \int _{0}^{\infty }|E(iy)|^{2}\frac{dy}{y}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{\mathbb{R}}|\unicode[STIX]{x1D6EC}(1/2+it,E)|^{2}\,dt\approx \int _{0}^{\infty }|E(iy)|^{2}\frac{dy}{y}.\end{eqnarray}$$Decomposing spectrally (and suppressing the continuous spectrum for notational simplicity), using Rankin–Selberg theory and Hecke’s integral representation again, this ‘equals’
 $$\begin{eqnarray}\int _{0}^{\infty }\mathop{\sum }_{j}\langle |E|^{2},\unicode[STIX]{x1D713}_{j}\rangle \unicode[STIX]{x1D713}_{j}(iy)\frac{dy}{y}\approx \int _{0}^{\infty }\mathop{\sum }_{j}\unicode[STIX]{x1D6EC}(1/2,\unicode[STIX]{x1D713}_{j}\times E)\unicode[STIX]{x1D713}_{j}(iy)\frac{dy}{y}\approx \mathop{\sum }_{j}\unicode[STIX]{x1D6EC}(1/2,\unicode[STIX]{x1D713}_{j})^{3}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{0}^{\infty }\mathop{\sum }_{j}\langle |E|^{2},\unicode[STIX]{x1D713}_{j}\rangle \unicode[STIX]{x1D713}_{j}(iy)\frac{dy}{y}\approx \int _{0}^{\infty }\mathop{\sum }_{j}\unicode[STIX]{x1D6EC}(1/2,\unicode[STIX]{x1D713}_{j}\times E)\unicode[STIX]{x1D713}_{j}(iy)\frac{dy}{y}\approx \mathop{\sum }_{j}\unicode[STIX]{x1D6EC}(1/2,\unicode[STIX]{x1D713}_{j})^{3}.\end{eqnarray}$$ This very beautiful idea comes with two technical challenges: first, none of the integrals converge and some regularization is necessary; and second, while this works very nicely for the special test function  $F(t)=|L_{\infty }(1/2+it,E)|^{2}$, it is not easy to spell out what happens for general test functions
$F(t)=|L_{\infty }(1/2+it,E)|^{2}$, it is not easy to spell out what happens for general test functions  $F$. (See, however, recent work by Nelson [Reference NelsonNel19] on this approach.)
$F$. (See, however, recent work by Nelson [Reference NelsonNel19] on this approach.)
In this paper we offer yet another proof of Motohashi’s identity, which has the advantage of working nicely in greater generality. The set-up we are interested in is as follows. For  $q\in \mathbb{N}$, consider
$q\in \mathbb{N}$, consider
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{\unicode[STIX]{x1D712}\hspace{-7.11317pt}\hspace{0.6em}({\rm mod}\hspace{0.2em}q)}F_{\text{fin}}(\unicode[STIX]{x1D712})\int _{\mathbb{R}}|L(1/2+it,\unicode[STIX]{x1D712})|^{4}F_{\infty }(t)\,dt & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{\unicode[STIX]{x1D712}\hspace{-7.11317pt}\hspace{0.6em}({\rm mod}\hspace{0.2em}q)}F_{\text{fin}}(\unicode[STIX]{x1D712})\int _{\mathbb{R}}|L(1/2+it,\unicode[STIX]{x1D712})|^{4}F_{\infty }(t)\,dt & & \displaystyle \nonumber\end{eqnarray}$$ for some function  $F_{\text{fin}}$. This can be seen as the proper adèlic analogue of (1.1), twisting
$F_{\text{fin}}$. This can be seen as the proper adèlic analogue of (1.1), twisting  $\unicode[STIX]{x1D701}(s)$ by the complete family of
$\unicode[STIX]{x1D701}(s)$ by the complete family of  $\text{GL}(1)$ characters
$\text{GL}(1)$ characters  $n^{it}\unicode[STIX]{x1D712}(n)$. By elementary Fourier analysis, every
$n^{it}\unicode[STIX]{x1D712}(n)$. By elementary Fourier analysis, every  $F_{\text{fin}}$ is a linear combination of character values. With applications in mind, we consider test functions of the shape
$F_{\text{fin}}$ is a linear combination of character values. With applications in mind, we consider test functions of the shape
 $$\begin{eqnarray}\displaystyle F_{\text{fin}}(\unicode[STIX]{x1D712})=\unicode[STIX]{x1D712}(a)\overline{\unicode[STIX]{x1D712}}(b) & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{\text{fin}}(\unicode[STIX]{x1D712})=\unicode[STIX]{x1D712}(a)\overline{\unicode[STIX]{x1D712}}(b) & & \displaystyle\end{eqnarray}$$ for some integers  $a,b\in \mathbb{N}$. It is straightforward to include a character average in Motohashi’s proof, which essentially results in a shifted convolution problem (1.3) where
$a,b\in \mathbb{N}$. It is straightforward to include a character average in Motohashi’s proof, which essentially results in a shifted convolution problem (1.3) where  $h$ is divisible by
$h$ is divisible by  $q$. It is much less straightforward to include a general test function (1.4), because then the shifted convolution problem becomes a sum over
$q$. It is much less straightforward to include a general test function (1.4), because then the shifted convolution problem becomes a sum over  $\unicode[STIX]{x1D70F}(n)\unicode[STIX]{x1D70F}(m)$ subject to the condition
$\unicode[STIX]{x1D70F}(n)\unicode[STIX]{x1D70F}(m)$ subject to the condition  $an\equiv bm\hspace{0.6em}({\rm mod}\hspace{0.2em}q).$ The difficulty of such an extension (with sufficient control on
$an\equiv bm\hspace{0.6em}({\rm mod}\hspace{0.2em}q).$ The difficulty of such an extension (with sufficient control on  $a,b$) was already observed in [Reference Duke, Friedlander and IwaniecDFI94, p. 210]. A heuristic argument based on a different strategy that we sketch in §1.4 suggests that we should expect something like
$a,b$) was already observed in [Reference Duke, Friedlander and IwaniecDFI94, p. 210]. A heuristic argument based on a different strategy that we sketch in §1.4 suggests that we should expect something like
 $$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D712}\hspace{-7.11317pt}\hspace{0.6em}({\rm mod}\hspace{0.2em}q)}\unicode[STIX]{x1D712}(a)\overline{\unicode[STIX]{x1D712}}(b)\int _{\mathbb{R}}|L(1/2+it,\unicode[STIX]{x1D712})|^{4}F(t)\,dt{\rightsquigarrow}\frac{q^{1/2}}{a^{1/2}}\mathop{\sum }_{\unicode[STIX]{x1D713}_{j}\text{ of level }ab}\unicode[STIX]{x1D706}_{j}(q)\unicode[STIX]{x1D706}_{j}(b)L(1/2,\unicode[STIX]{x1D713}_{j})^{3}\check{F}(t_{j}).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D712}\hspace{-7.11317pt}\hspace{0.6em}({\rm mod}\hspace{0.2em}q)}\unicode[STIX]{x1D712}(a)\overline{\unicode[STIX]{x1D712}}(b)\int _{\mathbb{R}}|L(1/2+it,\unicode[STIX]{x1D712})|^{4}F(t)\,dt{\rightsquigarrow}\frac{q^{1/2}}{a^{1/2}}\mathop{\sum }_{\unicode[STIX]{x1D713}_{j}\text{ of level }ab}\unicode[STIX]{x1D706}_{j}(q)\unicode[STIX]{x1D706}_{j}(b)L(1/2,\unicode[STIX]{x1D713}_{j})^{3}\check{F}(t_{j}).\end{eqnarray}$$ This indicates that the period integral approach will not be straightforward to extend because at the very least some non-trivial combinatorics in the Hecke algebra (see [Reference ZachariasZac19b] for how this could look in a slightly different situation) must happen in order to generate the Hecke eigenvalues on the right-hand side. As an aside, the left-hand side of (1.5) is symmetric in  $a,b$ as long as
$a,b$ as long as  $F$ is even, while this is not directly apparent on the right-hand side (which is only written in suggestive terms anyway). It follows from (2.3) that
$F$ is even, while this is not directly apparent on the right-hand side (which is only written in suggestive terms anyway). It follows from (2.3) that  $\unicode[STIX]{x1D706}_{j}(b)=\pm b^{-1/2}$, which to some extent restores the symmetry.
$\unicode[STIX]{x1D706}_{j}(b)=\pm b^{-1/2}$, which to some extent restores the symmetry.
We will present a proof of (1.5) in the spirit of recent reciprocity formulae of the first and third authors [Reference Blomer and KhanBK19a, Reference Blomer and KhanBK19b] that deal with this more general set-up without essential structural difficulties. We proceed to describe our first main result in detail. Let  $a,b,q\in \mathbb{N}$,
$a,b,q\in \mathbb{N}$,  $s,u,v\in \mathbb{C}$,
$s,u,v\in \mathbb{C}$,  $F$ be an even holomorphic function that is Schwartz class on fixed vertical lines, and
$F$ be an even holomorphic function that is Schwartz class on fixed vertical lines, and  $f$ an automorphic form for
$f$ an automorphic form for  $\text{SL}_{2}(\mathbb{Z})$ that is either cuspidal or the standard Eisenstein series
$\text{SL}_{2}(\mathbb{Z})$ that is either cuspidal or the standard Eisenstein series  $(d/ds)E(z,s)|_{s=1/2}$. We denote its Hecke eigenvalues by
$(d/ds)E(z,s)|_{s=1/2}$. We denote its Hecke eigenvalues by  $\unicode[STIX]{x1D706}(n)$, so that
$\unicode[STIX]{x1D706}(n)$, so that  $\unicode[STIX]{x1D706}(n)=\unicode[STIX]{x1D70F}(n):=\sum _{ab=n}1$ if
$\unicode[STIX]{x1D706}(n)=\unicode[STIX]{x1D70F}(n):=\sum _{ab=n}1$ if  $f$ is Eisenstein. We define
$f$ is Eisenstein. We define
 $$\begin{eqnarray}{\mathcal{T}}_{a,b,q}(s,u,v):=\mathop{\sum }_{\substack{ \unicode[STIX]{x1D712}\hspace{-7.11317pt}\hspace{0.6em}({\rm mod}\hspace{0.2em}q) \\ \unicode[STIX]{x1D712}\text{ primitive}}}\unicode[STIX]{x1D712}(a)\overline{\unicode[STIX]{x1D712}}(b)\int _{(0)}L(s+z,\unicode[STIX]{x1D712})L(u+z,\unicode[STIX]{x1D712})L(v-z,f\times \overline{\unicode[STIX]{x1D712}})F(z)\frac{dz}{2\unicode[STIX]{x1D70B}i},\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{T}}_{a,b,q}(s,u,v):=\mathop{\sum }_{\substack{ \unicode[STIX]{x1D712}\hspace{-7.11317pt}\hspace{0.6em}({\rm mod}\hspace{0.2em}q) \\ \unicode[STIX]{x1D712}\text{ primitive}}}\unicode[STIX]{x1D712}(a)\overline{\unicode[STIX]{x1D712}}(b)\int _{(0)}L(s+z,\unicode[STIX]{x1D712})L(u+z,\unicode[STIX]{x1D712})L(v-z,f\times \overline{\unicode[STIX]{x1D712}})F(z)\frac{dz}{2\unicode[STIX]{x1D70B}i},\end{eqnarray}$$ where the integration is over the vertical line  $\Re z=0$. We may assume without loss of generality that
$\Re z=0$. We may assume without loss of generality that  $(a,b)=(ab,q)=1$. It is convenient to assume that
$(a,b)=(ab,q)=1$. It is convenient to assume that  $F$ is divisible by
$F$ is divisible by  $(1-u)(v-1)^{2}\prod _{j=1}^{50}(j-s)$. A typical function we have in mind is
$(1-u)(v-1)^{2}\prod _{j=1}^{50}(j-s)$. A typical function we have in mind is
 $$\begin{eqnarray}F(z)=e^{z^{2}}(z^{2}-(1-u)^{2})^{2}(z^{2}-(v-1)^{2})^{2}\mathop{\prod }_{j=1}^{50}(z^{2}-(j-s)^{2}),\end{eqnarray}$$
$$\begin{eqnarray}F(z)=e^{z^{2}}(z^{2}-(1-u)^{2})^{2}(z^{2}-(v-1)^{2})^{2}\mathop{\prod }_{j=1}^{50}(z^{2}-(j-s)^{2}),\end{eqnarray}$$ which is positive for  $\Re z=0$,
$\Re z=0$,  $s=u=v=1/2$. To get a nice-looking formula, we also need to include non-primitive characters, and for simplicity we assume that
$s=u=v=1/2$. To get a nice-looking formula, we also need to include non-primitive characters, and for simplicity we assume that  $q$ is prime. For a suitable correction polynomial
$q$ is prime. For a suitable correction polynomial  $P_{q}(s,u,v,z)$ defined explicitly in (3.2) below and satisfying
$P_{q}(s,u,v,z)$ defined explicitly in (3.2) below and satisfying
 $$\begin{eqnarray}P_{q}(s,u,v,z)\ll 1+|\unicode[STIX]{x1D706}(q)|,\quad \Re s,\Re u,\Re v\geqslant 1/2,\quad \Re z=0,\end{eqnarray}$$
$$\begin{eqnarray}P_{q}(s,u,v,z)\ll 1+|\unicode[STIX]{x1D706}(q)|,\quad \Re s,\Re u,\Re v\geqslant 1/2,\quad \Re z=0,\end{eqnarray}$$we define the analogue for the trivial character
 $$\begin{eqnarray}{\mathcal{T}}_{q}^{\text{triv}}(s,u,v):=\int _{(0)}\unicode[STIX]{x1D701}(s+z)\unicode[STIX]{x1D701}(u+z)L(v-z,f)P_{q}(s,u,v,z)F(z)\frac{dz}{2\unicode[STIX]{x1D70B}i}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{T}}_{q}^{\text{triv}}(s,u,v):=\int _{(0)}\unicode[STIX]{x1D701}(s+z)\unicode[STIX]{x1D701}(u+z)L(v-z,f)P_{q}(s,u,v,z)F(z)\frac{dz}{2\unicode[STIX]{x1D70B}i}.\end{eqnarray}$$ Note that our assumptions on  $F$ imply that the integrand is holomorphic (since the poles of
$F$ imply that the integrand is holomorphic (since the poles of  $\unicode[STIX]{x1D701}$ are cancelled) and that we can shift the
$\unicode[STIX]{x1D701}$ are cancelled) and that we can shift the  $z$-contour in any way we want.
$z$-contour in any way we want.
On the spectral side, we define
 $$\begin{eqnarray}{\mathcal{M}}_{a,b,q}^{\text{Maa}\unicode[STIX]{x00DF}}(s,u,v):=\mathop{\sum }_{A\mid ab}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(A)}\unicode[STIX]{x1D6E9}_{a,b,q}^{\text{Maa}\unicode[STIX]{x00DF}}(s,u,v,\unicode[STIX]{x1D713})\frac{L(\frac{s+u-1+2v}{2},\unicode[STIX]{x1D713})L(\frac{1-s+u}{2},f\times \unicode[STIX]{x1D713})}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})},\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{M}}_{a,b,q}^{\text{Maa}\unicode[STIX]{x00DF}}(s,u,v):=\mathop{\sum }_{A\mid ab}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(A)}\unicode[STIX]{x1D6E9}_{a,b,q}^{\text{Maa}\unicode[STIX]{x00DF}}(s,u,v,\unicode[STIX]{x1D713})\frac{L(\frac{s+u-1+2v}{2},\unicode[STIX]{x1D713})L(\frac{1-s+u}{2},f\times \unicode[STIX]{x1D713})}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})},\end{eqnarray}$$ where  ${\mathcal{B}}^{\ast }(A)$ denotes an orthonormal Hecke basis of Maaß newforms of level
${\mathcal{B}}^{\ast }(A)$ denotes an orthonormal Hecke basis of Maaß newforms of level  $A$ and
$A$ and  $\unicode[STIX]{x1D6E9}_{a,b,q}^{\text{Maa}\unicode[STIX]{x00DF}}(s,u,v,\unicode[STIX]{x1D713})$ is a (complicated, but) completely explicit expression defined in (3.21) that satisfies
$\unicode[STIX]{x1D6E9}_{a,b,q}^{\text{Maa}\unicode[STIX]{x00DF}}(s,u,v,\unicode[STIX]{x1D713})$ is a (complicated, but) completely explicit expression defined in (3.21) that satisfies
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{a,b,q}^{\text{Maa}\unicode[STIX]{x00DF}}(s,u,v,\unicode[STIX]{x1D713})\;\ll _{s,u,v,F,\unicode[STIX]{x1D700}}\;q^{1/2}A^{-1/2}(1+|\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(q)|)(1+|t_{\unicode[STIX]{x1D713}}|)^{-30}(abq)^{\unicode[STIX]{x1D700}}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{a,b,q}^{\text{Maa}\unicode[STIX]{x00DF}}(s,u,v,\unicode[STIX]{x1D713})\;\ll _{s,u,v,F,\unicode[STIX]{x1D700}}\;q^{1/2}A^{-1/2}(1+|\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(q)|)(1+|t_{\unicode[STIX]{x1D713}}|)^{-30}(abq)^{\unicode[STIX]{x1D700}}\end{eqnarray}$$ for  $\Re s,\Re u,\Re v=1/2$ and
$\Re s,\Re u,\Re v=1/2$ and  $a\asymp b$. Similarly, we define
$a\asymp b$. Similarly, we define
 $$\begin{eqnarray}{\mathcal{M}}_{a,b,q}^{\text{hol}}(s,u,v):=\mathop{\sum }_{A\mid ab}\mathop{\sum }_{k\in 2\mathbb{N}}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}_{k}^{\ast }(A)}\unicode[STIX]{x1D6E9}_{a,b,q}^{\text{hol}}(s,u,v,\unicode[STIX]{x1D713})\frac{L(\frac{s+u-1+2v}{2},\unicode[STIX]{x1D713})L(\frac{1-s+u}{2},f\times \unicode[STIX]{x1D713})}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})},\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{M}}_{a,b,q}^{\text{hol}}(s,u,v):=\mathop{\sum }_{A\mid ab}\mathop{\sum }_{k\in 2\mathbb{N}}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}_{k}^{\ast }(A)}\unicode[STIX]{x1D6E9}_{a,b,q}^{\text{hol}}(s,u,v,\unicode[STIX]{x1D713})\frac{L(\frac{s+u-1+2v}{2},\unicode[STIX]{x1D713})L(\frac{1-s+u}{2},f\times \unicode[STIX]{x1D713})}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})},\end{eqnarray}$$ where  ${\mathcal{B}}_{k}^{\ast }(A)$ denotes an orthonormal Hecke basis of holomorphic newforms of weight
${\mathcal{B}}_{k}^{\ast }(A)$ denotes an orthonormal Hecke basis of holomorphic newforms of weight  $k$ and level
$k$ and level  $A$ and
$A$ and  $\unicode[STIX]{x1D6E9}_{a,b,q}^{\text{hol}}(s,u,v,\unicode[STIX]{x1D713})$ satisfies the analogous bound
$\unicode[STIX]{x1D6E9}_{a,b,q}^{\text{hol}}(s,u,v,\unicode[STIX]{x1D713})$ satisfies the analogous bound
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{a,b,q}^{\text{hol}}(s,u,v,\unicode[STIX]{x1D713})\;\ll _{s,u,v,F,\unicode[STIX]{x1D700}}\;q^{1/2}A^{-1/2}k^{-30}(abq)^{\unicode[STIX]{x1D700}}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{a,b,q}^{\text{hol}}(s,u,v,\unicode[STIX]{x1D713})\;\ll _{s,u,v,F,\unicode[STIX]{x1D700}}\;q^{1/2}A^{-1/2}k^{-30}(abq)^{\unicode[STIX]{x1D700}}\end{eqnarray}$$ for  $\Re s,\Re u,\Re v=1/2$ and
$\Re s,\Re u,\Re v=1/2$ and  $a\asymp b$. For simplicity, we assume that
$a\asymp b$. For simplicity, we assume that  $a,b$ are square-free, so that the Eisenstein spectrum is parametrized by
$a,b$ are square-free, so that the Eisenstein spectrum is parametrized by  $\unicode[STIX]{x1D70F}(ab)$ cusps. We define (initially in
$\unicode[STIX]{x1D70F}(ab)$ cusps. We define (initially in  $\Re (s+u+2v)>3$ and
$\Re (s+u+2v)>3$ and  $\Re (u-s)>1$)
$\Re (u-s)>1$)
 $$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{M}}_{a,b,q}^{\text{Eis}}(s,u,v)\nonumber\\ \displaystyle & & \displaystyle \quad :=\int _{\mathbb{R}}\unicode[STIX]{x1D6E9}_{a,b,q}^{\text{Eis}}(s,u,v,t)\frac{\unicode[STIX]{x1D701}(\frac{s+u-1+2v}{2}+it)\unicode[STIX]{x1D701}(\frac{s+u-1+2v}{2}-it)L(\frac{1-s+u}{2}+it,f)L(\frac{1-s+u}{2}-it,f)}{\unicode[STIX]{x1D701}(1+2it)\unicode[STIX]{x1D701}(1-2it)}\frac{dt}{2\unicode[STIX]{x1D70B}},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{M}}_{a,b,q}^{\text{Eis}}(s,u,v)\nonumber\\ \displaystyle & & \displaystyle \quad :=\int _{\mathbb{R}}\unicode[STIX]{x1D6E9}_{a,b,q}^{\text{Eis}}(s,u,v,t)\frac{\unicode[STIX]{x1D701}(\frac{s+u-1+2v}{2}+it)\unicode[STIX]{x1D701}(\frac{s+u-1+2v}{2}-it)L(\frac{1-s+u}{2}+it,f)L(\frac{1-s+u}{2}-it,f)}{\unicode[STIX]{x1D701}(1+2it)\unicode[STIX]{x1D701}(1-2it)}\frac{dt}{2\unicode[STIX]{x1D70B}},\nonumber\end{eqnarray}$$ where  $\unicode[STIX]{x1D6E9}_{a,b,q}^{\text{Eis}}(s,u,v,t)$ is defined in (3.26) and satisfies
$\unicode[STIX]{x1D6E9}_{a,b,q}^{\text{Eis}}(s,u,v,t)$ is defined in (3.26) and satisfies
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{a,b,q}^{\text{Eis}}(s,u,v,t)\;\ll _{s,u,v,\unicode[STIX]{x1D700},F}\;(abq)^{\unicode[STIX]{x1D700}}q^{1/2}(ab)^{\unicode[STIX]{x1D703}-1/2}(1+|t|)^{-30}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{a,b,q}^{\text{Eis}}(s,u,v,t)\;\ll _{s,u,v,\unicode[STIX]{x1D700},F}\;(abq)^{\unicode[STIX]{x1D700}}q^{1/2}(ab)^{\unicode[STIX]{x1D703}-1/2}(1+|t|)^{-30}\end{eqnarray}$$ for  $\Re s=\Re v=\Re u=1/2$,
$\Re s=\Re v=\Re u=1/2$,  $t\in \mathbb{R}$, where
$t\in \mathbb{R}$, where  $\unicode[STIX]{x1D703}\leqslant 7/64$ is an admissible exponent for the Ramanujan conjecture for the fixed form
$\unicode[STIX]{x1D703}\leqslant 7/64$ is an admissible exponent for the Ramanujan conjecture for the fixed form  $f$ (in particular,
$f$ (in particular,  $\unicode[STIX]{x1D703}=0$ if
$\unicode[STIX]{x1D703}=0$ if  $f$ is holomorphic or Eisenstein). The expressions
$f$ is holomorphic or Eisenstein). The expressions  ${\mathcal{M}}_{a,b,q}^{\ast }(s,u,v)$ for
${\mathcal{M}}_{a,b,q}^{\ast }(s,u,v)$ for  $\ast \in \{\text{Maa}\unicode[STIX]{x00DF},\text{hol}\}$ are obviously holomorphic in
$\ast \in \{\text{Maa}\unicode[STIX]{x00DF},\text{hol}\}$ are obviously holomorphic in  $\Re s,\Re u,\Re v\geqslant 1/2$. By contour shifts it is not hard to see that
$\Re s,\Re u,\Re v\geqslant 1/2$. By contour shifts it is not hard to see that  ${\mathcal{M}}_{a,b,q}^{\text{Eis}}(s,u,v)$ has meromorphic continuation to this region; see §3.9. In the intersection of
${\mathcal{M}}_{a,b,q}^{\text{Eis}}(s,u,v)$ has meromorphic continuation to this region; see §3.9. In the intersection of  $\Re s,\Re u,\Re v\geqslant 1/2$ with
$\Re s,\Re u,\Re v\geqslant 1/2$ with  $\Re (s+u+2v)<3,\Re (u-s)<1$ the meromorphic continuation is given explicitly by the same term plus an additional polar term, defined in (3.27). We define
$\Re (s+u+2v)<3,\Re (u-s)<1$ the meromorphic continuation is given explicitly by the same term plus an additional polar term, defined in (3.27). We define
 $$\begin{eqnarray}{\mathcal{M}}_{a,b,q}(s,u,v):={\mathcal{M}}_{a,b,q}^{\text{Maa}\unicode[STIX]{x00DF}}(s,u,v)+{\mathcal{M}}_{a,b,q}^{\text{hol}}(s,u,v)+{\mathcal{M}}_{a,b,q}^{\text{Eis}}(s,u,v).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{M}}_{a,b,q}(s,u,v):={\mathcal{M}}_{a,b,q}^{\text{Maa}\unicode[STIX]{x00DF}}(s,u,v)+{\mathcal{M}}_{a,b,q}^{\text{hol}}(s,u,v)+{\mathcal{M}}_{a,b,q}^{\text{Eis}}(s,u,v).\end{eqnarray}$$We are now ready to state the reciprocity formula to which we have already alluded.
Theorem 1. Let  $q,a,b\in \mathbb{N}$,
$q,a,b\in \mathbb{N}$,  $q$ be prime,
$q$ be prime,  $(ab,q)=(a,b)=1$,
$(ab,q)=(a,b)=1$,  $a,b$ be square-free,
$a,b$ be square-free,  $a\asymp b$. Let
$a\asymp b$. Let  $1/2\leqslant \Re s,\Re u,\Re v<3/4$ and
$1/2\leqslant \Re s,\Re u,\Re v<3/4$ and  $\Re s\leqslant \Re u$. Suppose that
$\Re s\leqslant \Re u$. Suppose that  $F$ is holomorphic, Schwartz class on vertical lines, and divisible by
$F$ is holomorphic, Schwartz class on vertical lines, and divisible by  $(1-u)(v-1)^{2}\prod _{j=1}^{50}(j-s)$. Then
$(1-u)(v-1)^{2}\prod _{j=1}^{50}(j-s)$. Then
 $$\begin{eqnarray}{\mathcal{T}}_{a,b,q}(s,u,v)+{\mathcal{T}}_{q}^{\text{triv}}(s,u,v)={\mathcal{P}}_{a,b,q}(s,u,v)+{\mathcal{M}}_{a,b,q}(s,u,v),\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{T}}_{a,b,q}(s,u,v)+{\mathcal{T}}_{q}^{\text{triv}}(s,u,v)={\mathcal{P}}_{a,b,q}(s,u,v)+{\mathcal{M}}_{a,b,q}(s,u,v),\end{eqnarray}$$ where the ‘main term’  ${\mathcal{P}}_{a,b,q}(s,u,v)$ is defined in (3.28) and satisfies
${\mathcal{P}}_{a,b,q}(s,u,v)$ is defined in (3.28) and satisfies
 $$\begin{eqnarray}{\mathcal{P}}_{a,b,q}(s,u,v)\;\ll _{s,u,v,\unicode[STIX]{x1D700},F}\;q(ab)^{-1/2+\unicode[STIX]{x1D703}}(abq)^{\unicode[STIX]{x1D700}}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{P}}_{a,b,q}(s,u,v)\;\ll _{s,u,v,\unicode[STIX]{x1D700},F}\;q(ab)^{-1/2+\unicode[STIX]{x1D703}}(abq)^{\unicode[STIX]{x1D700}}\end{eqnarray}$$ for  $\Re s=\Re u=\Re v=1/2$,
$\Re s=\Re u=\Re v=1/2$,  $a\asymp b$, where
$a\asymp b$, where  $\unicode[STIX]{x1D703}$ is an admissible exponent for the Ramanujan conjecture for
$\unicode[STIX]{x1D703}$ is an admissible exponent for the Ramanujan conjecture for  $f$.
$f$.
We emphasize that even though  ${\mathcal{M}}_{a,b,q}(s,u,v)$ depends on
${\mathcal{M}}_{a,b,q}(s,u,v)$ depends on  $q$, it only involves the spectrum of level
$q$, it only involves the spectrum of level  $ab$. This is the ultimate reason for the specific design of the term
$ab$. This is the ultimate reason for the specific design of the term  ${\mathcal{T}}_{q}^{\text{triv}}(s,u,v)$. In this sense, our formula is a clean reciprocity formula, where the pair (level, arithmetic of weight function) on the Dirichlet side is
${\mathcal{T}}_{q}^{\text{triv}}(s,u,v)$. In this sense, our formula is a clean reciprocity formula, where the pair (level, arithmetic of weight function) on the Dirichlet side is  $(q,ab)$ and on the spectral side is
$(q,ab)$ and on the spectral side is  $(ab,q)$.
$(ab,q)$.
Theorem 1 contains a number of simplifying assumptions, most of which can be removed without any structural difficulties at the cost of more technical work. If  $q$ is not prime, we need slightly more complicated correction terms for non-primitive characters. The assumption that
$q$ is not prime, we need slightly more complicated correction terms for non-primitive characters. The assumption that  $F$ has zeros at
$F$ has zeros at  $1-u,v-1,j-s$,
$1-u,v-1,j-s$,  $1\leqslant j\leqslant 50$, can be relaxed considerably, and probably entirely removed, but it saves us from computing several polar terms and buys us convergence without any trickery. The regularity assumptions on
$1\leqslant j\leqslant 50$, can be relaxed considerably, and probably entirely removed, but it saves us from computing several polar terms and buys us convergence without any trickery. The regularity assumptions on  $F$ can also be relaxed. The assumption that
$F$ can also be relaxed. The assumption that  $a$ is square-free is only to keep the formulae a little simpler. The assumption that
$a$ is square-free is only to keep the formulae a little simpler. The assumption that  $b$ is square-free is slightly more serious and enables us to use the Kuznetsov formula in a version that involves only Fourier expansions at infinity. For arbitrary
$b$ is square-free is slightly more serious and enables us to use the Kuznetsov formula in a version that involves only Fourier expansions at infinity. For arbitrary  $b$, one can use the analysis of Kıral and Young [Reference Kıral and YoungKY19, Lemma 2.5 and Theorem 3.4] instead. As mentioned before, the assumption
$b$, one can use the analysis of Kıral and Young [Reference Kıral and YoungKY19, Lemma 2.5 and Theorem 3.4] instead. As mentioned before, the assumption  $(ab,q)=(a,b)=1$ is without loss of generality, and if
$(ab,q)=(a,b)=1$ is without loss of generality, and if  $a$ and
$a$ and  $b$ are not of the same order of magnitude, our bounds may deteriorate by
$b$ are not of the same order of magnitude, our bounds may deteriorate by  $(\max (b,a)/\text{min}(b,a))^{O(1)}$ (this is unavoidable; see the sketch in §1.4).
$(\max (b,a)/\text{min}(b,a))^{O(1)}$ (this is unavoidable; see the sketch in §1.4).
The spectral side (1.2) of Motohashi’s original formula goes deeper in the spectrum (i.e. the support of  $\check{F}$ is larger) the more complicated the test function
$\check{F}$ is larger) the more complicated the test function  $F$ is (e.g. in terms of oscillation). Our formula features a similar phenomenon for the non-archimedean test function, except that the spectral support now increases, in some sense orthogonally, in terms of the level instead of the spectral parameter.
$F$ is (e.g. in terms of oscillation). Our formula features a similar phenomenon for the non-archimedean test function, except that the spectral support now increases, in some sense orthogonally, in terms of the level instead of the spectral parameter.
1.2 A sixth moment
In practice, we want to estimate the right-hand side of (1.5) for large  $q$ and somewhat large
$q$ and somewhat large  $a,b$, and a possible problem could be the occurrence of
$a,b$, and a possible problem could be the occurrence of  $\unicode[STIX]{x1D706}_{j}(q)$ in (1.11) for Maaß forms
$\unicode[STIX]{x1D706}_{j}(q)$ in (1.11) for Maaß forms  $\unicode[STIX]{x1D713}_{j}$ for which the Ramanujan conjecture is not known. The factor
$\unicode[STIX]{x1D713}_{j}$ for which the Ramanujan conjecture is not known. The factor  $\unicode[STIX]{x1D706}_{j}(b)$ is not a problem, since
$\unicode[STIX]{x1D706}_{j}(b)$ is not a problem, since  $b$ divides the level; see (2.3). A trivial bound on
$b$ divides the level; see (2.3). A trivial bound on  $\unicode[STIX]{x1D706}_{j}(q)$, however, may invoke an undesirable factor of
$\unicode[STIX]{x1D706}_{j}(q)$, however, may invoke an undesirable factor of  $q^{\unicode[STIX]{x1D703}}$ due to our limited knowledge of the Ramanujan conjecture. In order to avoid this, one may try to use the extra average over the forms of level
$q^{\unicode[STIX]{x1D703}}$ due to our limited knowledge of the Ramanujan conjecture. In order to avoid this, one may try to use the extra average over the forms of level  $ab$ and apply the Cauchy–Schwarz inequality.Footnote 1 This is successful if there is an additional average over
$ab$ and apply the Cauchy–Schwarz inequality.Footnote 1 This is successful if there is an additional average over  $a,b$, and to this end we will prove the following sixth moment bound, which is of independent interest.
$a,b$, and to this end we will prove the following sixth moment bound, which is of independent interest.
Theorem 2. Let  $Q,T\geqslant 1$, and for
$Q,T\geqslant 1$, and for  $q\in \mathbb{N}$, let
$q\in \mathbb{N}$, let  ${\mathcal{B}}^{\ast }(q)$ denote an orthonormal basis of Hecke–Maaß newforms
${\mathcal{B}}^{\ast }(q)$ denote an orthonormal basis of Hecke–Maaß newforms  $\unicode[STIX]{x1D713}$ of level
$\unicode[STIX]{x1D713}$ of level  $q$ having spectral parameter
$q$ having spectral parameter  $t_{\unicode[STIX]{x1D713}}$. Then
$t_{\unicode[STIX]{x1D713}}$. Then
 $$\begin{eqnarray}\mathop{\sum }_{q\leqslant Q}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(q) \\ |t_{\unicode[STIX]{x1D713}}|\leqslant T}}\frac{|L(1/2,\unicode[STIX]{x1D713})|^{6}}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})}\;\ll _{\unicode[STIX]{x1D700}}\;(QT)^{\unicode[STIX]{x1D700}}T^{8}Q^{2}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{q\leqslant Q}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(q) \\ |t_{\unicode[STIX]{x1D713}}|\leqslant T}}\frac{|L(1/2,\unicode[STIX]{x1D713})|^{6}}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})}\;\ll _{\unicode[STIX]{x1D700}}\;(QT)^{\unicode[STIX]{x1D700}}T^{8}Q^{2}.\end{eqnarray}$$ The emphasis here is on the  $Q$-aspect, which is sharp up to the presence of
$Q$-aspect, which is sharp up to the presence of  $Q^{\unicode[STIX]{x1D700}}$; the
$Q^{\unicode[STIX]{x1D700}}$; the  $T$-aspect only needs to be polynomial. For comparison, it is classical, although technically difficult, to understand the fourth moment for an individual large level
$T$-aspect only needs to be polynomial. For comparison, it is classical, although technically difficult, to understand the fourth moment for an individual large level  $q$. Our result is easier because we have an additional average over
$q$. Our result is easier because we have an additional average over  $q$ (which, however, is spectrally not easy to exploit), but also harder because we study a higher moment. Any spectral method will have to complete the discrete spectral sum to an entire spectral expression including Eisenstein series, and already in the fourth moment one of the biggest obstacles is the fact that the additional continuous contribution is quite large in the level aspect. It is not surprising that this becomes even worse for the sixth moment, and here the artificially added Eisenstein term exceeds the targeted bound by a substantial power of
$q$ (which, however, is spectrally not easy to exploit), but also harder because we study a higher moment. Any spectral method will have to complete the discrete spectral sum to an entire spectral expression including Eisenstein series, and already in the fourth moment one of the biggest obstacles is the fact that the additional continuous contribution is quite large in the level aspect. It is not surprising that this becomes even worse for the sixth moment, and here the artificially added Eisenstein term exceeds the targeted bound by a substantial power of  $Q$.
$Q$.
An overview of the method of proof and how the various technical and conceptual issues are addressed will be given in §1.4. We present an immediate application of Theorem 2.
Corollary 3. Let  $q$ be prime. Then
$q$ be prime. Then
 $$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(q)}L(1/2,\unicode[STIX]{x1D713})^{5}e^{-t_{\unicode[STIX]{x1D713}}^{2}}\;\ll _{\unicode[STIX]{x1D700}}\;q^{1+\unicode[STIX]{x1D703}/3+\unicode[STIX]{x1D700}}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(q)}L(1/2,\unicode[STIX]{x1D713})^{5}e^{-t_{\unicode[STIX]{x1D713}}^{2}}\;\ll _{\unicode[STIX]{x1D700}}\;q^{1+\unicode[STIX]{x1D703}/3+\unicode[STIX]{x1D700}}\end{eqnarray}$$ for every  $\unicode[STIX]{x1D700}>0$. In particular, for
$\unicode[STIX]{x1D700}>0$. In particular, for  $\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(q)$, we have
$\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(q)$, we have
 $$\begin{eqnarray}L(1/2,\unicode[STIX]{x1D713})\;\ll _{t_{\unicode[STIX]{x1D713}},\unicode[STIX]{x1D700}}\;q^{1/5+\unicode[STIX]{x1D703}/15+\unicode[STIX]{x1D700}}\ll q^{0.2073}.\end{eqnarray}$$
$$\begin{eqnarray}L(1/2,\unicode[STIX]{x1D713})\;\ll _{t_{\unicode[STIX]{x1D713}},\unicode[STIX]{x1D700}}\;q^{1/5+\unicode[STIX]{x1D703}/15+\unicode[STIX]{x1D700}}\ll q^{0.2073}.\end{eqnarray}$$ This improves the  $\unicode[STIX]{x1D703}$-dependence of the fifth moment bound in [Reference Blomer and KhanBK19b, Theorem 3] and provides the numerical subconvexity record for
$\unicode[STIX]{x1D703}$-dependence of the fifth moment bound in [Reference Blomer and KhanBK19b, Theorem 3] and provides the numerical subconvexity record for  $L(1/2,\unicode[STIX]{x1D713})$ in the level aspect (the previous exponent being
$L(1/2,\unicode[STIX]{x1D713})$ in the level aspect (the previous exponent being  $0.217$ from [Reference Blomer and KhanBK19b, Theorem 4]; cf. [Reference Kıral and YoungKY17]).
$0.217$ from [Reference Blomer and KhanBK19b, Theorem 4]; cf. [Reference Kıral and YoungKY17]).
1.3 Fourth moments twisted by Dirichlet polynomials
For many applications, in particular with respect to the amplification, mollification, or resonance method, one wishes to augment moment results on  $L$-functions by inserting well-chosen Dirichlet polynomials – ideally as long as possible – that in effect often act as additional fractional moments. This is classical for the Riemann zeta function, where Watt [Reference WattWat95], building on work of Deshouillers and Iwaniec [Reference Deshouillers and IwaniecDI82], proved
$L$-functions by inserting well-chosen Dirichlet polynomials – ideally as long as possible – that in effect often act as additional fractional moments. This is classical for the Riemann zeta function, where Watt [Reference WattWat95], building on work of Deshouillers and Iwaniec [Reference Deshouillers and IwaniecDI82], proved
 $$\begin{eqnarray}\int _{0}^{T}|\unicode[STIX]{x1D701}(1/2+it)|^{4}\biggl|\mathop{\sum }_{m\leqslant M}a_{m}m^{it}\biggr|^{2}\,dt\ll \Vert \mathbf{a}\Vert _{\infty }^{2}(MT)^{1+\unicode[STIX]{x1D700}}\end{eqnarray}$$
$$\begin{eqnarray}\int _{0}^{T}|\unicode[STIX]{x1D701}(1/2+it)|^{4}\biggl|\mathop{\sum }_{m\leqslant M}a_{m}m^{it}\biggr|^{2}\,dt\ll \Vert \mathbf{a}\Vert _{\infty }^{2}(MT)^{1+\unicode[STIX]{x1D700}}\end{eqnarray}$$ for  $M\leqslant T^{1/4}$ and an arbitrary sequence
$M\leqslant T^{1/4}$ and an arbitrary sequence  $\mathbf{a}=(a_{m})_{1\leqslant m\leqslant M}$. This can be turned into an asymptotic formula; see [Reference MotohashiMot96, Reference Hughes and YoungHY10, Reference Bettin, Bui, Li and RadziwiłłBBLR16]. Versions for Dirichlet
$\mathbf{a}=(a_{m})_{1\leqslant m\leqslant M}$. This can be turned into an asymptotic formula; see [Reference MotohashiMot96, Reference Hughes and YoungHY10, Reference Bettin, Bui, Li and RadziwiłłBBLR16]. Versions for Dirichlet  $L$-functions with conductors sufficiently small with respect to
$L$-functions with conductors sufficiently small with respect to  $T$ can be found in [Reference Harman, Watt and WongHWW04], along with applications to primes in arithmetic progressions and short intervals. We also mention [Reference Friedlander and IwaniecFI92] as an interesting variation if the sequence is factorizable in the ring of multiplicative functions.
$T$ can be found in [Reference Harman, Watt and WongHWW04], along with applications to primes in arithmetic progressions and short intervals. We also mention [Reference Friedlander and IwaniecFI92] as an interesting variation if the sequence is factorizable in the ring of multiplicative functions.
As an application of Theorems 1 and 2, we will prove the following analogous sharp upper bound for a fourth moment of Dirichlet  $L$-functions twisted by the square of a Dirichlet polynomial of length up to
$L$-functions twisted by the square of a Dirichlet polynomial of length up to  $q^{1/4}$.
$q^{1/4}$.
Theorem 4. Let  $q$ be a prime,
$q$ be a prime,  $1\leqslant M\leqslant q^{1/4}$, and
$1\leqslant M\leqslant q^{1/4}$, and  $\{a(m)\}_{1\leqslant m\leqslant M}$ a sequence of complex numbers supported on square-free numbers. Then
$\{a(m)\}_{1\leqslant m\leqslant M}$ a sequence of complex numbers supported on square-free numbers. Then
 $$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D712}\hspace{-7.11317pt}\hspace{0.6em}({\rm mod}\hspace{0.2em}q)}\biggl|\mathop{\sum }_{m\leqslant M}a(m)\unicode[STIX]{x1D712}(m)\biggr|^{2}|L(1/2,\unicode[STIX]{x1D712})|^{4}\;\ll _{\unicode[STIX]{x1D700}}\;\Vert \mathbf{a}\Vert _{\infty }^{2}(Mq)^{1+\unicode[STIX]{x1D700}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D712}\hspace{-7.11317pt}\hspace{0.6em}({\rm mod}\hspace{0.2em}q)}\biggl|\mathop{\sum }_{m\leqslant M}a(m)\unicode[STIX]{x1D712}(m)\biggr|^{2}|L(1/2,\unicode[STIX]{x1D712})|^{4}\;\ll _{\unicode[STIX]{x1D700}}\;\Vert \mathbf{a}\Vert _{\infty }^{2}(Mq)^{1+\unicode[STIX]{x1D700}}.\end{eqnarray}$$ To get a feeling for the strength of the result, we mention that it implies trivially the Burgess bound  $L(1/2,\unicode[STIX]{x1D712})\;\ll _{\unicode[STIX]{x1D700}}\;q^{3/16+\unicode[STIX]{x1D700}}$ for every non-trivial character modulo
$L(1/2,\unicode[STIX]{x1D712})\;\ll _{\unicode[STIX]{x1D700}}\;q^{3/16+\unicode[STIX]{x1D700}}$ for every non-trivial character modulo  $q$. The reader may wonder to what extent this upper bound can be turned into an asymptotic formula, but interestingly this is a much harder problem than in the case of the Riemann zeta function. The reason is that a
$q$. The reader may wonder to what extent this upper bound can be turned into an asymptotic formula, but interestingly this is a much harder problem than in the case of the Riemann zeta function. The reason is that a  $\unicode[STIX]{x1D6FF}$-mass at the point 1/2 is not a proper test function. On a technical level, the
$\unicode[STIX]{x1D6FF}$-mass at the point 1/2 is not a proper test function. On a technical level, the  $t$-integral with a holomorphic test function and the freedom to shift its contour is crucial to establish convergence throughout the argument, even in the special case
$t$-integral with a holomorphic test function and the freedom to shift its contour is crucial to establish convergence throughout the argument, even in the special case  $M=1$. Therefore, a corresponding asymptotic formula can be achieved if an additional
$M=1$. Therefore, a corresponding asymptotic formula can be achieved if an additional  $t$-average (essentially of constant length) is included, but for the central point individually, one has to use other methods (see, for example, [Reference HoughHou16, Reference ZachariasZac19a]) that yield much weaker results. See [Reference WattWat08] for a slightly more general result, which, however, is not independent of bounds towards the Ramanujan conjecture.
$t$-average (essentially of constant length) is included, but for the central point individually, one has to use other methods (see, for example, [Reference HoughHou16, Reference ZachariasZac19a]) that yield much weaker results. See [Reference WattWat08] for a slightly more general result, which, however, is not independent of bounds towards the Ramanujan conjecture.
1.4 Heuristics
We conclude this introduction with a heuristic argument supporting relation (1.5) and the bound in Theorem 2 as well as some additional comments. This section is not intended to provide proofs, but may serve as a roadmap.
We start with (1.5). For the sake of argument, we will use approximate functional equations, although our proof works with Dirichlet series in the region of absolute convergence and continues meromorphically only at the very end (the great advantage of this is that we do not have to deal with a root number term, and so we will ignore this term also in the present sketch). For simplicity, we will also ignore the  $t$-average whose purpose is to achieve convergence, as well as all ‘main terms’ that arise in the course of the computation. We have
$t$-average whose purpose is to achieve convergence, as well as all ‘main terms’ that arise in the course of the computation. We have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D712}\hspace{-7.11317pt}\hspace{0.6em}({\rm mod}\hspace{0.2em}q)}\unicode[STIX]{x1D712}(a)\overline{\unicode[STIX]{x1D712}}(b)|L(1/2,\unicode[STIX]{x1D712})|^{4}\nonumber\\ \displaystyle & & \displaystyle \quad \approx \mathop{\sum }_{\unicode[STIX]{x1D712}\hspace{-7.11317pt}\hspace{0.6em}({\rm mod}\hspace{0.2em}q)}\unicode[STIX]{x1D712}(a)\overline{\unicode[STIX]{x1D712}}(b)\mathop{\sum }_{n,m,r_{1},r_{2}\asymp q^{1/2}}\frac{\unicode[STIX]{x1D712}(nm)\overline{\unicode[STIX]{x1D712}}(r_{1}r_{2})}{(nmr_{1}r_{2})^{1/2}}\approx \mathop{\sum }_{\substack{ n,m,r_{1},r_{2}\asymp q^{1/2} \\ anm\equiv br_{1}r_{2}\hspace{-7.11317pt}\hspace{0.6em}({\rm mod}\hspace{0.2em}q)}}1.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D712}\hspace{-7.11317pt}\hspace{0.6em}({\rm mod}\hspace{0.2em}q)}\unicode[STIX]{x1D712}(a)\overline{\unicode[STIX]{x1D712}}(b)|L(1/2,\unicode[STIX]{x1D712})|^{4}\nonumber\\ \displaystyle & & \displaystyle \quad \approx \mathop{\sum }_{\unicode[STIX]{x1D712}\hspace{-7.11317pt}\hspace{0.6em}({\rm mod}\hspace{0.2em}q)}\unicode[STIX]{x1D712}(a)\overline{\unicode[STIX]{x1D712}}(b)\mathop{\sum }_{n,m,r_{1},r_{2}\asymp q^{1/2}}\frac{\unicode[STIX]{x1D712}(nm)\overline{\unicode[STIX]{x1D712}}(r_{1}r_{2})}{(nmr_{1}r_{2})^{1/2}}\approx \mathop{\sum }_{\substack{ n,m,r_{1},r_{2}\asymp q^{1/2} \\ anm\equiv br_{1}r_{2}\hspace{-7.11317pt}\hspace{0.6em}({\rm mod}\hspace{0.2em}q)}}1.\nonumber\end{eqnarray}$$ Rather than solving a shifted convolution problem, we take an asymmetric approach and apply Poisson summation only in one variable, say  $n$. This gives
$n$. This gives
 $$\begin{eqnarray}\frac{1}{q}\mathop{\sum }_{n,m,r_{1},r_{2}\asymp q^{1/2}}e\biggl(\frac{\overline{a}bn\overline{m}r_{1}r_{2}}{q}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{q}\mathop{\sum }_{n,m,r_{1},r_{2}\asymp q^{1/2}}e\biggl(\frac{\overline{a}bn\overline{m}r_{1}r_{2}}{q}\biggr).\end{eqnarray}$$ Suppose that  $a\asymp b$. Then
$a\asymp b$. Then  $bnr_{1}r_{2}\asymp amq$, so we can apply the additive reciprocity formula
$bnr_{1}r_{2}\asymp amq$, so we can apply the additive reciprocity formula
 $$\begin{eqnarray}e\biggl(\frac{n\overline{d}}{c}\biggr)=e\biggl(-\frac{n\overline{c}}{d}\biggr)e\biggl(\frac{n}{cd}\biggr)\end{eqnarray}$$
$$\begin{eqnarray}e\biggl(\frac{n\overline{d}}{c}\biggr)=e\biggl(-\frac{n\overline{c}}{d}\biggr)e\biggl(\frac{n}{cd}\biggr)\end{eqnarray}$$to obtain
 $$\begin{eqnarray}\frac{1}{q}\mathop{\sum }_{n,m,r_{1},r_{2}\asymp q^{1/2}}e\biggl(\frac{\overline{q}bnr_{1}r_{2}}{am}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{q}\mathop{\sum }_{n,m,r_{1},r_{2}\asymp q^{1/2}}e\biggl(\frac{\overline{q}bnr_{1}r_{2}}{am}\biggr).\end{eqnarray}$$ Applying Poisson summation in  $n,r_{1},r_{2}$, this gives roughly
$n,r_{1},r_{2}$, this gives roughly
 $$\begin{eqnarray}\frac{1}{a^{2}}\mathop{\sum }_{m\asymp q^{1/2}}\mathop{\sum }_{n,r_{1},r_{2}\asymp a}S(qr_{1}r_{2}\overline{b},n,am).\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{a^{2}}\mathop{\sum }_{m\asymp q^{1/2}}\mathop{\sum }_{n,r_{1},r_{2}\asymp a}S(qr_{1}r_{2}\overline{b},n,am).\end{eqnarray}$$ If we assume for simplicity that  $b$ is prime and coprime to
$b$ is prime and coprime to  $aqmr_{1}r_{2}$ (this is where the assumption ‘
$aqmr_{1}r_{2}$ (this is where the assumption ‘ $b$ square-free’ in Theorem 1 is used), then
$b$ square-free’ in Theorem 1 is used), then  $S(qr_{1}r_{2},bn,abm)=-S(qr_{1}r_{2}\overline{b},n,am)$ by twisted multiplicativity. For the Kloosterman sum on the left-hand side, we are in the ‘Linnik range’
$S(qr_{1}r_{2},bn,abm)=-S(qr_{1}r_{2}\overline{b},n,am)$ by twisted multiplicativity. For the Kloosterman sum on the left-hand side, we are in the ‘Linnik range’  $\sqrt{qr_{1}r_{2}bn}\asymp abm$, and an application of the Kuznetsov formula yields the right-hand side of (1.5).
$\sqrt{qr_{1}r_{2}bn}\asymp abm$, and an application of the Kuznetsov formula yields the right-hand side of (1.5).
A back-of-the-envelope computation for Theorem 2 looks as follows. By an approximate functional equation, we have roughly
 $$\begin{eqnarray}L(1/2,\unicode[STIX]{x1D713})^{6}\approx \mathop{\sum }_{n,m\ll Q^{3/2}}\frac{\unicode[STIX]{x1D70F}_{3}(n)\unicode[STIX]{x1D70F}_{3}(m)\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(n)\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(m)}{(nm)^{1/2}}\end{eqnarray}$$
$$\begin{eqnarray}L(1/2,\unicode[STIX]{x1D713})^{6}\approx \mathop{\sum }_{n,m\ll Q^{3/2}}\frac{\unicode[STIX]{x1D70F}_{3}(n)\unicode[STIX]{x1D70F}_{3}(m)\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(n)\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(m)}{(nm)^{1/2}}\end{eqnarray}$$ for  $\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(q)$,
$\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(q)$,  $q\asymp Q$, where for simplicity we regard
$q\asymp Q$, where for simplicity we regard  $T$ as fixed; here
$T$ as fixed; here  $\unicode[STIX]{x1D70F}_{3}(n):=\sum _{abc=n}1$. Summing
$\unicode[STIX]{x1D70F}_{3}(n):=\sum _{abc=n}1$. Summing  $\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(q)$ and
$\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(q)$ and  $q\asymp Q$ by the Kuznetsov formula, the diagonal term is of size
$q\asymp Q$ by the Kuznetsov formula, the diagonal term is of size  $Q^{2}$ and the off-diagonal term looks roughly like
$Q^{2}$ and the off-diagonal term looks roughly like
 $$\begin{eqnarray}Q\mathop{\sum }_{q\asymp Q}\mathop{\sum }_{n,m\ll Q^{3/2}}\frac{\unicode[STIX]{x1D70F}_{3}(n)\unicode[STIX]{x1D70F}_{3}(m)}{(nm)^{1/2}}\mathop{\sum }_{c\ll Q^{1/2}}\frac{S(n,m,qc)}{qc}.\end{eqnarray}$$
$$\begin{eqnarray}Q\mathop{\sum }_{q\asymp Q}\mathop{\sum }_{n,m\ll Q^{3/2}}\frac{\unicode[STIX]{x1D70F}_{3}(n)\unicode[STIX]{x1D70F}_{3}(m)}{(nm)^{1/2}}\mathop{\sum }_{c\ll Q^{1/2}}\frac{S(n,m,qc)}{qc}.\end{eqnarray}$$ The key idea is to switch the roles of  $q$ and
$q$ and  $c$ and to apply the Kuznetsov formula backwards, but this time viewed as a spectral summation formula of level
$c$ and to apply the Kuznetsov formula backwards, but this time viewed as a spectral summation formula of level  $c$. This switching principle is well known from sieve theory; here we apply it in an automorphic context, to some extent similar in spirit to [Reference Deshouillers and IwaniecDI82]. We obtain roughly
$c$. This switching principle is well known from sieve theory; here we apply it in an automorphic context, to some extent similar in spirit to [Reference Deshouillers and IwaniecDI82]. We obtain roughly
 $$\begin{eqnarray}Q^{1/2}\mathop{\sum }_{c\ll Q^{1/2}}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(c)}\mathop{\sum }_{n,m\ll Q^{3/2}}\frac{\unicode[STIX]{x1D70F}_{3}(n)\unicode[STIX]{x1D70F}_{3}(m)\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(n)\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(m)}{(nm)^{1/2}}.\end{eqnarray}$$
$$\begin{eqnarray}Q^{1/2}\mathop{\sum }_{c\ll Q^{1/2}}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(c)}\mathop{\sum }_{n,m\ll Q^{3/2}}\frac{\unicode[STIX]{x1D70F}_{3}(n)\unicode[STIX]{x1D70F}_{3}(m)\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(n)\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(m)}{(nm)^{1/2}}.\end{eqnarray}$$ Applying Voronoi summation on the long  $n,m$-sum, we may hope to get complete square root cancellation, obtaining the final bound
$n,m$-sum, we may hope to get complete square root cancellation, obtaining the final bound  $Q^{3/2}$ for the off-diagonal contribution.
$Q^{3/2}$ for the off-diagonal contribution.
Apart from neglecting oldforms, whose presence is technically challenging, this heuristic argument has an important deficiency: it ignores the continuous spectrum that needs to be added artificially before applying the Kuznetsov formula, and this contribution is of size  $Q^{5/2}$ and substantially exceeds our target bound. In particular, it is impossible to estimate (1.17) by
$Q^{5/2}$ and substantially exceeds our target bound. In particular, it is impossible to estimate (1.17) by  $Q^{3/2}$ as indicated, as we know in advance that it is of size
$Q^{3/2}$ as indicated, as we know in advance that it is of size  $Q^{5/2}$. This dilemma of a gigantic continuous spectrum contribution is well known to experts and was first encountered in [Reference Duke, Friedlander and IwaniecDFI02], where the contribution was carefully computed and matched with another main term that occurred at a different stage of the argument. In [Reference Blomer, Harcos and MichelBHM07], the problem was solved by introducing additional zeros in the Mellin transform of the weight function in the approximate functional equation. Unfortunately, this loses positivity (and therefore many convenient simplifications), and it is also a very technical task to find the initial zeros at the end of the argument where they are needed to make a certain main term disappear. In the present situation, we argue differently and find a rather soft way to match two Eisenstein terms without actually computing them.
$Q^{5/2}$. This dilemma of a gigantic continuous spectrum contribution is well known to experts and was first encountered in [Reference Duke, Friedlander and IwaniecDFI02], where the contribution was carefully computed and matched with another main term that occurred at a different stage of the argument. In [Reference Blomer, Harcos and MichelBHM07], the problem was solved by introducing additional zeros in the Mellin transform of the weight function in the approximate functional equation. Unfortunately, this loses positivity (and therefore many convenient simplifications), and it is also a very technical task to find the initial zeros at the end of the argument where they are needed to make a certain main term disappear. In the present situation, we argue differently and find a rather soft way to match two Eisenstein terms without actually computing them.
2 Preliminaries
2.1 Hecke theory
We generally denote Hecke eigenvalues, with or without subscript, by  $\unicode[STIX]{x1D706}(n)$. For newforms of level
$\unicode[STIX]{x1D706}(n)$. For newforms of level  $N$, we will often use the multiplicativity relation
$N$, we will often use the multiplicativity relation
 $$\begin{eqnarray}\unicode[STIX]{x1D706}(nm)=\mathop{\sum }_{\substack{ d\mid (m,n) \\ (d,N)=1}}\unicode[STIX]{x1D707}(d)\unicode[STIX]{x1D706}(m/d)\unicode[STIX]{x1D706}(n/d).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}(nm)=\mathop{\sum }_{\substack{ d\mid (m,n) \\ (d,N)=1}}\unicode[STIX]{x1D707}(d)\unicode[STIX]{x1D706}(m/d)\unicode[STIX]{x1D706}(n/d).\end{eqnarray}$$We have the general upper bound
 $$\begin{eqnarray}\unicode[STIX]{x1D706}(n)\;\ll _{\unicode[STIX]{x1D700}}\;n^{\unicode[STIX]{x1D703}+\unicode[STIX]{x1D700}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}(n)\;\ll _{\unicode[STIX]{x1D700}}\;n^{\unicode[STIX]{x1D703}+\unicode[STIX]{x1D700}}.\end{eqnarray}$$ For a newform of level  $N=N_{1}N_{2}$ and trivial central character with
$N=N_{1}N_{2}$ and trivial central character with  $N_{1}$ square-free,
$N_{1}$ square-free,  $(N_{1},N_{2})=1$, and some
$(N_{1},N_{2})=1$, and some  $n\mid N_{1}$, we have
$n\mid N_{1}$, we have
 $$\begin{eqnarray}|\unicode[STIX]{x1D706}(n)|=n^{-1/2}\end{eqnarray}$$
$$\begin{eqnarray}|\unicode[STIX]{x1D706}(n)|=n^{-1/2}\end{eqnarray}$$via [Reference OggOgg69, Theorem 2].
2.2 Functional equation for the Hurwitz zeta function
For  $\unicode[STIX]{x1D6FC}\in \mathbb{R}$,
$\unicode[STIX]{x1D6FC}\in \mathbb{R}$,  $\Re s>1$, let
$\Re s>1$, let
 $$\begin{eqnarray}\unicode[STIX]{x1D701}(s,\unicode[STIX]{x1D6FC}):=\mathop{\sum }_{n+\unicode[STIX]{x1D6FC}>0}(n+\unicode[STIX]{x1D6FC})^{-s}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D701}(s,\unicode[STIX]{x1D6FC}):=\mathop{\sum }_{n+\unicode[STIX]{x1D6FC}>0}(n+\unicode[STIX]{x1D6FC})^{-s}\end{eqnarray}$$ denote the Hurwitz zeta function. It has meromorphic continuation to all  $s\in \mathbb{C}$ with a simple pole at
$s\in \mathbb{C}$ with a simple pole at  $s=1$ of residue 1 and satisfies the functional equation
$s=1$ of residue 1 and satisfies the functional equation
 $$\begin{eqnarray}\unicode[STIX]{x1D701}(s,\unicode[STIX]{x1D6FC})=\mathop{\sum }_{\pm }G^{\mp }(1-s)\unicode[STIX]{x1D701}^{(\pm \unicode[STIX]{x1D6FC})}(1-s),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D701}(s,\unicode[STIX]{x1D6FC})=\mathop{\sum }_{\pm }G^{\mp }(1-s)\unicode[STIX]{x1D701}^{(\pm \unicode[STIX]{x1D6FC})}(1-s),\end{eqnarray}$$where
 $$\begin{eqnarray}G^{\pm }(s)=(2\unicode[STIX]{x1D70B})^{-s}\unicode[STIX]{x1D6E4}(s)\exp (\pm i\unicode[STIX]{x1D70B}s/2)\end{eqnarray}$$
$$\begin{eqnarray}G^{\pm }(s)=(2\unicode[STIX]{x1D70B})^{-s}\unicode[STIX]{x1D6E4}(s)\exp (\pm i\unicode[STIX]{x1D70B}s/2)\end{eqnarray}$$ and  $\unicode[STIX]{x1D701}^{(\unicode[STIX]{x1D6FC})}(s)$ is (the meromorphic continuation of)
$\unicode[STIX]{x1D701}^{(\unicode[STIX]{x1D6FC})}(s)$ is (the meromorphic continuation of)  $\sum _{n}e(\unicode[STIX]{x1D6FC}n)n^{-s}$. For
$\sum _{n}e(\unicode[STIX]{x1D6FC}n)n^{-s}$. For  $\unicode[STIX]{x1D6FC}\in \mathbb{Q}$, this is a reformulation of Poisson summation in residue classes.
$\unicode[STIX]{x1D6FC}\in \mathbb{Q}$, this is a reformulation of Poisson summation in residue classes.
2.3 Functional equation for twisted automorphic  $L$-functions
$L$-functions
For  $\unicode[STIX]{x1D6FC}\in \mathbb{R}$,
$\unicode[STIX]{x1D6FC}\in \mathbb{R}$,  $\Re s>1$, let
$\Re s>1$, let
 $$\begin{eqnarray}L(s,\unicode[STIX]{x1D6FC},f):=\mathop{\sum }_{n}\unicode[STIX]{x1D706}_{f}(n)e(\unicode[STIX]{x1D6FC}n)n^{-s},\end{eqnarray}$$
$$\begin{eqnarray}L(s,\unicode[STIX]{x1D6FC},f):=\mathop{\sum }_{n}\unicode[STIX]{x1D706}_{f}(n)e(\unicode[STIX]{x1D6FC}n)n^{-s},\end{eqnarray}$$ where, as before,  $f$ is a Hecke eigenform of the group
$f$ is a Hecke eigenform of the group  $\text{SL}_{2}(\mathbb{Z})$, either Maaß with spectral parameter
$\text{SL}_{2}(\mathbb{Z})$, either Maaß with spectral parameter  $t$ and parity
$t$ and parity  $\unicode[STIX]{x1D716}\in \{\pm 1\}$, or holomorphic of weight
$\unicode[STIX]{x1D716}\in \{\pm 1\}$, or holomorphic of weight  $k$, or the standard Eisenstein series with
$k$, or the standard Eisenstein series with  $\unicode[STIX]{x1D706}_{f}(n)=\unicode[STIX]{x1D70F}(n)$. If
$\unicode[STIX]{x1D706}_{f}(n)=\unicode[STIX]{x1D70F}(n)$. If  $\unicode[STIX]{x1D6FC}=a/c\in \mathbb{Q}$ with
$\unicode[STIX]{x1D6FC}=a/c\in \mathbb{Q}$ with  $(a,c)=1$, this
$(a,c)=1$, this  $L$-function has meromorphic continuation to all
$L$-function has meromorphic continuation to all  $s\in \mathbb{C}$ with a double pole at
$s\in \mathbb{C}$ with a double pole at  $s=1$ with Laurent expansion
$s=1$ with Laurent expansion
 $$\begin{eqnarray}\frac{1}{c}\biggl(\frac{1}{(s-1)^{2}}+\frac{2\unicode[STIX]{x1D6FE}-2\log c}{s-1}+O(1)\biggr)\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{c}\biggl(\frac{1}{(s-1)^{2}}+\frac{2\unicode[STIX]{x1D6FE}-2\log c}{s-1}+O(1)\biggr)\end{eqnarray}$$ if  $f$ is Eisenstein; note that this is independent of
$f$ is Eisenstein; note that this is independent of  $a$. The twisted
$a$. The twisted  $L$-function satisfies the functional equation (see, for example, [Reference Harcos and MichelHM06, §2.4])
$L$-function satisfies the functional equation (see, for example, [Reference Harcos and MichelHM06, §2.4])
 $$\begin{eqnarray}L(s,a/c,f)=\mathop{\sum }_{\pm }G_{f}^{\mp }(1-s)c^{1-2s}L(s,\pm \overline{a}/c,f),\end{eqnarray}$$
$$\begin{eqnarray}L(s,a/c,f)=\mathop{\sum }_{\pm }G_{f}^{\mp }(1-s)c^{1-2s}L(s,\pm \overline{a}/c,f),\end{eqnarray}$$where
 $$\begin{eqnarray}G_{f}^{+}(s)=i^{k}(2\unicode[STIX]{x1D70B})^{1-2s}\frac{\unicode[STIX]{x1D6E4}(s+(k-1)/2)}{\unicode[STIX]{x1D6E4}(1-s+(k-1)/2)},\quad G_{f}^{-}(s)=0\end{eqnarray}$$
$$\begin{eqnarray}G_{f}^{+}(s)=i^{k}(2\unicode[STIX]{x1D70B})^{1-2s}\frac{\unicode[STIX]{x1D6E4}(s+(k-1)/2)}{\unicode[STIX]{x1D6E4}(1-s+(k-1)/2)},\quad G_{f}^{-}(s)=0\end{eqnarray}$$ if  $f$ is holomorphic of weight
$f$ is holomorphic of weight  $k$ and
$k$ and
 $$\begin{eqnarray}G_{f}^{\pm }(s)=\unicode[STIX]{x1D716}^{(1\mp 1)/2}\frac{\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{2}}(s+it))\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{2}}(s-it))}{\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{2}}(1-s+it))\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{2}}(1-s-it))}\mp \frac{\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{2}}(1+s+it))\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{2}}(1+s-it))}{\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{2}}(2-s+it))\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{2}}(2-s-it))}\end{eqnarray}$$
$$\begin{eqnarray}G_{f}^{\pm }(s)=\unicode[STIX]{x1D716}^{(1\mp 1)/2}\frac{\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{2}}(s+it))\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{2}}(s-it))}{\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{2}}(1-s+it))\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{2}}(1-s-it))}\mp \frac{\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{2}}(1+s+it))\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{2}}(1+s-it))}{\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{2}}(2-s+it))\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{2}}(2-s-it))}\end{eqnarray}$$ if  $f$ is Maaß with spectral parameter
$f$ is Maaß with spectral parameter  $t$ and parity
$t$ and parity  $\unicode[STIX]{x1D716}\in \{\pm 1\}$. This also holds for
$\unicode[STIX]{x1D716}\in \{\pm 1\}$. This also holds for  $f$ equal to the standard Eisenstein series with
$f$ equal to the standard Eisenstein series with  $t=0$ and
$t=0$ and  $\unicode[STIX]{x1D716}=1$.
$\unicode[STIX]{x1D716}=1$.
2.4 Fourier coefficients
We quote from [Reference Blomer and KhanBK19b, §3] and refer to this source for more details and references. The cuspidal spectrum is parametrized by pairs  $(\unicode[STIX]{x1D713},M)$ of
$(\unicode[STIX]{x1D713},M)$ of  $\unicode[STIX]{x1D6E4}_{0}(N)$-normalized newforms
$\unicode[STIX]{x1D6E4}_{0}(N)$-normalized newforms  $\unicode[STIX]{x1D713}$ of level
$\unicode[STIX]{x1D713}$ of level  $N_{0}\mid N$ and integers
$N_{0}\mid N$ and integers  $M\mid N/N_{0}$. The corresponding Fourier coefficients are
$M\mid N/N_{0}$. The corresponding Fourier coefficients are
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},M,N}(n)=\frac{1}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})^{1/2}(N\unicode[STIX]{x1D708}(N))^{1/2}}\mathop{\prod }_{p\mid N_{0}}\biggl(1-\frac{1}{p^{2}}\biggr)^{1/2}\mathop{\sum }_{d\mid (M,n)}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}(M,d)\frac{d}{M^{1/2}}\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(n/d)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},M,N}(n)=\frac{1}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})^{1/2}(N\unicode[STIX]{x1D708}(N))^{1/2}}\mathop{\prod }_{p\mid N_{0}}\biggl(1-\frac{1}{p^{2}}\biggr)^{1/2}\mathop{\sum }_{d\mid (M,n)}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}(M,d)\frac{d}{M^{1/2}}\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(n/d)\end{eqnarray}$$ for  $n\in \mathbb{N}$, where
$n\in \mathbb{N}$, where  $\unicode[STIX]{x1D708}(N)=\prod _{p\mid N}(1+1/p)$ and the multiplicative function
$\unicode[STIX]{x1D708}(N)=\prod _{p\mid N}(1+1/p)$ and the multiplicative function  $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}$ is defined in [Reference Blomer and KhanBK19b, (3.10)] and satisfies in particular
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}$ is defined in [Reference Blomer and KhanBK19b, (3.10)] and satisfies in particular
 $$\begin{eqnarray}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}(p,p)=\biggl(1-\frac{\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(p)^{2}}{p(1+1/p)^{2}}\biggr)^{-1/2},\quad \unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}(p,1)=\frac{-\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(p)}{1+1/p^{2}},\quad \unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}(1,1)=1\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}(p,p)=\biggl(1-\frac{\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(p)^{2}}{p(1+1/p)^{2}}\biggr)^{-1/2},\quad \unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}(p,1)=\frac{-\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(p)}{1+1/p^{2}},\quad \unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}(1,1)=1\end{eqnarray}$$ for  $p\nmid N_{0}$ and in general
$p\nmid N_{0}$ and in general
 $$\begin{eqnarray}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}(M,d)\;\ll _{\unicode[STIX]{x1D700}}\;M^{\unicode[STIX]{x1D700}}(M/d)^{\unicode[STIX]{x1D703}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}(M,d)\;\ll _{\unicode[STIX]{x1D700}}\;M^{\unicode[STIX]{x1D700}}(M/d)^{\unicode[STIX]{x1D703}}.\end{eqnarray}$$ For  $-n\in \mathbb{N}$ we have
$-n\in \mathbb{N}$ we have  $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},M,N}(n)=\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},M,N}(-n)$ if
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},M,N}(n)=\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D713}}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},M,N}(-n)$ if  $\unicode[STIX]{x1D713}$ is Maaß of parity
$\unicode[STIX]{x1D713}$ is Maaß of parity  $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D713}}\in \{\pm 1\}$ and
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D713}}\in \{\pm 1\}$ and  $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},M,N}(n)=0$ if
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},M,N}(n)=0$ if  $\unicode[STIX]{x1D713}$ is holomorphic.
$\unicode[STIX]{x1D713}$ is holomorphic.
If  $N$ is square-free, the Fourier coefficients of Eisenstein series of level
$N$ is square-free, the Fourier coefficients of Eisenstein series of level  $N$ are easy to describe. They are parametrized by divisors
$N$ are easy to describe. They are parametrized by divisors  $v\mid N$ and a continuous parameter
$v\mid N$ and a continuous parameter  $s=1/2+it$. The corresponding Fourier coefficients are given by (see, for example, [Reference Conrey and IwaniecCI00, (3.25)])
$s=1/2+it$. The corresponding Fourier coefficients are given by (see, for example, [Reference Conrey and IwaniecCI00, (3.25)])
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{v,N}(n,t)=\frac{C(v,M,t)}{(Nv)^{1/2}\unicode[STIX]{x1D701}^{(N)}(1+2it)}\mathop{\sum }_{b\mid v}\mathop{\sum }_{\unicode[STIX]{x1D6FE}\mid N/v}\unicode[STIX]{x1D707}(b\unicode[STIX]{x1D6FE})b\biggl(\frac{b}{\unicode[STIX]{x1D6FE}}\biggr)^{it}\unicode[STIX]{x1D702}\biggl(\frac{|n|}{b\unicode[STIX]{x1D6FE}},t\biggr),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{v,N}(n,t)=\frac{C(v,M,t)}{(Nv)^{1/2}\unicode[STIX]{x1D701}^{(N)}(1+2it)}\mathop{\sum }_{b\mid v}\mathop{\sum }_{\unicode[STIX]{x1D6FE}\mid N/v}\unicode[STIX]{x1D707}(b\unicode[STIX]{x1D6FE})b\biggl(\frac{b}{\unicode[STIX]{x1D6FE}}\biggr)^{it}\unicode[STIX]{x1D702}\biggl(\frac{|n|}{b\unicode[STIX]{x1D6FE}},t\biggr),\end{eqnarray}$$ where  $\unicode[STIX]{x1D702}(n,t)=\sum _{d_{1}d_{2}=n}(d_{1}/d_{2})^{it}$ for
$\unicode[STIX]{x1D702}(n,t)=\sum _{d_{1}d_{2}=n}(d_{1}/d_{2})^{it}$ for  $n\in \mathbb{N}$ (and 0 otherwise) and
$n\in \mathbb{N}$ (and 0 otherwise) and  $|C(v,N,t)|=1$. For general
$|C(v,N,t)|=1$. For general  $N$, we follow [Reference Blomer and KhanBK19b, §3] and parametrize unitary Eisenstein series of
$N$, we follow [Reference Blomer and KhanBK19b, §3] and parametrize unitary Eisenstein series of  $\unicode[STIX]{x1D6E4}_{0}(N)$ by a continuous parameter
$\unicode[STIX]{x1D6E4}_{0}(N)$ by a continuous parameter  $s=1/2+it$ together with pairs
$s=1/2+it$ together with pairs  $(\unicode[STIX]{x1D712},M)$, where
$(\unicode[STIX]{x1D712},M)$, where  $\unicode[STIX]{x1D712}$ is a primitive Dirichlet character of conductor
$\unicode[STIX]{x1D712}$ is a primitive Dirichlet character of conductor  $c_{\unicode[STIX]{x1D712}}$ and
$c_{\unicode[STIX]{x1D712}}$ and  $M\in \mathbb{N}$ satisfies
$M\in \mathbb{N}$ satisfies  $c_{\unicode[STIX]{x1D712}}^{2}\mid M\mid N$. Note that the role of
$c_{\unicode[STIX]{x1D712}}^{2}\mid M\mid N$. Note that the role of  $M$ is different than in the cuspidal case. We write
$M$ is different than in the cuspidal case. We write
 $$\begin{eqnarray}\displaystyle \tilde{\mathfrak{n}}_{N}(M) & = & \displaystyle \biggl(\mathop{\prod }_{\substack{ p\mid N \\ p\nmid (M,N/M)}}\frac{p}{p+1}\mathop{\prod }_{p\mid (M,N/M)}\frac{p-1}{p+1}\biggr)^{1/2},\nonumber\\ \displaystyle M & = & \displaystyle c_{\unicode[STIX]{x1D712}}M_{1}M_{2},\quad \text{where }(M_{2},c_{\unicode[STIX]{x1D712}})=1,\quad M_{1}\mid c_{\unicode[STIX]{x1D712}}^{\infty },\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \tilde{\mathfrak{n}}_{N}(M) & = & \displaystyle \biggl(\mathop{\prod }_{\substack{ p\mid N \\ p\nmid (M,N/M)}}\frac{p}{p+1}\mathop{\prod }_{p\mid (M,N/M)}\frac{p-1}{p+1}\biggr)^{1/2},\nonumber\\ \displaystyle M & = & \displaystyle c_{\unicode[STIX]{x1D712}}M_{1}M_{2},\quad \text{where }(M_{2},c_{\unicode[STIX]{x1D712}})=1,\quad M_{1}\mid c_{\unicode[STIX]{x1D712}}^{\infty },\nonumber\end{eqnarray}$$ so that  $c_{\unicode[STIX]{x1D712}}\mid M_{1}$ and
$c_{\unicode[STIX]{x1D712}}\mid M_{1}$ and  $(M_{1},M_{2})=1$. The Fourier coefficients of the Eisenstein series attached to the data
$(M_{1},M_{2})=1$. The Fourier coefficients of the Eisenstein series attached to the data  $(N,M,t,\unicode[STIX]{x1D712})$ are
$(N,M,t,\unicode[STIX]{x1D712})$ are
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712},M,N}(n,t) & = & \displaystyle \frac{\tilde{C}(\unicode[STIX]{x1D712},M,t)|n|^{it}}{(N\unicode[STIX]{x1D708}(N))^{1/2}\tilde{\mathfrak{n}}_{N}(M)L^{(N)}(1+2it,\unicode[STIX]{x1D712}^{2})}\biggl(\frac{M_{1}}{M_{2}}\biggr)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{\unicode[STIX]{x1D6FF}\mid M_{2}}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D707}\biggl(\frac{M_{2}}{\unicode[STIX]{x1D6FF}}\biggr)\overline{\unicode[STIX]{x1D712}}(\unicode[STIX]{x1D6FF})\mathop{\sum }_{\substack{ cM_{1}\unicode[STIX]{x1D6FF}f=n \\ (c,N/M)=1}}\frac{\unicode[STIX]{x1D712}(c)}{c^{2it}}\overline{\unicode[STIX]{x1D712}}(f),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712},M,N}(n,t) & = & \displaystyle \frac{\tilde{C}(\unicode[STIX]{x1D712},M,t)|n|^{it}}{(N\unicode[STIX]{x1D708}(N))^{1/2}\tilde{\mathfrak{n}}_{N}(M)L^{(N)}(1+2it,\unicode[STIX]{x1D712}^{2})}\biggl(\frac{M_{1}}{M_{2}}\biggr)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{\unicode[STIX]{x1D6FF}\mid M_{2}}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D707}\biggl(\frac{M_{2}}{\unicode[STIX]{x1D6FF}}\biggr)\overline{\unicode[STIX]{x1D712}}(\unicode[STIX]{x1D6FF})\mathop{\sum }_{\substack{ cM_{1}\unicode[STIX]{x1D6FF}f=n \\ (c,N/M)=1}}\frac{\unicode[STIX]{x1D712}(c)}{c^{2it}}\overline{\unicode[STIX]{x1D712}}(f),\end{eqnarray}$$ where  $|\tilde{C}(\unicode[STIX]{x1D712},M,t)|=1$.
$|\tilde{C}(\unicode[STIX]{x1D712},M,t)|=1$.
2.5 The Kuznetsov formula
For  $x>0$, we define the integral kernels
$x>0$, we define the integral kernels
 $$\begin{eqnarray}\displaystyle {\mathcal{J}}^{+}(x,t) & := & \displaystyle \frac{\unicode[STIX]{x1D70B}i}{\sinh (\unicode[STIX]{x1D70B}t)}(J_{2it}(4\unicode[STIX]{x1D70B}x)-J_{-2it}(4\unicode[STIX]{x1D70B}x)),\nonumber\\ \displaystyle {\mathcal{J}}^{-}(x,t) & := & \displaystyle \frac{\unicode[STIX]{x1D70B}i}{\sinh (\unicode[STIX]{x1D70B}t)}(I_{2it}(4\unicode[STIX]{x1D70B}x)-I_{-2it}(4\unicode[STIX]{x1D70B}x))=4\cosh (\unicode[STIX]{x1D70B}t)K_{2it}(4\unicode[STIX]{x1D70B}x),\nonumber\\ \displaystyle {\mathcal{J}}^{\text{hol}}(x,k) & := & \displaystyle 2\unicode[STIX]{x1D70B}i^{k}J_{k-1}(4\unicode[STIX]{x1D70B}x)={\mathcal{J}}^{+}(x,(k-1)/(2i)),\quad k\in 2\mathbb{N}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{J}}^{+}(x,t) & := & \displaystyle \frac{\unicode[STIX]{x1D70B}i}{\sinh (\unicode[STIX]{x1D70B}t)}(J_{2it}(4\unicode[STIX]{x1D70B}x)-J_{-2it}(4\unicode[STIX]{x1D70B}x)),\nonumber\\ \displaystyle {\mathcal{J}}^{-}(x,t) & := & \displaystyle \frac{\unicode[STIX]{x1D70B}i}{\sinh (\unicode[STIX]{x1D70B}t)}(I_{2it}(4\unicode[STIX]{x1D70B}x)-I_{-2it}(4\unicode[STIX]{x1D70B}x))=4\cosh (\unicode[STIX]{x1D70B}t)K_{2it}(4\unicode[STIX]{x1D70B}x),\nonumber\\ \displaystyle {\mathcal{J}}^{\text{hol}}(x,k) & := & \displaystyle 2\unicode[STIX]{x1D70B}i^{k}J_{k-1}(4\unicode[STIX]{x1D70B}x)={\mathcal{J}}^{+}(x,(k-1)/(2i)),\quad k\in 2\mathbb{N}.\nonumber\end{eqnarray}$$ If  $H\in C^{3}((0,\infty ))$ satisfies
$H\in C^{3}((0,\infty ))$ satisfies  $x^{j}H^{(j)}(x)\ll \min (x,x^{-3/2})$ for
$x^{j}H^{(j)}(x)\ll \min (x,x^{-3/2})$ for  $0\leqslant j\leqslant 3$, we define
$0\leqslant j\leqslant 3$, we define
 $$\begin{eqnarray}\mathscr{L}^{\diamondsuit }H=\int _{0}^{\infty }{\mathcal{J}}^{\diamondsuit }(x,.)H(x)\frac{dx}{x}\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{L}^{\diamondsuit }H=\int _{0}^{\infty }{\mathcal{J}}^{\diamondsuit }(x,.)H(x)\frac{dx}{x}\end{eqnarray}$$ for  $\diamondsuit \in \{+,-,\text{hol}\}$, and for
$\diamondsuit \in \{+,-,\text{hol}\}$, and for  $n,m,N\in \mathbb{N}$, we have
$n,m,N\in \mathbb{N}$, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{N\mid c}\frac{S(\pm n,m,c)}{c}H\biggl(\frac{\sqrt{nm}}{c}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad ={\mathcal{A}}_{N}^{\text{Maa}\unicode[STIX]{x00DF}}(\pm n,m;\mathscr{L}^{\pm }H)+{\mathcal{A}}_{N}^{\text{Eis}}(\pm n,m;\mathscr{L}^{\pm }H)+{\mathcal{A}}_{N}^{\text{hol}}(\pm n,m;\mathscr{L}^{\text{hol}}H),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{N\mid c}\frac{S(\pm n,m,c)}{c}H\biggl(\frac{\sqrt{nm}}{c}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad ={\mathcal{A}}_{N}^{\text{Maa}\unicode[STIX]{x00DF}}(\pm n,m;\mathscr{L}^{\pm }H)+{\mathcal{A}}_{N}^{\text{Eis}}(\pm n,m;\mathscr{L}^{\pm }H)+{\mathcal{A}}_{N}^{\text{hol}}(\pm n,m;\mathscr{L}^{\text{hol}}H),\end{eqnarray}$$where
 $$\begin{eqnarray}\left.\begin{array}{@{}rcl@{}}{\mathcal{A}}_{N}^{\text{Maa}\unicode[STIX]{x00DF}}(n,m;h)\, & :=\, & \displaystyle \mathop{\sum }_{N_{0}M\mid N}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(N_{0})}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},M,N}(n)\overline{\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},M,N}(m)}h(t_{\unicode[STIX]{x1D713}}),\\ {\mathcal{A}}_{N}^{\text{Eis}}(n,m;h)\, & :=\, & \displaystyle \mathop{\sum }_{v\mid N}\int _{\mathbb{R}}\unicode[STIX]{x1D70C}_{v,N}(n,t)\overline{\unicode[STIX]{x1D70C}_{v,N}(m,t)}h(t)\frac{dt}{2\unicode[STIX]{x1D70B}}\quad (N\text{ square-free}),\\ {\mathcal{A}}_{N}^{\text{Eis}}(n,m;h)\, & :=\, & \displaystyle \mathop{\sum }_{c_{\unicode[STIX]{x1D712}}^{2}\mid M\mid N}\int _{\mathbb{R}}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712},M,N}(n,t)\overline{\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712},M,N}(m,t)}h(t)\frac{dt}{2\unicode[STIX]{x1D70B}}\quad (\text{in general}),\\ {\mathcal{A}}_{N}^{\text{hol}}(n,m;h)\, & :=\, & \displaystyle \mathop{\sum }_{N_{0}M\mid N}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}_{\text{hol}}^{\ast }(N_{0})}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},M,N}(n)\overline{\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},M,N}(m)}h(k_{\unicode[STIX]{x1D713}}).\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}rcl@{}}{\mathcal{A}}_{N}^{\text{Maa}\unicode[STIX]{x00DF}}(n,m;h)\, & :=\, & \displaystyle \mathop{\sum }_{N_{0}M\mid N}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(N_{0})}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},M,N}(n)\overline{\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},M,N}(m)}h(t_{\unicode[STIX]{x1D713}}),\\ {\mathcal{A}}_{N}^{\text{Eis}}(n,m;h)\, & :=\, & \displaystyle \mathop{\sum }_{v\mid N}\int _{\mathbb{R}}\unicode[STIX]{x1D70C}_{v,N}(n,t)\overline{\unicode[STIX]{x1D70C}_{v,N}(m,t)}h(t)\frac{dt}{2\unicode[STIX]{x1D70B}}\quad (N\text{ square-free}),\\ {\mathcal{A}}_{N}^{\text{Eis}}(n,m;h)\, & :=\, & \displaystyle \mathop{\sum }_{c_{\unicode[STIX]{x1D712}}^{2}\mid M\mid N}\int _{\mathbb{R}}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712},M,N}(n,t)\overline{\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712},M,N}(m,t)}h(t)\frac{dt}{2\unicode[STIX]{x1D70B}}\quad (\text{in general}),\\ {\mathcal{A}}_{N}^{\text{hol}}(n,m;h)\, & :=\, & \displaystyle \mathop{\sum }_{N_{0}M\mid N}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}_{\text{hol}}^{\ast }(N_{0})}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},M,N}(n)\overline{\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},M,N}(m)}h(k_{\unicode[STIX]{x1D713}}).\end{array}\right.\end{eqnarray}$$ (Recall that  $\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(N_{0})$ and
$\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(N_{0})$ and  $\unicode[STIX]{x1D713}\in {\mathcal{B}}_{\text{hol}}^{\ast }(N_{0})$ are
$\unicode[STIX]{x1D713}\in {\mathcal{B}}_{\text{hol}}^{\ast }(N_{0})$ are  $\unicode[STIX]{x1D6E4}_{0}(N)$-normalized.) Conversely, if
$\unicode[STIX]{x1D6E4}_{0}(N)$-normalized.) Conversely, if  $h$ is holomorphic in an
$h$ is holomorphic in an  $\unicode[STIX]{x1D700}$-neighbourhood of
$\unicode[STIX]{x1D700}$-neighbourhood of  $|\Im t|\leqslant 1/2$ and satisfies
$|\Im t|\leqslant 1/2$ and satisfies  $h(t)\ll (1+|t|)^{-2-\unicode[STIX]{x1D6FF}}$ in this region for some
$h(t)\ll (1+|t|)^{-2-\unicode[STIX]{x1D6FF}}$ in this region for some  $\unicode[STIX]{x1D6FF}>0$, then for
$\unicode[STIX]{x1D6FF}>0$, then for  $n,m\in \mathbb{N}$, we have [Reference Blomer and KhanBK19b, (3.14)]
$n,m\in \mathbb{N}$, we have [Reference Blomer and KhanBK19b, (3.14)]
 $$\begin{eqnarray}{\mathcal{A}}_{N}^{\text{Maa}\unicode[STIX]{x00DF}}(n,m;h)+{\mathcal{A}}_{N}^{\text{Eis}}(n,m;h)=\unicode[STIX]{x1D6FF}_{n,m}\int _{-\infty }^{\infty }h(t)\frac{t\tanh (\unicode[STIX]{x1D70B}t)\,dt}{2\unicode[STIX]{x1D70B}^{2}}+\mathop{\sum }_{N\mid c}\frac{S(n,m,c)}{c}\mathscr{K}h\biggl(\frac{\sqrt{nm}}{c}\biggr),\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}_{N}^{\text{Maa}\unicode[STIX]{x00DF}}(n,m;h)+{\mathcal{A}}_{N}^{\text{Eis}}(n,m;h)=\unicode[STIX]{x1D6FF}_{n,m}\int _{-\infty }^{\infty }h(t)\frac{t\tanh (\unicode[STIX]{x1D70B}t)\,dt}{2\unicode[STIX]{x1D70B}^{2}}+\mathop{\sum }_{N\mid c}\frac{S(n,m,c)}{c}\mathscr{K}h\biggl(\frac{\sqrt{nm}}{c}\biggr),\end{eqnarray}$$where
 $$\begin{eqnarray}\mathscr{K}h(x)=\int _{-\infty }^{\infty }{\mathcal{J}}^{+}(x,t)h(t)t\tanh (\unicode[STIX]{x1D70B}t)\frac{dt}{2\unicode[STIX]{x1D70B}^{2}}=\frac{i}{\unicode[STIX]{x1D70B}}\int _{-\infty }^{\infty }\frac{J_{2it}(4\unicode[STIX]{x1D70B}x)}{\cosh (\unicode[STIX]{x1D70B}t)}h(t)t\,dt.\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{K}h(x)=\int _{-\infty }^{\infty }{\mathcal{J}}^{+}(x,t)h(t)t\tanh (\unicode[STIX]{x1D70B}t)\frac{dt}{2\unicode[STIX]{x1D70B}^{2}}=\frac{i}{\unicode[STIX]{x1D70B}}\int _{-\infty }^{\infty }\frac{J_{2it}(4\unicode[STIX]{x1D70B}x)}{\cosh (\unicode[STIX]{x1D70B}t)}h(t)t\,dt.\end{eqnarray}$$2.6 Integral transforms
We generalize (2.17) slightly and define for  $s\in \mathbb{C}$ the transform
$s\in \mathbb{C}$ the transform  $\mathscr{K}_{s}h$ by
$\mathscr{K}_{s}h$ by  $\mathscr{K}_{s}h(x):=x^{s}\mathscr{K}h(x)$.
$\mathscr{K}_{s}h(x):=x^{s}\mathscr{K}h(x)$.
Lemma 1. Let  $s\in \mathbb{C}$ with
$s\in \mathbb{C}$ with  $\Re s<-10$, and suppose that
$\Re s<-10$, and suppose that  $h$ is holomorphic in
$h$ is holomorphic in  $|\Im t|<(-\Re s+15)/2$, satisfying
$|\Im t|<(-\Re s+15)/2$, satisfying  $h(t)\ll (1+|t|)^{-10}$ and having zeros at
$h(t)\ll (1+|t|)^{-10}$ and having zeros at  $\pm i(2n-1)/2$,
$\pm i(2n-1)/2$,  $n\in \mathbb{N}$, in this region. Then
$n\in \mathbb{N}$, in this region. Then  $H:=\mathscr{K}_{s}h$ satisfies the assumptions of (2.14), that is,
$H:=\mathscr{K}_{s}h$ satisfies the assumptions of (2.14), that is,  $x^{j}H^{(j)}(x)\;\ll _{s}\;\min (x,x^{-3/2})$ for
$x^{j}H^{(j)}(x)\;\ll _{s}\;\min (x,x^{-3/2})$ for  $0\leqslant j\leqslant 3$.
$0\leqslant j\leqslant 3$.
Proof. We record the formula [Reference Gradshteyn, Ryzhik, Jeffrey and ZwillingerGR07, (8.411.10)]
 $$\begin{eqnarray}\frac{J_{2it}(4\unicode[STIX]{x1D70B}x)}{\cosh (\unicode[STIX]{x1D70B}t)}=\frac{(2\unicode[STIX]{x1D70B}x)^{2it}}{\sqrt{\unicode[STIX]{x1D70B}}\unicode[STIX]{x1D6E4}(1/2+2it)\cosh (\unicode[STIX]{x1D70B}t)}\int _{-1}^{1}(1-y^{2})^{2it-1/2}\cos (4\unicode[STIX]{x1D70B}xy)\,dy\end{eqnarray}$$
$$\begin{eqnarray}\frac{J_{2it}(4\unicode[STIX]{x1D70B}x)}{\cosh (\unicode[STIX]{x1D70B}t)}=\frac{(2\unicode[STIX]{x1D70B}x)^{2it}}{\sqrt{\unicode[STIX]{x1D70B}}\unicode[STIX]{x1D6E4}(1/2+2it)\cosh (\unicode[STIX]{x1D70B}t)}\int _{-1}^{1}(1-y^{2})^{2it-1/2}\cos (4\unicode[STIX]{x1D70B}xy)\,dy\end{eqnarray}$$ for  $\Re (2it)>-1/2$,
$\Re (2it)>-1/2$,  $x>0$. In particular,
$x>0$. In particular,
 $$\begin{eqnarray}\frac{d^{j}}{dx^{j}}\frac{J_{2it}(4\unicode[STIX]{x1D70B}x)}{\cosh (\unicode[STIX]{x1D70B}t)}\;\ll _{j,A,\unicode[STIX]{x1D700}}\;\biggl(\frac{x}{1+|t|}\biggr)^{\Re (2it)}(1+|t|/x)^{j},\quad -1/2+\unicode[STIX]{x1D700}\leqslant \Re (2it)<A,\end{eqnarray}$$
$$\begin{eqnarray}\frac{d^{j}}{dx^{j}}\frac{J_{2it}(4\unicode[STIX]{x1D70B}x)}{\cosh (\unicode[STIX]{x1D70B}t)}\;\ll _{j,A,\unicode[STIX]{x1D700}}\;\biggl(\frac{x}{1+|t|}\biggr)^{\Re (2it)}(1+|t|/x)^{j},\quad -1/2+\unicode[STIX]{x1D700}\leqslant \Re (2it)<A,\end{eqnarray}$$ for  $j,A\in \mathbb{N}_{0}:=\mathbb{N}\cup \{0\}$,
$j,A\in \mathbb{N}_{0}:=\mathbb{N}\cup \{0\}$,  $\unicode[STIX]{x1D700}>0$. Let
$\unicode[STIX]{x1D700}>0$. Let  $s\in \mathbb{C}$ with
$s\in \mathbb{C}$ with  $\Re s<-10$ be fixed. For
$\Re s<-10$ be fixed. For  $x\geqslant 1$ and
$x\geqslant 1$ and  $0\leqslant j\leqslant 3$, we obtain
$0\leqslant j\leqslant 3$, we obtain
 $$\begin{eqnarray}x^{j}H^{(j)}(x)\ll x^{\Re s+j}\int _{-\infty }^{\infty }\biggl(1+\frac{|t|}{x}\biggr)^{j}|h(t)t|\,dt\ll x^{\Re s+j}\ll x^{-3/2},\end{eqnarray}$$
$$\begin{eqnarray}x^{j}H^{(j)}(x)\ll x^{\Re s+j}\int _{-\infty }^{\infty }\biggl(1+\frac{|t|}{x}\biggr)^{j}|h(t)t|\,dt\ll x^{\Re s+j}\ll x^{-3/2},\end{eqnarray}$$ and for  $x<1$, we shift the contour to
$x<1$, we shift the contour to  $\Re (2it)=-\Re s+10$ (not passing any pole by our assumption on
$\Re (2it)=-\Re s+10$ (not passing any pole by our assumption on  $h$), getting
$h$), getting

Lemma 2. Let  $s\in \mathbb{C}$ with
$s\in \mathbb{C}$ with  $\Re s<1$, and suppose that
$\Re s<1$, and suppose that  $h$ is even and holomorphic in
$h$ is even and holomorphic in  $|\Im t|<(-\Re s+15)/2$, satisfying
$|\Im t|<(-\Re s+15)/2$, satisfying  $h(t)\ll e^{-|t|}$ and having zeros at
$h(t)\ll e^{-|t|}$ and having zeros at  $\pm i(2n-1)/2$,
$\pm i(2n-1)/2$,  $n\in \mathbb{N}$, in this region.
$n\in \mathbb{N}$, in this region.
 $(\text{a})$ The transform
$(\text{a})$ The transform  $\mathscr{L}^{+}\mathscr{K}_{s}h$, defined for
$\mathscr{L}^{+}\mathscr{K}_{s}h$, defined for  $\Re s<-10$ by Lemma 1, has analytic continuation to
$\Re s<-10$ by Lemma 1, has analytic continuation to  $\Re s<1$, and we have the Sears–Titchmarsh inversion formula
$\Re s<1$, and we have the Sears–Titchmarsh inversion formula  $\mathscr{L}^{+}\mathscr{K}_{0}h=h$.
$\mathscr{L}^{+}\mathscr{K}_{0}h=h$.
 $(\text{b})$ We have the uniform bounds
$(\text{b})$ We have the uniform bounds
 $$\begin{eqnarray}\mathscr{L}^{+}\mathscr{K}_{s}h(t)\;\ll _{\Re s}\;\int _{-\infty }^{\infty }\biggl|h\biggl(\unicode[STIX]{x1D70F}-\frac{i}{2}(1-\Re s)\biggr)\biggr|(1+|\unicode[STIX]{x1D70F}|)\displaystyle \mathop{\prod }_{\pm }\biggl(1+\biggl|\frac{1}{2}\Im s-\unicode[STIX]{x1D70F}\pm \Re t\biggr|\biggr)^{-1+\Re s}\,d\unicode[STIX]{x1D70F}\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{L}^{+}\mathscr{K}_{s}h(t)\;\ll _{\Re s}\;\int _{-\infty }^{\infty }\biggl|h\biggl(\unicode[STIX]{x1D70F}-\frac{i}{2}(1-\Re s)\biggr)\biggr|(1+|\unicode[STIX]{x1D70F}|)\displaystyle \mathop{\prod }_{\pm }\biggl(1+\biggl|\frac{1}{2}\Im s-\unicode[STIX]{x1D70F}\pm \Re t\biggr|\biggr)^{-1+\Re s}\,d\unicode[STIX]{x1D70F}\end{eqnarray}$$ for  $t\in \mathbb{R}\cup [-i\unicode[STIX]{x1D703},i\unicode[STIX]{x1D703}]$ and
$t\in \mathbb{R}\cup [-i\unicode[STIX]{x1D703},i\unicode[STIX]{x1D703}]$ and  $\Re s<1$, and
$\Re s<1$, and
 $$\begin{eqnarray}\mathscr{L}^{\text{hol}}\mathscr{K}_{s}h(k)\;\ll _{\Re s}\;\int _{-\infty }^{\infty }\biggl|h\biggl(\unicode[STIX]{x1D70F}-\frac{i}{2}\max (2-k-\Re s,0)\biggr)\biggr|(1+|\unicode[STIX]{x1D70F}|)\displaystyle \mathop{\prod }_{\pm }\biggl(\biggl|\frac{1}{2}\Im s\pm \unicode[STIX]{x1D70F}\biggr|+k\biggr)^{-1+\Re s}\,d\unicode[STIX]{x1D70F}\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{L}^{\text{hol}}\mathscr{K}_{s}h(k)\;\ll _{\Re s}\;\int _{-\infty }^{\infty }\biggl|h\biggl(\unicode[STIX]{x1D70F}-\frac{i}{2}\max (2-k-\Re s,0)\biggr)\biggr|(1+|\unicode[STIX]{x1D70F}|)\displaystyle \mathop{\prod }_{\pm }\biggl(\biggl|\frac{1}{2}\Im s\pm \unicode[STIX]{x1D70F}\biggr|+k\biggr)^{-1+\Re s}\,d\unicode[STIX]{x1D70F}\end{eqnarray}$$ for  $k\in 2\mathbb{N}$, where the implied constants depend only on
$k\in 2\mathbb{N}$, where the implied constants depend only on  $\Re s$ (but not on
$\Re s$ (but not on  $t$,
$t$,  $k$,
$k$,  $h$,
$h$,  $\Im s$).
$\Im s$).
Proof. For  $\Re s<-10$, we have, by definition,
$\Re s<-10$, we have, by definition,
 $$\begin{eqnarray}\mathscr{K}_{s}h(x)=x^{s}\frac{i}{\unicode[STIX]{x1D70B}}\int _{\Re (i\unicode[STIX]{x1D70F})=(10-\Re s)/2}\frac{J_{2i\unicode[STIX]{x1D70F}}(4\unicode[STIX]{x1D70B}x)}{\cosh (\unicode[STIX]{x1D70B}\unicode[STIX]{x1D70F})}h(\unicode[STIX]{x1D70F})\unicode[STIX]{x1D70F}\,d\unicode[STIX]{x1D70F},\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{K}_{s}h(x)=x^{s}\frac{i}{\unicode[STIX]{x1D70B}}\int _{\Re (i\unicode[STIX]{x1D70F})=(10-\Re s)/2}\frac{J_{2i\unicode[STIX]{x1D70F}}(4\unicode[STIX]{x1D70B}x)}{\cosh (\unicode[STIX]{x1D70B}\unicode[STIX]{x1D70F})}h(\unicode[STIX]{x1D70F})\unicode[STIX]{x1D70F}\,d\unicode[STIX]{x1D70F},\end{eqnarray}$$and we have an absolutely convergent double integral
 $$\begin{eqnarray}\mathscr{L}^{+}\mathscr{K}_{s}h(t)=-\int _{0}^{\infty }\frac{1}{\sinh (\unicode[STIX]{x1D70B}t)}(J_{2it}(4\unicode[STIX]{x1D70B}x)-J_{-2it}(4\unicode[STIX]{x1D70B}x))x^{s}\int _{\Re (i\unicode[STIX]{x1D70F})=(10-\Re s)/2}\frac{J_{2i\unicode[STIX]{x1D70F}}(4\unicode[STIX]{x1D70B}x)}{\cosh (\unicode[STIX]{x1D70B}\unicode[STIX]{x1D70F})}h(\unicode[STIX]{x1D70F})\unicode[STIX]{x1D70F}\,d\unicode[STIX]{x1D70F}\frac{dx}{x}.\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{L}^{+}\mathscr{K}_{s}h(t)=-\int _{0}^{\infty }\frac{1}{\sinh (\unicode[STIX]{x1D70B}t)}(J_{2it}(4\unicode[STIX]{x1D70B}x)-J_{-2it}(4\unicode[STIX]{x1D70B}x))x^{s}\int _{\Re (i\unicode[STIX]{x1D70F})=(10-\Re s)/2}\frac{J_{2i\unicode[STIX]{x1D70F}}(4\unicode[STIX]{x1D70B}x)}{\cosh (\unicode[STIX]{x1D70B}\unicode[STIX]{x1D70F})}h(\unicode[STIX]{x1D70F})\unicode[STIX]{x1D70F}\,d\unicode[STIX]{x1D70F}\frac{dx}{x}.\end{eqnarray}$$ To see the absolute convergence, we use (2.19) with  $j=0$ to bound
$j=0$ to bound  $J_{\pm 2it}(x)\;\ll _{t}\;\min (x^{2\unicode[STIX]{x1D703}},x^{-2\unicode[STIX]{x1D703}})$ for
$J_{\pm 2it}(x)\;\ll _{t}\;\min (x^{2\unicode[STIX]{x1D703}},x^{-2\unicode[STIX]{x1D703}})$ for  $t\in \mathbb{R}\cup [-i\unicode[STIX]{x1D703},i\unicode[STIX]{x1D703}]$, and we combine (2.19) with the bound
$t\in \mathbb{R}\cup [-i\unicode[STIX]{x1D703},i\unicode[STIX]{x1D703}]$, and we combine (2.19) with the bound  $J_{\unicode[STIX]{x1D708}}(x)\ll x^{-1/2}$ for
$J_{\unicode[STIX]{x1D708}}(x)\ll x^{-1/2}$ for  $x\gg |\unicode[STIX]{x1D708}|^{2}$ (which follows from the asymptotic formula [Reference Gradshteyn, Ryzhik, Jeffrey and ZwillingerGR07, (8.451.1)]) to bound
$x\gg |\unicode[STIX]{x1D708}|^{2}$ (which follows from the asymptotic formula [Reference Gradshteyn, Ryzhik, Jeffrey and ZwillingerGR07, (8.451.1)]) to bound
 $$\begin{eqnarray}J_{2i\unicode[STIX]{x1D70F}}(x)\ll \min (x^{-\Re s+10},x^{-1/2}(1+|\unicode[STIX]{x1D70F}|)^{-\Re s+11}).\end{eqnarray}$$
$$\begin{eqnarray}J_{2i\unicode[STIX]{x1D70F}}(x)\ll \min (x^{-\Re s+10},x^{-1/2}(1+|\unicode[STIX]{x1D70F}|)^{-\Re s+11}).\end{eqnarray}$$ We can compute the  $x$-integral explicitly using [Reference Gradshteyn, Ryzhik, Jeffrey and ZwillingerGR07, (6.574.2)], getting
$x$-integral explicitly using [Reference Gradshteyn, Ryzhik, Jeffrey and ZwillingerGR07, (6.574.2)], getting
 $$\begin{eqnarray}\mathscr{L}^{+}\mathscr{K}_{s}h(t)=\int _{\Re (i\unicode[STIX]{x1D70F})=(10-\Re s)/2}\frac{\unicode[STIX]{x1D6E4}(1-s)\cos (i\unicode[STIX]{x1D70B}\unicode[STIX]{x1D70F}+\unicode[STIX]{x1D70B}s/2)h(\unicode[STIX]{x1D70F})\unicode[STIX]{x1D70F}}{(2\unicode[STIX]{x1D70B})^{s}\unicode[STIX]{x1D70B}i\cosh (\unicode[STIX]{x1D70B}\unicode[STIX]{x1D70F})}\mathop{\prod }_{\pm }\frac{\unicode[STIX]{x1D6E4}(\frac{s}{2}+i\unicode[STIX]{x1D70F}\pm it)}{\unicode[STIX]{x1D6E4}(1-\frac{s}{2}+i\unicode[STIX]{x1D70F}\pm it)}\,d\unicode[STIX]{x1D70F}.\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{L}^{+}\mathscr{K}_{s}h(t)=\int _{\Re (i\unicode[STIX]{x1D70F})=(10-\Re s)/2}\frac{\unicode[STIX]{x1D6E4}(1-s)\cos (i\unicode[STIX]{x1D70B}\unicode[STIX]{x1D70F}+\unicode[STIX]{x1D70B}s/2)h(\unicode[STIX]{x1D70F})\unicode[STIX]{x1D70F}}{(2\unicode[STIX]{x1D70B})^{s}\unicode[STIX]{x1D70B}i\cosh (\unicode[STIX]{x1D70B}\unicode[STIX]{x1D70F})}\mathop{\prod }_{\pm }\frac{\unicode[STIX]{x1D6E4}(\frac{s}{2}+i\unicode[STIX]{x1D70F}\pm it)}{\unicode[STIX]{x1D6E4}(1-\frac{s}{2}+i\unicode[STIX]{x1D70F}\pm it)}\,d\unicode[STIX]{x1D70F}.\end{eqnarray}$$ Here we can put any  $s$ with
$s$ with  $\Re s<1$ in the integrand (and also shift the contour to, say,
$\Re s<1$ in the integrand (and also shift the contour to, say,  $\Re (i\unicode[STIX]{x1D70F})=5$), in particular
$\Re (i\unicode[STIX]{x1D70F})=5$), in particular  $s=0$, so that
$s=0$, so that
 $$\begin{eqnarray}\mathscr{L}^{+}\mathscr{K}_{0}h(t)=\int _{\Re (i\unicode[STIX]{x1D70F})=5}\frac{h(\unicode[STIX]{x1D70F})\unicode[STIX]{x1D70F}}{t^{2}-\unicode[STIX]{x1D70F}^{2}}\frac{d\unicode[STIX]{x1D70F}}{\unicode[STIX]{x1D70B}i}.\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{L}^{+}\mathscr{K}_{0}h(t)=\int _{\Re (i\unicode[STIX]{x1D70F})=5}\frac{h(\unicode[STIX]{x1D70F})\unicode[STIX]{x1D70F}}{t^{2}-\unicode[STIX]{x1D70F}^{2}}\frac{d\unicode[STIX]{x1D70F}}{\unicode[STIX]{x1D70B}i}.\end{eqnarray}$$ The integrand is odd, so the integral equals half the sum of the two residues at  $\unicode[STIX]{x1D70F}=\pm t$ and part (a) of the lemma follows. To prove part (b) for
$\unicode[STIX]{x1D70F}=\pm t$ and part (a) of the lemma follows. To prove part (b) for  $\mathscr{L}^{+}\mathscr{K}_{s}h(t)$, we shift the
$\mathscr{L}^{+}\mathscr{K}_{s}h(t)$, we shift the  $\unicode[STIX]{x1D70F}$-contour to
$\unicode[STIX]{x1D70F}$-contour to  $\Re (i\unicode[STIX]{x1D70F})=(1-\Re (s))/2$ and estimate trivially in (2.20) using Stirling’s formula. For
$\Re (i\unicode[STIX]{x1D70F})=(1-\Re (s))/2$ and estimate trivially in (2.20) using Stirling’s formula. For  $\mathscr{L}^{\text{hol}}\mathscr{K}_{s}h(t)$, we have the similar expression
$\mathscr{L}^{\text{hol}}\mathscr{K}_{s}h(t)$, we have the similar expression
 $$\begin{eqnarray}\displaystyle \mathscr{L}^{\text{hol}}\mathscr{K}_{s}h(k)=i^{k+1}\int _{\Re (i\unicode[STIX]{x1D70F})=a}\frac{\unicode[STIX]{x1D6E4}(1-s)(2\unicode[STIX]{x1D70B})^{-s}\unicode[STIX]{x1D6E4}(\frac{k-1}{2}+\frac{s}{2}+i\unicode[STIX]{x1D70F})}{\unicode[STIX]{x1D6E4}(\frac{k+1}{2}-\frac{s}{2}-i\unicode[STIX]{x1D70F})\unicode[STIX]{x1D6E4}(\frac{3-k}{2}-\frac{s}{2}+i\unicode[STIX]{x1D70F})\unicode[STIX]{x1D6E4}(\frac{k+1}{2}-\frac{s}{2}+i\unicode[STIX]{x1D70F})}\frac{h(\unicode[STIX]{x1D70F})\unicode[STIX]{x1D70F}}{\cosh (\unicode[STIX]{x1D70B}\unicode[STIX]{x1D70F})}\,d\unicode[STIX]{x1D70F} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{L}^{\text{hol}}\mathscr{K}_{s}h(k)=i^{k+1}\int _{\Re (i\unicode[STIX]{x1D70F})=a}\frac{\unicode[STIX]{x1D6E4}(1-s)(2\unicode[STIX]{x1D70B})^{-s}\unicode[STIX]{x1D6E4}(\frac{k-1}{2}+\frac{s}{2}+i\unicode[STIX]{x1D70F})}{\unicode[STIX]{x1D6E4}(\frac{k+1}{2}-\frac{s}{2}-i\unicode[STIX]{x1D70F})\unicode[STIX]{x1D6E4}(\frac{3-k}{2}-\frac{s}{2}+i\unicode[STIX]{x1D70F})\unicode[STIX]{x1D6E4}(\frac{k+1}{2}-\frac{s}{2}+i\unicode[STIX]{x1D70F})}\frac{h(\unicode[STIX]{x1D70F})\unicode[STIX]{x1D70F}}{\cosh (\unicode[STIX]{x1D70B}\unicode[STIX]{x1D70F})}\,d\unicode[STIX]{x1D70F} & & \displaystyle \nonumber\end{eqnarray}$$ for any  $a\in \mathbb{R}$ satisfying
$a\in \mathbb{R}$ satisfying  $k-1+\Re s+2a>0$, say
$k-1+\Re s+2a>0$, say  $a=\max ((2-k-\Re s)/2,0)$. We can rewrite this as
$a=\max ((2-k-\Re s)/2,0)$. We can rewrite this as
 $$\begin{eqnarray}\int _{\Re (i\unicode[STIX]{x1D70F})=a}\frac{\unicode[STIX]{x1D6E4}(1-s)\cos (i\unicode[STIX]{x1D70B}\unicode[STIX]{x1D70F}+\textstyle \frac{1}{2}\unicode[STIX]{x1D70B}s)h(\unicode[STIX]{x1D70F})\unicode[STIX]{x1D70F}}{(2\unicode[STIX]{x1D70B})^{s}\unicode[STIX]{x1D70B}i\cosh (\unicode[STIX]{x1D70B}\unicode[STIX]{x1D70F})}\mathop{\prod }_{\pm }\frac{\unicode[STIX]{x1D6E4}(\frac{k-1}{2}+\frac{s}{2}\pm i\unicode[STIX]{x1D70F})}{\unicode[STIX]{x1D6E4}(\frac{k+1}{2}-\frac{s}{2}\pm i\unicode[STIX]{x1D70F})}\,d\unicode[STIX]{x1D70F}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{\Re (i\unicode[STIX]{x1D70F})=a}\frac{\unicode[STIX]{x1D6E4}(1-s)\cos (i\unicode[STIX]{x1D70B}\unicode[STIX]{x1D70F}+\textstyle \frac{1}{2}\unicode[STIX]{x1D70B}s)h(\unicode[STIX]{x1D70F})\unicode[STIX]{x1D70F}}{(2\unicode[STIX]{x1D70B})^{s}\unicode[STIX]{x1D70B}i\cosh (\unicode[STIX]{x1D70B}\unicode[STIX]{x1D70F})}\mathop{\prod }_{\pm }\frac{\unicode[STIX]{x1D6E4}(\frac{k-1}{2}+\frac{s}{2}\pm i\unicode[STIX]{x1D70F})}{\unicode[STIX]{x1D6E4}(\frac{k+1}{2}-\frac{s}{2}\pm i\unicode[STIX]{x1D70F})}\,d\unicode[STIX]{x1D70F}.\end{eqnarray}$$ The desired bound follows now from  $\unicode[STIX]{x1D6E4}(z+w)/\unicode[STIX]{x1D6E4}(z)\;\ll _{w}\;(1+|z|)^{w}$ for
$\unicode[STIX]{x1D6E4}(z+w)/\unicode[STIX]{x1D6E4}(z)\;\ll _{w}\;(1+|z|)^{w}$ for  $w\in \mathbb{R}$ and
$w\in \mathbb{R}$ and  $|z|$ sufficiently large; see, for example, [Reference Gradshteyn, Ryzhik, Jeffrey and ZwillingerGR07, (8.328.2)].☐
$|z|$ sufficiently large; see, for example, [Reference Gradshteyn, Ryzhik, Jeffrey and ZwillingerGR07, (8.328.2)].☐
3 Proof of Theorem 1
3.1 The set-up
We recall the definitions (1.6) and (1.9) for a prime  $q$ and integers
$q$ and integers  $a,b$ satisfying
$a,b$ satisfying  $(ab,q)=$
$(ab,q)=$ $(a,b)=1$,
$(a,b)=1$,  $a\asymp b$, and an even holomorphic test function
$a\asymp b$, and an even holomorphic test function  $F$ that is rapidly decaying on vertical lines and is divisible by
$F$ that is rapidly decaying on vertical lines and is divisible by  $(1-u)(v-1)^{2}\prod _{j=1}^{50}(j-s)$. Initially we assume
$(1-u)(v-1)^{2}\prod _{j=1}^{50}(j-s)$. Initially we assume
 $$\begin{eqnarray}2<\Re s,\quad \Re v<3,\quad 10<\Re u<11.\end{eqnarray}$$
$$\begin{eqnarray}2<\Re s,\quad \Re v<3,\quad 10<\Re u<11.\end{eqnarray}$$ In this section all implicit constants may depend on  $s,u,v,\unicode[STIX]{x1D700}$ and
$s,u,v,\unicode[STIX]{x1D700}$ and  $F$. Additional dependencies will be mentioned. We proceed to define the correction polynomial
$F$. Additional dependencies will be mentioned. We proceed to define the correction polynomial  $P_{q}(s,u,v,z)$, and to this end we define three auxiliary quantities
$P_{q}(s,u,v,z)$, and to this end we define three auxiliary quantities
 $$\begin{eqnarray}\displaystyle {\mathcal{T}}_{q}^{(1)}(s,u,v) & := & \displaystyle \int _{\mathbb{R}}\unicode[STIX]{x1D701}^{(q)}(s+z)\unicode[STIX]{x1D701}^{(q)}(u+z)L^{(q)}(v-z,f)F(z)\frac{dz}{2\unicode[STIX]{x1D70B}i},\nonumber\\ \displaystyle {\mathcal{T}}_{q}^{(2)}(s,u,v) & := & \displaystyle q^{1-s-v}\int _{\mathbb{R}}\biggl(\unicode[STIX]{x1D706}(q)-\frac{1}{q^{v-z}}\biggr)\unicode[STIX]{x1D701}(s+z)\unicode[STIX]{x1D701}^{(q)}(u+z)L(v-z,f)F(z)\frac{dt}{2\unicode[STIX]{x1D70B}i},\nonumber\\ \displaystyle {\mathcal{T}}_{q}^{(3)}(s,u,v) & := & \displaystyle \int _{\mathbb{R}}(q^{2-s-u-2v}-q^{1-u-2v+z})\unicode[STIX]{x1D701}(s+z)\unicode[STIX]{x1D701}(u+z)L(v-z,f)F(z)\frac{dz}{2\unicode[STIX]{x1D70B}i}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{T}}_{q}^{(1)}(s,u,v) & := & \displaystyle \int _{\mathbb{R}}\unicode[STIX]{x1D701}^{(q)}(s+z)\unicode[STIX]{x1D701}^{(q)}(u+z)L^{(q)}(v-z,f)F(z)\frac{dz}{2\unicode[STIX]{x1D70B}i},\nonumber\\ \displaystyle {\mathcal{T}}_{q}^{(2)}(s,u,v) & := & \displaystyle q^{1-s-v}\int _{\mathbb{R}}\biggl(\unicode[STIX]{x1D706}(q)-\frac{1}{q^{v-z}}\biggr)\unicode[STIX]{x1D701}(s+z)\unicode[STIX]{x1D701}^{(q)}(u+z)L(v-z,f)F(z)\frac{dt}{2\unicode[STIX]{x1D70B}i},\nonumber\\ \displaystyle {\mathcal{T}}_{q}^{(3)}(s,u,v) & := & \displaystyle \int _{\mathbb{R}}(q^{2-s-u-2v}-q^{1-u-2v+z})\unicode[STIX]{x1D701}(s+z)\unicode[STIX]{x1D701}(u+z)L(v-z,f)F(z)\frac{dz}{2\unicode[STIX]{x1D70B}i}.\nonumber\end{eqnarray}$$ Here  $\unicode[STIX]{x1D701}^{(q)}(s):=\unicode[STIX]{x1D701}(s)\prod _{p\mid q}(1-p^{-s})$ and
$\unicode[STIX]{x1D701}^{(q)}(s):=\unicode[STIX]{x1D701}(s)\prod _{p\mid q}(1-p^{-s})$ and  $L^{(q)}(s,f)=L(s,f)\prod _{p\mid q}(1-\unicode[STIX]{x1D706}_{f}(p)p^{-s}+p^{-2s})$ are the usual
$L^{(q)}(s,f)=L(s,f)\prod _{p\mid q}(1-\unicode[STIX]{x1D706}_{f}(p)p^{-s}+p^{-2s})$ are the usual  $L$-functions with the Euler factors dividing
$L$-functions with the Euler factors dividing  $q$ omitted. We define
$q$ omitted. We define
 $$\begin{eqnarray}{\mathcal{T}}_{q}^{\text{triv}}(s,u,v):=\mathop{\sum }_{j=1}^{3}{\mathcal{T}}_{q}^{(j)}(s,u,v),\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{T}}_{q}^{\text{triv}}(s,u,v):=\mathop{\sum }_{j=1}^{3}{\mathcal{T}}_{q}^{(j)}(s,u,v),\end{eqnarray}$$so that (1.9) holds with
 $$\begin{eqnarray}\displaystyle P_{q}(s,u,v,z) & = & \displaystyle \biggl(1-\frac{1}{q^{s+z}}\biggr)\biggl(1-\frac{1}{q^{u+z}}\biggr)\biggl(1-\frac{\unicode[STIX]{x1D706}(q)}{q^{v-z}}+\frac{1}{q^{2v-2z}}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,q^{1-s-v}\biggl(\unicode[STIX]{x1D706}(q)-\frac{1}{q^{v-z}}\biggr)\biggl(1-\frac{1}{q^{u+z}}\biggr)+q^{2-s-u-2v}-q^{1-u-2v+z}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P_{q}(s,u,v,z) & = & \displaystyle \biggl(1-\frac{1}{q^{s+z}}\biggr)\biggl(1-\frac{1}{q^{u+z}}\biggr)\biggl(1-\frac{\unicode[STIX]{x1D706}(q)}{q^{v-z}}+\frac{1}{q^{2v-2z}}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,q^{1-s-v}\biggl(\unicode[STIX]{x1D706}(q)-\frac{1}{q^{v-z}}\biggr)\biggl(1-\frac{1}{q^{u+z}}\biggr)+q^{2-s-u-2v}-q^{1-u-2v+z}.\end{eqnarray}$$It is easy to see that this satisfies (1.8). In the range (3.1), we can open the Dirichlet series and obtain
 $$\begin{eqnarray}\displaystyle {\mathcal{T}}_{a,b,q}(s,u,v)+{\mathcal{T}}_{q}^{(1)}(s,u,v) & = & \displaystyle q\int _{(0)}F(z)\mathop{\sum }_{\substack{ (nmr,q)=1 \\ anm\equiv br\hspace{-7.11317pt}\hspace{0.6em}({\rm mod}\hspace{0.2em}q)}}\frac{\unicode[STIX]{x1D706}(r)}{n^{s+z}m^{u+z}r^{v-z}}\frac{dz}{2\unicode[STIX]{x1D70B}i},\nonumber\\ \displaystyle {\mathcal{T}}_{q}^{(2)}(s,u,v) & = & \displaystyle q^{1-s-v}\int _{(0)}F(z)\biggl(\unicode[STIX]{x1D706}(q)-\frac{1}{q^{v-z}}\biggr)\mathop{\sum }_{n,r,(m,q)=1}\frac{\unicode[STIX]{x1D706}(r)}{n^{s+z}m^{u+z}r^{v-z}}\frac{dz}{2\unicode[STIX]{x1D70B}i},\nonumber\\ \displaystyle & = & \displaystyle q\int _{(0)}F(z)\mathop{\sum }_{n,r,(m,q)=1}\frac{\unicode[STIX]{x1D706}(qr)}{(qn)^{s+z}m^{u+z}(qr)^{v-z}}\frac{dz}{2\unicode[STIX]{x1D70B}i},\nonumber\\ \displaystyle {\mathcal{T}}_{q}^{(3)}(s,u,v) & = & \displaystyle q^{2-s-u-2v}\int _{(0)}F(z)(1-q^{s+z-1})\mathop{\sum }_{n,r,m}\frac{\unicode[STIX]{x1D706}(r)}{n^{s+z}m^{u+z}r^{v-z}}\frac{dz}{2\unicode[STIX]{x1D70B}i}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{T}}_{a,b,q}(s,u,v)+{\mathcal{T}}_{q}^{(1)}(s,u,v) & = & \displaystyle q\int _{(0)}F(z)\mathop{\sum }_{\substack{ (nmr,q)=1 \\ anm\equiv br\hspace{-7.11317pt}\hspace{0.6em}({\rm mod}\hspace{0.2em}q)}}\frac{\unicode[STIX]{x1D706}(r)}{n^{s+z}m^{u+z}r^{v-z}}\frac{dz}{2\unicode[STIX]{x1D70B}i},\nonumber\\ \displaystyle {\mathcal{T}}_{q}^{(2)}(s,u,v) & = & \displaystyle q^{1-s-v}\int _{(0)}F(z)\biggl(\unicode[STIX]{x1D706}(q)-\frac{1}{q^{v-z}}\biggr)\mathop{\sum }_{n,r,(m,q)=1}\frac{\unicode[STIX]{x1D706}(r)}{n^{s+z}m^{u+z}r^{v-z}}\frac{dz}{2\unicode[STIX]{x1D70B}i},\nonumber\\ \displaystyle & = & \displaystyle q\int _{(0)}F(z)\mathop{\sum }_{n,r,(m,q)=1}\frac{\unicode[STIX]{x1D706}(qr)}{(qn)^{s+z}m^{u+z}(qr)^{v-z}}\frac{dz}{2\unicode[STIX]{x1D70B}i},\nonumber\\ \displaystyle {\mathcal{T}}_{q}^{(3)}(s,u,v) & = & \displaystyle q^{2-s-u-2v}\int _{(0)}F(z)(1-q^{s+z-1})\mathop{\sum }_{n,r,m}\frac{\unicode[STIX]{x1D706}(r)}{n^{s+z}m^{u+z}r^{v-z}}\frac{dz}{2\unicode[STIX]{x1D70B}i}.\nonumber\end{eqnarray}$$We conclude that
 $$\begin{eqnarray}\displaystyle \tilde{{\mathcal{T}}}_{a,b,q}(s,u,v) & := & \displaystyle {\mathcal{T}}_{a,b,q}(s,u,v)+{\mathcal{T}}_{q}^{(1)}(s,u,v)+{\mathcal{T}}_{q}^{(2)}(s,u,v)\nonumber\\ \displaystyle & = & \displaystyle q\int _{(0)}F(z)\mathop{\sum }_{\substack{ (m,q)=1 \\ n\equiv \overline{am}br\hspace{-7.11317pt}\hspace{0.6em}({\rm mod}\hspace{0.2em}q)}}\frac{\unicode[STIX]{x1D706}(r)}{n^{s+z}m^{u+z}r^{v-z}}\frac{dz}{2\unicode[STIX]{x1D70B}i}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \tilde{{\mathcal{T}}}_{a,b,q}(s,u,v) & := & \displaystyle {\mathcal{T}}_{a,b,q}(s,u,v)+{\mathcal{T}}_{q}^{(1)}(s,u,v)+{\mathcal{T}}_{q}^{(2)}(s,u,v)\nonumber\\ \displaystyle & = & \displaystyle q\int _{(0)}F(z)\mathop{\sum }_{\substack{ (m,q)=1 \\ n\equiv \overline{am}br\hspace{-7.11317pt}\hspace{0.6em}({\rm mod}\hspace{0.2em}q)}}\frac{\unicode[STIX]{x1D706}(r)}{n^{s+z}m^{u+z}r^{v-z}}\frac{dz}{2\unicode[STIX]{x1D70B}i}.\nonumber\end{eqnarray}$$ Eventually the term  ${\mathcal{T}}_{q}^{(3)}(s,u,v)$ will remove the last coprimality condition
${\mathcal{T}}_{q}^{(3)}(s,u,v)$ will remove the last coprimality condition  $(m,q)=1$, but this has to wait until the end of argument. Until then, we transform
$(m,q)=1$, but this has to wait until the end of argument. Until then, we transform  $\tilde{{\mathcal{T}}}_{a,b,q}(s,u,v)$ and
$\tilde{{\mathcal{T}}}_{a,b,q}(s,u,v)$ and  ${\mathcal{T}}_{q}^{(3)}(s,u,v)$ in a parallel fashion.
${\mathcal{T}}_{q}^{(3)}(s,u,v)$ in a parallel fashion.
3.2 Poisson summation
We write the  $n$-sum in terms of the Hurwitz zeta function with
$n$-sum in terms of the Hurwitz zeta function with  $\unicode[STIX]{x1D6FC}=\overline{am}br/q$ and shift the
$\unicode[STIX]{x1D6FC}=\overline{am}br/q$ and shift the  $z$-contour to the left to
$z$-contour to the left to  $\Re z=-4$. Our assumption on
$\Re z=-4$. Our assumption on  $F$ implies that the potential pole at
$F$ implies that the potential pole at  $z=1-s$ is cancelled. The
$z=1-s$ is cancelled. The  $m,r$-sums are still absolutely convergent, and we apply the functional equation (2.4), getting
$m,r$-sums are still absolutely convergent, and we apply the functional equation (2.4), getting
 $$\begin{eqnarray}\tilde{{\mathcal{T}}}_{a,b,q}(s,u,v)=\mathop{\sum }_{\pm }\int _{(-4)}F(z)G^{\pm }(1-s-z)q^{1-s-z}\mathop{\sum }_{n,r,(m,q)=1}\frac{\unicode[STIX]{x1D706}(r)e(\mp \overline{a}brn\overline{m}/q)}{n^{1-s-z}m^{u+z}r^{v-z}}\frac{dz}{2\unicode[STIX]{x1D70B}i}\end{eqnarray}$$
$$\begin{eqnarray}\tilde{{\mathcal{T}}}_{a,b,q}(s,u,v)=\mathop{\sum }_{\pm }\int _{(-4)}F(z)G^{\pm }(1-s-z)q^{1-s-z}\mathop{\sum }_{n,r,(m,q)=1}\frac{\unicode[STIX]{x1D706}(r)e(\mp \overline{a}brn\overline{m}/q)}{n^{1-s-z}m^{u+z}r^{v-z}}\frac{dz}{2\unicode[STIX]{x1D70B}i}\end{eqnarray}$$and
 $$\begin{eqnarray}\displaystyle {\mathcal{T}}_{q}^{(3)}(s,u,v) & = & \displaystyle q^{2-s-u-2v}\int _{(-4)}F(z)(1-q^{s+z-1})G^{\pm }(1-s-z)\mathop{\sum }_{n,r,m}\frac{\unicode[STIX]{x1D706}(r)}{n^{1-s-z}m^{u+z}r^{v-z}}\frac{dz}{2\unicode[STIX]{x1D70B}i}\nonumber\\ \displaystyle & = & \displaystyle q^{2-s-u-2v}\int _{(-4)}F(z)G^{\pm }(1-s-z)\mathop{\sum }_{(n,q)=1,r,m}\frac{\unicode[STIX]{x1D706}(r)}{n^{1-s-z}m^{u+z}r^{v-z}}\frac{dz}{2\unicode[STIX]{x1D70B}i}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{T}}_{q}^{(3)}(s,u,v) & = & \displaystyle q^{2-s-u-2v}\int _{(-4)}F(z)(1-q^{s+z-1})G^{\pm }(1-s-z)\mathop{\sum }_{n,r,m}\frac{\unicode[STIX]{x1D706}(r)}{n^{1-s-z}m^{u+z}r^{v-z}}\frac{dz}{2\unicode[STIX]{x1D70B}i}\nonumber\\ \displaystyle & = & \displaystyle q^{2-s-u-2v}\int _{(-4)}F(z)G^{\pm }(1-s-z)\mathop{\sum }_{(n,q)=1,r,m}\frac{\unicode[STIX]{x1D706}(r)}{n^{1-s-z}m^{u+z}r^{v-z}}\frac{dz}{2\unicode[STIX]{x1D70B}i}.\end{eqnarray}$$3.3 Reciprocity
For  $\unicode[STIX]{x1D6FC}\in \mathbb{R}\setminus \{0\}$, we recall the absolutely convergent Mellin integral
$\unicode[STIX]{x1D6FC}\in \mathbb{R}\setminus \{0\}$, we recall the absolutely convergent Mellin integral
 $$\begin{eqnarray}e(\unicode[STIX]{x1D6FC})=\int _{{\mathcal{C}}}G^{\text{sgn}(\unicode[STIX]{x1D6FC})}(s)|\unicode[STIX]{x1D6FC}|^{-w}\frac{dw}{2\unicode[STIX]{x1D70B}i},\end{eqnarray}$$
$$\begin{eqnarray}e(\unicode[STIX]{x1D6FC})=\int _{{\mathcal{C}}}G^{\text{sgn}(\unicode[STIX]{x1D6FC})}(s)|\unicode[STIX]{x1D6FC}|^{-w}\frac{dw}{2\unicode[STIX]{x1D70B}i},\end{eqnarray}$$ where  ${\mathcal{C}}$ is the contour
${\mathcal{C}}$ is the contour
 $$\begin{eqnarray}{\mathcal{C}}=\textstyle (-\frac{3}{5}-i\infty ,-\frac{3}{5}-i]\cup [-\frac{3}{5}-i,\frac{1}{10}]\cup [\frac{1}{10},-\frac{3}{5}+i]\cup [-\frac{3}{5}+i,-\frac{3}{5}+i\infty ).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{C}}=\textstyle (-\frac{3}{5}-i\infty ,-\frac{3}{5}-i]\cup [-\frac{3}{5}-i,\frac{1}{10}]\cup [\frac{1}{10},-\frac{3}{5}+i]\cup [-\frac{3}{5}+i,-\frac{3}{5}+i\infty ).\end{eqnarray}$$In (3.3), we insert
 $$\begin{eqnarray}1=e\biggl(\pm \frac{brn}{amq}\biggr)\int _{{\mathcal{C}}}G^{\pm }(w)\biggl(\frac{brn}{amq}\biggr)^{-w}\frac{dw}{2\unicode[STIX]{x1D70B}i}\end{eqnarray}$$
$$\begin{eqnarray}1=e\biggl(\pm \frac{brn}{amq}\biggr)\int _{{\mathcal{C}}}G^{\pm }(w)\biggl(\frac{brn}{amq}\biggr)^{-w}\frac{dw}{2\unicode[STIX]{x1D70B}i}\end{eqnarray}$$and apply the additive reciprocity formula (1.16). This gives the absolutely convergent expression
 $$\begin{eqnarray}\displaystyle \tilde{{\mathcal{T}}}_{a,b,q}(s,u,v) & = & \displaystyle \mathop{\sum }_{\pm }\int _{(-4)}\int _{{\mathcal{C}}}F(z)\biggl(\frac{b}{a}\biggr)^{-w}G^{\pm }(w)G^{\pm }(1-s-z)q^{1-s-z+w}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{n,(m,q)=1,r}\frac{\unicode[STIX]{x1D706}(r)e(\pm \overline{q}brn/(am))}{n^{1-s-z+w}m^{u+z-w}r^{v-z+w}}\frac{dw}{2\unicode[STIX]{x1D70B}i}\frac{dz}{2\unicode[STIX]{x1D70B}i}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \tilde{{\mathcal{T}}}_{a,b,q}(s,u,v) & = & \displaystyle \mathop{\sum }_{\pm }\int _{(-4)}\int _{{\mathcal{C}}}F(z)\biggl(\frac{b}{a}\biggr)^{-w}G^{\pm }(w)G^{\pm }(1-s-z)q^{1-s-z+w}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{n,(m,q)=1,r}\frac{\unicode[STIX]{x1D706}(r)e(\pm \overline{q}brn/(am))}{n^{1-s-z+w}m^{u+z-w}r^{v-z+w}}\frac{dw}{2\unicode[STIX]{x1D70B}i}\frac{dz}{2\unicode[STIX]{x1D70B}i}.\nonumber\end{eqnarray}$$ We temporarily straighten the  ${\mathcal{C}}$-contour to
${\mathcal{C}}$-contour to  $\Re w=-3/5$, picking up the polar term
$\Re w=-3/5$, picking up the polar term
 $$\begin{eqnarray}\mathop{\sum }_{\pm }\int _{(-4)}F(z)G^{\pm }(1-s-z)q^{1-s-z}\mathop{\sum }_{n,(m,q)=1,r}\frac{\unicode[STIX]{x1D706}(r)e(\pm \overline{q}brn/(am))}{n^{1-s-z}m^{u+z}r^{v-z}}\frac{dz}{2\unicode[STIX]{x1D70B}i}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\pm }\int _{(-4)}F(z)G^{\pm }(1-s-z)q^{1-s-z}\mathop{\sum }_{n,(m,q)=1,r}\frac{\unicode[STIX]{x1D706}(r)e(\pm \overline{q}brn/(am))}{n^{1-s-z}m^{u+z}r^{v-z}}\frac{dz}{2\unicode[STIX]{x1D70B}i}.\end{eqnarray}$$ In the remaining double integral, we change variables  $w\mapsto w+z$ (so that
$w\mapsto w+z$ (so that  $\Re z=-4$,
$\Re z=-4$,  $\Re w=17/5$), exchange the two integrals, and in the inner
$\Re w=17/5$), exchange the two integrals, and in the inner  $z$-integral we bend the contour to the right to the contour
$z$-integral we bend the contour to the right to the contour
 $$\begin{eqnarray}\displaystyle {\mathcal{C}}(w)={\mathcal{C}}-w & = & \displaystyle \textstyle (-\frac{3}{5}-w-i\infty ,-\frac{3}{5}-w-i]\cup [-\frac{3}{5}-w-i,\frac{1}{10}-w]\nonumber\\ \displaystyle & & \displaystyle \cup \textstyle [\frac{1}{10}-w,-\frac{3}{5}-w+i]\cup [-\frac{3}{5}-w+i,-\frac{3}{5}-w+i\infty )\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{C}}(w)={\mathcal{C}}-w & = & \displaystyle \textstyle (-\frac{3}{5}-w-i\infty ,-\frac{3}{5}-w-i]\cup [-\frac{3}{5}-w-i,\frac{1}{10}-w]\nonumber\\ \displaystyle & & \displaystyle \cup \textstyle [\frac{1}{10}-w,-\frac{3}{5}-w+i]\cup [-\frac{3}{5}-w+i,-\frac{3}{5}-w+i\infty )\nonumber\end{eqnarray}$$consisting of a union of straight lines. This picks up a polar term
 $$\begin{eqnarray}-\mathop{\sum }_{\pm }\int _{(17/5)}F(-w)G^{\pm }(1-s+w)q^{1-s+w}\mathop{\sum }_{n,(m,q)=1,r}\frac{\unicode[STIX]{x1D706}(r)e(\pm \overline{q}brn/(am))}{n^{1-s+w}m^{u-w}r^{v+w}}\frac{dw}{2\unicode[STIX]{x1D70B}i},\end{eqnarray}$$
$$\begin{eqnarray}-\mathop{\sum }_{\pm }\int _{(17/5)}F(-w)G^{\pm }(1-s+w)q^{1-s+w}\mathop{\sum }_{n,(m,q)=1,r}\frac{\unicode[STIX]{x1D706}(r)e(\pm \overline{q}brn/(am))}{n^{1-s+w}m^{u-w}r^{v+w}}\frac{dw}{2\unicode[STIX]{x1D70B}i},\end{eqnarray}$$which cancels the previous one. This shows that
 $$\begin{eqnarray}\tilde{{\mathcal{T}}}_{a,b,q}(s,u,v)=\mathop{\sum }_{\pm }\int _{(17/5)}\unicode[STIX]{x1D6F7}_{a,b,s}^{\pm }(w)q^{1-s+w}\mathop{\sum }_{n,(m,q)=1,r}\frac{\unicode[STIX]{x1D706}(r)e(\pm \overline{q}brn/(am))}{n^{1-s+w}m^{u-w}r^{v+w}}\biggl(\frac{b}{a}\biggr)^{-w}\frac{dw}{2\unicode[STIX]{x1D70B}i},\end{eqnarray}$$
$$\begin{eqnarray}\tilde{{\mathcal{T}}}_{a,b,q}(s,u,v)=\mathop{\sum }_{\pm }\int _{(17/5)}\unicode[STIX]{x1D6F7}_{a,b,s}^{\pm }(w)q^{1-s+w}\mathop{\sum }_{n,(m,q)=1,r}\frac{\unicode[STIX]{x1D706}(r)e(\pm \overline{q}brn/(am))}{n^{1-s+w}m^{u-w}r^{v+w}}\biggl(\frac{b}{a}\biggr)^{-w}\frac{dw}{2\unicode[STIX]{x1D70B}i},\end{eqnarray}$$where
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}_{a,b,s}^{\pm }(w) & = & \displaystyle \int _{{\mathcal{C}}(w)}F(z)\biggl(\frac{b}{a}\biggr)^{-z}G^{\pm }(w+z)G^{\pm }(1-s-z)\frac{dz}{2\unicode[STIX]{x1D70B}i}\nonumber\\ \displaystyle & = & \displaystyle (2\unicode[STIX]{x1D70B})^{s-w-1}e^{\pm i\unicode[STIX]{x1D70B}(w+1-s)/2}\int _{{\mathcal{C}}(w)}F(z)\biggl(\frac{b}{a}\biggr)^{-z}\unicode[STIX]{x1D6E4}(w+z)\unicode[STIX]{x1D6E4}(1-s-z)\frac{dz}{2\unicode[STIX]{x1D70B}i}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}_{a,b,s}^{\pm }(w) & = & \displaystyle \int _{{\mathcal{C}}(w)}F(z)\biggl(\frac{b}{a}\biggr)^{-z}G^{\pm }(w+z)G^{\pm }(1-s-z)\frac{dz}{2\unicode[STIX]{x1D70B}i}\nonumber\\ \displaystyle & = & \displaystyle (2\unicode[STIX]{x1D70B})^{s-w-1}e^{\pm i\unicode[STIX]{x1D70B}(w+1-s)/2}\int _{{\mathcal{C}}(w)}F(z)\biggl(\frac{b}{a}\biggr)^{-z}\unicode[STIX]{x1D6E4}(w+z)\unicode[STIX]{x1D6E4}(1-s-z)\frac{dz}{2\unicode[STIX]{x1D70B}i}.\nonumber\end{eqnarray}$$ Here we can straighten the contour and shift it to the far left to  $\Re z=-A$, say. This gives a sum of polar terms of the shape
$\Re z=-A$, say. This gives a sum of polar terms of the shape
 $$\begin{eqnarray}p_{n}(w):=\frac{(-1)^{n}}{n!}(2\unicode[STIX]{x1D70B})^{s-w-1}e^{\pm i\unicode[STIX]{x1D70B}(w+1-s)/2}F(-w-n)\biggl(\frac{b}{a}\biggr)^{w+n}\unicode[STIX]{x1D6E4}(1-s+w+n),\quad n\in \mathbb{N}_{0},\end{eqnarray}$$
$$\begin{eqnarray}p_{n}(w):=\frac{(-1)^{n}}{n!}(2\unicode[STIX]{x1D70B})^{s-w-1}e^{\pm i\unicode[STIX]{x1D70B}(w+1-s)/2}F(-w-n)\biggl(\frac{b}{a}\biggr)^{w+n}\unicode[STIX]{x1D6E4}(1-s+w+n),\quad n\in \mathbb{N}_{0},\end{eqnarray}$$ and a remaining integral that is holomorphic in the half plane  $\Re w>-A$ and bounded by
$\Re w>-A$ and bounded by $\ll _{\Re w,A}\,(b/a)^{A}(1+|w|)^{\Re w-A-1/2}$. Since
$\ll _{\Re w,A}\,(b/a)^{A}(1+|w|)^{\Re w-A-1/2}$. Since  $F(1-s)=\cdots =F(50-s)=0$, we conclude that
$F(1-s)=\cdots =F(50-s)=0$, we conclude that  $\unicode[STIX]{x1D6F7}_{a,b,s}^{\pm }$ is
$\unicode[STIX]{x1D6F7}_{a,b,s}^{\pm }$ is
 $$\begin{eqnarray}\text{holomorphic in }|\Re w|<48\text{ and satisfies }\unicode[STIX]{x1D6F7}_{a,b,s}^{\pm }(w)\ll (1+|w|)^{-100}\end{eqnarray}$$
$$\begin{eqnarray}\text{holomorphic in }|\Re w|<48\text{ and satisfies }\unicode[STIX]{x1D6F7}_{a,b,s}^{\pm }(w)\ll (1+|w|)^{-100}\end{eqnarray}$$ as long as  $a\asymp b$ and
$a\asymp b$ and  $0<\Re s<3$. We also observe that
$0<\Re s<3$. We also observe that
 $$\begin{eqnarray}\mathop{\sum }_{\pm }\unicode[STIX]{x1D6F7}_{a,b,s}^{\pm }(s)=0.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\pm }\unicode[STIX]{x1D6F7}_{a,b,s}^{\pm }(s)=0.\end{eqnarray}$$Inserting
 $$\begin{eqnarray}1=e\biggl(\pm \frac{brn}{am}\biggr)\int _{{\mathcal{C}}}G^{\pm }(w)\biggl(\frac{brn}{am}\biggr)^{-w}\frac{dw}{2\unicode[STIX]{x1D70B}i}\end{eqnarray}$$
$$\begin{eqnarray}1=e\biggl(\pm \frac{brn}{am}\biggr)\int _{{\mathcal{C}}}G^{\pm }(w)\biggl(\frac{brn}{am}\biggr)^{-w}\frac{dw}{2\unicode[STIX]{x1D70B}i}\end{eqnarray}$$into (3.4) (similarly to (3.5), but with different variables), we obtain in the same way
 $$\begin{eqnarray}{\mathcal{T}}_{q}^{(3)}(s,u,v)=\mathop{\sum }_{\pm }\int _{(17/5)}\unicode[STIX]{x1D6F7}_{a,b,s}^{\pm }(w)q^{2-s-u-2v}\mathop{\sum }_{m,(n,q)=1,r}\frac{\unicode[STIX]{x1D706}(r)e(\pm brn/(am))}{n^{1-s+w}m^{u-w}r^{v+w}}\biggl(\frac{b}{a}\biggr)^{-w}\frac{dw}{2\unicode[STIX]{x1D70B}i}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{T}}_{q}^{(3)}(s,u,v)=\mathop{\sum }_{\pm }\int _{(17/5)}\unicode[STIX]{x1D6F7}_{a,b,s}^{\pm }(w)q^{2-s-u-2v}\mathop{\sum }_{m,(n,q)=1,r}\frac{\unicode[STIX]{x1D706}(r)e(\pm brn/(am))}{n^{1-s+w}m^{u-w}r^{v+w}}\biggl(\frac{b}{a}\biggr)^{-w}\frac{dw}{2\unicode[STIX]{x1D70B}i}.\end{eqnarray}$$ (The expression is still independent of  $a,b$, even though the right-hand side seems to depend on
$a,b$, even though the right-hand side seems to depend on  $a,b$.)
$a,b$.)
3.4 Poisson summation again
We return to (3.6), split the  $n$-sum into residue classes modulo
$n$-sum into residue classes modulo  $am$, express the
$am$, express the  $n$-sum in terms of the Hurwitz zeta function, shift the
$n$-sum in terms of the Hurwitz zeta function, shift the  $w$-contour to
$w$-contour to  $\Re w=0$, and apply the functional equation (2.4), getting
$\Re w=0$, and apply the functional equation (2.4), getting
 $$\begin{eqnarray}\displaystyle \tilde{{\mathcal{T}}}_{a,b,q}(s,u,v) & = & \displaystyle \mathop{\sum }_{\pm }\mathop{\sum }_{\unicode[STIX]{x1D70E}\in \{\pm \}}\int _{(0)}\unicode[STIX]{x1D6F7}_{a,b,s}^{\pm }(w)G^{-\unicode[STIX]{x1D70E}}(s-w)q^{1-s+w}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{(m,q)=1,r,n}\mathop{\sum }_{\unicode[STIX]{x1D708}\hspace{-7.11317pt}\hspace{0.6em}({\rm mod}\hspace{0.2em}am)}e\biggl(\frac{\pm \overline{q}br\unicode[STIX]{x1D708}}{am}\biggr)\frac{\unicode[STIX]{x1D706}(r)e(\unicode[STIX]{x1D70E}n\unicode[STIX]{x1D708}/(am))}{n^{s-w}m^{u-w}r^{v+w}}\biggl(\frac{b}{a}\biggr)^{-w}(am)^{s-w-1}\frac{dw}{2\unicode[STIX]{x1D70B}i}.\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \tilde{{\mathcal{T}}}_{a,b,q}(s,u,v) & = & \displaystyle \mathop{\sum }_{\pm }\mathop{\sum }_{\unicode[STIX]{x1D70E}\in \{\pm \}}\int _{(0)}\unicode[STIX]{x1D6F7}_{a,b,s}^{\pm }(w)G^{-\unicode[STIX]{x1D70E}}(s-w)q^{1-s+w}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{(m,q)=1,r,n}\mathop{\sum }_{\unicode[STIX]{x1D708}\hspace{-7.11317pt}\hspace{0.6em}({\rm mod}\hspace{0.2em}am)}e\biggl(\frac{\pm \overline{q}br\unicode[STIX]{x1D708}}{am}\biggr)\frac{\unicode[STIX]{x1D706}(r)e(\unicode[STIX]{x1D70E}n\unicode[STIX]{x1D708}/(am))}{n^{s-w}m^{u-w}r^{v+w}}\biggl(\frac{b}{a}\biggr)^{-w}(am)^{s-w-1}\frac{dw}{2\unicode[STIX]{x1D70B}i}.\qquad\end{eqnarray}$$ Note that the possible pole at  $w=s$ is cancelled by (3.8). Similarly,
$w=s$ is cancelled by (3.8). Similarly,
 $$\begin{eqnarray}\displaystyle {\mathcal{T}}_{q}^{(3)}(s,u,v) & = & \displaystyle \mathop{\sum }_{\pm }\mathop{\sum }_{\unicode[STIX]{x1D70E}\in \{\pm \}}\int _{(0)}\unicode[STIX]{x1D6F7}_{a,b,s}^{\pm }(w)G^{-\unicode[STIX]{x1D70E}}(s-w)q^{2-s-u-2v}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{r,m,n}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D708}\hspace{-7.11317pt}\hspace{0.6em}({\rm mod}\hspace{0.2em}qam) \\ (\unicode[STIX]{x1D708},q)=1}}e\biggl(\frac{\pm br\unicode[STIX]{x1D708}}{am}\biggr)\frac{\unicode[STIX]{x1D706}(r)e(\unicode[STIX]{x1D70E}n\unicode[STIX]{x1D708}/(amq))}{n^{s-w}m^{u-w}r^{v+w}}\biggl(\frac{b}{a}\biggr)^{-w}(amq)^{s-w-1}\frac{dw}{2\unicode[STIX]{x1D70B}i}.\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{T}}_{q}^{(3)}(s,u,v) & = & \displaystyle \mathop{\sum }_{\pm }\mathop{\sum }_{\unicode[STIX]{x1D70E}\in \{\pm \}}\int _{(0)}\unicode[STIX]{x1D6F7}_{a,b,s}^{\pm }(w)G^{-\unicode[STIX]{x1D70E}}(s-w)q^{2-s-u-2v}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{r,m,n}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D708}\hspace{-7.11317pt}\hspace{0.6em}({\rm mod}\hspace{0.2em}qam) \\ (\unicode[STIX]{x1D708},q)=1}}e\biggl(\frac{\pm br\unicode[STIX]{x1D708}}{am}\biggr)\frac{\unicode[STIX]{x1D706}(r)e(\unicode[STIX]{x1D70E}n\unicode[STIX]{x1D708}/(amq))}{n^{s-w}m^{u-w}r^{v+w}}\biggl(\frac{b}{a}\biggr)^{-w}(amq)^{s-w-1}\frac{dw}{2\unicode[STIX]{x1D70B}i}.\qquad\end{eqnarray}$$3.5 Voronoi summation
Our next aim is to apply the functional equation for the  $r$-sum. This requires some preparation because
$r$-sum. This requires some preparation because  $b\unicode[STIX]{x1D708}$ is not necessarily coprime to
$b\unicode[STIX]{x1D708}$ is not necessarily coprime to  $am$. Therefore we introduce various new variables. We write
$am$. Therefore we introduce various new variables. We write  $(m,b)=\unicode[STIX]{x1D6FD}_{1}$ and
$(m,b)=\unicode[STIX]{x1D6FD}_{1}$ and  $b=\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2}$,
$b=\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2}$,  $m=\unicode[STIX]{x1D6FD}_{1}m^{\prime }$,
$m=\unicode[STIX]{x1D6FD}_{1}m^{\prime }$,  $(m^{\prime },\unicode[STIX]{x1D6FD}_{2})=1$. Next, we write
$(m^{\prime },\unicode[STIX]{x1D6FD}_{2})=1$. Next, we write  $(\unicode[STIX]{x1D708},am^{\prime })=m_{1}$,
$(\unicode[STIX]{x1D708},am^{\prime })=m_{1}$,  $(m_{1},a)=\unicode[STIX]{x1D6FC}_{1}$, and
$(m_{1},a)=\unicode[STIX]{x1D6FC}_{1}$, and  $a=\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}$,
$a=\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}$,  $m_{1}=\unicode[STIX]{x1D6FC}_{1}m_{1}^{\prime }$,
$m_{1}=\unicode[STIX]{x1D6FC}_{1}m_{1}^{\prime }$,  $(m_{1}^{\prime },\unicode[STIX]{x1D6FC}_{2})=1$, and further
$(m_{1}^{\prime },\unicode[STIX]{x1D6FC}_{2})=1$, and further  $m^{\prime }=m_{1}^{\prime }m_{2}$,
$m^{\prime }=m_{1}^{\prime }m_{2}$,  $\unicode[STIX]{x1D708}=\unicode[STIX]{x1D6FC}_{1}m_{1}^{\prime }\unicode[STIX]{x1D708}^{\prime }$,
$\unicode[STIX]{x1D708}=\unicode[STIX]{x1D6FC}_{1}m_{1}^{\prime }\unicode[STIX]{x1D708}^{\prime }$,  $(\unicode[STIX]{x1D708}^{\prime },\unicode[STIX]{x1D6FC}_{2}m_{2})=1$. Dropping the primes for notational simplicity, we recast the second line in (3.9) as
$(\unicode[STIX]{x1D708}^{\prime },\unicode[STIX]{x1D6FC}_{2}m_{2})=1$. Dropping the primes for notational simplicity, we recast the second line in (3.9) as
 $$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2}=b}\mathop{\sum }_{r,n}\mathop{\sum }_{\substack{ (m_{1},\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{2}q)=1 \\ (m_{2},q\unicode[STIX]{x1D6FD}_{2})=1}}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D708}\hspace{-7.11317pt}\hspace{0.6em}({\rm mod}\hspace{0.2em}\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{1}m_{2}) \\ (\unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC}_{2}m_{2})=1}}e\biggl(\frac{\pm \overline{q}\unicode[STIX]{x1D6FD}_{2}r\unicode[STIX]{x1D708}}{\unicode[STIX]{x1D6FC}_{2}m_{2}}\biggr)\frac{\unicode[STIX]{x1D706}(r)e(\unicode[STIX]{x1D70E}n\unicode[STIX]{x1D708}/(\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{1}m_{2}))}{n^{s-w}(\unicode[STIX]{x1D6FD}_{1}m_{1}m_{2})^{u-s+1}r^{v+w}}\frac{a^{s-1}}{b^{w}}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2}=b}\mathop{\sum }_{r,n}\mathop{\sum }_{\substack{ (m_{1},\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{2}q)=1 \\ (m_{2},q\unicode[STIX]{x1D6FD}_{2})=1}}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D708}\hspace{-7.11317pt}\hspace{0.6em}({\rm mod}\hspace{0.2em}\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{1}m_{2}) \\ (\unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC}_{2}m_{2})=1}}e\biggl(\frac{\pm \overline{q}\unicode[STIX]{x1D6FD}_{2}r\unicode[STIX]{x1D708}}{\unicode[STIX]{x1D6FC}_{2}m_{2}}\biggr)\frac{\unicode[STIX]{x1D706}(r)e(\unicode[STIX]{x1D70E}n\unicode[STIX]{x1D708}/(\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{1}m_{2}))}{n^{s-w}(\unicode[STIX]{x1D6FD}_{1}m_{1}m_{2})^{u-s+1}r^{v+w}}\frac{a^{s-1}}{b^{w}}\end{eqnarray}$$and the second line in (3.10) as
 $$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2}=b}\mathop{\sum }_{r,n}\mathop{\sum }_{\substack{ (m_{1},\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{2}q)=1 \\ (m_{2},\unicode[STIX]{x1D6FD}_{2})=1}}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D708}\,(q\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{1}m_{2}) \\ (\unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC}_{2}m_{2}q)=1}}e\biggl(\frac{\pm \unicode[STIX]{x1D6FD}_{2}r\unicode[STIX]{x1D708}}{\unicode[STIX]{x1D6FC}_{2}m_{2}}\biggr)\frac{\unicode[STIX]{x1D706}(r)e(\unicode[STIX]{x1D70E}n\unicode[STIX]{x1D708}/(\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{1}m_{2}q))}{n^{s-w}(\unicode[STIX]{x1D6FD}_{1}m_{1}m_{2})^{u-s+1}r^{v+w}}\frac{a^{s-1}}{b^{w}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2}=b}\mathop{\sum }_{r,n}\mathop{\sum }_{\substack{ (m_{1},\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{2}q)=1 \\ (m_{2},\unicode[STIX]{x1D6FD}_{2})=1}}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D708}\,(q\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{1}m_{2}) \\ (\unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC}_{2}m_{2}q)=1}}e\biggl(\frac{\pm \unicode[STIX]{x1D6FD}_{2}r\unicode[STIX]{x1D708}}{\unicode[STIX]{x1D6FC}_{2}m_{2}}\biggr)\frac{\unicode[STIX]{x1D706}(r)e(\unicode[STIX]{x1D70E}n\unicode[STIX]{x1D708}/(\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{1}m_{2}q))}{n^{s-w}(\unicode[STIX]{x1D6FD}_{1}m_{1}m_{2})^{u-s+1}r^{v+w}}\frac{a^{s-1}}{b^{w}}.\end{eqnarray}$$ Note that in both cases the  $m_{1}$-sum is
$m_{1}$-sum is  $\unicode[STIX]{x1D701}^{(\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{2}q)}(1+u-s)$. Both terms are now in shape to apply Voronoi summation. We express the
$\unicode[STIX]{x1D701}^{(\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{2}q)}(1+u-s)$. Both terms are now in shape to apply Voronoi summation. We express the  $r$-sum in terms of the twisted
$r$-sum in terms of the twisted  $L$-function (2.5), shift the
$L$-function (2.5), shift the  $w$-contour to
$w$-contour to  $\Re w=-4$ (picking up a possible residue at
$\Re w=-4$ (picking up a possible residue at  $w=1-v$), and apply the functional equation (2.7). In this way we see that
$w=1-v$), and apply the functional equation (2.7). In this way we see that  $\tilde{{\mathcal{T}}}_{a,b,q}(s,u,v)$ equals
$\tilde{{\mathcal{T}}}_{a,b,q}(s,u,v)$ equals
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\pm }\mathop{\sum }_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\in \{\pm \}}\int _{(-4)}\unicode[STIX]{x1D6F7}_{a,b,s}^{\pm }(w)G^{-\unicode[STIX]{x1D70E}}(s-w)q^{1-s+w}\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2}=b}\unicode[STIX]{x1D701}^{(\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{2}q)}(1+u-s)\nonumber\\ \displaystyle & & \displaystyle \quad \times \,G_{f}^{-\unicode[STIX]{x1D70F}}(1-v-w)\mathop{\sum }_{r,n}\mathop{\sum }_{(m_{2},q\unicode[STIX]{x1D6FD}_{2})=1}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D708}\hspace{-7.11317pt}\hspace{0.6em}({\rm mod}\hspace{0.2em}\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{1}m_{2}) \\ (\unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC}_{2}m_{2})=1}}e\biggl(\frac{\pm \unicode[STIX]{x1D70F}q\overline{\unicode[STIX]{x1D6FD}_{2}\unicode[STIX]{x1D708}}r}{\unicode[STIX]{x1D6FC}_{2}m_{2}}\biggr)\frac{\unicode[STIX]{x1D706}(r)e(\unicode[STIX]{x1D70E}n\unicode[STIX]{x1D708}/(\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{1}m_{2}))}{n^{s-w}(\unicode[STIX]{x1D6FD}_{1}m_{2})^{u-s+1}r^{1-v-w}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\frac{a^{s-1}}{(\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2})^{w}}(\unicode[STIX]{x1D6FC}_{2}m_{2})^{1-2v-2w}\frac{dw}{2\unicode[STIX]{x1D70B}i}+{\mathcal{P}}_{a,b,q}^{(1)}(s,u,v),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\pm }\mathop{\sum }_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\in \{\pm \}}\int _{(-4)}\unicode[STIX]{x1D6F7}_{a,b,s}^{\pm }(w)G^{-\unicode[STIX]{x1D70E}}(s-w)q^{1-s+w}\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2}=b}\unicode[STIX]{x1D701}^{(\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{2}q)}(1+u-s)\nonumber\\ \displaystyle & & \displaystyle \quad \times \,G_{f}^{-\unicode[STIX]{x1D70F}}(1-v-w)\mathop{\sum }_{r,n}\mathop{\sum }_{(m_{2},q\unicode[STIX]{x1D6FD}_{2})=1}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D708}\hspace{-7.11317pt}\hspace{0.6em}({\rm mod}\hspace{0.2em}\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{1}m_{2}) \\ (\unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC}_{2}m_{2})=1}}e\biggl(\frac{\pm \unicode[STIX]{x1D70F}q\overline{\unicode[STIX]{x1D6FD}_{2}\unicode[STIX]{x1D708}}r}{\unicode[STIX]{x1D6FC}_{2}m_{2}}\biggr)\frac{\unicode[STIX]{x1D706}(r)e(\unicode[STIX]{x1D70E}n\unicode[STIX]{x1D708}/(\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{1}m_{2}))}{n^{s-w}(\unicode[STIX]{x1D6FD}_{1}m_{2})^{u-s+1}r^{1-v-w}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\frac{a^{s-1}}{(\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2})^{w}}(\unicode[STIX]{x1D6FC}_{2}m_{2})^{1-2v-2w}\frac{dw}{2\unicode[STIX]{x1D70B}i}+{\mathcal{P}}_{a,b,q}^{(1)}(s,u,v),\end{eqnarray}$$ where the polar term  ${\mathcal{P}}_{a,b,q}^{(1)}(s,u,v)$ vanishes unless
${\mathcal{P}}_{a,b,q}^{(1)}(s,u,v)$ vanishes unless  $f$ is Eisenstein, in which case it equals
$f$ is Eisenstein, in which case it equals
 $$\begin{eqnarray}\displaystyle {\mathcal{P}}_{a,b,q}^{(1)}(s,u,v) & = & \displaystyle \mathop{\{}_{w=1-v}\mathop{\sum }_{\pm }\mathop{\sum }_{\unicode[STIX]{x1D70E}\in \{\pm \}}\unicode[STIX]{x1D6F7}_{a,b,s}^{\pm }(w)G^{-\unicode[STIX]{x1D70E}}(s-w)q^{1-s+w}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2}=b}\unicode[STIX]{x1D701}^{(\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{2}q)}(1+u-s)\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}\mid n}\mathop{\sum }_{(m_{2},q\unicode[STIX]{x1D6FD}_{2})=1}\frac{a^{s-1}\unicode[STIX]{x1D6FD}_{1}r_{\unicode[STIX]{x1D6FC}_{2}m_{2}}(n/\unicode[STIX]{x1D6FD}_{1})}{(\unicode[STIX]{x1D6FD}_{1}m_{2})^{u-s+1}n^{s-w}b^{w}}L\biggl(v+w,\frac{\ast }{\unicode[STIX]{x1D6FC}_{2}m_{2}},f\biggr),\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{P}}_{a,b,q}^{(1)}(s,u,v) & = & \displaystyle \mathop{\{}_{w=1-v}\mathop{\sum }_{\pm }\mathop{\sum }_{\unicode[STIX]{x1D70E}\in \{\pm \}}\unicode[STIX]{x1D6F7}_{a,b,s}^{\pm }(w)G^{-\unicode[STIX]{x1D70E}}(s-w)q^{1-s+w}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2}=b}\unicode[STIX]{x1D701}^{(\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{2}q)}(1+u-s)\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}\mid n}\mathop{\sum }_{(m_{2},q\unicode[STIX]{x1D6FD}_{2})=1}\frac{a^{s-1}\unicode[STIX]{x1D6FD}_{1}r_{\unicode[STIX]{x1D6FC}_{2}m_{2}}(n/\unicode[STIX]{x1D6FD}_{1})}{(\unicode[STIX]{x1D6FD}_{1}m_{2})^{u-s+1}n^{s-w}b^{w}}L\biggl(v+w,\frac{\ast }{\unicode[STIX]{x1D6FC}_{2}m_{2}},f\biggr),\qquad\end{eqnarray}$$ where  $r_{c}(n)$ denotes the Ramanujan sum. (Recall that by (2.6) the residue is independent of the numerator
$r_{c}(n)$ denotes the Ramanujan sum. (Recall that by (2.6) the residue is independent of the numerator  $\ast$ in the twist of the
$\ast$ in the twist of the  $L$-function.) Similarly,
$L$-function.) Similarly,
 $$\begin{eqnarray}\displaystyle {\mathcal{T}}_{q}^{(3)}(s,u,v) & = & \displaystyle \mathop{\sum }_{\pm }\mathop{\sum }_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\in \{\pm \}}\int _{(-4)}\unicode[STIX]{x1D6F7}_{a,b,s}^{\pm }(w)G^{-\unicode[STIX]{x1D70E}}(s-w)q^{1-w-u-2v}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2}=b}\unicode[STIX]{x1D701}^{(\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{2}q)}(1+u-s)G_{f}^{-\unicode[STIX]{x1D70F}}(1-v-w)\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{r,n}\mathop{\sum }_{(m_{2},\unicode[STIX]{x1D6FD}_{2})=1}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D708}\hspace{-7.11317pt}\hspace{0.6em}({\rm mod}\hspace{0.2em}q\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{1}m_{2}) \\ (\unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC}_{2}m_{2}q)=1}}e\biggl(\frac{\pm \unicode[STIX]{x1D70F}\overline{\unicode[STIX]{x1D6FD}_{2}\unicode[STIX]{x1D708}}r}{\unicode[STIX]{x1D6FC}_{2}m_{2}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \times \,\frac{\unicode[STIX]{x1D706}(r)e(\unicode[STIX]{x1D70E}n\unicode[STIX]{x1D708}/(\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{1}m_{2}q))}{n^{s-w}(\unicode[STIX]{x1D6FD}_{1}m_{2})^{u-s+1}r^{1-v-w}}\frac{a^{s-1}}{b^{w}}(\unicode[STIX]{x1D6FC}_{2}m_{2})^{1-2v-2w}\frac{dw}{2\unicode[STIX]{x1D70B}i}+{\mathcal{P}}_{a,b,q}^{(2)}(s,u,v),\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{T}}_{q}^{(3)}(s,u,v) & = & \displaystyle \mathop{\sum }_{\pm }\mathop{\sum }_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\in \{\pm \}}\int _{(-4)}\unicode[STIX]{x1D6F7}_{a,b,s}^{\pm }(w)G^{-\unicode[STIX]{x1D70E}}(s-w)q^{1-w-u-2v}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2}=b}\unicode[STIX]{x1D701}^{(\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{2}q)}(1+u-s)G_{f}^{-\unicode[STIX]{x1D70F}}(1-v-w)\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{r,n}\mathop{\sum }_{(m_{2},\unicode[STIX]{x1D6FD}_{2})=1}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D708}\hspace{-7.11317pt}\hspace{0.6em}({\rm mod}\hspace{0.2em}q\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{1}m_{2}) \\ (\unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC}_{2}m_{2}q)=1}}e\biggl(\frac{\pm \unicode[STIX]{x1D70F}\overline{\unicode[STIX]{x1D6FD}_{2}\unicode[STIX]{x1D708}}r}{\unicode[STIX]{x1D6FC}_{2}m_{2}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \times \,\frac{\unicode[STIX]{x1D706}(r)e(\unicode[STIX]{x1D70E}n\unicode[STIX]{x1D708}/(\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{1}m_{2}q))}{n^{s-w}(\unicode[STIX]{x1D6FD}_{1}m_{2})^{u-s+1}r^{1-v-w}}\frac{a^{s-1}}{b^{w}}(\unicode[STIX]{x1D6FC}_{2}m_{2})^{1-2v-2w}\frac{dw}{2\unicode[STIX]{x1D70B}i}+{\mathcal{P}}_{a,b,q}^{(2)}(s,u,v),\qquad\end{eqnarray}$$where
 $$\begin{eqnarray}\displaystyle {\mathcal{P}}_{a,b,q}^{(2)}(s,u,v) & = & \displaystyle \mathop{\{}_{w=1-v}\mathop{\sum }_{\pm }\mathop{\sum }_{\unicode[STIX]{x1D70E}\in \{\pm \}}\unicode[STIX]{x1D6F7}_{a,b,s}^{\pm }(w)G^{-\unicode[STIX]{x1D70E}}(s-w)q^{1-w-u-2v}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2}=b}\unicode[STIX]{x1D701}^{(\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{2}q)}(1+u-s)\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}\mid n}\mathop{\sum }_{(m_{2},\unicode[STIX]{x1D6FD}_{2})=1}\frac{a^{s-1}\unicode[STIX]{x1D6FD}_{1}r_{\unicode[STIX]{x1D6FC}_{2}m_{2}q}(n/\unicode[STIX]{x1D6FD}_{1})}{(\unicode[STIX]{x1D6FD}_{1}m_{2})^{u-s+1}n^{s-w}b^{w}}L\biggl(v+w,\frac{\ast }{\unicode[STIX]{x1D6FC}_{2}m_{2}},f\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{P}}_{a,b,q}^{(2)}(s,u,v) & = & \displaystyle \mathop{\{}_{w=1-v}\mathop{\sum }_{\pm }\mathop{\sum }_{\unicode[STIX]{x1D70E}\in \{\pm \}}\unicode[STIX]{x1D6F7}_{a,b,s}^{\pm }(w)G^{-\unicode[STIX]{x1D70E}}(s-w)q^{1-w-u-2v}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2}=b}\unicode[STIX]{x1D701}^{(\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{2}q)}(1+u-s)\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}\mid n}\mathop{\sum }_{(m_{2},\unicode[STIX]{x1D6FD}_{2})=1}\frac{a^{s-1}\unicode[STIX]{x1D6FD}_{1}r_{\unicode[STIX]{x1D6FC}_{2}m_{2}q}(n/\unicode[STIX]{x1D6FD}_{1})}{(\unicode[STIX]{x1D6FD}_{1}m_{2})^{u-s+1}n^{s-w}b^{w}}L\biggl(v+w,\frac{\ast }{\unicode[STIX]{x1D6FC}_{2}m_{2}},f\biggr).\nonumber\end{eqnarray}$$ We will compute the two polar terms in a moment, but we observe already at this point that now the time has come to combine the two main terms. Indeed, the main term in (3.13) simply counteracts the condition  $(m_{2},q)=1$ of the main term in (3.11) and supplies the missing terms
$(m_{2},q)=1$ of the main term in (3.11) and supplies the missing terms  $q\mid m$. Combining the two, we see that
$q\mid m$. Combining the two, we see that
 $$\begin{eqnarray}\tilde{{\mathcal{T}}}_{a,b,q}(s,u,v)+{\mathcal{T}}_{q}^{(3)}(s,u,v)={\mathcal{T}}_{a,b,q}^{\ast }(s,u,v)+\mathop{\sum }_{j=1}^{2}{\mathcal{P}}_{a,b,q}^{(j)}(s,u,v),\end{eqnarray}$$
$$\begin{eqnarray}\tilde{{\mathcal{T}}}_{a,b,q}(s,u,v)+{\mathcal{T}}_{q}^{(3)}(s,u,v)={\mathcal{T}}_{a,b,q}^{\ast }(s,u,v)+\mathop{\sum }_{j=1}^{2}{\mathcal{P}}_{a,b,q}^{(j)}(s,u,v),\end{eqnarray}$$where
 $$\begin{eqnarray}\displaystyle {\mathcal{T}}_{a,b,q}^{\ast }(s,u,v) & = & \displaystyle \mathop{\sum }_{\pm }\mathop{\sum }_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\in \{\pm \}}\int _{(-4)}\unicode[STIX]{x1D6F7}_{a,b,s}^{\pm }(w)G^{-\unicode[STIX]{x1D70E}}(s-w)G_{f}^{-\unicode[STIX]{x1D70F}}(1-v-w)q^{1-w-u-2v}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2}=b}\unicode[STIX]{x1D701}^{(\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{2}q)}(1+u-s)\frac{\unicode[STIX]{x1D6FC}_{1}^{s-1}\unicode[STIX]{x1D6FC}_{2}^{s-2v-2w}}{\unicode[STIX]{x1D6FD}_{1}^{u-s+1+w}\unicode[STIX]{x1D6FD}_{2}^{w}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{r,n}\mathop{\sum }_{(m_{2},\unicode[STIX]{x1D6FD}_{2})=1}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D708}\hspace{-7.11317pt}\hspace{0.6em}({\rm mod}\hspace{0.2em}\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{1}m_{2}) \\ (\unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC}_{2}m_{2})=1}}e\biggl(\frac{\pm \unicode[STIX]{x1D70F}q\overline{\unicode[STIX]{x1D6FD}_{2}\unicode[STIX]{x1D708}}r}{\unicode[STIX]{x1D6FC}_{2}m_{2}}\biggr)\frac{\unicode[STIX]{x1D706}(r)e(\unicode[STIX]{x1D70E}n\unicode[STIX]{x1D708}/(\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{1}m_{2}))}{n^{s-w}m_{2}^{u-s+2v+2w}r^{1-v-w}}\frac{dw}{2\unicode[STIX]{x1D70B}i}.\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{T}}_{a,b,q}^{\ast }(s,u,v) & = & \displaystyle \mathop{\sum }_{\pm }\mathop{\sum }_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\in \{\pm \}}\int _{(-4)}\unicode[STIX]{x1D6F7}_{a,b,s}^{\pm }(w)G^{-\unicode[STIX]{x1D70E}}(s-w)G_{f}^{-\unicode[STIX]{x1D70F}}(1-v-w)q^{1-w-u-2v}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2}=b}\unicode[STIX]{x1D701}^{(\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{2}q)}(1+u-s)\frac{\unicode[STIX]{x1D6FC}_{1}^{s-1}\unicode[STIX]{x1D6FC}_{2}^{s-2v-2w}}{\unicode[STIX]{x1D6FD}_{1}^{u-s+1+w}\unicode[STIX]{x1D6FD}_{2}^{w}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{r,n}\mathop{\sum }_{(m_{2},\unicode[STIX]{x1D6FD}_{2})=1}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D708}\hspace{-7.11317pt}\hspace{0.6em}({\rm mod}\hspace{0.2em}\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{1}m_{2}) \\ (\unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC}_{2}m_{2})=1}}e\biggl(\frac{\pm \unicode[STIX]{x1D70F}q\overline{\unicode[STIX]{x1D6FD}_{2}\unicode[STIX]{x1D708}}r}{\unicode[STIX]{x1D6FC}_{2}m_{2}}\biggr)\frac{\unicode[STIX]{x1D706}(r)e(\unicode[STIX]{x1D70E}n\unicode[STIX]{x1D708}/(\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{1}m_{2}))}{n^{s-w}m_{2}^{u-s+2v+2w}r^{1-v-w}}\frac{dw}{2\unicode[STIX]{x1D70B}i}.\qquad\end{eqnarray}$$3.6 Computation of polar terms
In this subsection we compute  ${\mathcal{P}}_{a,b,q}^{(j)}(s,u,v)$ for
${\mathcal{P}}_{a,b,q}^{(j)}(s,u,v)$ for  $j=1,2$. We consider first
$j=1,2$. We consider first
 $$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2}=b}\unicode[STIX]{x1D701}^{(\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{2}q)}(1+u-s)\mathop{\sum }_{n}\mathop{\sum }_{(m_{2},q\unicode[STIX]{x1D6FD}_{2})=1}\frac{a^{s-1}\unicode[STIX]{x1D6FD}_{1}r_{\unicode[STIX]{x1D6FC}_{2}m_{2}}(n)}{(\unicode[STIX]{x1D6FD}_{1}m_{2})^{u-s+1}(\unicode[STIX]{x1D6FD}_{1}n)^{s-w}b^{w}}L\biggl(v+w,\frac{\ast }{\unicode[STIX]{x1D6FC}_{2}m_{2}},f\biggr)\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2}=b}\unicode[STIX]{x1D701}^{(\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{2}q)}(1+u-s)\mathop{\sum }_{n}\mathop{\sum }_{(m_{2},q\unicode[STIX]{x1D6FD}_{2})=1}\frac{a^{s-1}\unicode[STIX]{x1D6FD}_{1}r_{\unicode[STIX]{x1D6FC}_{2}m_{2}}(n)}{(\unicode[STIX]{x1D6FD}_{1}m_{2})^{u-s+1}(\unicode[STIX]{x1D6FD}_{1}n)^{s-w}b^{w}}L\biggl(v+w,\frac{\ast }{\unicode[STIX]{x1D6FC}_{2}m_{2}},f\biggr)\end{eqnarray}$$ corresponding to the last four sums in (3.12) for  $w$ in a neighbourhood of
$w$ in a neighbourhood of  $1-v$. Substituting
$1-v$. Substituting
 $$\begin{eqnarray}r_{\unicode[STIX]{x1D6FC}_{2}m_{2}}(n)=\mathop{\sum }_{\substack{ d_{1}d_{2}=\unicode[STIX]{x1D6FC}_{2}m \\ d_{1}\mid n}}d_{1}\unicode[STIX]{x1D707}(d_{2}),\end{eqnarray}$$
$$\begin{eqnarray}r_{\unicode[STIX]{x1D6FC}_{2}m_{2}}(n)=\mathop{\sum }_{\substack{ d_{1}d_{2}=\unicode[STIX]{x1D6FC}_{2}m \\ d_{1}\mid n}}d_{1}\unicode[STIX]{x1D707}(d_{2}),\end{eqnarray}$$we obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D701}(s-w)\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2}=b}\unicode[STIX]{x1D701}^{(\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{2}q)}(1+u-s)\frac{a^{s-1}}{\unicode[STIX]{x1D6FD}_{1}^{u}\unicode[STIX]{x1D6FD}_{2}^{w}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{(m_{2},q\unicode[STIX]{x1D6FD}_{2})=1}\mathop{\sum }_{d_{1}d_{2}=\unicode[STIX]{x1D6FC}_{2}m_{2}}\frac{\unicode[STIX]{x1D707}(d_{2})}{d_{1}^{s-w-1}}\frac{1}{m_{2}^{u-s+1}}L\biggl(v+w,\frac{\ast }{\unicode[STIX]{x1D6FC}_{2}m_{2}},f\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D701}(s-w)\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2}=b}\unicode[STIX]{x1D701}^{(\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{2}q)}(1+u-s)\frac{a^{s-1}}{\unicode[STIX]{x1D6FD}_{1}^{u}\unicode[STIX]{x1D6FD}_{2}^{w}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FC}_{2}\mid d_{1}d_{2} \\ (d_{1}d_{2}/\unicode[STIX]{x1D6FC}_{2},q\unicode[STIX]{x1D6FD}_{2})=1}}\frac{\unicode[STIX]{x1D707}(d_{2})}{d_{1}^{s-w-1}}\frac{\unicode[STIX]{x1D6FC}_{2}^{u-s+1}}{(d_{1}d_{2})^{u-s+1}}L\biggl(v+w,\frac{\ast }{d_{1}d_{2}},f\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D701}(s-w)\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2}=b}\unicode[STIX]{x1D701}^{(\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{2}q)}(1+u-s)\frac{a^{s-1}}{\unicode[STIX]{x1D6FD}_{1}^{u}\unicode[STIX]{x1D6FD}_{2}^{w}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{(m_{2},q\unicode[STIX]{x1D6FD}_{2})=1}\mathop{\sum }_{d_{1}d_{2}=\unicode[STIX]{x1D6FC}_{2}m_{2}}\frac{\unicode[STIX]{x1D707}(d_{2})}{d_{1}^{s-w-1}}\frac{1}{m_{2}^{u-s+1}}L\biggl(v+w,\frac{\ast }{\unicode[STIX]{x1D6FC}_{2}m_{2}},f\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D701}(s-w)\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2}=b}\unicode[STIX]{x1D701}^{(\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{2}q)}(1+u-s)\frac{a^{s-1}}{\unicode[STIX]{x1D6FD}_{1}^{u}\unicode[STIX]{x1D6FD}_{2}^{w}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FC}_{2}\mid d_{1}d_{2} \\ (d_{1}d_{2}/\unicode[STIX]{x1D6FC}_{2},q\unicode[STIX]{x1D6FD}_{2})=1}}\frac{\unicode[STIX]{x1D707}(d_{2})}{d_{1}^{s-w-1}}\frac{\unicode[STIX]{x1D6FC}_{2}^{u-s+1}}{(d_{1}d_{2})^{u-s+1}}L\biggl(v+w,\frac{\ast }{d_{1}d_{2}},f\biggr).\nonumber\end{eqnarray}$$ We write  $(d_{1},\unicode[STIX]{x1D6FC}_{2})=A_{1}$,
$(d_{1},\unicode[STIX]{x1D6FC}_{2})=A_{1}$,  $A_{1}A_{2}=\unicode[STIX]{x1D6FC}_{2}$,
$A_{1}A_{2}=\unicode[STIX]{x1D6FC}_{2}$,  $A_{2}\mid d_{2}$, eventually getting
$A_{2}\mid d_{2}$, eventually getting
 $$\begin{eqnarray}\displaystyle {\mathcal{P}}_{a,b,q}^{(1)}(s,u,v) & = & \displaystyle \mathop{\{}_{w=1-v}\mathop{\sum }_{\pm }\mathop{\sum }_{\unicode[STIX]{x1D70E}\in \{\pm \}}\unicode[STIX]{x1D6F7}_{a,b,s}^{\pm }(w)G^{-\unicode[STIX]{x1D70E}}(s-w)q^{1-s+w}\unicode[STIX]{x1D701}(s-w)\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}A_{1}A_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2}=b}\frac{\unicode[STIX]{x1D701}^{(A_{1}A_{2}\unicode[STIX]{x1D6FD}_{2}q)}(1+u-s)\unicode[STIX]{x1D707}(A_{2})A_{2}^{w}}{\unicode[STIX]{x1D6FD}_{1}^{u}\unicode[STIX]{x1D6FD}_{2}^{w}(\unicode[STIX]{x1D6FC}_{1}A_{2})^{1-s}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{(d_{1}d_{2},qA_{2}\unicode[STIX]{x1D6FD}_{2})=1}\frac{\unicode[STIX]{x1D707}(d_{2})L(v+w,\ast /A_{1}A_{2}d_{1}d_{2},f)}{d_{1}^{u-w}d_{2}^{u-s+1}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{P}}_{a,b,q}^{(1)}(s,u,v) & = & \displaystyle \mathop{\{}_{w=1-v}\mathop{\sum }_{\pm }\mathop{\sum }_{\unicode[STIX]{x1D70E}\in \{\pm \}}\unicode[STIX]{x1D6F7}_{a,b,s}^{\pm }(w)G^{-\unicode[STIX]{x1D70E}}(s-w)q^{1-s+w}\unicode[STIX]{x1D701}(s-w)\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}A_{1}A_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2}=b}\frac{\unicode[STIX]{x1D701}^{(A_{1}A_{2}\unicode[STIX]{x1D6FD}_{2}q)}(1+u-s)\unicode[STIX]{x1D707}(A_{2})A_{2}^{w}}{\unicode[STIX]{x1D6FD}_{1}^{u}\unicode[STIX]{x1D6FD}_{2}^{w}(\unicode[STIX]{x1D6FC}_{1}A_{2})^{1-s}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{(d_{1}d_{2},qA_{2}\unicode[STIX]{x1D6FD}_{2})=1}\frac{\unicode[STIX]{x1D707}(d_{2})L(v+w,\ast /A_{1}A_{2}d_{1}d_{2},f)}{d_{1}^{u-w}d_{2}^{u-s+1}}.\end{eqnarray}$$By (2.6), this is a linear combination of
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}A_{1}A_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2}=b}\unicode[STIX]{x1D6F7}_{a,b,q}^{\pm }(1-v)G^{-\unicode[STIX]{x1D70E}}(s+v-1)q^{2-v-s}\unicode[STIX]{x1D701}(s+v-1)\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\frac{\unicode[STIX]{x1D701}^{(A_{1}A_{2}\unicode[STIX]{x1D6FD}_{2}q)}(1-s+u)\unicode[STIX]{x1D701}^{(qA_{2}\unicode[STIX]{x1D6FD}_{2})}(u+v)}{\unicode[STIX]{x1D701}^{(qA_{2}\unicode[STIX]{x1D6FD}_{2})}(2+u-s)\unicode[STIX]{x1D6FC}_{1}^{1-s}A_{2}^{1+v-s}A_{1}\unicode[STIX]{x1D6FD}_{1}^{u}\unicode[STIX]{x1D6FD}_{2}^{1-v}}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}A_{1}A_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2}=b}\unicode[STIX]{x1D6F7}_{a,b,q}^{\pm }(1-v)G^{-\unicode[STIX]{x1D70E}}(s+v-1)q^{2-v-s}\unicode[STIX]{x1D701}(s+v-1)\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\frac{\unicode[STIX]{x1D701}^{(A_{1}A_{2}\unicode[STIX]{x1D6FD}_{2}q)}(1-s+u)\unicode[STIX]{x1D701}^{(qA_{2}\unicode[STIX]{x1D6FD}_{2})}(u+v)}{\unicode[STIX]{x1D701}^{(qA_{2}\unicode[STIX]{x1D6FD}_{2})}(2+u-s)\unicode[STIX]{x1D6FC}_{1}^{1-s}A_{2}^{1+v-s}A_{1}\unicode[STIX]{x1D6FD}_{1}^{u}\unicode[STIX]{x1D6FD}_{2}^{1-v}}\nonumber\end{eqnarray}$$and derivatives thereof. The same computation shows that
 $$\begin{eqnarray}\displaystyle {\mathcal{P}}_{a,b,q}^{(2)}(s,u,v) & = & \displaystyle \mathop{\{}_{w=1-v}\mathop{\sum }_{\pm }\mathop{\sum }_{\unicode[STIX]{x1D70E}\in \{\pm \}}\unicode[STIX]{x1D6F7}_{a,b,s}^{\pm }(w)G^{-\unicode[STIX]{x1D70E}}(s-w)q^{1-w-u-2v}\unicode[STIX]{x1D701}(s-w)\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{q_{1}q_{2}=q}\frac{1}{q_{1}^{s-w-1}}\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}A_{1}A_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2}=b}\frac{\unicode[STIX]{x1D701}^{(A_{1}A_{2}\unicode[STIX]{x1D6FD}_{2}q)}(1-s+u)\unicode[STIX]{x1D707}(A_{2}q_{2})A_{1}^{w}}{\unicode[STIX]{x1D6FD}_{1}^{u}\unicode[STIX]{x1D6FD}_{2}^{w}(\unicode[STIX]{x1D6FC}_{1}A_{2})^{1-s}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{\substack{ (d_{1},A_{2}\unicode[STIX]{x1D6FD}_{2}q_{2})=1 \\ (d_{2},A_{2}\unicode[STIX]{x1D6FD}_{2})=1}}\frac{\unicode[STIX]{x1D707}(d_{2})L(v+w,\ast /A_{1}A_{2}d_{1}d_{2},f)}{d_{1}^{u-w}d_{2}^{u-s+1}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{P}}_{a,b,q}^{(2)}(s,u,v) & = & \displaystyle \mathop{\{}_{w=1-v}\mathop{\sum }_{\pm }\mathop{\sum }_{\unicode[STIX]{x1D70E}\in \{\pm \}}\unicode[STIX]{x1D6F7}_{a,b,s}^{\pm }(w)G^{-\unicode[STIX]{x1D70E}}(s-w)q^{1-w-u-2v}\unicode[STIX]{x1D701}(s-w)\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{q_{1}q_{2}=q}\frac{1}{q_{1}^{s-w-1}}\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}A_{1}A_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2}=b}\frac{\unicode[STIX]{x1D701}^{(A_{1}A_{2}\unicode[STIX]{x1D6FD}_{2}q)}(1-s+u)\unicode[STIX]{x1D707}(A_{2}q_{2})A_{1}^{w}}{\unicode[STIX]{x1D6FD}_{1}^{u}\unicode[STIX]{x1D6FD}_{2}^{w}(\unicode[STIX]{x1D6FC}_{1}A_{2})^{1-s}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{\substack{ (d_{1},A_{2}\unicode[STIX]{x1D6FD}_{2}q_{2})=1 \\ (d_{2},A_{2}\unicode[STIX]{x1D6FD}_{2})=1}}\frac{\unicode[STIX]{x1D707}(d_{2})L(v+w,\ast /A_{1}A_{2}d_{1}d_{2},f)}{d_{1}^{u-w}d_{2}^{u-s+1}},\end{eqnarray}$$which is a linear combination of
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{q_{1}q_{2}=q}\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}A_{1}A_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2}=b}\unicode[STIX]{x1D6F7}_{a,b,q}^{\pm }(1-v)G^{-\unicode[STIX]{x1D70E}}(s+v-1)\unicode[STIX]{x1D701}(s+v-1)\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\frac{q_{1}^{2-s-u-2v}}{q_{2}^{u+v}}\frac{\unicode[STIX]{x1D701}^{(A_{1}A_{2}\unicode[STIX]{x1D6FD}_{2}q)}(1-s+u)\unicode[STIX]{x1D701}^{(A_{2}\unicode[STIX]{x1D6FD}_{2}q_{2})}(u+v-1)}{\unicode[STIX]{x1D701}^{(A_{2}\unicode[STIX]{x1D6FD}_{2})}(2+u-s)\unicode[STIX]{x1D6FC}_{1}^{1-s}A_{2}^{2-s}A_{1}^{v}\unicode[STIX]{x1D6FD}_{1}^{u}\unicode[STIX]{x1D6FD}_{2}^{1-v}}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{q_{1}q_{2}=q}\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}A_{1}A_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2}=b}\unicode[STIX]{x1D6F7}_{a,b,q}^{\pm }(1-v)G^{-\unicode[STIX]{x1D70E}}(s+v-1)\unicode[STIX]{x1D701}(s+v-1)\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\frac{q_{1}^{2-s-u-2v}}{q_{2}^{u+v}}\frac{\unicode[STIX]{x1D701}^{(A_{1}A_{2}\unicode[STIX]{x1D6FD}_{2}q)}(1-s+u)\unicode[STIX]{x1D701}^{(A_{2}\unicode[STIX]{x1D6FD}_{2}q_{2})}(u+v-1)}{\unicode[STIX]{x1D701}^{(A_{2}\unicode[STIX]{x1D6FD}_{2})}(2+u-s)\unicode[STIX]{x1D6FC}_{1}^{1-s}A_{2}^{2-s}A_{1}^{v}\unicode[STIX]{x1D6FD}_{1}^{u}\unicode[STIX]{x1D6FD}_{2}^{1-v}}\nonumber\end{eqnarray}$$and derivatives thereof.
3.7 Application of the Kuznetsov formula
We return to (3.14) and recognize the  $\unicode[STIX]{x1D708}$-sum as a Kloosterman sum. More precisely, the
$\unicode[STIX]{x1D708}$-sum as a Kloosterman sum. More precisely, the  $\unicode[STIX]{x1D708}$-sum vanishes unless
$\unicode[STIX]{x1D708}$-sum vanishes unless  $\unicode[STIX]{x1D6FD}_{1}\mid n$, so that the second and third lines of (3.14) equal
$\unicode[STIX]{x1D6FD}_{1}\mid n$, so that the second and third lines of (3.14) equal
 $$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2}=b}\unicode[STIX]{x1D701}^{(\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{2}q)}(1+u-s)\frac{\unicode[STIX]{x1D6FC}_{1}^{s-1}\unicode[STIX]{x1D6FC}_{2}^{s-2v-2w}}{\unicode[STIX]{x1D6FD}_{1}^{u}\unicode[STIX]{x1D6FD}_{2}^{w}}\mathop{\sum }_{r,n}\mathop{\sum }_{(m_{2},\unicode[STIX]{x1D6FD}_{2})=1}\frac{\unicode[STIX]{x1D706}(r)S(\pm \unicode[STIX]{x1D70F}q\overline{\unicode[STIX]{x1D6FD}_{2}}r,\unicode[STIX]{x1D70E}n,\unicode[STIX]{x1D6FC}_{2}m_{2})}{n^{s-w}m_{2}^{u-s+2v+2w}r^{1-v-w}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2}=b}\unicode[STIX]{x1D701}^{(\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{2}q)}(1+u-s)\frac{\unicode[STIX]{x1D6FC}_{1}^{s-1}\unicode[STIX]{x1D6FC}_{2}^{s-2v-2w}}{\unicode[STIX]{x1D6FD}_{1}^{u}\unicode[STIX]{x1D6FD}_{2}^{w}}\mathop{\sum }_{r,n}\mathop{\sum }_{(m_{2},\unicode[STIX]{x1D6FD}_{2})=1}\frac{\unicode[STIX]{x1D706}(r)S(\pm \unicode[STIX]{x1D70F}q\overline{\unicode[STIX]{x1D6FD}_{2}}r,\unicode[STIX]{x1D70E}n,\unicode[STIX]{x1D6FC}_{2}m_{2})}{n^{s-w}m_{2}^{u-s+2v+2w}r^{1-v-w}}.\end{eqnarray}$$ For  $(\unicode[STIX]{x1D6FD}_{2},q\unicode[STIX]{x1D6FC}_{2}m)=1$, we have, by the twisted multiplicativity of Kloosterman sums,
$(\unicode[STIX]{x1D6FD}_{2},q\unicode[STIX]{x1D6FC}_{2}m)=1$, we have, by the twisted multiplicativity of Kloosterman sums,
 $$\begin{eqnarray}S(\pm \unicode[STIX]{x1D70F}qr,\unicode[STIX]{x1D70E}\unicode[STIX]{x1D6FD}_{2}n,\unicode[STIX]{x1D6FD}_{2}\unicode[STIX]{x1D6FC}_{2}m)=r_{\unicode[STIX]{x1D6FD}_{2}}(r)S(\pm \unicode[STIX]{x1D70F}qr\overline{\unicode[STIX]{x1D6FD}_{2}},\unicode[STIX]{x1D70E}n,\unicode[STIX]{x1D6FC}_{2}m).\end{eqnarray}$$
$$\begin{eqnarray}S(\pm \unicode[STIX]{x1D70F}qr,\unicode[STIX]{x1D70E}\unicode[STIX]{x1D6FD}_{2}n,\unicode[STIX]{x1D6FD}_{2}\unicode[STIX]{x1D6FC}_{2}m)=r_{\unicode[STIX]{x1D6FD}_{2}}(r)S(\pm \unicode[STIX]{x1D70F}qr\overline{\unicode[STIX]{x1D6FD}_{2}},\unicode[STIX]{x1D70E}n,\unicode[STIX]{x1D6FC}_{2}m).\end{eqnarray}$$ At this point, we use the fact that  $b$ is square-free; in particular, the Ramanujan sum
$b$ is square-free; in particular, the Ramanujan sum  $r_{\unicode[STIX]{x1D6FD}_{2}}(r)$ does not vanish. Write
$r_{\unicode[STIX]{x1D6FD}_{2}}(r)$ does not vanish. Write  $B_{1}=(\unicode[STIX]{x1D6FD}_{2},r)$,
$B_{1}=(\unicode[STIX]{x1D6FD}_{2},r)$,  $B_{2}B_{1}=\unicode[STIX]{x1D6FD}_{2}$,
$B_{2}B_{1}=\unicode[STIX]{x1D6FD}_{2}$,  $r=r^{\prime }B_{1}$,
$r=r^{\prime }B_{1}$,  $(r^{\prime },B_{2})=1$. Then
$(r^{\prime },B_{2})=1$. Then
 $$\begin{eqnarray}\displaystyle S(\pm \unicode[STIX]{x1D70F}qr\overline{\unicode[STIX]{x1D6FD}_{2}},\unicode[STIX]{x1D70E}n,\unicode[STIX]{x1D6FC}_{2}m) & = & \displaystyle \frac{1}{r_{\unicode[STIX]{x1D6FD}_{2}}(r)}S(\pm \unicode[STIX]{x1D70F}qr^{\prime }B_{1},\unicode[STIX]{x1D70E}B_{1}B_{2}n,B_{1}B_{2}\unicode[STIX]{x1D6FC}_{2}m)\nonumber\\ \displaystyle & = & \displaystyle \frac{\unicode[STIX]{x1D719}(B_{1})}{\unicode[STIX]{x1D719}(B_{1})\unicode[STIX]{x1D707}(B_{2})}S(\pm \unicode[STIX]{x1D70F}qr^{\prime },\unicode[STIX]{x1D70E}B_{2}n,B_{2}\unicode[STIX]{x1D6FC}_{2}m),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S(\pm \unicode[STIX]{x1D70F}qr\overline{\unicode[STIX]{x1D6FD}_{2}},\unicode[STIX]{x1D70E}n,\unicode[STIX]{x1D6FC}_{2}m) & = & \displaystyle \frac{1}{r_{\unicode[STIX]{x1D6FD}_{2}}(r)}S(\pm \unicode[STIX]{x1D70F}qr^{\prime }B_{1},\unicode[STIX]{x1D70E}B_{1}B_{2}n,B_{1}B_{2}\unicode[STIX]{x1D6FC}_{2}m)\nonumber\\ \displaystyle & = & \displaystyle \frac{\unicode[STIX]{x1D719}(B_{1})}{\unicode[STIX]{x1D719}(B_{1})\unicode[STIX]{x1D707}(B_{2})}S(\pm \unicode[STIX]{x1D70F}qr^{\prime },\unicode[STIX]{x1D70E}B_{2}n,B_{2}\unicode[STIX]{x1D6FC}_{2}m),\nonumber\end{eqnarray}$$so that (3.17) is equal to
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}B_{1}B_{2}=b}\frac{\unicode[STIX]{x1D701}^{(\unicode[STIX]{x1D6FC}_{2}B_{1}B_{2}q)}(1+u-s)\unicode[STIX]{x1D707}(B_{2})\unicode[STIX]{x1D6FC}_{1}^{s-1}\unicode[STIX]{x1D6FC}_{2}^{s-2v-2w}}{\unicode[STIX]{x1D6FD}_{1}^{u}B_{2}^{w}B_{1}^{1-v}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\sum }_{(r,B_{2})=1,n}\mathop{\sum }_{(m_{2},\unicode[STIX]{x1D6FD}_{2})=1}\frac{\unicode[STIX]{x1D706}(rB_{1})S(\pm \unicode[STIX]{x1D70F}qr,\unicode[STIX]{x1D70E}B_{2}n,B_{2}\unicode[STIX]{x1D6FC}_{2}m_{2})}{n^{s-w}m_{2}^{u-s+2v+2w}r^{1-v-w}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}B_{1}B_{2}=b}\frac{\unicode[STIX]{x1D701}^{(\unicode[STIX]{x1D6FC}_{2}B_{1}B_{2}q)}(1+u-s)\unicode[STIX]{x1D707}(B_{2})\unicode[STIX]{x1D6FC}_{1}^{s-1}\unicode[STIX]{x1D6FC}_{2}^{s-2v-2w}}{\unicode[STIX]{x1D6FD}_{1}^{u}B_{2}^{w}B_{1}^{1-v}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\sum }_{(r,B_{2})=1,n}\mathop{\sum }_{(m_{2},\unicode[STIX]{x1D6FD}_{2})=1}\frac{\unicode[STIX]{x1D706}(rB_{1})S(\pm \unicode[STIX]{x1D70F}qr,\unicode[STIX]{x1D70E}B_{2}n,B_{2}\unicode[STIX]{x1D6FC}_{2}m_{2})}{n^{s-w}m_{2}^{u-s+2v+2w}r^{1-v-w}}.\nonumber\end{eqnarray}$$ Here we can drop the condition  $(m_{2},B_{2})=1$, since otherwise the Kloosterman sum vanishes (since
$(m_{2},B_{2})=1$, since otherwise the Kloosterman sum vanishes (since  $(r,B_{2})=1$). We remove the remaining condition
$(r,B_{2})=1$). We remove the remaining condition  $(m_{2},B_{1})=1$ by Möbius inversion, getting
$(m_{2},B_{1})=1$ by Möbius inversion, getting
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}B_{3}B_{4}B_{2}=b}\frac{\unicode[STIX]{x1D701}^{(\unicode[STIX]{x1D6FC}_{2}B_{2}B_{3}B_{4}q)}(1+u-s)\unicode[STIX]{x1D707}(B_{2})\unicode[STIX]{x1D707}(B_{3})\unicode[STIX]{x1D6FC}_{1}^{s-1}\unicode[STIX]{x1D6FC}_{2}^{s-2v-2w}}{\unicode[STIX]{x1D6FD}_{1}^{u}B_{2}^{w}B_{3}^{1+u-s+v+2w}B_{4}^{1-v}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \mathop{\sum }_{(r,B_{2})=1,n}\mathop{\sum }_{m_{2}}\frac{\unicode[STIX]{x1D706}(rB_{3}B_{4})S(\pm \unicode[STIX]{x1D70F}qr,\unicode[STIX]{x1D70E}B_{2}n,B_{2}B_{3}\unicode[STIX]{x1D6FC}_{2}m_{2})}{n^{s-w}m_{2}^{u-s+2v+2w}r^{1-v-w}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}B_{3}B_{4}B_{2}=b}\frac{\unicode[STIX]{x1D701}^{(\unicode[STIX]{x1D6FC}_{2}B_{2}B_{3}B_{4}q)}(1+u-s)\unicode[STIX]{x1D707}(B_{2})\unicode[STIX]{x1D707}(B_{3})\unicode[STIX]{x1D6FC}_{1}^{s-1}\unicode[STIX]{x1D6FC}_{2}^{s-2v-2w}}{\unicode[STIX]{x1D6FD}_{1}^{u}B_{2}^{w}B_{3}^{1+u-s+v+2w}B_{4}^{1-v}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \mathop{\sum }_{(r,B_{2})=1,n}\mathop{\sum }_{m_{2}}\frac{\unicode[STIX]{x1D706}(rB_{3}B_{4})S(\pm \unicode[STIX]{x1D70F}qr,\unicode[STIX]{x1D70E}B_{2}n,B_{2}B_{3}\unicode[STIX]{x1D6FC}_{2}m_{2})}{n^{s-w}m_{2}^{u-s+2v+2w}r^{1-v-w}}.\nonumber\end{eqnarray}$$Rearranging, we obtain the final expression
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\pm }\mathop{\sum }_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\in \{\pm \}}q^{(3-s-u-2v)/2}\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}B_{3}B_{4}B_{2}=b}\frac{\unicode[STIX]{x1D707}(B_{2})\unicode[STIX]{x1D707}(B_{3})\unicode[STIX]{x1D6FC}_{1}^{s-1}\unicode[STIX]{x1D6FC}_{2}^{u}\unicode[STIX]{x1D701}^{(\unicode[STIX]{x1D6FC}_{2}B_{2}B_{3}B_{4}q)}(1-s+u)}{\unicode[STIX]{x1D6FD}_{1}^{u}B_{2}^{(s-u-1-2v)/2}B_{3}^{1-v}B_{4}^{1-v}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\sum }_{(r,B_{2})=1,n}\frac{\unicode[STIX]{x1D706}(rB_{3}B_{4})}{n^{(s+u-1+2v)/2}r^{(1-s+u)/2}}\mathop{\sum }_{B_{2}B_{3}\unicode[STIX]{x1D6FC}_{2}\mid m_{2}}\frac{S(\pm \unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}qr,B_{2}n,m_{2})}{m_{2}}\unicode[STIX]{x1D6F9}_{a,b,s,u,v}^{\pm ,\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}}\biggl(\frac{\sqrt{qrB_{2}n}}{m_{2}}\biggr),\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\pm }\mathop{\sum }_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\in \{\pm \}}q^{(3-s-u-2v)/2}\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}B_{3}B_{4}B_{2}=b}\frac{\unicode[STIX]{x1D707}(B_{2})\unicode[STIX]{x1D707}(B_{3})\unicode[STIX]{x1D6FC}_{1}^{s-1}\unicode[STIX]{x1D6FC}_{2}^{u}\unicode[STIX]{x1D701}^{(\unicode[STIX]{x1D6FC}_{2}B_{2}B_{3}B_{4}q)}(1-s+u)}{\unicode[STIX]{x1D6FD}_{1}^{u}B_{2}^{(s-u-1-2v)/2}B_{3}^{1-v}B_{4}^{1-v}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\sum }_{(r,B_{2})=1,n}\frac{\unicode[STIX]{x1D706}(rB_{3}B_{4})}{n^{(s+u-1+2v)/2}r^{(1-s+u)/2}}\mathop{\sum }_{B_{2}B_{3}\unicode[STIX]{x1D6FC}_{2}\mid m_{2}}\frac{S(\pm \unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}qr,B_{2}n,m_{2})}{m_{2}}\unicode[STIX]{x1D6F9}_{a,b,s,u,v}^{\pm ,\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}}\biggl(\frac{\sqrt{qrB_{2}n}}{m_{2}}\biggr),\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$ for  ${\mathcal{T}}_{a,b,q}^{\ast }(s,u,v)$, where
${\mathcal{T}}_{a,b,q}^{\ast }(s,u,v)$, where
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F9}(x) & = & \displaystyle \unicode[STIX]{x1D6F9}_{a,b,s,u,v}^{\pm ,\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}}(x)=x^{u-s+2v-1}\int _{(-4)}\unicode[STIX]{x1D6F7}_{a,b,s}^{\pm }(w)G_{f}^{-\unicode[STIX]{x1D70F}}(1-v-w)G^{-\unicode[STIX]{x1D70E}}(s-w)x^{2w}\frac{dw}{2\unicode[STIX]{x1D70B}i}\nonumber\\ \displaystyle & = & \displaystyle \int _{(0)}\unicode[STIX]{x1D6F7}_{a,b,s}^{\pm }\biggl(\frac{1+s-u-2v-w}{2}\biggr)G_{f}^{-\unicode[STIX]{x1D70F}}\biggl(\frac{1-s+u+w}{2}\biggr)G^{-\unicode[STIX]{x1D70E}}\biggl(\frac{s+u+2v-1+w}{2}\biggr)\nonumber\\ \displaystyle & & \displaystyle \times \,x^{-w}\frac{dw}{2\unicode[STIX]{x1D70B}i}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F9}(x) & = & \displaystyle \unicode[STIX]{x1D6F9}_{a,b,s,u,v}^{\pm ,\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}}(x)=x^{u-s+2v-1}\int _{(-4)}\unicode[STIX]{x1D6F7}_{a,b,s}^{\pm }(w)G_{f}^{-\unicode[STIX]{x1D70F}}(1-v-w)G^{-\unicode[STIX]{x1D70E}}(s-w)x^{2w}\frac{dw}{2\unicode[STIX]{x1D70B}i}\nonumber\\ \displaystyle & = & \displaystyle \int _{(0)}\unicode[STIX]{x1D6F7}_{a,b,s}^{\pm }\biggl(\frac{1+s-u-2v-w}{2}\biggr)G_{f}^{-\unicode[STIX]{x1D70F}}\biggl(\frac{1-s+u+w}{2}\biggr)G^{-\unicode[STIX]{x1D70E}}\biggl(\frac{s+u+2v-1+w}{2}\biggr)\nonumber\\ \displaystyle & & \displaystyle \times \,x^{-w}\frac{dw}{2\unicode[STIX]{x1D70B}i}.\nonumber\end{eqnarray}$$ In the region (3.1), the integrand is holomorphic in  $2\unicode[STIX]{x1D703}-8<\Re w<34$ (recalling (2.8) and (3.7)) and rapidly decaying on vertical lines; in particular, the assumption
$2\unicode[STIX]{x1D703}-8<\Re w<34$ (recalling (2.8) and (3.7)) and rapidly decaying on vertical lines; in particular, the assumption  $x^{j}\unicode[STIX]{x1D6F9}^{(j)}(x)\ll \min (x,x^{-3/2})$ for
$x^{j}\unicode[STIX]{x1D6F9}^{(j)}(x)\ll \min (x,x^{-3/2})$ for  $0\leqslant j\leqslant 3$ of the Kuznetsov formula (2.14) is satisfied. By (2.14), the
$0\leqslant j\leqslant 3$ of the Kuznetsov formula (2.14) is satisfied. By (2.14), the  $m_{2}$-sum equals
$m_{2}$-sum equals
 $$\begin{eqnarray}{\mathcal{A}}_{B}^{\text{Maa}\unicode[STIX]{x00DF}}(\unicode[STIX]{x1D716}qr,B_{2}r;\mathscr{L}^{\unicode[STIX]{x1D716}}\unicode[STIX]{x1D6F9})+{\mathcal{A}}_{B}^{\text{Eis}}(\unicode[STIX]{x1D716}qr,B_{2}r;\mathscr{L}^{\unicode[STIX]{x1D716}}\unicode[STIX]{x1D6F9})+{\mathcal{A}}_{B}^{\text{hol}}(\unicode[STIX]{x1D716}qr,B_{2}r;\mathscr{L}^{\text{hol}}\unicode[STIX]{x1D6F9})\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}_{B}^{\text{Maa}\unicode[STIX]{x00DF}}(\unicode[STIX]{x1D716}qr,B_{2}r;\mathscr{L}^{\unicode[STIX]{x1D716}}\unicode[STIX]{x1D6F9})+{\mathcal{A}}_{B}^{\text{Eis}}(\unicode[STIX]{x1D716}qr,B_{2}r;\mathscr{L}^{\unicode[STIX]{x1D716}}\unicode[STIX]{x1D6F9})+{\mathcal{A}}_{B}^{\text{hol}}(\unicode[STIX]{x1D716}qr,B_{2}r;\mathscr{L}^{\text{hol}}\unicode[STIX]{x1D6F9})\end{eqnarray}$$ with  $B=B_{2}B_{3}\unicode[STIX]{x1D6FC}_{2}$ and
$B=B_{2}B_{3}\unicode[STIX]{x1D6FC}_{2}$ and  $\unicode[STIX]{x1D716}=\pm \unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}$. In the larger region
$\unicode[STIX]{x1D716}=\pm \unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}$. In the larger region
 $$\begin{eqnarray}1/2\leqslant \Re s,\Re v\leqslant 3,\quad \Re s\leqslant \Re u\leqslant 11,\end{eqnarray}$$
$$\begin{eqnarray}1/2\leqslant \Re s,\Re v\leqslant 3,\quad \Re s\leqslant \Re u\leqslant 11,\end{eqnarray}$$ the integrand of  $\unicode[STIX]{x1D6F9}$ is holomorphic in
$\unicode[STIX]{x1D6F9}$ is holomorphic in  $2\unicode[STIX]{x1D703}-1<\Re w<32$ (and meromorphic in
$2\unicode[STIX]{x1D703}-1<\Re w<32$ (and meromorphic in  $|\Re w|<32$) and rapidly decaying on vertical lines. By [Reference Blomer and KhanBK19b, Lemma 3a] and (3.7), we conclude that, uniformly in this region,
$|\Re w|<32$) and rapidly decaying on vertical lines. By [Reference Blomer and KhanBK19b, Lemma 3a] and (3.7), we conclude that, uniformly in this region,
 $$\begin{eqnarray}\mathscr{L}^{\pm }\unicode[STIX]{x1D6F9}(t)\ll (1+|t|)^{-30},\quad \mathscr{L}^{\text{hol}}\unicode[STIX]{x1D6F9}(k)\ll k^{-30}\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{L}^{\pm }\unicode[STIX]{x1D6F9}(t)\ll (1+|t|)^{-30},\quad \mathscr{L}^{\text{hol}}\unicode[STIX]{x1D6F9}(k)\ll k^{-30}\end{eqnarray}$$ as long as  $a\asymp b$ for
$a\asymp b$ for  $t\in \mathbb{R}\cup [-7i/64,7i/64]$ and
$t\in \mathbb{R}\cup [-7i/64,7i/64]$ and  $k\in 2\mathbb{N}$. Recall again that
$k\in 2\mathbb{N}$. Recall again that  $\unicode[STIX]{x1D6F9}$ depends on
$\unicode[STIX]{x1D6F9}$ depends on  $s,u,v$, which are currently restricted to (3.1).
$s,u,v$, which are currently restricted to (3.1).
3.8 The cuspidal contribution
We start with the analysis of the Maaß spectrum. Inserting definitions (2.15) and (2.9) and using the notation and conventions of §2.4, we obtain
 $$\begin{eqnarray}\displaystyle {\mathcal{A}}_{B}^{\text{Maa}\unicode[STIX]{x00DF}}(\unicode[STIX]{x1D716}qr,B_{2}r;\mathscr{L}^{\unicode[STIX]{x1D716}}\unicode[STIX]{x1D6F9}) & = & \displaystyle \mathop{\sum }_{B_{0}\mid B}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(B_{0})}\mathop{\sum }_{M\mid (B/B_{0})}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},M,B}(\unicode[STIX]{x1D716}qr)\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},M,B}(B_{2}n)\mathscr{L}^{\unicode[STIX]{x1D716}}\unicode[STIX]{x1D6F9}(t_{\unicode[STIX]{x1D713}})\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{B_{0}\mid B}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(B_{0})}\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D713}}^{(1-\unicode[STIX]{x1D716})/2}\mathop{\sum }_{M\mid (B/B_{0})}\frac{\mathop{\prod }_{p\mid B_{0}}(1-p^{-2})}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})B\unicode[STIX]{x1D708}(B)}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{d_{1},d_{2}\mid M}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}(M,d_{1})\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}(M,d_{2})\frac{d_{1}d_{2}}{M}\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}\biggl(\frac{qr}{d_{1}}\biggr)\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}\biggl(\frac{B_{2}n}{d_{2}}\biggr)\mathscr{L}^{\unicode[STIX]{x1D716}}\unicode[STIX]{x1D6F9}(t_{\unicode[STIX]{x1D713}}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{A}}_{B}^{\text{Maa}\unicode[STIX]{x00DF}}(\unicode[STIX]{x1D716}qr,B_{2}r;\mathscr{L}^{\unicode[STIX]{x1D716}}\unicode[STIX]{x1D6F9}) & = & \displaystyle \mathop{\sum }_{B_{0}\mid B}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(B_{0})}\mathop{\sum }_{M\mid (B/B_{0})}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},M,B}(\unicode[STIX]{x1D716}qr)\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},M,B}(B_{2}n)\mathscr{L}^{\unicode[STIX]{x1D716}}\unicode[STIX]{x1D6F9}(t_{\unicode[STIX]{x1D713}})\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{B_{0}\mid B}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(B_{0})}\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D713}}^{(1-\unicode[STIX]{x1D716})/2}\mathop{\sum }_{M\mid (B/B_{0})}\frac{\mathop{\prod }_{p\mid B_{0}}(1-p^{-2})}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})B\unicode[STIX]{x1D708}(B)}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{d_{1},d_{2}\mid M}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}(M,d_{1})\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}(M,d_{2})\frac{d_{1}d_{2}}{M}\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}\biggl(\frac{qr}{d_{1}}\biggr)\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}\biggl(\frac{B_{2}n}{d_{2}}\biggr)\mathscr{L}^{\unicode[STIX]{x1D716}}\unicode[STIX]{x1D6F9}(t_{\unicode[STIX]{x1D713}}).\nonumber\end{eqnarray}$$ Summing over  $n$ and
$n$ and  $r$ as in (3.18), we obtain
$r$ as in (3.18), we obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{B_{0}\mid B}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(B_{0})}\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D713}}^{(1-\unicode[STIX]{x1D716})/2}\mathop{\sum }_{M\mid (B/B_{0})}\frac{\mathop{\prod }_{p\mid B_{0}}(1-p^{-2})}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})B\unicode[STIX]{x1D708}(B)}\mathop{\sum }_{d_{1},d_{2}\mid M}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}(M,d_{1})\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}(M,d_{2})\frac{d_{1}d_{2}}{M}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\sum }_{(r,B_{2})=1}\frac{\unicode[STIX]{x1D706}(rB_{3}B_{4})\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(qr/d_{1})}{r^{(1-s+u)/2}}\mathop{\sum }_{n}\frac{\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(B_{2}n/d_{2})}{n^{(s+u-1+2v)/2}}\mathscr{L}^{\unicode[STIX]{x1D716}}\unicode[STIX]{x1D6F9}(t_{\unicode[STIX]{x1D713}}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{B_{0}\mid B}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(B_{0})}\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D713}}^{(1-\unicode[STIX]{x1D716})/2}\mathop{\sum }_{M\mid (B/B_{0})}\frac{\mathop{\prod }_{p\mid B_{0}}(1-p^{-2})}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})B\unicode[STIX]{x1D708}(B)}\mathop{\sum }_{d_{1},d_{2}\mid M}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}(M,d_{1})\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}(M,d_{2})\frac{d_{1}d_{2}}{M}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\sum }_{(r,B_{2})=1}\frac{\unicode[STIX]{x1D706}(rB_{3}B_{4})\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(qr/d_{1})}{r^{(1-s+u)/2}}\mathop{\sum }_{n}\frac{\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(B_{2}n/d_{2})}{n^{(s+u-1+2v)/2}}\mathscr{L}^{\unicode[STIX]{x1D716}}\unicode[STIX]{x1D6F9}(t_{\unicode[STIX]{x1D713}}).\nonumber\end{eqnarray}$$ Since  $(q,B)=1$, we have
$(q,B)=1$, we have  $(d_{1},q)=1$, and so by (2.1), the
$(d_{1},q)=1$, and so by (2.1), the  $r$-sum equals
$r$-sum equals
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x1D6FF}_{(d_{1},B_{2})=1}}{d_{1}^{(1-s+u)/2}}\mathop{\sum }_{(r,B_{2})=1}\frac{\unicode[STIX]{x1D706}(rd_{1}B_{3}B_{4})\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(qr)}{r^{(1-s+u)/2}}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\unicode[STIX]{x1D6FF}_{(d_{1},B_{2})=1}}{d_{1}^{(1-s+u)/2}}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FF}_{1}\mid d_{1}B_{3}B_{4} \\ (\unicode[STIX]{x1D6FF}_{1},B_{0})=1}}\frac{\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FF}_{1})\unicode[STIX]{x1D706}(d_{1}B_{3}B_{4}/\unicode[STIX]{x1D6FF}_{1})}{\unicode[STIX]{x1D6FF}_{1}^{(1-s+u)/2}}\mathop{\sum }_{\unicode[STIX]{x1D6FF}_{2}\mid q}\frac{\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FF}_{2})\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(q/\unicode[STIX]{x1D6FF})}{\unicode[STIX]{x1D6FF}_{2}^{(1-s+u)/2}}\frac{L^{(B_{2})}(f\times \unicode[STIX]{x1D713},(1-s+u)/2)}{\unicode[STIX]{x1D701}^{(B_{2})}(1-s+u)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x1D6FF}_{(d_{1},B_{2})=1}}{d_{1}^{(1-s+u)/2}}\mathop{\sum }_{(r,B_{2})=1}\frac{\unicode[STIX]{x1D706}(rd_{1}B_{3}B_{4})\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(qr)}{r^{(1-s+u)/2}}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\unicode[STIX]{x1D6FF}_{(d_{1},B_{2})=1}}{d_{1}^{(1-s+u)/2}}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FF}_{1}\mid d_{1}B_{3}B_{4} \\ (\unicode[STIX]{x1D6FF}_{1},B_{0})=1}}\frac{\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FF}_{1})\unicode[STIX]{x1D706}(d_{1}B_{3}B_{4}/\unicode[STIX]{x1D6FF}_{1})}{\unicode[STIX]{x1D6FF}_{1}^{(1-s+u)/2}}\mathop{\sum }_{\unicode[STIX]{x1D6FF}_{2}\mid q}\frac{\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FF}_{2})\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(q/\unicode[STIX]{x1D6FF})}{\unicode[STIX]{x1D6FF}_{2}^{(1-s+u)/2}}\frac{L^{(B_{2})}(f\times \unicode[STIX]{x1D713},(1-s+u)/2)}{\unicode[STIX]{x1D701}^{(B_{2})}(1-s+u)}.\nonumber\end{eqnarray}$$ Similarly, the  $n$-sum equals
$n$-sum equals
 $$\begin{eqnarray}\displaystyle & & \displaystyle \biggl(\frac{(B_{2},d_{2})}{d_{2}}\biggr)^{(s+u-1+2v)/2}\mathop{\sum }_{n}\frac{\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(B_{2}n/(d_{2},B_{2}))}{n^{(s+u-1+2v)/2}}\nonumber\\ \displaystyle & & \displaystyle \quad =\biggl(\frac{(B_{2},d_{2})}{d_{2}}\biggr)^{(s+u-1+2v)/2}\mathop{\sum }_{\substack{ B^{\ast }\mid B_{2}/(d_{2},B_{2}) \\ (B^{\ast },B_{0})=1}}\frac{\unicode[STIX]{x1D707}(B^{\ast })\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(B_{2}/((d_{2},B_{2})B^{\ast }))}{(B^{\ast })^{(s+u-1+2v)/2}}L(\unicode[STIX]{x1D713},(s+u-1+2v)/2).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \biggl(\frac{(B_{2},d_{2})}{d_{2}}\biggr)^{(s+u-1+2v)/2}\mathop{\sum }_{n}\frac{\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(B_{2}n/(d_{2},B_{2}))}{n^{(s+u-1+2v)/2}}\nonumber\\ \displaystyle & & \displaystyle \quad =\biggl(\frac{(B_{2},d_{2})}{d_{2}}\biggr)^{(s+u-1+2v)/2}\mathop{\sum }_{\substack{ B^{\ast }\mid B_{2}/(d_{2},B_{2}) \\ (B^{\ast },B_{0})=1}}\frac{\unicode[STIX]{x1D707}(B^{\ast })\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(B_{2}/((d_{2},B_{2})B^{\ast }))}{(B^{\ast })^{(s+u-1+2v)/2}}L(\unicode[STIX]{x1D713},(s+u-1+2v)/2).\nonumber\end{eqnarray}$$Putting everything together, the Maaß contribution to (3.18) equals
 $$\begin{eqnarray}\mathop{\sum }_{A\mid ab}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(A)}\unicode[STIX]{x1D6E9}_{a,b,q}^{\text{Maa}\unicode[STIX]{x00DF}}(s,u,v,\unicode[STIX]{x1D713})\frac{L(\frac{s+u-1+2v}{2},\unicode[STIX]{x1D713})L(\frac{1-s+u}{2},f\times \unicode[STIX]{x1D713})}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})},\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{A\mid ab}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(A)}\unicode[STIX]{x1D6E9}_{a,b,q}^{\text{Maa}\unicode[STIX]{x00DF}}(s,u,v,\unicode[STIX]{x1D713})\frac{L(\frac{s+u-1+2v}{2},\unicode[STIX]{x1D713})L(\frac{1-s+u}{2},f\times \unicode[STIX]{x1D713})}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})},\end{eqnarray}$$where
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6E9}_{a,b,q}^{\text{Maa}\unicode[STIX]{x00DF}}(s,u,v,\unicode[STIX]{x1D713})\nonumber\\ \displaystyle & & \displaystyle \quad :=\mathop{\sum }_{\pm }\mathop{\sum }_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\in \{\pm \}}\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D713}}^{(1\mp \unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F})/2}q^{(3-s-u-2v)/2}\underset{A\mid B_{2}B_{3}\unicode[STIX]{x1D6FC}_{2}}{\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}B_{3}B_{4}B_{2}=b}}\frac{\unicode[STIX]{x1D707}(B_{2})\unicode[STIX]{x1D707}(B_{3})\unicode[STIX]{x1D6FC}_{1}^{s-1}\unicode[STIX]{x1D6FC}_{2}^{u}}{\unicode[STIX]{x1D6FD}_{1}^{u}B_{2}^{(s-u-1-2v)/2}B_{3}^{1-v}B_{4}^{1-v}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{M\mid (B_{2}B_{3}\unicode[STIX]{x1D6FC}_{2}/A)}\mathop{\sum }_{\substack{ d_{1},d_{2}\mid M \\ (d_{1},B_{2})=1}}\frac{\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}(M,d_{1})\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}(M,d_{2})d_{1}d_{2}((B_{2},d_{2})/d_{2})^{(s+u-1+2v)/2}}{Md_{1}^{(1-s+u)/2}L_{B_{2}}(f\times \unicode[STIX]{x1D713},(1-s+u)/2)\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D6FC}_{2}B_{3}B_{4}q}(1-s+u)}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FF}_{1}\mid d_{1}B_{3}B_{4} \\ (\unicode[STIX]{x1D6FF}_{1},A)=1}}\frac{\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FF}_{1})\unicode[STIX]{x1D706}(d_{1}B_{3}B_{4}/\unicode[STIX]{x1D6FF}_{1})}{\unicode[STIX]{x1D6FF}_{1}^{(1-s+u)/2}}\mathop{\sum }_{\unicode[STIX]{x1D6FF}_{2}\mid q}\frac{\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FF}_{2})\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(q/\unicode[STIX]{x1D6FF})}{\unicode[STIX]{x1D6FF}_{2}^{(1-s+u)/2}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{\substack{ B^{\ast }\mid (B_{2}/(d_{2},B_{2})) \\ (B^{\ast },A)=1}}\frac{\unicode[STIX]{x1D707}(B^{\ast })\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(B_{2}/((d_{2},B_{2})B^{\ast }))}{(B^{\ast })^{(s+u-1+2v)/2}}\mathscr{L}^{\pm \unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D6F9}_{a,b,s,u,v}^{\pm ,\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}}(t_{\unicode[STIX]{x1D713}})\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6E9}_{a,b,q}^{\text{Maa}\unicode[STIX]{x00DF}}(s,u,v,\unicode[STIX]{x1D713})\nonumber\\ \displaystyle & & \displaystyle \quad :=\mathop{\sum }_{\pm }\mathop{\sum }_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\in \{\pm \}}\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D713}}^{(1\mp \unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F})/2}q^{(3-s-u-2v)/2}\underset{A\mid B_{2}B_{3}\unicode[STIX]{x1D6FC}_{2}}{\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}B_{3}B_{4}B_{2}=b}}\frac{\unicode[STIX]{x1D707}(B_{2})\unicode[STIX]{x1D707}(B_{3})\unicode[STIX]{x1D6FC}_{1}^{s-1}\unicode[STIX]{x1D6FC}_{2}^{u}}{\unicode[STIX]{x1D6FD}_{1}^{u}B_{2}^{(s-u-1-2v)/2}B_{3}^{1-v}B_{4}^{1-v}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{M\mid (B_{2}B_{3}\unicode[STIX]{x1D6FC}_{2}/A)}\mathop{\sum }_{\substack{ d_{1},d_{2}\mid M \\ (d_{1},B_{2})=1}}\frac{\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}(M,d_{1})\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}(M,d_{2})d_{1}d_{2}((B_{2},d_{2})/d_{2})^{(s+u-1+2v)/2}}{Md_{1}^{(1-s+u)/2}L_{B_{2}}(f\times \unicode[STIX]{x1D713},(1-s+u)/2)\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D6FC}_{2}B_{3}B_{4}q}(1-s+u)}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FF}_{1}\mid d_{1}B_{3}B_{4} \\ (\unicode[STIX]{x1D6FF}_{1},A)=1}}\frac{\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FF}_{1})\unicode[STIX]{x1D706}(d_{1}B_{3}B_{4}/\unicode[STIX]{x1D6FF}_{1})}{\unicode[STIX]{x1D6FF}_{1}^{(1-s+u)/2}}\mathop{\sum }_{\unicode[STIX]{x1D6FF}_{2}\mid q}\frac{\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FF}_{2})\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(q/\unicode[STIX]{x1D6FF})}{\unicode[STIX]{x1D6FF}_{2}^{(1-s+u)/2}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\sum }_{\substack{ B^{\ast }\mid (B_{2}/(d_{2},B_{2})) \\ (B^{\ast },A)=1}}\frac{\unicode[STIX]{x1D707}(B^{\ast })\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(B_{2}/((d_{2},B_{2})B^{\ast }))}{(B^{\ast })^{(s+u-1+2v)/2}}\mathscr{L}^{\pm \unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D6F9}_{a,b,s,u,v}^{\pm ,\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}}(t_{\unicode[STIX]{x1D713}})\end{eqnarray}$$ for  $\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(A)$ of spectral parameter
$\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(A)$ of spectral parameter  $t_{\unicode[STIX]{x1D713}}$ and parity
$t_{\unicode[STIX]{x1D713}}$ and parity  $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D713}}$. Clearly this expression is holomorphic in the region (3.19). We proceed to confirm the bound (1.11) for
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D713}}$. Clearly this expression is holomorphic in the region (3.19). We proceed to confirm the bound (1.11) for  $\Re s=\Re u=\Re v=1/2$. This requires a little more than a trivial bound of (3.21). The critical variable is
$\Re s=\Re u=\Re v=1/2$. This requires a little more than a trivial bound of (3.21). The critical variable is  $B_{2}$. In order to get enough saving, we need to exploit some cancellation. To this end, we write
$B_{2}$. In order to get enough saving, we need to exploit some cancellation. To this end, we write  $M=M_{1}M_{2}$, where
$M=M_{1}M_{2}$, where  $(M_{1},B_{2})=1$ and
$(M_{1},B_{2})=1$ and  $M_{2}\mid B_{2}$. (Recall that
$M_{2}\mid B_{2}$. (Recall that  $ab$ is square-free.) Since
$ab$ is square-free.) Since  $(d_{1},B_{2})=1$, we have
$(d_{1},B_{2})=1$, we have  $d_{1}\mid M_{1}$, and we write
$d_{1}\mid M_{1}$, and we write  $d_{2}=d_{2}^{\prime }d_{2}^{\prime \prime }$ with
$d_{2}=d_{2}^{\prime }d_{2}^{\prime \prime }$ with  $d_{2}^{\prime }\mid M_{1}$,
$d_{2}^{\prime }\mid M_{1}$,  $d_{2}^{\prime \prime }\mid M_{2}$. In this way, the
$d_{2}^{\prime \prime }\mid M_{2}$. In this way, the  $M_{2}$-sum becomes
$M_{2}$-sum becomes
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{d_{2}^{\prime \prime }\mid M_{2}\mid (B_{2}/(A,B_{2}))}\frac{\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}(M_{2},1)\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}(M_{2},d_{2}^{\prime \prime })d_{2}^{\prime \prime }((B_{2},d_{2}^{\prime \prime })/d_{2}^{\prime \prime })^{(s+u-1+2v)/2}}{M_{2}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\sum }_{\substack{ B^{\ast }\mid (B_{2}/(d_{2}^{\prime \prime },B_{2})) \\ (B^{\ast },A)=1}}\frac{\unicode[STIX]{x1D707}(B^{\ast })\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(B_{2}/((d_{2}^{\prime \prime },B_{2})B^{\ast }))}{(B^{\ast })^{(s+u-1+2v)/2}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{d_{2}^{\prime \prime }\mid M_{2}\mid (B_{2}/(A,B_{2}))}\frac{\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}(M_{2},1)\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}(M_{2},d_{2}^{\prime \prime })d_{2}^{\prime \prime }((B_{2},d_{2}^{\prime \prime })/d_{2}^{\prime \prime })^{(s+u-1+2v)/2}}{M_{2}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\sum }_{\substack{ B^{\ast }\mid (B_{2}/(d_{2}^{\prime \prime },B_{2})) \\ (B^{\ast },A)=1}}\frac{\unicode[STIX]{x1D707}(B^{\ast })\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(B_{2}/((d_{2}^{\prime \prime },B_{2})B^{\ast }))}{(B^{\ast })^{(s+u-1+2v)/2}}.\end{eqnarray}$$ If  $B_{2}\mid A$, this is equal to
$B_{2}\mid A$, this is equal to  $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(B_{2})\ll B_{2}^{-1/2}$ by (2.3). If
$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(B_{2})\ll B_{2}^{-1/2}$ by (2.3). If  $B_{2}\nmid A$, this is equal to
$B_{2}\nmid A$, this is equal to
 $$\begin{eqnarray}\mathop{\prod }_{p\mid B_{2}}\biggl(\biggl(\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(p)-\frac{1}{p^{(s+u-1+2v)/2}}\biggr)\biggl(1+\frac{\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}(p,1)^{2}}{p}\biggr)+\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}(p,1)\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}(p,p)\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{p\mid B_{2}}\biggl(\biggl(\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(p)-\frac{1}{p^{(s+u-1+2v)/2}}\biggr)\biggl(1+\frac{\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}(p,1)^{2}}{p}\biggr)+\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}(p,1)\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D713}}(p,p)\biggr).\end{eqnarray}$$ By (2.10), the leading term  $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(p)$ cancels (to first-order approximation), and each
$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(p)$ cancels (to first-order approximation), and each  $p$-factor in the preceding display is bounded by
$p$-factor in the preceding display is bounded by  $p^{-1/2}+p^{3\unicode[STIX]{x1D703}-1}\ll p^{-1/2}$ for
$p^{-1/2}+p^{3\unicode[STIX]{x1D703}-1}\ll p^{-1/2}$ for  $\Re s=\Re u=\Re v=1/2$. Hence in all cases the
$\Re s=\Re u=\Re v=1/2$. Hence in all cases the  $M_{2}$-sum is
$M_{2}$-sum is  $\ll B_{2}^{-1/2+\unicode[STIX]{x1D700}}$. Combining with (3.20) and (2.11), we obtain
$\ll B_{2}^{-1/2+\unicode[STIX]{x1D700}}$. Combining with (3.20) and (2.11), we obtain
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{a,b,q}^{\text{Maa}\unicode[STIX]{x00DF}}(s,u,v,\unicode[STIX]{x1D713})\ll \frac{(abq)^{\unicode[STIX]{x1D700}}q^{1/2}}{(1+|t_{\unicode[STIX]{x1D713}}|)^{30}}\underset{A\mid B_{2}B_{3}\unicode[STIX]{x1D6FC}_{2}}{\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}B_{3}B_{4}B_{2}=b}}\mathop{\sum }_{\substack{ d_{1},d_{2}\mid M\mid (B_{2}B_{3}\unicode[STIX]{x1D6FC}_{2}/A) \\ (M,B_{2})=1}}\frac{d_{1}^{1/2}d_{2}^{1/2-\unicode[STIX]{x1D703}}(1+|\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(q)|)}{\unicode[STIX]{x1D6FC}_{2}^{1/2}B_{3}^{3/2-\unicode[STIX]{x1D703}}M^{1-2\unicode[STIX]{x1D703}}B_{2}^{1/2}}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{a,b,q}^{\text{Maa}\unicode[STIX]{x00DF}}(s,u,v,\unicode[STIX]{x1D713})\ll \frac{(abq)^{\unicode[STIX]{x1D700}}q^{1/2}}{(1+|t_{\unicode[STIX]{x1D713}}|)^{30}}\underset{A\mid B_{2}B_{3}\unicode[STIX]{x1D6FC}_{2}}{\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}B_{3}B_{4}B_{2}=b}}\mathop{\sum }_{\substack{ d_{1},d_{2}\mid M\mid (B_{2}B_{3}\unicode[STIX]{x1D6FC}_{2}/A) \\ (M,B_{2})=1}}\frac{d_{1}^{1/2}d_{2}^{1/2-\unicode[STIX]{x1D703}}(1+|\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(q)|)}{\unicode[STIX]{x1D6FC}_{2}^{1/2}B_{3}^{3/2-\unicode[STIX]{x1D703}}M^{1-2\unicode[STIX]{x1D703}}B_{2}^{1/2}}\end{eqnarray}$$ for  $\Re s=\Re u=\Re v=1/2$. This is increasing in
$\Re s=\Re u=\Re v=1/2$. This is increasing in  $d_{1},d_{2}$, and the result is increasing in
$d_{1},d_{2}$, and the result is increasing in  $M$, so that one easily confirms (1.11).
$M$, so that one easily confirms (1.11).
The same formula holds for the holomorphic contribution to (3.18), except that the transform  $\mathscr{L}^{\pm \unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D6F9}_{a,b,s,u,v}^{\pm ,\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}}(t_{\unicode[STIX]{x1D713}})$ has to be replaced with
$\mathscr{L}^{\pm \unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D6F9}_{a,b,s,u,v}^{\pm ,\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}}(t_{\unicode[STIX]{x1D713}})$ has to be replaced with  $\mathscr{L}^{\text{hol}}\unicode[STIX]{x1D6F9}_{a,b,s,u,v}^{\pm ,\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}}(k_{\unicode[STIX]{x1D713}})$ and
$\mathscr{L}^{\text{hol}}\unicode[STIX]{x1D6F9}_{a,b,s,u,v}^{\pm ,\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}}(k_{\unicode[STIX]{x1D713}})$ and  $\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D713}}=0$ if
$\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D713}}=0$ if  $\pm \unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}=-1$. The corresponding bound (1.12) is even simpler to obtain because
$\pm \unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}=-1$. The corresponding bound (1.12) is even simpler to obtain because  $\unicode[STIX]{x1D703}=0$ in the holomorphic case.
$\unicode[STIX]{x1D703}=0$ in the holomorphic case.
3.9 The Eisenstein contribution
By (2.12), we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{A}}_{B_{2}B_{3}\unicode[STIX]{x1D6FC}_{2}}^{\text{Eis}}(\unicode[STIX]{x1D716}qr,B_{2}r;\mathscr{L}^{\unicode[STIX]{x1D716}}\unicode[STIX]{x1D6F9})\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{\mathbb{R}}\frac{1}{B|\unicode[STIX]{x1D701}^{(B_{2}B_{3}\unicode[STIX]{x1D6FC}_{2})}(1+2it)|^{2}}\mathop{\sum }_{v\mid B_{2}B_{3}\unicode[STIX]{x1D6FC}_{2}}\frac{1}{v}\mathop{\sum }_{b_{1},b_{2}\mid v}\mathop{\sum }_{\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2}\mid B_{2}B_{3}\unicode[STIX]{x1D6FC}_{2}/v}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\unicode[STIX]{x1D707}(b_{1}\unicode[STIX]{x1D6FE}_{1})\unicode[STIX]{x1D707}(b_{2}\unicode[STIX]{x1D6FE}_{2})b_{1}b_{2}\biggl(\frac{b_{1}\unicode[STIX]{x1D6FE}_{2}}{b_{2}\unicode[STIX]{x1D6FE}_{1}}\biggr)^{it}\unicode[STIX]{x1D702}\biggl(\frac{qr}{b_{1}\unicode[STIX]{x1D6FE}_{1}},t\biggr)\unicode[STIX]{x1D702}\biggl(\frac{B_{2}n}{b_{2}\unicode[STIX]{x1D6FE}_{2}},-t\biggr)\mathscr{L}^{\unicode[STIX]{x1D716}}\unicode[STIX]{x1D6F9}(t)\frac{dt}{2\unicode[STIX]{x1D70B}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{A}}_{B_{2}B_{3}\unicode[STIX]{x1D6FC}_{2}}^{\text{Eis}}(\unicode[STIX]{x1D716}qr,B_{2}r;\mathscr{L}^{\unicode[STIX]{x1D716}}\unicode[STIX]{x1D6F9})\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{\mathbb{R}}\frac{1}{B|\unicode[STIX]{x1D701}^{(B_{2}B_{3}\unicode[STIX]{x1D6FC}_{2})}(1+2it)|^{2}}\mathop{\sum }_{v\mid B_{2}B_{3}\unicode[STIX]{x1D6FC}_{2}}\frac{1}{v}\mathop{\sum }_{b_{1},b_{2}\mid v}\mathop{\sum }_{\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2}\mid B_{2}B_{3}\unicode[STIX]{x1D6FC}_{2}/v}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\unicode[STIX]{x1D707}(b_{1}\unicode[STIX]{x1D6FE}_{1})\unicode[STIX]{x1D707}(b_{2}\unicode[STIX]{x1D6FE}_{2})b_{1}b_{2}\biggl(\frac{b_{1}\unicode[STIX]{x1D6FE}_{2}}{b_{2}\unicode[STIX]{x1D6FE}_{1}}\biggr)^{it}\unicode[STIX]{x1D702}\biggl(\frac{qr}{b_{1}\unicode[STIX]{x1D6FE}_{1}},t\biggr)\unicode[STIX]{x1D702}\biggl(\frac{B_{2}n}{b_{2}\unicode[STIX]{x1D6FE}_{2}},-t\biggr)\mathscr{L}^{\unicode[STIX]{x1D716}}\unicode[STIX]{x1D6F9}(t)\frac{dt}{2\unicode[STIX]{x1D70B}}.\end{eqnarray}$$ We saw in the previous subsection that the  $B_{2}$-variable was the most critical variable, and we finally used the strong bound (2.3) to get a sufficient saving. We do not have a direct analogue of this bound in the Eisenstein case when we make the choice of basis arising from (2.12), but luckily we can obtain additional cancellation by summing non-trivially over the cusps
$B_{2}$-variable was the most critical variable, and we finally used the strong bound (2.3) to get a sufficient saving. We do not have a direct analogue of this bound in the Eisenstein case when we make the choice of basis arising from (2.12), but luckily we can obtain additional cancellation by summing non-trivially over the cusps  $v$. This again requires some subtle manipulations.
$v$. This again requires some subtle manipulations.
Since  $(B_{2},B_{3}\unicode[STIX]{x1D6FC}_{2})=1$, we write
$(B_{2},B_{3}\unicode[STIX]{x1D6FC}_{2})=1$, we write  $v=v_{1}v_{2}$ with
$v=v_{1}v_{2}$ with  $v_{1}\mid B_{3}\unicode[STIX]{x1D6FC}_{2}$,
$v_{1}\mid B_{3}\unicode[STIX]{x1D6FC}_{2}$,  $v_{2}\mid B_{3}\unicode[STIX]{x1D6FC}_{2}$,
$v_{2}\mid B_{3}\unicode[STIX]{x1D6FC}_{2}$,  $b_{j}=b_{j}^{\prime }b_{j}^{\prime \prime }$, where
$b_{j}=b_{j}^{\prime }b_{j}^{\prime \prime }$, where  $b_{j}^{\prime }\mid v_{1}$,
$b_{j}^{\prime }\mid v_{1}$,  $b_{j}^{\prime \prime }\mid v_{2}$, and
$b_{j}^{\prime \prime }\mid v_{2}$, and  $\unicode[STIX]{x1D6FE}_{j}=\unicode[STIX]{x1D6FE}_{j}^{\prime }\unicode[STIX]{x1D6FE}_{j}^{\prime \prime }$, where
$\unicode[STIX]{x1D6FE}_{j}=\unicode[STIX]{x1D6FE}_{j}^{\prime }\unicode[STIX]{x1D6FE}_{j}^{\prime \prime }$, where  $\unicode[STIX]{x1D6FE}_{j}^{\prime }\mid B_{2}/v_{1}$,
$\unicode[STIX]{x1D6FE}_{j}^{\prime }\mid B_{2}/v_{1}$,  $\unicode[STIX]{x1D6FE}_{j}^{\prime \prime }\mid B_{3}\unicode[STIX]{x1D6FC}_{2}/v_{2}$. The key observation is that
$\unicode[STIX]{x1D6FE}_{j}^{\prime \prime }\mid B_{3}\unicode[STIX]{x1D6FC}_{2}/v_{2}$. The key observation is that  $(qr,B_{2})=1$ in our application, so that
$(qr,B_{2})=1$ in our application, so that  $b_{1}^{\prime }=\unicode[STIX]{x1D6FE}_{1}^{\prime }=1$. In this way, we can recast the previous
$b_{1}^{\prime }=\unicode[STIX]{x1D6FE}_{1}^{\prime }=1$. In this way, we can recast the previous  $v,b_{1},b_{2},\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2}$-sum as
$v,b_{1},b_{2},\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2}$-sum as
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\substack{ b_{2}^{\prime }\mid v_{1}\mid B_{2} \\ b_{1}^{\prime \prime },b_{2}^{\prime \prime }\mid v_{2}\mid B_{3}\unicode[STIX]{x1D6FC}_{2}}}\mathop{\sum }_{\unicode[STIX]{x1D6FE}_{2}^{\prime }\mid (B_{2}/v_{1})}\mathop{\sum }_{\unicode[STIX]{x1D6FE}_{1}^{\prime \prime },\unicode[STIX]{x1D6FE}_{2}^{\prime \prime }\mid (B_{3}\unicode[STIX]{x1D6FC}_{2}/v_{2})}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\frac{\unicode[STIX]{x1D707}(b_{1}^{\prime \prime }\unicode[STIX]{x1D6FE}_{1}^{\prime \prime })\unicode[STIX]{x1D707}(b_{2}^{\prime }b_{2}^{\prime \prime }\unicode[STIX]{x1D6FE}_{2}^{\prime }\unicode[STIX]{x1D6FE}_{2}^{\prime \prime })b_{1}^{\prime \prime }b_{2}^{\prime }b_{2}^{\prime \prime }}{v_{1}v_{2}}\biggl(\frac{b_{1}^{\prime \prime }\unicode[STIX]{x1D6FE}_{2}^{\prime }\unicode[STIX]{x1D6FE}_{2}^{\prime \prime }}{b_{2}^{\prime }b_{2}^{\prime \prime }\unicode[STIX]{x1D6FE}_{1}^{\prime \prime }}\biggr)^{it}\unicode[STIX]{x1D702}\biggl(\frac{qr}{b_{1}^{\prime \prime }\unicode[STIX]{x1D6FE}_{1}^{\prime \prime }},t\biggr)\unicode[STIX]{x1D702}\biggl(\frac{B_{2}n}{b_{2}^{\prime }b_{2}^{\prime \prime }\unicode[STIX]{x1D6FE}_{2}^{\prime }\unicode[STIX]{x1D6FE}_{2}^{\prime \prime }},-t\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\substack{ b_{2}^{\prime }\mid v_{1}\mid B_{2} \\ b_{1}^{\prime \prime },b_{2}^{\prime \prime }\mid v_{2}\mid B_{3}\unicode[STIX]{x1D6FC}_{2}}}\mathop{\sum }_{\unicode[STIX]{x1D6FE}_{2}^{\prime }\mid (B_{2}/v_{1})}\mathop{\sum }_{\unicode[STIX]{x1D6FE}_{1}^{\prime \prime },\unicode[STIX]{x1D6FE}_{2}^{\prime \prime }\mid (B_{3}\unicode[STIX]{x1D6FC}_{2}/v_{2})}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\frac{\unicode[STIX]{x1D707}(b_{1}^{\prime \prime }\unicode[STIX]{x1D6FE}_{1}^{\prime \prime })\unicode[STIX]{x1D707}(b_{2}^{\prime }b_{2}^{\prime \prime }\unicode[STIX]{x1D6FE}_{2}^{\prime }\unicode[STIX]{x1D6FE}_{2}^{\prime \prime })b_{1}^{\prime \prime }b_{2}^{\prime }b_{2}^{\prime \prime }}{v_{1}v_{2}}\biggl(\frac{b_{1}^{\prime \prime }\unicode[STIX]{x1D6FE}_{2}^{\prime }\unicode[STIX]{x1D6FE}_{2}^{\prime \prime }}{b_{2}^{\prime }b_{2}^{\prime \prime }\unicode[STIX]{x1D6FE}_{1}^{\prime \prime }}\biggr)^{it}\unicode[STIX]{x1D702}\biggl(\frac{qr}{b_{1}^{\prime \prime }\unicode[STIX]{x1D6FE}_{1}^{\prime \prime }},t\biggr)\unicode[STIX]{x1D702}\biggl(\frac{B_{2}n}{b_{2}^{\prime }b_{2}^{\prime \prime }\unicode[STIX]{x1D6FE}_{2}^{\prime }\unicode[STIX]{x1D6FE}_{2}^{\prime \prime }},-t\biggr).\nonumber\end{eqnarray}$$ We consider only the  $B_{2}$-part,
$B_{2}$-part,
 $$\begin{eqnarray}\mathop{\sum }_{b_{2}^{\prime }\mid v_{1}\mid B_{2}}\mathop{\sum }_{\unicode[STIX]{x1D6FE}_{2}^{\prime }\mid (B_{2}/v_{1})}\frac{1}{v_{1}}\unicode[STIX]{x1D707}(b_{2}^{\prime }\unicode[STIX]{x1D6FE}_{2}^{\prime })b_{2}^{\prime }\biggl(\frac{\unicode[STIX]{x1D6FE}_{2}^{\prime }}{b_{2}^{\prime }}\biggr)^{it}\unicode[STIX]{x1D702}\biggl(\frac{B_{2}n}{b_{2}^{\prime }b_{2}^{\prime \prime }\unicode[STIX]{x1D6FE}_{2}^{\prime }\unicode[STIX]{x1D6FE}_{2}^{\prime \prime }},-t\biggr),\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{b_{2}^{\prime }\mid v_{1}\mid B_{2}}\mathop{\sum }_{\unicode[STIX]{x1D6FE}_{2}^{\prime }\mid (B_{2}/v_{1})}\frac{1}{v_{1}}\unicode[STIX]{x1D707}(b_{2}^{\prime }\unicode[STIX]{x1D6FE}_{2}^{\prime })b_{2}^{\prime }\biggl(\frac{\unicode[STIX]{x1D6FE}_{2}^{\prime }}{b_{2}^{\prime }}\biggr)^{it}\unicode[STIX]{x1D702}\biggl(\frac{B_{2}n}{b_{2}^{\prime }b_{2}^{\prime \prime }\unicode[STIX]{x1D6FE}_{2}^{\prime }\unicode[STIX]{x1D6FE}_{2}^{\prime \prime }},-t\biggr),\end{eqnarray}$$ for fixed  $b_{2}^{\prime \prime },\unicode[STIX]{x1D6FE}_{2}^{\prime \prime }$, where we parametrize
$b_{2}^{\prime \prime },\unicode[STIX]{x1D6FE}_{2}^{\prime \prime }$, where we parametrize  $v_{1}=b_{2}^{\prime }b^{\ast }$,
$v_{1}=b_{2}^{\prime }b^{\ast }$,  $B_{2}/v_{1}=\unicode[STIX]{x1D6FE}_{2}^{\prime }\unicode[STIX]{x1D6FE}^{\ast }$, getting
$B_{2}/v_{1}=\unicode[STIX]{x1D6FE}_{2}^{\prime }\unicode[STIX]{x1D6FE}^{\ast }$, getting
 $$\begin{eqnarray}\mathop{\sum }_{b_{2}^{\prime }b^{\ast }\unicode[STIX]{x1D6FE}_{2}^{\prime }\unicode[STIX]{x1D6FE}^{\ast }=B_{2}}\frac{1}{b^{\ast }}\unicode[STIX]{x1D707}(b_{2}^{\prime }\unicode[STIX]{x1D6FE}_{2}^{\prime })\biggl(\frac{\unicode[STIX]{x1D6FE}_{2}^{\prime }}{b_{2}^{\prime }}\biggr)^{it}\unicode[STIX]{x1D702}\biggl(b^{\ast }\unicode[STIX]{x1D6FE}^{\ast }\frac{n}{b_{2}^{\prime \prime }\unicode[STIX]{x1D6FE}_{2}^{\prime \prime }},-t\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{b_{2}^{\prime }b^{\ast }\unicode[STIX]{x1D6FE}_{2}^{\prime }\unicode[STIX]{x1D6FE}^{\ast }=B_{2}}\frac{1}{b^{\ast }}\unicode[STIX]{x1D707}(b_{2}^{\prime }\unicode[STIX]{x1D6FE}_{2}^{\prime })\biggl(\frac{\unicode[STIX]{x1D6FE}_{2}^{\prime }}{b_{2}^{\prime }}\biggr)^{it}\unicode[STIX]{x1D702}\biggl(b^{\ast }\unicode[STIX]{x1D6FE}^{\ast }\frac{n}{b_{2}^{\prime \prime }\unicode[STIX]{x1D6FE}_{2}^{\prime \prime }},-t\biggr).\end{eqnarray}$$ We must have  $b_{2}^{\prime \prime }\unicode[STIX]{x1D6FE}_{2}^{\prime \prime }\mid n$, so we write
$b_{2}^{\prime \prime }\unicode[STIX]{x1D6FE}_{2}^{\prime \prime }\mid n$, so we write  $n=b_{2}^{\prime \prime }\unicode[STIX]{x1D6FE}_{2}^{\prime \prime }n^{\ast }$. Applying the Hecke relation (2.1) for
$n=b_{2}^{\prime \prime }\unicode[STIX]{x1D6FE}_{2}^{\prime \prime }n^{\ast }$. Applying the Hecke relation (2.1) for  $\unicode[STIX]{x1D702}(n,t)$, we obtain
$\unicode[STIX]{x1D702}(n,t)$, we obtain
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ b_{2}^{\prime }b^{\ast }\unicode[STIX]{x1D6FE}_{2}^{\prime }\unicode[STIX]{x1D6FE}^{\ast }=B_{2} \\ \unicode[STIX]{x1D6FF}\mid (n^{\ast },b^{\ast }\unicode[STIX]{x1D6FE}^{\ast })}}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FF})\frac{1}{b^{\ast }}\unicode[STIX]{x1D707}(b_{2}^{\prime }\unicode[STIX]{x1D6FE}_{2}^{\prime })\biggl(\frac{\unicode[STIX]{x1D6FE}_{2}^{\prime }}{b_{2}^{\prime }}\biggr)^{it}\unicode[STIX]{x1D702}\biggl(\frac{b^{\ast }\unicode[STIX]{x1D6FE}^{\ast }}{\unicode[STIX]{x1D6FF}},-t\biggr)\unicode[STIX]{x1D702}\biggl(\frac{n^{\ast }}{\unicode[STIX]{x1D6FF}},-t\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ b_{2}^{\prime }b^{\ast }\unicode[STIX]{x1D6FE}_{2}^{\prime }\unicode[STIX]{x1D6FE}^{\ast }=B_{2} \\ \unicode[STIX]{x1D6FF}\mid (n^{\ast },b^{\ast }\unicode[STIX]{x1D6FE}^{\ast })}}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FF})\frac{1}{b^{\ast }}\unicode[STIX]{x1D707}(b_{2}^{\prime }\unicode[STIX]{x1D6FE}_{2}^{\prime })\biggl(\frac{\unicode[STIX]{x1D6FE}_{2}^{\prime }}{b_{2}^{\prime }}\biggr)^{it}\unicode[STIX]{x1D702}\biggl(\frac{b^{\ast }\unicode[STIX]{x1D6FE}^{\ast }}{\unicode[STIX]{x1D6FF}},-t\biggr)\unicode[STIX]{x1D702}\biggl(\frac{n^{\ast }}{\unicode[STIX]{x1D6FF}},-t\biggr).\end{eqnarray}$$ We parametrize  $\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6FF}_{2}$,
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6FF}_{2}$,  $b^{\ast }=\unicode[STIX]{x1D6FF}_{1}b_{0}$,
$b^{\ast }=\unicode[STIX]{x1D6FF}_{1}b_{0}$,  $\unicode[STIX]{x1D6FE}^{\ast }=\unicode[STIX]{x1D6FF}_{2}\unicode[STIX]{x1D6FE}_{0}$, so that the previous line is equal to
$\unicode[STIX]{x1D6FE}^{\ast }=\unicode[STIX]{x1D6FF}_{2}\unicode[STIX]{x1D6FE}_{0}$, so that the previous line is equal to
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ b_{2}^{\prime }\unicode[STIX]{x1D6FF}_{1}b_{0}\unicode[STIX]{x1D6FE}_{2}^{\prime }\unicode[STIX]{x1D6FF}_{2}\unicode[STIX]{x1D6FE}_{0}=B_{2} \\ \unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6FF}_{2}\mid n^{\ast }}}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6FF}_{2})\frac{1}{\unicode[STIX]{x1D6FF}_{1}b}\unicode[STIX]{x1D707}(b_{2}^{\prime }\unicode[STIX]{x1D6FE}_{2}^{\prime })\biggl(\frac{\unicode[STIX]{x1D6FE}_{2}^{\prime }}{b_{2}^{\prime }}\biggr)^{it}\unicode[STIX]{x1D702}(b_{0},-t)\unicode[STIX]{x1D702}(\unicode[STIX]{x1D6FE}_{0},-t)\unicode[STIX]{x1D702}\biggl(\frac{n^{\ast }}{\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6FF}_{2}},-t\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ b_{2}^{\prime }\unicode[STIX]{x1D6FF}_{1}b_{0}\unicode[STIX]{x1D6FE}_{2}^{\prime }\unicode[STIX]{x1D6FF}_{2}\unicode[STIX]{x1D6FE}_{0}=B_{2} \\ \unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6FF}_{2}\mid n^{\ast }}}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6FF}_{2})\frac{1}{\unicode[STIX]{x1D6FF}_{1}b}\unicode[STIX]{x1D707}(b_{2}^{\prime }\unicode[STIX]{x1D6FE}_{2}^{\prime })\biggl(\frac{\unicode[STIX]{x1D6FE}_{2}^{\prime }}{b_{2}^{\prime }}\biggr)^{it}\unicode[STIX]{x1D702}(b_{0},-t)\unicode[STIX]{x1D702}(\unicode[STIX]{x1D6FE}_{0},-t)\unicode[STIX]{x1D702}\biggl(\frac{n^{\ast }}{\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6FF}_{2}},-t\biggr).\end{eqnarray}$$ The key point is now that, by Möbius inversion, the  $b_{2}^{\prime },\unicode[STIX]{x1D6FE}_{2}^{\prime },\unicode[STIX]{x1D6FE}_{0}$-sum disappears, so that (3.24) is equal to
$b_{2}^{\prime },\unicode[STIX]{x1D6FE}_{2}^{\prime },\unicode[STIX]{x1D6FE}_{0}$-sum disappears, so that (3.24) is equal to
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FF}_{1}b_{0}\unicode[STIX]{x1D6FF}_{2}=B_{2} \\ \unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6FF}_{2}\mid n^{\ast }}}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6FF}_{2})\frac{1}{\unicode[STIX]{x1D6FF}_{1}b}\unicode[STIX]{x1D702}(b_{0},-t)\unicode[STIX]{x1D702}\biggl(\frac{n^{\ast }}{\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6FF}_{2}},-t\biggr),\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FF}_{1}b_{0}\unicode[STIX]{x1D6FF}_{2}=B_{2} \\ \unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6FF}_{2}\mid n^{\ast }}}\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6FF}_{2})\frac{1}{\unicode[STIX]{x1D6FF}_{1}b}\unicode[STIX]{x1D702}(b_{0},-t)\unicode[STIX]{x1D702}\biggl(\frac{n^{\ast }}{\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6FF}_{2}},-t\biggr),\end{eqnarray}$$and hence (3.23) is equal to
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\mathbb{R}}\underset{b_{2}\unicode[STIX]{x1D6FE}_{2}\mid n}{\mathop{\sum }_{b_{1},b_{2}\mid v\mid B_{3}\unicode[STIX]{x1D6FC}_{2}}\mathop{\sum }_{\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2}\mid B_{3}\unicode[STIX]{x1D6FC}_{2}/v}}\frac{\unicode[STIX]{x1D707}(b_{1}\unicode[STIX]{x1D6FE}_{1})\unicode[STIX]{x1D707}(b_{2}\unicode[STIX]{x1D6FE}_{2})b_{1}b_{2}}{vB_{2}B_{3}\unicode[STIX]{x1D6FC}_{2}|\unicode[STIX]{x1D701}^{(B_{2}B_{3}\unicode[STIX]{x1D6FC}_{2})}(1+2it)|^{2}}\biggl(\frac{b_{1}\unicode[STIX]{x1D6FE}_{2}}{b_{2}\unicode[STIX]{x1D6FE}_{1}}\biggr)^{it}\unicode[STIX]{x1D702}\biggl(\frac{qr}{b_{1}\unicode[STIX]{x1D6FE}_{1}},t\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FF}_{1}b_{0}\unicode[STIX]{x1D6FF}_{2}=B_{2} \\ \unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6FF}_{2}\mid n}}\frac{\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6FF}_{2})\unicode[STIX]{x1D702}(b_{0},-t)}{\unicode[STIX]{x1D6FF}_{1}b_{0}}\unicode[STIX]{x1D702}\biggl(\frac{n}{b_{2}\unicode[STIX]{x1D6FE}_{2}\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6FF}_{2}},-t\biggr)\mathscr{L}^{\unicode[STIX]{x1D716}}\unicode[STIX]{x1D6F9}(t)\frac{dt}{2\unicode[STIX]{x1D70B}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\mathbb{R}}\underset{b_{2}\unicode[STIX]{x1D6FE}_{2}\mid n}{\mathop{\sum }_{b_{1},b_{2}\mid v\mid B_{3}\unicode[STIX]{x1D6FC}_{2}}\mathop{\sum }_{\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2}\mid B_{3}\unicode[STIX]{x1D6FC}_{2}/v}}\frac{\unicode[STIX]{x1D707}(b_{1}\unicode[STIX]{x1D6FE}_{1})\unicode[STIX]{x1D707}(b_{2}\unicode[STIX]{x1D6FE}_{2})b_{1}b_{2}}{vB_{2}B_{3}\unicode[STIX]{x1D6FC}_{2}|\unicode[STIX]{x1D701}^{(B_{2}B_{3}\unicode[STIX]{x1D6FC}_{2})}(1+2it)|^{2}}\biggl(\frac{b_{1}\unicode[STIX]{x1D6FE}_{2}}{b_{2}\unicode[STIX]{x1D6FE}_{1}}\biggr)^{it}\unicode[STIX]{x1D702}\biggl(\frac{qr}{b_{1}\unicode[STIX]{x1D6FE}_{1}},t\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FF}_{1}b_{0}\unicode[STIX]{x1D6FF}_{2}=B_{2} \\ \unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6FF}_{2}\mid n}}\frac{\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6FF}_{2})\unicode[STIX]{x1D702}(b_{0},-t)}{\unicode[STIX]{x1D6FF}_{1}b_{0}}\unicode[STIX]{x1D702}\biggl(\frac{n}{b_{2}\unicode[STIX]{x1D6FE}_{2}\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6FF}_{2}},-t\biggr)\mathscr{L}^{\unicode[STIX]{x1D716}}\unicode[STIX]{x1D6F9}(t)\frac{dt}{2\unicode[STIX]{x1D70B}}.\nonumber\end{eqnarray}$$ After this manoeuvre, we are now in shape to sum over  $r$ and
$r$ and  $n$ as in (3.18). This gives
$n$ as in (3.18). This gives
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\mathbb{R}}\mathop{\sum }_{b_{1},b_{2}\mid v\mid B_{3}\unicode[STIX]{x1D6FC}_{2}}\mathop{\sum }_{\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2}\mid (B_{3}\unicode[STIX]{x1D6FC}_{2}/v)}\frac{\unicode[STIX]{x1D707}(b_{1}\unicode[STIX]{x1D6FE}_{1})\unicode[STIX]{x1D707}(b_{2}\unicode[STIX]{x1D6FE}_{2})b_{1}b_{2}}{vB_{2}B_{3}\unicode[STIX]{x1D6FC}_{2}|\unicode[STIX]{x1D701}^{(B_{2}B_{3}\unicode[STIX]{x1D6FC}_{2})}(1+2it)|^{2}}\biggl(\frac{b_{1}\unicode[STIX]{x1D6FE}_{2}}{b_{2}\unicode[STIX]{x1D6FE}_{1}}\biggr)^{it}\mathop{\sum }_{\unicode[STIX]{x1D6FF}_{1}b_{0}\unicode[STIX]{x1D6FF}_{2}=B_{2}}\frac{\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6FF}_{2})\unicode[STIX]{x1D702}(b_{0},-t)}{\unicode[STIX]{x1D6FF}_{1}b_{0}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\sum }_{(r,B_{2})=1}\frac{\unicode[STIX]{x1D706}(rb_{1}\unicode[STIX]{x1D6FE}_{1}B_{3}B_{4})\unicode[STIX]{x1D702}(qr,t)}{(b_{1}\unicode[STIX]{x1D6FE}_{1}r)^{(1-s+u)/2}}\mathop{\sum }_{n}\frac{\unicode[STIX]{x1D702}(n,-t)}{(b_{2}\unicode[STIX]{x1D6FE}_{2}\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6FF}_{2}n)^{(s+u-1+2v)/2}}\mathscr{L}^{\pm \unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D6F9}(t)\frac{dt}{2\unicode[STIX]{x1D70B}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\mathbb{R}}\mathop{\sum }_{b_{1},b_{2}\mid v\mid B_{3}\unicode[STIX]{x1D6FC}_{2}}\mathop{\sum }_{\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2}\mid (B_{3}\unicode[STIX]{x1D6FC}_{2}/v)}\frac{\unicode[STIX]{x1D707}(b_{1}\unicode[STIX]{x1D6FE}_{1})\unicode[STIX]{x1D707}(b_{2}\unicode[STIX]{x1D6FE}_{2})b_{1}b_{2}}{vB_{2}B_{3}\unicode[STIX]{x1D6FC}_{2}|\unicode[STIX]{x1D701}^{(B_{2}B_{3}\unicode[STIX]{x1D6FC}_{2})}(1+2it)|^{2}}\biggl(\frac{b_{1}\unicode[STIX]{x1D6FE}_{2}}{b_{2}\unicode[STIX]{x1D6FE}_{1}}\biggr)^{it}\mathop{\sum }_{\unicode[STIX]{x1D6FF}_{1}b_{0}\unicode[STIX]{x1D6FF}_{2}=B_{2}}\frac{\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6FF}_{2})\unicode[STIX]{x1D702}(b_{0},-t)}{\unicode[STIX]{x1D6FF}_{1}b_{0}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\sum }_{(r,B_{2})=1}\frac{\unicode[STIX]{x1D706}(rb_{1}\unicode[STIX]{x1D6FE}_{1}B_{3}B_{4})\unicode[STIX]{x1D702}(qr,t)}{(b_{1}\unicode[STIX]{x1D6FE}_{1}r)^{(1-s+u)/2}}\mathop{\sum }_{n}\frac{\unicode[STIX]{x1D702}(n,-t)}{(b_{2}\unicode[STIX]{x1D6FE}_{2}\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6FF}_{2}n)^{(s+u-1+2v)/2}}\mathscr{L}^{\pm \unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D6F9}(t)\frac{dt}{2\unicode[STIX]{x1D70B}}.\nonumber\end{eqnarray}$$ The  $n$-sum can be easily evaluated in terms of the Riemann zeta function. The
$n$-sum can be easily evaluated in terms of the Riemann zeta function. The  $r$-sum requires multiple applications of (2.1). Checking local factors, we confirm that, for
$r$-sum requires multiple applications of (2.1). Checking local factors, we confirm that, for  $(B,q)=(B_{2},Bq)=1$,
$(B,q)=(B_{2},Bq)=1$,  $B$ square-free, and
$B$ square-free, and  $q$ prime, we have
$q$ prime, we have
 $$\begin{eqnarray}\mathop{\sum }_{(B_{2},r)=1}\frac{\unicode[STIX]{x1D706}(rB)\unicode[STIX]{x1D702}(qr,t)}{r^{z}}=\frac{\unicode[STIX]{x1D702}(q,t)-\unicode[STIX]{x1D706}(q)q^{-z}}{1-q^{-2z}}\mathop{\prod }_{p\mid B}\frac{\unicode[STIX]{x1D706}(p)-\unicode[STIX]{x1D702}(p,t)p^{-z}}{1-p^{-2z}}\mathop{\sum }_{(B_{2},r)=1}\frac{\unicode[STIX]{x1D706}(r)\unicode[STIX]{x1D702}(r,t)}{r^{z}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{(B_{2},r)=1}\frac{\unicode[STIX]{x1D706}(rB)\unicode[STIX]{x1D702}(qr,t)}{r^{z}}=\frac{\unicode[STIX]{x1D702}(q,t)-\unicode[STIX]{x1D706}(q)q^{-z}}{1-q^{-2z}}\mathop{\prod }_{p\mid B}\frac{\unicode[STIX]{x1D706}(p)-\unicode[STIX]{x1D702}(p,t)p^{-z}}{1-p^{-2z}}\mathop{\sum }_{(B_{2},r)=1}\frac{\unicode[STIX]{x1D706}(r)\unicode[STIX]{x1D702}(r,t)}{r^{z}}.\end{eqnarray}$$Putting everything together, the Eisenstein contribution to (3.18) is equal to
 $$\begin{eqnarray}\int _{\mathbb{R}}\unicode[STIX]{x1D6E9}_{a,b,q}^{\text{Eis}}(s,u,v,t)\frac{\unicode[STIX]{x1D701}(\frac{s+u-1+2v}{2}+it)L(\frac{s+u-1+2v}{2}-it)\unicode[STIX]{x1D701}(\frac{1-s+u}{2}+it,f)L(\frac{1-s+u}{2}-it,f)}{\unicode[STIX]{x1D701}(1+2it)\unicode[STIX]{x1D701}(1-2it)}\frac{dt}{2\unicode[STIX]{x1D70B}},\end{eqnarray}$$
$$\begin{eqnarray}\int _{\mathbb{R}}\unicode[STIX]{x1D6E9}_{a,b,q}^{\text{Eis}}(s,u,v,t)\frac{\unicode[STIX]{x1D701}(\frac{s+u-1+2v}{2}+it)L(\frac{s+u-1+2v}{2}-it)\unicode[STIX]{x1D701}(\frac{1-s+u}{2}+it,f)L(\frac{1-s+u}{2}-it,f)}{\unicode[STIX]{x1D701}(1+2it)\unicode[STIX]{x1D701}(1-2it)}\frac{dt}{2\unicode[STIX]{x1D70B}},\end{eqnarray}$$where
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6E9}_{a,b,q}^{\text{Eis}}(s,u,v,t):=\mathop{\sum }_{\pm }\mathop{\sum }_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\in \{\pm \}}\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}B_{3}B_{4}B_{2}=b}\frac{q^{(3-s-u-2v)/2}\unicode[STIX]{x1D707}(B_{2})\unicode[STIX]{x1D707}(B_{3})\unicode[STIX]{x1D6FC}_{1}^{s-1}\unicode[STIX]{x1D6FC}_{2}^{u}}{\unicode[STIX]{x1D6FD}_{1}^{u}B_{2}^{(s-u-1-2v)/2}B_{3}^{1-v}B_{4}^{1-v}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\sum }_{b_{1},b_{2}\mid v\mid B_{3}\unicode[STIX]{x1D6FC}_{2}}\mathop{\sum }_{\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2}\mid (B_{3}\unicode[STIX]{x1D6FC}_{2}/v)}\frac{\unicode[STIX]{x1D707}(b_{1}\unicode[STIX]{x1D6FE}_{1})\unicode[STIX]{x1D707}(b_{2}\unicode[STIX]{x1D6FE}_{2})b_{1}b_{2}}{vB_{2}B_{3}\unicode[STIX]{x1D6FC}_{2}|\unicode[STIX]{x1D701}^{(B_{2}B_{3}\unicode[STIX]{x1D6FC}_{2})}(1+2it)|^{2}}\biggl(\frac{b_{1}\unicode[STIX]{x1D6FE}_{2}}{b_{2}\unicode[STIX]{x1D6FE}_{1}}\biggr)^{it}\frac{\unicode[STIX]{x1D702}(q,t)-\unicode[STIX]{x1D706}(q)q^{-(1-s+u)/2}}{1-q^{-(1-s+u)}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\sum }_{\unicode[STIX]{x1D6FF}_{1}b_{0}\unicode[STIX]{x1D6FF}_{2}=B_{2}}\frac{\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6FF}_{2})\unicode[STIX]{x1D702}(b_{0},-t)}{\unicode[STIX]{x1D6FF}_{1}b_{0}(b_{1}\unicode[STIX]{x1D6FE}_{1})^{(1-s+u)/2}(b_{2}\unicode[STIX]{x1D6FE}_{2}\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6FF}_{2})^{(s+u-1+2v)/2}}\mathop{\prod }_{p\mid b_{1}\unicode[STIX]{x1D6FE}_{1}B_{3}B_{4}}\frac{\unicode[STIX]{x1D706}(p)-\unicode[STIX]{x1D702}(p,t)p^{-(1-s+u)/2}}{1-p^{-(1-s+u)}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\frac{\unicode[STIX]{x1D701}_{B_{2}B_{3}\unicode[STIX]{x1D6FC}_{2}}(1+2it)\unicode[STIX]{x1D701}_{B_{2}B_{3}\unicode[STIX]{x1D6FC}_{2}}(1-2it)}{\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D6FC}_{2}B_{3}B_{4}q}(1-s+u)L_{B_{2}}(\frac{1-s+u}{2}+it,f)L_{B_{2}}(\frac{1-s+u}{2}-it,f)}\mathscr{L}^{\pm \unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D6F9}_{a,b,s,u,v}^{\pm ,\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}}(t).\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6E9}_{a,b,q}^{\text{Eis}}(s,u,v,t):=\mathop{\sum }_{\pm }\mathop{\sum }_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\in \{\pm \}}\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}=a}\mathop{\sum }_{\unicode[STIX]{x1D6FD}_{1}B_{3}B_{4}B_{2}=b}\frac{q^{(3-s-u-2v)/2}\unicode[STIX]{x1D707}(B_{2})\unicode[STIX]{x1D707}(B_{3})\unicode[STIX]{x1D6FC}_{1}^{s-1}\unicode[STIX]{x1D6FC}_{2}^{u}}{\unicode[STIX]{x1D6FD}_{1}^{u}B_{2}^{(s-u-1-2v)/2}B_{3}^{1-v}B_{4}^{1-v}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\sum }_{b_{1},b_{2}\mid v\mid B_{3}\unicode[STIX]{x1D6FC}_{2}}\mathop{\sum }_{\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2}\mid (B_{3}\unicode[STIX]{x1D6FC}_{2}/v)}\frac{\unicode[STIX]{x1D707}(b_{1}\unicode[STIX]{x1D6FE}_{1})\unicode[STIX]{x1D707}(b_{2}\unicode[STIX]{x1D6FE}_{2})b_{1}b_{2}}{vB_{2}B_{3}\unicode[STIX]{x1D6FC}_{2}|\unicode[STIX]{x1D701}^{(B_{2}B_{3}\unicode[STIX]{x1D6FC}_{2})}(1+2it)|^{2}}\biggl(\frac{b_{1}\unicode[STIX]{x1D6FE}_{2}}{b_{2}\unicode[STIX]{x1D6FE}_{1}}\biggr)^{it}\frac{\unicode[STIX]{x1D702}(q,t)-\unicode[STIX]{x1D706}(q)q^{-(1-s+u)/2}}{1-q^{-(1-s+u)}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\sum }_{\unicode[STIX]{x1D6FF}_{1}b_{0}\unicode[STIX]{x1D6FF}_{2}=B_{2}}\frac{\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6FF}_{2})\unicode[STIX]{x1D702}(b_{0},-t)}{\unicode[STIX]{x1D6FF}_{1}b_{0}(b_{1}\unicode[STIX]{x1D6FE}_{1})^{(1-s+u)/2}(b_{2}\unicode[STIX]{x1D6FE}_{2}\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6FF}_{2})^{(s+u-1+2v)/2}}\mathop{\prod }_{p\mid b_{1}\unicode[STIX]{x1D6FE}_{1}B_{3}B_{4}}\frac{\unicode[STIX]{x1D706}(p)-\unicode[STIX]{x1D702}(p,t)p^{-(1-s+u)/2}}{1-p^{-(1-s+u)}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\frac{\unicode[STIX]{x1D701}_{B_{2}B_{3}\unicode[STIX]{x1D6FC}_{2}}(1+2it)\unicode[STIX]{x1D701}_{B_{2}B_{3}\unicode[STIX]{x1D6FC}_{2}}(1-2it)}{\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D6FC}_{2}B_{3}B_{4}q}(1-s+u)L_{B_{2}}(\frac{1-s+u}{2}+it,f)L_{B_{2}}(\frac{1-s+u}{2}-it,f)}\mathscr{L}^{\pm \unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D6F9}_{a,b,s,u,v}^{\pm ,\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}}(t).\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$ The term (3.25) is clearly holomorphic in the range (3.1) and it can easily be extended as long as  $\Re (u-s)>1$ and
$\Re (u-s)>1$ and  $\Re (s+u+2v)>3$. To pass these two hyperplanes, we observe that the presence of the Riemann zeta function in the numerator contributes residues, and so we apply the argument of [Reference Blomer and KhanBK19b, Lemma 16] to show that the meromorphic continuation of (3.25) in the region
$\Re (s+u+2v)>3$. To pass these two hyperplanes, we observe that the presence of the Riemann zeta function in the numerator contributes residues, and so we apply the argument of [Reference Blomer and KhanBK19b, Lemma 16] to show that the meromorphic continuation of (3.25) in the region  $\Re (u-s)<1$ and
$\Re (u-s)<1$ and  $\Re (s+u+2v)<3$ is given by the same expression plus the polar term
$\Re (s+u+2v)<3$ is given by the same expression plus the polar term
 $$\begin{eqnarray}\displaystyle {\mathcal{P}}_{a,b,q}^{(3)}(s,u,v) & := & \displaystyle \sum \mathop{\{}_{\substack{ t=\pm i(1+s-u)/2 \\ t=\pm i(3-s-u-2v)/2}}(\pm i)\frac{\mathop{\unicode[STIX]{x1D6E9}}_{a,b,q}^{\text{Eis}}(s,u,v,t)\unicode[STIX]{x1D701}(\frac{s+u-1+2v}{2}+it)}{\unicode[STIX]{x1D701}(1+2it)\unicode[STIX]{x1D701}(1-2it)}\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D701}\biggl(\frac{s+u-1+2v}{2}-it\biggr)L\biggl(\frac{1-s+u}{2}+it,f\biggr)L\biggl(\frac{1-s+u}{2}-it,f\biggr).\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{P}}_{a,b,q}^{(3)}(s,u,v) & := & \displaystyle \sum \mathop{\{}_{\substack{ t=\pm i(1+s-u)/2 \\ t=\pm i(3-s-u-2v)/2}}(\pm i)\frac{\mathop{\unicode[STIX]{x1D6E9}}_{a,b,q}^{\text{Eis}}(s,u,v,t)\unicode[STIX]{x1D701}(\frac{s+u-1+2v}{2}+it)}{\unicode[STIX]{x1D701}(1+2it)\unicode[STIX]{x1D701}(1-2it)}\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D701}\biggl(\frac{s+u-1+2v}{2}-it\biggr)L\biggl(\frac{1-s+u}{2}+it,f\biggr)L\biggl(\frac{1-s+u}{2}-it,f\biggr).\qquad\end{eqnarray}$$ A trivial estimation confirms (1.13) for the term on the right-hand side of (3.25) with  $\Re s=\Re u=\Re v=1/2$,
$\Re s=\Re u=\Re v=1/2$,  $t\in \mathbb{R}$,
$t\in \mathbb{R}$,  $a\asymp b$ (which differs from the meromorphic continuation of (3.25) to this region by (3.27)).
$a\asymp b$ (which differs from the meromorphic continuation of (3.25) to this region by (3.27)).
It remains to meromorphically continue and bound the joint polar term
 $$\begin{eqnarray}{\mathcal{P}}_{a,b,q}(s,u,v):=\mathop{\sum }_{j=1}^{3}{\mathcal{P}}_{a,b,q}^{(j)}(s,u,v),\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{P}}_{a,b,q}(s,u,v):=\mathop{\sum }_{j=1}^{3}{\mathcal{P}}_{a,b,q}^{(j)}(s,u,v),\end{eqnarray}$$ where we recall (3.15) and (3.16) for  $j=1,2$. In these cases, it is easily seen that
$j=1,2$. In these cases, it is easily seen that  ${\mathcal{P}}_{a,b,q}^{(j)}(s,u,v)$ continues meromorphically to a neighbourhood of (3.19), and for
${\mathcal{P}}_{a,b,q}^{(j)}(s,u,v)$ continues meromorphically to a neighbourhood of (3.19), and for  $1/2-\unicode[STIX]{x1D700}<\Re s=\Re u=\Re v<1/2+\unicode[STIX]{x1D700}$,
$1/2-\unicode[STIX]{x1D700}<\Re s=\Re u=\Re v<1/2+\unicode[STIX]{x1D700}$,  $a\asymp b$, we have the bound
$a\asymp b$, we have the bound
 $$\begin{eqnarray}|{\mathcal{P}}_{a,b,q}^{(1)}(s,u,v)|+|{\mathcal{P}}_{a,b,q}^{(2)}(s,u,v)|\ll q(ab)^{-1/2}(abq)^{\unicode[STIX]{x1D700}}\end{eqnarray}$$
$$\begin{eqnarray}|{\mathcal{P}}_{a,b,q}^{(1)}(s,u,v)|+|{\mathcal{P}}_{a,b,q}^{(2)}(s,u,v)|\ll q(ab)^{-1/2}(abq)^{\unicode[STIX]{x1D700}}\end{eqnarray}$$ away from poles. The treatment of  ${\mathcal{P}}_{a,b,q}^{(3)}(s,u,v)$ requires slightly more effort, because we need to analyze
${\mathcal{P}}_{a,b,q}^{(3)}(s,u,v)$ requires slightly more effort, because we need to analyze  $\unicode[STIX]{x1D6E9}_{a,b,q}^{\text{Eis}}(s,u,v,t)$ for
$\unicode[STIX]{x1D6E9}_{a,b,q}^{\text{Eis}}(s,u,v,t)$ for  $|\Im t|\leqslant 1/2$. The meromorphic continuation of
$|\Im t|\leqslant 1/2$. The meromorphic continuation of  $\mathscr{L}^{\pm \unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D6F9}_{a,b,s,u,v}^{\pm ,\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}}(t)$ with at most finitely many poles (and hence of
$\mathscr{L}^{\pm \unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D6F9}_{a,b,s,u,v}^{\pm ,\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}}(t)$ with at most finitely many poles (and hence of  $\unicode[STIX]{x1D6E9}_{a,b,q}^{\text{Eis}}(s,u,v,t)$) to that region follows from [Reference Blomer and KhanBK19b, Lemma 3b]. Again, a trivial upper bound yields
$\unicode[STIX]{x1D6E9}_{a,b,q}^{\text{Eis}}(s,u,v,t)$) to that region follows from [Reference Blomer and KhanBK19b, Lemma 3b]. Again, a trivial upper bound yields
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{a,b,q}^{\text{Eis}}(s,u,v,t)\ll (abq)^{\unicode[STIX]{x1D700}}\frac{q}{(ab)^{1/2-\unicode[STIX]{x1D703}}}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{a,b,q}^{\text{Eis}}(s,u,v,t)\ll (abq)^{\unicode[STIX]{x1D700}}\frac{q}{(ab)^{1/2-\unicode[STIX]{x1D703}}}\end{eqnarray}$$ for fixed  $s,u,v,t$ with
$s,u,v,t$ with  $1/2-\unicode[STIX]{x1D700}<\Re s=\Re u=\Re v<1/2+\unicode[STIX]{x1D700}$,
$1/2-\unicode[STIX]{x1D700}<\Re s=\Re u=\Re v<1/2+\unicode[STIX]{x1D700}$,  $|\Im t|<1/2+\unicode[STIX]{x1D700}$,
$|\Im t|<1/2+\unicode[STIX]{x1D700}$,  $a\asymp b$ away from possible poles, so that also
$a\asymp b$ away from possible poles, so that also
 $$\begin{eqnarray}{\mathcal{P}}_{a,b,q}^{(3)}(s,u,v)\ll (abq)^{\unicode[STIX]{x1D700}}\frac{q}{(ab)^{1/2-\unicode[STIX]{x1D703}}}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{P}}_{a,b,q}^{(3)}(s,u,v)\ll (abq)^{\unicode[STIX]{x1D700}}\frac{q}{(ab)^{1/2-\unicode[STIX]{x1D703}}}\end{eqnarray}$$ in the region  $1/2-\unicode[STIX]{x1D700}<\Re s=\Re u=\Re v<1/2+\unicode[STIX]{x1D700}$, away from possible poles. We have established (1.14) as an equality of meromorphic functions, but since all terms except possibly
$1/2-\unicode[STIX]{x1D700}<\Re s=\Re u=\Re v<1/2+\unicode[STIX]{x1D700}$, away from possible poles. We have established (1.14) as an equality of meromorphic functions, but since all terms except possibly  ${\mathcal{P}}_{a,b,q}(s,u,v)$ are holomorphic for
${\mathcal{P}}_{a,b,q}(s,u,v)$ are holomorphic for  $\Re s=\Re u=\Re v=1/2$,
$\Re s=\Re u=\Re v=1/2$,  ${\mathcal{P}}_{a,b,q}(s,u,v)$ must also be holomorphic for
${\mathcal{P}}_{a,b,q}(s,u,v)$ must also be holomorphic for  $\Re s=\Re u=\Re v=1/2$, and the general bound (1.15) then follows by Cauchy’s integral theorem in the same way as at the end of [Reference Blomer and KhanBK19b, §10].
$\Re s=\Re u=\Re v=1/2$, and the general bound (1.15) then follows by Cauchy’s integral theorem in the same way as at the end of [Reference Blomer and KhanBK19b, §10].
Remark 1. We briefly discuss an alternate approach to dealing with the Eisenstein contribution suggested by the referee. Instead of inserting the expression (2.12) for the Fourier coefficients of the Eisenstein series into (3.23), we could use an identity akin to the expression (2.9) for the Fourier coefficients of cuspidal newforms. Such an identity follows from the work of Young [Reference YoungYou19, §8.5]. With this identity in hand, the treatment of the Eisenstein contribution can be done via the same process as for the cuspidal contribution, as in §3.8. A key difference is that when we arrive at an expression of the form (3.22), we cannot have  $B_{2}\mid A$, because there are no Eisenstein newforms of level
$B_{2}\mid A$, because there are no Eisenstein newforms of level  $N$ with trivial central character such that
$N$ with trivial central character such that  $p\Vert N$ for some prime
$p\Vert N$ for some prime  $p$. Thus instead of the bound
$p$. Thus instead of the bound  $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(B_{2})\ll B_{2}^{-1/2}$ when
$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(B_{2})\ll B_{2}^{-1/2}$ when  $B_{2}\mid A$ by (2.3), we have the stronger bound
$B_{2}\mid A$ by (2.3), we have the stronger bound  $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(B_{2})=0$, which gives us the requisite savings.
$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(B_{2})=0$, which gives us the requisite savings.
4 Proof of Theorem 2
4.1 Initial manipulations
Let  $P=TQ$. By ‘negligible’, we mean a quantity that is
$P=TQ$. By ‘negligible’, we mean a quantity that is  $O(P^{-100})$. By a dyadic decomposition, we may replace the conditions
$O(P^{-100})$. By a dyadic decomposition, we may replace the conditions  $q\leqslant Q$,
$q\leqslant Q$,  $|t_{\unicode[STIX]{x1D713}}|\leqslant T$ with
$|t_{\unicode[STIX]{x1D713}}|\leqslant T$ with  $\frac{1}{2}Q\leqslant q\leqslant Q$,
$\frac{1}{2}Q\leqslant q\leqslant Q$,  $\frac{1}{2}T\leqslant t_{\unicode[STIX]{x1D713}}\leqslant T$ or
$\frac{1}{2}T\leqslant t_{\unicode[STIX]{x1D713}}\leqslant T$ or  $t_{\unicode[STIX]{x1D713}}\in [0,1]\cup [-i\unicode[STIX]{x1D703},i\unicode[STIX]{x1D703}]$ where in the last case we formally put
$t_{\unicode[STIX]{x1D713}}\in [0,1]\cup [-i\unicode[STIX]{x1D703},i\unicode[STIX]{x1D703}]$ where in the last case we formally put  $T=1$.
$T=1$.
Let  $E_{3}$ denote the standard minimal Eisenstein series for
$E_{3}$ denote the standard minimal Eisenstein series for  $\text{SL}_{3}(\mathbb{Z})$ with Fourier coefficients
$\text{SL}_{3}(\mathbb{Z})$ with Fourier coefficients
 $$\begin{eqnarray}A(n,m)=\mathop{\sum }_{d\mid (n,m)}\unicode[STIX]{x1D707}(d)\unicode[STIX]{x1D70F}_{3}(n/d)\unicode[STIX]{x1D70F}_{3}(m/d).\end{eqnarray}$$
$$\begin{eqnarray}A(n,m)=\mathop{\sum }_{d\mid (n,m)}\unicode[STIX]{x1D707}(d)\unicode[STIX]{x1D70F}_{3}(n/d)\unicode[STIX]{x1D70F}_{3}(m/d).\end{eqnarray}$$ Then, for  $\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(q)$ with
$\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(q)$ with  $|t_{\unicode[STIX]{x1D713}}|\leqslant T$, we have
$|t_{\unicode[STIX]{x1D713}}|\leqslant T$, we have
 $$\begin{eqnarray}L(s,\unicode[STIX]{x1D713})^{3}=L(s,\unicode[STIX]{x1D713}\times E_{3})=\mathop{\sum }_{n}\mathop{\sum }_{(m,q)=1}\frac{A(n,m)\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(n)}{n^{s}m^{2s}}=P_{q}(s)\mathop{\sum }_{n,m}\frac{A(n,m)\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(n)}{n^{s}m^{2s}}\end{eqnarray}$$
$$\begin{eqnarray}L(s,\unicode[STIX]{x1D713})^{3}=L(s,\unicode[STIX]{x1D713}\times E_{3})=\mathop{\sum }_{n}\mathop{\sum }_{(m,q)=1}\frac{A(n,m)\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(n)}{n^{s}m^{2s}}=P_{q}(s)\mathop{\sum }_{n,m}\frac{A(n,m)\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(n)}{n^{s}m^{2s}}\end{eqnarray}$$ for  $\Re s>1$, where
$\Re s>1$, where
 $$\begin{eqnarray}P_{q}(s)=\mathop{\prod }_{p\mid q}\biggl(1-\frac{\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(p)}{p^{s}}\biggr)^{-3}\biggl(1-\frac{\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(p)}{p^{s}}+\frac{1}{p^{2s}}\biggr)^{3}\end{eqnarray}$$
$$\begin{eqnarray}P_{q}(s)=\mathop{\prod }_{p\mid q}\biggl(1-\frac{\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(p)}{p^{s}}\biggr)^{-3}\biggl(1-\frac{\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(p)}{p^{s}}+\frac{1}{p^{2s}}\biggr)^{3}\end{eqnarray}$$ is holomorphic and uniformly bounded in  $\Re s\geqslant 1/2$. By a standard approximate functional equation, we have
$\Re s\geqslant 1/2$. By a standard approximate functional equation, we have
 $$\begin{eqnarray}|L(1/2,\unicode[STIX]{x1D713})^{3}|\leqslant 2\biggl|\mathop{\sum }_{n,m}\frac{A(n,m)\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(n)}{n^{1/2}m}V_{\unicode[STIX]{x1D713}}\biggl(\frac{nm^{2}}{q^{3/2}}\biggr)\biggr|,\end{eqnarray}$$
$$\begin{eqnarray}|L(1/2,\unicode[STIX]{x1D713})^{3}|\leqslant 2\biggl|\mathop{\sum }_{n,m}\frac{A(n,m)\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(n)}{n^{1/2}m}V_{\unicode[STIX]{x1D713}}\biggl(\frac{nm^{2}}{q^{3/2}}\biggr)\biggr|,\end{eqnarray}$$where
 $$\begin{eqnarray}\displaystyle V_{\unicode[STIX]{x1D713}}(y) & = & \displaystyle \frac{1}{2\unicode[STIX]{x1D70B}i}\int _{(2)}P({\textstyle \frac{1}{2}}+u)\nonumber\\ \displaystyle & & \displaystyle \times \,\frac{\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{2}}({\textstyle \frac{1}{2}}+u+\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D713}}+it_{\unicode[STIX]{x1D713}}))^{3}\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{2}}({\textstyle \frac{1}{2}}+u+\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D713}}-it_{\unicode[STIX]{x1D713}}))^{3}}{\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{2}}({\textstyle \frac{1}{2}}+\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D713}}+it_{\unicode[STIX]{x1D713}}))^{3}\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{2}}({\textstyle \frac{1}{2}}+\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D713}}-it_{\unicode[STIX]{x1D713}}))^{3}}\unicode[STIX]{x1D70B}^{-3u}e^{u^{2}}y^{-u}\frac{du}{u}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle V_{\unicode[STIX]{x1D713}}(y) & = & \displaystyle \frac{1}{2\unicode[STIX]{x1D70B}i}\int _{(2)}P({\textstyle \frac{1}{2}}+u)\nonumber\\ \displaystyle & & \displaystyle \times \,\frac{\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{2}}({\textstyle \frac{1}{2}}+u+\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D713}}+it_{\unicode[STIX]{x1D713}}))^{3}\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{2}}({\textstyle \frac{1}{2}}+u+\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D713}}-it_{\unicode[STIX]{x1D713}}))^{3}}{\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{2}}({\textstyle \frac{1}{2}}+\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D713}}+it_{\unicode[STIX]{x1D713}}))^{3}\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{2}}({\textstyle \frac{1}{2}}+\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D713}}-it_{\unicode[STIX]{x1D713}}))^{3}}\unicode[STIX]{x1D70B}^{-3u}e^{u^{2}}y^{-u}\frac{du}{u}.\nonumber\end{eqnarray}$$ Shifting the contour to the far right, we see that  $V_{\unicode[STIX]{x1D713}}(y)$ is negligible if
$V_{\unicode[STIX]{x1D713}}(y)$ is negligible if  $y\geqslant T^{3}P^{\unicode[STIX]{x1D700}}$. Remembering this, we shift the contour to
$y\geqslant T^{3}P^{\unicode[STIX]{x1D700}}$. Remembering this, we shift the contour to  $\Re u=\unicode[STIX]{x1D700}$. There we may truncate the integral at
$\Re u=\unicode[STIX]{x1D700}$. There we may truncate the integral at  $|\Im u|\leqslant P^{\unicode[STIX]{x1D700}}$ at the cost of a negligible error. Applying a smooth dyadic decomposition, we have shown that
$|\Im u|\leqslant P^{\unicode[STIX]{x1D700}}$ at the cost of a negligible error. Applying a smooth dyadic decomposition, we have shown that
 $$\begin{eqnarray}L(1/2,\unicode[STIX]{x1D713})^{3}\;\ll _{\unicode[STIX]{x1D700}}\;P^{\unicode[STIX]{x1D700}}\int _{-P^{\unicode[STIX]{x1D700}}}^{P^{\unicode[STIX]{x1D700}}}\mathop{\sum }_{2^{\unicode[STIX]{x1D708}}=N\leqslant Q^{3/2}T^{3}P^{\unicode[STIX]{x1D700}}}\biggl|\mathop{\sum }_{n,m}\frac{A(n,m)\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(n)}{(nm^{2})^{1/2+iv}}V\biggl(\frac{nm^{2}}{N}\biggr)\biggr|\,dv,\end{eqnarray}$$
$$\begin{eqnarray}L(1/2,\unicode[STIX]{x1D713})^{3}\;\ll _{\unicode[STIX]{x1D700}}\;P^{\unicode[STIX]{x1D700}}\int _{-P^{\unicode[STIX]{x1D700}}}^{P^{\unicode[STIX]{x1D700}}}\mathop{\sum }_{2^{\unicode[STIX]{x1D708}}=N\leqslant Q^{3/2}T^{3}P^{\unicode[STIX]{x1D700}}}\biggl|\mathop{\sum }_{n,m}\frac{A(n,m)\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(n)}{(nm^{2})^{1/2+iv}}V\biggl(\frac{nm^{2}}{N}\biggr)\biggr|\,dv,\end{eqnarray}$$ where  $V$ has support in
$V$ has support in  $[1,2]$, is independent of
$[1,2]$, is independent of  $\unicode[STIX]{x1D713}$, and satisfies
$\unicode[STIX]{x1D713}$, and satisfies  $V^{(j)}(y)\;\ll _{j}\;1$ for all
$V^{(j)}(y)\;\ll _{j}\;1$ for all  $j\in \mathbb{N}_{0}$. Multiplying two such expressions together and using the Cauchy–Schwarz inequality, we obtain
$j\in \mathbb{N}_{0}$. Multiplying two such expressions together and using the Cauchy–Schwarz inequality, we obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle L(1/2,\unicode[STIX]{x1D713})^{6}\nonumber\\ \displaystyle & & \displaystyle \quad \;\ll _{\unicode[STIX]{x1D700}}\;P^{\unicode[STIX]{x1D700}}\max _{|v|\leqslant P^{\unicode[STIX]{x1D700}}}\max _{N\leqslant Q^{3/2}T^{3}P^{\unicode[STIX]{x1D700}}}\mathop{\sum }_{n_{1},n_{2},m_{1},m_{2}}\frac{A(n_{1},m_{1})A(n_{2},m_{2})\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(n_{1})\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(n_{2})}{(n_{1}m_{1}^{2})^{1/2+iv}(n_{2}m_{2}^{2})^{1/2-iv}}V\biggl(\frac{n_{1}m_{1}^{2}}{N}\biggr)\overline{V\biggl(\frac{n_{2}m_{2}^{2}}{N}\biggr)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle L(1/2,\unicode[STIX]{x1D713})^{6}\nonumber\\ \displaystyle & & \displaystyle \quad \;\ll _{\unicode[STIX]{x1D700}}\;P^{\unicode[STIX]{x1D700}}\max _{|v|\leqslant P^{\unicode[STIX]{x1D700}}}\max _{N\leqslant Q^{3/2}T^{3}P^{\unicode[STIX]{x1D700}}}\mathop{\sum }_{n_{1},n_{2},m_{1},m_{2}}\frac{A(n_{1},m_{1})A(n_{2},m_{2})\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(n_{1})\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(n_{2})}{(n_{1}m_{1}^{2})^{1/2+iv}(n_{2}m_{2}^{2})^{1/2-iv}}V\biggl(\frac{n_{1}m_{1}^{2}}{N}\biggr)\overline{V\biggl(\frac{n_{2}m_{2}^{2}}{N}\biggr)}.\nonumber\end{eqnarray}$$ For  $\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(q)$, we have
$\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(q)$, we have
 $$\begin{eqnarray}\frac{\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(n)\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(m)}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})}=q\mathop{\prod }_{p\mid q}\biggl(1-\frac{1}{p}\biggr)^{-1}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},1,q}(n)\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},1,q}(m)\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(n)\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(m)}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})}=q\mathop{\prod }_{p\mid q}\biggl(1-\frac{1}{p}\biggr)^{-1}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},1,q}(n)\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},1,q}(m)\end{eqnarray}$$by (2.9). For the purpose of Theorem 2, it therefore suffices to bound
 $$\begin{eqnarray}\displaystyle {\mathcal{S}}_{v}(Q,T,N) & := & \displaystyle \mathop{\sum }_{q}W\biggl(\frac{q}{Q}\biggr)Q\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(q)}h_{T}(t_{\unicode[STIX]{x1D713}})\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{n_{1},n_{2},m_{1},m_{2}}\frac{A(n_{1},m_{1})A(n_{2},m_{2})\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},1,q}(n_{1})\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},1,q}(n_{2})}{(n_{1}m_{1}^{2})^{1/2+iv}(n_{2}m_{2}^{2})^{1/2-iv}}V\biggl(\frac{n_{1}m_{1}^{2}}{N}\biggr)\overline{V\biggl(\frac{n_{2}m_{2}^{2}}{N}\biggr)},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{S}}_{v}(Q,T,N) & := & \displaystyle \mathop{\sum }_{q}W\biggl(\frac{q}{Q}\biggr)Q\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(q)}h_{T}(t_{\unicode[STIX]{x1D713}})\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{n_{1},n_{2},m_{1},m_{2}}\frac{A(n_{1},m_{1})A(n_{2},m_{2})\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},1,q}(n_{1})\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},1,q}(n_{2})}{(n_{1}m_{1}^{2})^{1/2+iv}(n_{2}m_{2}^{2})^{1/2-iv}}V\biggl(\frac{n_{1}m_{1}^{2}}{N}\biggr)\overline{V\biggl(\frac{n_{2}m_{2}^{2}}{N}\biggr)},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$ where  $N\leqslant Q^{3/2}T^{3}P^{\unicode[STIX]{x1D700}}$,
$N\leqslant Q^{3/2}T^{3}P^{\unicode[STIX]{x1D700}}$,  $|v|\leqslant P^{\unicode[STIX]{x1D700}}$, and
$|v|\leqslant P^{\unicode[STIX]{x1D700}}$, and
 $$\begin{eqnarray}h_{T}(t)=e^{-(t/T)^{2}}\mathop{\prod }_{n=1}^{\lfloor \unicode[STIX]{x1D700}^{-1}\rfloor }\biggl(\frac{1}{T^{2}}\biggl(t^{2}+\frac{(2n-1)^{2}}{4}\biggr)\biggr).\end{eqnarray}$$
$$\begin{eqnarray}h_{T}(t)=e^{-(t/T)^{2}}\mathop{\prod }_{n=1}^{\lfloor \unicode[STIX]{x1D700}^{-1}\rfloor }\biggl(\frac{1}{T^{2}}\biggl(t^{2}+\frac{(2n-1)^{2}}{4}\biggr)\biggr).\end{eqnarray}$$Note that this function satisfies the assumptions of Lemmas 1 and 2.
4.2 The Eisenstein contribution associated with the trivial character
The  $\unicode[STIX]{x1D713}$-sum in (4.1) can be evaluated by the Kuznetsov formula (2.16). To this end, we need to add, using positivity, the contribution from the oldforms and the continuous spectrum. As mentioned in the introduction, this manoeuvre is costly, and we single out the contribution of the continuous spectrum associated with the trivial character:
$\unicode[STIX]{x1D713}$-sum in (4.1) can be evaluated by the Kuznetsov formula (2.16). To this end, we need to add, using positivity, the contribution from the oldforms and the continuous spectrum. As mentioned in the introduction, this manoeuvre is costly, and we single out the contribution of the continuous spectrum associated with the trivial character:
 $$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{S}}_{v}^{\ast }(Q,T,N):=\mathop{\sum }_{q}W\biggl(\frac{q}{Q}\biggr)Q\mathop{\sum }_{M\mid q}\int _{\mathbb{R}}h_{T}(t)\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\sum }_{n_{1},n_{2},m_{1},m_{2}}\frac{A(n_{1},m_{1})A(n_{2},m_{2})\unicode[STIX]{x1D70C}_{\text{triv},M,q}(n_{1},t)\overline{\unicode[STIX]{x1D70C}_{\text{triv},M,q}(n_{2},t)}}{(n_{1}m_{1}^{2})^{1/2+iv}(n_{2}m_{2}^{2})^{1/2-iv}}V\biggl(\frac{n_{1}m_{1}^{2}}{N}\biggr)\overline{V\biggl(\frac{n_{2}m_{2}^{2}}{N}\biggr)}\frac{dt}{2\unicode[STIX]{x1D70B}},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{S}}_{v}^{\ast }(Q,T,N):=\mathop{\sum }_{q}W\biggl(\frac{q}{Q}\biggr)Q\mathop{\sum }_{M\mid q}\int _{\mathbb{R}}h_{T}(t)\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\sum }_{n_{1},n_{2},m_{1},m_{2}}\frac{A(n_{1},m_{1})A(n_{2},m_{2})\unicode[STIX]{x1D70C}_{\text{triv},M,q}(n_{1},t)\overline{\unicode[STIX]{x1D70C}_{\text{triv},M,q}(n_{2},t)}}{(n_{1}m_{1}^{2})^{1/2+iv}(n_{2}m_{2}^{2})^{1/2-iv}}V\biggl(\frac{n_{1}m_{1}^{2}}{N}\biggr)\overline{V\biggl(\frac{n_{2}m_{2}^{2}}{N}\biggr)}\frac{dt}{2\unicode[STIX]{x1D70B}},\nonumber\end{eqnarray}$$which we rewrite in more compact form as
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{(2)}\int _{(2)}\int _{(1)}\int _{\mathbb{R}}\widehat{V}(z_{1})\widehat{V}(z_{2})\widehat{W}(s)Q^{1+s}N^{z_{1}+z_{2}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\frac{{\mathcal{D}}_{t}(s,1/2+iv+z_{1},1/2-iv+z_{2};0,0)}{|\unicode[STIX]{x1D701}(1+2it)|^{2}}h_{T}(t)\frac{dt}{2\unicode[STIX]{x1D70B}}\frac{ds\,dz_{1}\,dz_{2}}{(2\unicode[STIX]{x1D70B}i)^{3}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{(2)}\int _{(2)}\int _{(1)}\int _{\mathbb{R}}\widehat{V}(z_{1})\widehat{V}(z_{2})\widehat{W}(s)Q^{1+s}N^{z_{1}+z_{2}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\frac{{\mathcal{D}}_{t}(s,1/2+iv+z_{1},1/2-iv+z_{2};0,0)}{|\unicode[STIX]{x1D701}(1+2it)|^{2}}h_{T}(t)\frac{dt}{2\unicode[STIX]{x1D70B}}\frac{ds\,dz_{1}\,dz_{2}}{(2\unicode[STIX]{x1D70B}i)^{3}},\end{eqnarray}$$where
 $$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{D}}_{t}(s,z_{1},z_{2};w_{1},w_{2})\nonumber\\ \displaystyle & & \displaystyle \quad =|\unicode[STIX]{x1D701}(1+2it)|^{2}\mathop{\sum }_{q,n_{1},n_{2},m_{1},m_{2}}\mathop{\sum }_{M\mid q}\frac{A(n_{1},m_{1})A(n_{2},m_{2})\unicode[STIX]{x1D70C}_{\text{triv},M,q}(n_{1},t)\overline{\unicode[STIX]{x1D70C}_{\text{triv},M,q}(n_{2},t)}}{q^{s}(n_{1}m_{1}^{2})^{z_{1}}(n_{2}m_{2}^{2})^{z_{2}}m_{1}^{2w_{1}}m_{2}^{2w_{2}}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{D}}_{t}(s,z_{1},z_{2};w_{1},w_{2})\nonumber\\ \displaystyle & & \displaystyle \quad =|\unicode[STIX]{x1D701}(1+2it)|^{2}\mathop{\sum }_{q,n_{1},n_{2},m_{1},m_{2}}\mathop{\sum }_{M\mid q}\frac{A(n_{1},m_{1})A(n_{2},m_{2})\unicode[STIX]{x1D70C}_{\text{triv},M,q}(n_{1},t)\overline{\unicode[STIX]{x1D70C}_{\text{triv},M,q}(n_{2},t)}}{q^{s}(n_{1}m_{1}^{2})^{z_{1}}(n_{2}m_{2}^{2})^{z_{2}}m_{1}^{2w_{1}}m_{2}^{2w_{2}}}.\nonumber\end{eqnarray}$$Recalling the definition (cf. (2.13))
 $$\begin{eqnarray}\displaystyle & & \displaystyle |\unicode[STIX]{x1D701}(1+2it)|^{2}\unicode[STIX]{x1D70C}_{\text{triv},M,q}(n_{1},t)\overline{\unicode[STIX]{x1D70C}_{\text{triv},M,q}(n_{2},t)}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{|\unicode[STIX]{x1D701}^{(q)}(1+2it)|^{2}(n_{1}/n_{2})^{it}}{q\unicode[STIX]{x1D708}(q)\tilde{\mathfrak{n}}_{q}(M)^{2}}\mathop{\sum }_{\unicode[STIX]{x1D6FF}_{1},\unicode[STIX]{x1D6FF}_{2}\mid M}\frac{\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6FF}_{2}\unicode[STIX]{x1D707}(M/\unicode[STIX]{x1D6FF}_{1})\unicode[STIX]{x1D707}(M/\unicode[STIX]{x1D6FF}_{2})}{M}\mathop{\sum }_{\substack{ c_{1}\unicode[STIX]{x1D6FF}_{1}f_{1}=n_{1} \\ (c_{1},q/M)=1}}\mathop{\sum }_{\substack{ c_{2}\unicode[STIX]{x1D6FF}_{2}f_{2}=n_{2} \\ (c_{2},q/M)=1}}\biggl(\frac{c_{2}}{c_{1}}\biggr)^{2it},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |\unicode[STIX]{x1D701}(1+2it)|^{2}\unicode[STIX]{x1D70C}_{\text{triv},M,q}(n_{1},t)\overline{\unicode[STIX]{x1D70C}_{\text{triv},M,q}(n_{2},t)}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{|\unicode[STIX]{x1D701}^{(q)}(1+2it)|^{2}(n_{1}/n_{2})^{it}}{q\unicode[STIX]{x1D708}(q)\tilde{\mathfrak{n}}_{q}(M)^{2}}\mathop{\sum }_{\unicode[STIX]{x1D6FF}_{1},\unicode[STIX]{x1D6FF}_{2}\mid M}\frac{\unicode[STIX]{x1D6FF}_{1}\unicode[STIX]{x1D6FF}_{2}\unicode[STIX]{x1D707}(M/\unicode[STIX]{x1D6FF}_{1})\unicode[STIX]{x1D707}(M/\unicode[STIX]{x1D6FF}_{2})}{M}\mathop{\sum }_{\substack{ c_{1}\unicode[STIX]{x1D6FF}_{1}f_{1}=n_{1} \\ (c_{1},q/M)=1}}\mathop{\sum }_{\substack{ c_{2}\unicode[STIX]{x1D6FF}_{2}f_{2}=n_{2} \\ (c_{2},q/M)=1}}\biggl(\frac{c_{2}}{c_{1}}\biggr)^{2it},\nonumber\end{eqnarray}$$ we see that (for  $t\in \mathbb{R}$) the series
$t\in \mathbb{R}$) the series  ${\mathcal{D}}_{t}(s,z_{1},z_{2};w_{1},w_{2})$ is absolutely convergent in
${\mathcal{D}}_{t}(s,z_{1},z_{2};w_{1},w_{2})$ is absolutely convergent in  $\Re s>0$,
$\Re s>0$,  $\Re z_{1},\Re z_{2}>1$,
$\Re z_{1},\Re z_{2}>1$,  $\Re (z_{1}+w_{1}),\Re (z_{2}+w_{2})>1/2$, and admits an Euler product of the shape
$\Re (z_{1}+w_{1}),\Re (z_{2}+w_{2})>1/2$, and admits an Euler product of the shape
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\prod }_{p} (1+\frac{1}{p^{s+1}}+\mathop{\sum }_{j=1,2}\mathop{\sum }_{\pm }\frac{3}{p^{z_{j}\pm it}}\nonumber\\ \displaystyle & & \displaystyle \quad +\,O\biggl(\frac{1}{p^{2\min (\Re z_{1},\Re z_{2},\Re (z_{1}+w_{1}),\Re (z_{2}+w_{2}))}}+\frac{1}{p^{\Re s+\min (\Re z_{1},1)+\min (\Re z_{2},1)}}\biggr)\!),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\prod }_{p} (1+\frac{1}{p^{s+1}}+\mathop{\sum }_{j=1,2}\mathop{\sum }_{\pm }\frac{3}{p^{z_{j}\pm it}}\nonumber\\ \displaystyle & & \displaystyle \quad +\,O\biggl(\frac{1}{p^{2\min (\Re z_{1},\Re z_{2},\Re (z_{1}+w_{1}),\Re (z_{2}+w_{2}))}}+\frac{1}{p^{\Re s+\min (\Re z_{1},1)+\min (\Re z_{2},1)}}\biggr)\!),\nonumber\end{eqnarray}$$where the bounds in the error term hold uniformly in
 $$\begin{eqnarray}\Re z_{1},\quad \Re z_{2},\quad \Re (z_{1}+w_{1}),\quad \Re (z_{2}+w_{2}),\quad \Re s+\min (\Re z_{1},1)+\min (\Re z_{2},1)>0.\end{eqnarray}$$
$$\begin{eqnarray}\Re z_{1},\quad \Re z_{2},\quad \Re (z_{1}+w_{1}),\quad \Re (z_{2}+w_{2}),\quad \Re s+\min (\Re z_{1},1)+\min (\Re z_{2},1)>0.\end{eqnarray}$$In particular, we have
 $$\begin{eqnarray}{\mathcal{D}}_{t}(s,z_{1},z_{2};w_{1},w_{2})=\unicode[STIX]{x1D701}(s+1)\unicode[STIX]{x1D701}(z_{1}+it)^{3}\unicode[STIX]{x1D701}(z_{1}-it)^{3}\unicode[STIX]{x1D701}(z_{2}+it)^{3}\unicode[STIX]{x1D701}(z_{2}-it)^{3}{\mathcal{E}}_{t}(s,z_{1},z_{2};w_{1},w_{2}),\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{D}}_{t}(s,z_{1},z_{2};w_{1},w_{2})=\unicode[STIX]{x1D701}(s+1)\unicode[STIX]{x1D701}(z_{1}+it)^{3}\unicode[STIX]{x1D701}(z_{1}-it)^{3}\unicode[STIX]{x1D701}(z_{2}+it)^{3}\unicode[STIX]{x1D701}(z_{2}-it)^{3}{\mathcal{E}}_{t}(s,z_{1},z_{2};w_{1},w_{2}),\end{eqnarray}$$ where  ${\mathcal{E}}_{t}(s,z_{1},z_{2};w_{1},w_{2})$ is holomorphic and uniformly bounded in
${\mathcal{E}}_{t}(s,z_{1},z_{2};w_{1},w_{2})$ is holomorphic and uniformly bounded in
 $$\begin{eqnarray}\Re z_{1},~\Re z_{2},~\Re (z_{1}+w_{1}),~\Re (z_{2}+w_{2})\geqslant 1/2+\unicode[STIX]{x1D700},\quad \Re s+\min (\Re z_{1},1)+\min (\Re z_{2},1)\geqslant 1+\unicode[STIX]{x1D700},\end{eqnarray}$$
$$\begin{eqnarray}\Re z_{1},~\Re z_{2},~\Re (z_{1}+w_{1}),~\Re (z_{2}+w_{2})\geqslant 1/2+\unicode[STIX]{x1D700},\quad \Re s+\min (\Re z_{1},1)+\min (\Re z_{2},1)\geqslant 1+\unicode[STIX]{x1D700},\end{eqnarray}$$ as long as  $\Im t=0$. Hence in (4.2), we may shift the contours to
$\Im t=0$. Hence in (4.2), we may shift the contours to  $\Re s=-1+\unicode[STIX]{x1D700}$ (picking up a residue at
$\Re s=-1+\unicode[STIX]{x1D700}$ (picking up a residue at  $s=0$), and in the remaining integral we shift the
$s=0$), and in the remaining integral we shift the  $z_{1},z_{2}$-contours to
$z_{1},z_{2}$-contours to  $\Re z_{1}=\Re z_{2}=1/2+\unicode[STIX]{x1D700}$, getting
$\Re z_{1}=\Re z_{2}=1/2+\unicode[STIX]{x1D700}$, getting
 $$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{S}}_{v}^{\ast }(Q,T,N)=\widehat{W}(0)Q\int _{(2)}\int _{(2)}\int _{\mathbb{R}}\mathop{\prod }_{\pm }\frac{\unicode[STIX]{x1D701}(1/2+iv+z_{1}\pm it)^{3}\unicode[STIX]{x1D701}(1/2-iv+z_{2}\pm it)^{3}}{\unicode[STIX]{x1D701}(1\pm 2it)}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,{\mathcal{E}}_{t}(0,1/2+iv+z_{1},1/2-iv+z_{2};0,0)\widehat{V}(z_{1})\widehat{V}(z_{2})N^{z_{1}+z_{2}}h_{T}(t)\frac{dz_{1}\,dz_{2}}{(2\unicode[STIX]{x1D70B}i)^{2}}\frac{dt}{2\unicode[STIX]{x1D70B}}+O(TNP^{\unicode[STIX]{x1D700}}).\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{S}}_{v}^{\ast }(Q,T,N)=\widehat{W}(0)Q\int _{(2)}\int _{(2)}\int _{\mathbb{R}}\mathop{\prod }_{\pm }\frac{\unicode[STIX]{x1D701}(1/2+iv+z_{1}\pm it)^{3}\unicode[STIX]{x1D701}(1/2-iv+z_{2}\pm it)^{3}}{\unicode[STIX]{x1D701}(1\pm 2it)}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,{\mathcal{E}}_{t}(0,1/2+iv+z_{1},1/2-iv+z_{2};0,0)\widehat{V}(z_{1})\widehat{V}(z_{2})N^{z_{1}+z_{2}}h_{T}(t)\frac{dz_{1}\,dz_{2}}{(2\unicode[STIX]{x1D70B}i)^{2}}\frac{dt}{2\unicode[STIX]{x1D70B}}+O(TNP^{\unicode[STIX]{x1D700}}).\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$4.3 Applying the Kuznetsov formula twice
By the Kuznetsov formula (and positivity), we obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{S}}_{v}(Q,T,N)+{\mathcal{S}}_{v}^{\ast }(Q,T,N)\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant Q\mathop{\sum }_{q}W\biggl(\frac{q}{Q}\biggr)\mathop{\sum }_{n_{1},n_{2},m_{1},m_{2}}\frac{A(n_{1},m_{1})A(n_{2},m_{2})}{(n_{1}m_{1}^{2})^{1/2+iv}(n_{2}m_{2}^{2})^{1/2-iv}}V\biggl(\frac{n_{1}m_{1}^{2}}{N}\biggr)\overline{V\biggl(\frac{n_{2}m_{2}^{2}}{N}\biggr)}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\biggl(\unicode[STIX]{x1D6FF}_{n_{1},n_{2}}\int _{-\infty }^{\infty }h_{T}(t)\frac{t\tanh (\unicode[STIX]{x1D70B}t)\,dt}{2\unicode[STIX]{x1D70B}^{2}}+\mathop{\sum }_{c}\frac{S(n_{1},n_{2},qc)}{qc}\mathscr{K}h_{T}\biggl(\frac{\sqrt{n_{1}n_{2}}}{qc}\biggr)\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{S}}_{v}(Q,T,N)+{\mathcal{S}}_{v}^{\ast }(Q,T,N)\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant Q\mathop{\sum }_{q}W\biggl(\frac{q}{Q}\biggr)\mathop{\sum }_{n_{1},n_{2},m_{1},m_{2}}\frac{A(n_{1},m_{1})A(n_{2},m_{2})}{(n_{1}m_{1}^{2})^{1/2+iv}(n_{2}m_{2}^{2})^{1/2-iv}}V\biggl(\frac{n_{1}m_{1}^{2}}{N}\biggr)\overline{V\biggl(\frac{n_{2}m_{2}^{2}}{N}\biggr)}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\biggl(\unicode[STIX]{x1D6FF}_{n_{1},n_{2}}\int _{-\infty }^{\infty }h_{T}(t)\frac{t\tanh (\unicode[STIX]{x1D70B}t)\,dt}{2\unicode[STIX]{x1D70B}^{2}}+\mathop{\sum }_{c}\frac{S(n_{1},n_{2},qc)}{qc}\mathscr{K}h_{T}\biggl(\frac{\sqrt{n_{1}n_{2}}}{qc}\biggr)\biggr).\nonumber\end{eqnarray}$$The diagonal term is easy to deal with and is trivially bounded by
 $$\begin{eqnarray}O_{\unicode[STIX]{x1D700}}(P^{\unicode[STIX]{x1D700}}Q^{2}T^{2}).\end{eqnarray}$$
$$\begin{eqnarray}O_{\unicode[STIX]{x1D700}}(P^{\unicode[STIX]{x1D700}}Q^{2}T^{2}).\end{eqnarray}$$By Mellin inversion, we can recast the off-diagonal term as
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{(-12)}Q^{s+1}\widehat{W}(s)\mathop{\sum }_{n_{1},n_{2},m_{1},m_{2}}\frac{A(n_{1},m_{1})A(n_{2},m_{2})}{(n_{1}m_{1}^{2})^{1/2+iv}(n_{2}m_{2}^{2})^{1/2-iv}(n_{1}n_{2})^{s/2}}V\biggl(\frac{n_{1}m_{1}^{2}}{N}\biggr)\overline{V\biggl(\frac{n_{2}m_{2}^{2}}{N}\biggr)}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\sum }_{c,q}c^{s}\frac{S(n_{1},n_{2},qc)}{qc}\mathscr{K}_{s}h_{T}\biggl(\frac{\sqrt{n_{1}n_{2}}}{qc}\biggr)\frac{ds}{2\unicode[STIX]{x1D70B}i}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{(-12)}Q^{s+1}\widehat{W}(s)\mathop{\sum }_{n_{1},n_{2},m_{1},m_{2}}\frac{A(n_{1},m_{1})A(n_{2},m_{2})}{(n_{1}m_{1}^{2})^{1/2+iv}(n_{2}m_{2}^{2})^{1/2-iv}(n_{1}n_{2})^{s/2}}V\biggl(\frac{n_{1}m_{1}^{2}}{N}\biggr)\overline{V\biggl(\frac{n_{2}m_{2}^{2}}{N}\biggr)}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\sum }_{c,q}c^{s}\frac{S(n_{1},n_{2},qc)}{qc}\mathscr{K}_{s}h_{T}\biggl(\frac{\sqrt{n_{1}n_{2}}}{qc}\biggr)\frac{ds}{2\unicode[STIX]{x1D70B}i}\nonumber\end{eqnarray}$$ with  $\mathscr{K}_{s}h_{T}(x)=x^{s}\mathscr{K}h_{T}(x)$ as in §2.6. Applying the Kuznetsov formula immediately in the other direction (which we may do by Lemma 1, but this time the summation is over
$\mathscr{K}_{s}h_{T}(x)=x^{s}\mathscr{K}h_{T}(x)$ as in §2.6. Applying the Kuznetsov formula immediately in the other direction (which we may do by Lemma 1, but this time the summation is over  $q$ instead of
$q$ instead of  $c$), we obtain by (2.14) that the previous expression is equal to
$c$), we obtain by (2.14) that the previous expression is equal to
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{(-12)}Q^{s+1}\widehat{W}(s)\mathop{\sum }_{n_{1},n_{2},m_{1},m_{2}}\frac{A(n_{1},m_{1})A(n_{2},m_{2})}{(n_{1}m_{1}^{2})^{1/2+iv}(n_{2}m_{2}^{2})^{1/2-iv}(n_{1}n_{2})^{s/2}}V\biggl(\frac{n_{1}m_{1}^{2}}{N}\biggr)\overline{V\biggl(\frac{n_{2}m_{2}^{2}}{N}\biggr)}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\sum }_{c}c^{s}({\mathcal{A}}_{c}^{\text{Maa}\unicode[STIX]{x00DF}}(n_{1},n_{2};\mathscr{L}^{+}\mathscr{K}_{s}h_{T})+{\mathcal{A}}_{c}^{\text{Eis}}(n_{1},n_{2};\mathscr{L}^{+}\mathscr{K}_{s}h_{T})+{\mathcal{A}}_{c}^{\text{hol}}(n_{1},n_{2};\mathscr{L}^{\text{hol}}\mathscr{K}_{s}h_{T}))\frac{ds}{2\unicode[STIX]{x1D70B}i}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{(-12)}Q^{s+1}\widehat{W}(s)\mathop{\sum }_{n_{1},n_{2},m_{1},m_{2}}\frac{A(n_{1},m_{1})A(n_{2},m_{2})}{(n_{1}m_{1}^{2})^{1/2+iv}(n_{2}m_{2}^{2})^{1/2-iv}(n_{1}n_{2})^{s/2}}V\biggl(\frac{n_{1}m_{1}^{2}}{N}\biggr)\overline{V\biggl(\frac{n_{2}m_{2}^{2}}{N}\biggr)}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\sum }_{c}c^{s}({\mathcal{A}}_{c}^{\text{Maa}\unicode[STIX]{x00DF}}(n_{1},n_{2};\mathscr{L}^{+}\mathscr{K}_{s}h_{T})+{\mathcal{A}}_{c}^{\text{Eis}}(n_{1},n_{2};\mathscr{L}^{+}\mathscr{K}_{s}h_{T})+{\mathcal{A}}_{c}^{\text{hol}}(n_{1},n_{2};\mathscr{L}^{\text{hol}}\mathscr{K}_{s}h_{T}))\frac{ds}{2\unicode[STIX]{x1D70B}i}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$ Lemma 2(b) implies that  $\mathscr{L}^{+}\mathscr{K}_{s}h_{T}(t)$ has analytic continuation to
$\mathscr{L}^{+}\mathscr{K}_{s}h_{T}(t)$ has analytic continuation to  $\Re s<1$, and we proceed to derive a uniform bound. If
$\Re s<1$, and we proceed to derive a uniform bound. If  $|t|\geqslant 10|\Im s|$ (so that
$|t|\geqslant 10|\Im s|$ (so that  $t\pm \frac{1}{2}|\Im s|\asymp t$), we have
$t\pm \frac{1}{2}|\Im s|\asymp t$), we have
 $$\begin{eqnarray}\displaystyle \mathscr{L}^{+}\mathscr{K}_{s}h_{T}(t) & \ll & \displaystyle \int _{\mathbb{R}}\frac{e^{-|\unicode[STIX]{x1D70F}|/T}(1+|\unicode[STIX]{x1D70F}|)}{(1+|t|+|\unicode[STIX]{x1D70F}|)^{2-2\Re s}}\,d\unicode[STIX]{x1D70F}+\frac{e^{-|t|/T}(1+|t|)}{(1+|t|)^{1-\Re s}}\int _{0}^{1+|t|}\frac{1}{(1+|\unicode[STIX]{x1D70F}|)^{1-\Re s}}\,d\unicode[STIX]{x1D70F}\nonumber\\ \displaystyle & \ll & \displaystyle \frac{T^{2}}{(1+|t|)^{2-2\Re s}}+e^{-|t|/T}((1+|t|)^{\Re s}+(1+|t|)^{2\Re s})\ll \frac{T^{2+\max (0,-\Re s)}}{(1+|t|)^{2-2\Re s}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{L}^{+}\mathscr{K}_{s}h_{T}(t) & \ll & \displaystyle \int _{\mathbb{R}}\frac{e^{-|\unicode[STIX]{x1D70F}|/T}(1+|\unicode[STIX]{x1D70F}|)}{(1+|t|+|\unicode[STIX]{x1D70F}|)^{2-2\Re s}}\,d\unicode[STIX]{x1D70F}+\frac{e^{-|t|/T}(1+|t|)}{(1+|t|)^{1-\Re s}}\int _{0}^{1+|t|}\frac{1}{(1+|\unicode[STIX]{x1D70F}|)^{1-\Re s}}\,d\unicode[STIX]{x1D70F}\nonumber\\ \displaystyle & \ll & \displaystyle \frac{T^{2}}{(1+|t|)^{2-2\Re s}}+e^{-|t|/T}((1+|t|)^{\Re s}+(1+|t|)^{2\Re s})\ll \frac{T^{2+\max (0,-\Re s)}}{(1+|t|)^{2-2\Re s}}.\nonumber\end{eqnarray}$$ If  $|t|\leqslant 10|\Im s|$, we have trivially
$|t|\leqslant 10|\Im s|$, we have trivially  $\mathscr{L}^{+}\mathscr{K}_{s}h_{T}(t)\ll T^{2}$, so that altogether we obtain the uniform bound
$\mathscr{L}^{+}\mathscr{K}_{s}h_{T}(t)\ll T^{2}$, so that altogether we obtain the uniform bound
 $$\begin{eqnarray}\mathscr{L}^{+}\mathscr{K}_{s}h_{T}(t)\;\ll _{\Re s}\;(1+|\Im s|)^{2-2\Re s}\frac{T^{2+\max (0,-\Re s)}}{(1+|t|)^{2-2\Re s}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{L}^{+}\mathscr{K}_{s}h_{T}(t)\;\ll _{\Re s}\;(1+|\Im s|)^{2-2\Re s}\frac{T^{2+\max (0,-\Re s)}}{(1+|t|)^{2-2\Re s}}.\end{eqnarray}$$ The problematic expression in (4.7) is the part of  ${\mathcal{A}}_{c}^{\text{Eis}}(n_{1},n_{2};\mathscr{L}^{+}\mathscr{K}_{s}h_{T})$ that is associated with the trivial character. We spell this out explicitly as
${\mathcal{A}}_{c}^{\text{Eis}}(n_{1},n_{2};\mathscr{L}^{+}\mathscr{K}_{s}h_{T})$ that is associated with the trivial character. We spell this out explicitly as
 $$\begin{eqnarray}\displaystyle {\mathcal{S}}_{v}^{\ast \ast }(Q,T,N) & = & \displaystyle \int _{(20)}\int _{(20)}\int _{(-12)}\int _{\mathbb{R}}\widehat{V}(z_{1})\widehat{V}(z_{2})\widehat{W}(s)Q^{1+s}N^{z_{1}+z_{2}}\nonumber\\ \displaystyle & & \displaystyle \times \,\frac{{\mathcal{D}}_{t}(-s,1/2+iv+s/2+z_{1},1/2-iv+s/2+z_{2};-s/2,-s/2)}{|\unicode[STIX]{x1D701}(1+2it)|^{2}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathscr{L}^{+}\mathscr{K}_{s}h_{T}(t)\frac{dt}{2\unicode[STIX]{x1D70B}}\frac{ds\,dz_{1}\,dz_{2}}{(2\unicode[STIX]{x1D70B}i)^{3}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{S}}_{v}^{\ast \ast }(Q,T,N) & = & \displaystyle \int _{(20)}\int _{(20)}\int _{(-12)}\int _{\mathbb{R}}\widehat{V}(z_{1})\widehat{V}(z_{2})\widehat{W}(s)Q^{1+s}N^{z_{1}+z_{2}}\nonumber\\ \displaystyle & & \displaystyle \times \,\frac{{\mathcal{D}}_{t}(-s,1/2+iv+s/2+z_{1},1/2-iv+s/2+z_{2};-s/2,-s/2)}{|\unicode[STIX]{x1D701}(1+2it)|^{2}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathscr{L}^{+}\mathscr{K}_{s}h_{T}(t)\frac{dt}{2\unicode[STIX]{x1D70B}}\frac{ds\,dz_{1}\,dz_{2}}{(2\unicode[STIX]{x1D70B}i)^{3}}.\nonumber\end{eqnarray}$$ Shifting the  $s$-contour to the far left and simultaneously the
$s$-contour to the far left and simultaneously the  $z_{1},z_{2}$-contours to
$z_{1},z_{2}$-contours to  $\Re z_{1}=\frac{1}{2}(1-\Re s)+\unicode[STIX]{x1D700}$, we see from (4.8) that the
$\Re z_{1}=\frac{1}{2}(1-\Re s)+\unicode[STIX]{x1D700}$, we see from (4.8) that the  $t$-integral is negligible for
$t$-integral is negligible for  $|t|\geqslant \sqrt{NT/Q}P^{\unicode[STIX]{x1D700}}$. In particular, we may truncate at
$|t|\geqslant \sqrt{NT/Q}P^{\unicode[STIX]{x1D700}}$. In particular, we may truncate at  $|t|\leqslant (T+\sqrt{NT/Q})P^{\unicode[STIX]{x1D700}}$.
$|t|\leqslant (T+\sqrt{NT/Q})P^{\unicode[STIX]{x1D700}}$.
Next we shift the  $s$-contour to
$s$-contour to  $\Re s=\unicode[STIX]{x1D700}$, past the pole at
$\Re s=\unicode[STIX]{x1D700}$, past the pole at  $s=0$. By Lemma 2(a), the residue matches exactly the main term in (4.5) except for the truncation of the
$s=0$. By Lemma 2(a), the residue matches exactly the main term in (4.5) except for the truncation of the  $t$-integral, but by the rapid decay of
$t$-integral, but by the rapid decay of  $\mathscr{L}^{+}\mathscr{K}_{0}h_{T}=h_{T}$ for
$\mathscr{L}^{+}\mathscr{K}_{0}h_{T}=h_{T}$ for  $|t|\geqslant T$, we may reinsert the tail at the cost of a negligible error.
$|t|\geqslant T$, we may reinsert the tail at the cost of a negligible error.
To estimate the remaining integral, we shift the  $z_{1},z_{2}$-contours to left, past the triple poles at
$z_{1},z_{2}$-contours to left, past the triple poles at  $z_{1}=1/2-iv-s/2\pm it$,
$z_{1}=1/2-iv-s/2\pm it$,  $z_{2}=1/2-iv-s/2\pm it$ to
$z_{2}=1/2-iv-s/2\pm it$ to  $\Re z_{1},\Re z_{2}=\unicode[STIX]{x1D700}$. Thus we need to bound the contributions from the remaining integral and the two residues. The remaining multiple integral contains a
$\Re z_{1},\Re z_{2}=\unicode[STIX]{x1D700}$. Thus we need to bound the contributions from the remaining integral and the two residues. The remaining multiple integral contains a  $t$-integral that can be bounded by
$t$-integral that can be bounded by
 $$\begin{eqnarray}\;\ll _{\unicode[STIX]{x1D700}}\;\int _{|t|\leqslant (T+\sqrt{NT/Q})P^{\unicode[STIX]{x1D700}}}\biggl|\unicode[STIX]{x1D701}\biggl(\frac{1}{2}+\unicode[STIX]{x1D700}+it+i\unicode[STIX]{x1D70F}\biggr)\biggr|^{12}\displaystyle \frac{T^{2}}{(1+|t|)^{2-\unicode[STIX]{x1D700}}}\,dt\;\ll _{\unicode[STIX]{x1D700}}\;T^{2}(1+|\unicode[STIX]{x1D70F}|)^{2}P^{\unicode[STIX]{x1D700}},\end{eqnarray}$$
$$\begin{eqnarray}\;\ll _{\unicode[STIX]{x1D700}}\;\int _{|t|\leqslant (T+\sqrt{NT/Q})P^{\unicode[STIX]{x1D700}}}\biggl|\unicode[STIX]{x1D701}\biggl(\frac{1}{2}+\unicode[STIX]{x1D700}+it+i\unicode[STIX]{x1D70F}\biggr)\biggr|^{12}\displaystyle \frac{T^{2}}{(1+|t|)^{2-\unicode[STIX]{x1D700}}}\,dt\;\ll _{\unicode[STIX]{x1D700}}\;T^{2}(1+|\unicode[STIX]{x1D70F}|)^{2}P^{\unicode[STIX]{x1D700}},\end{eqnarray}$$ where  $\unicode[STIX]{x1D70F}=\pm v+\Im z_{j}+\frac{1}{2}\Im s_{j}$ and we used Heath-Brown’s twelfth moment bound [Reference Heath-BrownHea78]. Thus the total contribution of the remaining integral is
$\unicode[STIX]{x1D70F}=\pm v+\Im z_{j}+\frac{1}{2}\Im s_{j}$ and we used Heath-Brown’s twelfth moment bound [Reference Heath-BrownHea78]. Thus the total contribution of the remaining integral is  $O_{\unicode[STIX]{x1D700}}(QT^{2}P^{\unicode[STIX]{x1D700}})$. It remains to deal with the two residues. Here the rapid decay of
$O_{\unicode[STIX]{x1D700}}(QT^{2}P^{\unicode[STIX]{x1D700}})$. It remains to deal with the two residues. Here the rapid decay of  $\widehat{W}$ and
$\widehat{W}$ and  $\widehat{V}_{1,2}$ and their derivatives at
$\widehat{V}_{1,2}$ and their derivatives at  $z=1/2\pm iv-s/2\pm it$ makes the
$z=1/2\pm iv-s/2\pm it$ makes the  $t$-integral rapidly convergent regardless of the real part of
$t$-integral rapidly convergent regardless of the real part of  $s$, so we may shift the contour to
$s$, so we may shift the contour to  $\Re s=1-\unicode[STIX]{x1D700}$ (so that
$\Re s=1-\unicode[STIX]{x1D700}$ (so that  $\Re z_{j}=\unicode[STIX]{x1D700}$), getting a contribution of
$\Re z_{j}=\unicode[STIX]{x1D700}$), getting a contribution of  $O_{\unicode[STIX]{x1D700}}(Q^{2}T^{2}P^{\unicode[STIX]{x1D700}})$.
$O_{\unicode[STIX]{x1D700}}(Q^{2}T^{2}P^{\unicode[STIX]{x1D700}})$.
Combining (4.6) and the error term in (4.5) with the previous two error terms, we have accomplished so far the bound
 $$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{S}}_{v}(Q,T,N)\;\ll _{\unicode[STIX]{x1D700}}\;P^{\unicode[STIX]{x1D700}}(Q^{2}T^{2}+NT)\nonumber\\ \displaystyle & & \displaystyle \quad +\, |\int _{(-12)}Q^{s+1}\widehat{W}(s)\mathop{\sum }_{n_{1},n_{2},m_{1},m_{2}}\frac{A(n_{1},m_{1})A(n_{2},m_{2})}{(n_{1}m_{1}^{2})^{1/2+iv}(n_{2}m_{2}^{2})^{1/2-iv}(n_{1}n_{2})^{s/2}}V\biggl(\frac{n_{1}m_{1}^{2}}{N}\biggr)\overline{V\biggl(\frac{n_{2}m_{2}^{2}}{N}\biggr)}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\sum }_{c}c^{s}({\mathcal{A}}_{c}^{\text{Maa}\unicode[STIX]{x00DF}}(n_{1},n_{2};\mathscr{L}^{+}\mathscr{K}_{s}h_{T})+{\mathcal{A}}_{c}^{\text{Eis},\ast }(n_{1},n_{2};\mathscr{L}^{+}\mathscr{K}_{s}h_{T})+{\mathcal{A}}_{c}^{\text{hol}}(n_{1},n_{2};\mathscr{L}^{\text{hol}}\mathscr{K}_{s}h_{T}))\frac{ds}{2\unicode[STIX]{x1D70B}i} |,\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{S}}_{v}(Q,T,N)\;\ll _{\unicode[STIX]{x1D700}}\;P^{\unicode[STIX]{x1D700}}(Q^{2}T^{2}+NT)\nonumber\\ \displaystyle & & \displaystyle \quad +\, |\int _{(-12)}Q^{s+1}\widehat{W}(s)\mathop{\sum }_{n_{1},n_{2},m_{1},m_{2}}\frac{A(n_{1},m_{1})A(n_{2},m_{2})}{(n_{1}m_{1}^{2})^{1/2+iv}(n_{2}m_{2}^{2})^{1/2-iv}(n_{1}n_{2})^{s/2}}V\biggl(\frac{n_{1}m_{1}^{2}}{N}\biggr)\overline{V\biggl(\frac{n_{2}m_{2}^{2}}{N}\biggr)}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\sum }_{c}c^{s}({\mathcal{A}}_{c}^{\text{Maa}\unicode[STIX]{x00DF}}(n_{1},n_{2};\mathscr{L}^{+}\mathscr{K}_{s}h_{T})+{\mathcal{A}}_{c}^{\text{Eis},\ast }(n_{1},n_{2};\mathscr{L}^{+}\mathscr{K}_{s}h_{T})+{\mathcal{A}}_{c}^{\text{hol}}(n_{1},n_{2};\mathscr{L}^{\text{hol}}\mathscr{K}_{s}h_{T}))\frac{ds}{2\unicode[STIX]{x1D70B}i} |,\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$ where  ${\mathcal{A}}_{c}^{\text{Eis},\ast }$ denotes the contribution of level-
${\mathcal{A}}_{c}^{\text{Eis},\ast }$ denotes the contribution of level- $c$ Eisenstein series without the trivial character.
$c$ Eisenstein series without the trivial character.
4.4 The endgame
We consider the Maaß contribution in (4.9) given by
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{(-12)}Q^{s+1}\widehat{W}(s)\mathop{\sum }_{c}c^{s}\mathop{\sum }_{c_{0}M\mid c}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(c_{0})}\mathop{\sum }_{n_{1},n_{2},m_{1},m_{2}}\frac{A(n_{1},m_{1})A(n_{2},m_{2})\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},M,N}(n)\overline{\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},M,N}(m)}}{(n_{1}m_{1}^{2})^{1/2+iv}(n_{2}m_{2}^{2})^{1/2-iv}(n_{1}n_{2})^{s/2}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,V\biggl(\frac{n_{1}m_{1}^{2}}{N}\biggr)\overline{V\biggl(\frac{n_{2}m_{2}^{2}}{N}\biggr)}\mathscr{L}^{+}\mathscr{K}_{s}h_{T}(t_{\unicode[STIX]{x1D713}})\frac{ds}{2\unicode[STIX]{x1D70B}i}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{(-12)}Q^{s+1}\widehat{W}(s)\mathop{\sum }_{c}c^{s}\mathop{\sum }_{c_{0}M\mid c}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(c_{0})}\mathop{\sum }_{n_{1},n_{2},m_{1},m_{2}}\frac{A(n_{1},m_{1})A(n_{2},m_{2})\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},M,N}(n)\overline{\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},M,N}(m)}}{(n_{1}m_{1}^{2})^{1/2+iv}(n_{2}m_{2}^{2})^{1/2-iv}(n_{1}n_{2})^{s/2}}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,V\biggl(\frac{n_{1}m_{1}^{2}}{N}\biggr)\overline{V\biggl(\frac{n_{2}m_{2}^{2}}{N}\biggr)}\mathscr{L}^{+}\mathscr{K}_{s}h_{T}(t_{\unicode[STIX]{x1D713}})\frac{ds}{2\unicode[STIX]{x1D70B}i}.\nonumber\end{eqnarray}$$ Shifting the  $s$-contour to the far left, we see that we can truncate both the
$s$-contour to the far left, we see that we can truncate both the  $c$-sum and the
$c$-sum and the  $\unicode[STIX]{x1D713}$-sum at
$\unicode[STIX]{x1D713}$-sum at  $c(1+|t_{\unicode[STIX]{x1D713}}|^{2})\leqslant P^{\unicode[STIX]{x1D700}}NT/Q$ at the cost of a negligible error (recall (4.8) and the rapid decay of
$c(1+|t_{\unicode[STIX]{x1D713}}|^{2})\leqslant P^{\unicode[STIX]{x1D700}}NT/Q$ at the cost of a negligible error (recall (4.8) and the rapid decay of  $\widehat{V}$). Having done this, we shift the
$\widehat{V}$). Having done this, we shift the  $s$-contour back to
$s$-contour back to  $\Re s=0$. By Mellin inversion, we obtain
$\Re s=0$. By Mellin inversion, we obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{(0)}Q^{s+1}\widehat{W}(s)\underset{c(1+|t_{\unicode[STIX]{x1D713}}|^{2})\leqslant P^{\unicode[STIX]{x1D700}}NT/Q}{\mathop{\sum }_{c}\mathop{\sum }_{c_{0}\mid c}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(c_{0})}}\frac{c^{s}}{c\unicode[STIX]{x1D708}(c)}\mathop{\prod }_{p\mid c_{0}}(1-p^{-2})\int _{(\unicode[STIX]{x1D700})}\int _{(\unicode[STIX]{x1D700})}N^{z_{1}+z_{2}}\widehat{V}(z_{1})\widehat{V}(z_{2})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\frac{{\mathcal{D}}_{\unicode[STIX]{x1D713},c}^{\text{Maa}\unicode[STIX]{x00DF}}(1/2+iv+s/2+z_{1},1/2-iv+s/2+z_{2},-s/2,-s/2)}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathscr{L}^{+}\mathscr{K}_{s}h_{T}(t_{\unicode[STIX]{x1D713}})\frac{dz_{1}\,dz_{2}}{(2\unicode[STIX]{x1D70B}i)^{2}}\frac{ds}{2\unicode[STIX]{x1D70B}i},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{(0)}Q^{s+1}\widehat{W}(s)\underset{c(1+|t_{\unicode[STIX]{x1D713}}|^{2})\leqslant P^{\unicode[STIX]{x1D700}}NT/Q}{\mathop{\sum }_{c}\mathop{\sum }_{c_{0}\mid c}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(c_{0})}}\frac{c^{s}}{c\unicode[STIX]{x1D708}(c)}\mathop{\prod }_{p\mid c_{0}}(1-p^{-2})\int _{(\unicode[STIX]{x1D700})}\int _{(\unicode[STIX]{x1D700})}N^{z_{1}+z_{2}}\widehat{V}(z_{1})\widehat{V}(z_{2})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\frac{{\mathcal{D}}_{\unicode[STIX]{x1D713},c}^{\text{Maa}\unicode[STIX]{x00DF}}(1/2+iv+s/2+z_{1},1/2-iv+s/2+z_{2},-s/2,-s/2)}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathscr{L}^{+}\mathscr{K}_{s}h_{T}(t_{\unicode[STIX]{x1D713}})\frac{dz_{1}\,dz_{2}}{(2\unicode[STIX]{x1D70B}i)^{2}}\frac{ds}{2\unicode[STIX]{x1D70B}i},\end{eqnarray}$$where (recalling the notation in (2.9))
 $$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{D}}_{\unicode[STIX]{x1D713},c}^{\text{Maa}\unicode[STIX]{x00DF}}(z_{1},z_{2},w_{1},w_{2})\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})c\unicode[STIX]{x1D708}(c)}{\mathop{\prod }_{p\mid c_{0}}(1-p^{-2})}\mathop{\sum }_{M\mid (c/c_{0})}\mathop{\sum }_{n_{1},n_{2},m_{1},m_{2}}\frac{A(n_{1},m_{1})A(n_{2},m_{2})\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},M,c}(n)\overline{\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},M,c}(m)}}{(n_{1}m_{1}^{2})^{z_{1}}(n_{2}m_{2}^{2})^{z_{2}}m_{1}^{2w_{1}}m_{2}^{2w_{2}}}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{D}}_{\unicode[STIX]{x1D713},c}^{\text{Maa}\unicode[STIX]{x00DF}}(z_{1},z_{2},w_{1},w_{2})\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})c\unicode[STIX]{x1D708}(c)}{\mathop{\prod }_{p\mid c_{0}}(1-p^{-2})}\mathop{\sum }_{M\mid (c/c_{0})}\mathop{\sum }_{n_{1},n_{2},m_{1},m_{2}}\frac{A(n_{1},m_{1})A(n_{2},m_{2})\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},M,c}(n)\overline{\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D713},M,c}(m)}}{(n_{1}m_{1}^{2})^{z_{1}}(n_{2}m_{2}^{2})^{z_{2}}m_{1}^{2w_{1}}m_{2}^{2w_{2}}}\nonumber\end{eqnarray}$$ for  $\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(c_{0})$ with
$\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(c_{0})$ with  $c_{0}\mid c$. Using (2.9) and (2.11) (with
$c_{0}\mid c$. Using (2.9) and (2.11) (with  $\unicode[STIX]{x1D703}\leqslant 1/2$), we see as in (4.3) that
$\unicode[STIX]{x1D703}\leqslant 1/2$), we see as in (4.3) that
 $$\begin{eqnarray}{\mathcal{D}}_{\unicode[STIX]{x1D713},c}^{\text{Maa}\unicode[STIX]{x00DF}}(z_{1},z_{2},w_{1},w_{2})=L(z_{1},\unicode[STIX]{x1D713})^{3}L(z_{2},\unicode[STIX]{x1D713})^{3}{\mathcal{E}}_{\unicode[STIX]{x1D713},c}^{\text{Maa}\unicode[STIX]{x00DF}}(z_{1},z_{2},w_{1},w_{2}),\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{D}}_{\unicode[STIX]{x1D713},c}^{\text{Maa}\unicode[STIX]{x00DF}}(z_{1},z_{2},w_{1},w_{2})=L(z_{1},\unicode[STIX]{x1D713})^{3}L(z_{2},\unicode[STIX]{x1D713})^{3}{\mathcal{E}}_{\unicode[STIX]{x1D713},c}^{\text{Maa}\unicode[STIX]{x00DF}}(z_{1},z_{2},w_{1},w_{2}),\end{eqnarray}$$where
 $$\begin{eqnarray}{\mathcal{E}}_{\unicode[STIX]{x1D713},c}^{\text{Maa}\unicode[STIX]{x00DF}}(z_{1},z_{2},w_{1},w_{2})\;\ll _{\unicode[STIX]{x1D700}}\;c^{\unicode[STIX]{x1D700}}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{E}}_{\unicode[STIX]{x1D713},c}^{\text{Maa}\unicode[STIX]{x00DF}}(z_{1},z_{2},w_{1},w_{2})\;\ll _{\unicode[STIX]{x1D700}}\;c^{\unicode[STIX]{x1D700}}\end{eqnarray}$$ uniformly in  $\Re z_{1},\Re z_{2},\Re (z_{1}+w_{1}),\Re (z_{2}+w_{2})\geqslant 1/2+\unicode[STIX]{x1D700}$. The convexity bound for
$\Re z_{1},\Re z_{2},\Re (z_{1}+w_{1}),\Re (z_{2}+w_{2})\geqslant 1/2+\unicode[STIX]{x1D700}$. The convexity bound for  $L(z,\unicode[STIX]{x1D713})$ is
$L(z,\unicode[STIX]{x1D713})$ is
 $$\begin{eqnarray}L(z,\unicode[STIX]{x1D713})\;\ll _{\unicode[STIX]{x1D700}}\;(c_{0}(1+|t_{\unicode[STIX]{x1D713}}|+|\Im z|)^{2})^{1/4+\unicode[STIX]{x1D700}},\quad \Re z\geqslant 1/2.\end{eqnarray}$$
$$\begin{eqnarray}L(z,\unicode[STIX]{x1D713})\;\ll _{\unicode[STIX]{x1D700}}\;(c_{0}(1+|t_{\unicode[STIX]{x1D713}}|+|\Im z|)^{2})^{1/4+\unicode[STIX]{x1D700}},\quad \Re z\geqslant 1/2.\end{eqnarray}$$ We can afford to use the convexity bound on four of the six  $L$-functions in (4.11). We may then truncate the
$L$-functions in (4.11). We may then truncate the  $s,z_{1},z_{2}$-contours at height
$s,z_{1},z_{2}$-contours at height  $P^{\unicode[STIX]{x1D700}}$, and after a trivial estimation, we bound (4.10) by
$P^{\unicode[STIX]{x1D700}}$, and after a trivial estimation, we bound (4.10) by
 $$\begin{eqnarray}\;\ll _{\unicode[STIX]{x1D700}}\;P^{\unicode[STIX]{x1D700}}Q\frac{NT}{Q}\max _{|\unicode[STIX]{x1D709}|\leqslant P^{\unicode[STIX]{x1D700}}}\underset{c(1+|t_{\unicode[STIX]{x1D713}}|^{2})\leqslant P^{\unicode[STIX]{x1D700}}NT/Q}{\mathop{\sum }_{c}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(c)}}\frac{1}{c}\biggl|L\biggl(\frac{1}{2}+\unicode[STIX]{x1D700}+i\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}\biggr)\biggr|^{2}\frac{T^{2}}{(1+|t_{\unicode[STIX]{x1D713}}|^{2})}.\end{eqnarray}$$
$$\begin{eqnarray}\;\ll _{\unicode[STIX]{x1D700}}\;P^{\unicode[STIX]{x1D700}}Q\frac{NT}{Q}\max _{|\unicode[STIX]{x1D709}|\leqslant P^{\unicode[STIX]{x1D700}}}\underset{c(1+|t_{\unicode[STIX]{x1D713}}|^{2})\leqslant P^{\unicode[STIX]{x1D700}}NT/Q}{\mathop{\sum }_{c}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(c)}}\frac{1}{c}\biggl|L\biggl(\frac{1}{2}+\unicode[STIX]{x1D700}+i\unicode[STIX]{x1D709},\unicode[STIX]{x1D713}\biggr)\biggr|^{2}\frac{T^{2}}{(1+|t_{\unicode[STIX]{x1D713}}|^{2})}.\end{eqnarray}$$ It is an easy exercise with the Kuznetsov formula or the spectral large sieve to obtain a Lindelöf on average bound for the second moment, which can safely be left to the reader: the length of the approximate functional equation in each factor is  $O_{\unicode[STIX]{x1D700}}(P^{\unicode[STIX]{x1D700}}c^{1/2}(1+|t_{\unicode[STIX]{x1D713}}|))$, so the Kloosterman term in the Kuznetsov formula is essentially invisible. Thus by Weyl’s law, the total contribution of the previous expression is
$O_{\unicode[STIX]{x1D700}}(P^{\unicode[STIX]{x1D700}}c^{1/2}(1+|t_{\unicode[STIX]{x1D713}}|))$, so the Kloosterman term in the Kuznetsov formula is essentially invisible. Thus by Weyl’s law, the total contribution of the previous expression is
 $$\begin{eqnarray}\;\ll _{\unicode[STIX]{x1D700}}\;P^{\unicode[STIX]{x1D700}}N^{2}T^{2}Q^{-1}\;\ll _{\unicode[STIX]{x1D700}}\;P^{\unicode[STIX]{x1D700}}Q^{2}T^{8}\end{eqnarray}$$
$$\begin{eqnarray}\;\ll _{\unicode[STIX]{x1D700}}\;P^{\unicode[STIX]{x1D700}}N^{2}T^{2}Q^{-1}\;\ll _{\unicode[STIX]{x1D700}}\;P^{\unicode[STIX]{x1D700}}Q^{2}T^{8}\end{eqnarray}$$ for  $N\leqslant Q^{3/2}T^{3}P^{\unicode[STIX]{x1D700}}$, and this majorizes all preceding error terms.
$N\leqslant Q^{3/2}T^{3}P^{\unicode[STIX]{x1D700}}$, and this majorizes all preceding error terms.
The contribution of  ${\mathcal{A}}_{c}^{\text{hol}}(n_{1},n_{2};\mathscr{L}^{\text{hol}}\mathscr{K}_{s}h_{T})$ can be bounded in same way using the analogous bound for
${\mathcal{A}}_{c}^{\text{hol}}(n_{1},n_{2};\mathscr{L}^{\text{hol}}\mathscr{K}_{s}h_{T})$ can be bounded in same way using the analogous bound for  $\mathscr{L}^{\text{hol}}\mathscr{K}_{s}h_{T}$ in Lemma 2(b).
$\mathscr{L}^{\text{hol}}\mathscr{K}_{s}h_{T}$ in Lemma 2(b).
Finally, for the contribution  ${\mathcal{A}}_{c}^{\text{Eis},\ast }(n_{1},n_{2};\mathscr{L}^{+}\mathscr{K}_{s}h_{T})$, we observe that after removing the trivial character, the analogously defined function
${\mathcal{A}}_{c}^{\text{Eis},\ast }(n_{1},n_{2};\mathscr{L}^{+}\mathscr{K}_{s}h_{T})$, we observe that after removing the trivial character, the analogously defined function
 $$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{D}}_{(\unicode[STIX]{x1D712},t),c}^{\text{Eis}}(z_{1},z_{2},w_{1},w_{2})\nonumber\\ \displaystyle & & \displaystyle \quad =|L(1+2it,\unicode[STIX]{x1D712}^{2})|^{2}c\unicode[STIX]{x1D708}(c)\mathop{\sum }_{c_{\unicode[STIX]{x1D712}}^{2}\mid M\mid c}\mathop{\sum }_{n_{1},n_{2},m_{1},m_{2}}\frac{A(n_{1},m_{1})A(n_{2},m_{2})\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712},M,c}(n)\overline{\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712},M,c}(m)}}{(n_{1}m_{1}^{2})^{z_{1}}(n_{2}m_{2}^{2})^{z_{2}}m_{1}^{2w_{1}}m_{2}^{2w_{2}}}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{D}}_{(\unicode[STIX]{x1D712},t),c}^{\text{Eis}}(z_{1},z_{2},w_{1},w_{2})\nonumber\\ \displaystyle & & \displaystyle \quad =|L(1+2it,\unicode[STIX]{x1D712}^{2})|^{2}c\unicode[STIX]{x1D708}(c)\mathop{\sum }_{c_{\unicode[STIX]{x1D712}}^{2}\mid M\mid c}\mathop{\sum }_{n_{1},n_{2},m_{1},m_{2}}\frac{A(n_{1},m_{1})A(n_{2},m_{2})\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712},M,c}(n)\overline{\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712},M,c}(m)}}{(n_{1}m_{1}^{2})^{z_{1}}(n_{2}m_{2}^{2})^{z_{2}}m_{1}^{2w_{1}}m_{2}^{2w_{2}}}\nonumber\end{eqnarray}$$ is pole-free in  $\Re z_{1},\Re z_{2},\Re (z_{1}+w_{1}),\Re (z_{2}+w_{2})\geqslant 1/2+\unicode[STIX]{x1D700}$ since
$\Re z_{1},\Re z_{2},\Re (z_{1}+w_{1}),\Re (z_{2}+w_{2})\geqslant 1/2+\unicode[STIX]{x1D700}$ since  $\unicode[STIX]{x1D712}$ is primitive of conductor
$\unicode[STIX]{x1D712}$ is primitive of conductor  ${>}1$, and it can be approximated by
${>}1$, and it can be approximated by  $L(z_{1}+it,\unicode[STIX]{x1D712})^{3}L(z_{1}-it,\overline{\unicode[STIX]{x1D712}})^{3}L(z_{2}+it,\unicode[STIX]{x1D712})^{3}L(z_{2}-it,\overline{\unicode[STIX]{x1D712}})^{3}$ in this region up to a holomorphic factor bounded by
$L(z_{1}+it,\unicode[STIX]{x1D712})^{3}L(z_{1}-it,\overline{\unicode[STIX]{x1D712}})^{3}L(z_{2}+it,\unicode[STIX]{x1D712})^{3}L(z_{2}-it,\overline{\unicode[STIX]{x1D712}})^{3}$ in this region up to a holomorphic factor bounded by  $O_{\unicode[STIX]{x1D700}}(c^{\unicode[STIX]{x1D700}})$. Here we can even afford to apply the convexity bound for all 12 Dirichlet
$O_{\unicode[STIX]{x1D700}}(c^{\unicode[STIX]{x1D700}})$. Here we can even afford to apply the convexity bound for all 12 Dirichlet  $L$-functions. The quantity corresponding to (4.12) is then
$L$-functions. The quantity corresponding to (4.12) is then
 $$\begin{eqnarray}P^{\unicode[STIX]{x1D700}}Q\biggl(\frac{NT}{Q}\biggr)^{3/2}\mathop{\sum }_{c}\int _{c(1+|t|)^{2}\leqslant P^{\unicode[STIX]{x1D700}}NT/Q}\frac{\#\{\unicode[STIX]{x1D712}:c_{\unicode[STIX]{x1D712}}^{2}\mid c\}T^{2}}{c(1+|t|^{2})}\,dt\;\ll _{\unicode[STIX]{x1D700}}\;P^{\unicode[STIX]{x1D700}}Q\biggl(\frac{NT}{Q}\biggr)^{3/2}\;\ll _{\unicode[STIX]{x1D700}}\;P^{\unicode[STIX]{x1D700}}Q^{7/4}T^{6}.\end{eqnarray}$$
$$\begin{eqnarray}P^{\unicode[STIX]{x1D700}}Q\biggl(\frac{NT}{Q}\biggr)^{3/2}\mathop{\sum }_{c}\int _{c(1+|t|)^{2}\leqslant P^{\unicode[STIX]{x1D700}}NT/Q}\frac{\#\{\unicode[STIX]{x1D712}:c_{\unicode[STIX]{x1D712}}^{2}\mid c\}T^{2}}{c(1+|t|^{2})}\,dt\;\ll _{\unicode[STIX]{x1D700}}\;P^{\unicode[STIX]{x1D700}}Q\biggl(\frac{NT}{Q}\biggr)^{3/2}\;\ll _{\unicode[STIX]{x1D700}}\;P^{\unicode[STIX]{x1D700}}Q^{7/4}T^{6}.\end{eqnarray}$$This completes the proof of Theorem 2.
5 Applications
It is now an easy task to prove Corollary 3 and Theorem 4. For both applications, we need the following auxiliary result.
Lemma 3. Let  $T\geqslant 1$,
$T\geqslant 1$,  $N,q\in \mathbb{N}$,
$N,q\in \mathbb{N}$,  $(N,q)=1$. Then
$(N,q)=1$. Then
 $$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(N)}\frac{\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(q)^{2}}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})}e^{-(t_{\unicode[STIX]{x1D713}}/T)^{2}}\;\ll _{\unicode[STIX]{x1D700}}\;(NTq)^{\unicode[STIX]{x1D700}}(T^{2}N+q^{1/2}).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(N)}\frac{\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(q)^{2}}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})}e^{-(t_{\unicode[STIX]{x1D713}}/T)^{2}}\;\ll _{\unicode[STIX]{x1D700}}\;(NTq)^{\unicode[STIX]{x1D700}}(T^{2}N+q^{1/2}).\end{eqnarray}$$This is a simple application of the Kuznetsov formula and Weil’s bounds for Kloosterman sums; see, for example, [Reference Blomer and MilićevićBM15, Lemma 12] or its ancestor [Reference MotohashiMot97, Lemma 2.4].
5.1 Proof of Corollary 3
From [Reference Blomer and KhanBK19b, §12.1], we quote
 $$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(q)}L(1/2,\unicode[STIX]{x1D713})^{5}e^{-t_{\unicode[STIX]{x1D713}}^{2}}\;\ll _{\unicode[STIX]{x1D700}}\;q^{\unicode[STIX]{x1D700}}\max _{|\unicode[STIX]{x1D70F}|\leqslant (\log q)^{2}}\mathop{\sum }_{\ell \leqslant q^{1/2+\unicode[STIX]{x1D700}}}\frac{1}{\ell ^{1/2}}\biggl|\mathop{\sum }_{f\in {\mathcal{B}}^{\ast }(q)}\frac{L(1/2,f)^{4}}{L(1,\text{Ad}^{2}f)}\unicode[STIX]{x1D706}_{f}(\ell )h_{\unicode[STIX]{x1D70F}}(t_{f})\biggr|+q^{-10},\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(q)}L(1/2,\unicode[STIX]{x1D713})^{5}e^{-t_{\unicode[STIX]{x1D713}}^{2}}\;\ll _{\unicode[STIX]{x1D700}}\;q^{\unicode[STIX]{x1D700}}\max _{|\unicode[STIX]{x1D70F}|\leqslant (\log q)^{2}}\mathop{\sum }_{\ell \leqslant q^{1/2+\unicode[STIX]{x1D700}}}\frac{1}{\ell ^{1/2}}\biggl|\mathop{\sum }_{f\in {\mathcal{B}}^{\ast }(q)}\frac{L(1/2,f)^{4}}{L(1,\text{Ad}^{2}f)}\unicode[STIX]{x1D706}_{f}(\ell )h_{\unicode[STIX]{x1D70F}}(t_{f})\biggr|+q^{-10},\end{eqnarray}$$where
 $$\begin{eqnarray}h_{\unicode[STIX]{x1D70F}}(t_{f})=\frac{L_{\infty }(1/2+\unicode[STIX]{x1D700}+i\unicode[STIX]{x1D70F},f)}{L_{\infty }(1/2,f)}\frac{G_{f}(\unicode[STIX]{x1D700}+i\unicode[STIX]{x1D70F})}{G_{f}(0)}e^{-t_{f}^{2}}(1+|t_{f}|)^{\unicode[STIX]{x1D700}}\end{eqnarray}$$
$$\begin{eqnarray}h_{\unicode[STIX]{x1D70F}}(t_{f})=\frac{L_{\infty }(1/2+\unicode[STIX]{x1D700}+i\unicode[STIX]{x1D70F},f)}{L_{\infty }(1/2,f)}\frac{G_{f}(\unicode[STIX]{x1D700}+i\unicode[STIX]{x1D70F})}{G_{f}(0)}e^{-t_{f}^{2}}(1+|t_{f}|)^{\unicode[STIX]{x1D700}}\end{eqnarray}$$with
 $$\begin{eqnarray}G_{f}(s)=\mathop{\prod }_{j=0}^{1000}\mathop{\prod }_{\unicode[STIX]{x1D716}_{1},\unicode[STIX]{x1D716}_{2}\in \{\pm 1\}}\biggl(\frac{1}{2}+\unicode[STIX]{x1D716}_{1}s+i\unicode[STIX]{x1D716}_{2}t_{f}+j\biggr).\end{eqnarray}$$
$$\begin{eqnarray}G_{f}(s)=\mathop{\prod }_{j=0}^{1000}\mathop{\prod }_{\unicode[STIX]{x1D716}_{1},\unicode[STIX]{x1D716}_{2}\in \{\pm 1\}}\biggl(\frac{1}{2}+\unicode[STIX]{x1D716}_{1}s+i\unicode[STIX]{x1D716}_{2}t_{f}+j\biggr).\end{eqnarray}$$ This is an application of a carefully designed approximate functional equation. Now the formula two displays below [Reference Blomer and KhanBK19b, (11.4)], together with [Reference Blomer and KhanBK19b, Lemma 1], shows that for  $q$ prime,
$q$ prime,
 $$\begin{eqnarray}\frac{\unicode[STIX]{x1D719}(q)}{q^{2}}\mathop{\sum }_{f\in {\mathcal{B}}^{\ast }(q)}\frac{L(1/2,f)^{4}}{L(1,\text{Ad}^{2}f)}\unicode[STIX]{x1D706}_{f}(\ell )h_{\unicode[STIX]{x1D70F}}(t_{f})=\mathop{\sum }_{ab=\ell }{\mathcal{M}}_{q,a}^{+}(1/2,1/2,\mathfrak{h}_{\unicode[STIX]{x1D70F}})\biggl(\frac{a}{b}\biggr)^{1/2}+O(\ell ^{\unicode[STIX]{x1D703}+\unicode[STIX]{x1D700}}q^{-1})\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D719}(q)}{q^{2}}\mathop{\sum }_{f\in {\mathcal{B}}^{\ast }(q)}\frac{L(1/2,f)^{4}}{L(1,\text{Ad}^{2}f)}\unicode[STIX]{x1D706}_{f}(\ell )h_{\unicode[STIX]{x1D70F}}(t_{f})=\mathop{\sum }_{ab=\ell }{\mathcal{M}}_{q,a}^{+}(1/2,1/2,\mathfrak{h}_{\unicode[STIX]{x1D70F}})\biggl(\frac{a}{b}\biggr)^{1/2}+O(\ell ^{\unicode[STIX]{x1D703}+\unicode[STIX]{x1D700}}q^{-1})\end{eqnarray}$$ with  $\mathfrak{h}_{\unicode[STIX]{x1D70F}}=(h_{\unicode[STIX]{x1D70F}},0)$ in the notation of [Reference Blomer and KhanBK19b, (1.3), (1.7)]. Here the error term also includes the oldforms of level 1. On the other hand, [Reference Blomer and KhanBK19b, (11.4)] states that
$\mathfrak{h}_{\unicode[STIX]{x1D70F}}=(h_{\unicode[STIX]{x1D70F}},0)$ in the notation of [Reference Blomer and KhanBK19b, (1.3), (1.7)]. Here the error term also includes the oldforms of level 1. On the other hand, [Reference Blomer and KhanBK19b, (11.4)] states that
 $$\begin{eqnarray}\mathop{\sum }_{ab=\ell }{\mathcal{M}}_{q,a}^{+}(1/2,1/2,\mathfrak{h}_{\unicode[STIX]{x1D70F}})\biggl(\frac{a}{b}\biggr)^{1/2}\;\ll _{\unicode[STIX]{x1D700}}\;(\ell q)^{\unicode[STIX]{x1D700}}\mathop{\sum }_{ab=\ell }\biggl(\frac{a}{b}\biggr)^{1/2}\biggl(\frac{1}{a}+\frac{1}{q}+\mathop{\sum }_{\pm }\big|{\mathcal{M}}_{a,q}^{\pm }(1/2,1/2;\mathscr{T}_{1/2,1/2}^{\pm }\mathfrak{h}_{\unicode[STIX]{x1D70F}})\big|\biggr)\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{ab=\ell }{\mathcal{M}}_{q,a}^{+}(1/2,1/2,\mathfrak{h}_{\unicode[STIX]{x1D70F}})\biggl(\frac{a}{b}\biggr)^{1/2}\;\ll _{\unicode[STIX]{x1D700}}\;(\ell q)^{\unicode[STIX]{x1D700}}\mathop{\sum }_{ab=\ell }\biggl(\frac{a}{b}\biggr)^{1/2}\biggl(\frac{1}{a}+\frac{1}{q}+\mathop{\sum }_{\pm }\big|{\mathcal{M}}_{a,q}^{\pm }(1/2,1/2;\mathscr{T}_{1/2,1/2}^{\pm }\mathfrak{h}_{\unicode[STIX]{x1D70F}})\big|\biggr)\end{eqnarray}$$ uniformly in  $|\unicode[STIX]{x1D70F}|\leqslant (\log q)^{2}$, and the analysis of [Reference Blomer and KhanBK19b, §11] shows
$|\unicode[STIX]{x1D70F}|\leqslant (\log q)^{2}$, and the analysis of [Reference Blomer and KhanBK19b, §11] shows
 $$\begin{eqnarray}{\mathcal{M}}_{a,q}^{\pm }(1/2,1/2;\mathscr{T}_{1/2,1/2}^{\pm }\mathfrak{h}_{\unicode[STIX]{x1D70F}})\;\ll _{\unicode[STIX]{x1D700}}\;(aq)^{\unicode[STIX]{x1D700}}\biggl(\frac{1}{q^{1/2}}+\frac{1}{aq^{1/2}}\mathop{\sum }_{a_{0}\mid a}\mathop{\sum }_{f\in {\mathcal{B}}^{\ast }(a_{0})}\frac{|L(1/2,f)|^{4}}{L(1,\text{Ad}^{2}f)}\frac{|\unicode[STIX]{x1D6EC}_{f}(q,1/2)|}{(1+|t_{f}|)^{15}}\biggr)\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{M}}_{a,q}^{\pm }(1/2,1/2;\mathscr{T}_{1/2,1/2}^{\pm }\mathfrak{h}_{\unicode[STIX]{x1D70F}})\;\ll _{\unicode[STIX]{x1D700}}\;(aq)^{\unicode[STIX]{x1D700}}\biggl(\frac{1}{q^{1/2}}+\frac{1}{aq^{1/2}}\mathop{\sum }_{a_{0}\mid a}\mathop{\sum }_{f\in {\mathcal{B}}^{\ast }(a_{0})}\frac{|L(1/2,f)|^{4}}{L(1,\text{Ad}^{2}f)}\frac{|\unicode[STIX]{x1D6EC}_{f}(q,1/2)|}{(1+|t_{f}|)^{15}}\biggr)\end{eqnarray}$$ (again uniformly in  $|\unicode[STIX]{x1D70F}|\leqslant (\log q)^{2}$) where
$|\unicode[STIX]{x1D70F}|\leqslant (\log q)^{2}$) where  $\unicode[STIX]{x1D6EC}_{f}(q,1/2):=\unicode[STIX]{x1D706}_{f}(q)-q^{-1/2}$ for
$\unicode[STIX]{x1D6EC}_{f}(q,1/2):=\unicode[STIX]{x1D706}_{f}(q)-q^{-1/2}$ for  $q$ prime. Combining these estimates, we obtain
$q$ prime. Combining these estimates, we obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x1D719}(q)}{q^{2}}\mathop{\sum }_{f\in {\mathcal{B}}^{\ast }(q)}\frac{L(1/2,f)^{4}}{L(1,\text{Ad}^{2}f)}\unicode[STIX]{x1D706}_{f}(\ell )h_{\unicode[STIX]{x1D70F}}(t_{f})\nonumber\\ \displaystyle & & \displaystyle \quad \;\ll _{\unicode[STIX]{x1D700}}\;(\ell q)^{\unicode[STIX]{x1D700}}\biggl(\frac{1}{\ell ^{1/2}}+\frac{\ell ^{1/2}}{q^{1/2}}+\frac{1}{(\ell q)^{1/2}}\mathop{\sum }_{a_{0}\mid \ell }\mathop{\sum }_{f\in {\mathcal{B}}^{\ast }(a_{0})}\frac{|L(1/2,f)|^{4}}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})}\frac{(1+|\unicode[STIX]{x1D706}_{f}(q)|)}{(1+|t_{f}|)^{15}}\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x1D719}(q)}{q^{2}}\mathop{\sum }_{f\in {\mathcal{B}}^{\ast }(q)}\frac{L(1/2,f)^{4}}{L(1,\text{Ad}^{2}f)}\unicode[STIX]{x1D706}_{f}(\ell )h_{\unicode[STIX]{x1D70F}}(t_{f})\nonumber\\ \displaystyle & & \displaystyle \quad \;\ll _{\unicode[STIX]{x1D700}}\;(\ell q)^{\unicode[STIX]{x1D700}}\biggl(\frac{1}{\ell ^{1/2}}+\frac{\ell ^{1/2}}{q^{1/2}}+\frac{1}{(\ell q)^{1/2}}\mathop{\sum }_{a_{0}\mid \ell }\mathop{\sum }_{f\in {\mathcal{B}}^{\ast }(a_{0})}\frac{|L(1/2,f)|^{4}}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})}\frac{(1+|\unicode[STIX]{x1D706}_{f}(q)|)}{(1+|t_{f}|)^{15}}\biggr).\nonumber\end{eqnarray}$$Substituting back into (5.1), this yields
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(q)}L(1/2,\unicode[STIX]{x1D713})^{5}e^{-t_{\unicode[STIX]{x1D713}}^{2}} & \;\ll _{\unicode[STIX]{x1D700}}\; & \displaystyle q^{1+\unicode[STIX]{x1D700}}\mathop{\sum }_{\ell \leqslant q^{1/2+\unicode[STIX]{x1D700}}}\biggl(\frac{1}{\ell }+\frac{1}{q^{1/2}}+\frac{1}{\ell q^{1/2}}\mathop{\sum }_{a\mid \ell }\mathop{\sum }_{f\in {\mathcal{B}}^{\ast }(a)}\frac{|L(1/2,f)|^{4}}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})}\frac{(1+|\unicode[STIX]{x1D706}_{f}(q)|)}{(1+|t_{f}|)^{15}}\biggr)\nonumber\\ \displaystyle & \;\ll _{\unicode[STIX]{x1D700}}\; & \displaystyle q^{1+\unicode[STIX]{x1D700}}+q^{1/2+\unicode[STIX]{x1D700}}\mathop{\sum }_{a\leqslant q^{1/2+\unicode[STIX]{x1D700}}}\frac{1}{a}\mathop{\sum }_{f\in {\mathcal{B}}^{\ast }(a)}\frac{|L(1/2,f)|^{4}}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})}\frac{(1+|\unicode[STIX]{x1D706}_{f}(q)|)}{(1+|t_{f}|)^{15}}\nonumber\\ \displaystyle & \;\ll _{\unicode[STIX]{x1D700}}\; & \displaystyle q^{1+\unicode[STIX]{x1D700}}+q^{1/2+\unicode[STIX]{x1D700}}\max _{A\leqslant q^{1/2+\unicode[STIX]{x1D700}}}\frac{1}{A}\mathop{\sum }_{a\asymp A}\mathop{\sum }_{f\in {\mathcal{B}}^{\ast }(a)}\frac{|L(1/2,f)|^{4}}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})}\frac{(1+|\unicode[STIX]{x1D706}_{f}(q)|)}{(1+|t_{f}|)^{15}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(q)}L(1/2,\unicode[STIX]{x1D713})^{5}e^{-t_{\unicode[STIX]{x1D713}}^{2}} & \;\ll _{\unicode[STIX]{x1D700}}\; & \displaystyle q^{1+\unicode[STIX]{x1D700}}\mathop{\sum }_{\ell \leqslant q^{1/2+\unicode[STIX]{x1D700}}}\biggl(\frac{1}{\ell }+\frac{1}{q^{1/2}}+\frac{1}{\ell q^{1/2}}\mathop{\sum }_{a\mid \ell }\mathop{\sum }_{f\in {\mathcal{B}}^{\ast }(a)}\frac{|L(1/2,f)|^{4}}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})}\frac{(1+|\unicode[STIX]{x1D706}_{f}(q)|)}{(1+|t_{f}|)^{15}}\biggr)\nonumber\\ \displaystyle & \;\ll _{\unicode[STIX]{x1D700}}\; & \displaystyle q^{1+\unicode[STIX]{x1D700}}+q^{1/2+\unicode[STIX]{x1D700}}\mathop{\sum }_{a\leqslant q^{1/2+\unicode[STIX]{x1D700}}}\frac{1}{a}\mathop{\sum }_{f\in {\mathcal{B}}^{\ast }(a)}\frac{|L(1/2,f)|^{4}}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})}\frac{(1+|\unicode[STIX]{x1D706}_{f}(q)|)}{(1+|t_{f}|)^{15}}\nonumber\\ \displaystyle & \;\ll _{\unicode[STIX]{x1D700}}\; & \displaystyle q^{1+\unicode[STIX]{x1D700}}+q^{1/2+\unicode[STIX]{x1D700}}\max _{A\leqslant q^{1/2+\unicode[STIX]{x1D700}}}\frac{1}{A}\mathop{\sum }_{a\asymp A}\mathop{\sum }_{f\in {\mathcal{B}}^{\ast }(a)}\frac{|L(1/2,f)|^{4}}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})}\frac{(1+|\unicode[STIX]{x1D706}_{f}(q)|)}{(1+|t_{f}|)^{15}}.\nonumber\end{eqnarray}$$So far this is essentially a restatement of the analysis in [Reference Blomer and KhanBK19b], but now we insert an additional application of Hölder’s inequality. In this way, we obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(q)}L(1/2,\unicode[STIX]{x1D713})^{5}e^{-t_{\unicode[STIX]{x1D713}}^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad \;\ll _{\unicode[STIX]{x1D700}}\;q^{1+\unicode[STIX]{x1D700}}+q^{1/2+\unicode[STIX]{x1D700}}\max _{A\leqslant q^{1/2+\unicode[STIX]{x1D700}}}\frac{1}{A}\biggl(\mathop{\sum }_{a\asymp A}\mathop{\sum }_{f\in {\mathcal{B}}^{\ast }(a)}\frac{|L(1/2,f)|^{6}}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})(1+|t_{f}|)^{15}}\biggr)^{2/3}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\biggl(\mathop{\sum }_{a\asymp A}\mathop{\sum }_{f\in {\mathcal{B}}^{\ast }(a)}\frac{(1+|\unicode[STIX]{x1D706}_{f}(q)|)^{3}}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})(1+|t_{f}|)^{15}}\biggr)^{1/3}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(q)}L(1/2,\unicode[STIX]{x1D713})^{5}e^{-t_{\unicode[STIX]{x1D713}}^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad \;\ll _{\unicode[STIX]{x1D700}}\;q^{1+\unicode[STIX]{x1D700}}+q^{1/2+\unicode[STIX]{x1D700}}\max _{A\leqslant q^{1/2+\unicode[STIX]{x1D700}}}\frac{1}{A}\biggl(\mathop{\sum }_{a\asymp A}\mathop{\sum }_{f\in {\mathcal{B}}^{\ast }(a)}\frac{|L(1/2,f)|^{6}}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})(1+|t_{f}|)^{15}}\biggr)^{2/3}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\biggl(\mathop{\sum }_{a\asymp A}\mathop{\sum }_{f\in {\mathcal{B}}^{\ast }(a)}\frac{(1+|\unicode[STIX]{x1D706}_{f}(q)|)^{3}}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})(1+|t_{f}|)^{15}}\biggr)^{1/3}.\nonumber\end{eqnarray}$$By Theorem 2 and Lemma 3, we obtain
 $$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(q)}L(1/2,\unicode[STIX]{x1D713})^{5}e^{-t_{\unicode[STIX]{x1D713}}^{2}}\;\ll _{\unicode[STIX]{x1D700}}\;q^{\unicode[STIX]{x1D700}}\biggl(q+q^{1/2}\max _{A\leqslant q^{1/2+\unicode[STIX]{x1D700}}}\frac{1}{A}A^{4/3}(A^{2}+q^{1/2})^{1/3}q^{\unicode[STIX]{x1D703}/3}\biggr)\;\ll _{\unicode[STIX]{x1D700}}\;q^{1+\unicode[STIX]{x1D703}/3+\unicode[STIX]{x1D700}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(q)}L(1/2,\unicode[STIX]{x1D713})^{5}e^{-t_{\unicode[STIX]{x1D713}}^{2}}\;\ll _{\unicode[STIX]{x1D700}}\;q^{\unicode[STIX]{x1D700}}\biggl(q+q^{1/2}\max _{A\leqslant q^{1/2+\unicode[STIX]{x1D700}}}\frac{1}{A}A^{4/3}(A^{2}+q^{1/2})^{1/3}q^{\unicode[STIX]{x1D703}/3}\biggr)\;\ll _{\unicode[STIX]{x1D700}}\;q^{1+\unicode[STIX]{x1D703}/3+\unicode[STIX]{x1D700}}.\end{eqnarray}$$5.2 Proof of Theorem 4
By a dyadic decomposition, we can replace the summation condition  $m\leqslant M$ by
$m\leqslant M$ by  $m\asymp M$. Let us also assume without loss of generality that
$m\asymp M$. Let us also assume without loss of generality that  $\Vert \mathbf{a}\Vert _{\infty }\leqslant 1$. In order to apply Theorem 1, we would like to bound
$\Vert \mathbf{a}\Vert _{\infty }\leqslant 1$. In order to apply Theorem 1, we would like to bound  $L(1/2,\unicode[STIX]{x1D712})$ by a small integral over the imaginary axis. This can be done by a standard argument based on the functional equation and the residue theorem (which seems to have been first applied by Heath-Brown [Reference Heath-BrownHea78, Lemma 3]) as follows. Fix
$L(1/2,\unicode[STIX]{x1D712})$ by a small integral over the imaginary axis. This can be done by a standard argument based on the functional equation and the residue theorem (which seems to have been first applied by Heath-Brown [Reference Heath-BrownHea78, Lemma 3]) as follows. Fix  $0<\unicode[STIX]{x1D700}<1/10$ and suppose that
$0<\unicode[STIX]{x1D700}<1/10$ and suppose that  $\unicode[STIX]{x1D712}$ is a primitive character modulo
$\unicode[STIX]{x1D712}$ is a primitive character modulo  $q$. We have
$q$. We have
 $$\begin{eqnarray}\displaystyle L(1/2,\unicode[STIX]{x1D712})^{4} & = & \displaystyle \int _{(\unicode[STIX]{x1D700})}L(1/2+s,\unicode[STIX]{x1D712})^{4}\frac{e^{2s^{2}}}{s}\frac{ds}{2\unicode[STIX]{x1D70B}i}+\int _{(\unicode[STIX]{x1D700})}L(1/2-s,\unicode[STIX]{x1D712})^{4}\frac{e^{2s^{2}}}{s}\frac{ds}{2\unicode[STIX]{x1D70B}i}\nonumber\\ \displaystyle & = & \displaystyle \int _{(\unicode[STIX]{x1D700})}L(1/2+s,\unicode[STIX]{x1D712})^{4}f(s)\frac{ds}{2\unicode[STIX]{x1D70B}i},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle L(1/2,\unicode[STIX]{x1D712})^{4} & = & \displaystyle \int _{(\unicode[STIX]{x1D700})}L(1/2+s,\unicode[STIX]{x1D712})^{4}\frac{e^{2s^{2}}}{s}\frac{ds}{2\unicode[STIX]{x1D70B}i}+\int _{(\unicode[STIX]{x1D700})}L(1/2-s,\unicode[STIX]{x1D712})^{4}\frac{e^{2s^{2}}}{s}\frac{ds}{2\unicode[STIX]{x1D70B}i}\nonumber\\ \displaystyle & = & \displaystyle \int _{(\unicode[STIX]{x1D700})}L(1/2+s,\unicode[STIX]{x1D712})^{4}f(s)\frac{ds}{2\unicode[STIX]{x1D70B}i},\nonumber\end{eqnarray}$$where
 $$\begin{eqnarray}f(s)=\biggl(1+\frac{\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{2}}({\textstyle \frac{1}{2}}+s+\mathfrak{a}))^{4}}{\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{2}}({\textstyle \frac{1}{2}}-s+\mathfrak{a}))^{4}}\biggl(\frac{q}{\unicode[STIX]{x1D70B}}\biggr)^{4s}\biggr)\frac{e^{2s^{2}}}{s}\end{eqnarray}$$
$$\begin{eqnarray}f(s)=\biggl(1+\frac{\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{2}}({\textstyle \frac{1}{2}}+s+\mathfrak{a}))^{4}}{\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{2}}({\textstyle \frac{1}{2}}-s+\mathfrak{a}))^{4}}\biggl(\frac{q}{\unicode[STIX]{x1D70B}}\biggr)^{4s}\biggr)\frac{e^{2s^{2}}}{s}\end{eqnarray}$$ with  $\mathfrak{a}=0$ if
$\mathfrak{a}=0$ if  $\unicode[STIX]{x1D712}$ is even and
$\unicode[STIX]{x1D712}$ is even and  $\mathfrak{a}=1$ if
$\mathfrak{a}=1$ if  $\unicode[STIX]{x1D712}$ is odd. Applying the same argument again, we have
$\unicode[STIX]{x1D712}$ is odd. Applying the same argument again, we have
 $$\begin{eqnarray}L(1/2+s,\unicode[STIX]{x1D712})^{4}=\int _{(-\unicode[STIX]{x1D700})}L(1/2+s+u,\unicode[STIX]{x1D712})^{4}g_{s}(u)\frac{ds}{2\unicode[STIX]{x1D70B}i},\end{eqnarray}$$
$$\begin{eqnarray}L(1/2+s,\unicode[STIX]{x1D712})^{4}=\int _{(-\unicode[STIX]{x1D700})}L(1/2+s+u,\unicode[STIX]{x1D712})^{4}g_{s}(u)\frac{ds}{2\unicode[STIX]{x1D70B}i},\end{eqnarray}$$where
 $$\begin{eqnarray}g_{s}(u)=-\biggl(1+\frac{\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{2}}({\textstyle \frac{1}{2}}+s+u+\mathfrak{a}))^{4}}{\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{2}}({\textstyle \frac{1}{2}}+s-u+\mathfrak{a}))^{4}}\biggl(\frac{q}{\unicode[STIX]{x1D70B}}\biggr)^{4u}\biggr)\frac{e^{2u^{2}}}{u}.\end{eqnarray}$$
$$\begin{eqnarray}g_{s}(u)=-\biggl(1+\frac{\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{2}}({\textstyle \frac{1}{2}}+s+u+\mathfrak{a}))^{4}}{\unicode[STIX]{x1D6E4}({\textstyle \frac{1}{2}}({\textstyle \frac{1}{2}}+s-u+\mathfrak{a}))^{4}}\biggl(\frac{q}{\unicode[STIX]{x1D70B}}\biggr)^{4u}\biggr)\frac{e^{2u^{2}}}{u}.\end{eqnarray}$$Inserting and changing variables, we obtain
 $$\begin{eqnarray}L(1/2,\unicode[STIX]{x1D712})^{4}=\int _{(0)}L(1/2+v,\unicode[STIX]{x1D712})^{4}h(v)\frac{dv}{2\unicode[STIX]{x1D70B}i},\end{eqnarray}$$
$$\begin{eqnarray}L(1/2,\unicode[STIX]{x1D712})^{4}=\int _{(0)}L(1/2+v,\unicode[STIX]{x1D712})^{4}h(v)\frac{dv}{2\unicode[STIX]{x1D70B}i},\end{eqnarray}$$where
 $$\begin{eqnarray}h(v)=\int _{(\unicode[STIX]{x1D700})}g_{s}(v-s)f(s)\frac{ds}{2\unicode[STIX]{x1D70B}i}\ll e^{-|v|^{2}}q^{4\unicode[STIX]{x1D700}}.\end{eqnarray}$$
$$\begin{eqnarray}h(v)=\int _{(\unicode[STIX]{x1D700})}g_{s}(v-s)f(s)\frac{ds}{2\unicode[STIX]{x1D70B}i}\ll e^{-|v|^{2}}q^{4\unicode[STIX]{x1D700}}.\end{eqnarray}$$ Now choosing  $F$ as in (1.7), we get
$F$ as in (1.7), we get
 $$\begin{eqnarray}|L(1/2,\unicode[STIX]{x1D712})|^{4}\;\ll _{\unicode[STIX]{x1D700}}\;q^{\unicode[STIX]{x1D700}}\int _{(0)}L(1/2+z,\unicode[STIX]{x1D712})^{2}L(1/2-z,\overline{\unicode[STIX]{x1D712}})^{2}F(z)\frac{dz}{2\unicode[STIX]{x1D70B}i}.\end{eqnarray}$$
$$\begin{eqnarray}|L(1/2,\unicode[STIX]{x1D712})|^{4}\;\ll _{\unicode[STIX]{x1D700}}\;q^{\unicode[STIX]{x1D700}}\int _{(0)}L(1/2+z,\unicode[STIX]{x1D712})^{2}L(1/2-z,\overline{\unicode[STIX]{x1D712}})^{2}F(z)\frac{dz}{2\unicode[STIX]{x1D70B}i}.\end{eqnarray}$$Opening the square, we have
 $$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D712}\hspace{-7.11317pt}\hspace{0.6em}({\rm mod}\hspace{0.2em}q)}\biggl|\mathop{\sum }_{m\asymp M}a(m)\unicode[STIX]{x1D712}(m)\biggr|^{2}|L(1/2,\unicode[STIX]{x1D712})|^{4}\;\ll _{\unicode[STIX]{x1D700}}\;M^{2}+q^{\unicode[STIX]{x1D700}}\mathop{\sum }_{d}\mathop{\sum }_{\substack{ m_{1},m_{2}\asymp M/d \\ (m_{1},m_{2})=1}}|{\mathcal{T}}_{m_{1},m_{2},q}(1/2,1/2,1/2)|\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D712}\hspace{-7.11317pt}\hspace{0.6em}({\rm mod}\hspace{0.2em}q)}\biggl|\mathop{\sum }_{m\asymp M}a(m)\unicode[STIX]{x1D712}(m)\biggr|^{2}|L(1/2,\unicode[STIX]{x1D712})|^{4}\;\ll _{\unicode[STIX]{x1D700}}\;M^{2}+q^{\unicode[STIX]{x1D700}}\mathop{\sum }_{d}\mathop{\sum }_{\substack{ m_{1},m_{2}\asymp M/d \\ (m_{1},m_{2})=1}}|{\mathcal{T}}_{m_{1},m_{2},q}(1/2,1/2,1/2)|\end{eqnarray}$$ with the notation as in (1.6) in the special case where  $f$ is the standard Eisenstein series with
$f$ is the standard Eisenstein series with  $\unicode[STIX]{x1D703}=0$. By Theorem 1 and (1.8) we have
$\unicode[STIX]{x1D703}=0$. By Theorem 1 and (1.8) we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D712}\hspace{-7.11317pt}\hspace{0.6em}({\rm mod}\hspace{0.2em}q)}\biggl|\mathop{\sum }_{m\asymp M}a(m)\unicode[STIX]{x1D712}(m)\biggr|^{2}|L(1/2,\unicode[STIX]{x1D712})|^{4}\nonumber\\ \displaystyle & & \displaystyle \quad \;\ll _{\unicode[STIX]{x1D700}}\;M^{2}+(Mq)^{1+\unicode[STIX]{x1D700}}+q^{\unicode[STIX]{x1D700}}\mathop{\sum }_{d}\mathop{\sum }_{\substack{ m_{1},m_{2}\asymp M/d \\ (m_{1},m_{2})=1}}\mathop{\sum }_{\ast \in \{\text{Maa}\unicode[STIX]{x00DF},\text{hol},\text{Eis}\}}|{\mathcal{M}}_{m_{1},m_{2},q}^{\ast }(1/2,1/2,1/2)|.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D712}\hspace{-7.11317pt}\hspace{0.6em}({\rm mod}\hspace{0.2em}q)}\biggl|\mathop{\sum }_{m\asymp M}a(m)\unicode[STIX]{x1D712}(m)\biggr|^{2}|L(1/2,\unicode[STIX]{x1D712})|^{4}\nonumber\\ \displaystyle & & \displaystyle \quad \;\ll _{\unicode[STIX]{x1D700}}\;M^{2}+(Mq)^{1+\unicode[STIX]{x1D700}}+q^{\unicode[STIX]{x1D700}}\mathop{\sum }_{d}\mathop{\sum }_{\substack{ m_{1},m_{2}\asymp M/d \\ (m_{1},m_{2})=1}}\mathop{\sum }_{\ast \in \{\text{Maa}\unicode[STIX]{x00DF},\text{hol},\text{Eis}\}}|{\mathcal{M}}_{m_{1},m_{2},q}^{\ast }(1/2,1/2,1/2)|.\nonumber\end{eqnarray}$$We only deal with the Maaß case; the other two cases are similar but easier. By (1.10) and (1.11), we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{d}\mathop{\sum }_{\substack{ m_{1},m_{2}\asymp M/d \\ (m_{1},m_{2})=1}}|{\mathcal{M}}_{m_{1},m_{2},q}^{\text{Maa}\unicode[STIX]{x00DF}}(1/2,1/2,1/2)|\nonumber\\ \displaystyle & & \displaystyle \quad \;\ll _{\unicode[STIX]{x1D700}}\;(qM)^{\unicode[STIX]{x1D700}}\mathop{\sum }_{d}\mathop{\sum }_{\substack{ m_{1},m_{2}\asymp M/d \\ (m_{1},m_{2})=1}}\mathop{\sum }_{N\mid m_{1}m_{2}}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(N)}\frac{q^{1/2}}{N^{1/2}}\frac{(1+|\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(q)|)}{(1+|t_{\unicode[STIX]{x1D713}}|)^{30}}\frac{L(1/2,\unicode[STIX]{x1D713})^{3}}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{d}\mathop{\sum }_{\substack{ m_{1},m_{2}\asymp M/d \\ (m_{1},m_{2})=1}}|{\mathcal{M}}_{m_{1},m_{2},q}^{\text{Maa}\unicode[STIX]{x00DF}}(1/2,1/2,1/2)|\nonumber\\ \displaystyle & & \displaystyle \quad \;\ll _{\unicode[STIX]{x1D700}}\;(qM)^{\unicode[STIX]{x1D700}}\mathop{\sum }_{d}\mathop{\sum }_{\substack{ m_{1},m_{2}\asymp M/d \\ (m_{1},m_{2})=1}}\mathop{\sum }_{N\mid m_{1}m_{2}}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(N)}\frac{q^{1/2}}{N^{1/2}}\frac{(1+|\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(q)|)}{(1+|t_{\unicode[STIX]{x1D713}}|)^{30}}\frac{L(1/2,\unicode[STIX]{x1D713})^{3}}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})}.\nonumber\end{eqnarray}$$ We drop the condition  $(m_{1},m_{2})=1$ and write
$(m_{1},m_{2})=1$ and write  $m_{1}m_{2}=m=NK$, obtaining by the standard divisor bound that the previous display is bounded by
$m_{1}m_{2}=m=NK$, obtaining by the standard divisor bound that the previous display is bounded by
 $$\begin{eqnarray}\displaystyle & \;\ll _{\unicode[STIX]{x1D700}}\; & \displaystyle (qM)^{\unicode[STIX]{x1D700}}\mathop{\sum }_{d}\mathop{\sum }_{NK\asymp M^{2}/d^{2}}\frac{q^{1/2}}{N^{1/2}}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(N)}\frac{(1+|\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(q)|)}{(1+|t_{\unicode[STIX]{x1D713}}|)^{30}}\frac{L(1/2,\unicode[STIX]{x1D713})^{3}}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})}\nonumber\\ \displaystyle & \;\ll _{\unicode[STIX]{x1D700}}\; & \displaystyle (qM)^{\unicode[STIX]{x1D700}}\mathop{\sum }_{d}\mathop{\sum }_{N\ll M^{2}/d^{2}}\frac{q^{1/2}M^{2}}{d^{2}N^{3/2}}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(N)}\frac{(1+|\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(q)|)}{(1+|t_{\unicode[STIX]{x1D713}}|)^{30}}\frac{L(1/2,\unicode[STIX]{x1D713})^{3}}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})}\nonumber\\ \displaystyle & \;\ll _{\unicode[STIX]{x1D700}}\; & \displaystyle (q^{1/2}M^{2})^{1+\unicode[STIX]{x1D700}}\max _{{\mathcal{N}}\ll M^{2}}\frac{1}{{\mathcal{N}}^{3/2}}\mathop{\sum }_{N\asymp {\mathcal{N}}}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(N)}\frac{(1+|\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(q)|)}{(1+|t_{\unicode[STIX]{x1D713}}|)^{30}}\frac{L(1/2,\unicode[STIX]{x1D713})^{3}}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \;\ll _{\unicode[STIX]{x1D700}}\; & \displaystyle (qM)^{\unicode[STIX]{x1D700}}\mathop{\sum }_{d}\mathop{\sum }_{NK\asymp M^{2}/d^{2}}\frac{q^{1/2}}{N^{1/2}}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(N)}\frac{(1+|\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(q)|)}{(1+|t_{\unicode[STIX]{x1D713}}|)^{30}}\frac{L(1/2,\unicode[STIX]{x1D713})^{3}}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})}\nonumber\\ \displaystyle & \;\ll _{\unicode[STIX]{x1D700}}\; & \displaystyle (qM)^{\unicode[STIX]{x1D700}}\mathop{\sum }_{d}\mathop{\sum }_{N\ll M^{2}/d^{2}}\frac{q^{1/2}M^{2}}{d^{2}N^{3/2}}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(N)}\frac{(1+|\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(q)|)}{(1+|t_{\unicode[STIX]{x1D713}}|)^{30}}\frac{L(1/2,\unicode[STIX]{x1D713})^{3}}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})}\nonumber\\ \displaystyle & \;\ll _{\unicode[STIX]{x1D700}}\; & \displaystyle (q^{1/2}M^{2})^{1+\unicode[STIX]{x1D700}}\max _{{\mathcal{N}}\ll M^{2}}\frac{1}{{\mathcal{N}}^{3/2}}\mathop{\sum }_{N\asymp {\mathcal{N}}}\mathop{\sum }_{\unicode[STIX]{x1D713}\in {\mathcal{B}}^{\ast }(N)}\frac{(1+|\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D713}}(q)|)}{(1+|t_{\unicode[STIX]{x1D713}}|)^{30}}\frac{L(1/2,\unicode[STIX]{x1D713})^{3}}{L(1,\text{Ad}^{2}\unicode[STIX]{x1D713})}.\nonumber\end{eqnarray}$$By the Cauchy–Schwarz inequality, Theorem 2, and Lemma 3, this is
 $$\begin{eqnarray}\;\ll _{\unicode[STIX]{x1D700}}\;(q^{1/2}M^{2})^{1+\unicode[STIX]{x1D700}}\max _{{\mathcal{N}}\ll M^{2}}\frac{1}{{\mathcal{N}}^{3/2}}({\mathcal{N}}+q^{1/4}{\mathcal{N}}^{1/2}){\mathcal{N}}\;\ll _{\unicode[STIX]{x1D700}}\;(q^{1/2}M^{2})^{1+\unicode[STIX]{x1D700}}(M+q^{1/4}).\end{eqnarray}$$
$$\begin{eqnarray}\;\ll _{\unicode[STIX]{x1D700}}\;(q^{1/2}M^{2})^{1+\unicode[STIX]{x1D700}}\max _{{\mathcal{N}}\ll M^{2}}\frac{1}{{\mathcal{N}}^{3/2}}({\mathcal{N}}+q^{1/4}{\mathcal{N}}^{1/2}){\mathcal{N}}\;\ll _{\unicode[STIX]{x1D700}}\;(q^{1/2}M^{2})^{1+\unicode[STIX]{x1D700}}(M+q^{1/4}).\end{eqnarray}$$ For  $M\leqslant q^{1/4}$, we obtain altogether
$M\leqslant q^{1/4}$, we obtain altogether
 $$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D712}\hspace{-7.11317pt}\hspace{0.6em}({\rm mod}\hspace{0.2em}q)}\biggl|\mathop{\sum }_{m\asymp M}a(m)\unicode[STIX]{x1D712}(m)\biggr|^{2}|L(1/2,\unicode[STIX]{x1D712})|^{4}\;\ll _{\unicode[STIX]{x1D700}}\;(Mq)^{1+\unicode[STIX]{x1D700}},\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D712}\hspace{-7.11317pt}\hspace{0.6em}({\rm mod}\hspace{0.2em}q)}\biggl|\mathop{\sum }_{m\asymp M}a(m)\unicode[STIX]{x1D712}(m)\biggr|^{2}|L(1/2,\unicode[STIX]{x1D712})|^{4}\;\ll _{\unicode[STIX]{x1D700}}\;(Mq)^{1+\unicode[STIX]{x1D700}},\end{eqnarray}$$as desired.
Acknowledgement
We would like to thank the referee for a careful reading as well as useful and enlightening suggestions.