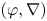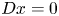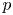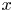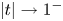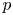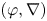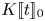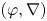Introduction
In the introduction, let ![]() $K$ be a complete discrete valuation field of mixed characteristic
$K$ be a complete discrete valuation field of mixed characteristic ![]() $(0,p)$ equipped with a valuation
$(0,p)$ equipped with a valuation ![]() $|\cdot |$ such that
$|\cdot |$ such that ![]() $|p|=p^{-1}$, with integer ring
$|p|=p^{-1}$, with integer ring ![]() $\mathcal {O}_K$ and residue field
$\mathcal {O}_K$ and residue field ![]() $k$. In this paper, we study the logarithmic growth (log-growth for short) filtrations for
$k$. In this paper, we study the logarithmic growth (log-growth for short) filtrations for ![]() $(\varphi ,\nabla )$-modules over the bounded Robba ring
$(\varphi ,\nabla )$-modules over the bounded Robba ring ![]() $\mathcal {R}^{\mathrm {bd}}$. Our main result is a proof of a generalization of Chiarellotto–Tsuzuki conjecture (Theorem 0.1). Recall that
$\mathcal {R}^{\mathrm {bd}}$. Our main result is a proof of a generalization of Chiarellotto–Tsuzuki conjecture (Theorem 0.1). Recall that ![]() $(\varphi ,\nabla )$-modules over
$(\varphi ,\nabla )$-modules over ![]() $\mathcal {R}^{\mathrm {bd}}$ naturally arise from Picard–Fuchs modules, in the sense of [Reference KedlayaKed10, Definition 22.1.1], associated with nice families
$\mathcal {R}^{\mathrm {bd}}$ naturally arise from Picard–Fuchs modules, in the sense of [Reference KedlayaKed10, Definition 22.1.1], associated with nice families ![]() $f:X\to \mathbb {P}^1_{K}$ of algebraic varieties [Reference KedlayaKed10, Theorem 22.2.1, Remark 22.2.2]. In the following, we recall Dwork's result of [Reference DworkDwo82], which illustrates Chiarellotto–Tsuzuki conjecture in the case where
$f:X\to \mathbb {P}^1_{K}$ of algebraic varieties [Reference KedlayaKed10, Theorem 22.2.1, Remark 22.2.2]. In the following, we recall Dwork's result of [Reference DworkDwo82], which illustrates Chiarellotto–Tsuzuki conjecture in the case where ![]() $f$ is given by Legendre family of elliptic curves.
$f$ is given by Legendre family of elliptic curves.
Dwork's result
In this paragraph, we assume that ![]() $k$ is algebraically closed of characteristic
$k$ is algebraically closed of characteristic ![]() $p\neq 2$, and
$p\neq 2$, and ![]() $\mathcal {O}_K$ is the ring of Witt vectors over
$\mathcal {O}_K$ is the ring of Witt vectors over ![]() $k$. Let
$k$. Let ![]() $X\to \mathbb {P}^1_K$ be Legendre family of elliptic curves defined by
$X\to \mathbb {P}^1_K$ be Legendre family of elliptic curves defined by ![]() $E_t:w^2=z(z-1)(z-t)$. Then, the associated (first) Picard–Fuchs module corresponds to Gaussian hypergeometric differential operator
$E_t:w^2=z(z-1)(z-t)$. Then, the associated (first) Picard–Fuchs module corresponds to Gaussian hypergeometric differential operator ![]() $H:=t(1-t)\partial ^2+(1-t)\partial -1/4$ (see [Reference KedlayaKed10, Examples 22.2.1, 22.2.3]). Let
$H:=t(1-t)\partial ^2+(1-t)\partial -1/4$ (see [Reference KedlayaKed10, Examples 22.2.1, 22.2.3]). Let ![]() $a\in \mathcal {O}_K$ be a lift of
$a\in \mathcal {O}_K$ be a lift of ![]() $\bar {a}\in k{\setminus} \{0,1\}$. We put
$\bar {a}\in k{\setminus} \{0,1\}$. We put ![]() $S_a:=\{x\in K[\![t-a]\!];t(1-t)d^2x/d(t-a)^2+(1-t){{d} x}/d(t-a)-x/4=0\}$, which is regarded as the set of local solutions of
$S_a:=\{x\in K[\![t-a]\!];t(1-t)d^2x/d(t-a)^2+(1-t){{d} x}/d(t-a)-x/4=0\}$, which is regarded as the set of local solutions of ![]() $Hx=0$ around
$Hx=0$ around ![]() $t=a$. We denote by
$t=a$. We denote by ![]() $K\{t-a\}$ the subring of
$K\{t-a\}$ the subring of ![]() $K[\![t-a]\!]$ consisting of series converging on the open unit disc
$K[\![t-a]\!]$ consisting of series converging on the open unit disc ![]() $|t-a|<1$. Then, we have
$|t-a|<1$. Then, we have ![]() $\dim _KS_a=2$, and
$\dim _KS_a=2$, and ![]() $S_a\subset K\{t-a\}$. That is, the differential equation
$S_a\subset K\{t-a\}$. That is, the differential equation ![]() $Hx=0$ is solvable on the open unit disc
$Hx=0$ is solvable on the open unit disc ![]() $|t-a|<1$. However, one can prove that no nonzero
$|t-a|<1$. However, one can prove that no nonzero ![]() $x\in S_a$ converges on the closed unit disc
$x\in S_a$ converges on the closed unit disc ![]() $|t-a|\leqslant 1$. To understand the asymptotic behavior of
$|t-a|\leqslant 1$. To understand the asymptotic behavior of ![]() $x\in S_a$ as
$x\in S_a$ as ![]() $|t-a|\to 1^{-}$, we introduce the log-growth filtration
$|t-a|\to 1^{-}$, we introduce the log-growth filtration ![]() $\mathrm {Fil}_{\bullet }K\{t-a\}$ of
$\mathrm {Fil}_{\bullet }K\{t-a\}$ of ![]() $K\{t-a\}$. Let
$K\{t-a\}$. Let ![]() $\lambda \in \mathbb {R}_{\geqslant 0}$. A formal power series
$\lambda \in \mathbb {R}_{\geqslant 0}$. A formal power series ![]() $x=\sum _{i\in \mathbb {N}}x_i(t-a)^i\in K[\![t-a]\!]$ with
$x=\sum _{i\in \mathbb {N}}x_i(t-a)^i\in K[\![t-a]\!]$ with ![]() $x_i\in K$ has log-growth
$x_i\in K$ has log-growth ![]() $\lambda$ if there exists
$\lambda$ if there exists ![]() $C\in \mathbb {R}$ such that
$C\in \mathbb {R}$ such that ![]() $|x_i|\leqslant Ci^{\lambda }$ for all
$|x_i|\leqslant Ci^{\lambda }$ for all ![]() $i\in \mathbb {N}$. Note that if
$i\in \mathbb {N}$. Note that if ![]() $x$ satisfies the condition, then
$x$ satisfies the condition, then ![]() $x\in K\{t-a\}$. We define
$x\in K\{t-a\}$. We define ![]() $\mathrm {Fil}_{\lambda }K\{t-a\}$ as the
$\mathrm {Fil}_{\lambda }K\{t-a\}$ as the ![]() $K$-subspace of
$K$-subspace of ![]() $K[\![t-a]\!]$ consisting of series having log-growth
$K[\![t-a]\!]$ consisting of series having log-growth ![]() $\lambda$. We put
$\lambda$. We put ![]() $\mathrm {Fil}_{\lambda }K\{t-a\}=0$ for
$\mathrm {Fil}_{\lambda }K\{t-a\}=0$ for ![]() $\lambda \in \mathbb {R}_{<0}$. Then, we put
$\lambda \in \mathbb {R}_{<0}$. Then, we put ![]() $S_{a,\lambda }:=S_a\cap \mathrm {Fil}_{\lambda }K\{t-a\}$ for
$S_{a,\lambda }:=S_a\cap \mathrm {Fil}_{\lambda }K\{t-a\}$ for ![]() $\lambda \in \mathbb {R}$. Dwork proves that the slope multiset of the filtration
$\lambda \in \mathbb {R}$. Dwork proves that the slope multiset of the filtration ![]() $S_{a,\bullet }$ is
$S_{a,\bullet }$ is ![]() $\{0,1\}$ if
$\{0,1\}$ if ![]() $E_{\bar {a}}$ is ordinary, and
$E_{\bar {a}}$ is ordinary, and ![]() $\{1/2,1/2\}$ if
$\{1/2,1/2\}$ if ![]() $E_{\bar {a}}$ is supersingular (see [Reference Chiarellotto and TsuzukiCT09, 7.4] for further explanation).
$E_{\bar {a}}$ is supersingular (see [Reference Chiarellotto and TsuzukiCT09, 7.4] for further explanation).
Chiarellotto–Tsuzuki conjecture
In [Reference Chiarellotto and TsuzukiCT09], Chiarellotto and Tsuzuki formulated a conjecture called the Chiarellotto–Tsuzuki conjecture in this paper, which is regarded as a generalization of Dwork's result. Let us briefly recall the statement of the conjecture. Let ![]() $q$ be a positive power of
$q$ be a positive power of ![]() $p$, and
$p$, and ![]() $\varphi _K$ an isometric ring endomorphism on
$\varphi _K$ an isometric ring endomorphism on ![]() $K$ which lifts the
$K$ which lifts the ![]() $q$-power map on
$q$-power map on ![]() $k$. We define
$k$. We define ![]() $K[\![t]\!]_0:=\mathcal {O}_K[\![t]\!]\otimes _{\mathcal {O}_K}K$, that is, the subring of
$K[\![t]\!]_0:=\mathcal {O}_K[\![t]\!]\otimes _{\mathcal {O}_K}K$, that is, the subring of ![]() $K\{t\}$ consisting of series
$K\{t\}$ consisting of series ![]() $x=\sum _{i\in \mathbb {N}}x_it^i$ with bounded coefficients, which is equipped with Gauss norm defined by
$x=\sum _{i\in \mathbb {N}}x_it^i$ with bounded coefficients, which is equipped with Gauss norm defined by ![]() $|x|_0=\sup _{i\in \mathbb {N}}|x_i|$. We endow
$|x|_0=\sup _{i\in \mathbb {N}}|x_i|$. We endow ![]() $K\{t\}$ with the
$K\{t\}$ with the ![]() $K$-linear derivation
$K$-linear derivation ![]() $\partial =d/dt:K\{t\}\to K\{t\}$ and a ring endomorphism
$\partial =d/dt:K\{t\}\to K\{t\}$ and a ring endomorphism ![]() $\varphi$ of the form
$\varphi$ of the form ![]() $\varphi (\sum _{i\in \mathbb {N}}x_it^i)=\sum _{i\in \mathbb {N}}\varphi _K(x_i)(S')^i$ for some
$\varphi (\sum _{i\in \mathbb {N}}x_it^i)=\sum _{i\in \mathbb {N}}\varphi _K(x_i)(S')^i$ for some ![]() $S'\in K[\![t]\!]_0$ with
$S'\in K[\![t]\!]_0$ with ![]() $|S'-t^q|_0<1$. Then, both
$|S'-t^q|_0<1$. Then, both ![]() $\varphi$ and
$\varphi$ and ![]() $\partial$ restrict to
$\partial$ restrict to ![]() $K[\![t]\!]_0$. Recall that for a ring
$K[\![t]\!]_0$. Recall that for a ring ![]() $R$ with a ring endomorphism
$R$ with a ring endomorphism ![]() $\varphi$, a
$\varphi$, a ![]() $\varphi$-module over
$\varphi$-module over ![]() $R$ is a finite free
$R$ is a finite free ![]() $R$-module
$R$-module ![]() $M$ equipped with a
$M$ equipped with a ![]() $\varphi$-semilinear endomorphism
$\varphi$-semilinear endomorphism ![]() $\varphi _M$ such that the
$\varphi _M$ such that the ![]() $R$-linear map
$R$-linear map ![]() $M\otimes _{R,\varphi }R\to M;m\otimes r\mapsto \varphi _M(m)r$ is an isomorphism. A
$M\otimes _{R,\varphi }R\to M;m\otimes r\mapsto \varphi _M(m)r$ is an isomorphism. A ![]() $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over ![]() $K[\![t]\!]_0$ is a
$K[\![t]\!]_0$ is a ![]() $\varphi$-module
$\varphi$-module ![]() $M$ over
$M$ over ![]() $K[\![t]\!]_0$ equipped with a
$K[\![t]\!]_0$ equipped with a ![]() $K$-linear differential operator
$K$-linear differential operator ![]() $\partial _M$ relative to
$\partial _M$ relative to ![]() $\partial$ satisfying the compatibility condition
$\partial$ satisfying the compatibility condition ![]() $\partial (\varphi (t))\cdot \varphi _M\circ \partial _M=\partial _M\circ \varphi _M$. We define the sets of analytic horizontal sections and analytic solutions of
$\partial (\varphi (t))\cdot \varphi _M\circ \partial _M=\partial _M\circ \varphi _M$. We define the sets of analytic horizontal sections and analytic solutions of ![]() $M$, respectively, by
$M$, respectively, by ![]() $V(M):=\ker {(\partial _M\otimes \mathrm {id}_{K\{t\}}+\mathrm {id}_M\otimes \partial :M\otimes _{K[\![t]\!]_0}K\{t\}\to M\otimes _{K[\![t]\!]_0}K\{t\})}$ and
$V(M):=\ker {(\partial _M\otimes \mathrm {id}_{K\{t\}}+\mathrm {id}_M\otimes \partial :M\otimes _{K[\![t]\!]_0}K\{t\}\to M\otimes _{K[\![t]\!]_0}K\{t\})}$ and ![]() $\mathrm {Sol}(M):=\{f\in \mathrm {Hom}_{K[\![t]\!]_0}(M,K\{t\});\partial \circ f=f\circ \partial _M\}$, which are equipped with a canonical perfect pairing
$\mathrm {Sol}(M):=\{f\in \mathrm {Hom}_{K[\![t]\!]_0}(M,K\{t\});\partial \circ f=f\circ \partial _M\}$, which are equipped with a canonical perfect pairing ![]() $V(M)\otimes _K\mathrm {Sol}(M)\to K$. By Dwork's trick [Reference KedlayaKed10, Corollary 17.2.2],
$V(M)\otimes _K\mathrm {Sol}(M)\to K$. By Dwork's trick [Reference KedlayaKed10, Corollary 17.2.2], ![]() $V(M)$ and
$V(M)$ and ![]() $\mathrm {Sol}(M)$ are regarded as
$\mathrm {Sol}(M)$ are regarded as ![]() $\varphi$-modules over
$\varphi$-modules over ![]() $K$ of dimension equal to the rank of
$K$ of dimension equal to the rank of ![]() $M$, where
$M$, where ![]() $\varphi _{V(M)}$ and
$\varphi _{V(M)}$ and ![]() $\varphi _{\mathrm {Sol}(M)}$ are defined as the restriction of
$\varphi _{\mathrm {Sol}(M)}$ are defined as the restriction of ![]() $\varphi _M\otimes \varphi$ and the unique
$\varphi _M\otimes \varphi$ and the unique ![]() $\varphi _K$-semilinear endomorphism on
$\varphi _K$-semilinear endomorphism on ![]() $\mathrm {Sol}(M)$ satisfying
$\mathrm {Sol}(M)$ satisfying ![]() $\varphi _{\mathrm {Sol}(M)}(f)(\varphi _M(m))=\varphi (f(m))$ for
$\varphi _{\mathrm {Sol}(M)}(f)(\varphi _M(m))=\varphi (f(m))$ for ![]() $f\in \mathrm {Sol}(M),m\in M$, respectively. Consequently,
$f\in \mathrm {Sol}(M),m\in M$, respectively. Consequently, ![]() $V(M)$ and
$V(M)$ and ![]() $\mathrm {Sol}(M)$ are endowed with the Frobenius slope filtrations
$\mathrm {Sol}(M)$ are endowed with the Frobenius slope filtrations ![]() $S_{\bullet }(V(M))$ and
$S_{\bullet }(V(M))$ and ![]() $S_{\bullet }(\mathrm {Sol}(M))$, respectively (see Theorem 1.5(ii)). We also define the growth filtrations
$S_{\bullet }(\mathrm {Sol}(M))$, respectively (see Theorem 1.5(ii)). We also define the growth filtrations ![]() $\mathrm {Sol}_{\bullet }(M)$ and
$\mathrm {Sol}_{\bullet }(M)$ and ![]() $V(M)^{\bullet }$ of
$V(M)^{\bullet }$ of ![]() $\mathrm {Sol}(M)$ and
$\mathrm {Sol}(M)$ and ![]() $V(M)$ respectively by
$V(M)$ respectively by ![]() $\mathrm {Sol}_{\lambda }(M)=\{f\in \mathrm {Sol}(M);f(M)\subset \mathrm {Fil}_{\lambda }K\{t\}\}$ and
$\mathrm {Sol}_{\lambda }(M)=\{f\in \mathrm {Sol}(M);f(M)\subset \mathrm {Fil}_{\lambda }K\{t\}\}$ and ![]() $V(M)^{\lambda }=\mathrm {Sol}_{\lambda }(M)^{\perp }$ for
$V(M)^{\lambda }=\mathrm {Sol}_{\lambda }(M)^{\perp }$ for ![]() $\lambda \in \mathbb {R}$, where
$\lambda \in \mathbb {R}$, where ![]() $\mathrm {Sol}_{\lambda }(M)^{\perp }$ denotes the orthogonal part of
$\mathrm {Sol}_{\lambda }(M)^{\perp }$ denotes the orthogonal part of ![]() $\mathrm {Sol}_{\lambda }(M)$ with respect to the canonical pairing
$\mathrm {Sol}_{\lambda }(M)$ with respect to the canonical pairing ![]() $V(M)\otimes _K \mathrm {Sol}(M)\to K$.
$V(M)\otimes _K \mathrm {Sol}(M)\to K$.
The Chiarellotto–Tsuzuki conjecture concerns a comparison between ![]() $V(M)^{\bullet }$ (respectively,
$V(M)^{\bullet }$ (respectively, ![]() $\mathrm {Sol}_{\bullet }(M)$) and
$\mathrm {Sol}_{\bullet }(M)$) and ![]() $S_{\bullet }(V(M))$ (respectively,
$S_{\bullet }(V(M))$ (respectively, ![]() $S_{\bullet }(\mathrm {Sol}(M))$). To state the conjecture precisely, we briefly recall the notion of being pure of bounded quotient (PBQ), which is a condition on the generic fiber of
$S_{\bullet }(\mathrm {Sol}(M))$). To state the conjecture precisely, we briefly recall the notion of being pure of bounded quotient (PBQ), which is a condition on the generic fiber of ![]() $M$ (see [Reference Chiarellotto and TsuzukiCT11, 5.1] for details). Let
$M$ (see [Reference Chiarellotto and TsuzukiCT11, 5.1] for details). Let ![]() $\mathcal {E}$ be the Amice ring, that is, the completion of the fraction field of
$\mathcal {E}$ be the Amice ring, that is, the completion of the fraction field of ![]() $K[\![t]\!]_0$ for the norm
$K[\![t]\!]_0$ for the norm ![]() $|\cdot |_0$, endowed with natural extensions of
$|\cdot |_0$, endowed with natural extensions of ![]() $\varphi$ and
$\varphi$ and ![]() $\partial$. We define
$\partial$. We define ![]() $\mathcal {E}[\![X-t]\!]_0$ as before with
$\mathcal {E}[\![X-t]\!]_0$ as before with ![]() $X-t$ a variable. We define the ring homomorphism
$X-t$ a variable. We define the ring homomorphism ![]() $\tau :\mathcal {E}\to \mathcal {E}[\![X-t]\!]_0;f\mapsto \sum _{i\in \mathbb {N}}\partial ^i(f)\cdot (X-t)^i/i!$. We endow
$\tau :\mathcal {E}\to \mathcal {E}[\![X-t]\!]_0;f\mapsto \sum _{i\in \mathbb {N}}\partial ^i(f)\cdot (X-t)^i/i!$. We endow ![]() $\mathcal {E}[\![X-t]\!]_0$ with the
$\mathcal {E}[\![X-t]\!]_0$ with the ![]() $\mathcal {E}$-linear derivation
$\mathcal {E}$-linear derivation ![]() $\partial =d/d(X-t):\mathcal {E}[\![X-t]\!]_0\to \mathcal {E}[\![X-t]\!]_0$ and a ring endomorphism
$\partial =d/d(X-t):\mathcal {E}[\![X-t]\!]_0\to \mathcal {E}[\![X-t]\!]_0$ and a ring endomorphism ![]() $\varphi$ defined by
$\varphi$ defined by ![]() $\varphi (\sum _{i\in \mathbb {N}}x_i(X-t)^i)=\sum _{i\in \mathbb {N}}\varphi (x_i)(\tau (\varphi (t))-S')^i$, which commute with
$\varphi (\sum _{i\in \mathbb {N}}x_i(X-t)^i)=\sum _{i\in \mathbb {N}}\varphi (x_i)(\tau (\varphi (t))-S')^i$, which commute with ![]() $\tau$. Let
$\tau$. Let ![]() $M'$ be a
$M'$ be a ![]() $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over ![]() $\mathcal {E}$. Let
$\mathcal {E}$. Let ![]() $\lambda _{\rm max}(M')$ denote the maximum Frobenius slope of
$\lambda _{\rm max}(M')$ denote the maximum Frobenius slope of ![]() $M'$ (see Definition 1.3). Regarding
$M'$ (see Definition 1.3). Regarding ![]() $\tau ^*(M'):=M'\otimes _{\mathcal {E},\tau }\mathcal {E}[\![X-t]\!]_0$ as a
$\tau ^*(M'):=M'\otimes _{\mathcal {E},\tau }\mathcal {E}[\![X-t]\!]_0$ as a ![]() $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over ![]() $\mathcal {E}[\![X-t]\!]_0$ (see § 4.1), we define a
$\mathcal {E}[\![X-t]\!]_0$ (see § 4.1), we define a ![]() $\varphi$-module
$\varphi$-module ![]() $V(\tau ^*(M'))$ over
$V(\tau ^*(M'))$ over ![]() $\mathcal {E}$ equipped with a growth filtration
$\mathcal {E}$ equipped with a growth filtration ![]() $V(\tau ^*(M'))^{\bullet }$ as before. For
$V(\tau ^*(M'))^{\bullet }$ as before. For ![]() $\lambda \in \mathbb {R}$, by a theorem of Robba, we have a (unique) subobject
$\lambda \in \mathbb {R}$, by a theorem of Robba, we have a (unique) subobject ![]() $(M')^{\lambda }$ of
$(M')^{\lambda }$ of ![]() $M'$ in the category of
$M'$ in the category of ![]() $(\varphi ,\nabla )$-modules over
$(\varphi ,\nabla )$-modules over ![]() $\mathcal {E}$ such that there exists a canonical isomorphism
$\mathcal {E}$ such that there exists a canonical isomorphism ![]() $V(\tau ^*(M'/(M')^{\lambda }))\cong V(\tau ^*(M'))^{\lambda }$, which forms a decreasing filtration of
$V(\tau ^*(M'/(M')^{\lambda }))\cong V(\tau ^*(M'))^{\lambda }$, which forms a decreasing filtration of ![]() $M'$ called the log-growth filtration of
$M'$ called the log-growth filtration of ![]() $M'$ (see [Reference Chiarellotto and TsuzukiCT09, 3.2 and 3.3]). We say that
$M'$ (see [Reference Chiarellotto and TsuzukiCT09, 3.2 and 3.3]). We say that ![]() $M'$ is PBQ if
$M'$ is PBQ if ![]() $M'/(M')^0$ is pure as a
$M'/(M')^0$ is pure as a ![]() $\varphi$-module over
$\varphi$-module over ![]() $\mathcal {E}$, that is, the Frobenius Newton polygon of
$\mathcal {E}$, that is, the Frobenius Newton polygon of ![]() $M'/(M')^0$ is a straight line.
$M'/(M')^0$ is a straight line.
Chiarellotto–Tsuzuki conjecture [Reference Chiarellotto and TsuzukiCT11, Conjecture 2.5]
Let ![]() $M$ be a
$M$ be a ![]() $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over ![]() $K[\![t]\!]_0$. We regard
$K[\![t]\!]_0$. We regard ![]() $M_{\mathcal {E}}:=M\otimes _{K[\![t]\!]_0}\mathcal {E}$ as a
$M_{\mathcal {E}}:=M\otimes _{K[\![t]\!]_0}\mathcal {E}$ as a ![]() $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over ![]() $\mathcal {E}$.
$\mathcal {E}$.
(i) We have
 $V(M)^{\lambda }=\bigcup _{\mu >\lambda }V(M)^{\mu }$ and
$V(M)^{\lambda }=\bigcup _{\mu >\lambda }V(M)^{\mu }$ and  $\mathrm {Sol}_{\lambda }(M)={\bigcap} _{\mu >\lambda }\mathrm {Sol}_{\mu }(M)$ for an arbitrary real number
$\mathrm {Sol}_{\lambda }(M)={\bigcap} _{\mu >\lambda }\mathrm {Sol}_{\mu }(M)$ for an arbitrary real number  $\lambda$. Moreover, the slope multisets of
$\lambda$. Moreover, the slope multisets of  $V(M)^{\bullet }$ and
$V(M)^{\bullet }$ and  $\mathrm {Sol}_{\bullet }(M)$, which coincide by definition, are consisting of rational numbers.
$\mathrm {Sol}_{\bullet }(M)$, which coincide by definition, are consisting of rational numbers.(ii) If
 $M_{\mathcal {E}}$ is PBQ, then
or, equivalently,
$M_{\mathcal {E}}$ is PBQ, then
or, equivalently, \[ V(M)^{\lambda}=\mathop{\bigcup}\limits_{\mu< \lambda_{\rm max}(M_{\mathcal{E}})-\lambda}S_{\mu}(V(M)), \]for an arbitrary real number
\[ V(M)^{\lambda}=\mathop{\bigcup}\limits_{\mu< \lambda_{\rm max}(M_{\mathcal{E}})-\lambda}S_{\mu}(V(M)), \]for an arbitrary real number \[ \mathrm{Sol}_{\lambda}(M)=S_{\lambda- \lambda_{\rm max}(M_{\mathcal{E}})}(\mathrm{Sol}(M)), \]
\[ \mathrm{Sol}_{\lambda}(M)=S_{\lambda- \lambda_{\rm max}(M_{\mathcal{E}})}(\mathrm{Sol}(M)), \] $\lambda$.
$\lambda$.
We quickly review known results on the Chiarellotto–Tsuzuki conjecture. If ![]() $M$ is of rank
$M$ is of rank ![]() $1$, then the conjecture obviously holds as
$1$, then the conjecture obviously holds as ![]() $M$ is trivial as a
$M$ is trivial as a ![]() $\nabla$-module over
$\nabla$-module over ![]() $K[\![t]\!]_0$ (see [Reference KedlayaKed10, Proposition 18.4.3]). If
$K[\![t]\!]_0$ (see [Reference KedlayaKed10, Proposition 18.4.3]). If ![]() $M$ arises from the Picard–Fuchs module associated with the Legendre family of elliptic curves, then Dwork's result implies part (ii) of the conjecture (see [Reference Chiarellotto and TsuzukiCT09, 7.4] for details). Chiarellotto and Tsuzuki proved the conjecture in the rank
$M$ arises from the Picard–Fuchs module associated with the Legendre family of elliptic curves, then Dwork's result implies part (ii) of the conjecture (see [Reference Chiarellotto and TsuzukiCT09, 7.4] for details). Chiarellotto and Tsuzuki proved the conjecture in the rank ![]() $2$ case [Reference Chiarellotto and TsuzukiCT09, Theorem 7.1(1)]. The present author proved part (i) of the conjecture without assumptions [Reference OhkuboOhk17, Theorem 3.7(i)].
$2$ case [Reference Chiarellotto and TsuzukiCT09, Theorem 7.1(1)]. The present author proved part (i) of the conjecture without assumptions [Reference OhkuboOhk17, Theorem 3.7(i)].
A generalization of Chiarellotto–Tsuzuki conjecture
In this paper, we prove Theorem 0.1, which is regarded as a generalization of the Chiarellotto–Tsuzuki conjecture to ![]() $(\varphi ,\nabla )$-modules over the bounded Robba ring
$(\varphi ,\nabla )$-modules over the bounded Robba ring ![]() $\mathcal {R}^{\mathrm {bd}}$. For
$\mathcal {R}^{\mathrm {bd}}$. For ![]() $r\in \mathbb {R}_{\geqslant 0}$ and a formal Laurent series over
$r\in \mathbb {R}_{\geqslant 0}$ and a formal Laurent series over ![]() $K$ denoted by
$K$ denoted by ![]() $x=\sum _{i\in \mathbb {Z}}x_it^i$ with
$x=\sum _{i\in \mathbb {Z}}x_it^i$ with ![]() $x_i\in K$, we put
$x_i\in K$, we put ![]() $|x|_r=\sup _{i\in \mathbb {Z}}|x_i|e^{-ri}\in [0,\infty ]$. We define the (respectively, bounded) Robba ring
$|x|_r=\sup _{i\in \mathbb {Z}}|x_i|e^{-ri}\in [0,\infty ]$. We define the (respectively, bounded) Robba ring ![]() $\mathcal {R}$ (respectively,
$\mathcal {R}$ (respectively, ![]() $\mathcal {R}^{\mathrm {bd}}$) as the ring consisting of series
$\mathcal {R}^{\mathrm {bd}}$) as the ring consisting of series ![]() $x$ such that there exists
$x$ such that there exists ![]() $r>0$ such that
$r>0$ such that ![]() $|x|_s<+\infty$ for all
$|x|_s<+\infty$ for all ![]() $s\in (0,r]$ (respectively,
$s\in (0,r]$ (respectively, ![]() $s\in [0,r]$). We fix an element
$s\in [0,r]$). We fix an element ![]() $X\in \mathcal {O}_K[\![t]\!]$ of the form
$X\in \mathcal {O}_K[\![t]\!]$ of the form ![]() $t^iv$ with
$t^iv$ with ![]() $i\in \mathbb {N}_{\geqslant 1}$ and
$i\in \mathbb {N}_{\geqslant 1}$ and ![]() $v\in \mathcal {O}_K[\![t]\!]^{\times }$, and define
$v\in \mathcal {O}_K[\![t]\!]^{\times }$, and define ![]() $\mathcal {R}_{\rm log}$ as the polynomial ring
$\mathcal {R}_{\rm log}$ as the polynomial ring ![]() $\mathcal {R}[\ell _X]$ with a variable
$\mathcal {R}[\ell _X]$ with a variable ![]() $\ell _X$. Then, the ring
$\ell _X$. Then, the ring ![]() $\mathcal {R}^{\mathrm {bd}}$ is a field, and we have the following commutative diagram of rings, where the hooked arrows denote the inclusions.
$\mathcal {R}^{\mathrm {bd}}$ is a field, and we have the following commutative diagram of rings, where the hooked arrows denote the inclusions.

We endow ![]() $\mathcal {R}$ with the
$\mathcal {R}$ with the ![]() $K$-linear derivation
$K$-linear derivation ![]() $\partial =d/dt:\mathcal {R}\to \mathcal {R}$ and a ring endomorphism
$\partial =d/dt:\mathcal {R}\to \mathcal {R}$ and a ring endomorphism ![]() $\varphi$ of the form
$\varphi$ of the form ![]() $\varphi (\sum _{i\in \mathbb {N}}x_it^i)=\sum _{i\in \mathbb {N}}\varphi _K(x_i)S^i$ for some
$\varphi (\sum _{i\in \mathbb {N}}x_it^i)=\sum _{i\in \mathbb {N}}\varphi _K(x_i)S^i$ for some ![]() $S\in \mathcal {R}^{\mathrm {bd}}$ with
$S\in \mathcal {R}^{\mathrm {bd}}$ with ![]() $|S-t^q|_0<1$. Then,
$|S-t^q|_0<1$. Then, ![]() $\varphi$ and
$\varphi$ and ![]() $\partial$ restrict to
$\partial$ restrict to ![]() $\mathcal {R}^{\mathrm {bd}}$, and extend to
$\mathcal {R}^{\mathrm {bd}}$, and extend to ![]() $\mathcal {E}$,
$\mathcal {E}$, ![]() $\mathcal {R}_{\rm log}$ by setting
$\mathcal {R}_{\rm log}$ by setting ![]() $\varphi (\ell _X)=\log {(\varphi (X)/X^q)}+q\ell _X$ and
$\varphi (\ell _X)=\log {(\varphi (X)/X^q)}+q\ell _X$ and ![]() $\partial (\ell _X)=\partial (X)/X$, respectively (see Definitions 2.1(ii), (iii), and 2.2). We define the log-growth filtrations of
$\partial (\ell _X)=\partial (X)/X$, respectively (see Definitions 2.1(ii), (iii), and 2.2). We define the log-growth filtrations of ![]() $\mathcal {R}$ and
$\mathcal {R}$ and ![]() $\mathcal {R}_{\rm log}$ by
$\mathcal {R}_{\rm log}$ by ![]() $\mathrm {Fil}_{\lambda }\mathcal {R}=\{x\in \mathcal {R};|x|_r=O(r^{-\lambda })\text { as }r\to +0\}$ if
$\mathrm {Fil}_{\lambda }\mathcal {R}=\{x\in \mathcal {R};|x|_r=O(r^{-\lambda })\text { as }r\to +0\}$ if ![]() $\lambda \in \mathbb {R}_{\geqslant 0}$,
$\lambda \in \mathbb {R}_{\geqslant 0}$, ![]() $\mathrm {Fil}_{\lambda }\mathcal {R}=0$ if
$\mathrm {Fil}_{\lambda }\mathcal {R}=0$ if ![]() $\lambda \in \mathbb {R}_{<0}$, and
$\lambda \in \mathbb {R}_{<0}$, and ![]() $\mathrm {Fil}_{\lambda }\mathcal {R}_{\rm log}:=\bigoplus _{i\in \mathbb {N}}\mathrm {Fil}_{\lambda -i}\mathcal {R}\cdot \ell _X^i$ for
$\mathrm {Fil}_{\lambda }\mathcal {R}_{\rm log}:=\bigoplus _{i\in \mathbb {N}}\mathrm {Fil}_{\lambda -i}\mathcal {R}\cdot \ell _X^i$ for ![]() $\lambda \in \mathbb {R}$. We can define the notion of
$\lambda \in \mathbb {R}$. We can define the notion of ![]() $(\varphi ,\nabla )$-modules over
$(\varphi ,\nabla )$-modules over ![]() $\mathcal {R}^{\mathrm {bd}}$ as before. For a literal generalization of the Chiarellotto–Tsuzuki conjecture, we should study the whole category of
$\mathcal {R}^{\mathrm {bd}}$ as before. For a literal generalization of the Chiarellotto–Tsuzuki conjecture, we should study the whole category of ![]() $(\varphi ,\nabla )$-modules
$(\varphi ,\nabla )$-modules ![]() $M$ over
$M$ over ![]() $\mathcal {R}^{\mathrm {bd}}$, where we encounter problems caused by the absence of a naïve analogue of Dwork's trick. To avoid complications, in this paper, we assume that
$\mathcal {R}^{\mathrm {bd}}$, where we encounter problems caused by the absence of a naïve analogue of Dwork's trick. To avoid complications, in this paper, we assume that ![]() $M_{\mathcal {R}}:=M\otimes _{\mathcal {R}^{\mathrm {bd}}}\mathcal {R}$ is unipotent as a
$M_{\mathcal {R}}:=M\otimes _{\mathcal {R}^{\mathrm {bd}}}\mathcal {R}$ is unipotent as a ![]() $\nabla$-module over
$\nabla$-module over ![]() $\mathcal {R}$. Thanks to the assumption, we can define
$\mathcal {R}$. Thanks to the assumption, we can define ![]() $V(M),\mathrm {Sol}(M)$, etc., as before, where
$V(M),\mathrm {Sol}(M)$, etc., as before, where ![]() $K[\![t]\!]_0$ and
$K[\![t]\!]_0$ and ![]() $K\{t\}$ are replaced by
$K\{t\}$ are replaced by ![]() $\mathcal {R}^{\mathrm {bd}}$ and
$\mathcal {R}^{\mathrm {bd}}$ and ![]() $\mathcal {R}_{\rm log}$, respectively. The main result of this paper is as follows.
$\mathcal {R}_{\rm log}$, respectively. The main result of this paper is as follows.
Theorem 0.1 (A generalization of the Chiarellotto–Tsuzuki conjecture) Let ![]() $M$ be a
$M$ be a ![]() $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over ![]() $\mathcal {R}^{\mathrm {bd}}$ such that
$\mathcal {R}^{\mathrm {bd}}$ such that ![]() $M_{\mathcal {R}}$ is unipotent as a
$M_{\mathcal {R}}$ is unipotent as a ![]() $\nabla$-module over
$\nabla$-module over ![]() $\mathcal {R}$. We regard
$\mathcal {R}$. We regard ![]() $M_{\mathcal {E}}:=M\otimes _{\mathcal {R}^{\mathrm {bd}}}\mathcal {E}$ as a
$M_{\mathcal {E}}:=M\otimes _{\mathcal {R}^{\mathrm {bd}}}\mathcal {E}$ as a ![]() $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over ![]() $\mathcal {E}$.
$\mathcal {E}$.
(i) We have
 $V(M)^{\lambda }=\bigcup _{\mu <\lambda }V(M)^{\mu }$ and
$V(M)^{\lambda }=\bigcup _{\mu <\lambda }V(M)^{\mu }$ and  $\mathrm {Sol}_{\lambda }(M)={\bigcap} _{\mu >\lambda }\mathrm {Sol}_{\mu }(M)$ for an arbitrary real number
$\mathrm {Sol}_{\lambda }(M)={\bigcap} _{\mu >\lambda }\mathrm {Sol}_{\mu }(M)$ for an arbitrary real number  $\lambda$. Moreover, the slope multisets of
$\lambda$. Moreover, the slope multisets of  $V(M)^{\bullet }$ and
$V(M)^{\bullet }$ and  $\mathrm {Sol}_{\bullet }(M)$, which coincide by definition, are consisting of rational numbers.
$\mathrm {Sol}_{\bullet }(M)$, which coincide by definition, are consisting of rational numbers.(ii) If
 $M_{\mathcal {E}}$ is PBQ, then
or, equivalently,
$M_{\mathcal {E}}$ is PBQ, then
or, equivalently, \[ V(M)^{\lambda}=\mathop{\bigcup}\limits_{\mu< \lambda_{\max}(M_{\mathcal{E}})-\lambda}S_{\mu}(V(M)), \]for an arbitrary real number
\[ V(M)^{\lambda}=\mathop{\bigcup}\limits_{\mu< \lambda_{\max}(M_{\mathcal{E}})-\lambda}S_{\mu}(V(M)), \]for an arbitrary real number \[ \mathrm{Sol}_{\lambda}(M)=S_{\lambda- \lambda_{\max}(M_{\mathcal{E}})}(\mathrm{Sol}(M)) \]
\[ \mathrm{Sol}_{\lambda}(M)=S_{\lambda- \lambda_{\max}(M_{\mathcal{E}})}(\mathrm{Sol}(M)) \] $\lambda$.
$\lambda$.
We prove part (ii) of Theorem 0.1 in § 8. We give two proofs of part (i) of Theorem 0.1; the first given in § 5 is done by a reduction to the case ![]() $X=t$, in which case the assertion is proved in [Reference OhkuboOhk17, Theorem 4.19], and the second given in § 10 is simple and self-contained.
$X=t$, in which case the assertion is proved in [Reference OhkuboOhk17, Theorem 4.19], and the second given in § 10 is simple and self-contained.
In the rest of this subsection, we put ![]() $S=S'\in K[\![t]\!]_0$ so that the inclusion
$S=S'\in K[\![t]\!]_0$ so that the inclusion ![]() $K[\![t]\!]_0\to \mathcal {R}^{\mathrm {bd}}$ is
$K[\![t]\!]_0\to \mathcal {R}^{\mathrm {bd}}$ is ![]() $\varphi$-equivariant. Moreover, we admit part (ii) of Theorem 0.1 and the property of the log-growth filtrations of
$\varphi$-equivariant. Moreover, we admit part (ii) of Theorem 0.1 and the property of the log-growth filtrations of ![]() $\mathcal {R}$ and
$\mathcal {R}$ and ![]() $\mathcal {R}_{\rm log}$ (see § 3.2). Under this setup, we will prove the following result.
$\mathcal {R}_{\rm log}$ (see § 3.2). Under this setup, we will prove the following result.
Theorem 0.2 Part (ii) of the Chiarellotto–Tsuzuki conjecture holds.
Note that even a log analogue of the Chiarellotto–Tsuzuki conjecture holds (Theorem 10.6).
Lemma 0.3 Let ![]() $M$ be a
$M$ be a ![]() $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over ![]() $K[\![t]\!]_0$. We put
$K[\![t]\!]_0$. We put ![]() $M_{\mathcal {R}^{\mathrm {bd}}}:=M\otimes _{K[\![t]\!]_0}\mathcal {R}^{\mathrm {bd}}$, which is regarded as a
$M_{\mathcal {R}^{\mathrm {bd}}}:=M\otimes _{K[\![t]\!]_0}\mathcal {R}^{\mathrm {bd}}$, which is regarded as a ![]() $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over ![]() $\mathcal {R}^{\mathrm {bd}}$. Then,
$\mathcal {R}^{\mathrm {bd}}$. Then, ![]() $(M_{\mathcal {R}^{\mathrm {bd}}})_{\mathcal {R}}$ is unipotent as a
$(M_{\mathcal {R}^{\mathrm {bd}}})_{\mathcal {R}}$ is unipotent as a ![]() $\nabla$-module over
$\nabla$-module over ![]() $\mathcal {R}$. Moreover, there exist canonical isomorphisms of
$\mathcal {R}$. Moreover, there exist canonical isomorphisms of ![]() $\varphi$-modules over
$\varphi$-modules over ![]() $K$
$K$
which are compatible with the canonical pairings. Furthermore, the maps ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$ induce isomorphisms
$\beta$ induce isomorphisms ![]() $V(M)^{\bullet }\to V(M_{\mathcal {R}^{\mathrm {bd}}})^{\bullet }$ and
$V(M)^{\bullet }\to V(M_{\mathcal {R}^{\mathrm {bd}}})^{\bullet }$ and ![]() $\mathrm {Sol}_{\bullet }(M)\to \mathrm {Sol}_{\bullet }(M_{\mathcal {R}^{\mathrm {bd}}})$ of filtrations, respectively. In particular, the log-growth Newton polygon
$\mathrm {Sol}_{\bullet }(M)\to \mathrm {Sol}_{\bullet }(M_{\mathcal {R}^{\mathrm {bd}}})$ of filtrations, respectively. In particular, the log-growth Newton polygon ![]() $\mathrm {NP}(M)$ of
$\mathrm {NP}(M)$ of ![]() $M$ (see [Reference Chiarellotto and TsuzukiCT11, 2.3] or the next subsection) coincides with the log-growth Newton polygon
$M$ (see [Reference Chiarellotto and TsuzukiCT11, 2.3] or the next subsection) coincides with the log-growth Newton polygon ![]() $\mathrm {NP}(M_{\mathcal {R}^{\mathrm {bd}}})$ of
$\mathrm {NP}(M_{\mathcal {R}^{\mathrm {bd}}})$ of ![]() $M_{\mathcal {R}^{\mathrm {bd}}}$ (Definition 10.1(i)).
$M_{\mathcal {R}^{\mathrm {bd}}}$ (Definition 10.1(i)).
Proof. As ![]() $M\otimes _{K[\![t]\!]_0}K\{t\}$ is trivial as a
$M\otimes _{K[\![t]\!]_0}K\{t\}$ is trivial as a ![]() $\nabla$-module over
$\nabla$-module over ![]() $K\{t\}$ by Dwork's trick [Reference KedlayaKed10, Corollary 17.2.2],
$K\{t\}$ by Dwork's trick [Reference KedlayaKed10, Corollary 17.2.2], ![]() $(M_{\mathcal {R}^{\mathrm {bd}}})_{\mathcal {R}}\cong (M\otimes _{K[\![t]\!]_0}K\{t\})\otimes _{K\{t\}}\mathcal {R}$ is unipotent (even trivial) as a
$(M_{\mathcal {R}^{\mathrm {bd}}})_{\mathcal {R}}\cong (M\otimes _{K[\![t]\!]_0}K\{t\})\otimes _{K\{t\}}\mathcal {R}$ is unipotent (even trivial) as a ![]() $\nabla$-module over
$\nabla$-module over ![]() $\mathcal {R}$. We define the maps
$\mathcal {R}$. We define the maps
 \begin{gather*} \alpha':M\otimes_{K[\![t]\!]_0}K\{t\}\to (M\otimes_{K[\![t]\!]_0}\mathcal{R}^{\mathrm{bd}})\otimes_{\mathcal{R}^{\mathrm{bd}}}\mathcal{R}_{{\rm log}};m\otimes r\mapsto m\otimes 1\otimes r,\\ \beta':\mathrm{Hom}_{K[\![t]\!]_0}(M,K\{t\})\to\mathrm{Hom}_{\mathcal{R}^{\mathrm{bd}}}(M\otimes_{K[\![t]\!]_0}\mathcal{R}^{\mathrm{bd}},\mathcal{R}_{{\rm log}});f\mapsto (m\otimes r\mapsto f(m)r), \end{gather*}
\begin{gather*} \alpha':M\otimes_{K[\![t]\!]_0}K\{t\}\to (M\otimes_{K[\![t]\!]_0}\mathcal{R}^{\mathrm{bd}})\otimes_{\mathcal{R}^{\mathrm{bd}}}\mathcal{R}_{{\rm log}};m\otimes r\mapsto m\otimes 1\otimes r,\\ \beta':\mathrm{Hom}_{K[\![t]\!]_0}(M,K\{t\})\to\mathrm{Hom}_{\mathcal{R}^{\mathrm{bd}}}(M\otimes_{K[\![t]\!]_0}\mathcal{R}^{\mathrm{bd}},\mathcal{R}_{{\rm log}});f\mapsto (m\otimes r\mapsto f(m)r), \end{gather*}
which are compatible with Frobenius actions and differential operators. Let ![]() $\alpha :V(M)\to V(M_{\mathcal {R}^{\mathrm {bd}}})$ and
$\alpha :V(M)\to V(M_{\mathcal {R}^{\mathrm {bd}}})$ and ![]() $\beta :\mathrm {Sol}(M)\to \mathrm {Sol}(M_{\mathcal {R}^{\mathrm {bd}}})$ be the morphisms of
$\beta :\mathrm {Sol}(M)\to \mathrm {Sol}(M_{\mathcal {R}^{\mathrm {bd}}})$ be the morphisms of ![]() $\varphi$-modules over
$\varphi$-modules over ![]() $K$ induced by
$K$ induced by ![]() $\alpha '$ and
$\alpha '$ and ![]() $\beta '$, respectively. As
$\beta '$, respectively. As ![]() $\alpha '$ and
$\alpha '$ and ![]() $\beta '$ are injective, the maps
$\beta '$ are injective, the maps ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$ are isomorphisms by comparing dimensions. By definition,
$\beta$ are isomorphisms by comparing dimensions. By definition, ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$ are compatible with the canonical pairings. To complete the proof, we have only to prove, by duality, that for
$\beta$ are compatible with the canonical pairings. To complete the proof, we have only to prove, by duality, that for ![]() $f\in \mathrm {Sol}(M)$, we have
$f\in \mathrm {Sol}(M)$, we have ![]() $f\in \mathrm {Sol}_{\lambda }(M)$ if and only if
$f\in \mathrm {Sol}_{\lambda }(M)$ if and only if ![]() $\beta (f)\in \mathrm {Sol}_{\lambda }(M_{\mathcal {R}^{\mathrm {bd}}})$. If
$\beta (f)\in \mathrm {Sol}_{\lambda }(M_{\mathcal {R}^{\mathrm {bd}}})$. If ![]() $f\in \mathrm {Sol}_{\lambda }(M)$, then
$f\in \mathrm {Sol}_{\lambda }(M)$, then ![]() $\beta (f)\in \mathrm {Sol}_{\lambda }(M_{\mathcal {R}^{\mathrm {bd}}})$ by
$\beta (f)\in \mathrm {Sol}_{\lambda }(M_{\mathcal {R}^{\mathrm {bd}}})$ by
where we use Corollary 3.7(i) and (iii). Conversely, if ![]() $\beta (f)\in \mathrm {Sol}_{\lambda }(M_{\mathcal {R}^{\mathrm {bd}}})$, then
$\beta (f)\in \mathrm {Sol}_{\lambda }(M_{\mathcal {R}^{\mathrm {bd}}})$, then ![]() $f\in \mathrm {Sol}_{\lambda }(M)$ by
$f\in \mathrm {Sol}_{\lambda }(M)$ by
where we use Corollary 3.6.
Proof of Theorem 0.2 Let ![]() $M$ be a
$M$ be a ![]() $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over ![]() $K[\![t]\!]_0$ such that
$K[\![t]\!]_0$ such that ![]() $M_{\mathcal {E}}$ is PBQ. Then, we can apply part (ii) of Theorem 0.1 to
$M_{\mathcal {E}}$ is PBQ. Then, we can apply part (ii) of Theorem 0.1 to ![]() $M_{\mathcal {R}^{\mathrm {bd}}}$ because
$M_{\mathcal {R}^{\mathrm {bd}}}$ because ![]() $(M_{\mathcal {R}^{\mathrm {bd}}})_{\mathcal {R}}$ is unipotent as a
$(M_{\mathcal {R}^{\mathrm {bd}}})_{\mathcal {R}}$ is unipotent as a ![]() $\nabla$-module over
$\nabla$-module over ![]() $\mathcal {R}$ by Lemma 0.3, and
$\mathcal {R}$ by Lemma 0.3, and ![]() $(M_{\mathcal {R}^{\mathrm {bd}}})_{\mathcal {E}}\cong M_{\mathcal {E}}$ is PBQ. Hence, we obtain the assertion by using Lemma 0.3.
$(M_{\mathcal {R}^{\mathrm {bd}}})_{\mathcal {E}}\cong M_{\mathcal {E}}$ is PBQ. Hence, we obtain the assertion by using Lemma 0.3.
Application to Dwork's conjecture
Recall that the Grothendieck–Katz specialization theorem for ![]() $\varphi$-modules
$\varphi$-modules ![]() $M$ over
$M$ over ![]() $K[\![t]\!]_0$ asserts that the Frobenius Newton polygon of
$K[\![t]\!]_0$ asserts that the Frobenius Newton polygon of ![]() $M/tM$ lies on or above the Frobenius Newton polygon of
$M/tM$ lies on or above the Frobenius Newton polygon of ![]() $M_{\mathcal {E}}$ with the same endpoints [Reference KedlayaKed10, Theorem 15.3.2]. Chiarellotto and Tsuzuki formulated Dwork's conjecture as an analogue of the Grothendieck–Katz specialization theorem for
$M_{\mathcal {E}}$ with the same endpoints [Reference KedlayaKed10, Theorem 15.3.2]. Chiarellotto and Tsuzuki formulated Dwork's conjecture as an analogue of the Grothendieck–Katz specialization theorem for ![]() $(\varphi ,\nabla )$-modules
$(\varphi ,\nabla )$-modules ![]() $M$ over
$M$ over ![]() $K[\![t]\!]_0$ (see also Remark 10.5). Recall that a slope of
$K[\![t]\!]_0$ (see also Remark 10.5). Recall that a slope of ![]() $V(M)^{\bullet }$ is a real number
$V(M)^{\bullet }$ is a real number ![]() $\lambda$ such that
$\lambda$ such that ![]() ${\bigcap} _{\mu <\lambda }V(M)^{\mu }\neq \bigcup _{\mu >\lambda }V(M)^{\mu }$. Let
${\bigcap} _{\mu <\lambda }V(M)^{\mu }\neq \bigcup _{\mu >\lambda }V(M)^{\mu }$. Let ![]() $\{s_1(M)\leqslant \cdots \leqslant s_n(M)\}$ denote the multiset of slopes
$\{s_1(M)\leqslant \cdots \leqslant s_n(M)\}$ denote the multiset of slopes ![]() $\lambda$ of
$\lambda$ of ![]() $V(M)^{\bullet }$ with multiplicity
$V(M)^{\bullet }$ with multiplicity ![]() $\dim _K{\bigcap} _{\mu <\lambda }V(M)^{\mu }-\dim _K\bigcup _{\mu >\lambda }V(M)^{\mu }$, where
$\dim _K{\bigcap} _{\mu <\lambda }V(M)^{\mu }-\dim _K\bigcup _{\mu >\lambda }V(M)^{\mu }$, where ![]() $n$ denotes the rank of
$n$ denotes the rank of ![]() $M$. Then, we define the log-growth Newton polygon
$M$. Then, we define the log-growth Newton polygon ![]() $\mathrm {NP}(M)$ of
$\mathrm {NP}(M)$ of ![]() $M$ as the boundary of the lower convex hull of the points
$M$ as the boundary of the lower convex hull of the points ![]() $(0,0)$ and
$(0,0)$ and ![]() $(i,s_1(M)+\dots +s_i(M))$ for
$(i,s_1(M)+\dots +s_i(M))$ for ![]() $i\in \{1,\dots ,n\}$. Similarly, we define the Newton polygon
$i\in \{1,\dots ,n\}$. Similarly, we define the Newton polygon ![]() $\mathrm {NP}(M)$ of a
$\mathrm {NP}(M)$ of a ![]() $(\varphi ,\nabla )$-module
$(\varphi ,\nabla )$-module ![]() $M$ over
$M$ over ![]() $\mathcal {E}$ (Definition 10.1(ii)).
$\mathcal {E}$ (Definition 10.1(ii)).
Dwork's conjecture [Reference Chiarellotto and TsuzukiCT11, Conjecture 2.7]
Let ![]() $M$ be a
$M$ be a ![]() $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over ![]() $K[\![t]\!]_0$. Then,
$K[\![t]\!]_0$. Then, ![]() $\mathrm {NP}(M)$ lies on or above
$\mathrm {NP}(M)$ lies on or above ![]() $\mathrm {NP}(M_{\mathcal {E}})$ with the same endpoints.
$\mathrm {NP}(M_{\mathcal {E}})$ with the same endpoints.
Dwork's conjecture is previously known in the case where the rank is less than or equal to two [Reference Chiarellotto and TsuzukiCT09, Corollary 7.3]. In § 10, we prove the following result.
Theorem 0.4 (A generalization of Dwork's conjecture) Let ![]() $M$ be a
$M$ be a ![]() $(\varphi ,\nabla )$-module of dimension
$(\varphi ,\nabla )$-module of dimension ![]() $n$ over
$n$ over ![]() $\mathcal {R}^{\mathrm {bd}}$ such that
$\mathcal {R}^{\mathrm {bd}}$ such that ![]() $M_{\mathcal {R}}$ is unipotent as a
$M_{\mathcal {R}}$ is unipotent as a ![]() $\nabla$-module over
$\nabla$-module over ![]() $\mathcal {R}$. Then, the Newton polygon
$\mathcal {R}$. Then, the Newton polygon ![]() $\mathrm {NP}(M)$ of
$\mathrm {NP}(M)$ of ![]() $M$ (Definition 10.1(i)) lies on or above
$M$ (Definition 10.1(i)) lies on or above ![]() $\mathrm {NP}(M_{\mathcal {E}})$ with the same endpoints. In particular, we have
$\mathrm {NP}(M_{\mathcal {E}})$ with the same endpoints. In particular, we have ![]() $s_n(M)\leqslant s_n(M_{\mathcal {E}})$, where
$s_n(M)\leqslant s_n(M_{\mathcal {E}})$, where ![]() $s_n(M_{(\mathcal {E})})$ denotes the maximum slope of
$s_n(M_{(\mathcal {E})})$ denotes the maximum slope of ![]() $\mathrm {NP}(M_{(\mathcal {E})})$.
$\mathrm {NP}(M_{(\mathcal {E})})$.
If we admit Theorem 0.4, then we have the following.
Theorem 0.5 Dwork's conjecture holds.
Proof. Let ![]() $M$ be a
$M$ be a ![]() $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over ![]() $K[\![t]\!]_0$. We can apply Theorem 0.4 to
$K[\![t]\!]_0$. We can apply Theorem 0.4 to ![]() $M_{\mathcal {R}^{\mathrm {bd}}}$ by using Lemma 0.3 as in the proof of Theorem 0.2. Moreover,
$M_{\mathcal {R}^{\mathrm {bd}}}$ by using Lemma 0.3 as in the proof of Theorem 0.2. Moreover, ![]() $\mathrm {NP}(M)$ (respectively,
$\mathrm {NP}(M)$ (respectively, ![]() $\mathrm {NP}(M_{\mathcal {E}})$) coincides with
$\mathrm {NP}(M_{\mathcal {E}})$) coincides with ![]() $\mathrm {NP}(M_{\mathcal {R}^{\mathrm {bd}}})$ (respectively,
$\mathrm {NP}(M_{\mathcal {R}^{\mathrm {bd}}})$ (respectively, ![]() $\mathrm {NP}((M_{\mathcal {R}^{\mathrm {bd}}})_{\mathcal {E}})$) by Lemma 0.3 (respectively, by definition), which implies the assertion.
$\mathrm {NP}((M_{\mathcal {R}^{\mathrm {bd}}})_{\mathcal {E}})$) by Lemma 0.3 (respectively, by definition), which implies the assertion.
Structure of the paper
We prove part (ii) of Theorem 0.1 in § 8. If the reader admits the key ingredients, that is, Propositions 3.11 and 7.2, then the (short) proof can be easily understood. We prove Propositions 3.11 and 7.2 in §§ 3 and 7 respectively, after giving preparations in §§ 1, 2 and §§ 4–6, respectively. We prove part (i) of Theorem 0.1 and Theorem 0.4 in § 10 by using the PBQ filtrations of ![]() $(\varphi ,\nabla )$-modules over
$(\varphi ,\nabla )$-modules over ![]() $\mathcal {R}^{\mathrm {bd}}$, which are studied in § 9.
$\mathcal {R}^{\mathrm {bd}}$, which are studied in § 9.
In § 6, we prove the invariance of the growth filtration under the base change of the coefficient field ![]() $K$, which can be skipped by assuming that
$K$, which can be skipped by assuming that ![]() $k$ is algebraically closed. Parts of §§ 2 and 3 (specifically, §§ 2.2, 2.3, 3.1, and 3.3) are rather technical because the extended Robba ring is involved. Hence, the reader may postpone these parts by admitting results proved there.
$k$ is algebraically closed. Parts of §§ 2 and 3 (specifically, §§ 2.2, 2.3, 3.1, and 3.3) are rather technical because the extended Robba ring is involved. Hence, the reader may postpone these parts by admitting results proved there.
Finally, we note that to make the paper concise, some results of an earlier version of this paper are not available in the current version, and will be included in a forthcoming paper(s).
Notation and terminology
(1) In this paper, a ring ![]() $R$ is a commutative ring with
$R$ is a commutative ring with ![]() $1$ unless otherwise mentioned. For a ring homomorphism
$1$ unless otherwise mentioned. For a ring homomorphism ![]() $\psi :R\to S$, we define the base change functor
$\psi :R\to S$, we define the base change functor ![]() $\psi ^*(-)$ from the category of
$\psi ^*(-)$ from the category of ![]() $R$-modules to the category of
$R$-modules to the category of ![]() $S$-modules by
$S$-modules by ![]() $M\mapsto \psi ^*M=M_S=M\otimes _RS$. When
$M\mapsto \psi ^*M=M_S=M\otimes _RS$. When ![]() $\psi$ is injective, we identify
$\psi$ is injective, we identify ![]() $R$ with
$R$ with ![]() $\psi (R)$, and regard
$\psi (R)$, and regard ![]() $\psi$ as the inclusion.
$\psi$ as the inclusion.
(2) We recall some terminology of difference modules [Reference KedlayaKed10, § 14]. A difference ring (respectively, field) is a ring (respectively, field) ![]() $R$ equipped with a ring endomorphism
$R$ equipped with a ring endomorphism ![]() $\phi$. Let
$\phi$. Let ![]() $R$ be a difference ring. A difference module over
$R$ be a difference ring. A difference module over ![]() $R$ is an
$R$ is an ![]() $R$-module
$R$-module ![]() $M$ equipped with a
$M$ equipped with a ![]() $\phi$-semilinear endomorphism
$\phi$-semilinear endomorphism ![]() $\phi _M$. A
$\phi _M$. A ![]() $\phi$-module over
$\phi$-module over ![]() $R$ is a difference module
$R$ is a difference module ![]() $M$ over
$M$ over ![]() $R$ such that
$R$ such that ![]() $M$ is finite free as an
$M$ is finite free as an ![]() $R$-module, and the
$R$-module, and the ![]() $R$-linear map
$R$-linear map ![]() $\phi ^*M=M\otimes _{R,\phi }R\to M;m\otimes r\mapsto r\phi _M(m)$ is an isomorphism. The category of
$\phi ^*M=M\otimes _{R,\phi }R\to M;m\otimes r\mapsto r\phi _M(m)$ is an isomorphism. The category of ![]() $\phi$-modules over
$\phi$-modules over ![]() $R$ is equipped with the following operations: the internal Hom
$R$ is equipped with the following operations: the internal Hom ![]() $\mathrm {Hom}_R(-,-)$, the tensor product
$\mathrm {Hom}_R(-,-)$, the tensor product ![]() $(-)\otimes _R(-)$, the dual
$(-)\otimes _R(-)$, the dual ![]() $(-)^\vee =\mathrm {Hom}_R(-,R)$, and the natural pairing
$(-)^\vee =\mathrm {Hom}_R(-,R)$, and the natural pairing ![]() $(-)\otimes _R(-)^\vee \to R$. For
$(-)\otimes _R(-)^\vee \to R$. For ![]() $c\in R^{\times }$, let
$c\in R^{\times }$, let ![]() $R(c)=Re_c$ be the
$R(c)=Re_c$ be the ![]() $\phi$-module over
$\phi$-module over ![]() $R$ defined by
$R$ defined by ![]() $\phi _{R(c)}(e_c)=ce_c$. We define the twist of a
$\phi _{R(c)}(e_c)=ce_c$. We define the twist of a ![]() $\phi$-module
$\phi$-module ![]() $M$ over
$M$ over ![]() $R$ by
$R$ by ![]() $c$ to be
$c$ to be ![]() $M(c)=M\otimes _R R(c)$. For
$M(c)=M\otimes _R R(c)$. For ![]() $d\in \mathbb {N}_{>0}$, we define the
$d\in \mathbb {N}_{>0}$, we define the ![]() $d$-pushforward functor
$d$-pushforward functor ![]() $[d]_*(-)$ from the category of
$[d]_*(-)$ from the category of ![]() $\phi$-modules over
$\phi$-modules over ![]() $R$ to the category of
$R$ to the category of ![]() $\phi ^d$-modules over
$\phi ^d$-modules over ![]() $R$ by
$R$ by ![]() $(M,\phi _M)\mapsto (M,\phi _M^d)$. For a morphism
$(M,\phi _M)\mapsto (M,\phi _M^d)$. For a morphism ![]() $\psi :R\to S$ of difference rings, we define a base change functor
$\psi :R\to S$ of difference rings, we define a base change functor ![]() $\psi ^*(-)$, as in part (1), from the category of
$\psi ^*(-)$, as in part (1), from the category of ![]() $\phi$-modules over
$\phi$-modules over ![]() $R$ to the category of
$R$ to the category of ![]() $\phi$-modules over
$\phi$-modules over ![]() $S$. Then, the
$S$. Then, the ![]() $d$-pushforward functor and the base change functor are compatible with internal Homs, tensor products, duals, and natural pairings in an obvious sense.
$d$-pushforward functor and the base change functor are compatible with internal Homs, tensor products, duals, and natural pairings in an obvious sense.
Let ![]() $F$ be a difference field with respect to a ring endomorphism
$F$ be a difference field with respect to a ring endomorphism ![]() $\phi$. We say that
$\phi$. We say that ![]() $F$ is inversive if
$F$ is inversive if ![]() $\phi$ is bijective. We say that
$\phi$ is bijective. We say that ![]() $F$ is weakly difference-closed if any equation of the form
$F$ is weakly difference-closed if any equation of the form ![]() $\phi (x)=cx$ with
$\phi (x)=cx$ with ![]() $c\in F^{\times }$ always has a solution
$c\in F^{\times }$ always has a solution ![]() $x\in F^{\times }$. We say that
$x\in F^{\times }$. We say that ![]() $F$ is strongly difference-closed if
$F$ is strongly difference-closed if ![]() $F$ is weakly difference-closed and inversive.
$F$ is weakly difference-closed and inversive.
(3) Let ![]() $V$ be a finite-dimensional vector space over a field
$V$ be a finite-dimensional vector space over a field ![]() $F$ with
$F$ with ![]() $n=\dim _FV$, equipped with a filtration of subspaces which is exhaustive and separated. We recall the definition of the Newton polygon associated with the filtration. For simplicity, we assume that our filtration is decreasing, which is denoted by
$n=\dim _FV$, equipped with a filtration of subspaces which is exhaustive and separated. We recall the definition of the Newton polygon associated with the filtration. For simplicity, we assume that our filtration is decreasing, which is denoted by ![]() $\{V^{\lambda };\lambda \in \mathbb {R}\}$. We put
$\{V^{\lambda };\lambda \in \mathbb {R}\}$. We put ![]() $m({\lambda })=\dim _F({\bigcap} _{\varepsilon >0}V^{\lambda -\varepsilon })/(\bigcup _{\varepsilon >0}V^{\lambda +\varepsilon })=\lim _{\varepsilon \to 0^+}\dim _FV^{\lambda -\varepsilon }-\lim _{\varepsilon \to 0^+}\dim _FV^{\lambda +\varepsilon }$. Note that
$m({\lambda })=\dim _F({\bigcap} _{\varepsilon >0}V^{\lambda -\varepsilon })/(\bigcup _{\varepsilon >0}V^{\lambda +\varepsilon })=\lim _{\varepsilon \to 0^+}\dim _FV^{\lambda -\varepsilon }-\lim _{\varepsilon \to 0^+}\dim _FV^{\lambda +\varepsilon }$. Note that ![]() $m({\lambda })=0$ for all but finitely many
$m({\lambda })=0$ for all but finitely many ![]() $\lambda$, and
$\lambda$, and ![]() $\sum _{\lambda \in \mathbb {R}}m(\lambda )=n$. If
$\sum _{\lambda \in \mathbb {R}}m(\lambda )=n$. If ![]() $m({\lambda })\neq 0$, then we call
$m({\lambda })\neq 0$, then we call ![]() $\lambda$ a slope of
$\lambda$ a slope of ![]() $V^{\bullet }$. The slope multiset of
$V^{\bullet }$. The slope multiset of ![]() $V^{\bullet }$ is the multiset consisting of slopes
$V^{\bullet }$ is the multiset consisting of slopes ![]() $\lambda$ of
$\lambda$ of ![]() $V^{\bullet }$ with multiplicity
$V^{\bullet }$ with multiplicity ![]() $m(\lambda )$, which is denoted by
$m(\lambda )$, which is denoted by ![]() $\{s_1\leqslant \cdots \leqslant s_n\}$. We define the Newton polygon
$\{s_1\leqslant \cdots \leqslant s_n\}$. We define the Newton polygon ![]() $\mathrm {NP}(V^{\bullet })$ of
$\mathrm {NP}(V^{\bullet })$ of ![]() $V^{\bullet }$ by the boundary of the lower convex hull in the
$V^{\bullet }$ by the boundary of the lower convex hull in the ![]() $xy$-plane of the set of points
$xy$-plane of the set of points ![]() $(0,0)$ and
$(0,0)$ and ![]() $(i,s_1+\dots +s_i)$ for
$(i,s_1+\dots +s_i)$ for ![]() $i\in \{1,\dots ,n\}$.
$i\in \{1,\dots ,n\}$.
1. Basic results on  $\phi$-modules over a complete discrete valuation field
$\phi$-modules over a complete discrete valuation field
We recall the definition of the slope filtrations ![]() $S_{\bullet }(M)$ of
$S_{\bullet }(M)$ of ![]() $\phi$-modules
$\phi$-modules ![]() $M$ over a complete discrete valuation field [Reference Chiarellotto and TsuzukiCT09, Reference Chiarellotto and TsuzukiCT11]: our slope filtration will be defined by renumbering a filtration of
$M$ over a complete discrete valuation field [Reference Chiarellotto and TsuzukiCT09, Reference Chiarellotto and TsuzukiCT11]: our slope filtration will be defined by renumbering a filtration of ![]() $M$ as in [Reference KedlayaKed10, Theorem 14.4.15] so that the indices of
$M$ as in [Reference KedlayaKed10, Theorem 14.4.15] so that the indices of ![]() $S_{\bullet }(M)$ represent the slopes of
$S_{\bullet }(M)$ represent the slopes of ![]() $M$. Then, we give basic properties of slope filtrations by rephrasing results of [Reference KedlayaKed10, § 14].
$M$. Then, we give basic properties of slope filtrations by rephrasing results of [Reference KedlayaKed10, § 14].
Definition 1.1 In this section, we fix a triple ![]() $(F,\phi ,q)$, where
$(F,\phi ,q)$, where ![]() $F$ is a complete discrete valuation field of mixed characteristic
$F$ is a complete discrete valuation field of mixed characteristic ![]() $(0,p)$ together with a valuation
$(0,p)$ together with a valuation ![]() $|\cdot |$,
$|\cdot |$, ![]() $\phi$ is an arbitrary isometric ring endomorphism on
$\phi$ is an arbitrary isometric ring endomorphism on ![]() $F$, and
$F$, and ![]() $q$ is a positive power of
$q$ is a positive power of ![]() $p$. Let
$p$. Let ![]() $\bar {\phi }$ denote the endomorphism on the residue field of
$\bar {\phi }$ denote the endomorphism on the residue field of ![]() $F$ induced by
$F$ induced by ![]() $\phi$. Unless otherwise mentioned, we regard
$\phi$. Unless otherwise mentioned, we regard ![]() $F$ and its residue field as difference rings with respect to
$F$ and its residue field as difference rings with respect to ![]() $\phi$ and
$\phi$ and ![]() $\bar {\phi }$, respectively. When
$\bar {\phi }$, respectively. When ![]() $\bar {\phi }$ is the
$\bar {\phi }$ is the ![]() $q$-power map, we call
$q$-power map, we call ![]() $\phi$ a
$\phi$ a ![]() $q$-power Frobenius lift, and we put the adjective Frobenius everywhere (for example, a slope is called a Frobenius slope).
$q$-power Frobenius lift, and we put the adjective Frobenius everywhere (for example, a slope is called a Frobenius slope).
An extension of ![]() $(F,\phi ,q)$ is a triple
$(F,\phi ,q)$ is a triple ![]() $(E,\phi ,q)$ as previously equipped with an isometric ring homomorphism
$(E,\phi ,q)$ as previously equipped with an isometric ring homomorphism ![]() $F\to E$ which is
$F\to E$ which is ![]() $\phi$-equivariant; in the case where
$\phi$-equivariant; in the case where ![]() $\phi :F\to F$ is a
$\phi :F\to F$ is a ![]() $q$-power Frobenius lift, we tacitly assume that
$q$-power Frobenius lift, we tacitly assume that ![]() $\phi :E\to E$ is also a
$\phi :E\to E$ is also a ![]() $q$-power Frobenius lift.
$q$-power Frobenius lift.
In the rest of this section, let ![]() $c\in F^{\times },d\in \mathbb {N}_{>0}$,
$c\in F^{\times },d\in \mathbb {N}_{>0}$, ![]() $\lambda \in \mathbb {R}$, and let
$\lambda \in \mathbb {R}$, and let ![]() $M,N$ be
$M,N$ be ![]() $\phi$-modules over
$\phi$-modules over ![]() $F$. Moreover, let
$F$. Moreover, let ![]() $(E,\phi ,q)$ be an extension of
$(E,\phi ,q)$ be an extension of ![]() $(F,\phi ,q)$ .
$(F,\phi ,q)$ .
Remark 1.2 There exists an extension ![]() $E$ of
$E$ of ![]() $F$ such that the value groups of
$F$ such that the value groups of ![]() $E$ and
$E$ and ![]() $F$ coincide, and the residue field of
$F$ coincide, and the residue field of ![]() $E$ is strongly difference-closed [Reference KedlayaKed08, Proposition 3.2.4]. Moreover, if
$E$ is strongly difference-closed [Reference KedlayaKed08, Proposition 3.2.4]. Moreover, if ![]() $\phi$ is a
$\phi$ is a ![]() $q$-power Frobenius lift on
$q$-power Frobenius lift on ![]() $F$, then we may assume that the residue field of
$F$, then we may assume that the residue field of ![]() $E$ is algebraically closed: for example, we consider the completion of a maximal unramified extension of the inductive limit
$E$ is algebraically closed: for example, we consider the completion of a maximal unramified extension of the inductive limit ![]() $\varinjlim {(F\xrightarrow []{\phi }F\xrightarrow []{\phi }\cdots )}$ (see [Reference KedlayaKed10, Hypothesis 14.4.1 and Proposition 14.3.4]).
$\varinjlim {(F\xrightarrow []{\phi }F\xrightarrow []{\phi }\cdots )}$ (see [Reference KedlayaKed10, Hypothesis 14.4.1 and Proposition 14.3.4]).
Definition 1.3 [Reference KedlayaKed10, Definitions 6.1.3, 14.4.6, and Remark 14.4.7]
We endow ![]() $M$ with the supremum norm with respect to a basis of
$M$ with the supremum norm with respect to a basis of ![]() $M$ (see [Reference KedlayaKed10, Definition 1.3.2]). We define the spectral radius of
$M$ (see [Reference KedlayaKed10, Definition 1.3.2]). We define the spectral radius of ![]() $\phi _M$ as
$\phi _M$ as ![]() $\lim _{n\to \infty }(\sup _{v\in M,v\neq 0}{|\phi _M^n(v)|/|v|})^{1/n}$, which is independent of the choice of the norm [Reference KedlayaKed10, Theorem 1.3.6, Proposition 6.1.5]. Let
$\lim _{n\to \infty }(\sup _{v\in M,v\neq 0}{|\phi _M^n(v)|/|v|})^{1/n}$, which is independent of the choice of the norm [Reference KedlayaKed10, Theorem 1.3.6, Proposition 6.1.5]. Let ![]() $\{M_i\}$ be the Jordan–Hölder constituents of
$\{M_i\}$ be the Jordan–Hölder constituents of ![]() $M$. We call
$M$. We call ![]() $M$ pure if there exists
$M$ pure if there exists ![]() $\lambda \in \mathbb {R}$ such that the
$\lambda \in \mathbb {R}$ such that the ![]() $\phi$-modules
$\phi$-modules ![]() $M_i$ have spectral radius
$M_i$ have spectral radius ![]() $|q|^{\lambda }$; in this case, we call
$|q|^{\lambda }$; in this case, we call ![]() $\lambda$ the slope of
$\lambda$ the slope of ![]() $M$. Note that
$M$. Note that ![]() $M=0$ and any irreducible
$M=0$ and any irreducible ![]() $\phi$-module over
$\phi$-module over ![]() $F$ are pure by definition: for example,
$F$ are pure by definition: for example, ![]() $F(c)$ is pure of slope
$F(c)$ is pure of slope ![]() $\log {|c|}/\log {|q|}$. We define the slope multiset of
$\log {|c|}/\log {|q|}$. We define the slope multiset of ![]() $M$ as the multiset consisting of the slopes of the
$M$ as the multiset consisting of the slopes of the ![]() $\phi$-modules
$\phi$-modules ![]() $M_i$ with multiplicity
$M_i$ with multiplicity ![]() $\dim _FM_i$. We define
$\dim _FM_i$. We define ![]() $\lambda _{\rm max}(M)$ as the maximum element in the slope multiset of
$\lambda _{\rm max}(M)$ as the maximum element in the slope multiset of ![]() $M$ if
$M$ if ![]() $M\neq 0$, and
$M\neq 0$, and ![]() $\lambda _{\rm max}(M)=0$ if
$\lambda _{\rm max}(M)=0$ if ![]() $M=0$. Unless otherwise mentioned, we calculate the slope multiset of the
$M=0$. Unless otherwise mentioned, we calculate the slope multiset of the ![]() $\phi ^d$-module
$\phi ^d$-module ![]() $[d]_*M$ over
$[d]_*M$ over ![]() $F$ (respectively, the
$F$ (respectively, the ![]() $\phi$-module
$\phi$-module ![]() $M\otimes _FE$ over
$M\otimes _FE$ over ![]() $E$) with respect to the triple
$E$) with respect to the triple ![]() $(F,\phi ^d,q^d)$ (respectively,
$(F,\phi ^d,q^d)$ (respectively, ![]() $(E,\phi ,q)$).
$(E,\phi ,q)$).
Lemma 1.4
(i) If we replace
 $(F,\phi ,q)$ in Definition 1.1 by
$(F,\phi ,q)$ in Definition 1.1 by  $(F,\phi ,q')$ with
$(F,\phi ,q')$ with  $q'$ a power of
$q'$ a power of  $p$, then the slope multiset of
$p$, then the slope multiset of  $M$ is multiplied by
$M$ is multiplied by  $\log {|q|}/\log {|q'|}$.
$\log {|q|}/\log {|q'|}$.(ii) If
 $0\to M'\to M\to M''\to 0$ is an exact sequence of
$0\to M'\to M\to M''\to 0$ is an exact sequence of  $\phi$-modules over
$\phi$-modules over  $F$, then the slope multiset of
$F$, then the slope multiset of  $M$ is equal to the disjoint union of those of
$M$ is equal to the disjoint union of those of  $M'$ and
$M'$ and  $M''$. In particular, the slope multiset of
$M''$. In particular, the slope multiset of  $M\oplus N$ is equal to the disjoint union of those of
$M\oplus N$ is equal to the disjoint union of those of  $M$ and
$M$ and  $N$.
$N$.(iii) (Rationality) The slope multiset of
 $M$ consists of rational numbers. In particular,
$M$ consists of rational numbers. In particular,  $\lambda _{\rm max}(M)$ is a rational number.
$\lambda _{\rm max}(M)$ is a rational number.(iv) (Base change) The slope multiset of
 $M\otimes _FE$ is equal to that of
$M\otimes _FE$ is equal to that of  $M$.
$M$.(v) (
 $d$-pushforward) The slope multiset of
$d$-pushforward) The slope multiset of  $[d]_*M$ is equal to that of
$[d]_*M$ is equal to that of  $M$.
$M$.(vi) (Tensor product) The slope multiset of
 $M\otimes _FN$ consists of
$M\otimes _FN$ consists of  $\lambda +\mu$ where
$\lambda +\mu$ where  $\lambda$,
$\lambda$,  $\mu$ respectively run over the slope multisets of
$\mu$ respectively run over the slope multisets of  $M$,
$M$,  $N$ with multiplicity.
$N$ with multiplicity.(vii) (Dual) The slope multiset of
 $M^\vee$ is equal to
$M^\vee$ is equal to  $(-1)$ times that of
$(-1)$ times that of  $M$. In particular,
$M$. In particular,  $M$ is pure of slope
$M$ is pure of slope  $\lambda$ if and only if
$\lambda$ if and only if  $M^\vee$ is pure of slope
$M^\vee$ is pure of slope  $-\lambda$.
$-\lambda$.
Proof. Parts (i), (ii), and (v) hold by definition. By part (ii), to prove the rest of the assertion, we may reduce to the irreducible case. Then, parts (iii), (iv), (vi), and (vii) follow from [Reference KedlayaKed10, Corollary 14.4.5, Lemma 14.4.3(c), Corollary 14.4.9, and Proposition 14.4.8] respectively.
Theorem 1.5
(i) [Reference KedlayaKed10, Theorem 14.4.13] Assume that
 $F$ is inversive. Then, there exists a unique internal direct sum decomposition
$F$ is inversive. Then, there exists a unique internal direct sum decomposition  $M=\bigoplus _{\lambda \in \mathbb {R}}M_{\lambda }$ of
$M=\bigoplus _{\lambda \in \mathbb {R}}M_{\lambda }$ of  $\phi$-modules, in which each nonzero
$\phi$-modules, in which each nonzero  $M_{\lambda }$ is pure of slope
$M_{\lambda }$ is pure of slope  $\lambda$. Moreover, the multiplicity of
$\lambda$. Moreover, the multiplicity of  $\lambda$ in the slope multiset of
$\lambda$ in the slope multiset of  $M$ is equal to
$M$ is equal to  $\dim _FM_{\lambda }$.
$\dim _FM_{\lambda }$.(ii) (Cf. [Reference Chiarellotto and TsuzukiCT09, Definition 2.3].) There exists a unique increasing filtration
 $\{S_{\lambda }(M);\lambda \in \mathbb {R}\}$ of
$\{S_{\lambda }(M);\lambda \in \mathbb {R}\}$ of  $\phi$-submodules of
$\phi$-submodules of  $M$, called the slope filtration of
$M$, called the slope filtration of  $M$, satisfying the following:
$M$, satisfying the following:
(a) the filtration
 $S_{\bullet }(M)$ is exhaustive and separated;
$S_{\bullet }(M)$ is exhaustive and separated;(b) (right continuity) we have
 $S_{\lambda }(M)={\bigcap} _{\mu >\lambda }S_{\mu }(M)$, i.e.
$S_{\lambda }(M)={\bigcap} _{\mu >\lambda }S_{\mu }(M)$, i.e. $S_{\lambda }(M)=S_{\lambda +\varepsilon }(M)$ for all sufficiently small
$S_{\lambda }(M)=S_{\lambda +\varepsilon }(M)$ for all sufficiently small  $\varepsilon \in \mathbb {R}_{>0}$;
$\varepsilon \in \mathbb {R}_{>0}$;(c) if
 $S_{\lambda }(M)/\bigcup _{\mu <\lambda }S_{\mu }(M)$ is nonzero, then it is pure of slope
$S_{\lambda }(M)/\bigcup _{\mu <\lambda }S_{\mu }(M)$ is nonzero, then it is pure of slope  $\lambda$.
$\lambda$.
 $M$ less than or equal to (respectively, strictly greater than)
$M$ less than or equal to (respectively, strictly greater than)  $\lambda$ coincides with the slope multiset of
$\lambda$ coincides with the slope multiset of  $S_{\lambda }(M)$ (respectively,
$S_{\lambda }(M)$ (respectively,  $M/S_{\lambda }(M)$); the multiplicity of
$M/S_{\lambda }(M)$); the multiplicity of  $\lambda$ in the slope multiset of
$\lambda$ in the slope multiset of  $M$ is equal to
$M$ is equal to  $\dim _F(S_{\lambda }(M)/\bigcup _{\mu <\lambda }S_{\mu }(M))$.
$\dim _F(S_{\lambda }(M)/\bigcup _{\mu <\lambda }S_{\mu }(M))$.(iii) If
 $F$ is inversive, then
$F$ is inversive, then  $S_{\lambda }(M)=\bigoplus _{\mu \leqslant \lambda }M_{\mu }$. In particular,
$S_{\lambda }(M)=\bigoplus _{\mu \leqslant \lambda }M_{\mu }$. In particular,  $S_{\lambda }(M)/\bigcup _{\mu <\lambda }S_{\mu }(M)\cong M_{\lambda }$.
$S_{\lambda }(M)/\bigcup _{\mu <\lambda }S_{\mu }(M)\cong M_{\lambda }$.(iv) (Functoriality) Let
 $f:M\to N$ be a morphism of
$f:M\to N$ be a morphism of  $\phi$-modules over
$\phi$-modules over  $F$. Then, we have
$F$. Then, we have  $f(M_{\lambda })\subset N_{\lambda }$ if
$f(M_{\lambda })\subset N_{\lambda }$ if  $F$ inversive, and
$F$ inversive, and  $f(S_{\lambda }(M))\subset S_{\lambda }(N)$.
$f(S_{\lambda }(M))\subset S_{\lambda }(N)$.
Lemma 1.6 If the slope multisets of ![]() $M$ and
$M$ and ![]() $N$ are disjoint, then
$N$ are disjoint, then ![]() $\mathrm {Hom}(M,N)=0$.
$\mathrm {Hom}(M,N)=0$.
Proof. By dévissage, we may assume that ![]() $M$ and
$M$ and ![]() $N$ are irreducible. By assumption,
$N$ are irreducible. By assumption, ![]() $M\ncong N$, hence,
$M\ncong N$, hence, ![]() $\mathrm {Hom}(M,N)=0$.
$\mathrm {Hom}(M,N)=0$.
Proof of Theorem 1.5 (ii) We prove the existence of ![]() $S_{\bullet }(M)$. By [Reference KedlayaKed10, Theorem 14.4.15], there exists a unique filtration
$S_{\bullet }(M)$. By [Reference KedlayaKed10, Theorem 14.4.15], there exists a unique filtration ![]() $0=\mathcal {F}_0M\subset \mathcal {F}_1M\subset \dots \subset \mathcal {F}_mM=M$ of
$0=\mathcal {F}_0M\subset \mathcal {F}_1M\subset \dots \subset \mathcal {F}_mM=M$ of ![]() $\phi$-modules such that
$\phi$-modules such that ![]() $\mathcal {F}_iM/\mathcal {F}_{i-1}M$ is pure of slope
$\mathcal {F}_iM/\mathcal {F}_{i-1}M$ is pure of slope ![]() $\lambda _i$ with
$\lambda _i$ with ![]() $\lambda _1<\cdots <\lambda _m$. We define
$\lambda _1<\cdots <\lambda _m$. We define ![]() $S_{\lambda }(M)=0$ if
$S_{\lambda }(M)=0$ if ![]() $\lambda \in (-\infty ,\lambda _1)$,
$\lambda \in (-\infty ,\lambda _1)$, ![]() $S_{\lambda }(M)=\mathcal {F}_iM$ if
$S_{\lambda }(M)=\mathcal {F}_iM$ if ![]() $\lambda \in [\lambda _i,\lambda _{i+1})$ for
$\lambda \in [\lambda _i,\lambda _{i+1})$ for ![]() $i=1,\dots ,m$, and
$i=1,\dots ,m$, and ![]() $S_{\lambda }(M)=M$ if
$S_{\lambda }(M)=M$ if ![]() $\lambda \in [\lambda _m,+\infty )$. Then,
$\lambda \in [\lambda _m,+\infty )$. Then, ![]() $S_{\bullet }(M)$ satisfies the required conditions. Let
$S_{\bullet }(M)$ satisfies the required conditions. Let ![]() $S'_{\bullet }(M)$ be another filtration satisfying conditions (a)–(c) as in part (ii). Then, the filtration
$S'_{\bullet }(M)$ be another filtration satisfying conditions (a)–(c) as in part (ii). Then, the filtration ![]() $\mathcal {F}_{\bullet }(M)$ can be recovered by using
$\mathcal {F}_{\bullet }(M)$ can be recovered by using ![]() $S'_{\bullet }(M)$ in an obvious way, which implies that
$S'_{\bullet }(M)$ in an obvious way, which implies that ![]() $S'_{\bullet }(M)=S_{\bullet }(M)$.
$S'_{\bullet }(M)=S_{\bullet }(M)$.
(iii) As the filtration ![]() $\{\bigoplus _{\mu \leqslant \lambda }M_{\mu };\lambda \in \mathbb {R}\}$ satisfies conditions (a)–(c) as in part (ii), the assertion follows from the uniqueness of
$\{\bigoplus _{\mu \leqslant \lambda }M_{\mu };\lambda \in \mathbb {R}\}$ satisfies conditions (a)–(c) as in part (ii), the assertion follows from the uniqueness of ![]() $S_{\bullet }(M)$.
$S_{\bullet }(M)$.
(iv) By Lemma 1.6, we have ![]() $\mathrm {Hom}(M_{\lambda },N_{\mu })=0$ for
$\mathrm {Hom}(M_{\lambda },N_{\mu })=0$ for ![]() $\mu \neq \lambda$ if
$\mu \neq \lambda$ if ![]() $F$ is inversive, and
$F$ is inversive, and ![]() $\mathrm {Hom}(S_{\lambda }(M),N/S_{\lambda }(N))=0$, which implies the assertion.
$\mathrm {Hom}(S_{\lambda }(M),N/S_{\lambda }(N))=0$, which implies the assertion.
For example, the slope filtration of ![]() $M=F(c)$ is given by
$M=F(c)$ is given by ![]() $S_{\lambda }(M)=M$ if
$S_{\lambda }(M)=M$ if ![]() $\lambda \geqslant \log {|c|}/\log {|q|}$, and
$\lambda \geqslant \log {|c|}/\log {|q|}$, and ![]() $S_{\lambda }(M)=0$ otherwise.
$S_{\lambda }(M)=0$ otherwise.
A pairing of ![]() $M$ and
$M$ and ![]() $N$ is a morphism
$N$ is a morphism ![]() $M\otimes _FN\to F$ of
$M\otimes _FN\to F$ of ![]() $\phi$-modules over
$\phi$-modules over ![]() $F$, which bijectively corresponds to, an
$F$, which bijectively corresponds to, an ![]() $F$-bilinear map
$F$-bilinear map ![]() $b:M\times N\to F$ such that
$b:M\times N\to F$ such that ![]() $b(\phi _M(m),\phi _N(n))=\phi (b(m,n))$ for
$b(\phi _M(m),\phi _N(n))=\phi (b(m,n))$ for ![]() $m\in M,n\in N$. Furthermore, the pairing is called perfect if
$m\in M,n\in N$. Furthermore, the pairing is called perfect if ![]() $b$ is nondegenerate. For example, the canonical map
$b$ is nondegenerate. For example, the canonical map ![]() $M\otimes _FM^\vee \to F$ is a perfect pairing of
$M\otimes _FM^\vee \to F$ is a perfect pairing of ![]() $M$ and
$M$ and ![]() $M^\vee$. We define the orthogonal part of a
$M^\vee$. We define the orthogonal part of a ![]() $\phi$-submodule
$\phi$-submodule ![]() $M_0$ of
$M_0$ of ![]() $M$ by
$M$ by ![]() $M_0^{\perp }:=\{n\in N;b(m_0,n)=0\ \forall m_0\in M_0\}$, which is a
$M_0^{\perp }:=\{n\in N;b(m_0,n)=0\ \forall m_0\in M_0\}$, which is a ![]() $\phi$-submodule of
$\phi$-submodule of ![]() $N$. We similarly define the orthogonal part of a
$N$. We similarly define the orthogonal part of a ![]() $\phi$-submodule
$\phi$-submodule ![]() $N_0$ of
$N_0$ of ![]() $N$.
$N$.
Lemma 1.7
(I) Assume that F is inversive.
(i) (Base change) There exists a canonical isomorphism
 $M_{\lambda }\otimes _FE\cong (M\otimes _FE)_{\lambda }.$
$M_{\lambda }\otimes _FE\cong (M\otimes _FE)_{\lambda }.$(ii) (
 $d$-pushforward) There exists a canonical isomorphism
$d$-pushforward) There exists a canonical isomorphism  $[d]_*(M_{\lambda })\cong ([d]_*M)_{\lambda }$.
$[d]_*(M_{\lambda })\cong ([d]_*M)_{\lambda }$.(iii) (Strictness) If
 $0\to M'\to M\to M''\to 0$ is an exact sequence of
$0\to M'\to M\to M''\to 0$ is an exact sequence of  $\phi$-modules over
$\phi$-modules over  $F$, then there exists an induced exact sequence
$F$, then there exists an induced exact sequence  $0\to M'_{\lambda }\to M_{\lambda }\to M''_{\lambda }\to 0$.
$0\to M'_{\lambda }\to M_{\lambda }\to M''_{\lambda }\to 0$.(iv) (Tensor product) There exists a canonical isomorphism
 $(M\otimes _F N)_{\lambda }\cong \bigoplus _{\mu +\nu =\lambda }(M_{\mu }\otimes _F N_{\nu })$.
$(M\otimes _F N)_{\lambda }\cong \bigoplus _{\mu +\nu =\lambda }(M_{\mu }\otimes _F N_{\nu })$.(v) (Twist) Put
 $\mu :=\log {|c|}/\log {|q|}\in \mathbb {Q}$. Then, there exists a canonical isomorphism
$\mu :=\log {|c|}/\log {|q|}\in \mathbb {Q}$. Then, there exists a canonical isomorphism  $M(c)_{\lambda }\cong M_{\lambda -\mu }(c)$.
$M(c)_{\lambda }\cong M_{\lambda -\mu }(c)$.(vi) (Duality) Let
 $M\otimes _FN\to F$ be a perfect pairing. Then, we have
$M\otimes _FN\to F$ be a perfect pairing. Then, we have  $(N_{-\lambda })^{\perp }=\bigoplus _{\mu \neq \lambda }M_{\mu }$.
$(N_{-\lambda })^{\perp }=\bigoplus _{\mu \neq \lambda }M_{\mu }$.
(II)
(i) (Base change) There exists a canonical isomorphism
 $S_{\lambda }(M)\otimes _FE\cong S_{\lambda }(M\otimes _FE)$.
$S_{\lambda }(M)\otimes _FE\cong S_{\lambda }(M\otimes _FE)$.(ii) (
 $d$-pushforward) There exists a canonical isomorphism
$d$-pushforward) There exists a canonical isomorphism  $[d]_*(S_{\lambda }(M))\cong S_{\lambda }([d]_*M)$.
$[d]_*(S_{\lambda }(M))\cong S_{\lambda }([d]_*M)$.(iii) (Strictness) If
 $0\to M'\to M\to M''\to 0$ is an exact sequence of
$0\to M'\to M\to M''\to 0$ is an exact sequence of  $\phi$-modules over
$\phi$-modules over  $F$, then there exists an induced exact sequence
$F$, then there exists an induced exact sequence  $0\to S_{\lambda }(M')\to S_{\lambda }(M)\to S_{\lambda }(M'')\to 0$.
$0\to S_{\lambda }(M')\to S_{\lambda }(M)\to S_{\lambda }(M'')\to 0$.(iv) (Tensor product) There exists a canonical isomorphism
 \[S_{\lambda }(M\otimes _F N)\cong \sum _{\mu +\nu =\lambda }S_{\mu }(M) \otimes _F S_{\nu }(N).\]
\[S_{\lambda }(M\otimes _F N)\cong \sum _{\mu +\nu =\lambda }S_{\mu }(M) \otimes _F S_{\nu }(N).\](v) (Twist) Put
 $\mu :=\log {|c|}/\log {|q|}\in \mathbb {Q}$. Then, there exists a canonical isomorphism
$\mu :=\log {|c|}/\log {|q|}\in \mathbb {Q}$. Then, there exists a canonical isomorphism  $S_{\lambda }(M(c))\cong S_{\lambda -\mu }(M)(c)$.
$S_{\lambda }(M(c))\cong S_{\lambda -\mu }(M)(c)$.(vi) (Duality) Let
 $M\otimes _FN\to F$ be a perfect pairing. Then, we have
$M\otimes _FN\to F$ be a perfect pairing. Then, we have  $S_{-\lambda }(N)^{\perp }=\bigcup _{\mu <\lambda }S_{\mu }(M)$.
$S_{-\lambda }(N)^{\perp }=\bigcup _{\mu <\lambda }S_{\mu }(M)$.
Proof. (I) Parts (i), (ii), and (iv) follow from the uniqueness of the decomposition given in Theorem 1.5(i). Part (iii) follows from Theorem 1.5(iv). Part (v) is a special case of part (iv). We prove part (vi). By Lemma 1.6, the image of ![]() $M_{\mu }\otimes _FN_{-\lambda }$ under the given pairing vanishes if
$M_{\mu }\otimes _FN_{-\lambda }$ under the given pairing vanishes if ![]() $\mu \neq \lambda$. Hence,
$\mu \neq \lambda$. Hence, ![]() $N_{-\lambda }\subset (\bigoplus _{\mu \neq \lambda }M_{\mu })^{\perp }$. By Theorem 1.5(i), we have
$N_{-\lambda }\subset (\bigoplus _{\mu \neq \lambda }M_{\mu })^{\perp }$. By Theorem 1.5(i), we have ![]() $(\bigoplus _{\mu \neq \lambda }M_{\mu })^{\perp }\cong (M/(\bigoplus _{\mu \neq \lambda }M_{\mu }))^\vee \cong (M_{\lambda })^\vee$. Hence,
$(\bigoplus _{\mu \neq \lambda }M_{\mu })^{\perp }\cong (M/(\bigoplus _{\mu \neq \lambda }M_{\mu }))^\vee \cong (M_{\lambda })^\vee$. Hence, ![]() $(\bigoplus _{\mu \neq \lambda }M_{\mu })^{\perp }$ is pure of slope
$(\bigoplus _{\mu \neq \lambda }M_{\mu })^{\perp }$ is pure of slope ![]() $-\lambda$. Therefore, the image of
$-\lambda$. Therefore, the image of ![]() $(\bigoplus _{\mu \neq \lambda }M_{\mu })^{\perp }$ under the projection
$(\bigoplus _{\mu \neq \lambda }M_{\mu })^{\perp }$ under the projection ![]() $N\to N/N_{-\lambda }$ vanishes by Lemma 1.6. Hence,
$N\to N/N_{-\lambda }$ vanishes by Lemma 1.6. Hence, ![]() $(\bigoplus _{\mu \neq \lambda }M_{\mu })^{\perp }\subset N_{-\lambda }$, which implies the assertion.
$(\bigoplus _{\mu \neq \lambda }M_{\mu })^{\perp }\subset N_{-\lambda }$, which implies the assertion.
(II) Part (i) follows from the uniqueness of the slope filtration. To prove the rest of the assertion, by performing a base change and using part (i), we may assume that ![]() $F$ is inversive, in which case
$F$ is inversive, in which case ![]() $S_{\lambda }(M),S_{\lambda }(N)$ etc., can be replaced by
$S_{\lambda }(M),S_{\lambda }(N)$ etc., can be replaced by ![]() $\bigoplus _{\mu \leqslant \lambda }M_{\lambda },\bigoplus _{\mu \leqslant \lambda }N_{\lambda }$, etc. Then, parts (ii)–(v) follow from parts (ii)–(v) of part (I), respectively. We prove part (vi). By part (I)(vi), we have
$\bigoplus _{\mu \leqslant \lambda }M_{\lambda },\bigoplus _{\mu \leqslant \lambda }N_{\lambda }$, etc. Then, parts (ii)–(v) follow from parts (ii)–(v) of part (I), respectively. We prove part (vi). By part (I)(vi), we have ![]() $S_{-\lambda }(N)^{\perp }=(\bigoplus _{\nu \geqslant \lambda }N_{-\nu })^{\perp }= {\bigcap} _{\nu \geqslant \lambda }(N_{-\nu })^{\perp }={\bigcap} _{\nu \geqslant \lambda }(\bigoplus _{\mu \neq \nu }M_{\mu })=\bigoplus _{\mu <\lambda }M_{\mu }$.
$S_{-\lambda }(N)^{\perp }=(\bigoplus _{\nu \geqslant \lambda }N_{-\nu })^{\perp }= {\bigcap} _{\nu \geqslant \lambda }(N_{-\nu })^{\perp }={\bigcap} _{\nu \geqslant \lambda }(\bigoplus _{\mu \neq \nu }M_{\mu })=\bigoplus _{\mu <\lambda }M_{\mu }$.
We gather miscellaneous results used later in this paper.
Definition 1.8 (Cf. [Reference KedlayaKed05b, Definition 4.2.1])
A ![]() $d$-eigenvector of
$d$-eigenvector of ![]() $M$ is a nonzero element
$M$ is a nonzero element ![]() $v\in M$ such that
$v\in M$ such that ![]() $\phi _M^d(v)=cv$ for some
$\phi _M^d(v)=cv$ for some ![]() $c\in F^{\times }$; we call the quotient
$c\in F^{\times }$; we call the quotient ![]() $\log {|c|}/\log {|q|^d}$ the slope of
$\log {|c|}/\log {|q|^d}$ the slope of ![]() $v$. Note that
$v$. Note that ![]() $v$ is regarded as a
$v$ is regarded as a ![]() $1$-eigenvector of
$1$-eigenvector of ![]() $[d]_*M$ whose slope is equal to that of
$[d]_*M$ whose slope is equal to that of ![]() $v$.
$v$.
Lemma 1.9 If ![]() $v\in M$ is a
$v\in M$ is a ![]() $d$-eigenvector of slope
$d$-eigenvector of slope ![]() $\lambda$, then
$\lambda$, then ![]() $v\in S_{\lambda }(M)$ and
$v\in S_{\lambda }(M)$ and ![]() $v\notin \bigcup _{\mu <\lambda }S_{\mu }(M)$. Moreover, if
$v\notin \bigcup _{\mu <\lambda }S_{\mu }(M)$. Moreover, if ![]() $M$ is pure, then the slope of
$M$ is pure, then the slope of ![]() $M$ is equal to
$M$ is equal to ![]() $\lambda$.
$\lambda$.
Proof. By Lemma 1.7(II)(ii), we may replace ![]() $M$ by
$M$ by ![]() $[d]_*M$. Thus, we may assume that
$[d]_*M$. Thus, we may assume that ![]() $d=1$. By Lemma 1.7(II)(iii), we may replace
$d=1$. By Lemma 1.7(II)(iii), we may replace ![]() $M$ by
$M$ by ![]() $Fv$. Thus, we may assume that
$Fv$. Thus, we may assume that ![]() $M=F(c)$ for some
$M=F(c)$ for some ![]() $c\in F^{\times }$ with
$c\in F^{\times }$ with ![]() $\lambda =\log {|c|}/\log {|q|}$, in which case the assertion is obvious.
$\lambda =\log {|c|}/\log {|q|}$, in which case the assertion is obvious.
Theorem 1.10 (Dieudonné–Manin classification theorem [Reference KedlayaKed10, Theorem14.6.3])
Assume that the residue field of ![]() $F$ is strongly difference closed. Then, there exists
$F$ is strongly difference closed. Then, there exists ![]() $d$ such that
$d$ such that ![]() $M$ admits an
$M$ admits an ![]() $F$-basis
$F$-basis ![]() $e_1,\dots ,e_n$ consisting of
$e_1,\dots ,e_n$ consisting of ![]() $d$-eigenvectors, where
$d$-eigenvectors, where ![]() $n=\dim _FM$; if
$n=\dim _FM$; if ![]() $M$ is pure of slope zero, i.e. étale, then we may assume that
$M$ is pure of slope zero, i.e. étale, then we may assume that ![]() $\phi _M(e_i)=e_i$ for all
$\phi _M(e_i)=e_i$ for all ![]() $i$. Moreover, if
$i$. Moreover, if ![]() $\mu _i$ denotes the slope of
$\mu _i$ denotes the slope of ![]() $e_i$, then the slope multiset of
$e_i$, then the slope multiset of ![]() $M$ coincides with the multiset
$M$ coincides with the multiset ![]() $\{\mu _i;1\leqslant i\leqslant n\}$, and
$\{\mu _i;1\leqslant i\leqslant n\}$, and ![]() $M_{\lambda }$ is spanned by
$M_{\lambda }$ is spanned by ![]() $\{e_i;\mu _i=\lambda \}$.
$\{e_i;\mu _i=\lambda \}$.
Definition 1.11 (Cf. [Reference LiuLiu13, Definition 1.6.6])
Assume that ![]() $F$ is inversive. Let
$F$ is inversive. Let ![]() $M=\bigoplus _{\lambda \in \mathbb {R}}M_{\lambda }$ be the decomposition given in Theorem 1.5(i). We define the reverse filtration
$M=\bigoplus _{\lambda \in \mathbb {R}}M_{\lambda }$ be the decomposition given in Theorem 1.5(i). We define the reverse filtration ![]() $S^{\bullet }(M)$ of
$S^{\bullet }(M)$ of ![]() $M$ by
$M$ by ![]() $S^{\lambda }(M)=\bigoplus _{\mu \geqslant \lambda }M_{\mu }$ for
$S^{\lambda }(M)=\bigoplus _{\mu \geqslant \lambda }M_{\mu }$ for ![]() $\lambda \in \mathbb {R}$.
$\lambda \in \mathbb {R}$.
Note that ![]() $S^{\bullet }(M)$ is a decreasing filtration of
$S^{\bullet }(M)$ is a decreasing filtration of ![]() $\phi$-submodules of
$\phi$-submodules of ![]() $M$, which is exhaustive and separated. Moreover, the slope multiset of
$M$, which is exhaustive and separated. Moreover, the slope multiset of ![]() $S^{\bullet }(M)$ coincides with that of
$S^{\bullet }(M)$ coincides with that of ![]() $M_{\bullet }$.
$M_{\bullet }$.
2. The Robba ring and the extended Robba ring
In this section, we recall basic facts on various analytic rings used in this paper, in particular, the extended Robba ring ![]() $\tilde {\mathcal {R}}$, which is introduced in [Reference KedlayaKed08], and studied further in [Reference LiuLiu13]. We also define a log analogue
$\tilde {\mathcal {R}}$, which is introduced in [Reference KedlayaKed08], and studied further in [Reference LiuLiu13]. We also define a log analogue ![]() $\tilde {\mathcal {R}}_{\rm log}$ of
$\tilde {\mathcal {R}}_{\rm log}$ of ![]() $\tilde {\mathcal {R}}$.
$\tilde {\mathcal {R}}$.
Notation 1. In the rest of the paper, let ![]() $p$ be fixed a prime number. Let
$p$ be fixed a prime number. Let ![]() $(K,\varphi _K,q)$ be a triple as in Definition 1.1. In §§ 2 and 3, as in [Reference KedlayaKed08, Reference LiuLiu13], we do not assume that
$(K,\varphi _K,q)$ be a triple as in Definition 1.1. In §§ 2 and 3, as in [Reference KedlayaKed08, Reference LiuLiu13], we do not assume that ![]() $\varphi _K$ is a
$\varphi _K$ is a ![]() $q$-power Frobenius lift. Let
$q$-power Frobenius lift. Let ![]() $\mathcal {O}_K$,
$\mathcal {O}_K$, ![]() $\mathfrak {m}_K$, and
$\mathfrak {m}_K$, and ![]() $k$ be the integer ring, maximal ideal, and residue field of
$k$ be the integer ring, maximal ideal, and residue field of ![]() $K$, respectively. Except in § 2, we normalize the valuation
$K$, respectively. Except in § 2, we normalize the valuation ![]() $|\cdot |$ of
$|\cdot |$ of ![]() $K$ by
$K$ by ![]() $|p|=p^{-1}$.
$|p|=p^{-1}$.
In this paper, when we denote rings associated to ![]() $K$, such as the Robba ring
$K$, such as the Robba ring ![]() $\mathcal {R}_K$, we omit the subscript
$\mathcal {R}_K$, we omit the subscript ![]() $K$ if no confusion arises.
$K$ if no confusion arises.
2.1 The Robba ring
Definition 2.1 (i) [Reference KedlayaKed08, Definitions 1.1.1, 1.2.3] For ![]() $r>0$, let
$r>0$, let ![]() $\mathcal {R}^r$ be the ring of formal Laurent series
$\mathcal {R}^r$ be the ring of formal Laurent series ![]() $\sum _{i\in \mathbb {Z}}a_it^i$ with
$\sum _{i\in \mathbb {Z}}a_it^i$ with ![]() $a_i\in K$ converging on
$a_i\in K$ converging on ![]() $e^{-r}\leqslant |t|<1$. We define the Robba ring
$e^{-r}\leqslant |t|<1$. We define the Robba ring ![]() $\mathcal {R}$ (over
$\mathcal {R}$ (over ![]() $K$) as the union of the
$K$) as the union of the ![]() $\mathcal {R}^r$'s, which is a Bézout domain. Explicitly, we have
$\mathcal {R}^r$'s, which is a Bézout domain. Explicitly, we have
 \begin{gather*} \mathcal{R}^r=\bigg\{\sum_{i\in\mathbb{Z}}a_it^i;\lim_{i\to\pm\infty}{|a_i|e^{{-}sn}}=0\ (s\in (0,r])\bigg\},\\ \mathcal{R}=\mathop{\bigcup}\limits_{r\in (0,+\infty)}\mathcal{R}^r. \end{gather*}
\begin{gather*} \mathcal{R}^r=\bigg\{\sum_{i\in\mathbb{Z}}a_it^i;\lim_{i\to\pm\infty}{|a_i|e^{{-}sn}}=0\ (s\in (0,r])\bigg\},\\ \mathcal{R}=\mathop{\bigcup}\limits_{r\in (0,+\infty)}\mathcal{R}^r. \end{gather*}
We equip ![]() $\mathcal {R}^r$ with the norm
$\mathcal {R}^r$ with the norm ![]() $|\cdot |_s$ for
$|\cdot |_s$ for ![]() $s\in (0,r]$ defined by
$s\in (0,r]$ defined by ![]() $|\sum _{i\in \mathbb {Z}}a_it^i|_s=\sup _{i\in \mathbb {Z}}\{|a_i|e^{-si}\}$.
$|\sum _{i\in \mathbb {Z}}a_it^i|_s=\sup _{i\in \mathbb {Z}}\{|a_i|e^{-si}\}$.
(ii) [Reference KedlayaKed08, Definition 1.1.3] We define the bounded (respectively, integral) Robba ring ![]() $\mathcal {R}^{\mathrm {bd}}$ (respectively,
$\mathcal {R}^{\mathrm {bd}}$ (respectively, ![]() $\mathcal {R}^{\mathrm {int}}$) as the subring of
$\mathcal {R}^{\mathrm {int}}$) as the subring of ![]() $\mathcal {R}$ consisting of series with bounded (respectively, integral) coefficients. We equip
$\mathcal {R}$ consisting of series with bounded (respectively, integral) coefficients. We equip ![]() $\mathcal {R}^{\mathrm {bd}}$ with Gauss norm
$\mathcal {R}^{\mathrm {bd}}$ with Gauss norm ![]() $|\cdot |_0$ defined by
$|\cdot |_0$ defined by ![]() $|\sum _{i\in \mathbb {Z}}a_it^i|_0=\sup _{i\in \mathbb {Z}}|a_i|$. Then, the ring
$|\sum _{i\in \mathbb {Z}}a_it^i|_0=\sup _{i\in \mathbb {Z}}|a_i|$. Then, the ring ![]() $\mathcal {R}^{\mathrm {bd}}$ is a henselian discrete valuation field of mixed characteristic
$\mathcal {R}^{\mathrm {bd}}$ is a henselian discrete valuation field of mixed characteristic ![]() $(0,p)$ with integer ring
$(0,p)$ with integer ring ![]() $\mathcal {R}^{\mathrm {int}}$ and residue field
$\mathcal {R}^{\mathrm {int}}$ and residue field ![]() $k((t))$ (see [Reference KedlayaKed08, Lemma 3.9]). We define the Amice ring
$k((t))$ (see [Reference KedlayaKed08, Lemma 3.9]). We define the Amice ring ![]() $\mathcal {E}$ as the completion of
$\mathcal {E}$ as the completion of ![]() $\mathcal {R}^{\mathrm {bd}}$ for Gauss norm. Explicitly, we have
$\mathcal {R}^{\mathrm {bd}}$ for Gauss norm. Explicitly, we have
 \begin{gather*} \mathcal{R}^{\mathrm{int}}=\bigg\{\sum_{i\in\mathbb{Z}}a_it^i\in\mathcal{R};a_i\in \mathcal{O}_K\bigg\},\\ \mathcal{R}^{\mathrm{bd}}=\bigg\{\sum_{i\in\mathbb{Z}}a_it^i\in\mathcal{R};\sup_{i\in\mathbb{Z}}{|a_i|}<\infty \bigg\}\cong\mathcal{R}^{\mathrm{int}}\otimes_{\mathcal{O}_K}K,\\ \mathcal{E}=\bigg\{\sum_{i\in\mathbb{Z}}a_it^i;\sup_{i\in\mathbb{Z}}|a_i|<\infty,\ \lim_{i\to-\infty}{|a_i|}=0\bigg\}. \end{gather*}
\begin{gather*} \mathcal{R}^{\mathrm{int}}=\bigg\{\sum_{i\in\mathbb{Z}}a_it^i\in\mathcal{R};a_i\in \mathcal{O}_K\bigg\},\\ \mathcal{R}^{\mathrm{bd}}=\bigg\{\sum_{i\in\mathbb{Z}}a_it^i\in\mathcal{R};\sup_{i\in\mathbb{Z}}{|a_i|}<\infty \bigg\}\cong\mathcal{R}^{\mathrm{int}}\otimes_{\mathcal{O}_K}K,\\ \mathcal{E}=\bigg\{\sum_{i\in\mathbb{Z}}a_it^i;\sup_{i\in\mathbb{Z}}|a_i|<\infty,\ \lim_{i\to-\infty}{|a_i|}=0\bigg\}. \end{gather*} (iii) Let ![]() $X=t^iv$ be an element of
$X=t^iv$ be an element of ![]() $\mathcal {O}_K[\![t]\!]$ with
$\mathcal {O}_K[\![t]\!]$ with ![]() $i\in \mathbb {N}_{\geqslant 1}$ and
$i\in \mathbb {N}_{\geqslant 1}$ and ![]() $v\in \mathcal {O}_K[\![t]\!]^{\times }$ such that
$v\in \mathcal {O}_K[\![t]\!]^{\times }$ such that ![]() $\varphi _K(v|_{t=0})/(v|_{t=0})^q\in 1+\mathfrak {m}_K$ (this always holds when
$\varphi _K(v|_{t=0})/(v|_{t=0})^q\in 1+\mathfrak {m}_K$ (this always holds when ![]() $\varphi _K$ is a
$\varphi _K$ is a ![]() $q$-power Frobenius lift). We define
$q$-power Frobenius lift). We define ![]() $\mathcal {R}_{\rm log}$ as the polynomial ring
$\mathcal {R}_{\rm log}$ as the polynomial ring ![]() $\mathcal {R}[\ell _X]$ with a variable
$\mathcal {R}[\ell _X]$ with a variable ![]() $\ell _X$ called the branch of log associated to
$\ell _X$ called the branch of log associated to ![]() $X$. We will endow
$X$. We will endow ![]() $\mathcal {R}_{\rm log}$ with extra structures by regarding
$\mathcal {R}_{\rm log}$ with extra structures by regarding ![]() $\ell _X$ as
$\ell _X$ as ![]() $\log {X}$ (Definitions 2.2 and 4.2).
$\log {X}$ (Definitions 2.2 and 4.2).
Definition 2.2 [Reference KedlayaKed08, Definition 1.2.1]
A relative (![]() $q$-power) Frobenius lift on
$q$-power) Frobenius lift on ![]() $\mathcal {R}$ is a ring endomorphism
$\mathcal {R}$ is a ring endomorphism ![]() $\varphi :\mathcal {R}\to \mathcal {R}$ of the form
$\varphi :\mathcal {R}\to \mathcal {R}$ of the form ![]() $\sum _{i\in \mathbb {Z}}a_it^i\mapsto \sum _{i\in \mathbb {Z}}\varphi _K(a_i)S^i$ for some
$\sum _{i\in \mathbb {Z}}a_it^i\mapsto \sum _{i\in \mathbb {Z}}\varphi _K(a_i)S^i$ for some ![]() $S\in \mathcal {R}^{\mathrm {bd}}$ satisfying
$S\in \mathcal {R}^{\mathrm {bd}}$ satisfying ![]() $|S-t^q|_0<1$. We show that
$|S-t^q|_0<1$. We show that ![]() $\varphi$ naturally induces ring endomorphisms on
$\varphi$ naturally induces ring endomorphisms on ![]() $\mathcal {R}^{\mathrm {int}},\mathcal {R}^{\mathrm {bd}},\mathcal {R}_{\rm log}$, and
$\mathcal {R}^{\mathrm {int}},\mathcal {R}^{\mathrm {bd}},\mathcal {R}_{\rm log}$, and ![]() $\mathcal {E}$, moreover, on
$\mathcal {E}$, moreover, on ![]() $K[\![t]\!]_0,K\{t\}$ if
$K[\![t]\!]_0,K\{t\}$ if ![]() $S\in K[\![t]\!]_0$, which we denote by
$S\in K[\![t]\!]_0$, which we denote by ![]() $\varphi$ for notational simplicity. Note that
$\varphi$ for notational simplicity. Note that ![]() $\varphi (X)/X^q\in 1+\mathfrak {m}_K\mathcal {R}^{\mathrm {int}}$ by
$\varphi (X)/X^q\in 1+\mathfrak {m}_K\mathcal {R}^{\mathrm {int}}$ by ![]() $\varphi (t)/t^q,\varphi (v)/v^q\in 1+\mathfrak {m}_K\mathcal {R}^{\mathrm {int}}$. We extend
$\varphi (t)/t^q,\varphi (v)/v^q\in 1+\mathfrak {m}_K\mathcal {R}^{\mathrm {int}}$. We extend ![]() $\varphi$ to
$\varphi$ to ![]() $\mathcal {R}_{\rm log}$ by setting
$\mathcal {R}_{\rm log}$ by setting ![]() $\varphi (\ell _X)=\log {(\varphi (X)/X^q)}+q\ell _X$, where
$\varphi (\ell _X)=\log {(\varphi (X)/X^q)}+q\ell _X$, where ![]() $\log :1+\mathfrak {m}_K\mathcal {R}^{\mathrm {int}}\to \mathcal {R}^{\mathrm {bd}};f\mapsto \sum _{n=1}^{\infty }(-1)^{n-1}(f-1)^n/n$. Obviously,
$\log :1+\mathfrak {m}_K\mathcal {R}^{\mathrm {int}}\to \mathcal {R}^{\mathrm {bd}};f\mapsto \sum _{n=1}^{\infty }(-1)^{n-1}(f-1)^n/n$. Obviously, ![]() $\varphi$ restricts to
$\varphi$ restricts to ![]() $\mathcal {R}^{\mathrm {int}},\mathcal {R}^{\mathrm {bd}}$, and to
$\mathcal {R}^{\mathrm {int}},\mathcal {R}^{\mathrm {bd}}$, and to ![]() $K[\![t]\!]_0,K\{t\}$ if
$K[\![t]\!]_0,K\{t\}$ if ![]() $S\in K[\![t]\!]_0$. Note that
$S\in K[\![t]\!]_0$. Note that ![]() $|\varphi (f)|_0=|f|_0$ for
$|\varphi (f)|_0=|f|_0$ for ![]() $f\in \mathcal {R}^{\mathrm {bd}}$. We define
$f\in \mathcal {R}^{\mathrm {bd}}$. We define ![]() $\varphi :\mathcal {E}\to \mathcal {E}$ as the completion of
$\varphi :\mathcal {E}\to \mathcal {E}$ as the completion of ![]() $\varphi :\mathcal {R}^{\mathrm {bd}}\to \mathcal {R}^{\mathrm {bd}}$ for Gauss norm.
$\varphi :\mathcal {R}^{\mathrm {bd}}\to \mathcal {R}^{\mathrm {bd}}$ for Gauss norm.
Convention 1. In the rest of the paper, unless otherwise mentioned, we fix a relative Frobenius lift ![]() $\varphi$ on
$\varphi$ on ![]() $\mathcal {R}$, and a branch
$\mathcal {R}$, and a branch ![]() $\ell _X$ of log. When we speak of
$\ell _X$ of log. When we speak of ![]() $K[\![t]\!]_0$ and
$K[\![t]\!]_0$ and ![]() $K\{t\}$, we tacitly assume that
$K\{t\}$, we tacitly assume that ![]() $\varphi (t)=S\in K[\![t]\!]_0$. Moreover, we apply results of § 1 to
$\varphi (t)=S\in K[\![t]\!]_0$. Moreover, we apply results of § 1 to ![]() $\varphi$-modules over
$\varphi$-modules over ![]() $K$,
$K$, ![]() $\mathcal {E}$, and
$\mathcal {E}$, and ![]() $\tilde {\mathcal {E}}$ (defined in § 2.2) with respect to the triples
$\tilde {\mathcal {E}}$ (defined in § 2.2) with respect to the triples ![]() $(K,\varphi _K,q)$,
$(K,\varphi _K,q)$, ![]() $(\mathcal {E},\varphi ,q)$, and
$(\mathcal {E},\varphi ,q)$, and ![]() $(\tilde {\mathcal {E}},\varphi ,q)$, respectively.
$(\tilde {\mathcal {E}},\varphi ,q)$, respectively.
2.2 The extended Robba ring
Throughout this subsection, we make the following assumption.
Assumption 2.3 We assume that ![]() $k$ is strongly difference-closed. As
$k$ is strongly difference-closed. As ![]() $K$ is inversive [Reference LiuLiu13, Lemma 1.3.2], our assumption coincides with [Reference KedlayaKed08, Hypothesis 2.1.1].
$K$ is inversive [Reference LiuLiu13, Lemma 1.3.2], our assumption coincides with [Reference KedlayaKed08, Hypothesis 2.1.1].
Definition 2.4 ([Reference KedlayaKed08, Definition 2.2.4 and Remark 2.2.5], [Reference LiuLiu13, Definition 1.4.1])
For ![]() ${r\,{>}\,0}$, let
${r\,{>}\,0}$, let ![]() $\tilde {\mathcal {R}}^r$ be the abelian group of formal sums
$\tilde {\mathcal {R}}^r$ be the abelian group of formal sums ![]() $\sum _{i\in \mathbb {Q}}a_iu^i$ with
$\sum _{i\in \mathbb {Q}}a_iu^i$ with ![]() $a_i\in K$ satisfying the following conditions.
$a_i\in K$ satisfying the following conditions.
(a) For each
 $c>0$, the set of
$c>0$, the set of  $i\in \mathbb {Q}$ such that
$i\in \mathbb {Q}$ such that  $|a_i|\geqslant c$ is well-ordered.
$|a_i|\geqslant c$ is well-ordered.(b) We have
 $\lim _{i\to -\infty }{|a_i|e^{-ri}}=0$.
$\lim _{i\to -\infty }{|a_i|e^{-ri}}=0$.(c) We have
 $\sup _{i\in (-\infty ,+\infty )}|a_i|e^{-ri}<\infty$.
$\sup _{i\in (-\infty ,+\infty )}|a_i|e^{-ri}<\infty$.(d) For all
 $s>0$, we have
$s>0$, we have  $\lim _{i\to +\infty }{|a_i|e^{-si}}=0$.
$\lim _{i\to +\infty }{|a_i|e^{-si}}=0$.
The group ![]() $\tilde {\mathcal {R}}^r$ forms a ring with multiplication given by convolution. We call the union
$\tilde {\mathcal {R}}^r$ forms a ring with multiplication given by convolution. We call the union ![]() $\tilde {\mathcal {R}}=\bigcup _{r\in (0,+\infty )}\tilde {\mathcal {R}}^r$ the extended Robba ring over
$\tilde {\mathcal {R}}=\bigcup _{r\in (0,+\infty )}\tilde {\mathcal {R}}^r$ the extended Robba ring over ![]() $K$, which is a Bézout domain. In the rest of this subsection, when we write
$K$, which is a Bézout domain. In the rest of this subsection, when we write ![]() $\sum _{i\in \mathbb {Q}}a_iu^i$, we tacitly assume that
$\sum _{i\in \mathbb {Q}}a_iu^i$, we tacitly assume that ![]() $a_i\in K$ for all
$a_i\in K$ for all ![]() $i\in \mathbb {Q}$. We equip
$i\in \mathbb {Q}$. We equip ![]() $\tilde {\mathcal {R}}^r$ with the norm
$\tilde {\mathcal {R}}^r$ with the norm ![]() $|\sum _{i\in \mathbb {Q}}a_iu^i|_r=\sup _{i\in \mathbb {Q}}\{|a_i|e^{-ri}\}$. We define
$|\sum _{i\in \mathbb {Q}}a_iu^i|_r=\sup _{i\in \mathbb {Q}}\{|a_i|e^{-ri}\}$. We define ![]() $\tilde {\mathcal {R}}_{\rm log}$ as the polynomial ring
$\tilde {\mathcal {R}}_{\rm log}$ as the polynomial ring ![]() $\tilde {\mathcal {R}}[\log {u}]$ over
$\tilde {\mathcal {R}}[\log {u}]$ over ![]() $\tilde {\mathcal {R}}$ with a variable
$\tilde {\mathcal {R}}$ with a variable ![]() $\log {u}$.
$\log {u}$.
We define the bounded (respectively, integral) extended Robba ring ![]() $\tilde {\mathcal {R}}^{\mathrm {bd}}$ (respectively,
$\tilde {\mathcal {R}}^{\mathrm {bd}}$ (respectively, ![]() $\tilde {\mathcal {R}}^{\mathrm {int}}$) as the subring of
$\tilde {\mathcal {R}}^{\mathrm {int}}$) as the subring of ![]() $\tilde {\mathcal {R}}$ consisting of series with bounded (respectively, integral) coefficients. We equip
$\tilde {\mathcal {R}}$ consisting of series with bounded (respectively, integral) coefficients. We equip ![]() $\tilde {\mathcal {R}}^{\mathrm {bd}}$ with Gauss norm
$\tilde {\mathcal {R}}^{\mathrm {bd}}$ with Gauss norm ![]() $|\cdot |_0$ defined by
$|\cdot |_0$ defined by ![]() $|\sum _{i\in \mathbb {Q}}a_iu^i|_0=\sup _{i\in \mathbb {Q}}|a_i|$. Then, the ring
$|\sum _{i\in \mathbb {Q}}a_iu^i|_0=\sup _{i\in \mathbb {Q}}|a_i|$. Then, the ring ![]() $\mathcal {R}^{\mathrm {bd}}$ is a henselian discrete valuation field with integer ring
$\mathcal {R}^{\mathrm {bd}}$ is a henselian discrete valuation field with integer ring ![]() $\mathcal {R}^{\mathrm {int}}$ and residue field
$\mathcal {R}^{\mathrm {int}}$ and residue field ![]() $k((u^{\mathbb {Q}}))$. Here,
$k((u^{\mathbb {Q}}))$. Here, ![]() $k((u^{\mathbb {Q}}))$ denotes the field of Hahn series over
$k((u^{\mathbb {Q}}))$ denotes the field of Hahn series over ![]() $k$ (see [Reference KedlayaKed08, Definition 2.2.1, Notation 2.5.1]). We define
$k$ (see [Reference KedlayaKed08, Definition 2.2.1, Notation 2.5.1]). We define ![]() $\tilde {\mathcal {E}}$ as the completion of
$\tilde {\mathcal {E}}$ as the completion of ![]() $\tilde {\mathcal {R}}^{\mathrm {bd}}$ for Gauss norm, which coincides with the set of formal sums
$\tilde {\mathcal {R}}^{\mathrm {bd}}$ for Gauss norm, which coincides with the set of formal sums ![]() $\sum _{i\in \mathbb {Q}}a_iu^i$ satisfying condition (a) as previously,
$\sum _{i\in \mathbb {Q}}a_iu^i$ satisfying condition (a) as previously, ![]() $\lim _{i\to -\infty }|a_i|=0$, and
$\lim _{i\to -\infty }|a_i|=0$, and ![]() $\sup _{i\in (-\infty ,+\infty )}|a_i|<0$ (see [Reference LiuLiu13, Definition 1.4.4 and Remark 1.4.5]).
$\sup _{i\in (-\infty ,+\infty )}|a_i|<0$ (see [Reference LiuLiu13, Definition 1.4.4 and Remark 1.4.5]).
We endow ![]() $\tilde {\mathcal {R}}$ with the ring automorphism
$\tilde {\mathcal {R}}$ with the ring automorphism ![]() $\varphi$ defined by
$\varphi$ defined by ![]() $\varphi (\sum _{i\in \mathbb {Q}}a_iu^i)=\sum _{i\in \mathbb {Q}}\varphi _K(a_i)u^{qi}$. Note that
$\varphi (\sum _{i\in \mathbb {Q}}a_iu^i)=\sum _{i\in \mathbb {Q}}\varphi _K(a_i)u^{qi}$. Note that ![]() $\varphi (\tilde {\mathcal {R}}^{qr})\subset \tilde {\mathcal {R}}^r$ and
$\varphi (\tilde {\mathcal {R}}^{qr})\subset \tilde {\mathcal {R}}^r$ and ![]() $|\varphi (f)|_r=|f|_{qr}$ for
$|\varphi (f)|_r=|f|_{qr}$ for ![]() $f\in \tilde {\mathcal {R}}^{qr}$. As in Definition 2.2,
$f\in \tilde {\mathcal {R}}^{qr}$. As in Definition 2.2, ![]() $\varphi$ induces ring endomorphisms on
$\varphi$ induces ring endomorphisms on ![]() $\tilde {\mathcal {R}}^{\mathrm {int}}$,
$\tilde {\mathcal {R}}^{\mathrm {int}}$, ![]() $\tilde {\mathcal {R}}^{\mathrm {bd}}$,
$\tilde {\mathcal {R}}^{\mathrm {bd}}$, ![]() $\tilde {\mathcal {E}}$, and
$\tilde {\mathcal {E}}$, and ![]() $\tilde {\mathcal {R}}_{\rm log}$ by setting
$\tilde {\mathcal {R}}_{\rm log}$ by setting ![]() $\varphi (\log {u})=q\log {u}$, which we denote by
$\varphi (\log {u})=q\log {u}$, which we denote by ![]() $\varphi$. Moreover, the field
$\varphi$. Moreover, the field ![]() $k((u^{\mathbb {Q}}))$ is strongly difference-closed with respect to the ring endomorphism induced by
$k((u^{\mathbb {Q}}))$ is strongly difference-closed with respect to the ring endomorphism induced by ![]() $\varphi :\tilde {\mathcal {R}}^{\mathrm {int}}\to \tilde {\mathcal {R}}^{\mathrm {int}}$ (see [Reference KedlayaKed08, Proposition 2.5.5]).
$\varphi :\tilde {\mathcal {R}}^{\mathrm {int}}\to \tilde {\mathcal {R}}^{\mathrm {int}}$ (see [Reference KedlayaKed08, Proposition 2.5.5]).
Lemma 2.5 Let ![]() $f=\sum _{i\in \mathbb {Q}}a_iu^i\in \tilde {\mathcal {R}}^{r'}$ with
$f=\sum _{i\in \mathbb {Q}}a_iu^i\in \tilde {\mathcal {R}}^{r'}$ with ![]() $r'>0$. Then, for any
$r'>0$. Then, for any ![]() $r\in (0,r']$ and
$r\in (0,r']$ and ![]() $i_0\in \mathbb {Q}$, we have
$i_0\in \mathbb {Q}$, we have
Proof. The assertion follows from
Lemma 2.6
(i) For
 $0<r\leqslant r'$, we have
$0<r\leqslant r'$, we have  $\tilde {\mathcal {R}}^{r'}\subset \tilde {\mathcal {R}}^r$. Consequently,
$\tilde {\mathcal {R}}^{r'}\subset \tilde {\mathcal {R}}^r$. Consequently,  $\tilde {\mathcal {R}}^{r'}$ is endowed with the family of the norms
$\tilde {\mathcal {R}}^{r'}$ is endowed with the family of the norms  $\{|\cdot |_r;r\in (0,r']\}$.
$\{|\cdot |_r;r\in (0,r']\}$.(ii) (Maximum modulus principle) Let
 $f\in \tilde {\mathcal {R}}^{r'}$. Then, for any closed interval
$f\in \tilde {\mathcal {R}}^{r'}$. Then, for any closed interval  $I=[r_1,r_2]\subset (0,r']$, we have
$I=[r_1,r_2]\subset (0,r']$, we have
 \begin{gather*} \sup_{r\in I}|f|_r=\max\{|f|_{r_1},|f|_{r_2}\},\\ \inf_{r\in I}|f|_r=\min\{|f|_{r_1},|f|_{r_2}\}. \end{gather*}
\begin{gather*} \sup_{r\in I}|f|_r=\max\{|f|_{r_1},|f|_{r_2}\},\\ \inf_{r\in I}|f|_r=\min\{|f|_{r_1},|f|_{r_2}\}. \end{gather*}
Proof. (i) Let ![]() $f=\sum _{i\in \mathbb {Q}}a_iu^i\in \tilde {\mathcal {R}}^{r'}$. It suffices to verify conditions (a)–(d) in Definition 2.4. We consider conditions (a)
$f=\sum _{i\in \mathbb {Q}}a_iu^i\in \tilde {\mathcal {R}}^{r'}$. It suffices to verify conditions (a)–(d) in Definition 2.4. We consider conditions (a)![]() $'$–(d)
$'$–(d)![]() $'$ as in Definition 2.4 with
$'$ as in Definition 2.4 with ![]() $r$ replaced by
$r$ replaced by ![]() $r'$, which hold by
$r'$, which hold by ![]() $f\in \tilde {\mathcal {R}}^{r'}$. By definition, conditions (a) and (d) coincide with conditions (a)
$f\in \tilde {\mathcal {R}}^{r'}$. By definition, conditions (a) and (d) coincide with conditions (a)![]() $'$ and (d)
$'$ and (d)![]() $'$ respectively, and condition (b) is weaker than condition (b)
$'$ respectively, and condition (b) is weaker than condition (b)![]() $'$. In particular, conditions (a), (b), and (d) hold. By condition (d)
$'$. In particular, conditions (a), (b), and (d) hold. By condition (d)![]() $'$, there exists
$'$, there exists ![]() $i_0\in \mathbb {Q}$ such that
$i_0\in \mathbb {Q}$ such that ![]() $\sup _{i\in [i_0,+\infty )}|a_i|e^{-ri}<\infty$. As
$\sup _{i\in [i_0,+\infty )}|a_i|e^{-ri}<\infty$. As ![]() $\sup _{i\in (-\infty ,i_0]}|a_i|e^{-ri}\leqslant |f|_{r'}e^{(r'-r)i_0}<\infty$ by Lemma 2.5, condition (c) holds.
$\sup _{i\in (-\infty ,i_0]}|a_i|e^{-ri}\leqslant |f|_{r'}e^{(r'-r)i_0}<\infty$ by Lemma 2.5, condition (c) holds.
(ii) We have only to prove ![]() $\min \{|f|_{r_1},|f|_{r_2}\}\leqslant |f|_r\leqslant \max \{|f|_{r_1},|f|_{r_2}\}$ for all
$\min \{|f|_{r_1},|f|_{r_2}\}\leqslant |f|_r\leqslant \max \{|f|_{r_1},|f|_{r_2}\}$ for all ![]() $r\in I$. Then, we may assume that
$r\in I$. Then, we may assume that ![]() $f$ is a monomial, in which case the assertion is obvious.
$f$ is a monomial, in which case the assertion is obvious.
Lemma 2.7 For ![]() $f\in \tilde {\mathcal {R}}^r$, we have
$f\in \tilde {\mathcal {R}}^r$, we have ![]() $f\in \tilde {\mathcal {R}}^{\mathrm {bd}}$ if and only if
$f\in \tilde {\mathcal {R}}^{\mathrm {bd}}$ if and only if ![]() $\sup _{s\in (0,r]}|f|_s<\infty$; in this case,
$\sup _{s\in (0,r]}|f|_s<\infty$; in this case, ![]() $\lim _{s\to 0+}|f|_s$ exists and
$\lim _{s\to 0+}|f|_s$ exists and ![]() $\lim _{s\to 0+}|f|_s=|f|_0$.
$\lim _{s\to 0+}|f|_s=|f|_0$.
Proof. Write ![]() $f=\sum _{i\in \mathbb {Q}}a_iu^i$, and put
$f=\sum _{i\in \mathbb {Q}}a_iu^i$, and put ![]() $|f|_0=\sup _{i\in \mathbb {Q}}|a_i|$ (it can be equal to
$|f|_0=\sup _{i\in \mathbb {Q}}|a_i|$ (it can be equal to ![]() $\infty$). Then, we have the equality in
$\infty$). Then, we have the equality in ![]() $\mathbb {R}\cup \{\infty \}$:
$\mathbb {R}\cup \{\infty \}$:
by
The first assertion is an immediate consequence of (2.7.1). We will prove the second assertion. Assume that ![]() $\sup _{s\in (0,r]}|f|_s<\infty$. Put
$\sup _{s\in (0,r]}|f|_s<\infty$. Put ![]() $f_+=\sum _{i\geqslant 0}a_iu^i$,
$f_+=\sum _{i\geqslant 0}a_iu^i$, ![]() $f_-=\sum _{i<0}a_iu^i$. As
$f_-=\sum _{i<0}a_iu^i$. As ![]() $|f|_s=\max \{|f_+|_s,|f_-|_s\}$ for all
$|f|_s=\max \{|f_+|_s,|f_-|_s\}$ for all ![]() $s\in [0,r]$, we may assume that
$s\in [0,r]$, we may assume that ![]() $f=f_{\pm }$. In the case
$f=f_{\pm }$. In the case ![]() $f=f_+$, the function
$f=f_+$, the function ![]() $s\mapsto |f|_s$ on
$s\mapsto |f|_s$ on ![]() $(0,r]$ is non-increasing and bounded above by
$(0,r]$ is non-increasing and bounded above by ![]() $|f|_0$. Hence,
$|f|_0$. Hence, ![]() $\lim _{s\to 0+}|f|_s$ exists and
$\lim _{s\to 0+}|f|_s$ exists and ![]() $\lim _{s\to 0+}|f|_s\leqslant |f|_0$. We also have
$\lim _{s\to 0+}|f|_s\leqslant |f|_0$. We also have ![]() $|f|_0\leqslant \lim _{s\to 0+}|f|_s$ by (2.7.1), which implies the assertion. In the case
$|f|_0\leqslant \lim _{s\to 0+}|f|_s$ by (2.7.1), which implies the assertion. In the case ![]() $f=f_-$, the function
$f=f_-$, the function ![]() $s\mapsto |f|_s$ on
$s\mapsto |f|_s$ on ![]() $(0,r]$ is non-decreasing and bounded below by
$(0,r]$ is non-decreasing and bounded below by ![]() $|f|_0$. Hence,
$|f|_0$. Hence, ![]() $\lim _{s\to 0+}|f|_s$ exists and
$\lim _{s\to 0+}|f|_s$ exists and ![]() $|f|_0\leqslant \lim _{s\to 0+}|f|_s$. To complete the proof, it suffices to prove that
$|f|_0\leqslant \lim _{s\to 0+}|f|_s$. To complete the proof, it suffices to prove that ![]() $\lim _{s\to 0+}|f|_s\leqslant |f|_0$. By condition (b) in Definition 2.4, there exists
$\lim _{s\to 0+}|f|_s\leqslant |f|_0$. By condition (b) in Definition 2.4, there exists ![]() $i_0<0$ such that
$i_0<0$ such that ![]() $\sup _{i\in (-\infty ,i_0]}{|a_i|e^{-ri}}\leqslant |f|_0$. Then, for any
$\sup _{i\in (-\infty ,i_0]}{|a_i|e^{-ri}}\leqslant |f|_0$. Then, for any ![]() $s\in (0,r]$, we have
$s\in (0,r]$, we have
 \begin{align*} |f|_s&=\max \Big\{\sup_{i\in (-\infty,i_0)}|a_i|e^{{-}si},\sup_{i\in [i_0,0]}|a_i|e^{{-}si} \Big\}\leqslant\max \Big\{\sup_{i\in (-\infty,i_0)}|a_i|e^{{-}ri},\sup_{i\in [i_0,0]}|a_i|e^{{-}si_0} \Big\}\\ &\leqslant\max\{|f|_0,|f|_0e^{{-}si_0}\}. \end{align*}
\begin{align*} |f|_s&=\max \Big\{\sup_{i\in (-\infty,i_0)}|a_i|e^{{-}si},\sup_{i\in [i_0,0]}|a_i|e^{{-}si} \Big\}\leqslant\max \Big\{\sup_{i\in (-\infty,i_0)}|a_i|e^{{-}ri},\sup_{i\in [i_0,0]}|a_i|e^{{-}si_0} \Big\}\\ &\leqslant\max\{|f|_0,|f|_0e^{{-}si_0}\}. \end{align*}
By taking the limit ![]() $s\to 0+$, we obtain the assertion.
$s\to 0+$, we obtain the assertion.
Lemma 2.8 For any ![]() $b\in \mathfrak {m}_K$, the map
$b\in \mathfrak {m}_K$, the map ![]() $\varphi -b:\tilde {\mathcal {R}}^{\mathrm {bd}}\to \tilde {\mathcal {R}}^{\mathrm {bd}}$ is bijective.
$\varphi -b:\tilde {\mathcal {R}}^{\mathrm {bd}}\to \tilde {\mathcal {R}}^{\mathrm {bd}}$ is bijective.
Proof. To prove the injectivity, we suppose, by way of contradiction, that there exists ![]() $x\in \tilde {\mathcal {R}}^{\mathrm {bd}}{\setminus} \{0\}$ such that
$x\in \tilde {\mathcal {R}}^{\mathrm {bd}}{\setminus} \{0\}$ such that ![]() $\varphi (x)=bx$. Then,
$\varphi (x)=bx$. Then, ![]() $|\varphi (x)|_0=|x|_0=|bx|_0<|x|_0$, which is a contradiction. To prove the surjectivity, we may replace
$|\varphi (x)|_0=|x|_0=|bx|_0<|x|_0$, which is a contradiction. To prove the surjectivity, we may replace ![]() $\varphi -b$ by
$\varphi -b$ by ![]() $1-\varphi _K^{-1}(b)\varphi ^{-1}(=\varphi ^{-1}\circ (\varphi -b))$. We have only to prove that for a given
$1-\varphi _K^{-1}(b)\varphi ^{-1}(=\varphi ^{-1}\circ (\varphi -b))$. We have only to prove that for a given ![]() $f=\sum _{i\in \mathbb {Q}}a_iu^i\in \tilde {\mathcal {R}}^{\mathrm {bd}}$, there exists
$f=\sum _{i\in \mathbb {Q}}a_iu^i\in \tilde {\mathcal {R}}^{\mathrm {bd}}$, there exists ![]() $g\in \tilde {\mathcal {R}}^{\mathrm {bd}}$ such that
$g\in \tilde {\mathcal {R}}^{\mathrm {bd}}$ such that ![]() $f=(1-\varphi _K^{-1}(b)\varphi ^{-1})g$. For
$f=(1-\varphi _K^{-1}(b)\varphi ^{-1})g$. For ![]() $i\in \mathbb {Q}$, we put
$i\in \mathbb {Q}$, we put ![]() $b_i:=\sum _{n\in \mathbb {N}}\varphi _K^{-1}(b)\cdot \dots \cdot \varphi _K^{-n}(b)\varphi _K^{-n}(a_{iq^n})\in K$. Since
$b_i:=\sum _{n\in \mathbb {N}}\varphi _K^{-1}(b)\cdot \dots \cdot \varphi _K^{-n}(b)\varphi _K^{-n}(a_{iq^n})\in K$. Since
the sequence ![]() $\{|b_i|\}_{i\in \mathbb {Q}}$ is bounded. Fix
$\{|b_i|\}_{i\in \mathbb {Q}}$ is bounded. Fix ![]() $r>0$ such that
$r>0$ such that ![]() $f\in \tilde {\mathcal {R}}^r$. We define conditions (a)
$f\in \tilde {\mathcal {R}}^r$. We define conditions (a)![]() $'$–(d)
$'$–(d)![]() $'$ as in Definition 2.4 with the
$'$ as in Definition 2.4 with the ![]() $a_i$'s replaced by the
$a_i$'s replaced by the ![]() $b_i$'s. We claim that conditions (a)
$b_i$'s. We claim that conditions (a)![]() $'$–(d)
$'$–(d)![]() $'$ hold. If the claim holds, then
$'$ hold. If the claim holds, then ![]() $g:=\sum _{i\in \mathbb {Q}}b_iu^i$ belongs to
$g:=\sum _{i\in \mathbb {Q}}b_iu^i$ belongs to ![]() $\tilde {\mathcal {R}}^{\mathrm {bd}}$, and
$\tilde {\mathcal {R}}^{\mathrm {bd}}$, and ![]() $f=(1-\varphi _K^{-1}(b)\varphi ^{-1})g$ by definition, which implies the assertion. Fix
$f=(1-\varphi _K^{-1}(b)\varphi ^{-1})g$ by definition, which implies the assertion. Fix ![]() $c>0$. Put
$c>0$. Put ![]() $I:=\{i\in \mathbb {Q};|a_i|\geqslant c\}$, which is well-ordered by
$I:=\{i\in \mathbb {Q};|a_i|\geqslant c\}$, which is well-ordered by ![]() $f\in \tilde {\mathcal {R}}^r$, and put
$f\in \tilde {\mathcal {R}}^r$, and put ![]() $I':=\{i\in \mathbb {Q};|b_i|\geqslant c\}$. Choose
$I':=\{i\in \mathbb {Q};|b_i|\geqslant c\}$. Choose ![]() $m\in \mathbb {N}$ sufficiently large such that
$m\in \mathbb {N}$ sufficiently large such that ![]() $|b|^{m+1}\cdot |f|_0<c/2$. If
$|b|^{m+1}\cdot |f|_0<c/2$. If ![]() $i\in I'$, then
$i\in I'$, then ![]() $\max \{|a_i|,|a_{iq}|,\dots ,|a_{iq^m}|\}\geqslant c$, i.e.
$\max \{|a_i|,|a_{iq}|,\dots ,|a_{iq^m}|\}\geqslant c$, i.e. ![]() $i\in I\cup \cdots \cup q^{-m}I$, by
$i\in I\cup \cdots \cup q^{-m}I$, by
where the second inequality follows from (2.8.1). Hence, ![]() $I'\subset I\cup \cdots \cup q^{-m}I$, which implies that
$I'\subset I\cup \cdots \cup q^{-m}I$, which implies that ![]() $I'$ is well-ordered. Thus, condition (a)
$I'$ is well-ordered. Thus, condition (a)![]() $'$ holds. For
$'$ holds. For ![]() $i\leqslant 0$, we have
$i\leqslant 0$, we have
where the first inequality follows from (2.8.1). Hence, condition (b)![]() $'$ holds by condition (b) in Definition 2.4. Moreover, by (2.8.1) and the displayed inequalities just above,
$'$ holds by condition (b) in Definition 2.4. Moreover, by (2.8.1) and the displayed inequalities just above,
 \begin{align*} \sup_{i\in \mathbb{Q}}|b_i|e^{{-}ri}&=\max \Big\{\sup_{i\in (-\infty,0]}|b_i|e^{{-}ri},\sup_{i\in [0,+\infty)}|b_i|e^{{-}ri} \Big\}\\ &\leqslant \max \Big\{\sup_{j\in (-\infty,0]}|a_{j}|e^{{-}rj},\sup_{i\in [0,+\infty)}|b_i| \Big\}\leqslant \max\{|f|_r,|f|_0\}<\infty. \end{align*}
\begin{align*} \sup_{i\in \mathbb{Q}}|b_i|e^{{-}ri}&=\max \Big\{\sup_{i\in (-\infty,0]}|b_i|e^{{-}ri},\sup_{i\in [0,+\infty)}|b_i|e^{{-}ri} \Big\}\\ &\leqslant \max \Big\{\sup_{j\in (-\infty,0]}|a_{j}|e^{{-}rj},\sup_{i\in [0,+\infty)}|b_i| \Big\}\leqslant \max\{|f|_r,|f|_0\}<\infty. \end{align*}
Hence, condition (c)![]() $'$ holds. Finally, condition (d)
$'$ holds. Finally, condition (d)![]() $'$ holds by the boundedness of
$'$ holds by the boundedness of ![]() $\{|b_i|\}_{i\in \mathbb {Q}}$.
$\{|b_i|\}_{i\in \mathbb {Q}}$.
Finally, we recall the reverse filtrations of ![]() $\varphi$-modules over
$\varphi$-modules over ![]() $\tilde {\mathcal {R}}^{\mathrm {bd}}$ constructed in [Reference LiuLiu13].
$\tilde {\mathcal {R}}^{\mathrm {bd}}$ constructed in [Reference LiuLiu13].
Definition 2.9 (Cf. Definition 1.8)
Let ![]() $\tilde {M}$ be a
$\tilde {M}$ be a ![]() $\varphi$-module over
$\varphi$-module over ![]() $\tilde {\mathcal {R}}^{\mathrm {bd}}$, and
$\tilde {\mathcal {R}}^{\mathrm {bd}}$, and ![]() $d$ a positive integer. A
$d$ a positive integer. A ![]() $d$-eigenvector of
$d$-eigenvector of ![]() $\tilde {M}$ is a nonzero element
$\tilde {M}$ is a nonzero element ![]() $v\in \tilde {M}$ such that
$v\in \tilde {M}$ such that ![]() $\varphi _M^d(v)=cv$ for some
$\varphi _M^d(v)=cv$ for some ![]() $c\in (\tilde {\mathcal {R}}^{\mathrm {bd}})^{\times }$; we call the quotient
$c\in (\tilde {\mathcal {R}}^{\mathrm {bd}})^{\times }$; we call the quotient ![]() $\log {|c|_0}/\log {|q|^d}$ the slope of
$\log {|c|_0}/\log {|q|^d}$ the slope of ![]() $v$. We also define the notion of
$v$. We also define the notion of ![]() $d$-eigenvectors of
$d$-eigenvectors of ![]() $\tilde {\mathcal {R}}_{\rm log}$ with
$\tilde {\mathcal {R}}_{\rm log}$ with ![]() $\tilde {M}$ replaced by
$\tilde {M}$ replaced by ![]() $\tilde {\mathcal {R}}_{\rm log}$.
$\tilde {\mathcal {R}}_{\rm log}$.
Proposition 2.10 [Reference LiuLiu13, Propositions 1.5.4, 1.6.9, and Theorem 1.5.8]
Let ![]() $\tilde {M}$ be a
$\tilde {M}$ be a ![]() $\varphi$-module over
$\varphi$-module over ![]() $\tilde {\mathcal {R}}^{\mathrm {bd}}$. Then, the reverse filtration of
$\tilde {\mathcal {R}}^{\mathrm {bd}}$. Then, the reverse filtration of ![]() $\tilde {M}_{\tilde {\mathcal {E}}}$ (Definition 1.11) descends to a filtration
$\tilde {M}_{\tilde {\mathcal {E}}}$ (Definition 1.11) descends to a filtration ![]() $S^{\bullet }(\tilde {M})$ of
$S^{\bullet }(\tilde {M})$ of ![]() $\tilde {M}$, which we call the reverse filtration of
$\tilde {M}$, which we call the reverse filtration of ![]() $\tilde {M}$. Moreover, there exists
$\tilde {M}$. Moreover, there exists ![]() $d\in \mathbb {N}_{>0}$ such that each graded piece
$d\in \mathbb {N}_{>0}$ such that each graded piece ![]() $S^{\lambda }(\tilde {M})/\bigcup _{\mu <\lambda }S^{\mu }(\tilde {M})$ admits a basis consisting of
$S^{\lambda }(\tilde {M})/\bigcup _{\mu <\lambda }S^{\mu }(\tilde {M})$ admits a basis consisting of ![]() $d$-eigenvectors of slope
$d$-eigenvectors of slope ![]() $\lambda$. In particular,
$\lambda$. In particular, ![]() $S^{\lambda _{\rm max}(\tilde {M}_{\tilde {\mathcal {E}}})}(\tilde {M})$ admits a basis consisting of
$S^{\lambda _{\rm max}(\tilde {M}_{\tilde {\mathcal {E}}})}(\tilde {M})$ admits a basis consisting of ![]() $d$-eigenvectors of slope
$d$-eigenvectors of slope ![]() $\lambda _{\rm max}(\tilde {M}_{\tilde {\mathcal {E}}})$.
$\lambda _{\rm max}(\tilde {M}_{\tilde {\mathcal {E}}})$.
2.3 Embeddings to extended rings
Proposition 2.11 We choose an extension ![]() $L$ of
$L$ of ![]() $K$ such that the residue field of
$K$ such that the residue field of ![]() $L$ is strongly difference-closed (Remark 1.2). We repeat the construction as in § 2.2 with
$L$ is strongly difference-closed (Remark 1.2). We repeat the construction as in § 2.2 with ![]() $K$ replaced by
$K$ replaced by ![]() $L$. Then, there exist a
$L$. Then, there exist a ![]() $\varphi$-equivariant embedding
$\varphi$-equivariant embedding ![]() $\tilde {\psi }_L:\mathcal {R}\hookrightarrow \tilde {\mathcal {R}}_L$ and
$\tilde {\psi }_L:\mathcal {R}\hookrightarrow \tilde {\mathcal {R}}_L$ and ![]() $r_0>0$ such that for any
$r_0>0$ such that for any ![]() $r\in (0,r_0)$,
$r\in (0,r_0)$, ![]() $\mathcal {R}^r$ maps to
$\mathcal {R}^r$ maps to ![]() $\tilde {\mathcal {R}}_L^r$ preserving
$\tilde {\mathcal {R}}_L^r$ preserving ![]() $|\cdot |_r$. Moreover,
$|\cdot |_r$. Moreover, ![]() $\mathcal {R}^{\mathrm {int}}$ (respectively,
$\mathcal {R}^{\mathrm {int}}$ (respectively, ![]() $\mathcal {R}^{\mathrm {bd}}$) maps
$\mathcal {R}^{\mathrm {bd}}$) maps ![]() $\tilde {\mathcal {R}}_L^{\mathrm {int}}$ (respectively,
$\tilde {\mathcal {R}}_L^{\mathrm {int}}$ (respectively, ![]() $\tilde {\mathcal {R}}_L^{\mathrm {bd}}$) preserving
$\tilde {\mathcal {R}}_L^{\mathrm {bd}}$) preserving ![]() $|\cdot |_0$.
$|\cdot |_0$.
Proof. By embedding ![]() $\mathcal {R}$ into
$\mathcal {R}$ into ![]() $\mathcal {R}_L$ via the inclusion, we may assume that
$\mathcal {R}_L$ via the inclusion, we may assume that ![]() $L=K$, in which case the assertion is proved in [Reference KedlayaKed08, Proposition 2.2.6] and [Reference LiuLiu13, Remark 1.4.10].
$L=K$, in which case the assertion is proved in [Reference KedlayaKed08, Proposition 2.2.6] and [Reference LiuLiu13, Remark 1.4.10].
Lemma 2.12 Let notation be as in Proposition 2.11.
(i) There exists a unique
 $c_0\in \tilde {\mathcal {R}}_L^{\mathrm {bd}}$ such that
$c_0\in \tilde {\mathcal {R}}_L^{\mathrm {bd}}$ such that  $\varphi (c_0)=qc_0+\tilde {\psi }_L(\log {(\varphi (X)/X^q)})$.
$\varphi (c_0)=qc_0+\tilde {\psi }_L(\log {(\varphi (X)/X^q)})$.(ii) Let
 $c_0$ be as in part (i), and
$c_0$ be as in part (i), and  $c_1\in (K^{\times })^{\varphi _K=1}$ (for example,
$c_1\in (K^{\times })^{\varphi _K=1}$ (for example,  $c_1=1$). We extend
$c_1=1$). We extend  $\tilde {\psi }_L:\mathcal {R}\hookrightarrow \tilde {\mathcal {R}}_L$ to
$\tilde {\psi }_L:\mathcal {R}\hookrightarrow \tilde {\mathcal {R}}_L$ to  $\mathcal {R}_{\rm log}\to \tilde {\mathcal {R}}_{L,{\rm log}}$ by setting
$\mathcal {R}_{\rm log}\to \tilde {\mathcal {R}}_{L,{\rm log}}$ by setting  $\tilde {\psi }_L(\ell _X):=c_0+c_1\log {u}$. Then,
$\tilde {\psi }_L(\ell _X):=c_0+c_1\log {u}$. Then,  $\tilde {\psi }_L$ is injective and
$\tilde {\psi }_L$ is injective and  $\varphi$-equivariant.
$\varphi$-equivariant.
Proof. As ![]() $\tilde {\psi }_L(\log (\varphi (X)/X^q))\in \tilde {\mathcal {R}}_L^{\mathrm {bd}}$ by Definitions 2.1(ii), 2.2, and Proposition 2.11, part (i) follows from Lemma 2.8 with
$\tilde {\psi }_L(\log (\varphi (X)/X^q))\in \tilde {\mathcal {R}}_L^{\mathrm {bd}}$ by Definitions 2.1(ii), 2.2, and Proposition 2.11, part (i) follows from Lemma 2.8 with ![]() $b=q$. Part (ii) follows from a direct computation.
$b=q$. Part (ii) follows from a direct computation.
Notation 2 In the rest of § 2, let ![]() $L,\tilde {\psi }_L,r_0,c_0$, and
$L,\tilde {\psi }_L,r_0,c_0$, and ![]() $c_1$ be as previously. By abuse of notation, let
$c_1$ be as previously. By abuse of notation, let ![]() $\tilde {\psi }_L$ denote the embedding
$\tilde {\psi }_L$ denote the embedding ![]() $\mathcal {E}\hookrightarrow \tilde {\mathcal {E}}_L$ obtained by completing
$\mathcal {E}\hookrightarrow \tilde {\mathcal {E}}_L$ obtained by completing ![]() $\tilde {\psi }_L:\mathcal {R}^{\mathrm {bd}}\hookrightarrow \tilde {\mathcal {R}}^{\mathrm {bd}}_L$ for Gauss norms.
$\tilde {\psi }_L:\mathcal {R}^{\mathrm {bd}}\hookrightarrow \tilde {\mathcal {R}}^{\mathrm {bd}}_L$ for Gauss norms.
Lemma 2.13
(i) [Reference KedlayaKed08, Propositions 3.2.4 and 3.5.2] The multiplication map
 $\tilde {\mathcal {R}}_L^{\mathrm {bd}}\otimes _{\mathcal {R}^{\mathrm {bd}}}\mathcal {R}\to \tilde {\mathcal {R}}_L;x\otimes y\mapsto x\tilde {\psi }_L(y)$ is injective and
$\tilde {\mathcal {R}}_L^{\mathrm {bd}}\otimes _{\mathcal {R}^{\mathrm {bd}}}\mathcal {R}\to \tilde {\mathcal {R}}_L;x\otimes y\mapsto x\tilde {\psi }_L(y)$ is injective and  $\varphi$-equivariant.
$\varphi$-equivariant.(ii) The multiplication map
 $\tilde {\mathcal {R}}_L^{\mathrm {bd}}\otimes _{\mathcal {R}^{\mathrm {bd}}}\mathcal {R}_{\rm log}\to \tilde {\mathcal {R}}_{L,{\rm log}};x\otimes y\mapsto x\tilde {\psi }_L(y)$ is injective and
$\tilde {\mathcal {R}}_L^{\mathrm {bd}}\otimes _{\mathcal {R}^{\mathrm {bd}}}\mathcal {R}_{\rm log}\to \tilde {\mathcal {R}}_{L,{\rm log}};x\otimes y\mapsto x\tilde {\psi }_L(y)$ is injective and  $\varphi$-equivariant.
$\varphi$-equivariant.(iii) (Cf. [Reference de JongdeJ98, Proposition 8.1]) The multiplication map
 $\tilde {\mathcal {R}}_L^{\mathrm {bd}}\otimes _{\mathcal {R}^{\mathrm {bd}}}\mathcal {E}\to \tilde {\mathcal {E}}_L;x\otimes y\mapsto x\tilde {\psi }_L(y)$ is injective and
$\tilde {\mathcal {R}}_L^{\mathrm {bd}}\otimes _{\mathcal {R}^{\mathrm {bd}}}\mathcal {E}\to \tilde {\mathcal {E}}_L;x\otimes y\mapsto x\tilde {\psi }_L(y)$ is injective and  $\varphi$-equivariant.
$\varphi$-equivariant.
Proof. (ii) We have only to prove the injectivity. Assume that ![]() $z\in \tilde {\mathcal {R}}_L^{\mathrm {bd}}\otimes _{\mathcal {R}^{\mathrm {bd}}}\mathcal {R}_{\rm log}$ belongs to the kernel of the multiplication map. Write
$z\in \tilde {\mathcal {R}}_L^{\mathrm {bd}}\otimes _{\mathcal {R}^{\mathrm {bd}}}\mathcal {R}_{\rm log}$ belongs to the kernel of the multiplication map. Write ![]() $z=\sum _{i=0}^nz_i(1\otimes \ell _X)^i$ with
$z=\sum _{i=0}^nz_i(1\otimes \ell _X)^i$ with ![]() $z_i\in \tilde {\mathcal {R}}^{\mathrm {bd}}_L\otimes _{\mathcal {R}^{\mathrm {bd}}}\mathcal {R}$. Then,
$z_i\in \tilde {\mathcal {R}}^{\mathrm {bd}}_L\otimes _{\mathcal {R}^{\mathrm {bd}}}\mathcal {R}$. Then, ![]() $z_n$ belongs to the kernel of the multiplication map in part (i) by assumption, hence,
$z_n$ belongs to the kernel of the multiplication map in part (i) by assumption, hence, ![]() $z_n=0$. By repeating this argument, we obtain
$z_n=0$. By repeating this argument, we obtain ![]() $z=0$.
$z=0$.
(iii) We claim that there exists a ![]() $\mathbb {Q}_p$-linear map
$\mathbb {Q}_p$-linear map ![]() $f_{\eta }:\tilde {\mathcal {E}}_L\to \mathcal {E}$ such that:
$f_{\eta }:\tilde {\mathcal {E}}_L\to \mathcal {E}$ such that:
(a)
 $^{\prime}$ we have
$^{\prime}$ we have  $f_{\eta }(\tilde {\psi }_L(y)w)=yf_{\eta }(w)$ for
$f_{\eta }(\tilde {\psi }_L(y)w)=yf_{\eta }(w)$ for  $y\in \mathcal {E}$,
$y\in \mathcal {E}$,  $w\in \tilde {\mathcal {E}}_L$.
$w\in \tilde {\mathcal {E}}_L$.
Let ![]() $f:\tilde {\mathcal {R}}_L\to \mathcal {R}$ be a natural projection as in [Reference KedlayaKed08, Definition 3.5.1]: recall that
$f:\tilde {\mathcal {R}}_L\to \mathcal {R}$ be a natural projection as in [Reference KedlayaKed08, Definition 3.5.1]: recall that ![]() $f$ restricts to
$f$ restricts to ![]() $\tilde {\mathcal {R}}^r_L\to \mathcal {R}^r$ for any
$\tilde {\mathcal {R}}^r_L\to \mathcal {R}^r$ for any ![]() $r\in (0,r_0)$, and:
$r\in (0,r_0)$, and:
(a) we have
 $f(\tilde {\psi }_L(y)w)=yf(w)$ for
$f(\tilde {\psi }_L(y)w)=yf(w)$ for  $y\in \mathcal {R}^{\mathrm {bd}}$,
$y\in \mathcal {R}^{\mathrm {bd}}$,  $w\in \tilde {\mathcal {R}}_L$;
$w\in \tilde {\mathcal {R}}_L$;(b) we have
 $|w|_r=\sup _{\alpha \in [0,1),a\in L^{\times }}\{|a|^{-1}e^{-\alpha }|f(au^{-\alpha }w)|_r\}$ for
$|w|_r=\sup _{\alpha \in [0,1),a\in L^{\times }}\{|a|^{-1}e^{-\alpha }|f(au^{-\alpha }w)|_r\}$ for  $w\in \tilde {\mathcal {R}}^r_L$,
$w\in \tilde {\mathcal {R}}^r_L$,
Fix ![]() $w\in \tilde {\mathcal {R}}^{\mathrm {bd}}_L$. We choose
$w\in \tilde {\mathcal {R}}^{\mathrm {bd}}_L$. We choose ![]() $r_1\in (0,r_0)$ such that
$r_1\in (0,r_0)$ such that ![]() $w\in \tilde {\mathcal {R}}^{r_1}_L$. By part (b) with
$w\in \tilde {\mathcal {R}}^{r_1}_L$. By part (b) with ![]() $\alpha =0$ and
$\alpha =0$ and ![]() $a=1$ on the right-hand side, we obtain
$a=1$ on the right-hand side, we obtain ![]() $|f(w)|_r\leqslant |w|_r$ for all
$|f(w)|_r\leqslant |w|_r$ for all ![]() $r\in (0,r_1]$. By Lemma 2.7, we have
$r\in (0,r_1]$. By Lemma 2.7, we have ![]() $f(w)\in \mathcal {R}^{\mathrm {bd}}$, and
$f(w)\in \mathcal {R}^{\mathrm {bd}}$, and ![]() $|f(w)|_0=\lim _{r\to 0+}|f(w)|_r\leqslant \lim _{r\to 0+}|w|_r=|w|_0$. Hence,
$|f(w)|_0=\lim _{r\to 0+}|f(w)|_r\leqslant \lim _{r\to 0+}|w|_r=|w|_0$. Hence, ![]() $f$ restricts to a
$f$ restricts to a ![]() $\mathbb {Q}_p$-linear map
$\mathbb {Q}_p$-linear map ![]() $\tilde {\mathcal {R}}^{\mathrm {bd}}_L\to \mathcal {R}^{\mathrm {bd}}$ bounded for Gauss norms. By taking the completion, we obtain a
$\tilde {\mathcal {R}}^{\mathrm {bd}}_L\to \mathcal {R}^{\mathrm {bd}}$ bounded for Gauss norms. By taking the completion, we obtain a ![]() $\mathbb {Q}_p$-linear map
$\mathbb {Q}_p$-linear map ![]() $f_{\eta }:\tilde {\mathcal {E}}_L\to \mathcal {E}$, which satisfies part (a)
$f_{\eta }:\tilde {\mathcal {E}}_L\to \mathcal {E}$, which satisfies part (a)![]() $'$ by definition. Thus, we obtain the claim.
$'$ by definition. Thus, we obtain the claim.
We suppose, by way of contradiction, that there exists a nonzero element ![]() $z$ belonging to the kernel of the multiplication map. Write
$z$ belonging to the kernel of the multiplication map. Write ![]() $z=\sum _{i=1}^nx_i\otimes y_i\in \tilde {\mathcal {R}}_L^{\mathrm {bd}}\otimes _{\mathcal {R}^{\mathrm {bd}}}\mathcal {E}$ with
$z=\sum _{i=1}^nx_i\otimes y_i\in \tilde {\mathcal {R}}_L^{\mathrm {bd}}\otimes _{\mathcal {R}^{\mathrm {bd}}}\mathcal {E}$ with ![]() $n$ minimal. Then,
$n$ minimal. Then, ![]() $y_1,\dots ,y_n$ are linearly independent over
$y_1,\dots ,y_n$ are linearly independent over ![]() $\mathcal {R}^{\mathrm {bd}}$ by [Reference KedlayaKed08, Corollary 3.4.3]. As
$\mathcal {R}^{\mathrm {bd}}$ by [Reference KedlayaKed08, Corollary 3.4.3]. As ![]() $x_1\neq 0$, there exist
$x_1\neq 0$, there exist ![]() $\alpha \in (0,1]$ and
$\alpha \in (0,1]$ and ![]() $a\in L^{\times }$ such that
$a\in L^{\times }$ such that ![]() $f(au^{-\alpha }x_1)\neq 0$ by part (b). By applying
$f(au^{-\alpha }x_1)\neq 0$ by part (b). By applying ![]() $f_{\eta }$ to
$f_{\eta }$ to ![]() $\sum _{i=1}^n au^{-\alpha }x_i\cdot \tilde {\psi }_L(y_i)=0$ and then using part (a)
$\sum _{i=1}^n au^{-\alpha }x_i\cdot \tilde {\psi }_L(y_i)=0$ and then using part (a)![]() $'$, we have
$'$, we have ![]() $\sum _{i=1}^n f(au^{-\alpha }x_i)\cdot y_i=0$, which is a nontrivial relation between the elements
$\sum _{i=1}^n f(au^{-\alpha }x_i)\cdot y_i=0$, which is a nontrivial relation between the elements ![]() $y_i$ over
$y_i$ over ![]() $\mathcal {R}^{\mathrm {bd}}$. This contradicts the choices of elements
$\mathcal {R}^{\mathrm {bd}}$. This contradicts the choices of elements ![]() $y_i$.
$y_i$.
The following lemma will only be used in the proof of Proposition 9.6. Hence, the reader may skip it if they are interested only in the proof of part (ii) of Theorem 0.1.
Lemma 2.14 (Cf. [Reference Chiarellotto and TsuzukiCT11, Lemma 5.7])
Let ![]() $M$ be a nonzero
$M$ be a nonzero ![]() $\varphi$-module over
$\varphi$-module over ![]() $\mathcal {R}^{\mathrm {bd}}$, and
$\mathcal {R}^{\mathrm {bd}}$, and ![]() $Q$ a
$Q$ a ![]() $\varphi$-module over
$\varphi$-module over ![]() $\mathcal {E}$ which is pure of slope
$\mathcal {E}$ which is pure of slope ![]() $\mu$. If there exists an
$\mu$. If there exists an ![]() $\mathcal {R}^{\mathrm {bd}}$-linear map
$\mathcal {R}^{\mathrm {bd}}$-linear map ![]() $f:M\to Q$ which is injective and
$f:M\to Q$ which is injective and ![]() $\varphi$-equivariant, then
$\varphi$-equivariant, then ![]() $\lambda _{\rm max}(M_{\mathcal {E}})=\mu$.
$\lambda _{\rm max}(M_{\mathcal {E}})=\mu$.
Proof. Put ![]() $\tilde {M}:=M\otimes _{\mathcal {R}^{\mathrm {bd}}}\tilde {\mathcal {R}}^{\mathrm {bd}}_L$ (respectively,
$\tilde {M}:=M\otimes _{\mathcal {R}^{\mathrm {bd}}}\tilde {\mathcal {R}}^{\mathrm {bd}}_L$ (respectively, ![]() $\tilde {Q}:=Q\otimes _{\mathcal {E}}\tilde {\mathcal {E}}_L$), which is regarded as a
$\tilde {Q}:=Q\otimes _{\mathcal {E}}\tilde {\mathcal {E}}_L$), which is regarded as a ![]() $\varphi$-module over
$\varphi$-module over ![]() $\tilde {\mathcal {R}}^{\mathrm {bd}}_L$ (respectively,
$\tilde {\mathcal {R}}^{\mathrm {bd}}_L$ (respectively, ![]() $\tilde {\mathcal {E}}_L$). We define the
$\tilde {\mathcal {E}}_L$). We define the ![]() $\tilde {\mathcal {R}}^{\mathrm {bd}}$-linear map
$\tilde {\mathcal {R}}^{\mathrm {bd}}$-linear map ![]() $\tilde {f}:\tilde {M}\to \tilde {Q}$ as the composition of the maps
$\tilde {f}:\tilde {M}\to \tilde {Q}$ as the composition of the maps
 \begin{gather*} M\otimes_{\mathcal{R}^{\mathrm{bd}}}\tilde{\mathcal{R}}^{\mathrm{bd}}_L\to Q\otimes_{\mathcal{E}}\mathcal{E}\otimes_{\mathcal{R}^{\mathrm{bd}}}\tilde{\mathcal{R}}_L^{\mathrm{bd}};m\otimes x\mapsto f(m)\otimes 1\otimes x,\\ Q\otimes_{\mathcal{E}}\mathcal{E}\otimes_{\mathcal{R}^{\mathrm{bd}}}\tilde{\mathcal{R}}_L^{\mathrm{bd}}\to Q\otimes_{\mathcal{E}}\tilde{\mathcal{E}}_L;w\otimes y\otimes x\mapsto w\otimes x\tilde{\psi}_L(y). \end{gather*}
\begin{gather*} M\otimes_{\mathcal{R}^{\mathrm{bd}}}\tilde{\mathcal{R}}^{\mathrm{bd}}_L\to Q\otimes_{\mathcal{E}}\mathcal{E}\otimes_{\mathcal{R}^{\mathrm{bd}}}\tilde{\mathcal{R}}_L^{\mathrm{bd}};m\otimes x\mapsto f(m)\otimes 1\otimes x,\\ Q\otimes_{\mathcal{E}}\mathcal{E}\otimes_{\mathcal{R}^{\mathrm{bd}}}\tilde{\mathcal{R}}_L^{\mathrm{bd}}\to Q\otimes_{\mathcal{E}}\tilde{\mathcal{E}}_L;w\otimes y\otimes x\mapsto w\otimes x\tilde{\psi}_L(y). \end{gather*}
Then, ![]() $\tilde {f}$ is injective and
$\tilde {f}$ is injective and ![]() $\varphi$-equivariant by assumption and Lemma 2.13(iii). By Proposition 2.10, there exists a
$\varphi$-equivariant by assumption and Lemma 2.13(iii). By Proposition 2.10, there exists a ![]() $d$-eigenvector
$d$-eigenvector ![]() $\tilde {v}\in \tilde {M}$ of slope
$\tilde {v}\in \tilde {M}$ of slope ![]() $\lambda _{\rm max}(M_{\mathcal {E}})(=\lambda _{\rm max}(\tilde {M}_{\tilde {\mathcal {E}}}))$ for some
$\lambda _{\rm max}(M_{\mathcal {E}})(=\lambda _{\rm max}(\tilde {M}_{\tilde {\mathcal {E}}}))$ for some ![]() $d>0$. Hence,
$d>0$. Hence, ![]() $\tilde {f}(\tilde {v})\in \tilde {Q}$ is also a
$\tilde {f}(\tilde {v})\in \tilde {Q}$ is also a ![]() $d$-eigenvector of slope
$d$-eigenvector of slope ![]() $\lambda _{\rm max}(M_{\mathcal {E}})$ (in the sense of Definition 1.8). Therefore, the assertion follows from Lemma 1.9.
$\lambda _{\rm max}(M_{\mathcal {E}})$ (in the sense of Definition 1.8). Therefore, the assertion follows from Lemma 1.9.
3. Logarithmic growth filtration
In § 3.1 (respectively, § 3.2), we define the log-growth filtrations of the rings ![]() $\mathcal {R},\mathcal {R}_{\rm log}$ (respectively,
$\mathcal {R},\mathcal {R}_{\rm log}$ (respectively, ![]() $\tilde {\mathcal {R}}$,
$\tilde {\mathcal {R}}$, ![]() $\tilde {\mathcal {R}}_{\rm log}$). In § 3.3, we study, in the viewpoint of log-growth, the images of certain homomorphisms of the forms
$\tilde {\mathcal {R}}_{\rm log}$). In § 3.3, we study, in the viewpoint of log-growth, the images of certain homomorphisms of the forms ![]() $M\to \mathcal {R}_{\rm log}$ and
$M\to \mathcal {R}_{\rm log}$ and ![]() $\tilde {M}\to \tilde {\mathcal {R}}_{\rm log}$, where
$\tilde {M}\to \tilde {\mathcal {R}}_{\rm log}$, where ![]() $M$ and
$M$ and ![]() $\tilde {M}$ denote
$\tilde {M}$ denote ![]() $\varphi$-modules over
$\varphi$-modules over ![]() $\mathcal {R}^{\mathrm {bd}}$ and
$\mathcal {R}^{\mathrm {bd}}$ and ![]() $\tilde {\mathcal {R}}^{\mathrm {bd}}$ respectively.
$\tilde {\mathcal {R}}^{\mathrm {bd}}$ respectively.
3.1 Logarithmic growth filtrations of  $\tilde {\mathcal {R}}$ and
$\tilde {\mathcal {R}}$ and  $\tilde {\mathcal {R}}_{\rm log}$
$\tilde {\mathcal {R}}_{\rm log}$
In this subsection, we keep Assumption 2.3.
Definition 3.1 Let ![]() $f\in \tilde {\mathcal {R}}$ and
$f\in \tilde {\mathcal {R}}$ and ![]() $\lambda \in \mathbb {R}_{\geqslant 0}$. We choose
$\lambda \in \mathbb {R}_{\geqslant 0}$. We choose ![]() $r'\in \mathbb {R}_{>0}$ such that
$r'\in \mathbb {R}_{>0}$ such that ![]() $f\in \tilde {\mathcal {R}}^{r'}$. We say that
$f\in \tilde {\mathcal {R}}^{r'}$. We say that ![]() $f$ has log-growth
$f$ has log-growth ![]() $\lambda$ if there exists a constant
$\lambda$ if there exists a constant ![]() $C$ such that
$C$ such that
The definition does not depend on the choice of ![]() $r'$ by Lemma 2.6(ii). We define the
$r'$ by Lemma 2.6(ii). We define the ![]() $\lambda$th log-growth filtration
$\lambda$th log-growth filtration ![]() $\mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}$ as the
$\mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}$ as the ![]() $K$-subspace of
$K$-subspace of ![]() $\tilde {\mathcal {R}}$ consisting of series having log-growth
$\tilde {\mathcal {R}}$ consisting of series having log-growth ![]() $\lambda$. For
$\lambda$. For ![]() $\lambda \in \mathbb {R}_{<0}$, we set
$\lambda \in \mathbb {R}_{<0}$, we set ![]() $\mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}=0$. Note that
$\mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}=0$. Note that ![]() $\mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}$ for
$\mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}$ for ![]() $\lambda >0$ is not closed under multiplication, hence, not a subring of
$\lambda >0$ is not closed under multiplication, hence, not a subring of ![]() $\tilde {\mathcal {R}}$.
$\tilde {\mathcal {R}}$.
We define the log-growth filtration of ![]() $\mathcal {R}_{\rm log}$ by
$\mathcal {R}_{\rm log}$ by
 \[ \mathrm{Fil}_{\lambda}\tilde{\mathcal{R}}_{{\rm log}}=\bigoplus_{n=0}^{\infty}\mathrm{Fil}_{\lambda-n}\tilde{\mathcal{R}}\cdot (\log{u})^n\subset \tilde{\mathcal{R}}_{{\rm log}}\quad \text{for}\ \lambda\in\mathbb{R}. \]
\[ \mathrm{Fil}_{\lambda}\tilde{\mathcal{R}}_{{\rm log}}=\bigoplus_{n=0}^{\infty}\mathrm{Fil}_{\lambda-n}\tilde{\mathcal{R}}\cdot (\log{u})^n\subset \tilde{\mathcal{R}}_{{\rm log}}\quad \text{for}\ \lambda\in\mathbb{R}. \]
Note that we have ![]() $\mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}_{\rm log}=0$ for
$\mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}_{\rm log}=0$ for ![]() $\lambda <0$ by definition. We say that
$\lambda <0$ by definition. We say that ![]() $f\in \tilde {\mathcal {R}}_{\rm log}$ has log-growth
$f\in \tilde {\mathcal {R}}_{\rm log}$ has log-growth ![]() $\lambda$ if
$\lambda$ if ![]() $f\in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}_{\rm log}$. Furthermore, if
$f\in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}_{\rm log}$. Furthermore, if ![]() $f\notin \mathrm {Fil}_{\mu }\tilde {\mathcal {R}}_{\rm log}$ for all
$f\notin \mathrm {Fil}_{\mu }\tilde {\mathcal {R}}_{\rm log}$ for all ![]() $\mu <\lambda$, then we say that
$\mu <\lambda$, then we say that ![]() $f$ has exact log-growth
$f$ has exact log-growth ![]() $\lambda$.
$\lambda$.
This definition may be rephrased in terms of the behavior of the norms of the coefficients of ![]() $f\in \tilde {\mathcal {R}}$.
$f\in \tilde {\mathcal {R}}$.
Lemma 3.2 Let ![]() $f=\sum _{i\in \mathbb {Q}}a_iu^i\in \tilde {\mathcal {R}}$ with
$f=\sum _{i\in \mathbb {Q}}a_iu^i\in \tilde {\mathcal {R}}$ with ![]() $a_i\in K$, and
$a_i\in K$, and ![]() $\lambda \in \mathbb {R}_{\geqslant 0}$. Then, the following are equivalent.
$\lambda \in \mathbb {R}_{\geqslant 0}$. Then, the following are equivalent.
(i) We have
 $f\in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}$.
$f\in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}$.(ii) We have
 $|a_i|=O(i^{\lambda })$ as
$|a_i|=O(i^{\lambda })$ as  $i\to +\infty$.
$i\to +\infty$.
Proof. In the following, fix ![]() $r'>0$ such that
$r'>0$ such that ![]() $f\in \tilde {\mathcal {R}}^{r'}$. Assume that condition (i) holds, i.e. there exists
$f\in \tilde {\mathcal {R}}^{r'}$. Assume that condition (i) holds, i.e. there exists ![]() $C\in \mathbb {R}$ such that
$C\in \mathbb {R}$ such that ![]() $r^{\lambda }|f|_r\leqslant C$ for
$r^{\lambda }|f|_r\leqslant C$ for ![]() $r\in (0,r']$. For arbitrary
$r\in (0,r']$. For arbitrary ![]() $i\in \mathbb {Q}$ and
$i\in \mathbb {Q}$ and ![]() $r\in (0,r']$, we have
$r\in (0,r']$, we have
Hence, ![]() $|a_i|\leqslant Ce\cdot i^{\lambda }$ for all
$|a_i|\leqslant Ce\cdot i^{\lambda }$ for all ![]() $i\geqslant 1/r'$ by (3.2.1) with
$i\geqslant 1/r'$ by (3.2.1) with ![]() $r=1/i$. Thus, condition (ii) holds.
$r=1/i$. Thus, condition (ii) holds.
Assume that condition (ii) holds, i.e. there exist ![]() $C\in \mathbb {R}$ and
$C\in \mathbb {R}$ and ![]() $i_0>0$ such that
$i_0>0$ such that ![]() $|a_i|\leqslant Ci^{\lambda }$ for all
$|a_i|\leqslant Ci^{\lambda }$ for all ![]() $i\in [i_0,+\infty )$. If we put
$i\in [i_0,+\infty )$. If we put ![]() $g_1=\sum _{i\in (-\infty ,i_0]}a_iu^i$ and
$g_1=\sum _{i\in (-\infty ,i_0]}a_iu^i$ and ![]() $g_2=\sum _{i\in [i_0,+\infty )}a_iu^i$, then
$g_2=\sum _{i\in [i_0,+\infty )}a_iu^i$, then ![]() $g_1$,
$g_1$, ![]() $g_2\in \tilde {\mathcal {R}}^{r'}$ and
$g_2\in \tilde {\mathcal {R}}^{r'}$ and ![]() $|f|_r=\max \{|g_1|_r,|g_2|_r\}$ for all
$|f|_r=\max \{|g_1|_r,|g_2|_r\}$ for all ![]() $r\in (0,r']$. Hence, to verify condition (i), we have only to prove
$r\in (0,r']$. Hence, to verify condition (i), we have only to prove ![]() $g_1,g_2\in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}$. Since
$g_1,g_2\in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}$. Since ![]() $|g_1|_r\leqslant |g_1|_{r'}e^{(r'-r)i_0}\leqslant |g_1|_{r'}e^{r'i_0}$ for
$|g_1|_r\leqslant |g_1|_{r'}e^{(r'-r)i_0}\leqslant |g_1|_{r'}e^{r'i_0}$ for ![]() $r\in (0,r']$ by Lemma 2.5, we have
$r\in (0,r']$ by Lemma 2.5, we have ![]() $g_1\in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}$. For
$g_1\in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}$. For ![]() $r\in (0,r']$, we have
$r\in (0,r']$, we have
which implies ![]() $g_2\in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}$.
$g_2\in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}$.
Lemma 3.3 (Cf. [Reference OhkuboOhk17, Lemma 4.7])
Let ![]() $R\in \{\tilde {\mathcal {R}},\tilde {\mathcal {R}}_{\rm log}\}$.
$R\in \{\tilde {\mathcal {R}},\tilde {\mathcal {R}}_{\rm log}\}$.
(i) The filtration
 $\mathrm {Fil}_{\bullet }R$ is an increasing filtration of
$\mathrm {Fil}_{\bullet }R$ is an increasing filtration of  $K$-subspaces of
$K$-subspaces of  $R$ satisfying
$R$ satisfying
 \[ \mathrm{Fil}_{\lambda}R\cdot \mathrm{Fil}_{\mu}R\subset \mathrm{Fil}_{\lambda+\mu}R\text{ for }\lambda,\mu\in\mathbb{R}. \]
\[ \mathrm{Fil}_{\lambda}R\cdot \mathrm{Fil}_{\mu}R\subset \mathrm{Fil}_{\lambda+\mu}R\text{ for }\lambda,\mu\in\mathbb{R}. \](ii) We have
 $\varphi (\mathrm {Fil}_{\lambda }R)\subset \mathrm {Fil}_{\lambda }R$ for
$\varphi (\mathrm {Fil}_{\lambda }R)\subset \mathrm {Fil}_{\lambda }R$ for  $\lambda \in \mathbb {R}$.
$\lambda \in \mathbb {R}$.(iii) We have
 $\mathrm {Fil}_{0}R=\tilde {\mathcal {R}}^{\mathrm {bd}}$.
$\mathrm {Fil}_{0}R=\tilde {\mathcal {R}}^{\mathrm {bd}}$.
Proof. By definition, we may reduce to the case ![]() $R=\tilde {\mathcal {R}}$. Then, part (i) follows from the multiplicativity of
$R=\tilde {\mathcal {R}}$. Then, part (i) follows from the multiplicativity of ![]() $|\cdot |_r$. To prove part (ii), we may assume
$|\cdot |_r$. To prove part (ii), we may assume ![]() $\lambda \geqslant 0$. Let
$\lambda \geqslant 0$. Let ![]() $f\in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}$. We choose
$f\in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}$. We choose ![]() $r'>0$ such that
$r'>0$ such that ![]() $f\in \tilde {\mathcal {R}}^{qr'}$. Then,
$f\in \tilde {\mathcal {R}}^{qr'}$. Then, ![]() $r^{\lambda }|\varphi (f)|_r=q^{-\lambda }(qr)^{\lambda }|f|_{qr}$ for
$r^{\lambda }|\varphi (f)|_r=q^{-\lambda }(qr)^{\lambda }|f|_{qr}$ for ![]() $r\in (0,r']$, which implies
$r\in (0,r']$, which implies ![]() $\varphi (f)\in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}$. In part (iii), we have
$\varphi (f)\in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}$. In part (iii), we have ![]() $\tilde {\mathcal {R}}^{\mathrm {bd}}\subset \mathrm {Fil}_0\tilde {\mathcal {R}}$ by Lemma 3.2, and the converse follows from Lemma 2.7.
$\tilde {\mathcal {R}}^{\mathrm {bd}}\subset \mathrm {Fil}_0\tilde {\mathcal {R}}$ by Lemma 3.2, and the converse follows from Lemma 2.7.
3.2 Logarithmic growth filtrations of  $\mathcal {R}$ and
$\mathcal {R}$ and  $\mathcal {R}_{\rm log}$
$\mathcal {R}_{\rm log}$
Definition 3.4 Let ![]() $\star \in \{\,,\log \}$. We define the log-growth filtration
$\star \in \{\,,\log \}$. We define the log-growth filtration ![]() $\mathrm {Fil}_{\bullet }\mathcal {R}_{\star }$ of
$\mathrm {Fil}_{\bullet }\mathcal {R}_{\star }$ of ![]() $\mathcal {R}_{\star }$ by repeating the construction as in Definition 3.1 after replacing
$\mathcal {R}_{\star }$ by repeating the construction as in Definition 3.1 after replacing ![]() $\tilde {\mathcal {R}}$ and
$\tilde {\mathcal {R}}$ and ![]() $\log {u}$ by
$\log {u}$ by ![]() $\mathcal {R}$ and
$\mathcal {R}$ and ![]() $\ell _X$, respectively. Note that
$\ell _X$, respectively. Note that ![]() $\mathrm {Fil}_{\bullet }\mathcal {R}_{\star }$ is independent of the choice of
$\mathrm {Fil}_{\bullet }\mathcal {R}_{\star }$ is independent of the choice of ![]() $\varphi$ by definition.
$\varphi$ by definition.
By the following lemma, the embedding ![]() $\tilde {\psi }_L:\mathcal {R}_{\star }\to \tilde {\mathcal {R}}_{L,\star }$ for
$\tilde {\psi }_L:\mathcal {R}_{\star }\to \tilde {\mathcal {R}}_{L,\star }$ for ![]() $\star \in \{\,,\log \}$ as in § 2.3 respects the log-growth filtration. Hence, some properties of
$\star \in \{\,,\log \}$ as in § 2.3 respects the log-growth filtration. Hence, some properties of ![]() $\mathrm {Fil}_{\bullet }\tilde {\mathcal {R}}_{L,\star }$ will automatically transmit to
$\mathrm {Fil}_{\bullet }\tilde {\mathcal {R}}_{L,\star }$ will automatically transmit to ![]() $\mathrm {Fil}_{\bullet }\mathcal {R}_{\star }$.
$\mathrm {Fil}_{\bullet }\mathcal {R}_{\star }$.
Lemma 3.5 Let notation be as in § 2.3. Let ![]() $\star \in \{\,,\log \}$, let
$\star \in \{\,,\log \}$, let ![]() $f\in \mathcal {R}_{\star }$, and
$f\in \mathcal {R}_{\star }$, and ![]() $\lambda \in \mathbb {R}$. Then,
$\lambda \in \mathbb {R}$. Then, ![]() $f\in \mathrm {Fil}_{\lambda }\mathcal {R}_{\star }$ if and only if
$f\in \mathrm {Fil}_{\lambda }\mathcal {R}_{\star }$ if and only if ![]() $\tilde {\psi }_L(f)\in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}_{L,\star }$.
$\tilde {\psi }_L(f)\in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}_{L,\star }$.
Proof. In the case ![]() $\star =(empty)$, the assertion immediately follows from the fact that
$\star =(empty)$, the assertion immediately follows from the fact that ![]() $\tilde {\psi }_L:\mathcal {R}^r\to \tilde {\mathcal {R}}^r_L$ preserves
$\tilde {\psi }_L:\mathcal {R}^r\to \tilde {\mathcal {R}}^r_L$ preserves ![]() $|\cdot |_r$ (Proposition 2.11). In the case
$|\cdot |_r$ (Proposition 2.11). In the case ![]() $\star =\log$, we write
$\star =\log$, we write ![]() $f=\sum _{i=0}^nf_i\ell _X^i$ with
$f=\sum _{i=0}^nf_i\ell _X^i$ with ![]() $f_i\in \mathcal {R}$, and prove by induction on
$f_i\in \mathcal {R}$, and prove by induction on ![]() $n$. In the base case
$n$. In the base case ![]() $n=0$, the assertion follows from the previous result. In the induction step, we first assume
$n=0$, the assertion follows from the previous result. In the induction step, we first assume ![]() $f\in \mathrm {Fil}_{\lambda }\mathcal {R}_{\rm log}$. Then, for all
$f\in \mathrm {Fil}_{\lambda }\mathcal {R}_{\rm log}$. Then, for all ![]() $i$, we have
$i$, we have ![]() $f_i\in \mathrm {Fil}_{\lambda -i}\mathcal {R}$ by assumption, which implies
$f_i\in \mathrm {Fil}_{\lambda -i}\mathcal {R}$ by assumption, which implies ![]() $\tilde {\psi }_L(f_i)\in \mathrm {Fil}_{\lambda -i}\tilde {\mathcal {R}}_{L}$ by the induction hypothesis. As
$\tilde {\psi }_L(f_i)\in \mathrm {Fil}_{\lambda -i}\tilde {\mathcal {R}}_{L}$ by the induction hypothesis. As ![]() $\tilde {\psi }_L(\ell _X)\in \mathrm {Fil}_1\tilde {\mathcal {R}}_{L,{\rm log}}$, we have
$\tilde {\psi }_L(\ell _X)\in \mathrm {Fil}_1\tilde {\mathcal {R}}_{L,{\rm log}}$, we have ![]() $\tilde {\psi }_L(f)=\sum _{i=0}^n\tilde {\psi }_L(f_i)\tilde {\psi }_L(\ell _X)^i\in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}_{L,{\rm log}}$ by Lemma 3.3(i). Conversely, we assume
$\tilde {\psi }_L(f)=\sum _{i=0}^n\tilde {\psi }_L(f_i)\tilde {\psi }_L(\ell _X)^i\in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}_{L,{\rm log}}$ by Lemma 3.3(i). Conversely, we assume ![]() $\tilde {\psi }_L(f)\in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}_{L,{\rm log}}$. As
$\tilde {\psi }_L(f)\in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}_{L,{\rm log}}$. As ![]() $\tilde {\psi }_L(f)=c_1^n\tilde {\psi }_L(f_n)(\log {u})^n+\dots \in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}_{L,{\rm log}}$ with
$\tilde {\psi }_L(f)=c_1^n\tilde {\psi }_L(f_n)(\log {u})^n+\dots \in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}_{L,{\rm log}}$ with ![]() $c_1\in K^{\times }$ as in Lemma 2.12(ii), we have
$c_1\in K^{\times }$ as in Lemma 2.12(ii), we have ![]() $c_1^n\tilde {\psi }_L(f_n)\in \mathrm {Fil}_{\lambda -n}\tilde {\mathcal {R}}_L$ by definition. Hence,
$c_1^n\tilde {\psi }_L(f_n)\in \mathrm {Fil}_{\lambda -n}\tilde {\mathcal {R}}_L$ by definition. Hence, ![]() $\tilde {\psi }_L(f_n)\in \mathrm {Fil}_{\lambda -n}\tilde {\mathcal {R}}_L$, which implies
$\tilde {\psi }_L(f_n)\in \mathrm {Fil}_{\lambda -n}\tilde {\mathcal {R}}_L$, which implies ![]() $f_n\in \mathrm {Fil}_{\lambda -n}\mathcal {R}$ by the previous result. By applying the induction hypothesis to
$f_n\in \mathrm {Fil}_{\lambda -n}\mathcal {R}$ by the previous result. By applying the induction hypothesis to ![]() $\tilde {\psi }_L(f-f_n\ell _X^n)=\tilde {\psi }_L(f)-\tilde {\psi }_L(f_n)\tilde {\psi }_L(\ell _X)^n\in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}_{\rm log}$, we have
$\tilde {\psi }_L(f-f_n\ell _X^n)=\tilde {\psi }_L(f)-\tilde {\psi }_L(f_n)\tilde {\psi }_L(\ell _X)^n\in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}_{\rm log}$, we have ![]() $f-f_n\ell _X^n\in \mathrm {Fil}_{\lambda }\mathcal {R}_{\rm log}$, which implies
$f-f_n\ell _X^n\in \mathrm {Fil}_{\lambda }\mathcal {R}_{\rm log}$, which implies ![]() $f=f-f_n\ell _X^n+f_n\ell _X^n\in \mathrm {Fil}_{\lambda }\mathcal {R}_{\rm log}$.
$f=f-f_n\ell _X^n+f_n\ell _X^n\in \mathrm {Fil}_{\lambda }\mathcal {R}_{\rm log}$.
Corollary 3.6 Let ![]() $f=\sum _{i\in \mathbb {Z}}a_it^i\in \mathcal {R}$ with
$f=\sum _{i\in \mathbb {Z}}a_it^i\in \mathcal {R}$ with ![]() $a_i\in K$, and
$a_i\in K$, and ![]() $\lambda \in \mathbb {R}_{\geqslant 0}$. Then,
$\lambda \in \mathbb {R}_{\geqslant 0}$. Then, ![]() $f\in \mathrm {Fil}_{\lambda }\mathcal {R}$ if and only if
$f\in \mathrm {Fil}_{\lambda }\mathcal {R}$ if and only if ![]() $|a_i|=O(i^{\lambda })$ as
$|a_i|=O(i^{\lambda })$ as ![]() $i\to +\infty$.
$i\to +\infty$.
Proof. As ![]() $\mathrm {Fil}_{\bullet }\mathcal {R}$ is independent of the choice of
$\mathrm {Fil}_{\bullet }\mathcal {R}$ is independent of the choice of ![]() $\varphi$, we may assume that
$\varphi$, we may assume that ![]() $\varphi (t)=S=t^q$, in which case
$\varphi (t)=S=t^q$, in which case ![]() $\tilde {\psi }_L:\mathcal {R}\to \tilde {\mathcal {R}}_L$ is regarded as the inclusion. Then, the assertion follows from Lemmas 3.2 and 3.5. An alternative proof is given by simply repeating the argument as in the proof of Lemma 3.2.
$\tilde {\psi }_L:\mathcal {R}\to \tilde {\mathcal {R}}_L$ is regarded as the inclusion. Then, the assertion follows from Lemmas 3.2 and 3.5. An alternative proof is given by simply repeating the argument as in the proof of Lemma 3.2.
Corollary 3.7 Let ![]() $R\in \{\mathcal {R},\mathcal {R}_{\rm log}\}$.
$R\in \{\mathcal {R},\mathcal {R}_{\rm log}\}$.
(i) The filtration
 $\mathrm {Fil}_{\bullet }R$ is an increasing filtration of
$\mathrm {Fil}_{\bullet }R$ is an increasing filtration of  $K$-subspaces of
$K$-subspaces of  $R$ satisfying
$R$ satisfying
 \[ \mathrm{Fil}_{\lambda}R\cdot \mathrm{Fil}_{\mu}R\subset \mathrm{Fil}_{\lambda+\mu}R \quad \text{for }\lambda,\mu\in\mathbb{R}. \]
\[ \mathrm{Fil}_{\lambda}R\cdot \mathrm{Fil}_{\mu}R\subset \mathrm{Fil}_{\lambda+\mu}R \quad \text{for }\lambda,\mu\in\mathbb{R}. \](ii) We have
 $\varphi (\mathrm {Fil}_{\lambda }R)\subset \mathrm {Fil}_{\lambda }R$ for
$\varphi (\mathrm {Fil}_{\lambda }R)\subset \mathrm {Fil}_{\lambda }R$ for  $\lambda \in \mathbb {R}$.
$\lambda \in \mathbb {R}$.(iii) We have
 $\mathrm {Fil}_{0}R=\mathcal {R}^{\mathrm {bd}}$.
$\mathrm {Fil}_{0}R=\mathcal {R}^{\mathrm {bd}}$.
3.3 Technical results
In this subsection, we keep Assumption 2.3.
Lemma 3.8 (Cf. [Reference Chiarellotto and TsuzukiCT11, Lemma 4.8])
Assume that ![]() $g,h\in \tilde {\mathcal {R}}_{\rm log}$ satisfy a relation of the form
$g,h\in \tilde {\mathcal {R}}_{\rm log}$ satisfy a relation of the form
If we have ![]() $h\in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}_{\rm log}$ for some
$h\in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}_{\rm log}$ for some ![]() $\lambda \geqslant \log {|c|_0}/\log {|q|^d}$, then
$\lambda \geqslant \log {|c|_0}/\log {|q|^d}$, then ![]() $g\in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}_{\rm log}$.
$g\in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}_{\rm log}$.
Proof. After replacing ![]() $\varphi$ by
$\varphi$ by ![]() $\varphi ^d$, we may assume
$\varphi ^d$, we may assume ![]() $d=1$. We reduce to the case where
$d=1$. We reduce to the case where ![]() $g,h\in \tilde {\mathcal {R}}$ and
$g,h\in \tilde {\mathcal {R}}$ and ![]() $c\in K^{\times }$. Write
$c\in K^{\times }$. Write ![]() $g=\sum _{i=0}^ng_i(\log {u})^i,h=\sum _{i=0}^nh_i(\log {u})^i$ with
$g=\sum _{i=0}^ng_i(\log {u})^i,h=\sum _{i=0}^nh_i(\log {u})^i$ with ![]() $g_i,h_i\in \tilde {\mathcal {R}}$. Then,
$g_i,h_i\in \tilde {\mathcal {R}}$. Then, ![]() $(\varphi -c/q^i)g_i=h_i/q^i$, and
$(\varphi -c/q^i)g_i=h_i/q^i$, and ![]() $h_i\in \mathrm {Fil}_{\lambda -i}\tilde {\mathcal {R}}$. Moreover,
$h_i\in \mathrm {Fil}_{\lambda -i}\tilde {\mathcal {R}}$. Moreover, ![]() $g\in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}_{\rm log}$ if and only if
$g\in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}_{\rm log}$ if and only if ![]() $g_i\in \mathrm {Fil}_{\lambda -i}\tilde {\mathcal {R}}$ for all
$g_i\in \mathrm {Fil}_{\lambda -i}\tilde {\mathcal {R}}$ for all ![]() $i$. Hence, after replacing
$i$. Hence, after replacing ![]() $(g,h,c,\lambda )$ by
$(g,h,c,\lambda )$ by ![]() $(g_i,h_i/q^i,c/q^i,\lambda -i)$, we may assume
$(g_i,h_i/q^i,c/q^i,\lambda -i)$, we may assume ![]() $g,h\in \tilde {\mathcal {R}}$. We can choose
$g,h\in \tilde {\mathcal {R}}$. We can choose ![]() $c'\in K^{\times }$ such that
$c'\in K^{\times }$ such that ![]() $|c'|=|c|_0$, since
$|c'|=|c|_0$, since ![]() $K$ is discretely valued. As
$K$ is discretely valued. As ![]() $\tilde {\mathcal {E}}(c'/c)$ is pure of slope
$\tilde {\mathcal {E}}(c'/c)$ is pure of slope ![]() $0$ as a
$0$ as a ![]() $\varphi$-module over
$\varphi$-module over ![]() $\tilde {\mathcal {E}}$, there exists
$\tilde {\mathcal {E}}$, there exists ![]() $b\in \tilde {\mathcal {E}}^{\times }$ such that
$b\in \tilde {\mathcal {E}}^{\times }$ such that ![]() $b=(c'/c)\varphi (b)$ by Dieudonné–Manin classification theorem 1.10 (recall that the residue field
$b=(c'/c)\varphi (b)$ by Dieudonné–Manin classification theorem 1.10 (recall that the residue field ![]() $k((t^{\mathbb {Q}}))$ of
$k((t^{\mathbb {Q}}))$ of ![]() $\tilde {\mathcal {E}}$ is strongly difference-closed). We have
$\tilde {\mathcal {E}}$ is strongly difference-closed). We have ![]() $b\in (\tilde {\mathcal {R}}^{\mathrm {bd}})^{\times }$ by [Reference KedlayaKed08, Proposition 2.5.8], and
$b\in (\tilde {\mathcal {R}}^{\mathrm {bd}})^{\times }$ by [Reference KedlayaKed08, Proposition 2.5.8], and ![]() $(\varphi -c')(g/b)=c'h/cb$. Hence, by Lemma 3.3(i) and (iii), we have
$(\varphi -c')(g/b)=c'h/cb$. Hence, by Lemma 3.3(i) and (iii), we have ![]() $g,h\in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}_{\rm log}$, respectively, if and only if
$g,h\in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}_{\rm log}$, respectively, if and only if ![]() $g/b,c'h/cb\in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}_{\rm log}$, respectively. Therefore, after replacing
$g/b,c'h/cb\in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}_{\rm log}$, respectively. Therefore, after replacing ![]() $(g,h,c)$ by
$(g,h,c)$ by ![]() $(g/b,c'h/cb,c')$, we may assume
$(g/b,c'h/cb,c')$, we may assume ![]() $c\in K^{\times }$ as desired.
$c\in K^{\times }$ as desired.
We choose ![]() $r_0\in (0,+\infty )$ such that
$r_0\in (0,+\infty )$ such that ![]() $g,h\in \tilde {\mathcal {R}}^{r_0}$. Then,
$g,h\in \tilde {\mathcal {R}}^{r_0}$. Then,
by Lemma 2.6(ii). Hence, we can choose ![]() $C\in \mathbb {R}$ sufficiently large such that
$C\in \mathbb {R}$ sufficiently large such that
 \begin{gather*} |g|_r\leqslant C/|c|\cdot r^{-\lambda}\ \forall r\in [r_0/q,r_0],\\ |h|_r\leqslant C\cdot r^{-\lambda}\ \forall r\in (0,r_0]. \end{gather*}
\begin{gather*} |g|_r\leqslant C/|c|\cdot r^{-\lambda}\ \forall r\in [r_0/q,r_0],\\ |h|_r\leqslant C\cdot r^{-\lambda}\ \forall r\in (0,r_0]. \end{gather*}Then, it suffices to prove
by induction on ![]() $n\in \mathbb {N}$. In the base case
$n\in \mathbb {N}$. In the base case ![]() $n=0$, we have nothing to prove. In the induction step, the assertion follows from
$n=0$, we have nothing to prove. In the induction step, the assertion follows from
Lemma 3.9 (Cf. [Reference OhkuboOhk17, Theorem 6.1])
If ![]() $g\in \tilde {\mathcal {R}}_{\rm log}$ is a
$g\in \tilde {\mathcal {R}}_{\rm log}$ is a ![]() $d$-eigenvector of slope
$d$-eigenvector of slope ![]() $\lambda$ (Definition 2.9), then we have
$\lambda$ (Definition 2.9), then we have ![]() $\lambda \geqslant 0$, and
$\lambda \geqslant 0$, and ![]() $g$ has exact log-growth
$g$ has exact log-growth ![]() $\lambda$.
$\lambda$.
Proof. By definition, there exists ![]() $c\in (\tilde {\mathcal {R}}^{\mathrm {bd}})^{\times }$ such that
$c\in (\tilde {\mathcal {R}}^{\mathrm {bd}})^{\times }$ such that ![]() $(\varphi ^d-c)g=0$ and
$(\varphi ^d-c)g=0$ and ![]() $\lambda =\log {|c|_0}/\log {|q|^d}$. By Lemma 3.8, we have
$\lambda =\log {|c|_0}/\log {|q|^d}$. By Lemma 3.8, we have ![]() $g\in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}_{\rm log}$. Hence,
$g\in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}_{\rm log}$. Hence, ![]() $\lambda \geqslant 0$ by
$\lambda \geqslant 0$ by ![]() $g\neq 0$. To prove the second assertion, we have only to prove that
$g\neq 0$. To prove the second assertion, we have only to prove that ![]() $g$ does not have log-growth
$g$ does not have log-growth ![]() $\mu$ for any
$\mu$ for any ![]() $\mu <\lambda$. As in the proof of Lemma 3.8, we may assume
$\mu <\lambda$. As in the proof of Lemma 3.8, we may assume ![]() $d=1$,
$d=1$, ![]() $g\in \tilde {\mathcal {R}}$, and
$g\in \tilde {\mathcal {R}}$, and ![]() $c\in K^{\times }$. We choose
$c\in K^{\times }$. We choose ![]() $r_0>0$ such that
$r_0>0$ such that ![]() $g\in \tilde {\mathcal {R}}^{r_0}$. As we have
$g\in \tilde {\mathcal {R}}^{r_0}$. As we have
by Lemma 2.6(ii), we can choose ![]() $C'>0$ sufficiently small such that
$C'>0$ sufficiently small such that ![]() $|g|_r\geqslant C'/|c|\cdot r^{-\lambda }$ for all
$|g|_r\geqslant C'/|c|\cdot r^{-\lambda }$ for all ![]() $r\in [r_0/q,r_0]$. Then, it suffices to prove
$r\in [r_0/q,r_0]$. Then, it suffices to prove
by induction on ![]() $n\in \mathbb {N}$. In the base case
$n\in \mathbb {N}$. In the base case ![]() $n=0$, we have nothing to prove. In the induction step, the assertion follows from
$n=0$, we have nothing to prove. In the induction step, the assertion follows from ![]() $|cg|_r=|\varphi (g)|_r=|g|_{qr}\geqslant C'/|c|\cdot (qr)^{-\lambda }=C'r^{-\lambda }$.
$|cg|_r=|\varphi (g)|_r=|g|_{qr}\geqslant C'/|c|\cdot (qr)^{-\lambda }=C'r^{-\lambda }$.
Proposition 3.10 Let ![]() $\tilde {M}$ be a nonzero
$\tilde {M}$ be a nonzero ![]() $\varphi$-module over
$\varphi$-module over ![]() $\tilde {\mathcal {R}}^{\mathrm {bd}}$. Put
$\tilde {\mathcal {R}}^{\mathrm {bd}}$. Put ![]() $\tilde {M}_{\tilde {\mathcal {E}}}:=\tilde {M}\otimes _{\tilde {\mathcal {R}}^{\mathrm {bd}}}\tilde {\mathcal {E}}$, which is regarded as a
$\tilde {M}_{\tilde {\mathcal {E}}}:=\tilde {M}\otimes _{\tilde {\mathcal {R}}^{\mathrm {bd}}}\tilde {\mathcal {E}}$, which is regarded as a ![]() $\varphi$-module over
$\varphi$-module over ![]() $\tilde {\mathcal {E}}$. Let
$\tilde {\mathcal {E}}$. Let ![]() $\tilde {f}:\tilde {M}\to \tilde {\mathcal {R}}_{\rm log}$ be an
$\tilde {f}:\tilde {M}\to \tilde {\mathcal {R}}_{\rm log}$ be an ![]() $\tilde {\mathcal {R}}^{\mathrm {bd}}$-linear map such that
$\tilde {\mathcal {R}}^{\mathrm {bd}}$-linear map such that ![]() $\varphi \circ \tilde {f}=c\tilde {f}\circ \varphi _{\tilde {M}}$ for some
$\varphi \circ \tilde {f}=c\tilde {f}\circ \varphi _{\tilde {M}}$ for some ![]() $c\in (\tilde {\mathcal {R}}^{\mathrm {bd}})^{\times }$. Put
$c\in (\tilde {\mathcal {R}}^{\mathrm {bd}})^{\times }$. Put ![]() $\mu :=\log {|c|_0}/\log {|q|}$.
$\mu :=\log {|c|_0}/\log {|q|}$.
(i) We have
 $\tilde {f}(\tilde {M})\subset \mathrm {Fil}_{\mu +\lambda _{\rm max}(\tilde {M}_{\tilde {\mathcal {E}}})}\tilde {\mathcal {R}}_{\rm log}$.
$\tilde {f}(\tilde {M})\subset \mathrm {Fil}_{\mu +\lambda _{\rm max}(\tilde {M}_{\tilde {\mathcal {E}}})}\tilde {\mathcal {R}}_{\rm log}$.(ii) Assume that
 $\tilde {f}$ is injective. If
$\tilde {f}$ is injective. If  $\tilde {f}(\tilde {M})\subset \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}_{\rm log}$, then
$\tilde {f}(\tilde {M})\subset \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}_{\rm log}$, then  $\mu +\lambda _{\rm max}(\tilde {M}_{\tilde {\mathcal {E}}})\leqslant \lambda$.
$\mu +\lambda _{\rm max}(\tilde {M}_{\tilde {\mathcal {E}}})\leqslant \lambda$.
Proof. We reduce to the case ![]() $c=1$, where
$c=1$, where ![]() $\tilde {f}$ is
$\tilde {f}$ is ![]() $\varphi$-equivariant, and
$\varphi$-equivariant, and ![]() $\mu =0$. Put
$\mu =0$. Put ![]() $\tilde {N}=\tilde {M}(c)$, which is a
$\tilde {N}=\tilde {M}(c)$, which is a ![]() $\varphi$-module over
$\varphi$-module over ![]() $\tilde {\mathcal {R}}^{\mathrm {bd}}$ such that
$\tilde {\mathcal {R}}^{\mathrm {bd}}$ such that ![]() $\lambda _{\rm max}(\tilde {N}_{\tilde {\mathcal {E}}})=\mu +\lambda _{\rm max}(\tilde {M}_{\tilde {\mathcal {E}}})$. We define the
$\lambda _{\rm max}(\tilde {N}_{\tilde {\mathcal {E}}})=\mu +\lambda _{\rm max}(\tilde {M}_{\tilde {\mathcal {E}}})$. We define the ![]() $\tilde {\mathcal {R}}^{\mathrm {bd}}$-linear map
$\tilde {\mathcal {R}}^{\mathrm {bd}}$-linear map ![]() $\tilde {f}':\tilde {N}\to \mathcal {R}_{\rm log};m\otimes e_c\mapsto \tilde {f}(m)$. It is straightforward to see that
$\tilde {f}':\tilde {N}\to \mathcal {R}_{\rm log};m\otimes e_c\mapsto \tilde {f}(m)$. It is straightforward to see that ![]() $\varphi \circ \tilde {f}'=\tilde {f}'\circ \varphi _{\tilde {N}}$ and
$\varphi \circ \tilde {f}'=\tilde {f}'\circ \varphi _{\tilde {N}}$ and ![]() $\tilde {f}'(\tilde {N})=\tilde {f}(\tilde {M})$. Moreover,
$\tilde {f}'(\tilde {N})=\tilde {f}(\tilde {M})$. Moreover, ![]() $\tilde {f}'$ is injective if and only if so is
$\tilde {f}'$ is injective if and only if so is ![]() $\tilde {f}$. Hence, after replacing
$\tilde {f}$. Hence, after replacing ![]() $\tilde {f}$ by
$\tilde {f}$ by ![]() $\tilde {f}'$, we may assume
$\tilde {f}'$, we may assume ![]() $c=1$ as desired.
$c=1$ as desired.
(i) Let ![]() $F_0=0\subsetneq F_1\subsetneq \dots \subsetneq F_m=\tilde {M}$ denote the reverse filtration of
$F_0=0\subsetneq F_1\subsetneq \dots \subsetneq F_m=\tilde {M}$ denote the reverse filtration of ![]() $\tilde {M}$ (Proposition 2.10). We have only to prove
$\tilde {M}$ (Proposition 2.10). We have only to prove ![]() $\tilde {f}(F_i)\subset \mathrm {Fil}_{\lambda _{\rm max}(\tilde {M}_{\tilde {\mathcal {E}}})}\tilde {\mathcal {R}}_{\rm log}$ by induction on
$\tilde {f}(F_i)\subset \mathrm {Fil}_{\lambda _{\rm max}(\tilde {M}_{\tilde {\mathcal {E}}})}\tilde {\mathcal {R}}_{\rm log}$ by induction on ![]() $i\in \{0,\dots ,m\}$. In the base case
$i\in \{0,\dots ,m\}$. In the base case ![]() $i=0$, the assertion is trivial. In the induction step, for some
$i=0$, the assertion is trivial. In the induction step, for some ![]() $d$, there exists a set of generator of
$d$, there exists a set of generator of ![]() $F_{i+1}/F_i$ consisting of
$F_{i+1}/F_i$ consisting of ![]() $d$-eigenvectors of slopes less than or equal to
$d$-eigenvectors of slopes less than or equal to ![]() $\lambda _{\rm max}(\tilde {M}_{\tilde {\mathcal {E}}})$. We choose a lift
$\lambda _{\rm max}(\tilde {M}_{\tilde {\mathcal {E}}})$. We choose a lift ![]() $S$ of such a set to
$S$ of such a set to ![]() $F_{i+1}$. For
$F_{i+1}$. For ![]() $v\in S$, we have
$v\in S$, we have ![]() $v':=(\varphi _{\tilde {M}}^d-c')v\in F_i$ for some
$v':=(\varphi _{\tilde {M}}^d-c')v\in F_i$ for some ![]() $c'\in (\tilde {\mathcal {R}}^{\mathrm {bd}})^{\times }$ (depending on
$c'\in (\tilde {\mathcal {R}}^{\mathrm {bd}})^{\times }$ (depending on ![]() $v$), and
$v$), and ![]() $\log {|c'|_0}/\log {|q|^d}\leqslant \lambda _{\rm max}(\tilde {M}_{\tilde {\mathcal {E}}})$. Then,
$\log {|c'|_0}/\log {|q|^d}\leqslant \lambda _{\rm max}(\tilde {M}_{\tilde {\mathcal {E}}})$. Then, ![]() $(\varphi ^d-c')(\tilde {f}(v))=\tilde {f}((\varphi ^d_{\tilde {M}}-c')v)=\tilde {f}(v')\in \tilde {f}(F_i)\subset \mathrm {Fil}_{\lambda _{\rm max}(\tilde {M}_{\tilde {\mathcal {E}}})}\tilde {\mathcal {R}}_{\rm log}$ by the induction hypothesis. Hence, by applying Lemma 3.8 to
$(\varphi ^d-c')(\tilde {f}(v))=\tilde {f}((\varphi ^d_{\tilde {M}}-c')v)=\tilde {f}(v')\in \tilde {f}(F_i)\subset \mathrm {Fil}_{\lambda _{\rm max}(\tilde {M}_{\tilde {\mathcal {E}}})}\tilde {\mathcal {R}}_{\rm log}$ by the induction hypothesis. Hence, by applying Lemma 3.8 to ![]() $(g,h)=(\tilde {f}(v),\tilde {f}(v'))$, we have
$(g,h)=(\tilde {f}(v),\tilde {f}(v'))$, we have ![]() $\tilde {f}(v)\in \mathrm {Fil}_{\lambda _{\rm max}(M_{\tilde {\mathcal {E}}})}\tilde {\mathcal {R}}_{\rm log}$. We complete the proof by
$\tilde {f}(v)\in \mathrm {Fil}_{\lambda _{\rm max}(M_{\tilde {\mathcal {E}}})}\tilde {\mathcal {R}}_{\rm log}$. We complete the proof by ![]() $\tilde {f}(F_{i+1})=\tilde {f}(F_i+\tilde {\mathcal {R}}^{\mathrm {bd}}\cdot S)=\tilde {f}(F_i)+\tilde {\mathcal {R}}^{\mathrm {bd}}\cdot \tilde {f}(S)\subset \mathrm {Fil}_{\lambda _{\rm max}(\tilde {M}_{\tilde {\mathcal {E}}})}\tilde {\mathcal {R}}_{\rm log}$.
$\tilde {f}(F_{i+1})=\tilde {f}(F_i+\tilde {\mathcal {R}}^{\mathrm {bd}}\cdot S)=\tilde {f}(F_i)+\tilde {\mathcal {R}}^{\mathrm {bd}}\cdot \tilde {f}(S)\subset \mathrm {Fil}_{\lambda _{\rm max}(\tilde {M}_{\tilde {\mathcal {E}}})}\tilde {\mathcal {R}}_{\rm log}$.
(ii) By Proposition 2.10, there exists a ![]() $d$-eigenvector
$d$-eigenvector ![]() $v\in \tilde {M}$ of slope
$v\in \tilde {M}$ of slope ![]() $\lambda _{\rm max}(\tilde {M}_{\tilde {\mathcal {E}}})$. As
$\lambda _{\rm max}(\tilde {M}_{\tilde {\mathcal {E}}})$. As ![]() $\tilde {f}$ is
$\tilde {f}$ is ![]() $\varphi$-equivariant and injective,
$\varphi$-equivariant and injective, ![]() $\tilde {f}(v)\in \tilde {\mathcal {R}}_{\rm log}$ is also a
$\tilde {f}(v)\in \tilde {\mathcal {R}}_{\rm log}$ is also a ![]() $d$-eigenvector of slope
$d$-eigenvector of slope ![]() $\lambda _{\rm max}(\tilde {M}_{\tilde {\mathcal {E}}})$. Hence,
$\lambda _{\rm max}(\tilde {M}_{\tilde {\mathcal {E}}})$. Hence, ![]() $\tilde {f}(v)$ has exact log-growth
$\tilde {f}(v)$ has exact log-growth ![]() $\lambda _{\rm max}(\tilde {M}_{\tilde {\mathcal {E}}})$ by Lemma 3.9. As
$\lambda _{\rm max}(\tilde {M}_{\tilde {\mathcal {E}}})$ by Lemma 3.9. As ![]() $\tilde {f}(v)\in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}_{\rm log}$, we have
$\tilde {f}(v)\in \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}_{\rm log}$, we have ![]() $\lambda \geqslant \lambda _{\rm max}(\tilde {M}_{\tilde {\mathcal {E}}})$.
$\lambda \geqslant \lambda _{\rm max}(\tilde {M}_{\tilde {\mathcal {E}}})$.
Proposition 3.11 Let ![]() $M$ be a nonzero
$M$ be a nonzero ![]() $\varphi$-module over
$\varphi$-module over ![]() $\mathcal {R}^{\mathrm {bd}}$. Let
$\mathcal {R}^{\mathrm {bd}}$. Let ![]() $f:M\to \mathcal {R}_{\rm log}$ be an
$f:M\to \mathcal {R}_{\rm log}$ be an ![]() $\mathcal {R}^{\mathrm {bd}}$-linear map such that
$\mathcal {R}^{\mathrm {bd}}$-linear map such that ![]() $\varphi \circ f=cf\circ \varphi _M$ for some
$\varphi \circ f=cf\circ \varphi _M$ for some ![]() $c\in (\mathcal {R}^{\mathrm {bd}})^{\times }$. Put
$c\in (\mathcal {R}^{\mathrm {bd}})^{\times }$. Put ![]() $\mu :=\log {|c|_0}/\log {|q|}$.
$\mu :=\log {|c|_0}/\log {|q|}$.
(i) We have
 $f(M)\subset \mathrm {Fil}_{\mu +\lambda _{\rm max}(M_{\mathcal {E}})}\mathcal {R}_{\rm log}$.
$f(M)\subset \mathrm {Fil}_{\mu +\lambda _{\rm max}(M_{\mathcal {E}})}\mathcal {R}_{\rm log}$.(ii) Assume that
 $f$ is injective. If
$f$ is injective. If  $f(M)\subset \mathrm {Fil}_{\lambda }\mathcal {R}_{\rm log}$, then
$f(M)\subset \mathrm {Fil}_{\lambda }\mathcal {R}_{\rm log}$, then  $\mu +\lambda _{\rm max}(M_{\mathcal {E}})\leqslant \lambda$.
$\mu +\lambda _{\rm max}(M_{\mathcal {E}})\leqslant \lambda$.
Proof. (i) Let ![]() $\tilde {\psi }_K:\mathcal {R}_{\rm log}\to \tilde {\mathcal {R}}_{\rm log}$ be an embedding as in § 2.3 with
$\tilde {\psi }_K:\mathcal {R}_{\rm log}\to \tilde {\mathcal {R}}_{\rm log}$ be an embedding as in § 2.3 with ![]() $L=K$. Put
$L=K$. Put ![]() $\tilde {M}=M\otimes _{\mathcal {R}^{\mathrm {bd}}}\tilde {\mathcal {R}}^{\mathrm {bd}}$, which is regarded as a
$\tilde {M}=M\otimes _{\mathcal {R}^{\mathrm {bd}}}\tilde {\mathcal {R}}^{\mathrm {bd}}$, which is regarded as a ![]() $\varphi$-module over
$\varphi$-module over ![]() $\tilde {\mathcal {R}}^{\mathrm {bd}}$. Let
$\tilde {\mathcal {R}}^{\mathrm {bd}}$. Let ![]() $\tilde {f}:\tilde {M}\to \tilde {\mathcal {R}}_{\rm log}$ be the composition
$\tilde {f}:\tilde {M}\to \tilde {\mathcal {R}}_{\rm log}$ be the composition
where the second morphism is a multiplication map as in Lemma 2.13(ii). Then, ![]() $\varphi ^d\circ \tilde {f}=c\tilde {f}\circ \varphi _{\tilde {M}}^d$ by assumption. Hence,
$\varphi ^d\circ \tilde {f}=c\tilde {f}\circ \varphi _{\tilde {M}}^d$ by assumption. Hence, ![]() $\tilde {f}(\tilde {M})\subset \mathrm {Fil}_{\mu +\lambda _{\rm max}(M_{\mathcal {E}})}\tilde {\mathcal {R}}_{\rm log}$ by Proposition 3.10(i). As
$\tilde {f}(\tilde {M})\subset \mathrm {Fil}_{\mu +\lambda _{\rm max}(M_{\mathcal {E}})}\tilde {\mathcal {R}}_{\rm log}$ by Proposition 3.10(i). As ![]() $\tilde {\psi }_K(f(M))=\tilde {f}(M\otimes _{\mathcal {R}^{\mathrm {bd}}}\mathcal {R}^{\mathrm {bd}})\subset \tilde {f}(\tilde {M})$ by the definition of
$\tilde {\psi }_K(f(M))=\tilde {f}(M\otimes _{\mathcal {R}^{\mathrm {bd}}}\mathcal {R}^{\mathrm {bd}})\subset \tilde {f}(\tilde {M})$ by the definition of ![]() $\tilde {f}$, we have
$\tilde {f}$, we have ![]() $f(M)\subset \mathrm {Fil}_{\mu +\lambda _{\rm max}(M_{\mathcal {E}})}\mathcal {R}_{\rm log}$ by Lemma 3.5.
$f(M)\subset \mathrm {Fil}_{\mu +\lambda _{\rm max}(M_{\mathcal {E}})}\mathcal {R}_{\rm log}$ by Lemma 3.5.
(ii) Let notation be as previously. As ![]() $f$ is injective, so is
$f$ is injective, so is ![]() $\tilde {f}$ by definition. Moreover, we have
$\tilde {f}$ by definition. Moreover, we have ![]() $\tilde {f}(\tilde {M})\subset \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}_{\rm log}$ by
$\tilde {f}(\tilde {M})\subset \mathrm {Fil}_{\lambda }\tilde {\mathcal {R}}_{\rm log}$ by
where we use Lemmas 3.3(i), 3.3(iii), and 3.5. Hence, we obtain the assertion by Proposition 3.10(ii).
4. Preliminaries on  $(\varphi ,\nabla )$-modules over the Robba ring
$(\varphi ,\nabla )$-modules over the Robba ring
We give the formalism of ![]() $\nabla$-modules and
$\nabla$-modules and ![]() $(\phi ,\nabla )$-modules over certain rings in § 4.1, and recall basic results on unipotent
$(\phi ,\nabla )$-modules over certain rings in § 4.1, and recall basic results on unipotent ![]() $\nabla$-modules over
$\nabla$-modules over ![]() $\mathcal {R}$ in § 4.2.
$\mathcal {R}$ in § 4.2.
4.1 Definition of  $(\varphi ,\nabla )$-modules over the Robba ring
$(\varphi ,\nabla )$-modules over the Robba ring
Definition 4.1 Let ![]() $R$ be a ring, and
$R$ be a ring, and ![]() $A\subset R$ a subring. Let
$A\subset R$ a subring. Let ![]() $\partial :R\to R$ be an
$\partial :R\to R$ be an ![]() $A$-linear derivation, and
$A$-linear derivation, and ![]() $x$ an element of
$x$ an element of ![]() $R$ such that
$R$ such that ![]() $\partial (x)=1$.
$\partial (x)=1$.
(i) We define a ![]() $\nabla$-module over
$\nabla$-module over ![]() $R$ (relative to
$R$ (relative to ![]() $A$) as a finite free
$A$) as a finite free ![]() $R$-module
$R$-module ![]() $M$ endowed with an
$M$ endowed with an ![]() $A$-linear differential operator
$A$-linear differential operator ![]() $\partial _M$ relative to
$\partial _M$ relative to ![]() $\partial$, that is,
$\partial$, that is, ![]() $\partial _M:M\to M$ is an
$\partial _M:M\to M$ is an ![]() $A$-linear map satisfying
$A$-linear map satisfying ![]() $\partial _M(rm)=\partial (r)m+r\partial _M(m)$ for
$\partial _M(rm)=\partial (r)m+r\partial _M(m)$ for ![]() $r\in R$ and
$r\in R$ and ![]() $m\in M$. We may regard a
$m\in M$. We may regard a ![]() $\nabla$-module over
$\nabla$-module over ![]() $R$ as a differential module over
$R$ as a differential module over ![]() $R$ in the sense of [Reference KedlayaKed10, Definition 5.1.2]. We define basic operations in the category of
$R$ in the sense of [Reference KedlayaKed10, Definition 5.1.2]. We define basic operations in the category of ![]() $\nabla$-modules over
$\nabla$-modules over ![]() $R$, such as the internal Hom
$R$, such as the internal Hom ![]() $\mathrm {Hom}_R(-,-)$, the tensor product
$\mathrm {Hom}_R(-,-)$, the tensor product ![]() $-\otimes _R-$, and the dual
$-\otimes _R-$, and the dual ![]() $(-)^\vee$ as in [Reference KedlayaKed10, 5.3]. We also define the natural pairing
$(-)^\vee$ as in [Reference KedlayaKed10, 5.3]. We also define the natural pairing ![]() $M\otimes _RM^\vee \to R;v\otimes f\mapsto f(v)$. We put
$M\otimes _RM^\vee \to R;v\otimes f\mapsto f(v)$. We put ![]() $M^{\nabla }:=\ker {\partial _M}$, which is regarded as an
$M^{\nabla }:=\ker {\partial _M}$, which is regarded as an ![]() $A$-submodule of
$A$-submodule of ![]() $M$.
$M$.
(ii) Let ![]() $\phi$ be a ring endomorphism on
$\phi$ be a ring endomorphism on ![]() $R$ such that
$R$ such that ![]() $\partial (\phi (x))\phi \circ \partial =\partial \circ \phi$, and
$\partial (\phi (x))\phi \circ \partial =\partial \circ \phi$, and ![]() $\phi (A)\subset A$. We define a
$\phi (A)\subset A$. We define a ![]() $(\phi ,\nabla )$-module over
$(\phi ,\nabla )$-module over ![]() $R$ (relative to
$R$ (relative to ![]() $A$) as a
$A$) as a ![]() $\phi$-module
$\phi$-module ![]() $M$ over
$M$ over ![]() $R$ endowed with an
$R$ endowed with an ![]() $A$-linear differential operator
$A$-linear differential operator ![]() $\partial _M$ relative to
$\partial _M$ relative to ![]() $\partial$ satisfying the compatibility condition
$\partial$ satisfying the compatibility condition ![]() $\partial (\phi (x))\cdot \phi _M\circ \partial _M=\partial _M\circ \phi _M$. We define the forgetful functor from the category of
$\partial (\phi (x))\cdot \phi _M\circ \partial _M=\partial _M\circ \phi _M$. We define the forgetful functor from the category of ![]() $(\phi ,\nabla )$-modules over
$(\phi ,\nabla )$-modules over ![]() $R$ to the category of
$R$ to the category of ![]() $\phi$-modules (respectively,
$\phi$-modules (respectively, ![]() $\nabla$-modules) over
$\nabla$-modules) over ![]() $R$ by
$R$ by ![]() $(M,\phi _M,\partial _M)\mapsto (M,\phi _M)$ (respectively,
$(M,\phi _M,\partial _M)\mapsto (M,\phi _M)$ (respectively, ![]() $(M,\phi _M,\partial _M)\mapsto (M,\partial _M)$). In the category of
$(M,\phi _M,\partial _M)\mapsto (M,\partial _M)$). In the category of ![]() $(\phi ,\nabla )$-modules over
$(\phi ,\nabla )$-modules over ![]() $R$, we can naturally define the internal Hom, the tensor product, the dual, and the natural pairing in such a way that these operations are preserved under the above forgetful functors. Let
$R$, we can naturally define the internal Hom, the tensor product, the dual, and the natural pairing in such a way that these operations are preserved under the above forgetful functors. Let ![]() $M$ be a
$M$ be a ![]() $(\phi ,\nabla )$-module over
$(\phi ,\nabla )$-module over ![]() $R$. We define the
$R$. We define the ![]() $d$-pushforward
$d$-pushforward ![]() $[d]_*M$ of
$[d]_*M$ of ![]() $M$ to be
$M$ to be ![]() $(\phi ^d,\nabla )$-module over
$(\phi ^d,\nabla )$-module over ![]() $R$ given by
$R$ given by ![]() $(M,\phi _M^d,\partial _M)$. For
$(M,\phi _M^d,\partial _M)$. For ![]() $c\in A^{\times }$, let
$c\in A^{\times }$, let ![]() $R(c)=Re_c$ be the
$R(c)=Re_c$ be the ![]() $(\phi ,\nabla )$-module over
$(\phi ,\nabla )$-module over ![]() $R$ defined by
$R$ defined by ![]() $\phi _{R(c)}(e_c)=ce_c$ and
$\phi _{R(c)}(e_c)=ce_c$ and ![]() $\partial _{R(c)}(e_c)=0$, and
$\partial _{R(c)}(e_c)=0$, and ![]() $M(c):=M\otimes _RR(c)$. As in part (i), we put
$M(c):=M\otimes _RR(c)$. As in part (i), we put ![]() $M^{\nabla }:=\ker {\partial _M}$, which is regarded as a difference module over
$M^{\nabla }:=\ker {\partial _M}$, which is regarded as a difference module over ![]() $A=(A,\phi |_A)$.
$A=(A,\phi |_A)$.
Let ![]() $(R,A,\partial ,\phi ,x)$ be a
$(R,A,\partial ,\phi ,x)$ be a ![]() $5$-tuple as above. We give a few remarks on base changes of
$5$-tuple as above. We give a few remarks on base changes of ![]() $(\phi ,\nabla )$-modules over
$(\phi ,\nabla )$-modules over ![]() $R$, which also applies to
$R$, which also applies to ![]() $\nabla$-modules over
$\nabla$-modules over ![]() $R$ by regarding the category of
$R$ by regarding the category of ![]() $\nabla$-modules over
$\nabla$-modules over ![]() $R$ as a full subcategory of
$R$ as a full subcategory of ![]() $(\mathrm {id}_R,\nabla )$-modules over
$(\mathrm {id}_R,\nabla )$-modules over ![]() $R$ via the correspondence
$R$ via the correspondence ![]() $(M,\partial _M)\mapsto (M,\mathrm {id}_M,\partial _M)$. Let
$(M,\partial _M)\mapsto (M,\mathrm {id}_M,\partial _M)$. Let ![]() $(R',A',\partial ',\phi ',x')$ be another
$(R',A',\partial ',\phi ',x')$ be another ![]() $5$-tuple as in Definition 4.1, and
$5$-tuple as in Definition 4.1, and ![]() $\psi :R\to R'$ a ring homomorphism such that
$\psi :R\to R'$ a ring homomorphism such that ![]() $\psi \circ \phi =\phi '\circ \psi$,
$\psi \circ \phi =\phi '\circ \psi$, ![]() $\partial '\circ \psi =\psi \circ \partial$,
$\partial '\circ \psi =\psi \circ \partial$, ![]() $\psi (x)\in x'+A'$, and
$\psi (x)\in x'+A'$, and ![]() $\psi (A)\subset A'$. We define the base change functor
$\psi (A)\subset A'$. We define the base change functor ![]() $\psi ^*(-)$ from the category of
$\psi ^*(-)$ from the category of ![]() $(\phi ,\nabla )$-modules over
$(\phi ,\nabla )$-modules over ![]() $R$ to the category of
$R$ to the category of ![]() $(\phi ,\nabla )$-modules over
$(\phi ,\nabla )$-modules over ![]() $R'$ by the correspondence
$R'$ by the correspondence ![]() $(M,\phi _M,\partial _M)\mapsto (\psi ^*M,\phi _M\otimes \phi ',\partial _M\otimes \mathrm {id}_{R'}+\mathrm {id}_M\otimes \partial ')$. Note that the base change functor is compatible with compositions. Precisely speaking, let
$(M,\phi _M,\partial _M)\mapsto (\psi ^*M,\phi _M\otimes \phi ',\partial _M\otimes \mathrm {id}_{R'}+\mathrm {id}_M\otimes \partial ')$. Note that the base change functor is compatible with compositions. Precisely speaking, let ![]() $(R'',A'',\partial '',\phi '',x'')$ be a
$(R'',A'',\partial '',\phi '',x'')$ be a ![]() $5$-tuple with a ring homomorphism
$5$-tuple with a ring homomorphism ![]() $\psi ':R'\to R''$ as previously. Then, we have a natural isomorphism
$\psi ':R'\to R''$ as previously. Then, we have a natural isomorphism ![]() $(\psi '\circ \psi )^*\cong (\psi ')^*\circ \psi ^*$.
$(\psi '\circ \psi )^*\cong (\psi ')^*\circ \psi ^*$.
Definition 4.2 Let ![]() $R$ denote any one of
$R$ denote any one of ![]() $K[\![t]\!]_0,K\{t\},\mathcal {R}^{\mathrm {bd}},\mathcal {R},\mathcal {R}_{\rm log}$, and
$K[\![t]\!]_0,K\{t\},\mathcal {R}^{\mathrm {bd}},\mathcal {R},\mathcal {R}_{\rm log}$, and ![]() $\mathcal {E}$. Let
$\mathcal {E}$. Let ![]() $\partial :=d/dt:R\to R$ be the natural derivation for
$\partial :=d/dt:R\to R$ be the natural derivation for ![]() $R\neq \mathcal {R}_{\rm log}$. We extend
$R\neq \mathcal {R}_{\rm log}$. We extend ![]() $\partial :R\to R$ to
$\partial :R\to R$ to ![]() $\mathcal {R}_{\rm log}\to \mathcal {R}_{\rm log}$ by setting
$\mathcal {R}_{\rm log}\to \mathcal {R}_{\rm log}$ by setting ![]() $\partial (\ell _X):=\partial (X)/X=i/t+\partial (v)/v$ with notation as in Definition 2.1(iii). We can see that
$\partial (\ell _X):=\partial (X)/X=i/t+\partial (v)/v$ with notation as in Definition 2.1(iii). We can see that ![]() $\partial (\varphi (t))\varphi \circ \partial =\partial \circ \varphi$. We define the category of
$\partial (\varphi (t))\varphi \circ \partial =\partial \circ \varphi$. We define the category of ![]() $(\varphi ,\nabla )$-modules over
$(\varphi ,\nabla )$-modules over ![]() $R$ by applying Definition 4.1(ii) to the
$R$ by applying Definition 4.1(ii) to the ![]() $5$-tuple
$5$-tuple ![]() $(R,K,\partial ,\varphi ,t)$. Any inclusion between the rings
$(R,K,\partial ,\varphi ,t)$. Any inclusion between the rings ![]() $K[\![t]\!]_0,K\{t\},\mathcal {R}^{\mathrm {bd}},\mathcal {R},\mathcal {R}_{\rm log}$, and
$K[\![t]\!]_0,K\{t\},\mathcal {R}^{\mathrm {bd}},\mathcal {R},\mathcal {R}_{\rm log}$, and ![]() $\mathcal {E}$ (see the commutative diagram in the Appendix) induces a base change functor between the corresponding categories of
$\mathcal {E}$ (see the commutative diagram in the Appendix) induces a base change functor between the corresponding categories of ![]() $(\varphi ,\nabla )$-modules.
$(\varphi ,\nabla )$-modules.
We endow the ring ![]() $\mathcal {E}[\![X-t]\!]_0$ with
$\mathcal {E}[\![X-t]\!]_0$ with ![]() $\varphi$ and
$\varphi$ and ![]() $\partial$ as in the introduction. Then, we can define the notion of
$\partial$ as in the introduction. Then, we can define the notion of ![]() $(\varphi ,\nabla )$-modules over
$(\varphi ,\nabla )$-modules over ![]() $\mathcal {E}[\![X-t]\!]_0$ as previously. Moreover, the ring homomorphism
$\mathcal {E}[\![X-t]\!]_0$ as previously. Moreover, the ring homomorphism ![]() $\tau :\mathcal {E}\to \mathcal {E}[\![X-t]\!]_0$ as in the introduction induces the base change functor from the category of
$\tau :\mathcal {E}\to \mathcal {E}[\![X-t]\!]_0$ as in the introduction induces the base change functor from the category of ![]() $(\varphi ,\nabla )$-modules over
$(\varphi ,\nabla )$-modules over ![]() $\mathcal {E}$ to the category of
$\mathcal {E}$ to the category of ![]() $(\varphi ,\nabla )$-modules over
$(\varphi ,\nabla )$-modules over ![]() $\mathcal {E}[\![X-t]\!]_0$.
$\mathcal {E}[\![X-t]\!]_0$.
4.2 Unipotent  $\nabla$-modules over the Robba ring
$\nabla$-modules over the Robba ring
We start with proving that in the category of differential rings, the isomorphism class of the differential ring ![]() $(\mathcal {R}_{\rm log},\partial )$ is independent of the choice of
$(\mathcal {R}_{\rm log},\partial )$ is independent of the choice of ![]() $\ell _X$. Let
$\ell _X$. Let ![]() $\ell _{X'}$ be another branch of log associated to
$\ell _{X'}$ be another branch of log associated to ![]() $X'=t^jv'$ with
$X'=t^jv'$ with ![]() $v'\in \mathcal {O}_K[\![t]\!]^{\times }$ and
$v'\in \mathcal {O}_K[\![t]\!]^{\times }$ and ![]() $j\in \mathbb {N}_{\geqslant 1}$. Put
$j\in \mathbb {N}_{\geqslant 1}$. Put ![]() $c'_1=i/j$, and
$c'_1=i/j$, and ![]() $g:=\partial (X)/X-c'_1\partial (X')/X'=\partial (v)/v-c'_1\partial (v')/v'\in K[\![t]\!]_0$. Then, there exists
$g:=\partial (X)/X-c'_1\partial (X')/X'=\partial (v)/v-c'_1\partial (v')/v'\in K[\![t]\!]_0$. Then, there exists ![]() $c'_0\in K\{t\}$ (unique up to modulo
$c'_0\in K\{t\}$ (unique up to modulo ![]() $K$) such that
$K$) such that ![]() $\partial (c'_0)=g$ by considering an antidifferential of
$\partial (c'_0)=g$ by considering an antidifferential of ![]() $g$. Note that we have
$g$. Note that we have ![]() $c'_0\in K\{t\}\cap \mathrm {Fil}_1\mathcal {R}$ by
$c'_0\in K\{t\}\cap \mathrm {Fil}_1\mathcal {R}$ by ![]() $g\in K[\![t]\!]_0$ and Corollary 3.6(or by using [Reference Chiarellotto and TsuzukiCT09, Proposition 1.2(5)]). We define the
$g\in K[\![t]\!]_0$ and Corollary 3.6(or by using [Reference Chiarellotto and TsuzukiCT09, Proposition 1.2(5)]). We define the ![]() $\mathcal {R}$-algebra homomorphism
$\mathcal {R}$-algebra homomorphism ![]() $T_{X,X'}:\mathcal {R}[\ell _X]\to \mathcal {R}[\ell _{X'}];\ell _X\mapsto c'_0+c'_1\ell _{X'}$.
$T_{X,X'}:\mathcal {R}[\ell _X]\to \mathcal {R}[\ell _{X'}];\ell _X\mapsto c'_0+c'_1\ell _{X'}$.
Lemma 4.3 Let notation be as previously.
(i) We have the following commutative diagram.

(ii) The map
 $T_{X,X'}$ is bijective.
$T_{X,X'}$ is bijective.(iii) The map
 $T_{X,X'}$ induces a bijection
$T_{X,X'}$ induces a bijection  $\mathrm {Fil}_{\lambda }\mathcal {R}[\ell _X]\to \mathrm {Fil}_{\lambda }\mathcal {R}[\ell _{X'}]$ for
$\mathrm {Fil}_{\lambda }\mathcal {R}[\ell _X]\to \mathrm {Fil}_{\lambda }\mathcal {R}[\ell _{X'}]$ for  $\lambda \in \mathbb {R}$.
$\lambda \in \mathbb {R}$.
Proof. Part (i) is verified directly. We define the ![]() $\mathcal {R}$-algebra homomorphism
$\mathcal {R}$-algebra homomorphism ![]() $T_{X',X}:\mathcal {R}[\ell _{X'}]\to \mathcal {R}[\ell _X];\ell _{X'}\mapsto -c'_0/c'_1+1/c'_1\cdot \ell _{X}$. Then,
$T_{X',X}:\mathcal {R}[\ell _{X'}]\to \mathcal {R}[\ell _X];\ell _{X'}\mapsto -c'_0/c'_1+1/c'_1\cdot \ell _{X}$. Then, ![]() $T_{X',X}$ gives an inverse of
$T_{X',X}$ gives an inverse of ![]() $T_{X,X'}$, which implies part (ii). Since
$T_{X,X'}$, which implies part (ii). Since ![]() $T_{X,X'}(\ell _X)\in \mathrm {Fil}_1\mathcal {R}[\ell _{X'}]$, we have
$T_{X,X'}(\ell _X)\in \mathrm {Fil}_1\mathcal {R}[\ell _{X'}]$, we have ![]() $T_{X,X'}(\mathrm {Fil}_{\lambda }\mathcal {R}[\ell _X])\subset \mathrm {Fil}_{\lambda }\mathcal {R}[\ell _{X'}]$ for
$T_{X,X'}(\mathrm {Fil}_{\lambda }\mathcal {R}[\ell _X])\subset \mathrm {Fil}_{\lambda }\mathcal {R}[\ell _{X'}]$ for ![]() $\lambda \in \mathbb {R}$. Similarly, we have
$\lambda \in \mathbb {R}$. Similarly, we have ![]() $T_{X',X}(\mathrm {Fil}_{\lambda }\mathcal {R}[\ell _{X'}])\subset \mathrm {Fil}_{\lambda }\mathcal {R}[\ell _{X}]$ for
$T_{X',X}(\mathrm {Fil}_{\lambda }\mathcal {R}[\ell _{X'}])\subset \mathrm {Fil}_{\lambda }\mathcal {R}[\ell _{X}]$ for ![]() $\lambda \in \mathbb {R}$, which implies part (iii).
$\lambda \in \mathbb {R}$, which implies part (iii).
Lemma 4.4 The ![]() $K$-linear derivation
$K$-linear derivation ![]() $\partial :\mathcal {R}_{\rm log}\to \mathcal {R}_{\rm log}$ is surjective.
$\partial :\mathcal {R}_{\rm log}\to \mathcal {R}_{\rm log}$ is surjective.
Proof. By Lemma 4.3(i) and (ii), we may assume ![]() $X=t$, in which case the assertion is trivial.
$X=t$, in which case the assertion is trivial.
Definition 4.5 Let ![]() $M$ be a
$M$ be a ![]() $\nabla$-module over
$\nabla$-module over ![]() $\mathcal {R}$. We put
$\mathcal {R}$. We put ![]() $\mathbf {V}(M):=(M\otimes _{\mathcal {R}}\mathcal {R}_{\rm log})^{\nabla }$, which is regarded as a vector space over
$\mathbf {V}(M):=(M\otimes _{\mathcal {R}}\mathcal {R}_{\rm log})^{\nabla }$, which is regarded as a vector space over ![]() $K$. We define the monodromy operator
$K$. We define the monodromy operator ![]() $N_X$ as the
$N_X$ as the ![]() $K$-linear endomorphism on
$K$-linear endomorphism on ![]() $\mathbf {V}(M)$ induced by
$\mathbf {V}(M)$ induced by ![]() $\mathrm {id}_M\otimes d/d\ell _X$, where
$\mathrm {id}_M\otimes d/d\ell _X$, where ![]() $d/d\ell _X:\mathcal {R}_{\rm log}\to \mathcal {R}_{\rm log}$ is the unique (locally nilpotent)
$d/d\ell _X:\mathcal {R}_{\rm log}\to \mathcal {R}_{\rm log}$ is the unique (locally nilpotent) ![]() $\mathcal {R}$-linear derivation sending
$\mathcal {R}$-linear derivation sending ![]() $\ell _X$ to
$\ell _X$ to ![]() $1$.
$1$.
Let ![]() $\mathcal {C}$ denote the category of
$\mathcal {C}$ denote the category of ![]() $\nabla$-modules over
$\nabla$-modules over ![]() $\mathcal {R}$. Recall that
$\mathcal {R}$. Recall that ![]() $\mathcal {C}$ is an abelian tensor category whose objects admit composition series [Reference CrewCre98, 6.2]. Moreover, the correspondence
$\mathcal {C}$ is an abelian tensor category whose objects admit composition series [Reference CrewCre98, 6.2]. Moreover, the correspondence ![]() $M\mapsto \mathbf {V}(M)$ gives a left-exact covariant functor from
$M\mapsto \mathbf {V}(M)$ gives a left-exact covariant functor from ![]() $\mathcal {C}$ to the category of vector spaces over
$\mathcal {C}$ to the category of vector spaces over ![]() $K$. Recall that
$K$. Recall that ![]() $M\in \mathcal {C}$ is trivial (respectively, unipotent) if
$M\in \mathcal {C}$ is trivial (respectively, unipotent) if ![]() $M$ is isomorphic to a finite direct sum (respectively, a successive extension) of copies of
$M$ is isomorphic to a finite direct sum (respectively, a successive extension) of copies of ![]() $\mathcal {R}$, where
$\mathcal {R}$, where ![]() $\mathcal {R}$ is equipped with the trivial differential operator
$\mathcal {R}$ is equipped with the trivial differential operator ![]() $\partial$ (see [Reference KedlayaKed05a, Definition 4.27]). Then, the unipotent objects form an abelian full subcategory
$\partial$ (see [Reference KedlayaKed05a, Definition 4.27]). Then, the unipotent objects form an abelian full subcategory ![]() $\mathcal {C}^{\mathrm {unip}}$ of
$\mathcal {C}^{\mathrm {unip}}$ of ![]() $\mathcal {C}$, which is closed under formation of direct sums, tensor products, duals, subobjects, quotients, and extensions [Reference KedlayaKed04, Definition 4.27].
$\mathcal {C}$, which is closed under formation of direct sums, tensor products, duals, subobjects, quotients, and extensions [Reference KedlayaKed04, Definition 4.27].
Lemma 4.6 Let ![]() $M$ be a
$M$ be a ![]() $\nabla$-module over
$\nabla$-module over ![]() $\mathcal {R}$.
$\mathcal {R}$.
(i) We have
 $M^{\nabla }=0$ if and only if
$M^{\nabla }=0$ if and only if  $\mathbf {V}(M)=0$.
$\mathbf {V}(M)=0$.(ii) If
 $M$ is irreducible in
$M$ is irreducible in  $\mathcal {C}$, then we have either
$\mathcal {C}$, then we have either  $\mathbf {V}(M)=0$ or
$\mathbf {V}(M)=0$ or  $M\cong \mathcal {R}$.
$M\cong \mathcal {R}$.(iii) The canonical maps
are injective. In particular, \[ M^{\nabla}\otimes_K\mathcal{R}\to M,\quad \mathbf{V}(M)\otimes_K\mathcal{R}_{{\rm log}}\to M\otimes_{\mathcal{R}}\mathcal{R}_{{\rm log}} \]
\[ M^{\nabla}\otimes_K\mathcal{R}\to M,\quad \mathbf{V}(M)\otimes_K\mathcal{R}_{{\rm log}}\to M\otimes_{\mathcal{R}}\mathcal{R}_{{\rm log}} \] $\dim _K\mathbf {V}(M)\leqslant \mathrm {rank}_{\mathcal {R}}M$, and
$\dim _K\mathbf {V}(M)\leqslant \mathrm {rank}_{\mathcal {R}}M$, and  $N_X$ is nilpotent.
$N_X$ is nilpotent.
Proof. Part (i) follows from ![]() $\mathbf {V}(M)^{N_X=0}=M^{\nabla }$ and the local nilpotency of
$\mathbf {V}(M)^{N_X=0}=M^{\nabla }$ and the local nilpotency of ![]() $N_X$. Part (ii) can be proved by using part (i) and a canonical isomorphism
$N_X$. Part (ii) can be proved by using part (i) and a canonical isomorphism ![]() $M^{\nabla }\cong \mathrm {Hom}_{\mathcal {C}}(\mathcal {R},M)$ (see [Reference KedlayaKed10, Deifnition 5.3.2]). To prove part (iii), by dévissage, we may assume that
$M^{\nabla }\cong \mathrm {Hom}_{\mathcal {C}}(\mathcal {R},M)$ (see [Reference KedlayaKed10, Deifnition 5.3.2]). To prove part (iii), by dévissage, we may assume that ![]() $M$ is irreducible in
$M$ is irreducible in ![]() $\mathcal {C}$, in which case the assertion immediately follows from parts (i) and (ii).
$\mathcal {C}$, in which case the assertion immediately follows from parts (i) and (ii).
Corollary 4.7 The restriction of the functor ![]() $\mathbf {V}(-)$ to
$\mathbf {V}(-)$ to ![]() $\mathcal {C}^{\mathrm {unip}}$ is faithfully exact, compatible with tensor products and direct sums, and preserves the rank. Moreover, if
$\mathcal {C}^{\mathrm {unip}}$ is faithfully exact, compatible with tensor products and direct sums, and preserves the rank. Moreover, if ![]() $M\in \mathcal {C}^{\mathrm {unip}}$, then there exists a functorial isomorphism
$M\in \mathcal {C}^{\mathrm {unip}}$, then there exists a functorial isomorphism ![]() $\mathbf {V}(M)\otimes _K\mathcal {R}_{\rm log}\cong M\otimes _{\mathcal {R}}\mathcal {R}_{\rm log}$ of
$\mathbf {V}(M)\otimes _K\mathcal {R}_{\rm log}\cong M\otimes _{\mathcal {R}}\mathcal {R}_{\rm log}$ of ![]() $\nabla$-modules over
$\nabla$-modules over ![]() $\mathcal {R}_{\rm log}$.
$\mathcal {R}_{\rm log}$.
Proof. Note that if ![]() $M\in \mathcal {C}^{\mathrm {unip}}$, then the differential operator
$M\in \mathcal {C}^{\mathrm {unip}}$, then the differential operator ![]() $\partial _{M\otimes _{\mathcal {R}}\mathcal {R}_{\rm log}}:M\otimes _{\mathcal {R}}\mathcal {R}_{\rm log}\to M\otimes _{\mathcal {R}}\mathcal {R}_{\rm log}$ is surjective, which is easily seen by reducing to Lemma 4.4. This fact implies the faithful exactness of the restriction of
$\partial _{M\otimes _{\mathcal {R}}\mathcal {R}_{\rm log}}:M\otimes _{\mathcal {R}}\mathcal {R}_{\rm log}\to M\otimes _{\mathcal {R}}\mathcal {R}_{\rm log}$ is surjective, which is easily seen by reducing to Lemma 4.4. This fact implies the faithful exactness of the restriction of ![]() $\mathbf {V}(-)$ to
$\mathbf {V}(-)$ to ![]() $\mathcal {C}^{\mathrm {unip}}$. Hence, by dévissage, we can easily see that
$\mathcal {C}^{\mathrm {unip}}$. Hence, by dévissage, we can easily see that ![]() $\mathbf {V}(M)\otimes _K\mathcal {R}_{\rm log}\cong M\otimes _{\mathcal {R}}\mathcal {R}_{\rm log}$ for
$\mathbf {V}(M)\otimes _K\mathcal {R}_{\rm log}\cong M\otimes _{\mathcal {R}}\mathcal {R}_{\rm log}$ for ![]() $M\in \mathcal {C}^{\mathrm {unip}}$, which implies the rest of the assertion.
$M\in \mathcal {C}^{\mathrm {unip}}$, which implies the rest of the assertion.
Lemma 4.8 Let ![]() $M$ be a
$M$ be a ![]() $\nabla$-module over
$\nabla$-module over ![]() $\mathcal {R}$.
$\mathcal {R}$.
(i) There exists a maximum unipotent subobject
 $U(M)$ of
$U(M)$ of  $M$. Moreover, we have a canonical isomorphism
$M$. Moreover, we have a canonical isomorphism  $\mathbf {V}(U(M))\cong \mathbf {V}(M)$, and
$\mathbf {V}(U(M))\cong \mathbf {V}(M)$, and  $\mathbf {V}(M/U(M))=0$.
$\mathbf {V}(M/U(M))=0$.(ii) Let
 $n:=\mathrm {rank}_{\mathcal {R}}M$. Then,
$n:=\mathrm {rank}_{\mathcal {R}}M$. Then,  $M$ is unipotent (respectively, trivial) if and only if
$M$ is unipotent (respectively, trivial) if and only if  $\dim _K\mathbf {V}(M)=n$ (respectively,
$\dim _K\mathbf {V}(M)=n$ (respectively,  $\dim _KM^{\nabla }=n$).
$\dim _KM^{\nabla }=n$).
Proof. (i) Let ![]() $N$ is any maximal unipotent subobject of
$N$ is any maximal unipotent subobject of ![]() $M$. If
$M$. If ![]() $N'$ is a unipotent subobject of
$N'$ is a unipotent subobject of ![]() $M$, then
$M$, then ![]() $N+N'$ is also unipotent, hence,
$N+N'$ is also unipotent, hence, ![]() $N+N'=N$, i.e.
$N+N'=N$, i.e. ![]() $N'\subset N$. Hence,
$N'\subset N$. Hence, ![]() $N$ is a maximum unipotent subobject of
$N$ is a maximum unipotent subobject of ![]() $M$. For the rest of the assertion, it suffices to prove that
$M$. For the rest of the assertion, it suffices to prove that ![]() $\mathbf {V}(M/U(M))=0$. The inverse image
$\mathbf {V}(M/U(M))=0$. The inverse image ![]() $U'$ of
$U'$ of ![]() $U(M/U(M))$ under the projection
$U(M/U(M))$ under the projection ![]() $M\to M/U(M)$ is a unipotent subobject of
$M\to M/U(M)$ is a unipotent subobject of ![]() $M$. Hence,
$M$. Hence, ![]() $U'=U(M)$, that is,
$U'=U(M)$, that is, ![]() $U(M/U(M))=0$. Therefore, any morphism
$U(M/U(M))=0$. Therefore, any morphism ![]() $\mathcal {R}\to M/U(M)$ of
$\mathcal {R}\to M/U(M)$ of ![]() $\nabla$-modules over
$\nabla$-modules over ![]() $\mathcal {R}$ has image
$\mathcal {R}$ has image ![]() $0$, i.e.
$0$, i.e.![]() $(M/U(M))^{\nabla }\cong \mathrm {Hom}_{\mathcal {C}}(\mathcal {R},M/U(M))=0$, which implies the assertion by Lemma 4.6(ii).
$(M/U(M))^{\nabla }\cong \mathrm {Hom}_{\mathcal {C}}(\mathcal {R},M/U(M))=0$, which implies the assertion by Lemma 4.6(ii).
(ii) As ![]() $\dim _K\mathbf {V}(M)=\mathrm {rank}_{\mathcal {R}}U(M)$ by part (i) and Corollary 4.7,
$\dim _K\mathbf {V}(M)=\mathrm {rank}_{\mathcal {R}}U(M)$ by part (i) and Corollary 4.7, ![]() $M$ is unipotent if and only if
$M$ is unipotent if and only if ![]() $\dim _K\mathbf {V}(M)=n$. If
$\dim _K\mathbf {V}(M)=n$. If ![]() $M$ is trivial, then we obviously have
$M$ is trivial, then we obviously have ![]() $\dim _KM^{\nabla }=n$. Conversely, if
$\dim _KM^{\nabla }=n$. Conversely, if ![]() $\dim _KM^{\nabla }=n$, then
$\dim _KM^{\nabla }=n$, then ![]() $M$ is trivial since the injection
$M$ is trivial since the injection ![]() $M^{\nabla }\otimes _K\mathcal {R}\hookrightarrow M$ in Lemma 4.6(iii) is an isomorphism by comparing ranks.
$M^{\nabla }\otimes _K\mathcal {R}\hookrightarrow M$ in Lemma 4.6(iii) is an isomorphism by comparing ranks.
In the rest of this subsection, we study the behavior of ![]() $\nabla$-modules over
$\nabla$-modules over ![]() $\mathcal {R}$ under base changes of the coefficient field
$\mathcal {R}$ under base changes of the coefficient field ![]() $K$.
$K$.
Notation 3 Let ![]() $(K',\varphi _{K'},q)$ be an extension of
$(K',\varphi _{K'},q)$ be an extension of ![]() $(K,\varphi _K,q)$ in the sense of Definition 1.1. We put
$(K,\varphi _K,q)$ in the sense of Definition 1.1. We put ![]() $\mathcal {R}_{K',{\rm log}}=\mathcal {R}_{K'}[\ell _X]$, where we regard
$\mathcal {R}_{K',{\rm log}}=\mathcal {R}_{K'}[\ell _X]$, where we regard ![]() $X$ as an element of
$X$ as an element of ![]() $\mathcal {O}_{K'}[\![t]\!]$. By abuse of notation, we denote the inclusions
$\mathcal {O}_{K'}[\![t]\!]$. By abuse of notation, we denote the inclusions ![]() $\mathcal {R}\to \mathcal {R}_{K'}$ and
$\mathcal {R}\to \mathcal {R}_{K'}$ and ![]() $\mathcal {R}_{\rm log}\to \mathcal {R}_{K',{\rm log}}$ by
$\mathcal {R}_{\rm log}\to \mathcal {R}_{K',{\rm log}}$ by ![]() $\psi$.
$\psi$.
Lemma 4.9 Let ![]() $M$ be a
$M$ be a ![]() $\nabla$-module over
$\nabla$-module over ![]() $\mathcal {R}$. If
$\mathcal {R}$. If ![]() $M^{\nabla }=0$, then
$M^{\nabla }=0$, then ![]() $(\psi ^*M)^{\nabla }=0$.
$(\psi ^*M)^{\nabla }=0$.
Proof. Assume that ![]() $(\psi ^*M)\neq 0$. We prove that
$(\psi ^*M)\neq 0$. We prove that ![]() $M^{\nabla }\neq 0$. We extend
$M^{\nabla }\neq 0$. We extend ![]() $\mathrm {id}_K:K\to K$ to a bounded
$\mathrm {id}_K:K\to K$ to a bounded ![]() $K$-linear map
$K$-linear map ![]() $\chi :K'\to K$ by the
$\chi :K'\to K$ by the ![]() $p$-adic Hahn–Banach theorem [Reference RobertRob00, 4.7]. We define the
$p$-adic Hahn–Banach theorem [Reference RobertRob00, 4.7]. We define the ![]() $\mathcal {R}$-linear map
$\mathcal {R}$-linear map ![]() $\chi ':\mathcal {R}_{K'}\to \mathcal {R};\sum _{i\in \mathbb {Z}}x_it^i\mapsto \sum _{i\in \mathbb {Z}}\chi (x_i)t^i$. Then, the map
$\chi ':\mathcal {R}_{K'}\to \mathcal {R};\sum _{i\in \mathbb {Z}}x_it^i\mapsto \sum _{i\in \mathbb {Z}}\chi (x_i)t^i$. Then, the map ![]() $M\otimes _{\mathcal {R}}\mathcal {R}_{K'}\to M;m\otimes r'\mapsto \chi '(r')m$ commutes with differential operators. Thus, we obtain a map
$M\otimes _{\mathcal {R}}\mathcal {R}_{K'}\to M;m\otimes r'\mapsto \chi '(r')m$ commutes with differential operators. Thus, we obtain a map ![]() $\chi '':(\psi ^*M)^{\nabla }\to M^{\nabla }$. We have only to prove
$\chi '':(\psi ^*M)^{\nabla }\to M^{\nabla }$. We have only to prove ![]() $\chi ''\neq 0$. Let
$\chi ''\neq 0$. Let ![]() $x$ be a nonzero element of
$x$ be a nonzero element of ![]() $(\psi ^*M)^{\nabla }$, and
$(\psi ^*M)^{\nabla }$, and ![]() $e_1,\dots ,e_n$ a basis of
$e_1,\dots ,e_n$ a basis of ![]() $M$. We write
$M$. We write ![]() $x=e_1\otimes r_1+\dots +e_n\otimes r_n$ with
$x=e_1\otimes r_1+\dots +e_n\otimes r_n$ with ![]() $r_j=\sum _{i\in \mathbb {Z}}r_{ij}t^i\in \mathcal {R}_{K'}$. By
$r_j=\sum _{i\in \mathbb {Z}}r_{ij}t^i\in \mathcal {R}_{K'}$. By ![]() $x\neq 0$, we have
$x\neq 0$, we have ![]() $r_{ij}\in (K')^{\times }$ for some
$r_{ij}\in (K')^{\times }$ for some ![]() $i,j$. Then,
$i,j$. Then, ![]() $\chi ''(x/r_{ij})=\chi '(r_1/r_{ij})e_1+\dots +\chi '(r_j/r_{ij})e_j+\dots +\chi '(r_n/r_{ij})e_n$ is nonzero because the coefficient of
$\chi ''(x/r_{ij})=\chi '(r_1/r_{ij})e_1+\dots +\chi '(r_j/r_{ij})e_j+\dots +\chi '(r_n/r_{ij})e_n$ is nonzero because the coefficient of ![]() $t^i$ in
$t^i$ in ![]() $\chi '(r_j/r_{ij})$ is equal to
$\chi '(r_j/r_{ij})$ is equal to ![]() $1$.
$1$.
Proposition 4.10 Let ![]() $M$ be a
$M$ be a ![]() $\nabla$-module over
$\nabla$-module over ![]() $\mathcal {R}$. Then, the canonical maps
$\mathcal {R}$. Then, the canonical maps
are isomorphisms. In particular, ![]() $M$ is unipotent (respectively, trivial) if and only if
$M$ is unipotent (respectively, trivial) if and only if ![]() $\psi ^*M$ is unipotent (respectively, trivial).
$\psi ^*M$ is unipotent (respectively, trivial).
Proof. Since ![]() $M^{\nabla }\cong \mathbf {V}(M)^{N_X=0}$ and
$M^{\nabla }\cong \mathbf {V}(M)^{N_X=0}$ and ![]() $(\psi ^*M)^{\nabla }\cong \mathbf {V}(\psi ^*M)^{N_X=0}$, we have only to prove that the second map is an isomorphism. We have
$(\psi ^*M)^{\nabla }\cong \mathbf {V}(\psi ^*M)^{N_X=0}$, we have only to prove that the second map is an isomorphism. We have ![]() $\mathbf {V}(M/U(M))=0$ by Lemma 4.8(i), hence,
$\mathbf {V}(M/U(M))=0$ by Lemma 4.8(i), hence, ![]() $\mathbf {V}(\psi ^*M/\psi ^*(U(M)))=0$ by Lemma 4.9. Therefore, we have a canonical isomorphism
$\mathbf {V}(\psi ^*M/\psi ^*(U(M)))=0$ by Lemma 4.9. Therefore, we have a canonical isomorphism ![]() $\mathbf {V}(\psi ^*(U(M)))\cong \mathbf {V}(\psi ^*M)$. Hence, after replacing
$\mathbf {V}(\psi ^*(U(M)))\cong \mathbf {V}(\psi ^*M)$. Hence, after replacing ![]() $M$ by
$M$ by ![]() $U(M)$, we may assume that
$U(M)$, we may assume that ![]() $M\in \mathcal {C}^{\mathrm {unip}}$. Then, by dévissage, we may reduce to the case
$M\in \mathcal {C}^{\mathrm {unip}}$. Then, by dévissage, we may reduce to the case ![]() $M=\mathcal {R}$, in which case the assertion is trivial.
$M=\mathcal {R}$, in which case the assertion is trivial.
5. Logarithmic growth filtrations for  $(\varphi ,\nabla )$-modules over
$(\varphi ,\nabla )$-modules over  $\mathcal {R}^{\mathrm {bd}}$
$\mathcal {R}^{\mathrm {bd}}$
Assumption 5.1 In the rest of the paper, we assume that ![]() $\varphi _K$ is a
$\varphi _K$ is a ![]() $q$-power Frobenius lift on
$q$-power Frobenius lift on ![]() $K$. We also fix an extension
$K$. We also fix an extension ![]() $L$ of
$L$ of ![]() $K$ such that the residue field of
$K$ such that the residue field of ![]() $L$ is algebraically closed (Remark 1.2). Note that the residue field of
$L$ is algebraically closed (Remark 1.2). Note that the residue field of ![]() $L$ is strongly difference-closed [Reference KedlayaKed10, Proposition 14.3.4], i.e. satisfies Assumption 2.3.
$L$ is strongly difference-closed [Reference KedlayaKed10, Proposition 14.3.4], i.e. satisfies Assumption 2.3.
Convention 2. In the rest of this paper, unless otherwise is mentioned, a subquotient of a ![]() $(\varphi ,\nabla )$-module
$(\varphi ,\nabla )$-module ![]() $M$ over
$M$ over ![]() $\mathcal {R}^{\mathrm {bd}}$ (respectively,
$\mathcal {R}^{\mathrm {bd}}$ (respectively, ![]() $\mathcal {E}$) means a subquotient of
$\mathcal {E}$) means a subquotient of ![]() $M$ in the category of
$M$ in the category of ![]() $(\varphi ,\nabla )$-modules over
$(\varphi ,\nabla )$-modules over ![]() $\mathcal {R}^{\mathrm {bd}}$ (respectively,
$\mathcal {R}^{\mathrm {bd}}$ (respectively, ![]() $\mathcal {E}$).
$\mathcal {E}$).
In the following, we study ![]() $(\varphi ,\nabla )$-modules
$(\varphi ,\nabla )$-modules ![]() $M$ over
$M$ over ![]() $\mathcal {R}^{\mathrm {bd}}$ such that
$\mathcal {R}^{\mathrm {bd}}$ such that ![]() $M_{\mathcal {R}}$ is unipotent as a
$M_{\mathcal {R}}$ is unipotent as a ![]() $\nabla$-module over
$\nabla$-module over ![]() $\mathcal {R}$. Note that these
$\mathcal {R}$. Note that these ![]() $M$ form an abelian full subcategory of the category of
$M$ form an abelian full subcategory of the category of ![]() $(\varphi ,\nabla )$-modules over
$(\varphi ,\nabla )$-modules over ![]() $\mathcal {R}^{\mathrm {bd}}$, which is closed under formation of direct sums, extensions, internal Homs, duals, and tensor products. We define
$\mathcal {R}^{\mathrm {bd}}$, which is closed under formation of direct sums, extensions, internal Homs, duals, and tensor products. We define ![]() $V(M)$ and
$V(M)$ and ![]() $\mathrm {Sol}(M)$, which are
$\mathrm {Sol}(M)$, which are ![]() $\varphi$-modules over
$\varphi$-modules over ![]() $K$ called the sets of analytic horizontal sections and analytic solutions, respectively, equipped with a perfect pairing
$K$ called the sets of analytic horizontal sections and analytic solutions, respectively, equipped with a perfect pairing ![]() $V(M)\otimes _K \mathrm {Sol}(M)\to K$ called the canonical pairing. We put
$V(M)\otimes _K \mathrm {Sol}(M)\to K$ called the canonical pairing. We put
 \begin{gather*} V(M):=(M\otimes_{\mathcal{R}^{\mathrm{bd}}}\mathcal{R}_{{\rm log}})^{\nabla},\\ \mathrm{Sol}(M):=\{f\in\mathrm{Hom}_{\mathcal{R}^{\mathrm{bd}}}(M,\mathcal{R}_{{\rm log}});\partial\circ f=f\circ\partial_M\}. \end{gather*}
\begin{gather*} V(M):=(M\otimes_{\mathcal{R}^{\mathrm{bd}}}\mathcal{R}_{{\rm log}})^{\nabla},\\ \mathrm{Sol}(M):=\{f\in\mathrm{Hom}_{\mathcal{R}^{\mathrm{bd}}}(M,\mathcal{R}_{{\rm log}});\partial\circ f=f\circ\partial_M\}. \end{gather*}
Then, both ![]() $V(M)$ and
$V(M)$ and ![]() $\mathrm {Sol}(M)$ are regarded as
$\mathrm {Sol}(M)$ are regarded as ![]() $\varphi$-modules over
$\varphi$-modules over ![]() $K$, where
$K$, where ![]() $\varphi _{\mathrm {Sol}(M)}$ is defined as the unique
$\varphi _{\mathrm {Sol}(M)}$ is defined as the unique ![]() $\varphi _K$-semilinear map satisfying
$\varphi _K$-semilinear map satisfying ![]() $\varphi _{\mathrm {Sol}(M)}(f)(\varphi _M(m))=\varphi (f(m))$ for
$\varphi _{\mathrm {Sol}(M)}(f)(\varphi _M(m))=\varphi (f(m))$ for ![]() $f\in \mathrm {Sol}(M)$ and
$f\in \mathrm {Sol}(M)$ and ![]() $m\in M$. We define the canonical pairing as that induced by the
$m\in M$. We define the canonical pairing as that induced by the ![]() $K$-bilinear map
$K$-bilinear map
where ![]() $f'$ denotes the linear extension of
$f'$ denotes the linear extension of ![]() $f$ to
$f$ to ![]() $M\otimes _{\mathcal {R}^{\mathrm {bd}}}\mathcal {R}_{\rm log}\to \mathcal {R}_{\rm log}$. It is straightforward to check that the canonical pairing is perfect, and
$M\otimes _{\mathcal {R}^{\mathrm {bd}}}\mathcal {R}_{\rm log}\to \mathcal {R}_{\rm log}$. It is straightforward to check that the canonical pairing is perfect, and ![]() $V(-)$ (respectively,
$V(-)$ (respectively, ![]() $\mathrm {Sol}(-)$) forms a covariant (respectively, contravariant) functor, which is faithfully exact, compatible with direct sums and tensor products, and preserves the rank. In the following, unless otherwise mentioned, when
$\mathrm {Sol}(-)$) forms a covariant (respectively, contravariant) functor, which is faithfully exact, compatible with direct sums and tensor products, and preserves the rank. In the following, unless otherwise mentioned, when ![]() $S$ is a subset of
$S$ is a subset of ![]() $\mathrm {Sol}(M)$, let
$\mathrm {Sol}(M)$, let ![]() $S^{\perp }$ denote the orthogonal part of
$S^{\perp }$ denote the orthogonal part of ![]() $S$ with respect to the above bilinear map
$S$ with respect to the above bilinear map ![]() $V(M)\times \mathrm {Sol}(M)\to K$.
$V(M)\times \mathrm {Sol}(M)\to K$.
We define the Frobenius slope filtration ![]() $S_{\bullet }(V(M))$ and
$S_{\bullet }(V(M))$ and ![]() $S_{\bullet }(\mathrm {Sol}(M))$ of
$S_{\bullet }(\mathrm {Sol}(M))$ of ![]() $V(M)$ and
$V(M)$ and ![]() $\mathrm {Sol}(M)$, respectively, as in § 1. For
$\mathrm {Sol}(M)$, respectively, as in § 1. For ![]() $\lambda \in \mathbb {R}$, we have the natural duality
$\lambda \in \mathbb {R}$, we have the natural duality
We define the growth filtrations ![]() $\mathrm {Sol}_{\bullet }(M)$ and
$\mathrm {Sol}_{\bullet }(M)$ and ![]() $V(M)^{\bullet }$ of
$V(M)^{\bullet }$ of ![]() $\mathrm {Sol}(M)$ and
$\mathrm {Sol}(M)$ and ![]() $V(M)$, respectively, by
$V(M)$, respectively, by ![]() $\mathrm {Sol}_{\lambda }(M):=\{f\in \mathrm {Sol}(M);f(M)\subset \mathrm {Fil}_{\lambda }\mathcal {R}_{\rm log}\}$ and
$\mathrm {Sol}_{\lambda }(M):=\{f\in \mathrm {Sol}(M);f(M)\subset \mathrm {Fil}_{\lambda }\mathcal {R}_{\rm log}\}$ and ![]() $V(M)^{\lambda }=\mathrm {Sol}_{\lambda }(M)^{\perp }$ for
$V(M)^{\lambda }=\mathrm {Sol}_{\lambda }(M)^{\perp }$ for ![]() $\lambda \in \mathbb {R}$. As in the literature, we may call
$\lambda \in \mathbb {R}$. As in the literature, we may call ![]() $V(M)^{\bullet }$ the special log-growth filtration of
$V(M)^{\bullet }$ the special log-growth filtration of ![]() $M$. Then,
$M$. Then, ![]() $V(M)^{\bullet }$ (respectively,
$V(M)^{\bullet }$ (respectively, ![]() $\mathrm {Sol}_{\bullet }(M)$) is a decreasing (respectively, increasing) filtration of
$\mathrm {Sol}_{\bullet }(M)$) is a decreasing (respectively, increasing) filtration of ![]() $\varphi$-submodules of
$\varphi$-submodules of ![]() $V(M)$ (respectively,
$V(M)$ (respectively, ![]() $\mathrm {Sol}(M)$) by Corollary 3.7(ii), and
$\mathrm {Sol}(M)$) by Corollary 3.7(ii), and ![]() $V(-)/V(-)^{\lambda }$ (respectively,
$V(-)/V(-)^{\lambda }$ (respectively, ![]() $\mathrm {Sol}_{\lambda }(-)$) is regarded as a right-exact quotient functor (respectively, left-exact subfunctor) of
$\mathrm {Sol}_{\lambda }(-)$) is regarded as a right-exact quotient functor (respectively, left-exact subfunctor) of ![]() $V(-)$ (respectively,
$V(-)$ (respectively, ![]() $\mathrm {Sol}(-)$), which commutes with direct sums and
$\mathrm {Sol}(-)$), which commutes with direct sums and ![]() $d$-pushforwards.
$d$-pushforwards.
Remark 5.2 (Independence of the choice of the branch of log) As a consequence of Lemma 4.3, the isomorphism class of ![]() $V(M)^{\bullet }$ (respectively,
$V(M)^{\bullet }$ (respectively, ![]() $\mathrm {Sol}_{\bullet }(M)$) in the category of vector spaces over
$\mathrm {Sol}_{\bullet }(M)$) in the category of vector spaces over ![]() $K$ with decreasing (respectively, increasing) filtrations is independent of the choice of the branch
$K$ with decreasing (respectively, increasing) filtrations is independent of the choice of the branch ![]() $\ell _X$ of log. Note that the growth filtrations for
$\ell _X$ of log. Note that the growth filtrations for ![]() $M$ in the case
$M$ in the case ![]() $X=t$ are already studied in [Reference OhkuboOhk17], where
$X=t$ are already studied in [Reference OhkuboOhk17], where ![]() $\mathcal {R}_{\rm log},V(M)^{(\bullet )}$, and
$\mathcal {R}_{\rm log},V(M)^{(\bullet )}$, and ![]() $\mathrm {Sol}_{(\bullet )}(M)$ are denoted by
$\mathrm {Sol}_{(\bullet )}(M)$ are denoted by ![]() $\Gamma _{\log ,\mathrm {an},\mathrm {con}},\mathcal {V}(M)^{(\bullet )}$, and
$\Gamma _{\log ,\mathrm {an},\mathrm {con}},\mathcal {V}(M)^{(\bullet )}$, and ![]() $\mathfrak {Sol}_{(\bullet )}(M)$, respectively.
$\mathfrak {Sol}_{(\bullet )}(M)$, respectively.
First proof of part (i) of Theorem 0.1 By Remark 5.2, we may assume that ![]() $X=t$, in which case the assertion is nothing but [Reference OhkuboOhk17, Theorem 4.19].
$X=t$, in which case the assertion is nothing but [Reference OhkuboOhk17, Theorem 4.19].
We have the following relations between growth filtrations and Frobenius slope filtrations, which are analogues of [Reference Chiarellotto and TsuzukiCT11, Theorem 2.3 (2)] for ![]() $(\varphi ,\nabla )$-modules over
$(\varphi ,\nabla )$-modules over ![]() $\mathcal {R}^{\mathrm {bd}}$.
$\mathcal {R}^{\mathrm {bd}}$.
Proposition 5.3 (Cf. [Reference OhkuboOhk17, Proposition 4.1(i)])
Let ![]() $M$ be a
$M$ be a ![]() $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over ![]() $\mathcal {R}^{\mathrm {bd}}$ such that
$\mathcal {R}^{\mathrm {bd}}$ such that ![]() $M_{\mathcal {R}}$ is unipotent as a
$M_{\mathcal {R}}$ is unipotent as a ![]() $\nabla$-module over
$\nabla$-module over ![]() $\mathcal {R}$. Then, we have
$\mathcal {R}$. Then, we have
or, equivalently,
for an arbitrary real number ![]() $\lambda$.
$\lambda$.
See § 8 for the proof.
Remark 5.4 (i) The first displayed relation may be written as ![]() $V(M)^{\lambda }\subset S_{\lambda -\lambda _{\rm max}(M_{\mathcal {E}})}(V(M^\vee ))^{\perp }$ à la [Reference Chiarellotto and TsuzukiCT11, Theorem 2.3(2)] by Lemma 1.7(II)(vi), where the orthogonal part is taken with respect to the natural
$V(M)^{\lambda }\subset S_{\lambda -\lambda _{\rm max}(M_{\mathcal {E}})}(V(M^\vee ))^{\perp }$ à la [Reference Chiarellotto and TsuzukiCT11, Theorem 2.3(2)] by Lemma 1.7(II)(vi), where the orthogonal part is taken with respect to the natural ![]() $K$-bilinear map
$K$-bilinear map ![]() $V(M)\times V(M^\vee )\to K$.
$V(M)\times V(M^\vee )\to K$.
(ii) In terms of Newton polygons, Proposition 5.3 says that the Newton polygon of ![]() $V(M)^{\bullet }$ lies on or below that of
$V(M)^{\bullet }$ lies on or below that of ![]() $S_{\lambda _{\rm max}(M_{\mathcal {E}})-\bullet }(V(M))$ (Proposition 10.3(i)).
$S_{\lambda _{\rm max}(M_{\mathcal {E}})-\bullet }(V(M))$ (Proposition 10.3(i)).
Corollary 5.5 Let notation be as in Proposition 5.3. Then, the filtrations ![]() $V(M)^{\bullet }$ and
$V(M)^{\bullet }$ and ![]() $\mathrm {Sol}_{\bullet }(M)$ are exhaustive and separated.
$\mathrm {Sol}_{\bullet }(M)$ are exhaustive and separated.
Proof. By duality, we have only to prove the exhaustivity of ![]() $\mathrm {Sol}_{\bullet }(M)$. Let
$\mathrm {Sol}_{\bullet }(M)$. Let ![]() $\mu$ denote the maximum Frobenius slope of
$\mu$ denote the maximum Frobenius slope of ![]() $\mathrm {Sol}(M)$. Then, we have
$\mathrm {Sol}(M)$. Then, we have ![]() $\mathrm {Sol}_{\mu +\lambda _{\rm max}(M_{\mathcal {E}})}(M)=\mathrm {Sol}(M)$ by the second displayed relation in Proposition 5.3 with
$\mathrm {Sol}_{\mu +\lambda _{\rm max}(M_{\mathcal {E}})}(M)=\mathrm {Sol}(M)$ by the second displayed relation in Proposition 5.3 with ![]() $\lambda =\mu +\lambda _{\rm max}(M_{\mathcal {E}})$.
$\lambda =\mu +\lambda _{\rm max}(M_{\mathcal {E}})$.
Finally, we briefly recall some results on the log-growth filtrations of ![]() $(\varphi ,\nabla )$-modules over
$(\varphi ,\nabla )$-modules over ![]() $\mathcal {E}$. In the rest of this section, let
$\mathcal {E}$. In the rest of this section, let ![]() $M$ be a
$M$ be a ![]() $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over ![]() $\mathcal {E}$. The log-growth filtration
$\mathcal {E}$. The log-growth filtration ![]() $M^{\bullet }$ (see the introduction) is a decreasing filtration of subobjects of
$M^{\bullet }$ (see the introduction) is a decreasing filtration of subobjects of ![]() $M$ indexed by
$M$ indexed by ![]() $\mathbb {R}$, which is exhaustive and separated. Moreover, the correspondence
$\mathbb {R}$, which is exhaustive and separated. Moreover, the correspondence ![]() $M\mapsto M^{\lambda }$ forms a covariant endofunctor on the category of
$M\mapsto M^{\lambda }$ forms a covariant endofunctor on the category of ![]() $(\varphi ,\nabla )$-modules over
$(\varphi ,\nabla )$-modules over ![]() $\mathcal {E}$ (see [Reference Chiarellotto and TsuzukiCT09, Proposition 3.6]). Furthermore,
$\mathcal {E}$ (see [Reference Chiarellotto and TsuzukiCT09, Proposition 3.6]). Furthermore, ![]() $M\neq 0$ implies
$M\neq 0$ implies ![]() $M^{\lambda }\neq M$ for
$M^{\lambda }\neq M$ for ![]() $\lambda \geqslant 0$ (see [Reference Chiarellotto and TsuzukiCT09, Theorem 3.2(4)]). Recall that we say that
$\lambda \geqslant 0$ (see [Reference Chiarellotto and TsuzukiCT09, Theorem 3.2(4)]). Recall that we say that ![]() $M$ is PBQ if
$M$ is PBQ if ![]() $M/M^0$ is pure as a
$M/M^0$ is pure as a ![]() $\varphi$-module over
$\varphi$-module over ![]() $\mathcal {E}$ (see [Reference Chiarellotto and TsuzukiCT11, Definition 5.1(1)]). As a consequence of functoriality, if
$\mathcal {E}$ (see [Reference Chiarellotto and TsuzukiCT11, Definition 5.1(1)]). As a consequence of functoriality, if ![]() $M$ is PBQ, then so is any quotient of
$M$ is PBQ, then so is any quotient of ![]() $M$ (see [Reference Chiarellotto and TsuzukiCT11, Proposition 5.3]). We define the Frobenius slope filtration
$M$ (see [Reference Chiarellotto and TsuzukiCT11, Proposition 5.3]). We define the Frobenius slope filtration ![]() $S_{\bullet }(M)$ of
$S_{\bullet }(M)$ of ![]() $M$ as in § 1. Then, we have analogues of Proposition 5.3 and Theorem 0.1.
$M$ as in § 1. Then, we have analogues of Proposition 5.3 and Theorem 0.1.
Theorem 5.6 [Reference Chiarellotto and TsuzukiCT11, Theorems 2.3(1) and 7.1]
(i) We have
 $M^{\lambda }\subset \bigcup _{\mu <\lambda _{\rm max}(M)-\lambda }S_{\mu }(M)$ for an arbitrary real number
$M^{\lambda }\subset \bigcup _{\mu <\lambda _{\rm max}(M)-\lambda }S_{\mu }(M)$ for an arbitrary real number  $\lambda$ with equality when
$\lambda$ with equality when  $M$ is PBQ.
$M$ is PBQ.(ii) We have
 $M^{\lambda }=\bigcup _{\mu >\lambda }M^{\mu }$ for an arbitrary real number
$M^{\lambda }=\bigcup _{\mu >\lambda }M^{\mu }$ for an arbitrary real number  $\lambda$. Moreover, the slope multiset of
$\lambda$. Moreover, the slope multiset of  $M^{\bullet }$ consists of rational numbers.
$M^{\bullet }$ consists of rational numbers.
6. Base change of the coefficient field
In this section, let notation be as in Notation 3. By abuse of notation, we denote the inclusions ![]() $\mathcal {R}^{\mathrm {bd}}\to \mathcal {R}_{K'}^{\mathrm {bd}}$ and
$\mathcal {R}^{\mathrm {bd}}\to \mathcal {R}_{K'}^{\mathrm {bd}}$ and ![]() $\mathcal {E}\to \mathcal {E}_{K'}$ by
$\mathcal {E}\to \mathcal {E}_{K'}$ by ![]() $\psi$. We prove that the base change functor
$\psi$. We prove that the base change functor ![]() $\psi ^*(-)$ respects the growth filtration (Lemma 6.2).
$\psi ^*(-)$ respects the growth filtration (Lemma 6.2).
Lemma 6.1 (Cf. [Reference Chiarellotto and TsuzukiCT11, Proposition 2.1])
Let ![]() $\star \in \{\,,\log \}$.
$\star \in \{\,,\log \}$.
(i) The canonical ring homomorphism
 $\mathcal {R}_{\star }\otimes _K{K'}\to \mathcal {R}_{K',\star }$ is injective. Moreover,
$\mathcal {R}_{\star }\otimes _K{K'}\to \mathcal {R}_{K',\star }$ is injective. Moreover,  $(\mathrm {Fil}_{\lambda }\mathcal {R}_{\star })\otimes _KK'$ maps
$(\mathrm {Fil}_{\lambda }\mathcal {R}_{\star })\otimes _KK'$ maps  $\mathrm {Fil}_{\lambda }\mathcal {R}_{K',\star }$.
$\mathrm {Fil}_{\lambda }\mathcal {R}_{K',\star }$.(ii) Let
 $c_1,\dots ,c_n\in K'$ be
$c_1,\dots ,c_n\in K'$ be  $K$-linearly independent, and
$K$-linearly independent, and  $r_1,\dots ,r_n\in \mathcal {R}_{\star }$. If
$r_1,\dots ,r_n\in \mathcal {R}_{\star }$. If  $\sum _{j=1}^nc_jr_j\in \mathrm {Fil}_{\lambda }\mathcal {R}_{K',\star }$, then we have
$\sum _{j=1}^nc_jr_j\in \mathrm {Fil}_{\lambda }\mathcal {R}_{K',\star }$, then we have  $r_j\in \mathrm {Fil}_{\lambda }\mathcal {R}_{\star }$ for all
$r_j\in \mathrm {Fil}_{\lambda }\mathcal {R}_{\star }$ for all  $j$.
$j$.
Proof. We may easily reduce to the case ![]() $\star =(empty)$.
$\star =(empty)$.
(i) The second assertion follows from Corollary 3.7. We prove the first. Assume that ![]() $x$ belongs to the kernel of the map
$x$ belongs to the kernel of the map ![]() $\mathcal {R}\otimes _KK'\to \mathcal {R}_{K'}$. Write
$\mathcal {R}\otimes _KK'\to \mathcal {R}_{K'}$. Write ![]() $x=\sum _{j=1}^nr_j\otimes c_j\in \mathcal {R}\otimes _KK'$ with
$x=\sum _{j=1}^nr_j\otimes c_j\in \mathcal {R}\otimes _KK'$ with ![]() $n$ minimal. Then, the
$n$ minimal. Then, the ![]() $c_{j}$'s are
$c_{j}$'s are ![]() $K$-linearly independent. Write
$K$-linearly independent. Write ![]() $r_j=\sum _{i\in \mathbb {Z}}r_{ij}t^i\in \mathcal {R}_K$ with
$r_j=\sum _{i\in \mathbb {Z}}r_{ij}t^i\in \mathcal {R}_K$ with ![]() $r_{ij}\in K$. By
$r_{ij}\in K$. By ![]() $0=\sum _{j=1}^nc_jr_j=\sum _{i\in \mathbb {Z}}(\sum _{j=1}^nc_jr_{ij})t^i$, we have
$0=\sum _{j=1}^nc_jr_j=\sum _{i\in \mathbb {Z}}(\sum _{j=1}^nc_jr_{ij})t^i$, we have ![]() $\sum _{j=1}^nc_jr_{ij}=0$, which implies
$\sum _{j=1}^nc_jr_{ij}=0$, which implies ![]() $r_{ij}=0$ for all
$r_{ij}=0$ for all ![]() $i,j$, i.e.
$i,j$, i.e. ![]() $x=0$.
$x=0$.
(ii) Write ![]() $r_j\in \mathcal {R}$ as above. Then,
$r_j\in \mathcal {R}$ as above. Then, ![]() $\sup _{i\geqslant 1}i^{-\lambda }|\sum _{j=1}^nc_jr_{ij}|<\infty$ by assumption and Corollary 3.6. By [Reference KedlayaKed10, Theorem 1.3.6], there exists a constant
$\sup _{i\geqslant 1}i^{-\lambda }|\sum _{j=1}^nc_jr_{ij}|<\infty$ by assumption and Corollary 3.6. By [Reference KedlayaKed10, Theorem 1.3.6], there exists a constant ![]() $C$ such that
$C$ such that
 \[ \sup\{|\alpha_1|,\dots,|\alpha_n|\}\leqslant C\bigg|\sum_{j=1}^nc_j\alpha_j\bigg| \forall \alpha_1,\dots,\alpha_n\in K. \]
\[ \sup\{|\alpha_1|,\dots,|\alpha_n|\}\leqslant C\bigg|\sum_{j=1}^nc_j\alpha_j\bigg| \forall \alpha_1,\dots,\alpha_n\in K. \]
Then, ![]() $r_1,\dots ,r_n\in \mathrm {Fil}_{\lambda }\mathcal {R}$ by
$r_1,\dots ,r_n\in \mathrm {Fil}_{\lambda }\mathcal {R}$ by
 \[ \sup_{j=1,\dots,n}\sup_{i\geqslant 1}i^{-\lambda}|r_{ij}|=\sup_{i\geqslant 1}\sup_{j=1,\dots,n}i^{-\lambda}|r_{ij}|\leqslant\sup_{i\geqslant 1}i^{-\lambda}C\bigg|\sum_{j=1}^nc_jr_{ij}\bigg|<\infty. \]
\[ \sup_{j=1,\dots,n}\sup_{i\geqslant 1}i^{-\lambda}|r_{ij}|=\sup_{i\geqslant 1}\sup_{j=1,\dots,n}i^{-\lambda}|r_{ij}|\leqslant\sup_{i\geqslant 1}i^{-\lambda}C\bigg|\sum_{j=1}^nc_jr_{ij}\bigg|<\infty. \]Lemma 6.2 (Cf. [Reference Chiarellotto and TsuzukiCT09, Proposition 1.10])
(i) Let
 $M$ be a
$M$ be a  $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over  $\mathcal {R}^{\mathrm {bd}}$ such that
$\mathcal {R}^{\mathrm {bd}}$ such that  $M_{\mathcal {R}}$ is unipotent as a
$M_{\mathcal {R}}$ is unipotent as a  $\nabla$-module over
$\nabla$-module over  $\mathcal {R}$. Then,
$\mathcal {R}$. Then,  $(\psi ^*M)_{\mathcal {R}_{K'}}$ is unipotent as a
$(\psi ^*M)_{\mathcal {R}_{K'}}$ is unipotent as a  $\nabla$-module over
$\nabla$-module over  $\mathcal {R}_{K'}$, and there exist canonical isomorphisms of
$\mathcal {R}_{K'}$, and there exist canonical isomorphisms of  $\varphi$-modules over
$\varphi$-modules over  $K'$
which are compatible with the canonical pairings. Moreover, these isomorphisms respectively induce isomorphisms
$K'$
which are compatible with the canonical pairings. Moreover, these isomorphisms respectively induce isomorphisms \begin{gather*} V(M)\otimes_K K'\to V(\psi^*M),\\ \mathrm{Sol}(M)\otimes_KK'\to \mathrm{Sol}(\psi^*M), \end{gather*}
\begin{gather*} V(M)\otimes_K K'\to V(\psi^*M),\\ \mathrm{Sol}(M)\otimes_KK'\to \mathrm{Sol}(\psi^*M), \end{gather*} \begin{gather*} V(M)^{{\bullet}}\otimes_K K'\cong V(\psi^*M)^{{\bullet}},\\ \mathrm{Sol}_{{\bullet}}(M)\otimes_K K'\cong \mathrm{Sol}_{{\bullet}}(\psi^*M). \end{gather*}
\begin{gather*} V(M)^{{\bullet}}\otimes_K K'\cong V(\psi^*M)^{{\bullet}},\\ \mathrm{Sol}_{{\bullet}}(M)\otimes_K K'\cong \mathrm{Sol}_{{\bullet}}(\psi^*M). \end{gather*}(ii) (See [Reference Chiarellotto and TsuzukiCT09, Proposition 1.10] and [Reference Chiarellotto and TsuzukiCT11, Proposition 2.1].) Let
 $M$ be a
$M$ be a  $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over  $K[\![t]\!]_0$. Then, we have analogous isomorphisms as in part (i).
$K[\![t]\!]_0$. Then, we have analogous isomorphisms as in part (i).(iii) Let
 $M$ be a
$M$ be a  $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over  $\mathcal {E}$. Then, there exists a canonical isomorphism
$\mathcal {E}$. Then, there exists a canonical isomorphism
 \[ \psi^*(M^{{\bullet}})\cong (\psi^*M)^{{\bullet}}. \]
\[ \psi^*(M^{{\bullet}})\cong (\psi^*M)^{{\bullet}}. \]
Proof. (i) The first assertion follows from Proposition 4.10. To prove the second assertion, by duality, we have only to prove that ![]() $\mathrm {Sol}_{\lambda }(M)\otimes _KK'\cong \mathrm {Sol}_{\lambda }(\psi ^*M)$ for
$\mathrm {Sol}_{\lambda }(M)\otimes _KK'\cong \mathrm {Sol}_{\lambda }(\psi ^*M)$ for ![]() $\lambda \in \mathbb {R}$. For
$\lambda \in \mathbb {R}$. For ![]() $f\in \mathrm {Sol}(M)$, let
$f\in \mathrm {Sol}(M)$, let ![]() $\beta (f)\in \mathrm {Sol}(\psi ^*M)$ be the image of
$\beta (f)\in \mathrm {Sol}(\psi ^*M)$ be the image of ![]() $f\otimes 1$ under the map
$f\otimes 1$ under the map ![]() $\mathrm {Sol}(M)\otimes _KK'\to \mathrm {Sol}(\psi ^*M)$. We claim that
$\mathrm {Sol}(M)\otimes _KK'\to \mathrm {Sol}(\psi ^*M)$. We claim that ![]() $f\in \mathrm {Sol}_{\lambda }(M)$ if and only if
$f\in \mathrm {Sol}_{\lambda }(M)$ if and only if ![]() $\beta (f)\in \mathrm {Sol}_{\lambda }(\psi ^*M)$. By definition,
$\beta (f)\in \mathrm {Sol}_{\lambda }(\psi ^*M)$. By definition, ![]() $\beta (f)$ coincides with the composition
$\beta (f)$ coincides with the composition
where the second map is the multiplication map. Hence, ![]() $\beta (f)(\psi ^*M)=f(M)\cdot \mathcal {R}_{K'}^{\mathrm {bd}}=f(M)\cdot \mathrm {Fil}_{0}\mathcal {R}_{K',{\rm log}}$ by Corollary 3.7(iii). Therefore, we obtain the claim by using Corollary 3.7(i) and the fact
$\beta (f)(\psi ^*M)=f(M)\cdot \mathcal {R}_{K'}^{\mathrm {bd}}=f(M)\cdot \mathrm {Fil}_{0}\mathcal {R}_{K',{\rm log}}$ by Corollary 3.7(iii). Therefore, we obtain the claim by using Corollary 3.7(i) and the fact ![]() $\mathcal {R}_{\rm log}\cap \mathrm {Fil}_{\lambda }\mathcal {R}_{K',{\rm log}}=\mathrm {Fil}_{\lambda }\mathcal {R}_{\rm log}$.
$\mathcal {R}_{\rm log}\cap \mathrm {Fil}_{\lambda }\mathcal {R}_{K',{\rm log}}=\mathrm {Fil}_{\lambda }\mathcal {R}_{\rm log}$.
We fix a basis ![]() $\{c_j\}_{j\in J}$ of
$\{c_j\}_{j\in J}$ of ![]() $K'$ as a vector space over
$K'$ as a vector space over ![]() $K$. Let
$K$. Let ![]() $F\in \mathrm {Sol}(\psi ^*M)$. We can uniquely write
$F\in \mathrm {Sol}(\psi ^*M)$. We can uniquely write ![]() $F=\sum _{j\in J}c_j\beta (f_{j})$ with
$F=\sum _{j\in J}c_j\beta (f_{j})$ with ![]() $f_j\in \mathrm {Sol}(M)$ such that
$f_j\in \mathrm {Sol}(M)$ such that ![]() $f_{j}=0$ for all but finitely many
$f_{j}=0$ for all but finitely many ![]() $j$. By Lemma 6.1(ii),
$j$. By Lemma 6.1(ii), ![]() $F\in \mathrm {Sol}_{\lambda }(\psi ^*M)$ if and only if
$F\in \mathrm {Sol}_{\lambda }(\psi ^*M)$ if and only if ![]() $\beta (f_{j})\in \mathrm {Sol}_{\lambda }(\psi ^*M)$ for all
$\beta (f_{j})\in \mathrm {Sol}_{\lambda }(\psi ^*M)$ for all ![]() $j\in J$. Moreover, by the claim, the latter condition is equivalent to
$j\in J$. Moreover, by the claim, the latter condition is equivalent to ![]() $f_j\in \mathrm {Sol}_{\lambda }(M)$ for all
$f_j\in \mathrm {Sol}_{\lambda }(M)$ for all ![]() $j\in J$, which implies the assertion.
$j\in J$, which implies the assertion.
(ii) We may reduce to part (i) by Lemma 0.3.
(iii) Let notation be as in the introduction. We naturally extend ![]() $\tau :\mathcal {E}\to \mathcal {E}[\![X-t]\!]_0$ (respectively,
$\tau :\mathcal {E}\to \mathcal {E}[\![X-t]\!]_0$ (respectively, ![]() $\psi :\mathcal {E}\to \mathcal {E}_{K'}$) to
$\psi :\mathcal {E}\to \mathcal {E}_{K'}$) to ![]() $\mathcal {E}_{K'}\to \mathcal {E}_{K'}[\![X-t]\!]_0$ (respectively,
$\mathcal {E}_{K'}\to \mathcal {E}_{K'}[\![X-t]\!]_0$ (respectively, ![]() $\mathcal {E}[\![X-t]\!]_0\to \mathcal {E}_{K'}[\![X-t]\!]_0;X-t\mapsto X-t$), which is denoted by
$\mathcal {E}[\![X-t]\!]_0\to \mathcal {E}_{K'}[\![X-t]\!]_0;X-t\mapsto X-t$), which is denoted by ![]() $\tau$ (respectively,
$\tau$ (respectively, ![]() $\psi$) for simplicity. As
$\psi$) for simplicity. As ![]() $\psi \circ \tau =\tau \circ \psi$, we have a natural isomorphism
$\psi \circ \tau =\tau \circ \psi$, we have a natural isomorphism ![]() $\psi ^*\circ \tau ^*\cong \tau ^*\circ \psi ^*$. Let
$\psi ^*\circ \tau ^*\cong \tau ^*\circ \psi ^*$. Let ![]() $\lambda \in \mathbb {R}$. By the definition of the log-growth filtration,
$\lambda \in \mathbb {R}$. By the definition of the log-growth filtration, ![]() $(\psi ^*M)^{\lambda }$ is characterized as a unique subobject
$(\psi ^*M)^{\lambda }$ is characterized as a unique subobject ![]() $U$ of
$U$ of ![]() $\psi ^*M$ such that there exists a canonical isomorphism
$\psi ^*M$ such that there exists a canonical isomorphism ![]() $V(\tau ^*U)\cong V(\tau ^*\psi ^*M)^{\lambda }$. Hence, we have only to prove
$V(\tau ^*U)\cong V(\tau ^*\psi ^*M)^{\lambda }$. Hence, we have only to prove ![]() $V(\tau ^*\psi ^*(M^{\lambda }))\cong V(\tau ^*\psi ^*M)^{\lambda }$. We have
$V(\tau ^*\psi ^*(M^{\lambda }))\cong V(\tau ^*\psi ^*M)^{\lambda }$. We have ![]() $V(\tau ^*\psi ^*(M^{\lambda }))\cong V(\psi ^*\tau ^*(M^{\lambda }))$ and
$V(\tau ^*\psi ^*(M^{\lambda }))\cong V(\psi ^*\tau ^*(M^{\lambda }))$ and ![]() $V(\tau ^*\psi ^*M)^{\lambda }\cong V(\psi ^*\tau ^*M)^{\lambda }$. By applying part (ii) to
$V(\tau ^*\psi ^*M)^{\lambda }\cong V(\psi ^*\tau ^*M)^{\lambda }$. By applying part (ii) to ![]() $\psi :\mathcal {E}[\![X-t]\!]_0\to \mathcal {E}_{K'}[\![X-t]\!]_0$, we have
$\psi :\mathcal {E}[\![X-t]\!]_0\to \mathcal {E}_{K'}[\![X-t]\!]_0$, we have ![]() $V(\psi ^*\tau ^*(M^{\lambda }))\cong V(\tau ^*(M^{\lambda }))\otimes _{\mathcal {E}}\mathcal {E}_{K'}\cong V(\tau ^*M)^{\lambda }\otimes _{\mathcal {E}}\mathcal {E}_{K'}\cong V(\psi ^*\tau ^*M)^{\lambda }$, which implies the assertion.
$V(\psi ^*\tau ^*(M^{\lambda }))\cong V(\tau ^*(M^{\lambda }))\otimes _{\mathcal {E}}\mathcal {E}_{K'}\cong V(\tau ^*M)^{\lambda }\otimes _{\mathcal {E}}\mathcal {E}_{K'}\cong V(\psi ^*\tau ^*M)^{\lambda }$, which implies the assertion.
Corollary 6.3 Let ![]() $M$ be a
$M$ be a ![]() $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over ![]() $\mathcal {E}$. Then,
$\mathcal {E}$. Then, ![]() $M$ is PBQ if and only if
$M$ is PBQ if and only if ![]() $\psi ^*M$ is PBQ.
$\psi ^*M$ is PBQ.
Proof. As we have a canonical isomorphism ![]() $\psi ^*M/(\psi ^*M)^0\cong \psi ^*(M/M^0)$ by Lemma 6.2(iii),
$\psi ^*M/(\psi ^*M)^0\cong \psi ^*(M/M^0)$ by Lemma 6.2(iii), ![]() $M/M^0$ is pure as a
$M/M^0$ is pure as a ![]() $\varphi$-module over
$\varphi$-module over ![]() $\mathcal {E}$ if and only if
$\mathcal {E}$ if and only if ![]() $\psi ^*M/(\psi ^*M)^0$ is pure as a
$\psi ^*M/(\psi ^*M)^0$ is pure as a ![]() $\varphi$-module over
$\varphi$-module over ![]() $\mathcal {E}_{K'}$.
$\mathcal {E}_{K'}$.
7. Slope criterion
Lemma 7.1 (Cf. [Reference OhkuboOhk17, Lemma 7.3])
Let ![]() $M$ be a
$M$ be a ![]() $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over ![]() $\mathcal {E}$. Then,
$\mathcal {E}$. Then, ![]() $\lambda _{\rm max}(M/M^0)=\lambda _{\rm max}(M)$.
$\lambda _{\rm max}(M/M^0)=\lambda _{\rm max}(M)$.
Proof. It suffices to prove ![]() $\lambda _{\rm max}(M/M^0)\geqslant \lambda _{\rm max}(M)$. As we have a canonical surjection
$\lambda _{\rm max}(M/M^0)\geqslant \lambda _{\rm max}(M)$. As we have a canonical surjection ![]() $M/M^0\to M/\bigcup _{\mu <\lambda _{\rm max}(M)}S_{\mu }(M)$ by Theorem 5.6(i), we have
$M/M^0\to M/\bigcup _{\mu <\lambda _{\rm max}(M)}S_{\mu }(M)$ by Theorem 5.6(i), we have ![]() $\lambda _{\rm max}(M/M^0)\geqslant \lambda _{\rm max}(M/\bigcup _{\mu <\lambda _{\rm max}(M)}S_{\mu }(M)) =\lambda _{\rm max}(M)$.
$\lambda _{\rm max}(M/M^0)\geqslant \lambda _{\rm max}(M/\bigcup _{\mu <\lambda _{\rm max}(M)}S_{\mu }(M)) =\lambda _{\rm max}(M)$.
Proposition 7.2 (Slope criterion) For a ![]() $(\varphi ,\nabla )$-module
$(\varphi ,\nabla )$-module ![]() $M$ over
$M$ over ![]() $\mathcal {E}$, we consider the following conditions.
$\mathcal {E}$, we consider the following conditions.
(i) The
 $(\varphi ,\nabla )$-module
$(\varphi ,\nabla )$-module  $M$ over
$M$ over  $\mathcal {E}$ is PBQ.
$\mathcal {E}$ is PBQ.(ii) For any nonzero quotient
 $Q$ of
$Q$ of  $M$, we have
$M$, we have  $\lambda _{\rm max}(Q)=\lambda _{\rm max}(M)$.
$\lambda _{\rm max}(Q)=\lambda _{\rm max}(M)$.
Then, condition (i) implies condition (ii). Moreover, if ![]() $k$ is perfect, then condition (ii) implies condition (i).
$k$ is perfect, then condition (ii) implies condition (i).
Proof. Let (i)![]() $'$ and (ii)
$'$ and (ii)![]() $'$ denote conditions (i) and (ii) for
$'$ denote conditions (i) and (ii) for ![]() $M/M^0$ respectively, that is:
$M/M^0$ respectively, that is:
(i)
 $^{\prime}$ the
$^{\prime}$ the  $(\varphi ,\nabla )$-module
$(\varphi ,\nabla )$-module  $M/M^0$ over
$M/M^0$ over  $\mathcal {E}$ is PBQ;
$\mathcal {E}$ is PBQ;(ii)
 $^{\prime}$ for any nonzero quotient
$^{\prime}$ for any nonzero quotient  $Q$ of
$Q$ of  $M/M^0$, we have
$M/M^0$, we have  $\lambda _{\rm max}(Q)=\lambda _{\rm max}(M/M^0)$.
$\lambda _{\rm max}(Q)=\lambda _{\rm max}(M/M^0)$.
We claim that conditions (i) and (i)![]() $'$ (respectively, (ii) and (ii)
$'$ (respectively, (ii) and (ii)![]() $'$) are equivalent. Note that
$'$) are equivalent. Note that ![]() $(M/M^0)^0=0$ because
$(M/M^0)^0=0$ because ![]() $\tau ^*(M/M^0)$ is trivial as a
$\tau ^*(M/M^0)$ is trivial as a ![]() $\nabla$-module over
$\nabla$-module over ![]() $\mathcal {E}[\![X-t]\!]_0$. Hence, conditions (i) and (i)
$\mathcal {E}[\![X-t]\!]_0$. Hence, conditions (i) and (i)![]() $'$ are equivalent. By Lemma 7.1, condition (ii) implies condition (ii)
$'$ are equivalent. By Lemma 7.1, condition (ii) implies condition (ii)![]() $'$. Conversely, assume that condition (ii)
$'$. Conversely, assume that condition (ii)![]() $'$ holds. Let
$'$ holds. Let ![]() $Q$ be a nonzero quotient of
$Q$ be a nonzero quotient of ![]() $M$. We have
$M$. We have ![]() $\lambda _{\rm max}(Q)=\lambda _{\rm max}(Q/Q^0),\lambda _{\rm max}(M)=\lambda _{\rm max}(M/M^0)$ by Lemma 7.1, and
$\lambda _{\rm max}(Q)=\lambda _{\rm max}(Q/Q^0),\lambda _{\rm max}(M)=\lambda _{\rm max}(M/M^0)$ by Lemma 7.1, and ![]() $\lambda _{\rm max}(Q/Q^0)=\lambda _{\rm max}(M/M^0)$ by condition (ii)
$\lambda _{\rm max}(Q/Q^0)=\lambda _{\rm max}(M/M^0)$ by condition (ii)![]() $'$, where
$'$, where ![]() $Q/Q^0$ is regarded as a nonzero quotient of
$Q/Q^0$ is regarded as a nonzero quotient of ![]() $M/M^0$. Hence, condition (ii) holds. Thus, we obtain the claim.
$M/M^0$. Hence, condition (ii) holds. Thus, we obtain the claim.
To prove the assertion, we may replace ![]() $M$ by
$M$ by ![]() $M/M^0$ in virtue of the claim. Thus, we may assume that
$M/M^0$ in virtue of the claim. Thus, we may assume that ![]() $M^0=0$. Then, condition (i) is equivalent to saying that
$M^0=0$. Then, condition (i) is equivalent to saying that ![]() $M$ is pure as a
$M$ is pure as a ![]() $\varphi$-module over
$\varphi$-module over ![]() $\mathcal {E}$. Hence, condition (i) implies condition (ii). We assume that
$\mathcal {E}$. Hence, condition (i) implies condition (ii). We assume that ![]() $k$ is perfect and condition (ii) holds. Let
$k$ is perfect and condition (ii) holds. Let ![]() $\mu _1$ be the least Frobenius slope of
$\mu _1$ be the least Frobenius slope of ![]() $M$. Then,
$M$. Then, ![]() $S_{\mu _1}(M)$ is regarded as a quotient of
$S_{\mu _1}(M)$ is regarded as a quotient of ![]() $M$ by Theorem 7.3. By applying condition (ii) to
$M$ by Theorem 7.3. By applying condition (ii) to ![]() $Q=S_{\mu _1}(M)$, we obtain
$Q=S_{\mu _1}(M)$, we obtain ![]() $\mu _1=\lambda _{\rm max}(M)$, which implies that
$\mu _1=\lambda _{\rm max}(M)$, which implies that ![]() $M=S_{\lambda _{\rm max}(M)}(M)=S_{\mu _1}(M)$ is pure (of slope
$M=S_{\lambda _{\rm max}(M)}(M)=S_{\mu _1}(M)$ is pure (of slope ![]() $\mu _1$) as a
$\mu _1$) as a ![]() $\varphi$-module over
$\varphi$-module over ![]() $\mathcal {E}$.
$\mathcal {E}$.
Theorem 7.3 (Splitting theorem [Reference Chiarellotto and TsuzukiCT11, Theorem 4.1])
Let ![]() $M$ be a
$M$ be a ![]() $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over ![]() $\mathcal {E}$. Assume that
$\mathcal {E}$. Assume that ![]() $k$ is perfect. Then,
$k$ is perfect. Then, ![]() $M$ is bounded in the sense of [Reference Chiarellotto and TsuzukiCT11, 2.2], that is,
$M$ is bounded in the sense of [Reference Chiarellotto and TsuzukiCT11, 2.2], that is, ![]() $M^0=0$ if and only if the Frobenius slope filtration of
$M^0=0$ if and only if the Frobenius slope filtration of ![]() $M$ splits, that is, there exists an isomorphism of
$M$ splits, that is, there exists an isomorphism of ![]() $(\varphi ,\nabla )$-modules over
$(\varphi ,\nabla )$-modules over ![]() $\mathcal {E}$
$\mathcal {E}$
 \[ M\cong\mathop{\bigoplus}\limits_{i=1,\dots,m}S_{\mu_i}(M)\bigg/\mathop{\bigcup}\limits_{\mu<\mu_i}S_{\mu}(M), \]
\[ M\cong\mathop{\bigoplus}\limits_{i=1,\dots,m}S_{\mu_i}(M)\bigg/\mathop{\bigcup}\limits_{\mu<\mu_i}S_{\mu}(M), \]
where ![]() $\mu _1<\cdots <\mu _m$ denote the Frobenius slopes of
$\mu _1<\cdots <\mu _m$ denote the Frobenius slopes of ![]() $M$ without multiplicity. In particular,
$M$ without multiplicity. In particular, ![]() $S_{\mu _1}(M)$ is regarded a quotient of
$S_{\mu _1}(M)$ is regarded a quotient of ![]() $M$.
$M$.
8. Proofs of Proposition 5.3 and part (ii) of Theorem 0.1
Proof of Proposition 5.3 We may assume that ![]() $M\neq 0$. By duality, we have only to prove that
$M\neq 0$. By duality, we have only to prove that ![]() $\mathrm {Sol}_{\lambda -\lambda _{\rm max}(M_{\mathcal {E}})}(\mathrm {Sol}(M))\subset \mathrm {Sol}(M)$ for
$\mathrm {Sol}_{\lambda -\lambda _{\rm max}(M_{\mathcal {E}})}(\mathrm {Sol}(M))\subset \mathrm {Sol}(M)$ for ![]() $\lambda \in \mathbb {R}$. By Lemma 6.2(i), we may reduce to the case
$\lambda \in \mathbb {R}$. By Lemma 6.2(i), we may reduce to the case ![]() $K=L$. Thus, we may assume that
$K=L$. Thus, we may assume that ![]() $k$ is algebraically closed. As the functors
$k$ is algebraically closed. As the functors ![]() $S_{\bullet }(-)$ and
$S_{\bullet }(-)$ and ![]() $\mathrm {Sol}_{\bullet }(-)$ commute with
$\mathrm {Sol}_{\bullet }(-)$ commute with ![]() $d$-pushforwards, after replacing
$d$-pushforwards, after replacing ![]() $M$ by
$M$ by ![]() $[d]_*M$, we may assume that
$[d]_*M$, we may assume that ![]() $S_{\lambda -\lambda _{\rm max}(M_{\mathcal {E}})}(\mathrm {Sol}(M))$ admits a
$S_{\lambda -\lambda _{\rm max}(M_{\mathcal {E}})}(\mathrm {Sol}(M))$ admits a ![]() $K$-basis
$K$-basis ![]() $B$ consisting of Frobenius
$B$ consisting of Frobenius ![]() $1$-eigenvectors
$1$-eigenvectors ![]() $f$ of slopes
$f$ of slopes ![]() $\mu _f$. Let
$\mu _f$. Let ![]() $f\in B$. Then, we have
$f\in B$. Then, we have ![]() $\varphi _{\mathrm {Sol}(M)}(f)=c_ff$ with
$\varphi _{\mathrm {Sol}(M)}(f)=c_ff$ with ![]() $c_f\in K^{\times }$, i.e.
$c_f\in K^{\times }$, i.e. ![]() $\varphi \circ f=c_ff\circ \varphi _M$, and
$\varphi \circ f=c_ff\circ \varphi _M$, and ![]() $\mu _f=\log {|c_f|}/\log {|q|}\leqslant \lambda -\lambda _{\rm max}(M_{\mathcal {E}})$. By applying Proposition 3.11(i) to
$\mu _f=\log {|c_f|}/\log {|q|}\leqslant \lambda -\lambda _{\rm max}(M_{\mathcal {E}})$. By applying Proposition 3.11(i) to ![]() $f$, we have
$f$, we have ![]() $f\in \mathrm {Sol}_{\mu _f+\lambda _{\rm max}(M_{\mathcal {E}})}(M)\subset \mathrm {Sol}_{\lambda }(M)$. Hence,
$f\in \mathrm {Sol}_{\mu _f+\lambda _{\rm max}(M_{\mathcal {E}})}(M)\subset \mathrm {Sol}_{\lambda }(M)$. Hence, ![]() $S_{\lambda -\lambda _{\rm max}(M_{\mathcal {E}})}(\mathrm {Sol}(M))=\sum _{f\in B}Kf\subset \mathrm {Sol}_{\lambda }(M)$.
$S_{\lambda -\lambda _{\rm max}(M_{\mathcal {E}})}(\mathrm {Sol}(M))=\sum _{f\in B}Kf\subset \mathrm {Sol}_{\lambda }(M)$.
Proof of part (ii) of Theorem 0.1 We may assume that ![]() $M\neq 0$. By duality and Proposition 5.3, we have only to prove that
$M\neq 0$. By duality and Proposition 5.3, we have only to prove that ![]() $\mathrm {Sol}(M)\subset \mathrm {Sol}_{\lambda -\lambda _{\rm max}(M_{\mathcal {E}})}(\mathrm {Sol}(M))$ for
$\mathrm {Sol}(M)\subset \mathrm {Sol}_{\lambda -\lambda _{\rm max}(M_{\mathcal {E}})}(\mathrm {Sol}(M))$ for ![]() $\lambda \in \mathbb {R}$. By Corollary 6.3 and a reduction argument as previously, we may assume that
$\lambda \in \mathbb {R}$. By Corollary 6.3 and a reduction argument as previously, we may assume that ![]() $k$ is algebraically closed, and
$k$ is algebraically closed, and ![]() $\mathrm {Sol}_{\lambda }(M)$ admits a
$\mathrm {Sol}_{\lambda }(M)$ admits a ![]() $K$-basis
$K$-basis ![]() $B$ consisting of Frobenius
$B$ consisting of Frobenius ![]() $1$-eigenvectors
$1$-eigenvectors ![]() $f$ of slopes
$f$ of slopes ![]() $\mu _f$. Let
$\mu _f$. Let ![]() $f\in B$, and
$f\in B$, and ![]() $c_f\in K^{\times }$ be as previously. Let
$c_f\in K^{\times }$ be as previously. Let ![]() $N$ be the kernel of the map
$N$ be the kernel of the map ![]() $f:M\to \mathcal {R}_{\rm log}$. Then,
$f:M\to \mathcal {R}_{\rm log}$. Then, ![]() $N$ is regarded as a subobject of
$N$ is regarded as a subobject of ![]() $M$ because
$M$ because ![]() $N$ is stable under
$N$ is stable under ![]() $\varphi _M$ and
$\varphi _M$ and ![]() $\partial _M$. Moreover, we have
$\partial _M$. Moreover, we have ![]() $N\neq M$ by
$N\neq M$ by ![]() $f\neq 0$. Hence, we may regard
$f\neq 0$. Hence, we may regard ![]() $Q:=M/N$ as a nonzero quotient of
$Q:=M/N$ as a nonzero quotient of ![]() $M$. By Slope criterion 7.2,
$M$. By Slope criterion 7.2, ![]() $\lambda _{\rm max}(Q_{\mathcal {E}})=\lambda _{\rm max}(M_{\mathcal {E}})$. Let
$\lambda _{\rm max}(Q_{\mathcal {E}})=\lambda _{\rm max}(M_{\mathcal {E}})$. Let ![]() $f'\in \mathrm {Sol}(Q)$ be the solution induced by
$f'\in \mathrm {Sol}(Q)$ be the solution induced by ![]() $f$. By definition,
$f$. By definition, ![]() $f'$ is injective,
$f'$ is injective, ![]() $\varphi \circ f'=c_ff'\circ \varphi _{\mathrm {Sol}(Q)}$, and
$\varphi \circ f'=c_ff'\circ \varphi _{\mathrm {Sol}(Q)}$, and ![]() $f'(Q)=f(M)\subset \mathrm {Fil}_{\lambda }\mathcal {R}_{\rm log}$. By applying Proposition 3.11(ii) to
$f'(Q)=f(M)\subset \mathrm {Fil}_{\lambda }\mathcal {R}_{\rm log}$. By applying Proposition 3.11(ii) to ![]() $f'$, we obtain
$f'$, we obtain ![]() $\mu _f\leqslant \lambda -\lambda _{\rm max}(Q_{\mathcal {E}})=\lambda -\lambda _{\rm max}(M_{\mathcal {E}})$. Hence, we have
$\mu _f\leqslant \lambda -\lambda _{\rm max}(Q_{\mathcal {E}})=\lambda -\lambda _{\rm max}(M_{\mathcal {E}})$. Hence, we have ![]() $f\in S_{\mu _f}(\mathrm {Sol}(M))\subset S_{\lambda -\lambda _{\rm max}(M_{\mathcal {E}})}(\mathrm {Sol}(M))$. Therefore,
$f\in S_{\mu _f}(\mathrm {Sol}(M))\subset S_{\lambda -\lambda _{\rm max}(M_{\mathcal {E}})}(\mathrm {Sol}(M))$. Therefore, ![]() $\mathrm {Sol}_{\lambda }(M)=\sum _{f\in B}Kf\subset S_{\lambda -\lambda _{\rm max}(M_{\mathcal {E}})}(\mathrm {Sol}(M))$.
$\mathrm {Sol}_{\lambda }(M)=\sum _{f\in B}Kf\subset S_{\lambda -\lambda _{\rm max}(M_{\mathcal {E}})}(\mathrm {Sol}(M))$.
9. The PBQ filtration
The PBQ filtration of an arbitrary ![]() $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over ![]() $K[\![t]\!]_0$ is constructed in [Reference Chiarellotto and TsuzukiCT11]. We generalize the construction to an arbitrary
$K[\![t]\!]_0$ is constructed in [Reference Chiarellotto and TsuzukiCT11]. We generalize the construction to an arbitrary ![]() $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over ![]() $\mathcal {R}^{\mathrm {bd}}$.
$\mathcal {R}^{\mathrm {bd}}$.
Assumption 9.1 In this section, as in [Reference Chiarellotto and TsuzukiCT11, 5.2 and 5.3] we assume that ![]() $k$ is perfect.
$k$ is perfect.
Definition 9.2 Let ![]() $M$ be a
$M$ be a ![]() $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over ![]() $\mathcal {E}$, and
$\mathcal {E}$, and ![]() $N\subset M$ a subobject. Then,
$N\subset M$ a subobject. Then, ![]() $N^0\subset M^0$ by the functoriality of the log-growth filtration, and
$N^0\subset M^0$ by the functoriality of the log-growth filtration, and ![]() $M^0\subset \bigcup _{\mu <\lambda _{\rm max}(M)}S_{\mu }(M)$ by Theorem 5.6(i). Thus, we obtain the canonical morphism
$M^0\subset \bigcup _{\mu <\lambda _{\rm max}(M)}S_{\mu }(M)$ by Theorem 5.6(i). Thus, we obtain the canonical morphism
 \[ \sigma_{N,M}:N/N^0\to M\bigg/\mathop{\bigcup}\limits_{\mu< \lambda_{\rm max}(M)}S_{\mu}(M). \]
\[ \sigma_{N,M}:N/N^0\to M\bigg/\mathop{\bigcup}\limits_{\mu< \lambda_{\rm max}(M)}S_{\mu}(M). \]Proposition 9.3 (Cf. [Reference Chiarellotto and TsuzukiCT11, Proposition 5.4])
Let ![]() $M$ be a
$M$ be a ![]() $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over ![]() $\mathcal {E}$. Then, there exists a unique subobject
$\mathcal {E}$. Then, there exists a unique subobject ![]() $N$ of
$N$ of ![]() $M$ such that
$M$ such that ![]() $\sigma _{N,M}$ is an isomorphism. Moreover,
$\sigma _{N,M}$ is an isomorphism. Moreover, ![]() $N$ is PBQ with
$N$ is PBQ with ![]() $\lambda _{\rm max}(N)=\lambda _{\rm max}(M)$, and
$\lambda _{\rm max}(N)=\lambda _{\rm max}(M)$, and ![]() $N\neq 0$ if
$N\neq 0$ if ![]() $M\neq 0$. We call
$M\neq 0$. We call ![]() $N$ the maximally PBQ submodule of
$N$ the maximally PBQ submodule of ![]() $M$.
$M$.
Proof. We may assume that ![]() $M\neq 0$. The first assertion is proved in the reference. As
$M\neq 0$. The first assertion is proved in the reference. As ![]() $\sigma _{N,M}$ is an isomorphism,
$\sigma _{N,M}$ is an isomorphism, ![]() $N/N^0$ is pure of slope
$N/N^0$ is pure of slope ![]() $\lambda _{\rm max}(M)$. Hence,
$\lambda _{\rm max}(M)$. Hence, ![]() $N$ is PBQ, and
$N$ is PBQ, and ![]() $\lambda _{\rm max}(N)=\lambda _{\rm max}(N/N^0)=\lambda _{\rm max}(M)$ by Lemma 7.1.
$\lambda _{\rm max}(N)=\lambda _{\rm max}(N/N^0)=\lambda _{\rm max}(M)$ by Lemma 7.1.
Definition 9.4 [Reference Chiarellotto and TsuzukiCT11, Corollary 5.5]
Let ![]() $M$ be a
$M$ be a ![]() $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over ![]() $\mathcal {E}$. We define
$\mathcal {E}$. We define ![]() $P_i(M)$ for
$P_i(M)$ for ![]() $i\in \mathbb {N}$ as follows. We put
$i\in \mathbb {N}$ as follows. We put ![]() $P_0(M)=0$,
$P_0(M)=0$, ![]() $P_1(M)=N$ with notation as in Proposition 9.3. For
$P_1(M)=N$ with notation as in Proposition 9.3. For ![]() $i\geqslant 2$, we inductively define
$i\geqslant 2$, we inductively define ![]() $P_i(M)$ as the inverse image of
$P_i(M)$ as the inverse image of ![]() $P_1(M/P_{i-1}(M))$ under the canonical projection
$P_1(M/P_{i-1}(M))$ under the canonical projection ![]() $M\to M/P_{i-1}(M)$. By definition, we have a canonical isomorphism
$M\to M/P_{i-1}(M)$. By definition, we have a canonical isomorphism ![]() $P_i(M)/P_{i-1}(M)\cong P_1(M/P_{i-1}(M))$. Thus,
$P_i(M)/P_{i-1}(M)\cong P_1(M/P_{i-1}(M))$. Thus, ![]() $P_{\bullet }(M)$ forms an increasing filtration of subobjects of
$P_{\bullet }(M)$ forms an increasing filtration of subobjects of ![]() $M$, which is called the PBQ filtration of
$M$, which is called the PBQ filtration of ![]() $M$.
$M$.
Lemma 9.5 Let ![]() $M$ be a
$M$ be a ![]() $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over ![]() $\mathcal {E}$.
$\mathcal {E}$.
(i) The
 $(\varphi ,\nabla )$-module
$(\varphi ,\nabla )$-module  $P_1(M)$ over
$P_1(M)$ over  $\mathcal {E}$ is PBQ with
$\mathcal {E}$ is PBQ with  $\lambda _{\rm max}(P_1(M))=\lambda _{\rm max}(M)$, and
$\lambda _{\rm max}(P_1(M))=\lambda _{\rm max}(M)$, and  $P_1(M)\neq 0$ if
$P_1(M)\neq 0$ if  $M\neq 0$.
$M\neq 0$.(ii) We have
 $P_1(M)=M$ if and only if
$P_1(M)=M$ if and only if  $M$ is PBQ. In particular, if
$M$ is PBQ. In particular, if  $M$ is not PBQ, then
$M$ is not PBQ, then  $P_1(M)\neq M$.
$P_1(M)\neq M$.(iii) The filtration
 $P_{\bullet }(M)$ is separated and exhaustive, and each graded piece
$P_{\bullet }(M)$ is separated and exhaustive, and each graded piece  $P_{i+1}(M)/P_{i}(M)$ is PBQ.
$P_{i+1}(M)/P_{i}(M)$ is PBQ.(iv) If
 $M$ is not PBQ, then
$M$ is not PBQ, then  $\lambda _{\rm max}(M/P_1(M))<\lambda _{\rm max}(M)$.
$\lambda _{\rm max}(M/P_1(M))<\lambda _{\rm max}(M)$.
Proof. Part (i) is a part of Proposition 9.3. We prove part (ii). If ![]() $P_1(M)=M$, then
$P_1(M)=M$, then ![]() $M$ is PBQ by part (i). Conversely, if
$M$ is PBQ by part (i). Conversely, if ![]() $M$ is PBQ, then
$M$ is PBQ, then ![]() $\sigma _{M,M}$ is an isomorphism by using Theorem 5.6(i) with
$\sigma _{M,M}$ is an isomorphism by using Theorem 5.6(i) with ![]() $\lambda =0$, which implies that
$\lambda =0$, which implies that ![]() $P_1(M)=M$ by uniqueness. In part (iii), the separatedness is trivial, and the rest of the assertion follows from
$P_1(M)=M$ by uniqueness. In part (iii), the separatedness is trivial, and the rest of the assertion follows from ![]() $P_i(M)/P_{i-1}(M)\cong P_1(M/P_{i-1}(M))$ and part (i). We prove part (iv). As
$P_i(M)/P_{i-1}(M)\cong P_1(M/P_{i-1}(M))$ and part (i). We prove part (iv). As ![]() $M=P_1(M)+\bigcup _{\mu <\lambda _{\rm max}(M)}S_{\mu }(M)$ by the surjectivity of
$M=P_1(M)+\bigcup _{\mu <\lambda _{\rm max}(M)}S_{\mu }(M)$ by the surjectivity of ![]() $\sigma _{P_1(M),M}$, we have
$\sigma _{P_1(M),M}$, we have ![]() $M/P_1(M)=\bigcup _{\mu <\lambda _{\rm max}(M)}S_{\mu }(M/P_1(M))$ by Lemma 1.7(II)(iii), which implies the assertion.
$M/P_1(M)=\bigcup _{\mu <\lambda _{\rm max}(M)}S_{\mu }(M/P_1(M))$ by Lemma 1.7(II)(iii), which implies the assertion.
Proposition 9.6 Let ![]() $M$ be a
$M$ be a ![]() $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over ![]() $\mathcal {R}^{\mathrm {bd}}$. Then,
$\mathcal {R}^{\mathrm {bd}}$. Then, ![]() $P_{\bullet }(M_{\mathcal {E}})$ descends to a filtration
$P_{\bullet }(M_{\mathcal {E}})$ descends to a filtration ![]() $P_{\bullet }(M)$ of subobjects of
$P_{\bullet }(M)$ of subobjects of ![]() $M$. We call
$M$. We call ![]() $P_1(M)$ (respectively,
$P_1(M)$ (respectively, ![]() $P_{\bullet }(M)$) the maximally PBQ submodule (respectively, the PBQ filtration) of
$P_{\bullet }(M)$) the maximally PBQ submodule (respectively, the PBQ filtration) of ![]() $M$.
$M$.
Proof. By the definition of ![]() $P_{\bullet }(M_{\mathcal {E}})$, we have only to prove that
$P_{\bullet }(M_{\mathcal {E}})$, we have only to prove that ![]() $P_1(M_{\mathcal {E}})$ descends to
$P_1(M_{\mathcal {E}})$ descends to ![]() $\mathcal {R}^{\mathrm {bd}}$. We may assume that
$\mathcal {R}^{\mathrm {bd}}$. We may assume that ![]() $M\neq 0$. We proceed by induction on
$M\neq 0$. We proceed by induction on ![]() $n=\dim _{\mathcal {R}^{\mathrm {bd}}}M$. In the case where
$n=\dim _{\mathcal {R}^{\mathrm {bd}}}M$. In the case where ![]() $M_{\mathcal {E}}$ is PBQ (including the base case
$M_{\mathcal {E}}$ is PBQ (including the base case ![]() $n=1$), we have
$n=1$), we have ![]() $P_1(M)=M$ by
$P_1(M)=M$ by ![]() $P_1(M_{\mathcal {E}})=M_{\mathcal {E}}$ (Lemma 9.5(ii)). In the induction step, we may assume that
$P_1(M_{\mathcal {E}})=M_{\mathcal {E}}$ (Lemma 9.5(ii)). In the induction step, we may assume that ![]() $M_{\mathcal {E}}$ is not PBQ. It suffices to construct a subobject
$M_{\mathcal {E}}$ is not PBQ. It suffices to construct a subobject ![]() $N$ of
$N$ of ![]() $M$ satisfying the following conditions: (a)
$M$ satisfying the following conditions: (a) ![]() $N\neq M$; (b)
$N\neq M$; (b) ![]() $\lambda _{\rm max}(N_{\mathcal {E}})=\lambda _{\rm max}(M_{\mathcal {E}})$; (c) the canonical morphism
$\lambda _{\rm max}(N_{\mathcal {E}})=\lambda _{\rm max}(M_{\mathcal {E}})$; (c) the canonical morphism ![]() $i:N_{\mathcal {E}}/\bigcup _{\mu <\lambda _{\rm max}(M_{\mathcal {E}})}S_{\mu }(N_{\mathcal {E}})\to M_{\mathcal {E}}/\bigcup _{\mu <\lambda _{\rm max}(M_{\mathcal {E}})}S_{\mu }(M_{\mathcal {E}})$ is an isomorphism. Indeed, if this is the case, then
$i:N_{\mathcal {E}}/\bigcup _{\mu <\lambda _{\rm max}(M_{\mathcal {E}})}S_{\mu }(N_{\mathcal {E}})\to M_{\mathcal {E}}/\bigcup _{\mu <\lambda _{\rm max}(M_{\mathcal {E}})}S_{\mu }(M_{\mathcal {E}})$ is an isomorphism. Indeed, if this is the case, then ![]() $P_1(N_{\mathcal {E}})$ descends to
$P_1(N_{\mathcal {E}})$ descends to ![]() $P_1(N)$ by condition (a) and the induction hypothesis. As
$P_1(N)$ by condition (a) and the induction hypothesis. As ![]() $\sigma _{P_1(N_{\mathcal {E}}),M_{\mathcal {E}}}=i\circ \sigma _{P_1(N_{\mathcal {E}}),N_{\mathcal {E}}}$ by condition (b), the morphism
$\sigma _{P_1(N_{\mathcal {E}}),M_{\mathcal {E}}}=i\circ \sigma _{P_1(N_{\mathcal {E}}),N_{\mathcal {E}}}$ by condition (b), the morphism ![]() $\sigma _{P_1(N_{\mathcal {E}}),M_{\mathcal {E}}}$ is an isomorphism by condition (c). Hence,
$\sigma _{P_1(N_{\mathcal {E}}),M_{\mathcal {E}}}$ is an isomorphism by condition (c). Hence, ![]() $P_1(M_{\mathcal {E}})=P_1(N_{\mathcal {E}})$ by uniqueness. Thus,
$P_1(M_{\mathcal {E}})=P_1(N_{\mathcal {E}})$ by uniqueness. Thus, ![]() $P_1(M_{\mathcal {E}})$ descends to
$P_1(M_{\mathcal {E}})$ descends to ![]() $P_1(N)$. We construct
$P_1(N)$. We construct ![]() $N$, and then verify conditions (a)–(c). Let
$N$, and then verify conditions (a)–(c). Let ![]() $\mu$ denote the minimum Frobenius slope of
$\mu$ denote the minimum Frobenius slope of ![]() $M_{\mathcal {E}}/M_{\mathcal {E}}^0$. Then,
$M_{\mathcal {E}}/M_{\mathcal {E}}^0$. Then, ![]() $\mu <\lambda _{\rm max}(M_{\mathcal {E}})$ by assumption, and
$\mu <\lambda _{\rm max}(M_{\mathcal {E}})$ by assumption, and ![]() $Q:=S_{\mu }(M_{\mathcal {E}}/M_{\mathcal {E}}^0)$ is regarded as a quotient of
$Q:=S_{\mu }(M_{\mathcal {E}}/M_{\mathcal {E}}^0)$ is regarded as a quotient of ![]() $M_{\mathcal {E}}/M_{\mathcal {E}}^0$ by Theorem 7.3. Let
$M_{\mathcal {E}}/M_{\mathcal {E}}^0$ by Theorem 7.3. Let ![]() $f:M\to Q$ be the composition of the canonical map
$f:M\to Q$ be the composition of the canonical map ![]() $M\to M_{\mathcal {E}}$ followed by the projection
$M\to M_{\mathcal {E}}$ followed by the projection ![]() $M_{\mathcal {E}}\to Q$. We have
$M_{\mathcal {E}}\to Q$. We have ![]() $f\neq 0$ because
$f\neq 0$ because ![]() $f(M)$ generates
$f(M)$ generates ![]() $Q(\neq 0)$ as a vector space over
$Q(\neq 0)$ as a vector space over ![]() $\mathcal {E}$. Let
$\mathcal {E}$. Let ![]() $N$ denote the kernel of
$N$ denote the kernel of ![]() $f$. Then,
$f$. Then, ![]() $N$ is a nonzero subobject of
$N$ is a nonzero subobject of ![]() $M$. By applying Lemma 2.14 to the map
$M$. By applying Lemma 2.14 to the map ![]() $M/N\hookrightarrow Q$ induced by
$M/N\hookrightarrow Q$ induced by ![]() $f$, we have
$f$, we have ![]() $\lambda _{\rm max}((M/N)_{\mathcal {E}})=\lambda _{\rm max}(Q)=\mu <\lambda _{\rm max}(M_{\mathcal {E}})$. Hence,
$\lambda _{\rm max}((M/N)_{\mathcal {E}})=\lambda _{\rm max}(Q)=\mu <\lambda _{\rm max}(M_{\mathcal {E}})$. Hence, ![]() $\lambda _{\rm max}(N_{\mathcal {E}})=\lambda _{\rm max}(M_{\mathcal {E}})$ and
$\lambda _{\rm max}(N_{\mathcal {E}})=\lambda _{\rm max}(M_{\mathcal {E}})$ and ![]() $(M/N)_{\mathcal {E}}=\bigcup _{\mu <\lambda _{\rm max}(M_{\mathcal {E}})}S_{\mu }((M/N)_{\mathcal {E}})$. Therefore, the morphism
$(M/N)_{\mathcal {E}}=\bigcup _{\mu <\lambda _{\rm max}(M_{\mathcal {E}})}S_{\mu }((M/N)_{\mathcal {E}})$. Therefore, the morphism ![]() $i$ is an isomorphism by Lemma 1.7(II)(iii).
$i$ is an isomorphism by Lemma 1.7(II)(iii).
We record the following consequence though it is not used in the paper.
Corollary 9.7 If ![]() $M$ is an irreducible object in the category of
$M$ is an irreducible object in the category of ![]() $(\varphi ,\nabla )$-modules over
$(\varphi ,\nabla )$-modules over ![]() $\mathcal {R}^{\mathrm {bd}}$, then
$\mathcal {R}^{\mathrm {bd}}$, then ![]() $M_{\mathcal {E}}$ is PBQ.
$M_{\mathcal {E}}$ is PBQ.
Proof. If ![]() $M_{\mathcal {E}}$ is not PBQ, then
$M_{\mathcal {E}}$ is not PBQ, then ![]() $0\subsetneq P_1(M_{\mathcal {E}})\subsetneq M_{\mathcal {E}}$ by Lemma 9.5(i) and (ii), which implies that
$0\subsetneq P_1(M_{\mathcal {E}})\subsetneq M_{\mathcal {E}}$ by Lemma 9.5(i) and (ii), which implies that ![]() $0\subsetneq P_1(M)\subsetneq M$. In particular,
$0\subsetneq P_1(M)\subsetneq M$. In particular, ![]() $M$ is reducible.
$M$ is reducible.
Lemma 9.8 Let ![]() $0\to M'\to M\to M''\to 0$ be an exact sequence of
$0\to M'\to M\to M''\to 0$ be an exact sequence of ![]() $(\varphi ,\nabla )$-modules over
$(\varphi ,\nabla )$-modules over ![]() $\mathcal {R}^{\mathrm {bd}}$ such that
$\mathcal {R}^{\mathrm {bd}}$ such that ![]() $M_{\mathcal {R}}$ is unipotent as a
$M_{\mathcal {R}}$ is unipotent as a ![]() $\nabla$-module over
$\nabla$-module over ![]() $\mathcal {R}$. Let
$\mathcal {R}$. Let ![]() $\lambda \in \mathbb {R}$.
$\lambda \in \mathbb {R}$.
(i) Assume that
 $V(M')^{\lambda }=\bigcup _{\mu <\lambda _{\rm max}(M_{\mathcal {E}})-\lambda }S_{\mu }(V(M'))$, or, equivalently,
$V(M')^{\lambda }=\bigcup _{\mu <\lambda _{\rm max}(M_{\mathcal {E}})-\lambda }S_{\mu }(V(M'))$, or, equivalently,  $\mathrm {Sol}_{\lambda }(M')=S_{\lambda -\lambda _{\rm max}(M_{\mathcal {E}})} (\mathrm {Sol}(M'))$. Then, there exist canonical exact sequences
$\mathrm {Sol}_{\lambda }(M')=S_{\lambda -\lambda _{\rm max}(M_{\mathcal {E}})} (\mathrm {Sol}(M'))$. Then, there exist canonical exact sequences
 \begin{gather*} 0\to V(M')^{\lambda}\to V(M)^{\lambda}\to V(M'')^{\lambda}\to 0,\\ 0\to \mathrm{Sol}_{\lambda}(M'')\to \mathrm{Sol}_{\lambda}(M)\to \mathrm{Sol}_{\lambda}(M')\to 0. \end{gather*}
\begin{gather*} 0\to V(M')^{\lambda}\to V(M)^{\lambda}\to V(M'')^{\lambda}\to 0,\\ 0\to \mathrm{Sol}_{\lambda}(M'')\to \mathrm{Sol}_{\lambda}(M)\to \mathrm{Sol}_{\lambda}(M')\to 0. \end{gather*}(ii) There exist canonical exact sequences
In particular, the slope multisets of \begin{gather*} 0\to V(P_1(M))^{\lambda}\to V(M)^{\lambda}\to V(M/P_1(M))^{\lambda}\to 0,\\ 0\to\mathrm{Sol}_{\lambda}(M/P_1(M))\to\mathrm{Sol}_{\lambda}(M)\to\mathrm{Sol}_{\lambda}(P_1(M))\to 0. \end{gather*}
\begin{gather*} 0\to V(P_1(M))^{\lambda}\to V(M)^{\lambda}\to V(M/P_1(M))^{\lambda}\to 0,\\ 0\to\mathrm{Sol}_{\lambda}(M/P_1(M))\to\mathrm{Sol}_{\lambda}(M)\to\mathrm{Sol}_{\lambda}(P_1(M))\to 0. \end{gather*} $V(M)^{\bullet }$ and
$V(M)^{\bullet }$ and  $\mathrm {Sol}_{\bullet }(M)$, which coincide by definition, are equal to the disjoint union of those of
$\mathrm {Sol}_{\bullet }(M)$, which coincide by definition, are equal to the disjoint union of those of  $V(P_1(M))^{\bullet }$ and
$V(P_1(M))^{\bullet }$ and  $V(M/P_1(M))^{\bullet }$.
$V(M/P_1(M))^{\bullet }$.
Proof. (i) We proceed as in the proof of [Reference Chiarellotto and TsuzukiCT11, Proposition 2.6(1)]. By duality and the left exactness of ![]() $\mathrm {Sol}_{\lambda }(-)$, we have only to prove the surjectivity of
$\mathrm {Sol}_{\lambda }(-)$, we have only to prove the surjectivity of ![]() $\mathrm {Sol}_{\lambda }(M)\to \mathrm {Sol}_{\lambda }(M')$. By assumption and Proposition 5.3, we obtain the following commutative diagram.
$\mathrm {Sol}_{\lambda }(M)\to \mathrm {Sol}_{\lambda }(M')$. By assumption and Proposition 5.3, we obtain the following commutative diagram.

Then, the bottom horizontal arrow is surjective by Lemma 1.7(II)(iii), which implies the assertion.
(ii) As ![]() $P_1(M)_{\mathcal {E}}$ is PBQ with
$P_1(M)_{\mathcal {E}}$ is PBQ with ![]() $\lambda _{\rm max}(P_1(M)_{\mathcal {E}})=\lambda _{\rm max}(M_{\mathcal {E}})$ (Lemma 9.5(i)), we have
$\lambda _{\rm max}(P_1(M)_{\mathcal {E}})=\lambda _{\rm max}(M_{\mathcal {E}})$ (Lemma 9.5(i)), we have ![]() $V(P_1(M))=\bigcup _{\mu <\lambda _{\rm max}(M_{\mathcal {E}})-\lambda }S_{\mu }(V(P_1(M)))$ by Theorem 0.1(ii). Hence, we obtain the assertion by applying part (i) to
$V(P_1(M))=\bigcup _{\mu <\lambda _{\rm max}(M_{\mathcal {E}})-\lambda }S_{\mu }(V(P_1(M)))$ by Theorem 0.1(ii). Hence, we obtain the assertion by applying part (i) to ![]() $M'=P_1(M)$.
$M'=P_1(M)$.
Lemma 9.9
(i) [Reference Chiarellotto and TsuzukiCT11, Proposition 2.6 (1)] Let
 $0\to M'\to M\to M''\to 0$ be an exact sequence of
$0\to M'\to M\to M''\to 0$ be an exact sequence of  $(\varphi ,\nabla )$-modules over
$(\varphi ,\nabla )$-modules over  $\mathcal {E}$, and
$\mathcal {E}$, and  $\lambda \in \mathbb {R}$. Assume that
$\lambda \in \mathbb {R}$. Assume that  $(M')^{\lambda }=\bigcup _{\mu <\lambda _{\rm max}(M)-\lambda }S_{\mu }(M')$. Then, there exists a canonical exact sequence
$(M')^{\lambda }=\bigcup _{\mu <\lambda _{\rm max}(M)-\lambda }S_{\mu }(M')$. Then, there exists a canonical exact sequence  $0\to (M')^{\lambda }\to M^{\lambda }\to (M'')^{\lambda }\to 0$.
$0\to (M')^{\lambda }\to M^{\lambda }\to (M'')^{\lambda }\to 0$.(ii) Let
 $M$ be a
$M$ be a  $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over  $\mathcal {E}$, and
$\mathcal {E}$, and  $\lambda \in \mathbb {R}$. Then, there exists a canonical exact sequence
$\lambda \in \mathbb {R}$. Then, there exists a canonical exact sequence  $0\to P_1(M)^{\lambda }\to M^{\lambda }\to (M/P_1(M))^{\lambda }\to 0$. In particular, the slope multiset of
$0\to P_1(M)^{\lambda }\to M^{\lambda }\to (M/P_1(M))^{\lambda }\to 0$. In particular, the slope multiset of  $M^{\bullet }$ is equal to the disjoint union of those of
$M^{\bullet }$ is equal to the disjoint union of those of  $P_1(M)^{\bullet }$ and
$P_1(M)^{\bullet }$ and  $(M/P_1(M))^{\bullet }$.
$(M/P_1(M))^{\bullet }$.
10. Proof of Theorem 0.4
We start with a simple alternative proof of part (i) of Theorem 0.1 by using the PBQ filtration.
Second proof of part (i) of Theorem 0.1 We may assume that ![]() $M\neq 0$. By duality, we have only to prove that the filtration
$M\neq 0$. By duality, we have only to prove that the filtration ![]() $\mathrm {Sol}_{\bullet }(M)$ is right continuous, and has rational slopes. As in the proof of Proposition 5.3, we may assume that
$\mathrm {Sol}_{\bullet }(M)$ is right continuous, and has rational slopes. As in the proof of Proposition 5.3, we may assume that ![]() $k$ is algebraically closed. We prove by induction on
$k$ is algebraically closed. We prove by induction on ![]() $n=\dim _{\mathcal {R}^{\mathrm {bd}}}M$. In the case where
$n=\dim _{\mathcal {R}^{\mathrm {bd}}}M$. In the case where ![]() $M$ is PBQ (including the base case
$M$ is PBQ (including the base case ![]() $n=1$), we have
$n=1$), we have ![]() $\mathrm {Sol}_{\lambda }(M)=S_{\lambda -\lambda _{\rm max}(M_{\mathcal {E}})}(\mathrm {Sol}(M))$ by Theorem 0.1(ii). Hence, the assertion follows from Lemma 1.4(iii) and Theorem 1.5(ii)(b). In the induction step, we may assume that
$\mathrm {Sol}_{\lambda }(M)=S_{\lambda -\lambda _{\rm max}(M_{\mathcal {E}})}(\mathrm {Sol}(M))$ by Theorem 0.1(ii). Hence, the assertion follows from Lemma 1.4(iii) and Theorem 1.5(ii)(b). In the induction step, we may assume that ![]() $M_{\mathcal {E}}$ is not PBQ. Then, we have
$M_{\mathcal {E}}$ is not PBQ. Then, we have ![]() $0\subsetneq P_1(M)\subsetneq M$ by Lemma 9.5(i) and (ii). Hence, by the second exact sequence in Lemma 9.8(ii), the assertion follows from the induction hypothesis for
$0\subsetneq P_1(M)\subsetneq M$ by Lemma 9.5(i) and (ii). Hence, by the second exact sequence in Lemma 9.8(ii), the assertion follows from the induction hypothesis for ![]() $P_1(M)$ and
$P_1(M)$ and ![]() $M/P_1(M)$.
$M/P_1(M)$.
Definition 10.1 (i) Let ![]() $M$ be a
$M$ be a ![]() $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over ![]() $\mathcal {R}^{\mathrm {bd}}$ of dimension
$\mathcal {R}^{\mathrm {bd}}$ of dimension ![]() $n$ such that
$n$ such that ![]() $M_{\mathcal {R}}$ is unipotent as a
$M_{\mathcal {R}}$ is unipotent as a ![]() $\nabla$-module over
$\nabla$-module over ![]() $\mathcal {R}$. We define the log-growth Newton polygon
$\mathcal {R}$. We define the log-growth Newton polygon ![]() $\mathrm {NP}(M)$ of
$\mathrm {NP}(M)$ of ![]() $M$ as the Newton polygon of
$M$ as the Newton polygon of ![]() $V(M)^{\bullet }$. Let
$V(M)^{\bullet }$. Let ![]() $\{s_1(M)\leqslant \cdots \leqslant s_n(M)\}$ denote the slope multiset of
$\{s_1(M)\leqslant \cdots \leqslant s_n(M)\}$ denote the slope multiset of ![]() $V(M)^{\bullet }$. Put
$V(M)^{\bullet }$. Put ![]() $h_i(M):=s_1(M)+\dots +s_i(M)$ for
$h_i(M):=s_1(M)+\dots +s_i(M)$ for ![]() $i\in \{1,\dots ,n\}$, and
$i\in \{1,\dots ,n\}$, and ![]() $h_0(M):=0$.
$h_0(M):=0$.
(ii) Let ![]() $M$ be a
$M$ be a ![]() $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over ![]() $\mathcal {E}$ of dimension
$\mathcal {E}$ of dimension ![]() $n$. We define the log-growth Newton polygon
$n$. We define the log-growth Newton polygon ![]() $\mathrm {NP}(M)$ of
$\mathrm {NP}(M)$ of ![]() $M$ as the Newton polygon of
$M$ as the Newton polygon of ![]() $M^{\bullet }$. We also define
$M^{\bullet }$. We also define ![]() $s_i(M)$ for
$s_i(M)$ for ![]() $i\in \{1,\dots ,n\}$, and
$i\in \{1,\dots ,n\}$, and ![]() $h_i(M)$ for
$h_i(M)$ for ![]() $i\in \{0,\dots ,n\}$ as previously.
$i\in \{0,\dots ,n\}$ as previously.
Notation 4. For ![]() $M$ a
$M$ a ![]() $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over ![]() $\mathcal {R}$, let
$\mathcal {R}$, let ![]() $S_{\bullet }(M)$ be the slope filtration of
$S_{\bullet }(M)$ be the slope filtration of ![]() $M$ in the sense of [Reference TsuzukiTsu98, Definition 5.1.1], whose existence is proved in [Reference KedlayaKed04]. Note that Tsuzuki's definition of the slopes [Reference TsuzukiTsu98, Definition 3.1.5(1)] is compatible with that given in Definition 1.3.
$M$ in the sense of [Reference TsuzukiTsu98, Definition 5.1.1], whose existence is proved in [Reference KedlayaKed04]. Note that Tsuzuki's definition of the slopes [Reference TsuzukiTsu98, Definition 3.1.5(1)] is compatible with that given in Definition 1.3.
Lemma 10.2 Let ![]() $M$ be a
$M$ be a ![]() $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over ![]() $\mathcal {R}$ which is unipotent as a
$\mathcal {R}$ which is unipotent as a ![]() $\nabla$-module over
$\nabla$-module over ![]() $\mathcal {R}$. Let notation be as in § 4.2. We regard
$\mathcal {R}$. Let notation be as in § 4.2. We regard ![]() $\mathbf {V}(M)$ as a
$\mathbf {V}(M)$ as a ![]() $\varphi$-module over
$\varphi$-module over ![]() $K$ as is the case of
$K$ as is the case of ![]() $V(M)$ (see § 5). Then,
$V(M)$ (see § 5). Then, ![]() $\dim _KS_{\lambda }(\mathbf {V}(M))=\mathrm {rank}_{\mathcal {R}}S_{\lambda }(M)$ for
$\dim _KS_{\lambda }(\mathbf {V}(M))=\mathrm {rank}_{\mathcal {R}}S_{\lambda }(M)$ for ![]() $\lambda \in \mathbb {R}$.
$\lambda \in \mathbb {R}$.
Proof. By dévissage, we may assume that ![]() $M$ is irreducible in the category of
$M$ is irreducible in the category of ![]() $(\varphi ,\nabla )$-modules over
$(\varphi ,\nabla )$-modules over ![]() $\mathcal {R}$. The difference module
$\mathcal {R}$. The difference module ![]() $M^{\nabla }$ over
$M^{\nabla }$ over ![]() $K$ is a
$K$ is a ![]() $\varphi$-module over
$\varphi$-module over ![]() $K$ since
$K$ since ![]() $M^{\nabla }$ is isomorphic to
$M^{\nabla }$ is isomorphic to ![]() $\mathbf {V}(M)^{N_X=0}$, which is a
$\mathbf {V}(M)^{N_X=0}$, which is a ![]() $\varphi$-submodule of
$\varphi$-submodule of ![]() $\mathbf {V}(M)$ by
$\mathbf {V}(M)$ by ![]() $N_X\circ \varphi _{\mathbf {V}(M)}=q\varphi _{\mathbf {V}(M)}\circ N_X$. Hence, the canonical injection
$N_X\circ \varphi _{\mathbf {V}(M)}=q\varphi _{\mathbf {V}(M)}\circ N_X$. Hence, the canonical injection ![]() $i:M^{\nabla }\otimes _K\mathcal {R}\to M$ as in Lemma 4.6(ii) is an isomorphism of
$i:M^{\nabla }\otimes _K\mathcal {R}\to M$ as in Lemma 4.6(ii) is an isomorphism of ![]() $(\varphi ,\nabla )$-modules over
$(\varphi ,\nabla )$-modules over ![]() $\mathcal {R}$ by the irreducibility of
$\mathcal {R}$ by the irreducibility of ![]() $M$. Hence,
$M$. Hence, ![]() $i$ induces isomorphisms
$i$ induces isomorphisms ![]() $M^{\nabla }\cong \mathbf {V}(M^{\nabla }\otimes _K\mathcal {R})\cong \mathbf {V}(M)$ of
$M^{\nabla }\cong \mathbf {V}(M^{\nabla }\otimes _K\mathcal {R})\cong \mathbf {V}(M)$ of ![]() $\varphi$-modules over
$\varphi$-modules over ![]() $K$, and an isomorphism
$K$, and an isomorphism ![]() $S_{\lambda }(M^{\nabla })\otimes _K\mathcal {R}\cong S_{\lambda }(M)$ of
$S_{\lambda }(M^{\nabla })\otimes _K\mathcal {R}\cong S_{\lambda }(M)$ of ![]() $\mathcal {R}$-modules by the uniqueness of the slope filtration of
$\mathcal {R}$-modules by the uniqueness of the slope filtration of ![]() $M$. Hence,
$M$. Hence, ![]() $\dim _KS_{\lambda }(\mathbf {V}(M))=\dim _KS_{\lambda }(M^{\nabla })=\mathrm {rank}_{\mathcal {R}}S_{\lambda }(M)$.
$\dim _KS_{\lambda }(\mathbf {V}(M))=\dim _KS_{\lambda }(M^{\nabla })=\mathrm {rank}_{\mathcal {R}}S_{\lambda }(M)$.
Proposition 10.3 (i) Let ![]() $M$ be a
$M$ be a ![]() $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over ![]() $\mathcal {R}^{\mathrm {bd}}$ of dimension
$\mathcal {R}^{\mathrm {bd}}$ of dimension ![]() $n$ such that
$n$ such that ![]() $M_{\mathcal {R}}$ is unipotent as a
$M_{\mathcal {R}}$ is unipotent as a ![]() $\nabla$-module over
$\nabla$-module over ![]() $\mathcal {R}$. Let
$\mathcal {R}$. Let ![]() $\{s'_1(M)\leqslant \cdots \leqslant s'_n(M)\}$ denote the slope multiset of
$\{s'_1(M)\leqslant \cdots \leqslant s'_n(M)\}$ denote the slope multiset of ![]() $S_{\bullet }(M_{\mathcal {R}})$, which coincides with that of
$S_{\bullet }(M_{\mathcal {R}})$, which coincides with that of ![]() $S_{\bullet }(V(M))$ by Lemma 10.2. Then, for
$S_{\bullet }(V(M))$ by Lemma 10.2. Then, for ![]() $i\in \{1,\dots ,n\}$, we have
$i\in \{1,\dots ,n\}$, we have ![]() $s_i(M)\leqslant \lambda _{\rm max}(M_{\mathcal {E}})-s'_{n-i+1}(M)$ with equality when
$s_i(M)\leqslant \lambda _{\rm max}(M_{\mathcal {E}})-s'_{n-i+1}(M)$ with equality when ![]() $M_{\mathcal {E}}$ is PBQ. In particular,
$M_{\mathcal {E}}$ is PBQ. In particular, ![]() $\mathrm {NP}(M)$ lies on or below the Newton polygon of
$\mathrm {NP}(M)$ lies on or below the Newton polygon of ![]() $S_{\lambda _{\rm max}(M_{\mathcal {E}})-\bullet }(M_{\mathcal {R}})$, and the two polygons coincide if
$S_{\lambda _{\rm max}(M_{\mathcal {E}})-\bullet }(M_{\mathcal {R}})$, and the two polygons coincide if ![]() $M_{\mathcal {E}}$ is PBQ.
$M_{\mathcal {E}}$ is PBQ.
(ii) Let ![]() $M$ be a
$M$ be a ![]() $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over ![]() $\mathcal {E}$ of dimension
$\mathcal {E}$ of dimension ![]() $n$. Let
$n$. Let ![]() $\{s'_1(M)\leqslant \cdots \leqslant s'_n(M)\}$ denote the slope multiset of
$\{s'_1(M)\leqslant \cdots \leqslant s'_n(M)\}$ denote the slope multiset of ![]() $S_{\bullet }(M)$. Then, for
$S_{\bullet }(M)$. Then, for ![]() $i\in \{1,\dots ,n\}$, we have
$i\in \{1,\dots ,n\}$, we have ![]() $s_i(M)\leqslant \lambda _{\rm max}(M)-s'_{n-i+1}(M)$ with equality when
$s_i(M)\leqslant \lambda _{\rm max}(M)-s'_{n-i+1}(M)$ with equality when ![]() $M$ is PBQ. In particular,
$M$ is PBQ. In particular, ![]() $\mathrm {NP}(M)$ lies on or below the Newton polygon of
$\mathrm {NP}(M)$ lies on or below the Newton polygon of ![]() $S_{\lambda _{\rm max}(M)-\bullet }(M)$, and the two polygons coincide if
$S_{\lambda _{\rm max}(M)-\bullet }(M)$, and the two polygons coincide if ![]() $M$ is PBQ.
$M$ is PBQ.
Proof. (i) We remark that as a consequence of the right continuity of ![]() $V(M)^{\bullet }$ (respectively,
$V(M)^{\bullet }$ (respectively, ![]() $S_{\bullet }(V(M))$) proved in Theorem 0.1(i), we have
$S_{\bullet }(V(M))$) proved in Theorem 0.1(i), we have ![]() $s_i(M)\leqslant \lambda$ (respectively,
$s_i(M)\leqslant \lambda$ (respectively, ![]() $s'_i(M)\leqslant \lambda$) if and only if
$s'_i(M)\leqslant \lambda$) if and only if ![]() $n-\dim _KV(M)^{\lambda }\geqslant i$ (respectively,
$n-\dim _KV(M)^{\lambda }\geqslant i$ (respectively, ![]() $\dim _KS_{\lambda }(V(M))\geqslant i$); moreover, we have
$\dim _KS_{\lambda }(V(M))\geqslant i$); moreover, we have ![]() $s_i(M)\geqslant \lambda$ (respectively,
$s_i(M)\geqslant \lambda$ (respectively, ![]() $s'_i(M)\geqslant \lambda$) if and only if for any
$s'_i(M)\geqslant \lambda$) if and only if for any ![]() $\mu \in (-\infty ,\lambda )$, we have
$\mu \in (-\infty ,\lambda )$, we have ![]() $i>n-\dim _KV(M)^{\mu }$ (respectively,
$i>n-\dim _KV(M)^{\mu }$ (respectively, ![]() $i>\dim _KS_{\mu }(V(M))$).
$i>\dim _KS_{\mu }(V(M))$).
We have
 \[ \dim_KV(M)^{\lambda_{\rm max}(M_{\mathcal{E}})-s'_{n-i+1}(M)}\leqslant \dim_K{\bigg(\mathop{\bigcup}\limits_{\mu<s'_{n-i+1}(M)}S_{\mu}(V(M))\bigg)}<n-i+1, \]
\[ \dim_KV(M)^{\lambda_{\rm max}(M_{\mathcal{E}})-s'_{n-i+1}(M)}\leqslant \dim_K{\bigg(\mathop{\bigcup}\limits_{\mu<s'_{n-i+1}(M)}S_{\mu}(V(M))\bigg)}<n-i+1, \]
where the first (respectively, second) inequality follows from Proposition 5.3 (respectively, the above remark). Hence, ![]() $s_i(M)\leqslant \lambda _{\rm max}(M_{\mathcal {E}})-s'_{n-i+1}(M)$ by the previous remark. Assume that
$s_i(M)\leqslant \lambda _{\rm max}(M_{\mathcal {E}})-s'_{n-i+1}(M)$ by the previous remark. Assume that ![]() $M_{\mathcal {E}}$ is PBQ. Then, for any
$M_{\mathcal {E}}$ is PBQ. Then, for any ![]() $\mu \in (-\infty ,\lambda _{\rm max}(M_{\mathcal {E}})-s'_{n-i+1}(M))$, we have
$\mu \in (-\infty ,\lambda _{\rm max}(M_{\mathcal {E}})-s'_{n-i+1}(M))$, we have
 \[ \dim_KV(M)^{\mu}=\dim_K \bigg(\mathop{\bigcup}\limits_{\eta< \lambda_{\rm max}(M_{\mathcal{E}})-\mu}S_{\eta}(V(M))\bigg)\geqslant \dim_K{S_{s'_{n-i+1}(M)}(V(M))}=n-i+1, \]
\[ \dim_KV(M)^{\mu}=\dim_K \bigg(\mathop{\bigcup}\limits_{\eta< \lambda_{\rm max}(M_{\mathcal{E}})-\mu}S_{\eta}(V(M))\bigg)\geqslant \dim_K{S_{s'_{n-i+1}(M)}(V(M))}=n-i+1, \]
where the first (respectively, second) equality follows from Theorem 0.1(ii) (respectively, the previous remark). Hence, ![]() $s_i(M)\geqslant \lambda _{\rm max}(M_{\mathcal {E}})-s'_{n-i+1}(M)$ by the previous remark, which implies the assertion.
$s_i(M)\geqslant \lambda _{\rm max}(M_{\mathcal {E}})-s'_{n-i+1}(M)$ by the previous remark, which implies the assertion.
(ii) We can prove as previously with Proposition 5.3 and Theorem 0.1(ii) replaced by Theorem 5.6.
Remark 10.4 (Non-coincidence of the right endpoints) In part (i) (respectively, part (ii)) of Proposition 10.3, the right endpoints of the two polygons may not coincide if ![]() $M_{\mathcal {E}}$ (respectively,
$M_{\mathcal {E}}$ (respectively, ![]() $M$) is not PBQ. For example, let
$M$) is not PBQ. For example, let ![]() $M$ be the
$M$ be the ![]() $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over ![]() $\mathcal {R}^{\mathrm {bd}}$ defined by
$\mathcal {R}^{\mathrm {bd}}$ defined by ![]() $\mathcal {R}^{\mathrm {bd}}\oplus \mathcal {R}^{\mathrm {bd}}(q)$. As
$\mathcal {R}^{\mathrm {bd}}\oplus \mathcal {R}^{\mathrm {bd}}(q)$. As ![]() $M$ is trivial as a
$M$ is trivial as a ![]() $\nabla$-module over
$\nabla$-module over ![]() $\mathcal {R}^{\mathrm {bd}}$, we have
$\mathcal {R}^{\mathrm {bd}}$, we have ![]() $s_1(M_{(\mathcal {E})})=s_2(M_{(\mathcal {E})})=0$. Moreover, we obviously have
$s_1(M_{(\mathcal {E})})=s_2(M_{(\mathcal {E})})=0$. Moreover, we obviously have ![]() $s'_1(M_{(\mathcal {E})})=0,s'_2(M_{(\mathcal {E})})=1$, and
$s'_1(M_{(\mathcal {E})})=0,s'_2(M_{(\mathcal {E})})=1$, and ![]() $\lambda _{\rm max}(M_{\mathcal {E}})=1$. Hence,
$\lambda _{\rm max}(M_{\mathcal {E}})=1$. Hence, ![]() $\mathrm {NP}(M_{(\mathcal {E})})$ has right endpoint
$\mathrm {NP}(M_{(\mathcal {E})})$ has right endpoint ![]() $(2,0)$, and the Newton polygons of
$(2,0)$, and the Newton polygons of ![]() $S_{\lambda _{\rm max}(M_{\mathcal {E}})-\bullet }(M_{\mathcal {R}})$ and
$S_{\lambda _{\rm max}(M_{\mathcal {E}})-\bullet }(M_{\mathcal {R}})$ and ![]() $S_{\lambda _{\rm max}(M_{\mathcal {E}})-\bullet }(M_{\mathcal {E}})$ have right endpoints
$S_{\lambda _{\rm max}(M_{\mathcal {E}})-\bullet }(M_{\mathcal {E}})$ have right endpoints ![]() $(2,1)$. Note that
$(2,1)$. Note that ![]() $M_{\mathcal {E}}$ is not PBQ by
$M_{\mathcal {E}}$ is not PBQ by ![]() $M_{\mathcal {E}}^0=0$, and the PBQ filtration of
$M_{\mathcal {E}}^0=0$, and the PBQ filtration of ![]() $M_{(\mathcal {E})}$ is given by
$M_{(\mathcal {E})}$ is given by ![]() $P_1(M)=\mathcal {R}^{\mathrm {bd}}(q),P_2(M)=M$ (respectively,
$P_1(M)=\mathcal {R}^{\mathrm {bd}}(q),P_2(M)=M$ (respectively, ![]() $P_1(M_{\mathcal {E}})=\mathcal {E}(q),P_2(M_{\mathcal {E}})=M_{\mathcal {E}}$).
$P_1(M_{\mathcal {E}})=\mathcal {E}(q),P_2(M_{\mathcal {E}})=M_{\mathcal {E}}$).
Proof of Theorem 0.4 As in the proof of Proposition 5.3, we may assume that ![]() $k$ is algebraically closed. We have only to prove that
$k$ is algebraically closed. We have only to prove that ![]() $h_i(M)\geqslant h_i(M_{\mathcal {E}})$ for all
$h_i(M)\geqslant h_i(M_{\mathcal {E}})$ for all ![]() $i$ with equality when
$i$ with equality when ![]() $i=n$. We prove by induction on
$i=n$. We prove by induction on ![]() $n$. In the case where
$n$. In the case where ![]() $M_{\mathcal {E}}$ is PBQ (including the base case
$M_{\mathcal {E}}$ is PBQ (including the base case ![]() $n=1$), the assertion follows from Proposition 10.3 and the specialization theorem for Frobenius Newton polygons [Reference KedlayaKed10, Theorem 16.4.6], that is,
$n=1$), the assertion follows from Proposition 10.3 and the specialization theorem for Frobenius Newton polygons [Reference KedlayaKed10, Theorem 16.4.6], that is, ![]() $s'_{n-i+1}(M)+\dots +s'_n(M)\leqslant s'_{n-i+1}(M_{\mathcal {E}})+\cdots +s'_n(M_{\mathcal {E}})$ with equality when
$s'_{n-i+1}(M)+\dots +s'_n(M)\leqslant s'_{n-i+1}(M_{\mathcal {E}})+\cdots +s'_n(M_{\mathcal {E}})$ with equality when ![]() $i=n$. In the induction step, we may assume that
$i=n$. In the induction step, we may assume that ![]() $M_{\mathcal {E}}$ is not PBQ. Then,
$M_{\mathcal {E}}$ is not PBQ. Then, ![]() $0\subsetneq P_1(M)\subsetneq M$ by Lemma 9.5(i) and (ii). As
$0\subsetneq P_1(M)\subsetneq M$ by Lemma 9.5(i) and (ii). As ![]() $h_i(M)$ is equal to the minimum of the sums of
$h_i(M)$ is equal to the minimum of the sums of ![]() $i$ elements in the slope multiset of
$i$ elements in the slope multiset of ![]() $V(M)^{\bullet }$, we have
$V(M)^{\bullet }$, we have ![]() $h_i(M)=\min \{h_j(M/P_1(M))+h_l(P_1(M));j,l\in \mathbb {N},j+l=i\}$ by Lemma 9.8(ii). Similarly, we have
$h_i(M)=\min \{h_j(M/P_1(M))+h_l(P_1(M));j,l\in \mathbb {N},j+l=i\}$ by Lemma 9.8(ii). Similarly, we have ![]() $h_i(M_{\mathcal {E}})=\min \{h_j((M/P_1(M))_{\mathcal {E}})+h_l(P_1(M)_{\mathcal {E}});j,l\in \mathbb {N},j+l=i\}$ by Lemma 9.9(ii). Hence, the assertion follows from the induction hypothesis for
$h_i(M_{\mathcal {E}})=\min \{h_j((M/P_1(M))_{\mathcal {E}})+h_l(P_1(M)_{\mathcal {E}});j,l\in \mathbb {N},j+l=i\}$ by Lemma 9.9(ii). Hence, the assertion follows from the induction hypothesis for ![]() $M/P_1(M)$ and
$M/P_1(M)$ and ![]() $P_1(M)$.
$P_1(M)$.
Note that the inequality ![]() $s_n(M)\leqslant s_n(M_{\mathcal {E}})$ in Theorem 0.4 may be regarded as a partial generalization of Christol's transfer theorem [Reference Chiarellotto and TsuzukiCT09, Proposition 4.3], which asserts an analogous inequality for a
$s_n(M)\leqslant s_n(M_{\mathcal {E}})$ in Theorem 0.4 may be regarded as a partial generalization of Christol's transfer theorem [Reference Chiarellotto and TsuzukiCT09, Proposition 4.3], which asserts an analogous inequality for a ![]() $\nabla$-module over
$\nabla$-module over ![]() $K[\![t]\!]_0$ such that
$K[\![t]\!]_0$ such that ![]() $M\otimes _{K[\![t]\!]_0}K\{t\}$ is trivial as a
$M\otimes _{K[\![t]\!]_0}K\{t\}$ is trivial as a ![]() $\nabla$-module over
$\nabla$-module over ![]() $K\{t\}$.
$K\{t\}$.
Remark 10.5 (André's theorem, cf. [Reference Chiarellotto and TsuzukiCT11, Remark 2.8])
In [Reference DworkDwo73, pp. 45–46], Dwork gives a primitive version of Proposition 10.3 as a conjectural statement for ![]() $p$-adic differential equations. Then, as an analogue of Grothendieck–Katz theorem in the sense of the introduction, Dwork states the following.
$p$-adic differential equations. Then, as an analogue of Grothendieck–Katz theorem in the sense of the introduction, Dwork states the following.
Conjecture [Reference DworkDwo73, Conjecture 2]
The [log-growth] Newton polygon (at ![]() $b$) rises under specialization.
$b$) rises under specialization.
André proved this conjecture. Precisely speaking, let ![]() $M$ be a
$M$ be a ![]() $\nabla$-module of rank
$\nabla$-module of rank ![]() $n$ over
$n$ over ![]() $K[\![t]\!]_0$ such that
$K[\![t]\!]_0$ such that ![]() $M\otimes _{K[\![t]\!]_0}K\{t\}$ is trivial as a
$M\otimes _{K[\![t]\!]_0}K\{t\}$ is trivial as a ![]() $\nabla$-module over
$\nabla$-module over ![]() $K\{t\}$. We can define
$K\{t\}$. We can define ![]() $\mathrm {NP}(M_{(\mathcal {E})})$ and
$\mathrm {NP}(M_{(\mathcal {E})})$ and ![]() $h_n(M_{(\mathcal {E})})$ as in Definition 10.1. Let
$h_n(M_{(\mathcal {E})})$ as in Definition 10.1. Let ![]() $NP_{\log ,\bar {0}}(M)$ (respectively,
$NP_{\log ,\bar {0}}(M)$ (respectively, ![]() $NP_{\log ,\bar {t}}(M_{\bar {t}})$) be the translation of
$NP_{\log ,\bar {t}}(M_{\bar {t}})$) be the translation of ![]() $\mathrm {NP}(M)$ (respectively,
$\mathrm {NP}(M)$ (respectively, ![]() $\mathrm {NP}(M_{\mathcal {E}})$) by
$\mathrm {NP}(M_{\mathcal {E}})$) by ![]() $-h_n(M)$ (respectively,
$-h_n(M)$ (respectively, ![]() $-h_n(M_{\mathcal {E}})$) along the
$-h_n(M_{\mathcal {E}})$) along the ![]() $y$-axis so that the right endpoint coincides with
$y$-axis so that the right endpoint coincides with ![]() $(n,0)$, which is called the special (respectively, generic) log-growth Newton polygon of
$(n,0)$, which is called the special (respectively, generic) log-growth Newton polygon of ![]() $M$ in [Reference AndréAnd08, 3.4]. Then, André proves that
$M$ in [Reference AndréAnd08, 3.4]. Then, André proves that ![]() $NP_{\log ,\bar {0}}(M)$ lies on or above
$NP_{\log ,\bar {0}}(M)$ lies on or above ![]() $NP_{\log ,\bar {t}}(M_{\bar {t}})$ (see [Reference AndréAnd08, Theorem 4.1.1]); we consequently have
$NP_{\log ,\bar {t}}(M_{\bar {t}})$ (see [Reference AndréAnd08, Theorem 4.1.1]); we consequently have ![]() $h_n(M)\leqslant h_n(M_{\mathcal {E}})$. Dwork's conjecture in the introduction is an analogue of the above conjecture for
$h_n(M)\leqslant h_n(M_{\mathcal {E}})$. Dwork's conjecture in the introduction is an analogue of the above conjecture for ![]() $(\varphi ,\nabla )$-modules
$(\varphi ,\nabla )$-modules ![]() $M$ over
$M$ over ![]() $K[\![t]\!]_0$, which is equivalent to saying, under André's notation, that
$K[\![t]\!]_0$, which is equivalent to saying, under André's notation, that ![]() $NP_{\log ,\bar {0}}(M)$ lies on or above
$NP_{\log ,\bar {0}}(M)$ lies on or above ![]() $NP_{\log ,\bar {t}}(M_{\bar {t}})$ with the same left endpoints, i.e.
$NP_{\log ,\bar {t}}(M_{\bar {t}})$ with the same left endpoints, i.e. ![]() $h_n(M)=h_n(M_{\mathcal {E}})$; note that the equality
$h_n(M)=h_n(M_{\mathcal {E}})$; note that the equality ![]() $h_n(M)=h_n(M_{\mathcal {E}})$ does not always hold for
$h_n(M)=h_n(M_{\mathcal {E}})$ does not always hold for ![]() $\nabla$-modules
$\nabla$-modules ![]() $M$ over
$M$ over ![]() $K[\![t]\!]_0$ such that
$K[\![t]\!]_0$ such that ![]() $M\otimes _{K[\![t]\!]_0}K\{t\}$ are trivial as
$M\otimes _{K[\![t]\!]_0}K\{t\}$ are trivial as ![]() $\nabla$-modules over
$\nabla$-modules over ![]() $K\{t\}$ (see [Reference OhkuboOhk15]). To the best of the author's knowledge, at this point, there is no alternative proof of Dwork's conjecture or
$K\{t\}$ (see [Reference OhkuboOhk15]). To the best of the author's knowledge, at this point, there is no alternative proof of Dwork's conjecture or ![]() $h_n(M)=h_n(M_{\mathcal {E}})$ exploiting Andre's theorem in an essential way.
$h_n(M)=h_n(M_{\mathcal {E}})$ exploiting Andre's theorem in an essential way.
Finally, we give applications to log-![]() $(\varphi ,\nabla )$-modules over
$(\varphi ,\nabla )$-modules over ![]() $K[\![t]\!]_0$. We put
$K[\![t]\!]_0$. We put ![]() $K\{t\}_{\rm log}:=K\{t\}[\ell _X]$, which is regarded as a
$K\{t\}_{\rm log}:=K\{t\}[\ell _X]$, which is regarded as a ![]() $K\{t\}$-subalgebra of
$K\{t\}$-subalgebra of ![]() $\mathcal {R}_{\rm log}$. Let
$\mathcal {R}_{\rm log}$. Let ![]() $R$ denote either
$R$ denote either ![]() $K[\![t]\!]_0$ or
$K[\![t]\!]_0$ or ![]() $K\{t\}_{\rm log}$. As in Convention 2, we assume that
$K\{t\}_{\rm log}$. As in Convention 2, we assume that ![]() $\varphi$ on
$\varphi$ on ![]() $\mathcal {R}$ satisfies
$\mathcal {R}$ satisfies ![]() $\varphi (t)=S\in K[\![t]\!]_0$. Then,
$\varphi (t)=S\in K[\![t]\!]_0$. Then, ![]() $R$ is stable under both
$R$ is stable under both ![]() $\varphi$ and
$\varphi$ and ![]() $\partial _{\rm log}:=t\partial =t d/dt$ by
$\partial _{\rm log}:=t\partial =t d/dt$ by ![]() $\partial _{\rm log}(\ell _X)=\partial _{\rm log}(X)/X=i+\partial _{\rm log}(v)/v\in K[\![t]\!]_0$, where we write
$\partial _{\rm log}(\ell _X)=\partial _{\rm log}(X)/X=i+\partial _{\rm log}(v)/v\in K[\![t]\!]_0$, where we write ![]() $X=t^iv$ as in Definition 2.1(iii). Moreover, we have
$X=t^iv$ as in Definition 2.1(iii). Moreover, we have ![]() $\partial _{\rm log}(\varphi (t))/\varphi (t)\cdot \varphi \circ \partial _{\rm log}=\partial _{\rm log}\circ \varphi$. We define a log-
$\partial _{\rm log}(\varphi (t))/\varphi (t)\cdot \varphi \circ \partial _{\rm log}=\partial _{\rm log}\circ \varphi$. We define a log-![]() $\nabla$-module over
$\nabla$-module over ![]() $R$ as a finite free
$R$ as a finite free ![]() $R$-module equipped with a differential operator relative to
$R$-module equipped with a differential operator relative to ![]() $\partial _{\rm log}$. We define a log-
$\partial _{\rm log}$. We define a log-![]() $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over ![]() $R$ as a
$R$ as a ![]() $\varphi$-module
$\varphi$-module ![]() $M$ over
$M$ over ![]() $R$ equipped with a differential operator
$R$ equipped with a differential operator ![]() $\partial _{\log ,M}$ relative to
$\partial _{\log ,M}$ relative to ![]() $\partial _{\rm log}$ satisfying the compatibility condition
$\partial _{\rm log}$ satisfying the compatibility condition ![]() $\partial _{\rm log}(\varphi (t))/\varphi (t)\cdot \varphi _M\circ \partial _{\log ,M}=\partial _{\log ,M}\circ \varphi _M$ (cf. Definition 4.1(ii)). We put
$\partial _{\rm log}(\varphi (t))/\varphi (t)\cdot \varphi _M\circ \partial _{\log ,M}=\partial _{\log ,M}\circ \varphi _M$ (cf. Definition 4.1(ii)). We put ![]() $R'=\mathcal {R}^{\mathrm {bd}}$ if
$R'=\mathcal {R}^{\mathrm {bd}}$ if ![]() $R=K[\![t]\!]_0$, and
$R=K[\![t]\!]_0$, and ![]() $R'=\mathcal {R}_{\rm log}$ if
$R'=\mathcal {R}_{\rm log}$ if ![]() $R=K\{t\}_{\rm log}$. Then,
$R=K\{t\}_{\rm log}$. Then, ![]() $M':=M\otimes _RR'$ is regarded as a
$M':=M\otimes _RR'$ is regarded as a ![]() $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over ![]() $R'$ by setting
$R'$ by setting ![]() $\varphi _{M'}=\varphi _M\otimes \varphi$ and
$\varphi _{M'}=\varphi _M\otimes \varphi$ and ![]() $\partial _{M'}=\partial _{\log ,M}\otimes t\cdot \mathrm {id}_{R'}+\mathrm {id}_M\otimes \partial$. Moreover, we have an obvious base change functor from the category of log-
$\partial _{M'}=\partial _{\log ,M}\otimes t\cdot \mathrm {id}_{R'}+\mathrm {id}_M\otimes \partial$. Moreover, we have an obvious base change functor from the category of log-![]() $(\varphi ,\nabla )$-modules over
$(\varphi ,\nabla )$-modules over ![]() $K[\![t]\!]_0$ to the category of log-
$K[\![t]\!]_0$ to the category of log-![]() $(\varphi ,\nabla )$-modules over
$(\varphi ,\nabla )$-modules over ![]() $K\{t\}_{\rm log}$ as in § 4.1. Thus, we obtain the following diagram of functors, which is commutative up to a natural isomorphism.
$K\{t\}_{\rm log}$ as in § 4.1. Thus, we obtain the following diagram of functors, which is commutative up to a natural isomorphism.

We claim that if ![]() $M$ is a log-
$M$ is a log-![]() $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over ![]() $K[\![t]\!]_0$, then
$K[\![t]\!]_0$, then ![]() $M\otimes _{K[\![t]\!]_0}K\{t\}_{\rm log}$ is trivial as a log-
$M\otimes _{K[\![t]\!]_0}K\{t\}_{\rm log}$ is trivial as a log-![]() $\nabla$-module over
$\nabla$-module over ![]() $K\{t\}_{\rm log}$. As in Remark 5.2, we may assume that
$K\{t\}_{\rm log}$. As in Remark 5.2, we may assume that ![]() $X=t$, in which case the claim follows from a nilpotent analogue of Dwork's trick [Reference KedlayaKed10, Corollary 17.2.4]: note that a log-
$X=t$, in which case the claim follows from a nilpotent analogue of Dwork's trick [Reference KedlayaKed10, Corollary 17.2.4]: note that a log-![]() $(\varphi ,\nabla )$-module over
$(\varphi ,\nabla )$-module over ![]() $K[\![t]\!]_0$ is regarded as a finite differential module over the differential ring
$K[\![t]\!]_0$ is regarded as a finite differential module over the differential ring ![]() $(K[\![t]\!]_0,td/dt)$ with a Frobenius structure in the sense of [Reference KedlayaKed10, Remark 17.1.2].
$(K[\![t]\!]_0,td/dt)$ with a Frobenius structure in the sense of [Reference KedlayaKed10, Remark 17.1.2].
We define the log-growth filtration of ![]() $K\{t\}_{\rm log}$ by
$K\{t\}_{\rm log}$ by ![]() $\mathrm {Fil}_{\lambda }K\{t\}_{\rm log}:=K\{t\}_{\rm log}\cap \mathrm {Fil}_{\lambda }\mathcal {R}_{\rm log}$ for
$\mathrm {Fil}_{\lambda }K\{t\}_{\rm log}:=K\{t\}_{\rm log}\cap \mathrm {Fil}_{\lambda }\mathcal {R}_{\rm log}$ for ![]() $\lambda \in \mathbb {R}$ (cf.[Reference OhkuboOhk17, Definition 4.11]). By using the claim, we can define
$\lambda \in \mathbb {R}$ (cf.[Reference OhkuboOhk17, Definition 4.11]). By using the claim, we can define ![]() $V(M),\mathrm {Sol}(M)$, etc., for log-
$V(M),\mathrm {Sol}(M)$, etc., for log-![]() $(\varphi ,\nabla )$-modules
$(\varphi ,\nabla )$-modules ![]() $M$ over
$M$ over ![]() $K[\![t]\!]_0$ as in § 5. Moreover, an analogue of Lemma 0.3 holds: note that the unipotence of
$K[\![t]\!]_0$ as in § 5. Moreover, an analogue of Lemma 0.3 holds: note that the unipotence of ![]() $(M_{\mathcal {R}^{\mathrm {bd}}})_{\mathcal {R}}$ follows from the above claim and Lemma 4.8(ii). Hence, we can prove the following result as in the proof of Theorem 0.2 given in the introduction.
$(M_{\mathcal {R}^{\mathrm {bd}}})_{\mathcal {R}}$ follows from the above claim and Lemma 4.8(ii). Hence, we can prove the following result as in the proof of Theorem 0.2 given in the introduction.
Theorem 10.6 Analogues of Proposition 5.3, Chiarellotto–Tsuzuki conjecture, and Dwork's conjecture hold for log-![]() $(\varphi ,\nabla )$-modules
$(\varphi ,\nabla )$-modules ![]() $M$ over
$M$ over ![]() $K[\![t]\!]_0$, where we define
$K[\![t]\!]_0$, where we define ![]() $M_{\mathcal {E}}:=(M\otimes _{K[\![t]\!]_0}\mathcal {R}^{\mathrm {bd}})_{\mathcal {E}}$.
$M_{\mathcal {E}}:=(M\otimes _{K[\![t]\!]_0}\mathcal {R}^{\mathrm {bd}})_{\mathcal {E}}$.
Acknowledgements
The author thanks Nobuo Tsuzuki for discussion and many comments. The author thanks Daxin Xu for useful discussion. The author also thanks the anonymous referee(s) for valuable comments. This work is supported by JSPS KAKENHI Grant-in-Aid for Young Scientists (B) JP17K14161.
Appendix
The following is a list of notation used in the paper.
§ 1
 $(F,\phi ,q)$,
$(F,\phi ,q)$,  $\lambda _{\rm max}(-)$,
$\lambda _{\rm max}(-)$,  $S_{\bullet }(-)$,
$S_{\bullet }(-)$,  $S^{\bullet }(-)$
$S^{\bullet }(-)$§ 2
 $(K,\varphi _K,q)$,
$(K,\varphi _K,q)$,  $\mathcal {O}_K$,
$\mathcal {O}_K$,  $\mathfrak {m}_K$,
$\mathfrak {m}_K$,  $k$
$k$§ 2.1
 $\mathcal {R}^r$,
$\mathcal {R}^r$,  $\mathcal {R}$,
$\mathcal {R}$,  $|\cdot |_r:\mathcal {R}^r\to \mathbb {R}_{\geqslant 0}$,
$|\cdot |_r:\mathcal {R}^r\to \mathbb {R}_{\geqslant 0}$,  $\mathcal {R}^{\mathrm {bd}}$,
$\mathcal {R}^{\mathrm {bd}}$,  $\mathcal {R}^{\mathrm {int}}$,
$\mathcal {R}^{\mathrm {int}}$,  $|\cdot |_0:\mathcal {R}^{\mathrm {bd}}\to \mathbb {R}_{\geqslant 0}$,
$|\cdot |_0:\mathcal {R}^{\mathrm {bd}}\to \mathbb {R}_{\geqslant 0}$,  $\mathcal {E}$,
$\mathcal {E}$,  $X$,
$X$,  $\ell _X$,
$\ell _X$,  $\mathcal {R}_{\rm log}$,
$\mathcal {R}_{\rm log}$,  $\varphi :\mathcal {R}\to \mathcal {R}$,
$\varphi :\mathcal {R}\to \mathcal {R}$,  $S$
$S$§ 2.2
 $\tilde {\mathcal {R}}^r$,
$\tilde {\mathcal {R}}^r$,  $\tilde {\mathcal {R}}$,
$\tilde {\mathcal {R}}$,  $|\cdot |_r:\tilde {\mathcal {R}}^r\to \mathbb {R}_{\geqslant 0}$,
$|\cdot |_r:\tilde {\mathcal {R}}^r\to \mathbb {R}_{\geqslant 0}$,  $\tilde {\mathcal {R}}^{\mathrm {bd}}$,
$\tilde {\mathcal {R}}^{\mathrm {bd}}$,  $\tilde {\mathcal {R}}^{\mathrm {int}}$,
$\tilde {\mathcal {R}}^{\mathrm {int}}$,  $|\cdot |_0:\tilde {\mathcal {R}}^{\mathrm {bd}}\to \mathbb {R}_{\geqslant 0}$,
$|\cdot |_0:\tilde {\mathcal {R}}^{\mathrm {bd}}\to \mathbb {R}_{\geqslant 0}$,  $k((u^{\mathbb {Q}}))$,
$k((u^{\mathbb {Q}}))$,  $\tilde {\mathcal {E}}$,
$\tilde {\mathcal {E}}$,  $\tilde {\mathcal {R}}_{\rm log}$,
$\tilde {\mathcal {R}}_{\rm log}$,  $\varphi :\tilde {\mathcal {R}}\to \tilde {\mathcal {R}}$
$\varphi :\tilde {\mathcal {R}}\to \tilde {\mathcal {R}}$§ 2.3
 $L$,
$L$,  $\tilde {\psi }_L$,
$\tilde {\psi }_L$,  $r_0$,
$r_0$,  $c_0$,
$c_0$,  $c_1$
$c_1$§ 3.1
 $\mathrm {Fil}_{\bullet }\tilde {\mathcal {R}}$,
$\mathrm {Fil}_{\bullet }\tilde {\mathcal {R}}$,  $\mathrm {Fil}_{\bullet }\tilde {\mathcal {R}}_{\rm log}$
$\mathrm {Fil}_{\bullet }\tilde {\mathcal {R}}_{\rm log}$§ 3.2
 $\mathrm {Fil}_{\bullet }\mathcal {R}$,
$\mathrm {Fil}_{\bullet }\mathcal {R}$,  $\mathrm {Fil}_{\bullet }\mathcal {R}_{\rm log}$
$\mathrm {Fil}_{\bullet }\mathcal {R}_{\rm log}$§ 4.1
 $\partial$,
$\partial$,  $\partial _M$,
$\partial _M$,  $\phi _M$,
$\phi _M$,  $(-)^{\nabla }$
$(-)^{\nabla }$§ 4.2
 $T_{X,X'}$,
$T_{X,X'}$,  $\mathbf {V}(-)$,
$\mathbf {V}(-)$,  $N_X$,
$N_X$,  $K'$,
$K'$,  $\psi$,
$\psi$,  $U(-)$
$U(-)$§ 5
 $V(-)$,
$V(-)$,  $\mathrm {Sol}(-)$,
$\mathrm {Sol}(-)$,  $V(-)^{\bullet }$,
$V(-)^{\bullet }$,  $\mathrm {Sol}_{\bullet }(-)$,
$\mathrm {Sol}_{\bullet }(-)$,  $M^{\bullet }$
$M^{\bullet }$§ 9
 $\sigma _{N,M}$,
$\sigma _{N,M}$,  $P_{\bullet }(-)$
$P_{\bullet }(-)$§ 10
 $\mathrm {NP}(-)$,
$\mathrm {NP}(-)$,  $s_{\bullet }(-)$,
$s_{\bullet }(-)$,  $h_{\bullet }(-)$,
$h_{\bullet }(-)$,  $s'_{\bullet }(-)$,
$s'_{\bullet }(-)$,  $K\{t\}_{\rm log}$,
$K\{t\}_{\rm log}$,  $\partial _{\rm log}$,
$\partial _{\rm log}$,  $\partial _{\log ,M}$,
$\partial _{\log ,M}$,  $\mathrm {Fil}_{\bullet }K\{t\}_{\rm log}$
$\mathrm {Fil}_{\bullet }K\{t\}_{\rm log}$
The following is a commutative diagram of rings, where the hooked arrows denote the inclusions, and all morphisms are injective.