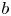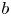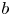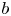Introduction
The notion of a ![]() $b$-divisor was introduced by Shokurov and has found striking applications in algebraic geometry and singularity theory [Reference ShokurovSho96, Reference ShokurovSho03, Reference AmbroAmb05, Reference CortiCor07, Reference FujinoFuj12, Reference Boucksom, de Fernex and FavreBdFF12, Reference ZhangZha14, Reference Boucksom, Favre and JonssonBFJ14, Reference Hacon and LiuHL21], and in algebraic dynamical systems [Reference Boucksom, Favre and JonssonBFJ08a, Reference CantatCan11, Reference Gignac and RuggieroGR14, Reference XieXie15, Reference Blanc and CantatBC16, Reference Dang and FavreDF21]. It provides the right setting to construct Zariski decomposition of divisors [Reference Boucksom, Favre and JonssonBFJ09, Reference Küronya and MacleanKM13] and of higher codimension cycles [Reference Fulger and LehmannFL17b]. It is also deeply tied with some recent developments in pluripotential analysis on non-Archimedean analytic varieties (see [Reference ZhangZha95, Reference GublerGub98, Reference Chambert-LoirCha06, Reference Boucksom, Favre and JonssonBFJ16, Reference Boucksom and JonssonBJ18, Reference Gubler, Jell, Künnemann and MartinGJKM19] and the references therein).
$b$-divisor was introduced by Shokurov and has found striking applications in algebraic geometry and singularity theory [Reference ShokurovSho96, Reference ShokurovSho03, Reference AmbroAmb05, Reference CortiCor07, Reference FujinoFuj12, Reference Boucksom, de Fernex and FavreBdFF12, Reference ZhangZha14, Reference Boucksom, Favre and JonssonBFJ14, Reference Hacon and LiuHL21], and in algebraic dynamical systems [Reference Boucksom, Favre and JonssonBFJ08a, Reference CantatCan11, Reference Gignac and RuggieroGR14, Reference XieXie15, Reference Blanc and CantatBC16, Reference Dang and FavreDF21]. It provides the right setting to construct Zariski decomposition of divisors [Reference Boucksom, Favre and JonssonBFJ09, Reference Küronya and MacleanKM13] and of higher codimension cycles [Reference Fulger and LehmannFL17b]. It is also deeply tied with some recent developments in pluripotential analysis on non-Archimedean analytic varieties (see [Reference ZhangZha95, Reference GublerGub98, Reference Chambert-LoirCha06, Reference Boucksom, Favre and JonssonBFJ16, Reference Boucksom and JonssonBJ18, Reference Gubler, Jell, Künnemann and MartinGJKM19] and the references therein).
A ![]() $b$-divisor class is by definition a collection of Néron–Severi classes in all birational models of a fixed projective variety satisfying natural compatibility conditions under pushforward morphisms. It is thus in essence an ‘infinite’ object and defining the intersection product of two such objects always requires a limiting process which may be guaranteed only under special circumstances.
$b$-divisor class is by definition a collection of Néron–Severi classes in all birational models of a fixed projective variety satisfying natural compatibility conditions under pushforward morphisms. It is thus in essence an ‘infinite’ object and defining the intersection product of two such objects always requires a limiting process which may be guaranteed only under special circumstances.
Such an intersection theory has been successfully developed for special classes of ![]() $b$-divisors: Cartier
$b$-divisors: Cartier ![]() $b$-divisors in [Reference Kaveh and KhovanskiiKK14], relatively nef
$b$-divisors in [Reference Kaveh and KhovanskiiKK14], relatively nef ![]() $b$-divisors over a closed point in [Reference Boucksom, Favre and JonssonBFJ08b], and over the spectrum of a valuation ring [Reference Boucksom, Favre and JonssonBFJ16, Reference Boucksom and JonssonBJ18, Reference Gubler, Jell, Künnemann and MartinGJKM19]. In this paper, we focus on nef
$b$-divisors over a closed point in [Reference Boucksom, Favre and JonssonBFJ08b], and over the spectrum of a valuation ring [Reference Boucksom, Favre and JonssonBFJ16, Reference Boucksom and JonssonBJ18, Reference Gubler, Jell, Künnemann and MartinGJKM19]. In this paper, we focus on nef ![]() $b$-divisors over a projective variety, and show that one can develop a natural intersection calculus for them. We proceed with proving a Hodge index theorem in this context, and invert the operator
$b$-divisors over a projective variety, and show that one can develop a natural intersection calculus for them. We proceed with proving a Hodge index theorem in this context, and invert the operator ![]() $\alpha \mapsto \alpha ^{d-1}$ (
$\alpha \mapsto \alpha ^{d-1}$ (![]() $d$ being the dimension of the ambient variety) which may be viewed as an analog of the complex Monge–Ampère operator.
$d$ being the dimension of the ambient variety) which may be viewed as an analog of the complex Monge–Ampère operator.
We work under the following setup, and borrow the terminology from [Reference Boucksom, Favre and JonssonBFJ08a, Reference Dang and FavreDF21].
Let ![]() $X$ be any smooth projective variety of dimension
$X$ be any smooth projective variety of dimension ![]() $d$ defined over an algebraically closed field
$d$ defined over an algebraically closed field ![]() $K$ of characteristic
$K$ of characteristic ![]() $0$. A Weil
$0$. A Weil ![]() $b$-divisor class
$b$-divisor class ![]() $\alpha$ is a family of real Néron–Severi classes
$\alpha$ is a family of real Néron–Severi classes ![]() $\alpha _{X'}\in \operatorname {NS}(X')$ that are compatible under pushforward. Here
$\alpha _{X'}\in \operatorname {NS}(X')$ that are compatible under pushforward. Here ![]() $X'$ runs over all smooth birational models lying over
$X'$ runs over all smooth birational models lying over ![]() $X$.
$X$.
The space ![]() $\operatorname {w-N}^{1}({ \mathcal {X} })$ (where
$\operatorname {w-N}^{1}({ \mathcal {X} })$ (where ![]() ${ \mathcal {X} }$ stands for the Riemann–Zariski space of
${ \mathcal {X} }$ stands for the Riemann–Zariski space of ![]() $X$) of Weil
$X$) of Weil ![]() $b$-divisor classes forms an infinite-dimensional vector space. It can be identified with the projective limit of the real Néron–Severi spaces of all models, hence carries a natural locally convex topology in which every bounded set is relatively compact.
$b$-divisor classes forms an infinite-dimensional vector space. It can be identified with the projective limit of the real Néron–Severi spaces of all models, hence carries a natural locally convex topology in which every bounded set is relatively compact.
Cartier ![]() $b$-divisors are Weil
$b$-divisors are Weil ![]() $b$-divisors for which there exists a model
$b$-divisors for which there exists a model ![]() $X'$ such that
$X'$ such that ![]() $\alpha _{X''} = \pi ^{*} \alpha _{X'}$ for any model such that the induced birational map
$\alpha _{X''} = \pi ^{*} \alpha _{X'}$ for any model such that the induced birational map ![]() $\pi \colon X''\to X'$ is regular. In this situation we say that
$\pi \colon X''\to X'$ is regular. In this situation we say that ![]() $\alpha$ is determined by
$\alpha$ is determined by ![]() $\alpha _{X'}$ in
$\alpha _{X'}$ in ![]() $X'$. The space
$X'$. The space ![]() $\operatorname {c-N}^{1}({ \mathcal {X} })$ of Cartier
$\operatorname {c-N}^{1}({ \mathcal {X} })$ of Cartier ![]() $b$-divisors is dense in
$b$-divisors is dense in ![]() $\operatorname {w-N}^{1}({ \mathcal {X} })$.
$\operatorname {w-N}^{1}({ \mathcal {X} })$.
As the nef property is stable by pullback, one can define nef Cartier classes as those determined by nef classes in some model. We say that a class ![]() $\alpha \in \operatorname {w-N}^{1}({ \mathcal {X} })$ is nef if it lies in the closure of the set of nef classes in
$\alpha \in \operatorname {w-N}^{1}({ \mathcal {X} })$ is nef if it lies in the closure of the set of nef classes in ![]() $\operatorname {w-N}^{1}({ \mathcal {X} })$.
$\operatorname {w-N}^{1}({ \mathcal {X} })$.
Our main aim is to explore in depth the structure of the convex cone ![]() $\operatorname {Nef^{1}}({ \mathcal {X} })$ of nef
$\operatorname {Nef^{1}}({ \mathcal {X} })$ of nef ![]() $b$-divisors. To that end, we first prove a fundamental approximation result for arbitrary nef classes.
$b$-divisors. To that end, we first prove a fundamental approximation result for arbitrary nef classes.
Theorem A Let ![]() $\alpha \in \operatorname {Nef^{1}}({ \mathcal {X} })$ be any nef class. Then there exists a sequence of nef Cartier
$\alpha \in \operatorname {Nef^{1}}({ \mathcal {X} })$ be any nef class. Then there exists a sequence of nef Cartier ![]() $b$-divisor classes
$b$-divisor classes ![]() $\alpha _n \in \operatorname {c-Nef^{1}}({ \mathcal {X} })$ decreasing to
$\alpha _n \in \operatorname {c-Nef^{1}}({ \mathcal {X} })$ decreasing to ![]() $\alpha$.
$\alpha$.
The crucial point in this statement is the fact that the approximating sequence is decreasing meaning that it satisfies the condition ![]() $\alpha _n \geqslant \alpha$ in the sense that
$\alpha _n \geqslant \alpha$ in the sense that ![]() $\alpha _n - \alpha$ is pseudo-effective (psef) for all
$\alpha _n - \alpha$ is pseudo-effective (psef) for all ![]() $n$. The proof relies on the asymptotic construction of multiplier ideals and is completely analogous to (and, in fact, simpler than) the approximation results of relatively nef
$n$. The proof relies on the asymptotic construction of multiplier ideals and is completely analogous to (and, in fact, simpler than) the approximation results of relatively nef ![]() $b$-divisors (over a smooth point [Reference Boucksom, Favre and JonssonBFJ08b], or over a curve [Reference Boucksom, Favre and JonssonBFJ16, Reference Boucksom and JonssonBJ18, Reference Gubler, Jell, Künnemann and MartinGJKM19]). A similar approximation result is proved in a toroidal context in [Reference Botero and Burgos GilBBG22, Lemma 5.9] which does not use multiplier ideals techniques.
$b$-divisors (over a smooth point [Reference Boucksom, Favre and JonssonBFJ08b], or over a curve [Reference Boucksom, Favre and JonssonBFJ16, Reference Boucksom and JonssonBJ18, Reference Gubler, Jell, Künnemann and MartinGJKM19]). A similar approximation result is proved in a toroidal context in [Reference Botero and Burgos GilBBG22, Lemma 5.9] which does not use multiplier ideals techniques.
After we released a first version of this paper, and using the same technics based on multiplier ideal sheaves, Boucksom and Jonsson have been able to prove an approximation result for plurisubharmonic functions on the Berkovich analytification of projective varieties defined over a trivially valued field. As explained in [Reference Boucksom and JonssonBJ21, § 10.3], their far-reaching result implies our theorem.
In order to intersect nef ![]() $b$-divisors, it is necessary to discuss an appropriate notion of positivity for classes of arbitrary codimension.
$b$-divisors, it is necessary to discuss an appropriate notion of positivity for classes of arbitrary codimension.
We first define a ![]() $b$-numerical class of codimension
$b$-numerical class of codimension ![]() $k$ as a collection of numerical classes
$k$ as a collection of numerical classes ![]() $\alpha _{X'}\in \operatorname {N}^{k}(X')$ for any proper birational model
$\alpha _{X'}\in \operatorname {N}^{k}(X')$ for any proper birational model ![]() $X'\to X$ that are invariant under pushforward morphisms. Cartier
$X'\to X$ that are invariant under pushforward morphisms. Cartier ![]() $b$-classes are defined analogously as in codimension one. We obtain a locally convex topological space
$b$-classes are defined analogously as in codimension one. We obtain a locally convex topological space ![]() $\operatorname {w-N}^{k}({ \mathcal {X} })$ containing
$\operatorname {w-N}^{k}({ \mathcal {X} })$ containing ![]() $\operatorname {c-N}^{k}({ \mathcal {X} })$ as a dense subset and we have a natural perfect intersection pairing
$\operatorname {c-N}^{k}({ \mathcal {X} })$ as a dense subset and we have a natural perfect intersection pairing ![]() $\operatorname {w-N}^{k}({ \mathcal {X} }) \times \operatorname {c-N}^{d-k}({ \mathcal {X} }) \to \mathbb {R}$.
$\operatorname {w-N}^{k}({ \mathcal {X} }) \times \operatorname {c-N}^{d-k}({ \mathcal {X} }) \to \mathbb {R}$.
Several notions of positivity have been explored in ![]() $\operatorname {N}^{k}(X')$, see [Reference Fulger and LehmannFL17a]. Among those, we shall use the notion of basepoint-free (BPF) classes which seems appropriate in several contexts, in particular for applications to dynamical systems, see [Reference DangDan20, Reference Dang and FavreDF21].
$\operatorname {N}^{k}(X')$, see [Reference Fulger and LehmannFL17a]. Among those, we shall use the notion of basepoint-free (BPF) classes which seems appropriate in several contexts, in particular for applications to dynamical systems, see [Reference DangDan20, Reference Dang and FavreDF21].
By definition, a numerical class ![]() $\operatorname {N}^{k}(X')$ is BPF if it can be approximated by images under flat morphisms of complete intersection ample classes. As previously, this notion leads to the definition of codimension-
$\operatorname {N}^{k}(X')$ is BPF if it can be approximated by images under flat morphisms of complete intersection ample classes. As previously, this notion leads to the definition of codimension-![]() $k$ BPF numerical
$k$ BPF numerical ![]() $b$-classes.
$b$-classes.
Note that a class in ![]() $\operatorname {N}^{1}(X')$ is BPF if and only if it is nef, so that
$\operatorname {N}^{1}(X')$ is BPF if and only if it is nef, so that ![]() $\operatorname {BPF}^{1}({ \mathcal {X} })=\operatorname {Nef^{1}}({ \mathcal {X} })$. We further prove in § 5.1 that a
$\operatorname {BPF}^{1}({ \mathcal {X} })=\operatorname {Nef^{1}}({ \mathcal {X} })$. We further prove in § 5.1 that a ![]() $b$-numerical class
$b$-numerical class ![]() $\alpha \in \operatorname {w-N}^{k}({ \mathcal {X} })$ is BPF iff for all models
$\alpha \in \operatorname {w-N}^{k}({ \mathcal {X} })$ is BPF iff for all models ![]() $X'$ the class
$X'$ the class ![]() $\alpha _{X'}$ is movable (see Theorem 5.2). These results generalize [Reference Boucksom, de Fernex and FavreBdFF12, Lemma 2.10], and suggest the following duality conjecture that is proved by Lehmann [Reference LehmannLeh11, Theorem 1.5] when
$\alpha _{X'}$ is movable (see Theorem 5.2). These results generalize [Reference Boucksom, de Fernex and FavreBdFF12, Lemma 2.10], and suggest the following duality conjecture that is proved by Lehmann [Reference LehmannLeh11, Theorem 1.5] when ![]() $k=1$, and that we extend to the case
$k=1$, and that we extend to the case ![]() $k=d-1$ (Proposition 5.6).
$k=d-1$ (Proposition 5.6).
(i) A
 $b$-numerical class
$b$-numerical class  $\alpha \in \operatorname {w-N}^{k}({ \mathcal {X} })$ is psef iff for any
$\alpha \in \operatorname {w-N}^{k}({ \mathcal {X} })$ is psef iff for any  $b$-numerical class
$b$-numerical class  $\beta \in \operatorname {c-BPF}^{d-k}({ \mathcal {X} })$ we have
$\beta \in \operatorname {c-BPF}^{d-k}({ \mathcal {X} })$ we have  $(\alpha \cdot \beta )\geqslant 0$.
$(\alpha \cdot \beta )\geqslant 0$.(ii) A
 $b$-numerical class
$b$-numerical class  $\alpha \in \operatorname {w-N}^{k}({ \mathcal {X} })$ belongs to
$\alpha \in \operatorname {w-N}^{k}({ \mathcal {X} })$ belongs to  $\operatorname {BPF}^{k}({ \mathcal {X} })$ iff for any psef Cartier
$\operatorname {BPF}^{k}({ \mathcal {X} })$ iff for any psef Cartier  $b$-numerical class
$b$-numerical class  $\beta \in \operatorname {c-N}^{d-k}({ \mathcal {X} })$, we have
$\beta \in \operatorname {c-N}^{d-k}({ \mathcal {X} })$, we have  $(\alpha \cdot \beta )\geqslant 0$.
$(\alpha \cdot \beta )\geqslant 0$.
With these notions at hand and using Theorem A, one can follow the construction of positive intersection classes developed in [Reference Boucksom, Favre and JonssonBFJ09, Reference Boucksom, Demailly, Păun and PeternellBDPP13], and define a generalized intersection product of nef ![]() $b$-divisor classes which takes the following form.
$b$-divisor classes which takes the following form.
Given any collection of nef classes ![]() $\{\alpha _i\}_{1\leqslant i \leqslant k}\in \operatorname {Nef^{1}}({ \mathcal {X} })$, we define
$\{\alpha _i\}_{1\leqslant i \leqslant k}\in \operatorname {Nef^{1}}({ \mathcal {X} })$, we define ![]() $(\alpha _1\cdot \ldots \cdot \alpha _k)\in \operatorname {BPF}^{k}({ \mathcal {X} })$ as the infimum
$(\alpha _1\cdot \ldots \cdot \alpha _k)\in \operatorname {BPF}^{k}({ \mathcal {X} })$ as the infimum ![]() $(\beta _1\cdot \ldots \cdot \beta _k)$ over all nef Cartier
$(\beta _1\cdot \ldots \cdot \beta _k)$ over all nef Cartier ![]() $b$-classes
$b$-classes ![]() $\beta _i\geqslant \alpha _i$. That this intersection product is multilinear and extends the natural one on Cartier classes is a consequence of Theorem A.
$\beta _i\geqslant \alpha _i$. That this intersection product is multilinear and extends the natural one on Cartier classes is a consequence of Theorem A.
Of crucial importance to applications is the fact that the intersection product satisfies various forms of the Hodge index theorem. In particular, we shall prove the following result.
Theorem B Any two ![]() $b$-divisor classes
$b$-divisor classes ![]() $\alpha, \beta \in \operatorname {Nef^{1}}({ \mathcal {X} })$ such that
$\alpha, \beta \in \operatorname {Nef^{1}}({ \mathcal {X} })$ such that ![]() $\alpha \cdot \beta =0$ are proportional.
$\alpha \cdot \beta =0$ are proportional.
We also obtain a far-reaching generalization of [Reference Dinh and SibonyDS04a, Corollary 3.5] for ![]() $b$-divisors, see Theorem 3.14 below. We hope that this result will find applications to the study of birational group actions on projective varieties.
$b$-divisors, see Theorem 3.14 below. We hope that this result will find applications to the study of birational group actions on projective varieties.
Let ![]() ${{\omega }}$ be any Cartier
${{\omega }}$ be any Cartier ![]() $b$-divisor class determined by an ample class in
$b$-divisor class determined by an ample class in ![]() $X$. For any
$X$. For any ![]() $k\geqslant 1$, let us call big any class
$k\geqslant 1$, let us call big any class ![]() $\alpha \in \operatorname {w-N}^{k}({ \mathcal {X} })$ such that
$\alpha \in \operatorname {w-N}^{k}({ \mathcal {X} })$ such that ![]() $\alpha \geqslant c{{\omega }}^{k}$ for some
$\alpha \geqslant c{{\omega }}^{k}$ for some ![]() $c>0$. As two ample classes are comparable, the notion of bigness does not depend on the choice of
$c>0$. As two ample classes are comparable, the notion of bigness does not depend on the choice of ![]() ${{\omega }}$. It follows from Siu's inequalities that for any two big BPF classes
${{\omega }}$. It follows from Siu's inequalities that for any two big BPF classes ![]() $\alpha, \beta \in \operatorname {BPF}^{k}({ \mathcal {X} })$ there exists a constant
$\alpha, \beta \in \operatorname {BPF}^{k}({ \mathcal {X} })$ there exists a constant ![]() $C>1$ such that
$C>1$ such that ![]() $C^{-1} \alpha \leqslant \beta \leqslant C \alpha$. We prove that any big BPF class of dimension one can be realized as a
$C^{-1} \alpha \leqslant \beta \leqslant C \alpha$. We prove that any big BPF class of dimension one can be realized as a ![]() $(d-1)$th power of a nef
$(d-1)$th power of a nef ![]() $b$-divisor. Our precise result reads as follows.
$b$-divisor. Our precise result reads as follows.
Theorem C The map ![]() $\alpha \mapsto \alpha ^{d-1}$ induces a bijection from the convex cone of big
$\alpha \mapsto \alpha ^{d-1}$ induces a bijection from the convex cone of big ![]() $b$-divisor classes
$b$-divisor classes ![]() $\alpha \in \operatorname {Nef^{1}}({ \mathcal {X} })$ onto the convex cone of big
$\alpha \in \operatorname {Nef^{1}}({ \mathcal {X} })$ onto the convex cone of big ![]() $b$-numerical curve classes in
$b$-numerical curve classes in ![]() $\operatorname {BPF}^{d-1}({ \mathcal {X} })$.
$\operatorname {BPF}^{d-1}({ \mathcal {X} })$.
Our proof is variational in nature, and follows the same line of arguments as in [Reference Boucksom, Favre and JonssonBFJ15] (whose proof is itself inspired by [Reference AlexandrovAle96, Reference Berman, Boucksom, Guedj and ZeriahiBBGZ13]). A key point in the proof is the differentiability of the volume function, see [Reference Boucksom, Favre and JonssonBFJ09, Reference Lazarsfeld and MustaţăLM09, Reference Witt NyströmWN19]. Over a toric variety, a big curve (torus-invariant) class can be identified to a positive measure on a sphere, and our statement reduces in that case to Minkowski's theorem which states the existence of a convex body with a prescribed surface area measure [Reference SchneiderSch14, Theorem 8.2.2].
Recently several decompositions of sufficiently positive curve classes on projective varieties have been introduced [Reference Lehmann and XiaoLX16, Reference Fulger and LehmannFL17b, Reference Lehmann and XiaoLX19] which generalizes the Zariski decomposition of psef divisors. Theorem C gives a new perspective on these decompositions as we now explain.
First Lehmann and Xiao [Reference Lehmann and XiaoLX16] have shown that for any big curve class ![]() $\alpha \in \operatorname {N}^{d-1}(X)$ there exists a unique nef class
$\alpha \in \operatorname {N}^{d-1}(X)$ there exists a unique nef class ![]() $\operatorname {LX}(\alpha ) \in \operatorname {N}^{1}(X)$ such that
$\operatorname {LX}(\alpha ) \in \operatorname {N}^{1}(X)$ such that
We prove (Theorem 5.8) that for any big BPF class ![]() $\alpha$ the family of nef Cartier classes
$\alpha$ the family of nef Cartier classes ![]() $\operatorname {LX}(\alpha _{X'})$ where
$\operatorname {LX}(\alpha _{X'})$ where ![]() $X'$ ranges over all models over
$X'$ ranges over all models over ![]() $X$ converges to the unique nef class
$X$ converges to the unique nef class ![]() $\gamma$ solving
$\gamma$ solving ![]() $\gamma ^{d-1} = \alpha$. As a consequence of [Reference Lehmann and XiaoLX16, Theorem 5.29], we also obtain a characterization of big curve classes in terms of the functional
$\gamma ^{d-1} = \alpha$. As a consequence of [Reference Lehmann and XiaoLX16, Theorem 5.29], we also obtain a characterization of big curve classes in terms of the functional ![]() $\operatorname {\widehat {\operatorname {vol}}}$ that was introduced by Xiao in [Reference XiaoXia17] (Theorem 5.11).
$\operatorname {\widehat {\operatorname {vol}}}$ that was introduced by Xiao in [Reference XiaoXia17] (Theorem 5.11).
We then discuss a second decomposition based on the functional ![]() ${{\mathfrak {M}}}$ defined on movable curve classes and introduced by Xiao. We prove (Theorem 5.12) yet another convergence result
${{\mathfrak {M}}}$ defined on movable curve classes and introduced by Xiao. We prove (Theorem 5.12) yet another convergence result ![]() $\operatorname {Mv}(\alpha _{X'})\to \gamma$ where
$\operatorname {Mv}(\alpha _{X'})\to \gamma$ where ![]() $\operatorname {Mv}(\alpha _{X'})\in \operatorname {N}^{1}(X')$ is the movable divisor class computing
$\operatorname {Mv}(\alpha _{X'})\in \operatorname {N}^{1}(X')$ is the movable divisor class computing ![]() ${{\mathfrak {M}}}(\alpha _{X'})$ given by [Reference Lehmann and XiaoLX19, Theorem 3.14].
${{\mathfrak {M}}}(\alpha _{X'})$ given by [Reference Lehmann and XiaoLX19, Theorem 3.14].
The intersection theory of ![]() $b$-divisors and the techniques presented in this paper lead to a better understanding of the structure of the space of
$b$-divisors and the techniques presented in this paper lead to a better understanding of the structure of the space of ![]() $b$-classes. The most natural norm on
$b$-classes. The most natural norm on ![]() $\operatorname {c-N}^{k}({ \mathcal {X} })$ is arguably defined by
$\operatorname {c-N}^{k}({ \mathcal {X} })$ is arguably defined by ![]() $\lVert {\alpha } \rVert _{\omega }:= \inf \{ C>0, -C {{\omega }}^{k} \leqslant \alpha \leqslant C {{\omega }}^{k}\}$, and we may thus look at the Banach space
$\lVert {\alpha } \rVert _{\omega }:= \inf \{ C>0, -C {{\omega }}^{k} \leqslant \alpha \leqslant C {{\omega }}^{k}\}$, and we may thus look at the Banach space ![]() $\operatorname {N}^{k}_+({ \mathcal {X} })$ obtained as the completion of
$\operatorname {N}^{k}_+({ \mathcal {X} })$ obtained as the completion of ![]() $\operatorname {c-N}^{k}({ \mathcal {X} })$ with respect to this norm. The underlying topological space of
$\operatorname {c-N}^{k}({ \mathcal {X} })$ with respect to this norm. The underlying topological space of ![]() $\operatorname {N}^{k}_+({ \mathcal {X} })$ is independent of the choice of
$\operatorname {N}^{k}_+({ \mathcal {X} })$ is independent of the choice of ![]() ${{\omega }}$ as all such norms are equivalent.
${{\omega }}$ as all such norms are equivalent.
In a previous paper [Reference Dang and FavreDF21], we also introduced other Banach spaces ![]() $\operatorname {N}_{\operatorname {BPF}}^{k}({ \mathcal {X} }), \operatorname {N}^{{k},\vee }_{\operatorname {BPF}}({ \mathcal {X} }) \subset \operatorname {w-N}^{k}({ \mathcal {X} })$ for
$\operatorname {N}_{\operatorname {BPF}}^{k}({ \mathcal {X} }), \operatorname {N}^{{k},\vee }_{\operatorname {BPF}}({ \mathcal {X} }) \subset \operatorname {w-N}^{k}({ \mathcal {X} })$ for ![]() $0\leqslant k\leqslant d$ and
$0\leqslant k\leqslant d$ and ![]() $\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} }) \subset \operatorname {w-N}^{1}({ \mathcal {X} })$ which played a crucial role in our approach to analyze the degree growth of rational self-maps.
$\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} }) \subset \operatorname {w-N}^{1}({ \mathcal {X} })$ which played a crucial role in our approach to analyze the degree growth of rational self-maps.
First ![]() $\operatorname {N}_{\operatorname {BPF}}^{k}({ \mathcal {X} })$ is obtained as the completion of the space of Cartier
$\operatorname {N}_{\operatorname {BPF}}^{k}({ \mathcal {X} })$ is obtained as the completion of the space of Cartier ![]() $b$-divisor classes for the norm induced by the BPF cone. The space
$b$-divisor classes for the norm induced by the BPF cone. The space ![]() $\operatorname {N}^{{k},\vee }_{\operatorname {BPF}}({ \mathcal {X} })$ is similarly defined as the completion of
$\operatorname {N}^{{k},\vee }_{\operatorname {BPF}}({ \mathcal {X} })$ is similarly defined as the completion of ![]() $\operatorname {c-N}^{k}({ \mathcal {X} })$ for the dual norm induced by the BPF cone.
$\operatorname {c-N}^{k}({ \mathcal {X} })$ for the dual norm induced by the BPF cone.
Let us review briefly the definition of ![]() $\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$ referring to § 1.4 for more details. When
$\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$ referring to § 1.4 for more details. When ![]() $X$ is a surface, then
$X$ is a surface, then ![]() $\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$ is the Picard–Manin space introduced by Cantat [Reference CantatCan11] and [Reference Boucksom, Favre and JonssonBFJ08a]. It is a Hilbert space which is equipped with a natural intersection form
$\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$ is the Picard–Manin space introduced by Cantat [Reference CantatCan11] and [Reference Boucksom, Favre and JonssonBFJ08a]. It is a Hilbert space which is equipped with a natural intersection form ![]() $\langle \cdot, \cdot \rangle$ of Minkowski's type for which the Hodge index theorem extends naturally. It contains
$\langle \cdot, \cdot \rangle$ of Minkowski's type for which the Hodge index theorem extends naturally. It contains ![]() $\operatorname {N}_{\operatorname {BPF}}^{1}({ \mathcal {X} })$ and is contained in
$\operatorname {N}_{\operatorname {BPF}}^{1}({ \mathcal {X} })$ and is contained in ![]() $\operatorname {N}^{{1},\vee }_{\operatorname {BPF}}({ \mathcal {X} })$, and its importance stems from the fact that birational surface maps induce isometries for the pairing
$\operatorname {N}^{{1},\vee }_{\operatorname {BPF}}({ \mathcal {X} })$, and its importance stems from the fact that birational surface maps induce isometries for the pairing ![]() $\langle \cdot, \cdot \rangle$.
$\langle \cdot, \cdot \rangle$.
In higher dimension, ![]() $\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$ is defined as the completion of
$\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$ is defined as the completion of ![]() $\operatorname {c-N}^{1}({ \mathcal {X} })$ with respect to a family of semi-norms obtained by restricting classes to sufficiently general surfaces in birational models of
$\operatorname {c-N}^{1}({ \mathcal {X} })$ with respect to a family of semi-norms obtained by restricting classes to sufficiently general surfaces in birational models of ![]() $X$. In [Reference Dang and FavreDF21], we proved that a version of the Hodge index theorem still holds in this Banach space.
$X$. In [Reference Dang and FavreDF21], we proved that a version of the Hodge index theorem still holds in this Banach space.
We use Theorem A and a version of Diskant inequalities for ![]() $b$-divisors extending [Reference Boucksom, Favre and JonssonBFJ09, Theorem F] to prove the following inclusions.
$b$-divisors extending [Reference Boucksom, Favre and JonssonBFJ09, Theorem F] to prove the following inclusions.
Theorem D One has the following sequence of continuous injections:
The first and last injections were proved in [Reference Dang and FavreDF21, Proposition 2.10] whereas the equality ![]() $\operatorname {N}^{1}_+({ \mathcal {X} }) =\operatorname {N}^{{1},\vee }_{\operatorname {BPF}}({ \mathcal {X} })$ and the two injections
$\operatorname {N}^{1}_+({ \mathcal {X} }) =\operatorname {N}^{{1},\vee }_{\operatorname {BPF}}({ \mathcal {X} })$ and the two injections ![]() $\operatorname {Vect}(\operatorname {Nef^{1}}({ \mathcal {X} })) \hookrightarrow \operatorname {N^{1}_{\Sigma }}({ \mathcal {X} }) \hookrightarrow \operatorname {N}^{{1},\vee }_{\operatorname {BPF}}({ \mathcal {X} })$ are new.
$\operatorname {Vect}(\operatorname {Nef^{1}}({ \mathcal {X} })) \hookrightarrow \operatorname {N^{1}_{\Sigma }}({ \mathcal {X} }) \hookrightarrow \operatorname {N}^{{1},\vee }_{\operatorname {BPF}}({ \mathcal {X} })$ are new.
Conjecture 2 For any projective manifold ![]() $X$ of dimension at least two, all inclusions in (1) are strict.
$X$ of dimension at least two, all inclusions in (1) are strict.
The injection ![]() $\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} }) \hookrightarrow \operatorname {N}^{{1},\vee }_{\operatorname {BPF}}({ \mathcal {X} })$ can be viewed as an analog of the Sobolev injection of
$\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} }) \hookrightarrow \operatorname {N}^{{1},\vee }_{\operatorname {BPF}}({ \mathcal {X} })$ can be viewed as an analog of the Sobolev injection of ![]() $W^{1,2}([0,1])$ into
$W^{1,2}([0,1])$ into ![]() $\mathcal {C}^{0}([0,1])$. This analogy takes its root in the context of toric geometry, and we plan to discuss these links in detail in a forthcoming work.
$\mathcal {C}^{0}([0,1])$. This analogy takes its root in the context of toric geometry, and we plan to discuss these links in detail in a forthcoming work.
Let us discuss some of the restrictions of our approach. As in our companion paper [Reference Dang and FavreDF21], we suppose ![]() $K$ to be of characteristic zero. We use the assumption on the characteristic for the existence of smooth models and for the uniform generation of multiplier ideals which eventually relies on Kodaira vanishing theorem. We expect though that our results extend verbatim to positive characteristics with multiplier ideals being replaced by test ideals as in [Reference Gubler, Jell, Künnemann and MartinGJKM19].
$K$ to be of characteristic zero. We use the assumption on the characteristic for the existence of smooth models and for the uniform generation of multiplier ideals which eventually relies on Kodaira vanishing theorem. We expect though that our results extend verbatim to positive characteristics with multiplier ideals being replaced by test ideals as in [Reference Gubler, Jell, Künnemann and MartinGJKM19].
It is very tempting to extend our results to compact Kähler manifolds. In this case, the natural objects to consider are projective limits of Dolbeault cohomology spaces ![]() $H^{k,k}_\mathbb {R}(X')$ where
$H^{k,k}_\mathbb {R}(X')$ where ![]() $\mu \colon X'\to X$ ranges over all bimeromorphic proper holomorphic maps. Observe that one obtains a space which is, in general, much bigger than
$\mu \colon X'\to X$ ranges over all bimeromorphic proper holomorphic maps. Observe that one obtains a space which is, in general, much bigger than ![]() $\operatorname {w-N}^{k}({ \mathcal {X} })$ even when
$\operatorname {w-N}^{k}({ \mathcal {X} })$ even when ![]() $X$ is projective as one needs to deal with potentially transcendental classes.
$X$ is projective as one needs to deal with potentially transcendental classes.
The notion of volume and the Zariski decomposition of big ![]() $(1,1)$-cohomological classes (which in the projective case play important roles in our approach) have been defined by Boucksom [Reference BoucksomBou04] and further characterized by DiNezza, Floris, and Trapani [Reference Di Nezza, Floris and TrapaniDNFT17] (see also [Reference NakayamaNak04, Reference Darvas, Di Nezza and LuDDNL21, Reference TosattiTos19]). Even so, we face a serious obstacle in extending our results because the differentiability of volume function is not known for arbitrary Kähler manifolds. This property is equivalent to the so-called transcendental Morse inequalities (that we call Siu's inequalities here) by an argument of Xiao, see also [Reference Witt NyströmWN19, Appendix A]. Much progress have been made recently towards the proof of these inequalities (see [Reference XiaoXia15, Reference TosattiTos16, Reference PopoviciPop16, Reference ChioseChi16, Reference PopoviciPop17]) but they remain open in general. Note that the duality between the movable curves and psef classes is also very much related to these problems, and is not known except in the projective case (see [Reference Witt NyströmWN19]).
$(1,1)$-cohomological classes (which in the projective case play important roles in our approach) have been defined by Boucksom [Reference BoucksomBou04] and further characterized by DiNezza, Floris, and Trapani [Reference Di Nezza, Floris and TrapaniDNFT17] (see also [Reference NakayamaNak04, Reference Darvas, Di Nezza and LuDDNL21, Reference TosattiTos19]). Even so, we face a serious obstacle in extending our results because the differentiability of volume function is not known for arbitrary Kähler manifolds. This property is equivalent to the so-called transcendental Morse inequalities (that we call Siu's inequalities here) by an argument of Xiao, see also [Reference Witt NyströmWN19, Appendix A]. Much progress have been made recently towards the proof of these inequalities (see [Reference XiaoXia15, Reference TosattiTos16, Reference PopoviciPop16, Reference ChioseChi16, Reference PopoviciPop17]) but they remain open in general. Note that the duality between the movable curves and psef classes is also very much related to these problems, and is not known except in the projective case (see [Reference Witt NyströmWN19]).
It would be interesting to investigate analogs of Theorem A for a class ![]() $\alpha \in \operatorname {BPF}^{k}({ \mathcal {X} })$ with
$\alpha \in \operatorname {BPF}^{k}({ \mathcal {X} })$ with ![]() $k\geqslant 2$. The work of Dinh and Sibony [Reference Dinh and SibonyDS04b] on the regularization of positive closed currents suggests that one might expect the existence of a sequence
$k\geqslant 2$. The work of Dinh and Sibony [Reference Dinh and SibonyDS04b] on the regularization of positive closed currents suggests that one might expect the existence of a sequence ![]() $\alpha _n^{\pm } \in \operatorname {c-BPF}^{k}({ \mathcal {X} })$ such that
$\alpha _n^{\pm } \in \operatorname {c-BPF}^{k}({ \mathcal {X} })$ such that ![]() $\alpha = \lim _n (\alpha _n^{+} - \alpha _n^{-})$, and
$\alpha = \lim _n (\alpha _n^{+} - \alpha _n^{-})$, and ![]() $\sup _n (\alpha ^{\pm }_n\cdot {{\omega }}^{d-k})\leqslant C (\alpha \cdot {{\omega }}^{d-k})$ for some universal
$\sup _n (\alpha ^{\pm }_n\cdot {{\omega }}^{d-k})\leqslant C (\alpha \cdot {{\omega }}^{d-k})$ for some universal ![]() $C>0$.
$C>0$.
One might also want to generalize Theorem C and try to solve the equation ![]() $(\alpha ^{k}\cdot {{\omega }}^{d-k-1}) =\theta$ where
$(\alpha ^{k}\cdot {{\omega }}^{d-k-1}) =\theta$ where ![]() ${{\omega }}\in \operatorname {Nef^{1}}({ \mathcal {X} })$ and
${{\omega }}\in \operatorname {Nef^{1}}({ \mathcal {X} })$ and ![]() $\theta \in \operatorname {BPF}^{d-1}({ \mathcal {X} })$ are fixed and
$\theta \in \operatorname {BPF}^{d-1}({ \mathcal {X} })$ are fixed and ![]() $\alpha$ lie in an appropriate subspace of numerical divisor
$\alpha$ lie in an appropriate subspace of numerical divisor ![]() $b$-classes. This would be analogous to solving mixed Monge–Ampere equations in the complex domain (see [Reference Dinew and KołodziejDK14, Reference Lu and NguyenLN15, Reference Benali and ZeriahiBZ20, Reference Benali and ZeriahiBZ21] and the references therein for recent developments on this problem).
$b$-classes. This would be analogous to solving mixed Monge–Ampere equations in the complex domain (see [Reference Dinew and KołodziejDK14, Reference Lu and NguyenLN15, Reference Benali and ZeriahiBZ20, Reference Benali and ZeriahiBZ21] and the references therein for recent developments on this problem).
Finally one can look at relative situations where ![]() $X$ is a (non-necessarily Noetherian) scheme,
$X$ is a (non-necessarily Noetherian) scheme, ![]() $Z$ is a strict subscheme of
$Z$ is a strict subscheme of ![]() $X$, and consider all proper morphisms
$X$, and consider all proper morphisms ![]() $X' \to X$ that are isomorphisms over
$X' \to X$ that are isomorphisms over ![]() $X\setminus Z$. A case of interest arises when
$X\setminus Z$. A case of interest arises when ![]() $X$ is a flat projective scheme over
$X$ is a flat projective scheme over ![]() $\operatorname {spec}(K^{\circ })$ where
$\operatorname {spec}(K^{\circ })$ where ![]() $K^{\circ }$ is the ring of integers of a complete non-Archimedean metrized field. Then Theorem A follows from the so-called continuity of envelopes, a key problem in the development of non-Archimedean pluripotential theory. We refer to [Reference Boucksom, Favre and JonssonBFJ16, Reference Boucksom and JonssonBJ18, Reference Boucksom and JonssonBJ21, Reference Gubler, Jell, Künnemann and MartinGJKM19] for a detailed discussion of this important problem.
$K^{\circ }$ is the ring of integers of a complete non-Archimedean metrized field. Then Theorem A follows from the so-called continuity of envelopes, a key problem in the development of non-Archimedean pluripotential theory. We refer to [Reference Boucksom, Favre and JonssonBFJ16, Reference Boucksom and JonssonBJ18, Reference Boucksom and JonssonBJ21, Reference Gubler, Jell, Künnemann and MartinGJKM19] for a detailed discussion of this important problem.
1. Basics on  $b$-classes
$b$-classes
In this section, we review briefly some notions on ![]() $b$-classes following the discussion in [Reference Dang and FavreDF21], see also [Reference Boucksom, Favre and JonssonBFJ08a, Reference Boucksom, Favre and JonssonBFJ08b, Reference Küronya and MacleanKM13]. We fix a smooth projective variety
$b$-classes following the discussion in [Reference Dang and FavreDF21], see also [Reference Boucksom, Favre and JonssonBFJ08a, Reference Boucksom, Favre and JonssonBFJ08b, Reference Küronya and MacleanKM13]. We fix a smooth projective variety ![]() $X$ of dimension
$X$ of dimension ![]() $d$ defined over an algebraically closed field
$d$ defined over an algebraically closed field ![]() ${K}$ of characteristic
${K}$ of characteristic ![]() $0$.
$0$.
1.1 Numerical classes of cycles
Let ![]() $Z^{k}(X)$ be the
$Z^{k}(X)$ be the ![]() $\mathbb {R}$-vector space freely generated by irreducible subvarieties of pure codimension
$\mathbb {R}$-vector space freely generated by irreducible subvarieties of pure codimension ![]() $k$ in
$k$ in ![]() $X$. Given any two cycles
$X$. Given any two cycles ![]() $\alpha,\beta$ of complementary dimension in
$\alpha,\beta$ of complementary dimension in ![]() $X$, we denote by
$X$, we denote by ![]() $(\alpha \cdot \beta )\in \mathbb {R}$ their intersection number as defined in [Reference FultonFul98].
$(\alpha \cdot \beta )\in \mathbb {R}$ their intersection number as defined in [Reference FultonFul98].
The numerical space of cycles of codimension ![]() $k$, denoted by
$k$, denoted by ![]() $\operatorname {N}^{k}(X)$, is defined as the quotient of
$\operatorname {N}^{k}(X)$, is defined as the quotient of ![]() $Z^{k}(X)$ by the vector space of cycles
$Z^{k}(X)$ by the vector space of cycles ![]() $z$ such that
$z$ such that ![]() $(\alpha \cdot z) = 0$ for all cycle
$(\alpha \cdot z) = 0$ for all cycle ![]() $\alpha$ of dimension
$\alpha$ of dimension ![]() $k$. It is a finite-dimensional
$k$. It is a finite-dimensional ![]() $\mathbb {R}$-vector space, and the pairing
$\mathbb {R}$-vector space, and the pairing ![]() $\operatorname {N}^{k}(X) \times \operatorname {N}^{d-k}(X) \to \mathbb {R}$ is perfect.
$\operatorname {N}^{k}(X) \times \operatorname {N}^{d-k}(X) \to \mathbb {R}$ is perfect.
The space ![]() $\operatorname {N}^{1}(X)$ is the tensor product of the Néron–Severi group of
$\operatorname {N}^{1}(X)$ is the tensor product of the Néron–Severi group of ![]() $X$ with
$X$ with ![]() $\mathbb {R}$. Intersection products of
$\mathbb {R}$. Intersection products of ![]() $k$ divisors define numerical cycle classes of codimension
$k$ divisors define numerical cycle classes of codimension ![]() $k$ but these classes do not span
$k$ but these classes do not span ![]() $\operatorname {N}^{k}(X)$ in general.
$\operatorname {N}^{k}(X)$ in general.
A class in ![]() $\operatorname {N}^{k}(X)$ is called psef, if it belongs to the closure of the convex cone spanned by effective cycle classes. When
$\operatorname {N}^{k}(X)$ is called psef, if it belongs to the closure of the convex cone spanned by effective cycle classes. When ![]() $\alpha \in \operatorname {N}^{k}(X)$ is psef, we write
$\alpha \in \operatorname {N}^{k}(X)$ is psef, we write ![]() $\alpha \geqslant 0$. The set of psef classes forms a closed salient convex cone
$\alpha \geqslant 0$. The set of psef classes forms a closed salient convex cone ![]() $\operatorname {Psef}^{k}(X)$ inside
$\operatorname {Psef}^{k}(X)$ inside ![]() $\operatorname {N}^{k}(X)$ with non-empty interior.
$\operatorname {N}^{k}(X)$ with non-empty interior.
A class lying in the interior of the cone of psef classes in ![]() $\operatorname {N}^{1}(X)$ is said to be big. An ample class
$\operatorname {N}^{1}(X)$ is said to be big. An ample class ![]() ${{\omega }}$ is big. A class
${{\omega }}$ is big. A class ![]() $\alpha \in \operatorname {N}^{1}(X)$ is big iff one can find
$\alpha \in \operatorname {N}^{1}(X)$ is big iff one can find ![]() $\epsilon >0$ such that
$\epsilon >0$ such that ![]() $\alpha \geqslant \epsilon {{\omega }}$.
$\alpha \geqslant \epsilon {{\omega }}$.
A class ![]() $\alpha \in \operatorname {N}^{1}(X)$ is nef if its intersection with any psef curve class is non-negative. The nef cone
$\alpha \in \operatorname {N}^{1}(X)$ is nef if its intersection with any psef curve class is non-negative. The nef cone ![]() $\operatorname {Nef}^{1}(X)$ is the interior of the cone of real ample classes. A nef class
$\operatorname {Nef}^{1}(X)$ is the interior of the cone of real ample classes. A nef class ![]() $\alpha$ is big iff
$\alpha$ is big iff ![]() $(\alpha ^{d})>0$.
$(\alpha ^{d})>0$.
The negativity lemma (see, e.g., [Reference FujinoFuj11, Lemma 4.16]) states that for any proper birational morphism ![]() $\pi \colon X \to Y$ and any nef class
$\pi \colon X \to Y$ and any nef class ![]() $\alpha \in \operatorname {Nef}^{1}(X)$, we have
$\alpha \in \operatorname {Nef}^{1}(X)$, we have ![]() $\pi ^{*} (\pi _*\alpha ) \geqslant \alpha$.
$\pi ^{*} (\pi _*\alpha ) \geqslant \alpha$.
A class ![]() $\alpha \in \operatorname {N}^{k}(X)$ with
$\alpha \in \operatorname {N}^{k}(X)$ with ![]() $k\geqslant 1$ is called strongly BPF if it is the pushforward under a flat proper morphism of relative dimension
$k\geqslant 1$ is called strongly BPF if it is the pushforward under a flat proper morphism of relative dimension ![]() $e$ of the intersection of
$e$ of the intersection of ![]() $k+e$ ample divisor classes of the intersection of
$k+e$ ample divisor classes of the intersection of ![]() $k+e$ ample divisors.Footnote 1 The closure of the cone generated by strongly BPF classes is called the BPF cone of codimension
$k+e$ ample divisors.Footnote 1 The closure of the cone generated by strongly BPF classes is called the BPF cone of codimension ![]() $k$. We denote it by
$k$. We denote it by ![]() $\operatorname {BPF}^{k}(X)$. When
$\operatorname {BPF}^{k}(X)$. When ![]() $k=1$, BPF classes coincide with nef classes (i.e.
$k=1$, BPF classes coincide with nef classes (i.e. ![]() $\operatorname {Nef^{1}}(X) = \operatorname {BPF}^{1}(X)$). Any BPF class of arbitrary codimension is both psef and nef (i.e. intersects non-negatively the fundamental class of any irreducible subvariety
$\operatorname {Nef^{1}}(X) = \operatorname {BPF}^{1}(X)$). Any BPF class of arbitrary codimension is both psef and nef (i.e. intersects non-negatively the fundamental class of any irreducible subvariety ![]() $V$ of codimension
$V$ of codimension ![]() $d-k$), and the pullback of BPF classes by a proper morphism remains BPF. Note, however, that a nef class need not be psef when
$d-k$), and the pullback of BPF classes by a proper morphism remains BPF. Note, however, that a nef class need not be psef when ![]() $d-2\geqslant k\geqslant 2$, see [Reference Debarre, Ein, Lazarsfeld and VoisinDELV11].
$d-2\geqslant k\geqslant 2$, see [Reference Debarre, Ein, Lazarsfeld and VoisinDELV11].
A class ![]() $\alpha \in \operatorname {N}^{k}(X)$ is big iff one can find
$\alpha \in \operatorname {N}^{k}(X)$ is big iff one can find ![]() $\epsilon >0$ such that
$\epsilon >0$ such that ![]() $\alpha \geqslant \epsilon {{\omega }}^{k}$ for some ample class
$\alpha \geqslant \epsilon {{\omega }}^{k}$ for some ample class ![]() ${{\omega }}$. A class is big iff it belongs to the interior of the psef cone, see [Reference Fulger and LehmannFL17a, Lemma 2.12].
${{\omega }}$. A class is big iff it belongs to the interior of the psef cone, see [Reference Fulger and LehmannFL17a, Lemma 2.12].
The image under a proper birational map of a BPF class is not BPF in general. This motivates the introduction of the notion of ‘movable’ classes. We discuss this notion in detail in § 5.1 following Fulger and Lehmann [Reference Fulger and LehmannFL17b, § 3]. We present here the case of curve classes which is needed in the proof of Proposition 1.9. We insist on working with closed cones, and therefore introduce a slight twist in the usual terminology by introducing first ‘strongly movable’ classes.
One says that a class ![]() $\alpha \in \operatorname {N}^{d-1}(X)$ is strongly movable if there exists a birational proper morphism
$\alpha \in \operatorname {N}^{d-1}(X)$ is strongly movable if there exists a birational proper morphism ![]() $\pi \colon X \to Y$, and real ample classes
$\pi \colon X \to Y$, and real ample classes ![]() $\beta _1, \ldots, \beta _{d-1} \in \operatorname {N}^{d-1}(Y)$ such that
$\beta _1, \ldots, \beta _{d-1} \in \operatorname {N}^{d-1}(Y)$ such that ![]() $\alpha = \pi _*( \beta _1\cdot \cdots \cdot \beta _{d-1})$. A class in
$\alpha = \pi _*( \beta _1\cdot \cdots \cdot \beta _{d-1})$. A class in ![]() $\operatorname {N}^{d-1}(X)$ is movable if it is the limit of a sequence of positive linear combinations of strongly movable classes. By [Reference Boucksom, Demailly, Păun and PeternellBDPP13, Corollary 2.5], a class
$\operatorname {N}^{d-1}(X)$ is movable if it is the limit of a sequence of positive linear combinations of strongly movable classes. By [Reference Boucksom, Demailly, Păun and PeternellBDPP13, Corollary 2.5], a class ![]() $\alpha \in \operatorname {N}^{d-1}(X)$ is movable iff
$\alpha \in \operatorname {N}^{d-1}(X)$ is movable iff ![]() $(\alpha \cdot \gamma )\geqslant 0$ for all nef divisor classes
$(\alpha \cdot \gamma )\geqslant 0$ for all nef divisor classes ![]() $\gamma \in \operatorname {N}^{1}(X)$.
$\gamma \in \operatorname {N}^{1}(X)$.
We now present a key estimate, called Siu's inequalities, which allows one to compare a BPF class with a complete intersection class. We refer to [Reference DangDan20, Proposition 3.4.6] for a proof.
Proposition 1.1 There exists a constant ![]() $C_d>0$ such that for all classes
$C_d>0$ such that for all classes ![]() $\alpha \in \operatorname {BPF}^{k}(X)$ and all big and nef divisor classes
$\alpha \in \operatorname {BPF}^{k}(X)$ and all big and nef divisor classes ![]() $\beta$ on
$\beta$ on ![]() $X$, one has
$X$, one has
1.2 Weil and Cartier numerical  $b$-classes
$b$-classes
A model over ![]() $X$ is a projective birational morphism
$X$ is a projective birational morphism ![]() $\pi \colon X' \to X$ from a smooth projective variety
$\pi \colon X' \to X$ from a smooth projective variety ![]() $X'$. Any such model is obtained as the blow-up of some ideal sheaf on
$X'$. Any such model is obtained as the blow-up of some ideal sheaf on ![]() $X$ so that the category
$X$ so that the category ![]() ${ \mathcal {M}}_X$ of all models over
${ \mathcal {M}}_X$ of all models over ![]() $X$ is naturally a poset for which
$X$ is naturally a poset for which ![]() $X' \geqslant X''$ iff the canonical map
$X' \geqslant X''$ iff the canonical map ![]() $X' \dashrightarrow X''$ is a morphism. When
$X' \dashrightarrow X''$ is a morphism. When ![]() $X'\geqslant X''$ we say that
$X'\geqslant X''$ we say that ![]() $X'$ dominates
$X'$ dominates ![]() $X''$. The poset
$X''$. The poset ![]() ${ \mathcal {M}}_X$ is inductive in the sense that any two models are simultaneously dominated by a third. The projective limit over the inductive system defined by
${ \mathcal {M}}_X$ is inductive in the sense that any two models are simultaneously dominated by a third. The projective limit over the inductive system defined by ![]() ${ \mathcal {M}}_X$ where each model is endowed with the Zariski topology is a quasi-compact topological space called the Riemann–Zariski space of
${ \mathcal {M}}_X$ where each model is endowed with the Zariski topology is a quasi-compact topological space called the Riemann–Zariski space of ![]() $X$ that we denote by
$X$ that we denote by ![]() ${ \mathcal {X} }$. We refer to [Reference VaquiéVaq00] for an interpretation of this space in terms of valuations.
${ \mathcal {X} }$. We refer to [Reference VaquiéVaq00] for an interpretation of this space in terms of valuations.
A Weil numerical ![]() $b$-class
$b$-class ![]() $\alpha$ of codimension
$\alpha$ of codimension ![]() $k$ is a map which assigns to any smooth model
$k$ is a map which assigns to any smooth model ![]() $X'\in { \mathcal {M}}_X$ a numerical class
$X'\in { \mathcal {M}}_X$ a numerical class ![]() $\alpha _{X'}\in \operatorname {N}^{k}(X')$, such that
$\alpha _{X'}\in \operatorname {N}^{k}(X')$, such that ![]() $\pi _*(\alpha _{X'})=\alpha _{X''}$ for any pair of smooth models
$\pi _*(\alpha _{X'})=\alpha _{X''}$ for any pair of smooth models ![]() $X'\geqslant X''$ with
$X'\geqslant X''$ with ![]() $\pi = (\pi '')^{-1}\circ \pi '$. In the rest of the paper, we also refer to codimension-one
$\pi = (\pi '')^{-1}\circ \pi '$. In the rest of the paper, we also refer to codimension-one ![]() $b$-classes as
$b$-classes as ![]() $b$-divisor classes. The class
$b$-divisor classes. The class ![]() $\alpha _{X'}$ is called the incarnation of
$\alpha _{X'}$ is called the incarnation of ![]() $\alpha$ in
$\alpha$ in ![]() $X'$.
$X'$.
A Cartier ![]() $b$-class is a numerical
$b$-class is a numerical ![]() $b$-class
$b$-class ![]() $\alpha$ for which one can find a model
$\alpha$ for which one can find a model ![]() $X''$ such that
$X''$ such that ![]() $\alpha _{X'} = \pi ^{*}(\alpha _{X''})$ for any model
$\alpha _{X'} = \pi ^{*}(\alpha _{X''})$ for any model ![]() $X'\geqslant X''$. When it is the case, we say that
$X'\geqslant X''$. When it is the case, we say that ![]() $\alpha$ is determined in
$\alpha$ is determined in ![]() $X''$. Conversely for any class
$X''$. Conversely for any class ![]() $\alpha \in \operatorname {N}^{k}(X')$, we let
$\alpha \in \operatorname {N}^{k}(X')$, we let ![]() $[\alpha ]$ be the Cartier
$[\alpha ]$ be the Cartier ![]() $b$-class determined by
$b$-class determined by ![]() $\alpha$ in
$\alpha$ in ![]() $X'$.
$X'$.
The space of Weil numerical ![]() $b$-classes is an infinite-dimensional real vector space, which we denote by
$b$-classes is an infinite-dimensional real vector space, which we denote by ![]() $\operatorname {w-N}^{k}({ \mathcal {X} })$. It contains the set of Cartier numerical
$\operatorname {w-N}^{k}({ \mathcal {X} })$. It contains the set of Cartier numerical ![]() $b$-classes
$b$-classes ![]() $\operatorname {c-N}^{k}({ \mathcal {X} })$ as a subspace, and for each smooth model
$\operatorname {c-N}^{k}({ \mathcal {X} })$ as a subspace, and for each smooth model ![]() $X'$ the map
$X'$ the map ![]() $\alpha \mapsto [\alpha ]$ induces an injective linear map
$\alpha \mapsto [\alpha ]$ induces an injective linear map ![]() $\operatorname {N}^{k}(X')\to \operatorname {c-N}^{k}({ \mathcal {X} })$.
$\operatorname {N}^{k}(X')\to \operatorname {c-N}^{k}({ \mathcal {X} })$.
The space ![]() $\operatorname {w-N}^{k}({ \mathcal {X} })$ is a locally convex topological vector space when endowed with its natural product topology, and such that every bounded set is relatively compact. Note that when
$\operatorname {w-N}^{k}({ \mathcal {X} })$ is a locally convex topological vector space when endowed with its natural product topology, and such that every bounded set is relatively compact. Note that when ![]() $K$ is countable this space is also separable and metrizable, but these properties do not hold when
$K$ is countable this space is also separable and metrizable, but these properties do not hold when ![]() $K$ is uncountable.
$K$ is uncountable.
In this topology, a sequence ![]() $\alpha _n \in \operatorname {w-N}^{k}({ \mathcal {X} })$ converges to
$\alpha _n \in \operatorname {w-N}^{k}({ \mathcal {X} })$ converges to ![]() $\beta \in \operatorname {w-N}^{k}({ \mathcal {X} })$ iff for any (smooth) model
$\beta \in \operatorname {w-N}^{k}({ \mathcal {X} })$ iff for any (smooth) model ![]() $X'$ we have
$X'$ we have ![]() $(\alpha _n)_{X'} \to \beta _{X'}$ in
$(\alpha _n)_{X'} \to \beta _{X'}$ in ![]() $\operatorname {N}^{k}(X')$. As for any
$\operatorname {N}^{k}(X')$. As for any ![]() $\alpha \in \operatorname {w-N}^{k}({ \mathcal {X} })$ the sequence of Cartier
$\alpha \in \operatorname {w-N}^{k}({ \mathcal {X} })$ the sequence of Cartier ![]() $b$-classes
$b$-classes ![]() $[\alpha _{X'}]$ converges to
$[\alpha _{X'}]$ converges to ![]() $\alpha$, the space
$\alpha$, the space ![]() $\operatorname {c-N}^{k}({ \mathcal {X} })$ is dense in
$\operatorname {c-N}^{k}({ \mathcal {X} })$ is dense in ![]() $\operatorname {w-N}^{k}({ \mathcal {X} })$.
$\operatorname {w-N}^{k}({ \mathcal {X} })$.
Pick ![]() $\alpha \in \operatorname {c-N}^{k}({ \mathcal {X} })$ and
$\alpha \in \operatorname {c-N}^{k}({ \mathcal {X} })$ and ![]() $\beta \in \operatorname {w-N}^{l}({ \mathcal {X} })$. Suppose
$\beta \in \operatorname {w-N}^{l}({ \mathcal {X} })$. Suppose ![]() $\alpha$ is determined in a model
$\alpha$ is determined in a model ![]() $X_0$. For any other smooth model
$X_0$. For any other smooth model ![]() $X'\geqslant X_0$, we set
$X'\geqslant X_0$, we set ![]() $(\alpha \cdot \beta )_{X'} := \alpha _{X'} \cdot \beta _{X'} \in \operatorname {N}^{k+l}(X')$. By the projection formula,
$(\alpha \cdot \beta )_{X'} := \alpha _{X'} \cdot \beta _{X'} \in \operatorname {N}^{k+l}(X')$. By the projection formula, ![]() $\pi _* (\alpha \cdot \beta )_{X''} = (\alpha \cdot \beta )_{X'}$ for any smooth model
$\pi _* (\alpha \cdot \beta )_{X''} = (\alpha \cdot \beta )_{X'}$ for any smooth model ![]() $X''\geqslant X'$ so that we may define the class
$X''\geqslant X'$ so that we may define the class ![]() $\alpha \cdot \beta \in \operatorname {w-N}^{k+l}({ \mathcal {X} })$ as the unique Weil numerical
$\alpha \cdot \beta \in \operatorname {w-N}^{k+l}({ \mathcal {X} })$ as the unique Weil numerical ![]() $b$-class whose incarnation in any smooth model dominating
$b$-class whose incarnation in any smooth model dominating ![]() $X_0$ is equal to
$X_0$ is equal to ![]() $(\alpha \cdot \beta )_{X'}$.
$(\alpha \cdot \beta )_{X'}$.
The ring ![]() $\operatorname {c-N}^{\bullet }({ \mathcal {X} }) = \oplus \operatorname {c-N}^{k}({ \mathcal {X} })$ is a graded ring over which
$\operatorname {c-N}^{\bullet }({ \mathcal {X} }) = \oplus \operatorname {c-N}^{k}({ \mathcal {X} })$ is a graded ring over which ![]() $\operatorname {w-N}^{\bullet }({ \mathcal {X} }) = \oplus \operatorname {w-N}^{k}({ \mathcal {X} })$ is a graded module.
$\operatorname {w-N}^{\bullet }({ \mathcal {X} }) = \oplus \operatorname {w-N}^{k}({ \mathcal {X} })$ is a graded module.
Lemma 1.2 The pairing ![]() $\operatorname {c-N}^{\bullet }({ \mathcal {X} }) \times \operatorname {w-N}^{\bullet }({ \mathcal {X} })\to \mathbb {R}$ is perfect in the sense that for any integer
$\operatorname {c-N}^{\bullet }({ \mathcal {X} }) \times \operatorname {w-N}^{\bullet }({ \mathcal {X} })\to \mathbb {R}$ is perfect in the sense that for any integer ![]() $k\in \{0, \ldots, d\}$:
$k\in \{0, \ldots, d\}$:
(i) the canonical map from
 $\operatorname {w-N}^{d-k}({ \mathcal {X} })$ to the dual space
$\operatorname {w-N}^{d-k}({ \mathcal {X} })$ to the dual space  $\operatorname {c-N}^{k}({ \mathcal {X} })^{*}$ is an isomorphism;
$\operatorname {c-N}^{k}({ \mathcal {X} })^{*}$ is an isomorphism;(ii) and the canonical map from
 $\operatorname {c-N}^{d-k}({ \mathcal {X} })$ to the space of weakly continuous linear forms on
$\operatorname {c-N}^{d-k}({ \mathcal {X} })$ to the space of weakly continuous linear forms on  $\operatorname {w-N}^{k}({ \mathcal {X} })$ is also an isomorphism.
$\operatorname {w-N}^{k}({ \mathcal {X} })$ is also an isomorphism.
We thank the referee for pointing out to us the following neat proof of the previous lemma.
Proof. The first statement follows from Poincaré duality. Pick any linear form ![]() $\ell$ on
$\ell$ on ![]() $\operatorname {c-N}^{d-k}({ \mathcal {X} })$. For each model
$\operatorname {c-N}^{d-k}({ \mathcal {X} })$. For each model ![]() $X'$, there exists a unique class
$X'$, there exists a unique class ![]() $\alpha _{X'}\in \operatorname {N}^{k}(X')$ such that
$\alpha _{X'}\in \operatorname {N}^{k}(X')$ such that ![]() $\ell ([\beta ]) = (\alpha _{X'}\cdot \beta )$ for all
$\ell ([\beta ]) = (\alpha _{X'}\cdot \beta )$ for all ![]() $\beta \in \operatorname {N}^{d-k}(X')$. For any proper birational morphism
$\beta \in \operatorname {N}^{d-k}(X')$. For any proper birational morphism ![]() $\pi \colon X'' \to X'$ and any class
$\pi \colon X'' \to X'$ and any class ![]() $\beta \in \operatorname {N}^{d-k}(X')$, we have
$\beta \in \operatorname {N}^{d-k}(X')$, we have ![]() $(\alpha _{X'}\cdot \beta ) = \ell ([\beta ]) = (\alpha _{X''}\cdot \pi ^{*}\beta )$ hence
$(\alpha _{X'}\cdot \beta ) = \ell ([\beta ]) = (\alpha _{X''}\cdot \pi ^{*}\beta )$ hence ![]() $\pi _*\alpha _{X''}=\alpha _{X'}$. The collection of numerical classes
$\pi _*\alpha _{X''}=\alpha _{X'}$. The collection of numerical classes ![]() $(\alpha _{X'})$ thus defines a Weil class
$(\alpha _{X'})$ thus defines a Weil class ![]() $\alpha$ which satisfies
$\alpha$ which satisfies ![]() $\ell (\gamma ) = (\alpha \cdot \gamma )$ for any Cartier class
$\ell (\gamma ) = (\alpha \cdot \gamma )$ for any Cartier class ![]() $\gamma$.
$\gamma$.
Before we prove the second statement, note that a basis of neighborhoods of ![]() $0$ for the weak topology on
$0$ for the weak topology on ![]() $\operatorname {w-N}^{d-k}({ \mathcal {X} })$ is given by sets of the form
$\operatorname {w-N}^{d-k}({ \mathcal {X} })$ is given by sets of the form ![]() $[U,X']:=\{\alpha \in \operatorname {w-N}^{d-k}({ \mathcal {X} }) \mid \alpha _{X'} \in U\}$ where
$[U,X']:=\{\alpha \in \operatorname {w-N}^{d-k}({ \mathcal {X} }) \mid \alpha _{X'} \in U\}$ where ![]() $X'$ is a smooth model and
$X'$ is a smooth model and ![]() $U$ is an open neighborhood of
$U$ is an open neighborhood of ![]() $0$ in
$0$ in ![]() $\operatorname {N}^{d-k}(X')$. As the latter space is finite dimensional, it is isomorphic to the dual of
$\operatorname {N}^{d-k}(X')$. As the latter space is finite dimensional, it is isomorphic to the dual of ![]() $\operatorname {N}^{k}(X')$. It follows that the family of open sets
$\operatorname {N}^{k}(X')$. It follows that the family of open sets
also forms a basis of neighborhood of ![]() $0$, where
$0$, where ![]() $\beta _i$ are classes in
$\beta _i$ are classes in ![]() $\operatorname {N}^{k}(X')$ for some model
$\operatorname {N}^{k}(X')$ for some model ![]() $X'$ and
$X'$ and ![]() $r_i$ are positive real numbers.
$r_i$ are positive real numbers.
Now take any weakly continuous linear form ![]() $\ell$ on
$\ell$ on ![]() $\operatorname {w-N}^{d-k}({ \mathcal {X} })$. By what precedes, we may find a model
$\operatorname {w-N}^{d-k}({ \mathcal {X} })$. By what precedes, we may find a model ![]() $X'$, classes
$X'$, classes ![]() $\beta _i\in \operatorname {N}^{k}(X')$ and
$\beta _i\in \operatorname {N}^{k}(X')$ and ![]() $r_i>0$ such that
$r_i>0$ such that ![]() $|\ell (\alpha )|<1$ if
$|\ell (\alpha )|<1$ if ![]() $|(\alpha \cdot [\beta _i])| < r_i$ for all
$|(\alpha \cdot [\beta _i])| < r_i$ for all ![]() $i$. Write
$i$. Write ![]() $\ell _i(\alpha ) := (\alpha \cdot [\beta _i])$. Then we first infer
$\ell _i(\alpha ) := (\alpha \cdot [\beta _i])$. Then we first infer ![]() $| \ell | \leqslant C \max |\ell _i|$ with
$| \ell | \leqslant C \max |\ell _i|$ with ![]() $C= \max r^{-1}_i$, hence
$C= \max r^{-1}_i$, hence ![]() $\ell =0$ on
$\ell =0$ on ![]() $\cap _i \{ \ell _i =0\}$. This implies
$\cap _i \{ \ell _i =0\}$. This implies ![]() $\ell$ is a linear combination of the
$\ell$ is a linear combination of the ![]() $\ell _i$'s (see, e.g., [Reference RudinRud91, Lemma 3.9]). We obtain a family of real numbers
$\ell _i$'s (see, e.g., [Reference RudinRud91, Lemma 3.9]). We obtain a family of real numbers ![]() $a_i$ such that
$a_i$ such that
for all ![]() $\alpha \in \operatorname {w-N}^{d-k}({ \mathcal {X} })$ as required.
$\alpha \in \operatorname {w-N}^{d-k}({ \mathcal {X} })$ as required.
1.3 Positive cones of  $b$-numerical classes
$b$-numerical classes
We discuss here some positivity notions on ![]() $b$-classes that are inherited from those defined on particular models.
$b$-classes that are inherited from those defined on particular models.
A class ![]() $\alpha \in \operatorname {w-N}^{k}({ \mathcal {X} })$ is said to be psef (and we write
$\alpha \in \operatorname {w-N}^{k}({ \mathcal {X} })$ is said to be psef (and we write ![]() $\alpha \geqslant 0$) when
$\alpha \geqslant 0$) when ![]() $\alpha _{X'}\geqslant 0$ for any model
$\alpha _{X'}\geqslant 0$ for any model ![]() $X'$. Note that the pseudo-effectivity is only preserved by pushforward, and not by pullback, so that it may happen that a Cartier
$X'$. Note that the pseudo-effectivity is only preserved by pushforward, and not by pullback, so that it may happen that a Cartier ![]() $b$-class determined by a psef class in a smooth model
$b$-class determined by a psef class in a smooth model ![]() $X$ is not psef in
$X$ is not psef in ![]() $\operatorname {w-N}^{k}({ \mathcal {X} })$. However a Cartier
$\operatorname {w-N}^{k}({ \mathcal {X} })$. However a Cartier ![]() $b$-divisor class
$b$-divisor class ![]() $\alpha \in \operatorname {c-N}^{1}({ \mathcal {X} })$ is psef iff its incarnation in one (or all) of its determination on a smooth model is psef.
$\alpha \in \operatorname {c-N}^{1}({ \mathcal {X} })$ is psef iff its incarnation in one (or all) of its determination on a smooth model is psef.
The notion of BPF ![]() $b$-class is defined as follows. We let
$b$-class is defined as follows. We let ![]() $\operatorname {c-BPF}^{k}({ \mathcal {X} })$ be the convex cone in
$\operatorname {c-BPF}^{k}({ \mathcal {X} })$ be the convex cone in ![]() $\operatorname {c-N}^{k}({ \mathcal {X} })$ generated by Cartier numerical
$\operatorname {c-N}^{k}({ \mathcal {X} })$ generated by Cartier numerical ![]() $b$-classes
$b$-classes ![]() $[\alpha ]$ with
$[\alpha ]$ with ![]() $\alpha \in \operatorname {BPF}(X')$ for some model
$\alpha \in \operatorname {BPF}(X')$ for some model ![]() $X'$. As BPF classes are stable by pullback, a class
$X'$. As BPF classes are stable by pullback, a class ![]() $\alpha \in \operatorname {c-N}^{k}({ \mathcal {X} })$ is BPF iff it is BPF in one of its determination.
$\alpha \in \operatorname {c-N}^{k}({ \mathcal {X} })$ is BPF iff it is BPF in one of its determination.
Definition 1.3 The cone ![]() $\operatorname {BPF}^{k}({ \mathcal {X} })$ is the (weak) closure in
$\operatorname {BPF}^{k}({ \mathcal {X} })$ is the (weak) closure in ![]() $\operatorname {w-N}^{k}({ \mathcal {X} })$ of the cone
$\operatorname {w-N}^{k}({ \mathcal {X} })$ of the cone ![]() $\operatorname {c-BPF}^{k}({ \mathcal {X} })$.
$\operatorname {c-BPF}^{k}({ \mathcal {X} })$.
As the cone ![]() $\operatorname {BPF}^{1}(X')$ coincides with the nef cone for all model
$\operatorname {BPF}^{1}(X')$ coincides with the nef cone for all model ![]() $X'$, we write
$X'$, we write ![]() $\operatorname {Nef^{1}}({ \mathcal {X} })=\operatorname {BPF}^{1}({ \mathcal {X} })$, and
$\operatorname {Nef^{1}}({ \mathcal {X} })=\operatorname {BPF}^{1}({ \mathcal {X} })$, and ![]() $\operatorname {c-Nef^{1}}({ \mathcal {X} })=\operatorname {c-BPF}^{1}({ \mathcal {X} })$. The next lemma is clear but we provide a proof for completeness.
$\operatorname {c-Nef^{1}}({ \mathcal {X} })=\operatorname {c-BPF}^{1}({ \mathcal {X} })$. The next lemma is clear but we provide a proof for completeness.
Lemma 1.4 A class ![]() $\alpha \in \operatorname {w-N}^{k}({ \mathcal {X} })$ is BPF iff there exists a net of classes
$\alpha \in \operatorname {w-N}^{k}({ \mathcal {X} })$ is BPF iff there exists a net of classes ![]() $\alpha _i \in \operatorname {c-BPF}^{k}({ \mathcal {X} })$ such that
$\alpha _i \in \operatorname {c-BPF}^{k}({ \mathcal {X} })$ such that ![]() $(\alpha _i)_{X'} \to \alpha _{X'}$ for all model
$(\alpha _i)_{X'} \to \alpha _{X'}$ for all model ![]() $X'$.
$X'$.
Proof. Pick any class ![]() $\alpha \in \operatorname {w-N}^{k}({ \mathcal {X} })$. For any model
$\alpha \in \operatorname {w-N}^{k}({ \mathcal {X} })$. For any model ![]() $X'$, and for any open subset
$X'$, and for any open subset ![]() $U$ of
$U$ of ![]() $\operatorname {N}^{k}(X')$, let
$\operatorname {N}^{k}(X')$, let ![]() $[U,X'] = \{ \beta \in \operatorname {w-N}^{k} ({ \mathcal {X} }), \beta _{X'} \in U\}$ as previously. Then the collection
$[U,X'] = \{ \beta \in \operatorname {w-N}^{k} ({ \mathcal {X} }), \beta _{X'} \in U\}$ as previously. Then the collection ![]() $I_\alpha$ of all sets containing
$I_\alpha$ of all sets containing ![]() $\alpha$ and of the form
$\alpha$ and of the form ![]() $[U,X']$ forms a basis of neighborhood of
$[U,X']$ forms a basis of neighborhood of ![]() $\alpha$. It is also an inductive set for the order relation
$\alpha$. It is also an inductive set for the order relation ![]() $[U_0,X_0] \leqslant [U_1,X_1]$ iff
$[U_0,X_0] \leqslant [U_1,X_1]$ iff ![]() $X_0 \leqslant X_1$ and the preimage of
$X_0 \leqslant X_1$ and the preimage of ![]() $U_0$ by the pullback morphism
$U_0$ by the pullback morphism ![]() $\operatorname {N}^{k}(X_0)\to \operatorname {N}^{k}(X_1)$ contains
$\operatorname {N}^{k}(X_0)\to \operatorname {N}^{k}(X_1)$ contains ![]() $U_1$.
$U_1$.
Suppose that ![]() $\alpha$ is BPF. Then for each
$\alpha$ is BPF. Then for each ![]() $i=[U,X']\in I_\alpha$ we may choose a Cartier BPF
$i=[U,X']\in I_\alpha$ we may choose a Cartier BPF ![]() $b$-class
$b$-class ![]() $\alpha _i$ in
$\alpha _i$ in ![]() $[U,X']$. By construction, we have
$[U,X']$. By construction, we have ![]() $(\alpha _i)_{X'} \to \alpha _{X'}$ for all model
$(\alpha _i)_{X'} \to \alpha _{X'}$ for all model ![]() $X'$. The converse statement is clear.
$X'$. The converse statement is clear.
Lemma 1.5 For any class ![]() $\alpha \in \operatorname {Nef}^{1}({ \mathcal {X} })$, and for any model
$\alpha \in \operatorname {Nef}^{1}({ \mathcal {X} })$, and for any model ![]() $X''\geqslant X'$ we have
$X''\geqslant X'$ we have
Proof. This is a rephrasing of the negativity lemma alluded to previously.
1.4 Banach spaces  $\operatorname {N}_{\operatorname {BPF}}^{k}({ \mathcal {X} })$,
$\operatorname {N}_{\operatorname {BPF}}^{k}({ \mathcal {X} })$,  $\operatorname {N}^{{k},\vee }_{\operatorname {BPF}}({ \mathcal {X} })$, and
$\operatorname {N}^{{k},\vee }_{\operatorname {BPF}}({ \mathcal {X} })$, and  $\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$
$\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$
Let ![]() ${{\omega }}$ be any fixed big and nef Cartier
${{\omega }}$ be any fixed big and nef Cartier ![]() $b$-divisor class. For any class
$b$-divisor class. For any class ![]() $\alpha \in \operatorname {c-N}^{k}({ \mathcal {X} })$, we define
$\alpha \in \operatorname {c-N}^{k}({ \mathcal {X} })$, we define
 \begin{align} \lVert {\alpha} \rVert_{\operatorname{BPF}}^{\vee} &:= \sup_{\substack{\gamma \in \operatorname{c-BPF}^{d-k}({ \mathcal{X} })\\ (\omega^{k} \cdot \gamma) =1 }} |(\alpha \cdot \gamma)|. \end{align}
\begin{align} \lVert {\alpha} \rVert_{\operatorname{BPF}}^{\vee} &:= \sup_{\substack{\gamma \in \operatorname{c-BPF}^{d-k}({ \mathcal{X} })\\ (\omega^{k} \cdot \gamma) =1 }} |(\alpha \cdot \gamma)|. \end{align}
Note that ![]() $\lVert {\cdot } \rVert _{\operatorname {BPF}}^{\vee }$ is the dual norm of
$\lVert {\cdot } \rVert _{\operatorname {BPF}}^{\vee }$ is the dual norm of ![]() $\lVert {\cdot } \rVert _{\operatorname {BPF}}$ on
$\lVert {\cdot } \rVert _{\operatorname {BPF}}$ on ![]() $\operatorname {c-N}^{d-k}({ \mathcal {X} })$. When
$\operatorname {c-N}^{d-k}({ \mathcal {X} })$. When ![]() $\alpha \in \operatorname {c-N}^{1}({ \mathcal {X} })$, we also set
$\alpha \in \operatorname {c-N}^{1}({ \mathcal {X} })$, we also set
 \begin{equation} \lVert {\alpha} \rVert_{\Sigma} :=\sup_{ \substack{\gamma \in \operatorname{c-BPF}^{d-2}({ \mathcal{X} }) \\ (\gamma \cdot {{\omega}}^{2}) = 1}} ( 2 (\alpha \cdot {{\omega}} \cdot \gamma )^{2} - ( \alpha^{2} \cdot \gamma) )^{1/2}. \end{equation}
\begin{equation} \lVert {\alpha} \rVert_{\Sigma} :=\sup_{ \substack{\gamma \in \operatorname{c-BPF}^{d-2}({ \mathcal{X} }) \\ (\gamma \cdot {{\omega}}^{2}) = 1}} ( 2 (\alpha \cdot {{\omega}} \cdot \gamma )^{2} - ( \alpha^{2} \cdot \gamma) )^{1/2}. \end{equation}
We showed in [Reference Dang and FavreDF21, §§ 2–3] that these functions induce norms on ![]() $\operatorname {c-N}^{k}({ \mathcal {X} })$ and
$\operatorname {c-N}^{k}({ \mathcal {X} })$ and ![]() $\operatorname {c-N}^{1}({ \mathcal {X} })$, respectively.
$\operatorname {c-N}^{1}({ \mathcal {X} })$, respectively.
One defines the spaces ![]() $\operatorname {N}_{\operatorname {BPF}}^{k}({ \mathcal {X} })$,
$\operatorname {N}_{\operatorname {BPF}}^{k}({ \mathcal {X} })$, ![]() $\operatorname {N}^{{k},\vee }_{\operatorname {BPF}}({ \mathcal {X} })$ as the completions of
$\operatorname {N}^{{k},\vee }_{\operatorname {BPF}}({ \mathcal {X} })$ as the completions of ![]() $\operatorname {c-N}^{k}({ \mathcal {X} })$ with respect to
$\operatorname {c-N}^{k}({ \mathcal {X} })$ with respect to ![]() $\lVert {\cdot } \rVert _{\operatorname {BPF}}$ and
$\lVert {\cdot } \rVert _{\operatorname {BPF}}$ and ![]() $\lVert {\cdot } \rVert _{\operatorname {BPF}}^{\vee }$, respectively. The space
$\lVert {\cdot } \rVert _{\operatorname {BPF}}^{\vee }$, respectively. The space ![]() $\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$ is similarly obtained as the completion of
$\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$ is similarly obtained as the completion of ![]() $\operatorname {c-N}^{1}({ \mathcal {X} })$ with respect to the norm
$\operatorname {c-N}^{1}({ \mathcal {X} })$ with respect to the norm ![]() $\lVert {\cdot } \rVert _{\Sigma }$.
$\lVert {\cdot } \rVert _{\Sigma }$.
In fact, all three norms only depend on ![]() ${{\omega }}$ up to equivalence, so that the corresponding completions are independent of the choice of
${{\omega }}$ up to equivalence, so that the corresponding completions are independent of the choice of ![]() $\omega$ (for the norm
$\omega$ (for the norm ![]() $\lVert {\cdot } \rVert _{\Sigma }$, we refer to [Reference Dang and FavreDF21, Theorem 3.3]). We also obtained in [Reference Dang and FavreDF21, Theorem 4.11] the following statement.
$\lVert {\cdot } \rVert _{\Sigma }$, we refer to [Reference Dang and FavreDF21, Theorem 3.3]). We also obtained in [Reference Dang and FavreDF21, Theorem 4.11] the following statement.
Theorem 1.6 The intersection product ![]() $\operatorname {c-N}^{1}(X)\times \operatorname {c-N}^{1}({ \mathcal {X} }) \to \operatorname {c-N}^{2}({ \mathcal {X} })$ extends continuously to a symmetric bilinear map:
$\operatorname {c-N}^{1}(X)\times \operatorname {c-N}^{1}({ \mathcal {X} }) \to \operatorname {c-N}^{2}({ \mathcal {X} })$ extends continuously to a symmetric bilinear map:
In [Reference Dang and FavreDF21, Propositions 2.10 and 2.11 and Theorem 3.16], we proved the following continuous injections:
 \begin{equation} \begin{array}{cl} \operatorname{N}_{\operatorname{BPF}}^{k}({ \mathcal{X} }) & \hookrightarrow \operatorname{N}^{{k},\vee}_{\operatorname{BPF}}({ \mathcal{X} }) \hookrightarrow \operatorname{N}_{\operatorname{BPF}}^{d-k}({ \mathcal{X} })^{*} \hookrightarrow \operatorname{w-N}^{k}({ \mathcal{X} }), \\ \operatorname{N}_{\operatorname{BPF}}^{1}({ \mathcal{X} }) & \hookrightarrow \operatorname{N^{1}_{\Sigma}}({ \mathcal{X} }) \hookrightarrow \operatorname{w-N}^{1}({ \mathcal{X} }). \end{array} \end{equation}
\begin{equation} \begin{array}{cl} \operatorname{N}_{\operatorname{BPF}}^{k}({ \mathcal{X} }) & \hookrightarrow \operatorname{N}^{{k},\vee}_{\operatorname{BPF}}({ \mathcal{X} }) \hookrightarrow \operatorname{N}_{\operatorname{BPF}}^{d-k}({ \mathcal{X} })^{*} \hookrightarrow \operatorname{w-N}^{k}({ \mathcal{X} }), \\ \operatorname{N}_{\operatorname{BPF}}^{1}({ \mathcal{X} }) & \hookrightarrow \operatorname{N^{1}_{\Sigma}}({ \mathcal{X} }) \hookrightarrow \operatorname{w-N}^{1}({ \mathcal{X} }). \end{array} \end{equation}Let us record the following useful lemma.
Lemma 1.7 For any ![]() $\alpha \in \operatorname {Nef^{1}}({ \mathcal {X} })$, one has
$\alpha \in \operatorname {Nef^{1}}({ \mathcal {X} })$, one has ![]() $(\alpha \cdot {{\omega }}^{d-1}) = \lVert {\alpha } \rVert _{\operatorname {BPF}}$.
$(\alpha \cdot {{\omega }}^{d-1}) = \lVert {\alpha } \rVert _{\operatorname {BPF}}$.
Proof. Fix a class ![]() $\alpha \in \operatorname {Nef^{1}}({ \mathcal {X} })$, and note that it follows from the definition that
$\alpha \in \operatorname {Nef^{1}}({ \mathcal {X} })$, and note that it follows from the definition that
Conversely, write ![]() $\alpha = \alpha _+ - \alpha _-$ where
$\alpha = \alpha _+ - \alpha _-$ where ![]() $\alpha _\pm \in \operatorname {Nef^{1}}({ \mathcal {X} })$ are chosen so that
$\alpha _\pm \in \operatorname {Nef^{1}}({ \mathcal {X} })$ are chosen so that ![]() $(\alpha _+ \cdot {{\omega }}^{d-1}) + (\alpha _- \cdot {{\omega }}^{d-1}) \leqslant \lVert {\alpha } \rVert _{\operatorname {BPF}} + \epsilon$ with
$(\alpha _+ \cdot {{\omega }}^{d-1}) + (\alpha _- \cdot {{\omega }}^{d-1}) \leqslant \lVert {\alpha } \rVert _{\operatorname {BPF}} + \epsilon$ with ![]() $\epsilon >0$. Then
$\epsilon >0$. Then ![]() $(\alpha \cdot {{\omega }}^{d-1}) \leqslant (\alpha _+ \cdot {{\omega }}^{d-1}) + (\alpha _- \cdot {{\omega }}^{d-1})\leqslant \lVert {\alpha } \rVert _{\operatorname {BPF}} +\epsilon$, and this implies the reverse inequality.
$(\alpha \cdot {{\omega }}^{d-1}) \leqslant (\alpha _+ \cdot {{\omega }}^{d-1}) + (\alpha _- \cdot {{\omega }}^{d-1})\leqslant \lVert {\alpha } \rVert _{\operatorname {BPF}} +\epsilon$, and this implies the reverse inequality.
1.5 Banach space  $\operatorname {N}^{k}_+({ \mathcal {X} })$
$\operatorname {N}^{k}_+({ \mathcal {X} })$
As in the previous section, ![]() ${{\omega }}$ is a big and nef Cartier
${{\omega }}$ is a big and nef Cartier ![]() $b$-divisor class. For any class
$b$-divisor class. For any class ![]() $\alpha \in \operatorname {c-N}^{k}({ \mathcal {X} })$, we set
$\alpha \in \operatorname {c-N}^{k}({ \mathcal {X} })$, we set
As the psef cone is closed in any model, note that the infimum is actually attained, and the function ![]() $\lVert {\cdot } \rVert _{\omega }$ defines a norm on
$\lVert {\cdot } \rVert _{\omega }$ defines a norm on ![]() $\operatorname {c-N}^{k}({ \mathcal {X} })$.
$\operatorname {c-N}^{k}({ \mathcal {X} })$.
Lemma 1.8 There exists a positive constant ![]() $C_d>0$ depending only on
$C_d>0$ depending only on ![]() $d$ such that the following hold: for any class
$d$ such that the following hold: for any class ![]() $\alpha \in \operatorname {c-BPF}^{k}({ \mathcal {X} })$,
$\alpha \in \operatorname {c-BPF}^{k}({ \mathcal {X} })$,
and for any class ![]() $\alpha \in \operatorname {c-N}^{k}({ \mathcal {X} })$,
$\alpha \in \operatorname {c-N}^{k}({ \mathcal {X} })$,
Proof. Suppose ![]() $\alpha$ is BPF. By Siu's inequalities (Proposition 1.1), we obtain
$\alpha$ is BPF. By Siu's inequalities (Proposition 1.1), we obtain ![]() $0\leqslant \alpha \leqslant C_d (\alpha \cdot {{\omega }}^{d-k}) {{\omega }}^{k}$ so that
$0\leqslant \alpha \leqslant C_d (\alpha \cdot {{\omega }}^{d-k}) {{\omega }}^{k}$ so that ![]() $\lVert {\alpha } \rVert _{\omega } \leqslant C_d (\alpha \cdot {{\omega }}^{d-k})$. Conversely,
$\lVert {\alpha } \rVert _{\omega } \leqslant C_d (\alpha \cdot {{\omega }}^{d-k})$. Conversely, ![]() $\alpha \leqslant C {{\omega }}^{k}$ implies
$\alpha \leqslant C {{\omega }}^{k}$ implies ![]() $(\alpha \cdot {{\omega }}^{d-k})\leqslant C ({{\omega }}^{d})$ hence (8) holds.
$(\alpha \cdot {{\omega }}^{d-k})\leqslant C ({{\omega }}^{d})$ hence (8) holds.
Pick any Cartier ![]() $b$-class
$b$-class ![]() $\alpha$, and write
$\alpha$, and write ![]() $\alpha = \alpha _+ - \alpha _-$ with
$\alpha = \alpha _+ - \alpha _-$ with ![]() $\alpha _\pm \in \operatorname {BPF}^{k}({ \mathcal {X} })$. The previous arguments show
$\alpha _\pm \in \operatorname {BPF}^{k}({ \mathcal {X} })$. The previous arguments show
and, similarly, ![]() $\alpha \geqslant - C_d \lVert {\alpha } \rVert _{\operatorname {BPF}}$, hence
$\alpha \geqslant - C_d \lVert {\alpha } \rVert _{\operatorname {BPF}}$, hence ![]() $\lVert {\alpha } \rVert _{\omega } \leqslant C_d \lVert {\alpha } \rVert _{\operatorname {BPF}}$.
$\lVert {\alpha } \rVert _{\omega } \leqslant C_d \lVert {\alpha } \rVert _{\operatorname {BPF}}$.
Suppose that ![]() $- C {{\omega }} \leqslant \alpha \leqslant C {{\omega }}$ for some positive constant
$- C {{\omega }} \leqslant \alpha \leqslant C {{\omega }}$ for some positive constant ![]() $C>0$, and pick any class
$C>0$, and pick any class ![]() $\gamma \in \operatorname {BPF}^{d-1}({ \mathcal {X} })$. We obtain
$\gamma \in \operatorname {BPF}^{d-1}({ \mathcal {X} })$. We obtain ![]() $|(\alpha \cdot \gamma )|\leqslant C ({{\omega }}\cdot \gamma )$, hence
$|(\alpha \cdot \gamma )|\leqslant C ({{\omega }}\cdot \gamma )$, hence ![]() $\lVert {\alpha } \rVert _{\operatorname {BPF}}^{\vee }\leqslant C$.
$\lVert {\alpha } \rVert _{\operatorname {BPF}}^{\vee }\leqslant C$.
Observe that replacing ![]() ${{\omega }}$ by another ample class gives an equivalent norm. We denote by
${{\omega }}$ by another ample class gives an equivalent norm. We denote by ![]() $\operatorname {N}^{k}_+({ \mathcal {X} })$ the completion of
$\operatorname {N}^{k}_+({ \mathcal {X} })$ the completion of ![]() $\operatorname {c-N}^{k}({ \mathcal {X} })$ for the norm
$\operatorname {c-N}^{k}({ \mathcal {X} })$ for the norm ![]() $\lVert {\cdot } \rVert _{\omega }$.
$\lVert {\cdot } \rVert _{\omega }$.
The previous estimate proves that we have the following continuous injections:
We observe that both in dimension and codimension one, the norm ![]() $\lVert {\cdot } \rVert _{\omega }$ is identical to the dual BPF norm.
$\lVert {\cdot } \rVert _{\omega }$ is identical to the dual BPF norm.
Proposition 1.9 For every class ![]() $\alpha \in \operatorname {c-N}^{1}({ \mathcal {X} })\cup \operatorname {c-N}^{d-1}({ \mathcal {X} })$, we have
$\alpha \in \operatorname {c-N}^{1}({ \mathcal {X} })\cup \operatorname {c-N}^{d-1}({ \mathcal {X} })$, we have
In particular, ![]() $\operatorname {N}^{1}_+({ \mathcal {X} }) = \operatorname {N}^{{1},\vee }_{\operatorname {BPF}}({ \mathcal {X} })$ and
$\operatorname {N}^{1}_+({ \mathcal {X} }) = \operatorname {N}^{{1},\vee }_{\operatorname {BPF}}({ \mathcal {X} })$ and ![]() $\operatorname {N}^{d-1}_+({ \mathcal {X} }) = \operatorname {N}^{{d-1},\vee }_{\operatorname {BPF}}({ \mathcal {X} })$.
$\operatorname {N}^{d-1}_+({ \mathcal {X} }) = \operatorname {N}^{{d-1},\vee }_{\operatorname {BPF}}({ \mathcal {X} })$.
Proof. Suppose ![]() $\alpha$ is a Cartier class determined in some smooth model
$\alpha$ is a Cartier class determined in some smooth model ![]() $X'$. We only need to show that
$X'$. We only need to show that ![]() $\lVert {\alpha } \rVert _{\omega }\leqslant \lVert {\alpha } \rVert _{\operatorname {BPF}}^{\vee }$.
$\lVert {\alpha } \rVert _{\omega }\leqslant \lVert {\alpha } \rVert _{\operatorname {BPF}}^{\vee }$.
Let us first treat the case ![]() $\alpha \in \operatorname {c-N}^{d-1}({ \mathcal {X} })$. For any nef class
$\alpha \in \operatorname {c-N}^{d-1}({ \mathcal {X} })$. For any nef class ![]() $\gamma \in \operatorname {Nef}(X')$ such that
$\gamma \in \operatorname {Nef}(X')$ such that ![]() ${(\gamma \cdot {{\omega }}^{d-1})=1}$ we have
${(\gamma \cdot {{\omega }}^{d-1})=1}$ we have
hence the class ![]() $(\alpha + \lVert {\alpha } \rVert _{\operatorname {BPF}}^{\vee } {{\omega }}^{d-1})_{X'}$ is psef by duality. Similarly, we obtain
$(\alpha + \lVert {\alpha } \rVert _{\operatorname {BPF}}^{\vee } {{\omega }}^{d-1})_{X'}$ is psef by duality. Similarly, we obtain ![]() $(-\alpha + \lVert {\alpha } \rVert _{\operatorname {BPF}}^{\vee } {{\omega }}^{d-1})_{X'}\geqslant 0$, hence
$(-\alpha + \lVert {\alpha } \rVert _{\operatorname {BPF}}^{\vee } {{\omega }}^{d-1})_{X'}\geqslant 0$, hence ![]() $\lVert {\alpha } \rVert _{\omega }\leqslant \lVert {\alpha } \rVert _{\operatorname {BPF}}^{\vee }$ as required.
$\lVert {\alpha } \rVert _{\omega }\leqslant \lVert {\alpha } \rVert _{\operatorname {BPF}}^{\vee }$ as required.
Let us now treat the case where ![]() $\alpha$ is a
$\alpha$ is a ![]() $b$-divisor. Recall from [Reference Boucksom, Demailly, Păun and PeternellBDPP13] that a class
$b$-divisor. Recall from [Reference Boucksom, Demailly, Păun and PeternellBDPP13] that a class ![]() $\alpha _0\in \operatorname {N}^{1}(X)$ is psef if and only if
$\alpha _0\in \operatorname {N}^{1}(X)$ is psef if and only if ![]() $(\alpha _0\cdot \gamma _0)\geqslant 0$ for any strongly movable curve class
$(\alpha _0\cdot \gamma _0)\geqslant 0$ for any strongly movable curve class ![]() $\gamma _0\in \operatorname {N}^{d-1}(X)$.
$\gamma _0\in \operatorname {N}^{d-1}(X)$.
Suppose first that ![]() $\alpha$ is a Cartier
$\alpha$ is a Cartier ![]() $b$-divisor determined in some smooth model
$b$-divisor determined in some smooth model ![]() $X'$. For any strongly movable class
$X'$. For any strongly movable class ![]() $\gamma _0\in \operatorname {N}^{d-1}(X')$, there exists a class
$\gamma _0\in \operatorname {N}^{d-1}(X')$, there exists a class ![]() $\gamma \in \operatorname {c-BPF}^{d-1}({ \mathcal {X} })$ such that
$\gamma \in \operatorname {c-BPF}^{d-1}({ \mathcal {X} })$ such that ![]() $\gamma _{X'} = \gamma _0$. It follows that
$\gamma _{X'} = \gamma _0$. It follows that
hence ![]() $\alpha + \lVert {\alpha } \rVert _{\operatorname {BPF}}^{\vee } {{\omega }}\geqslant 0$ as required.
$\alpha + \lVert {\alpha } \rVert _{\operatorname {BPF}}^{\vee } {{\omega }}\geqslant 0$ as required.
2. Approximation of nef  $b$-divisor classes
$b$-divisor classes
In this section, we prove a version of our approximation result from the introduction in terms of nets. In § 3.2 we show that we can replace nets by sequences and obtain Theorem A.
Theorem 2.1 Let ![]() $\alpha \in \operatorname {Nef^{1}}({ \mathcal {X} })$ be any nef class. There exists an inductive set
$\alpha \in \operatorname {Nef^{1}}({ \mathcal {X} })$ be any nef class. There exists an inductive set ![]() $I$ and a non-increasing net of nef Cartier
$I$ and a non-increasing net of nef Cartier ![]() $b$-divisor classes
$b$-divisor classes ![]() $(\alpha _i)_{i\in I} \in \operatorname {c-Nef^{1}}({ \mathcal {X} })$ that is converging to
$(\alpha _i)_{i\in I} \in \operatorname {c-Nef^{1}}({ \mathcal {X} })$ that is converging to ![]() $\alpha$.
$\alpha$.
In §§ 2.1 and 2.2 we first collect some general facts on ideal sheaves, and nef envelopes. The proof of Theorem 2.1 is then given in § 2.3. In § 2.4, we give a first application of this theorem and prove that a nef divisor ![]() $b$-class which is Cartier is determined by a nef class in some model.
$b$-class which is Cartier is determined by a nef class in some model.
2.1 Coherent ideal sheaves
To any coherent ideal sheaf ![]() $\mathfrak {A}$ on
$\mathfrak {A}$ on ![]() $X$, we attach a Cartier
$X$, we attach a Cartier ![]() $b$-divisor
$b$-divisor ![]() $[\mathfrak {A}]$ as follows. Choose a log-resolution
$[\mathfrak {A}]$ as follows. Choose a log-resolution ![]() $X'$ of
$X'$ of ![]() $\mathfrak {A}$ so that one can write
$\mathfrak {A}$ so that one can write ![]() $\mathcal {O}_{X'}(-D) =\mathfrak {A}\cdot \mathcal {O}_{X'}$ for some divisor
$\mathcal {O}_{X'}(-D) =\mathfrak {A}\cdot \mathcal {O}_{X'}$ for some divisor ![]() $D$. Then we let
$D$. Then we let ![]() $[\mathfrak {A}]$ be the Cartier
$[\mathfrak {A}]$ be the Cartier ![]() $b$-divisor determined by
$b$-divisor determined by ![]() $[D]$ in
$[D]$ in ![]() $X'$. Note that this definition does not depend on the choice of resolution, and because
$X'$. Note that this definition does not depend on the choice of resolution, and because ![]() $D$ is effective that
$D$ is effective that ![]() $[\mathfrak {A}] \geqslant 0$.
$[\mathfrak {A}] \geqslant 0$.
For any pair of ideal sheaves ![]() $\mathfrak {A}, \mathfrak {B}$ on
$\mathfrak {A}, \mathfrak {B}$ on ![]() $X$, we have:
$X$, we have:
(i)
 $[\mathfrak {A}]\geqslant [\mathfrak {B}]$ when
$[\mathfrak {A}]\geqslant [\mathfrak {B}]$ when  $\mathfrak {A} \subset \mathfrak {B}$; and
$\mathfrak {A} \subset \mathfrak {B}$; and(ii)
 $[\mathfrak {A}\cdot \mathfrak {B}]=[\mathfrak {A}]+[\mathfrak {B}]$.
$[\mathfrak {A}\cdot \mathfrak {B}]=[\mathfrak {A}]+[\mathfrak {B}]$.
The notion of multiplier ideal sheaf will play an essential role in the paper. We briefly discuss the basic definitions and properties that are necessary for our purposes, referring the interested reader to [Reference LazarsfeldLaz04] for an extensive treatment of this notion.
Let ![]() $\mathfrak {A}$ be any coherent ideal sheaf on
$\mathfrak {A}$ be any coherent ideal sheaf on ![]() $X$, and let
$X$, and let ![]() $c>0$ be any positive constant. If
$c>0$ be any positive constant. If ![]() $X' \overset {\pi }{\to } X$ is a resolution of
$X' \overset {\pi }{\to } X$ is a resolution of ![]() $\mathfrak {A}$ as previously, then we let
$\mathfrak {A}$ as previously, then we let ![]() $\mathcal {J}(\mathfrak {A}^{c})=\pi _* (K_{X'/X} - \lfloor {c\cdot D}\rfloor )$ where
$\mathcal {J}(\mathfrak {A}^{c})=\pi _* (K_{X'/X} - \lfloor {c\cdot D}\rfloor )$ where ![]() $K_{X'/X}= \pi ^{*} K_X- K_{X'}$ is the relative canonical sheaf, and
$K_{X'/X}= \pi ^{*} K_X- K_{X'}$ is the relative canonical sheaf, and ![]() $\lfloor {c\cdot D}\rfloor$ is the round-down of the divisor
$\lfloor {c\cdot D}\rfloor$ is the round-down of the divisor ![]() $c\cdot D$. This definition does not depend on the resolution.
$c\cdot D$. This definition does not depend on the resolution.
A graded sequence of coherent ideal sheaves ![]() $\mathfrak {A}_\bullet = (\mathfrak {A}_m)$ is, by definition, a sequence of coherent ideal sheaves such that
$\mathfrak {A}_\bullet = (\mathfrak {A}_m)$ is, by definition, a sequence of coherent ideal sheaves such that ![]() $\mathfrak {A}_0 = { \mathcal {O} }_X$ and
$\mathfrak {A}_0 = { \mathcal {O} }_X$ and ![]() $\mathfrak {A}_n\cdot \mathfrak {A}_m\subset \mathfrak {A}_{n+m}$ for all
$\mathfrak {A}_n\cdot \mathfrak {A}_m\subset \mathfrak {A}_{n+m}$ for all ![]() $n,m\geqslant 0$. For any
$n,m\geqslant 0$. For any ![]() $c>0$, one can show that
$c>0$, one can show that ![]() ${ \mathcal {J} }(\mathfrak {A}_m^{c/m}) \subset { \mathcal {J} }(\mathfrak {A}_n^{c/n})$ whenever
${ \mathcal {J} }(\mathfrak {A}_m^{c/m}) \subset { \mathcal {J} }(\mathfrak {A}_n^{c/n})$ whenever ![]() $m$ divides
$m$ divides ![]() $n$, and one defines the multiplier ideal sheaf
$n$, and one defines the multiplier ideal sheaf ![]() ${ \mathcal {J} }(\mathfrak {A}_\bullet ^{c})$ as the unique (coherent) ideal sheaf equal to
${ \mathcal {J} }(\mathfrak {A}_\bullet ^{c})$ as the unique (coherent) ideal sheaf equal to ![]() ${ \mathcal {J} }(\mathfrak {A}_m^{c/m})$ for all sufficiently divisible
${ \mathcal {J} }(\mathfrak {A}_m^{c/m})$ for all sufficiently divisible ![]() $m$. This definition makes sense by Noetherianity. Moreover, we have
$m$. This definition makes sense by Noetherianity. Moreover, we have
for all ![]() $m>0$ by [Reference LazarsfeldLaz04, Theorem 11.1.19], and the following fundamental sub-additivity property holds (see [Reference LazarsfeldLaz04, Theorem 11.2.3]):
$m>0$ by [Reference LazarsfeldLaz04, Theorem 11.1.19], and the following fundamental sub-additivity property holds (see [Reference LazarsfeldLaz04, Theorem 11.2.3]):
for any graded sequence of coherent ideal sheaves ![]() $\mathfrak {A}_\bullet$.
$\mathfrak {A}_\bullet$.
Suppose now that ![]() $L\to X$ is a big line bundle. For
$L\to X$ is a big line bundle. For ![]() $n$ large enough, the space of global sections
$n$ large enough, the space of global sections ![]() $H^{0}(X,L^{\otimes n})$ is non-zero, and we may consider the base ideal
$H^{0}(X,L^{\otimes n})$ is non-zero, and we may consider the base ideal ![]() $\mathfrak {b}_n(L)$ which is the coherent ideal sheaf locally defined by the vanishing of global sections of
$\mathfrak {b}_n(L)$ which is the coherent ideal sheaf locally defined by the vanishing of global sections of ![]() $L^{\otimes n}$. The sequence
$L^{\otimes n}$. The sequence ![]() $\mathfrak {b}_\bullet (L):=\{\mathfrak {b}_n(L)\}$ forms a graded sequence of ideal sheaves and Nadel's vanishing theorem implies the following theorem, see [Reference LazarsfeldLaz04, Corollary 11.2.13].
$\mathfrak {b}_\bullet (L):=\{\mathfrak {b}_n(L)\}$ forms a graded sequence of ideal sheaves and Nadel's vanishing theorem implies the following theorem, see [Reference LazarsfeldLaz04, Corollary 11.2.13].
Theorem 2.2 Fix any very ample line bundle ![]() $A$ on
$A$ on ![]() $X$. For any big line bundle
$X$. For any big line bundle ![]() $L\to X$, and for any
$L\to X$, and for any ![]() $m \geqslant 1$, the sheaf
$m \geqslant 1$, the sheaf
is globally generated.
2.2 Nef envelopes
In this section, we gather some facts on the notion of nef envelopes following [Reference Boucksom, Favre and JonssonBFJ09, Reference Boucksom, de Fernex and FavreBdFF12, Reference Küronya and MacleanKM13].
Let us fix any big Cartier ![]() $b$-divisor class
$b$-divisor class ![]() $\beta \in \operatorname {c-N}^{1}({ \mathcal {X} })$. Consider the set
$\beta \in \operatorname {c-N}^{1}({ \mathcal {X} })$. Consider the set ![]() $\mathcal {D}(\beta )$ of classes
$\mathcal {D}(\beta )$ of classes ![]() $\gamma \in \operatorname {c-Nef^{1}}({ \mathcal {X} })_\mathbb {Q}$ such that
$\gamma \in \operatorname {c-Nef^{1}}({ \mathcal {X} })_\mathbb {Q}$ such that ![]() $\gamma \leqslant \beta$. By [Reference Boucksom, Favre and JonssonBFJ09, Lemma 2.6] or [Reference Küronya and MacleanKM13, Lemma 3.4], for any
$\gamma \leqslant \beta$. By [Reference Boucksom, Favre and JonssonBFJ09, Lemma 2.6] or [Reference Küronya and MacleanKM13, Lemma 3.4], for any ![]() $\gamma _1, \gamma _2\in \mathcal {D}(\beta )$ one can find a third element
$\gamma _1, \gamma _2\in \mathcal {D}(\beta )$ one can find a third element ![]() $\gamma _3\in \mathcal {D}(\beta )$ such that
$\gamma _3\in \mathcal {D}(\beta )$ such that ![]() $\gamma _3 \geqslant \gamma _1$ and
$\gamma _3 \geqslant \gamma _1$ and ![]() $\gamma _3\geqslant \gamma _2$. For any model
$\gamma _3\geqslant \gamma _2$. For any model ![]() $X'$ over
$X'$ over ![]() $X$, we may thus define
$X$, we may thus define ![]() $P(\beta )_{X'}$ as the least upper bound of the set
$P(\beta )_{X'}$ as the least upper bound of the set ![]() $\{ \gamma _{X'} \in \operatorname {N}^{1}(X'), \gamma \in \mathcal {D}(\beta )\}$ (see [Reference Boucksom, Favre and JonssonBFJ09, Lemma 2.7]). The collection of classes
$\{ \gamma _{X'} \in \operatorname {N}^{1}(X'), \gamma \in \mathcal {D}(\beta )\}$ (see [Reference Boucksom, Favre and JonssonBFJ09, Lemma 2.7]). The collection of classes ![]() $\{P(\beta )_{X'}\}$ defines a nef
$\{P(\beta )_{X'}\}$ defines a nef ![]() $b$-divisor class (called the nef envelope of
$b$-divisor class (called the nef envelope of ![]() $\beta$) such that for any
$\beta$) such that for any ![]() $\gamma \in \operatorname {c-Nef^{1}}({ \mathcal {X} })$ satisfying
$\gamma \in \operatorname {c-Nef^{1}}({ \mathcal {X} })$ satisfying ![]() $\gamma \leqslant \beta$, we have
$\gamma \leqslant \beta$, we have ![]() $\gamma \leqslant P(\beta )$.
$\gamma \leqslant P(\beta )$.
Lemma 2.3 For any ![]() $\gamma \in \operatorname {Nef^{1}}({ \mathcal {X} })$ such that
$\gamma \in \operatorname {Nef^{1}}({ \mathcal {X} })$ such that ![]() $\gamma \leqslant \beta$, we have
$\gamma \leqslant \beta$, we have ![]() $\gamma \leqslant P(\beta )$; and the nef envelope is the least nef class satisfying this property (in particular, this class is unique).
$\gamma \leqslant P(\beta )$; and the nef envelope is the least nef class satisfying this property (in particular, this class is unique).
Remark 2.4 The nef envelope coincides with the positive product intersection ![]() $\langle \beta \rangle$ of [Reference Boucksom, Favre and JonssonBFJ09, § 2.2]. It is also the nef part of the Zariski decomposition defined in [Reference Küronya and MacleanKM13].
$\langle \beta \rangle$ of [Reference Boucksom, Favre and JonssonBFJ09, § 2.2]. It is also the nef part of the Zariski decomposition defined in [Reference Küronya and MacleanKM13].
Proof. Suppose ![]() $\beta \geqslant \gamma \in \operatorname {Nef^{1}}({ \mathcal {X} })$, and
$\beta \geqslant \gamma \in \operatorname {Nef^{1}}({ \mathcal {X} })$, and ![]() $\beta$ is determined in
$\beta$ is determined in ![]() $X'$. Then
$X'$. Then ![]() $\beta _{X'}\geqslant \gamma _{X'}$ and by Lemma 1.4 there exists a net
$\beta _{X'}\geqslant \gamma _{X'}$ and by Lemma 1.4 there exists a net ![]() $\gamma _i\in \operatorname {c-Nef^{1}}({ \mathcal {X} })$ such that
$\gamma _i\in \operatorname {c-Nef^{1}}({ \mathcal {X} })$ such that ![]() $\gamma _{i,X'} \to \gamma _{X'}$. As
$\gamma _{i,X'} \to \gamma _{X'}$. As ![]() $\beta _{X'}$ is big, we have
$\beta _{X'}$ is big, we have ![]() $\gamma _{i,X'}\leqslant (1+\epsilon )\beta _{X'}$ for any
$\gamma _{i,X'}\leqslant (1+\epsilon )\beta _{X'}$ for any ![]() $\epsilon >0$ and for
$\epsilon >0$ and for ![]() $i \in I_\epsilon$ in a tail set. We infer from Lemma 1.5
$i \in I_\epsilon$ in a tail set. We infer from Lemma 1.5 ![]() $\gamma _i\leqslant [\gamma _{i,X'}] \leqslant (1+\epsilon )\beta$, hence
$\gamma _i\leqslant [\gamma _{i,X'}] \leqslant (1+\epsilon )\beta$, hence ![]() $\gamma _i\leqslant (1+\epsilon ) P(\beta )$ for
$\gamma _i\leqslant (1+\epsilon ) P(\beta )$ for ![]() $i \in I_\epsilon$. We conclude that
$i \in I_\epsilon$. We conclude that ![]() $\gamma \leqslant P(\beta )$ by taking the limit of the net and then
$\gamma \leqslant P(\beta )$ by taking the limit of the net and then ![]() $\epsilon \to 0$.
$\epsilon \to 0$.
Suppose that ![]() $\beta '$ is a nef
$\beta '$ is a nef ![]() $b$-divisor class such that
$b$-divisor class such that ![]() $\gamma \leqslant \beta '$ for any
$\gamma \leqslant \beta '$ for any ![]() $\gamma \in \operatorname {Nef^{1}}({ \mathcal {X} })$ satisfying
$\gamma \in \operatorname {Nef^{1}}({ \mathcal {X} })$ satisfying ![]() $\gamma \leqslant \beta$. Applying these inequalities to Cartier
$\gamma \leqslant \beta$. Applying these inequalities to Cartier ![]() $b$-divisor classes, we get
$b$-divisor classes, we get ![]() $P(\beta )_{X'} \leqslant \beta '_{X'}$ in each model, which concludes the proof.
$P(\beta )_{X'} \leqslant \beta '_{X'}$ in each model, which concludes the proof.
We shall use the following characterization of the nef envelope.
Proposition 2.5 Let ![]() $L\to X$ be any big line bundle. Then
$L\to X$ be any big line bundle. Then
where ![]() $\mathfrak {b}_n(L)$ denotes, as above, the base ideal of the line bundle
$\mathfrak {b}_n(L)$ denotes, as above, the base ideal of the line bundle ![]() $L^{\otimes n}$.
$L^{\otimes n}$.
See [Reference Küronya and MacleanKM13, Proposition 3.7] for the proof.
2.3 Proof of Theorem 2.1
We fix any Cartier ![]() $b$-divisor class
$b$-divisor class ![]() ${{\omega }}$ determined by an ample class in
${{\omega }}$ determined by an ample class in ![]() $X$. We rely on the following proposition whose proof is given below.
$X$. We rely on the following proposition whose proof is given below.
Proposition 2.6 For any nef ![]() $b$-divisor class
$b$-divisor class ![]() $\alpha$, and any big class
$\alpha$, and any big class ![]() $\gamma \in \operatorname {N}^{1}(X')$ in a model
$\gamma \in \operatorname {N}^{1}(X')$ in a model ![]() $X'$, there exists a nef Cartier
$X'$, there exists a nef Cartier ![]() $b$-divisor class
$b$-divisor class ![]() $\beta$ such that
$\beta$ such that
Pick any class ![]() $\alpha \in \operatorname {Nef^{1}}({ \mathcal {X} })$. Denote by
$\alpha \in \operatorname {Nef^{1}}({ \mathcal {X} })$. Denote by ![]() $I$ the set of all nef Cartier
$I$ the set of all nef Cartier ![]() $b$-divisor classes
$b$-divisor classes ![]() $\beta$ such that
$\beta$ such that ![]() $\beta \geqslant \alpha + \epsilon {{\omega }}$ for some
$\beta \geqslant \alpha + \epsilon {{\omega }}$ for some ![]() $\epsilon >0$. We endow the set
$\epsilon >0$. We endow the set ![]() $I$ with a partial order by declaring that
$I$ with a partial order by declaring that ![]() $\beta$ is less or equal to
$\beta$ is less or equal to ![]() $\beta '$ iff
$\beta '$ iff ![]() $\beta ' \leqslant \beta$.
$\beta ' \leqslant \beta$.
Let us first justify that ![]() $I$ is an inductive set. Pick any two nef Cartier
$I$ is an inductive set. Pick any two nef Cartier ![]() $b$-divisor classes
$b$-divisor classes ![]() $\beta, \beta ' \in I$. We need to exhibit a class
$\beta, \beta ' \in I$. We need to exhibit a class ![]() $\beta '' \in I$ such that
$\beta '' \in I$ such that ![]() $\beta ''\leqslant \beta$ and
$\beta ''\leqslant \beta$ and ![]() $\beta ''\leqslant \beta '$.
$\beta ''\leqslant \beta '$.
We may suppose that both classes are determined by a class in the same model ![]() $X'$ and that
$X'$ and that ![]() $\beta \geqslant \alpha + \epsilon {{\omega }}$ and
$\beta \geqslant \alpha + \epsilon {{\omega }}$ and ![]() $\beta ' \geqslant \alpha + \epsilon {{\omega }}$ for the same constant
$\beta ' \geqslant \alpha + \epsilon {{\omega }}$ for the same constant ![]() $\epsilon >0$. By Proposition 2.6, there exists a nef Cartier
$\epsilon >0$. By Proposition 2.6, there exists a nef Cartier ![]() $b$-divisor class
$b$-divisor class ![]() $\beta ''$ such that
$\beta ''$ such that ![]() $\alpha + ({\epsilon }/2) {{\omega }} \leqslant \beta ''$ and
$\alpha + ({\epsilon }/2) {{\omega }} \leqslant \beta ''$ and ![]() $\beta ''_{X'} \leqslant \alpha _{X'} + \epsilon {{\omega }}_{X'}$. By Lemma 1.5, this implies
$\beta ''_{X'} \leqslant \alpha _{X'} + \epsilon {{\omega }}_{X'}$. By Lemma 1.5, this implies ![]() $\beta '' \leqslant \beta$ and
$\beta '' \leqslant \beta$ and ![]() $\beta ''\leqslant \beta '$ proving that
$\beta ''\leqslant \beta '$ proving that ![]() $I$ is an inductive set.
$I$ is an inductive set.
In order to make a distinction between nef classes and the poset ![]() $I$ parameterizing the approximants of
$I$ parameterizing the approximants of ![]() $\alpha$, let us denote by
$\alpha$, let us denote by ![]() $\beta _i$ the class associated with the element
$\beta _i$ the class associated with the element ![]() $i\in I$. Pick any model
$i\in I$. Pick any model ![]() $X'$, and choose an open neighborhood
$X'$, and choose an open neighborhood ![]() $U$ of
$U$ of ![]() $\alpha _{X'}$ in
$\alpha _{X'}$ in ![]() $\operatorname {N}^{1}(X')$. One can find
$\operatorname {N}^{1}(X')$. One can find ![]() $\epsilon >0$ such that any class
$\epsilon >0$ such that any class ![]() $\gamma \in \operatorname {N}^{1}(X')$ satisfying
$\gamma \in \operatorname {N}^{1}(X')$ satisfying ![]() $\alpha _{X'} \leqslant \gamma \leqslant \alpha _{X'} + 3 \epsilon {{\omega }}_{X'}$ belongs to
$\alpha _{X'} \leqslant \gamma \leqslant \alpha _{X'} + 3 \epsilon {{\omega }}_{X'}$ belongs to ![]() $U$. By Proposition 2.6, there exists a nef Cartier
$U$. By Proposition 2.6, there exists a nef Cartier ![]() $b$-divisor class
$b$-divisor class ![]() $\beta _i$ such that
$\beta _i$ such that ![]() $\alpha + \epsilon {{\omega }} \leqslant \beta _i$ and
$\alpha + \epsilon {{\omega }} \leqslant \beta _i$ and ![]() $\beta _{i,X'} \leqslant \alpha _{X'} + 3 \epsilon {{\omega }}_{X'}$ For any index
$\beta _{i,X'} \leqslant \alpha _{X'} + 3 \epsilon {{\omega }}_{X'}$ For any index ![]() $j \geqslant i$, we have
$j \geqslant i$, we have
hence ![]() $(\beta _j)_{X'}$ belongs to
$(\beta _j)_{X'}$ belongs to ![]() $U$. This proves the net
$U$. This proves the net ![]() $\beta _i$ is converging to
$\beta _i$ is converging to ![]() $\alpha$. We conclude by observing that the net is decreasing by construction.
$\alpha$. We conclude by observing that the net is decreasing by construction.
Proof of Proposition 2.6 As the big cone is open in ![]() $\operatorname {N}^{1}(X')$, one can find a big line bundle
$\operatorname {N}^{1}(X')$, one can find a big line bundle ![]() $L\to X'$ and an integer
$L\to X'$ and an integer ![]() $l\in \mathbb {N}$ such that
$l\in \mathbb {N}$ such that ![]() $\alpha _{X'} \leqslant ({1}/{l}) c_1(L) \leqslant \alpha _{X'} + {\gamma }/{2}$. By Proposition 2.7, there exists a sequence of nef Cartier
$\alpha _{X'} \leqslant ({1}/{l}) c_1(L) \leqslant \alpha _{X'} + {\gamma }/{2}$. By Proposition 2.7, there exists a sequence of nef Cartier ![]() $b$-divisor classes
$b$-divisor classes ![]() $\beta _n$ decreasing to
$\beta _n$ decreasing to ![]() $P(({1}/{l}) c_1(L))$. Set
$P(({1}/{l}) c_1(L))$. Set ![]() $\beta := \beta _N$ for a sufficiently large integer
$\beta := \beta _N$ for a sufficiently large integer ![]() $N$ so that
$N$ so that ![]() $\beta _{X'} \leqslant \alpha _{X'} + \gamma$. We infer from Lemma 2.3 that
$\beta _{X'} \leqslant \alpha _{X'} + \gamma$. We infer from Lemma 2.3 that ![]() $\beta \geqslant P( ({1}/{l})c_1(L)) \geqslant \alpha$ and the proof is complete.
$\beta \geqslant P( ({1}/{l})c_1(L)) \geqslant \alpha$ and the proof is complete.
Proposition 2.7 Let ![]() $L\to X$ be any big line bundle and set
$L\to X$ be any big line bundle and set ![]() $\alpha := [c_1(L)] \in \operatorname {c-N}^{1}({ \mathcal {X} })$. Then there exists a non-increasing sequence of Cartier
$\alpha := [c_1(L)] \in \operatorname {c-N}^{1}({ \mathcal {X} })$. Then there exists a non-increasing sequence of Cartier ![]() $b$-divisor classes
$b$-divisor classes ![]() $\beta _n\in \operatorname {c-Nef^{1}}({ \mathcal {X} })$ converging to the envelope
$\beta _n\in \operatorname {c-Nef^{1}}({ \mathcal {X} })$ converging to the envelope ![]() $P(\alpha )$. Moreover, for any
$P(\alpha )$. Moreover, for any ![]() $\epsilon >0$ we have
$\epsilon >0$ we have ![]() $P(\alpha ) \leqslant \beta _n\leqslant (1+\epsilon ) P(\alpha )$ for all
$P(\alpha ) \leqslant \beta _n\leqslant (1+\epsilon ) P(\alpha )$ for all ![]() $n$ large enough.
$n$ large enough.
Proof of Proposition 2.7 Replacing ![]() $L$ by one of its multiple, we may (and shall) find an effective divisor
$L$ by one of its multiple, we may (and shall) find an effective divisor ![]() $D$ such that
$D$ such that ![]() $L = { \mathcal {O} }_X(D)$. Let
$L = { \mathcal {O} }_X(D)$. Let ![]() $\mathfrak {b}_\bullet :=\{\mathfrak {b}_n(L)\}$ be the graded sequence of ideal sheaves defined by the base loci of
$\mathfrak {b}_\bullet :=\{\mathfrak {b}_n(L)\}$ be the graded sequence of ideal sheaves defined by the base loci of ![]() $L^{\otimes n}$. Fix any very ample line bundle
$L^{\otimes n}$. Fix any very ample line bundle ![]() $A$ on
$A$ on ![]() $X$ such that
$X$ such that ![]() $K_X + (d+1)A$ is effective. By Theorem 2.2, the sheaf
$K_X + (d+1)A$ is effective. By Theorem 2.2, the sheaf
is globally generated so that we may find a nef divisor ![]() $D_m$ on a log-resolution
$D_m$ on a log-resolution ![]() $X_m$ of the sheaf of ideals
$X_m$ of the sheaf of ideals ![]() $J(\mathfrak {b}_\bullet ^{m})$ such that
$J(\mathfrak {b}_\bullet ^{m})$ such that
If ![]() $\beta '_m$ denotes the nef Cartier
$\beta '_m$ denotes the nef Cartier ![]() $b$-divisor class determined by
$b$-divisor class determined by ![]() $D_m$ in
$D_m$ in ![]() $X_m$, then the incarnation of
$X_m$, then the incarnation of ![]() $\beta '_m$ in
$\beta '_m$ in ![]() $X$ is less effective than
$X$ is less effective than ![]() $K_X+ (d+1) A+ mD$, hence
$K_X+ (d+1) A+ mD$, hence
for any fixed ![]() $\epsilon >0$, and any
$\epsilon >0$, and any ![]() $m$ large enough.
$m$ large enough.
Now by the sub-additivity of multiplier ideals (11), we have ![]() ${ \mathcal {J} }(\mathfrak {b}_\bullet ^{n+m})\subset { \mathcal {J} }(\mathfrak {b}_\bullet ^{m})\cdot { \mathcal {J} }(\mathfrak {b}_\bullet ^{n})$, hence
${ \mathcal {J} }(\mathfrak {b}_\bullet ^{n+m})\subset { \mathcal {J} }(\mathfrak {b}_\bullet ^{m})\cdot { \mathcal {J} }(\mathfrak {b}_\bullet ^{n})$, hence ![]() $-[{ \mathcal {J} }(\mathfrak {b}_\bullet ^{n+m})]\leqslant -[{ \mathcal {J} }(\mathfrak {b}_\bullet ^{m})]- [{ \mathcal {J} }(\mathfrak {b}_\bullet ^{n})]$ and the sequence
$-[{ \mathcal {J} }(\mathfrak {b}_\bullet ^{n+m})]\leqslant -[{ \mathcal {J} }(\mathfrak {b}_\bullet ^{m})]- [{ \mathcal {J} }(\mathfrak {b}_\bullet ^{n})]$ and the sequence ![]() $-({1}/{2^{m}}) [{ \mathcal {J} }(\mathfrak {b}_\bullet ^{2^{m}})]$ is decreasing. It follows that
$-({1}/{2^{m}}) [{ \mathcal {J} }(\mathfrak {b}_\bullet ^{2^{m}})]$ is decreasing. It follows that ![]() $\beta _n:= ({1}/{2^{n}}) \beta '_{2^{n}}$ is also decreasing. By (10), we have
$\beta _n:= ({1}/{2^{n}}) \beta '_{2^{n}}$ is also decreasing. By (10), we have ![]() $\mathfrak {b}_m \subset \mathcal {J}(\mathfrak {b}_\bullet ^{m})$, and we infer using the effectivity of the class
$\mathfrak {b}_m \subset \mathcal {J}(\mathfrak {b}_\bullet ^{m})$, and we infer using the effectivity of the class ![]() $K_X + (d+1) A$
$K_X + (d+1) A$
By Proposition 2.5, we have ![]() $\alpha - ({1}/{2^{m}})[\mathfrak {b}_{2^{m}}]\to P(\alpha )$ and combining this information with (13) we conclude that
$\alpha - ({1}/{2^{m}})[\mathfrak {b}_{2^{m}}]\to P(\alpha )$ and combining this information with (13) we conclude that ![]() $\beta _n \to P(\alpha )$.
$\beta _n \to P(\alpha )$.
2.4 Application of the approximation theorem
Our next result is an analog of [Reference Boucksom, Favre and JonssonBFJ08b, Proposition 2.2], [Reference Boucksom, Favre and JonssonBFJ16, Theorem 5.11], [Reference Boucksom and JonssonBJ18, Theorem 5.19], [Reference Gubler and MartinGM19, Theorem 1.3], and [Reference Botero and Burgos GilBBG22, Lemma 4.24].
Theorem 2.8 We have
In other words any Cartier numerical ![]() $b$-divisor class lying in the weak closure of nef classes is determined by a nef class in some model.
$b$-divisor class lying in the weak closure of nef classes is determined by a nef class in some model.
Proof. Pick any ![]() $\alpha \in \operatorname {c-N}^{1}({ \mathcal {X} }) \cap \operatorname {Nef^{1}}({ \mathcal {X} })$. Without loss of generality, we may suppose that
$\alpha \in \operatorname {c-N}^{1}({ \mathcal {X} }) \cap \operatorname {Nef^{1}}({ \mathcal {X} })$. Without loss of generality, we may suppose that ![]() $\alpha$ is determined in
$\alpha$ is determined in ![]() $X$, and we need to show that
$X$, and we need to show that ![]() $\alpha _X$ is nef. By adding a small real ample class of
$\alpha _X$ is nef. By adding a small real ample class of ![]() $X$, we may suppose that
$X$, we may suppose that ![]() $\alpha _X = c_1(L)$ for some big line bundle
$\alpha _X = c_1(L)$ for some big line bundle ![]() $L\to X$. As
$L\to X$. As ![]() $\alpha$ is nef, we have
$\alpha$ is nef, we have ![]() $P(\alpha _X)=\alpha$. Redoing the proof of Proposition 2.7, we find a sequence of elements
$P(\alpha _X)=\alpha$. Redoing the proof of Proposition 2.7, we find a sequence of elements
which converges weakly to ![]() $\alpha$. This implies
$\alpha$. This implies ![]() $- ({1}/{2^{m}}) [\mathcal {J}(\mathfrak {b}_\bullet ^{2^{m}})]$ to tend to
$- ({1}/{2^{m}}) [\mathcal {J}(\mathfrak {b}_\bullet ^{2^{m}})]$ to tend to ![]() $0$ weakly. As the sequence
$0$ weakly. As the sequence ![]() $- ({1}/{2^{m}}) [\mathcal {J}(\mathfrak {b}_\bullet ^{2^{m}})]\leqslant 0$ is decreasing, we obtain
$- ({1}/{2^{m}}) [\mathcal {J}(\mathfrak {b}_\bullet ^{2^{m}})]\leqslant 0$ is decreasing, we obtain ![]() ${ \mathcal {J} }(\mathfrak {b}_\bullet ^{2^{m}})=0$ for all
${ \mathcal {J} }(\mathfrak {b}_\bullet ^{2^{m}})=0$ for all ![]() $m$, and
$m$, and ![]() $\beta _{m}$ is thus a nef class determined in
$\beta _{m}$ is thus a nef class determined in ![]() $X$. This implies
$X$. This implies ![]() $\alpha _X$ to be nef as required.
$\alpha _X$ to be nef as required.
Remark 2.9 We prove an analogous statement for BPF curve ![]() $b$-numerical classes, see Proposition 5.4. The equality
$b$-numerical classes, see Proposition 5.4. The equality ![]() $\operatorname {c-N}^{k}({ \mathcal {X} }) \cap \operatorname {BPF}^{k}({ \mathcal {X} }) = \operatorname {c-BPF}^{k}({ \mathcal {X} })$ remains however unclear when
$\operatorname {c-N}^{k}({ \mathcal {X} }) \cap \operatorname {BPF}^{k}({ \mathcal {X} }) = \operatorname {c-BPF}^{k}({ \mathcal {X} })$ remains however unclear when ![]() $2\leqslant k \leqslant d-2$.
$2\leqslant k \leqslant d-2$.
3. Intersection of nef  $b$-divisor classes
$b$-divisor classes
3.1 Definition
Proposition-Definition 3.1 Let ![]() $\alpha _1, \ldots, \alpha _k$ be any family of nef
$\alpha _1, \ldots, \alpha _k$ be any family of nef ![]() $b$-divisor classes, and pick
$b$-divisor classes, and pick ![]() $\gamma \in \operatorname {BPF}^{l}({ \mathcal {X} })$. Then there exists a unique class
$\gamma \in \operatorname {BPF}^{l}({ \mathcal {X} })$. Then there exists a unique class ![]() $\Delta \in \operatorname {BPF}^{k+l}({ \mathcal {X} })$ satisfying the following properties.
$\Delta \in \operatorname {BPF}^{k+l}({ \mathcal {X} })$ satisfying the following properties.
(i) For any nef Cartier
 $b$-divisor classes
$b$-divisor classes  $\beta _i\geqslant \alpha _i$, we have
(14)
$\beta _i\geqslant \alpha _i$, we have
(14) \begin{equation} \Delta \leqslant (\beta_1\cdot \beta_2 \cdot \cdots \cdot \beta_k\cdot\gamma). \end{equation}
\begin{equation} \Delta \leqslant (\beta_1\cdot \beta_2 \cdot \cdots \cdot \beta_k\cdot\gamma). \end{equation}(ii) For any net of nef Cartier
 $b$-divisor classes
$b$-divisor classes  $\beta ^{(i)}_1, \ldots, \beta ^{(i)}_k$ decreasing to
$\beta ^{(i)}_1, \ldots, \beta ^{(i)}_k$ decreasing to  $\alpha _1, \ldots, \alpha _k$, we have
(15)
$\alpha _1, \ldots, \alpha _k$, we have
(15) \begin{equation} ( \beta^{(i)}_1\cdot \beta^{(i)}_2 \cdot \cdots \cdot \beta^{(i)}_k\cdot\gamma)\downarrow \Delta. \end{equation}
\begin{equation} ( \beta^{(i)}_1\cdot \beta^{(i)}_2 \cdot \cdots \cdot \beta^{(i)}_k\cdot\gamma)\downarrow \Delta. \end{equation}
This intersection product was defined in [Reference Boucksom, Favre and JonssonBFJ09, § 2] following the construction in the complex setting of positive intersection products introduced by Boucksom in [Reference BoucksomBou02, § 3.2], see also [Reference Boucksom, Demailly, Păun and PeternellBDPP13]. It bears a strong analogy with the definition of wedge products of currents ![]() $dd^{c} u_i$ in complex geometry.
$dd^{c} u_i$ in complex geometry.
Proof of Proposition–Definition 3.1 By Theorem 2.1 one can find a net of nef Cartier ![]() $b$-divisor classes
$b$-divisor classes ![]() $\alpha ^{(i)}_l\downarrow \alpha _l$ for all
$\alpha ^{(i)}_l\downarrow \alpha _l$ for all ![]() $l=1, \ldots, k$. As
$l=1, \ldots, k$. As ![]() $\gamma$ is BPF, for any
$\gamma$ is BPF, for any ![]() $j\geqslant i$ we have
$j\geqslant i$ we have
hence the net ![]() $(\alpha ^{(i)}_1\cdot \alpha ^{(i)}_2 \cdot \cdots \cdot \alpha ^{(i)}_k \cdot \gamma )$ is decreasing. Let
$(\alpha ^{(i)}_1\cdot \alpha ^{(i)}_2 \cdot \cdots \cdot \alpha ^{(i)}_k \cdot \gamma )$ is decreasing. Let ![]() $\Delta$ be its (weak) limit.
$\Delta$ be its (weak) limit.
To prove (14), take nef Cartier ![]() $b$-divisor classes
$b$-divisor classes ![]() $\beta _l\geqslant \alpha _l$,
$\beta _l\geqslant \alpha _l$, ![]() $l=1, \ldots, k$. Choose a model
$l=1, \ldots, k$. Choose a model ![]() $X'$ in which all classes
$X'$ in which all classes ![]() $\beta _1, \ldots, \beta _k$ are determined. Fix any Cartier
$\beta _1, \ldots, \beta _k$ are determined. Fix any Cartier ![]() $b$-divisor class
$b$-divisor class ![]() ${{\omega }}$ determined in
${{\omega }}$ determined in ![]() $X$ by an ample class and a positive constant
$X$ by an ample class and a positive constant ![]() $C>0$ such that
$C>0$ such that ![]() $\beta _l \leqslant C {{\omega }}$ for all
$\beta _l \leqslant C {{\omega }}$ for all ![]() $l =1, \ldots, k$. Pick any
$l =1, \ldots, k$. Pick any ![]() $\epsilon >0$. We have
$\epsilon >0$. We have ![]() $(\alpha _l^{(i)})_{X'} \to \alpha _{l,X'}$ in
$(\alpha _l^{(i)})_{X'} \to \alpha _{l,X'}$ in ![]() $\operatorname {N}^{1}(X')$, hence
$\operatorname {N}^{1}(X')$, hence ![]() $(\alpha _l^{(i)})_{X'} \leqslant \alpha _{l,X'} + \epsilon {{\omega }}_{X'}\leqslant (\beta _l)_{X'}+ \epsilon {{\omega }}_{X'}$ for all
$(\alpha _l^{(i)})_{X'} \leqslant \alpha _{l,X'} + \epsilon {{\omega }}_{X'}\leqslant (\beta _l)_{X'}+ \epsilon {{\omega }}_{X'}$ for all ![]() $i$ large enough, hence
$i$ large enough, hence ![]() $\alpha _l^{(i)} \leqslant \beta _l+\epsilon {{\omega }}_{X'}$ by Lemma 1.5. This proves
$\alpha _l^{(i)} \leqslant \beta _l+\epsilon {{\omega }}_{X'}$ by Lemma 1.5. This proves
and we conclude by letting ![]() $\epsilon \to 0$.
$\epsilon \to 0$.
Finally, pick any net of nef Cartier ![]() $b$-divisor classes
$b$-divisor classes ![]() $\beta ^{(i)}_1, \ldots, \beta ^{(i)}_k$ decreasing to
$\beta ^{(i)}_1, \ldots, \beta ^{(i)}_k$ decreasing to ![]() $\alpha _1, \ldots, \alpha _k$, and let
$\alpha _1, \ldots, \alpha _k$, and let ![]() $\Delta '$ be the limit of the net of decreasing classes
$\Delta '$ be the limit of the net of decreasing classes ![]() $(\beta ^{(i)}_1\cdot \beta ^{(i)}_2 \cdot \cdots \cdot \beta ^{(i)}_k \cdot \gamma )$. By (14) we have
$(\beta ^{(i)}_1\cdot \beta ^{(i)}_2 \cdot \cdots \cdot \beta ^{(i)}_k \cdot \gamma )$. By (14) we have ![]() $\Delta \leqslant \Delta '$. However, the same argument applies when reversing the role of the nets
$\Delta \leqslant \Delta '$. However, the same argument applies when reversing the role of the nets ![]() $\alpha ^{(i)}_l$ and
$\alpha ^{(i)}_l$ and ![]() $\beta ^{(i)}_l$ which implies
$\beta ^{(i)}_l$ which implies ![]() $\Delta = \Delta '$, and proves (15).
$\Delta = \Delta '$, and proves (15).
We conclude by observing that because any nef ![]() $b$-divisor class is the limit of a decreasing net of nef Cartier
$b$-divisor class is the limit of a decreasing net of nef Cartier ![]() $b$-divisor classes, (14) and (15) characterize a unique class.
$b$-divisor classes, (14) and (15) characterize a unique class.
The following result is the main statement of the section. It can be viewed as a vague ‘algebraic’ analog of Bedford and Taylor's intersection theory.
Theorem 3.2
(i) The intersection product of nef divisor classes coincides with the usual intersection when all classes are Cartier. It is non-negative, symmetric, multilinear in the variables
 $\alpha _1, \ldots, \alpha _k\in \operatorname {Nef}({ \mathcal {X} })$, linear in the variable
$\alpha _1, \ldots, \alpha _k\in \operatorname {Nef}({ \mathcal {X} })$, linear in the variable  $\gamma$ and increasing in each variable.
$\gamma$ and increasing in each variable.(ii) The intersection product of nef classes is upper-semicontinuous: for any net of divisor classes such that
 $\alpha ^{(j)}_i\to \alpha _i$ in the weak topology, then we have
for any class
$\alpha ^{(j)}_i\to \alpha _i$ in the weak topology, then we have
for any class \[ \limsup_j (\alpha_1^{(j)}\cdot \cdots \cdot \alpha_k^{(j)}\cdot\gamma ) \leqslant (\alpha_1\cdot \cdots \cdot \alpha_k\cdot\gamma) \]
\[ \limsup_j (\alpha_1^{(j)}\cdot \cdots \cdot \alpha_k^{(j)}\cdot\gamma ) \leqslant (\alpha_1\cdot \cdots \cdot \alpha_k\cdot\gamma) \]
 $\gamma \in \operatorname {BPF}^{d-k}({ \mathcal {X} })$.
$\gamma \in \operatorname {BPF}^{d-k}({ \mathcal {X} })$.(iii) The intersection product of nef divisor classes is continuous along decreasing sequences: if
 $\alpha ^{(j)}_i$ is a net of divisor classes decreasing to
$\alpha ^{(j)}_i$ is a net of divisor classes decreasing to  $\alpha _i$, then
in
$\alpha _i$, then
in \[ \lim_j (\alpha_1^{(j)}\cdot \cdots \cdot \alpha_k^{(j)} \cdot\gamma) = (\alpha_1\cdot \cdots \cdot \alpha_k \cdot\gamma) \]
\[ \lim_j (\alpha_1^{(j)}\cdot \cdots \cdot \alpha_k^{(j)} \cdot\gamma) = (\alpha_1\cdot \cdots \cdot \alpha_k \cdot\gamma) \]
 $\operatorname {N}_+^{k+l}({ \mathcal {X} })$ where
$\operatorname {N}_+^{k+l}({ \mathcal {X} })$ where  $\gamma \in \operatorname {BPF}^{l}({ \mathcal {X} })$.
$\gamma \in \operatorname {BPF}^{l}({ \mathcal {X} })$.(iv) The intersection product of nef classes is continuous in the
 $\lVert {\cdot } \rVert _{\omega }$-norm. In other words, if
$\lVert {\cdot } \rVert _{\omega }$-norm. In other words, if  $\big \lVert {\alpha ^{(j)}_i-\alpha _i} \big \rVert _{\omega }\to 0$, then we have
in
$\big \lVert {\alpha ^{(j)}_i-\alpha _i} \big \rVert _{\omega }\to 0$, then we have
in \[ \lim_j (\alpha_1^{(j)}\cdot \cdots \cdot \alpha_k^{(j)} \cdot\gamma) = (\alpha_1\cdot \cdots \cdot \alpha_k \cdot\gamma) \]
\[ \lim_j (\alpha_1^{(j)}\cdot \cdots \cdot \alpha_k^{(j)} \cdot\gamma) = (\alpha_1\cdot \cdots \cdot \alpha_k \cdot\gamma) \]
 $\operatorname {N}_+^{k+l}({ \mathcal {X} })$.
$\operatorname {N}_+^{k+l}({ \mathcal {X} })$.
Example 3.3 This intersection product is not continuous with respect to the weak topology. Take ![]() $X = \mathbb {P}^{2}$ and a general line
$X = \mathbb {P}^{2}$ and a general line ![]() $L$ and choose a sequence of point
$L$ and choose a sequence of point ![]() $p_n\in \mathbb {P}^{2}$ converging to the generic point (i.e. for any curve
$p_n\in \mathbb {P}^{2}$ converging to the generic point (i.e. for any curve ![]() $C$, the set
$C$, the set ![]() $\{n, p_n\in C\}$ is finite). For each
$\{n, p_n\in C\}$ is finite). For each ![]() $n$, consider the blow-up
$n$, consider the blow-up ![]() $\pi _n\colon X_n \to \mathbb {P}^{2}$ at
$\pi _n\colon X_n \to \mathbb {P}^{2}$ at ![]() $p_n$, and let
$p_n$, and let ![]() $\alpha _n$ be the nef Cartier class attached to
$\alpha _n$ be the nef Cartier class attached to ![]() $\pi ^{*}_n (c_1({ \mathcal {O} }(1))) - [E_n]$ where
$\pi ^{*}_n (c_1({ \mathcal {O} }(1))) - [E_n]$ where ![]() $E_n$ is the exceptional divisor of
$E_n$ is the exceptional divisor of ![]() $\pi _n$. Then the sequence
$\pi _n$. Then the sequence ![]() $\alpha _n$ converges weakly to the Cartier class attached to
$\alpha _n$ converges weakly to the Cartier class attached to ![]() $c_1({ \mathcal {O} }(1))$ as
$c_1({ \mathcal {O} }(1))$ as ![]() $n\rightarrow +\infty$, but
$n\rightarrow +\infty$, but ![]() $\alpha _n^{2}=0$ whereas
$\alpha _n^{2}=0$ whereas ![]() $c_1({ \mathcal {O} }(1))^{2}=1$.
$c_1({ \mathcal {O} }(1))^{2}=1$.
Proof. Compatibility with the intersection of Cartier ![]() $b$-divisor classes is obvious from the definition. The symmetry and multilinearity follows from the corresponding properties for the intersection product of divisors. The fact that it is increasing is a consequence of the observation that
$b$-divisor classes is obvious from the definition. The symmetry and multilinearity follows from the corresponding properties for the intersection product of divisors. The fact that it is increasing is a consequence of the observation that ![]() $(\alpha '_1\cdot \alpha _2 \cdot \cdots \cdot \alpha _k \cdot \gamma ) \geqslant (\alpha _1\cdot \alpha _2 \cdot \cdots \cdot \alpha _k \cdot \gamma )$ as soon as
$(\alpha '_1\cdot \alpha _2 \cdot \cdots \cdot \alpha _k \cdot \gamma ) \geqslant (\alpha _1\cdot \alpha _2 \cdot \cdots \cdot \alpha _k \cdot \gamma )$ as soon as ![]() $\alpha '_1\geqslant \alpha _1$. These arguments prove part (i).
$\alpha '_1\geqslant \alpha _1$. These arguments prove part (i).
We fix a class ![]() ${{\omega }}\in \operatorname {Nef^{1}}({ \mathcal {X} })$ determined by an ample class in
${{\omega }}\in \operatorname {Nef^{1}}({ \mathcal {X} })$ determined by an ample class in ![]() $X$, and prove part (ii). Suppose
$X$, and prove part (ii). Suppose ![]() $\alpha ^{(i)}_l\to \alpha _l$ weakly. Pick any class
$\alpha ^{(i)}_l\to \alpha _l$ weakly. Pick any class ![]() $\Delta$ in the accumulation locus of the net
$\Delta$ in the accumulation locus of the net ![]() $(\alpha _1^{(j)}\cdot \cdots \cdot \alpha _k^{(j)} \cdot \gamma )$. We may replace the net
$(\alpha _1^{(j)}\cdot \cdots \cdot \alpha _k^{(j)} \cdot \gamma )$. We may replace the net ![]() $I$ by one indexed by the family of open neighborhoods of
$I$ by one indexed by the family of open neighborhoods of ![]() $\Delta$ (endowed with the partial ordering given by the inclusion) and assume that
$\Delta$ (endowed with the partial ordering given by the inclusion) and assume that ![]() $(\alpha _1^{(j)}\cdot \cdots \cdot \alpha _k^{(j)} \cdot \gamma ) \to \Delta$.
$(\alpha _1^{(j)}\cdot \cdots \cdot \alpha _k^{(j)} \cdot \gamma ) \to \Delta$.
Let ![]() $\beta ^{(i)}_l$ be nets of nef Cartier
$\beta ^{(i)}_l$ be nets of nef Cartier ![]() $b$-divisor classes decreasing to
$b$-divisor classes decreasing to ![]() $\alpha _l$. Fix any large index
$\alpha _l$. Fix any large index ![]() $i$, and choose a model
$i$, and choose a model ![]() $X'$ in which
$X'$ in which ![]() $\beta ^{(i)}_l$,
$\beta ^{(i)}_l$, ![]() $l=1, \ldots, k$ are all determined. As
$l=1, \ldots, k$ are all determined. As ![]() $(\alpha _l^{(j)})_{X'} \to (\alpha _l)_{X'}$ in
$(\alpha _l^{(j)})_{X'} \to (\alpha _l)_{X'}$ in ![]() $\operatorname {N}^{1}(X')$ we have
$\operatorname {N}^{1}(X')$ we have ![]() $(\alpha _l^{(j)})_{X'}\leqslant (\beta ^{(i)}_l)_{X'} + \epsilon {{\omega }}$ for an arbitrary small
$(\alpha _l^{(j)})_{X'}\leqslant (\beta ^{(i)}_l)_{X'} + \epsilon {{\omega }}$ for an arbitrary small ![]() $\epsilon >0$ and all
$\epsilon >0$ and all ![]() $j$ large enough, hence
$j$ large enough, hence ![]() $\alpha _l^{(j)} \leqslant \beta ^{(i)}_l + \epsilon {{\omega }}$ by Lemma 1.5. We infer
$\alpha _l^{(j)} \leqslant \beta ^{(i)}_l + \epsilon {{\omega }}$ by Lemma 1.5. We infer
where ![]() $C>0$ is a any constant such that
$C>0$ is a any constant such that ![]() $\beta _l^{(i_0)}\leqslant C{{\omega }}$,
$\beta _l^{(i_0)}\leqslant C{{\omega }}$, ![]() $l=1,\ldots,k$, and
$l=1,\ldots,k$, and ![]() $i_0$ is a fixed index. We now let successively
$i_0$ is a fixed index. We now let successively ![]() $j$ tend to infinity in the net
$j$ tend to infinity in the net ![]() $I$, then
$I$, then ![]() $\epsilon \to 0$, and finally let
$\epsilon \to 0$, and finally let ![]() $l$ tend to infinity in
$l$ tend to infinity in ![]() $I$. We conclude that
$I$. We conclude that ![]() $\Delta \leqslant (\alpha _1\cdot \cdots \cdot \alpha _k \cdot \gamma )$ as required.
$\Delta \leqslant (\alpha _1\cdot \cdots \cdot \alpha _k \cdot \gamma )$ as required.
Now suppose that ![]() $\alpha ^{(j)}_i$ is a net of nef
$\alpha ^{(j)}_i$ is a net of nef ![]() $b$-divisor classes (not necessarily Cartier) decreasing to
$b$-divisor classes (not necessarily Cartier) decreasing to ![]() $\alpha _i$. We claim that there exists a constant
$\alpha _i$. We claim that there exists a constant ![]() $C>0$ such that for any
$C>0$ such that for any ![]() $\epsilon >0$ one has
$\epsilon >0$ one has
for all ![]() $j$ large enough. Indeed, the first inequality is a consequence of the fact that the intersection product is increasing in each variable, and the second inequality follows from the previous proof. These estimates imply the convergence
$j$ large enough. Indeed, the first inequality is a consequence of the fact that the intersection product is increasing in each variable, and the second inequality follows from the previous proof. These estimates imply the convergence ![]() $(\alpha _1^{(j)}\cdot \cdots \cdot \alpha _k^{(j)} \cdot \gamma ) \to (\alpha _1\cdot \cdots \cdot \alpha _k \cdot \gamma )$ to hold in
$(\alpha _1^{(j)}\cdot \cdots \cdot \alpha _k^{(j)} \cdot \gamma ) \to (\alpha _1\cdot \cdots \cdot \alpha _k \cdot \gamma )$ to hold in ![]() $\operatorname {N}_+^{k+l}({ \mathcal {X} })$ which proves part (iii).
$\operatorname {N}_+^{k+l}({ \mathcal {X} })$ which proves part (iii).
Finally, we observe that if ![]() $\alpha$ and
$\alpha$ and ![]() $\alpha '$ are two nef classes such that
$\alpha '$ are two nef classes such that ![]() $\lVert {\alpha - \alpha '} \rVert _{\omega }\leqslant \epsilon$, then
$\lVert {\alpha - \alpha '} \rVert _{\omega }\leqslant \epsilon$, then ![]() $- \epsilon {{\omega }} \leqslant (\alpha - \alpha ')\leqslant \epsilon {{\omega }}$ so that part (iv) follows from part (iii).
$- \epsilon {{\omega }} \leqslant (\alpha - \alpha ')\leqslant \epsilon {{\omega }}$ so that part (iv) follows from part (iii).
Proposition 1.1 together with Theorem 2.1 yield the next two results.
Corollary 3.4 There exists a constant ![]() $C_d>0$ depending only on
$C_d>0$ depending only on ![]() $d$ such that for any set of classes
$d$ such that for any set of classes ![]() $\alpha _1, \ldots, \alpha _k, \beta \in \operatorname {Nef^{1}}({ \mathcal {X} })$ with
$\alpha _1, \ldots, \alpha _k, \beta \in \operatorname {Nef^{1}}({ \mathcal {X} })$ with ![]() $(\beta ^{d})>0$ and any
$(\beta ^{d})>0$ and any ![]() $\gamma \in \operatorname {BPF}^{l}({ \mathcal {X} })$ we have
$\gamma \in \operatorname {BPF}^{l}({ \mathcal {X} })$ we have
We obtain a ‘numerical’ or cohomological version of the Chern–Levine–Nirenberg inequalities [Reference Chern, Levine and NirenbergCLN69] and [Reference DemaillyDem97, (3.3)].
Corollary 3.5 There exists a constant ![]() $C_{d,\omega }>0$ depending only on
$C_{d,\omega }>0$ depending only on ![]() $d$ and on the choice of
$d$ and on the choice of ![]() $\omega$ such that for any
$\omega$ such that for any ![]() $\alpha _1, \ldots, \alpha _k \in \operatorname {Nef^{1}}({ \mathcal {X} })$ and for any
$\alpha _1, \ldots, \alpha _k \in \operatorname {Nef^{1}}({ \mathcal {X} })$ and for any ![]() $\gamma \in \operatorname {BPF}^{d-k}({ \mathcal {X} })$, we have
$\gamma \in \operatorname {BPF}^{d-k}({ \mathcal {X} })$, we have
3.2 Diskant inequalities and applications
Theorem 3.6 Pick any two classes ![]() $\alpha,\beta \in \operatorname {Nef^{1}}({ \mathcal {X} })$ such that
$\alpha,\beta \in \operatorname {Nef^{1}}({ \mathcal {X} })$ such that ![]() $(\alpha ^{d})>0$ and
$(\alpha ^{d})>0$ and ![]() $(\beta ^{d})>0$ (i.e. both classes
$(\beta ^{d})>0$ (i.e. both classes ![]() $\alpha,\beta$ are big). Let
$\alpha,\beta$ are big). Let ![]() $s> 0$ be the largest positive number such that
$s> 0$ be the largest positive number such that ![]() $\alpha - s \beta \geqslant 0$. Then we have
$\alpha - s \beta \geqslant 0$. Then we have
Proof. Pick any two nets ![]() $\alpha _j, \beta _j\in \operatorname {c-Nef^{1}}({ \mathcal {X} })$ parametrized by an inductive set
$\alpha _j, \beta _j\in \operatorname {c-Nef^{1}}({ \mathcal {X} })$ parametrized by an inductive set ![]() $J$ and decreasing to
$J$ and decreasing to ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$, respectively. Fix any
$\beta$, respectively. Fix any ![]() $\epsilon >0$.
$\epsilon >0$.
Observe that ![]() $(\alpha _j^{d}) \geqslant (\alpha ^{d})>0$ and
$(\alpha _j^{d}) \geqslant (\alpha ^{d})>0$ and ![]() $(\beta _j^{d}) \geqslant (\beta ^{d})>0$ so that
$(\beta _j^{d}) \geqslant (\beta ^{d})>0$ so that ![]() $\alpha _j$ and
$\alpha _j$ and ![]() $\beta _j$ are big. The largest non-negative number
$\beta _j$ are big. The largest non-negative number ![]() $s_j$ such that
$s_j$ such that ![]() $\alpha _j - s_j \beta _j\geqslant 0$ is, thus, positive. By [Reference Boucksom, Favre and JonssonBFJ09, Theorem F], we have
$\alpha _j - s_j \beta _j\geqslant 0$ is, thus, positive. By [Reference Boucksom, Favre and JonssonBFJ09, Theorem F], we have
In other words, ![]() $s_j\geqslant \tau _j$ where
$s_j\geqslant \tau _j$ where
By Theorem 3.2(iii), we have
and we obtain ![]() $\alpha - \tau \beta \geqslant 0$ as required.
$\alpha - \tau \beta \geqslant 0$ as required.
We now complete the proof of Theorem A.
Proof of Theorem A Let ![]() $\alpha$ be any nef
$\alpha$ be any nef ![]() $b$-divisor class. By adding
$b$-divisor class. By adding ![]() $({1}/{n}){{\omega }}$ with
$({1}/{n}){{\omega }}$ with ![]() ${{\omega }}$ a fixed Cartier
${{\omega }}$ a fixed Cartier ![]() $b$-divisor class determined in
$b$-divisor class determined in ![]() $X$ by an ample divisor, we may suppose that
$X$ by an ample divisor, we may suppose that ![]() $\alpha$ is big so that
$\alpha$ is big so that ![]() $(\alpha ^{d})>0$.
$(\alpha ^{d})>0$.
Let ![]() $\alpha _j$ be a net of nef Cartier
$\alpha _j$ be a net of nef Cartier ![]() $b$-divisor classes decreasing to
$b$-divisor classes decreasing to ![]() $\alpha$. Diskant inequalities yield
$\alpha$. Diskant inequalities yield ![]() $\alpha \geqslant s_j \alpha _j$ with
$\alpha \geqslant s_j \alpha _j$ with
As ![]() $(\alpha _j^{d})\to (\alpha ^{d})$, and
$(\alpha _j^{d})\to (\alpha ^{d})$, and ![]() $(\alpha ^{d-1}\cdot \alpha _j)\to (\alpha ^{d})$, we may extract a subsequence
$(\alpha ^{d-1}\cdot \alpha _j)\to (\alpha ^{d})$, we may extract a subsequence ![]() $i_n$ such that
$i_n$ such that ![]() $\alpha _{i_n}$ is still decreasing, and
$\alpha _{i_n}$ is still decreasing, and ![]() $s_{i_n} \to 1$ which implies
$s_{i_n} \to 1$ which implies ![]() $\alpha _{i_n} \to \alpha$.
$\alpha _{i_n} \to \alpha$.
The same arguments yield the following result.
Corollary 3.7 For any class ![]() $\alpha \in \operatorname {Nef^{1}}({ \mathcal {X} })$ such that
$\alpha \in \operatorname {Nef^{1}}({ \mathcal {X} })$ such that ![]() $(\alpha ^{d})>0$ and for any
$(\alpha ^{d})>0$ and for any ![]() $\epsilon >0$, there exists a class
$\epsilon >0$, there exists a class ![]() $\alpha '\in \operatorname {c-Nef^{1}}({ \mathcal {X} })$ such that
$\alpha '\in \operatorname {c-Nef^{1}}({ \mathcal {X} })$ such that ![]() $(1-\epsilon ) \alpha ' \leqslant \alpha \leqslant \alpha '$.
$(1-\epsilon ) \alpha ' \leqslant \alpha \leqslant \alpha '$.
This corollary allows one to obtain better continuity properties of the intersection product.
Corollary 3.8 For any ![]() $\alpha _1, \ldots, \alpha _k\in \operatorname {Nef^{1}}({ \mathcal {X} })$, the map
$\alpha _1, \ldots, \alpha _k\in \operatorname {Nef^{1}}({ \mathcal {X} })$, the map
is weakly continuous.
Proof. When ![]() $\alpha _i$ are Cartier, the result is clear. By multilinearity and by replacing
$\alpha _i$ are Cartier, the result is clear. By multilinearity and by replacing ![]() $\alpha _i$ by
$\alpha _i$ by ![]() $\alpha _i + {{\omega }}$, we may suppose that
$\alpha _i + {{\omega }}$, we may suppose that ![]() $(\alpha _i^{d})>0$ for all
$(\alpha _i^{d})>0$ for all ![]() $i$. Pick any
$i$. Pick any ![]() $\epsilon >0$. By the previous corollary, one can find
$\epsilon >0$. By the previous corollary, one can find ![]() $\alpha '_i\in \operatorname {c-Nef^{1}}({ \mathcal {X} })$ such that
$\alpha '_i\in \operatorname {c-Nef^{1}}({ \mathcal {X} })$ such that ![]() $(1-\epsilon ) \alpha _i' \leqslant \alpha _i \leqslant \alpha _i'$. It follows that
$(1-\epsilon ) \alpha _i' \leqslant \alpha _i \leqslant \alpha _i'$. It follows that
 \begin{align*} 0\leqslant (\alpha'_1 \cdot \cdots \cdot \alpha'_k\cdot\gamma) -(\alpha_1\cdot \cdots \cdot \alpha_k\cdot\gamma) &\leqslant ((1-\epsilon)^{-k} -1) (\alpha_1\cdot \cdots \cdot \alpha_k\cdot\gamma)\\ &\leqslant C \epsilon ({{\omega}}^{k}\cdot\gamma). \end{align*}
\begin{align*} 0\leqslant (\alpha'_1 \cdot \cdots \cdot \alpha'_k\cdot\gamma) -(\alpha_1\cdot \cdots \cdot \alpha_k\cdot\gamma) &\leqslant ((1-\epsilon)^{-k} -1) (\alpha_1\cdot \cdots \cdot \alpha_k\cdot\gamma)\\ &\leqslant C \epsilon ({{\omega}}^{k}\cdot\gamma). \end{align*}
Suppose ![]() $\gamma _i \to \gamma$ is a net of classes converging weakly in
$\gamma _i \to \gamma$ is a net of classes converging weakly in ![]() $\operatorname {BPF}^{l}({ \mathcal {X} })$. Then
$\operatorname {BPF}^{l}({ \mathcal {X} })$. Then
 \begin{align*} \liminf_i (\alpha_1\cdot \cdots \cdot \alpha_k\cdot\gamma_i) &\geqslant \liminf_i (\alpha'_1 \cdot \cdots \cdot \alpha'_k\cdot\gamma_i) - C \epsilon ({{\omega}}^{k}\cdot\gamma_i)\\ &= (\alpha'_1 \cdot \cdots \cdot \alpha'_k\cdot\gamma) - C \epsilon ({{\omega}}^{k}\cdot\gamma) \geqslant (\alpha_1 \cdot \cdots \cdot \alpha_k\cdot\gamma) - C \epsilon ({{\omega}}^{k}\cdot\gamma), \end{align*}
\begin{align*} \liminf_i (\alpha_1\cdot \cdots \cdot \alpha_k\cdot\gamma_i) &\geqslant \liminf_i (\alpha'_1 \cdot \cdots \cdot \alpha'_k\cdot\gamma_i) - C \epsilon ({{\omega}}^{k}\cdot\gamma_i)\\ &= (\alpha'_1 \cdot \cdots \cdot \alpha'_k\cdot\gamma) - C \epsilon ({{\omega}}^{k}\cdot\gamma) \geqslant (\alpha_1 \cdot \cdots \cdot \alpha_k\cdot\gamma) - C \epsilon ({{\omega}}^{k}\cdot\gamma), \end{align*}
which implies ![]() $\liminf _i (\alpha _1\cdot \cdots \cdot \alpha _k\cdot \gamma _i)\geqslant (\alpha _1\cdot \cdots \cdot \alpha _k\cdot \gamma )$.
$\liminf _i (\alpha _1\cdot \cdots \cdot \alpha _k\cdot \gamma _i)\geqslant (\alpha _1\cdot \cdots \cdot \alpha _k\cdot \gamma )$.
We conclude using Theorem 3.2(i).
Recall the definition of ![]() $\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$ from § 1.4.
$\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$ from § 1.4.
Corollary 3.9 The following inclusion holds:
More precisely, for any nef class ![]() $\alpha \in \operatorname {Nef^{1}}({ \mathcal {X} })$ there exists a sequence of nef Cartier
$\alpha \in \operatorname {Nef^{1}}({ \mathcal {X} })$ there exists a sequence of nef Cartier ![]() $b$-divisor classes
$b$-divisor classes ![]() $\alpha _n\in \operatorname {c-Nef^{1}}({ \mathcal {X} })$ such that
$\alpha _n\in \operatorname {c-Nef^{1}}({ \mathcal {X} })$ such that ![]() $\lVert {\alpha -\alpha _n} \rVert _{\Sigma } \to 0$.
$\lVert {\alpha -\alpha _n} \rVert _{\Sigma } \to 0$.
In particular, we have following continuous injection
Proof. Let ![]() $\alpha$ be any nef class. As any Cartier class belongs to
$\alpha$ be any nef class. As any Cartier class belongs to ![]() $\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$, by adding
$\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$, by adding ![]() ${{\omega }}$ if necessary, we may assume that
${{\omega }}$ if necessary, we may assume that ![]() $(\alpha ^{d})>0$. By Corollary 3.7, for each
$(\alpha ^{d})>0$. By Corollary 3.7, for each ![]() $n$, one can take a nef Cartier class
$n$, one can take a nef Cartier class ![]() $\alpha _n$ such that
$\alpha _n$ such that ![]() $(1+ {1}/{n})^{-1} \alpha _n\leqslant \alpha \leqslant \alpha _n$. Using Corollary 3.5, we infer for all integers
$(1+ {1}/{n})^{-1} \alpha _n\leqslant \alpha \leqslant \alpha _n$. Using Corollary 3.5, we infer for all integers ![]() $m\geqslant n$:
$m\geqslant n$:
 \begin{align*} \lVert {\alpha_n - \alpha_m} \rVert_{\Sigma}^{2} &=\sup_{ \substack{\gamma \in \operatorname{c-BPF}^{d-2}({ \mathcal{X} }) \\ (\gamma \cdot {{\omega}}^{2}) = 1}} 2 ((\alpha_n - \alpha_m)\cdot {{\omega}} \cdot \gamma )^{2} - ( (\alpha_n - \alpha_m)^{2} \cdot \gamma)\\ &\leqslant \sup_{ \substack{\gamma \in \operatorname{c-BPF}^{d-2}({ \mathcal{X} }) \\ (\gamma \cdot {{\omega}}^{2}) = 1}} \frac 2{n^{2}} (\alpha_m \cdot {{\omega}} \cdot \gamma )^{2} + \frac 2{n} (\alpha_m^{2}\cdot \gamma) \leqslant \frac{C}n \end{align*}
\begin{align*} \lVert {\alpha_n - \alpha_m} \rVert_{\Sigma}^{2} &=\sup_{ \substack{\gamma \in \operatorname{c-BPF}^{d-2}({ \mathcal{X} }) \\ (\gamma \cdot {{\omega}}^{2}) = 1}} 2 ((\alpha_n - \alpha_m)\cdot {{\omega}} \cdot \gamma )^{2} - ( (\alpha_n - \alpha_m)^{2} \cdot \gamma)\\ &\leqslant \sup_{ \substack{\gamma \in \operatorname{c-BPF}^{d-2}({ \mathcal{X} }) \\ (\gamma \cdot {{\omega}}^{2}) = 1}} \frac 2{n^{2}} (\alpha_m \cdot {{\omega}} \cdot \gamma )^{2} + \frac 2{n} (\alpha_m^{2}\cdot \gamma) \leqslant \frac{C}n \end{align*}
for some constant ![]() $C>0$. This shows that
$C>0$. This shows that ![]() $(\alpha _n)$ is a Cauchy sequence in
$(\alpha _n)$ is a Cauchy sequence in ![]() $\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$. However, because it converges weakly to
$\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$. However, because it converges weakly to ![]() $\alpha$ we conclude that
$\alpha$ we conclude that ![]() $\alpha$ belongs to
$\alpha$ belongs to ![]() $\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$ and
$\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$ and ![]() $\lVert {\alpha _n-\alpha } \rVert _{\Sigma } \to 0$.
$\lVert {\alpha _n-\alpha } \rVert _{\Sigma } \to 0$.
By linearity, we obtain ![]() $\operatorname {Vect}(\operatorname {Nef^{1}}({ \mathcal {X} })) \subset \operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$ and the continuity follows from the fact that
$\operatorname {Vect}(\operatorname {Nef^{1}}({ \mathcal {X} })) \subset \operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$ and the continuity follows from the fact that ![]() $\lVert {\alpha } \rVert _{\operatorname {BPF}} = (\alpha \cdot {{\omega }}^{d-1})$ for all
$\lVert {\alpha } \rVert _{\operatorname {BPF}} = (\alpha \cdot {{\omega }}^{d-1})$ for all ![]() $\alpha \in \operatorname {Nef^{1}}({ \mathcal {X} })$ by Lemma 1.7.
$\alpha \in \operatorname {Nef^{1}}({ \mathcal {X} })$ by Lemma 1.7.
We now relate the intersection product of nef divisors with the intersection product ![]() $\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} }) \times \operatorname {N^{1}_{\Sigma }}({ \mathcal {X} }) \to \operatorname {N}^{{2},\vee }_{\operatorname {BPF}}({ \mathcal {X} })$ recalled in Theorem 1.6. Denote by
$\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} }) \times \operatorname {N^{1}_{\Sigma }}({ \mathcal {X} }) \to \operatorname {N}^{{2},\vee }_{\operatorname {BPF}}({ \mathcal {X} })$ recalled in Theorem 1.6. Denote by ![]() $\imath \colon \operatorname {Nef^{1}}(X)\to \operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$ the natural inclusion map given be the previous corollary.
$\imath \colon \operatorname {Nef^{1}}(X)\to \operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$ the natural inclusion map given be the previous corollary.
Corollary 3.10 For any two nef ![]() $b$-divisor classes
$b$-divisor classes ![]() $\alpha,\beta$, the class
$\alpha,\beta$, the class ![]() $\alpha \cdot \beta \in \operatorname {BPF}^{2}({ \mathcal {X} })$ defined by Proposition–Definition 3.1 is identical to the intersection product
$\alpha \cdot \beta \in \operatorname {BPF}^{2}({ \mathcal {X} })$ defined by Proposition–Definition 3.1 is identical to the intersection product ![]() $\imath (\alpha )\cdot \imath (\beta )\in \operatorname {N}^{{2},\vee }_{\operatorname {BPF}}({ \mathcal {X} })$ given by Theorem 1.6.
$\imath (\alpha )\cdot \imath (\beta )\in \operatorname {N}^{{2},\vee }_{\operatorname {BPF}}({ \mathcal {X} })$ given by Theorem 1.6.
Proof. Take two sequences of nef Cartier ![]() $b$-divisor classes such that
$b$-divisor classes such that ![]() $\lVert {\alpha _n-\alpha } \rVert _{\Sigma }\to 0$ and
$\lVert {\alpha _n-\alpha } \rVert _{\Sigma }\to 0$ and ![]() $\lVert {\beta _n-\beta } \rVert _{\Sigma }\to 0$. By continuity of the intersection product in
$\lVert {\beta _n-\beta } \rVert _{\Sigma }\to 0$. By continuity of the intersection product in ![]() $\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$, we have
$\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$, we have ![]() $\imath (\alpha )\cdot \imath (\beta ) = \lim _n \lim _m \alpha _n\cdot \beta _m$. By Corollary 3.8, we obtain
$\imath (\alpha )\cdot \imath (\beta ) = \lim _n \lim _m \alpha _n\cdot \beta _m$. By Corollary 3.8, we obtain ![]() $\lim _m \alpha _n\cdot \beta _m = \alpha _n\cdot \beta$; and then
$\lim _m \alpha _n\cdot \beta _m = \alpha _n\cdot \beta$; and then ![]() $\lim _n \alpha _n\cdot \beta = \alpha \cdot \beta$ which proves the result.
$\lim _n \alpha _n\cdot \beta = \alpha \cdot \beta$ which proves the result.
3.3 Variations on the Hodge index theorem
Theorem B Any two ![]() $b$-divisor classes
$b$-divisor classes ![]() $\alpha, \beta \in \operatorname {Nef^{1}}({ \mathcal {X} })$ such that
$\alpha, \beta \in \operatorname {Nef^{1}}({ \mathcal {X} })$ such that ![]() $\alpha \cdot \beta =0$ are proportional.
$\alpha \cdot \beta =0$ are proportional.
Proof. In view of Corollary 3.10, the statement is a direct consequence of the version of Hodge index theorem holding in ![]() $\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$, see [Reference Dang and FavreDF21, Theorem 3.13].
$\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$, see [Reference Dang and FavreDF21, Theorem 3.13].
Proposition 3.11 For any two nef classes ![]() $\alpha, \beta$, the sequence
$\alpha, \beta$, the sequence ![]() $e_k:= (\alpha ^{k}\cdot \beta ^{d-k})$ is log-concave. Moreover, if
$e_k:= (\alpha ^{k}\cdot \beta ^{d-k})$ is log-concave. Moreover, if ![]() $\alpha$ or
$\alpha$ or ![]() $\beta$ are nef and big, and the sequence
$\beta$ are nef and big, and the sequence ![]() $(\log e_k)_k$ is affine, then
$(\log e_k)_k$ is affine, then ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$ are proportional.
$\beta$ are proportional.
Proof. Write ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$ as decreasing limits of sequences of nef Cartier classes
$\beta$ as decreasing limits of sequences of nef Cartier classes ![]() $\alpha _n\downarrow \alpha$ and
$\alpha _n\downarrow \alpha$ and ![]() $\beta _n\downarrow \beta$. By the Khovanskii–Teissier inequalities, the sequence
$\beta _n\downarrow \beta$. By the Khovanskii–Teissier inequalities, the sequence ![]() $(\alpha _n^{k}\cdot \beta _n^{d-k})$ is log-concave which implies by Theorem 3.2 the log-concavity of the sequence
$(\alpha _n^{k}\cdot \beta _n^{d-k})$ is log-concave which implies by Theorem 3.2 the log-concavity of the sequence ![]() $e_k=(\alpha ^{k}\cdot \beta ^{d-k})$ by letting
$e_k=(\alpha ^{k}\cdot \beta ^{d-k})$ by letting ![]() $n\to \infty$.
$n\to \infty$.
Suppose now that ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$ are big and nef, and that the sequence
$\beta$ are big and nef, and that the sequence ![]() $e_k$ is linear. Scale both classes such that
$e_k$ is linear. Scale both classes such that ![]() $(\alpha ^{d})=(\beta ^{d}) =1$ so that
$(\alpha ^{d})=(\beta ^{d}) =1$ so that ![]() $(\alpha ^{d-1}\cdot \beta )=1$ too. Then
$(\alpha ^{d-1}\cdot \beta )=1$ too. Then ![]() $\alpha =\beta$ by Diskant's inequalities.
$\alpha =\beta$ by Diskant's inequalities.
Recall from § 1.4 that given any two classes ![]() $\theta, \theta '\in \operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$ the pairing
$\theta, \theta '\in \operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$ the pairing ![]() $\alpha \cdot \beta$ belongs to
$\alpha \cdot \beta$ belongs to ![]() $\operatorname {N}^{{2},\vee }_{\operatorname {BPF}}({ \mathcal {X} })$ which is included in
$\operatorname {N}^{{2},\vee }_{\operatorname {BPF}}({ \mathcal {X} })$ which is included in ![]() $\operatorname {N}_{\operatorname {BPF}}^{d-2}({ \mathcal {X} })^{*}$. It follows that for any class
$\operatorname {N}_{\operatorname {BPF}}^{d-2}({ \mathcal {X} })^{*}$. It follows that for any class ![]() $\gamma \in \operatorname {BPF}^{d-2}({ \mathcal {X} })$, the pairing
$\gamma \in \operatorname {BPF}^{d-2}({ \mathcal {X} })$, the pairing ![]() $\theta \cdot \theta '\cdot \gamma \in \mathbb {R}$ is well-defined.
$\theta \cdot \theta '\cdot \gamma \in \mathbb {R}$ is well-defined.
Proposition 3.12 Let ![]() $\gamma \in \operatorname {BPF}^{d-2}({ \mathcal {X} })$, and
$\gamma \in \operatorname {BPF}^{d-2}({ \mathcal {X} })$, and ![]() $\alpha \in \operatorname {Nef^{1}}({ \mathcal {X} })$. Suppose that
$\alpha \in \operatorname {Nef^{1}}({ \mathcal {X} })$. Suppose that ![]() $\alpha \cdot \gamma \neq 0$, and that there exists a sequence
$\alpha \cdot \gamma \neq 0$, and that there exists a sequence ![]() $\gamma _n\in \operatorname {c-BPF}^{d-2}({ \mathcal {X} })$ decreasing to
$\gamma _n\in \operatorname {c-BPF}^{d-2}({ \mathcal {X} })$ decreasing to ![]() $\gamma$.
$\gamma$.
Then the quadratic form
is semi-negative on the hyperplane ![]() $H_\alpha := \{\theta \in \operatorname {N^{1}_{\Sigma }}({ \mathcal {X} }), (\theta \cdot \alpha \cdot \gamma )=0\}$. In particular, we obtain
$H_\alpha := \{\theta \in \operatorname {N^{1}_{\Sigma }}({ \mathcal {X} }), (\theta \cdot \alpha \cdot \gamma )=0\}$. In particular, we obtain
Remark 3.13 We believe the assumption on the existence of a sequence of Cartier BPF classes approximating ![]() $\gamma$ to be superfluous. Note that it is satisfied when
$\gamma$ to be superfluous. Note that it is satisfied when ![]() $\gamma$ is a positive linear combination of intersections of nef classes or when the codimension of
$\gamma$ is a positive linear combination of intersections of nef classes or when the codimension of ![]() $\gamma$ is one by Theorem A.
$\gamma$ is one by Theorem A.
Proof. Observe that the last statement is a consequence of Cauchy–Schwarz inequality. Let us prove that ![]() $q$ is semi-negative on
$q$ is semi-negative on ![]() $H_\alpha$.
$H_\alpha$.
Pick any decreasing sequence ![]() $\alpha _n\in \operatorname {c-Nef^{1}}({ \mathcal {X} })$ converging to
$\alpha _n\in \operatorname {c-Nef^{1}}({ \mathcal {X} })$ converging to ![]() $\alpha$. Pick any sequence of models
$\alpha$. Pick any sequence of models ![]() $X_{n+1}\geqslant X_n$ such that for each
$X_{n+1}\geqslant X_n$ such that for each ![]() $n$, the classes
$n$, the classes ![]() $\gamma _n$ and
$\gamma _n$ and ![]() $\alpha _n$ are determined in
$\alpha _n$ are determined in ![]() $X_n$. By perturbing slightly
$X_n$. By perturbing slightly ![]() $\gamma _n$, we may assume it is represented by a surface
$\gamma _n$, we may assume it is represented by a surface ![]() $\Sigma$ in
$\Sigma$ in ![]() $X_n$. We may also assume that
$X_n$. We may also assume that ![]() $\gamma _n \leqslant \omega ^{d-2}$ for some fixed ample class
$\gamma _n \leqslant \omega ^{d-2}$ for some fixed ample class ![]() $\omega$ in
$\omega$ in ![]() $X$. Note that
$X$. Note that
Pick any class ![]() $\theta \in \operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$ such that
$\theta \in \operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$ such that ![]() $(\theta \cdot \alpha \cdot \gamma )=0$. Take any sequence of Cartier classes
$(\theta \cdot \alpha \cdot \gamma )=0$. Take any sequence of Cartier classes ![]() $\theta ^{(j)}\to \theta$ in
$\theta ^{(j)}\to \theta$ in ![]() $\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$. By Theorem 1.6, we have
$\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$. By Theorem 1.6, we have ![]() $(\theta ^{(j)} \cdot \beta )\to (\theta \cdot \beta )$ in
$(\theta ^{(j)} \cdot \beta )\to (\theta \cdot \beta )$ in ![]() $\operatorname {N}^{{2},\vee }_{\operatorname {BPF}}({ \mathcal {X} })$ for any class
$\operatorname {N}^{{2},\vee }_{\operatorname {BPF}}({ \mathcal {X} })$ for any class ![]() $\beta \in \operatorname {Nef^{1}} ({ \mathcal {X} })$.
$\beta \in \operatorname {Nef^{1}} ({ \mathcal {X} })$.
Fix ![]() $\epsilon >0$, and take
$\epsilon >0$, and take ![]() $n$ large enough such that
$n$ large enough such that ![]() $|(\theta \cdot \alpha _n\cdot \gamma _n)|\leqslant \epsilon$. For all
$|(\theta \cdot \alpha _n\cdot \gamma _n)|\leqslant \epsilon$. For all ![]() $j\gg 1$, we have
$j\gg 1$, we have ![]() $|(\theta ^{(j)} \cdot \alpha _n\cdot \gamma _n)|\leqslant 2\epsilon$. Set
$|(\theta ^{(j)} \cdot \alpha _n\cdot \gamma _n)|\leqslant 2\epsilon$. Set ![]() $\tilde {\theta }_j= \theta ^{(j)} - \eta _j \omega$ so that
$\tilde {\theta }_j= \theta ^{(j)} - \eta _j \omega$ so that ![]() $(\tilde {\theta }_j \cdot \alpha _n\cdot \gamma _n)=0$, and observe that
$(\tilde {\theta }_j \cdot \alpha _n\cdot \gamma _n)=0$, and observe that
By the Hodge index theorem, we obtain
As the sequence ![]() $\eta _j$ is bounded, we may extract a subsequence converging to some
$\eta _j$ is bounded, we may extract a subsequence converging to some ![]() $0<\eta \leqslant 2c^{-1}\epsilon$ and letting
$0<\eta \leqslant 2c^{-1}\epsilon$ and letting ![]() $j\to \infty$, we obtain
$j\to \infty$, we obtain
We conclude by letting first ![]() $n\to \infty$ and then
$n\to \infty$ and then ![]() $\epsilon \to 0$.
$\epsilon \to 0$.
An analog of the Hodge index theorem was used by Dinh and Sibony in [Reference Dinh and SibonyDS04a] to study commutative subgroups of the group of automorphisms on compact Kähler manifolds. Following [Reference Dinh and SibonyDS04a, Corollary 3.5], we extend their result to arbitrary ![]() $b$-divisor classes.
$b$-divisor classes.
Theorem 3.14 Pick any class ![]() $0\neq \gamma \in \operatorname {BPF}^{k}({ \mathcal {X} })$ such that there exists a sequence
$0\neq \gamma \in \operatorname {BPF}^{k}({ \mathcal {X} })$ such that there exists a sequence ![]() $\gamma _n\in \operatorname {c-BPF}^{k}({ \mathcal {X} })$ decreasing to
$\gamma _n\in \operatorname {c-BPF}^{k}({ \mathcal {X} })$ decreasing to ![]() $\gamma$.
$\gamma$.
If ![]() $\theta, \theta ' \in \operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$ satisfy
$\theta, \theta ' \in \operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$ satisfy ![]() $(\theta ^{2}\cdot \gamma )\geqslant 0$,
$(\theta ^{2}\cdot \gamma )\geqslant 0$, ![]() $((\theta ')^{2} \cdot \gamma ) \geqslant 0$, and
$((\theta ')^{2} \cdot \gamma ) \geqslant 0$, and ![]() $(\theta \cdot \theta ' \cdot \gamma ) =0$, then there exist
$(\theta \cdot \theta ' \cdot \gamma ) =0$, then there exist ![]() $(a, a')\neq (0)$ such that
$(a, a')\neq (0)$ such that ![]() $(a \theta + a' \theta ') \cdot \gamma =0$.
$(a \theta + a' \theta ') \cdot \gamma =0$.
Remark 3.15 Note that the conditions ![]() $(\theta ^{2}\cdot \gamma )\geqslant 0$,
$(\theta ^{2}\cdot \gamma )\geqslant 0$, ![]() $((\theta ')^{2} \cdot \gamma ) \geqslant 0$ are automatically satisfied when
$((\theta ')^{2} \cdot \gamma ) \geqslant 0$ are automatically satisfied when ![]() $\theta, \theta '\in \operatorname {Nef^{1}}({ \mathcal {X} })$.
$\theta, \theta '\in \operatorname {Nef^{1}}({ \mathcal {X} })$.
Proof. We may suppose that ![]() $\theta \cdot \gamma \neq 0$,
$\theta \cdot \gamma \neq 0$, ![]() $\theta '\cdot \gamma \neq 0$.
$\theta '\cdot \gamma \neq 0$.
We claim that
To see this pick any class ![]() $\beta \in \operatorname {c-BPF}^{d-k-2}({ \mathcal {X} })$ such that the curve classes
$\beta \in \operatorname {c-BPF}^{d-k-2}({ \mathcal {X} })$ such that the curve classes ![]() $\theta \cdot \gamma \cdot \beta$ and
$\theta \cdot \gamma \cdot \beta$ and ![]() $\theta '\cdot \gamma \cdot \beta$ are both non-zero. Observe that
$\theta '\cdot \gamma \cdot \beta$ are both non-zero. Observe that
Pick any big and nef class ![]() $\alpha \in \operatorname {c-Nef^{1}}({ \mathcal {X} })$ such that
$\alpha \in \operatorname {c-Nef^{1}}({ \mathcal {X} })$ such that ![]() $(\theta \cdot \gamma \cdot \beta \cdot \alpha ) \neq 0$, and
$(\theta \cdot \gamma \cdot \beta \cdot \alpha ) \neq 0$, and ![]() $(\theta '\cdot \gamma \cdot \beta \cdot \alpha ) \neq 0$. By Proposition 3.12, we have
$(\theta '\cdot \gamma \cdot \beta \cdot \alpha ) \neq 0$. By Proposition 3.12, we have ![]() $q_\gamma \leqslant 0$ on the hyperplane
$q_\gamma \leqslant 0$ on the hyperplane ![]() $H:= (\gamma \cdot \beta \cdot \alpha )^{\perp }$. One can thus find a pair
$H:= (\gamma \cdot \beta \cdot \alpha )^{\perp }$. One can thus find a pair ![]() $a,a' \neq 0$ such that
$a,a' \neq 0$ such that ![]() $a\theta + a'\theta ' \in H$ is non-zero and such that
$a\theta + a'\theta ' \in H$ is non-zero and such that ![]() $q_\gamma (a\theta + a'\theta ')=0$, and it follows that
$q_\gamma (a\theta + a'\theta ')=0$, and it follows that ![]() $(\theta ^{2}\cdot \gamma \cdot \beta ) = ((\theta ')^{2}\cdot \gamma \cdot \beta ) = 0$. As
$(\theta ^{2}\cdot \gamma \cdot \beta ) = ((\theta ')^{2}\cdot \gamma \cdot \beta ) = 0$. As ![]() $\beta$ is arbitrary, the claim is proved.
$\beta$ is arbitrary, the claim is proved.
Pick any class ![]() $\beta \in \operatorname {c-BPF}^{d-k-2}({ \mathcal {X} })$ such that both curve classes
$\beta \in \operatorname {c-BPF}^{d-k-2}({ \mathcal {X} })$ such that both curve classes ![]() $\theta \cdot \Omega$ and
$\theta \cdot \Omega$ and ![]() $\theta '\cdot \Omega$ are non-zero with
$\theta '\cdot \Omega$ are non-zero with ![]() $\Omega =\beta \cdot \gamma$. We shall prove that
$\Omega =\beta \cdot \gamma$. We shall prove that ![]() $\theta \cdot \gamma \cdot \beta = c(\beta ) \theta '\cdot \gamma \cdot \beta$ for some
$\theta \cdot \gamma \cdot \beta = c(\beta ) \theta '\cdot \gamma \cdot \beta$ for some ![]() $c(\beta )>0$. By adding a small multiple of
$c(\beta )>0$. By adding a small multiple of ![]() ${{\omega }}^{k}$ to
${{\omega }}^{k}$ to ![]() $\gamma _n$ and
$\gamma _n$ and ![]() ${{\omega }}^{d-k-2}$ to
${{\omega }}^{d-k-2}$ to ![]() $\beta$, we may assume that
$\beta$, we may assume that ![]() $\Omega _n:= \gamma _n\cdot \beta$ is strongly BPF, and determined in some model by a surface
$\Omega _n:= \gamma _n\cdot \beta$ is strongly BPF, and determined in some model by a surface ![]() $\Sigma _n$ which is the image under a flat map of a complete intersection of ample divisors. We may also impose that
$\Sigma _n$ which is the image under a flat map of a complete intersection of ample divisors. We may also impose that ![]() $\theta \cdot \Omega \cdot {{\omega }} \neq 0$.
$\theta \cdot \Omega \cdot {{\omega }} \neq 0$.
Choose any ![]() $t_n$ such that
$t_n$ such that ![]() $(\theta _n^{2}\cdot \Omega _n) =0$ with
$(\theta _n^{2}\cdot \Omega _n) =0$ with ![]() $\theta _n = \theta + t_n {{\omega }}$. Observe that
$\theta _n = \theta + t_n {{\omega }}$. Observe that
 \begin{align*} 0 = (\theta_n^{2}\cdot \Omega_n) &= (\theta^{2}\cdot \Omega_n) + 2 t_n ({{\omega}}\cdot \theta\cdot \Omega_n) +t_n^{2} ({{\omega}}^{2}\cdot \Omega_n)\\ &=(\theta^{2}\cdot (\Omega_n-\Omega)) + 2 t_n ({{\omega}}\cdot \theta\cdot \Omega_n) +t_n^{2} ({{\omega}}^{2}\cdot \Omega_n). \end{align*}
\begin{align*} 0 = (\theta_n^{2}\cdot \Omega_n) &= (\theta^{2}\cdot \Omega_n) + 2 t_n ({{\omega}}\cdot \theta\cdot \Omega_n) +t_n^{2} ({{\omega}}^{2}\cdot \Omega_n)\\ &=(\theta^{2}\cdot (\Omega_n-\Omega)) + 2 t_n ({{\omega}}\cdot \theta\cdot \Omega_n) +t_n^{2} ({{\omega}}^{2}\cdot \Omega_n). \end{align*}
As ![]() $({{\omega }}^{2}\cdot \Omega _n)$ is uniformly bounded from below by
$({{\omega }}^{2}\cdot \Omega _n)$ is uniformly bounded from below by ![]() $({{\omega }}^{2} \cdot \gamma \cdot \beta )$, and
$({{\omega }}^{2} \cdot \gamma \cdot \beta )$, and ![]() $(\theta ^{2}\cdot \Omega _n)\sim (\theta ^{2}\cdot \Omega ) =0$, such a constant
$(\theta ^{2}\cdot \Omega _n)\sim (\theta ^{2}\cdot \Omega ) =0$, such a constant ![]() $t_n$ exists and we may choose
$t_n$ exists and we may choose ![]() $t_n\to 0$ as
$t_n\to 0$ as ![]() $n\to \infty$.
$n\to \infty$.
Now pick another big and nef class ![]() ${{\omega }}'$ such that
${{\omega }}'$ such that ![]() ${{\omega }} \cdot \Omega$ and
${{\omega }} \cdot \Omega$ and ![]() ${{\omega }}' \cdot \Omega$ are not proportional, normalized by
${{\omega }}' \cdot \Omega$ are not proportional, normalized by ![]() $({{\omega }} \cdot \Omega \cdot \theta )= ({{\omega }}' \cdot \Omega \cdot \theta )\neq 0$. Choose
$({{\omega }} \cdot \Omega \cdot \theta )= ({{\omega }}' \cdot \Omega \cdot \theta )\neq 0$. Choose ![]() $r_n, r'_n$ such that
$r_n, r'_n$ such that
with ![]() $\theta '_n = \theta ' + r_n {{\omega }}+ r'_n {{\omega }}'$.
$\theta '_n = \theta ' + r_n {{\omega }}+ r'_n {{\omega }}'$.
Lemma 3.16 One can find constants ![]() $r_n , r_n'$ satisfying (17) and (18) converging to zero as
$r_n , r_n'$ satisfying (17) and (18) converging to zero as ![]() $n\to \infty$.
$n\to \infty$.
From ![]() $\theta _n^{2}\cdot \Sigma _n = (\theta '_n)^{2}\cdot \Sigma _n =\theta _n\cdot \theta '_n\cdot \Sigma _n=0$ we infer that
$\theta _n^{2}\cdot \Sigma _n = (\theta '_n)^{2}\cdot \Sigma _n =\theta _n\cdot \theta '_n\cdot \Sigma _n=0$ we infer that ![]() $\theta _n\cdot \Sigma _n$ and
$\theta _n\cdot \Sigma _n$ and ![]() $\theta '_n\cdot \Sigma _n$ are proportional by the usual Hodge index theorem. Letting
$\theta '_n\cdot \Sigma _n$ are proportional by the usual Hodge index theorem. Letting ![]() $n\to \infty$ proves that
$n\to \infty$ proves that ![]() $\theta \cdot \gamma \cdot \beta = c(\beta ) \theta '\cdot \gamma \cdot \beta$ for some
$\theta \cdot \gamma \cdot \beta = c(\beta ) \theta '\cdot \gamma \cdot \beta$ for some ![]() $c(\beta )>0$.
$c(\beta )>0$.
We claim that the proportionality constant ![]() $c(\beta )$ is, in fact, independent on
$c(\beta )$ is, in fact, independent on ![]() $\beta$ so that
$\beta$ so that ![]() $\theta \cdot \gamma = c \theta '\cdot \gamma$ for some
$\theta \cdot \gamma = c \theta '\cdot \gamma$ for some ![]() $c>0$ as required.
$c>0$ as required.
To prove our claim we suppose first that ![]() $\beta = {{\omega }}_1\cdot {{\omega }}_2\cdot \cdots \cdot {{\omega }}_{d-k-2}$, and
$\beta = {{\omega }}_1\cdot {{\omega }}_2\cdot \cdots \cdot {{\omega }}_{d-k-2}$, and ![]() $\beta ' = {{\omega }}'_1\cdot {{\omega }}_2\cdot \cdots \cdot {{\omega }}_{d-k-2}$ for some big and nef classes
$\beta ' = {{\omega }}'_1\cdot {{\omega }}_2\cdot \cdots \cdot {{\omega }}_{d-k-2}$ for some big and nef classes ![]() ${{\omega }}'_1, {{\omega }}_1, \ldots, {{\omega }}_{d-k-2}$. Then
${{\omega }}'_1, {{\omega }}_1, \ldots, {{\omega }}_{d-k-2}$. Then
hence ![]() $c(\beta ) =c(\beta ')$ in this case. As flat pushforwards of complete intersection classes of ample divisors generate
$c(\beta ) =c(\beta ')$ in this case. As flat pushforwards of complete intersection classes of ample divisors generate ![]() $\operatorname {c-Nef^{1}}({ \mathcal {X} })$, we get the result (compare with the proof of [Reference Dang and FavreDF21, Theorem 3.13]).
$\operatorname {c-Nef^{1}}({ \mathcal {X} })$, we get the result (compare with the proof of [Reference Dang and FavreDF21, Theorem 3.13]).
Proof of Lemma 3.16 Write ![]() $r=r_n$ and
$r=r_n$ and ![]() $r'=r'_n$. Note that (17) implies
$r'=r'_n$. Note that (17) implies ![]() $r'= \epsilon _n - \kappa _n r$ with
$r'= \epsilon _n - \kappa _n r$ with
and
Replacing ![]() $r'$ in (18), we obtain the following second-degree equation:
$r'$ in (18), we obtain the following second-degree equation:
 \begin{align*} &r^{2} \big[({{\omega}}^{2}\cdot\hat{\Omega}_n) + \kappa_n^{2} (({{\omega}}')^{2}\cdot\hat{\Omega}_n) - 2\kappa_n ({{\omega}}\cdot{{\omega}}'\cdot\hat{\Omega}_n) \big]\\ &\quad + 2r \big[({{\omega}}\cdot\theta'\cdot\hat{\Omega}_n) + \epsilon_n({{\omega}}\cdot{{\omega}}'\cdot\hat{\Omega}_n) - \kappa_n ({{\omega}}'\cdot\theta'\cdot\hat{\Omega}_n) \big]\\ &\quad+ \big[ ((\theta')^{2}\cdot\hat{\Omega}_n) + \epsilon_n^{2} (({{\omega}}')^{2}\cdot\hat{\Omega}_n) + 2\epsilon_n ({{\omega}}'\cdot\theta'\cdot\hat{\Omega}_n) \big]=0 \end{align*}
\begin{align*} &r^{2} \big[({{\omega}}^{2}\cdot\hat{\Omega}_n) + \kappa_n^{2} (({{\omega}}')^{2}\cdot\hat{\Omega}_n) - 2\kappa_n ({{\omega}}\cdot{{\omega}}'\cdot\hat{\Omega}_n) \big]\\ &\quad + 2r \big[({{\omega}}\cdot\theta'\cdot\hat{\Omega}_n) + \epsilon_n({{\omega}}\cdot{{\omega}}'\cdot\hat{\Omega}_n) - \kappa_n ({{\omega}}'\cdot\theta'\cdot\hat{\Omega}_n) \big]\\ &\quad+ \big[ ((\theta')^{2}\cdot\hat{\Omega}_n) + \epsilon_n^{2} (({{\omega}}')^{2}\cdot\hat{\Omega}_n) + 2\epsilon_n ({{\omega}}'\cdot\theta'\cdot\hat{\Omega}_n) \big]=0 \end{align*}
with ![]() $\hat {\Omega }_n=\theta _n\cdot \Omega _n$. As the constant term tends to zero and the leading term is bounded away from zero by Hodge index theorem (using that
$\hat {\Omega }_n=\theta _n\cdot \Omega _n$. As the constant term tends to zero and the leading term is bounded away from zero by Hodge index theorem (using that ![]() ${{\omega }} \cdot \Omega$ and
${{\omega }} \cdot \Omega$ and ![]() ${{\omega }}'\cdot \Omega$ are not proportional), we may choose a solution
${{\omega }}'\cdot \Omega$ are not proportional), we may choose a solution ![]() $r_n\to 0$, and this forces
$r_n\to 0$, and this forces ![]() $r'_n\to 0$.
$r'_n\to 0$.
4. Minkowski's problem and applications
Let ![]() ${{\omega }}\in \operatorname {c-Nef^{1}}({ \mathcal {X} })$ be any Cartier
${{\omega }}\in \operatorname {c-Nef^{1}}({ \mathcal {X} })$ be any Cartier ![]() $b$-divisor class determined by an ample class in
$b$-divisor class determined by an ample class in ![]() $X$.
$X$.
4.1 Inverting  $\alpha \mapsto \alpha ^{d-1}$
$\alpha \mapsto \alpha ^{d-1}$
Theorem C The map ![]() $\alpha \mapsto \alpha ^{d-1}$ induces a bijection from the convex cone of big
$\alpha \mapsto \alpha ^{d-1}$ induces a bijection from the convex cone of big ![]() $b$-divisor classes
$b$-divisor classes ![]() $\alpha \in \operatorname {Nef^{1}}({ \mathcal {X} })$ onto the convex cone of big
$\alpha \in \operatorname {Nef^{1}}({ \mathcal {X} })$ onto the convex cone of big ![]() $b$-numerical curve classes in
$b$-numerical curve classes in ![]() $\operatorname {BPF}^{d-1}({ \mathcal {X} })$.
$\operatorname {BPF}^{d-1}({ \mathcal {X} })$.
Remark 4.1 The map ![]() $\alpha \mapsto \alpha ^{d-1}$ is continuous for the
$\alpha \mapsto \alpha ^{d-1}$ is continuous for the ![]() $\lVert {\cdot } \rVert _{\operatorname {BPF}}^{\vee }$-norm (hence, for the
$\lVert {\cdot } \rVert _{\operatorname {BPF}}^{\vee }$-norm (hence, for the ![]() $\lVert {\cdot } \rVert _{\Sigma }$-norm too) and along decreasing limits. It is not continuous in the weak topology (pullback Example 3.3 by a map
$\lVert {\cdot } \rVert _{\Sigma }$-norm too) and along decreasing limits. It is not continuous in the weak topology (pullback Example 3.3 by a map ![]() $C \times \mathbb {P}^{2} \to \mathbb {P}^{2}$ where
$C \times \mathbb {P}^{2} \to \mathbb {P}^{2}$ where ![]() $C$ is any projective curve).
$C$ is any projective curve).
Proof. Let us prove that ![]() $M(\alpha ) := \alpha ^{d-1}$ is injective on the cone of big and nef classes. Recall that by Corollary 3.4, a nef class
$M(\alpha ) := \alpha ^{d-1}$ is injective on the cone of big and nef classes. Recall that by Corollary 3.4, a nef class ![]() $\alpha$ satisfies
$\alpha$ satisfies ![]() $\alpha \geqslant c{{\omega }}$ for some
$\alpha \geqslant c{{\omega }}$ for some ![]() $c>0$ iff
$c>0$ iff ![]() $(\alpha ^{d})>0$.
$(\alpha ^{d})>0$.
If ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$ are two nef classes such that
$\beta$ are two nef classes such that ![]() $\alpha ^{d-1}= \beta ^{d-1}$, then
$\alpha ^{d-1}= \beta ^{d-1}$, then ![]() $(\alpha ^{d}) = (\alpha \cdot \beta ^{d-1})$, and
$(\alpha ^{d}) = (\alpha \cdot \beta ^{d-1})$, and ![]() $(\alpha ^{d-1}\cdot \beta ) = (\beta ^{d})$. By the log-concavity of the sequence
$(\alpha ^{d-1}\cdot \beta ) = (\beta ^{d})$. By the log-concavity of the sequence ![]() $k\mapsto \log (\alpha ^{k}\cdot \beta ^{d-k})$ we obtain
$k\mapsto \log (\alpha ^{k}\cdot \beta ^{d-k})$ we obtain ![]() $0<(\alpha ^{d})= (\beta ^{d}) = (\alpha ^{k}\cdot \beta ^{d-k})$ for all
$0<(\alpha ^{d})= (\beta ^{d}) = (\alpha ^{k}\cdot \beta ^{d-k})$ for all ![]() $k$. This implies the equality between
$k$. This implies the equality between ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$ by Proposition 3.11.
$\beta$ by Proposition 3.11.
We now prove the surjectivity. Fix any class ![]() $\gamma \in \operatorname {BPF}^{d-1}({ \mathcal {X} })$ such that
$\gamma \in \operatorname {BPF}^{d-1}({ \mathcal {X} })$ such that ![]() $\gamma \geqslant c {{\omega }}^{d-1}$ for some
$\gamma \geqslant c {{\omega }}^{d-1}$ for some ![]() $c>0$. We follow the classical variational method to solve a Monge-Ampère equation. Let
$c>0$. We follow the classical variational method to solve a Monge-Ampère equation. Let ![]() $K:= \{ \alpha \in \operatorname {Nef^{1}}({ \mathcal {X} }) \,|\,(\alpha \cdot \gamma ) = 1\}$. Note that
$K:= \{ \alpha \in \operatorname {Nef^{1}}({ \mathcal {X} }) \,|\,(\alpha \cdot \gamma ) = 1\}$. Note that ![]() $K$ is compact for the weak topology of
$K$ is compact for the weak topology of ![]() $\operatorname {w-N}^{1}({ \mathcal {X} })$ by [Reference Dang and FavreDF21, Proposition 2.13], as
$\operatorname {w-N}^{1}({ \mathcal {X} })$ by [Reference Dang and FavreDF21, Proposition 2.13], as ![]() $K\subset \{ \alpha \in \operatorname {Nef^{1}}({ \mathcal {X} }), (\alpha \cdot {{\omega }}^{d-1}) \leqslant c^{-1}\}$. As the function
$K\subset \{ \alpha \in \operatorname {Nef^{1}}({ \mathcal {X} }), (\alpha \cdot {{\omega }}^{d-1}) \leqslant c^{-1}\}$. As the function ![]() $\alpha \mapsto (\alpha ^{d})$ is upper-semicontinuous by Theorem 3.2(ii), there exists a class
$\alpha \mapsto (\alpha ^{d})$ is upper-semicontinuous by Theorem 3.2(ii), there exists a class ![]() $\alpha _\star \in K$ such that
$\alpha _\star \in K$ such that ![]() $(\alpha _\star ^{d})= \sup _K (\alpha ^{d})$.
$(\alpha _\star ^{d})= \sup _K (\alpha ^{d})$.
Observe that ![]() $(\alpha _\star ^{d})>0$. Pick any Cartier class
$(\alpha _\star ^{d})>0$. Pick any Cartier class ![]() $\beta \in \operatorname {c-N}^{1}({ \mathcal {X} })$. For
$\beta \in \operatorname {c-N}^{1}({ \mathcal {X} })$. For ![]() $t$ small enough, the class
$t$ small enough, the class ![]() $\alpha _\star + t\beta$ is psef by Siu's inequality. Consider the nef envelope
$\alpha _\star + t\beta$ is psef by Siu's inequality. Consider the nef envelope ![]() $P(\alpha _\star + t\beta )$ as defined in § 2.2.
$P(\alpha _\star + t\beta )$ as defined in § 2.2.
Pick any big and nef class ![]() ${{\omega }}'\in \operatorname {c-Nef^{1}}({ \mathcal {X} })$ such that
${{\omega }}'\in \operatorname {c-Nef^{1}}({ \mathcal {X} })$ such that ![]() $\alpha _\star \leqslant \omega '$, and
$\alpha _\star \leqslant \omega '$, and ![]() $\omega ' \pm \beta$ are both nef (any sufficiently large ample class in a model in which
$\omega ' \pm \beta$ are both nef (any sufficiently large ample class in a model in which ![]() $\beta$ is determined does the job). Using [Reference Boucksom, Favre and JonssonBFJ09, Corollary 3.4] and by taking limits of Cartier nef classes decreasing to
$\beta$ is determined does the job). Using [Reference Boucksom, Favre and JonssonBFJ09, Corollary 3.4] and by taking limits of Cartier nef classes decreasing to ![]() $\alpha _\star$, we have
$\alpha _\star$, we have
for some ![]() $C>0$ which depends only on
$C>0$ which depends only on ![]() $(\omega ^{d})$ and for any
$(\omega ^{d})$ and for any ![]() $0 \leqslant t \leqslant 1$. Observe now that
$0 \leqslant t \leqslant 1$. Observe now that
which implies
 \begin{align*} (\alpha_\star^{d}) \geqslant \frac{P(\alpha_\star+ t\beta)^{d}}{(P(\alpha_\star+ t\beta)\cdot \gamma)^{d}} &\geqslant \frac{(\alpha_\star^{d}) + d t (\alpha_\star^{(d-1)}\cdot \beta) - C t^{2}}{((\alpha_\star+ t\beta)\cdot \gamma)^{d}}\\ &\geqslant (\alpha_\star^{d}) + d t (\alpha_\star^{(d-1)}\cdot \beta) - d t (\beta\cdot \gamma) (\alpha_\star^{d}) +O(t^{2}), \end{align*}
\begin{align*} (\alpha_\star^{d}) \geqslant \frac{P(\alpha_\star+ t\beta)^{d}}{(P(\alpha_\star+ t\beta)\cdot \gamma)^{d}} &\geqslant \frac{(\alpha_\star^{d}) + d t (\alpha_\star^{(d-1)}\cdot \beta) - C t^{2}}{((\alpha_\star+ t\beta)\cdot \gamma)^{d}}\\ &\geqslant (\alpha_\star^{d}) + d t (\alpha_\star^{(d-1)}\cdot \beta) - d t (\beta\cdot \gamma) (\alpha_\star^{d}) +O(t^{2}), \end{align*}
hence ![]() $(\alpha _\star ^{(d-1)}\cdot \beta ) \leqslant (\beta \cdot \gamma ) (\alpha _\star ^{d})$. Since this is true for
$(\alpha _\star ^{(d-1)}\cdot \beta ) \leqslant (\beta \cdot \gamma ) (\alpha _\star ^{d})$. Since this is true for ![]() $\pm \beta$ we infer
$\pm \beta$ we infer ![]() $(\alpha _\star ^{(d-1)}\cdot \beta ) = (\beta \cdot \gamma ) (\alpha _\star ^{d})$. Rescaling
$(\alpha _\star ^{(d-1)}\cdot \beta ) = (\beta \cdot \gamma ) (\alpha _\star ^{d})$. Rescaling ![]() $\alpha _\star$, we find a nef class such that
$\alpha _\star$, we find a nef class such that ![]() $(\alpha ^{d-1}) = \gamma$ as required.
$(\alpha ^{d-1}) = \gamma$ as required.
4.2 An example of the  $(d-1)$th root of a Cartier class which is not Cartier
$(d-1)$th root of a Cartier class which is not Cartier
For the sake of completeness, we include the following clever observation of Li [Reference LiLi21, Lemma 4.2]. We are indebted to Boucksom and Jonsson for pointing this reference to us, and for letting us include it here.
Proposition 4.2 (Li)
For any big line bundle ![]() $L\to X$, the
$L\to X$, the ![]() $b$-numerical curve class
$b$-numerical curve class
is Cartier.
Proof. Let ![]() $\pi \colon X'\to X$ be any composition of blow-ups of smooth centers, and let
$\pi \colon X'\to X$ be any composition of blow-ups of smooth centers, and let ![]() $E$ be any
$E$ be any ![]() $\pi$-exceptional prime divisor in
$\pi$-exceptional prime divisor in ![]() $X'$. It follows from [Reference Boucksom, Favre and JonssonBFJ09, Theorem B] that
$X'$. It follows from [Reference Boucksom, Favre and JonssonBFJ09, Theorem B] that
where
Observe that
and because ![]() $\dim (\pi _*(E)) < d-1$, the asymptotic Riemann–Roch theorem implies
$\dim (\pi _*(E)) < d-1$, the asymptotic Riemann–Roch theorem implies ![]() $\dim _\mathbb {C} (V_n)= o(n^{d-1})$, hence
$\dim _\mathbb {C} (V_n)= o(n^{d-1})$, hence ![]() $P([\pi ^{*}c_1(L)])^{d-1}\cdot E =0$.
$P([\pi ^{*}c_1(L)])^{d-1}\cdot E =0$.
Define the class ![]() $\alpha := P([c_1(L)])^{d-1}$. The previous computation shows
$\alpha := P([c_1(L)])^{d-1}$. The previous computation shows
for any ![]() $\pi$-exceptional divisor
$\pi$-exceptional divisor ![]() $E$. As
$E$. As ![]() $\pi$ is a composition of blow-ups with smooth centers, there is a decomposition
$\pi$ is a composition of blow-ups with smooth centers, there is a decomposition ![]() $\operatorname {N}^{1}(X') = \pi ^{*} \operatorname {N}^{1}(X) \oplus F$ where
$\operatorname {N}^{1}(X') = \pi ^{*} \operatorname {N}^{1}(X) \oplus F$ where ![]() $F$ is the subspace spanned by classes of exceptional divisors. As the intersection of
$F$ is the subspace spanned by classes of exceptional divisors. As the intersection of ![]() $\alpha _{X'}$ with any element in
$\alpha _{X'}$ with any element in ![]() $F$ is zero, we have
$F$ is zero, we have ![]() $\alpha _{X'} = \pi ^{*} \pi _*(\alpha _{X'})= \pi ^{*}\alpha _{X}$, hence
$\alpha _{X'} = \pi ^{*} \pi _*(\alpha _{X'})= \pi ^{*}\alpha _{X}$, hence ![]() $\alpha$ is a Cartier class determined in
$\alpha$ is a Cartier class determined in ![]() $X$.
$X$.
Example 4.3 It follows from the work of Nakayama [Reference NakayamaNak04, Theorem IV.2.10] that there exists a big line bundle on a projective ![]() $4$-fold
$4$-fold ![]() $L\to X$ such that
$L\to X$ such that ![]() $P(L)$ is a nef and big
$P(L)$ is a nef and big ![]() $b$-divisor class which is not Cartier. The
$b$-divisor class which is not Cartier. The ![]() $b$-numerical curve class
$b$-numerical curve class ![]() $\alpha = P(L)^{3}$ is BPF and Cartier whereas its unique third root is not.
$\alpha = P(L)^{3}$ is BPF and Cartier whereas its unique third root is not.
Remark 4.4 It is not difficult to find a nef class ![]() $\alpha$ that is not Cartier and such that
$\alpha$ that is not Cartier and such that ![]() $\alpha ^{d-1}=0$, for example in a toric situation.
$\alpha ^{d-1}=0$, for example in a toric situation.
4.3 Proof of Theorem D
Recall that we aim at proving the inclusions
The first and last inclusions hold by definition, see [Reference Dang and FavreDF21, § 2]. The second inclusion is Corollary 3.9. It thus remains to prove the continuous inclusion ![]() $\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} }) \subset \operatorname {N}^{{1},\vee }_{\operatorname {BPF}}({ \mathcal {X} })$. This fact follows from the next theorem of independent interest.
$\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} }) \subset \operatorname {N}^{{1},\vee }_{\operatorname {BPF}}({ \mathcal {X} })$. This fact follows from the next theorem of independent interest.
Theorem 4.5 For any ![]() $\alpha \in \operatorname {c-N}^{1}({ \mathcal {X} })$, and for any
$\alpha \in \operatorname {c-N}^{1}({ \mathcal {X} })$, and for any ![]() $\gamma \in \operatorname {BPF}^{d-1}({ \mathcal {X} })$, we have
$\gamma \in \operatorname {BPF}^{d-1}({ \mathcal {X} })$, we have
Let ![]() $\alpha _n\in \operatorname {c-N}^{1}({ \mathcal {X} })$ be any Cauchy sequence for the norm
$\alpha _n\in \operatorname {c-N}^{1}({ \mathcal {X} })$ be any Cauchy sequence for the norm ![]() $\lVert {\cdot } \rVert _{\Sigma }$. Then (19) implies that
$\lVert {\cdot } \rVert _{\Sigma }$. Then (19) implies that ![]() $\alpha _n$ is a Cauchy sequence for
$\alpha _n$ is a Cauchy sequence for ![]() $\lVert {\cdot } \rVert _{\operatorname {BPF}}^{\vee }$, proving the continuous injection
$\lVert {\cdot } \rVert _{\operatorname {BPF}}^{\vee }$, proving the continuous injection ![]() $\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} }) \subset \operatorname {N}^{{1},\vee }_{\operatorname {BPF}}({ \mathcal {X} })$.
$\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} }) \subset \operatorname {N}^{{1},\vee }_{\operatorname {BPF}}({ \mathcal {X} })$.
Proof. Pick any ![]() $\gamma \in \operatorname {BPF}^{d-1}({ \mathcal {X} })$. By Theorem C, for any
$\gamma \in \operatorname {BPF}^{d-1}({ \mathcal {X} })$. By Theorem C, for any ![]() $t>0$ we may find a class
$t>0$ we may find a class ![]() $\delta _t\in \operatorname {Nef^{1}}({ \mathcal {X} })$ such that
$\delta _t\in \operatorname {Nef^{1}}({ \mathcal {X} })$ such that ![]() $\gamma + t{{\omega }}^{d-1} = (\delta _t^{d-1})$. Let
$\gamma + t{{\omega }}^{d-1} = (\delta _t^{d-1})$. Let ![]() $s = (\delta _t^{d-2}\cdot {{\omega }}^{2})$. We now estimate using [Reference Dang and FavreDF21, Theorem 3.11]:
$s = (\delta _t^{d-2}\cdot {{\omega }}^{2})$. We now estimate using [Reference Dang and FavreDF21, Theorem 3.11]:
 \begin{align*} | (\alpha\cdot (\gamma+t{{\omega}}^{d-1})) |^{2} &= | (\alpha\cdot \delta_t^{d-1}) |^{2}\\ &\leqslant 9 q_{{{\omega}}, ({1}/{s}) \delta_t^{d-2}}(\alpha) q_{{{\omega}}, ({1}/{s}) \delta_t^{d-2}}(s \delta_t)\\ &\leqslant 18 ( (\gamma+t{{\omega}}^{d-1}) \cdot{{\omega}})^{2} \lVert {\alpha} \rVert_{\Sigma}^{2}, \end{align*}
\begin{align*} | (\alpha\cdot (\gamma+t{{\omega}}^{d-1})) |^{2} &= | (\alpha\cdot \delta_t^{d-1}) |^{2}\\ &\leqslant 9 q_{{{\omega}}, ({1}/{s}) \delta_t^{d-2}}(\alpha) q_{{{\omega}}, ({1}/{s}) \delta_t^{d-2}}(s \delta_t)\\ &\leqslant 18 ( (\gamma+t{{\omega}}^{d-1}) \cdot{{\omega}})^{2} \lVert {\alpha} \rVert_{\Sigma}^{2}, \end{align*}
and we conclude by letting ![]() $t\to 0$.
$t\to 0$.
Corollary 4.6 For any ![]() $\alpha,\beta \in \operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$, the maps
$\alpha,\beta \in \operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$, the maps
are weakly continuous.
Proof. Pick ![]() $\alpha \in \operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$ and choose a sequence
$\alpha \in \operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$ and choose a sequence ![]() $\alpha _n\in \operatorname {c-N}^{1}({ \mathcal {X} })$ such that
$\alpha _n\in \operatorname {c-N}^{1}({ \mathcal {X} })$ such that ![]() $\lVert {\alpha -\alpha _n} \rVert _{\Sigma } \to 0$. Suppose
$\lVert {\alpha -\alpha _n} \rVert _{\Sigma } \to 0$. Suppose ![]() $\gamma _i\in \operatorname {BPF}^{k}({ \mathcal {X} })$ is a net of BPF classes converging weakly to
$\gamma _i\in \operatorname {BPF}^{k}({ \mathcal {X} })$ is a net of BPF classes converging weakly to ![]() $\gamma$. We may suppose that
$\gamma$. We may suppose that ![]() $C:= \sup _i(\gamma _i\cdot {{\omega }}^{d-k})< \infty$. Pick any BPF Cartier
$C:= \sup _i(\gamma _i\cdot {{\omega }}^{d-k})< \infty$. Pick any BPF Cartier ![]() $b$-numerical class
$b$-numerical class ![]() $\beta \in \operatorname {c-BPF}^{d-k-1}({ \mathcal {X} })$. By (19) and Corollary 3.4, we have
$\beta \in \operatorname {c-BPF}^{d-k-1}({ \mathcal {X} })$. By (19) and Corollary 3.4, we have
Pick any ![]() $\epsilon >0$. Choose
$\epsilon >0$. Choose ![]() $n_0$ large enough such that
$n_0$ large enough such that ![]() $CC_d (\beta \cdot {{\omega }}^{k+1}) \lVert {\alpha -\alpha _{n_0}} \rVert _{\Sigma } \leqslant \epsilon$. As the class
$CC_d (\beta \cdot {{\omega }}^{k+1}) \lVert {\alpha -\alpha _{n_0}} \rVert _{\Sigma } \leqslant \epsilon$. As the class ![]() $\alpha _{n_0}$ is Cartier, the map
$\alpha _{n_0}$ is Cartier, the map ![]() $\eta \mapsto \alpha _{n_0}\cdot \eta$ is weakly continuous, hence for
$\eta \mapsto \alpha _{n_0}\cdot \eta$ is weakly continuous, hence for ![]() $i$ large enough we have
$i$ large enough we have
This proves ![]() $\gamma \in \operatorname {BPF}^{k}({ \mathcal {X} })\mapsto \alpha \cdot \gamma$ is weakly continuous.
$\gamma \in \operatorname {BPF}^{k}({ \mathcal {X} })\mapsto \alpha \cdot \gamma$ is weakly continuous.
The fact that ![]() $\gamma \mapsto \alpha \cdot \beta \cdot \gamma$ is continuous follows by the same token and [Reference Dang and FavreDF21, Theorem 3.16].
$\gamma \mapsto \alpha \cdot \beta \cdot \gamma$ is continuous follows by the same token and [Reference Dang and FavreDF21, Theorem 3.16].
4.4 Approximation of classes in  $\operatorname {BPF}^{d-1}({ \mathcal {X} })$
$\operatorname {BPF}^{d-1}({ \mathcal {X} })$
The resolution of the operator ![]() $\alpha \mapsto \alpha ^{d-1}$ yields interesting consequences for the structure of
$\alpha \mapsto \alpha ^{d-1}$ yields interesting consequences for the structure of ![]() $\operatorname {BPF}^{d-1}({ \mathcal {X} })$.
$\operatorname {BPF}^{d-1}({ \mathcal {X} })$.
Corollary 4.7 For any ![]() $\alpha \in \operatorname {BPF}^{d-1}({ \mathcal {X} })$ there exists a sequence of classes
$\alpha \in \operatorname {BPF}^{d-1}({ \mathcal {X} })$ there exists a sequence of classes ![]() $\alpha _n\in \operatorname {c-BPF}^{d-1}({ \mathcal {X} })$ which is decreasing to
$\alpha _n\in \operatorname {c-BPF}^{d-1}({ \mathcal {X} })$ which is decreasing to ![]() $\alpha$. If, moreover,
$\alpha$. If, moreover, ![]() $\alpha$ is big, then for any
$\alpha$ is big, then for any ![]() $\epsilon >0$ there exists a class
$\epsilon >0$ there exists a class ![]() $\alpha '\in \operatorname {c-BPF}^{d-1}({ \mathcal {X} })$ such that
$\alpha '\in \operatorname {c-BPF}^{d-1}({ \mathcal {X} })$ such that ![]() $(1-\epsilon ) \alpha ' \leqslant \alpha \leqslant \alpha '$.
$(1-\epsilon ) \alpha ' \leqslant \alpha \leqslant \alpha '$.
Proof. We may suppose that ![]() $\alpha \leqslant {{\omega }}^{d-1}$. We claim that for each integer
$\alpha \leqslant {{\omega }}^{d-1}$. We claim that for each integer ![]() $n$, there exists a class
$n$, there exists a class ![]() $\alpha _n\in \operatorname {c-BPF}^{d-1}({ \mathcal {X} })$ such that
$\alpha _n\in \operatorname {c-BPF}^{d-1}({ \mathcal {X} })$ such that
As for all ![]() $n\geqslant 2$
$n\geqslant 2$
 \begin{align*} \alpha_{n+1} &\leqslant \bigg(1+\frac 1{2^{n+1}}\bigg) \bigg(\alpha + \frac 1{n+1} {{\omega}}^{d-1}\bigg)\\ &\leqslant \alpha_n - \frac 1{n(n+1)} {{\omega}}^{d-1} +\frac 1{2^{n+1}} \bigg(\alpha + \frac 1{n+1} {{\omega}}^{d-1}\bigg)\leqslant \alpha_n \end{align*}
\begin{align*} \alpha_{n+1} &\leqslant \bigg(1+\frac 1{2^{n+1}}\bigg) \bigg(\alpha + \frac 1{n+1} {{\omega}}^{d-1}\bigg)\\ &\leqslant \alpha_n - \frac 1{n(n+1)} {{\omega}}^{d-1} +\frac 1{2^{n+1}} \bigg(\alpha + \frac 1{n+1} {{\omega}}^{d-1}\bigg)\leqslant \alpha_n \end{align*}
the sequence ![]() $\alpha _n$ is decreasing to
$\alpha _n$ is decreasing to ![]() $\alpha$ as required. When
$\alpha$ as required. When ![]() $\alpha$ is big, then for any
$\alpha$ is big, then for any ![]() $\epsilon >0$, we have
$\epsilon >0$, we have ![]() ${{\omega }}^{d-1}/n \leqslant \epsilon \alpha$ for all
${{\omega }}^{d-1}/n \leqslant \epsilon \alpha$ for all ![]() $n$ large enough, hence it remains to prove (20).
$n$ large enough, hence it remains to prove (20).
By Theorem C, one can find a nef and big class ![]() $\beta ' \in \operatorname {Nef^{1}}({ \mathcal {X} })$ such that
$\beta ' \in \operatorname {Nef^{1}}({ \mathcal {X} })$ such that ![]() $(\beta ')^{d-1} = \alpha + ({1}/{n}){{\omega }}^{d-1}$. By Corollary 3.7, one can find a nef Cartier class
$(\beta ')^{d-1} = \alpha + ({1}/{n}){{\omega }}^{d-1}$. By Corollary 3.7, one can find a nef Cartier class ![]() $\beta (\epsilon )$ such that
$\beta (\epsilon )$ such that ![]() $\beta ' \leqslant \beta (\epsilon ) \leqslant (1+\epsilon ) \beta '$ and we conclude by taking
$\beta ' \leqslant \beta (\epsilon ) \leqslant (1+\epsilon ) \beta '$ and we conclude by taking ![]() $\alpha _n := \beta (\epsilon )^{d-1}$ with
$\alpha _n := \beta (\epsilon )^{d-1}$ with ![]() $(1+\epsilon )^{d-1} \leqslant 1+ {1}/{n}$.
$(1+\epsilon )^{d-1} \leqslant 1+ {1}/{n}$.
Recall from the definition of the space ![]() $\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$ [Reference Dang and FavreDF21, § 3.2] that the topological dual of the Banach space
$\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$ [Reference Dang and FavreDF21, § 3.2] that the topological dual of the Banach space ![]() $\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$ is characterized as follows:
$\operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$ is characterized as follows:
As (19) holds for any class ![]() $\alpha \in \operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$ by density, we obtain the following.
$\alpha \in \operatorname {N^{1}_{\Sigma }}({ \mathcal {X} })$ by density, we obtain the following.
Corollary 4.8 We have
5. Movable cones and Lehmann–Xiao decompositions of curve classes
In § 5.1, we discuss the notion of movable classes as defined in § 1.1 and relate it to positivity properties of ![]() $b$-numerical classes. In the last two sections §§ 5.2 and 5.3, we compare the
$b$-numerical classes. In the last two sections §§ 5.2 and 5.3, we compare the ![]() $(d-1)$th root of a BPF
$(d-1)$th root of a BPF ![]() $b$-curve class given by Theorem C to two divisor classes introduced by Lehmann and Xiao in [Reference Lehmann and XiaoLX16, Reference Lehmann and XiaoLX19].
$b$-curve class given by Theorem C to two divisor classes introduced by Lehmann and Xiao in [Reference Lehmann and XiaoLX16, Reference Lehmann and XiaoLX19].
5.1 Movable classes
Let us first introduce the notion of movable classes in the sense of Fulger and Lehmann, see [Reference Fulger and LehmannFL17b, § 3]. An effective ![]() $k$-cycle
$k$-cycle ![]() $Z$ in
$Z$ in ![]() $X$ is said to be strictly movable if there exists a variety
$X$ is said to be strictly movable if there exists a variety ![]() $\Lambda$ and a reduced closed subscheme
$\Lambda$ and a reduced closed subscheme ![]() $V$ of
$V$ of ![]() $X\times \Lambda$ such that for each irreducible component
$X\times \Lambda$ such that for each irreducible component ![]() $V_i$ of
$V_i$ of ![]() $V$:
$V$:
(i) the first projection map
 $V_i \to X$ is dominant for each
$V_i \to X$ is dominant for each  $i$;
$i$;(ii) the second projection map
 $\pi _i\colon V_i \to \Lambda$ is flat and dominant of relative dimension
$\pi _i\colon V_i \to \Lambda$ is flat and dominant of relative dimension  $k$ for each
$k$ for each  $i$; and
$i$; and(iii)
 $Z= \sum a_i [\pi _i^{-1}(\lambda )]$ for some
$Z= \sum a_i [\pi _i^{-1}(\lambda )]$ for some  $\lambda \in \Lambda$ and some
$\lambda \in \Lambda$ and some  $a_i \in \mathbb {N}$.
$a_i \in \mathbb {N}$.
A class ![]() $\alpha \in \operatorname {N}^{k}(X)$ is strictly movable if it is the class of a strictly movable
$\alpha \in \operatorname {N}^{k}(X)$ is strictly movable if it is the class of a strictly movable ![]() $(d-k)$-cycle. Roughly speaking, a strictly movable class is one represented by a
$(d-k)$-cycle. Roughly speaking, a strictly movable class is one represented by a ![]() $k$-cycle which moves in a family covering
$k$-cycle which moves in a family covering ![]() $X$.
$X$.
Definition 5.1 The movable cone is the closed convex cone in ![]() $\operatorname {N}^{k}(X)$ generated by strictly movable classes.
$\operatorname {N}^{k}(X)$ generated by strictly movable classes.
It is not difficult to see that we have the following characterization of movable divisor classes. A class ![]() $\alpha \in \operatorname {N}^{1}(X)$ is movable if it lies in the closure of the convex cone generated by integral classes
$\alpha \in \operatorname {N}^{1}(X)$ is movable if it lies in the closure of the convex cone generated by integral classes ![]() $\alpha = c_1(L) \in \operatorname {N}^{1}(X)$ such that the base locus of a multiple of the line bundle
$\alpha = c_1(L) \in \operatorname {N}^{1}(X)$ such that the base locus of a multiple of the line bundle ![]() $L\to X$ has codimension
$L\to X$ has codimension ![]() $\geqslant 2$.
$\geqslant 2$.
It also follows from [Reference Fulger and LehmannFL17b, Proposition 3.13] that the movable cone is equal to the closure of ![]() $\sum _\pi \pi _* \operatorname {BPF}^{k}(X')$ where
$\sum _\pi \pi _* \operatorname {BPF}^{k}(X')$ where ![]() $\pi \colon X' \to X$ varies over all (smooth) birational models over
$\pi \colon X' \to X$ varies over all (smooth) birational models over ![]() $X$.
$X$.
We have the following interpretation of movable classes in terms of ![]() $b$-numerical classes.
$b$-numerical classes.
Theorem 5.2 For any class ![]() $\alpha \in \operatorname {N}^{k}(X)$ the following are equivalent:
$\alpha \in \operatorname {N}^{k}(X)$ the following are equivalent:
(i)
 $\alpha$ is movable;
$\alpha$ is movable;(ii) there exists a
 $b$-numerical class
$b$-numerical class  $\beta \in \operatorname {BPF}^{k}({ \mathcal {X} })$ such that
$\beta \in \operatorname {BPF}^{k}({ \mathcal {X} })$ such that  $\beta _X = \alpha$.
$\beta _X = \alpha$.
In particular, a ![]() $b$-numerical class
$b$-numerical class ![]() $\beta \in \operatorname {w-N}^{k}({ \mathcal {X} })$ is BPF iff
$\beta \in \operatorname {w-N}^{k}({ \mathcal {X} })$ is BPF iff ![]() $\beta _{X'}$ is movable for any model
$\beta _{X'}$ is movable for any model ![]() $X'$.
$X'$.
Remark 5.3 As the cone ![]() $\operatorname {BPF}^{d-1}({ \mathcal {X} })$ is the (weak) closure of classes
$\operatorname {BPF}^{d-1}({ \mathcal {X} })$ is the (weak) closure of classes ![]() $[\alpha _{X'}]^{d-1}$ with
$[\alpha _{X'}]^{d-1}$ with ![]() $\alpha _{X'}\in \operatorname {N}^{1}(X')$ ample, we see that Definition 5.1 is also consistent with that given in § 1.1 in the case
$\alpha _{X'}\in \operatorname {N}^{1}(X')$ ample, we see that Definition 5.1 is also consistent with that given in § 1.1 in the case ![]() $k=d-1$.
$k=d-1$.
Proof. Suppose ![]() $\alpha \in \operatorname {N}^{k}(X)$ is movable. As recalled previously, by [Reference Fulger and LehmannFL17b, Proposition 3.13], we can find a sequence of models
$\alpha \in \operatorname {N}^{k}(X)$ is movable. As recalled previously, by [Reference Fulger and LehmannFL17b, Proposition 3.13], we can find a sequence of models ![]() $\pi _n\colon X_n \to X$ and classes
$\pi _n\colon X_n \to X$ and classes ![]() $\beta _n\in \operatorname {BPF}^{k}(X_n)$ such that
$\beta _n\in \operatorname {BPF}^{k}(X_n)$ such that ![]() $(\pi _n)_*\beta _n \to \alpha$. Note that
$(\pi _n)_*\beta _n \to \alpha$. Note that ![]() $(\beta _n\cdot {{\omega }}^{d-k})$ is uniformly bounded, hence the Banach–Alaoglu theorem implies that the set
$(\beta _n\cdot {{\omega }}^{d-k})$ is uniformly bounded, hence the Banach–Alaoglu theorem implies that the set ![]() $F_p= \overline {\{\beta _n, n\geqslant p\}}$ is weakly compact for all
$F_p= \overline {\{\beta _n, n\geqslant p\}}$ is weakly compact for all ![]() $p$. Pick any class
$p$. Pick any class ![]() $\beta \in \cap _{p\geqslant 1} F_p$. Then
$\beta \in \cap _{p\geqslant 1} F_p$. Then ![]() $\beta$ lies in
$\beta$ lies in ![]() $\operatorname {BPF}^{k}({ \mathcal {X} })$ and we have
$\operatorname {BPF}^{k}({ \mathcal {X} })$ and we have ![]() $\beta _X = \alpha$ which proves
$\beta _X = \alpha$ which proves ![]() $\rm (i)\Rightarrow (ii)$.
$\rm (i)\Rightarrow (ii)$.
Conversely, suppose ![]() $\beta \in \operatorname {BPF}^{k}({ \mathcal {X} })$. By definition, we can find a sequence of classes
$\beta \in \operatorname {BPF}^{k}({ \mathcal {X} })$. By definition, we can find a sequence of classes ![]() $\beta _n\in \operatorname {c-BPF}^{k}(X)$ such that
$\beta _n\in \operatorname {c-BPF}^{k}(X)$ such that ![]() $(\beta _n)_X \to \beta _X$. As
$(\beta _n)_X \to \beta _X$. As ![]() $(\beta _n)_X$ is the image under a proper birational morphism of a BPF class, it is movable, hence
$(\beta _n)_X$ is the image under a proper birational morphism of a BPF class, it is movable, hence ![]() $\beta _X$ is movable too. This proves
$\beta _X$ is movable too. This proves ![]() $\rm (ii)\Rightarrow (i)$.
$\rm (ii)\Rightarrow (i)$.
Finally pick any class ![]() $\beta \in \operatorname {w-N}^{k}({ \mathcal {X} })$, and suppose that
$\beta \in \operatorname {w-N}^{k}({ \mathcal {X} })$, and suppose that ![]() $\beta _{X'}$ is movable for any model
$\beta _{X'}$ is movable for any model ![]() $X'$. By what precedes, for each
$X'$. By what precedes, for each ![]() $X'$ there exists a class
$X'$ there exists a class ![]() $\tilde {\beta }(X')\in \operatorname {BPF}^{k}({ \mathcal {X} })$ such that
$\tilde {\beta }(X')\in \operatorname {BPF}^{k}({ \mathcal {X} })$ such that ![]() $\tilde {\beta }(X')_{X'}=\beta _{X'}\in \operatorname {N}^{k}(X')$. This implies that the net
$\tilde {\beta }(X')_{X'}=\beta _{X'}\in \operatorname {N}^{k}(X')$. This implies that the net ![]() $\tilde {\beta }(X')$ converges (as
$\tilde {\beta }(X')$ converges (as ![]() $b$-numerical classes) to
$b$-numerical classes) to ![]() $\beta$, hence
$\beta$, hence ![]() $\beta$ is BPF.
$\beta$ is BPF.
An easy consequence of the previous theorem is the following analog of Theorem 2.8.
Proposition 5.4 We have
In other words any Cartier ![]() $b$-numerical curve class that is BPF as a
$b$-numerical curve class that is BPF as a ![]() $b$-numerical curve class is determined by a BPF class in some model.
$b$-numerical curve class is determined by a BPF class in some model.
Proof. Pick any ![]() $\alpha \in \operatorname {c-BPF}^{d-1}({ \mathcal {X} })$, and suppose that
$\alpha \in \operatorname {c-BPF}^{d-1}({ \mathcal {X} })$, and suppose that ![]() $\alpha$ is determined in some model
$\alpha$ is determined in some model ![]() $X'$ and
$X'$ and ![]() $\alpha _{X'}\in \operatorname {N}^{d-1}(X')$ is not BPF. By the previous result,
$\alpha _{X'}\in \operatorname {N}^{d-1}(X')$ is not BPF. By the previous result, ![]() $\alpha _{X'}$ is not movable, hence by the duality theorem [Reference Boucksom, Demailly, Păun and PeternellBDPP13, Corollary 2.5], one can find a psef class
$\alpha _{X'}$ is not movable, hence by the duality theorem [Reference Boucksom, Demailly, Păun and PeternellBDPP13, Corollary 2.5], one can find a psef class ![]() $\beta \in \operatorname {N}^{1}(X')$ such that
$\beta \in \operatorname {N}^{1}(X')$ such that ![]() $(\alpha _{X'}\cdot \beta ) <0$.
$(\alpha _{X'}\cdot \beta ) <0$.
Observe that the Cartier ![]() $b$-divisor class
$b$-divisor class ![]() $[\beta ]$ is psef because the pullback of any psef divisor remains psef. We then obtain
$[\beta ]$ is psef because the pullback of any psef divisor remains psef. We then obtain ![]() $(\alpha \cdot [\beta ]) < 0$ which implies that
$(\alpha \cdot [\beta ]) < 0$ which implies that ![]() $\alpha$ cannot belong to
$\alpha$ cannot belong to ![]() $\operatorname {BPF}^{d-1}({ \mathcal {X} })$.
$\operatorname {BPF}^{d-1}({ \mathcal {X} })$.
Recall that a ![]() $b$-numerical class
$b$-numerical class ![]() $\alpha$ is psef iff
$\alpha$ is psef iff ![]() $\alpha _{X'}\geqslant 0$ for all models
$\alpha _{X'}\geqslant 0$ for all models ![]() $X'$. When it is the case, we write
$X'$. When it is the case, we write ![]() $\alpha \geqslant 0$. Beware that, in general, a Cartier class which is determined by a psef class is not psef (as a
$\alpha \geqslant 0$. Beware that, in general, a Cartier class which is determined by a psef class is not psef (as a ![]() $b$-numerical class).
$b$-numerical class).
We conclude this section by exploring duality statements between the BPF and the psef cone in the space of ![]() $b$-numerical classes.
$b$-numerical classes.
Proposition 5.5 Pick any ![]() $b$-numerical class
$b$-numerical class ![]() $\alpha \in \operatorname {w-N}^{k}({ \mathcal {X} })$. If
$\alpha \in \operatorname {w-N}^{k}({ \mathcal {X} })$. If ![]() $\alpha$ is psef (respectively, BPF), then for any BPF (respectively, psef) Cartier
$\alpha$ is psef (respectively, BPF), then for any BPF (respectively, psef) Cartier ![]() $b$-numerical class
$b$-numerical class ![]() $\beta$ we have
$\beta$ we have ![]() $(\alpha \cdot \beta )\geqslant 0$.
$(\alpha \cdot \beta )\geqslant 0$.
Proof. Suppose ![]() $\alpha$ is psef and pick any BPF Cartier
$\alpha$ is psef and pick any BPF Cartier ![]() $b$-numerical class
$b$-numerical class ![]() $\beta$ determined in a model
$\beta$ determined in a model ![]() $X'$. Then
$X'$. Then ![]() $(\alpha \cdot \beta )= (\alpha _{X'} \cdot \beta _{X'})\geqslant 0$.
$(\alpha \cdot \beta )= (\alpha _{X'} \cdot \beta _{X'})\geqslant 0$.
Pick now any psef Cartier ![]() $b$-numerical class
$b$-numerical class ![]() $\beta$ determined in a model
$\beta$ determined in a model ![]() $X'$. If
$X'$. If ![]() $\alpha$ is a Cartier BPF class determined in a model
$\alpha$ is a Cartier BPF class determined in a model ![]() $X''$, then
$X''$, then ![]() $(\alpha _{X'} \cdot \beta _{X'})=(\alpha \cdot \beta )= (\alpha _{X''} \cdot \beta _{X''})\geqslant 0$. We obtain
$(\alpha _{X'} \cdot \beta _{X'})=(\alpha \cdot \beta )= (\alpha _{X''} \cdot \beta _{X''})\geqslant 0$. We obtain ![]() $(\alpha \cdot \beta )=(\alpha _{X'} \cdot \beta _{X'})\geqslant 0$ by density for any nef
$(\alpha \cdot \beta )=(\alpha _{X'} \cdot \beta _{X'})\geqslant 0$ by density for any nef ![]() $b$-numerical classes.
$b$-numerical classes.
Recall from the introduction that we stated a duality between the cones of BPF ![]() $b$-classes and psef
$b$-classes and psef ![]() $b$-classes (Conjecture 1). We prove it here for curve and divisor classes.
$b$-classes (Conjecture 1). We prove it here for curve and divisor classes.
Proposition 5.6 For ![]() $k=1$ and
$k=1$ and ![]() $k=d-1$, the following two statements hold.
$k=d-1$, the following two statements hold.
(i) A
 $b$-numerical class
$b$-numerical class  $\alpha \in \operatorname {w-N}^{k}({ \mathcal {X} })$ is psef iff for any
$\alpha \in \operatorname {w-N}^{k}({ \mathcal {X} })$ is psef iff for any  $b$-numerical class
$b$-numerical class  $\beta \in \operatorname {c-BPF}^{d-k}({ \mathcal {X} })$ we have
$\beta \in \operatorname {c-BPF}^{d-k}({ \mathcal {X} })$ we have  $(\alpha \cdot \beta )\geqslant 0$.
$(\alpha \cdot \beta )\geqslant 0$.(ii) A
 $b$-numerical class
$b$-numerical class  $\alpha \in \operatorname {w-N}^{k}({ \mathcal {X} })$ belongs to
$\alpha \in \operatorname {w-N}^{k}({ \mathcal {X} })$ belongs to  $\operatorname {BPF}^{k}({ \mathcal {X} })$ iff for any psef Cartier
$\operatorname {BPF}^{k}({ \mathcal {X} })$ iff for any psef Cartier  $b$-numerical class
$b$-numerical class  $\beta \in \operatorname {c-N}^{d-k}({ \mathcal {X} })$, we have
$\beta \in \operatorname {c-N}^{d-k}({ \mathcal {X} })$, we have  $(\alpha \cdot \beta )\geqslant 0$.
$(\alpha \cdot \beta )\geqslant 0$.
Remark 5.7 The fact that a ![]() $b$-divisor class is nef if it intersects non-negatively psef
$b$-divisor class is nef if it intersects non-negatively psef ![]() $b$-numerical curve classes is due to Lehmann who formulated this fact in terms of movable classes, see [Reference LehmannLeh11, Theorem 1.5].
$b$-numerical curve classes is due to Lehmann who formulated this fact in terms of movable classes, see [Reference LehmannLeh11, Theorem 1.5].
Proof. In view of Proposition 5.5, we need to prove four implications.
Suppose first that a class ![]() $\alpha \in \operatorname {w-N}^{1}({ \mathcal {X} })$ intersects non-negatively all
$\alpha \in \operatorname {w-N}^{1}({ \mathcal {X} })$ intersects non-negatively all ![]() $b$-numerical classes
$b$-numerical classes ![]() $\beta \in \operatorname {c-BPF}^{d-1}({ \mathcal {X} })$. By Theorem 5.2, for any model
$\beta \in \operatorname {c-BPF}^{d-1}({ \mathcal {X} })$. By Theorem 5.2, for any model ![]() $X'$ the class
$X'$ the class ![]() $\alpha _{X'}$ lies in the dual cone of movable curve classes, hence it is psef. This proves
$\alpha _{X'}$ lies in the dual cone of movable curve classes, hence it is psef. This proves ![]() $\alpha \geqslant 0$.
$\alpha \geqslant 0$.
Suppose next that ![]() $\alpha \in \operatorname {w-N}^{d-1}({ \mathcal {X} })$ intersects non-negatively all nef Cartier
$\alpha \in \operatorname {w-N}^{d-1}({ \mathcal {X} })$ intersects non-negatively all nef Cartier ![]() $b$-divisor classes. As the nef cone
$b$-divisor classes. As the nef cone ![]() $\operatorname {Nef^{1}}(X')$ is dual to the psef cone in
$\operatorname {Nef^{1}}(X')$ is dual to the psef cone in ![]() $\operatorname {N}^{d-1}(X')$, the class
$\operatorname {N}^{d-1}(X')$, the class ![]() $\alpha _{X'}$ is effective for all
$\alpha _{X'}$ is effective for all ![]() $X'$, hence
$X'$, hence ![]() $\alpha \geqslant 0$.
$\alpha \geqslant 0$.
Take now a class ![]() $\alpha \in \operatorname {w-N}^{d-1}({ \mathcal {X} })$ intersecting non-negatively all psef
$\alpha \in \operatorname {w-N}^{d-1}({ \mathcal {X} })$ intersecting non-negatively all psef ![]() $b$-divisor classes. Pick any model
$b$-divisor classes. Pick any model ![]() $X'$ and any effective divisor class
$X'$ and any effective divisor class ![]() $\gamma \in \operatorname {N}^{1}(X')$. As the pullback of an effective divisor remains effective, the Cartier class
$\gamma \in \operatorname {N}^{1}(X')$. As the pullback of an effective divisor remains effective, the Cartier class ![]() $[\gamma ]$ is psef, hence
$[\gamma ]$ is psef, hence ![]() $(\alpha _{X'}\cdot \gamma )= (\alpha \cdot [\gamma ]) \geqslant 0$. As the psef cone is dual to the movable cone in
$(\alpha _{X'}\cdot \gamma )= (\alpha \cdot [\gamma ]) \geqslant 0$. As the psef cone is dual to the movable cone in ![]() $\operatorname {N}^{d-1}(X')$, we conclude that
$\operatorname {N}^{d-1}(X')$, we conclude that ![]() $\alpha _{X'}$ is movable for all
$\alpha _{X'}$ is movable for all ![]() $X'$, hence
$X'$, hence ![]() $\alpha$ is BPF by Theorem 5.2.
$\alpha$ is BPF by Theorem 5.2.
It remains to prove that a ![]() $b$-divisor class is nef iff it intersects non-negatively all psef Cartier
$b$-divisor class is nef iff it intersects non-negatively all psef Cartier ![]() $b$-numerical curve classes. Denote by
$b$-numerical curve classes. Denote by ![]() $\mathcal {C}\subset \operatorname {w-N}^{1}({ \mathcal {X} })$ the dual of the cone of psef Cartier
$\mathcal {C}\subset \operatorname {w-N}^{1}({ \mathcal {X} })$ the dual of the cone of psef Cartier ![]() $b$-numerical curve classes. It is weakly closed and contains
$b$-numerical curve classes. It is weakly closed and contains ![]() $\operatorname {Nef^{1}}({ \mathcal {X} })$. Suppose there exists a class
$\operatorname {Nef^{1}}({ \mathcal {X} })$. Suppose there exists a class ![]() $\alpha \in \mathcal {C}$ which is not nef. By the Hahn–Banach theorem there exists a linear form
$\alpha \in \mathcal {C}$ which is not nef. By the Hahn–Banach theorem there exists a linear form ![]() $\ell \in \operatorname {w-N}^{1}({ \mathcal {X} })^{*}$ which is continuous for the weak topology and such that
$\ell \in \operatorname {w-N}^{1}({ \mathcal {X} })^{*}$ which is continuous for the weak topology and such that ![]() $\ell (\alpha ) <0$ and
$\ell (\alpha ) <0$ and ![]() $\ell |_{\operatorname {Nef^{1}}({ \mathcal {X} })} \geqslant 0$.
$\ell |_{\operatorname {Nef^{1}}({ \mathcal {X} })} \geqslant 0$.
By Lemma 1.2, there exists a Cartier curve class ![]() $\beta$ such that
$\beta$ such that ![]() $\ell (\alpha ) = (\beta \cdot \alpha )$ for all
$\ell (\alpha ) = (\beta \cdot \alpha )$ for all ![]() $\alpha \in \operatorname {w-N}^{1}({ \mathcal {X} })$.
$\alpha \in \operatorname {w-N}^{1}({ \mathcal {X} })$.
Then we have ![]() $(\alpha \cdot \beta ) <0$ and
$(\alpha \cdot \beta ) <0$ and ![]() $(\theta \cdot \beta )\geqslant 0$ for all
$(\theta \cdot \beta )\geqslant 0$ for all ![]() $\theta \in \operatorname {Nef^{1}}({ \mathcal {X} })$. By duality, we infer
$\theta \in \operatorname {Nef^{1}}({ \mathcal {X} })$. By duality, we infer ![]() $\beta _{X'}\geqslant 0$ for all model
$\beta _{X'}\geqslant 0$ for all model ![]() $X'$ which proves
$X'$ which proves ![]() $\beta \geqslant 0$. This gives a contradiction and concludes the proof.
$\beta \geqslant 0$. This gives a contradiction and concludes the proof.
5.2 Lehmann–Xiao decompositions of curve classes
Our objective is to relate our Theorem C to the results of Lehmann and Xiao [Reference Lehmann and XiaoLX16]. Let us review briefly their construction.
Let ![]() $\alpha$ be any big class in
$\alpha$ be any big class in ![]() $\operatorname {N}^{d-1}(X')$ for some model
$\operatorname {N}^{d-1}(X')$ for some model ![]() $X'$ so that
$X'$ so that ![]() $\alpha \geqslant c {{\omega }}^{d-1}$ for some
$\alpha \geqslant c {{\omega }}^{d-1}$ for some ![]() $c>0$. Then [Reference Lehmann and XiaoLX16, Theorem 1.3] states the existence of a unique class
$c>0$. Then [Reference Lehmann and XiaoLX16, Theorem 1.3] states the existence of a unique class ![]() $\operatorname {LX}(\alpha )\in \operatorname {Nef^{1}}(X')$ such that
$\operatorname {LX}(\alpha )\in \operatorname {Nef^{1}}(X')$ such that
Our next result relies on the extension to ![]() $b$-classes of the functional
$b$-classes of the functional ![]() $\operatorname {\widehat {\operatorname {vol}}}$ introduced in [Reference XiaoXia17]. Recall that for any psef class
$\operatorname {\widehat {\operatorname {vol}}}$ introduced in [Reference XiaoXia17]. Recall that for any psef class ![]() $\alpha \in \operatorname {N}^{d-1}(X')$, Xiao defined the following quantity:
$\alpha \in \operatorname {N}^{d-1}(X')$, Xiao defined the following quantity:
 \begin{equation} \operatorname{\widehat{\operatorname{vol}}}_{X'}(\alpha) :=\Bigg(\inf_{\substack{\beta \in\operatorname{Nef^{1}}(X')\\ (\beta^{d})>0}} \frac{(\alpha\cdot \beta)}{(\beta^{d})^{1/d}}\Bigg)^{d/(d-1)}\in \mathbb{R}_+. \end{equation}
\begin{equation} \operatorname{\widehat{\operatorname{vol}}}_{X'}(\alpha) :=\Bigg(\inf_{\substack{\beta \in\operatorname{Nef^{1}}(X')\\ (\beta^{d})>0}} \frac{(\alpha\cdot \beta)}{(\beta^{d})^{1/d}}\Bigg)^{d/(d-1)}\in \mathbb{R}_+. \end{equation}
We extend this functional to any psef class ![]() $\alpha \in \operatorname {Vect}(\operatorname {BPF}^{d-1}({ \mathcal {X} }))$ by setting
$\alpha \in \operatorname {Vect}(\operatorname {BPF}^{d-1}({ \mathcal {X} }))$ by setting
 \begin{equation} \operatorname{\widehat{\operatorname{vol}}}(\alpha) :=\Bigg(\inf_{\substack{\beta \in\operatorname{Nef^{1}}({ \mathcal{X} })\\ (\beta^{d})>0}} \frac{(\alpha\cdot \beta)}{(\beta^{d})^{1/d}}\Bigg)^{d/(d-1)}\in \mathbb{R}_+. \end{equation}
\begin{equation} \operatorname{\widehat{\operatorname{vol}}}(\alpha) :=\Bigg(\inf_{\substack{\beta \in\operatorname{Nef^{1}}({ \mathcal{X} })\\ (\beta^{d})>0}} \frac{(\alpha\cdot \beta)}{(\beta^{d})^{1/d}}\Bigg)^{d/(d-1)}\in \mathbb{R}_+. \end{equation}Theorem 5.8 For any big curve class ![]() $\alpha \in \operatorname {BPF}^{d-1}({ \mathcal {X} })$, the family of Cartier
$\alpha \in \operatorname {BPF}^{d-1}({ \mathcal {X} })$, the family of Cartier ![]() $b$-divisor classes
$b$-divisor classes ![]() $\big [\operatorname {LX}(\alpha _{X'})\big ]$ converges weakly to
$\big [\operatorname {LX}(\alpha _{X'})\big ]$ converges weakly to ![]() $\beta$ which is the unique nef
$\beta$ which is the unique nef ![]() $b$-divisor class satisfying
$b$-divisor class satisfying ![]() $\alpha = (\beta ^{d-1})$.
$\alpha = (\beta ^{d-1})$.
In other words, for any ![]() $\gamma \in \operatorname {c-N}^{d-1}({ \mathcal {X} })$ and for any
$\gamma \in \operatorname {c-N}^{d-1}({ \mathcal {X} })$ and for any ![]() $\epsilon >0$, there exists a model
$\epsilon >0$, there exists a model ![]() $X'$ such that for any model
$X'$ such that for any model ![]() $X''\geqslant X'$ we have
$X''\geqslant X'$ we have
Proof. Suppose that ![]() $\alpha \in \operatorname {BPF}^{d-1}({ \mathcal {X} })$ is big. By Theorem C, one can write
$\alpha \in \operatorname {BPF}^{d-1}({ \mathcal {X} })$ is big. By Theorem C, one can write ![]() $\alpha = \gamma ^{d-1}$ for some big curve class
$\alpha = \gamma ^{d-1}$ for some big curve class ![]() $\gamma \in \operatorname {Nef^{1}}({ \mathcal {X} })$. We claim that
$\gamma \in \operatorname {Nef^{1}}({ \mathcal {X} })$. We claim that ![]() $\gamma$ is the unique minimizer computing
$\gamma$ is the unique minimizer computing ![]() $\operatorname {\widehat {\operatorname {vol}}}(\alpha )$.
$\operatorname {\widehat {\operatorname {vol}}}(\alpha )$.
Pick any class ![]() $\beta \in \operatorname {Nef^{1}}({ \mathcal {X} })$ such that
$\beta \in \operatorname {Nef^{1}}({ \mathcal {X} })$ such that ![]() $(\beta ^{d})>0$, and normalize it by
$(\beta ^{d})>0$, and normalize it by ![]() $(\beta \cdot {{\omega }}^{d-1}) =+1$. By the proof of Theorem C, the class
$(\beta \cdot {{\omega }}^{d-1}) =+1$. By the proof of Theorem C, the class ![]() $\gamma /(\alpha \cdot \gamma )$ is the unique class in
$\gamma /(\alpha \cdot \gamma )$ is the unique class in ![]() $\{\beta '\in \operatorname {Nef^{1}}({ \mathcal {X} }), (\beta '\cdot {{\omega }}^{d-1}) =+1\}$ maximizing
$\{\beta '\in \operatorname {Nef^{1}}({ \mathcal {X} }), (\beta '\cdot {{\omega }}^{d-1}) =+1\}$ maximizing ![]() $(\beta ^{'d})$. It follows that
$(\beta ^{'d})$. It follows that
hence by Proposition 3.11, we obtain
which proves the claim.
For any model ![]() $X'$, we have
$X'$, we have
 \begin{align*} \operatorname{\widehat{\operatorname{vol}}}_{X'}(\alpha_{X'}) = \Bigg(\inf_{\substack{\beta \in \operatorname{Nef^{1}}(X')\\ (\beta^{d})>0}} \frac{(\alpha_{X'}\cdot \beta)}{(\beta^{d})^{1/d}}\Bigg)^{d/(d-1)} &= \Bigg(\inf_{\substack{\beta \in \operatorname{Nef^{1}}(X')\\ (\beta^{d})>0}} \frac{(\alpha\cdot [\beta_{X'}])}{(\beta^{d})^{(1/d)}}\Bigg)^{d/(d-1)}\\ &\geqslant\Bigg(\inf_{\substack{\beta \in \operatorname{Nef^{1}}({ \mathcal{X} })\\ (\beta^{d})>0}} \frac{(\alpha \cdot \beta)}{(\beta^{d})^{1/d}}\Bigg)^{d/(d-1)} = \operatorname{\widehat{\operatorname{vol}}}(\alpha). \end{align*}
\begin{align*} \operatorname{\widehat{\operatorname{vol}}}_{X'}(\alpha_{X'}) = \Bigg(\inf_{\substack{\beta \in \operatorname{Nef^{1}}(X')\\ (\beta^{d})>0}} \frac{(\alpha_{X'}\cdot \beta)}{(\beta^{d})^{1/d}}\Bigg)^{d/(d-1)} &= \Bigg(\inf_{\substack{\beta \in \operatorname{Nef^{1}}(X')\\ (\beta^{d})>0}} \frac{(\alpha\cdot [\beta_{X'}])}{(\beta^{d})^{(1/d)}}\Bigg)^{d/(d-1)}\\ &\geqslant\Bigg(\inf_{\substack{\beta \in \operatorname{Nef^{1}}({ \mathcal{X} })\\ (\beta^{d})>0}} \frac{(\alpha \cdot \beta)}{(\beta^{d})^{1/d}}\Bigg)^{d/(d-1)} = \operatorname{\widehat{\operatorname{vol}}}(\alpha). \end{align*}
Lemma 5.9 For any ![]() $\epsilon >0$, there exists a model
$\epsilon >0$, there exists a model ![]() $X'$ such that for any
$X'$ such that for any ![]() $X''\geqslant X'$ we have
$X''\geqslant X'$ we have ![]() $\operatorname {\widehat {\operatorname {vol}}}_{X''}(\alpha _{X''}) \leqslant \operatorname {\widehat {\operatorname {vol}}}(\alpha ) +\epsilon$.
$\operatorname {\widehat {\operatorname {vol}}}_{X''}(\alpha _{X''}) \leqslant \operatorname {\widehat {\operatorname {vol}}}(\alpha ) +\epsilon$.
Fix any model ![]() $X'$ as in the lemma. As
$X'$ as in the lemma. As ![]() $\alpha _{X'}$ is big, it follows from [Reference Lehmann and XiaoLX16, Theorem 1.3] that
$\alpha _{X'}$ is big, it follows from [Reference Lehmann and XiaoLX16, Theorem 1.3] that ![]() $\operatorname {LX}(\alpha _{X'})$ is the unique minimizer for
$\operatorname {LX}(\alpha _{X'})$ is the unique minimizer for ![]() $\operatorname {\widehat {\operatorname {vol}}}_{X'}(\alpha _{X'})$. From the previous lemma, and the relation
$\operatorname {\widehat {\operatorname {vol}}}_{X'}(\alpha _{X'})$. From the previous lemma, and the relation ![]() $(\alpha _{X'}- \operatorname {LX}(\alpha _{X'})^{d-1})\cdot \operatorname {LX}(\alpha _{X'})=0$, we obtain
$(\alpha _{X'}- \operatorname {LX}(\alpha _{X'})^{d-1})\cdot \operatorname {LX}(\alpha _{X'})=0$, we obtain
We conclude using the Diskant inequality (16).
Proof of Lemma 5.9 Pick any sequence ![]() $\gamma _n\in \operatorname {c-Nef^{1}}({ \mathcal {X} })$ decreasing to
$\gamma _n\in \operatorname {c-Nef^{1}}({ \mathcal {X} })$ decreasing to ![]() $\gamma$. By Theorem 3.2(iii), we have
$\gamma$. By Theorem 3.2(iii), we have
 \[ \lim_{n\to\infty} \bigg(\frac{(\alpha\cdot \gamma_n)}{(\gamma_n^{d})^{1/d}}\bigg)^{d/(d-1)} = \operatorname{\widehat{\operatorname{vol}}}(\alpha) . \]
\[ \lim_{n\to\infty} \bigg(\frac{(\alpha\cdot \gamma_n)}{(\gamma_n^{d})^{1/d}}\bigg)^{d/(d-1)} = \operatorname{\widehat{\operatorname{vol}}}(\alpha) . \]
Choose ![]() $n$ large enough such that
$n$ large enough such that
 \[ \bigg(\frac{(\alpha\cdot \gamma_n)}{(\gamma_n^{d})^{1/d}}\bigg)^{d/(d-1)} \leqslant \operatorname{\widehat{\operatorname{vol}}}(\alpha) + \epsilon . \]
\[ \bigg(\frac{(\alpha\cdot \gamma_n)}{(\gamma_n^{d})^{1/d}}\bigg)^{d/(d-1)} \leqslant \operatorname{\widehat{\operatorname{vol}}}(\alpha) + \epsilon . \]
Then in any model ![]() $X''$ dominating a model in which
$X''$ dominating a model in which ![]() $\gamma _n$ is determined, we obtain
$\gamma _n$ is determined, we obtain ![]() $\operatorname {\widehat {\operatorname {vol}}}_{X''}(\alpha _{X''})\leqslant \operatorname {\widehat {\operatorname {vol}}}(\alpha ) + \epsilon$.
$\operatorname {\widehat {\operatorname {vol}}}_{X''}(\alpha _{X''})\leqslant \operatorname {\widehat {\operatorname {vol}}}(\alpha ) + \epsilon$.
Remark 5.10 Suppose that ![]() $\alpha _n \to \alpha \geqslant {{\omega }}^{d-1}$. Then we can write
$\alpha _n \to \alpha \geqslant {{\omega }}^{d-1}$. Then we can write ![]() $\alpha _n =\gamma _n^{d-1}$ and
$\alpha _n =\gamma _n^{d-1}$ and ![]() $\alpha =\gamma ^{d-1}$ for some unique
$\alpha =\gamma ^{d-1}$ for some unique ![]() $\gamma _n , \gamma \in \operatorname {Nef^{1}}({ \mathcal {X} })$. If
$\gamma _n , \gamma \in \operatorname {Nef^{1}}({ \mathcal {X} })$. If ![]() $\operatorname {\widehat {\operatorname {vol}}}(\alpha _n)\to \operatorname {\widehat {\operatorname {vol}}}(\alpha )$, then it is possible to show that
$\operatorname {\widehat {\operatorname {vol}}}(\alpha _n)\to \operatorname {\widehat {\operatorname {vol}}}(\alpha )$, then it is possible to show that ![]() $\gamma _n \to \gamma$ in the weak topology. It would be interesting to find more general criteria ensuring the convergence
$\gamma _n \to \gamma$ in the weak topology. It would be interesting to find more general criteria ensuring the convergence ![]() $\gamma _n \to \gamma$.
$\gamma _n \to \gamma$.
We conclude this section by relating the big curve ![]() $b$-classes with the positivity of the functional
$b$-classes with the positivity of the functional ![]() $\operatorname {\widehat {\operatorname {vol}}}$. The following result is a natural generalization of [Reference Lehmann and XiaoLX16, Theorem 5.2] to
$\operatorname {\widehat {\operatorname {vol}}}$. The following result is a natural generalization of [Reference Lehmann and XiaoLX16, Theorem 5.2] to ![]() $b$-classes. A similar statement holds in codimension one, which is a direct application of Siu's inequalities.
$b$-classes. A similar statement holds in codimension one, which is a direct application of Siu's inequalities.
Theorem 5.11 Pick any curve ![]() $b$-numerical class
$b$-numerical class ![]() $\alpha \in \operatorname {BPF}^{d-1}({ \mathcal {X} })$, and let
$\alpha \in \operatorname {BPF}^{d-1}({ \mathcal {X} })$, and let ![]() ${{\omega }}$ be any big nef Cartier
${{\omega }}$ be any big nef Cartier ![]() $b$-divisor class. Then the following are equivalent:
$b$-divisor class. Then the following are equivalent:
(i)
 $\operatorname {\widehat {\operatorname {vol}}}(\alpha ) >0$;
$\operatorname {\widehat {\operatorname {vol}}}(\alpha ) >0$;(ii)
 $\alpha$ is big.
$\alpha$ is big.
Proof. The implication ![]() $\rm (ii) \Rightarrow (i)$ is easy because
$\rm (ii) \Rightarrow (i)$ is easy because ![]() $\operatorname {\widehat {\operatorname {vol}}}$ is increasing. Suppose conversely that
$\operatorname {\widehat {\operatorname {vol}}}$ is increasing. Suppose conversely that ![]() $\operatorname {\widehat {\operatorname {vol}}}(\alpha )>0$. Pick
$\operatorname {\widehat {\operatorname {vol}}}(\alpha )>0$. Pick ![]() $\epsilon >0$ and write
$\epsilon >0$ and write ![]() $\alpha _\epsilon = \alpha + \epsilon {{\omega }}^{d-1}$. We apply [Reference Lehmann and XiaoLX16, Theorem 5.19] to the big class
$\alpha _\epsilon = \alpha + \epsilon {{\omega }}^{d-1}$. We apply [Reference Lehmann and XiaoLX16, Theorem 5.19] to the big class ![]() $(\alpha _\epsilon )_{X'}$ and the movable class
$(\alpha _\epsilon )_{X'}$ and the movable class ![]() ${{\omega }}^{d-1}$. Write
${{\omega }}^{d-1}$. Write ![]() $B := \operatorname {LX}([(\alpha _\epsilon )_{X'}])\in \operatorname {Nef^{1}}(X')$ so that
$B := \operatorname {LX}([(\alpha _\epsilon )_{X'}])\in \operatorname {Nef^{1}}(X')$ so that ![]() $(B^{d})= \operatorname {\widehat {\operatorname {vol}}}_{X'}((\alpha _\epsilon )_{X'})$. We obtain
$(B^{d})= \operatorname {\widehat {\operatorname {vol}}}_{X'}((\alpha _\epsilon )_{X'})$. We obtain
 \[ [(\alpha_\epsilon)_{X'}] \geqslant \frac{\operatorname{\widehat{\operatorname{vol}}}([(\alpha_\epsilon)_{X'}])}{d (B\cdot {{\omega}}^{d-1})} {{\omega}}^{d-1} \]
\[ [(\alpha_\epsilon)_{X'}] \geqslant \frac{\operatorname{\widehat{\operatorname{vol}}}([(\alpha_\epsilon)_{X'}])}{d (B\cdot {{\omega}}^{d-1})} {{\omega}}^{d-1} \]
By Khovanskii–Teissier inequalities, we obtain ![]() $(B\cdot {{\omega }}^{d-1}) \leqslant {(B^{d-1}\cdot {{\omega }})^{d-1}}/{(B^{d})^{d-2}}$, hence
$(B\cdot {{\omega }}^{d-1}) \leqslant {(B^{d-1}\cdot {{\omega }})^{d-1}}/{(B^{d})^{d-2}}$, hence
 \[ [(\alpha_\epsilon)_{X'}] \geqslant {{\omega}}^{d-1} \frac{(B^{d})^{d-1}}{d (B^{d-1}\cdot {{\omega}})^{d-1}} \mathop{\geqslant}^{(25)} {{\omega}}^{d-1} \frac{\operatorname{\widehat{\operatorname{vol}}}(\alpha_\epsilon)^{d-1}}{d (\alpha_\epsilon\cdot {{\omega}})^{d-1}}, \]
\[ [(\alpha_\epsilon)_{X'}] \geqslant {{\omega}}^{d-1} \frac{(B^{d})^{d-1}}{d (B^{d-1}\cdot {{\omega}})^{d-1}} \mathop{\geqslant}^{(25)} {{\omega}}^{d-1} \frac{\operatorname{\widehat{\operatorname{vol}}}(\alpha_\epsilon)^{d-1}}{d (\alpha_\epsilon\cdot {{\omega}})^{d-1}}, \]
because ![]() $B^{d-1}= \operatorname {LX}([(\alpha _\epsilon )_{X'}])^{d-1} \leqslant (\alpha _\epsilon )_{X'}$. Now
$B^{d-1}= \operatorname {LX}([(\alpha _\epsilon )_{X'}])^{d-1} \leqslant (\alpha _\epsilon )_{X'}$. Now ![]() $[(\alpha _\epsilon )_{X'}]$ converges weakly to
$[(\alpha _\epsilon )_{X'}]$ converges weakly to ![]() $\alpha _\epsilon$, so that
$\alpha _\epsilon$, so that
 \[ \alpha_\epsilon \geqslant {{\omega}}^{d-1} \frac{\operatorname{\widehat{\operatorname{vol}}}(\alpha_\epsilon)^{d-1}}{d (\alpha_\epsilon\cdot {{\omega}})^{d-1}} \geqslant {{\omega}}^{d-1} \frac{\operatorname{\widehat{\operatorname{vol}}}(\alpha)^{d-1}}{d (\alpha_\epsilon\cdot {{\omega}})^{d-1}}. \]
\[ \alpha_\epsilon \geqslant {{\omega}}^{d-1} \frac{\operatorname{\widehat{\operatorname{vol}}}(\alpha_\epsilon)^{d-1}}{d (\alpha_\epsilon\cdot {{\omega}})^{d-1}} \geqslant {{\omega}}^{d-1} \frac{\operatorname{\widehat{\operatorname{vol}}}(\alpha)^{d-1}}{d (\alpha_\epsilon\cdot {{\omega}})^{d-1}}. \]
Letting ![]() $\epsilon \to 0$, we get
$\epsilon \to 0$, we get ![]() $\alpha \geqslant {{\omega }}^{d-1} {\operatorname {\widehat {\operatorname {vol}}}(\alpha )^{d-1}}/{d (\alpha \cdot {{\omega }})^{d-1}}$ which concludes the proof.
$\alpha \geqslant {{\omega }}^{d-1} {\operatorname {\widehat {\operatorname {vol}}}(\alpha )^{d-1}}/{d (\alpha \cdot {{\omega }})^{d-1}}$ which concludes the proof.
5.3 Positive intersections and  $(d-1)$th root
$(d-1)$th root
Xiao associated to any movable class ![]() $\alpha \in \operatorname {N}^{d-1}(X)$ the following quantity:
$\alpha \in \operatorname {N}^{d-1}(X)$ the following quantity:
 \begin{equation} {{\mathfrak{M}}}_{X}(\alpha) = \inf_{\substack{\gamma\in \operatorname{N}^{1}(X)\\ \text{big and movable}}} \bigg(\frac{(\gamma\cdot\alpha)}{\operatorname{vol}(\gamma)^{1/d}} \bigg)^{d/(d-1)} , \end{equation}
\begin{equation} {{\mathfrak{M}}}_{X}(\alpha) = \inf_{\substack{\gamma\in \operatorname{N}^{1}(X)\\ \text{big and movable}}} \bigg(\frac{(\gamma\cdot\alpha)}{\operatorname{vol}(\gamma)^{1/d}} \bigg)^{d/(d-1)} , \end{equation}
where ![]() $\operatorname {vol}(\gamma )$ is the standard volume function on the cone of big divisor classes (which is defined by
$\operatorname {vol}(\gamma )$ is the standard volume function on the cone of big divisor classes (which is defined by ![]() $\operatorname {vol}(\gamma ):=\langle P(\gamma )^{d}\rangle$).
$\operatorname {vol}(\gamma ):=\langle P(\gamma )^{d}\rangle$).
Lehmann and Xiao then proved that if ![]() ${{\mathfrak {M}}}_{X}(\alpha )>0$, then there exists a unique class
${{\mathfrak {M}}}_{X}(\alpha )>0$, then there exists a unique class ![]() $\operatorname {Mv}_{X}(\alpha )\in \operatorname {N}^{1}(X)$ minimizing the right-hand side of (26), and that this class satisfies
$\operatorname {Mv}_{X}(\alpha )\in \operatorname {N}^{1}(X)$ minimizing the right-hand side of (26), and that this class satisfies ![]() $\alpha = \langle P([\operatorname {Mv}_{X}(\alpha )])^{d-1}\rangle _{X}$, see [Reference Lehmann and XiaoLX19, Theorem 3.14].
$\alpha = \langle P([\operatorname {Mv}_{X}(\alpha )])^{d-1}\rangle _{X}$, see [Reference Lehmann and XiaoLX19, Theorem 3.14].
If ![]() $\alpha \in \operatorname {BPF}^{d-1}(X)$ is now a
$\alpha \in \operatorname {BPF}^{d-1}(X)$ is now a ![]() $b$-numerical curve class, then
$b$-numerical curve class, then ![]() $\alpha _{X'}$ is movable for any model
$\alpha _{X'}$ is movable for any model ![]() $X'$ and we may set
$X'$ and we may set ![]() ${{\mathfrak {M}}}_{X'}(\alpha ):={{\mathfrak {M}}}_{X'}(\alpha _{X'})$.
${{\mathfrak {M}}}_{X'}(\alpha ):={{\mathfrak {M}}}_{X'}(\alpha _{X'})$.
Theorem 5.12 Pick any big curve class ![]() $\alpha \in \operatorname {BPF}^{d-1}({ \mathcal {X} })$. Then for any model
$\alpha \in \operatorname {BPF}^{d-1}({ \mathcal {X} })$. Then for any model ![]() $X'$, the class
$X'$, the class ![]() $\alpha _{X'}$ is movable and
$\alpha _{X'}$ is movable and ![]() ${{\mathfrak {M}}}_{X'}(\alpha _{X'})>0$. The family of Cartier
${{\mathfrak {M}}}_{X'}(\alpha _{X'})>0$. The family of Cartier ![]() $b$-divisor classes
$b$-divisor classes ![]() $\big [\operatorname {Mv}_{X'}(\alpha )\big ]$ converges weakly to
$\big [\operatorname {Mv}_{X'}(\alpha )\big ]$ converges weakly to ![]() $\beta$ which is the unique nef
$\beta$ which is the unique nef ![]() $b$-divisor class satisfying
$b$-divisor class satisfying ![]() $\alpha = (\beta ^{d-1})$.
$\alpha = (\beta ^{d-1})$.
Proof. Choose any big curve class ![]() $\alpha \in \operatorname {BPF}^{d-1}({ \mathcal {X} })$, and write
$\alpha \in \operatorname {BPF}^{d-1}({ \mathcal {X} })$, and write ![]() $\alpha = (\beta ^{d-1})$ with
$\alpha = (\beta ^{d-1})$ with ![]() $\beta \in \operatorname {Nef^{1}}({ \mathcal {X} })$. Pick any model
$\beta \in \operatorname {Nef^{1}}({ \mathcal {X} })$. Pick any model ![]() $X'$ and any big and movable class
$X'$ and any big and movable class ![]() $\gamma \in \operatorname {N}^{1}(X')$. As
$\gamma \in \operatorname {N}^{1}(X')$. As ![]() $\gamma$ is movable, we have
$\gamma$ is movable, we have ![]() $P([\gamma ])_{X'} =\gamma$, and
$P([\gamma ])_{X'} =\gamma$, and ![]() $\operatorname {vol}(P([\gamma ]))=\operatorname {vol}(\gamma )$. We thus obtain
$\operatorname {vol}(P([\gamma ]))=\operatorname {vol}(\gamma )$. We thus obtain
 \[
\bigg(\frac{(\gamma\cdot\alpha_{X'})}{\operatorname{vol}(\gamma)^{1/d}}
\bigg)^{d/(d-1)} =
\bigg(\frac{(P([\gamma])\cdot[\alpha_{X'}])}{\operatorname{vol}(P([\gamma]))^{1/d}}
\bigg)^{d/(d-1)}
\mathop{\geqslant}\limits^{\text{Lemma 1.5}}\bigg(
\frac{(P([\gamma])\cdot\alpha)}{\operatorname{vol}(P([\gamma]))^{1/d}}
\bigg)^{d/(d-1)} \geqslant
\operatorname{\widehat{\operatorname{vol}}}(\alpha),
\]
\[
\bigg(\frac{(\gamma\cdot\alpha_{X'})}{\operatorname{vol}(\gamma)^{1/d}}
\bigg)^{d/(d-1)} =
\bigg(\frac{(P([\gamma])\cdot[\alpha_{X'}])}{\operatorname{vol}(P([\gamma]))^{1/d}}
\bigg)^{d/(d-1)}
\mathop{\geqslant}\limits^{\text{Lemma 1.5}}\bigg(
\frac{(P([\gamma])\cdot\alpha)}{\operatorname{vol}(P([\gamma]))^{1/d}}
\bigg)^{d/(d-1)} \geqslant
\operatorname{\widehat{\operatorname{vol}}}(\alpha),
\]
which proves ![]() ${{\mathfrak {M}}}_{X'}(\alpha ) \geqslant \operatorname {\widehat {\operatorname {vol}}}(\alpha ) >0$.
${{\mathfrak {M}}}_{X'}(\alpha ) \geqslant \operatorname {\widehat {\operatorname {vol}}}(\alpha ) >0$.
On the other hand, we claim that
 \begin{equation} \lim_{X'} \bigg(\frac{([\beta_{X'}]\cdot\alpha)}{\operatorname{vol}(\beta_{X'})^{1/d}} \bigg)^{d/(d-1)} =\operatorname{\widehat{\operatorname{vol}}}(\alpha) . \end{equation}
\begin{equation} \lim_{X'} \bigg(\frac{([\beta_{X'}]\cdot\alpha)}{\operatorname{vol}(\beta_{X'})^{1/d}} \bigg)^{d/(d-1)} =\operatorname{\widehat{\operatorname{vol}}}(\alpha) . \end{equation}
Indeed, because ![]() $\operatorname {vol}(\beta _{X'})=\langle P([\beta _{X'}])^{d}\rangle$ and
$\operatorname {vol}(\beta _{X'})=\langle P([\beta _{X'}])^{d}\rangle$ and ![]() $P([\beta _{X'}])$ is a decreasing net of nef divisor classes converging to
$P([\beta _{X'}])$ is a decreasing net of nef divisor classes converging to ![]() $\beta$, we have
$\beta$, we have ![]() $\operatorname {vol}(\beta _{X'})\to \operatorname {vol}(\beta )$ by Theorem 3.2. We also have
$\operatorname {vol}(\beta _{X'})\to \operatorname {vol}(\beta )$ by Theorem 3.2. We also have ![]() $([\beta _{X'}]\cdot \alpha )\to (\beta \cdot \alpha )$ as
$([\beta _{X'}]\cdot \alpha )\to (\beta \cdot \alpha )$ as ![]() $X'$ tends to infinity in the net of all models. Indeed this fact is obvious when
$X'$ tends to infinity in the net of all models. Indeed this fact is obvious when ![]() $\alpha$ is Cartier, and the general case follows from Corollary 4.7. This proves (27). As
$\alpha$ is Cartier, and the general case follows from Corollary 4.7. This proves (27). As
 \[ {{\mathfrak{M}}}_{X'}(\alpha)\leqslant \bigg(\frac{([\beta_{X'}]\cdot\alpha)}{\operatorname{vol}(\beta_{X'})^{1/d}} \bigg)^{d/(d-1)} \]
\[ {{\mathfrak{M}}}_{X'}(\alpha)\leqslant \bigg(\frac{([\beta_{X'}]\cdot\alpha)}{\operatorname{vol}(\beta_{X'})^{1/d}} \bigg)^{d/(d-1)} \]
we conclude that ![]() $\lim _{X'} {{\mathfrak {M}}}_{X'}(\alpha ) = \operatorname {\widehat {\operatorname {vol}}}(\alpha )$.
$\lim _{X'} {{\mathfrak {M}}}_{X'}(\alpha ) = \operatorname {\widehat {\operatorname {vol}}}(\alpha )$.
We obtain
and
 \begin{align*} (\beta^{d-1}\cdot P([\operatorname{Mv}_{X'}(\alpha)])) &= (\alpha\cdot P([\operatorname{Mv}_{X'}(\alpha)])) \leqslant([\alpha_{X'}]\cdot P([\operatorname{Mv}_{X'}(\alpha)]))\\ &\leqslant (P([\operatorname{Mv}_{X'}(\alpha)])^{d}), \end{align*}
\begin{align*} (\beta^{d-1}\cdot P([\operatorname{Mv}_{X'}(\alpha)])) &= (\alpha\cdot P([\operatorname{Mv}_{X'}(\alpha)])) \leqslant([\alpha_{X'}]\cdot P([\operatorname{Mv}_{X'}(\alpha)]))\\ &\leqslant (P([\operatorname{Mv}_{X'}(\alpha)])^{d}), \end{align*}
and Diskant's estimates (16) imply ![]() $P([\operatorname {Mv}_{X'}(\alpha )])\to \beta$. As
$P([\operatorname {Mv}_{X'}(\alpha )])\to \beta$. As ![]() $P([\operatorname {Mv}_{X'}(\alpha )])_{X'} = \operatorname {Mv}_{X'}(\alpha )$, it follows that
$P([\operatorname {Mv}_{X'}(\alpha )])_{X'} = \operatorname {Mv}_{X'}(\alpha )$, it follows that ![]() $[\operatorname {Mv}_{X'}(\alpha )]\to \beta$.
$[\operatorname {Mv}_{X'}(\alpha )]\to \beta$.
Remark 5.13 Fulger and Lehmann [Reference Fulger and LehmannFL17b] have also introduced a notion of Zariski decomposition of a big class ![]() $\alpha \in \operatorname {N}^{k}(X)$ for any
$\alpha \in \operatorname {N}^{k}(X)$ for any ![]() $k$. This decomposition is based on the mobility functional which is not invariant under birational pullbacks. We do not know how to extend this functional to the space of Cartier
$k$. This decomposition is based on the mobility functional which is not invariant under birational pullbacks. We do not know how to extend this functional to the space of Cartier ![]() $b$-numerical cycles, not to mention to the BPF cone.
$b$-numerical cycles, not to mention to the BPF cone.
Acknowledgements
We would like to thank Sébastien Boucksom, Mattias Jonsson for their comments and for letting us include in § 4.2 an example of a BPF curve class which is Cartier whereas its root is not. We also thank Ana Maria Botero and Jian Xiao for their numerous remarks on a first version of this paper. We express our gratitude to the anonymous referee for the careful reading and thoughtful suggestions.