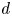1. Introduction
The preprojective algebras of quivers are important algebras that appear in various areas of mathematics, e.g. Cohen–Macaulay modules [Reference AuslanderAus86, Reference Geigle and LenzingGL91], Kleinian singularities [Reference Crawley-BoeveyCra00], cluster algebras [Reference Geiss, Leclerc and SchröerGLS13], quantum groups [Reference Kashiwara and SaitoKS97, Reference LusztigLus91], and quiver varieties [Reference NakajimaNak94]. They were first introduced by Gelfand and Ponomarev [Reference Gelfand and PonomarevGP79] (see also [Reference Dlab and RingelDR80]) by explicit quivers with relations: the algebra ![]() $\Pi$ of a quiver
$\Pi$ of a quiver ![]() $Q$ is the path algebra
$Q$ is the path algebra ![]() $\mathbb {F} \bar {Q}$ of the double quiver
$\mathbb {F} \bar {Q}$ of the double quiver ![]() $\bar {Q}$ of
$\bar {Q}$ of ![]() $Q$ modulo the ideal generated by
$Q$ modulo the ideal generated by ![]() $\sum _{x\in Q_1}(xx^{*}-x^{*}x)$. Baer, Geigle, and Lenzing gave a more conceptual construction of
$\sum _{x\in Q_1}(xx^{*}-x^{*}x)$. Baer, Geigle, and Lenzing gave a more conceptual construction of ![]() $\Pi$ based on the representation theory of the quiver
$\Pi$ based on the representation theory of the quiver ![]() $Q$ [Reference Baer, Geigle and LenzingBGL87]: their algebra is the direct sum of spaces
$Q$ [Reference Baer, Geigle and LenzingBGL87]: their algebra is the direct sum of spaces ![]() $\operatorname {Hom} _{\Lambda }(\Lambda ,\tau ^{-\ell }(\Lambda ))$ for the inverse Auslander–Reiten translate
$\operatorname {Hom} _{\Lambda }(\Lambda ,\tau ^{-\ell }(\Lambda ))$ for the inverse Auslander–Reiten translate ![]() $\tau ^{-}$, with an obvious multiplication. The algebras of Gelfand–Ponomarev and Baer–Geigle–Lenzing are isomorphic, as shown in [Reference RingelRin98, Reference Crawley-BoeveyCra99].
$\tau ^{-}$, with an obvious multiplication. The algebras of Gelfand–Ponomarev and Baer–Geigle–Lenzing are isomorphic, as shown in [Reference RingelRin98, Reference Crawley-BoeveyCra99].
Preprojective algebras enjoy very nice homological properties. They enjoy a certain 2-Calabi–Yau property [Reference Crawley-BoeveyCra98]: if ![]() $Q$ is non-Dynkin, then
$Q$ is non-Dynkin, then ![]() $\Pi$ is a
$\Pi$ is a ![]() $2$-Calabi–Yau algebra in the sense of Ginzburg. If
$2$-Calabi–Yau algebra in the sense of Ginzburg. If ![]() $Q$ is Dynkin, then
$Q$ is Dynkin, then ![]() $\Pi$ is a self-injective algebra and its stable category is 2-Calabi–Yau. They also enjoy a certain Koszul property: If
$\Pi$ is a self-injective algebra and its stable category is 2-Calabi–Yau. They also enjoy a certain Koszul property: If ![]() $Q$ is non-Dynkin, then
$Q$ is non-Dynkin, then ![]() $\Pi$ is a Koszul algebra. If
$\Pi$ is a Koszul algebra. If ![]() $Q$ is Dynkin, then
$Q$ is Dynkin, then ![]() $\Pi$ is twisted periodic of period
$\Pi$ is twisted periodic of period ![]() $3$ [Reference Ringel and SchofieldRS], and moreover it is an almost Koszul algebra in the sense of Brenner, Butler, and King [Reference Brenner, Butler and KingBBK02].
$3$ [Reference Ringel and SchofieldRS], and moreover it is an almost Koszul algebra in the sense of Brenner, Butler, and King [Reference Brenner, Butler and KingBBK02].
Recently, an analogue of preprojective algebras was studied in cluster theory [Reference KellerKel11] and higher-dimensional Auslander–Reiten theory [Reference IyamaIya07]. For a finite-dimensional algebra ![]() $\Lambda$ of global dimension
$\Lambda$ of global dimension ![]() $d$, its preprojective algebra is defined as
$d$, its preprojective algebra is defined as ![]() $\operatorname {Hom} _{\Lambda }(\Lambda ,\tau _d^{-\ell }(\Lambda ))$, where
$\operatorname {Hom} _{\Lambda }(\Lambda ,\tau _d^{-\ell }(\Lambda ))$, where ![]() $\tau _d$ and
$\tau _d$ and ![]() $\tau _d^{-}$ are higher analogues of the Auslander–Reiten translates. This algebra is the zeroth cohomology of the
$\tau _d^{-}$ are higher analogues of the Auslander–Reiten translates. This algebra is the zeroth cohomology of the ![]() $(d+1)$-Calabi–Yau completion [Reference KellerKel11], which is a
$(d+1)$-Calabi–Yau completion [Reference KellerKel11], which is a ![]() $(d+1)$-Calabi–Yau differential graded algebra. When
$(d+1)$-Calabi–Yau differential graded algebra. When ![]() $\Lambda$ is a so-called
$\Lambda$ is a so-called ![]() $d$-hereditary algebra, its higher preprojective algebra enjoys nice homological properties, including the
$d$-hereditary algebra, its higher preprojective algebra enjoys nice homological properties, including the ![]() $(d+1)$-Calabi–Yau property [Reference Amiot and OppermannAO14, Reference Herschend and IyamaHI11, Reference Iyama and OppermannIO11, Reference Iyama and OppermannIO13, Reference Herschend, Iyama and OppermannHIO14]. Higher preprojective algebras also appear in conformal field theory [Reference Evans and PughEP12a, Reference Evans and PughEP12b] and in commutative and non-commutative algebraic geometry [Reference Buchweitz and HilleBH14, Reference Bridgeland and SternBS10, Reference Herschend, Iyama, Minamoto and OppermannHIMO14, Reference MinamotoMin12, Reference Minamoto and MoriMM11] where they are non-commutative analogues of anticanonical bundles.
$(d+1)$-Calabi–Yau property [Reference Amiot and OppermannAO14, Reference Herschend and IyamaHI11, Reference Iyama and OppermannIO11, Reference Iyama and OppermannIO13, Reference Herschend, Iyama and OppermannHIO14]. Higher preprojective algebras also appear in conformal field theory [Reference Evans and PughEP12a, Reference Evans and PughEP12b] and in commutative and non-commutative algebraic geometry [Reference Buchweitz and HilleBH14, Reference Bridgeland and SternBS10, Reference Herschend, Iyama, Minamoto and OppermannHIMO14, Reference MinamotoMin12, Reference Minamoto and MoriMM11] where they are non-commutative analogues of anticanonical bundles.
A natural question arises: can we describe these higher preprojective algebras by quivers and relations, generalizing the description of Gelfand and Ponomarev? This is important in practice because having a description by a quiver and relations often makes calculations much easier to perform. When ![]() $\Lambda$ has global dimension exactly
$\Lambda$ has global dimension exactly ![]() $2$, the higher preprojective algebra is isomorphic to the Jacobi algebra of a certain quiver with potential [Reference KellerKel11, Reference Herschend and IyamaHI11], whose relations are given by taking formal partial differentials of the potential. Quivers with potential appeared in physicists’ study of mirror symmetry, and also played a key role in categorification of Fomin–Zelevinsky cluster algebras [Reference Derksen, Weyman and ZelevinskyDWZ08].
$2$, the higher preprojective algebra is isomorphic to the Jacobi algebra of a certain quiver with potential [Reference KellerKel11, Reference Herschend and IyamaHI11], whose relations are given by taking formal partial differentials of the potential. Quivers with potential appeared in physicists’ study of mirror symmetry, and also played a key role in categorification of Fomin–Zelevinsky cluster algebras [Reference Derksen, Weyman and ZelevinskyDWZ08].
It is a difficult problem to give a description of the higher preprojective algebra of a general finite-dimensional algebra in terms of a quiver and relations. Here, we impose the restriction that ![]() $\Lambda$ should be a Koszul algebra, which ensures its homological algebra is easier to understand. Then we are able to describe the quivers of the higher preprojective algebras, and to show that the new relations in the higher preprojective algebra come from taking higher formal partial differentials of a superpotential (see Theorem 3.13). If we further assume that
$\Lambda$ should be a Koszul algebra, which ensures its homological algebra is easier to understand. Then we are able to describe the quivers of the higher preprojective algebras, and to show that the new relations in the higher preprojective algebra come from taking higher formal partial differentials of a superpotential (see Theorem 3.13). If we further assume that ![]() $\Lambda$ is a
$\Lambda$ is a ![]() $d$-hereditary algebra [Reference Herschend, Iyama and OppermannHIO14], then all the relations come from higher differentials of the superpotential, as in the known cases
$d$-hereditary algebra [Reference Herschend, Iyama and OppermannHIO14], then all the relations come from higher differentials of the superpotential, as in the known cases ![]() $d=1,2$.
$d=1,2$.
Theorem A (Corollary 4.3) If ![]() $\Lambda \cong \mathbb {F} Q/(R)$ is Koszul and
$\Lambda \cong \mathbb {F} Q/(R)$ is Koszul and ![]() $d$-hereditary, then
$d$-hereditary, then
where the quiver ![]() $\bar {Q}$ is a quiver obtained from
$\bar {Q}$ is a quiver obtained from ![]() $Q$ by adding new arrows, and the relations
$Q$ by adding new arrows, and the relations ![]() $\partial _pW$ are obtained by differentiating a certain superpotential
$\partial _pW$ are obtained by differentiating a certain superpotential ![]() $W$ with respect to length
$W$ with respect to length ![]() $d-1$ paths of
$d-1$ paths of ![]() $\bar {Q}$.
$\bar {Q}$.
In fact, our Theorem 3.14 is more general because ![]() $\Lambda$ can be a factor algebra of the tensor algebra
$\Lambda$ can be a factor algebra of the tensor algebra ![]() $\operatorname {T} _S(V)$ for a separable
$\operatorname {T} _S(V)$ for a separable ![]() $\mathbb {F}$-algebra
$\mathbb {F}$-algebra ![]() $S$. Higher Jacobi algebras have been considered previously in representation theory, notably in work of Van den Bergh [Reference Van den BerghVan15], and Bocklandt, Schedler, and Wemyss [Reference Bocklandt, Schedler and WemyssBSW10] (see also [Reference Dubois-VioletteDub07, Reference Mori and SmithMS16]). In the
$S$. Higher Jacobi algebras have been considered previously in representation theory, notably in work of Van den Bergh [Reference Van den BerghVan15], and Bocklandt, Schedler, and Wemyss [Reference Bocklandt, Schedler and WemyssBSW10] (see also [Reference Dubois-VioletteDub07, Reference Mori and SmithMS16]). In the ![]() $d$-representation infinite case, which makes up half of the dichotomy of
$d$-representation infinite case, which makes up half of the dichotomy of ![]() $d$-hereditary algebras, we recover the description of Calabi–Yau Koszul algebras given in [Reference Bocklandt, Schedler and WemyssBSW10]. In the case where
$d$-hereditary algebras, we recover the description of Calabi–Yau Koszul algebras given in [Reference Bocklandt, Schedler and WemyssBSW10]. In the case where ![]() $\Lambda$ is a basic Koszul
$\Lambda$ is a basic Koszul ![]() $d$-representation-infinite algebra over an algebraically closed field of characteristic 0, this description was also given by Thibault [Reference ThibaultThi20]. These previous works only deals with the case when
$d$-representation-infinite algebra over an algebraically closed field of characteristic 0, this description was also given by Thibault [Reference ThibaultThi20]. These previous works only deals with the case when ![]() $\Lambda$ is Morita equivalent to a quotient of the path algebra of a quiver, whereas our Theorem 3.14 is much more general because
$\Lambda$ is Morita equivalent to a quotient of the path algebra of a quiver, whereas our Theorem 3.14 is much more general because ![]() $\Lambda$ can be a factor algebra of the tensor algebra
$\Lambda$ can be a factor algebra of the tensor algebra ![]() $\operatorname {T} _S(V)$ for a separable
$\operatorname {T} _S(V)$ for a separable ![]() $\mathbb {F}$-algebra
$\mathbb {F}$-algebra ![]() $S$. We give definitions of superpotentials in
$S$. We give definitions of superpotentials in ![]() $\operatorname {T} _S(V)$ and the associated higher Jacobi algebras that work in this generality, by using the zeroth Hochschild homology (Definitions 3.4 and 3.5). This requires some technical machinery prepared in § 3.2. Although other definitions of (ordinary) Jacobi algebras for
$\operatorname {T} _S(V)$ and the associated higher Jacobi algebras that work in this generality, by using the zeroth Hochschild homology (Definitions 3.4 and 3.5). This requires some technical machinery prepared in § 3.2. Although other definitions of (ordinary) Jacobi algebras for ![]() $\operatorname {T} _S(V)$ were given in [Reference NguefackNgu10, Reference Labardini-Fragoso and ZelevinskyLZ16, Reference Bautista and López-AguayoBL15], our definition seems to be more convenient.
$\operatorname {T} _S(V)$ were given in [Reference NguefackNgu10, Reference Labardini-Fragoso and ZelevinskyLZ16, Reference Bautista and López-AguayoBL15], our definition seems to be more convenient.
We also obtain homological information about higher preprojective algebras. Under the assumption that ![]() $\Lambda$ is
$\Lambda$ is ![]() $d$-hereditary, we are able to describe the projective resolutions of all simple
$d$-hereditary, we are able to describe the projective resolutions of all simple ![]() $\Pi$-modules using the higher Auslander–Reiten theory of
$\Pi$-modules using the higher Auslander–Reiten theory of ![]() $\Lambda$. In fact, we show that they are induced from
$\Lambda$. In fact, we show that they are induced from ![]() $d$-almost split sequences (see Theorem 4.12). As applications, we have the following results.
$d$-almost split sequences (see Theorem 4.12). As applications, we have the following results.
Theorem B (Corollaries 4.13 and 4.14 and Theorem 4.21) Let ![]() $\Lambda$ be a
$\Lambda$ be a ![]() $d$-hereditary algebra and
$d$-hereditary algebra and ![]() $\Pi$ the
$\Pi$ the ![]() $(d+1)$-preprojective algebra of
$(d+1)$-preprojective algebra of ![]() $\Lambda$.
$\Lambda$.
(a) If
 $\Lambda$ is
$\Lambda$ is  $d$-representation finite, then
$d$-representation finite, then  $\Pi$ is self-injective, and the simple
$\Pi$ is self-injective, and the simple  $\Pi$-modules have periodic projective resolutions. If, moreover,
$\Pi$-modules have periodic projective resolutions. If, moreover,  $\Lambda$ is Koszul, then
$\Lambda$ is Koszul, then  $\Pi$ is almost Koszul.
$\Pi$ is almost Koszul.(b) If
 $\Lambda$ is
$\Lambda$ is  $d$-representation infinite, then
$d$-representation infinite, then  $\Pi$ has global dimension
$\Pi$ has global dimension  $d+1$ (cf. the Appendix), and the
$d+1$ (cf. the Appendix), and the  $\mathbb {Z}$-graded simple
$\mathbb {Z}$-graded simple  $\Pi$-modules
$\Pi$-modules  $S$ satisfy
$S$ satisfy  $\mathbb {R}\strut \kern -.2em\operatorname {Hom} _{\Pi }(S,\Pi )\cong S^{*}(1)[-d-1]$. If, moreover,
$\mathbb {R}\strut \kern -.2em\operatorname {Hom} _{\Pi }(S,\Pi )\cong S^{*}(1)[-d-1]$. If, moreover,  $\Lambda$ is Koszul, then so is
$\Lambda$ is Koszul, then so is  $\Pi$.
$\Pi$.
As a corollary, we deduce that in the ![]() $d$-representation finite case
$d$-representation finite case ![]() $\Pi$ is twisted periodic of period
$\Pi$ is twisted periodic of period ![]() $d+2$. This recovers a result of Dugas [Reference DugasDug12] and is related to the stably Calabi–Yau property [Reference Iyama and OppermannIO13]. In the
$d+2$. This recovers a result of Dugas [Reference DugasDug12] and is related to the stably Calabi–Yau property [Reference Iyama and OppermannIO13]. In the ![]() $d$-representation infinite case, we deduce that
$d$-representation infinite case, we deduce that ![]() $\Pi$ is a generalized Artin–Schelter regular algebra of dimension
$\Pi$ is a generalized Artin–Schelter regular algebra of dimension ![]() $d+1$ and Gorenstein parameter
$d+1$ and Gorenstein parameter ![]() $1$ in the sense of [Reference Martínez-VillaMV98, Reference Martínez-Villa and SolbergMS11, Reference Minamoto and MoriMM11, Reference Reyes and RogalskiRR18] (see also [Reference Artin and SchelterAS87]). This recovers a result of Minamoto and Mori [Reference Minamoto and MoriMM11]. Our results show that higher Auslander–Reiten theory is essential in the study of Artin–Schelter regular algebras.
$1$ in the sense of [Reference Martínez-VillaMV98, Reference Martínez-Villa and SolbergMS11, Reference Minamoto and MoriMM11, Reference Reyes and RogalskiRR18] (see also [Reference Artin and SchelterAS87]). This recovers a result of Minamoto and Mori [Reference Minamoto and MoriMM11]. Our results show that higher Auslander–Reiten theory is essential in the study of Artin–Schelter regular algebras.
Next we consider quadratic duals. We show that, when ![]() $\Lambda$ is Koszul, there is a natural map from the quadratic dual of the preprojective algebra to a graded trivial extension algebra of the quadratic dual of
$\Lambda$ is Koszul, there is a natural map from the quadratic dual of the preprojective algebra to a graded trivial extension algebra of the quadratic dual of ![]() $\Lambda$. Moreover, we characterize when this map is surjective (respectively, an isomorphism) (see Theorem 5.2). In particular, we prove the following result.
$\Lambda$. Moreover, we characterize when this map is surjective (respectively, an isomorphism) (see Theorem 5.2). In particular, we prove the following result.
Theorem C (Theorems 5.2 and 5.4) Let ![]() $\Lambda =\operatorname {T} _S(V)/(R)$ be a Koszul algebra of global dimension
$\Lambda =\operatorname {T} _S(V)/(R)$ be a Koszul algebra of global dimension ![]() $d$ over a separable
$d$ over a separable ![]() $\mathbb {F}$-algebra
$\mathbb {F}$-algebra ![]() $S$.
$S$.
(a) There exists a morphism
 $\phi :\Pi ^{!}\to \operatorname {Triv} _{d+1}(\Lambda ^{!})$ of
$\phi :\Pi ^{!}\to \operatorname {Triv} _{d+1}(\Lambda ^{!})$ of  $\mathbb {Z}$-graded
$\mathbb {Z}$-graded  $\mathbb {F}$-algebras.
$\mathbb {F}$-algebras.(b) If
 $\Lambda$ is
$\Lambda$ is  $d$-hereditary, then
$d$-hereditary, then  $\phi$ is surjective, and in this case
$\phi$ is surjective, and in this case  $\phi$ is an isomorphism if and only if
$\phi$ is an isomorphism if and only if  $\operatorname {Triv} _{d+1}(\Lambda ^{!})$ is quadratic.
$\operatorname {Triv} _{d+1}(\Lambda ^{!})$ is quadratic.
In the ![]() $d=1$ case where
$d=1$ case where ![]() $\Lambda =\mathbb {F} Q$ for
$\Lambda =\mathbb {F} Q$ for ![]() $Q$ any connected acyclic quiver, we show that the map is an isomorphism whenever the underlying graph of
$Q$ any connected acyclic quiver, we show that the map is an isomorphism whenever the underlying graph of ![]() $Q$ is not of type
$Q$ is not of type ![]() $A_1$ or
$A_1$ or ![]() $A_2$. We finish by applying our results to the type
$A_2$. We finish by applying our results to the type ![]() $A$
$A$ ![]() $d$-hereditary algebras
$d$-hereditary algebras ![]() $\Lambda ^{(d,s)}$ [Reference Iyama and OppermannIO11] and use Theorem B to deduce that the type
$\Lambda ^{(d,s)}$ [Reference Iyama and OppermannIO11] and use Theorem B to deduce that the type ![]() $A$ higher preprojective algebras are almost Koszul algebras with parameters
$A$ higher preprojective algebras are almost Koszul algebras with parameters ![]() $(s-1,d+1)$, thus obtaining examples of
$(s-1,d+1)$, thus obtaining examples of ![]() $(p,q)$-Koszul algebras for all
$(p,q)$-Koszul algebras for all ![]() $p,q\geq 2$.
$p,q\geq 2$.
Note that a special case of Theorem C was independently obtained by Guo [Reference GuoGuo20, Theorem 5.3]. His result corresponds to the ‘if’ part of our Theorem 5.2(c) under the assumption that ![]() $\Lambda ^{!}$ is given by a quiver with relations and
$\Lambda ^{!}$ is given by a quiver with relations and ![]() $\operatorname {Triv} _{d+1}(\Lambda ^{!})$ is Koszul. In addition, Theorem C is closely related to [Reference HilleHil95, Section 5].
$\operatorname {Triv} _{d+1}(\Lambda ^{!})$ is Koszul. In addition, Theorem C is closely related to [Reference HilleHil95, Section 5].
2. Preliminaries
Let ![]() $\Lambda$ be a finite-dimensional algebra over a field
$\Lambda$ be a finite-dimensional algebra over a field ![]() $\mathbb {F}$. By default, a
$\mathbb {F}$. By default, a ![]() $\Lambda$-module will mean a finitely generated left
$\Lambda$-module will mean a finitely generated left ![]() $\Lambda$-module, and we denote the category of such modules by
$\Lambda$-module, and we denote the category of such modules by ![]() $\Lambda \operatorname {-mod}$. The corresponding category of right modules is denoted
$\Lambda \operatorname {-mod}$. The corresponding category of right modules is denoted ![]() $\operatorname {mod-}\Lambda$. If
$\operatorname {mod-}\Lambda$. If ![]() $\mathscr {X}$ is a set of left or right modules, we denote by
$\mathscr {X}$ is a set of left or right modules, we denote by ![]() $\operatorname {add} \mathscr {X}$ the additive subcategory of modules isomorphic to summands of sums of elements of
$\operatorname {add} \mathscr {X}$ the additive subcategory of modules isomorphic to summands of sums of elements of ![]() $\mathscr {X}$. We sometimes write
$\mathscr {X}$. We sometimes write ![]() $\operatorname {add} M$ for
$\operatorname {add} M$ for ![]() $\operatorname {add} \{M\}$. We denote by
$\operatorname {add} \{M\}$. We denote by ![]() $gf$ the composition of morphisms
$gf$ the composition of morphisms ![]() $f:X\to Y$ and
$f:X\to Y$ and ![]() $g:Y\to Z$.
$g:Y\to Z$.
We denote the enveloping algebra ![]() $\Lambda \otimes _{\mathbb {F}}\Lambda ^{{\operatorname {op} }}$ of
$\Lambda \otimes _{\mathbb {F}}\Lambda ^{{\operatorname {op} }}$ of ![]() $\Lambda$ by
$\Lambda$ by ![]() $\Lambda ^{{\operatorname {en} }}$. We assume that
$\Lambda ^{{\operatorname {en} }}$. We assume that ![]() $\mathbb {F}$ acts centrally on all bimodules, and then we can identify the category
$\mathbb {F}$ acts centrally on all bimodules, and then we can identify the category ![]() $\Lambda ^{{\operatorname {en} }}\operatorname {-mod}$ of left
$\Lambda ^{{\operatorname {en} }}\operatorname {-mod}$ of left ![]() $\Lambda ^{{\operatorname {en} }}$-modules with the category
$\Lambda ^{{\operatorname {en} }}$-modules with the category ![]() $\Lambda \operatorname {-mod-}\Lambda$ of
$\Lambda \operatorname {-mod-}\Lambda$ of ![]() $\Lambda ^{{\operatorname {en} }}$-modules. We have a duality
$\Lambda ^{{\operatorname {en} }}$-modules. We have a duality ![]() $(-)^{*}=\operatorname {Hom} _{\mathbb {F}}(-,\mathbb {F}):\Lambda \operatorname {-mod}\overset {\sim }{\rightarrow } \operatorname {mod-}\Lambda$ which sends left modules to right modules and vice versa. It extends to a duality
$(-)^{*}=\operatorname {Hom} _{\mathbb {F}}(-,\mathbb {F}):\Lambda \operatorname {-mod}\overset {\sim }{\rightarrow } \operatorname {mod-}\Lambda$ which sends left modules to right modules and vice versa. It extends to a duality ![]() $\Lambda ^{{\operatorname {en} }}\operatorname {-mod}\overset {\sim }{\rightarrow }\Lambda ^{{\operatorname {en} }}\operatorname {-mod}$ of bimodules.
$\Lambda ^{{\operatorname {en} }}\operatorname {-mod}\overset {\sim }{\rightarrow }\Lambda ^{{\operatorname {en} }}\operatorname {-mod}$ of bimodules.
2.1 Tensor algebras
Let ![]() $M$ be a
$M$ be a ![]() $\Lambda ^{{\operatorname {en} }}$-module. Recall that the tensor algebra
$\Lambda ^{{\operatorname {en} }}$-module. Recall that the tensor algebra ![]() $\operatorname {T} _{\Lambda} (M)$ of
$\operatorname {T} _{\Lambda} (M)$ of ![]() $M$ is the
$M$ is the ![]() $\mathbb {Z}$-graded vector space
$\mathbb {Z}$-graded vector space
where ![]() $M^{i}=M\otimes _{\Lambda} \cdots \otimes _{\Lambda} M$ is the tensor product of
$M^{i}=M\otimes _{\Lambda} \cdots \otimes _{\Lambda} M$ is the tensor product of ![]() $i$ copies of
$i$ copies of ![]() $M$ so, in particular,
$M$ so, in particular, ![]() $M^{0}=\Lambda$. There is an obvious graded multiplication map
$M^{0}=\Lambda$. There is an obvious graded multiplication map ![]() $M^{i}\times M^{j}\to M^{i+j}$ which sends the pair
$M^{i}\times M^{j}\to M^{i+j}$ which sends the pair ![]() $(\lambda _1\otimes \lambda _2\otimes \cdots \otimes \lambda _i,\lambda _{i+1}\otimes \cdots \otimes \lambda _{i+j})$ of standard basis vectors to the concatenated vector
$(\lambda _1\otimes \lambda _2\otimes \cdots \otimes \lambda _i,\lambda _{i+1}\otimes \cdots \otimes \lambda _{i+j})$ of standard basis vectors to the concatenated vector ![]() $\lambda _1\otimes \lambda _2\otimes \cdots \otimes \lambda _{i+j}$, and so
$\lambda _1\otimes \lambda _2\otimes \cdots \otimes \lambda _{i+j}$, and so ![]() $\operatorname {T} _{\Lambda} (M)$ is a non-negatively
$\operatorname {T} _{\Lambda} (M)$ is a non-negatively ![]() $\mathbb {Z}$-graded algebra. For later use, we prepare the following basic observations, the proofs of which are left to the reader.
$\mathbb {Z}$-graded algebra. For later use, we prepare the following basic observations, the proofs of which are left to the reader.
Lemma 2.1 Let ![]() $M$ be a
$M$ be a ![]() $\Lambda ^{{\operatorname {en} }}$-module,
$\Lambda ^{{\operatorname {en} }}$-module, ![]() $T:=\operatorname {T} _{\Lambda} (M)$, and
$T:=\operatorname {T} _{\Lambda} (M)$, and ![]() $I$ an ideal of
$I$ an ideal of ![]() $\Lambda$.
$\Lambda$.
(a) For a
 $\Lambda ^{{\operatorname {en} }}$-module
$\Lambda ^{{\operatorname {en} }}$-module  $N$, we have
$N$, we have  $\operatorname {T} _T(T\otimes _{\Lambda} N\otimes _{\Lambda} T)\cong \operatorname {T} _{\Lambda} (M\oplus N)$.
$\operatorname {T} _T(T\otimes _{\Lambda} N\otimes _{\Lambda} T)\cong \operatorname {T} _{\Lambda} (M\oplus N)$.(b) For a
 $\Lambda ^{{\operatorname {en} }}$-submodule
$\Lambda ^{{\operatorname {en} }}$-submodule  $L$ of
$L$ of  $M$, we have
$M$, we have  $\operatorname {T} _{\Lambda} (M)/(I+L)\cong \operatorname {T} _{\Lambda /I}(M/(IM+MI+L))$.
$\operatorname {T} _{\Lambda} (M)/(I+L)\cong \operatorname {T} _{\Lambda /I}(M/(IM+MI+L))$.
Let ![]() $\Lambda$ be a basic
$\Lambda$ be a basic ![]() $\mathbb {F}$-algebra with Jacobson radical
$\mathbb {F}$-algebra with Jacobson radical ![]() $J$. We assume that
$J$. We assume that ![]() $S$ is a semisimple subalgebra of
$S$ is a semisimple subalgebra of ![]() $\Lambda$ such that
$\Lambda$ such that ![]() $\Lambda =S\oplus J$. Then we can write
$\Lambda =S\oplus J$. Then we can write ![]() $\Lambda =\operatorname {T} _S(V)/I$ for an
$\Lambda =\operatorname {T} _S(V)/I$ for an ![]() $S^{{\operatorname {en} }}$-module
$S^{{\operatorname {en} }}$-module ![]() $V$ and an ideal
$V$ and an ideal ![]() $I$ of
$I$ of ![]() $\operatorname {T} _S(V)$. If
$\operatorname {T} _S(V)$. If ![]() $I$ is a homogeneous ideal, then
$I$ is a homogeneous ideal, then ![]() $\Lambda$ inherits a grading from
$\Lambda$ inherits a grading from ![]() $\operatorname {T} _S(V)$. Any such non-negatively
$\operatorname {T} _S(V)$. Any such non-negatively ![]() $\mathbb {Z}$-graded algebra
$\mathbb {Z}$-graded algebra ![]() $\Lambda$ has a minimal
$\Lambda$ has a minimal ![]() $\mathbb {Z}$-graded projective
$\mathbb {Z}$-graded projective ![]() $\Lambda ^{{\operatorname {en} }}$-module resolution
$\Lambda ^{{\operatorname {en} }}$-module resolution
where each projective module ![]() $P_i$ is generated in degrees greater than or equal to
$P_i$ is generated in degrees greater than or equal to ![]() $i$. Immediately, we have the following property.
$i$. Immediately, we have the following property.
Lemma 2.2 For any ![]() $i\ge 0$, the
$i\ge 0$, the ![]() $\mathbb {Z}$-graded
$\mathbb {Z}$-graded ![]() $\Lambda ^{{\operatorname {en} }}$-module
$\Lambda ^{{\operatorname {en} }}$-module ![]() $\operatorname {Ext} ^{i}_{\Lambda ^{{\operatorname {en} }}}(\Lambda ,\Lambda ^{{\operatorname {en} }})$ is generated in degrees greater than or equal to
$\operatorname {Ext} ^{i}_{\Lambda ^{{\operatorname {en} }}}(\Lambda ,\Lambda ^{{\operatorname {en} }})$ is generated in degrees greater than or equal to ![]() $-i$.
$-i$.
We can write each projective ![]() $\Lambda ^{{\operatorname {en} }}$-module in the form
$\Lambda ^{{\operatorname {en} }}$-module in the form ![]() $\Lambda \otimes _S K\otimes _S \Lambda$ for some
$\Lambda \otimes _S K\otimes _S \Lambda$ for some ![]() $\mathbb {Z}$-graded projective
$\mathbb {Z}$-graded projective ![]() $S^{{\operatorname {en} }}$-module
$S^{{\operatorname {en} }}$-module ![]() $K$, where we consider
$K$, where we consider ![]() $S$ as a
$S$ as a ![]() $\mathbb {Z}$-graded algebra concentrated in degree
$\mathbb {Z}$-graded algebra concentrated in degree ![]() $0$; see [Reference Butler and KingBK99]. In particular, we write
$0$; see [Reference Butler and KingBK99]. In particular, we write ![]() $P_i=\Lambda \otimes _S K_i\otimes _S \Lambda$ for
$P_i=\Lambda \otimes _S K_i\otimes _S \Lambda$ for ![]() $\mathbb {Z}$-graded projective
$\mathbb {Z}$-graded projective ![]() $S^{{\operatorname {en} }}$-modules
$S^{{\operatorname {en} }}$-modules ![]() $K_i$, for
$K_i$, for ![]() $0\leq i$.
$0\leq i$.
In general ![]() $K_i\cong \operatorname {Tor} ^{\Lambda }_i(S,S)$, and explicit descriptions for these spaces are known. For
$K_i\cong \operatorname {Tor} ^{\Lambda }_i(S,S)$, and explicit descriptions for these spaces are known. For ![]() $m\geq 0$,
$m\geq 0$,
For more information and references, see the introduction to [Reference Butler and KingBK99]. For certain kinds of algebras there are nicer descriptions of these spaces: see § 2.2 and the final chapters of [Reference Butler and KingBK99].
As well as our vector-space duality ![]() $(-)^{*}$, we have dualities
$(-)^{*}$, we have dualities
 \begin{align*} (-)^{{\vee}} &:= \operatorname{Hom}_{S^{{\operatorname{en}}}}(-,S^{{\operatorname{en}}}):S^{{\operatorname{en}}}\operatorname{-mod}\overset{\sim}{\rightarrow} S^{{\operatorname{en}}}\operatorname{-mod},\\ (-)^{*\ell} &:= \operatorname{Hom}_S(-,S):S^{{\operatorname{en}}}\operatorname{-mod}\overset{\sim}{\rightarrow} S^{{\operatorname{en}}}\operatorname{-mod},\\ (-)^{*r} &:= \operatorname{Hom}_{S^{{\operatorname{op}}}}(-,S):S^{{\operatorname{en}}}\operatorname{-mod}\overset{\sim}{\rightarrow} S^{{\operatorname{en}}}\operatorname{-mod}. \end{align*}
\begin{align*} (-)^{{\vee}} &:= \operatorname{Hom}_{S^{{\operatorname{en}}}}(-,S^{{\operatorname{en}}}):S^{{\operatorname{en}}}\operatorname{-mod}\overset{\sim}{\rightarrow} S^{{\operatorname{en}}}\operatorname{-mod},\\ (-)^{*\ell} &:= \operatorname{Hom}_S(-,S):S^{{\operatorname{en}}}\operatorname{-mod}\overset{\sim}{\rightarrow} S^{{\operatorname{en}}}\operatorname{-mod},\\ (-)^{*r} &:= \operatorname{Hom}_{S^{{\operatorname{op}}}}(-,S):S^{{\operatorname{en}}}\operatorname{-mod}\overset{\sim}{\rightarrow} S^{{\operatorname{en}}}\operatorname{-mod}. \end{align*}
For ![]() $S^{{\operatorname {en} }}$-modules
$S^{{\operatorname {en} }}$-modules ![]() $X$ and
$X$ and ![]() $Y$, we have functorial isomorphisms
$Y$, we have functorial isomorphisms
sending ![]() $f\otimes g$ to
$f\otimes g$ to ![]() $(x\otimes y\mapsto g(xf(y))$,
$(x\otimes y\mapsto g(xf(y))$,
sending ![]() $f\otimes g$ to
$f\otimes g$ to ![]() $(x\otimes y\mapsto f(g(x)y))$, and
$(x\otimes y\mapsto f(g(x)y))$, and
sending ![]() $f\otimes g$ to
$f\otimes g$ to ![]() $(x\otimes y\mapsto \sum _is_i\otimes f(s'_iy))$ for
$(x\otimes y\mapsto \sum _is_i\otimes f(s'_iy))$ for ![]() $g(x)=\sum _is_i\otimes s'_i$. For example, (4) can be checked as follows: as
$g(x)=\sum _is_i\otimes s'_i$. For example, (4) can be checked as follows: as ![]() $\operatorname {Hom} _{S^{{\operatorname {op} }}}(Y,S^{{\operatorname {en} }})\cong S\otimes _{\mathbb {F}} Y^{*r}\in S^{{\operatorname {en} }}\operatorname {-proj}$, we have
$\operatorname {Hom} _{S^{{\operatorname {op} }}}(Y,S^{{\operatorname {en} }})\cong S\otimes _{\mathbb {F}} Y^{*r}\in S^{{\operatorname {en} }}\operatorname {-proj}$, we have
Note the following simple lemma.
Lemma 2.3 Let ![]() $L$ be a
$L$ be a ![]() $\Lambda \otimes _{\mathbb {F}} S^{{\operatorname {op} }}$-module,
$\Lambda \otimes _{\mathbb {F}} S^{{\operatorname {op} }}$-module, ![]() $X$ be a projective
$X$ be a projective ![]() $S^{{\operatorname {en} }}$-module, and
$S^{{\operatorname {en} }}$-module, and ![]() $M$ be a
$M$ be a ![]() $S\otimes _{\mathbb {F}} \Lambda ^{{\operatorname {op} }}$-module. Then there is an isomorphism of
$S\otimes _{\mathbb {F}} \Lambda ^{{\operatorname {op} }}$-module. Then there is an isomorphism of ![]() $\Lambda ^{{\operatorname {en} }}$-modules that is natural in
$\Lambda ^{{\operatorname {en} }}$-modules that is natural in ![]() $L$,
$L$, ![]() $X$, and
$X$, and ![]() $M$:
$M$:
In particular, for any projective ![]() $S^{{\operatorname {en} }}$-module
$S^{{\operatorname {en} }}$-module ![]() $X$, there is a functorial isomorphism of
$X$, there is a functorial isomorphism of ![]() $\Lambda ^{{\operatorname {en} }}$-modules
$\Lambda ^{{\operatorname {en} }}$-modules
Proof. We include a complete proof for the convenience of the reader. Using the tensor-hom adjunctions, for any ![]() $X\in S^{{\operatorname {en} }}\operatorname {-mod}$ we have isomorphisms of
$X\in S^{{\operatorname {en} }}\operatorname {-mod}$ we have isomorphisms of ![]() $\Lambda ^{{\operatorname {en} }}$-modules
$\Lambda ^{{\operatorname {en} }}$-modules
 \begin{align*} & \operatorname{Hom}_{\Lambda^{{\operatorname{en}}}}(L\otimes_S X\otimes_SM,\Lambda^{{\operatorname{en}}}) \cong\operatorname{Hom}_{\Lambda^{{\operatorname{en}}}}((L\otimes_{\mathbb {F}} M)\otimes_{S^{{\operatorname{en}}}}X,\Lambda^{{\operatorname{en}}})\\ &\quad \cong\operatorname{Hom}_{S^{{\operatorname{en}}}}(X,\operatorname{Hom}_{\Lambda^{{\operatorname{en}}}}(L\otimes_{\mathbb {F}} M,\Lambda^{{\operatorname{en}}})) \cong X^{{\vee}}\otimes_{S^{{\operatorname{en}}}}\operatorname{Hom}_{\Lambda^{{\operatorname{en}}}}(L\otimes_{\mathbb {F}} M,\Lambda^{{\operatorname{en}}})\\ &\quad \cong X^{{\vee}}\otimes_{S^{{\operatorname{en}}}}(\operatorname{Hom}_{\Lambda}(L,\Lambda) \otimes_{\mathbb {F}}\operatorname{Hom}_{\Lambda^{{\operatorname{op}}}}(M,\Lambda))\cong\operatorname{Hom}_{\Lambda}(M,\Lambda) \otimes_S X^{{\vee}}\otimes_S\operatorname{Hom}_{\Lambda^{{\operatorname{op}}}}(L,\Lambda). \end{align*}
\begin{align*} & \operatorname{Hom}_{\Lambda^{{\operatorname{en}}}}(L\otimes_S X\otimes_SM,\Lambda^{{\operatorname{en}}}) \cong\operatorname{Hom}_{\Lambda^{{\operatorname{en}}}}((L\otimes_{\mathbb {F}} M)\otimes_{S^{{\operatorname{en}}}}X,\Lambda^{{\operatorname{en}}})\\ &\quad \cong\operatorname{Hom}_{S^{{\operatorname{en}}}}(X,\operatorname{Hom}_{\Lambda^{{\operatorname{en}}}}(L\otimes_{\mathbb {F}} M,\Lambda^{{\operatorname{en}}})) \cong X^{{\vee}}\otimes_{S^{{\operatorname{en}}}}\operatorname{Hom}_{\Lambda^{{\operatorname{en}}}}(L\otimes_{\mathbb {F}} M,\Lambda^{{\operatorname{en}}})\\ &\quad \cong X^{{\vee}}\otimes_{S^{{\operatorname{en}}}}(\operatorname{Hom}_{\Lambda}(L,\Lambda) \otimes_{\mathbb {F}}\operatorname{Hom}_{\Lambda^{{\operatorname{op}}}}(M,\Lambda))\cong\operatorname{Hom}_{\Lambda}(M,\Lambda) \otimes_S X^{{\vee}}\otimes_S\operatorname{Hom}_{\Lambda^{{\operatorname{op}}}}(L,\Lambda). \end{align*}All our isomorphisms are natural.
The four duals ![]() $(-)^{*}$,
$(-)^{*}$, ![]() $(-)^{*\ell }$,
$(-)^{*\ell }$, ![]() $(-)^{*r}$, and
$(-)^{*r}$, and ![]() $(-)^{\vee }$ are isomorphic to each other (see, e.g., [Reference RickardRic02, Section 3, Reference Bocklandt, Schedler and WemyssBSW10, Section 2.1]). In fact, because
$(-)^{\vee }$ are isomorphic to each other (see, e.g., [Reference RickardRic02, Section 3, Reference Bocklandt, Schedler and WemyssBSW10, Section 2.1]). In fact, because ![]() $S$ is a symmetric
$S$ is a symmetric ![]() $\mathbb {F}$-algebra, there exists an
$\mathbb {F}$-algebra, there exists an ![]() $\mathbb {F}$-linear form
$\mathbb {F}$-linear form ![]() $t:S\to \mathbb {F}$ such that
$t:S\to \mathbb {F}$ such that ![]() $t(xy)=t(yx)$ and the map
$t(xy)=t(yx)$ and the map ![]() $S\to S^{*}$ sending
$S\to S^{*}$ sending ![]() $x$ to
$x$ to ![]() $(y\mapsto t(xy))$ is an isomorphism. This gives isomorphisms
$(y\mapsto t(xy))$ is an isomorphism. This gives isomorphisms
of functors.
For later use in § 5, we now show that these isomorphisms are compatible with module structures in the following sense: let ![]() $L={\bigoplus} _{i\in \mathbb {Z}}L_i$ be a
$L={\bigoplus} _{i\in \mathbb {Z}}L_i$ be a ![]() $\mathbb {Z}$-graded
$\mathbb {Z}$-graded ![]() $\operatorname {T} _S(V^{*\ell })^{{{\operatorname {op} }}}$-module, and let
$\operatorname {T} _S(V^{*\ell })^{{{\operatorname {op} }}}$-module, and let
Then ![]() $L^{(*)}$ and
$L^{(*)}$ and ![]() $L^{(*\ell )}$ are
$L^{(*\ell )}$ are ![]() $\mathbb {Z}$-graded
$\mathbb {Z}$-graded ![]() $\operatorname {T} _S(V^{*\ell })$-modules, and
$\operatorname {T} _S(V^{*\ell })$-modules, and ![]() $L^{(*r)}$ and
$L^{(*r)}$ and ![]() $L^{(\vee )}$ are
$L^{(\vee )}$ are ![]() $\mathbb {Z}$-graded
$\mathbb {Z}$-graded ![]() $\operatorname {T} _S(V^{*r})$-modules as follows: the action of
$\operatorname {T} _S(V^{*r})$-modules as follows: the action of ![]() $\operatorname {T} _S(V^{*\ell })^{{{\operatorname {op} }}}$ on
$\operatorname {T} _S(V^{*\ell })^{{{\operatorname {op} }}}$ on ![]() $L$ is given by a morphism
$L$ is given by a morphism ![]() $a_i:L_i\otimes _SV^{*\ell }\to L_{i+1}$ of
$a_i:L_i\otimes _SV^{*\ell }\to L_{i+1}$ of ![]() $S^{{\operatorname {en} }}$-modules for
$S^{{\operatorname {en} }}$-modules for ![]() $i\in \mathbb {Z}$. This corresponds to a morphism
$i\in \mathbb {Z}$. This corresponds to a morphism ![]() $b_i:L_i\to L_{i+1}\otimes _SV$ of
$b_i:L_i\to L_{i+1}\otimes _SV$ of ![]() $S^{{\operatorname {en} }}$-modules via Hom-tensor adjunction
$S^{{\operatorname {en} }}$-modules via Hom-tensor adjunction ![]() $\operatorname {Hom} _{S^{{\operatorname {en} }}}(A\otimes _SB,C)\cong \operatorname {Hom} _{S^{{\operatorname {en} }}}(A,\operatorname {Hom} _{S^{{\operatorname {op} }}}(B,C))$. Applying
$\operatorname {Hom} _{S^{{\operatorname {en} }}}(A\otimes _SB,C)\cong \operatorname {Hom} _{S^{{\operatorname {en} }}}(A,\operatorname {Hom} _{S^{{\operatorname {op} }}}(B,C))$. Applying ![]() $(-)^{{\dagger}ger }$ for
$(-)^{{\dagger}ger }$ for ![]() ${\dagger}ger =*,*\ell ,*r,\vee$, we obtain morphisms
${\dagger}ger =*,*\ell ,*r,\vee$, we obtain morphisms
 \begin{align*} & V^{*\ell}\otimes_SL_{i+1}^{{\dagger}}\stackrel{(1)(2)}{\cong}(L_{i+1}\otimes_SV)^{{\dagger}} \xrightarrow{b_i^{{\dagger}}} L_i^{{\dagger}}\quad \mbox{for } \dagger{=}* \hbox{ or } *\ell,\\ & V^{*r}\otimes_SL_{i+1}^{{\dagger}}\stackrel{(3)(4)}{\cong}(L_{i+1}\otimes_SV)^{{\dagger}} \xrightarrow{b_i^{{\dagger}}} L_i^{{\dagger}}\quad \mbox{for } \dagger{=}*\!r \,\hbox{ or } \vee \end{align*}
\begin{align*} & V^{*\ell}\otimes_SL_{i+1}^{{\dagger}}\stackrel{(1)(2)}{\cong}(L_{i+1}\otimes_SV)^{{\dagger}} \xrightarrow{b_i^{{\dagger}}} L_i^{{\dagger}}\quad \mbox{for } \dagger{=}* \hbox{ or } *\ell,\\ & V^{*r}\otimes_SL_{i+1}^{{\dagger}}\stackrel{(3)(4)}{\cong}(L_{i+1}\otimes_SV)^{{\dagger}} \xrightarrow{b_i^{{\dagger}}} L_i^{{\dagger}}\quad \mbox{for } \dagger{=}*\!r \,\hbox{ or } \vee \end{align*}
of ![]() $S^{{\operatorname {en} }}$-modules, which give the desired structures on
$S^{{\operatorname {en} }}$-modules, which give the desired structures on ![]() $L^{(*)}$,
$L^{(*)}$, ![]() $L^{(*\ell )}$,
$L^{(*\ell )}$, ![]() $L^{(*r)}$, and
$L^{(*r)}$, and ![]() $L^{(\vee )}$.
$L^{(\vee )}$.
Lemma 2.4
(a) We have isomorphisms
 $L^{(*)}\cong L^{(*\ell )}$ of
$L^{(*)}\cong L^{(*\ell )}$ of  $\mathbb {Z}$-graded
$\mathbb {Z}$-graded  $\operatorname {T} _S(V^{*\ell })$-modules, and
$\operatorname {T} _S(V^{*\ell })$-modules, and  $L^{(*r)}\cong L^{(\vee )}$ of
$L^{(*r)}\cong L^{(\vee )}$ of  $\mathbb {Z}$-graded
$\mathbb {Z}$-graded  $\operatorname {T} _S(V^{*r})$-modules.
$\operatorname {T} _S(V^{*r})$-modules.(b) Under the isomorphism
 $\operatorname {T} _S(V^{*r})\cong \operatorname {T} _S(V^{*\ell })$ of algebras given by
$\operatorname {T} _S(V^{*r})\cong \operatorname {T} _S(V^{*\ell })$ of algebras given by  $\alpha _V^{-1}\beta _V:V^{*r}\cong V^{*\ell }$, we have isomorphisms
$\alpha _V^{-1}\beta _V:V^{*r}\cong V^{*\ell }$, we have isomorphisms  $L^{(*)}\cong L^{(*\ell )}\cong L^{(*r)}\cong L^{(\vee )}$ of
$L^{(*)}\cong L^{(*\ell )}\cong L^{(*r)}\cong L^{(\vee )}$ of  $\mathbb {Z}$-graded
$\mathbb {Z}$-graded  $\operatorname {T} _S(V^{*r})$-modules.
$\operatorname {T} _S(V^{*r})$-modules.
Proof. The assertions follow from the following commutative diagram.

The right squares commute because ![]() $\alpha ,\beta ,\gamma$ are morphisms of functors. The top left square commutes because both the north-east composition and the south-west composition send
$\alpha ,\beta ,\gamma$ are morphisms of functors. The top left square commutes because both the north-east composition and the south-west composition send ![]() $f\otimes g\in V^{*r}\otimes _SL_{i+1}^{\vee }$ to
$f\otimes g\in V^{*r}\otimes _SL_{i+1}^{\vee }$ to ![]() $(L_{i+1}\otimes _SV\ni x\otimes v\mapsto \sum _it(s_i)f(s'_iv)\in S)$, where
$(L_{i+1}\otimes _SV\ni x\otimes v\mapsto \sum _it(s_i)f(s'_iv)\in S)$, where ![]() $g(x)=\sum _is_i\otimes s'_i$. The bottom left square also commutes because both the north-west composition and the south-east composition send
$g(x)=\sum _is_i\otimes s'_i$. The bottom left square also commutes because both the north-west composition and the south-east composition send ![]() $f\otimes g\in V^{*\ell }\otimes _SL_{i+1}^{*\ell }$ to
$f\otimes g\in V^{*\ell }\otimes _SL_{i+1}^{*\ell }$ to ![]() $(L_{i+1}\otimes _SV\ni x\otimes v\mapsto t(g(xf(v)))\in \mathbb {F})$.
$(L_{i+1}\otimes _SV\ni x\otimes v\mapsto t(g(xf(v)))\in \mathbb {F})$.
To check that the left middle square commutes, fix ![]() $f\otimes g\in V^{*r}\otimes _SL_{i+1}^{*r}$. The north-east composition sends
$f\otimes g\in V^{*r}\otimes _SL_{i+1}^{*r}$. The north-east composition sends ![]() $f\otimes g$ to
$f\otimes g$ to ![]() $(x\otimes v\mapsto t(f(g(x)v)))$. The south-west composition sends
$(x\otimes v\mapsto t(f(g(x)v)))$. The south-west composition sends ![]() $f\otimes g$ to
$f\otimes g$ to ![]() $(x\otimes v\mapsto t(g(xf'(v))))$, where
$(x\otimes v\mapsto t(g(xf'(v))))$, where ![]() $f'=\alpha _V^{-1}\beta _V(f)\in V^{*\ell }$ satisfies
$f'=\alpha _V^{-1}\beta _V(f)\in V^{*\ell }$ satisfies ![]() $t\circ f=t\circ f'$. These two elements coincide because
$t\circ f=t\circ f'$. These two elements coincide because ![]() $t(f(g(x)v)))=t(f'(g(x)v))=t(g(x)f'(v))=t(g(xf'(v)))$.
$t(f(g(x)v)))=t(f'(g(x)v))=t(g(x)f'(v))=t(g(xf'(v)))$.
2.2 Graded algebras and Koszul algebras
In this section, we give preliminaries on Koszul algebras, which were introduced in [Reference PriddyPri70] and studied extensively in [Reference Beilinson, Ginzburg and SoergelBGS96].
Let ![]() $\Lambda ={\bigoplus} _{i\geq 0}\Lambda _i$ be a positively
$\Lambda ={\bigoplus} _{i\geq 0}\Lambda _i$ be a positively ![]() $\mathbb {Z}$-graded
$\mathbb {Z}$-graded ![]() $\mathbb {F}$-algebra satisfying the following conditions:
$\mathbb {F}$-algebra satisfying the following conditions:
•
 $S:=\Lambda _0$ is a finite-dimensional semisimple
$S:=\Lambda _0$ is a finite-dimensional semisimple  $\mathbb {F}$-algebra or, equivalently, the
$\mathbb {F}$-algebra or, equivalently, the  $\mathbb {Z}$-graded radical of
$\mathbb {Z}$-graded radical of  $\Lambda$ coincides with
$\Lambda$ coincides with  $\Lambda _{>0}:={\bigoplus} _{i>0}\Lambda _i$;
$\Lambda _{>0}:={\bigoplus} _{i>0}\Lambda _i$;•
 $\Lambda$ is generated in degree
$\Lambda$ is generated in degree  $1$, that is, the multiplication map
$1$, that is, the multiplication map  $\Lambda _1\otimes _{\mathbb {F}} \Lambda _1\otimes _{\mathbb {F}} \cdots \otimes _{\mathbb {F}} \Lambda _1\to \Lambda _j$ is surjective for each
$\Lambda _1\otimes _{\mathbb {F}} \Lambda _1\otimes _{\mathbb {F}} \cdots \otimes _{\mathbb {F}} \Lambda _1\to \Lambda _j$ is surjective for each  $j$.
$j$.
In this case, we call the grading a radical grading.
We assume, for simplicity, that ![]() $\Lambda$ is basic. Our assumptions ensure that
$\Lambda$ is basic. Our assumptions ensure that ![]() $\Lambda$ is a quotient of the tensor algebra
$\Lambda$ is a quotient of the tensor algebra ![]() $\operatorname {T} _S(V)$ where
$\operatorname {T} _S(V)$ where ![]() $V$ is the
$V$ is the ![]() $S^{{\operatorname {en} }}$-module
$S^{{\operatorname {en} }}$-module ![]() $\Lambda _1$. When
$\Lambda _1$. When ![]() $\Lambda$ is finite-dimensional and
$\Lambda$ is finite-dimensional and ![]() $\mathbb {F}$ is algebraically closed, we can identify
$\mathbb {F}$ is algebraically closed, we can identify ![]() $S$ with the space
$S$ with the space ![]() $\mathbb {F} Q_0$ of vertices, and
$\mathbb {F} Q_0$ of vertices, and ![]() $V$ with the space
$V$ with the space ![]() $\mathbb {F} Q_1$ of arrows, of the Gabriel quiver
$\mathbb {F} Q_1$ of arrows, of the Gabriel quiver ![]() $Q$ of
$Q$ of ![]() $\Lambda$.
$\Lambda$.
For a ![]() $\mathbb {Z}$-graded
$\mathbb {Z}$-graded ![]() $\Lambda$-module
$\Lambda$-module ![]() $M$ and
$M$ and ![]() $j\in \mathbb {Z}$, let
$j\in \mathbb {Z}$, let ![]() $M({j})$ denote the shifted
$M({j})$ denote the shifted ![]() $\mathbb {Z}$-graded
$\mathbb {Z}$-graded ![]() $\Lambda$-module where
$\Lambda$-module where ![]() $M({j})_i = M_{i+j}$. A complex
$M({j})_i = M_{i+j}$. A complex
of ![]() $\mathbb {Z}$-graded
$\mathbb {Z}$-graded ![]() $\Lambda$-modules is linear if each module
$\Lambda$-modules is linear if each module ![]() $M_i$ is generated in degree
$M_i$ is generated in degree ![]() $i$ and each map is homogeneous of degree
$i$ and each map is homogeneous of degree ![]() $0$. The algebra
$0$. The algebra ![]() $\Lambda$ is Koszul if each simple module
$\Lambda$ is Koszul if each simple module ![]() $S_i$ has a linear projective resolution.
$S_i$ has a linear projective resolution.
All Koszul algebras are quadratic in the sense that they can be written as a quotient of a tensor algebra:
where ![]() $V$ is an
$V$ is an ![]() $S^{{\operatorname {en} }}$-module,
$S^{{\operatorname {en} }}$-module, ![]() $R$ is a subset of
$R$ is a subset of ![]() $V\otimes _SV$, and
$V\otimes _SV$, and ![]() $(R)$ is the ideal in
$(R)$ is the ideal in ![]() $\operatorname {T} _S(V)$ generated by R. To simplify the proofs, we sometimes assume that
$\operatorname {T} _S(V)$ generated by R. To simplify the proofs, we sometimes assume that ![]() $R$ is a sub-
$R$ is a sub-![]() $S^{{\operatorname {en} }}$-module of
$S^{{\operatorname {en} }}$-module of ![]() $V\otimes _SV$ instead of just a subset. In particular, it is a vector subspace. This is no real restriction.
$V\otimes _SV$ instead of just a subset. In particular, it is a vector subspace. This is no real restriction.
We view ![]() $S$ as a
$S$ as a ![]() $\mathbb {Z}$-graded
$\mathbb {Z}$-graded ![]() $\mathbb {F}$-algebra concentrated in degree
$\mathbb {F}$-algebra concentrated in degree ![]() $0$, and
$0$, and ![]() $V$ as a
$V$ as a ![]() $\mathbb {Z}$-graded
$\mathbb {Z}$-graded ![]() $S^{{\operatorname {en} }}$-module concentrated in degree
$S^{{\operatorname {en} }}$-module concentrated in degree ![]() $1$. Then the tensor grading and the grading coming from
$1$. Then the tensor grading and the grading coming from ![]() $\Lambda$ coincide, and so we can safely refer to just the grading on
$\Lambda$ coincide, and so we can safely refer to just the grading on ![]() $\Lambda$.
$\Lambda$.
We record a useful lemma on quadratic algebras that can be checked easily.
Lemma 2.5 Let ![]() $\phi :\operatorname {T} _S(V)/(R)\to \operatorname {T} _{S'}(V')/(R')$ be a morphism of
$\phi :\operatorname {T} _S(V)/(R)\to \operatorname {T} _{S'}(V')/(R')$ be a morphism of ![]() $\mathbb {Z}$-graded quadratic
$\mathbb {Z}$-graded quadratic ![]() $\mathbb {F}$-algebras. If
$\mathbb {F}$-algebras. If ![]() $\phi$ is an isomorphism in degrees
$\phi$ is an isomorphism in degrees ![]() $0$,
$0$, ![]() $1$, and
$1$, and ![]() $2$, then it is an isomorphism.
$2$, then it is an isomorphism.
In the rest of this subsection, let ![]() $\Lambda \cong \operatorname {T} _S(V)/(R)$ be a quadratic algebra. We have
$\Lambda \cong \operatorname {T} _S(V)/(R)$ be a quadratic algebra. We have ![]() $S^{{\operatorname {en} }}$-modules
$S^{{\operatorname {en} }}$-modules ![]() $K_0=S$,
$K_0=S$, ![]() $K_1=V$,
$K_1=V$, ![]() $K_2=R$, and
$K_2=R$, and
 \[ K_j=(V\otimes_SK_{j-1})\cap(K_{j-1}\otimes_SV)=\mathop{\bigcap}\limits_{i=0}^{j-2}V^{i}\otimes_SR\otimes_SV^{j-2-i} \]
\[ K_j=(V\otimes_SK_{j-1})\cap(K_{j-1}\otimes_SV)=\mathop{\bigcap}\limits_{i=0}^{j-2}V^{i}\otimes_SR\otimes_SV^{j-2-i} \]
for ![]() $j\geq 3$. Here,
$j\geq 3$. Here, ![]() $V^{i}$ denotes the
$V^{i}$ denotes the ![]() $i$th tensor power
$i$th tensor power ![]() $V\otimes _S\cdots \otimes _SV$. Note that
$V\otimes _S\cdots \otimes _SV$. Note that ![]() $K_i$ is concentrated in degree
$K_i$ is concentrated in degree ![]() $i$ and that for
$i$ and that for ![]() $i<0$, we set
$i<0$, we set ![]() $K_i=0$. We have obvious inclusions
$K_i=0$. We have obvious inclusions ![]() $\iota^\ell_i:K_i\hookrightarrow V\otimes_SK_{i-1}$ and
$\iota^\ell_i:K_i\hookrightarrow V\otimes_SK_{i-1}$ and ![]() $\iota^r_i:K_i\hookrightarrow K_{i-1}\otimes_SV$ of
$\iota^r_i:K_i\hookrightarrow K_{i-1}\otimes_SV$ of ![]() $S^{\operatorname{en}}$-modules.
$S^{\operatorname{en}}$-modules.
Recall [Reference Beilinson, Ginzburg and SoergelBGS96, Section 2.7] that if ![]() $U$ is a subset of
$U$ is a subset of ![]() $V^{i}$, the right orthogonal complement of
$V^{i}$, the right orthogonal complement of ![]() $U$ is
$U$ is ![]() $U^{\perp }=\{f\in (V^{*\ell })^{i}\;|\; f(U)=0\}$, where we identify
$U^{\perp }=\{f\in (V^{*\ell })^{i}\;|\; f(U)=0\}$, where we identify ![]() $(V^{*\ell })^{i}$ with
$(V^{*\ell })^{i}$ with ![]() $(V^{i})^{*\ell }$ by (2). The quadratic dual of a quadratic algebra
$(V^{i})^{*\ell }$ by (2). The quadratic dual of a quadratic algebra ![]() $\Lambda =\operatorname {T} _S(V)/(R)$ is
$\Lambda =\operatorname {T} _S(V)/(R)$ is
It is again quadratic. If moreover ![]() $\Lambda$ is Koszul, then
$\Lambda$ is Koszul, then ![]() $\Lambda ^{!}$ is also Koszul and it coincides with the opposite ext algebra
$\Lambda ^{!}$ is also Koszul and it coincides with the opposite ext algebra ![]() $\big ({\bigoplus} _{i\geq 0}\operatorname {Ext} ^{i}_{\Lambda} (S,S)\big )^{{\operatorname {op} }}$ (see [Reference Beilinson, Ginzburg and SoergelBGS96, Proposition 2.10.1]). In this case,
$\big ({\bigoplus} _{i\geq 0}\operatorname {Ext} ^{i}_{\Lambda} (S,S)\big )^{{\operatorname {op} }}$ (see [Reference Beilinson, Ginzburg and SoergelBGS96, Proposition 2.10.1]). In this case, ![]() $\Lambda ^{!}$ has the following description.
$\Lambda ^{!}$ has the following description.
Lemma 2.6 [BGS96, Section 2.8] For a Koszul algebra ![]() $\Lambda$, we have an isomorphism of
$\Lambda$, we have an isomorphism of ![]() $\mathbb {Z}$-graded algebras
$\mathbb {Z}$-graded algebras
where the ![]() $\mathbb {Z}$-graded algebra structure on
$\mathbb {Z}$-graded algebra structure on ![]() ${\bigoplus} _{i\geq 0}K_i^{*\ell }$ is given by the duals
${\bigoplus} _{i\geq 0}K_i^{*\ell }$ is given by the duals ![]() $(\iota ^{\ell }_i)^{*\ell }$ and
$(\iota ^{\ell }_i)^{*\ell }$ and ![]() $(\iota ^{r}_i)^{*\ell }$.
$(\iota ^{r}_i)^{*\ell }$.
Now we assume that ![]() $S$ is a separable
$S$ is a separable ![]() $\mathbb {F}$-algebra, that is,
$\mathbb {F}$-algebra, that is, ![]() $S\otimes _{\mathbb {F}}\mathbb {F}'$ is semisimple for all field extensions
$S\otimes _{\mathbb {F}}\mathbb {F}'$ is semisimple for all field extensions ![]() $\mathbb {F}\subset \mathbb {F}'$ or, equivalently,
$\mathbb {F}\subset \mathbb {F}'$ or, equivalently, ![]() $S^{{\operatorname {en} }}$ is semisimple [Reference WeibelWei94, Theorem 9.2.11]. Let
$S^{{\operatorname {en} }}$ is semisimple [Reference WeibelWei94, Theorem 9.2.11]. Let
This is a projective ![]() $\Lambda ^{{\operatorname {en} }}$-module because
$\Lambda ^{{\operatorname {en} }}$-module because ![]() $S^{{\operatorname {en} }}$ is semisimple by our assumption. Combining
$S^{{\operatorname {en} }}$ is semisimple by our assumption. Combining ![]() $\iota_i^\ell$ and
$\iota_i^\ell$ and ![]() $\iota_i^r$ with the multiplication for
$\iota_i^r$ with the multiplication for ![]() $\Lambda$, they induce maps
$\Lambda$, they induce maps ![]() $\hat {\iota }^{\ell }_i,\hat {\iota }^{r}_i:P_i\to P_{i-1}$. Let
$\hat {\iota }^{\ell }_i,\hat {\iota }^{r}_i:P_i\to P_{i-1}$. Let
One can check that these maps give a chain complex
which is called the Koszul bimodule complex. Note that, as ![]() $K_i\subseteq V^{i}$ and
$K_i\subseteq V^{i}$ and ![]() $V$ is concentrated in degree
$V$ is concentrated in degree ![]() $1$, each
$1$, each ![]() $P_i$ is generated in degree
$P_i$ is generated in degree ![]() $i$, i.e. the complex is linear.
$i$, i.e. the complex is linear.
The next result is an important characterization of Koszul algebras. It can be found as, for example, [Reference Braverman and GaitsgoryBG96, Proposition A.2, Reference Butler and KingBK99, Theorem 9.2].
Theorem 2.7 The algebra ![]() $\Lambda$ is Koszul if and only if the Koszul bimodule complex (5) is its minimal projective resolution as a
$\Lambda$ is Koszul if and only if the Koszul bimodule complex (5) is its minimal projective resolution as a ![]() $\Lambda ^{{\operatorname {en} }}$-module.
$\Lambda ^{{\operatorname {en} }}$-module.
In this paper, we need separability of ![]() $S$ when we consider bimodule resolutions including the Koszul bimodule resolutions. We assume separability in Theorems C and 2.7, §§ 3.1 and 3.3, Corollary 4.3, and § 5.1.
$S$ when we consider bimodule resolutions including the Koszul bimodule resolutions. We assume separability in Theorems C and 2.7, §§ 3.1 and 3.3, Corollary 4.3, and § 5.1.
2.3 Higher preprojective algebras
Let
denote the Auslander–Reiten translation, which is a functor from the stable category of modules over ![]() $\Lambda$ to the costable category, and
$\Lambda$ to the costable category, and
the inverse Auslander–Reiten translation. Note that if ![]() $\Lambda$ is hereditary, then the Auslander–Reiten translation in fact can be regarded as an endofunctor of the module category:
$\Lambda$ is hereditary, then the Auslander–Reiten translation in fact can be regarded as an endofunctor of the module category: ![]() $\tau = \operatorname{Ext}_\Lambda^1(-,\Lambda )^{*}$ and
$\tau = \operatorname{Ext}_\Lambda^1(-,\Lambda )^{*}$ and ![]() $\tau ^{-} = \operatorname {Ext} ^{1}_{\Lambda} (\Lambda ^{*},-)$. Moreover,
$\tau ^{-} = \operatorname {Ext} ^{1}_{\Lambda} (\Lambda ^{*},-)$. Moreover, ![]() $\tau ^{-}$ is left adjoint to
$\tau ^{-}$ is left adjoint to ![]() $\tau$.
$\tau$.
Recall [Reference IyamaIya07] that the ![]() $d$-Auslander–Reiten translation and inverse
$d$-Auslander–Reiten translation and inverse ![]() $d$-Auslander–Reiten translation are defined as
$d$-Auslander–Reiten translation are defined as
where ![]() $\Omega :\Lambda \operatorname {-\underline {mod}}\to \Lambda \operatorname {-\underline {mod}}$ denotes the syzygy functor and
$\Omega :\Lambda \operatorname {-\underline {mod}}\to \Lambda \operatorname {-\underline {mod}}$ denotes the syzygy functor and ![]() $\Omega ^{-}:\Lambda \operatorname {-\overline {mod}}\to \Lambda \operatorname {-\overline {mod}}$ the cosyzygy functor. If
$\Omega ^{-}:\Lambda \operatorname {-\overline {mod}}\to \Lambda \operatorname {-\overline {mod}}$ the cosyzygy functor. If ![]() $\operatorname {gldim}\Lambda \leq d$, then we regard
$\operatorname {gldim}\Lambda \leq d$, then we regard ![]() $\tau _d$ and
$\tau _d$ and ![]() $\tau _d^{-}$ as the endofunctors
$\tau _d^{-}$ as the endofunctors
of ![]() $\Lambda \operatorname {-mod}$.
$\Lambda \operatorname {-mod}$.
Generalizing the classical case, we have two distinguished classes of modules.
Definition 2.8 [HIO14, Definition 4.7] We have the following two full subcategories ![]() $\mathscr {P}$ and
$\mathscr {P}$ and ![]() $\mathscr {I}$ of
$\mathscr {I}$ of ![]() $\Lambda \operatorname {-mod}$:
$\Lambda \operatorname {-mod}$:
Any module in ![]() $\mathscr {P}$ is called
$\mathscr {P}$ is called ![]() $d$-preprojective and any module in
$d$-preprojective and any module in ![]() $\mathscr {I}$ is called
$\mathscr {I}$ is called ![]() $d$-preinjective.
$d$-preinjective.
In the rest of this section, we assume that ![]() $\Lambda$ has global dimension
$\Lambda$ has global dimension ![]() $d$. The
$d$. The ![]() $\Lambda ^{{\operatorname {en} }}$-module
$\Lambda ^{{\operatorname {en} }}$-module
plays a central role in this paper. We take this opportunity to record a useful lemma, which makes the ![]() $\Lambda ^{{\operatorname {en} }}$-module structure of
$\Lambda ^{{\operatorname {en} }}$-module structure of ![]() $E$ clearer.
$E$ clearer.
Lemma 2.9 We have isomorphisms
of ![]() $\Lambda ^{{\operatorname {en} }}$-modules.
$\Lambda ^{{\operatorname {en} }}$-modules.
Proof. For each finite-dimensional ![]() $\Lambda$-module
$\Lambda$-module ![]() $M$, there is a natural isomorphism
$M$, there is a natural isomorphism ![]() $M\cong M^{**}$. Then we use the natural isomorphism of finite-dimensional vector spaces
$M\cong M^{**}$. Then we use the natural isomorphism of finite-dimensional vector spaces ![]() $V^{*}\otimes _{\mathbb {F}} W\cong \operatorname {Hom} _{\mathbb {F}}(V,W)$ to see that we have an isomorphism of
$V^{*}\otimes _{\mathbb {F}} W\cong \operatorname {Hom} _{\mathbb {F}}(V,W)$ to see that we have an isomorphism of ![]() $\Lambda ^{{\operatorname {en} }}$-modules
$\Lambda ^{{\operatorname {en} }}$-modules
Finally, we use the tensor-hom adjunctions to obtain
The second isomorphism is shown similarly.
Using ![]() $E$, one can describe the functors
$E$, one can describe the functors ![]() $\tau _d$ and
$\tau _d$ and ![]() $\tau _d^{-}$ as follows.
$\tau _d^{-}$ as follows.
Proposition 2.10 If ![]() $\operatorname {gldim}\Lambda \leq d$ then we have isomorphisms of functors
$\operatorname {gldim}\Lambda \leq d$ then we have isomorphisms of functors
In particular, ![]() $\tau _d^{-}$ is left adjoint to
$\tau _d^{-}$ is left adjoint to ![]() $\tau _d$.
$\tau _d$.
Proof. See the proof of [Reference Iyama and OppermannIO13, Lemma 2.13]. The latter assertion follows from the former.
Now we recall the definition of higher preprojective algebras as given in [Reference Iyama and OppermannIO11].
Definition 2.11 The higher preprojective algebra (or, more precisely, the ![]() $(d+1)$-preprojective algebra) of
$(d+1)$-preprojective algebra) of ![]() $\Lambda$ is the tensor algebra of the
$\Lambda$ is the tensor algebra of the ![]() $\Lambda ^{{\operatorname {en} }}$-module
$\Lambda ^{{\operatorname {en} }}$-module ![]() $E$:
$E$:
As this is a tensor algebra, it comes with a natural grading that we call the tensor grading, i.e., the degree ![]() $i$ part of
$i$ part of ![]() $\Pi$ is
$\Pi$ is ![]() $E^{i}$.
$E^{i}$.
The following result justifies the name of the higher preprojective algebra.
Proposition 2.12 As both a left and a right ![]() $\Lambda$-module,
$\Lambda$-module, ![]() $\Pi$ is the direct sum of all indecomposable
$\Pi$ is the direct sum of all indecomposable ![]() $d$-preprojective
$d$-preprojective ![]() $\Lambda$-modules.
$\Lambda$-modules.
Proof. The statement is immediate from the definition of ![]() $\Pi$ and Proposition 2.10.
$\Pi$ and Proposition 2.10.
As in the global dimension ![]() $1$ case, the preprojective algebra can be identified with
$1$ case, the preprojective algebra can be identified with
where the composition of ![]() $f:\Lambda \to \tau _d^{-i}(\Lambda )$ and
$f:\Lambda \to \tau _d^{-i}(\Lambda )$ and ![]() $g:\Lambda \to \tau _d^{-j}(\Lambda )$ is given by
$g:\Lambda \to \tau _d^{-j}(\Lambda )$ is given by
The ![]() $i$th part of the tensor grading is just
$i$th part of the tensor grading is just ![]() $\operatorname {Hom} _{\Lambda} \big (\Lambda ,\tau _d^{-i}(\Lambda )\big )$.
$\operatorname {Hom} _{\Lambda} \big (\Lambda ,\tau _d^{-i}(\Lambda )\big )$.
3. Description of higher preprojective algebras as higher Jacobi algebras
The aim of this section is to give some basic properties of higher preprojective algebras, including presentations of these algebras by generators and relations.
3.1 Preliminaries
In this subsection, let ![]() $\Lambda$ be a finite-dimensional
$\Lambda$ be a finite-dimensional ![]() $\mathbb {F}$-algebra
$\mathbb {F}$-algebra ![]() $\Lambda$ with global dimension at most
$\Lambda$ with global dimension at most ![]() $d$, where
$d$, where ![]() $d$ is a positive integer. Moreover, we assume that
$d$ is a positive integer. Moreover, we assume that
for a separable ![]() $\mathbb {F}$-algebra
$\mathbb {F}$-algebra ![]() $S$. Thus,
$S$. Thus, ![]() $S^{{\operatorname {en} }}$ is semisimple, and the projective dimension of the
$S^{{\operatorname {en} }}$ is semisimple, and the projective dimension of the ![]() $\Lambda ^{{\operatorname {en} }}$-module
$\Lambda ^{{\operatorname {en} }}$-module ![]() $\Lambda$ coincides with the global dimension of
$\Lambda$ coincides with the global dimension of ![]() $\Lambda$, which is at most
$\Lambda$, which is at most ![]() $d$. As before, let
$d$. As before, let
We take a minimal projective resolution of the ![]() $\Lambda ^{{{\operatorname {en} }}}$-module
$\Lambda ^{{{\operatorname {en} }}}$-module ![]() $\Lambda$:
$\Lambda$:
where ![]() $K_i$ is an
$K_i$ is an ![]() $S^{{\operatorname {en} }}$-module. For each
$S^{{\operatorname {en} }}$-module. For each ![]() $i\ge 1$, we define a map
$i\ge 1$, we define a map ![]() $\delta '_i$ by the commutative diagram
$\delta '_i$ by the commutative diagram

where the vertical maps are given by Lemma 2.3.
Proposition 3.1 We have isomorphisms ![]() $E\cong \big (\Lambda \otimes _SK_d^{\vee }\otimes _S\Lambda \big )/\operatorname {Im} \delta _d'$ of
$E\cong \big (\Lambda \otimes _SK_d^{\vee }\otimes _S\Lambda \big )/\operatorname {Im} \delta _d'$ of ![]() $\Lambda ^{{\operatorname {en} }}$-modules and
$\Lambda ^{{\operatorname {en} }}$-modules and ![]() $\operatorname {head} E\cong K_d^{\vee }$ of
$\operatorname {head} E\cong K_d^{\vee }$ of ![]() $S^{{\operatorname {en} }}$-modules.
$S^{{\operatorname {en} }}$-modules.
Proof. The former isomorphism is immediate from (7). As the resolution (6) is minimal, ![]() $\operatorname {Im} \operatorname {Hom} _{\Lambda ^{{\operatorname {en} }}}(\delta _d,\Lambda ^{{\operatorname {en} }})\subseteq J^{{\operatorname {en} }}\big (\Lambda \otimes _S K_d^{\vee }\otimes _S\Lambda \big )$ holds. Thus,
$\operatorname {Im} \operatorname {Hom} _{\Lambda ^{{\operatorname {en} }}}(\delta _d,\Lambda ^{{\operatorname {en} }})\subseteq J^{{\operatorname {en} }}\big (\Lambda \otimes _S K_d^{\vee }\otimes _S\Lambda \big )$ holds. Thus, ![]() $\operatorname {head} E\cong \operatorname {head} \big (\Lambda \otimes _S K_d^{\vee }\otimes _S\Lambda \big )=K_d^{\vee }$ because
$\operatorname {head} E\cong \operatorname {head} \big (\Lambda \otimes _S K_d^{\vee }\otimes _S\Lambda \big )=K_d^{\vee }$ because ![]() $S^{{\operatorname {en} }}$ is semisimple.
$S^{{\operatorname {en} }}$ is semisimple.
Let ![]() $\bar {V}$ be the
$\bar {V}$ be the ![]() $S^{{\operatorname {en} }}$-module
$S^{{\operatorname {en} }}$-module
This notation is meant to be reminiscent of ![]() $\bar {Q}$, which, in the global dimension
$\bar {Q}$, which, in the global dimension ![]() $1$ case, is used to denote the doubled quiver of the underlying quiver
$1$ case, is used to denote the doubled quiver of the underlying quiver ![]() $Q$. For
$Q$. For ![]() $T:=\operatorname {T} _S(V)$, we have an isomorphism
$T:=\operatorname {T} _S(V)$, we have an isomorphism
by Lemma 2.1(a). Regarding ![]() $T\otimes _SK_d^{\vee }\otimes _ST$ as a subspace of
$T\otimes _SK_d^{\vee }\otimes _ST$ as a subspace of ![]() $\operatorname {T} _S(\bar {V})$, we have the following description of
$\operatorname {T} _S(\bar {V})$, we have the following description of ![]() $\Pi$.
$\Pi$.
Proposition 3.2 Let ![]() $\Lambda =T/I$ with
$\Lambda =T/I$ with ![]() $T=\operatorname {T} _S(V)$ and
$T=\operatorname {T} _S(V)$ and ![]() $I\subset V^{\ge 2}$.
$I\subset V^{\ge 2}$.
(a) We have a surjective morphism of algebras:
which is bijective on restriction to \[ \operatorname{T}_S(\bar{V})\twoheadrightarrow\Pi, \]
\[ \operatorname{T}_S(\bar{V})\twoheadrightarrow\Pi, \] $S\oplus \bar {V}$.
$S\oplus \bar {V}$.(b) Let
 $L$ be a subspace of
$L$ be a subspace of  $T\otimes _SK_d^{\vee }\otimes _ST$ whose image under the natural surjection
$T\otimes _SK_d^{\vee }\otimes _ST$ whose image under the natural surjection  $T\otimes _SK_d^{\vee }\otimes _ST\twoheadrightarrow \Lambda \otimes _SK_d^{\vee }\otimes _S\Lambda$ is
$T\otimes _SK_d^{\vee }\otimes _ST\twoheadrightarrow \Lambda \otimes _SK_d^{\vee }\otimes _S\Lambda$ is  $\delta _d'(K_{d-1}^{\vee })$. Then we have an isomorphism of algebras:
$\delta _d'(K_{d-1}^{\vee })$. Then we have an isomorphism of algebras:
 \[ \operatorname{T}_S(\bar{V})/(I+L)\cong\Pi. \]
\[ \operatorname{T}_S(\bar{V})/(I+L)\cong\Pi. \]
Proof. We only need to prove part (b) of the proposition, from which part (a) follows. By Proposition 3.1, we have
 \begin{align*} E &\cong \operatorname{Cok}\delta_d' = \big(\Lambda\otimes_SK_d^{{\vee}}\otimes_S\Lambda\big)/\Lambda\delta_d'\big(K_{d-1}^{{\vee}}\big)\Lambda\\ &\cong \big(T\otimes_SK_d^{{\vee}}\otimes_ST\big)/\big(I\otimes_SK_d^{{\vee}}\otimes_ST+T\otimes_SK_d^{{\vee}}\otimes_SI+TLT\big). \end{align*}
\begin{align*} E &\cong \operatorname{Cok}\delta_d' = \big(\Lambda\otimes_SK_d^{{\vee}}\otimes_S\Lambda\big)/\Lambda\delta_d'\big(K_{d-1}^{{\vee}}\big)\Lambda\\ &\cong \big(T\otimes_SK_d^{{\vee}}\otimes_ST\big)/\big(I\otimes_SK_d^{{\vee}}\otimes_ST+T\otimes_SK_d^{{\vee}}\otimes_SI+TLT\big). \end{align*}Thus, applying Lemma 2.1(a) and (b), we have
 \begin{align*} \operatorname{T}_S(\bar{V})/(I+L) &\cong\operatorname{T}_T\big(T\otimes_SK_d^{{\vee}}\otimes_ST\big)/(I+TLT)\\ &\cong\operatorname{T}_{\Lambda}\big(\big(T\otimes_SK_d^{{\vee}}\otimes_ST\big)/\big(I\otimes_SK_d^{{\vee}} \otimes_ST+T\otimes_SK_d^{{\vee}}\otimes_SI+TLT\big)\big)\\ &\cong\operatorname{T}_{\Lambda}(E)=\Pi \end{align*}
\begin{align*} \operatorname{T}_S(\bar{V})/(I+L) &\cong\operatorname{T}_T\big(T\otimes_SK_d^{{\vee}}\otimes_ST\big)/(I+TLT)\\ &\cong\operatorname{T}_{\Lambda}\big(\big(T\otimes_SK_d^{{\vee}}\otimes_ST\big)/\big(I\otimes_SK_d^{{\vee}} \otimes_ST+T\otimes_SK_d^{{\vee}}\otimes_SI+TLT\big)\big)\\ &\cong\operatorname{T}_{\Lambda}(E)=\Pi \end{align*}as desired.
Consider the case where ![]() $\mathbb {F}$ is algebraically closed, so we can describe
$\mathbb {F}$ is algebraically closed, so we can describe ![]() $\Lambda$ as
$\Lambda$ as ![]() $\mathbb {F} Q/I$. Let
$\mathbb {F} Q/I$. Let ![]() $\{k_1,\ldots ,k_r\}$ be a basis of
$\{k_1,\ldots ,k_r\}$ be a basis of ![]() $K_d$, each with a unique source and target
$K_d$, each with a unique source and target ![]() $s(k_i)$ and
$s(k_i)$ and ![]() $t(k_i)$, and let
$t(k_i)$, and let ![]() $\bar {Q}$ be the quiver obtained by adding
$\bar {Q}$ be the quiver obtained by adding ![]() $r$ arrows
$r$ arrows ![]() $k_i^{*}:t(k_i)\to s(k_i)$ to
$k_i^{*}:t(k_i)\to s(k_i)$ to ![]() $Q$. Then, just as
$Q$. Then, just as ![]() $V$ is the arrow space of
$V$ is the arrow space of ![]() $Q$,
$Q$, ![]() $\bar {V}$ is the arrow space of
$\bar {V}$ is the arrow space of ![]() $\bar {Q}$, and Proposition 3.2 says that
$\bar {Q}$, and Proposition 3.2 says that ![]() $\bar {Q}$ is the Gabriel quiver of
$\bar {Q}$ is the Gabriel quiver of ![]() $\Pi$.
$\Pi$.
We can therefore calculate the Gabriel quiver ![]() $\bar {Q}$ of
$\bar {Q}$ of ![]() $\Pi$ as follows. First, for each vertex
$\Pi$ as follows. First, for each vertex ![]() $i$ of
$i$ of ![]() $Q$, compute the projective resolution
$Q$, compute the projective resolution
of the simple left ![]() $\Lambda$-module
$\Lambda$-module ![]() $S_i$, where some projective modules
$S_i$, where some projective modules ![]() $P_{i,h}$ may be zero. Then, for each
$P_{i,h}$ may be zero. Then, for each ![]() $i$ and for each summand of the projective module
$i$ and for each summand of the projective module ![]() $P_{i,n}$ that is isomorphic to the projective cover of
$P_{i,n}$ that is isomorphic to the projective cover of ![]() $S_j$, add an arrow
$S_j$, add an arrow ![]() $i\to j$ to the quiver
$i\to j$ to the quiver ![]() $Q$. The resulting quiver is
$Q$. The resulting quiver is ![]() $\bar {Q}$.
$\bar {Q}$.
Example 3.3 Let
and ![]() $\Lambda =\mathbb {F} Q/(\beta \gamma \delta ,\gamma \delta \varepsilon )$. Let
$\Lambda =\mathbb {F} Q/(\beta \gamma \delta ,\gamma \delta \varepsilon )$. Let ![]() $S_i$ denote the simple left
$S_i$ denote the simple left ![]() $\Lambda$-module associated to the vertex
$\Lambda$-module associated to the vertex ![]() $i$, and
$i$, and ![]() $P(S_i)$ its projective cover. One can check that
$P(S_i)$ its projective cover. One can check that ![]() $\Lambda$ has global dimension
$\Lambda$ has global dimension ![]() $3$ and the only simple module with projective dimension
$3$ and the only simple module with projective dimension ![]() $3$ is
$3$ is ![]() $S_6$. Its projective resolution is
$S_6$. Its projective resolution is
where ![]() $\cdot a$ denotes right multiplication by
$\cdot a$ denotes right multiplication by ![]() $a$. Thus, the quiver
$a$. Thus, the quiver ![]() $\bar {Q}$ of
$\bar {Q}$ of ![]() $\Pi$ is just
$\Pi$ is just ![]() $Q$ with an extra arrow from
$Q$ with an extra arrow from ![]() $6$ to
$6$ to ![]() $2$, which we label
$2$, which we label ![]() $(\beta \gamma \delta \varepsilon )^{*}$.
$(\beta \gamma \delta \varepsilon )^{*}$.
3.2 Superpotentials and higher Jacobi algebras
To introduce our main notions of superpotentials, we need preparations. For an ![]() $\mathbb {F}$-algebra
$\mathbb {F}$-algebra ![]() $A$ and an
$A$ and an ![]() $A^{{\operatorname {en} }}$-module
$A^{{\operatorname {en} }}$-module ![]() $M$, we write
$M$, we write
for the zeroth Hochschild homology ![]() $H_0(A,M)$ of
$H_0(A,M)$ of ![]() $A$. This can be naturally identified with the quotient of
$A$. This can be naturally identified with the quotient of ![]() $M$ modulo the subgroup generated by
$M$ modulo the subgroup generated by ![]() $am-ma$ with
$am-ma$ with ![]() $a\in A$ and
$a\in A$ and ![]() $m\in M$. Therefore, we have a natural surjective map
$m\in M$. Therefore, we have a natural surjective map ![]() $\pi :M\twoheadrightarrow A\otimes _{A^{{\operatorname {en} }}}M$ of
$\pi :M\twoheadrightarrow A\otimes _{A^{{\operatorname {en} }}}M$ of ![]() $\mathbb {F}$-modules.
$\mathbb {F}$-modules.
For ![]() $A^{{\operatorname {en} }}$-modules
$A^{{\operatorname {en} }}$-modules ![]() $M_1,\ldots ,M_{\ell}$, we clearly have functorial isomorphisms
$M_1,\ldots ,M_{\ell}$, we clearly have functorial isomorphisms
given by ![]() $m_1\otimes\cdots\otimes m_\ell\mapsto m_2\otimes\cdots\otimes m_\ell\otimes m_1\mapsto\cdots\mapsto m_\ell\otimes m_1\otimes\cdots\otimes m_{\ell-1}$. For
$m_1\otimes\cdots\otimes m_\ell\mapsto m_2\otimes\cdots\otimes m_\ell\otimes m_1\mapsto\cdots\mapsto m_\ell\otimes m_1\otimes\cdots\otimes m_{\ell-1}$. For ![]() $M,N\in A^{{\operatorname {en} }}\operatorname {-mod}$, there is a functorial isomorphism
$M,N\in A^{{\operatorname {en} }}\operatorname {-mod}$, there is a functorial isomorphism
given by ![]() $a\otimes (m\otimes n)\mapsto am\otimes n= m\otimes na$, whose inverse is
$a\otimes (m\otimes n)\mapsto am\otimes n= m\otimes na$, whose inverse is ![]() $m\otimes n\mapsto 1\otimes (m\otimes n)$. It gives a functorial morphism
$m\otimes n\mapsto 1\otimes (m\otimes n)$. It gives a functorial morphism
which is an isomorphism if ![]() $M$ is a finitely generated projective
$M$ is a finitely generated projective ![]() $A^{{\operatorname {en} }}$-module.
$A^{{\operatorname {en} }}$-module.
Setting ![]() $M=A^{{\operatorname {en} }}$ in (9), we have a functorial isomorphism of
$M=A^{{\operatorname {en} }}$ in (9), we have a functorial isomorphism of ![]() $A^{{\operatorname {en} }}$-modules
$A^{{\operatorname {en} }}$-modules
For ![]() $M,N\in A^{{\operatorname {en} }}\operatorname {-mod}$, we have a well-defined pairing
$M,N\in A^{{\operatorname {en} }}\operatorname {-mod}$, we have a well-defined pairing
given as the composition ![]() $M^{\vee }\otimes _{\mathbb {F}} c(M\otimes _AN)\to c(A^{{\operatorname {en} }}\otimes _AN)\xrightarrow {(11)} N$, where the first map sends
$M^{\vee }\otimes _{\mathbb {F}} c(M\otimes _AN)\to c(A^{{\operatorname {en} }}\otimes _AN)\xrightarrow {(11)} N$, where the first map sends ![]() $f\otimes (1_A\otimes (m\otimes n))$ to
$f\otimes (1_A\otimes (m\otimes n))$ to ![]() $f(m) n$.
$f(m) n$.
Now we are ready to introduce the following, which is a central notion in this paper.
Definition 3.4 Let ![]() $S$ be a semisimple
$S$ be a semisimple ![]() $\mathbb {F}$-algebra and
$\mathbb {F}$-algebra and ![]() $U$ an
$U$ an ![]() $S^{{\operatorname {en} }}$-module. A superpotential of degree
$S^{{\operatorname {en} }}$-module. A superpotential of degree ![]() $\ell$ for
$\ell$ for ![]() $T=\operatorname {T} _S(U)$ is an element of
$T=\operatorname {T} _S(U)$ is an element of ![]() $c(U^{\ell })=S\otimes _{S^{{\operatorname {en} }}}U^{\ell }$, where
$c(U^{\ell })=S\otimes _{S^{{\operatorname {en} }}}U^{\ell }$, where ![]() $U^{\ell }$ is the
$U^{\ell }$ is the ![]() $\ell$th tensor power
$\ell$th tensor power ![]() $U\otimes _S\cdots \otimes _S U$ as before.
$U\otimes _S\cdots \otimes _S U$ as before.
By (8), we have a well-defined automorphism
Using ![]() $\rho$, we define
$\rho$, we define ![]() $\varphi$ by
$\varphi$ by
 \[ \varphi:=\sum_{i=0}^{\ell-1}({-}1)^{(\ell-1)i}\rho^{i}:S\otimes_{S^{{\operatorname{en}}}}U^{\ell}\to S\otimes_{S^{{\operatorname{en}}}}U^{\ell}. \]
\[ \varphi:=\sum_{i=0}^{\ell-1}({-}1)^{(\ell-1)i}\rho^{i}:S\otimes_{S^{{\operatorname{en}}}}U^{\ell}\to S\otimes_{S^{{\operatorname{en}}}}U^{\ell}. \]
By (12), for ![]() $0\leq k\leq \ell$, we have a well-defined pairing
$0\leq k\leq \ell$, we have a well-defined pairing
For ![]() $f\in (U^{k})^{\vee }$ and
$f\in (U^{k})^{\vee }$ and ![]() $x\in c(U^{\ell })$, we simply write
$x\in c(U^{\ell })$, we simply write ![]() $f\cdot x:=\operatorname {ev} _{U^{k}}\otimes 1_{U^{\ell -k}}(f\otimes x)$.
$f\cdot x:=\operatorname {ev} _{U^{k}}\otimes 1_{U^{\ell -k}}(f\otimes x)$.
Definition 3.5 Let ![]() $S$ be a semisimple
$S$ be a semisimple ![]() $\mathbb {F}$-algebra,
$\mathbb {F}$-algebra, ![]() $U$ an
$U$ an ![]() $S^{{\operatorname {en} }}$-module, and
$S^{{\operatorname {en} }}$-module, and ![]() $T=\operatorname {T} _S(U)$. For a superpotential
$T=\operatorname {T} _S(U)$. For a superpotential ![]() $W$ of degree
$W$ of degree ![]() $\ell$ and a non-negative integer
$\ell$ and a non-negative integer ![]() $k\le \ell$, the
$k\le \ell$, the ![]() $k$-Jacobi ideal of
$k$-Jacobi ideal of ![]() $T$ is the two-sided ideal
$T$ is the two-sided ideal
The ![]() $k$-Jacobi algebra is the quotient algebra
$k$-Jacobi algebra is the quotient algebra
We now explain a connection to notation used elsewhere.
Remark 3.6 Given a quiver ![]() $Q$, we have a semisimple algebra
$Q$, we have a semisimple algebra ![]() $S=\mathbb {F} Q_0$ with basis the vertices of
$S=\mathbb {F} Q_0$ with basis the vertices of ![]() $Q$ and an
$Q$ and an ![]() $S^{{\operatorname {en} }}$-module
$S^{{\operatorname {en} }}$-module ![]() $U=\mathbb {F} Q_1$ with basis the arrows. For each
$U=\mathbb {F} Q_1$ with basis the arrows. For each ![]() $i\geq 0$, let
$i\geq 0$, let ![]() $Q_i$ be the set of all paths of length
$Q_i$ be the set of all paths of length ![]() $i$ on
$i$ on ![]() $Q$. Then
$Q$. Then ![]() $Q_i$ gives a basis of the
$Q_i$ gives a basis of the ![]() $S^{{\operatorname {en} }}$-module
$S^{{\operatorname {en} }}$-module ![]() $U^{i}$, and we denote by
$U^{i}$, and we denote by ![]() $\{p^{\vee }\mid p\in Q_i\}$ the dual basis of
$\{p^{\vee }\mid p\in Q_i\}$ the dual basis of ![]() $(U^{i})^{\vee }$ in the obvious sense.
$(U^{i})^{\vee }$ in the obvious sense.
Let ![]() $W$ be a superpotential for
$W$ be a superpotential for ![]() $\mathbb {F} Q=\operatorname {T} _S(U)$. Define
$\mathbb {F} Q=\operatorname {T} _S(U)$. Define
Then the ![]() $k$-Jacobi ideal is the ideal of
$k$-Jacobi ideal is the ideal of ![]() $\operatorname {T} _S(U)$ generated by
$\operatorname {T} _S(U)$ generated by ![]() $\{\partial _{p}W\;|\; p\in Q_k\}$. Note that when
$\{\partial _{p}W\;|\; p\in Q_k\}$. Note that when ![]() $k=1$ and the superpotential
$k=1$ and the superpotential ![]() $W$ is of odd degree we recover the usual notion of the Jacobi algebra of a quiver with potential
$W$ is of odd degree we recover the usual notion of the Jacobi algebra of a quiver with potential ![]() $(Q,W)$.
$(Q,W)$.
Note also that some sources, such as [Reference Bocklandt, Schedler and WemyssBSW10], define the superpotential to be ![]() $\varphi (W)$ rather than
$\varphi (W)$ rather than ![]() $W$.
$W$.
In the remainder of this section, we give general observations that are used later. Let ![]() $A$ be an
$A$ be an ![]() $\mathbb {F}$-algebra.
$\mathbb {F}$-algebra.
Lemma 3.7 For ![]() $A^{{\operatorname {en} }}$-modules
$A^{{\operatorname {en} }}$-modules ![]() $X,Y,Z$, we have functorial morphisms
$X,Y,Z$, we have functorial morphisms
The left (respectively, right) one is an isomorphism if ![]() $X$ (respectively,
$X$ (respectively, ![]() $Y$) is a projective
$Y$) is a projective ![]() $A^{{\operatorname {en} }}$-module.
$A^{{\operatorname {en} }}$-module.
Proof. Using (10), we have functorial morphisms ![]() $c(X\otimes _AY\otimes _AZ)\to \operatorname {Hom} _{A^{{\operatorname {en} }}}(X^{\vee },Y\otimes _AZ)$ and
$c(X\otimes _AY\otimes _AZ)\to \operatorname {Hom} _{A^{{\operatorname {en} }}}(X^{\vee },Y\otimes _AZ)$ and ![]() $c(X\otimes _AY\otimes _AZ)\stackrel {(8)}{\cong }c(Y\otimes _AZ\otimes _AX)\to \operatorname {Hom} _{A^{{\operatorname {en} }}}(Y^{\vee },Z\otimes _AX)$.
$c(X\otimes _AY\otimes _AZ)\stackrel {(8)}{\cong }c(Y\otimes _AZ\otimes _AX)\to \operatorname {Hom} _{A^{{\operatorname {en} }}}(Y^{\vee },Z\otimes _AX)$.
As in (4) when ![]() $A$ is semisimple, for
$A$ is semisimple, for ![]() $A^{{\operatorname {en} }}$-modules
$A^{{\operatorname {en} }}$-modules ![]() $X,Y,Z$, we have functorial isomorphisms
$X,Y,Z$, we have functorial isomorphisms
The first map sends ![]() $f\otimes g$ to
$f\otimes g$ to ![]() $(x\otimes y\mapsto \sum _ig(xs_i)\otimes s'_i)$ where
$(x\otimes y\mapsto \sum _ig(xs_i)\otimes s'_i)$ where ![]() $f(y)=\sum _is_i\otimes s'_i$, and the second one sends
$f(y)=\sum _is_i\otimes s'_i$, and the second one sends ![]() $f'\otimes g'$ to
$f'\otimes g'$ to ![]() $(x\otimes y\mapsto \sum _jt_j\otimes f'(t'_jy))$ where
$(x\otimes y\mapsto \sum _jt_j\otimes f'(t'_jy))$ where ![]() $g'(x)=\sum _jt_j\otimes t'_j$. We have the following commutative diagram.
$g'(x)=\sum _jt_j\otimes t'_j$. We have the following commutative diagram.

3.3 Higher preprojective algebras of Koszul algebras
Now we go back to the setting in § 3.1, that is, ![]() $\Lambda$ is a finite-dimensional
$\Lambda$ is a finite-dimensional ![]() $\mathbb {F}$-algebra with global dimension
$\mathbb {F}$-algebra with global dimension ![]() $d>0$. Moreover, we assume that
$d>0$. Moreover, we assume that ![]() $\Lambda$ is a Koszul algebra and
$\Lambda$ is a Koszul algebra and
for a separable ![]() $\mathbb {F}$-algebra
$\mathbb {F}$-algebra ![]() $S$. Then the minimal
$S$. Then the minimal ![]() $\mathbb {Z}$-graded projective resolution (6) of the
$\mathbb {Z}$-graded projective resolution (6) of the ![]() $\Lambda ^{{\operatorname {en} }}$-module
$\Lambda ^{{\operatorname {en} }}$-module ![]() $\Lambda$ is given by the Koszul bimodule complex (5). Let
$\Lambda$ is given by the Koszul bimodule complex (5). Let ![]() $\bar {V}=V\oplus K_d^{\vee }$.
$\bar {V}=V\oplus K_d^{\vee }$.
Definition 3.8 We define a superpotential ![]() $W$ of degree
$W$ of degree ![]() $d+1$ for
$d+1$ for ![]() $\operatorname {T} _S(\bar {V})$ as the image of
$\operatorname {T} _S(\bar {V})$ as the image of ![]() $1_{\mathbb {F}}\in \mathbb {F}$ under the composition
$1_{\mathbb {F}}\in \mathbb {F}$ under the composition
where ![]() $\operatorname {coev} _{K_d}:\mathbb {F}\to \operatorname {End} _{S^{{\operatorname {en} }}}(K_d)\cong K_d\otimes _{S^{{\operatorname {en} }}}K_d^{\vee }\cong c\big (K_d\otimes _SK_d^{\vee }\big )$ is the coevaluation map. We call
$\operatorname {coev} _{K_d}:\mathbb {F}\to \operatorname {End} _{S^{{\operatorname {en} }}}(K_d)\cong K_d\otimes _{S^{{\operatorname {en} }}}K_d^{\vee }\cong c\big (K_d\otimes _SK_d^{\vee }\big )$ is the coevaluation map. We call ![]() $W$ the superpotential associated to
$W$ the superpotential associated to ![]() $\Lambda$, or the associated superpotential.
$\Lambda$, or the associated superpotential.
By Lemma 3.7, we have isomorphisms ![]() $\operatorname {Hom} _{S^{{\operatorname {en} }}}(K_i,V\otimes _SK_{i-1})\cong \operatorname {Hom} _{S^{{\operatorname {en} }}}(K_{i-1}^{\vee },K_i^{\vee }\otimes _SV)$ and
$\operatorname {Hom} _{S^{{\operatorname {en} }}}(K_i,V\otimes _SK_{i-1})\cong \operatorname {Hom} _{S^{{\operatorname {en} }}}(K_{i-1}^{\vee },K_i^{\vee }\otimes _SV)$ and ![]() $\operatorname {Hom} _{S^{{\operatorname {en} }}}(K_i,K_{i-1}\otimes _SV)\cong \operatorname {Hom} _{S^{{\operatorname {en} }}}(K_{i-1}^{\vee },V\otimes _SK_i^{\vee })$. Thus, the inclusions
$\operatorname {Hom} _{S^{{\operatorname {en} }}}(K_i,K_{i-1}\otimes _SV)\cong \operatorname {Hom} _{S^{{\operatorname {en} }}}(K_{i-1}^{\vee },V\otimes _SK_i^{\vee })$. Thus, the inclusions ![]() $\iota _i^{\ell }:K_i\to V\otimes _SK_{i-1}$ and
$\iota _i^{\ell }:K_i\to V\otimes _SK_{i-1}$ and ![]() $\iota _i^{r}:K_i\to K_{i-1}\otimes _SV$ give rise to
$\iota _i^{r}:K_i\to K_{i-1}\otimes _SV$ give rise to
We need the following observations.
Lemma 3.9 The following assertions hold.
(a) The map
 $(\bar {V}^{d-1})^{\vee }\twoheadrightarrow K_{d-1}^{\vee }\xrightarrow {\theta _d^{r}}V\otimes _SK_d^{\vee }\hookrightarrow \bar {V}^{2}$ coincides with
$(\bar {V}^{d-1})^{\vee }\twoheadrightarrow K_{d-1}^{\vee }\xrightarrow {\theta _d^{r}}V\otimes _SK_d^{\vee }\hookrightarrow \bar {V}^{2}$ coincides with  $-\cdot W:(\bar {V}^{d-1})^{\vee }\to \bar {V}^{2}$.
$-\cdot W:(\bar {V}^{d-1})^{\vee }\to \bar {V}^{2}$.(b) The map
 $(\bar {V}^{d-1})^{\vee }\twoheadrightarrow K_{d-1}^{\vee }\xrightarrow {\theta _d^{\ell }}K_d^{\vee }\otimes _SV\hookrightarrow \bar {V}^{2}$ coincides with
$(\bar {V}^{d-1})^{\vee }\twoheadrightarrow K_{d-1}^{\vee }\xrightarrow {\theta _d^{\ell }}K_d^{\vee }\otimes _SV\hookrightarrow \bar {V}^{2}$ coincides with  $-\cdot \rho (W):(\bar {V}^{d-1})^{\vee }\to \bar {V}^{2}$.
$-\cdot \rho (W):(\bar {V}^{d-1})^{\vee }\to \bar {V}^{2}$.
Proof. (a) By definition, ![]() $W$ belongs to the subspace
$W$ belongs to the subspace ![]() $c\big (K_{d-1}\otimes _SV\otimes _SK_d^{\vee }\big )$ of
$c\big (K_{d-1}\otimes _SV\otimes _SK_d^{\vee }\big )$ of ![]() $c(\bar {V}^{d+1})$, and coincides with
$c(\bar {V}^{d+1})$, and coincides with ![]() $\iota _d^{r}$ under the isomorphism
$\iota _d^{r}$ under the isomorphism ![]() $\operatorname {Hom} _{S^{{\operatorname {en} }}}(K_d,K_{d-1}\otimes _SV)\cong c\big (K_{d-1}\otimes _SV\otimes _SK_d^{\vee }\big )$ in Lemma 3.7. By definition,
$\operatorname {Hom} _{S^{{\operatorname {en} }}}(K_d,K_{d-1}\otimes _SV)\cong c\big (K_{d-1}\otimes _SV\otimes _SK_d^{\vee }\big )$ in Lemma 3.7. By definition, ![]() $\theta _d^{r}$ is the image of
$\theta _d^{r}$ is the image of ![]() $W$ under the isomorphism
$W$ under the isomorphism ![]() $c\big (K_{d-1}\otimes _SV\otimes _SK_d^{\vee }\big )\cong \operatorname {Hom} _{S^{{\operatorname {en} }}}\big (K_{d-1}^{\vee },V\otimes _SK_d^{\vee }\big )$ in Lemma 3.7. Thus,
$c\big (K_{d-1}\otimes _SV\otimes _SK_d^{\vee }\big )\cong \operatorname {Hom} _{S^{{\operatorname {en} }}}\big (K_{d-1}^{\vee },V\otimes _SK_d^{\vee }\big )$ in Lemma 3.7. Thus, ![]() $\theta _d^{r}$ coincides with
$\theta _d^{r}$ coincides with
On the other hand, because ![]() $W$ belongs to
$W$ belongs to ![]() $c\big (K_{d-1}\otimes _SV\otimes _SK_d^{\vee }\big )$, the map
$c\big (K_{d-1}\otimes _SV\otimes _SK_d^{\vee }\big )$, the map ![]() $-\cdot W$ factors through the surjection
$-\cdot W$ factors through the surjection ![]() $(\bar{V}^{d-1})^\vee\to K_{d-1}^\vee$. Thus, the assertion follows.
$(\bar{V}^{d-1})^\vee\to K_{d-1}^\vee$. Thus, the assertion follows.
(b) Although the argument is mostly the same as (a), we record the details.
By definition, ![]() $W$ belongs to the subspace
$W$ belongs to the subspace ![]() $c\big (V\otimes _SK_{d-1}\otimes _SK_d^{\vee }\big )$ of
$c\big (V\otimes _SK_{d-1}\otimes _SK_d^{\vee }\big )$ of ![]() $c(\bar {V}^{d+1})$, and coincides with
$c(\bar {V}^{d+1})$, and coincides with ![]() $\iota _d^{\ell }$ under the isomorphism
$\iota _d^{\ell }$ under the isomorphism ![]() $\operatorname {Hom} _{S^{{\operatorname {en} }}}(K_d,V\otimes _SK_{d-1})\cong c\big (V\otimes _SK_{d-1}\otimes _SK_d^{\vee }\big )$ in Lemma 3.7. By definition,
$\operatorname {Hom} _{S^{{\operatorname {en} }}}(K_d,V\otimes _SK_{d-1})\cong c\big (V\otimes _SK_{d-1}\otimes _SK_d^{\vee }\big )$ in Lemma 3.7. By definition, ![]() $\theta _d^{\ell }$ is the image of
$\theta _d^{\ell }$ is the image of ![]() $W$ under the isomorphism
$W$ under the isomorphism ![]() $c\big (V\otimes _SK_{d-1}\otimes _SK_d^{\vee }\big )\cong \operatorname {Hom} _{S^{{\operatorname {en} }}}\big (K_{d-1}^{\vee },K_d^{\vee }\otimes _SV\big )$ in Lemma 3.7. Thus,
$c\big (V\otimes _SK_{d-1}\otimes _SK_d^{\vee }\big )\cong \operatorname {Hom} _{S^{{\operatorname {en} }}}\big (K_{d-1}^{\vee },K_d^{\vee }\otimes _SV\big )$ in Lemma 3.7. Thus, ![]() $\theta _d^{\ell }$ coincides with
$\theta _d^{\ell }$ coincides with
which equals ![]() $K_{d-1}^{\vee }\xrightarrow {1\otimes \rho (W)}K_{d-1}^{\vee }\otimes _{\mathbb {F}} c\big (K_{d-1}\otimes _SK_d^{\vee }\otimes _SV\big )\xrightarrow {\operatorname {ev} _{K_{d-1}}\otimes 1\otimes 1}V\otimes _SK_d^{\vee }$.
$K_{d-1}^{\vee }\xrightarrow {1\otimes \rho (W)}K_{d-1}^{\vee }\otimes _{\mathbb {F}} c\big (K_{d-1}\otimes _SK_d^{\vee }\otimes _SV\big )\xrightarrow {\operatorname {ev} _{K_{d-1}}\otimes 1\otimes 1}V\otimes _SK_d^{\vee }$.
On the other hand, because ![]() $\rho (W)$ belongs to
$\rho (W)$ belongs to ![]() $c\big (K_{d-1}\otimes _SK_d^{\vee }\otimes _SV\big )$, the map
$c\big (K_{d-1}\otimes _SK_d^{\vee }\otimes _SV\big )$, the map ![]() $-\cdot \rho (W)$ factors through the surjection
$-\cdot \rho (W)$ factors through the surjection ![]() $(\bar{V}^{d-1})^\vee\to K_{d-1}^\vee$. Thus, the assertion follows.
$(\bar{V}^{d-1})^\vee\to K_{d-1}^\vee$. Thus, the assertion follows.
On the other hand, ![]() $\theta _i^{\ell }$ and
$\theta _i^{\ell }$ and ![]() $\theta _i^{r}$ induce morphisms
$\theta _i^{r}$ induce morphisms ![]() $\hat {\theta }^{\ell }_i$ and
$\hat {\theta }^{\ell }_i$ and ![]() ${\hat {\theta }^{r}_i:\Lambda \otimes _SK_{i-1}^{\vee }\otimes _S\Lambda \to \Lambda \otimes _SK_{i}^{\vee }\otimes _S\Lambda}$ of
${\hat {\theta }^{r}_i:\Lambda \otimes _SK_{i-1}^{\vee }\otimes _S\Lambda \to \Lambda \otimes _SK_{i}^{\vee }\otimes _S\Lambda}$ of ![]() $\Lambda ^{{\operatorname {en} }}$-modules. This gives an explicit construction of
$\Lambda ^{{\operatorname {en} }}$-modules. This gives an explicit construction of ![]() $\delta _i'$ in (7) by the following observation.
$\delta _i'$ in (7) by the following observation.
Lemma 3.10 If ![]() $\Lambda$ is Koszul, then we have a commutative diagram
$\Lambda$ is Koszul, then we have a commutative diagram

and therefore ![]() $\delta _i'=\hat {\theta }^{\ell }_i+(-1)^{i}\hat {\theta }^{r}_i$.
$\delta _i'=\hat {\theta }^{\ell }_i+(-1)^{i}\hat {\theta }^{r}_i$.
To prove this, we prepare the following observation.
Lemma 3.11 For ![]() $S^{{\operatorname {en} }}$-modules
$S^{{\operatorname {en} }}$-modules ![]() $X$ and
$X$ and ![]() $Y$, we have the following commutative diagram.
$Y$, we have the following commutative diagram.

where we write ![]() $(-)^{\vee _{\Lambda} }=\operatorname {Hom} _{\Lambda ^{{\operatorname {en} }}}(-,\Lambda ^{{\operatorname {en} }})$.
$(-)^{\vee _{\Lambda} }=\operatorname {Hom} _{\Lambda ^{{\operatorname {en} }}}(-,\Lambda ^{{\operatorname {en} }})$.
Proof. Fix ![]() $y\otimes v\otimes f\in c(Y\otimes _SV\otimes _SX^{\vee })$, and let
$y\otimes v\otimes f\in c(Y\otimes _SV\otimes _SX^{\vee })$, and let ![]() $a\in \operatorname {Hom} _{\Lambda ^{{\operatorname {en} }}}(\Lambda \otimes _SX\otimes _S\Lambda ,\Lambda \otimes _SY\otimes _S\Lambda )$ and
$a\in \operatorname {Hom} _{\Lambda ^{{\operatorname {en} }}}(\Lambda \otimes _SX\otimes _S\Lambda ,\Lambda \otimes _SY\otimes _S\Lambda )$ and ![]() $b\in \operatorname {Hom} _{\Lambda ^{{\operatorname {en} }}}(\Lambda \otimes _SY^{\vee }\otimes _S\Lambda ,\Lambda \otimes _SX^{\vee }\otimes _S\Lambda )$ be the corresponding maps. Let
$b\in \operatorname {Hom} _{\Lambda ^{{\operatorname {en} }}}(\Lambda \otimes _SY^{\vee }\otimes _S\Lambda ,\Lambda \otimes _SX^{\vee }\otimes _S\Lambda )$ be the corresponding maps. Let ![]() $a'$ and
$a'$ and ![]() $b'$ be the maps in
$b'$ be the maps in ![]() $\operatorname {Hom} _{\Lambda ^{{\operatorname {en} }}}((\Lambda \otimes _SY\otimes _S\Lambda )^{\vee _{\Lambda} },(\Lambda \otimes _SX\otimes _S\Lambda )^{\vee _{\Lambda} })$ corresponding to
$\operatorname {Hom} _{\Lambda ^{{\operatorname {en} }}}((\Lambda \otimes _SY\otimes _S\Lambda )^{\vee _{\Lambda} },(\Lambda \otimes _SX\otimes _S\Lambda )^{\vee _{\Lambda} })$ corresponding to ![]() $a$ and
$a$ and ![]() $b$, respectively. To prove
$b$, respectively. To prove ![]() $a'=b'$, it suffices to show that
$a'=b'$, it suffices to show that ![]() $a'(g^\prime)=b'(g^\prime)$ holds for all
$a'(g^\prime)=b'(g^\prime)$ holds for all ![]() $g\in Y^{\vee }$, where
$g\in Y^{\vee }$, where ![]() $g^\prime\in (\Lambda \otimes _SY\otimes _S\Lambda )^{\vee _{\Lambda} }$ is the natural extension of
$g^\prime\in (\Lambda \otimes _SY\otimes _S\Lambda )^{\vee _{\Lambda} }$ is the natural extension of ![]() $g$.
$g$.
As ![]() $a(1\otimes x\otimes 1)=(1\otimes y\otimes v)f(x)=(1\otimes y\otimes 1)((v\otimes 1)f(x))$ holds for all
$a(1\otimes x\otimes 1)=(1\otimes y\otimes v)f(x)=(1\otimes y\otimes 1)((v\otimes 1)f(x))$ holds for all ![]() $x\in X$, we have
$x\in X$, we have ![]() $(a'(g^\prime))(1\otimes x\otimes 1)=g(y)(v\otimes 1)f(x)$. On the other hand, since
$(a'(g^\prime))(1\otimes x\otimes 1)=g(y)(v\otimes 1)f(x)$. On the other hand, since ![]() $b(g^\prime)=g(y)(v\otimes f\otimes 1)=(g(y)(v\otimes 1))(1\otimes f\otimes 1)$ holds for all
$b(g^\prime)=g(y)(v\otimes f\otimes 1)=(g(y)(v\otimes 1))(1\otimes f\otimes 1)$ holds for all ![]() $g\in Y^{\vee }$, we have
$g\in Y^{\vee }$, we have ![]() $(b'(g^\prime))(1\otimes x\otimes 1)=g(y)(v\otimes 1)f(x)$. Thus,
$(b'(g^\prime))(1\otimes x\otimes 1)=g(y)(v\otimes 1)f(x)$. Thus, ![]() $a'=b'$ holds.
$a'=b'$ holds.
Proof of Lemma 3.10 As ![]() $\delta _i=\hat {\iota }_i^{\ell }+(-1)^{i}\hat {\iota }_i^{r}$, it suffices to show that the following diagram commutes for
$\delta _i=\hat {\iota }_i^{\ell }+(-1)^{i}\hat {\iota }_i^{r}$, it suffices to show that the following diagram commutes for ![]() $s\in \{\ell ,r\}$.
$s\in \{\ell ,r\}$.

We just show the ![]() $s=r$ version;
$s=r$ version; ![]() $s=\ell$ is the dual. We apply Lemma 3.11 to
$s=\ell$ is the dual. We apply Lemma 3.11 to ![]() $X:=K_i$ and
$X:=K_i$ and ![]() $Y:=K_{i-1}$. As
$Y:=K_{i-1}$. As ![]() $\iota _i^{r}\in \operatorname {Hom} _{S^{{\operatorname {en} }}}(K_i,K_{i-1}\otimes _SV)$ corresponds to
$\iota _i^{r}\in \operatorname {Hom} _{S^{{\operatorname {en} }}}(K_i,K_{i-1}\otimes _SV)$ corresponds to ![]() $\theta _i^{r}\in \operatorname {Hom} _{S^{{\operatorname {en} }}}(K_{i-1}^{\vee },V\otimes _SK_i^{\vee })$, the map
$\theta _i^{r}\in \operatorname {Hom} _{S^{{\operatorname {en} }}}(K_{i-1}^{\vee },V\otimes _SK_i^{\vee })$, the map ![]() ${}_{\Lambda ^{{\operatorname {en} }}}(\hat {\iota }_i^{r},\Lambda ^{{\operatorname {en} }})$ coincides with
${}_{\Lambda ^{{\operatorname {en} }}}(\hat {\iota }_i^{r},\Lambda ^{{\operatorname {en} }})$ coincides with ![]() $\hat {\theta }_i^{r}$ up to the isomorphisms in Lemma 2.3. This gives the commutativity of the diagram.
$\hat {\theta }_i^{r}$ up to the isomorphisms in Lemma 2.3. This gives the commutativity of the diagram.
As ![]() $\Lambda$ is Koszul, we can regard
$\Lambda$ is Koszul, we can regard ![]() $\delta _d'(K_{d-1}^{\vee })\subset V\otimes _SK_d^{\vee }\otimes _SS+S\otimes _SK_d^{\vee }\otimes _SV$ as a subspace of
$\delta _d'(K_{d-1}^{\vee })\subset V\otimes _SK_d^{\vee }\otimes _SS+S\otimes _SK_d^{\vee }\otimes _SV$ as a subspace of ![]() $T\otimes _SK_d^{\vee }\otimes _ST\subset \operatorname {T} _S(\bar {V})$ naturally. Now we show the following assertion.
$T\otimes _SK_d^{\vee }\otimes _ST\subset \operatorname {T} _S(\bar {V})$ naturally. Now we show the following assertion.
Proposition 3.12 If ![]() $\Lambda =\operatorname {T} _S(V)/(R)$ is a finite-dimensional Koszul algebra of global dimension
$\Lambda =\operatorname {T} _S(V)/(R)$ is a finite-dimensional Koszul algebra of global dimension ![]() $d$ with
$d$ with ![]() $R\subset V^{2}$, then we have an isomorphism of algebras:
$R\subset V^{2}$, then we have an isomorphism of algebras:
In particular, ![]() $\Pi$ is quadratic.
$\Pi$ is quadratic.
Proof. The first assertion is immediate from Proposition 3.2(b). The second assertion is immediate from the first because both ![]() $R$ and
$R$ and ![]() $\delta _d'(K_{d-1}^{\vee })$ are contained in
$\delta _d'(K_{d-1}^{\vee })$ are contained in ![]() $\bar {V}^{2}$.
$\bar {V}^{2}$.
Now we are ready to prove the following.
Theorem 3.13 If ![]() $\Lambda =\operatorname {T} _S(V)/(R)$ is a finite-dimensional Koszul algebra of global dimension
$\Lambda =\operatorname {T} _S(V)/(R)$ is a finite-dimensional Koszul algebra of global dimension ![]() $d$, then we have an isomorphism of algebras:
$d$, then we have an isomorphism of algebras:
Proof. The left-hand side is ![]() $\operatorname {T} _S(\bar {V})/(R+\delta _d'(K_{d-1}^{\vee }))$ by Proposition 3.12, and the right-hand side is
$\operatorname {T} _S(\bar {V})/(R+\delta _d'(K_{d-1}^{\vee }))$ by Proposition 3.12, and the right-hand side is ![]() $\operatorname {T} _S(\bar {V})/(R+(\bar {V}^{d-1})^{\vee }\cdot \varphi (W))$ by definition. It suffices to prove
$\operatorname {T} _S(\bar {V})/(R+(\bar {V}^{d-1})^{\vee }\cdot \varphi (W))$ by definition. It suffices to prove ![]() $R+\delta _d'(K_{d-1}^{\vee })=R+(\bar {V}^{d-1})^{\vee }\cdot \varphi (W)$.
$R+\delta _d'(K_{d-1}^{\vee })=R+(\bar {V}^{d-1})^{\vee }\cdot \varphi (W)$.
As ![]() $K_d={\bigcap} _{i=2}^{d}V^{i-2}\otimes _SR\otimes _SV^{d-i}$, for each
$K_d={\bigcap} _{i=2}^{d}V^{i-2}\otimes _SR\otimes _SV^{d-i}$, for each ![]() $2\le i\le d$ we have
$2\le i\le d$ we have
and, hence, ![]() $\rho ^{i}(W)\in c\big (V^{d-i}\otimes _SK_d^{\vee }\otimes _SV^{i-2}\otimes _SR\big )$. Therefore,
$\rho ^{i}(W)\in c\big (V^{d-i}\otimes _SK_d^{\vee }\otimes _SV^{i-2}\otimes _SR\big )$. Therefore, ![]() $(\bar {V}^{d-1})^{\vee }\cdot \rho ^{i}(W)\subset R$ holds. In particular,
$(\bar {V}^{d-1})^{\vee }\cdot \rho ^{i}(W)\subset R$ holds. In particular,
 \begin{align*} R+(\bar{V}^{d-1})^{{\vee}}\cdot\varphi(W) &= R+(\bar{V}^{d-1})^{{\vee}} \cdot(W+({-}1)^{d}\rho(W))\stackrel{\text{Lemma (3.9)}}{=}R+(\theta_d^{r}+({-}1)^{d}\theta_d^{\ell}) (K_{d-1}^{{\vee}})\\ &\hspace{-1.6pc}\stackrel{\text{Lemma (3.10)}}{=} R+\delta_d'(K_{d-1}^{{\vee}}) \end{align*}
\begin{align*} R+(\bar{V}^{d-1})^{{\vee}}\cdot\varphi(W) &= R+(\bar{V}^{d-1})^{{\vee}} \cdot(W+({-}1)^{d}\rho(W))\stackrel{\text{Lemma (3.9)}}{=}R+(\theta_d^{r}+({-}1)^{d}\theta_d^{\ell}) (K_{d-1}^{{\vee}})\\ &\hspace{-1.6pc}\stackrel{\text{Lemma (3.10)}}{=} R+\delta_d'(K_{d-1}^{{\vee}}) \end{align*}holds as desired.
The extension condition in the following theorem is a special case of the following property of [Reference Iyama and OppermannIO13, Section 3]. Given a ![]() $d$-cluster tilting subcategory
$d$-cluster tilting subcategory ![]() $\mathscr {U}$ of
$\mathscr {U}$ of ![]() ${{D^{b}}}(\Lambda )$, we say that
${{D^{b}}}(\Lambda )$, we say that ![]() $\mathscr {U}$ has the vosnex property (‘vanishing of small negative extensions’) if
$\mathscr {U}$ has the vosnex property (‘vanishing of small negative extensions’) if ![]() $\operatorname {Hom} _{{{D^{b}}}(\Lambda )}(\mathscr {U}[j],\mathscr {U})=0$ for
$\operatorname {Hom} _{{{D^{b}}}(\Lambda )}(\mathscr {U}[j],\mathscr {U})=0$ for ![]() $j\in \{1,2,\ldots , d-2\}$. In this case, because
$j\in \{1,2,\ldots , d-2\}$. In this case, because ![]() $\Lambda ,\Lambda ^{*}[-d]\in \mathscr {U}$, we have
$\Lambda ,\Lambda ^{*}[-d]\in \mathscr {U}$, we have ![]() $\operatorname {Ext} ^{d-j}_{\Lambda ^{{\operatorname {en} }}}(\Lambda ,\Lambda ^{{\operatorname {en} }})\cong \operatorname {Ext} ^{d-j}_{\Lambda }(\Lambda ^{*},\Lambda )\cong \operatorname {Hom} _{{{D^{b}}}(\Lambda )}(\Lambda ^{*}[j-d],\Lambda )=0$ for
$\operatorname {Ext} ^{d-j}_{\Lambda ^{{\operatorname {en} }}}(\Lambda ,\Lambda ^{{\operatorname {en} }})\cong \operatorname {Ext} ^{d-j}_{\Lambda }(\Lambda ^{*},\Lambda )\cong \operatorname {Hom} _{{{D^{b}}}(\Lambda )}(\Lambda ^{*}[j-d],\Lambda )=0$ for ![]() $j\in \{1,2,\ldots , d-2\}$.
$j\in \{1,2,\ldots , d-2\}$.
Theorem 3.14 Suppose ![]() $\Lambda$ is a finite-dimensional Koszul algebra of global dimension
$\Lambda$ is a finite-dimensional Koszul algebra of global dimension ![]() $d$. If
$d$. If ![]() $\operatorname {Ext} ^{i}_{\Lambda ^{{\operatorname {en} }}}(\Lambda ,\Lambda ^{{\operatorname {en} }})_{-i}=0$ for
$\operatorname {Ext} ^{i}_{\Lambda ^{{\operatorname {en} }}}(\Lambda ,\Lambda ^{{\operatorname {en} }})_{-i}=0$ for ![]() $2\leq i\leq d-1$, then we have an isomorphism of algebras:
$2\leq i\leq d-1$, then we have an isomorphism of algebras:
Proof. By Theorem 3.13, it suffices to prove ![]() $(\bar {V}^{d-1})^{\vee }\cdot \varphi (W)\supseteq R$. In fact, for each
$(\bar {V}^{d-1})^{\vee }\cdot \varphi (W)\supseteq R$. In fact, for each ![]() $2\le i\le d$, we prove by downwards induction
$2\le i\le d$, we prove by downwards induction
First we prove (16) for ![]() $i=d$. Consider the decomposition
$i=d$. Consider the decomposition ![]() $\bar {V}^{\vee }=V^{\vee }\oplus K_d$. Since
$\bar {V}^{\vee }=V^{\vee }\oplus K_d$. Since ![]() $W=\operatorname {coev} _{K_d}(1_{\mathbb {F}})$, we have
$W=\operatorname {coev} _{K_d}(1_{\mathbb {F}})$, we have ![]() $K_d\cdot \rho ^{d}(W)=K_d$ and
$K_d\cdot \rho ^{d}(W)=K_d$ and ![]() $K_d\cdot \rho ^{i}(W)=0$ for each
$K_d\cdot \rho ^{i}(W)=0$ for each ![]() $0\le i\le d-1$. Thus,
$0\le i\le d-1$. Thus, ![]() $\bar {V}^{\vee }\cdot \varphi (W)\supseteq K_d\cdot \varphi (W)=K_d$ holds.
$\bar {V}^{\vee }\cdot \varphi (W)\supseteq K_d\cdot \varphi (W)=K_d$ holds.
Next, for each ![]() $3\le i\le d$, we prove
$3\le i\le d$, we prove
where ![]() $\cdot$ are the maps
$\cdot$ are the maps ![]() $\operatorname {Hom} _{S^{{\operatorname {op} }}}(V,S)\otimes _SV^{i}\to V^{i-1}$ and
$\operatorname {Hom} _{S^{{\operatorname {op} }}}(V,S)\otimes _SV^{i}\to V^{i-1}$ and ![]() $V^{i}\otimes _S\operatorname {Hom} _{S}(V,S)\to V^{i-1}$ given by the evaluations. We use the Koszul resolution together with Lemma 3.10. These tell us that
$V^{i}\otimes _S\operatorname {Hom} _{S}(V,S)\to V^{i-1}$ given by the evaluations. We use the Koszul resolution together with Lemma 3.10. These tell us that ![]() $\operatorname {Ext} ^{i-1}_{\Lambda ^{{\operatorname {en} }}}(\Lambda ,\Lambda ^{{\operatorname {en} }})$ is the
$\operatorname {Ext} ^{i-1}_{\Lambda ^{{\operatorname {en} }}}(\Lambda ,\Lambda ^{{\operatorname {en} }})$ is the ![]() $(i-1)$th homology of the complex
$(i-1)$th homology of the complex
where the differentials are induced by the maps
This is injective since its kernel is ![]() $\operatorname {Ext} ^{i-1}_{\Lambda ^{{\operatorname {en} }}}(\Lambda ,\Lambda ^{{\operatorname {en} }})_{1-i}=0$ by our assumption. Applying
$\operatorname {Ext} ^{i-1}_{\Lambda ^{{\operatorname {en} }}}(\Lambda ,\Lambda ^{{\operatorname {en} }})_{1-i}=0$ by our assumption. Applying ![]() $(-)^{\vee }$, we have a surjective map
$(-)^{\vee }$, we have a surjective map
This is a restriction of the map ![]() $(\operatorname {Hom} _{S^{{\operatorname {op} }}}(V,S)\otimes _SV^{i})\oplus (V^{i}\otimes _S\operatorname {Hom} _{S}(V,S))\to V^{i-1}$ given by the evaluations. Thus, (17) holds.
$(\operatorname {Hom} _{S^{{\operatorname {op} }}}(V,S)\otimes _SV^{i})\oplus (V^{i}\otimes _S\operatorname {Hom} _{S}(V,S))\to V^{i-1}$ given by the evaluations. Thus, (17) holds.
Now assume (16) holds. Applying the upper part of (14) to ![]() $(X,Y,Z)=(\bar {V}^{d-i+1},\bar {V},\bar {V}^{i-1})$ and the lower part to
$(X,Y,Z)=(\bar {V}^{d-i+1},\bar {V},\bar {V}^{i-1})$ and the lower part to ![]() $(X,Y,Z)=(\bar {V},\bar {V}^{d-i+1},\bar {V}^{i-1})$, we obtain
$(X,Y,Z)=(\bar {V},\bar {V}^{d-i+1},\bar {V}^{i-1})$, we obtain
 \begin{align*} & (\bar{V}^{d-i+2})^{{\vee}}\cdot\varphi(W)\stackrel{(14)}{=} \operatorname{Hom}_{S^{{\operatorname{op}}}}(\bar{V},S)\cdot((\bar{V}^{d-i+1})^{{\vee}}\cdot\varphi(W)) \stackrel{(16)}{\supseteq} \operatorname{Hom}_{S^{{\operatorname{op}}}}(\bar{V},S)\cdot K_i,\\ & (\bar{V}^{d-i+2})^{{\vee}}\cdot\varphi(W)\stackrel{(14)}{=} ((\bar{V}^{d-i+1})^{{\vee}}\cdot\varphi(W))\cdot\operatorname{Hom}_S(\bar{V},S) \stackrel{(16)}{\supseteq} K_i\cdot\operatorname{Hom}_S(\bar{V},S). \end{align*}
\begin{align*} & (\bar{V}^{d-i+2})^{{\vee}}\cdot\varphi(W)\stackrel{(14)}{=} \operatorname{Hom}_{S^{{\operatorname{op}}}}(\bar{V},S)\cdot((\bar{V}^{d-i+1})^{{\vee}}\cdot\varphi(W)) \stackrel{(16)}{\supseteq} \operatorname{Hom}_{S^{{\operatorname{op}}}}(\bar{V},S)\cdot K_i,\\ & (\bar{V}^{d-i+2})^{{\vee}}\cdot\varphi(W)\stackrel{(14)}{=} ((\bar{V}^{d-i+1})^{{\vee}}\cdot\varphi(W))\cdot\operatorname{Hom}_S(\bar{V},S) \stackrel{(16)}{\supseteq} K_i\cdot\operatorname{Hom}_S(\bar{V},S). \end{align*}
Thus, ![]() $(\bar {V}^{d-i+2})^{\vee }\cdot \varphi (W)\supseteq \operatorname {Hom} _{S^{{\operatorname {op} }}}(V,S)\cdot K_i+K_i\cdot \operatorname {Hom} _S(V,S)\stackrel {(17)}{=}K_{i-1}$ holds, which completes the induction.
$(\bar {V}^{d-i+2})^{\vee }\cdot \varphi (W)\supseteq \operatorname {Hom} _{S^{{\operatorname {op} }}}(V,S)\cdot K_i+K_i\cdot \operatorname {Hom} _S(V,S)\stackrel {(17)}{=}K_{i-1}$ holds, which completes the induction.
Note that the condition of Theorem 3.14 is vacuous when ![]() $d=2$, so this result agrees with Keller's description of
$d=2$, so this result agrees with Keller's description of ![]() $3$-preprojective algebras (see [Reference KellerKel11, Theorem 6.10, Reference Herschend and IyamaHI11, Section 2.2]).
$3$-preprojective algebras (see [Reference KellerKel11, Theorem 6.10, Reference Herschend and IyamaHI11, Section 2.2]).
We will see in Corollary 4.3 that this theorem is particularly applicable to ![]() $d$-hereditary algebras.
$d$-hereditary algebras.
Example 3.15 (a) Consider the quiver
and the algebra ![]() $\Lambda =\mathbb {F} Q/(\alpha \beta ,\beta \gamma )$. One can check that it satisfies the conditions of Theorem 3.14 for
$\Lambda =\mathbb {F} Q/(\alpha \beta ,\beta \gamma )$. One can check that it satisfies the conditions of Theorem 3.14 for ![]() $d=3$. (In fact,
$d=3$. (In fact, ![]() $\Lambda$ is Koszul and
$\Lambda$ is Koszul and ![]() $3$-representation finite, see Definition 4.4.) We have
$3$-representation finite, see Definition 4.4.) We have ![]() $K_3=\langle {\alpha \beta \gamma }\rangle$ so the quiver
$K_3=\langle {\alpha \beta \gamma }\rangle$ so the quiver ![]() $\bar {Q}$ of
$\bar {Q}$ of ![]() $\Pi =\Pi (\Lambda )$ is
$\Pi =\Pi (\Lambda )$ is

where ![]() $\eta =(\alpha \beta \gamma )^{*}$. The superpotential
$\eta =(\alpha \beta \gamma )^{*}$. The superpotential ![]() $W$ is represented by
$W$ is represented by ![]() $\alpha \beta \gamma {\eta }$ and the space of relations of
$\alpha \beta \gamma {\eta }$ and the space of relations of ![]() $\Pi$ is given by
$\Pi$ is given by ![]() $\bar {V}^{-2}\cdot \varphi (W) =\langle {\alpha \beta ,\beta \gamma ,\gamma {\eta },{\eta }\alpha }\rangle$.
$\bar {V}^{-2}\cdot \varphi (W) =\langle {\alpha \beta ,\beta \gamma ,\gamma {\eta },{\eta }\alpha }\rangle$.
(b) Next consider the quiver
and the algebra ![]() $\Lambda =\mathbb {F} Q/(R)$ with
$\Lambda =\mathbb {F} Q/(R)$ with ![]() $R=\langle \alpha \beta ,\beta \gamma ,\delta \varepsilon \rangle$. One can check that
$R=\langle \alpha \beta ,\beta \gamma ,\delta \varepsilon \rangle$. One can check that ![]() $\Lambda$ has global dimension
$\Lambda$ has global dimension ![]() $3$ and is Koszul, but it does not satisfy the condition of Theorem 3.14 as
$3$ and is Koszul, but it does not satisfy the condition of Theorem 3.14 as ![]() $\operatorname {Ext} ^{2}_{\Lambda }(\Lambda ^{*} e_6,\Lambda e_4)_{-2}\neq 0$. Again, we have
$\operatorname {Ext} ^{2}_{\Lambda }(\Lambda ^{*} e_6,\Lambda e_4)_{-2}\neq 0$. Again, we have ![]() $K_3=\langle {\alpha \beta \gamma }\rangle$ so the quiver
$K_3=\langle {\alpha \beta \gamma }\rangle$ so the quiver ![]() $\bar {Q}$ of
$\bar {Q}$ of ![]() $\Pi (\Lambda )$ is
$\Pi (\Lambda )$ is

where ![]() ${\eta =}(\alpha \beta \gamma )^{*}$. The superpotential
${\eta =}(\alpha \beta \gamma )^{*}$. The superpotential ![]() $W$ is represented by
$W$ is represented by ![]() $\alpha \beta \gamma {\eta }$ and the
$\alpha \beta \gamma {\eta }$ and the ![]() $2$-Jacobi ideal is generated by
$2$-Jacobi ideal is generated by ![]() $\bar {V}^{-2}\cdot \varphi (W) =\langle {\alpha \beta ,\beta \gamma ,\gamma {\eta },{\eta }\alpha }\rangle$. We see that this does not include
$\bar {V}^{-2}\cdot \varphi (W) =\langle {\alpha \beta ,\beta \gamma ,\gamma {\eta },{\eta }\alpha }\rangle$. We see that this does not include ![]() $\delta \varepsilon$, and so to obtain the whole space of relations of
$\delta \varepsilon$, and so to obtain the whole space of relations of ![]() $\Pi$ we need to consider
$\Pi$ we need to consider ![]() $R+\bar {V}^{-2}\cdot \varphi (W)$.
$R+\bar {V}^{-2}\cdot \varphi (W)$.
Remark 3.16 It is worth pointing out that higher preprojective algebras are sometimes higher Jacobi algebras even in the non-Koszul case. For example, consider the following example, due to Vaso [Reference VasoVas19, Example 5.3], of an algebra of global dimension 4 that satisfies the Ext-vanishing condition of Theorem 3.14. (In fact, ![]() $\Lambda$ is
$\Lambda$ is ![]() $4$-representation finite, see Definition 4.4.) We take the quiver
$4$-representation finite, see Definition 4.4.) We take the quiver
and the algebra ![]() $\Lambda =\mathbb {F} Q/(\operatorname {rad} \mathbb {F} Q)^{4}=\mathbb {F} Q/(\alpha \beta \gamma \delta , \beta \gamma \delta \varepsilon , \gamma \delta \varepsilon \zeta , \delta \varepsilon \zeta \eta , \varepsilon \zeta \eta \theta )$. We know from Proposition 3.2 that the quiver for
$\Lambda =\mathbb {F} Q/(\operatorname {rad} \mathbb {F} Q)^{4}=\mathbb {F} Q/(\alpha \beta \gamma \delta , \beta \gamma \delta \varepsilon , \gamma \delta \varepsilon \zeta , \delta \varepsilon \zeta \eta , \varepsilon \zeta \eta \theta )$. We know from Proposition 3.2 that the quiver for ![]() $\Pi$ is
$\Pi$ is

where ![]() $\iota =(\alpha \beta \gamma \delta \varepsilon \zeta \eta \theta )^{*}$, and one can check that
$\iota =(\alpha \beta \gamma \delta \varepsilon \zeta \eta \theta )^{*}$, and one can check that ![]() $\Pi$ is, in fact, a
$\Pi$ is, in fact, a ![]() $5$-Jacobi algebra: we obtain its relations by differentiating the superpotential represented by
$5$-Jacobi algebra: we obtain its relations by differentiating the superpotential represented by ![]() $W=\alpha \beta \gamma \delta \varepsilon \zeta \eta \theta \iota$ with respect to paths of length
$W=\alpha \beta \gamma \delta \varepsilon \zeta \eta \theta \iota$ with respect to paths of length ![]() $5$.
$5$.
We do not know an example of a non-Koszul algebra that satisfies the Ext-vanishing condition of Theorem 3.14 but is not a higher Jacobi algebra.
4. Resolutions of simple modules over higher preprojective algebras
The aim of this section is to construct projective resolutions of simple modules for preprojective algebras of ![]() $d$-hereditary algebras.
$d$-hereditary algebras.
4.1 Preliminaries on  $d$-hereditary algebras
$d$-hereditary algebras
Let ![]() $\Lambda$ be a finite-dimensional
$\Lambda$ be a finite-dimensional ![]() $\mathbb {F}$-algebra with
$\mathbb {F}$-algebra with ![]() $\mathop {\textrm {gl.dim}} \Lambda \le d$, and
$\mathop {\textrm {gl.dim}} \Lambda \le d$, and ![]() ${{D^{b}}}(\Lambda )$ the derived category of finitely generated left
${{D^{b}}}(\Lambda )$ the derived category of finitely generated left ![]() $\Lambda$-modules with bounded homology. Then we have the following result on formality.
$\Lambda$-modules with bounded homology. Then we have the following result on formality.
Lemma 4.1 [Iya11, Lemma 5.2] If ![]() $X\in {{D^{b}}}(\Lambda )$ satisfies
$X\in {{D^{b}}}(\Lambda )$ satisfies ![]() $H^{i}(X)=0$ for any
$H^{i}(X)=0$ for any ![]() $i\notin d\mathbb {Z}$, then
$i\notin d\mathbb {Z}$, then ![]() $X\cong {\bigoplus} _{i\in d\mathbb {Z}}H^{i}(X)[-i]$.
$X\cong {\bigoplus} _{i\in d\mathbb {Z}}H^{i}(X)[-i]$.
Let ![]() $\nu$ denote the Nakayama functor
$\nu$ denote the Nakayama functor
of ![]() $\Lambda$ and let
$\Lambda$ and let ![]() $\nu ^{-1}$ denote its quasi-inverse, defined using the internal hom,
$\nu ^{-1}$ denote its quasi-inverse, defined using the internal hom,
Let ![]() $\nu _d$ denote the shifted Nakayama functor
$\nu _d$ denote the shifted Nakayama functor ![]() $\nu _d=\nu \circ [-d]$ and
$\nu _d=\nu \circ [-d]$ and ![]() $\nu _d^{-1}=\nu ^{-1}\circ [d]$. Then we have
$\nu _d^{-1}=\nu ^{-1}\circ [d]$. Then we have
Definition 4.2 [HIO14, Definition 3.2] A finite-dimensional algebra ![]() $\Lambda$ with
$\Lambda$ with ![]() $\operatorname {gldim}\Lambda = d$ is
$\operatorname {gldim}\Lambda = d$ is ![]() $d$-hereditary if
$d$-hereditary if ![]() $H^{i}(\nu _d^{j}(\Lambda ))=0$ for all
$H^{i}(\nu _d^{j}(\Lambda ))=0$ for all ![]() $i,j\in \mathbb {Z}$ such that
$i,j\in \mathbb {Z}$ such that ![]() $i\notin d\mathbb {Z}$.
$i\notin d\mathbb {Z}$.
One of the important properties of ![]() $d$-hereditary algebras
$d$-hereditary algebras ![]() $\Lambda$ follows from Lemma 4.1: for any
$\Lambda$ follows from Lemma 4.1: for any ![]() $j\in \mathbb {Z}$ and an indecomposable projective
$j\in \mathbb {Z}$ and an indecomposable projective ![]() $\Lambda$-module
$\Lambda$-module ![]() $P$, there exists
$P$, there exists ![]() $i\in \mathbb {Z}$ such that
$i\in \mathbb {Z}$ such that
Note that in [Reference Herschend, Iyama and OppermannHIO14], the weaker condition ![]() $\operatorname {gldim}\Lambda \leq d$ instead of
$\operatorname {gldim}\Lambda \leq d$ instead of ![]() $\operatorname {gldim}\Lambda =d$ was imposed. The only difference between the two definitions is whether we allow
$\operatorname {gldim}\Lambda =d$ was imposed. The only difference between the two definitions is whether we allow ![]() $\Lambda$ to be semisimple, which is a case we are not interested in. Therefore, we always assume
$\Lambda$ to be semisimple, which is a case we are not interested in. Therefore, we always assume ![]() $\operatorname {gldim}\Lambda =d$.
$\operatorname {gldim}\Lambda =d$.
The following result is an immediate consequence of Theorem 3.14.
Corollary 4.3 Let ![]() $\Lambda =\operatorname {T} _S(V)/(R)$ be a Koszul
$\Lambda =\operatorname {T} _S(V)/(R)$ be a Koszul ![]() $d$-hereditary algebra over a separable
$d$-hereditary algebra over a separable ![]() $\mathbb {F}$-algebra
$\mathbb {F}$-algebra ![]() $S$ and
$S$ and ![]() $(\bar {V},W)$ the associated superpotential. Then we have
$(\bar {V},W)$ the associated superpotential. Then we have ![]() $\Pi \cong P_S^{d}(\bar {V},W)$.
$\Pi \cong P_S^{d}(\bar {V},W)$.
Proof. The assertion is immediate from Theorem 3.14 because
holds for any ![]() $0 < i < d$.
$0 < i < d$.
Definition 4.4 [IO13, HIO14] We say that a finite-dimensional ![]() $\mathbb {F}$-algebra
$\mathbb {F}$-algebra ![]() $\Lambda$ with
$\Lambda$ with ![]() $\operatorname {gldim}\Lambda =d$ is:
$\operatorname {gldim}\Lambda =d$ is:
•
 $d$-representation finite (or
$d$-representation finite (or  $d$-RF) if there exists an
$d$-RF) if there exists an  $d$-cluster tilting
$d$-cluster tilting  $\Lambda$-module
$\Lambda$-module  $M$, that is,
$M$, that is,
 \begin{align*} \operatorname{add} M &= \big\{X\in\Lambda\operatorname{-mod} \;|\; \operatorname{Ext}_{\Lambda}^{i}(X,M)=0\text{ for all }0 < i < d\big\} \\ &= \big\{Y\in\Lambda\operatorname{-mod} \;|\; \operatorname{Ext}_{\Lambda}^{i}(M,Y)=0\text{ for all }0 < i < d\big\}\text{.} \end{align*}
\begin{align*} \operatorname{add} M &= \big\{X\in\Lambda\operatorname{-mod} \;|\; \operatorname{Ext}_{\Lambda}^{i}(X,M)=0\text{ for all }0 < i < d\big\} \\ &= \big\{Y\in\Lambda\operatorname{-mod} \;|\; \operatorname{Ext}_{\Lambda}^{i}(M,Y)=0\text{ for all }0 < i < d\big\}\text{.} \end{align*}•
 $d$-representation infinite (or
$d$-representation infinite (or  $d$-RI) if
$d$-RI) if  $\nu _d^{-i}(\Lambda )$ is concentrated in degree
$\nu _d^{-i}(\Lambda )$ is concentrated in degree  $0$ for any
$0$ for any  $i\geq 0$.
$i\geq 0$.
Then we have a dichotomy theorem.
Theorem 4.5 [HIO14, Theorem 3.4] Every ring-indecomposable finite-dimensional ![]() $\mathbb {F}$-algebra is
$\mathbb {F}$-algebra is ![]() $d$-hereditary if and only if it is either
$d$-hereditary if and only if it is either ![]() $d$-RF or
$d$-RF or ![]() $d$-RI.
$d$-RI.
In the study of ![]() $d$-hereditary algebras, the subcategory
$d$-hereditary algebras, the subcategory
of ![]() ${{D^{b}}}(\Lambda )$ plays an important role.
${{D^{b}}}(\Lambda )$ plays an important role.
We give a few properties of ![]() $\mathscr {U}$ and the categories
$\mathscr {U}$ and the categories ![]() $\mathscr {P}$ and
$\mathscr {P}$ and ![]() $\mathscr {I}$ of
$\mathscr {I}$ of ![]() $d$-preprojective
$d$-preprojective ![]() $\Lambda$-modules and
$\Lambda$-modules and ![]() $d$-preinjective
$d$-preinjective ![]() $\Lambda$-modules (Definition 2.8). By the following result, any
$\Lambda$-modules (Definition 2.8). By the following result, any ![]() $d$-RF algebra has a unique
$d$-RF algebra has a unique ![]() $d$-cluster tilting module up to additive equivalence, which is given by
$d$-cluster tilting module up to additive equivalence, which is given by ![]() $\Pi$. For a full subcategory
$\Pi$. For a full subcategory ![]() $\mathscr {X}$ and
$\mathscr {X}$ and ![]() $\mathscr {Y}$ of an additive category
$\mathscr {Y}$ of an additive category ![]() $\mathscr {C}$, we denote by
$\mathscr {C}$, we denote by ![]() $\mathscr {X}\vee \mathscr {Y}$ the full subcategory
$\mathscr {X}\vee \mathscr {Y}$ the full subcategory ![]() $\operatorname {add} (\mathscr {X}\cup \mathscr {Y})$ of
$\operatorname {add} (\mathscr {X}\cup \mathscr {Y})$ of ![]() $\mathscr {C}$.
$\mathscr {C}$.
Proposition 4.6
(a) [Reference IyamaIya11, Theorem 1.6] If
 $\Lambda$ is
$\Lambda$ is  $d$-RF, then
$d$-RF, then  $\Pi$ is a
$\Pi$ is a  $d$-cluster tilting
$d$-cluster tilting  $\Lambda$-module,
$\Lambda$-module,  $\mathscr {P}=\mathscr {I}=\operatorname {add} \Pi$, and
$\mathscr {P}=\mathscr {I}=\operatorname {add} \Pi$, and  $\mathscr {U}=\operatorname {add} \{\Pi [di]\mid i\in \mathbb {Z}\}$.
$\mathscr {U}=\operatorname {add} \{\Pi [di]\mid i\in \mathbb {Z}\}$.(b) [Reference Herschend, Iyama and OppermannHIO14, Proposition 4.10(d)] If
 $\Lambda$ is
$\Lambda$ is  $d$-RI, then
$d$-RI, then  $\mathscr {P}=\operatorname {add} \big \{\nu _d^{-i}(\Lambda )\mid i\ge 0\big \}$,
$\mathscr {P}=\operatorname {add} \big \{\nu _d^{-i}(\Lambda )\mid i\ge 0\big \}$,  $\mathscr {I}=\operatorname {add} \big \{\nu _d^{i}(D\Lambda )\mid i\ge 0\big \}$, and
$\mathscr {I}=\operatorname {add} \big \{\nu _d^{i}(D\Lambda )\mid i\ge 0\big \}$, and  $\mathscr {U}=\mathscr {I}[-d]\vee \mathscr {P}$. Moreover,
$\mathscr {U}=\mathscr {I}[-d]\vee \mathscr {P}$. Moreover,  $\operatorname {Hom} _{\Lambda} (\mathscr {I},\mathscr {P})=0$ and
$\operatorname {Hom} _{\Lambda} (\mathscr {I},\mathscr {P})=0$ and  $\mathscr {P}\cap \mathscr {I}=0$.
$\mathscr {P}\cap \mathscr {I}=0$.
In the final part of our preparations for this section, we recall the generalization of almost split sequences, or Auslander–Reiten sequences, to ![]() $d$-hereditary algebras.
$d$-hereditary algebras.
Definition 4.7 [Iya07] Let ![]() $\mathscr {C}$ be a Krull–Schmidt
$\mathscr {C}$ be a Krull–Schmidt ![]() $\mathbb {F}$-linear category with Jacobson radical
$\mathbb {F}$-linear category with Jacobson radical ![]() $\operatorname {rad} _{\mathscr{C}}$ and let
$\operatorname {rad} _{\mathscr{C}}$ and let
be a complex in ![]() $\mathscr {C}$ where
$\mathscr {C}$ where ![]() $X$ and
$X$ and ![]() $Y$ are indecomposable and each
$Y$ are indecomposable and each ![]() $f_i$ belongs to
$f_i$ belongs to ![]() $\operatorname {rad} _{\mathscr{C}}$. Then we say the sequence (20) is
$\operatorname {rad} _{\mathscr{C}}$. Then we say the sequence (20) is ![]() $d$-almost split in
$d$-almost split in ![]() $\mathscr {C}$ if both of the following sequences are exact for all objects
$\mathscr {C}$ if both of the following sequences are exact for all objects ![]() $M$ in
$M$ in ![]() $\mathscr {C}$:
$\mathscr {C}$:
 \begin{align*} & 0\to\operatorname{Hom}_{\mathscr{C}}(M,Y)\xrightarrow{{f_{d}}_*} \operatorname{Hom}_{\mathscr{C}}(M,C_{d-1})\xrightarrow{{f_{d-1}}_*} \cdots\xrightarrow{{f_{1}}_*} \operatorname{Hom}_{\mathscr{C}}(M,C_0)\xrightarrow{{f_{0}}_*} \operatorname{rad}_{\mathscr{C}}(M,X)\to 0;\\ & 0\to\operatorname{Hom}_{\mathscr{C}}(X,M)\xrightarrow{{f_{0}}^{*}} \operatorname{Hom}_{\mathscr{C}}(C_0,M)\xrightarrow{{f_{1}}^{*}} \cdots\xrightarrow{{f_{d-1}}^{*}} \operatorname{Hom}_{\mathscr{C}}(C_{d-1},M)\xrightarrow{{f_{d}}^{*}} \operatorname{rad}_{\mathscr{C}}(Y,M) \to 0. \end{align*}
\begin{align*} & 0\to\operatorname{Hom}_{\mathscr{C}}(M,Y)\xrightarrow{{f_{d}}_*} \operatorname{Hom}_{\mathscr{C}}(M,C_{d-1})\xrightarrow{{f_{d-1}}_*} \cdots\xrightarrow{{f_{1}}_*} \operatorname{Hom}_{\mathscr{C}}(M,C_0)\xrightarrow{{f_{0}}_*} \operatorname{rad}_{\mathscr{C}}(M,X)\to 0;\\ & 0\to\operatorname{Hom}_{\mathscr{C}}(X,M)\xrightarrow{{f_{0}}^{*}} \operatorname{Hom}_{\mathscr{C}}(C_0,M)\xrightarrow{{f_{1}}^{*}} \cdots\xrightarrow{{f_{d-1}}^{*}} \operatorname{Hom}_{\mathscr{C}}(C_{d-1},M)\xrightarrow{{f_{d}}^{*}} \operatorname{rad}_{\mathscr{C}}(Y,M) \to 0. \end{align*}
More generally, we say the sequence (20) is weak ![]() $d$-almost split in
$d$-almost split in ![]() $\mathscr {C}$ if these sequences are exact except at
$\mathscr {C}$ if these sequences are exact except at ![]() $\operatorname{Hom}_{\mathscr{C}}(M,Y)$ and
$\operatorname{Hom}_{\mathscr{C}}(M,Y)$ and ![]() $\operatorname{Hom}_{\mathscr{C}}(X,M)$, respectively.
$\operatorname{Hom}_{\mathscr{C}}(X,M)$, respectively.
Example 4.8 Let ![]() $Q=[1\to 2]$ and
$Q=[1\to 2]$ and ![]() $\Lambda =\mathbb {F} Q$. Then the short exact sequence corresponding to the non-split extension of one simple module by the other is
$\Lambda =\mathbb {F} Q$. Then the short exact sequence corresponding to the non-split extension of one simple module by the other is ![]() $1$-almost split in
$1$-almost split in ![]() $\Lambda \operatorname {-mod}$ but is only weak
$\Lambda \operatorname {-mod}$ but is only weak ![]() $1$-almost split in
$1$-almost split in ![]() ${{D^{b}}}(\Lambda )$.
${{D^{b}}}(\Lambda )$.
It was shown in [Reference Herschend, Iyama and OppermannHIO14] (respectively, [Reference IyamaIya07]) that the category ![]() $\mathscr {P}\vee \mathscr {I}$ has
$\mathscr {P}\vee \mathscr {I}$ has ![]() $d$-almost split sequences when
$d$-almost split sequences when ![]() $\Lambda$ is
$\Lambda$ is ![]() $d$-RI (respectively,
$d$-RI (respectively, ![]() $d$-RF). In addition, it was shown in [Reference Iyama and YoshinoIY08, Reference Iyama and OppermannIO13] that
$d$-RF). In addition, it was shown in [Reference Iyama and YoshinoIY08, Reference Iyama and OppermannIO13] that ![]() $d$-cluster tilting subcategories of triangulated categories have certain analogue of
$d$-cluster tilting subcategories of triangulated categories have certain analogue of ![]() $d$-almost split sequences called AR
$d$-almost split sequences called AR ![]() $(d+2)$-angles. From these results, one can deduce the following results on
$(d+2)$-angles. From these results, one can deduce the following results on ![]() $d$-almost split sequences in the category
$d$-almost split sequences in the category ![]() $\mathscr {U}$, which play a key role in this section.
$\mathscr {U}$, which play a key role in this section.
Theorem 4.9 Let ![]() $\Lambda$ be a
$\Lambda$ be a ![]() $d$-hereditary algebra.
$d$-hereditary algebra.
(a) If ![]() $\Lambda$ is
$\Lambda$ is ![]() $d$-RI, then any indecomposable object
$d$-RI, then any indecomposable object ![]() $X$ (respectively,
$X$ (respectively, ![]() $Y$) in
$Y$) in ![]() $\mathscr {U}$ has a
$\mathscr {U}$ has a ![]() $d$-almost split sequence in
$d$-almost split sequence in ![]() $\mathscr {U}$
$\mathscr {U}$
Moreover, we have ![]() $Y\cong \nu _d(X)$ (respectively,
$Y\cong \nu _d(X)$ (respectively, ![]() $X\cong \nu _d^{-1}(Y)$).
$X\cong \nu _d^{-1}(Y)$).
(b) If ![]() $\Lambda$ is
$\Lambda$ is ![]() $d$-RF, then any indecomposable object
$d$-RF, then any indecomposable object ![]() $X$ (respectively,
$X$ (respectively, ![]() $Y$) in
$Y$) in ![]() $\mathscr {U}$ has a weak
$\mathscr {U}$ has a weak ![]() $d$-almost split sequence in
$d$-almost split sequence in ![]() $\mathscr {U}$
$\mathscr {U}$
Moreover, we have ![]() $Y\cong \nu _d(X)$ (respectively,
$Y\cong \nu _d(X)$ (respectively, ![]() $X\cong \nu _d^{-1}(Y)$),
$X\cong \nu _d^{-1}(Y)$), ![]() $\operatorname {Ker} (f_d{}_*)=\operatorname {soc} \operatorname {Hom} _{\mathscr {U}}(-,Y)$ and
$\operatorname {Ker} (f_d{}_*)=\operatorname {soc} \operatorname {Hom} _{\mathscr {U}}(-,Y)$ and ![]() $\operatorname {Ker} (f_0{}^{*})=\operatorname {soc} \operatorname {Hom} _{\mathscr {U}}(X,-)$.
$\operatorname {Ker} (f_0{}^{*})=\operatorname {soc} \operatorname {Hom} _{\mathscr {U}}(X,-)$.
Proof. In both cases, we only show the assertion for ![]() $X$ because the assertion for
$X$ because the assertion for ![]() $Y$ is the dual.
$Y$ is the dual.
(a) Let ![]() $X\in \mathscr {U}$ be an indecomposable object. If
$X\in \mathscr {U}$ be an indecomposable object. If ![]() $X$ is a projective
$X$ is a projective ![]() $\Lambda$-module, then
$\Lambda$-module, then ![]() $\nu _d^{-1}(X)$ is not projective, as otherwise
$\nu _d^{-1}(X)$ is not projective, as otherwise ![]() $X\cong \nu _d\nu _d^{-1}(X)$ would be concentrated in degree
$X\cong \nu _d\nu _d^{-1}(X)$ would be concentrated in degree ![]() $d$ which contradicts our assumption that
$d$ which contradicts our assumption that ![]() $\Lambda$ is
$\Lambda$ is ![]() $d$-RI. As
$d$-RI. As ![]() $\nu _d:\mathscr {U}\to \mathscr {U}$ is an equivalence, it preserves
$\nu _d:\mathscr {U}\to \mathscr {U}$ is an equivalence, it preserves ![]() $d$-almost split sequences in
$d$-almost split sequences in ![]() $\mathscr {U}$. Thus, we can assume that
$\mathscr {U}$. Thus, we can assume that ![]() $X$ is a non-projective object in
$X$ is a non-projective object in ![]() $\mathscr {P}$.
$\mathscr {P}$.
It was shown in [Reference Herschend, Iyama and OppermannHIO14, Theorem 4.25] that there exists an exact sequence
in ![]() $\operatorname {mod} \Lambda$ that has terms in
$\operatorname {mod} \Lambda$ that has terms in ![]() $\mathscr {P}$,
$\mathscr {P}$, ![]() $Y=\nu _d(X)$, and gives a
$Y=\nu _d(X)$, and gives a ![]() $d$-almost split sequence in
$d$-almost split sequence in ![]() $\mathscr {P}\vee \mathscr {I}$. Thus, because Proposition 4.6(b) implies
$\mathscr {P}\vee \mathscr {I}$. Thus, because Proposition 4.6(b) implies ![]() $Y\notin \mathscr {I}$, which implies
$Y\notin \mathscr {I}$, which implies ![]() $\operatorname{rad}_{\Lambda} (Y,\mathscr {I})=\operatorname {Hom}_{\Lambda} (Y,\mathscr {I})$, the following sequences are exact:
$\operatorname{rad}_{\Lambda} (Y,\mathscr {I})=\operatorname {Hom}_{\Lambda} (Y,\mathscr {I})$, the following sequences are exact:
 \begin{align*} & 0\to\operatorname{Hom}_{\Lambda}(\mathscr{P},Y)\xrightarrow{{f_{d}}_*} \operatorname{Hom}_{\Lambda}(\mathscr{P},C_{d-1})\xrightarrow{{f_{d-1}}_*} \cdots\xrightarrow{{f_{1}}_*} \operatorname{Hom}_{\Lambda}(\mathscr{P},C_0)\xrightarrow{{f_{0}}_*} \operatorname{rad}_{\Lambda}(\mathscr{P},X)\to 0; \\ & 0\to\operatorname{Hom}_{\Lambda}(X,\mathscr{I})\xrightarrow{{f_{0}}^{*}} \operatorname{Hom}_{\Lambda}(C_0,\mathscr{I})\xrightarrow{{f_{1}}^{*}} \cdots\xrightarrow{{f_{d-1}}^{*}} \operatorname{Hom}_{\Lambda}(C_{d-1},\mathscr{I})\xrightarrow{{f_{d}}^{*}} \operatorname{Hom}_{\Lambda}(Y,\mathscr{I}) \to 0. \end{align*}
\begin{align*} & 0\to\operatorname{Hom}_{\Lambda}(\mathscr{P},Y)\xrightarrow{{f_{d}}_*} \operatorname{Hom}_{\Lambda}(\mathscr{P},C_{d-1})\xrightarrow{{f_{d-1}}_*} \cdots\xrightarrow{{f_{1}}_*} \operatorname{Hom}_{\Lambda}(\mathscr{P},C_0)\xrightarrow{{f_{0}}_*} \operatorname{rad}_{\Lambda}(\mathscr{P},X)\to 0; \\ & 0\to\operatorname{Hom}_{\Lambda}(X,\mathscr{I})\xrightarrow{{f_{0}}^{*}} \operatorname{Hom}_{\Lambda}(C_0,\mathscr{I})\xrightarrow{{f_{1}}^{*}} \cdots\xrightarrow{{f_{d-1}}^{*}} \operatorname{Hom}_{\Lambda}(C_{d-1},\mathscr{I})\xrightarrow{{f_{d}}^{*}} \operatorname{Hom}_{\Lambda}(Y,\mathscr{I}) \to 0. \end{align*}
Using Serre duality, we have ![]() $\operatorname {Hom} _{\Lambda} (\mathscr {P},\mathscr {I})=\operatorname {Hom} _{\mathscr {U}}(\nu ^{-1}_d(\mathscr {I})[-d],\mathscr {P})^{*}$. As
$\operatorname {Hom} _{\Lambda} (\mathscr {P},\mathscr {I})=\operatorname {Hom} _{\mathscr {U}}(\nu ^{-1}_d(\mathscr {I})[-d],\mathscr {P})^{*}$. As ![]() $\Lambda$ is
$\Lambda$ is ![]() $d$-RI, we have
$d$-RI, we have ![]() $\mathscr {I}\subseteq \nu ^{-1}_d(\mathscr {I})$ by Proposition 4.6(b). Therefore, the latter exact sequence gives an exact sequence
$\mathscr {I}\subseteq \nu ^{-1}_d(\mathscr {I})$ by Proposition 4.6(b). Therefore, the latter exact sequence gives an exact sequence
 \begin{align*} 0\to\operatorname{Hom}_{\mathscr{U}}(\mathscr{I}[{-}d],Y)\xrightarrow{{f_{d}}_*} \operatorname{Hom}_{\mathscr{U}}(\mathscr{I}[{-}d],C_{d-1})\xrightarrow{{f_{d-1}}_*}\cdots &\xrightarrow{{f_{1}}_*} \operatorname{Hom}_{\mathscr{U}}(\mathscr{I}[{-}d],C_0)\\ &\xrightarrow{{f_{0}}_*} \operatorname{Hom}_{\mathscr{U}}(\mathscr{I}[{-}d],X)\to 0. \end{align*}
\begin{align*} 0\to\operatorname{Hom}_{\mathscr{U}}(\mathscr{I}[{-}d],Y)\xrightarrow{{f_{d}}_*} \operatorname{Hom}_{\mathscr{U}}(\mathscr{I}[{-}d],C_{d-1})\xrightarrow{{f_{d-1}}_*}\cdots &\xrightarrow{{f_{1}}_*} \operatorname{Hom}_{\mathscr{U}}(\mathscr{I}[{-}d],C_0)\\ &\xrightarrow{{f_{0}}_*} \operatorname{Hom}_{\mathscr{U}}(\mathscr{I}[{-}d],X)\to 0. \end{align*}
As ![]() $\mathscr {U}=\mathscr {I}[-d]\vee \mathscr {P}$ by [Reference Herschend, Iyama and OppermannHIO14, Proposition 4.10(c)], the above exact sequences give an exact sequence
$\mathscr {U}=\mathscr {I}[-d]\vee \mathscr {P}$ by [Reference Herschend, Iyama and OppermannHIO14, Proposition 4.10(c)], the above exact sequences give an exact sequence
Dually, the following sequence is exact:
Thus, the sequence (21) is a ![]() $d$-almost split sequence in
$d$-almost split sequence in ![]() $\mathscr {U}$.
$\mathscr {U}$.
(b) By [Reference IyamaIya11, Theorem 1.23], ![]() $\mathscr {U}$ is a
$\mathscr {U}$ is a ![]() $d$-cluster tilting subcategory of
$d$-cluster tilting subcategory of ![]() ${{D^{b}}}(\Lambda )$. By [Reference Iyama and YoshinoIY08, Theorem 3.10], there exist triangles
${{D^{b}}}(\Lambda )$. By [Reference Iyama and YoshinoIY08, Theorem 3.10], there exist triangles
in ![]() ${{D^{b}}}(\Lambda )$ for
${{D^{b}}}(\Lambda )$ for ![]() $0\le i\le d-1$ satisfying the following conditions:
$0\le i\le d-1$ satisfying the following conditions:
•
 $X_0=X$,
$X_0=X$,  $X_{d}=\nu _d(X)$, and
$X_{d}=\nu _d(X)$, and  $C_i\in \mathscr {U}$ for any
$C_i\in \mathscr {U}$ for any  $0\le i\le d-1$;
$0\le i\le d-1$;•
 $\operatorname {Hom} _{\mathscr{U}}(\mathscr {U},C_0)\xrightarrow {{g_{0}}_*} \operatorname {rad} _{\mathscr {U}}(\mathscr {U},X)\to 0$ and
$\operatorname {Hom} _{\mathscr{U}}(\mathscr {U},C_0)\xrightarrow {{g_{0}}_*} \operatorname {rad} _{\mathscr {U}}(\mathscr {U},X)\to 0$ and  $\operatorname {Hom} _{\mathscr{U}}(C_{d-1},\mathscr {U})\xrightarrow {{h_{d}}^{*}} \operatorname {rad} _{\mathscr {U}}(\nu _d(X),\mathscr {U})\to 0$ are exact.
$\operatorname {Hom} _{\mathscr{U}}(C_{d-1},\mathscr {U})\xrightarrow {{h_{d}}^{*}} \operatorname {rad} _{\mathscr {U}}(\nu _d(X),\mathscr {U})\to 0$ are exact.
Let ![]() $f_d:=h_d$,
$f_d:=h_d$, ![]() $f_i:=h_ig_i$, and
$f_i:=h_ig_i$, and ![]() $f_0:=g_0$. Then we have a complex
$f_0:=g_0$. Then we have a complex
Moreover, as ![]() $\Lambda$ is
$\Lambda$ is ![]() $d$-RF,
$d$-RF, ![]() $\nu (\mathscr {U})=\mathscr {U}$ by [Reference Iyama and OppermannIO13, Theorem 3.1(1)
$\nu (\mathscr {U})=\mathscr {U}$ by [Reference Iyama and OppermannIO13, Theorem 3.1(1)![]() $\Rightarrow$(3)] and hence
$\Rightarrow$(3)] and hence ![]() $\mathscr {U}[d]=\mathscr {U}$. Thus, by [Reference Iyama and OppermannIO13, Lemma 4.3], we have an exact sequence
$\mathscr {U}[d]=\mathscr {U}$. Thus, by [Reference Iyama and OppermannIO13, Lemma 4.3], we have an exact sequence
 \begin{align*} &\cdots\to\operatorname{Hom}_{\mathscr{U}}(\mathscr{U},C_0[{-}d])\xrightarrow{{f_{0}[{-}d]}_*}\operatorname{Hom}_{\mathscr{U}}(\mathscr{U},X[{-}d])\to\\ &\operatorname{Hom}_{\mathscr{U}}(\mathscr{U},\nu_d(X))\xrightarrow{{f_{d}}_*} \operatorname{Hom}_{\mathscr{U}}(\mathscr{U},C_{d-1})\xrightarrow{{f_{d-1}}_*} \cdots\xrightarrow{{f_{1}}_*} \operatorname{Hom}_{\mathscr{U}}(\mathscr{U},C_0)\xrightarrow{{f_{0}}_*} \operatorname{rad}_{\mathscr{U}}(\mathscr{U},X)\to 0. \end{align*}
\begin{align*} &\cdots\to\operatorname{Hom}_{\mathscr{U}}(\mathscr{U},C_0[{-}d])\xrightarrow{{f_{0}[{-}d]}_*}\operatorname{Hom}_{\mathscr{U}}(\mathscr{U},X[{-}d])\to\\ &\operatorname{Hom}_{\mathscr{U}}(\mathscr{U},\nu_d(X))\xrightarrow{{f_{d}}_*} \operatorname{Hom}_{\mathscr{U}}(\mathscr{U},C_{d-1})\xrightarrow{{f_{d-1}}_*} \cdots\xrightarrow{{f_{1}}_*} \operatorname{Hom}_{\mathscr{U}}(\mathscr{U},C_0)\xrightarrow{{f_{0}}_*} \operatorname{rad}_{\mathscr{U}}(\mathscr{U},X)\to 0. \end{align*}
Thus, ![]() $\operatorname {Cok} (f_{0}{}_*:\operatorname {Hom} _{\mathscr{U}}(-,C_0)\to \operatorname {Hom} _{\mathscr {U}}(-,X))$ is a simple
$\operatorname {Cok} (f_{0}{}_*:\operatorname {Hom} _{\mathscr{U}}(-,C_0)\to \operatorname {Hom} _{\mathscr {U}}(-,X))$ is a simple ![]() $\mathscr {U}$-module, and hence
$\mathscr {U}$-module, and hence ![]() $\operatorname {Ker} (f_d{}_*)=\operatorname {Cok} (f_{0}[-d]{}_*)$ is a simple
$\operatorname {Ker} (f_d{}_*)=\operatorname {Cok} (f_{0}[-d]{}_*)$ is a simple ![]() $\mathscr {U}$-module because
$\mathscr {U}$-module because ![]() $[d]:\mathscr {U}\to \mathscr {U}$ is an autoequivalence. As
$[d]:\mathscr {U}\to \mathscr {U}$ is an autoequivalence. As ![]() $X[-d]\in \mathscr {U}$ is indecomposable,
$X[-d]\in \mathscr {U}$ is indecomposable, ![]() $\operatorname {Hom} _{\mathscr {U}}(X[-d],-)$ is an indecomposable projective functor and, thus, it has a simple top. Hence, the
$\operatorname {Hom} _{\mathscr {U}}(X[-d],-)$ is an indecomposable projective functor and, thus, it has a simple top. Hence, the ![]() $\mathscr {U}$-module
$\mathscr {U}$-module ![]() $\operatorname {Hom} _{\mathscr {U}}(-,\nu _d(X))\cong \operatorname {Hom} _{\mathscr {U}}(X[-d],-)^{*}$ has a simple socle. Therefore,
$\operatorname {Hom} _{\mathscr {U}}(-,\nu _d(X))\cong \operatorname {Hom} _{\mathscr {U}}(X[-d],-)^{*}$ has a simple socle. Therefore, ![]() $\operatorname {Ker} (f_d{}_*)=\operatorname {soc} \operatorname {Hom} _{\mathscr {U}}(\mathscr {U},\nu _d(X))$.
$\operatorname {Ker} (f_d{}_*)=\operatorname {soc} \operatorname {Hom} _{\mathscr {U}}(\mathscr {U},\nu _d(X))$.
Dually, we have an exact sequence
such that ![]() $\operatorname {Ker} ({f_{0}}^{*})=\operatorname {soc} \operatorname {Hom} _{\mathscr{U}}(X,\mathscr {U})$. Thus, the assertions hold.
$\operatorname {Ker} ({f_{0}}^{*})=\operatorname {soc} \operatorname {Hom} _{\mathscr{U}}(X,\mathscr {U})$. Thus, the assertions hold.
4.2 Resolutions of simple modules over higher preprojective algebras
For the rest of this section, ![]() $\Lambda$ is a
$\Lambda$ is a ![]() $d$-hereditary algebra and
$d$-hereditary algebra and ![]() $\Pi$ is its higher preprojective algebra. We assume that
$\Pi$ is its higher preprojective algebra. We assume that ![]() $\Lambda$ is basic and ring-indecomposable. We regard
$\Lambda$ is basic and ring-indecomposable. We regard ![]() $\Pi$ as a
$\Pi$ as a ![]() $\mathbb {Z}$-graded algebra with the tensor grading. Then we have an isomorphism
$\mathbb {Z}$-graded algebra with the tensor grading. Then we have an isomorphism
of ![]() $\mathbb {Z}$-graded algebras.
$\mathbb {Z}$-graded algebras.
For a group ![]() $\Psi$ and a
$\Psi$ and a ![]() $\Psi$-graded ring
$\Psi$-graded ring ![]() $\Gamma$, we denote by
$\Gamma$, we denote by ![]() $\Gamma \operatorname {-mod^{\Psi }}$ (respectively,
$\Gamma \operatorname {-mod^{\Psi }}$ (respectively, ![]() $\Gamma \operatorname {-proj^{\Psi }}$) the category of finitely generated (respectively, finitely generated projective)
$\Gamma \operatorname {-proj^{\Psi }}$) the category of finitely generated (respectively, finitely generated projective) ![]() $\Psi$-graded
$\Psi$-graded ![]() $\Gamma$-modules. We start with the following easy observation.
$\Gamma$-modules. We start with the following easy observation.
Lemma 4.10 Let ![]() $\mathscr {C}$ be an additive category and
$\mathscr {C}$ be an additive category and ![]() $\Psi$ a group acting on
$\Psi$ a group acting on ![]() $\mathscr {C}$. Assume that
$\mathscr {C}$. Assume that ![]() $M\in \mathscr {C}$ is an object satisfying
$M\in \mathscr {C}$ is an object satisfying ![]() $\mathscr {C}=\operatorname {add} \{\psi M\mid \psi \in \Psi \}$. Define a
$\mathscr {C}=\operatorname {add} \{\psi M\mid \psi \in \Psi \}$. Define a ![]() $\Psi$-graded ring by
$\Psi$-graded ring by ![]() $\Gamma :={\bigoplus} _{\psi \in \Psi }\operatorname {Hom} _{\mathscr {C}}(M,\psi M)$. Then there are equivalences of additive categories
$\Gamma :={\bigoplus} _{\psi \in \Psi }\operatorname {Hom} _{\mathscr {C}}(M,\psi M)$. Then there are equivalences of additive categories
Applying Lemma 4.10 to the category ![]() $\mathscr {U}$ and the group
$\mathscr {U}$ and the group ![]() $\big \{\nu _d^{-i}\mid i\in \mathbb {Z}\big \}\cong \mathbb {Z}$, we have the following description of the category
$\big \{\nu _d^{-i}\mid i\in \mathbb {Z}\big \}\cong \mathbb {Z}$, we have the following description of the category ![]() $\mathscr {U}$.
$\mathscr {U}$.
Proposition 4.11 (a) There are equivalences of additive categories
 \begin{align*} & G:=\mathop{\bigoplus}\limits_{i\in\mathbb{Z}}\operatorname{Hom}_{{{D^{b}}}(\Lambda)}\big(\Lambda,\nu_d^{{-}i}(-)\big):\mathscr{U}\to\operatorname{proj^{\mathbb{Z}}-}\Pi,\\ & H:=\mathop{\bigoplus}\limits_{i\in\mathbb{Z}}\operatorname{Hom}_{{{D^{b}}}(\Lambda)}\big(-,\nu_d^{{-}i}(\Lambda)\big):\mathscr{U}\to\Pi\operatorname{-proj^{\mathbb{Z}}}. \end{align*}
\begin{align*} & G:=\mathop{\bigoplus}\limits_{i\in\mathbb{Z}}\operatorname{Hom}_{{{D^{b}}}(\Lambda)}\big(\Lambda,\nu_d^{{-}i}(-)\big):\mathscr{U}\to\operatorname{proj^{\mathbb{Z}}-}\Pi,\\ & H:=\mathop{\bigoplus}\limits_{i\in\mathbb{Z}}\operatorname{Hom}_{{{D^{b}}}(\Lambda)}\big(-,\nu_d^{{-}i}(\Lambda)\big):\mathscr{U}\to\Pi\operatorname{-proj^{\mathbb{Z}}}. \end{align*}In particular, there are equivalences of additive categories
(b) The following diagram commutes up to natural isomorphism.

Now we are ready to state the main result of this subsection. It asserts that minimal projective resolutions of ![]() $\mathbb {Z}$-graded simple modules over the higher preprojective algebra
$\mathbb {Z}$-graded simple modules over the higher preprojective algebra ![]() $\Pi$ of a
$\Pi$ of a ![]() $d$-hereditary algebra
$d$-hereditary algebra ![]() $\Lambda$ are induced from
$\Lambda$ are induced from ![]() $d$-almost split sequences in
$d$-almost split sequences in ![]() $\mathscr {U}$.
$\mathscr {U}$.
Theorem 4.12 Let ![]() $X$ be an indecomposable object in
$X$ be an indecomposable object in ![]() $\mathscr {U}$, and
$\mathscr {U}$, and
a weak ![]() $d$-almost split sequence in
$d$-almost split sequence in ![]() $\mathscr {U}$.
$\mathscr {U}$.
(a) There exist exact sequences
in \begin{gather*} GY\xrightarrow{Gf_d} GC_{d-1}\xrightarrow{Gf_{d-1}}\cdots\xrightarrow{Gf_2} GC_1\xrightarrow{Gf_1} GC_0\xrightarrow{Gf_0} GX\to T\to 0,\\ HX\xrightarrow{Hf_0} HC_0\xrightarrow{Hf_1}HC_1\xrightarrow{Hf_2}\cdots\xrightarrow{Hf_{d-1}} HC_{d-1}\xrightarrow{Hf_d} HY\to U\to 0 \end{gather*}
\begin{gather*} GY\xrightarrow{Gf_d} GC_{d-1}\xrightarrow{Gf_{d-1}}\cdots\xrightarrow{Gf_2} GC_1\xrightarrow{Gf_1} GC_0\xrightarrow{Gf_0} GX\to T\to 0,\\ HX\xrightarrow{Hf_0} HC_0\xrightarrow{Hf_1}HC_1\xrightarrow{Hf_2}\cdots\xrightarrow{Hf_{d-1}} HC_{d-1}\xrightarrow{Hf_d} HY\to U\to 0 \end{gather*} $\operatorname {mod^{\mathbb {Z}}-}\Pi$ and
$\operatorname {mod^{\mathbb {Z}}-}\Pi$ and  $\Pi \operatorname {-mod^{\mathbb {Z}}}$, where
$\Pi \operatorname {-mod^{\mathbb {Z}}}$, where  $T$ and
$T$ and  $U$ are simple.
$U$ are simple.(b) If
 $\Lambda$ is
$\Lambda$ is  $d$-RI, then
$d$-RI, then  $Gf_d$ and
$Gf_d$ and  $Hf_0$ are monomorphisms.
$Hf_0$ are monomorphisms.(c) If
 $\Lambda$ is
$\Lambda$ is  $d$-RF, then
$d$-RF, then  $\operatorname {Ker} Gf_d=\operatorname {soc} GY$ and
$\operatorname {Ker} Gf_d=\operatorname {soc} GY$ and  $\operatorname {Ker} Hf_0=\operatorname {soc} HX$. Moreover, these are simple.
$\operatorname {Ker} Hf_0=\operatorname {soc} HX$. Moreover, these are simple.
Proof. (a) By Theorem 4.9(a) and (b), we have an exact sequence
 \begin{align*} \mathop{\bigoplus}\limits_{i\in\mathbb{Z}}\operatorname{Hom}_{\mathscr{U}}\big(\nu_d^{i}(\Lambda),Y\big)\xrightarrow{f_d{}_*} \mathop{\bigoplus}\limits_{i\in\mathbb{Z}}\operatorname{Hom}_{\mathscr{U}}\big(\nu_d^{i}(\Lambda),C_{d-1}\big)\xrightarrow{f_{d-1}{}_*}\cdots &\xrightarrow{f_1{}_*}\mathop{\bigoplus}\limits_{i\in\mathbb{Z}}\operatorname{Hom}_{\mathscr{U}}\big(\nu_d^{i}(\Lambda),C_0\big)\\ &\xrightarrow{f_0{}_*}\mathop{\bigoplus}\limits_{i\in\mathbb{Z}}\operatorname{rad}_{\mathscr{U}}\big(\nu_d^{i}(\Lambda),X\big)\to 0. \end{align*}
\begin{align*} \mathop{\bigoplus}\limits_{i\in\mathbb{Z}}\operatorname{Hom}_{\mathscr{U}}\big(\nu_d^{i}(\Lambda),Y\big)\xrightarrow{f_d{}_*} \mathop{\bigoplus}\limits_{i\in\mathbb{Z}}\operatorname{Hom}_{\mathscr{U}}\big(\nu_d^{i}(\Lambda),C_{d-1}\big)\xrightarrow{f_{d-1}{}_*}\cdots &\xrightarrow{f_1{}_*}\mathop{\bigoplus}\limits_{i\in\mathbb{Z}}\operatorname{Hom}_{\mathscr{U}}\big(\nu_d^{i}(\Lambda),C_0\big)\\ &\xrightarrow{f_0{}_*}\mathop{\bigoplus}\limits_{i\in\mathbb{Z}}\operatorname{rad}_{\mathscr{U}}\big(\nu_d^{i}(\Lambda),X\big)\to 0. \end{align*}
This gives the first sequence. Dually, we obtain the second sequence. It follows from Proposition 4.11(a) that ![]() $T$ and
$T$ and ![]() $U$ are simple.
$U$ are simple.
(b),(c) These follow from Theorem 4.9(a) and (b). It follows from Proposition 4.11(a) that ![]() $\operatorname {Ker} Gf_d$ and
$\operatorname {Ker} Gf_d$ and ![]() $\operatorname {Ker} Hf_0$ are simple if
$\operatorname {Ker} Hf_0$ are simple if ![]() $\Lambda$ is
$\Lambda$ is ![]() $d$-RF.
$d$-RF.
We say that an algebra ![]() $A$ is twisted-periodic if, for some
$A$ is twisted-periodic if, for some ![]() $i\geq 1$,
$i\geq 1$, ![]() $\Omega _{A^{{\operatorname {en} }}}^{i}(A)\cong A_{\sigma}$ as
$\Omega _{A^{{\operatorname {en} }}}^{i}(A)\cong A_{\sigma}$ as ![]() $A^{{\operatorname {en} }}$-modules for some
$A^{{\operatorname {en} }}$-modules for some ![]() $\sigma \in \operatorname {Aut} (A)$, i.e., the projective resolution of the identity bimodule is periodic up to a twist by some algebra automorphism.
$\sigma \in \operatorname {Aut} (A)$, i.e., the projective resolution of the identity bimodule is periodic up to a twist by some algebra automorphism.
As an application of our results, we have the following result for ![]() $d$-RF case. The self-injectivity was first proved in [Reference Iyama and OppermannIO13], and the twisted-periodicity was first proved by Dugas [Reference DugasDug12].
$d$-RF case. The self-injectivity was first proved in [Reference Iyama and OppermannIO13], and the twisted-periodicity was first proved by Dugas [Reference DugasDug12].
Corollary 4.13 Let ![]() $\Lambda$ be a
$\Lambda$ be a ![]() $d$-RF algebra and
$d$-RF algebra and ![]() $\Pi$ its
$\Pi$ its ![]() $(d+1)$-preprojective algebra:
$(d+1)$-preprojective algebra:
(a)
 $\Pi$ is self-injective;
$\Pi$ is self-injective;(b)
 $\Pi$ is twisted-periodic of period
$\Pi$ is twisted-periodic of period  $d+2$.
$d+2$.
Proof. (a) It follows from Theorem 4.12 that ![]() $\operatorname {Ext} ^{i}_{\Pi }(T,\Pi )=0$ holds for any
$\operatorname {Ext} ^{i}_{\Pi }(T,\Pi )=0$ holds for any ![]() $\mathbb {Z}$-graded simple
$\mathbb {Z}$-graded simple ![]() $\Pi$-modules and
$\Pi$-modules and ![]() $0 < i < d+1$. Thus,
$0 < i < d+1$. Thus, ![]() $\operatorname {Ext} ^{1}_{\Pi }(-,\Pi )=0$ holds on
$\operatorname {Ext} ^{1}_{\Pi }(-,\Pi )=0$ holds on ![]() $\operatorname {mod} \Pi$ and, therefore,
$\operatorname {mod} \Pi$ and, therefore, ![]() $\Pi$ is injective as a
$\Pi$ is injective as a ![]() $\Pi$-module.
$\Pi$-module.
(b) As ![]() $\Lambda$ is a factor algebra of
$\Lambda$ is a factor algebra of ![]() $\Pi$ by the ideal
$\Pi$ by the ideal ![]() ${\bigoplus} _{i>0}\Pi _i$ contained in the radical, each simple
${\bigoplus} _{i>0}\Pi _i$ contained in the radical, each simple ![]() $\Pi$-module
$\Pi$-module ![]() $S$ is realized as the top of
$S$ is realized as the top of ![]() $GP$, where
$GP$, where ![]() $P$ is an indecomposable projective
$P$ is an indecomposable projective ![]() $\Lambda$-module. Thus, by Theorem 4.12(c), the sum
$\Lambda$-module. Thus, by Theorem 4.12(c), the sum ![]() $S={\bigoplus} S_i$ of the simple
$S={\bigoplus} S_i$ of the simple ![]() $\Pi$-modules is periodic of period
$\Pi$-modules is periodic of period ![]() $d+2$. This implies the assertion by [Reference Green, Snashall and SolbergGSS03, Theorem 1.4].
$d+2$. This implies the assertion by [Reference Green, Snashall and SolbergGSS03, Theorem 1.4].
We note that the twisted-periodicity is closely related to the stably Calabi–Yau property (e.g. [Reference Ivanov and VolkovIV14, Theorem 1.8]). In fact, ![]() $\Pi$ is known to be stably
$\Pi$ is known to be stably ![]() $(d+1)$-Calabi–Yau [Reference Iyama and OppermannIO13, Theorem 1.1(a)].
$(d+1)$-Calabi–Yau [Reference Iyama and OppermannIO13, Theorem 1.1(a)].
As another application our results, we have the following result for ![]() $d$-RI case.
$d$-RI case.
Corollary 4.14 Let ![]() $\Lambda$ be a
$\Lambda$ be a ![]() $d$-RI algebra and
$d$-RI algebra and ![]() $\Pi$ its
$\Pi$ its ![]() $(d+1)$-preprojective algebra:
$(d+1)$-preprojective algebra:
(a)
 $\Pi$ has left and right global dimension
$\Pi$ has left and right global dimension  $d+1$ (cf. the Appendix);
$d+1$ (cf. the Appendix);(b) any
 $\mathbb {Z}$-graded simple right
$\mathbb {Z}$-graded simple right  $\Pi$-module
$\Pi$-module  $T$ satisfies
$T$ satisfies
 \[ \operatorname{Ext}^{i}_{\Pi^{{{\operatorname{op}}}}}(T,\Pi) \cong \begin{cases} T^{*}({1}) & \text{if } i=d+1;\\ 0 & \text{otherwise;} \end{cases} \]
\[ \operatorname{Ext}^{i}_{\Pi^{{{\operatorname{op}}}}}(T,\Pi) \cong \begin{cases} T^{*}({1}) & \text{if } i=d+1;\\ 0 & \text{otherwise;} \end{cases} \](c) any
 $\mathbb {Z}$-graded simple left
$\mathbb {Z}$-graded simple left  $\Pi$-module
$\Pi$-module  $U$ satisfies
$U$ satisfies
 \[ \operatorname{Ext}^{i}_{\Pi}(U,\Pi) \cong \begin{cases} U^{*}({1}) & \text{if } i=d+1;\\ 0 & \text{otherwise.} \end{cases} \]
\[ \operatorname{Ext}^{i}_{\Pi}(U,\Pi) \cong \begin{cases} U^{*}({1}) & \text{if } i=d+1;\\ 0 & \text{otherwise.} \end{cases} \]
Proof. It follows from Theorem 4.12 that any ![]() $\mathbb {Z}$-graded simple
$\mathbb {Z}$-graded simple ![]() $\Pi ^{{{\operatorname {op} }}}$-module
$\Pi ^{{{\operatorname {op} }}}$-module ![]() $T$ has projective dimension
$T$ has projective dimension ![]() $d+1$ and satisfies the equalities of extension groups. Thus, part (b) holds, and dually part (c) holds. They imply part (a) by Theorem A.1.
$d+1$ and satisfies the equalities of extension groups. Thus, part (b) holds, and dually part (c) holds. They imply part (a) by Theorem A.1.
Corollary 4.14 says that ![]() $\Pi$, with the tensor grading, is a generalized Artin–Schelter regular algebra of dimension
$\Pi$, with the tensor grading, is a generalized Artin–Schelter regular algebra of dimension ![]() $d+1$ and Gorenstein parameter
$d+1$ and Gorenstein parameter ![]() $1$ in the sense of [Reference Martínez-VillaMV98, Reference Martínez-Villa and SolbergMS11, Reference Minamoto and MoriMM11, Reference Reyes and RogalskiRR18] (see also [Reference Artin and SchelterAS87]). This is equivalent to a result [Reference Minamoto and MoriMM11, Theorem 4.2] of Minamoto and Mori up to [Reference Reyes and RogalskiRR18, Theorem 5.2], and also can be deduced from results of Keller [Reference KellerKel11].
$1$ in the sense of [Reference Martínez-VillaMV98, Reference Martínez-Villa and SolbergMS11, Reference Minamoto and MoriMM11, Reference Reyes and RogalskiRR18] (see also [Reference Artin and SchelterAS87]). This is equivalent to a result [Reference Minamoto and MoriMM11, Theorem 4.2] of Minamoto and Mori up to [Reference Reyes and RogalskiRR18, Theorem 5.2], and also can be deduced from results of Keller [Reference KellerKel11].
4.3  $\mathbb {Z}^{2}$-graded higher preprojective algebras
$\mathbb {Z}^{2}$-graded higher preprojective algebras
Here, we consider gradings on higher preprojective algebras, which are used in § 4.4. Let ![]() $\Lambda$ be a
$\Lambda$ be a ![]() $\mathbb {Z}$-graded algebra
$\mathbb {Z}$-graded algebra
The enveloping algebra ![]() $\Lambda ^{{\operatorname {en} }}$ of
$\Lambda ^{{\operatorname {en} }}$ of ![]() $\Lambda$ has a
$\Lambda$ has a ![]() $\mathbb {Z}$-grading given by
$\mathbb {Z}$-grading given by
Using the ![]() $\mathbb {Z}$-grading on
$\mathbb {Z}$-grading on ![]() $\Lambda$, we define a new
$\Lambda$, we define a new ![]() $\mathbb {Z}$-grading on the higher preprojective algebra
$\mathbb {Z}$-grading on the higher preprojective algebra ![]() $\Pi$.
$\Pi$.
For ![]() $i>0$ and finitely generated
$i>0$ and finitely generated ![]() $\mathbb {Z}$-graded
$\mathbb {Z}$-graded ![]() $\Lambda$-modules
$\Lambda$-modules ![]() $M$ and
$M$ and ![]() $N$, let
$N$, let ![]() $\operatorname {ext} ^{i}_{\Lambda} (M,N)$ denote the
$\operatorname {ext} ^{i}_{\Lambda} (M,N)$ denote the ![]() $\mathbb {Z}$-graded
$\mathbb {Z}$-graded ![]() $i$th ext space (our notation follows [Reference Beilinson, Ginzburg and SoergelBGS96, Section 2.1]). Then we have an equality
$i$th ext space (our notation follows [Reference Beilinson, Ginzburg and SoergelBGS96, Section 2.1]). Then we have an equality
Hence, ![]() $\operatorname {Ext} ^{i}_{\Lambda} (M,N)$ has a
$\operatorname {Ext} ^{i}_{\Lambda} (M,N)$ has a ![]() $\mathbb {Z}$-grading whose degree
$\mathbb {Z}$-grading whose degree ![]() $j$ part is
$j$ part is ![]() $\operatorname {ext} ^{i}_{\Lambda} (M,N({j}))$.
$\operatorname {ext} ^{i}_{\Lambda} (M,N({j}))$.
Now we define the ![]() $\mathbb {Z}$-grading on the
$\mathbb {Z}$-grading on the ![]() $\Lambda ^{{\operatorname {en} }}$-module
$\Lambda ^{{\operatorname {en} }}$-module ![]() $E=\operatorname {Ext} ^{d}_{\Lambda} (\Lambda ^{*},\Lambda )$ by
$E=\operatorname {Ext} ^{d}_{\Lambda} (\Lambda ^{*},\Lambda )$ by
Then, as in Lemma 2.9, we can show that there are isomorphisms
of ![]() $\mathbb {Z}$-graded
$\mathbb {Z}$-graded ![]() $\Lambda ^{{\operatorname {en} }}$-modules. Let
$\Lambda ^{{\operatorname {en} }}$-modules. Let ![]() $\Lambda \operatorname {-mod^{\mathbb {Z}}}$ denote the category of finitely generated
$\Lambda \operatorname {-mod^{\mathbb {Z}}}$ denote the category of finitely generated ![]() $\mathbb {Z}$-graded left
$\mathbb {Z}$-graded left ![]() $\Lambda$-modules. We lift the functors
$\Lambda$-modules. We lift the functors ![]() $\tau _d$ and
$\tau _d$ and ![]() $\tau _d^{-}$ to
$\tau _d^{-}$ to ![]() $\mathbb {Z}$-graded
$\mathbb {Z}$-graded ![]() $\Lambda$-modules as follows:
$\Lambda$-modules as follows:
Definition 4.15 (a) The ![]() $\mathbb {Z}^{2}$-graded
$\mathbb {Z}^{2}$-graded ![]() $(d+1)$-preprojective algebra of a
$(d+1)$-preprojective algebra of a ![]() $\mathbb {Z}$-graded algebra
$\mathbb {Z}$-graded algebra ![]() $\Lambda ={\bigoplus} _{i\in \mathbb {Z}}\Lambda _i$ is the tensor algebra of the
$\Lambda ={\bigoplus} _{i\in \mathbb {Z}}\Lambda _i$ is the tensor algebra of the ![]() $\mathbb {Z}$-graded
$\mathbb {Z}$-graded ![]() $\Lambda ^{{\operatorname {en} }}$-module
$\Lambda ^{{\operatorname {en} }}$-module ![]() $E$:
$E$:
The first part of the ![]() $\mathbb {Z}^{2}$-grading is the tensor grading (Definition 2.11). The second part of the
$\mathbb {Z}^{2}$-grading is the tensor grading (Definition 2.11). The second part of the ![]() $\mathbb {Z}^{2}$-grading is called the
$\mathbb {Z}^{2}$-grading is called the ![]() $\Lambda$-grading, which is a natural grading on
$\Lambda$-grading, which is a natural grading on ![]() $E^{i}$ for any
$E^{i}$ for any ![]() $i\ge 0$ given by the
$i\ge 0$ given by the ![]() $\mathbb {Z}$-grading on
$\mathbb {Z}$-grading on ![]() $E$ in (22).
$E$ in (22).
(b) We consider a single ![]() $\mathbb {Z}$-grading on
$\mathbb {Z}$-grading on ![]() $\Pi$, called the
$\Pi$, called the ![]() $(d+1)$-total grading, by defining
$(d+1)$-total grading, by defining
where ![]() $\Pi _{i,j}=(E^{i})_j$ denotes the
$\Pi _{i,j}=(E^{i})_j$ denotes the ![]() $j$th graded component of
$j$th graded component of ![]() $E^{i}$.
$E^{i}$.
Later we use the following observation.
Proposition 4.16 If ![]() $\Lambda$ is a Koszul algebra with radical grading (see § 2.2), then
$\Lambda$ is a Koszul algebra with radical grading (see § 2.2), then ![]() $E$ is generated in degree
$E$ is generated in degree ![]() $-d$. Therefore, the
$-d$. Therefore, the ![]() $(d+1)$-total grading of
$(d+1)$-total grading of ![]() $\Pi$ gives a radical grading.
$\Pi$ gives a radical grading.
Proof. If ![]() $\Lambda$ is Koszul, then
$\Lambda$ is Koszul, then ![]() $P_d$ is generated in degree
$P_d$ is generated in degree ![]() $d$ by Theorem 2.7, and the former assertion follows. As
$d$ by Theorem 2.7, and the former assertion follows. As ![]() $\Pi _0=\Lambda _0$,
$\Pi _0=\Lambda _0$, ![]() $\Pi _1=\Lambda _1\oplus E_{-d}$ and
$\Pi _1=\Lambda _1\oplus E_{-d}$ and ![]() $E_{-d}=\operatorname {head} _{\Lambda ^{{\operatorname {en} }}}E$, the latter assertion follows.
$E_{-d}=\operatorname {head} _{\Lambda ^{{\operatorname {en} }}}E$, the latter assertion follows.
4.4 Koszul properties of higher preprojective algebras
Let ![]() $\Lambda$ be a
$\Lambda$ be a ![]() $d$-hereditary
$d$-hereditary ![]() $\mathbb {F}$-algebra. In this section, we further assume that
$\mathbb {F}$-algebra. In this section, we further assume that ![]() $\Lambda$ is a
$\Lambda$ is a ![]() $\mathbb {Z}$-graded algebra
$\mathbb {Z}$-graded algebra ![]() $\Lambda ={\bigoplus} _{i\in \mathbb {Z}}\Lambda _i$. We denote by
$\Lambda ={\bigoplus} _{i\in \mathbb {Z}}\Lambda _i$. We denote by ![]() ${{D^{b}}}(\Lambda \operatorname {-mod^{\mathbb{Z}}})$ the bounded derived category of
${{D^{b}}}(\Lambda \operatorname {-mod^{\mathbb{Z}}})$ the bounded derived category of ![]() $\Lambda \operatorname {-mod^{\mathbb{Z}}}$. As in the ungraded case, we define an autoequivalence
$\Lambda \operatorname {-mod^{\mathbb{Z}}}$. As in the ungraded case, we define an autoequivalence
and a full subcategory
We have the following graded version of Theorem 4.9.
Theorem 4.17 Let ![]() $\Lambda$ be a
$\Lambda$ be a ![]() $\mathbb {Z}$-graded
$\mathbb {Z}$-graded ![]() $d$-hereditary algebra.
$d$-hereditary algebra.
(a) If ![]() $\Lambda$ is
$\Lambda$ is ![]() $d$-RI, then any indecomposable object
$d$-RI, then any indecomposable object ![]() $X$ (respectively,
$X$ (respectively, ![]() $Y$) in
$Y$) in ![]() $\mathscr {U}^{\mathbb {Z}}$ has a
$\mathscr {U}^{\mathbb {Z}}$ has a ![]() $d$-almost split sequence in
$d$-almost split sequence in ![]() $\mathscr {U}^{\mathbb {Z}}$
$\mathscr {U}^{\mathbb {Z}}$
Moreover, we have ![]() $Y\cong \nu _d(X)$ (respectively,
$Y\cong \nu _d(X)$ (respectively, ![]() $X\cong \nu _d^{-1}(Y)$).
$X\cong \nu _d^{-1}(Y)$).
(b) If ![]() $\Lambda$ is
$\Lambda$ is ![]() $d$-RF, then any indecomposable object
$d$-RF, then any indecomposable object ![]() $X$ (respectively,
$X$ (respectively, ![]() $Y$) in
$Y$) in ![]() $\mathscr {U}^{\mathbb {Z}}$ has a weak
$\mathscr {U}^{\mathbb {Z}}$ has a weak ![]() $d$-almost split sequence in
$d$-almost split sequence in ![]() $\mathscr {U}^{\mathbb {Z}}$
$\mathscr {U}^{\mathbb {Z}}$
Moreover, we have ![]() $Y\cong \nu _d(X)$ (respectively,
$Y\cong \nu _d(X)$ (respectively, ![]() $X\cong \nu _d^{-1}(Y)$),
$X\cong \nu _d^{-1}(Y)$), ![]() $\operatorname {Ker} (f_d{}_*)=\operatorname {soc} \operatorname {Hom} _{\mathscr {U}}(-,Y)$ and
$\operatorname {Ker} (f_d{}_*)=\operatorname {soc} \operatorname {Hom} _{\mathscr {U}}(-,Y)$ and ![]() $\operatorname {Ker} (f_0{}^{*})=\operatorname {soc} \operatorname {Hom} _{\mathscr {U}}(X,-)$.
$\operatorname {Ker} (f_0{}^{*})=\operatorname {soc} \operatorname {Hom} _{\mathscr {U}}(X,-)$.
Proof. The proof is very similar to Theorem 4.9.
Let ![]() $\Pi$ be the
$\Pi$ be the ![]() $\mathbb {Z}^{2}$-graded
$\mathbb {Z}^{2}$-graded ![]() $(d+1)$-preprojective algebra. Recall from Definition 4.15 that the first entry of the
$(d+1)$-preprojective algebra. Recall from Definition 4.15 that the first entry of the ![]() $\mathbb {Z}^{2}$-grading is the tensor grading, and the second is the
$\mathbb {Z}^{2}$-grading is the tensor grading, and the second is the ![]() $\Lambda$-grading.
$\Lambda$-grading.
On the other hand, we consider the action of ![]() $\mathbb {Z}^{2}$ on
$\mathbb {Z}^{2}$ on ![]() $\mathscr {U}^{\mathbb {Z}}$ given by
$\mathscr {U}^{\mathbb {Z}}$ given by ![]() $(i,j)\mapsto \nu _d^{-i}(j)$. The following description of the category
$(i,j)\mapsto \nu _d^{-i}(j)$. The following description of the category ![]() $\mathscr {U}^{\mathbb {Z}}$ follows directly from Lemma 4.10 and the definition.
$\mathscr {U}^{\mathbb {Z}}$ follows directly from Lemma 4.10 and the definition.
Proposition 4.18 (a) There are equivalences of additive categories
 \begin{align*} & G^{\mathbb{Z}}=\mathop{\bigoplus}\limits_{i,j\in\mathbb{Z}}\operatorname{Hom}_{{{D^{b}}}(\Lambda\operatorname{-mod^{\mathbb{Z}}})}\big(\Lambda,\nu_d^{{-}i}(-)(j)\big):\mathscr{U}^{\mathbb{Z}}\cong\operatorname{proj^{\mathbb{Z}^{2}}-}\Pi,\\ & H^{\mathbb{Z}}=\mathop{\bigoplus}\limits_{i,j\in\mathbb{Z}}\operatorname{Hom}_{{{D^{b}}}(\Lambda\operatorname{-mod^{\mathbb{Z}}})}\big(-,\nu_d^{{-}i}(\Lambda)(j)\big):\mathscr{U}^{\mathbb{Z}}\cong\Pi\operatorname{-proj^{\mathbb{Z}^{2}}}. \end{align*}
\begin{align*} & G^{\mathbb{Z}}=\mathop{\bigoplus}\limits_{i,j\in\mathbb{Z}}\operatorname{Hom}_{{{D^{b}}}(\Lambda\operatorname{-mod^{\mathbb{Z}}})}\big(\Lambda,\nu_d^{{-}i}(-)(j)\big):\mathscr{U}^{\mathbb{Z}}\cong\operatorname{proj^{\mathbb{Z}^{2}}-}\Pi,\\ & H^{\mathbb{Z}}=\mathop{\bigoplus}\limits_{i,j\in\mathbb{Z}}\operatorname{Hom}_{{{D^{b}}}(\Lambda\operatorname{-mod^{\mathbb{Z}}})}\big(-,\nu_d^{{-}i}(\Lambda)(j)\big):\mathscr{U}^{\mathbb{Z}}\cong\Pi\operatorname{-proj^{\mathbb{Z}^{2}}}. \end{align*}(b) The following diagram commutes up to natural isomorphism.

(c) We have the following commutative diagrams.

Immediately, we have the following ![]() $\mathbb {Z}$-graded version of Theorem 4.12.
$\mathbb {Z}$-graded version of Theorem 4.12.
Theorem 4.19 Let ![]() $\Lambda$ be a
$\Lambda$ be a ![]() $\mathbb {Z}$-graded
$\mathbb {Z}$-graded ![]() $d$-hereditary algebra. For an indecomposable object
$d$-hereditary algebra. For an indecomposable object ![]() $X$ in
$X$ in ![]() $\mathscr {U}^{\mathbb {Z}}$, we consider a weak
$\mathscr {U}^{\mathbb {Z}}$, we consider a weak ![]() $d$-almost split sequence in
$d$-almost split sequence in ![]() $\mathscr {U}^{\mathbb {Z}}$:
$\mathscr {U}^{\mathbb {Z}}$:
(a) There exist exact sequences
in \begin{gather*} G^{\mathbb{Z}}Y\xrightarrow{G^{\mathbb{Z}}f_d} G^{\mathbb{Z}}C_{d-1}\xrightarrow{G^{\mathbb{Z}}f_{d-1}}\cdots\xrightarrow{G^{\mathbb{Z}}f_2} G^{\mathbb{Z}}C_1\xrightarrow{G^{\mathbb{Z}}f_1} G^{\mathbb{Z}}C_0\xrightarrow{G^{\mathbb{Z}}f_0} G^{\mathbb{Z}}X\to S\to 0,\\ H^{\mathbb{Z}}X\xrightarrow{H^{\mathbb{Z}}f_0} H^{\mathbb{Z}}C_0\xrightarrow{H^{\mathbb{Z}}f_1}H^{\mathbb{Z}}C_1\xrightarrow{H^{\mathbb{Z}}f_2}\cdots\xrightarrow{H^{\mathbb{Z}}f_{d-1}} H^{\mathbb{Z}}C_{d-1}\xrightarrow{H^{\mathbb{Z}}f_d} H^{\mathbb{Z}}Y\to T\to 0 \end{gather*}
\begin{gather*} G^{\mathbb{Z}}Y\xrightarrow{G^{\mathbb{Z}}f_d} G^{\mathbb{Z}}C_{d-1}\xrightarrow{G^{\mathbb{Z}}f_{d-1}}\cdots\xrightarrow{G^{\mathbb{Z}}f_2} G^{\mathbb{Z}}C_1\xrightarrow{G^{\mathbb{Z}}f_1} G^{\mathbb{Z}}C_0\xrightarrow{G^{\mathbb{Z}}f_0} G^{\mathbb{Z}}X\to S\to 0,\\ H^{\mathbb{Z}}X\xrightarrow{H^{\mathbb{Z}}f_0} H^{\mathbb{Z}}C_0\xrightarrow{H^{\mathbb{Z}}f_1}H^{\mathbb{Z}}C_1\xrightarrow{H^{\mathbb{Z}}f_2}\cdots\xrightarrow{H^{\mathbb{Z}}f_{d-1}} H^{\mathbb{Z}}C_{d-1}\xrightarrow{H^{\mathbb{Z}}f_d} H^{\mathbb{Z}}Y\to T\to 0 \end{gather*} $\operatorname {mod^{\mathbb {Z}^{2}}-}\Pi$ and
$\operatorname {mod^{\mathbb {Z}^{2}}-}\Pi$ and  $\Pi \operatorname {-mod^{\mathbb {Z}^{2}}}$, where
$\Pi \operatorname {-mod^{\mathbb {Z}^{2}}}$, where  $S$ and
$S$ and  $T$ are simple.
$T$ are simple.(b) If
 $\Lambda$ is
$\Lambda$ is  $d$-RI, then
$d$-RI, then  $G^{\mathbb {Z}}f_d$ and
$G^{\mathbb {Z}}f_d$ and  $H^{\mathbb {Z}}f_0$ are monomorphisms.
$H^{\mathbb {Z}}f_0$ are monomorphisms.(c) If
 $\Lambda$ is
$\Lambda$ is  $d$-RF, then
$d$-RF, then  $\operatorname {Ker} G^{\mathbb {Z}}f_d=\operatorname {soc} G^{\mathbb {Z}}Y$ and
$\operatorname {Ker} G^{\mathbb {Z}}f_d=\operatorname {soc} G^{\mathbb {Z}}Y$ and  $\operatorname {Ker} H^{\mathbb {Z}}f_0=\operatorname {soc} H^{\mathbb {Z}}X$ hold. Moreover, these are simple.
$\operatorname {Ker} H^{\mathbb {Z}}f_0=\operatorname {soc} H^{\mathbb {Z}}X$ hold. Moreover, these are simple.
We now recall the theory of almost Koszul duality due to Brenner, Butler, and King [Reference Brenner, Butler and KingBBK02]. Let ![]() $S$ be a semisimple finite-dimensional
$S$ be a semisimple finite-dimensional ![]() $\mathbb {F}$-algebra and
$\mathbb {F}$-algebra and ![]() $A={\bigoplus} _{i\geq 0}A_i$ a non-negatively
$A={\bigoplus} _{i\geq 0}A_i$ a non-negatively ![]() $\mathbb {Z}$-graded
$\mathbb {Z}$-graded ![]() $S$-algebra with
$S$-algebra with ![]() $A_0=S$.
$A_0=S$.
Definition 4.20 The ![]() $\mathbb {Z}$-graded algebra
$\mathbb {Z}$-graded algebra ![]() $A$ is almost Koszul, or
$A$ is almost Koszul, or ![]() $(p,q)$-Koszul, if there exist integers
$(p,q)$-Koszul, if there exist integers ![]() $p,q\geq 1$ such that
$p,q\geq 1$ such that ![]() $A_i=0$ for all
$A_i=0$ for all ![]() $i>p$ and there is an exact sequence
$i>p$ and there is an exact sequence
of ![]() $\mathbb {Z}$-graded
$\mathbb {Z}$-graded ![]() $A$-modules with projective
$A$-modules with projective ![]() $A$-modules
$A$-modules ![]() $P_i$ generated in degree
$P_i$ generated in degree ![]() $i$ and a semisimple
$i$ and a semisimple ![]() $A$-module
$A$-module ![]() $S'$ concentrated in degree
$S'$ concentrated in degree ![]() $p+q$.
$p+q$.
Note that it does not matter whether we consider left or right ![]() $A$-modules [Reference Brenner, Butler and KingBBK02, Proposition 3.4].
$A$-modules [Reference Brenner, Butler and KingBBK02, Proposition 3.4].
Theorem 4.21 Let ![]() $\Lambda$ be a Koszul
$\Lambda$ be a Koszul ![]() $d$-hereditary algebra with radical grading, and
$d$-hereditary algebra with radical grading, and ![]() $\Pi$ its
$\Pi$ its ![]() $(d+1)$-preprojective algebra with the
$(d+1)$-preprojective algebra with the ![]() $(d+1)$-total grading given in Definition 4.15.
$(d+1)$-total grading given in Definition 4.15.
(a) If
 $\Lambda$ is
$\Lambda$ is  $d$-RI, then
$d$-RI, then  $\Pi$ is Koszul.
$\Pi$ is Koszul.(b) If
 $\Lambda$ is
$\Lambda$ is  $d$-RF, then
$d$-RF, then  $\Pi$ is almost Koszul. It is
$\Pi$ is almost Koszul. It is  $(p,d+1)$-Koszul, where
$(p,d+1)$-Koszul, where  $p=\max \{i\ge 0\mid \Pi _i\neq 0\}$ with respect to the total grading.
$p=\max \{i\ge 0\mid \Pi _i\neq 0\}$ with respect to the total grading.
Proof. Let ![]() $\operatorname {mod^{\mathbb{Z}}-}\Pi$ be the category of
$\operatorname {mod^{\mathbb{Z}}-}\Pi$ be the category of ![]() $\mathbb {Z}$-graded
$\mathbb {Z}$-graded ![]() $\Pi$-modules with respect to the
$\Pi$-modules with respect to the ![]() $(d+1)$-total grading on
$(d+1)$-total grading on ![]() $\Pi$. Let
$\Pi$. Let ![]() $S$ be a
$S$ be a ![]() $\mathbb {Z}$-graded simple
$\mathbb {Z}$-graded simple ![]() $\Pi$-module
$\Pi$-module ![]() $S$ concentrated in degree 0. Consider the functor
$S$ concentrated in degree 0. Consider the functor ![]() $F:\operatorname {mod^{\mathbb {Z}^{2}}-}\Pi \to \operatorname {mod^{\mathbb{Z}}-}\Pi$ given by
$F:\operatorname {mod^{\mathbb {Z}^{2}}-}\Pi \to \operatorname {mod^{\mathbb{Z}}-}\Pi$ given by ![]() ${\bigoplus} _{(i,j)\in \mathbb {Z}^{2}}X_{i,j}\mapsto {\bigoplus} _{\ell \in \mathbb {Z}}X_{\ell}$, where
${\bigoplus} _{(i,j)\in \mathbb {Z}^{2}}X_{i,j}\mapsto {\bigoplus} _{\ell \in \mathbb {Z}}X_{\ell}$, where ![]() $X_{\ell} ={\bigoplus} _{(d+1)i+j=\ell }X_{i,j}$. Let
$X_{\ell} ={\bigoplus} _{(d+1)i+j=\ell }X_{i,j}$. Let ![]() $G'=F\circ G^{\mathbb {Z}}$ and
$G'=F\circ G^{\mathbb {Z}}$ and ![]() $H'=F\circ H^{\mathbb {Z}}$. Then Theorem 4.19(a) gives the first
$H'=F\circ H^{\mathbb {Z}}$. Then Theorem 4.19(a) gives the first ![]() $d+1$ terms of minimal
$d+1$ terms of minimal ![]() $\mathbb {Z}$-graded projective resolutions
$\mathbb {Z}$-graded projective resolutions
To prove both assertions, we only have to show that ![]() $G'C_i$ is generated in degree
$G'C_i$ is generated in degree ![]() $i+1$. As
$i+1$. As ![]() $\Lambda$ is Koszul, by Proposition 4.16, the
$\Lambda$ is Koszul, by Proposition 4.16, the ![]() $(d+1)$-total grading gives a radical grading on
$(d+1)$-total grading gives a radical grading on ![]() $\Pi$. As
$\Pi$. As ![]() $G'X$ is generated in degree
$G'X$ is generated in degree ![]() $0$ and (23) is minimal,
$0$ and (23) is minimal, ![]() $G'C_i$ is generated in degrees at least
$G'C_i$ is generated in degrees at least ![]() $i+1$.
$i+1$.
By Proposition 4.18(c), we have ![]() $G^{\mathbb {Z}}Y=G^{\mathbb {Z}}\nu _d(X)=(G^{\mathbb {Z}}X)(-1,0)$ and hence
$G^{\mathbb {Z}}Y=G^{\mathbb {Z}}\nu _d(X)=(G^{\mathbb {Z}}X)(-1,0)$ and hence ![]() $G'Y=(G'X)(-d-1)$. Thus,
$G'Y=(G'X)(-d-1)$. Thus, ![]() $G'Y$ is generated in degree
$G'Y$ is generated in degree ![]() $d+1$ and, hence,
$d+1$ and, hence, ![]() $H'Y$ is generated in degree
$H'Y$ is generated in degree ![]() $-d-1$ by Proposition 4.18(b). As (24) is minimal,
$-d-1$ by Proposition 4.18(b). As (24) is minimal, ![]() $H'C_i$ is generated in degrees at least
$H'C_i$ is generated in degrees at least ![]() $-i-1$ and, hence,
$-i-1$ and, hence, ![]() $G'C_i$ is generated in degrees at most
$G'C_i$ is generated in degrees at most ![]() $i+1$. Thus, the assertion follows.
$i+1$. Thus, the assertion follows.
5. Quadratic duals of higher preprojective algebras
The aim of this section is to compare the quadratic duals of the higher preprojective algebras and certain twisted trivial extension algebras of the quadratic duals for Koszul algebras.
5.1 Graded trivial extension algebras
For any finite-dimensional ![]() $\mathbb {F}$-algebra
$\mathbb {F}$-algebra ![]() $\Gamma$, there is a well-known way to construct a new algebra called the trivial extension algebra. We describe a graded version of this, which can be seen as an extension of
$\Gamma$, there is a well-known way to construct a new algebra called the trivial extension algebra. We describe a graded version of this, which can be seen as an extension of ![]() $\Gamma$ by a twist of the dual bimodule
$\Gamma$ by a twist of the dual bimodule ![]() $\Gamma ^{*}$.
$\Gamma ^{*}$.
Definition 5.1 Let ![]() $\Gamma$ be a non-negatively
$\Gamma$ be a non-negatively ![]() $\mathbb {Z}$-graded finite-dimensional algebra and
$\mathbb {Z}$-graded finite-dimensional algebra and ![]() $n\in \mathbb {Z}$. The graded
$n\in \mathbb {Z}$. The graded ![]() $(d+1)$-trivial extension algebra of
$(d+1)$-trivial extension algebra of ![]() $\Gamma$, denoted
$\Gamma$, denoted ![]() $\operatorname {Triv} _{d+1}(\Gamma )$, is the
$\operatorname {Triv} _{d+1}(\Gamma )$, is the ![]() $\mathbb {Z}$-graded vector space
$\mathbb {Z}$-graded vector space ![]() $\Gamma \oplus \Gamma ^{*}({-d-1})$ with multiplication given by
$\Gamma \oplus \Gamma ^{*}({-d-1})$ with multiplication given by
when ![]() $b\in \Gamma _i$ is a homogeneous element of degree
$b\in \Gamma _i$ is a homogeneous element of degree ![]() $i$.
$i$.
We have used the fact that ![]() $\Gamma$, and hence
$\Gamma$, and hence ![]() $\Gamma ^{*}$, has a natural structure of a
$\Gamma ^{*}$, has a natural structure of a ![]() $\Gamma ^{{\operatorname {en} }}$-module.
$\Gamma ^{{\operatorname {en} }}$-module.
One can interpret ![]() $\mathbb {Z}$-graded
$\mathbb {Z}$-graded ![]() $d$-trivial extensions in the following way. First, let
$d$-trivial extensions in the following way. First, let ![]() $\sigma :\Gamma \to \Gamma$ be the algebra automorphism defined by
$\sigma :\Gamma \to \Gamma$ be the algebra automorphism defined by ![]() $\sigma (a)=(-1)^{i}a$ for
$\sigma (a)=(-1)^{i}a$ for ![]() $a\in \Gamma _i$. Then
$a\in \Gamma _i$. Then ![]() $\operatorname {Triv} _{d+1}(\Gamma )$ is the trivial extension of
$\operatorname {Triv} _{d+1}(\Gamma )$ is the trivial extension of ![]() $\Gamma$ by the twisted bimodule
$\Gamma$ by the twisted bimodule ![]() ${}_{\sigma ^{d}}\Gamma ^{*}$. Note that another multiplication rule
${}_{\sigma ^{d}}\Gamma ^{*}$. Note that another multiplication rule ![]() $(a,f)\cdot (b,g)=(ab,(-1)^{di}ag+fb))$ with
$(a,f)\cdot (b,g)=(ab,(-1)^{di}ag+fb))$ with ![]() $a\in \Gamma _i$ used in [Reference GrantGra19] gives an isomorphic
$a\in \Gamma _i$ used in [Reference GrantGra19] gives an isomorphic ![]() $\mathbb {Z}$-graded algebra.
$\mathbb {Z}$-graded algebra.
In the rest of this section, we assume that
is a Koszul algebra with a separable ![]() $\mathbb {F}$-algebra
$\mathbb {F}$-algebra ![]() $S$, and
$S$, and ![]() $\Gamma$ is its quadratic dual
$\Gamma$ is its quadratic dual ![]() $\Gamma =\Lambda ^{!}$. Recall that we have
$\Gamma =\Lambda ^{!}$. Recall that we have ![]() $S^{{\operatorname {en} }}$-modules
$S^{{\operatorname {en} }}$-modules ![]() $K_i$ with
$K_i$ with ![]() $K_0=S$,
$K_0=S$, ![]() $K_1=V$ and
$K_1=V$ and ![]() $K_2=R$ and maps
$K_2=R$ and maps ![]() $\iota ^{\ell }_i:K_i\hookrightarrow V\otimes _SK_{i-1}$ and
$\iota ^{\ell }_i:K_i\hookrightarrow V\otimes _SK_{i-1}$ and ![]() $\iota ^{r}_i:K_i\hookrightarrow K_{i-1}\otimes _SV$. By Lemma 2.6, we have an isomorphism of
$\iota ^{r}_i:K_i\hookrightarrow K_{i-1}\otimes _SV$. By Lemma 2.6, we have an isomorphism of ![]() $\mathbb {Z}$-graded algebras
$\mathbb {Z}$-graded algebras
where the algebra structure on ![]() ${\bigoplus} _{i\geq 0}K_i^{*\ell }$ is given by
${\bigoplus} _{i\geq 0}K_i^{*\ell }$ is given by ![]() $(\iota ^{\ell }_i)^{*\ell }:K_{i-1}^{*\ell }\otimes _SV^{*\ell }\to K_i^{*\ell }$ and
$(\iota ^{\ell }_i)^{*\ell }:K_{i-1}^{*\ell }\otimes _SV^{*\ell }\to K_i^{*\ell }$ and ![]() $(\iota ^{r}_i)^{*\ell }:V^{*\ell }\otimes _SK_{i-1}^{*\ell }\to K_i^{*\ell }$. As
$(\iota ^{r}_i)^{*\ell }:V^{*\ell }\otimes _SK_{i-1}^{*\ell }\to K_i^{*\ell }$. As ![]() $(\Lambda ^{!})_i=\operatorname {Ext} ^{i}_{\Lambda} (S,S)$, the global dimension
$(\Lambda ^{!})_i=\operatorname {Ext} ^{i}_{\Lambda} (S,S)$, the global dimension ![]() $d$ of
$d$ of ![]() $\Lambda$ is the maximal
$\Lambda$ is the maximal ![]() $i$ such that
$i$ such that ![]() $(\Lambda ^{!})_i\neq 0$, and we have
$(\Lambda ^{!})_i\neq 0$, and we have
where ![]() $K_i=0$ for
$K_i=0$ for ![]() $i<0$ or
$i<0$ or ![]() $i>d$, and
$i>d$, and ![]() $\operatorname {Triv} _{d+1}(\Lambda ^{!})$ is concentrated in degrees
$\operatorname {Triv} _{d+1}(\Lambda ^{!})$ is concentrated in degrees ![]() $0$ to
$0$ to ![]() $d+1$.
$d+1$.
Recall from Proposition 3.12 that if ![]() $\Lambda$ is a Koszul algebra, then its higher preprojective algebra
$\Lambda$ is a Koszul algebra, then its higher preprojective algebra ![]() $\Pi$ is quadratic. We are now able to state the following result for the quadratic dual
$\Pi$ is quadratic. We are now able to state the following result for the quadratic dual ![]() $\Pi ^{!}$ of
$\Pi ^{!}$ of ![]() $\Pi$.
$\Pi$.
Theorem 5.2 Let ![]() $\Lambda$ be a finite-dimensional Koszul
$\Lambda$ be a finite-dimensional Koszul ![]() $\mathbb {F}$-algebra of global dimension
$\mathbb {F}$-algebra of global dimension ![]() $d$ such that
$d$ such that ![]() $S=\Lambda _0$ is a separable
$S=\Lambda _0$ is a separable ![]() $\mathbb {F}$-algebra, and let
$\mathbb {F}$-algebra, and let ![]() $\Pi$ be its higher preprojective algebra with radical grading:
$\Pi$ be its higher preprojective algebra with radical grading:
(a) there exists a morphism
 $\phi :\Pi ^{!}\to \operatorname {Triv} _{d+1}(\Lambda ^{!})$ of
$\phi :\Pi ^{!}\to \operatorname {Triv} _{d+1}(\Lambda ^{!})$ of  $\mathbb {Z}$-graded
$\mathbb {Z}$-graded  $\mathbb {F}$-algebras, which is an isomorphism in degrees
$\mathbb {F}$-algebras, which is an isomorphism in degrees  $0$ and
$0$ and  $1$ and is injective in degree
$1$ and is injective in degree  $2$;
$2$;(b)
 $\phi$ is surjective if and only if
$\phi$ is surjective if and only if  $(\Lambda ^{!})_d=\operatorname {soc} _{\Lambda ^{!{{\operatorname {en} }}}}(\Lambda ^{!})$; in this case
$(\Lambda ^{!})_d=\operatorname {soc} _{\Lambda ^{!{{\operatorname {en} }}}}(\Lambda ^{!})$; in this case  $\phi$ is an isomorphism in degrees
$\phi$ is an isomorphism in degrees  $0$,
$0$,  $1$, and
$1$, and  $2$;
$2$;(c)
 $\phi$ is an isomorphism if and only if
$\phi$ is an isomorphism if and only if  $(\Lambda ^{!})_d=\operatorname {soc} _{\Lambda ^{!{{\operatorname {en} }}}}(\Lambda ^{!})$ holds and
$(\Lambda ^{!})_d=\operatorname {soc} _{\Lambda ^{!{{\operatorname {en} }}}}(\Lambda ^{!})$ holds and  $\operatorname {Triv} _{d+1}(\Lambda ^{!})$ is quadratic.
$\operatorname {Triv} _{d+1}(\Lambda ^{!})$ is quadratic.
To prove this, we need the following technical observation. Consider the ![]() $\mathbb {Z}$-graded
$\mathbb {Z}$-graded ![]() $\Lambda ^{!{{\operatorname {en} }}}$-module
$\Lambda ^{!{{\operatorname {en} }}}$-module
whose structure is given by ![]() $(\theta _i^{\ell })^{*\ell }:V^{*\ell }\otimes _SK_{i-1}^{\vee *\ell }\to K_i^{\vee *\ell }$ and
$(\theta _i^{\ell })^{*\ell }:V^{*\ell }\otimes _SK_{i-1}^{\vee *\ell }\to K_i^{\vee *\ell }$ and ![]() $(\theta _i^{r})^{*\ell }:K_{i-1}^{\vee *\ell }\otimes _SV^{*\ell }\to K_i^{\vee *\ell }$ obtained from (15).
$(\theta _i^{r})^{*\ell }:K_{i-1}^{\vee *\ell }\otimes _SV^{*\ell }\to K_i^{\vee *\ell }$ obtained from (15).
Lemma 5.3 We have an isomorphism ![]() $\Lambda^{!*}(-d-1)\cong L$ of
$\Lambda^{!*}(-d-1)\cong L$ of ![]() $\mathbb {Z}$-graded
$\mathbb {Z}$-graded ![]() $\Lambda ^{!{{\operatorname {en} }}}$-modules.
$\Lambda ^{!{{\operatorname {en} }}}$-modules.
Proof. Applying Lemma 2.4 and its dual to the ![]() $\mathbb {Z}$-graded
$\mathbb {Z}$-graded ![]() $\Lambda ^{!{{\operatorname {en} }}}$-module
$\Lambda ^{!{{\operatorname {en} }}}$-module ![]() ${\bigoplus} _{i\in \mathbb {Z}}K_i^{*\ell }$, we obtain isomorphisms of
${\bigoplus} _{i\in \mathbb {Z}}K_i^{*\ell }$, we obtain isomorphisms of ![]() $\mathbb {Z}$-graded
$\mathbb {Z}$-graded ![]() $\Lambda ^{!{{\operatorname {en} }}}$-modules
$\Lambda ^{!{{\operatorname {en} }}}$-modules ![]() $\Lambda ^{!*}={\bigoplus} _{i\in \mathbb {Z}}K_{-i}^{*\ell *}\cong {\bigoplus} _{i\in \mathbb {Z}}K_{-i}^{*\ell *r}\cong {\bigoplus} _{i\in \mathbb {Z}}K_{-i}$. Similarly, we obtain isomorphisms of
$\Lambda ^{!*}={\bigoplus} _{i\in \mathbb {Z}}K_{-i}^{*\ell *}\cong {\bigoplus} _{i\in \mathbb {Z}}K_{-i}^{*\ell *r}\cong {\bigoplus} _{i\in \mathbb {Z}}K_{-i}$. Similarly, we obtain isomorphisms of ![]() $\mathbb {Z}$-graded
$\mathbb {Z}$-graded ![]() $\Lambda ^{!{{\operatorname {en} }}}$-modules
$\Lambda ^{!{{\operatorname {en} }}}$-modules ![]() $L={\bigoplus} _{i\in \mathbb {Z}}K_{d+1-i}^{\vee *\ell }\cong {\bigoplus} _{i\in \mathbb {Z}}K_{d+1-i}^{\vee \vee }\cong {\bigoplus} _{i\in \mathbb {Z}}K_{d+1-i}$. Thus, the assertion follows.
$L={\bigoplus} _{i\in \mathbb {Z}}K_{d+1-i}^{\vee *\ell }\cong {\bigoplus} _{i\in \mathbb {Z}}K_{d+1-i}^{\vee \vee }\cong {\bigoplus} _{i\in \mathbb {Z}}K_{d+1-i}$. Thus, the assertion follows.
We are ready to prove Theorem 5.2.
Proof of Theorem 5.2. Twisting the right action of ![]() $\Lambda ^{!}$ on
$\Lambda ^{!}$ on ![]() $L$ as
$L$ as ![]() $f\cdot a:=(-1)^{di}fa$ for
$f\cdot a:=(-1)^{di}fa$ for ![]() $f\in L$ and
$f\in L$ and ![]() $a\in (\Lambda ^{!})_i$, we obtain an
$a\in (\Lambda ^{!})_i$, we obtain an ![]() $\Lambda ^{!{{\operatorname {en} }}}$-module
$\Lambda ^{!{{\operatorname {en} }}}$-module ![]() $L'$. Thanks to Lemma 5.3, we can regard
$L'$. Thanks to Lemma 5.3, we can regard ![]() $\operatorname {Triv} _{d+1}(\Lambda ^{!})$ as
$\operatorname {Triv} _{d+1}(\Lambda ^{!})$ as ![]() $\operatorname {Triv} _{d+1}(\Lambda ^{!})=\Lambda ^{!}\oplus L'={\bigoplus} _{i\in \mathbb {Z}}\big (K_i^{*\ell }\oplus K_{d+1-i}^{\vee *\ell }\big )$.
$\operatorname {Triv} _{d+1}(\Lambda ^{!})=\Lambda ^{!}\oplus L'={\bigoplus} _{i\in \mathbb {Z}}\big (K_i^{*\ell }\oplus K_{d+1-i}^{\vee *\ell }\big )$.
(a) By Proposition 3.2, ![]() $\Pi$ is a quotient of
$\Pi$ is a quotient of ![]() $\operatorname {T} _S(\bar {V})$, so
$\operatorname {T} _S(\bar {V})$, so ![]() $\Pi ^{!}$ is a quotient of
$\Pi ^{!}$ is a quotient of ![]() $\operatorname {T} _S(\bar {V}^{*\ell })$. As
$\operatorname {T} _S(\bar {V}^{*\ell })$. As
we have a morphism ![]() $\phi ':\operatorname {T} _S(\bar {V}^{*\ell })\to \operatorname {Triv} _{d+1}(\Lambda ^{!})$ of
$\phi ':\operatorname {T} _S(\bar {V}^{*\ell })\to \operatorname {Triv} _{d+1}(\Lambda ^{!})$ of ![]() $\mathbb {F}$-algebras
$\mathbb {F}$-algebras
By Proposition 3.12, ![]() $\Pi$ is a quadratic algebra whose degree
$\Pi$ is a quadratic algebra whose degree ![]() $2$ part is
$2$ part is
 \[ \Pi_2={\frac{V\otimes_SV}{R}\oplus\frac{\big(V\otimes_SK_d^{{\vee}}\big) \oplus\big(K_d^{{\vee}}\otimes_SV\big)}{\delta_d'\big(K_{d-1}^{{\vee}}\big)}\oplus K_d^{{\vee}}\otimes_SK_d^{{\vee}}}, \]
\[ \Pi_2={\frac{V\otimes_SV}{R}\oplus\frac{\big(V\otimes_SK_d^{{\vee}}\big) \oplus\big(K_d^{{\vee}}\otimes_SV\big)}{\delta_d'\big(K_{d-1}^{{\vee}}\big)}\oplus K_d^{{\vee}}\otimes_SK_d^{{\vee}}}, \]
where we use the notation (25). Therefore, ![]() $\Pi ^{!}$ is also a quadratic algebra whose degree
$\Pi ^{!}$ is also a quadratic algebra whose degree ![]() $2$ part is
$2$ part is
On the other hand, we have
Now we compare ![]() $(\Pi ^{!})_2$ with
$(\Pi ^{!})_2$ with ![]() $\operatorname {Triv} _{d+1}(\Lambda ^{!})_2$. To prove that
$\operatorname {Triv} _{d+1}(\Lambda ^{!})_2$. To prove that ![]() $\phi '$ induces the desired morphism
$\phi '$ induces the desired morphism ![]() $\phi :\Pi ^{!}\to \operatorname {Triv} _{d+1}(\Lambda ^{!})$, it suffices to show that the following sequence is exact:
$\phi :\Pi ^{!}\to \operatorname {Triv} _{d+1}(\Lambda ^{!})$, it suffices to show that the following sequence is exact:
By our definition of the ![]() $\Lambda ^{!{{\operatorname {en} }}}$-module structure on
$\Lambda ^{!{{\operatorname {en} }}}$-module structure on ![]() $L'$, the morphism
$L'$, the morphism ![]() $\phi '$ in (26) is
$\phi '$ in (26) is ![]() $(\theta _d^{\ell }+(-1)^{d}\theta _d^{r})^{*\ell }$. As
$(\theta _d^{\ell }+(-1)^{d}\theta _d^{r})^{*\ell }$. As ![]() $\theta _d^{\ell }+(-1)^{d}\theta _d^{r}:K_{d-1}^{\vee }\to \big (K_d^{\vee }\otimes _SV\big )\oplus \big (V\otimes _SK_d^{\vee }\big )$ is the restriction of
$\theta _d^{\ell }+(-1)^{d}\theta _d^{r}:K_{d-1}^{\vee }\to \big (K_d^{\vee }\otimes _SV\big )\oplus \big (V\otimes _SK_d^{\vee }\big )$ is the restriction of ![]() $\delta _d'$, the sequence (26) is exact. In fact, for a morphism
$\delta _d'$, the sequence (26) is exact. In fact, for a morphism ![]() $\gamma :X\to Y$ of
$\gamma :X\to Y$ of ![]() $S^{{\operatorname {en} }}$-modules, the sequence
$S^{{\operatorname {en} }}$-modules, the sequence ![]() $0\to \gamma (X)^{\perp }\to Y^{*\ell }\xrightarrow {\gamma ^{*\ell }}X^{*\ell }$ is clearly exact. This completes the proof.
$0\to \gamma (X)^{\perp }\to Y^{*\ell }\xrightarrow {\gamma ^{*\ell }}X^{*\ell }$ is clearly exact. This completes the proof.
(b) As ![]() $\phi$ is an isomorphism in degrees 0 and 1 by part (a), we have that
$\phi$ is an isomorphism in degrees 0 and 1 by part (a), we have that ![]() $\phi$ is surjective if and only if
$\phi$ is surjective if and only if ![]() $\operatorname {Triv} _{d+1}(\Lambda ^{!})$ is generated in degrees 0 and 1 as an algebra. We know that the algebras
$\operatorname {Triv} _{d+1}(\Lambda ^{!})$ is generated in degrees 0 and 1 as an algebra. We know that the algebras ![]() $\Pi ^{!}$ and
$\Pi ^{!}$ and ![]() $\operatorname {Triv} _{d+1}(\Lambda ^{!})$ are generated by
$\operatorname {Triv} _{d+1}(\Lambda ^{!})$ are generated by ![]() $V^{*\ell }\oplus K_d^{\vee *\ell }$ and
$V^{*\ell }\oplus K_d^{\vee *\ell }$ and ![]() $V^{*\ell }\oplus \operatorname {head} _{\Lambda ^{!{{\operatorname {en} }}}}L'$, respectively. Thus,
$V^{*\ell }\oplus \operatorname {head} _{\Lambda ^{!{{\operatorname {en} }}}}L'$, respectively. Thus, ![]() $\phi$ is surjective if and only if
$\phi$ is surjective if and only if ![]() $\phi$ gives a surjection
$\phi$ gives a surjection ![]() $V^{*\ell }\oplus K_d^{\vee *\ell }\to V^{*\ell }\oplus \operatorname {head} _{\Lambda ^{!{{\operatorname {en} }}}}L'$ if and only if
$V^{*\ell }\oplus K_d^{\vee *\ell }\to V^{*\ell }\oplus \operatorname {head} _{\Lambda ^{!{{\operatorname {en} }}}}L'$ if and only if ![]() $L'_1=\operatorname {head} _{\Lambda ^{!{{\operatorname {en} }}}}L'$ if and only if
$L'_1=\operatorname {head} _{\Lambda ^{!{{\operatorname {en} }}}}L'$ if and only if ![]() $(\Lambda ^{!*})_1=\operatorname {head} _{\Lambda ^{!{{\operatorname {en} }}}}(\Lambda ^{!*})$. Applying
$(\Lambda ^{!*})_1=\operatorname {head} _{\Lambda ^{!{{\operatorname {en} }}}}(\Lambda ^{!*})$. Applying ![]() $(-)^{*}$, this is equivalent to
$(-)^{*}$, this is equivalent to ![]() $(\Lambda ^{!})_d=\operatorname {soc} _{\Lambda ^{!{{\operatorname {en} }}}}(\Lambda ^{!})$.
$(\Lambda ^{!})_d=\operatorname {soc} _{\Lambda ^{!{{\operatorname {en} }}}}(\Lambda ^{!})$.
The latter assertion is immediate from part (a).
(c) The ‘only if’ part is clear from part (b) and the fact that ![]() $\Pi ^{!}$ is quadratic. The ‘if’ part follows from Lemma 2.5 because both algebras are quadratic and
$\Pi ^{!}$ is quadratic. The ‘if’ part follows from Lemma 2.5 because both algebras are quadratic and ![]() $\phi$ is an isomorphism in degrees
$\phi$ is an isomorphism in degrees ![]() $0$,
$0$, ![]() $1$, and
$1$, and ![]() $2$.
$2$.
We have the following nice property of ![]() $\phi$.
$\phi$.
Theorem 5.4 If ![]() $\Lambda$ is Koszul and
$\Lambda$ is Koszul and ![]() $d$-hereditary, then the natural morphism
$d$-hereditary, then the natural morphism ![]() $\phi :\Pi ^{!}\twoheadrightarrow \operatorname {Triv} _{d+1}(\Lambda ^{!})$ is surjective.
$\phi :\Pi ^{!}\twoheadrightarrow \operatorname {Triv} _{d+1}(\Lambda ^{!})$ is surjective.
To prove this, we need the following.
Lemma 5.5 Let ![]() $\Lambda$ be a Koszul algebra and
$\Lambda$ be a Koszul algebra and ![]() $i\ge 0$. Then
$i\ge 0$. Then ![]() $\operatorname {Ext} ^{i}_{\Lambda ^{{\operatorname {en} }}}(\Lambda ,\Lambda ^{{\operatorname {en} }})_{-i}\cong (\operatorname {soc} _{\Lambda ^{!{{\operatorname {en} }}}}(\Lambda ^{!}))_i$.
$\operatorname {Ext} ^{i}_{\Lambda ^{{\operatorname {en} }}}(\Lambda ,\Lambda ^{{\operatorname {en} }})_{-i}\cong (\operatorname {soc} _{\Lambda ^{!{{\operatorname {en} }}}}(\Lambda ^{!}))_i$.
Proof. Recall that ![]() $\operatorname {Ext} ^{i}_{\Lambda ^{{\operatorname {en} }}}(\Lambda ,\Lambda ^{{\operatorname {en} }})$ is the cohomology of the complex
$\operatorname {Ext} ^{i}_{\Lambda ^{{\operatorname {en} }}}(\Lambda ,\Lambda ^{{\operatorname {en} }})$ is the cohomology of the complex
Taking the degree ![]() $-i$ part,
$-i$ part, ![]() $\operatorname {Ext} ^{i}_{\Lambda ^{{\operatorname {en} }}}(\Lambda ,\Lambda ^{{\operatorname {en} }})_{-i}$ is the kernel of the morphism
$\operatorname {Ext} ^{i}_{\Lambda ^{{\operatorname {en} }}}(\Lambda ,\Lambda ^{{\operatorname {en} }})_{-i}$ is the kernel of the morphism
By adjunctions, ![]() $f\in K_i^{\vee }$ is in the kernel if and only if
$f\in K_i^{\vee }$ is in the kernel if and only if ![]() $V^{*r}\cdot f=0=f\cdot V^{*\ell }$.
$V^{*r}\cdot f=0=f\cdot V^{*\ell }$.
On the other hand, we have ![]() $(\Lambda ^{!})_i=K_i^{*\ell }$ and
$(\Lambda ^{!})_i=K_i^{*\ell }$ and ![]() $(\operatorname {soc} _{\Lambda ^{!{{\operatorname {en} }}}}(\Lambda ^{!}))_i=\big \{f\in K_i^{*\ell }\mid V^{*\ell }\cdot f=0=f\cdot V^{*\ell }\big \}$. By Lemma 2.4 and its dual, the isomorphism
$(\operatorname {soc} _{\Lambda ^{!{{\operatorname {en} }}}}(\Lambda ^{!}))_i=\big \{f\in K_i^{*\ell }\mid V^{*\ell }\cdot f=0=f\cdot V^{*\ell }\big \}$. By Lemma 2.4 and its dual, the isomorphism ![]() $K_i^{*\ell }\cong K_i^{\vee }$ induces an isomorphism
$K_i^{*\ell }\cong K_i^{\vee }$ induces an isomorphism
Now we are ready to prove Theorem 5.4.
Proof of Theorem 5.4. Suppose ![]() $\phi$ is not surjective, so
$\phi$ is not surjective, so ![]() $\operatorname {soc} _{\Lambda ^{!{{\operatorname {en} }}}}(\Lambda ^{!})\neq (\Lambda ^{!})_d$ holds by Theorem 5.2(b). By Lemma 5.5, we have
$\operatorname {soc} _{\Lambda ^{!{{\operatorname {en} }}}}(\Lambda ^{!})\neq (\Lambda ^{!})_d$ holds by Theorem 5.2(b). By Lemma 5.5, we have ![]() $\operatorname {Ext} ^{i}_{\Lambda ^{{\operatorname {en} }}}(\Lambda ,\Lambda ^{{\operatorname {en} }})\neq 0$, a contradiction to our assumption that
$\operatorname {Ext} ^{i}_{\Lambda ^{{\operatorname {en} }}}(\Lambda ,\Lambda ^{{\operatorname {en} }})\neq 0$, a contradiction to our assumption that ![]() $\Lambda$ is
$\Lambda$ is ![]() $d$-hereditary.
$d$-hereditary.
Now we look at the case ![]() $d=1$.
$d=1$.
Example 5.6 Let ![]() $Q$ be a connected quiver and
$Q$ be a connected quiver and ![]() $\Lambda =\mathbb {F} Q$. Assume that
$\Lambda =\mathbb {F} Q$. Assume that ![]() $\Lambda$ is 1-hereditary, that is,
$\Lambda$ is 1-hereditary, that is, ![]() $Q$ is not of type
$Q$ is not of type ![]() $A_1$ by our convention.
$A_1$ by our convention.
Then ![]() $\Pi ^{!}$ is given by the double quiver
$\Pi ^{!}$ is given by the double quiver ![]() $\bar {Q}$ with the following relations, where we denote by
$\bar {Q}$ with the following relations, where we denote by ![]() $(-)^{*}$ the canonical involution of
$(-)^{*}$ the canonical involution of ![]() $\bar {Q}$: For any arrows
$\bar {Q}$: For any arrows ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$ in
$\beta$ in ![]() $\bar {Q}$,
$\bar {Q}$, ![]() $\alpha \beta =0$ if
$\alpha \beta =0$ if ![]() $\beta \neq \alpha ^{*}$, and
$\beta \neq \alpha ^{*}$, and ![]() $\alpha \alpha ^{*}=\pm \beta \beta ^{*}$ if
$\alpha \alpha ^{*}=\pm \beta \beta ^{*}$ if ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$ start at the same vertex.
$\beta$ start at the same vertex.
This implies that, if ![]() $Q$ is not of type
$Q$ is not of type ![]() $A_2$, then
$A_2$, then ![]() $(\Pi ^{!})_i$ is non-zero if and only if
$(\Pi ^{!})_i$ is non-zero if and only if ![]() $i=0$,
$i=0$, ![]() $1$, or
$1$, or ![]() $2$.
$2$.
If ![]() $Q$ is of type
$Q$ is of type ![]() $A_2$, then
$A_2$, then ![]() $\Pi ^{!}$ is the path algebra of
$\Pi ^{!}$ is the path algebra of ![]() and, hence, infinite-dimensional, whereas
and, hence, infinite-dimensional, whereas ![]() $\operatorname {Triv} _2(\Lambda ^{!})$ is the factor algebra of
$\operatorname {Triv} _2(\Lambda ^{!})$ is the factor algebra of ![]() $\Pi ^{!}$ by the ideal generated by paths of length 3.
$\Pi ^{!}$ by the ideal generated by paths of length 3.
For other cases in ![]() $d=1$, we have the following.
$d=1$, we have the following.
Theorem 5.7 Let ![]() $Q$ be a connected acyclic quiver that is not of type
$Q$ be a connected acyclic quiver that is not of type ![]() $A_1$ and
$A_1$ and ![]() $\Lambda :=\mathbb {F} Q$ its path algebra. Then the natural morphism
$\Lambda :=\mathbb {F} Q$ its path algebra. Then the natural morphism ![]() $\phi :\Pi ^{!}\to \operatorname {Triv} _2(\Lambda ^{!})$ is an isomorphism if and only if
$\phi :\Pi ^{!}\to \operatorname {Triv} _2(\Lambda ^{!})$ is an isomorphism if and only if ![]() $Q$ is not of type
$Q$ is not of type ![]() $A_2$.
$A_2$.
Proof. By Example 5.6, we only have to show the ‘if’ part. Clearly ![]() $\Lambda ^{!}$ is the factor algebra of
$\Lambda ^{!}$ is the factor algebra of ![]() $\mathbb {F} Q^{{{\operatorname {op} }}}$ by the ideal generated by all paths of length 2. Thus,
$\mathbb {F} Q^{{{\operatorname {op} }}}$ by the ideal generated by all paths of length 2. Thus, ![]() $(\Lambda ^{!})_i$ is non-zero only when
$(\Lambda ^{!})_i$ is non-zero only when ![]() $i=0$ or
$i=0$ or ![]() $1$, and
$1$, and ![]() $(\Lambda ^{!})_1=\operatorname {soc} {}_{\Lambda ^{!{{\operatorname {en} }}}}(\Lambda ^{!})$ holds because
$(\Lambda ^{!})_1=\operatorname {soc} {}_{\Lambda ^{!{{\operatorname {en} }}}}(\Lambda ^{!})$ holds because ![]() $Q$ is not of type
$Q$ is not of type ![]() $A_1$. By Theorem 5.2(b), we have that
$A_1$. By Theorem 5.2(b), we have that ![]() $\phi$ is surjective morphism,which is an isomorphism in degrees
$\phi$ is surjective morphism,which is an isomorphism in degrees ![]() $0$,
$0$, ![]() $1$, and
$1$, and ![]() $2$. On the other hand,
$2$. On the other hand, ![]() $\operatorname {Triv} _2(\Lambda ^{!})_i$ is non-zero only when
$\operatorname {Triv} _2(\Lambda ^{!})_i$ is non-zero only when ![]() $i=0$,
$i=0$, ![]() $1$, or
$1$, or ![]() $2$, whereas
$2$, whereas ![]() $(\Pi ^{!})_i$ is non-zero only when
$(\Pi ^{!})_i$ is non-zero only when ![]() $i=0$,
$i=0$, ![]() $1$, or
$1$, or ![]() $2$ by Example 5.6. Thus, the assertion follows.
$2$ by Example 5.6. Thus, the assertion follows.
As an application of Theorem 5.7, we recover a well-known result, which is mentioned in § 5.1 of [Reference Brenner, Butler and KingBBK02] and in the introduction of [Reference Huerfano and KhovanovHK01].
Corollary 5.8 Let ![]() $Q$ be a connected quiver that is not of type
$Q$ be a connected quiver that is not of type ![]() $A_1$ or
$A_1$ or ![]() $A_2$ and has bipartite orientation, and
$A_2$ and has bipartite orientation, and ![]() $\Lambda :=\mathbb {F} Q$ be its path algebra. Then
$\Lambda :=\mathbb {F} Q$ be its path algebra. Then
Proof. This is a consequence of Theorem 5.7 because, when ![]() $Q$ has bipartite orientation, we have
$Q$ has bipartite orientation, we have ![]() $\Lambda ^{!}\cong \Lambda ^{{\operatorname {op} }}$ and
$\Lambda ^{!}\cong \Lambda ^{{\operatorname {op} }}$ and ![]() $\operatorname {Triv} (\Lambda ^{{\operatorname {op} }})\cong \operatorname {Triv} (\Lambda )$. Moreover, as
$\operatorname {Triv} (\Lambda ^{{\operatorname {op} }})\cong \operatorname {Triv} (\Lambda )$. Moreover, as ![]() $Q$ is bipartite, the algebra automorphism
$Q$ is bipartite, the algebra automorphism ![]() $\sigma$ is inner: it is induced by a change of sign at either the sources or the sinks. Thus,
$\sigma$ is inner: it is induced by a change of sign at either the sources or the sinks. Thus, ![]() $\operatorname {Triv} _2(\Lambda )\cong \operatorname {Triv} (\Lambda )$.
$\operatorname {Triv} _2(\Lambda )\cong \operatorname {Triv} (\Lambda )$.
Example 5.9 Note that our map ![]() $\phi$ is not necessarily injective nor surjective. Let
$\phi$ is not necessarily injective nor surjective. Let ![]() $\Lambda$ be the Koszul algebra given by taking the quotient of the path algebra of the quiver
$\Lambda$ be the Koszul algebra given by taking the quotient of the path algebra of the quiver
by the ideal ![]() $(\alpha \beta )$. Then
$(\alpha \beta )$. Then ![]() $\Pi ^{!}$ is infinite-dimensional and
$\Pi ^{!}$ is infinite-dimensional and ![]() $\operatorname {Triv} _3(\Lambda ^{!})$ is
$\operatorname {Triv} _3(\Lambda ^{!})$ is ![]() $16$-dimensional. The kernel of
$16$-dimensional. The kernel of ![]() $\phi$ is the infinite-dimensional space
$\phi$ is the infinite-dimensional space ![]() $(\Pi ^{!})_{\geq 4}$ and the cokernel is
$(\Pi ^{!})_{\geq 4}$ and the cokernel is ![]() $2$-dimensional, generated by
$2$-dimensional, generated by ![]() $\gamma \in K_1\subseteq \operatorname {Triv} _3(\Lambda ^{!})_2$ and
$\gamma \in K_1\subseteq \operatorname {Triv} _3(\Lambda ^{!})_2$ and ![]() $e_4\in K_0\subseteq \operatorname {Triv} _3(\Lambda ^{!})_3$.
$e_4\in K_0\subseteq \operatorname {Triv} _3(\Lambda ^{!})_3$.
5.2 Type  $A$ examples
$A$ examples
We finish this article by applying our theory to higher type A ![]() $d$-representation finite algebras [Reference IyamaIya11, Reference Iyama and OppermannIO11].
$d$-representation finite algebras [Reference IyamaIya11, Reference Iyama and OppermannIO11].
Let ![]() $1\leq d<\infty$ and
$1\leq d<\infty$ and ![]() $2\leq s<\infty$. Let
$2\leq s<\infty$. Let ![]() $\bar {Q}^{(d,s)}$ denote the quiver whose vertices are
$\bar {Q}^{(d,s)}$ denote the quiver whose vertices are ![]() $d+1$-tuples
$d+1$-tuples ![]() $x=(x_1,\ldots ,x_{d+1})$ of non-negative integers that sum to
$x=(x_1,\ldots ,x_{d+1})$ of non-negative integers that sum to ![]() $s-1$, and whose arrows are
$s-1$, and whose arrows are
for ![]() $1\leq i\leq d+1$ whenever
$1\leq i\leq d+1$ whenever ![]() $x_i\geq 1$, where
$x_i\geq 1$, where
Let ![]() $Q^{(d,s)}$ be the quiver obtained by removing all arrows of the form
$Q^{(d,s)}$ be the quiver obtained by removing all arrows of the form ![]() $\alpha _{x,d+1}$ from
$\alpha _{x,d+1}$ from ![]() $\bar {Q}^{(d,s)}$. For example, the quivers
$\bar {Q}^{(d,s)}$. For example, the quivers ![]() $\bar {Q}^{(2,5)}$ and
$\bar {Q}^{(2,5)}$ and ![]() $Q^{(2,5)}$ are as follows.
$Q^{(2,5)}$ are as follows.

Let ![]() $I^{(d,s)}$ denote the ideal of
$I^{(d,s)}$ denote the ideal of ![]() $\mathbb {F} Q^{(d,s)}$ generated by elements:
$\mathbb {F} Q^{(d,s)}$ generated by elements:
where ![]() $x\in Q^{(d,s)}_0$ and
$x\in Q^{(d,s)}_0$ and ![]() $1 \le i < j \le d$.
$1 \le i < j \le d$.
For a field ![]() $\mathbb {F}$, let
$\mathbb {F}$, let
Then ![]() $\Lambda ^{(d,s)}$ is
$\Lambda ^{(d,s)}$ is ![]() $d$-RF [Reference IyamaIya11, Theorems 1.18, 6.12]. In addition, as
$d$-RF [Reference IyamaIya11, Theorems 1.18, 6.12]. In addition, as ![]() $I^{(d,s)}$ is a homogeneous ideal with respect to the path length grading on
$I^{(d,s)}$ is a homogeneous ideal with respect to the path length grading on ![]() $\mathbb {F} Q^{(d,s)}$,
$\mathbb {F} Q^{(d,s)}$, ![]() $\Lambda ^{(d,s)}$ inherits this grading.
$\Lambda ^{(d,s)}$ inherits this grading.
The following notation will be useful: for a vertex ![]() $x$ in
$x$ in ![]() $Q^{(d,s)}$, let
$Q^{(d,s)}$, let ![]() $e_x$ denote the idempotent of
$e_x$ denote the idempotent of ![]() $\Lambda$ corresponding to the vertex
$\Lambda$ corresponding to the vertex ![]() $x$, and let
$x$, and let
Then the relations in ![]() $\Lambda ^{(d,s)}$ can be rewritten as
$\Lambda ^{(d,s)}$ can be rewritten as
We have a natural morphism ![]() $\phi :\Pi ^{!}\to \operatorname {Triv} _{d+1}(\Lambda ^{!})$. We know by Theorem 5.2 and Corollary 5.4 that
$\phi :\Pi ^{!}\to \operatorname {Triv} _{d+1}(\Lambda ^{!})$. We know by Theorem 5.2 and Corollary 5.4 that ![]() $\phi$ is always surjective. If
$\phi$ is always surjective. If ![]() $s\geq 3$, then it is shown in [Reference GrantGra19, Section 3] that
$s\geq 3$, then it is shown in [Reference GrantGra19, Section 3] that ![]() $\phi$ is an isomorphism.
$\phi$ is an isomorphism.
We will make use of the following result.
Proposition 5.10 [Gra19, Proposition 3.4] The algebra ![]() $\Lambda$ is Koszul
$\Lambda$ is Koszul
Lemma 5.11 The space ![]() $K_d$ has an
$K_d$ has an ![]() $S^{{\operatorname {en} }}$-module basis
$S^{{\operatorname {en} }}$-module basis ![]() $\{k_x\;|\; x\in Q_0,\ x_1\neq 0\}$, where
$\{k_x\;|\; x\in Q_0,\ x_1\neq 0\}$, where
Proof. Fix ![]() $0\leq r\leq d-2$. First we show that
$0\leq r\leq d-2$. First we show that ![]() $k_x\in V^{r} R V^{d-r-2}$. For any vertex
$k_x\in V^{r} R V^{d-r-2}$. For any vertex ![]() $y$ and any
$y$ and any ![]() $i\neq j$ we have
$i\neq j$ we have ![]() $e_y(\alpha _i\alpha _j-\alpha _j\alpha _i)\in R$. Thus, for any indices
$e_y(\alpha _i\alpha _j-\alpha _j\alpha _i)\in R$. Thus, for any indices ![]() $i_1,\ldots ,i_{d-2}$ such that
$i_1,\ldots ,i_{d-2}$ such that ![]() $\{i,j, i_1,\ldots ,i_{d-2}\}=\{1,2,\ldots ,d\}$ we have
$\{i,j, i_1,\ldots ,i_{d-2}\}=\{1,2,\ldots ,d\}$ we have ![]() $e_x\alpha _{i_1}\cdots \alpha _{i_r}(\alpha _i\alpha _j-\alpha _j\alpha _i)\alpha _{r+1}\cdots \alpha _{d-2}\in V^{r} R V^{d-r-2}$. Summing over all such sets
$e_x\alpha _{i_1}\cdots \alpha _{i_r}(\alpha _i\alpha _j-\alpha _j\alpha _i)\alpha _{r+1}\cdots \alpha _{d-2}\in V^{r} R V^{d-r-2}$. Summing over all such sets ![]() $\{i_1,\ldots ,i_{d-2}\}$, with sign, we get that
$\{i_1,\ldots ,i_{d-2}\}$, with sign, we get that ![]() $k_x\in V^{r} R V^{d-r-2}$. But this did not depend on
$k_x\in V^{r} R V^{d-r-2}$. But this did not depend on ![]() $r$, so we have
$r$, so we have ![]() $k_x\in K_d={\bigcap} _{r=0}^{d-2}V^{r} R V^{d-r-2}$.
$k_x\in K_d={\bigcap} _{r=0}^{d-2}V^{r} R V^{d-r-2}$.
Conversely, consider an element ![]() $k\in K_d$. Without loss of generality,
$k\in K_d$. Without loss of generality, ![]() $k=e_xk$ for some vertex
$k=e_xk$ for some vertex ![]() $x$. No summand of
$x$. No summand of ![]() $k$ can be of the form
$k$ can be of the form ![]() $p\alpha _i\alpha _iq$ with
$p\alpha _i\alpha _iq$ with ![]() $p\in V^{r}$ and
$p\in V^{r}$ and ![]() $q\in V^{d-r-2}$, otherwise
$q\in V^{d-r-2}$, otherwise ![]() $k\notin V^{r} R V^{d-r-2}$. Thus, we must have
$k\notin V^{r} R V^{d-r-2}$. Thus, we must have
for some scalars ![]() $\lambda _{\sigma} \in \mathbb {F}$. But this can only be in
$\lambda _{\sigma} \in \mathbb {F}$. But this can only be in ![]() $RV^{d-2}$ if
$RV^{d-2}$ if ![]() $\lambda _{\sigma} +\lambda _{(12)\sigma }=0$. Similarly, we have
$\lambda _{\sigma} +\lambda _{(12)\sigma }=0$. Similarly, we have ![]() $\lambda _{\sigma} +\lambda _{(i,i+1)\sigma }=0$ for all
$\lambda _{\sigma} +\lambda _{(i,i+1)\sigma }=0$ for all ![]() $1\leq i < d$. Thus,
$1\leq i < d$. Thus, ![]() $\textrm {sgn}\,\sigma =\textrm {sgn}\,\tau$ implies
$\textrm {sgn}\,\sigma =\textrm {sgn}\,\tau$ implies ![]() $\lambda _{\sigma} =\lambda _{\tau}$, and
$\lambda _{\sigma} =\lambda _{\tau}$, and ![]() $\textrm {sgn}\,\sigma =-\textrm {sgn}\,\tau$ implies
$\textrm {sgn}\,\sigma =-\textrm {sgn}\,\tau$ implies ![]() $\lambda _{\sigma} =-\lambda _{\tau}$. Thus,
$\lambda _{\sigma} =-\lambda _{\tau}$. Thus, ![]() $k$ is a scalar multiple of
$k$ is a scalar multiple of ![]() $k_x$.
$k_x$.
Let ![]() $\bar {I}^{(d,s)}$ denote the ideal of
$\bar {I}^{(d,s)}$ denote the ideal of ![]() $\mathbb {F}\bar {Q}^{(d,s)}$ generated by elements:
$\mathbb {F}\bar {Q}^{(d,s)}$ generated by elements:
where ![]() $x\in \bar {Q}^{(d,s)}_0$ and
$x\in \bar {Q}^{(d,s)}_0$ and ![]() $1\le i < j \le d+1$. Here,
$1\le i < j \le d+1$. Here, ![]() $\alpha _{x+f_{d+1},d+2}$ should be interpreted as
$\alpha _{x+f_{d+1},d+2}$ should be interpreted as ![]() $\alpha _{x+f_{d+1},1}$. As an application of our results in this paper, we give the following description of the higher preprojective algebra of
$\alpha _{x+f_{d+1},1}$. As an application of our results in this paper, we give the following description of the higher preprojective algebra of ![]() $\Lambda$, which recovers the quiver with relations in [Reference Iyama and OppermannIO11, Definition 5.1, Proposition 5.48].
$\Lambda$, which recovers the quiver with relations in [Reference Iyama and OppermannIO11, Definition 5.1, Proposition 5.48].
Theorem 5.12 Let ![]() $\Pi =\Pi (\Lambda )$. The quiver
$\Pi =\Pi (\Lambda )$. The quiver ![]() $\bar {Q}$ of
$\bar {Q}$ of ![]() $\Pi$ is
$\Pi$ is ![]() $\bar {Q}^{(d,s)}$, and we have an isomorphism
$\bar {Q}^{(d,s)}$, and we have an isomorphism
Proof. The former statement follows from Proposition 3.2. We prove the latter. From Lemma 5.11 we obtain the superpotential
for ![]() $\bar {Q}$. By differentiating this superpotential with respect to all paths of length
$\bar {Q}$. By differentiating this superpotential with respect to all paths of length ![]() $d-1$ in
$d-1$ in ![]() $\bar {Q}$, we have the isomorphism.
$\bar {Q}$, we have the isomorphism.
We now apply Theorem 4.21 to obtain a large family of pairs of almost Koszul algebras. This statement generalizes [Reference Brenner, Butler and KingBBK02, Corollary 4.3] for type ![]() $A$ quivers. It appears to be the first construction of
$A$ quivers. It appears to be the first construction of ![]() $(p,q)$-Koszul algebras for all
$(p,q)$-Koszul algebras for all ![]() $p,q\geq 2$.
$p,q\geq 2$.
Proposition 5.13 If ![]() $s\geq 3$ and
$s\geq 3$ and ![]() $n\geq 1$, then
$n\geq 1$, then ![]() $\Pi$ and
$\Pi$ and ![]() $\Pi ^{!}$ are an almost Koszul pair:
$\Pi ^{!}$ are an almost Koszul pair: ![]() $\Pi$ is
$\Pi$ is ![]() $(s-1,d+1)$-Koszul and
$(s-1,d+1)$-Koszul and ![]() $\Pi ^{!}$ is
$\Pi ^{!}$ is ![]() $(d+1,s-1)$-Koszul.
$(d+1,s-1)$-Koszul.
Proof. Theorem 4.21 tells us that ![]() $\Pi$ is
$\Pi$ is ![]() $(p,d+1)$-Koszul if
$(p,d+1)$-Koszul if ![]() $\Pi$ is concentrated in degrees
$\Pi$ is concentrated in degrees ![]() $0$ to
$0$ to ![]() $p$, and [Reference Brenner, Butler and KingBBK02, Proposition 3.11] tells us that the quadratic dual of a
$p$, and [Reference Brenner, Butler and KingBBK02, Proposition 3.11] tells us that the quadratic dual of a ![]() $(p,q)$-Koszul ring with
$(p,q)$-Koszul ring with ![]() $p,q\geq 2$ is a
$p,q\geq 2$ is a ![]() $(q,p)$-Koszul ring. Thus, we just need to show that
$(q,p)$-Koszul ring. Thus, we just need to show that ![]() $\Pi$ is concentrated in degrees
$\Pi$ is concentrated in degrees ![]() $0$ to
$0$ to ![]() $s-1$.
$s-1$.
We use Martínez-Villa's result that all projective modules for a ![]() $\mathbb {Z}$-graded self-injective algebra have the same Loewy length [Reference Martínez-VillaMar99, Theorem 3.3]. Thus we only need to show that there is a projective
$\mathbb {Z}$-graded self-injective algebra have the same Loewy length [Reference Martínez-VillaMar99, Theorem 3.3]. Thus we only need to show that there is a projective ![]() $\Pi$-module concentrated in degrees
$\Pi$-module concentrated in degrees ![]() $0$ to
$0$ to ![]() $s-1$. Consider the left projective
$s-1$. Consider the left projective ![]() $\Pi$-module
$\Pi$-module ![]() $\Pi e_{(s-1,0,\ldots ,0)}$ associated to the vertex
$\Pi e_{(s-1,0,\ldots ,0)}$ associated to the vertex ![]() $x=(s-1,0,\ldots ,0)$. First we claim that all paths starting at
$x=(s-1,0,\ldots ,0)$. First we claim that all paths starting at ![]() $x$ are of the form
$x$ are of the form ![]() $e_x\alpha _1^{d}$. To see this, note that the arrows in
$e_x\alpha _1^{d}$. To see this, note that the arrows in ![]() $\bar {Q}$ ensure that every path not of this form starting at
$\bar {Q}$ ensure that every path not of this form starting at ![]() $x$ must begin
$x$ must begin ![]() $e_x\alpha _1^{m}\alpha _2$ for some
$e_x\alpha _1^{m}\alpha _2$ for some ![]() $m\geq 1$. But then the commutation relations in
$m\geq 1$. But then the commutation relations in ![]() $\Pi$ show that
$\Pi$ show that ![]() $e_x\alpha _1^{m}\alpha _2=e_x\alpha _1\alpha _2\alpha _1^{m-1}$. But
$e_x\alpha _1^{m}\alpha _2=e_x\alpha _1\alpha _2\alpha _1^{m-1}$. But ![]() $e_x\alpha _1\alpha _2=0$. Next we note that
$e_x\alpha _1\alpha _2=0$. Next we note that ![]() $e_x\alpha _1^{d}$ is non-zero for
$e_x\alpha _1^{d}$ is non-zero for ![]() $0\leq d\leq s-1$ and is zero for
$0\leq d\leq s-1$ and is zero for ![]() $d\geq s$. So
$d\geq s$. So ![]() $\Pi e_{(s-1,0,\ldots ,0)}$ is non-zero precisely in degrees
$\Pi e_{(s-1,0,\ldots ,0)}$ is non-zero precisely in degrees ![]() $0$ to
$0$ to ![]() $s-1$.
$s-1$.
Acknowledgements
Early versions of these results were obtained when the first author was a JSPS Postdoctoral Fellow at Nagoya University during 2010 and 2011. Some results were presented at meetings in Newcastle University (2012), University of Cambridge (2015), and Isaac Newton Institute (2017). The authors thank them for supporting our project. They also acknowledge the hospitality of Syracuse University, Isaac Newton Institute, and Czech Technical University in Prague.
On global dimension of  $\mathbb {Z}$-graded rings
$\mathbb {Z}$-graded rings
The aim of this appendix is to remark that several possible definitions of global dimensions of ![]() $\mathbb {Z}$-graded rings coincide.
$\mathbb {Z}$-graded rings coincide.
For a ring ![]() $A$, we denote by
$A$, we denote by ![]() $A\operatorname {-Mod}$ the abelian category of all left
$A\operatorname {-Mod}$ the abelian category of all left ![]() $A$-modules. For a
$A$-modules. For a ![]() $\mathbb {Z}$-graded ring
$\mathbb {Z}$-graded ring ![]() $A={\bigoplus} _{i\in \mathbb {Z}}A_i$, we denote by
$A={\bigoplus} _{i\in \mathbb {Z}}A_i$, we denote by ![]() $A\operatorname {-Mod^{\mathbb {Z}}}$ the abelian category of all
$A\operatorname {-Mod^{\mathbb {Z}}}$ the abelian category of all ![]() $\mathbb {Z}$-graded left
$\mathbb {Z}$-graded left ![]() $A$-modules. We denote by
$A$-modules. We denote by ![]() $\operatorname {Mod-} A$ and
$\operatorname {Mod-} A$ and ![]() $\operatorname {Mod^{\mathbb {Z}}-} A$ the right versions. If
$\operatorname {Mod^{\mathbb {Z}}-} A$ the right versions. If ![]() $A_i=0$ for all
$A_i=0$ for all ![]() $i<0$, then by [Reference Nastasescu and Van OystaeyenNV79, I.7.8] (see also [Reference McConnell and RobsonMR01, 7.6.18(ii)]) and [Reference Nastasescu and Van OystaeyenNV04, 2.4.8], we have
$i<0$, then by [Reference Nastasescu and Van OystaeyenNV79, I.7.8] (see also [Reference McConnell and RobsonMR01, 7.6.18(ii)]) and [Reference Nastasescu and Van OystaeyenNV04, 2.4.8], we have
The aim of this section is to prove the following general observation.
Theorem A.1 Let ![]() $A={\bigoplus} _{i\ge 0}A_i$ be a
$A={\bigoplus} _{i\ge 0}A_i$ be a ![]() $\mathbb {Z}$-graded ring. If
$\mathbb {Z}$-graded ring. If ![]() $A_0$ is artinian, then
$A_0$ is artinian, then
 \begin{align*} \mathop{{\rm gl.dim\,}}(A\operatorname{-Mod})&=\sup\{\operatorname{proj.dim}_AX\mid X\in A\operatorname{-Mod^{\mathbb{Z}}}\ \text{: simple}\}\\ &=\mathop{{\rm gl.dim\,}}(\operatorname{Mod-} A)=\sup\{\operatorname{proj.dim} X_A\mid X\in \operatorname{Mod^{\mathbb{Z}}-} A\ \text{: simple}\}. \end{align*}
\begin{align*} \mathop{{\rm gl.dim\,}}(A\operatorname{-Mod})&=\sup\{\operatorname{proj.dim}_AX\mid X\in A\operatorname{-Mod^{\mathbb{Z}}}\ \text{: simple}\}\\ &=\mathop{{\rm gl.dim\,}}(\operatorname{Mod-} A)=\sup\{\operatorname{proj.dim} X_A\mid X\in \operatorname{Mod^{\mathbb{Z}}-} A\ \text{: simple}\}. \end{align*}It is well-known that (A.1) fails if we drop the condition ![]() $A_i=0$ for
$A_i=0$ for ![]() $i<0$, e.g.
$i<0$, e.g. ![]() $A=k[x,x^{-1}]$ with field
$A=k[x,x^{-1}]$ with field ![]() $A_0=k$ and
$A_0=k$ and ![]() $\deg x=1$. In addition, Theorem A.1 fails if
$\deg x=1$. In addition, Theorem A.1 fails if ![]() $A_0$ is not artinian, e.g.
$A_0$ is not artinian, e.g.![]() $A=A_0\oplus A_1=\mathbb {Z}\oplus \mathbb {Q} x$ is a subring of
$A=A_0\oplus A_1=\mathbb {Z}\oplus \mathbb {Q} x$ is a subring of ![]() $\mathbb {Q}[x]/(x^{2})$.
$\mathbb {Q}[x]/(x^{2})$.
Theorem A.1 follows immediately from (A.1), (A.2) and the following observation.
Lemma A.2 Let ![]() $A={\bigoplus} _{i\ge 0}A_i$ be a
$A={\bigoplus} _{i\ge 0}A_i$ be a ![]() $\mathbb {Z}$-graded ring. If
$\mathbb {Z}$-graded ring. If ![]() $A_0$ is left artinian, then
$A_0$ is left artinian, then
To prove this, we need some preparation. For ![]() $i\in \mathbb {Z}$, let
$i\in \mathbb {Z}$, let ![]() $\mathscr {P}^{i}$ be the full subcategory of
$\mathscr {P}^{i}$ be the full subcategory of ![]() $A\operatorname {-Mod^{\mathbb{Z}}}$ consisting of arbitrary direct sums of modules of the form
$A\operatorname {-Mod^{\mathbb{Z}}}$ consisting of arbitrary direct sums of modules of the form ![]() $Ae(-i)$ for some idempotents
$Ae(-i)$ for some idempotents ![]() $e\in A_0$. Let
$e\in A_0$. Let ![]() $\mathscr {P}$ be the full subcategory of
$\mathscr {P}$ be the full subcategory of ![]() $A\operatorname {-Mod^{\mathbb{Z}}}$ consisting of arbitrary direct sums of objects from
$A\operatorname {-Mod^{\mathbb{Z}}}$ consisting of arbitrary direct sums of objects from ![]() $\mathscr {P}^{i}$ for all
$\mathscr {P}^{i}$ for all ![]() $i\in \mathbb {Z}$.
$i\in \mathbb {Z}$.
Lemma A.3 Let ![]() $A={\bigoplus} _{i\ge 0}A_i$ be a
$A={\bigoplus} _{i\ge 0}A_i$ be a ![]() $\mathbb {Z}$-graded ring such that
$\mathbb {Z}$-graded ring such that ![]() $A_0$ is left artinian, and
$A_0$ is left artinian, and ![]() $J:=(\operatorname {rad} A_0)\oplus ({\bigoplus} _{i\ge 1}A_i)$. For any
$J:=(\operatorname {rad} A_0)\oplus ({\bigoplus} _{i\ge 1}A_i)$. For any ![]() $X\in A\operatorname {-Mod^{\mathbb{Z}}}$ such that
$X\in A\operatorname {-Mod^{\mathbb{Z}}}$ such that ![]() $X_j=0$ for
$X_j=0$ for ![]() $j\ll 0$, there exists a surjective morphism
$j\ll 0$, there exists a surjective morphism ![]() $f:P\to X$ in
$f:P\to X$ in ![]() $A\operatorname {-Mod^{\mathbb{Z}}}$ with
$A\operatorname {-Mod^{\mathbb{Z}}}$ with ![]() $P\in \mathscr {P}$ such that
$P\in \mathscr {P}$ such that ![]() $\operatorname {Ker} f\subset JP$ and
$\operatorname {Ker} f\subset JP$ and ![]() $(\operatorname {Ker} f)_j=0$ for
$(\operatorname {Ker} f)_j=0$ for ![]() $j\ll 0$.
$j\ll 0$.
Proof. Without loss of generality, we can assume ![]() $X_j=0$ for all
$X_j=0$ for all ![]() $j < 0$. We take a morphism
$j < 0$. We take a morphism ![]() $f^{0}:P^{0}\to X$ in
$f^{0}:P^{0}\to X$ in ![]() $A\operatorname {-Mod^{\mathbb{Z}}}$ with
$A\operatorname {-Mod^{\mathbb{Z}}}$ with ![]() $P^{0}\in \mathscr {P}^{0}$ such that
$P^{0}\in \mathscr {P}^{0}$ such that ![]() $(f^{0})_0:(P^{0})_0\to X_0$ is a projective cover of the
$(f^{0})_0:(P^{0})_0\to X_0$ is a projective cover of the ![]() $A_0$-module
$A_0$-module ![]() $X_0$. Assume that
$X_0$. Assume that ![]() $f^{j}:P^{j}\to X$ with
$f^{j}:P^{j}\to X$ with ![]() $P^{j}\in \mathscr {P}^{j}$ are constructed for
$P^{j}\in \mathscr {P}^{j}$ are constructed for ![]() $0 \le j < i$ such that
$0 \le j < i$ such that
satisfies ![]() $(\operatorname {Cok} f^{[0,i)})_j=0$ for all
$(\operatorname {Cok} f^{[0,i)})_j=0$ for all ![]() $j < i$. We take a morphism
$j < i$. We take a morphism ![]() $g^{i}:P^{i}\to \operatorname {Cok} f^{[0,i)}$ in
$g^{i}:P^{i}\to \operatorname {Cok} f^{[0,i)}$ in ![]() $A\operatorname {-Mod^{\mathbb{Z}}}$ with
$A\operatorname {-Mod^{\mathbb{Z}}}$ with ![]() $P^{i}\in \mathscr {P}^{i}$ such that
$P^{i}\in \mathscr {P}^{i}$ such that ![]() $(g^{i})_i:(P^{i})_i\to (\operatorname {Cok} f^{[0,i)})_i$ is a projective cover of the
$(g^{i})_i:(P^{i})_i\to (\operatorname {Cok} f^{[0,i)})_i$ is a projective cover of the ![]() $A_0$-module
$A_0$-module ![]() $(\operatorname {Cok} f^{[0,i)})_i$. We lift
$(\operatorname {Cok} f^{[0,i)})_i$. We lift ![]() $g^{i}$ to
$g^{i}$ to ![]() $f^{i}:P^{i}\to X$. Then
$f^{i}:P^{i}\to X$. Then ![]() $f^{j}$ with
$f^{j}$ with ![]() $0\le j\le i$ satisfy the same assumption.
$0\le j\le i$ satisfy the same assumption.
Now we show that the morphism ![]() $f:=(f^{j})_{j\le 0}:P:={\bigoplus} _{0\le j}P^{j}\to X$ satisfies the desired properties. Clearly
$f:=(f^{j})_{j\le 0}:P:={\bigoplus} _{0\le j}P^{j}\to X$ satisfies the desired properties. Clearly ![]() $f$ is surjective, and
$f$ is surjective, and ![]() $P\in \mathscr {P}$ and
$P\in \mathscr {P}$ and ![]() $(\operatorname {Ker} f)_j=0$ hold for all
$(\operatorname {Ker} f)_j=0$ hold for all ![]() $j<0$. It remains to show
$j<0$. It remains to show ![]() $\operatorname {Ker} f\subset JP$. Take any
$\operatorname {Ker} f\subset JP$. Take any ![]() $x=(x^{j})_{j\ge 0}\in \operatorname {Ker} f$ with
$x=(x^{j})_{j\ge 0}\in \operatorname {Ker} f$ with ![]() $x^{j}\in P^{j}$. Then the composition
$x^{j}\in P^{j}$. Then the composition ![]() $P\xrightarrow {f}X\to \operatorname {Cok} f^{[0,i)}$ sends
$P\xrightarrow {f}X\to \operatorname {Cok} f^{[0,i)}$ sends ![]() $(x^{j})_{j\ge i}$ to zero, and
$(x^{j})_{j\ge i}$ to zero, and ![]() $(x^{j})_{j>i}$ to an element in
$(x^{j})_{j>i}$ to an element in ![]() $(\operatorname {Cok} f^{[0,i)})_{>i}$. Thus,
$(\operatorname {Cok} f^{[0,i)})_{>i}$. Thus, ![]() $g^{i}(x^{i})$ belongs to
$g^{i}(x^{i})$ belongs to ![]() $(\operatorname {Cok} f^{[0,i)})_{>i}$. Since
$(\operatorname {Cok} f^{[0,i)})_{>i}$. Since ![]() $(g^{i})_i:(P^{i})_i\to (\operatorname {Cok} f^{[0,i)})_i$ is a projective cover,
$(g^{i})_i:(P^{i})_i\to (\operatorname {Cok} f^{[0,i)})_i$ is a projective cover, ![]() $x^{i}\in JP^{i}$ holds, as desired.
$x^{i}\in JP^{i}$ holds, as desired.
Now we are ready to prove Lemma A.2.
Proof of Lemma A.2. As ![]() $A_0$ is left artinian,
$A_0$ is left artinian, ![]() $A/J=A_0/\operatorname {rad} A_0$ is a semisimple ring and
$A/J=A_0/\operatorname {rad} A_0$ is a semisimple ring and ![]() $A/J$ is a semisimple right
$A/J$ is a semisimple right ![]() $A$-module. Let
$A$-module. Let ![]() $\ell =\operatorname {proj.dim} (A/J)_A$. Thanks to (A.1), it suffices to show that
$\ell =\operatorname {proj.dim} (A/J)_A$. Thanks to (A.1), it suffices to show that ![]() $\operatorname {proj.dim} _AX\le \ell$ holds for any
$\operatorname {proj.dim} _AX\le \ell$ holds for any ![]() $X\in A\operatorname {-Mod^{\mathbb{Z}}}$ that is cyclic. As
$X\in A\operatorname {-Mod^{\mathbb{Z}}}$ that is cyclic. As ![]() $X_i=0$ holds for
$X_i=0$ holds for ![]() $i\ll 0$, by applying Lemma A.3 to
$i\ll 0$, by applying Lemma A.3 to ![]() $X$ and its syzygies repeatedly, we obtain an exact sequence
$X$ and its syzygies repeatedly, we obtain an exact sequence
such that ![]() $Q^{i}\in \mathscr {P}$ and
$Q^{i}\in \mathscr {P}$ and ![]() $f^{i}(Q^{i})\subset JQ^{i-1}$ for all
$f^{i}(Q^{i})\subset JQ^{i-1}$ for all ![]() $i$. As
$i$. As ![]() $(A/J)\otimes f^{i}=0$ for all
$(A/J)\otimes f^{i}=0$ for all ![]() $i>0$, we have
$i>0$, we have
Thus, ![]() $Q^{\ell +1}=0$ and, hence,
$Q^{\ell +1}=0$ and, hence, ![]() $\operatorname {proj.dim} _AX\le \ell$.
$\operatorname {proj.dim} _AX\le \ell$.