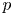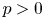Introduction
Recall that a Fano variety ![]() $X$ is a variety with mild (at worst klt) singularities such that
$X$ is a variety with mild (at worst klt) singularities such that ![]() $-K_X$ is ample. The index of
$-K_X$ is ample. The index of ![]() $X$ is the largest number
$X$ is the largest number ![]() $r$ such that
$r$ such that ![]() $-K_X \equiv rH$ for an ample Weil divisor
$-K_X \equiv rH$ for an ample Weil divisor ![]() $H$. Iskovskikh and Manin [Reference Iskovskikh and ManinIM71] showed that the birational automorphism group,
$H$. Iskovskikh and Manin [Reference Iskovskikh and ManinIM71] showed that the birational automorphism group, ![]() ${\mathrm {Bir}}(X)$, of a smooth quartic threefold is finite, which implied that a smooth quartic threefold is not rational. Given a rational map of Fano varieties, their approach relied on a detailed study of singularities of divisors in the corresponding linear series. This approach is now referred to as the Noether–Fano method (using ideas of Fano [Reference FanoFan08, Reference FanoFan15]). An immense amount of work has been devoted to proving the birational rigidity, and thus finiteness, of
${\mathrm {Bir}}(X)$, of a smooth quartic threefold is finite, which implied that a smooth quartic threefold is not rational. Given a rational map of Fano varieties, their approach relied on a detailed study of singularities of divisors in the corresponding linear series. This approach is now referred to as the Noether–Fano method (using ideas of Fano [Reference FanoFan08, Reference FanoFan15]). An immense amount of work has been devoted to proving the birational rigidity, and thus finiteness, of ![]() ${\mathrm {Bir}}(X)$ for other Fano varieties of index one. From the contributions of many authors (cf. [Reference CheltsovChe00, Reference CortiCor95, Reference de FernexdF13, Reference de FernexdF16, Reference de Fernex, Ein and MustaţădFEM03, Reference PukhlikovPuk87, Reference PukhlikovPuk02]) we now know that in characteristic zero any smooth Fano hypersurface
${\mathrm {Bir}}(X)$ for other Fano varieties of index one. From the contributions of many authors (cf. [Reference CheltsovChe00, Reference CortiCor95, Reference de FernexdF13, Reference de FernexdF16, Reference de Fernex, Ein and MustaţădFEM03, Reference PukhlikovPuk87, Reference PukhlikovPuk02]) we now know that in characteristic zero any smooth Fano hypersurface ![]() $X \subset {\mathbb {C}}{\mathbb {P}}^{n+1}$ of degree
$X \subset {\mathbb {C}}{\mathbb {P}}^{n+1}$ of degree ![]() $n+1$ is superrigid. As a consequence, these index-one Fano hypersurfaces have finite birational automorphism groups. For index-two Fano varieties, Pukhlikov has a number of results on finiteness of birational automorphisms [Reference PukhlikovPuk10, Reference PukhlikovPuk16, Reference PukhlikovPuk20, Reference PukhlikovPuk21]. These results classify rationally connected fibrations of these varieties with base of dimension one. Little is known about
$n+1$ is superrigid. As a consequence, these index-one Fano hypersurfaces have finite birational automorphism groups. For index-two Fano varieties, Pukhlikov has a number of results on finiteness of birational automorphisms [Reference PukhlikovPuk10, Reference PukhlikovPuk16, Reference PukhlikovPuk20, Reference PukhlikovPuk21]. These results classify rationally connected fibrations of these varieties with base of dimension one. Little is known about ![]() ${\mathrm {Bir}}(X)$ for higher index Fano varieties. Here we give the first examples of higher index Fano varieties with finite birational automorphism groups.Footnote 1
${\mathrm {Bir}}(X)$ for higher index Fano varieties. Here we give the first examples of higher index Fano varieties with finite birational automorphism groups.Footnote 1
Theorem A For every characteristic ![]() $p>0$ there are singular Fano varieties of arbitrarily large index over a field of characteristic
$p>0$ there are singular Fano varieties of arbitrarily large index over a field of characteristic ![]() $p$ with trivial birational automorphism groups.
$p$ with trivial birational automorphism groups.
In positive characteristic, Kollár [Reference KollárKol95] observed that certain Fano varieties that are ![]() $p$-cyclic covers in characteristic
$p$-cyclic covers in characteristic ![]() $p$ carry global differential forms, and used these to deduce that a very general hypersurface
$p$ carry global differential forms, and used these to deduce that a very general hypersurface ![]() $X \subset {\mathbb {C}}{\mathbb {P}}^{n+1}$ of degree at least
$X \subset {\mathbb {C}}{\mathbb {P}}^{n+1}$ of degree at least ![]() $2\lceil (n+3)/3 \rceil$ is not rational. These forms have also been used to show that Fano hypersurfaces of high degree are far from being rational in other ways. For example, Totaro [Reference TotaroTot16] used these forms to prove that hypersurfaces in a slightly larger range are not even stably rational. Using unramified cohomology as an obstruction, Schreieder [Reference SchreiederSch19] improved these results and showed that a very general hypersurface of degree
$2\lceil (n+3)/3 \rceil$ is not rational. These forms have also been used to show that Fano hypersurfaces of high degree are far from being rational in other ways. For example, Totaro [Reference TotaroTot16] used these forms to prove that hypersurfaces in a slightly larger range are not even stably rational. Using unramified cohomology as an obstruction, Schreieder [Reference SchreiederSch19] improved these results and showed that a very general hypersurface of degree ![]() $d\ge \log _2(n)+2$ is not stably rational. The arguments of Totaro and Schreieder both involve the specialization property of decomposition of the diagonal, which was developed by Voisin [Reference VoisinVoi13] and expanded upon in work of Colliot-Thélène and Pirutka [Reference Colliot-Thélene and PirutkaCP16]. In other degree ranges, by studying the positivity properties of these forms in more detail, the authors demonstrated that the degrees of irrationality of complex Fano hypersurfaces can be arbitrarily large and, in a different range, the degrees of possible rational endomorphisms on complex Fano hypersurfaces must satisfy certain congruence conditions (see [Reference Chen and StapletonCS20, Reference Chen and StapletonCS21]).
$d\ge \log _2(n)+2$ is not stably rational. The arguments of Totaro and Schreieder both involve the specialization property of decomposition of the diagonal, which was developed by Voisin [Reference VoisinVoi13] and expanded upon in work of Colliot-Thélène and Pirutka [Reference Colliot-Thélene and PirutkaCP16]. In other degree ranges, by studying the positivity properties of these forms in more detail, the authors demonstrated that the degrees of irrationality of complex Fano hypersurfaces can be arbitrarily large and, in a different range, the degrees of possible rational endomorphisms on complex Fano hypersurfaces must satisfy certain congruence conditions (see [Reference Chen and StapletonCS20, Reference Chen and StapletonCS21]).
We work with the ![]() $p$-cyclic covers that Kollár used:
$p$-cyclic covers that Kollár used:
They have mild (terminal) isolated singularities and admit a straightforward resolution of singularities:
An important step in proving Theorem A is the computation of the space of global ![]() $(n-1)$-forms on
$(n-1)$-forms on ![]() $Z$. In doing so, we show that the only global
$Z$. In doing so, we show that the only global ![]() $(n-1)$-forms are the forms that Kollár found.
$(n-1)$-forms are the forms that Kollár found.
Theorem B Let ![]() $k$ be an algebraically closed field of characteristic
$k$ be an algebraically closed field of characteristic ![]() $p>0$. Let
$p>0$. Let ![]() $n\ge 3$ (if
$n\ge 3$ (if ![]() $p=2$, then assume
$p=2$, then assume ![]() $n$ is even). Let
$n$ is even). Let ![]() $X\subset {\mathbb {P}}^{n+1}_k$ be a smooth degree
$X\subset {\mathbb {P}}^{n+1}_k$ be a smooth degree ![]() $e$ hypersurface, fix an integer
$e$ hypersurface, fix an integer ![]() $d>0$, and let
$d>0$, and let ![]() $Y$ be a
$Y$ be a ![]() $p$-cyclic cover branched over a general section of
$p$-cyclic cover branched over a general section of ![]() ${\mathcal {O}}_X(pd)$. There exists a resolution of singularities
${\mathcal {O}}_X(pd)$. There exists a resolution of singularities ![]() $Z$ of
$Z$ of ![]() $Y$. Moreover, if
$Y$. Moreover, if
then ![]() $H^0(Z,{\bigwedge} ^{n-1}\Omega _Z) \cong H^0(X,\omega _X(pd))$.
$H^0(Z,{\bigwedge} ^{n-1}\Omega _Z) \cong H^0(X,\omega _X(pd))$.
The first inequality implies that ![]() $Y$ is Fano of index at least two. The second inequality implies that
$Y$ is Fano of index at least two. The second inequality implies that ![]() $\omega _X(pd)$ is very ample.
$\omega _X(pd)$ is very ample.
We introduce the notion of birational equivariance for line bundles, which arises naturally in this setting. We show that the existence of a nontrivial birationally equivariant line bundle is a strong condition. In particular, the global sections of a birationally equivariant line bundle ![]() ${\mathcal {L}}$ on
${\mathcal {L}}$ on ![]() $Y$ are naturally a representation of
$Y$ are naturally a representation of ![]() ${\mathrm {Bir}}(Y)$. This allows us to show the following result.
${\mathrm {Bir}}(Y)$. This allows us to show the following result.
Corollary C In the setting of Theorem B, let ![]() $\nu \colon Y \rightarrow X$ denote the
$\nu \colon Y \rightarrow X$ denote the ![]() $p$-cyclic cover. Then
$p$-cyclic cover. Then ![]() $\nu ^*(\omega _X(pd))$ is an ample and birationally equivariant line bundle on
$\nu ^*(\omega _X(pd))$ is an ample and birationally equivariant line bundle on ![]() $Y$, and there is an injection
$Y$, and there is an injection ![]() ${\mathrm {Bir}}(Y)\cong {\mathrm {Aut}}(Y) \hookrightarrow {\mathrm {Aut}}(X)$.
${\mathrm {Bir}}(Y)\cong {\mathrm {Aut}}(Y) \hookrightarrow {\mathrm {Aut}}(X)$.
For an alternative perspective on these results, in [Reference KollárKol96, V.5.20] Kollár views the map ![]() $Y\rightarrow X$ as a birational invariant of
$Y\rightarrow X$ as a birational invariant of ![]() $Y$.
$Y$.
These theorems are proved in slightly greater generality and apply to other ![]() $p$-cyclic covers with appropriate hypotheses. The results lead us to ask the following question:
$p$-cyclic covers with appropriate hypotheses. The results lead us to ask the following question:
Question Can finiteness of birational automorphisms of Fano varieties in characteristic ![]() $p$ be used to prove that complex Fano varieties have finitely many birational automorphisms?
$p$ be used to prove that complex Fano varieties have finitely many birational automorphisms?
Outline and conventions
We begin in § 1 by defining birational equivariance for line bundles ![]() ${\mathcal {L}}$ and giving some properties and relevant examples. In § 2, we describe the resolutions of certain
${\mathcal {L}}$ and giving some properties and relevant examples. In § 2, we describe the resolutions of certain ![]() $p$-cyclic covers and check that they have terminal singularities. Finally, in § 3 we prove Theorem B by computing the
$p$-cyclic covers and check that they have terminal singularities. Finally, in § 3 we prove Theorem B by computing the ![]() $(n-1)$-forms on the cyclic covers, which leads to a proof of Theorem A and Corollary C.
$(n-1)$-forms on the cyclic covers, which leads to a proof of Theorem A and Corollary C.
Throughout we work over an algebraically closed field ![]() $k$. A variety is an integral
$k$. A variety is an integral ![]() $k$-scheme of finite type. We do not give the birational automorphism group any scheme structure.
$k$-scheme of finite type. We do not give the birational automorphism group any scheme structure.
1. Birationally equivariant line bundles
The goal of this section is to introduce the notion of a birationally equivariant line bundle, to give some examples, to state some basic properties, and explain how they can be used to study the birational automorphism group. We consider ![]() ${\mathrm {Bir}}(X)$ as an abstract group, without any scheme structure.
${\mathrm {Bir}}(X)$ as an abstract group, without any scheme structure.
Let ![]() $k$ be an algebraically closed field, and let
$k$ be an algebraically closed field, and let ![]() $X$ be a normal projective algebraic variety over
$X$ be a normal projective algebraic variety over ![]() $k$. By variety, we mean an integral scheme of finite type over
$k$. By variety, we mean an integral scheme of finite type over ![]() $k$. Let
$k$. Let
be a rational endomorphism. The map ![]() $f$ is defined on some open set
$f$ is defined on some open set ![]() $i{\colon } U\hookrightarrow X$ such that
$i{\colon } U\hookrightarrow X$ such that ![]() $X\setminus U$ has codimension two in
$X\setminus U$ has codimension two in ![]() $X$. To start we define the pullback of a line bundle along
$X$. To start we define the pullback of a line bundle along ![]() $f$.
$f$.
Definition 1.1 Let ![]() ${\mathcal {L}}$ be a line bundle on
${\mathcal {L}}$ be a line bundle on ![]() $X$. The pullback of
$X$. The pullback of ![]() ${\mathcal {L}}$ along
${\mathcal {L}}$ along ![]() $f$ is defined by (1) first pulling back to a line bundle
$f$ is defined by (1) first pulling back to a line bundle ![]() $f^*({\mathcal {L}})\in {\mathrm {Pic}}(U)$, and then (2) pushing forward
$f^*({\mathcal {L}})\in {\mathrm {Pic}}(U)$, and then (2) pushing forward ![]() $i_*(f^*({\mathcal {L}}))$ to get a reflexive rank-one sheaf. This gives a group homomorphism:
$i_*(f^*({\mathcal {L}}))$ to get a reflexive rank-one sheaf. This gives a group homomorphism:
(where we identify the divisor class group with the group of reflexive rank-one sheaves with reflexive tensor product).
Definition 1.2 We say that ![]() ${\mathcal {L}}$ is equipped with a birationally equivariant structure (or simply
${\mathcal {L}}$ is equipped with a birationally equivariant structure (or simply ![]() ${\mathcal {L}}$ is birationally equivariant) if for every
${\mathcal {L}}$ is birationally equivariant) if for every ![]() $g\in {\mathrm {Bir}}(X)$ there is a choice of an isomorphism
$g\in {\mathrm {Bir}}(X)$ there is a choice of an isomorphism
subject to the following compatibility condition: for all ![]() $g_1, g_2 \in {\mathrm {Bir}}(X)$, there is the following commutative diagram.
$g_1, g_2 \in {\mathrm {Bir}}(X)$, there is the following commutative diagram.

Remark 1.3 It also makes sense to talk about ![]() $G$-birationally equivariant line bundles for any subgroup
$G$-birationally equivariant line bundles for any subgroup ![]() $G\le {\mathrm {Bir}}(X)$ and any group homomorphism
$G\le {\mathrm {Bir}}(X)$ and any group homomorphism ![]() $G\rightarrow {\mathrm {Bir}}(X)$, as well as birationally equivariant vector bundles on
$G\rightarrow {\mathrm {Bir}}(X)$, as well as birationally equivariant vector bundles on ![]() $X$.
$X$.
Example 1.4 For ![]() $n \geq 2$, the Cremona involution
$n \geq 2$, the Cremona involution ![]() $\tau {\colon } {\mathbb {P}}^n \dashrightarrow {\mathbb {P}}^n$ is defined by
$\tau {\colon } {\mathbb {P}}^n \dashrightarrow {\mathbb {P}}^n$ is defined by
The pullback ![]() $\tau ^*{\colon } {\mathrm {Pic}}({\mathbb {P}}^n)\rightarrow {\mathrm {Pic}}({\mathbb {P}}^n)$ is multiplication by
$\tau ^*{\colon } {\mathrm {Pic}}({\mathbb {P}}^n)\rightarrow {\mathrm {Pic}}({\mathbb {P}}^n)$ is multiplication by ![]() $n$. However,
$n$. However, ![]() $\tau ^{\circ 2} = {\mathrm {id}}\in {\mathrm {Bir}}({\mathbb {P}}^n)$. Thus, even if
$\tau ^{\circ 2} = {\mathrm {id}}\in {\mathrm {Bir}}({\mathbb {P}}^n)$. Thus, even if ![]() ${\mathrm {Pic}}(X) = {\mathrm {Cl}}(X)$, the map
${\mathrm {Pic}}(X) = {\mathrm {Cl}}(X)$, the map
is only a map of sets: it does not always respect composition. This also shows that ![]() ${\mathbb {P}}^n$ does not admit any nontrivial birationally equivariant line bundles when
${\mathbb {P}}^n$ does not admit any nontrivial birationally equivariant line bundles when ![]() $n\ge 2$.
$n\ge 2$.
Theorem 1.5 (Basic properties of birationally equivariant line bundles)
(i) If
 ${\mathcal {L}}_1$ and
${\mathcal {L}}_1$ and  ${\mathcal {L}}_2$ are birationally equivariant line bundles on
${\mathcal {L}}_2$ are birationally equivariant line bundles on  $X$, then so is
$X$, then so is  ${\mathcal {L}}_1\otimes {\mathcal {L}}_2$.
${\mathcal {L}}_1\otimes {\mathcal {L}}_2$.(ii) Likewise, the inverse of a birationally equivariant line bundle is naturally birationally equivariant. In particular,
is a group under tensor product and the forgetful map \[ {\mathrm{Pic}_{{\mathrm{Bir}}(X)}}(X):=\{\text{line bundles with birational equivariant structure}\} \]is a group homomorphism with kernel equal to the group of one-dimensional
\[ {\mathrm{Pic}_{{\mathrm{Bir}}(X)}}(X):=\{\text{line bundles with birational equivariant structure}\} \]is a group homomorphism with kernel equal to the group of one-dimensional \[ {\mathrm{Pic}_{{\mathrm{Bir}}(X)}}(X)\rightarrow {\mathrm{Pic}}(X) \]
\[ {\mathrm{Pic}_{{\mathrm{Bir}}(X)}}(X)\rightarrow {\mathrm{Pic}}(X) \] $k$-representations of
$k$-representations of  ${\mathrm {Bir}}(X)$ under tensor product.
${\mathrm {Bir}}(X)$ under tensor product.(iii) Let
 $\mu {\colon } {\widetilde {X}} \rightarrow X$ be a proper birational morphism. If
$\mu {\colon } {\widetilde {X}} \rightarrow X$ be a proper birational morphism. If  ${\mathcal {L}}$ is a line bundle on
${\mathcal {L}}$ is a line bundle on  $X$ and
$X$ and  $\mu ^{\ast }{\mathcal {L}}$ has a birationally equivariant structure, then
$\mu ^{\ast }{\mathcal {L}}$ has a birationally equivariant structure, then  ${\mathcal {L}}$ is naturally birationally equivariant.
${\mathcal {L}}$ is naturally birationally equivariant.(iv) If
 ${\mathcal {L}}$ is a birationally equivariant line bundle on
${\mathcal {L}}$ is a birationally equivariant line bundle on  $X$ and
$X$ and  $H^0(X,{\mathcal {L}})\ne 0$, then there is a representation
$H^0(X,{\mathcal {L}})\ne 0$, then there is a representation  $\rho {\colon } {\mathrm {Bir}}(X)\rightarrow {\mathrm {GL}}(H^0(X,{\mathcal {L}})^\vee )$ such that the following diagram commutes.
$\rho {\colon } {\mathrm {Bir}}(X)\rightarrow {\mathrm {GL}}(H^0(X,{\mathcal {L}})^\vee )$ such that the following diagram commutes.

(v) In the setting of property (iv), let
 $X'\subset {\mathrm {PGL}}(H^0({\mathcal {L}})^\vee )$ be the closure of the image of
$X'\subset {\mathrm {PGL}}(H^0({\mathcal {L}})^\vee )$ be the closure of the image of  $X$. For all
$X$. For all  $g\in {\mathrm {Bir}}(X)$,
$g\in {\mathrm {Bir}}(X)$,  $\rho (g)$ restricts to an automorphism of
$\rho (g)$ restricts to an automorphism of  $X'$, which induces a group homomorphism:
and the kernel consists of
$X'$, which induces a group homomorphism:
and the kernel consists of \[ {\mathrm{Bir}}(X)\rightarrow {\mathrm{Aut}}(X'), \]
\[ {\mathrm{Bir}}(X)\rightarrow {\mathrm{Aut}}(X'), \] $g\in {\mathrm {Bir}}(X)$ such that
$g\in {\mathrm {Bir}}(X)$ such that  $\pi \circ g = \pi.$
$\pi \circ g = \pi.$(vi) In the setting of property (iv), if there is a nonempty open set
 $U\subset X$ such that
$U\subset X$ such that  $\pi |_U$ is injective on the
$\pi |_U$ is injective on the  $k$-points of
$k$-points of  $U$ (e.g. if
$U$ (e.g. if  $\pi$ is birational or generically finite and purely inseparable), then the homomorphism
$\pi$ is birational or generically finite and purely inseparable), then the homomorphism  ${\mathrm {Bir}}(X)\rightarrow {\mathrm {Aut}}(X')$ is injective.
${\mathrm {Bir}}(X)\rightarrow {\mathrm {Aut}}(X')$ is injective.(vii) If
 $X$ has an ample birationally equivariant line bundle, then
$X$ has an ample birationally equivariant line bundle, then  ${\mathrm {Bir}}(X)\cong {\mathrm {Aut}}(X)$.
${\mathrm {Bir}}(X)\cong {\mathrm {Aut}}(X)$.
Proof. For property (i), to give the tensor product ![]() ${\mathcal {L}}_1\otimes {\mathcal {L}}_2$ a birationally equivariant structure, one may assign
${\mathcal {L}}_1\otimes {\mathcal {L}}_2$ a birationally equivariant structure, one may assign
Note that the first isomorphism is canonical. The compatibility condition is easy to check.
In property (ii), if ![]() ${\mathcal {L}}$ is birationally equivariant with isomorphisms
${\mathcal {L}}$ is birationally equivariant with isomorphisms ![]() $\phi _g$, then there are isomorphisms
$\phi _g$, then there are isomorphisms
Compatibility is easy to check. It is clear that the map
is a group homomorphism. The kernel is given by equivariant structures on the trivial line bundle. These give rise to one-dimensional representations on ![]() $H^0(X,{\mathcal {O}}_X)$ which determine the birationally equivariant bundle up to isomorphism.
$H^0(X,{\mathcal {O}}_X)$ which determine the birationally equivariant bundle up to isomorphism.
To prove property (iii), let ![]() $g\in {\mathrm {Bir}}(X)$ let
$g\in {\mathrm {Bir}}(X)$ let ![]() ${\tilde {g}}\in {\mathrm {Bir}}({\widetilde {X}})$ be the corresponding birational automorphism. Assume that both
${\tilde {g}}\in {\mathrm {Bir}}({\widetilde {X}})$ be the corresponding birational automorphism. Assume that both ![]() $g$ and
$g$ and ![]() ${\tilde {g}}$ are defined away from codimension two. Let
${\tilde {g}}$ are defined away from codimension two. Let ![]() $U\subset X$ be an open set so that (a)
$U\subset X$ be an open set so that (a) ![]() $X\setminus U$ has codimension at least two in
$X\setminus U$ has codimension at least two in ![]() $X$, (b)
$X$, (b) ![]() $\pi ^{-1}$ is defined on
$\pi ^{-1}$ is defined on ![]() $U$, (c)
$U$, (c) ![]() $g$ is defined on
$g$ is defined on ![]() $U$, and (d)
$U$, and (d) ![]() ${\tilde {g}}$ is defined on
${\tilde {g}}$ is defined on ![]() $\pi ^{-1}(U)$. By assumption, there is an isomorphism
$\pi ^{-1}(U)$. By assumption, there is an isomorphism
This gives an isomorphism
which uniquely extends to an isomorphism
Lastly, compatibility follows as it can be checked on any nonempty open set (such as ![]() $U$).
$U$).
For property (iv), the isomorphisms ![]() $\phi _g$ give rise to isomorphisms of global sections:
$\phi _g$ give rise to isomorphisms of global sections:
Let ![]() $\rho (g)^{\vee }$ denote the composition. The compatibility implies that the dual isomorphisms satisfy
$\rho (g)^{\vee }$ denote the composition. The compatibility implies that the dual isomorphisms satisfy
Commutativity of the diagram follows from the fact that for a general ![]() $x\in X$, the map
$x\in X$, the map ![]() $\rho (g)^\vee$ gives an isomorphism between sections of
$\rho (g)^\vee$ gives an isomorphism between sections of ![]() $H^0(X,{\mathcal {L}})$ vanishing at
$H^0(X,{\mathcal {L}})$ vanishing at ![]() $x$ and those vanishing at
$x$ and those vanishing at ![]() $g(x)$.
$g(x)$.
To prove property (v), it suffices to observe that the matrix ![]() $\rho (g)$ preserves the closure of the image
$\rho (g)$ preserves the closure of the image ![]() $\pi (X)$, which is clear from commutativity.
$\pi (X)$, which is clear from commutativity.
For property (iv), by the Nullstellensatz any birational automorphism ![]() $g\in {\mathrm {Bir}}(X)$ which is equal to the identity on the
$g\in {\mathrm {Bir}}(X)$ which is equal to the identity on the ![]() $k$-points of some nonempty open subset
$k$-points of some nonempty open subset ![]() $U \subset X$ must be equal to the identity on
$U \subset X$ must be equal to the identity on ![]() $U$. Therefore,
$U$. Therefore, ![]() $g={\mathrm {id}}\in {\mathrm {Bir}}(X)$.
$g={\mathrm {id}}\in {\mathrm {Bir}}(X)$.
Part (vii) is proved by taking a tensor power of ![]() ${\mathcal {L}}$ that is very ample and applying property (vi).
${\mathcal {L}}$ that is very ample and applying property (vi).
Now we shift our focus to giving examples of birationally equivariant line bundles.
Proposition 1.6 Let ![]() $X$ be a smooth projective variety.
$X$ be a smooth projective variety.
(i) If
 $\omega _X$ is a globally generated line bundle, then it is birationally equivariant.
$\omega _X$ is a globally generated line bundle, then it is birationally equivariant.(ii) More generally, if the image of the evaluation map
is a line bundle \[ H^0(X,{\bigwedge}^i \Omega_X)\otimes_k {\mathcal{O}}_X \rightarrow {\bigwedge}^i \Omega_X \]
\[ H^0(X,{\bigwedge}^i \Omega_X)\otimes_k {\mathcal{O}}_X \rightarrow {\bigwedge}^i \Omega_X \] ${\mathcal {L}}\subset {\bigwedge} ^i \Omega _X$ (which is necessarily globally generated), then
${\mathcal {L}}\subset {\bigwedge} ^i \Omega _X$ (which is necessarily globally generated), then  ${\mathcal {L}}$ is birationally equivariant.
${\mathcal {L}}$ is birationally equivariant.
Proof. Part (ii) implies part (i), so we just prove part (ii). Let ![]() $g\in {\mathrm {Bir}}(X)$ and let
$g\in {\mathrm {Bir}}(X)$ and let ![]() $i_g {\colon } U_g\hookrightarrow X$ denote the inclusion of the open set on which
$i_g {\colon } U_g\hookrightarrow X$ denote the inclusion of the open set on which ![]() $g$ is defined (so the complement
$g$ is defined (so the complement ![]() $X\setminus U_g$ has codimension
$X\setminus U_g$ has codimension ![]() $\ge 2$).
$\ge 2$).
The derivative map
pushes forward to an inclusion
This gives an injection on global sections:
Now ![]() $i_{g*} g^*({\bigwedge} ^i \Omega _X)$ contains the line bundle
$i_{g*} g^*({\bigwedge} ^i \Omega _X)$ contains the line bundle ![]() $g^*{\mathcal {L}}$ (here we use smoothness of
$g^*{\mathcal {L}}$ (here we use smoothness of ![]() $X$ to say that Weil divisors are Cartier). Moreover, every global section of
$X$ to say that Weil divisors are Cartier). Moreover, every global section of ![]() ${\mathcal {L}}$ pulls back to a global section of
${\mathcal {L}}$ pulls back to a global section of ![]() $g^*{\mathcal {L}}$. Thus, we have a commuting diagram of inclusions as follows.
$g^*{\mathcal {L}}$. Thus, we have a commuting diagram of inclusions as follows.

As the spaces on the left and the right are of the same dimension and the maps are all inclusions, it follows that every map is an isomorphism. Lastly, the commutative diagram of evaluation maps

shows that the image of ![]() $g^*{\mathcal {L}}$ in
$g^*{\mathcal {L}}$ in ![]() ${\bigwedge} ^i\Omega _X$ contains
${\bigwedge} ^i\Omega _X$ contains ![]() ${\mathcal {L}}$. It remains to show that the natural inclusion
${\mathcal {L}}$. It remains to show that the natural inclusion ![]() ${\mathcal {L}}\hookrightarrow \phi _g(g^*{\mathcal {L}}) \cong g^*{\mathcal {L}}$ is an isomorphism.
${\mathcal {L}}\hookrightarrow \phi _g(g^*{\mathcal {L}}) \cong g^*{\mathcal {L}}$ is an isomorphism.
Suppose for contradiction that ![]() $g^*{\mathcal {L}} \cong {\mathcal {L}}(\Delta )$ for some effective divisor
$g^*{\mathcal {L}} \cong {\mathcal {L}}(\Delta )$ for some effective divisor ![]() $\Delta$. As
$\Delta$. As ![]() $H^0(X,{\mathcal {L}})$ and
$H^0(X,{\mathcal {L}})$ and ![]() $H^0(X,g^*{\mathcal {L}})$ have the same dimension it follows that the fixed component of the linear series
$H^0(X,g^*{\mathcal {L}})$ have the same dimension it follows that the fixed component of the linear series ![]() $|g^*{\mathcal {L}}|$ equals
$|g^*{\mathcal {L}}|$ equals ![]() $\Delta$. However, the sections in
$\Delta$. However, the sections in ![]() $H^0(X,g^*{\mathcal {L}})$ globally generate
$H^0(X,g^*{\mathcal {L}})$ globally generate ![]() $g^*{\mathcal {L}}$ on
$g^*{\mathcal {L}}$ on ![]() $U_g$, which has a complement of codimension at least two in
$U_g$, which has a complement of codimension at least two in ![]() $X$, so there is no fixed component. Therefore,
$X$, so there is no fixed component. Therefore, ![]() $\phi _g$ defines an isomorphism between
$\phi _g$ defines an isomorphism between ![]() $g^*{\mathcal {L}}$ and
$g^*{\mathcal {L}}$ and ![]() ${\mathcal {L}}$.
${\mathcal {L}}$.
To check equality of isomorphisms
it suffices to check on any nonempty open set (as global automorphisms of a line bundle on a projective variety are constant). This reduces to the chain rule:
on an open set where everything is defined.
2.  $p$-cyclic covers and their resolutions
$p$-cyclic covers and their resolutions
The goal of this section is to define ![]() $p$-cyclic covers in characteristic
$p$-cyclic covers in characteristic ![]() $p$, present Kollár's resolution [Reference KollárKol95, § 21], and check that they have terminal singularities (by further passing to a log resolution, and computing discrepancies). Throughout we work over an algebraically closed field
$p$, present Kollár's resolution [Reference KollárKol95, § 21], and check that they have terminal singularities (by further passing to a log resolution, and computing discrepancies). Throughout we work over an algebraically closed field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p>0$.
$p>0$.
First we define cyclic covers. Fix a ![]() $k$-scheme
$k$-scheme ![]() $X$ together with a line bundle
$X$ together with a line bundle ![]() ${\mathcal {L}}$ on
${\mathcal {L}}$ on ![]() $X$. Let
$X$. Let
 \[ {\mathbb{L}}={\mathrm{Spec}}_{{\mathcal{O}}_X}\biggl(\bigoplus_{i\ge 0} {\mathcal{L}}^{-i}\cdot y^i\biggr) \]
\[ {\mathbb{L}}={\mathrm{Spec}}_{{\mathcal{O}}_X}\biggl(\bigoplus_{i\ge 0} {\mathcal{L}}^{-i}\cdot y^i\biggr) \]
(respectively, ![]() ${\mathbb {L}}^{\otimes m}$) be the total space of the line bundle
${\mathbb {L}}^{\otimes m}$) be the total space of the line bundle ![]() ${\mathcal {L}}$ (respectively,
${\mathcal {L}}$ (respectively, ![]() ${\mathcal {L}}^{\otimes m}$). Let
${\mathcal {L}}^{\otimes m}$). Let ![]() $s\in H^0(X,{\mathcal {L}}^{\otimes m})$ be a section, which corresponds to the following map.
$s\in H^0(X,{\mathcal {L}}^{\otimes m})$ be a section, which corresponds to the following map.

There is also an ![]() $m$th power map,
$m$th power map, ![]() ${\mathbb {L}}\xrightarrow {p_m}{\mathbb {L}}^{\otimes m}$, which is a
${\mathbb {L}}\xrightarrow {p_m}{\mathbb {L}}^{\otimes m}$, which is a ![]() $\mu _m$-quotient.
$\mu _m$-quotient.
Definition 2.1 The ![]() $m$-cyclic cover branched over
$m$-cyclic cover branched over ![]() $s$ is
$s$ is ![]() $Y := p_m^{-1}(s(X))$ with the map
$Y := p_m^{-1}(s(X))$ with the map ![]() $\nu {\colon } Y\rightarrow X$. We say that the cyclic cover
$\nu {\colon } Y\rightarrow X$. We say that the cyclic cover ![]() $Y$ has branch divisor
$Y$ has branch divisor ![]() $(s=0)\subset X$.
$(s=0)\subset X$.
It follows that ![]() $Y\cong {\mathrm {Spec}}_{{\mathcal {O}}_X}\big (\bigoplus _{i\ge 0} {\mathcal {L}}^{-i} \cdot y^i/(y^m-s)\big )$.
$Y\cong {\mathrm {Spec}}_{{\mathcal {O}}_X}\big (\bigoplus _{i\ge 0} {\mathcal {L}}^{-i} \cdot y^i/(y^m-s)\big )$.
Let ![]() $X$ be a smooth projective
$X$ be a smooth projective ![]() $k$-variety with a line bundle
$k$-variety with a line bundle ![]() ${\mathcal {L}}$ and let
${\mathcal {L}}$ and let ![]() $s\in H^0(X,{\mathcal {L}}^{\otimes p})$ be a section. The
$s\in H^0(X,{\mathcal {L}}^{\otimes p})$ be a section. The ![]() $p$-cyclic cover
$p$-cyclic cover ![]() $Y$ branched along
$Y$ branched along ![]() $s$ is inseparable and typically singular. However, if
$s$ is inseparable and typically singular. However, if ![]() $s$ is general then Kollár shows how to resolve these singularities. We say
$s$ is general then Kollár shows how to resolve these singularities. We say ![]() $s$ has non-degenerate critical points [Reference KollárKol96, 17.3] if when we locally describe
$s$ has non-degenerate critical points [Reference KollárKol96, 17.3] if when we locally describe ![]() $s$ as a function, any critical point of
$s$ as a function, any critical point of ![]() $s$ has a non-degenerate Hessian matrix (when the characteristic is two this forces the dimension to be even, we leave out the odd-dimensional case here). In this case, any critical point of
$s$ has a non-degenerate Hessian matrix (when the characteristic is two this forces the dimension to be even, we leave out the odd-dimensional case here). In this case, any critical point of ![]() $s$ gives rise to an isolated hypersurface singularity on
$s$ gives rise to an isolated hypersurface singularity on ![]() $Y$ of the form
$Y$ of the form
where ![]() $f_2$ and
$f_2$ and ![]() $f_3$ are functions on
$f_3$ are functions on ![]() $X$,
$X$, ![]() $f_3$ vanishes to order three, and
$f_3$ vanishes to order three, and ![]() $f_2({x_1,\ldots,x_n})$ is a quadratic polynomial with non-degenerate Hessian. Kollár shows that these isolated singularities can be resolved by a sequence of blow-ups at points.
$f_2({x_1,\ldots,x_n})$ is a quadratic polynomial with non-degenerate Hessian. Kollár shows that these isolated singularities can be resolved by a sequence of blow-ups at points.
If ![]() $p=2$ then
$p=2$ then ![]() $Y$ is resolved after one blow-up of each singular point, and this is a log-resolution (the exceptional divisor over each point is given by the quadric:
$Y$ is resolved after one blow-up of each singular point, and this is a log-resolution (the exceptional divisor over each point is given by the quadric:
which can be checked to be smooth).
If ![]() $p>2$, then Kollár shows that a sequence of
$p>2$, then Kollár shows that a sequence of ![]() $(p-1)/2$ blow-ups of isolated double points resolves the singularities of
$(p-1)/2$ blow-ups of isolated double points resolves the singularities of ![]() $Y$. At the
$Y$. At the ![]() $i$th step, the new exceptional divisor over
$i$th step, the new exceptional divisor over ![]() $Y$ is a quadric in the new exceptional divisor over
$Y$ is a quadric in the new exceptional divisor over ![]() ${\mathbb {L}}$ whose equation is given by
${\mathbb {L}}$ whose equation is given by
where ![]() ${\mathbb {P}}^n$ has coordinates
${\mathbb {P}}^n$ has coordinates ![]() $[x_1:\cdots :x_n:y]$. This exceptional divisor is smooth away from the point
$[x_1:\cdots :x_n:y]$. This exceptional divisor is smooth away from the point ![]() $[0:\cdots :0:1]$. The only exceptional divisor it intersects is the one from the step before, and the intersection is given by
$[0:\cdots :0:1]$. The only exceptional divisor it intersects is the one from the step before, and the intersection is given by ![]() $(y=0)\cap (f_2=0)\subset {\mathbb {P}}^n$, which is smooth. Here the strict transform of
$(y=0)\cap (f_2=0)\subset {\mathbb {P}}^n$, which is smooth. Here the strict transform of ![]() $Y$ has the new local equation:
$Y$ has the new local equation:
Thus, it is resolved after ![]() $(p-1)/2$ steps. To give a log resolution, that is, to resolve the singularity of the
$(p-1)/2$ steps. To give a log resolution, that is, to resolve the singularity of the ![]() $(p-1)/2$th exceptional divisor, we must blow-up one more time at the point
$(p-1)/2$th exceptional divisor, we must blow-up one more time at the point ![]() $[0:\cdots :0:1]$. The last exceptional divisor over
$[0:\cdots :0:1]$. The last exceptional divisor over ![]() $Y$ is a smooth projective space
$Y$ is a smooth projective space ![]() ${\mathbb {P}}^{n-1}$ with coordinates
${\mathbb {P}}^{n-1}$ with coordinates ![]() $[x_1:\cdots :x_n]$, and the intersection of the last two exceptional divisors is again the quadric
$[x_1:\cdots :x_n]$, and the intersection of the last two exceptional divisors is again the quadric ![]() $f_2({x_1,\ldots,x_n}) = 0\subset {\mathbb {P}}^{n-1}$. This shows that the total exceptional divisor is simple normal crossing.
$f_2({x_1,\ldots,x_n}) = 0\subset {\mathbb {P}}^{n-1}$. This shows that the total exceptional divisor is simple normal crossing.
Call this log-resolution ![]() $Z$. This gives a log resolution of
$Z$. This gives a log resolution of ![]() $Y$ which fits into the following diagram.
$Y$ which fits into the following diagram.

Proposition 2.2 Let ![]() $X$ be a smooth
$X$ be a smooth ![]() $k$-variety of dimension
$k$-variety of dimension ![]() $n\ge 3$ with a line bundle
$n\ge 3$ with a line bundle ![]() ${\mathcal {L}}$. If
${\mathcal {L}}$. If
is a section with non-degenerate critical points then the ![]() $p$-cyclic cover branched over
$p$-cyclic cover branched over ![]() $s$ has terminal singularities.
$s$ has terminal singularities.
Proof. This can be checked locally at each singularity of the form
First, when the characteristic of ![]() $k$ is two (with
$k$ is two (with ![]() $n$ even), if
$n$ even), if ![]() $\sigma {\colon } Z\rightarrow Y$ is the resolution of singularities and
$\sigma {\colon } Z\rightarrow Y$ is the resolution of singularities and ![]() $E$ is the unique exceptional divisor it suffices to compute the coefficient
$E$ is the unique exceptional divisor it suffices to compute the coefficient ![]() $\alpha$ of
$\alpha$ of ![]() $E$ in the equation
$E$ in the equation
If ![]() $n\ge 3$, then
$n\ge 3$, then ![]() $\alpha >0$.
$\alpha >0$.
When ![]() $p$ is odd, let
$p$ is odd, let ![]() $E_i\subset Z$ denote the strict transform of the exceptional divisor of the
$E_i\subset Z$ denote the strict transform of the exceptional divisor of the ![]() $i$th blow-up of
$i$th blow-up of ![]() $T$. Let
$T$. Let ![]() $r=(p-1)/2$. Then it suffices to compute the coefficients
$r=(p-1)/2$. Then it suffices to compute the coefficients ![]() $\alpha _i$ of
$\alpha _i$ of ![]() $E_i$:
$E_i$:
This gives ![]() $\alpha _i = i(n-2)$ for
$\alpha _i = i(n-2)$ for ![]() $0\le i\le r$ and
$0\le i\le r$ and ![]() $\alpha _{r+1} = (r+1)n-p$. These are all positive for
$\alpha _{r+1} = (r+1)n-p$. These are all positive for ![]() $n\ge 3$.
$n\ge 3$.
3. Computing the space of  $(n-1)$-forms
$(n-1)$-forms
Again, assume ![]() $k$ has characteristic
$k$ has characteristic ![]() $p>0$. In this section we prove a slightly more general version of Theorem B. Specifically we consider the following situation:
$p>0$. In this section we prove a slightly more general version of Theorem B. Specifically we consider the following situation:
(i)
 $X$ is a smooth projective
$X$ is a smooth projective  $k$-variety of dimension
$k$-variety of dimension  $n\ge 3$;
$n\ge 3$;(ii)
 ${\mathcal {L}}$ is an effective line bundle on
${\mathcal {L}}$ is an effective line bundle on  $X$ with total space
$X$ with total space  ${\mathbb {L}}$;
${\mathbb {L}}$;(iii)
 $s\in H^0(X,{\mathcal {L}}^{\otimes p})$ is a global section with non-degenerate critical points;
$s\in H^0(X,{\mathcal {L}}^{\otimes p})$ is a global section with non-degenerate critical points;(iv)
 $\nu \colon Y \rightarrow X$ is the
$\nu \colon Y \rightarrow X$ is the  $p$-cyclic cover branched over
$p$-cyclic cover branched over  $s$;
$s$;(v) and assume that
 $-K_Y$ is ample (i.e.
$-K_Y$ is ample (i.e.  $Y$ is Fano).
$Y$ is Fano).
In Proposition 3.2, assuming that
we show
As a consequence, we show the line bundle ![]() $\mu ^*(\omega _X\otimes {\mathcal {L}}^p)|_Y$ is birationally equivariant on
$\mu ^*(\omega _X\otimes {\mathcal {L}}^p)|_Y$ is birationally equivariant on ![]() $Y$. Theorems A and B and Corollary C follow from results in § 1.
$Y$. Theorems A and B and Corollary C follow from results in § 1.
Let ![]() $Z\subset {\widetilde {{\mathbb {L}}}}$ be the log-resolution of the cyclic cover as in § 2. Following Kollár, consider the relative cotangent sequence for
$Z\subset {\widetilde {{\mathbb {L}}}}$ be the log-resolution of the cyclic cover as in § 2. Following Kollár, consider the relative cotangent sequence for ![]() ${\widetilde {{\mathbb {L}}}}/X$ restricted to
${\widetilde {{\mathbb {L}}}}/X$ restricted to ![]() $Z$ and the cotangent sequence for
$Z$ and the cotangent sequence for ![]() $Z\subset {\widetilde {{\mathbb {L}}}}$. This gives rise to the following diagram.
$Z\subset {\widetilde {{\mathbb {L}}}}$. This gives rise to the following diagram.

Here, ![]() $\tau$ (respectively,
$\tau$ (respectively, ![]() $B$) is the torsion (respectively, torsion-free) part of
$B$) is the torsion (respectively, torsion-free) part of ![]() $\Omega _{{\widetilde {{\mathbb {L}}}}/X}|_Z$. To check that there is a map
$\Omega _{{\widetilde {{\mathbb {L}}}}/X}|_Z$. To check that there is a map ![]() $\rho _2$ that makes the diagram commute, it suffices to check that
$\rho _2$ that makes the diagram commute, it suffices to check that ![]() $I/I^2$ maps to
$I/I^2$ maps to ![]() $0$ in
$0$ in ![]() $B$ which can be done generically as these are both torsion-free. Generically, this follows from the fact that the
$B$ which can be done generically as these are both torsion-free. Generically, this follows from the fact that the ![]() $y$-derivative of the equation of the cyclic cover
$y$-derivative of the equation of the cyclic cover
vanishes (as we are in characteristic ![]() $p$). Here
$p$). Here ![]() $Q$ is defined to be the kernel of
$Q$ is defined to be the kernel of ![]() $\rho _2$.
$\rho _2$.
Proposition 3.1 In the setting described previously:
(i) the natural map
is surjective outside of codimension two; \[ {\bigwedge}^{n-1}\Omega_Z\cong \Omega_Z^{\vee}\otimes \omega_Z\rightarrow Q^\vee\otimes \omega_Z \]
\[ {\bigwedge}^{n-1}\Omega_Z\cong \Omega_Z^{\vee}\otimes \omega_Z\rightarrow Q^\vee\otimes \omega_Z \](ii) the kernel is isomorphic to
 $\det (Q)$;
$\det (Q)$;(iii) if
 $H^0(X,T_X\otimes \omega _X\otimes {\mathcal {L}}^{p-1})=0$ then
$H^0(X,T_X\otimes \omega _X\otimes {\mathcal {L}}^{p-1})=0$ then  $H^0(Z,{\bigwedge} ^{n-1}\Omega _Z) \cong H^0(Z,\det (Q))$.
$H^0(Z,{\bigwedge} ^{n-1}\Omega _Z) \cong H^0(Z,\det (Q))$.
Proof. For part (i), the map
only fails to be surjective on the locus where ![]() $B$ is not locally free (which has codimension at least two as
$B$ is not locally free (which has codimension at least two as ![]() $B$ is torsion-free). Letting
$B$ is torsion-free). Letting ![]() $A$ denote the kernel of the map above, we observe that
$A$ denote the kernel of the map above, we observe that ![]() $A$ reflexive as it is the kernel of a map of reflexive sheaves.
$A$ reflexive as it is the kernel of a map of reflexive sheaves. ![]() $A$ is therefore a line bundle as it is rank one.
$A$ is therefore a line bundle as it is rank one.
Now that we know the kernel is a line bundle, part (ii) can be verified outside codimension two where the sequence
becomes exact. Thus, we have
which gives ![]() $c_1(A) = c_1(Q)$, that is,
$c_1(A) = c_1(Q)$, that is, ![]() $A \cong \det Q$.
$A \cong \det Q$.
It remains to check part (iii). By (1) and part (ii) it suffices to show that ![]() $Q^\vee \otimes \omega _Z$ has no global sections. There is an inclusion
$Q^\vee \otimes \omega _Z$ has no global sections. There is an inclusion
so it suffices to show
As ![]() $Y$ has terminal singularities there is an exact sequence
$Y$ has terminal singularities there is an exact sequence
(where ![]() $\Delta$ is an effective exceptional divisor in
$\Delta$ is an effective exceptional divisor in ![]() $Z$). Pushing forward to
$Z$). Pushing forward to ![]() $Y$ shows
$Y$ shows ![]() $\omega _Y\cong \sigma _*\omega _Z$ (as they are isomorphic outside of points, torsion-free, and the first is a line bundle). By the projection formula,
$\omega _Y\cong \sigma _*\omega _Z$ (as they are isomorphic outside of points, torsion-free, and the first is a line bundle). By the projection formula,
is an isomorphism. Therefore, as push-forward preserves global sections it suffices to show that
Now ![]() $\omega _Y = \nu ^*(\omega _X\otimes {\mathcal {L}}^{p-1})$. As
$\omega _Y = \nu ^*(\omega _X\otimes {\mathcal {L}}^{p-1})$. As ![]() $Y$ is a
$Y$ is a ![]() $p$-cyclic cover,
$p$-cyclic cover,
 \[ \nu_*({\mathcal{O}}_Y)\cong \bigoplus_{i=0}^{p-1} {\mathcal{L}}^{-i}. \]
\[ \nu_*({\mathcal{O}}_Y)\cong \bigoplus_{i=0}^{p-1} {\mathcal{L}}^{-i}. \]
Pushing forward ![]() $\nu ^*(T_X) \otimes \omega _Y$ gives
$\nu ^*(T_X) \otimes \omega _Y$ gives
 \[ H^0(Y,\nu^*(T_X)\otimes \omega_Y) = \bigoplus_{i=0}^{p-1}H^0(X,T_X\otimes \omega_X\otimes {\mathcal{L}}^{i}). \]
\[ H^0(Y,\nu^*(T_X)\otimes \omega_Y) = \bigoplus_{i=0}^{p-1}H^0(X,T_X\otimes \omega_X\otimes {\mathcal{L}}^{i}). \]
This vanishes by the assumptions that ![]() $H^0(X,T_X\otimes \omega _X\otimes {\mathcal {L}}^{p-1})=0$ (here we use that
$H^0(X,T_X\otimes \omega _X\otimes {\mathcal {L}}^{p-1})=0$ (here we use that ![]() ${\mathcal {L}}$ is effective to show the other summands vanish).
${\mathcal {L}}$ is effective to show the other summands vanish).
Proposition 3.2 Assume:
(i)
 $H^0(X,T_X\otimes \omega _X\otimes {\mathcal {L}}^{p-1})=0$;
$H^0(X,T_X\otimes \omega _X\otimes {\mathcal {L}}^{p-1})=0$;(ii)
 $\omega _X\otimes {\mathcal {L}}^{p}$ is globally generated; and
$\omega _X\otimes {\mathcal {L}}^{p}$ is globally generated; and(iii)
 $Y$ is Fano (or that
$Y$ is Fano (or that  $H^{0}(Y, \omega _{Y}) = 0$).
$H^{0}(Y, \omega _{Y}) = 0$).
Then
for some effective divisor ![]() $\Delta$ that is exceptional for the birational map
$\Delta$ that is exceptional for the birational map ![]() $\sigma$, and
$\sigma$, and
Proof. By Kollár's work ([Reference KollárKol95, § 23]) there is an injection:
The line bundle ![]() ${\tilde {\mu }}^*(\omega _X\otimes {\mathcal {L}}^p)|_Z$ is globally generated, so it must land inside of
${\tilde {\mu }}^*(\omega _X\otimes {\mathcal {L}}^p)|_Z$ is globally generated, so it must land inside of ![]() $\det (Q)$. Hence,
$\det (Q)$. Hence, ![]() $\det (Q) = {\tilde {\mu }}^*(\omega _X\otimes {\mathcal {L}}^p)|_Z (\Delta )$ for some effective divisor
$\det (Q) = {\tilde {\mu }}^*(\omega _X\otimes {\mathcal {L}}^p)|_Z (\Delta )$ for some effective divisor ![]() $\Delta$. On the other hand, away from the exceptional divisors of
$\Delta$. On the other hand, away from the exceptional divisors of ![]() $\sigma$, the vector bundle
$\sigma$, the vector bundle ![]() $Q$ is the pull-back of a vector bundle on the complement of the singular locus of
$Q$ is the pull-back of a vector bundle on the complement of the singular locus of ![]() $Y$ with determinant
$Y$ with determinant ![]() $\nu ^*(\omega _X\otimes {\mathcal {L}}^p)$. Thus, the line bundles are isomorphic away from the exceptional divisors. Thus,
$\nu ^*(\omega _X\otimes {\mathcal {L}}^p)$. Thus, the line bundles are isomorphic away from the exceptional divisors. Thus, ![]() $\Delta$ is exceptional for
$\Delta$ is exceptional for ![]() $\sigma$.
$\sigma$.
Pushing forward along ![]() $\sigma$ gives a map on
$\sigma$ gives a map on ![]() $Y$:
$Y$:
which is necessarily an isomorphism, as ![]() $\sigma _*(\det (Q))$ is torsion-free and they are isomorphic away from points. It follows that
$\sigma _*(\det (Q))$ is torsion-free and they are isomorphic away from points. It follows that
Lastly, we have
 \begin{equation} \nu_*(\nu^*(\omega_X\otimes {\mathcal{L}}^p)) \cong \bigoplus_{i=0}^{p-1} \big(\omega_X \otimes {\mathcal{L}}^{p-i}\big). \end{equation}
\begin{equation} \nu_*(\nu^*(\omega_X\otimes {\mathcal{L}}^p)) \cong \bigoplus_{i=0}^{p-1} \big(\omega_X \otimes {\mathcal{L}}^{p-i}\big). \end{equation}
By the Fano assumption, ![]() $H^{0}(Y, \omega _{Y}) = 0$. We also have
$H^{0}(Y, \omega _{Y}) = 0$. We also have ![]() $\omega _{Y} = \nu ^{\ast }(\omega _{X} \otimes {\mathcal {L}}^{p-1})$. Thus,
$\omega _{Y} = \nu ^{\ast }(\omega _{X} \otimes {\mathcal {L}}^{p-1})$. Thus,
 \[ \nu_{\ast}(\omega_{Y}) = \bigoplus_{i=0}^{p-1} \big(\omega_X \otimes {\mathcal{L}}^{p-1-i}\big) \]
\[ \nu_{\ast}(\omega_{Y}) = \bigoplus_{i=0}^{p-1} \big(\omega_X \otimes {\mathcal{L}}^{p-1-i}\big) \]
has no global sections. It follows that the only global sections on the right-hand side of (4) come from ![]() $\omega _X \otimes {\mathcal {L}}^p$, giving:
$\omega _X \otimes {\mathcal {L}}^p$, giving:
which completes the proof.
Proof of Theorem B We check that in the setting of Theorem B, the assumptions of Proposition 3.2 are satisfied. Let ![]() $e$ be a positive integer such that
$e$ be a positive integer such that
Consider a hypersurface ![]() $X \subset {\mathbb {P}}^{n+1}_{k}$ of degree
$X \subset {\mathbb {P}}^{n+1}_{k}$ of degree ![]() $e$ and let
$e$ and let ![]() ${\mathcal {L}} = {\mathcal {O}}_{X}(d)$ for some
${\mathcal {L}} = {\mathcal {O}}_{X}(d)$ for some ![]() $d \geq 1$. We claim that
$d \geq 1$. We claim that
The Euler sequence restricted to ![]() $X$
$X$
 \begin{gather*} 0 \rightarrow {\mathcal{O}}_{X}(e+(p-1)d-n-2) \rightarrow {\mathcal{O}}_{X}^{\oplus(n+2)}(e+(p-1)d-n-1)\\ \rightarrow T_{{\mathbb{P}}^{n+1}}(e+(p-1)d-n-2)|_X \rightarrow 0 \end{gather*}
\begin{gather*} 0 \rightarrow {\mathcal{O}}_{X}(e+(p-1)d-n-2) \rightarrow {\mathcal{O}}_{X}^{\oplus(n+2)}(e+(p-1)d-n-1)\\ \rightarrow T_{{\mathbb{P}}^{n+1}}(e+(p-1)d-n-2)|_X \rightarrow 0 \end{gather*}
can be used to show that ![]() $T_{{\mathbb {P}}^{n+1}}(e+(p-1)d-n-2)|_X$ has no global sections. Thus, the above vanishing follows from taking global sections for the inclusion of tangent bundles:
$T_{{\mathbb {P}}^{n+1}}(e+(p-1)d-n-2)|_X$ has no global sections. Thus, the above vanishing follows from taking global sections for the inclusion of tangent bundles:
Next, observe that
so the inequality ![]() $e+pd-3\ge n$ implies that
$e+pd-3\ge n$ implies that ![]() $\omega _{X} \otimes {\mathcal {L}}^{p}$ is globally generated.
$\omega _{X} \otimes {\mathcal {L}}^{p}$ is globally generated.
Now for any point ![]() $x\in X$ the restriction map
$x\in X$ the restriction map ![]() $H^0(X,{\mathcal {L}}^p)\rightarrow {\mathcal {L}}^p/{\mathfrak {m}}_x^3$ is surjective as
$H^0(X,{\mathcal {L}}^p)\rightarrow {\mathcal {L}}^p/{\mathfrak {m}}_x^3$ is surjective as ![]() $p\ge 2$ and
$p\ge 2$ and ![]() ${\mathcal {L}}^p = {\mathcal {O}}_X(pd)$ (this follows from the analogous result for
${\mathcal {L}}^p = {\mathcal {O}}_X(pd)$ (this follows from the analogous result for ![]() ${\mathbb {P}}^{n+1}$ by restricting sections). Therefore, by [Reference KollárKol96, V.5.7.1], a general section
${\mathbb {P}}^{n+1}$ by restricting sections). Therefore, by [Reference KollárKol96, V.5.7.1], a general section ![]() $s\in H^0(X,{\mathcal {O}}_X(pd))$ has non-degenerate critical points.
$s\in H^0(X,{\mathcal {O}}_X(pd))$ has non-degenerate critical points. ![]() $Y$ is Fano as
$Y$ is Fano as ![]() $\omega _Y = \nu ^*({\mathcal {O}}_X(e+(p-1)d-n-2)).$ By Proposition 3.2, it follows that
$\omega _Y = \nu ^*({\mathcal {O}}_X(e+(p-1)d-n-2)).$ By Proposition 3.2, it follows that
Proof of Corollary C By § 2, ![]() $Y$ admits a log resolution
$Y$ admits a log resolution ![]() $\sigma \colon Z \rightarrow Y$ and by Theorem B there is an injection
$\sigma \colon Z \rightarrow Y$ and by Theorem B there is an injection
which induces the isomorphism on global sections in (2). In particular, the image of the evaluation map
is precisely the line bundle
so by Proposition 1.6(ii) it is birationally equivariant on ![]() $Z$. Theorem 1.5(iii) shows that
$Z$. Theorem 1.5(iii) shows that ![]() $\mu ^{\ast }(\omega _X(pd))|_{Y}$ is birationally equivariant on
$\mu ^{\ast }(\omega _X(pd))|_{Y}$ is birationally equivariant on ![]() $Y$. The map
$Y$. The map ![]() $\nu$ is purely inseparable and the sections of
$\nu$ is purely inseparable and the sections of ![]() $\nu ^{\ast }(\omega _X(pd))$ define a map
$\nu ^{\ast }(\omega _X(pd))$ define a map
Therefore, Theorem 1.5(vi) and (vii) imply that ![]() ${\mathrm {Bir}}(Y) \cong {\mathrm {Aut}}(Y) \hookrightarrow {\mathrm {Aut}}(X)$.
${\mathrm {Bir}}(Y) \cong {\mathrm {Aut}}(Y) \hookrightarrow {\mathrm {Aut}}(X)$.
We are now ready to give the following proof.
Proof of Theorem A Let ![]() $X$ be a general degree
$X$ be a general degree ![]() $e\ge 3$ hypersurface over an algebraically closed field of characteristic
$e\ge 3$ hypersurface over an algebraically closed field of characteristic ![]() $p>0$ and fix the line bundle
$p>0$ and fix the line bundle ![]() ${\mathcal {L}} := {\mathcal {O}}_{X}(d)$. Assume (as in Corollary C) that
${\mathcal {L}} := {\mathcal {O}}_{X}(d)$. Assume (as in Corollary C) that ![]() $n\ge 3$ and
$n\ge 3$ and
Let ![]() $Y$ be a cyclic cover branched over a general section of
$Y$ be a cyclic cover branched over a general section of ![]() $H^0(X,{\mathcal {O}}_X(pd))$. By Corollary C,
$H^0(X,{\mathcal {O}}_X(pd))$. By Corollary C,
By the work of Matsumura and Monsky [Reference Matsumura and MonskyMM63] (see [Reference PoonenPoo05, Corollary 1.9] for a more modern treatment), we may assume that ![]() ${\mathrm {Aut}}(X) = \{ 1 \}$. The index of such a
${\mathrm {Aut}}(X) = \{ 1 \}$. The index of such a ![]() $Y$ is
$Y$ is ![]() $n+2-e-(p-1)d$. For appropriate choices of
$n+2-e-(p-1)d$. For appropriate choices of ![]() $e$ and
$e$ and ![]() $n$ this can be made arbitrarily large. For example,
$n$ this can be made arbitrarily large. For example, ![]() $p=2$,
$p=2$, ![]() $e=3$,
$e=3$, ![]() $d=3$, and
$d=3$, and ![]() $n = 6$ give index-two examples. When
$n = 6$ give index-two examples. When ![]() $p=2$,
$p=2$, ![]() $e=3$,
$e=3$, ![]() $d=4$, and
$d=4$, and ![]() $n=8$, there are index-three examples.
$n=8$, there are index-three examples.
Remark 3.3 Fixing a prime number ![]() $p$. There are examples of Fano varieties of dimension
$p$. There are examples of Fano varieties of dimension ![]() $n$, index equal to
$n$, index equal to ![]() $i\ge 2$, and trivial birational automorphisms once
$i\ge 2$, and trivial birational automorphisms once
Indeed, setting ![]() $d=i+1$, there are always solutions to
$d=i+1$, there are always solutions to ![]() $n+3-e=pd$ with
$n+3-e=pd$ with ![]() $e\ge 3$ once
$e\ge 3$ once ![]() $n$ satisfies the above inequality. For such values of
$n$ satisfies the above inequality. For such values of ![]() $n$,
$n$, ![]() $e$, and
$e$, and ![]() $d$, the index is
$d$, the index is
Acknowledgements
We would like to thank J. Kollár, M. Mustaţă, A. Perry, A. Pukhlikov, and B. Totaro for valuable comments and discussions. We especially thank the referees for a thorough report and helpful suggestions.