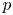1. Introduction
1.1 Representation theory of reductive algebraic groups and the Hecke category
Let ![]() $G$ be a connected reductive algebraic group over an algebraically closed field
$G$ be a connected reductive algebraic group over an algebraically closed field ![]() $\Bbbk$ of characteristic
$\Bbbk$ of characteristic ![]() $p$ (assumed to be strictly bigger than the Coxeter number of
$p$ (assumed to be strictly bigger than the Coxeter number of ![]() $G$), and let
$G$), and let ![]() ${W_{\mathrm {aff}}}$ be the associated affine Weyl group. A choice of a Borel subgroup
${W_{\mathrm {aff}}}$ be the associated affine Weyl group. A choice of a Borel subgroup ![]() $B$ in
$B$ in ![]() $G$ determines a subset
$G$ determines a subset ![]() ${S_{\mathrm {aff}}} \subset {W_{\mathrm {aff}}}$ of ‘simple reflections’ such that
${S_{\mathrm {aff}}} \subset {W_{\mathrm {aff}}}$ of ‘simple reflections’ such that ![]() $({W_{\mathrm {aff}}}, {S_{\mathrm {aff}}})$ is a Coxeter system. It has long been expected (following ideas of Verma [Reference VermaVer75], later expanded by Lusztig [Reference LusztigLus80] in particular) that the combinatorics of the category
$({W_{\mathrm {aff}}}, {S_{\mathrm {aff}}})$ is a Coxeter system. It has long been expected (following ideas of Verma [Reference VermaVer75], later expanded by Lusztig [Reference LusztigLus80] in particular) that the combinatorics of the category ![]() $\mathsf {Rep}(G)$ of finite-dimensional algebraic
$\mathsf {Rep}(G)$ of finite-dimensional algebraic ![]() $G$-modules should be expressible in terms of the Kazhdan–Lusztig combinatorics of
$G$-modules should be expressible in terms of the Kazhdan–Lusztig combinatorics of ![]() $({W_{\mathrm {aff}}}, {S_{\mathrm {aff}}})$. This expectation is now known to be exact if
$({W_{\mathrm {aff}}}, {S_{\mathrm {aff}}})$. This expectation is now known to be exact if ![]() $p$ is large (thanks to work of Kazhdan and Lusztig, Kashiwara and Tanisaki, and Andersen, Jantzen and Soergel, or a later version of Fiebig), but not for some smaller values of
$p$ is large (thanks to work of Kazhdan and Lusztig, Kashiwara and Tanisaki, and Andersen, Jantzen and Soergel, or a later version of Fiebig), but not for some smaller values of ![]() $p$ (as shown by Williamson); see [Reference Riche and WilliamsonRW18] for details and references.
$p$ (as shown by Williamson); see [Reference Riche and WilliamsonRW18] for details and references.
In [Reference Riche and WilliamsonRW18], G. Williamson and the second author of the present paper started advocating the idea that the combinatorics of ![]() $\mathsf {Rep}(G)$ should rather be expressed in terms of the
$\mathsf {Rep}(G)$ should rather be expressed in terms of the ![]() $p$-Kazhdan–Lusztig combinatorics, introduced a few years before by G. Williamson (partly in collaboration; see [Reference Juteau, Mautner and WilliamsonJMW14, Reference Jensen and WilliamsonJW17]) as some ‘combinatorial shadow’ of the Hecke category
$p$-Kazhdan–Lusztig combinatorics, introduced a few years before by G. Williamson (partly in collaboration; see [Reference Juteau, Mautner and WilliamsonJMW14, Reference Jensen and WilliamsonJW17]) as some ‘combinatorial shadow’ of the Hecke category ![]() $\mathsf {D}_{\mathrm {BS}}$ over
$\mathsf {D}_{\mathrm {BS}}$ over ![]() $\Bbbk$ attached to
$\Bbbk$ attached to ![]() $({W_{\mathrm {aff}}}, {S_{\mathrm {aff}}})$. (Here by ‘Hecke category’ we mean the diagrammatic category introduced by Elias and Williamson in [Reference Elias and WilliamsonEW16]; this category is closely related to those of Soergel bimodules and parity complexes on flag varieties.) In that paper it was observed in particular that a concrete incarnation of this idea (a character formula for indecomposable tilting modules in the principal block, in terms of antispherical
$({W_{\mathrm {aff}}}, {S_{\mathrm {aff}}})$. (Here by ‘Hecke category’ we mean the diagrammatic category introduced by Elias and Williamson in [Reference Elias and WilliamsonEW16]; this category is closely related to those of Soergel bimodules and parity complexes on flag varieties.) In that paper it was observed in particular that a concrete incarnation of this idea (a character formula for indecomposable tilting modules in the principal block, in terms of antispherical ![]() $p$-Kazhdan–Lusztig polynomials) was a consequence of the following conjecture, where for
$p$-Kazhdan–Lusztig polynomials) was a consequence of the following conjecture, where for ![]() $s \in {S_{\mathrm {aff}}}$ we denote by
$s \in {S_{\mathrm {aff}}}$ we denote by ![]() $B_s$ the object of
$B_s$ the object of ![]() $\mathsf {D}_{\mathrm {BS}}$ naturally associated with
$\mathsf {D}_{\mathrm {BS}}$ naturally associated with ![]() $s$.
$s$.
Conjecture 1.1 [Reference Riche and WilliamsonRW18]
There exists a (![]() $\Bbbk$-linear) right action of the monoidal category
$\Bbbk$-linear) right action of the monoidal category ![]() $\mathsf {D}_{\mathrm {BS}}$ on the principal block
$\mathsf {D}_{\mathrm {BS}}$ on the principal block ![]() $\mathsf {Rep}_0(G)$ of
$\mathsf {Rep}_0(G)$ of ![]() $\mathsf {Rep}(G)$ such that for any
$\mathsf {Rep}(G)$ such that for any ![]() $s \in {S_{\mathrm {aff}}}$ the object
$s \in {S_{\mathrm {aff}}}$ the object ![]() $B_s$ acts via a functor isomorphic to the wall-crossing functor associated with
$B_s$ acts via a functor isomorphic to the wall-crossing functor associated with ![]() $s$.
$s$.
The formulation of Conjecture 1.1 was motivated in particular by the philosophy of categorical actions of Lie algebras; it was proved in [Reference Riche and WilliamsonRW18, Part II] (and independently by Elias and Losev [Reference Elias and LosevEL17]) in the special case when ![]() $G=\mathrm {GL}_n(\Bbbk )$ for some
$G=\mathrm {GL}_n(\Bbbk )$ for some ![]() $n$, using the machinery of
$n$, using the machinery of ![]() $2$-Kac–Moody algebras [Reference RouquierRou08].
$2$-Kac–Moody algebras [Reference RouquierRou08].
Later the ‘combinatorial’ consequence of Conjecture 1.1 (the tilting character formula) was proved for general ![]() $G$ (in fact, in two very different ways; see [Reference Achar, Makisumi, Riche and WilliamsonAMRW19, Reference Riche and WilliamsonRW20]), but these proofs use other tools, and none of them implies the original categorical conjecture. The main result of the present paper is a proof of Conjecture 1.1 (which, as explained above, provides in particular a third general proof of the tilting character formula). In contrast to the other approaches to such questions, our proof does not involve constructible sheaves in any way; it uses coherent sheaves, but mostly over affine schemes, and hence can be considered essentially algebraic.
$G$ (in fact, in two very different ways; see [Reference Achar, Makisumi, Riche and WilliamsonAMRW19, Reference Riche and WilliamsonRW20]), but these proofs use other tools, and none of them implies the original categorical conjecture. The main result of the present paper is a proof of Conjecture 1.1 (which, as explained above, provides in particular a third general proof of the tilting character formula). In contrast to the other approaches to such questions, our proof does not involve constructible sheaves in any way; it uses coherent sheaves, but mostly over affine schemes, and hence can be considered essentially algebraic.
1.2 Localization for Harish-Chandra bimodules
The action from Conjecture 1.1 will be constructed from the natural action of Harish-Chandra ![]() $\mathcal {U} \mathfrak {g}$-bimodules (where
$\mathcal {U} \mathfrak {g}$-bimodules (where ![]() $\mathcal {U} \mathfrak {g}$ is the enveloping algebra of the Lie algebra
$\mathcal {U} \mathfrak {g}$ is the enveloping algebra of the Lie algebra ![]() $\mathfrak {g}$ of
$\mathfrak {g}$ of ![]() $G$), that is,
$G$), that is, ![]() $G$-equivariant finitely generated
$G$-equivariant finitely generated ![]() $\mathcal {U} \mathfrak {g}$-bimodules on which the diagonal action of
$\mathcal {U} \mathfrak {g}$-bimodules on which the diagonal action of ![]() $\mathcal {U} \mathfrak {g}$ is the differential of the
$\mathcal {U} \mathfrak {g}$ is the differential of the ![]() $G$-action (see § 3.4 for details). Namely, the category
$G$-action (see § 3.4 for details). Namely, the category ![]() $\mathsf {Rep}(G)$ can be naturally seen as a full subcategory of the category of
$\mathsf {Rep}(G)$ can be naturally seen as a full subcategory of the category of ![]() $G$-equivariant
$G$-equivariant ![]() $\mathcal {U} \mathfrak {g}$-modules via differentiation. Thus it admits an action of the monoidal category of Harish-Chandra bimodules; moreover, wall-crossing functors (and, more generally, translation functors) can be described as the action of certain specific completed Harish-Chandra bimodules.
$\mathcal {U} \mathfrak {g}$-modules via differentiation. Thus it admits an action of the monoidal category of Harish-Chandra bimodules; moreover, wall-crossing functors (and, more generally, translation functors) can be described as the action of certain specific completed Harish-Chandra bimodules.
More specifically, recall that (under suitable assumptions on ![]() $p$) the center of
$p$) the center of ![]() $\mathcal {U} \mathfrak {g}$ identifies with functions on the fiber product
$\mathcal {U} \mathfrak {g}$ identifies with functions on the fiber product
where the superscript ![]() $(1)$ denotes Frobenius twist,
$(1)$ denotes Frobenius twist, ![]() $\mathfrak {t}$ is the Lie algebra of a maximal torus
$\mathfrak {t}$ is the Lie algebra of a maximal torus ![]() $T$ contained in
$T$ contained in ![]() $B$, and
$B$, and ![]() $W$ is the Weyl group of
$W$ is the Weyl group of ![]() $(G,T)$, acting on
$(G,T)$, acting on ![]() $\mathfrak {t}^{*}$ via the ‘dot action’
$\mathfrak {t}^{*}$ via the ‘dot action’ ![]() $\bullet$. The subalgebra
$\bullet$. The subalgebra ![]() $\mathscr {O}(\mathfrak {g}^{*(1)})$ is realized as the ‘Frobenius center’ and the subalgebra
$\mathscr {O}(\mathfrak {g}^{*(1)})$ is realized as the ‘Frobenius center’ and the subalgebra ![]() $\mathscr {O}(\mathfrak {t}^{*}/(W,\bullet ))$ as the ‘Harish-Chandra center’. For
$\mathscr {O}(\mathfrak {t}^{*}/(W,\bullet ))$ as the ‘Harish-Chandra center’. For ![]() $\lambda, \mu \in X^{*}(T)$, in §§ 3.5–3.7 we will construct a certain monoidal category
$\lambda, \mu \in X^{*}(T)$, in §§ 3.5–3.7 we will construct a certain monoidal category
of ‘completed Harish-Chandra bimodules’, which are certain ![]() $G$-equivariant finitely generated modules over
$G$-equivariant finitely generated modules over
where ![]() $\mathscr {O}(\mathfrak {t}^{*}/(W,\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W,\bullet ))^{\hat {\lambda },\hat {\mu }}$ is the completion of
$\mathscr {O}(\mathfrak {t}^{*}/(W,\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W,\bullet ))^{\hat {\lambda },\hat {\mu }}$ is the completion of ![]() $\mathscr {O}(\mathfrak {t}^{*}/(W,\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W,\bullet ))$ with respect to the maximal ideal determined by
$\mathscr {O}(\mathfrak {t}^{*}/(W,\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W,\bullet ))$ with respect to the maximal ideal determined by ![]() $(\lambda,\mu )$. Once this definition is in place, to construct the desired action it therefore suffices to construct a monoidal functor from the Hecke category
$(\lambda,\mu )$. Once this definition is in place, to construct the desired action it therefore suffices to construct a monoidal functor from the Hecke category ![]() $\mathsf {D}_{\mathrm {BS}}$ to the category
$\mathsf {D}_{\mathrm {BS}}$ to the category ![]() $\mathsf {HC}^{\hat {0},\hat {0}}$ sending each
$\mathsf {HC}^{\hat {0},\hat {0}}$ sending each ![]() $B_s$ to an object isomorphic to the completed bimodule realizing the corresponding wall-crossing functor. This will be realized in Theorem 6.3.
$B_s$ to an object isomorphic to the completed bimodule realizing the corresponding wall-crossing functor. This will be realized in Theorem 6.3.
The main tool we will use for this construction is a localization theory for Harish-Chandra bimodules. Even though in the end we are interested in ![]() $G$-modules, which when seen as
$G$-modules, which when seen as ![]() $\mathcal {U} \mathfrak {g}$-modules have a trivial Frobenius central character, we will localize our bimodules on the regular part of
$\mathcal {U} \mathfrak {g}$-modules have a trivial Frobenius central character, we will localize our bimodules on the regular part of ![]() $\mathscr {O}(\mathfrak {g}^{*(1)})$, and more precisely on a Kostant section
$\mathscr {O}(\mathfrak {g}^{*(1)})$, and more precisely on a Kostant section ![]() $\mathbf {S}^{*} \subset \mathfrak {g}^{*(1)}$ to the (co)adjoint quotient. We will therefore set
$\mathbf {S}^{*} \subset \mathfrak {g}^{*(1)}$ to the (co)adjoint quotient. We will therefore set ![]() $\mathcal {U}_\mathbf {S} \mathfrak {g}:=\mathcal {U} \mathfrak {g} \otimes _{\mathscr {O}(\mathfrak {g}^{*(1)})} \mathscr {O}(\mathbf {S}^{*})$, and consider a certain group scheme over
$\mathcal {U}_\mathbf {S} \mathfrak {g}:=\mathcal {U} \mathfrak {g} \otimes _{\mathscr {O}(\mathfrak {g}^{*(1)})} \mathscr {O}(\mathbf {S}^{*})$, and consider a certain group scheme over ![]() $\mathfrak {t}^{*}/(W,\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W,\bullet )$ constructed out of the universal centralizer group scheme
$\mathfrak {t}^{*}/(W,\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W,\bullet )$ constructed out of the universal centralizer group scheme ![]() $\mathbb {J}^{*}_\mathbf {S}$ over
$\mathbb {J}^{*}_\mathbf {S}$ over ![]() $\mathbf {S}^{*} \cong \mathfrak {t}^{*(1)}/W$. For
$\mathbf {S}^{*} \cong \mathfrak {t}^{*(1)}/W$. For ![]() $\lambda, \mu \in X^{*}(T)$, we will define a certain monoidal category
$\lambda, \mu \in X^{*}(T)$, we will define a certain monoidal category ![]() $\mathsf {HC}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$ of finitely generated equivariant modules over
$\mathsf {HC}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$ of finitely generated equivariant modules over
see § 3.9 for the precise definition. By construction we have a natural monoidal functor
and the main result of § 3 (Proposition 3.7) states that this functor is fully faithful on a certain subcategory ![]() $\mathsf {HC}^{\hat {\lambda },\hat {\mu }}_\mathrm {diag}$ of ‘diagonally induced’ bimodules which contains the objects realizing translation and wall-crossing functors.
$\mathsf {HC}^{\hat {\lambda },\hat {\mu }}_\mathrm {diag}$ of ‘diagonally induced’ bimodules which contains the objects realizing translation and wall-crossing functors.
It is a classical observation that ![]() $\mathcal {U}_\mathbf {S} \mathfrak {g}$ is an Azumaya algebra over its center (see Proposition 4.1 for details and references); as a consequence, the category of (finitely generated) bimodules over this algebra such that the left and right actions of its center coincide is equivalent to the category of (finitely generated) modules over this center (see § 4.1 for details and references). This property is not directly applicable to our problem, since the two actions of this center on Harish-Chandra bimodules do not coincide in general; however, by using bimodules realizing translation to and from the ‘most singular’ Harish-Chandra character (namely, the opposite of the half-sum of the positive roots), we construct in § 4 an equivariant splitting bundle for
$\mathcal {U}_\mathbf {S} \mathfrak {g}$ is an Azumaya algebra over its center (see Proposition 4.1 for details and references); as a consequence, the category of (finitely generated) bimodules over this algebra such that the left and right actions of its center coincide is equivalent to the category of (finitely generated) modules over this center (see § 4.1 for details and references). This property is not directly applicable to our problem, since the two actions of this center on Harish-Chandra bimodules do not coincide in general; however, by using bimodules realizing translation to and from the ‘most singular’ Harish-Chandra character (namely, the opposite of the half-sum of the positive roots), we construct in § 4 an equivariant splitting bundle for ![]() $\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$ in the case where
$\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$ in the case where ![]() $\lambda$ and
$\lambda$ and ![]() $\mu$ belong to the lower closure of the fundamental alcove. As a consequence, for such
$\mu$ belong to the lower closure of the fundamental alcove. As a consequence, for such ![]() $\lambda,\mu$ we obtain an equivalence of categories between
$\lambda,\mu$ we obtain an equivalence of categories between ![]() $\mathsf {HC}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$ and the category of coherent representations of the pullback of
$\mathsf {HC}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$ and the category of coherent representations of the pullback of ![]() $\mathbb {J}^{*}_\mathbf {S}$ to the spectrum of
$\mathbb {J}^{*}_\mathbf {S}$ to the spectrum of ![]() $\mathscr {O}(\mathfrak {t}^{*}/(W,\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W,\bullet ))^{\hat {\lambda },\hat {\mu }}$; see Corollary 4.8.
$\mathscr {O}(\mathfrak {t}^{*}/(W,\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W,\bullet ))^{\hat {\lambda },\hat {\mu }}$; see Corollary 4.8.
A general theory of localization for modules over ![]() $\mathcal {U} \mathfrak {g}$ has been developed by the first author with Mirković and Rumynin; see [Reference Bezrukavnikov, Mirković and RumyninBMR06, Reference Bezrukavnikov, Mirković and RumyninBMR08, Reference Bezrukavnikov and MirkovićBM13]. The localization that we require here is, however, slightly different, and the present paper does not formally rely on any substantial result from [Reference Bezrukavnikov, Mirković and RumyninBMR06, Reference Bezrukavnikov, Mirković and RumyninBMR08, Reference Bezrukavnikov and MirkovićBM13]. One difference is that we are interested not in modules but in bimodules, which are equivariant for the diagonal
$\mathcal {U} \mathfrak {g}$ has been developed by the first author with Mirković and Rumynin; see [Reference Bezrukavnikov, Mirković and RumyninBMR06, Reference Bezrukavnikov, Mirković and RumyninBMR08, Reference Bezrukavnikov and MirkovićBM13]. The localization that we require here is, however, slightly different, and the present paper does not formally rely on any substantial result from [Reference Bezrukavnikov, Mirković and RumyninBMR06, Reference Bezrukavnikov, Mirković and RumyninBMR08, Reference Bezrukavnikov and MirkovićBM13]. One difference is that we are interested not in modules but in bimodules, which are equivariant for the diagonal ![]() $G$-action. Some of the constructions in [Reference Bezrukavnikov, Mirković and RumyninBMR06, Reference Bezrukavnikov, Mirković and RumyninBMR08, Reference Bezrukavnikov and MirkovićBM13] (in particular, the non-canonicity of the choice of splitting bundle) make this theory difficult to use in an equivariant setting, and our construction is slightly different. Finally, as explained above, we only need to consider the regular part of the Frobenius center, which simplifies the situation a lot, and in particular allows us to work completely at the level of abelian categories, without having to consider the more involved derived categories.
$G$-action. Some of the constructions in [Reference Bezrukavnikov, Mirković and RumyninBMR06, Reference Bezrukavnikov, Mirković and RumyninBMR08, Reference Bezrukavnikov and MirkovićBM13] (in particular, the non-canonicity of the choice of splitting bundle) make this theory difficult to use in an equivariant setting, and our construction is slightly different. Finally, as explained above, we only need to consider the regular part of the Frobenius center, which simplifies the situation a lot, and in particular allows us to work completely at the level of abelian categories, without having to consider the more involved derived categories.
1.3 The Hecke category and representations of the universal centralizer
The other crucial ingredient of our proof is a new incarnation of the Hecke category (for any Coxeter system ![]() $(\mathcal {W},\mathcal {S})$) recently found by Abe [Reference AbeAbe21].
$(\mathcal {W},\mathcal {S})$) recently found by Abe [Reference AbeAbe21].
The Hecke category is a categorification of the Hecke algebra of ![]() $(\mathcal {W},\mathcal {S})$, depending on a choice of extra data (comprising a representation
$(\mathcal {W},\mathcal {S})$, depending on a choice of extra data (comprising a representation ![]() $V$ of
$V$ of ![]() $\mathcal {W}$), which admits several different incarnations. An early definition of this category in terms of Soergel bimodules [Reference SoergelSoe07] applies to ‘reflection faithful’ representations of Coxeter systems, which include natural examples of representations over fields of characteristic
$\mathcal {W}$), which admits several different incarnations. An early definition of this category in terms of Soergel bimodules [Reference SoergelSoe07] applies to ‘reflection faithful’ representations of Coxeter systems, which include natural examples of representations over fields of characteristic ![]() $0$ (e.g. geometric representations of finite Coxeter systems and representations appearing in the theory of Kac–Moody Lie algebras for crystallographic Coxeter systems), but does not include important examples over fields of positive characteristic (e.g. some natural representations of affine Weyl groups of reductive groups). Under this assumption Soergel bimodules can be defined as a full subcategory of the category of graded bimodules over the polynomial algebra
$0$ (e.g. geometric representations of finite Coxeter systems and representations appearing in the theory of Kac–Moody Lie algebras for crystallographic Coxeter systems), but does not include important examples over fields of positive characteristic (e.g. some natural representations of affine Weyl groups of reductive groups). Under this assumption Soergel bimodules can be defined as a full subcategory of the category of graded bimodules over the polynomial algebra ![]() $\mathscr {O}(V)$. More recently Elias and Williamson [Reference Elias and WilliamsonEW16] have proposed a definition of the Hecke category in terms of generators and relations which applies (and behaves as one might expect) in a much greater generality, encompassing the representation of the affine Weyl group that we require. It is in terms of this construction that Conjecture 1.1 was stated. (For more on the Hecke category, see also [Reference Jensen and WilliamsonJW17, Reference WilliamsonWil18].)
$\mathscr {O}(V)$. More recently Elias and Williamson [Reference Elias and WilliamsonEW16] have proposed a definition of the Hecke category in terms of generators and relations which applies (and behaves as one might expect) in a much greater generality, encompassing the representation of the affine Weyl group that we require. It is in terms of this construction that Conjecture 1.1 was stated. (For more on the Hecke category, see also [Reference Jensen and WilliamsonJW17, Reference WilliamsonWil18].)
The main drawback of the construction in [Reference Elias and WilliamsonEW16], however, is that it is much less concrete than Soergel's original definition, and does not involve ![]() $\mathscr {O}(V)$-bimodules. This drawback is exactly compensated by Abe's work; under minor technical assumptions he proves in [Reference AbeAbe21] that the category of Elias and Williamson identifies with a category of ‘enhanced Soergel bimodules’, which are certain graded bimodules over
$\mathscr {O}(V)$-bimodules. This drawback is exactly compensated by Abe's work; under minor technical assumptions he proves in [Reference AbeAbe21] that the category of Elias and Williamson identifies with a category of ‘enhanced Soergel bimodules’, which are certain graded bimodules over ![]() $\mathscr {O}(V)$ endowed with a decomposition of its tensor product with
$\mathscr {O}(V)$ endowed with a decomposition of its tensor product with ![]() $\mathrm {Frac}(\mathscr {O}(V))$ (on the right) parametrized by
$\mathrm {Frac}(\mathscr {O}(V))$ (on the right) parametrized by ![]() $\mathcal {W}$.
$\mathcal {W}$.
Based on Abe's work, in the case of the affine Weyl group acting on ![]() $X^{*}(T) \otimes _\mathbb {Z} \Bbbk$ through the natural action of
$X^{*}(T) \otimes _\mathbb {Z} \Bbbk$ through the natural action of ![]() $W$, we realize the Hecke category as a full subcategory in (
$W$, we realize the Hecke category as a full subcategory in (![]() $\mathbb {G}_{\mathrm {m}}$-equivariant) coherent representations of the pullback of
$\mathbb {G}_{\mathrm {m}}$-equivariant) coherent representations of the pullback of ![]() $\mathbb {J}^{*}_\mathbf {S}$ to
$\mathbb {J}^{*}_\mathbf {S}$ to ![]() $\mathfrak {t}^{*(1)} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*(1)}$; see Theorem 2.10. This construction allows us to define a monoidal functor from the Hecke category to the category of representations considered in § 1.2, and then (using our localization theorem) a monoidal functor
$\mathfrak {t}^{*(1)} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*(1)}$; see Theorem 2.10. This construction allows us to define a monoidal functor from the Hecke category to the category of representations considered in § 1.2, and then (using our localization theorem) a monoidal functor
(This construction applies more generally for the category ![]() $\mathsf {HC}_\mathbf {S}^{\hat {\lambda },\hat {\lambda }}$ when
$\mathsf {HC}_\mathbf {S}^{\hat {\lambda },\hat {\lambda }}$ when ![]() $\lambda$ belongs to the fundamental alcove; in this case natural étale maps allow us to identify the completions of the schemes
$\lambda$ belongs to the fundamental alcove; in this case natural étale maps allow us to identify the completions of the schemes ![]() $\mathfrak {t}^{*}/(W,\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W,\bullet )$ and
$\mathfrak {t}^{*}/(W,\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W,\bullet )$ and ![]() $\mathfrak {t}^{*(1)} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*(1)}$ at the images of
$\mathfrak {t}^{*(1)} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*(1)}$ at the images of ![]() $(\lambda,\lambda )$.)
$(\lambda,\lambda )$.)
Remark 1.2 Although the concrete incarnation of this idea that is relevant in the present paper is new, the fact that affine Soergel bimodules are closely related to representations of the universal centralizer was already known: it dates back (at least) to [Reference DoddDod11]; see also [Reference Mautner and RicheMR18] for an adaptation of these ideas to positive characteristic coefficients.
At this point, to conclude our proof it only remains to show that our functor (1.1) sends the objects of the Hecke category labeled by simple reflections to the images in ![]() $\mathsf {HC}_\mathbf {S}^{\hat {0},\hat {0}}$ of the bimodules realizing the wall-crossing functors. (In fact, this property will also ensure that the functor takes values in the essential image of our fully faithful functor
$\mathsf {HC}_\mathbf {S}^{\hat {0},\hat {0}}$ of the bimodules realizing the wall-crossing functors. (In fact, this property will also ensure that the functor takes values in the essential image of our fully faithful functor ![]() $\mathsf {HC}_\mathrm {diag}^{\hat {0},\hat {0}} \to \mathsf {HC}_\mathbf {S}^{\hat {0},\hat {0}}$, which will imply that it ‘lifts’ to a functor from
$\mathsf {HC}_\mathrm {diag}^{\hat {0},\hat {0}} \to \mathsf {HC}_\mathbf {S}^{\hat {0},\hat {0}}$, which will imply that it ‘lifts’ to a functor from ![]() $\mathsf {D}_{\mathrm {BS}}$ to
$\mathsf {D}_{\mathrm {BS}}$ to ![]() $\mathsf {HC}^{\hat {0},\hat {0}}$.) In the case when the simple reflection belongs to the finite Weyl group
$\mathsf {HC}^{\hat {0},\hat {0}}$.) In the case when the simple reflection belongs to the finite Weyl group ![]() $W$, this can be checked explicitly, using localization at a character involving a weight on the corresponding wall of the fundamental alcove; see Proposition 6.6. The general case is reduced to this one using a standard trick (used, for example, in [Reference RicheRic10, Reference Bezrukavnikov and MirkovićBM13]), based on the observation that in the extended affine Weyl group each simple reflection is conjugate to a simple reflection which belongs to
$W$, this can be checked explicitly, using localization at a character involving a weight on the corresponding wall of the fundamental alcove; see Proposition 6.6. The general case is reduced to this one using a standard trick (used, for example, in [Reference RicheRic10, Reference Bezrukavnikov and MirkovićBM13]), based on the observation that in the extended affine Weyl group each simple reflection is conjugate to a simple reflection which belongs to ![]() $W$. The concrete proof involves the study of an analogue of the affine braid group action from [Reference Bezrukavnikov and RicheBR12] in our present context; in this case the situation simplifies, however (once again because we work over the regular part of the Frobenius center), and this action in fact factors through an action of the extended affine Weyl group.
$W$. The concrete proof involves the study of an analogue of the affine braid group action from [Reference Bezrukavnikov and RicheBR12] in our present context; in this case the situation simplifies, however (once again because we work over the regular part of the Frobenius center), and this action in fact factors through an action of the extended affine Weyl group.
Remark 1.3 One of the motivations for Abe's work [Reference AbeAbe21] was an attempt to prove Conjecture 1.1. What Abe was actually able to construct is rather an action on the principal block of the category of ![]() $G_1 T$-modules (where
$G_1 T$-modules (where ![]() $G_1$ is the first Frobenius kernel of
$G_1$ is the first Frobenius kernel of ![]() $G$), which is interesting but less applicable to character computations; see [Reference AbeAbe19].
$G$), which is interesting but less applicable to character computations; see [Reference AbeAbe19].
1.4 Towards a coherent realization of the Hecke category
Thanks to work of Kazhdan and Lusztig [Reference Kazhdan and LusztigKL87] and Ginzburg [Reference Chriss and GinzburgCG97], it is known that the Hecke algebra of ![]() $({W_{\mathrm {aff}}},{S_{\mathrm {aff}}})$ identifies with the Grothendieck group of the category of equivariant coherent sheaves on the Steinberg variety of triples
$({W_{\mathrm {aff}}},{S_{\mathrm {aff}}})$ identifies with the Grothendieck group of the category of equivariant coherent sheaves on the Steinberg variety of triples ![]() $\mathrm {St}$.Footnote 1 The fiber product
$\mathrm {St}$.Footnote 1 The fiber product ![]() $\mathfrak {t}^{*(1)} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*(1)}$ considered in § 1.3 identifies with the preimage of the Kostant section
$\mathfrak {t}^{*(1)} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*(1)}$ considered in § 1.3 identifies with the preimage of the Kostant section ![]() $\mathbf {S}^{*}$ in the Frobenius twist of
$\mathbf {S}^{*}$ in the Frobenius twist of ![]() $\mathrm {St}$, and the construction of § 1.3 can be seen to provide a fully faithful monoidal functor from the Hecke category to the category of equivariant coherent sheaves on the regular part of
$\mathrm {St}$, and the construction of § 1.3 can be seen to provide a fully faithful monoidal functor from the Hecke category to the category of equivariant coherent sheaves on the regular part of ![]() $\mathrm {St}$. In future work we will upgrade this construction to a fully faithful monoidal functor to the category of equivariant coherent sheaves on the whole Steinberg variety.Footnote 2 This construction will be part of our project (in part jointly with L. Rider) of constructing a ‘modular’ version of the equivalence constructed by the first author in [Reference BezrukavnikovBez16]; see [Reference Bezrukavnikov, Riche and RiderBRR20] for a first step towards this goal.
$\mathrm {St}$. In future work we will upgrade this construction to a fully faithful monoidal functor to the category of equivariant coherent sheaves on the whole Steinberg variety.Footnote 2 This construction will be part of our project (in part jointly with L. Rider) of constructing a ‘modular’ version of the equivalence constructed by the first author in [Reference BezrukavnikovBez16]; see [Reference Bezrukavnikov, Riche and RiderBRR20] for a first step towards this goal.
1.5 Contents
In § 2 we recall Abe's results, and use them to construct our monoidal functor from the Hecke category to the appropriate category of representations of the universal centralizer. In § 3 we introduce the categories of completed Harish-Chandra bimodules we will work with, and prove that restriction to a Kostant section is fully faithful on diagonally induced bimodules. In § 4 we develop our localization theory for Harish-Chandra bimodules. In § 5 we prove (for later use) some technical results using the relation between ![]() $\mathcal {U} \mathfrak {g}$ and differential operators on the flag variety of
$\mathcal {U} \mathfrak {g}$ and differential operators on the flag variety of ![]() $G$. In § 6 we prove the main result of the paper, that is, we construct the Hecke action on the principal block and prove that objects associated with simple reflections act via wall-crossing functors. Finally, Appendix A contains an index of the main notation used in the paper.
$G$. In § 6 we prove the main result of the paper, that is, we construct the Hecke action on the principal block and prove that objects associated with simple reflections act via wall-crossing functors. Finally, Appendix A contains an index of the main notation used in the paper.
2. The affine Hecke category and representations of the regular centralizer
In this section we explain that the affine Hecke category attached to a connected reductive algebraic group ![]() $\mathbf {G}$ can be described as a category of representations of (a pullback of) the universal centralizer attached to
$\mathbf {G}$ can be described as a category of representations of (a pullback of) the universal centralizer attached to ![]() $\mathbf {G}$. Our main tool will be a description of the Hecke as a category of ‘enhanced Soergel bimodules’ recently obtained by Abe [Reference AbeAbe21]. In later sections the group
$\mathbf {G}$. Our main tool will be a description of the Hecke as a category of ‘enhanced Soergel bimodules’ recently obtained by Abe [Reference AbeAbe21]. In later sections the group ![]() $\mathbf {G}$ will be chosen as the Frobenius twist of the group
$\mathbf {G}$ will be chosen as the Frobenius twist of the group ![]() $G$ appearing in Conjecture 1.1; however, this construction applies in a slightly more general context, and might be of independent interest.
$G$ appearing in Conjecture 1.1; however, this construction applies in a slightly more general context, and might be of independent interest.
2.1 The affine Weyl group and the associated Hecke category
We let ![]() $\Bbbk$ be an algebraically closed field of characteristic
$\Bbbk$ be an algebraically closed field of characteristic ![]() $p$ (possibly equal to
$p$ (possibly equal to ![]() $0$), and
$0$), and ![]() $\mathbf {G}$ be a connected reductive algebraic group over
$\mathbf {G}$ be a connected reductive algebraic group over ![]() $\Bbbk$. We fix a Borel subgroup
$\Bbbk$. We fix a Borel subgroup ![]() $\mathbf {B} \subset \mathbf {G}$ and a maximal torus
$\mathbf {B} \subset \mathbf {G}$ and a maximal torus ![]() $\mathbf {T} \subset \mathbf {B}$. The Lie algebras of
$\mathbf {T} \subset \mathbf {B}$. The Lie algebras of ![]() $\mathbf {G}$,
$\mathbf {G}$, ![]() $\mathbf {B}$,
$\mathbf {B}$, ![]() $\mathbf {T}$ will be denoted
$\mathbf {T}$ will be denoted ![]() $\mathbf {g}$,
$\mathbf {g}$, ![]() $\mathbf {b}$ and
$\mathbf {b}$ and ![]() $\mathbf {t}$ respectively. We set
$\mathbf {t}$ respectively. We set ![]() $\mathbf {X}:=X^{*}(\mathbf {T})$ (respectively,
$\mathbf {X}:=X^{*}(\mathbf {T})$ (respectively, ![]() $\mathbf {X}^{\vee } := X_*(\mathbf {T})$), and denote by
$\mathbf {X}^{\vee } := X_*(\mathbf {T})$), and denote by ![]() $\Phi \subset \mathbf {X}$ (respectively,
$\Phi \subset \mathbf {X}$ (respectively, ![]() $\Phi ^{\vee } \subset \mathbf {X}^{\vee }$) the root system (respectively, coroot system) of
$\Phi ^{\vee } \subset \mathbf {X}^{\vee }$) the root system (respectively, coroot system) of ![]() $(\mathbf {G},\mathbf {T})$. The canonical bijection
$(\mathbf {G},\mathbf {T})$. The canonical bijection ![]() $\Phi \xrightarrow {\sim } \Phi ^{\vee }$ will be denoted
$\Phi \xrightarrow {\sim } \Phi ^{\vee }$ will be denoted ![]() $\alpha \mapsto \alpha ^{\vee }$. The choice of
$\alpha \mapsto \alpha ^{\vee }$. The choice of ![]() $\mathbf {B}$ determines a subset
$\mathbf {B}$ determines a subset ![]() $\Phi ^{+} \subset \Phi$ of positive roots, consisting of the
$\Phi ^{+} \subset \Phi$ of positive roots, consisting of the ![]() $\mathbf {T}$-weights in
$\mathbf {T}$-weights in ![]() $\mathbf {g}/\mathbf {b}$; the corresponding basis of
$\mathbf {g}/\mathbf {b}$; the corresponding basis of ![]() $\Phi$ will be denoted
$\Phi$ will be denoted ![]() $\Phi ^{\mathrm {s}}$. In this section we will make the following assumptions.
$\Phi ^{\mathrm {s}}$. In this section we will make the following assumptions.
(i)
 $p$ is good for
$p$ is good for  $\mathbf {G}$.
$\mathbf {G}$.(ii) Neither
 $\mathbf {X}/\mathbb {Z}\Phi$ nor
$\mathbf {X}/\mathbb {Z}\Phi$ nor  $\mathbf {X}^{\vee }/\mathbb {Z}\Phi ^{\vee }$ has
$\mathbf {X}^{\vee }/\mathbb {Z}\Phi ^{\vee }$ has  $p$-torsion.
$p$-torsion.(iii) There exists a
 $\mathbf {G}$-equivariant isomorphism
$\mathbf {G}$-equivariant isomorphism  $\mathbf {g} \xrightarrow {\sim } \mathbf {g}^{*}$.
$\mathbf {g} \xrightarrow {\sim } \mathbf {g}^{*}$.
For simplicity we will fix once and for all a ![]() $\mathbf {G}$-equivariant isomorphism
$\mathbf {G}$-equivariant isomorphism ![]() $\kappa : \mathbf {g} \xrightarrow {\sim } \mathbf {g}^{*}$. By equivariance this also provides an identification of
$\kappa : \mathbf {g} \xrightarrow {\sim } \mathbf {g}^{*}$. By equivariance this also provides an identification of ![]() $\mathbf {t}$ and
$\mathbf {t}$ and ![]() $\mathbf {t}^{*}$ (where
$\mathbf {t}^{*}$ (where ![]() $\mathbf {t}^{*}$ is identified with the subspace in
$\mathbf {t}^{*}$ is identified with the subspace in ![]() $\mathbf {g}^{*}$ consisting of linear forms that vanish on all root subspaces).
$\mathbf {g}^{*}$ consisting of linear forms that vanish on all root subspaces).
Let ![]() $\mathbf {W}=N_{\mathbf {G}}(\mathbf {T})/\mathbf {T}$ be the Weyl group of
$\mathbf {W}=N_{\mathbf {G}}(\mathbf {T})/\mathbf {T}$ be the Weyl group of ![]() $(\mathbf {G},\mathbf {T})$. The associated affine Weyl group is the semi-direct product
$(\mathbf {G},\mathbf {T})$. The associated affine Weyl group is the semi-direct product
where ![]() $\mathbb {Z} \Phi \subset \mathbf {X}$ is the lattice generated by the roots. For
$\mathbb {Z} \Phi \subset \mathbf {X}$ is the lattice generated by the roots. For ![]() $\lambda \in \mathbb {Z}\Phi$ we will denote by
$\lambda \in \mathbb {Z}\Phi$ we will denote by ![]() $t_\lambda$ the image of
$t_\lambda$ the image of ![]() $\lambda$ in
$\lambda$ in ![]() ${W_{\mathrm {aff}}}$. It is well known that
${W_{\mathrm {aff}}}$. It is well known that ![]() ${W_{\mathrm {aff}}}$ is generated by the subset
${W_{\mathrm {aff}}}$ is generated by the subset ![]() ${S_{\mathrm {aff}}}$ consisting of the reflections
${S_{\mathrm {aff}}}$ consisting of the reflections ![]() $s_\alpha$ with
$s_\alpha$ with ![]() $\alpha \in \Phi ^{\mathrm {s}}$, together with the products
$\alpha \in \Phi ^{\mathrm {s}}$, together with the products ![]() $t_\beta s_\beta$ where
$t_\beta s_\beta$ where ![]() $\beta \in \Phi$ is such that
$\beta \in \Phi$ is such that ![]() $\beta ^{\vee }$ is a maximal coroot. Moreover, the pair
$\beta ^{\vee }$ is a maximal coroot. Moreover, the pair ![]() $({W_{\mathrm {aff}}},{S_{\mathrm {aff}}})$ is a Coxeter system; see [Reference JantzenJan03, §II.6.3]. We will sometimes need to ‘enlarge’ this group by considering translations by all elements of
$({W_{\mathrm {aff}}},{S_{\mathrm {aff}}})$ is a Coxeter system; see [Reference JantzenJan03, §II.6.3]. We will sometimes need to ‘enlarge’ this group by considering translations by all elements of ![]() $\mathbf {X}$. Namely, the extended affine Weyl group is the semi-direct product
$\mathbf {X}$. Namely, the extended affine Weyl group is the semi-direct product
Then ![]() ${W_{\mathrm {aff}}}$ is a normal subgroup in
${W_{\mathrm {aff}}}$ is a normal subgroup in ![]() ${W_{\mathrm {ext}}}$.
${W_{\mathrm {ext}}}$.
We will consider the balanced ‘realization’ of ![]() ${W_{\mathrm {aff}}}$ over
${W_{\mathrm {aff}}}$ over ![]() $\Bbbk$ (in the sense of [Reference Elias and WilliamsonEW16]) defined as follows.
$\Bbbk$ (in the sense of [Reference Elias and WilliamsonEW16]) defined as follows.
– The underlying
 $\Bbbk$-vector space is
$\Bbbk$-vector space is  $\mathbf {t}^{*}$.
$\mathbf {t}^{*}$.– If
 $\alpha \in \Phi ^{\mathrm {s}}$ and
$\alpha \in \Phi ^{\mathrm {s}}$ and  $s=s_\alpha$, then the ‘root’
$s=s_\alpha$, then the ‘root’  $\alpha _s \in \mathbf {t}$ (respectively, ‘coroot’
$\alpha _s \in \mathbf {t}$ (respectively, ‘coroot’  $\alpha _s^{\vee } \in \mathbf {t}^{*}$) associated with
$\alpha _s^{\vee } \in \mathbf {t}^{*}$) associated with  $s$ is the differential of
$s$ is the differential of  $\alpha ^{\vee }$ (respectively, of
$\alpha ^{\vee }$ (respectively, of  $\alpha$).
$\alpha$).– If
 $\beta \in \Phi ^{+}$ is such that
$\beta \in \Phi ^{+}$ is such that  $\beta ^{\vee }$ is a maximal coroot and
$\beta ^{\vee }$ is a maximal coroot and  $s=t_\beta s_\beta$ then the ‘root’
$s=t_\beta s_\beta$ then the ‘root’  $\alpha _s$ (respectively, ‘coroot’
$\alpha _s$ (respectively, ‘coroot’  $\alpha _s^{\vee }$) associated with
$\alpha _s^{\vee }$) associated with  $s$ is the differential of
$s$ is the differential of  $-\beta ^{\vee }$ (respectively, of
$-\beta ^{\vee }$ (respectively, of  $-\beta$).
$-\beta$).
This realization is an example of a Cartan realization in the sense of [Reference Achar, Makisumi, Riche and WilliamsonAMRW17, § 10.1]. Our assumption (ii) implies that this realization satisfies the ‘Demazure surjectivity’ condition of [Reference Elias and WilliamsonEW16]. There is an associated action of ![]() ${W_{\mathrm {aff}}}$ on
${W_{\mathrm {aff}}}$ on ![]() $\mathbf {t}^{*}$, which is simply the natural action of
$\mathbf {t}^{*}$, which is simply the natural action of ![]() $\mathbf {W}$, seen as an action of
$\mathbf {W}$, seen as an action of ![]() ${W_{\mathrm {aff}}}$ via the projection
${W_{\mathrm {aff}}}$ via the projection ![]() ${W_{\mathrm {aff}}} \to \mathbf {W}$.
${W_{\mathrm {aff}}} \to \mathbf {W}$.
We will denote by ![]() $\mathsf {D}_{\mathrm {BS}}$ the diagrammatic Hecke category defined by Elias–Williamson [Reference Elias and WilliamsonEW16] for the Coxeter system
$\mathsf {D}_{\mathrm {BS}}$ the diagrammatic Hecke category defined by Elias–Williamson [Reference Elias and WilliamsonEW16] for the Coxeter system ![]() $({W_{\mathrm {aff}}},{S_{\mathrm {aff}}})$ and this choice of realization. (For a discussion of this definition, see also [Reference Achar, Makisumi, Riche and WilliamsonAMRW17, Chap. 2].) The technical conditions necessary for this category to be defined (and well behaved) are somewhat subtle, and not all of them are made explicit in [Reference Elias and WilliamsonEW16]; see [Reference Elias and WilliamsonEW20, § 5] for a detailed discussion of this question. As explained in [Reference Elias and WilliamsonEW20, § 5.1], a sufficient condition (in addition to the fact that the data define a realization satisfying Demazure surjectivity) that ensures that all the results of [Reference Elias and WilliamsonEW16] are applicable is that for any pair of distinct simple reflections
$({W_{\mathrm {aff}}},{S_{\mathrm {aff}}})$ and this choice of realization. (For a discussion of this definition, see also [Reference Achar, Makisumi, Riche and WilliamsonAMRW17, Chap. 2].) The technical conditions necessary for this category to be defined (and well behaved) are somewhat subtle, and not all of them are made explicit in [Reference Elias and WilliamsonEW16]; see [Reference Elias and WilliamsonEW20, § 5] for a detailed discussion of this question. As explained in [Reference Elias and WilliamsonEW20, § 5.1], a sufficient condition (in addition to the fact that the data define a realization satisfying Demazure surjectivity) that ensures that all the results of [Reference Elias and WilliamsonEW16] are applicable is that for any pair of distinct simple reflections ![]() $s,t$ such that
$s,t$ such that ![]() $st$ has finite order, the restriction of the action to the subgroup generated by
$st$ has finite order, the restriction of the action to the subgroup generated by ![]() $s$ and
$s$ and ![]() $t$ is faithful. It follows from [Reference Achar, Makisumi, Riche and WilliamsonAMRW17, Lemma 8.1.1] that this condition is satisfied in our context, except possibly if
$t$ is faithful. It follows from [Reference Achar, Makisumi, Riche and WilliamsonAMRW17, Lemma 8.1.1] that this condition is satisfied in our context, except possibly if ![]() $p=2$ and
$p=2$ and ![]() $st=ts$. (The assumptions of [Reference Achar, Makisumi, Riche and WilliamsonAMRW17, Lemma 8.1.1] are easily checked by hand for Cartan realizations in good characteristic.) However, in this case
$st=ts$. (The assumptions of [Reference Achar, Makisumi, Riche and WilliamsonAMRW17, Lemma 8.1.1] are easily checked by hand for Cartan realizations in good characteristic.) However, in this case ![]() $s$ and
$s$ and ![]() $t$ act non-trivially by Demazure surjectivity, and
$t$ act non-trivially by Demazure surjectivity, and ![]() $st$ acts non-trivially since
$st$ acts non-trivially since ![]() $\alpha _s^{\vee }$ and
$\alpha _s^{\vee }$ and ![]() $\alpha _t^{\vee }$ are not collinear thanks to assumption (ii).
$\alpha _t^{\vee }$ are not collinear thanks to assumption (ii).
The category ![]() $\mathsf {D}_{\mathrm {BS}}$ is a
$\mathsf {D}_{\mathrm {BS}}$ is a ![]() $\Bbbk$-linear (non-additive) monoidal category. By definition its objects are pairs
$\Bbbk$-linear (non-additive) monoidal category. By definition its objects are pairs ![]() $(\underline {w},n)$ where
$(\underline {w},n)$ where ![]() $\underline {w}$ is a word in
$\underline {w}$ is a word in ![]() ${S_{\mathrm {aff}}}$ and
${S_{\mathrm {aff}}}$ and ![]() $n \in \mathbb {Z}$; the product is given by concatenation of words and addition of integers, and for any words
$n \in \mathbb {Z}$; the product is given by concatenation of words and addition of integers, and for any words ![]() $\underline {w},\underline {w}'$ the direct sum of morphism spaces
$\underline {w},\underline {w}'$ the direct sum of morphism spaces
is a graded bimodule over ![]() $R:=\mathscr {O}(\mathbf {t}^{*}) = \mathrm {Sym}(\mathbf {t})$ (where the grading is such that elements in
$R:=\mathscr {O}(\mathbf {t}^{*}) = \mathrm {Sym}(\mathbf {t})$ (where the grading is such that elements in ![]() $\mathbf {t}$ have degree
$\mathbf {t}$ have degree ![]() $2$). Following usual conventions, the object
$2$). Following usual conventions, the object ![]() $(\underline {w},n)$ will rather be denoted
$(\underline {w},n)$ will rather be denoted ![]() $B_{\underline {w}}(n)$. Then there exists a natural ‘grading shift’ autoequivalence of
$B_{\underline {w}}(n)$. Then there exists a natural ‘grading shift’ autoequivalence of ![]() $\mathsf {D}_{\mathrm {BS}}$ such that
$\mathsf {D}_{\mathrm {BS}}$ such that ![]() $(B_{\underline {w}}(n))(1)=B_{\underline {w}}(n+1)$ for any
$(B_{\underline {w}}(n))(1)=B_{\underline {w}}(n+1)$ for any ![]() $\underline {w}$ and any
$\underline {w}$ and any ![]() $n \in \mathbb {Z}$.
$n \in \mathbb {Z}$.
Remark 2.1 The Hecke category ![]() $\mathsf {D}_{\mathrm {BS}}$ (as, more generally, Hecke categories attached to Cartan realizations of crystallographic Coxeter systems) admits an incarnation in terms of parity complexes on a flag variety; see [Reference Riche and WilliamsonRW18, Part III]. Although important for some other purposes, this realization of the Hecke category will not play any role in the present paper. (The relation between Soergel bimodules and constructible sheaves on flag varieties was first obtained, in a characteristic-
$\mathsf {D}_{\mathrm {BS}}$ (as, more generally, Hecke categories attached to Cartan realizations of crystallographic Coxeter systems) admits an incarnation in terms of parity complexes on a flag variety; see [Reference Riche and WilliamsonRW18, Part III]. Although important for some other purposes, this realization of the Hecke category will not play any role in the present paper. (The relation between Soergel bimodules and constructible sheaves on flag varieties was first obtained, in a characteristic-![]() $0$ context, by Soergel [Reference SoergelSoe01] in the case of finite crystallographic groups (using the earlier definition of Soergel bimodules in this case in [Reference SoergelSoe92]) and by Härterich for Kac–Moody groups [Reference HärterichHar99].)
$0$ context, by Soergel [Reference SoergelSoe01] in the case of finite crystallographic groups (using the earlier definition of Soergel bimodules in this case in [Reference SoergelSoe92]) and by Härterich for Kac–Moody groups [Reference HärterichHar99].)
2.2 Abe's incarnation of the Hecke category
For our present purposes we will need a description of ![]() $\mathsf {D}_{\mathrm {BS}}$ in terms of
$\mathsf {D}_{\mathrm {BS}}$ in terms of ![]() $R$-bimodules due to Abe [Reference AbeAbe21], which is close to the definition of Soergel bimodules [Reference SoergelSoe07], and which we now recall. Once again, in order to apply these results one needs some technical assumptions. A sufficient condition (in terms of vanishing of quantum binomial coefficients) for the results of [Reference AbeAbe21] to be applicable is given in [Reference AbeAbe20]. One can check by explicit computation that this condition is automatically satisfied for Cartan realizations.
$R$-bimodules due to Abe [Reference AbeAbe21], which is close to the definition of Soergel bimodules [Reference SoergelSoe07], and which we now recall. Once again, in order to apply these results one needs some technical assumptions. A sufficient condition (in terms of vanishing of quantum binomial coefficients) for the results of [Reference AbeAbe21] to be applicable is given in [Reference AbeAbe20]. One can check by explicit computation that this condition is automatically satisfied for Cartan realizations.
We will denote by ![]() $Q$ the fraction field of
$Q$ the fraction field of ![]() $R$. Following [Reference AbeAbe21], we denote by
$R$. Following [Reference AbeAbe21], we denote by ![]() $\mathsf {C}'$ the category defined as follows. Objects are pairs consisting of a graded
$\mathsf {C}'$ the category defined as follows. Objects are pairs consisting of a graded ![]() $R$-bimodule
$R$-bimodule ![]() $M$ together with a decomposition
$M$ together with a decomposition
as ![]() $(R,Q)$-bimodules such that:
$(R,Q)$-bimodules such that:
– there exist only finitely many elements
 $w$ such that
$w$ such that  $M_Q^{w} \neq 0$;
$M_Q^{w} \neq 0$;– for any
 $w \in {W_{\mathrm {aff}}}$,
$w \in {W_{\mathrm {aff}}}$,  $r \in R$ and
$r \in R$ and  $m \in M_Q^{w}$ we have
(2.2)
$m \in M_Q^{w}$ we have
(2.2) \begin{equation} m \cdot r=w(r) \cdot m. \end{equation}
\begin{equation} m \cdot r=w(r) \cdot m. \end{equation}
Morphisms in ![]() $\mathsf {C}'$ are defined in the obvious way, as morphisms of graded bimodules compatible with the decompositions (2.1). We also denote by
$\mathsf {C}'$ are defined in the obvious way, as morphisms of graded bimodules compatible with the decompositions (2.1). We also denote by ![]() $\mathsf {C}$ the full subcategory of
$\mathsf {C}$ the full subcategory of ![]() $\mathsf {C}'$ whose objects are those whose underlying graded
$\mathsf {C}'$ whose objects are those whose underlying graded ![]() $R$-bimodule
$R$-bimodule ![]() $M$ is finitely generated as an
$M$ is finitely generated as an ![]() $R$-bimodule and flat as a right
$R$-bimodule and flat as a right ![]() $R$-module. As explained in [Reference AbeAbe21, Lemma 2.6], the underlying
$R$-module. As explained in [Reference AbeAbe21, Lemma 2.6], the underlying ![]() $R$-bimodule of any object in
$R$-bimodule of any object in ![]() $\mathsf {C}$ is in fact finitely generated as a left and as a right
$\mathsf {C}$ is in fact finitely generated as a left and as a right ![]() $R$-module; this property shows that the tensor product over
$R$-module; this property shows that the tensor product over ![]() $R$ induces in a natural way a monoidal product on
$R$ induces in a natural way a monoidal product on ![]() $\mathsf {C}$. We also have a ‘grading shift’ autoequivalence of
$\mathsf {C}$. We also have a ‘grading shift’ autoequivalence of ![]() $\mathsf {C}$, which only changes the grading of the underlying graded
$\mathsf {C}$, which only changes the grading of the underlying graded ![]() $R$-bimodule in such a way that
$R$-bimodule in such a way that ![]() $M(1)^{i}=M^{i+1}$.
$M(1)^{i}=M^{i+1}$.
For ![]() $s \in {S_{\mathrm {aff}}}$, we consider the
$s \in {S_{\mathrm {aff}}}$, we consider the ![]() $s$-invariants
$s$-invariants ![]() $R^{s} \subset R$, and the graded
$R^{s} \subset R$, and the graded ![]() $R$-bimodule
$R$-bimodule ![]() $B_s^{\mathrm {Bim}} := R \otimes _{R^{s}} R (1)$. This object has a natural ‘lift’ as an object in
$B_s^{\mathrm {Bim}} := R \otimes _{R^{s}} R (1)$. This object has a natural ‘lift’ as an object in ![]() $\mathsf {C}$, which will also be denoted by
$\mathsf {C}$, which will also be denoted by ![]() $B_s^{\mathrm {Bim}}$ (see [Reference AbeAbe21, § 2.4]).
$B_s^{\mathrm {Bim}}$ (see [Reference AbeAbe21, § 2.4]).
The following result is a special case of [Reference AbeAbe21, Theorem 5.9]; see also [Reference AbeAbe20, Theorem 1.3].
Theorem 2.2 There exists a canonical fully faithful monoidal functor
sending ![]() $B_s$ to
$B_s$ to ![]() $B_s^{\mathrm {Bim}}$ for any
$B_s^{\mathrm {Bim}}$ for any ![]() $s \in {S_{\mathrm {aff}}}$ and intertwining the grading shifts
$s \in {S_{\mathrm {aff}}}$ and intertwining the grading shifts ![]() $(1)$.
$(1)$.
It will be convenient to consider also a slight extension of the category ![]() $\mathsf {C}$, adapted to the group
$\mathsf {C}$, adapted to the group ![]() ${W_{\mathrm {ext}}}$. Namely, the action of
${W_{\mathrm {ext}}}$. Namely, the action of ![]() ${W_{\mathrm {aff}}}$ on
${W_{\mathrm {aff}}}$ on ![]() $\mathbf {t}^{*}$ extends in a natural way to
$\mathbf {t}^{*}$ extends in a natural way to ![]() ${W_{\mathrm {ext}}}$ (using now the projection
${W_{\mathrm {ext}}}$ (using now the projection ![]() ${W_{\mathrm {ext}}} \to \mathbf {W}$). We will denote by
${W_{\mathrm {ext}}} \to \mathbf {W}$). We will denote by ![]() $\mathsf {C}'_{\mathrm {ext}}$ the category whose objects are pairs consisting a graded
$\mathsf {C}'_{\mathrm {ext}}$ the category whose objects are pairs consisting a graded ![]() $R$-bimodule
$R$-bimodule ![]() $M$ together with a decomposition
$M$ together with a decomposition
as ![]() $(R,Q)$-bimodules such that:
$(R,Q)$-bimodules such that:
– there exist only finitely many elements
 $w$ such that
$w$ such that  $M_Q^{w} \neq 0$;
$M_Q^{w} \neq 0$;– for any
 $w \in {W_{\mathrm {ext}}}$,
$w \in {W_{\mathrm {ext}}}$,  $r \in R$ and
$r \in R$ and  $m \in M_Q^{w}$ we have
$m \in M_Q^{w}$ we have  $m \cdot r=w(r) \cdot m$,
$m \cdot r=w(r) \cdot m$,
and where morphisms are defined in the obvious way. We will also denote by ![]() $\mathsf {C}_\mathrm {ext}$ the full subcategory of
$\mathsf {C}_\mathrm {ext}$ the full subcategory of ![]() $\mathsf {C}'_\mathrm {ext}$ whose objects are those whose underlying graded
$\mathsf {C}'_\mathrm {ext}$ whose objects are those whose underlying graded ![]() $R$-bimodule
$R$-bimodule ![]() $M$ is finitely generated as an
$M$ is finitely generated as an ![]() $R$-bimodule and flat as a right
$R$-bimodule and flat as a right ![]() $R$-module. It is clear that
$R$-module. It is clear that ![]() $\mathsf {C}'$ is a full subcategory in
$\mathsf {C}'$ is a full subcategory in ![]() $\mathsf {C}'_\mathrm {ext}$, that
$\mathsf {C}'_\mathrm {ext}$, that ![]() $\mathsf {C}$ is a full subcategory in
$\mathsf {C}$ is a full subcategory in ![]() $\mathsf {C}_\mathrm {ext}$, and that the tensor product
$\mathsf {C}_\mathrm {ext}$, and that the tensor product ![]() $\otimes _R$ defines a monoidal structure on
$\otimes _R$ defines a monoidal structure on ![]() $\mathsf {C}_\mathrm {ext}$.
$\mathsf {C}_\mathrm {ext}$.
Remark 2.3 Some adaptations of the ‘Soergel calculus’ of [Reference Elias and WilliamsonEW16] to extended affine Weyl groups have been discussed in work of Mackaay and Thiel [Reference Mackaay and ThielMT17] and Elias [Reference EliasEli18, § 3]. The analogue of Theorem 2.2 in this context is most likely true, but since it is not needed in this paper we will not investigate this question further.
In addition to the objects ![]() $B_s^{\mathrm {Bim}}$ considered above, the category
$B_s^{\mathrm {Bim}}$ considered above, the category ![]() $\mathsf {C}_\mathrm {ext}$ possesses ‘standard’ objects
$\mathsf {C}_\mathrm {ext}$ possesses ‘standard’ objects ![]() $(\Delta _x : x \in {W_{\mathrm {ext}}})$ defined as follows. For any
$(\Delta _x : x \in {W_{\mathrm {ext}}})$ defined as follows. For any ![]() $x \in {W_{\mathrm {ext}}}$,
$x \in {W_{\mathrm {ext}}}$, ![]() $\Delta _x$ is isomorphic to
$\Delta _x$ is isomorphic to ![]() $R$ as a graded vector space, and the
$R$ as a graded vector space, and the ![]() $R$-bimodule structure is given by
$R$-bimodule structure is given by
for ![]() $r,r' \in R$ and
$r,r' \in R$ and ![]() $m \in \Delta _x$. The decomposition of
$m \in \Delta _x$. The decomposition of ![]() $\Delta _x \otimes _R Q$ is defined so that this object is concentrated in degree
$\Delta _x \otimes _R Q$ is defined so that this object is concentrated in degree ![]() $x$. For any
$x$. For any ![]() $x,y \in {W_{\mathrm {ext}}}$ we have a canonical isomorphism
$x,y \in {W_{\mathrm {ext}}}$ we have a canonical isomorphism
in ![]() $\mathsf {C}_\mathrm {ext}$, defined by
$\mathsf {C}_\mathrm {ext}$, defined by ![]() $m \otimes m' \mapsto mx(m')$.
$m \otimes m' \mapsto mx(m')$.
Lemma 2.4 Let ![]() $s,t \in {S_{\mathrm {aff}}}$ and
$s,t \in {S_{\mathrm {aff}}}$ and ![]() $x \in {W_{\mathrm {ext}}}$ be such that
$x \in {W_{\mathrm {ext}}}$ be such that ![]() $s=xtx^{-1}$. Then there exists a canonical isomorphism
$s=xtx^{-1}$. Then there exists a canonical isomorphism
Proof. The isomorphism of ![]() $R$-bimodules
$R$-bimodules
is defined by
We leave it to the reader to check that this morphism is well defined, and indeed defines an isomorphism in ![]() $\mathsf {C}_\mathrm {ext}$.
$\mathsf {C}_\mathrm {ext}$.
In § 6 we will also need the following standard claim, for which we refer to [Reference Elias and WilliamsonEW16, § 3.4].
Lemma 2.5 For any ![]() $s \in {S_{\mathrm {aff}}}$, there exist exact sequences of
$s \in {S_{\mathrm {aff}}}$, there exist exact sequences of ![]() $R$-bimodules
$R$-bimodules
2.3 Universal centralizer and Kostant section
We will denote by ![]() $\mathbf {g}_{\mathrm {reg}} \subset \mathbf {g}$ the open subset consisting of regular elements, that is, elements whose centralizer has dimension
$\mathbf {g}_{\mathrm {reg}} \subset \mathbf {g}$ the open subset consisting of regular elements, that is, elements whose centralizer has dimension ![]() $\dim (T)$. The ‘regular universal centralizer’ is the affine group scheme
$\dim (T)$. The ‘regular universal centralizer’ is the affine group scheme
over ![]() $\mathbf {g}_{\mathrm {reg}}$, where the morphism
$\mathbf {g}_{\mathrm {reg}}$, where the morphism ![]() $\mathbf {g}_{\mathrm {reg}} \to \mathbf {g}_{\mathrm {reg}} \times \mathbf {g}_{\mathrm {reg}}$ is the diagonal embedding, and the map
$\mathbf {g}_{\mathrm {reg}} \to \mathbf {g}_{\mathrm {reg}} \times \mathbf {g}_{\mathrm {reg}}$ is the diagonal embedding, and the map ![]() $\mathbf {G} \times \mathbf {g}_{\mathrm {reg}} \to \mathbf {g}_{\mathrm {reg}}$ sends
$\mathbf {G} \times \mathbf {g}_{\mathrm {reg}} \to \mathbf {g}_{\mathrm {reg}}$ sends ![]() $(g,x)$ to
$(g,x)$ to ![]() $(g \cdot x, x)$. For any
$(g \cdot x, x)$. For any ![]() $x \in \mathbf {g}_{\mathrm {reg}}$, the fiber of
$x \in \mathbf {g}_{\mathrm {reg}}$, the fiber of ![]() $\mathbb {J}_\mathrm {reg}$ over
$\mathbb {J}_\mathrm {reg}$ over ![]() $x$ is the scheme-theoretic centralizer of
$x$ is the scheme-theoretic centralizer of ![]() $x$ for the adjoint
$x$ for the adjoint ![]() $\mathbf {G}$-action. By construction
$\mathbf {G}$-action. By construction ![]() $\mathbb {J}_\mathrm {reg}$ is a closed subgroup scheme in
$\mathbb {J}_\mathrm {reg}$ is a closed subgroup scheme in ![]() $\mathbf {G} \times \mathbf {g}_{\mathrm {reg}}$, and as explained in [Reference RicheRic17, Corollary 3.3.6] it is smooth over
$\mathbf {G} \times \mathbf {g}_{\mathrm {reg}}$, and as explained in [Reference RicheRic17, Corollary 3.3.6] it is smooth over ![]() $\mathbf {g}_{\mathrm {reg}}$. We will also denote by
$\mathbf {g}_{\mathrm {reg}}$. We will also denote by ![]() $\mathbf {g}_{\mathrm {reg}}^{*}$ the image of
$\mathbf {g}_{\mathrm {reg}}^{*}$ the image of ![]() $\mathbf {g}_{\mathrm {reg}}$ under
$\mathbf {g}_{\mathrm {reg}}$ under ![]() $\kappa$, and by
$\kappa$, and by ![]() $\mathbb {J}_\mathrm {reg}^{*}$ the smooth affine group scheme over
$\mathbb {J}_\mathrm {reg}^{*}$ the smooth affine group scheme over ![]() $\mathbf {g}_{\mathrm {reg}}^{*}$ obtained by pushforward from
$\mathbf {g}_{\mathrm {reg}}^{*}$ obtained by pushforward from ![]() $\mathbb {J}_\mathrm {reg}$. (It is easily seen that these objects do not depend on the choice of
$\mathbb {J}_\mathrm {reg}$. (It is easily seen that these objects do not depend on the choice of ![]() $\kappa$.)
$\kappa$.)
There exists a canonical morphism
of group schemes over ![]() $\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {g}_{\mathrm {reg}}^{*}$, whose construction we now explain. Let
$\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {g}_{\mathrm {reg}}^{*}$, whose construction we now explain. Let ![]() $\mathbf {n}$ be the Lie algebra of the unipotent radical
$\mathbf {n}$ be the Lie algebra of the unipotent radical ![]() $\mathbf {U}$ of
$\mathbf {U}$ of ![]() $\mathbf {B}$. Recall that the Grothendieck resolution is the
$\mathbf {B}$. Recall that the Grothendieck resolution is the ![]() $\mathbf {G}$-equivariant vector bundle over
$\mathbf {G}$-equivariant vector bundle over ![]() $\mathbf {G}/\mathbf {B}$ given by
$\mathbf {G}/\mathbf {B}$ given by
We have natural maps
(The morphism ![]() $\pi$ is induced by the first projection. The morphism
$\pi$ is induced by the first projection. The morphism ![]() $\vartheta$ sends a pair
$\vartheta$ sends a pair ![]() $(\xi,g\mathbf {B})$ to
$(\xi,g\mathbf {B})$ to ![]() $\xi _{|g \cdot \mathbf {b}}$, seen as an element in
$\xi _{|g \cdot \mathbf {b}}$, seen as an element in ![]() $(g \cdot \mathbf {b} / g \cdot \mathbf {n})^{*} \cong (\mathbf {b}/\mathbf {n})^{*} \cong \mathbf {t}^{*}$, where the first isomorphism is induced by conjugation by the inverse of any representative for the coset
$(g \cdot \mathbf {b} / g \cdot \mathbf {n})^{*} \cong (\mathbf {b}/\mathbf {n})^{*} \cong \mathbf {t}^{*}$, where the first isomorphism is induced by conjugation by the inverse of any representative for the coset ![]() $g\mathbf {B}$.) If we denote by
$g\mathbf {B}$.) If we denote by ![]() $\tilde {\mathbf {g}}_{\mathrm {reg}}$ the preimage of
$\tilde {\mathbf {g}}_{\mathrm {reg}}$ the preimage of ![]() $\mathbf {g}_{\mathrm {reg}}^{*}$ in
$\mathbf {g}_{\mathrm {reg}}^{*}$ in ![]() $\tilde {\mathbf {g}}$, then these maps induce an isomorphism of schemes
$\tilde {\mathbf {g}}$, then these maps induce an isomorphism of schemes
see [Reference RicheRic17, Lemma 3.5.3]. Moreover, under this identification, by [Reference RicheRic17, Proposition 3.5.6] the group scheme ![]() $\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_\mathrm {reg}$ identifies with the universal stabilizer associated with the action of
$\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_\mathrm {reg}$ identifies with the universal stabilizer associated with the action of ![]() $\mathbf {G}$ on
$\mathbf {G}$ on ![]() $\tilde {\mathbf {g}}_{\mathrm {reg}}$ (defined by the same procedure as for
$\tilde {\mathbf {g}}_{\mathrm {reg}}$ (defined by the same procedure as for ![]() $\mathbb {J}_\mathrm {reg}$ above), which is such that the fiber over
$\mathbb {J}_\mathrm {reg}$ above), which is such that the fiber over ![]() $(\xi,g\mathbf {B})$ is the scheme-theoretic stabilizer of
$(\xi,g\mathbf {B})$ is the scheme-theoretic stabilizer of ![]() $\xi$ for the action of
$\xi$ for the action of ![]() $g\mathbf {B} g^{-1}$. Now as above in the definition of
$g\mathbf {B} g^{-1}$. Now as above in the definition of ![]() $\vartheta$, there exists for any
$\vartheta$, there exists for any ![]() $g \in \mathbf {G}$ a canonical isomorphism
$g \in \mathbf {G}$ a canonical isomorphism ![]() $g\mathbf {B} g^{-1} / g\mathbf {U} g^{-1} \cong \mathbf {T}$, which allows us to define the wished-for morphism (2.4).
$g\mathbf {B} g^{-1} / g\mathbf {U} g^{-1} \cong \mathbf {T}$, which allows us to define the wished-for morphism (2.4).
Let ![]() $\mathbf {g}_{\mathrm {rs}} \subset \mathbf {g}$ denote the open subset of semisimple regular elements, and set
$\mathbf {g}_{\mathrm {rs}} \subset \mathbf {g}$ denote the open subset of semisimple regular elements, and set ![]() $\mathbf {g}_{\mathrm {rs}}^{*}:=\kappa (\mathbf {g}_{\mathrm {rs}})$. We will denote by
$\mathbf {g}_{\mathrm {rs}}^{*}:=\kappa (\mathbf {g}_{\mathrm {rs}})$. We will denote by ![]() $\mathbb {J}_\mathrm {rs}$ (respectively,
$\mathbb {J}_\mathrm {rs}$ (respectively, ![]() $\mathbb {J}^{*}_\mathrm {rs}$) the restriction of
$\mathbb {J}^{*}_\mathrm {rs}$) the restriction of ![]() $\mathbb {J}_\mathrm {reg}$ (respectively,
$\mathbb {J}_\mathrm {reg}$ (respectively, ![]() $\mathbb {J}^{*}_\mathrm {reg}$) to
$\mathbb {J}^{*}_\mathrm {reg}$) to ![]() $\mathbf {g}_{\mathrm {rs}}$ (respectively,
$\mathbf {g}_{\mathrm {rs}}$ (respectively, ![]() $\mathbf {g}_{\mathrm {rs}}^{*}$). Recall that the adjoint quotient
$\mathbf {g}_{\mathrm {rs}}^{*}$). Recall that the adjoint quotient ![]() $\mathbf {g}/\mathbf {G}$ identifies canonically with
$\mathbf {g}/\mathbf {G}$ identifies canonically with ![]() $\mathbf {t}/\mathbf {W}$ (see [Reference Bouthier and CesnaviciusBC19, § 4.1]); as a consequence, under our assumptions the coadjoint quotient
$\mathbf {t}/\mathbf {W}$ (see [Reference Bouthier and CesnaviciusBC19, § 4.1]); as a consequence, under our assumptions the coadjoint quotient ![]() $\mathbf {g}^{*}/\mathbf {G}$ identifies canonically with
$\mathbf {g}^{*}/\mathbf {G}$ identifies canonically with ![]() $\mathbf {t}^{*}/\mathbf {W}$.
$\mathbf {t}^{*}/\mathbf {W}$.
Lemma 2.6 The morphism (2.4) restricts to an isomorphism
of group schemes over ![]() $\mathbf {g}_{\mathrm {rs}}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*}$.
$\mathbf {g}_{\mathrm {rs}}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*}$.
Proof. It is sufficient to prove the analogous statement for ![]() $\mathbf {g}$ in place of
$\mathbf {g}$ in place of ![]() $\mathbf {g}^{*}$. If we denote by
$\mathbf {g}^{*}$. If we denote by ![]() $\tilde {\mathbf {g}}_\mathrm {rs}$ the inverse image of
$\tilde {\mathbf {g}}_\mathrm {rs}$ the inverse image of ![]() $\mathbf {g}_{\mathrm {rs}}$ under
$\mathbf {g}_{\mathrm {rs}}$ under ![]() $\pi$, then by [Reference JantzenJan04, Lemma 13.4] there exists a canonical isomorphism
$\pi$, then by [Reference JantzenJan04, Lemma 13.4] there exists a canonical isomorphism
where ![]() $\mathbf {t}_\mathrm {rs} := \mathbf {t} \cap \mathbf {g}_\mathrm {rs}$. From the comments above and the compatibility of universal stabilizers with open embeddings,
$\mathbf {t}_\mathrm {rs} := \mathbf {t} \cap \mathbf {g}_\mathrm {rs}$. From the comments above and the compatibility of universal stabilizers with open embeddings, ![]() $\mathbf {t} \times _{\mathbf {t}/\mathbf {W}} \mathbb {J}_\mathrm {rs}$ identifies with the universal stabilizer associated with the action of
$\mathbf {t} \times _{\mathbf {t}/\mathbf {W}} \mathbb {J}_\mathrm {rs}$ identifies with the universal stabilizer associated with the action of ![]() $\mathbf {G}$ on
$\mathbf {G}$ on ![]() $\tilde {\mathbf {g}}_\mathrm {rs}$. Since the latter scheme identifies with
$\tilde {\mathbf {g}}_\mathrm {rs}$. Since the latter scheme identifies with ![]() $\mathbf {G} \times ^{\mathbf{T}} \mathbf {t}_\mathrm {rs} = \mathbf {G}/\mathbf {T} \times \mathbf {t}_\mathrm {rs}$, the universal stabilizer identifies with
$\mathbf {G} \times ^{\mathbf{T}} \mathbf {t}_\mathrm {rs} = \mathbf {G}/\mathbf {T} \times \mathbf {t}_\mathrm {rs}$, the universal stabilizer identifies with ![]() $\mathbf {T} \times \tilde {\mathbf {g}}_\mathrm {rs}$, as desired.
$\mathbf {T} \times \tilde {\mathbf {g}}_\mathrm {rs}$, as desired.
Let us choose a Kostant section to the adjoint quotient, that is, a closed subscheme ![]() $\mathbf {S} \subset \mathbf {g}$ contained in
$\mathbf {S} \subset \mathbf {g}$ contained in ![]() $\mathbf {g}_{\mathrm {reg}}$ and such that the composition
$\mathbf {g}_{\mathrm {reg}}$ and such that the composition ![]() $\mathbf {S} \hookrightarrow \mathbf {g} \to \mathbf {g}/\mathbf {G}$ (where the second map is the adjoint quotient morphism) is an isomorphism. (For a construction of such a section in the present generality, see [Reference RicheRic17, § 3].) We will denote by
$\mathbf {S} \hookrightarrow \mathbf {g} \to \mathbf {g}/\mathbf {G}$ (where the second map is the adjoint quotient morphism) is an isomorphism. (For a construction of such a section in the present generality, see [Reference RicheRic17, § 3].) We will denote by ![]() $\mathbf {S}^{*}$ the image of
$\mathbf {S}^{*}$ the image of ![]() $\mathbf {S}$ under
$\mathbf {S}$ under ![]() $\kappa$, so that the composition
$\kappa$, so that the composition ![]() $\mathbf {S}^{*} \hookrightarrow \mathbf {g}^{*} \to \mathbf {g}^{*}/\mathbf {G}$ is an isomorphism, and by
$\mathbf {S}^{*} \hookrightarrow \mathbf {g}^{*} \to \mathbf {g}^{*}/\mathbf {G}$ is an isomorphism, and by ![]() $\mathbb {J}^{*}_\mathbf {S}$ the restriction of
$\mathbb {J}^{*}_\mathbf {S}$ the restriction of ![]() $\mathbb {J}_\mathrm {reg}^{*}$ to
$\mathbb {J}_\mathrm {reg}^{*}$ to ![]() $\mathbf {S}^{*}$ (a closed subgroup scheme of
$\mathbf {S}^{*}$ (a closed subgroup scheme of ![]() $\mathbf {G} \times \mathbf {S}^{*}$, smooth over
$\mathbf {G} \times \mathbf {S}^{*}$, smooth over ![]() $\mathbf {S}^{*}$).
$\mathbf {S}^{*}$).
As explained in [Reference Mautner and RicheMR18, § 4.4], for example, there exists a natural action of the multiplicative group ![]() $\mathbb {G}_{\mathrm {m}}$ on
$\mathbb {G}_{\mathrm {m}}$ on ![]() $\mathbf {S}^{*}$ such that the isomorphism
$\mathbf {S}^{*}$ such that the isomorphism ![]() $\mathbf {S}^{*} \xrightarrow {\sim } \mathbf {g}^{*}/\mathbf {G}$ is
$\mathbf {S}^{*} \xrightarrow {\sim } \mathbf {g}^{*}/\mathbf {G}$ is ![]() $\mathbb {G}_{\mathrm {m}}$-equivariant, where
$\mathbb {G}_{\mathrm {m}}$-equivariant, where ![]() $t \in \Bbbk ^{\times }$ acts on
$t \in \Bbbk ^{\times }$ acts on ![]() $\mathbf {g}^{*}$ by multiplication by
$\mathbf {g}^{*}$ by multiplication by ![]() $t^{-2}$, and on
$t^{-2}$, and on ![]() $\mathbf {g}^{*}/\mathbf {G}$ by the induced action. The isomorphism
$\mathbf {g}^{*}/\mathbf {G}$ by the induced action. The isomorphism ![]() $\mathbf {t}^{*}/\mathbf {W} \xrightarrow {\sim } \mathbf {g}^{*}/\mathbf {G}$ is also
$\mathbf {t}^{*}/\mathbf {W} \xrightarrow {\sim } \mathbf {g}^{*}/\mathbf {G}$ is also ![]() $\mathbb {G}_{\mathrm {m}}$-equivariant, where the action on
$\mathbb {G}_{\mathrm {m}}$-equivariant, where the action on ![]() $\mathbf {t}^{*}/\mathbf {W}$ is induced by the action on
$\mathbf {t}^{*}/\mathbf {W}$ is induced by the action on ![]() $\mathbf {t}^{*}$ where
$\mathbf {t}^{*}$ where ![]() $t \in \Bbbk ^{\times }$ acts by multiplication by
$t \in \Bbbk ^{\times }$ acts by multiplication by ![]() $t^{-2}$. As explained in [Reference Mautner and RicheMR18, § 4.5, p. 2302] there exists a natural
$t^{-2}$. As explained in [Reference Mautner and RicheMR18, § 4.5, p. 2302] there exists a natural ![]() $\mathbb {G}_{\mathrm {m}}$-action on
$\mathbb {G}_{\mathrm {m}}$-action on ![]() $\mathbb {J}^{*}_{\mathbf {S}}$ such that the structure morphism
$\mathbb {J}^{*}_{\mathbf {S}}$ such that the structure morphism ![]() $\mathbb {J}^{*}_{\mathbf {S}} \to \mathbf {S}^{*}$, the multiplication map
$\mathbb {J}^{*}_{\mathbf {S}} \to \mathbf {S}^{*}$, the multiplication map ![]() $\mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {S}^{*}} \mathbb {J}^{*}_{\mathbf {S}} \to \mathbb {J}^{*}_{\mathbf {S}}$ and the inversion morphism
$\mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {S}^{*}} \mathbb {J}^{*}_{\mathbf {S}} \to \mathbb {J}^{*}_{\mathbf {S}}$ and the inversion morphism ![]() $\mathbb {J}^{*}_{\mathbf {S}} \to \mathbb {J}^{*}_{\mathbf {S}}$ are
$\mathbb {J}^{*}_{\mathbf {S}} \to \mathbb {J}^{*}_{\mathbf {S}}$ are ![]() $\mathbb {G}_{\mathrm {m}}$-equivariant.
$\mathbb {G}_{\mathrm {m}}$-equivariant.
2.4 Representations of the universal centralizer and Abe's category
The actions of ![]() $\mathbb {G}_{\mathrm {m}}$ on
$\mathbb {G}_{\mathrm {m}}$ on ![]() $\mathbf {t}^{*}$ and
$\mathbf {t}^{*}$ and ![]() $\mathbf {t}^{*}/\mathbf {W}$ considered in § 2.3 provide an action on the fiber product
$\mathbf {t}^{*}/\mathbf {W}$ considered in § 2.3 provide an action on the fiber product ![]() $\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*}$. Let us now consider the category
$\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*}$. Let us now consider the category
of ![]() $\mathbb {G}_{\mathrm {m}}$-equivariant coherent representations of the smooth affine group scheme
$\mathbb {G}_{\mathrm {m}}$-equivariant coherent representations of the smooth affine group scheme
over ![]() $\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*}$ (where the morphism
$\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*}$ (where the morphism ![]() $\mathbb {J}^{*}_\mathbf {S} \to \mathbf {t}^{*}/\mathbf {W}$ is obtained via the identification
$\mathbb {J}^{*}_\mathbf {S} \to \mathbf {t}^{*}/\mathbf {W}$ is obtained via the identification ![]() $\mathbf {S}^{*} \xrightarrow {\sim } \mathbf {t}^{*}/\mathbf {W}$), that is,
$\mathbf {S}^{*} \xrightarrow {\sim } \mathbf {t}^{*}/\mathbf {W}$), that is, ![]() $\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*}$-modules equipped with a structure of
$\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*}$-modules equipped with a structure of ![]() $\mathbb {G}_{\mathrm {m}}$-equivariant coherent sheaf on
$\mathbb {G}_{\mathrm {m}}$-equivariant coherent sheaf on ![]() $\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*}$, such that the action map is
$\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*}$, such that the action map is ![]() $\mathbb {G}_{\mathrm {m}}$-equivariant. Since
$\mathbb {G}_{\mathrm {m}}$-equivariant. Since ![]() $R$ is finite over
$R$ is finite over ![]() $R^{\mathbf{W}}$, this category admits a natural convolution product
$R^{\mathbf{W}}$, this category admits a natural convolution product ![]() $\star$, such that the
$\star$, such that the ![]() $\mathscr {O}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*})$-module underlying the product
$\mathscr {O}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*})$-module underlying the product ![]() $M \star N$ is the tensor product
$M \star N$ is the tensor product ![]() $M \otimes _{R} N$ (where
$M \otimes _{R} N$ (where ![]() $R=\mathscr {O}(\mathbf {t}^{*})$ acts on
$R=\mathscr {O}(\mathbf {t}^{*})$ acts on ![]() $M$ via the second projection
$M$ via the second projection ![]() $\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*} \to \mathbf {t}^{*}$ and on
$\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*} \to \mathbf {t}^{*}$ and on ![]() $N$ via the first projection
$N$ via the first projection ![]() $\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*} \to \mathbf {t}^{*}$). In this way,
$\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*} \to \mathbf {t}^{*}$). In this way, ![]() $(\mathsf {Rep}^{\mathbb {G}_{\mathrm {m}}}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*}), \star )$ is a monoidal category. We will denote by
$(\mathsf {Rep}^{\mathbb {G}_{\mathrm {m}}}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*}), \star )$ is a monoidal category. We will denote by
the full subcategory of ![]() $\mathsf {Rep}^{\mathbb {G}_{\mathrm {m}}}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*})$ whose objects are the representations whose underlying coherent sheaves are flat with respect to the second projection
$\mathsf {Rep}^{\mathbb {G}_{\mathrm {m}}}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*})$ whose objects are the representations whose underlying coherent sheaves are flat with respect to the second projection ![]() $\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*} \to \mathbf {t}^{*}$. It is not difficult to check that this subcategory is stable under
$\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*} \to \mathbf {t}^{*}$. It is not difficult to check that this subcategory is stable under ![]() $\star$, hence also admits a canonical monoidal category structure.
$\star$, hence also admits a canonical monoidal category structure.
Proposition 2.7 There exists a canonical fully faithful monoidal functor
Proof. We start by constructing a functor
By definition, any object in ![]() $\mathsf {Rep}^{\mathbb {G}_{\mathrm {m}}}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*})$ is in particular a
$\mathsf {Rep}^{\mathbb {G}_{\mathrm {m}}}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*})$ is in particular a ![]() $\mathbb {G}_{\mathrm {m}}$-equivariant coherent sheaf on
$\mathbb {G}_{\mathrm {m}}$-equivariant coherent sheaf on ![]() $\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*}$, hence can be seen as a graded
$\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*}$, hence can be seen as a graded ![]() $R$-bimodule. To equip this graded bimodule with the structure of an object in
$R$-bimodule. To equip this graded bimodule with the structure of an object in ![]() $\mathsf {C}'_\mathrm {ext}$, we must provide a decomposition of its tensor product with
$\mathsf {C}'_\mathrm {ext}$, we must provide a decomposition of its tensor product with ![]() $Q$ parametrized by
$Q$ parametrized by ![]() ${W_{\mathrm {ext}}}$. In fact, we will provide such a decomposition for its tensor product with
${W_{\mathrm {ext}}}$. In fact, we will provide such a decomposition for its tensor product with ![]() $\mathscr {O}(\mathbf {t}^{*}_\mathrm {rs})$, where
$\mathscr {O}(\mathbf {t}^{*}_\mathrm {rs})$, where ![]() $\mathbf {t}^{*}_\mathrm {rs} := \mathbf {t}^{*} \cap \mathbf {g}^{*}_\mathrm {rs}$ (which is sufficient since
$\mathbf {t}^{*}_\mathrm {rs} := \mathbf {t}^{*} \cap \mathbf {g}^{*}_\mathrm {rs}$ (which is sufficient since ![]() $Q$ is a further localization of
$Q$ is a further localization of ![]() $\mathscr {O}(\mathbf {t}^{*}_\mathrm {rs})$).
$\mathscr {O}(\mathbf {t}^{*}_\mathrm {rs})$).
First, the open subset ![]() $\mathbf {t}^{*}_{\mathrm {rs}} \subset \mathbf {t}^{*}$ is the complement of the kernels of the differentials of the coroots. This open subset is stable under the action of
$\mathbf {t}^{*}_{\mathrm {rs}} \subset \mathbf {t}^{*}$ is the complement of the kernels of the differentials of the coroots. This open subset is stable under the action of ![]() $\mathbf {W}$, and the restriction of this action is free; see [Reference RicheRic17, Lemma 2.3.3]. In particular, we have an open subset
$\mathbf {W}$, and the restriction of this action is free; see [Reference RicheRic17, Lemma 2.3.3]. In particular, we have an open subset ![]() $\mathbf {t}^{*}_{\mathrm {rs}} / \mathbf {W} \subset \mathbf {t}^{*}/\mathbf {W}$, the morphism
$\mathbf {t}^{*}_{\mathrm {rs}} / \mathbf {W} \subset \mathbf {t}^{*}/\mathbf {W}$, the morphism ![]() $\mathbf {t}^{*}_\mathrm {rs} \to \mathbf {t}^{*}_\mathrm {rs}/\mathbf {W}$ is étale, and the map
$\mathbf {t}^{*}_\mathrm {rs} \to \mathbf {t}^{*}_\mathrm {rs}/\mathbf {W}$ is étale, and the map ![]() $(w,x) \mapsto (x,w(x))$ induces an isomorphism of schemes
$(w,x) \mapsto (x,w(x))$ induces an isomorphism of schemes
see [SGA1, Exp. V, § 2]. As a consequence, for any coherent sheaf ![]() $\mathscr {F}$ on
$\mathscr {F}$ on ![]() $\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*}$, the tensor product
$\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*}$, the tensor product
admits a canonical decomposition (as an ![]() $\mathscr {O}(\mathbf {t}^{*}_\mathrm {rs})$-bimodule) parametrized by
$\mathscr {O}(\mathbf {t}^{*}_\mathrm {rs})$-bimodule) parametrized by ![]() $\mathbf {W}$, such that the action on the factor corresponding to
$\mathbf {W}$, such that the action on the factor corresponding to ![]() $w \in \mathbf {W}$ factors through the quotient
$w \in \mathbf {W}$ factors through the quotient
(where on the right-hand side ![]() $\mathrm {Gr}(w,\mathbf {t}^{*}_\mathrm {rs})$ denotes the graph of
$\mathrm {Gr}(w,\mathbf {t}^{*}_\mathrm {rs})$ denotes the graph of ![]() $w$ acting on
$w$ acting on ![]() $\mathbf {t}^{*}_\mathrm {rs}$), that is, satisfies the condition in (2.2).
$\mathbf {t}^{*}_\mathrm {rs}$), that is, satisfies the condition in (2.2).
Next, let us explain how this decomposition can be refined if ![]() $\mathscr {F}$ belongs to
$\mathscr {F}$ belongs to ![]() $\mathsf {Rep}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*})$. For this, we consider the restriction
$\mathsf {Rep}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*})$. For this, we consider the restriction ![]() $\mathbf {M}_w$ of
$\mathbf {M}_w$ of ![]() $\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*}$ to
$\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*}$ to ![]() $\mathrm {Gr}(w,\mathbf {t}^{*}_\mathrm {rs})$. Identifying the latter subscheme with
$\mathrm {Gr}(w,\mathbf {t}^{*}_\mathrm {rs})$. Identifying the latter subscheme with ![]() $\mathbf {t}^{*}_\mathrm {rs}$ via the first projection and using Lemma 2.6, we obtain a canonical isomorphism of group schemes
$\mathbf {t}^{*}_\mathrm {rs}$ via the first projection and using Lemma 2.6, we obtain a canonical isomorphism of group schemes
This means that the category of representations of ![]() $\mathbf {M}_w$ on coherent sheaves on
$\mathbf {M}_w$ on coherent sheaves on ![]() $\mathrm {Gr}(w,\mathbf {t}^{*}_\mathrm {rs})$ is canonically equivalent to the category of
$\mathrm {Gr}(w,\mathbf {t}^{*}_\mathrm {rs})$ is canonically equivalent to the category of ![]() $\mathbf {X}$-graded coherent sheaves on
$\mathbf {X}$-graded coherent sheaves on ![]() $\mathbf {t}^{*}_\mathrm {rs}$. Starting with an object
$\mathbf {t}^{*}_\mathrm {rs}$. Starting with an object ![]() $\mathscr {F}$ in
$\mathscr {F}$ in ![]() $\mathsf {Rep}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*})$, we therefore obtain a decomposition of
$\mathsf {Rep}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*})$, we therefore obtain a decomposition of ![]() $\Gamma (\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*}, \mathscr {F}) \otimes _R \mathscr {O}(\mathbf {t}^{*}_\mathrm {rs})$ parametrized by
$\Gamma (\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*}, \mathscr {F}) \otimes _R \mathscr {O}(\mathbf {t}^{*}_\mathrm {rs})$ parametrized by ![]() ${W_{\mathrm {ext}}}$ by defining, for
${W_{\mathrm {ext}}}$ by defining, for ![]() $\lambda \in \mathbf {X}$ and
$\lambda \in \mathbf {X}$ and ![]() $w \in \mathbf {W}$, the summand associated with
$w \in \mathbf {W}$, the summand associated with ![]() $t_\lambda w$ as the
$t_\lambda w$ as the ![]() $\lambda$-graded part in the summand associated with
$\lambda$-graded part in the summand associated with ![]() $w$ (which is a representation of
$w$ (which is a representation of ![]() $\mathbf {M}_w$). This finishes the description of the functor (2.6).
$\mathbf {M}_w$). This finishes the description of the functor (2.6).
It is clear from construction that this functor sends objects in ![]() $\mathsf {Rep}^{\mathbb {G}_{\mathrm {m}}}_{\mathrm {fl}}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*})$ to objects in
$\mathsf {Rep}^{\mathbb {G}_{\mathrm {m}}}_{\mathrm {fl}}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*})$ to objects in ![]() $\mathsf {C}_{\mathrm {ext}}$, which therefore provides the functor of the statement. This functor is also easily seen to be monoidal. Let us now explain why it is fully faithful. Consider
$\mathsf {C}_{\mathrm {ext}}$, which therefore provides the functor of the statement. This functor is also easily seen to be monoidal. Let us now explain why it is fully faithful. Consider ![]() $\mathscr {F},\mathscr {G}$ in
$\mathscr {F},\mathscr {G}$ in ![]() $\mathsf {Rep}^{\mathbb {G}_{\mathrm {m}}}_{\mathrm {fl}}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*})$, and denote their images by
$\mathsf {Rep}^{\mathbb {G}_{\mathrm {m}}}_{\mathrm {fl}}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*})$, and denote their images by ![]() $M,N$—so that the underlying graded bimodule of
$M,N$—so that the underlying graded bimodule of ![]() $M$ (respectively,
$M$ (respectively, ![]() $N$) is
$N$) is ![]() $\Gamma (\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*},\mathscr {F})$ (respectively,
$\Gamma (\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*},\mathscr {F})$ (respectively, ![]() $\Gamma (\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*},\mathscr {G})$). By construction, morphisms in
$\Gamma (\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*},\mathscr {G})$). By construction, morphisms in ![]() $\mathsf {C}_{\mathrm {ext}}$ from
$\mathsf {C}_{\mathrm {ext}}$ from ![]() $M$ to
$M$ to ![]() $N$ are morphisms of graded bimodules from
$N$ are morphisms of graded bimodules from ![]() $\Gamma (\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*},\mathscr {F})$ to
$\Gamma (\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*},\mathscr {F})$ to ![]() $\Gamma (\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*},\mathscr {G})$ whose restriction to
$\Gamma (\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*},\mathscr {G})$ whose restriction to ![]() $\mathbf {t}^{*} \times \{\eta \}$ (where
$\mathbf {t}^{*} \times \{\eta \}$ (where ![]() $\eta$ is the generic point of
$\eta$ is the generic point of ![]() $\mathbf {t}^{*}$) commutes with the action of the restriction of
$\mathbf {t}^{*}$) commutes with the action of the restriction of ![]() $\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*}$. Now, since by assumption
$\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*}$. Now, since by assumption ![]() $\Gamma (\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*},\mathscr {G})$ is flat as a right
$\Gamma (\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*},\mathscr {G})$ is flat as a right ![]() $R$-module and
$R$-module and ![]() $\mathscr {O}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*})$ is flat over
$\mathscr {O}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*})$ is flat over ![]() $\mathscr {O}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*})$, such a morphism is automatically a morphism of
$\mathscr {O}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*})$, such a morphism is automatically a morphism of ![]() $\mathscr {O}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*})$-comodules. This proves the desired full faithfulness.
$\mathscr {O}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*})$-comodules. This proves the desired full faithfulness.
Lemma 2.8 For any ![]() $w \in {W_{\mathrm {ext}}}$, the object
$w \in {W_{\mathrm {ext}}}$, the object ![]() $\Delta _w$ belongs to the essential image of the functor of Proposition 2.7.
$\Delta _w$ belongs to the essential image of the functor of Proposition 2.7.
Proof. The isomorphism (2.3) reduces the proof to the case where ![]() $w$ belongs to either
$w$ belongs to either ![]() $\mathbf {W}$ or
$\mathbf {W}$ or ![]() $\mathbf {X}$. The case
$\mathbf {X}$. The case ![]() $w \in \mathbf {W}$ is obvious: in this case
$w \in \mathbf {W}$ is obvious: in this case ![]() $\Delta _w$ is the image of its underlying graded
$\Delta _w$ is the image of its underlying graded ![]() $R$-bimodule, endowed with the trivial structure as a representation. For the case
$R$-bimodule, endowed with the trivial structure as a representation. For the case ![]() $w \in \mathbf {X}$, in view of the construction of the functor in Proposition 2.7, the claim follows from the fact that the isomorphism of Lemma 2.6 is the restriction of the morphism (2.4).
$w \in \mathbf {X}$, in view of the construction of the functor in Proposition 2.7, the claim follows from the fact that the isomorphism of Lemma 2.6 is the restriction of the morphism (2.4).
For ![]() $w \in {W_{\mathrm {ext}}}$, we will denote by
$w \in {W_{\mathrm {ext}}}$, we will denote by ![]() $\Delta _w^{\mathbb {J}}$ the unique object in
$\Delta _w^{\mathbb {J}}$ the unique object in ![]() $\mathsf {Rep}_{\mathrm {fl}}^{\mathbb {G}_{\mathrm {m}}}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*})$ which is sent to
$\mathsf {Rep}_{\mathrm {fl}}^{\mathbb {G}_{\mathrm {m}}}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*})$ which is sent to ![]() $\Delta _w$.
$\Delta _w$.
2.5 Representations of the universal centralizer and the Hecke category
By Proposition 2.7 the category ![]() $\mathsf {Rep}_{\mathrm {fl}}^{\mathbb {G}_{\mathrm {m}}}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*})$ can be seen as a full monoidal subcategory in Abe's category
$\mathsf {Rep}_{\mathrm {fl}}^{\mathbb {G}_{\mathrm {m}}}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*})$ can be seen as a full monoidal subcategory in Abe's category ![]() $\mathsf {C}_\mathrm {ext}$, and by Theorem 2.2 the same is true for the Hecke category
$\mathsf {C}_\mathrm {ext}$, and by Theorem 2.2 the same is true for the Hecke category ![]() $\mathsf {D}_{\mathrm {BS}}$. We now investigate the relation between these two subcategories.
$\mathsf {D}_{\mathrm {BS}}$. We now investigate the relation between these two subcategories.
Lemma 2.9 The essential image of the functor of Theorem 2.2 is contained in the essential image of the functor of Proposition 2.7.
Proof. By definition, the category ![]() $\mathsf {D}_{\mathrm {BS}}$ is generated under convolution and grading shift by the objects
$\mathsf {D}_{\mathrm {BS}}$ is generated under convolution and grading shift by the objects ![]() $(B_s : s \in {S_{\mathrm {aff}}})$. Hence, to prove the lemma it suffices to prove each
$(B_s : s \in {S_{\mathrm {aff}}})$. Hence, to prove the lemma it suffices to prove each ![]() $B_s^{\mathrm{Bim}}$ belongs to the essential image of the functor of Proposition 2.7.
$B_s^{\mathrm{Bim}}$ belongs to the essential image of the functor of Proposition 2.7.
If ![]() $s=s_\alpha$ for some
$s=s_\alpha$ for some ![]() $\alpha \in \Phi ^{\mathrm {s}}$, then
$\alpha \in \Phi ^{\mathrm {s}}$, then ![]() $B_s^{\mathrm{Bim}}$ is the image of the appropriate shift of
$B_s^{\mathrm{Bim}}$ is the image of the appropriate shift of ![]() $\mathscr {O}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\{e,s\}} \mathbf {t}^{*})$, endowed with the trivial structure as a representation of
$\mathscr {O}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\{e,s\}} \mathbf {t}^{*})$, endowed with the trivial structure as a representation of ![]() $\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*}$. If
$\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*}$. If ![]() $s \in \mathbf {S}_{\mathrm {aff}}$ is not of this form, then there exist
$s \in \mathbf {S}_{\mathrm {aff}}$ is not of this form, then there exist ![]() $x \in {W_{\mathrm {ext}}}$ and
$x \in {W_{\mathrm {ext}}}$ and ![]() $t \in {S_{\mathrm {aff}}}$ such that
$t \in {S_{\mathrm {aff}}}$ such that ![]() $t=s_\alpha$ for some
$t=s_\alpha$ for some ![]() $\alpha \in \Phi ^{\mathrm {s}}$ and
$\alpha \in \Phi ^{\mathrm {s}}$ and ![]() $s=xtx^{-1}$. (In fact, such a statement is even true in the braid group associated with
$s=xtx^{-1}$. (In fact, such a statement is even true in the braid group associated with ![]() ${W_{\mathrm {ext}}}$; see [Reference RicheRic10, Lemma 6.1.2] or [Reference Bezrukavnikov and MirkovićBM13, Lemma 2.1.1] for the proof in the setting where
${W_{\mathrm {ext}}}$; see [Reference RicheRic10, Lemma 6.1.2] or [Reference Bezrukavnikov and MirkovićBM13, Lemma 2.1.1] for the proof in the setting where ![]() $\mathbf {G}$ is semisimple and simply connected, from which one can deduce the general case using restriction to the derived subgroup.) By Lemma 2.4 we then have
$\mathbf {G}$ is semisimple and simply connected, from which one can deduce the general case using restriction to the derived subgroup.) By Lemma 2.4 we then have ![]() $B_s^{\mathrm{Bim}} \cong \Delta _x \otimes _R B_t^{\mathrm{Bim}} \otimes _R \Delta _{x^{-1}}$; since
$B_s^{\mathrm{Bim}} \cong \Delta _x \otimes _R B_t^{\mathrm{Bim}} \otimes _R \Delta _{x^{-1}}$; since ![]() $B_t^{\mathrm{Bim}}$ is now known to belong to the essential image of our functor, and since
$B_t^{\mathrm{Bim}}$ is now known to belong to the essential image of our functor, and since ![]() $\Delta _x$ also satisfies this property by Lemma 2.8, this finishes the proof.
$\Delta _x$ also satisfies this property by Lemma 2.8, this finishes the proof.
From this lemma we deduce the following claim, which will be crucial for our constructions in § 6.
Theorem 2.10 There exists a canonical fully faithful monoidal functor
3. Some categories of equivariant  $\mathcal {U} \mathfrak {g}$-bimodules
$\mathcal {U} \mathfrak {g}$-bimodules
3.1 Weights
From now on we assume that ![]() $p>0$. We consider a simply connected semisimple algebraic group
$p>0$. We consider a simply connected semisimple algebraic group ![]() $G$ over
$G$ over ![]() $\Bbbk$, and its category
$\Bbbk$, and its category
of finite-dimensional algebraic representations.
For a ![]() $\Bbbk$-scheme
$\Bbbk$-scheme ![]() $X$ we will denote by
$X$ we will denote by ![]() $X^{(1)}$ the associated Frobenius twist, defined as the fiber product
$X^{(1)}$ the associated Frobenius twist, defined as the fiber product ![]() $X^{(1)}:=X \times _{\mathrm {Spec}(\Bbbk )} \,\mathrm {Spec}(\Bbbk )$, where the morphism
$X^{(1)}:=X \times _{\mathrm {Spec}(\Bbbk )} \,\mathrm {Spec}(\Bbbk )$, where the morphism ![]() $\mathrm {Spec}(\Bbbk ) \to \mathrm {Spec}(\Bbbk )$ is associated with the map
$\mathrm {Spec}(\Bbbk ) \to \mathrm {Spec}(\Bbbk )$ is associated with the map ![]() $x \mapsto x^{p}$. (The projection
$x \mapsto x^{p}$. (The projection ![]() $X^{(1)} \to X$ is an isomorphism of
$X^{(1)} \to X$ is an isomorphism of ![]() $\mathbb {F}_p$-schemes, but not of
$\mathbb {F}_p$-schemes, but not of ![]() $\Bbbk$-schemes.) We will assume that
$\Bbbk$-schemes.) We will assume that
Then the group ![]() $\mathbf {G} := G^{(1)}$ satisfies the assumptions of § 2. We will denote by
$\mathbf {G} := G^{(1)}$ satisfies the assumptions of § 2. We will denote by ![]() $\mathrm {Fr} : G \to \mathbf {G}$ the Frobenius morphism of
$\mathrm {Fr} : G \to \mathbf {G}$ the Frobenius morphism of ![]() $G$, and will use the same notation for its restriction to the various subgroups considered below.
$G$, and will use the same notation for its restriction to the various subgroups considered below.
The subgroups ![]() $\mathbf {B}$,
$\mathbf {B}$, ![]() $\mathbf {T}$,
$\mathbf {T}$, ![]() $\mathbf {U}$ of
$\mathbf {U}$ of ![]() $\mathbf {G}$, when seen as subschemes in
$\mathbf {G}$, when seen as subschemes in ![]() $G$, determine subgroups
$G$, determine subgroups ![]() $B$,
$B$, ![]() $T$,
$T$, ![]() $U$ whose Frobenius twists are
$U$ whose Frobenius twists are ![]() $\mathbf {B}$,
$\mathbf {B}$, ![]() $\mathbf {T}$,
$\mathbf {T}$, ![]() $\mathbf {U}$, respectively. We will denote by
$\mathbf {U}$, respectively. We will denote by ![]() $\mathfrak {g}$,
$\mathfrak {g}$, ![]() $\mathfrak {b}$,
$\mathfrak {b}$, ![]() $\mathfrak {t}$,
$\mathfrak {t}$, ![]() $\mathfrak {n}$ the respective Lie algebras of
$\mathfrak {n}$ the respective Lie algebras of ![]() $G$,
$G$, ![]() $B$,
$B$, ![]() $T$,
$T$, ![]() $U$ (so that
$U$ (so that ![]() $\mathbf {g}=\mathfrak {g}^{(1)}$, and similarly for
$\mathbf {g}=\mathfrak {g}^{(1)}$, and similarly for ![]() $B$,
$B$, ![]() $U$,
$U$, ![]() $T$), and by
$T$), and by ![]() $W$ the Weyl group of
$W$ the Weyl group of ![]() $(G,T)$. We set
$(G,T)$. We set ![]() $\mathbb {X}:=X^{*}(T)$, and denote by
$\mathbb {X}:=X^{*}(T)$, and denote by ![]() $\mathfrak {R} \subset \mathbb {X}$ the root system of
$\mathfrak {R} \subset \mathbb {X}$ the root system of ![]() $(G,T)$. The choice of
$(G,T)$. The choice of ![]() $B$ determines a system of positive roots
$B$ determines a system of positive roots ![]() $\mathfrak {R}^{+} \subset \mathfrak {R}$, chosen as the
$\mathfrak {R}^{+} \subset \mathfrak {R}$, chosen as the ![]() $T$-weights in
$T$-weights in ![]() $\mathfrak {g}/\mathfrak {b}$. We will denote by
$\mathfrak {g}/\mathfrak {b}$. We will denote by ![]() $\mathfrak {R}^{\mathrm {s}} \subset \mathfrak {R}$ the corresponding subset of simple roots, and by
$\mathfrak {R}^{\mathrm {s}} \subset \mathfrak {R}$ the corresponding subset of simple roots, and by ![]() $\rho \in \mathbb {X}$ the half-sum of the positive roots. We also set
$\rho \in \mathbb {X}$ the half-sum of the positive roots. We also set ![]() $\mathbb {X}^{\vee } := X_*(T)$, and denote by
$\mathbb {X}^{\vee } := X_*(T)$, and denote by ![]() $\mathfrak {R}^{\vee } \subset \mathbb {X}^{\vee }$ the coroot system. The canonical bijection
$\mathfrak {R}^{\vee } \subset \mathbb {X}^{\vee }$ the coroot system. The canonical bijection ![]() $\mathfrak {R} \xrightarrow {\sim } \mathfrak {R}^{\vee }$ will be denoted as usual
$\mathfrak {R} \xrightarrow {\sim } \mathfrak {R}^{\vee }$ will be denoted as usual ![]() $\alpha \mapsto \alpha ^{\vee }$.
$\alpha \mapsto \alpha ^{\vee }$.
The Frobenius morphism ![]() $\mathrm {Fr}$ induces an isomorphism
$\mathrm {Fr}$ induces an isomorphism
which allows us to identify the Weyl group ![]() $\mathbf {W}$ of
$\mathbf {W}$ of ![]() $\mathbf {G}$ with
$\mathbf {G}$ with ![]() $W$. It is a standard fact that the morphism from
$W$. It is a standard fact that the morphism from ![]() $\mathbf {X}=X^{*}(T^{(1)})$ to
$\mathbf {X}=X^{*}(T^{(1)})$ to ![]() $\mathbb {X}$ induced by
$\mathbb {X}$ induced by ![]() $\mathrm {Fr} : T \to \mathbf {T}$ is injective, and that its image is
$\mathrm {Fr} : T \to \mathbf {T}$ is injective, and that its image is ![]() $p \cdot \mathbb {X}$, which allows us to identify
$p \cdot \mathbb {X}$, which allows us to identify ![]() $\mathbf {X}$ with
$\mathbf {X}$ with ![]() $p \cdot \mathbb {X}$. The identification
$p \cdot \mathbb {X}$. The identification ![]() $\mathbf {X} = p \cdot \mathbb {X}$ is
$\mathbf {X} = p \cdot \mathbb {X}$ is ![]() $W$-equivariant, and the root system
$W$-equivariant, and the root system ![]() $\Phi$ of
$\Phi$ of ![]() $(\mathbf {G},\mathbf {T})$ is
$(\mathbf {G},\mathbf {T})$ is ![]() $\Phi = \{p \cdot \alpha : \alpha \in \mathfrak {R}\}$; similarly, we have
$\Phi = \{p \cdot \alpha : \alpha \in \mathfrak {R}\}$; similarly, we have ![]() $\Phi ^{+}=p\mathfrak {R}^{+}$ and
$\Phi ^{+}=p\mathfrak {R}^{+}$ and ![]() $\Phi ^{\mathrm {s}}=p\mathfrak {R}^{\mathrm {s}}$. In particular, the affine Weyl group
$\Phi ^{\mathrm {s}}=p\mathfrak {R}^{\mathrm {s}}$. In particular, the affine Weyl group ![]() ${W_{\mathrm {aff}}}$ of § 2.1 identifies with
${W_{\mathrm {aff}}}$ of § 2.1 identifies with ![]() $W \ltimes (p \mathbb {Z}\mathfrak {R})$, and the extended affine Weyl group
$W \ltimes (p \mathbb {Z}\mathfrak {R})$, and the extended affine Weyl group ![]() ${W_{\mathrm {ext}}}$ identifies with
${W_{\mathrm {ext}}}$ identifies with ![]() $W \ltimes (p \cdot \mathbb {X})$. Recall also our subset of Coxeter generators
$W \ltimes (p \cdot \mathbb {X})$. Recall also our subset of Coxeter generators ![]() ${S_{\mathrm {aff}}} \subset {W_{\mathrm {aff}}}$. The subgroup
${S_{\mathrm {aff}}} \subset {W_{\mathrm {aff}}}$. The subgroup ![]() $W \subset {W_{\mathrm {aff}}}$ is a parabolic subgroup; its longest element will be denoted (as usual) by
$W \subset {W_{\mathrm {aff}}}$ is a parabolic subgroup; its longest element will be denoted (as usual) by ![]() $w_0$. We will consider the ‘dot’ action of
$w_0$. We will consider the ‘dot’ action of ![]() ${W_{\mathrm {ext}}}$ (or its subgroup
${W_{\mathrm {ext}}}$ (or its subgroup ![]() ${W_{\mathrm {aff}}}$) on
${W_{\mathrm {aff}}}$) on ![]() $\mathbb {X}$ defined by
$\mathbb {X}$ defined by
for ![]() $\mu \in p\mathbb {X}$,
$\mu \in p\mathbb {X}$, ![]() $w \in W$ and
$w \in W$ and ![]() $\lambda \in \mathbb {X}$.
$\lambda \in \mathbb {X}$.
Given a character ![]() $\lambda \in \mathbb {X}$, we will denote by
$\lambda \in \mathbb {X}$, we will denote by ![]() ${{\bar {\lambda }}} \in \mathfrak {t}^{*}$ the differential of
${{\bar {\lambda }}} \in \mathfrak {t}^{*}$ the differential of ![]() $\lambda$. We set
$\lambda$. We set
In this way, the map ![]() $\lambda \mapsto {{\bar {\lambda }}}$ induces an isomorphism of abelian groups
$\lambda \mapsto {{\bar {\lambda }}}$ induces an isomorphism of abelian groups
(In particular, ![]() $\mathfrak {t}^{*}_{\mathbb {F}_p}$ is finite.)
$\mathfrak {t}^{*}_{\mathbb {F}_p}$ is finite.)
The group ![]() $W$ naturally acts on
$W$ naturally acts on ![]() $\mathfrak {t}^{*}$. We also have a ‘dot’ action of
$\mathfrak {t}^{*}$. We also have a ‘dot’ action of ![]() $W$ on
$W$ on ![]() $\mathfrak {t}^{*}$, defined by
$\mathfrak {t}^{*}$, defined by
With this definition the map ![]() $\mathbb {X} \to \mathfrak {t}^{*}$ sending
$\mathbb {X} \to \mathfrak {t}^{*}$ sending ![]() $\lambda$ to
$\lambda$ to ![]() ${{\bar {\lambda }}}$ is
${{\bar {\lambda }}}$ is ![]() ${W_{\mathrm {ext}}}$-equivariant, where
${W_{\mathrm {ext}}}$-equivariant, where ![]() ${W_{\mathrm {ext}}}$ acts on
${W_{\mathrm {ext}}}$ acts on ![]() $\mathbb {X}$ via the dot action and on
$\mathbb {X}$ via the dot action and on ![]() $\mathfrak {t}^{*}$ via the projection
$\mathfrak {t}^{*}$ via the projection ![]() ${W_{\mathrm {ext}}} \to W$ and the dot action of
${W_{\mathrm {ext}}} \to W$ and the dot action of ![]() $W$ on
$W$ on ![]() $\mathfrak {t}^{*}$. This observation legitimates the use of the same notation for these actions. It also shows that the subset
$\mathfrak {t}^{*}$. This observation legitimates the use of the same notation for these actions. It also shows that the subset ![]() $\mathfrak {t}^{*}_{\mathbb {F}_p} \subset \mathfrak {t}^{*}$ is stable under the dot action of
$\mathfrak {t}^{*}_{\mathbb {F}_p} \subset \mathfrak {t}^{*}$ is stable under the dot action of ![]() $W$. Below we will consider the quotient
$W$. Below we will consider the quotient ![]() $\mathfrak {t}^{*}/(W,\bullet )$ of the dot action of
$\mathfrak {t}^{*}/(W,\bullet )$ of the dot action of ![]() $W$ on
$W$ on ![]() $\mathfrak {t}^{*}$. For
$\mathfrak {t}^{*}$. For ![]() $\lambda \in \mathbb {X}$, we will denote by
$\lambda \in \mathbb {X}$, we will denote by ![]() ${{\tilde {\lambda }}}$ the image of
${{\tilde {\lambda }}}$ the image of ![]() ${{\bar {\lambda }}}$ in
${{\bar {\lambda }}}$ in ![]() $\mathfrak {t}^{*}/(W,\bullet )$.
$\mathfrak {t}^{*}/(W,\bullet )$.
As mentioned above, our assumption that ![]() $p$ is very good for
$p$ is very good for ![]() $G$ implies in particular that the quotient
$G$ implies in particular that the quotient ![]() $\mathbb {X}/\mathbb {Z}\mathfrak {R}$ has no
$\mathbb {X}/\mathbb {Z}\mathfrak {R}$ has no ![]() $p$-torsion, or in other words that
$p$-torsion, or in other words that
This equality has the following consequences.
Lemma 3.1 Let ![]() $\lambda \in \mathbb {X}$.
$\lambda \in \mathbb {X}$.
(i) We have
 \[ {W_{\mathrm{aff}}} \bullet \lambda = ({W_{\mathrm{ext}}} \bullet \lambda) \cap (\lambda+\mathbb{Z}\mathfrak{R}). \]
\[ {W_{\mathrm{aff}}} \bullet \lambda = ({W_{\mathrm{ext}}} \bullet \lambda) \cap (\lambda+\mathbb{Z}\mathfrak{R}). \](ii) The stabilizer of
 ${{\bar {\lambda }}}$ for the dot action of
${{\bar {\lambda }}}$ for the dot action of  $W$ on
$W$ on  $\mathfrak {t}^{*}$ is the image under the natural surjection
$\mathfrak {t}^{*}$ is the image under the natural surjection  ${W_{\mathrm {aff}}} \to W$ of the stabilizer of
${W_{\mathrm {aff}}} \to W$ of the stabilizer of  $\lambda$ for the dot action of
$\lambda$ for the dot action of  ${W_{\mathrm {aff}}}$ on
${W_{\mathrm {aff}}}$ on  $\mathbb {X}$.
$\mathbb {X}$.
Proof. (i) Since ![]() $W \bullet \lambda \subset \lambda +\mathbb {Z}\mathfrak {R}$, we have
$W \bullet \lambda \subset \lambda +\mathbb {Z}\mathfrak {R}$, we have
In view of (3.1), the right-hand side equals ![]() $W \bullet \lambda + p\mathbb {Z}\mathfrak {R} = {W_{\mathrm {aff}}} \bullet \lambda$, as desired.
$W \bullet \lambda + p\mathbb {Z}\mathfrak {R} = {W_{\mathrm {aff}}} \bullet \lambda$, as desired.
(ii) For ![]() $w \in W$ we have
$w \in W$ we have
so that ![]() $w \bullet {{\bar {\lambda }}}={{\bar {\lambda }}}$ if and only if
$w \bullet {{\bar {\lambda }}}={{\bar {\lambda }}}$ if and only if ![]() $w \bullet \lambda \in \lambda +p\mathbb {X}$. Since
$w \bullet \lambda \in \lambda +p\mathbb {X}$. Since ![]() $w \bullet \lambda \in \lambda +\mathbb {Z}\mathfrak {R}$, as above this condition is equivalent to
$w \bullet \lambda \in \lambda +\mathbb {Z}\mathfrak {R}$, as above this condition is equivalent to ![]() $w \bullet \lambda \in \lambda +p\mathbb {Z}\mathfrak {R}$, that is, to the existence of
$w \bullet \lambda \in \lambda +p\mathbb {Z}\mathfrak {R}$, that is, to the existence of ![]() $\mu \in p\mathbb {Z}\mathfrak {R}$ such that
$\mu \in p\mathbb {Z}\mathfrak {R}$ such that ![]() $t_\mu w \in {W_{\mathrm {aff}}}$ stabilizes
$t_\mu w \in {W_{\mathrm {aff}}}$ stabilizes ![]() $\lambda$.
$\lambda$.
For any subset ![]() $I \subset \mathfrak {R}^{\mathrm {s}}$, we will denote by
$I \subset \mathfrak {R}^{\mathrm {s}}$, we will denote by ![]() $W_I \subset W$ the subgroup generated by the reflections
$W_I \subset W$ the subgroup generated by the reflections ![]() $\{s_\alpha : \alpha \in I\}$. Recall that an element of
$\{s_\alpha : \alpha \in I\}$. Recall that an element of ![]() $\mathbb {X}$ is called regular if its stabilizer in
$\mathbb {X}$ is called regular if its stabilizer in ![]() ${W_{\mathrm {aff}}}$ (for the dot action) is trivial. As a consequence of Lemma 3.1, we obtain, in particular, the following claim.
${W_{\mathrm {aff}}}$ (for the dot action) is trivial. As a consequence of Lemma 3.1, we obtain, in particular, the following claim.
Lemma 3.2 Let ![]() $\lambda \in \mathbb {X}$, and assume that the stabilizer of
$\lambda \in \mathbb {X}$, and assume that the stabilizer of ![]() $\lambda$ for the dot action of
$\lambda$ for the dot action of ![]() ${W_{\mathrm {aff}}}$ is
${W_{\mathrm {aff}}}$ is ![]() $W_I$. Then the morphism
$W_I$. Then the morphism
induced by the quotient morphism ![]() $\mathfrak {t}^{*} \to \mathfrak {t}^{*}/(W,\bullet )$ is étale at the image of
$\mathfrak {t}^{*} \to \mathfrak {t}^{*}/(W,\bullet )$ is étale at the image of ![]() ${{\bar {\lambda }}}$. In particular, if
${{\bar {\lambda }}}$. In particular, if ![]() $\lambda$ is regular then the quotient morphism
$\lambda$ is regular then the quotient morphism ![]() $\mathfrak {t}^{*} \to \mathfrak {t}^{*}/(W,\bullet )$ is étale at
$\mathfrak {t}^{*} \to \mathfrak {t}^{*}/(W,\bullet )$ is étale at ![]() ${{\bar {\lambda }}}$.
${{\bar {\lambda }}}$.
3.2 The center of the enveloping algebra
Consider the universal enveloping algebra ![]() $\mathcal {U} \mathfrak {g}$ of
$\mathcal {U} \mathfrak {g}$ of ![]() $\mathfrak {g}$. Its center
$\mathfrak {g}$. Its center ![]() $Z(\mathcal {U}\mathfrak {g})$ can be described as follows. We set
$Z(\mathcal {U}\mathfrak {g})$ can be described as follows. We set
(Here, the subscript ‘![]() $\mathrm {HC}$’ stands for Harish-Chandra.) Next, as the Lie algebra of an algebraic group over a field of characteristic
$\mathrm {HC}$’ stands for Harish-Chandra.) Next, as the Lie algebra of an algebraic group over a field of characteristic ![]() $p$,
$p$, ![]() $\mathfrak {g}$ admits a ‘restricted
$\mathfrak {g}$ admits a ‘restricted ![]() $p$th power’ operation
$p$th power’ operation ![]() $x \mapsto x^{[p]}$, which stabilizes the Lie algebra of any algebraic subgroup of
$x \mapsto x^{[p]}$, which stabilizes the Lie algebra of any algebraic subgroup of ![]() $G$. We will denote by
$G$. We will denote by
the ![]() $\Bbbk$-subalgebra of
$\Bbbk$-subalgebra of ![]() $\mathcal {U}\mathfrak {g}$ generated by the elements of the form
$\mathcal {U}\mathfrak {g}$ generated by the elements of the form ![]() $x^{p}-x^{[p]}$ for
$x^{p}-x^{[p]}$ for ![]() $x \in \mathfrak {g}$. Then by [Reference Mirković and RumyninMR99, Theorem 2] multiplication induces an isomorphism
$x \in \mathfrak {g}$. Then by [Reference Mirković and RumyninMR99, Theorem 2] multiplication induces an isomorphism
It is well known that ![]() $\mathcal {U} \mathfrak {g}$ is finite as a
$\mathcal {U} \mathfrak {g}$ is finite as a ![]() ${Z_{\mathrm {Fr}}}$-algebra (hence a fortiori as a
${Z_{\mathrm {Fr}}}$-algebra (hence a fortiori as a ![]() $Z(\mathcal {U} \mathfrak {g})$-algebra).
$Z(\mathcal {U} \mathfrak {g})$-algebra).
These central subalgebras can be described geometrically as follows. It is well known that the map ![]() $x \mapsto x^{p}-x^{[p]}$ induces a
$x \mapsto x^{p}-x^{[p]}$ induces a ![]() $\Bbbk$-algebra isomorphism
$\Bbbk$-algebra isomorphism
We also have ![]() ${Z_{\mathrm {Fr}}} \cap {Z_{\mathrm {HC}}} = ({Z_{\mathrm {Fr}}})^{G}$, and the
${Z_{\mathrm {Fr}}} \cap {Z_{\mathrm {HC}}} = ({Z_{\mathrm {Fr}}})^{G}$, and the ![]() $G$-action on
$G$-action on ![]() $\mathfrak {g}^{*(1)}$ factors through the Frobenius morphism
$\mathfrak {g}^{*(1)}$ factors through the Frobenius morphism ![]() $\mathrm {Fr}$, so that we obtain an isomorphism
$\mathrm {Fr}$, so that we obtain an isomorphism
On the other hand, the ‘Harish-Chandra isomorphism’ provides a ![]() $\Bbbk$-algebra isomorphism
$\Bbbk$-algebra isomorphism
see [Reference Mirković and RumyninMR99, Theorem 1(2)].
The Artin–Schreier morphism
is the morphism associated with the algebra map ![]() $\mathscr {O}(\mathfrak {t}^{*(1)}) \to \mathscr {O}(\mathfrak {t}^{*})$ defined by
$\mathscr {O}(\mathfrak {t}^{*(1)}) \to \mathscr {O}(\mathfrak {t}^{*})$ defined by ![]() $h \mapsto h^{p}-h^{[p]}$ for
$h \mapsto h^{p}-h^{[p]}$ for ![]() $h \in \mathfrak {t}$. It is well known that
$h \in \mathfrak {t}$. It is well known that ![]() $\mathrm {AS}$ is a Galois covering with Galois group
$\mathrm {AS}$ is a Galois covering with Galois group ![]() $\mathfrak {t}^{*}_{\mathbb {F}_p}$ (acting on
$\mathfrak {t}^{*}_{\mathbb {F}_p}$ (acting on ![]() $\mathfrak {t}^{*}$ via addition). The morphism
$\mathfrak {t}^{*}$ via addition). The morphism ![]() $\mathrm {AS}$ is
$\mathrm {AS}$ is ![]() $W$-equivariant, where
$W$-equivariant, where ![]() $W$ acts on
$W$ acts on ![]() $\mathfrak {t}^{*}$ via the dot action and on
$\mathfrak {t}^{*}$ via the dot action and on ![]() $\mathfrak {t}^{*(1)}$ via the natural action. It therefore induces a morphism
$\mathfrak {t}^{*(1)}$ via the natural action. It therefore induces a morphism
Recall the Chevalley isomorphism
already encountered in § 2.3. Under this identification, the embedding ![]() ${Z_{\mathrm {Fr}}} \cap {Z_{\mathrm {HC}}} \hookrightarrow {Z_{\mathrm {HC}}}$ is induced by (3.4).
${Z_{\mathrm {Fr}}} \cap {Z_{\mathrm {HC}}} \hookrightarrow {Z_{\mathrm {HC}}}$ is induced by (3.4).
Combining all these descriptions, and setting
we therefore obtain a ![]() $\Bbbk$-algebra isomorphism
$\Bbbk$-algebra isomorphism
see [Reference Mirković and RumyninMR99, Corollary 3].
Using this identification one can consider ![]() $\mathcal {U} \mathfrak {g}$ as an
$\mathcal {U} \mathfrak {g}$ as an ![]() $\mathscr {O}(\mathfrak {C})$-algebra. The
$\mathscr {O}(\mathfrak {C})$-algebra. The ![]() $G$-action on
$G$-action on ![]() $\mathfrak {C}$ induced by the adjoint
$\mathfrak {C}$ induced by the adjoint ![]() $G$-action on
$G$-action on ![]() $\mathcal {U} \mathfrak {g}$ is the action obtained by pullback via the Frobenius morphism
$\mathcal {U} \mathfrak {g}$ is the action obtained by pullback via the Frobenius morphism ![]() $\mathrm {Fr}$ of the
$\mathrm {Fr}$ of the ![]() $G^{(1)}$-action on
$G^{(1)}$-action on ![]() $\mathfrak {C}$ induced by the coadjoint
$\mathfrak {C}$ induced by the coadjoint ![]() $G^{(1)}$-action on
$G^{(1)}$-action on ![]() $\mathfrak {g}^{*(1)}$. Using this action, one can therefore see
$\mathfrak {g}^{*(1)}$. Using this action, one can therefore see ![]() $\mathcal {U} \mathfrak {g}$ as a
$\mathcal {U} \mathfrak {g}$ as a ![]() $G$-equivariant
$G$-equivariant ![]() $\mathscr {O}(\mathfrak {C})$-algebra.
$\mathscr {O}(\mathfrak {C})$-algebra.
3.3 Central reductions
In view of (3.2), the maximal ideals in ![]() ${Z_{\mathrm {Fr}}}$ are in a canonical bijection with elements in
${Z_{\mathrm {Fr}}}$ are in a canonical bijection with elements in ![]() $\mathfrak {g}^{*(1)}$. Given
$\mathfrak {g}^{*(1)}$. Given ![]() $\eta \in \mathfrak {g}^{*(1)}$, we will denote by
$\eta \in \mathfrak {g}^{*(1)}$, we will denote by ![]() $\mathfrak {m}_\eta \subset {Z_{\mathrm {Fr}}}$ the corresponding maximal ideal, and set
$\mathfrak {m}_\eta \subset {Z_{\mathrm {Fr}}}$ the corresponding maximal ideal, and set
Similarly, in view of (3.3) the maximal ideals in ![]() ${Z_{\mathrm {HC}}}$ are in a canonical bijection with closed points in
${Z_{\mathrm {HC}}}$ are in a canonical bijection with closed points in ![]() $\mathfrak {t}^{*}/(W,\bullet )$, that is, with
$\mathfrak {t}^{*}/(W,\bullet )$, that is, with ![]() $(W,\bullet )$-orbits in
$(W,\bullet )$-orbits in ![]() $\mathfrak {t}^{*}$. Given a closed point
$\mathfrak {t}^{*}$. Given a closed point ![]() $\xi \in \mathfrak {t}^{*}/(W,\bullet )$, we will denote by
$\xi \in \mathfrak {t}^{*}/(W,\bullet )$, we will denote by ![]() $\mathfrak {m}^{\xi } \subset {Z_{\mathrm {HC}}}$ the corresponding maximal ideal, and set
$\mathfrak {m}^{\xi } \subset {Z_{\mathrm {HC}}}$ the corresponding maximal ideal, and set
If ![]() $\eta$ and
$\eta$ and ![]() $\xi$ have the same image in
$\xi$ have the same image in ![]() $\mathfrak {t}^{*(1)}/W$, then
$\mathfrak {t}^{*(1)}/W$, then ![]() $\mathfrak {m}_\eta \cdot Z(\mathcal {U} \mathfrak {g}) + \mathfrak {m}^{\xi } \cdot Z(\mathcal {U} \mathfrak {g})$ is a maximal ideal in
$\mathfrak {m}_\eta \cdot Z(\mathcal {U} \mathfrak {g}) + \mathfrak {m}^{\xi } \cdot Z(\mathcal {U} \mathfrak {g})$ is a maximal ideal in ![]() $Z(\mathcal {U} \mathfrak {g})$, and we can also set
$Z(\mathcal {U} \mathfrak {g})$, and we can also set
In the cases we will encounter more specifically below, the point ![]() $\xi$ will often be the image
$\xi$ will often be the image ![]() $\tilde {\lambda }$ of the differential of a character
$\tilde {\lambda }$ of the differential of a character ![]() $\lambda \in \mathbb {X}$. In this setting we will write
$\lambda \in \mathbb {X}$. In this setting we will write ![]() $\mathfrak {m}^{\lambda }$,
$\mathfrak {m}^{\lambda }$, ![]() $\mathcal {U}^{\lambda } \mathfrak {g}$ and
$\mathcal {U}^{\lambda } \mathfrak {g}$ and ![]() $\mathcal {U}_{\eta }^{\lambda }\mathfrak {g}$ instead of
$\mathcal {U}_{\eta }^{\lambda }\mathfrak {g}$ instead of ![]() $\mathfrak {m}^{\tilde {\lambda }}$,
$\mathfrak {m}^{\tilde {\lambda }}$, ![]() $\mathcal {U}^{\tilde {\lambda }} \mathfrak {g}$ and
$\mathcal {U}^{\tilde {\lambda }} \mathfrak {g}$ and ![]() $\mathcal {U}_{\eta }^{\tilde {\lambda }}\mathfrak {g}$. The image of any element of
$\mathcal {U}_{\eta }^{\tilde {\lambda }}\mathfrak {g}$. The image of any element of ![]() $\mathfrak {t}^{*}_{\mathbb {F}_p}$ under the Artin–Schreier map is
$\mathfrak {t}^{*}_{\mathbb {F}_p}$ under the Artin–Schreier map is ![]() $0$; therefore, if we denote by
$0$; therefore, if we denote by
the preimage under the coadjoint morphism ![]() $\mathfrak {g}^{*} \to \mathfrak {t}^{*}/W$ of the image of
$\mathfrak {g}^{*} \to \mathfrak {t}^{*}/W$ of the image of ![]() $0$, then, given any
$0$, then, given any ![]() $\lambda \in \mathbb {X}$, the elements
$\lambda \in \mathbb {X}$, the elements ![]() $\eta \in \mathfrak {g}^{*(1)}$ whose image in
$\eta \in \mathfrak {g}^{*(1)}$ whose image in ![]() $\mathfrak {t}^{*(1)}/W$ coincides with that of
$\mathfrak {t}^{*(1)}/W$ coincides with that of ![]() $\tilde {\lambda }$ are exactly those in
$\tilde {\lambda }$ are exactly those in ![]() $\mathcal {N}^{*(1)}$.
$\mathcal {N}^{*(1)}$.
3.4 Harish-Chandra bimodules
We will denote by ![]() $\mathsf {HC}$ the category whose objects are the
$\mathsf {HC}$ the category whose objects are the ![]() $\mathcal {U} \mathfrak {g}$-bimodules
$\mathcal {U} \mathfrak {g}$-bimodules ![]() $V$ endowed with an (algebraic) action of
$V$ endowed with an (algebraic) action of ![]() $G$ which satisfy the following conditions.
$G$ which satisfy the following conditions.
(i) The action morphisms
 $\mathcal {U} \mathfrak {g} \otimes V \to V$ and
$\mathcal {U} \mathfrak {g} \otimes V \to V$ and  $V \otimes \mathcal {U} \mathfrak {g} \to V$ are
$V \otimes \mathcal {U} \mathfrak {g} \to V$ are  $G$-equivariant (for the diagonal actions on
$G$-equivariant (for the diagonal actions on  $\mathcal {U} \mathfrak {g} \otimes V$ and
$\mathcal {U} \mathfrak {g} \otimes V$ and  $V \otimes \mathcal {U} \mathfrak {g}$).
$V \otimes \mathcal {U} \mathfrak {g}$).(ii) The
 $\mathfrak {g}$-action on
$\mathfrak {g}$-action on  $V$ obtained by differentiating the
$V$ obtained by differentiating the  $G$-action is given by
$G$-action is given by  $(x,v) \mapsto x \cdot v - v \cdot x$.
$(x,v) \mapsto x \cdot v - v \cdot x$.(iii)
 $V$ is finitely generated both as a left and as a right
$V$ is finitely generated both as a left and as a right  $\mathcal {U} \mathfrak {g}$-module.
$\mathcal {U} \mathfrak {g}$-module.
Morphisms in the category ![]() $\mathsf {HC}$ are morphisms of bimodules which also commute with the
$\mathsf {HC}$ are morphisms of bimodules which also commute with the ![]() $G$-actions. Objects in this category are called Harish-Chandra bimodules. It is easily seen that the tensor product
$G$-actions. Objects in this category are called Harish-Chandra bimodules. It is easily seen that the tensor product ![]() $\otimes _{\mathcal {U} \mathfrak {g}}$ of bimodules endows
$\otimes _{\mathcal {U} \mathfrak {g}}$ of bimodules endows ![]() $\mathsf {HC}$ with the structure of a monoidal category, where the
$\mathsf {HC}$ with the structure of a monoidal category, where the ![]() $G$-action on the tensor product is the diagonal action.
$G$-action on the tensor product is the diagonal action.
If ![]() $M$ belongs to
$M$ belongs to ![]() $\mathsf {HC}$, the
$\mathsf {HC}$, the ![]() $\mathcal {U} \mathfrak {g}$-action obtained by differentiating the
$\mathcal {U} \mathfrak {g}$-action obtained by differentiating the ![]() $G$-action must vanish on
$G$-action must vanish on ![]() ${Z_{\mathrm {Fr}}} \cap (\mathfrak {g} \cdot \mathcal {U} \mathfrak {g})$. In view of condition (ii) above, this implies that the two actions of
${Z_{\mathrm {Fr}}} \cap (\mathfrak {g} \cdot \mathcal {U} \mathfrak {g})$. In view of condition (ii) above, this implies that the two actions of ![]() ${Z_{\mathrm {Fr}}}$ on
${Z_{\mathrm {Fr}}}$ on ![]() $M$ obtained by restriction of the left and right
$M$ obtained by restriction of the left and right ![]() $\mathcal {U} \mathfrak {g}$-actions coincide; in other words, the action of
$\mathcal {U} \mathfrak {g}$-actions coincide; in other words, the action of ![]() $\mathcal {U} \mathfrak {g} \otimes _\Bbbk \mathcal {U} \mathfrak {g}^{\mathrm {op}}$ on
$\mathcal {U} \mathfrak {g} \otimes _\Bbbk \mathcal {U} \mathfrak {g}^{\mathrm {op}}$ on ![]() $M$ must factor through an action of
$M$ must factor through an action of ![]() $\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm {op}}$. However, the two actions of
$\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm {op}}$. However, the two actions of ![]() ${Z_{\mathrm {HC}}}$ on a Harish-Chandra bimodule might differ. Note that
${Z_{\mathrm {HC}}}$ on a Harish-Chandra bimodule might differ. Note that ![]() $\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm {op}}$ is in a natural way a finite algebra over the commutative ring
$\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm {op}}$ is in a natural way a finite algebra over the commutative ring
Note also that since ![]() $\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm {op}}$ is finitely generated both as a left and as a right
$\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm {op}}$ is finitely generated both as a left and as a right ![]() $\mathcal {U} \mathfrak {g}$-module, condition (iii) above can be equivalently replaced by the condition that the object is finitely generated as a
$\mathcal {U} \mathfrak {g}$-module, condition (iii) above can be equivalently replaced by the condition that the object is finitely generated as a ![]() $\mathcal {U} \mathfrak {g}$-bimodule (or as a left
$\mathcal {U} \mathfrak {g}$-bimodule (or as a left ![]() $\mathcal {U} \mathfrak {g}$-module, or as a right
$\mathcal {U} \mathfrak {g}$-module, or as a right ![]() $\mathcal {U} \mathfrak {g}$-module). It is easily seen that forgetting the right (respectively, left) action of
$\mathcal {U} \mathfrak {g}$-module). It is easily seen that forgetting the right (respectively, left) action of ![]() $\mathcal {U} \mathfrak {g}$ defines an equivalence of categories
$\mathcal {U} \mathfrak {g}$ defines an equivalence of categories
where ![]() $\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U} \mathfrak {g})$ is the category of
$\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U} \mathfrak {g})$ is the category of ![]() $G$-equivariant finitely generated
$G$-equivariant finitely generated ![]() $\mathcal {U} \mathfrak {g}$-modules, and similarly for
$\mathcal {U} \mathfrak {g}$-modules, and similarly for ![]() $\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U} \mathfrak {g}^{\mathrm {op}})$. For instance, for the first functor, one can reconstruct the right action of
$\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U} \mathfrak {g}^{\mathrm {op}})$. For instance, for the first functor, one can reconstruct the right action of ![]() $\mathcal {U} \mathfrak {g}$ on a
$\mathcal {U} \mathfrak {g}$ on a ![]() $G$-equivariant
$G$-equivariant ![]() $\mathcal {U} \mathfrak {g}$-module
$\mathcal {U} \mathfrak {g}$-module ![]() $M$ by setting
$M$ by setting ![]() $m \cdot x := x \cdot m -\varrho (x)(m)$ for
$m \cdot x := x \cdot m -\varrho (x)(m)$ for ![]() $m \in M$ and
$m \in M$ and ![]() $x \in \mathfrak {g}$, where
$x \in \mathfrak {g}$, where ![]() $\varrho$ denotes the differential of the
$\varrho$ denotes the differential of the ![]() $G$-action.
$G$-action.
We will also denote by ![]() $\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm {op}})$ the category of
$\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm {op}})$ the category of ![]() $G$-equivariant finitely generated (left) modules over
$G$-equivariant finitely generated (left) modules over ![]() $\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm {op}}$. As above, since
$\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm {op}}$. As above, since ![]() $\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm {op}}$ is finitely generated both as a left and as a right
$\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm {op}}$ is finitely generated both as a left and as a right ![]() $\mathcal {U} \mathfrak {g}$-module, the tensor product
$\mathcal {U} \mathfrak {g}$-module, the tensor product ![]() $\otimes _{\mathcal {U} \mathfrak {g}}$ endows this category with a monoidal structure, and as explained above we have a fully faithful monoidal functor
$\otimes _{\mathcal {U} \mathfrak {g}}$ endows this category with a monoidal structure, and as explained above we have a fully faithful monoidal functor
If ![]() $M$ belongs to
$M$ belongs to ![]() $\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm {op}})$, then one obtains an extra
$\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm {op}})$, then one obtains an extra ![]() $\mathcal {U}_0 \mathfrak {g}$-action on
$\mathcal {U}_0 \mathfrak {g}$-action on ![]() $M$ by setting
$M$ by setting ![]() $x \cdot m = (x \otimes 1 - 1 \otimes x)m$ for
$x \cdot m = (x \otimes 1 - 1 \otimes x)m$ for ![]() $x \in \mathfrak {g}$ and
$x \in \mathfrak {g}$ and ![]() $m \in M$. Since
$m \in M$. Since ![]() $\mathcal {U}_0 \mathfrak {g}$ identifies canonically with the distribution algebra
$\mathcal {U}_0 \mathfrak {g}$ identifies canonically with the distribution algebra ![]() $\mathrm {Dist}(G_1)$ of the kernel
$\mathrm {Dist}(G_1)$ of the kernel ![]() $G_1$ of
$G_1$ of ![]() $\mathrm {Fr}$,
$\mathrm {Fr}$, ![]() $M$ becomes in this way a
$M$ becomes in this way a ![]() $G \ltimes G_1$-equivariant
$G \ltimes G_1$-equivariant ![]() $\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm {op}}$-module, where the action of
$\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm {op}}$-module, where the action of ![]() $G \ltimes G_1$ on
$G \ltimes G_1$ on ![]() $\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm {op}}$ is obtained from the
$\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm {op}}$ is obtained from the ![]() $G$-action by composition with the product morphism
$G$-action by composition with the product morphism ![]() $G \ltimes G_1 \to G$. As for (3.5), forgetting the right (respectively, left) action of
$G \ltimes G_1 \to G$. As for (3.5), forgetting the right (respectively, left) action of ![]() $\mathcal {U} \mathfrak {g}$ defines an equivalence of categories
$\mathcal {U} \mathfrak {g}$ defines an equivalence of categories
From the point of view of these equivalences and those in (3.5), the essential image of (3.6) consists of equivariant modules on which the action of ![]() $G \ltimes G_1$ factors through the product morphism
$G \ltimes G_1$ factors through the product morphism ![]() $G \ltimes G_1 \to G$.
$G \ltimes G_1 \to G$.
One can construct interesting objects in ![]() $\mathsf {HC}$ from
$\mathsf {HC}$ from ![]() $G$-modules as follows. Given
$G$-modules as follows. Given ![]() $V$ in
$V$ in ![]() $\mathsf {Rep}(G)$, we consider the Harish-Chandra bimodule
$\mathsf {Rep}(G)$, we consider the Harish-Chandra bimodule
where the left ![]() $\mathcal {U} \mathfrak {g}$-action is diagonal (with respect to the action on
$\mathcal {U} \mathfrak {g}$-action is diagonal (with respect to the action on ![]() $V$ obtained by differentiation, and the action on
$V$ obtained by differentiation, and the action on ![]() $\mathcal {U} \mathfrak {g}$ by left multiplication), the right
$\mathcal {U} \mathfrak {g}$ by left multiplication), the right ![]() $\mathcal {U} \mathfrak {g}$-action is induced by right multiplication on
$\mathcal {U} \mathfrak {g}$-action is induced by right multiplication on ![]() $\mathcal {U} \mathfrak {g}$, and the
$\mathcal {U} \mathfrak {g}$, and the ![]() $G$-action is diagonal (with respect to the given action on
$G$-action is diagonal (with respect to the given action on ![]() $V$ and the adjoint action on
$V$ and the adjoint action on ![]() $\mathcal {U} \mathfrak {g}$). In particular, for
$\mathcal {U} \mathfrak {g}$). In particular, for ![]() $x,y,z \in \mathcal {U} \mathfrak {g}$ and
$x,y,z \in \mathcal {U} \mathfrak {g}$ and ![]() $v \in V$ we have
$v \in V$ we have
where we use Sweedler's notation for the comultiplication in the Hopf algebra ![]() $\mathcal {U} \mathfrak {g}$. It is easily seen that the map
$\mathcal {U} \mathfrak {g}$. It is easily seen that the map ![]() $(x \otimes y) \otimes v \mapsto (x_{(1)} \cdot v) \otimes (x_{(2)} y)$ induces an isomorphism of
$(x \otimes y) \otimes v \mapsto (x_{(1)} \cdot v) \otimes (x_{(2)} y)$ induces an isomorphism of ![]() $G$-equivariant
$G$-equivariant ![]() $\mathcal {U} \mathfrak {g}$-bimodules
$\mathcal {U} \mathfrak {g}$-bimodules
where the tensor product over ![]() $\mathcal {U} \mathfrak {g}$ on the left-hand side is taken with respect to the morphism
$\mathcal {U} \mathfrak {g}$ on the left-hand side is taken with respect to the morphism ![]() $\mathcal {U} \mathfrak {g} \to \mathcal {U} \mathfrak {g} \otimes \mathcal {U} \mathfrak {g}^{\mathrm{op}}$ defined by
$\mathcal {U} \mathfrak {g} \to \mathcal {U} \mathfrak {g} \otimes \mathcal {U} \mathfrak {g}^{\mathrm{op}}$ defined by ![]() $x \mapsto x_{(1)} \otimes S(x_{(2)})$, where
$x \mapsto x_{(1)} \otimes S(x_{(2)})$, where ![]() $S$ is the antipode. In particular, the modules
$S$ is the antipode. In particular, the modules ![]() $V \otimes \mathcal {U} \mathfrak {g}$ are ‘induced from the diagonal’. For
$V \otimes \mathcal {U} \mathfrak {g}$ are ‘induced from the diagonal’. For ![]() $V,V'$ in
$V,V'$ in ![]() $\mathsf {Rep}(G)$, we have a canonical isomorphism of Harish-Chandra bimodules
$\mathsf {Rep}(G)$, we have a canonical isomorphism of Harish-Chandra bimodules
One can similarly consider, again for ![]() $V$ in
$V$ in ![]() $\mathsf {Rep}(G)$, the Harish-Chandra bimodule
$\mathsf {Rep}(G)$, the Harish-Chandra bimodule
where now the actions of ![]() $\mathcal {U} \mathfrak {g}$ are defined by
$\mathcal {U} \mathfrak {g}$ are defined by
for ![]() $x,y,z \in \mathcal {U} \mathfrak {g}$ and
$x,y,z \in \mathcal {U} \mathfrak {g}$ and ![]() $v \in V$ (and the
$v \in V$ (and the ![]() $G$-action is still diagonal). As above, we have an isomorphism of
$G$-action is still diagonal). As above, we have an isomorphism of ![]() $G$-equivariant
$G$-equivariant ![]() $\mathcal {U} \mathfrak {g}$-bimodules
$\mathcal {U} \mathfrak {g}$-bimodules
now given by ![]() $(x \otimes y) \otimes v \mapsto (xy_{(1)}) \otimes (S(y_{(2)}) \cdot v)$ for
$(x \otimes y) \otimes v \mapsto (xy_{(1)}) \otimes (S(y_{(2)}) \cdot v)$ for ![]() $x,y \in \mathcal {U} \mathfrak {g}$ and
$x,y \in \mathcal {U} \mathfrak {g}$ and ![]() $v \in V$. In particular, the objects
$v \in V$. In particular, the objects ![]() $V \otimes \mathcal {U} \mathfrak {g}$ and
$V \otimes \mathcal {U} \mathfrak {g}$ and ![]() $\mathcal {U} \mathfrak {g} \otimes V$ are isomorphic; explicitly, the isomorphism is given by
$\mathcal {U} \mathfrak {g} \otimes V$ are isomorphic; explicitly, the isomorphism is given by
for ![]() $x \in \mathcal {U} \mathfrak {g}$ and
$x \in \mathcal {U} \mathfrak {g}$ and ![]() $v \in V$.
$v \in V$.
3.5 Completed Harish-Chandra bimodules
We now need to adapt the considerations of § 3.4 to the setting of completed Harish-Chandra characters.
Let us set
so that ![]() $\mathcal {Z} = \mathscr {O}(\mathfrak {g}^{*(1)} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {D})$. For
$\mathcal {Z} = \mathscr {O}(\mathfrak {g}^{*(1)} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {D})$. For ![]() $\lambda,\mu \in \mathbb {X}$, we will also set
$\lambda,\mu \in \mathbb {X}$, we will also set
and will denote by ![]() $\mathfrak {D}^{\hat {\lambda },\hat {\mu }}$ the spectrum of the completion of
$\mathfrak {D}^{\hat {\lambda },\hat {\mu }}$ the spectrum of the completion of ![]() $\mathscr {O}(\mathfrak {D})$ with respect to the maximal ideal
$\mathscr {O}(\mathfrak {D})$ with respect to the maximal ideal ![]() $\mathcal {I}^{\lambda,\mu }$. Finally, we set
$\mathcal {I}^{\lambda,\mu }$. Finally, we set
(Note that ![]() $\mathcal {U}^{\hat {\lambda },\hat {\mu }}$ is not the completion of
$\mathcal {U}^{\hat {\lambda },\hat {\mu }}$ is not the completion of ![]() $\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm {op}}$ with respect to the ideal generated by
$\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm {op}}$ with respect to the ideal generated by ![]() $\mathcal {I}^{\lambda,\mu }$, since
$\mathcal {I}^{\lambda,\mu }$, since ![]() $\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm {op}}$ is not of finite type as an
$\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm {op}}$ is not of finite type as an ![]() $\mathscr {O}(\mathfrak {D})$-module.)
$\mathscr {O}(\mathfrak {D})$-module.)
The algebra ![]() $\mathscr {O}(\mathfrak {D}^{\hat {\lambda },\hat {\mu }})$ is Noetherian (see [Sta20, Tag 05GH]), hence
$\mathscr {O}(\mathfrak {D}^{\hat {\lambda },\hat {\mu }})$ is Noetherian (see [Sta20, Tag 05GH]), hence ![]() $\mathscr {O}(\mathfrak {g}^{*(1)} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {D}^{\hat {\lambda },\hat {\mu }})$ is Noetherian too, being finitely generated over
$\mathscr {O}(\mathfrak {g}^{*(1)} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {D}^{\hat {\lambda },\hat {\mu }})$ is Noetherian too, being finitely generated over ![]() $\mathscr {O}(\mathfrak {D}^{\hat {\lambda },\hat {\mu }})$ (see [Sta20, Tag 00FN]). Finally, since
$\mathscr {O}(\mathfrak {D}^{\hat {\lambda },\hat {\mu }})$ (see [Sta20, Tag 00FN]). Finally, since ![]() $\mathcal {U}^{\hat {\lambda },\hat {\mu }}$ is finitely generated as an
$\mathcal {U}^{\hat {\lambda },\hat {\mu }}$ is finitely generated as an ![]() $\mathscr {O}(\mathfrak {g}^{*(1)} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {D}^{\hat {\lambda },\hat {\mu }})$-module it is left and right Noetherian (as a non-commutative ring), and a
$\mathscr {O}(\mathfrak {g}^{*(1)} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {D}^{\hat {\lambda },\hat {\mu }})$-module it is left and right Noetherian (as a non-commutative ring), and a ![]() $\mathcal {U}^{\hat {\lambda },\hat {\mu }}$-module is finitely generated if and only if it is finitely generated as an
$\mathcal {U}^{\hat {\lambda },\hat {\mu }}$-module is finitely generated if and only if it is finitely generated as an ![]() $\mathscr {O}(\mathfrak {g}^{*(1)} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {D}^{\hat {\lambda },\hat {\mu }})$-module.
$\mathscr {O}(\mathfrak {g}^{*(1)} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {D}^{\hat {\lambda },\hat {\mu }})$-module.
The ![]() $G$-action on
$G$-action on ![]() $\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm {op}}$ induces an algebraic
$\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm {op}}$ induces an algebraic ![]() $G$-module structure on
$G$-module structure on ![]() $\mathcal {U}^{\hat {\lambda },\hat {\mu }}$, and we can consider the category of
$\mathcal {U}^{\hat {\lambda },\hat {\mu }}$, and we can consider the category of ![]() $G$-equivariant finitely generated modules over this algebra; this (abelian) category will be denoted by
$G$-equivariant finitely generated modules over this algebra; this (abelian) category will be denoted by ![]() $\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\hat {\lambda },\hat {\mu }})$. The full subcategory whose objects are the modules
$\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\hat {\lambda },\hat {\mu }})$. The full subcategory whose objects are the modules ![]() $M$ such that the differential of the
$M$ such that the differential of the ![]() $G$-action coincides with the action given by
$G$-action coincides with the action given by ![]() $x \cdot m=xm-mx$ for
$x \cdot m=xm-mx$ for ![]() $x \in \mathfrak {g}$ and
$x \in \mathfrak {g}$ and ![]() $m \in M$ will be denoted
$m \in M$ will be denoted ![]() $\mathsf {HC}^{\hat {\lambda },\hat {\mu }}$; its objects will be called completed Harish-Chandra bimodules.
$\mathsf {HC}^{\hat {\lambda },\hat {\mu }}$; its objects will be called completed Harish-Chandra bimodules.
Given ![]() $\lambda,\mu \in \mathbb {X}$, we have a natural exact functor
$\lambda,\mu \in \mathbb {X}$, we have a natural exact functor
defined by
which restricts to a functor ![]() $\mathsf {HC} \to \mathsf {HC}^{\hat {\lambda },\hat {\mu }}$. (Exactness of this functor follows from the fact that
$\mathsf {HC} \to \mathsf {HC}^{\hat {\lambda },\hat {\mu }}$. (Exactness of this functor follows from the fact that ![]() $\mathscr {O}(\mathfrak {D}^{\hat {\lambda },\hat {\mu }})$ is flat over
$\mathscr {O}(\mathfrak {D}^{\hat {\lambda },\hat {\mu }})$ is flat over ![]() $\mathscr {O}(\mathfrak {D})$; see [Sta20, Tag 00MB].) We will denote by
$\mathscr {O}(\mathfrak {D})$; see [Sta20, Tag 00MB].) We will denote by
the full additive subcategory of ![]() $\mathsf {HC}^{\hat {\lambda },\hat {\mu }}$ whose objects are direct summands of objects of the form
$\mathsf {HC}^{\hat {\lambda },\hat {\mu }}$ whose objects are direct summands of objects of the form ![]() $\mathsf {C}^{\lambda,\mu } (V \otimes \mathcal {U} \mathfrak {g})$ with
$\mathsf {C}^{\lambda,\mu } (V \otimes \mathcal {U} \mathfrak {g})$ with ![]() $V$ in
$V$ in ![]() $\mathsf {Rep}(G)$. (In view of the comments at the end of § 3.4, objects in this category will sometimes be referred to as completed diagonally induced Harish-Chandra bimodules.) In the case where
$\mathsf {Rep}(G)$. (In view of the comments at the end of § 3.4, objects in this category will sometimes be referred to as completed diagonally induced Harish-Chandra bimodules.) In the case where ![]() $\lambda =\mu$, we will set
$\lambda =\mu$, we will set
where ![]() $\Bbbk$ is the trivial
$\Bbbk$ is the trivial ![]() $G$-module.
$G$-module.
For later use, we also introduce some completed bimodules which are closely related to the translation functors for ![]() $G$-modules (see § 6.3 below for details). Recall that a weight
$G$-modules (see § 6.3 below for details). Recall that a weight ![]() $\lambda \in \mathbb {X}$ is said to belong to the fundamental alcove (respectively, to the closure of the fundamental alcove) if it satisfies
$\lambda \in \mathbb {X}$ is said to belong to the fundamental alcove (respectively, to the closure of the fundamental alcove) if it satisfies
for any positive root ![]() $\alpha$. With this notation, the set of weights which belong to the closure of the fundamental alcove is a fundamental domain for the
$\alpha$. With this notation, the set of weights which belong to the closure of the fundamental alcove is a fundamental domain for the ![]() $({W_{\mathrm {aff}}},\bullet )$-action on
$({W_{\mathrm {aff}}},\bullet )$-action on ![]() $\mathbb {X}$. Moreover, if
$\mathbb {X}$. Moreover, if ![]() $\lambda \in \mathbb {X}$ belongs to the closure of the fundamental alcove, then its stabilizer in
$\lambda \in \mathbb {X}$ belongs to the closure of the fundamental alcove, then its stabilizer in ![]() ${W_{\mathrm {aff}}}$ is the parabolic subgroup generated by the elements
${W_{\mathrm {aff}}}$ is the parabolic subgroup generated by the elements ![]() $s \in {S_{\mathrm {aff}}}$ such that
$s \in {S_{\mathrm {aff}}}$ such that ![]() $s \bullet \lambda =\lambda$; see [Reference JantzenJan03, §II.6.3].
$s \bullet \lambda =\lambda$; see [Reference JantzenJan03, §II.6.3].
Remark 3.3 The weight lattice ![]() $\mathbb {X}$ contains weights which belong to the fundamental alcove if and only if
$\mathbb {X}$ contains weights which belong to the fundamental alcove if and only if ![]() $p \geq h$, where
$p \geq h$, where ![]() $h$ is the Coxeter number of
$h$ is the Coxeter number of ![]() $G$; see [Reference JantzenJan03, § 6.2]. Even though this condition will be imposed only in § 6, some of our statements in § 5 involve weights in the fundamental alcove; these statements will simply be empty in the case where
$G$; see [Reference JantzenJan03, § 6.2]. Even though this condition will be imposed only in § 6, some of our statements in § 5 involve weights in the fundamental alcove; these statements will simply be empty in the case where ![]() $p< h$.
$p< h$.
Let ![]() $\mathbb {X}^{+} \subset \mathbb {X}$ be the subset of dominant weights determined by
$\mathbb {X}^{+} \subset \mathbb {X}$ be the subset of dominant weights determined by ![]() $\mathfrak {R}^{+}$. For any
$\mathfrak {R}^{+}$. For any ![]() $\nu \in \mathbb {X}^{+}$, we will denote by
$\nu \in \mathbb {X}^{+}$, we will denote by ![]() $\mathsf {L}(\nu )$ the simple
$\mathsf {L}(\nu )$ the simple ![]() $G$-module with highest weight
$G$-module with highest weight ![]() $\nu$, that is, the unique simple submodule in
$\nu$, that is, the unique simple submodule in ![]() $\mathrm {Ind}_{B}^{G}(\nu )$. Given two weights
$\mathrm {Ind}_{B}^{G}(\nu )$. Given two weights ![]() $\lambda,\mu \in \mathbb {X}$ which belong to the closure of the fundamental alcove, we set
$\lambda,\mu \in \mathbb {X}$ which belong to the closure of the fundamental alcove, we set
where ![]() $\nu$ is the unique dominant
$\nu$ is the unique dominant ![]() $W$-translate of
$W$-translate of ![]() $\lambda -\mu$.
$\lambda -\mu$.
3.6 Comparison of completions
For notational simplicity, let us now fix a subset ![]() $\Lambda \subset \mathbb {X}$ such that the map
$\Lambda \subset \mathbb {X}$ such that the map ![]() $\lambda \mapsto {{\tilde {\lambda }}}$ restricts to a bijection
$\lambda \mapsto {{\tilde {\lambda }}}$ restricts to a bijection ![]() $\Lambda \xrightarrow {\sim } \mathfrak {t}^{*}_{\mathbb {F}_p}/(W,\bullet )$. (In other words,
$\Lambda \xrightarrow {\sim } \mathfrak {t}^{*}_{\mathbb {F}_p}/(W,\bullet )$. (In other words, ![]() $\Lambda$ is a set of representatives for the
$\Lambda$ is a set of representatives for the ![]() $\bullet$-action of
$\bullet$-action of ![]() ${W_{\mathrm {ext}}}$ on
${W_{\mathrm {ext}}}$ on ![]() $\mathbb {X}$.)
$\mathbb {X}$.)
We will denote by ![]() $\mathcal {I} \subset \mathscr {O}(\mathfrak {t}^{*(1)}/W)={Z_{\mathrm {HC}}} \cap {Z_{\mathrm {Fr}}}$ the maximal ideal corresponding to the image of
$\mathcal {I} \subset \mathscr {O}(\mathfrak {t}^{*(1)}/W)={Z_{\mathrm {HC}}} \cap {Z_{\mathrm {Fr}}}$ the maximal ideal corresponding to the image of ![]() $0 \in \mathfrak {t}^{*(1)}$. Then, in the notation of § 3.2,
$0 \in \mathfrak {t}^{*(1)}$. Then, in the notation of § 3.2, ![]() $\mathcal {I} \cdot {Z_{\mathrm {Fr}}}$ is the ideal of definition of
$\mathcal {I} \cdot {Z_{\mathrm {Fr}}}$ is the ideal of definition of ![]() $\mathcal {N}^{*(1)} \subset \mathfrak {g}^{*(1)}$, and each ideal
$\mathcal {N}^{*(1)} \subset \mathfrak {g}^{*(1)}$, and each ideal ![]() $\mathcal {I}^{\lambda,\mu }$ contains
$\mathcal {I}^{\lambda,\mu }$ contains ![]() $\mathcal {I} \cdot \mathscr {O}(\mathfrak {D})$. We will denote by
$\mathcal {I} \cdot \mathscr {O}(\mathfrak {D})$. We will denote by ![]() $\mathfrak {D}^{\wedge }$ the spectrum of the completion of
$\mathfrak {D}^{\wedge }$ the spectrum of the completion of ![]() $\mathscr {O}(\mathfrak {D})$ with respect to the ideal
$\mathscr {O}(\mathfrak {D})$ with respect to the ideal ![]() $\mathcal {I} \cdot \mathscr {O}(\mathfrak {D})$. Note that since
$\mathcal {I} \cdot \mathscr {O}(\mathfrak {D})$. Note that since ![]() $\mathscr {O}(\mathfrak {D})$ is finite as an
$\mathscr {O}(\mathfrak {D})$ is finite as an ![]() $\mathscr {O}(\mathfrak {t}^{*(1)}/W)$-module (because the morphisms
$\mathscr {O}(\mathfrak {t}^{*(1)}/W)$-module (because the morphisms ![]() $\mathfrak {t}^{*} \to \mathfrak {t}^{*(1)}$ and
$\mathfrak {t}^{*} \to \mathfrak {t}^{*(1)}$ and ![]() $\mathfrak {t}^{*(1)} \to \mathfrak {t}^{*(1)}/W$ are finite), if we denote by
$\mathfrak {t}^{*(1)} \to \mathfrak {t}^{*(1)}/W$ are finite), if we denote by ![]() $\mathscr {O}(\mathfrak {t}^{*(1)}/W)^{\wedge }$ the completion of
$\mathscr {O}(\mathfrak {t}^{*(1)}/W)^{\wedge }$ the completion of ![]() $\mathscr {O}(\mathfrak {t}^{*(1)}/W)$ with respect to
$\mathscr {O}(\mathfrak {t}^{*(1)}/W)$ with respect to ![]() $\mathcal {I}$ we have a canonical isomorphism
$\mathcal {I}$ we have a canonical isomorphism
Lemma 3.4 The natural morphism
is a ring isomorphism.
Proof. The lemma will basically follow from the observation that the closed points in the fiber of the morphism (3.4) over the (closed) point corresponding to ![]() $\mathcal {I}$ are those corresponding to the ideals
$\mathcal {I}$ are those corresponding to the ideals ![]() $\mathfrak {m}^{\lambda }$ with
$\mathfrak {m}^{\lambda }$ with ![]() $\lambda \in \mathbb {X}$, which itself follows from the fact that the fiber of
$\lambda \in \mathbb {X}$, which itself follows from the fact that the fiber of ![]() $\mathrm {AS} : \mathfrak {t}^{*} \to \mathfrak {t}^{*(1)}$ over
$\mathrm {AS} : \mathfrak {t}^{*} \to \mathfrak {t}^{*(1)}$ over ![]() $0$ is
$0$ is ![]() $\mathfrak {t}^{*}_{\mathbb {F}_p}$.
$\mathfrak {t}^{*}_{\mathbb {F}_p}$.
More precisely, the morphism considered in this statement is the product of the morphisms ![]() $\mathscr {O}(\mathfrak {D}^{\wedge }) \to \mathscr {O}(\mathfrak {D}^{\hat {\lambda },\hat {\mu }})$ induced by the natural morphisms
$\mathscr {O}(\mathfrak {D}^{\wedge }) \to \mathscr {O}(\mathfrak {D}^{\hat {\lambda },\hat {\mu }})$ induced by the natural morphisms ![]() $\mathscr {O}(\mathfrak {D})/(\mathcal {I}^{n} \cdot \mathscr {O}(\mathfrak {D})) \twoheadrightarrow \mathscr {O}(\mathfrak {D})/(\mathcal {I}^{\lambda,\mu })^{n}$. This morphism is clearly a ring morphism; to prove that it is invertible we will construct its inverse.
$\mathscr {O}(\mathfrak {D})/(\mathcal {I}^{n} \cdot \mathscr {O}(\mathfrak {D})) \twoheadrightarrow \mathscr {O}(\mathfrak {D})/(\mathcal {I}^{\lambda,\mu })^{n}$. This morphism is clearly a ring morphism; to prove that it is invertible we will construct its inverse.
Let us fix some ![]() $n \geq 1$, and consider the quotient
$n \geq 1$, and consider the quotient ![]() $\mathscr {O}(\mathfrak {D})/(\mathcal {I}^{n} \cdot \mathscr {O}(\mathfrak {D}))$. Here, as explained above,
$\mathscr {O}(\mathfrak {D})/(\mathcal {I}^{n} \cdot \mathscr {O}(\mathfrak {D}))$. Here, as explained above, ![]() $\mathscr {O}(\mathfrak {D})={Z_{\mathrm {HC}}} \otimes _{{Z_{\mathrm {HC}}} \cap {Z_{\mathrm {Fr}}}} {Z_{\mathrm {HC}}}$ is a finite
$\mathscr {O}(\mathfrak {D})={Z_{\mathrm {HC}}} \otimes _{{Z_{\mathrm {HC}}} \cap {Z_{\mathrm {Fr}}}} {Z_{\mathrm {HC}}}$ is a finite ![]() $\mathscr {O}(\mathfrak {t}^{*(1)}/W)$-module; therefore, this algebra is finite-dimensional. Its maximal ideals are in bijection with the maximal ideals of
$\mathscr {O}(\mathfrak {t}^{*(1)}/W)$-module; therefore, this algebra is finite-dimensional. Its maximal ideals are in bijection with the maximal ideals of ![]() $\mathscr {O}(\mathfrak {D})$ containing
$\mathscr {O}(\mathfrak {D})$ containing ![]() $\mathcal {I} \cdot \mathscr {O}(\mathfrak {D})$, hence with
$\mathcal {I} \cdot \mathscr {O}(\mathfrak {D})$, hence with ![]() $\Lambda \times \Lambda$ through
$\Lambda \times \Lambda$ through ![]() $(\lambda,\mu ) \mapsto \mathcal {I}^{\lambda,\mu } / \mathcal {I}^{n} \cdot \mathscr {O}(\mathfrak {D})$. In view of the general theory of Artin rings (see, for example, [Reference Atiyah and MacdonaldAM69, Chap. 8]), for any
$(\lambda,\mu ) \mapsto \mathcal {I}^{\lambda,\mu } / \mathcal {I}^{n} \cdot \mathscr {O}(\mathfrak {D})$. In view of the general theory of Artin rings (see, for example, [Reference Atiyah and MacdonaldAM69, Chap. 8]), for any ![]() $\lambda,\mu \in \Lambda$ the quotient
$\lambda,\mu \in \Lambda$ the quotient
does not depend on ![]() $m$ for
$m$ for ![]() $m \gg 0$, and the natural morphism from
$m \gg 0$, and the natural morphism from ![]() $\mathscr {O}(\mathfrak {D})/(\mathcal {I}^{n} \cdot \mathscr {O}(\mathfrak {D}))$ to the product of these rings (over
$\mathscr {O}(\mathfrak {D})/(\mathcal {I}^{n} \cdot \mathscr {O}(\mathfrak {D}))$ to the product of these rings (over ![]() $\Lambda \times \Lambda$) is an isomorphism.
$\Lambda \times \Lambda$) is an isomorphism.
We are now ready to define the wished-for inverse morphism
For this it suffices to define, for any ![]() $n \geq 1$, a ring morphism
$n \geq 1$, a ring morphism
We fix ![]() $m$ such that the natural morphism
$m$ such that the natural morphism
is an isomorphism. Then we have natural ring morphisms
Composing with the inverse of (3.10), we deduce the desired map (3.9).
It is easy (and left to the reader) to check that the two morphisms considered above are inverse to each other.
Remark 3.5 If we denote by ![]() ${Z^{\wedge}_{\mathrm {HC}}}$ the completion of
${Z^{\wedge}_{\mathrm {HC}}}$ the completion of ![]() ${Z_{\mathrm {HC}}}$ with respect to the ideal
${Z_{\mathrm {HC}}}$ with respect to the ideal ![]() $\mathcal {I} \cdot {Z_{\mathrm {HC}}}$, then we have as in (3.8) a canonical isomorphism
$\mathcal {I} \cdot {Z_{\mathrm {HC}}}$, then we have as in (3.8) a canonical isomorphism ![]() $\mathscr {O}(\mathfrak {t}^{*(1)}/W)^{\wedge } \otimes _{\mathscr {O}(\mathfrak {t}^{*(1)}/W)} {Z_{\mathrm {HC}}} \xrightarrow {\sim } {Z^{\wedge }_{\mathrm {HC}}}$, and therefore a canonical isomorphism
$\mathscr {O}(\mathfrak {t}^{*(1)}/W)^{\wedge } \otimes _{\mathscr {O}(\mathfrak {t}^{*(1)}/W)} {Z_{\mathrm {HC}}} \xrightarrow {\sim } {Z^{\wedge }_{\mathrm {HC}}}$, and therefore a canonical isomorphism
Denoting by ![]() ${Z^{\hat {\lambda }}_{\mathrm {HC}}}$ the completion of
${Z^{\hat {\lambda }}_{\mathrm {HC}}}$ the completion of ![]() ${Z_{\mathrm {HC}}}$ with respect to the ideal
${Z_{\mathrm {HC}}}$ with respect to the ideal ![]() $\mathfrak {m}^{\lambda }$, for
$\mathfrak {m}^{\lambda }$, for ![]() $\lambda \in \mathbb {X}$, the same considerations as for Lemma 3.4 show that we have a canonical isomorphism
$\lambda \in \mathbb {X}$, the same considerations as for Lemma 3.4 show that we have a canonical isomorphism
from which we obtain a decomposition
This decomposition is in fact ‘the same’ as the decomposition of Lemma 3.4, in the sense that for any ![]() $\lambda,\mu \in \Lambda$ we have an identification
$\lambda,\mu \in \Lambda$ we have an identification
We will also set
where the isomorphism uses (3.8). Then, as in § 3.5, ![]() $\mathcal {U}^{\wedge }$ is a left and right Noetherian ring, endowed with a structure of an algebraic
$\mathcal {U}^{\wedge }$ is a left and right Noetherian ring, endowed with a structure of an algebraic ![]() $G$-module, and Lemma 3.4 implies that the natural morphism
$G$-module, and Lemma 3.4 implies that the natural morphism
is an algebra isomorphism. Below we will consider various categories of ![]() $\mathcal {U}^{\wedge }$-modules; in fact we have
$\mathcal {U}^{\wedge }$-modules; in fact we have
 \begin{align*} \mathcal{U}^{\wedge} &\cong ( \mathcal{U} \mathfrak{g} \otimes_{\mathscr{O}(\mathfrak{t}^{*(1)}/W)} \mathscr{O}(\mathfrak{t}^{*(1)}/W)^{\wedge} ) \otimes_{{Z_{\mathrm{Fr}}} \otimes_{\mathscr{O}(\mathfrak{t}^{*(1)}/W)} \mathscr{O}(\mathfrak{t}^{*(1)}/W)^{\wedge}}\\ &\quad \times ( \mathcal{U} \mathfrak{g} \otimes_{\mathscr{O}(\mathfrak{t}^{*(1)}/W)} \mathscr{O}(\mathfrak{t}^{*(1)}/W)^{\wedge} )^{\mathrm{op}}; \end{align*}
\begin{align*} \mathcal{U}^{\wedge} &\cong ( \mathcal{U} \mathfrak{g} \otimes_{\mathscr{O}(\mathfrak{t}^{*(1)}/W)} \mathscr{O}(\mathfrak{t}^{*(1)}/W)^{\wedge} ) \otimes_{{Z_{\mathrm{Fr}}} \otimes_{\mathscr{O}(\mathfrak{t}^{*(1)}/W)} \mathscr{O}(\mathfrak{t}^{*(1)}/W)^{\wedge}}\\ &\quad \times ( \mathcal{U} \mathfrak{g} \otimes_{\mathscr{O}(\mathfrak{t}^{*(1)}/W)} \mathscr{O}(\mathfrak{t}^{*(1)}/W)^{\wedge} )^{\mathrm{op}}; \end{align*}
a ![]() $\mathcal {U}^{\wedge }$-module is therefore the same as a
$\mathcal {U}^{\wedge }$-module is therefore the same as a ![]() $(\mathcal {U} \mathfrak {g} \otimes _{\mathscr {O}(\mathfrak {t}^{*(1)}/W)} \mathscr {O}(\mathfrak {t}^{*(1)}/W)^{\wedge })$-bimodule on which the left and right actions of
$(\mathcal {U} \mathfrak {g} \otimes _{\mathscr {O}(\mathfrak {t}^{*(1)}/W)} \mathscr {O}(\mathfrak {t}^{*(1)}/W)^{\wedge })$-bimodule on which the left and right actions of ![]() ${Z_{\mathrm {Fr}}} \otimes _{\mathscr {O}(\mathfrak {t}^{*(1)}/W)} \mathscr {O}(\mathfrak {t}^{*(1)}/W)^{\wedge }$ coincide.
${Z_{\mathrm {Fr}}} \otimes _{\mathscr {O}(\mathfrak {t}^{*(1)}/W)} \mathscr {O}(\mathfrak {t}^{*(1)}/W)^{\wedge }$ coincide.
We will denote by ![]() $\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\wedge })$ the abelian category of
$\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\wedge })$ the abelian category of ![]() $G$-equivariant finitely generated
$G$-equivariant finitely generated ![]() $\mathcal {U}^{\wedge }$-modules. In view of (3.12), we have a canonical equivalence of categories
$\mathcal {U}^{\wedge }$-modules. In view of (3.12), we have a canonical equivalence of categories
We also have a canonical exact functor
defined by ![]() $\mathsf {C}^{\wedge }(M)=\mathscr {O}(\mathfrak {D}^{\wedge }) \otimes _{\mathscr {O}(\mathfrak {D})} M$. For the same reasons as above, for any
$\mathsf {C}^{\wedge }(M)=\mathscr {O}(\mathfrak {D}^{\wedge }) \otimes _{\mathscr {O}(\mathfrak {D})} M$. For the same reasons as above, for any ![]() $M$ in
$M$ in ![]() $\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm {op}})$ we have a canonical isomorphism
$\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm {op}})$ we have a canonical isomorphism
An object ![]() $M$ in
$M$ in ![]() $\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\wedge })$ will be called a completed Harish-Chandra bimodule if the differential of the
$\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\wedge })$ will be called a completed Harish-Chandra bimodule if the differential of the ![]() $G$-action coincides with the action given by
$G$-action coincides with the action given by ![]() $x \cdot m = xm-mx$ for
$x \cdot m = xm-mx$ for ![]() $x \in \mathfrak {g}$ and
$x \in \mathfrak {g}$ and ![]() $m \in M$, and we will denote by
$m \in M$, and we will denote by ![]() $\mathsf {HC}^{\wedge }$ the full subcategory of
$\mathsf {HC}^{\wedge }$ the full subcategory of ![]() $\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\wedge })$ consisting of such objects; this terminology is compatible with that of § 3.5 in the sense that (3.13) restricts to an equivalence of categories
$\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\wedge })$ consisting of such objects; this terminology is compatible with that of § 3.5 in the sense that (3.13) restricts to an equivalence of categories
We will denote by ![]() $\mathsf {HC}^{\wedge }_\mathrm {diag}$ the full additive subcategory of
$\mathsf {HC}^{\wedge }_\mathrm {diag}$ the full additive subcategory of ![]() $\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\wedge })$ whose objects are the direct summands of objects of the form
$\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\wedge })$ whose objects are the direct summands of objects of the form ![]() $\mathsf {C}^{\wedge }(V \otimes \mathcal {U} \mathfrak {g})$ with
$\mathsf {C}^{\wedge }(V \otimes \mathcal {U} \mathfrak {g})$ with ![]() $V$ in
$V$ in ![]() $\mathsf {Rep}(G)$. With this definition, (3.13) restricts further to an equivalence of categories
$\mathsf {Rep}(G)$. With this definition, (3.13) restricts further to an equivalence of categories
3.7 Monoidal structure
We now want to define some analogue of the monoidal structure on ![]() $\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm {op}})$ for the categories
$\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm {op}})$ for the categories ![]() $\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\hat {\lambda },\hat {\mu }})$. More specifically, given
$\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\hat {\lambda },\hat {\mu }})$. More specifically, given ![]() $\lambda,\mu,\nu$ in
$\lambda,\mu,\nu$ in ![]() $\mathbb {X}$, we want to define a canonical bifunctor
$\mathbb {X}$, we want to define a canonical bifunctor
right exact on both sides, which restricts to a bifunctor
these bifunctors satisfying natural unit and associativity axioms. Explicitly, we require that:
– if
 $\mu =\lambda$ we have a canonical isomorphism of functors
and if
$\mu =\lambda$ we have a canonical isomorphism of functors
and if \[ \mathcal{U}^{\hat{\lambda}} {\widehat{\otimes}}_{\mathcal{U} \mathfrak{g}} (-) \cong \mathrm{id}, \]
\[ \mathcal{U}^{\hat{\lambda}} {\widehat{\otimes}}_{\mathcal{U} \mathfrak{g}} (-) \cong \mathrm{id}, \] $\nu =\mu$ we have a canonical isomorphism
$\nu =\mu$ we have a canonical isomorphism
 \[ (-) {\widehat{\otimes}}_{\mathcal{U} \mathfrak{g}} \mathcal{U}^{\hat{\mu}} \cong \mathrm{id}; \]
\[ (-) {\widehat{\otimes}}_{\mathcal{U} \mathfrak{g}} \mathcal{U}^{\hat{\mu}} \cong \mathrm{id}; \]– for four weights
 $\lambda,\mu,\nu,\eta \in \mathbb {X}$ we have an isomorphism
of functors from
$\lambda,\mu,\nu,\eta \in \mathbb {X}$ we have an isomorphism
of functors from \[ ( (-) {\widehat{\otimes}}_{\mathcal{U} \mathfrak{g}} (-) ) {\widehat{\otimes}}_{\mathcal{U} \mathfrak{g}} (-) \xrightarrow{\sim} (-) {\widehat{\otimes}}_{\mathcal{U} \mathfrak{g}} ( (-) {\widehat{\otimes}}_{\mathcal{U} \mathfrak{g}} (-) ) \]to
\[ ( (-) {\widehat{\otimes}}_{\mathcal{U} \mathfrak{g}} (-) ) {\widehat{\otimes}}_{\mathcal{U} \mathfrak{g}} (-) \xrightarrow{\sim} (-) {\widehat{\otimes}}_{\mathcal{U} \mathfrak{g}} ( (-) {\widehat{\otimes}}_{\mathcal{U} \mathfrak{g}} (-) ) \]to \[ \mathsf{Mod}^{G}_{\mathrm{fg}}(\mathcal{U}^{\hat{\lambda},\hat{\mu}}) \times \mathsf{Mod}^{G}_{\mathrm{fg}}(\mathcal{U}^{\hat{\mu},\hat{\nu}}) \times \mathsf{Mod}^{G}_{\mathrm{fg}}(\mathcal{U}^{\hat{\nu},\hat{\eta}}) \]
\[ \mathsf{Mod}^{G}_{\mathrm{fg}}(\mathcal{U}^{\hat{\lambda},\hat{\mu}}) \times \mathsf{Mod}^{G}_{\mathrm{fg}}(\mathcal{U}^{\hat{\mu},\hat{\nu}}) \times \mathsf{Mod}^{G}_{\mathrm{fg}}(\mathcal{U}^{\hat{\nu},\hat{\eta}}) \] $\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\hat {\lambda },\hat {\eta }})$.
$\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\hat {\lambda },\hat {\eta }})$.
In particular, in the case where ![]() $\lambda =\mu =\nu$, this construction will equip
$\lambda =\mu =\nu$, this construction will equip ![]() $\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\hat {\lambda },\hat {\lambda }})$ with the structure of a monoidal category.
$\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\hat {\lambda },\hat {\lambda }})$ with the structure of a monoidal category.
For this we can assume that all the weights involved belong to the subset ![]() $\Lambda$ chosen in § 3.6. It therefore suffices to construct a monoidal structure of the category
$\Lambda$ chosen in § 3.6. It therefore suffices to construct a monoidal structure of the category ![]() $\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\wedge })$, with monoidal unit
$\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\wedge })$, with monoidal unit ![]() $\mathsf {C}^{\wedge }(\Bbbk \otimes \mathcal {U} \mathfrak {g})$; the bifunctor (3.15) will then be deduced by restriction to the factor
$\mathsf {C}^{\wedge }(\Bbbk \otimes \mathcal {U} \mathfrak {g})$; the bifunctor (3.15) will then be deduced by restriction to the factor ![]() $\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\hat {\lambda },\hat {\mu }}) \times \mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\hat {\mu },\hat {\nu }})$ in the decomposition (3.13).
$\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\hat {\lambda },\hat {\mu }}) \times \mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\hat {\mu },\hat {\nu }})$ in the decomposition (3.13).
Recall that we have
Given ![]() $M,N$ in
$M,N$ in ![]() $\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\wedge })$, we set
$\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\wedge })$, we set
where the right action of ![]() $\mathcal {U} \mathfrak {g} \otimes _{\mathscr {O}(\mathfrak {t}^{*(1)}/W)} \mathscr {O}(\mathfrak {t}^{*(1)}/W)^{\wedge }$ on
$\mathcal {U} \mathfrak {g} \otimes _{\mathscr {O}(\mathfrak {t}^{*(1)}/W)} \mathscr {O}(\mathfrak {t}^{*(1)}/W)^{\wedge }$ on ![]() $M$ is induced by the action of the second copy of
$M$ is induced by the action of the second copy of ![]() $\mathcal {U} \mathfrak {g}$, and the left action on
$\mathcal {U} \mathfrak {g}$, and the left action on ![]() $N$ is induced by the action of the first copy of
$N$ is induced by the action of the first copy of ![]() $\mathcal {U} \mathfrak {g}$. This tensor product admits compatible actions of
$\mathcal {U} \mathfrak {g}$. This tensor product admits compatible actions of ![]() $\mathcal {U}\mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U}\mathfrak {g}^{\mathrm{op}}$ (induced by the action of the first copy of
$\mathcal {U}\mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U}\mathfrak {g}^{\mathrm{op}}$ (induced by the action of the first copy of ![]() $\mathcal {U} \mathfrak {g}$ on
$\mathcal {U} \mathfrak {g}$ on ![]() $M$, and of the second copy of
$M$, and of the second copy of ![]() $\mathcal {U} \mathfrak {g}$ on
$\mathcal {U} \mathfrak {g}$ on ![]() $N$) and of
$N$) and of ![]() $\mathscr {O}(\mathfrak {t}^{*(1)}/W)^{\wedge }$, hence of
$\mathscr {O}(\mathfrak {t}^{*(1)}/W)^{\wedge }$, hence of ![]() $\mathcal {U}^{\wedge }$. This module is, moreover, finitely generated, since it is finitely generated over
$\mathcal {U}^{\wedge }$. This module is, moreover, finitely generated, since it is finitely generated over ![]() $\mathscr {O}(\mathfrak {g}^{*(1)}) \otimes _{\mathscr {O}(\mathfrak {t}^{*(1)}/W)} \mathscr {O}(\mathfrak {t}^{*(1)}/W)^{\wedge }$, and it admits a canonical (diagonal)
$\mathscr {O}(\mathfrak {g}^{*(1)}) \otimes _{\mathscr {O}(\mathfrak {t}^{*(1)}/W)} \mathscr {O}(\mathfrak {t}^{*(1)}/W)^{\wedge }$, and it admits a canonical (diagonal) ![]() $G$-module structure. In this way we obtain a bifunctor
$G$-module structure. In this way we obtain a bifunctor
which is easily seen to provide a monoidal structure with monoidal unit ![]() $\mathsf {C}^{\wedge }(\Bbbk \otimes \mathcal {U} \mathfrak {g})$. It is easily seen also that the functor (3.14) has a canonical monoidal structure; using (3.7), we deduce that the full subcategory
$\mathsf {C}^{\wedge }(\Bbbk \otimes \mathcal {U} \mathfrak {g})$. It is easily seen also that the functor (3.14) has a canonical monoidal structure; using (3.7), we deduce that the full subcategory ![]() $\mathsf {HC}^{\wedge }_\mathrm {diag}$ is a monoidal subcategory.
$\mathsf {HC}^{\wedge }_\mathrm {diag}$ is a monoidal subcategory.
If ![]() $\lambda,\mu,\nu \in \mathbb {X}$ and if
$\lambda,\mu,\nu \in \mathbb {X}$ and if ![]() $M$ belongs to
$M$ belongs to ![]() $\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\hat {\lambda },\hat {\mu }})$ and
$\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\hat {\lambda },\hat {\mu }})$ and ![]() $N$ belongs to
$N$ belongs to ![]() $\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\hat {\mu },\hat {\nu }})$, then seeing
$\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\hat {\mu },\hat {\nu }})$, then seeing ![]() $M$ and
$M$ and ![]() $N$ as objects in
$N$ as objects in ![]() $\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\wedge })$ via (3.13), the product
$\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\wedge })$ via (3.13), the product ![]() $M {\widehat{\otimes}}_{\mathcal {U} \mathfrak {g}} N$ belongs to the factor
$M {\widehat{\otimes}}_{\mathcal {U} \mathfrak {g}} N$ belongs to the factor ![]() $\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\hat {\lambda },\hat {\nu }})$, which provides the desired bifunctor (3.15). (In fact, the action of the left copy of
$\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\hat {\lambda },\hat {\nu }})$, which provides the desired bifunctor (3.15). (In fact, the action of the left copy of ![]() ${Z_{\mathrm {HC}}}$ factors through an action of
${Z_{\mathrm {HC}}}$ factors through an action of ![]() ${Z^{\hat {\lambda }}_{\mathrm {HC}}}$, and that of the right copy factors through an action of
${Z^{\hat {\lambda }}_{\mathrm {HC}}}$, and that of the right copy factors through an action of ![]() ${Z^{\hat {\nu }}_{\mathrm {HC}}}$, which justifies the claim in view of (3.11).) From the corresponding property for
${Z^{\hat {\nu }}_{\mathrm {HC}}}$, which justifies the claim in view of (3.11).) From the corresponding property for ![]() $\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\wedge })$ we deduce that the subcategories
$\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\wedge })$ we deduce that the subcategories ![]() $\mathsf {HC}^{\hat {\lambda },\hat {\mu }}$ and
$\mathsf {HC}^{\hat {\lambda },\hat {\mu }}$ and ![]() $\mathsf {HC}^{\hat {\lambda },\hat {\mu }}_\mathrm {diag}$ are stable (in the obvious sense) under this bifunctor. In this setting the functor
$\mathsf {HC}^{\hat {\lambda },\hat {\mu }}_\mathrm {diag}$ are stable (in the obvious sense) under this bifunctor. In this setting the functor ![]() $\mathsf {C}^{\hat {\lambda },\hat {\mu }}$ satisfies
$\mathsf {C}^{\hat {\lambda },\hat {\mu }}$ satisfies
for any ![]() $M,N$ in
$M,N$ in ![]() $\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm {op}})$.
$\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm {op}})$.
3.8 Restriction to the Kostant section
Recall the constructions of § 2.3 applied to the group ![]() $\mathbf {G}=G^{(1)}$. In particular, we have a Kostant section
$\mathbf {G}=G^{(1)}$. In particular, we have a Kostant section ![]() $\mathbf {S}^{*} \subset \mathbf {g}^{*}=\mathfrak {g}^{*(1)}$, and group schemes
$\mathbf {S}^{*} \subset \mathbf {g}^{*}=\mathfrak {g}^{*(1)}$, and group schemes ![]() $\mathbb {J}^{*}_\mathrm {reg}$ over
$\mathbb {J}^{*}_\mathrm {reg}$ over ![]() $\mathfrak {g}_\mathrm {reg}^{*(1)}$ and
$\mathfrak {g}_\mathrm {reg}^{*(1)}$ and ![]() $\mathbb {J}^{*}_\mathbf {S}$ over
$\mathbb {J}^{*}_\mathbf {S}$ over ![]() $\mathbf {S}^{*}$.
$\mathbf {S}^{*}$.
We also set
where the map ![]() $G \times \mathbf {S}^{*} \to G^{(1)} \times \mathbf {S}^{*}$ is the product of the Frobenius morphism of
$G \times \mathbf {S}^{*} \to G^{(1)} \times \mathbf {S}^{*}$ is the product of the Frobenius morphism of ![]() $G$ and the identity of
$G$ and the identity of ![]() $\mathbf {S}^{*}$. Since
$\mathbf {S}^{*}$. Since ![]() $G$ is smooth its Frobenius morphism is flat (see, for example, [Reference Brion and KumarBK05, § 1.1]), and therefore
$G$ is smooth its Frobenius morphism is flat (see, for example, [Reference Brion and KumarBK05, § 1.1]), and therefore ![]() $\mathbb {I}^{*}_\mathbf {S}$ is a flat affine group scheme over
$\mathbb {I}^{*}_\mathbf {S}$ is a flat affine group scheme over ![]() $\mathbf {S}^{*}$. By construction
$\mathbf {S}^{*}$. By construction ![]() $\mathbb {I}^{*}_\mathbf {S}$ contains
$\mathbb {I}^{*}_\mathbf {S}$ contains ![]() $G_1 \times \mathbf {S}^{*}$ as a normal subgroup, and the quotient identifies with
$G_1 \times \mathbf {S}^{*}$ as a normal subgroup, and the quotient identifies with ![]() $\mathbb {J}^{*}_\mathbf {S}$. Note also that the morphism (2.4) induces (after restriction to
$\mathbb {J}^{*}_\mathbf {S}$. Note also that the morphism (2.4) induces (after restriction to ![]() $\mathbf {S}$ and composition with the projection
$\mathbf {S}$ and composition with the projection ![]() $\mathbb {I}^{*}_\mathbf {S} \to \mathbb {J}^{*}_\mathbf {S}$) a group-scheme morphism
$\mathbb {I}^{*}_\mathbf {S} \to \mathbb {J}^{*}_\mathbf {S}$) a group-scheme morphism
Finally, we set
where ![]() $\mathscr {O}(\mathbf {S}^{*})$ is seen as a
$\mathscr {O}(\mathbf {S}^{*})$ is seen as a ![]() ${Z_{\mathrm {Fr}}}$-algebra via the identification (3.2). If we set
${Z_{\mathrm {Fr}}}$-algebra via the identification (3.2). If we set
then the projection ![]() $\mathfrak {C}_\mathbf {S} \to \mathfrak {t}^{*}/(W,\bullet )$ is an isomorphism, and
$\mathfrak {C}_\mathbf {S} \to \mathfrak {t}^{*}/(W,\bullet )$ is an isomorphism, and ![]() $\mathcal {U}_{\mathbf {S}}\mathfrak {g}$ is an
$\mathcal {U}_{\mathbf {S}}\mathfrak {g}$ is an ![]() $\mathscr {O}(\mathfrak {C}_\mathbf {S})$-algebra. Recall that the algebra
$\mathscr {O}(\mathfrak {C}_\mathbf {S})$-algebra. Recall that the algebra ![]() $\mathcal {U}\mathfrak {g}$ can be seen as a
$\mathcal {U}\mathfrak {g}$ can be seen as a ![]() $G$-equivariant
$G$-equivariant ![]() $\mathscr {O}(\mathfrak {C})$-algebra (see § 3.2). Using the general construction recalled in [Reference Mautner and RicheMR18, § 2.2], from this we deduce on
$\mathscr {O}(\mathfrak {C})$-algebra (see § 3.2). Using the general construction recalled in [Reference Mautner and RicheMR18, § 2.2], from this we deduce on ![]() $\mathcal {U}_{\mathbf {S}} \mathfrak {g}$ a natural module structure for the flat affine group scheme
$\mathcal {U}_{\mathbf {S}} \mathfrak {g}$ a natural module structure for the flat affine group scheme ![]() $\mathfrak {C}_\mathbf {S} \times _{\mathbf {S}^{*}} \mathbb {I}^{*}_\mathbf {S}$ over
$\mathfrak {C}_\mathbf {S} \times _{\mathbf {S}^{*}} \mathbb {I}^{*}_\mathbf {S}$ over ![]() $\mathfrak {C}_\mathbf {S}$, such that the multiplication morphism is equivariant.
$\mathfrak {C}_\mathbf {S}$, such that the multiplication morphism is equivariant.
3.9 (Completed) Harish-Chandra bimodules for  $\mathcal {U}_{\mathbf {S}}\mathfrak {g}$
$\mathcal {U}_{\mathbf {S}}\mathfrak {g}$
We now want to define, given ![]() $\lambda,\mu \in \mathbb {X}$, categories analogous to
$\lambda,\mu \in \mathbb {X}$, categories analogous to ![]() $\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\hat {\lambda },\hat {\mu }})$ and
$\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\hat {\lambda },\hat {\mu }})$ and ![]() $\mathsf {HC}^{\hat {\lambda },\hat {\mu }}$ but for the algebra
$\mathsf {HC}^{\hat {\lambda },\hat {\mu }}$ but for the algebra ![]() $\mathcal {U}_{\mathbf {S}}\mathfrak {g}$ in place of
$\mathcal {U}_{\mathbf {S}}\mathfrak {g}$ in place of ![]() $\mathcal {U} \mathfrak {g}$. We start with the non-completed version.
$\mathcal {U} \mathfrak {g}$. We start with the non-completed version.
Let us consider the category ![]() $\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {U}_\mathbf {S} \mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} \mathcal {U}_\mathbf {S} \mathfrak {g}^{\mathrm {op}})$ of finitely generated
$\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {U}_\mathbf {S} \mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} \mathcal {U}_\mathbf {S} \mathfrak {g}^{\mathrm {op}})$ of finitely generated ![]() $\mathcal {U}_\mathbf {S} \mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} \mathcal {U}_\mathbf {S} \mathfrak {g}^{\mathrm {op}}$-modules endowed with a compatible
$\mathcal {U}_\mathbf {S} \mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} \mathcal {U}_\mathbf {S} \mathfrak {g}^{\mathrm {op}}$-modules endowed with a compatible ![]() $\mathbb {I}^{*}_\mathbf {S}$-module structure. Since
$\mathbb {I}^{*}_\mathbf {S}$-module structure. Since ![]() $\mathbb {I}^{*}_\mathbf {S}$ is flat over
$\mathbb {I}^{*}_\mathbf {S}$ is flat over ![]() $\mathbf {S}^{*}$, this category is abelian. Here
$\mathbf {S}^{*}$, this category is abelian. Here ![]() $\mathcal {U}_\mathbf {S} \mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} (\mathcal {U}_\mathbf {S} \mathfrak {g})^{\mathrm {op}}$ is an algebra over
$\mathcal {U}_\mathbf {S} \mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} (\mathcal {U}_\mathbf {S} \mathfrak {g})^{\mathrm {op}}$ is an algebra over
which identifies with ![]() $\mathscr {O}(\mathfrak {D})$ via the composition of natural algebra morphisms
$\mathscr {O}(\mathfrak {D})$ via the composition of natural algebra morphisms
As in § 3.4, the tensor product ![]() $\otimes _{\mathcal {U}_\mathbf {S} \mathfrak {g}}$ defines a monoidal structure on this category, and, using the construction of [Reference Mautner and RicheMR18, § 2.2] considered above, the functor
$\otimes _{\mathcal {U}_\mathbf {S} \mathfrak {g}}$ defines a monoidal structure on this category, and, using the construction of [Reference Mautner and RicheMR18, § 2.2] considered above, the functor ![]() $\mathscr {O}(\mathbf {S}^{*}) \otimes _{{Z_{\mathrm {Fr}}}} (-)$ defines a monoidal functor
$\mathscr {O}(\mathbf {S}^{*}) \otimes _{{Z_{\mathrm {Fr}}}} (-)$ defines a monoidal functor
An object ![]() $M$ in
$M$ in ![]() $\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {U}_\mathbf {S} \mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} \mathcal {U}_\mathbf {S} \mathfrak {g}^{\mathrm {op}})$ will be called a Harish-Chandra
$\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {U}_\mathbf {S} \mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} \mathcal {U}_\mathbf {S} \mathfrak {g}^{\mathrm {op}})$ will be called a Harish-Chandra ![]() $\mathcal {U}_\mathbf {S} \mathfrak {g}$-bimodule if the restriction of the action of
$\mathcal {U}_\mathbf {S} \mathfrak {g}$-bimodule if the restriction of the action of ![]() $\mathbb {I}^{*}_\mathbf {S}$ to
$\mathbb {I}^{*}_\mathbf {S}$ to ![]() $G_1 \times \mathbf {S}^{*}$, seen as an action of the algebra
$G_1 \times \mathbf {S}^{*}$, seen as an action of the algebra ![]() $\mathrm {Dist}(G_1) = \mathcal {U}_0 \mathfrak {g}$, coincides with the action determined by the rule
$\mathrm {Dist}(G_1) = \mathcal {U}_0 \mathfrak {g}$, coincides with the action determined by the rule ![]() $x \cdot m = xm-mx$ for
$x \cdot m = xm-mx$ for ![]() $x \in \mathfrak {g}$ and
$x \in \mathfrak {g}$ and ![]() $m \in M$. We will denote by
$m \in M$. We will denote by ![]() $\mathsf {HC}_\mathbf {S}$ the full subcategory of
$\mathsf {HC}_\mathbf {S}$ the full subcategory of ![]() $\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {U}_\mathbf {S} \mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} \mathcal {U}_\mathbf {S} \mathfrak {g}^{\mathrm {op}})$ consisting of such objects; then the functor (3.17) restricts to a functor
$\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {U}_\mathbf {S} \mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} \mathcal {U}_\mathbf {S} \mathfrak {g}^{\mathrm {op}})$ consisting of such objects; then the functor (3.17) restricts to a functor
As in § 3.4, for any ![]() $M$ in
$M$ in ![]() $\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {U}_\mathbf {S} \mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} \mathcal {U}_\mathbf {S} \mathfrak {g}^{\mathrm {op}})$ the action of
$\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {U}_\mathbf {S} \mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} \mathcal {U}_\mathbf {S} \mathfrak {g}^{\mathrm {op}})$ the action of ![]() $\mathbb {I}^{*}_\mathbf {S}$ on
$\mathbb {I}^{*}_\mathbf {S}$ on ![]() $M$ extends to an action of the semi-direct product
$M$ extends to an action of the semi-direct product
the Harish-Chandra ![]() $\mathcal {U}_\mathbf {S} \mathfrak {g}$-bimodules are those objects on which this action factors through the multiplication morphism
$\mathcal {U}_\mathbf {S} \mathfrak {g}$-bimodules are those objects on which this action factors through the multiplication morphism ![]() $\mathbb {I}^{*}_\mathbf {S} \ltimes G_1 \to \mathbb {I}^{*}_\mathbf {S}$.
$\mathbb {I}^{*}_\mathbf {S} \ltimes G_1 \to \mathbb {I}^{*}_\mathbf {S}$.
Now we add completions to the picture. Given ![]() $\lambda,\mu \in \mathbb {X}$, we will denote by
$\lambda,\mu \in \mathbb {X}$, we will denote by ![]() $\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$ the completion of
$\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$ the completion of ![]() $\mathcal {Z}_\mathbf {S}$ with respect to the maximal ideal
$\mathcal {Z}_\mathbf {S}$ with respect to the maximal ideal ![]() $\mathcal {I}^{\lambda,\mu }_\mathbf {S} := \mathcal {I}^{\lambda,\mu } \cdot \mathcal {Z}_\mathbf {S}$, so that we have a canonical isomorphism
$\mathcal {I}^{\lambda,\mu }_\mathbf {S} := \mathcal {I}^{\lambda,\mu } \cdot \mathcal {Z}_\mathbf {S}$, so that we have a canonical isomorphism ![]() $\mathscr {O}(\mathfrak {D}^{\hat {\lambda },\hat {\mu }}) \xrightarrow {\sim } \mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$. We also set
$\mathscr {O}(\mathfrak {D}^{\hat {\lambda },\hat {\mu }}) \xrightarrow {\sim } \mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$. We also set
In this setting ![]() $\mathcal {U}_\mathbf {S} \mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} \mathcal {U}_\mathbf {S} \mathfrak {g}^{\mathrm{op}}$ is finitely generated as a
$\mathcal {U}_\mathbf {S} \mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} \mathcal {U}_\mathbf {S} \mathfrak {g}^{\mathrm{op}}$ is finitely generated as a ![]() $\mathcal {Z}_\mathbf {S}$-module, so that
$\mathcal {Z}_\mathbf {S}$-module, so that ![]() $\mathcal {U}^{\hat {\lambda },\hat {\mu }}_\mathbf {S}$ identifies with the completion of
$\mathcal {U}^{\hat {\lambda },\hat {\mu }}_\mathbf {S}$ identifies with the completion of ![]() $\mathcal {U}_\mathbf {S} \mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} \mathcal {U}_\mathbf {S} \mathfrak {g}^{\mathrm{op}}$ with respect to the ideal
$\mathcal {U}_\mathbf {S} \mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} \mathcal {U}_\mathbf {S} \mathfrak {g}^{\mathrm{op}}$ with respect to the ideal ![]() $\mathcal {I}^{\lambda,\mu } \cdot (\mathcal {U}_\mathbf {S} \mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} \mathcal {U}_\mathbf {S} \mathfrak {g}^{\mathrm{op}})$. If we denote by
$\mathcal {I}^{\lambda,\mu } \cdot (\mathcal {U}_\mathbf {S} \mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} \mathcal {U}_\mathbf {S} \mathfrak {g}^{\mathrm{op}})$. If we denote by ![]() $\mathbb {I}^{\hat {\lambda },\hat {\mu }}_\mathbf {S}$ the pullback of
$\mathbb {I}^{\hat {\lambda },\hat {\mu }}_\mathbf {S}$ the pullback of ![]() $\mathbb {I}^{*}_\mathbf {S}$ under the natural morphism
$\mathbb {I}^{*}_\mathbf {S}$ under the natural morphism ![]() $\mathrm {Spec}(\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}) \to \mathbf {S}^{*}$, then
$\mathrm {Spec}(\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}) \to \mathbf {S}^{*}$, then ![]() $\mathbb {I}^{\hat {\lambda },\hat {\mu }}_\mathbf {S}$ is a flat group scheme over
$\mathbb {I}^{\hat {\lambda },\hat {\mu }}_\mathbf {S}$ is a flat group scheme over ![]() $\mathrm {Spec}(\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$, and the
$\mathrm {Spec}(\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$, and the ![]() $\mathbb {I}^{*}_\mathbf {S}$-module structure on
$\mathbb {I}^{*}_\mathbf {S}$-module structure on ![]() $\mathcal {U}_\mathbf {S} \mathfrak {g}$ induces a natural
$\mathcal {U}_\mathbf {S} \mathfrak {g}$ induces a natural ![]() $\mathbb {I}^{\hat {\lambda },\hat {\mu }}_\mathbf {S}$-module structure on
$\mathbb {I}^{\hat {\lambda },\hat {\mu }}_\mathbf {S}$-module structure on ![]() $\mathcal {U}^{\hat {\lambda },\hat {\mu }}_\mathbf {S}$.
$\mathcal {U}^{\hat {\lambda },\hat {\mu }}_\mathbf {S}$.
The algebra ![]() $\mathcal {U}^{\hat {\lambda },\hat {\mu }}_\mathbf {S}$ is left and right Noetherian, and we will denote by
$\mathcal {U}^{\hat {\lambda },\hat {\mu }}_\mathbf {S}$ is left and right Noetherian, and we will denote by ![]() $\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$ the abelian category of
$\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$ the abelian category of ![]() $\mathbb {I}^{\hat {\lambda },\hat {\mu }}_\mathbf {S}$-equivariant finitely generated
$\mathbb {I}^{\hat {\lambda },\hat {\mu }}_\mathbf {S}$-equivariant finitely generated ![]() $\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$-modules. Note that we have
$\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$-modules. Note that we have
in particular, the functor ![]() $\mathscr {O}(\mathbf {S}^{*}) \otimes _{{Z_{\mathrm {Fr}}}} (-)$ defines a natural functor
$\mathscr {O}(\mathbf {S}^{*}) \otimes _{{Z_{\mathrm {Fr}}}} (-)$ defines a natural functor
(Standard arguments show that this functor is exact, but this will not play any role below.) If ![]() $\lambda,\mu \in \mathbb {X}$ belong to the closure of the fundamental alcove, we will also set
$\lambda,\mu \in \mathbb {X}$ belong to the closure of the fundamental alcove, we will also set
One defines the notion of completed Harish-Chandra ![]() $\mathcal {U}_\mathbf {S} \mathfrak {g}$-bimodules by imposing the same condition as for
$\mathcal {U}_\mathbf {S} \mathfrak {g}$-bimodules by imposing the same condition as for ![]() $\mathsf {HC}_\mathbf {S}$. The full subcategory of
$\mathsf {HC}_\mathbf {S}$. The full subcategory of ![]() $\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$ consisting of such objects will be denoted by
$\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$ consisting of such objects will be denoted by ![]() $\mathsf {HC}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$; it is clear that the functor (3.18) restricts to a functor
$\mathsf {HC}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$; it is clear that the functor (3.18) restricts to a functor
Using considerations similar to those of § 3.7, one constructs, again for ![]() $\lambda,\mu,\nu \in \mathbb {X}$, a canonical bifunctor
$\lambda,\mu,\nu \in \mathbb {X}$, a canonical bifunctor
which factors through a bifunctor
this construction being unital, associative and compatible in the natural way with the bifunctors ![]() $(-) {\widehat{\otimes}}_{\mathcal {U} \mathfrak {g}} (-)$ via the functors (3.18). More explicitly, one remarks that if
$(-) {\widehat{\otimes}}_{\mathcal {U} \mathfrak {g}} (-)$ via the functors (3.18). More explicitly, one remarks that if ![]() $\mathcal {Z}_\mathbf {S}^{\wedge }$ is the completion of
$\mathcal {Z}_\mathbf {S}^{\wedge }$ is the completion of ![]() $\mathcal {Z}_\mathbf {S}$ with respect to the ideal
$\mathcal {Z}_\mathbf {S}$ with respect to the ideal ![]() $\mathcal {I} \cdot \mathcal {Z}_\mathbf {S}$, then if we set
$\mathcal {I} \cdot \mathcal {Z}_\mathbf {S}$, then if we set
as in (3.12) we have a canonical algebra isomorphism
If we denote by ![]() $\mathbb {I}_\mathbf {S}^{\wedge }$ the pullback of
$\mathbb {I}_\mathbf {S}^{\wedge }$ the pullback of ![]() $\mathbb {I}^{*}_\mathbf {S}$ to
$\mathbb {I}^{*}_\mathbf {S}$ to ![]() $\mathrm {Spec}(\mathcal {Z}_\mathbf {S}^{\wedge })$, then we can consider the abelian category
$\mathrm {Spec}(\mathcal {Z}_\mathbf {S}^{\wedge })$, then we can consider the abelian category ![]() $\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\mathcal {U}_\mathbf {S}^{\wedge })$ of finitely generated
$\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\mathcal {U}_\mathbf {S}^{\wedge })$ of finitely generated ![]() $\mathbb {I}_\mathbf {S}^{\wedge }$-equivariant
$\mathbb {I}_\mathbf {S}^{\wedge }$-equivariant ![]() $\mathcal {U}_\mathbf {S}^{\wedge }$-modules, and the bifunctor
$\mathcal {U}_\mathbf {S}^{\wedge }$-modules, and the bifunctor
defined by
defines a monoidal structure on this category. Note that any finitely generated ![]() $\mathcal {U}_\mathbf {S}^{\wedge }$-module
$\mathcal {U}_\mathbf {S}^{\wedge }$-module ![]() $M$ is also finitely generated as a
$M$ is also finitely generated as a ![]() $\mathcal {Z}_\mathbf {S}^{\wedge }$-module, so that the natural morphism
$\mathcal {Z}_\mathbf {S}^{\wedge }$-module, so that the natural morphism ![]() $M \to \varprojlim _n M/\mathcal {I}^{n} \cdot M$ is an isomorphism (see [Sta20, Tag 00MA]); the monoidal product considered above therefore satisfies
$M \to \varprojlim _n M/\mathcal {I}^{n} \cdot M$ is an isomorphism (see [Sta20, Tag 00MA]); the monoidal product considered above therefore satisfies
as ![]() $\mathcal {U}_\mathbf {S}^{\wedge }$-modules, for any
$\mathcal {U}_\mathbf {S}^{\wedge }$-modules, for any ![]() $M,N$ in
$M,N$ in ![]() $\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\mathcal {U}_\mathbf {S}^{\wedge })$. The functor
$\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\mathcal {U}_\mathbf {S}^{\wedge })$. The functor ![]() $\mathscr {O}(\mathbf {S}^{*}) \otimes _{{Z_{\mathrm {Fr}}}} (-)$ also induces a functor
$\mathscr {O}(\mathbf {S}^{*}) \otimes _{{Z_{\mathrm {Fr}}}} (-)$ also induces a functor
which admits a canonical monoidal structure. The composition of this functor with the functor ![]() $\mathsf {C}^{\wedge }$ of (3.14) will be denoted by
$\mathsf {C}^{\wedge }$ of (3.14) will be denoted by ![]() $\mathsf {C}^{\wedge }_\mathbf {S}$.
$\mathsf {C}^{\wedge }_\mathbf {S}$.
As in (3.13), we have
and the bifunctor (3.19) is then obtained by restriction of (3.20) to the appropriate summands. In the case where ![]() $\lambda =\mu =\nu$, this bifunctor equips
$\lambda =\mu =\nu$, this bifunctor equips ![]() $\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\lambda }})$ with a monoidal category structure, with unit object
$\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\lambda }})$ with a monoidal category structure, with unit object
It is clear that the functor (3.18) is compatible with the bifunctors ![]() $(-) {\widehat{\otimes}}_{\mathcal {U} \mathfrak {g}} (-)$ and
$(-) {\widehat{\otimes}}_{\mathcal {U} \mathfrak {g}} (-)$ and ![]() $(-) {\widehat{\otimes}}_{\mathcal {U}_\mathbf {S} \mathfrak {g}} (-)$ in the obvious way.
$(-) {\widehat{\otimes}}_{\mathcal {U}_\mathbf {S} \mathfrak {g}} (-)$ in the obvious way.
Lemma 3.6 For any ![]() $\lambda,\mu \in \mathbb {X}$ which belong to the closure of the fundamental alcove and any
$\lambda,\mu \in \mathbb {X}$ which belong to the closure of the fundamental alcove and any ![]() $\nu \in \mathbb {X}$, the functor
$\nu \in \mathbb {X}$, the functor
is both left and right adjoint to the functor
A similar property holds for the functors ![]() $(-) {\widehat{\otimes}}_{\mathcal {U}_\mathbf {S} \mathfrak {g}} \mathsf {P}^{\lambda,\mu }_\mathbf {S}$ and
$(-) {\widehat{\otimes}}_{\mathcal {U}_\mathbf {S} \mathfrak {g}} \mathsf {P}^{\lambda,\mu }_\mathbf {S}$ and ![]() $(-) {\widehat{\otimes}}_{\mathcal {U}_\mathbf {S} \mathfrak {g}} \mathsf {P}^{\mu,\lambda }_\mathbf {S}$.
$(-) {\widehat{\otimes}}_{\mathcal {U}_\mathbf {S} \mathfrak {g}} \mathsf {P}^{\mu,\lambda }_\mathbf {S}$.
Proof. We prove the case of convolution on the left; convolution on the right can be treated similarly. We remark that for any ![]() $V \in \mathsf {Rep}(G)$, the functor
$V \in \mathsf {Rep}(G)$, the functor
is both left and right adjoint to the functor
(In fact, these functors can be realized more concretely as tensor product with ![]() $V$ and
$V$ and ![]() $V^{*}$ respectively.) On the other hand, the inclusion functor
$V^{*}$ respectively.) On the other hand, the inclusion functor
(see (3.22)) is both left and right adjoint to the corresponding projection functor
and similarly for ![]() $\mu$ in place of
$\mu$ in place of ![]() $\lambda$. The desired claim follows, since the functors
$\lambda$. The desired claim follows, since the functors ![]() $\mathsf {P}^{\lambda,\mu }_\mathbf {S} {\widehat{\otimes}}_{\mathcal {U}_\mathbf {S} \mathfrak {g}} (-)$ and
$\mathsf {P}^{\lambda,\mu }_\mathbf {S} {\widehat{\otimes}}_{\mathcal {U}_\mathbf {S} \mathfrak {g}} (-)$ and ![]() $\mathsf {P}^{\mu,\lambda }_\mathbf {S} {\widehat{\otimes}}_{\mathcal {U}_\mathbf {S} \mathfrak {g}} (-)$ are isomorphic to compositions of functors of this form. (More specifically, if
$\mathsf {P}^{\mu,\lambda }_\mathbf {S} {\widehat{\otimes}}_{\mathcal {U}_\mathbf {S} \mathfrak {g}} (-)$ are isomorphic to compositions of functors of this form. (More specifically, if ![]() $\nu \in \mathbb {X}$ is the only dominant
$\nu \in \mathbb {X}$ is the only dominant ![]() $W$-translate of
$W$-translate of ![]() $\mu -\lambda$, the functor
$\mu -\lambda$, the functor ![]() $\mathsf {P}^{\lambda,\mu }_\mathbf {S} {\widehat{\otimes}}_{\mathcal {U}_\mathbf {S} \mathfrak {g}} (-)$ involves the module
$\mathsf {P}^{\lambda,\mu }_\mathbf {S} {\widehat{\otimes}}_{\mathcal {U}_\mathbf {S} \mathfrak {g}} (-)$ involves the module ![]() $\mathsf {L}(\nu )$, and the functor
$\mathsf {L}(\nu )$, and the functor ![]() $\mathsf {P}^{\mu,\lambda }_\mathbf {S} {\widehat{\otimes}}_{\mathcal {U}_\mathbf {S} \mathfrak {g}} (-)$ involves the module
$\mathsf {P}^{\mu,\lambda }_\mathbf {S} {\widehat{\otimes}}_{\mathcal {U}_\mathbf {S} \mathfrak {g}} (-)$ involves the module ![]() $\mathsf {L}(-w_0(\nu ))$; here we fix an isomorphism
$\mathsf {L}(-w_0(\nu ))$; here we fix an isomorphism ![]() $\mathsf {L}(\nu )^{*} \cong \mathsf {L}(-w_0(\nu ))$.)
$\mathsf {L}(\nu )^{*} \cong \mathsf {L}(-w_0(\nu ))$.)
3.10 Restriction to the Kostant section for diagonally induced bimodules
In this subsection we aim to prove the following claim.
Proposition 3.7 For any ![]() $\lambda,\mu \in \mathbb {X}$, the functor (3.18) is fully faithful on the subcategory
$\lambda,\mu \in \mathbb {X}$, the functor (3.18) is fully faithful on the subcategory ![]() $\mathsf {HC}^{\hat {\lambda },\hat {\mu }}_\mathrm {diag}$.
$\mathsf {HC}^{\hat {\lambda },\hat {\mu }}_\mathrm {diag}$.
The proof of this proposition will use some standard properties stated in the following lemma. Here, ![]() $k$ is a commutative ring,
$k$ is a commutative ring, ![]() $A$ is a left Noetherian
$A$ is a left Noetherian ![]() $k$-algebra, and
$k$-algebra, and ![]() $H$ is an affine
$H$ is an affine ![]() $k$-group scheme. For any commutative
$k$-group scheme. For any commutative ![]() $k$-algebra
$k$-algebra ![]() $k'$ we set
$k'$ we set ![]() $H_{k'}:=\mathrm {Spec}(k') \times _{\mathrm {Spec}(k)} H$. If
$H_{k'}:=\mathrm {Spec}(k') \times _{\mathrm {Spec}(k)} H$. If ![]() $A$ admits an action of
$A$ admits an action of ![]() $H$ by algebra automorphisms, we denote by
$H$ by algebra automorphisms, we denote by ![]() $\mathsf {Mod}^{H}(A)$ the category of
$\mathsf {Mod}^{H}(A)$ the category of ![]() $H$-equivariant
$H$-equivariant ![]() $A$-modules. (This category is abelian if
$A$-modules. (This category is abelian if ![]() $H$ is flat over
$H$ is flat over ![]() $k$.)
$k$.)
Lemma 3.8
(i) If
 $M,N$ are
$M,N$ are  $A$-modules with
$A$-modules with  $M$ finitely generated, for any flat
$M$ finitely generated, for any flat  $k$-module
$k$-module  $V$ we have a canonical isomorphism
where
$V$ we have a canonical isomorphism
where \[ {{\rm Hom}}_A(M,N \otimes_k V) \xrightarrow{\sim} {{\rm Hom}}_A(M,N) \otimes_k V \]
\[ {{\rm Hom}}_A(M,N \otimes_k V) \xrightarrow{\sim} {{\rm Hom}}_A(M,N) \otimes_k V \] $N \otimes _k V$ is regarded as an
$N \otimes _k V$ is regarded as an  $A$-module for the action on the first factor.
$A$-module for the action on the first factor.(ii) If
 $H$ is flat over
$H$ is flat over  $k$, and if
$k$, and if  $M,N$ are
$M,N$ are  $H$-equivariant
$H$-equivariant  $A$-modules, with
$A$-modules, with  $M$ finitely generated as an
$M$ finitely generated as an  $A$-module, then the
$A$-module, then the  $k$-module
$k$-module  ${{\rm Hom}}_A(M,N)$ admits a canonical
${{\rm Hom}}_A(M,N)$ admits a canonical  $H$-module structure, and we have a canonical isomorphism
$H$-module structure, and we have a canonical isomorphism
 \[ {{\rm Hom}}_{\mathsf{Mod}^{H}(A)}(M,N) \xrightarrow{\sim} ( {{\rm Hom}}_A(M,N) )^{H}. \]
\[ {{\rm Hom}}_{\mathsf{Mod}^{H}(A)}(M,N) \xrightarrow{\sim} ( {{\rm Hom}}_A(M,N) )^{H}. \](iii) If
 $k'$ is a flat commutative
$k'$ is a flat commutative  $k$-algebra, for any
$k$-algebra, for any  $H$-module we have a canonical isomorphism
$H$-module we have a canonical isomorphism
 \[ (k' \otimes_k M)^{H_{k'}} \xrightarrow{\sim} k' \otimes_k M^{H}. \]
\[ (k' \otimes_k M)^{H_{k'}} \xrightarrow{\sim} k' \otimes_k M^{H}. \]
Proof. (i) We consider a presentation ![]() $A^{\oplus n} \to A^{\oplus m} \to M \to 0$; we then have exact sequences
$A^{\oplus n} \to A^{\oplus m} \to M \to 0$; we then have exact sequences
and
where we use the flatness of ![]() $V$. It is clear that the second and third terms in these exact sequences identify, and we deduce an identification of the first terms.
$V$. It is clear that the second and third terms in these exact sequences identify, and we deduce an identification of the first terms.
(ii) We consider the morphism
which sends a morphism ![]() $\varphi : M \to N$ to the composition
$\varphi : M \to N$ to the composition
where the third morphism sends ![]() $n \otimes g$ to
$n \otimes g$ to ![]() $n_{(1)} \otimes f_{(2)} g$ in Sweedler's notation. By (i) we have
$n_{(1)} \otimes f_{(2)} g$ in Sweedler's notation. By (i) we have ![]() ${{\rm Hom}}_A(M,N \otimes _k \mathscr {O}(H)) \cong {{\rm Hom}}_A(M,N) \otimes _k \mathscr {O}(H)$, so that this morphism can be seen as a morphism
${{\rm Hom}}_A(M,N \otimes _k \mathscr {O}(H)) \cong {{\rm Hom}}_A(M,N) \otimes _k \mathscr {O}(H)$, so that this morphism can be seen as a morphism ![]() ${{\rm Hom}}_A(M,N) \to {{\rm Hom}}_A(M,N) \otimes _k \mathscr {O}(H)$, which can be checked to provide an
${{\rm Hom}}_A(M,N) \to {{\rm Hom}}_A(M,N) \otimes _k \mathscr {O}(H)$, which can be checked to provide an ![]() $\mathscr {O}(H)$-comodule structure (i.e. an
$\mathscr {O}(H)$-comodule structure (i.e. an ![]() $H$-module structure) on
$H$-module structure) on ![]() ${{\rm Hom}}_A(M,N)$. The isomorphism
${{\rm Hom}}_A(M,N)$. The isomorphism
is then clear from definitions.
(iii) See [Reference JantzenJan03, § I.2.10, equation (3)].
With these tools we can give the proof of the proposition.
Proof of Proposition 3.7 To prove the proposition, it suffices to prove that the functor (3.21) is fully faithful on the subcategory ![]() $\mathsf {HC}^{\wedge }_\mathrm {diag}$, which will follow if we prove that it induces an isomorphism
$\mathsf {HC}^{\wedge }_\mathrm {diag}$, which will follow if we prove that it induces an isomorphism
for any ![]() $M$ in
$M$ in ![]() $\mathsf {Mod}^{G}_\mathrm {fg}(\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm{op}})$ and
$\mathsf {Mod}^{G}_\mathrm {fg}(\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm{op}})$ and ![]() $V \in \mathsf {Rep}(G)$.
$V \in \mathsf {Rep}(G)$.
For ![]() $N$ in
$N$ in ![]() $\mathsf {Mod}^{G}_\mathrm {fg}(\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm{op}})$, we have
$\mathsf {Mod}^{G}_\mathrm {fg}(\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm{op}})$, we have
 \begin{align*} {{\rm Hom}}_{\mathsf{Mod}^{G}_{\mathrm{fg}}(\mathcal{U}^{\wedge})}(\mathsf{C}^{\wedge}(M),\mathsf{C}^{\wedge}(N)) &\cong ( {{\rm Hom}}_{\mathcal{U}^{\wedge}}(\mathsf{C}^{\wedge}(M),\mathsf{C}^{\wedge}(N)) )^{G}\\ &\cong \big( {{\rm Hom}}_{\mathcal{U} \mathfrak{g} \otimes_{{Z_{\mathrm{Fr}}}} \mathcal{U} \mathfrak{g}^{\mathrm{op}}}(M,\mathsf{C}^{\wedge}(N)) \big)^{G} \\ &\cong \big( {{\rm Hom}}_{\mathcal{U} \mathfrak{g} \otimes_{{Z_{\mathrm{Fr}}}} \mathcal{U} \mathfrak{g}^{\mathrm{op}}}(M,N) \otimes_{\mathscr{O}(\mathfrak{D})} \mathscr{O}(\mathfrak{D}^{\wedge}) \big)^{G}, \end{align*}
\begin{align*} {{\rm Hom}}_{\mathsf{Mod}^{G}_{\mathrm{fg}}(\mathcal{U}^{\wedge})}(\mathsf{C}^{\wedge}(M),\mathsf{C}^{\wedge}(N)) &\cong ( {{\rm Hom}}_{\mathcal{U}^{\wedge}}(\mathsf{C}^{\wedge}(M),\mathsf{C}^{\wedge}(N)) )^{G}\\ &\cong \big( {{\rm Hom}}_{\mathcal{U} \mathfrak{g} \otimes_{{Z_{\mathrm{Fr}}}} \mathcal{U} \mathfrak{g}^{\mathrm{op}}}(M,\mathsf{C}^{\wedge}(N)) \big)^{G} \\ &\cong \big( {{\rm Hom}}_{\mathcal{U} \mathfrak{g} \otimes_{{Z_{\mathrm{Fr}}}} \mathcal{U} \mathfrak{g}^{\mathrm{op}}}(M,N) \otimes_{\mathscr{O}(\mathfrak{D})} \mathscr{O}(\mathfrak{D}^{\wedge}) \big)^{G}, \end{align*}where the first isomorphism uses Lemma 3.8(ii), and the third one uses Lemma 3.8(i). Using Lemma 3.8(iii), we deduce isomorphisms
 \begin{align*} {{\rm Hom}}_{\mathsf{Mod}^{G}_{\mathrm{fg}}(\mathcal{U}^{\wedge})}(\mathsf{C}^{\wedge}(M),\mathsf{C}^{\wedge}(N)) &\cong \big( {{\rm Hom}}_{\mathcal{U} \mathfrak{g} \otimes_{{Z_{\mathrm{Fr}}}} \mathcal{U} \mathfrak{g}^{\mathrm{op}}}(M,N) \big)^{G} \otimes_{\mathscr{O}(\mathfrak{D})} \mathscr{O}(\mathfrak{D}^{\wedge})\\ &\cong {{\rm Hom}}_{\mathsf{Mod}^{G}(\mathcal{U} \mathfrak{g} \otimes_{{Z_{\mathrm{Fr}}}} \mathcal{U} \mathfrak{g}^{\mathrm{op}})}(M,N) \otimes_{\mathscr{O}(\mathfrak{D})} \mathscr{O}(\mathfrak{D}^{\wedge}). \end{align*}
\begin{align*} {{\rm Hom}}_{\mathsf{Mod}^{G}_{\mathrm{fg}}(\mathcal{U}^{\wedge})}(\mathsf{C}^{\wedge}(M),\mathsf{C}^{\wedge}(N)) &\cong \big( {{\rm Hom}}_{\mathcal{U} \mathfrak{g} \otimes_{{Z_{\mathrm{Fr}}}} \mathcal{U} \mathfrak{g}^{\mathrm{op}}}(M,N) \big)^{G} \otimes_{\mathscr{O}(\mathfrak{D})} \mathscr{O}(\mathfrak{D}^{\wedge})\\ &\cong {{\rm Hom}}_{\mathsf{Mod}^{G}(\mathcal{U} \mathfrak{g} \otimes_{{Z_{\mathrm{Fr}}}} \mathcal{U} \mathfrak{g}^{\mathrm{op}})}(M,N) \otimes_{\mathscr{O}(\mathfrak{D})} \mathscr{O}(\mathfrak{D}^{\wedge}). \end{align*} Assuming now that ![]() $N=V \otimes \mathcal {U} \mathfrak {g}$, we claim that the functor
$N=V \otimes \mathcal {U} \mathfrak {g}$, we claim that the functor ![]() $\mathscr {O}(\mathbf {S}^{*}) \otimes _{{Z_{\mathrm {Fr}}}} (-)$ induces an isomorphism
$\mathscr {O}(\mathbf {S}^{*}) \otimes _{{Z_{\mathrm {Fr}}}} (-)$ induces an isomorphism
 \begin{align} &{{\rm Hom}}_{\mathsf{Mod}^{G}_\mathrm{fg}(\mathcal{U} \mathfrak{g} \otimes_{{Z_{\mathrm{Fr}}}} \mathcal{U} \mathfrak{g}^{\mathrm{op}})}(M,V \otimes \mathcal{U} \mathfrak{g}) \nonumber\\ &\quad \xrightarrow{\sim} {{\rm Hom}}_{\mathsf{Mod}^{\mathbb{I}}_\mathrm{fg}(\mathcal{U}_\mathbf{S} \mathfrak{g} \otimes_{\mathscr{O}(\mathbf{S}^{*})} \mathcal{U}_\mathbf{S} \mathfrak{g}^{\mathrm{op}})}(\mathscr{O}(\mathbf{S}^{*}) \otimes_{{Z_{\mathrm{Fr}}}} M, V \otimes \mathcal{U}_{\mathbf{S}} \mathfrak{g}). \end{align}
\begin{align} &{{\rm Hom}}_{\mathsf{Mod}^{G}_\mathrm{fg}(\mathcal{U} \mathfrak{g} \otimes_{{Z_{\mathrm{Fr}}}} \mathcal{U} \mathfrak{g}^{\mathrm{op}})}(M,V \otimes \mathcal{U} \mathfrak{g}) \nonumber\\ &\quad \xrightarrow{\sim} {{\rm Hom}}_{\mathsf{Mod}^{\mathbb{I}}_\mathrm{fg}(\mathcal{U}_\mathbf{S} \mathfrak{g} \otimes_{\mathscr{O}(\mathbf{S}^{*})} \mathcal{U}_\mathbf{S} \mathfrak{g}^{\mathrm{op}})}(\mathscr{O}(\mathbf{S}^{*}) \otimes_{{Z_{\mathrm{Fr}}}} M, V \otimes \mathcal{U}_{\mathbf{S}} \mathfrak{g}). \end{align}
In fact, the algebra ![]() $\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm{op}}$ is a
$\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm{op}}$ is a ![]() $G$-equivariant finite
$G$-equivariant finite ![]() $\mathscr {O}(\mathfrak {g}^{*(1)})$-algebra. Therefore, it identifies with the global sections of a
$\mathscr {O}(\mathfrak {g}^{*(1)})$-algebra. Therefore, it identifies with the global sections of a ![]() $G$-equivariant coherent sheaf of
$G$-equivariant coherent sheaf of ![]() $\mathscr {O}_{\mathfrak {g}^{*(1)}}$-algebras
$\mathscr {O}_{\mathfrak {g}^{*(1)}}$-algebras ![]() $\mathscr {U}$ on
$\mathscr {U}$ on ![]() $\mathfrak {g}^{*(1)}$. Moreover, the restriction
$\mathfrak {g}^{*(1)}$. Moreover, the restriction ![]() $\mathscr {U}_\mathbf {S}$ of
$\mathscr {U}_\mathbf {S}$ of ![]() $\mathscr {U}$ to
$\mathscr {U}$ to ![]() $\mathbf {S}^{*}$ is an
$\mathbf {S}^{*}$ is an ![]() $\mathbb {I}^{*}_\mathbf {S}$-equivariant sheaf of
$\mathbb {I}^{*}_\mathbf {S}$-equivariant sheaf of ![]() $\mathscr {O}_{\mathbf {S}^{*}}$-algebras on
$\mathscr {O}_{\mathbf {S}^{*}}$-algebras on ![]() $\mathbf {S}^{*}$, whose global sections are
$\mathbf {S}^{*}$, whose global sections are ![]() $\mathcal {U}_\mathbf {S} \mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} (\mathcal {U}_\mathbf {S} \mathfrak {g})^{\mathrm{op}}$. Consider the open embedding
$\mathcal {U}_\mathbf {S} \mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} (\mathcal {U}_\mathbf {S} \mathfrak {g})^{\mathrm{op}}$. Consider the open embedding ![]() $j : \mathfrak {g}^{*(1)}_\mathrm {reg} \hookrightarrow \mathfrak {g}^{*(1)}$, and set
$j : \mathfrak {g}^{*(1)}_\mathrm {reg} \hookrightarrow \mathfrak {g}^{*(1)}$, and set ![]() $\mathscr {U}_\mathrm {reg} := j^{*}(\mathscr {U})$. Let us denote by
$\mathscr {U}_\mathrm {reg} := j^{*}(\mathscr {U})$. Let us denote by ![]() $\mathsf {QCoh}^{G}(\mathfrak {g}^{*(1)}_\mathrm {reg}, \mathscr {U}_\mathrm {reg})$ the category of
$\mathsf {QCoh}^{G}(\mathfrak {g}^{*(1)}_\mathrm {reg}, \mathscr {U}_\mathrm {reg})$ the category of ![]() $G$-equivariant quasi-coherent sheaves on
$G$-equivariant quasi-coherent sheaves on ![]() $\mathfrak {g}^{*(1)}_\mathrm {reg}$ equipped with a
$\mathfrak {g}^{*(1)}_\mathrm {reg}$ equipped with a ![]() $\mathscr {U}_\mathrm {reg}$-module structure, compatible with the
$\mathscr {U}_\mathrm {reg}$-module structure, compatible with the ![]() $G$-equivariant structure in the natural way, and by
$G$-equivariant structure in the natural way, and by ![]() $\mathsf {Coh}^{G}(\mathfrak {g}^{*(1)}_\mathrm {reg}, \mathscr {U}_\mathrm {reg})$ the subcategory of coherent modules. Then we have a restriction functor
$\mathsf {Coh}^{G}(\mathfrak {g}^{*(1)}_\mathrm {reg}, \mathscr {U}_\mathrm {reg})$ the subcategory of coherent modules. Then we have a restriction functor
which admits a right adjoint
coinciding with the usual pushforward functor at the level of quasi-coherent sheaves on ![]() $\mathfrak {g}^{*(1)}_\mathrm {reg}$ and
$\mathfrak {g}^{*(1)}_\mathrm {reg}$ and ![]() $\mathfrak {g}^{*(1)}$. Since the complement of
$\mathfrak {g}^{*(1)}$. Since the complement of ![]() $\mathfrak {g}^{*(1)}_\mathrm {reg}$ has codimension at least
$\mathfrak {g}^{*(1)}_\mathrm {reg}$ has codimension at least ![]() $2$, the natural morphism
$2$, the natural morphism ![]() $\mathscr {O}_{\mathfrak {g}^{*(1)}} \to j_* j^{*} \mathscr {O}_{\mathfrak {g}^{*(1)}}$ is an isomorphism. Since
$\mathscr {O}_{\mathfrak {g}^{*(1)}} \to j_* j^{*} \mathscr {O}_{\mathfrak {g}^{*(1)}}$ is an isomorphism. Since ![]() $\mathcal {U} \mathfrak {g}$ is free over
$\mathcal {U} \mathfrak {g}$ is free over ![]() ${Z_{\mathrm {Fr}}}$ it follows that the morphism
${Z_{\mathrm {Fr}}}$ it follows that the morphism ![]() $V \otimes \mathcal {U} \mathfrak {g} \to j_* j^{*} (V \otimes \mathcal {U} \mathfrak {g})$ is also an isomorphism, and then that the functor
$V \otimes \mathcal {U} \mathfrak {g} \to j_* j^{*} (V \otimes \mathcal {U} \mathfrak {g})$ is also an isomorphism, and then that the functor ![]() $j^{*}$ induces an isomorphism
$j^{*}$ induces an isomorphism
It is a standard observation (see [Reference RicheRic17, Proposition 3.3.11]) that restriction to ![]() $\mathbf {S}^{*}$ induces an equivalence of abelian categories
$\mathbf {S}^{*}$ induces an equivalence of abelian categories
where the right-hand side denotes the category of representations of the affine group scheme ![]() $\mathbb {J}^{*}_{\mathbf {S}}$ (see § 3.8) on coherent
$\mathbb {J}^{*}_{\mathbf {S}}$ (see § 3.8) on coherent ![]() $\mathscr {O}_{\mathbf {S}^{*}}$-modules. The same considerations provide an equivalence of categories
$\mathscr {O}_{\mathbf {S}^{*}}$-modules. The same considerations provide an equivalence of categories
(Here we use the fact that the Frobenius morphism of ![]() $G$ is flat and surjective, hence faithfully flat.) This equivalence is monoidal with respect to the natural tensor product on each side, and the image of the algebra
$G$ is flat and surjective, hence faithfully flat.) This equivalence is monoidal with respect to the natural tensor product on each side, and the image of the algebra ![]() $\mathscr {U}_\mathrm {reg}$ is
$\mathscr {U}_\mathrm {reg}$ is ![]() $\mathscr {U}_\mathbf {S}$; therefore, it induces an equivalence of abelian categories
$\mathscr {U}_\mathbf {S}$; therefore, it induces an equivalence of abelian categories
From this we finally obtain that (3.23) is an isomorphism.
Combining (3.23) with the preceding isomorphisms, we obtain a canonical isomorphism
 \begin{align*} &{{\rm Hom}}_{\mathsf{Mod}^{G}_{\mathrm{fg}}(\mathcal{U}^{\wedge})}(\mathsf{C}^{\wedge}(M),\mathsf{C}^{\wedge}(V \otimes \mathcal{U} \mathfrak{g})) \\ &\quad \cong {{\rm Hom}}_{\mathsf{Mod}^{\mathbb{I}}_\mathrm{fg}(\mathcal{U}_\mathbf{S} \mathfrak{g} \otimes_{\mathscr{O}(\mathbf{S}^{*})} \mathcal{U}_\mathbf{S} \mathfrak{g}^{\mathrm{op}})}(\mathscr{O}(\mathbf{S}^{*}) \otimes_{{Z_{\mathrm{Fr}}}} M, V \otimes \mathcal{U}_{\mathbf{S}} \mathfrak{g}) \otimes_{\mathscr{O}(\mathfrak{D})} \mathscr{O}(\mathfrak{D}^{\wedge}). \end{align*}
\begin{align*} &{{\rm Hom}}_{\mathsf{Mod}^{G}_{\mathrm{fg}}(\mathcal{U}^{\wedge})}(\mathsf{C}^{\wedge}(M),\mathsf{C}^{\wedge}(V \otimes \mathcal{U} \mathfrak{g})) \\ &\quad \cong {{\rm Hom}}_{\mathsf{Mod}^{\mathbb{I}}_\mathrm{fg}(\mathcal{U}_\mathbf{S} \mathfrak{g} \otimes_{\mathscr{O}(\mathbf{S}^{*})} \mathcal{U}_\mathbf{S} \mathfrak{g}^{\mathrm{op}})}(\mathscr{O}(\mathbf{S}^{*}) \otimes_{{Z_{\mathrm{Fr}}}} M, V \otimes \mathcal{U}_{\mathbf{S}} \mathfrak{g}) \otimes_{\mathscr{O}(\mathfrak{D})} \mathscr{O}(\mathfrak{D}^{\wedge}). \end{align*}Considerations similar to those of the beginning of the proof allow us to identify the right-hand side with
which finishes the proof.
4. Localization for Harish-Chandra bimodules
4.1 Azumaya algebras
We start by recalling the basic theory of Azumaya algebras.
Let ![]() $R$ be a commutative ring. Recall that an
$R$ be a commutative ring. Recall that an ![]() $R$-module
$R$-module ![]() $P$ is called faithfully projective if it is projective of finite type and if, moreover, the only
$P$ is called faithfully projective if it is projective of finite type and if, moreover, the only ![]() $R$-module
$R$-module ![]() $M$ such that
$M$ such that ![]() $P \otimes _R M = 0$ is
$P \otimes _R M = 0$ is ![]() $M=0$. By [Reference Knus and OjangurenKO74, Chap. I, Lemme 6.2] this condition is equivalent to requiring that
$M=0$. By [Reference Knus and OjangurenKO74, Chap. I, Lemme 6.2] this condition is equivalent to requiring that ![]() $P$ is projective of finite type and faithful (i.e. its annihilator in
$P$ is projective of finite type and faithful (i.e. its annihilator in ![]() $R$ is trivial). An
$R$ is trivial). An ![]() $R$-module
$R$-module ![]() $P$ is finitely generated and projective if and only if it is finitely presented and, moreover, the localization
$P$ is finitely generated and projective if and only if it is finitely presented and, moreover, the localization ![]() $P_{\mathfrak {p}}$ is free over
$P_{\mathfrak {p}}$ is free over ![]() $R_{\mathfrak {p}}$ for any
$R_{\mathfrak {p}}$ for any ![]() $\mathfrak {p} \in \mathrm {Spec}(R)$; see [Reference Knus and OjangurenKO74, Chap. I, Lemme 5.2] or [Sta20, Tag 00NX]. In this setting,
$\mathfrak {p} \in \mathrm {Spec}(R)$; see [Reference Knus and OjangurenKO74, Chap. I, Lemme 5.2] or [Sta20, Tag 00NX]. In this setting, ![]() $P$ is faithful if and only if the rank of
$P$ is faithful if and only if the rank of ![]() $P_{\mathfrak {p}}$ is positive for any
$P_{\mathfrak {p}}$ is positive for any ![]() $\mathfrak {p}$; see [Reference Knus and OjangurenKO74, Chap. I, Lemme 6.1]. This notion is important in Morita theory since if
$\mathfrak {p}$; see [Reference Knus and OjangurenKO74, Chap. I, Lemme 6.1]. This notion is important in Morita theory since if ![]() $P$ is a faithfully projective
$P$ is a faithfully projective ![]() $R$-module, then we obtain quasi-inverse equivalences of categories
$R$-module, then we obtain quasi-inverse equivalences of categories
given by ![]() $M \mapsto P \otimes _R M$ and
$M \mapsto P \otimes _R M$ and ![]() $N \mapsto {{\rm Hom}}_R(P,R) \otimes _{{{\rm End}}_R(P)} N$ where
$N \mapsto {{\rm Hom}}_R(P,R) \otimes _{{{\rm End}}_R(P)} N$ where ![]() $\mathsf {Mod}(A)$ is the category of left
$\mathsf {Mod}(A)$ is the category of left ![]() $A$-modules for any ring
$A$-modules for any ring ![]() $A$; see [Reference Knus and OjangurenKO74, Chap. I, Lemme 7.2]. In the case where
$A$; see [Reference Knus and OjangurenKO74, Chap. I, Lemme 7.2]. In the case where ![]() $R$ is Noetherian, the ring
$R$ is Noetherian, the ring ![]() ${{\rm End}}_R(P)$ is left Noetherian (as a non-commutative ring), and these equivalences restrict to equivalences
${{\rm End}}_R(P)$ is left Noetherian (as a non-commutative ring), and these equivalences restrict to equivalences
between subcategories of finitely generated modules. (Here, a left ![]() ${{\rm End}}_R(P)$-module is finitely generated if and only if it is finitely generated as an
${{\rm End}}_R(P)$-module is finitely generated if and only if it is finitely generated as an ![]() $R$-module.)
$R$-module.)
Let ![]() $A$ be an
$A$ be an ![]() $R$-algebra.Footnote 3 Recall (see [Reference Knus and OjangurenKO74, § III.5]) that
$R$-algebra.Footnote 3 Recall (see [Reference Knus and OjangurenKO74, § III.5]) that ![]() $A$ is called an Azumaya
$A$ is called an Azumaya ![]() $R$-algebra if it satisfies one of the following equivalent conditions.
$R$-algebra if it satisfies one of the following equivalent conditions.
–
 $A$ is faithfully projective as an
$A$ is faithfully projective as an  $R$-module, and the morphism sending
$R$-module, and the morphism sending  $a \otimes b$ to the map
$a \otimes b$ to the map  $x \mapsto axb$ is an isomorphism of
$x \mapsto axb$ is an isomorphism of  $R$-algebras
$R$-algebras
 \[ A \otimes_R A^{\mathrm{op}} \xrightarrow{\sim} \mathrm{End}_R(A) . \]
\[ A \otimes_R A^{\mathrm{op}} \xrightarrow{\sim} \mathrm{End}_R(A) . \]–
 $A$ is finite as an
$A$ is finite as an  $R$-module, the ring morphism
$R$-module, the ring morphism  $R \to A$ is injective, and for any maximal ideal
$R \to A$ is injective, and for any maximal ideal  $\mathfrak {m} \subset R$ the finite-dimensional
$\mathfrak {m} \subset R$ the finite-dimensional  $R/\mathfrak {m}$-algebra
$R/\mathfrak {m}$-algebra  $A/\mathfrak {m} A$ is a central simple algebra.
$A/\mathfrak {m} A$ is a central simple algebra.
In particular, the first characterization and the facts recalled above show that in this case we have canonical equivalences of categories
4.2 Azumaya property of  $\mathcal {U}_\mathbf {S}\mathfrak {g}$
$\mathcal {U}_\mathbf {S}\mathfrak {g}$
The following property is standard (see [Reference Brown and GoodearlBG97, Reference Brown and GordonBG01]); we recall its proof for the reader's convenience.
Proposition 4.1 The ![]() $\mathscr {O}(\mathfrak {C}_\mathbf {S})$-algebra
$\mathscr {O}(\mathfrak {C}_\mathbf {S})$-algebra ![]() $\mathcal {U}_\mathbf {S} \mathfrak {g}$ is Azumaya.
$\mathcal {U}_\mathbf {S} \mathfrak {g}$ is Azumaya.
Proof. We will use the second characterization of Azumaya algebras recalled in § 4.1. Since ![]() $\mathcal {U} \mathfrak {g}$ is finite over
$\mathcal {U} \mathfrak {g}$ is finite over ![]() $Z(\mathcal {U} \mathfrak {g})=\mathscr {O}(\mathfrak {C})$,
$Z(\mathcal {U} \mathfrak {g})=\mathscr {O}(\mathfrak {C})$, ![]() $\mathcal {U}_\mathbf {S} \mathfrak {g}$ is finite over
$\mathcal {U}_\mathbf {S} \mathfrak {g}$ is finite over ![]() $\mathscr {O}(\mathfrak {C}_\mathbf {S})$. To prove that the morphism
$\mathscr {O}(\mathfrak {C}_\mathbf {S})$. To prove that the morphism ![]() $\mathscr {O}(\mathfrak {C}_\mathbf {S}) \to \mathcal {U}_\mathbf {S} \mathfrak {g}$ is injective, we consider the composition
$\mathscr {O}(\mathfrak {C}_\mathbf {S}) \to \mathcal {U}_\mathbf {S} \mathfrak {g}$ is injective, we consider the composition
Here the first morphism is flat since ![]() $G$ is smooth (see § 3.8), the second morphism is smooth by [Reference RicheRic17, Lemma 3.3.1], and the third one is an open embedding; this composition is therefore flat. The algebras
$G$ is smooth (see § 3.8), the second morphism is smooth by [Reference RicheRic17, Lemma 3.3.1], and the third one is an open embedding; this composition is therefore flat. The algebras ![]() $Z(\mathcal {U} \mathfrak {g})$ and
$Z(\mathcal {U} \mathfrak {g})$ and ![]() $\mathcal {U} \mathfrak {g}$ can be considered as
$\mathcal {U} \mathfrak {g}$ can be considered as ![]() $G$-equivariant coherent sheaves on
$G$-equivariant coherent sheaves on ![]() $\mathfrak {g}^{*(1)}$, and the induced morphism
$\mathfrak {g}^{*(1)}$, and the induced morphism ![]() $\mathscr {O}(\mathfrak {C}_\mathbf {S}) \to \mathcal {U}_\mathbf {S} \mathfrak {g}$ is obtained from the embedding
$\mathscr {O}(\mathfrak {C}_\mathbf {S}) \to \mathcal {U}_\mathbf {S} \mathfrak {g}$ is obtained from the embedding ![]() $Z(\mathcal {U} \mathfrak {g}) \to \mathcal {U} \mathfrak {g}$ by the pullback functor
$Z(\mathcal {U} \mathfrak {g}) \to \mathcal {U} \mathfrak {g}$ by the pullback functor
associated with the flat morphism considered above, followed by the obvious equivalences
it is therefore injective.
What is left to prove is that if ![]() $\mathfrak {m} \subset Z(\mathcal {U} \mathfrak {g})$ is a maximal ideal which belongs to
$\mathfrak {m} \subset Z(\mathcal {U} \mathfrak {g})$ is a maximal ideal which belongs to ![]() $\mathfrak {C}_\mathbf {S}=\mathbf {S}^{*(1)} \times _{\mathfrak {t}^{*(1)} / W} \mathfrak {t}^{*}/(W,\bullet )$, then
$\mathfrak {C}_\mathbf {S}=\mathbf {S}^{*(1)} \times _{\mathfrak {t}^{*(1)} / W} \mathfrak {t}^{*}/(W,\bullet )$, then ![]() $\mathcal {U} \mathfrak {g}/\mathfrak {m} \mathcal {U} \mathfrak {g}$ is a central simple algebra. In fact, this property holds more generally if
$\mathcal {U} \mathfrak {g}/\mathfrak {m} \mathcal {U} \mathfrak {g}$ is a central simple algebra. In fact, this property holds more generally if ![]() $\mathfrak {m}$ belongs to
$\mathfrak {m}$ belongs to ![]() $\mathfrak {C}_\mathrm {reg} := \mathfrak {g}_\mathrm {reg}^{*(1)} \times _{\mathfrak {t}^{*}{}^{(1)} / W} \mathfrak {t}^{*}/(W,\bullet )$. Indeed, let
$\mathfrak {C}_\mathrm {reg} := \mathfrak {g}_\mathrm {reg}^{*(1)} \times _{\mathfrak {t}^{*}{}^{(1)} / W} \mathfrak {t}^{*}/(W,\bullet )$. Indeed, let ![]() $N$ be the maximal dimension of a simple
$N$ be the maximal dimension of a simple ![]() $\mathcal {U} \mathfrak {g}$-module. By [Reference Brown and GoodearlBG97, Proposition 3.1], if
$\mathcal {U} \mathfrak {g}$-module. By [Reference Brown and GoodearlBG97, Proposition 3.1], if ![]() $\mathfrak {m} \subset Z(\mathcal {U} \mathfrak {g})$ is a maximal ideal such that
$\mathfrak {m} \subset Z(\mathcal {U} \mathfrak {g})$ is a maximal ideal such that ![]() $\mathcal {U} \mathfrak {g}/\mathfrak {m} \mathcal {U} \mathfrak {g}$ admits a simple module
$\mathcal {U} \mathfrak {g}/\mathfrak {m} \mathcal {U} \mathfrak {g}$ admits a simple module ![]() $V$ of dimension
$V$ of dimension ![]() $N$, then
$N$, then ![]() $\mathcal {U} \mathfrak {g}/\mathfrak {m} \mathcal {U} \mathfrak {g}$ is a central simple algebra; more specifically, the algebra morphism
$\mathcal {U} \mathfrak {g}/\mathfrak {m} \mathcal {U} \mathfrak {g}$ is a central simple algebra; more specifically, the algebra morphism ![]() $\mathcal {U} \mathfrak {g}/\mathfrak {m} \mathcal {U} \mathfrak {g} \to {{\rm End}}_\Bbbk (V)$ is an isomorphism. Now by [Reference Premet and SkryabinPS99, Theorem 4.4] we have
$\mathcal {U} \mathfrak {g}/\mathfrak {m} \mathcal {U} \mathfrak {g} \to {{\rm End}}_\Bbbk (V)$ is an isomorphism. Now by [Reference Premet and SkryabinPS99, Theorem 4.4] we have ![]() $N=p^{\# \mathfrak {R}^{+}}$. And by [Reference Premet and SkryabinPS99, Theorem 5.6], if
$N=p^{\# \mathfrak {R}^{+}}$. And by [Reference Premet and SkryabinPS99, Theorem 5.6], if ![]() $\mathfrak {m}$ belongs to
$\mathfrak {m}$ belongs to ![]() $\mathfrak {C}_\mathrm {reg}$ then any simple
$\mathfrak {C}_\mathrm {reg}$ then any simple ![]() $\mathcal {U} \mathfrak {g}/\mathfrak {m} \mathcal {U} \mathfrak {g}$-module has dimension divisible by
$\mathcal {U} \mathfrak {g}/\mathfrak {m} \mathcal {U} \mathfrak {g}$-module has dimension divisible by ![]() $p^{\# \mathfrak {R}^{+}}$, hence equal to
$p^{\# \mathfrak {R}^{+}}$, hence equal to ![]() $N$.
$N$.
It follows in particular from Proposition 4.1 that ![]() $\mathcal {U}_{\mathbf {S}} \mathfrak {g}$ is faithfully projective as an
$\mathcal {U}_{\mathbf {S}} \mathfrak {g}$ is faithfully projective as an ![]() $\mathscr {O}(\mathfrak {C}_\mathbf {S})$-module.
$\mathscr {O}(\mathfrak {C}_\mathbf {S})$-module.
Below we will use a slightly more concrete version of Proposition 4.1, as follows. First we need to recall the definition of baby Verma modules. Consider some element ![]() $\eta \in \mathfrak {g}^{*(1)}$, and some Borel subgroup
$\eta \in \mathfrak {g}^{*(1)}$, and some Borel subgroup ![]() $B' \subset G$ with unipotent radical
$B' \subset G$ with unipotent radical ![]() $U'$ such that
$U'$ such that ![]() $\eta$ vanishes on
$\eta$ vanishes on ![]() $\mathrm {Lie}(U')^{(1)}$. (Such a Borel subgroup exists for any
$\mathrm {Lie}(U')^{(1)}$. (Such a Borel subgroup exists for any ![]() $\eta$; see [Reference JantzenJan98, Lemma 6.6].) Then
$\eta$; see [Reference JantzenJan98, Lemma 6.6].) Then ![]() $\eta$ defines an element
$\eta$ defines an element ![]() $\eta '$ in
$\eta '$ in ![]() $(\mathrm {Lie}(B')/\mathrm {Lie}(U'))^{*(1)}$. Let
$(\mathrm {Lie}(B')/\mathrm {Lie}(U'))^{*(1)}$. Let ![]() $\xi \in \mathfrak {t}^{*}$ be an element whose image under the map
$\xi \in \mathfrak {t}^{*}$ be an element whose image under the map
is ![]() $\eta '$, where the second map is induced by conjugation by an element
$\eta '$, where the second map is induced by conjugation by an element ![]() $g \in G$ such that
$g \in G$ such that ![]() $gBg^{-1}=B'$ (it is well known that the isomorphism does not depend on the choice of
$gBg^{-1}=B'$ (it is well known that the isomorphism does not depend on the choice of ![]() $g$), and the second one is the Artin–Schreier map associated with the torus
$g$), and the second one is the Artin–Schreier map associated with the torus ![]() $B'/U'$. Then we can consider the associated baby Verma module
$B'/U'$. Then we can consider the associated baby Verma module
where ![]() $\mathcal {U}_\eta \,\mathrm {Lie}(B')$ is the central reduction (with respect to the Frobenius center) of the enveloping algebra of
$\mathcal {U}_\eta \,\mathrm {Lie}(B')$ is the central reduction (with respect to the Frobenius center) of the enveloping algebra of ![]() $\mathrm {Lie}(B')$ at the image of
$\mathrm {Lie}(B')$ at the image of ![]() $\eta$ in
$\eta$ in ![]() $\mathrm {Lie}(B')^{*(1)}$, and
$\mathrm {Lie}(B')^{*(1)}$, and ![]() $\Bbbk _\xi$ is its one-dimensional module defined by the image of
$\Bbbk _\xi$ is its one-dimensional module defined by the image of ![]() $\xi$ in
$\xi$ in ![]() $(\mathrm {Lie}(B')/\mathrm {Lie}(U'))^{*}$. This module has dimension
$(\mathrm {Lie}(B')/\mathrm {Lie}(U'))^{*}$. This module has dimension ![]() $p^{\# \mathfrak {R}^{+}}$; furthermore, if we assume that
$p^{\# \mathfrak {R}^{+}}$; furthermore, if we assume that ![]() $\eta \in \mathfrak {g}^{*(1)}_\mathrm {reg}$, then the considerations in the proof of Proposition 4.1 imply that this module is simple, and that the algebra morphism
$\eta \in \mathfrak {g}^{*(1)}_\mathrm {reg}$, then the considerations in the proof of Proposition 4.1 imply that this module is simple, and that the algebra morphism
is an isomorphism, where we denote by ![]() $\xi '$ the image of
$\xi '$ the image of ![]() $\xi$ in
$\xi$ in ![]() $\mathfrak {t}^{*}/(W,\bullet )$.
$\mathfrak {t}^{*}/(W,\bullet )$.
4.3 Splitting bundles for the algebras  $\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$
$\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$
Our goal in this section is to construct some tools that will allow us to study the categories ![]() $\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\hat {\lambda },\hat {\mu }})$ and
$\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\hat {\lambda },\hat {\mu }})$ and ![]() $\mathsf {HC}^{\hat {\lambda },\hat {\mu }}$ via geometric methods. First we introduce the categories of modules that will be involved in these constructions. Our model will be the category
$\mathsf {HC}^{\hat {\lambda },\hat {\mu }}$ via geometric methods. First we introduce the categories of modules that will be involved in these constructions. Our model will be the category ![]() $\mathsf {Coh}^{G}(\mathfrak {C} \times _{\mathfrak {g}^{*(1)}} \mathfrak {C})$ of
$\mathsf {Coh}^{G}(\mathfrak {C} \times _{\mathfrak {g}^{*(1)}} \mathfrak {C})$ of ![]() $G$-equivariant coherent sheaves on
$G$-equivariant coherent sheaves on ![]() $\mathfrak {C} \times _{\mathfrak {g}^{*(1)}} \mathfrak {C}$, or in other words of
$\mathfrak {C} \times _{\mathfrak {g}^{*(1)}} \mathfrak {C}$, or in other words of ![]() $G$-equivariant finitely generated
$G$-equivariant finitely generated ![]() $\mathcal {Z}$-modules, which is a monoidal category for the operation sending a pair
$\mathcal {Z}$-modules, which is a monoidal category for the operation sending a pair ![]() $(M,N)$ to
$(M,N)$ to
where in the tensor product ![]() $Z(\mathcal {U} \mathfrak {g})$ acts on
$Z(\mathcal {U} \mathfrak {g})$ acts on ![]() $M$ via the right action and on
$M$ via the right action and on ![]() $N$ via the left action. The
$N$ via the left action. The ![]() $\mathcal {Z}$-action on
$\mathcal {Z}$-action on ![]() $M \otimes _{Z(\mathcal {U} \mathfrak {g})} N$ comes from the left action of
$M \otimes _{Z(\mathcal {U} \mathfrak {g})} N$ comes from the left action of ![]() $Z(\mathcal {U} \mathfrak {g})$ on
$Z(\mathcal {U} \mathfrak {g})$ on ![]() $M$ and the right action on
$M$ and the right action on ![]() $N$. In practice, however, we will have to restrict to
$N$. In practice, however, we will have to restrict to ![]() $\mathbf {S}^{*}$, and add generalized characters to this picture.
$\mathbf {S}^{*}$, and add generalized characters to this picture.
First, recall the group scheme ![]() $\mathbb {I}^{\wedge }_\mathbf {S}$ over
$\mathbb {I}^{\wedge }_\mathbf {S}$ over ![]() $\mathrm {Spec}(\mathcal {Z}_\mathbf {S}^{\wedge })$ introduced in § 3.9. We consider the abelian category
$\mathrm {Spec}(\mathcal {Z}_\mathbf {S}^{\wedge })$ introduced in § 3.9. We consider the abelian category ![]() $\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {Z}_\mathbf {S}^{\wedge })$ of representations of the flat affine group scheme
$\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {Z}_\mathbf {S}^{\wedge })$ of representations of the flat affine group scheme ![]() $\mathbb {I}^{\wedge }_\mathbf {S}$ on finitely generated
$\mathbb {I}^{\wedge }_\mathbf {S}$ on finitely generated ![]() $\mathcal {Z}_\mathbf {S}^{\wedge }$-modules. Here a
$\mathcal {Z}_\mathbf {S}^{\wedge }$-modules. Here a ![]() $\mathcal {Z}_\mathbf {S}^{\wedge }$-module is a
$\mathcal {Z}_\mathbf {S}^{\wedge }$-module is a ![]() ${Z_{\mathrm {HC}}} \otimes _{\mathscr {O}(\mathfrak {t}^{*(1)}/W)} \mathscr {O}(\mathfrak {t}^{*(1)}/W)^{\wedge }$-bimodule on which the left and right actions of
${Z_{\mathrm {HC}}} \otimes _{\mathscr {O}(\mathfrak {t}^{*(1)}/W)} \mathscr {O}(\mathfrak {t}^{*(1)}/W)^{\wedge }$-bimodule on which the left and right actions of ![]() $\mathscr {O}(\mathfrak {t}^{*(1)}/W)^{\wedge }$ coincide; the category of such modules therefore admits a canonical tensor product, which preserves finitely generated modules, and induces a monoidal product
$\mathscr {O}(\mathfrak {t}^{*(1)}/W)^{\wedge }$ coincide; the category of such modules therefore admits a canonical tensor product, which preserves finitely generated modules, and induces a monoidal product
with unit object ![]() ${Z_{\mathrm {HC}}} \otimes _{\mathscr {O}(\mathfrak {t}^{*(1)}/W)} \mathscr {O}(\mathfrak {t}^{*(1)}/W)^{\wedge }$, with diagonal
${Z_{\mathrm {HC}}} \otimes _{\mathscr {O}(\mathfrak {t}^{*(1)}/W)} \mathscr {O}(\mathfrak {t}^{*(1)}/W)^{\wedge }$, with diagonal ![]() $\mathcal {Z}_\mathbf {S}^{\wedge }$-module structure and trivial action of
$\mathcal {Z}_\mathbf {S}^{\wedge }$-module structure and trivial action of ![]() $\mathbb {I}^{\wedge }_\mathbf {S}$. If we set
$\mathbb {I}^{\wedge }_\mathbf {S}$. If we set
then we can also consider the abelian category ![]() $\mathsf {Mod}^{\mathbb {J}}_{\mathrm {fg}}(\mathcal {Z}_\mathbf {S}^{\wedge })$ of representations of
$\mathsf {Mod}^{\mathbb {J}}_{\mathrm {fg}}(\mathcal {Z}_\mathbf {S}^{\wedge })$ of representations of ![]() $\mathbb {J}_{\mathbf{S}}^{\wedge }$ on finitely generated
$\mathbb {J}_{\mathbf{S}}^{\wedge }$ on finitely generated ![]() $\mathcal {Z}_\mathbf {S}^{\wedge }$-modules; the quotient morphism
$\mathcal {Z}_\mathbf {S}^{\wedge }$-modules; the quotient morphism ![]() $\mathbb {I}_\mathbf {S}^{\wedge } \to \mathbb {J}^{\wedge }_\mathbf {S}$ induces an exact and fully faithful functor
$\mathbb {I}_\mathbf {S}^{\wedge } \to \mathbb {J}^{\wedge }_\mathbf {S}$ induces an exact and fully faithful functor
whose image is stabilized by the convolution product ![]() $\mathbin {\hat {\star }}_\mathbf {S}$.
$\mathbin {\hat {\star }}_\mathbf {S}$.
Next, for ![]() $\lambda,\mu \in \mathbb {X}$ we have the affine group scheme
$\lambda,\mu \in \mathbb {X}$ we have the affine group scheme ![]() $\mathbb {I}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$ over
$\mathbb {I}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$ over ![]() $\mathrm {Spec}(\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$ also introduced in § 3.9, and we can consider the abelian category
$\mathrm {Spec}(\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$ also introduced in § 3.9, and we can consider the abelian category ![]() $\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$ of representations of this affine group scheme on finitely generated
$\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$ of representations of this affine group scheme on finitely generated ![]() $\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$-modules. As in (3.22), we have a decomposition
$\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$-modules. As in (3.22), we have a decomposition
Given ![]() $M$ in
$M$ in ![]() $\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$ and
$\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$ and ![]() $N$ in
$N$ in ![]() $\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {Z}_\mathbf {S}^{\hat {\mu },\hat {\nu }})$, seen as objects in
$\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {Z}_\mathbf {S}^{\hat {\mu },\hat {\nu }})$, seen as objects in ![]() $\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {Z}_\mathbf {S}^{\wedge })$, the object
$\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {Z}_\mathbf {S}^{\wedge })$, the object ![]() $M \mathbin {\hat {\star }}_{\mathbf {S}} N$ belongs to
$M \mathbin {\hat {\star }}_{\mathbf {S}} N$ belongs to ![]() $\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\nu }})$; in other words, the bifunctor
$\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\nu }})$; in other words, the bifunctor ![]() $\mathbin {\hat {\star }}_{\mathbf {S}}$ restricts to a bifunctor
$\mathbin {\hat {\star }}_{\mathbf {S}}$ restricts to a bifunctor
for any ![]() $\lambda,\mu,\nu \in \mathbb {X}$. In particular, each category
$\lambda,\mu,\nu \in \mathbb {X}$. In particular, each category ![]() $\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\lambda }})$ admits a monoidal structure; the unit object
$\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\lambda }})$ admits a monoidal structure; the unit object ![]() $\mathcal {Z}_\mathbf {S}^{\hat {\lambda }}$ for this structure is
$\mathcal {Z}_\mathbf {S}^{\hat {\lambda }}$ for this structure is ![]() ${Z^{\hat {\lambda }}_{\mathrm {HC}}}$, endowed with the natural structure of a
${Z^{\hat {\lambda }}_{\mathrm {HC}}}$, endowed with the natural structure of a ![]() $\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\lambda }}$-module (induced by the product morphism
$\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\lambda }}$-module (induced by the product morphism ![]() ${Z_{\mathrm {HC}}} \otimes _{{Z_{\mathrm {HC}}} \cap {Z_{\mathrm {Fr}}}} {Z_{\mathrm {HC}}} \to {Z_{\mathrm {HC}}}$) and the trivial structure as a representation of
${Z_{\mathrm {HC}}} \otimes _{{Z_{\mathrm {HC}}} \cap {Z_{\mathrm {Fr}}}} {Z_{\mathrm {HC}}} \to {Z_{\mathrm {HC}}}$) and the trivial structure as a representation of ![]() $\mathbb {I}^{\hat {\lambda },\hat {\lambda }}_\mathbf {S}$.
$\mathbb {I}^{\hat {\lambda },\hat {\lambda }}_\mathbf {S}$.
We can also play the same game starting with ![]() $\mathbb {J}^{*}_\mathbf {S}$ in place of
$\mathbb {J}^{*}_\mathbf {S}$ in place of ![]() $\mathbb {I}^{*}_\mathbf {S}$; we obtain in this way affine group schemes
$\mathbb {I}^{*}_\mathbf {S}$; we obtain in this way affine group schemes ![]() $\mathbb {J}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$, categories
$\mathbb {J}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$, categories ![]() $\mathsf {Mod}^{\mathbb {J}}_{\mathrm {fg}}(\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$ and exact fully faithful functors
$\mathsf {Mod}^{\mathbb {J}}_{\mathrm {fg}}(\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$ and exact fully faithful functors
whose essential images are stabilized by the bifunctor (4.3) in the obvious sense.
Remark 4.2 In view of (3.11), for any ![]() $\lambda,\mu$ we have an algebra isomorphism
$\lambda,\mu$ we have an algebra isomorphism
From this point of view, the bifunctor (4.3) is induced by the tensor product ![]() $(-) \otimes _{{Z_{\mathrm {HC}}^{\hat {\mu }}}} (-)$.
$(-) \otimes _{{Z_{\mathrm {HC}}^{\hat {\mu }}}} (-)$.
Recall that a weight ![]() $\lambda \in \mathbb {X}$ is said to belong to the lower closure of the fundamental alcove if it satisfies
$\lambda \in \mathbb {X}$ is said to belong to the lower closure of the fundamental alcove if it satisfies
for any positive root ![]() $\alpha$. Recall also the completed bimodules introduced in § 3.5. In particular, given
$\alpha$. Recall also the completed bimodules introduced in § 3.5. In particular, given ![]() $\lambda,\mu \in \mathbb {X}$ which belong to the lower closure of the fundamental alcove, we have the objects
$\lambda,\mu \in \mathbb {X}$ which belong to the lower closure of the fundamental alcove, we have the objects
 \begin{align*} \mathsf{P}^{\lambda,-\rho} &= \mathsf{C}^{\lambda,-\rho} ( \mathsf{L}(\lambda+\rho) \otimes \mathcal{U} \mathfrak{g} ) \in \mathsf{HC}^{\hat{\lambda},\widehat{-\rho}}_\mathrm{diag},\\ \mathsf{P}^{-\rho,\mu} &= \mathsf{C}^{-\rho,\mu} (\mathsf{L}(-w_0 \mu+\rho) \otimes \mathcal{U} \mathfrak{g} ) \in \mathsf{HC}^{\widehat{-\rho},\hat{\mu}}_\mathrm{diag}. \end{align*}
\begin{align*} \mathsf{P}^{\lambda,-\rho} &= \mathsf{C}^{\lambda,-\rho} ( \mathsf{L}(\lambda+\rho) \otimes \mathcal{U} \mathfrak{g} ) \in \mathsf{HC}^{\hat{\lambda},\widehat{-\rho}}_\mathrm{diag},\\ \mathsf{P}^{-\rho,\mu} &= \mathsf{C}^{-\rho,\mu} (\mathsf{L}(-w_0 \mu+\rho) \otimes \mathcal{U} \mathfrak{g} ) \in \mathsf{HC}^{\widehat{-\rho},\hat{\mu}}_\mathrm{diag}. \end{align*}We set
We also set ![]() $\mathsf {M}^{\lambda,\mu }_\mathbf {S} := \mathscr {O}(\mathbf {S}^{*}) \otimes _{\mathscr {O}(\mathfrak {g}^{*(1)})} \mathsf {M}^{\lambda,\mu }$, so that
$\mathsf {M}^{\lambda,\mu }_\mathbf {S} := \mathscr {O}(\mathbf {S}^{*}) \otimes _{\mathscr {O}(\mathfrak {g}^{*(1)})} \mathsf {M}^{\lambda,\mu }$, so that
where we use the notation of § 3.9.
The main technical result of this section is the following theorem. Its proof will be given in § 4.5, after some preliminaries treated in § 4.4.
Theorem 4.3 For any ![]() $\lambda,\mu \in \mathbb {X}$ in the lower closure of the fundamental alcove, the
$\lambda,\mu \in \mathbb {X}$ in the lower closure of the fundamental alcove, the ![]() $\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$-module
$\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$-module ![]() $\mathsf {M}^{\lambda,\mu }_\mathbf {S}$ is faithfully projective, and the natural algebra morphism
$\mathsf {M}^{\lambda,\mu }_\mathbf {S}$ is faithfully projective, and the natural algebra morphism
is an isomorphism.
4.4 Study of some stalks
Recall that ![]() $\mathrm {Spec}(\mathcal {Z}_\mathbf {S})$ identifies naturally with
$\mathrm {Spec}(\mathcal {Z}_\mathbf {S})$ identifies naturally with
see § 3.9. We also set
Since the Artin–Schreier map ![]() $\mathfrak {t}^{*} \to \mathfrak {t}^{*(1)}$ is a Galois covering with Galois group
$\mathfrak {t}^{*} \to \mathfrak {t}^{*(1)}$ is a Galois covering with Galois group ![]() $\mathfrak {t}^{*}_{\mathbb {F}_p}$, we have a canonical isomorphism
$\mathfrak {t}^{*}_{\mathbb {F}_p}$, we have a canonical isomorphism
defined by ![]() $(\eta,\xi ) \mapsto (\eta +\xi,\xi )$. For
$(\eta,\xi ) \mapsto (\eta +\xi,\xi )$. For ![]() $\lambda \in \mathbb {X}$ we will denote by
$\lambda \in \mathbb {X}$ we will denote by ![]() $\tilde {\mathfrak {D}}(\lambda )$ the image of
$\tilde {\mathfrak {D}}(\lambda )$ the image of ![]() $\{\overline {\lambda + \rho }\} \times \mathfrak {t}^{*}$ in
$\{\overline {\lambda + \rho }\} \times \mathfrak {t}^{*}$ in ![]() $\tilde {\mathfrak {D}}$; if
$\tilde {\mathfrak {D}}$; if ![]() $\tilde {\Lambda } \subset \mathbb {X}$ is a subset of representatives for the quotient
$\tilde {\Lambda } \subset \mathbb {X}$ is a subset of representatives for the quotient ![]() $\mathfrak {t}^{*}_{\mathbb {F}_p}=\mathbb {X}/p \mathbb {X}$, we then have
$\mathfrak {t}^{*}_{\mathbb {F}_p}=\mathbb {X}/p \mathbb {X}$, we then have
Recall that if ![]() $A$ is a finitely generated
$A$ is a finitely generated ![]() $\Bbbk$-algebra, then by [Sta20, Tag 02J6]
$\Bbbk$-algebra, then by [Sta20, Tag 02J6] ![]() $\mathrm {Spec}(A)$ is a Jacobson space in the sense of [Sta20, Tag 005T]; in other words, closed points are dense in any closed subset of
$\mathrm {Spec}(A)$ is a Jacobson space in the sense of [Sta20, Tag 005T]; in other words, closed points are dense in any closed subset of ![]() $\mathrm {Spec}(A)$. Here we have a natural finite morphism
$\mathrm {Spec}(A)$. Here we have a natural finite morphism
and it is easily seen that the image of this morphism contains all the closed points of ![]() $\mathfrak {D}$; this morphism is therefore surjective. For any
$\mathfrak {D}$; this morphism is therefore surjective. For any ![]() $\lambda \in \mathbb {X}$ we denote by
$\lambda \in \mathbb {X}$ we denote by ![]() $\mathfrak {D}(\lambda )$ the scheme-theoretic image of
$\mathfrak {D}(\lambda )$ the scheme-theoretic image of ![]() $\tilde {\mathfrak {D}}(\lambda )$ in
$\tilde {\mathfrak {D}}(\lambda )$ in ![]() $\mathfrak {D}$; in other words,
$\mathfrak {D}$; in other words, ![]() $\mathscr {O}(\mathfrak {D}(\lambda ))$ is the image of the composition
$\mathscr {O}(\mathfrak {D}(\lambda ))$ is the image of the composition
see [Sta20, Tag 056A]. The morphism (4.4) then factors through a finite morphism ![]() $\tilde {\mathfrak {D}}(\lambda ) \to \mathfrak {D}(\lambda )$, which is surjective since its image is closed and dense; see [Sta20, Tag 01R8]. Since
$\tilde {\mathfrak {D}}(\lambda ) \to \mathfrak {D}(\lambda )$, which is surjective since its image is closed and dense; see [Sta20, Tag 01R8]. Since ![]() $\tilde {\mathfrak {D}}(\lambda )$ is integral, so is
$\tilde {\mathfrak {D}}(\lambda )$ is integral, so is ![]() $\mathfrak {D}(\lambda )$. Moreover, we can check that
$\mathfrak {D}(\lambda )$. Moreover, we can check that
where the operation ![]() $\lambda \mapsto {{\tilde {\lambda }}}$ is as in § 3.1. If
$\lambda \mapsto {{\tilde {\lambda }}}$ is as in § 3.1. If ![]() $\Lambda \subset \mathbb {X}$ is (as in § 3.6) a subset of representatives for
$\Lambda \subset \mathbb {X}$ is (as in § 3.6) a subset of representatives for ![]() $\mathfrak {t}^{*}_{\mathbb {F}_p}/(W,\bullet )$, we therefore have
$\mathfrak {t}^{*}_{\mathbb {F}_p}/(W,\bullet )$, we therefore have
and this constitutes the decomposition of ![]() $\mathfrak {D}$ into its irreducible components.
$\mathfrak {D}$ into its irreducible components.
Let us consider the open subset
Then ![]() $\mathfrak {t}^{*}_\circ$ is stable under the
$\mathfrak {t}^{*}_\circ$ is stable under the ![]() $(W,\bullet )$-action, and is in fact the pullback of an open subset of
$(W,\bullet )$-action, and is in fact the pullback of an open subset of ![]() $\mathfrak {t}^{*}/(W,\bullet )$, which therefore identifies with the quotient
$\mathfrak {t}^{*}/(W,\bullet )$, which therefore identifies with the quotient ![]() $\mathfrak {t}^{*}_\circ / (W,\bullet )$.
$\mathfrak {t}^{*}_\circ / (W,\bullet )$.
Recall the Grothendieck resolution ![]() $\tilde {\mathbf {g}}$Footnote 4 (for the reductive group
$\tilde {\mathbf {g}}$Footnote 4 (for the reductive group ![]() $\mathbf {G}=G^{(1)}$) and the morphism
$\mathbf {G}=G^{(1)}$) and the morphism ![]() $\vartheta : \tilde {\mathbf {g}} \to \mathfrak {t}^{*(1)}$; see § 2.3 and § 3.8. If we denote by
$\vartheta : \tilde {\mathbf {g}} \to \mathfrak {t}^{*(1)}$; see § 2.3 and § 3.8. If we denote by ![]() $\tilde {\mathbf {S}}^{*}$ the (scheme-theoretic) preimage of
$\tilde {\mathbf {S}}^{*}$ the (scheme-theoretic) preimage of ![]() $\mathbf {S}^{*}$ in
$\mathbf {S}^{*}$ in ![]() $\tilde {\mathbf {g}}$, then by [Reference RicheRic17, Proposition 3.5.5] the morphism
$\tilde {\mathbf {g}}$, then by [Reference RicheRic17, Proposition 3.5.5] the morphism ![]() $\vartheta$ restricts to an isomorphism
$\vartheta$ restricts to an isomorphism ![]() $\tilde {\mathbf {S}}^{*} \xrightarrow {\sim } \mathfrak {t}^{*(1)}$. In concrete terms, this means that, given
$\tilde {\mathbf {S}}^{*} \xrightarrow {\sim } \mathfrak {t}^{*(1)}$. In concrete terms, this means that, given ![]() $\zeta \in \mathfrak {t}^{*(1)}/W$ identified with an element in
$\zeta \in \mathfrak {t}^{*(1)}/W$ identified with an element in ![]() $\mathbf {S}^{*}$, the datum of a preimage of
$\mathbf {S}^{*}$, the datum of a preimage of ![]() $\zeta$ in
$\zeta$ in ![]() $\mathfrak {t}^{*(1)}$ is equivalent to the datum of a Borel subgroup
$\mathfrak {t}^{*(1)}$ is equivalent to the datum of a Borel subgroup ![]() $B' \subset G$ such that
$B' \subset G$ such that ![]() $\zeta _{|\mathrm {Lie}(U')^{(1)}}=0$, where
$\zeta _{|\mathrm {Lie}(U')^{(1)}}=0$, where ![]() $U'$ is the unipotent radical of
$U'$ is the unipotent radical of ![]() $B'$.
$B'$.
Proposition 4.4 Let ![]() $\lambda \in \mathbb {X}$ be a weight which belongs to the lower closure of the fundamental alcove. Consider some element
$\lambda \in \mathbb {X}$ be a weight which belongs to the lower closure of the fundamental alcove. Consider some element ![]() $\xi \in \mathfrak {t}^{*}_\circ$, and denote by
$\xi \in \mathfrak {t}^{*}_\circ$, and denote by ![]() $(\zeta _1,\zeta _2) \in \mathfrak {D}(\lambda )$ the image of
$(\zeta _1,\zeta _2) \in \mathfrak {D}(\lambda )$ the image of ![]() $(\xi + \overline {\lambda +\rho },\xi ) \in \tilde {\mathfrak {D}}(\lambda )$ in
$(\xi + \overline {\lambda +\rho },\xi ) \in \tilde {\mathfrak {D}}(\lambda )$ in ![]() $\mathfrak {D}$ and by
$\mathfrak {D}$ and by ![]() $\eta \in \mathbf {S}^{*}$ the element corresponding to the images of
$\eta \in \mathbf {S}^{*}$ the element corresponding to the images of ![]() $\zeta _1$ and
$\zeta _1$ and ![]() $\zeta _2$ in
$\zeta _2$ in ![]() $\mathfrak {t}^{*(1)}/W$. As explained above, the image of
$\mathfrak {t}^{*(1)}/W$. As explained above, the image of ![]() $\xi$ in
$\xi$ in ![]() $\mathfrak {t}^{*(1)}$ determines a Borel subgroup
$\mathfrak {t}^{*(1)}$ determines a Borel subgroup ![]() $B' \subset G$ with unipotent radical
$B' \subset G$ with unipotent radical ![]() $U'$ such that
$U'$ such that ![]() $\eta _{|\mathrm {Lie}(U')^{(1)}}=0$.
$\eta _{|\mathrm {Lie}(U')^{(1)}}=0$.
If we denote by ![]() $i : \mathrm {Spec}(\Bbbk ) \to \mathfrak {D}$ the morphism defined by
$i : \mathrm {Spec}(\Bbbk ) \to \mathfrak {D}$ the morphism defined by ![]() $(\zeta _1,\zeta _2)$, there exists an isomorphism of
$(\zeta _1,\zeta _2)$, there exists an isomorphism of ![]() $\mathcal {U}_\eta ^{\zeta _1} \mathfrak {g} \otimes (\mathcal {U}_\eta ^{\zeta _2} \mathfrak {g})^{\mathrm {op}}$-modules
$\mathcal {U}_\eta ^{\zeta _1} \mathfrak {g} \otimes (\mathcal {U}_\eta ^{\zeta _2} \mathfrak {g})^{\mathrm {op}}$-modules
Proof. By definition we have
By construction, the image of ![]() $\xi$ in
$\xi$ in ![]() $\mathfrak {t}^{*(1)}$ corresponds to the element in
$\mathfrak {t}^{*(1)}$ corresponds to the element in ![]() $(\mathrm {Lie}(B')/\mathrm {Lie}(U'))^{*(1)}$ defined by
$(\mathrm {Lie}(B')/\mathrm {Lie}(U'))^{*(1)}$ defined by ![]() $\eta$; by (4.2), we therefore have a canonical isomorphism
$\eta$; by (4.2), we therefore have a canonical isomorphism
under which the action of ![]() $\mathcal {U}\mathfrak {g}$ induced by left multiplication on the left-hand side corresponds to the natural action on
$\mathcal {U}\mathfrak {g}$ induced by left multiplication on the left-hand side corresponds to the natural action on ![]() $\mathsf {Z}_{\eta, B'}(\xi )$. We deduce an isomorphism
$\mathsf {Z}_{\eta, B'}(\xi )$. We deduce an isomorphism
which shows that to conclude the proof it suffices to construct an isomorphism of ![]() $\mathcal {U}_\eta ^{\zeta _1}$-modules
$\mathcal {U}_\eta ^{\zeta _1}$-modules
As above, we have a canonical isomorphism
therefore, any ![]() $\mathcal {U}_\eta ^{\zeta _1} \mathfrak {g}$-module is isomorphic to a direct sum of copies of
$\mathcal {U}_\eta ^{\zeta _1} \mathfrak {g}$-module is isomorphic to a direct sum of copies of ![]() $\mathsf {Z}_{\eta, B'}(\xi +\overline {\lambda +\rho })$. To analyze how many copies we have for the specific module in the left-hand side of (4.5), we observe that
$\mathsf {Z}_{\eta, B'}(\xi +\overline {\lambda +\rho })$. To analyze how many copies we have for the specific module in the left-hand side of (4.5), we observe that
 \begin{align*} &{{\rm Hom}}_{\mathcal{U}_\eta^{\zeta_1} \mathfrak{g}}(\Bbbk_{\zeta_1} \otimes_{{Z_{\mathrm{HC}}}} ( \mathsf{L}(\lambda+\rho) \otimes \mathsf{Z}_{\eta, B'}(\xi) ), \mathsf{Z}_{\eta,B'}(\xi + \overline{\lambda+\rho})) \\ &\quad ={{\rm Hom}}_{\mathcal{U}_\eta \mathfrak{g}}( \mathsf{L}(\lambda+\rho) \otimes \mathsf{Z}_{\eta, B'}(\xi), \mathsf{Z}_{\eta,B'}(\xi + \overline{\lambda+\rho})) \\ &\quad \cong{{\rm Hom}}_{\mathcal{U}_\eta \mathfrak{g}}( \mathsf{Z}_{\eta, B'}(\xi), \mathsf{L}(-w_0\lambda+\rho) \otimes \mathsf{Z}_{\eta,B'}(\xi + \overline{\lambda+\rho})). \end{align*}
\begin{align*} &{{\rm Hom}}_{\mathcal{U}_\eta^{\zeta_1} \mathfrak{g}}(\Bbbk_{\zeta_1} \otimes_{{Z_{\mathrm{HC}}}} ( \mathsf{L}(\lambda+\rho) \otimes \mathsf{Z}_{\eta, B'}(\xi) ), \mathsf{Z}_{\eta,B'}(\xi + \overline{\lambda+\rho})) \\ &\quad ={{\rm Hom}}_{\mathcal{U}_\eta \mathfrak{g}}( \mathsf{L}(\lambda+\rho) \otimes \mathsf{Z}_{\eta, B'}(\xi), \mathsf{Z}_{\eta,B'}(\xi + \overline{\lambda+\rho})) \\ &\quad \cong{{\rm Hom}}_{\mathcal{U}_\eta \mathfrak{g}}( \mathsf{Z}_{\eta, B'}(\xi), \mathsf{L}(-w_0\lambda+\rho) \otimes \mathsf{Z}_{\eta,B'}(\xi + \overline{\lambda+\rho})). \end{align*} We now consider the ![]() $\mathcal {U}_\eta \mathfrak {g}$-module
$\mathcal {U}_\eta \mathfrak {g}$-module ![]() $\mathsf {L}(-w_0\lambda +\rho ) \otimes \mathsf {Z}_{\eta,B'}(\xi + \overline {\lambda +\rho })$, and more specifically the direct summand on which
$\mathsf {L}(-w_0\lambda +\rho ) \otimes \mathsf {Z}_{\eta,B'}(\xi + \overline {\lambda +\rho })$, and more specifically the direct summand on which ![]() ${Z_{\mathrm {HC}}}$ acts with a generalized character corresponding to
${Z_{\mathrm {HC}}}$ acts with a generalized character corresponding to ![]() $\zeta _2$. We have a canonical isomorphism of
$\zeta _2$. We have a canonical isomorphism of ![]() $\mathcal {U}_\eta \mathfrak {g}$-modules
$\mathcal {U}_\eta \mathfrak {g}$-modules
The ![]() $B'$-module
$B'$-module ![]() $\mathsf {L}(-w_0\lambda +\rho )_{|B'}$ admits a filtration
$\mathsf {L}(-w_0\lambda +\rho )_{|B'}$ admits a filtration
where each ![]() $M_i/M_{i-1}$ is one-dimensional; moreover, these modules are associated with the characters of
$M_i/M_{i-1}$ is one-dimensional; moreover, these modules are associated with the characters of ![]() $B'/U' \cong B/U \cong T$ corresponding to the
$B'/U' \cong B/U \cong T$ corresponding to the ![]() $T$-weights of
$T$-weights of ![]() $\mathsf {L}(-w_0\lambda +\rho )$, counted with multiplicities. This filtration induces a filtration of
$\mathsf {L}(-w_0\lambda +\rho )$, counted with multiplicities. This filtration induces a filtration of ![]() $\mathsf {L}(-w_0\lambda +\rho )_{|B'} \otimes \Bbbk _{\xi +\overline {\lambda +\rho }}$, and then of
$\mathsf {L}(-w_0\lambda +\rho )_{|B'} \otimes \Bbbk _{\xi +\overline {\lambda +\rho }}$, and then of ![]() $\mathsf {L}(-w_0\lambda +\rho ) \otimes \mathsf {Z}_{\eta, B'}(\xi +\overline {\lambda +\rho })$, whose subquotients are of the form
$\mathsf {L}(-w_0\lambda +\rho ) \otimes \mathsf {Z}_{\eta, B'}(\xi +\overline {\lambda +\rho })$, whose subquotients are of the form ![]() $\mathsf {Z}_{\eta,B'}(\xi +\overline {\lambda +\rho +\mu })$, where
$\mathsf {Z}_{\eta,B'}(\xi +\overline {\lambda +\rho +\mu })$, where ![]() $\mu$ runs over the
$\mu$ runs over the ![]() $T$-weights of
$T$-weights of ![]() $\mathsf {L}(-w_0\lambda +\rho )$, counted with multiplicities.
$\mathsf {L}(-w_0\lambda +\rho )$, counted with multiplicities.
We claim that there exists exactly one subquotient in this filtration on which ![]() ${Z_{\mathrm {HC}}}$ acts via the character
${Z_{\mathrm {HC}}}$ acts via the character ![]() $\zeta _2$, corresponding to the multiplicity-
$\zeta _2$, corresponding to the multiplicity-![]() $1$ weight
$1$ weight ![]() $-\lambda -\rho$ of
$-\lambda -\rho$ of ![]() $\mathsf {L}(-w_0\lambda +\rho )$. Indeed, assume that
$\mathsf {L}(-w_0\lambda +\rho )$. Indeed, assume that ![]() ${Z_{\mathrm {HC}}}$ acts with character
${Z_{\mathrm {HC}}}$ acts with character ![]() $\zeta _2$ on
$\zeta _2$ on ![]() $\mathsf {Z}_{\eta,B'}(\xi +\overline {\lambda +\rho +\mu })$. Then there exists
$\mathsf {Z}_{\eta,B'}(\xi +\overline {\lambda +\rho +\mu })$. Then there exists ![]() $w \in W$ such that
$w \in W$ such that ![]() $\xi +\overline {\lambda +\rho +\mu }=w \bullet \xi$. Since
$\xi +\overline {\lambda +\rho +\mu }=w \bullet \xi$. Since ![]() $\xi$ belongs to
$\xi$ belongs to ![]() $\mathfrak {t}^{*}_\circ$, this condition implies that
$\mathfrak {t}^{*}_\circ$, this condition implies that ![]() $\xi +\overline {\lambda +\rho +\mu }=\xi$, hence that
$\xi +\overline {\lambda +\rho +\mu }=\xi$, hence that ![]() $\lambda +\rho +\mu \in p \mathbb {X}$. On the other hand,
$\lambda +\rho +\mu \in p \mathbb {X}$. On the other hand, ![]() $\mu$ is a weight of
$\mu$ is a weight of ![]() $\mathsf {L}(-w_0\lambda +\rho )$, hence it belongs to
$\mathsf {L}(-w_0\lambda +\rho )$, hence it belongs to ![]() $-w_0\lambda +\rho + \mathbb {Z}\mathfrak {R} = -\lambda - \rho +\mathbb {Z}\mathfrak {R}$. In view of (3.1) these conditions imply that
$-w_0\lambda +\rho + \mathbb {Z}\mathfrak {R} = -\lambda - \rho +\mathbb {Z}\mathfrak {R}$. In view of (3.1) these conditions imply that ![]() $\lambda +\rho +\mu \in p\mathbb {Z}\mathfrak {R}$, that is, that
$\lambda +\rho +\mu \in p\mathbb {Z}\mathfrak {R}$, that is, that ![]() $\lambda +\mu \in -\rho +p\mathbb {Z}\mathfrak {R}={W_{\mathrm {aff}}} \bullet (-\rho )$. By [Reference JantzenJan03, Lemma II.7.7] (applied to the pair of elements
$\lambda +\mu \in -\rho +p\mathbb {Z}\mathfrak {R}={W_{\mathrm {aff}}} \bullet (-\rho )$. By [Reference JantzenJan03, Lemma II.7.7] (applied to the pair of elements ![]() $(\lambda,-\rho )$), there must then exist
$(\lambda,-\rho )$), there must then exist ![]() $w \in {W_{\mathrm {aff}}}$ such that
$w \in {W_{\mathrm {aff}}}$ such that ![]() $w \bullet \lambda =\lambda$ and
$w \bullet \lambda =\lambda$ and ![]() $\lambda +\mu = w \bullet (-\rho )$. Here, since
$\lambda +\mu = w \bullet (-\rho )$. Here, since ![]() $\lambda$ belongs to the lower closure of the fundamental alcove, the first condition implies that
$\lambda$ belongs to the lower closure of the fundamental alcove, the first condition implies that ![]() $w \in W$ (see § 3.5); it follows that
$w \in W$ (see § 3.5); it follows that ![]() $w \bullet (-\rho )=-\rho$, hence that
$w \bullet (-\rho )=-\rho$, hence that ![]() $\lambda +\mu =-\rho$, which finishes the proof of our claim.
$\lambda +\mu =-\rho$, which finishes the proof of our claim.
This claim implies that the direct summand of ![]() $\mathsf {L}(-w_0\lambda +\rho ) \otimes \mathsf {Z}_{\eta,B'}(\xi + \overline {\lambda +\rho })$ corresponding to the generalized character of
$\mathsf {L}(-w_0\lambda +\rho ) \otimes \mathsf {Z}_{\eta,B'}(\xi + \overline {\lambda +\rho })$ corresponding to the generalized character of ![]() ${Z_{\mathrm {HC}}}$ given by
${Z_{\mathrm {HC}}}$ given by ![]() $\zeta _2$ is isomorphic to
$\zeta _2$ is isomorphic to ![]() $\mathsf {Z}_{\eta, B'}(\xi )$; it follows that
$\mathsf {Z}_{\eta, B'}(\xi )$; it follows that
is one-dimensional, which finally proves (4.5).
The statement of Proposition 4.4 is not symmetric, in that the conditions we impose imply that ![]() $\zeta _2$ necessarily belongs to
$\zeta _2$ necessarily belongs to ![]() $\mathfrak {t}^{*}_\circ / (W,\bullet )$, whereas
$\mathfrak {t}^{*}_\circ / (W,\bullet )$, whereas ![]() $\zeta _1$ might not. Below we will also need the other variant of this statement, in which the first component has to belong to
$\zeta _1$ might not. Below we will also need the other variant of this statement, in which the first component has to belong to ![]() $\mathfrak {t}^{*}_\circ / (W,\bullet )$. Its proof is analogous to that of Proposition 4.4. (More precisely, in this case the counterpart of (4.5) can be obtained directly, without recourse to the computation in the paragraph following this equation.)
$\mathfrak {t}^{*}_\circ / (W,\bullet )$. Its proof is analogous to that of Proposition 4.4. (More precisely, in this case the counterpart of (4.5) can be obtained directly, without recourse to the computation in the paragraph following this equation.)
Proposition 4.5 Let ![]() $\mu \in \mathbb {X}$ be a weight which belongs to the lower closure of the fundamental alcove. Consider some element
$\mu \in \mathbb {X}$ be a weight which belongs to the lower closure of the fundamental alcove. Consider some element ![]() $\xi \in \mathfrak {t}^{*}_\circ$, and denote by
$\xi \in \mathfrak {t}^{*}_\circ$, and denote by ![]() $(\zeta _1,\zeta _2) \in \mathfrak {D}(-w_0 \mu )$ the image of
$(\zeta _1,\zeta _2) \in \mathfrak {D}(-w_0 \mu )$ the image of ![]() $(\xi,\xi + \overline {\mu +\rho }) \in \tilde {\mathfrak {D}}(-w_0 \mu )$ in
$(\xi,\xi + \overline {\mu +\rho }) \in \tilde {\mathfrak {D}}(-w_0 \mu )$ in ![]() $\mathfrak {D}$ and by
$\mathfrak {D}$ and by ![]() $\eta \in \mathbf {S}^{*}$ the element corresponding to the images of
$\eta \in \mathbf {S}^{*}$ the element corresponding to the images of ![]() $\zeta _1$ and
$\zeta _1$ and ![]() $\zeta _2$ in
$\zeta _2$ in ![]() $\mathfrak {t}^{*(1)}/W$. As explained above Proposition 4.4, the image of
$\mathfrak {t}^{*(1)}/W$. As explained above Proposition 4.4, the image of ![]() $\xi$ in
$\xi$ in ![]() $\mathfrak {t}^{*(1)}$ determines a Borel subgroup
$\mathfrak {t}^{*(1)}$ determines a Borel subgroup ![]() $B' \subset G$ with unipotent radical
$B' \subset G$ with unipotent radical ![]() $U'$ such that
$U'$ such that ![]() $\eta _{|\mathrm {Lie}(U')^{(1)}}=0$.
$\eta _{|\mathrm {Lie}(U')^{(1)}}=0$.
If we denote by ![]() $i : \mathrm {Spec}(\Bbbk ) \to \mathfrak {D}$ the morphism defined by
$i : \mathrm {Spec}(\Bbbk ) \to \mathfrak {D}$ the morphism defined by ![]() $(\zeta _1,\zeta _2)$, there exists an isomorphism of
$(\zeta _1,\zeta _2)$, there exists an isomorphism of ![]() $\mathcal {U}_\eta ^{\zeta _1} \mathfrak {g} \otimes (\mathcal {U}_\eta ^{\zeta _2} \mathfrak {g})^{\mathrm {op}}$-modules
$\mathcal {U}_\eta ^{\zeta _1} \mathfrak {g} \otimes (\mathcal {U}_\eta ^{\zeta _2} \mathfrak {g})^{\mathrm {op}}$-modules
4.5 Proof of Theorem 4.3
The proof of Theorem 4.3 will require two more preliminary lemmas.
Lemma 4.6 Let ![]() $X$ be a reduced scheme locally of finite type over
$X$ be a reduced scheme locally of finite type over ![]() $\Bbbk$, and let
$\Bbbk$, and let ![]() $\mathscr {F}$ be a coherent sheaf on
$\mathscr {F}$ be a coherent sheaf on ![]() $X$. Assume that there exists
$X$. Assume that there exists ![]() $d \geq 0$ such that for any morphism
$d \geq 0$ such that for any morphism ![]() $i : \mathrm {Spec}(\Bbbk ) \to X$ the pullback
$i : \mathrm {Spec}(\Bbbk ) \to X$ the pullback ![]() $i^{*}(\mathscr {F}) \in \mathsf {Coh}(\mathrm {Spec}(\Bbbk ))=\mathsf {Vect}_\Bbbk$ has dimension
$i^{*}(\mathscr {F}) \in \mathsf {Coh}(\mathrm {Spec}(\Bbbk ))=\mathsf {Vect}_\Bbbk$ has dimension ![]() $d$. Then
$d$. Then ![]() $\mathscr {F}$ is a locally free
$\mathscr {F}$ is a locally free ![]() $\mathscr {O}_X$-module of rank
$\mathscr {O}_X$-module of rank ![]() $d$.
$d$.
Proof. Of course we can assume that ![]() $X$ is also affine and of finite type, that is, that
$X$ is also affine and of finite type, that is, that ![]() $X=\mathrm {Spec}(A)$ for some finitely generated reduced
$X=\mathrm {Spec}(A)$ for some finitely generated reduced ![]() $\Bbbk$-algebra
$\Bbbk$-algebra ![]() $A$. With this notation, recall that closed points are dense in any closed subset of
$A$. With this notation, recall that closed points are dense in any closed subset of ![]() $\mathrm {Spec}(A)$; see § 4.4.
$\mathrm {Spec}(A)$; see § 4.4.
Let us denote by ![]() $M$ the
$M$ the ![]() $A$-module corresponding to
$A$-module corresponding to ![]() $\mathscr {F}$. In this setting the datum of a morphism
$\mathscr {F}$. In this setting the datum of a morphism ![]() $i : \mathrm {Spec}(\Bbbk ) \to X$ is equivalent to the datum of a maximal ideal
$i : \mathrm {Spec}(\Bbbk ) \to X$ is equivalent to the datum of a maximal ideal ![]() $\mathfrak {m} \subset A$, and we have
$\mathfrak {m} \subset A$, and we have ![]() $i^{*}(\mathscr {F})=M/\mathfrak {m} \cdot M$. In view of [Sta20, Tag 0FWG], to show that
$i^{*}(\mathscr {F})=M/\mathfrak {m} \cdot M$. In view of [Sta20, Tag 0FWG], to show that ![]() $M$ is locally free of rank
$M$ is locally free of rank ![]() $d$ it suffices to prove that for any
$d$ it suffices to prove that for any ![]() $\mathfrak {p} \in \mathrm {Spec}(A)$ we have
$\mathfrak {p} \in \mathrm {Spec}(A)$ we have
Now by [Reference PeskinePes96, Theorem 7.33], the function
is upper semi-continuous. By assumption, this function is constant (equal to ![]() $d$) on the subset of
$d$) on the subset of ![]() $\mathrm {Spec}(A)$ consisting of maximal ideals, that is, of closed points. Hence, the open subset
$\mathrm {Spec}(A)$ consisting of maximal ideals, that is, of closed points. Hence, the open subset
contains all closed points, hence is the whole of ![]() $\mathrm {Spec}(A)$. On the other hand, the open subset
$\mathrm {Spec}(A)$. On the other hand, the open subset
does not contain any closed point, hence is empty.
Lemma 4.7 The morphism
induced by projection on the first and third factors is étale at any point of the form ![]() $(\tilde {\lambda },\widetilde {-\rho },\tilde {\mu })$ with
$(\tilde {\lambda },\widetilde {-\rho },\tilde {\mu })$ with ![]() $\lambda,\mu \in \mathbb {X}$.
$\lambda,\mu \in \mathbb {X}$.
Proof. To prove this claim it suffices to prove that the morphism ![]() $\mathfrak {t}^{*}/(W,\bullet ) \to \mathfrak {t}^{*(1)}/W$ is étale at
$\mathfrak {t}^{*}/(W,\bullet ) \to \mathfrak {t}^{*(1)}/W$ is étale at ![]() $\widetilde {-\rho }$. The dot action of
$\widetilde {-\rho }$. The dot action of ![]() $W$ and the natural action of
$W$ and the natural action of ![]() $\mathfrak {t}^{*}_{\mathbb {F}_p}$ on
$\mathfrak {t}^{*}_{\mathbb {F}_p}$ on ![]() $\mathfrak {t}^{*}$ combine to provide an action of the semi-direct product
$\mathfrak {t}^{*}$ combine to provide an action of the semi-direct product ![]() $\mathfrak {t}^{*}_{\mathbb {F}_p} \rtimes W$ (where
$\mathfrak {t}^{*}_{\mathbb {F}_p} \rtimes W$ (where ![]() $W$ acts on
$W$ acts on ![]() $\mathfrak {t}^{*}_{\mathbb {F}_p}$ through the natural, unshifted, action) defined by
$\mathfrak {t}^{*}_{\mathbb {F}_p}$ through the natural, unshifted, action) defined by ![]() $({{\bar {\lambda }}}w) \bullet \xi = w(\xi +\bar {\rho })-\bar {\rho }+{{\bar {\lambda }}}$ for
$({{\bar {\lambda }}}w) \bullet \xi = w(\xi +\bar {\rho })-\bar {\rho }+{{\bar {\lambda }}}$ for ![]() ${{\bar {\lambda }}} \in \mathfrak {t}^{*}_{\mathbb {F}_p}$ and
${{\bar {\lambda }}} \in \mathfrak {t}^{*}_{\mathbb {F}_p}$ and ![]() $w \in W$. Moreover, the composition
$w \in W$. Moreover, the composition ![]() $\mathfrak {t}^{*} \to \mathfrak {t}^{*}/(W,\bullet ) \to \mathfrak {t}^{*(1)}/W$ is the quotient morphism for this action. Since
$\mathfrak {t}^{*} \to \mathfrak {t}^{*}/(W,\bullet ) \to \mathfrak {t}^{*(1)}/W$ is the quotient morphism for this action. Since ![]() $\overline {-\rho }$ is stabilized by
$\overline {-\rho }$ is stabilized by ![]() $W$, the claim then follows from [SGA1, Exp. V, Proposition 2.2].
$W$, the claim then follows from [SGA1, Exp. V, Proposition 2.2].
For ![]() $\lambda \in \mathbb {X}$, whose image in
$\lambda \in \mathbb {X}$, whose image in ![]() $\mathfrak {t}^{*}_{\mathbb {F}_p}/(W,\bullet )$ is that of
$\mathfrak {t}^{*}_{\mathbb {F}_p}/(W,\bullet )$ is that of ![]() $\lambda ' \in \Lambda$, we set
$\lambda ' \in \Lambda$, we set
 \[ \mathfrak{D}_\circ(\lambda) := (\mathfrak{t}^{*} / (W,\bullet) \times_{\mathfrak{t}^{*(1)}/W} \mathfrak{t}^{*}_\circ / (W,\bullet) ) \smallsetminus \bigg( \bigcup_{\mu \in \Lambda \smallsetminus \{\lambda'\}} \mathfrak{D}(\mu) \bigg). \]
\[ \mathfrak{D}_\circ(\lambda) := (\mathfrak{t}^{*} / (W,\bullet) \times_{\mathfrak{t}^{*(1)}/W} \mathfrak{t}^{*}_\circ / (W,\bullet) ) \smallsetminus \bigg( \bigcup_{\mu \in \Lambda \smallsetminus \{\lambda'\}} \mathfrak{D}(\mu) \bigg). \]
Then ![]() $\mathfrak {D}_\circ (\lambda )$ is an open subset of
$\mathfrak {D}_\circ (\lambda )$ is an open subset of ![]() $\mathfrak {D}$, contained in
$\mathfrak {D}$, contained in ![]() $\mathfrak {D}(\lambda )$. We will denote by
$\mathfrak {D}(\lambda )$. We will denote by ![]() $j_\lambda : \mathfrak {D}_\circ (\lambda ) \to \mathfrak {D}$ the embedding. Continuing with the same notation, we also set
$j_\lambda : \mathfrak {D}_\circ (\lambda ) \to \mathfrak {D}$ the embedding. Continuing with the same notation, we also set
 \[ \mathfrak{D}_\circ'(\lambda) := (\mathfrak{t}_\circ^{*} / (W,\bullet) \times_{\mathfrak{t}^{*(1)}/W} \mathfrak{t}^{*} / (W,\bullet) ) \smallsetminus \bigg( \bigcup_{\mu \in \Lambda \smallsetminus \{\lambda'\}} \mathfrak{D}(\mu) \bigg), \]
\[ \mathfrak{D}_\circ'(\lambda) := (\mathfrak{t}_\circ^{*} / (W,\bullet) \times_{\mathfrak{t}^{*(1)}/W} \mathfrak{t}^{*} / (W,\bullet) ) \smallsetminus \bigg( \bigcup_{\mu \in \Lambda \smallsetminus \{\lambda'\}} \mathfrak{D}(\mu) \bigg), \]
and we denote by ![]() $j_\lambda ' : \mathfrak {D}_\circ '(\lambda ) \to \mathfrak {D}$ the open embedding.
$j_\lambda ' : \mathfrak {D}_\circ '(\lambda ) \to \mathfrak {D}$ the open embedding.
Proof of Theorem 4.3 Let ![]() $\lambda,\mu \in \mathbb {X}$ belong to the lower closure of the fundamental alcove. The vector
$\lambda,\mu \in \mathbb {X}$ belong to the lower closure of the fundamental alcove. The vector ![]() $\overline {-\rho }$ belongs to
$\overline {-\rho }$ belongs to ![]() $\mathfrak {t}^{*}_\circ$ since this point is stable under the dot action of
$\mathfrak {t}^{*}_\circ$ since this point is stable under the dot action of ![]() $W$. On the other hand, if
$W$. On the other hand, if ![]() $\nu \in \mathbb {X}$ is such that
$\nu \in \mathbb {X}$ is such that ![]() $(\tilde {\lambda },\widetilde {-\rho }) \in \mathfrak {D}(\nu )$, then there exists
$(\tilde {\lambda },\widetilde {-\rho }) \in \mathfrak {D}(\nu )$, then there exists ![]() $\xi \in \mathfrak {t}^{*}$ such that the point
$\xi \in \mathfrak {t}^{*}$ such that the point ![]() $(\xi +\overline {\nu +\rho },\xi ) \in \tilde {\mathfrak {D}}$ has image
$(\xi +\overline {\nu +\rho },\xi ) \in \tilde {\mathfrak {D}}$ has image ![]() $(\tilde {\lambda },\widetilde {-\rho })$ in
$(\tilde {\lambda },\widetilde {-\rho })$ in ![]() $\mathfrak {D}$; we then have
$\mathfrak {D}$; we then have ![]() $\xi \in W \bullet \overline {-\rho } = \{\overline {-\rho }\}$ and
$\xi \in W \bullet \overline {-\rho } = \{\overline {-\rho }\}$ and ![]() $\xi + \overline {\nu +\rho } \in W \bullet \bar {\lambda }$, so that
$\xi + \overline {\nu +\rho } \in W \bullet \bar {\lambda }$, so that ![]() ${{\tilde {\lambda }}}=\tilde {\nu }$. We have finally checked that
${{\tilde {\lambda }}}=\tilde {\nu }$. We have finally checked that ![]() $(\tilde {\lambda },\widetilde {-\rho }) \in \mathfrak {D}_\circ (\lambda )$; similar considerations show that
$(\tilde {\lambda },\widetilde {-\rho }) \in \mathfrak {D}_\circ (\lambda )$; similar considerations show that ![]() $(\widetilde {-\rho },\tilde {\mu }) \in \mathfrak {D}'_\circ (-w_0\mu )$.
$(\widetilde {-\rho },\tilde {\mu }) \in \mathfrak {D}'_\circ (-w_0\mu )$.
By construction, ![]() $\mathfrak {D}_\circ (\lambda ) \times _{\mathfrak {t}^{*}/(W,\bullet )} \mathfrak {D}'_\circ (-w_0\mu )$ is an open subscheme in the fiber product
$\mathfrak {D}_\circ (\lambda ) \times _{\mathfrak {t}^{*}/(W,\bullet )} \mathfrak {D}'_\circ (-w_0\mu )$ is an open subscheme in the fiber product
Consider the morphism
induced by projection on the middle factor. The algebra ![]() $\mathcal {U}_\mathbf {S} \mathfrak {g}$ is an
$\mathcal {U}_\mathbf {S} \mathfrak {g}$ is an ![]() $\mathscr {O}(\mathfrak {t}^{*}/(W,\bullet ))$-algebra; it therefore defines a coherent sheaf of
$\mathscr {O}(\mathfrak {t}^{*}/(W,\bullet ))$-algebra; it therefore defines a coherent sheaf of ![]() $\mathscr {O}_{\mathfrak {t}^{*}/(W,\bullet )}$-algebras
$\mathscr {O}_{\mathfrak {t}^{*}/(W,\bullet )}$-algebras ![]() $\mathscr {A}$ on
$\mathscr {A}$ on ![]() $\mathfrak {t}^{*}/(W,\bullet )$. Consider also the projections
$\mathfrak {t}^{*}/(W,\bullet )$. Consider also the projections
 \begin{align*} p &: \mathfrak{D}_\circ(\lambda) \times_{\mathfrak{t}^{*}/(W,\bullet)} \mathfrak{D}'_\circ(-w_0\mu) \to \mathfrak{D}_\circ(\lambda), \\ q &: \mathfrak{D}_\circ(\lambda) \times_{\mathfrak{t}^{*}/(W,\bullet)} \mathfrak{D}'_\circ(-w_0\mu) \to \mathfrak{D}'_\circ(-w_0 \mu). \end{align*}
\begin{align*} p &: \mathfrak{D}_\circ(\lambda) \times_{\mathfrak{t}^{*}/(W,\bullet)} \mathfrak{D}'_\circ(-w_0\mu) \to \mathfrak{D}_\circ(\lambda), \\ q &: \mathfrak{D}_\circ(\lambda) \times_{\mathfrak{t}^{*}/(W,\bullet)} \mathfrak{D}'_\circ(-w_0\mu) \to \mathfrak{D}'_\circ(-w_0 \mu). \end{align*}
The sheaves ![]() $p^{*} j_\lambda ^{*} ( \mathsf {L}(\lambda +\rho ) \otimes \mathcal {U}_\mathbf {S} \mathfrak {g} )$ and
$p^{*} j_\lambda ^{*} ( \mathsf {L}(\lambda +\rho ) \otimes \mathcal {U}_\mathbf {S} \mathfrak {g} )$ and ![]() $q^{*} (j'_{-w_0\mu })^{*} (\mathsf {L}(-w_0\mu +\rho ) \otimes \mathcal {U}_\mathbf {S} \mathfrak {g})$ are naturally sheaves of (right and left, respectively) modules for
$q^{*} (j'_{-w_0\mu })^{*} (\mathsf {L}(-w_0\mu +\rho ) \otimes \mathcal {U}_\mathbf {S} \mathfrak {g})$ are naturally sheaves of (right and left, respectively) modules for ![]() $f^{*} \mathscr {A}$, so that we can consider the tensor product
$f^{*} \mathscr {A}$, so that we can consider the tensor product
We claim that this sheaf is a locally free ![]() $\mathscr {O}_{\mathfrak {D}_\circ (\lambda ) \times _{\mathfrak {t}^{*}/(W,\bullet )} \mathfrak {D}'_\circ (-w_0\mu )}$-module, of rank
$\mathscr {O}_{\mathfrak {D}_\circ (\lambda ) \times _{\mathfrak {t}^{*}/(W,\bullet )} \mathfrak {D}'_\circ (-w_0\mu )}$-module, of rank ![]() $p^{2\# \mathfrak {R}^{+}}$. In fact, by Lemma 4.6, to prove this it suffices to prove that for any closed point
$p^{2\# \mathfrak {R}^{+}}$. In fact, by Lemma 4.6, to prove this it suffices to prove that for any closed point ![]() $(\zeta _1,\zeta _2,\zeta _3) \in \mathfrak {D}_\circ (\lambda ) \times _{\mathfrak {t}^{*}/(W,\bullet )} \mathfrak {D}'_\circ (-w_0\mu )$, denoting by
$(\zeta _1,\zeta _2,\zeta _3) \in \mathfrak {D}_\circ (\lambda ) \times _{\mathfrak {t}^{*}/(W,\bullet )} \mathfrak {D}'_\circ (-w_0\mu )$, denoting by ![]() $i : \mathrm {Spec}(\Bbbk ) \to \mathfrak {D}_\circ (\lambda ) \times _{\mathfrak {t}^{*}/(W,\bullet )} \mathfrak {D}'_\circ (-w_0\mu )$ the corresponding morphism, the vector space
$i : \mathrm {Spec}(\Bbbk ) \to \mathfrak {D}_\circ (\lambda ) \times _{\mathfrak {t}^{*}/(W,\bullet )} \mathfrak {D}'_\circ (-w_0\mu )$ the corresponding morphism, the vector space
has dimension ![]() $p^{2\#\mathfrak {R}^{+}}$. If we denote by
$p^{2\#\mathfrak {R}^{+}}$. If we denote by ![]() $i_1 : \mathrm {Spec}(\Bbbk ) \to \mathfrak {D}$ and
$i_1 : \mathrm {Spec}(\Bbbk ) \to \mathfrak {D}$ and ![]() $i_2 : \mathrm {Spec}(\Bbbk ) \to \mathfrak {D}$ the embeddings of the points
$i_2 : \mathrm {Spec}(\Bbbk ) \to \mathfrak {D}$ the embeddings of the points ![]() $(\zeta _1,\zeta _2)$ and
$(\zeta _1,\zeta _2)$ and ![]() $(\zeta _2,\zeta _3)$ respectively, then this vector space can be written as
$(\zeta _2,\zeta _3)$ respectively, then this vector space can be written as
where ![]() $\eta \in \mathbf {S}^{*}$ is the image of the elements
$\eta \in \mathbf {S}^{*}$ is the image of the elements ![]() $\zeta _i$. Let
$\zeta _i$. Let ![]() $\xi \in \mathfrak {t}^{*}$ be such that
$\xi \in \mathfrak {t}^{*}$ be such that ![]() $(\zeta _1,\zeta _2)$ is the image of
$(\zeta _1,\zeta _2)$ is the image of ![]() $(\xi + \overline {\lambda +\rho },\xi )$, and let
$(\xi + \overline {\lambda +\rho },\xi )$, and let ![]() $B' \subset G$ be the Borel subgroup with unipotent radical
$B' \subset G$ be the Borel subgroup with unipotent radical ![]() $U'$ such that
$U'$ such that ![]() $\eta _{|\mathrm {Lie}(U')^{(1)}}=0$ determined by the image of
$\eta _{|\mathrm {Lie}(U')^{(1)}}=0$ determined by the image of ![]() $\xi$ in
$\xi$ in ![]() $\mathfrak {t}^{*(1)}$ (see the comments above Proposition 4.4). By Proposition 4.4 we have
$\mathfrak {t}^{*(1)}$ (see the comments above Proposition 4.4). By Proposition 4.4 we have
Similarly, if ![]() $\xi ' \in \mathfrak {t}^{*}$ is such that
$\xi ' \in \mathfrak {t}^{*}$ is such that ![]() $(\zeta _2,\zeta _3)$ is the image of
$(\zeta _2,\zeta _3)$ is the image of ![]() $(\xi ',\xi ' + \overline {\mu +\rho })$, and if
$(\xi ',\xi ' + \overline {\mu +\rho })$, and if ![]() $B'' \subset G$ is the Borel subgroup with unipotent radical
$B'' \subset G$ is the Borel subgroup with unipotent radical ![]() $U''$ such that
$U''$ such that ![]() $\eta _{|\mathrm {Lie}(U'')^{(1)}}=0$ determined by the image of
$\eta _{|\mathrm {Lie}(U'')^{(1)}}=0$ determined by the image of ![]() $\xi '$ in
$\xi '$ in ![]() $\mathfrak {t}^{*(1)}$, then by Proposition 4.5 we have
$\mathfrak {t}^{*(1)}$, then by Proposition 4.5 we have
Here ![]() $\mathsf {Z}_{\eta,B'}(\xi )$ and
$\mathsf {Z}_{\eta,B'}(\xi )$ and ![]() $\mathsf {Z}_{\eta,B''}(\xi ')$ are two simple modules over the matrix algebra
$\mathsf {Z}_{\eta,B''}(\xi ')$ are two simple modules over the matrix algebra ![]() $\mathcal {U}_\eta ^{\zeta _2} \mathfrak {g}$, see § 4.2; they must therefore be isomorphic. Fixing an isomorphism
$\mathcal {U}_\eta ^{\zeta _2} \mathfrak {g}$, see § 4.2; they must therefore be isomorphic. Fixing an isomorphism ![]() $\varphi : \mathsf {Z}_{\eta,B'}(\xi ) \xrightarrow {\sim } \mathsf {Z}_{\eta,B''}(\xi ')$, we obtain a pairing
$\varphi : \mathsf {Z}_{\eta,B'}(\xi ) \xrightarrow {\sim } \mathsf {Z}_{\eta,B''}(\xi ')$, we obtain a pairing
defined by ![]() $f \otimes v \mapsto f(\varphi ^{-1}(v))$, which induces an isomorphism
$f \otimes v \mapsto f(\varphi ^{-1}(v))$, which induces an isomorphism
Combining these observations, we obtain that the vector space in (4.7) is isomorphic to
hence has dimension ![]() $p^{2\#\mathfrak {R}^{+}}$, as desired.
$p^{2\#\mathfrak {R}^{+}}$, as desired.
We now consider the morphism
obtained from that of Lemma 4.7 by restriction to the open subset
This lemma ensures that this morphism is étale at ![]() $(\tilde {\lambda },\widetilde {-\rho },\tilde {\mu })$; it therefore identifies the completion of
$(\tilde {\lambda },\widetilde {-\rho },\tilde {\mu })$; it therefore identifies the completion of ![]() $\mathfrak {D}_\circ (\lambda ) \times _{\mathfrak {t}^{*}/(W,\bullet )} \mathfrak {D}'_\circ (-w_0\mu )$ at
$\mathfrak {D}_\circ (\lambda ) \times _{\mathfrak {t}^{*}/(W,\bullet )} \mathfrak {D}'_\circ (-w_0\mu )$ at ![]() $(\tilde {\lambda },\widetilde {-\rho },\tilde {\mu })$ with the completion of
$(\tilde {\lambda },\widetilde {-\rho },\tilde {\mu })$ with the completion of ![]() $\mathfrak {D}$ at
$\mathfrak {D}$ at ![]() $(\tilde {\lambda },\tilde {\mu })$, that is, with the spectrum of
$(\tilde {\lambda },\tilde {\mu })$, that is, with the spectrum of ![]() $\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$. By construction the completion of the sheaf (4.6) at
$\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$. By construction the completion of the sheaf (4.6) at ![]() $(\tilde {\lambda },\widetilde {-\rho },\tilde {\mu })$ is
$(\tilde {\lambda },\widetilde {-\rho },\tilde {\mu })$ is ![]() $\mathsf {M}^{\lambda,\mu }_\mathbf {S}$; since this sheaf is locally free this proves that
$\mathsf {M}^{\lambda,\mu }_\mathbf {S}$; since this sheaf is locally free this proves that ![]() $\mathsf {M}^{\lambda,\mu }_\mathbf {S}$ is faithfully projective. In fact, since the ring
$\mathsf {M}^{\lambda,\mu }_\mathbf {S}$ is faithfully projective. In fact, since the ring ![]() $\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$ is local, this module is even free (of rank
$\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$ is local, this module is even free (of rank ![]() $p^{2\#\mathfrak {R}^{+}}$) by [Sta20, Tag 00NZ].
$p^{2\#\mathfrak {R}^{+}}$) by [Sta20, Tag 00NZ].
Finally, we consider the natural morphism
Here, both sides are finite free as modules over ![]() $\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$. In fact, for the right-hand side this follows from the same property for the module
$\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$. In fact, for the right-hand side this follows from the same property for the module ![]() $\mathsf {M}^{\lambda,\mu }_\mathbf {S}$, which we have seen above. For the left-hand side, we observe that
$\mathsf {M}^{\lambda,\mu }_\mathbf {S}$, which we have seen above. For the left-hand side, we observe that ![]() $\mathcal {U}_\mathbf {S} \mathfrak {g}$ is finite projective over
$\mathcal {U}_\mathbf {S} \mathfrak {g}$ is finite projective over ![]() $\mathscr {O}(\mathfrak {C}_\mathbf {S})$ by Proposition 4.1; it follows that
$\mathscr {O}(\mathfrak {C}_\mathbf {S})$ by Proposition 4.1; it follows that ![]() $\mathcal {U}_\mathbf {S} \mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} \mathcal {U}_\mathbf {S} \mathfrak {g}^{\mathrm{op}}$ is finite projective over
$\mathcal {U}_\mathbf {S} \mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} \mathcal {U}_\mathbf {S} \mathfrak {g}^{\mathrm{op}}$ is finite projective over ![]() $\mathcal {Z}_\mathbf {S}$, and finally that
$\mathcal {Z}_\mathbf {S}$, and finally that ![]() $\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$ is finite projective, hence finite free (again by [Sta20, Tag 00NZ]), over the local ring
$\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$ is finite projective, hence finite free (again by [Sta20, Tag 00NZ]), over the local ring ![]() $\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$. Given this property, to prove that our morphism is an isomorphism it suffices to prove that it is invertible after application of the functor
$\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$. Given this property, to prove that our morphism is an isomorphism it suffices to prove that it is invertible after application of the functor ![]() $\Bbbk \otimes _{\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}} (-)$. Now if we denote by
$\Bbbk \otimes _{\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}} (-)$. Now if we denote by ![]() $\chi \in \mathfrak {g}^{*(1)}$ the point corresponding to the image of
$\chi \in \mathfrak {g}^{*(1)}$ the point corresponding to the image of ![]() $0$ in
$0$ in ![]() $\mathfrak {t}^{*(1)}/W$ under the identification
$\mathfrak {t}^{*(1)}/W$ under the identification ![]() $\mathbf {S}^{*} \xrightarrow {\sim } \mathfrak {t}^{*(1)}/W$, we have
$\mathbf {S}^{*} \xrightarrow {\sim } \mathfrak {t}^{*(1)}/W$, we have
On the other hand, since ![]() $\mathsf {M}^{\lambda,\mu }_\mathbf {S}$ is a free module we have
$\mathsf {M}^{\lambda,\mu }_\mathbf {S}$ is a free module we have
and, applying the considerations above with ![]() $\xi =\xi '=\overline {-\rho }$, we have
$\xi =\xi '=\overline {-\rho }$, we have
where ![]() $B' \subset G$ is the unique Borel subgroup with unipotent radical
$B' \subset G$ is the unique Borel subgroup with unipotent radical ![]() $U'$ such that
$U'$ such that ![]() $\chi _{|\mathrm {Lie}(U')^{(1)}}=0$. By (4.2) our morphism is indeed an isomorphism, which finishes the proof.
$\chi _{|\mathrm {Lie}(U')^{(1)}}=0$. By (4.2) our morphism is indeed an isomorphism, which finishes the proof.
4.6 Localization for Harish-Chandra bimodules
The main consequence of Theorem 4.3 that will be used below is the following statement. (See § 3.9 for the definition of ![]() $\mathcal {U}_\mathbf {S}^{\hat {\lambda }}$, and § 4.3 for that of
$\mathcal {U}_\mathbf {S}^{\hat {\lambda }}$, and § 4.3 for that of ![]() $\mathcal {Z}_\mathbf {S}^{\hat {\lambda }}$.)
$\mathcal {Z}_\mathbf {S}^{\hat {\lambda }}$.)
Corollary 4.8 For any ![]() $\lambda,\mu \in \mathbb {X}$ in the lower closure of the fundamental alcove, the functor
$\lambda,\mu \in \mathbb {X}$ in the lower closure of the fundamental alcove, the functor ![]() $\mathsf {M}^{\lambda,\mu }_\mathbf {S} \otimes _{\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}} (-)$ induces an equivalence of abelian categories
$\mathsf {M}^{\lambda,\mu }_\mathbf {S} \otimes _{\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}} (-)$ induces an equivalence of abelian categories
which restricts to an equivalence of abelian subcategories
Moreover, in the case where ![]() $\lambda =\mu$, there exists a canonical isomorphism
$\lambda =\mu$, there exists a canonical isomorphism
Proof. The properties stated in Theorem 4.3 ensure that the functor
induces an equivalence of abelian categories
see (4.1). Adding the ![]() $\mathbb {I}^{\hat {\lambda },\hat {\mu }}_\mathbf {S}$-actions in the picture, we obtain the desired equivalence
$\mathbb {I}^{\hat {\lambda },\hat {\mu }}_\mathbf {S}$-actions in the picture, we obtain the desired equivalence
Let us now identify the subcategory corresponding to completed Harish-Chandra ![]() $\mathcal {U}_\mathbf {S} \mathfrak {g}$-bimodules under this equivalence. Recall that any object in
$\mathcal {U}_\mathbf {S} \mathfrak {g}$-bimodules under this equivalence. Recall that any object in ![]() $\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$ has a canonical action of
$\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$ has a canonical action of ![]() $\mathbb {I}^{\hat {\lambda },\hat {\mu }}_\mathbf {S} \ltimes G_1$, and that such an object is a Harish-Chandra bimodule if and only if this action factors through the product morphism
$\mathbb {I}^{\hat {\lambda },\hat {\mu }}_\mathbf {S} \ltimes G_1$, and that such an object is a Harish-Chandra bimodule if and only if this action factors through the product morphism ![]() $\mathbb {I}^{\hat {\lambda },\hat {\mu }}_\mathbf {S} \ltimes G_1 \to \mathbb {I}^{\hat {\lambda },\hat {\mu }}_\mathbf {S}$, that is, if and only if the action of the kernel
$\mathbb {I}^{\hat {\lambda },\hat {\mu }}_\mathbf {S} \ltimes G_1 \to \mathbb {I}^{\hat {\lambda },\hat {\mu }}_\mathbf {S}$, that is, if and only if the action of the kernel ![]() $\mathbb {K}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$ of this map is trivial. Now if
$\mathbb {K}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$ of this map is trivial. Now if ![]() $V$ is in
$V$ is in ![]() $\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$, the action of
$\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$, the action of ![]() $\mathbb {I}^{\hat {\lambda },\hat {\mu }}_\mathbf {S} \ltimes G_1$ on
$\mathbb {I}^{\hat {\lambda },\hat {\mu }}_\mathbf {S} \ltimes G_1$ on ![]() $\mathsf {M}^{\lambda,\mu }_\mathbf {S} \otimes _{\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}} V$ is diagonal, induced by the action on
$\mathsf {M}^{\lambda,\mu }_\mathbf {S} \otimes _{\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}} V$ is diagonal, induced by the action on ![]() $\mathsf {M}^{\lambda,\mu }_\mathbf {S}$ and the action on
$\mathsf {M}^{\lambda,\mu }_\mathbf {S}$ and the action on ![]() $V$ obtained by pullback under the morphism
$V$ obtained by pullback under the morphism ![]() $\mathbb {I}^{\hat {\lambda },\hat {\mu }}_\mathbf {S} \ltimes G_1 \to \mathbb {I}^{\hat {\lambda },\hat {\mu }}_\mathbf {S}$ given by projection on the first factor. By construction the module
$\mathbb {I}^{\hat {\lambda },\hat {\mu }}_\mathbf {S} \ltimes G_1 \to \mathbb {I}^{\hat {\lambda },\hat {\mu }}_\mathbf {S}$ given by projection on the first factor. By construction the module ![]() $\mathsf {M}^{\lambda,\mu }_\mathbf {S}$ is a completed Harish-Chandra
$\mathsf {M}^{\lambda,\mu }_\mathbf {S}$ is a completed Harish-Chandra ![]() $\mathcal {U}_\mathbf {S} \mathfrak {g}$-bimodule, so that the action on this factor does factor though the product morphism
$\mathcal {U}_\mathbf {S} \mathfrak {g}$-bimodule, so that the action on this factor does factor though the product morphism ![]() $\mathbb {I}^{\hat {\lambda },\hat {\mu }}_\mathbf {S} \ltimes G_1 \to \mathbb {I}^{\hat {\lambda },\hat {\mu }}_\mathbf {S}$, and, moreover,
$\mathbb {I}^{\hat {\lambda },\hat {\mu }}_\mathbf {S} \ltimes G_1 \to \mathbb {I}^{\hat {\lambda },\hat {\mu }}_\mathbf {S}$, and, moreover, ![]() $\mathsf {M}^{\lambda,\mu }_\mathbf {S}$ is free over
$\mathsf {M}^{\lambda,\mu }_\mathbf {S}$ is free over ![]() $\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$. Hence,
$\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$. Hence, ![]() $\mathsf {M}^{\lambda,\mu }_\mathbf {S} \otimes _{\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}} V$ is a completed Harish-Chandra bimodule if and only if the action of
$\mathsf {M}^{\lambda,\mu }_\mathbf {S} \otimes _{\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}} V$ is a completed Harish-Chandra bimodule if and only if the action of ![]() $\mathbb {K}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$ on
$\mathbb {K}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$ on ![]() $V$ is trivial, or in other words if and only if the action of the subgroup scheme
$V$ is trivial, or in other words if and only if the action of the subgroup scheme ![]() $G_1 \times \mathrm {Spec}(\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$ on
$G_1 \times \mathrm {Spec}(\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$ on ![]() $V$ is trivial, or finally if and only if the action of
$V$ is trivial, or finally if and only if the action of ![]() $\mathbb {I}^{\hat {\lambda },\hat {\mu }}_\mathbf {S}$ factors through the quotient morphism
$\mathbb {I}^{\hat {\lambda },\hat {\mu }}_\mathbf {S}$ factors through the quotient morphism ![]() $\mathbb {I}^{\hat {\lambda },\hat {\mu }}_\mathbf {S} \to \mathbb {J}^{\hat {\lambda },\hat {\mu }}_\mathbf {S}$. This proves that our equivalence restricts to an equivalence
$\mathbb {I}^{\hat {\lambda },\hat {\mu }}_\mathbf {S} \to \mathbb {J}^{\hat {\lambda },\hat {\mu }}_\mathbf {S}$. This proves that our equivalence restricts to an equivalence ![]() $\mathsf {Mod}^{\mathbb {J}}_{\mathrm {fg}}(\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}) \xrightarrow {\sim } \mathsf {HC}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$.
$\mathsf {Mod}^{\mathbb {J}}_{\mathrm {fg}}(\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}) \xrightarrow {\sim } \mathsf {HC}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$.
Finally, we consider the special case ![]() $\lambda =\mu$, and construct a canonical isomorphism
$\lambda =\mu$, and construct a canonical isomorphism
Adjunction (see Lemma 3.6) provides a canonical morphism
which factors through a morphism
Here, by the same considerations as in the proof of Theorem 4.3, both sides are finite free modules over the local ring ![]() $\mathcal {Z}_\mathbf {S}^{\hat {\lambda }}$; to prove that this morphism is an isomorphism it therefore suffices to check that the induced morphism
$\mathcal {Z}_\mathbf {S}^{\hat {\lambda }}$; to prove that this morphism is an isomorphism it therefore suffices to check that the induced morphism
is invertible. The right-hand side identifies with ![]() $\mathcal {U}_\chi ^{\lambda } \mathfrak {g}$, where
$\mathcal {U}_\chi ^{\lambda } \mathfrak {g}$, where ![]() $\chi$ is as at the end of the proof of Theorem 4.3, and by (4.8) the left-hand side identifies with
$\chi$ is as at the end of the proof of Theorem 4.3, and by (4.8) the left-hand side identifies with ![]() $\mathsf {Z}_{\chi,B'}(\bar {\lambda }) \otimes \mathsf {Z}_{\chi,B'}(\bar {\lambda })^{*}$, where
$\mathsf {Z}_{\chi,B'}(\bar {\lambda }) \otimes \mathsf {Z}_{\chi,B'}(\bar {\lambda })^{*}$, where ![]() $B' \subset G$ is the unique Borel subgroup with unipotent radical
$B' \subset G$ is the unique Borel subgroup with unipotent radical ![]() $U'$ such that
$U'$ such that ![]() $\chi _{|\mathrm {Lie}(U')^{(1)}}=0$; the desired claim is therefore clear from the isomorphism (4.2).
$\chi _{|\mathrm {Lie}(U')^{(1)}}=0$; the desired claim is therefore clear from the isomorphism (4.2).
Remark 4.9 We will prove later (at least in the special case when ![]() $\mu$ belongs to the fundamental alcove; see § 5.5) that for any
$\mu$ belongs to the fundamental alcove; see § 5.5) that for any ![]() $\lambda,\mu,\nu \in \mathbb {X}$ in the lower closure of the fundamental alcove the equivalences of Corollary 4.8 intertwine the bifunctors
$\lambda,\mu,\nu \in \mathbb {X}$ in the lower closure of the fundamental alcove the equivalences of Corollary 4.8 intertwine the bifunctors
(see § 3.9) and
(see § 4.3).
5.  $\mathcal {U} \mathfrak {g}$ and differential operators on the flag variety
$\mathcal {U} \mathfrak {g}$ and differential operators on the flag variety
In this section we study the equivalences ![]() $\mathscr {L}_{\lambda,\mu }$ of Corollary 4.8 further, using the relation between the algebra
$\mathscr {L}_{\lambda,\mu }$ of Corollary 4.8 further, using the relation between the algebra ![]() $\mathcal {U} \mathfrak {g}$ and differential operators on the flag variety of
$\mathcal {U} \mathfrak {g}$ and differential operators on the flag variety of ![]() $G$.
$G$.
5.1 Universal twisted differential operators
Set ![]() $\mathcal {B}:=G/B$, and consider the natural projection morphism
$\mathcal {B}:=G/B$, and consider the natural projection morphism
Here ![]() $G/U$ admits a natural action of
$G/U$ admits a natural action of ![]() $T$ induced by multiplication on the right on
$T$ induced by multiplication on the right on ![]() $G$, and
$G$, and ![]() $\omega$ is a (Zariski locally trivial)
$\omega$ is a (Zariski locally trivial) ![]() $T$-torsor. The sheaf of universal twisted differential operators on
$T$-torsor. The sheaf of universal twisted differential operators on ![]() $\mathcal {B}$ is the quasi-coherent sheaf of algebras
$\mathcal {B}$ is the quasi-coherent sheaf of algebras
where the exponent means ![]() $T$-invariants. The actions of
$T$-invariants. The actions of ![]() $G$ and
$G$ and ![]() $T$ on
$T$ on ![]() $G/U$ induce a canonical algebra morphism
$G/U$ induce a canonical algebra morphism
see [Reference Bezrukavnikov, Mirković and RumyninBMR08, Lemma 3.1.5].
Recall the Grothendieck resolution ![]() $\tilde {\mathbf {g}}$ for the group
$\tilde {\mathbf {g}}$ for the group ![]() $\mathbf {G}=G^{(1)}$ and the morphism
$\mathbf {G}=G^{(1)}$ and the morphism ![]() $\vartheta : \tilde {\mathbf {g}} \to \mathfrak {t}^{*(1)}$; see §§ 2.3 and 3.8. Consider the Frobenius morphism
$\vartheta : \tilde {\mathbf {g}} \to \mathfrak {t}^{*(1)}$; see §§ 2.3 and 3.8. Consider the Frobenius morphism ![]() $\mathrm {Fr}_\mathcal {B} : \mathcal {B} \to \mathcal {B}^{(1)}$ and the natural morphism
$\mathrm {Fr}_\mathcal {B} : \mathcal {B} \to \mathcal {B}^{(1)}$ and the natural morphism ![]() $f : \tilde {\mathbf {g}} \times _{\mathfrak {t}^{*(1)}} \mathfrak {t}^{*} \to \mathcal {B}^{(1)}$. As explained in [Reference Bezrukavnikov, Mirković and RumyninBMR08, § 2.3], there exists a canonical algebra morphism
$f : \tilde {\mathbf {g}} \times _{\mathfrak {t}^{*(1)}} \mathfrak {t}^{*} \to \mathcal {B}^{(1)}$. As explained in [Reference Bezrukavnikov, Mirković and RumyninBMR08, § 2.3], there exists a canonical algebra morphism
which takes values in the center of ![]() $(\mathrm {Fr}_\mathcal {B})_* \tilde {\mathscr {D}}$, and which makes
$(\mathrm {Fr}_\mathcal {B})_* \tilde {\mathscr {D}}$, and which makes ![]() $(\mathrm {Fr}_\mathcal {B})_* \tilde {\mathscr {D}}$ a locally finitely generated
$(\mathrm {Fr}_\mathcal {B})_* \tilde {\mathscr {D}}$ a locally finitely generated ![]() $f_* \mathscr {O}_{\tilde {\mathbf {g}} \times _{\mathfrak {t}^{*(1)}} \mathfrak {t}^{*}}$-module. Since all the morphisms involved in this construction are affine, using this morphism one can consider
$f_* \mathscr {O}_{\tilde {\mathbf {g}} \times _{\mathfrak {t}^{*(1)}} \mathfrak {t}^{*}}$-module. Since all the morphisms involved in this construction are affine, using this morphism one can consider ![]() $\tilde {\mathscr {D}}$ as a coherent sheaf of
$\tilde {\mathscr {D}}$ as a coherent sheaf of ![]() $\mathscr {O}_{\tilde {\mathbf {g}} \times _{\mathfrak {t}^{*(1)}} \mathfrak {t}^{*}}$-algebras on
$\mathscr {O}_{\tilde {\mathbf {g}} \times _{\mathfrak {t}^{*(1)}} \mathfrak {t}^{*}}$-algebras on ![]() $\tilde {\mathbf {g}} \times _{\mathfrak {t}^{*(1)}} \mathfrak {t}^{*}$. (We will not introduce a different notation for this sheaf of algebras.)
$\tilde {\mathbf {g}} \times _{\mathfrak {t}^{*(1)}} \mathfrak {t}^{*}$. (We will not introduce a different notation for this sheaf of algebras.)
Recall also (see § 4.4) that we denote by ![]() $\tilde {\mathbf {S}}^{*}$ the preimage of
$\tilde {\mathbf {S}}^{*}$ the preimage of ![]() $\mathbf {S}^{*}$ under the natural morphism
$\mathbf {S}^{*}$ under the natural morphism ![]() $\pi : \tilde {\mathbf {g}} \to \mathfrak {g}^{*(1)}$, and that the morphism
$\pi : \tilde {\mathbf {g}} \to \mathfrak {g}^{*(1)}$, and that the morphism ![]() $\vartheta$ restricts to an isomorphism
$\vartheta$ restricts to an isomorphism ![]() $\tilde {\mathbf {S}}^{*} \xrightarrow {\sim } \mathfrak {t}^{*(1)}$; in particular,
$\tilde {\mathbf {S}}^{*} \xrightarrow {\sim } \mathfrak {t}^{*(1)}$; in particular, ![]() $\tilde {\mathbf {S}}^{*}$ is an affine scheme. We set
$\tilde {\mathbf {S}}^{*}$ is an affine scheme. We set
We will also set
Lemma 5.1 The morphism (5.1) induces an algebra isomorphism
Proof. Consider the natural morphism
If we still denote by ![]() $\mathcal {U}_\mathbf {S}\mathfrak {g}$ the sheaf of
$\mathcal {U}_\mathbf {S}\mathfrak {g}$ the sheaf of ![]() $\mathscr {O}_{\mathbf {S}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W,\bullet )}$-algebras associated with the
$\mathscr {O}_{\mathbf {S}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W,\bullet )}$-algebras associated with the ![]() $\mathscr {O}(\mathbf {S}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W,\bullet ))$-algebra
$\mathscr {O}(\mathbf {S}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W,\bullet ))$-algebra ![]() $\mathcal {U}_\mathbf {S}\mathfrak {g}$, then as in [Reference Bezrukavnikov, Mirković and RumyninBMR08, Proposition 5.2.1] the morphism (5.1) induces a canonical isomorphism of sheaves of algebras
$\mathcal {U}_\mathbf {S}\mathfrak {g}$, then as in [Reference Bezrukavnikov, Mirković and RumyninBMR08, Proposition 5.2.1] the morphism (5.1) induces a canonical isomorphism of sheaves of algebras
Now ![]() $h$ induces an isomorphism
$h$ induces an isomorphism
(in fact, both sides identify canonically with ![]() $\mathfrak {t}^{*}$) so that the claim follows by taking global sections.
$\mathfrak {t}^{*}$) so that the claim follows by taking global sections.
Remark 5.2 One can give a different proof of Lemma 5.1 as follows. By [Reference Bezrukavnikov, Mirković and RumyninBMR08, Proposition 3.4.1], the morphism (5.1) is an isomorphism; in other words, identifying quasi-coherent sheaves on ![]() $\mathfrak {g}^{*(1)}$ and
$\mathfrak {g}^{*(1)}$ and ![]() $\mathscr {O}(\mathfrak {g}^{*(1)})$-modules, we have a canonical isomorphism of sheaves of
$\mathscr {O}(\mathfrak {g}^{*(1)})$-modules, we have a canonical isomorphism of sheaves of ![]() $\mathscr {O}_{\mathfrak {g}^{*(1)}}$-algebras
$\mathscr {O}_{\mathfrak {g}^{*(1)}}$-algebras
where ![]() $g : \tilde {\mathbf {g}} \times _{\mathfrak {t}^{*(1)}} \mathfrak {t}^{*} \to \mathfrak {g}^{*(1)} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}$ is the morphism induced by
$g : \tilde {\mathbf {g}} \times _{\mathfrak {t}^{*(1)}} \mathfrak {t}^{*} \to \mathfrak {g}^{*(1)} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}$ is the morphism induced by ![]() $\pi$. Restricting this isomorphism first to
$\pi$. Restricting this isomorphism first to ![]() $\mathfrak {g}^{*(1)}_\mathrm {reg} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}$ and then to
$\mathfrak {g}^{*(1)}_\mathrm {reg} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}$ and then to ![]() $\mathbf {S}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}$ we deduce the isomorphism of the lemma, since
$\mathbf {S}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}$ we deduce the isomorphism of the lemma, since ![]() $g$ restricts to an isomorphism on the preimage of
$g$ restricts to an isomorphism on the preimage of ![]() $\mathfrak {g}^{*(1)}_\mathrm {reg} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}$ (see (2.5)).
$\mathfrak {g}^{*(1)}_\mathrm {reg} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}$ (see (2.5)).
5.2 Study of some equivariant  $\mathcal {U}_\mathbf{S}\mathfrak {g}$-bimodules
$\mathcal {U}_\mathbf{S}\mathfrak {g}$-bimodules
Given any ![]() $\lambda \in \mathbb {X}$, we have a line bundle
$\lambda \in \mathbb {X}$, we have a line bundle ![]() $\mathscr {O}_{\mathcal {B}}(\lambda )$ on
$\mathscr {O}_{\mathcal {B}}(\lambda )$ on ![]() $\mathcal {B}$ attached naturally to
$\mathcal {B}$ attached naturally to ![]() $\lambda$. (Our normalization is that of [Reference JantzenJan03], so that line bundles attached to dominant weights are ample.) This line bundle identifies with the direct summand of
$\lambda$. (Our normalization is that of [Reference JantzenJan03], so that line bundles attached to dominant weights are ample.) This line bundle identifies with the direct summand of ![]() $\omega _* \mathscr {O}_{G/U}$ consisting of sections which have weight
$\omega _* \mathscr {O}_{G/U}$ consisting of sections which have weight ![]() $\lambda$ for the
$\lambda$ for the ![]() $T$-action induced by right multiplication on
$T$-action induced by right multiplication on ![]() $G$; it therefore admits a natural action of the sheaf of algebras
$G$; it therefore admits a natural action of the sheaf of algebras ![]() $\tilde {\mathscr {D}}$. Using this action and the natural action on
$\tilde {\mathscr {D}}$. Using this action and the natural action on ![]() $\tilde {\mathscr {D}}$, we obtain a left action of
$\tilde {\mathscr {D}}$, we obtain a left action of ![]() $\tilde {\mathscr {D}}$ on the tensor product
$\tilde {\mathscr {D}}$ on the tensor product
As for ![]() $\tilde {\mathscr {D}}$ itself, this module can be also considered as a sheaf of modules on
$\tilde {\mathscr {D}}$ itself, this module can be also considered as a sheaf of modules on ![]() $\tilde {\mathbf {g}} \times _{\mathfrak {t}^{*(1)}} \mathfrak {t}^{*}$. We can therefore consider the
$\tilde {\mathbf {g}} \times _{\mathfrak {t}^{*(1)}} \mathfrak {t}^{*}$. We can therefore consider the ![]() $\Bbbk$-vector space
$\Bbbk$-vector space
which in view of Lemma 5.1 admits a natural left action of ![]() $\tilde {\mathcal {U}}_\mathbf {S}\mathfrak {g}$. The tensor product
$\tilde {\mathcal {U}}_\mathbf {S}\mathfrak {g}$. The tensor product ![]() $\mathscr {O}_\mathcal {B}(\lambda ) \otimes _{\mathscr {O}_\mathcal {B}} \tilde {\mathscr {D}}$ also admits a natural right action of
$\mathscr {O}_\mathcal {B}(\lambda ) \otimes _{\mathscr {O}_\mathcal {B}} \tilde {\mathscr {D}}$ also admits a natural right action of ![]() $\tilde {\mathscr {D}}$, induced by right multiplication on the second factor. The action of
$\tilde {\mathscr {D}}$, induced by right multiplication on the second factor. The action of ![]() $\pi _* \mathscr {O}_{\tilde {\mathbf {g}}}$ on
$\pi _* \mathscr {O}_{\tilde {\mathbf {g}}}$ on ![]() $(\mathrm {Fr}_\mathcal {B})_* \mathscr {O}_\mathcal {B}(\lambda )$ being trivial, the two actions of this subalgebra on
$(\mathrm {Fr}_\mathcal {B})_* \mathscr {O}_\mathcal {B}(\lambda )$ being trivial, the two actions of this subalgebra on ![]() $(\mathrm {Fr}_\mathcal {B})_* (\mathscr {O}_\mathcal {B}(\lambda ) \otimes _{\mathscr {O}_\mathcal {B}} \tilde {\mathscr {D}})$ coincide, and the space (5.2) therefore also admits a right action of
$(\mathrm {Fr}_\mathcal {B})_* (\mathscr {O}_\mathcal {B}(\lambda ) \otimes _{\mathscr {O}_\mathcal {B}} \tilde {\mathscr {D}})$ coincide, and the space (5.2) therefore also admits a right action of ![]() $\tilde {\mathcal {U}}_\mathbf {S}\mathfrak {g}$; moreover, these actions combine to provide an action of
$\tilde {\mathcal {U}}_\mathbf {S}\mathfrak {g}$; moreover, these actions combine to provide an action of ![]() $\tilde {\mathcal {U}}_\mathbf {S}\mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} (\tilde {\mathcal {U}}_\mathbf {S}\mathfrak {g})^{\mathrm{op}}$. By construction the action of the central subalgebra
$\tilde {\mathcal {U}}_\mathbf {S}\mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} (\tilde {\mathcal {U}}_\mathbf {S}\mathfrak {g})^{\mathrm{op}}$. By construction the action of the central subalgebra
factors through an action of the image of the closed embedding ![]() $\mathfrak {t}^{*} \to \mathfrak {t}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}$ given by
$\mathfrak {t}^{*} \to \mathfrak {t}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}$ given by
The object ![]() $\mathscr {O}_\mathcal {B}(\lambda ) \otimes _{\mathscr {O}_\mathcal {B}} \tilde {\mathscr {D}}$ also admits a natural
$\mathscr {O}_\mathcal {B}(\lambda ) \otimes _{\mathscr {O}_\mathcal {B}} \tilde {\mathscr {D}}$ also admits a natural ![]() $G$-equivariant quasi-coherent sheaf structure, compatible with the actions considered above. The module (5.2) therefore also admits a natural and compatible module structure for the group scheme
$G$-equivariant quasi-coherent sheaf structure, compatible with the actions considered above. The module (5.2) therefore also admits a natural and compatible module structure for the group scheme
For ![]() $\lambda,\mu \in \mathbb {X}$, we will denote by
$\lambda,\mu \in \mathbb {X}$, we will denote by
the completion of the ![]() $\mathscr {O}(\mathfrak {t}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*})$-algebra
$\mathscr {O}(\mathfrak {t}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*})$-algebra ![]() $\tilde {\mathcal {U}}_\mathbf {S}\mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} (\tilde {\mathcal {U}}_\mathbf {S}\mathfrak {g})^{\mathrm{op}}$ at the ideal corresponding to the point
$\tilde {\mathcal {U}}_\mathbf {S}\mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} (\tilde {\mathcal {U}}_\mathbf {S}\mathfrak {g})^{\mathrm{op}}$ at the ideal corresponding to the point ![]() $({{\bar {\lambda }}},{{\bar {\mu }}}) \in \mathfrak {t}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}$. Copying the constructions in § 3.9 (replacing
$({{\bar {\lambda }}},{{\bar {\mu }}}) \in \mathfrak {t}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}$. Copying the constructions in § 3.9 (replacing ![]() $\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$ by
$\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$ by ![]() $\tilde {\mathcal {U}}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$ and
$\tilde {\mathcal {U}}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$ and ![]() $\mathfrak {t}^{*}/(W,\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathbb {I}_\mathbf {S}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*} /(W,\bullet )$ by
$\mathfrak {t}^{*}/(W,\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathbb {I}_\mathbf {S}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*} /(W,\bullet )$ by ![]() $\mathfrak {t}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathbb {I}_\mathbf {S}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}$), we define the category
$\mathfrak {t}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathbb {I}_\mathbf {S}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}$), we define the category ![]() $\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\tilde {\mathcal {U}}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$. Copying the definition of
$\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\tilde {\mathcal {U}}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$. Copying the definition of ![]() ${\widehat{\otimes}}_{\mathcal {U}_\mathbf {S} \mathfrak {g}}$, we obtain, for
${\widehat{\otimes}}_{\mathcal {U}_\mathbf {S} \mathfrak {g}}$, we obtain, for ![]() $\lambda,\mu,\nu \in \mathbb {X}$, a bifunctor
$\lambda,\mu,\nu \in \mathbb {X}$, a bifunctor
For any ![]() $\lambda,\mu \in \mathbb {X}$ we have a natural ‘forgetful’ functor
$\lambda,\mu \in \mathbb {X}$ we have a natural ‘forgetful’ functor
which we will usually omit from the notation. In the case where ![]() $\lambda$ and
$\lambda$ and ![]() $\mu$ are regular, this functor is an equivalence by Lemma 3.2. In the case where
$\mu$ are regular, this functor is an equivalence by Lemma 3.2. In the case where ![]() $\mu$ is regular, for
$\mu$ is regular, for ![]() $M \in \mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\tilde {\mathcal {U}}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$ and
$M \in \mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\tilde {\mathcal {U}}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$ and ![]() $N \in \mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\tilde {\mathcal {U}}_\mathbf {S}^{\hat {\mu },\hat {\nu }})$ we also have a canonical identification
$N \in \mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\tilde {\mathcal {U}}_\mathbf {S}^{\hat {\mu },\hat {\nu }})$ we also have a canonical identification
For ![]() $\lambda,\mu \in \mathbb {X}$, we will denote by
$\lambda,\mu \in \mathbb {X}$, we will denote by ![]() $\mathsf {Q}_{\lambda,\mu }$ the completion of the module
$\mathsf {Q}_{\lambda,\mu }$ the completion of the module
at the ideal of ![]() $\mathscr {O}(\mathfrak {t}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*})$ corresponding to the element
$\mathscr {O}(\mathfrak {t}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*})$ corresponding to the element ![]() $({{\bar {\lambda }}},{{\bar {\mu }}})$. In view of the remarks above, this object can equivalently be obtained by completing this module at the ideal of
$({{\bar {\lambda }}},{{\bar {\mu }}})$. In view of the remarks above, this object can equivalently be obtained by completing this module at the ideal of ![]() $\mathscr {O}(\mathfrak {t}^{*})$ corresponding to
$\mathscr {O}(\mathfrak {t}^{*})$ corresponding to ![]() ${{\bar {\lambda }}}$ for the left action, or at the ideal of
${{\bar {\lambda }}}$ for the left action, or at the ideal of ![]() $\mathscr {O}(\mathfrak {t}^{*})$ corresponding to
$\mathscr {O}(\mathfrak {t}^{*})$ corresponding to ![]() ${{\bar {\mu }}}$ for the right action. This construction provides an object in
${{\bar {\mu }}}$ for the right action. This construction provides an object in ![]() $\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\tilde {\mathcal {U}}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$, hence a fortiori an object in
$\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\tilde {\mathcal {U}}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$, hence a fortiori an object in ![]() $\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$.
$\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$.
Lemma 5.3 For ![]() $\lambda,\mu,\nu \in \mathbb {X}$, there exists a canonical isomorphism
$\lambda,\mu,\nu \in \mathbb {X}$, there exists a canonical isomorphism
in ![]() $\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\tilde {\mathcal {U}}_\mathbf {S}^{\hat {\lambda },\hat {\nu }})$. In particular, in the case where
$\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\tilde {\mathcal {U}}_\mathbf {S}^{\hat {\lambda },\hat {\nu }})$. In particular, in the case where ![]() $\mu$ is regular there exists a canonical isomorphism
$\mu$ is regular there exists a canonical isomorphism
in ![]() $\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\nu }})$.
$\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\nu }})$.
Proof. There exist canonical isomorphisms
 \begin{align*} &(\mathscr{O}_\mathcal{B}(\lambda-\mu) \otimes_{\mathscr{O}_\mathcal{B}} \tilde{\mathscr{D}} ) \otimes_{\tilde{\mathscr{D}}} ( \mathscr{O}_\mathcal{B}(\mu-\nu) \otimes_{\mathscr{O}_\mathcal{B}} \tilde{\mathscr{D}} ) \\ &\quad \xrightarrow{\sim}\mathscr{O}_\mathcal{B}(\lambda-\mu) \otimes_{\mathscr{O}_\mathcal{B}} \mathscr{O}_\mathcal{B}(\mu-\nu) \otimes_{\mathscr{O}_\mathcal{B}} \tilde{\mathscr{D}} \cong \mathscr{O}_\mathcal{B}(\lambda-\nu) \otimes_{\mathscr{O}_\mathcal{B}} \tilde{\mathscr{D}}.\end{align*}
\begin{align*} &(\mathscr{O}_\mathcal{B}(\lambda-\mu) \otimes_{\mathscr{O}_\mathcal{B}} \tilde{\mathscr{D}} ) \otimes_{\tilde{\mathscr{D}}} ( \mathscr{O}_\mathcal{B}(\mu-\nu) \otimes_{\mathscr{O}_\mathcal{B}} \tilde{\mathscr{D}} ) \\ &\quad \xrightarrow{\sim}\mathscr{O}_\mathcal{B}(\lambda-\mu) \otimes_{\mathscr{O}_\mathcal{B}} \mathscr{O}_\mathcal{B}(\mu-\nu) \otimes_{\mathscr{O}_\mathcal{B}} \tilde{\mathscr{D}} \cong \mathscr{O}_\mathcal{B}(\lambda-\nu) \otimes_{\mathscr{O}_\mathcal{B}} \tilde{\mathscr{D}}.\end{align*}
The desired isomorphism follows by restriction to ![]() $\tilde {\mathbf {S}}^{*} \times _{\mathfrak {t}^{*(1)}} \mathfrak {t}^{*}$ and then completion at
$\tilde {\mathbf {S}}^{*} \times _{\mathfrak {t}^{*(1)}} \mathfrak {t}^{*}$ and then completion at ![]() $({{\bar {\lambda }}},\bar {\nu })$.
$({{\bar {\lambda }}},\bar {\nu })$.
If ![]() $\lambda \in \mathbb {X}$ is regular, Lemmas 3.2 and 5.1 imply that we have
$\lambda \in \mathbb {X}$ is regular, Lemmas 3.2 and 5.1 imply that we have
where the left-hand side is as in § 3.9. Hence, the functor of convolution on the left (respectively, right) with ![]() $\mathsf {Q}_{\lambda,\lambda }$ is isomorphic to the identity functor of
$\mathsf {Q}_{\lambda,\lambda }$ is isomorphic to the identity functor of ![]() $\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$ (respectively,
$\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$ (respectively, ![]() $\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\mathcal {U}_\mathbf {S}^{\hat {\mu },\hat {\lambda }})$), for any
$\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\mathcal {U}_\mathbf {S}^{\hat {\mu },\hat {\lambda }})$), for any ![]() $\mu \in \mathbb {X}$. Combining this observation with Lemma 5.3, we see that if
$\mu \in \mathbb {X}$. Combining this observation with Lemma 5.3, we see that if ![]() $\lambda \in \mathbb {X}$ belongs to the fundamental alcove, then for any
$\lambda \in \mathbb {X}$ belongs to the fundamental alcove, then for any ![]() $w \in {W_{\mathrm {ext}}}$ the object
$w \in {W_{\mathrm {ext}}}$ the object ![]() $\mathsf {Q}_{\lambda, w \bullet \lambda }$ is invertible in the monoidal category
$\mathsf {Q}_{\lambda, w \bullet \lambda }$ is invertible in the monoidal category ![]() $\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\lambda }})$, with inverse
$\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\lambda }})$, with inverse ![]() $\mathsf {Q}_{w \bullet \lambda, \lambda }$.
$\mathsf {Q}_{w \bullet \lambda, \lambda }$.
Recall from (3.16) that we have a canonical morphism of group schemes
Taking the fiber product with the morphism ![]() $\mathfrak {t}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*} \to \mathfrak {t}^{*} \xrightarrow {\mathrm {AS}} \mathfrak {t}^{*(1)}$ (where the first morphism is the first projection), we obtain a morphism of group schemes
$\mathfrak {t}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*} \to \mathfrak {t}^{*} \xrightarrow {\mathrm {AS}} \mathfrak {t}^{*(1)}$ (where the first morphism is the first projection), we obtain a morphism of group schemes
Using this morphism, for any character ![]() $\eta$ of
$\eta$ of ![]() $T^{(1)}$ we obtain a structure of representation of
$T^{(1)}$ we obtain a structure of representation of ![]() $\mathfrak {t}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathbb {I}_\mathbf {S}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}$ on
$\mathfrak {t}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathbb {I}_\mathbf {S}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}$ on ![]() $\mathscr {O}(\mathfrak {t}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*})$ defined by this character. Tensoring with this representation we obtain an autoequivalence of
$\mathscr {O}(\mathfrak {t}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*})$ defined by this character. Tensoring with this representation we obtain an autoequivalence of ![]() $\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\tilde {\mathcal {U}}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$, which we denote by
$\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\tilde {\mathcal {U}}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$, which we denote by ![]() $M \mapsto M \langle \eta \rangle$.
$M \mapsto M \langle \eta \rangle$.
Recall from § 3.1 that we identify the lattice of characters of ![]() $T^{(1)}$ with
$T^{(1)}$ with ![]() $p \cdot \mathbb {X}$.
$p \cdot \mathbb {X}$.
Lemma 5.4 For any ![]() $\lambda,\nu \in \mathbb {X}$, there exists a canonical isomorphism
$\lambda,\nu \in \mathbb {X}$, there exists a canonical isomorphism
in ![]() $\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\tilde {\mathcal {U}}_\mathbf {S}^{\hat {\lambda },\hat {\lambda }})$.
$\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\tilde {\mathcal {U}}_\mathbf {S}^{\hat {\lambda },\hat {\lambda }})$.
Proof. By definition, ![]() $\mathsf {Q}_{\lambda +p\nu,\lambda }$ is the completion at the ideal corresponding to
$\mathsf {Q}_{\lambda +p\nu,\lambda }$ is the completion at the ideal corresponding to ![]() $({{\bar {\lambda }}},{{\bar {\lambda }}})$ of the
$({{\bar {\lambda }}},{{\bar {\lambda }}})$ of the ![]() $\tilde {\mathcal {U}}_\mathbf {S}\mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} (\tilde {\mathcal {U}}_\mathbf {S}\mathfrak {g})^{\mathrm{op}}$-module
$\tilde {\mathcal {U}}_\mathbf {S}\mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} (\tilde {\mathcal {U}}_\mathbf {S}\mathfrak {g})^{\mathrm{op}}$-module
If we denote by ![]() $U^{+}$ the unipotent radical of the Borel subgroup opposite to
$U^{+}$ the unipotent radical of the Borel subgroup opposite to ![]() $B$, then
$B$, then ![]() $U^{+}B/B \subset \mathcal {B}$ is an open subvariety isomorphic to
$U^{+}B/B \subset \mathcal {B}$ is an open subvariety isomorphic to ![]() $U^{+}$, and the projection
$U^{+}$, and the projection ![]() $\tilde {\mathbf {S}}^{*} \to \mathcal {B}$ factors through a morphism
$\tilde {\mathbf {S}}^{*} \to \mathcal {B}$ factors through a morphism ![]() $\tilde {\mathbf {S}}^{*} \to U^{+}B/B$; see [Reference Mautner and RicheMR18, Lemma 4.8]. As a consequence, the sheaf
$\tilde {\mathbf {S}}^{*} \to U^{+}B/B$; see [Reference Mautner and RicheMR18, Lemma 4.8]. As a consequence, the sheaf ![]() $(\mathscr {O}_\mathcal {B}(p\nu ) \otimes _{\mathscr {O}_\mathcal {B}} \tilde {\mathscr {D}})_{|\tilde {\mathbf {S}}^{*} \times _{\mathfrak {t}^{*(1)}} \mathfrak {t}^{*}}$ can be obtained as a further restriction of
$(\mathscr {O}_\mathcal {B}(p\nu ) \otimes _{\mathscr {O}_\mathcal {B}} \tilde {\mathscr {D}})_{|\tilde {\mathbf {S}}^{*} \times _{\mathfrak {t}^{*(1)}} \mathfrak {t}^{*}}$ can be obtained as a further restriction of ![]() $(\mathscr {O}_\mathcal {B}(p\nu ) \otimes _{\mathscr {O}_\mathcal {B}} \tilde {\mathscr {D}})_{|U^{+}B/B}$.
$(\mathscr {O}_\mathcal {B}(p\nu ) \otimes _{\mathscr {O}_\mathcal {B}} \tilde {\mathscr {D}})_{|U^{+}B/B}$.
Since ![]() $\tilde {\mathscr {D}}$ acts on
$\tilde {\mathscr {D}}$ acts on ![]() $\mathscr {O}_{\mathcal {B}}(p\nu )$, we have an action of the algebra
$\mathscr {O}_{\mathcal {B}}(p\nu )$, we have an action of the algebra ![]() $\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {HC}}}} \mathscr {O}(\mathfrak {t}^{*})$ on the space
$\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {HC}}}} \mathscr {O}(\mathfrak {t}^{*})$ on the space ![]() $\Gamma (U^{+}B/B, \mathscr {O}_\mathcal {B}(p\nu ))$, see (5.1). We have
$\Gamma (U^{+}B/B, \mathscr {O}_\mathcal {B}(p\nu ))$, see (5.1). We have
In this space we have a canonical vector, namely the function ![]() $f : U^{+}B \to \Bbbk$ defined by
$f : U^{+}B \to \Bbbk$ defined by ![]() $f(u_1 t u_2)=(p\nu )^{-1}(t)$ for all
$f(u_1 t u_2)=(p\nu )^{-1}(t)$ for all ![]() $u_1 \in U^{+}$,
$u_1 \in U^{+}$, ![]() $t \in T$ and
$t \in T$ and ![]() $u_2 \in U$. This section does not vanish on
$u_2 \in U$. This section does not vanish on ![]() $U^{+}B/B$, hence induces an isomorphism of line bundles
$U^{+}B/B$, hence induces an isomorphism of line bundles ![]() $\mathscr {O}_{U^{+}B/B} \xrightarrow {\sim } \mathscr {O}_{\mathcal {B}}(p\nu )_{|U^{+}B/B}$. We claim, furthermore, that it is annihilated by the action of
$\mathscr {O}_{U^{+}B/B} \xrightarrow {\sim } \mathscr {O}_{\mathcal {B}}(p\nu )_{|U^{+}B/B}$. We claim, furthermore, that it is annihilated by the action of ![]() $\mathfrak {g} \subset \mathcal {U} \mathfrak {g}$ and
$\mathfrak {g} \subset \mathcal {U} \mathfrak {g}$ and ![]() $\mathfrak {t} \subset \mathscr {O}(\mathfrak {t}^{*})$. In fact, the second case is clear. For the action of
$\mathfrak {t} \subset \mathscr {O}(\mathfrak {t}^{*})$. In fact, the second case is clear. For the action of ![]() $\mathfrak {g}$, in the case where
$\mathfrak {g}$, in the case where ![]() $\nu \in \mathbb {X}^{+}$ the claim follows from the fact that our vector is the restriction of the unique (up to scalar) vector of weight
$\nu \in \mathbb {X}^{+}$ the claim follows from the fact that our vector is the restriction of the unique (up to scalar) vector of weight ![]() $p\nu$ in
$p\nu$ in ![]() $\Gamma ( \mathcal {B}, \mathscr {O}_\mathcal {B}(p\nu ) )$ (see [Reference JantzenJan03, proof of Proposition II.2.6]), and that this vector belongs to the
$\Gamma ( \mathcal {B}, \mathscr {O}_\mathcal {B}(p\nu ) )$ (see [Reference JantzenJan03, proof of Proposition II.2.6]), and that this vector belongs to the ![]() $G$-submodule
$G$-submodule ![]() $\mathsf {L}(p\nu )$, on which the action of
$\mathsf {L}(p\nu )$, on which the action of ![]() $\mathfrak {g}$ is well known to vanish. From this we deduce the general case by using the Leibniz rule for the action on tensor products of line bundles.
$\mathfrak {g}$ is well known to vanish. From this we deduce the general case by using the Leibniz rule for the action on tensor products of line bundles.
Tensoring this section with the unit in ![]() $\tilde {\mathscr {D}}$, we obtain a section of
$\tilde {\mathscr {D}}$, we obtain a section of ![]() $(\mathscr {O}_\mathcal {B}(p\nu ) \otimes _{\mathscr {O}_\mathcal {B}} \tilde {\mathscr {D}})_{|U^{+}B/B}$. The right action on this section provides an isomorphism
$(\mathscr {O}_\mathcal {B}(p\nu ) \otimes _{\mathscr {O}_\mathcal {B}} \tilde {\mathscr {D}})_{|U^{+}B/B}$. The right action on this section provides an isomorphism
which commutes with the natural left and right actions of ![]() $\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {HC}}}} \mathscr {O}(\mathfrak {t}^{*})$. Restricting further, we obtain an isomorphism
$\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {HC}}}} \mathscr {O}(\mathfrak {t}^{*})$. Restricting further, we obtain an isomorphism
and then, taking global sections and completing, an isomorphism of ![]() $\tilde {\mathcal {U}}_\mathbf {S}^{\hat {\lambda },\hat {\lambda }}$-modules
$\tilde {\mathcal {U}}_\mathbf {S}^{\hat {\lambda },\hat {\lambda }}$-modules ![]() $\mathsf {Q}_{\lambda,\lambda } \xrightarrow {\sim } \mathsf {Q}_{\lambda +p\nu,\lambda }$. Taking the action of
$\mathsf {Q}_{\lambda,\lambda } \xrightarrow {\sim } \mathsf {Q}_{\lambda +p\nu,\lambda }$. Taking the action of ![]() $\mathfrak {t}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathbb {I}_\mathbf {S}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}$ into account, this provides the desired isomorphism
$\mathfrak {t}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathbb {I}_\mathbf {S}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}$ into account, this provides the desired isomorphism ![]() $\mathsf {Q}_{\lambda,\lambda } \langle p\nu \rangle \xrightarrow {\sim } \mathsf {Q}_{\lambda +p\nu,\lambda }$.
$\mathsf {Q}_{\lambda,\lambda } \langle p\nu \rangle \xrightarrow {\sim } \mathsf {Q}_{\lambda +p\nu,\lambda }$.
5.3 Relation with translation bimodules
Recall from § 3.5 the notation ![]() $\mathfrak {D}=\mathfrak {t}^{*}/(W,\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W,\bullet )$. In our constructions below we will also have to work with variants of this scheme where one of the two copies of
$\mathfrak {D}=\mathfrak {t}^{*}/(W,\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W,\bullet )$. In our constructions below we will also have to work with variants of this scheme where one of the two copies of ![]() $\mathfrak {t}^{*}/(W,\bullet )$ is replaced by
$\mathfrak {t}^{*}/(W,\bullet )$ is replaced by ![]() $\mathfrak {t}^{*}$. We therefore introduce the notation
$\mathfrak {t}^{*}$. We therefore introduce the notation
We now explain the relation between the objects ![]() $\mathsf {Q}_{\lambda,\mu }$ and the ‘translation bimodules’ introduced in § 3.5.
$\mathsf {Q}_{\lambda,\mu }$ and the ‘translation bimodules’ introduced in § 3.5.
Lemma 5.5 Let ![]() $\lambda,\mu \in \mathbb {X}$ in the closure of the fundamental alcove, with one of them in the fundamental alcove itself. Then for any
$\lambda,\mu \in \mathbb {X}$ in the closure of the fundamental alcove, with one of them in the fundamental alcove itself. Then for any ![]() $w \in {W_{\mathrm {ext}}}$ we have
$w \in {W_{\mathrm {ext}}}$ we have
in ![]() $\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\mathcal {U}_\mathbf {S}^{\hat {\mu },\hat {\lambda }})$.
$\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\mathcal {U}_\mathbf {S}^{\hat {\mu },\hat {\lambda }})$.
Proof. To fix notation we assume that ![]() $\lambda$ is in the fundamental alcove; the other case can be obtained similarly. It is clear that we can assume that
$\lambda$ is in the fundamental alcove; the other case can be obtained similarly. It is clear that we can assume that ![]() $w \in W$. Let
$w \in W$. Let ![]() $\nu \in \mathbb {X}$ be the unique dominant weight which belongs to
$\nu \in \mathbb {X}$ be the unique dominant weight which belongs to ![]() $W(\mu -\lambda )$. Then by definition,
$W(\mu -\lambda )$. Then by definition, ![]() $\mathsf {P}_\mathbf {S}^{\mu,\lambda }$ is the completion of the module
$\mathsf {P}_\mathbf {S}^{\mu,\lambda }$ is the completion of the module
at the ideal corresponding to the point ![]() $({{\tilde {\mu }}},{{\tilde {\lambda }}}) \in \mathfrak {t}^{*}/(W,\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W,\bullet )$. Now by Lemma 3.2 the quotient morphism
$({{\tilde {\mu }}},{{\tilde {\lambda }}}) \in \mathfrak {t}^{*}/(W,\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W,\bullet )$. Now by Lemma 3.2 the quotient morphism ![]() $\mathfrak {t}^{*} \to \mathfrak {t}^{*}/(W,\bullet )$ is étale at
$\mathfrak {t}^{*} \to \mathfrak {t}^{*}/(W,\bullet )$ is étale at ![]() $w \bullet {{\bar {\lambda }}}$. It follows that
$w \bullet {{\bar {\lambda }}}$. It follows that ![]() $\mathsf {P}_\mathbf {S}^{\mu,\lambda }$ can also be obtained as the completion of the
$\mathsf {P}_\mathbf {S}^{\mu,\lambda }$ can also be obtained as the completion of the ![]() $\mathcal {U}_\mathbf {S} \mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} (\tilde {\mathcal {U}}_\mathbf {S}\mathfrak {g})^{\mathrm{op}}$-module
$\mathcal {U}_\mathbf {S} \mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} (\tilde {\mathcal {U}}_\mathbf {S}\mathfrak {g})^{\mathrm{op}}$-module
with respect to the ideal of ![]() $\mathscr {O}(\mathfrak {E}')$ corresponding to
$\mathscr {O}(\mathfrak {E}')$ corresponding to ![]() $({{\tilde {\mu }}},w \bullet {{\bar {\lambda }}})$.
$({{\tilde {\mu }}},w \bullet {{\bar {\lambda }}})$.
By Lemma 5.1 we have canonical isomorphisms
It is a classical fact that the coherent sheaf ![]() $\mathsf {L}(\nu ) \otimes \mathscr {O}_\mathcal {B}$ on
$\mathsf {L}(\nu ) \otimes \mathscr {O}_\mathcal {B}$ on ![]() $\mathcal {B}$ admits a filtration whose subquotients have the form
$\mathcal {B}$ admits a filtration whose subquotients have the form ![]() $\mathscr {O}_\mathcal {B}(\eta )$, where
$\mathscr {O}_\mathcal {B}(\eta )$, where ![]() $\eta$ runs over the weights of
$\eta$ runs over the weights of ![]() $\mathsf {L}(\nu )$ (counted with multiplicities). We deduce a similar filtration for the sheaf
$\mathsf {L}(\nu )$ (counted with multiplicities). We deduce a similar filtration for the sheaf ![]() $\mathsf {L}(\nu ) \otimes \tilde {\mathscr {D}}$, and then for its restriction to
$\mathsf {L}(\nu ) \otimes \tilde {\mathscr {D}}$, and then for its restriction to ![]() $\tilde {\mathbf {S}}^{*} \times _{\mathfrak {t}^{*(1)}} \mathfrak {t}^{*}$. (Here we use the fact that restriction along the closed embedding
$\tilde {\mathbf {S}}^{*} \times _{\mathfrak {t}^{*(1)}} \mathfrak {t}^{*}$. (Here we use the fact that restriction along the closed embedding ![]() $\tilde {\mathbf {S}}^{*} \hookrightarrow \tilde {\mathbf {g}}$ is exact on the category
$\tilde {\mathbf {S}}^{*} \hookrightarrow \tilde {\mathbf {g}}$ is exact on the category ![]() $\mathsf {QCoh}^{G}(\tilde {\mathbf {g}})$, which follows from the same arguments as those used at the beginning of the proof of Proposition 4.1.) In other words, we have obtained a filtration of
$\mathsf {QCoh}^{G}(\tilde {\mathbf {g}})$, which follows from the same arguments as those used at the beginning of the proof of Proposition 4.1.) In other words, we have obtained a filtration of ![]() $\mathsf {L}(\nu ) \otimes \tilde {\mathcal {U}}_\mathbf{S}\mathfrak {g}$ with subquotients
$\mathsf {L}(\nu ) \otimes \tilde {\mathcal {U}}_\mathbf{S}\mathfrak {g}$ with subquotients
where ![]() $\eta$ runs over the weights of
$\eta$ runs over the weights of ![]() $\mathsf {L}(\nu )$ (counted with multiplicities). This filtration is clearly compatible with the action of
$\mathsf {L}(\nu )$ (counted with multiplicities). This filtration is clearly compatible with the action of ![]() $\mathcal {U}_\mathbf {S} \mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} (\tilde {\mathcal {U}}_\mathbf {S}\mathfrak {g})^{\mathrm{op}}$ and the natural module structure over the group scheme
$\mathcal {U}_\mathbf {S} \mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} (\tilde {\mathcal {U}}_\mathbf {S}\mathfrak {g})^{\mathrm{op}}$ and the natural module structure over the group scheme ![]() $\mathfrak {t}^{*}/(W,\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathbb {I}_\mathbf {S}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}$.
$\mathfrak {t}^{*}/(W,\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathbb {I}_\mathbf {S}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}$.
Let us denote by ![]() $\varpi : \mathfrak {t}^{*} \to \mathfrak {t}^{*}/(W,\bullet )$ the quotient morphism. The irreducible components of
$\varpi : \mathfrak {t}^{*} \to \mathfrak {t}^{*}/(W,\bullet )$ the quotient morphism. The irreducible components of ![]() $\mathfrak {E}'$ are parametrized by
$\mathfrak {E}'$ are parametrized by ![]() $\mathfrak {t}^{*}_{\mathbb {F}_p}$, with the component corresponding to
$\mathfrak {t}^{*}_{\mathbb {F}_p}$, with the component corresponding to ![]() $\bar {\gamma }$ being the image of the closed embedding
$\bar {\gamma }$ being the image of the closed embedding ![]() $\mathfrak {t}^{*} \to \mathfrak {E}'$ given by
$\mathfrak {t}^{*} \to \mathfrak {E}'$ given by ![]() $\xi \mapsto (\varpi (\xi +\bar {\gamma }),\xi )$. The components containing the point
$\xi \mapsto (\varpi (\xi +\bar {\gamma }),\xi )$. The components containing the point ![]() $({{\tilde {\mu }}},w \bullet {{\bar {\lambda }}})$ correspond to the elements
$({{\tilde {\mu }}},w \bullet {{\bar {\lambda }}})$ correspond to the elements ![]() $\bar {\gamma } \in \mathfrak {t}^{*}_{\mathbb {F}_p}$ such that
$\bar {\gamma } \in \mathfrak {t}^{*}_{\mathbb {F}_p}$ such that ![]() $w \bullet {{\bar {\lambda }}}+\bar {\gamma } \in W \bullet {{\bar {\mu }}}$, that is,
$w \bullet {{\bar {\lambda }}}+\bar {\gamma } \in W \bullet {{\bar {\mu }}}$, that is, ![]() ${{\bar {\lambda }}} + w^{-1}\bar {\gamma } \in W \bullet {{\bar {\mu }}}$. On the other hand, the module (5.3) is supported on the component corresponding to
${{\bar {\lambda }}} + w^{-1}\bar {\gamma } \in W \bullet {{\bar {\mu }}}$. On the other hand, the module (5.3) is supported on the component corresponding to ![]() $\bar {\eta }$. Hence, after completion at
$\bar {\eta }$. Hence, after completion at ![]() $({{\tilde {\mu }}},w \bullet {{\bar {\lambda }}})$, the only subquotients that survive are those corresponding to the weights
$({{\tilde {\mu }}},w \bullet {{\bar {\lambda }}})$, the only subquotients that survive are those corresponding to the weights ![]() $\eta$ such that
$\eta$ such that ![]() ${{\bar {\lambda }}} + w^{-1}\bar {\eta } \in W \bullet {{\bar {\mu }}}$, namely,
${{\bar {\lambda }}} + w^{-1}\bar {\eta } \in W \bullet {{\bar {\mu }}}$, namely, ![]() $\lambda +w^{-1}\eta \in {W_{\mathrm {ext}}} \bullet \mu$. Since
$\lambda +w^{-1}\eta \in {W_{\mathrm {ext}}} \bullet \mu$. Since ![]() $w^{-1}\eta$ is a weight of
$w^{-1}\eta$ is a weight of ![]() $\mathsf {L}(\nu )$, it belongs to
$\mathsf {L}(\nu )$, it belongs to ![]() $\mu -\lambda +\mathbb {Z}\mathfrak {R}$, so that
$\mu -\lambda +\mathbb {Z}\mathfrak {R}$, so that ![]() $\lambda +w^{-1}\eta \in \mu +\mathbb {Z}\mathfrak {R}$. By Lemma 3.1(i) the condition that
$\lambda +w^{-1}\eta \in \mu +\mathbb {Z}\mathfrak {R}$. By Lemma 3.1(i) the condition that ![]() $\lambda +w^{-1}\eta \in {W_{\mathrm {ext}}} \bullet \mu$ is therefore equivalent to
$\lambda +w^{-1}\eta \in {W_{\mathrm {ext}}} \bullet \mu$ is therefore equivalent to ![]() $\lambda +w^{-1}\eta \in {W_{\mathrm {aff}}} \bullet \mu$. Now by [Reference JantzenJan03, Lemma II.7.7] this condition is satisfied only when
$\lambda +w^{-1}\eta \in {W_{\mathrm {aff}}} \bullet \mu$. Now by [Reference JantzenJan03, Lemma II.7.7] this condition is satisfied only when ![]() $\lambda +w^{-1}\eta =\mu$, that is,
$\lambda +w^{-1}\eta =\mu$, that is, ![]() $\eta =w(\mu -\lambda )$. We deduce the desired isomorphism, since
$\eta =w(\mu -\lambda )$. We deduce the desired isomorphism, since ![]() $w \bullet \mu -w \bullet \lambda =w(\mu -\lambda )$.
$w \bullet \mu -w \bullet \lambda =w(\mu -\lambda )$.
Remark 5.6 Let ![]() $\lambda,\mu \in \mathbb {X}$ belonging to the closure of the fundamental alcove, and assume that the stabilizer of
$\lambda,\mu \in \mathbb {X}$ belonging to the closure of the fundamental alcove, and assume that the stabilizer of ![]() $\lambda$ for the dot action of
$\lambda$ for the dot action of ![]() ${W_{\mathrm {aff}}}$ is contained in the stabilizer of
${W_{\mathrm {aff}}}$ is contained in the stabilizer of ![]() $\mu$. Then, if we denote by
$\mu$. Then, if we denote by ![]() $\mathscr {O}(\mathfrak {E})^{\hat {\lambda },\hat {\mu }}$ the completion of
$\mathscr {O}(\mathfrak {E})^{\hat {\lambda },\hat {\mu }}$ the completion of ![]() $\mathscr {O}(\mathfrak {E})$ at the ideal corresponding to
$\mathscr {O}(\mathfrak {E})$ at the ideal corresponding to ![]() $({{\bar {\lambda }}},{{\tilde {\mu }}})$, the same considerations as in the proof of Lemma 5.5 show that there exists an isomorphism
$({{\bar {\lambda }}},{{\tilde {\mu }}})$, the same considerations as in the proof of Lemma 5.5 show that there exists an isomorphism
Recall that, given a simple reflection ![]() $s \in {S_{\mathrm {aff}}}$, a weight
$s \in {S_{\mathrm {aff}}}$, a weight ![]() $\lambda \in \mathbb {X}$ belonging to the closure of the fundamental alcove is said to be on the wall corresponding to
$\lambda \in \mathbb {X}$ belonging to the closure of the fundamental alcove is said to be on the wall corresponding to ![]() $s$ if
$s$ if ![]() $s \bullet \lambda =\lambda$.
$s \bullet \lambda =\lambda$.
Lemma 5.7 Let ![]() $\lambda,\mu \in \mathbb {X}$, with
$\lambda,\mu \in \mathbb {X}$, with ![]() $\lambda$ belonging to the fundamental alcove and
$\lambda$ belonging to the fundamental alcove and ![]() $\mu$ on exactly one wall of the fundamental alcove, attached to the simple reflection
$\mu$ on exactly one wall of the fundamental alcove, attached to the simple reflection ![]() $s$. Let also
$s$. Let also ![]() $w \in W$.
$w \in W$.
(i) If
 $ws \bullet \lambda > w \bullet \lambda$, then there exists an exact sequence
in
$ws \bullet \lambda > w \bullet \lambda$, then there exists an exact sequence
in \[ \mathsf{Q}_{w \bullet \lambda, w \bullet \lambda} \hookrightarrow \mathsf{P}_\mathbf{S}^{\lambda,\mu} {\widehat{\otimes}}_{\mathcal{U}_\mathbf{S}\mathfrak{g}} \mathsf{P}_\mathbf{S}^{\mu,\lambda} \twoheadrightarrow \mathsf{Q}_{ws \bullet \lambda, w \bullet \lambda} \]
\[ \mathsf{Q}_{w \bullet \lambda, w \bullet \lambda} \hookrightarrow \mathsf{P}_\mathbf{S}^{\lambda,\mu} {\widehat{\otimes}}_{\mathcal{U}_\mathbf{S}\mathfrak{g}} \mathsf{P}_\mathbf{S}^{\mu,\lambda} \twoheadrightarrow \mathsf{Q}_{ws \bullet \lambda, w \bullet \lambda} \] $\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\lambda }})$.
$\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\lambda }})$.(ii) If
 $ws \bullet \lambda < w \bullet \lambda$, then there exists an exact sequence
in
$ws \bullet \lambda < w \bullet \lambda$, then there exists an exact sequence
in \[ \mathsf{Q}_{ws \bullet \lambda, w \bullet \lambda} \hookrightarrow \mathsf{P}_\mathbf{S}^{\lambda,\mu} {\widehat{\otimes}}_{\mathcal{U}_\mathbf{S}\mathfrak{g}} \mathsf{P}_\mathbf{S}^{\mu,\lambda} \twoheadrightarrow \mathsf{Q}_{w \bullet \lambda, w \bullet \lambda} \]
\[ \mathsf{Q}_{ws \bullet \lambda, w \bullet \lambda} \hookrightarrow \mathsf{P}_\mathbf{S}^{\lambda,\mu} {\widehat{\otimes}}_{\mathcal{U}_\mathbf{S}\mathfrak{g}} \mathsf{P}_\mathbf{S}^{\mu,\lambda} \twoheadrightarrow \mathsf{Q}_{w \bullet \lambda, w \bullet \lambda} \] $\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\lambda }})$.
$\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\lambda }})$.
Proof. By Lemma 5.5 we have
Hence, if we denote by ![]() $\nu$ the unique dominant weight in
$\nu$ the unique dominant weight in ![]() $W(\lambda -\mu )$, this object can be obtained by completing the bimodule
$W(\lambda -\mu )$, this object can be obtained by completing the bimodule
 \begin{align*} &\mathsf{L}(\nu) \otimes \Gamma \big( \tilde{\mathbf{S}}^{*} \times_{\mathfrak{t}^{*(1)}} \mathfrak{t}^{*}, (\mathscr{O}_\mathcal{B}(w \bullet \mu - w \bullet \lambda) \otimes_{\mathscr{O}_\mathcal{B}} \tilde{\mathscr{D}})_{|\tilde{\mathbf{S}}^{*} \times_{\mathfrak{t}^{*(1)}} \mathfrak{t}^{*}} \big)\\ &\quad \cong\Gamma \big( \tilde{\mathbf{S}}^{*} \times_{\mathfrak{t}^{*(1)}} \mathfrak{t}^{*}, \mathsf{L}(\nu) \otimes (\mathscr{O}_\mathcal{B}(w \bullet \mu - w \bullet \lambda) \otimes_{\mathscr{O}_\mathcal{B}} \tilde{\mathscr{D}})_{|\tilde{\mathbf{S}}^{*} \times_{\mathfrak{t}^{*(1)}} \mathfrak{t}^{*}} \big) \end{align*}
\begin{align*} &\mathsf{L}(\nu) \otimes \Gamma \big( \tilde{\mathbf{S}}^{*} \times_{\mathfrak{t}^{*(1)}} \mathfrak{t}^{*}, (\mathscr{O}_\mathcal{B}(w \bullet \mu - w \bullet \lambda) \otimes_{\mathscr{O}_\mathcal{B}} \tilde{\mathscr{D}})_{|\tilde{\mathbf{S}}^{*} \times_{\mathfrak{t}^{*(1)}} \mathfrak{t}^{*}} \big)\\ &\quad \cong\Gamma \big( \tilde{\mathbf{S}}^{*} \times_{\mathfrak{t}^{*(1)}} \mathfrak{t}^{*}, \mathsf{L}(\nu) \otimes (\mathscr{O}_\mathcal{B}(w \bullet \mu - w \bullet \lambda) \otimes_{\mathscr{O}_\mathcal{B}} \tilde{\mathscr{D}})_{|\tilde{\mathbf{S}}^{*} \times_{\mathfrak{t}^{*(1)}} \mathfrak{t}^{*}} \big) \end{align*}
with respect to the ideal of ![]() $\mathscr {O}(\mathfrak {E}')$ corresponding to
$\mathscr {O}(\mathfrak {E}')$ corresponding to ![]() $({{\tilde {\lambda }}}, w \bullet {{\bar {\lambda }}})$. Hence, as in the proof of Lemma 5.5, if we choose an enumeration
$({{\tilde {\lambda }}}, w \bullet {{\bar {\lambda }}})$. Hence, as in the proof of Lemma 5.5, if we choose an enumeration ![]() $\eta _1, \ldots, \eta _n$ of the
$\eta _1, \ldots, \eta _n$ of the ![]() $T$-weights of
$T$-weights of ![]() $\mathsf {L}(\nu )$ (counted with multiplicities) such that
$\mathsf {L}(\nu )$ (counted with multiplicities) such that ![]() $\eta _i < \eta _j$ implies
$\eta _i < \eta _j$ implies ![]() $i< j$, then this bimodule admits a filtration
$i< j$, then this bimodule admits a filtration
such that
for any ![]() $i$. The subquotient
$i$. The subquotient ![]() $M_i/M_{i-1}$ survives after completion at the ideal corresponding to
$M_i/M_{i-1}$ survives after completion at the ideal corresponding to ![]() $({{\tilde {\lambda }}}, w \bullet {{\bar {\lambda }}})$ if and only if
$({{\tilde {\lambda }}}, w \bullet {{\bar {\lambda }}})$ if and only if
that is, if and only if
Here ![]() $w^{-1} \eta _i$ is a weight of
$w^{-1} \eta _i$ is a weight of ![]() $\mathsf {L}(\nu )$, hence
$\mathsf {L}(\nu )$, hence ![]() $\mu + w^{-1} \eta _i$ belongs to
$\mu + w^{-1} \eta _i$ belongs to ![]() $\lambda +\mathbb {Z}\mathfrak {R}$; in view of Lemma 3.1(i), this condition is therefore equivalent to
$\lambda +\mathbb {Z}\mathfrak {R}$; in view of Lemma 3.1(i), this condition is therefore equivalent to ![]() $\mu + w^{-1}\eta _i \in {W_{\mathrm {aff}}} \bullet \lambda$. Since the stabilizer of
$\mu + w^{-1}\eta _i \in {W_{\mathrm {aff}}} \bullet \lambda$. Since the stabilizer of ![]() $\mu$ for the dot action of
$\mu$ for the dot action of ![]() ${W_{\mathrm {aff}}}$ is
${W_{\mathrm {aff}}}$ is ![]() $\{e,s\}$, by [Reference JantzenJan03, Lemma II.7.7] this condition is satisfied for two values of
$\{e,s\}$, by [Reference JantzenJan03, Lemma II.7.7] this condition is satisfied for two values of ![]() $\eta _i$, corresponding to
$\eta _i$, corresponding to
that is,
Hence, ![]() $\mathsf {P}_\mathbf {S}^{\lambda,\mu } {\widehat{\otimes}}_{\mathcal {U}_\mathbf {S}\mathfrak {g}} \mathsf {P}_\mathbf {S}^{\mu,\lambda }$ admits a two-step filtration, with subquotients isomorphic respectively to
$\mathsf {P}_\mathbf {S}^{\lambda,\mu } {\widehat{\otimes}}_{\mathcal {U}_\mathbf {S}\mathfrak {g}} \mathsf {P}_\mathbf {S}^{\mu,\lambda }$ admits a two-step filtration, with subquotients isomorphic respectively to ![]() $\mathsf {Q}_{w \bullet \lambda, w \bullet \lambda }$ and
$\mathsf {Q}_{w \bullet \lambda, w \bullet \lambda }$ and ![]() $\mathsf {Q}_{ws \bullet \lambda, w \bullet \lambda }$. The order in which these subquotients appear depends on whether
$\mathsf {Q}_{ws \bullet \lambda, w \bullet \lambda }$. The order in which these subquotients appear depends on whether ![]() $ws \bullet \lambda > w \bullet \lambda$ or
$ws \bullet \lambda > w \bullet \lambda$ or ![]() $ws \bullet \lambda < w \bullet \lambda$, and is as indicated in the statement.
$ws \bullet \lambda < w \bullet \lambda$, and is as indicated in the statement.
5.4 Convolution with translation bimodules
Let ![]() $\lambda,\mu \in \mathbb {X}$, and assume that
$\lambda,\mu \in \mathbb {X}$, and assume that ![]() $\lambda$ is regular. Then there exists a canonical algebra morphism
$\lambda$ is regular. Then there exists a canonical algebra morphism
which can be defined as follows. The algebra ![]() $\mathcal {Z}_\mathbf {S}^{\hat {\mu },\hat {\lambda }}$ is by definition the completion of
$\mathcal {Z}_\mathbf {S}^{\hat {\mu },\hat {\lambda }}$ is by definition the completion of ![]() $\mathscr {O}(\mathfrak {D})$ at the ideal corresponding to
$\mathscr {O}(\mathfrak {D})$ at the ideal corresponding to ![]() $({{\tilde {\mu }}},{{\tilde {\lambda }}})$. Hence, it admits a canonical morphism to the completion
$({{\tilde {\mu }}},{{\tilde {\lambda }}})$. Hence, it admits a canonical morphism to the completion ![]() $\mathscr {O}(\mathfrak {E})^{\hat {\mu },\hat {\lambda }}$ of
$\mathscr {O}(\mathfrak {E})^{\hat {\mu },\hat {\lambda }}$ of ![]() $\mathscr {O}(\mathfrak {E})$ at the ideal corresponding to
$\mathscr {O}(\mathfrak {E})$ at the ideal corresponding to ![]() $({{\bar {\mu }}},{{\tilde {\lambda }}})$. Now the morphism
$({{\bar {\mu }}},{{\tilde {\lambda }}})$. Now the morphism ![]() $\mathfrak {t}^{*} \to \mathfrak {t}^{*}$ defined by
$\mathfrak {t}^{*} \to \mathfrak {t}^{*}$ defined by ![]() $\xi \mapsto \xi +{{\bar {\mu }}}-{{\bar {\lambda }}}$ induces an automorphism of
$\xi \mapsto \xi +{{\bar {\mu }}}-{{\bar {\lambda }}}$ induces an automorphism of ![]() $\mathfrak {E}$ sending
$\mathfrak {E}$ sending ![]() $({{\bar {\lambda }}},{{\tilde {\lambda }}})$ to
$({{\bar {\lambda }}},{{\tilde {\lambda }}})$ to ![]() $({{\bar {\mu }}},{{\tilde {\lambda }}})$, which therefore induces an isomorphism
$({{\bar {\mu }}},{{\tilde {\lambda }}})$, which therefore induces an isomorphism
where the right-hand side is the completion of ![]() $\mathscr {O}(\mathfrak {E})$ at the ideal corresponding to
$\mathscr {O}(\mathfrak {E})$ at the ideal corresponding to ![]() $({{\bar {\lambda }}},{{\tilde {\lambda }}})$. Finally, the natural morphism
$({{\bar {\lambda }}},{{\tilde {\lambda }}})$. Finally, the natural morphism
is an isomorphism by Lemma 3.2, since ![]() $\lambda$ is regular; combining these constructions, we obtain the wished-for morphism (5.4).
$\lambda$ is regular; combining these constructions, we obtain the wished-for morphism (5.4).
Our goal in this subsection is to prove the following claim, which involves the equivalence constructed in Corollary 4.8.
Proposition 5.8 Let ![]() $\lambda,\mu \in \mathbb {X}$, with
$\lambda,\mu \in \mathbb {X}$, with ![]() $\lambda$ belonging to the fundamental alcove and
$\lambda$ belonging to the fundamental alcove and ![]() $\mu$ on exactly one wall of the fundamental alcove, attached to a simple reflection
$\mu$ on exactly one wall of the fundamental alcove, attached to a simple reflection ![]() $s$ which belongs to
$s$ which belongs to ![]() $W$. Then there exists an isomorphism
$W$. Then there exists an isomorphism
in ![]() $\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\lambda }})$, where
$\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\lambda }})$, where ![]() $\mathcal {Z}_\mathbf {S}^{\hat {\lambda }}$ is regarded as a
$\mathcal {Z}_\mathbf {S}^{\hat {\lambda }}$ is regarded as a ![]() $\mathcal {Z}_\mathbf {S}^{\hat {\mu },\hat {\lambda }}$-module via the morphism (5.4) and
$\mathcal {Z}_\mathbf {S}^{\hat {\mu },\hat {\lambda }}$-module via the morphism (5.4) and ![]() $\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\lambda }} \otimes _{\mathcal {Z}_\mathbf {S}^{\hat {\mu },\hat {\lambda }}} \mathcal {Z}_\mathbf {S}^{\hat {\lambda }}$ is endowed with the trivial structure as a representation.
$\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\lambda }} \otimes _{\mathcal {Z}_\mathbf {S}^{\hat {\mu },\hat {\lambda }}} \mathcal {Z}_\mathbf {S}^{\hat {\lambda }}$ is endowed with the trivial structure as a representation.
Remark 5.9 From the proof below one can check that the isomorphism in Proposition 5.8 is ‘canonical’ in that it depends only on the choice of an adjunction ![]() $(\mathsf {P}_\mathbf {S}^{\lambda,\mu } {\widehat{\otimes}}_{\mathcal {U}_\mathbf {S}\mathfrak {g}} (-), \mathsf {P}_\mathbf {S}^{\mu,\lambda } {\widehat{\otimes}}_{\mathcal {U}_\mathbf {S}\mathfrak {g}} (-))$, which can be defined by a choice of an isomorphism
$(\mathsf {P}_\mathbf {S}^{\lambda,\mu } {\widehat{\otimes}}_{\mathcal {U}_\mathbf {S}\mathfrak {g}} (-), \mathsf {P}_\mathbf {S}^{\mu,\lambda } {\widehat{\otimes}}_{\mathcal {U}_\mathbf {S}\mathfrak {g}} (-))$, which can be defined by a choice of an isomorphism ![]() $\mathsf {L}(\nu )^{*} \cong \mathsf {L}(-w_0(\nu ))$ where
$\mathsf {L}(\nu )^{*} \cong \mathsf {L}(-w_0(\nu ))$ where ![]() $\nu$ is the only
$\nu$ is the only ![]() $W$-translate of
$W$-translate of ![]() $\mu -\lambda$; see the proof of Lemma 3.6. From this proof it is clear also that the morphism
$\mu -\lambda$; see the proof of Lemma 3.6. From this proof it is clear also that the morphism
defined by this adjunction corresponds under ![]() $\mathscr {L}_{\lambda,\lambda }$ to the morphism
$\mathscr {L}_{\lambda,\lambda }$ to the morphism
given by the action of ![]() $\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\lambda }}$ on
$\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\lambda }}$ on ![]() $\mathcal {Z}_\mathbf {S}^{\hat {\lambda }}$.
$\mathcal {Z}_\mathbf {S}^{\hat {\lambda }}$.
The proof of this proposition will use two preliminary lemmas.
Lemma 5.10 If ![]() $s$ is a simple reflection in
$s$ is a simple reflection in ![]() $W$, then
$W$, then ![]() $\mathscr {O}(\mathfrak {t}^{*})$ is free of rank
$\mathscr {O}(\mathfrak {t}^{*})$ is free of rank ![]() $2$ as a module over
$2$ as a module over ![]() $\mathscr {O}(\mathfrak {t}^{*}/(\{e,s\},\bullet ))$.
$\mathscr {O}(\mathfrak {t}^{*}/(\{e,s\},\bullet ))$.
Proof. First, translating by ![]() $\rho$, we can reduce the
$\rho$, we can reduce the ![]() $\bullet$-action to the standard action; it therefore suffices to prove that
$\bullet$-action to the standard action; it therefore suffices to prove that ![]() $\mathscr {O}(\mathfrak {t}^{*})$ is free of rank
$\mathscr {O}(\mathfrak {t}^{*})$ is free of rank ![]() $2$ over the subalgebra
$2$ over the subalgebra ![]() $\mathscr {O}(\mathfrak {t}^{*})^{s}$ of
$\mathscr {O}(\mathfrak {t}^{*})^{s}$ of ![]() $s$-invariants. Next, recall that we have a
$s$-invariants. Next, recall that we have a ![]() $W$-equivariant isomorphism
$W$-equivariant isomorphism ![]() $\mathfrak {t} \xrightarrow {\sim } \mathfrak {t}^{*}$, induced by a choice of
$\mathfrak {t} \xrightarrow {\sim } \mathfrak {t}^{*}$, induced by a choice of ![]() $G$-equivariant isomorphism
$G$-equivariant isomorphism ![]() $\mathfrak {g} \xrightarrow {\sim } \mathfrak {g}^{*}$. We are therefore reduced to proving that
$\mathfrak {g} \xrightarrow {\sim } \mathfrak {g}^{*}$. We are therefore reduced to proving that ![]() $\mathscr {O}(\mathfrak {t})$ is free of rank
$\mathscr {O}(\mathfrak {t})$ is free of rank ![]() $2$ over
$2$ over ![]() $\mathscr {O}(\mathfrak {t})^{s}$. Now, standard arguments show that
$\mathscr {O}(\mathfrak {t})^{s}$. Now, standard arguments show that ![]() $(1,\bar {\rho })$ is a basis of
$(1,\bar {\rho })$ is a basis of ![]() $\mathscr {O}(\mathfrak {t})$ over
$\mathscr {O}(\mathfrak {t})$ over ![]() $\mathscr {O}(\mathfrak {t})^{s}$; see, for example, [Reference Elias and WilliamsonEW16, Claim 3.11].
$\mathscr {O}(\mathfrak {t})^{s}$; see, for example, [Reference Elias and WilliamsonEW16, Claim 3.11].
Lemma 5.11 Let ![]() $\lambda,\mu \in \mathbb {X}$, with
$\lambda,\mu \in \mathbb {X}$, with ![]() $\lambda$ belonging to the fundamental alcove and
$\lambda$ belonging to the fundamental alcove and ![]() $\mu$ on exactly one wall of the fundamental alcove, attached to a simple reflection
$\mu$ on exactly one wall of the fundamental alcove, attached to a simple reflection ![]() $s$ which belongs to
$s$ which belongs to ![]() $W$. Then there exist isomorphisms of functors which make the following diagrams commutative, where the upper horizontal arrow on the left-hand side is the restriction-of-scalars functor associated with the morphism (5.4):
$W$. Then there exist isomorphisms of functors which make the following diagrams commutative, where the upper horizontal arrow on the left-hand side is the restriction-of-scalars functor associated with the morphism (5.4):

Proof. By definition we have
Using Lemmas 5.3 and 5.5, we deduce that
Hence, to prove the commutativity of the diagram of the left it suffices to construct an isomorphism
or, in other words (in view of (5.5) and (5.6)), an isomorphism
To construct a morphism as in (5.7) it suffices to construct a morphism
in ![]() $\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\mathcal {U}_\mathbf {S}^{\hat {\mu },\hat {\lambda }})$. By Remark 5.6 we have
$\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\mathcal {U}_\mathbf {S}^{\hat {\mu },\hat {\lambda }})$. By Remark 5.6 we have
in particular, there exists a natural morphism ![]() $\mathsf {P}_\mathbf {S}^{\mu,-\rho } \to \mathsf {Q}_{\mu,-\rho }$, which allows to define the wished-for morphism (5.8), hence the morphism (5.7).
$\mathsf {P}_\mathbf {S}^{\mu,-\rho } \to \mathsf {Q}_{\mu,-\rho }$, which allows to define the wished-for morphism (5.8), hence the morphism (5.7).
Now we claim that ![]() $\mathscr {O}(\mathfrak {E})^{\hat {\mu },\hat {\lambda }}$ (respectively,
$\mathscr {O}(\mathfrak {E})^{\hat {\mu },\hat {\lambda }}$ (respectively, ![]() $\mathscr {O}(\mathfrak {E})^{\hat {\mu },\widehat {-\rho }}$) is free of rank
$\mathscr {O}(\mathfrak {E})^{\hat {\mu },\widehat {-\rho }}$) is free of rank ![]() $2$ over the algebra
$2$ over the algebra ![]() $\mathcal {Z}_\mathbf {S}^{\hat {\mu },\hat {\lambda }}$ (respectively,
$\mathcal {Z}_\mathbf {S}^{\hat {\mu },\hat {\lambda }}$ (respectively, ![]() $\mathcal {Z}_\mathbf {S}^{\hat {\mu },\widehat {-\rho }}$), which in view of (5.9) will imply that the morphism (5.7) is an isomorphism. The two cases are similar, so we only consider
$\mathcal {Z}_\mathbf {S}^{\hat {\mu },\widehat {-\rho }}$), which in view of (5.9) will imply that the morphism (5.7) is an isomorphism. The two cases are similar, so we only consider ![]() $\mathscr {O}(\mathfrak {E})^{\hat {\mu },\hat {\lambda }}$. It follows from Lemma 3.2 that
$\mathscr {O}(\mathfrak {E})^{\hat {\mu },\hat {\lambda }}$. It follows from Lemma 3.2 that ![]() $\mathcal {Z}_\mathbf {S}^{\hat {\mu },\hat {\lambda }}$ identifies with the completion
$\mathcal {Z}_\mathbf {S}^{\hat {\mu },\hat {\lambda }}$ identifies with the completion
of ![]() $\mathscr {O}(\mathfrak {t}^{*}/(\{e,s\},\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W,\bullet ))$ with respect to the ideal corresponding to the image of
$\mathscr {O}(\mathfrak {t}^{*}/(\{e,s\},\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W,\bullet ))$ with respect to the ideal corresponding to the image of ![]() $({{\bar {\mu }}},{{\tilde {\lambda }}})$. Now
$({{\bar {\mu }}},{{\tilde {\lambda }}})$. Now ![]() $\mathscr {O}(\mathfrak {E})$ is free of rank
$\mathscr {O}(\mathfrak {E})$ is free of rank ![]() $2$ over
$2$ over ![]() $\mathscr {O}(\mathfrak {t}^{*}/(\{e,s\},\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W,\bullet ))$ by Lemma 5.10, and its completion with respect to the ideal corresponding to
$\mathscr {O}(\mathfrak {t}^{*}/(\{e,s\},\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W,\bullet ))$ by Lemma 5.10, and its completion with respect to the ideal corresponding to ![]() $({{\bar {\mu }}},{{\tilde {\lambda }}})$ coincides with its completion with respect to the ideal of
$({{\bar {\mu }}},{{\tilde {\lambda }}})$ coincides with its completion with respect to the ideal of ![]() $\mathscr {O}(\mathfrak {t}^{*}/(\{e,s\},\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W,\bullet ))$ corresponding to the image of
$\mathscr {O}(\mathfrak {t}^{*}/(\{e,s\},\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W,\bullet ))$ corresponding to the image of ![]() $({{\bar {\mu }}},{{\tilde {\lambda }}})$ (because
$({{\bar {\mu }}},{{\tilde {\lambda }}})$ (because ![]() $({{\bar {\mu }}},{{\tilde {\lambda }}})$ is the only closed point in the fiber over its image in
$({{\bar {\mu }}},{{\tilde {\lambda }}})$ is the only closed point in the fiber over its image in ![]() $\mathfrak {t}^{*}/(\{e,s\},\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W,\bullet )$). The desired claim follows.
$\mathfrak {t}^{*}/(\{e,s\},\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W,\bullet )$). The desired claim follows.
We have finally proved the commutativity of the left diagram of the lemma. The commutativity of the right diagram follows from that of the left one by adjunction, in view of Lemma 3.6.
Proof of Proposition 5.8 Lemma 5.11 provides isomorphisms
The desired claim follows, using the isomorphism (4.9).
5.5 Monoidality of the functors  $\mathscr {L}_{\lambda,\lambda }$
$\mathscr {L}_{\lambda,\lambda }$
Our goal in this subsection is to prove the following claim, announced in Remark 4.9.
Proposition 5.12 Let ![]() $\lambda,\nu \in \mathbb {X}$ in the lower closure of the fundamental alcove, and let
$\lambda,\nu \in \mathbb {X}$ in the lower closure of the fundamental alcove, and let ![]() $\mu \in \mathbb {X}$ be in the fundamental alcove. Then for
$\mu \in \mathbb {X}$ be in the fundamental alcove. Then for ![]() $M \in \mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$ and
$M \in \mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$ and ![]() $N \in \mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\mathcal {Z}_\mathbf {S}^{\hat {\mu },\hat {\nu }})$ there exists a canonical (in particular, bifunctorial) isomorphism
$N \in \mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\mathcal {Z}_\mathbf {S}^{\hat {\mu },\hat {\nu }})$ there exists a canonical (in particular, bifunctorial) isomorphism
In the case where ![]() $\lambda =\mu =\nu$, this isomorphism and (4.9) define on
$\lambda =\mu =\nu$, this isomorphism and (4.9) define on ![]() $\mathscr {L}_{\lambda,\lambda }$ the structure of a monoidal functor.
$\mathscr {L}_{\lambda,\lambda }$ the structure of a monoidal functor.
Proof. Recall the completion ![]() $\mathscr {O}(\mathfrak {t}^{*(1)}/W)^{\wedge }$ introduced in § 3.6. By definition and Remark 3.5, if we set
$\mathscr {O}(\mathfrak {t}^{*(1)}/W)^{\wedge }$ introduced in § 3.6. By definition and Remark 3.5, if we set ![]() $\mathcal {U}_\mathbf{S}\mathfrak {g}^{\wedge } :=\mathcal {U}_\mathbf{S} \mathfrak {g} \otimes _{\mathscr {O}(\mathfrak {t}^{*(1)}/W)} \mathscr {O}(\mathfrak {t}^{*(1)}/W)^{\wedge }$ we have
$\mathcal {U}_\mathbf{S}\mathfrak {g}^{\wedge } :=\mathcal {U}_\mathbf{S} \mathfrak {g} \otimes _{\mathscr {O}(\mathfrak {t}^{*(1)}/W)} \mathscr {O}(\mathfrak {t}^{*(1)}/W)^{\wedge }$ we have
and
We deduce that
 \begin{align*} \mathscr{L}_{\lambda,\mu}(M) {\widehat{\otimes}}_{\mathcal{U}_\mathbf{S}\mathfrak{g}} \mathscr{L}_{\mu,\nu}(N) &\cong( \mathsf{P}_\mathbf{S}^{\lambda,-\rho} \otimes_{\mathcal{U}_\mathbf{S}\mathfrak{g}^{\wedge}} \mathsf{P}_\mathbf{S}^{-\rho,\mu} \otimes_{\mathcal{U}_\mathbf{S}\mathfrak{g}^{\wedge}} \mathsf{P}_\mathbf{S}^{\mu,-\rho} \otimes_{\mathcal{U}_\mathbf{S}\mathfrak{g}^{\wedge}} \mathsf{P}_\mathbf{S}^{-\rho,\nu}) \\ &\quad \otimes_{{Z^{\hat{\lambda}}_{\mathrm{HC}}} \otimes_{\mathscr{O}(\mathfrak{t}^{*(1)}/W)^{\wedge}} {Z^{\hat{\mu}}_{\mathrm{HC}}} \otimes_{\mathscr{O}(\mathfrak{t}^{*(1)}/W)^{\wedge}} {Z_{\mathrm{HC}}^{\hat{\nu}}}} (M \otimes_{{Z_{\mathrm{HC}}^{\hat{\mu}}}} N). \end{align*}
\begin{align*} \mathscr{L}_{\lambda,\mu}(M) {\widehat{\otimes}}_{\mathcal{U}_\mathbf{S}\mathfrak{g}} \mathscr{L}_{\mu,\nu}(N) &\cong( \mathsf{P}_\mathbf{S}^{\lambda,-\rho} \otimes_{\mathcal{U}_\mathbf{S}\mathfrak{g}^{\wedge}} \mathsf{P}_\mathbf{S}^{-\rho,\mu} \otimes_{\mathcal{U}_\mathbf{S}\mathfrak{g}^{\wedge}} \mathsf{P}_\mathbf{S}^{\mu,-\rho} \otimes_{\mathcal{U}_\mathbf{S}\mathfrak{g}^{\wedge}} \mathsf{P}_\mathbf{S}^{-\rho,\nu}) \\ &\quad \otimes_{{Z^{\hat{\lambda}}_{\mathrm{HC}}} \otimes_{\mathscr{O}(\mathfrak{t}^{*(1)}/W)^{\wedge}} {Z^{\hat{\mu}}_{\mathrm{HC}}} \otimes_{\mathscr{O}(\mathfrak{t}^{*(1)}/W)^{\wedge}} {Z_{\mathrm{HC}}^{\hat{\nu}}}} (M \otimes_{{Z_{\mathrm{HC}}^{\hat{\mu}}}} N). \end{align*}
(Here, ![]() ${Z^{\hat {\lambda }}_{\mathrm {HC}}} \otimes _{\mathscr {O}(\mathfrak {t}^{*(1)}/W)^{\wedge }} {Z^{\hat {\mu }}_{\mathrm {HC}}} \otimes _{\mathscr {O}(\mathfrak {t}^{*(1)}/W)^{\wedge }} {Z^{\hat {\nu }}_{\mathrm {HC}}}$ identifies with the completion of the algebra
${Z^{\hat {\lambda }}_{\mathrm {HC}}} \otimes _{\mathscr {O}(\mathfrak {t}^{*(1)}/W)^{\wedge }} {Z^{\hat {\mu }}_{\mathrm {HC}}} \otimes _{\mathscr {O}(\mathfrak {t}^{*(1)}/W)^{\wedge }} {Z^{\hat {\nu }}_{\mathrm {HC}}}$ identifies with the completion of the algebra ![]() $\mathscr {O}(\mathfrak {t}^{*}/(W,\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W,\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W,\bullet ))$ with respect to the ideal corresponding to
$\mathscr {O}(\mathfrak {t}^{*}/(W,\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W,\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W,\bullet ))$ with respect to the ideal corresponding to ![]() $({{\tilde {\lambda }}},{{\tilde {\mu }}},\tilde {\nu })$.) By Lemmas 5.5 and 5.3 we have
$({{\tilde {\lambda }}},{{\tilde {\mu }}},\tilde {\nu })$.) By Lemmas 5.5 and 5.3 we have
By Lemma 5.1, ![]() $\mathsf {Q}_{-\rho,-\rho }$ identifies with the completion of
$\mathsf {Q}_{-\rho,-\rho }$ identifies with the completion of ![]() $\tilde {\mathcal {U}}_\mathbf {S}\mathfrak {g}$ with respect to the ideal of
$\tilde {\mathcal {U}}_\mathbf {S}\mathfrak {g}$ with respect to the ideal of ![]() $\mathscr {O}(\mathfrak {t}^{*})$ corresponding to
$\mathscr {O}(\mathfrak {t}^{*})$ corresponding to ![]() $\overline {-\rho }$. Via this identification, the action of
$\overline {-\rho }$. Via this identification, the action of ![]() ${Z^{\hat {\mu }}_{\mathrm {HC}}}$ is given by the composition
${Z^{\hat {\mu }}_{\mathrm {HC}}}$ is given by the composition
where ![]() $\mathscr {O}(\mathfrak {t}^{*})^{\hat {\mu }}$ and
$\mathscr {O}(\mathfrak {t}^{*})^{\hat {\mu }}$ and ![]() $\mathscr {O}(\mathfrak {t}^{*})^{\widehat {-\rho }}$ are the completions of
$\mathscr {O}(\mathfrak {t}^{*})^{\widehat {-\rho }}$ are the completions of ![]() $\mathscr {O}(\mathfrak {t}^{*})$ with respect to the ideals corresponding to
$\mathscr {O}(\mathfrak {t}^{*})$ with respect to the ideals corresponding to ![]() $\bar {\lambda }$ and
$\bar {\lambda }$ and ![]() $\overline {-\rho }$ respectively, the first map is induced by the embedding
$\overline {-\rho }$ respectively, the first map is induced by the embedding ![]() ${Z_{\mathrm {HC}}} \cong \mathscr {O}(\mathfrak {t}^{*}/(W,\bullet )) \to \mathscr {O}(\mathfrak {t}^{*})$, and the second one is defined in terms of translation, in a way similar to that considered at the beginning of § 5.4. Here the first map is an isomorphism by Lemma 3.2, from which we obtain an isomorphism
${Z_{\mathrm {HC}}} \cong \mathscr {O}(\mathfrak {t}^{*}/(W,\bullet )) \to \mathscr {O}(\mathfrak {t}^{*})$, and the second one is defined in terms of translation, in a way similar to that considered at the beginning of § 5.4. Here the first map is an isomorphism by Lemma 3.2, from which we obtain an isomorphism
 \begin{align*} &\mathscr{L}_{\lambda,\mu}(M) {\widehat{\otimes}}_{\mathcal{U}_\mathbf{S}\mathfrak{g}} \mathscr{L}_{\mu,\nu}(N) \\ &\quad \cong ( \mathsf{P}_\mathbf{S}^{\lambda,-\rho} \otimes_{\mathcal{U}_\mathbf{S}\mathfrak{g}^{\wedge}} \mathsf{P}_\mathbf{S}^{-\rho,\nu}) \otimes_{{Z^{\hat{\lambda}}_{\mathrm{HC}}} \otimes_{\mathscr{O}(\mathfrak{t}^{*(1)}/W)^{\wedge}} {Z_{\mathrm{HC}}^{\widehat{-\rho}}} \otimes_{\mathscr{O}(\mathfrak{t}^{*(1)}/W)^{\wedge}} {Z_{\mathrm{HC}}^{\hat{\nu}}}} (M \otimes_{Z_{\mathrm{HC}}^{\hat{\mu}}} N). \end{align*}
\begin{align*} &\mathscr{L}_{\lambda,\mu}(M) {\widehat{\otimes}}_{\mathcal{U}_\mathbf{S}\mathfrak{g}} \mathscr{L}_{\mu,\nu}(N) \\ &\quad \cong ( \mathsf{P}_\mathbf{S}^{\lambda,-\rho} \otimes_{\mathcal{U}_\mathbf{S}\mathfrak{g}^{\wedge}} \mathsf{P}_\mathbf{S}^{-\rho,\nu}) \otimes_{{Z^{\hat{\lambda}}_{\mathrm{HC}}} \otimes_{\mathscr{O}(\mathfrak{t}^{*(1)}/W)^{\wedge}} {Z_{\mathrm{HC}}^{\widehat{-\rho}}} \otimes_{\mathscr{O}(\mathfrak{t}^{*(1)}/W)^{\wedge}} {Z_{\mathrm{HC}}^{\hat{\nu}}}} (M \otimes_{Z_{\mathrm{HC}}^{\hat{\mu}}} N). \end{align*}
Finally, we use the fact that the morphism ![]() $\mathscr {O}(\mathfrak {t}^{*(1)}/W)^{\wedge } \to {Z^{\widehat {-\rho }}_{\mathrm {HC}}}$ is an isomorphism (see the proof of Lemma 4.7) to deduce the wished-for isomorphism
$\mathscr {O}(\mathfrak {t}^{*(1)}/W)^{\wedge } \to {Z^{\widehat {-\rho }}_{\mathrm {HC}}}$ is an isomorphism (see the proof of Lemma 4.7) to deduce the wished-for isomorphism
In the case where ![]() $\lambda =\mu =\nu$, the fact that the relevant isomorphisms define a monoidal structure on
$\lambda =\mu =\nu$, the fact that the relevant isomorphisms define a monoidal structure on ![]() $\mathscr {L}_{\lambda,\lambda }$ is clear from constructions.
$\mathscr {L}_{\lambda,\lambda }$ is clear from constructions.
5.6 Singular analogues
Let ![]() $I \subset \mathfrak {R}^{\mathrm {s}}$ be a subset, and let
$I \subset \mathfrak {R}^{\mathrm {s}}$ be a subset, and let ![]() $P_I \subset G$ be the associated standard (i.e. containing
$P_I \subset G$ be the associated standard (i.e. containing ![]() $B$) parabolic subgroup of
$B$) parabolic subgroup of ![]() $G$. (In practice, only the case
$G$. (In practice, only the case ![]() $\#I=1$ will be considered below.) Let
$\#I=1$ will be considered below.) Let ![]() $U_I \subset P_I$ be the unipotent radical of
$U_I \subset P_I$ be the unipotent radical of ![]() $P_I$, and let
$P_I$, and let ![]() $L_I$ be the Levi factor containing
$L_I$ be the Levi factor containing ![]() $T$, so that
$T$, so that ![]() $P_I \cong L_I \ltimes U_I$. Let
$P_I \cong L_I \ltimes U_I$. Let ![]() $\mathcal {P}_I:=G/P_I$, and consider the natural projection
$\mathcal {P}_I:=G/P_I$, and consider the natural projection
The group ![]() $L_I$ acts naturally on
$L_I$ acts naturally on ![]() $G/U_I$ on the right, via the action induced by multiplication on the right on
$G/U_I$ on the right, via the action induced by multiplication on the right on ![]() $G$; this action makes
$G$; this action makes ![]() $\omega _I$ a (Zariski locally trivial)
$\omega _I$ a (Zariski locally trivial) ![]() $L_I$-torsor. We set
$L_I$-torsor. We set
where the exponent means ![]() $L_I$-invariants. The actions of
$L_I$-invariants. The actions of ![]() $G$ and
$G$ and ![]() $L_I$ on
$L_I$ on ![]() $G/U_I$ induce a canonical algebra morphism
$G/U_I$ induce a canonical algebra morphism
see [Reference Bezrukavnikov, Mirković and RumyninBMR06, Proposition 1.2.3].
Let also ![]() $\mathbf {P}_I:=P_I^{(1)}$, a parabolic subgroup of
$\mathbf {P}_I:=P_I^{(1)}$, a parabolic subgroup of ![]() $\mathbf {G}=G^{(1)}$ with unipotent radical
$\mathbf {G}=G^{(1)}$ with unipotent radical ![]() $\mathbf {U}_I:=U_I^{(1)}$. Let
$\mathbf {U}_I:=U_I^{(1)}$. Let ![]() $\tilde {\mathbf {g}}_I$ be the parabolic Grothendieck resolution (for the group
$\tilde {\mathbf {g}}_I$ be the parabolic Grothendieck resolution (for the group ![]() $\mathbf {G}$) associated with
$\mathbf {G}$) associated with ![]() $I$, defined as
$I$, defined as
Here ![]() $\tilde {\mathbf {g}}_I$ is a vector bundle over
$\tilde {\mathbf {g}}_I$ is a vector bundle over ![]() $\mathbf {G}/\mathbf {P}_I = \mathcal {P}_I^{(1)}$, and if
$\mathbf {G}/\mathbf {P}_I = \mathcal {P}_I^{(1)}$, and if ![]() $\mathbf {L}_I:=L_I^{(1)}$ there is a natural morphism
$\mathbf {L}_I:=L_I^{(1)}$ there is a natural morphism
where ![]() $W_I \subset W$ is as in § 3.1 (seen here as the Weyl group of
$W_I \subset W$ is as in § 3.1 (seen here as the Weyl group of ![]() $(\mathbf {L}_I,\mathbf {T})$).
$(\mathbf {L}_I,\mathbf {T})$).
Consider the induced morphism ![]() $f_I : \tilde {\mathbf {g}}_I \times _{\mathfrak {t}^{*(1)}/W_I} \mathfrak {t}^{*}/(W_I,\bullet ) \to \mathcal {P}_I^{(1)}$, and the Frobenius morphism
$f_I : \tilde {\mathbf {g}}_I \times _{\mathfrak {t}^{*(1)}/W_I} \mathfrak {t}^{*}/(W_I,\bullet ) \to \mathcal {P}_I^{(1)}$, and the Frobenius morphism ![]() $\mathrm {Fr}_{\mathcal {P}_I} : \mathcal {P}_I \to \mathcal {P}_I^{(1)}$. As explained in [Reference Bezrukavnikov, Mirković and RumyninBMR06, § 1.2.1], there exists a canonical algebra morphism
$\mathrm {Fr}_{\mathcal {P}_I} : \mathcal {P}_I \to \mathcal {P}_I^{(1)}$. As explained in [Reference Bezrukavnikov, Mirković and RumyninBMR06, § 1.2.1], there exists a canonical algebra morphism
where the morphism ![]() $\mathfrak {t}^{*}/(W_I,\bullet ) \to \mathfrak {t}^{*(1)}/W_I$ is induced by the Artin–Schreier map. This morphism takes values in the center of
$\mathfrak {t}^{*}/(W_I,\bullet ) \to \mathfrak {t}^{*(1)}/W_I$ is induced by the Artin–Schreier map. This morphism takes values in the center of ![]() $(\mathrm {Fr}_{\mathcal {P}_I})_* \tilde {\mathscr {D}}_I$, and makes
$(\mathrm {Fr}_{\mathcal {P}_I})_* \tilde {\mathscr {D}}_I$, and makes ![]() $(\mathrm {Fr}_{\mathcal {P}_I})_* \tilde {\mathscr {D}}_I$ a locally finitely generated
$(\mathrm {Fr}_{\mathcal {P}_I})_* \tilde {\mathscr {D}}_I$ a locally finitely generated ![]() $(f_I)_* \mathscr {O}_{\tilde {\mathbf {g}}_I \times _{\mathfrak {t}^{*(1)}/W_I} \mathfrak {t}^{*}/(W_I,\bullet )}$-module. Since all the morphisms involved in this construction are affine, using this morphism one can consider
$(f_I)_* \mathscr {O}_{\tilde {\mathbf {g}}_I \times _{\mathfrak {t}^{*(1)}/W_I} \mathfrak {t}^{*}/(W_I,\bullet )}$-module. Since all the morphisms involved in this construction are affine, using this morphism one can consider ![]() $\tilde {\mathscr {D}}_I$ as a coherent sheaf of
$\tilde {\mathscr {D}}_I$ as a coherent sheaf of ![]() $\mathscr {O}_{\tilde {\mathbf {g}}_I \times _{\mathfrak {t}^{*(1)}/W_I} \mathfrak {t}^{*}/(W_I,\bullet )}$-algebras on
$\mathscr {O}_{\tilde {\mathbf {g}}_I \times _{\mathfrak {t}^{*(1)}/W_I} \mathfrak {t}^{*}/(W_I,\bullet )}$-algebras on ![]() $\tilde {\mathbf {g}}_I \times _{\mathfrak {t}^{*(1)}/W_I} \mathfrak {t}^{*}/(W_I,\bullet )$. (We will not introduce a different notation for this sheaf of algebras.)
$\tilde {\mathbf {g}}_I \times _{\mathfrak {t}^{*(1)}/W_I} \mathfrak {t}^{*}/(W_I,\bullet )$. (We will not introduce a different notation for this sheaf of algebras.)
We also have a canonical morphism ![]() $\tilde {\mathbf {g}}_I \to \mathfrak {g}^{*(1)}$, and we denote by
$\tilde {\mathbf {g}}_I \to \mathfrak {g}^{*(1)}$, and we denote by ![]() $\tilde {\mathbf {S}}^{*}_I$ the (scheme-theoretic) inverse image of
$\tilde {\mathbf {S}}^{*}_I$ the (scheme-theoretic) inverse image of ![]() $\mathbf {S}^{*}$ under this morphism. As in the case
$\mathbf {S}^{*}$ under this morphism. As in the case ![]() $I=\varnothing$, using [Reference RicheRic17, Remark 3.5.4] one can check that the morphism
$I=\varnothing$, using [Reference RicheRic17, Remark 3.5.4] one can check that the morphism ![]() $\tilde {\mathbf {g}}_I \to \mathfrak {t}^{*(1)}/W_I$ considered above restricts to an isomorphism
$\tilde {\mathbf {g}}_I \to \mathfrak {t}^{*(1)}/W_I$ considered above restricts to an isomorphism ![]() $\tilde {\mathbf {S}}^{*}_I \xrightarrow {\sim } \mathfrak {t}^{*(1)}/W_I$; in particular, this scheme is affine. We set
$\tilde {\mathbf {S}}^{*}_I \xrightarrow {\sim } \mathfrak {t}^{*(1)}/W_I$; in particular, this scheme is affine. We set
The following lemma is a parabolic analogue of Lemma 5.1, for which the same proof applies.
Lemma 5.14 The morphism (5.10) induces an algebra isomorphism
Let
so that ![]() $\mathbb {X}_I$ identifies with the character lattice of
$\mathbb {X}_I$ identifies with the character lattice of ![]() $L_I$. Then any
$L_I$. Then any ![]() $\lambda \in \mathbb {X}_I$ defines a line bundle
$\lambda \in \mathbb {X}_I$ defines a line bundle ![]() $\mathscr {O}_{\mathcal {P}_I}(\lambda )$ on
$\mathscr {O}_{\mathcal {P}_I}(\lambda )$ on ![]() $\mathcal {P}_I$, from which one can define the space
$\mathcal {P}_I$, from which one can define the space
This object admits a natural action of the algebra
and of the group scheme
Since ![]() $\lambda$ is
$\lambda$ is ![]() $W_I$-invariant, the map
$W_I$-invariant, the map ![]() $\xi \mapsto {{\bar {\lambda }}} + \xi$ factors through an isomorphism
$\xi \mapsto {{\bar {\lambda }}} + \xi$ factors through an isomorphism
and the action of the subalgebra ![]() $\mathscr {O}(\mathfrak {t}^{*}/(W_I,\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W_I,\bullet ))$ on (5.11) factors through the morphism induced by the closed embedding
$\mathscr {O}(\mathfrak {t}^{*}/(W_I,\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W_I,\bullet ))$ on (5.11) factors through the morphism induced by the closed embedding
Given ![]() $\lambda,\mu \in \mathbb {X}$ such that
$\lambda,\mu \in \mathbb {X}$ such that ![]() $\lambda -\mu \in \mathbb {X}_I$, one can then define the object
$\lambda -\mu \in \mathbb {X}_I$, one can then define the object
as the completion of the module
at the ideal of ![]() $\mathscr {O}(\mathfrak {t}^{*}/(W_I,\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W_I,\bullet ))$ corresponding to the image of
$\mathscr {O}(\mathfrak {t}^{*}/(W_I,\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W_I,\bullet ))$ corresponding to the image of ![]() $({{\bar {\lambda }}},{{\bar {\mu }}})$. As for
$({{\bar {\lambda }}},{{\bar {\mu }}})$. As for ![]() $\mathsf {Q}_{\lambda,\mu }$, this object can be obtained by completing the module at the ideal of
$\mathsf {Q}_{\lambda,\mu }$, this object can be obtained by completing the module at the ideal of ![]() $\mathscr {O}(\mathfrak {t}^{*}/(W_I,\bullet ))$ corresponding to the image of
$\mathscr {O}(\mathfrak {t}^{*}/(W_I,\bullet ))$ corresponding to the image of ![]() ${{\bar {\lambda }}}$ with respect to the left action, or at the ideal of
${{\bar {\lambda }}}$ with respect to the left action, or at the ideal of ![]() $\mathscr {O}(\mathfrak {t}^{*}/(W_I,\bullet ))$ corresponding to the image of
$\mathscr {O}(\mathfrak {t}^{*}/(W_I,\bullet ))$ corresponding to the image of ![]() ${{\bar {\mu }}}$ with respect to the right action.
${{\bar {\mu }}}$ with respect to the right action.
Lemma 5.15 Let ![]() $\lambda,\mu,\nu \in \mathbb {X}$.
$\lambda,\mu,\nu \in \mathbb {X}$.
(i) Assume that the stabilizer of
 $\mu$ for the dot action of
$\mu$ for the dot action of  ${W_{\mathrm {aff}}}$ is
${W_{\mathrm {aff}}}$ is  $W_I$, and that
$W_I$, and that  $\nu \in -\rho + \mathbb {X}_I$. Then there exists a canonical isomorphism
in
$\nu \in -\rho + \mathbb {X}_I$. Then there exists a canonical isomorphism
in \[ \mathsf{Q}_{\lambda,\mu} {\widehat{\otimes}}_{\mathcal{U}_\mathbf{S} \mathfrak{g}} \mathsf{Q}_{\mu,\nu}^{I} \xrightarrow{\sim} \mathsf{Q}_{\lambda,\nu} \]
\[ \mathsf{Q}_{\lambda,\mu} {\widehat{\otimes}}_{\mathcal{U}_\mathbf{S} \mathfrak{g}} \mathsf{Q}_{\mu,\nu}^{I} \xrightarrow{\sim} \mathsf{Q}_{\lambda,\nu} \] $\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\nu }})$. Similarly, if the stabilizer of
$\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\nu }})$. Similarly, if the stabilizer of  $\mu$ for the dot action of
$\mu$ for the dot action of  ${W_{\mathrm {aff}}}$ is
${W_{\mathrm {aff}}}$ is  $W_I$, and
$W_I$, and  $\lambda \in -\rho + \mathbb {X}_I$, then there exists a canonical isomorphism
in
$\lambda \in -\rho + \mathbb {X}_I$, then there exists a canonical isomorphism
in \[ \mathsf{Q}^{I}_{\lambda,\mu} {\widehat{\otimes}}_{\mathcal{U}_\mathbf{S} \mathfrak{g}} \mathsf{Q}_{\mu,\nu} \xrightarrow{\sim} \mathsf{Q}_{\lambda,\nu} \]
\[ \mathsf{Q}^{I}_{\lambda,\mu} {\widehat{\otimes}}_{\mathcal{U}_\mathbf{S} \mathfrak{g}} \mathsf{Q}_{\mu,\nu} \xrightarrow{\sim} \mathsf{Q}_{\lambda,\nu} \] $\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\nu }})$.
$\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\nu }})$.(ii) Assume that the stabilizer of
 $\mu$ for the dot action of
$\mu$ for the dot action of  ${W_{\mathrm {aff}}}$ is
${W_{\mathrm {aff}}}$ is  $W_I$, and that
$W_I$, and that  $\lambda,\nu \in -\rho + \mathbb {X}_I$. Then there exists a canonical isomorphism
in
$\lambda,\nu \in -\rho + \mathbb {X}_I$. Then there exists a canonical isomorphism
in \[ \mathsf{Q}^{I}_{\lambda,\mu} {\widehat{\otimes}}_{\mathcal{U}_\mathbf{S} \mathfrak{g}} \mathsf{Q}_{\mu,\nu}^{I} \xrightarrow{\sim} \mathsf{Q}^{I}_{\lambda,\nu} \]
\[ \mathsf{Q}^{I}_{\lambda,\mu} {\widehat{\otimes}}_{\mathcal{U}_\mathbf{S} \mathfrak{g}} \mathsf{Q}_{\mu,\nu}^{I} \xrightarrow{\sim} \mathsf{Q}^{I}_{\lambda,\nu} \] $\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\nu }})$.
$\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\nu }})$.
Proof. (i) We only prove the first isomorphism; the proof of the second one is similar. Our assumptions ensure that ![]() $\mu -\nu \in \mathbb {X}_I$, so that the object
$\mu -\nu \in \mathbb {X}_I$, so that the object ![]() $\mathsf {Q}_{\mu,\nu }^{I}$ is well defined. Consider the natural morphism
$\mathsf {Q}_{\mu,\nu }^{I}$ is well defined. Consider the natural morphism ![]() $a_I : \mathcal {B} \to \mathcal {P}_I$. By [Reference Bezrukavnikov, Mirković and RumyninBMR06, Proposition 1.2.3] there exists a canonical morphism of sheaves of algebras
$a_I : \mathcal {B} \to \mathcal {P}_I$. By [Reference Bezrukavnikov, Mirković and RumyninBMR06, Proposition 1.2.3] there exists a canonical morphism of sheaves of algebras
By the projection formula, and since ![]() $(a_I)_* \mathscr {O}_\mathcal {B} \cong \mathscr {O}_{\mathcal {P}_I}$, we also have
$(a_I)_* \mathscr {O}_\mathcal {B} \cong \mathscr {O}_{\mathcal {P}_I}$, we also have
and via this isomorphism the action of ![]() $\tilde {\mathscr {D}}_I$ on
$\tilde {\mathscr {D}}_I$ on ![]() $\mathscr {O}_{\mathcal {P}_I}(\mu -\nu )$ is obtained by restriction of scalars along (5.12) from the natural action of
$\mathscr {O}_{\mathcal {P}_I}(\mu -\nu )$ is obtained by restriction of scalars along (5.12) from the natural action of ![]() $(a_I)_* \tilde {\mathscr {D}}$ on
$(a_I)_* \tilde {\mathscr {D}}$ on ![]() $(a_I)_* \mathscr {O}_{\mathcal {B}}(\mu -\nu )$. We deduce a natural isomorphism
$(a_I)_* \mathscr {O}_{\mathcal {B}}(\mu -\nu )$. We deduce a natural isomorphism
defined by a formula similar to that considered in the proof of Lemma 5.3. The desired isomorphism follows by restricting to ![]() $\tilde {\mathbf {S}}_I^{*} \times _{\mathfrak {t}^{*(1)}/W_I} \mathfrak {t}^{*}/(W_I,\bullet )$ and then completing, using Lemma 5.14 and the fact that the natural morphism
$\tilde {\mathbf {S}}_I^{*} \times _{\mathfrak {t}^{*(1)}/W_I} \mathfrak {t}^{*}/(W_I,\bullet )$ and then completing, using Lemma 5.14 and the fact that the natural morphism ![]() $\mathfrak {t}^{*}/(W_I,\bullet ) \to \mathfrak {t}^{*}/(W,\bullet )$ is étale at the image of
$\mathfrak {t}^{*}/(W_I,\bullet ) \to \mathfrak {t}^{*}/(W,\bullet )$ is étale at the image of ![]() ${{\bar {\mu }}}$, see Lemma 3.2.
${{\bar {\mu }}}$, see Lemma 3.2.
(ii) The proof is similar to that of Lemma 5.3.
5.7 Conjugation of wall-crossing bimodules
The following proposition will eventually reduce the question of the description of the bimodules realizing wall-crossing functors for ![]() $G$ to the case of wall-crossing functors attached to simple reflections which belong to
$G$ to the case of wall-crossing functors attached to simple reflections which belong to ![]() $W$.
$W$.
Proposition 5.16 Consider elements ![]() $s \in {S_{\mathrm {aff}}}$,
$s \in {S_{\mathrm {aff}}}$, ![]() $s' \in {S_{\mathrm {aff}}} \cap W$ and
$s' \in {S_{\mathrm {aff}}} \cap W$ and ![]() $w \in {W_{\mathrm {ext}}}$ such that
$w \in {W_{\mathrm {ext}}}$ such that ![]() $s'=wsw^{-1}$. Let
$s'=wsw^{-1}$. Let ![]() $\lambda, \mu, \mu ' \in \mathbb {X}$, with
$\lambda, \mu, \mu ' \in \mathbb {X}$, with ![]() $\lambda$ belonging to the fundamental alcove, and
$\lambda$ belonging to the fundamental alcove, and ![]() $\mu$ (respectively,
$\mu$ (respectively, ![]() $\mu '$) belonging to the wall of the fundamental alcove attached to
$\mu '$) belonging to the wall of the fundamental alcove attached to ![]() $s$ (respectively,
$s$ (respectively, ![]() $s'$), and on no other wall. Then there exists an isomorphism
$s'$), and on no other wall. Then there exists an isomorphism
in ![]() $\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\lambda }})$.
$\mathsf {Mod}_{\mathrm {fg}}^{\mathbb {I}}(\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\lambda }})$.
Proof. By Lemma 5.5 we have isomorphisms
Using Lemma 5.3, we deduce isomorphisms
 \begin{align*} &\mathsf{Q}_{\lambda, w \bullet \lambda} {\widehat{\otimes}}_{\mathcal{U}_\mathbf{S} \mathfrak{g}} ( \mathsf{P}_\mathbf{S}^{\lambda,\mu} {\widehat{\otimes}}_{\mathcal{U}_\mathbf{S} \mathfrak{g}} \mathsf{P}_\mathbf{S}^{\mu,\lambda} ) {\widehat{\otimes}}_{\mathcal{U}_\mathbf{S} \mathfrak{g}} \mathsf{Q}_{w \bullet \lambda, \lambda}\\ &\quad \cong \mathsf{Q}_{\lambda, w \bullet \lambda} {\widehat{\otimes}}_{\mathcal{U}_\mathbf{S} \mathfrak{g}} \mathsf{Q}_{w \bullet \lambda, w \bullet \mu} {\widehat{\otimes}}_{\mathcal{U}_\mathbf{S} \mathfrak{g}} \mathsf{Q}_{w \bullet \mu, w \bullet \lambda} {\widehat{\otimes}}_{\mathcal{U}_\mathbf{S} \mathfrak{g}} \mathsf{Q}_{w \bullet \lambda, \lambda}\\ &\quad \cong \mathsf{Q}_{\lambda,w \bullet \mu} {\widehat{\otimes}}_{\mathcal{U}_\mathbf{S} \mathfrak{g}} \mathsf{Q}_{w \bullet \mu, \lambda}. \end{align*}
\begin{align*} &\mathsf{Q}_{\lambda, w \bullet \lambda} {\widehat{\otimes}}_{\mathcal{U}_\mathbf{S} \mathfrak{g}} ( \mathsf{P}_\mathbf{S}^{\lambda,\mu} {\widehat{\otimes}}_{\mathcal{U}_\mathbf{S} \mathfrak{g}} \mathsf{P}_\mathbf{S}^{\mu,\lambda} ) {\widehat{\otimes}}_{\mathcal{U}_\mathbf{S} \mathfrak{g}} \mathsf{Q}_{w \bullet \lambda, \lambda}\\ &\quad \cong \mathsf{Q}_{\lambda, w \bullet \lambda} {\widehat{\otimes}}_{\mathcal{U}_\mathbf{S} \mathfrak{g}} \mathsf{Q}_{w \bullet \lambda, w \bullet \mu} {\widehat{\otimes}}_{\mathcal{U}_\mathbf{S} \mathfrak{g}} \mathsf{Q}_{w \bullet \mu, w \bullet \lambda} {\widehat{\otimes}}_{\mathcal{U}_\mathbf{S} \mathfrak{g}} \mathsf{Q}_{w \bullet \lambda, \lambda}\\ &\quad \cong \mathsf{Q}_{\lambda,w \bullet \mu} {\widehat{\otimes}}_{\mathcal{U}_\mathbf{S} \mathfrak{g}} \mathsf{Q}_{w \bullet \mu, \lambda}. \end{align*}
Now the stabilizer of both ![]() $\mu '$ and
$\mu '$ and ![]() $w \bullet \mu$ for the dot action of
$w \bullet \mu$ for the dot action of ![]() ${W_{\mathrm {aff}}}$ is
${W_{\mathrm {aff}}}$ is ![]() $W_{\{\alpha \}}$, where
$W_{\{\alpha \}}$, where ![]() $\alpha \in \mathfrak {R}^{\mathrm {s}}$ is the simple reflection such that
$\alpha \in \mathfrak {R}^{\mathrm {s}}$ is the simple reflection such that ![]() $s'=s_\alpha$. By Lemma 5.15(i), it follows that we have isomorphisms
$s'=s_\alpha$. By Lemma 5.15(i), it follows that we have isomorphisms
from which we obtain an isomorphism
Then by Lemma 5.15(ii) we have
which implies (again using Lemma 5.15(i)) that
The desired claim follows, again using Lemma 5.5.
6. Hecke action on the principal block
In this section we assume that ![]() $p>h$, where
$p>h$, where ![]() $h$ is the Coxeter number of
$h$ is the Coxeter number of ![]() $G$ (see Remark 3.3). In particular, this ensures that
$G$ (see Remark 3.3). In particular, this ensures that ![]() $p$ is very good for
$p$ is very good for ![]() $G$, so that the results of the previous sections are applicable.
$G$, so that the results of the previous sections are applicable.
6.1 Categories of  $G$-modules and
$G$-modules and  $G$-equivariant
$G$-equivariant  $\mathcal {U} \mathfrak {g}$-modules
$\mathcal {U} \mathfrak {g}$-modules
We now take a closer look at the category ![]() $\mathsf {Rep}(G)$ of finite-dimensional algebraic
$\mathsf {Rep}(G)$ of finite-dimensional algebraic ![]() $G$-modules, and review its decomposition into ‘blocks’. This will involve the notation introduced in §§ 3.1–3.3.
$G$-modules, and review its decomposition into ‘blocks’. This will involve the notation introduced in §§ 3.1–3.3.
Recall (see § 3.5) that for any ![]() $\lambda \in \mathbb {X}^{+}$ we have a simple
$\lambda \in \mathbb {X}^{+}$ we have a simple ![]() $G$-module
$G$-module ![]() $\mathsf {L}(\lambda )$ of highest weight
$\mathsf {L}(\lambda )$ of highest weight ![]() $\lambda$, and that all simple
$\lambda$, and that all simple ![]() $G$-modules are of this form. The linkage principle (see [Reference JantzenJan03, Corollary II.6.17]) states that for
$G$-modules are of this form. The linkage principle (see [Reference JantzenJan03, Corollary II.6.17]) states that for ![]() $\lambda,\mu \in \mathbb {X}^{+}$ we have
$\lambda,\mu \in \mathbb {X}^{+}$ we have
As a consequence, if for a ![]() ${W_{\mathrm {aff}}}$-orbit
${W_{\mathrm {aff}}}$-orbit ![]() $\mathbf {c} \subset \mathbb {X}$ we denote by
$\mathbf {c} \subset \mathbb {X}$ we denote by ![]() $\mathsf {Rep}_{\mathbf {c}}(G)$ the Serre subcategory of
$\mathsf {Rep}_{\mathbf {c}}(G)$ the Serre subcategory of ![]() $\mathsf {Rep}(G)$ generated by the simple objects
$\mathsf {Rep}(G)$ generated by the simple objects ![]() $\mathsf {L}(\lambda )$ with
$\mathsf {L}(\lambda )$ with ![]() $\lambda \in \mathbf {c} \cap \mathbb {X}^{+}$, then we have a direct sum decomposition
$\lambda \in \mathbf {c} \cap \mathbb {X}^{+}$, then we have a direct sum decomposition
For ![]() $\lambda \in \mathbb {X}$, we will write
$\lambda \in \mathbb {X}$, we will write ![]() $[\lambda ]$ for the
$[\lambda ]$ for the ![]() ${W_{\mathrm {aff}}}$-orbit of
${W_{\mathrm {aff}}}$-orbit of ![]() $\lambda$. We will also set
$\lambda$. We will also set
 \[ \mathsf{Rep}_{\langle \lambda \rangle}(G) = \bigoplus_{\substack{\mathbf{c} \in \mathbb{X}/({W_{\mathrm{aff}}},\bullet) \\ \mathbf{c} \subset {W_{\mathrm{ext}}} \bullet \lambda}} \mathsf{Rep}_{\mathbf{c}}(G). \]
\[ \mathsf{Rep}_{\langle \lambda \rangle}(G) = \bigoplus_{\substack{\mathbf{c} \in \mathbb{X}/({W_{\mathrm{aff}}},\bullet) \\ \mathbf{c} \subset {W_{\mathrm{ext}}} \bullet \lambda}} \mathsf{Rep}_{\mathbf{c}}(G). \]
Consider the category ![]() $\mathsf {Mod}_{\mathrm {fg}}^{G}(\mathcal {U} \mathfrak {g})$ of
$\mathsf {Mod}_{\mathrm {fg}}^{G}(\mathcal {U} \mathfrak {g})$ of ![]() $G$-equivariant finitely generated
$G$-equivariant finitely generated ![]() $\mathcal {U} \mathfrak {g}$-modules. For
$\mathcal {U} \mathfrak {g}$-modules. For ![]() $\xi \in \mathfrak {t}^{*}/(W,\bullet )$, we will denote by
$\xi \in \mathfrak {t}^{*}/(W,\bullet )$, we will denote by
the full subcategory of ![]() $\mathsf {Mod}_{\mathrm {fg}}^{G}(\mathcal {U} \mathfrak {g})$ whose objects are the modules annihilated by a power of the ideal
$\mathsf {Mod}_{\mathrm {fg}}^{G}(\mathcal {U} \mathfrak {g})$ whose objects are the modules annihilated by a power of the ideal ![]() $\mathfrak {m}^{\xi } \subset {Z_{\mathrm {HC}}}$. As for other similar notation, in the case where
$\mathfrak {m}^{\xi } \subset {Z_{\mathrm {HC}}}$. As for other similar notation, in the case where ![]() $\xi =\tilde {\lambda }$ for some
$\xi =\tilde {\lambda }$ for some ![]() $\lambda \in \mathbb {X}$, we will write
$\lambda \in \mathbb {X}$, we will write ![]() $\mathsf {Mod}_{\mathrm {fg}}^{G,\lambda }(\mathcal {U} \mathfrak {g})$ for
$\mathsf {Mod}_{\mathrm {fg}}^{G,\lambda }(\mathcal {U} \mathfrak {g})$ for ![]() $\mathsf {Mod}_{\mathrm {fg}}^{G,\tilde {\lambda }}(\mathcal {U} \mathfrak {g})$. If we denote by
$\mathsf {Mod}_{\mathrm {fg}}^{G,\tilde {\lambda }}(\mathcal {U} \mathfrak {g})$. If we denote by ![]() $\mathsf {Mod}_{\mathrm {fg}}^{G,\wedge }(\mathcal {U} \mathfrak {g})$ the category of
$\mathsf {Mod}_{\mathrm {fg}}^{G,\wedge }(\mathcal {U} \mathfrak {g})$ the category of ![]() $G$-equivariant finitely generated
$G$-equivariant finitely generated ![]() $\mathcal {U} \mathfrak {g}$-modules annihilated by a power of the ideal
$\mathcal {U} \mathfrak {g}$-modules annihilated by a power of the ideal ![]() $\mathcal {I} \subset {Z_{\mathrm {HC}}} \cap {Z_{\mathrm {Fr}}}$ defined in § 3.6, then, as for example in (3.13), we have a canonical decomposition
$\mathcal {I} \subset {Z_{\mathrm {HC}}} \cap {Z_{\mathrm {Fr}}}$ defined in § 3.6, then, as for example in (3.13), we have a canonical decomposition
where ![]() $\Lambda \subset \mathbb {X}$ is as in (3.13).
$\Lambda \subset \mathbb {X}$ is as in (3.13).
There is a natural fully faithful functor
sending a ![]() $G$-module
$G$-module ![]() $V$ to itself, with its
$V$ to itself, with its ![]() $G$-module structure, and with the
$G$-module structure, and with the ![]() $\mathcal {U} \mathfrak {g}$-module structure obtained by differentiating the
$\mathcal {U} \mathfrak {g}$-module structure obtained by differentiating the ![]() $G$-action. The essential image of this functor consists of the finite-dimensional
$G$-action. The essential image of this functor consists of the finite-dimensional ![]() $G$-equivariant
$G$-equivariant ![]() $\mathcal {U} \mathfrak {g}$-modules having the property that their
$\mathcal {U} \mathfrak {g}$-modules having the property that their ![]() $\mathcal {U} \mathfrak {g}$-module structure is obtained from their
$\mathcal {U} \mathfrak {g}$-module structure is obtained from their ![]() $G$-module structure by differentiation. Since, for any
$G$-module structure by differentiation. Since, for any ![]() $\lambda \in \mathbb {X}^{+}$, the action of
$\lambda \in \mathbb {X}^{+}$, the action of ![]() ${Z_{\mathrm {HC}}}$ on
${Z_{\mathrm {HC}}}$ on ![]() $\mathsf {L}(\lambda )$ factors through the quotient
$\mathsf {L}(\lambda )$ factors through the quotient ![]() ${Z_{\mathrm {HC}}}/\mathfrak {m}^{\lambda }$, the functor (6.2) restricts to a functor
${Z_{\mathrm {HC}}}/\mathfrak {m}^{\lambda }$, the functor (6.2) restricts to a functor
for any ![]() $\lambda \in \mathbb {X}$. Since
$\lambda \in \mathbb {X}$. Since ![]() $\mathfrak {m}^{\lambda }$ only depends on the orbit
$\mathfrak {m}^{\lambda }$ only depends on the orbit ![]() ${W_{\mathrm {ext}}} \bullet \lambda$, in this way we also obtain a fully faithful functor
${W_{\mathrm {ext}}} \bullet \lambda$, in this way we also obtain a fully faithful functor
6.2 Action of completed bimodules
Recall the category ![]() $\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\wedge })$ introduced in § 3.6. There exists a canonical bifunctor
$\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\wedge })$ introduced in § 3.6. There exists a canonical bifunctor
which can be defined as follows. Consider some ![]() $M$ in
$M$ in ![]() $\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\wedge })$ and some
$\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\wedge })$ and some ![]() $V$ in
$V$ in ![]() $\mathsf {Mod}_{\mathrm {fg}}^{G,\wedge }(\mathcal {U} \mathfrak {g})$. By definition, there exists
$\mathsf {Mod}_{\mathrm {fg}}^{G,\wedge }(\mathcal {U} \mathfrak {g})$. By definition, there exists ![]() $m \in \mathbb {Z}_{\geq 1}$ such that
$m \in \mathbb {Z}_{\geq 1}$ such that ![]() $\mathcal {I}^{m}$ acts trivially on
$\mathcal {I}^{m}$ acts trivially on ![]() $V$. Then the tensor product
$V$. Then the tensor product
is a finitely generated left ![]() $\mathcal {U} \mathfrak {g}$-module (where in the tensor product we consider the right
$\mathcal {U} \mathfrak {g}$-module (where in the tensor product we consider the right ![]() $\mathcal {U} \mathfrak {g}$-action on
$\mathcal {U} \mathfrak {g}$-action on ![]() $M/\mathcal {I}^{m} \cdot M$), which does not depend on the choice of
$M/\mathcal {I}^{m} \cdot M$), which does not depend on the choice of ![]() $m$, and which admits a natural (diagonal) algebraic
$m$, and which admits a natural (diagonal) algebraic ![]() $G$-module structure. Moreover, the action of
$G$-module structure. Moreover, the action of ![]() $\mathcal {I}$ on this module is nilpotent. We can therefore take this as the definition of
$\mathcal {I}$ on this module is nilpotent. We can therefore take this as the definition of ![]() $M {\widehat{\otimes}}_{\mathcal {U} \mathfrak {g}} V$.
$M {\widehat{\otimes}}_{\mathcal {U} \mathfrak {g}} V$.
The bifunctor ![]() ${\widehat{\otimes}}_{\mathcal {U} \mathfrak {g}}$ defines on
${\widehat{\otimes}}_{\mathcal {U} \mathfrak {g}}$ defines on ![]() $\mathsf {Mod}_{\mathrm {fg}}^{G,\wedge }(\mathcal {U} \mathfrak {g})$ a module category structure for the monoidal category
$\mathsf {Mod}_{\mathrm {fg}}^{G,\wedge }(\mathcal {U} \mathfrak {g})$ a module category structure for the monoidal category ![]() $\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\wedge })$. It is also easily seen that for
$\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\wedge })$. It is also easily seen that for ![]() $\lambda,\mu \in \mathbb {X}$ this bifunctor restricts to a bifunctor
$\lambda,\mu \in \mathbb {X}$ this bifunctor restricts to a bifunctor
(where the category ![]() $\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\hat {\lambda },\hat {\mu }})$ is as in § 3.5), which itself restricts to a bifunctor
$\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\hat {\lambda },\hat {\mu }})$ is as in § 3.5), which itself restricts to a bifunctor
under the embeddings ![]() $\mathsf {HC}^{\hat {\lambda },\hat {\mu }} \to \mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\hat {\lambda },\hat {\mu }})$ and (6.3).
$\mathsf {HC}^{\hat {\lambda },\hat {\mu }} \to \mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\hat {\lambda },\hat {\mu }})$ and (6.3).
6.3 Relation with translation functors
Recall the definition of the translation functors for ![]() $G$-modules from [Reference JantzenJan03, Chap. II.7]. Fix
$G$-modules from [Reference JantzenJan03, Chap. II.7]. Fix ![]() $\lambda,\mu \in \mathbb {X}$, and denote by
$\lambda,\mu \in \mathbb {X}$, and denote by ![]() $\nu$ the only dominant
$\nu$ the only dominant ![]() $W$-translate of
$W$-translate of ![]() $\lambda -\mu$. Then the translation functor
$\lambda -\mu$. Then the translation functor
is the functor sending an object ![]() $V$ to the direct summand of
$V$ to the direct summand of ![]() $\mathsf {L}(\nu ) \otimes V$ which belongs to
$\mathsf {L}(\nu ) \otimes V$ which belongs to ![]() $\mathsf {Rep}_{[\lambda ]}(G)$ in the decomposition provided by (6.1). We will consider these functors only in the case where
$\mathsf {Rep}_{[\lambda ]}(G)$ in the decomposition provided by (6.1). We will consider these functors only in the case where ![]() $\lambda$ and
$\lambda$ and ![]() $\mu$ both belong to the closure of the fundamental alcove. In this setting, we have defined in § 3.5 an object
$\mu$ both belong to the closure of the fundamental alcove. In this setting, we have defined in § 3.5 an object ![]() $\mathsf {P}^{\lambda,\mu } \in \mathsf {HC}_{\mathrm {diag}}^{\hat {\lambda },\hat {\mu }}$.
$\mathsf {P}^{\lambda,\mu } \in \mathsf {HC}_{\mathrm {diag}}^{\hat {\lambda },\hat {\mu }}$.
Lemma 6.1 Let ![]() $\lambda,\mu \in \mathbb {X}$ belonging to the closure of the fundamental alcove. The composition
$\lambda,\mu \in \mathbb {X}$ belonging to the closure of the fundamental alcove. The composition
is canonically isomorphic to the composition
Proof. By definition, the first functor sends a module ![]() $V$ in
$V$ in ![]() $\mathsf {Rep}_{[\mu ]}(G)$ to the quotient
$\mathsf {Rep}_{[\mu ]}(G)$ to the quotient
for ![]() $n \gg 0$, that is, to the direct sum of the factors in
$n \gg 0$, that is, to the direct sum of the factors in ![]() $\mathsf {L}(\nu ) \otimes V$ corresponding to orbits included in
$\mathsf {L}(\nu ) \otimes V$ corresponding to orbits included in ![]() ${W_{\mathrm {ext}}} \bullet \lambda$ in the decomposition provided by (6.1). However, all the
${W_{\mathrm {ext}}} \bullet \lambda$ in the decomposition provided by (6.1). However, all the ![]() $T$-weights in
$T$-weights in ![]() $\mathsf {L}(\nu ) \otimes V$ belong to
$\mathsf {L}(\nu ) \otimes V$ belong to ![]() $\lambda + \mathbb {Z} \mathfrak {R}$. In view of Lemma 3.1(i), this implies that
$\lambda + \mathbb {Z} \mathfrak {R}$. In view of Lemma 3.1(i), this implies that ![]() $[\lambda ]$ is the only
$[\lambda ]$ is the only ![]() ${W_{\mathrm {aff}}}$-orbit contained in
${W_{\mathrm {aff}}}$-orbit contained in ![]() ${W_{\mathrm {ext}}} \bullet \lambda$ that can contribute to the direct sum above.
${W_{\mathrm {ext}}} \bullet \lambda$ that can contribute to the direct sum above.
Remark 6.2 See [Reference RicheRic10, Lemma 4.3.1] for a different proof of this claim, under more restrictive assumptions which would be sufficient for our present purposes.
6.4 Main result
We now consider the category ![]() $\mathsf {D}_{\mathrm {BS}}$ of § 2.1 associated with the group
$\mathsf {D}_{\mathrm {BS}}$ of § 2.1 associated with the group ![]() $\mathbf {G}=G^{(1)}$. We also fix a weight
$\mathbf {G}=G^{(1)}$. We also fix a weight ![]() $\lambda$ in the fundamental alcove. (Such a weight exists since
$\lambda$ in the fundamental alcove. (Such a weight exists since ![]() $p \geq h$.) For any
$p \geq h$.) For any ![]() $s \in {S_{\mathrm {aff}}}$, we choose a weight
$s \in {S_{\mathrm {aff}}}$, we choose a weight ![]() $\mu _s \in \mathbb {X}$ in the closure of the fundamental alcove, which lies on the wall associated with
$\mu _s \in \mathbb {X}$ in the closure of the fundamental alcove, which lies on the wall associated with ![]() $s$ but on no other wall. (For the existence of such a weight, see [Reference JantzenJan03, §II.6.3].) Once these choices have been made, the wall-crossing functor associated with
$s$ but on no other wall. (For the existence of such a weight, see [Reference JantzenJan03, §II.6.3].) Once these choices have been made, the wall-crossing functor associated with ![]() $s \in {S_{\mathrm {aff}}}$ is the composition
$s \in {S_{\mathrm {aff}}}$ is the composition
The main result of the present section (and of this paper) is the following theorem.
Theorem 6.3 There exists a monoidal functor
such that
for any ![]() $s \in {S_{\mathrm {aff}}}$.
$s \in {S_{\mathrm {aff}}}$.
We explain the proof of this theorem in § 6.5. Before we do so, we show that (as explained in the introduction) this theorem implies the main conjecture of [Reference Riche and WilliamsonRW18].
Corollary 6.4 There exists a ![]() $\Bbbk$-linear right action of the monoidal category
$\Bbbk$-linear right action of the monoidal category ![]() $\mathsf {D}_{\mathrm {BS}}$ on
$\mathsf {D}_{\mathrm {BS}}$ on ![]() $\mathsf {Rep}_{[\lambda ]}(G)$ such that for any
$\mathsf {Rep}_{[\lambda ]}(G)$ such that for any ![]() $s \in {S_{\mathrm {aff}}}$ the action of the object
$s \in {S_{\mathrm {aff}}}$ the action of the object ![]() $B_s$ is isomorphic to
$B_s$ is isomorphic to ![]() $\Theta _s$.
$\Theta _s$.
Proof. As explained in § 6.2, there exists a canonical (left) action of the category ![]() $\mathsf {HC}^{\hat {\lambda },\hat {\lambda }}$ on the category
$\mathsf {HC}^{\hat {\lambda },\hat {\lambda }}$ on the category ![]() $\mathsf {Rep}_{\langle \lambda \rangle }(G)$. The category
$\mathsf {Rep}_{\langle \lambda \rangle }(G)$. The category ![]() $\mathsf {D}_{\mathrm {BS}}$ admits a canonical autoequivalence
$\mathsf {D}_{\mathrm {BS}}$ admits a canonical autoequivalence ![]() $\imath$ which satisfies
$\imath$ which satisfies ![]() $\imath (X \cdot Y)=\imath (Y) \cdot \imath (X)$ for any
$\imath (X \cdot Y)=\imath (Y) \cdot \imath (X)$ for any ![]() $X,Y \in \mathsf {D}_{\mathrm {BS}}$; see, for example, [Reference Riche and WilliamsonRW18, § 4.2]. Using this autoequivalence, the functor of Theorem 6.3 therefore provides a right action of
$X,Y \in \mathsf {D}_{\mathrm {BS}}$; see, for example, [Reference Riche and WilliamsonRW18, § 4.2]. Using this autoequivalence, the functor of Theorem 6.3 therefore provides a right action of ![]() $\mathsf {D}_{\mathrm {BS}}$ on
$\mathsf {D}_{\mathrm {BS}}$ on ![]() $\mathsf {Rep}_{\langle \lambda \rangle }(G)$ such that
$\mathsf {Rep}_{\langle \lambda \rangle }(G)$ such that ![]() $B_s$ acts via the bimodule
$B_s$ acts via the bimodule ![]() $\mathsf {P}^{\lambda,\mu _s} {\widehat{\otimes}}_{\mathcal {U} \mathfrak {g}} \mathsf {P}^{\mu _s,\lambda }$, for any
$\mathsf {P}^{\lambda,\mu _s} {\widehat{\otimes}}_{\mathcal {U} \mathfrak {g}} \mathsf {P}^{\mu _s,\lambda }$, for any ![]() $s \in {S_{\mathrm {aff}}}$. By Lemma 6.1, the action of this bimodule stabilizes the subcategory
$s \in {S_{\mathrm {aff}}}$. By Lemma 6.1, the action of this bimodule stabilizes the subcategory ![]() $\mathsf {Rep}_{[\lambda ]}(G)$, and its action on this summand is isomorphic to
$\mathsf {Rep}_{[\lambda ]}(G)$, and its action on this summand is isomorphic to ![]() $\Theta _s$. We have therefore constructed the desired action.
$\Theta _s$. We have therefore constructed the desired action.
Remark 6.5 It is clear from the proof of Corollary 6.4 that the existence of a right action of ![]() $\mathsf {D}_{\mathrm {BS}}$ with the required action of each
$\mathsf {D}_{\mathrm {BS}}$ with the required action of each ![]() $B_s$ is equivalent to the existence of a left action with the same property. The reason why Conjecture 1.1 mentions a right action is that it makes the comparison with the combinatorics of the category
$B_s$ is equivalent to the existence of a left action with the same property. The reason why Conjecture 1.1 mentions a right action is that it makes the comparison with the combinatorics of the category ![]() $\mathsf {Rep}_{[\lambda]}(G)$ easier.
$\mathsf {Rep}_{[\lambda]}(G)$ easier.
See § 6.6 for a discussion of what can be said about the images under ![]() $\Psi ^{\lambda }$ of the generating morphisms of
$\Psi ^{\lambda }$ of the generating morphisms of ![]() $\mathsf {D}_{\mathrm {BS}}$.
$\mathsf {D}_{\mathrm {BS}}$.
6.5 Proof of Theorem 6.3
Recall that Theorem 2.10 provides a monoidal functor
Since ![]() $\lambda$ belongs to the fundamental alcove, its stabilizer for the dot action on
$\lambda$ belongs to the fundamental alcove, its stabilizer for the dot action on ![]() $\mathbb {X}$ is trivial, so that the quotient morphism
$\mathbb {X}$ is trivial, so that the quotient morphism
is étale at ![]() ${{\bar {\lambda }}}$; see Lemma 3.2. Similarly, the Artin–Schreier map
${{\bar {\lambda }}}$; see Lemma 3.2. Similarly, the Artin–Schreier map
is étale (everywhere, hence in particular at ![]() ${{\bar {\lambda }}}$), and sends
${{\bar {\lambda }}}$), and sends ![]() ${{\bar {\lambda }}}$ to
${{\bar {\lambda }}}$ to ![]() $0$. Using these maps, we obtain morphisms
$0$. Using these maps, we obtain morphisms
étale at ![]() $({{\bar {\lambda }}},{{\bar {\lambda }}})$, which identify the algebra
$({{\bar {\lambda }}},{{\bar {\lambda }}})$, which identify the algebra ![]() $\mathcal {Z}_{\mathbf {S}}^{\hat {\lambda },\hat {\lambda }}$ from § 3.9 with the completion
$\mathcal {Z}_{\mathbf {S}}^{\hat {\lambda },\hat {\lambda }}$ from § 3.9 with the completion ![]() $\mathscr {O}(\mathfrak {t}^{*(1)} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*(1)})^{\hat {0},\hat {0}}$ of
$\mathscr {O}(\mathfrak {t}^{*(1)} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*(1)})^{\hat {0},\hat {0}}$ of ![]() $\mathscr {O}(\mathfrak {t}^{*(1)} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*(1)})$ with respect to the maximal ideal corresponding to
$\mathscr {O}(\mathfrak {t}^{*(1)} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*(1)})$ with respect to the maximal ideal corresponding to ![]() $(0,0)$. Using this identification, the pullback functor associated with the natural morphism
$(0,0)$. Using this identification, the pullback functor associated with the natural morphism
induces a monoidal functor
where the category on the right-hand side is as in § 4.3. Precomposing this functor with (6.4), and then composing with the equivalence of Corollary 4.8, we obtain a monoidal functor
Proposition 6.6 For any ![]() $s \in {S_{\mathrm {aff}}} \cap W$, there exists an isomorphism
$s \in {S_{\mathrm {aff}}} \cap W$, there exists an isomorphism
Proof. In the course of the proof of Lemma 2.9 we have seen that the image of ![]() $B_s$ in the category
$B_s$ in the category ![]() $\mathsf {Rep}^{\mathbb {G}_{\mathrm {m}}}(\mathfrak {t}^{*(1)} \times _{\mathfrak {t}^{*(1)}/W} \mathbb {J}^{*}_\mathbf {S} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*(1)})$ is
$\mathsf {Rep}^{\mathbb {G}_{\mathrm {m}}}(\mathfrak {t}^{*(1)} \times _{\mathfrak {t}^{*(1)}/W} \mathbb {J}^{*}_\mathbf {S} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*(1)})$ is ![]() $\mathscr {O}(\mathfrak {t}^{*(1)} \times _{\mathfrak {t}^{*(1)}/\{e,s\}} \mathfrak {t}^{*(1)})$, endowed with the trivial structure as a representation. On the other hand, by Proposition 5.8 the wall-crossing bimodule
$\mathscr {O}(\mathfrak {t}^{*(1)} \times _{\mathfrak {t}^{*(1)}/\{e,s\}} \mathfrak {t}^{*(1)})$, endowed with the trivial structure as a representation. On the other hand, by Proposition 5.8 the wall-crossing bimodule ![]() $\mathsf {P}_\mathbf {S}^{\lambda,\mu _s} {\widehat{\otimes}}_{\mathcal {U}_\mathbf {S}\mathfrak {g}} \mathsf {P}_\mathbf {S}^{\mu _s,\lambda }$ corresponds to the object
$\mathsf {P}_\mathbf {S}^{\lambda,\mu _s} {\widehat{\otimes}}_{\mathcal {U}_\mathbf {S}\mathfrak {g}} \mathsf {P}_\mathbf {S}^{\mu _s,\lambda }$ corresponds to the object ![]() $\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\lambda }} \otimes _{\mathcal {Z}_\mathbf {S}^{\hat {\mu },\hat {\lambda }}} \mathcal {Z}_\mathbf {S}^{\hat {\lambda }}$ (again endowed with the trivial structure as a representation) under the equivalence
$\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\lambda }} \otimes _{\mathcal {Z}_\mathbf {S}^{\hat {\mu },\hat {\lambda }}} \mathcal {Z}_\mathbf {S}^{\hat {\lambda }}$ (again endowed with the trivial structure as a representation) under the equivalence ![]() $\mathscr {L}_{\lambda,\lambda }$. Recall that
$\mathscr {L}_{\lambda,\lambda }$. Recall that ![]() $\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\lambda }}$ identifies with the completion of
$\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\lambda }}$ identifies with the completion of ![]() $\mathscr {O}(\mathfrak {t}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*})$ at the ideal corresponding to
$\mathscr {O}(\mathfrak {t}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*})$ at the ideal corresponding to ![]() $({{\bar {\lambda }}},{{\bar {\lambda }}})$. The considerations in the proof of Lemma 5.11, together with the fact that the quotient morphism
$({{\bar {\lambda }}},{{\bar {\lambda }}})$. The considerations in the proof of Lemma 5.11, together with the fact that the quotient morphism ![]() $\mathfrak {t}^{*} \to \mathfrak {t}^{*}/(W,\bullet )$ is étale at
$\mathfrak {t}^{*} \to \mathfrak {t}^{*}/(W,\bullet )$ is étale at ![]() ${{\bar {\lambda }}}$, imply that the algebra
${{\bar {\lambda }}}$, imply that the algebra ![]() $\mathcal {Z}_\mathbf {S}^{\hat {\mu },\hat {\lambda }}$ identifies with the completion of
$\mathcal {Z}_\mathbf {S}^{\hat {\mu },\hat {\lambda }}$ identifies with the completion of ![]() $\mathscr {O}(\mathfrak {t}^{*}/(\{e,s\},\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*})$ at the ideal corresponding to the image of
$\mathscr {O}(\mathfrak {t}^{*}/(\{e,s\},\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*})$ at the ideal corresponding to the image of ![]() $({{\bar {\mu }}},{{\bar {\lambda }}})$, and that via this identification the morphism
$({{\bar {\mu }}},{{\bar {\lambda }}})$, and that via this identification the morphism ![]() $\mathcal {Z}_\mathbf {S}^{\hat {\mu },\hat {\lambda }} \to \mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\lambda }}$ is induced by the natural morphism
$\mathcal {Z}_\mathbf {S}^{\hat {\mu },\hat {\lambda }} \to \mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\lambda }}$ is induced by the natural morphism
sending ![]() $({{\bar {\lambda }}},{{\bar {\lambda }}})$ to the image of
$({{\bar {\lambda }}},{{\bar {\lambda }}})$ to the image of ![]() $({{\bar {\mu }}},{{\bar {\lambda }}})$. This morphism fits in a natural commutative diagram
$({{\bar {\mu }}},{{\bar {\lambda }}})$. This morphism fits in a natural commutative diagram

where the right vertical arrow is induced by the natural quotient morphism ![]() $\mathfrak {t}^{*(1)} \to \mathfrak {t}^{*(1)}/\{e,s\}$ and the horizontal arrows are induced by the Artin–Schreier map. Here the morphism on the upper row is étale at
$\mathfrak {t}^{*(1)} \to \mathfrak {t}^{*(1)}/\{e,s\}$ and the horizontal arrows are induced by the Artin–Schreier map. Here the morphism on the upper row is étale at ![]() $({{\bar {\lambda }}},{{\bar {\lambda }}})$, and that on the lower row is étale at the image of
$({{\bar {\lambda }}},{{\bar {\lambda }}})$, and that on the lower row is étale at the image of ![]() $({{\bar {\mu }}},{{\bar {\lambda }}})$ by the same arguments as for Lemma 4.7. This observation shows that
$({{\bar {\mu }}},{{\bar {\lambda }}})$ by the same arguments as for Lemma 4.7. This observation shows that ![]() $\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\lambda }} \otimes _{\mathcal {Z}_\mathbf {S}^{\hat {\mu },\hat {\lambda }}} \mathcal {Z}_\mathbf {S}^{\hat {\lambda }}$ identifies with the
$\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\lambda }} \otimes _{\mathcal {Z}_\mathbf {S}^{\hat {\mu },\hat {\lambda }}} \mathcal {Z}_\mathbf {S}^{\hat {\lambda }}$ identifies with the ![]() $\mathscr {O}(\mathfrak {t}^{*(1)} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*(1)})^{\hat {0},\hat {0}}$-module
$\mathscr {O}(\mathfrak {t}^{*(1)} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*(1)})^{\hat {0},\hat {0}}$-module
where ![]() $\mathscr {O}(\mathfrak {t}^{*(1)}/\{e,s\} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*(1)})^{\hat {0},\hat {0}}$ is the completion of
$\mathscr {O}(\mathfrak {t}^{*(1)}/\{e,s\} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*(1)})^{\hat {0},\hat {0}}$ is the completion of ![]() $\mathscr {O}(\mathfrak {t}^{*(1)}/\{e,s\} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*(1)})$ at the ideal corresponding to the image of
$\mathscr {O}(\mathfrak {t}^{*(1)}/\{e,s\} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*(1)})$ at the ideal corresponding to the image of ![]() $(0,0)$, and
$(0,0)$, and ![]() $\mathscr {O}(\mathfrak {t}^{*(1)})^{\hat {0}}$ is the completion of
$\mathscr {O}(\mathfrak {t}^{*(1)})^{\hat {0}}$ is the completion of ![]() $\mathscr {O}(\mathfrak {t}^{*(1)})$ (seen as an
$\mathscr {O}(\mathfrak {t}^{*(1)})$ (seen as an ![]() $\mathscr {O}(\mathfrak {t}^{*(1)}/\{e,s\} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*(1)})$-module in the natural way) at the ideal corresponding to
$\mathscr {O}(\mathfrak {t}^{*(1)}/\{e,s\} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*(1)})$-module in the natural way) at the ideal corresponding to ![]() $0$. Using the same considerations as in the proof of Lemma 5.11, it is easily seen that this module identifies with the completion of
$0$. Using the same considerations as in the proof of Lemma 5.11, it is easily seen that this module identifies with the completion of ![]() $\mathscr {O}(\mathfrak {t}^{*(1)} \times _{\mathfrak {t}^{*(1)}/\{e,s\}} \mathfrak {t}^{*(1)})$, which finishes the proof of our claim.
$\mathscr {O}(\mathfrak {t}^{*(1)} \times _{\mathfrak {t}^{*(1)}/\{e,s\}} \mathfrak {t}^{*(1)})$, which finishes the proof of our claim.
Remark 6.7 The isomorphism constructed in the proof of Proposition 6.6 is essentially canonical, in the sense that it only depends on the isomorphism of Proposition 5.8 (for the pair ![]() $(\lambda,\mu _s)$), which itself only depends on a choice of isomorphism
$(\lambda,\mu _s)$), which itself only depends on a choice of isomorphism ![]() $\mathsf {L}(\nu _s)^{*} \cong \mathsf {L}(-w_0(\nu _s))$ where
$\mathsf {L}(\nu _s)^{*} \cong \mathsf {L}(-w_0(\nu _s))$ where ![]() $\nu _s$ is the only dominant
$\nu _s$ is the only dominant ![]() $W$-translate of
$W$-translate of ![]() $\mu _s-\lambda$; see Remark 5.9.
$\mu _s-\lambda$; see Remark 5.9.
Recall the objects ![]() $(\Delta _w^{\mathbb {J}} : w \in W_\mathrm {ext})$ introduced at the end of § 2.4, and the objects
$(\Delta _w^{\mathbb {J}} : w \in W_\mathrm {ext})$ introduced at the end of § 2.4, and the objects ![]() $(\mathsf {Q}_{\nu,\eta } : \nu,\eta \in \mathbb {X})$ introduced in § 5.2.
$(\mathsf {Q}_{\nu,\eta } : \nu,\eta \in \mathbb {X})$ introduced in § 5.2.
Lemma 6.8 For any ![]() $w \in {W_{\mathrm {ext}}}$, the object
$w \in {W_{\mathrm {ext}}}$, the object ![]() $\mathscr {L}_{\lambda,\lambda }^{-1}(\mathsf {Q}_{\lambda,w \bullet \lambda })$ is isomorphic to the image of
$\mathscr {L}_{\lambda,\lambda }^{-1}(\mathsf {Q}_{\lambda,w \bullet \lambda })$ is isomorphic to the image of ![]() $\Delta _w^{\mathbb {J}}$ under the functor (6.5).
$\Delta _w^{\mathbb {J}}$ under the functor (6.5).
Proof. Write ![]() $w = t_\nu x$ with
$w = t_\nu x$ with ![]() $\nu \in p\mathbb {X}$ and
$\nu \in p\mathbb {X}$ and ![]() $x \in W$. Then by Lemma 5.3 we have
$x \in W$. Then by Lemma 5.3 we have
It follows from Lemma 5.4 and the proof of Lemma 2.8 that ![]() $\mathscr {L}_{\lambda,\lambda }^{-1}(\mathsf {Q}_{x \bullet \lambda,x \bullet \lambda +p\nu })$ is the image of
$\mathscr {L}_{\lambda,\lambda }^{-1}(\mathsf {Q}_{x \bullet \lambda,x \bullet \lambda +p\nu })$ is the image of ![]() $\Delta _{t_\nu }^{\mathbb{J}}$. In view of (2.3) and the monoidality of
$\Delta _{t_\nu }^{\mathbb{J}}$. In view of (2.3) and the monoidality of ![]() $\mathscr {L}_{\lambda,\lambda }^{-1}$ (see Proposition 5.12), to conclude it therefore suffices to prove that
$\mathscr {L}_{\lambda,\lambda }^{-1}$ (see Proposition 5.12), to conclude it therefore suffices to prove that ![]() $\mathscr {L}_{\lambda,\lambda }^{-1}(\mathsf {Q}_{\lambda,x \bullet \lambda })$ is the image of
$\mathscr {L}_{\lambda,\lambda }^{-1}(\mathsf {Q}_{\lambda,x \bullet \lambda })$ is the image of ![]() $\Delta _x^{\mathbb{J}}$. In turn, if
$\Delta _x^{\mathbb{J}}$. In turn, if ![]() $x=s_1 \cdots s_r$ is a reduced expression (with each
$x=s_1 \cdots s_r$ is a reduced expression (with each ![]() $s_i$ in
$s_i$ in ![]() $W \cap {S_{\mathrm {aff}}}$) then again by Lemma 5.3 we have
$W \cap {S_{\mathrm {aff}}}$) then again by Lemma 5.3 we have
If we write ![]() $y_j = s_1 \cdots s_{j}$ for
$y_j = s_1 \cdots s_{j}$ for ![]() $j \in \{0, \ldots, r\}$ then, by monoidality of
$j \in \{0, \ldots, r\}$ then, by monoidality of ![]() $\mathscr {L}_{\lambda,\lambda }$, to conclude it suffices to prove that
$\mathscr {L}_{\lambda,\lambda }$, to conclude it suffices to prove that ![]() $\mathscr {L}_{\lambda,\lambda }^{-1}(\mathsf {Q}_{y_{i-1} \bullet \lambda,y_i \bullet \lambda })$ is the image of
$\mathscr {L}_{\lambda,\lambda }^{-1}(\mathsf {Q}_{y_{i-1} \bullet \lambda,y_i \bullet \lambda })$ is the image of ![]() $\Delta _{s_i}^{\mathbb{J}}$ for any
$\Delta _{s_i}^{\mathbb{J}}$ for any ![]() $i \in \{1, \ldots, r\}$.
$i \in \{1, \ldots, r\}$.
Fix ![]() $i \in \{1, \ldots, r\}$. We have
$i \in \{1, \ldots, r\}$. We have ![]() $y_i \bullet \lambda < y_{i-1} \bullet \lambda$. By Lemma 5.7 we therefore have an exact sequence
$y_i \bullet \lambda < y_{i-1} \bullet \lambda$. By Lemma 5.7 we therefore have an exact sequence
As seen in the course of the proof of Proposition 6.6, ![]() $\mathscr {L}_{\lambda,\lambda }^{-1}(\mathsf {P}_\mathbf {S}^{\lambda,\mu _{s_i}}\, {\widehat{\otimes}}_{\mathcal {U}_\mathbf {S}\mathfrak {g}}\, \mathsf {P}_\mathbf {S}^{\mu _{s_i},\lambda })$ corresponds to the completion of
$\mathscr {L}_{\lambda,\lambda }^{-1}(\mathsf {P}_\mathbf {S}^{\lambda,\mu _{s_i}}\, {\widehat{\otimes}}_{\mathcal {U}_\mathbf {S}\mathfrak {g}}\, \mathsf {P}_\mathbf {S}^{\mu _{s_i},\lambda })$ corresponds to the completion of ![]() $\mathscr {O}(\mathfrak {t}^{*(1)} \times _{\mathfrak {t}^{*(1)}/\{e,s_i\}} \mathfrak {t}^{*(1)})$ (with the trivial structure as a representation of the appropriate group scheme), and it is clear that
$\mathscr {O}(\mathfrak {t}^{*(1)} \times _{\mathfrak {t}^{*(1)}/\{e,s_i\}} \mathfrak {t}^{*(1)})$ (with the trivial structure as a representation of the appropriate group scheme), and it is clear that ![]() $\mathscr {L}_{\lambda,\lambda }^{-1}(\mathsf {Q}_{y_{i-1} \bullet \lambda, y_{i-1} \bullet \lambda })$ is the completion of
$\mathscr {L}_{\lambda,\lambda }^{-1}(\mathsf {Q}_{y_{i-1} \bullet \lambda, y_{i-1} \bullet \lambda })$ is the completion of ![]() $\mathscr {O}(\mathfrak {t}^{*(1)})$. The object
$\mathscr {O}(\mathfrak {t}^{*(1)})$. The object ![]() $\mathscr {L}_{\lambda,\lambda }^{-1}(\mathsf {Q}_{y_i \bullet \lambda,y_{i-1} \bullet \lambda })$ is therefore the kernel of a surjection from the former completion to the latter completion. However, up to an automorphism of the completion of
$\mathscr {L}_{\lambda,\lambda }^{-1}(\mathsf {Q}_{y_i \bullet \lambda,y_{i-1} \bullet \lambda })$ is therefore the kernel of a surjection from the former completion to the latter completion. However, up to an automorphism of the completion of ![]() $\mathscr {O}(\mathfrak {t}^{*(1)})$ there exists only one such surjection, and its kernel corresponds to the completion of
$\mathscr {O}(\mathfrak {t}^{*(1)})$ there exists only one such surjection, and its kernel corresponds to the completion of ![]() $\Delta _{s_i}^{\mathbb {J}}$ by Lemma 2.5.
$\Delta _{s_i}^{\mathbb {J}}$ by Lemma 2.5.
Once Lemma 6.8 is proved, one also obtains that ![]() $\mathscr {L}_{\lambda,\lambda }^{-1}(\mathsf {Q}_{w \bullet \lambda,\lambda })$, which is the inverse of
$\mathscr {L}_{\lambda,\lambda }^{-1}(\mathsf {Q}_{w \bullet \lambda,\lambda })$, which is the inverse of ![]() $\mathscr {L}_{\lambda,\lambda }^{-1}(\mathsf {Q}_{\lambda,w \bullet \lambda })$ (see § 5.2), is isomorphic to the image of
$\mathscr {L}_{\lambda,\lambda }^{-1}(\mathsf {Q}_{\lambda,w \bullet \lambda })$ (see § 5.2), is isomorphic to the image of ![]() $\Delta _{w^{-1}}^{\mathbb {J}}$ under (6.5). (In fact, one can then check that, for any
$\Delta _{w^{-1}}^{\mathbb {J}}$ under (6.5). (In fact, one can then check that, for any ![]() $\mu \in W_\mathrm {ext} \bullet \lambda$,
$\mu \in W_\mathrm {ext} \bullet \lambda$, ![]() $\mathscr {L}_{\lambda,\lambda }^{-1}(\mathsf {Q}_{\mu,w \bullet \mu })$ is isomorphic to the image of
$\mathscr {L}_{\lambda,\lambda }^{-1}(\mathsf {Q}_{\mu,w \bullet \mu })$ is isomorphic to the image of ![]() $\Delta _{w}^{\mathbb {J}}$.)
$\Delta _{w}^{\mathbb {J}}$.)
We can finally complete the proof of Theorem 6.3.
Proof of Theorem 6.3 Consider the functor ![]() $\Psi _\mathbf {S}^{\lambda }$ from (6.6). We claim that for any
$\Psi _\mathbf {S}^{\lambda }$ from (6.6). We claim that for any ![]() $s \in {S_{\mathrm {aff}}}$ we have
$s \in {S_{\mathrm {aff}}}$ we have
In fact, if ![]() $s \in W$ this is the content of Proposition 6.6. Otherwise, as already seen in the course of the proof of Lemma 2.9, there exist
$s \in W$ this is the content of Proposition 6.6. Otherwise, as already seen in the course of the proof of Lemma 2.9, there exist ![]() $x \in {W_{\mathrm {ext}}}$ and
$x \in {W_{\mathrm {ext}}}$ and ![]() $t \in {S_{\mathrm {aff}}} \cap W$ such that
$t \in {S_{\mathrm {aff}}} \cap W$ such that ![]() $s=xtx^{-1}$. Then, by Lemma 2.4, the image of
$s=xtx^{-1}$. Then, by Lemma 2.4, the image of ![]() $B_s$ in
$B_s$ in ![]() $\mathsf {C}_\mathrm {ext}$ is
$\mathsf {C}_\mathrm {ext}$ is
using Lemma 6.8 (together with the remark following it) and the known description of ![]() $\Psi _\mathbf {S}^{\lambda }(B_t)$, we deduce that
$\Psi _\mathbf {S}^{\lambda }(B_t)$, we deduce that
In view of Proposition 5.16, this implies (6.7).
Since each object of ![]() $\mathsf {D}_{\mathrm {BS}}$ is isomorphic to a shift of a product of objects
$\mathsf {D}_{\mathrm {BS}}$ is isomorphic to a shift of a product of objects ![]() $B_s$, and since both of the functors involved are monoidal, our claim implies that
$B_s$, and since both of the functors involved are monoidal, our claim implies that ![]() $\Psi _\mathbf {S}^{\lambda }$ takes values in the essential image of the fully faithful functor
$\Psi _\mathbf {S}^{\lambda }$ takes values in the essential image of the fully faithful functor
(see Proposition 3.7). It follows that ![]() $\Psi _\mathbf {S}^{\lambda }$ factors in a canonical way through a monoidal functor
$\Psi _\mathbf {S}^{\lambda }$ factors in a canonical way through a monoidal functor
sending ![]() $B_s$ to
$B_s$ to ![]() $\mathsf {P}^{\lambda,\mu _s} {\widehat{\otimes}}_{\mathcal {U} \mathfrak {g}} \mathsf {P}^{\mu _s,\lambda }$ for any
$\mathsf {P}^{\lambda,\mu _s} {\widehat{\otimes}}_{\mathcal {U} \mathfrak {g}} \mathsf {P}^{\mu _s,\lambda }$ for any ![]() $s \in {S_{\mathrm {aff}}}$, which finishes the proof.
$s \in {S_{\mathrm {aff}}}$, which finishes the proof.
6.6 Images of generating morphisms
The category ![]() $\mathsf {D}_{\mathrm {BS}}$ is defined in [Reference Elias and WilliamsonEW16] in terms of generators and relations. In Theorem 6.3 we have explained what are the images of the generating objects under
$\mathsf {D}_{\mathrm {BS}}$ is defined in [Reference Elias and WilliamsonEW16] in terms of generators and relations. In Theorem 6.3 we have explained what are the images of the generating objects under ![]() $\Psi ^{\lambda }$ (at least, up to isomorphism); by monoidality this determines the image of any object in
$\Psi ^{\lambda }$ (at least, up to isomorphism); by monoidality this determines the image of any object in ![]() $\mathsf {D}_{\mathrm {BS}}$ (again, up to isomorphism). We finish the paper with a discussion of what can be said about the image under
$\mathsf {D}_{\mathrm {BS}}$ (again, up to isomorphism). We finish the paper with a discussion of what can be said about the image under ![]() $\Psi ^{\lambda }$ of the generating morphisms of
$\Psi ^{\lambda }$ of the generating morphisms of ![]() $\mathsf {D}_{\mathrm {BS}}$.
$\mathsf {D}_{\mathrm {BS}}$.
Remark 6.9 As explained in [Reference Riche and WilliamsonRW18, Remark 5.1.2(3)], although the original version of Conjecture 1.1 contained information about these images, this information is not needed for the applications considered in [Reference Riche and WilliamsonRW18, Part I], and in particular the character formula for tilting modules in ![]() $\mathsf {Rep}_{[\lambda ]}(G)$.
$\mathsf {Rep}_{[\lambda ]}(G)$.
Recall that these generating morphisms fall into four families:
– the polynomials (morphisms from
 $B_\varnothing$ to a shift of
$B_\varnothing$ to a shift of  $B_\varnothing$, determined by homogeneous elements in
$B_\varnothing$, determined by homogeneous elements in  $R=\mathscr {O}(\mathfrak {t}^{*(1)})$);
$R=\mathscr {O}(\mathfrak {t}^{*(1)})$);– the ‘dot’ morphisms for
 $s \in {S_{\mathrm {aff}}}$
(morphisms from
$s \in {S_{\mathrm {aff}}}$
(morphisms from
 $B_s$ to a shift of
$B_s$ to a shift of  $B_\varnothing$ and from
$B_\varnothing$ and from  $B_\varnothing$ to a shift of
$B_\varnothing$ to a shift of  $B_s$);
$B_s$);– the ‘trivalent’ morphisms for
 $s \in {S_{\mathrm {aff}}}$
(morphisms from
$s \in {S_{\mathrm {aff}}}$
(morphisms from
 $B_s$ to a shift of
$B_s$ to a shift of  $B_{ss}$ and from
$B_{ss}$ and from  $B_{ss}$ to a shift of
$B_{ss}$ to a shift of  $B_s$);
$B_s$);– the ‘
 $2m_{s,t}$-valent’ morphisms, for pairs
$2m_{s,t}$-valent’ morphisms, for pairs  $(s,t)$ of distinct elements of
$(s,t)$ of distinct elements of  ${S_{\mathrm {aff}}}$ generating a finite subgroup of
${S_{\mathrm {aff}}}$ generating a finite subgroup of  ${W_{\mathrm {aff}}}$.
${W_{\mathrm {aff}}}$.
The information we can give concerns only the first two families of morphisms.
The image of polynomials is easy to describe: we have ![]() $\Psi ^{\lambda }(B_\varnothing )=\mathcal {U}^{\hat {\lambda }}$. If
$\Psi ^{\lambda }(B_\varnothing )=\mathcal {U}^{\hat {\lambda }}$. If ![]() ${Z^{\hat {\lambda }}_{\mathrm {HC}}}$ is as in Remark 3.5, any element in
${Z^{\hat {\lambda }}_{\mathrm {HC}}}$ is as in Remark 3.5, any element in ![]() ${Z^{\hat {\lambda }}_{\mathrm {HC}}}$ determines an endomorphism of
${Z^{\hat {\lambda }}_{\mathrm {HC}}}$ determines an endomorphism of ![]() $\mathcal {U}^{\hat {\lambda }}$. Now the natural morphisms
$\mathcal {U}^{\hat {\lambda }}$. Now the natural morphisms
are étale at ![]() ${{\bar {\lambda }}}$; they therefore determine an isomorphism between
${{\bar {\lambda }}}$; they therefore determine an isomorphism between ![]() ${Z^{\hat {\lambda }}_{\mathrm {HC}}}$ and the completion
${Z^{\hat {\lambda }}_{\mathrm {HC}}}$ and the completion ![]() $\mathscr {O}(\mathfrak {t}^{*(1)})^{\hat {0}}$ of
$\mathscr {O}(\mathfrak {t}^{*(1)})^{\hat {0}}$ of ![]() $\mathscr {O}(\mathfrak {t}^{*(1)})$ with respect to the ideal of
$\mathscr {O}(\mathfrak {t}^{*(1)})$ with respect to the ideal of ![]() $0$. The image under
$0$. The image under ![]() $\Psi ^{\lambda }$ of a homogenous polynomial in
$\Psi ^{\lambda }$ of a homogenous polynomial in ![]() $R$ is the endomorphism of
$R$ is the endomorphism of ![]() $\mathcal {U}^{\hat {\lambda }}$ determined by the corresponding element in
$\mathcal {U}^{\hat {\lambda }}$ determined by the corresponding element in ![]() ${Z^{\hat {\lambda }}_{\mathrm {HC}}}$.
${Z^{\hat {\lambda }}_{\mathrm {HC}}}$.
To describe the image of the other morphisms, we must be more specific about the isomorphism ![]() $\Psi ^{\lambda }(B_s) \cong \mathsf {P}^{\lambda,\mu _s} {\widehat{\otimes}}_{\mathcal {U} \mathfrak {g}} \mathsf {P}^{\mu _s,\lambda }$. First, assume that
$\Psi ^{\lambda }(B_s) \cong \mathsf {P}^{\lambda,\mu _s} {\widehat{\otimes}}_{\mathcal {U} \mathfrak {g}} \mathsf {P}^{\mu _s,\lambda }$. First, assume that ![]() $s \in W$. In this case, after choosing an isomorphism
$s \in W$. In this case, after choosing an isomorphism ![]() $\mathsf {L}(\nu _s)^{*} \cong \mathsf {L}(-w_0(\nu _s))$ we obtain a canonical such isomorphism; see Remark 6.7. Using this isomorphism, Remark 5.9 shows that the image of the upper dot morphism
$\mathsf {L}(\nu _s)^{*} \cong \mathsf {L}(-w_0(\nu _s))$ we obtain a canonical such isomorphism; see Remark 6.7. Using this isomorphism, Remark 5.9 shows that the image of the upper dot morphism
is the morphism ![]() $\varphi _s : \mathsf {P}^{\lambda,\mu _s}\, {\widehat{\otimes}}_{\mathcal {U} \mathfrak {g}} \mathsf {P}^{\mu _s,\lambda } \to \mathcal {U}^{\hat {\lambda }}$ determined by the adjunction
$\varphi _s : \mathsf {P}^{\lambda,\mu _s}\, {\widehat{\otimes}}_{\mathcal {U} \mathfrak {g}} \mathsf {P}^{\mu _s,\lambda } \to \mathcal {U}^{\hat {\lambda }}$ determined by the adjunction
defined by our choice of isomorphism ![]() $\mathsf {L}(\nu _s)^{*} \cong \mathsf {L}(-w_0(\nu _s))$. (Here we use an obvious variant of Lemma 3.6 for
$\mathsf {L}(\nu _s)^{*} \cong \mathsf {L}(-w_0(\nu _s))$. (Here we use an obvious variant of Lemma 3.6 for ![]() $\mathcal {U} \mathfrak {g}$ in place of
$\mathcal {U} \mathfrak {g}$ in place of ![]() $\mathcal {U}_\mathbf {S}\mathfrak {g}$.)
$\mathcal {U}_\mathbf {S}\mathfrak {g}$.)
Proposition 3.7, Corollary 4.8 and Proposition 5.8 (together with the various étale maps considered above) show that the ![]() $\mathscr {O}(\mathfrak {t}^{*(1)})^{\hat {0}}$-modules
$\mathscr {O}(\mathfrak {t}^{*(1)})^{\hat {0}}$-modules
are both free of rank ![]() $1$; from this one can check that there exists a unique morphism
$1$; from this one can check that there exists a unique morphism
whose composition with ![]() $\varphi _s$ is the differential of the coroot of
$\varphi _s$ is the differential of the coroot of ![]() $(\mathbf {G},\mathbf {T})$ associated with
$(\mathbf {G},\mathbf {T})$ associated with ![]() $s$ (seen as an endomorphism of
$s$ (seen as an endomorphism of ![]() $\mathcal {U}^{\hat {\lambda }}$), and that this morphism is a generator of
$\mathcal {U}^{\hat {\lambda }}$), and that this morphism is a generator of ![]() ${{\rm Hom}}_{\mathsf {HC}^{\hat {\lambda },\hat {\lambda }}}(\mathcal {U}^{\hat {\lambda }},\mathsf {P}^{\lambda,\mu _s} {\widehat{\otimes}}_{\mathcal {U} \mathfrak {g}} \mathsf {P}^{\mu _s,\lambda })$. In view of the ‘barbell relation’ in
${{\rm Hom}}_{\mathsf {HC}^{\hat {\lambda },\hat {\lambda }}}(\mathcal {U}^{\hat {\lambda }},\mathsf {P}^{\lambda,\mu _s} {\widehat{\otimes}}_{\mathcal {U} \mathfrak {g}} \mathsf {P}^{\mu _s,\lambda })$. In view of the ‘barbell relation’ in ![]() $\mathsf {D}_{\mathrm {BS}}$, the image of the lower dot morphism
$\mathsf {D}_{\mathrm {BS}}$, the image of the lower dot morphism
is ![]() $\psi _s$.
$\psi _s$.
In the case where ![]() $s \notin {W_{\mathrm {aff}}}$, we do not have a canonical choice of isomorphism
$s \notin {W_{\mathrm {aff}}}$, we do not have a canonical choice of isomorphism ![]() $\Psi ^{\lambda }(B_s) \cong \mathsf {P}^{\lambda,\mu _s} {\widehat{\otimes}}_{\mathcal {U} \mathfrak {g}} \mathsf {P}^{\mu _s,\lambda }$. What we can say is that there exists a choice of such an isomorphism (not unique) such that the images of the dot morphisms are described by the same rules as above.
$\Psi ^{\lambda }(B_s) \cong \mathsf {P}^{\lambda,\mu _s} {\widehat{\otimes}}_{\mathcal {U} \mathfrak {g}} \mathsf {P}^{\mu _s,\lambda }$. What we can say is that there exists a choice of such an isomorphism (not unique) such that the images of the dot morphisms are described by the same rules as above.
Acknowledgements
We thank Ivan Losev for his active interest in our work and useful discussions on the subject of this paper, and the referee for his/her careful reading and useful suggestions, which both helped improve the exposition of the paper.
While we were in the final stages of our work, we were informed that J. Ciappara had obtained a radically different proof of Conjecture 1.1. His construction of the action relies on the geometric Satake equivalence and the Smith–Treumann theory of [Reference Riche and WilliamsonRW20]; these results have now appeared in [Reference CiapparaCia21]. We thank G. Williamson for keeping us informed of this work, and for useful comments.
The project realized in this paper was conceived during the Modular Representation Theory workshop organized in Oxford by the Clay Mathematical Institute. We thank the organizers of this conference (G. Williamson, I. Losev and M. Emerton) for the fruitful working atmosphere they created, and the participants for the inspiring talks. A later part of this work was accomplished at the Institut Henri Poincaré, as part of the thematic program Representation Theory organized by D. Hernandez, N. Jacon, E. Letellier, S. R., and É. Vasserot, and an even later part was done while both authors were members of the Institute for Advanced Study during the Special Year on Geometric and Modular Representation Theory organized by G. Williamson.
Appendix A. Index of notation
Below is a list of the main notation used in the paper, listed by section of appearance. (We sometimes omit notation used only in one specific subsection.)
A.1 Section 2
![]() $\Bbbk$: algebraically closed field of characteristic
$\Bbbk$: algebraically closed field of characteristic ![]() $p$, § 2.1.
$p$, § 2.1.
![]() $\mathbf {G}$: connected reductive algebraic group over
$\mathbf {G}$: connected reductive algebraic group over ![]() $\Bbbk$, § 2.1.
$\Bbbk$, § 2.1.
![]() $\mathbf {B}$,
$\mathbf {B}$, ![]() $\mathbf {T}$: Borel subgroup and maximal torus in
$\mathbf {T}$: Borel subgroup and maximal torus in ![]() $\mathbf {G}$, § 2.1.
$\mathbf {G}$, § 2.1.
![]() $\mathbf {g}$,
$\mathbf {g}$, ![]() $\mathbf {b}$,
$\mathbf {b}$, ![]() $\mathbf {t}$: Lie algebras of
$\mathbf {t}$: Lie algebras of ![]() $\mathbf {G}$,
$\mathbf {G}$, ![]() $\mathbf {B}$,
$\mathbf {B}$, ![]() $\mathbf {T}$, § 2.1.
$\mathbf {T}$, § 2.1.
![]() $\mathbf {X}$,
$\mathbf {X}$, ![]() $\mathbf {X}^{\vee }$: weight and coweight lattices of
$\mathbf {X}^{\vee }$: weight and coweight lattices of ![]() $\mathbf {T}$, § 2.1.
$\mathbf {T}$, § 2.1.
![]() $\Phi$,
$\Phi$, ![]() $\Phi ^{\vee }$,
$\Phi ^{\vee }$, ![]() $\Phi ^{+}$,
$\Phi ^{+}$, ![]() $\Phi ^{\mathrm {s}}$: roots, coroots, positive roots, simple roots of
$\Phi ^{\mathrm {s}}$: roots, coroots, positive roots, simple roots of ![]() $(\mathbf {G},\mathbf {B},\mathbf {T})$, § 2.1.
$(\mathbf {G},\mathbf {B},\mathbf {T})$, § 2.1.
![]() $\kappa$: choice of isomorphism
$\kappa$: choice of isomorphism ![]() $\mathbf {g} \xrightarrow {\sim } \mathbf {g}^{*}$, § 2.1.
$\mathbf {g} \xrightarrow {\sim } \mathbf {g}^{*}$, § 2.1.
![]() $\mathbf {W}$: Weyl group of
$\mathbf {W}$: Weyl group of ![]() $(\mathbf {G},\mathbf {T})$, § 2.1.
$(\mathbf {G},\mathbf {T})$, § 2.1.
![]() ${W_{\mathrm {aff}}}$,
${W_{\mathrm {aff}}}$, ![]() ${W_{\mathrm {ext}}}$: affine and extended affine Weyl groups of
${W_{\mathrm {ext}}}$: affine and extended affine Weyl groups of ![]() $(\mathbf {G},\mathbf {T})$, § 2.1.
$(\mathbf {G},\mathbf {T})$, § 2.1.
![]() ${S_{\mathrm {aff}}}$,
${S_{\mathrm {aff}}}$, ![]() ${W_{\mathrm {ext}}}$: simple reflections in
${W_{\mathrm {ext}}}$: simple reflections in ![]() ${W_{\mathrm {aff}}}$, § 2.1.
${W_{\mathrm {aff}}}$, § 2.1.
![]() $\mathsf {D}_{\mathrm {BS}}$: diagrammatic Hecke category attached to
$\mathsf {D}_{\mathrm {BS}}$: diagrammatic Hecke category attached to ![]() $\mathbf {G}$, § 2.1.
$\mathbf {G}$, § 2.1.
![]() $B_{\underline {w}}$: object of
$B_{\underline {w}}$: object of ![]() $\mathsf {D}_{\mathrm {BS}}$ attached to
$\mathsf {D}_{\mathrm {BS}}$ attached to ![]() $\underline {w}$, § 2.1.
$\underline {w}$, § 2.1.
![]() $R=\mathscr {O}(\mathbf {t}^{*})$, § 2.1.
$R=\mathscr {O}(\mathbf {t}^{*})$, § 2.1.
![]() $Q$: fraction field of
$Q$: fraction field of ![]() $R$, § 2.2.
$R$, § 2.2.
![]() $\mathsf {C}$,
$\mathsf {C}$, ![]() $\mathsf {C}'$,
$\mathsf {C}'$, ![]() $\mathsf {C}_\mathrm {ext}$,
$\mathsf {C}_\mathrm {ext}$, ![]() $\mathsf {C}'_\mathrm {ext}$: Abe's categories, § 2.2.
$\mathsf {C}'_\mathrm {ext}$: Abe's categories, § 2.2.
![]() $B_s^{\mathrm {Bim}}$: bimodule in
$B_s^{\mathrm {Bim}}$: bimodule in ![]() $\mathsf {C}$ attached to
$\mathsf {C}$ attached to ![]() $s$, § 2.2.
$s$, § 2.2.
![]() $\Delta _x$: ‘standard’ object in
$\Delta _x$: ‘standard’ object in ![]() $\mathsf {C}_\mathrm {ext}$ attached to
$\mathsf {C}_\mathrm {ext}$ attached to ![]() $x$, § 2.2.
$x$, § 2.2.
![]() $\mathbf {U}$: unipotent radical in
$\mathbf {U}$: unipotent radical in ![]() $\mathbf {B}$, § 2.3.
$\mathbf {B}$, § 2.3.
![]() $\mathbf {n}$: Lie algebra of
$\mathbf {n}$: Lie algebra of ![]() $\mathbf {U}$, § 2.3.
$\mathbf {U}$, § 2.3.
![]() $\mathbf {g}_\mathrm {reg}$,
$\mathbf {g}_\mathrm {reg}$, ![]() $\mathbf {g}^{*}_\mathrm {reg}$: regular parts in
$\mathbf {g}^{*}_\mathrm {reg}$: regular parts in ![]() $\mathbf {g}$ and
$\mathbf {g}$ and ![]() $\mathbf {g}^{*}$, § 2.3.
$\mathbf {g}^{*}$, § 2.3.
![]() $\mathbb {J}_\mathrm {reg}$,
$\mathbb {J}_\mathrm {reg}$, ![]() $\mathbb {J}^{*}_\mathrm {reg}$: universal centralizers over
$\mathbb {J}^{*}_\mathrm {reg}$: universal centralizers over ![]() $\mathbf {g}_\mathrm {reg}$ and
$\mathbf {g}_\mathrm {reg}$ and ![]() $\mathbf {g}^{*}_\mathrm {reg}$, § 2.3.
$\mathbf {g}^{*}_\mathrm {reg}$, § 2.3.
![]() $\tilde {\mathbf {g}}$: Grothendieck resolution attached to
$\tilde {\mathbf {g}}$: Grothendieck resolution attached to ![]() $\mathbf {G}$, § 2.3.
$\mathbf {G}$, § 2.3.
![]() $\tilde {\mathbf {g}}_\mathrm {reg}$: regular part in
$\tilde {\mathbf {g}}_\mathrm {reg}$: regular part in ![]() $\tilde {\mathbf {g}}$, § 2.3.
$\tilde {\mathbf {g}}$, § 2.3.
![]() $\pi$: natural morphism
$\pi$: natural morphism ![]() $\tilde {\mathbf {g}} \to \mathbf {g}^{*}$, § 2.3.
$\tilde {\mathbf {g}} \to \mathbf {g}^{*}$, § 2.3.
![]() $\vartheta$: natural morphism
$\vartheta$: natural morphism ![]() $\tilde {\mathbf {g}} \to \mathbf {t}^{*}$, § 2.3.
$\tilde {\mathbf {g}} \to \mathbf {t}^{*}$, § 2.3.
![]() $\mathbf {g}_\mathrm {rs}$,
$\mathbf {g}_\mathrm {rs}$, ![]() $\mathbf {g}^{*}_\mathrm {rs}$: regular semisimple parts in
$\mathbf {g}^{*}_\mathrm {rs}$: regular semisimple parts in ![]() $\mathbf {g}$ and
$\mathbf {g}$ and ![]() $\mathbf {g}^{*}$, § 2.3.
$\mathbf {g}^{*}$, § 2.3.
![]() $\mathbb {J}_\mathrm {rs}$,
$\mathbb {J}_\mathrm {rs}$, ![]() $\mathbb {J}^{*}_\mathrm {rs}$: restrictions of
$\mathbb {J}^{*}_\mathrm {rs}$: restrictions of ![]() $\mathbb {J}_\mathrm {reg}$,
$\mathbb {J}_\mathrm {reg}$, ![]() $\mathbb {J}^{*}_\mathrm {reg}$ to
$\mathbb {J}^{*}_\mathrm {reg}$ to ![]() $\mathbf {g}_\mathrm {rs}$,
$\mathbf {g}_\mathrm {rs}$, ![]() $\mathbf {g}^{*}_\mathrm {rs}$, § 2.3.
$\mathbf {g}^{*}_\mathrm {rs}$, § 2.3.
![]() $\mathbf {S}$,
$\mathbf {S}$, ![]() $\mathbf {S}^{*}$: Kostant sections in
$\mathbf {S}^{*}$: Kostant sections in ![]() $\mathbf {g}$ and
$\mathbf {g}$ and ![]() $\mathbf {g}^{*}$, § 2.3.
$\mathbf {g}^{*}$, § 2.3.
![]() $\mathbb {J}^{*}_\mathbf {S}$: restriction of
$\mathbb {J}^{*}_\mathbf {S}$: restriction of ![]() $\mathbb {J}^{*}_\mathrm {reg}$ to
$\mathbb {J}^{*}_\mathrm {reg}$ to ![]() $\mathbf {S}^{*}$, § 2.3.
$\mathbf {S}^{*}$, § 2.3.
![]() $\mathsf {Rep}^{\mathbb {G}_{\mathrm {m}}}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*})$: category of
$\mathsf {Rep}^{\mathbb {G}_{\mathrm {m}}}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*})$: category of ![]() $\mathbb {G}_{\mathrm {m}}$-equivariant representations of
$\mathbb {G}_{\mathrm {m}}$-equivariant representations of ![]() $\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*}$ on coherent sheaves on
$\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*}$ on coherent sheaves on ![]() $\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*}$, § 2.4.
$\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*}$, § 2.4.
![]() $\star$: monoidal product on
$\star$: monoidal product on ![]() $\mathsf {Rep}^{\mathbb {G}_{\mathrm {m}}}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*})$, § 2.4.
$\mathsf {Rep}^{\mathbb {G}_{\mathrm {m}}}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*})$, § 2.4.
![]() $\mathsf {Rep}^{\mathbb {G}_{\mathrm {m}}}_{\mathrm {fl}}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*})$: subcategory of
$\mathsf {Rep}^{\mathbb {G}_{\mathrm {m}}}_{\mathrm {fl}}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*})$: subcategory of ![]() $\mathsf {Rep}^{\mathbb {G}_{\mathrm {m}}}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*})$ consisting of modules flat with respect to the second projection
$\mathsf {Rep}^{\mathbb {G}_{\mathrm {m}}}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*})$ consisting of modules flat with respect to the second projection ![]() $\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*} \to \mathbf {t}^{*}$, § 2.4.
$\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*} \to \mathbf {t}^{*}$, § 2.4.
![]() $\Delta ^{\mathbb{J}}_w$: object in
$\Delta ^{\mathbb{J}}_w$: object in ![]() $\mathsf {Rep}^{\mathbb {G}_{\mathrm {m}}}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*})$ corresponding to
$\mathsf {Rep}^{\mathbb {G}_{\mathrm {m}}}(\mathbf {t}^{*} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbb {J}^{*}_{\mathbf {S}} \times _{\mathbf {t}^{*}/\mathbf {W}} \mathbf {t}^{*})$ corresponding to ![]() $\Delta _w$, § 2.4.
$\Delta _w$, § 2.4.
A.2 Section 3
![]() $G$: connected reductive algebraic group such that
$G$: connected reductive algebraic group such that ![]() $\mathbf {G}=G^{(1)}$, § 3.1.
$\mathbf {G}=G^{(1)}$, § 3.1.
![]() $\mathrm {Fr}$: Frobenius morphism of
$\mathrm {Fr}$: Frobenius morphism of ![]() $G$, § 3.1.
$G$, § 3.1.
![]() $B$,
$B$, ![]() $T$,
$T$, ![]() $U$: subgroups of
$U$: subgroups of ![]() $G$ corresponding to
$G$ corresponding to ![]() $\mathbf {B}$,
$\mathbf {B}$, ![]() $\mathbf {T}$,
$\mathbf {T}$, ![]() $\mathbf {U}$, § 3.1.
$\mathbf {U}$, § 3.1.
![]() $\mathfrak {g}$,
$\mathfrak {g}$, ![]() $\mathfrak {b}$,
$\mathfrak {b}$, ![]() $\mathfrak {t}$,
$\mathfrak {t}$, ![]() $\mathfrak {n}$: Lie algebras of
$\mathfrak {n}$: Lie algebras of ![]() $G$,
$G$, ![]() $B$,
$B$, ![]() $T$,
$T$, ![]() $U$, § 3.1.
$U$, § 3.1.
![]() $W$: Weyl group of
$W$: Weyl group of ![]() $(G,T)$, § 3.1.
$(G,T)$, § 3.1.
![]() $\mathbf {X}$,
$\mathbf {X}$, ![]() $\mathbf {X}^{\vee }$: weight and coweight lattices of
$\mathbf {X}^{\vee }$: weight and coweight lattices of ![]() $T$, § 3.1.
$T$, § 3.1.
![]() $\mathfrak {R}$,
$\mathfrak {R}$, ![]() $\mathfrak {R}^{\vee }$,
$\mathfrak {R}^{\vee }$, ![]() $\mathfrak {R}^{+}$,
$\mathfrak {R}^{+}$, ![]() $\mathfrak {R}^{\mathrm {s}}$: roots, coroots, positive roots, simple roots of
$\mathfrak {R}^{\mathrm {s}}$: roots, coroots, positive roots, simple roots of ![]() $(G,B,T)$, § 3.1.
$(G,B,T)$, § 3.1.
![]() $w_0$: longest element in
$w_0$: longest element in ![]() $W$, § 3.1.
$W$, § 3.1.
![]() $\rho$: half-sum of the positive roots, § 3.1.
$\rho$: half-sum of the positive roots, § 3.1.
![]() $\bullet$: dot action of
$\bullet$: dot action of ![]() $W_\mathrm {ext}$ on
$W_\mathrm {ext}$ on ![]() $\mathbb {X}$ and
$\mathbb {X}$ and ![]() $W$ on
$W$ on ![]() $\mathfrak {t}^{*}$, § 3.1.
$\mathfrak {t}^{*}$, § 3.1.
![]() ${{\bar {\lambda }}}$: element of
${{\bar {\lambda }}}$: element of ![]() $\mathfrak {t}^{*}$ associated with
$\mathfrak {t}^{*}$ associated with ![]() $\lambda \in \mathbb {X}$, § 3.1.
$\lambda \in \mathbb {X}$, § 3.1.
![]() $\tilde {\lambda }$: image of
$\tilde {\lambda }$: image of ![]() ${{\bar {\lambda }}}$ in
${{\bar {\lambda }}}$ in ![]() $\mathfrak {t}^{*}/(W,\bullet )$, § 3.1.
$\mathfrak {t}^{*}/(W,\bullet )$, § 3.1.
![]() $\mathfrak {t}^{*}_{\mathbb {F}_p}$: ‘integral’ part of
$\mathfrak {t}^{*}_{\mathbb {F}_p}$: ‘integral’ part of ![]() $\mathfrak {t}^{*}$, § 3.1.
$\mathfrak {t}^{*}$, § 3.1.
![]() $W_I$: subgroup of
$W_I$: subgroup of ![]() $W$ associated with
$W$ associated with ![]() $I \subset \mathfrak {R}^{\mathrm {s}}$, § 3.1.
$I \subset \mathfrak {R}^{\mathrm {s}}$, § 3.1.
![]() $\mathcal {U} \mathfrak {g}$: universal enveloping algebra of
$\mathcal {U} \mathfrak {g}$: universal enveloping algebra of ![]() $\mathfrak {g}$, § 3.2.
$\mathfrak {g}$, § 3.2.
![]() ${Z_{\mathrm {HC}}}$,
${Z_{\mathrm {HC}}}$, ![]() ${Z_{\mathrm {Fr}}}$: Harish-Chandra and Frobenius centers of
${Z_{\mathrm {Fr}}}$: Harish-Chandra and Frobenius centers of ![]() $\mathcal {U} \mathfrak {g}$, § 3.2.
$\mathcal {U} \mathfrak {g}$, § 3.2.
![]() $\mathrm {AS}$: Artin–Schreier morphism, § 3.2.
$\mathrm {AS}$: Artin–Schreier morphism, § 3.2.
![]() $\mathfrak {C}$: spectrum of
$\mathfrak {C}$: spectrum of ![]() $Z(\mathcal {U} \mathfrak {g})$, § 3.2.
$Z(\mathcal {U} \mathfrak {g})$, § 3.2.
![]() $\mathfrak {m}_\eta$: ideal in
$\mathfrak {m}_\eta$: ideal in ![]() ${Z_{\mathrm {Fr}}}$ associated with
${Z_{\mathrm {Fr}}}$ associated with ![]() $\eta \in \mathfrak {g}^{*(1)}$, § 3.3.
$\eta \in \mathfrak {g}^{*(1)}$, § 3.3.
![]() $\mathfrak {m}^{\xi }$: ideal in
$\mathfrak {m}^{\xi }$: ideal in ![]() ${Z_{\mathrm {HC}}}$ associated with
${Z_{\mathrm {HC}}}$ associated with ![]() $\xi \in \mathfrak {t}^{*}/(W,\bullet )$, § 3.3.
$\xi \in \mathfrak {t}^{*}/(W,\bullet )$, § 3.3.
![]() $\mathcal {U}_\eta \mathfrak {g}$,
$\mathcal {U}_\eta \mathfrak {g}$, ![]() $\mathcal {U}^{\xi } \mathfrak {g}$,
$\mathcal {U}^{\xi } \mathfrak {g}$, ![]() $\mathcal {U}_\eta ^{\xi } \mathfrak {g}$: central reductions of
$\mathcal {U}_\eta ^{\xi } \mathfrak {g}$: central reductions of ![]() $\mathcal {U} \mathfrak {g}$, § 3.3.
$\mathcal {U} \mathfrak {g}$, § 3.3.
![]() $\mathcal {N}^{*}$: nilpotent cone in
$\mathcal {N}^{*}$: nilpotent cone in ![]() $\mathfrak {g}^{*}$, § 3.3.
$\mathfrak {g}^{*}$, § 3.3.
![]() $\mathsf {HC}$: category of Harish-Chandra bimodules for
$\mathsf {HC}$: category of Harish-Chandra bimodules for ![]() $G$, § 3.4.
$G$, § 3.4.
![]() $\mathcal {Z} = Z(\mathcal {U} \mathfrak {g}) \otimes _{{Z_{\mathrm {Fr}}}} Z(\mathcal {U} \mathfrak {g})$, § 3.4.
$\mathcal {Z} = Z(\mathcal {U} \mathfrak {g}) \otimes _{{Z_{\mathrm {Fr}}}} Z(\mathcal {U} \mathfrak {g})$, § 3.4.
![]() $\mathsf {Mod}^{G}_\mathrm {fg}(\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm{op}})$: category of
$\mathsf {Mod}^{G}_\mathrm {fg}(\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm{op}})$: category of ![]() $G$-equivariant finitely generated
$G$-equivariant finitely generated ![]() $\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm{op}}$-modules, § 3.4.
$\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm{op}}$-modules, § 3.4.
![]() $\mathfrak {D} = \mathfrak {t}^{*}/(W,\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W,\bullet )$, § 3.5.
$\mathfrak {D} = \mathfrak {t}^{*}/(W,\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W,\bullet )$, § 3.5.
![]() $\mathcal {I}^{\lambda,\mu }$: ideal in
$\mathcal {I}^{\lambda,\mu }$: ideal in ![]() $\mathscr {O}(\mathfrak {D})$ associated with
$\mathscr {O}(\mathfrak {D})$ associated with ![]() $\lambda,\mu \in \mathbb {X}$, § 3.5.
$\lambda,\mu \in \mathbb {X}$, § 3.5.
![]() $\mathfrak {D}^{\hat {\lambda },\hat {\mu }}$: spectrum of the completion of
$\mathfrak {D}^{\hat {\lambda },\hat {\mu }}$: spectrum of the completion of ![]() $\mathscr {O}(\mathfrak {D})$ with respect to
$\mathscr {O}(\mathfrak {D})$ with respect to ![]() $\mathcal {I}^{\lambda,\mu }$, § 3.5.
$\mathcal {I}^{\lambda,\mu }$, § 3.5.
![]() $\mathcal {U}^{\hat {\lambda },\hat {\mu }} = (\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm{op}}) \otimes _{\mathscr {O}(\mathfrak {D})} \mathscr {O}(\mathfrak {D}^{\hat {\lambda },\hat {\mu }})$, § 3.5.
$\mathcal {U}^{\hat {\lambda },\hat {\mu }} = (\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm{op}}) \otimes _{\mathscr {O}(\mathfrak {D})} \mathscr {O}(\mathfrak {D}^{\hat {\lambda },\hat {\mu }})$, § 3.5.
![]() $\mathsf {Mod}^{G}_\mathrm {fg}(\mathcal {U}^{\hat {\lambda },\hat {\mu }})$: category of
$\mathsf {Mod}^{G}_\mathrm {fg}(\mathcal {U}^{\hat {\lambda },\hat {\mu }})$: category of ![]() $G$-equivariant finitely generated
$G$-equivariant finitely generated ![]() $\mathcal {U}^{\hat {\lambda },\hat {\mu }}$-modules, § 3.5.
$\mathcal {U}^{\hat {\lambda },\hat {\mu }}$-modules, § 3.5.
![]() $\mathsf {HC}^{\hat {\lambda },\hat {\mu }}$: subcategory of
$\mathsf {HC}^{\hat {\lambda },\hat {\mu }}$: subcategory of ![]() $\mathsf {Mod}^{G}_\mathrm {fg}(\mathcal {U}^{\hat {\lambda },\hat {\mu }})$ of Harish-Chandra bimodules, § 3.5.
$\mathsf {Mod}^{G}_\mathrm {fg}(\mathcal {U}^{\hat {\lambda },\hat {\mu }})$ of Harish-Chandra bimodules, § 3.5.
![]() $\mathsf {HC}^{\hat {\lambda },\hat {\mu }}_\mathrm {diag}$: subcategory of
$\mathsf {HC}^{\hat {\lambda },\hat {\mu }}_\mathrm {diag}$: subcategory of ![]() $\mathsf {HC}^{\hat {\lambda },\hat {\mu }}$ of diagonally induced bimodules, § 3.5.
$\mathsf {HC}^{\hat {\lambda },\hat {\mu }}$ of diagonally induced bimodules, § 3.5.
![]() $\mathsf {C}^{\lambda,\mu }(-)=\mathscr {O}(\mathfrak {D}^{\hat {\lambda },\hat {\mu }}) \otimes _{\mathscr {O}(\mathfrak {D})} (-)$, § 3.5.
$\mathsf {C}^{\lambda,\mu }(-)=\mathscr {O}(\mathfrak {D}^{\hat {\lambda },\hat {\mu }}) \otimes _{\mathscr {O}(\mathfrak {D})} (-)$, § 3.5.
![]() $\mathcal {U}^{\hat {\lambda }} = \mathsf {C}^{\lambda,\lambda }(\Bbbk \otimes \mathcal {U} \mathfrak {g})$, § 3.5.
$\mathcal {U}^{\hat {\lambda }} = \mathsf {C}^{\lambda,\lambda }(\Bbbk \otimes \mathcal {U} \mathfrak {g})$, § 3.5.
![]() $h$: Coxeter number of
$h$: Coxeter number of ![]() $G$, § 3.5.
$G$, § 3.5.
![]() $\mathsf {P}^{\lambda,\mu }$: translation bimodule attached to
$\mathsf {P}^{\lambda,\mu }$: translation bimodule attached to ![]() $\lambda,\mu \in \mathbb {X}$, § 3.5.
$\lambda,\mu \in \mathbb {X}$, § 3.5.
![]() $\Lambda$: set of representatives for the
$\Lambda$: set of representatives for the ![]() $({W_{\mathrm {ext}}},\bullet )$-orbits on
$({W_{\mathrm {ext}}},\bullet )$-orbits on ![]() $\mathbb {X}$, § 3.6.
$\mathbb {X}$, § 3.6.
![]() $\mathcal {I}$: ideal of
$\mathcal {I}$: ideal of ![]() $\mathscr {O}(\mathfrak {t}^{*(1)}/W)$ corresponding to the image of
$\mathscr {O}(\mathfrak {t}^{*(1)}/W)$ corresponding to the image of ![]() $0$, § 3.6.
$0$, § 3.6.
![]() $\mathfrak {D}^{\wedge }$: spectrum of the completion of
$\mathfrak {D}^{\wedge }$: spectrum of the completion of ![]() $\mathscr {O}(\mathfrak {D})$ with respect to
$\mathscr {O}(\mathfrak {D})$ with respect to ![]() $\mathcal {I} \cdot \mathscr {O}(\mathfrak {D})$, § 3.6.
$\mathcal {I} \cdot \mathscr {O}(\mathfrak {D})$, § 3.6.
![]() $\mathscr {O}(\mathfrak {t}^{*(1)}/W)^{\wedge }$: completion of
$\mathscr {O}(\mathfrak {t}^{*(1)}/W)^{\wedge }$: completion of ![]() $\mathscr {O}(\mathfrak {t}^{*(1)}/W)$ with respect to
$\mathscr {O}(\mathfrak {t}^{*(1)}/W)$ with respect to ![]() $\mathcal {I}$, § 3.6.
$\mathcal {I}$, § 3.6.
![]() ${Z^{\wedge }_{\mathrm {HC}}}$: completion of
${Z^{\wedge }_{\mathrm {HC}}}$: completion of ![]() ${Z_{\mathrm {HC}}}$ with respect to
${Z_{\mathrm {HC}}}$ with respect to ![]() $\mathcal {I} \cdot {Z_{\mathrm {HC}}}$, § 3.6.
$\mathcal {I} \cdot {Z_{\mathrm {HC}}}$, § 3.6.
![]() ${Z^{\hat {\lambda }}_{\mathrm {HC}}}$: completion of
${Z^{\hat {\lambda }}_{\mathrm {HC}}}$: completion of ![]() ${Z_{\mathrm {HC}}}$ with respect to
${Z_{\mathrm {HC}}}$ with respect to ![]() $\mathfrak {m}^{\lambda }$, § 3.6.
$\mathfrak {m}^{\lambda }$, § 3.6.
![]() $\mathcal {U}^{\wedge }=(\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm{op}}) \otimes _{\mathscr {O}(\mathfrak {D})} \mathscr {O}(\mathfrak {D}^{\wedge })$, § 3.6.
$\mathcal {U}^{\wedge }=(\mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathcal {U} \mathfrak {g}^{\mathrm{op}}) \otimes _{\mathscr {O}(\mathfrak {D})} \mathscr {O}(\mathfrak {D}^{\wedge })$, § 3.6.
![]() $\mathsf {Mod}^{G}_\mathrm {fg}(\mathcal {U}^{\wedge })$: category of
$\mathsf {Mod}^{G}_\mathrm {fg}(\mathcal {U}^{\wedge })$: category of ![]() $G$-equivariant finitely generated
$G$-equivariant finitely generated ![]() $\mathcal {U}^{\wedge }$-modules, § 3.6.
$\mathcal {U}^{\wedge }$-modules, § 3.6.
![]() $\mathsf {HC}^{\wedge }$: subcategory of
$\mathsf {HC}^{\wedge }$: subcategory of ![]() $\mathsf {Mod}^{G}_\mathrm {fg}(\mathcal {U}^{\wedge })$ of Harish-Chandra bimodules, § 3.6.
$\mathsf {Mod}^{G}_\mathrm {fg}(\mathcal {U}^{\wedge })$ of Harish-Chandra bimodules, § 3.6.
![]() $\mathsf {HC}^{\wedge }_\mathrm {diag}$: subcategory of
$\mathsf {HC}^{\wedge }_\mathrm {diag}$: subcategory of ![]() $\mathsf {HC}^{\wedge }$ of diagonally induced bimodules, § 3.6.
$\mathsf {HC}^{\wedge }$ of diagonally induced bimodules, § 3.6.
![]() $\mathsf {C}^{\wedge }(-)=\mathscr {O}(\mathfrak {D}^{\wedge }) \otimes _{\mathscr {O}(\mathfrak {D})} (-)$, § 3.6.
$\mathsf {C}^{\wedge }(-)=\mathscr {O}(\mathfrak {D}^{\wedge }) \otimes _{\mathscr {O}(\mathfrak {D})} (-)$, § 3.6.
![]() $(-) {\widehat{\otimes}}_{\mathcal{U} \mathfrak{g}} (-)$: monoidal product for the categories
$(-) {\widehat{\otimes}}_{\mathcal{U} \mathfrak{g}} (-)$: monoidal product for the categories ![]() $\mathsf {Mod}^{G}_\mathrm {fg}(\mathcal {U}^{\hat {\lambda },\hat {\mu }})$, § 3.7.
$\mathsf {Mod}^{G}_\mathrm {fg}(\mathcal {U}^{\hat {\lambda },\hat {\mu }})$, § 3.7.
![]() $\mathbb {I}^{*}_\mathbf {S}$: group scheme over
$\mathbb {I}^{*}_\mathbf {S}$: group scheme over ![]() $\mathbf {S}^{*}$, § 3.8.
$\mathbf {S}^{*}$, § 3.8.
![]() $\mathcal {U}_{\mathbf {S}}\mathfrak {g} := \mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathscr {O}(\mathbf {S}^{*})$, § 3.8.
$\mathcal {U}_{\mathbf {S}}\mathfrak {g} := \mathcal {U} \mathfrak {g} \otimes _{{Z_{\mathrm {Fr}}}} \mathscr {O}(\mathbf {S}^{*})$, § 3.8.
![]() $\mathfrak {C}_\mathbf {S} := \mathbf {S}^{*} \times _{\mathfrak {t}^{*(1)} / W} \mathfrak {t}^{*}/(W,\bullet )$, § 3.8.
$\mathfrak {C}_\mathbf {S} := \mathbf {S}^{*} \times _{\mathfrak {t}^{*(1)} / W} \mathfrak {t}^{*}/(W,\bullet )$, § 3.8.
![]() $\mathcal {Z}_\mathbf {S} = \mathcal {Z} \otimes _{{Z_{\mathrm {Fr}}}} \mathscr {O}(\mathbf {S}^{*})$, § 3.9.
$\mathcal {Z}_\mathbf {S} = \mathcal {Z} \otimes _{{Z_{\mathrm {Fr}}}} \mathscr {O}(\mathbf {S}^{*})$, § 3.9.
![]() $\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {U}_\mathbf {S} \mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} \mathcal {U}_\mathbf {S} \mathfrak {g}^{\mathrm {op}})$: category of
$\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {U}_\mathbf {S} \mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} \mathcal {U}_\mathbf {S} \mathfrak {g}^{\mathrm {op}})$: category of ![]() $\mathbb {I}^{*}_\mathbf {S}$-equivariant finitely generated
$\mathbb {I}^{*}_\mathbf {S}$-equivariant finitely generated ![]() $\mathcal {U}_\mathbf {S} \mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} \mathcal {U}_\mathbf {S} \mathfrak {g}^{\mathrm {op}}$-modules, § 3.9.
$\mathcal {U}_\mathbf {S} \mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} \mathcal {U}_\mathbf {S} \mathfrak {g}^{\mathrm {op}}$-modules, § 3.9.
![]() $\mathsf {HC}_\mathbf {S}$: subcategory of
$\mathsf {HC}_\mathbf {S}$: subcategory of ![]() $\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {U}_\mathbf {S} \mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} \mathcal {U}_\mathbf {S} \mathfrak {g}^{\mathrm {op}})$ of Harish-Chandra bimodules, § 3.9.
$\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {U}_\mathbf {S} \mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} \mathcal {U}_\mathbf {S} \mathfrak {g}^{\mathrm {op}})$ of Harish-Chandra bimodules, § 3.9.
![]() $\mathcal {I}^{\lambda,\mu }_\mathbf {S} = \mathcal {I}^{\lambda,\mu } \cdot \mathcal {Z}_\mathbf {S}$, § 3.9.
$\mathcal {I}^{\lambda,\mu }_\mathbf {S} = \mathcal {I}^{\lambda,\mu } \cdot \mathcal {Z}_\mathbf {S}$, § 3.9.
![]() $\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$: completion of
$\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$: completion of ![]() $\mathcal {Z}_\mathbf {S}$ with respect to
$\mathcal {Z}_\mathbf {S}$ with respect to ![]() $\mathcal {I}^{\lambda,\mu }_\mathbf {S}$, § 3.9.
$\mathcal {I}^{\lambda,\mu }_\mathbf {S}$, § 3.9.
![]() $\mathcal {U}^{\hat {\lambda },\hat {\mu }}_\mathbf {S} = \mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }} \otimes _{\mathcal {Z}_\mathbf {S}} ( \mathcal {U}_\mathbf {S} \mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} \mathcal {U}_\mathbf {S} \mathfrak {g}^{\mathrm{op}} )$, § 3.9.
$\mathcal {U}^{\hat {\lambda },\hat {\mu }}_\mathbf {S} = \mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }} \otimes _{\mathcal {Z}_\mathbf {S}} ( \mathcal {U}_\mathbf {S} \mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} \mathcal {U}_\mathbf {S} \mathfrak {g}^{\mathrm{op}} )$, § 3.9.
![]() $\mathbb {I}_\mathbf {S}^{\hat {\lambda },\hat {\mu }} = \mathrm {Spec}(\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}) \times _{\mathbf {S}^{*}} \mathbb {I}^{*}_\mathbf {S}$, § 3.9.
$\mathbb {I}_\mathbf {S}^{\hat {\lambda },\hat {\mu }} = \mathrm {Spec}(\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}) \times _{\mathbf {S}^{*}} \mathbb {I}^{*}_\mathbf {S}$, § 3.9.
![]() $\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$: category of
$\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$: category of ![]() $\mathbb {I}^{\hat {\lambda },\hat {\mu }}_\mathbf {S}$-equivariant finitely generated
$\mathbb {I}^{\hat {\lambda },\hat {\mu }}_\mathbf {S}$-equivariant finitely generated ![]() $\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$-modules, § 3.9.
$\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$-modules, § 3.9.
![]() $\mathsf {HC}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$: subcategory of
$\mathsf {HC}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$: subcategory of ![]() $\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$ of Harish-Chandra bimodules, § 3.9.
$\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$ of Harish-Chandra bimodules, § 3.9.
![]() $\mathsf {P}^{\lambda,\mu }_\mathbf {S} = \mathscr {O}(\mathbf {S}^{*}) \otimes _{\mathscr {O}(\mathfrak {g}^{*(1)})} \mathsf {P}^{\lambda,\mu }$, § 3.9.
$\mathsf {P}^{\lambda,\mu }_\mathbf {S} = \mathscr {O}(\mathbf {S}^{*}) \otimes _{\mathscr {O}(\mathfrak {g}^{*(1)})} \mathsf {P}^{\lambda,\mu }$, § 3.9.
![]() $(-) {\widehat{\otimes}}_{\mathcal {U}_\mathbf {S} \mathfrak {g}} (-)$: monoidal product for the categories
$(-) {\widehat{\otimes}}_{\mathcal {U}_\mathbf {S} \mathfrak {g}} (-)$: monoidal product for the categories ![]() $\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$, § 3.9.
$\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {U}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$, § 3.9.
![]() $\mathcal {Z}_\mathbf {S}^{\wedge }$: completion of
$\mathcal {Z}_\mathbf {S}^{\wedge }$: completion of ![]() $\mathcal {Z}_\mathbf {S}$ with respect to
$\mathcal {Z}_\mathbf {S}$ with respect to ![]() $\mathcal {I} \cdot \mathcal {Z}_\mathbf {S}$, § 3.9.
$\mathcal {I} \cdot \mathcal {Z}_\mathbf {S}$, § 3.9.
![]() $\mathcal {U}^{\wedge }_\mathbf {S} = \mathcal {Z}_\mathbf {S}^{\wedge } \otimes _{\mathcal {Z}_\mathbf {S}} ( \mathcal {U}_\mathbf {S} \mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} \mathcal {U}_\mathbf {S} \mathfrak {g}^{\mathrm{op}} )$, § 3.9.
$\mathcal {U}^{\wedge }_\mathbf {S} = \mathcal {Z}_\mathbf {S}^{\wedge } \otimes _{\mathcal {Z}_\mathbf {S}} ( \mathcal {U}_\mathbf {S} \mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} \mathcal {U}_\mathbf {S} \mathfrak {g}^{\mathrm{op}} )$, § 3.9.
![]() $\mathbb {I}_\mathbf {S}^{\wedge } = \mathrm {Spec}(\mathcal {Z}_\mathbf {S}^{\wedge }) \times _{\mathbf {S}^{*}} \mathbb {I}^{*}_\mathbf {S}$, § 3.9.
$\mathbb {I}_\mathbf {S}^{\wedge } = \mathrm {Spec}(\mathcal {Z}_\mathbf {S}^{\wedge }) \times _{\mathbf {S}^{*}} \mathbb {I}^{*}_\mathbf {S}$, § 3.9.
![]() $\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {U}_\mathbf {S}^{\wedge })$: category of
$\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {U}_\mathbf {S}^{\wedge })$: category of ![]() $\mathbb {I}^{\wedge }_\mathbf {S}$-equivariant finitely generated
$\mathbb {I}^{\wedge }_\mathbf {S}$-equivariant finitely generated ![]() $\mathcal {U}_\mathbf {S}^{\wedge }$-modules, § 3.9.
$\mathcal {U}_\mathbf {S}^{\wedge }$-modules, § 3.9.
![]() $\mathsf {C}_\mathbf {S}^{\wedge } (-) = \mathscr {O}(\mathbf {S}^{*}) \otimes _{{Z_{\mathrm {Fr}}}} \mathsf {C}^{\wedge }(-)$, § 3.9.
$\mathsf {C}_\mathbf {S}^{\wedge } (-) = \mathscr {O}(\mathbf {S}^{*}) \otimes _{{Z_{\mathrm {Fr}}}} \mathsf {C}^{\wedge }(-)$, § 3.9.
![]() $\mathcal {U}_\mathbf {S}^{\hat {\lambda }} = \mathscr {O}(\mathbf {S}^{*}) \otimes _{\mathscr {O}(\mathfrak {g}^{*(1)})} \mathcal {U}^{\hat {\lambda }}$, § 3.9.
$\mathcal {U}_\mathbf {S}^{\hat {\lambda }} = \mathscr {O}(\mathbf {S}^{*}) \otimes _{\mathscr {O}(\mathfrak {g}^{*(1)})} \mathcal {U}^{\hat {\lambda }}$, § 3.9.
A.3 Section 4
![]() $\mathsf {Z}_{\eta,B'}(\xi )$: baby Verma module, § 4.2.
$\mathsf {Z}_{\eta,B'}(\xi )$: baby Verma module, § 4.2.
![]() $\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {Z}_\mathbf {S}^{\wedge })$: category of representations of
$\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {Z}_\mathbf {S}^{\wedge })$: category of representations of ![]() $\mathbb {I}^{\wedge }_\mathbf {S}$ on finitely generated
$\mathbb {I}^{\wedge }_\mathbf {S}$ on finitely generated ![]() $\mathcal {Z}_\mathbf {S}^{\wedge }$-modules, § 4.3.
$\mathcal {Z}_\mathbf {S}^{\wedge }$-modules, § 4.3.
![]() $(-) \mathbin {\hat {\star }}_{\mathbf {S}} (-)$: monoidal product on
$(-) \mathbin {\hat {\star }}_{\mathbf {S}} (-)$: monoidal product on ![]() $\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {Z}_\mathbf {S}^{\wedge })$, § 4.3.
$\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {Z}_\mathbf {S}^{\wedge })$, § 4.3.
![]() $\mathbb {J}_\mathbf {S}^{\wedge } = \mathrm {Spec}(\mathcal {Z}_\mathbf {S}^{\wedge }) \times _{\mathbf {S}^{*}} \mathbb {J}^{*}_\mathbf {S}$, § 4.3.
$\mathbb {J}_\mathbf {S}^{\wedge } = \mathrm {Spec}(\mathcal {Z}_\mathbf {S}^{\wedge }) \times _{\mathbf {S}^{*}} \mathbb {J}^{*}_\mathbf {S}$, § 4.3.
![]() $\mathsf {Mod}^{\mathbb {J}}_{\mathrm {fg}}(\mathcal {Z}_\mathbf {S}^{\wedge })$: category of representations of
$\mathsf {Mod}^{\mathbb {J}}_{\mathrm {fg}}(\mathcal {Z}_\mathbf {S}^{\wedge })$: category of representations of ![]() $\mathbb {J}^{\wedge }_\mathbf {S}$ on finitely generated
$\mathbb {J}^{\wedge }_\mathbf {S}$ on finitely generated ![]() $\mathcal {Z}_\mathbf {S}^{\wedge }$-modules, § 4.3.
$\mathcal {Z}_\mathbf {S}^{\wedge }$-modules, § 4.3.
![]() $\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$: category of representations of
$\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$: category of representations of ![]() $\mathbb {I}^{\hat {\lambda },\hat {\mu }}_\mathbf {S}$ on finitely generated
$\mathbb {I}^{\hat {\lambda },\hat {\mu }}_\mathbf {S}$ on finitely generated ![]() $\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$-modules, § 4.3.
$\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$-modules, § 4.3.
![]() $\mathbb {J}_\mathbf {S}^{\hat {\lambda },\hat {\mu }} = \mathrm {Spec}(\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}) \times _{\mathbf {S}^{*}} \mathbb {J}^{*}_\mathbf {S}$, § 4.3.
$\mathbb {J}_\mathbf {S}^{\hat {\lambda },\hat {\mu }} = \mathrm {Spec}(\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}) \times _{\mathbf {S}^{*}} \mathbb {J}^{*}_\mathbf {S}$, § 4.3.
![]() $\mathsf {Mod}^{\mathbb {J}}_{\mathrm {fg}}(\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$: category of representations of
$\mathsf {Mod}^{\mathbb {J}}_{\mathrm {fg}}(\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$: category of representations of ![]() $\mathbb {J}^{\hat {\lambda },\hat {\mu }}_\mathbf {S}$ on finitely generated
$\mathbb {J}^{\hat {\lambda },\hat {\mu }}_\mathbf {S}$ on finitely generated ![]() $\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$-modules, § 4.3.
$\mathcal {Z}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$-modules, § 4.3.
![]() $\mathsf {M}^{\lambda,\mu } = \mathsf {P}^{\lambda,-\rho } {\widehat{\otimes}}_{\mathcal {U} \mathfrak {g}} \mathsf {P}^{-\rho,\mu }$, § 4.3.
$\mathsf {M}^{\lambda,\mu } = \mathsf {P}^{\lambda,-\rho } {\widehat{\otimes}}_{\mathcal {U} \mathfrak {g}} \mathsf {P}^{-\rho,\mu }$, § 4.3.
![]() $\mathsf {M}^{\lambda,\mu }_\mathbf {S} = \mathscr {O}(\mathbf {S}^{*}) \otimes _{\mathscr {O}(\mathfrak {g}^{*(1)})} \mathsf {M}^{\lambda,\mu }$, § 4.3.
$\mathsf {M}^{\lambda,\mu }_\mathbf {S} = \mathscr {O}(\mathbf {S}^{*}) \otimes _{\mathscr {O}(\mathfrak {g}^{*(1)})} \mathsf {M}^{\lambda,\mu }$, § 4.3.
![]() $\tilde {\mathfrak {D}} = \mathfrak {t}^{*} \times _{\mathfrak {t}^{*(1)}} \mathfrak {t}^{*}$, § 4.4.
$\tilde {\mathfrak {D}} = \mathfrak {t}^{*} \times _{\mathfrak {t}^{*(1)}} \mathfrak {t}^{*}$, § 4.4.
![]() $\tilde {\mathfrak {D}}(\lambda )$,
$\tilde {\mathfrak {D}}(\lambda )$, ![]() $\mathfrak {D}(\lambda )$: irreducible components associated with
$\mathfrak {D}(\lambda )$: irreducible components associated with ![]() $\lambda \in \mathbb {X}$, § 4.4.
$\lambda \in \mathbb {X}$, § 4.4.
![]() $\tilde {\Lambda }$: set of representatives for
$\tilde {\Lambda }$: set of representatives for ![]() $\mathbb {X}/p\mathbb {X}$, § 4.4.
$\mathbb {X}/p\mathbb {X}$, § 4.4.
![]() $\mathfrak {t}^{*}_\circ$, open subset in
$\mathfrak {t}^{*}_\circ$, open subset in ![]() $\mathfrak {t}^{*}$, § 4.4.
$\mathfrak {t}^{*}$, § 4.4.
![]() $\tilde {\mathbf {S}}^{*}$: preimage of
$\tilde {\mathbf {S}}^{*}$: preimage of ![]() $\mathbf {S}^{*}$ in
$\mathbf {S}^{*}$ in ![]() $\tilde {\mathbf {g}}$, § 4.4.
$\tilde {\mathbf {g}}$, § 4.4.
![]() $\mathscr {L}_{\lambda,\mu }$: localization equivalence, § 4.6.
$\mathscr {L}_{\lambda,\mu }$: localization equivalence, § 4.6.
A.4 Section 5
![]() $\mathcal {B}=G/B$, § 5.1.
$\mathcal {B}=G/B$, § 5.1.
![]() $\omega$: natural morphism
$\omega$: natural morphism ![]() $G/U \to \mathcal {B}$, § 5.1.
$G/U \to \mathcal {B}$, § 5.1.
![]() $\tilde {\mathscr {D}}$: universal twisted differential operators on
$\tilde {\mathscr {D}}$: universal twisted differential operators on ![]() $\mathcal {B}$, § 5.1.
$\mathcal {B}$, § 5.1.
![]() $\tilde {\mathscr {D}}_\mathbf {S} := \tilde {\mathscr {D}}_{|\tilde {\mathbf {S}}^{*} \times _{\mathfrak {t}^{*(1)}} \mathfrak {t}^{*}}$, § 5.1.
$\tilde {\mathscr {D}}_\mathbf {S} := \tilde {\mathscr {D}}_{|\tilde {\mathbf {S}}^{*} \times _{\mathfrak {t}^{*(1)}} \mathfrak {t}^{*}}$, § 5.1.
![]() $\tilde {\mathcal {U}}_\mathbf {S}\mathfrak {g} := \mathcal {U}_\mathbf {S}\mathfrak {g} \otimes _{{Z_{\mathrm {HC}}}} \mathscr {O}(\mathfrak {t}^{*})$, § 5.1.
$\tilde {\mathcal {U}}_\mathbf {S}\mathfrak {g} := \mathcal {U}_\mathbf {S}\mathfrak {g} \otimes _{{Z_{\mathrm {HC}}}} \mathscr {O}(\mathfrak {t}^{*})$, § 5.1.
![]() $\mathscr {O}_{\mathcal {B}}(\lambda )$: line bundle on
$\mathscr {O}_{\mathcal {B}}(\lambda )$: line bundle on ![]() $\mathcal {B}$ attached to
$\mathcal {B}$ attached to ![]() $\lambda \in \mathbb {X}$, § 5.2.
$\lambda \in \mathbb {X}$, § 5.2.
![]() $\tilde {\mathcal {U}}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$: completion of
$\tilde {\mathcal {U}}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$: completion of ![]() $\tilde {\mathcal {U}}_\mathbf {S}\mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} (\tilde {\mathcal {U}}_\mathbf {S}\mathfrak {g})^{\mathrm{op}}$ at the ideal corresponding to
$\tilde {\mathcal {U}}_\mathbf {S}\mathfrak {g} \otimes _{\mathscr {O}(\mathbf {S}^{*})} (\tilde {\mathcal {U}}_\mathbf {S}\mathfrak {g})^{\mathrm{op}}$ at the ideal corresponding to ![]() $({{\bar {\lambda }}},{{\bar {\mu }}}) \in \mathfrak {t}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}$, § 5.2.
$({{\bar {\lambda }}},{{\bar {\mu }}}) \in \mathfrak {t}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}$, § 5.2.
![]() $\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\tilde {\mathcal {U}}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$: category of equivariant finitely generated
$\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\tilde {\mathcal {U}}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$: category of equivariant finitely generated ![]() $\tilde {\mathcal {U}}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$-modules, § 5.2.
$\tilde {\mathcal {U}}_\mathbf {S}^{\hat {\lambda },\hat {\mu }}$-modules, § 5.2.
![]() $(-) {\widehat{\otimes}}_{\tilde {\mathcal {U}}_\mathbf{S} \mathfrak {g}} (-)$: monoidal product for the categories
$(-) {\widehat{\otimes}}_{\tilde {\mathcal {U}}_\mathbf{S} \mathfrak {g}} (-)$: monoidal product for the categories ![]() $\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\tilde {\mathcal {U}}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$, § 5.2.
$\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\tilde {\mathcal {U}}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$, § 5.2.
![]() $\mathsf {Q}_{\lambda,\mu }$: completion of
$\mathsf {Q}_{\lambda,\mu }$: completion of ![]() $\Gamma \bigl ( \tilde {\mathbf {S}}^{*} \times _{\mathfrak {t}^{*(1)}} \mathfrak {t}^{*}, (\mathscr {O}_\mathcal {B}(\lambda -\mu ) \otimes _{\mathscr {O}_\mathcal {B}} \tilde {\mathscr {D}})_{|\tilde {\mathbf {S}}^{*} \times _{\mathfrak {t}^{*(1)}} \mathfrak {t}^{*}} \bigr )$, § 5.2.
$\Gamma \bigl ( \tilde {\mathbf {S}}^{*} \times _{\mathfrak {t}^{*(1)}} \mathfrak {t}^{*}, (\mathscr {O}_\mathcal {B}(\lambda -\mu ) \otimes _{\mathscr {O}_\mathcal {B}} \tilde {\mathscr {D}})_{|\tilde {\mathbf {S}}^{*} \times _{\mathfrak {t}^{*(1)}} \mathfrak {t}^{*}} \bigr )$, § 5.2.
![]() $\langle \eta \rangle$: twist functor on
$\langle \eta \rangle$: twist functor on ![]() $\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\tilde {\mathcal {U}}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$, § 5.2.
$\mathsf {Mod}^{\mathbb {I}}_{\mathrm {fg}}(\tilde {\mathcal {U}}_\mathbf {S}^{\hat {\lambda },\hat {\mu }})$, § 5.2.
![]() $\mathfrak {E}=\mathfrak {t}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W,\bullet )$, § 5.3.
$\mathfrak {E}=\mathfrak {t}^{*} \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}/(W,\bullet )$, § 5.3.
![]() $\mathfrak {E}':=\mathfrak {t}^{*}/(W,\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}$, § 5.3.
$\mathfrak {E}':=\mathfrak {t}^{*}/(W,\bullet ) \times _{\mathfrak {t}^{*(1)}/W} \mathfrak {t}^{*}$, § 5.3.
![]() $\mathscr {O}(\mathfrak {E})^{\hat {\lambda },\hat {\mu }}$: completion of
$\mathscr {O}(\mathfrak {E})^{\hat {\lambda },\hat {\mu }}$: completion of ![]() $\mathscr {O}(\mathfrak {E})$ at the ideal corresponding to
$\mathscr {O}(\mathfrak {E})$ at the ideal corresponding to ![]() $({{\bar {\lambda }}},\tilde {\mu })$, § 5.3.
$({{\bar {\lambda }}},\tilde {\mu })$, § 5.3.
![]() $P_I$,
$P_I$, ![]() $\mathbf {P}_I$: standard parabolic subgroups in
$\mathbf {P}_I$: standard parabolic subgroups in ![]() $G$ and
$G$ and ![]() $\mathbf {G}$ associated with
$\mathbf {G}$ associated with ![]() $I \subset \mathfrak {R}^{\mathrm {s}}$, § 5.6.
$I \subset \mathfrak {R}^{\mathrm {s}}$, § 5.6.
![]() $L_I$,
$L_I$, ![]() $\mathbf {L}_I$,
$\mathbf {L}_I$, ![]() $U_I$,
$U_I$, ![]() $\mathbf {U}_I$: Levi factor and unipotent radical of
$\mathbf {U}_I$: Levi factor and unipotent radical of ![]() $P_I$ and
$P_I$ and ![]() $\mathbf {P}_I$, § 5.6.
$\mathbf {P}_I$, § 5.6.
![]() $\mathcal {P}_I=G/P_I$, § 5.6.
$\mathcal {P}_I=G/P_I$, § 5.6.
![]() $\omega _I$: natural morphism
$\omega _I$: natural morphism ![]() $G/U_I \to \mathcal {P}_I$, § 5.6.
$G/U_I \to \mathcal {P}_I$, § 5.6.
![]() $\tilde {\mathscr {D}}_I$: twisted differential operators on
$\tilde {\mathscr {D}}_I$: twisted differential operators on ![]() $\mathcal {P}_I$, § 5.6.
$\mathcal {P}_I$, § 5.6.
![]() $\tilde {\mathbf {g}}_I$: parabolic Grothendieck resolution for
$\tilde {\mathbf {g}}_I$: parabolic Grothendieck resolution for ![]() $\mathbf {G}$, § 5.6.
$\mathbf {G}$, § 5.6.
![]() $\tilde {\mathbf {S}}^{*}_I$: preimage of
$\tilde {\mathbf {S}}^{*}_I$: preimage of ![]() $\mathbf {S}^{*}$ in
$\mathbf {S}^{*}$ in ![]() $\tilde {\mathbf {g}}_I$, § 5.6.
$\tilde {\mathbf {g}}_I$, § 5.6.
![]() $\tilde {\mathscr {D}}_{I,\mathbf {S}} = (\tilde {\mathscr {D}}_I)_{|\tilde {\mathbf {S}}_I^{*} \times _{\mathfrak {t}^{*(1)}/W_I} \mathfrak {t}^{*}/(W_I,\bullet )}$, § 5.6.
$\tilde {\mathscr {D}}_{I,\mathbf {S}} = (\tilde {\mathscr {D}}_I)_{|\tilde {\mathbf {S}}_I^{*} \times _{\mathfrak {t}^{*(1)}/W_I} \mathfrak {t}^{*}/(W_I,\bullet )}$, § 5.6.
![]() $\mathsf {Q}^{I}_{\lambda,\mu }$: completion of
$\mathsf {Q}^{I}_{\lambda,\mu }$: completion of ![]() $\Gamma \bigl ( \tilde {\mathbf {S}}_I^{*} \times _{\mathfrak {t}^{*(1)}/W_I} \mathfrak {t}^{*}/(W_I,\bullet ), (\mathscr {O}_{\mathcal {P}_I}(\lambda -\mu ) \otimes \tilde {\mathscr {D}}_I)_{|\tilde {\mathbf {S}}_I^{*} \times _{\mathfrak {t}^{*(1)}/W_I} \mathfrak {t}^{*}/(W_I,\bullet )} \bigr )$, § 5.6.
$\Gamma \bigl ( \tilde {\mathbf {S}}_I^{*} \times _{\mathfrak {t}^{*(1)}/W_I} \mathfrak {t}^{*}/(W_I,\bullet ), (\mathscr {O}_{\mathcal {P}_I}(\lambda -\mu ) \otimes \tilde {\mathscr {D}}_I)_{|\tilde {\mathbf {S}}_I^{*} \times _{\mathfrak {t}^{*(1)}/W_I} \mathfrak {t}^{*}/(W_I,\bullet )} \bigr )$, § 5.6.
A.5 Section 6
![]() $\mathsf {Rep}_{\mathbf {c}}(G)$: subcategory of
$\mathsf {Rep}_{\mathbf {c}}(G)$: subcategory of ![]() $\mathsf {Rep}(G)$ associated with a
$\mathsf {Rep}(G)$ associated with a ![]() ${W_{\mathrm {aff}}}$-orbit
${W_{\mathrm {aff}}}$-orbit ![]() $\mathbf {c} \subset \mathbb {X}$, § 6.1.
$\mathbf {c} \subset \mathbb {X}$, § 6.1.
![]() $[\lambda ]$:
$[\lambda ]$: ![]() ${W_{\mathrm {aff}}}$-orbit of
${W_{\mathrm {aff}}}$-orbit of ![]() $\lambda \in \mathbb {X}$, § 6.1.
$\lambda \in \mathbb {X}$, § 6.1.
![]() $\mathsf {Rep}_{\langle \lambda \rangle }(G)$: sum of the categories
$\mathsf {Rep}_{\langle \lambda \rangle }(G)$: sum of the categories ![]() $\mathsf {Rep}_{\mathbf {c}}(G)$ with
$\mathsf {Rep}_{\mathbf {c}}(G)$ with ![]() $\mathbf {c} \subset {W_{\mathrm {ext}}} \bullet \lambda$, § 6.1.
$\mathbf {c} \subset {W_{\mathrm {ext}}} \bullet \lambda$, § 6.1.
![]() $\mathsf {Mod}^{G}_\mathrm {fg}(\mathcal {U} \mathfrak {g})$: category of
$\mathsf {Mod}^{G}_\mathrm {fg}(\mathcal {U} \mathfrak {g})$: category of ![]() $G$-equivariant finitely generated
$G$-equivariant finitely generated ![]() $\mathcal {U} \mathfrak {g}$-modules, § 6.1.
$\mathcal {U} \mathfrak {g}$-modules, § 6.1.
![]() $\mathsf {Mod}^{G,\xi }_\mathrm {fg}(\mathcal {U} \mathfrak {g})$: full subcategory of
$\mathsf {Mod}^{G,\xi }_\mathrm {fg}(\mathcal {U} \mathfrak {g})$: full subcategory of ![]() $\mathsf {Mod}^{G}_\mathrm {fg}(\mathcal {U} \mathfrak {g})$ of modules annihilated by a power of
$\mathsf {Mod}^{G}_\mathrm {fg}(\mathcal {U} \mathfrak {g})$ of modules annihilated by a power of ![]() $\mathfrak {m}^{\xi }$, § 6.1.
$\mathfrak {m}^{\xi }$, § 6.1.
![]() $\mathsf {Mod}^{G,\wedge }_\mathrm {fg}(\mathcal {U} \mathfrak {g})$: full subcategory of
$\mathsf {Mod}^{G,\wedge }_\mathrm {fg}(\mathcal {U} \mathfrak {g})$: full subcategory of ![]() $\mathsf {Mod}^{G}_\mathrm {fg}(\mathcal {U} \mathfrak {g})$ of modules annihilated by a power of
$\mathsf {Mod}^{G}_\mathrm {fg}(\mathcal {U} \mathfrak {g})$ of modules annihilated by a power of ![]() $\mathcal {I}$, § 6.1.
$\mathcal {I}$, § 6.1.
![]() $(-) {\widehat{\otimes}}_{\mathcal {U} \mathfrak {g}} (-)$: bifunctor defining the action of
$(-) {\widehat{\otimes}}_{\mathcal {U} \mathfrak {g}} (-)$: bifunctor defining the action of ![]() $\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\wedge })$ on
$\mathsf {Mod}^{G}_{\mathrm {fg}}(\mathcal {U}^{\wedge })$ on ![]() $\mathsf {Mod}_{\mathrm {fg}}^{G,\wedge }(\mathcal {U} \mathfrak {g})$, § 6.2.
$\mathsf {Mod}_{\mathrm {fg}}^{G,\wedge }(\mathcal {U} \mathfrak {g})$, § 6.2.
![]() $T_\lambda ^{\mu }$: translation functor (for
$T_\lambda ^{\mu }$: translation functor (for ![]() $G$-modules) associated with
$G$-modules) associated with ![]() $\lambda,\mu \in \mathbb {X}$, § 6.3.
$\lambda,\mu \in \mathbb {X}$, § 6.3.
![]() $\Theta _s$: wall-crossing functor associated with
$\Theta _s$: wall-crossing functor associated with ![]() $s \in {S_{\mathrm {aff}}}$, § 6.4.
$s \in {S_{\mathrm {aff}}}$, § 6.4.
![]() $\Psi ^{\lambda }$: functor from
$\Psi ^{\lambda }$: functor from ![]() $\mathsf {D}_{\mathrm {BS}}$ to
$\mathsf {D}_{\mathrm {BS}}$ to ![]() $\mathsf {HC}^{\hat {\lambda },\hat {\lambda }}$, § 6.4.
$\mathsf {HC}^{\hat {\lambda },\hat {\lambda }}$, § 6.4.
![]() $\Psi ^{\lambda }_\mathbf {S}$: functor from
$\Psi ^{\lambda }_\mathbf {S}$: functor from ![]() $\mathsf {D}_{\mathrm {BS}}$ to
$\mathsf {D}_{\mathrm {BS}}$ to ![]() $\mathsf {HC}_\mathbf {S}^{\hat {\lambda },\hat {\lambda }}$, § 6.5.
$\mathsf {HC}_\mathbf {S}^{\hat {\lambda },\hat {\lambda }}$, § 6.5.