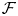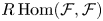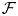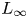1. Introduction
The main goal of this paper is to provide an elementary proof of the following theorem, which extends an analogous result for K3 surfaces [Reference Budur and ZhangBZ18].
Theorem 1.1 (=Theorem 5.3) Let ![]() $X$ be a smooth minimal projective surface of Kodaira dimension
$X$ be a smooth minimal projective surface of Kodaira dimension ![]() $0$, and consider a polystable sheaf
$0$, and consider a polystable sheaf ![]() $\mathcal {F}$ on
$\mathcal {F}$ on ![]() $X$. Then the differential graded (DG) Lie algebra
$X$. Then the differential graded (DG) Lie algebra ![]() $R\mspace {-2mu}\operatorname {Hom}_X(\mathcal {F},\mathcal {F})$ is formal.
$R\mspace {-2mu}\operatorname {Hom}_X(\mathcal {F},\mathcal {F})$ is formal.
Moduli spaces of coherent sheaves on K3 surfaces and Abelian surfaces have been intensively studied in recent decades. Among the reasons for the interest in these objects there is certainly the fact due to Mukai that the smooth locus of the moduli space inherits a holomorphic symplectic structure from the symplectic form on the surface [Reference MukaiMuk84]. In particular, provided that such a moduli space is smooth and projective, it yields an example of an irreducible holomorphic symplectic manifold. In general the moduli space is singular at a point corresponding to a strictly semistable sheaf; these singularities arise either when the Mukai vector is not primitive or when the polarization on the surface is not general (i.e. it lies on a wall with respect to the walls and chambers decomposition of the ample cone [Reference Kaledin, Lehn and SorgerKLS06, Reference YoshiokaYos01]). Nevertheless, in some cases there exist symplectic resolutions, which have been investigated for moduli spaces with general polarization and non-primitive Mukai vector. First, O'Grady found two new examples of irreducible holomorphic symplectic manifolds [Reference O'GradyO'Gr99, Reference O'GradyO'Gr03] by exhibiting symplectic resolutions of moduli spaces of sheaves on a K3 surface and on an Abelian surface. A few years later Kaledin, Lehn and Sorger showed that, other than the ones in O'Grady's examples, such moduli spaces do not admit symplectic resolutions [Reference Kaledin, Lehn and SorgerKLS06].
More recently, in [Reference Arbarello and SaccàAS18] Arbarello and Saccà turned their attention to the case of a K3 surface with a non-general polarization and Mukai vector ![]() $(0, c_1, \chi )$. The corresponding moduli space admits a symplectic resolution, given by moving the polarization (hence changing the notion of stability) into a chamber, and they give a local description of the moduli space around the singularity in terms of a suitable Nakajima quiver variety.
$(0, c_1, \chi )$. The corresponding moduli space admits a symplectic resolution, given by moving the polarization (hence changing the notion of stability) into a chamber, and they give a local description of the moduli space around the singularity in terms of a suitable Nakajima quiver variety.
By general deformation theory, an easy description of an analytic neighborhood around a singular point ![]() $[\mathcal {F}]$ in the moduli space corresponding to a given (possibly non-general) polarization can be deduced from the formality of the derived endomorphisms of the sheaf
$[\mathcal {F}]$ in the moduli space corresponding to a given (possibly non-general) polarization can be deduced from the formality of the derived endomorphisms of the sheaf ![]() $\mathcal {F}$ on the surface
$\mathcal {F}$ on the surface ![]() $X$. We now briefly recall the main steps that led to the so-called Kaledin–Lehn formality conjecture. It is well known that the base space of the formal semiuniversal deformation of
$X$. We now briefly recall the main steps that led to the so-called Kaledin–Lehn formality conjecture. It is well known that the base space of the formal semiuniversal deformation of ![]() $[\mathcal {F}]$ is the scheme-theoretic fiber of the Kuranishi map
$[\mathcal {F}]$ is the scheme-theoretic fiber of the Kuranishi map
which can be chosen to be ![]() $G$-equivariant (see, for example, [Reference Arbarello and SaccàAS18, Reference Bandiera, Manetti and MeazziniBMM20, Reference RimRim80]) with respect to the action of the automorphisms group modulo the action of the scalars:
$G$-equivariant (see, for example, [Reference Arbarello and SaccàAS18, Reference Bandiera, Manetti and MeazziniBMM20, Reference RimRim80]) with respect to the action of the automorphisms group modulo the action of the scalars: ![]() $G=\operatorname {Aut}(\mathcal {F})/\mathbb {C}^{\ast }$. Often it is definitely not trivial to compute the null-fiber of the Kuranishi map; on the other hand. its quadratic part
$G=\operatorname {Aut}(\mathcal {F})/\mathbb {C}^{\ast }$. Often it is definitely not trivial to compute the null-fiber of the Kuranishi map; on the other hand. its quadratic part ![]() $k_2$ is nothing more than the Yoneda pairing, so that in general it is much easier to understand
$k_2$ is nothing more than the Yoneda pairing, so that in general it is much easier to understand ![]() $k_2^{-1}(0)$ instead of
$k_2^{-1}(0)$ instead of ![]() $k^{-1}(0)$. In [Reference Kaledin and LehnKL07], Kaledin and Lehn essentially conjectured that for a polystable sheaf on a K3 surface the Kuranishi map is quadratic, namely
$k^{-1}(0)$. In [Reference Kaledin and LehnKL07], Kaledin and Lehn essentially conjectured that for a polystable sheaf on a K3 surface the Kuranishi map is quadratic, namely ![]() $k_2^{-1}(0)\cong k^{-1}(0)$. If this condition is satisfied then the moduli space, locally around
$k_2^{-1}(0)\cong k^{-1}(0)$. If this condition is satisfied then the moduli space, locally around ![]() $[\mathcal {F}]$, is isomorphic to the geometric invariant theory quotient
$[\mathcal {F}]$, is isomorphic to the geometric invariant theory quotient ![]() $k^{-1}_2(0)\! // \! G$.
$k^{-1}_2(0)\! // \! G$.
In their original paper Kaledin and Lehn gave a first example motivating and inspiring the future work on the subject. The conjecture was then proven in full generality by Yoshioka [Reference YoshiokaYos17], and partially by Arbarello and Saccà [Reference Arbarello and SaccàAS18]. Let us make a few remarks before continuing. First, recall that to any (homotopy class of a) DG Lie algebra there is associated a deformation functor (see, for example, [Reference ManettiMan09, Reference ManettiMan20]), which in turn provides a Kuranishi map via the Maurer–Cartan equation. Moreover, if the DG Lie algebra ![]() $L$ is formal (i.e. it is quasi-isomorphic to its cohomology) then the associated Kuranishi space
$L$ is formal (i.e. it is quasi-isomorphic to its cohomology) then the associated Kuranishi space ![]() $k^{-1}(0)$ is the null-fiber of the cup product in cohomology
$k^{-1}(0)$ is the null-fiber of the cup product in cohomology ![]() $H^1(L)\to H^2(L)$. Hence, by showing the formality of the DG Lie algebra
$H^1(L)\to H^2(L)$. Hence, by showing the formality of the DG Lie algebra ![]() $R\operatorname {Hom}(\mathcal {F},\mathcal {F})$ one also proves the quadraticity of the Kuranishi map. Notice that since our approach involves techniques of
$R\operatorname {Hom}(\mathcal {F},\mathcal {F})$ one also proves the quadraticity of the Kuranishi map. Notice that since our approach involves techniques of ![]() $L_{\infty }$-algebras we investigate derived endomorphisms as a DG Lie algebra, while the papers [Reference Kaledin and LehnKL07, Reference Budur and ZhangBZ18] consider
$L_{\infty }$-algebras we investigate derived endomorphisms as a DG Lie algebra, while the papers [Reference Kaledin and LehnKL07, Reference Budur and ZhangBZ18] consider ![]() $R\operatorname {Hom}(\mathcal {F},\mathcal {F})$ as an associative DG algebra and also Kaledin's refinement of the Massey products works in the associative setting [Reference KaledinKal07]. It is important to point out that the formality in the associative case is a stronger statement, but on the other hand the DG Lie formality is the one needed for applications to moduli spaces.
$R\operatorname {Hom}(\mathcal {F},\mathcal {F})$ as an associative DG algebra and also Kaledin's refinement of the Massey products works in the associative setting [Reference KaledinKal07]. It is important to point out that the formality in the associative case is a stronger statement, but on the other hand the DG Lie formality is the one needed for applications to moduli spaces.
It is worth mentioning that formality is in general much stronger and harder to prove than the quadraticity property; from the point of view of derived algebraic geometry this can be easily understood since formality implies that the derived moduli space is locally quadratic. Nevertheless, formality of ![]() $R\operatorname {Hom}(\mathcal {F},\mathcal {F})$ has been conjectured for polystable sheaves again by Kaledin and Lehn in [Reference Kaledin and LehnKL07], it has been studied in some cases by Zhang [Reference ZhangZha12], and finally completely solved by Budur and Zhang [Reference Budur and ZhangBZ18] who proved that the conjecture holds true for any polystable sheaf using results about strong uniqueness of DG enhancements.
$R\operatorname {Hom}(\mathcal {F},\mathcal {F})$ has been conjectured for polystable sheaves again by Kaledin and Lehn in [Reference Kaledin and LehnKL07], it has been studied in some cases by Zhang [Reference ZhangZha12], and finally completely solved by Budur and Zhang [Reference Budur and ZhangBZ18] who proved that the conjecture holds true for any polystable sheaf using results about strong uniqueness of DG enhancements.
It is interesting to notice that all of the above-cited formality results actually rely on the famous result due to Kaledin about formality in families [Reference KaledinKal07, Reference LuntsLun10]. Even if the vanishing of Massey products does not guarantee the formality of a DG algebra ![]() $A$ (see, for example, [Reference Halperin and StasheffHS79]), Kaledin determined a refinement of them defining the so-called Kaledin class in a certain (reduced) Hochschild homology group depending on
$A$ (see, for example, [Reference Halperin and StasheffHS79]), Kaledin determined a refinement of them defining the so-called Kaledin class in a certain (reduced) Hochschild homology group depending on ![]() $A$. Furthermore, he proved that the variation of such a class in a suitable family of DG algebras
$A$. Furthermore, he proved that the variation of such a class in a suitable family of DG algebras ![]() $\mathcal {A}\to S$ over an irreducible base
$\mathcal {A}\to S$ over an irreducible base ![]() $S$ glues to a global section of a certain obstruction bundle
$S$ glues to a global section of a certain obstruction bundle ![]() $\mathcal {O} b_S$ defined on
$\mathcal {O} b_S$ defined on ![]() $S$. It follows that if
$S$. It follows that if ![]() $\mathcal {O} b_S$ does not admit non-trivial global sections then all the fibers
$\mathcal {O} b_S$ does not admit non-trivial global sections then all the fibers ![]() $\mathcal {A}_s$ are formal [Reference KaledinKal07, Theorem 4.3].
$\mathcal {A}_s$ are formal [Reference KaledinKal07, Theorem 4.3].
Applying Kaledin's result and twistor spaces, in the paper [Reference Kaledin and LehnKL07] Kaledin and Lehn first obtained the formality of ![]() $R\mspace {-2mu}\operatorname {Hom}(\mathcal {F},\mathcal {F})$ for sheaves of the form
$R\mspace {-2mu}\operatorname {Hom}(\mathcal {F},\mathcal {F})$ for sheaves of the form ![]() $\mathcal {F}=\mathcal {I}_Z^{\oplus n}$, where
$\mathcal {F}=\mathcal {I}_Z^{\oplus n}$, where ![]() $\mathcal {I}_Z$ denotes the ideal sheaf of some zero-dimensional closed subscheme
$\mathcal {I}_Z$ denotes the ideal sheaf of some zero-dimensional closed subscheme ![]() $Z$. Later, Zhang showed that Kaledin's theorem may be applied to polystable sheaves with some constraints on the ranks of the corresponding stable summands [Reference ZhangZha12, Proposition 1.3], hence enlarging the class of polystable sheaves for which the formality conjecture holds. Eventually in [Reference Budur and ZhangBZ18] Budur and Zhang established a very interesting result, namely that the formality of derived endomorphisms of any object in
$Z$. Later, Zhang showed that Kaledin's theorem may be applied to polystable sheaves with some constraints on the ranks of the corresponding stable summands [Reference ZhangZha12, Proposition 1.3], hence enlarging the class of polystable sheaves for which the formality conjecture holds. Eventually in [Reference Budur and ZhangBZ18] Budur and Zhang established a very interesting result, namely that the formality of derived endomorphisms of any object in ![]() $D^b(X)$ is preserved under derived equivalences; hence the formality conjecture follows since by [Reference YoshiokaYos09] any polystable sheaf can be mapped via a Fourier–Mukai transform to another polystable sheaf satisfying the hypothesis of [Reference ZhangZha12, Proposition 3.1].
$D^b(X)$ is preserved under derived equivalences; hence the formality conjecture follows since by [Reference YoshiokaYos09] any polystable sheaf can be mapped via a Fourier–Mukai transform to another polystable sheaf satisfying the hypothesis of [Reference ZhangZha12, Proposition 3.1].
In our recent paper [Reference Bandiera, Manetti and MeazziniBMM20], we proved that for a sheaf ![]() $\mathcal {F}$ whose automorphisms group is reductive (e.g. for any
$\mathcal {F}$ whose automorphisms group is reductive (e.g. for any ![]() $\mathcal {F}$ polystable), the quadraticity of the Kuranishi map and the formality of the DG Lie algebra
$\mathcal {F}$ polystable), the quadraticity of the Kuranishi map and the formality of the DG Lie algebra ![]() $R\operatorname {Hom}(\mathcal {F},\mathcal {F})$ are in fact equivalent conditions; our proof has the advantage of relaxing the hypothesis on the surface which no longer needs to be a K3. This provides further evidence of the formality conjecture without involving powerful methods of DG category theory, but instead relying on the work of Yoshioka [Reference YoshiokaYos17] and of Arbarello and Saccà [Reference Arbarello and SaccàAS18]. Actually, both the papers [Reference Arbarello and SaccàAS18, Reference YoshiokaYos17] base their proofs of the quadraticity property on the fundamental work [Reference ZhangZha12], hence again Kaledin's theorem [Reference KaledinKal07] seems to be essential.
$R\operatorname {Hom}(\mathcal {F},\mathcal {F})$ are in fact equivalent conditions; our proof has the advantage of relaxing the hypothesis on the surface which no longer needs to be a K3. This provides further evidence of the formality conjecture without involving powerful methods of DG category theory, but instead relying on the work of Yoshioka [Reference YoshiokaYos17] and of Arbarello and Saccà [Reference Arbarello and SaccàAS18]. Actually, both the papers [Reference Arbarello and SaccàAS18, Reference YoshiokaYos17] base their proofs of the quadraticity property on the fundamental work [Reference ZhangZha12], hence again Kaledin's theorem [Reference KaledinKal07] seems to be essential.
The present paper aims to prove the formality conjecture for polystable sheaves on a smooth minimal projective surface of Kodaira dimension ![]() $0$. Examples of such surfaces include projective K3 surfaces, Enriques surfaces, bielliptic surfaces and Abelian surfaces [Reference Barth, Hulek, Peters and van de VenBHPV04, Reference BeauvilleBea94]. One of the main innovations of our proof is that we translate the problem into a purely algebraic statement (see Theorem 3.8) about the formality of DG Lie algebras endowed with some additional structure (see Definition 3.6), which will be proved using only elementary techniques of (strong homotopic) DG Lie algebras. In particular, perhaps surprisingly, in the case of K3 and Abelian surfaces our proof of the formality conjecture only requires a basic knowledge of
$0$. Examples of such surfaces include projective K3 surfaces, Enriques surfaces, bielliptic surfaces and Abelian surfaces [Reference Barth, Hulek, Peters and van de VenBHPV04, Reference BeauvilleBea94]. One of the main innovations of our proof is that we translate the problem into a purely algebraic statement (see Theorem 3.8) about the formality of DG Lie algebras endowed with some additional structure (see Definition 3.6), which will be proved using only elementary techniques of (strong homotopic) DG Lie algebras. In particular, perhaps surprisingly, in the case of K3 and Abelian surfaces our proof of the formality conjecture only requires a basic knowledge of ![]() $L_\infty$ algebras and is self-contained, meaning that it does not involve either Kaledin's result about formality in families or the geometric situations considered by Zhang in [Reference ZhangZha12]. As pointed out by one of the referees, it is similar in spirit to Neisendorfer and Miller's proof of the fact that any six-dimensional simply connected Poincaré duality space is formal [Reference Neisendorfer and MillerNM78].
$L_\infty$ algebras and is self-contained, meaning that it does not involve either Kaledin's result about formality in families or the geometric situations considered by Zhang in [Reference ZhangZha12]. As pointed out by one of the referees, it is similar in spirit to Neisendorfer and Miller's proof of the fact that any six-dimensional simply connected Poincaré duality space is formal [Reference Neisendorfer and MillerNM78].
The plan of the paper is as follows. In § 2 we fix notation and briefly summarize the results needed in the rest of the paper about formality and ![]() $L_{\infty }$ algebras. In § 3 we introduce the notion of quasi-cyclic DG Lie algebras and discuss examples arising from geometric situations: a DG Lie algebra
$L_{\infty }$ algebras. In § 3 we introduce the notion of quasi-cyclic DG Lie algebras and discuss examples arising from geometric situations: a DG Lie algebra ![]() $(L,d,[-,-])$ with finite-dimensional cohomology equipped with a degree
$(L,d,[-,-])$ with finite-dimensional cohomology equipped with a degree ![]() $-n$ symmetric bilinear form
$-n$ symmetric bilinear form ![]() $(-,-)\colon L^{\odot 2}\to \mathbb {K}[-n]$ is called quasi-cyclic of degree
$(-,-)\colon L^{\odot 2}\to \mathbb {K}[-n]$ is called quasi-cyclic of degree ![]() $n$ provided that
$n$ provided that
and the form induced in cohomology ![]() $(-,-)\colon H(L)^{\odot 2} \to \mathbb {K}[-n]$ is non-degenerate.
$(-,-)\colon H(L)^{\odot 2} \to \mathbb {K}[-n]$ is non-degenerate.
The typical example of a quasi-cyclic DG Lie algebra of degree ![]() $n$ is given by the Dolbeault resolution
$n$ is given by the Dolbeault resolution ![]() $L=A^{0,*}_X({{\mathcal {H}}om}(\mathcal {E},\mathcal {E}))$ of the sheaf of endomorphisms of a locally free sheaf
$L=A^{0,*}_X({{\mathcal {H}}om}(\mathcal {E},\mathcal {E}))$ of the sheaf of endomorphisms of a locally free sheaf ![]() $\mathcal {E}$ on an
$\mathcal {E}$ on an ![]() $n$-dimensional manifold
$n$-dimensional manifold ![]() $X$ equipped with a nowhere vanishing holomorphic volume form
$X$ equipped with a nowhere vanishing holomorphic volume form ![]() $\omega _X$, with the pairing
$\omega _X$, with the pairing ![]() $(f,g)=\int _X \omega _X\wedge \operatorname {Tr}(fg)$; see Example 3.7. A similar construction can be also performed when
$(f,g)=\int _X \omega _X\wedge \operatorname {Tr}(fg)$; see Example 3.7. A similar construction can be also performed when ![]() $\mathcal {E}$ is replaced by any coherent sheaf; see § 5.
$\mathcal {E}$ is replaced by any coherent sheaf; see § 5.
Then § 4 is entirely devoted to the proof of our main algebraic result.
Theorem 1.2 (=Theorem 3.8) Let ![]() $(L,d,[-,-],(-,-))$ be a quasi-cyclic DG Lie algebra of degree
$(L,d,[-,-],(-,-))$ be a quasi-cyclic DG Lie algebra of degree ![]() $n\leqslant 2$. Assume that there exists a splitting
$n\leqslant 2$. Assume that there exists a splitting ![]() $L=H\oplus d(K)\oplus K$ such that:
$L=H\oplus d(K)\oplus K$ such that:
(i)
 $H^i=0$ for
$H^i=0$ for  $i<0$ (and hence also
$i<0$ (and hence also  $H^i=0$ for
$H^i=0$ for  $i>n$);
$i>n$);(ii)
 $H^0\subset L^0$ is closed with respect to the bracket
$H^0\subset L^0$ is closed with respect to the bracket  $[-,-]$;
$[-,-]$;(iii)
 $H^i,K^i\subset L^i$ are
$H^i,K^i\subset L^i$ are  $H^0$-submodules (with respect to the adjoint action) for all
$H^0$-submodules (with respect to the adjoint action) for all  $i>0$.
$i>0$.
Then the DG Lie algebra ![]() $(L,d,[-,-])$ is formal.
$(L,d,[-,-])$ is formal.
Finally, in § 5 we discuss the applications to moduli spaces of sheaves on minimal projective surfaces of Kodaira dimension 0. We will first prove the formality conjecture for polystable sheaves on K3 and Abelian surfaces as an immediate consequence of Theorem 1.2, where the polystability assumption ensures the existence of the splitting with the required properties.
Then we will extend the formality result to polystable sheaves on surfaces with torsion canonical bundle. Here the idea is to use the cyclic covering trick in order to construct the DG Lie algebra ![]() $R\mspace {-2mu}\operatorname {Hom}_X(\mathcal {F},\mathcal {F})$ as a subalgebra of a suitable quasi-cyclic DG Lie algebra satisfying the assumptions of Theorem 1.2 and then use the formality transfer theorem due to the second named author [Reference ManettiMan15, Theorem 3.4].
$R\mspace {-2mu}\operatorname {Hom}_X(\mathcal {F},\mathcal {F})$ as a subalgebra of a suitable quasi-cyclic DG Lie algebra satisfying the assumptions of Theorem 1.2 and then use the formality transfer theorem due to the second named author [Reference ManettiMan15, Theorem 3.4].
2. Review of formality and minimal models of DG Lie algebras
We work over a field ![]() $\mathbb {K}$ of characteristic
$\mathbb {K}$ of characteristic ![]() $0$ for the algebraic part and over the field
$0$ for the algebraic part and over the field ![]() $\mathbb {C}$ of complex numbers for the geometric applications. Every complex of vector spaces is intended as a cochain complex.
$\mathbb {C}$ of complex numbers for the geometric applications. Every complex of vector spaces is intended as a cochain complex.
By definition a DG Lie algebra ![]() $L$ is formal if it is quasi-isomorphic to its cohomology DG Lie algebra
$L$ is formal if it is quasi-isomorphic to its cohomology DG Lie algebra ![]() $H^*(L)$, equipped with the trivial differential and the induced bracket. In order to avoid possible mistakes, it is useful to keep in mind that not every DG Lie algebra is formal and that if
$H^*(L)$, equipped with the trivial differential and the induced bracket. In order to avoid possible mistakes, it is useful to keep in mind that not every DG Lie algebra is formal and that if ![]() $L$ is formal, then in general there does not exist any direct quasi-isomorphism of DG Lie algebras
$L$ is formal, then in general there does not exist any direct quasi-isomorphism of DG Lie algebras ![]() $H^*(L)\to L$. However, since the category of DG Lie algebras admits a model structure where the fibrations (respectively, the weak equivalences) are the surjective maps (respectively, the quasi-isomorphisms) it follows that a DG Lie algebra
$H^*(L)\to L$. However, since the category of DG Lie algebras admits a model structure where the fibrations (respectively, the weak equivalences) are the surjective maps (respectively, the quasi-isomorphisms) it follows that a DG Lie algebra ![]() $L$ is formal if and only if there exists a span of surjective quasi-isomorphisms of DG Lie algebras
$L$ is formal if and only if there exists a span of surjective quasi-isomorphisms of DG Lie algebras ![]() $L\xleftarrow {}M\xrightarrow {}H^*(L)$.
$L\xleftarrow {}M\xrightarrow {}H^*(L)$.
Since two DG Lie algebras are quasi-isomorphic if and only if they are weak equivalent as ![]() $L_{\infty }$ algebras, we also have that a DG Lie algebra
$L_{\infty }$ algebras, we also have that a DG Lie algebra ![]() $L$ is formal if and only if there exist an
$L$ is formal if and only if there exist an ![]() $L_{\infty }$ algebra
$L_{\infty }$ algebra ![]() $H$ and a span of
$H$ and a span of ![]() $L_{\infty }$ weak equivalences
$L_{\infty }$ weak equivalences
We assume that the reader is familiar with the notion and basic properties of ![]() $L_{\infty }$ algebras; see, for example, [Reference GetzlerGet09, Reference KontsevichKon03, Reference Lada and MarklLM95, Reference Lada and StasheffLS93, Reference ManettiMan20]. For the reader's convenience and to fix the sign convention, we briefly recall here the definition of
$L_{\infty }$ algebras; see, for example, [Reference GetzlerGet09, Reference KontsevichKon03, Reference Lada and MarklLM95, Reference Lada and StasheffLS93, Reference ManettiMan20]. For the reader's convenience and to fix the sign convention, we briefly recall here the definition of ![]() $L_{\infty }$ algebra in the version used for the explicit computations that we shall perform in § 4.
$L_{\infty }$ algebra in the version used for the explicit computations that we shall perform in § 4.
Let ![]() $V$ be a graded vector space. Given homogeneous vectors
$V$ be a graded vector space. Given homogeneous vectors ![]() $v_1,\ldots ,v_n$ of
$v_1,\ldots ,v_n$ of ![]() $V$ and a permutation
$V$ and a permutation ![]() $\sigma$ of
$\sigma$ of ![]() $\{1,\ldots ,n\}$, we denote by
$\{1,\ldots ,n\}$, we denote by ![]() $\chi (\sigma ;v_1,\ldots ,v_n)=\pm 1$ the antisymmetric Koszul sign, defined by the relation
$\chi (\sigma ;v_1,\ldots ,v_n)=\pm 1$ the antisymmetric Koszul sign, defined by the relation
in the ![]() $n$th exterior power
$n$th exterior power ![]() $V^{\wedge n}$. We shall simply write
$V^{\wedge n}$. We shall simply write ![]() $\chi (\sigma )$ instead of
$\chi (\sigma )$ instead of ![]() $\chi (\sigma ;v_1,\ldots ,v_n)$ when the vectors
$\chi (\sigma ;v_1,\ldots ,v_n)$ when the vectors ![]() $v_1,\ldots ,v_n$ are clear from the context. For instance, if
$v_1,\ldots ,v_n$ are clear from the context. For instance, if ![]() $\sigma$ is the transposition exchanging 1 and 2 we have
$\sigma$ is the transposition exchanging 1 and 2 we have ![]() $\chi (\sigma )=-(-1)^{|v_1|\,|v_2|}$ where
$\chi (\sigma )=-(-1)^{|v_1|\,|v_2|}$ where ![]() $|v|$ denotes the degree of the homogeneous vector
$|v|$ denotes the degree of the homogeneous vector ![]() $v$. Notice that if every
$v$. Notice that if every ![]() $v_i$ has odd degree, then
$v_i$ has odd degree, then ![]() $\chi (\sigma )=1$ for every
$\chi (\sigma )=1$ for every ![]() $\sigma$.
$\sigma$.
Because of the universal property of wedge powers, we shall constantly interpret every linear map ![]() $V^{\wedge p}\to W$ as a graded skew-symmetric
$V^{\wedge p}\to W$ as a graded skew-symmetric ![]() $p$-linear map
$p$-linear map ![]() $V\times \cdots \times V\to W$.
$V\times \cdots \times V\to W$.
Definition 2.1 An ![]() $L_{\infty }$ algebra is the data of a graded vector space
$L_{\infty }$ algebra is the data of a graded vector space ![]() $V$ together with a sequence of (multi)linear maps
$V$ together with a sequence of (multi)linear maps ![]() $\{\cdots \}_n\colon V^{\wedge n}\to V$,
$\{\cdots \}_n\colon V^{\wedge n}\to V$, ![]() $n\geqslant 1$, such that for every
$n\geqslant 1$, such that for every ![]() $n$:
$n$:
(i)
 $\{\cdots \}_n$ has degree
$\{\cdots \}_n$ has degree  $2-n$;
$2-n$;(ii) for every
 $v_1,\ldots ,v_n\in V$ homogeneous,
(2.2)where
$v_1,\ldots ,v_n\in V$ homogeneous,
(2.2)where \begin{equation} \sum_{k=1}^n(-1)^{n-k}\sum_{\sigma\in S(k,n-k)}\chi(\sigma)\, \{\{v_{\sigma(1)},\ldots,v_{\sigma(k)}\}_k,v_{\sigma(k+1)},\ldots,v_{\sigma(n)}\}_{n-k+1}=0, \end{equation}
\begin{equation} \sum_{k=1}^n(-1)^{n-k}\sum_{\sigma\in S(k,n-k)}\chi(\sigma)\, \{\{v_{\sigma(1)},\ldots,v_{\sigma(k)}\}_k,v_{\sigma(k+1)},\ldots,v_{\sigma(n)}\}_{n-k+1}=0, \end{equation} $S(k,n-k)=\{\sigma \in S_n\mid \sigma (i)<\sigma (i+1),\ \forall \, i\neq k \}$ is the set of
$S(k,n-k)=\{\sigma \in S_n\mid \sigma (i)<\sigma (i+1),\ \forall \, i\neq k \}$ is the set of  $(k,n-k)$-shuffles.
$(k,n-k)$-shuffles.
In the above definition we used the sign convention of [Reference GetzlerGet09, Reference KontsevichKon03, Reference ManettiMan20], while in [Reference Lada and MarklLM95, Reference Lada and StasheffLS93] the maps ![]() $\{\cdots \}_k$ differ by the sign
$\{\cdots \}_k$ differ by the sign ![]() $(-1)^{k(k-1)/2}$. Every DG Lie algebra
$(-1)^{k(k-1)/2}$. Every DG Lie algebra ![]() $(L,d,[-,-])$ is an
$(L,d,[-,-])$ is an ![]() $L_{\infty }$ algebra where
$L_{\infty }$ algebra where ![]() $\{\cdot \}_1=d$,
$\{\cdot \}_1=d$, ![]() $\{\cdot \,\cdot \}_2=[-,-]$ and
$\{\cdot \,\cdot \}_2=[-,-]$ and ![]() $\{\cdots \}_n=0$ for every
$\{\cdots \}_n=0$ for every ![]() $n>2$. If
$n>2$. If ![]() $\{\cdot \}_1=0$ the
$\{\cdot \}_1=0$ the ![]() $L_{\infty }$ algebra is called minimal.
$L_{\infty }$ algebra is called minimal.
There exists a general notion of ![]() $L_{\infty }$ morphism (see, for example, [Reference ManettiMan20]), but for simplicity of exposition we only recall here the case of morphisms from an
$L_{\infty }$ morphism (see, for example, [Reference ManettiMan20]), but for simplicity of exposition we only recall here the case of morphisms from an ![]() $L_{\infty }$ algebra to a DG Lie algebra; this particular case will be sufficient for our purposes.
$L_{\infty }$ algebra to a DG Lie algebra; this particular case will be sufficient for our purposes.
Definition 2.2 Let ![]() $(V,\{\cdot \}_1,\{\cdot \,\cdot \}_2,\{\cdots \}_3,\ldots )$ be an
$(V,\{\cdot \}_1,\{\cdot \,\cdot \}_2,\{\cdots \}_3,\ldots )$ be an ![]() $L_{\infty }$ algebra and
$L_{\infty }$ algebra and ![]() $(L,d,[-,-])$ a DG Lie algebra. An
$(L,d,[-,-])$ a DG Lie algebra. An ![]() $L_{\infty }$ morphism
$L_{\infty }$ morphism ![]() $g\colon V\to L$ is a sequence of maps
$g\colon V\to L$ is a sequence of maps ![]() $g_n\colon V^{\wedge n}\to L$,
$g_n\colon V^{\wedge n}\to L$, ![]() $n\geqslant 1$, with
$n\geqslant 1$, with ![]() $g_n$ of degree
$g_n$ of degree ![]() $1-n$ such that, for every
$1-n$ such that, for every ![]() $n$ and every
$n$ and every ![]() $v_1,\ldots ,v_n\in V$ homogeneous, we have
$v_1,\ldots ,v_n\in V$ homogeneous, we have
 \begin{align*} &\frac{1}{2}\sum_{p=1}^{n-1} \!\!\!\!\!\sum_{\quad\sigma\in S(p,n-p)}\chi(\sigma) (-1)^{(1-n+p)(|v_{\sigma(1)}|+\cdots+ |v_{\sigma(p)}|-p)} [g_p(v_{\sigma(1)},\ldots, v_{\sigma(p)}),\vphantom{\sum} g_{n-p}(v_{\sigma(p+1)},\ldots,v_{\sigma(n)})]\\ &\quad +dg_n(v_1,\ldots,v_n)= \sum_{k=1}^{n}(-1)^{n-k}\sum_{\sigma\in S(k,n-k)}\chi(\sigma)g_{n-k+1}(\{v_{\sigma(1)},\ldots,v_{\sigma(k)}\}_k,\ldots,v_{\sigma(n)}).\end{align*}
\begin{align*} &\frac{1}{2}\sum_{p=1}^{n-1} \!\!\!\!\!\sum_{\quad\sigma\in S(p,n-p)}\chi(\sigma) (-1)^{(1-n+p)(|v_{\sigma(1)}|+\cdots+ |v_{\sigma(p)}|-p)} [g_p(v_{\sigma(1)},\ldots, v_{\sigma(p)}),\vphantom{\sum} g_{n-p}(v_{\sigma(p+1)},\ldots,v_{\sigma(n)})]\\ &\quad +dg_n(v_1,\ldots,v_n)= \sum_{k=1}^{n}(-1)^{n-k}\sum_{\sigma\in S(k,n-k)}\chi(\sigma)g_{n-k+1}(\{v_{\sigma(1)},\ldots,v_{\sigma(k)}\}_k,\ldots,v_{\sigma(n)}).\end{align*} An ![]() $L_{\infty }$ morphism
$L_{\infty }$ morphism ![]() $g$ as in Definition 2.2 is called a weak equivalence or a quasi-isomorphism if
$g$ as in Definition 2.2 is called a weak equivalence or a quasi-isomorphism if ![]() $g_1\colon (V,\{\cdot \}_1)\to (L,d)$ is a quasi-isomorphism of cochain complexes.
$g_1\colon (V,\{\cdot \}_1)\to (L,d)$ is a quasi-isomorphism of cochain complexes.
By homotopy classification of ![]() $L_{\infty }$ algebras [Reference KontsevichKon03], for every DG Lie algebra
$L_{\infty }$ algebras [Reference KontsevichKon03], for every DG Lie algebra ![]() $L$ there exist a minimal
$L$ there exist a minimal ![]() $L_{\infty }$ algebra
$L_{\infty }$ algebra ![]() $H$ and an
$H$ and an ![]() $L_{\infty }$ weak equivalence
$L_{\infty }$ weak equivalence ![]() $\imath \colon H\to L$. The algebra
$\imath \colon H\to L$. The algebra ![]() $H$ is called the
$H$ is called the ![]() $L_{\infty }$ minimal model of
$L_{\infty }$ minimal model of ![]() $L$ and it is unique up to isomorphism, while the
$L$ and it is unique up to isomorphism, while the ![]() $L_{\infty }$ morphism
$L_{\infty }$ morphism ![]() $i$ is unique up to homotopy. By homological perturbation theory, every splitting of the complex
$i$ is unique up to homotopy. By homological perturbation theory, every splitting of the complex ![]() $(L,d)$ induces canonically a morphism
$(L,d)$ induces canonically a morphism ![]() $\imath \colon H\to L$ as above.
$\imath \colon H\to L$ as above.
Recall that a splitting of ![]() $(L,d)$ is a direct sum decomposition
$(L,d)$ is a direct sum decomposition ![]() $L=H\oplus d(K)\oplus K$ such that
$L=H\oplus d(K)\oplus K$ such that ![]() $H,K$ are graded vector subspaces of
$H,K$ are graded vector subspaces of ![]() $L$ and the restrictions of the differential
$L$ and the restrictions of the differential ![]() $d$ to
$d$ to ![]() $H$ and
$H$ and ![]() $K$ are respectively zero and injective; see [Reference WeibelWei94, § 1.4]. In particular,
$K$ are respectively zero and injective; see [Reference WeibelWei94, § 1.4]. In particular, ![]() $d(L)=d(K)$,
$d(L)=d(K)$, ![]() $Z(L)=H\oplus d(K)$ and the natural map
$Z(L)=H\oplus d(K)$ and the natural map ![]() $H\to H^*(L)$ is an isomorphism of graded vector spaces. Denoting by
$H\to H^*(L)$ is an isomorphism of graded vector spaces. Denoting by ![]() $\hookrightarrow$ and
$\hookrightarrow$ and ![]() $\twoheadrightarrow$ the inclusions and the projections given by the splitting
$\twoheadrightarrow$ the inclusions and the projections given by the splitting ![]() $L=H\oplus d(K)\oplus K$, we define the maps
$L=H\oplus d(K)\oplus K$, we define the maps
that satisfy the contraction identities
Then a minimal ![]() $L_{\infty }$ algebra
$L_{\infty }$ algebra ![]() $(H,0,\{\cdot \,\cdot \}_2,\{\cdots \}_3,\ldots )$ and an extension of
$(H,0,\{\cdot \,\cdot \}_2,\{\cdots \}_3,\ldots )$ and an extension of ![]() $\imath _1$ to an
$\imath _1$ to an ![]() $L_{\infty }$ quasi-isomorphism
$L_{\infty }$ quasi-isomorphism ![]() $\imath \colon H\to L$ are defined by the recursive equations
$\imath \colon H\to L$ are defined by the recursive equations
 \begin{align} \imath_p(\xi_1,\ldots,\xi_p) = \frac{1}{2}\sum_{k=1}^{p-1}\sum_{\sigma\in S(k,p-k)}\chi(\sigma)(-1)^{\alpha(\sigma)} h[\imath_k(\xi_{\sigma(1)},\ldots),\imath_{p-k}(\ldots,\xi_{\sigma(p)})],\quad p\geqslant2, \end{align}
\begin{align} \imath_p(\xi_1,\ldots,\xi_p) = \frac{1}{2}\sum_{k=1}^{p-1}\sum_{\sigma\in S(k,p-k)}\chi(\sigma)(-1)^{\alpha(\sigma)} h[\imath_k(\xi_{\sigma(1)},\ldots),\imath_{p-k}(\ldots,\xi_{\sigma(p)})],\quad p\geqslant2, \end{align} \begin{align} \{\xi_1,\ldots,\xi_p\}_p = \frac{1}{2}\sum_{k=1}^{p-1}\sum_{\sigma\in S(k,p-k)} \chi(\sigma)(-1)^{\alpha(\sigma)} \pi[\imath_k(\xi_{\sigma(1)},\ldots),\imath_{p-k}(\ldots,\xi_{\sigma(p)})], \quad p\geqslant2, \end{align}
\begin{align} \{\xi_1,\ldots,\xi_p\}_p = \frac{1}{2}\sum_{k=1}^{p-1}\sum_{\sigma\in S(k,p-k)} \chi(\sigma)(-1)^{\alpha(\sigma)} \pi[\imath_k(\xi_{\sigma(1)},\ldots),\imath_{p-k}(\ldots,\xi_{\sigma(p)})], \quad p\geqslant2, \end{align}where
 \[ \alpha(\sigma)=(1-p+k)\bigg(k+\sum_{i=1}^k|\xi_{\sigma(i)}|\bigg). \]
\[ \alpha(\sigma)=(1-p+k)\bigg(k+\sum_{i=1}^k|\xi_{\sigma(i)}|\bigg). \]
Notice that for every ![]() $\xi ,\eta \in H$ we have
$\xi ,\eta \in H$ we have
the integer ![]() $\alpha (\sigma )$ is even for
$\alpha (\sigma )$ is even for ![]() $p=2$ and
$p=2$ and ![]() $\chi (\sigma )(-1)^{\alpha (\sigma )}=1$ if
$\chi (\sigma )(-1)^{\alpha (\sigma )}=1$ if ![]() $|\xi _i|$ is odd for every
$|\xi _i|$ is odd for every ![]() $i$. Formulas (2.3) and (2.4) are well known and essentially date back to Kadeishvili's paper [Reference KadeishviliKad82]: the choice of signs comes from standard décalage isomorphisms applied to the explicit formulas used in [Reference Bandiera and ManettiBM18, Theorem 3.7] and [Reference ManettiMan20].
$i$. Formulas (2.3) and (2.4) are well known and essentially date back to Kadeishvili's paper [Reference KadeishviliKad82]: the choice of signs comes from standard décalage isomorphisms applied to the explicit formulas used in [Reference Bandiera and ManettiBM18, Theorem 3.7] and [Reference ManettiMan20].
In [Reference ManettiMan15] the second named author proved a series of formality criteria for DG Lie algebras. As a consequence of these criteria we have the following formality transfer theorem, where ![]() $H_{CE}^*(A,B)$ denotes the Chevalley–Eilenberg cohomology of the graded Lie algebra
$H_{CE}^*(A,B)$ denotes the Chevalley–Eilenberg cohomology of the graded Lie algebra ![]() $A$ with coefficient in the
$A$ with coefficient in the ![]() $A$-module
$A$-module ![]() $B$.
$B$.
Theorem 2.3 [Reference ManettiMan15, Theorem 3.4]
Let ![]() $f\colon M\to L$ be a morphism of DG Lie algebras. Assume that
$f\colon M\to L$ be a morphism of DG Lie algebras. Assume that
(i)
 $L$ is formal;
$L$ is formal;(ii) the induced map
 $f\colon H^2_{CE}(H^*(M),H^*(M))\to H^2_{CE}(H^*(M),H^*(L))$ is injective.
$f\colon H^2_{CE}(H^*(M),H^*(M))\to H^2_{CE}(H^*(M),H^*(L))$ is injective.
Then ![]() $M$ is also formal. In particular, if
$M$ is also formal. In particular, if ![]() $L$ is formal,
$L$ is formal, ![]() $f$ is injective and
$f$ is injective and ![]() $f(M)$ is a direct summand of
$f(M)$ is a direct summand of ![]() $L$ as
$L$ as ![]() $M$-module, then
$M$-module, then ![]() $M$ is also formal.
$M$ is also formal.
It should be noted that for ![]() $L=0$ the above theorem reduces to the classical criterion for intrinsic formality of graded Lie algebras.
$L=0$ the above theorem reduces to the classical criterion for intrinsic formality of graded Lie algebras.
3. Cyclic and quasi-cyclic DG Lie algebras
The general notion of cyclic (DG) algebra [Reference Getzler and KapranovGK95] specialized to DG Lie algebras gives the following definition; see also [Reference Lazarev and SchedlerLS12].
Definition 3.1 Let ![]() $n$ be an integer. A cyclic DG Lie algebra
$n$ be an integer. A cyclic DG Lie algebra ![]() $(L,d,[-,-],(-,-))$ of degree
$(L,d,[-,-],(-,-))$ of degree ![]() $n$ is a finite-dimensional DG Lie algebra
$n$ is a finite-dimensional DG Lie algebra ![]() $(L,d,[-,-])$ equipped with a degree
$(L,d,[-,-])$ equipped with a degree ![]() $-n$ non-degenerate graded symmetric bilinear form
$-n$ non-degenerate graded symmetric bilinear form ![]() $(-,-)\colon L^{\odot 2}\to \mathbb {K}[-n]$ such that
$(-,-)\colon L^{\odot 2}\to \mathbb {K}[-n]$ such that
The condition ![]() $({{d} x},y)=\pm (x,{{d} y})$ implies in particular that
$({{d} x},y)=\pm (x,{{d} y})$ implies in particular that ![]() $d(L)^{\perp }=\ker (d)$; since
$d(L)^{\perp }=\ker (d)$; since ![]() $L$ is finite-dimensional we have
$L$ is finite-dimensional we have ![]() $d(L)=\ker (d)^{\perp }$, and this implies that also the induced bilinear form in the cohomology
$d(L)=\ker (d)^{\perp }$, and this implies that also the induced bilinear form in the cohomology ![]() $H^*(L)$ is non-degenerate.
$H^*(L)$ is non-degenerate.
Example 3.2 Symplectic representations Let ![]() $(V,\omega )$ be a finite-dimensional symplectic vector space and let
$(V,\omega )$ be a finite-dimensional symplectic vector space and let ![]() $\mathfrak {g}$ be a finite-dimensional Lie algebra. Recall that a left action
$\mathfrak {g}$ be a finite-dimensional Lie algebra. Recall that a left action
is called symplectic if for every ![]() $v,w\in V$ and every
$v,w\in V$ and every ![]() $g\in \mathfrak {g}$ we have
$g\in \mathfrak {g}$ we have
There exists a natural correspondence between (isomorphism classes of) symplectic representations and (isomorphism classes of) cyclic DG Lie algebras of degree 2 with trivial differential and without elements of negative degree: given a symplectic action as above, consider the graded Lie algebra ![]() $L=H(L)=L^0\oplus L^1\oplus L^2$ whose cyclic Lie structure is defined as follows.
$L=H(L)=L^0\oplus L^1\oplus L^2$ whose cyclic Lie structure is defined as follows.
(i)
 $L^0=\mathfrak {g}$,
$L^0=\mathfrak {g}$,  $L^1=V$, and
$L^1=V$, and  $L^2=\mathfrak {g}^{\vee }=\operatorname {Hom}_{\mathbb {K}}(\mathfrak {g},\mathbb {K})$.
$L^2=\mathfrak {g}^{\vee }=\operatorname {Hom}_{\mathbb {K}}(\mathfrak {g},\mathbb {K})$.(ii) The Lie bracket is defined by
–
 $[g,v]=gv$ for every
$[g,v]=gv$ for every  $g\in L^0$,
$g\in L^0$,  $v\in L^1$,
$v\in L^1$,–
 $[v,w] \colon h\mapsto \omega (hv,w)$ for every
$[v,w] \colon h\mapsto \omega (hv,w)$ for every  $v,w\in L^1$,
$v,w\in L^1$,  $h\in \mathfrak {g}$,
$h\in \mathfrak {g}$,–
 $[g,y]\colon h\mapsto y([h,g]_{\mathfrak {g}})$ for every
$[g,y]\colon h\mapsto y([h,g]_{\mathfrak {g}})$ for every  $g,h\in \mathfrak {g}$,
$g,h\in \mathfrak {g}$,  $y\in \mathfrak {g}^{\vee }$.
$y\in \mathfrak {g}^{\vee }$.
(iii) The pairing is defined by
–
 $(-,-)\colon L^0\times L^2\to \mathbb {K}$ is the natural pairing,
$(-,-)\colon L^0\times L^2\to \mathbb {K}$ is the natural pairing,–
 $(v,w)=\omega (v,w)$ for every
$(v,w)=\omega (v,w)$ for every  $v,w\in L^1$.
$v,w\in L^1$.
The relations below easily follow from the above conditions:
 \begin{gather*} (h,[g,y]_L)=([h,g]_{\mathfrak{g}},y) \quad \mbox{for every } h,g\in L^0,\, y\in L^2,\\(g,[v,w]_L)=\omega(gv,w)=\omega([g,v]_L,w) \quad \mbox{for every } g\in L^0,\, v,w\in L^1. \end{gather*}
\begin{gather*} (h,[g,y]_L)=([h,g]_{\mathfrak{g}},y) \quad \mbox{for every } h,g\in L^0,\, y\in L^2,\\(g,[v,w]_L)=\omega(gv,w)=\omega([g,v]_L,w) \quad \mbox{for every } g\in L^0,\, v,w\in L^1. \end{gather*}Moreover, the equalities
show that the symplectic condition ![]() $\omega (gv,w)+\omega (v,gw)=0$ is equivalent to the cyclicity condition
$\omega (gv,w)+\omega (v,gw)=0$ is equivalent to the cyclicity condition ![]() $(g,[v,w])=([g,v],w)$. The proof that the data
$(g,[v,w])=([g,v],w)$. The proof that the data ![]() $(L,0,[-,-],(-,-))$ defined above provides an example of a cyclic DG Lie algebra of degree 2 is now straightforward.
$(L,0,[-,-],(-,-))$ defined above provides an example of a cyclic DG Lie algebra of degree 2 is now straightforward.
Notice that the Maurer–Cartan functional ![]() $\frac {1}{2}[v,v]$ coincides by definition with the moment map
$\frac {1}{2}[v,v]$ coincides by definition with the moment map ![]() $\mu \colon V\to \mathfrak {g}^{\vee }$ of the symplectic representation.
$\mu \colon V\to \mathfrak {g}^{\vee }$ of the symplectic representation.
Example 3.3 Consider the following complex of vector spaces in degrees 0,1,2:
equipped with the bilinear form ![]() $(-,-)\colon L^{\odot 2}\to \mathbb {K}[-2]$, where the only nontrivial products between basis vectors are
$(-,-)\colon L^{\odot 2}\to \mathbb {K}[-2]$, where the only nontrivial products between basis vectors are
Next consider the bracket ![]() $[-,-]\colon L^{\wedge 2}\to L$, where the only nontrivial brackets between basis vectors are
$[-,-]\colon L^{\wedge 2}\to L$, where the only nontrivial brackets between basis vectors are
The next proposition summarizes the properties or the above example that are relevant for this paper.
Proposition 3.4 In the above setup:
(i)
 $L$ is a cyclic DG Lie algebra of degree 2;
$L$ is a cyclic DG Lie algebra of degree 2;(ii)
 $L$ is not a formal DG Lie algebra;
$L$ is not a formal DG Lie algebra;(iii) there does not exist any splitting
 $L=H\oplus d(K)\oplus K$ such that
$L=H\oplus d(K)\oplus K$ such that  $[H^0,H^1]\subset H^1$.
$[H^0,H^1]\subset H^1$.
Proof. The first item is a tedious but straightforward computation. For the second item we observe that the triple Massey power of ![]() $x$ is non-trivial since
$x$ is non-trivial since ![]() $dp=[x,x]$ and
$dp=[x,x]$ and ![]() $[p,x]=z$. The third item is clear since for every splitting there exists
$[p,x]=z$. The third item is clear since for every splitting there exists ![]() $\alpha \in \mathbb {K}$ such that
$\alpha \in \mathbb {K}$ such that ![]() $x+\alpha db\in H^1$ and therefore
$x+\alpha db\in H^1$ and therefore ![]() $[a,x+\alpha db]=[a,x]=db\not \in H^1$.
$[a,x+\alpha db]=[a,x]=db\not \in H^1$.
Example 3.5 Consider the following complex of vector spaces in degrees 1,2:
equipped with the closed bilinear form ![]() $(-,-)\colon L^{\odot 2}\to \mathbb {K}[-3]$, where the only non-trivial products between basis vectors are
$(-,-)\colon L^{\odot 2}\to \mathbb {K}[-3]$, where the only non-trivial products between basis vectors are ![]() $(a,x)=(b,db)=1$. Next consider the bracket
$(a,x)=(b,db)=1$. Next consider the bracket ![]() $[-,-]\colon L^{\wedge 2}\to L$, where the only non-trivial brackets between basis vectors are
$[-,-]\colon L^{\wedge 2}\to L$, where the only non-trivial brackets between basis vectors are ![]() $[a,a]=db$,
$[a,a]=db$, ![]() $[a,b]=x$. The same argument used in the proof of Proposition 3.4 shows that
$[a,b]=x$. The same argument used in the proof of Proposition 3.4 shows that ![]() $L$ is a cyclic non-formal DG Lie algebra of degree 3.
$L$ is a cyclic non-formal DG Lie algebra of degree 3.
It is useful to enlarge the class of cyclic DG Lie algebras by removing the assumption that ![]() $L$ is finite-dimensional, which is not satisfied in most geometrical situations. The same weakening of assumption was considered by Kontsevich [Reference KontsevichKon94] in the associative case.
$L$ is finite-dimensional, which is not satisfied in most geometrical situations. The same weakening of assumption was considered by Kontsevich [Reference KontsevichKon94] in the associative case.
Definition 3.6 A quasi-cyclic DG Lie algebra ![]() $(L,d,[-,-],(-,-))$ of degree
$(L,d,[-,-],(-,-))$ of degree ![]() $n$ is a DG Lie algebra
$n$ is a DG Lie algebra ![]() $(L,d,[-,-])$ with finite-dimensional cohomology, together with a degree
$(L,d,[-,-])$ with finite-dimensional cohomology, together with a degree ![]() $-n$ symmetric bilinear form
$-n$ symmetric bilinear form ![]() $(-,-)\colon L^{\odot 2}\to \mathbb {K}[-n]$ which satisfies
$(-,-)\colon L^{\odot 2}\to \mathbb {K}[-n]$ which satisfies
and such that the induced form ![]() $(-,-)\colon H(L)^{\odot 2} \to \mathbb {K}[-n]$ is non-degenerate.
$(-,-)\colon H(L)^{\odot 2} \to \mathbb {K}[-n]$ is non-degenerate.
If ![]() $(L,d,[-,-],(-,-))$ is a quasi-cyclic DG Lie algebra then its cohomology
$(L,d,[-,-],(-,-))$ is a quasi-cyclic DG Lie algebra then its cohomology ![]() $H^*(L)$ is naturally endowed with a structure of cyclic graded Lie algebra of the same degree.
$H^*(L)$ is naturally endowed with a structure of cyclic graded Lie algebra of the same degree.
Example 3.7 Vector bundles on manifolds with trivial canonical bundle Let ![]() $\mathcal {E}$ be a locally free sheaf of a smooth complex projective manifold
$\mathcal {E}$ be a locally free sheaf of a smooth complex projective manifold ![]() $X$ of dimension
$X$ of dimension ![]() $n$ with trivial canonical bundle, and denote by
$n$ with trivial canonical bundle, and denote by ![]() $\omega _X$ be a holomorphic volume form. Then the Dolbeault complex
$\omega _X$ be a holomorphic volume form. Then the Dolbeault complex
of the sheaf of endomorphisms of ![]() $\mathcal {E}$ is a quasi-cyclic DG Lie algebra of degree
$\mathcal {E}$ is a quasi-cyclic DG Lie algebra of degree ![]() $n$, where
$n$, where
We have ![]() $H^i(L)=\operatorname {Ext}^i_X(\mathcal {E},\mathcal {E})$ and by Serre duality the induced pairing
$H^i(L)=\operatorname {Ext}^i_X(\mathcal {E},\mathcal {E})$ and by Serre duality the induced pairing
is non-degenerate. In § 5 we extend this construction to coherent sheaves.
We are now ready to state one of the main results of this paper, namely a sufficient condition for formality of quasi-cyclic DG Lie algebras of degree at most ![]() $2$.
$2$.
Theorem 3.8 Let ![]() $(L,d,[-,-],(-,-))$ be a quasi-cyclic DG Lie algebra of degree
$(L,d,[-,-],(-,-))$ be a quasi-cyclic DG Lie algebra of degree ![]() $n\leqslant 2$. Assume that there exists a splitting
$n\leqslant 2$. Assume that there exists a splitting ![]() $L=H\oplus d(K)\oplus K$ such that:
$L=H\oplus d(K)\oplus K$ such that:
(i)
 $H^i=0$ for
$H^i=0$ for  $i<0$ (and hence also
$i<0$ (and hence also  $H^i=0$ for
$H^i=0$ for  $i>n$);
$i>n$);(ii)
 $H^0\subset L^0$ is closed with respect to the bracket
$H^0\subset L^0$ is closed with respect to the bracket  $[-,-]$;
$[-,-]$;(iii)
 $H^i,K^i\subset L^i$ are
$H^i,K^i\subset L^i$ are  $H^0$-submodules (with respect to the adjoint action) for all
$H^0$-submodules (with respect to the adjoint action) for all  $i>0$.
$i>0$.
Then the DG Lie algebra ![]() $(L,d,[-,-])$ is formal.
$(L,d,[-,-])$ is formal.
For ![]() $n\leqslant 0$ the above theorem is trivial since
$n\leqslant 0$ the above theorem is trivial since ![]() $H^i=0$ for every
$H^i=0$ for every ![]() $i>0$ and then the embedding
$i>0$ and then the embedding ![]() $H^0\to L$ is a quasi-isomorphism of DG Lie algebras. The next section will be entirely devoted to the (long) proof in the case
$H^0\to L$ is a quasi-isomorphism of DG Lie algebras. The next section will be entirely devoted to the (long) proof in the case ![]() $n=2$, whose first step also provides a complete proof for
$n=2$, whose first step also provides a complete proof for ![]() $n=1$. Examples 3.5 and 3.3 show that formality fails if either
$n=1$. Examples 3.5 and 3.3 show that formality fails if either ![]() $n>2$ or without the assumption (iii), even for cyclic DG Lie algebras.
$n>2$ or without the assumption (iii), even for cyclic DG Lie algebras.
4. Proof of Theorem 3.8
Let ![]() $(L,d,[-,-],(-,-))$ be as in Theorem 3.8. If
$(L,d,[-,-],(-,-))$ be as in Theorem 3.8. If ![]() $A,B$ are two subsets of
$A,B$ are two subsets of ![]() $L$ we shall write
$L$ we shall write ![]() $A\perp B$ if
$A\perp B$ if ![]() $(x,y)=0$ for every
$(x,y)=0$ for every ![]() $x\in A$,
$x\in A$, ![]() $y\in B$. For instance, it follows immediately from the relation
$y\in B$. For instance, it follows immediately from the relation ![]() $({{d} x},y)=(-1)^{|x|+1}(x,{{d} y})$ that
$({{d} x},y)=(-1)^{|x|+1}(x,{{d} y})$ that ![]() $d(K)\perp d(K)$ and
$d(K)\perp d(K)$ and ![]() $H\perp d(K)$.
$H\perp d(K)$.
Lemma 4.1 Up to a possible restriction to a quasi-isomorphic DG Lie subalgebra of ![]() $L$ we may assume that the splitting
$L$ we may assume that the splitting ![]() $L=H\oplus d(K)\oplus K$ satisfies the following conditions:
$L=H\oplus d(K)\oplus K$ satisfies the following conditions:
(i)
 $H^i=0$ for
$H^i=0$ for  $i<0$;
$i<0$;(ii)
 $H^0\subset L^0$ is closed with respect to the bracket
$H^0\subset L^0$ is closed with respect to the bracket  $[-,-]$;
$[-,-]$;(iii)
 $H^i,K^i\subset L^i$ are
$H^i,K^i\subset L^i$ are  $H^0$-submodules (with respect to the adjoint action) for all
$H^0$-submodules (with respect to the adjoint action) for all  $i\in \mathbb {Z}$;
$i\in \mathbb {Z}$;(iv)
 $H\perp K$.
$H\perp K$.
Proof. Since ![]() $H^i=0$ for every
$H^i=0$ for every ![]() $i<0$ the DG Lie subalgebra
$i<0$ the DG Lie subalgebra
is quasi-cyclic and quasi-isomorphic to ![]() $L$. This proves that, up to a possible restriction to a quasi-isomorphic DG Lie subalgebra, it is not restrictive to assume the validity of condition (iii). Next, for every integer
$L$. This proves that, up to a possible restriction to a quasi-isomorphic DG Lie subalgebra, it is not restrictive to assume the validity of condition (iii). Next, for every integer ![]() $i$ consider the vector subspace
$i$ consider the vector subspace
Since ![]() $(-,-)\colon H^i\times H^{n-i}\to \mathbb {K}$ is a perfect pairing, the map
$(-,-)\colon H^i\times H^{n-i}\to \mathbb {K}$ is a perfect pairing, the map
 \[ \begin{aligned} H^i\oplus C^i & \to H^i\oplus K^i \\ (h_1,h_2,k) & \mapsto (h_1-h_2,k) \end{aligned} \]
\[ \begin{aligned} H^i\oplus C^i & \to H^i\oplus K^i \\ (h_1,h_2,k) & \mapsto (h_1-h_2,k) \end{aligned} \]
is an isomorphism. If ![]() $x\in C^i$ and
$x\in C^i$ and ![]() $a\in H^0$, then
$a\in H^0$, then ![]() $[a,x]\in H^i\oplus K^i$; for every
$[a,x]\in H^i\oplus K^i$; for every ![]() $y\in H^{n-i}$ we have
$y\in H^{n-i}$ we have ![]() $(y,[a,x])=([y,a],x)=0$ and therefore
$(y,[a,x])=([y,a],x)=0$ and therefore ![]() $[a,x]\in C^i$. Finally, replacing
$[a,x]\in C^i$. Finally, replacing ![]() $K^i$ with
$K^i$ with ![]() $C^i$, we may assume
$C^i$, we may assume ![]() $H\perp K$.
$H\perp K$.
For later use it should be pointed out that the non-degeneracy of ![]() $(-,-)\colon H^{\odot 2}\to \mathbb {K}$ immediately implies
$(-,-)\colon H^{\odot 2}\to \mathbb {K}$ immediately implies
From now on we assume that ![]() $(L,d,[-,-],(-,-))$ is a quasi-cyclic DG Lie algebra of degree
$(L,d,[-,-],(-,-))$ is a quasi-cyclic DG Lie algebra of degree ![]() $n\leqslant 2$ equipped with a splitting
$n\leqslant 2$ equipped with a splitting ![]() $L=H\oplus d(K)\oplus K$ satisfying the conditions of Lemma 4.1. The fist step is to use such a splitting in order to produce a minimal
$L=H\oplus d(K)\oplus K$ satisfying the conditions of Lemma 4.1. The fist step is to use such a splitting in order to produce a minimal ![]() $L_{\infty }$ model of
$L_{\infty }$ model of ![]() $L$. Following the recipe described in § 2, we introduce the maps
$L$. Following the recipe described in § 2, we introduce the maps
that satisfy the relations
The first one is obvious and the second one follows from the orthogonality condition ![]() $H\perp K$. Since
$H\perp K$. Since ![]() $\operatorname {Im}(\imath _1)=H$,
$\operatorname {Im}(\imath _1)=H$, ![]() $\operatorname {Im}(h)=K$ and
$\operatorname {Im}(h)=K$ and ![]() $H\perp d(K)\oplus K$, the first two imply the third:
$H\perp d(K)\oplus K$, the first two imply the third:
The maps ![]() $\imath _1,\pi ,h$ induce via homotopy transfer a minimal
$\imath _1,\pi ,h$ induce via homotopy transfer a minimal ![]() $L_\infty$-algebra structure on
$L_\infty$-algebra structure on ![]() $H$, together with an
$H$, together with an ![]() $L_\infty$ quasi-isomorphism
$L_\infty$ quasi-isomorphism ![]() $\imath \colon H(L)\to L$ of
$\imath \colon H(L)\to L$ of ![]() $L_\infty$-algebras with linear part
$L_\infty$-algebras with linear part ![]() $\imath _1$. The quadratic components are given by
$\imath _1$. The quadratic components are given by
while the higher brackets ![]() $\{\cdots \}_p\colon H^{\wedge p}\to H[2-p]$ and the higher Taylor coefficients
$\{\cdots \}_p\colon H^{\wedge p}\to H[2-p]$ and the higher Taylor coefficients ![]() $\imath _p\colon H^{\wedge p}\to L[1-p]$,
$\imath _p\colon H^{\wedge p}\to L[1-p]$, ![]() $p\geqslant 2$, are explicitly (and recursively) defined by
$p\geqslant 2$, are explicitly (and recursively) defined by
 \begin{align} \imath_p(\xi_1,\ldots,\xi_p) = \frac{1}{2}\sum_{k=1}^{p-1}\sum_{\sigma\in S(k,p-k)} \pm\, h[\imath_k(\xi_\sigma(1),\ldots),\imath_{p-k}(\ldots,\xi_{\sigma(p)})], \end{align}
\begin{align} \imath_p(\xi_1,\ldots,\xi_p) = \frac{1}{2}\sum_{k=1}^{p-1}\sum_{\sigma\in S(k,p-k)} \pm\, h[\imath_k(\xi_\sigma(1),\ldots),\imath_{p-k}(\ldots,\xi_{\sigma(p)})], \end{align} \begin{align} \{\xi_1,\ldots,\xi_p\}_p = \frac{1}{2}\sum_{k=1}^{p-1}\sum_{\sigma\in S(k,p-k)} \pm\, \pi[\imath_k(\xi_\sigma(1),\ldots),\imath_{p-k}(\ldots,\xi_{\sigma(p)})], \end{align}
\begin{align} \{\xi_1,\ldots,\xi_p\}_p = \frac{1}{2}\sum_{k=1}^{p-1}\sum_{\sigma\in S(k,p-k)} \pm\, \pi[\imath_k(\xi_\sigma(1),\ldots),\imath_{p-k}(\ldots,\xi_{\sigma(p)})], \end{align}
where ![]() $\pm$ is the appropriate Koszul sign described explicitly in (2.3) and (2.4). These signs will simplify in our specific case, for instance
$\pm$ is the appropriate Koszul sign described explicitly in (2.3) and (2.4). These signs will simplify in our specific case, for instance ![]() $\pm 1=+1$ whenever
$\pm 1=+1$ whenever ![]() $\xi _i\in H^1$ for every
$\xi _i\in H^1$ for every ![]() $i$, and we do not need to make them explicit.
$i$, and we do not need to make them explicit.
Notice that ![]() $\{a,b\}_2=[a,b]$ for
$\{a,b\}_2=[a,b]$ for ![]() $a,b\in H^0$ and under the natural isomorphism
$a,b\in H^0$ and under the natural isomorphism ![]() $H\cong H^*(L)$, the quadratic bracket
$H\cong H^*(L)$, the quadratic bracket ![]() $\{x,y\}_2=\pi [\imath _1(x),\imath _1(y)]$ on
$\{x,y\}_2=\pi [\imath _1(x),\imath _1(y)]$ on ![]() $H$ is just the bracket induced by
$H$ is just the bracket induced by ![]() $[-,-]$ in cohomology.
$[-,-]$ in cohomology.
Lemma 4.2 In the above setup, for every ![]() $p\geqslant 2$ and every
$p\geqslant 2$ and every ![]() $g\in H^0$ we have
$g\in H^0$ we have
Proof. If ![]() $g\in H^0$, then
$g\in H^0$, then ![]() $[\imath _1(g),\imath _1(\xi )]\in H \subset \operatorname {Ker}(h)$ for all
$[\imath _1(g),\imath _1(\xi )]\in H \subset \operatorname {Ker}(h)$ for all ![]() $\xi \in H$, since
$\xi \in H$, since ![]() $H$ is an
$H$ is an ![]() $H^0$-submodule of
$H^0$-submodule of ![]() $L$, thus
$L$, thus ![]() $\imath _2(g,\xi )=0$ for all
$\imath _2(g,\xi )=0$ for all ![]() $g\in H^0$ and
$g\in H^0$ and ![]() $\xi \in H$. In general, by formulas (4.2), (4.3) and induction on
$\xi \in H$. In general, by formulas (4.2), (4.3) and induction on ![]() $p$, for all
$p$, for all ![]() $p\geqslant 2$,
$p\geqslant 2$, ![]() $g\in H^0$ and
$g\in H^0$ and ![]() $\xi _1,\ldots ,\xi _p\in H$, we have
$\xi _1,\ldots ,\xi _p\in H$, we have
Finally, notice that for ![]() $p\geqslant 2$ we have
$p\geqslant 2$ we have ![]() $\operatorname {Im}(\imath _p)\subset K\subset \operatorname {Ker}(h)\bigcap \operatorname {Ker}(\pi )$, and that
$\operatorname {Im}(\imath _p)\subset K\subset \operatorname {Ker}(h)\bigcap \operatorname {Ker}(\pi )$, and that ![]() $K$ is by hypothesis an
$K$ is by hypothesis an ![]() $H^0$-submodule of
$H^0$-submodule of ![]() $L$. This implies that
$L$. This implies that ![]() $[\imath _p(\xi _1,\ldots ,\xi _p),\imath _1(g)]\in K$ and therefore
$[\imath _p(\xi _1,\ldots ,\xi _p),\imath _1(g)]\in K$ and therefore
Lemma 4.2 provides a complete proof of formality for ![]() $n=1$, since
$n=1$, since ![]() $H^i=0$ for every
$H^i=0$ for every ![]() $i\not =0,1$ and therefore for degree reasons
$i\not =0,1$ and therefore for degree reasons ![]() $\{\cdots \}_{p+1}=0$ for every
$\{\cdots \}_{p+1}=0$ for every ![]() $p\geqslant 2$. From now on we assume that the degree of the quasi-cyclic DG Lie algebra
$p\geqslant 2$. From now on we assume that the degree of the quasi-cyclic DG Lie algebra ![]() $L$ of Theorem 3.8 is equal to
$L$ of Theorem 3.8 is equal to ![]() $n=2$.
$n=2$.
Lemma 4.3 In the above situation, for every ![]() $\xi _1,\ldots ,\xi _p\in H^1$,
$\xi _1,\ldots ,\xi _p\in H^1$, ![]() $p\geqslant 3$, we have
$p\geqslant 3$, we have
 \begin{gather} \{\xi_1,\ldots,\xi_p\}_p = \frac{1}{2}\sum_{k=2}^{p-2}\ \sum_{\sigma\in S(k,p-k)} \pi[\imath_k(\xi_\sigma(1),\ldots),\imath_{p-k}(\ldots,\xi_{\sigma(p)})], \end{gather}
\begin{gather} \{\xi_1,\ldots,\xi_p\}_p = \frac{1}{2}\sum_{k=2}^{p-2}\ \sum_{\sigma\in S(k,p-k)} \pi[\imath_k(\xi_\sigma(1),\ldots),\imath_{p-k}(\ldots,\xi_{\sigma(p)})], \end{gather}
and therefore ![]() $\{\xi _1,\xi _2,\xi _3\}_3=0$ for every
$\{\xi _1,\xi _2,\xi _3\}_3=0$ for every ![]() $\xi _1,\xi _2,\xi _3\in H^1$.
$\xi _1,\xi _2,\xi _3\in H^1$.
Proof. It is sufficient to prove (4.4). We first note that the image of ![]() $\imath _1$ is contained in
$\imath _1$ is contained in ![]() $H$ and the image of
$H$ and the image of ![]() $\imath _j$ is contained in
$\imath _j$ is contained in ![]() $K$ for every
$K$ for every ![]() $j>1$. Moreover, we can rewrite (4.1) in the form
$j>1$. Moreover, we can rewrite (4.1) in the form ![]() $\pi (x)=0$ if and only if
$\pi (x)=0$ if and only if ![]() $(x,y)=0$ for every
$(x,y)=0$ for every ![]() $y\in H$: now it is sufficient to observe that for any
$y\in H$: now it is sufficient to observe that for any ![]() $g\in H^0$,
$g\in H^0$, ![]() $x\in H^1$ and
$x\in H^1$ and ![]() $y\in K^1$ we have
$y\in K^1$ we have ![]() $(g,[x,y])=([g,x],y)=0$ since
$(g,[x,y])=([g,x],y)=0$ since ![]() $H^1$ is an
$H^1$ is an ![]() $H^0$-module and
$H^0$-module and ![]() $K^1$ is orthogonal to
$K^1$ is orthogonal to ![]() $H^1$.
$H^1$.
For degree reasons, Lemma 4.2 implies that for ![]() $p\geqslant 2$ we have
$p\geqslant 2$ we have ![]() $\{\xi _1,\ldots ,\xi _{p+1}\}_{p+1}=0$ unless
$\{\xi _1,\ldots ,\xi _{p+1}\}_{p+1}=0$ unless ![]() $\xi _1,\ldots ,\xi _{p+1}\in H^1$, and then by Lemma 4.3 we have
$\xi _1,\ldots ,\xi _{p+1}\in H^1$, and then by Lemma 4.3 we have ![]() $\{\cdots \}_3\equiv 0$. However, it should be noted that in general the higher brackets
$\{\cdots \}_3\equiv 0$. However, it should be noted that in general the higher brackets ![]() $\{\cdots \}_p$ will not vanish for
$\{\cdots \}_p$ will not vanish for ![]() $p\geqslant 4$ and therefore the proof of Theorem 3.8 is still very far from concluded.
$p\geqslant 4$ and therefore the proof of Theorem 3.8 is still very far from concluded.
Notation From now on we shall denote by ![]() $\mathfrak {g}$ the Lie algebra
$\mathfrak {g}$ the Lie algebra ![]() $(H^0,\{-,-\})$.
$(H^0,\{-,-\})$.
Now we notice that item (iii) in the hypotheses of Lemma 4.1 implies that the maps ![]() $\imath \colon H\to L$,
$\imath \colon H\to L$, ![]() $\pi \colon L\to H$ and
$\pi \colon L\to H$ and ![]() $h:L\to L[-1]$ are equivariant with respect to the induced
$h:L\to L[-1]$ are equivariant with respect to the induced ![]() $\mathfrak {g}$-module structures.
$\mathfrak {g}$-module structures.
Since ![]() $\imath =(\imath _1,\imath _2,\ldots )$ is a morphism of
$\imath =(\imath _1,\imath _2,\ldots )$ is a morphism of ![]() $L_\infty$ algebras we have
$L_\infty$ algebras we have
 \begin{align*} &\sum_{k=1}^{p}\sum_{\sigma\in S(p+2-k,k-1)} \pm \imath_k(\{\xi_{\sigma(1)},\ldots\}_{p+2-k},\ldots,\xi_{\sigma(p+1)}) \\ &\quad = \pm d\imath_{p+1}(\xi_1,\ldots,\xi_{p+1})+\frac{1}{2}\sum_{j=1}^{p}\sum_{ \sigma\in S(j,p+1-j)}\pm[ \imath_j(\xi_{\sigma(1)},\ldots),\imath_{p+1-j}(\ldots,\xi_{\sigma(p+1)}) ], \end{align*}
\begin{align*} &\sum_{k=1}^{p}\sum_{\sigma\in S(p+2-k,k-1)} \pm \imath_k(\{\xi_{\sigma(1)},\ldots\}_{p+2-k},\ldots,\xi_{\sigma(p+1)}) \\ &\quad = \pm d\imath_{p+1}(\xi_1,\ldots,\xi_{p+1})+\frac{1}{2}\sum_{j=1}^{p}\sum_{ \sigma\in S(j,p+1-j)}\pm[ \imath_j(\xi_{\sigma(1)},\ldots),\imath_{p+1-j}(\ldots,\xi_{\sigma(p+1)}) ], \end{align*}
and taking ![]() $p\geqslant 2$,
$p\geqslant 2$, ![]() $\xi _1,\ldots ,\xi _p\in H^1$,
$\xi _1,\ldots ,\xi _p\in H^1$, ![]() $\xi _{p+1}=g\in \mathfrak {g}$, by Lemma 4.2 the above expression reduces to
$\xi _{p+1}=g\in \mathfrak {g}$, by Lemma 4.2 the above expression reduces to
Notice that formula (4.6) is also trivially satisfied for ![]() $p=1$. For later use it is useful to introduce, for every
$p=1$. For later use it is useful to introduce, for every ![]() $0 < j < p$, the function
$0 < j < p$, the function
Then for every ![]() $0 < j < p$,
$0 < j < p$, ![]() $\xi _1,\ldots ,\xi _p\in H^1$ and
$\xi _1,\ldots ,\xi _p\in H^1$ and ![]() $g\in \mathfrak {g}$, we have
$g\in \mathfrak {g}$, we have
 \begin{equation} \sum_{i=1}^pI_j^p(\xi_1,\ldots,\{\xi_i,g\}_2,\ldots,\xi_p)=0. \end{equation}
\begin{equation} \sum_{i=1}^pI_j^p(\xi_1,\ldots,\{\xi_i,g\}_2,\ldots,\xi_p)=0. \end{equation}
The proof of (4.7) is an immediate consequence of (4.6) together with the identity ![]() $([l_1,\imath _1(g)],l_2)+(l_1,[l_2,\imath _1(g)])=0$ for all
$([l_1,\imath _1(g)],l_2)+(l_1,[l_2,\imath _1(g)])=0$ for all ![]() $g\in \mathfrak {g}$,
$g\in \mathfrak {g}$, ![]() $l_1,l_2\in L^1$. Moreover, the orthogonality condition
$l_1,l_2\in L^1$. Moreover, the orthogonality condition ![]() $H\perp K$ implies that for every
$H\perp K$ implies that for every ![]() $p\geqslant 2$ we have
$p\geqslant 2$ we have ![]() $I^{p+1}_1=I^{p+1}_p=0$.
$I^{p+1}_1=I^{p+1}_p=0$.
Notation We denote by ![]() $\{-,-\}\colon H^*(L)^{\wedge 2}\to H^*(L)$ the Lie bracket induced by the bracket
$\{-,-\}\colon H^*(L)^{\wedge 2}\to H^*(L)$ the Lie bracket induced by the bracket ![]() $[-,-]\colon L^{\wedge 2}\to L$ on
$[-,-]\colon L^{\wedge 2}\to L$ on ![]() $L$. We have already observed that via the natural identification
$L$. We have already observed that via the natural identification ![]() $H=H^*(L)$ we have
$H=H^*(L)$ we have ![]() $\{-,-\}=\{\cdot \,\cdot \}_2$ and it is straightforward to check that it continues to satisfy the condition
$\{-,-\}=\{\cdot \,\cdot \}_2$ and it is straightforward to check that it continues to satisfy the condition ![]() $(\{x,y\},z)=(x,\{y,z\})$ for all
$(\{x,y\},z)=(x,\{y,z\})$ for all ![]() $x,y,z\in H^*(L)$.
$x,y,z\in H^*(L)$.
By homotopy classification of DG Lie and ![]() $L_\infty$ algebras, in order to prove the formality of
$L_\infty$ algebras, in order to prove the formality of ![]() $L$ it is enough to exhibit an
$L$ it is enough to exhibit an ![]() $L_\infty$ isomorphism
$L_\infty$ isomorphism
between ![]() $H$ with the transferred
$H$ with the transferred ![]() $L_\infty$ algebra structure and
$L_\infty$ algebra structure and ![]() $H^*(L)$ with the induced graded Lie algebra structure. Denoting by
$H^*(L)$ with the induced graded Lie algebra structure. Denoting by ![]() $f_p\colon H^{\wedge p}\to H[1-p]$ the Taylor coefficients of
$f_p\colon H^{\wedge p}\to H[1-p]$ the Taylor coefficients of ![]() $f$, the necessary relations these have to satisfy in order for
$f$, the necessary relations these have to satisfy in order for ![]() $f$ to be an
$f$ to be an ![]() $L_\infty$ morphism read
$L_\infty$ morphism read
 \begin{align} &\sum_{k=1}^{p}\sum_{\sigma\in S(p+2-k,k-1)} \pm f_k(\{\xi_{\sigma(1)},\ldots\},\ldots,\xi_{\sigma(p+1)}) \nonumber\\ &\quad = \frac{1}{2}\sum_{j=1}^{p}\sum_{\sigma\in S(j,p+1-j)}\pm\{ f_j(\xi_{\sigma(1)},\ldots),f_{p+1-j}(\ldots,\xi_{\sigma(p+1)}) \} \end{align}
\begin{align} &\sum_{k=1}^{p}\sum_{\sigma\in S(p+2-k,k-1)} \pm f_k(\{\xi_{\sigma(1)},\ldots\},\ldots,\xi_{\sigma(p+1)}) \nonumber\\ &\quad = \frac{1}{2}\sum_{j=1}^{p}\sum_{\sigma\in S(j,p+1-j)}\pm\{ f_j(\xi_{\sigma(1)},\ldots),f_{p+1-j}(\ldots,\xi_{\sigma(p+1)}) \} \end{align}
for all ![]() $p\geqslant 2$ and
$p\geqslant 2$ and ![]() $\xi _1,\ldots ,\xi _{p+1}\in H$. If these are satisfied, for
$\xi _1,\ldots ,\xi _{p+1}\in H$. If these are satisfied, for ![]() $f$ to be an isomorphism of
$f$ to be an isomorphism of ![]() $L_\infty$ algebras it is necessary and sufficient that its linear part
$L_\infty$ algebras it is necessary and sufficient that its linear part ![]() $f_1\colon H\to H$ is an isomorphism of graded spaces. We look for an
$f_1\colon H\to H$ is an isomorphism of graded spaces. We look for an ![]() $L_\infty$ isomorphism
$L_\infty$ isomorphism ![]() $f$ as above such that moreover
$f$ as above such that moreover ![]() $f_1=\operatorname {id}_H$ and
$f_1=\operatorname {id}_H$ and ![]() $f_p(\xi _1,\ldots ,\xi _p)=0$ for
$f_p(\xi _1,\ldots ,\xi _p)=0$ for ![]() $p\geqslant 2$ unless
$p\geqslant 2$ unless ![]() $p\geqslant 3$ and
$p\geqslant 3$ and ![]() $\xi _1,\ldots ,\xi _p\in H^1$. With these hypotheses, many of the previous relations (4.8) become trivial, and the only non-trivial ones we are left to verify are
$\xi _1,\ldots ,\xi _p\in H^1$. With these hypotheses, many of the previous relations (4.8) become trivial, and the only non-trivial ones we are left to verify are
 \begin{gather} \big\{ \xi_1,\ldots,\xi_{p+1} \big\}_{p+1} = \frac{1}{2}\sum_{j=1}^{p}\sum_{\sigma\in S(j,p+1-j)}\big\{ f_j(\xi_{\sigma(1)},\ldots),f_{p+1-j}(\ldots,\xi_{\sigma(p+1)})\big\}, \end{gather}
\begin{gather} \big\{ \xi_1,\ldots,\xi_{p+1} \big\}_{p+1} = \frac{1}{2}\sum_{j=1}^{p}\sum_{\sigma\in S(j,p+1-j)}\big\{ f_j(\xi_{\sigma(1)},\ldots),f_{p+1-j}(\ldots,\xi_{\sigma(p+1)})\big\}, \end{gather}
for all ![]() $p\geqslant 2$,
$p\geqslant 2$, ![]() $\xi _1,\ldots ,\xi _{p+1}\in H^1$ and
$\xi _1,\ldots ,\xi _{p+1}\in H^1$ and ![]() $g\in \mathfrak {g}$ (as in the case of transfer formulas, Koszul signs have disappeared since
$g\in \mathfrak {g}$ (as in the case of transfer formulas, Koszul signs have disappeared since ![]() $|\xi _1|=\cdots =|\xi _{p+1}|=1$). Since
$|\xi _1|=\cdots =|\xi _{p+1}|=1$). Since ![]() $f_2=0$ by definition and we already know that
$f_2=0$ by definition and we already know that ![]() $\{\cdots \}_3=0$, relations (4.9) and (4.10) are trivially satisfied for
$\{\cdots \}_3=0$, relations (4.9) and (4.10) are trivially satisfied for ![]() $p=2$.
$p=2$.
For every ![]() $p\geqslant 3$ and every
$p\geqslant 3$ and every ![]() $1<j<p$, we define recursively the linear maps
$1<j<p$, we define recursively the linear maps
by the formulas
 \begin{gather} \big(f_p(\xi_1,\ldots,\xi_p),\xi_{p+1}\big)= \frac{1}{2} \sum_{j=2}^{p-1}\sum_{\sigma\in S(j,p-j)} (I^{p+1}_j-F^{p+1}_j)(\xi_{\sigma(1)},\ldots,\xi_{\sigma(p)},\xi_{p+1}), \end{gather}
\begin{gather} \big(f_p(\xi_1,\ldots,\xi_p),\xi_{p+1}\big)= \frac{1}{2} \sum_{j=2}^{p-1}\sum_{\sigma\in S(j,p-j)} (I^{p+1}_j-F^{p+1}_j)(\xi_{\sigma(1)},\ldots,\xi_{\sigma(p)},\xi_{p+1}), \end{gather}
for all ![]() $\xi _1,\ldots ,\xi _{p+1}\in H^1$. The validity of (4.9) is proved in the following lemma.
$\xi _1,\ldots ,\xi _{p+1}\in H^1$. The validity of (4.9) is proved in the following lemma.
Lemma 4.4 In the above situation, for every ![]() $p\geqslant 2$, every
$p\geqslant 2$, every ![]() $1 < j < p$, every
$1 < j < p$, every ![]() $\xi _1,\ldots ,\xi _{p+1}\in H^1$ and every
$\xi _1,\ldots ,\xi _{p+1}\in H^1$ and every ![]() $g\in \mathfrak {g}$, we have
$g\in \mathfrak {g}$, we have
 \begin{gather} \sum_{i=1}^{p}f_{p}(\xi_1,\ldots,\{\xi_i,g\},\ldots,\xi_{p})=\{ f_p(\xi_1,\ldots,\xi_p),g \}, \end{gather}
\begin{gather} \sum_{i=1}^{p}f_{p}(\xi_1,\ldots,\{\xi_i,g\},\ldots,\xi_{p})=\{ f_p(\xi_1,\ldots,\xi_p),g \}, \end{gather} \begin{gather} \sum_{i=1}^{p+1}F_j^{p+1}(\xi_1,\ldots,\{\xi_i,g\},\ldots,\xi_{p+1})=0. \end{gather}
\begin{gather} \sum_{i=1}^{p+1}F_j^{p+1}(\xi_1,\ldots,\{\xi_i,g\},\ldots,\xi_{p+1})=0. \end{gather}Proof. The above formula are trivially satisfied for ![]() $p=2$, since
$p=2$, since ![]() $f_2=0$ and (4.14) is empty. Assuming (4.13) valid for all integers smaller than
$f_2=0$ and (4.14) is empty. Assuming (4.13) valid for all integers smaller than ![]() $p$, we have
$p$, we have
 \begin{align*} &\sum_{i=1}^{p+1}F_j^{p+1}(\xi_1,\ldots,\{\xi_i,g\},\ldots,\xi_{p+1})\\ &\quad=(\{f_j(\xi_1,\ldots,\xi_j),g\},f_{p-j-1}(\xi_1,\ldots,\xi_j))+ (f_j(\xi_1,\ldots,\xi_j),\{f_{p-j-1}(\xi_1,\ldots,\xi_j),g\})=0, \end{align*}
\begin{align*} &\sum_{i=1}^{p+1}F_j^{p+1}(\xi_1,\ldots,\{\xi_i,g\},\ldots,\xi_{p+1})\\ &\quad=(\{f_j(\xi_1,\ldots,\xi_j),g\},f_{p-j-1}(\xi_1,\ldots,\xi_j))+ (f_j(\xi_1,\ldots,\xi_j),\{f_{p-j-1}(\xi_1,\ldots,\xi_j),g\})=0, \end{align*}
where the second equality follows from the cyclic condition ![]() $(\{x,g\},y)+(x,\{y,g\})=0$ for all
$(\{x,g\},y)+(x,\{y,g\})=0$ for all ![]() $g\in \mathfrak {g}$ and
$g\in \mathfrak {g}$ and ![]() $x,y\in H^1$. For the same reason we have
$x,y\in H^1$. For the same reason we have
 \begin{align*} \big(\big\{f_p(\xi_1,\ldots,\xi_p),g\big\},\xi_{p+1}\big)&= - \big(f_p(\xi_1,\ldots,\xi_p),\big\{\xi_{p+1},g\big\}\big)\\ &= \Big(- \frac{1}{2}\Big) \sum_{j=2}^{p-1}\sum_{\sigma\in S(j,p-j)} (I^{p+1}_j-F^{p+1}_j)\big(\xi_{\sigma(1)},\ldots,\xi_{\sigma(p)},\big\{\xi_{p+1},g\big\}\big)\\ &=\frac{1}{2}\sum_{i=1}^p\sum_{j=2}^{p-1}\sum_{\sigma\in S(j,p-j)} (I^{p+1}_j-F^{p+1}_j)\big(\xi_{\sigma(1)},\ldots,\big\{\xi_{\sigma(i)},g\big\},\ldots,\xi_{p+1}\big)\\ &=\sum_{h=1}^p \big(f_p(\xi_1,\ldots,\{\xi_h,g\},\ldots,\xi_p),\xi_{p+1}\big), \end{align*}
\begin{align*} \big(\big\{f_p(\xi_1,\ldots,\xi_p),g\big\},\xi_{p+1}\big)&= - \big(f_p(\xi_1,\ldots,\xi_p),\big\{\xi_{p+1},g\big\}\big)\\ &= \Big(- \frac{1}{2}\Big) \sum_{j=2}^{p-1}\sum_{\sigma\in S(j,p-j)} (I^{p+1}_j-F^{p+1}_j)\big(\xi_{\sigma(1)},\ldots,\xi_{\sigma(p)},\big\{\xi_{p+1},g\big\}\big)\\ &=\frac{1}{2}\sum_{i=1}^p\sum_{j=2}^{p-1}\sum_{\sigma\in S(j,p-j)} (I^{p+1}_j-F^{p+1}_j)\big(\xi_{\sigma(1)},\ldots,\big\{\xi_{\sigma(i)},g\big\},\ldots,\xi_{p+1}\big)\\ &=\sum_{h=1}^p \big(f_p(\xi_1,\ldots,\{\xi_h,g\},\ldots,\xi_p),\xi_{p+1}\big), \end{align*}
where in the second and fourth equalities we have used the defining formula (4.12), while the third equality is a consequence of (4.7) and (4.14). Since ![]() $(-,-)$ is non-degenerate in
$(-,-)$ is non-degenerate in ![]() $H^1$, the formula
$H^1$, the formula
 \[ \big(\big\{f_p(\xi_1,\ldots,\xi_p),g\big\},\xi_{p+1}\big)= \sum_{h=1}^p \big(f_p(\xi_1,\ldots,\{\xi_h,g\},\ldots,\xi_p),\xi_{p+1}\big) \]
\[ \big(\big\{f_p(\xi_1,\ldots,\xi_p),g\big\},\xi_{p+1}\big)= \sum_{h=1}^p \big(f_p(\xi_1,\ldots,\{\xi_h,g\},\ldots,\xi_p),\xi_{p+1}\big) \]is completely equivalent to (4.13).
Finally, we prove (4.10), or equivalently that
 \[ 2\big(\big\{ \xi_1,\ldots,\xi_{p+1} \big\}_{p+1},g\big) = \sum_{j=1}^{p}\sum_{\sigma\in S(j,p+1-j)}\big(\big\{ f_j(\xi_{\sigma(1)},\ldots),f_{p+1-j}(\ldots,\xi_{\sigma(p+1)})\big\},g\big), \]
\[ 2\big(\big\{ \xi_1,\ldots,\xi_{p+1} \big\}_{p+1},g\big) = \sum_{j=1}^{p}\sum_{\sigma\in S(j,p+1-j)}\big(\big\{ f_j(\xi_{\sigma(1)},\ldots),f_{p+1-j}(\ldots,\xi_{\sigma(p+1)})\big\},g\big), \]
for every ![]() $\xi _1,\ldots ,\xi _{p+1}\in H^1$ and
$\xi _1,\ldots ,\xi _{p+1}\in H^1$ and ![]() $g\in \mathfrak {g}$. By (4.5) we have
$g\in \mathfrak {g}$. By (4.5) we have
 \begin{align*} 2\big(\big\{ \xi_1,\ldots,\xi_{p+1} \big\}_{p+1}, g \big) &= \sum_{j=2}^{p-1}\sum_{\sigma\in S(j,p+1-j)}\big(\pi\big[ \imath_j\big(\xi_{\sigma(1)},\ldots\big) ,\imath_{p+1-j} \big(\ldots,\xi_{\sigma(p+1)}\big) \big],g\big)\\ &= \sum_{j=2}^{p-1}\sum_{\sigma\in S(j,p+1-j)}\big(\big[ \imath_j\big(\xi_{\sigma(1)},\ldots\big) ,\imath_{p+1-j} \big(\ldots,\xi_{\sigma(p+1)}\big) \big],\imath_1(g)\big) . \end{align*}
\begin{align*} 2\big(\big\{ \xi_1,\ldots,\xi_{p+1} \big\}_{p+1}, g \big) &= \sum_{j=2}^{p-1}\sum_{\sigma\in S(j,p+1-j)}\big(\pi\big[ \imath_j\big(\xi_{\sigma(1)},\ldots\big) ,\imath_{p+1-j} \big(\ldots,\xi_{\sigma(p+1)}\big) \big],g\big)\\ &= \sum_{j=2}^{p-1}\sum_{\sigma\in S(j,p+1-j)}\big(\big[ \imath_j\big(\xi_{\sigma(1)},\ldots\big) ,\imath_{p+1-j} \big(\ldots,\xi_{\sigma(p+1)}\big) \big],\imath_1(g)\big) . \end{align*}
By using the cyclic relation ![]() $([l_1,l_2],l_3)=(l_1,[l_2,l_3])$,
$([l_1,l_2],l_3)=(l_1,[l_2,l_3])$, ![]() $\forall \;l_1,l_2,l_3\in L$, and (4.6) we get
$\forall \;l_1,l_2,l_3\in L$, and (4.6) we get
 \begin{align*} 2\big(\big\{ \xi_1,\ldots,\xi_{p+1} \big\}_{p+1}, g \big) &= \sum_{j=2}^{p-1}\sum_{\sigma\in S(j,p+1-j)}\big(\imath_j\big(\xi_{\sigma(1)},\ldots\big) ,[\imath_{p+1-j} \big(\ldots,\xi_{\sigma(p+1)}\big),\imath(g)]\big) \\ &= \sum_{j=2}^{p-1}\sum_{\sigma\in S(j,p-j,1)}\big( \imath_j\big(\xi_{\sigma(1)}, \ldots\big),\imath_{p+1-j}\big(\ldots,\xi_{\sigma(p)}, \big\{ \xi_{\sigma(p+1)},g \big\}\big) \big)\\ &=\sum_{j=2}^{p-1}\sum_{\sigma\in S(j,p-j,1)}I^{p+1}_j\big(\xi_{\sigma(1)},\ldots, \xi_{\sigma(p)}, \big\{ \xi_{\sigma(p+1)},g \big\}\big), \end{align*}
\begin{align*} 2\big(\big\{ \xi_1,\ldots,\xi_{p+1} \big\}_{p+1}, g \big) &= \sum_{j=2}^{p-1}\sum_{\sigma\in S(j,p+1-j)}\big(\imath_j\big(\xi_{\sigma(1)},\ldots\big) ,[\imath_{p+1-j} \big(\ldots,\xi_{\sigma(p+1)}\big),\imath(g)]\big) \\ &= \sum_{j=2}^{p-1}\sum_{\sigma\in S(j,p-j,1)}\big( \imath_j\big(\xi_{\sigma(1)}, \ldots\big),\imath_{p+1-j}\big(\ldots,\xi_{\sigma(p)}, \big\{ \xi_{\sigma(p+1)},g \big\}\big) \big)\\ &=\sum_{j=2}^{p-1}\sum_{\sigma\in S(j,p-j,1)}I^{p+1}_j\big(\xi_{\sigma(1)},\ldots, \xi_{\sigma(p)}, \big\{ \xi_{\sigma(p+1)},g \big\}\big), \end{align*}
where ![]() $S(j,p-j,1)$ is the set of permutations
$S(j,p-j,1)$ is the set of permutations ![]() $\sigma$ of
$\sigma$ of ![]() $1,\ldots ,p+1$ such that
$1,\ldots ,p+1$ such that
On the other hand,
 \begin{align*} &\sum_{j=1}^{p}\sum_{\sigma\in S(j,p+1-j)}\big( \big\{ f_j(\xi_{\sigma(1)},\ldots),f_{p+1-j}(\ldots, \xi_{\sigma(p+1)})\big\},g\big)\\ &\quad =\sum_{j=1}^{p}\sum_{\sigma\in S(j,p+1-j)} \big( f_j(\xi_{\sigma(1)},\ldots),\{f_{p+1-j}(\ldots,\xi_{\sigma(p+1)}),g\}\big)\\ &\quad = \sum_{j=2}^{p-1}\sum_{\sigma\in S(j,p-j,1)} \big( f_j(\xi_{\sigma(1)},\ldots), \{f_{p+1-j}(\ldots,\xi_{\sigma(p+1)}),g\}\big)\\ &\qquad+\sum_{\sigma\in S(p,1)} \big( f_p\big(\xi_{\sigma(1)},\ldots,\xi_{\sigma(p)}\big), \big\{\xi_{\sigma(p+1)},g\big\} \big). \end{align*}
\begin{align*} &\sum_{j=1}^{p}\sum_{\sigma\in S(j,p+1-j)}\big( \big\{ f_j(\xi_{\sigma(1)},\ldots),f_{p+1-j}(\ldots, \xi_{\sigma(p+1)})\big\},g\big)\\ &\quad =\sum_{j=1}^{p}\sum_{\sigma\in S(j,p+1-j)} \big( f_j(\xi_{\sigma(1)},\ldots),\{f_{p+1-j}(\ldots,\xi_{\sigma(p+1)}),g\}\big)\\ &\quad = \sum_{j=2}^{p-1}\sum_{\sigma\in S(j,p-j,1)} \big( f_j(\xi_{\sigma(1)},\ldots), \{f_{p+1-j}(\ldots,\xi_{\sigma(p+1)}),g\}\big)\\ &\qquad+\sum_{\sigma\in S(p,1)} \big( f_p\big(\xi_{\sigma(1)},\ldots,\xi_{\sigma(p)}\big), \big\{\xi_{\sigma(p+1)},g\big\} \big). \end{align*}Reasoning as before and using the already proved (4.9), we have
 \begin{align*} &\sum_{j=1}^{p}\sum_{\sigma\in S(j,p+1-j)}\big( \big\{ f_j(\xi_{\sigma(1)},\ldots),f_{p+1-j}(\ldots,\xi_{\sigma(p+1)})\big\},g\big)\\ &\quad = \sum_{j=2}^{p-1}\sum_{\sigma\in S(j,p-j,1)} \big( f_j\big(\xi_{\sigma(1)},\ldots \big), f_{p+1-j}\big(\ldots, \xi_{\sigma(p)},\big\{ \xi_{\sigma(p+1)},g\big\}\big) \big)\\ &\qquad+\sum_{\sigma\in S(p,1)} \big( f_p\big(\xi_{\sigma(1)},\ldots,\xi_{\sigma(p)}\big), \big\{\xi_{\sigma(p+1)},g\big\} \big) \\ &\quad = \sum_{j=2}^{p-1}\sum_{\sigma\in S(j,p-j,1)} F^{p+1}_j\big(\xi_{\sigma(1)},\ldots,\xi_{\sigma(p)}, \big\{ \xi_{\sigma(p+1)},g\big\}\big) \\ &\qquad+\sum_{\sigma\in S(p,1)} \big( f_p\big(\xi_{\sigma(1)},\ldots,\xi_{\sigma(p)}\big), \big\{\xi_{\sigma(p+1)},g\big\} \big) \\ &\quad =\sum_{j=2}^{p-1}\sum_{\sigma\in S(j,p-j,1)} I^{p+1}_j\big(\xi_{\sigma(1)},\ldots, \xi_{\sigma(p)}, \big\{ \xi_{\sigma(p+1)},g \big\}\big), \end{align*}
\begin{align*} &\sum_{j=1}^{p}\sum_{\sigma\in S(j,p+1-j)}\big( \big\{ f_j(\xi_{\sigma(1)},\ldots),f_{p+1-j}(\ldots,\xi_{\sigma(p+1)})\big\},g\big)\\ &\quad = \sum_{j=2}^{p-1}\sum_{\sigma\in S(j,p-j,1)} \big( f_j\big(\xi_{\sigma(1)},\ldots \big), f_{p+1-j}\big(\ldots, \xi_{\sigma(p)},\big\{ \xi_{\sigma(p+1)},g\big\}\big) \big)\\ &\qquad+\sum_{\sigma\in S(p,1)} \big( f_p\big(\xi_{\sigma(1)},\ldots,\xi_{\sigma(p)}\big), \big\{\xi_{\sigma(p+1)},g\big\} \big) \\ &\quad = \sum_{j=2}^{p-1}\sum_{\sigma\in S(j,p-j,1)} F^{p+1}_j\big(\xi_{\sigma(1)},\ldots,\xi_{\sigma(p)}, \big\{ \xi_{\sigma(p+1)},g\big\}\big) \\ &\qquad+\sum_{\sigma\in S(p,1)} \big( f_p\big(\xi_{\sigma(1)},\ldots,\xi_{\sigma(p)}\big), \big\{\xi_{\sigma(p+1)},g\big\} \big) \\ &\quad =\sum_{j=2}^{p-1}\sum_{\sigma\in S(j,p-j,1)} I^{p+1}_j\big(\xi_{\sigma(1)},\ldots, \xi_{\sigma(p)}, \big\{ \xi_{\sigma(p+1)},g \big\}\big), \end{align*}
where in the last equality we used the recursive definition (4.12) of ![]() $f_p$. The proof of Theorem 3.8 is now complete.
$f_p$. The proof of Theorem 3.8 is now complete.
Corollary 4.5 Let ![]() $(L,d,[-,-],(-,-))$ be a quasi-cyclic DG Lie algebra of degree
$(L,d,[-,-],(-,-))$ be a quasi-cyclic DG Lie algebra of degree ![]() $2$ with
$2$ with ![]() $H^i(L)=0$ for every
$H^i(L)=0$ for every ![]() $i\not =0,1,2$. Assume that there exists a Lie subalgebra
$i\not =0,1,2$. Assume that there exists a Lie subalgebra ![]() $H^0\subset Z^0(L)$ such that:
$H^0\subset Z^0(L)$ such that:
(i) the projection
 $Z^0(L)\to H^0(L)$ induces an isomorphism
$Z^0(L)\to H^0(L)$ induces an isomorphism  $H^0\simeq H^0(L)$;
$H^0\simeq H^0(L)$;(ii)
 $L^i$ is a completely reducible
$L^i$ is a completely reducible  $H^0$-module (with respect to the adjoint action) for all
$H^0$-module (with respect to the adjoint action) for all  $i$.
$i$.
Then the DG Lie algebra ![]() $(L,d,[-,-])$ is formal.
$(L,d,[-,-])$ is formal.
Proof. Construct a splitting by choosing for every ![]() $i\not =0$ a direct sum decomposition
$i\not =0$ a direct sum decomposition ![]() $Z^i(L)=B^i(L)\oplus H^i$ of
$Z^i(L)=B^i(L)\oplus H^i$ of ![]() $H^0$-modules and then, for every
$H^0$-modules and then, for every ![]() $i$, a direct sum decomposition
$i$, a direct sum decomposition ![]() $L^i=Z^i(L)\oplus K^i$ of
$L^i=Z^i(L)\oplus K^i$ of ![]() $H^0$-modules. This splitting satisfies the conditions of Theorem 3.8.
$H^0$-modules. This splitting satisfies the conditions of Theorem 3.8.
5. Derived endomorphisms and their formality
For every coherent sheaf ![]() $\mathcal {F}$ on a smooth complex projective manifold
$\mathcal {F}$ on a smooth complex projective manifold ![]() $X$ there is a well-defined homotopy class of DG Lie algebras denoted by
$X$ there is a well-defined homotopy class of DG Lie algebras denoted by ![]() $R\mspace {-2mu}\operatorname {Hom}_X(\mathcal {F},\mathcal {F})$ and called, with a little abuse of language, the DG Lie algebra of derived endomorphisms of
$R\mspace {-2mu}\operatorname {Hom}_X(\mathcal {F},\mathcal {F})$ and called, with a little abuse of language, the DG Lie algebra of derived endomorphisms of ![]() $\mathcal {F}$. There exist several possible (quasi-isomorphic) representatives for
$\mathcal {F}$. There exist several possible (quasi-isomorphic) representatives for ![]() $R\mspace {-2mu}\operatorname {Hom}_X(\mathcal {F},\mathcal {F})$, and we refer to [Reference MeazziniMea18] for an explicit and concrete description of many of them. The importance of the DG Lie algebra of derived endomorphisms relies on the fact that it controls the deformation theory of
$R\mspace {-2mu}\operatorname {Hom}_X(\mathcal {F},\mathcal {F})$, and we refer to [Reference MeazziniMea18] for an explicit and concrete description of many of them. The importance of the DG Lie algebra of derived endomorphisms relies on the fact that it controls the deformation theory of ![]() $\mathcal {F}$ in the usual way via Maurer–Cartan equation modulus gauge action; cf. [Reference Arbarello and SaccàAS18, Reference Budur and ZhangBZ18, Reference Iacono and ManettiIM19, Reference MeazziniMea18]. Moreover,
$\mathcal {F}$ in the usual way via Maurer–Cartan equation modulus gauge action; cf. [Reference Arbarello and SaccàAS18, Reference Budur and ZhangBZ18, Reference Iacono and ManettiIM19, Reference MeazziniMea18]. Moreover, ![]() $H^i(R\mspace {-2mu}\operatorname {Hom}_X(\mathcal {F},\mathcal {F}))=\operatorname {Ext}^i(\mathcal {F},\mathcal {F})$ for every
$H^i(R\mspace {-2mu}\operatorname {Hom}_X(\mathcal {F},\mathcal {F}))=\operatorname {Ext}^i(\mathcal {F},\mathcal {F})$ for every ![]() $i$.
$i$.
Since the notion of quasi-cyclic DG Lie algebra is not stable under general quasi-isomorphisms, in view of a possible application of Theorem 3.8 it is useful to consider the Dolbeault representatives for ![]() $R\mspace {-2mu}\operatorname {Hom}_X(\mathcal {F},\mathcal {F})$. Consider a finite locally free resolution
$R\mspace {-2mu}\operatorname {Hom}_X(\mathcal {F},\mathcal {F})$. Consider a finite locally free resolution ![]() $\mathcal {E}^*=\{\cdots \mathcal {E}^{-1}\to \mathcal {E}^0\}\to \mathcal {F}$ and denote by
$\mathcal {E}^*=\{\cdots \mathcal {E}^{-1}\to \mathcal {E}^0\}\to \mathcal {F}$ and denote by
the (DG) sheaf of endomorphisms of ![]() $\mathcal {E}^*$. Then
$\mathcal {E}^*$. Then ![]() ${{\mathcal {H}}om}^*_{\mathcal {O}_X}(\mathcal {E}^*,\mathcal {E}^*)$ is a sheaf of DG Lie algebras over
${{\mathcal {H}}om}^*_{\mathcal {O}_X}(\mathcal {E}^*,\mathcal {E}^*)$ is a sheaf of DG Lie algebras over ![]() $X$. It is important to notice that the bracket
$X$. It is important to notice that the bracket ![]() $[f,g]=fg-(-1)^{|f|\,|g|}gf$ is
$[f,g]=fg-(-1)^{|f|\,|g|}gf$ is ![]() $\mathcal {O}_X$-bilinear and therefore it can be extended naturally to Dolbeault's resolution
$\mathcal {O}_X$-bilinear and therefore it can be extended naturally to Dolbeault's resolution
where ![]() $A^{0,p}_X(\mathcal {G})$ denotes the space of global differential forms of type
$A^{0,p}_X(\mathcal {G})$ denotes the space of global differential forms of type ![]() $(0,q)$ with values in the locally free sheaf
$(0,q)$ with values in the locally free sheaf ![]() $\mathcal {G}$. Similarly, the usual trace map (see, for example, [Reference Iacono and ManettiIM19] and references therein)
$\mathcal {G}$. Similarly, the usual trace map (see, for example, [Reference Iacono and ManettiIM19] and references therein)
is a morphism of sheaves of DG Lie algebras, and extends to a morphism of DG Lie algebras
Since the bracket on ![]() $A^{0,*}_X$ is trivial we have
$A^{0,*}_X$ is trivial we have
for every ![]() $f,g\in L$, and this immediately implies that
$f,g\in L$, and this immediately implies that ![]() $\operatorname {Tr}([f,g]h)=\operatorname {Tr}(f[h,g])$ for every
$\operatorname {Tr}([f,g]h)=\operatorname {Tr}(f[h,g])$ for every ![]() $f,g,h\in L$. If
$f,g,h\in L$. If ![]() $\omega$ is a non-trivial section of the canonical bundle of
$\omega$ is a non-trivial section of the canonical bundle of ![]() $X$, the graded symmetric bilinear form
$X$, the graded symmetric bilinear form
is a cyclic bilinear form, where this means that it satisfies the conditions ![]() $(df,g)+(-1)^{|f|}(f,dg)=0$ and
$(df,g)+(-1)^{|f|}(f,dg)=0$ and ![]() $([f,g],h)=(f,[g,h])$. Finally, if
$([f,g],h)=(f,[g,h])$. Finally, if ![]() $\omega$ is a holomorphic volume form, by Serre duality the above bilinear form is non-degenerate in cohomology and therefore
$\omega$ is a holomorphic volume form, by Serre duality the above bilinear form is non-degenerate in cohomology and therefore ![]() $(L,(-,-))$ is a quasi-cyclic DG Lie algebra of degree
$(L,(-,-))$ is a quasi-cyclic DG Lie algebra of degree ![]() $\dim X$.
$\dim X$.
From now on we consider only coherent sheaves on projective surfaces with torsion canonical bundle. According to the Enriques–Kodaira classification of surfaces (see, for example, [Reference Barth, Hulek, Peters and van de VenBHPV04, Reference BeauvilleBea94]), a smooth projective surface has torsion canonical bundle ![]() $K$ if and only if it is minimal of Kodaira dimension
$K$ if and only if it is minimal of Kodaira dimension ![]() $0$. According to the values of irregularity
$0$. According to the values of irregularity ![]() $q$ and geometric genus
$q$ and geometric genus ![]() $p_g$, these surfaces are classified into four (non-empty) distinguished classes:
$p_g$, these surfaces are classified into four (non-empty) distinguished classes:
– projective K3 surfaces, with
 $q=0$,
$q=0$,  $p_g=1$ and
$p_g=1$ and  $K=0$;
$K=0$;– Enriques surfaces, with
 $q=0$,
$q=0$,  $p_g=0$ and
$p_g=0$ and  $2K=0$;
$2K=0$;– bielliptic surfaces, with
 $q=1$,
$q=1$,  $p_g=0$ and
$p_g=0$ and  $nK=0$ for some
$nK=0$ for some  $n=2,3,4,6$;
$n=2,3,4,6$;– Abelian surfaces, with
 $q=2$,
$q=2$,  $p_g=1$ and
$p_g=1$ and  $K=0$.
$K=0$.
We are now ready to prove the Kaledin–Lehn formality conjecture for the above surfaces, namely that ![]() $R\mspace {-2mu}\operatorname {Hom}_X(\mathcal {F},\mathcal {F})$ is formal whenever
$R\mspace {-2mu}\operatorname {Hom}_X(\mathcal {F},\mathcal {F})$ is formal whenever ![]() $\mathcal {F}$ is polystable with respect to any (possibly non-generic) polarization; see, for example, [Reference Huybrechts and LehnHL10, Chapter 1]. It is useful and instructive to give first a separate proof for the cases of K3 and Abelian surfaces.
$\mathcal {F}$ is polystable with respect to any (possibly non-generic) polarization; see, for example, [Reference Huybrechts and LehnHL10, Chapter 1]. It is useful and instructive to give first a separate proof for the cases of K3 and Abelian surfaces.
Theorem 5.1 Let ![]() $X$ be a complex projective surface with trivial canonical bundle and let
$X$ be a complex projective surface with trivial canonical bundle and let ![]() $\mathcal {F}$ be a coherent sheaf on
$\mathcal {F}$ be a coherent sheaf on ![]() $X$. If the group of automorphisms of
$X$. If the group of automorphisms of ![]() $\mathcal {F}$ is linearly reductive (e.g. if
$\mathcal {F}$ is linearly reductive (e.g. if ![]() $\mathcal {F}$ is polystable), then the DG Lie algebra
$\mathcal {F}$ is polystable), then the DG Lie algebra ![]() $R\mspace {-2mu}\operatorname {Hom}_X(\mathcal {F},\mathcal {F})$ is formal.
$R\mspace {-2mu}\operatorname {Hom}_X(\mathcal {F},\mathcal {F})$ is formal.
Proof. Let us denote by ![]() $G$ the linearly reductive group of automorphisms of
$G$ the linearly reductive group of automorphisms of ![]() $\mathcal {F}$. Since
$\mathcal {F}$. Since ![]() $X$ is smooth projective it is not difficult to see that there exists a
$X$ is smooth projective it is not difficult to see that there exists a ![]() $G$-equivariant finite locally free resolution
$G$-equivariant finite locally free resolution ![]() $\mathcal {E}^*=\{0\to \mathcal {E}^{-2}\to \mathcal {E}^{-1}\to \mathcal {E}^0\}\to \mathcal {F}$; a detailed proof is given, for instance, in [Reference Bandiera, Manetti and MeazziniBMM20]. We claim that the DG Lie algebra
$\mathcal {E}^*=\{0\to \mathcal {E}^{-2}\to \mathcal {E}^{-1}\to \mathcal {E}^0\}\to \mathcal {F}$; a detailed proof is given, for instance, in [Reference Bandiera, Manetti and MeazziniBMM20]. We claim that the DG Lie algebra ![]() $L=A^{0,*}_X({{\mathcal {H}}om}^*_{\mathcal {O}_X}(\mathcal {E}^*,\mathcal {E}^*))$ satisfies the condition of Theorem 3.8, when equipped with the cyclic non-degenerate structure (5.1).
$L=A^{0,*}_X({{\mathcal {H}}om}^*_{\mathcal {O}_X}(\mathcal {E}^*,\mathcal {E}^*))$ satisfies the condition of Theorem 3.8, when equipped with the cyclic non-degenerate structure (5.1).
Assume for the moment that the induced action of ![]() $G$ on
$G$ on ![]() $L^i$ is rational for every
$L^i$ is rational for every ![]() $i$; since the action of
$i$; since the action of ![]() $G$ commutes with the differential of the resolution
$G$ commutes with the differential of the resolution ![]() $\mathcal {E}^*$. we have a natural inclusion
$\mathcal {E}^*$. we have a natural inclusion ![]() $G\subset Z^0(L)$ and we can take
$G\subset Z^0(L)$ and we can take ![]() $H^0=T_{\operatorname {Id}}G\subset Z^0(L)\subset L^0$ as the Lie algebra of
$H^0=T_{\operatorname {Id}}G\subset Z^0(L)\subset L^0$ as the Lie algebra of ![]() $G$. Then, since
$G$. Then, since ![]() $G$ is assumed to be linearly reductive we may extend
$G$ is assumed to be linearly reductive we may extend ![]() $H^0$ to a
$H^0$ to a ![]() $G$-equivariant splitting of
$G$-equivariant splitting of ![]() $L$ that clearly satisfies the hypotheses of Theorem 3.8.
$L$ that clearly satisfies the hypotheses of Theorem 3.8.
It remains to be shown that ![]() $L^i$ is a rational representation of
$L^i$ is a rational representation of ![]() $G$ for every
$G$ for every ![]() $i$. This follows immediately from the results of [Reference Bandiera, Manetti and MeazziniBMM20], and we give here only a sketch of the proof. The key point is that if
$i$. This follows immediately from the results of [Reference Bandiera, Manetti and MeazziniBMM20], and we give here only a sketch of the proof. The key point is that if ![]() $G$ acts on a coherent sheaf
$G$ acts on a coherent sheaf ![]() $\mathcal {G}$ then, for every open affine subset
$\mathcal {G}$ then, for every open affine subset ![]() $U$, the space
$U$, the space ![]() $\mathcal {G}(U)$ is a rational finitely supported representation of
$\mathcal {G}(U)$ is a rational finitely supported representation of ![]() $G$ [Reference Bandiera, Manetti and MeazziniBMM20, Lemma 3.5]. Recall that a representation is finitely supported if it is isomorphic to a finite direct sum
$G$ [Reference Bandiera, Manetti and MeazziniBMM20, Lemma 3.5]. Recall that a representation is finitely supported if it is isomorphic to a finite direct sum ![]() ${\bigoplus _{i=1}^nH_i\otimes W_i}$, for some irreducible rational (hence finite-dimensional) representations
${\bigoplus _{i=1}^nH_i\otimes W_i}$, for some irreducible rational (hence finite-dimensional) representations ![]() $H_i$ and some trivial representations
$H_i$ and some trivial representations ![]() $W_i$; every subrepresentation and every quotient of a rational finitely supported representation remains finitely supported [Reference Bandiera, Manetti and MeazziniBMM20, Lemma 2.7 and Remark 2.8].
$W_i$; every subrepresentation and every quotient of a rational finitely supported representation remains finitely supported [Reference Bandiera, Manetti and MeazziniBMM20, Lemma 2.7 and Remark 2.8].
Let ![]() $X=\bigcup _j U_j$ be a finite open affine cover such that
$X=\bigcup _j U_j$ be a finite open affine cover such that ![]() $\mathcal {E}^*$ is free over
$\mathcal {E}^*$ is free over ![]() $U_j$ for every
$U_j$ for every ![]() $j$. Then
$j$. Then ![]() $\Gamma \big (U_j,{{\mathcal {H}}om}^*_{\mathcal {O}_X}(\mathcal {E}^*,\mathcal {E}^*)\big )$ is rational and finitely supported for every
$\Gamma \big (U_j,{{\mathcal {H}}om}^*_{\mathcal {O}_X}(\mathcal {E}^*,\mathcal {E}^*)\big )$ is rational and finitely supported for every ![]() $j$, therefore
$j$, therefore
is also a rational finitely supported representation of ![]() $G$.
$G$.
Let us now return to our initial situation, namely with ![]() $\mathcal {F}$ a polystable sheaf on a smooth projective surface
$\mathcal {F}$ a polystable sheaf on a smooth projective surface ![]() $X$ with torsion canonical bundle
$X$ with torsion canonical bundle ![]() $K_X=\Omega ^2_X$. We denote by
$K_X=\Omega ^2_X$. We denote by ![]() $n$ be the smallest positive integer such that
$n$ be the smallest positive integer such that ![]() $K_X^{\otimes n}\simeq \mathcal {O}_X$ (we already know that
$K_X^{\otimes n}\simeq \mathcal {O}_X$ (we already know that ![]() $n=1,2,3,4,6$).
$n=1,2,3,4,6$).
Every choice of an isomorphism ![]() $K_X^{\otimes n}\xrightarrow {\simeq }\mathcal {O}_X$ induces naturally a structure of commutative
$K_X^{\otimes n}\xrightarrow {\simeq }\mathcal {O}_X$ induces naturally a structure of commutative ![]() $\mathcal {O}_X$-algebra on the locally free sheaf of rank
$\mathcal {O}_X$-algebra on the locally free sheaf of rank ![]() $n$,
$n$,
Since ![]() $K_X$ is a torsion line bundle we have that
$K_X$ is a torsion line bundle we have that ![]() $\mathcal {F}\otimes \mathcal {C}$ is also polystable.
$\mathcal {F}\otimes \mathcal {C}$ is also polystable.
Let ![]() $\mathcal {E}^*=\{\cdots \mathcal {E}^{-1}\to \mathcal {E}^0\}\to \mathcal {F}$ be any finite locally free resolution. Then
$\mathcal {E}^*=\{\cdots \mathcal {E}^{-1}\to \mathcal {E}^0\}\to \mathcal {F}$ be any finite locally free resolution. Then ![]() $\mathcal {E}^*\otimes \mathcal {C}$ is a finite locally free resolution of
$\mathcal {E}^*\otimes \mathcal {C}$ is a finite locally free resolution of ![]() $\mathcal {F}\otimes \mathcal {C}$. Moreover,
$\mathcal {F}\otimes \mathcal {C}$. Moreover,
 \[ {{\mathcal{H}}om}^*_{\mathcal{O}_X}(\mathcal{E}^*\otimes\mathcal{C},\mathcal{E}^*\otimes\mathcal{C})=\bigoplus_{i,j=0}^{n-1} {{\mathcal{H}}om}^*_{\mathcal{O}_X}\big(\mathcal{E}^*\otimes K_X^{\otimes i},\mathcal{E}^*\otimes K_X^{\otimes j}\big), \]
\[ {{\mathcal{H}}om}^*_{\mathcal{O}_X}(\mathcal{E}^*\otimes\mathcal{C},\mathcal{E}^*\otimes\mathcal{C})=\bigoplus_{i,j=0}^{n-1} {{\mathcal{H}}om}^*_{\mathcal{O}_X}\big(\mathcal{E}^*\otimes K_X^{\otimes i},\mathcal{E}^*\otimes K_X^{\otimes j}\big), \]
and every direct summand is a ![]() ${{\mathcal {H}}om}^*_{\mathcal {O}_X}(\mathcal {E}^*,\mathcal {E}^*)$-module via the adjoint action. The trace map extends naturally to a morphism of sheaves
${{\mathcal {H}}om}^*_{\mathcal {O}_X}(\mathcal {E}^*,\mathcal {E}^*)$-module via the adjoint action. The trace map extends naturally to a morphism of sheaves
with components
The DG Lie algebra ![]() $L=A^{0,*}_X({{\mathcal {H}}om}^*_{\mathcal {O}_X}(\mathcal {E}^*\otimes \mathcal {C},\mathcal {E}^*\otimes \mathcal {C}))$ is quasi-cyclic of degree 2, when equipped with the pairing
$L=A^{0,*}_X({{\mathcal {H}}om}^*_{\mathcal {O}_X}(\mathcal {E}^*\otimes \mathcal {C},\mathcal {E}^*\otimes \mathcal {C}))$ is quasi-cyclic of degree 2, when equipped with the pairing
where ![]() $p_K\colon A^{0,*}_X(\mathcal {C})\to A^{0,2}_X(K_X)=A^{2,2}_X$ is the projection. In fact, for every
$p_K\colon A^{0,*}_X(\mathcal {C})\to A^{0,2}_X(K_X)=A^{2,2}_X$ is the projection. In fact, for every ![]() $0\leqslant i,j < n$ the above pairing induces the Serre duality isomorphism
$0\leqslant i,j < n$ the above pairing induces the Serre duality isomorphism
so that it is non-degenerate in cohomology.
Lemma 5.2 In the above situation there exists a finite locally free resolution ![]() $\mathcal {E}^*\to \mathcal {F}$ such that every endomorphism of
$\mathcal {E}^*\to \mathcal {F}$ such that every endomorphism of ![]() $\mathcal {F}\otimes \mathcal {C}$ lifts canonically to an endomorphism of the complex
$\mathcal {F}\otimes \mathcal {C}$ lifts canonically to an endomorphism of the complex ![]() $\mathcal {E}^*\otimes \mathcal {C}$.
$\mathcal {E}^*\otimes \mathcal {C}$.
Proof. By assumption ![]() $\mathcal {F}$ is a pure coherent sheaf that is a direct sum of stable sheaves with the same reduced Hilbert polynomial:
$\mathcal {F}$ is a pure coherent sheaf that is a direct sum of stable sheaves with the same reduced Hilbert polynomial:
In particular, ![]() $\operatorname {Hom}_{\mathcal {O}_X}(\mathcal {F}_i,\mathcal {F}_j)=0$ for every
$\operatorname {Hom}_{\mathcal {O}_X}(\mathcal {F}_i,\mathcal {F}_j)=0$ for every ![]() $i\not =j$ and
$i\not =j$ and ![]() $\operatorname {Hom}_{\mathcal {O}_X}(\mathcal {F}_i,\mathcal {F}_i)=\mathbb {C}$ for every
$\operatorname {Hom}_{\mathcal {O}_X}(\mathcal {F}_i,\mathcal {F}_i)=\mathbb {C}$ for every ![]() $i$. Consider the following equivalence relation on the set of direct summands
$i$. Consider the following equivalence relation on the set of direct summands
Equivalently, ![]() $\mathcal {F}_i\sim \mathcal {F}_j$ if and only if
$\mathcal {F}_i\sim \mathcal {F}_j$ if and only if ![]() $\mathcal {F}_i$ is isomorphic to
$\mathcal {F}_i$ is isomorphic to ![]() $\mathcal {F}_j\otimes K^{\otimes h}$ for some
$\mathcal {F}_j\otimes K^{\otimes h}$ for some ![]() $h$. Up to permutation of indices we may assume that
$h$. Up to permutation of indices we may assume that ![]() $\mathcal {F}_1,\ldots ,\mathcal {F}_r$ are a set or representatives for this equivalence relation. We may write
$\mathcal {F}_1,\ldots ,\mathcal {F}_r$ are a set or representatives for this equivalence relation. We may write
 \[ \mathcal{F}=\bigoplus_{i=1}^r \mathcal{F}_i\otimes \mathcal{W}_i, \]
\[ \mathcal{F}=\bigoplus_{i=1}^r \mathcal{F}_i\otimes \mathcal{W}_i, \]
where every ![]() $\mathcal {W}_i$ is a direct sum of line bundles of type
$\mathcal {W}_i$ is a direct sum of line bundles of type ![]() $K_X^{\otimes h}$. We have
$K_X^{\otimes h}$. We have ![]() $\mathcal {F}\otimes \mathcal {C}=\bigoplus _{i=1}^r \mathcal {F}_i\otimes \mathcal {C}^{\oplus w_i}$ where
$\mathcal {F}\otimes \mathcal {C}=\bigoplus _{i=1}^r \mathcal {F}_i\otimes \mathcal {C}^{\oplus w_i}$ where ![]() $w_i$ is the rank of
$w_i$ is the rank of ![]() $\mathcal {W}_i$. Every non-trivial endomorphism of
$\mathcal {W}_i$. Every non-trivial endomorphism of ![]() $\mathcal {F}_i$ is a scalar multiple of the identity and then the group of automorphisms of
$\mathcal {F}_i$ is a scalar multiple of the identity and then the group of automorphisms of ![]() $\mathcal {F}\otimes \mathcal {C}$ is the product of
$\mathcal {F}\otimes \mathcal {C}$ is the product of ![]() $n$ copies of
$n$ copies of ![]() $\prod _{i=1}^r{\rm GL}_{w_i}(\mathbb {C})$.
$\prod _{i=1}^r{\rm GL}_{w_i}(\mathbb {C})$.
Choose ![]() $r$ a finite locally free resolution
$r$ a finite locally free resolution ![]() $\mathcal {E}_i^*\to \mathcal {F}_i$: every endomorphism of
$\mathcal {E}_i^*\to \mathcal {F}_i$: every endomorphism of ![]() $\mathcal {F}_i$ is a scalar multiple of the identity and then lifts canonically to
$\mathcal {F}_i$ is a scalar multiple of the identity and then lifts canonically to ![]() $\mathcal {E}_i^*$. It is now easy to verify that
$\mathcal {E}_i^*$. It is now easy to verify that
 \[ \mathcal{E}^*=\bigoplus_{i=1}^r \mathcal{E}^*_j\otimes \mathcal{W}_i \]
\[ \mathcal{E}^*=\bigoplus_{i=1}^r \mathcal{E}^*_j\otimes \mathcal{W}_i \]
is resolution of ![]() $\mathcal {F}$ with the required properties.
$\mathcal {F}$ with the required properties.
Theorem 5.3 In the above situation both the DG Lie algebras ![]() $R\mspace {-2mu}\operatorname {Hom}_X(\mathcal {F}\otimes \mathcal {C},\mathcal {F}\otimes \mathcal {C})$ and
$R\mspace {-2mu}\operatorname {Hom}_X(\mathcal {F}\otimes \mathcal {C},\mathcal {F}\otimes \mathcal {C})$ and ![]() $R\mspace {-2mu}\operatorname {Hom}_X(\mathcal {F},\mathcal {F})$ are formal.
$R\mspace {-2mu}\operatorname {Hom}_X(\mathcal {F},\mathcal {F})$ are formal.
Proof. Let ![]() $\mathcal {E}\to \mathcal {F}$ be a resolution as in Lemma 5.2 and consider the quasi-cyclic DG Lie algebra
$\mathcal {E}\to \mathcal {F}$ be a resolution as in Lemma 5.2 and consider the quasi-cyclic DG Lie algebra
as a representative in the homotopy class of ![]() $R\operatorname {Hom}(\mathcal {F}\otimes \mathcal {C},\mathcal {F}\otimes \mathcal {C})$. The same arguments used in the proof of Theorem 5.1 imply that
$R\operatorname {Hom}(\mathcal {F}\otimes \mathcal {C},\mathcal {F}\otimes \mathcal {C})$. The same arguments used in the proof of Theorem 5.1 imply that ![]() $L$ is a rational and finitely supported representation of the linearly reductive group of automorphisms of
$L$ is a rational and finitely supported representation of the linearly reductive group of automorphisms of ![]() $\mathcal {F}\otimes \mathcal {C}$.
$\mathcal {F}\otimes \mathcal {C}$.
By assumption there exists a natural inclusion of Lie algebras
that induces an isomorphism ![]() $H^0\simeq H^0(L)$. The adjoint action of
$H^0\simeq H^0(L)$. The adjoint action of ![]() $\operatorname {Hom}_X(\mathcal {F}\otimes \mathcal {C},\mathcal {F}\otimes \mathcal {C})$ on
$\operatorname {Hom}_X(\mathcal {F}\otimes \mathcal {C},\mathcal {F}\otimes \mathcal {C})$ on ![]() $L$ is induced by a rational action of a linearly reductive algebraic group, hence the action of
$L$ is induced by a rational action of a linearly reductive algebraic group, hence the action of ![]() $H^0$ on
$H^0$ on ![]() $L$ is completely reducible and the formality of
$L$ is completely reducible and the formality of ![]() $L$ follows from Corollary 4.5.
$L$ follows from Corollary 4.5.
Taking
as a representative in the homotopy class of ![]() $R\operatorname {Hom}(\mathcal {F},\mathcal {F})$, we have already observed that there exists a natural inclusion of DG Lie algebra
$R\operatorname {Hom}(\mathcal {F},\mathcal {F})$, we have already observed that there exists a natural inclusion of DG Lie algebra ![]() $M\subset L$ together a decomposition of
$M\subset L$ together a decomposition of ![]() $L$ as a direct sum of
$L$ as a direct sum of ![]() $M$-modules:
$M$-modules:
 \[ L=\bigoplus_{i,j=0}^{n-1} A_X^{0,*}\big({{\mathcal{H}}om}^*_{\mathcal{O}_X}\big(\mathcal{E}^*\otimes K_X^{\otimes i},\mathcal{E}^*\otimes K_X^{\otimes j}\big)\big). \]
\[ L=\bigoplus_{i,j=0}^{n-1} A_X^{0,*}\big({{\mathcal{H}}om}^*_{\mathcal{O}_X}\big(\mathcal{E}^*\otimes K_X^{\otimes i},\mathcal{E}^*\otimes K_X^{\otimes j}\big)\big). \]
Now the formality of ![]() $M$ is a direct consequence of the formality of
$M$ is a direct consequence of the formality of ![]() $L$ and of the formality transfer theorem (Theorem 2.3).
$L$ and of the formality transfer theorem (Theorem 2.3).
Acknowledgements
This work has been carried out in the framework of the PRIN project ‘Moduli and Lie theory’ 2017YRA3LK.