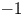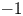1. Introduction
1.1 Motivations
For a Calabi–Yau ![]() $3$-fold
$3$-fold ![]() $X$, Thomas introduced enumerative invariants in [Reference ThomasTho00], now called the Donaldson–Thomas (DT) invariants, which virtually count stable sheaves on
$X$, Thomas introduced enumerative invariants in [Reference ThomasTho00], now called the Donaldson–Thomas (DT) invariants, which virtually count stable sheaves on ![]() $X$. Later several variations and generalizations of DT invariants were introduced. One such example are the DT invariants for quivers with potentials first introduced in [Reference SzendröiSze08], which are now understood as the local version of the original DT invariants. Another example is cohomological Donaldson–Thomas (CoDT) theory, which studies the sheaf-theoretic categorification of DT invariants.
$X$. Later several variations and generalizations of DT invariants were introduced. One such example are the DT invariants for quivers with potentials first introduced in [Reference SzendröiSze08], which are now understood as the local version of the original DT invariants. Another example is cohomological Donaldson–Thomas (CoDT) theory, which studies the sheaf-theoretic categorification of DT invariants.
CoDT theory was initiated by the work of Kontsevich and Soibelman [Reference Kontsevich and SoibelmanKS11] in the case of quivers with potentials. It studies the vanishing cycle cohomologies of the moduli stacks of representations over Jacobi algebras associated with quivers with potentials. Later [Reference Ben-Bassat, Brav, Bussi and JoyceBBBJ15, Reference Brav, Bussi, Dupont, Joyce and SzeondröiBBDJS15, Reference Joyce and UpmeierJU21] opened the door to CoDT theory for Calabi–Yau 3-folds by defining a natural perverse sheaf ![]() $\varphi _{\mathfrak {M}_X^{H\text {-ss}}}$ (respectively,
$\varphi _{\mathfrak {M}_X^{H\text {-ss}}}$ (respectively, ![]() $\varphi _{\mathcal {M}_X^{H\text {-st}}}$) on the moduli stack
$\varphi _{\mathcal {M}_X^{H\text {-st}}}$) on the moduli stack ![]() $\mathfrak {M}_X^{H\text {-ss}}$ of compactly supported
$\mathfrak {M}_X^{H\text {-ss}}$ of compactly supported ![]() $H$-semistable sheaves (respectively, the moduli scheme
$H$-semistable sheaves (respectively, the moduli scheme ![]() $\mathcal {M}_X^{H\text {-st}}$ of
$\mathcal {M}_X^{H\text {-st}}$ of ![]() $H$-stable sheaves) on a Calabi–Yau
$H$-stable sheaves) on a Calabi–Yau ![]() $3$-fold
$3$-fold ![]() $X$ with a fixed ample divisor
$X$ with a fixed ample divisor ![]() $H$, which can be regarded as a categorification of the original DT invariant in the following sense: for a compact component
$H$, which can be regarded as a categorification of the original DT invariant in the following sense: for a compact component ![]() $\mathcal {N} \subset \mathcal {M}_X^{H\text {-st}}$, we have
$\mathcal {N} \subset \mathcal {M}_X^{H\text {-st}}$, we have
where ![]() $[\mathcal {N}]^{\mathrm {vir}}$ denotes the virtual fundamental class of
$[\mathcal {N}]^{\mathrm {vir}}$ denotes the virtual fundamental class of ![]() $\mathcal {N}$.
$\mathcal {N}$.
CoDT theory for quivers with potentials is well developed and shown to have a rich theory. For example, Kontsevich and Soibelman in [Reference Kontsevich and SoibelmanKS11] constructed algebra structures called critical cohomological Hall algebras (critical CoHAs) on the CoDT invariants for quivers with potentials. Later, Davison and Meinhardt in [Reference Davison and MeinhardtDM20] proved the wall crossing formulas for CoDT invariants of quivers with potentials, and realized them as natural maps induced by the CoHA multiplications. In contrast to these developments, almost nothing is known concerning CoDT theory for Calabi–Yau ![]() $3$-folds though it is expected that the local theory as above can be extended to the global settings. The aim of this paper is to take the first step towards the development of CoDT theory for local surfaces (i.e. Calabi–Yau
$3$-folds though it is expected that the local theory as above can be extended to the global settings. The aim of this paper is to take the first step towards the development of CoDT theory for local surfaces (i.e. Calabi–Yau ![]() $3$-folds of the form
$3$-folds of the form ![]() $\mathop {\mathrm {Tot}}\nolimits _S(\omega _S)$ where
$\mathop {\mathrm {Tot}}\nolimits _S(\omega _S)$ where ![]() $S$ is a smooth surface) by proving a global version of the dimensional reduction theorem [Reference DavisonDav17, Theorem A.1].
$S$ is a smooth surface) by proving a global version of the dimensional reduction theorem [Reference DavisonDav17, Theorem A.1].
1.2 Dimensional reduction
In this paper we always use the term ‘dimensional reduction’ as a statement that relates three-dimensional things to two-dimensional things. A dimensional reduction in DT theory was first observed by the work of [Reference Behrend, Bryan and SzendröiBBS13] in the motivic context. They computed the motivic refinement of the DT invariant of zero-dimensional closed subschemes of ![]() $\mathbb {C}^{3}$ by relating it to the motive of the moduli stack of zero-dimensional sheaves on
$\mathbb {C}^{3}$ by relating it to the motive of the moduli stack of zero-dimensional sheaves on ![]() $\mathbb {C}^{2}$. Later Davison proved a categorified version of the dimensional reduction theorem in [Reference DavisonDav17], which we briefly recall now. Let
$\mathbb {C}^{2}$. Later Davison proved a categorified version of the dimensional reduction theorem in [Reference DavisonDav17], which we briefly recall now. Let ![]() $U$ be a scheme,
$U$ be a scheme, ![]() $E$ be a vector bundle on
$E$ be a vector bundle on ![]() $U$,
$U$, ![]() $s \in \Gamma (U, E)$ be a section, and
$s \in \Gamma (U, E)$ be a section, and ![]() $\bar {s}$ be the regular function on
$\bar {s}$ be the regular function on ![]() $\mathop {\mathrm {Tot}}\nolimits _U(E^{\vee })$ corresponding to
$\mathop {\mathrm {Tot}}\nolimits _U(E^{\vee })$ corresponding to ![]() $s$. Denote the projection by
$s$. Denote the projection by ![]() $\pi \colon \mathop {\mathrm {Tot}}\nolimits _U(E^{\vee }) \to U$. Write
$\pi \colon \mathop {\mathrm {Tot}}\nolimits _U(E^{\vee }) \to U$. Write ![]() $Z = s^{-1}(0)$. Then [Reference DavisonDav17, Theorem A.1] states that we have an isomorphism
$Z = s^{-1}(0)$. Then [Reference DavisonDav17, Theorem A.1] states that we have an isomorphism
where ![]() $\varphi ^{p}_{\bar {s}}$ denotes the vanishing cycle functor. This statement has many applications in CoDT theory for quiver with potentials. For example, Davison in [Reference DavisonDav16] computed the vanishing cycle cohomology for the Hilbert scheme of points in
$\varphi ^{p}_{\bar {s}}$ denotes the vanishing cycle functor. This statement has many applications in CoDT theory for quiver with potentials. For example, Davison in [Reference DavisonDav16] computed the vanishing cycle cohomology for the Hilbert scheme of points in ![]() $\mathbb {C}^{3}$ by using the quiver description and applying (1.1). Another interesting application of the isomorphism (1.1) also discussed in [Reference DavisonDav16] is the study of compactly supported cohomologies of the moduli stacks of representations of preprojective algebras, for example the purity of their Hodge structures. Therefore the isomorphism (1.1) not only allows us to compute the vanishing cycle cohomology but also can be used to import three-dimensional techniques to the study of two-dimensional objects.
$\mathbb {C}^{3}$ by using the quiver description and applying (1.1). Another interesting application of the isomorphism (1.1) also discussed in [Reference DavisonDav16] is the study of compactly supported cohomologies of the moduli stacks of representations of preprojective algebras, for example the purity of their Hodge structures. Therefore the isomorphism (1.1) not only allows us to compute the vanishing cycle cohomology but also can be used to import three-dimensional techniques to the study of two-dimensional objects.
The main theme of this paper is to globalize the isomorphism (1.1) so that it can be applied to the study of CoDT theory for local surfaces. Before stating the main theorem of this paper, we briefly recall the construction of the perverse sheaves introduced in [Reference Ben-Bassat, Brav, Bussi and JoyceBBBJ15, Reference Brav, Bussi, Dupont, Joyce and SzeondröiBBDJS15]. Let ![]() $(\boldsymbol {\mathfrak {X}}, \omega )$ be a
$(\boldsymbol {\mathfrak {X}}, \omega )$ be a ![]() $-1$-shifted symplectic derived Artin stack. By the work of [Reference Pantev, Toën, Vaquié and VezzosiPTVV13, Reference Brav and DyckerhoffBD21], the derived moduli stacks of coherent sheaves with proper supports on smooth Calabi–Yau
$-1$-shifted symplectic derived Artin stack. By the work of [Reference Pantev, Toën, Vaquié and VezzosiPTVV13, Reference Brav and DyckerhoffBD21], the derived moduli stacks of coherent sheaves with proper supports on smooth Calabi–Yau ![]() $3$-folds give such examples. It is shown in [Reference Ben-Bassat, Brav, Bussi and JoyceBBBJ15] that
$3$-folds give such examples. It is shown in [Reference Ben-Bassat, Brav, Bussi and JoyceBBBJ15] that ![]() $\boldsymbol {\mathfrak {X}}$ is locally (in the smooth topology) written as a critical locus. Given a square root of the line bundle
$\boldsymbol {\mathfrak {X}}$ is locally (in the smooth topology) written as a critical locus. Given a square root of the line bundle ![]() $\mathop {\mathrm {det}}\nolimits (\mathbb {L}_{\boldsymbol {\mathfrak {X}}} |_{\boldsymbol {\mathfrak {X}} ^{\mathrm {red}}})$
$\mathop {\mathrm {det}}\nolimits (\mathbb {L}_{\boldsymbol {\mathfrak {X}}} |_{\boldsymbol {\mathfrak {X}} ^{\mathrm {red}}})$
which is called an orientation for ![]() $\boldsymbol {\mathfrak {X}}$, we can construct a natural perverse sheaf
$\boldsymbol {\mathfrak {X}}$, we can construct a natural perverse sheaf
on ![]() $t_0(\boldsymbol {\mathfrak {X}})$ locally isomorphic to the vanishing cycle complex twisted by a certain local system. Our main theorem in this paper is as follows.
$t_0(\boldsymbol {\mathfrak {X}})$ locally isomorphic to the vanishing cycle complex twisted by a certain local system. Our main theorem in this paper is as follows.
Theorem (Theorem 4.14)
Let ![]() $\boldsymbol {\mathfrak {Y}}$ be a quasi-smooth derived Artin stack, and
$\boldsymbol {\mathfrak {Y}}$ be a quasi-smooth derived Artin stack, and ![]() $\mathbf {T}^{*}[-1] \boldsymbol {\mathfrak {Y}} := \mathop {\mathbf {Spec}}\nolimits _{\boldsymbol {\mathfrak {Y}}}(\mathop {\mathrm {Sym}}\nolimits (\mathbb {T}_{\boldsymbol {\mathfrak {Y}}}[1]))$ be the
$\mathbf {T}^{*}[-1] \boldsymbol {\mathfrak {Y}} := \mathop {\mathbf {Spec}}\nolimits _{\boldsymbol {\mathfrak {Y}}}(\mathop {\mathrm {Sym}}\nolimits (\mathbb {T}_{\boldsymbol {\mathfrak {Y}}}[1]))$ be the ![]() $-1$-shifted cotangent stack. Equip
$-1$-shifted cotangent stack. Equip ![]() $\mathbf {T}^{*}[-1] \boldsymbol {\mathfrak {Y}}$ with the canonical
$\mathbf {T}^{*}[-1] \boldsymbol {\mathfrak {Y}}$ with the canonical ![]() $-1$-shifted symplectic structure
$-1$-shifted symplectic structure ![]() $\omega _{\mathbf {T}^{*}[-1] \boldsymbol {\mathfrak {Y}}}$ and the canonical orientation
$\omega _{\mathbf {T}^{*}[-1] \boldsymbol {\mathfrak {Y}}}$ and the canonical orientation ![]() $o_{\mathbf {T}^{*}[-1] \boldsymbol {\mathfrak {Y}}}$ (see Examples 2.6 and 2.15). If we write
$o_{\mathbf {T}^{*}[-1] \boldsymbol {\mathfrak {Y}}}$ (see Examples 2.6 and 2.15). If we write ![]() $\pi \colon t_0( \mathbf {T}^{*}[-1] \boldsymbol {\mathfrak {Y}}) \to t_0(\boldsymbol {\mathfrak {Y}})$ for the projection, we have a natural isomorphism
$\pi \colon t_0( \mathbf {T}^{*}[-1] \boldsymbol {\mathfrak {Y}}) \to t_0(\boldsymbol {\mathfrak {Y}})$ for the projection, we have a natural isomorphism
We now return to the story of the dimensional reduction in CoDT theory. Consider a smooth surface ![]() $S$ and write
$S$ and write ![]() $X = \mathop {\mathrm {Tot}}\nolimits _S(\omega _S)$. Denote by
$X = \mathop {\mathrm {Tot}}\nolimits _S(\omega _S)$. Denote by ![]() $\boldsymbol {\mathfrak {M}}_{S}$ (respectively,
$\boldsymbol {\mathfrak {M}}_{S}$ (respectively, ![]() $\boldsymbol {\mathfrak {M}}_{X}$) the derived moduli stack of compactly supported coherent sheaves on
$\boldsymbol {\mathfrak {M}}_{X}$) the derived moduli stack of compactly supported coherent sheaves on ![]() $S$ (respectively,
$S$ (respectively, ![]() $X$), and we write
$X$), and we write ![]() $\mathfrak {M}_{S} = t_0(\boldsymbol {\mathfrak {M}}_{S})$ and
$\mathfrak {M}_{S} = t_0(\boldsymbol {\mathfrak {M}}_{S})$ and ![]() $\mathfrak {M}_{X} = t_0(\boldsymbol {\mathfrak {M}}_{X})$. By applying the work of [Reference Bozec, Calaque and ScherotzkeBCS20, Reference Ikeda and QiuIQ18], we can show that there is a natural equivalence between
$\mathfrak {M}_{X} = t_0(\boldsymbol {\mathfrak {M}}_{X})$. By applying the work of [Reference Bozec, Calaque and ScherotzkeBCS20, Reference Ikeda and QiuIQ18], we can show that there is a natural equivalence between ![]() $\boldsymbol {\mathfrak {M}}_{X}$ and
$\boldsymbol {\mathfrak {M}}_{X}$ and ![]() $\mathbf {T}^{*}[-1] \boldsymbol {\mathfrak {M}}_{S}$ over
$\mathbf {T}^{*}[-1] \boldsymbol {\mathfrak {M}}_{S}$ over ![]() $\boldsymbol {\mathfrak {M}}_{S}$ preserving the
$\boldsymbol {\mathfrak {M}}_{S}$ preserving the ![]() $-1$-shifted symplectic structure. Therefore we obtain the following corollary.
$-1$-shifted symplectic structure. Therefore we obtain the following corollary.
Corollary (Corollary 5.2)
Let ![]() $\boldsymbol {\mathfrak {M}}_{X}$ and
$\boldsymbol {\mathfrak {M}}_{X}$ and ![]() $\boldsymbol {\mathfrak {M}}_{S}$ be as above, and equip
$\boldsymbol {\mathfrak {M}}_{S}$ be as above, and equip ![]() $\boldsymbol {\mathfrak {M}}_{X}$ with the orientation induced by the canonical orientationFootnote 1 on
$\boldsymbol {\mathfrak {M}}_{X}$ with the orientation induced by the canonical orientationFootnote 1 on ![]() $\mathbf {T}^{*}[-1] \boldsymbol {\mathfrak {M}}_{S}$. If we write
$\mathbf {T}^{*}[-1] \boldsymbol {\mathfrak {M}}_{S}$. If we write ![]() $\pi \colon \mathfrak {M}_{X} \to \mathfrak {M}_{S}$ for the canonical projection, we have an isomorphism
$\pi \colon \mathfrak {M}_{X} \to \mathfrak {M}_{S}$ for the canonical projection, we have an isomorphism
By the Verdier self-duality of ![]() $\varphi ^{p}_{\boldsymbol {\mathfrak {M}}_{X}}$, the isomorphism (1.3) implies
$\varphi ^{p}_{\boldsymbol {\mathfrak {M}}_{X}}$, the isomorphism (1.3) implies
where ![]() $\mathrm {H}^{\mathrm {BM}}$ denotes the Borel–Moore homology. Since it is shown in [Reference Kapranov and VasserotKV19] that
$\mathrm {H}^{\mathrm {BM}}$ denotes the Borel–Moore homology. Since it is shown in [Reference Kapranov and VasserotKV19] that ![]() $\mathrm {H}^{\mathrm {BM}}_{*}(\boldsymbol {\mathfrak {M}}_{S})$ carries a convolution product, the isomorphism (1.4) induces an algebra structure on
$\mathrm {H}^{\mathrm {BM}}_{*}(\boldsymbol {\mathfrak {M}}_{S})$ carries a convolution product, the isomorphism (1.4) induces an algebra structure on ![]() $\mathrm {H}^{*}(\boldsymbol {\mathfrak {M}}_{X}; \varphi ^{p}_{\boldsymbol {\mathfrak {M}}_{X}})$. We expect that this is isomorphic to the conjectural critical CoHA for
$\mathrm {H}^{*}(\boldsymbol {\mathfrak {M}}_{X}; \varphi ^{p}_{\boldsymbol {\mathfrak {M}}_{X}})$. We expect that this is isomorphic to the conjectural critical CoHA for ![]() $X$ and it is useful in the study of wall-crossing formulas for CoDT invariants of
$X$ and it is useful in the study of wall-crossing formulas for CoDT invariants of ![]() $X$ as in the local case. Further, as the local dimensional reduction isomorphism (1.1) plays an important role in the cohomological study of moduli stacks of representations of preprojective algebras in [Reference DavisonDav16], we expect that its global variant (1.3) will be useful in the cohomological study of moduli stacks of coherent sheaves on K3 surfaces or Higgs sheaves on curves. These directions will be pursued in future work.
$X$ as in the local case. Further, as the local dimensional reduction isomorphism (1.1) plays an important role in the cohomological study of moduli stacks of representations of preprojective algebras in [Reference DavisonDav16], we expect that its global variant (1.3) will be useful in the cohomological study of moduli stacks of coherent sheaves on K3 surfaces or Higgs sheaves on curves. These directions will be pursued in future work.
1.3 Thom isomorphism
For a quasi-smooth derived scheme ![]() $\boldsymbol {Y}$, the dimensional reduction isomorphism (1.2) has another interpretation: a version of the Thom isomorphism for the dual obstruction cone. By imitating the construction of the Euler class, we construct a class
$\boldsymbol {Y}$, the dimensional reduction isomorphism (1.2) has another interpretation: a version of the Thom isomorphism for the dual obstruction cone. By imitating the construction of the Euler class, we construct a class ![]() $e(\mathbf {T}^{*}[-1] \boldsymbol {Y}) \in \mathrm {H}^{\mathrm {BM}}_{2\operatorname {vdim} \boldsymbol {Y}}(Y)$ where we write
$e(\mathbf {T}^{*}[-1] \boldsymbol {Y}) \in \mathrm {H}^{\mathrm {BM}}_{2\operatorname {vdim} \boldsymbol {Y}}(Y)$ where we write ![]() $Y = t_0(\boldsymbol {Y})$ as follows. Consider the natural morphism
$Y = t_0(\boldsymbol {Y})$ as follows. Consider the natural morphism
By taking the Verdier dual of the isomorphism (1.2), we have
Therefore the map (1.5) defines an element in ![]() $\mathrm {H}^{\mathrm {BM}}_{2\operatorname {vdim} \boldsymbol {Y}}(Y)$, which we name
$\mathrm {H}^{\mathrm {BM}}_{2\operatorname {vdim} \boldsymbol {Y}}(Y)$, which we name ![]() $e(\mathbf {T}^{*}[-1] \boldsymbol {Y})$. Since the virtual fundamental class is a generalization of the Euler class, it is natural to compare
$e(\mathbf {T}^{*}[-1] \boldsymbol {Y})$. Since the virtual fundamental class is a generalization of the Euler class, it is natural to compare ![]() $e(\mathbf {T}^{*}[-1] \boldsymbol {Y})$ with the virtual fundamental class
$e(\mathbf {T}^{*}[-1] \boldsymbol {Y})$ with the virtual fundamental class ![]() $[\boldsymbol {Y}]^{\mathrm {vir}}$. Concerning this, we have obtained the following claim, which will be proved in a subsequent paper.
$[\boldsymbol {Y}]^{\mathrm {vir}}$. Concerning this, we have obtained the following claim, which will be proved in a subsequent paper.
Theorem [Reference KinjoKin21]
Assume ![]() $Y$ is quasi-projective. Then we have
$Y$ is quasi-projective. Then we have
In other words, this theorem gives a new construction of the virtual fundamental class (at least for quasi-projective cases). It is an interesting problem to construct other enumerative invariants (e.g. Donaldson–Thomas type invariants for Calabi–Yau ![]() $4$-folds constructed in [Reference Cao and LeungCL14, Reference Borisov and JoyceBJ17, Reference Oh and ThomasOT20]) based on the isomorphism (1.2) or its variant. This direction will be investigated in future work.
$4$-folds constructed in [Reference Cao and LeungCL14, Reference Borisov and JoyceBJ17, Reference Oh and ThomasOT20]) based on the isomorphism (1.2) or its variant. This direction will be investigated in future work.
1.4 Plan of the paper
This paper is organized as follows. In § 2 we recall some basic facts used in CoDT theory. In § 3 we prove the dimensional reduction theorem for quasi-smooth derived schemes, by gluing the local dimensional reduction isomorphisms in [Reference DavisonDav17, Theorem A.1]. In § 4 we extend the dimensional reduction theorem to quasi-smooth derived Artin stacks. The key point of the proof is the observation that the canonical ![]() $-1$-shifted symplectic structure and the canonical orientation for
$-1$-shifted symplectic structure and the canonical orientation for ![]() $-1$-shifted cotangent stacks are preserved by smooth base changes. In § 5 we discuss some applications of the dimensional reduction theorem. In Appendix A we collect some basic facts on the determinant of perfect complexes.
$-1$-shifted cotangent stacks are preserved by smooth base changes. In § 5 we discuss some applications of the dimensional reduction theorem. In Appendix A we collect some basic facts on the determinant of perfect complexes.
Notation and convention.
• All commutative differential graded algebras (cdgas) sit in non-positive degree with respect to the cohomological grading.
• All derived or underived Artin stacks are assumed to be
 $1$-Artin, and to have quasi-compact and quasi-separated diagonals.
$1$-Artin, and to have quasi-compact and quasi-separated diagonals.• All cdgas and derived Artin stacks are assumed to be locally of finite presentation over the complex number field
 $\mathbb {C}$.
$\mathbb {C}$.• Denote by
 $\mathbb {S}$,
$\mathbb {S}$,  $\mathop {\mathbf {dSch}}\nolimits$, and
$\mathop {\mathbf {dSch}}\nolimits$, and  $\mathop {\mathbf {dSt}}\nolimits$ the
$\mathop {\mathbf {dSt}}\nolimits$ the  $\infty$-categories of spaces, derived schemes, and derived stacks, respectively.
$\infty$-categories of spaces, derived schemes, and derived stacks, respectively.• For a derived scheme or a derived Artin stack
 $\boldsymbol {X}$,
$\boldsymbol {X}$,  $t_0(\boldsymbol {X})$ denotes the classical truncation. Denote by
$t_0(\boldsymbol {X})$ denotes the classical truncation. Denote by  $\boldsymbol {X}^{\mathrm{red}} = t_0(\boldsymbol {X})^{\mathrm{red}}$ the reduction of
$\boldsymbol {X}^{\mathrm{red}} = t_0(\boldsymbol {X})^{\mathrm{red}}$ the reduction of  $\boldsymbol {X}$.
$\boldsymbol {X}$.• For a morphism of derived Artin stacks
 $\boldsymbol {f} \colon \boldsymbol {X} \to \boldsymbol {Y}$,
$\boldsymbol {f} \colon \boldsymbol {X} \to \boldsymbol {Y}$,  $\mathbb {L}_{\boldsymbol {f}}$ denotes the relative cotangent complex. We write
$\mathbb {L}_{\boldsymbol {f}}$ denotes the relative cotangent complex. We write  $\mathbb {L}_{\boldsymbol {X}}$ for the absolute cotangent complex of
$\mathbb {L}_{\boldsymbol {X}}$ for the absolute cotangent complex of  $\boldsymbol {X}$, and
$\boldsymbol {X}$, and  $\mathbb {T}_{\boldsymbol {X}} := \mathbb {L}_{\boldsymbol {X}}^{\vee }$ for the tangent complex.
$\mathbb {T}_{\boldsymbol {X}} := \mathbb {L}_{\boldsymbol {X}}^{\vee }$ for the tangent complex.• For a derived Artin stack
 $\boldsymbol {\mathfrak {X}}$,
$\boldsymbol {\mathfrak {X}}$,  $\operatorname {vdim} \boldsymbol {\mathfrak {X}}$ denotes the locally constant function on
$\operatorname {vdim} \boldsymbol {\mathfrak {X}}$ denotes the locally constant function on  $t_0(\boldsymbol {\mathfrak {X}})$ whose value at
$t_0(\boldsymbol {\mathfrak {X}})$ whose value at  $p \in t_0(\boldsymbol {\mathfrak {X}})$ is
$p \in t_0(\boldsymbol {\mathfrak {X}})$ is  $\sum (-1)^{i} \mathrm {H}^{i}(\mathbb {L}_{\boldsymbol {\mathfrak {X}}} |_p)$. We define
$\sum (-1)^{i} \mathrm {H}^{i}(\mathbb {L}_{\boldsymbol {\mathfrak {X}}} |_p)$. We define  $\operatorname {vdim} \boldsymbol {f}$ for a morphism locally of finite presentation between derived Artin stacks
$\operatorname {vdim} \boldsymbol {f}$ for a morphism locally of finite presentation between derived Artin stacks  $\boldsymbol {f}$ in a similar manner.
$\boldsymbol {f}$ in a similar manner.• For a derived Artin stack
 $\boldsymbol {\mathfrak {X}}$ and a perfect complex
$\boldsymbol {\mathfrak {X}}$ and a perfect complex  $E$ on
$E$ on  $\boldsymbol {\mathfrak {X}}$, we define
$\boldsymbol {\mathfrak {X}}$, we define  $\mathop {\widehat {\mathrm {det}}}\nolimits (E) := \mathop {\mathrm {det}}\nolimits (E |_{\boldsymbol {\mathfrak {X}}^{\mathrm{red}}})$.
$\mathop {\widehat {\mathrm {det}}}\nolimits (E) := \mathop {\mathrm {det}}\nolimits (E |_{\boldsymbol {\mathfrak {X}}^{\mathrm{red}}})$.• For a complex analytic space or a scheme
 $X$, we will only consider (analytically) constructible sheaves or perverse sheaves which are of
$X$, we will only consider (analytically) constructible sheaves or perverse sheaves which are of  $\mathbb {Q}$-coefficients. Denote by
$\mathbb {Q}$-coefficients. Denote by  $D^{b} _c(X, \mathbb {Q})$ the full subcategory of the bounded derived category of sheaves of
$D^{b} _c(X, \mathbb {Q})$ the full subcategory of the bounded derived category of sheaves of  $\mathbb {Q}$-vector spaces
$\mathbb {Q}$-vector spaces  $D^{b}(X, \mathbb {Q})$ spanned by the complexes with (analytically) constructible cohomology sheaves.
$D^{b}(X, \mathbb {Q})$ spanned by the complexes with (analytically) constructible cohomology sheaves.• Concerning sign conventions for derived categories, we always follow [Sta20, Tag 0FNG].
• If there is no confusion, we use expressions such as
 $f_*$,
$f_*$,  $f_!$, and
$f_!$, and  $\mathop {\mathcal {H}\! \mathit {om}}\nolimits$ for the derived functors
$\mathop {\mathcal {H}\! \mathit {om}}\nolimits$ for the derived functors  $Rf_*$,
$Rf_*$,  $Rf_!$, and
$Rf_!$, and  $\mathop {\mathit {R}\mathcal {H}\! \mathit {om}}\nolimits$.
$\mathop {\mathit {R}\mathcal {H}\! \mathit {om}}\nolimits$.
2. Shifted symplectic structures and vanishing cycles
In this section we briefly recall the notion of shifted symplectic structures introduced by [Reference Pantev, Toën, Vaquié and VezzosiPTVV13], and some facts about vanishing cycle functors which will be needed later.
2.1 Shifted symplectic geometry
Here we briefly recall some notions in derived algebraic geometry and shifted symplectic geometry.
Definition 2.1 A derived Artin stack ![]() $\boldsymbol {\mathfrak {X}}$ is called quasi-smooth if the cotangent complex
$\boldsymbol {\mathfrak {X}}$ is called quasi-smooth if the cotangent complex ![]() $\mathbb {L}_{\boldsymbol {\mathfrak {X}}}$ is perfect of amplitude
$\mathbb {L}_{\boldsymbol {\mathfrak {X}}}$ is perfect of amplitude ![]() $[-1, 1]$.
$[-1, 1]$.
Let ![]() $U$ be a smooth scheme, and
$U$ be a smooth scheme, and ![]() $s \in \Gamma (U, E)$ be a section of a vector bundle
$s \in \Gamma (U, E)$ be a section of a vector bundle ![]() $E$ on
$E$ on ![]() $U$. Write
$U$. Write ![]() $\boldsymbol {Z}(s)$ for the derived zero locus of
$\boldsymbol {Z}(s)$ for the derived zero locus of ![]() $s$. We have the following Cartesian diagram in
$s$. We have the following Cartesian diagram in ![]() $\mathop {\mathbf {dSch}}\nolimits$.
$\mathop {\mathbf {dSch}}\nolimits$.

Since ![]() $\mathbb {L}_g[-1]$ and
$\mathbb {L}_g[-1]$ and ![]() $g^{*} \mathbb {L}_U$ are locally free sheaves concentrated in degree zero, we conclude that
$g^{*} \mathbb {L}_U$ are locally free sheaves concentrated in degree zero, we conclude that ![]() $\boldsymbol {Z}(s)$ is quasi-smooth.
$\boldsymbol {Z}(s)$ is quasi-smooth.
Definition 2.2 For a quasi-smooth derived scheme ![]() $\boldsymbol {X}$, a Kuranishi chart is a tuple
$\boldsymbol {X}$, a Kuranishi chart is a tuple ![]() $(Z, U, E, s, \boldsymbol {\iota })$ where
$(Z, U, E, s, \boldsymbol {\iota })$ where ![]() $Z$ is an open subscheme of
$Z$ is an open subscheme of ![]() $t_0(\boldsymbol {X})$,
$t_0(\boldsymbol {X})$, ![]() $U$ is a smooth scheme,
$U$ is a smooth scheme, ![]() $E$ is a vector bundle on
$E$ is a vector bundle on ![]() $U$,
$U$, ![]() $s$ is a section of
$s$ is a section of ![]() $E$, and
$E$, and ![]() ${\boldsymbol {\iota }} \colon {\boldsymbol {Z}(s)} \to {\boldsymbol {X}}$ is an open immersion whose image is
${\boldsymbol {\iota }} \colon {\boldsymbol {Z}(s)} \to {\boldsymbol {X}}$ is an open immersion whose image is ![]() $Z$. A Kuranishi chart is said to be minimal at
$Z$. A Kuranishi chart is said to be minimal at ![]() $p = \boldsymbol {\iota }(q) \in Z$ if the differential
$p = \boldsymbol {\iota }(q) \in Z$ if the differential ![]() ${(ds)_q} \colon {T_q U} \to {E_q}$ is zero. A Kuranishi chart
${(ds)_q} \colon {T_q U} \to {E_q}$ is zero. A Kuranishi chart ![]() $(Z, U, E, s, \boldsymbol {\iota })$ is called good if
$(Z, U, E, s, \boldsymbol {\iota })$ is called good if ![]() $U$ is affine and has global étale coordinate, that is, regular functions
$U$ is affine and has global étale coordinate, that is, regular functions ![]() $x_1, x_2, \ldots, x_n$ such that
$x_1, x_2, \ldots, x_n$ such that ![]() ${d_{\mathrm {dR}}}x_1, {d_{\mathrm {dR}}}x_2, \ldots, {d_{\mathrm {dR}}}x_n$ form a basis of
${d_{\mathrm {dR}}}x_1, {d_{\mathrm {dR}}}x_2, \ldots, {d_{\mathrm {dR}}}x_n$ form a basis of ![]() $\Omega _U$, and
$\Omega _U$, and ![]() $E$ is a trivial vector bundle of a constant rank.
$E$ is a trivial vector bundle of a constant rank.
Proposition 2.3 Let ![]() $\boldsymbol {X}$ be a quasi-smooth derived scheme, and
$\boldsymbol {X}$ be a quasi-smooth derived scheme, and ![]() $p \in \boldsymbol {X}$ be a point.
$p \in \boldsymbol {X}$ be a point.
(i) [Reference Brav, Bussi and JoyceBBJ19, Theorem 4.1] There exists a Kuranishi chart
 $(Z, U, E, s, \boldsymbol {\iota })$ of
$(Z, U, E, s, \boldsymbol {\iota })$ of  $\boldsymbol {X}$ minimal at
$\boldsymbol {X}$ minimal at  $p \in Z$.
$p \in Z$.(ii) [Reference Brav, Bussi and JoyceBBJ19, Theorem 4.2] For
 $i=1,2$, let
$i=1,2$, let  $(Z_i, U_i, E_i, s_i, \boldsymbol {\iota }_i)$ be a Kuranishi chart on
$(Z_i, U_i, E_i, s_i, \boldsymbol {\iota }_i)$ be a Kuranishi chart on  $\boldsymbol {X}$ minimal at
$\boldsymbol {X}$ minimal at  $p = \boldsymbol {\iota }_i(q_i)$. Then there exist a third Kuranishi chart
$p = \boldsymbol {\iota }_i(q_i)$. Then there exist a third Kuranishi chart  $(Z', U', E', s', \boldsymbol {\iota }')$ of
$(Z', U', E', s', \boldsymbol {\iota }')$ of  $\boldsymbol {X}$ minimal at
$\boldsymbol {X}$ minimal at  $p = \boldsymbol {\iota }'(q')$, étale morphisms
$p = \boldsymbol {\iota }'(q')$, étale morphisms  ${\eta _i} \colon {U'} \to {U_i}$, and isomorphisms
${\eta _i} \colon {U'} \to {U_i}$, and isomorphisms  ${\tau _i} \colon {E'} \to {\eta _i ^{*} E_i}$ with the following properties:
${\tau _i} \colon {E'} \to {\eta _i ^{*} E_i}$ with the following properties:–
 $\tau _i (s') = \eta _i ^{*} s_i$;
$\tau _i (s') = \eta _i ^{*} s_i$;– the composition
 $\boldsymbol {Z}(s') \to \boldsymbol {Z}(s_i) \xrightarrow {\boldsymbol {\iota }_i} \boldsymbol {X}$ is equivalent to
$\boldsymbol {Z}(s') \to \boldsymbol {Z}(s_i) \xrightarrow {\boldsymbol {\iota }_i} \boldsymbol {X}$ is equivalent to  $\boldsymbol {\iota }'$ where the first map is induced by
$\boldsymbol {\iota }'$ where the first map is induced by  $\eta _i$ and
$\eta _i$ and  $\tau _i$.
$\tau _i$.
Proof. (i) is a direct consequence of [Reference Brav, Bussi and JoyceBBJ19, Theorem 4.1].
(ii) follows from [Reference Brav, Bussi and JoyceBBJ19, Theorem 4.2] except for ![]() $\eta _i$ being étale and
$\eta _i$ being étale and ![]() $\tau _i$ being isomorphism. Since
$\tau _i$ being isomorphism. Since ![]() $(Z_i, U_i, E_i, s_i, \boldsymbol {f}_i)$ is minimal at
$(Z_i, U_i, E_i, s_i, \boldsymbol {f}_i)$ is minimal at ![]() $q_i$, we have
$q_i$, we have
Similarly, we have
Since the open immersion ![]() $\boldsymbol {Z}(s') \to \boldsymbol {Z}(s_i)$ induces a quasi-isomorphism
$\boldsymbol {Z}(s') \to \boldsymbol {Z}(s_i)$ induces a quasi-isomorphism ![]() $\mathbb {L}_{\boldsymbol {Z}(s_i)} |_{q_i} \simeq \mathbb {L}_{\boldsymbol {Z}(s')} |_{q'}$, we see that
$\mathbb {L}_{\boldsymbol {Z}(s_i)} |_{q_i} \simeq \mathbb {L}_{\boldsymbol {Z}(s')} |_{q'}$, we see that ![]() $\eta _i$ is étale at
$\eta _i$ is étale at ![]() $q'$ and
$q'$ and ![]() $\tau _i$ is invertible at
$\tau _i$ is invertible at ![]() $q'$. Thus by shrinking
$q'$. Thus by shrinking ![]() $U'$ around
$U'$ around ![]() $q'$ if necessary, we obtain the required properties.
$q'$ if necessary, we obtain the required properties.
Let ![]() $A$ be a cdga, and take a semi-free resolution
$A$ be a cdga, and take a semi-free resolution ![]() $A' \to A$. We define the space of
$A' \to A$. We define the space of ![]() $n$-shifted
$n$-shifted ![]() $p$-forms and the space of
$p$-forms and the space of ![]() $n$-shifted closed
$n$-shifted closed ![]() $p$-forms by
$p$-forms by
 \begin{align*} \mathcal{A}^{p}(A, n) & := \lvert ({\wedge} ^{p} \Omega_{A'} [n], d) \rvert,\\ \mathcal{A}^{p,cl}(A, n) & := \bigg\lvert \bigg(\prod_{i \geq 0} \wedge^{p + i} \Omega_{A'} [{-}i + n], d + {d_{\mathrm{dR}}}\bigg) \bigg\rvert ,\end{align*}
\begin{align*} \mathcal{A}^{p}(A, n) & := \lvert ({\wedge} ^{p} \Omega_{A'} [n], d) \rvert,\\ \mathcal{A}^{p,cl}(A, n) & := \bigg\lvert \bigg(\prod_{i \geq 0} \wedge^{p + i} \Omega_{A'} [{-}i + n], d + {d_{\mathrm{dR}}}\bigg) \bigg\rvert ,\end{align*}
respectively, where ![]() $d$ is the internal differential induced by the differential of
$d$ is the internal differential induced by the differential of ![]() $\Omega _{A'}$, and
$\Omega _{A'}$, and ![]() ${d_{\mathrm {dR}}}$ is the de Rham differential. Here for a differential graded (dg) module
${d_{\mathrm {dR}}}$ is the de Rham differential. Here for a differential graded (dg) module ![]() $E$,
$E$, ![]() $\lvert E \rvert$ denotes the simplicial set corresponding to the truncation
$\lvert E \rvert$ denotes the simplicial set corresponding to the truncation ![]() $\tau ^{\leq 0}(E)$ by the Dold–Kan correspondence. These constructions can be made
$\tau ^{\leq 0}(E)$ by the Dold–Kan correspondence. These constructions can be made ![]() $\infty$-functorial, and they satisfy the sheaf condition with respect to the étale topology (see [Reference Pantev, Toën, Vaquié and VezzosiPTVV13, Proposition 1.11]). Therefore we obtain
$\infty$-functorial, and they satisfy the sheaf condition with respect to the étale topology (see [Reference Pantev, Toën, Vaquié and VezzosiPTVV13, Proposition 1.11]). Therefore we obtain ![]() $\infty$-functors
$\infty$-functors
We write ![]() $\boldsymbol {f}^{\star }$ for
$\boldsymbol {f}^{\star }$ for ![]() $\mathcal {A}^{p}(\boldsymbol {f}, n)$ and also for
$\mathcal {A}^{p}(\boldsymbol {f}, n)$ and also for ![]() $\mathcal {A}^{p,cl}(\boldsymbol {f}, n)$. For a derived Artin stack
$\mathcal {A}^{p,cl}(\boldsymbol {f}, n)$. For a derived Artin stack ![]() $\boldsymbol {\mathfrak {X}}$, it is shown in [Reference Pantev, Toën, Vaquié and VezzosiPTVV13, Proposition 1.14] that we have an equivalence
$\boldsymbol {\mathfrak {X}}$, it is shown in [Reference Pantev, Toën, Vaquié and VezzosiPTVV13, Proposition 1.14] that we have an equivalence
We have natural morphisms
 \begin{align*} \pi &\colon \mathcal{A}^{p,cl}(-, n) \to \mathcal{A}^{p}(-, n), \\ {{\mathrm d}}_{\mathrm{dR}} &\colon \mathcal{A}^{p}(-, n) \to \mathcal{A}^{p+1,cl}(-, n), \end{align*}
\begin{align*} \pi &\colon \mathcal{A}^{p,cl}(-, n) \to \mathcal{A}^{p}(-, n), \\ {{\mathrm d}}_{\mathrm{dR}} &\colon \mathcal{A}^{p}(-, n) \to \mathcal{A}^{p+1,cl}(-, n), \end{align*}
where ![]() $\pi$ is induced by the projection
$\pi$ is induced by the projection ![]() $\prod _{i \geq 0} \wedge ^{p + i} \Omega _{A'} [-i + n] \to \wedge ^{p} \Omega _{A'} [p]$, and
$\prod _{i \geq 0} \wedge ^{p + i} \Omega _{A'} [-i + n] \to \wedge ^{p} \Omega _{A'} [p]$, and ![]() ${{\mathrm d}}_{\mathrm {dR}}$ is induced by the map
${{\mathrm d}}_{\mathrm {dR}}$ is induced by the map
Definition 2.4 Let ![]() $\boldsymbol {\mathfrak {X}}$ be a derived Artin stack. A closed
$\boldsymbol {\mathfrak {X}}$ be a derived Artin stack. A closed ![]() $n$-shifted
$n$-shifted ![]() $2$-form
$2$-form ![]() $\omega \in \mathcal {A}^{2,cl}(\boldsymbol {\mathfrak {X}}, n)$ is called an
$\omega \in \mathcal {A}^{2,cl}(\boldsymbol {\mathfrak {X}}, n)$ is called an ![]() $n$-shifted symplectic structure if
$n$-shifted symplectic structure if ![]() $\pi (\omega )$ is non-degenerate (i.e. the morphism
$\pi (\omega )$ is non-degenerate (i.e. the morphism ![]() $\mathbb {T}_{\boldsymbol {\mathfrak {X}}} \to \mathbb {L}_{\boldsymbol {\mathfrak {X}}}[n]$ induced by
$\mathbb {T}_{\boldsymbol {\mathfrak {X}}} \to \mathbb {L}_{\boldsymbol {\mathfrak {X}}}[n]$ induced by ![]() $\pi (\omega )$ using the identification (2.1) is an equivalence). An
$\pi (\omega )$ using the identification (2.1) is an equivalence). An ![]() $n$-shifted symplectic derived Artin stack is a derived Artin stack equipped with an
$n$-shifted symplectic derived Artin stack is a derived Artin stack equipped with an ![]() $n$-shifted symplectic structure on it.
$n$-shifted symplectic structure on it.
We say that two shifted symplectic derived Artin stacks ![]() $(\boldsymbol {\mathfrak {X}}_1, \omega _{\boldsymbol {X}_1})$ and
$(\boldsymbol {\mathfrak {X}}_1, \omega _{\boldsymbol {X}_1})$ and ![]() $(\boldsymbol {\mathfrak {X}}_2, \omega _{\boldsymbol {\mathfrak {X}}_2})$ are equivalent if there exist an equivalence
$(\boldsymbol {\mathfrak {X}}_2, \omega _{\boldsymbol {\mathfrak {X}}_2})$ are equivalent if there exist an equivalence ![]() $\boldsymbol {\Phi } \colon \boldsymbol {\mathfrak {X}}_1 \xrightarrow {\sim } \boldsymbol {\mathfrak {X}}_2$ as derived stacks and an equivalence
$\boldsymbol {\Phi } \colon \boldsymbol {\mathfrak {X}}_1 \xrightarrow {\sim } \boldsymbol {\mathfrak {X}}_2$ as derived stacks and an equivalence ![]() $\boldsymbol {\Phi } ^{\star } \omega _{\boldsymbol {\mathfrak {X}}_2} \sim \omega _{\boldsymbol {\mathfrak {X}}_1}$.
$\boldsymbol {\Phi } ^{\star } \omega _{\boldsymbol {\mathfrak {X}}_2} \sim \omega _{\boldsymbol {\mathfrak {X}}_1}$.
Example 2.5 Let ![]() $U = \mathop {\mathrm {Spec}}\nolimits A$ be a smooth affine scheme and
$U = \mathop {\mathrm {Spec}}\nolimits A$ be a smooth affine scheme and ![]() ${f} \colon {U} \to {\mathbb {C}}$ be a regular function on it. Denote by
${f} \colon {U} \to {\mathbb {C}}$ be a regular function on it. Denote by ![]() $\boldsymbol {X}$ the derived critical locus
$\boldsymbol {X}$ the derived critical locus ![]() $\mathop {\mathbf {Crit}}\nolimits (f)$. Since
$\mathop {\mathbf {Crit}}\nolimits (f)$. Since ![]() $\boldsymbol {X}$ is the derived zero locus of the section
$\boldsymbol {X}$ is the derived zero locus of the section ![]() ${{d_{\mathrm {dR}}}f} \colon {U} \to {\Omega _U}$, the derived scheme
${{d_{\mathrm {dR}}}f} \colon {U} \to {\Omega _U}$, the derived scheme ![]() $\boldsymbol {X}$ is equivalent to
$\boldsymbol {X}$ is equivalent to ![]() $\mathop {\mathbf {Spec}}\nolimits B$ where
$\mathop {\mathbf {Spec}}\nolimits B$ where ![]() $B$ is a cdga defined by the Koszul complex
$B$ is a cdga defined by the Koszul complex
Assume there exists a global étale coordinate ![]() $(x_1, \ldots, x_n)$ on
$(x_1, \ldots, x_n)$ on ![]() $U$. We write the dual basis of
$U$. We write the dual basis of ![]() ${d_{\mathrm {dR}}}x_1, \ldots, {d_{\mathrm {dR}}}x_n$ as
${d_{\mathrm {dR}}}x_1, \ldots, {d_{\mathrm {dR}}}x_n$ as ![]() ${\partial }/{\partial x_1}, \ldots, {\partial }/{\partial x_n}$, and
${\partial }/{\partial x_1}, \ldots, {\partial }/{\partial x_n}$, and ![]() $y_i \in B^{-1}$ denotes the element of degree
$y_i \in B^{-1}$ denotes the element of degree ![]() $-1$ corresponding to
$-1$ corresponding to ![]() ${\partial }/{\partial x_i}$ for each
${\partial }/{\partial x_i}$ for each ![]() $i=1,\ldots, n$. Although
$i=1,\ldots, n$. Although ![]() $B$ is not semi-free in general, one can see that
$B$ is not semi-free in general, one can see that ![]() $\Omega _B$ gives a model for
$\Omega _B$ gives a model for ![]() $\mathbb {L}_B$. Define an element
$\mathbb {L}_B$. Define an element ![]() $\omega _{\boldsymbol {X}}' \in (\wedge ^{2} \Omega _B)^{-1}$ of degree
$\omega _{\boldsymbol {X}}' \in (\wedge ^{2} \Omega _B)^{-1}$ of degree ![]() $-1$ by
$-1$ by
This defines a ![]() $-1$-shifted
$-1$-shifted ![]() $2$-form, which is clearly non-degenerate. Since we also have
$2$-form, which is clearly non-degenerate. Since we also have ![]() ${d_{\mathrm {dR}}} \omega _{\boldsymbol {X}}' =0$, the closed form
${d_{\mathrm {dR}}} \omega _{\boldsymbol {X}}' =0$, the closed form ![]() $\omega _{\boldsymbol {X}} := (\omega _{\boldsymbol {X}}', 0, \ldots )$ defines a
$\omega _{\boldsymbol {X}} := (\omega _{\boldsymbol {X}}', 0, \ldots )$ defines a ![]() $-1$-shifted symplectic structure on
$-1$-shifted symplectic structure on ![]() $\boldsymbol {X}$.
$\boldsymbol {X}$.
Example 2.6 Let ![]() $\boldsymbol {\mathfrak {Y}}$ be a derived Artin stack, and
$\boldsymbol {\mathfrak {Y}}$ be a derived Artin stack, and ![]() $n$ be an integer. Define the
$n$ be an integer. Define the ![]() $n$-shifted cotangent stack of
$n$-shifted cotangent stack of ![]() $\boldsymbol {\mathfrak {Y}}$ by
$\boldsymbol {\mathfrak {Y}}$ by ![]() $\mathbf {T}^{*}[n]\boldsymbol {\mathfrak {Y}} := \mathop {\mathbf {Spec}}\nolimits _{\boldsymbol {\mathfrak {Y}}}(\mathop {\mathrm {Sym}}\nolimits (\mathbb {T}_{\boldsymbol {\mathfrak {Y}}}[-n]))$. Let
$\mathbf {T}^{*}[n]\boldsymbol {\mathfrak {Y}} := \mathop {\mathbf {Spec}}\nolimits _{\boldsymbol {\mathfrak {Y}}}(\mathop {\mathrm {Sym}}\nolimits (\mathbb {T}_{\boldsymbol {\mathfrak {Y}}}[-n]))$. Let ![]() ${\boldsymbol {\pi }} \colon {\mathbf {T}^{*}[n]\boldsymbol {\mathfrak {Y}}} \to {\boldsymbol {\mathfrak {Y}}}$ be the projection. We have a tautological
${\boldsymbol {\pi }} \colon {\mathbf {T}^{*}[n]\boldsymbol {\mathfrak {Y}}} \to {\boldsymbol {\mathfrak {Y}}}$ be the projection. We have a tautological ![]() $n$-shifted
$n$-shifted ![]() $1$-form
$1$-form ![]() $\lambda _{\mathbf {T}^{*}[n]\boldsymbol {\mathfrak {Y}}}$ on
$\lambda _{\mathbf {T}^{*}[n]\boldsymbol {\mathfrak {Y}}}$ on ![]() $\mathbf {T}^{*} [n]\boldsymbol {\mathfrak {Y}}$ defined by the image of the tautological section of
$\mathbf {T}^{*} [n]\boldsymbol {\mathfrak {Y}}$ defined by the image of the tautological section of ![]() $\boldsymbol {\pi }^{*} \mathbb {L}_{\boldsymbol {\mathfrak {Y}}}[n]$ under the canonical map
$\boldsymbol {\pi }^{*} \mathbb {L}_{\boldsymbol {\mathfrak {Y}}}[n]$ under the canonical map ![]() $\boldsymbol {\pi }^{*} \mathbb {L}_{\boldsymbol {\mathfrak {Y}}}[n] \to \mathbb {L}_{\mathbf {T}^{*}[n]\boldsymbol {\mathfrak {Y}}}[n]$. In [Reference CalaqueCal19, Theorem 2.2] it is shown that
$\boldsymbol {\pi }^{*} \mathbb {L}_{\boldsymbol {\mathfrak {Y}}}[n] \to \mathbb {L}_{\mathbf {T}^{*}[n]\boldsymbol {\mathfrak {Y}}}[n]$. In [Reference CalaqueCal19, Theorem 2.2] it is shown that ![]() $\omega _{\mathbf {T}^{*}[n]\boldsymbol {\mathfrak {Y}}} := {{\mathrm d}}_{\mathrm {dR}}{\lambda _{\mathbf {T}^{*}[n]\boldsymbol {\mathfrak {Y}}}}$ is non-degenerate, and we obtain the canonical
$\omega _{\mathbf {T}^{*}[n]\boldsymbol {\mathfrak {Y}}} := {{\mathrm d}}_{\mathrm {dR}}{\lambda _{\mathbf {T}^{*}[n]\boldsymbol {\mathfrak {Y}}}}$ is non-degenerate, and we obtain the canonical ![]() $n$-shifted symplectic structure on
$n$-shifted symplectic structure on ![]() $\mathbf {T}^{*}[n]\boldsymbol {\mathfrak {Y}}$.
$\mathbf {T}^{*}[n]\boldsymbol {\mathfrak {Y}}$.
It is proved in [Reference Brav, Bussi and JoyceBBJ19, Theorem 5.18] that any ![]() $-1$-shifted symplectic derived scheme is Zariski locally modeled on a derived critical locus. For a
$-1$-shifted symplectic derived scheme is Zariski locally modeled on a derived critical locus. For a ![]() $-1$-shifted symplectic derived scheme of the form
$-1$-shifted symplectic derived scheme of the form ![]() $\mathbf {T}^{*}[-1]\boldsymbol {Y}$ for some quasi-smooth derived scheme
$\mathbf {T}^{*}[-1]\boldsymbol {Y}$ for some quasi-smooth derived scheme ![]() $\boldsymbol {Y}$, its local model as a derived critical locus can be described by combining Proposition 2.3 and the following lemma.
$\boldsymbol {Y}$, its local model as a derived critical locus can be described by combining Proposition 2.3 and the following lemma.
Lemma 2.7 Let ![]() $U = \mathop {\mathrm {Spec}}\nolimits A$ be a smooth affine scheme admitting a global étale coordinate,
$U = \mathop {\mathrm {Spec}}\nolimits A$ be a smooth affine scheme admitting a global étale coordinate, ![]() $E$ be a trivial vector bundle on
$E$ be a trivial vector bundle on ![]() $U$, and
$U$, and ![]() $s \in \Gamma (U, E)$ be a section. Denote by
$s \in \Gamma (U, E)$ be a section. Denote by ![]() $\bar {s}$ the regular function on
$\bar {s}$ the regular function on ![]() $\mathop {\mathrm {Tot}}\nolimits _U(E ^{\vee })$ corresponding to
$\mathop {\mathrm {Tot}}\nolimits _U(E ^{\vee })$ corresponding to ![]() $s$. Then we have an equivalence of
$s$. Then we have an equivalence of ![]() $-1$-shifted symplectic derived schemes
$-1$-shifted symplectic derived schemes
equipped with the ![]() $-1$-shifted symplectic structures constructed in Examples 2.5 and 2.6, respectively.
$-1$-shifted symplectic structures constructed in Examples 2.5 and 2.6, respectively.
Proof. Fix a global étale coordinate ![]() $x_1, \ldots, x_n$ on
$x_1, \ldots, x_n$ on ![]() $U$ and a basis
$U$ and a basis ![]() $e_1, \ldots, e_m$ of
$e_1, \ldots, e_m$ of ![]() $M := \Gamma (U, E)$. Write
$M := \Gamma (U, E)$. Write ![]() $s = a_1 e_1 + \cdots + a_m e_m$. If we write
$s = a_1 e_1 + \cdots + a_m e_m$. If we write ![]() $\alpha _i := {d_{\mathrm {dR}}}x_i$, then
$\alpha _i := {d_{\mathrm {dR}}}x_i$, then ![]() $\alpha _1, \ldots, \alpha _n$ defines a basis of
$\alpha _1, \ldots, \alpha _n$ defines a basis of ![]() $\Omega _U$. Denote by
$\Omega _U$. Denote by ![]() $e_1^{\vee }, \ldots, e_m^{\vee }$ and
$e_1^{\vee }, \ldots, e_m^{\vee }$ and ![]() $\alpha _1^{\vee }, \ldots, \alpha _n^{\vee }$ the dual bases of
$\alpha _1^{\vee }, \ldots, \alpha _n^{\vee }$ the dual bases of ![]() $e_1, \ldots, e_m$ and
$e_1, \ldots, e_m$ and ![]() $\alpha _1, \ldots, \alpha _n$, respectively. Define a cdga
$\alpha _1, \ldots, \alpha _n$, respectively. Define a cdga ![]() $C$ by the Koszul complex
$C$ by the Koszul complex
Now it is clear that ![]() $\mathop {\mathbf {Spec}}\nolimits C$ gives models for both
$\mathop {\mathbf {Spec}}\nolimits C$ gives models for both ![]() $\mathop {\mathbf {Crit}}\nolimits (\bar {s})$ and
$\mathop {\mathbf {Crit}}\nolimits (\bar {s})$ and ![]() $\mathbf {T}^{*}[-1]{\boldsymbol {Z}(s)}$. The tautological
$\mathbf {T}^{*}[-1]{\boldsymbol {Z}(s)}$. The tautological ![]() $1$-form
$1$-form ![]() $\lambda _{\mathbf {T}^{*}[-1]{\boldsymbol {Z}(s)}}$ is represented by
$\lambda _{\mathbf {T}^{*}[-1]{\boldsymbol {Z}(s)}}$ is represented by
 \[ \sum _{i=1} ^{n} \alpha_i^{{\vee}} ({d_{\mathrm{dR}}}x_i ) + \sum _{j=1} ^{m} z_j({d_{\mathrm{dR}}}e_j ^{{\vee}}) \in \mathcal{A}^{1}(\mathop{\mathbf{Spec}}\nolimits C, -1). \]
\[ \sum _{i=1} ^{n} \alpha_i^{{\vee}} ({d_{\mathrm{dR}}}x_i ) + \sum _{j=1} ^{m} z_j({d_{\mathrm{dR}}}e_j ^{{\vee}}) \in \mathcal{A}^{1}(\mathop{\mathbf{Spec}}\nolimits C, -1). \]
A direct computation shows that ![]() ${{\mathrm d}}_{\mathrm {dR}} \lambda _{\mathbf {T}^{*}[-1]{\boldsymbol {Z}(s)}} \sim \omega _{\mathop {\mathbf {Crit}}\nolimits (\bar {s})}$, which implies the lemma.
${{\mathrm d}}_{\mathrm {dR}} \lambda _{\mathbf {T}^{*}[-1]{\boldsymbol {Z}(s)}} \sim \omega _{\mathop {\mathbf {Crit}}\nolimits (\bar {s})}$, which implies the lemma.
2.2 D-critical schemes
In this section we briefly recall the notion of d-critical structures introduced in [Reference JoyceJoy15], which constitute a classical model for ![]() $-1$-shifted symplectic structures. D-critical structures are easier to treat than
$-1$-shifted symplectic structures. D-critical structures are easier to treat than ![]() $-1$-shifted symplectic structures and are enough to apply in cohomological Donaldson–Thomas theory.
$-1$-shifted symplectic structures and are enough to apply in cohomological Donaldson–Thomas theory.
For any complex analytic space ![]() $X$, Joyce in [Reference JoyceJoy15, Theorem 2.1] introduced a sheaf
$X$, Joyce in [Reference JoyceJoy15, Theorem 2.1] introduced a sheaf
of ![]() $\mathbb {C}$-vector space on
$\mathbb {C}$-vector space on ![]() $X$ with the following property: for any open subset
$X$ with the following property: for any open subset ![]() $R \subset X$ and any closed embedding
$R \subset X$ and any closed embedding ![]() $i \colon R \hookrightarrow U$ where
$i \colon R \hookrightarrow U$ where ![]() $U$ is a complex manifold, we have an exact sequence of sheaves on
$U$ is a complex manifold, we have an exact sequence of sheaves on ![]() $R$,
$R$,
Here ![]() $I_{R, U}$ is the ideal sheaf of
$I_{R, U}$ is the ideal sheaf of ![]() $i^{-1} \mathcal {O}_U$ corresponding to
$i^{-1} \mathcal {O}_U$ corresponding to ![]() $R$. The composition
$R$. The composition
glues to define a morphism ![]() ${\beta _X} \colon {\mathcal {S}_X} \to {\mathcal {O}_X}$, and we define a subsheaf
${\beta _X} \colon {\mathcal {S}_X} \to {\mathcal {O}_X}$, and we define a subsheaf ![]() $\mathcal {S}_X ^{0}$ of
$\mathcal {S}_X ^{0}$ of ![]() $\mathcal {S}_X$ by the kernel of the composition
$\mathcal {S}_X$ by the kernel of the composition
It can be shown that we have a decomposition ![]() $\mathcal {S}_X = \mathbb {C}_X \oplus \mathcal {S}_X ^{0}$ where
$\mathcal {S}_X = \mathbb {C}_X \oplus \mathcal {S}_X ^{0}$ where ![]() $\mathbb {C}_X$ is the constant sheaf and
$\mathbb {C}_X$ is the constant sheaf and ![]() $\mathbb {C}_X \hookrightarrow \mathcal {S}_X$ is induced by the inclusion
$\mathbb {C}_X \hookrightarrow \mathcal {S}_X$ is induced by the inclusion ![]() $\mathbb {C}_U \hookrightarrow \mathcal {O}_U$ identifying
$\mathbb {C}_U \hookrightarrow \mathcal {O}_U$ identifying ![]() $\mathbb {C}_U$ with the sheaf of locally constant functions on
$\mathbb {C}_U$ with the sheaf of locally constant functions on ![]() $U$. If
$U$. If ![]() $X$ is the critical locus of some function
$X$ is the critical locus of some function ![]() $f$ on a complex manifold
$f$ on a complex manifold ![]() $U$ such that
$U$ such that ![]() $f \vert _{X ^{\mathrm {red}}} = 0$, then
$f \vert _{X ^{\mathrm {red}}} = 0$, then ![]() $f + I_{X, U}^{2}$ defines an element of
$f + I_{X, U}^{2}$ defines an element of ![]() $\Gamma (X, \mathcal {S}_X^{0})$ since
$\Gamma (X, \mathcal {S}_X^{0})$ since ![]() ${d_{\mathrm {dR}}}f \vert _X = 0$.
${d_{\mathrm {dR}}}f \vert _X = 0$.
Definition 2.8 [Reference JoyceJoy15, Definition 2.5]
Let ![]() $X$ be a complex analytic space. A section
$X$ be a complex analytic space. A section ![]() $s \in \Gamma (X, \mathcal {S}_X ^{0})$ is called an (analytic) d-critical structure if for any closed point
$s \in \Gamma (X, \mathcal {S}_X ^{0})$ is called an (analytic) d-critical structure if for any closed point ![]() $x \in X$ there exist an open neighborhood
$x \in X$ there exist an open neighborhood ![]() $x \in R \subset X$, a complex manifold
$x \in R \subset X$, a complex manifold ![]() $U$, a regular function
$U$, a regular function ![]() $f$ on
$f$ on ![]() $U$ with
$U$ with ![]() $f \vert _{R^{\mathrm {red}}} = 0$, and a closed embedding
$f \vert _{R^{\mathrm {red}}} = 0$, and a closed embedding ![]() ${i} \colon {R} \to {U}$ such that
${i} \colon {R} \to {U}$ such that ![]() $i(R) = \mathop {\mathrm {Crit}}\nolimits (f)$ and
$i(R) = \mathop {\mathrm {Crit}}\nolimits (f)$ and ![]() $f + I_{R, U}^{2} = s \vert _R$. The tuple
$f + I_{R, U}^{2} = s \vert _R$. The tuple ![]() $(R, U, f, i)$ as above is called a d-critical chart for
$(R, U, f, i)$ as above is called a d-critical chart for ![]() $(X, s)$. A d-critical scheme is a scheme equipped with a d-critical structure on its analytification.
$(X, s)$. A d-critical scheme is a scheme equipped with a d-critical structure on its analytification.
Remark 2.9 Joyce [Reference JoyceJoy15, Definition 2.5] also introduced the algebraic version of the d-critical structure, and some authors define a d-critical scheme as a scheme equipped with an algebraic d-critical structure. We always work with analytic d-critical structures since they are enough for our purposes.
For a d-critical chart ![]() $(R, U, f, i)$ of a d-critical scheme
$(R, U, f, i)$ of a d-critical scheme ![]() $(X, s)$ and an open subset
$(X, s)$ and an open subset ![]() $U' \subset U$, define
$U' \subset U$, define ![]() $R' = i^{-1}(U')$,
$R' = i^{-1}(U')$, ![]() $f' = f|_{U'}$, and
$f' = f|_{U'}$, and ![]() $i' = i |_{R'} \colon R' \hookrightarrow U'$. Then
$i' = i |_{R'} \colon R' \hookrightarrow U'$. Then ![]() $(R', U', f', i')$ defines a d-critical chart on
$(R', U', f', i')$ defines a d-critical chart on ![]() $(X, s)$. We call
$(X, s)$. We call ![]() $(R', U', f', i')$ an open subchart of
$(R', U', f', i')$ an open subchart of ![]() $(R, U, f, i)$.
$(R, U, f, i)$.
In order to compare two d-critical charts, Joyce introduced the notion of embedding: for a d-critical scheme ![]() $(X, s)$ and its d-critical charts
$(X, s)$ and its d-critical charts ![]() $(R_1, U_1, f_1, i_1)$ and
$(R_1, U_1, f_1, i_1)$ and ![]() $(R_2, U_2, f_2, i_2)$ such that
$(R_2, U_2, f_2, i_2)$ such that ![]() $R_1 \subset R_2$, an embedding
$R_1 \subset R_2$, an embedding ![]() ${(R_1, U_1, f_1, i_1)}\hookrightarrow {(R_2, U_2, f_2, i_2)}$ is defined by a locally closed embedding
${(R_1, U_1, f_1, i_1)}\hookrightarrow {(R_2, U_2, f_2, i_2)}$ is defined by a locally closed embedding ![]() $\Phi \colon {U_1}\hookrightarrow {U_2}$ such that
$\Phi \colon {U_1}\hookrightarrow {U_2}$ such that ![]() $f_1 = f_2 \circ {\Phi }$ and
$f_1 = f_2 \circ {\Phi }$ and ![]() $\Phi \circ i_1 = i_2 \vert _{R_2}$. The following theorem is useful when comparing two d-critical charts.
$\Phi \circ i_1 = i_2 \vert _{R_2}$. The following theorem is useful when comparing two d-critical charts.
Theorem 2.10 Let ![]() $(X, s)$ be a d-critical scheme.
$(X, s)$ be a d-critical scheme.
(i) [Reference JoyceJoy15, Theorem 2.20] Let
 $(R_1, U_1, f_1, i_1)$ and
$(R_1, U_1, f_1, i_1)$ and  $(R_2, U_2, f_2, i_2)$ be d-critical charts, and
$(R_2, U_2, f_2, i_2)$ be d-critical charts, and  $x \in R_1 \cap R_2$ be a point. Then, by shrinking these d-critical charts around
$x \in R_1 \cap R_2$ be a point. Then, by shrinking these d-critical charts around  $x$ if necessary, we can find a third d-critical chart
$x$ if necessary, we can find a third d-critical chart  $(R_3, U_3, f_3, i_3)$ with
$(R_3, U_3, f_3, i_3)$ with  $x \in R_3$ and embeddings
$x \in R_3$ and embeddings  ${(R_1, U_1, f_1, i_1)}\hookrightarrow {(R_3, U_3, f_3, i_3)}$ and
${(R_1, U_1, f_1, i_1)}\hookrightarrow {(R_3, U_3, f_3, i_3)}$ and  ${(R_2, U_2, f_2, i_2)}\hookrightarrow {(R_3, U_3, f_3, i_3)}$.
${(R_2, U_2, f_2, i_2)}\hookrightarrow {(R_3, U_3, f_3, i_3)}$.(ii) [Reference JoyceJoy15, Theorem 2.22] Let
 $\Phi \colon (R_1, U_1, f_1, i_1) \hookrightarrow (R_2, U_2, f_2, i_2)$ be an embedding of d-critical charts, and
$\Phi \colon (R_1, U_1, f_1, i_1) \hookrightarrow (R_2, U_2, f_2, i_2)$ be an embedding of d-critical charts, and  $x \in R_1$ be a point. Then, by shrinking these d-critical charts around
$x \in R_1$ be a point. Then, by shrinking these d-critical charts around  $x$ keeping
$x$ keeping  $\Phi (U_1) \subset U_2$ if necessary and replacing
$\Phi (U_1) \subset U_2$ if necessary and replacing  $\Phi$ by its restriction, we can find holomorphic maps
$\Phi$ by its restriction, we can find holomorphic maps  $\alpha \colon U_2 \to U_1$ and
$\alpha \colon U_2 \to U_1$ and  $\beta \colon U_2 \to \mathbb {C}^{n}$ for
$\beta \colon U_2 \to \mathbb {C}^{n}$ for  $n = \dim U_2 - \dim U_1$, such that
$n = \dim U_2 - \dim U_1$, such that  $(\alpha, \beta ) \colon U_2 \to U_1 \times \mathbb {C}^{n}$ is biholomorphic onto its image, and we have
$(\alpha, \beta ) \colon U_2 \to U_1 \times \mathbb {C}^{n}$ is biholomorphic onto its image, and we have  $\alpha \circ \Phi =\mathop {\mathrm {id}}\nolimits$,
$\alpha \circ \Phi =\mathop {\mathrm {id}}\nolimits$,  $\beta \circ \Phi = 0$, and
$\beta \circ \Phi = 0$, and  $f_2 = f_1 \circ \alpha + (z_1^{2}+ \cdots +z_n^{2})\circ \beta$ where
$f_2 = f_1 \circ \alpha + (z_1^{2}+ \cdots +z_n^{2})\circ \beta$ where  $z_i$ is the
$z_i$ is the  $i$th coordinate of
$i$th coordinate of  $\mathbb {C}^{n}$.
$\mathbb {C}^{n}$.
For an embedding of d-critical charts ![]() $\Phi \colon (R_1, U_1, f_1, i_1) \hookrightarrow (R_2, U_2, f_2, i_2)$ of a d-critical scheme
$\Phi \colon (R_1, U_1, f_1, i_1) \hookrightarrow (R_2, U_2, f_2, i_2)$ of a d-critical scheme ![]() $(X, s)$, Joyce defined in [Reference JoyceJoy15, Definition 2.26] a natural isomorphism
$(X, s)$, Joyce defined in [Reference JoyceJoy15, Definition 2.26] a natural isomorphism
If there exist ![]() $\alpha, \beta$ as in Theorem 2.10(ii),
$\alpha, \beta$ as in Theorem 2.10(ii), ![]() $J_{\Phi }$ is defined as follows. Firstly, we have isomorphisms
$J_{\Phi }$ is defined as follows. Firstly, we have isomorphisms
where the final isomorphism is defined by the trivialization
Then, by taking the square of this composition and pulling back to ![]() $R_1$, we obtain the desired isomorphism.
$R_1$, we obtain the desired isomorphism.
Using this preparation, we can construct a natural line bundle ![]() $K_{X, s}$ on
$K_{X, s}$ on ![]() $X^{\mathrm {red}}$, which is a d-critical version of the canonical line bundle as follows.
$X^{\mathrm {red}}$, which is a d-critical version of the canonical line bundle as follows.
Theorem 2.11 [Reference JoyceJoy15, Theorem 2.28]
For a d-critical scheme ![]() $(X, s)$, one can define a line bundle
$(X, s)$, one can define a line bundle ![]() $K_{X, s}$ on
$K_{X, s}$ on ![]() $X^{\mathrm {red}}$ which we call the virtual canonical bundle of
$X^{\mathrm {red}}$ which we call the virtual canonical bundle of ![]() $(X, s)$ characterized by the following properties.
$(X, s)$ characterized by the following properties.
(i) For a d-critical chart
 $\mathscr {R} = (R, U, f, i)$ of
$\mathscr {R} = (R, U, f, i)$ of  $(X, s)$, we have an isomorphism
$(X, s)$, we have an isomorphism
 \[ \iota_{\mathscr{R}} \colon K_{X, s} \vert_{R^{\mathrm{red}}} \cong (i^{*} K_U) ^{{\otimes}^{2}} \vert_{R^{\mathrm{red}}}. \]
\[ \iota_{\mathscr{R}} \colon K_{X, s} \vert_{R^{\mathrm{red}}} \cong (i^{*} K_U) ^{{\otimes}^{2}} \vert_{R^{\mathrm{red}}}. \](ii) For an embedding of d-critical charts
we have \[ \Phi \colon \mathscr{R}_1 = (R_1, U_1, f_1, i_1) \hookrightarrow \mathscr{R}_2 = (R_2, U_2, f_2, i_2), \]
\[ \Phi \colon \mathscr{R}_1 = (R_1, U_1, f_1, i_1) \hookrightarrow \mathscr{R}_2 = (R_2, U_2, f_2, i_2), \] \[ \iota_{\mathscr{R}_2} \vert_{R^{\mathrm{red}}_1} = J_{\Phi} \circ \iota_{\mathscr{R}_1}. \]
\[ \iota_{\mathscr{R}_2} \vert_{R^{\mathrm{red}}_1} = J_{\Phi} \circ \iota_{\mathscr{R}_1}. \]
Definition 2.12 [Reference JoyceJoy15, Definition 2.31]
An orientation ![]() $o$ of a d-critical scheme
$o$ of a d-critical scheme ![]() $(X, s)$ is a choice of a line bundle
$(X, s)$ is a choice of a line bundle ![]() $L$ on
$L$ on ![]() $X^{\mathrm {red}}$ and an isomorphism
$X^{\mathrm {red}}$ and an isomorphism
As we have seen in the previous section, ![]() $-1$-shifted symplectic derived schemes are locally modeled on derived critical loci. Therefore we can regard the notion of d-critical schemes as an underived version of the
$-1$-shifted symplectic derived schemes are locally modeled on derived critical loci. Therefore we can regard the notion of d-critical schemes as an underived version of the ![]() $-1$-shifted symplectic derived scheme. The following theorem gives the rigorous statement of this fact.
$-1$-shifted symplectic derived scheme. The following theorem gives the rigorous statement of this fact.
Theorem 2.13 [Reference Brav, Bussi and JoyceBBJ19, Theorem 6.6]
Let ![]() $(\boldsymbol {X}, \omega _{\boldsymbol {X}})$ be a
$(\boldsymbol {X}, \omega _{\boldsymbol {X}})$ be a ![]() $-1$-shifted symplectic derived scheme. Then its underlying scheme
$-1$-shifted symplectic derived scheme. Then its underlying scheme ![]() $X = t_0 (\boldsymbol {X})$ carries a canonical d-critical structure
$X = t_0 (\boldsymbol {X})$ carries a canonical d-critical structure ![]() $s_X$ with the following property: for any
$s_X$ with the following property: for any ![]() $-1$ shifted symplectic derived scheme
$-1$ shifted symplectic derived scheme ![]() $(\boldsymbol {R}, \omega _{\boldsymbol {R}})$ of the form
$(\boldsymbol {R}, \omega _{\boldsymbol {R}})$ of the form ![]() $\boldsymbol {R} = \mathop {\mathbf {Crit}}\nolimits (f)$ where
$\boldsymbol {R} = \mathop {\mathbf {Crit}}\nolimits (f)$ where ![]() $f$ is a regular function on a smooth scheme
$f$ is a regular function on a smooth scheme ![]() $U$,
$U$, ![]() $\omega _{\boldsymbol {R}}$ the
$\omega _{\boldsymbol {R}}$ the ![]() $-1$-shifted symplectic form on
$-1$-shifted symplectic form on ![]() $\boldsymbol {R}$ constructed in Example 2.5, and an open inclusion
$\boldsymbol {R}$ constructed in Example 2.5, and an open inclusion ![]() $\boldsymbol {\iota } \colon \boldsymbol {R} \hookrightarrow \boldsymbol {X}$ such that
$\boldsymbol {\iota } \colon \boldsymbol {R} \hookrightarrow \boldsymbol {X}$ such that ![]() $\boldsymbol {\iota } ^{*} \omega _{\boldsymbol {X}} \sim \omega _{\boldsymbol {R}}$, the tuple
$\boldsymbol {\iota } ^{*} \omega _{\boldsymbol {X}} \sim \omega _{\boldsymbol {R}}$, the tuple ![]() $(R, U, f, i)$ gives a d-critical chart for
$(R, U, f, i)$ gives a d-critical chart for ![]() $(X, s_X)$ where we write
$(X, s_X)$ where we write ![]() $R = t_0(\boldsymbol {R})$ and
$R = t_0(\boldsymbol {R})$ and ![]() $i \colon R \hookrightarrow U$ for the natural closed embedding. Furthermore, there exists a canonical isomorphism of line bundles
$i \colon R \hookrightarrow U$ for the natural closed embedding. Furthermore, there exists a canonical isomorphism of line bundles
where ![]() $\mathop {\widehat {\mathrm {det}}}\nolimits (\mathbb {L}_{\boldsymbol {X}}) = \mathop {\mathrm {det}}\nolimits (\mathbb {L}_{\boldsymbol {X}} |_{X^{\mathrm{red}}})$ by definition.
$\mathop {\widehat {\mathrm {det}}}\nolimits (\mathbb {L}_{\boldsymbol {X}}) = \mathop {\mathrm {det}}\nolimits (\mathbb {L}_{\boldsymbol {X}} |_{X^{\mathrm{red}}})$ by definition.
We define the notion of orientations for ![]() $-1$-shifted symplectic derived schemes to be that of the underlying d-critical schemes.
$-1$-shifted symplectic derived schemes to be that of the underlying d-critical schemes.
For later use, we explain the construction of ![]() $\Lambda _{\boldsymbol {X}}$ in the above theorem for
$\Lambda _{\boldsymbol {X}}$ in the above theorem for ![]() $\boldsymbol {X} = \mathop {\mathbf {Crit}}\nolimits (f)$ where
$\boldsymbol {X} = \mathop {\mathbf {Crit}}\nolimits (f)$ where ![]() $f$ is a regular function on a smooth scheme
$f$ is a regular function on a smooth scheme ![]() $U$. In this case,
$U$. In this case, ![]() $\mathbb {L}_{\boldsymbol {X}}|_{X}$ is represented by the two-term complex
$\mathbb {L}_{\boldsymbol {X}}|_{X}$ is represented by the two-term complex
where ![]() $\mathrm {Hess}(f)$ denotes the Hessian of
$\mathrm {Hess}(f)$ denotes the Hessian of ![]() $f$. We define
$f$. We define ![]() $\Lambda _{\boldsymbol {X}}$ by the following composition:
$\Lambda _{\boldsymbol {X}}$ by the following composition:
 \begin{align} \mathop{\widehat{\mathrm{det}}}\nolimits(\mathbb{L}_{\boldsymbol{X}}) &\cong \mathop{\mathrm{det}}\nolimits(\Omega_U \vert _{X^{\mathrm{red}}}) \otimes \mathop{\mathrm{det}}\nolimits(T_U \vert _{X^{\mathrm{red}}})^{{-}1} \nonumber\\ &\cong (i^{*} K_U) \vert _{X^{\mathrm{red}}} ^{{\otimes}^{2}} \xrightarrow{\cdot \big(\frac{1}{2}\big)^{\dim U}} (i^{*} K_U) \vert _{X^{\mathrm{red}}} ^{{\otimes}^{2}} \cong K_{X, s}. \end{align}
\begin{align} \mathop{\widehat{\mathrm{det}}}\nolimits(\mathbb{L}_{\boldsymbol{X}}) &\cong \mathop{\mathrm{det}}\nolimits(\Omega_U \vert _{X^{\mathrm{red}}}) \otimes \mathop{\mathrm{det}}\nolimits(T_U \vert _{X^{\mathrm{red}}})^{{-}1} \nonumber\\ &\cong (i^{*} K_U) \vert _{X^{\mathrm{red}}} ^{{\otimes}^{2}} \xrightarrow{\cdot \big(\frac{1}{2}\big)^{\dim U}} (i^{*} K_U) \vert _{X^{\mathrm{red}}} ^{{\otimes}^{2}} \cong K_{X, s}. \end{align}
where ![]() $\mathop {\mathrm {det}}\nolimits (T_U)^{-1} \cong K_U$ is locally defined by
$\mathop {\mathrm {det}}\nolimits (T_U)^{-1} \cong K_U$ is locally defined by
The constant ![]() $(\frac {1}{2})^{\dim U}$ is just a convention, and it corresponds to the fact that
$(\frac {1}{2})^{\dim U}$ is just a convention, and it corresponds to the fact that ![]() $\mathrm {Hess} (z^{2}) = 2({{\mathrm d}}z)^{\otimes ^{2}}$.
$\mathrm {Hess} (z^{2}) = 2({{\mathrm d}}z)^{\otimes ^{2}}$.
We now we discuss the canonical orientation for ![]() $-1$-shifted cotangent schemes. To do this we recall basic facts on the determinant of perfect complexes, which are proved in Appendix A.
$-1$-shifted cotangent schemes. To do this we recall basic facts on the determinant of perfect complexes, which are proved in Appendix A.
Lemma 2.14 Let ![]() $\boldsymbol {\mathfrak {X}}$ be a derived Artin stack.
$\boldsymbol {\mathfrak {X}}$ be a derived Artin stack.
(i) For a perfect complex
 $E$ on
$E$ on  $\boldsymbol {\mathfrak {X}}$ and an integer
$\boldsymbol {\mathfrak {X}}$ and an integer  $m$, we have natural isomorphisms
$m$, we have natural isomorphisms
 \[ \hat{\eta}_E \colon \mathop{\widehat{\mathrm{det}}}\nolimits(E^{{\vee}}) \cong \mathop{\widehat{\mathrm{det}}}\nolimits(E)^{{-}1},\quad \hat{\chi}_E^{(m)} \colon \mathop{\widehat{\mathrm{det}}}\nolimits{(E[m])} \cong \mathop{\widehat{\mathrm{det}}}\nolimits(E)^{({-}1)^{m}}. \]
\[ \hat{\eta}_E \colon \mathop{\widehat{\mathrm{det}}}\nolimits(E^{{\vee}}) \cong \mathop{\widehat{\mathrm{det}}}\nolimits(E)^{{-}1},\quad \hat{\chi}_E^{(m)} \colon \mathop{\widehat{\mathrm{det}}}\nolimits{(E[m])} \cong \mathop{\widehat{\mathrm{det}}}\nolimits(E)^{({-}1)^{m}}. \](ii) For a distinguished triangle
 $\Delta \colon E \to F \to G \to E[1]$ of perfect complexes on
$\Delta \colon E \to F \to G \to E[1]$ of perfect complexes on  $\boldsymbol {\mathfrak {X}}$, we have a natural isomorphism
$\boldsymbol {\mathfrak {X}}$, we have a natural isomorphism
 \[ \hat{\imath}(\Delta) \colon \mathop{\widehat{\mathrm{det}}}\nolimits(E) \otimes \mathop{\widehat{\mathrm{det}}}\nolimits(G) \cong \mathop{\widehat{\mathrm{det}}}\nolimits(F). \]
\[ \hat{\imath}(\Delta) \colon \mathop{\widehat{\mathrm{det}}}\nolimits(E) \otimes \mathop{\widehat{\mathrm{det}}}\nolimits(G) \cong \mathop{\widehat{\mathrm{det}}}\nolimits(F). \]
We write ![]() $\hat {\chi }_E = \hat {\chi }_E^{(1)}$. The following example defines the canonical orientation for
$\hat {\chi }_E = \hat {\chi }_E^{(1)}$. The following example defines the canonical orientation for ![]() $-1$-shifted cotangent schemes.
$-1$-shifted cotangent schemes.
Example 2.15 [Reference TodaTod19, Lemma 4.3]
Let ![]() $\boldsymbol {Y}$ be a quasi-smooth derived scheme,
$\boldsymbol {Y}$ be a quasi-smooth derived scheme, ![]() ${\boldsymbol {\pi }} \colon {\mathbf {T}^{*}[-1]\boldsymbol {Y}} \to {\boldsymbol {Y}}$ be the projection, and write
${\boldsymbol {\pi }} \colon {\mathbf {T}^{*}[-1]\boldsymbol {Y}} \to {\boldsymbol {Y}}$ be the projection, and write ![]() $s_{\mathbf {T}^{*}[-1]\boldsymbol {Y}}$ for the d-critical structure associated with the canonical
$s_{\mathbf {T}^{*}[-1]\boldsymbol {Y}}$ for the d-critical structure associated with the canonical ![]() $-1$-shifted symplectic form constructed in Example 2.6. We have a natural distinguished triangle
$-1$-shifted symplectic form constructed in Example 2.6. We have a natural distinguished triangle
Define an isomorphism
by the composition of the isomorphisms
 \begin{align*} (\pi^{\mathrm{red}} )^{*} \mathop{\widehat{\mathrm{det}}}\nolimits(\mathbb{L}_{\boldsymbol{Y}})^{{\otimes}^{2}} &\xrightarrow{\mathop{\mathrm{id}}\nolimits \otimes \hat{\eta}_{\boldsymbol{\pi}^{*} \mathbb{T}_{\boldsymbol{Y}}}} (\pi^{\mathrm{red}} )^{*} \mathop{\widehat{\mathrm{det}}}\nolimits(\mathbb{L}_{\boldsymbol{Y}}) \otimes (\pi^{\mathrm{red}} )^{*} \mathop{\widehat{\mathrm{det}}}\nolimits(\mathbb{T}_{\boldsymbol{Y}})^{{-}1} \\ &\xrightarrow{\mathop{\mathrm{id}}\nolimits \otimes \hat{\chi}_{\boldsymbol{\pi}^{*} \mathbb{T}_{\boldsymbol{Y}}}^{{-}1}} (\pi^{\mathrm{red}} )^{*} \mathop{\widehat{\mathrm{det}}}\nolimits(\mathbb{L}_{\boldsymbol{Y}}) \otimes (\pi^{\mathrm{red}} )^{*} \mathop{\widehat{\mathrm{det}}}\nolimits(\mathbb{T}_{\boldsymbol{Y}}[1]) \\ &\xrightarrow{\hat{\imath}(\Delta_{\boldsymbol{\pi}})} \mathop{\widehat{\mathrm{det}}}\nolimits(\mathbb{L}_{\mathbf{T}^{*}[{-}1]\boldsymbol{Y}}) \end{align*}
\begin{align*} (\pi^{\mathrm{red}} )^{*} \mathop{\widehat{\mathrm{det}}}\nolimits(\mathbb{L}_{\boldsymbol{Y}})^{{\otimes}^{2}} &\xrightarrow{\mathop{\mathrm{id}}\nolimits \otimes \hat{\eta}_{\boldsymbol{\pi}^{*} \mathbb{T}_{\boldsymbol{Y}}}} (\pi^{\mathrm{red}} )^{*} \mathop{\widehat{\mathrm{det}}}\nolimits(\mathbb{L}_{\boldsymbol{Y}}) \otimes (\pi^{\mathrm{red}} )^{*} \mathop{\widehat{\mathrm{det}}}\nolimits(\mathbb{T}_{\boldsymbol{Y}})^{{-}1} \\ &\xrightarrow{\mathop{\mathrm{id}}\nolimits \otimes \hat{\chi}_{\boldsymbol{\pi}^{*} \mathbb{T}_{\boldsymbol{Y}}}^{{-}1}} (\pi^{\mathrm{red}} )^{*} \mathop{\widehat{\mathrm{det}}}\nolimits(\mathbb{L}_{\boldsymbol{Y}}) \otimes (\pi^{\mathrm{red}} )^{*} \mathop{\widehat{\mathrm{det}}}\nolimits(\mathbb{T}_{\boldsymbol{Y}}[1]) \\ &\xrightarrow{\hat{\imath}(\Delta_{\boldsymbol{\pi}})} \mathop{\widehat{\mathrm{det}}}\nolimits(\mathbb{L}_{\mathbf{T}^{*}[{-}1]\boldsymbol{Y}}) \end{align*}
where we write ![]() $\pi = t_0(\boldsymbol {\pi } )$. Define
$\pi = t_0(\boldsymbol {\pi } )$. Define
by the composition ![]() $\Lambda _{\mathbf {T}^{*}[-1]\boldsymbol {Y}} \circ o_{\mathbf {T}^{*}[-1]\boldsymbol {Y}}'$, and we call this the canonical orientation for
$\Lambda _{\mathbf {T}^{*}[-1]\boldsymbol {Y}} \circ o_{\mathbf {T}^{*}[-1]\boldsymbol {Y}}'$, and we call this the canonical orientation for ![]() $\mathbf {T}^{*}[-1]\boldsymbol {Y}$.
$\mathbf {T}^{*}[-1]\boldsymbol {Y}$.
2.3 Vanishing cycle complexes
Let ![]() $f$ be a holomorphic function on a complex manifold
$f$ be a holomorphic function on a complex manifold ![]() $U$, and set
$U$, and set ![]() $U_0 = f^{-1}(0)$ and
$U_0 = f^{-1}(0)$ and ![]() $U_{\leq 0} = f^{-1}(\{z\in \mathbb {C} \mid \mathrm {Re}(z) \leq 0\})$. The (shifted) vanishing cycle functor
$U_{\leq 0} = f^{-1}(\{z\in \mathbb {C} \mid \mathrm {Re}(z) \leq 0\})$. The (shifted) vanishing cycle functor ![]() ${\varphi _f ^{p}} \colon {D^{b} _c(U, \mathbb {Q})} \to {D^{b} (U_0, \mathbb {Q})}$ is defined by the composition of the functors
${\varphi _f ^{p}} \colon {D^{b} _c(U, \mathbb {Q})} \to {D^{b} (U_0, \mathbb {Q})}$ is defined by the composition of the functors
The functor ![]() $\varphi _f ^{p}$ preserves the constructibility (see, for example, [Reference DimcaDim04, Definition 4.2.4, Proposition 4.2.9]). The canonical morphism
$\varphi _f ^{p}$ preserves the constructibility (see, for example, [Reference DimcaDim04, Definition 4.2.4, Proposition 4.2.9]). The canonical morphism ![]() $(U_{\leq 0} \hookrightarrow U)^{!} \to (U_{\leq 0} \hookrightarrow U)^{*}$ induces a natural transform
$(U_{\leq 0} \hookrightarrow U)^{!} \to (U_{\leq 0} \hookrightarrow U)^{*}$ induces a natural transform
Here we list basic properties of the functor ![]() $\varphi _f ^{p}$ we use later.
$\varphi _f ^{p}$ we use later.
Proposition 2.16 Let ![]() $U$ be a complex manifold and
$U$ be a complex manifold and ![]() $f$ be a holomorphic function on it. Write
$f$ be a holomorphic function on it. Write ![]() $U_0 =f^{-1}(0)$.
$U_0 =f^{-1}(0)$.
(i) If
 $F$ is a perverse sheaf on
$F$ is a perverse sheaf on  $U$, then
$U$, then  $\varphi _f^{p} (F)$ is also a perverse sheaf.
$\varphi _f^{p} (F)$ is also a perverse sheaf.(ii) The support of
 $\varphi _f ^{p} (\mathbb {Q}_U)$ is contained in
$\varphi _f ^{p} (\mathbb {Q}_U)$ is contained in  $\mathop {\mathrm {Crit}}\nolimits (f)$.
$\mathop {\mathrm {Crit}}\nolimits (f)$.(iii) Let
 ${q} \colon {V} \to {U}$ be a holomorphic map where
${q} \colon {V} \to {U}$ be a holomorphic map where  $V$ is a complex manifold, and
$V$ is a complex manifold, and  ${q_0} \colon {V_0} \to {U_0}$ denotes the restriction of
${q_0} \colon {V_0} \to {U_0}$ denotes the restriction of  $q$ where
$q$ where  $V_0 = (f \circ q)^{-1}(0)$. Then we have a canonical morphism
$V_0 = (f \circ q)^{-1}(0)$. Then we have a canonical morphism  ${\Theta _{q, f}} \colon {q_0 ^{*} \varphi _f^{p} (F)} \to {\varphi _{f\circ q} ^{p} (q^{*}F)}$ for each
${\Theta _{q, f}} \colon {q_0 ^{*} \varphi _f^{p} (F)} \to {\varphi _{f\circ q} ^{p} (q^{*}F)}$ for each  $F \in D^{b} _c(U,\mathbb {Q})$, which is an isomorphism if
$F \in D^{b} _c(U,\mathbb {Q})$, which is an isomorphism if  $q$ is a submersion. Further, the following diagram commutes.
(2.9)
$q$ is a submersion. Further, the following diagram commutes.
(2.9)
(iv) (Thom and Sebastiani) Let
 $V$ be a complex manifold,
$V$ be a complex manifold,  $g$ be a holomorphic function on it, and
$g$ be a holomorphic function on it, and  $f \boxplus g$ be the function on
$f \boxplus g$ be the function on  $U \times V$ defined by
$U \times V$ defined by  $(f \boxplus g)(u, v) = f(u) + g(v)$. For
$(f \boxplus g)(u, v) = f(u) + g(v)$. For  $F \in D^{b} _c(U,\mathbb {Q})$ and
$F \in D^{b} _c(U,\mathbb {Q})$ and  $G \in D^{b} _c(V,\mathbb {Q})$, we have a canonical isomorphism
where
$G \in D^{b} _c(V,\mathbb {Q})$, we have a canonical isomorphism
where \[ \mathcal{TS}_{f, g, F, G} \colon \varphi_{f \boxplus g}^{p}(F \boxtimes G) \vert_{U_0 \times V_0} \cong \varphi_f^{p} (F) \boxtimes \varphi_g^{p} (G) \]
\[ \mathcal{TS}_{f, g, F, G} \colon \varphi_{f \boxplus g}^{p}(F \boxtimes G) \vert_{U_0 \times V_0} \cong \varphi_f^{p} (F) \boxtimes \varphi_g^{p} (G) \] $V_0 = g^{-1}(0)$. Further, the following diagram commutes.
(2.10)
$V_0 = g^{-1}(0)$. Further, the following diagram commutes.
(2.10)
(v) (Verdier duality) For
 $F \in D^{b}_c(U,\mathbb {Q})$, there exists a canonical isomorphism
where
$F \in D^{b}_c(U,\mathbb {Q})$, there exists a canonical isomorphism
where \[ \mathbb{D}_{U_0}(\varphi_f^{p}(F)) \cong \varphi_f^{p}(\mathbb{D}_U(F)) \]
\[ \mathbb{D}_{U_0}(\varphi_f^{p}(F)) \cong \varphi_f^{p}(\mathbb{D}_U(F)) \] $\mathbb {D}_{U_0}$ and
$\mathbb {D}_{U_0}$ and  $\mathbb {D}_U$ denote the Verdier duality functors on
$\mathbb {D}_U$ denote the Verdier duality functors on  $U_0$ and
$U_0$ and  $U$, respectively.
$U$, respectively.
Proof. (i) is proved in [Reference Kashiwara and SchapiraKS90, Corollary 10.3.13]. (ii) easily follows from the definition. (iii) follows from the smooth base-change theorem. (iv) is proved in [Reference SchürmanSch03, Corollary 1.3.4]. (v) is proved in [Reference MasseyMas16].
By an abuse of notation, we write ![]() $\varphi _f ^{p} = \varphi _f ^{p} (\mathbb {Q}_U[\dim U])$ if there is no confusion. We identify the
$\varphi _f ^{p} = \varphi _f ^{p} (\mathbb {Q}_U[\dim U])$ if there is no confusion. We identify the ![]() $i$th cohomology of the stalk of
$i$th cohomology of the stalk of ![]() $\varphi _f ^{p}$ at some point with the
$\varphi _f ^{p}$ at some point with the ![]() $(i + \dim U)$th relative cohomology of a ball modulo the Milnor fiber at a small positive value. We regard
$(i + \dim U)$th relative cohomology of a ball modulo the Milnor fiber at a small positive value. We regard ![]() $\varphi _f ^{p}$ as a perverse sheaf on
$\varphi _f ^{p}$ as a perverse sheaf on ![]() $U$,
$U$, ![]() $U_0$, or
$U_0$, or ![]() $\mathop {\mathrm {Crit}}\nolimits (f)$ depending on each situation.
$\mathop {\mathrm {Crit}}\nolimits (f)$ depending on each situation.
If we write ![]() $z \colon \mathbb {C} \to \mathbb {C}$ for the identity map, we have natural isomorphisms
$z \colon \mathbb {C} \to \mathbb {C}$ for the identity map, we have natural isomorphisms
 \begin{align} (\varphi _{z^{2}} ^{p})_0 &\cong \mathrm{H}^{1} (\mathbb{C}, \{z \in \mathbb{C} \mid \mathrm{Re}(z^{2}) >0 \}; \mathbb{Q}) \nonumber\\ &\cong \mathrm{H}^{1} (\mathbb{R}, \mathbb{R} \setminus 0; \mathbb{Q}). \end{align}
\begin{align} (\varphi _{z^{2}} ^{p})_0 &\cong \mathrm{H}^{1} (\mathbb{C}, \{z \in \mathbb{C} \mid \mathrm{Re}(z^{2}) >0 \}; \mathbb{Q}) \nonumber\\ &\cong \mathrm{H}^{1} (\mathbb{R}, \mathbb{R} \setminus 0; \mathbb{Q}). \end{align}The latter isomorphism is induced by the inclusion
The orientation of ![]() $\mathbb {R}$ given by the positive direction defines a cohomology class
$\mathbb {R}$ given by the positive direction defines a cohomology class ![]() $a_+ \in \mathrm {H}^{1} (\mathbb {R}, \mathbb {R} \setminus 0; \mathbb {Q})$, hence a trivialization
$a_+ \in \mathrm {H}^{1} (\mathbb {R}, \mathbb {R} \setminus 0; \mathbb {Q})$, hence a trivialization
Let ![]() $(z_1, \ldots, z_n)$ be the standard coordinate of
$(z_1, \ldots, z_n)$ be the standard coordinate of ![]() $\mathbb {C}^{n}$. Then the Thom–Sebastiani theorem and (2.12) give an isomorphism
$\mathbb {C}^{n}$. Then the Thom–Sebastiani theorem and (2.12) give an isomorphism
We now recall the construction of the globalization of the vanishing cycle complexes associated with oriented d-critical schemes introduced in [Reference Brav, Bussi, Dupont, Joyce and SzeondröiBBDJS15]. To do this we introduce the following notation. For a scheme ![]() $X$, a principal
$X$, a principal ![]() $\mathbb {Z}/2\mathbb {Z}$-bundle
$\mathbb {Z}/2\mathbb {Z}$-bundle ![]() $P$ on
$P$ on ![]() $X$, and
$X$, and ![]() $F \in D^{b} _c (X, \mathbb {Q})$, one defines
$F \in D^{b} _c (X, \mathbb {Q})$, one defines
where the ![]() $\mathbb {Z}_X/2\mathbb {Z}_X$-module structure on
$\mathbb {Z}_X/2\mathbb {Z}_X$-module structure on ![]() $\mathbb {Q}_X$ is defined by multiplication by
$\mathbb {Q}_X$ is defined by multiplication by ![]() $-1$. For a d-critical scheme
$-1$. For a d-critical scheme ![]() $(X, s)$ with a fixed orientation
$(X, s)$ with a fixed orientation ![]() $o \colon {L^{\otimes ^{2}}} \xrightarrow {\sim }{K_{X,s}}$ and its d-critical chart
$o \colon {L^{\otimes ^{2}}} \xrightarrow {\sim }{K_{X,s}}$ and its d-critical chart ![]() $\mathscr {R} = (R, U, f, i)$, we define a principal
$\mathscr {R} = (R, U, f, i)$, we define a principal ![]() $\mathbb {Z}/2\mathbb {Z}$-bundle
$\mathbb {Z}/2\mathbb {Z}$-bundle
over ![]() $R$ whose sections are local isomorphisms
$R$ whose sections are local isomorphisms
such that ![]() $a^{\otimes ^{2}} = \iota _{R, U, f, i} \circ o$. For an embedding of d-critical charts
$a^{\otimes ^{2}} = \iota _{R, U, f, i} \circ o$. For an embedding of d-critical charts
such that ![]() $\alpha \colon U_2 \to U_1$ and
$\alpha \colon U_2 \to U_1$ and ![]() $\beta \colon U_1 \to \mathbb {C}^{n}$ as in Theorem 2.10(ii) exist,
$\beta \colon U_1 \to \mathbb {C}^{n}$ as in Theorem 2.10(ii) exist,
parameterizes square roots of
Thus the choice ![]() $i_1^{*} \beta ^{*} ({{\mathrm d}}z_1\wedge \cdots \wedge {{\mathrm d}}z_n) |_{R^{\mathrm{red}}}$ gives an isomorphism
$i_1^{*} \beta ^{*} ({{\mathrm d}}z_1\wedge \cdots \wedge {{\mathrm d}}z_n) |_{R^{\mathrm{red}}}$ gives an isomorphism
On the other hand, we have isomorphisms
where the first one is defined using (2.12) and the second one is a Thom–Sebastiani isomorphism.
With this notation, the globalized vanishing cycle complex is defined by the following theorem.
Theorem 2.17 [Reference Brav, Bussi, Dupont, Joyce and SzeondröiBBDJS15, Theorem 6.9]
Let ![]() $(X, s, o)$ be an oriented d-critical scheme, and let
$(X, s, o)$ be an oriented d-critical scheme, and let ![]() $\mathscr {R}_1 = (R_1, U_1, f_1, i_1)$ and
$\mathscr {R}_1 = (R_1, U_1, f_1, i_1)$ and ![]() $\mathscr {R}_2 = (R_2, U_2, f_2, i_2)$ be any d-critical charts with
$\mathscr {R}_2 = (R_2, U_2, f_2, i_2)$ be any d-critical charts with ![]() $R_1 \subset R_2$. Then there exists a natural isomorphism
$R_1 \subset R_2$. Then there exists a natural isomorphism
with the following properties.
(i) Given another d-critical chart
 $\mathscr {R}_3 = (R_3, U_3, f_3, i_3)$ with
$\mathscr {R}_3 = (R_3, U_3, f_3, i_3)$ with  $R_2 \subset R_3$, we have
$R_2 \subset R_3$, we have
 \[ \Upsilon_{\mathscr{R}_3, \mathscr{R}_1} =\Upsilon_{\mathscr{R}_3, \mathscr{R}_2} \vert _{R_1} \circ \Upsilon_{\mathscr{R}_2, \mathscr{R}_1}. \]
\[ \Upsilon_{\mathscr{R}_3, \mathscr{R}_1} =\Upsilon_{\mathscr{R}_3, \mathscr{R}_2} \vert _{R_1} \circ \Upsilon_{\mathscr{R}_2, \mathscr{R}_1}. \](ii) If
 $\mathscr {R}_1$ is an open subchart of
$\mathscr {R}_1$ is an open subchart of  $\mathscr {R}_2$, then
$\mathscr {R}_2$, then  $\Upsilon _{\mathscr {R}_2, \mathscr {R}_1}$ is defined by the canonical isomorphisms
$\Upsilon _{\mathscr {R}_2, \mathscr {R}_1}$ is defined by the canonical isomorphisms
 \[ \varphi_{f_1}^{p} \cong \varphi_{f_2}^{p} |_{U_1},\quad Q^{o}_{\mathscr{R}_1} \cong Q^{o}_{\mathscr{R}_1} |_{U_1}. \]
\[ \varphi_{f_1}^{p} \cong \varphi_{f_2}^{p} |_{U_1},\quad Q^{o}_{\mathscr{R}_1} \cong Q^{o}_{\mathscr{R}_1} |_{U_1}. \](iii) For an embedding of d-critical charts
such that \[ \mathscr{R}_1 = (R, U_1, f_1, i_1) \hookrightarrow \mathscr{R}_2 = (R, U_2, f_2, i_2) \]
\[ \mathscr{R}_1 = (R, U_1, f_1, i_1) \hookrightarrow \mathscr{R}_2 = (R, U_2, f_2, i_2) \] $\alpha \colon U_2 \to U_1$ and
$\alpha \colon U_2 \to U_1$ and  $\beta \colon U_1 \to \mathbb {C}^{n}$ as in Theorem 2.10(ii) exist,
$\beta \colon U_1 \to \mathbb {C}^{n}$ as in Theorem 2.10(ii) exist,  $\Upsilon _{\mathscr {R}_2, \mathscr {R}_1}$ is defined by isomorphisms (2.15) and (2.16).
$\Upsilon _{\mathscr {R}_2, \mathscr {R}_1}$ is defined by isomorphisms (2.15) and (2.16).
Using (i), we can define a perverse sheaf ![]() $\varphi _{X, s, o}^{p}$ on
$\varphi _{X, s, o}^{p}$ on ![]() $X$ such that for a given d-critical chart
$X$ such that for a given d-critical chart ![]() $\mathscr {R} = (R, U, f, i)$ there exists a natural isomorphism
$\mathscr {R} = (R, U, f, i)$ there exists a natural isomorphism
Moreover, there exists an isomorphism ![]() $\sigma _{X, s, o} \colon \mathbb {D}_X(\varphi _{X, s, o}^{p}) \cong \varphi _{X, s, o}^{p}$.
$\sigma _{X, s, o} \colon \mathbb {D}_X(\varphi _{X, s, o}^{p}) \cong \varphi _{X, s, o}^{p}$.
For later use, we recall the construction of ![]() $\sigma _{X, s, o}$. For a d-critical chart
$\sigma _{X, s, o}$. For a d-critical chart ![]() $\mathscr {R} = (R, U, f, i)$, the Verdier self-duality of
$\mathscr {R} = (R, U, f, i)$, the Verdier self-duality of ![]() $\varphi _f^{p}$ induces an isomorphism
$\varphi _f^{p}$ induces an isomorphism
If we define
we can show that it glues to define an isomorphism ![]() $\sigma _{X, s, o}$ (the necessity of the sign intervention is due to the fact that the first diagram in [Reference Brav, Bussi, Dupont, Joyce and SzeondröiBBDJS15, Theorem 2.13] commutes up to the sign
$\sigma _{X, s, o}$ (the necessity of the sign intervention is due to the fact that the first diagram in [Reference Brav, Bussi, Dupont, Joyce and SzeondröiBBDJS15, Theorem 2.13] commutes up to the sign ![]() $(-1)^{\dim U \cdot \dim V}$). If there is no confusion, we write
$(-1)^{\dim U \cdot \dim V}$). If there is no confusion, we write ![]() $\sigma _{X} = \sigma _{X, s, o}$.
$\sigma _{X} = \sigma _{X, s, o}$.
For an oriented ![]() $-1$-shifted symplectic derived scheme
$-1$-shifted symplectic derived scheme ![]() $(\boldsymbol {X}, \omega _{\boldsymbol {X}}, o)$, define
$(\boldsymbol {X}, \omega _{\boldsymbol {X}}, o)$, define ![]() $\varphi _{\boldsymbol {X}, \omega _{\boldsymbol {X}}, o}$ to be the perverse sheaf
$\varphi _{\boldsymbol {X}, \omega _{\boldsymbol {X}}, o}$ to be the perverse sheaf ![]() $\varphi ^{p}_{X, s_X, o}$ on
$\varphi ^{p}_{X, s_X, o}$ on ![]() $X = t_0(\boldsymbol {X})$ where
$X = t_0(\boldsymbol {X})$ where ![]() $s_X$ is the d-critical structure associated with
$s_X$ is the d-critical structure associated with ![]() $\omega _{\boldsymbol {X}}$. If there is no confusion, we simply write
$\omega _{\boldsymbol {X}}$. If there is no confusion, we simply write ![]() $\varphi _{\boldsymbol {X}, o}$ or
$\varphi _{\boldsymbol {X}, o}$ or ![]() $\varphi _{\boldsymbol {X}}$ instead of
$\varphi _{\boldsymbol {X}}$ instead of ![]() $\varphi _{\boldsymbol {X}, \omega _{\boldsymbol {X}}, o}$.
$\varphi _{\boldsymbol {X}, \omega _{\boldsymbol {X}}, o}$.
2.4 Dimensional reduction
Let ![]() $U$ be a smooth variety of dimension
$U$ be a smooth variety of dimension ![]() $n$, and
$n$, and ![]() $s$ be a section of a trivial vector bundle
$s$ be a section of a trivial vector bundle ![]() $E$ of rank
$E$ of rank ![]() $r$ on
$r$ on ![]() $U$. Denote by
$U$. Denote by ![]() $\bar {s} \colon \mathop {\mathrm {Tot}}\nolimits _U(E^{\vee }) \to \mathbb {A}^{1}$ the regular function corresponding to
$\bar {s} \colon \mathop {\mathrm {Tot}}\nolimits _U(E^{\vee }) \to \mathbb {A}^{1}$ the regular function corresponding to ![]() $s$. We have a canonical morphism
$s$. We have a canonical morphism
Define ![]() $Z := Z(s)$ to be the zero locus of
$Z := Z(s)$ to be the zero locus of ![]() $s$, and
$s$, and ![]() $\tilde {Z} := (\pi _{E^{\vee }})^{-1}(Z)$ where
$\tilde {Z} := (\pi _{E^{\vee }})^{-1}(Z)$ where ![]() $\pi _{E^{\vee }} \colon \mathop {\mathrm {Tot}}\nolimits _U(E^{\vee }) \to U$ is the projection. By restricting (2.18) to
$\pi _{E^{\vee }} \colon \mathop {\mathrm {Tot}}\nolimits _U(E^{\vee }) \to U$ is the projection. By restricting (2.18) to ![]() $\tilde {Z}$, we obtain
$\tilde {Z}$, we obtain
Here we identify ![]() $\varphi _{\bar {s}}^{p}$ and
$\varphi _{\bar {s}}^{p}$ and ![]() $\varphi _{\bar {s}}^{p} | _{\tilde {Z}}$ since the support of
$\varphi _{\bar {s}}^{p} | _{\tilde {Z}}$ since the support of ![]() $\varphi _{\bar {s}}^{p}$ is contained in
$\varphi _{\bar {s}}^{p}$ is contained in ![]() $\tilde {Z}$.
$\tilde {Z}$.
Theorem 2.18 [Reference DavisonDav17, Theorem A.1]
The natural map
is an isomorphism.
We want to globalize this statement for the ![]() $-1$-shifted cotangent space using Lemma 2.7. To do this, we first need to prove the triviality of the
$-1$-shifted cotangent space using Lemma 2.7. To do this, we first need to prove the triviality of the ![]() $\mathbb {Z} / 2\mathbb {Z}$-bundle introduced in (2.14) associated with the canonical orientations for shifted cotangent schemes and certain d-critical charts.
$\mathbb {Z} / 2\mathbb {Z}$-bundle introduced in (2.14) associated with the canonical orientations for shifted cotangent schemes and certain d-critical charts.
Lemma 2.19 Let ![]() $U, s$ be as above, and
$U, s$ be as above, and ![]() $\boldsymbol {Z} := \boldsymbol {Z}(s)$ be the derived zero locus of
$\boldsymbol {Z} := \boldsymbol {Z}(s)$ be the derived zero locus of ![]() $s$. Assume
$s$. Assume ![]() $U$ is affine and carries a global étale coordinate. Denote by
$U$ is affine and carries a global étale coordinate. Denote by ![]() $o^{} _{\mathbf {T}^{*}[-1]\boldsymbol {Z}}$ the canonical orientation constructed in Example 2.15 and by
$o^{} _{\mathbf {T}^{*}[-1]\boldsymbol {Z}}$ the canonical orientation constructed in Example 2.15 and by
the d-critical chart induced by the equivalence (2.2). Then ![]() $Q^{o^{} _{\mathbf {T}^{*}[-1]\boldsymbol {Z}}}_{\tilde {\mathscr {Z}}}$ is a trivial
$Q^{o^{} _{\mathbf {T}^{*}[-1]\boldsymbol {Z}}}_{\tilde {\mathscr {Z}}}$ is a trivial ![]() $\mathbb {Z} / 2\mathbb {Z}$-bundle.
$\mathbb {Z} / 2\mathbb {Z}$-bundle.
Proof. The distinguished triangle (2.6) for ![]() $\boldsymbol {Z}$ restricted to
$\boldsymbol {Z}$ restricted to ![]() $\mathop {\mathrm {Crit}}\nolimits (\bar {s})$ is represented by the following short exact sequence of two-term complexes:
$\mathop {\mathrm {Crit}}\nolimits (\bar {s})$ is represented by the following short exact sequence of two-term complexes:

Thus the canonical orientation (2.7) for ![]() $\mathop {\mathbf {Crit}}\nolimits (\bar {s})$ is identified with
$\mathop {\mathbf {Crit}}\nolimits (\bar {s})$ is identified with
where
and
are defined in the same manner as (2.5). On the other hand, we have an isomorphism
 \begin{align} \nu \colon \mathop{\widehat{\mathrm{det}}}\nolimits(\pi_{E^{{\vee}}}^{*} \Omega_U) \otimes \mathop{\widehat{\mathrm{det}}}\nolimits(\pi_{E^{{\vee}}}^{*} E^{{\vee}})^{{-}1} &\cong \mathop{\widehat{\mathrm{det}}}\nolimits(\pi_{E^{{\vee}}}^{*} \Omega_U) \otimes \mathop{\widehat{\mathrm{det}}}\nolimits(\pi_{E^{{\vee}}}^{*} E) \nonumber\\ &\cong \mathop{\widehat{\mathrm{det}}}\nolimits(\Omega_{\mathop{\mathrm{Tot}}\nolimits_U(E^{{\vee}})}), \end{align}
\begin{align} \nu \colon \mathop{\widehat{\mathrm{det}}}\nolimits(\pi_{E^{{\vee}}}^{*} \Omega_U) \otimes \mathop{\widehat{\mathrm{det}}}\nolimits(\pi_{E^{{\vee}}}^{*} E^{{\vee}})^{{-}1} &\cong \mathop{\widehat{\mathrm{det}}}\nolimits(\pi_{E^{{\vee}}}^{*} \Omega_U) \otimes \mathop{\widehat{\mathrm{det}}}\nolimits(\pi_{E^{{\vee}}}^{*} E) \nonumber\\ &\cong \mathop{\widehat{\mathrm{det}}}\nolimits(\Omega_{\mathop{\mathrm{Tot}}\nolimits_U(E^{{\vee}})}), \end{align}
where the first isomorphism is defined as (2.5) and the second isomorphism is induced by the lower short exact sequence in (2.21). By the definition of ![]() $o^{} _{\mathbf {T}^{*}[-1]\boldsymbol {Z}}$ and (2.4) we see that
$o^{} _{\mathbf {T}^{*}[-1]\boldsymbol {Z}}$ and (2.4) we see that
where we write ![]() $n = \dim U$ and
$n = \dim U$ and ![]() $r = \mathop {\mathrm {rank}}\nolimits E$. The appearance of the sign
$r = \mathop {\mathrm {rank}}\nolimits E$. The appearance of the sign ![]() $(-1)^{ (n+r)(n+r-1)/2 }$ is caused by the difference of the maps (2.5) and (A.2), and the difference of the symmetric monoidal structure for the category of graded line bundles (A.1) and the standard symmetric monoidal structure for the category of ungraded line bundles. Equation (2.24) implies the triviality of
$(-1)^{ (n+r)(n+r-1)/2 }$ is caused by the difference of the maps (2.5) and (A.2), and the difference of the symmetric monoidal structure for the category of graded line bundles (A.1) and the standard symmetric monoidal structure for the category of ungraded line bundles. Equation (2.24) implies the triviality of ![]() $Q^{o^{} _{\mathbf {T}^{*}[-1]\boldsymbol {Z}}}_{\tilde {\mathscr {Z}}}$.
$Q^{o^{} _{\mathbf {T}^{*}[-1]\boldsymbol {Z}}}_{\tilde {\mathscr {Z}}}$.
For later use, we explicitly choose a trivialization of ![]() $Q^{o^{} _{\mathbf {T}^{*}[-1]\boldsymbol {Z}}}_{\tilde {\mathscr {Z}}}$. For each
$Q^{o^{} _{\mathbf {T}^{*}[-1]\boldsymbol {Z}}}_{\tilde {\mathscr {Z}}}$. For each ![]() $(a, b) \in \mathbb {Z}_{\geq 0}^{2}$, take
$(a, b) \in \mathbb {Z}_{\geq 0}^{2}$, take ![]() $\epsilon _{a, b} \in \{1, -1, \sqrt {-1}, -\sqrt {-1}\}$ so that
$\epsilon _{a, b} \in \{1, -1, \sqrt {-1}, -\sqrt {-1}\}$ so that
•
 $\epsilon _{0, 0} = 1$,
$\epsilon _{0, 0} = 1$,•
 $\epsilon _{a, b} = (-1)^{b} \sqrt {-1} \epsilon _{a-1, b-1}$,
$\epsilon _{a, b} = (-1)^{b} \sqrt {-1} \epsilon _{a-1, b-1}$,•
 $\epsilon _{a+1, b} = (-\sqrt {-1})^{a - b}\epsilon _{a, b}$.
$\epsilon _{a+1, b} = (-\sqrt {-1})^{a - b}\epsilon _{a, b}$.
Then
gives a square root of ![]() $\mu$, hence a trivialization of
$\mu$, hence a trivialization of ![]() $Q^{o^{} _{\mathbf {T}^{*}[-1]\boldsymbol {Z}}}_{\tilde {\mathscr {Z}}}$.
$Q^{o^{} _{\mathbf {T}^{*}[-1]\boldsymbol {Z}}}_{\tilde {\mathscr {Z}}}$.
Corollary 2.20 Let ![]() $\boldsymbol {Y}$ be a quasi-smooth derived scheme,
$\boldsymbol {Y}$ be a quasi-smooth derived scheme, ![]() $\boldsymbol {\pi }_{\boldsymbol {Y}} \colon \mathbf {T}^{*}[-1]\boldsymbol {Y} \to \boldsymbol {Y}$ the projection, and write
$\boldsymbol {\pi }_{\boldsymbol {Y}} \colon \mathbf {T}^{*}[-1]\boldsymbol {Y} \to \boldsymbol {Y}$ the projection, and write ![]() $\pi _{\boldsymbol {Y}} = t_0(\boldsymbol {\pi }_{\boldsymbol {Y}})$. Then
$\pi _{\boldsymbol {Y}} = t_0(\boldsymbol {\pi }_{\boldsymbol {Y}})$. Then ![]() $({\pi _{\boldsymbol {Y}}})_! \varphi _{\mathbf {T}^{*}[-1]\boldsymbol {Y}}^{p}$ is a rank-one local system shifted by
$({\pi _{\boldsymbol {Y}}})_! \varphi _{\mathbf {T}^{*}[-1]\boldsymbol {Y}}^{p}$ is a rank-one local system shifted by ![]() $\operatorname {vdim} \boldsymbol {Y}$.
$\operatorname {vdim} \boldsymbol {Y}$.
Proof. Since the statement is local, we may assume ![]() $\boldsymbol {Y}$ is a derived zero locus
$\boldsymbol {Y}$ is a derived zero locus ![]() $\boldsymbol {Z}(s)$ as in the previous lemma. The conclusion of the lemma implies that
$\boldsymbol {Z}(s)$ as in the previous lemma. The conclusion of the lemma implies that ![]() $\varphi _{\mathbf {T}^{*}[-1]\boldsymbol {Y}}^{p}$ is isomorphic to
$\varphi _{\mathbf {T}^{*}[-1]\boldsymbol {Y}}^{p}$ is isomorphic to ![]() $\varphi _{\bar {s}}^{p}$, hence the statement follows from Theorem 2.18.
$\varphi _{\bar {s}}^{p}$, hence the statement follows from Theorem 2.18.
3. Dimensional reduction for schemes
In this section we will prove that the local system appearing in Corollary 2.20 is in fact trivial, by showing that the local dimensional reduction isomorphism (2.20) is independent of the choice of the Kuranishi chart.
Let ![]() $\boldsymbol {Y}$ be a quasi-smooth derived scheme and
$\boldsymbol {Y}$ be a quasi-smooth derived scheme and ![]() $\boldsymbol {\pi }_{\boldsymbol {Y}} \colon \mathbf {T}^{*}[-1]\boldsymbol {Y} \to \boldsymbol {Y}$ be the projection. We always equip
$\boldsymbol {\pi }_{\boldsymbol {Y}} \colon \mathbf {T}^{*}[-1]\boldsymbol {Y} \to \boldsymbol {Y}$ be the projection. We always equip ![]() $\mathbf {T}^{*}[-1]\boldsymbol {Y}$ with the
$\mathbf {T}^{*}[-1]\boldsymbol {Y}$ with the ![]() $-1$-shifted symplectic form constructed in Example 2.6 and the canonical orientation
$-1$-shifted symplectic form constructed in Example 2.6 and the canonical orientation
Write ![]() ${\pi _{\boldsymbol {Y}}} = t_0(\boldsymbol {\pi }_{\boldsymbol {Y}} )$,
${\pi _{\boldsymbol {Y}}} = t_0(\boldsymbol {\pi }_{\boldsymbol {Y}} )$, ![]() $\tilde {Y} = t_0(\mathbf {T}^{*}[-1]\boldsymbol {Y})$, and
$\tilde {Y} = t_0(\mathbf {T}^{*}[-1]\boldsymbol {Y})$, and ![]() $Y = t_0(\boldsymbol {Y})$. Take a good Kuranishi chart
$Y = t_0(\boldsymbol {Y})$. Take a good Kuranishi chart
of ![]() $\boldsymbol {Y}$. The map
$\boldsymbol {Y}$. The map ![]() $\boldsymbol {\iota }$ induces an open immersion
$\boldsymbol {\iota }$ induces an open immersion ![]() $\tilde {\boldsymbol {\iota }} \colon \mathbf {T}^{*}[-1]\boldsymbol {Z}(s) \hookrightarrow \mathbf {T}^{*}[-1]\boldsymbol {Y}$ with the image
$\tilde {\boldsymbol {\iota }} \colon \mathbf {T}^{*}[-1]\boldsymbol {Z}(s) \hookrightarrow \mathbf {T}^{*}[-1]\boldsymbol {Y}$ with the image ![]() $\tilde {Z} := \pi _{\boldsymbol {Y}}^{-1}(Z)$. Lemma 2.7 shows that there exists a natural embedding
$\tilde {Z} := \pi _{\boldsymbol {Y}}^{-1}(Z)$. Lemma 2.7 shows that there exists a natural embedding ![]() $\tilde {i} \colon \tilde {Z} \hookrightarrow \mathop {\mathrm {Tot}}\nolimits _U(E^{\vee })$ such that
$\tilde {i} \colon \tilde {Z} \hookrightarrow \mathop {\mathrm {Tot}}\nolimits _U(E^{\vee })$ such that
gives a d-critical chart on ![]() $\tilde {Y}$.
$\tilde {Y}$.
We now have an isomorphism
where ![]() $\pi _{E^{\vee }} \colon \mathop {\mathrm {Tot}}\nolimits _U(E^{\vee }) \to U$ is the projection and
$\pi _{E^{\vee }} \colon \mathop {\mathrm {Tot}}\nolimits _U(E^{\vee }) \to U$ is the projection and ![]() $i \colon Z \hookrightarrow U$ is the natural embedding. By the definition of
$i \colon Z \hookrightarrow U$ is the natural embedding. By the definition of ![]() $\varphi _{\mathbf {T}^{*}[-1]\boldsymbol {Y}}^{p}$ in Theorem 2.17 we also have an isomorphism
$\varphi _{\mathbf {T}^{*}[-1]\boldsymbol {Y}}^{p}$ in Theorem 2.17 we also have an isomorphism
By combining isomorphisms (3.1) and (3.2), the trivialization of ![]() $Q^{o}_{\tilde {\mathscr {Z}}}$ in (2.25), and Theorem 2.18, we obtain the following isomorphism:
$Q^{o}_{\tilde {\mathscr {Z}}}$ in (2.25), and Theorem 2.18, we obtain the following isomorphism:
Theorem 3.1 For ![]() $i=1, 2$, let
$i=1, 2$, let ![]() $\mathscr {Z}_i = (Z_i, U_i, E_i, s_i, \boldsymbol {\iota }_i)$ be good Kuranishi charts on
$\mathscr {Z}_i = (Z_i, U_i, E_i, s_i, \boldsymbol {\iota }_i)$ be good Kuranishi charts on ![]() $\boldsymbol{Y}\!$. Then we have
$\boldsymbol{Y}\!$. Then we have ![]() $\bar {\gamma }_{\mathscr {Z}_1} |_{Z_1 \cap Z_2} = \bar {\gamma }_{\mathscr {Z}_2} |_{Z_1 \cap Z_2}$. Therefore there exists a natural isomorphism
$\bar {\gamma }_{\mathscr {Z}_1} |_{Z_1 \cap Z_2} = \bar {\gamma }_{\mathscr {Z}_2} |_{Z_1 \cap Z_2}$. Therefore there exists a natural isomorphism
We say that two Kuranishi charts ![]() $\mathscr {Z}_1 = (Z_1, U_1, E_1, s_1, \boldsymbol {\iota }_1)$ and
$\mathscr {Z}_1 = (Z_1, U_1, E_1, s_1, \boldsymbol {\iota }_1)$ and ![]() $\mathscr {Z}_2 = (Z_2, U_2, E_2, s_2, \boldsymbol {\iota }_2)$ have compatible dimensional reductions at
$\mathscr {Z}_2 = (Z_2, U_2, E_2, s_2, \boldsymbol {\iota }_2)$ have compatible dimensional reductions at ![]() $p \in Z_1 \cap Z_2$ if there exists an analytic open neighborhood
$p \in Z_1 \cap Z_2$ if there exists an analytic open neighborhood ![]() $p \in W \subset Z_1 \cap Z_2$ such that
$p \in W \subset Z_1 \cap Z_2$ such that ![]() $\bar {\gamma }_{\mathscr {Z}_1} |_{W} = \bar {\gamma }_{\mathscr {Z}_2} |_{W}$.
$\bar {\gamma }_{\mathscr {Z}_1} |_{W} = \bar {\gamma }_{\mathscr {Z}_2} |_{W}$.
Lemma 3.2 Let ![]() $\mathscr {Z}_1 = (Z_1, U_1, E_1, s_1, \boldsymbol {\iota }_1)$ and
$\mathscr {Z}_1 = (Z_1, U_1, E_1, s_1, \boldsymbol {\iota }_1)$ and ![]() $\mathscr {Z}_2 = (Z_2, U_2, E_2, s_2, \boldsymbol {\iota }_2)$ be good Kuranishi charts on
$\mathscr {Z}_2 = (Z_2, U_2, E_2, s_2, \boldsymbol {\iota }_2)$ be good Kuranishi charts on ![]() $\boldsymbol {Y}$. Assume that these Kuranishi charts are minimal at
$\boldsymbol {Y}$. Assume that these Kuranishi charts are minimal at ![]() $p \in Z_1 \cap Z_2$. Then they have compatible dimensional reductions at
$p \in Z_1 \cap Z_2$. Then they have compatible dimensional reductions at ![]() $p$.
$p$.
Proof. Denote by ![]() $i_1 \colon Z_1 \hookrightarrow U_1$ and
$i_1 \colon Z_1 \hookrightarrow U_1$ and ![]() $i_2 \colon Z_2 \hookrightarrow U_2$ the natural embeddings, and let
$i_2 \colon Z_2 \hookrightarrow U_2$ the natural embeddings, and let
be d-critical charts associated with ![]() $\mathscr {Z}_1$ and
$\mathscr {Z}_1$ and ![]() $\mathscr {Z}_2$, respectively. Using Proposition 2.3(ii), we may assume that we have the commutative diagram
$\mathscr {Z}_2$, respectively. Using Proposition 2.3(ii), we may assume that we have the commutative diagram

such that ![]() $\eta$ is étale and
$\eta$ is étale and ![]() $\eta (i_1(p)) = i_2(p)$. The natural isomorphism
$\eta (i_1(p)) = i_2(p)$. The natural isomorphism
induces an isomorphism
which identifies the trivializations (2.25). Then Theorem 2.17(ii) implies that the composition
is the natural isomorphism
given in Proposition 2.16(iii) pulled back to ![]() $\widetilde {Z_1}$. Hence the commutativity of diagram (2.9) implies the lemma.
$\widetilde {Z_1}$. Hence the commutativity of diagram (2.9) implies the lemma.
Proposition 3.3 Let ![]() $\mathscr {Z} = (Z, U, E, s, \boldsymbol {\iota })$ be a good Kuranishi chart on
$\mathscr {Z} = (Z, U, E, s, \boldsymbol {\iota })$ be a good Kuranishi chart on ![]() $\boldsymbol {Y}$, which is not minimal at
$\boldsymbol {Y}$, which is not minimal at ![]() $p \in Z$. Then there exists another good Kuranishi chart
$p \in Z$. Then there exists another good Kuranishi chart ![]() $\mathscr {Z}' = (Z', U', E', s', \boldsymbol {\iota }')$ with
$\mathscr {Z}' = (Z', U', E', s', \boldsymbol {\iota }')$ with ![]() $p \in Z'$ and
$p \in Z'$ and ![]() $\dim U' < \dim U$ such that
$\dim U' < \dim U$ such that ![]() $\mathscr {Z}$ and
$\mathscr {Z}$ and ![]() $\mathscr {Z}'$ have compatible dimensional reductions at
$\mathscr {Z}'$ have compatible dimensional reductions at ![]() $p$.
$p$.
Proof. Take a trivialization
and write
By the non-minimality assumption, we may assume that ![]() $f_1 \neq 0$ and the zero locus
$f_1 \neq 0$ and the zero locus ![]() $Z(f_1)$ is smooth at
$Z(f_1)$ is smooth at ![]() $p$. Take a smooth affine open neighborhood
$p$. Take a smooth affine open neighborhood ![]() $p \in U' \subset Z(f_1)$ and define a vector bundle
$p \in U' \subset Z(f_1)$ and define a vector bundle ![]() $E'$ on
$E'$ on ![]() $U'$ by
$U'$ by
Let ![]() $s' \in \Gamma (U', E')$ be the section induced by
$s' \in \Gamma (U', E')$ be the section induced by ![]() $s|_{U'}$. Then we obtain a natural open immersion of the derived zero loci
$s|_{U'}$. Then we obtain a natural open immersion of the derived zero loci ![]() $\boldsymbol {Z}(s') \hookrightarrow \boldsymbol {Z}(s)$. Define
$\boldsymbol {Z}(s') \hookrightarrow \boldsymbol {Z}(s)$. Define ![]() $\boldsymbol {\iota }' \colon \boldsymbol {Z}(s') \to \boldsymbol {Y}$ by the composition
$\boldsymbol {\iota }' \colon \boldsymbol {Z}(s') \to \boldsymbol {Y}$ by the composition ![]() $\boldsymbol {Z}(s') \hookrightarrow \boldsymbol {Z}(s) \xrightarrow {\boldsymbol {\iota }} \boldsymbol {Y}$, and denote its image by
$\boldsymbol {Z}(s') \hookrightarrow \boldsymbol {Z}(s) \xrightarrow {\boldsymbol {\iota }} \boldsymbol {Y}$, and denote its image by ![]() $Z'$. By shrinking around
$Z'$. By shrinking around ![]() $p$ if necessary, we may assume that
$p$ if necessary, we may assume that
is a good Kuranishi chart. We prove that this Kuranishi chart has the desired property.
Firstly take a local coordinate ![]() $x_1, \ldots, x_n$ of
$x_1, \ldots, x_n$ of ![]() $U$ around
$U$ around ![]() $p_U = \boldsymbol {\iota }^{-1}(p)$ with
$p_U = \boldsymbol {\iota }^{-1}(p)$ with ![]() $x_1 = f_1$ and an analytic open neighborhood
$x_1 = f_1$ and an analytic open neighborhood ![]() $p_U \in V$ in
$p_U \in V$ in ![]() $U$ which maps biholomorphically to a polydisc
$U$ which maps biholomorphically to a polydisc ![]() $B_{\epsilon }^{n} \subset \mathbb {C}^{n}$ under
$B_{\epsilon }^{n} \subset \mathbb {C}^{n}$ under ![]() $(x_1, \ldots, x_n)$. Write
$(x_1, \ldots, x_n)$. Write ![]() $V' = V \cap U'$. By shrinking
$V' = V \cap U'$. By shrinking ![]() $V$ if necessary, we can write
$V$ if necessary, we can write
for each ![]() $i \in \{ 2, \ldots, n\}$, where
$i \in \{ 2, \ldots, n\}$, where ![]() $h_i$ is a holomorphic function on
$h_i$ is a holomorphic function on ![]() $V$,
$V$, ![]() $r_i$ is a holomorphic function on
$r_i$ is a holomorphic function on ![]() $V'$, and
$V'$, and ![]() $\bar {\alpha } \colon V \to V'$ is the map identified with the projection
$\bar {\alpha } \colon V \to V'$ is the map identified with the projection ![]() $B_{\epsilon }^{n} \to B_{\epsilon }^{n-1}$.
$B_{\epsilon }^{n} \to B_{\epsilon }^{n-1}$.
Let
be d-critical charts on ![]() $\tilde {Y}$ associated with
$\tilde {Y}$ associated with ![]() $\mathscr {Z}$ and
$\mathscr {Z}$ and ![]() $\mathscr {Z}'$, respectively. Write
$\mathscr {Z}'$, respectively. Write
for the restrictions of ![]() $\tilde {\mathscr {Z}}$ and
$\tilde {\mathscr {Z}}$ and ![]() $\widetilde {\mathscr {Z}'}$, where we define
$\widetilde {\mathscr {Z}'}$, where we define
To simplify the notation, we write
Define a closed immersion linear over ![]() $V' \hookrightarrow V$,
$V' \hookrightarrow V$,
by
where ![]() $e_1^{\vee }, \ldots, e_r^{\vee }$ is the dual basis of
$e_1^{\vee }, \ldots, e_r^{\vee }$ is the dual basis of ![]() $e_1, \ldots, e_r$. A direct computation shows that
$e_1, \ldots, e_r$. A direct computation shows that ![]() $\Phi$ defines an embedding of d-critical charts
$\Phi$ defines an embedding of d-critical charts
in other words, we have the commutative diagram

such that
Now define a map linear over the projection ![]() $\bar {\alpha } \colon V \twoheadrightarrow V'$,
$\bar {\alpha } \colon V \twoheadrightarrow V'$,
by
and a map linear over the projection ![]() $x_1 \colon V \twoheadrightarrow B_{\epsilon }$,
$x_1 \colon V \twoheadrightarrow B_{\epsilon }$,
by
It is clear by the construction that
the map ![]() $(\alpha, \beta ) \colon \tilde {V} \to \tilde {V}' \times (B_{\epsilon } \times \mathbb {C})$ is invertible, and the following diagram commutes.
$(\alpha, \beta ) \colon \tilde {V} \to \tilde {V}' \times (B_{\epsilon } \times \mathbb {C})$ is invertible, and the following diagram commutes.

Here ![]() $\pi _V$ and
$\pi _V$ and ![]() $\pi _{V'}$ are natural projections.
$\pi _{V'}$ are natural projections.
Consider the following composition of morphisms of perverse sheaves on ![]() $\tilde{W}$:
$\tilde{W}$:
where the first and final isomorphisms are induced by (2.25), and the second and third isomorphisms are ![]() $\omega ^{-1}_{\tilde {\mathscr {Z}}}$ and
$\omega ^{-1}_{\tilde {\mathscr {Z}}}$ and ![]() $\omega _{\widetilde {\mathscr {Z}'}}$ defined in Theorem 2.17, respectively. We now show that this is equal to the composition
$\omega _{\widetilde {\mathscr {Z}'}}$ defined in Theorem 2.17, respectively. We now show that this is equal to the composition
where the first map is the Thom–Sebastiani isomorphism, and the second map is constructed by substituting ![]() $z_1 = (x_1 - y) / 2 \sqrt {-1}$ and
$z_1 = (x_1 - y) / 2 \sqrt {-1}$ and ![]() $z_2 = (x_1 + y) / 2$ for
$z_2 = (x_1 + y) / 2$ for ![]() $h_{2,(z_1, z_2)}$ in (2.13). To do this, it suffices to prove the commutativity of the following diagram, thanks to Theorem 2.17(iii).
$h_{2,(z_1, z_2)}$ in (2.13). To do this, it suffices to prove the commutativity of the following diagram, thanks to Theorem 2.17(iii).

Here the right vertical map is (2.15) and
are constructed in the same manner as (2.23). The commutativity of the diagram above is equivalent to the commutativity of the following diagram.

The commutativity of this diagram follows by the definitions of ![]() $\nu$ and
$\nu$ and ![]() $\nu '$, and the equations
$\nu '$, and the equations ![]() $\epsilon _{n, r}/\epsilon _{n-1, r-1}=(-1)^{r} \sqrt {-1}$ and
$\epsilon _{n, r}/\epsilon _{n-1, r-1}=(-1)^{r} \sqrt {-1}$ and ![]() ${{\mathrm d}}z_1 \wedge {{\mathrm d}}z_2 = (-\sqrt {-1}/2) {{\mathrm d}}x_1 \wedge {{\mathrm d}}y$. Therefore we have obtained the equality of isomorphisms (3.5) and (3.6).
${{\mathrm d}}z_1 \wedge {{\mathrm d}}z_2 = (-\sqrt {-1}/2) {{\mathrm d}}x_1 \wedge {{\mathrm d}}y$. Therefore we have obtained the equality of isomorphisms (3.5) and (3.6).
Now consider the commutative diagram

where the left vertical map is induced by the Thom–Sebastiani isomorphism. The commutativity follows from the commutativity of diagram (2.10). By applying the functor ![]() $(\pi _{V})_!$, we obtain the following commutative diagram.
$(\pi _{V})_!$, we obtain the following commutative diagram.

By combining the commutativity of the diagram above and the equality of isomorphisms (3.5) and (3.6), the proposition follows from the next lemma.
Lemma 3.4 The following diagram commutes:

where we use ![]() $z_1 = (x_1 - y) / 2 \sqrt {-1}$ and
$z_1 = (x_1 - y) / 2 \sqrt {-1}$ and ![]() $z_2 = (x_1 + y) / 2$.
$z_2 = (x_1 + y) / 2$.
Proof. Since ![]() $x_1y$ is homogeneous and
$x_1y$ is homogeneous and ![]() $\mathop {\mathrm {Crit}}\nolimits (x_1 y)$ has compact support, we have natural isomorphisms
$\mathop {\mathrm {Crit}}\nolimits (x_1 y)$ has compact support, we have natural isomorphisms
 \begin{align} \mathrm{H}^{0}(\mathbb{C}, (x_1)_!\varphi_{x_1y}^{p}) &\cong \mathrm{H}^{2}(\mathbb{C}^{2}, \{(x_1, y) \in \mathbb{C}^{2} \mid \mathrm{Re}(x_1 y)>0\};\mathbb{Q}) \nonumber\\ &\cong \mathrm{H}^{2}(\mathbb{C}^{2}, \mathbb{C}^{2} \setminus \mathbb{C} \times \{ 0 \};\mathbb{Q}). \end{align}
\begin{align} \mathrm{H}^{0}(\mathbb{C}, (x_1)_!\varphi_{x_1y}^{p}) &\cong \mathrm{H}^{2}(\mathbb{C}^{2}, \{(x_1, y) \in \mathbb{C}^{2} \mid \mathrm{Re}(x_1 y)>0\};\mathbb{Q}) \nonumber\\ &\cong \mathrm{H}^{2}(\mathbb{C}^{2}, \mathbb{C}^{2} \setminus \mathbb{C} \times \{ 0 \};\mathbb{Q}). \end{align}
The left vertical map in (3.7) is given by the Thom class of ![]() $\mathrm {H}^{2}(\mathbb {C}^{2},\mathbb {C}^{2} \setminus \mathbb {C} \times \{ 0 \};\mathbb {Q})$ and (3.8). Now consider the following composition of isomorphisms:
$\mathrm {H}^{2}(\mathbb {C}^{2},\mathbb {C}^{2} \setminus \mathbb {C} \times \{ 0 \};\mathbb {Q})$ and (3.8). Now consider the following composition of isomorphisms:
 \begin{align} \mathrm{H}^{0}(\mathbb{C}, (x_1)_!\varphi_{x_1y}^{p}) &\cong \mathrm{H}^{2}(\mathbb{C}^{2}, \{(x_1, y) \in \mathbb{C}^{2} \mid \mathrm{Re}(x_1 y)>0\};\mathbb{Q}) \nonumber\\ &= \mathrm{H}^{2}(\mathbb{C}^{2}, \{(z_1, z_2) \in \mathbb{C}^{2} \mid \mathrm{Re}(z_1^{2} + z_2^{2})>0\};\mathbb{Q}) \nonumber\\ &\cong \mathrm{H}^{2}(\mathbb{C}^{2},\{(z_1, z_2) \in \mathbb{C}^{2} \mid \mathrm{Re}(z_1^{2})>0,\ \text{or} \ \mathrm{Re}(z_2^{2})>0\};\mathbb{Q}) \nonumber\\ &\cong \mathrm{H}^{1}(\mathbb{C}, \{z_1 \in \mathbb{C} \mid \mathrm{Re}(z_1 ^{2})>0 \};\mathbb{Q}) \otimes \mathrm{H}^{1}(\mathbb{C}, \{z_2 \in \mathbb{C} \mid \mathrm{Re}(z_2 ^{2})>0) \};\mathbb{Q}) \nonumber\\ &\cong \mathbb{Q} \otimes \mathbb{Q} \cong \mathbb{Q}. \end{align}
\begin{align} \mathrm{H}^{0}(\mathbb{C}, (x_1)_!\varphi_{x_1y}^{p}) &\cong \mathrm{H}^{2}(\mathbb{C}^{2}, \{(x_1, y) \in \mathbb{C}^{2} \mid \mathrm{Re}(x_1 y)>0\};\mathbb{Q}) \nonumber\\ &= \mathrm{H}^{2}(\mathbb{C}^{2}, \{(z_1, z_2) \in \mathbb{C}^{2} \mid \mathrm{Re}(z_1^{2} + z_2^{2})>0\};\mathbb{Q}) \nonumber\\ &\cong \mathrm{H}^{2}(\mathbb{C}^{2},\{(z_1, z_2) \in \mathbb{C}^{2} \mid \mathrm{Re}(z_1^{2})>0,\ \text{or} \ \mathrm{Re}(z_2^{2})>0\};\mathbb{Q}) \nonumber\\ &\cong \mathrm{H}^{1}(\mathbb{C}, \{z_1 \in \mathbb{C} \mid \mathrm{Re}(z_1 ^{2})>0 \};\mathbb{Q}) \otimes \mathrm{H}^{1}(\mathbb{C}, \{z_2 \in \mathbb{C} \mid \mathrm{Re}(z_2 ^{2})>0) \};\mathbb{Q}) \nonumber\\ &\cong \mathbb{Q} \otimes \mathbb{Q} \cong \mathbb{Q}. \end{align}
The third isomorphism is the relative Künneth isomorphism and the fourth isomorphism is given by (2.12). Since the Thom–Sebastiani isomorphism is induced by the relative Künneth isomorphism (see [Reference SchürmanSch03, p. 62]), this composition corresponds to ![]() $h_{2, (z_1, z_2)}$. Therefore we only need to show that
$h_{2, (z_1, z_2)}$. Therefore we only need to show that
constructed by combining (3.8) and (3.9), gives the Thom class. Consider the composition
If we equip ![]() $\mathbb {R}^{2}$ with the product orientation of the positive directions, this composition preserves the orientation. This proves the claim.
$\mathbb {R}^{2}$ with the product orientation of the positive directions, this composition preserves the orientation. This proves the claim.
By repeatedly using Proposition 3.3, we obtain the following corollary.
Corollary 3.5 Under the assumption of Proposition 3.3, there exists a good Kuranishi chart ![]() $\mathscr {Z'} = (Z', U', E', s', \boldsymbol {\iota }')$ containing and minimal at
$\mathscr {Z'} = (Z', U', E', s', \boldsymbol {\iota }')$ containing and minimal at ![]() $p$, such that
$p$, such that ![]() $\mathscr {Z}$ and
$\mathscr {Z}$ and ![]() $\mathscr {Z'}$ have compatible dimensional reductions at
$\mathscr {Z'}$ have compatible dimensional reductions at ![]() $p$.
$p$.
Proof Proof of Theorem 3.1
By the sheaf property, it suffices to show that ![]() $\mathscr {Z}_1$ and
$\mathscr {Z}_1$ and ![]() $\mathscr {Z}_2$ have compatible dimensional reductions at each
$\mathscr {Z}_2$ have compatible dimensional reductions at each ![]() $p \in Z_1 \cap Z_2$. By Corollary 3.5, we may assume these Kuranishi charts are minimal at
$p \in Z_1 \cap Z_2$. By Corollary 3.5, we may assume these Kuranishi charts are minimal at ![]() $p$, and then the claim follows from Lemma 3.2.
$p$, and then the claim follows from Lemma 3.2.
Remark 3.6 For a d-critical scheme ![]() $(X, s)$, it is shown in [Reference Brav, Bussi, Dupont, Joyce and SzeondröiBBDJS15, § 6.4] that
$(X, s)$, it is shown in [Reference Brav, Bussi, Dupont, Joyce and SzeondröiBBDJS15, § 6.4] that ![]() $\varphi _{X, s}$ has a natural extension to a mixed Hodge module. We can extend Theorem 3.1 to an isomorphism in the derived category of mixed Hodge modules.
$\varphi _{X, s}$ has a natural extension to a mixed Hodge module. We can extend Theorem 3.1 to an isomorphism in the derived category of mixed Hodge modules.
4. Dimensional reduction for stacks
The aim of this section is to extend Theorem 3.1 to quasi-smooth derived Artin stacks.
4.1 Lisse-analytic topology
We briefly recall the theory of lisse-analytic topos introduced in [Reference SunSun17], which is a complex analytic analogue of the lisse-étale topos. All statements in this section can be deduced in the same manner as in [Reference OlssonOls07] or [Reference Laszlo and OlssonLO08], so we do not give detailed proofs.
Let ![]() $\mathbf {AnSp}$ denote the site of complex analytic spaces equipped with the analytic topology. A stack in groupoid
$\mathbf {AnSp}$ denote the site of complex analytic spaces equipped with the analytic topology. A stack in groupoid ![]() $\mathcal {X}$ over
$\mathcal {X}$ over ![]() $\mathbf {AnSp}$ is called a complex analytic stack if the following conditions hold.
$\mathbf {AnSp}$ is called a complex analytic stack if the following conditions hold.
(i) The diagonal morphism
 $\mathcal {X} \to \mathcal {X} \times \mathcal {X}$ is representable by complex analytic spaces.
$\mathcal {X} \to \mathcal {X} \times \mathcal {X}$ is representable by complex analytic spaces.(ii) There exists a smooth surjection
 $U \to \mathcal {X}$ from a complex analytic space
$U \to \mathcal {X}$ from a complex analytic space  $U$.
$U$.
Definition 4.1 Let ![]() $\mathcal {X}$ be a complex analytic stack. The lisse-analytic site
$\mathcal {X}$ be a complex analytic stack. The lisse-analytic site ![]() $\mathop {\text {Lis-An}}\nolimits (\mathcal {X})$ is the site defined as follows.
$\mathop {\text {Lis-An}}\nolimits (\mathcal {X})$ is the site defined as follows.
• The underlying category of
 $\mathop {\text {Lis-An}} \nolimits (\mathcal {X})$ is the full subcategory of complex analytic spaces over
$\mathop {\text {Lis-An}} \nolimits (\mathcal {X})$ is the full subcategory of complex analytic spaces over  $\mathcal {X}$ spanned by ones smooth over
$\mathcal {X}$ spanned by ones smooth over  $\mathcal {X}$.
$\mathcal {X}$.• A family of morphisms
 $\{(U_i \to \mathcal {X}) \to (U \to \mathcal {X})\}_{i \in I}$ is a covering if
$\{(U_i \to \mathcal {X}) \to (U \to \mathcal {X})\}_{i \in I}$ is a covering if  $\{U_i \to U\}_{i \in I}$ is an open covering.
$\{U_i \to U\}_{i \in I}$ is an open covering.
The topos ![]() $\mathcal {X}_{\text {lis-an}}$ associated with
$\mathcal {X}_{\text {lis-an}}$ associated with ![]() $\mathop {\text {Lis-An}} \nolimits (\mathcal {X})$ is called the lisse-analytic topos of
$\mathop {\text {Lis-An}} \nolimits (\mathcal {X})$ is called the lisse-analytic topos of ![]() $\mathcal {X}$.
$\mathcal {X}$.
It can easily be seen that a sheaf ![]() $F \in \mathcal {X}_{\text {lis-an}}$ is given by the following data:
$F \in \mathcal {X}_{\text {lis-an}}$ is given by the following data:
• a sheaf
 $F_{(U, u)}$ on
$F_{(U, u)}$ on  $U$ for each
$U$ for each  $(u \colon U \to \mathcal {X}) \in \mathop {\text {Lis-An}} \nolimits (\mathcal {X})$ and
$(u \colon U \to \mathcal {X}) \in \mathop {\text {Lis-An}} \nolimits (\mathcal {X})$ and• a morphism
 $c_f \colon f^{-1} F_{(V, v)} \to F_{(U, u)}$ for each
$c_f \colon f^{-1} F_{(V, v)} \to F_{(U, u)}$ for each  $f \colon (u \colon U \to \mathcal {X}) \to (v \colon V \to \mathcal {X})$ in
$f \colon (u \colon U \to \mathcal {X}) \to (v \colon V \to \mathcal {X})$ in  $\mathop {\text {Lis-An}} \nolimits (\mathcal {X})$
$\mathop {\text {Lis-An}} \nolimits (\mathcal {X})$
such that the following conditions hold.
–
 $c_f$ is an isomorphism if
$c_f$ is an isomorphism if  $f$ is an open immersion.
$f$ is an open immersion.– Given a composition
we have \[ (u \colon U \to \mathcal{X}) \xrightarrow{f} (v \colon V \to \mathcal{X}) \xrightarrow{g} (w \colon W \to \mathcal{X}), \]
\[ (u \colon U \to \mathcal{X}) \xrightarrow{f} (v \colon V \to \mathcal{X}) \xrightarrow{g} (w \colon W \to \mathcal{X}), \] $c_{g \circ f} = c_f \circ f^{-1}c_g$.
$c_{g \circ f} = c_f \circ f^{-1}c_g$.
Denote by ![]() $\mathrm {Mod}(\mathcal {X}_{\text {lis-an}}, \mathbb {Q})$ the category of sheaves of
$\mathrm {Mod}(\mathcal {X}_{\text {lis-an}}, \mathbb {Q})$ the category of sheaves of ![]() $\mathbb {Q}$-vector spaces over
$\mathbb {Q}$-vector spaces over ![]() $\mathcal {X}$ and by
$\mathcal {X}$ and by ![]() $D(\mathcal {X}_{\text {lis-an}}, \mathbb {Q})$ the derived category of
$D(\mathcal {X}_{\text {lis-an}}, \mathbb {Q})$ the derived category of ![]() $\mathrm {Mod}(\mathcal {X}_{\text {lis-an}}, \mathbb {Q})$.
$\mathrm {Mod}(\mathcal {X}_{\text {lis-an}}, \mathbb {Q})$.
Definition 4.2 A sheaf ![]() $F \in \mathrm {Mod}(\mathcal {X}_{\text {lis-an}}, \mathbb {Q})$ is called Cartesian if, for any morphism
$F \in \mathrm {Mod}(\mathcal {X}_{\text {lis-an}}, \mathbb {Q})$ is called Cartesian if, for any morphism ![]() $f \colon (U \to \mathcal {X}) \to (V \to \mathcal {X})$ in
$f \colon (U \to \mathcal {X}) \to (V \to \mathcal {X})$ in ![]() $\mathop {\text {Lis-An}} \nolimits (\mathcal {X})$,
$\mathop {\text {Lis-An}} \nolimits (\mathcal {X})$, ![]() $c_f$ is an isomorphism. A Cartesian sheaf
$c_f$ is an isomorphism. A Cartesian sheaf ![]() $F \in \mathrm {Mod}(\mathcal {X}_{\text {lis-an}}, \mathbb {Q})$ is called (analytically) constructible if for any
$F \in \mathrm {Mod}(\mathcal {X}_{\text {lis-an}}, \mathbb {Q})$ is called (analytically) constructible if for any ![]() $U \to \mathcal {X}$ in
$U \to \mathcal {X}$ in ![]() $\mathop {\text {Lis-An}} \nolimits (\mathcal {X})$ the restriction
$\mathop {\text {Lis-An}} \nolimits (\mathcal {X})$ the restriction ![]() $F |_{U_{\mathrm {an}}}$ to the analytic topos of
$F |_{U_{\mathrm {an}}}$ to the analytic topos of ![]() $U$ is (analytically) constructible.
$U$ is (analytically) constructible.
Denote by ![]() $D_{\mathrm {cart}}(\mathcal {X}_{\text {lis-an}}, \mathbb {Q})$ (respectively,
$D_{\mathrm {cart}}(\mathcal {X}_{\text {lis-an}}, \mathbb {Q})$ (respectively, ![]() $D_c(\mathcal {X}_{\text {lis-an}}, \mathbb {Q})$) the full subcategory of
$D_c(\mathcal {X}_{\text {lis-an}}, \mathbb {Q})$) the full subcategory of ![]() $D(\mathcal {X}_{\text {lis-an}}, \mathbb {Q})$ spanned by complexes whose cohomologies are Cartesian sheaves (respectively, constructible sheaves).
$D(\mathcal {X}_{\text {lis-an}}, \mathbb {Q})$ spanned by complexes whose cohomologies are Cartesian sheaves (respectively, constructible sheaves).
For an Artin stack ![]() $\mathfrak {X}$, one can define its associated complex analytic stack
$\mathfrak {X}$, one can define its associated complex analytic stack ![]() $\mathfrak {X}^{\mathrm {an}}$ as in [Reference SunSun17, 3.2.2]. By an abuse of notation, we write
$\mathfrak {X}^{\mathrm {an}}$ as in [Reference SunSun17, 3.2.2]. By an abuse of notation, we write ![]() $\mathop {\text {Lis-An}} \nolimits (\mathfrak {X})$ (respectively,
$\mathop {\text {Lis-An}} \nolimits (\mathfrak {X})$ (respectively, ![]() $\mathfrak {X}_{\text {lis-an}}$) instead of
$\mathfrak {X}_{\text {lis-an}}$) instead of ![]() $\mathop {\text {Lis-An}} \nolimits (\mathfrak {X}^{\mathrm {an}})$ (respectively,
$\mathop {\text {Lis-An}} \nolimits (\mathfrak {X}^{\mathrm {an}})$ (respectively, ![]() ${\mathfrak {X}}^{\mathrm {an}}_{\text {lis-an}}$). For
${\mathfrak {X}}^{\mathrm {an}}_{\text {lis-an}}$). For ![]() $* \in \{b, +, -\}$,
$* \in \{b, +, -\}$, ![]() $D^{(*)}(\mathfrak {X}_{\text {lis-an}}, \mathbb {Q})$ denotes the full subcategory of
$D^{(*)}(\mathfrak {X}_{\text {lis-an}}, \mathbb {Q})$ denotes the full subcategory of ![]() $D(\mathfrak {X}_{\text {lis-an}}, \mathbb {Q})$ consisting of complexes
$D(\mathfrak {X}_{\text {lis-an}}, \mathbb {Q})$ consisting of complexes ![]() $K$ such that
$K$ such that ![]() $K|_\mathfrak {U} \in D^{*}(\mathfrak {U}_{\text {lis-an}}, \mathbb {Q})$ for any quasi-compact Zariski open subset
$K|_\mathfrak {U} \in D^{*}(\mathfrak {U}_{\text {lis-an}}, \mathbb {Q})$ for any quasi-compact Zariski open subset ![]() $\mathfrak {U} \subset \mathfrak {X}$. Define
$\mathfrak {U} \subset \mathfrak {X}$. Define ![]() $D^{(*)}_{\mathrm {cart}}(\mathfrak {X}_{\text {lis-an}}, \mathbb {Q})$ and
$D^{(*)}_{\mathrm {cart}}(\mathfrak {X}_{\text {lis-an}}, \mathbb {Q})$ and ![]() $D^{(*)}_c(\mathfrak {X}_{\text {lis-an}}, \mathbb {Q})$ in a similar manner.
$D^{(*)}_c(\mathfrak {X}_{\text {lis-an}}, \mathbb {Q})$ in a similar manner.
Arguing as in [Reference Laszlo and OlssonLO08], if we are given a morphism ![]() $f \colon \mathfrak {X} \to \mathfrak {Y}$ of finite type between Artin stacks, we can construct six functors:
$f \colon \mathfrak {X} \to \mathfrak {Y}$ of finite type between Artin stacks, we can construct six functors:
 \begin{gather*} Rf_* \colon D^{(+)}_{c}(\mathfrak{X}_{\text{lis-an}}, \mathbb{Q}) \to D^{(+)}_{c}(\mathfrak{Y}_{\text{lis-an}}, \mathbb{Q}),\quad f^{*} \colon D_{c}(\mathfrak{Y}_{\text{lis-an}}, \mathbb{Q}) \to D_{c} (\mathfrak{X}_{\text{lis-an}}, \mathbb{Q}),\\ Rf_! \colon D^{(-)}_{c}(\mathfrak{X}_{\text{lis-an}}, \mathbb{Q}) \to D^{(-)}_{c}(\mathfrak{Y}_{\text{lis-an}}, \mathbb{Q}),\quad f^{!} \colon D_{c}(\mathfrak{Y}_{\text{lis-an}}, \mathbb{Q}) \to D_{c}(\mathfrak{X}_{\text{lis-an}}, \mathbb{Q}),\\ (-) \otimes (-) \colon D^{(-)}_{c}(\mathfrak{X}_{\text{lis-an}}, \mathbb{Q}) \times D^{(-)}_{c}(\mathfrak{X}_{\text{lis-an}}, \mathbb{Q}) \to D^{(-)}_{c}(\mathfrak{X}_{\text{lis-an}}, \mathbb{Q}), \\ \mathop{\mathit{R}\mathcal{H}\! \mathit{om}}\nolimits \colon D^{(-)}_{c}(\mathfrak{X}_{\text{lis-an}}, \mathbb{Q})^{\mathrm{op}} \times D^{(+)}_{c}(\mathfrak{X}_{\text{lis-an}}, \mathbb{Q}) \to D^{(+)}_{c}(\mathfrak{X}_{\text{lis-an}}, \mathbb{Q}). \end{gather*}
\begin{gather*} Rf_* \colon D^{(+)}_{c}(\mathfrak{X}_{\text{lis-an}}, \mathbb{Q}) \to D^{(+)}_{c}(\mathfrak{Y}_{\text{lis-an}}, \mathbb{Q}),\quad f^{*} \colon D_{c}(\mathfrak{Y}_{\text{lis-an}}, \mathbb{Q}) \to D_{c} (\mathfrak{X}_{\text{lis-an}}, \mathbb{Q}),\\ Rf_! \colon D^{(-)}_{c}(\mathfrak{X}_{\text{lis-an}}, \mathbb{Q}) \to D^{(-)}_{c}(\mathfrak{Y}_{\text{lis-an}}, \mathbb{Q}),\quad f^{!} \colon D_{c}(\mathfrak{Y}_{\text{lis-an}}, \mathbb{Q}) \to D_{c}(\mathfrak{X}_{\text{lis-an}}, \mathbb{Q}),\\ (-) \otimes (-) \colon D^{(-)}_{c}(\mathfrak{X}_{\text{lis-an}}, \mathbb{Q}) \times D^{(-)}_{c}(\mathfrak{X}_{\text{lis-an}}, \mathbb{Q}) \to D^{(-)}_{c}(\mathfrak{X}_{\text{lis-an}}, \mathbb{Q}), \\ \mathop{\mathit{R}\mathcal{H}\! \mathit{om}}\nolimits \colon D^{(-)}_{c}(\mathfrak{X}_{\text{lis-an}}, \mathbb{Q})^{\mathrm{op}} \times D^{(+)}_{c}(\mathfrak{X}_{\text{lis-an}}, \mathbb{Q}) \to D^{(+)}_{c}(\mathfrak{X}_{\text{lis-an}}, \mathbb{Q}). \end{gather*}
We briefly recall the construction of ![]() $Rf_*$,
$Rf_*$, ![]() $f^{*}$,
$f^{*}$, ![]() $Rf_!$ and
$Rf_!$ and ![]() $f^{!}$. Firstly define
$f^{!}$. Firstly define
by the rule that ![]() $f_* F(U) = F(U \times _{\mathfrak {Y}} \mathfrak {X})$. By taking the derived functor of
$f_* F(U) = F(U \times _{\mathfrak {Y}} \mathfrak {X})$. By taking the derived functor of ![]() $f_*$ we obtain
$f_*$ we obtain ![]() $Rf_*$. When
$Rf_*$. When ![]() $f$ is a smooth morphism,
$f$ is a smooth morphism, ![]() $f^{*}$ is nothing but the restriction functor. In general,
$f^{*}$ is nothing but the restriction functor. In general, ![]() $f^{*}$ is constructed by taking simplicial covers, but we use pullback functors only for smooth morphisms in this paper, so we do not need this general construction. To define
$f^{*}$ is constructed by taking simplicial covers, but we use pullback functors only for smooth morphisms in this paper, so we do not need this general construction. To define ![]() $Rf_!$ and
$Rf_!$ and ![]() $f^{!}$ we use the Verdier duality functor. Arguing as in [Reference Laszlo and OlssonLO08, § 3], we can construct the dualizing complex
$f^{!}$ we use the Verdier duality functor. Arguing as in [Reference Laszlo and OlssonLO08, § 3], we can construct the dualizing complex
and define the Verdier duality functor
Now define ![]() $Rf_! := \mathbb {D}_{\mathfrak {Y}} \circ f_* \circ \mathbb {D}_{\mathfrak {X}}$ and
$Rf_! := \mathbb {D}_{\mathfrak {Y}} \circ f_* \circ \mathbb {D}_{\mathfrak {X}}$ and ![]() $f^{!} := \mathbb {D}_{\mathfrak {X}} \circ f^{*} \circ \mathbb {D}_{\mathfrak {Y}}$. If
$f^{!} := \mathbb {D}_{\mathfrak {X}} \circ f^{*} \circ \mathbb {D}_{\mathfrak {Y}}$. If ![]() $f$ is a smooth morphism of relative dimension
$f$ is a smooth morphism of relative dimension ![]() $d$, we have natural isomorphisms
$d$, we have natural isomorphisms
 \begin{align} f^{*}\mathbb{D}_{\mathfrak{X}}(F) &= f^{*}\mathop{\mathit{R}\mathcal{H}\! \mathit{om}}\nolimits(F, \omega_{\mathfrak{Y}}) \xrightarrow{\sim} \mathop{\mathit{R}\mathcal{H}\! \mathit{om}}\nolimits(f^{*}F, f^{*}\omega_{\mathfrak{Y}}) \nonumber\\ &\xrightarrow{\sim} \mathop{\mathit{R}\mathcal{H}\! \mathit{om}}\nolimits(f^{*}F, \omega_{\mathfrak{X}}[{-}2d]) \cong \mathbb{D}_{\mathfrak{Y}}(f^{*}F)[{-}2d] \end{align}
\begin{align} f^{*}\mathbb{D}_{\mathfrak{X}}(F) &= f^{*}\mathop{\mathit{R}\mathcal{H}\! \mathit{om}}\nolimits(F, \omega_{\mathfrak{Y}}) \xrightarrow{\sim} \mathop{\mathit{R}\mathcal{H}\! \mathit{om}}\nolimits(f^{*}F, f^{*}\omega_{\mathfrak{Y}}) \nonumber\\ &\xrightarrow{\sim} \mathop{\mathit{R}\mathcal{H}\! \mathit{om}}\nolimits(f^{*}F, \omega_{\mathfrak{X}}[{-}2d]) \cong \mathbb{D}_{\mathfrak{Y}}(f^{*}F)[{-}2d] \end{align}
for ![]() $F \in D_c(\mathfrak {Y}, \mathbb {Q})$. Therefore we have
$F \in D_c(\mathfrak {Y}, \mathbb {Q})$. Therefore we have ![]() $f^{!} \cong f^{*}[2d]$.
$f^{!} \cong f^{*}[2d]$.
If we are given a ![]() $2$-morphism
$2$-morphism ![]() $\xi \colon f \Rightarrow g$ between morphisms of finite type of Artin stacks, we have a natural isomorphism
$\xi \colon f \Rightarrow g$ between morphisms of finite type of Artin stacks, we have a natural isomorphism ![]() $\xi _* \colon Rf_* \Rightarrow Rg_*$ compatible with the vertical and horizontal compositions. The same statement also holds for
$\xi _* \colon Rf_* \Rightarrow Rg_*$ compatible with the vertical and horizontal compositions. The same statement also holds for ![]() $Rf_!$,
$Rf_!$, ![]() $f^{*}$ and
$f^{*}$ and ![]() $f^{!}$.
$f^{!}$.
We now discuss the base-change isomorphisms. Consider the following ![]() $2$-Cartesian diagram of Artin stacks.
$2$-Cartesian diagram of Artin stacks.

By adjunction, we have the base-change map
which is an isomorphism if ![]() $g$ is smooth. Now assume that
$g$ is smooth. Now assume that ![]() $f$ is of finite type and
$f$ is of finite type and ![]() $g$ is smooth with relative dimension
$g$ is smooth with relative dimension ![]() $d$, and take
$d$, and take ![]() $F \in D^{(-)}_c(\mathfrak {X}, \mathbb {Q})$. Then we can construct the proper base-change map
$F \in D^{(-)}_c(\mathfrak {X}, \mathbb {Q})$. Then we can construct the proper base-change map
by the composition
 \begin{align*} g^{*} Rf_! F &= g^{*} \mathbb{D}_{\mathfrak{Y}} Rf_* \mathbb{D}_{\mathfrak{X}} F \\ &\cong \mathbb{D}_{\mathfrak{Y}'} g^{*} Rf_* \mathbb{D}_{\mathfrak{X}} F [2d] \\ &\cong \mathbb{D}_{\mathfrak{Y}'} Rf'_* g'^{*} \mathbb{D}_{\mathfrak{X}} F [2d] \\ &\cong \mathbb{D}_{\mathfrak{Y}'} Rf'_* \mathbb{D}_{\mathfrak{X}'} g'^{*} F = Rf'_! g'^{*} F, \end{align*}
\begin{align*} g^{*} Rf_! F &= g^{*} \mathbb{D}_{\mathfrak{Y}} Rf_* \mathbb{D}_{\mathfrak{X}} F \\ &\cong \mathbb{D}_{\mathfrak{Y}'} g^{*} Rf_* \mathbb{D}_{\mathfrak{X}} F [2d] \\ &\cong \mathbb{D}_{\mathfrak{Y}'} Rf'_* g'^{*} \mathbb{D}_{\mathfrak{X}} F [2d] \\ &\cong \mathbb{D}_{\mathfrak{Y}'} Rf'_* \mathbb{D}_{\mathfrak{X}'} g'^{*} F = Rf'_! g'^{*} F, \end{align*}
where the first and third isomorphisms are defined by using (4.1) and the second isomorphism is the base-change map (4.2). Now consider the following composition of ![]() $2$-Cartesian diagrams:
$2$-Cartesian diagrams:

where ![]() $f$ is of finite type, and
$f$ is of finite type, and ![]() $g$ and
$g$ and ![]() $h$ are smooth. We define
$h$ are smooth. We define ![]() $\eta \colon f \circ k' \Rightarrow k \circ f''$ by composing
$\eta \colon f \circ k' \Rightarrow k \circ f''$ by composing ![]() $2$-morphisms in the diagram. Arguing as [Reference Laszlo and OlssonLO08, Lemma 5.1.2], we can show the commutativity of the following diagram.
$2$-morphisms in the diagram. Arguing as [Reference Laszlo and OlssonLO08, Lemma 5.1.2], we can show the commutativity of the following diagram.

For an Artin stack ![]() $\mathfrak {X}$, we define a full subcategory
$\mathfrak {X}$, we define a full subcategory ![]() $\mathrm {Perv}(\mathfrak {X}) \hookrightarrow D_c(\mathfrak {X}, \mathbb {Q})$ consisting of objects
$\mathrm {Perv}(\mathfrak {X}) \hookrightarrow D_c(\mathfrak {X}, \mathbb {Q})$ consisting of objects ![]() $K$ such that, for any smooth morphism
$K$ such that, for any smooth morphism ![]() $f \colon U \to \mathfrak {X}$ from a scheme,
$f \colon U \to \mathfrak {X}$ from a scheme, ![]() $f^{*} K [\dim f]$ is a perverse sheaf on
$f^{*} K [\dim f]$ is a perverse sheaf on ![]() $U$. An object in
$U$. An object in ![]() $\mathrm {Perv}(\mathfrak {X})$ is called a perverse sheaf on
$\mathrm {Perv}(\mathfrak {X})$ is called a perverse sheaf on ![]() $\mathfrak {X}$. Arguing as [Reference Laszlo and OlssonLO09, Proposition 7.1], we see that
$\mathfrak {X}$. Arguing as [Reference Laszlo and OlssonLO09, Proposition 7.1], we see that ![]() $U \mapsto \mathrm {Perv}(U)$ defines a stack on
$U \mapsto \mathrm {Perv}(U)$ defines a stack on ![]() $\mathop {\text {Lis-An}} \nolimits (\mathfrak {X})$ whose global section category is
$\mathop {\text {Lis-An}} \nolimits (\mathfrak {X})$ whose global section category is ![]() $\mathrm {Perv}(\mathfrak {X})$.
$\mathrm {Perv}(\mathfrak {X})$.
4.2 D-critical stacks
In this section we first recall the notion of d-critical stacks introduced in [Reference JoyceJoy15, § 2.8], which is a stacky generalization of d-critical schemes. And then we prove that the canonical d-critical structures and the canonical orientations for ![]() $-1$-shifted cotangent stacks are preserved under smooth base changes. This is the key ingredient in the proof of the dimensional reduction theorem for quasi-smooth derived Artin stacks.
$-1$-shifted cotangent stacks are preserved under smooth base changes. This is the key ingredient in the proof of the dimensional reduction theorem for quasi-smooth derived Artin stacks.
We first explain the functorial behavior of the d-critical structure.
Proposition 4.3 [Reference JoyceJoy15, Propositions 2.3, 2.8]
Let ![]() $f \colon X \to Y$ be a morphism of complex analytic spaces, and
$f \colon X \to Y$ be a morphism of complex analytic spaces, and ![]() $\mathcal {S}_X$ (respectively,
$\mathcal {S}_X$ (respectively, ![]() $\mathcal {S}_Y$) be the sheaf on
$\mathcal {S}_Y$) be the sheaf on ![]() $X$ (respectively,
$X$ (respectively, ![]() $Y$) defined in (2.3). Then there exists a natural map
$Y$) defined in (2.3). Then there exists a natural map ![]() $\theta _f \colon f^{-1}\mathcal {S}_Y \to \mathcal {S}_X$ with the following property. If
$\theta _f \colon f^{-1}\mathcal {S}_Y \to \mathcal {S}_X$ with the following property. If ![]() $R \subset X$ and
$R \subset X$ and ![]() $S \subset Y$ are open subsets with
$S \subset Y$ are open subsets with ![]() $f(R) \subset S$,
$f(R) \subset S$, ![]() $i \colon R \hookrightarrow U$ and
$i \colon R \hookrightarrow U$ and ![]() $j \colon S \hookrightarrow V$ are closed embeddings into complex manifolds, and
$j \colon S \hookrightarrow V$ are closed embeddings into complex manifolds, and ![]() $\tilde {f} \colon U \to V$ is a holomorphic map with
$\tilde {f} \colon U \to V$ is a holomorphic map with ![]() $j \circ f |_R = \tilde {f} \circ i$, then the following diagram commutes.
$j \circ f |_R = \tilde {f} \circ i$, then the following diagram commutes.

Here horizontal maps are induced by the natural inclusions, and the right vertical map is induced by ![]() $\tilde {f}^{\sharp } \colon \tilde {f}^{-1}\mathcal {O}_V \to \mathcal {O}_U$. The map
$\tilde {f}^{\sharp } \colon \tilde {f}^{-1}\mathcal {O}_V \to \mathcal {O}_U$. The map ![]() $\theta _f$ induces natural map
$\theta _f$ induces natural map ![]() $f^{-1}\mathcal {S}_Y ^{0} \to \mathcal {S}_X ^{0}$ (also written as
$f^{-1}\mathcal {S}_Y ^{0} \to \mathcal {S}_X ^{0}$ (also written as ![]() $\theta _f$). If
$\theta _f$). If ![]() $f$ is smooth and
$f$ is smooth and ![]() $s \in \Gamma (Y, \mathcal {S}_Y^ 0)$ is a d-critical structure,
$s \in \Gamma (Y, \mathcal {S}_Y^ 0)$ is a d-critical structure, ![]() $f^{\star } s := \theta _f(f^{-1}s)$ is also a d-critical structure.
$f^{\star } s := \theta _f(f^{-1}s)$ is also a d-critical structure.
We now explain that the definition of the sheaf ![]() $\mathcal {S}_X ^{0}$ can be extended to complex analytic stacks.
$\mathcal {S}_X ^{0}$ can be extended to complex analytic stacks.
Proposition 4.4 [Reference JoyceJoy15, Corollary 2.52]
Let ![]() $\mathcal {X}$ be a complex analytic stack. Then there exists a sheaf of complex vector spaces
$\mathcal {X}$ be a complex analytic stack. Then there exists a sheaf of complex vector spaces ![]() $\mathcal {S}_\mathcal {X} ^{0}$ in
$\mathcal {S}_\mathcal {X} ^{0}$ in ![]() $ {\text {Lis-an}}(\mathcal {X})$ with the following properties.
$ {\text {Lis-an}}(\mathcal {X})$ with the following properties.
• For
 $(u \colon U \to \mathcal {X}) \in {\text {Lis-an}}(\mathcal {X})$, we have an isomorphism
$(u \colon U \to \mathcal {X}) \in {\text {Lis-an}}(\mathcal {X})$, we have an isomorphism
 \[ \theta_u \colon \mathcal{S}_{\mathcal{X}}^{0} |_{U_{\mathrm{an}}} \cong \mathcal{S}_U ^{0}. \]
\[ \theta_u \colon \mathcal{S}_{\mathcal{X}}^{0} |_{U_{\mathrm{an}}} \cong \mathcal{S}_U ^{0}. \]• For a morphism
 $f \colon (u \colon U \to \mathcal {X}) \to (v \colon V \to \mathcal {X})$ in
$f \colon (u \colon U \to \mathcal {X}) \to (v \colon V \to \mathcal {X})$ in  ${\text {Lis-an}}(\mathcal {X})$, the following diagram commutes.
${\text {Lis-an}}(\mathcal {X})$, the following diagram commutes.

Definition 4.5 Let ![]() $\mathcal {X}$ be a complex analytic stack. A section
$\mathcal {X}$ be a complex analytic stack. A section ![]() $s \in \Gamma (\mathcal {X_{\text {lis-an}}}, \mathcal {S}_\mathcal {X}^{0})$ is called a d-critical structure if, for any
$s \in \Gamma (\mathcal {X_{\text {lis-an}}}, \mathcal {S}_\mathcal {X}^{0})$ is called a d-critical structure if, for any ![]() $(u\colon U \to \mathcal {X}) \in \mathop {\text {Lis-An}}\nolimits (\mathcal {X})$,
$(u\colon U \to \mathcal {X}) \in \mathop {\text {Lis-An}}\nolimits (\mathcal {X})$, ![]() $u^{\star } s := \theta _u(s |_{U_\mathrm {an}})$ is a d-critical structure on
$u^{\star } s := \theta _u(s |_{U_\mathrm {an}})$ is a d-critical structure on ![]() $U$. A d-critical Artin stack is an Artin stack
$U$. A d-critical Artin stack is an Artin stack ![]() $\mathfrak {X}$ with a d-critical structure on its analytification.
$\mathfrak {X}$ with a d-critical structure on its analytification.
We have a stacky version of Theorem 2.13.
Theorem 4.6 [Reference Ben-Bassat, Brav, Bussi and JoyceBBBJ15, Theorem 3.18(a)]
Let ![]() $(\boldsymbol {\mathfrak {X}}, \omega _{\boldsymbol {\mathfrak {X}}})$ be a
$(\boldsymbol {\mathfrak {X}}, \omega _{\boldsymbol {\mathfrak {X}}})$ be a ![]() $-1$-shifted symplectic derived Artin stack. Then there exists a natural d-critical structure
$-1$-shifted symplectic derived Artin stack. Then there exists a natural d-critical structure ![]() $s_{\mathfrak {X}}$ on
$s_{\mathfrak {X}}$ on ![]() $\mathfrak {X} := t_0(\boldsymbol {\mathfrak {X}})$ uniquely characterized by the following property.
$\mathfrak {X} := t_0(\boldsymbol {\mathfrak {X}})$ uniquely characterized by the following property.
Assume we are given derived schemes ![]() $\boldsymbol {X}$ and
$\boldsymbol {X}$ and ![]() $\hat {\boldsymbol {X}}$, and morphisms
$\hat {\boldsymbol {X}}$, and morphisms ![]() $\boldsymbol {g} \colon \boldsymbol {X} \to \boldsymbol {\mathfrak {X}}$ and
$\boldsymbol {g} \colon \boldsymbol {X} \to \boldsymbol {\mathfrak {X}}$ and ![]() $\boldsymbol {\tau } \colon \boldsymbol {X} \to \hat {\boldsymbol {X}}$ such that
$\boldsymbol {\tau } \colon \boldsymbol {X} \to \hat {\boldsymbol {X}}$ such that ![]() $\boldsymbol {g}$ is smooth. Further assume that there exist a
$\boldsymbol {g}$ is smooth. Further assume that there exist a ![]() $-1$-shifted symplectic structure
$-1$-shifted symplectic structure ![]() $\omega _{\hat {\boldsymbol {X}}}$ and an equivalence
$\omega _{\hat {\boldsymbol {X}}}$ and an equivalence ![]() $\boldsymbol {g}^{\star } \omega _{\boldsymbol {\mathfrak {X}}} \sim \boldsymbol {\tau }^{\star } \omega _{\hat {\boldsymbol {X}}}$. If we write
$\boldsymbol {g}^{\star } \omega _{\boldsymbol {\mathfrak {X}}} \sim \boldsymbol {\tau }^{\star } \omega _{\hat {\boldsymbol {X}}}$. If we write ![]() $g = t_0(\boldsymbol {g})$,
$g = t_0(\boldsymbol {g})$, ![]() $\tau = t_0 (\boldsymbol {\tau })$, and
$\tau = t_0 (\boldsymbol {\tau })$, and ![]() $s_{\hat {X}}$ for the d-critical structure on
$s_{\hat {X}}$ for the d-critical structure on ![]() $\hat {X} = t_0(\hat {\boldsymbol {X}})$ associated with
$\hat {X} = t_0(\hat {\boldsymbol {X}})$ associated with ![]() $\omega _{\hat {\boldsymbol {X}}}$, we have
$\omega _{\hat {\boldsymbol {X}}}$, we have ![]() $g^{\star } s_{\mathfrak {X}} = \tau ^{\star } s_{\hat {X}}$.
$g^{\star } s_{\mathfrak {X}} = \tau ^{\star } s_{\hat {X}}$.
Proof. The uniqueness part is proved in [Reference Ben-Bassat, Brav, Bussi and JoyceBBBJ15, Theorem 3.18(a)]. We now verify that the d-critical structure constructed there satisfies the property as above. Using [Reference Ben-Bassat, Brav, Bussi and JoyceBBBJ15, Theorem 2.10], we have derived schemes ![]() $\boldsymbol {U}$ and
$\boldsymbol {U}$ and ![]() $\hat {\boldsymbol {U}}$, a smooth surjection
$\hat {\boldsymbol {U}}$, a smooth surjection ![]() $\boldsymbol {u} \colon \boldsymbol {U} \to \boldsymbol {\mathfrak {X}}$, a morphism
$\boldsymbol {u} \colon \boldsymbol {U} \to \boldsymbol {\mathfrak {X}}$, a morphism ![]() $\boldsymbol {\tau }_{\boldsymbol {U}} \colon \boldsymbol {U} \to \hat {\boldsymbol {U}}$, and a
$\boldsymbol {\tau }_{\boldsymbol {U}} \colon \boldsymbol {U} \to \hat {\boldsymbol {U}}$, and a ![]() $-1$-shifted symplectic form
$-1$-shifted symplectic form ![]() $\omega _{\hat {\boldsymbol {U}}}$ on
$\omega _{\hat {\boldsymbol {U}}}$ on ![]() $\hat {\boldsymbol {U}}$ such that
$\hat {\boldsymbol {U}}$ such that ![]() $\boldsymbol {u}^{\star } \omega _{\boldsymbol {X}} \sim \boldsymbol {\tau }_{\boldsymbol {U}}^{\star } \omega _{\hat {\boldsymbol {U}}}$. Further, if we write
$\boldsymbol {u}^{\star } \omega _{\boldsymbol {X}} \sim \boldsymbol {\tau }_{\boldsymbol {U}}^{\star } \omega _{\hat {\boldsymbol {U}}}$. Further, if we write ![]() $s_{\hat {U}}$ for the d-critical structure associated with
$s_{\hat {U}}$ for the d-critical structure associated with ![]() $\omega _{\hat {\boldsymbol {U}}}$, we may assume
$\omega _{\hat {\boldsymbol {U}}}$, we may assume ![]() $t_0(\boldsymbol {u})^{\star } s_{\mathfrak {X}} = t_0(\boldsymbol {\tau }_{\boldsymbol {U}})^{\star } s_{\hat {U}}$. We have the following diagram of derived stacks.
$t_0(\boldsymbol {u})^{\star } s_{\mathfrak {X}} = t_0(\boldsymbol {\tau }_{\boldsymbol {U}})^{\star } s_{\hat {U}}$. We have the following diagram of derived stacks.

Now take any point ![]() $x \in t_0(\boldsymbol {X})$ and an étale morphism from a derived scheme
$x \in t_0(\boldsymbol {X})$ and an étale morphism from a derived scheme ![]() $\boldsymbol {\eta } \colon \boldsymbol {W} \to \boldsymbol {U} \times _{\boldsymbol {\mathfrak {X}}} \boldsymbol {X}$ such that the image of
$\boldsymbol {\eta } \colon \boldsymbol {W} \to \boldsymbol {U} \times _{\boldsymbol {\mathfrak {X}}} \boldsymbol {X}$ such that the image of ![]() $t_0(\boldsymbol {u}' \circ \boldsymbol {\eta })$ contains
$t_0(\boldsymbol {u}' \circ \boldsymbol {\eta })$ contains ![]() $x$. Since
$x$. Since ![]() $t_0(\boldsymbol {u}' \circ \boldsymbol {\eta })$ is a smooth morphism, it suffices to show that
$t_0(\boldsymbol {u}' \circ \boldsymbol {\eta })$ is a smooth morphism, it suffices to show that
This follows by arguing as in [Reference Brav, Bussi and JoyceBBJ19, Example 5.22] since we have ![]() $(\boldsymbol {\tau }_{\boldsymbol {U}} \circ \boldsymbol {g}' \circ \boldsymbol {\eta })^{\star } \omega _{\hat {\boldsymbol {U}}} \sim (\boldsymbol {\tau } \circ \boldsymbol {u}' \circ \boldsymbol {\eta }) ^{\star } \omega _{\hat {\boldsymbol {X}}}$.
$(\boldsymbol {\tau }_{\boldsymbol {U}} \circ \boldsymbol {g}' \circ \boldsymbol {\eta })^{\star } \omega _{\hat {\boldsymbol {U}}} \sim (\boldsymbol {\tau } \circ \boldsymbol {u}' \circ \boldsymbol {\eta }) ^{\star } \omega _{\hat {\boldsymbol {X}}}$.
We now discuss the behavior of the d-critical structure associated with the canonical ![]() $-1$-shifted symplectic structures on
$-1$-shifted symplectic structures on ![]() $-1$-shifted cotangent stacks constructed in Example 2.6 under smooth pullbacks. Let
$-1$-shifted cotangent stacks constructed in Example 2.6 under smooth pullbacks. Let ![]() $\boldsymbol {f}\colon \boldsymbol {Y} \to \boldsymbol {\mathfrak {Y}}$ be a smooth morphism from a derived scheme
$\boldsymbol {f}\colon \boldsymbol {Y} \to \boldsymbol {\mathfrak {Y}}$ be a smooth morphism from a derived scheme ![]() $\boldsymbol {Y}$ to a quasi-smooth derived Artin stack
$\boldsymbol {Y}$ to a quasi-smooth derived Artin stack ![]() $\boldsymbol {\mathfrak {Y}}$. Consider the following diagram.
$\boldsymbol {\mathfrak {Y}}$. Consider the following diagram.

Here ![]() $\boldsymbol {f}^{*}\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}$ is the total space
$\boldsymbol {f}^{*}\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}$ is the total space ![]() $\mathop {\mathrm {Tot}}\nolimits _{\boldsymbol {Y}}(\mathbb {L}_{\boldsymbol {\boldsymbol {f}^{*} \mathfrak {Y}}}[-1])$,
$\mathop {\mathrm {Tot}}\nolimits _{\boldsymbol {Y}}(\mathbb {L}_{\boldsymbol {\boldsymbol {f}^{*} \mathfrak {Y}}}[-1])$, ![]() $\pi _{\boldsymbol {Y}}$,
$\pi _{\boldsymbol {Y}}$, ![]() $\pi _{\boldsymbol {\mathfrak {Y}}}$, and
$\pi _{\boldsymbol {\mathfrak {Y}}}$, and ![]() $\pi _{\boldsymbol {\mathfrak {Y}}, \boldsymbol {f}}$ are the projections,
$\pi _{\boldsymbol {\mathfrak {Y}}, \boldsymbol {f}}$ are the projections, ![]() $\boldsymbol {\tau }$ is induced by the canonical map
$\boldsymbol {\tau }$ is induced by the canonical map ![]() $\boldsymbol {f}^{*} \mathbb {L}_{\boldsymbol {\mathfrak {Y}}}[-1] \to \mathbb {L}_{\boldsymbol {Y}}[-1]$, and
$\boldsymbol {f}^{*} \mathbb {L}_{\boldsymbol {\mathfrak {Y}}}[-1] \to \mathbb {L}_{\boldsymbol {Y}}[-1]$, and ![]() $\tilde {\boldsymbol {f}} \colon \boldsymbol {f}^{*}\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}} \to \mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}$ is the base change of
$\tilde {\boldsymbol {f}} \colon \boldsymbol {f}^{*}\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}} \to \mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}$ is the base change of ![]() $\boldsymbol {f}$. The smoothness of
$\boldsymbol {f}$. The smoothness of ![]() $\boldsymbol {f}$ implies that
$\boldsymbol {f}$ implies that ![]() $\boldsymbol {\tau }$ induces an isomorphism on underlying schemes, so we use the identification
$\boldsymbol {\tau }$ induces an isomorphism on underlying schemes, so we use the identification
throughout the paper.
Proposition 4.7 Consider the situation as above. Denote by ![]() $s_{\mathbf {T}^{*}[-1]\boldsymbol {Y}}$ (respectively,
$s_{\mathbf {T}^{*}[-1]\boldsymbol {Y}}$ (respectively, ![]() $s_{\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}}$) the d-critical structure associated with the canonical
$s_{\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}}$) the d-critical structure associated with the canonical ![]() $-1$-shifted symplectic form
$-1$-shifted symplectic form ![]() $\omega _{\mathbf {T}^{*}[-1]\boldsymbol {Y}}$ (respectively,
$\omega _{\mathbf {T}^{*}[-1]\boldsymbol {Y}}$ (respectively, ![]() $\omega _{\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}}$) constructed in Example 2.6. Then we have
$\omega _{\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}}$) constructed in Example 2.6. Then we have ![]() $s_{\mathbf {T}^{*}[-1]\boldsymbol {Y}} = \tilde {f}^{\star } s_{\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}}$, where we write
$s_{\mathbf {T}^{*}[-1]\boldsymbol {Y}} = \tilde {f}^{\star } s_{\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}}$, where we write ![]() $\tilde {f} = t_0(\tilde {\boldsymbol {f}})$ and use the identification (4.5).
$\tilde {f} = t_0(\tilde {\boldsymbol {f}})$ and use the identification (4.5).
Proof. By Theorem 4.6, we only need to show that ![]() $\boldsymbol {\tau }^{\star } \omega _{\mathbf {T}^{*}[-1]\boldsymbol {Y}} \sim \tilde {\boldsymbol {f}}^{\star } \omega _{\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}}$. If we write
$\boldsymbol {\tau }^{\star } \omega _{\mathbf {T}^{*}[-1]\boldsymbol {Y}} \sim \tilde {\boldsymbol {f}}^{\star } \omega _{\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}}$. If we write ![]() $\lambda _{\mathbf {T}^{*}[-1]\boldsymbol {Y}}$ and
$\lambda _{\mathbf {T}^{*}[-1]\boldsymbol {Y}}$ and ![]() $\lambda _{\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}}$ for the tautological
$\lambda _{\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}}$ for the tautological ![]() $1$-forms on
$1$-forms on ![]() $\mathbf {T}^{*}[-1]\boldsymbol {Y}$ and
$\mathbf {T}^{*}[-1]\boldsymbol {Y}$ and ![]() $\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}$ respectively, we have
$\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}$ respectively, we have ![]() ${{\mathrm d}}_{\mathrm {dR}} \lambda _{\mathbf {T}^{*}[-1]\boldsymbol {Y}} = \omega _{\mathbf {T}^{*}[-1]\boldsymbol {Y}}$ and
${{\mathrm d}}_{\mathrm {dR}} \lambda _{\mathbf {T}^{*}[-1]\boldsymbol {Y}} = \omega _{\mathbf {T}^{*}[-1]\boldsymbol {Y}}$ and ![]() ${d_{\mathrm {dR}}} \lambda _{\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}} = \omega _{\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}}$ by definition. Therefore we only need to prove
${d_{\mathrm {dR}}} \lambda _{\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}} = \omega _{\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}}$ by definition. Therefore we only need to prove
By the functoriality of the cotangent complex, we have the following homotopy commutative diagram.

Here ![]() $a$ and
$a$ and ![]() $b$ are defined by using
$b$ are defined by using ![]() $\boldsymbol {f} \circ \boldsymbol {\pi }_{\boldsymbol {\mathfrak {Y}}, \boldsymbol {f}} \simeq \boldsymbol {\pi }_{\boldsymbol {\mathfrak {Y}}} \circ \tilde {\boldsymbol {f}}$ and
$\boldsymbol {f} \circ \boldsymbol {\pi }_{\boldsymbol {\mathfrak {Y}}, \boldsymbol {f}} \simeq \boldsymbol {\pi }_{\boldsymbol {\mathfrak {Y}}} \circ \tilde {\boldsymbol {f}}$ and ![]() $\boldsymbol {\pi }_{\boldsymbol {\mathfrak {Y}}, \boldsymbol {f}} \simeq \boldsymbol {\pi }_{\boldsymbol {Y}} \circ \boldsymbol {\tau }$ respectively, and other morphisms are induced by the functoriality of the cotangent complex. Now write
$\boldsymbol {\pi }_{\boldsymbol {\mathfrak {Y}}, \boldsymbol {f}} \simeq \boldsymbol {\pi }_{\boldsymbol {Y}} \circ \boldsymbol {\tau }$ respectively, and other morphisms are induced by the functoriality of the cotangent complex. Now write ![]() $\gamma _{\boldsymbol {f}^{*}\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}}$,
$\gamma _{\boldsymbol {f}^{*}\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}}$, ![]() $\gamma _{\mathbf {T}^{*}[-1]\boldsymbol {Y}}$, and
$\gamma _{\mathbf {T}^{*}[-1]\boldsymbol {Y}}$, and ![]() $\gamma _{\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}}$ for the tautological sections of
$\gamma _{\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}}$ for the tautological sections of ![]() $(\boldsymbol {\pi }_{\boldsymbol {\mathfrak {Y}}, \boldsymbol {f}})^{*} \boldsymbol {f}^{*} \mathbb {L}_{\boldsymbol {\mathfrak {Y}}}[-1]$,
$(\boldsymbol {\pi }_{\boldsymbol {\mathfrak {Y}}, \boldsymbol {f}})^{*} \boldsymbol {f}^{*} \mathbb {L}_{\boldsymbol {\mathfrak {Y}}}[-1]$, ![]() $\boldsymbol {\pi }_{\boldsymbol {\mathfrak {Y}}}^{*} \mathbb {L}_{\boldsymbol {\mathfrak {Y}}}[-1]$, and
$\boldsymbol {\pi }_{\boldsymbol {\mathfrak {Y}}}^{*} \mathbb {L}_{\boldsymbol {\mathfrak {Y}}}[-1]$, and ![]() $\boldsymbol {\pi }_{\boldsymbol {Y}}^{*} \mathbb {L}_{\boldsymbol {Y}}[-1]$, respectively. By definition, we have
$\boldsymbol {\pi }_{\boldsymbol {Y}}^{*} \mathbb {L}_{\boldsymbol {Y}}[-1]$, respectively. By definition, we have
 \begin{align*} \tilde{\boldsymbol{f}}^{{\star}} \lambda_{\mathbf{T}^{*}[{-}1]\boldsymbol{\mathfrak{Y}}} \sim \theta_{\tilde{\boldsymbol{f}}}(\tilde{\boldsymbol{f}}^{*} \lambda_{\mathbf{T}^{*}[{-}1]\boldsymbol{\mathfrak{Y}}}) &\sim \theta_{\tilde{\boldsymbol{f}}} \circ \tilde{\boldsymbol{f}}^{*} \theta_{\boldsymbol{\pi}_{\boldsymbol{\mathfrak{Y}}}} (\tilde{\boldsymbol{f}}^{*} \gamma_{\mathbf{T}^{*}[{-}1]\boldsymbol{\mathfrak{Y}}}), \\ \boldsymbol{\tau}^{{\star}} \lambda_{\mathbf{T}^{*}[{-}1]\boldsymbol{Y}} \sim \theta_{\boldsymbol{\tau}}(\boldsymbol{\tau}^{*} \lambda_{\mathbf{T}^{*}[{-}1]\boldsymbol{Y}}) &\sim \theta_{\boldsymbol{\tau}} \circ \boldsymbol{\tau}^{*} \theta_{\boldsymbol{\pi}_{\boldsymbol{Y}}} (\boldsymbol{\tau}^{*} \gamma_{\mathbf{T}^{*}[{-}1]\boldsymbol{Y}}). \end{align*}
\begin{align*} \tilde{\boldsymbol{f}}^{{\star}} \lambda_{\mathbf{T}^{*}[{-}1]\boldsymbol{\mathfrak{Y}}} \sim \theta_{\tilde{\boldsymbol{f}}}(\tilde{\boldsymbol{f}}^{*} \lambda_{\mathbf{T}^{*}[{-}1]\boldsymbol{\mathfrak{Y}}}) &\sim \theta_{\tilde{\boldsymbol{f}}} \circ \tilde{\boldsymbol{f}}^{*} \theta_{\boldsymbol{\pi}_{\boldsymbol{\mathfrak{Y}}}} (\tilde{\boldsymbol{f}}^{*} \gamma_{\mathbf{T}^{*}[{-}1]\boldsymbol{\mathfrak{Y}}}), \\ \boldsymbol{\tau}^{{\star}} \lambda_{\mathbf{T}^{*}[{-}1]\boldsymbol{Y}} \sim \theta_{\boldsymbol{\tau}}(\boldsymbol{\tau}^{*} \lambda_{\mathbf{T}^{*}[{-}1]\boldsymbol{Y}}) &\sim \theta_{\boldsymbol{\tau}} \circ \boldsymbol{\tau}^{*} \theta_{\boldsymbol{\pi}_{\boldsymbol{Y}}} (\boldsymbol{\tau}^{*} \gamma_{\mathbf{T}^{*}[{-}1]\boldsymbol{Y}}). \end{align*}Since we have the tautological relations
the proposition follows.
We now discuss the notion of the virtual canonical bundles and the orientations for d-critical stacks. Before doing this, we recall a property of the virtual canonical bundle of d-critical schemes. For a d-critical chart ![]() $(R, U, f, i)$ of a d-critical scheme
$(R, U, f, i)$ of a d-critical scheme ![]() $(X, s)$ and a point
$(X, s)$ and a point ![]() $x \in R$, consider the following complex concentrated in degree
$x \in R$, consider the following complex concentrated in degree ![]() $-1$ and
$-1$ and ![]() $0$:
$0$:
Since ![]() $\mathrm {H}^{0}(L_x) \cong \Omega _X |_x$ and
$\mathrm {H}^{0}(L_x) \cong \Omega _X |_x$ and ![]() $\mathrm {H}^{-1}(L_x) \cong (\Omega _X |_x)^{\vee }$, we can define an isomorphism
$\mathrm {H}^{-1}(L_x) \cong (\Omega _X |_x)^{\vee }$, we can define an isomorphism
Here the final isomorphism is defined in the same manner as (2.5). It is proved in [Reference JoyceJoy15, Theorem 2.28] that ![]() $\kappa _x$ does not depend on the choice of a d-critical chart. Now the virtual canonical bundle for a d-critical stack is defined by the following proposition.
$\kappa _x$ does not depend on the choice of a d-critical chart. Now the virtual canonical bundle for a d-critical stack is defined by the following proposition.
Proposition 4.8 [Reference JoyceJoy15, Theorem 2.56]
Let ![]() $(\mathfrak {X}, s)$ be a d-critical stack. Then there exists a line bundle
$(\mathfrak {X}, s)$ be a d-critical stack. Then there exists a line bundle ![]() $K_{\mathfrak {X}, s}$ on
$K_{\mathfrak {X}, s}$ on ![]() $\mathfrak {X}^{\mathrm{red}}$, which we call the virtual canonical bundle of
$\mathfrak {X}^{\mathrm{red}}$, which we call the virtual canonical bundle of ![]() $(\mathfrak {X}, s)$, characterized uniquely up to unique isomorphism by the following properties.
$(\mathfrak {X}, s)$, characterized uniquely up to unique isomorphism by the following properties.
(i) For
 $x\in \mathfrak {X}$, there exists an isomorphism
(4.7)
$x\in \mathfrak {X}$, there exists an isomorphism
(4.7) \begin{equation} \kappa_x \colon K_{\mathfrak{X}, s} |_x \cong \mathop{\mathrm{det}}\nolimits(\tau^{{\geq} 0}(\mathbb{L}_{\mathfrak{X}})|_x)^{{\otimes} ^{2}} . \end{equation}
\begin{equation} \kappa_x \colon K_{\mathfrak{X}, s} |_x \cong \mathop{\mathrm{det}}\nolimits(\tau^{{\geq} 0}(\mathbb{L}_{\mathfrak{X}})|_x)^{{\otimes} ^{2}} . \end{equation}(ii) For a smooth morphism
 $u \colon U \to \mathfrak {X}$ from a scheme
$u \colon U \to \mathfrak {X}$ from a scheme  $U$, there exists an isomorphism
(4.8)
$U$, there exists an isomorphism
(4.8) \begin{equation} \Gamma_{U, u} \colon (u^{\mathrm{red}})^{*} K_{\mathfrak{X}, s} \cong K_{U, u^{{\star}} s} \otimes \mathop{\widehat{\mathrm{det}}}\nolimits(\Omega_{U/\mathfrak{X}}) ^{{\otimes} ^{{-}2}}. \end{equation}
\begin{equation} \Gamma_{U, u} \colon (u^{\mathrm{red}})^{*} K_{\mathfrak{X}, s} \cong K_{U, u^{{\star}} s} \otimes \mathop{\widehat{\mathrm{det}}}\nolimits(\Omega_{U/\mathfrak{X}}) ^{{\otimes} ^{{-}2}}. \end{equation}(iii) In the situation of (ii), take any
 $p \in U$. The distinguished triangle
induces an isomorphism
$p \in U$. The distinguished triangle
induces an isomorphism \[ \Delta \colon u^{*} \tau^{{\geq} 0} (\mathbb{L}_{\mathfrak{X}}) \to \Omega_U \to \Omega_{U/\mathfrak{X}} \to u^{*} \tau^{{\geq} 0} (\mathbb{L}_{\mathfrak{X}})[1] \]
\[ \Delta \colon u^{*} \tau^{{\geq} 0} (\mathbb{L}_{\mathfrak{X}}) \to \Omega_U \to \Omega_{U/\mathfrak{X}} \to u^{*} \tau^{{\geq} 0} (\mathbb{L}_{\mathfrak{X}})[1] \] $\hat {\imath }(\Delta )_p \colon \mathop {\mathrm {det}}\nolimits (\tau ^{\geq 0} (\mathbb {L}_{\mathfrak {X}})|_{u(p)}) \otimes \mathop {\mathrm {det}}\nolimits (\Omega _{U/\mathfrak {X}}|_p) \cong \mathop {\mathrm {det}}\nolimits (\Omega _U |_p)$ where
$\hat {\imath }(\Delta )_p \colon \mathop {\mathrm {det}}\nolimits (\tau ^{\geq 0} (\mathbb {L}_{\mathfrak {X}})|_{u(p)}) \otimes \mathop {\mathrm {det}}\nolimits (\Omega _{U/\mathfrak {X}}|_p) \cong \mathop {\mathrm {det}}\nolimits (\Omega _U |_p)$ where  $\hat {\imath }$ is defined in Lemma 2.14. Then the following diagram commutes.
Here the bottom horizontal map is defined by using
$\hat {\imath }$ is defined in Lemma 2.14. Then the following diagram commutes.
Here the bottom horizontal map is defined by using
 $\hat {\imath }(\Delta )_p$.
$\hat {\imath }(\Delta )_p$.
An orientation ![]() $o$ of a d-critical stack
$o$ of a d-critical stack ![]() $(\mathfrak {X}, s)$ is the choice of a line bundle
$(\mathfrak {X}, s)$ is the choice of a line bundle ![]() $L$ on
$L$ on ![]() $\mathfrak {X}^{\mathrm{red}}$ and an isomorphism
$\mathfrak {X}^{\mathrm{red}}$ and an isomorphism ![]() $o \colon L^{\otimes ^{2}} \cong K_{\mathfrak {X}, s}$. An isomorphism between orientations
$o \colon L^{\otimes ^{2}} \cong K_{\mathfrak {X}, s}$. An isomorphism between orientations ![]() $o_1\colon L_1^{\otimes ^{2}} \cong K_{\mathfrak {X}, s}$ and
$o_1\colon L_1^{\otimes ^{2}} \cong K_{\mathfrak {X}, s}$ and ![]() $o_2 \colon L_2^{\otimes ^{2}} \cong K_{\mathfrak {X}, s}$ is defined by an isomorphism
$o_2 \colon L_2^{\otimes ^{2}} \cong K_{\mathfrak {X}, s}$ is defined by an isomorphism ![]() $\phi \colon L_1 \cong L_2$ such that
$\phi \colon L_1 \cong L_2$ such that ![]() $o_1 = o_2 \circ {\phi }^{\otimes ^{2}}$. If there exists a smooth morphism
$o_1 = o_2 \circ {\phi }^{\otimes ^{2}}$. If there exists a smooth morphism ![]() $u \colon U \to \mathfrak {X}$, we define an orientation
$u \colon U \to \mathfrak {X}$, we define an orientation ![]() $u^{\star } o$ for
$u^{\star } o$ for ![]() $(U, u^{\star } s)$ by the following composition:
$(U, u^{\star } s)$ by the following composition:
If we are given a smooth morphism ![]() $q \colon (u \colon U \to \mathfrak {X}) \to (v \colon V \to \mathfrak {X})$ in
$q \colon (u \colon U \to \mathfrak {X}) \to (v \colon V \to \mathfrak {X})$ in ![]() $\mathop {\text {Lis-An}} \nolimits (\mathfrak {X})$, define an isomorphism
$\mathop {\text {Lis-An}} \nolimits (\mathfrak {X})$, define an isomorphism
by using the natural isomorphism
We now discuss the relation of the cotangent complex of a ![]() $-1$-shifted symplectic derived Artin stack and the virtual canonical bundle of the associated d-critical stack.
$-1$-shifted symplectic derived Artin stack and the virtual canonical bundle of the associated d-critical stack.
Theorem 4.9 [Reference Ben-Bassat, Brav, Bussi and JoyceBBBJ15, Theorem 3.18(b)]
Let ![]() $(\boldsymbol {\mathfrak {X}}, \omega _{\boldsymbol {\mathfrak {X}}})$ be a
$(\boldsymbol {\mathfrak {X}}, \omega _{\boldsymbol {\mathfrak {X}}})$ be a ![]() $-1$-shifted symplectic derived Artin stack, and
$-1$-shifted symplectic derived Artin stack, and ![]() $(\mathfrak {X}, s_{\mathfrak {X}})$ the associated d-critical stack. Then there exists a natural isomorphism
$(\mathfrak {X}, s_{\mathfrak {X}})$ the associated d-critical stack. Then there exists a natural isomorphism
characterized by the following property.
Assume we are given derived schemes ![]() $\boldsymbol {X}$ and
$\boldsymbol {X}$ and ![]() $\hat {\boldsymbol {X}}$, and morphisms
$\hat {\boldsymbol {X}}$, and morphisms ![]() $\boldsymbol {g} \colon \boldsymbol {X} \to \boldsymbol {\mathfrak {X}}$ and
$\boldsymbol {g} \colon \boldsymbol {X} \to \boldsymbol {\mathfrak {X}}$ and ![]() $\boldsymbol {\tau } \colon \boldsymbol {X} \to \hat {\boldsymbol {X}}$ such that
$\boldsymbol {\tau } \colon \boldsymbol {X} \to \hat {\boldsymbol {X}}$ such that ![]() $\boldsymbol {g}$ is smooth and
$\boldsymbol {g}$ is smooth and ![]() $\mathbb {L}_{\boldsymbol {\tau }} |_{x}$ is concentrated in degree
$\mathbb {L}_{\boldsymbol {\tau }} |_{x}$ is concentrated in degree ![]() $-2$ for each
$-2$ for each ![]() $x \in \boldsymbol {X}$. Note that it automatically follows that
$x \in \boldsymbol {X}$. Note that it automatically follows that ![]() $\tau = t_0(\boldsymbol {\tau })$ is étale. Further assume that there exist a
$\tau = t_0(\boldsymbol {\tau })$ is étale. Further assume that there exist a ![]() $-1$-shifted symplectic structure
$-1$-shifted symplectic structure ![]() $\omega _{\hat {\boldsymbol {X}}}$ on
$\omega _{\hat {\boldsymbol {X}}}$ on ![]() $\hat {\boldsymbol {X}}$ with associated d-critical locus
$\hat {\boldsymbol {X}}$ with associated d-critical locus ![]() $(\hat {X}, s_{\hat {X}})$ and an equivalence
$(\hat {X}, s_{\hat {X}})$ and an equivalence ![]() $\boldsymbol {g}^{\star } \omega _{\boldsymbol {\mathfrak {X}}} \sim \boldsymbol {\tau }^{\star } \omega _{\hat {\boldsymbol {X}}}$. This equivalence induces a homotopy between the composition
$\boldsymbol {g}^{\star } \omega _{\boldsymbol {\mathfrak {X}}} \sim \boldsymbol {\tau }^{\star } \omega _{\hat {\boldsymbol {X}}}$. This equivalence induces a homotopy between the composition
and ![]() $0$, hence an isomorphism
$0$, hence an isomorphism
Then the composition
 \begin{align*} \mathop{\widehat{\mathrm{det}}}\nolimits(\boldsymbol{g}^{*} \mathbb{L}_{\boldsymbol{\mathfrak{X}}}) &\cong \mathop{\widehat{\mathrm{det}}} (\mathbb{L}_{\boldsymbol{X}}) \otimes \mathop{\widehat{\mathrm{det}}}\nolimits(\mathbb{L}_{\boldsymbol{g}})^{{-}1} \\ &\cong \mathop{\widehat{\mathrm{det}}}\nolimits(\boldsymbol{\tau}^{*} \mathbb{L}_{\hat{\boldsymbol{X}}}) \otimes \mathop{\widehat{\mathrm{det}}}\nolimits(\mathbb{L}_{\boldsymbol{\tau}}) \otimes \mathop{\widehat{\mathrm{det}}}\nolimits(\mathbb{L}_{\boldsymbol{g}})^{{-}1} \\ &\cong \mathop{\widehat{\mathrm{det}}}\nolimits(\boldsymbol{\tau}^{*} \mathbb{L}_{\hat{\boldsymbol{X}}}) \otimes \mathop{\widehat{\mathrm{det}}}\nolimits(\mathbb{L}_{\boldsymbol{g}})^{{\otimes} ^{{-}2}}\\
&\cong (\tau^{\mathrm{red}})^{*} K_{\hat{X}, s_{\hat{X}}} \otimes \mathop{\widehat{\mathrm{det}}}\nolimits(\mathbb{L}_{\boldsymbol{g}})^{{\otimes} ^{{-}2}} \\ &\cong K_{X,\tau^{{\star}} s_{\hat{X}}} \otimes \mathop{\widehat{\mathrm{det}}}\nolimits(\mathbb{L}_{\boldsymbol{g}})^{{\otimes} ^{{-}2}}\\ &\cong (g^{\mathrm{red}})^{*}K_{\mathfrak{X}, s_{\mathfrak{X}}} \end{align*}
\begin{align*} \mathop{\widehat{\mathrm{det}}}\nolimits(\boldsymbol{g}^{*} \mathbb{L}_{\boldsymbol{\mathfrak{X}}}) &\cong \mathop{\widehat{\mathrm{det}}} (\mathbb{L}_{\boldsymbol{X}}) \otimes \mathop{\widehat{\mathrm{det}}}\nolimits(\mathbb{L}_{\boldsymbol{g}})^{{-}1} \\ &\cong \mathop{\widehat{\mathrm{det}}}\nolimits(\boldsymbol{\tau}^{*} \mathbb{L}_{\hat{\boldsymbol{X}}}) \otimes \mathop{\widehat{\mathrm{det}}}\nolimits(\mathbb{L}_{\boldsymbol{\tau}}) \otimes \mathop{\widehat{\mathrm{det}}}\nolimits(\mathbb{L}_{\boldsymbol{g}})^{{-}1} \\ &\cong \mathop{\widehat{\mathrm{det}}}\nolimits(\boldsymbol{\tau}^{*} \mathbb{L}_{\hat{\boldsymbol{X}}}) \otimes \mathop{\widehat{\mathrm{det}}}\nolimits(\mathbb{L}_{\boldsymbol{g}})^{{\otimes} ^{{-}2}}\\
&\cong (\tau^{\mathrm{red}})^{*} K_{\hat{X}, s_{\hat{X}}} \otimes \mathop{\widehat{\mathrm{det}}}\nolimits(\mathbb{L}_{\boldsymbol{g}})^{{\otimes} ^{{-}2}} \\ &\cong K_{X,\tau^{{\star}} s_{\hat{X}}} \otimes \mathop{\widehat{\mathrm{det}}}\nolimits(\mathbb{L}_{\boldsymbol{g}})^{{\otimes} ^{{-}2}}\\ &\cong (g^{\mathrm{red}})^{*}K_{\mathfrak{X}, s_{\mathfrak{X}}} \end{align*}
is equal to ![]() $(-1)^{\mathop {\mathrm {rank}}\nolimits (\Omega _{g})} {(g^{\mathrm{red}})}^{*}\Lambda _{\boldsymbol {\mathfrak {X}}}$, where we write
$(-1)^{\mathop {\mathrm {rank}}\nolimits (\Omega _{g})} {(g^{\mathrm{red}})}^{*}\Lambda _{\boldsymbol {\mathfrak {X}}}$, where we write ![]() $g = t_0(\boldsymbol {g})$. Here the first and second isomorphisms are defined by using
$g = t_0(\boldsymbol {g})$. Here the first and second isomorphisms are defined by using ![]() $\hat {\imath }(\Delta _{\boldsymbol {g}})$ and
$\hat {\imath }(\Delta _{\boldsymbol {g}})$ and ![]() $\hat {\imath }(\Delta _{\boldsymbol {\tau }})$ respectively, where
$\hat {\imath }(\Delta _{\boldsymbol {\tau }})$ respectively, where ![]() $\Delta _{\boldsymbol {g}}$ and
$\Delta _{\boldsymbol {g}}$ and ![]() $\Delta _{\boldsymbol {\tau }}$ are distinguished triangles
$\Delta _{\boldsymbol {\tau }}$ are distinguished triangles
The third isomorphism is defined in the same manner as (2.5) using ![]() $\ell$ (without any sign intervention used in Appendix A), the fourth isomorphism is
$\ell$ (without any sign intervention used in Appendix A), the fourth isomorphism is ![]() $\Lambda _{\hat {\boldsymbol {X}}}$ in Theorem 2.13, and the fifth isomorphism is
$\Lambda _{\hat {\boldsymbol {X}}}$ in Theorem 2.13, and the fifth isomorphism is ![]() $\Gamma _{X, \tau }$ defined in Proposition 4.8. The final isomorphism is
$\Gamma _{X, \tau }$ defined in Proposition 4.8. The final isomorphism is ![]() $\Gamma _{X, g}$, where we use the fact that
$\Gamma _{X, g}$, where we use the fact that ![]() $\tau ^{\star } s_{\hat {X}} = g^{\star } s_{\mathfrak {X}}$ proved in Theorem 4.6.
$\tau ^{\star } s_{\hat {X}} = g^{\star } s_{\mathfrak {X}}$ proved in Theorem 4.6.
Proof. The proof is essentially same as one in [Reference Ben-Bassat, Brav, Bussi and JoyceBBBJ15], but we include it for the reader's convenience and to fix the sign. Suppose we are given ![]() $\boldsymbol {X}$,
$\boldsymbol {X}$, ![]() $\hat {\boldsymbol {X}}$,
$\hat {\boldsymbol {X}}$, ![]() $\boldsymbol {g}$, and
$\boldsymbol {g}$, and ![]() $\boldsymbol {\tau }$ as above. Define
$\boldsymbol {\tau }$ as above. Define
by the composition as above multiplied by ![]() $(-1)^{\mathop {\mathrm {rank}}\nolimits (\Omega _{g})}$. Write
$(-1)^{\mathop {\mathrm {rank}}\nolimits (\Omega _{g})}$. Write ![]() $\mathrm {pr}_1, \mathrm {pr}_2 \colon R = X \times _{\mathfrak {X}} X \rightrightarrows X$ for the first and second projections. We have a natural
$\mathrm {pr}_1, \mathrm {pr}_2 \colon R = X \times _{\mathfrak {X}} X \rightrightarrows X$ for the first and second projections. We have a natural ![]() $2$-morphism
$2$-morphism ![]() $\xi \colon g \circ \mathrm {pr}_1 \Rightarrow g \circ \mathrm {pr}_2$. We now prove the commutativity of the following diagram.
$\xi \colon g \circ \mathrm {pr}_1 \Rightarrow g \circ \mathrm {pr}_2$. We now prove the commutativity of the following diagram.

By the reducedness of ![]() $R^{\mathrm{red}}$, we only need to prove the commutativity at each point
$R^{\mathrm{red}}$, we only need to prove the commutativity at each point ![]() $r \in R$. Write
$r \in R$. Write ![]() $\mathrm {pr}_1(r) = x_1$ and
$\mathrm {pr}_1(r) = x_1$ and ![]() $\mathrm {pr}_2(r) = x_2$. Now consider the following diagram.
$\mathrm {pr}_2(r) = x_2$. Now consider the following diagram.

Here (A)![]() $_i$ is defined by the quasi-isomorphism
$_i$ is defined by the quasi-isomorphism ![]() $\boldsymbol {g}^{*} \mathbb {L}_{\boldsymbol {\mathfrak {X}}} |_{x_i} \simeq \mathrm {H}^{*}(\boldsymbol {g}^{*}\mathbb {L}_{\boldsymbol {\mathfrak {X}}} |_{x_i} )$ and (B)
$\boldsymbol {g}^{*} \mathbb {L}_{\boldsymbol {\mathfrak {X}}} |_{x_i} \simeq \mathrm {H}^{*}(\boldsymbol {g}^{*}\mathbb {L}_{\boldsymbol {\mathfrak {X}}} |_{x_i} )$ and (B)![]() $_i$ is defined by
$_i$ is defined by ![]() $\kappa _{g(x_i)}$ in Proposition 4.8 and the quasi-isomorphism
$\kappa _{g(x_i)}$ in Proposition 4.8 and the quasi-isomorphism ![]() $\tau ^{\geq 0}(g^{*}\mathbb {L}_{\mathfrak {X}})|_{x_i} \simeq \mathrm {H}^{*}(\tau ^{\geq 0}(g^{*}\mathbb {L}_{\mathfrak {X}})|_{x_i})$. The map (C)
$\tau ^{\geq 0}(g^{*}\mathbb {L}_{\mathfrak {X}})|_{x_i} \simeq \mathrm {H}^{*}(\tau ^{\geq 0}(g^{*}\mathbb {L}_{\mathfrak {X}})|_{x_i})$. The map (C)![]() $_i$ is defined in the same manner as (2.5) using the isomorphisms
$_i$ is defined in the same manner as (2.5) using the isomorphisms
 \[ \mathrm{H}^{n}(\boldsymbol{g}^{*}\mathbb{L}_{\boldsymbol{\mathfrak{X}}} |_{x_i}) \cong \begin{cases} \mathrm{H}^{n}(\tau^{{\geq} 0}(g^{*}\mathbb{L}_{\mathfrak{X}})|_{x_i}) & n = 0,1 \\ \mathrm{H}^{{-}n-1}(\tau^{{\geq} 0}(g^{*}\mathbb{L}_{\mathfrak{X}})|_{x_i})^{{\vee}} & n ={-}2, -1. \end{cases} \]
\[ \mathrm{H}^{n}(\boldsymbol{g}^{*}\mathbb{L}_{\boldsymbol{\mathfrak{X}}} |_{x_i}) \cong \begin{cases} \mathrm{H}^{n}(\tau^{{\geq} 0}(g^{*}\mathbb{L}_{\mathfrak{X}})|_{x_i}) & n = 0,1 \\ \mathrm{H}^{{-}n-1}(\tau^{{\geq} 0}(g^{*}\mathbb{L}_{\mathfrak{X}})|_{x_i})^{{\vee}} & n ={-}2, -1. \end{cases} \]
The commutativity of the left trapezoid and middle square is obvious, and the commutativity of the right trapezoid follows from the proof of [Reference JoyceJoy15, Theorem 2.56]. It is easy to see that the upper and lower trapezoids commute up to the sign ![]() $(-1)^{\mathop {\mathrm {rank}}\nolimits (\mathrm {H}^{1}(\mathbb {L}_{\mathfrak {X}} |_{g(x_i)}))}$ by using the equality (A.3). These commutativity properties imply the commutativity of the outer square, and hence the commutativity of diagram (
$(-1)^{\mathop {\mathrm {rank}}\nolimits (\mathrm {H}^{1}(\mathbb {L}_{\mathfrak {X}} |_{g(x_i)}))}$ by using the equality (A.3). These commutativity properties imply the commutativity of the outer square, and hence the commutativity of diagram (
).
By Darboux's theorem [Reference Ben-Bassat, Brav, Bussi and JoyceBBBJ15, Theorem 2.10], we can take ![]() $\boldsymbol {X}$,
$\boldsymbol {X}$, ![]() $\hat {\boldsymbol {X}}$,
$\hat {\boldsymbol {X}}$, ![]() $\boldsymbol {g}$, and
$\boldsymbol {g}$, and ![]() $\boldsymbol {\tau }$ in the proposition so that
$\boldsymbol {\tau }$ in the proposition so that ![]() $g$ is surjective. By the commutativity of diagram (4.12),
$g$ is surjective. By the commutativity of diagram (4.12), ![]() $\Lambda _{\boldsymbol {X}, \hat {\boldsymbol {X}}, \boldsymbol {g}, \boldsymbol {\tau }}$ descends to
$\Lambda _{\boldsymbol {X}, \hat {\boldsymbol {X}}, \boldsymbol {g}, \boldsymbol {\tau }}$ descends to ![]() $\Lambda _{\boldsymbol {\mathfrak {X}}} \colon \mathop {\widehat {\mathrm {det}}}\nolimits (\mathbb {L}_{\boldsymbol {\mathfrak {X}}}) \cong K_{\mathfrak {X}, s_{\mathfrak {X}}}$ satisfying the property in the proposition. The uniqueness of
$\Lambda _{\boldsymbol {\mathfrak {X}}} \colon \mathop {\widehat {\mathrm {det}}}\nolimits (\mathbb {L}_{\boldsymbol {\mathfrak {X}}}) \cong K_{\mathfrak {X}, s_{\mathfrak {X}}}$ satisfying the property in the proposition. The uniqueness of ![]() $\Lambda _{\boldsymbol {\mathfrak {X}}}$ as in the theorem is clear from the construction.
$\Lambda _{\boldsymbol {\mathfrak {X}}}$ as in the theorem is clear from the construction.
The notion of orientation for ![]() $-1$-shifted symplectic derived Artin stacks is defined by that of the associated d-critical stacks. Let
$-1$-shifted symplectic derived Artin stacks is defined by that of the associated d-critical stacks. Let ![]() $\boldsymbol {\mathfrak {Y}}$ be a quasi-smooth derived Artin stack. The argument in Example 2.15 works also for the stacky case and defines a natural isomorphism
$\boldsymbol {\mathfrak {Y}}$ be a quasi-smooth derived Artin stack. The argument in Example 2.15 works also for the stacky case and defines a natural isomorphism
We define the canonical orientation ![]() $o^{}_{\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}}$ for
$o^{}_{\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}}$ for ![]() $\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}$ by the composition
$\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}$ by the composition ![]() $o^{}_{\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}} := \Lambda _{\boldsymbol {\mathfrak {Y}}} \circ o'_{\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}}$.
$o^{}_{\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}} := \Lambda _{\boldsymbol {\mathfrak {Y}}} \circ o'_{\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}}$.
Proposition 4.10 In the notation as in Proposition 4.7, we have an isomorphism
Proof. Throughout the proof we use the following notation: for a morphism ![]() $\boldsymbol {h} \colon {\boldsymbol {\mathfrak {Z}}} \to \boldsymbol {\mathfrak {W}}$ of derived Artin stacks, we write
$\boldsymbol {h} \colon {\boldsymbol {\mathfrak {Z}}} \to \boldsymbol {\mathfrak {W}}$ of derived Artin stacks, we write
for the natural distinguished triangle of cotangent complexes.
Define
by using ![]() $\hat {\imath }(\Delta _{\boldsymbol {f}})$ and the identification
$\hat {\imath }(\Delta _{\boldsymbol {f}})$ and the identification ![]() $(\boldsymbol {\pi }_{\boldsymbol {\mathfrak {Y}}, \boldsymbol {f}})^{*} \mathbb {L}_{\boldsymbol {f}} \cong \mathbb {L}_{\tilde {\boldsymbol {f}}}$. Write
$(\boldsymbol {\pi }_{\boldsymbol {\mathfrak {Y}}, \boldsymbol {f}})^{*} \mathbb {L}_{\boldsymbol {f}} \cong \mathbb {L}_{\tilde {\boldsymbol {f}}}$. Write
Now it is enough to prove the commutativity of the following diagram of line bundles on ![]() $\mathbf {T}^{*}[-1]\boldsymbol {Y}^{\mathrm {red}}$.
$\mathbf {T}^{*}[-1]\boldsymbol {Y}^{\mathrm {red}}$.

Here ![]() $\Lambda _{\mathbf {T}^{*}[-1]\boldsymbol {Y}}$ and
$\Lambda _{\mathbf {T}^{*}[-1]\boldsymbol {Y}}$ and ![]() $\Lambda _{\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}}$ are defined in Theorems 2.13 and 4.9 respectively, and the bottom arrow is defined by using
$\Lambda _{\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}}$ are defined in Theorems 2.13 and 4.9 respectively, and the bottom arrow is defined by using ![]() $\Gamma _{t_0(\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}) ,\tilde {f}}$ in (4.8) and the identification
$\Gamma _{t_0(\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}) ,\tilde {f}}$ in (4.8) and the identification
Consider the following diagram in ![]() $\mathrm {Perf}(\boldsymbol {f}^{*} \mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}})$:
$\mathrm {Perf}(\boldsymbol {f}^{*} \mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}})$:

where the top vertical arrows are identified with a part of the natural morphism between distinguished triangles
by the natural isomorphisms
and ![]() $k$ is taken so that the right horizontal arrows define a morphism between distinguished triangles
$k$ is taken so that the right horizontal arrows define a morphism between distinguished triangles
Here ![]() $\Delta _{\boldsymbol {f}, \mathrm {rot}}^{\vee }$ denotes the right vertical distinguished triangle in the diagram above. Now we claim that
$\Delta _{\boldsymbol {f}, \mathrm {rot}}^{\vee }$ denotes the right vertical distinguished triangle in the diagram above. Now we claim that
where ![]() $\ell \colon \mathbb {T}_{\tilde {\boldsymbol {f}}} \xrightarrow {\sim } \mathbb {L}_{\boldsymbol {\tau }}[-2]$ is defined in (4.11), and
$\ell \colon \mathbb {T}_{\tilde {\boldsymbol {f}}} \xrightarrow {\sim } \mathbb {L}_{\boldsymbol {\tau }}[-2]$ is defined in (4.11), and ![]() $\phi \colon (\boldsymbol {\pi }_{\boldsymbol {\mathfrak {Y}}, \boldsymbol {f}})^{*} \mathbb {T}_{\tilde {\boldsymbol {f}}} \xrightarrow {\sim } \mathbb {T}_{\boldsymbol {f}}$ is the natural isomorphism. To see this, consider the following commutative diagram.
$\phi \colon (\boldsymbol {\pi }_{\boldsymbol {\mathfrak {Y}}, \boldsymbol {f}})^{*} \mathbb {T}_{\tilde {\boldsymbol {f}}} \xrightarrow {\sim } \mathbb {T}_{\boldsymbol {f}}$ is the natural isomorphism. To see this, consider the following commutative diagram.

By using [Reference Knudsen and MumfordKM76, Proposition 6], it is enough to prove the equalities
 \begin{gather*} \boldsymbol{\tau}^{*} \zeta_{\boldsymbol{\pi}_{\boldsymbol{Y}}} \circ ({\cdot} \boldsymbol{\tau}^{*} \omega_{\mathbf{T}^{*}[{-}1]\boldsymbol{Y}})[1] \circ \theta_{\boldsymbol{\tau}}^{{\vee}}[1]= \theta_{\boldsymbol{\pi}_{\boldsymbol{\mathfrak{Y}}, \boldsymbol{f}}}^{{\vee}} [1], \\ \zeta_{\boldsymbol{\pi}_{\boldsymbol{\mathfrak{Y}}, \boldsymbol{f}}} \circ \theta_{\tilde{\boldsymbol{f}}} \circ ({\cdot} \tilde{\boldsymbol{f}}^{*} \omega_{\mathbf{T}^{*}[{-}1]\boldsymbol{\mathfrak{Y}}})[1] = \tilde{\boldsymbol{f}}^{*} \theta_{\boldsymbol{\pi}_{\boldsymbol{\mathfrak{Y}}}}^{{\vee}} [1], \end{gather*}
\begin{gather*} \boldsymbol{\tau}^{*} \zeta_{\boldsymbol{\pi}_{\boldsymbol{Y}}} \circ ({\cdot} \boldsymbol{\tau}^{*} \omega_{\mathbf{T}^{*}[{-}1]\boldsymbol{Y}})[1] \circ \theta_{\boldsymbol{\tau}}^{{\vee}}[1]= \theta_{\boldsymbol{\pi}_{\boldsymbol{\mathfrak{Y}}, \boldsymbol{f}}}^{{\vee}} [1], \\ \zeta_{\boldsymbol{\pi}_{\boldsymbol{\mathfrak{Y}}, \boldsymbol{f}}} \circ \theta_{\tilde{\boldsymbol{f}}} \circ ({\cdot} \tilde{\boldsymbol{f}}^{*} \omega_{\mathbf{T}^{*}[{-}1]\boldsymbol{\mathfrak{Y}}})[1] = \tilde{\boldsymbol{f}}^{*} \theta_{\boldsymbol{\pi}_{\boldsymbol{\mathfrak{Y}}}}^{{\vee}} [1], \end{gather*}but these are consequences of [Reference CalaqueCal19, Remark 2.5].
Now consider the following diagram of line bundles on ![]() $\boldsymbol {f}^{*} \mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}^{\mathrm {red}}$, in which we omit the pullback functors
$\boldsymbol {f}^{*} \mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}^{\mathrm {red}}$, in which we omit the pullback functors ![]() $\boldsymbol {\tau }^{*}$,
$\boldsymbol {\tau }^{*}$, ![]() $\boldsymbol {\pi }_{\boldsymbol {\mathfrak {Y}}, \boldsymbol {f}}^{*}$, and
$\boldsymbol {\pi }_{\boldsymbol {\mathfrak {Y}}, \boldsymbol {f}}^{*}$, and ![]() $(\boldsymbol {f} \circ \boldsymbol {\pi }_{\boldsymbol {\mathfrak {Y}}, \boldsymbol {f}} )^{*}$ to simplify the notation.
$(\boldsymbol {f} \circ \boldsymbol {\pi }_{\boldsymbol {\mathfrak {Y}}, \boldsymbol {f}} )^{*}$ to simplify the notation.

Here ![]() $\hat {\eta }, \hat {\chi }$ are defined in Lemma 2.14. The commutativity of diagram (4.17), equality (4.18), and [Reference Knudsen and MumfordKM76, Theorem 1] implies the commutativity of the upper square. By applying Propositions A.1 and A.4 we see that the lower square also commutes. Next consider the following commutative diagram in
$\hat {\eta }, \hat {\chi }$ are defined in Lemma 2.14. The commutativity of diagram (4.17), equality (4.18), and [Reference Knudsen and MumfordKM76, Theorem 1] implies the commutativity of the upper square. By applying Propositions A.1 and A.4 we see that the lower square also commutes. Next consider the following commutative diagram in ![]() $\mathrm {Perf}(\boldsymbol {f}^{*} \mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}})$.
$\mathrm {Perf}(\boldsymbol {f}^{*} \mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}})$.

The upper vertical arrows are identified with a part of the natural morphism of distinguished triangles
by the natural isomorphisms
and the left horizontal arrows are identified with a part of the natural morphism
by the natural isomorphism
Now consider the following diagram of line bundles on ![]() $\boldsymbol {f}^{*} \mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}^{\mathrm {red}}$, in which we omit pullback functors as previous.
$\boldsymbol {f}^{*} \mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}^{\mathrm {red}}$, in which we omit pullback functors as previous.

The commutativity of diagram (
4.20) and [Reference Knudsen and MumfordKM76, Theorem 1] implies the commutativity of the upper square, and the commutativity of the lower square is obvious. By combining the commutativity of the diagrams (
4.19) and (
4.21), we obtain the commutativity of diagram (4.16) (the sign ![]() $(-1)^{{\operatorname {vdim} \boldsymbol {f} \cdot (\operatorname {vdim} \boldsymbol {f} - 1) / 2}}$ appears due to the difference of the maps (2.5) and (A.2)).
$(-1)^{{\operatorname {vdim} \boldsymbol {f} \cdot (\operatorname {vdim} \boldsymbol {f} - 1) / 2}}$ appears due to the difference of the maps (2.5) and (A.2)).
Remark 4.11 In the situation of the proposition above, assume further that there exists a smooth morphism ![]() $\boldsymbol {q} \colon \boldsymbol {Y}' \to \boldsymbol {Y}$, and write
$\boldsymbol {q} \colon \boldsymbol {Y}' \to \boldsymbol {Y}$, and write ![]() $\tilde {q} \colon t_0(\mathbf {T}^{*}[-1]\boldsymbol {Y}') \to t_0(\mathbf {T}^{*}[-1]\boldsymbol {Y})$ for the base change of
$\tilde {q} \colon t_0(\mathbf {T}^{*}[-1]\boldsymbol {Y}') \to t_0(\mathbf {T}^{*}[-1]\boldsymbol {Y})$ for the base change of ![]() $q = t_0(\boldsymbol {q})$. Then it is clear that the composition
$q = t_0(\boldsymbol {q})$. Then it is clear that the composition
is equal to ![]() $\Xi _{\boldsymbol {f} \circ \boldsymbol {q}}$.
$\Xi _{\boldsymbol {f} \circ \boldsymbol {q}}$.
4.3 Dimensional reduction for Artin stacks
We first recall the definition of the vanishing cycle complexes associated with d-critical stacks. To do this, we discuss the functorial behavior of the vanishing cycle complexes associated with d-critical schemes with respect to smooth morphisms.
Proposition 4.12 [Reference Ben-Bassat, Brav, Bussi and JoyceBBBJ15, Proposition 4.5]
Let ![]() $(Y, s, o)$ be an oriented d-critical scheme, and
$(Y, s, o)$ be an oriented d-critical scheme, and ![]() $q \colon X \to Y$ be a smooth morphism. Then there exists a natural isomorphism
$q \colon X \to Y$ be a smooth morphism. Then there exists a natural isomorphism
characterized by the following property: for a d-critical chart ![]() $\mathscr {R} = (R, U, f, i)$ of
$\mathscr {R} = (R, U, f, i)$ of ![]() $(X, s)$, a d-critical chart
$(X, s)$, a d-critical chart ![]() $\mathscr {S} = (S, V, g, j)$ of
$\mathscr {S} = (S, V, g, j)$ of ![]() $(Y, s)$ such that
$(Y, s)$ such that ![]() $q(R) \subset S$, and a smooth morphism
$q(R) \subset S$, and a smooth morphism ![]() $\tilde {q} \colon U \to V$ such that
$\tilde {q} \colon U \to V$ such that ![]() $f = g \circ \tilde {q}$ and
$f = g \circ \tilde {q}$ and ![]() $j \circ q = \tilde {q} \circ i$, the following diagram commutes:
$j \circ q = \tilde {q} \circ i$, the following diagram commutes:

where ![]() $\Theta _{\tilde {q}, f}$ is defined in Proposition 2.16(iii), and
$\Theta _{\tilde {q}, f}$ is defined in Proposition 2.16(iii), and ![]() $\rho _q$ is defined by using the natural isomorphism
$\rho _q$ is defined by using the natural isomorphism ![]() $K_U \cong \tilde {q}^{*} K_V \otimes \mathop {\mathrm {det}}\nolimits (\Omega _{U/V})$.
$K_U \cong \tilde {q}^{*} K_V \otimes \mathop {\mathrm {det}}\nolimits (\Omega _{U/V})$.
Theorem 4.13 [Reference Ben-Bassat, Brav, Bussi and JoyceBBBJ15, Theorem 4.8]
Let ![]() $(\mathfrak {X}, s, o)$ be an oriented d-critical stack. Then there exists a natural perverse sheaf
$(\mathfrak {X}, s, o)$ be an oriented d-critical stack. Then there exists a natural perverse sheaf ![]() $\varphi _{\mathfrak {X}, s, o}$ with the following property: for each
$\varphi _{\mathfrak {X}, s, o}$ with the following property: for each ![]() $(u \colon U \to \mathfrak {X}) \in \mathop {\text {Lis-An}} \nolimits (\mathfrak {X})$ there exists an isomorphism
$(u \colon U \to \mathfrak {X}) \in \mathop {\text {Lis-An}} \nolimits (\mathfrak {X})$ there exists an isomorphism
satisfying ![]() $\Theta _{u, s, o} = q^{*}\Theta _{v, s, o}[\dim q] \circ \Theta _{q, v^{\star } s, v^{\star } o}$ for any smooth morphism
$\Theta _{u, s, o} = q^{*}\Theta _{v, s, o}[\dim q] \circ \Theta _{q, v^{\star } s, v^{\star } o}$ for any smooth morphism ![]() $q \colon (u\colon U \to \mathfrak {X}) \to (v\colon V \to \mathfrak {X})$ in
$q \colon (u\colon U \to \mathfrak {X}) \to (v\colon V \to \mathfrak {X})$ in ![]() $\mathop {\text {Lis-An}} \nolimits (\mathfrak {X})$. Here we identify
$\mathop {\text {Lis-An}} \nolimits (\mathfrak {X})$. Here we identify ![]() $q^{\star } v^{\star } o$ and
$q^{\star } v^{\star } o$ and ![]() $u^{\star } o$ by using (4.9).
$u^{\star } o$ by using (4.9).
Let ![]() $(\mathfrak {X}, s)$ be a d-critical stack, and
$(\mathfrak {X}, s)$ be a d-critical stack, and ![]() $\Xi \colon o_1 \cong o_2$ be an isomorphism between orientations on
$\Xi \colon o_1 \cong o_2$ be an isomorphism between orientations on ![]() $(\mathfrak {X},s)$. We write
$(\mathfrak {X},s)$. We write
for the isomorphism induced by ![]() $\Xi$.
$\Xi$.
We now state our main theorem.
Theorem 4.14 Let ![]() $\boldsymbol {\mathfrak {Y}}$ be a quasi-smooth derived Artin stack, and equip
$\boldsymbol {\mathfrak {Y}}$ be a quasi-smooth derived Artin stack, and equip ![]() $\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}$ with the canonical
$\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}$ with the canonical ![]() $-1$-shifted symplectic structure and the canonical orientation. Then we have a natural isomorphism
$-1$-shifted symplectic structure and the canonical orientation. Then we have a natural isomorphism
where we write ![]() $\mathfrak {Y} = t_0(\boldsymbol {\mathfrak {Y}})$ and
$\mathfrak {Y} = t_0(\boldsymbol {\mathfrak {Y}})$ and ![]() ${\pi _{\boldsymbol {\mathfrak {Y}}}} = t_0(\boldsymbol {\pi }_{\boldsymbol {\mathfrak {Y}}})$.
${\pi _{\boldsymbol {\mathfrak {Y}}}} = t_0(\boldsymbol {\pi }_{\boldsymbol {\mathfrak {Y}}})$.
Proof. Take a smooth surjective morphism ![]() $\boldsymbol {v} \colon \boldsymbol {V} \to \boldsymbol {\mathfrak {Y}}$ and an étale morphism
$\boldsymbol {v} \colon \boldsymbol {V} \to \boldsymbol {\mathfrak {Y}}$ and an étale morphism ![]() $\boldsymbol {\eta } \colon \boldsymbol {U} \to \boldsymbol {V} \times _{\boldsymbol {\mathfrak {Y}}} \boldsymbol {V}$ where
$\boldsymbol {\eta } \colon \boldsymbol {U} \to \boldsymbol {V} \times _{\boldsymbol {\mathfrak {Y}}} \boldsymbol {V}$ where ![]() $\boldsymbol {V}$ and
$\boldsymbol {V}$ and ![]() $\boldsymbol {U}$ are derived schemes.
$\boldsymbol {U}$ are derived schemes. ![]() $\boldsymbol {q}_1, \boldsymbol {q}_2 \colon \boldsymbol {U} \to \boldsymbol {V}$ denote the composition of
$\boldsymbol {q}_1, \boldsymbol {q}_2 \colon \boldsymbol {U} \to \boldsymbol {V}$ denote the composition of ![]() $\boldsymbol {\eta }$ and the first and second projections, respectively. Write
$\boldsymbol {\eta }$ and the first and second projections, respectively. Write ![]() $U = t_0(\boldsymbol {U})$,
$U = t_0(\boldsymbol {U})$, ![]() $\tilde {U} = t_0(\mathbf {T}^{*}[-1]\boldsymbol {U})$,
$\tilde {U} = t_0(\mathbf {T}^{*}[-1]\boldsymbol {U})$, ![]() $V = t_0(\boldsymbol {V})$,
$V = t_0(\boldsymbol {V})$, ![]() $\tilde {V} = t_0(\mathbf {T}^{*}[-1]\boldsymbol {V})$,
$\tilde {V} = t_0(\mathbf {T}^{*}[-1]\boldsymbol {V})$, ![]() $\widetilde {\mathfrak {Y}} = t_0(\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}})$,
$\widetilde {\mathfrak {Y}} = t_0(\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}})$, ![]() $v = t_0(\boldsymbol {v})$, and
$v = t_0(\boldsymbol {v})$, and ![]() $q_i = t_0(\boldsymbol {q}_i)$ for
$q_i = t_0(\boldsymbol {q}_i)$ for ![]() $i =1, 2$. Denote by
$i =1, 2$. Denote by ![]() $\pi _{\mathfrak {Y}} \colon \widetilde {\mathfrak {Y}} \to \mathfrak {Y}$,
$\pi _{\mathfrak {Y}} \colon \widetilde {\mathfrak {Y}} \to \mathfrak {Y}$, ![]() $\pi _{U} \colon \tilde {U} \to U$, and
$\pi _{U} \colon \tilde {U} \to U$, and ![]() $\pi _{V} \colon \tilde {V} \to V$ the projections, and by
$\pi _{V} \colon \tilde {V} \to V$ the projections, and by ![]() $\tilde {v} \colon \tilde {V} \to \widetilde {\mathfrak {Y}}$ (respectively,
$\tilde {v} \colon \tilde {V} \to \widetilde {\mathfrak {Y}}$ (respectively, ![]() $\tilde {q}_i \colon \tilde {U} \to \tilde {V}$) the base change of
$\tilde {q}_i \colon \tilde {U} \to \tilde {V}$) the base change of ![]() $v$ (respectively,
$v$ (respectively, ![]() $q_i$). Denote by
$q_i$). Denote by ![]() $s$ the d-critical structure on
$s$ the d-critical structure on ![]() $\widetilde {\mathfrak {Y}}$ associated with the canonical
$\widetilde {\mathfrak {Y}}$ associated with the canonical ![]() $-1$-shifted symplectic structure
$-1$-shifted symplectic structure ![]() $\omega _{\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}}$.
$\omega _{\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}}}$.
Define
by the following composition:
 \begin{align*} v^{*}({\pi_{\mathfrak{Y}}})_! \varphi^{p}_{\mathbf{T}^{*}[{-}1]\boldsymbol{\mathfrak{Y}}} &\cong (\pi_{{V}})_! \tilde{v}^{*} \varphi^{p}_{\mathbf{T}^{*}[{-}1]\boldsymbol{\mathfrak{Y}}} \\ &\cong (\pi_{{V}})_! \varphi^{p}_{\mathbf{T}^{*}[{-}1]\boldsymbol{V}}[-\dim v] \\ &\cong v^{*} \mathbb{Q}_{\mathfrak{Y}}[\operatorname{vdim} \boldsymbol{\mathfrak{Y}}], \end{align*}
\begin{align*} v^{*}({\pi_{\mathfrak{Y}}})_! \varphi^{p}_{\mathbf{T}^{*}[{-}1]\boldsymbol{\mathfrak{Y}}} &\cong (\pi_{{V}})_! \tilde{v}^{*} \varphi^{p}_{\mathbf{T}^{*}[{-}1]\boldsymbol{\mathfrak{Y}}} \\ &\cong (\pi_{{V}})_! \varphi^{p}_{\mathbf{T}^{*}[{-}1]\boldsymbol{V}}[-\dim v] \\ &\cong v^{*} \mathbb{Q}_{\mathfrak{Y}}[\operatorname{vdim} \boldsymbol{\mathfrak{Y}}], \end{align*}
where the first isomorphism is the proper base-change map, the second isomorphism is ![]() $(\pi _{V})_! ( a_{\Xi _{\boldsymbol {v}}} \circ \Theta _{\tilde {v}}^{-1}) [-\dim v]$, and the third isomorphism is
$(\pi _{V})_! ( a_{\Xi _{\boldsymbol {v}}} \circ \Theta _{\tilde {v}}^{-1}) [-\dim v]$, and the third isomorphism is ![]() $\bar {\gamma }_{\boldsymbol {V}} [-\dim v]$. By the sheaf property, it is enough to prove the commutativity of the diagram
$\bar {\gamma }_{\boldsymbol {V}} [-\dim v]$. By the sheaf property, it is enough to prove the commutativity of the diagram

where ![]() $\xi \colon v \circ q_1 \Rightarrow v \circ q_2$ is the natural
$\xi \colon v \circ q_1 \Rightarrow v \circ q_2$ is the natural ![]() $2$-morphism. We define
$2$-morphism. We define
for ![]() $i =1, 2$ in the same manner as
$i =1, 2$ in the same manner as ![]() $\bar {\gamma }_{\boldsymbol {\mathfrak {Y}}, \boldsymbol {v}}$. The commutativity of diagram (4.3) implies the commutativity of the following diagram.
$\bar {\gamma }_{\boldsymbol {\mathfrak {Y}}, \boldsymbol {v}}$. The commutativity of diagram (4.3) implies the commutativity of the following diagram.

Therefore the commutativity of diagram (
4.22) follows once we prove the commutativity of the diagram

for each ![]() $i = 1, 2$. We drop
$i = 1, 2$. We drop ![]() $i$ from the notation, and write
$i$ from the notation, and write ![]() $q = q_i$ and
$q = q_i$ and ![]() $\tilde {q} = \tilde {q}_i$. By Remark 4.11, the following diagram commutes.
$\tilde {q} = \tilde {q}_i$. By Remark 4.11, the following diagram commutes.

Using this and the commutativity of diagram (4.3) again, the commutativity of diagram (
4.23) is implied by the commutativity of the diagram

where ![]() $\mathfrak {pbc}_q$ denotes the base-change map. Arguing as in the proof of [Reference Ben-Bassat, Brav, Bussi and JoyceBBBJ15, Theorem 2.9] and by shrinking if necessary, we may assume that there exist a smooth morphism
$\mathfrak {pbc}_q$ denotes the base-change map. Arguing as in the proof of [Reference Ben-Bassat, Brav, Bussi and JoyceBBBJ15, Theorem 2.9] and by shrinking if necessary, we may assume that there exist a smooth morphism ![]() $\hbox{$F \colon M \to N$}$ with a constant relative dimension between smooth schemes, a vector bundle
$\hbox{$F \colon M \to N$}$ with a constant relative dimension between smooth schemes, a vector bundle ![]() $E$ of rank
$E$ of rank ![]() $r$ on
$r$ on ![]() $N$, and its section
$N$, and its section ![]() $e \in \Gamma (N, E)$ such that
$e \in \Gamma (N, E)$ such that ![]() $\boldsymbol {V} = \boldsymbol {Z}(e)$,
$\boldsymbol {V} = \boldsymbol {Z}(e)$, ![]() $\boldsymbol {U} = \boldsymbol {Z}(F^{*} e)$, and
$\boldsymbol {U} = \boldsymbol {Z}(F^{*} e)$, and ![]() $\boldsymbol {q} \colon \boldsymbol {Z}(F^{*} e) \to \boldsymbol {Z}(e)$ is the base change of
$\boldsymbol {q} \colon \boldsymbol {Z}(F^{*} e) \to \boldsymbol {Z}(e)$ is the base change of ![]() $F$. Write
$F$. Write ![]() $\tilde {F} \colon \mathop {\mathrm {Tot}}\nolimits _M(F^{*}E^{\vee }) \to \mathop {\mathrm {Tot}}\nolimits _N(E^{\vee })$ for the base change of
$\tilde {F} \colon \mathop {\mathrm {Tot}}\nolimits _M(F^{*}E^{\vee }) \to \mathop {\mathrm {Tot}}\nolimits _N(E^{\vee })$ for the base change of ![]() $F$, and denote by
$F$, and denote by ![]() $\bar {e} \colon \mathop {\mathrm {Tot}}\nolimits _N(E^{\vee }) \to \mathbb {A}^{1}$ the regular function corresponding to
$\bar {e} \colon \mathop {\mathrm {Tot}}\nolimits _N(E^{\vee }) \to \mathbb {A}^{1}$ the regular function corresponding to ![]() $e$. Then
$e$. Then
define d-critical charts on ![]() $\tilde {U}$ and
$\tilde {U}$ and ![]() $\tilde {V}$ respectively, where
$\tilde {V}$ respectively, where ![]() $i$ and
$i$ and ![]() $j$ denote the natural embeddings. Consider the composition
$j$ denote the natural embeddings. Consider the composition
where the first map is induced by ![]() $\Xi _{\boldsymbol {q}}$. Recall that we have chosen trivializations of
$\Xi _{\boldsymbol {q}}$. Recall that we have chosen trivializations of ![]() $Q_{\mathscr {U}}^{o^{}_{\mathbf {T}^{*}[-1]\boldsymbol {U}}}$ and
$Q_{\mathscr {U}}^{o^{}_{\mathbf {T}^{*}[-1]\boldsymbol {U}}}$ and ![]() $Q_{\mathscr {V}}^{o^{}_{\mathbf {T}^{*}[-1]\boldsymbol {V}}}$ in (2.25). Since we have
$Q_{\mathscr {V}}^{o^{}_{\mathbf {T}^{*}[-1]\boldsymbol {V}}}$ in (2.25). Since we have
these trivializations are identified by ![]() $\rho _{\tilde {q}}'$. This shows the commutativity of the diagram
$\rho _{\tilde {q}}'$. This shows the commutativity of the diagram

where the two ![]() $\text {triv}$ in the right horizontal arrows denote the trivialization as above. Then the commutativity of diagram (
$\text {triv}$ in the right horizontal arrows denote the trivialization as above. Then the commutativity of diagram (
) follows from the commutativity of diagram (2.9).
5. Applications
In this section we will discuss two applications of Theorem 3.1 and its stacky generalization, Theorem 4.14. Firstly, we will apply it to prove the dimensional reduction theorem for the vanishing cycle cohomology of the moduli stacks of sheaves on local surfaces. Secondly, we will propose a sheaf-theoretic construction of virtual fundamental classes of quasi-smooth derived schemes by regarding Theorem 3.1 as a version of the Thom isomorphism for ![]() $-1$-shifted cotangent stacks.
$-1$-shifted cotangent stacks.
5.1 Cohomological Donaldson–Thomas theory for local surfaces
Let ![]() $S$ be a smooth quasi-projective surface and denote by
$S$ be a smooth quasi-projective surface and denote by ![]() $p \colon X = \mathop {\mathrm {Tot}}\nolimits _S(\omega _S) \to S$ the projection from the total space of the canonical bundle. Denote by
$p \colon X = \mathop {\mathrm {Tot}}\nolimits _S(\omega _S) \to S$ the projection from the total space of the canonical bundle. Denote by ![]() $\boldsymbol {\mathfrak {M}}_{S}$ (respectively,
$\boldsymbol {\mathfrak {M}}_{S}$ (respectively, ![]() $\boldsymbol {\mathfrak {M}}_{X}$) the derived moduli stack of coherent sheaves on
$\boldsymbol {\mathfrak {M}}_{X}$) the derived moduli stack of coherent sheaves on ![]() $S$ (respectively,
$S$ (respectively, ![]() $X$) with proper supports, and by
$X$) with proper supports, and by ![]() $\boldsymbol {\pi }_{p} \colon \boldsymbol {\mathfrak {M}}_{X} \to \boldsymbol {\mathfrak {M}}_{S}$ the projection defined by
$\boldsymbol {\pi }_{p} \colon \boldsymbol {\mathfrak {M}}_{X} \to \boldsymbol {\mathfrak {M}}_{S}$ the projection defined by ![]() $p_*$. By applying the main theorem of [Reference Brav and DyckerhoffBD19],
$p_*$. By applying the main theorem of [Reference Brav and DyckerhoffBD19], ![]() $\boldsymbol {\mathfrak {M}}_{X}$ carries a canonical
$\boldsymbol {\mathfrak {M}}_{X}$ carries a canonical ![]() $-1$-shifted symplectic structure
$-1$-shifted symplectic structure ![]() $\omega _{\boldsymbol {\mathfrak {M}}_{S}}$.
$\omega _{\boldsymbol {\mathfrak {M}}_{S}}$.
Theorem 5.1 There exists an equivalence of ![]() $-1$-shifted symplectic derived Artin stacks
$-1$-shifted symplectic derived Artin stacks
such that ![]() $\boldsymbol {\pi }_{p} \simeq \boldsymbol {\pi }_{\boldsymbol {\mathfrak {M}}_{S}} \circ \Phi$.
$\boldsymbol {\pi }_{p} \simeq \boldsymbol {\pi }_{\boldsymbol {\mathfrak {M}}_{S}} \circ \Phi$.
Proof. Let ![]() $G$ be a compact generator of
$G$ be a compact generator of ![]() $D(\mathop {\mathrm {Qcoh}}(S))$, and
$D(\mathop {\mathrm {Qcoh}}(S))$, and ![]() $A = \mathop {R\mathrm {Hom}}\nolimits (G, G)$ and
$A = \mathop {R\mathrm {Hom}}\nolimits (G, G)$ and ![]() $B = \mathop {R\mathrm {Hom}}\nolimits (p^{*}G, p^{*}G)$ be the derived endomorphism algebras. It is clear that
$B = \mathop {R\mathrm {Hom}}\nolimits (p^{*}G, p^{*}G)$ be the derived endomorphism algebras. It is clear that ![]() $p^{*}G$ is a compact generator of
$p^{*}G$ is a compact generator of ![]() $D(\mathop {\mathrm {Qcoh}}(X))$. Then it follows from a result of Schwede and Shipley [Reference Schwede and ShipleySS03, Theorem 3.1.1] that we have quasi-equivalences
$D(\mathop {\mathrm {Qcoh}}(X))$. Then it follows from a result of Schwede and Shipley [Reference Schwede and ShipleySS03, Theorem 3.1.1] that we have quasi-equivalences
where ![]() $L_{\mathrm {qcoh}}(S)$ (respectively,
$L_{\mathrm {qcoh}}(S)$ (respectively, ![]() $L_{\mathrm {qcoh}}(X)$) denotes the derived dg-category of
$L_{\mathrm {qcoh}}(X)$) denotes the derived dg-category of ![]() $\mathop {\mathrm {Qcoh}}(S)$ (respectively,
$\mathop {\mathrm {Qcoh}}(S)$ (respectively, ![]() $\mathop {\mathrm {Qcoh}}(X)$), and
$\mathop {\mathrm {Qcoh}}(X)$), and ![]() $\mathrm {RMod} A$ (respectively,
$\mathrm {RMod} A$ (respectively, ![]() $\mathrm {RMod} B$) denotes the derived dg-category of right
$\mathrm {RMod} B$) denotes the derived dg-category of right ![]() $A$-modules (respectively, right
$A$-modules (respectively, right ![]() $B$-modules). By taking the full dg-subcategories of compact objects of dg-categories appearing in the above quasi-equivalences, we obtain quasi-equivalences
$B$-modules). By taking the full dg-subcategories of compact objects of dg-categories appearing in the above quasi-equivalences, we obtain quasi-equivalences
where ![]() $L_{\mathrm {coh}}(S)$ (respectively,
$L_{\mathrm {coh}}(S)$ (respectively, ![]() $L_{\mathrm {coh}}(X)$) denotes the derived dg-category of
$L_{\mathrm {coh}}(X)$) denotes the derived dg-category of ![]() $\mathrm {Coh}(S)$ (respectively,
$\mathrm {Coh}(S)$ (respectively, ![]() $\mathrm {Coh}(X)$), and
$\mathrm {Coh}(X)$), and ![]() $\mathrm {per}_{\mathrm {dg}}A$ (respectively,
$\mathrm {per}_{\mathrm {dg}}A$ (respectively, ![]() $\mathrm {per}_{\mathrm {dg}} B$) denotes the derived dg-category of perfect
$\mathrm {per}_{\mathrm {dg}} B$) denotes the derived dg-category of perfect ![]() $A$-modules (respectively, perfect
$A$-modules (respectively, perfect ![]() $B$-modules). It is proved in [Reference Ikeda and QiuIQ18, § 2.5] that
$B$-modules). It is proved in [Reference Ikeda and QiuIQ18, § 2.5] that ![]() $B$ is equivalent to the
$B$ is equivalent to the ![]() $3$-Calabi–Yau completion of
$3$-Calabi–Yau completion of ![]() $A$. Note that
$A$. Note that ![]() $\boldsymbol {\mathfrak {M}}_{S}$ (respectively,
$\boldsymbol {\mathfrak {M}}_{S}$ (respectively, ![]() $\boldsymbol {\mathfrak {M}}_{X}$) is the derived moduli space of objects in
$\boldsymbol {\mathfrak {M}}_{X}$) is the derived moduli space of objects in ![]() $L_{\mathrm {coh}}(S)$ (respectively,
$L_{\mathrm {coh}}(S)$ (respectively, ![]() $L_{\mathrm {coh}}(X)$) in the sense of [Reference Toën and VaquiéTV07, Definition 3.2]. Therefore, by applying [Reference Bozec, Calaque and ScherotzkeBCS20, Theorem 6.17], we obtain an equivalence of derived Artin stacks
$L_{\mathrm {coh}}(X)$) in the sense of [Reference Toën and VaquiéTV07, Definition 3.2]. Therefore, by applying [Reference Bozec, Calaque and ScherotzkeBCS20, Theorem 6.17], we obtain an equivalence of derived Artin stacks ![]() $\boldsymbol {\mathfrak {M}}_{X} \simeq \mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {M}}_{S}$ and all we need to prove is the coincidence of two left Calabi–Yau structures
$\boldsymbol {\mathfrak {M}}_{X} \simeq \mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {M}}_{S}$ and all we need to prove is the coincidence of two left Calabi–Yau structures
where ![]() $c_1$ is induced by the Calabi–Yau completion description and
$c_1$ is induced by the Calabi–Yau completion description and ![]() $c_2$ corresponds to the canonical Calabi–Yau form on
$c_2$ corresponds to the canonical Calabi–Yau form on ![]() $X$. Since the statement is local on
$X$. Since the statement is local on ![]() $S$, we may assume
$S$, we may assume ![]() $S$ is affine. By the discussion after [Reference Bozec, Calaque and ScherotzkeBCS20, Theorem 5.8], we see that
$S$ is affine. By the discussion after [Reference Bozec, Calaque and ScherotzkeBCS20, Theorem 5.8], we see that ![]() $c_1 = \delta c$ where
$c_1 = \delta c$ where ![]() $\delta$ denotes the mixed differential and
$\delta$ denotes the mixed differential and
corresponds to the tautological ![]() $2$-form on
$2$-form on ![]() $X$ under the Hochschild–Kostant–Rosenberg isomorphism. Since the Hochschild–Kostant–Rosenberg isomorphism identifies the mixed differential on the Hochschild homology and the de Rham differential (see [Reference Toën and VezzosiTV11]), the theorem is proved.
$X$ under the Hochschild–Kostant–Rosenberg isomorphism. Since the Hochschild–Kostant–Rosenberg isomorphism identifies the mixed differential on the Hochschild homology and the de Rham differential (see [Reference Toën and VezzosiTV11]), the theorem is proved.
We always equip ![]() $\boldsymbol {\mathfrak {M}}_{X}$ with the canonical
$\boldsymbol {\mathfrak {M}}_{X}$ with the canonical ![]() $-1$-shifted symplectic structure as above and the orientation
$-1$-shifted symplectic structure as above and the orientation ![]() $t_0(\boldsymbol {\Psi })^{\star } o^{}_{\mathbf {T}^{*}[-1] \boldsymbol {\mathfrak {M}}_{S}}$. The following statement is a direct consequence of Theorem 4.14.
$t_0(\boldsymbol {\Psi })^{\star } o^{}_{\mathbf {T}^{*}[-1] \boldsymbol {\mathfrak {M}}_{S}}$. The following statement is a direct consequence of Theorem 4.14.
Corollary 5.2 We have an isomorphism
where we write ![]() $\mathfrak {M}_{X} = t_0(\boldsymbol {\mathfrak {M}}_{X})$,
$\mathfrak {M}_{X} = t_0(\boldsymbol {\mathfrak {M}}_{X})$, ![]() $\mathfrak {M}_{S} = t_0(\boldsymbol {\mathfrak {M}}_{S})$, and
$\mathfrak {M}_{S} = t_0(\boldsymbol {\mathfrak {M}}_{S})$, and ![]() $\pi _{p} = t_0(\boldsymbol {\pi }_{p})$.
$\pi _{p} = t_0(\boldsymbol {\pi }_{p})$.
Now assume ![]() $S$ is quasi-projective and
$S$ is quasi-projective and ![]() $\omega _S$ is trivial. Take an ample divisor
$\omega _S$ is trivial. Take an ample divisor ![]() $H$ on
$H$ on ![]() $S$ and denote by
$S$ and denote by ![]() $\mathfrak {M}_{S}^{H {\text {-ss}}} \subset \boldsymbol {\mathfrak {M}}_{S}$ (respectively,
$\mathfrak {M}_{S}^{H {\text {-ss}}} \subset \boldsymbol {\mathfrak {M}}_{S}$ (respectively, ![]() $\mathfrak {M}_{X}^{p^{*}H {\text {-ss}}} \subset \mathfrak {M}_{X}$) the moduli stack of
$\mathfrak {M}_{X}^{p^{*}H {\text {-ss}}} \subset \mathfrak {M}_{X}$) the moduli stack of ![]() $H$-semistable sheaves on
$H$-semistable sheaves on ![]() $S$ (respectively,
$S$ (respectively, ![]() $p^{*}H$-semistable sheaves on
$p^{*}H$-semistable sheaves on ![]() $X$) with proper supports. By the triviality of
$X$) with proper supports. By the triviality of ![]() $\omega _S$, we have an equality
$\omega _S$, we have an equality ![]() $\pi _{p}^{-1} (\mathfrak {M}_{S}^{H {\text {-ss}}}) = \mathfrak {M}_{X}^{p^{*}H {\text {-ss}}}$. This observation and the Verdier self-duality of
$\pi _{p}^{-1} (\mathfrak {M}_{S}^{H {\text {-ss}}}) = \mathfrak {M}_{X}^{p^{*}H {\text {-ss}}}$. This observation and the Verdier self-duality of ![]() $\varphi ^{p} _{\boldsymbol {\mathfrak {M}}_{X}}$ together imply the following corollary.
$\varphi ^{p} _{\boldsymbol {\mathfrak {M}}_{X}}$ together imply the following corollary.
Corollary 5.3 Write ![]() $\varphi ^{p}_{\boldsymbol {\mathfrak {M}}_{X}^{p^{*}H {\text {-ss}}}} := \varphi ^{p}_{\boldsymbol {\mathfrak {M}}_{X}} |_{\mathfrak {M}_{X}^{p^{*}H {\text {-ss}}}}$. Then we have following isomorphisms:
$\varphi ^{p}_{\boldsymbol {\mathfrak {M}}_{X}^{p^{*}H {\text {-ss}}}} := \varphi ^{p}_{\boldsymbol {\mathfrak {M}}_{X}} |_{\mathfrak {M}_{X}^{p^{*}H {\text {-ss}}}}$. Then we have following isomorphisms:
 \begin{align*} \mathrm{H}^{*}_c (\mathfrak{M}_{X}^{p^{*}H {\text{-ss}}}; \varphi^{p}_{\mathfrak{M}_{X}^{p^{*}H {\text{-ss}}}}) &\cong \mathrm{H}_c^{* + \operatorname{vdim} \boldsymbol{\mathfrak{M}}_{S}^{H {\text{-ss}}}}(\mathfrak{M}_{S}^{H {\text{-ss}}}), \\ \mathrm{H}^{*} (\mathfrak{M}_{X}^{p^{*}H {\text{-ss}}}; \varphi^{p}_{\mathfrak{M}_{X}^{p^{*}H {\text{-ss}}}}) &\cong \mathrm{H}_{\operatorname{vdim} \boldsymbol{\mathfrak{M}}_{S}^{H {\text{-ss}}}-*}^{\mathrm{BM}}(\mathfrak{M}_{S}^{H {\text{-ss}}}). \end{align*}
\begin{align*} \mathrm{H}^{*}_c (\mathfrak{M}_{X}^{p^{*}H {\text{-ss}}}; \varphi^{p}_{\mathfrak{M}_{X}^{p^{*}H {\text{-ss}}}}) &\cong \mathrm{H}_c^{* + \operatorname{vdim} \boldsymbol{\mathfrak{M}}_{S}^{H {\text{-ss}}}}(\mathfrak{M}_{S}^{H {\text{-ss}}}), \\ \mathrm{H}^{*} (\mathfrak{M}_{X}^{p^{*}H {\text{-ss}}}; \varphi^{p}_{\mathfrak{M}_{X}^{p^{*}H {\text{-ss}}}}) &\cong \mathrm{H}_{\operatorname{vdim} \boldsymbol{\mathfrak{M}}_{S}^{H {\text{-ss}}}-*}^{\mathrm{BM}}(\mathfrak{M}_{S}^{H {\text{-ss}}}). \end{align*}
Here ![]() $\mathrm {H}_c$ denotes the cohomology with compact support, and
$\mathrm {H}_c$ denotes the cohomology with compact support, and ![]() $\mathrm {H}^{\mathrm {BM}}$ denotes the Borel–Moore homology.
$\mathrm {H}^{\mathrm {BM}}$ denotes the Borel–Moore homology.
5.2 Thom isomorphism
Let ![]() $\boldsymbol {Y}$ be a quasi-smooth derived scheme, and write
$\boldsymbol {Y}$ be a quasi-smooth derived scheme, and write ![]() $Y = t_0(\boldsymbol {Y})$ and
$Y = t_0(\boldsymbol {Y})$ and ![]() $\tilde {Y} = t_0(\mathbf {T}^{*}[-1]\boldsymbol {Y})$. Thanks to Theorem 3.1, we have the following isomorphism:
$\tilde {Y} = t_0(\mathbf {T}^{*}[-1]\boldsymbol {Y})$. Thanks to Theorem 3.1, we have the following isomorphism:
Since ![]() $\varphi _{\mathbf {T}^{*}[-1]\boldsymbol {Y}}^{p}$ is conical, by using Theorem 3.1 and [Reference Kashiwara and SchapiraKS90, Proposition 3.7.5], we also have the following isomorphism:
$\varphi _{\mathbf {T}^{*}[-1]\boldsymbol {Y}}^{p}$ is conical, by using Theorem 3.1 and [Reference Kashiwara and SchapiraKS90, Proposition 3.7.5], we also have the following isomorphism:
This isomorphism can be regarded as a version of the Thom isomorphism. Indeed, if ![]() $\boldsymbol {Y} = M \times ^{\mathbf {R}}_{0_E, E, 0_E} M$ where
$\boldsymbol {Y} = M \times ^{\mathbf {R}}_{0_E, E, 0_E} M$ where ![]() $M$ is a smooth scheme,
$M$ is a smooth scheme, ![]() $E$ is a vector bundle on
$E$ is a vector bundle on ![]() $M$, and
$M$, and ![]() $0_E$ is the zero section of
$0_E$ is the zero section of ![]() $E$, the isomorphism (5.3) is the usual Thom isomorphism. By imitating the construction of the Euler class, we construct a class
$E$, the isomorphism (5.3) is the usual Thom isomorphism. By imitating the construction of the Euler class, we construct a class
by the image of ![]() $1 \in \mathrm {H}^{0}(Y)$ under the following composition:
$1 \in \mathrm {H}^{0}(Y)$ under the following composition:
Denote by ![]() $[\boldsymbol {Y}]^{\mathrm {vir}} \in \mathrm {H}^{\mathrm {BM}}_{2\operatorname {vdim} \boldsymbol {Y}}(Y)$ the virtual fundamental class of
$[\boldsymbol {Y}]^{\mathrm {vir}} \in \mathrm {H}^{\mathrm {BM}}_{2\operatorname {vdim} \boldsymbol {Y}}(Y)$ the virtual fundamental class of ![]() $\boldsymbol {Y}$ constructed in [Reference Behrend and FantechiBF97, Reference KreshKre99]. We have the following conjecture.
$\boldsymbol {Y}$ constructed in [Reference Behrend and FantechiBF97, Reference KreshKre99]. We have the following conjecture.
Conjecture 5.4
In other words, we expect that this gives a new construction of the virtual fundamental class.
Example 5.5 Assume ![]() $\boldsymbol {Y} = M \times ^{\mathbf {R}}_{0_E, E, 0_E} M$. In this case, we have
$\boldsymbol {Y} = M \times ^{\mathbf {R}}_{0_E, E, 0_E} M$. In this case, we have ![]() $\tilde {Y} \cong \mathop {\mathrm {Tot}}\nolimits _{N}(E^{\vee })$ and
$\tilde {Y} \cong \mathop {\mathrm {Tot}}\nolimits _{N}(E^{\vee })$ and ![]() $\varphi ^{p}_{\mathbf {T}^{*}[-1]\boldsymbol {Y}} \cong \mathbb {Q}_{\tilde {Y}}[\dim \tilde {Y}]$, and the construction of the Verdier duality isomorphism
$\varphi ^{p}_{\mathbf {T}^{*}[-1]\boldsymbol {Y}} \cong \mathbb {Q}_{\tilde {Y}}[\dim \tilde {Y}]$, and the construction of the Verdier duality isomorphism ![]() $\sigma _{\tilde {Y}}$ in (2.17) implies that the following diagram commutes.
$\sigma _{\tilde {Y}}$ in (2.17) implies that the following diagram commutes.

Therefore, we have
 \begin{align*} e(\mathbf{T}^{*}[{-}1] \boldsymbol{Y}) &= ({-}1)^{\dim \tilde{Y}\cdot (\dim \tilde{Y}-1)/2} e(E^{{\vee}}) \cap [M] \\ &= ({-}1)^{(\dim \tilde{Y}\cdot (\dim \tilde{Y}-1)/2) + \mathop{\mathrm{rank}}\nolimits E} e(E) \cap [M] \\ &= ({-}1)^{\operatorname{vdim} \boldsymbol{Y} \cdot (\operatorname{vdim} \boldsymbol{Y} - 1) /2} [\boldsymbol{Y}]^{\mathrm{vir}}. \end{align*}
\begin{align*} e(\mathbf{T}^{*}[{-}1] \boldsymbol{Y}) &= ({-}1)^{\dim \tilde{Y}\cdot (\dim \tilde{Y}-1)/2} e(E^{{\vee}}) \cap [M] \\ &= ({-}1)^{(\dim \tilde{Y}\cdot (\dim \tilde{Y}-1)/2) + \mathop{\mathrm{rank}}\nolimits E} e(E) \cap [M] \\ &= ({-}1)^{\operatorname{vdim} \boldsymbol{Y} \cdot (\operatorname{vdim} \boldsymbol{Y} - 1) /2} [\boldsymbol{Y}]^{\mathrm{vir}}. \end{align*}The author has verified Conjecture 5.4 under a certain assumption.
Theorem 5.6 [Reference KinjoKin21]
If ![]() $\mathbb {L}_{\boldsymbol {Y}} |_Y$ is represented by a two-term complex of vector bundles, then Conjecture 5.4 is true. In particular, Conjecture 5.4 holds when
$\mathbb {L}_{\boldsymbol {Y}} |_Y$ is represented by a two-term complex of vector bundles, then Conjecture 5.4 is true. In particular, Conjecture 5.4 holds when ![]() $Y$ is quasi-projective.
$Y$ is quasi-projective.
Remark 5.7 We can extend the above construction for stacky cases as follows. Let ![]() $\boldsymbol {\mathfrak {Y}}$ be a quasi-smooth derived Artin stack and write
$\boldsymbol {\mathfrak {Y}}$ be a quasi-smooth derived Artin stack and write ![]() $\mathfrak {Y} = t_0(\boldsymbol {\mathfrak {Y}})$ and
$\mathfrak {Y} = t_0(\boldsymbol {\mathfrak {Y}})$ and ![]() $\widetilde {\mathfrak {Y}} = t_0(\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}})$. Denote by
$\widetilde {\mathfrak {Y}} = t_0(\mathbf {T}^{*}[-1]\boldsymbol {\mathfrak {Y}})$. Denote by ![]() $\pi \colon \widetilde {\mathfrak {Y}} \to \mathfrak {Y}$ the projection and by
$\pi \colon \widetilde {\mathfrak {Y}} \to \mathfrak {Y}$ the projection and by ![]() $i \colon \mathfrak {Y} \to \widetilde {\mathfrak {Y}}$ the zero section. Then for a conic sheaf
$i \colon \mathfrak {Y} \to \widetilde {\mathfrak {Y}}$ the zero section. Then for a conic sheaf ![]() $F \in D^{b}_c(\widetilde {\mathfrak {Y}}_{\text {lis-an}}, \mathbb {Q})$ [Reference Kashiwara and SchapiraKS90, Proposition 3.7.5], and the smooth base-change theorem implies isomorphisms
$F \in D^{b}_c(\widetilde {\mathfrak {Y}}_{\text {lis-an}}, \mathbb {Q})$ [Reference Kashiwara and SchapiraKS90, Proposition 3.7.5], and the smooth base-change theorem implies isomorphisms
Therefore Theorem 4.14 implies isomorphisms
 \begin{align*} i^{!} \varphi_{\mathbf{T}^{*}[{-}1]\boldsymbol{\mathfrak{Y}}} &\cong \mathbb{Q}_{\mathfrak{Y}}[\operatorname{vdim} \boldsymbol{\mathfrak{Y}}], \\ i^{*} \varphi_{\mathbf{T}^{*}[{-}1]\boldsymbol{\mathfrak{Y}}} &\cong \omega_{\mathfrak{Y}}[- \operatorname{vdim} \boldsymbol{\mathfrak{Y}}]. \end{align*}
\begin{align*} i^{!} \varphi_{\mathbf{T}^{*}[{-}1]\boldsymbol{\mathfrak{Y}}} &\cong \mathbb{Q}_{\mathfrak{Y}}[\operatorname{vdim} \boldsymbol{\mathfrak{Y}}], \\ i^{*} \varphi_{\mathbf{T}^{*}[{-}1]\boldsymbol{\mathfrak{Y}}} &\cong \omega_{\mathfrak{Y}}[- \operatorname{vdim} \boldsymbol{\mathfrak{Y}}]. \end{align*}Consider the following composition of natural transforms:
where the first map is the ![]() $*$-unit, the second map is defined in the same manner as in [Reference Laszlo and OlssonLO08, Proposition 4.6.2], and the third map is the inverse of the
$*$-unit, the second map is defined in the same manner as in [Reference Laszlo and OlssonLO08, Proposition 4.6.2], and the third map is the inverse of the ![]() $!$-unit. This composition defines an element
$!$-unit. This composition defines an element
We conjecture that this is equal (up to the sign ![]() $(-1)^{\operatorname {vdim} \boldsymbol {\mathfrak {Y}} \cdot (\operatorname {vdim} \boldsymbol {\mathfrak {Y}} - 1) /2}$) to the stacky virtual fundamental class recently constructed by [Reference Aranha and PstrgowskiAP19] under the resolution property and by [Reference KhanKha19] in general.
$(-1)^{\operatorname {vdim} \boldsymbol {\mathfrak {Y}} \cdot (\operatorname {vdim} \boldsymbol {\mathfrak {Y}} - 1) /2}$) to the stacky virtual fundamental class recently constructed by [Reference Aranha and PstrgowskiAP19] under the resolution property and by [Reference KhanKha19] in general.
Remark 5.8 By [Reference CalaqueCal19, Theorem 2.2], the zero section ![]() $\boldsymbol {Y} \hookrightarrow \mathbf {T}^{*}[-1]\boldsymbol {Y}$ carries a canonical Lagrangian structure. Further, arguing as Example 2.15, we see that this Lagrangian structure admits a canonical orientation with respect to
$\boldsymbol {Y} \hookrightarrow \mathbf {T}^{*}[-1]\boldsymbol {Y}$ carries a canonical Lagrangian structure. Further, arguing as Example 2.15, we see that this Lagrangian structure admits a canonical orientation with respect to ![]() $o^{}_{\mathbf {T}^{*}[-1] \boldsymbol {Y}}$. The isomorphism (5.3) can be regarded as [Reference Amorim and Ben-BassatAB17, Conjecture 5.18] for this oriented Lagrangian structure.
$o^{}_{\mathbf {T}^{*}[-1] \boldsymbol {Y}}$. The isomorphism (5.3) can be regarded as [Reference Amorim and Ben-BassatAB17, Conjecture 5.18] for this oriented Lagrangian structure.
Acknowledgements
I am deeply grateful to my supervisor Yukinobu Toda for introducing cohomological Donaldson–Thomas theory to me, for sharing many ideas, and for useful comments on this paper. I also thank Ben Davison for answering several questions related to this work. I am grateful to the anonymous referee for corrections. I was partly supported by the WINGS-FMSP program at the Graduate School of Mathematical Science, the University of Tokyo.
Appendix A. Remarks on the determinant functor
In this appendix we prove some results on the determinant of perfect complexes. All results follow easily from [Reference Knudsen and MumfordKM76], but we include this for completeness and to fix the sign conventions.
Let ![]() $X$ be a scheme. Denote by
$X$ be a scheme. Denote by ![]() $\mathscr {P}is_X$ the category of invertible sheaves on
$\mathscr {P}is_X$ the category of invertible sheaves on ![]() $X$ with the isomorphisms, and
$X$ with the isomorphisms, and ![]() $\mathscr {P}_{\mathrm {gr}}is_X$ by the category of locally
$\mathscr {P}_{\mathrm {gr}}is_X$ by the category of locally ![]() $\mathbb {Z}/2\mathbb {Z}$-graded invertible sheaves with the isomorphisms defined as follows.
$\mathbb {Z}/2\mathbb {Z}$-graded invertible sheaves with the isomorphisms defined as follows.
• Objects of
 $\mathscr {P}_{\mathrm {gr}}is_X$ are pairs
$\mathscr {P}_{\mathrm {gr}}is_X$ are pairs  $(L, \alpha )$ where
$(L, \alpha )$ where  $L$ is an invertible sheaf on
$L$ is an invertible sheaf on  $X$ and
$X$ and  $\alpha$ is a locally constant
$\alpha$ is a locally constant  $\mathbb {Z}/2\mathbb {Z}$-valued function.
$\mathbb {Z}/2\mathbb {Z}$-valued function.• A morphism from
 $(L, \alpha )$ to
$(L, \alpha )$ to  $(M, \beta )$ is an isomorphism from
$(M, \beta )$ is an isomorphism from  $L$ to
$L$ to  $M$ when
$M$ when  $\alpha = \beta$, and otherwise there is no morphism between them.
$\alpha = \beta$, and otherwise there is no morphism between them.
If there is no confusion, we omit the local grading. We define a monoidal structure on ![]() $\mathscr {P}_{\mathrm {gr}}is_X$ by
$\mathscr {P}_{\mathrm {gr}}is_X$ by
with the monoidal unit ![]() $(\mathcal {O}_X, 0)$ and the obvious associator. By the Koszul sign rule with respect to the local grading, we define the symmetrizer
$(\mathcal {O}_X, 0)$ and the obvious associator. By the Koszul sign rule with respect to the local grading, we define the symmetrizer
This makes ![]() $\mathscr {P}_{\mathrm {gr}}is_X$ a symmetric monoidal category. In this paper we do not equip
$\mathscr {P}_{\mathrm {gr}}is_X$ a symmetric monoidal category. In this paper we do not equip ![]() $\mathscr {P}_{\mathrm {gr}}is_X$ with any other symmetric monoidal structure. Note that the forgetful functor
$\mathscr {P}_{\mathrm {gr}}is_X$ with any other symmetric monoidal structure. Note that the forgetful functor ![]() $\mathscr {P}_{\mathrm {gr}}is_X \to \mathscr {P}is_X$ is monoidal but not symmetric monoidal with respect to the standard symmetric monoidal structure on
$\mathscr {P}_{\mathrm {gr}}is_X \to \mathscr {P}is_X$ is monoidal but not symmetric monoidal with respect to the standard symmetric monoidal structure on ![]() $\mathscr {P}is_X$. For
$\mathscr {P}is_X$. For ![]() $(L, \alpha ) \in \mathscr {P}_{\mathrm {gr}}is_X$, define its (right) inverse by
$(L, \alpha ) \in \mathscr {P}_{\mathrm {gr}}is_X$, define its (right) inverse by ![]() $(L, \alpha )^{-1} := (L^{-1}, - \alpha )$, and define morphisms
$(L, \alpha )^{-1} := (L^{-1}, - \alpha )$, and define morphisms ![]() $\delta ^{\flat }_{(L, \alpha )}, (\delta _{(L, \alpha )}')^{\flat }$ as follows:
$\delta ^{\flat }_{(L, \alpha )}, (\delta _{(L, \alpha )}')^{\flat }$ as follows:
 \begin{align*} \delta^{\flat}_{(L, \alpha)} &\colon (L, \alpha) \otimes (L, \alpha)^{{-}1} \cong (L \otimes L^{{-}1}, 0) \cong (\mathcal{O}_X, 0),\\ (\delta_{(L, \alpha)}')^{\flat} &\colon (L, \alpha)^{{-}1} \otimes (L, \alpha) \xrightarrow{s^{\flat}_{(L, \alpha)^{{-}1}, (L, \alpha)}} (L, \alpha) \otimes (L, \alpha)^{{-}1} \xrightarrow{\delta^{\flat}_{(L, \alpha)}} (\mathcal{O}_X, 0). \end{align*}
\begin{align*} \delta^{\flat}_{(L, \alpha)} &\colon (L, \alpha) \otimes (L, \alpha)^{{-}1} \cong (L \otimes L^{{-}1}, 0) \cong (\mathcal{O}_X, 0),\\ (\delta_{(L, \alpha)}')^{\flat} &\colon (L, \alpha)^{{-}1} \otimes (L, \alpha) \xrightarrow{s^{\flat}_{(L, \alpha)^{{-}1}, (L, \alpha)}} (L, \alpha) \otimes (L, \alpha)^{{-}1} \xrightarrow{\delta^{\flat}_{(L, \alpha)}} (\mathcal{O}_X, 0). \end{align*}Define
so that the following diagram commutes.

Note that the map ![]() $\mu ^{\flat }_{(L, \alpha )}$ differs from the natural isomorphism of the ungraded line bundles
$\mu ^{\flat }_{(L, \alpha )}$ differs from the natural isomorphism of the ungraded line bundles ![]() $(L^{-1})^{-1} \to L$ by the sign
$(L^{-1})^{-1} \to L$ by the sign ![]() $(-1)^{\alpha }$. For
$(-1)^{\alpha }$. For ![]() $L, M \in \mathscr {P}_{\mathrm {gr}}is_X$, define
$L, M \in \mathscr {P}_{\mathrm {gr}}is_X$, define
so that the following diagram commutes.

Note that the map ![]() $\theta ^{\flat }_{(L, \alpha ), (M, \beta )}$ differs from the natural isomorphism
$\theta ^{\flat }_{(L, \alpha ), (M, \beta )}$ differs from the natural isomorphism ![]() $(L \otimes M)^{-1} \to L^{-1} \otimes M^{-1}$ defined by using the standard symmetric monoidal structure on the category of ungraded line bundles by
$(L \otimes M)^{-1} \to L^{-1} \otimes M^{-1}$ defined by using the standard symmetric monoidal structure on the category of ungraded line bundles by ![]() $(-1)^{\alpha \cdot \beta }$.
$(-1)^{\alpha \cdot \beta }$.
Write ![]() $\mathscr {C}_X^{\bullet }$ for the category of bounded complexes of finite locally free
$\mathscr {C}_X^{\bullet }$ for the category of bounded complexes of finite locally free ![]() $\mathcal {O}_X$-modules, and
$\mathcal {O}_X$-modules, and ![]() $\mathscr {C}is_X^{\bullet }$ for the subcategory of
$\mathscr {C}is_X^{\bullet }$ for the subcategory of ![]() $\mathscr {C}_X^{\bullet }$ with the same objects and where the morphisms are quasi-isomorphisms. For a locally free
$\mathscr {C}_X^{\bullet }$ with the same objects and where the morphisms are quasi-isomorphisms. For a locally free ![]() $\mathcal {O}_X$-module
$\mathcal {O}_X$-module ![]() $F$, define a graded line bundle
$F$, define a graded line bundle ![]() $\mathop {\mathrm {det}}\nolimits ^{\flat }(F) \in \mathscr {P}_{\mathrm {gr}}is_X$ by
$\mathop {\mathrm {det}}\nolimits ^{\flat }(F) \in \mathscr {P}_{\mathrm {gr}}is_X$ by
Clearly, ![]() $\mathop {\mathrm {det}}\nolimits ^{\flat }$ is functorial with respect to isomorphisms. For
$\mathop {\mathrm {det}}\nolimits ^{\flat }$ is functorial with respect to isomorphisms. For ![]() $F^{\bullet } \in \mathscr {C}is_X^{\bullet }$, define a graded line bundle
$F^{\bullet } \in \mathscr {C}is_X^{\bullet }$, define a graded line bundle ![]() $\mathop {\mathrm {det}}\nolimits ^{\flat } (F^{\bullet }) \in \mathscr {P}_{\mathrm {gr}}is_X$ by
$\mathop {\mathrm {det}}\nolimits ^{\flat } (F^{\bullet }) \in \mathscr {P}_{\mathrm {gr}}is_X$ by
In [Reference Knudsen and MumfordKM76, Theorem 1], it is shown that ![]() $\mathop {\mathrm {det}}\nolimits ^{\flat }$ extends naturally to a functor
$\mathop {\mathrm {det}}\nolimits ^{\flat }$ extends naturally to a functor ![]() $\mathscr {C}is_X^{\bullet } \to \mathscr {P}_{\mathrm {gr}}is_X$, which we also write as
$\mathscr {C}is_X^{\bullet } \to \mathscr {P}_{\mathrm {gr}}is_X$, which we also write as ![]() $\mathop {\mathrm {det}}\nolimits ^{\flat }$. Define a functor
$\mathop {\mathrm {det}}\nolimits ^{\flat }$. Define a functor ![]() $\mathop {\mathrm {det}}\nolimits \colon \mathscr {C}is_X^{\bullet } \to \mathscr {P}is_X$ by the composition
$\mathop {\mathrm {det}}\nolimits \colon \mathscr {C}is_X^{\bullet } \to \mathscr {P}is_X$ by the composition
where the latter functor is the forgetful one. For a short exact sequence ![]() ${0 \to E^{\bullet } \xrightarrow {u^{\bullet }} F^{\bullet } \xrightarrow {v^{\bullet }} G^{\bullet } \to 0}$ in
${0 \to E^{\bullet } \xrightarrow {u^{\bullet }} F^{\bullet } \xrightarrow {v^{\bullet }} G^{\bullet } \to 0}$ in ![]() $\mathscr {C}_X^{\bullet }$, define
$\mathscr {C}_X^{\bullet }$, define
by the following composition:
 \begin{align*} \mathop{\mathrm{det}}\nolimits^{\flat}(E^{{\bullet}}) \otimes \mathop{\mathrm{det}}\nolimits^{\flat}(G^{{\bullet}}) &= \bigg(\bigotimes_{i} \mathop{\mathrm{det}}\nolimits^{\flat}(E^{i})^{({-}1)^{i}}\bigg) \otimes \bigg(\bigotimes_i \mathop{\mathrm{det}}\nolimits^{\flat}(G^{i})^{({-}1)^{i}}\bigg) \\ &\overset{(\mathrm{i})}{\cong} \bigotimes_i(\mathop{\mathrm{det}}\nolimits^{\flat}(E^{i})^{({-}1)^{i}} \otimes \mathop{\mathrm{det}}\nolimits^{\flat}(G^{i})^{({-}1)^{i}}) \\ &\overset{(\mathrm{ii})}{\cong} \bigotimes_i(\mathop{\mathrm{det}}\nolimits^{\flat}(E^{i}) \otimes \mathop{\mathrm{det}}\nolimits^{\flat}(G^{i}))^{({-}1)^{i}} \\ &\overset{(\mathrm{iii})}{\cong}\bigotimes_i\mathop{\mathrm{det}}\nolimits^{\flat}(F^{i})^{({-}1)^{i}} = \mathop{\mathrm{det}}\nolimits^{\flat}(F^{{\bullet}}). \end{align*}
\begin{align*} \mathop{\mathrm{det}}\nolimits^{\flat}(E^{{\bullet}}) \otimes \mathop{\mathrm{det}}\nolimits^{\flat}(G^{{\bullet}}) &= \bigg(\bigotimes_{i} \mathop{\mathrm{det}}\nolimits^{\flat}(E^{i})^{({-}1)^{i}}\bigg) \otimes \bigg(\bigotimes_i \mathop{\mathrm{det}}\nolimits^{\flat}(G^{i})^{({-}1)^{i}}\bigg) \\ &\overset{(\mathrm{i})}{\cong} \bigotimes_i(\mathop{\mathrm{det}}\nolimits^{\flat}(E^{i})^{({-}1)^{i}} \otimes \mathop{\mathrm{det}}\nolimits^{\flat}(G^{i})^{({-}1)^{i}}) \\ &\overset{(\mathrm{ii})}{\cong} \bigotimes_i(\mathop{\mathrm{det}}\nolimits^{\flat}(E^{i}) \otimes \mathop{\mathrm{det}}\nolimits^{\flat}(G^{i}))^{({-}1)^{i}} \\ &\overset{(\mathrm{iii})}{\cong}\bigotimes_i\mathop{\mathrm{det}}\nolimits^{\flat}(F^{i})^{({-}1)^{i}} = \mathop{\mathrm{det}}\nolimits^{\flat}(F^{{\bullet}}). \end{align*}
Here (i) is defined by the symmetric monoidal structure on ![]() $\mathscr {P}_{\mathrm {gr}}is_X$, (ii) is defined using
$\mathscr {P}_{\mathrm {gr}}is_X$, (ii) is defined using ![]() $\theta ^{\flat }_{\mathop {\mathrm {det}}\nolimits (E^{i}), \mathop {\mathrm {det}}\nolimits (G^{i})}$, and (iii) is defined by the natural isomorphisms
$\theta ^{\flat }_{\mathop {\mathrm {det}}\nolimits (E^{i}), \mathop {\mathrm {det}}\nolimits (G^{i})}$, and (iii) is defined by the natural isomorphisms ![]() $\mathop {\mathrm {det}}\nolimits (E_i) \otimes \mathop {\mathrm {det}}\nolimits (G_i) \cong \mathop {\mathrm {det}}\nolimits (F_i)$. We define
$\mathop {\mathrm {det}}\nolimits (E_i) \otimes \mathop {\mathrm {det}}\nolimits (G_i) \cong \mathop {\mathrm {det}}\nolimits (F_i)$. We define ![]() $i(u^{\bullet }, v^{\bullet }) \colon \mathop {\mathrm {det}}\nolimits (E^{\bullet }) \otimes \mathop {\mathrm {det}}\nolimits (G^{\bullet }) \cong \mathop {\mathrm {det}}\nolimits (F^{\bullet })$ by forgetting the local grading from
$i(u^{\bullet }, v^{\bullet }) \colon \mathop {\mathrm {det}}\nolimits (E^{\bullet }) \otimes \mathop {\mathrm {det}}\nolimits (G^{\bullet }) \cong \mathop {\mathrm {det}}\nolimits (F^{\bullet })$ by forgetting the local grading from ![]() $i^{\flat }(u^{\bullet }, v^{\bullet })$.
$i^{\flat }(u^{\bullet }, v^{\bullet })$.
A.1 Compatibility with the derived dual functor
For a free ![]() $\mathcal {O}_X$-module
$\mathcal {O}_X$-module ![]() $E$ with a fixed basis
$E$ with a fixed basis ![]() $e_1,\ldots,e_n$, define
$e_1,\ldots,e_n$, define ![]() $\eta _E \colon \mathop {\mathrm {det}}\nolimits (E^{\vee }) \xrightarrow {\cong } \mathop {\mathrm {det}}\nolimits (E)^{-1}$ by the rule
$\eta _E \colon \mathop {\mathrm {det}}\nolimits (E^{\vee }) \xrightarrow {\cong } \mathop {\mathrm {det}}\nolimits (E)^{-1}$ by the rule
where ![]() $e_1^{\vee },\ldots,e_n^{\vee }$ denotes the dual basis of
$e_1^{\vee },\ldots,e_n^{\vee }$ denotes the dual basis of ![]() $e_1,\ldots,e_n$ and
$e_1,\ldots,e_n$ and ![]() $(e_n \wedge \cdots \wedge e_1)^{\vee }$ denotes the dual of
$(e_n \wedge \cdots \wedge e_1)^{\vee }$ denotes the dual of ![]() $e_n \wedge \cdots \wedge e_1$. Clearly
$e_n \wedge \cdots \wedge e_1$. Clearly ![]() $\eta _E$ is independent of the choice of the basis, and we can define
$\eta _E$ is independent of the choice of the basis, and we can define ![]() $\eta _E$ for any locally free
$\eta _E$ for any locally free ![]() $\mathcal {O}_X$-module. For
$\mathcal {O}_X$-module. For ![]() $E^{\bullet } \in \mathscr {C}_X^{\bullet }$, define
$E^{\bullet } \in \mathscr {C}_X^{\bullet }$, define
by the following composition:
 \[ \mathop{\mathrm{det}}\nolimits^{\flat}({E^{{\bullet}}}^{{\vee}}) = \bigotimes_i \mathop{\mathrm{det}}\nolimits^{\flat}((E^{{-}i})^{{\vee}})^{({-}1)^{i}} \overset{(\mathrm{i})}{\cong} \bigotimes_i (\mathop{\mathrm{det}}\nolimits^{\flat}(E^{{-}i})^{({-}1)^{i}})^{{-}1} \overset{(\mathrm{ii})}{\cong} (\mathop{\mathrm{det}}\nolimits^{\flat}(E^{{\bullet}}))^{{-}1}. \]
\[ \mathop{\mathrm{det}}\nolimits^{\flat}({E^{{\bullet}}}^{{\vee}}) = \bigotimes_i \mathop{\mathrm{det}}\nolimits^{\flat}((E^{{-}i})^{{\vee}})^{({-}1)^{i}} \overset{(\mathrm{i})}{\cong} \bigotimes_i (\mathop{\mathrm{det}}\nolimits^{\flat}(E^{{-}i})^{({-}1)^{i}})^{{-}1} \overset{(\mathrm{ii})}{\cong} (\mathop{\mathrm{det}}\nolimits^{\flat}(E^{{\bullet}}))^{{-}1}. \]
Here (i) is defined by ![]() $\eta _{E_i}$ and (ii) is defined by iterating
$\eta _{E_i}$ and (ii) is defined by iterating ![]() $\theta ^{\flat }$. Write
$\theta ^{\flat }$. Write ![]() $\epsilon (E^{\bullet }) := \sum _{i \equiv 1, 2 \mathrm {mod}4} \mathrm {rank}(E^{i})$ and define
$\epsilon (E^{\bullet }) := \sum _{i \equiv 1, 2 \mathrm {mod}4} \mathrm {rank}(E^{i})$ and define
Proposition A.1
(i) For a short exact sequence
 $0 \to E^{\bullet } \xrightarrow {u^{\bullet }} F^{\bullet } \xrightarrow {v^{\bullet }} G^{\bullet } \to 0$ in
$0 \to E^{\bullet } \xrightarrow {u^{\bullet }} F^{\bullet } \xrightarrow {v^{\bullet }} G^{\bullet } \to 0$ in  $\mathscr {C}_X^{\bullet }$, the following diagram commutes.
$\mathscr {C}_X^{\bullet }$, the following diagram commutes.

(ii) For a quasi-isomorphism
 $u^{\bullet } \colon E^{\bullet } \to F^{\bullet }$ in
$u^{\bullet } \colon E^{\bullet } \to F^{\bullet }$ in  $\mathscr {C}is_X$, the following diagram commutes.
$\mathscr {C}is_X$, the following diagram commutes.

Proof. (i) Clearly we may assume that these three complexes are concentrated in a single degree ![]() $i$. Then the claim follows from a direct computation.
$i$. Then the claim follows from a direct computation.
(ii) Arguing as the proof of [Reference Knudsen and MumfordKM76, Lemma 2] and using (i), we may assume that ![]() $E^{\bullet }$ is an acyclic complex and
$E^{\bullet }$ is an acyclic complex and ![]() $F^{\bullet } = 0$. Further, by localizing
$F^{\bullet } = 0$. Further, by localizing ![]() $X$ if necessary and using (i), we may assume that
$X$ if necessary and using (i), we may assume that ![]() $E^{\bullet }$ has length two, but then the claim follows from a direct computation (note the sign convention of the dual complex).
$E^{\bullet }$ has length two, but then the claim follows from a direct computation (note the sign convention of the dual complex).
In [Reference Knudsen and MumfordKM76, Theorem 2], the determinant functor is defined for the category of perfect complexes with quasi-isomorphisms. By using the proposition above, we can define ![]() $\eta ^{\flat }_{E} \colon \mathop {\mathrm {det}}\nolimits ^{\flat }({E}^{\vee }) \xrightarrow {\cong } \mathop {\mathrm {det}}\nolimits ^{\flat }(E)^{-1}$ for any perfect complex
$\eta ^{\flat }_{E} \colon \mathop {\mathrm {det}}\nolimits ^{\flat }({E}^{\vee }) \xrightarrow {\cong } \mathop {\mathrm {det}}\nolimits ^{\flat }(E)^{-1}$ for any perfect complex ![]() $E$. We define
$E$. We define
by forgetting the local grading from ![]() $\eta ^{\flat }_{E}$.
$\eta ^{\flat }_{E}$.
A.2 Compatibility with the shift functor
For ![]() $E^{\bullet } \in \mathscr {C}is_X$, define
$E^{\bullet } \in \mathscr {C}is_X$, define
by the following composition:
 \[ \mathop{\mathrm{det}}\nolimits^{\flat}(E^{{\bullet}}[1]) = \bigotimes_i \mathop{\mathrm{det}}\nolimits^{\flat}(E^{i+1})^{({-}1)^{i}} \overset{(\mathrm{i})}{\cong}\bigotimes_i (\mathop{\mathrm{det}}\nolimits^{\flat}(E^{i+1})^{({-}1)^{i+1}})^{{-}1} \overset{(\mathrm{ii})}{\cong} \mathop{\mathrm{det}}\nolimits^{\flat}(E^{{\bullet}})^{{-}1}. \]
\[ \mathop{\mathrm{det}}\nolimits^{\flat}(E^{{\bullet}}[1]) = \bigotimes_i \mathop{\mathrm{det}}\nolimits^{\flat}(E^{i+1})^{({-}1)^{i}} \overset{(\mathrm{i})}{\cong}\bigotimes_i (\mathop{\mathrm{det}}\nolimits^{\flat}(E^{i+1})^{({-}1)^{i+1}})^{{-}1} \overset{(\mathrm{ii})}{\cong} \mathop{\mathrm{det}}\nolimits^{\flat}(E^{{\bullet}})^{{-}1}. \]
Here (i) is defined by using ![]() $\mu ^{\flat }_{\mathop {\mathrm {det}}\nolimits ^{\flat }(E_i)}$ and (ii) is defined by iterating
$\mu ^{\flat }_{\mathop {\mathrm {det}}\nolimits ^{\flat }(E_i)}$ and (ii) is defined by iterating ![]() $\theta ^{\flat }$. The following proposition can be shown similarly to Proposition A.1.
$\theta ^{\flat }$. The following proposition can be shown similarly to Proposition A.1.
Proposition A.2
(i) For a short exact sequence
 $0 \to E^{\bullet } \xrightarrow {u^{\bullet }} F^{\bullet } \xrightarrow {v^{\bullet }} G^{\bullet } \to 0$ in
$0 \to E^{\bullet } \xrightarrow {u^{\bullet }} F^{\bullet } \xrightarrow {v^{\bullet }} G^{\bullet } \to 0$ in  $\mathscr {C}_X^{\bullet }$, the following diagram commutes.
$\mathscr {C}_X^{\bullet }$, the following diagram commutes.

(ii) For a quasi-isomorphism
 $u^{\bullet } \colon E^{\bullet } \to F^{\bullet }$ in
$u^{\bullet } \colon E^{\bullet } \to F^{\bullet }$ in  $\mathscr {C}is_X$, the following diagram commutes.
$\mathscr {C}is_X$, the following diagram commutes.

This proposition implies that we can define ![]() $\chi ^{\flat }_{E } \colon \mathop {\mathrm {det}}\nolimits ^{\flat }(E [1]) \cong \mathop {\mathrm {det}}\nolimits ^{\flat }(E )^{-1}$ for any perfect complex
$\chi ^{\flat }_{E } \colon \mathop {\mathrm {det}}\nolimits ^{\flat }(E [1]) \cong \mathop {\mathrm {det}}\nolimits ^{\flat }(E )^{-1}$ for any perfect complex ![]() $E$. We define
$E$. We define
by forgetting the local grading from ![]() $\chi ^{\flat }_{E}$. We also define
$\chi ^{\flat }_{E}$. We also define
for each ![]() $n \in \mathbb {Z}$ so that
$n \in \mathbb {Z}$ so that ![]() $\chi _{E }^{(1)} =\chi _{E }$ and
$\chi _{E }^{(1)} =\chi _{E }$ and ![]() $\chi _{E }^{(n+m)} = (\chi _{E[n]}^{(m)})^{(-1)^{{}^{\otimes ^{n}}}} \circ \chi _{E }^{(n)}$ holds for each
$\chi _{E }^{(n+m)} = (\chi _{E[n]}^{(m)})^{(-1)^{{}^{\otimes ^{n}}}} \circ \chi _{E }^{(n)}$ holds for each ![]() $n, m \in \mathbb {Z}$, where we identify
$n, m \in \mathbb {Z}$, where we identify ![]() $(\mathop {\mathrm {det}}\nolimits (E)^{(-1)^{n}})^{(-1)^{m}}$ and
$(\mathop {\mathrm {det}}\nolimits (E)^{(-1)^{n}})^{(-1)^{m}}$ and ![]() $\mathop {\mathrm {det}}\nolimits (E)^{(-1)^{n + m}}$ by using
$\mathop {\mathrm {det}}\nolimits (E)^{(-1)^{n + m}}$ by using ![]() $\mu ^{\flat }_{\mathop {\mathrm {det}}\nolimits (E)^{\flat }}$ if both
$\mu ^{\flat }_{\mathop {\mathrm {det}}\nolimits (E)^{\flat }}$ if both ![]() $n$ and
$n$ and ![]() $m$ are odd.
$m$ are odd.
A.3 Compatibility with distinguished triangles
Consider a distinguished triangle ![]() $E \to F \to G \to E[1]$ of perfect complexes on
$E \to F \to G \to E[1]$ of perfect complexes on ![]() $X$. In [Reference Knudsen and MumfordKM76] it is observed that there exists an isomorphism
$X$. In [Reference Knudsen and MumfordKM76] it is observed that there exists an isomorphism ![]() $\mathop {\mathrm {det}}\nolimits ^{\flat } (E) \otimes \mathop {\mathrm {det}}\nolimits ^{\flat }(G) \cong \mathop {\mathrm {det}}\nolimits ^{\flat }(F)$, though there is no natural choice in general.Footnote 2 However, it is also observed in [Reference Knudsen and MumfordKM76] that there is a canonical choice when
$\mathop {\mathrm {det}}\nolimits ^{\flat } (E) \otimes \mathop {\mathrm {det}}\nolimits ^{\flat }(G) \cong \mathop {\mathrm {det}}\nolimits ^{\flat }(F)$, though there is no natural choice in general.Footnote 2 However, it is also observed in [Reference Knudsen and MumfordKM76] that there is a canonical choice when ![]() $X$ is reduced.
$X$ is reduced.
Proposition A.3 [Reference Knudsen and MumfordKM76, Proposition 7]
For each distinguished triangle of perfect complexes ![]() $\Delta \colon E \xrightarrow {u} F \xrightarrow {v} G \xrightarrow {w} E[1]$ on a reduced scheme
$\Delta \colon E \xrightarrow {u} F \xrightarrow {v} G \xrightarrow {w} E[1]$ on a reduced scheme ![]() $X$, there exists a unique isomorphism
$X$, there exists a unique isomorphism
characterized by the following properties.
• If
 $E \xrightarrow {u} F \xrightarrow {v} G \xrightarrow {w} E[1]$ is represented by a short exact sequence of complexes of locally free sheaves
$E \xrightarrow {u} F \xrightarrow {v} G \xrightarrow {w} E[1]$ is represented by a short exact sequence of complexes of locally free sheaves  $0 \to E^{\bullet } \xrightarrow {u^{\bullet }} F^{\bullet } \xrightarrow {v^{\bullet }} G^{\bullet } \to 0$, then
$0 \to E^{\bullet } \xrightarrow {u^{\bullet }} F^{\bullet } \xrightarrow {v^{\bullet }} G^{\bullet } \to 0$, then  $i^{\flat }(u, v, w) = i^{\flat }(u^{\bullet }, v^{\bullet })$.
$i^{\flat }(u, v, w) = i^{\flat }(u^{\bullet }, v^{\bullet })$.• If there exists a morphism of reduced schemes
 $f \colon Y \to X$, then
$f \colon Y \to X$, then  $f^{*} i^{\flat }(u, v, w) = i(f^{*}u, f^{*}v, f^{*}w)$.
$f^{*} i^{\flat }(u, v, w) = i(f^{*}u, f^{*}v, f^{*}w)$.
We define ![]() $i(\Delta ) = i(u, v, w) \colon \mathop {\mathrm {det}}\nolimits (E) \otimes \mathop {\mathrm {det}}\nolimits (G) \cong \mathop {\mathrm {det}}\nolimits (F)$ by forgetting the local grading from
$i(\Delta ) = i(u, v, w) \colon \mathop {\mathrm {det}}\nolimits (E) \otimes \mathop {\mathrm {det}}\nolimits (G) \cong \mathop {\mathrm {det}}\nolimits (F)$ by forgetting the local grading from ![]() $i^{\flat }(u, v, w)$. The following statement follows by a direct computation.
$i^{\flat }(u, v, w)$. The following statement follows by a direct computation.
Proposition A.4 Let ![]() $X$ be a reduced scheme,
$X$ be a reduced scheme, ![]() $\Delta \colon E \xrightarrow {u} F \xrightarrow {v} G \xrightarrow {w} E[1]$ a distinguished triangle of perfect complexes over
$\Delta \colon E \xrightarrow {u} F \xrightarrow {v} G \xrightarrow {w} E[1]$ a distinguished triangle of perfect complexes over ![]() $X$, and
$X$, and ![]() $\Delta ' \colon F \xrightarrow {v} G \xrightarrow {w} E[1] \xrightarrow {-u[1]} F[1]$ the rotated triangle. Then the following diagram commutes.
$\Delta ' \colon F \xrightarrow {v} G \xrightarrow {w} E[1] \xrightarrow {-u[1]} F[1]$ the rotated triangle. Then the following diagram commutes.

Here the right vertical map is defined by unit map for the standard symmetric monoidal structure on ![]() $\mathscr {P}is_X$.
$\mathscr {P}is_X$.
Let ![]() $k$ be a field, and
$k$ be a field, and ![]() $E$ be a perfect complex over
$E$ be a perfect complex over ![]() $\mathop {\mathrm {Spec}}\nolimits k$. Write
$\mathop {\mathrm {Spec}}\nolimits k$. Write ![]() $\mathrm {H}^{*}(E) := \bigoplus _i \mathrm {H}^{i}(E)[-i]$, considered as a complex with zero differential. The natural isomorphism
$\mathrm {H}^{*}(E) := \bigoplus _i \mathrm {H}^{i}(E)[-i]$, considered as a complex with zero differential. The natural isomorphism ![]() $\mathrm {H}^{*}(E) \simeq E$ in
$\mathrm {H}^{*}(E) \simeq E$ in ![]() $D(k)$ induces an isomorphism
$D(k)$ induces an isomorphism
Let ![]() $E \xrightarrow {u} F \xrightarrow {v} G \xrightarrow {w} E[1]$ be a distinguished triangle of perfect complexes over
$E \xrightarrow {u} F \xrightarrow {v} G \xrightarrow {w} E[1]$ be a distinguished triangle of perfect complexes over ![]() $\mathop {\mathrm {Spec}}\nolimits k$. By decomposing the long exact sequence induced by the above distinguished triangle into short exact sequences, we can construct
$\mathop {\mathrm {Spec}}\nolimits k$. By decomposing the long exact sequence induced by the above distinguished triangle into short exact sequences, we can construct
Define
The maps ![]() $i(u, v, w)$ and
$i(u, v, w)$ and ![]() $i'(u, v, w)$ do not coincide in general because we used the symmetric monoidal structure on
$i'(u, v, w)$ do not coincide in general because we used the symmetric monoidal structure on ![]() $\mathscr {P}_{\mathrm {gr}}is_X$ to construct
$\mathscr {P}_{\mathrm {gr}}is_X$ to construct ![]() $i(u, v, w)$. However we can explicitly write down the difference between
$i(u, v, w)$. However we can explicitly write down the difference between ![]() $i(u, v, w)$ and
$i(u, v, w)$ and ![]() $i'(u, v, w)$ as follows: write
$i'(u, v, w)$ as follows: write ![]() $a_i := \mathop {\mathrm {rank}}\nolimits \ker \mathrm {H}^{i}(u)$,
$a_i := \mathop {\mathrm {rank}}\nolimits \ker \mathrm {H}^{i}(u)$, ![]() $b_i := \mathop {\mathrm {rank}}\nolimits \ker \mathrm {H}^{i}(v)$, and
$b_i := \mathop {\mathrm {rank}}\nolimits \ker \mathrm {H}^{i}(v)$, and ![]() $c_i := \mathop {\mathrm {rank}}\nolimits \ker \mathrm {H}^{i}(w)$. Then we have
$c_i := \mathop {\mathrm {rank}}\nolimits \ker \mathrm {H}^{i}(w)$. Then we have
 \begin{align} i(u, v, w) &= ({-}1)^{T} i'(u, v, w),\nonumber\\ &\hspace{-9.6pc}\text{where} \nonumber\\ T &= \sum_{i \colon \text{even}}\bigg(\sum_{j \leq i-1}a_i a_j + \sum_{j \leq i} a_i b_j + \sum_{j \leq i+1} c_i a_j +\sum_{j \leq i-1} c_i b_j\bigg) \nonumber\\ &\quad + \sum_{i \colon \text{odd}}\bigg(\sum_{j \leq i}a_i a_j + \sum_{j \leq i-1} a_i b_j + \sum_{j \leq i} c_i a_j + \sum_{j \leq i} c_i b_j\bigg). \end{align}
\begin{align} i(u, v, w) &= ({-}1)^{T} i'(u, v, w),\nonumber\\ &\hspace{-9.6pc}\text{where} \nonumber\\ T &= \sum_{i \colon \text{even}}\bigg(\sum_{j \leq i-1}a_i a_j + \sum_{j \leq i} a_i b_j + \sum_{j \leq i+1} c_i a_j +\sum_{j \leq i-1} c_i b_j\bigg) \nonumber\\ &\quad + \sum_{i \colon \text{odd}}\bigg(\sum_{j \leq i}a_i a_j + \sum_{j \leq i-1} a_i b_j + \sum_{j \leq i} c_i a_j + \sum_{j \leq i} c_i b_j\bigg). \end{align}A.4 Extension to Artin stacks
Since the determinant functor commutes with base change, we can extend the determinant functor to the category of perfect complexes on Artin stacks with quasi-isomorphisms. Clearly, ![]() $\eta _E$ and
$\eta _E$ and ![]() $\chi _E$ commutes with base change, and we can define
$\chi _E$ commutes with base change, and we can define ![]() $\eta _{E} \colon \mathop {\mathrm {det}}\nolimits (E^{\vee }) \cong \mathop {\mathrm {det}}\nolimits (E)^{-1}$ and
$\eta _{E} \colon \mathop {\mathrm {det}}\nolimits (E^{\vee }) \cong \mathop {\mathrm {det}}\nolimits (E)^{-1}$ and ![]() $\chi _{E} \colon \mathop {\mathrm {det}}\nolimits (E[1]) \cong \mathop {\mathrm {det}}\nolimits (E)^{-1}$ for any perfect complex
$\chi _{E} \colon \mathop {\mathrm {det}}\nolimits (E[1]) \cong \mathop {\mathrm {det}}\nolimits (E)^{-1}$ for any perfect complex ![]() $E$ over an Artin stack
$E$ over an Artin stack ![]() $\mathfrak {X}$. By similar reasoning, we can define
$\mathfrak {X}$. By similar reasoning, we can define ![]() $i(u, v, w) \colon \mathop {\mathrm {det}}\nolimits (E) \otimes \mathop {\mathrm {det}}\nolimits (G) \cong \mathop {\mathrm {det}}\nolimits (F)$ for a distinguished triangle of perfect complexes
$i(u, v, w) \colon \mathop {\mathrm {det}}\nolimits (E) \otimes \mathop {\mathrm {det}}\nolimits (G) \cong \mathop {\mathrm {det}}\nolimits (F)$ for a distinguished triangle of perfect complexes ![]() $E \xrightarrow {u} F \xrightarrow {v} G \xrightarrow {w} E[1]$ over a reduced Artin stack
$E \xrightarrow {u} F \xrightarrow {v} G \xrightarrow {w} E[1]$ over a reduced Artin stack ![]() $\mathfrak {X}$.
$\mathfrak {X}$.