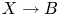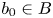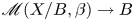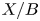1. Introduction
1.1 Statement of results
One of the main goals of logarithmic Gromov–Witten theory is to relate the Gromov–Witten invariants of a smooth projective variety to invariants of a degenerate variety ![]() $X_0$.
$X_0$.
Consider a logarithmically smooth and projective morphism ![]() $X \longrightarrow B$, with
$X \longrightarrow B$, with ![]() $B$ a logarithmically smooth curve having a single closed point
$B$ a logarithmically smooth curve having a single closed point ![]() $b_0\in B$ where the logarithmic structure is non-trivial. In the language of [Reference Kempf, Knudsen, Mumford and Saint-DonatKKMS73, Reference Abramovich and KaruAK00], this is the same as saying that the underlying schemes
$b_0\in B$ where the logarithmic structure is non-trivial. In the language of [Reference Kempf, Knudsen, Mumford and Saint-DonatKKMS73, Reference Abramovich and KaruAK00], this is the same as saying that the underlying schemes ![]() $\underline {X}$ and
$\underline {X}$ and ![]() $\underline {B}$ are provided with a toroidal structure such that
$\underline {B}$ are provided with a toroidal structure such that ![]() $\underline {X} \longrightarrow \underline {B}$ is a toroidal morphism, and
$\underline {X} \longrightarrow \underline {B}$ is a toroidal morphism, and ![]() $\underline {\{b_0\}}\subset \underline {B}$ is the toroidal divisor. One defines as in [Reference Gross and SiebertGS13], see also [Reference ChenChe14, Reference Abramovich and ChenAC14], an algebraic stack
$\underline {\{b_0\}}\subset \underline {B}$ is the toroidal divisor. One defines as in [Reference Gross and SiebertGS13], see also [Reference ChenChe14, Reference Abramovich and ChenAC14], an algebraic stack ![]() $\mathscr {M}(X/B,\beta )$ parameterizing stable logarithmic maps
$\mathscr {M}(X/B,\beta )$ parameterizing stable logarithmic maps ![]() $f: C \longrightarrow X$ with discrete data
$f: C \longrightarrow X$ with discrete data ![]() $\beta = (g,A,u_{p_1},\ldots ,u_{p_k})$ from logarithmically smooth curves to
$\beta = (g,A,u_{p_1},\ldots ,u_{p_k})$ from logarithmically smooth curves to ![]() $X$. Here:
$X$. Here:
•
 $g$ is the genus of
$g$ is the genus of  $C$;
$C$;•
 $A$ is the homology class
$A$ is the homology class  $\underline {f}_*[\underline {C}]$, which we assume is supported on fibres of
$\underline {f}_*[\underline {C}]$, which we assume is supported on fibres of  $\underline {X} \longrightarrow \underline {B}$; and
$\underline {X} \longrightarrow \underline {B}$; and•
 $u_{p_1},\ldots ,u_{p_k}$ are the contact orders of the marked points with the logarithmic strata of
$u_{p_1},\ldots ,u_{p_k}$ are the contact orders of the marked points with the logarithmic strata of  $X$.
$X$.
Writing ![]() $\underline \beta = (g,k,A)$ for the non-logarithmic discrete data, there is a natural morphism
$\underline \beta = (g,k,A)$ for the non-logarithmic discrete data, there is a natural morphism ![]() $\mathscr {M}(X/B,\beta ) \longrightarrow \mathscr {M}(\underline {X}/\underline {B},{\underline{ \beta} })$ ‘forgetting the logarithmic structures’, which is proper and representable [Reference Abramovich, Chen, Marcus and WiseACMW17, Theorem 1.1.1]. The map
$\mathscr {M}(X/B,\beta ) \longrightarrow \mathscr {M}(\underline {X}/\underline {B},{\underline{ \beta} })$ ‘forgetting the logarithmic structures’, which is proper and representable [Reference Abramovich, Chen, Marcus and WiseACMW17, Theorem 1.1.1]. The map ![]() $\mathscr {M}(X/B,\beta ) \longrightarrow \mathscr {M}(\underline {X}/\underline {B},{\underline{\beta} })$ is in fact finite, see [Reference WiseWis19, Corollary 1.2]. There is also a natural morphism
$\mathscr {M}(X/B,\beta ) \longrightarrow \mathscr {M}(\underline {X}/\underline {B},{\underline{\beta} })$ is in fact finite, see [Reference WiseWis19, Corollary 1.2]. There is also a natural morphism ![]() $\mathscr {M}(X/B,\beta ) \longrightarrow B$, and we denote its fibre over
$\mathscr {M}(X/B,\beta ) \longrightarrow B$, and we denote its fibre over ![]() $b\in B$ by
$b\in B$ by ![]() $\mathscr {M}(X_b/b,\beta )$.
$\mathscr {M}(X_b/b,\beta )$.
Since ![]() $X \longrightarrow B$ is logarithmically smooth there is a perfect relative obstruction theory
$X \longrightarrow B$ is logarithmically smooth there is a perfect relative obstruction theory ![]() $\mathbf {E}^\bullet \longrightarrow \mathbf {L}_{\mathscr {M}(X/B,\beta )/{\operatorname {Log}}_B}$ in the sense of [Reference Behrend and FantechiBF97], hence defining a virtual fundamental class
$\mathbf {E}^\bullet \longrightarrow \mathbf {L}_{\mathscr {M}(X/B,\beta )/{\operatorname {Log}}_B}$ in the sense of [Reference Behrend and FantechiBF97], hence defining a virtual fundamental class ![]() $[\mathscr {M}(X/B,\beta )]^{\operatorname {virt}}$ and logarithmic Gromov–Witten invariants.
$[\mathscr {M}(X/B,\beta )]^{\operatorname {virt}}$ and logarithmic Gromov–Witten invariants.
An immediate consequence of the formalism is the following (this is indicated after [Reference Gross and SiebertGS13, Theorem 0.3]).
Theorem 1.1 (Logarithmic deformation invariance) For any point ![]() $\{b\}\stackrel {j_b}\hookrightarrow B$ one has
$\{b\}\stackrel {j_b}\hookrightarrow B$ one has
This implies, in particular, that Gromov–Witten invariants of ![]() $X_b$ agree with those of
$X_b$ agree with those of ![]() $X_0=X_{b_0}$. Now holomorphic curves in
$X_0=X_{b_0}$. Now holomorphic curves in ![]() $X_0$ come in various families depending on the intersection pattern with the irreducible components of
$X_0$ come in various families depending on the intersection pattern with the irreducible components of ![]() $X_0$. Thus one may hope that logarithmic Gromov–Witten invariants similarly group according to some discrete data reflecting such intersection patterns. The main result of this paper shows that this is indeed the case, with the intersection patterns recorded in an interesting and very transparent fashion in terms of the underlying tropical geometry.
$X_0$. Thus one may hope that logarithmic Gromov–Witten invariants similarly group according to some discrete data reflecting such intersection patterns. The main result of this paper shows that this is indeed the case, with the intersection patterns recorded in an interesting and very transparent fashion in terms of the underlying tropical geometry.
Theorem 1.2 (The logarithmic decomposition formula; Theorem 3.11 below) Suppose the morphism ![]() $X_0 \longrightarrow b_0$ is logarithmically smooth and
$X_0 \longrightarrow b_0$ is logarithmically smooth and ![]() $X_0$ is simple. Then we have the following equality in the Chow group of
$X_0$ is simple. Then we have the following equality in the Chow group of ![]() $\mathscr {M}(X_0/b_0,\beta )$ with coefficients in
$\mathscr {M}(X_0/b_0,\beta )$ with coefficients in ![]() $\mathbb {Q}$:
$\mathbb {Q}$:
See Definition 2.1 for the notion of simple logarithmic structures. The notations ![]() $\mathscr {M}(X_0,{\boldsymbol{\tau }})$,
$\mathscr {M}(X_0,{\boldsymbol{\tau }})$, ![]() $m_\tau$ and
$m_\tau$ and ![]() $j_{\boldsymbol{\tau }}$ are briefly explained as follows. First, the tropicalization of
$j_{\boldsymbol{\tau }}$ are briefly explained as follows. First, the tropicalization of ![]() $X_0 \longrightarrow b_0$ defines a polyhedral complex
$X_0 \longrightarrow b_0$ defines a polyhedral complex ![]() $\Delta (X_0)$ (§§ 2.1.4 and 2.5.4), and
$\Delta (X_0)$ (§§ 2.1.4 and 2.5.4), and ![]() $\tau$ stands for a rigid tropical map to
$\tau$ stands for a rigid tropical map to ![]() $\Delta (X)$ (Definition 3.6). Each such rigid
$\Delta (X)$ (Definition 3.6). Each such rigid ![]() $\tau$ comes with a multiplicity
$\tau$ comes with a multiplicity ![]() $m_{\tau } \in \mathbb {N}$, the smallest integer such that scaling
$m_{\tau } \in \mathbb {N}$, the smallest integer such that scaling ![]() $\Delta (X)$ by
$\Delta (X)$ by ![]() $m_\tau$ leads to a tropical curve with integral vertices and edge lengths.
$m_\tau$ leads to a tropical curve with integral vertices and edge lengths.
The symbol ![]() $\mathbf {A}$ stands for a partition of the curve class
$\mathbf {A}$ stands for a partition of the curve class ![]() $A\in H_2(X)$ into classes
$A\in H_2(X)$ into classes ![]() $\mathbf {A}(v)$, one for each vertex
$\mathbf {A}(v)$, one for each vertex ![]() $v$ in the graph underlying
$v$ in the graph underlying ![]() $\tau$.
$\tau$.
The moduli stack ![]() $\mathscr {M}(X_0,{\boldsymbol{\tau }})$ is the stack parameterizing basic stable logarithmic maps to
$\mathscr {M}(X_0,{\boldsymbol{\tau }})$ is the stack parameterizing basic stable logarithmic maps to ![]() $X_0$ over
$X_0$ over ![]() $b_0$ decorated by
$b_0$ decorated by ![]() ${\boldsymbol{\tau }}=(\tau ,\mathbf {A})$ (Definition 2.31). The marking exhibits
${\boldsymbol{\tau }}=(\tau ,\mathbf {A})$ (Definition 2.31). The marking exhibits ![]() ${\boldsymbol{\tau }}$ as a degeneration of the tropicalization of any stable logarithmic map in this moduli stack. The map
${\boldsymbol{\tau }}$ as a degeneration of the tropicalization of any stable logarithmic map in this moduli stack. The map ![]() $j_{\boldsymbol{\tau }}:\mathscr {M}(X_0,{\boldsymbol{\tau }}) \longrightarrow \mathscr {M}(X_0/b_0,\beta )$ forgets the marking by
$j_{\boldsymbol{\tau }}:\mathscr {M}(X_0,{\boldsymbol{\tau }}) \longrightarrow \mathscr {M}(X_0/b_0,\beta )$ forgets the marking by ![]() ${\boldsymbol{\tau }}$. The sum runs over all isomorphism classes of decorated rigid tropical maps
${\boldsymbol{\tau }}$. The sum runs over all isomorphism classes of decorated rigid tropical maps ![]() $\boldsymbol{\tau} = (\tau,\mathbf{A})$.
$\boldsymbol{\tau} = (\tau,\mathbf{A})$.
Remark 1.3 In general, the sum over ![]() ${\boldsymbol{\tau }}$ will be infinite, but because the moduli space
${\boldsymbol{\tau }}$ will be infinite, but because the moduli space ![]() $\mathscr {M}(X_0/b_0,\beta )$ is of finite type, all but a finite number of the moduli spaces
$\mathscr {M}(X_0/b_0,\beta )$ is of finite type, all but a finite number of the moduli spaces ![]() $\mathscr {M}(X_0,{\boldsymbol{\tau }})$ will be empty. In practice one uses the balancing condition [Reference Gross and SiebertGS13, Proposition 1.15] to control how curves can break up into strata of
$\mathscr {M}(X_0,{\boldsymbol{\tau }})$ will be empty. In practice one uses the balancing condition [Reference Gross and SiebertGS13, Proposition 1.15] to control how curves can break up into strata of ![]() $X_0$. This is carried out in some of the examples in § 5.
$X_0$. This is carried out in some of the examples in § 5.
Theorems 1.1 and 1.2 form the first two steps toward a general logarithmic degeneration formula. In many cases this is sufficient for meaningful computations, as we show in § 5. These results have precise analogies with results in [Reference LiLi02], as explained in § 5.1. Theorem 1.1 is a generalization of [Reference LiLi02, Lemma 3.10], while Theorem 1.2 is a generalization of part of [Reference LiLi02, Corollary 3.13], where the notation ![]() ${\mathfrak M}(\mathfrak {Y}_1^{\textrm {rel}}\cup \mathfrak {Y}_2^{\textrm {rel}},\eta )$ describes an object playing the role of our
${\mathfrak M}(\mathfrak {Y}_1^{\textrm {rel}}\cup \mathfrak {Y}_2^{\textrm {rel}},\eta )$ describes an object playing the role of our ![]() $\mathscr {M}(X_0,{\boldsymbol{\tau }})$.
$\mathscr {M}(X_0,{\boldsymbol{\tau }})$.
The current paper does not, however, include a description of the moduli stack ![]() $\mathscr {M}(X_0,{\boldsymbol{\tau }})$ analogous to that given in the proof of [Reference LiLi02, Lemma 3.14]. There, the moduli space is described by gluing together relative stable maps to the individual components of
$\mathscr {M}(X_0,{\boldsymbol{\tau }})$ analogous to that given in the proof of [Reference LiLi02, Lemma 3.14]. There, the moduli space is described by gluing together relative stable maps to the individual components of ![]() $X_0$. However, in general this will not be the case: while a curve in
$X_0$. However, in general this will not be the case: while a curve in ![]() $\mathscr {M}(X_0,{\boldsymbol{\tau }})$ may be glued schematically from stable maps to individual components of
$\mathscr {M}(X_0,{\boldsymbol{\tau }})$ may be glued schematically from stable maps to individual components of ![]() $X_0$, it is not possible to do this at the logarithmic level, in the sense that the maps to individual components of
$X_0$, it is not possible to do this at the logarithmic level, in the sense that the maps to individual components of ![]() $X_0$ may not be interpretable as relative maps. We give an example in § 5.2 in which
$X_0$ may not be interpretable as relative maps. We give an example in § 5.2 in which ![]() $X_0$ has three components meeting normally, with one triple point. Our example features a log curve contributing to the Gromov–Witten invariant which has a component contracting to the triple point, and this curve cannot be interpreted as a relative curve on any of the three irreducible components of
$X_0$ has three components meeting normally, with one triple point. Our example features a log curve contributing to the Gromov–Witten invariant which has a component contracting to the triple point, and this curve cannot be interpreted as a relative curve on any of the three irreducible components of ![]() $X_0$.
$X_0$.
In fact, a new theory is needed to give a more detailed description of the moduli spaces ![]() $\mathscr {M}(X_0,{\boldsymbol{\tau }})$ in terms of pieces of simpler curves. In the follow-up paper [Reference Abramovich, Chen, Gross and SiebertACGS20] we define stable punctured maps admitting negative contact orders to replace the relative curves in Jun Li's gluing formula. Crucially, we will explain how punctured curves can be glued together to describe the moduli spaces
$\mathscr {M}(X_0,{\boldsymbol{\tau }})$ in terms of pieces of simpler curves. In the follow-up paper [Reference Abramovich, Chen, Gross and SiebertACGS20] we define stable punctured maps admitting negative contact orders to replace the relative curves in Jun Li's gluing formula. Crucially, we will explain how punctured curves can be glued together to describe the moduli spaces ![]() $\mathscr {M}(X_0,{\boldsymbol{\tau }})$.
$\mathscr {M}(X_0,{\boldsymbol{\tau }})$.
The results described here are analogous to results of Brett Parker proved in his category of exploded manifolds. He defines Gromov–Witten invariants in this category in the series of papers [Reference ParkerPar15, Reference ParkerPar19a, Reference ParkerPar19b, Reference ParkerPar19c]. The analogue of logarithmic deformation invariance, Theorem 1.1 above, is proved in [Reference ParkerPar19c, Theorems 5.20 and 5.22], while Theorem 1.2 is analogous to parts of [Reference ParkerPar19c, Theorem 5.22 and Lemma 7.3]. A gluing formula in terms of Gromov–Witten invariants of individual irreducible components of ![]() $X_0$ is given in [Reference ParkerPar17, Theorems 4.7 and 5.2]. The aim in proving a general gluing formula is a full logarithmic analogue of these theorems.
$X_0$ is given in [Reference ParkerPar17, Theorems 4.7 and 5.2]. The aim in proving a general gluing formula is a full logarithmic analogue of these theorems.
This paper has a somewhat long genesis, with the main ideas contained in draft versions first presented in a talk by B.S. at the conference ‘Algebraic, Analytic, and Tropical Geometry’ in Ein Gedi, Israel, in Spring 2013. A first full version was posted on Q.C.'s website in October 2016. The follow-up paper [Reference Abramovich, Chen, Gross and SiebertACGS20] has furthermore been distributed via M.G.'s website since March 2017.
Several related works have appeared during this long period of preparation. The 2016 version has been used in [Reference Mandel and RuddatMR20]. Concerning the decomposition formula, the one closest to our point of view is [Reference Kim, Lho and RuddatKLR18], giving a formula of logarithmic Gromov–Witten invariants of the central fiber ![]() $X_0$ of a degeneration with smooth singular locus in terms of Gromov–Witten invariants of the reducible components. This paper is a full logarithmic analogue of Jun Li's formula in [Reference LiLi02], without using expanded degenerations. This case is considerably simpler than the case with points of multiplicity greater than 2 and in particular does not require the introduction of punctured Gromov–Witten invariants, see § 5.1 and [Reference Abramovich, Chen, Gross and SiebertACGS20].
$X_0$ of a degeneration with smooth singular locus in terms of Gromov–Witten invariants of the reducible components. This paper is a full logarithmic analogue of Jun Li's formula in [Reference LiLi02], without using expanded degenerations. This case is considerably simpler than the case with points of multiplicity greater than 2 and in particular does not require the introduction of punctured Gromov–Witten invariants, see § 5.1 and [Reference Abramovich, Chen, Gross and SiebertACGS20].
A gluing formula for a special case has also been proved by Tony Yue Yu in his developing theory of Gromov–Witten invariants in rigid analytic geometry [Reference YuYu20, Theorem 1.2].
Very recently, Ranganathan has suggested an alternative approach to fully general gluing formulas for logarithmic Gromov–Witten invariants using expanded degenerations [Reference RanganathanRan20].
The structure of the paper is as follows. In § 2, we review various aspects of logarithmic Gromov–Witten theory, with a special emphasis on the relationship with tropical geometry. We develop tropical geometry in the setup of generalized cone complexes, introduced in § 2.1. While this point of view was present in [Reference Gross and SiebertGS13], we make it more explicit here, and in particular discuss tropicalization in a sufficient degree of generality as needed here. As an application, in § 2.6 we introduce the refined moduli spaces ![]() $\mathfrak {M}(X_0,{\boldsymbol{\tau }})$ appearing in the decomposition formula. Section 2.2 reviews the notion of Artin fans, an algebraic stack associated to any generalized cone complex. Our decomposition result is based on a decomposition of the fundamental class in a moduli space of stable log maps to the Artin fan of
$\mathfrak {M}(X_0,{\boldsymbol{\tau }})$ appearing in the decomposition formula. Section 2.2 reviews the notion of Artin fans, an algebraic stack associated to any generalized cone complex. Our decomposition result is based on a decomposition of the fundamental class in a moduli space of stable log maps to the Artin fan of ![]() $X_0$ over
$X_0$ over ![]() $b_0$.
$b_0$.
Section 3 proves the main theorem, the decomposition formula. In § 3.1 we first prove a general decomposition of the fundamental class for a space log smooth over the standard log point. The main insight in § 3.2 is that replacing ![]() $X_0$ with its relative Artin fan the moduli space of stable log maps becomes unobstructed, and hence has a fundamental class that can be decomposed. The main theorem then follows in § 3.3 by lifting this decomposition to the virtual level.
$X_0$ with its relative Artin fan the moduli space of stable log maps becomes unobstructed, and hence has a fundamental class that can be decomposed. The main theorem then follows in § 3.3 by lifting this decomposition to the virtual level.
The remainder of the paper is devoted to applications. As a preparation, § 4 closes a gap in the literature, building on work of Nishinou and Siebert in [Reference Nishinou and SiebertNS06]. This concerns the logarithmic enhancement problem, the problem of constructing stable logarithmic maps with a given usual stable map, previously considered only in special cases. We address the problem through a two-step process. In the first step, we use the tropical geometry of the situation to identify a proper, birational, logarithmically étale map, i.e. a logarithmic modification, which reduces the problem to a situation where no irreducible component of the domain curve maps into the singular locus of ![]() $X_0$ and maps no node into strata of
$X_0$ and maps no node into strata of ![]() $X_0$ of codimension larger than 1. The second step is the main result of § 4, Theorem 4.13, giving the number of logarithmic enhancements in fully general situations, including non-reduced
$X_0$ of codimension larger than 1. The second step is the main result of § 4, Theorem 4.13, giving the number of logarithmic enhancements in fully general situations, including non-reduced ![]() $X_0$.
$X_0$.
Section 5 employs these formulas in the discussion of a number of hopefully instructive examples. Section 5.1 contains the already announced discussion of our decomposition formula in the traditional situation of [Reference LiLi02]. In § 5.2 we retrieve the classical number ![]() $12$ of nodal plane sections of a cubic surface passing through two points via a degeneration into three copies of
$12$ of nodal plane sections of a cubic surface passing through two points via a degeneration into three copies of ![]() $\mathbb {P}^2$, blown up in zero, three and six points, respectively. The topic of § 5.3 is an interpretation of the imposing of point conditions in tropical geometry via degenerating scheme-theoretic point conditions in the trivial product
$\mathbb {P}^2$, blown up in zero, three and six points, respectively. The topic of § 5.3 is an interpretation of the imposing of point conditions in tropical geometry via degenerating scheme-theoretic point conditions in the trivial product ![]() $Y\times \mathbb {A}^1$. The decomposition formula in this case (Theorem 5.4) provides an alternative view on tropical map counting with point conditions as in [Reference MikhalkinMik05, Reference Nishinou and SiebertNS06]. The final section § 5.4 features an example with two rigid tropical maps such that only one of them arises as the tropicalization of a stable log map, but the contribution to the virtual count comes from the other, non-realizable rigid tropical map.
$Y\times \mathbb {A}^1$. The decomposition formula in this case (Theorem 5.4) provides an alternative view on tropical map counting with point conditions as in [Reference MikhalkinMik05, Reference Nishinou and SiebertNS06]. The final section § 5.4 features an example with two rigid tropical maps such that only one of them arises as the tropicalization of a stable log map, but the contribution to the virtual count comes from the other, non-realizable rigid tropical map.
1.2 Conventions
All logarithmic schemes and stacks we consider here are fine and saturated and defined over an algebraically closed field ![]() $\Bbbk$ of characteristic
$\Bbbk$ of characteristic ![]() $0$. We will usually only consider toric monoids, i.e. monoids of the form
$0$. We will usually only consider toric monoids, i.e. monoids of the form ![]() $P=P_{\mathbb {R}}\cap M$ for
$P=P_{\mathbb {R}}\cap M$ for ![]() $M\simeq \mathbb {Z}^n$,
$M\simeq \mathbb {Z}^n$, ![]() $P_{\mathbb {R}}\subset M_{\mathbb {R}}=M\otimes _{\mathbb {Z}} \mathbb {R}$ a rational polyhedral cone. For
$P_{\mathbb {R}}\subset M_{\mathbb {R}}=M\otimes _{\mathbb {Z}} \mathbb {R}$ a rational polyhedral cone. For ![]() $P$ a toric monoid, we write
$P$ a toric monoid, we write
For ![]() $Q$ a toric monoid and
$Q$ a toric monoid and ![]() $\varphi :Q\to R$ a homomorphism to the multiplicative monoid of the
$\varphi :Q\to R$ a homomorphism to the multiplicative monoid of the ![]() $\Bbbk$-algebra
$\Bbbk$-algebra ![]() $R$, the notation
$R$, the notation ![]() $\operatorname {Spec}(Q \longrightarrow R)$ denotes
$\operatorname {Spec}(Q \longrightarrow R)$ denotes ![]() $\operatorname {Spec} R$ with the log structure induced by
$\operatorname {Spec} R$ with the log structure induced by ![]() $\varphi$. For our conventions concerning graphs see § 2.3.6.
$\varphi$. For our conventions concerning graphs see § 2.3.6.
2. Preliminaries
2.1 Cone complexes associated to logarithmic stacks
2.1.1 The category of cones
We consider the category of rational polyhedral cones, which we denote by ![]() $\mathbf {Cones}$. The objects of
$\mathbf {Cones}$. The objects of ![]() $\mathbf {Cones}$ are pairs
$\mathbf {Cones}$ are pairs ![]() $\sigma = (\sigma _\mathbb {R}, N)$ where
$\sigma = (\sigma _\mathbb {R}, N)$ where ![]() $N\simeq \mathbb {Z}^n$ is a lattice and
$N\simeq \mathbb {Z}^n$ is a lattice and ![]() $\sigma _\mathbb {R}\subset N_{\mathbb {R}}=N\otimes _{\mathbb {Z}}\mathbb {R}$ is a top-dimensional strictly convex rational polyhedral cone. A morphism of cones
$\sigma _\mathbb {R}\subset N_{\mathbb {R}}=N\otimes _{\mathbb {Z}}\mathbb {R}$ is a top-dimensional strictly convex rational polyhedral cone. A morphism of cones ![]() $\varphi :\sigma _1 \longrightarrow \sigma _2$ is a homomorphism
$\varphi :\sigma _1 \longrightarrow \sigma _2$ is a homomorphism ![]() $\varphi :N_1 \longrightarrow N_2$ which takes
$\varphi :N_1 \longrightarrow N_2$ which takes ![]() ${\sigma _1}_\mathbb {R}$ into
${\sigma _1}_\mathbb {R}$ into ![]() ${\sigma _2}_\mathbb {R}$. Such a morphism is a face morphism if it identifies
${\sigma _2}_\mathbb {R}$. Such a morphism is a face morphism if it identifies ![]() ${\sigma _1}_\mathbb {R}$ with a face of
${\sigma _1}_\mathbb {R}$ with a face of ![]() ${\sigma _2}_\mathbb {R}$ and
${\sigma _2}_\mathbb {R}$ and ![]() $N_1$ with a saturated sublattice of
$N_1$ with a saturated sublattice of ![]() $N_2$. If we need to specify that
$N_2$. If we need to specify that ![]() $N$ is associated to
$N$ is associated to ![]() $\sigma$ we write
$\sigma$ we write ![]() $N_\sigma$ instead.
$N_\sigma$ instead.
2.1.2 Generalized cone complexes
Recall from [Reference Kempf, Knudsen, Mumford and Saint-DonatKKMS73, II.1] and [Reference Abramovich, Caporaso and PayneACP15] that a generalized cone complex is a topological space with a presentation as the colimit of an arbitrary finite diagram in the category ![]() $\mathbf {Cones}$ with all morphisms being face morphisms. If
$\mathbf {Cones}$ with all morphisms being face morphisms. If ![]() $\Sigma$ denotes a generalized cone complex, we write
$\Sigma$ denotes a generalized cone complex, we write ![]() $\sigma \in \Sigma$ if
$\sigma \in \Sigma$ if ![]() $\sigma$ is a cone in the diagram yielding
$\sigma$ is a cone in the diagram yielding ![]() $\Sigma$, and write
$\Sigma$, and write ![]() $|\Sigma |$ for the underlying topological space. A morphism of generalized cone complexes
$|\Sigma |$ for the underlying topological space. A morphism of generalized cone complexes ![]() $f:\Sigma \longrightarrow \Sigma '$ is a continuous map
$f:\Sigma \longrightarrow \Sigma '$ is a continuous map ![]() $f:|\Sigma | \longrightarrow |\Sigma '|$ such that for each
$f:|\Sigma | \longrightarrow |\Sigma '|$ such that for each ![]() $\sigma _\mathbb {R}\in \Sigma$, the induced map
$\sigma _\mathbb {R}\in \Sigma$, the induced map ![]() $\sigma \longrightarrow |\Sigma '|$ factors through a morphism
$\sigma \longrightarrow |\Sigma '|$ factors through a morphism ![]() $\sigma \longrightarrow \sigma '\in \Sigma '$. For a cone
$\sigma \longrightarrow \sigma '\in \Sigma '$. For a cone ![]() $\sigma \in \mathbf {Cones}$, we use the same symbol
$\sigma \in \mathbf {Cones}$, we use the same symbol ![]() $\sigma$ to also denote the cone complex of all its faces.
$\sigma$ to also denote the cone complex of all its faces.
Note that two generalized cone complexes can be isomorphic yet not have the same presentation. This phenomenon does not occur for so-called reduced presentations, which have the defining property that every face of a cone in the diagram is in the diagram, and every isomorphism in the diagram is a self-map. By [Reference Abramovich, Caporaso and PayneACP15, Proposition 2.6.2] any generalized cone complex has such a reduced presentation. In this paper we only work with reduced presentations of generalized cone complexes.
2.1.3 Generalized polyhedral complexes
We can similarly define a generalized polyhedral complex, where in the above set of definitions pairs ![]() $(\sigma _\mathbb {R},N)$ live in the category
$(\sigma _\mathbb {R},N)$ live in the category ![]() $\textbf {Poly}$ of rationally defined polyhedra. This is more general than cones, as any cone
$\textbf {Poly}$ of rationally defined polyhedra. This is more general than cones, as any cone ![]() $\sigma$ is in particular a polyhedron (usually unbounded). For example, an affine slice of a fan is a polyhedral complex.
$\sigma$ is in particular a polyhedron (usually unbounded). For example, an affine slice of a fan is a polyhedral complex.
2.1.4 The tropicalization of a logarithmic scheme
Now let ![]() $X$ be a Zariski fine saturated (fs) log scheme of finite type. For the generic point
$X$ be a Zariski fine saturated (fs) log scheme of finite type. For the generic point ![]() $\eta$ of a stratum of
$\eta$ of a stratum of ![]() $X$, its characteristic monoid
$X$, its characteristic monoid ![]() $\overline{\mathcal {M}}_{X,\eta }$ defines a dual monoid
$\overline{\mathcal {M}}_{X,\eta }$ defines a dual monoid ![]() $(\overline{\mathcal {M}}_{X,\eta })^{\vee } := {\operatorname {Hom}}(\overline{\mathcal {M}}_{X,\eta }, \mathbb {N})$ lying in the group
$(\overline{\mathcal {M}}_{X,\eta })^{\vee } := {\operatorname {Hom}}(\overline{\mathcal {M}}_{X,\eta }, \mathbb {N})$ lying in the group ![]() $(\overline{\mathcal {M}}_{X,\eta })^* := {\operatorname {Hom}}(\overline{\mathcal {M}}_{X,\eta }, \mathbb {Z})$, see § 1.2, and hence a dual cone
$(\overline{\mathcal {M}}_{X,\eta })^* := {\operatorname {Hom}}(\overline{\mathcal {M}}_{X,\eta }, \mathbb {Z})$, see § 1.2, and hence a dual cone
If ![]() $\eta$ is a specialization of
$\eta$ is a specialization of ![]() $\eta '$, then there is a well-defined generization map
$\eta '$, then there is a well-defined generization map ![]() $\overline{\mathcal {M}}_{X,\eta } \longrightarrow \overline{\mathcal {M}}_{X,\eta '}$ since we assumed
$\overline{\mathcal {M}}_{X,\eta } \longrightarrow \overline{\mathcal {M}}_{X,\eta '}$ since we assumed ![]() $X$ is a Zariski logarithmic scheme. Dualizing, we obtain a face morphism
$X$ is a Zariski logarithmic scheme. Dualizing, we obtain a face morphism ![]() $\sigma _{\eta '} \longrightarrow \sigma _{\eta }$. This gives a diagram of cones indexed by strata of
$\sigma _{\eta '} \longrightarrow \sigma _{\eta }$. This gives a diagram of cones indexed by strata of ![]() $X$ with face morphisms, and hence gives a generalized cone complex
$X$ with face morphisms, and hence gives a generalized cone complex ![]() $\Sigma (X)$. We call this the tropicalization of
$\Sigma (X)$. We call this the tropicalization of ![]() $X$, following [Reference Gross and SiebertGS13, Appendix B].Footnote 1 For
$X$, following [Reference Gross and SiebertGS13, Appendix B].Footnote 1 For ![]() $\sigma \in \Sigma (X)$ we denote by
$\sigma \in \Sigma (X)$ we denote by
the closure of the corresponding stratum of ![]() $X$, endowed with the reduced induced scheme structure. We refer to these subschemes with reduced induced structure as closed strata of
$X$, endowed with the reduced induced scheme structure. We refer to these subschemes with reduced induced structure as closed strata of ![]() $X$.
$X$.
This construction is functorial: given a morphism of log schemes ![]() $f:X \longrightarrow Y$, the map
$f:X \longrightarrow Y$, the map ![]() $f^{\flat }:f^{-1}\overline{\mathcal{M}}_Y \longrightarrow \overline{\mathcal{M}}_X$ induces a map of generalized cone complexes
$f^{\flat }:f^{-1}\overline{\mathcal{M}}_Y \longrightarrow \overline{\mathcal{M}}_X$ induces a map of generalized cone complexes ![]() $\Sigma (f):\Sigma (X) \longrightarrow \Sigma (Y)$.
$\Sigma (f):\Sigma (X) \longrightarrow \Sigma (Y)$.
Definition 2.1 [GS13, Definition B.2] We say ![]() $X$ is monodromy free if
$X$ is monodromy free if ![]() $X$ is a Zariski log scheme and for every
$X$ is a Zariski log scheme and for every ![]() $\sigma \in \Sigma (X)$, the natural map
$\sigma \in \Sigma (X)$, the natural map ![]() $\sigma \longrightarrow |\Sigma (X)|$ is injective on the interior of any face of
$\sigma \longrightarrow |\Sigma (X)|$ is injective on the interior of any face of ![]() $\sigma$. We say
$\sigma$. We say ![]() $X$ is simple if the map is injective on every
$X$ is simple if the map is injective on every ![]() $\sigma$.
$\sigma$.
Here is an example of a Zariski log structure that is monodromy free, but not simple. Take ![]() $X$ to be the Neron
$X$ to be the Neron ![]() $2$-gon, the fibred sum of two copies of
$2$-gon, the fibred sum of two copies of ![]() $\mathbb {P}^1$ joined at two pairs of points. Thus
$\mathbb {P}^1$ joined at two pairs of points. Thus ![]() $X$ has two irreducible components
$X$ has two irreducible components ![]() $X_1,X_2$ and two nodes
$X_1,X_2$ and two nodes ![]() $q_1,q_2$. Take a log structure
$q_1,q_2$. Take a log structure ![]() $\mathcal {M}_X$ on
$\mathcal {M}_X$ on ![]() $X$ with
$X$ with ![]() $\overline{\mathcal{M}}_X$ constant with fibres
$\overline{\mathcal{M}}_X$ constant with fibres ![]() $\mathbb {N}^2$ along
$\mathbb {N}^2$ along ![]() $X_1$, with fibers
$X_1$, with fibers ![]() $\mathbb {N}$ on
$\mathbb {N}$ on ![]() $X_2\setminus \{q_1,q_2\}$ and with generization maps
$X_2\setminus \{q_1,q_2\}$ and with generization maps ![]() $\overline{\mathcal{M}}_{X,q_i}=\mathbb {N}^2\to \mathbb {N}$ to the generic point of
$\overline{\mathcal{M}}_{X,q_i}=\mathbb {N}^2\to \mathbb {N}$ to the generic point of ![]() $X_2$ the two projections. See also [Reference Gross and SiebertGS13, Expl. B.1] for another example.
$X_2$ the two projections. See also [Reference Gross and SiebertGS13, Expl. B.1] for another example.
Simplicity is, however, true in the Zariski log smooth case over a trivial log point. Such log schemes can in fact be viewed as toroidal pairs without self-intersections and the following statement follows readily from the classical treatment in [Reference Kempf, Knudsen, Mumford and Saint-DonatKKMS73, pp. 70–72].
Proposition 2.2 Let ![]() $X$ be a Zariski log scheme, log smooth over
$X$ be a Zariski log scheme, log smooth over ![]() $\operatorname {Spec} \Bbbk$ with the trivial log structure. Then
$\operatorname {Spec} \Bbbk$ with the trivial log structure. Then ![]() $X$ is simple.
$X$ is simple.
As remarked in [Reference Gross and SiebertGS13], more generally we can define the generalized cone complex associated with a finite type logarithmic stack ![]() $X$, in particular allowing for logarithmic schemes
$X$, in particular allowing for logarithmic schemes ![]() $X$ in the étale topology. In fact, one can always find a cover
$X$ in the étale topology. In fact, one can always find a cover ![]() $X' \longrightarrow X$ in the smooth topology with
$X' \longrightarrow X$ in the smooth topology with ![]() $X'$ a union of simple log schemes, and with
$X'$ a union of simple log schemes, and with ![]() $X''=X'\times _{X} X'$; then define
$X''=X'\times _{X} X'$; then define ![]() $\Sigma (X)$ to be the colimit of
$\Sigma (X)$ to be the colimit of ![]() $\Sigma (X'')\rightrightarrows \Sigma (X')$. The resulting generalized cone complex is independent of the choice of cover. This process is explicitly carried out in [Reference Abramovich, Caporaso and PayneACP15, Reference UlirschUli15].
$\Sigma (X'')\rightrightarrows \Sigma (X')$. The resulting generalized cone complex is independent of the choice of cover. This process is explicitly carried out in [Reference Abramovich, Caporaso and PayneACP15, Reference UlirschUli15].
Examples 2.3 (1) If ![]() $X$ is a toric variety with the canonical toric logarithmic structure, then
$X$ is a toric variety with the canonical toric logarithmic structure, then ![]() $\Sigma (X)$ is abstractly the fan defining
$\Sigma (X)$ is abstractly the fan defining ![]() $X$. It is missing the embedding of
$X$. It is missing the embedding of ![]() $|\Sigma (X)|$ as a fan in a vector space
$|\Sigma (X)|$ as a fan in a vector space ![]() $N_{\mathbb {R}}$, and should be viewed as a piecewise linear object.
$N_{\mathbb {R}}$, and should be viewed as a piecewise linear object.
(2) Let ![]() $\Bbbk$ be a field and
$\Bbbk$ be a field and ![]() $X=\operatorname {Spec}(\mathbb {N} \longrightarrow \Bbbk )$ the standard log point with
$X=\operatorname {Spec}(\mathbb {N} \longrightarrow \Bbbk )$ the standard log point with ![]() $\mathcal {M}_X=\Bbbk ^{\times } \times \mathbb {N}$. Then
$\mathcal {M}_X=\Bbbk ^{\times } \times \mathbb {N}$. Then ![]() $\Sigma (X)$ consists of the ray
$\Sigma (X)$ consists of the ray ![]() $\mathbb {R}_{\ge 0}$.
$\mathbb {R}_{\ge 0}$.
(3) Let ![]() $C$ be a curve with an étale logarithmic structure with the property that
$C$ be a curve with an étale logarithmic structure with the property that ![]() $\overline{\mathcal {M}}_C$ has stalk
$\overline{\mathcal {M}}_C$ has stalk ![]() $\mathbb {N}^2$ at any geometric point, but has monodromy of the form
$\mathbb {N}^2$ at any geometric point, but has monodromy of the form ![]() $(a,b)\mapsto (b,a)$, so that the pull-back of
$(a,b)\mapsto (b,a)$, so that the pull-back of ![]() $\overline{\mathcal {M}}_C$ to an unramified double cover
$\overline{\mathcal {M}}_C$ to an unramified double cover ![]() $C' \longrightarrow C$ is constant but
$C' \longrightarrow C$ is constant but ![]() $\overline{\mathcal {M}}_C$ is only locally constant. Then
$\overline{\mathcal {M}}_C$ is only locally constant. Then ![]() $\Sigma (C)$ can be described as the quotient of
$\Sigma (C)$ can be described as the quotient of ![]() $\mathbb {R}_{\ge 0}^2$ by the automorphism
$\mathbb {R}_{\ge 0}^2$ by the automorphism ![]() $(a,b)\mapsto (b,a)$. If we use the reduced presentation,
$(a,b)\mapsto (b,a)$. If we use the reduced presentation, ![]() $\Sigma (C)$ has three cones, one each of dimension
$\Sigma (C)$ has three cones, one each of dimension ![]() $0$,
$0$, ![]() $1$ and
$1$ and ![]() $2$.
$2$.
2.2 Artin fans
Let ![]() $X$ be a fine and saturated algebraic log stack. We are quite permissive with algebraic stacks, as delineated in [Reference OlssonOls03, (1.2.4)–(1.2.5)], since we need to work with stacks with non-separated diagonal. An Artin stack logarithmically étale over
$X$ be a fine and saturated algebraic log stack. We are quite permissive with algebraic stacks, as delineated in [Reference OlssonOls03, (1.2.4)–(1.2.5)], since we need to work with stacks with non-separated diagonal. An Artin stack logarithmically étale over ![]() $\operatorname {Spec}\Bbbk$ is called an Artin fan.
$\operatorname {Spec}\Bbbk$ is called an Artin fan.
The logarithmic structure of ![]() $X$ is encoded by a morphism
$X$ is encoded by a morphism ![]() $X \longrightarrow {\operatorname {Log}}$ to Olsson's stack
$X \longrightarrow {\operatorname {Log}}$ to Olsson's stack ![]() ${\operatorname {Log}}$ of fine log structures, see [Reference OlssonOls03]. One crucial idea developed in the context of the present paper is a refinement of the stack
${\operatorname {Log}}$ of fine log structures, see [Reference OlssonOls03]. One crucial idea developed in the context of the present paper is a refinement of the stack ![]() ${\operatorname {Log}}$ by an Artin fan that takes into account the stratification of
${\operatorname {Log}}$ by an Artin fan that takes into account the stratification of ![]() $X$ defined by
$X$ defined by ![]() $\overline{\mathcal {M}}_X$. Following preliminary notes written by two of us (Chen and Gross), the paper [Reference Abramovich and WiseAW18] introduces a canonical Artin fan
$\overline{\mathcal {M}}_X$. Following preliminary notes written by two of us (Chen and Gross), the paper [Reference Abramovich and WiseAW18] introduces a canonical Artin fan ![]() $\mathcal {A}_X$ associated to a logarithmically smooth fs log scheme
$\mathcal {A}_X$ associated to a logarithmically smooth fs log scheme ![]() $X$. This was generalized in [Reference Abramovich, Chen, Marcus and WiseACMW17, Proposition 3.1.1] as follows.
$X$. This was generalized in [Reference Abramovich, Chen, Marcus and WiseACMW17, Proposition 3.1.1] as follows.
Theorem 2.4 Let ![]() $X$ be a logarithmic algebraic stack over
$X$ be a logarithmic algebraic stack over ![]() $\operatorname {Spec}\Bbbk$ which is locally connected in the smooth topology. Then there is an initial strict étale morphism
$\operatorname {Spec}\Bbbk$ which is locally connected in the smooth topology. Then there is an initial strict étale morphism ![]() $\mathcal {A}_X \longrightarrow {\operatorname {Log}}$ over which
$\mathcal {A}_X \longrightarrow {\operatorname {Log}}$ over which ![]() $X \longrightarrow {\operatorname {Log}}$ factors. Moreover, the morphism
$X \longrightarrow {\operatorname {Log}}$ factors. Moreover, the morphism ![]() $\mathcal {A}_X \longrightarrow {\operatorname {Log}}$ is representable by algebraic spaces.
$\mathcal {A}_X \longrightarrow {\operatorname {Log}}$ is representable by algebraic spaces.
Note that ![]() $\mathcal {A}_X$ in the theorem is indeed an Artin fan because
$\mathcal {A}_X$ in the theorem is indeed an Artin fan because ![]() ${\operatorname {Log}}$ is logarithmically étale over
${\operatorname {Log}}$ is logarithmically étale over ![]() $\operatorname {Spec}\Bbbk$.
$\operatorname {Spec}\Bbbk$.
If ![]() $X$ is a Deligne–Mumford stack,
$X$ is a Deligne–Mumford stack, ![]() $\mathcal {A}_X$ can be constructed from the cone complex
$\mathcal {A}_X$ can be constructed from the cone complex ![]() $\Sigma (X)$ as follows. For any cone
$\Sigma (X)$ as follows. For any cone ![]() $\sigma \subset N_{\mathbb {R}}$, let
$\sigma \subset N_{\mathbb {R}}$, let ![]() $P=\sigma ^{\vee }\cap M$ be the corresponding monoid. We write
$P=\sigma ^{\vee }\cap M$ be the corresponding monoid. We write
This stack carries the standard toric logarithmic structure induced by descent from the global chart ![]() $P \longrightarrow \Bbbk [P]$. Then
$P \longrightarrow \Bbbk [P]$. Then ![]() $\mathcal {A}_X$ is the colimit
$\mathcal {A}_X$ is the colimit
in the category of sheaves over ![]() ${\operatorname {Log}}$.
${\operatorname {Log}}$.
Remark 2.5 Unlike ![]() $\Sigma (X)$, the formation of
$\Sigma (X)$, the formation of ![]() $\mathcal {A}_X$ is not functorial for all logarithmic morphisms
$\mathcal {A}_X$ is not functorial for all logarithmic morphisms ![]() $Y \longrightarrow X$. This is a result of the fact that the morphism
$Y \longrightarrow X$. This is a result of the fact that the morphism ![]() $Y \longrightarrow {\operatorname {Log}}$ is not the composition
$Y \longrightarrow {\operatorname {Log}}$ is not the composition ![]() $Y \longrightarrow X \longrightarrow {\operatorname {Log}}$, unless
$Y \longrightarrow X \longrightarrow {\operatorname {Log}}$, unless ![]() $Y \longrightarrow X$ is strict. Note also that not all Artin fans
$Y \longrightarrow X$ is strict. Note also that not all Artin fans ![]() $\mathcal {A}$ are of the form
$\mathcal {A}$ are of the form ![]() $\mathcal {A}_X$, since
$\mathcal {A}_X$, since ![]() $\mathcal {A} \longrightarrow {\operatorname {Log}}$ may fail to be representable.
$\mathcal {A} \longrightarrow {\operatorname {Log}}$ may fail to be representable.
Our next aim is to prove functoriality of the formation of Artin fans for maps with Zariski log smooth domains, stated as Proposition 2.8 below. We need two lemmas.
Lemma 2.6 Suppose ![]() $X$ is a log smooth scheme over the trivial log point
$X$ is a log smooth scheme over the trivial log point ![]() $\operatorname {Spec}\Bbbk$ and with Zariski log structure. Then
$\operatorname {Spec}\Bbbk$ and with Zariski log structure. Then ![]() $\mathcal {A}_X$ admits a Zariski open covering
$\mathcal {A}_X$ admits a Zariski open covering ![]() $\{\mathcal {A}_{\sigma } \subset \mathcal {A}_X\,|\, \sigma \in \Sigma (X)\}$.
$\{\mathcal {A}_{\sigma } \subset \mathcal {A}_X\,|\, \sigma \in \Sigma (X)\}$.
Proof. Since ![]() $X$ has Zariski log structure, we may select a covering
$X$ has Zariski log structure, we may select a covering ![]() $\{U \longrightarrow X\}$ by Zariski open sets such that
$\{U \longrightarrow X\}$ by Zariski open sets such that ![]() $U \longrightarrow \mathcal {A}_{\sigma _U}$ is the Artin fan of
$U \longrightarrow \mathcal {A}_{\sigma _U}$ is the Artin fan of ![]() $U$. By the log smoothness of
$U$. By the log smoothness of ![]() $X$, the morphism
$X$, the morphism ![]() $X \longrightarrow \mathcal {A}_{X}$ is smooth, and hence the image
$X \longrightarrow \mathcal {A}_{X}$ is smooth, and hence the image ![]() $\tilde U \subset \mathcal {A}_X$ of
$\tilde U \subset \mathcal {A}_X$ of ![]() $U$ is an open substack.
$U$ is an open substack.
It remains to show that ![]() $\tilde U$ is the Artin fan of
$\tilde U$ is the Artin fan of ![]() $U$. By [Reference Abramovich and WiseAW18, § 2.3 and Definition 2.3.2(2)], this amounts to showing that
$U$. By [Reference Abramovich and WiseAW18, § 2.3 and Definition 2.3.2(2)], this amounts to showing that ![]() $\tilde U$ parameterizes the connected components of the fibres of
$\tilde U$ parameterizes the connected components of the fibres of ![]() $U \longrightarrow {\operatorname {Log}}$. Since both
$U \longrightarrow {\operatorname {Log}}$. Since both ![]() $X \longrightarrow {\operatorname {Log}}$ and
$X \longrightarrow {\operatorname {Log}}$ and ![]() $U \longrightarrow {\operatorname {Log}}$ are smooth morphisms between reduced stacks, it suffices to consider each geometric point
$U \longrightarrow {\operatorname {Log}}$ are smooth morphisms between reduced stacks, it suffices to consider each geometric point ![]() $T \longrightarrow {\operatorname {Log}}$. Since
$T \longrightarrow {\operatorname {Log}}$. Since ![]() $U \subset X$ is Zariski open,
$U \subset X$ is Zariski open, ![]() $U_T = T\times _{{\operatorname {Log}}}U \subset X_{T} = T\times _{{\operatorname {Log}}}X$ is also Zariski open. Thus, for each connected component
$U_T = T\times _{{\operatorname {Log}}}U \subset X_{T} = T\times _{{\operatorname {Log}}}X$ is also Zariski open. Thus, for each connected component ![]() $V \subset U_T$, there is a unique connected component
$V \subset U_T$, there is a unique connected component ![]() $V' \subset X_T$ containing
$V' \subset X_T$ containing ![]() $V$ as a Zariski open dense set. As the set of connected components of
$V$ as a Zariski open dense set. As the set of connected components of ![]() $X_T$ is parameterized by
$X_T$ is parameterized by ![]() $T\times _{{\operatorname {Log}}}\mathcal {A}_X$, we observe that the set of connected components of
$T\times _{{\operatorname {Log}}}\mathcal {A}_X$, we observe that the set of connected components of ![]() $U_T$ is parameterized by the subscheme
$U_T$ is parameterized by the subscheme ![]() $T\times _{{\operatorname {Log}}}\tilde U \subset T\times _{{\operatorname {Log}}}\mathcal{A}_X$.
$T\times _{{\operatorname {Log}}}\tilde U \subset T\times _{{\operatorname {Log}}}\mathcal{A}_X$.
Lemma 2.7 Suppose ![]() $X$ is a log smooth scheme with Zariski log structure and
$X$ is a log smooth scheme with Zariski log structure and ![]() $\tau \in \mathbf {Cones}$. Then any morphism
$\tau \in \mathbf {Cones}$. Then any morphism ![]() $X \longrightarrow \mathcal {A}_{\tau }$ has a canonical factorization through
$X \longrightarrow \mathcal {A}_{\tau }$ has a canonical factorization through ![]() $\mathcal {A}_{X} \longrightarrow \mathcal {A}_{\tau }$.
$\mathcal {A}_{X} \longrightarrow \mathcal {A}_{\tau }$.
Proof. By Lemma 2.6, we may select a Zariski covering ![]() $\mathcal {C} := \{\mathcal {A}_\sigma \subset \mathcal {A}_X\}$ of
$\mathcal {C} := \{\mathcal {A}_\sigma \subset \mathcal {A}_X\}$ of ![]() $\mathcal {A}_X$, and hence a Zariski covering
$\mathcal {A}_X$, and hence a Zariski covering ![]() $\{U_{\sigma } := \mathcal {A}_{\sigma }\times _{\mathcal {A}_X}X \subset X\}$ of
$\{U_{\sigma } := \mathcal {A}_{\sigma }\times _{\mathcal {A}_X}X \subset X\}$ of ![]() $X$. We may assume that if
$X$. We may assume that if ![]() $\sigma ' \subset \sigma$ is a face, then
$\sigma ' \subset \sigma$ is a face, then ![]() $\mathcal {A}_{\sigma '} \subset \mathcal {A}_{\sigma } \subset \mathcal {A}_X$ is also in
$\mathcal {A}_{\sigma '} \subset \mathcal {A}_{\sigma } \subset \mathcal {A}_X$ is also in ![]() $\mathcal {C}$.
$\mathcal {C}$.
Locally, the morphism ![]() $U_{\sigma } \longrightarrow \mathcal {A}_{\tau }$ induces a morphism
$U_{\sigma } \longrightarrow \mathcal {A}_{\tau }$ induces a morphism ![]() $\tau ^{\vee } \longrightarrow \Gamma (U_{\sigma },\overline{\mathcal{M}}_{U_{\sigma }}) = \sigma ^{\vee }$, and hence a canonical
$\tau ^{\vee } \longrightarrow \Gamma (U_{\sigma },\overline{\mathcal{M}}_{U_{\sigma }}) = \sigma ^{\vee }$, and hence a canonical ![]() $\phi _{\sigma }: \mathcal {A}_{\sigma } \longrightarrow \mathcal {A}_{\tau }$ through which
$\phi _{\sigma }: \mathcal {A}_{\sigma } \longrightarrow \mathcal {A}_{\tau }$ through which ![]() $U_{\sigma } \longrightarrow \mathcal {A}_{\tau }$ factors.
$U_{\sigma } \longrightarrow \mathcal {A}_{\tau }$ factors.
To see the local construction glues, observe that the intersection ![]() $\mathcal {A}_{\sigma _1}\cap \mathcal {A}_{\sigma _2}$ of two Zariski charts in
$\mathcal {A}_{\sigma _1}\cap \mathcal {A}_{\sigma _2}$ of two Zariski charts in ![]() $\mathcal {C}$ is again covered by elements in
$\mathcal {C}$ is again covered by elements in ![]() $\mathcal {C}$. It suffices to verify that
$\mathcal {C}$. It suffices to verify that ![]() $\phi _{\sigma _1},\phi _{\sigma _2}$ agree on
$\phi _{\sigma _1},\phi _{\sigma _2}$ agree on ![]() $\mathcal {A}_{\sigma '} \in \mathcal {C}$ if
$\mathcal {A}_{\sigma '} \in \mathcal {C}$ if ![]() $\mathcal {A}_{\sigma '} \subset \mathcal {A}_{\sigma _1}\cap \mathcal {A}_{\sigma _2}$. Taking global sections, we observe that the composition
$\mathcal {A}_{\sigma '} \subset \mathcal {A}_{\sigma _1}\cap \mathcal {A}_{\sigma _2}$. Taking global sections, we observe that the composition ![]() $\tau ^{\vee } \longrightarrow \Gamma (U_{\sigma _i},\overline{\mathcal{M}}_{U_{\sigma _i}}) \longrightarrow \Gamma (U_{\sigma '},\overline{\mathcal{M}}_{U_{\sigma '}}) = (\sigma ')^{\vee }$ is independent of
$\tau ^{\vee } \longrightarrow \Gamma (U_{\sigma _i},\overline{\mathcal{M}}_{U_{\sigma _i}}) \longrightarrow \Gamma (U_{\sigma '},\overline{\mathcal{M}}_{U_{\sigma '}}) = (\sigma ')^{\vee }$ is independent of ![]() $i = 1,2$ as they are determined by the restriction of
$i = 1,2$ as they are determined by the restriction of ![]() $U_{\sigma _i} \longrightarrow \mathcal {A}_{\tau }$ to the common Zariski open
$U_{\sigma _i} \longrightarrow \mathcal {A}_{\tau }$ to the common Zariski open ![]() $U_{\sigma '}$. Hence
$U_{\sigma '}$. Hence ![]() $\phi _{\sigma _1}|_{U_{\sigma '}} = \phi _{\sigma _2}|_{U_{\sigma '}}$.
$\phi _{\sigma _1}|_{U_{\sigma '}} = \phi _{\sigma _2}|_{U_{\sigma '}}$.
Proposition 2.8 Let ![]() $X \longrightarrow Y$ be a morphism of log schemes. Suppose
$X \longrightarrow Y$ be a morphism of log schemes. Suppose ![]() $X$ is log smooth with Zariski log structure. Then there is a canonical morphism
$X$ is log smooth with Zariski log structure. Then there is a canonical morphism ![]() $\mathcal {A}_X \longrightarrow \mathcal {A}_Y$ such that the following diagram commutes.
$\mathcal {A}_X \longrightarrow \mathcal {A}_Y$ such that the following diagram commutes.

Proof. By the claimed uniqueness and étale descent, the statement can be checked étale locally on ![]() $\mathcal {A}_Y$. We may then assume
$\mathcal {A}_Y$. We may then assume ![]() $\mathcal {A}_Y = \mathcal {A}_{\tau }$ for some
$\mathcal {A}_Y = \mathcal {A}_{\tau }$ for some ![]() $\tau \in \mathbf {Cones}$, for which the statement is exactly Lemma 2.7.
$\tau \in \mathbf {Cones}$, for which the statement is exactly Lemma 2.7.
Using Proposition 2.8 we can also define a relative notion of Artin fan for maps with log smooth domains.
Definition 2.9 The relative Artin fan for a morphism ![]() $X \longrightarrow B$ of log schemes with
$X \longrightarrow B$ of log schemes with ![]() $X$ log smooth with Zariski log structure is defined as the fibre product
$X$ log smooth with Zariski log structure is defined as the fibre product
While not, strictly speaking, needed for this paper, we end this subsection with the instructive result that giving a log morphism to the Artin fan ![]() $\mathcal {A}_X$ of a log scheme
$\mathcal {A}_X$ of a log scheme ![]() $X$ is combinatorial in nature, captured entirely by the induced map of cone complexes.
$X$ is combinatorial in nature, captured entirely by the induced map of cone complexes.
Proposition 2.10 Let ![]() $X$ be a Zariski fs log scheme log smooth over
$X$ be a Zariski fs log scheme log smooth over ![]() $\operatorname {Spec}\Bbbk$. Then for any fs log scheme
$\operatorname {Spec}\Bbbk$. Then for any fs log scheme ![]() $T$ there is a canonical bijection
$T$ there is a canonical bijection
which is functorial in ![]() $T$.
$T$.
Proof. Step I. Description of ![]() $\mathcal {A}_X$. By Lemma 2.6, we may select a Zariski covering
$\mathcal {A}_X$. By Lemma 2.6, we may select a Zariski covering ![]() $\mathcal {C} := \{\mathcal {A}_\sigma \subset \mathcal {A}_X\}$, and hence a Zariski covering
$\mathcal {C} := \{\mathcal {A}_\sigma \subset \mathcal {A}_X\}$, and hence a Zariski covering ![]() $\{U_{\sigma } := \mathcal {A}_{\sigma }\times _{\mathcal {A}_X}X \subset X\}$. We may assume that if
$\{U_{\sigma } := \mathcal {A}_{\sigma }\times _{\mathcal {A}_X}X \subset X\}$. We may assume that if ![]() $\sigma ' \subset \sigma$ is a face, then
$\sigma ' \subset \sigma$ is a face, then ![]() $\mathcal {A}_{\sigma '} \subset \mathcal {A}_{\sigma } \subset \mathcal {A}_X$ is also in
$\mathcal {A}_{\sigma '} \subset \mathcal {A}_{\sigma } \subset \mathcal {A}_X$ is also in ![]() $\mathcal {C}$. Thus
$\mathcal {C}$. Thus ![]() $\Sigma (X)$ can be presented by the collection of cones
$\Sigma (X)$ can be presented by the collection of cones ![]() $\{\sigma \}$ glued along face maps
$\{\sigma \}$ glued along face maps ![]() $\sigma ' \longrightarrow \sigma$. In particular, this shows that
$\sigma ' \longrightarrow \sigma$. In particular, this shows that ![]() $\Sigma (X)=\Sigma (\mathcal {A}_X)$. Since
$\Sigma (X)=\Sigma (\mathcal {A}_X)$. Since ![]() $\Sigma$ is functorial, there is then a map
$\Sigma$ is functorial, there is then a map ![]() ${\operatorname {Hom}}(T,\mathcal {A}_X) \longrightarrow {\operatorname {Hom}}(\Sigma (T),\Sigma (X))$. We need to construct the inverse.
${\operatorname {Hom}}(T,\mathcal {A}_X) \longrightarrow {\operatorname {Hom}}(\Sigma (T),\Sigma (X))$. We need to construct the inverse.
Step II. ![]() $T$ is atomic. Suppose
$T$ is atomic. Suppose ![]() $T$ has unique closed stratum
$T$ has unique closed stratum ![]() $T_0$ and a global chart
$T_0$ and a global chart ![]() $P \longrightarrow \mathcal {M}_T$ inducing an isomorphism
$P \longrightarrow \mathcal {M}_T$ inducing an isomorphism ![]() $P\simeq \overline{\mathcal{M}}_{T,\bar t}$ at some point
$P\simeq \overline{\mathcal{M}}_{T,\bar t}$ at some point ![]() $\bar t\in T_0$; in the language of [Reference Abramovich and WiseAW18, Definition 2.2.4] the logarithmic scheme
$\bar t\in T_0$; in the language of [Reference Abramovich and WiseAW18, Definition 2.2.4] the logarithmic scheme ![]() $T$ is atomic. Then with
$T$ is atomic. Then with ![]() $\tau :={\operatorname {Hom}}(P,\mathbb {R}_{\ge 0})$,
$\tau :={\operatorname {Hom}}(P,\mathbb {R}_{\ge 0})$, ![]() $\Sigma (T)=\tau$.
$\Sigma (T)=\tau$.
Using the presentation of ![]() $\Sigma (X)$ described in Step I, a map
$\Sigma (X)$ described in Step I, a map ![]() $\alpha :\Sigma (T) \longrightarrow \Sigma (X)$ has image
$\alpha :\Sigma (T) \longrightarrow \Sigma (X)$ has image ![]() $\alpha (\tau ) \subset \sigma _i\in \Sigma (X)$ for some
$\alpha (\tau ) \subset \sigma _i\in \Sigma (X)$ for some ![]() $i$. Observe that
$i$. Observe that ![]() ${\operatorname {Hom}}(T,\mathcal {A}_{\sigma _i})={\operatorname {Hom}}(Q_i,\Gamma (T,\overline{\mathcal{M}}_T))$ by [Reference OlssonOls03, Proposition 5.17]. Now
${\operatorname {Hom}}(T,\mathcal {A}_{\sigma _i})={\operatorname {Hom}}(Q_i,\Gamma (T,\overline{\mathcal{M}}_T))$ by [Reference OlssonOls03, Proposition 5.17]. Now ![]() $\Gamma (T,\overline{\mathcal{M}}_T)=P$, and giving a homomorphism
$\Gamma (T,\overline{\mathcal{M}}_T)=P$, and giving a homomorphism ![]() $Q_i \longrightarrow P$ is equivalent to giving a morphism of cones
$Q_i \longrightarrow P$ is equivalent to giving a morphism of cones ![]() $\tau \longrightarrow \sigma _i$. Thus
$\tau \longrightarrow \sigma _i$. Thus ![]() ${\operatorname {Hom}}(T,\mathcal {A}_{\sigma _i})={\operatorname {Hom}}(\tau ,\sigma _i)$. In particular,
${\operatorname {Hom}}(T,\mathcal {A}_{\sigma _i})={\operatorname {Hom}}(\tau ,\sigma _i)$. In particular, ![]() $\alpha$ induces a composed map
$\alpha$ induces a composed map ![]() $T \longrightarrow \mathcal {A}_{\sigma _i}\subset \mathcal {A}_X$, yielding the desired inverse map
$T \longrightarrow \mathcal {A}_{\sigma _i}\subset \mathcal {A}_X$, yielding the desired inverse map ![]() ${\operatorname {Hom}}(\Sigma (T),\Sigma (X)) \longrightarrow {\operatorname {Hom}}(T,\mathcal {A}_X)$.
${\operatorname {Hom}}(\Sigma (T),\Sigma (X)) \longrightarrow {\operatorname {Hom}}(T,\mathcal {A}_X)$.
Step III. ![]() $T$ general. In general
$T$ general. In general ![]() $T$ has an étale cover
$T$ has an étale cover ![]() $\{T_i\}$ by atomic logarithmic schemes, and each
$\{T_i\}$ by atomic logarithmic schemes, and each ![]() $T_{ij}:=T_i\times _T T_j$ also has such a covering
$T_{ij}:=T_i\times _T T_j$ also has such a covering ![]() $\{T_{ij}^k \}$ by atomic logarithmic schemes. This gives a presentation
$\{T_{ij}^k \}$ by atomic logarithmic schemes. This gives a presentation ![]() $\coprod {\Sigma (T_{ij}^k)}\rightrightarrows \coprod \Sigma (T_i)$ of
$\coprod {\Sigma (T_{ij}^k)}\rightrightarrows \coprod \Sigma (T_i)$ of ![]() $\Sigma (T)$. In particular, a morphism of cone complexes
$\Sigma (T)$. In particular, a morphism of cone complexes ![]() $\Sigma (T) \longrightarrow \Sigma (X)$ induces morphisms
$\Sigma (T) \longrightarrow \Sigma (X)$ induces morphisms ![]() $\Sigma (T_i) \longrightarrow \Sigma (X)$ compatible with the maps
$\Sigma (T_i) \longrightarrow \Sigma (X)$ compatible with the maps ![]() ${\Sigma (T_{ij}^k)} \longrightarrow \Sigma (T_i),\Sigma (T_j)$. Thus we obtain unique morphisms
${\Sigma (T_{ij}^k)} \longrightarrow \Sigma (T_i),\Sigma (T_j)$. Thus we obtain unique morphisms ![]() $T_i \longrightarrow \mathcal {A}_X$ compatible with the morphisms
$T_i \longrightarrow \mathcal {A}_X$ compatible with the morphisms ![]() ${T_{ij}^k} \longrightarrow T_i, T_j$, inducing a morphism
${T_{ij}^k} \longrightarrow T_i, T_j$, inducing a morphism ![]() $T \longrightarrow \mathcal {A}_X$.
$T \longrightarrow \mathcal {A}_X$.
Example 2.11 Let ![]() $X=\mathbb {A}^1$ with the toric log structure. Then
$X=\mathbb {A}^1$ with the toric log structure. Then ![]() $\mathcal {A}_X=\mathcal {A}_\mathbb {N} = [\mathbb {A}^1/\mathbb {G}_m]$. Given an ordinary scheme
$\mathcal {A}_X=\mathcal {A}_\mathbb {N} = [\mathbb {A}^1/\mathbb {G}_m]$. Given an ordinary scheme ![]() $\underline{T}$, a morphism
$\underline{T}$, a morphism ![]() $\underline{f}:\underline{T} \longrightarrow \mathcal {A}_X$ is equivalent to giving a strict log morphism
$\underline{f}:\underline{T} \longrightarrow \mathcal {A}_X$ is equivalent to giving a strict log morphism ![]() $T \longrightarrow \mathcal {A}_X$, by endowing
$T \longrightarrow \mathcal {A}_X$, by endowing ![]() $\underline{T}$ with the pull-back
$\underline{T}$ with the pull-back ![]() $f^*\mathcal {M}_{\mathcal {A}_\mathbb {N}}$ of the log structure on
$f^*\mathcal {M}_{\mathcal {A}_\mathbb {N}}$ of the log structure on ![]() $\mathcal {A}_\mathbb {N}$. From this point of view, the universal
$\mathcal {A}_\mathbb {N}$. From this point of view, the universal ![]() $\mathbb {G}_m$-torsor
$\mathbb {G}_m$-torsor ![]() $\mathcal {P}$ on
$\mathcal {P}$ on ![]() $\mathcal {A}_\mathbb {N}$ agrees with the
$\mathcal {A}_\mathbb {N}$ agrees with the ![]() $\mathbb {G}_m$-torsor subsheaf of
$\mathbb {G}_m$-torsor subsheaf of ![]() $\mathcal {M}_{\mathcal {A}_\mathbb {N}}$ defined by the generating section of
$\mathcal {M}_{\mathcal {A}_\mathbb {N}}$ defined by the generating section of ![]() $\overline{\mathcal {M}}_{\mathcal {A}_\mathbb {N}}$. Thus the pull-back log structure
$\overline{\mathcal {M}}_{\mathcal {A}_\mathbb {N}}$. Thus the pull-back log structure ![]() $\underline{f}^*\mathcal {M}_{\mathcal {A}_\mathbb {N}}$ is given by a line bundle
$\underline{f}^*\mathcal {M}_{\mathcal {A}_\mathbb {N}}$ is given by a line bundle ![]() $\mathcal {L}$ on
$\mathcal {L}$ on ![]() $\underline{T}$, the line bundle with associated torsor
$\underline{T}$, the line bundle with associated torsor ![]() $\mathcal {L}^\times = \underline{f}^* \mathcal {P}$, and a homomorphism
$\mathcal {L}^\times = \underline{f}^* \mathcal {P}$, and a homomorphism ![]() $\mathcal {L}\to \mathcal {O}_{\underline{T}}$ of
$\mathcal {L}\to \mathcal {O}_{\underline{T}}$ of ![]() $\mathcal {O}_{\underline{T}}$-modules defining the structure morphism, or its restriction to
$\mathcal {O}_{\underline{T}}$-modules defining the structure morphism, or its restriction to ![]() $\mathcal {L}^\times$. Conversely, the morphism
$\mathcal {L}^\times$. Conversely, the morphism ![]() $\underline{f}$ from
$\underline{f}$ from ![]() $\underline{T}$ to the quotient stack
$\underline{T}$ to the quotient stack ![]() $\mathcal {A}_\mathbb {N}= [\mathbb {A}^1/\mathbb {G}_m]$ can be recovered from
$\mathcal {A}_\mathbb {N}= [\mathbb {A}^1/\mathbb {G}_m]$ can be recovered from ![]() $\mathcal {L}\to \mathcal {O}_{\underline{T}}$ by the associated
$\mathcal {L}\to \mathcal {O}_{\underline{T}}$ by the associated ![]() $\mathbb {G}_m$-equivariant morphism from the
$\mathbb {G}_m$-equivariant morphism from the ![]() $\mathbb {G}_m$-torsor
$\mathbb {G}_m$-torsor ![]() $\operatorname {Spec}_{\underline{T}}\big (\bigoplus _{d\in \mathbb {Z}}\mathcal {L}^{\otimes -d}\big )$ to
$\operatorname {Spec}_{\underline{T}}\big (\bigoplus _{d\in \mathbb {Z}}\mathcal {L}^{\otimes -d}\big )$ to ![]() $\mathbb {A}^1_{\underline{T}}$.
$\mathbb {A}^1_{\underline{T}}$.
Thus for an arbitrary log structure ![]() $\mathcal {M}_T$ on
$\mathcal {M}_T$ on ![]() $\underline{T}$, a log morphism
$\underline{T}$, a log morphism ![]() $f:(\underline{T},\mathcal {M}_T) \longrightarrow \mathcal {A}_\mathbb {N}$ is the same data as the restriction of
$f:(\underline{T},\mathcal {M}_T) \longrightarrow \mathcal {A}_\mathbb {N}$ is the same data as the restriction of ![]() $\mathcal {M}_T\to \mathcal {O}_T$ to a
$\mathcal {M}_T\to \mathcal {O}_T$ to a ![]() $\mathbb {G}_m$-torsor subsheaf
$\mathbb {G}_m$-torsor subsheaf ![]() $\mathcal {L}^\times \subset \mathcal {M}_T$. Indeed, such an isomorphism yields the identification of
$\mathcal {L}^\times \subset \mathcal {M}_T$. Indeed, such an isomorphism yields the identification of ![]() $\underline{f}^*\mathcal {P}$ with a
$\underline{f}^*\mathcal {P}$ with a ![]() $\mathbb {G}_m$-torsor subsheaf
$\mathbb {G}_m$-torsor subsheaf ![]() $\mathcal {L}^\times \subset \mathcal {M}_T$, and the property of being a log morphism forces
$\mathcal {L}^\times \subset \mathcal {M}_T$, and the property of being a log morphism forces ![]() $\underline{f}$ to be associated to the restriction of the structure morphism
$\underline{f}$ to be associated to the restriction of the structure morphism ![]() $\mathcal {M}_T \longrightarrow \mathcal {O}_{\underline{T}}$ to
$\mathcal {M}_T \longrightarrow \mathcal {O}_{\underline{T}}$ to ![]() $\mathcal {L}^\times$.
$\mathcal {L}^\times$.
Now Proposition 2.10 assumes a log structure ![]() $\mathcal {M}_T$ on
$\mathcal {M}_T$ on ![]() $\underline{T}$ is already given and then says that the set of log morphisms
$\underline{T}$ is already given and then says that the set of log morphisms ![]() $T=(\underline{T},\mathcal {M}_T) \longrightarrow \mathcal {A}_X$ equals the set of morphisms
$T=(\underline{T},\mathcal {M}_T) \longrightarrow \mathcal {A}_X$ equals the set of morphisms ![]() $\Sigma (T)\to \mathbb {R}_{\ge 0}=\Sigma (X)$ of cone complexes. Indeed, such a morphism of cone complexes is equivalent to specifying
$\Sigma (T)\to \mathbb {R}_{\ge 0}=\Sigma (X)$ of cone complexes. Indeed, such a morphism of cone complexes is equivalent to specifying ![]() $\bar m\in \Gamma (T,\overline{\mathcal {M}}_T)$, and then the
$\bar m\in \Gamma (T,\overline{\mathcal {M}}_T)$, and then the ![]() $\mathbb {G}_m$-torsor subsheaf
$\mathbb {G}_m$-torsor subsheaf ![]() $\mathcal {L}^\times \subset \mathcal {M}_T$ is simply defined by the preimage of
$\mathcal {L}^\times \subset \mathcal {M}_T$ is simply defined by the preimage of ![]() $\bar m$ under
$\bar m$ under ![]() $\mathcal {M}_T\to \overline{\mathcal {M}}_T$.
$\mathcal {M}_T\to \overline{\mathcal {M}}_T$.
2.3 Stable logarithmic maps and their moduli
This section reviews the theory of stable logarithmic maps developed in [Reference Gross and SiebertGS13, Reference ChenChe14, Reference Abramovich and ChenAC14], emphasizing the tropical language from [Reference Gross and SiebertGS13]. Most references in the following are therefore to [Reference Gross and SiebertGS13], but of course all results have analogues in [Reference ChenChe14, Reference Abramovich and ChenAC14] under the slightly stronger assumption of global generatedness of ![]() $\overline{\mathcal {M}}_X$. Note that the restriction on global generatedness has been removed in [Reference Abramovich, Chen, Marcus and WiseACMW17] by base changing to a refinement of the Artin fan
$\overline{\mathcal {M}}_X$. Note that the restriction on global generatedness has been removed in [Reference Abramovich, Chen, Marcus and WiseACMW17] by base changing to a refinement of the Artin fan ![]() $\mathcal {A}_X$ of
$\mathcal {A}_X$ of ![]() $X$.
$X$.
2.3.1 Definition
We fix a log morphism ![]() $X \longrightarrow B$ with the logarithmic structure on
$X \longrightarrow B$ with the logarithmic structure on ![]() $X$ being defined in the Zariski topology. Recall the following from [Reference Gross and SiebertGS13, Definition 1.6].
$X$ being defined in the Zariski topology. Recall the following from [Reference Gross and SiebertGS13, Definition 1.6].
Definition 2.12 A stable logarithmic map ![]() $(C/S,\mathbf {p}, f)$ is a commutative diagram
$(C/S,\mathbf {p}, f)$ is a commutative diagram

where the following hold.
(i)
 $\pi :C \longrightarrow S$ is a proper, logarithmically smooth and integral morphism of log schemes together with a tuple of sections
$\pi :C \longrightarrow S$ is a proper, logarithmically smooth and integral morphism of log schemes together with a tuple of sections  ${\mathbf {p}}=(p_1,\ldots ,p_{k})$ of
${\mathbf {p}}=(p_1,\ldots ,p_{k})$ of  $\underline {\pi }$ such that every geometric fibre of
$\underline {\pi }$ such that every geometric fibre of  $\pi$ is a reduced and connected curve, and if
$\pi$ is a reduced and connected curve, and if  $U\subset \underline {C}$ is the non-critical locus of
$U\subset \underline {C}$ is the non-critical locus of  $\underline {\pi }$ then
$\underline {\pi }$ then  $\overline{\mathcal{M}}_C|_U \simeq \underline {\pi }^*\overline{\mathcal{M}}_S\oplus \bigoplus _{i=1}^{k}p_{i*}\mathbb {N}_S$.
$\overline{\mathcal{M}}_C|_U \simeq \underline {\pi }^*\overline{\mathcal{M}}_S\oplus \bigoplus _{i=1}^{k}p_{i*}\mathbb {N}_S$.(ii) For every geometric point
 $\bar s \longrightarrow \underline {S}$, the restriction of
$\bar s \longrightarrow \underline {S}$, the restriction of  $\underline {f}$ to
$\underline {f}$ to  $\underline {C}_{\bar s}$ together with
$\underline {C}_{\bar s}$ together with  ${\mathbf {p}}$ is an ordinary stable map.
${\mathbf {p}}$ is an ordinary stable map.
2.3.2 Basic maps
The crucial concept for defining moduli of stable logarithmic maps is the notion of basic stable logarithmic maps. To explain this in tropical terms, we begin by summarizing the discussion of [Reference Gross and SiebertGS13, § 1] where more details are available. The terminology used in [Reference ChenChe14, Reference Abramovich and ChenAC14] is minimal stable logarithmic maps.
2.3.3 Induced maps of monoids
Suppose given ![]() $(C/S, \mathbf {p}, f)$ a stable logarithmic map with
$(C/S, \mathbf {p}, f)$ a stable logarithmic map with ![]() $S=\operatorname {Spec}(Q' \longrightarrow \Bbbk )$, with
$S=\operatorname {Spec}(Q' \longrightarrow \Bbbk )$, with ![]() $Q'$ an arbitrary sharp fs monoid and
$Q'$ an arbitrary sharp fs monoid and ![]() $\Bbbk$ an algebraically closed field. We will use the convention that a point denoted
$\Bbbk$ an algebraically closed field. We will use the convention that a point denoted ![]() $p\in C$ is always a marked point, and a point denoted
$p\in C$ is always a marked point, and a point denoted ![]() $q\in C$ is always a nodal point. Denoting
$q\in C$ is always a nodal point. Denoting ![]() $\underline {Q}' = \pi ^{-1} Q'$, the morphism
$\underline {Q}' = \pi ^{-1} Q'$, the morphism ![]() $\pi ^\flat$ of logarithmic structures induces a homomorphism of sheaves of monoids
$\pi ^\flat$ of logarithmic structures induces a homomorphism of sheaves of monoids ![]() $\psi = \bar \pi ^\flat :\underline {Q}' \longrightarrow \overline{\mathcal{M}}_{C}$. Similarly
$\psi = \bar \pi ^\flat :\underline {Q}' \longrightarrow \overline{\mathcal{M}}_{C}$. Similarly ![]() $f^\flat$ induces
$f^\flat$ induces ![]() $\varphi = \bar f^\flat :f^{-1}\overline{\mathcal{M}}_X \longrightarrow \overline{\mathcal{M}}_{C}$.
$\varphi = \bar f^\flat :f^{-1}\overline{\mathcal{M}}_X \longrightarrow \overline{\mathcal{M}}_{C}$.
2.3.4 Structure of  $\psi$
$\psi$
The homomorphism ![]() $\psi$ is an isomorphism when restricted to the complement of the special (nodal or marked) points of
$\psi$ is an isomorphism when restricted to the complement of the special (nodal or marked) points of ![]() $C$. The sheaf
$C$. The sheaf ![]() $\overline{\mathcal{M}}_C$ has stalks
$\overline{\mathcal{M}}_C$ has stalks ![]() $Q'\oplus \mathbb {N}$ and
$Q'\oplus \mathbb {N}$ and ![]() $Q'\oplus _{\mathbb {N}}\mathbb {N}^2$ at marked points and nodal points, respectively. The latter fibred sum is determined by a map
$Q'\oplus _{\mathbb {N}}\mathbb {N}^2$ at marked points and nodal points, respectively. The latter fibred sum is determined by a map
and the diagonal map ![]() $\mathbb {N} \longrightarrow \mathbb {N}^2$, see [Reference Gross and SiebertGS13, Definition 1.5]. The map
$\mathbb {N} \longrightarrow \mathbb {N}^2$, see [Reference Gross and SiebertGS13, Definition 1.5]. The map ![]() $\psi$ at these special points is given by the inclusion
$\psi$ at these special points is given by the inclusion ![]() $Q' \longrightarrow Q'\oplus \mathbb {N}$ and
$Q' \longrightarrow Q'\oplus \mathbb {N}$ and ![]() $Q' \longrightarrow Q'\oplus _{\mathbb {N}}\mathbb {N}^2$ into the first component for marked and nodal points, respectively.
$Q' \longrightarrow Q'\oplus _{\mathbb {N}}\mathbb {N}^2$ into the first component for marked and nodal points, respectively.
2.3.5 Structure of  $\varphi$
$\varphi$
For ![]() $\bar x\in C$ a geometric point with underlying scheme-theoretic point
$\bar x\in C$ a geometric point with underlying scheme-theoretic point ![]() $x$, the map
$x$, the map ![]() $\varphi$ induces maps
$\varphi$ induces maps ![]() $\varphi _{\bar x}:P_{x} \longrightarrow \overline{\mathcal{M}}_{C,\bar x}$ for
$\varphi _{\bar x}:P_{x} \longrightarrow \overline{\mathcal{M}}_{C,\bar x}$ for
Note that ![]() $\overline{\mathcal{M}}_{X,\underline{f}(\bar x)}$ is independent of the choice of
$\overline{\mathcal{M}}_{X,\underline{f}(\bar x)}$ is independent of the choice of ![]() $\bar x \longrightarrow x$ since the logarithmic structure on
$\bar x \longrightarrow x$ since the logarithmic structure on ![]() $X$ is Zariski. Following Discussion 1.8 of [Reference Gross and SiebertGS13], we have the following behaviour at three types of points on
$X$ is Zariski. Following Discussion 1.8 of [Reference Gross and SiebertGS13], we have the following behaviour at three types of points on ![]() $C$.
$C$.
(i)
 $x=\eta$ is a generic point, giving a local homomorphismFootnote 2 of monoids
(2.6)
$x=\eta$ is a generic point, giving a local homomorphismFootnote 2 of monoids
(2.6) \begin{equation} \varphi_{\bar\eta}:P_{\eta}\longrightarrow Q'. \end{equation}
\begin{equation} \varphi_{\bar\eta}:P_{\eta}\longrightarrow Q'. \end{equation}(ii)
 $x=p$ is a marked point, giving the composition
(2.7)The element
$x=p$ is a marked point, giving the composition
(2.7)The element \begin{equation} u_p:P_p\stackrel{\varphi_{\bar p}}{\longrightarrow} Q'\oplus\mathbb{N}\stackrel{\operatorname{pr}_2}{\longrightarrow} \mathbb{N}. \end{equation}
\begin{equation} u_p:P_p\stackrel{\varphi_{\bar p}}{\longrightarrow} Q'\oplus\mathbb{N}\stackrel{\operatorname{pr}_2}{\longrightarrow} \mathbb{N}. \end{equation} $u_p\in P_p^{\vee }$ is called the contact order at
$u_p\in P_p^{\vee }$ is called the contact order at  $p$.
$p$.(iii)
 $x=q$ is a node contained in the closures of
$x=q$ is a node contained in the closures of  $\eta _1$,
$\eta _1$,  $\eta _2$. If
$\eta _2$. If  $\chi _i:P_q \longrightarrow P_{\eta _i}$ are the generization maps there exists a homomorphism
called contact order at
$\chi _i:P_q \longrightarrow P_{\eta _i}$ are the generization maps there exists a homomorphism
called contact order at \[ u_q:P_q \longrightarrow \mathbb{Z}, \]
\[ u_q:P_q \longrightarrow \mathbb{Z}, \] $q$, such that
(2.8)with
$q$, such that
(2.8)with \begin{equation} \varphi_{\bar\eta_2}(\chi_2(m))-\varphi_{\bar \eta_1}(\chi_1(m) )=u_q(m)\cdot \rho_q, \end{equation}
\begin{equation} \varphi_{\bar\eta_2}(\chi_2(m))-\varphi_{\bar \eta_1}(\chi_1(m) )=u_q(m)\cdot \rho_q, \end{equation} $\rho _q\neq 0$ given in (2.5), see [Reference Gross and SiebertGS13, (1.8)]. The maps
$\rho _q\neq 0$ given in (2.5), see [Reference Gross and SiebertGS13, (1.8)]. The maps  $\varphi _{\bar \eta }\circ \chi _i$ and
$\varphi _{\bar \eta }\circ \chi _i$ and  $u_q$ are equivalent to providing the local homomorphism
$u_q$ are equivalent to providing the local homomorphism  $\varphi _{\bar q}:P_q \longrightarrow Q'\oplus _{\mathbb {N}} \mathbb {N}^2$.
$\varphi _{\bar q}:P_q \longrightarrow Q'\oplus _{\mathbb {N}} \mathbb {N}^2$.
The choice of ordering ![]() $\eta _1,\eta _2$ for the branches of
$\eta _1,\eta _2$ for the branches of ![]() $C$ containing a node is called an orientation of the node. We note that reversing the orientation of a node
$C$ containing a node is called an orientation of the node. We note that reversing the orientation of a node ![]() $q$ (by interchanging
$q$ (by interchanging ![]() $\eta _1$ and
$\eta _1$ and ![]() $\eta _2$) results in reversing the sign of
$\eta _2$) results in reversing the sign of ![]() $u_q$.
$u_q$.
2.3.6 Dual graphs and combinatorial type
In this paper, a graph ![]() $G$ consists of a set of vertices
$G$ consists of a set of vertices ![]() $V(G)$, a set of edges
$V(G)$, a set of edges ![]() $E(G)$ and a separate set of legs or half-edges
$E(G)$ and a separate set of legs or half-edges ![]() $L(G)$, with appropriate incidence relations between vertices and edges, and between vertices and half-edges. We admit multiple edges, loops and legs. In order to obtain the correct notion of automorphisms, we also implicitly use the convention that every edge
$L(G)$, with appropriate incidence relations between vertices and edges, and between vertices and half-edges. We admit multiple edges, loops and legs. In order to obtain the correct notion of automorphisms, we also implicitly use the convention that every edge ![]() $E \in E(G)$ of
$E \in E(G)$ of ![]() $G$ is a pair of orientations of
$G$ is a pair of orientations of ![]() $E$ or a pair of half-edges of
$E$ or a pair of half-edges of ![]() $E$ (disjoint from
$E$ (disjoint from ![]() $L(G)$), so that the automorphism group of a graph with a single loop is
$L(G)$), so that the automorphism group of a graph with a single loop is ![]() $\mathbb {Z}/2\mathbb {Z}$.
$\mathbb {Z}/2\mathbb {Z}$.
Given a stable logarithmic map ![]() $(C/S,\mathbf {p},f)$ over a logarithmic point, let
$(C/S,\mathbf {p},f)$ over a logarithmic point, let ![]() $G_C$ be the dual intersection graph of
$G_C$ be the dual intersection graph of ![]() $C$. This is the graph which has a vertex
$C$. This is the graph which has a vertex ![]() $v_{\eta }$ for each generic point
$v_{\eta }$ for each generic point ![]() $\eta$ of
$\eta$ of ![]() $C$, an edge
$C$, an edge ![]() $E_q$ joining
$E_q$ joining ![]() $v_{\eta _1}, v_{\eta _2}$ for each node
$v_{\eta _1}, v_{\eta _2}$ for each node ![]() $q$ contained in the closures of both
$q$ contained in the closures of both ![]() $\eta _1$ and
$\eta _1$ and ![]() $\eta _2$, and where
$\eta _2$, and where ![]() $E_q$ is a loop if
$E_q$ is a loop if ![]() $q$ is a double point in an irreducible component of
$q$ is a double point in an irreducible component of ![]() $C$. Note that an ordering of the two branches of
$C$. Note that an ordering of the two branches of ![]() $\underline{C}$ at a node gives rise to an orientation on the corresponding edge. Finally,
$\underline{C}$ at a node gives rise to an orientation on the corresponding edge. Finally, ![]() $G_C$ has a leg
$G_C$ has a leg ![]() $L_p$ with endpoint
$L_p$ with endpoint ![]() $v_{\eta }$ for each marked point
$v_{\eta }$ for each marked point ![]() $p$ contained in the closure of
$p$ contained in the closure of ![]() $\eta$. Occasionally we view
$\eta$. Occasionally we view ![]() $V(G), E(G)$ and
$V(G), E(G)$ and ![]() $L(G)$ as subsets of
$L(G)$ as subsets of ![]() $C$ and then write
$C$ and then write ![]() $x\in C$ for a vertex, edge or leg of
$x\in C$ for a vertex, edge or leg of ![]() $G$ corresponding to a generic point, node or marked point of
$G$ corresponding to a generic point, node or marked point of ![]() $C$ respectively.
$C$ respectively.
Definition 2.13 Let ![]() $(C/S,\mathbf {p},f)$ be a stable logarithmic map over a logarithmic point
$(C/S,\mathbf {p},f)$ be a stable logarithmic map over a logarithmic point ![]() $S=\operatorname {Spec}(Q \longrightarrow \Bbbk )$. The combinatorial type of
$S=\operatorname {Spec}(Q \longrightarrow \Bbbk )$. The combinatorial type of ![]() $(C/S,\mathbf {p},f)$ consists of the following data:
$(C/S,\mathbf {p},f)$ consists of the following data:
(1) the dual intersection graph
 $G=G_C$ of
$G=G_C$ of  $C$;
$C$;(2) the genus functionFootnote 3
 $\mathbf {g}: V(G) \longrightarrow \mathbb {N}$ associating to
$\mathbf {g}: V(G) \longrightarrow \mathbb {N}$ associating to  $v\in V(G)$ the genus of the irreducible component
$v\in V(G)$ the genus of the irreducible component  $C(v)\subset C$;
$C(v)\subset C$;(3) the map
 $\boldsymbol {\sigma }: V(G)\cup E(G)\cup L(G) \longrightarrow \Sigma (X)$ mapping
$\boldsymbol {\sigma }: V(G)\cup E(G)\cup L(G) \longrightarrow \Sigma (X)$ mapping  $x\in C$ to
$x\in C$ to  $\big (\overline{\mathcal {M}}_{X,f(x)}\big )_\mathbb {R}^\vee \in \Sigma (X)$;
$\big (\overline{\mathcal {M}}_{X,f(x)}\big )_\mathbb {R}^\vee \in \Sigma (X)$;(4) the contact data
 $\mathbf {u}=\{u_p,u_q\}$ at marked points
$\mathbf {u}=\{u_p,u_q\}$ at marked points  $p$ and nodes
$p$ and nodes  $q$ of
$q$ of  $C$.
$C$.
2.3.7 The basic monoid
Given a combinatorial type of a stable logarithmic map ![]() $(C/S,\mathbf {p},f)$, we define a monoid
$(C/S,\mathbf {p},f)$, we define a monoid ![]() $Q$ by first defining its dual
$Q$ by first defining its dual
Here the sum is over generic points ![]() $\eta$ of
$\eta$ of ![]() $C$ and nodes
$C$ and nodes ![]() $q$ of
$q$ of ![]() $C$. Readers with background in tropical geometry should recognize this monoid as the moduli cone of tropical curves of fixed combinatorial type, as will be discussed in § 2.5. We then set
$C$. Readers with background in tropical geometry should recognize this monoid as the moduli cone of tropical curves of fixed combinatorial type, as will be discussed in § 2.5. We then set
It is shown in [Reference Gross and SiebertGS13, § 1.5], that ![]() $Q$ is a sharp monoid, fine and saturated by construction as the dual of a finitely generated submonoid of a free abelian group. Note also that
$Q$ is a sharp monoid, fine and saturated by construction as the dual of a finitely generated submonoid of a free abelian group. Note also that ![]() $Q$ indeed only depends on the combinatorial type of
$Q$ indeed only depends on the combinatorial type of ![]() $(C/S,\mathbf {p},f)$.
$(C/S,\mathbf {p},f)$.
Given a stable logarithmic map ![]() $(C'/S',\mathbf {p}',f')$ over
$(C'/S',\mathbf {p}',f')$ over ![]() $S'=\operatorname {Spec}(Q' \longrightarrow \Bbbk )$ of the same combinatorial type, we obtain a canonically defined map
$S'=\operatorname {Spec}(Q' \longrightarrow \Bbbk )$ of the same combinatorial type, we obtain a canonically defined map
which is most easily defined as the transpose of the map
with ![]() $\varphi _{\bar \eta }$ and
$\varphi _{\bar \eta }$ and ![]() $\rho _q$ defined in (2.6) and (2.5), respectively.
$\rho _q$ defined in (2.6) and (2.5), respectively.
Definition 2.14 (Basic maps) Let ![]() $(C/S, \mathbf {p}, f)$ be a stable logarithmic map. We say
$(C/S, \mathbf {p}, f)$ be a stable logarithmic map. We say ![]() $f$ is basic if at every geometric point
$f$ is basic if at every geometric point ![]() $\bar s$ of
$\bar s$ of ![]() $S$, the map
$S$, the map ![]() $Q \longrightarrow Q'=\overline{\mathcal {M}}_{S,\bar s}$ from (2.10) defined by the restriction
$Q \longrightarrow Q'=\overline{\mathcal {M}}_{S,\bar s}$ from (2.10) defined by the restriction ![]() $(C_{\bar s}/\bar s, \mathbf {p}_{\bar s}, f|_{C_{\bar s}})$ is an isomorphism.
$(C_{\bar s}/\bar s, \mathbf {p}_{\bar s}, f|_{C_{\bar s}})$ is an isomorphism.
2.3.8 Degree data and class
In what follows, ![]() $H_2^+(X)$ denotes a semigroup carrying degree data for curves in
$H_2^+(X)$ denotes a semigroup carrying degree data for curves in ![]() $X$, which are locally constant in flat families, such as effective
$X$, which are locally constant in flat families, such as effective ![]() $1$-cycles on
$1$-cycles on ![]() $X$ modulo algebraic or numerical equivalence or, working over
$X$ modulo algebraic or numerical equivalence or, working over ![]() $\mathbb {C}$, classes in singular homology
$\mathbb {C}$, classes in singular homology ![]() $H_2(X,\mathbb {Z})$ pairing non-negatively with a Kähler form. We require that the moduli spaces of ordinary stable maps of fixed curve class, genus and number of marked points are of finite type.
$H_2(X,\mathbb {Z})$ pairing non-negatively with a Kähler form. We require that the moduli spaces of ordinary stable maps of fixed curve class, genus and number of marked points are of finite type.
Definition 2.15 A class ![]() $\beta$ of stable logarithmic maps to
$\beta$ of stable logarithmic maps to ![]() $X$ consists of the following:
$X$ consists of the following:
(i) the data
 $\underline {\beta }$ of an underlying ordinary stable map, i.e. the genus
$\underline {\beta }$ of an underlying ordinary stable map, i.e. the genus  $g$, a curve class
$g$, a curve class  $A\in H_2^+(X)$, and the number of marked points
$A\in H_2^+(X)$, and the number of marked points  $k$;
$k$;(ii) integral elements
 $u_{p_1},\ldots ,u_{p_k}\in |\Sigma (X)|$.Footnote 4
$u_{p_1},\ldots ,u_{p_k}\in |\Sigma (X)|$.Footnote 4
We say a stable logarithmic map ![]() $(C/S,\mathbf {p},f)$ is of class
$(C/S,\mathbf {p},f)$ is of class ![]() $\beta$ if two conditions are satisfied. First, the underlying ordinary stable map must be of type
$\beta$ if two conditions are satisfied. First, the underlying ordinary stable map must be of type ![]() $\underline{\beta} =(g,A,k)$. Second, define the closed subset
$\underline{\beta} =(g,A,k)$. Second, define the closed subset ![]() $\underline{Z}_i\subset \underline{X}$ to be the union of strata with generic points
$\underline{Z}_i\subset \underline{X}$ to be the union of strata with generic points ![]() $\eta$ such that
$\eta$ such that ![]() $u_{p_i}$ lies in the image of
$u_{p_i}$ lies in the image of ![]() $\sigma _{\eta } \longrightarrow |\Sigma (X)|$. Then for any
$\sigma _{\eta } \longrightarrow |\Sigma (X)|$. Then for any ![]() $i$ we have
$i$ we have ![]() $\operatorname {im}(\underline {f}\circ p_i)\subset \underline {Z}_i$ and for any geometric point
$\operatorname {im}(\underline {f}\circ p_i)\subset \underline {Z}_i$ and for any geometric point ![]() $\bar s \longrightarrow \underline {S}$ such that
$\bar s \longrightarrow \underline {S}$ such that ![]() $p_i(\bar s)$ lies in the stratum of
$p_i(\bar s)$ lies in the stratum of ![]() $X$ with generic point
$X$ with generic point ![]() $\eta$, there exists
$\eta$, there exists ![]() $u\in \sigma _\eta ={\operatorname {Hom}}(\overline{\mathcal {M}}_{X,\bar \eta },\mathbb {N})$ mapping to
$u\in \sigma _\eta ={\operatorname {Hom}}(\overline{\mathcal {M}}_{X,\bar \eta },\mathbb {N})$ mapping to ![]() $u_{p_i}\in |\Sigma (X)|$ making the following diagram commute.
$u_{p_i}\in |\Sigma (X)|$ making the following diagram commute.

Here ![]() $\chi$ is the generization map. In particular,
$\chi$ is the generization map. In particular, ![]() $s_i$ specifies the contact order
$s_i$ specifies the contact order ![]() $u_{p_i}$ at the marked point
$u_{p_i}$ at the marked point ![]() $p_i(\bar s)$ as defined in (2.7).
$p_i(\bar s)$ as defined in (2.7).
We emphasize that the class ![]() $\beta$ does not specify the contact orders
$\beta$ does not specify the contact orders ![]() $u_q$ at nodes.
$u_q$ at nodes.
Definition 2.16 Let ![]() $\mathscr {M}(X/B,\beta )$ denote the stack of basic stable logarithmic maps of class
$\mathscr {M}(X/B,\beta )$ denote the stack of basic stable logarithmic maps of class ![]() $\beta$. This is the category whose objects are basic stable logarithmic maps
$\beta$. This is the category whose objects are basic stable logarithmic maps ![]() $(C/S,\mathbf {p},f)$ of class
$(C/S,\mathbf {p},f)$ of class ![]() $\beta$, and whose morphisms
$\beta$, and whose morphisms ![]() $(C/S,\mathbf {p},f) \longrightarrow (C'/S',\mathbf {p}',f')$ are commutative diagrams
$(C/S,\mathbf {p},f) \longrightarrow (C'/S',\mathbf {p}',f')$ are commutative diagrams

with the left-hand square cartesian, ![]() $S \longrightarrow S'$ strict, and
$S \longrightarrow S'$ strict, and ![]() $f=f'\circ g$,
$f=f'\circ g$, ![]() $g\circ {\mathbf {p}}= {\mathbf {p}}'\circ h$.
$g\circ {\mathbf {p}}= {\mathbf {p}}'\circ h$.
Theorem 2.17 If ![]() $X \longrightarrow B$ is proper, then
$X \longrightarrow B$ is proper, then ![]() $\mathscr {M}(X/B,\beta )$ is a proper Deligne–Mumford stack. If furthermore
$\mathscr {M}(X/B,\beta )$ is a proper Deligne–Mumford stack. If furthermore ![]() $X \longrightarrow B$ is logarithmically smooth, then
$X \longrightarrow B$ is logarithmically smooth, then ![]() $\mathscr {M}(X/B,\beta )$ carries a perfect obstruction theory, defining a virtual fundamental class
$\mathscr {M}(X/B,\beta )$ carries a perfect obstruction theory, defining a virtual fundamental class ![]() $[\mathscr {M}(X/B,\beta )]^{{\operatorname {virt}}}$ in the rational Chow group of
$[\mathscr {M}(X/B,\beta )]^{{\operatorname {virt}}}$ in the rational Chow group of ![]() $\mathscr {M}(X/B,\beta )$.
$\mathscr {M}(X/B,\beta )$.
Proof. Under the given assumption that ![]() $X$ is a Zariski log scheme, [Reference Gross and SiebertGS13, Theorem 2.4] proves that
$X$ is a Zariski log scheme, [Reference Gross and SiebertGS13, Theorem 2.4] proves that ![]() $\mathscr {M}(X/B,\beta )$ is a Deligne–Mumford stack. Properness was shown in [Reference Gross and SiebertGS13, Theorem 2.4] under a technical assumption, and in general in [Reference Abramovich, Chen, Marcus and WiseACMW17].
$\mathscr {M}(X/B,\beta )$ is a Deligne–Mumford stack. Properness was shown in [Reference Gross and SiebertGS13, Theorem 2.4] under a technical assumption, and in general in [Reference Abramovich, Chen, Marcus and WiseACMW17].
The existence of a perfect obstruction theory when ![]() $X \longrightarrow B$ is logarithmically smooth was proved in [Reference Gross and SiebertGS13, § 5].
$X \longrightarrow B$ is logarithmically smooth was proved in [Reference Gross and SiebertGS13, § 5].
2.4 Stacks of pre-stable logarithmic curves
For the obstruction theory in Theorem 2.17 one works over the Artin stack ![]() $\mathfrak {M}_B$ of pre-stable logarithmically smooth curves defined over
$\mathfrak {M}_B$ of pre-stable logarithmically smooth curves defined over ![]() $B$. Since this stack will be important later on, let us briefly recall its construction. First, working over a field
$B$. Since this stack will be important later on, let us briefly recall its construction. First, working over a field ![]() $\Bbbk$, there is a stack
$\Bbbk$, there is a stack ![]() ${\mathbf {M}}$ of pre-stable basic logarithmic curves over
${\mathbf {M}}$ of pre-stable basic logarithmic curves over ![]() $\operatorname {Spec}\Bbbk$, essentially constructed by Kato in [Reference KatoKat00]. Endowing
$\operatorname {Spec}\Bbbk$, essentially constructed by Kato in [Reference KatoKat00]. Endowing ![]() ${\mathbf {M}}$ with its basic log structure, the fibre product
${\mathbf {M}}$ with its basic log structure, the fibre product ![]() ${\mathbf {M}}\times _{\operatorname {Spec}\Bbbk } B$ in the category of log stacks is a fs log stack. We can then define
${\mathbf {M}}\times _{\operatorname {Spec}\Bbbk } B$ in the category of log stacks is a fs log stack. We can then define ![]() $\mathfrak {M}_B$ using Olsson's stack over
$\mathfrak {M}_B$ using Olsson's stack over ![]() ${\mathbf {M}}\times B$:
${\mathbf {M}}\times B$:
Indeed, an object in this stack is a log scheme ![]() $T$ with two morphisms
$T$ with two morphisms ![]() $T\to {\mathbf {M}}$ and
$T\to {\mathbf {M}}$ and ![]() $T \longrightarrow B$. The corresponding pre-stable log smooth curve over
$T \longrightarrow B$. The corresponding pre-stable log smooth curve over ![]() $T$ is the logarithmic pull-back to
$T$ is the logarithmic pull-back to ![]() $T$ of the universal pre-stable curve over
$T$ of the universal pre-stable curve over ![]() ${\mathbf {M}}$.
${\mathbf {M}}$.
We also consider the following refinements of ![]() $\mathbf {M}$ introduced in [Reference Behrend and ManinBM96, Definition 2.6] and further discussed in [Reference BehrendBeh97, p. 603]. Let
$\mathbf {M}$ introduced in [Reference Behrend and ManinBM96, Definition 2.6] and further discussed in [Reference BehrendBeh97, p. 603]. Let ![]() $G$ be a graph decorated by a map
$G$ be a graph decorated by a map
associating to each vertex its genus. Then there is an algebraic stack
with objects over a ![]() $B$-scheme
$B$-scheme ![]() $S$ given by:
$S$ given by:
(1) for each
 $v\in V(G)$, a family of pre-stable curves
$v\in V(G)$, a family of pre-stable curves  $C_v\to S$ of genus
$C_v\to S$ of genus  $\mathbf {g}(v)$, together with marked sections
$\mathbf {g}(v)$, together with marked sections  $x_L:S\to C_v$ defined by the legs
$x_L:S\to C_v$ defined by the legs  $L\in L(G)$ with
$L\in L(G)$ with  $v\in L$;
$v\in L$;(2) for each edge
 $E\in E(G)$ with vertices
$E\in E(G)$ with vertices  $v,w$, a pair of marked sections
$v,w$, a pair of marked sections  $y_v, y_w$ of
$y_v, y_w$ of  $C_v\to S$,
$C_v\to S$,  $C_w\to S$, respectively.
$C_w\to S$, respectively.
All marked sections are required to be mutually disjoint and to have image in the non-critical locus of ![]() $\coprod _v C_v \longrightarrow S$. Taking the fibred sum of
$\coprod _v C_v \longrightarrow S$. Taking the fibred sum of ![]() $\coprod _v C_v$ along the pairs of marked sections associated to the edges, we may as well view the objects of
$\coprod _v C_v$ along the pairs of marked sections associated to the edges, we may as well view the objects of ![]() $\mathbf {M}(G,\mathbf {g})$ as families of marked nodal curves
$\mathbf {M}(G,\mathbf {g})$ as families of marked nodal curves
from this point of view, each edge ![]() $E$ defines a nodal section
$E$ defines a nodal section ![]() $y_E:S\to C$ and each vertex a closed embedding
$y_E:S\to C$ and each vertex a closed embedding ![]() $C_v\to C$ of a family of pre-stable curves of genus
$C_v\to C$ of a family of pre-stable curves of genus ![]() $g(v)$ and with image a union of irreducible components. Thus we have a morphism of algebraic stacks
$g(v)$ and with image a union of irreducible components. Thus we have a morphism of algebraic stacks
turning ![]() $\textbf {M}(G,\mathbf {g})$ into a logarithmic algebraic stack by pulling back the log structure from
$\textbf {M}(G,\mathbf {g})$ into a logarithmic algebraic stack by pulling back the log structure from ![]() $\textbf {M}$. Note that on the level of the underlying stacks, (2.13) induces the identification of the stack quotient
$\textbf {M}$. Note that on the level of the underlying stacks, (2.13) induces the identification of the stack quotient ![]() $[\mathbf {M}(G,\mathbf {g})/ \operatorname {Aut}(G,\mathbf {g})]$ with the normalization of a closed substack of
$[\mathbf {M}(G,\mathbf {g})/ \operatorname {Aut}(G,\mathbf {g})]$ with the normalization of a closed substack of ![]() $\mathbf {M}$, defining the well-known stratified structure of
$\mathbf {M}$, defining the well-known stratified structure of ![]() $\mathbf {M}$. See [Reference Arbarello, Cornalba and GriffithsACG11, XII, § 10] for a detailed discussion. Now define
$\mathbf {M}$. See [Reference Arbarello, Cornalba and GriffithsACG11, XII, § 10] for a detailed discussion. Now define
An important feature of the collection of stacks ![]() $\mathbf {M}(G,\mathbf {g})$ and in turn of
$\mathbf {M}(G,\mathbf {g})$ and in turn of ![]() $\mathfrak {M}_B(G,\mathbf {g})$ is their functorial behaviour under contraction morphisms of decorated graphs
$\mathfrak {M}_B(G,\mathbf {g})$ is their functorial behaviour under contraction morphisms of decorated graphs
that is, an isomorphism of ![]() $G'$ with the graph
$G'$ with the graph ![]() $G/E_\phi$ contracting a subset of edges
$G/E_\phi$ contracting a subset of edges ![]() $E_\phi \subset E(G)$ such thatFootnote 5
$E_\phi \subset E(G)$ such thatFootnote 5
holds for all ![]() $v'\in V(G')$ [Reference Behrend and ManinBM96, Definition 1.3]. Here
$v'\in V(G')$ [Reference Behrend and ManinBM96, Definition 1.3]. Here ![]() $V(\phi ):V(G) \longrightarrow V(G')$ is the surjection on the set of vertices defined by
$V(\phi ):V(G) \longrightarrow V(G')$ is the surjection on the set of vertices defined by ![]() $\phi$, and we have in addition a compatible inclusion
$\phi$, and we have in addition a compatible inclusion ![]() $E(\phi ): E(G')\smash {\mathop {\longrightarrow }\limits ^{\simeq }} E(G)\setminus E_\phi \subset E(G)$ of the sets of edges and a bijection
$E(\phi ): E(G')\smash {\mathop {\longrightarrow }\limits ^{\simeq }} E(G)\setminus E_\phi \subset E(G)$ of the sets of edges and a bijection ![]() $L(\phi ):L(G')\to L(G)$ on the sets of legs. This notion of morphism captures the behaviour of the combinatorial type of pre-stable curves under generization and is indeed compatible with the finite maps (2.13) to
$L(\phi ):L(G')\to L(G)$ on the sets of legs. This notion of morphism captures the behaviour of the combinatorial type of pre-stable curves under generization and is indeed compatible with the finite maps (2.13) to ![]() $\mathbf {M}$.
$\mathbf {M}$.
Proposition 2.18 For any contraction morphism ![]() $(G,\mathbf {g}) \longrightarrow (G',\mathbf {g}')$ of genus-decorated graphs, there are finite unramified morphisms of ordinary stacks
$(G,\mathbf {g}) \longrightarrow (G',\mathbf {g}')$ of genus-decorated graphs, there are finite unramified morphisms of ordinary stacks ![]() $\mathbf {M}(G,\mathbf {g}) \longrightarrow \mathbf {M}(G',\mathbf {g}')$ and
$\mathbf {M}(G,\mathbf {g}) \longrightarrow \mathbf {M}(G',\mathbf {g}')$ and
Proof. By base change and the definition of the log structures it is enough to prove the statement for the morphism of stacks underlying ![]() $\mathbf {M}(G,\mathbf {g}) \longrightarrow \mathbf {M}(G',\mathbf {g}')$. In this case the statement follows by iterated application of the clutching morphisms of [Reference KnudsenKnu83, Corollary 3.9].
$\mathbf {M}(G,\mathbf {g}) \longrightarrow \mathbf {M}(G',\mathbf {g}')$. In this case the statement follows by iterated application of the clutching morphisms of [Reference KnudsenKnu83, Corollary 3.9].
We emphasize that Proposition 2.18 is purely on the level of stacks with no log structures involved. Incorporating log structures in the picture is more subtle and is part of the gluing formalism developed in [Reference Abramovich, Chen, Gross and SiebertACGS20].
2.5 The tropical interpretation
The basic monoid ![]() $Q$ was originally derived from its tropical interpretation, which will play an important role here. We review this in our general setting. Given a stable logarithmic map
$Q$ was originally derived from its tropical interpretation, which will play an important role here. We review this in our general setting. Given a stable logarithmic map ![]() $(C/S,\mathbf {p},f)$, we obtain an associated diagram of cone complexes.
$(C/S,\mathbf {p},f)$, we obtain an associated diagram of cone complexes.

This diagram can be viewed as giving a family of tropical curves mapping to ![]() $\Sigma (X)$, parameterized by the cone complex
$\Sigma (X)$, parameterized by the cone complex ![]() $\Sigma (S)$. Indeed, a fibre of
$\Sigma (S)$. Indeed, a fibre of ![]() $\Sigma (\pi )$ is a graph and the restriction of
$\Sigma (\pi )$ is a graph and the restriction of ![]() $\Sigma (f)$ to such a fibre can be viewed as a tropical curve mapping to
$\Sigma (f)$ to such a fibre can be viewed as a tropical curve mapping to ![]() $\Sigma (X)$. We make this precise.
$\Sigma (X)$. We make this precise.
To avoid difficulties in notation, we shall assume that ![]() $X$ is simple (Definition 2.1). This is not a restrictive assumption in this paper since we assume
$X$ is simple (Definition 2.1). This is not a restrictive assumption in this paper since we assume ![]() $X$ to be log smooth over the trivial log point
$X$ to be log smooth over the trivial log point ![]() $\operatorname {Spec}\Bbbk$, and as
$\operatorname {Spec}\Bbbk$, and as ![]() $X$ is assumed to be Zariski in any event, it follows that
$X$ is assumed to be Zariski in any event, it follows that ![]() $X$ is simple (Proposition 2.2). We use the reduced presentation of
$X$ is simple (Proposition 2.2). We use the reduced presentation of ![]() $\Sigma (X)$ from 2.1.2. Then simplicity implies that if
$\Sigma (X)$ from 2.1.2. Then simplicity implies that if ![]() $\tau ,\sigma \in \Sigma (X)$ and the image of
$\tau ,\sigma \in \Sigma (X)$ and the image of ![]() $\tau$ in
$\tau$ in ![]() $|\Sigma (X)|$ is a face of the image of
$|\Sigma (X)|$ is a face of the image of ![]() $\sigma$, then there is a unique face map
$\sigma$, then there is a unique face map ![]() $\tau \longrightarrow \sigma$ in the diagram.
$\tau \longrightarrow \sigma$ in the diagram.
The left-hand vertical arrow of (2.16) is a family of abstract tropical curves according to the following definition, cf. also [Reference Cavalieri, Chan, Ulirsch and WiseCCUW20, Definition 3.2].
Definition 2.19 A (family of) tropical curves ![]() $(G,\mathbf {g},\ell )$ over a cone
$(G,\mathbf {g},\ell )$ over a cone ![]() $\omega \in \mathbf {Cones}$ is a connected graph
$\omega \in \mathbf {Cones}$ is a connected graph ![]() $G$ together with a bijection
$G$ together with a bijection ![]() $L(G) \longrightarrow \{1,\ldots ,k\}$ (leg ordering) and two maps
$L(G) \longrightarrow \{1,\ldots ,k\}$ (leg ordering) and two maps
For ![]() $v\in V(G)$ and
$v\in V(G)$ and ![]() $E\in E(G)$ we call
$E\in E(G)$ we call ![]() $g(v)$ the genus of
$g(v)$ the genus of ![]() $v$ and
$v$ and ![]() $\ell (E)$ the length function of
$\ell (E)$ the length function of ![]() $E$.
$E$.
The genus of a family of tropical curves ![]() $(G,\mathbf {g},\ell )$ is defined by
$(G,\mathbf {g},\ell )$ is defined by
Note that given a tropical curve ![]() $(G,\mathbf {g},\ell )$ over a cone
$(G,\mathbf {g},\ell )$ over a cone ![]() $\omega$ and
$\omega$ and ![]() $s\in \omega$ not contained in any proper face, then
$s\in \omega$ not contained in any proper face, then ![]() $s\circ \ell$ assigns a strictly positive real number to each edge. Together with the convention that legs are infinite length,
$s\circ \ell$ assigns a strictly positive real number to each edge. Together with the convention that legs are infinite length, ![]() $(G,s\circ \ell )$ therefore specifies a metric graph, reproducing the traditional definition of an abstract tropical curve. Hence our definition makes precise the notion of a family of abstract tropical curves parameterized by
$(G,s\circ \ell )$ therefore specifies a metric graph, reproducing the traditional definition of an abstract tropical curve. Hence our definition makes precise the notion of a family of abstract tropical curves parameterized by ![]() $\omega \in \mathbf {Cones}$.
$\omega \in \mathbf {Cones}$.
Construction 2.20 We suppress the genus decoration in the notation ![]() $(G,\mathbf {g},\ell )$ and conflate
$(G,\mathbf {g},\ell )$ and conflate ![]() $(G,\mathbf {g},\ell )$ with its associated morphism of cone complexes
$(G,\mathbf {g},\ell )$ with its associated morphism of cone complexes
constructed as follows. For each ![]() $v\in V(G)$ take one copy
$v\in V(G)$ take one copy ![]() $\omega _v$ of
$\omega _v$ of ![]() $\omega$, while for each
$\omega$, while for each ![]() $E\in E(G)$ take the cone
$E\in E(G)$ take the cone
The cone ![]() $\omega _E$ has two facets, each isomorphic to
$\omega _E$ has two facets, each isomorphic to ![]() $\omega$ via projection to the first factor. The corresponding inclusions,
$\omega$ via projection to the first factor. The corresponding inclusions,
define face morphisms ![]() $\omega _v,\omega _{v'} \longrightarrow \omega _E$ for the two vertices
$\omega _v,\omega _{v'} \longrightarrow \omega _E$ for the two vertices ![]() $v,v'$ adjacent to
$v,v'$ adjacent to ![]() $E$. Note this definition is independent of the chosen labellings
$E$. Note this definition is independent of the chosen labellings ![]() $v,v'$ and works also for graphs with loops. Finally, for each
$v,v'$ and works also for graphs with loops. Finally, for each ![]() $L\in L(G)$ with adjacent vertex
$L\in L(G)$ with adjacent vertex ![]() $v$ take
$v$ take ![]() $\omega _L=\omega \times \mathbb {R}_{\ge 0}$ with face morphism
$\omega _L=\omega \times \mathbb {R}_{\ge 0}$ with face morphism ![]() $\omega _v\to \omega _L$ defined by the facet
$\omega _v\to \omega _L$ defined by the facet ![]() $\omega \times \{0\}\subset \omega _L$. Then
$\omega \times \{0\}\subset \omega _L$. Then ![]() $\Gamma$ is the generalized cone complex defined by this directed system in
$\Gamma$ is the generalized cone complex defined by this directed system in ![]() $\mathbf {Cones}$. The morphism to
$\mathbf {Cones}$. The morphism to ![]() $\omega$ is defined on each
$\omega$ is defined on each ![]() $\omega _E$ by the projection to the first factor.
$\omega _E$ by the projection to the first factor.
By construction, each vertex ![]() $v\in V(G)$ defines a section of
$v\in V(G)$ defines a section of ![]() $\pi _\Gamma : \Gamma \to \omega$ denoted as follows:
$\pi _\Gamma : \Gamma \to \omega$ denoted as follows:
Then for ![]() $s\in \omega$ not contained in a proper face, the fibre
$s\in \omega$ not contained in a proper face, the fibre ![]() ${\pi _\Gamma }^{-1}(s)$ is the metric graph
${\pi _\Gamma }^{-1}(s)$ is the metric graph ![]() $(G,s\circ \ell )$ previously defined.
$(G,s\circ \ell )$ previously defined.
It is also not hard to replace individual cones as base spaces for families of tropical curves by cone complexes. See [Reference Cavalieri, Chan, Ulirsch and WiseCCUW20, § 3] for an elaboration of such ideas.
Definition 2.21 A (family of) tropical maps (from a tropical curve) to ![]() $\Sigma (X)$ over a cone
$\Sigma (X)$ over a cone ![]() $\omega \in \mathbf {Cones}$ is a tropical curve
$\omega \in \mathbf {Cones}$ is a tropical curve ![]() $(G,\mathbf {g},\ell )$ over
$(G,\mathbf {g},\ell )$ over ![]() $\omega$ (Definition 2.19) with associated cone complex
$\omega$ (Definition 2.19) with associated cone complex ![]() $\Gamma =\Gamma (G,\ell )$ (Construction 2.20), together with a morphism of cone complexes
$\Gamma =\Gamma (G,\ell )$ (Construction 2.20), together with a morphism of cone complexes
Remark 2.22 There are a number of discrete data that we can extract from a tropical map ![]() $h:\Gamma \longrightarrow \Sigma (X)$ over
$h:\Gamma \longrightarrow \Sigma (X)$ over ![]() $\omega \in \mathbf {Cones}$ which are of importance in the sequel.
$\omega \in \mathbf {Cones}$ which are of importance in the sequel.
(1) Image cones. For a vertex, edge, or leg ![]() $x$ of
$x$ of ![]() $G$, let
$G$, let ![]() $\omega _x\in \Gamma$ be the cone associated to
$\omega _x\in \Gamma$ be the cone associated to ![]() $x$. Define
$x$. Define
by mapping ![]() $x$ to the minimal cone
$x$ to the minimal cone ![]() $\tau \in \Sigma (X)$ containing
$\tau \in \Sigma (X)$ containing ![]() $h(\omega _x)$. Note that if
$h(\omega _x)$. Note that if ![]() $E$ is a leg or edge incident to a vertex
$E$ is a leg or edge incident to a vertex ![]() $v$, then there is an inclusion of faces
$v$, then there is an inclusion of faces ![]() $\boldsymbol {\sigma }(v)\subset \boldsymbol {\sigma }(E)$ in the (reduced) presentation of
$\boldsymbol {\sigma }(v)\subset \boldsymbol {\sigma }(E)$ in the (reduced) presentation of ![]() $\Sigma (X)$.
$\Sigma (X)$.
(2) Contact orders at edges. Let ![]() $E_q\in E(G)$ be an edge with a chosen order of vertices
$E_q\in E(G)$ be an edge with a chosen order of vertices ![]() $v,v'$ (orientation). Then by the definition of the cone
$v,v'$ (orientation). Then by the definition of the cone ![]() $\omega _{E_q}$ of
$\omega _{E_q}$ of ![]() $\Gamma$ associated to
$\Gamma$ associated to ![]() $E_q$ in (2.19), the image of
$E_q$ in (2.19), the image of ![]() $(0,1)\in N_{\omega _{E_q}}= N_\omega \times \mathbb {R}$ under
$(0,1)\in N_{\omega _{E_q}}= N_\omega \times \mathbb {R}$ under ![]() $h$ defines
$h$ defines ![]() $u_q\in N_{\boldsymbol {\sigma }(E_q)}$ such that in
$u_q\in N_{\boldsymbol {\sigma }(E_q)}$ such that in ![]() $N_{\boldsymbol {\sigma }(E_q)}$,
$N_{\boldsymbol {\sigma }(E_q)}$,
holds for any ![]() $s\in \omega _{E_q}$. Here
$s\in \omega _{E_q}$. Here ![]() $v(s)\in \Gamma$ is the section of
$v(s)\in \Gamma$ is the section of ![]() $\Gamma \to \omega$ defined in (2.20). Reversing the orientation of
$\Gamma \to \omega$ defined in (2.20). Reversing the orientation of ![]() $E_q$ results in replacing
$E_q$ results in replacing ![]() $u_q$ by
$u_q$ by ![]() $-u_q$.
$-u_q$.
(3) Contact orders at marked points. Similarly, for a leg ![]() $L_p\in L(G)$, the image of
$L_p\in L(G)$, the image of ![]() $(0,1)\in N_{\omega _{L_p}}= N_\omega \times \mathbb {R}$ defines
$(0,1)\in N_{\omega _{L_p}}= N_\omega \times \mathbb {R}$ defines ![]() $u_p \in N_{\boldsymbol {\sigma }(L_p)}\cap \boldsymbol {\sigma }(L_p)$ with
$u_p \in N_{\boldsymbol {\sigma }(L_p)}\cap \boldsymbol {\sigma }(L_p)$ with ![]() $h(\operatorname {Int}(\omega _{L_p}))\subset \operatorname {Int}(\boldsymbol {\sigma }(L_p))$.
$h(\operatorname {Int}(\omega _{L_p}))\subset \operatorname {Int}(\boldsymbol {\sigma }(L_p))$.
Definition 2.23 (1) The type of a family of tropical maps ![]() $h:\Gamma \longrightarrow \Sigma (X)$ over
$h:\Gamma \longrightarrow \Sigma (X)$ over ![]() $Q^\vee _\mathbb {R}\in \mathbf {Cones}$ is the quadruple
$Q^\vee _\mathbb {R}\in \mathbf {Cones}$ is the quadruple ![]() $\tau =(G,\mathbf {g},\boldsymbol {\sigma },\mathbf {u})$ consisting of the associated genus decorated graph
$\tau =(G,\mathbf {g},\boldsymbol {\sigma },\mathbf {u})$ consisting of the associated genus decorated graph ![]() $(G,\mathbf {g})$, the map
$(G,\mathbf {g})$, the map ![]() $\boldsymbol {\sigma }$ from (2.21) recording the strata and the contact orders
$\boldsymbol {\sigma }$ from (2.21) recording the strata and the contact orders ![]() $\mathbf {u}=\{ u_p,u_q\}$ as defined in Remark 2.22. Note that we are suppressing the leg numbering, viewing the set
$\mathbf {u}=\{ u_p,u_q\}$ as defined in Remark 2.22. Note that we are suppressing the leg numbering, viewing the set ![]() $L(G)$ as identical with
$L(G)$ as identical with ![]() $\{1,\ldots ,k\}$.
$\{1,\ldots ,k\}$.
(2) For a type ![]() $\tau$ of a family of tropical maps,
$\tau$ of a family of tropical maps, ![]() $\operatorname {Aut}(\tau )$ denotes the subset of automorphisms of
$\operatorname {Aut}(\tau )$ denotes the subset of automorphisms of ![]() $G$ commuting with the maps
$G$ commuting with the maps ![]() $\mathbf {g},\boldsymbol {\sigma },\mathbf {u}$.
$\mathbf {g},\boldsymbol {\sigma },\mathbf {u}$.
(3) Given a type ![]() $\tau$ of a family of tropical maps, the associated basic monoid
$\tau$ of a family of tropical maps, the associated basic monoid ![]() $Q(\tau )$ is the dual of the monoid
$Q(\tau )$ is the dual of the monoid ![]() $Q^\vee$ defined in (2.9), depending only on
$Q^\vee$ defined in (2.9), depending only on ![]() $G,\boldsymbol {\sigma }$ and
$G,\boldsymbol {\sigma }$ and ![]() $\mathbf {u}$.
$\mathbf {u}$.
(4) If in addition we have given a map
we call ![]() ${\boldsymbol{\tau }}=(\tau ,\mathbf {A})$ the decorated type of a family of tropical maps, the pair
${\boldsymbol{\tau }}=(\tau ,\mathbf {A})$ the decorated type of a family of tropical maps, the pair ![]() $(h,\mathbf {A})$ a decorated family of tropical maps and
$(h,\mathbf {A})$ a decorated family of tropical maps and
the total curve class of ![]() $\mathbf {A}$.
$\mathbf {A}$.
Generalizing (2.15) we have a notion of contraction morphism for (decorated) types of families of tropical maps needed below.
Definition 2.24 Let ![]() $\tau =(G,\mathbf {g},\boldsymbol {\sigma },\mathbf {u})$ and
$\tau =(G,\mathbf {g},\boldsymbol {\sigma },\mathbf {u})$ and ![]() $\tau '=(G',\mathbf {g}',\boldsymbol {\sigma }',\mathbf {u}')$ be types of families of tropical maps. A contraction morphism
$\tau '=(G',\mathbf {g}',\boldsymbol {\sigma }',\mathbf {u}')$ be types of families of tropical maps. A contraction morphism ![]() $\tau \to \tau '$ is a contraction morphism
$\tau \to \tau '$ is a contraction morphism ![]() $\phi :(G,\mathbf {g})\to (G',\mathbf {g}')$ of decorated graphs (2.15) with the following additional properties.
$\phi :(G,\mathbf {g})\to (G',\mathbf {g}')$ of decorated graphs (2.15) with the following additional properties.
(i) For all
 $x\in V(G)\cup E(G)\cup L(G)$ the cone
$x\in V(G)\cup E(G)\cup L(G)$ the cone  $\boldsymbol {\sigma }'(\phi (x))\in \Sigma (X)$ is a face of
$\boldsymbol {\sigma }'(\phi (x))\in \Sigma (X)$ is a face of  $\boldsymbol {\sigma }(x)$.
$\boldsymbol {\sigma }(x)$.(ii) For all
 $x\in E(G')\cup L(G')$ it holds that
$x\in E(G')\cup L(G')$ it holds that  $\mathbf{u}'(x)=\mathbf{u}((E(\phi)\cup L(\phi))(x))$.
$\mathbf{u}'(x)=\mathbf{u}((E(\phi)\cup L(\phi))(x))$.
Similarly, a contraction morphism ![]() ${\boldsymbol{\tau }}=(\tau ,\mathbf {A}) \longrightarrow {\boldsymbol{\tau }}'=(\tau ',\mathbf {A}')$ of decorated types of families of tropical maps is a contraction morphism
${\boldsymbol{\tau }}=(\tau ,\mathbf {A}) \longrightarrow {\boldsymbol{\tau }}'=(\tau ',\mathbf {A}')$ of decorated types of families of tropical maps is a contraction morphism ![]() $\tau \longrightarrow \tau '$ such that
$\tau \longrightarrow \tau '$ such that ![]() $\mathbf {A}'(v')=\sum _{v\in V(\phi )^{-1}(v')} \mathbf {A}(v)$ holds for all
$\mathbf {A}'(v')=\sum _{v\in V(\phi )^{-1}(v')} \mathbf {A}(v)$ holds for all ![]() $v'\in V(G')$.
$v'\in V(G')$.
2.5.1 Families of tropical curves from logarithmically smooth curves
Now suppose
for some monoid ![]() $Q$ and
$Q$ and ![]() $(C/S,\textbf {p})$ is a family of marked log smooth curves, as in Definition 2.12(i).
$(C/S,\textbf {p})$ is a family of marked log smooth curves, as in Definition 2.12(i).
Proposition 2.25 The tropicalization
of ![]() $(C/S,\textbf {p})$ naturally has the structure of a family of tropical curves
$(C/S,\textbf {p})$ naturally has the structure of a family of tropical curves ![]() $(G,\mathbf {g},\ell )$ over
$(G,\mathbf {g},\ell )$ over ![]() $Q^\vee _\mathbb {R}$.
$Q^\vee _\mathbb {R}$.
Proof. Take for ![]() $G$ the dual intersection graph of
$G$ the dual intersection graph of ![]() $C$. If
$C$. If ![]() $\eta$ is a generic point of
$\eta$ is a generic point of ![]() $C$, then
$C$, then ![]() $\omega _{\eta }=Q^{\vee }_{\mathbb {R}}$ and
$\omega _{\eta }=Q^{\vee }_{\mathbb {R}}$ and ![]() $\Sigma (\pi )|_{\omega _{\eta }}$ is the identity. Thus each fibre of
$\Sigma (\pi )|_{\omega _{\eta }}$ is the identity. Thus each fibre of ![]() $\Sigma (\pi )|_{\omega _{\eta }}$ is a point
$\Sigma (\pi )|_{\omega _{\eta }}$ is a point ![]() $v$. We take the weight
$v$. We take the weight ![]() $\mathbf {g}(v) = g(C(v))$, the geometric genus of the component
$\mathbf {g}(v) = g(C(v))$, the geometric genus of the component ![]() $C(v)$ with generic point
$C(v)$ with generic point ![]() $\eta$. The cone of
$\eta$. The cone of ![]() $\Sigma (C)$ defined by a node
$\Sigma (C)$ defined by a node ![]() $q$ of
$q$ of ![]() $C$ is
$C$ is
where the maps ![]() $Q^{\vee }_{\mathbb {R}} \longrightarrow \mathbb {R}_{\ge 0}$ and
$Q^{\vee }_{\mathbb {R}} \longrightarrow \mathbb {R}_{\ge 0}$ and ![]() $\mathbb {R}^2_{\ge 0} \longrightarrow \mathbb {R}_{\ge 0}$ are given by evaluation at
$\mathbb {R}^2_{\ge 0} \longrightarrow \mathbb {R}_{\ge 0}$ are given by evaluation at ![]() $\rho _q\in Q\setminus \{0\}$ and by
$\rho _q\in Q\setminus \{0\}$ and by ![]() $(a,b)\mapsto a+b$, respectively. The projection
$(a,b)\mapsto a+b$, respectively. The projection ![]() $\mathbb {R}^2_{\ge 0} \longrightarrow \mathbb {R}_{\ge 0}$ to, say, the first factor, defines an isomorphism
$\mathbb {R}^2_{\ge 0} \longrightarrow \mathbb {R}_{\ge 0}$ to, say, the first factor, defines an isomorphism
Thus defining ![]() $\ell (E_q)= \rho _q$, we have a canonical isomorphism
$\ell (E_q)= \rho _q$, we have a canonical isomorphism ![]() $\omega _q\simeq \omega _{E_q}$ with
$\omega _q\simeq \omega _{E_q}$ with ![]() $\omega _{E_q}$ defined in (2.19). For a marked point
$\omega _{E_q}$ defined in (2.19). For a marked point ![]() $p_i\in C$, we have
$p_i\in C$, we have ![]() $\omega _{p_i}=Q^{\vee }_{\mathbb {R}} \times \mathbb {R}_{\ge 0}$, and
$\omega _{p_i}=Q^{\vee }_{\mathbb {R}} \times \mathbb {R}_{\ge 0}$, and ![]() $\Sigma (\pi )|_{\omega _{p_i}}$ is the projection onto the first component, again compatible with the definition of
$\Sigma (\pi )|_{\omega _{p_i}}$ is the projection onto the first component, again compatible with the definition of ![]() $\Gamma =\Gamma (G,\ell )$ in Construction 2.20.
$\Gamma =\Gamma (G,\ell )$ in Construction 2.20.
2.5.2 Families of tropical maps to  $\Sigma (X)$ from stable logarithmic maps
$\Sigma (X)$ from stable logarithmic maps
We continue working over a logarithmic point ![]() $S=\operatorname {Spec}(Q \longrightarrow \Bbbk )$ and assume in addition given an fs log scheme
$S=\operatorname {Spec}(Q \longrightarrow \Bbbk )$ and assume in addition given an fs log scheme ![]() $X$, which is simple in the sense of Definition 2.1.
$X$, which is simple in the sense of Definition 2.1.
Proposition 2.26 The tropicalization of a stable logarithmic map ![]() $(C/S,\textbf {p},f)$ over the logarithmic point
$(C/S,\textbf {p},f)$ over the logarithmic point ![]() $S=\operatorname {Spec}(Q \longrightarrow \Bbbk )$ defines a family of tropical maps to
$S=\operatorname {Spec}(Q \longrightarrow \Bbbk )$ defines a family of tropical maps to ![]() $\Sigma (X)$ over
$\Sigma (X)$ over ![]() $Q_\mathbb {R}^\vee$.
$Q_\mathbb {R}^\vee$.
Proof. In view of Proposition 2.25 the statement follows readily from the definitions.
Remark 2.27 An element ![]() $x\in V(G)\cup E(G)\cup L(G)$ corresponds to a point
$x\in V(G)\cup E(G)\cup L(G)$ corresponds to a point ![]() $x\in C$ – either a generic point, a double point, or a marked point. The cone
$x\in C$ – either a generic point, a double point, or a marked point. The cone ![]() $\boldsymbol {\sigma }(x)$ introduced in Remark 2.22 is
$\boldsymbol {\sigma }(x)$ introduced in Remark 2.22 is
for any geometric point ![]() $\bar x$ mapping to
$\bar x$ mapping to ![]() $x$. With this identification of cones understood, it is a matter of unravelling the definitions that the other discrete data introduced in Remark 2.22, the contact orders
$x$. With this identification of cones understood, it is a matter of unravelling the definitions that the other discrete data introduced in Remark 2.22, the contact orders ![]() $u_{L_p},u_{E_q}$, agree with
$u_{L_p},u_{E_q}$, agree with ![]() $u_p,u_q$ defined in § 2.3.5. Note in particular how (2.22) appears as the tropical manifestation of (2.8). Thus the type of the tropicalization of a stable logarithmic map, as a family of tropical maps (Definition 2.23), agrees with its combinatorial type from Definition 2.13.
$u_p,u_q$ defined in § 2.3.5. Note in particular how (2.22) appears as the tropical manifestation of (2.8). Thus the type of the tropicalization of a stable logarithmic map, as a family of tropical maps (Definition 2.23), agrees with its combinatorial type from Definition 2.13.
2.5.3 Traditional tropical maps: the relative situation
A situation of particular interest arises when working over the standard log point ![]() $b_0=\operatorname {Spec}(\mathbb {N}\to \Bbbk [\mathbb {N}]))$. Then all generalized cone complexes come with a morphism
$b_0=\operatorname {Spec}(\mathbb {N}\to \Bbbk [\mathbb {N}]))$. Then all generalized cone complexes come with a morphism ![]() $\pi$ to
$\pi$ to ![]() $\Sigma (b_0)=\mathbb {R}_{\ge 0}$. Taking the fiber of
$\Sigma (b_0)=\mathbb {R}_{\ge 0}$. Taking the fiber of ![]() $\pi$ over
$\pi$ over ![]() $1\in \mathbb {R}_{\ge 0}$ then produces a generalized polyhedral complex as introduced in § 2.1.3. Conversely, let
$1\in \mathbb {R}_{\ge 0}$ then produces a generalized polyhedral complex as introduced in § 2.1.3. Conversely, let ![]() $\pi :\Sigma \to \mathbb {R}_{\ge 0}$ be a map of generalized cone complexes such that no maximal cone of
$\pi :\Sigma \to \mathbb {R}_{\ge 0}$ be a map of generalized cone complexes such that no maximal cone of ![]() $\Sigma$ maps to
$\Sigma$ maps to ![]() $0\in \mathbb {R}_{\ge 0}$. Then
$0\in \mathbb {R}_{\ge 0}$. Then ![]() $\Sigma$ and
$\Sigma$ and ![]() $\pi$ can be recovered from the generalized polyhedral complex
$\pi$ can be recovered from the generalized polyhedral complex ![]() $\pi ^{-1}(1)$ by replacing each polyhedron
$\pi ^{-1}(1)$ by replacing each polyhedron ![]() $\sigma =(\sigma _\mathbb {R},N)$ by the closure of
$\sigma =(\sigma _\mathbb {R},N)$ by the closure of ![]() $\mathbb {R}_{\ge 0}(\sigma \times \{1\})$ in
$\mathbb {R}_{\ge 0}(\sigma \times \{1\})$ in ![]() $N_\mathbb {R}\times \mathbb {R}$.
$N_\mathbb {R}\times \mathbb {R}$.
If ![]() $X$ is a finite type logarithmic stack over the standard log point
$X$ is a finite type logarithmic stack over the standard log point ![]() $b_0$ with associated tropicalization
$b_0$ with associated tropicalization ![]() $\pi :\Sigma (X) \longrightarrow \Sigma (B_0)=\mathbb {R}_{\ge 0}$, we now write
$\pi :\Sigma (X) \longrightarrow \Sigma (B_0)=\mathbb {R}_{\ge 0}$, we now write
for the associated polyhedral complex.
In particular, this discussion applies to the logarithmic scheme ![]() $X_0$ and logarithmically smooth morphism
$X_0$ and logarithmically smooth morphism ![]() $X_0 \longrightarrow b_0$ from the main theorem in this paper, Theorem 1.2. Let
$X_0 \longrightarrow b_0$ from the main theorem in this paper, Theorem 1.2. Let ![]() $(C/S,\mathbf {p},f)$ be a stable log map to
$(C/S,\mathbf {p},f)$ be a stable log map to ![]() $X_0$ with
$X_0$ with ![]() $S=\operatorname {Spec}(Q\to \Bbbk )$ a log point as in § 2.5.2, but now coming with a map to
$S=\operatorname {Spec}(Q\to \Bbbk )$ a log point as in § 2.5.2, but now coming with a map to ![]() $b_0$. Let
$b_0$. Let ![]() $\pi _S:Q^\vee \to \mathbb {N}$ be the tropicalization of
$\pi _S:Q^\vee \to \mathbb {N}$ be the tropicalization of ![]() $S \longrightarrow b_0$. Then the family of tropical maps
$S \longrightarrow b_0$. Then the family of tropical maps ![]() $\Sigma (C) \longrightarrow \Sigma (X_0)$ over
$\Sigma (C) \longrightarrow \Sigma (X_0)$ over ![]() $Q^\vee$ carries the same information as its restriction to the fiber over
$Q^\vee$ carries the same information as its restriction to the fiber over ![]() $1\in \mathbb {R}_{\ge 0}$, a family of maps from metric graphs to
$1\in \mathbb {R}_{\ge 0}$, a family of maps from metric graphs to ![]() $\Delta (X)$ parameterized by the polyhedron
$\Delta (X)$ parameterized by the polyhedron ![]() $\pi _S^{-1}(1)\subset Q^\vee$.
$\pi _S^{-1}(1)\subset Q^\vee$.
The transition from cone complexes to polyhedral complexes provides the link to more traditional tropical language. In the remainder of this paper we use cone complexes for most of the general results and polyhedral complexes for explicit computations. With regards to using both cones and polyhedra as parameter spaces for families of tropical maps, note that there is no conflict of language: a family of tropical maps to ![]() $\Sigma (X_0)$ over a cone
$\Sigma (X_0)$ over a cone ![]() $\sigma$ can be viewed as a family of maps of metric graphs to
$\sigma$ can be viewed as a family of maps of metric graphs to ![]() $\Sigma (X_0)$ interpreted as a polyhedral complex, now parameterized by
$\Sigma (X_0)$ interpreted as a polyhedral complex, now parameterized by ![]() $\sigma$ as a polyhedron.Footnote 6
$\sigma$ as a polyhedron.Footnote 6
As a matter of notation, we indicate the transition from cone complexes to polyhedral complexes by overlining. Thus a family of tropical maps ![]() $h:\Gamma \longrightarrow \Sigma (X_0)$ over a cone
$h:\Gamma \longrightarrow \Sigma (X_0)$ over a cone ![]() $\sigma$ with a map
$\sigma$ with a map ![]() $\pi _S: \sigma \longrightarrow \mathbb {R}_{\ge 0}$ induces the family of tropical maps
$\pi _S: \sigma \longrightarrow \mathbb {R}_{\ge 0}$ induces the family of tropical maps
over the polyhedron ![]() $\bar \sigma =\pi _S^{-1}(1)$.
$\bar \sigma =\pi _S^{-1}(1)$.
2.5.4 Basic maps and tropical universal families
Basicness of a stable logarithmic map ![]() $(C/S,\mathbf {p},f)$ over a logarithmic point can then be recast as follows.
$(C/S,\mathbf {p},f)$ over a logarithmic point can then be recast as follows.
Proposition 2.28 Let ![]() $(C/S,\mathbf {p},f)$ be a stable logarithmic map over a logarithmic point
$(C/S,\mathbf {p},f)$ be a stable logarithmic map over a logarithmic point ![]() $S=\operatorname {Spec}(Q \longrightarrow \Bbbk )$ and
$S=\operatorname {Spec}(Q \longrightarrow \Bbbk )$ and ![]() $\tau$ its combinatorial type (Definition 2.13). Then
$\tau$ its combinatorial type (Definition 2.13). Then ![]() $(C/S,\mathbf {p},f)$ is basic if and only if the family of tropical maps in Proposition 2.26 is universal among families of tropical maps to
$(C/S,\mathbf {p},f)$ is basic if and only if the family of tropical maps in Proposition 2.26 is universal among families of tropical maps to ![]() $\Sigma (X)$ of type
$\Sigma (X)$ of type ![]() $\tau$.
$\tau$.
Proof. The definition of the dual of the basic monoid ![]() $Q^{\vee }$ precisely encodes the data of a family of tropical maps to
$Q^{\vee }$ precisely encodes the data of a family of tropical maps to ![]() $\Sigma (X)$ over
$\Sigma (X)$ over ![]() $\sigma =\mathbb {R}_{\ge 0}$ of type
$\sigma =\mathbb {R}_{\ge 0}$ of type ![]() $\tau$ (Definition 2.23). Indeed, let
$\tau$ (Definition 2.23). Indeed, let ![]() $G_C$ be the dual intersection graph of
$G_C$ be the dual intersection graph of ![]() $C$ from § 2.3.6, with vertices
$C$ from § 2.3.6, with vertices ![]() $v_\eta$, edges
$v_\eta$, edges ![]() $E_q$ and legs
$E_q$ and legs ![]() $L_p$. Then a tuple
$L_p$. Then a tuple ![]() $((V_{\eta })_{\eta }, (e_q)_q)\in \operatorname {Int}(Q^{\vee }_{\mathbb {R}})$ specifies a family of tropical maps
$((V_{\eta })_{\eta }, (e_q)_q)\in \operatorname {Int}(Q^{\vee }_{\mathbb {R}})$ specifies a family of tropical maps
over ![]() $\mathbb {R}_{\ge 0}$ of the given type, by defining
$\mathbb {R}_{\ge 0}$ of the given type, by defining ![]() $\ell (E_q)=e_q$ and
$\ell (E_q)=e_q$ and ![]() $h|_{\omega _v}$ by mapping
$h|_{\omega _v}$ by mapping ![]() $1\in \mathbb {R}_{\ge 0}=\omega _{v_\eta }$ to
$1\in \mathbb {R}_{\ge 0}=\omega _{v_\eta }$ to ![]() $V_{\eta }\in \Sigma (X)$. The type also determines
$V_{\eta }\in \Sigma (X)$. The type also determines ![]() $h$ on each leg
$h$ on each leg ![]() $L_p$. It is shown in [Reference Gross and SiebertGS13, Proposition 1.9] that if one such tropical map to
$L_p$. It is shown in [Reference Gross and SiebertGS13, Proposition 1.9] that if one such tropical map to ![]() $\Sigma (X)$ of a certain type exists then there exists one over
$\Sigma (X)$ of a certain type exists then there exists one over ![]() $Q_\mathbb {R}^\vee$; moreover, any other tropical map of the same type, say over
$Q_\mathbb {R}^\vee$; moreover, any other tropical map of the same type, say over ![]() $\sigma \in \mathbf {Cones}$, is obtained from this one by pull-back via a homomorphism
$\sigma \in \mathbf {Cones}$, is obtained from this one by pull-back via a homomorphism ![]() $\sigma \to Q_{\mathbb{R}}^\vee$.
$\sigma \to Q_{\mathbb{R}}^\vee$.
Remark 2.29 Note that if ![]() $S$ is not a log point, the diagram (2.16) still exists, but the fibres of
$S$ is not a log point, the diagram (2.16) still exists, but the fibres of ![]() $\Sigma (\pi )$ may not be the expected ones. In particular, if
$\Sigma (\pi )$ may not be the expected ones. In particular, if ![]() $\bar s$ is a geometric point of
$\bar s$ is a geometric point of ![]() $S$, there is a functorial diagram
$S$, there is a functorial diagram

but this diagram need not be Cartesian due to monodromy in the family ![]() $S$. For example, it is easy to imagine a situation where
$S$. For example, it is easy to imagine a situation where ![]() $C_{\bar s}$ has two irreducible components and two nodes for every geometric point
$C_{\bar s}$ has two irreducible components and two nodes for every geometric point ![]() $\bar s$, but the nodal locus of
$\bar s$, but the nodal locus of ![]() $C \longrightarrow S$ is irreducible, as there is monodromy interchanging the two nodes. Then a fibre of
$C \longrightarrow S$ is irreducible, as there is monodromy interchanging the two nodes. Then a fibre of ![]() $\Sigma (C) \longrightarrow \Sigma (S)$ may consist of two vertices joined by a single edge, while a fibre of
$\Sigma (C) \longrightarrow \Sigma (S)$ may consist of two vertices joined by a single edge, while a fibre of ![]() $\Sigma (C_{\bar s}) \longrightarrow \Sigma (\bar s)$ will have two vertices joined by two edges. Similarly, there may be monodromy interchanging irreducible components, and hence a fibre of
$\Sigma (C_{\bar s}) \longrightarrow \Sigma (\bar s)$ will have two vertices joined by two edges. Similarly, there may be monodromy interchanging irreducible components, and hence a fibre of ![]() $\Sigma (C) \longrightarrow \Sigma (S)$ may have fewer vertices than
$\Sigma (C) \longrightarrow \Sigma (S)$ may have fewer vertices than ![]() $C_{\bar w}$ has irreducible components. This issue can be resolved by redefining moduli of tropical curves as stacks, following [Reference Cavalieri, Chan, Ulirsch and WiseCCUW20].
$C_{\bar w}$ has irreducible components. This issue can be resolved by redefining moduli of tropical curves as stacks, following [Reference Cavalieri, Chan, Ulirsch and WiseCCUW20].
2.5.5 Decorated tropical maps from stable logarithmic maps
In the situation of Proposition 2.26, the tropical map ![]() $h:\Sigma (C)\to \Sigma (X)$ comes with the natural decoration
$h:\Sigma (C)\to \Sigma (X)$ comes with the natural decoration
Here ![]() $C(v)\subset C$ is the irreducible component corresponding to the vertex
$C(v)\subset C$ is the irreducible component corresponding to the vertex ![]() $v$ and
$v$ and ![]() $[f(C(v))]$ is the class of
$[f(C(v))]$ is the class of ![]() $f(C(v))$ in
$f(C(v))$ in ![]() $H_2^+(X)$. The decoration by curve classes is compatible with the contraction morphisms of decorated graphs (Definition 2.24) defined by generization.
$H_2^+(X)$. The decoration by curve classes is compatible with the contraction morphisms of decorated graphs (Definition 2.24) defined by generization.
Lemma 2.30 Let ![]() $(C/S,\mathbf {p},f)$ be a stable logarithmic map to
$(C/S,\mathbf {p},f)$ be a stable logarithmic map to ![]() $X$ over some logarithmic scheme
$X$ over some logarithmic scheme ![]() $S$ and
$S$ and ![]() $(\tau _{\bar s},\mathbf {A}_{\bar s})$ with
$(\tau _{\bar s},\mathbf {A}_{\bar s})$ with ![]() $\tau _{\bar s}= (G_{\bar s},\mathbf {g}_{\bar s},\boldsymbol {\sigma }_{\bar s},\mathbf {u}_{\bar s})$ its decorated type at the geometric point
$\tau _{\bar s}= (G_{\bar s},\mathbf {g}_{\bar s},\boldsymbol {\sigma }_{\bar s},\mathbf {u}_{\bar s})$ its decorated type at the geometric point ![]() $\bar s\to S$ according to Definition 2.23 and (2.25). Then if
$\bar s\to S$ according to Definition 2.23 and (2.25). Then if ![]() $\bar s,\bar s'\to S$ are two geometric points with
$\bar s,\bar s'\to S$ are two geometric points with ![]() $\bar s$ a generization of
$\bar s$ a generization of ![]() $\bar s'$, the induced map
$\bar s'$, the induced map
is a contraction morphism (Definition 2.24).
Proof. [Reference Gross and SiebertGS13, Lemma 1.11] says that ![]() $\tau _{\bar s'}\to \tau _{\bar s}$ is a contraction morphism. To check the statement on the curve classes, recall that the preimage of
$\tau _{\bar s'}\to \tau _{\bar s}$ is a contraction morphism. To check the statement on the curve classes, recall that the preimage of ![]() $v\in G_{\bar s}$ in
$v\in G_{\bar s}$ in ![]() $G_{\bar s}'$ consists of those vertices
$G_{\bar s}'$ consists of those vertices ![]() $v'\in G_{\bar s'}$ with
$v'\in G_{\bar s'}$ with ![]() $C_{\bar s'}(v')$ contained in the closure of
$C_{\bar s'}(v')$ contained in the closure of ![]() $C_{\bar s}(v)$. Since this closure defines a flat family of curves, invariance of classes in
$C_{\bar s}(v)$. Since this closure defines a flat family of curves, invariance of classes in ![]() $H_2^+(X)$ in flat families then implies
$H_2^+(X)$ in flat families then implies
as claimed.
2.6 Stacks of stable logarithmic maps marked by tropical types
We now put ourselves in the situation of the main result in this paper, Theorem 1.2, and assume ![]() $X_0 \longrightarrow b_0$ is logarithmically smooth and
$X_0 \longrightarrow b_0$ is logarithmically smooth and ![]() $X_0$ is simple. In particular, curve classes are understood to take values in
$X_0$ is simple. In particular, curve classes are understood to take values in ![]() $H_2^+(X_0)$.
$H_2^+(X_0)$.
Similar to ![]() $\mathbf {M}(G,\mathbf {g})$, we can now define stacks of stable logarithmic maps to
$\mathbf {M}(G,\mathbf {g})$, we can now define stacks of stable logarithmic maps to ![]() $X_0$ over
$X_0$ over ![]() $b_0$ with restricted decorated types of tropicalizations.
$b_0$ with restricted decorated types of tropicalizations.
Definition 2.31 Let ![]() ${\boldsymbol{\tau }}=(G,\mathbf {g},\boldsymbol {\sigma },\mathbf {u},\mathbf {A})=(\tau ,\mathbf {A})$ be the decorated type of a tropical map as defined in Definition 2.23. A marking by
${\boldsymbol{\tau }}=(G,\mathbf {g},\boldsymbol {\sigma },\mathbf {u},\mathbf {A})=(\tau ,\mathbf {A})$ be the decorated type of a tropical map as defined in Definition 2.23. A marking by ![]() ${\boldsymbol{\tau }}$ of a stable logarithmic map
${\boldsymbol{\tau }}$ of a stable logarithmic map ![]() $(C/S,\mathbf {p},f)$ to
$(C/S,\mathbf {p},f)$ to ![]() $X_0$ over a logarithmic base scheme
$X_0$ over a logarithmic base scheme ![]() $S$ over
$S$ over ![]() $b_0$ is the following data:
$b_0$ is the following data:
(1) an isomorphism of
 $\underline{C}/\underline{S}$ with a
$\underline{C}/\underline{S}$ with a  $(G,\mathbf {g})$-marked pre-stable curve (2.12);
$(G,\mathbf {g})$-marked pre-stable curve (2.12);(2) the restriction of
 $\underline{f}$ to the closed subscheme
$\underline{f}$ to the closed subscheme  $Z\subset \underline{C}$ (a subcurve or nodal or punctured section of
$Z\subset \underline{C}$ (a subcurve or nodal or punctured section of  $C$) defined by
$C$) defined by  $x\in V(G)\cup E(G)\cup L(G)$ factors through
$x\in V(G)\cup E(G)\cup L(G)$ factors through  $X_{\boldsymbol {\sigma }(x)}\subset X_0$;
$X_{\boldsymbol {\sigma }(x)}\subset X_0$;(3) for each geometric point
 $\bar s \longrightarrow S$ with decorated type
$\bar s \longrightarrow S$ with decorated type  ${\boldsymbol{\tau }}_{\bar s}=(G_{\bar s},\mathbf {g}_{\bar s},\boldsymbol {\sigma }_{\bar s},\mathbf {u}_{\bar s},\mathbf {A}_{\bar s})$ of
${\boldsymbol{\tau }}_{\bar s}=(G_{\bar s},\mathbf {g}_{\bar s},\boldsymbol {\sigma }_{\bar s},\mathbf {u}_{\bar s},\mathbf {A}_{\bar s})$ of  $(C/S,\mathbf {p},f)$, the morphism
$(C/S,\mathbf {p},f)$, the morphism  $(G_{\bar s},\mathbf {g}_{\bar s}) \longrightarrow (G,\mathbf {g})$ of decorated graphs from (1) defines a morphism
of decorated types of tropical maps; in particular, there is an associated localization map
$(G_{\bar s},\mathbf {g}_{\bar s}) \longrightarrow (G,\mathbf {g})$ of decorated graphs from (1) defines a morphism
of decorated types of tropical maps; in particular, there is an associated localization map \[ {\boldsymbol{\tau}}_{\bar s}=(\tau_{\bar s},\mathbf{A}_{\bar s}) \longrightarrow {\boldsymbol{\tau}}=(\tau,\mathbf{A}) \]of the corresponding basic monoids;
\[ {\boldsymbol{\tau}}_{\bar s}=(\tau_{\bar s},\mathbf{A}_{\bar s}) \longrightarrow {\boldsymbol{\tau}}=(\tau,\mathbf{A}) \]of the corresponding basic monoids; \[ \chi_{\tau\tau_{\bar s}}: Q_{\tau_{\bar s}} \longrightarrow Q_\tau \]
\[ \chi_{\tau\tau_{\bar s}}: Q_{\tau_{\bar s}} \longrightarrow Q_\tau \](4) in the situation of (3), the preimage
 $\mathcal {K}_{{\boldsymbol{\tau }},\bar s}\subset \mathcal {M}_{S,\bar s}$ of
$\mathcal {K}_{{\boldsymbol{\tau }},\bar s}\subset \mathcal {M}_{S,\bar s}$ of  $Q_\tau \setminus \{0\}$ under the composition
maps to
$Q_\tau \setminus \{0\}$ under the composition
maps to \[ \mathcal{M}_{S,\bar s} \longrightarrow \overline{\mathcal{M}}_{S,\bar s}= Q_{\tau_{\bar s}}\stackrel{\chi_{\tau\tau_{\bar s}}}{ \longrightarrow} Q_\tau \]
\[ \mathcal{M}_{S,\bar s} \longrightarrow \overline{\mathcal{M}}_{S,\bar s}= Q_{\tau_{\bar s}}\stackrel{\chi_{\tau\tau_{\bar s}}}{ \longrightarrow} Q_\tau \] $0$ under the structure morphism
$0$ under the structure morphism  $\mathcal {M}_{S,\bar s} \longrightarrow \mathcal {O}_{S,\bar s}$.
$\mathcal {M}_{S,\bar s} \longrightarrow \mathcal {O}_{S,\bar s}$.
Remark 2.32 Definition 2.31 calls for some explanations. The isomorphism in (1) just identifies a contraction of the dual intersection graph of each geometric fiber of ![]() $\underline{C}\to \underline{S}$ with a fixed genus-decorated graph
$\underline{C}\to \underline{S}$ with a fixed genus-decorated graph ![]() $(G,\mathbf {g})$, in a way compatible with generization. Then (2) and (3) ask that the decorated graphs associated to geometric fibers of the stable log map
$(G,\mathbf {g})$, in a way compatible with generization. Then (2) and (3) ask that the decorated graphs associated to geometric fibers of the stable log map ![]() $(C/S,\mathbf {p},f)$ are refinements of the decorated type
$(C/S,\mathbf {p},f)$ are refinements of the decorated type ![]() $(\tau ,\mathbf {A})$. Condition (4) is maybe the least obvious, but is necessary to restrict the decorated type on a schematic level. It effectively takes the reduction of the moduli space in unobstructed situations, or on a virtual level later on. We could, in fact, omit Condition (4) at the expense of taking reductions in some formulas below, e.g. in
$(\tau ,\mathbf {A})$. Condition (4) is maybe the least obvious, but is necessary to restrict the decorated type on a schematic level. It effectively takes the reduction of the moduli space in unobstructed situations, or on a virtual level later on. We could, in fact, omit Condition (4) at the expense of taking reductions in some formulas below, e.g. in ![]() $\mathfrak{M}(\mathcal{X}_0,\tau)$ in Corollary 3.8.
$\mathfrak{M}(\mathcal{X}_0,\tau)$ in Corollary 3.8.
Given a decorated type ![]() ${\boldsymbol{\tau }}=(\tau ,\mathbf {A})$ of tropical maps, we define
${\boldsymbol{\tau }}=(\tau ,\mathbf {A})$ of tropical maps, we define
as the stack with objects over a scheme ![]() $S$ basic stable logarithmic maps
$S$ basic stable logarithmic maps ![]() $(C/S,\mathbf {p},f)$ over
$(C/S,\mathbf {p},f)$ over ![]() $b_0$ marked by the decorated type
$b_0$ marked by the decorated type ![]() ${\boldsymbol{\tau }}$. We emphasize
${\boldsymbol{\tau }}$. We emphasize ![]() $\mathscr {M}(X_0,{\boldsymbol{\tau }})$ is a moduli space of stable maps over
$\mathscr {M}(X_0,{\boldsymbol{\tau }})$ is a moduli space of stable maps over ![]() $b_0$, but we suppress
$b_0$, but we suppress ![]() $/b_0$ in the notation for simplicity. Similarly, we henceforth write
$/b_0$ in the notation for simplicity. Similarly, we henceforth write ![]() $\mathscr {M}(X_0,\beta )$ instead of
$\mathscr {M}(X_0,\beta )$ instead of ![]() $\mathscr {M}(X_0/b_0,\beta )$.
$\mathscr {M}(X_0/b_0,\beta )$.
For later use let us also show here that the monoid ideals in Definition 2.31(4) define a coherent sheaf of ideals [Reference OgusOgu18, Proposition II.2.6.1] in ![]() $\mathcal {M}_{\mathscr {M}(X_0,{\boldsymbol{\tau }})}$.
$\mathcal {M}_{\mathscr {M}(X_0,{\boldsymbol{\tau }})}$.
Lemma 2.33 For each decorated type ![]() ${\boldsymbol{\tau }}$ of tropical maps, there exists a unique coherent sheaf of ideals
${\boldsymbol{\tau }}$ of tropical maps, there exists a unique coherent sheaf of ideals ![]() $\mathcal {K}_{\boldsymbol{\tau }}\subset \mathcal {M}_{\mathscr {M}(X_0,{\boldsymbol{\tau }})}$ with stalks
$\mathcal {K}_{\boldsymbol{\tau }}\subset \mathcal {M}_{\mathscr {M}(X_0,{\boldsymbol{\tau }})}$ with stalks ![]() $\mathcal {K}_{{\boldsymbol{\tau }},\bar s}$ as defined in Definition 2.31(4).
$\mathcal {K}_{{\boldsymbol{\tau }},\bar s}$ as defined in Definition 2.31(4).
Proof. The statement follows by [Reference OgusOgu18, Proposition II.2.6.1(2)] since ![]() $\mathcal {K}_{\bar s}$ is defined by a monoid ideal in a chart.
$\mathcal {K}_{\bar s}$ is defined by a monoid ideal in a chart.
Let ![]() $\beta =(g,A,u_{p_1},\ldots ,u_{p_k})$ with
$\beta =(g,A,u_{p_1},\ldots ,u_{p_k})$ with ![]() $g=|\mathbf {g}|$,
$g=|\mathbf {g}|$, ![]() $A=|\mathbf {A}|$,
$A=|\mathbf {A}|$, ![]() $k=|L(G)|$.
$k=|L(G)|$.
(1) The stack
 $\mathscr {M}(X_0,{\boldsymbol{\tau }})$ is a proper Deligne–Mumford stack.
$\mathscr {M}(X_0,{\boldsymbol{\tau }})$ is a proper Deligne–Mumford stack.(2) The morphism
 $\mathscr {M}(X_0,{\boldsymbol{\tau }}) \longrightarrow \mathscr {M}(X_0,\beta )$ is finite and unramified.
$\mathscr {M}(X_0,{\boldsymbol{\tau }}) \longrightarrow \mathscr {M}(X_0,\beta )$ is finite and unramified.
Proof. By condition (1) in Definition 2.31, we have a morphism of stacks
Conditions (2) and (4) in Definition 2.31 defines a closed substack of the fibre product on the right-hand side. Prescribing the contact orders ![]() $u_p, u_q$ at
$u_p, u_q$ at ![]() $p\in L(G)$,
$p\in L(G)$, ![]() $q\in E(G)$ and the curve classes for the subcurves of
$q\in E(G)$ and the curve classes for the subcurves of ![]() $C$ defined by each
$C$ defined by each ![]() $v\in V(G)$ imposes locally constant conditions, and hence select a union of connected components of this closed substack. Thus
$v\in V(G)$ imposes locally constant conditions, and hence select a union of connected components of this closed substack. Thus ![]() $\mathscr {M}(X_0,{\boldsymbol{\tau }})$ is isomorphic to a closed substack of the algebraic stack
$\mathscr {M}(X_0,{\boldsymbol{\tau }})$ is isomorphic to a closed substack of the algebraic stack ![]() $\mathscr {M}(X_0,\beta )\times _\mathbf {M} \mathbf {M}(G,\mathbf {g})$, proving (1). The second statement follows since
$\mathscr {M}(X_0,\beta )\times _\mathbf {M} \mathbf {M}(G,\mathbf {g})$, proving (1). The second statement follows since ![]() $\mathfrak {M}(G,\mathbf {g}) \longrightarrow \mathfrak {M}$ is finite and unramified (Proposition 2.18).
$\mathfrak {M}(G,\mathbf {g}) \longrightarrow \mathfrak {M}$ is finite and unramified (Proposition 2.18).
3. From toric decomposition to virtual decomposition
Throughout this section, denote by ![]() $b_0= (\operatorname {Spec}\Bbbk ,\Bbbk ^\times \oplus \mathbb {N})$ the standard log point over
$b_0= (\operatorname {Spec}\Bbbk ,\Bbbk ^\times \oplus \mathbb {N})$ the standard log point over ![]() $\Bbbk$. We also fix a logarithmically smooth and projective morphism
$\Bbbk$. We also fix a logarithmically smooth and projective morphism ![]() $X_0\to b_0$ of log schemes.
$X_0\to b_0$ of log schemes.
3.1 Decomposition in the log smooth case
The decomposition formula is based on the following simple fact in toric geometry. Let ![]() $\pi : W \longrightarrow \mathbb {A}^1$ be a morphism of toric varieties with
$\pi : W \longrightarrow \mathbb {A}^1$ be a morphism of toric varieties with ![]() $\Sigma _\pi :\Sigma _W\to \Sigma _{\mathbb {A}^1}$ the corresponding morphism of fans, defined by a homomorphism
$\Sigma _\pi :\Sigma _W\to \Sigma _{\mathbb {A}^1}$ the corresponding morphism of fans, defined by a homomorphism ![]() $N \longrightarrow N_{\mathbb {A}^1}$ of co-character lattices. We identify
$N \longrightarrow N_{\mathbb {A}^1}$ of co-character lattices. We identify ![]() $\Sigma _W$ with the cone complex
$\Sigma _W$ with the cone complex ![]() $\Sigma (W)$ associated to
$\Sigma (W)$ associated to ![]() $W$ with its toric log structure, by forgetting the embedding of
$W$ with its toric log structure, by forgetting the embedding of ![]() $|\Sigma _W|$ into
$|\Sigma _W|$ into ![]() $N_\mathbb {R}$, and similarly for
$N_\mathbb {R}$, and similarly for ![]() $\Sigma _{\mathbb {A}^1}$. For a ray
$\Sigma _{\mathbb {A}^1}$. For a ray ![]() $\gamma \in \Sigma _W$ denote by
$\gamma \in \Sigma _W$ denote by ![]() $D_\gamma \subset W$ the corresponding toric divisor and by
$D_\gamma \subset W$ the corresponding toric divisor and by ![]() $m_\gamma \in \mathbb {N}$ the generator of the image of
$m_\gamma \in \mathbb {N}$ the generator of the image of
Proposition 3.1 We have the following equality of Weil divisors on ![]() $W$:
$W$:
Proof. The map ![]() $\Sigma (\pi ):N \longrightarrow \mathbb {Z}$ defines a monomial function
$\Sigma (\pi ):N \longrightarrow \mathbb {Z}$ defines a monomial function ![]() $z^m$,
$z^m$, ![]() $m\in {\operatorname {Hom}}(N,\mathbb {Z})$ on
$m\in {\operatorname {Hom}}(N,\mathbb {Z})$ on ![]() $W$. It is standard that the order of vanishing of
$W$. It is standard that the order of vanishing of ![]() $z^m$ on the divisor
$z^m$ on the divisor ![]() $D_{\gamma }$ is the value of
$D_{\gamma }$ is the value of ![]() $m$ on the generator of
$m$ on the generator of ![]() $\gamma \cap N_{\gamma }$. But this value is precisely
$\gamma \cap N_{\gamma }$. But this value is precisely ![]() $m_{\gamma }$, giving the result.
$m_{\gamma }$, giving the result.
Proposition 3.1 can equivalently be stated as a decomposition of the fundamental class of ![]() $W_0=\pi ^{-1}(0)$. Our decomposition theorem is based on the generalization of this statement to a log smooth morphism
$W_0=\pi ^{-1}(0)$. Our decomposition theorem is based on the generalization of this statement to a log smooth morphism ![]() $W_0 \longrightarrow b_0$ of logarithmic algebraic stacks locally of finite type. Note first that in this situation,
$W_0 \longrightarrow b_0$ of logarithmic algebraic stacks locally of finite type. Note first that in this situation, ![]() $W_0$ is locally pure-dimensional by log smoothness over
$W_0$ is locally pure-dimensional by log smoothness over ![]() $b_0$. Thus it makes sense to define the fundamental cycle
$b_0$. Thus it makes sense to define the fundamental cycle ![]() $[W_0]$ as locally finite formal linear combination of locally top-dimensional integral substacks.
$[W_0]$ as locally finite formal linear combination of locally top-dimensional integral substacks.
Next, to define the multiplicities ![]() $m_\gamma$, consider the morphism of generalized cone complexes
$m_\gamma$, consider the morphism of generalized cone complexes ![]() $\Sigma (W_0) \to \Sigma (b_0)$ associated to
$\Sigma (W_0) \to \Sigma (b_0)$ associated to ![]() $W_0 \longrightarrow b_0$ as defined after Proposition 2.2. We have
$W_0 \longrightarrow b_0$ as defined after Proposition 2.2. We have ![]() $\Sigma (b_0) \simeq \mathbb {R}_{\geq 0}$ with the lattice
$\Sigma (b_0) \simeq \mathbb {R}_{\geq 0}$ with the lattice ![]() $N_{b_0} \simeq \mathbb {Z}$. Working in charts, there is still a correspondence between rays
$N_{b_0} \simeq \mathbb {Z}$. Working in charts, there is still a correspondence between rays ![]() $\gamma \in \Sigma (W_0)$ and integral substacks
$\gamma \in \Sigma (W_0)$ and integral substacks ![]() $W_\gamma \subset W_0$, now locally of top dimension. Note that if
$W_\gamma \subset W_0$, now locally of top dimension. Note that if ![]() $\sigma \in \Sigma (W_0)$ and
$\sigma \in \Sigma (W_0)$ and ![]() $\gamma \to \sigma$ is a morphism in
$\gamma \to \sigma$ is a morphism in ![]() $\Sigma (X)$, then the pull-back of
$\Sigma (X)$, then the pull-back of ![]() $W_\gamma$ to a chart for
$W_\gamma$ to a chart for ![]() $W_0$ at a geometric point of the stratum
$W_0$ at a geometric point of the stratum ![]() $W_0(\sigma )$ is contained in the union of all toric divisors for rays
$W_0(\sigma )$ is contained in the union of all toric divisors for rays ![]() $\gamma '\subset \sigma$ with
$\gamma '\subset \sigma$ with ![]() $\gamma \simeq \gamma '$ in
$\gamma \simeq \gamma '$ in ![]() $\Sigma (W_0)$. Hence
$\Sigma (W_0)$. Hence ![]() $W_\gamma$ may not be locally irreducible if
$W_\gamma$ may not be locally irreducible if ![]() $\Sigma (W_0)$ has cones with self-identifications. But since we work with cone complexes with reduced presentations, such rays
$\Sigma (W_0)$ has cones with self-identifications. But since we work with cone complexes with reduced presentations, such rays ![]() $\gamma ,\gamma '\subset \sigma$ define the same one-dimensional cone in
$\gamma ,\gamma '\subset \sigma$ define the same one-dimensional cone in ![]() $\Sigma (W_0)$. These rays may be identified by self-maps of
$\Sigma (W_0)$. These rays may be identified by self-maps of ![]() $\sigma$ or simply correspond to several maps
$\sigma$ or simply correspond to several maps ![]() $\sigma ^\vee \to \gamma ^\vee$ defined by generization in
$\sigma ^\vee \to \gamma ^\vee$ defined by generization in ![]() $\overline{\mathcal{M}}_{W_0}$.
$\overline{\mathcal{M}}_{W_0}$.
For a ray ![]() $\gamma$ with integral lattice
$\gamma$ with integral lattice ![]() $N_{\gamma }$, we have
$N_{\gamma }$, we have ![]() $\gamma \cap N_{\gamma }\simeq \mathbb {N}$, and the homomorphism
$\gamma \cap N_{\gamma }\simeq \mathbb {N}$, and the homomorphism ![]() $\mathbb {Z}\simeq N_\gamma \longrightarrow N_{b_0}\simeq \mathbb {Z}$ is multiplication by an integer
$\mathbb {Z}\simeq N_\gamma \longrightarrow N_{b_0}\simeq \mathbb {Z}$ is multiplication by an integer ![]() $m_\gamma$.
$m_\gamma$.
For the following statement recall also the notion of idealized log structures and idealized log smoothness from [Reference OgusOgu18, III.1.3 and IV.3]. In a nutshell, this notion is designed to treat strata of logarithmic spaces, by adding sheaves of ideals ![]() $\mathcal {K}\subset \mathcal {M}_X$ defining these strata as part of the data.
$\mathcal {K}\subset \mathcal {M}_X$ defining these strata as part of the data.
Corollary 3.2 Let ![]() $\pi :W_0 \longrightarrow b_0$ be a log smooth morphism locally of finite type from a logarithmic algebraic stack to the standard log point
$\pi :W_0 \longrightarrow b_0$ be a log smooth morphism locally of finite type from a logarithmic algebraic stack to the standard log point ![]() $b_0$. Denote by
$b_0$. Denote by ![]() $[W_0]$ the fundamental cycle of
$[W_0]$ the fundamental cycle of ![]() $W_0$, well-defined since
$W_0$, well-defined since ![]() $W_0$ is locally pure-dimensional. Then the following formula holds
$W_0$ is locally pure-dimensional. Then the following formula holds
in the group of locally top-dimensional algebraic cycles on ![]() $W_0$ [Reference KreschKre99]. The sum runs over the one-dimensional cones in the generalized cone complex
$W_0$ [Reference KreschKre99]. The sum runs over the one-dimensional cones in the generalized cone complex ![]() $\Sigma (W_0)$ of
$\Sigma (W_0)$ of ![]() $W_0$.
$W_0$.
Moreover, ![]() $W_\gamma$ is idealized log smooth over
$W_\gamma$ is idealized log smooth over ![]() $b_0$ for some sheaf of ideals
$b_0$ for some sheaf of ideals ![]() $\mathcal {K}_\gamma \subset \mathcal {M}_{W_\gamma }$.
$\mathcal {K}_\gamma \subset \mathcal {M}_{W_\gamma }$.
Proof. The claimed equality of cycles can be checked on a cover by smooth charts. We may thus assume that ![]() $W_0$ is covered by a neat chart, that is, that we have a commutative diagram
$W_0$ is covered by a neat chart, that is, that we have a commutative diagram

where (i) ![]() $h$ is an étale surjection, (ii)
$h$ is an étale surjection, (ii) ![]() $\operatorname {Spec}\Bbbk \longrightarrow \mathbb {A}^1$ is the inclusion of the origin and
$\operatorname {Spec}\Bbbk \longrightarrow \mathbb {A}^1$ is the inclusion of the origin and ![]() $g:U\to \operatorname {Spec}\Bbbk \times _{\mathbb {A}^1} V= \pi _V^{-1}(0)$ is smooth, (iii)
$g:U\to \operatorname {Spec}\Bbbk \times _{\mathbb {A}^1} V= \pi _V^{-1}(0)$ is smooth, (iii) ![]() $V$ is the affine toric variety
$V$ is the affine toric variety ![]() $\operatorname {Spec}\Bbbk [\sigma ^\vee \cap N^*]$ defined by
$\operatorname {Spec}\Bbbk [\sigma ^\vee \cap N^*]$ defined by ![]() $(\sigma _\mathbb {R},N)\in \Sigma (W_0)$ and
$(\sigma _\mathbb {R},N)\in \Sigma (W_0)$ and ![]() $\pi _V:V\to \mathbb {A}^1$ is a toric morphism. Thus we have
$\pi _V:V\to \mathbb {A}^1$ is a toric morphism. Thus we have
via flat pull-back, where ![]() $V_0=\pi ^{-1}(0)$. Now Proposition 3.1 describes
$V_0=\pi ^{-1}(0)$. Now Proposition 3.1 describes ![]() $[V_0]$ in terms of the toric divisors
$[V_0]$ in terms of the toric divisors ![]() $D_{\gamma '}\subset V$ defined by the rays
$D_{\gamma '}\subset V$ defined by the rays ![]() $\gamma '\subset \sigma$. Thus
$\gamma '\subset \sigma$. Thus
with ![]() $m_{\gamma '}$ the generator of the image of
$m_{\gamma '}$ the generator of the image of ![]() $\mathbb {Z}\simeq N_{\gamma '}\to N_{\mathbb {A}^1}=\mathbb {Z}$. Each such
$\mathbb {Z}\simeq N_{\gamma '}\to N_{\mathbb {A}^1}=\mathbb {Z}$. Each such ![]() $\gamma '$ defines a one-dimensional cone
$\gamma '$ defines a one-dimensional cone ![]() $\gamma \in \Sigma (W_0)$ with
$\gamma \in \Sigma (W_0)$ with ![]() $m_\gamma =m_{\gamma '}$. Moreover, for two different rays
$m_\gamma =m_{\gamma '}$. Moreover, for two different rays ![]() $\gamma ',\gamma ''\subset \sigma$, the geometric generic points of
$\gamma ',\gamma ''\subset \sigma$, the geometric generic points of ![]() $D_{\gamma '}$,
$D_{\gamma '}$, ![]() $D_{\gamma ''}$ map to the same geometric generic point of
$D_{\gamma ''}$ map to the same geometric generic point of ![]() $W_0$ if and only if there exists a one-dimensional cone
$W_0$ if and only if there exists a one-dimensional cone ![]() $\gamma \in \Sigma (W_0)$ and morphisms
$\gamma \in \Sigma (W_0)$ and morphisms ![]() $\gamma \to \gamma '$ and
$\gamma \to \gamma '$ and ![]() $\gamma \to \gamma ''$. Since
$\gamma \to \gamma ''$. Since ![]() $\Sigma (x)$ is the colimit of such
$\Sigma (x)$ is the colimit of such ![]() $\sigma$ appearing in neat charts of
$\sigma$ appearing in neat charts of ![]() $W_0$, the equality (3.1) in a chart verifies the claimed equation of cycles.
$W_0$, the equality (3.1) in a chart verifies the claimed equation of cycles.
The claim on idealized log smoothness of ![]() $W_\gamma$ follows from the local description as a union of toric strata and the criteria in [Reference OgusOgu18, IV.3.1.21 and IV.3.1.22].
$W_\gamma$ follows from the local description as a union of toric strata and the criteria in [Reference OgusOgu18, IV.3.1.21 and IV.3.1.22].
3.2 Logarithmic maps to the relative Artin fan  $\mathcal {X}_0$
$\mathcal {X}_0$
To lift the decomposition result Corollary 3.2 to the moduli space ![]() $\mathscr {M}(X_0,\beta ) =\mathscr {M}(X_0/b_0,\beta )$ of stable logarithmic maps in Theorem 1.2, we factor the map
$\mathscr {M}(X_0,\beta ) =\mathscr {M}(X_0/b_0,\beta )$ of stable logarithmic maps in Theorem 1.2, we factor the map ![]() $\mathscr {M}(X_0,\beta ) \to \mathfrak {M}_{b_0}$ forgetting the logarithmic map to
$\mathscr {M}(X_0,\beta ) \to \mathfrak {M}_{b_0}$ forgetting the logarithmic map to ![]() $X_0$ via an intermediate log stack that is log étale over
$X_0$ via an intermediate log stack that is log étale over ![]() $\mathfrak {M}_{b_0}=\mathfrak {M}_B\times _B b_0$. This intermediate log stack is the stack
$\mathfrak {M}_{b_0}=\mathfrak {M}_B\times _B b_0$. This intermediate log stack is the stack ![]() $\mathfrak {M}(\mathcal {X}_0,\beta ')$ of basic logarithmic maps to the relative Artin fan
$\mathfrak {M}(\mathcal {X}_0,\beta ')$ of basic logarithmic maps to the relative Artin fan ![]() $\mathcal {X}_0 = b_0\times _B \mathcal {X}$ of
$\mathcal {X}_0 = b_0\times _B \mathcal {X}$ of ![]() $X_0$ over
$X_0$ over ![]() $b_0$ (Definition 2.9). Since curve classes do not make sense on
$b_0$ (Definition 2.9). Since curve classes do not make sense on ![]() $\mathcal {X}_0$, we have no stability in
$\mathcal {X}_0$, we have no stability in ![]() $\mathfrak {M}(\mathcal {X}_0,\beta ')$ and
$\mathfrak {M}(\mathcal {X}_0,\beta ')$ and
only keeps the genus and the contact orders at the marked points from ![]() $\beta =(g,A,u_{p_1},\ldots ,u_{p_k})$. The point is that
$\beta =(g,A,u_{p_1},\ldots ,u_{p_k})$. The point is that ![]() $\mathfrak {M}(\mathcal {X}_0,\beta ')$ is pure-dimensional, has unobstructed deformations and captures the tropical geometry of the situation, while the decomposition according to Corollary 3.2 has a simple tropical interpretation on this stack.
$\mathfrak {M}(\mathcal {X}_0,\beta ')$ is pure-dimensional, has unobstructed deformations and captures the tropical geometry of the situation, while the decomposition according to Corollary 3.2 has a simple tropical interpretation on this stack.
(1) The stack of basic logarithmic maps
 $\mathfrak {M}(\mathcal {X}_0,\beta ')$ to
$\mathfrak {M}(\mathcal {X}_0,\beta ')$ to  $\mathcal {X}_0$ over
$\mathcal {X}_0$ over  $b_0$ is algebraic.
$b_0$ is algebraic.(2) The morphism
 $\mathfrak {M}(\mathcal {X}_0,\beta ) \longrightarrow \mathfrak {M}_{b_0}$ forgetting the logarithmic map to
$\mathfrak {M}(\mathcal {X}_0,\beta ) \longrightarrow \mathfrak {M}_{b_0}$ forgetting the logarithmic map to  $\mathcal {X}_0$ is strict and étale.
$\mathcal {X}_0$ is strict and étale.
Proof. Let ![]() $\mathfrak {C}_{b_0}$ denote the universal curve over
$\mathfrak {C}_{b_0}$ denote the universal curve over ![]() $\mathfrak {M}_{b_0}$. By openness of basicness,
$\mathfrak {M}_{b_0}$. By openness of basicness, ![]() $\mathfrak {M}(\mathcal {X}_0,\beta ')$ is an open substack of
$\mathfrak {M}(\mathcal {X}_0,\beta ')$ is an open substack of ![]() ${\operatorname {Hom}}_{\mathfrak {M}_{b_0}}(\mathfrak {C}_{b_0}, \mathfrak {M}_{b_0}\times _{b_0} \mathcal {X}_0)$. This Hom-stack is algebraic by [Reference WiseWis16, Corollary 1.1.1], proving (1).
${\operatorname {Hom}}_{\mathfrak {M}_{b_0}}(\mathfrak {C}_{b_0}, \mathfrak {M}_{b_0}\times _{b_0} \mathcal {X}_0)$. This Hom-stack is algebraic by [Reference WiseWis16, Corollary 1.1.1], proving (1).
For (2), the morphism ![]() $\mathfrak {M}(\mathcal {X}_0,\beta ') \longrightarrow \mathfrak {M}_{b_0}$ is strict by definition. Since
$\mathfrak {M}(\mathcal {X}_0,\beta ') \longrightarrow \mathfrak {M}_{b_0}$ is strict by definition. Since ![]() $\mathcal {A}_X\to \mathcal {A}_B$ is logarithmically étale, it follows that
$\mathcal {A}_X\to \mathcal {A}_B$ is logarithmically étale, it follows that ![]() $\mathcal {X}_0$ is logarithmically étale over
$\mathcal {X}_0$ is logarithmically étale over ![]() $b_0$. Now [Reference Abramovich and WiseAW18, Propostion 3.2] implies that
$b_0$. Now [Reference Abramovich and WiseAW18, Propostion 3.2] implies that ![]() $\mathfrak {M}(\mathcal {X}_0,\beta ')\to \mathfrak {M}_{b_0}$ is logarithmically étale.
$\mathfrak {M}(\mathcal {X}_0,\beta ')\to \mathfrak {M}_{b_0}$ is logarithmically étale.
Note that Proposition 3.3(2) also shows that ![]() $\mathfrak {M}(\mathcal {X}_0,\beta ')$ is log smooth over
$\mathfrak {M}(\mathcal {X}_0,\beta ')$ is log smooth over ![]() $b_0$, because
$b_0$, because ![]() $\mathfrak {M}_{b_0}$ is, and that the obstruction theory of
$\mathfrak {M}_{b_0}$ is, and that the obstruction theory of ![]() $\mathscr {M}(X_0,\beta )$ over
$\mathscr {M}(X_0,\beta )$ over ![]() $\mathfrak {M}_{b_0}$ induces an obstruction theory for
$\mathfrak {M}_{b_0}$ induces an obstruction theory for ![]() $\mathscr {M}(X_0,\beta )$ over
$\mathscr {M}(X_0,\beta )$ over ![]() $\mathfrak {M}(\mathcal {X}_0,\beta ')$.
$\mathfrak {M}(\mathcal {X}_0,\beta ')$.
Remark 3.4 Implicit in the discussion in Proposition 2.28 applied with ![]() $X=\operatorname {Spec}\Bbbk$ and in Remark 2.29 is the fact that log-smoothness of
$X=\operatorname {Spec}\Bbbk$ and in Remark 2.29 is the fact that log-smoothness of ![]() $\mathbf {M}$ can be used to relate the moduli space of abstract tropical curves to the tropicalization of
$\mathbf {M}$ can be used to relate the moduli space of abstract tropical curves to the tropicalization of ![]() $\mathbf{M}$, properly interpreted as a stacky cone complex [Reference Cavalieri, Chan, Ulirsch and WiseCCUW20]; see the precise statement in [Theorem 3.14, Reference UlirschUli20]. In view of Proposition 3.3(2) we can now similarly relate the moduli space of tropical maps to
$\mathbf{M}$, properly interpreted as a stacky cone complex [Reference Cavalieri, Chan, Ulirsch and WiseCCUW20]; see the precise statement in [Theorem 3.14, Reference UlirschUli20]. In view of Proposition 3.3(2) we can now similarly relate the moduli space of tropical maps to ![]() $\Sigma (X_0)=\Sigma (\mathcal {X}_0)$ of class
$\Sigma (X_0)=\Sigma (\mathcal {X}_0)$ of class ![]() $\beta '$ to the stacky cone complex associated to
$\beta '$ to the stacky cone complex associated to ![]() $\mathfrak {M}(\mathcal {X}_0,\beta ')$. While we do not develop the details of this picture here, it should be clear that this interpretation is at the basis of many arguments in this paper.
$\mathfrak {M}(\mathcal {X}_0,\beta ')$. While we do not develop the details of this picture here, it should be clear that this interpretation is at the basis of many arguments in this paper.
We also need the ![]() $\tau$-marked refinements
$\tau$-marked refinements ![]() $\mathfrak {M}(\mathcal {X}_0,\tau )$ of
$\mathfrak {M}(\mathcal {X}_0,\tau )$ of ![]() $\mathfrak {M}(\mathcal {X}_0,\beta ')$, similar to
$\mathfrak {M}(\mathcal {X}_0,\beta ')$, similar to ![]() $\mathscr {M}(X_0,{\boldsymbol{\tau }})$ for
$\mathscr {M}(X_0,{\boldsymbol{\tau }})$ for ![]() $\mathscr {M}(X_0,\beta )$. Omitting the curve class,
$\mathscr {M}(X_0,\beta )$. Omitting the curve class, ![]() $\tau$ is now a type of tropical map to
$\tau$ is now a type of tropical map to ![]() $\Sigma (X_0)$ of total genus
$\Sigma (X_0)$ of total genus ![]() $g$ and with
$g$ and with ![]() $k$ legs (Definition 2.23(1)). Then
$k$ legs (Definition 2.23(1)). Then
is defined as in Definition 2.31 with ![]() $\mathcal {X}_0$ replacing
$\mathcal {X}_0$ replacing ![]() $X_0$ and disregarding the curve classes in Definition 2.31(3). Analogous to
$X_0$ and disregarding the curve classes in Definition 2.31(3). Analogous to ![]() $\mathcal {K}_{\boldsymbol{\tau }}$ for
$\mathcal {K}_{\boldsymbol{\tau }}$ for ![]() $\mathscr {M}(X_0,{\boldsymbol{\tau }})$ constructed in Lemma 2.33, we have a sheaf of ideals
$\mathscr {M}(X_0,{\boldsymbol{\tau }})$ constructed in Lemma 2.33, we have a sheaf of ideals
We first observe the following analogue of Proposition 2.34.
Proposition 3.5
(1) The stack
 $\mathfrak {M}(\mathcal {X}_0,\tau )$ is algebraic.
$\mathfrak {M}(\mathcal {X}_0,\tau )$ is algebraic.(2) The morphism
 $\iota _\tau :\mathfrak {M}(\mathcal {X}_0,\tau ) \longrightarrow \mathfrak {M}(\mathcal {X}_0,\beta ')$ forgetting the marking by
$\iota _\tau :\mathfrak {M}(\mathcal {X}_0,\tau ) \longrightarrow \mathfrak {M}(\mathcal {X}_0,\beta ')$ forgetting the marking by  $\tau$ is finite and unramified.
$\tau$ is finite and unramified.
Proof. The proof is identical to the proof of Proposition 2.34.
We are now in position to apply Corollary 3.2 to ![]() $\mathfrak {M}(\mathcal {X}_0,\beta ')\to b_0$. The key is the description of the components
$\mathfrak {M}(\mathcal {X}_0,\beta ')\to b_0$. The key is the description of the components ![]() $W_\gamma$ in this corollary in terms of rigid tropical maps.
$W_\gamma$ in this corollary in terms of rigid tropical maps.
Definition 3.6 A family of tropical maps ![]() $h:\Gamma \to \Sigma (X_0)$ of type
$h:\Gamma \to \Sigma (X_0)$ of type ![]() $\tau$ is rigid if the corresponding basic monoid
$\tau$ is rigid if the corresponding basic monoid ![]() $Q(\tau )$ from Definition 2.23(3) is isomorphic to
$Q(\tau )$ from Definition 2.23(3) is isomorphic to ![]() $\mathbb {N}$.
$\mathbb {N}$.
In the language of polyhedral complexes, being rigid is equivalent to saying that the restriction ![]() $\bar h: \bar \Gamma \longrightarrow \Delta (X)$ of
$\bar h: \bar \Gamma \longrightarrow \Delta (X)$ of ![]() $h$ to the fiber over
$h$ to the fiber over ![]() $1\in \mathbb {R}_{\ge 0}=\Sigma (b_0)$ cannot be deformed as a map of generalized polyhedral complexes. In other words, as a traditional tropical map, any deformation of
$1\in \mathbb {R}_{\ge 0}=\Sigma (b_0)$ cannot be deformed as a map of generalized polyhedral complexes. In other words, as a traditional tropical map, any deformation of ![]() $\bar h$ keeping the combinatorial data (i.e. of constant type) is trivial.
$\bar h$ keeping the combinatorial data (i.e. of constant type) is trivial.
The following decomposition of the Artin stack ![]() $\mathfrak {M}(\mathcal {X}_0,\beta ')$ according to rigid tropical curves is the main result of this section.
$\mathfrak {M}(\mathcal {X}_0,\beta ')$ according to rigid tropical curves is the main result of this section.
Theorem 3.7 (Virtual decomposition) For each irreducible component ![]() $W_\gamma$ of
$W_\gamma$ of ![]() $\mathfrak {M}(\mathcal {X}_0,\beta ')$ according to Corollary 3.2 there exists a unique type
$\mathfrak {M}(\mathcal {X}_0,\beta ')$ according to Corollary 3.2 there exists a unique type ![]() $\tau$ of a rigid tropical map such that
$\tau$ of a rigid tropical map such that ![]() $W_\gamma$ is an irreducible component of the image of the finite map
$W_\gamma$ is an irreducible component of the image of the finite map ![]() $\iota _\tau :\mathfrak {M}(\mathcal {X}_0,\tau ) \longrightarrow \mathfrak {M}(\mathcal {X}_0,\beta ')$ from Proposition 3.5.
$\iota _\tau :\mathfrak {M}(\mathcal {X}_0,\tau ) \longrightarrow \mathfrak {M}(\mathcal {X}_0,\beta ')$ from Proposition 3.5.
In particular, ![]() $\mathfrak {M}(\mathcal {X}_0,\tau )$ with the sheaf of ideals
$\mathfrak {M}(\mathcal {X}_0,\tau )$ with the sheaf of ideals ![]() $\mathcal {K}_\tau \subset \mathcal {M}_{\mathfrak {M}(\mathcal {X}_0,\tau )}$ from (3.2) is idealized.
$\mathcal {K}_\tau \subset \mathcal {M}_{\mathfrak {M}(\mathcal {X}_0,\tau )}$ from (3.2) is idealized.
Proof. The logarithmic stack ![]() $\mathfrak {M}(\mathcal {X}_0,\beta ')$ is logarithmically smooth over
$\mathfrak {M}(\mathcal {X}_0,\beta ')$ is logarithmically smooth over ![]() $b_0$ by Proposition 3.3 and since
$b_0$ by Proposition 3.3 and since ![]() $\mathfrak {M}_{b_0}/b_0$ is logarithmically smooth. Up to a smooth factor, the map
$\mathfrak {M}_{b_0}/b_0$ is logarithmically smooth. Up to a smooth factor, the map
is locally given by base change to the central fibre of the map of toric varieties ![]() $\operatorname {Spec} \Bbbk [Q] \longrightarrow \operatorname {Spec} \Bbbk [\mathbb {N}]$ with
$\operatorname {Spec} \Bbbk [Q] \longrightarrow \operatorname {Spec} \Bbbk [\mathbb {N}]$ with ![]() $Q$ the basic monoid of a tropical map to
$Q$ the basic monoid of a tropical map to ![]() $\Sigma (X)$ of some type
$\Sigma (X)$ of some type ![]() $\tau '$ and
$\tau '$ and ![]() $\mathbb {N}\to Q$ induced by the structure map
$\mathbb {N}\to Q$ induced by the structure map
Locally the subschemes ![]() $W_\gamma$ are defined by the toric divisors in
$W_\gamma$ are defined by the toric divisors in ![]() $\operatorname {Spec}\Bbbk [Q]$, which are in bijection to extremal rays in
$\operatorname {Spec}\Bbbk [Q]$, which are in bijection to extremal rays in ![]() $Q_\mathbb {R}^\vee$. Each extremal ray defines a rigid tropical map, say of type
$Q_\mathbb {R}^\vee$. Each extremal ray defines a rigid tropical map, say of type ![]() $\tau$. Any localization map of the associated basic monoids
$\tau$. Any localization map of the associated basic monoids ![]() $Q_{\tau '} \longrightarrow Q_\tau =\mathbb {N}$ is the contraction of the codimension one face dual to the one-dimensional cone in
$Q_{\tau '} \longrightarrow Q_\tau =\mathbb {N}$ is the contraction of the codimension one face dual to the one-dimensional cone in ![]() $Q_{\tau '}^\vee$ defined by
$Q_{\tau '}^\vee$ defined by ![]() $\tau$. By the definition of
$\tau$. By the definition of ![]() $\mathcal {K}_\tau$, the monoid ideal defining the corresponding toric prime divisor agrees with the ideal in
$\mathcal {K}_\tau$, the monoid ideal defining the corresponding toric prime divisor agrees with the ideal in ![]() $Q_{\tau '}$ given by
$Q_{\tau '}$ given by ![]() $\mathcal {K}_\tau$. Since this description is compatible with the restriction of charts, the first statement follows.
$\mathcal {K}_\tau$. Since this description is compatible with the restriction of charts, the first statement follows.
Corollary 3.2 also shows that ![]() $W_\gamma \to b_0$ is idealized log-smooth. The corresponding sheaf of ideals has just been checked to agree with
$W_\gamma \to b_0$ is idealized log-smooth. The corresponding sheaf of ideals has just been checked to agree with ![]() $\mathcal {K}_\tau$ locally along
$\mathcal {K}_\tau$ locally along ![]() $W_\gamma$.
$W_\gamma$.
Corollary 3.8 We have the following equality of top-dimensional algebraic cycles in the pure-dimensional algebraic stack ![]() $\mathfrak {M}(\mathcal {X}_0,\beta ')$:
$\mathfrak {M}(\mathcal {X}_0,\beta ')$:
The sum is over all types ![]() $\tau$ of rigid tropical maps to
$\tau$ of rigid tropical maps to ![]() $\Sigma (X)$ and
$\Sigma (X)$ and ![]() $m_\tau \in \mathbb {N}\setminus \{0\}$ is the projection of the generator of the dual basic monoid
$m_\tau \in \mathbb {N}\setminus \{0\}$ is the projection of the generator of the dual basic monoid ![]() $Q_\tau ^\vee \simeq \mathbb {N}$ to
$Q_\tau ^\vee \simeq \mathbb {N}$ to ![]() $\Sigma (b_0)=\mathbb {R}_{\ge 0}$.
$\Sigma (b_0)=\mathbb {R}_{\ge 0}$.
Proof. The statement merely spells out the definition of the multiplicities ![]() $m_\tau$ in Corollary 3.2.
$m_\tau$ in Corollary 3.2.
3.3 Proof of the decomposition theorem
To prove the main theorem, Theorem 1.2, it remains to apply the virtual bivariant machinery developed by Costello [Reference CostelloCos06] and Manolache [Reference ManolacheMan12]. We need two lemmas.
Lemma 3.9 The degree of the finite map
from Proposition 3.5(2) over any irreducible component of the image is ![]() $|\operatorname {Aut}(\tau )|$.
$|\operatorname {Aut}(\tau )|$.
Proof. The description of the smooth cover of ![]() $\mathfrak {M}(\mathcal {X}_0,\beta ')$ given in the proof of Theorem 3.7 shows that each geometric generic point
$\mathfrak {M}(\mathcal {X}_0,\beta ')$ given in the proof of Theorem 3.7 shows that each geometric generic point ![]() $\operatorname {Spec} K\to \mathfrak {M}(\mathcal {X}_0,\beta ')$ of
$\operatorname {Spec} K\to \mathfrak {M}(\mathcal {X}_0,\beta ')$ of ![]() $\iota _\tau (\mathfrak {M}(\mathcal {X}_0,\tau ))$ is a basic logarithmic map to
$\iota _\tau (\mathfrak {M}(\mathcal {X}_0,\tau ))$ is a basic logarithmic map to ![]() $\mathcal {X}_0$ over
$\mathcal {X}_0$ over ![]() $b_0$, defined over
$b_0$, defined over ![]() $K$ and with basic monoid
$K$ and with basic monoid ![]() $Q(\tau )=\mathbb {N}$ and tropical type isomorphic to
$Q(\tau )=\mathbb {N}$ and tropical type isomorphic to ![]() $\tau$. Thus a geometric generic point of
$\tau$. Thus a geometric generic point of ![]() $\mathfrak {M}(\mathcal {X}_0,\tau )$ is a basic logarithmic map
$\mathfrak {M}(\mathcal {X}_0,\tau )$ is a basic logarithmic map ![]() $(C/S,\mathbf {p},f)$ to
$(C/S,\mathbf {p},f)$ to ![]() $\mathcal {X}_0$ over a standard logarithmic point
$\mathcal {X}_0$ over a standard logarithmic point ![]() $S=\operatorname {Spec}(\mathbb {N} \longrightarrow K)$. Writing
$S=\operatorname {Spec}(\mathbb {N} \longrightarrow K)$. Writing ![]() $\tau =(G,\mathbf {g},\boldsymbol {\sigma },\mathbf {u})$, the fibre of
$\tau =(G,\mathbf {g},\boldsymbol {\sigma },\mathbf {u})$, the fibre of ![]() $\iota _\tau$ over
$\iota _\tau$ over ![]() $(C/S,\mathbf {p},f)$ is an isomorphism of the dual intersection graph of
$(C/S,\mathbf {p},f)$ is an isomorphism of the dual intersection graph of ![]() $C$ with
$C$ with ![]() $G$ identifying
$G$ identifying ![]() $\mathbf {g},\boldsymbol {\sigma },\mathbf {u}$ with the genera, strata and contact orders of
$\mathbf {g},\boldsymbol {\sigma },\mathbf {u}$ with the genera, strata and contact orders of ![]() $(C/S,\mathbf {p},f)$. The statement now follows by observing that the automorphism group
$(C/S,\mathbf {p},f)$. The statement now follows by observing that the automorphism group ![]() $\operatorname {Aut}(\tau )$ of the decorated graph
$\operatorname {Aut}(\tau )$ of the decorated graph ![]() $\tau$ acts simply transitively on this set of isomorphisms of graphs.
$\tau$ acts simply transitively on this set of isomorphisms of graphs.
As an intermediate object we define the stack of basic stable logarithmic maps marked by a tropical type ![]() $\tau$ by
$\tau$ by
Compared to ![]() $\mathscr {M}(X_0,{\boldsymbol{\tau }})$, this stack keeps the total curve class
$\mathscr {M}(X_0,{\boldsymbol{\tau }})$, this stack keeps the total curve class ![]() $A$ from
$A$ from ![]() $\beta =(g,A,u_{p_1},\ldots ,u_{p_k})$, but drops the restriction on the distribution of
$\beta =(g,A,u_{p_1},\ldots ,u_{p_k})$, but drops the restriction on the distribution of ![]() $A$ to the subcurves given by the vertices.
$A$ to the subcurves given by the vertices.
For the following statement recall that ![]() $\mathscr {M}(X_0,{\boldsymbol{\tau }})$ is the stack defined in (2.26) of basic stable log maps over
$\mathscr {M}(X_0,{\boldsymbol{\tau }})$ is the stack defined in (2.26) of basic stable log maps over ![]() $b_0$ marked by the decorated type
$b_0$ marked by the decorated type ![]() ${\boldsymbol{\tau }}$ and
${\boldsymbol{\tau }}$ and
is the morphism forgetting the marking.
Lemma 3.10 Let ![]() $\tau =(G,\mathbf {g},\boldsymbol {\sigma },\mathbf {u})$ be the type of a tropical map to
$\tau =(G,\mathbf {g},\boldsymbol {\sigma },\mathbf {u})$ be the type of a tropical map to ![]() $\Sigma (X_0)$ and
$\Sigma (X_0)$ and ![]() $\beta =(g,A,u_{p_1},\ldots ,u_{p_k})$. Then we have the decomposition
$\beta =(g,A,u_{p_1},\ldots ,u_{p_k})$. Then we have the decomposition
where the sum is over all ![]() $\mathbf {A}: V(G)\to H_2^+(X_0)$ with
$\mathbf {A}: V(G)\to H_2^+(X_0)$ with ![]() $|\mathbf {A}|=A$ and
$|\mathbf {A}|=A$ and ![]() ${\boldsymbol{\tau }}=(\tau ,\mathbf {A})$.
${\boldsymbol{\tau }}=(\tau ,\mathbf {A})$.
Proof. The result follows since the map ![]() $\mathbf {A}: V(G)\to H_2^+(X_0)$ of curve classes is locally constant on
$\mathbf {A}: V(G)\to H_2^+(X_0)$ of curve classes is locally constant on ![]() $\mathscr {M}_\tau (X_0,\beta )$.
$\mathscr {M}_\tau (X_0,\beta )$.
Before stating the main theorem, we note that ![]() $\mathscr {M}_\tau (X_0,\beta )$ inherits a perfect obstruction theoryFootnote 7
$\mathscr {M}_\tau (X_0,\beta )$ inherits a perfect obstruction theoryFootnote 7 ![]() $\mathfrak {E}_\tau$ over
$\mathfrak {E}_\tau$ over ![]() $\mathfrak {M}(\mathcal {X}_0,\tau )$ from the perfect obstruction theory
$\mathfrak {M}(\mathcal {X}_0,\tau )$ from the perfect obstruction theory ![]() $\mathfrak {E}$ of
$\mathfrak {E}$ of ![]() $\mathscr {M}(X_0,\beta )$ over
$\mathscr {M}(X_0,\beta )$ over ![]() $\mathfrak {M}(\mathcal {X}_0,\beta ')$ by base change by
$\mathfrak {M}(\mathcal {X}_0,\beta ')$ by base change by ![]() $\iota _\tau : \mathfrak {M}(\mathcal {X}_0,\tau )\to \mathfrak {M}(\mathcal {X}_0,\beta ')$. Restricting to the open substacks
$\iota _\tau : \mathfrak {M}(\mathcal {X}_0,\tau )\to \mathfrak {M}(\mathcal {X}_0,\beta ')$. Restricting to the open substacks ![]() $\mathscr {M}(X_0,{\boldsymbol{\tau }})\subset \mathscr {M}_\tau (X_0,\beta )$ in Lemma 3.10, we also have an obstruction theory
$\mathscr {M}(X_0,{\boldsymbol{\tau }})\subset \mathscr {M}_\tau (X_0,\beta )$ in Lemma 3.10, we also have an obstruction theory ![]() $\mathfrak {E}_{\boldsymbol{\tau }}$ on
$\mathfrak {E}_{\boldsymbol{\tau }}$ on ![]() $\mathscr {M}(X_0,{\boldsymbol{\tau }})$. If
$\mathscr {M}(X_0,{\boldsymbol{\tau }})$. If ![]() $\tau$ is rigid,
$\tau$ is rigid, ![]() $\mathfrak {M}(\mathcal {X}_0,\tau )$ is pure-dimensional of the same dimension as
$\mathfrak {M}(\mathcal {X}_0,\tau )$ is pure-dimensional of the same dimension as ![]() $\mathfrak {M}(\mathcal {X}_0,\beta ')$. Thus we have virtual fundamental classes
$\mathfrak {M}(\mathcal {X}_0,\beta ')$. Thus we have virtual fundamental classes
on the moduli spaces ![]() $\mathscr {M}(X_0,\beta )$,
$\mathscr {M}(X_0,\beta )$, ![]() $\mathscr {M}_\tau (X_0,\beta )$ and
$\mathscr {M}_\tau (X_0,\beta )$ and ![]() $\mathscr {M}(X_0,{\boldsymbol{\tau }})$.
$\mathscr {M}(X_0,{\boldsymbol{\tau }})$.
Here is our main theorem, stated as Theorem 1.2 in the introduction.
Theorem 3.11 For any ![]() $\beta =(g,A,u_{p_1},\ldots ,u_{p_k})$ we have the equality
$\beta =(g,A,u_{p_1},\ldots ,u_{p_k})$ we have the equality
in the Chow group of the underlying stack ![]() $\underline{\mathscr {M}}(X_0,\beta )$ with coefficients in
$\underline{\mathscr {M}}(X_0,\beta )$ with coefficients in ![]() $\mathbb {Q}$. The sum is over all isomorphism classes of decorated types of rigid tropical maps
$\mathbb {Q}$. The sum is over all isomorphism classes of decorated types of rigid tropical maps ![]() ${\boldsymbol{\tau }}=(G,\mathbf {g},\boldsymbol {\sigma },\mathbf {u},\mathbf {A})=(\tau ,\mathbf {A})$ of total genus
${\boldsymbol{\tau }}=(G,\mathbf {g},\boldsymbol {\sigma },\mathbf {u},\mathbf {A})=(\tau ,\mathbf {A})$ of total genus ![]() $|\mathbf {g}|=g$, total curve class
$|\mathbf {g}|=g$, total curve class ![]() $|\mathbf {A}|=A$ and
$|\mathbf {A}|=A$ and ![]() $|L(G)|=k$.
$|L(G)|=k$.
Proof. By Corollary 3.8 and Lemma 3.9 we can write the fundamental class of ![]() $\mathfrak {M}(\mathcal {X}_0,\beta ')$ as
$\mathfrak {M}(\mathcal {X}_0,\beta ')$ as
For each ![]() $\tau$, compatibility of virtual pull-back with push-forward [Reference ManolacheMan12, Theorem 4.1(3)] applied to the cartesian square
$\tau$, compatibility of virtual pull-back with push-forward [Reference ManolacheMan12, Theorem 4.1(3)] applied to the cartesian square

yields
Moreover, from Lemma 3.10 and the definition of ![]() $\mathfrak {E}_{\boldsymbol{\tau }}$ by restriction of
$\mathfrak {E}_{\boldsymbol{\tau }}$ by restriction of ![]() $\mathfrak {E}_\tau$, we have
$\mathfrak {E}_\tau$, we have
Plugging the last two equalities into (3.4) now gives the desired result:
 \begin{align*} [\mathscr{M}(X_0,\beta)]^{\operatorname{virt}} &= p_\mathfrak{E}^![\mathfrak{M}(\mathcal{X}_0,\beta')] = \sum_\tau \frac{m_\tau}{|\operatorname{Aut}(\tau)|}\, p_\mathfrak{E}^!{\iota_\tau}_*[\mathfrak{M}(\mathcal{X}_0,\tau)]\\ &= \sum_\tau \frac{m_\tau}{|\operatorname{Aut}(\tau)|}\, {j_\tau}_* [\mathscr{M}_\tau(X_0,\beta)]^{\operatorname{virt}}\\ &= \sum_{{\boldsymbol{\tau}}=(\tau,\mathbf{A})} \frac{m_\tau}{|\operatorname{Aut}(\boldsymbol{\tau})|}\, {j_{\boldsymbol{\tau}}}_*[\mathscr{M}(X_0,{\boldsymbol{\tau}})]^{\operatorname{virt}}. \end{align*}
\begin{align*} [\mathscr{M}(X_0,\beta)]^{\operatorname{virt}} &= p_\mathfrak{E}^![\mathfrak{M}(\mathcal{X}_0,\beta')] = \sum_\tau \frac{m_\tau}{|\operatorname{Aut}(\tau)|}\, p_\mathfrak{E}^!{\iota_\tau}_*[\mathfrak{M}(\mathcal{X}_0,\tau)]\\ &= \sum_\tau \frac{m_\tau}{|\operatorname{Aut}(\tau)|}\, {j_\tau}_* [\mathscr{M}_\tau(X_0,\beta)]^{\operatorname{virt}}\\ &= \sum_{{\boldsymbol{\tau}}=(\tau,\mathbf{A})} \frac{m_\tau}{|\operatorname{Aut}(\boldsymbol{\tau})|}\, {j_{\boldsymbol{\tau}}}_*[\mathscr{M}(X_0,{\boldsymbol{\tau}})]^{\operatorname{virt}}. \end{align*}4. Logarithmic modifications and transversal maps
There is a general strategy which is often useful for constructing stable logarithmic maps. This is the most powerful tool we have at our disposal at the moment; eventually, the hope is that gluing technology will replace this construction. However, we expect it to be generally useful, as illustrated by the examples in the next section.
Suppose we wish to construct a stable logarithmic map to ![]() $X/B$, with, as usual,
$X/B$, with, as usual, ![]() $X$ logarithmically smooth with a Zariski logarithmic structure over one-dimensional
$X$ logarithmically smooth with a Zariski logarithmic structure over one-dimensional ![]() $B$ with logarithmic structure induced by
$B$ with logarithmic structure induced by ![]() $b_0\in B$. Suppose further we wish the stable logarithmic map to map into the fibre
$b_0\in B$. Suppose further we wish the stable logarithmic map to map into the fibre ![]() $X_{0}$ over
$X_{0}$ over ![]() $b_0$. Generalizing a method introduced in [Reference Nishinou and SiebertNS06], this construction is accomplished by the following two-step process: (i) apply a logarithmic modificationFootnote 8 of
$b_0$. Generalizing a method introduced in [Reference Nishinou and SiebertNS06], this construction is accomplished by the following two-step process: (i) apply a logarithmic modificationFootnote 8 of ![]() $X$ to reduce to a transverse situation; (ii) study logarithmic enhancements in the transverse case.
$X$ to reduce to a transverse situation; (ii) study logarithmic enhancements in the transverse case.
4.1 Logarithmic modifications
First, we will choose a logarithmic modification ![]() $h:\tilde X \longrightarrow X$. The modification
$h:\tilde X \longrightarrow X$. The modification ![]() $h$ is chosen to accommodate a situation at hand, in our applications the datum of a rigid tropical map.
$h$ is chosen to accommodate a situation at hand, in our applications the datum of a rigid tropical map.
Given a modification ![]() $h$, [Reference Abramovich and WiseAW18] constructed a morphism
$h$, [Reference Abramovich and WiseAW18] constructed a morphism ![]() $\mathscr {M}(h):\mathscr {M}(\tilde X/B) \longrightarrow \mathscr {M}(X/B)$ of moduli stacks of basic stable logarithmic maps, satisfying
$\mathscr {M}(h):\mathscr {M}(\tilde X/B) \longrightarrow \mathscr {M}(X/B)$ of moduli stacks of basic stable logarithmic maps, satisfying
The construction of ![]() $\mathscr {M}(h)$ is as follows. Given a stable logarithmic map
$\mathscr {M}(h)$ is as follows. Given a stable logarithmic map ![]() $\tilde f:\tilde C/S \longrightarrow \tilde X/B$, one obtains on the level of schemes the stabilization of
$\tilde f:\tilde C/S \longrightarrow \tilde X/B$, one obtains on the level of schemes the stabilization of ![]() $h\circ \tilde f$, i.e. a factorization of
$h\circ \tilde f$, i.e. a factorization of ![]() $h\circ \tilde f$ given by
$h\circ \tilde f$ given by
such that ![]() $\underline {C}/\underline {S} \longrightarrow \underline {X}$ is a stable map. One gives
$\underline {C}/\underline {S} \longrightarrow \underline {X}$ is a stable map. One gives ![]() $\underline {C}$ the logarithmic structure
$\underline {C}$ the logarithmic structure ![]() $\mathcal {M}_{C}:=g_*\mathcal {M}_{\tilde C}$, and with this logarithmic structure one obtains a factorization of
$\mathcal {M}_{C}:=g_*\mathcal {M}_{\tilde C}$, and with this logarithmic structure one obtains a factorization of ![]() $h\circ \tilde f$ through
$h\circ \tilde f$ through ![]() $C$ at the level of log schemes, giving
$C$ at the level of log schemes, giving ![]() $f:C/S \longrightarrow X/B$. Note that this is one of the rare occasions where push-forward of logarithmic structures behaves well. If
$f:C/S \longrightarrow X/B$. Note that this is one of the rare occasions where push-forward of logarithmic structures behaves well. If ![]() $\tilde f$ was basic, there is no expectation that
$\tilde f$ was basic, there is no expectation that ![]() $f$ is basic, but by [Reference Gross and SiebertGS13, Proposition 1.22] there is a unique basic map with the same underlying stable map of schemes such that the above constructed
$f$ is basic, but by [Reference Gross and SiebertGS13, Proposition 1.22] there is a unique basic map with the same underlying stable map of schemes such that the above constructed ![]() $f$ is obtained by pull-back from the basic map. This yields the map
$f$ is obtained by pull-back from the basic map. This yields the map ![]() $\mathscr {M}(h)$.
$\mathscr {M}(h)$.
4.2 Transverse maps, logarithmic enhancements, and strata
Second, if we have a stable map to ![]() $\underline {X}_0$ which interacts sufficiently well with the strata, we will compute in Theorem 4.13 the number of log enhancements of this curve. This generalizes a key argument of Nishinou and Siebert in [Reference Nishinou and SiebertNS06]. There are two differences: our degeneration
$\underline {X}_0$ which interacts sufficiently well with the strata, we will compute in Theorem 4.13 the number of log enhancements of this curve. This generalizes a key argument of Nishinou and Siebert in [Reference Nishinou and SiebertNS06]. There are two differences: our degeneration ![]() $X \longrightarrow B$ is only logarithmically smooth and not necessarily toric; and the fibre
$X \longrightarrow B$ is only logarithmically smooth and not necessarily toric; and the fibre ![]() $X_0$ is not required to be reduced. Not requiring
$X_0$ is not required to be reduced. Not requiring ![]() $X_0$ to be reduced makes the situation more complex and perhaps explains why it was avoided in the past; we hope our treatment here will find further uses. The precise meaning of ‘interacting well with logarithmic strata’ is as follows.
$X_0$ to be reduced makes the situation more complex and perhaps explains why it was avoided in the past; we hope our treatment here will find further uses. The precise meaning of ‘interacting well with logarithmic strata’ is as follows.
Definition 4.1 (Transverse maps and constrained points) Let ![]() $X \longrightarrow B$ be a logarithmically smooth morphism over
$X \longrightarrow B$ be a logarithmically smooth morphism over ![]() $B$ one-dimensional carrying the divisorial logarithmic structure
$B$ one-dimensional carrying the divisorial logarithmic structure ![]() $b_0\in B$ as usual. Let
$b_0\in B$ as usual. Let ![]() $X_0^{[d]}$ denote the union of the codimension
$X_0^{[d]}$ denote the union of the codimension ![]() $d$ logarithmic strata of
$d$ logarithmic strata of ![]() $X_0$. Suppose
$X_0$. Suppose ![]() $\underline {f}:\underline {C}/\operatorname {Spec} \Bbbk \longrightarrow \underline {X}_0$ is a stable map. We say that
$\underline {f}:\underline {C}/\operatorname {Spec} \Bbbk \longrightarrow \underline {X}_0$ is a stable map. We say that ![]() $\underline {f}$ is a transverse map if the image of
$\underline {f}$ is a transverse map if the image of ![]() $\underline {f}$ is contained in
$\underline {f}$ is contained in ![]() $X_0^{[0]}\cup X_0^{[1]}$, and
$X_0^{[0]}\cup X_0^{[1]}$, and ![]() $\underline {f}^{-1}(X_0^{[1]})$ is a finite set.
$\underline {f}^{-1}(X_0^{[1]})$ is a finite set.
We call a node ![]() $q\in \underline {C}$ a constrained node if
$q\in \underline {C}$ a constrained node if ![]() $\underline {f}(q)\in X^{[1]}_0$, otherwise it is a free node. Similarly a marked point
$\underline {f}(q)\in X^{[1]}_0$, otherwise it is a free node. Similarly a marked point ![]() $x\in \underline {C}$ with
$x\in \underline {C}$ with ![]() $\underline {f}(x)\in X^{[1]}_0$ is a constrained marking, otherwise it is a free marking.
$\underline {f}(x)\in X^{[1]}_0$ is a constrained marking, otherwise it is a free marking.
The term ‘transverse map’ is shorthand for ‘a map meeting strata in a logarithmically transverse way’.
4.2.1 Cones and strata in the transverse setting
For the rest of this section strata of higher codimension are irrelevant and we henceforth assume ![]() $X_0= X_0^{[0]} \cup X_0^{[1]}$. Then
$X_0= X_0^{[0]} \cup X_0^{[1]}$. Then ![]() $\Sigma (X_0)$ is a purely two-dimensional cone complex, with rays in bijection with the irreducible components of
$\Sigma (X_0)$ is a purely two-dimensional cone complex, with rays in bijection with the irreducible components of ![]() $X_0$. There are two types of two-dimensional cones: first, there is one cone for each component of the double locus
$X_0$. There are two types of two-dimensional cones: first, there is one cone for each component of the double locus ![]() $X_0^{[1]}$; second, there is one cone for each other component of
$X_0^{[1]}$; second, there is one cone for each other component of ![]() $X_0^{[1]}$, forming a smooth divisor in the regular locus of
$X_0^{[1]}$, forming a smooth divisor in the regular locus of ![]() $X_0$.
$X_0$.
4.2.2 Logarithmic enhancement of a map
We codify what it means to take a stable map and endow it with a logarithmic structure.
Definition 4.2 Let ![]() $X \longrightarrow B$ be as above and
$X \longrightarrow B$ be as above and ![]() $\underline {f}: \underline {C} \longrightarrow \underline {X}_0$ a stable map. A logarithmic enhancement
$\underline {f}: \underline {C} \longrightarrow \underline {X}_0$ a stable map. A logarithmic enhancement ![]() $f: C \longrightarrow X$ is a stable logarithmic map whose underlying map is
$f: C \longrightarrow X$ is a stable logarithmic map whose underlying map is ![]() $\underline {f}$. Two logarithmic enhancements
$\underline {f}$. Two logarithmic enhancements ![]() $f_1,f_2$ are isomorphic enhancements if there is an isomorphism between
$f_1,f_2$ are isomorphic enhancements if there is an isomorphism between ![]() $f_1$ and
$f_1$ and ![]() $f_2$ which is the identity on the underlying
$f_2$ which is the identity on the underlying ![]() $\underline {f}$. Otherwise we say they are non-isomorphic or distinct enhancements.
$\underline {f}$. Otherwise we say they are non-isomorphic or distinct enhancements.
4.2.3 Discrete invariants in the transverse case
Notation 4.3 Let ![]() $\underline {f}: \underline{C}/\operatorname {Spec}\Bbbk \longrightarrow \underline{X}_0$ be a transverse map and
$\underline {f}: \underline{C}/\operatorname {Spec}\Bbbk \longrightarrow \underline{X}_0$ be a transverse map and ![]() $x\in \underline{C}$ a closed point with
$x\in \underline{C}$ a closed point with ![]() $\underline {f}(x)$ contained in a stratum
$\underline {f}(x)$ contained in a stratum ![]() $S\subset X_0^{[1]}$ and let
$S\subset X_0^{[1]}$ and let ![]() $\eta \in \underline{C}$ be a generic point with
$\eta \in \underline{C}$ be a generic point with ![]() $x\in \mathrm {cl}(\eta )$. We now associate a number of invariants to the pair
$x\in \mathrm {cl}(\eta )$. We now associate a number of invariants to the pair ![]() $(\eta ,x)$, all related to the rank two toric monoid
$(\eta ,x)$, all related to the rank two toric monoid ![]() $P_x=\overline{\mathcal{M}}_{X,\underline {f}(x)}$. Denote by
$P_x=\overline{\mathcal{M}}_{X,\underline {f}(x)}$. Denote by ![]() $m_{\eta ,x}\in P_x$ the generator of the kernel of the localization map
$m_{\eta ,x}\in P_x$ the generator of the kernel of the localization map ![]() $P_x \longrightarrow \overline{\mathcal{M}}_{X,\underline {f}(\eta )}\simeq \mathbb {N}$ and by
$P_x \longrightarrow \overline{\mathcal{M}}_{X,\underline {f}(\eta )}\simeq \mathbb {N}$ and by ![]() $m'_{\eta ,x}\in P_x$ the generator of the other extremal ray. Denote by
$m'_{\eta ,x}\in P_x$ the generator of the other extremal ray. Denote by ![]() $n_{\eta ,x},n'_{\eta ,x}\in P_x^\vee$ the dual generators of the extremal rays of
$n_{\eta ,x},n'_{\eta ,x}\in P_x^\vee$ the dual generators of the extremal rays of ![]() $P_x^\vee$, satisfying
$P_x^\vee$, satisfying ![]() $\langle n_{\eta ,x},m_{\eta ,x}\rangle =0$. A third distinguished element
$\langle n_{\eta ,x},m_{\eta ,x}\rangle =0$. A third distinguished element ![]() $\rho _x\in P_x$ is defined by pulling back the generator of
$\rho _x\in P_x$ is defined by pulling back the generator of ![]() $\Gamma (B,\overline{\mathcal{M}}_B)=\mathbb {N}$ under the log morphism
$\Gamma (B,\overline{\mathcal{M}}_B)=\mathbb {N}$ under the log morphism ![]() $X \longrightarrow B$.
$X \longrightarrow B$.
For the following discussion denote by ![]() $\ell (m)$ the integral length of an element
$\ell (m)$ the integral length of an element ![]() $m\in M\otimes _\mathbb {Z}\mathbb {Q}$, that is, for
$m\in M\otimes _\mathbb {Z}\mathbb {Q}$, that is, for ![]() $m\neq 0$ the maximum of
$m\neq 0$ the maximum of ![]() $\alpha \in \mathbb {Q}_{>0}$ with
$\alpha \in \mathbb {Q}_{>0}$ with ![]() $\alpha ^{-1}\cdot m\in M$, while
$\alpha ^{-1}\cdot m\in M$, while ![]() $\ell (0)=0$.
$\ell (0)=0$.
Definition 4.4
(1) The index of
 $x\in \underline{C}$ or of the stratum
$x\in \underline{C}$ or of the stratum  $S\subset X_0^{[1]}$ containing
$S\subset X_0^{[1]}$ containing  $\underline {f}(x)$ is the index of the sublattices in
$\underline {f}(x)$ is the index of the sublattices in  $P_x^{\mathrm {gp}}$ or in
$P_x^{\mathrm {gp}}$ or in  $P_x^*$ generated by
$P_x^*$ generated by  $m_{\eta ,x},m'_{\eta ,x}$ and
$m_{\eta ,x},m'_{\eta ,x}$ and  $n_{\eta ,x},n'_{\eta ,x}$, respectively, that is,
For a constrained node
$n_{\eta ,x},n'_{\eta ,x}$, respectively, that is,
For a constrained node \[ \operatorname{Ind}(S)= \operatorname{Ind}_x = \langle n_{\eta,x},m'_{\eta,x}\rangle = \langle n'_{\eta,x}, m_{\eta,x}\rangle. \]
\[ \operatorname{Ind}(S)= \operatorname{Ind}_x = \langle n_{\eta,x},m'_{\eta,x}\rangle = \langle n'_{\eta,x}, m_{\eta,x}\rangle. \] $x=q$, the length
$x=q$, the length  $\lambda (q)=\lambda (S)\in \mathbb {Q}$ is the integral length of the interval
$\lambda (q)=\lambda (S)\in \mathbb {Q}$ is the integral length of the interval  $\rho _q^{-1}(1)$ when viewing
$\rho _q^{-1}(1)$ when viewing  $\rho _q$ as a map
$\rho _q$ as a map  $P^*_q\otimes _\mathbb {Z}\mathbb {Q} \to \mathbb {Q}$.
$P^*_q\otimes _\mathbb {Z}\mathbb {Q} \to \mathbb {Q}$.(2) If
 $\eta \in \underline{C}$ is a generic point with
$\eta \in \underline{C}$ is a generic point with  $x\in \mathrm {cl}(\eta )$, denote by
$x\in \mathrm {cl}(\eta )$, denote by  $w_{\eta ,x}\in \mathbb {N}\setminus \{0\}$ the local intersection number of
$w_{\eta ,x}\in \mathbb {N}\setminus \{0\}$ the local intersection number of  $\underline{f}|_{\mathrm {cl}(\eta )}$ at
$\underline{f}|_{\mathrm {cl}(\eta )}$ at  $x$ with
$x$ with  $S$ inside the irreducible component of
$S$ inside the irreducible component of  $X_0$ containing
$X_0$ containing  $\underline {f}(\eta )$.
$\underline {f}(\eta )$.
When the choice of ![]() $x$ and
$x$ and ![]() $\eta$ is understood we write
$\eta$ is understood we write ![]() $m_1=m_{\eta ,x}$,
$m_1=m_{\eta ,x}$, ![]() $m_2=m'_{\eta ,x}$,
$m_2=m'_{\eta ,x}$, ![]() $n_1=n_{\eta ,x}$,
$n_1=n_{\eta ,x}$, ![]() $n_2=n'_{\eta ,x}$,
$n_2=n'_{\eta ,x}$, ![]() $\rho _x\in P_x$ and
$\rho _x\in P_x$ and ![]() $w_1=w_{\eta ,x}$.
$w_1=w_{\eta ,x}$.
4.2.4 Relations between discrete invariants
Lemma 4.5 In the situation of Definition 4.4 denote by ![]() $\mu _1$ the multiplicity of the irreducible component of
$\mu _1$ the multiplicity of the irreducible component of ![]() $\underline{X}_0$ containing
$\underline{X}_0$ containing ![]() $\underline {f}(\eta )$. If the stratum
$\underline {f}(\eta )$. If the stratum ![]() $S\subset X_0^{[1]}$ is contained in two irreducible components of
$S\subset X_0^{[1]}$ is contained in two irreducible components of ![]() $\underline{X}_0$, denote by
$\underline{X}_0$, denote by ![]() $\mu _2$ the multiplicity of the other component and otherwise define
$\mu _2$ the multiplicity of the other component and otherwise define ![]() $\mu _2=0$.
$\mu _2=0$.
(1)
 $\mu _i= \langle n_i,\rho _x\rangle$;
$\mu _i= \langle n_i,\rho _x\rangle$;(2)
 $\operatorname {Ind}_x \cdot \rho _x =\mu _2 m_1+\mu _1 m_2$;
$\operatorname {Ind}_x \cdot \rho _x =\mu _2 m_1+\mu _1 m_2$;(3)
 $\lambda (q)=\tfrac {\ell (\rho _q)\cdot \operatorname {Ind}_q}{\mu _1\mu _2}$.
$\lambda (q)=\tfrac {\ell (\rho _q)\cdot \operatorname {Ind}_q}{\mu _1\mu _2}$.
In particular, if ![]() $X_0$ is reduced then
$X_0$ is reduced then ![]() $\mu _i\in \{0,1\}$ for all
$\mu _i\in \{0,1\}$ for all ![]() $i$ and
$i$ and
Proof. For (1) note that since ![]() $n_i\in P_x^\vee$ is a primitive vector with
$n_i\in P_x^\vee$ is a primitive vector with ![]() $\langle n_i,m_i\rangle =0$, the pairing with
$\langle n_i,m_i\rangle =0$, the pairing with ![]() $n_i$ computes the integral distance from the face
$n_i$ computes the integral distance from the face ![]() $\mathbb {N} \cdot m_i$ of
$\mathbb {N} \cdot m_i$ of ![]() $P_x$. Now étale locally, the log smooth morphism
$P_x$. Now étale locally, the log smooth morphism ![]() $X \longrightarrow B$ is the composition of a smooth map with
$X \longrightarrow B$ is the composition of a smooth map with ![]() $\operatorname {Spec} \Bbbk [P_x] \longrightarrow \operatorname {Spec}\Bbbk [t]$ defined by sending
$\operatorname {Spec} \Bbbk [P_x] \longrightarrow \operatorname {Spec}\Bbbk [t]$ defined by sending ![]() $t$ to
$t$ to ![]() $z^{\rho _x}\in \Bbbk [P_x]$. Hence the multiplicity
$z^{\rho _x}\in \Bbbk [P_x]$. Hence the multiplicity ![]() $\mu _i$ equals the integral distance of
$\mu _i$ equals the integral distance of ![]() $\rho _x$ to
$\rho _x$ to ![]() $\mathbb {N}\cdot m_i$, that is, the image of
$\mathbb {N}\cdot m_i$, that is, the image of ![]() $\rho _x$ under the quotient map
$\rho _x$ under the quotient map ![]() $P_x\to P_x/\mathbb {N} m_i\simeq \mathbb {N}$.
$P_x\to P_x/\mathbb {N} m_i\simeq \mathbb {N}$.
For (2), since the sublattice of ![]() $P^{\mathrm {gp}}$ generated by
$P^{\mathrm {gp}}$ generated by ![]() $m_1, m_2$ is of index
$m_1, m_2$ is of index ![]() $\operatorname {Ind}_x$, there are
$\operatorname {Ind}_x$, there are ![]() $a_1,a_2\in \mathbb {Z}$ with
$a_1,a_2\in \mathbb {Z}$ with ![]() $\operatorname {Ind}_x\cdot \rho _x= a_1 m_1+a_2 m_2$. Pairing with
$\operatorname {Ind}_x\cdot \rho _x= a_1 m_1+a_2 m_2$. Pairing with ![]() $n_1$ and using (1) and the definition of
$n_1$ and using (1) and the definition of ![]() $\operatorname {Ind}_x$ yields
$\operatorname {Ind}_x$ yields
This shows ![]() $a_2=\mu _1$, and similarly
$a_2=\mu _1$, and similarly ![]() $a_1=\mu _2$, yielding the claim.
$a_1=\mu _2$, yielding the claim.
To prove (3) note that (1) implies
Hence ![]() $\rho _q: P_q^*\to \mathbb {N}$ maps both
$\rho _q: P_q^*\to \mathbb {N}$ maps both ![]() $\mu _2 n_1$ and
$\mu _2 n_1$ and ![]() $\mu _1 n_2$ to
$\mu _1 n_2$ to ![]() $\mu _1\mu _2$. Since
$\mu _1\mu _2$. Since ![]() $\lambda (q)$ is defined as the integral length of
$\lambda (q)$ is defined as the integral length of ![]() $\rho _q^{-1}(1)$, we see that
$\rho _q^{-1}(1)$, we see that ![]() $\mu _1\mu _2\cdot \lambda (q)$ equals the integral length of
$\mu _1\mu _2\cdot \lambda (q)$ equals the integral length of ![]() $\mu _2 n_1-\mu _1 n_2$. Choosing an isomorphism of
$\mu _2 n_1-\mu _1 n_2$. Choosing an isomorphism of ![]() $P_q$ with
$P_q$ with
with ![]() $r,s>0$ pairwise prime and
$r,s>0$ pairwise prime and ![]() $\rho _q$ mapping to
$\rho _q$ mapping to ![]() $(a,c)$, then
$(a,c)$, then
In the dual lattice ![]() $P_q^*\simeq \mathbb {Z}^2$ we have
$P_q^*\simeq \mathbb {Z}^2$ we have ![]() $n_1=(0,1)$,
$n_1=(0,1)$, ![]() $n_2=(s,-r)$ and
$n_2=(s,-r)$ and ![]() $\mu _2 n_1-\mu _1 n_2= s\cdot (-c,a)$ has integral length
$\mu _2 n_1-\mu _1 n_2= s\cdot (-c,a)$ has integral length ![]() $\operatorname {Ind}_q\ell (\rho _q)$. Thus
$\operatorname {Ind}_q\ell (\rho _q)$. Thus ![]() $\lambda (q)= \operatorname {Ind}_q\ell (\rho _q)/\mu _1\mu _2$ as claimed.
$\lambda (q)= \operatorname {Ind}_q\ell (\rho _q)/\mu _1\mu _2$ as claimed.
4.2.5 Necessary conditions for enhancement
As we now show, the data listed in Definition 4.4 determine the discrete invariant ![]() $u_x\in P_x^\vee$ at each special point
$u_x\in P_x^\vee$ at each special point ![]() $x\in \underline{C}$. Recall that (2.8) characterizing
$x\in \underline{C}$. Recall that (2.8) characterizing ![]() $u_q$ implies
$u_q$ implies ![]() $\langle u_q, \rho _x\rangle =0$. To fix the sign of
$\langle u_q, \rho _x\rangle =0$. To fix the sign of ![]() $u_q$ we use the convention that
$u_q$ we use the convention that ![]() $\chi _1$ in the defining equation is the generization map to
$\chi _1$ in the defining equation is the generization map to ![]() $\eta$. Similarly, for each marked point
$\eta$. Similarly, for each marked point ![]() $p$, it holds that
$p$, it holds that ![]() $\langle u_p, \rho _p \rangle =0$ by definition of
$\langle u_p, \rho _p \rangle =0$ by definition of ![]() $u_p$. We now deduce a number of necessary conditions for a logarithmic enhancement of a transverse stable map to exist.
$u_p$. We now deduce a number of necessary conditions for a logarithmic enhancement of a transverse stable map to exist.
Proposition 4.6 Let ![]() $f:C \longrightarrow X$ be a logarithmic enhancement of a transverse stable map
$f:C \longrightarrow X$ be a logarithmic enhancement of a transverse stable map ![]() $\underline{f}:\underline{C} \longrightarrow \underline{X}_0$. Let
$\underline{f}:\underline{C} \longrightarrow \underline{X}_0$. Let ![]() $\eta \in \underline{C}$ be a generic point and
$\eta \in \underline{C}$ be a generic point and ![]() $x\in \mathrm {cl}(\eta )$. If
$x\in \mathrm {cl}(\eta )$. If ![]() $\underline {f}(x)\in X_0^{[1]}$ then following Definition 4.4 write
$\underline {f}(x)\in X_0^{[1]}$ then following Definition 4.4 write ![]() $m_1=m_{\eta ,x}$,
$m_1=m_{\eta ,x}$, ![]() $m_2=m'_{\eta ,x}$,
$m_2=m'_{\eta ,x}$, ![]() $n_1=n_{\eta ,x}$,
$n_1=n_{\eta ,x}$, ![]() $n_2=n'_{\eta ,x}$,
$n_2=n'_{\eta ,x}$, ![]() $\rho _x\in P_x$ and
$\rho _x\in P_x$ and ![]() $w_1=w_{\eta ,x}$.
$w_1=w_{\eta ,x}$.
(I) Node. If ![]() $x=q$ is a constrained nodal point of
$x=q$ is a constrained nodal point of ![]() $\underline{C}$, then the second generic point
$\underline{C}$, then the second generic point ![]() $\eta '$ of
$\eta '$ of ![]() $C$ with
$C$ with ![]() $x\in \mathrm {cl}(\eta ')$ maps to a different irreducible component of
$x\in \mathrm {cl}(\eta ')$ maps to a different irreducible component of ![]() $X_0$ than
$X_0$ than ![]() $\eta$. Moreover, with
$\eta$. Moreover, with ![]() $w_2=w_{\eta ',x}$ the following hold:
$w_2=w_{\eta ',x}$ the following hold:
(1)
 $\displaystyle u_q={1}/{\operatorname {Ind}_q}\cdot (w_1 n_2-w_2 n_1)$;
$\displaystyle u_q={1}/{\operatorname {Ind}_q}\cdot (w_1 n_2-w_2 n_1)$;(2)
 $u_q(m_1)=w_1$,
$u_q(m_1)=w_1$,  $u_q(m_2)=-w_2$;
$u_q(m_2)=-w_2$;(3)
 $\mu _1 w_2=\mu _2 w_1$;
$\mu _1 w_2=\mu _2 w_1$;(4) the integral length of
 $u_q$ equals
$u_q$ equals  $\ell (u_q)={\mu _2 w_1\lambda (q)}/{\operatorname {Ind}_q} = ({w_1}/{\mu _1})\ell (\rho _q)$.
$\ell (u_q)={\mu _2 w_1\lambda (q)}/{\operatorname {Ind}_q} = ({w_1}/{\mu _1})\ell (\rho _q)$.
If ![]() $x=q$ is a free node then
$x=q$ is a free node then ![]() $u_q=0$.
$u_q=0$.
(II) Marked point. If ![]() $x$ is a smooth point of
$x$ is a smooth point of ![]() $\underline{C}$, then
$\underline{C}$, then ![]() $\underline {f}(x)$ is contained in only one irreducible component of
$\underline {f}(x)$ is contained in only one irreducible component of ![]() $X_0$. Moreover, if
$X_0$. Moreover, if ![]() $x=p$ is a marked point then
$x=p$ is a marked point then ![]() $u_p=0$ in the free case, while in the constrained case the following hold:
$u_p=0$ in the free case, while in the constrained case the following hold:
(1)
 $w_1$ is a multiple of
$w_1$ is a multiple of  $\operatorname {Ind}_p$;
$\operatorname {Ind}_p$;(2)
 $u_p= ({w_1}/{\operatorname {Ind}_p})n_2$.
$u_p= ({w_1}/{\operatorname {Ind}_p})n_2$.
Proof. Setup for (I). Let ![]() $C$ be defined over the log point
$C$ be defined over the log point ![]() $S=\operatorname {Spec}(Q \longrightarrow \Bbbk )$. For any generic point
$S=\operatorname {Spec}(Q \longrightarrow \Bbbk )$. For any generic point ![]() $\eta \in \underline{C}$, there is a commutative square as follows.
$\eta \in \underline{C}$, there is a commutative square as follows.

Free node. In the case of a free node, both generic points ![]() $\eta ,\eta '\in \underline{C}$ containing
$\eta ,\eta '\in \underline{C}$ containing ![]() $q$ in their closure map to the same irreducible component of
$q$ in their closure map to the same irreducible component of ![]() $X_0$. Thus
$X_0$. Thus ![]() $u_q=0$ by the defining equation (2.8).
$u_q=0$ by the defining equation (2.8).
Image components of constrained node. Let now ![]() $x=q$ be a constrained node. Since the generization map
$x=q$ be a constrained node. Since the generization map ![]() $\chi _\eta :P_q \longrightarrow P_\eta$ is a localization of fine monoids there exists
$\chi _\eta :P_q \longrightarrow P_\eta$ is a localization of fine monoids there exists ![]() $m\in P_q\setminus \{0\}$ with
$m\in P_q\setminus \{0\}$ with ![]() $\chi _\eta (m)=0$. Then also
$\chi _\eta (m)=0$. Then also ![]() $\bar f^\flat _q(m)$ is a non-zero element in
$\bar f^\flat _q(m)$ is a non-zero element in ![]() $\overline{\mathcal {M}}_{C,q}$ with vanishing generization at
$\overline{\mathcal {M}}_{C,q}$ with vanishing generization at ![]() $\eta$. But
$\eta$. But ![]() $\overline{\mathcal {M}}_C$ has no local section with isolated support at
$\overline{\mathcal {M}}_C$ has no local section with isolated support at ![]() $q$. Hence
$q$. Hence ![]() $\chi _{\eta '}(m)\neq 0$, which implies that the two branches of
$\chi _{\eta '}(m)\neq 0$, which implies that the two branches of ![]() $C$ at
$C$ at ![]() $q$ map to different irreducible components of
$q$ map to different irreducible components of ![]() $X_0$.
$X_0$.
Computations for a constrained node. (1) follows from (2) by pairing both sides with ![]() $m_1$,
$m_1$, ![]() $m_2$ since these elements generate
$m_2$ since these elements generate ![]() $P_q\otimes _\mathbb {Z}\mathbb {Q}$. We now prove (2). Since
$P_q\otimes _\mathbb {Z}\mathbb {Q}$. We now prove (2). Since ![]() $u_q$ is preserved under base-change, we may assume
$u_q$ is preserved under base-change, we may assume ![]() $C$ is defined over the standard log point
$C$ is defined over the standard log point ![]() $\operatorname {Spec}(\mathbb {N}\to \Bbbk )$. Then
$\operatorname {Spec}(\mathbb {N}\to \Bbbk )$. Then ![]() $\overline{\mathcal{M}}_{C,q}\simeq S_e$ for some
$\overline{\mathcal{M}}_{C,q}\simeq S_e$ for some ![]() $e\in \mathbb {N}\setminus \{0\}$ with
$e\in \mathbb {N}\setminus \{0\}$ with ![]() $S_e$ the submonoid of
$S_e$ the submonoid of ![]() $\mathbb {Z}^2$ generated by
$\mathbb {Z}^2$ generated by ![]() $(e,0),(0,e),(1,1)$, see e.g. [Reference Gross and SiebertGS13, § 1.3]. The generator
$(e,0),(0,e),(1,1)$, see e.g. [Reference Gross and SiebertGS13, § 1.3]. The generator ![]() $1\in \mathbb {N}$ of the standard log point maps to
$1\in \mathbb {N}$ of the standard log point maps to ![]() $(1,1)$, while a chart at
$(1,1)$, while a chart at ![]() $q$ maps
$q$ maps ![]() $(e,0)$ to a function restricting to a coordinate on one of the two branches of
$(e,0)$ to a function restricting to a coordinate on one of the two branches of ![]() $C$, say on
$C$, say on ![]() $\mathrm {cl}(\eta )$, while vanishing on the other. Similarly,
$\mathrm {cl}(\eta )$, while vanishing on the other. Similarly, ![]() $(0,e)$ restricts to a coordinate on
$(0,e)$ restricts to a coordinate on ![]() $\mathrm {cl}(\eta ')$. By transversality we conclude
$\mathrm {cl}(\eta ')$. By transversality we conclude
Equation (2.8) defining ![]() $u_q$ says
$u_q$ says
with ![]() $\chi _i: S_e\to \mathbb {N}$ the generization maps. With our presentation,
$\chi _i: S_e\to \mathbb {N}$ the generization maps. With our presentation, ![]() $\chi _1$ and
$\chi _1$ and ![]() $\chi _2$ are induced by the projections
$\chi _2$ are induced by the projections ![]() $S_e\subset \mathbb {Z}^2\to \mathbb {Z}$ to the second and first factors, respectively. Hence
$S_e\subset \mathbb {Z}^2\to \mathbb {Z}$ to the second and first factors, respectively. Hence
 \begin{align*} \big(\chi_2\circ\bar f_q^\flat-\chi_1\circ \bar f_q^\flat\big) (m_1)&= w_1\cdot e,\\ \big(\chi_2\circ\bar f_q^\flat-\chi_1\circ \bar f_q^\flat\big) (m_2)&= -w_2\cdot e, \end{align*}
\begin{align*} \big(\chi_2\circ\bar f_q^\flat-\chi_1\circ \bar f_q^\flat\big) (m_1)&= w_1\cdot e,\\ \big(\chi_2\circ\bar f_q^\flat-\chi_1\circ \bar f_q^\flat\big) (m_2)&= -w_2\cdot e, \end{align*}showing (2).
Statement (3) is obtained by evaluating (1) on ![]() $\rho _q$:
$\rho _q$:
For (4) observe from (1) that ![]() $\operatorname {Ind}_q\cdot u_q$ is the vector connecting the extremal elements
$\operatorname {Ind}_q\cdot u_q$ is the vector connecting the extremal elements ![]() $w_2n_1$ and
$w_2n_1$ and ![]() $w_1 n_2$ of
$w_1 n_2$ of ![]() $P_q^\vee$. Thus
$P_q^\vee$. Thus ![]() $\operatorname {Ind}_q\cdot \ell (u_q)$ equals the integral length of
$\operatorname {Ind}_q\cdot \ell (u_q)$ equals the integral length of ![]() $\rho _q^{-1}(h)$ for
$\rho _q^{-1}(h)$ for ![]() $h=\langle w_1 n_2,\rho _q\rangle = \mu _2 w_1= \mu _1 w_2= \langle w_2 n_1,\rho _q\rangle$. This length equals
$h=\langle w_1 n_2,\rho _q\rangle = \mu _2 w_1= \mu _1 w_2= \langle w_2 n_1,\rho _q\rangle$. This length equals ![]() $h\cdot \lambda (q)$, yielding the stated formula. This finishes the proof of (I).
$h\cdot \lambda (q)$, yielding the stated formula. This finishes the proof of (I).
Marked point. Turning to (II), let ![]() $x\in \underline{C}$ be a smooth point with
$x\in \underline{C}$ be a smooth point with ![]() $\underline {f}(x)\in X_0^{[1]}$ and again assume without restriction
$\underline {f}(x)\in X_0^{[1]}$ and again assume without restriction ![]() $C$ is defined over the standard log point. If
$C$ is defined over the standard log point. If ![]() $s_u\in \mathcal {M}_{X,\underline {f}(x)}$ is a lift of
$s_u\in \mathcal {M}_{X,\underline {f}(x)}$ is a lift of ![]() $m_1$, then by transversality,
$m_1$, then by transversality, ![]() $f_x^\flat (s_u)\in \mathcal {M}_{C,x}$ maps under the structure homomorphism
$f_x^\flat (s_u)\in \mathcal {M}_{C,x}$ maps under the structure homomorphism ![]() $\mathcal {M}_{C,x} \longrightarrow \mathcal {O}_{C,x}$ to
$\mathcal {M}_{C,x} \longrightarrow \mathcal {O}_{C,x}$ to ![]() $z^{w_1}$, with
$z^{w_1}$, with ![]() $z$ a local coordinate of
$z$ a local coordinate of ![]() $\underline{C}$ at
$\underline{C}$ at ![]() $x$. Thus
$x$. Thus ![]() $x=p$ is a marked point,
$x=p$ is a marked point, ![]() $\overline{\mathcal{M}}_{C,x}=\mathbb {N}^2$ and
$\overline{\mathcal{M}}_{C,x}=\mathbb {N}^2$ and
maps ![]() $m_1$ to
$m_1$ to ![]() $(0,w_1)$. Here we are taking the morphism
$(0,w_1)$. Here we are taking the morphism ![]() $C \longrightarrow \operatorname {Spec}(\mathbb {N}\to \Bbbk )$ to be defined by
$C \longrightarrow \operatorname {Spec}(\mathbb {N}\to \Bbbk )$ to be defined by ![]() $\mathbb {N}\to \mathbb {N}^2$,
$\mathbb {N}\to \mathbb {N}^2$, ![]() $1\mapsto (1,0)$. Moreover, by compatibility of
$1\mapsto (1,0)$. Moreover, by compatibility of ![]() $f_p^\flat$ with the morphism of standard log points that
$f_p^\flat$ with the morphism of standard log points that ![]() $C$ and
$C$ and ![]() $X_0$ are defined over,
$X_0$ are defined over, ![]() $\bar f_p^\flat (\rho _p)=(b,0)$ for some
$\bar f_p^\flat (\rho _p)=(b,0)$ for some ![]() $b\in \mathbb {N}\setminus \{0\}$. Thus by Lemma 4.5(2),
$b\in \mathbb {N}\setminus \{0\}$. Thus by Lemma 4.5(2), ![]() $\rho _p=({\mu _1}/{\operatorname {Ind}_p} )m_2$ spans an extremal ray of
$\rho _p=({\mu _1}/{\operatorname {Ind}_p} )m_2$ spans an extremal ray of ![]() $P_p$. In particular,
$P_p$. In particular, ![]() $\underline {f}(p)$ is contained in only one irreducible component of
$\underline {f}(p)$ is contained in only one irreducible component of ![]() $X_0$ and
$X_0$ and ![]() $u_p(m_2)=0$. Thus
$u_p(m_2)=0$. Thus
This shows (2), which implies (1) since ![]() $n_2$ is a primitive vector.
$n_2$ is a primitive vector.
Finally, at a free marked point ![]() $p\in \underline{C}$, commutativity over the standard log point again readily implies
$p\in \underline{C}$, commutativity over the standard log point again readily implies ![]() $u_p=0$.
$u_p=0$.
Remark 4.7 If ![]() $X_0$ is reduced, then in Proposition 4.6(I) there is a well-defined contact order
$X_0$ is reduced, then in Proposition 4.6(I) there is a well-defined contact order ![]() $w=w_1=w_2$ of
$w=w_1=w_2$ of ![]() $\underline{f}$ with the double locus, and the formulas simplify to
$\underline{f}$ with the double locus, and the formulas simplify to
4.2.6 Transverse pre-logarithmic maps
Summarizing the necessary conditions of Proposition 4.6, we are led to the following definition.
Definition 4.8 Let ![]() $X \longrightarrow B$ be as above, and let
$X \longrightarrow B$ be as above, and let ![]() $\underline {f}:\underline {C}/ \operatorname {Spec}\Bbbk \longrightarrow \underline {X}_0$ be a transverse map. We say
$\underline {f}:\underline {C}/ \operatorname {Spec}\Bbbk \longrightarrow \underline {X}_0$ be a transverse map. We say ![]() $\underline {f}$ is a transverse pre-logarithmic map if any
$\underline {f}$ is a transverse pre-logarithmic map if any ![]() $x\in \underline{C}$ with
$x\in \underline{C}$ with ![]() $\underline {f}(x)\in X_0^{[1]}$ is a special point and if in the notation of Proposition 4.6 the following holds.
$\underline {f}(x)\in X_0^{[1]}$ is a special point and if in the notation of Proposition 4.6 the following holds.
(I) Constrained node. If ![]() $x=q$ is a constrained node then the two branches of
$x=q$ is a constrained node then the two branches of ![]() $C$ at
$C$ at ![]() $q$ map to different irreducible components of
$q$ map to different irreducible components of ![]() $X_0$. In addition,
$X_0$. In addition, ![]() $\mu _1 w_2=\mu _2 w_1$ and the reduced branching order
$\mu _1 w_2=\mu _2 w_1$ and the reduced branching order
is an integer.
(II) Constrained marking. If ![]() $x=p$ is a constrained marking then
$x=p$ is a constrained marking then ![]() $\underline{f}(x)$ is a smooth point of
$\underline{f}(x)$ is a smooth point of ![]() $X_0$ and
$X_0$ and ![]() $w_1/\operatorname {Ind}_p\in \mathbb {N}$.
$w_1/\operatorname {Ind}_p\in \mathbb {N}$.
Note that if a logarithmic enhancement of ![]() $\underline{f}$ exists, then by Proposition 4.6 the reduced branching order
$\underline{f}$ exists, then by Proposition 4.6 the reduced branching order ![]() $\bar w_q$ agrees with
$\bar w_q$ agrees with ![]() $\ell (u_q)$. Note also that in the case of reduced
$\ell (u_q)$. Note also that in the case of reduced ![]() $X_0$, we have
$X_0$, we have ![]() $\ell (\rho _q)=1$ and all
$\ell (\rho _q)=1$ and all ![]() $\mu _i=1$, and hence
$\mu _i=1$, and hence ![]() $\bar w_q=w_1=w_2$.
$\bar w_q=w_1=w_2$.
Definition 4.9 (Base order) For a transverse pre-logarithmic map ![]() $\underline {f}:\underline {C}/ \operatorname {Spec}\Bbbk \longrightarrow \underline {X}_0$ define its base order
$\underline {f}:\underline {C}/ \operatorname {Spec}\Bbbk \longrightarrow \underline {X}_0$ define its base order ![]() $b\in \mathbb {N}$ to be the least common multiple of the following natural numbers: (1) all multiplicities of irreducible components of
$b\in \mathbb {N}$ to be the least common multiple of the following natural numbers: (1) all multiplicities of irreducible components of ![]() $X_0$ intersecting
$X_0$ intersecting ![]() $\underline {f}(\underline{C})$ and; (2) for each constrained node
$\underline {f}(\underline{C})$ and; (2) for each constrained node ![]() $q\in \underline{C}$ the quotient
$q\in \underline{C}$ the quotient ![]() $\mu _1 w_2/\gcd (\operatorname {Ind}_q, \mu _1 w_2)$, notation as in Proposition 4.6.
$\mu _1 w_2/\gcd (\operatorname {Ind}_q, \mu _1 w_2)$, notation as in Proposition 4.6.
Theorem 4.10 Let ![]() $X \longrightarrow B$ be as above, and let
$X \longrightarrow B$ be as above, and let ![]() $\underline {f}:\underline {C}/ \operatorname {Spec}\Bbbk \longrightarrow \underline {X}_0$ be a transverse map. Suppose that there is an enhancement of
$\underline {f}:\underline {C}/ \operatorname {Spec}\Bbbk \longrightarrow \underline {X}_0$ be a transverse map. Suppose that there is an enhancement of ![]() $\underline {f}$ to a basic stable logarithmic map
$\underline {f}$ to a basic stable logarithmic map ![]() $f:C/S \longrightarrow X/B$. Then we have the following.
$f:C/S \longrightarrow X/B$. Then we have the following.
(1)
 $\underline {f}$ is a transverse pre-logarithmic map.
$\underline {f}$ is a transverse pre-logarithmic map.(2) The combinatorial type of
 $f$ is uniquely determined up to possibly a number of marked points
$f$ is uniquely determined up to possibly a number of marked points  $p$ with
$p$ with  $u_p=0$, and the basic monoid
$u_p=0$, and the basic monoid  $Q$ is
$Q$ is
 \[ Q=\mathbb{N}\oplus \bigoplus_{q\ \text{a free node}} \mathbb{N}. \]
\[ Q=\mathbb{N}\oplus \bigoplus_{q\ \text{a free node}} \mathbb{N}. \](3) The map
 $S=\operatorname {Spec}(Q \longrightarrow \Bbbk ) \longrightarrow B$ induces the map
$S=\operatorname {Spec}(Q \longrightarrow \Bbbk ) \longrightarrow B$ induces the map  $\overline{\mathcal {M}}_{b_0}=\mathbb {N} \longrightarrow Q$ given by
$\overline{\mathcal {M}}_{b_0}=\mathbb {N} \longrightarrow Q$ given by  $1\mapsto (b,0,\ldots ,0)$, where the integer
$1\mapsto (b,0,\ldots ,0)$, where the integer  $b\in \mathbb {N}$ is the base order of
$b\in \mathbb {N}$ is the base order of  $\underline {f}$.
$\underline {f}$.
Proof. Parts (1) and (2) follow readily from Proposition 4.6. For (3), recall that the basic monoid ![]() $Q$ is dual to the monoid
$Q$ is dual to the monoid ![]() $Q^{\vee } \subset Q_{\mathbb {R}}^{\vee }$, the latter being the moduli space of tropical maps
$Q^{\vee } \subset Q_{\mathbb {R}}^{\vee }$, the latter being the moduli space of tropical maps ![]() $h:\Gamma \longrightarrow \Sigma (X)$ of the given combinatorial type, and
$h:\Gamma \longrightarrow \Sigma (X)$ of the given combinatorial type, and ![]() $Q^{\vee }$ consists of those tropical maps whose edge lengths are integral and whose vertices map to integral points of
$Q^{\vee }$ consists of those tropical maps whose edge lengths are integral and whose vertices map to integral points of ![]() $\Sigma (X)$.
$\Sigma (X)$.
If ![]() $\eta$ is a generic point of
$\eta$ is a generic point of ![]() $\underline {C}$, denote by
$\underline {C}$, denote by ![]() $\mu _{\eta }$ the multiplicity of the irreducible component of
$\mu _{\eta }$ the multiplicity of the irreducible component of ![]() $(X_0)_{{\mathrm {red}}}$ in
$(X_0)_{{\mathrm {red}}}$ in ![]() $X_0$ containing
$X_0$ containing ![]() $\underline {f}(\eta )$. Thus the induced map
$\underline {f}(\eta )$. Thus the induced map ![]() $\mathbb {N} \longrightarrow P_{\eta }\simeq \mathbb {N}$ coming from the structure map
$\mathbb {N} \longrightarrow P_{\eta }\simeq \mathbb {N}$ coming from the structure map ![]() $X \longrightarrow B$ is multiplication by
$X \longrightarrow B$ is multiplication by ![]() $\mu _{\eta }$. Write
$\mu _{\eta }$. Write ![]() $\rho :\Sigma (X) \longrightarrow \Sigma (B)$ for the tropicalization of
$\rho :\Sigma (X) \longrightarrow \Sigma (B)$ for the tropicalization of ![]() $X \longrightarrow B$. The restriction of
$X \longrightarrow B$. The restriction of ![]() $\rho$ to the ray
$\rho$ to the ray ![]() ${\operatorname {Hom}}(P_\eta ,\mathbb {R}_{\ge 0})$ of
${\operatorname {Hom}}(P_\eta ,\mathbb {R}_{\ge 0})$ of ![]() $\Sigma (X)$ corresponding to the irreducible component of
$\Sigma (X)$ corresponding to the irreducible component of ![]() $X_0$ containing
$X_0$ containing ![]() $\underline {f}(\eta )$ is multiplication by
$\underline {f}(\eta )$ is multiplication by ![]() $\mu _{\eta }$. Thus given a tropical map
$\mu _{\eta }$. Thus given a tropical map ![]() $h:\Gamma \longrightarrow \Sigma (X)$ with vertex
$h:\Gamma \longrightarrow \Sigma (X)$ with vertex ![]() $v_\eta$ for
$v_\eta$ for ![]() $\eta \in \underline{C}$ and
$\eta \in \underline{C}$ and ![]() $b$ the image of
$b$ the image of ![]() $\rho \circ h$ in
$\rho \circ h$ in ![]() $\Sigma (B)$, we see that
$\Sigma (B)$, we see that ![]() $h(v_{\eta })$ is integral if and only if
$h(v_{\eta })$ is integral if and only if ![]() $\mu _{\eta }|b$.
$\mu _{\eta }|b$.
The edges of ![]() $\Gamma$ corresponding to free nodes have arbitrary length independent of
$\Gamma$ corresponding to free nodes have arbitrary length independent of ![]() $\mu$. But an edge corresponding to a constrained node
$\mu$. But an edge corresponding to a constrained node ![]() $q$ must have length
$q$ must have length
This must also be integral for ![]() $h$ to represent a point in
$h$ to represent a point in ![]() $Q^{\vee }$. Thus the map
$Q^{\vee }$. Thus the map ![]() $\Sigma (S) \longrightarrow \Sigma (B)$ must be given by
$\Sigma (S) \longrightarrow \Sigma (B)$ must be given by ![]() $(\alpha , (\alpha _q)_q)\mapsto b\alpha$ where
$(\alpha , (\alpha _q)_q)\mapsto b\alpha$ where ![]() $b$ is as given in the statement of the theorem. Dually, we obtain the stated description of the map
$b$ is as given in the statement of the theorem. Dually, we obtain the stated description of the map ![]() $S \longrightarrow B$.
$S \longrightarrow B$.
4.3 Existence and count of enhancements of transverse pre-logarithmic maps
We now turn to count the number of logarithmic enhancements of a transverse stable map ![]() $\underline{f}:\underline{C} \longrightarrow \underline{X}_0$. Denote by
$\underline{f}:\underline{C} \longrightarrow \underline{X}_0$. Denote by ![]() $\mathcal {M}:= \underline{f}^*\mathcal {M}_{X_0}$ the pull-back log structure on
$\mathcal {M}:= \underline{f}^*\mathcal {M}_{X_0}$ the pull-back log structure on ![]() $\underline{C}$ and by
$\underline{C}$ and by ![]() $\mathcal {M}^{\text {Zar}}$ the corresponding sheaf of monoids in the Zariski topology, noting that the log structure on
$\mathcal {M}^{\text {Zar}}$ the corresponding sheaf of monoids in the Zariski topology, noting that the log structure on ![]() $X_0$ is assumed to be defined in the Zariski topology.
$X_0$ is assumed to be defined in the Zariski topology.
4.3.1 The torsor of roots
The count of logarithmic enhancements involves a torsor ![]() $\mathcal {F}$ under a sheaf of finite cyclic groups
$\mathcal {F}$ under a sheaf of finite cyclic groups ![]() $\mathcal {G}$ on a finite topological space encoding compatible choices of roots of elements occurring in the construction of logarithmic enhancements. The following discussion is trivial if
$\mathcal {G}$ on a finite topological space encoding compatible choices of roots of elements occurring in the construction of logarithmic enhancements. The following discussion is trivial if ![]() $X_0$ is reduced and can be skipped by the reader only interested in this case. Given a transverse map
$X_0$ is reduced and can be skipped by the reader only interested in this case. Given a transverse map ![]() $\underline {f}:\underline{C}/\operatorname {Spec}\Bbbk \longrightarrow \underline{X}_0$, the finite topological space consists of the set of constrained nodes
$\underline {f}:\underline{C}/\operatorname {Spec}\Bbbk \longrightarrow \underline{X}_0$, the finite topological space consists of the set of constrained nodes ![]() $q\in \underline{C}$ and generic points
$q\in \underline{C}$ and generic points ![]() $\eta \in \underline{C}$. As basis for the topology we take the sets
$\eta \in \underline{C}$. As basis for the topology we take the sets ![]() $U_\eta = \{\eta \}\cup \{q\in \mathrm {cl}(\eta )\}$ and
$U_\eta = \{\eta \}\cup \{q\in \mathrm {cl}(\eta )\}$ and ![]() $U_q=\{q\}$ (which is opposite to the topology as a subset of
$U_q=\{q\}$ (which is opposite to the topology as a subset of ![]() $\underline{C}$). Let
$\underline{C}$). Let ![]() $\rho \in \Gamma (\underline{C},\mathcal {M})$ be the preimage of a generator
$\rho \in \Gamma (\underline{C},\mathcal {M})$ be the preimage of a generator ![]() $\rho _0$ of
$\rho _0$ of ![]() $\mathcal {M}_{B,b_0}$, that we assume fixed in this subsection. The stalks at a constrained node
$\mathcal {M}_{B,b_0}$, that we assume fixed in this subsection. The stalks at a constrained node ![]() $q\in \underline{C}$ and at a generic point
$q\in \underline{C}$ and at a generic point ![]() $\eta \in \underline{C}$ are various roots of the germs
$\eta \in \underline{C}$ are various roots of the germs ![]() $\rho _x$ of
$\rho _x$ of ![]() $\rho$:
$\rho$:
 \begin{align*} \mathcal{F}_q&=\{ \sigma_q\in\mathcal{M}_q^{\text{Zar}}\,|\, \sigma_q^{\ell(\rho_q)}=\rho_q\},\\ \mathcal{F}_\eta&=\{ \sigma_\eta\in\mathcal{M}_\eta^{\text{Zar}}\, |\, \sigma_\eta^{\mu_\eta} =\rho_\eta\}. \end{align*}
\begin{align*} \mathcal{F}_q&=\{ \sigma_q\in\mathcal{M}_q^{\text{Zar}}\,|\, \sigma_q^{\ell(\rho_q)}=\rho_q\},\\ \mathcal{F}_\eta&=\{ \sigma_\eta\in\mathcal{M}_\eta^{\text{Zar}}\, |\, \sigma_\eta^{\mu_\eta} =\rho_\eta\}. \end{align*}
We note that any of these sets may be empty, as Example 4.12 below shows. In such case we do not define a sheaf ![]() $\mathcal {F}$ and declare
$\mathcal {F}$ and declare ![]() $|\Gamma (\mathcal {F})| = \emptyset$ in what follows. Otherwise we define the sheaf
$|\Gamma (\mathcal {F})| = \emptyset$ in what follows. Otherwise we define the sheaf ![]() $\mathcal {F}$ as follows. For
$\mathcal {F}$ as follows. For ![]() $q\in \mathrm {cl}(\eta )$, a choice
$q\in \mathrm {cl}(\eta )$, a choice ![]() $\sigma _\eta$ with
$\sigma _\eta$ with ![]() $\sigma _\eta ^{\mu _\eta }= \rho _\eta$ determines a unique
$\sigma _\eta ^{\mu _\eta }= \rho _\eta$ determines a unique ![]() $\sigma _{\eta ,q}\in \mathcal {F}_q$ with restriction to
$\sigma _{\eta ,q}\in \mathcal {F}_q$ with restriction to ![]() $\eta$ equal to
$\eta$ equal to ![]() $\sigma _\eta ^{\mu _\eta /\ell (\rho _q)}$. Note that by Lemma 4.5(1) we have
$\sigma _\eta ^{\mu _\eta /\ell (\rho _q)}$. Note that by Lemma 4.5(1) we have ![]() $\mu _\eta / \ell (\rho _q) \in \mathbb {N}$. We define the generization map
$\mu _\eta / \ell (\rho _q) \in \mathbb {N}$. We define the generization map ![]() $\mathcal {F}_\eta \to \mathcal {F}_q$ by mapping
$\mathcal {F}_\eta \to \mathcal {F}_q$ by mapping ![]() $\sigma _\eta$ to
$\sigma _\eta$ to ![]() $\sigma _{\eta ,q}$. Observe that a different choice of
$\sigma _{\eta ,q}$. Observe that a different choice of ![]() $\rho$ leads to an isomorphic sheaf
$\rho$ leads to an isomorphic sheaf ![]() $\mathcal {F}$.
$\mathcal {F}$.
Replacing the elements ![]() $\rho _q$ and
$\rho _q$ and ![]() $\rho _\eta$ in the definition of
$\rho _\eta$ in the definition of ![]() $\mathcal {F}$ by the element
$\mathcal {F}$ by the element ![]() $1$, we obtain a sheaf
$1$, we obtain a sheaf ![]() $\mathcal {G}$ of abelian groups, for which
$\mathcal {G}$ of abelian groups, for which ![]() $\mathcal {F}$ is evidently a torsor.
$\mathcal {F}$ is evidently a torsor.
4.3.2 Global sections of  $\mathcal {G}$ and
$\mathcal {G}$ and  $\mathcal {F}$
$\mathcal {F}$
General theory [SP17, Tag 03AH], or direct computation, implies that the set of global sections ![]() $\Gamma (\mathcal {F})$ is a pseudo-torsor for the group
$\Gamma (\mathcal {F})$ is a pseudo-torsor for the group ![]() $G:= \Gamma (\mathcal {G})$. Here
$G:= \Gamma (\mathcal {G})$. Here ![]() $G$ is computed as the kernel of the sheaf-axiom homomorphism
$G$ is computed as the kernel of the sheaf-axiom homomorphism
Here ![]() $\eta (q),\eta '(q)$ are the generic points of the two adjacent branches of a constrained node
$\eta (q),\eta '(q)$ are the generic points of the two adjacent branches of a constrained node ![]() $q\in \underline{C}$, viewed in the étale topology. The notation implies a chosen order of branches. Multiplication of
$q\in \underline{C}$, viewed in the étale topology. The notation implies a chosen order of branches. Multiplication of ![]() $\sigma _q$ by
$\sigma _q$ by ![]() $\zeta _q$ and of
$\zeta _q$ and of ![]() $\sigma _\eta$ by
$\sigma _\eta$ by ![]() $\zeta _\eta$ describes the natural action of
$\zeta _\eta$ describes the natural action of ![]() $G= \Gamma (\mathcal {G})$ on
$G= \Gamma (\mathcal {G})$ on ![]() $\Gamma (\mathcal {F})$. Note that if
$\Gamma (\mathcal {F})$. Note that if ![]() $X_0$ is reduced then all
$X_0$ is reduced then all ![]() $\mu _i=1$ and
$\mu _i=1$ and ![]() $G$ is the trivial group.
$G$ is the trivial group.
Lemma 4.11 If ![]() $\Gamma (\mathcal {F})\neq \emptyset$ the action of
$\Gamma (\mathcal {F})\neq \emptyset$ the action of ![]() $G$ on
$G$ on ![]() $\Gamma (\mathcal {F})$ is simply transitive. In particular, it then holds
$\Gamma (\mathcal {F})$ is simply transitive. In particular, it then holds ![]() $|\Gamma (\mathcal {F})|= |G|$. If the dual intersection graph of
$|\Gamma (\mathcal {F})|= |G|$. If the dual intersection graph of ![]() $C$ is a tree or if
$C$ is a tree or if ![]() $X_0$ is reduced then
$X_0$ is reduced then ![]() $\Gamma (\mathcal {F})\neq \emptyset$.
$\Gamma (\mathcal {F})\neq \emptyset$.
Proof. Simple transitivity is the fact that ![]() $\Gamma (\mathcal {F})$ is a pseudo-torsor for
$\Gamma (\mathcal {F})$ is a pseudo-torsor for ![]() $G$.
$G$.
If ![]() $X_0$ is reduced then
$X_0$ is reduced then ![]() $\mu _\eta =1$ for all
$\mu _\eta =1$ for all ![]() $\eta$ and
$\eta$ and ![]() $\Gamma (\mathcal {F})=\prod _q \mathcal {F}_q$ is non-empty. If
$\Gamma (\mathcal {F})=\prod _q \mathcal {F}_q$ is non-empty. If ![]() $C$ is rational we can construct a section by inductive extension over the irreducible components. Indeed, if
$C$ is rational we can construct a section by inductive extension over the irreducible components. Indeed, if ![]() $\sigma _q\in \mathcal {F}_q$ and
$\sigma _q\in \mathcal {F}_q$ and ![]() $\eta$ is the generic point of the next irreducible component, we can define
$\eta$ is the generic point of the next irreducible component, we can define ![]() $\sigma _\eta$ as any
$\sigma _\eta$ as any ![]() $\mu _\eta /\ell (\rho _q)$-th root of the restriction of
$\mu _\eta /\ell (\rho _q)$-th root of the restriction of ![]() $\sigma _q$ to
$\sigma _q$ to ![]() $\eta$. By the definition of
$\eta$. By the definition of ![]() $\mathcal {F}$ this choice then also defines
$\mathcal {F}$ this choice then also defines ![]() $\sigma _{q'}$ for all other
$\sigma _{q'}$ for all other ![]() $q'\in \mathrm {cl}(\eta )$.
$q'\in \mathrm {cl}(\eta )$.
Example 4.12 Here is a simple example with ![]() $\Gamma (\mathcal {F})=\emptyset$, in fact
$\Gamma (\mathcal {F})=\emptyset$, in fact ![]() $\mathcal {F}_\eta =\emptyset$ for the unique point
$\mathcal {F}_\eta =\emptyset$ for the unique point ![]() $\eta$ in our space. Let
$\eta$ in our space. Let ![]() $\underline{X} \longrightarrow \underline{B}=\mathbb {A}^1$ be an elliptically fibred surface with
$\underline{X} \longrightarrow \underline{B}=\mathbb {A}^1$ be an elliptically fibred surface with ![]() $\underline{X}_0\subset \underline{X}$ a
$\underline{X}_0\subset \underline{X}$ a ![]() $b$-fold multiple fibre with smooth reduction. Endow
$b$-fold multiple fibre with smooth reduction. Endow ![]() $\underline{X}$ and
$\underline{X}$ and ![]() $\underline{B}$ with the divisorial log structures for the divisors
$\underline{B}$ with the divisorial log structures for the divisors ![]() $\underline{X}_0\subset \underline{X}$ and
$\underline{X}_0\subset \underline{X}$ and ![]() $\{0\}\subset \underline{B}$. Then the generator
$\{0\}\subset \underline{B}$. Then the generator ![]() $\bar \rho _0\in \overline{\mathcal {M}}_{B,0}$ maps to
$\bar \rho _0\in \overline{\mathcal {M}}_{B,0}$ maps to ![]() $b$ times the generator
$b$ times the generator ![]() $\bar \sigma \in \Gamma (\underline{X}_0,\overline{\mathcal {M}}_{X_0})=\mathbb {N}$. The preimage of
$\bar \sigma \in \Gamma (\underline{X}_0,\overline{\mathcal {M}}_{X_0})=\mathbb {N}$. The preimage of ![]() $\bar \sigma$ under
$\bar \sigma$ under ![]() $\mathcal {M}_{X_0^{\mathrm {red}}} \longrightarrow \overline{\mathcal {M}}_{X_0^{\mathrm {red}}}$ is the torsor with associated line bundle the conormal bundle
$\mathcal {M}_{X_0^{\mathrm {red}}} \longrightarrow \overline{\mathcal {M}}_{X_0^{\mathrm {red}}}$ is the torsor with associated line bundle the conormal bundle ![]() $N^{\vee }_{X_0^{\mathrm {red}}|X}$. This conormal bundle is not trivial, but has order
$N^{\vee }_{X_0^{\mathrm {red}}|X}$. This conormal bundle is not trivial, but has order ![]() $b$ in
$b$ in ![]() $\operatorname {Pic}(\underline{X}_0^{\mathrm {red}})$. Thus there exists no section
$\operatorname {Pic}(\underline{X}_0^{\mathrm {red}})$. Thus there exists no section ![]() $\sigma _\eta$ with
$\sigma _\eta$ with ![]() $\sigma _\eta ^b$ extending to a global section
$\sigma _\eta ^b$ extending to a global section ![]() $\rho$ of
$\rho$ of ![]() $\mathcal {M}_{X_0}$ lifting
$\mathcal {M}_{X_0}$ lifting ![]() $\bar \rho = b\cdot \bar \sigma$.
$\bar \rho = b\cdot \bar \sigma$.
The following statement generalizes and gives a more structural proof of [Reference Nishinou and SiebertNS06, Proposition 7.1], which treated a special case with reduced central fibre.
Theorem 4.13 Suppose given ![]() $X \longrightarrow B$ as above, and let
$X \longrightarrow B$ as above, and let
be a transverse pre-logarithmic map. Suppose further that the marked points ![]() $\{p_i\}$ include all points of
$\{p_i\}$ include all points of ![]() $\underline {f}^{-1}(X_0^{[1]})$ mapping to non-singular points of
$\underline {f}^{-1}(X_0^{[1]})$ mapping to non-singular points of ![]() $(X_0)_{{\mathrm {red}}}$.
$(X_0)_{{\mathrm {red}}}$.
Then there exists an enhancement of ![]() $\underline {f}$ to a basic stable logarithmic map if and only if
$\underline {f}$ to a basic stable logarithmic map if and only if ![]() $\Gamma (\mathcal {F})\neq \emptyset$, in which case the number of pairwise non-isomorphic enhancements is
$\Gamma (\mathcal {F})\neq \emptyset$, in which case the number of pairwise non-isomorphic enhancements is
 \[ \frac{|G|}{b} \prod_q \bar w_q. \]
\[ \frac{|G|}{b} \prod_q \bar w_q. \]
Here ![]() $G$ is as in (4.4), the integer
$G$ is as in (4.4), the integer ![]() $b$ is the base order (Definition 4.9), and the product is taken over the reduced branching orders (4.2) at constrained nodes.
$b$ is the base order (Definition 4.9), and the product is taken over the reduced branching orders (4.2) at constrained nodes.
If ![]() $X_0$ is reduced there is no obstruction to the existence of an enhancement and the count is
$X_0$ is reduced there is no obstruction to the existence of an enhancement and the count is ![]() $b^{-1}\prod _q \bar w_q$ and
$b^{-1}\prod _q \bar w_q$ and ![]() $\bar w_q=w_1=w_2$ either of the two contact orders in Definition 4.4 and Proposition 4.6.
$\bar w_q=w_1=w_2$ either of the two contact orders in Definition 4.4 and Proposition 4.6.
Proof. Counting rigidified objects. We are going to count diagrams of the form

with ![]() $p$ and
$p$ and ![]() $\underline {f}$ given by assumption and
$\underline {f}$ given by assumption and ![]() $g$ determined by
$g$ determined by ![]() $b$ as in Theorem 4.10(3) uniquely up to isomorphism. For the final count we will divide out the
$b$ as in Theorem 4.10(3) uniquely up to isomorphism. For the final count we will divide out the ![]() $\mathbb {Z}/b$-action coming from the automorphisms of
$\mathbb {Z}/b$-action coming from the automorphisms of ![]() $\operatorname {Spec}(Q\to \Bbbk ) \longrightarrow B$.
$\operatorname {Spec}(Q\to \Bbbk ) \longrightarrow B$.
Simplifying the base. By Theorem 4.10 we have ![]() $Q=\mathbb {N}\oplus \bigoplus _{\text {free nodes}}\mathbb {N}$ and the map
$Q=\mathbb {N}\oplus \bigoplus _{\text {free nodes}}\mathbb {N}$ and the map ![]() $\mathbb {N}=\overline{\mathcal{M}}_{B,b_0} \longrightarrow Q$ is the inclusion of the first factor multiplied by the base order
$\mathbb {N}=\overline{\mathcal{M}}_{B,b_0} \longrightarrow Q$ is the inclusion of the first factor multiplied by the base order ![]() $b$. Pulling back by any fixed sharp map
$b$. Pulling back by any fixed sharp map ![]() $Q\to \mathbb {N}$ replaces the lower left corner by the standard log point
$Q\to \mathbb {N}$ replaces the lower left corner by the standard log point ![]() $O^\dagger =\operatorname {Spec}(\mathbb {N} \longrightarrow \Bbbk )$. To be explicit, we take
$O^\dagger =\operatorname {Spec}(\mathbb {N} \longrightarrow \Bbbk )$. To be explicit, we take ![]() $Q\to \mathbb {N}$ to restrict to the identity on each summand. Since this map
$Q\to \mathbb {N}$ to restrict to the identity on each summand. Since this map ![]() $Q \longrightarrow \mathbb {N}$ is surjective we do not introduce automorphisms or ramification. The universal property of basic objects guarantees that the number of liftings is not changed.
$Q \longrightarrow \mathbb {N}$ is surjective we do not introduce automorphisms or ramification. The universal property of basic objects guarantees that the number of liftings is not changed.
The composition ![]() $\overline{\mathcal {M}}_{B,b_0} \longrightarrow Q \longrightarrow \mathbb {N}$ is then multiplication by
$\overline{\mathcal {M}}_{B,b_0} \longrightarrow Q \longrightarrow \mathbb {N}$ is then multiplication by ![]() $b$. We have now arrived at a counting problem over a standard log point. Note also that the given data already determines (4.5) at the level of ghost monoids, that is, the data determines the sheaf
$b$. We have now arrived at a counting problem over a standard log point. Note also that the given data already determines (4.5) at the level of ghost monoids, that is, the data determines the sheaf ![]() $\overline{\mathcal {M}}_C$, and maps
$\overline{\mathcal {M}}_C$, and maps ![]() $\bar f^\flat : \overline{\mathcal {M}}= \underline{f}^*\overline{\mathcal {M}}_{X_0} \longrightarrow \overline{\mathcal {M}}_C$ and
$\bar f^\flat : \overline{\mathcal {M}}= \underline{f}^*\overline{\mathcal {M}}_{X_0} \longrightarrow \overline{\mathcal {M}}_C$ and ![]() $\bar \pi ^\flat : \overline{\mathcal {M}}_{O^\dagger } \longrightarrow \overline{\mathcal {M}}_C$, uniquely.
$\bar \pi ^\flat : \overline{\mathcal {M}}_{O^\dagger } \longrightarrow \overline{\mathcal {M}}_C$, uniquely.
Pulling back the target monoid. Pull-back yields the two log structures ![]() $\mathcal {M}=\underline{f}^*\mathcal {M}_{X_0}$ and
$\mathcal {M}=\underline{f}^*\mathcal {M}_{X_0}$ and ![]() $\pi ^*\mathcal {M}_{O^\dagger }$ on
$\pi ^*\mathcal {M}_{O^\dagger }$ on ![]() $\underline{C}$. Recall our choice of generator
$\underline{C}$. Recall our choice of generator ![]() $\rho _0$ of
$\rho _0$ of ![]() $\mathcal {M}_{B, b_0}$ and its pull-back
$\mathcal {M}_{B, b_0}$ and its pull-back ![]() $\rho \in \Gamma (\underline{C},\mathcal {M})$, introduced earlier in § 4.3. For later use let also
$\rho \in \Gamma (\underline{C},\mathcal {M})$, introduced earlier in § 4.3. For later use let also ![]() $\tau _0\in \mathcal {M}_{O^\dagger ,0}$ be a generator with
$\tau _0\in \mathcal {M}_{O^\dagger ,0}$ be a generator with ![]() $g^\flat (\rho _0)= \tau _0^b$. Then for any log smooth structure
$g^\flat (\rho _0)= \tau _0^b$. Then for any log smooth structure ![]() $\mathcal {M}_C$ on
$\mathcal {M}_C$ on ![]() $\underline{C}$ over
$\underline{C}$ over ![]() $O^\dagger$ we have a distinguished section
$O^\dagger$ we have a distinguished section ![]() $\tau =\pi ^\flat (\tau _0)$.
$\tau =\pi ^\flat (\tau _0)$.
Simplifying the target monoid. Now define ![]() $\mathcal {M}'_C$ as the fine monoid sheaf given by pushout of these two monoid sheaves over
$\mathcal {M}'_C$ as the fine monoid sheaf given by pushout of these two monoid sheaves over ![]() ${\underline \pi} ^*{\underline g}^*\mathcal {M}_B$:
${\underline \pi} ^*{\underline g}^*\mathcal {M}_B$:
Since ![]() $\overline{\mathcal{M}}_{B,b_0} = \mathbb {N}$, by [Reference KatoKat89, (4.4)(ii)]
$\overline{\mathcal{M}}_{B,b_0} = \mathbb {N}$, by [Reference KatoKat89, (4.4)(ii)] ![]() $X_0 \longrightarrow B$ is an integral morphism. Hence the pushout
$X_0 \longrightarrow B$ is an integral morphism. Hence the pushout ![]() $\mathcal {M}'_C$ in the category of fine monoid sheaves agrees with the ordinary pushout. In particular, the structure morphisms of
$\mathcal {M}'_C$ in the category of fine monoid sheaves agrees with the ordinary pushout. In particular, the structure morphisms of ![]() $X_0$ and
$X_0$ and ![]() $O^\dagger$ define a structure morphism
$O^\dagger$ define a structure morphism ![]() $\alpha '_C: \mathcal {M}'_C\to \mathcal {O}_C$.
$\alpha '_C: \mathcal {M}'_C\to \mathcal {O}_C$.
Restating the counting problem. Classifying diagrams (4.5) amounts to finding an fs log structure ![]() $\mathcal {M}_C$ on
$\mathcal {M}_C$ on ![]() $\underline{C}$ together with a morphism of monoid sheaves
$\underline{C}$ together with a morphism of monoid sheaves
compatible with ![]() $f^\sharp$ and such that the composition
$f^\sharp$ and such that the composition ![]() $\pi ^*\mathcal {M}_{O^\dagger } \longrightarrow \mathcal {M}_C$ of
$\pi ^*\mathcal {M}_{O^\dagger } \longrightarrow \mathcal {M}_C$ of ![]() $\phi$ with
$\phi$ with ![]() $\pi ^*\mathcal {M}_{O^\dagger } \longrightarrow \mathcal {M}'_C$ is log smooth.
$\pi ^*\mathcal {M}_{O^\dagger } \longrightarrow \mathcal {M}'_C$ is log smooth.
We will soon see that ![]() $\bar \phi :(\overline{\mathcal{M}}'_C)^{\mathrm {gp}}\longrightarrow \overline{\mathcal{M}}_C^{\mathrm {gp}}$ necessarily decomposes into the quotient by some finite torsion part and the inclusion of a finite index subgroup.
$\bar \phi :(\overline{\mathcal{M}}'_C)^{\mathrm {gp}}\longrightarrow \overline{\mathcal{M}}_C^{\mathrm {gp}}$ necessarily decomposes into the quotient by some finite torsion part and the inclusion of a finite index subgroup.
Lifting the quotient morphism to ![]() $\mathcal {M}'_C$ leads to the factor
$\mathcal {M}'_C$ leads to the factor ![]() $|G|$, while the finite extension of the resulting log structure to
$|G|$, while the finite extension of the resulting log structure to ![]() $\mathcal {M}_C$ receives a contribution by the reduced branching order
$\mathcal {M}_C$ receives a contribution by the reduced branching order ![]() $\bar w_q$ from each constrained node. Note that
$\bar w_q$ from each constrained node. Note that ![]() $\bar w_q = \ell (u_q)$ by Proposition 4.6(I)(4); it is in this form that it appears in the proof.
$\bar w_q = \ell (u_q)$ by Proposition 4.6(I)(4); it is in this form that it appears in the proof.
The ghost kernel. To understand the torsion part to be divided out, note that ![]() $(\overline {\mathcal {M}'_{C,x}})^{\mathrm {gp}}$ at
$(\overline {\mathcal {M}'_{C,x}})^{\mathrm {gp}}$ at ![]() $x\in \underline{C}$ equals
$x\in \underline{C}$ equals ![]() $P_x^{\mathrm {gp}}\oplus _\mathbb {Z} \mathbb {Z}$ with
$P_x^{\mathrm {gp}}\oplus _\mathbb {Z} \mathbb {Z}$ with ![]() $1\in \mathbb {Z}$ mapping to
$1\in \mathbb {Z}$ mapping to ![]() $\bar \rho _x\in P_x^{\mathrm {gp}}$ and to the base order
$\bar \rho _x\in P_x^{\mathrm {gp}}$ and to the base order ![]() $b\in \mathbb {Z}$, respectively. Since
$b\in \mathbb {Z}$, respectively. Since ![]() $\ell (\bar \rho _x)$ divides the multiplicities of some irreducible components of
$\ell (\bar \rho _x)$ divides the multiplicities of some irreducible components of ![]() $\underline{X}_0$, Theorem 4.10(3) implies
$\underline{X}_0$, Theorem 4.10(3) implies ![]() $b/\ell (\bar \rho _x)\in \mathbb {N}$. If
$b/\ell (\bar \rho _x)\in \mathbb {N}$. If ![]() $\bar \rho _x$ has integral length
$\bar \rho _x$ has integral length ![]() $\ell (\bar \rho _x)>1$, then
$\ell (\bar \rho _x)>1$, then ![]() $(\bar \rho _x/ \ell (\bar \rho _x),-b/ \ell (\bar \rho _x))$ is a generator of the torsion subgroup
$(\bar \rho _x/ \ell (\bar \rho _x),-b/ \ell (\bar \rho _x))$ is a generator of the torsion subgroup ![]() $((\overline {\mathcal {M}'_{C,x}})^{\mathrm {gp}})_{\operatorname {tor}}$, which has order
$((\overline {\mathcal {M}'_{C,x}})^{\mathrm {gp}})_{\operatorname {tor}}$, which has order ![]() $\ell (\bar \rho _x)$. This element has to be in the kernel of the map to the torsion-free monoid
$\ell (\bar \rho _x)$. This element has to be in the kernel of the map to the torsion-free monoid ![]() $\overline{\mathcal {M}}_C$.
$\overline{\mathcal {M}}_C$.
The ![]() $|G|$ embodiments of the ghost image. The interesting fact is that the lift of
$|G|$ embodiments of the ghost image. The interesting fact is that the lift of ![]() $(\bar \rho _x/\ell (\bar \rho _x),-b/ \ell (\bar \rho _x))$ to
$(\bar \rho _x/\ell (\bar \rho _x),-b/ \ell (\bar \rho _x))$ to ![]() $(\mathcal {M}'_{C,x})^{\mathrm {gp}}$ is only unique up to an
$(\mathcal {M}'_{C,x})^{\mathrm {gp}}$ is only unique up to an ![]() $\ell (\bar \rho _x)$-torsion element in
$\ell (\bar \rho _x)$-torsion element in ![]() $\mathcal {O}_{\underline{C},x}^\times$, that is, up to an
$\mathcal {O}_{\underline{C},x}^\times$, that is, up to an ![]() $\ell (\bar \rho _x)$-th root of unity
$\ell (\bar \rho _x)$-th root of unity ![]() $\zeta _x\in \Bbbk ^\times$. Explicitly, the lift is equivalent to a choice
$\zeta _x\in \Bbbk ^\times$. Explicitly, the lift is equivalent to a choice ![]() $\sigma _x\in \mathcal {M}_x$ with
$\sigma _x\in \mathcal {M}_x$ with ![]() $\sigma _x^{\ell (\bar \rho _x)}=\rho _x$ by taking the torsion subsheaf in
$\sigma _x^{\ell (\bar \rho _x)}=\rho _x$ by taking the torsion subsheaf in ![]() $(\mathcal {M}'_C)^{\mathrm {gp}}$ generated by
$(\mathcal {M}'_C)^{\mathrm {gp}}$ generated by ![]() $(\sigma _x,\tau _x^{-b/\ell (\bar \rho _x)})$. The quotient by this subsheaf means that we upgrade the relation
$(\sigma _x,\tau _x^{-b/\ell (\bar \rho _x)})$. The quotient by this subsheaf means that we upgrade the relation ![]() $f^\flat (\rho _x)=\tau _x^b$ coming from the commutativity of (4.5) to
$f^\flat (\rho _x)=\tau _x^b$ coming from the commutativity of (4.5) to ![]() $f^\flat (\sigma _x)= \tau _x^{b/\ell (\bar \rho _x)}$.
$f^\flat (\sigma _x)= \tau _x^{b/\ell (\bar \rho _x)}$.
To define this quotient of the monoid ![]() $\mathcal {M}'_C$ globally amounts to choosing the roots
$\mathcal {M}'_C$ globally amounts to choosing the roots ![]() $\sigma _x$ of
$\sigma _x$ of ![]() $\rho _x$ compatibly with the generization maps, leading to a global section of the sheaf
$\rho _x$ compatibly with the generization maps, leading to a global section of the sheaf ![]() $\mathcal {F}$ introduced directly before the statement of the theorem. For this statement note that for
$\mathcal {F}$ introduced directly before the statement of the theorem. For this statement note that for ![]() $x=\eta$ a generic point,
$x=\eta$ a generic point, ![]() $\ell (\bar \rho _\eta )$ equals the multiplicity
$\ell (\bar \rho _\eta )$ equals the multiplicity ![]() $\mu _\eta$ of the irreducible component of
$\mu _\eta$ of the irreducible component of ![]() $\underline{X}_0$ containing
$\underline{X}_0$ containing ![]() $\underline{f}(\eta )$.
$\underline{f}(\eta )$.
The quotient is a logarithmic structure. Assume now ![]() $\sigma \in \Gamma (\mathcal {F})$ has been chosen and denote by
$\sigma \in \Gamma (\mathcal {F})$ has been chosen and denote by ![]() $\mathcal {M}''_C$ the quotient of
$\mathcal {M}''_C$ the quotient of ![]() $\mathcal {M}'_C$ by the corresponding torsion subgroup of
$\mathcal {M}'_C$ by the corresponding torsion subgroup of ![]() $(\mathcal {M}'_C)^{\mathrm {gp}}$. Since
$(\mathcal {M}'_C)^{\mathrm {gp}}$. Since ![]() $\alpha '_C(\sigma _x)=\alpha '_C(\tau _x)=0$, the homomorphism
$\alpha '_C(\sigma _x)=\alpha '_C(\tau _x)=0$, the homomorphism ![]() $\alpha '_C$ descends to the quotient, thus defining a structure homomorphism
$\alpha '_C$ descends to the quotient, thus defining a structure homomorphism ![]() $\alpha ''_C: \mathcal {M}''_C\to \mathcal {O}_C$.
$\alpha ''_C: \mathcal {M}''_C\to \mathcal {O}_C$.
The log structure ![]() $\mathcal {M}_C$ is determined at smooth points. Note that the map
$\mathcal {M}_C$ is determined at smooth points. Note that the map ![]() $(\pi ^*\mathcal {M}_{O^\dagger })_\eta \to \mathcal {M}''_{C,\eta }$ is an isomorphism and hence we must have
$(\pi ^*\mathcal {M}_{O^\dagger })_\eta \to \mathcal {M}''_{C,\eta }$ is an isomorphism and hence we must have ![]() $\mathcal {M}_{C,\eta }=\mathcal {M}''_{C,\eta }$. The log structure
$\mathcal {M}_{C,\eta }=\mathcal {M}''_{C,\eta }$. The log structure ![]() $\mathcal {M}_C$ is then also defined at each marked point
$\mathcal {M}_C$ is then also defined at each marked point ![]() $p\in \underline{C}$ by adding a generator of the maximal ideal in
$p\in \underline{C}$ by adding a generator of the maximal ideal in ![]() $\mathcal {O}_{\underline{C},p}$ as an additional generator to
$\mathcal {O}_{\underline{C},p}$ as an additional generator to ![]() $\mathcal {M}_{C,p}$. It is also clear that
$\mathcal {M}_{C,p}$. It is also clear that ![]() $\mathcal {M}''_{C,p} \longrightarrow \mathcal {M}_{C,p}$ exists and is determined by the corresponding map at
$\mathcal {M}''_{C,p} \longrightarrow \mathcal {M}_{C,p}$ exists and is determined by the corresponding map at ![]() $\eta$ and by
$\eta$ and by ![]() $f^\sharp$.
$f^\sharp$.
The log structure ![]() $\mathcal {M}_C$ is determined at free nodes. At a free node
$\mathcal {M}_C$ is determined at free nodes. At a free node ![]() $q$ we have
$q$ we have ![]() $\underline{f}(q)\in (X_0)_\mathrm {reg}$ and hence there is a unique specialization
$\underline{f}(q)\in (X_0)_\mathrm {reg}$ and hence there is a unique specialization ![]() $\sigma _q\in \mathcal {M}_q$ of
$\sigma _q\in \mathcal {M}_q$ of ![]() $\sigma _\eta$ for the two generic points
$\sigma _\eta$ for the two generic points ![]() $\eta \in \underline{C}$ with
$\eta \in \underline{C}$ with ![]() $q\in \mathrm {cl}(\eta )$. The log structure
$q\in \mathrm {cl}(\eta )$. The log structure ![]() $\mathcal {M}_C$ on
$\mathcal {M}_C$ on ![]() $C$ is then determined by
$C$ is then determined by ![]() $f^\flat _\eta$ and by the universal log structure
$f^\flat _\eta$ and by the universal log structure ![]() $\mathcal {M}_C^\circ$ of
$\mathcal {M}_C^\circ$ of ![]() $\underline{C}$ as follows. Let
$\underline{C}$ as follows. Let ![]() $x,y\in \mathcal {O}_{C,q}$ be coordinates of the two branches of
$x,y\in \mathcal {O}_{C,q}$ be coordinates of the two branches of ![]() $\underline{C}$ at
$\underline{C}$ at ![]() $q$ in the étale topology. Then there exist unique lifts
$q$ in the étale topology. Then there exist unique lifts ![]() $s_x,s_y\in \mathcal {M}^\circ _{C,q}$ such that
$s_x,s_y\in \mathcal {M}^\circ _{C,q}$ such that ![]() $s_x\cdot s_y$ is the pull-back of a generator
$s_x\cdot s_y$ is the pull-back of a generator ![]() $\epsilon _q$ of the
$\epsilon _q$ of the ![]() $q$-th factor in the universal base log structure
$q$-th factor in the universal base log structure ![]() ${\rm Spec} \big(\oplus _{{\rm nodes\,of\, }{\rm \underline{C} }}{\mathbb N}\to {\rm \Bbbk } \big )$. Our choice of pull-back
${\rm Spec} \big(\oplus _{{\rm nodes\,of\, }{\rm \underline{C} }}{\mathbb N}\to {\rm \Bbbk } \big )$. Our choice of pull-back ![]() $O^\dagger \longrightarrow \operatorname {Spec}(Q \longrightarrow \Bbbk )$ turns
$O^\dagger \longrightarrow \operatorname {Spec}(Q \longrightarrow \Bbbk )$ turns ![]() $\epsilon _q$ into
$\epsilon _q$ into ![]() $\lambda \tau _0^{e_q}$ for some
$\lambda \tau _0^{e_q}$ for some ![]() $\lambda \in \Bbbk ^\times$ and
$\lambda \in \Bbbk ^\times$ and ![]() $e_q\in \mathbb {N}$ determined by basicness as in (4.3). Thus
$e_q\in \mathbb {N}$ determined by basicness as in (4.3). Thus ![]() $\mathcal {M}_{C,q}$ is generated by
$\mathcal {M}_{C,q}$ is generated by ![]() $s_x,s_y$ and
$s_x,s_y$ and ![]() $\tau _q$ with single relation
$\tau _q$ with single relation ![]() $s_x\cdot s_y=\lambda \tau _q^{e_q}$ and mapping to
$s_x\cdot s_y=\lambda \tau _q^{e_q}$ and mapping to ![]() $x,y$ and
$x,y$ and ![]() $0$ under the structure homomorphism, respectively. The morphism
$0$ under the structure homomorphism, respectively. The morphism ![]() $f^\flat :\mathcal {M}_q \longrightarrow \mathcal {M}_{C,q}$ factors over
$f^\flat :\mathcal {M}_q \longrightarrow \mathcal {M}_{C,q}$ factors over ![]() $\pi ^*\mathcal {M}_{O^\dagger }$ and is therefore completely determined by
$\pi ^*\mathcal {M}_{O^\dagger }$ and is therefore completely determined by ![]() $f^\flat _\eta (\sigma _q)= \tau _q^{b/\mu _\eta }$.
$f^\flat _\eta (\sigma _q)= \tau _q^{b/\mu _\eta }$.
Constrained nodes: Study of the image log structure ![]() $\mathcal {M}''_C$. It remains to extend
$\mathcal {M}''_C$. It remains to extend ![]() $\mathcal {M}''_C$ to the correct log structure at each constrained node
$\mathcal {M}''_C$ to the correct log structure at each constrained node ![]() $q\in \underline{C}$. On the level of ghost sheaves we have the following situation, where we include the above description of the kernel for completeness.
$q\in \underline{C}$. On the level of ghost sheaves we have the following situation, where we include the above description of the kernel for completeness.
Proposition 4.14 The homomorphism of abelian groups
has kernel generated by ![]() $(\bar \rho _q/\ell (\bar \rho _q),-b/\ell (\bar \rho _q))$ and cokernel a cyclic group of order
$(\bar \rho _q/\ell (\bar \rho _q),-b/\ell (\bar \rho _q))$ and cokernel a cyclic group of order ![]() $\ell (u_q)$.
$\ell (u_q)$.
Proof The kernel is described in the discussion above. Indeed, if ![]() $(m,k)\in P_q^{\mathrm {gp}}\oplus \mathbb {Z}$ lies in the kernel then
$(m,k)\in P_q^{\mathrm {gp}}\oplus \mathbb {Z}$ lies in the kernel then ![]() $\bar f^\flat _q(m)\in \mathbb {Z}\cdot \bar \tau _q$. Because
$\bar f^\flat _q(m)\in \mathbb {Z}\cdot \bar \tau _q$. Because ![]() $\bar f^\flat _q$ is injective and
$\bar f^\flat _q$ is injective and ![]() $\bar f^\flat _q(\bar \rho _q)=\bar \tau _q^b$ we conclude that
$\bar f^\flat _q(\bar \rho _q)=\bar \tau _q^b$ we conclude that ![]() $(m,k)$ is proportional to
$(m,k)$ is proportional to ![]() $(\bar \rho _q, -b)$. The stated element is a primitive element of this one-dimensional subspace.
$(\bar \rho _q, -b)$. The stated element is a primitive element of this one-dimensional subspace.
For the determination of the cokernel observe that the composition
equals ![]() $u_q$ up to sign. Indeed, the quotient by
$u_q$ up to sign. Indeed, the quotient by ![]() $\mathbb {Z}\bar \tau _q$ maps the two generators of extremal rays of
$\mathbb {Z}\bar \tau _q$ maps the two generators of extremal rays of ![]() $\overline{\mathcal {M}}_{C,q}$ to
$\overline{\mathcal {M}}_{C,q}$ to ![]() $\pm 1\in \mathbb {Z}$. Hence
$\pm 1\in \mathbb {Z}$. Hence ![]() $m_i\in P_q^{\mathrm {gp}}$ maps to
$m_i\in P_q^{\mathrm {gp}}$ maps to ![]() $\pm w_i$, which by Proposition 4.6(I)(2) agrees with
$\pm w_i$, which by Proposition 4.6(I)(2) agrees with ![]() $\pm u_q(m_i)$. The order of the cokernel now agrees with the greatest common divisor of the components of
$\pm u_q(m_i)$. The order of the cokernel now agrees with the greatest common divisor of the components of ![]() $u_q$, that is, with
$u_q$, that is, with ![]() $\ell (u_q)$.
$\ell (u_q)$.
Once again we follow [Reference Gross and SiebertGS13, § 1.3] and denote by ![]() $S_e\subset \mathbb {Z}^2$ the submonoid generated by
$S_e\subset \mathbb {Z}^2$ the submonoid generated by ![]() $(e,0),(1,1),(0,e)$, for
$(e,0),(1,1),(0,e)$, for ![]() $e\in \mathbb {N}\setminus \{0\}$. Up to a choice of ordering of extremal rays there is a canonical isomorphism
$e\in \mathbb {N}\setminus \{0\}$. Up to a choice of ordering of extremal rays there is a canonical isomorphism
Using Proposition 4.14 we can now determine the saturation of ![]() $\overline{\mathcal {M}}''_{C,q}$. For readability we write
$\overline{\mathcal {M}}''_{C,q}$. For readability we write ![]() $\ell =\ell (u_q)$.
$\ell =\ell (u_q)$.
Corollary 4.15 Using the description (4.6), the saturation of ![]() $\overline{\mathcal {M}}''_{C,q}$ equals
$\overline{\mathcal {M}}''_{C,q}$ equals ![]() $S_{\ell (u_q)e_q}\subset S_{e_q}$.
$S_{\ell (u_q)e_q}\subset S_{e_q}$.
Proof. By construction of ![]() $\mathcal {M}''_C$, the image of the homomorphism in Proposition 4.14 equals
$\mathcal {M}''_C$, the image of the homomorphism in Proposition 4.14 equals ![]() $(\overline{\mathcal {M}}''_{C,q})^{\mathrm {gp}}$. In the notation of (4.6), the statement now follows from the fact that by the proposition, the image has index
$(\overline{\mathcal {M}}''_{C,q})^{\mathrm {gp}}$. In the notation of (4.6), the statement now follows from the fact that by the proposition, the image has index ![]() $\ell (u_q)$ in
$\ell (u_q)$ in ![]() $\overline{\mathcal {M}}_{C,q}^{\mathrm {gp}}$ and
$\overline{\mathcal {M}}_{C,q}^{\mathrm {gp}}$ and ![]() $(e_q,0)\in S_{e_q}$. Hence
$(e_q,0)\in S_{e_q}$. Hence ![]() $(\ell e_q,0)\in (\overline{\mathcal {M}}''_{C,q})^{\mathrm {gp}}$, which together with
$(\ell e_q,0)\in (\overline{\mathcal {M}}''_{C,q})^{\mathrm {gp}}$, which together with ![]() $(1,1)\in (\overline{\mathcal {M}}''_{C,q})^{\mathrm {gp}}$ generates
$(1,1)\in (\overline{\mathcal {M}}''_{C,q})^{\mathrm {gp}}$ generates ![]() $S_{\ell e_q}\subset S_{e_q}$.
$S_{\ell e_q}\subset S_{e_q}$.
The saturation is then computed by taking all integral points in the real cone in ![]() $\overline{\mathcal {M}}_{C,q}^{\mathrm {gp}}\otimes _\mathbb {Z} \mathbb {R}$ spanned by
$\overline{\mathcal {M}}_{C,q}^{\mathrm {gp}}\otimes _\mathbb {Z} \mathbb {R}$ spanned by ![]() $\overline{\mathcal {M}}''_{C,q}$.
$\overline{\mathcal {M}}''_{C,q}$.
Constrained nodes: Extending the log structure. In this step we extend the log structure to the saturation of ![]() $\mathcal {M}''_C$, described in Corollary 4.15.
$\mathcal {M}''_C$, described in Corollary 4.15.
Lemma 4.16 The log structure ![]() $\alpha '':\mathcal {M}''_C\to \mathcal {O}_C$ extends uniquely to the saturation
$\alpha '':\mathcal {M}''_C\to \mathcal {O}_C$ extends uniquely to the saturation ![]() $(\mathcal {M}''_C)^{\mathrm {sat}}$.
$(\mathcal {M}''_C)^{\mathrm {sat}}$.
Proof. We continue to write ![]() $\ell =\ell (u_q)$. The saturation can at most be non-trivial at a constrained node
$\ell =\ell (u_q)$. The saturation can at most be non-trivial at a constrained node ![]() $q$. By Corollary 4.15 we have an isomorphism
$q$. By Corollary 4.15 we have an isomorphism ![]() $(\overline{\mathcal {M}}''_{C,q})^{\mathrm {sat}}\simeq S_{\ell e_q}$. The definition of the weights
$(\overline{\mathcal {M}}''_{C,q})^{\mathrm {sat}}\simeq S_{\ell e_q}$. The definition of the weights ![]() $w_i$ implies
$w_i$ implies ![]() $(w_1 e_q,0),(0,w_2 e_q)\in \overline{\mathcal {M}}''_{C,q}$, for the appropriate ordering of the branches of
$(w_1 e_q,0),(0,w_2 e_q)\in \overline{\mathcal {M}}''_{C,q}$, for the appropriate ordering of the branches of ![]() $C$ at
$C$ at ![]() $q$. As a sanity check, notice that
$q$. As a sanity check, notice that ![]() $w_i$ divides
$w_i$ divides ![]() $\ell$ by Proposition 4.6(I)(2). Let
$\ell$ by Proposition 4.6(I)(2). Let ![]() $\beta _q: \overline{\mathcal {M}}''_{C,q} \longrightarrow \mathcal {O}_{C,q}$ be the composition of a choice of splitting
$\beta _q: \overline{\mathcal {M}}''_{C,q} \longrightarrow \mathcal {O}_{C,q}$ be the composition of a choice of splitting ![]() $\overline{\mathcal {M}}''_{C,q} \longrightarrow \mathcal {M}''_{C,q}$ and the structure morphism
$\overline{\mathcal {M}}''_{C,q} \longrightarrow \mathcal {M}''_{C,q}$ and the structure morphism ![]() $\mathcal {M}''_{C,q} \longrightarrow \mathcal {O}_{C,q}$. Then
$\mathcal {M}''_{C,q} \longrightarrow \mathcal {O}_{C,q}$. Then ![]() $\beta _q ((w_1 e_q,0))$ vanishes at
$\beta _q ((w_1 e_q,0))$ vanishes at ![]() $q$ to order
$q$ to order ![]() $w_1$ on one branch of
$w_1$ on one branch of ![]() $C$ and
$C$ and ![]() $\beta _q((0,w_2 e_q))$ vanishes to order
$\beta _q((0,w_2 e_q))$ vanishes to order ![]() $w_2$ on the other branch. Thus, étale locally there exist generators
$w_2$ on the other branch. Thus, étale locally there exist generators ![]() $x,y\in \mathcal {O}_{C,q}$ for the maximal ideal at
$x,y\in \mathcal {O}_{C,q}$ for the maximal ideal at ![]() $q$ with
$q$ with
Thus any extension ![]() $\beta _q^{\mathrm {sat}}$ of
$\beta _q^{\mathrm {sat}}$ of ![]() $\beta _q$ to a chart for
$\beta _q$ to a chart for ![]() $(\mathcal {M}_{C,q}'')^{\mathrm {sat}}$ has to fulfill
$(\mathcal {M}_{C,q}'')^{\mathrm {sat}}$ has to fulfill
with ![]() $\zeta _i\in \Bbbk$,
$\zeta _i\in \Bbbk$, ![]() $\zeta _i^{w_1/\ell }=1$. On the other hand, the
$\zeta _i^{w_1/\ell }=1$. On the other hand, the ![]() $\zeta _i$ are uniquely determined by compatibility of
$\zeta _i$ are uniquely determined by compatibility of ![]() $\beta _q^{\mathrm {sat}}$ with
$\beta _q^{\mathrm {sat}}$ with ![]() $\beta$ at the generic points of the two branches of
$\beta$ at the generic points of the two branches of ![]() $C$ at
$C$ at ![]() $q$ since
$q$ since ![]() $(\ell e_q,0),(0,\ell e_q)\in \overline{\mathcal {M}}_{C,q}$. Conversely, with this choice of the
$(\ell e_q,0),(0,\ell e_q)\in \overline{\mathcal {M}}_{C,q}$. Conversely, with this choice of the ![]() $\zeta _i$, the equations (4.7) provide the requested extension of
$\zeta _i$, the equations (4.7) provide the requested extension of ![]() $\alpha ''$.
$\alpha ''$.
Finally, we extend ![]() $\mathcal {M}''_C$ to a log structure of a log smooth curve over the standard log point. The situation is largely the same as with admissible covers, see, e.g. [Reference MochizukiMoc95, § 3].
$\mathcal {M}''_C$ to a log structure of a log smooth curve over the standard log point. The situation is largely the same as with admissible covers, see, e.g. [Reference MochizukiMoc95, § 3].
Lemma 4.17 Up to isomorphism of log structures over the standard log point, there are ![]() $\ell =\ell (u_q)$ pairwise non-isomorphic extensions
$\ell =\ell (u_q)$ pairwise non-isomorphic extensions ![]() $\alpha _q:\mathcal {M}_{C,q}\to \mathcal {O}_{C,q}$ of the image log structure
$\alpha _q:\mathcal {M}_{C,q}\to \mathcal {O}_{C,q}$ of the image log structure ![]() $\alpha ''_q:\mathcal {M}''_{C,q}\to \mathcal {O}_{C,q}$ at the constrained node
$\alpha ''_q:\mathcal {M}''_{C,q}\to \mathcal {O}_{C,q}$ at the constrained node ![]() $q$ to a log structure of a log smooth curve.
$q$ to a log structure of a log smooth curve.
Proof. Let
be a chart for the log structure ![]() $(\mathcal {M}''_C)^{\mathrm {sat}}$ at
$(\mathcal {M}''_C)^{\mathrm {sat}}$ at ![]() $q$. The task is to classify extensions to a chart
$q$. The task is to classify extensions to a chart ![]() $\tilde \beta _q: S_{e_q} \longrightarrow \mathcal {O}_{C,q}$ up to isomorphisms of induced log structures. Similar to the reasoning in Lemma 4.16, in terms of coordinates
$\tilde \beta _q: S_{e_q} \longrightarrow \mathcal {O}_{C,q}$ up to isomorphisms of induced log structures. Similar to the reasoning in Lemma 4.16, in terms of coordinates ![]() $x,y\in \mathcal {O}_{C,q}$ with
$x,y\in \mathcal {O}_{C,q}$ with
we have to define
with ![]() $\zeta _i\in \Bbbk$,
$\zeta _i\in \Bbbk$, ![]() $\zeta _i^\ell =1$. Dividing out isomorphisms amounts to working modulo
$\zeta _i^\ell =1$. Dividing out isomorphisms amounts to working modulo ![]() $\varphi \in {\operatorname {Hom}}(S_{e_q},\mathbb {Z}/\ell )$ with
$\varphi \in {\operatorname {Hom}}(S_{e_q},\mathbb {Z}/\ell )$ with ![]() $\varphi ( (1,1))=1$. In other words, we can change
$\varphi ( (1,1))=1$. In other words, we can change ![]() $\zeta _1,\zeta _2$ by
$\zeta _1,\zeta _2$ by ![]() $\zeta \zeta _1,\zeta ^{-1}\zeta _2$ for any
$\zeta \zeta _1,\zeta ^{-1}\zeta _2$ for any ![]() $\ell$-th root of unity
$\ell$-th root of unity ![]() $\zeta$. This leaves us with
$\zeta$. This leaves us with ![]() $\ell$ pairwise non-isomorphic extensions of the log structure at
$\ell$ pairwise non-isomorphic extensions of the log structure at ![]() $q$.
$q$.
Counting non-rigidified lifts. For the final count we need to divide out the action of ![]() $\mathbb {Z}/b$ by composition with automorphisms of
$\mathbb {Z}/b$ by composition with automorphisms of ![]() $\operatorname {Spec}(Q\to \Bbbk )$ over
$\operatorname {Spec}(Q\to \Bbbk )$ over ![]() $B$. The stated count follows once we prove that this action is free. The action changes
$B$. The stated count follows once we prove that this action is free. The action changes ![]() $\tau _0$ to
$\tau _0$ to ![]() $\zeta \cdot \tau _0$ for
$\zeta \cdot \tau _0$ for ![]() $\zeta$ a
$\zeta$ a ![]() $b$-th root of unity. For this change to lead to an isomorphic log structure
$b$-th root of unity. For this change to lead to an isomorphic log structure ![]() $\mathcal {M}_C$ requires
$\mathcal {M}_C$ requires ![]() $\zeta _1\zeta _2\in \Bbbk ^\times$ in (4.8) to be unchanged at any constrained node
$\zeta _1\zeta _2\in \Bbbk ^\times$ in (4.8) to be unchanged at any constrained node ![]() $q\in \underline{C}$. This shows
$q\in \underline{C}$. This shows ![]() $\zeta ^{e_q}=1$ for all
$\zeta ^{e_q}=1$ for all ![]() $q$. Similarly, for the map
$q$. Similarly, for the map ![]() $\mathcal {M}_{X_0,\underline {f}(\eta )} \longrightarrow \mathcal {M}_{C,\eta }$ to stay unchanged relative
$\mathcal {M}_{X_0,\underline {f}(\eta )} \longrightarrow \mathcal {M}_{C,\eta }$ to stay unchanged relative ![]() $\mathcal {M}_{B,b_0} \longrightarrow \mathcal {M}_{O^\dagger ,0}$ requires
$\mathcal {M}_{B,b_0} \longrightarrow \mathcal {M}_{O^\dagger ,0}$ requires ![]() $f^\flat _\eta (\sigma _\eta ) =\tau _\eta ^{b/\mu _\eta }$ to stay unchanged. Thus also
$f^\flat _\eta (\sigma _\eta ) =\tau _\eta ^{b/\mu _\eta }$ to stay unchanged. Thus also ![]() $\zeta ^{b/\mu _\eta }=1$ for all generic points
$\zeta ^{b/\mu _\eta }=1$ for all generic points ![]() $\eta \in \underline{C}$. But by Theorem 4.10 the base order
$\eta \in \underline{C}$. But by Theorem 4.10 the base order ![]() $b$ is the smallest natural number with all
$b$ is the smallest natural number with all ![]() $e_q= b\cdot \operatorname {Ind}_q/\mu _2 w_1$ and all
$e_q= b\cdot \operatorname {Ind}_q/\mu _2 w_1$ and all ![]() $b/\mu _\eta$ integers. Thus the
$b/\mu _\eta$ integers. Thus the ![]() $e_q$ and
$e_q$ and ![]() $b/\mu _\eta$ have no common factor. This shows that
$b/\mu _\eta$ have no common factor. This shows that ![]() $\zeta ^{e_q}=1$ and
$\zeta ^{e_q}=1$ and ![]() $\zeta ^{b/\mu _\eta }=1$ for all
$\zeta ^{b/\mu _\eta }=1$ for all ![]() $q, \eta$ implies
$q, \eta$ implies ![]() $\zeta =1$. We conclude that the action of
$\zeta =1$. We conclude that the action of ![]() $\mathbb {Z}/b$ is free as claimed
$\mathbb {Z}/b$ is free as claimed
Remark 4.18 The obstruction to the existence of a logarithmic enhancement in Theorem 4.13 can be interpreted geometrically as follows.
Let ![]() $\bar \mu$ be a positive integer and
$\bar \mu$ be a positive integer and ![]() $\underline {\tilde {B}} \longrightarrow {\underline{B}}$ be the degree
$\underline {\tilde {B}} \longrightarrow {\underline{B}}$ be the degree ![]() $d$ cyclic cover branched with ramification index
$d$ cyclic cover branched with ramification index ![]() $d$ over
$d$ over ![]() $b_0$. Let
$b_0$. Let ![]() $\underline {\bar {X}}=\underline {X}\times _{\underline{B}}\underline {\tilde {B}}$, and let
$\underline {\bar {X}}=\underline {X}\times _{\underline{B}}\underline {\tilde {B}}$, and let ![]() $\underline {\tilde {X}} \longrightarrow \underline {\bar {X}}$ be the normalization, giving a family
$\underline {\tilde {X}} \longrightarrow \underline {\bar {X}}$ be the normalization, giving a family ![]() $\underline {\tilde {X}} \longrightarrow \underline {\tilde {B}}$. It is a standard computation that the inverse image of a multiplicity
$\underline {\tilde {X}} \longrightarrow \underline {\tilde {B}}$. It is a standard computation that the inverse image of a multiplicity ![]() $\mu$ irreducible component of
$\mu$ irreducible component of ![]() $\underline {X}_0$ in
$\underline {X}_0$ in ![]() $\underline {\tilde X}$ is a union of irreducible components of
$\underline {\tilde X}$ is a union of irreducible components of ![]() $\underline {\tilde X}_0$, each with multiplicity
$\underline {\tilde X}_0$, each with multiplicity ![]() $\mu /\gcd (\mu ,d)$.
$\mu /\gcd (\mu ,d)$.
At the level of log schemes, in fact ![]() $\bar {X}$ carries a fine but not saturated logarithmic structure via the description
$\bar {X}$ carries a fine but not saturated logarithmic structure via the description ![]() $\bar {X}=X\times _B \tilde {B}$ in the category of fine log schemes, while
$\bar {X}=X\times _B \tilde {B}$ in the category of fine log schemes, while ![]() $\tilde X$ carries an fs logarithmic structure via the description
$\tilde X$ carries an fs logarithmic structure via the description ![]() $\tilde {X}=X\times _B\tilde {B}$ in the category of fs logarithmic structures. Here
$\tilde {X}=X\times _B\tilde {B}$ in the category of fs logarithmic structures. Here ![]() $\tilde {B}$ carries the divisorial logarithmic structure given by
$\tilde {B}$ carries the divisorial logarithmic structure given by ![]() $\tilde b_0\in \tilde B$, the unique point mapping to
$\tilde b_0\in \tilde B$, the unique point mapping to ![]() $b_0$.
$b_0$.
Similarly, the central fibres are related as follows. The map ![]() $\tilde B \longrightarrow B$ induces a morphism on standard log points
$\tilde B \longrightarrow B$ induces a morphism on standard log points ![]() $\tilde b_0 \longrightarrow b_0$ induced by
$\tilde b_0 \longrightarrow b_0$ induced by ![]() $\mathbb {N} \longrightarrow \mathbb {N}, 1\mapsto d$ for some integer
$\mathbb {N} \longrightarrow \mathbb {N}, 1\mapsto d$ for some integer ![]() $d$. Then
$d$. Then ![]() $\bar X_0 =X_0\times _{b_0}\tilde b_0$ in the category of fine log schemes, and
$\bar X_0 =X_0\times _{b_0}\tilde b_0$ in the category of fine log schemes, and ![]() $\tilde X_0=X_0\times _{b_0}\tilde b_0$ in the category of fs log schemes.
$\tilde X_0=X_0\times _{b_0}\tilde b_0$ in the category of fs log schemes.
Given a transverse pre-logarithmic map ![]() $\underline {f}:\underline {C}/\operatorname {Spec}\Bbbk \longrightarrow \underline {X}$, take the integer
$\underline {f}:\underline {C}/\operatorname {Spec}\Bbbk \longrightarrow \underline {X}$, take the integer ![]() $d$ above to be the positive integer
$d$ above to be the positive integer ![]() $b$ given by Theorem 4.10(3). Then one checks readily that
$b$ given by Theorem 4.10(3). Then one checks readily that ![]() $\underline {f}$ has a logarithmic enhancement if and only if there is a lift
$\underline {f}$ has a logarithmic enhancement if and only if there is a lift ![]() $\underline {\tilde {f}}:\underline {C} \longrightarrow \underline {\tilde {X}}_0$ of
$\underline {\tilde {f}}:\underline {C} \longrightarrow \underline {\tilde {X}}_0$ of ![]() $\underline {f}$. Indeed, if
$\underline {f}$. Indeed, if ![]() $\underline {f}$ has a logarithmic enhancement
$\underline {f}$ has a logarithmic enhancement ![]() $f:C/S \longrightarrow X_0$ with
$f:C/S \longrightarrow X_0$ with ![]() $S$ carrying the basic log structure, the morphism
$S$ carrying the basic log structure, the morphism ![]() $S \longrightarrow b_0$ factors through
$S \longrightarrow b_0$ factors through ![]() $\tilde b_0$ by the description of Theorem 4.10. Thus the universal property of fibred product gives a morphism
$\tilde b_0$ by the description of Theorem 4.10. Thus the universal property of fibred product gives a morphism ![]() $\tilde f:C \longrightarrow \tilde X_0$. Conversely, given a lift, it follows again from the definition of
$\tilde f:C \longrightarrow \tilde X_0$. Conversely, given a lift, it follows again from the definition of ![]() $b$ in Theorem 4.10 that the multiplicity
$b$ in Theorem 4.10 that the multiplicity ![]() $\mu$ of any irreducible component of
$\mu$ of any irreducible component of ![]() $\underline {X}_0$ meeting
$\underline {X}_0$ meeting ![]() $\underline {f}(\underline {C})$ divides
$\underline {f}(\underline {C})$ divides ![]() $b$. So the multiplicity of any component of
$b$. So the multiplicity of any component of ![]() $\underline {\tilde {X}}_0$ meeting
$\underline {\tilde {X}}_0$ meeting ![]() $\underline {\tilde {f}}(\underline {C})$ is
$\underline {\tilde {f}}(\underline {C})$ is ![]() $1$ and by shrinking
$1$ and by shrinking ![]() $\underline {X}_0$ we can assume that
$\underline {X}_0$ we can assume that ![]() $\underline {\tilde {X}}_0$ is reduced. One also checks that the reduced branching order
$\underline {\tilde {X}}_0$ is reduced. One also checks that the reduced branching order ![]() $\bar {w}_q$ associated to a node
$\bar {w}_q$ associated to a node ![]() $q$ is the same for
$q$ is the same for ![]() $\underline {f}$ and
$\underline {f}$ and ![]() $\underline {\tilde {f}}$, and thus
$\underline {\tilde {f}}$, and thus ![]() $\underline {\tilde {f}}$ is still transverse pre-logarithmic. By Lemma 4.11 and Theorem 4.13,
$\underline {\tilde {f}}$ is still transverse pre-logarithmic. By Lemma 4.11 and Theorem 4.13, ![]() $\underline {\tilde {f}}$ has a logarithmic enhancement, and then the composed morphism
$\underline {\tilde {f}}$ has a logarithmic enhancement, and then the composed morphism ![]() $C\smash {\mathop {\longrightarrow }\limits ^{\tilde f}}\tilde {X}_0 \smash {\mathop {\longrightarrow }\limits ^{}} X_0$ gives the desired logarithmic enhancement of
$C\smash {\mathop {\longrightarrow }\limits ^{\tilde f}}\tilde {X}_0 \smash {\mathop {\longrightarrow }\limits ^{}} X_0$ gives the desired logarithmic enhancement of ![]() $\underline {f}$.
$\underline {f}$.
5. Examples
We will now study explicit examples of the decomposition formula for a logarithmically smooth morphism ![]() $X\to B$. We mostly use the traditional tropical language of polyhedral complexes and metric graphs discussed in § 2.5.3.
$X\to B$. We mostly use the traditional tropical language of polyhedral complexes and metric graphs discussed in § 2.5.3.
5.1 The classical case
Suppose ![]() $X \longrightarrow B$ is a simple normal crossings degeneration with
$X \longrightarrow B$ is a simple normal crossings degeneration with ![]() $X_0=Y_1\cup Y_2$ a reduced union of two irreducible components, with
$X_0=Y_1\cup Y_2$ a reduced union of two irreducible components, with ![]() $Y_1\cap Y_2=D$ a smooth divisor in both
$Y_1\cap Y_2=D$ a smooth divisor in both ![]() $Y_1$ and
$Y_1$ and ![]() $Y_2$. In this case,
$Y_2$. In this case, ![]() $\Sigma (X)=(\mathbb {R}_{\ge 0})^2$ and the map
$\Sigma (X)=(\mathbb {R}_{\ge 0})^2$ and the map ![]() $\Sigma (X) \longrightarrow \Sigma (B)=\mathbb {R}_{\ge 0}$ is given by
$\Sigma (X) \longrightarrow \Sigma (B)=\mathbb {R}_{\ge 0}$ is given by ![]() $(x,y)\mapsto x+y$. Thus
$(x,y)\mapsto x+y$. Thus ![]() $\Delta (X)$ admits an affine-linear isomorphism with the unit interval
$\Delta (X)$ admits an affine-linear isomorphism with the unit interval ![]() $[0,1]$, see Figure 1.
$[0,1]$, see Figure 1.
Proposition 5.1 In the above situation, let ![]() $f:\Gamma \longrightarrow \Delta (X)$ be a decorated tropical map. Then
$f:\Gamma \longrightarrow \Delta (X)$ be a decorated tropical map. Then ![]() $f$ is rigid if and only if every vertex
$f$ is rigid if and only if every vertex ![]() $v$ of
$v$ of ![]() $\Gamma$ maps to the endpoints of
$\Gamma$ maps to the endpoints of ![]() $\Delta (X)$ and every edge of
$\Delta (X)$ and every edge of ![]() $\Gamma$ surjects onto
$\Gamma$ surjects onto ![]() $\Delta (X)$.
$\Delta (X)$.

Figure 1. The cones ![]() $\Sigma (X)$ and
$\Sigma (X)$ and ![]() $\Sigma (B)$ and the interval
$\Sigma (B)$ and the interval ![]() $\Delta (X)$.
$\Delta (X)$.
Note that necessarily every leg of ![]() $\Gamma$ is contracted, as
$\Gamma$ is contracted, as ![]() $\Delta (X)$ is compact.
$\Delta (X)$ is compact.
Proof. First note that if an edge ![]() $E_q$ is contracted, then
$E_q$ is contracted, then ![]() $u_q=0$ and the length of the edge is arbitrary. By changing the length, one sees
$u_q=0$ and the length of the edge is arbitrary. By changing the length, one sees ![]() $f$ is not rigid, see Figure 2 on the left.
$f$ is not rigid, see Figure 2 on the left.

Figure 2. A graph with a contracted bounded edge or an interior vertex is not rigid.
Next, suppose ![]() $v$ is a vertex with
$v$ is a vertex with ![]() $f(v)$ lying in the interior of
$f(v)$ lying in the interior of ![]() $\Delta (X)$. Identifying the latter with
$\Delta (X)$. Identifying the latter with ![]() $[0,1]$, we can view
$[0,1]$, we can view ![]() $u_q\in \mathbb {Z}$ for any
$u_q\in \mathbb {Z}$ for any ![]() $q$. Let
$q$. Let ![]() $E_{q_1},\ldots ,E_{q_r}$ be the edges of
$E_{q_1},\ldots ,E_{q_r}$ be the edges of ![]() $\Gamma$ adjacent to
$\Gamma$ adjacent to ![]() $v$ with lengths
$v$ with lengths ![]() $\ell _1,\ldots ,\ell _r$, oriented to point away from
$\ell _1,\ldots ,\ell _r$, oriented to point away from ![]() $v$. We can then write down a family
$v$. We can then write down a family ![]() $f_t$ of tropical maps,
$f_t$ of tropical maps, ![]() $t$ a real number close to
$t$ a real number close to ![]() $0$, with
$0$, with ![]() $f=f_0$,
$f=f_0$, ![]() $f_t(v')=f(v')$ for any vertex
$f_t(v')=f(v')$ for any vertex ![]() $v'\not =v$, and
$v'\not =v$, and ![]() $f_t(v)=f(v)+t$. In doing so, we also need to modify the lengths of the edges
$f_t(v)=f(v)+t$. In doing so, we also need to modify the lengths of the edges ![]() $E_{q_i}$, as indicated in Figure 2 on the right. Any unbounded edge attached to
$E_{q_i}$, as indicated in Figure 2 on the right. Any unbounded edge attached to ![]() $v$ is contracted to
$v$ is contracted to ![]() $f_t(v)$. So
$f_t(v)$. So ![]() $f$ is not rigid. Thus if
$f$ is not rigid. Thus if ![]() $f$ is rigid, we see that all vertices of
$f$ is rigid, we see that all vertices of ![]() $\Gamma$ map to endpoints of
$\Gamma$ map to endpoints of ![]() $\Delta (X)$, and any compact edge is not contracted, and hence surjects onto
$\Delta (X)$, and any compact edge is not contracted, and hence surjects onto ![]() $\Delta (X)$. The converse is clear.
$\Delta (X)$. The converse is clear.
A choice of decorated rigid tropical map in this situation is then exactly what Jun Li terms an admissible triple in [Reference LiLi02]. Indeed, by removing ![]() $f^{-1}(1/2)$ from
$f^{-1}(1/2)$ from ![]() $\Gamma$, one obtains two graphs (possibly disconnected)
$\Gamma$, one obtains two graphs (possibly disconnected) ![]() $\Gamma _1, \Gamma _2$ with legs and what Jun Li terms roots (the half-edges mapping non-trivially to
$\Gamma _1, \Gamma _2$ with legs and what Jun Li terms roots (the half-edges mapping non-trivially to ![]() $\Delta (X)$). The weights of a root, in Li's terminology, coincide with the absolute value of the corresponding
$\Delta (X)$). The weights of a root, in Li's terminology, coincide with the absolute value of the corresponding ![]() $u_q$. The set
$u_q$. The set ![]() $I$ in the definition of admissible triple indicates which labels occur for unbounded edges mapping to, say,
$I$ in the definition of admissible triple indicates which labels occur for unbounded edges mapping to, say, ![]() $0\in \Delta (X)$. An illustration is given in Figure 3.
$0\in \Delta (X)$. An illustration is given in Figure 3.

Figure 3. A rigid tropical map is depicted with four edges and two legs, the latter corresponding to marked points with contact order ![]() $0$. The corresponding admissible triple of Jun Li is depicted on the right, with roots corresponding to half-edges and legs corresponding to the legs of the original graph. The half-edges marked
$0$. The corresponding admissible triple of Jun Li is depicted on the right, with roots corresponding to half-edges and legs corresponding to the legs of the original graph. The half-edges marked ![]() $1$ and
$1$ and ![]() $3$ have
$3$ have ![]() $u=2$.
$u=2$.
We emphasize that our virtual decomposition of the moduli space of stable logarithmic maps in terms of rigid tropical maps does not depend on transversality. Already in this simple situation, the tropicalization of a basic stable logarithmic map parameterizes a family of tropical maps with several rigid limits, one for each facet of the basic monoid. The main result of this paper refines the virtual counting problem in providing a count for each such choice of rigid limit. This count applies even in more general situations where the vertices of the tropical curve do not necessarily map to vertices of the polyhedron associated to the target, as the next section shows. Note also that this case has been carried out in detail and with somewhat different notation after distribution of a first version of this paper in [Reference Kim, Lho and RuddatKLR18].
5.2 Rational curves in a pencil of cubics
It is well known that if one fixes eight general points in ![]() $\mathbb {P}^2$, the pencil of cubics passing through these eight points contains precisely
$\mathbb {P}^2$, the pencil of cubics passing through these eight points contains precisely ![]() $12$ nodal rational curves. Blowing up six of these eight points, we get a cubic surface we denote
$12$ nodal rational curves. Blowing up six of these eight points, we get a cubic surface we denote ![]() $X_1' \subset \mathbb {P}^3$, and the enumeration of
$X_1' \subset \mathbb {P}^3$, and the enumeration of ![]() $12$ nodal rational cubics translates to the enumeration of
$12$ nodal rational cubics translates to the enumeration of ![]() $12$ nodal plane sections of
$12$ nodal plane sections of ![]() $X_1'$ passing through the remaining two points
$X_1'$ passing through the remaining two points ![]() $p_1,p_2$.
$p_1,p_2$.
We will give here a non-trivial demonstration of the decomposition formula by degenerating the cubic surface to a normal crossings union ![]() $H_1\cup H_2\cup H_3$ of three blown-up planes.
$H_1\cup H_2\cup H_3$ of three blown-up planes.
5.2.1 Degenerating a cubic to three planes
Using coordinates ![]() $x_0,\ldots ,x_3$ on
$x_0,\ldots ,x_3$ on ![]() $\mathbb {P}^3$, consider a smooth cubic surface
$\mathbb {P}^3$, consider a smooth cubic surface ![]() $X_1'\subset \mathbb {P}^3$ with equation
$X_1'\subset \mathbb {P}^3$ with equation
We then have a family ![]() $X' \longrightarrow B=\mathbb {A}^1$ given by
$X' \longrightarrow B=\mathbb {A}^1$ given by ![]() $X'\subset \mathbb {A}^1\times \mathbb {P}^3$ defined by
$X'\subset \mathbb {A}^1\times \mathbb {P}^3$ defined by ![]() $tf_3+x_1x_2x_3=0$. The fibre
$tf_3+x_1x_2x_3=0$. The fibre ![]() $X'_0$ is the union of three planes
$X'_0$ is the union of three planes ![]() $H'_1\cup H'_2\cup H'_3$. Pick two sections
$H'_1\cup H'_2\cup H'_3$. Pick two sections ![]() $p_1,p_2:B \longrightarrow X'$ such that
$p_1,p_2:B \longrightarrow X'$ such that ![]() $p_i(0)\in H'_i$. This can be achieved by choosing two appropriate points on the base locus
$p_i(0)\in H'_i$. This can be achieved by choosing two appropriate points on the base locus ![]() $f_3(x_0,x_1,x_2,x_3)=x_1x_2x_3=0$.
$f_3(x_0,x_1,x_2,x_3)=x_1x_2x_3=0$.
5.2.2 Resolving to obtain a normal crossings family
The total space of ![]() $X'$ is not a normal crossings family: it has nine ordinary double points over
$X'$ is not a normal crossings family: it has nine ordinary double points over ![]() $t=0$, assuming
$t=0$, assuming ![]() $f_3$ is chosen generally: these are the points of intersection of the singular lines
$f_3$ is chosen generally: these are the points of intersection of the singular lines ![]() $H_i'\cap H_j'$ with
$H_i'\cap H_j'$ with ![]() $f_3=0$. One manifestation is the fact that
$f_3=0$. One manifestation is the fact that ![]() $H_i'$ are Weil divisors which are not Cartier. By blowing up
$H_i'$ are Weil divisors which are not Cartier. By blowing up ![]() $H'_1$ followed by
$H'_1$ followed by ![]() $H'_2$, we resolve the ordinary double points. We obtain a family
$H'_2$, we resolve the ordinary double points. We obtain a family ![]() $X \longrightarrow B$, which is normal crossings, hence logarithmically smooth, in a neighbourhood of
$X \longrightarrow B$, which is normal crossings, hence logarithmically smooth, in a neighbourhood of ![]() $t=0$, as depicted on the left in Figure 4. Denote by
$t=0$, as depicted on the left in Figure 4. Denote by ![]() $H_i$ the proper transform of
$H_i$ the proper transform of ![]() $H_i'$.
$H_i'$.

Figure 4. The left-hand picture depicts ![]() $X_0$ as a union of three copies of
$X_0$ as a union of three copies of ![]() $\mathbb {P}^2$, blown up at six, three or zero points. The right-hand picture depicts
$\mathbb {P}^2$, blown up at six, three or zero points. The right-hand picture depicts ![]() $\Delta (X)$.
$\Delta (X)$.
We identify ![]() $\Sigma (X)$ with
$\Sigma (X)$ with ![]() $(\mathbb {R}_{\ge 0})^3$, so that
$(\mathbb {R}_{\ge 0})^3$, so that ![]() $\Delta (X)$ is identified with the standard simplex
$\Delta (X)$ is identified with the standard simplex ![]() $\{(x_1,x_2,x_3)\,|\,x_1+x_2+x_3=1, x_1,x_2,x_3\ge 0\}$, as depicted on the right in Figure 4.
$\{(x_1,x_2,x_3)\,|\,x_1+x_2+x_3=1, x_1,x_2,x_3\ge 0\}$, as depicted on the right in Figure 4.
5.2.3 Limiting curves: triangles
Since the limit of plane curves on ![]() $X'_t = X_t$ should be a plane curve on
$X'_t = X_t$ should be a plane curve on ![]() $X'_0$, limiting curves on
$X'_0$, limiting curves on ![]() $X_0$ would map to plane sections of
$X_0$ would map to plane sections of ![]() $X_0'$ through
$X_0'$ through ![]() $p_1,p_2$. This greatly limits the possible limiting curves, in particular the image in each of
$p_1,p_2$. This greatly limits the possible limiting curves, in particular the image in each of ![]() $H_i'$ is a line.
$H_i'$ is a line.
General triangles do not occur. It is easy to see that a plane section of ![]() $X'_0$ passing through
$X'_0$ passing through ![]() $p_1, p_2$ whose proper transform in
$p_1, p_2$ whose proper transform in ![]() $X_0$ is a triangle of lines cannot be the image of a stable logarithmic curve
$X_0$ is a triangle of lines cannot be the image of a stable logarithmic curve ![]() $C \longrightarrow X_0$ of genus
$C \longrightarrow X_0$ of genus ![]() $0$. Indeed, there would be a smooth point of
$0$. Indeed, there would be a smooth point of ![]() $\underline{C}$ mapping to
$\underline{C}$ mapping to ![]() $(X_0)_\mathrm {sing}$, contradicting Proposition 4.6(II).
$(X_0)_\mathrm {sing}$, contradicting Proposition 4.6(II).
Triangles through double points. On the other hand, consider the total transform of a triangle in ![]() $X_0'$ passing through
$X_0'$ passing through ![]() $p_1$,
$p_1$, ![]() $p_2$, and one of the nine ordinary double points of
$p_2$, and one of the nine ordinary double points of ![]() $X'$. The resulting curve will be a cycle of four rational curves, one of the curves being part of the exceptional set of the blowup of
$X'$. The resulting curve will be a cycle of four rational curves, one of the curves being part of the exceptional set of the blowup of ![]() $H_1'$ and
$H_1'$ and ![]() $H_2'$. We can partially normalize this curve at the node contained in the smooth part of
$H_2'$. We can partially normalize this curve at the node contained in the smooth part of ![]() $X_0$, getting a stable logarithmic curve of genus
$X_0$, getting a stable logarithmic curve of genus ![]() $0$. See Figure 5 for one such case.
$0$. See Figure 5 for one such case.

Figure 5. Proper transform of a triangle through a double point. The curve is normalized where ![]() $C_1$ and
$C_1$ and ![]() $C_4$ meet.
$C_4$ meet.
Tropical picture. We depict to the right the associated rigid tropical curve. Here the lengths of each edge are ![]() $1$, and the contact data
$1$, and the contact data ![]() $u_q$ take the values
$u_q$ take the values ![]() $(-1,1,0)$,
$(-1,1,0)$, ![]() $(0,-1,1)$ and
$(0,-1,1)$ and ![]() $(1,0,-1)$. This accounts for nine curves.
$(1,0,-1)$. This accounts for nine curves.
Logarithmic enhancement and logarithmic unobstructedness. Note that the above curves are transverse pre-logarithmic curves, and, by Theorem 4.13, each of these curves has precisely one basic logarithmic enhancement. Since the curve is immersed it has no automorphisms. One can use a natural absolute, rather than relative, obstruction theory to define the virtual fundamental class, which is governed by the logarithmic normal bundle. In this case each curve is unobstructed: since it is transverse with contact order 1, the logarithmic normal bundle coincides with the usual normal bundle. The normal bundle restricts to ![]() $\mathcal {O}_{\mathbb {P}^1},\mathcal {O}_{\mathbb {P}^1}(1),\mathcal {O}_{\mathbb {P}^1}(1)$, and
$\mathcal {O}_{\mathbb {P}^1},\mathcal {O}_{\mathbb {P}^1}(1),\mathcal {O}_{\mathbb {P}^1}(1)$, and ![]() $\mathcal {O}_{\mathbb {P}^1}(-1)$ on the respective four components
$\mathcal {O}_{\mathbb {P}^1}(-1)$ on the respective four components ![]() $C_1,C_2,C_3$ and
$C_1,C_2,C_3$ and ![]() $C_4$, and hence it is non-special. We note that this does not account for the incidence condition that the marked points land at
$C_4$, and hence it is non-special. We note that this does not account for the incidence condition that the marked points land at ![]() $p_i$. This can be arranged, for instance, using (5.1) in 5.3.2.
$p_i$. This can be arranged, for instance, using (5.1) in 5.3.2.
It follows that indeed each of these nine curves contributes precisely once to the desired Gromov–Witten invariant.
5.2.4 Limiting curves: the plane section through the origin
The far more interesting case is when the plane section of ![]() $X_0'$ passes through the triple point. Then one has a stable map from a union of four projective lines, with the central component contracted to the triple point, see Figure 6 on the left.
$X_0'$ passes through the triple point. Then one has a stable map from a union of four projective lines, with the central component contracted to the triple point, see Figure 6 on the left.

Figure 6. A curve mapping to a plane section through the origin, and its tropicalization.
There is in fact a one-parameter family ![]() $\underline {W}$ of such stable maps, as the line in
$\underline {W}$ of such stable maps, as the line in ![]() $H_3$ is unconstrained and can be chosen to be any element in a pencil of lines. Only one member of this family lies in a plane, and we will see below that indeed only one member of the family admits a logarithmic enhancement.
$H_3$ is unconstrained and can be chosen to be any element in a pencil of lines. Only one member of this family lies in a plane, and we will see below that indeed only one member of the family admits a logarithmic enhancement.
Tropical picture. To understand the nature of such a logarithmic curve, we first analyse the corresponding tropical map. The image of such a map will be as depicted in Figure 6 on the right, with the central vertex corresponding to the contracted component landing somewhere in the interior of the triangle. However, the tropical balancing condition must hold at this central vertex, by [Reference Gross and SiebertGS13, Proposition 1.14]. From this one determines that the only possibility for the values of ![]() $u_q$ are
$u_q$ are ![]() $(-2,1,1)$,
$(-2,1,1)$, ![]() $(1,1,-2)$ and
$(1,1,-2)$ and ![]() $(1,-2,1)$, all lengths are
$(1,-2,1)$, all lengths are ![]() $1/3$, and the central vertex is
$1/3$, and the central vertex is ![]() $(1/3,1/3,1/3)$. The multiplicity of this rigid tropical map
$(1/3,1/3,1/3)$. The multiplicity of this rigid tropical map ![]() $\Gamma$ according to Corollary 3.8 then is
$\Gamma$ according to Corollary 3.8 then is ![]() $m_{\Gamma }=3$.
$m_{\Gamma }=3$.
5.2.5 Logarithmic enhancement using a logarithmic modification
We now show that only one of the stable maps in the family ![]() $\underline {S}$ has a logarithmic enhancement. To do so, we use the techniques of § 4, first refining
$\underline {S}$ has a logarithmic enhancement. To do so, we use the techniques of § 4, first refining ![]() $\Sigma (X)$ to obtain a logarithmic modification of
$\Sigma (X)$ to obtain a logarithmic modification of ![]() $X$. The subdivision visible in Figure 6 gives a refinement of
$X$. The subdivision visible in Figure 6 gives a refinement of ![]() $\Sigma (X)$, the central star subdivision of
$\Sigma (X)$, the central star subdivision of ![]() $\Sigma (X)$. This corresponds to the ordinary blow-up
$\Sigma (X)$. This corresponds to the ordinary blow-up ![]() $h:\tilde X \longrightarrow X$ at the triple point of
$h:\tilde X \longrightarrow X$ at the triple point of ![]() $X_0$. We may then identify logarithmic curves in
$X_0$. We may then identify logarithmic curves in ![]() $\tilde X$ and use the induced morphism
$\tilde X$ and use the induced morphism ![]() $\mathscr {M}(\tilde X/B) \longrightarrow \mathscr {M}(X/B)$.
$\mathscr {M}(\tilde X/B) \longrightarrow \mathscr {M}(X/B)$.
Lifting the map to ![]() $\tilde X_0$. The central fibre
$\tilde X_0$. The central fibre ![]() $\tilde X_0$ is now as depicted in Figure 7. We then try to build a transverse pre-logarithmic curve in
$\tilde X_0$ is now as depicted in Figure 7. We then try to build a transverse pre-logarithmic curve in ![]() $\tilde X$ lifting one of the stable maps of Figure 6. Writing
$\tilde X$ lifting one of the stable maps of Figure 6. Writing ![]() $C=C_1\cup C_2\cup C_3\cup C_4$, with
$C=C_1\cup C_2\cup C_3\cup C_4$, with ![]() $C_4$ the central component, we map
$C_4$ the central component, we map ![]() $C_1$ and
$C_1$ and ![]() $C_2$ to the lines
$C_2$ to the lines ![]() $L_1$ and
$L_1$ and ![]() $L_2$ containing the preimages of
$L_2$ containing the preimages of ![]() $p_1$ and
$p_1$ and ![]() $p_2$, respectively, as depicted in Figure 7, while
$p_2$, respectively, as depicted in Figure 7, while ![]() $C_3$ maps to some line
$C_3$ maps to some line ![]() $L_3$ in
$L_3$ in ![]() $H_3$. On the other hand, by (4.2) in the definition of transverse pre-logarithmic maps,
$H_3$. On the other hand, by (4.2) in the definition of transverse pre-logarithmic maps, ![]() $C_4$ must map to the exceptional
$C_4$ must map to the exceptional ![]() $\mathbb {P}^2=E$, which is of multiplicity
$\mathbb {P}^2=E$, which is of multiplicity ![]() $3$, in such a way that it is triply tangent to
$3$, in such a way that it is triply tangent to ![]() $\partial E$ precisely at the points of intersection with
$\partial E$ precisely at the points of intersection with ![]() $L_i$,
$L_i$, ![]() $i=1,2,3$.
$i=1,2,3$.

Figure 7. The lifted map. The middle figure is only a sketch: the nodal cubic curve ![]() $C_4$ meets each of the visible coordinate lines at one point with multiplicity 3. Moreover, these three points are collinear.
$C_4$ meets each of the visible coordinate lines at one point with multiplicity 3. Moreover, these three points are collinear.
Uniqueness of liftable map. We claim that there is precisely one such map, necessarily with image containing a curve of degree ![]() $3$ in the exceptional
$3$ in the exceptional ![]() $\mathbb {P}^2$, with image as depicted in Figure 7. The number of transverse pre-logarithmic maps can be determined by considering linear series as follows. The three contact points on
$\mathbb {P}^2$, with image as depicted in Figure 7. The number of transverse pre-logarithmic maps can be determined by considering linear series as follows. The three contact points on ![]() $C_4 \simeq \mathbb {P}^1$ can be taken to be
$C_4 \simeq \mathbb {P}^1$ can be taken to be ![]() $0,1$ and
$0,1$ and ![]() $\infty$, and the map
$\infty$, and the map ![]() $C_4 \longrightarrow \mathbb {P}^2$ corresponds, up to a choice of basis, to the unique linear system on
$C_4 \longrightarrow \mathbb {P}^2$ corresponds, up to a choice of basis, to the unique linear system on ![]() $\mathbb {P}^1$ spanned by the divisors
$\mathbb {P}^1$ spanned by the divisors ![]() $3\{0\}$,
$3\{0\}$, ![]() $3\{1\}$ and
$3\{1\}$ and ![]() $3\{\infty \}$. Since these points map to the coordinate lines, the choice of basis is limited to rescaling the defining sections. The choice of scaling of the defining sections results in fixing the images of
$3\{\infty \}$. Since these points map to the coordinate lines, the choice of basis is limited to rescaling the defining sections. The choice of scaling of the defining sections results in fixing the images of ![]() $0$ and
$0$ and ![]() $1$, and the image point of
$1$, and the image point of ![]() $\infty$ is then uniquely determined.
$\infty$ is then uniquely determined.
This determines uniquely the point ![]() $L_3\cap E$. In particular, the line
$L_3\cap E$. In particular, the line ![]() $L_3$ is determined. Thus we see that there is a unique transverse prelogarithmic map
$L_3$ is determined. Thus we see that there is a unique transverse prelogarithmic map ![]() $\underline {f}:C \longrightarrow \tilde{\underline{X}}_0$ such that
$\underline {f}:C \longrightarrow \tilde{\underline{X}}_0$ such that ![]() $\underline {h}\circ \underline {f}$ lies in the family
$\underline {h}\circ \underline {f}$ lies in the family ![]() $\underline {S}$ of stable maps to
$\underline {S}$ of stable maps to ![]() $X$.
$X$.
Logarithmic enhancement. Since the curve is rational, Theorem 4.13 assures the existence of a logarithmic enhancement. Only the exceptional component is non-reduced, of multiplicity ![]() $\mu =3$, and for each node
$\mu =3$, and for each node ![]() $q\in C$ we have
$q\in C$ we have ![]() $\operatorname {Ind}_q=1$ and
$\operatorname {Ind}_q=1$ and ![]() $\bar w_q=1/1=3/3=1$. Hence
$\bar w_q=1/1=3/3=1$. Hence ![]() $b=3$,
$b=3$, ![]() $G=\mathbb {Z}/\mu =\mathbb {Z}/3$ and the count of Theorem 4.13 gives
$G=\mathbb {Z}/\mu =\mathbb {Z}/3$ and the count of Theorem 4.13 gives
 \[ \frac{|G|}{b}\prod_q\bar w_q= \frac{3}{3}\cdot 1^3=1 \]
\[ \frac{|G|}{b}\prod_q\bar w_q= \frac{3}{3}\cdot 1^3=1 \]
basic log enhancement of this transverse prelogarithmic curve. This gives one more basic stable logarithmic map ![]() $h\circ f$.
$h\circ f$.
Unobstructedness. Once again we check that ![]() $h\circ f$ is unobstructed, if one makes use of an absolute obstruction theory: the logarithmic normal bundle has degree 0 on each line, hence degree 1 on
$h\circ f$ is unobstructed, if one makes use of an absolute obstruction theory: the logarithmic normal bundle has degree 0 on each line, hence degree 1 on ![]() $C_4$, and is non-special. Again the map has no automorphisms, which accounts for one curve, with multiplicity
$C_4$, and is non-special. Again the map has no automorphisms, which accounts for one curve, with multiplicity ![]() $3$, because
$3$, because ![]() $m_{\Gamma }=3$. Hence the final accounting according to Theorem 3.11 is
$m_{\Gamma }=3$. Hence the final accounting according to Theorem 3.11 is
which is the desired result.
5.2.6 Impossibility of other contributions
Note our presentation has not been thorough in ruling out other possibilities for stable logarithmic maps, possibly obstructed, contributing to the total. For example, ![]() $\underline {S}$ includes curves where
$\underline {S}$ includes curves where ![]() $L_3$ falls into the double point locus of
$L_3$ falls into the double point locus of ![]() $X_0$, but a more detailed analysis of the tropical possibilities rules out a possible log enhancement. We leave it to the reader to confirm that we have found all possibilities.
$X_0$, but a more detailed analysis of the tropical possibilities rules out a possible log enhancement. We leave it to the reader to confirm that we have found all possibilities.
5.3 Degeneration of point conditions
We now consider a situation which is common in applications of tropical geometry; this includes tropical counting of curves on toric varieties [Reference MikhalkinMik05, Reference Nishinou and SiebertNS06]. We fix a pair ![]() $(Y,D)$ where
$(Y,D)$ where ![]() $Y$ is a variety over a field
$Y$ is a variety over a field ![]() $\Bbbk$ and
$\Bbbk$ and ![]() $D$ is a reduced Weil divisor such that the divisorial logarithmic structure on
$D$ is a reduced Weil divisor such that the divisorial logarithmic structure on ![]() $Y$ is logarithmically smooth over the trivial point
$Y$ is logarithmically smooth over the trivial point ![]() $\operatorname {Spec}\Bbbk$. We then consider the trivial family
$\operatorname {Spec}\Bbbk$. We then consider the trivial family
where now ![]() $X$ is given the divisorial logarithmic structure with respect to the divisor
$X$ is given the divisorial logarithmic structure with respect to the divisor ![]() $(D\times B)\cup (Y\times \{0\})$.
$(D\times B)\cup (Y\times \{0\})$.
5.3.1 Evaluation maps and moduli
Fix a type ![]() $\beta$ of stable logarithmic maps to
$\beta$ of stable logarithmic maps to ![]() $X$ over
$X$ over ![]() $B$, getting a moduli space
$B$, getting a moduli space ![]() ${\mathscr M}(X/B,\beta )$. We assume that the curves of type
${\mathscr M}(X/B,\beta )$. We assume that the curves of type ![]() $\beta$ have
$\beta$ have ![]() $n$ marked points
$n$ marked points ![]() $p_1,\ldots ,p_n$ with
$p_1,\ldots ,p_n$ with ![]() $u_{p_i}=0$ (and possibly some additional marked points
$u_{p_i}=0$ (and possibly some additional marked points ![]() $x_1,\ldots ,x_m$ with non-trivial contact orders with
$x_1,\ldots ,x_m$ with non-trivial contact orders with ![]() $D$). Given a stable map
$D$). Given a stable map ![]() $(C/S,\textbf {x},\mathbf {p},f)$, a priori for each
$(C/S,\textbf {x},\mathbf {p},f)$, a priori for each ![]() $i\in \{1,\ldots ,n\}$ we have an evaluation map
$i\in \{1,\ldots ,n\}$ we have an evaluation map ![]() $\mathrm {ev}_i:(\underline{S},p_i^*\mathcal {M}_C) \longrightarrow X$ obtained by restricting
$\mathrm {ev}_i:(\underline{S},p_i^*\mathcal {M}_C) \longrightarrow X$ obtained by restricting ![]() $f$ to the section
$f$ to the section ![]() $p_i$. Noting that
$p_i$. Noting that ![]() $u_{p_i}=0$, the map
$u_{p_i}=0$, the map ![]() $\mathrm {ev}_i^{\flat }:(f\circ p_i)^{-1}\overline{\mathcal{M}}_X \longrightarrow \overline{\mathcal{M}}_S\oplus \mathbb {N}$ factors through
$\mathrm {ev}_i^{\flat }:(f\circ p_i)^{-1}\overline{\mathcal{M}}_X \longrightarrow \overline{\mathcal{M}}_S\oplus \mathbb {N}$ factors through ![]() $\overline{\mathcal{M}}_S$, and thus we have a factorization
$\overline{\mathcal{M}}_S$, and thus we have a factorization ![]() $\mathrm {ev}_i:(\underline{S},p_i^*\mathcal {M}_C) \longrightarrow S \longrightarrow X$. In a slight abuse of notation we write
$\mathrm {ev}_i:(\underline{S},p_i^*\mathcal {M}_C) \longrightarrow S \longrightarrow X$. In a slight abuse of notation we write ![]() $\mathrm {ev}_i$ for the morphism
$\mathrm {ev}_i$ for the morphism ![]() $S \longrightarrow X$ also, and thus obtain a morphism
$S \longrightarrow X$ also, and thus obtain a morphism
If we choose sections ![]() $\sigma _1,\ldots ,\sigma _n:B \longrightarrow X$, we obtain a map
$\sigma _1,\ldots ,\sigma _n:B \longrightarrow X$, we obtain a map
 \[ \sigma:=\prod_{i=1}^n \sigma_i:B \longrightarrow X^n. \]
\[ \sigma:=\prod_{i=1}^n \sigma_i:B \longrightarrow X^n. \]This allows us to define the moduli space of curves passing through the given sections,
where the two maps are ![]() $\mathrm {ev}$ and
$\mathrm {ev}$ and ![]() $\sigma$.Footnote 9
$\sigma$.Footnote 9
5.3.2 Virtual fundamental class on  $\mathscr {M}(X/B,\beta ,\sigma )$
$\mathscr {M}(X/B,\beta ,\sigma )$
We note that the moduli space ![]() $\mathscr {M}(X/B,\beta ,\sigma )$ of curves passing through the given sections carries a virtual fundamental class. The perfect obstruction theory is defined by
$\mathscr {M}(X/B,\beta ,\sigma )$ of curves passing through the given sections carries a virtual fundamental class. The perfect obstruction theory is defined by
 \begin{equation} \mathfrak{E}^{\bullet} = \Big(R\pi_*\Bigl[f^*\Theta_{X/B} \longrightarrow \bigoplus_{i=1}^n (f^*\Theta_{X/B})|_{p_i(S)}\Big]\Big)^{\vee}, \end{equation}
\begin{equation} \mathfrak{E}^{\bullet} = \Big(R\pi_*\Bigl[f^*\Theta_{X/B} \longrightarrow \bigoplus_{i=1}^n (f^*\Theta_{X/B})|_{p_i(S)}\Big]\Big)^{\vee}, \end{equation}
for the stable map ![]() $(\pi :C \longrightarrow S, \textbf {x}, \mathbf {p}, f)$. Here the map of sheaves above is just restriction. See [Reference Abramovich, Chen, Gross and SiebertACGS20, § 4] for a detailed discussion of how to impose logarithmic point conditions on a virtual level, cf. also [Reference Bryan and LeungBL00, Proposition A.1] for an earlier study in ordinary Gromov–Witten theory.
$(\pi :C \longrightarrow S, \textbf {x}, \mathbf {p}, f)$. Here the map of sheaves above is just restriction. See [Reference Abramovich, Chen, Gross and SiebertACGS20, § 4] for a detailed discussion of how to impose logarithmic point conditions on a virtual level, cf. also [Reference Bryan and LeungBL00, Proposition A.1] for an earlier study in ordinary Gromov–Witten theory.
5.3.3 Choice of sections and  $\Delta (X)$
$\Delta (X)$
We can now use the techniques of previous sections to produce a virtual decomposition of the fibre over ![]() $b_0=0$ of
$b_0=0$ of ![]() $\mathscr {M}(X/B,\beta ,\sigma ) \longrightarrow B$. However, to be interesting, we should in general choose the sections to interact with
$\mathscr {M}(X/B,\beta ,\sigma ) \longrightarrow B$. However, to be interesting, we should in general choose the sections to interact with ![]() $D$ in a very degenerate way over
$D$ in a very degenerate way over ![]() $b_0$. In particular, restricting to
$b_0$. In particular, restricting to ![]() $b_0$ (which is now the standard log point), we obtain maps
$b_0$ (which is now the standard log point), we obtain maps
where ![]() $Y^\dagger = Y \times O^\dagger$ is the product with the standard log point. Note that
$Y^\dagger = Y \times O^\dagger$ is the product with the standard log point. Note that
with ![]() $\Sigma (X) \longrightarrow \Sigma (B)$ the projection to the second factor. So
$\Sigma (X) \longrightarrow \Sigma (B)$ the projection to the second factor. So ![]() $\Delta (X)=\Sigma (Y)$ and
$\Delta (X)=\Sigma (Y)$ and ![]() $\Sigma (\sigma _i):\Sigma (B) \longrightarrow \Sigma (X)$ is a section of
$\Sigma (\sigma _i):\Sigma (B) \longrightarrow \Sigma (X)$ is a section of ![]() $\Sigma (X) \longrightarrow \Sigma (B)$ and hence is determined by a point
$\Sigma (X) \longrightarrow \Sigma (B)$ and hence is determined by a point ![]() $P_i\in \Delta (X)$, necessarily rationally defined.
$P_i\in \Delta (X)$, necessarily rationally defined.
5.3.4 Tropical fibred product
We wish to understand the fibred product
at a tropical level. We observe the following.
Proposition 5.2 Let ![]() $X,Y$ and
$X,Y$ and ![]() $S$ be fs log schemes, with morphisms
$S$ be fs log schemes, with morphisms ![]() $f_1:X \longrightarrow S$,
$f_1:X \longrightarrow S$, ![]() $f_2:Y \longrightarrow S$. Let
$f_2:Y \longrightarrow S$. Let ![]() $Z=X\times _S Y$ in the category of fs log schemes,
$Z=X\times _S Y$ in the category of fs log schemes, ![]() $p_1,p_2$ the projections. Suppose
$p_1,p_2$ the projections. Suppose ![]() $\bar z\in Z$ with
$\bar z\in Z$ with ![]() $\bar x= p_1(\bar z)$,
$\bar x= p_1(\bar z)$, ![]() $\bar y=p_2(\bar z)$, and
$\bar y=p_2(\bar z)$, and ![]() $\bar s=f_1(p_1(\bar z))=f_2(p_2(\bar z))$. Then
$\bar s=f_1(p_1(\bar z))=f_2(p_2(\bar z))$. Then
and
Proof. The first statement follows immediately from the universal property of fibred product applied to maps ![]() $\bar z^{\dagger } \longrightarrow Z$, where
$\bar z^{\dagger } \longrightarrow Z$, where ![]() $\bar z^{\dagger }$ denotes a geometric point
$\bar z^{\dagger }$ denotes a geometric point ![]() $\bar z$ with standard logarithmic structure. The second statement then follows from the first.
$\bar z$ with standard logarithmic structure. The second statement then follows from the first.
5.3.5 Tropical moduli space
We now provide a simple interpretation for the tropicalization of ![]() $S:=\mathscr {M}(X/B,\beta ,\sigma )$. If
$S:=\mathscr {M}(X/B,\beta ,\sigma )$. If ![]() $\bar s\in S$ is a geometric point, let
$\bar s\in S$ is a geometric point, let ![]() $Q$ be the basic monoid associated with
$Q$ be the basic monoid associated with ![]() $\bar s$ as a stable logarithmic map to
$\bar s$ as a stable logarithmic map to ![]() $X$. Then by Proposition 5.2, we have
$X$. Then by Proposition 5.2, we have
Here as usual ![]() $P_{p_i}=\overline{\mathcal{M}}_{X,\underline{f}(p_i)}$, which here equals
$P_{p_i}=\overline{\mathcal{M}}_{X,\underline{f}(p_i)}$, which here equals ![]() $\overline{\mathcal {M}}_{Y,\underline{f}(p_i)}\oplus \mathbb {N}$. The maps defining the fibred product are as follows. The map
$\overline{\mathcal {M}}_{Y,\underline{f}(p_i)}\oplus \mathbb {N}$. The maps defining the fibred product are as follows. The map ![]() ${\operatorname {Hom}}(Q,\mathbb {R}_{\ge 0}) \longrightarrow \prod _i{\operatorname {Hom}}(P_{p_i},\mathbb {R}_{\ge 0})$ can be interpreted as taking a tropical map
${\operatorname {Hom}}(Q,\mathbb {R}_{\ge 0}) \longrightarrow \prod _i{\operatorname {Hom}}(P_{p_i},\mathbb {R}_{\ge 0})$ can be interpreted as taking a tropical map ![]() $\Gamma \longrightarrow \Sigma (X)=\Sigma (Y)\times \mathbb {R}_{\ge 0}$ to the point of
$\Gamma \longrightarrow \Sigma (X)=\Sigma (Y)\times \mathbb {R}_{\ge 0}$ to the point of ![]() ${\operatorname {Hom}}(P_{p_i},\mathbb {R}_{\ge 0})$ which is the image of the contracted edge corresponding to the marked point
${\operatorname {Hom}}(P_{p_i},\mathbb {R}_{\ge 0})$ which is the image of the contracted edge corresponding to the marked point ![]() $p_i$. The map
$p_i$. The map ![]() $\mathbb {R}_{\ge 0} \longrightarrow \prod _i{\operatorname {Hom}}(P_{p_i},\mathbb {R}_{\ge 0})$ is
$\mathbb {R}_{\ge 0} \longrightarrow \prod _i{\operatorname {Hom}}(P_{p_i},\mathbb {R}_{\ge 0})$ is ![]() $\prod _i \Sigma (\sigma _i)$ and hence takes
$\prod _i \Sigma (\sigma _i)$ and hence takes ![]() $1$ to
$1$ to ![]() $((P_1,1),\ldots ,(P_n,1)$.
$((P_1,1),\ldots ,(P_n,1)$.
This yields the following.
Proposition 5.3 Let ![]() $m\in \Delta (S)$, and let
$m\in \Delta (S)$, and let ![]() $\Gamma _C= \Sigma (\pi )^{-1}(m)$. Then
$\Gamma _C= \Sigma (\pi )^{-1}(m)$. Then ![]() $\Sigma (f):\Gamma _C \longrightarrow \Delta (X)$ is a tropical map with the unbounded edges
$\Sigma (f):\Gamma _C \longrightarrow \Delta (X)$ is a tropical map with the unbounded edges ![]() $E_{p_i}$ being mapped to the points
$E_{p_i}$ being mapped to the points ![]() $P_i$. Furthermore, as
$P_i$. Furthermore, as ![]() $m$ varies within its cell of
$m$ varies within its cell of ![]() $\Delta (S)$, we obtain the universal family of tropical maps of the same combinatorial type mapping to
$\Delta (S)$, we obtain the universal family of tropical maps of the same combinatorial type mapping to ![]() $\Delta (X)$ and with the edges
$\Delta (X)$ and with the edges ![]() $E_{p_i}$ being mapped to
$E_{p_i}$ being mapped to ![]() $P_i$.
$P_i$.
5.3.6 Restatement of the decomposition formula
Write
and, for ![]() ${\boldsymbol{\tau }}=(\tau ,\mathbf {A})$ a decorated type of a rigid tropical map (Definition 2.23),
${\boldsymbol{\tau }}=(\tau ,\mathbf {A})$ a decorated type of a rigid tropical map (Definition 2.23),
Theorem 3.11 now translates to the following.
Theorem 5.4 (The logarithmic decomposition formula for point conditions) Suppose ![]() $Y$ is logarithmically smooth. Then
$Y$ is logarithmically smooth. Then
Example 5.5 The above discussion allows a reformulation of the approach of [Reference Nishinou and SiebertNS06] to tropical counts of curves in toric varieties. Take ![]() $Y$ to be a toric variety with the toric logarithmic structure, and fix a curve class
$Y$ to be a toric variety with the toric logarithmic structure, and fix a curve class ![]() $\beta$. By fixing an appropriate number
$\beta$. By fixing an appropriate number ![]() $n$ of points in
$n$ of points in ![]() $Y$, one can assume that the expected dimension of the moduli space of curves of genus
$Y$, one can assume that the expected dimension of the moduli space of curves of genus ![]() $0$ and class
$0$ and class ![]() $\beta$ passing through these points is
$\beta$ passing through these points is ![]() $0$. Next, after choosing suitable degenerating sections
$0$. Next, after choosing suitable degenerating sections ![]() $\sigma _1,\ldots ,\sigma _n$, one obtains points
$\sigma _1,\ldots ,\sigma _n$, one obtains points ![]() $P_1,\ldots ,P_n \in \Sigma (Y)$, the fan for
$P_1,\ldots ,P_n \in \Sigma (Y)$, the fan for ![]() $Y$. Finally, one explicitly describes
$Y$. Finally, one explicitly describes ![]() $\mathscr {M}(X/B,\beta ,\sigma )$ through an analysis for each rigid tropical map to
$\mathscr {M}(X/B,\beta ,\sigma )$ through an analysis for each rigid tropical map to ![]() $\Sigma (Y)$ with the correct topology. In particular, the domain curve is rational and should have
$\Sigma (Y)$ with the correct topology. In particular, the domain curve is rational and should have ![]() $D_{\rho }\cdot \beta$ unbounded edges parallel to a ray
$D_{\rho }\cdot \beta$ unbounded edges parallel to a ray ![]() $\rho \in \Sigma (Y)$, where
$\rho \in \Sigma (Y)$, where ![]() $D_{\rho }\subset Y$ is the corresponding divisor. The argument of [Reference Nishinou and SiebertNS06] essentially carries out an explicit analysis of possible logarithmic curves associated with each such rigid curve after a log blow-up
$D_{\rho }\subset Y$ is the corresponding divisor. The argument of [Reference Nishinou and SiebertNS06] essentially carries out an explicit analysis of possible logarithmic curves associated with each such rigid curve after a log blow-up ![]() $\tilde Y^\dagger \longrightarrow Y^\dagger$. Theorem 5.4 also generalizes part of [Reference Nishinou and SiebertNS06] to some higher genus cases, with the determination of the contribution of individual maps left open.
$\tilde Y^\dagger \longrightarrow Y^\dagger$. Theorem 5.4 also generalizes part of [Reference Nishinou and SiebertNS06] to some higher genus cases, with the determination of the contribution of individual maps left open.
5.4 An example in  $\mathbb {F}_2$
$\mathbb {F}_2$
We now consider a very specific case of § 5.3 above. This example deliberately deviates slightly from the toric case of Example 5.5 and exhibits new phenomena.
5.4.1 A non-toric logarithmic structure on a Hirzebruch surface
Let ![]() $Y$ be the Hirzebruch surface
$Y$ be the Hirzebruch surface ![]() $\mathbb {F}_2$. Viewed as a toric surface, it has four toric divisors, which we write as
$\mathbb {F}_2$. Viewed as a toric surface, it has four toric divisors, which we write as ![]() $f_0$,
$f_0$, ![]() $f_{\infty }$,
$f_{\infty }$, ![]() $C_0$ and
$C_0$ and ![]() $C_{\infty }$. Here
$C_{\infty }$. Here ![]() $f_0,f_{\infty }$ are the fibres of
$f_0,f_{\infty }$ are the fibres of ![]() $\mathbb {F}_2 \longrightarrow \mathbb {P}^1$ over
$\mathbb {F}_2 \longrightarrow \mathbb {P}^1$ over ![]() $0$ and
$0$ and ![]() $\infty$,
$\infty$, ![]() $C_0$ is the unique section with self-intersection
$C_0$ is the unique section with self-intersection ![]() $-2$, and
$-2$, and ![]() $C_{\infty }$ is a section disjoint from
$C_{\infty }$ is a section disjoint from ![]() $C_0$, with
$C_0$, with ![]() $C_{\infty }$ linearly equivalent to
$C_{\infty }$ linearly equivalent to ![]() $f_0+f_{\infty }+C_0$.
$f_0+f_{\infty }+C_0$.
We will give ![]() $Y$ the (non-toric) divisorial logarithmic structure coming from the divisor
$Y$ the (non-toric) divisorial logarithmic structure coming from the divisor ![]() $D=f_0+f_{\infty }+C_{\infty }$, deliberately omitting
$D=f_0+f_{\infty }+C_{\infty }$, deliberately omitting ![]() $C_0$.
$C_0$.
5.4.2 The curves and their marked points
We will consider rational curves representing the class ![]() $C_{\infty }$ passing through three points
$C_{\infty }$ passing through three points ![]() $y_1,y_2,y_3$. Of course there should be precisely one such curve.
$y_1,y_2,y_3$. Of course there should be precisely one such curve.
A general curve of class ![]() $C_{\infty }$ will intersect
$C_{\infty }$ will intersect ![]() $D$ in four points, so we will set this up as a logarithmic Gromov–Witten problem by considering genus
$D$ in four points, so we will set this up as a logarithmic Gromov–Witten problem by considering genus ![]() $0$ stable logarithmic maps
$0$ stable logarithmic maps
imposing the condition that ![]() $f(p_i)=y_i$, and
$f(p_i)=y_i$, and ![]() $f$ is constrained to be transversal to
$f$ is constrained to be transversal to ![]() $f_0, f_{\infty }, C_{\infty }$ and
$f_0, f_{\infty }, C_{\infty }$ and ![]() $C_{\infty }$ at
$C_{\infty }$ at ![]() $x_i$ for
$x_i$ for ![]() $i=1,\ldots , 4$, respectively. This transversality determines the vectors
$i=1,\ldots , 4$, respectively. This transversality determines the vectors ![]() $u_{x_i}$, while we take the contact data
$u_{x_i}$, while we take the contact data ![]() $u_{p_i}=0$.
$u_{p_i}=0$.
Since the maps have the points ![]() $x_3$ and
$x_3$ and ![]() $x_4$ ordered, we expect the final count to amount to two rather than one.
$x_4$ ordered, we expect the final count to amount to two rather than one.
5.4.3 Choice of degeneration
We will now see what happens when we degenerate the point conditions as in § 5.3, by taking ![]() $X=Y\times \mathbb {A}^1$ and considering sections
$X=Y\times \mathbb {A}^1$ and considering sections ![]() $\sigma _i:\mathbb {A}^1 \longrightarrow X$,
$\sigma _i:\mathbb {A}^1 \longrightarrow X$, ![]() $1\le i \le 3$. We choose these sections to be general subject to the condition that
$1\le i \le 3$. We choose these sections to be general subject to the condition that
Since ![]() $C_0\cap C_{\infty }=\emptyset$, any curve in the linear system
$C_0\cap C_{\infty }=\emptyset$, any curve in the linear system ![]() $|C_{\infty }|$ which passes through this special choice of three points must contain
$|C_{\infty }|$ which passes through this special choice of three points must contain ![]() $C_0$, and hence be the curve
$C_0$, and hence be the curve ![]() $f_0+f_{\infty }+C_0$.
$f_0+f_{\infty }+C_0$.
5.4.4 The complex  $\Delta (X)$ and the tropical sections
$\Delta (X)$ and the tropical sections
Note that ![]() $\Delta (X)$ is as depicted in Figure 8, an abstract gluing of two quadrants, not linearly embedded in the plane. The choice of sections
$\Delta (X)$ is as depicted in Figure 8, an abstract gluing of two quadrants, not linearly embedded in the plane. The choice of sections ![]() $\sigma _i$ determines points
$\sigma _i$ determines points ![]() $P_i\in \Sigma (X)$ as explained in § 5.3. For example, if, say, the section
$P_i\in \Sigma (X)$ as explained in § 5.3. For example, if, say, the section ![]() $\sigma _1$ is transversal to
$\sigma _1$ is transversal to ![]() $f_0\times \mathbb {A}^1$, then
$f_0\times \mathbb {A}^1$, then ![]() $P_1$ is the point at distance
$P_1$ is the point at distance ![]() $1$ from the origin along the ray corresponding to
$1$ from the origin along the ray corresponding to ![]() $f_0$. Since
$f_0$. Since ![]() $C_0$ is not part of the divisor determining the logarithmic structure,
$C_0$ is not part of the divisor determining the logarithmic structure, ![]() $P_3$ is in fact the origin.
$P_3$ is in fact the origin.

Figure 8. The polyhedral complex ![]() $\Delta (X)=\Sigma (Y)$ and a potential tropical map. The small arrows indicate
$\Delta (X)=\Sigma (Y)$ and a potential tropical map. The small arrows indicate ![]() $E_{p_i}$ which are contracted to
$E_{p_i}$ which are contracted to ![]() $P_i$. The suggested positions of
$P_i$. The suggested positions of ![]() $E_{x_3}$ and
$E_{x_3}$ and ![]() $E_{x_4}$ are shown below to contribute
$E_{x_4}$ are shown below to contribute ![]() $0$ to the virtual count.
$0$ to the virtual count.
5.4.5 The tropical maps
One then considers rigid decorated tropical maps passing through these points.
• The curves must have seven unbounded edges,
 $E_{p_i}$,
$E_{p_i}$,  $E_{x_j}$.
$E_{x_j}$.• The map contracts
 $E_{p_i}$ to
$E_{p_i}$ to  $P_i$.
$P_i$.• Each
 $E_{x_j}$ is mapped to an unbounded ray going to infinity in the direction indicating which of the three irreducible components of
$E_{x_j}$ is mapped to an unbounded ray going to infinity in the direction indicating which of the three irreducible components of  $D$ the point
$D$ the point  $x_j$ is mapped to.
$x_j$ is mapped to.
5.4.6 Rigid tropical maps
It is then easy to see that to be rigid, the domain of the tropical map must have three vertices, ![]() $v_1,v_2,v_3$, with the edge
$v_1,v_2,v_3$, with the edge ![]() $E_{p_i}$ attached to
$E_{p_i}$ attached to ![]() $v_i$ and
$v_i$ and ![]() $v_i$ necessarily being mapped to
$v_i$ necessarily being mapped to ![]() $P_i$.
$P_i$.
The location of the ![]() $E_{x_i}$ is less clear. One can show using the balancing condition [Reference Gross and SiebertGS13, Proposition 1.15] that
$E_{x_i}$ is less clear. One can show using the balancing condition [Reference Gross and SiebertGS13, Proposition 1.15] that ![]() $E_{x_1}$ must be attached to
$E_{x_1}$ must be attached to ![]() $v_1$ and
$v_1$ and ![]() $E_{x_2}$ must be attached to
$E_{x_2}$ must be attached to ![]() $v_2$. There remains, however, some choice about the location of
$v_2$. There remains, however, some choice about the location of ![]() $E_{x_3}$ and
$E_{x_3}$ and ![]() $E_{x_4}$. Indeed, they may be attached to the vertices
$E_{x_4}$. Indeed, they may be attached to the vertices ![]() $v_1$,
$v_1$, ![]() $v_2$ or
$v_2$ or ![]() $v_3$ in any manner. Figure 8 shows one such choice.
$v_3$ in any manner. Figure 8 shows one such choice.
5.4.7 Decorated rigid tropical maps
We must however consider decorated rigid tropical maps, and in particular we need to assign curve classes ![]() $\mathbf {A}(v)$ to each vertex
$\mathbf {A}(v)$ to each vertex ![]() $v$. Let
$v$. Let ![]() $n_i$ be the number of edges in
$n_i$ be the number of edges in ![]() $\{E_{x_3},E_{x_4}\}$ attached to the vertex
$\{E_{x_3},E_{x_4}\}$ attached to the vertex ![]() $v_i$. Since
$v_i$. Since ![]() $E_{x_3}$ and
$E_{x_3}$ and ![]() $E_{x_4}$ indicate which ‘virtual’ components of the domain curve have marked points mapping to
$E_{x_4}$ indicate which ‘virtual’ components of the domain curve have marked points mapping to ![]() $C_{\infty }$, it then becomes clear that
$C_{\infty }$, it then becomes clear that
where ![]() $n_1+n_2+n_3 = 2$.
$n_1+n_2+n_3 = 2$.
5.4.8 The seeming contradiction
In fact, as we shall see shortly, there are logarithmic curves whose tropicalization yields any one of the curves with ![]() $n_1=n_2=1$, and there is no logarithmic curve over the standard log point whose tropicalization is the tropical map with
$n_1=n_2=1$, and there is no logarithmic curve over the standard log point whose tropicalization is the tropical map with ![]() $n_3=2$. Surprisingly at first glance, the only decorated rigid tropical map which provides a non-trivial contribution to the Gromov–Witten invariant is the one which cannot be realized, with
$n_3=2$. Surprisingly at first glance, the only decorated rigid tropical map which provides a non-trivial contribution to the Gromov–Witten invariant is the one which cannot be realized, with ![]() $n_3=2$. We will also see that the case
$n_3=2$. We will also see that the case ![]() $n_1=2$ or
$n_1=2$ or ![]() $n_2=2$ plays no role. Before we exhibit this counterintuitive behaviour, we point out that this is no contradiction. Indeed, consider a stable log map to
$n_2=2$ plays no role. Before we exhibit this counterintuitive behaviour, we point out that this is no contradiction. Indeed, consider a stable log map to ![]() $X_0$ with non-rigid tropicalization. This stable log map will lie in the intersection of the images in
$X_0$ with non-rigid tropicalization. This stable log map will lie in the intersection of the images in ![]() $\mathscr {M}(X_0,\beta )$ of more than one subspace
$\mathscr {M}(X_0,\beta )$ of more than one subspace ![]() $\mathscr {M}_\tau (X_0,\beta )$ from (3.3). Tropical geometry cannot thus tell how these stable log maps with non-rigid tropicalizations contribute to the virtual count on any of these components.
$\mathscr {M}_\tau (X_0,\beta )$ from (3.3). Tropical geometry cannot thus tell how these stable log maps with non-rigid tropicalizations contribute to the virtual count on any of these components.
5.4.9 Curves with  $n_1=n_2=1$ contribute zero
$n_1=n_2=1$ contribute zero
To exhibit this seemingly contradictory behaviour, first recall the standard fact that there is a flat family ![]() $\underline {W} \longrightarrow \underline {\mathbb {A}}^1$ such that
$\underline {W} \longrightarrow \underline {\mathbb {A}}^1$ such that ![]() $\underline {W}_0\simeq \underline{X}_0=\mathbb {F}_2$ and
$\underline {W}_0\simeq \underline{X}_0=\mathbb {F}_2$ and ![]() $\underline {W}_t\simeq \underline {\mathbb {P}}^1\times \underline {\mathbb {P}}^1$ for
$\underline {W}_t\simeq \underline {\mathbb {P}}^1\times \underline {\mathbb {P}}^1$ for ![]() $t\not =0$. Furthermore, the divisor
$t\not =0$. Furthermore, the divisor ![]() $f_0\cup f_{\infty }\cup C_{\infty }$ extends to a normal crossings divisor on
$f_0\cup f_{\infty }\cup C_{\infty }$ extends to a normal crossings divisor on ![]() $\underline {W}$ with three irreducible components:
$\underline {W}$ with three irreducible components: ![]() $\{0\}\times \mathbb {P}^1, \{\infty \}\times \mathbb {P}^1,$ and a curve of type
$\{0\}\times \mathbb {P}^1, \{\infty \}\times \mathbb {P}^1,$ and a curve of type ![]() $(1,1)$. This endows
$(1,1)$. This endows ![]() $\underline {W}$ with a divisorial logarithmic structure, logarithmically smooth over
$\underline {W}$ with a divisorial logarithmic structure, logarithmically smooth over ![]() $\mathbb {A}^1$ with the trivial logarithmic structure. However, no curve of class
$\mathbb {A}^1$ with the trivial logarithmic structure. However, no curve of class ![]() $C_0$ in
$C_0$ in ![]() $W_0$ deforms to
$W_0$ deforms to ![]() $W_t$ for
$W_t$ for ![]() $t\not =0$. Hence no curve representing a point in the moduli space
$t\not =0$. Hence no curve representing a point in the moduli space ![]() $\mathscr {M}_{\tau }(X_0,\beta )$ for
$\mathscr {M}_{\tau }(X_0,\beta )$ for ![]() $\tau$ one of the decorated rigid tropical maps with
$\tau$ one of the decorated rigid tropical maps with ![]() $n_3=0$ deforms. The usual deformation invariance of Gromov–Witten invariants then implies that the contribution to the Gromov–Witten invariant from such a
$n_3=0$ deforms. The usual deformation invariance of Gromov–Witten invariants then implies that the contribution to the Gromov–Witten invariant from such a ![]() $\tau$ is zero.
$\tau$ is zero.
Another transparent explanation for the vanishing of this count is given by the gluing formalism further developed in [Reference Abramovich, Chen, Gross and SiebertACGS20]: the moduli space of punctured stable maps corresponding to the ![]() $(-2)$-curve has negative virtual dimension and by [Reference Gross and SiebertGS19, Theorem A.16] any moduli space of stable maps with such a component has vanishing virtual count.
$(-2)$-curve has negative virtual dimension and by [Reference Gross and SiebertGS19, Theorem A.16] any moduli space of stable maps with such a component has vanishing virtual count.
5.4.10 Expansion and description of moduli space for  $n_1=n_2=1$
$n_1=n_2=1$
To explore the existence of the relevant logarithmic curves, we again turn to § 4. First let us construct a curve whose decorated tropical map has ![]() $n_1=n_2=1$. The image of this curve in
$n_1=n_2=1$. The image of this curve in ![]() $\Delta (X)$ yields a subdivision of
$\Delta (X)$ yields a subdivision of ![]() $\Delta (X)$ which in turn yields a refinement of
$\Delta (X)$ which in turn yields a refinement of ![]() $\Sigma (X)$, and hence a log étale morphism
$\Sigma (X)$, and hence a log étale morphism ![]() $\tilde X \longrightarrow X$. It is easy to see that this is just a weighted blow-up of
$\tilde X \longrightarrow X$. It is easy to see that this is just a weighted blow-up of ![]() $f_0\times \{0\}$ and
$f_0\times \{0\}$ and ![]() $f_{\infty }\times \{0\}$ in
$f_{\infty }\times \{0\}$ in ![]() $X=Y\times \mathbb {A}^1$; the weights depend on the precise location of
$X=Y\times \mathbb {A}^1$; the weights depend on the precise location of ![]() $P_1$ and
$P_1$ and ![]() $P_2$, but if they are taken to have distance 1 from the origin, the subdivision will correspond to an ordinary blow-up. The central fibre is now as depicted in Figure 9, with the proper transforms of the sections meeting the central fibre at the points
$P_2$, but if they are taken to have distance 1 from the origin, the subdivision will correspond to an ordinary blow-up. The central fibre is now as depicted in Figure 9, with the proper transforms of the sections meeting the central fibre at the points ![]() $p_1,p_2,p_3$ as depicted.
$p_1,p_2,p_3$ as depicted.

Figure 9. A central fiber with ![]() $n_1=n_2=1$.
$n_1=n_2=1$.
The logarithmic curve then has three irreducible components, one mapping to ![]() $C_0$ and the other two mapping to the two exceptional divisors, each isomorphic to
$C_0$ and the other two mapping to the two exceptional divisors, each isomorphic to ![]() $\mathbb {P}^1\times \mathbb {P}^1$. These latter two components each map isomorphically to a curve of class
$\mathbb {P}^1\times \mathbb {P}^1$. These latter two components each map isomorphically to a curve of class ![]() $(1,1)$ on the exceptional divisor, and is constrained to pass through
$(1,1)$ on the exceptional divisor, and is constrained to pass through ![]() $p_i$ and the point where
$p_i$ and the point where ![]() $C_0$ meets the exceptional divisor. There is in fact a pencil of such curves. We remark that all seven marked points are visible in Figure 9, but the curves in the exceptional divisors meet the left-most and right-most curves transversally, and not tangent as it appears in the picture. By Theorem 4.13, any such stable map then has a log enhancement, and composing with the map
$C_0$ meets the exceptional divisor. There is in fact a pencil of such curves. We remark that all seven marked points are visible in Figure 9, but the curves in the exceptional divisors meet the left-most and right-most curves transversally, and not tangent as it appears in the picture. By Theorem 4.13, any such stable map then has a log enhancement, and composing with the map ![]() $\tilde X \longrightarrow X$ gives a stable logarithmic map over the standard log point whose tropicalization is one of the rigid curves with
$\tilde X \longrightarrow X$ gives a stable logarithmic map over the standard log point whose tropicalization is one of the rigid curves with ![]() $n_1=n_2=1$. Thus the relevant moduli space of stable log maps to
$n_1=n_2=1$. Thus the relevant moduli space of stable log maps to ![]() $\tilde X_0$ has two components, each isomorphic to
$\tilde X_0$ has two components, each isomorphic to ![]() $\mathbb {P}^1 \times \mathbb {P}^1$, depending on which sides
$\mathbb {P}^1 \times \mathbb {P}^1$, depending on which sides ![]() $x_3$ and
$x_3$ and ![]() $x_4$ lie. This moduli space maps injectively to the moduli space of stable log maps to
$x_4$ lie. This moduli space maps injectively to the moduli space of stable log maps to ![]() $X_0$.
$X_0$.
To see that the virtual count gives zero, one can again consider the absolute deformation and obstruction theory of all the maps parameterized by ![]() $\mathbb {P}^1 \times \mathbb {P}^1$. Over the open subset
$\mathbb {P}^1 \times \mathbb {P}^1$. Over the open subset ![]() $\mathbb {C}^* \times \mathbb {C}^*$ the maps admit a normal line bundle with degrees
$\mathbb {C}^* \times \mathbb {C}^*$ the maps admit a normal line bundle with degrees ![]() $2,-2,2$ on the three components of the curve. To account for the point conditions we twist down by the points
$2,-2,2$ on the three components of the curve. To account for the point conditions we twist down by the points ![]() $x_i$, obtaining a line bundle
$x_i$, obtaining a line bundle ![]() $N$ of degrees
$N$ of degrees ![]() $1,-3,1$ respectively. Restricting to the middle components gives an isomorphism of the obstruction space
$1,-3,1$ respectively. Restricting to the middle components gives an isomorphism of the obstruction space ![]() $H^1(C, N) \to H^1(\mathbb {P}^1, \mathcal {O}(-3)) = \mathbb {C}^2$. One checks that the isomorphism extends across the boundary of
$H^1(C, N) \to H^1(\mathbb {P}^1, \mathcal {O}(-3)) = \mathbb {C}^2$. One checks that the isomorphism extends across the boundary of ![]() $\mathbb {P}^1 \times \mathbb {P}^1$, giving a trivial obstruction bundle with zero Chern classes representing the virtual fundamental class 0.
$\mathbb {P}^1 \times \mathbb {P}^1$, giving a trivial obstruction bundle with zero Chern classes representing the virtual fundamental class 0.
5.4.11 Curves with  $n_1=n_2=0$
$n_1=n_2=0$
Now consider the case that ![]() $n_1=n_2=0$ and
$n_1=n_2=0$ and ![]() $n_3=2$. This rigid tropical curve cannot be realized as the tropicalization of a stable logarithmic map over the standard log point. Indeed, to be realized, the curve must have an irreducible component of class
$n_3=2$. This rigid tropical curve cannot be realized as the tropicalization of a stable logarithmic map over the standard log point. Indeed, to be realized, the curve must have an irreducible component of class ![]() $C_0+2f=C_{\infty }$, and we know there is no such curve passing through
$C_0+2f=C_{\infty }$, and we know there is no such curve passing through ![]() $\sigma _3(0)$, a general point on
$\sigma _3(0)$, a general point on ![]() $C_0$. However, this tropical map can in fact be realized as a degeneration of a different, non-rigid tropical map, as depicted in Figure 10.
$C_0$. However, this tropical map can in fact be realized as a degeneration of a different, non-rigid tropical map, as depicted in Figure 10.

Figure 10. A realizable tropical map with ![]() $n_1=n_2=0$.
$n_1=n_2=0$.
To construct an actual logarithmic curve with ![]() $n_1=n_2=0$, we use refinements again. Assume for simplicity of the discussion that
$n_1=n_2=0$, we use refinements again. Assume for simplicity of the discussion that ![]() $P_1$ and
$P_1$ and ![]() $P_2$ have been taken to have distance
$P_2$ have been taken to have distance ![]() $2$ from the origin. Subdivide
$2$ from the origin. Subdivide ![]() $\Delta (X)$ by introducing vertical rays with endpoints
$\Delta (X)$ by introducing vertical rays with endpoints ![]() $P_1$ and
$P_1$ and ![]() $P_2$, and in addition introduce vertical rays which are the images
$P_2$, and in addition introduce vertical rays which are the images ![]() $E_{x_3}$ and
$E_{x_3}$ and ![]() $E_{x_4}$; again for simplicity of the discussion take the endpoints of these rays to be at distance
$E_{x_4}$; again for simplicity of the discussion take the endpoints of these rays to be at distance ![]() $1$ from the origin.
$1$ from the origin.
This corresponds to a blow-up ![]() $\tilde X \longrightarrow X$ involving four exceptional components, and Figure 11 shows the central fibre of
$\tilde X \longrightarrow X$ involving four exceptional components, and Figure 11 shows the central fibre of ![]() $\tilde X \longrightarrow \mathbb {A}^1$, along with the image of a stable logarithmic map which tropicalizes appropriately (once again the curves on the second and fourth components of
$\tilde X \longrightarrow \mathbb {A}^1$, along with the image of a stable logarithmic map which tropicalizes appropriately (once again the curves on the second and fourth components of ![]() $\tilde X$ meet the first and fifth components with order 1, and no tangency). Composing this stable logarithmic map with
$\tilde X$ meet the first and fifth components with order 1, and no tangency). Composing this stable logarithmic map with ![]() $\tilde X \longrightarrow X$ then gives a non-basic stable logarithmic map to
$\tilde X \longrightarrow X$ then gives a non-basic stable logarithmic map to ![]() $X$ over the standard log point. It is not hard to see that the corresponding basic monoid
$X$ over the standard log point. It is not hard to see that the corresponding basic monoid ![]() $Q$ has rank
$Q$ has rank ![]() $3$, parameterizing the image of the curve in
$3$, parameterizing the image of the curve in ![]() $\Sigma (B)$ as well as the location of the edges
$\Sigma (B)$ as well as the location of the edges ![]() $E_{x_3}$ and
$E_{x_3}$ and ![]() $E_{x_4}$. The degenerate tropical curve where the edges
$E_{x_4}$. The degenerate tropical curve where the edges ![]() $E_{x_3}$ and
$E_{x_3}$ and ![]() $E_{x_4}$ are attached to the vertex
$E_{x_4}$ are attached to the vertex ![]() $v_3$ represents a one-dimensional face of
$v_3$ represents a one-dimensional face of ![]() $Q^{\vee }$, so the rigid tropical map with
$Q^{\vee }$, so the rigid tropical map with ![]() $n_3=2$ does appear in the family
$n_3=2$ does appear in the family ![]() $Q^{\vee }$, but only as a degeneration of a tropical map which is realisable by an actual stable logarithmic curve over the standard log point.
$Q^{\vee }$, but only as a degeneration of a tropical map which is realisable by an actual stable logarithmic curve over the standard log point.

Figure 11. A logarithmic map with ![]() $n_1=n_2=0$.
$n_1=n_2=0$.
One can again show that the relevant moduli space in ![]() $\tilde X_0$ has two components isomorphic to
$\tilde X_0$ has two components isomorphic to ![]() $\mathbb {P}^1 \times \mathbb {P}^1$. This time the virtual fundamental class of each component is the top Chern class of
$\mathbb {P}^1 \times \mathbb {P}^1$. This time the virtual fundamental class of each component is the top Chern class of ![]() $\mathcal {O}(1)\boxplus \mathcal {O}(1)$, which has degree 1. Each of these maps to
$\mathcal {O}(1)\boxplus \mathcal {O}(1)$, which has degree 1. Each of these maps to ![]() $\tilde X_0$ define the same map to
$\tilde X_0$ define the same map to ![]() $X_0$, and indeed the corresponding moduli space
$X_0$, and indeed the corresponding moduli space ![]() $\mathscr {M}_{n_i=0}(X_0)$ is discrete and unobstructed.
$\mathscr {M}_{n_i=0}(X_0)$ is discrete and unobstructed.
5.4.12 Curves with  $n_1+n_2=1$
$n_1+n_2=1$
In this case ![]() $\mathbf {A}(v_3)=C_0+n_3 f=C_0+f$ and either
$\mathbf {A}(v_3)=C_0+n_3 f=C_0+f$ and either ![]() $\mathbf {A}(v_1)=f,\mathbf {A}(v_2)=0$ or
$\mathbf {A}(v_1)=f,\mathbf {A}(v_2)=0$ or ![]() $\mathbf {A}(v_1)=0,\mathbf {A}(v_2)=f$. The expanded degeneration picture then looks like a hybrid of Figures 9 and 10, with the depicted behaviour describing one end each. A computation similar to the one presented for the case
$\mathbf {A}(v_1)=0,\mathbf {A}(v_2)=f$. The expanded degeneration picture then looks like a hybrid of Figures 9 and 10, with the depicted behaviour describing one end each. A computation similar to the one presented for the case ![]() $n_1=n_2=1$ shows vanishing of this count as well.
$n_1=n_2=1$ shows vanishing of this count as well.
5.4.13 Curves with  $n_i=2$
$n_i=2$
To complete the analysis, we end by noting that the case ![]() $n_1=2$ or
$n_1=2$ or ![]() $n_2=2$ cannot occur. Consider the case
$n_2=2$ cannot occur. Consider the case ![]() $n_1=2$. Any stable logarithmic curve over the standard log point with a tropicalization which degenerates to such a rigid tropical map must have a decomposition into unions of irreducible components corresponding to the vertices
$n_1=2$. Any stable logarithmic curve over the standard log point with a tropicalization which degenerates to such a rigid tropical map must have a decomposition into unions of irreducible components corresponding to the vertices ![]() $v_1, v_2$ and
$v_1, v_2$ and ![]() $v_3$, with the homology class of the image of the stable map restricted to each of these unions of irreducible components being
$v_3$, with the homology class of the image of the stable map restricted to each of these unions of irreducible components being ![]() $2[f_0]$,
$2[f_0]$, ![]() $0$ and
$0$ and ![]() $[C_0]$ respectively. In particular, this will prevent the possibility of having any irreducible component whose image contains
$[C_0]$ respectively. In particular, this will prevent the possibility of having any irreducible component whose image contains ![]() $\sigma _2(0)$. Thus this case does not occur.
$\sigma _2(0)$. Thus this case does not occur.
Acknowledgements
That there are analogies with Parker's work is not an accident: we received a great deal of inspiration from his work and had many fruitful discussions with him. We also benefited from discussions with Steffen Marcus, Dhruv Ranganathan, Ilya Tyomkin, Martin Ulirsch and Jonathan Wise.