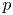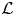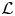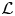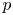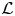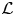Introduction
Let ![]() $f=\sum _{n=1}^{\infty } a_n q^{n}$ be a normalized newform of weight
$f=\sum _{n=1}^{\infty } a_n q^{n}$ be a normalized newform of weight ![]() $2$ and level
$2$ and level ![]() $\Gamma _0(M)$ such that
$\Gamma _0(M)$ such that ![]() $M=pN$ with
$M=pN$ with ![]() $p$ prime,
$p$ prime, ![]() $p\nmid N$ and
$p\nmid N$ and ![]() $a_p=1$. Inspired by Teitelbaum's work (cf. [Reference TeitelbaumTei90]) on
$a_p=1$. Inspired by Teitelbaum's work (cf. [Reference TeitelbaumTei90]) on ![]() $\mathcal {L}$-invariants for automorphic forms on definite quaternion groups, Darmon in [Reference DarmonDar01] constructed the automorphic
$\mathcal {L}$-invariants for automorphic forms on definite quaternion groups, Darmon in [Reference DarmonDar01] constructed the automorphic ![]() $\mathcal {L}$-invariant
$\mathcal {L}$-invariant ![]() $\mathcal {L}(f)^{\pm }$ of
$\mathcal {L}(f)^{\pm }$ of ![]() $f$, depending a priori on a choice of sign at infinity. Let
$f$, depending a priori on a choice of sign at infinity. Let ![]() $a_p(k)$ be the
$a_p(k)$ be the ![]() $U_p$-eigenvalue of the
$U_p$-eigenvalue of the ![]() $p$-adic family passing through
$p$-adic family passing through ![]() $f$. In [Reference Bertolini, Darmon and IovitaBDI10] Bertolini, Darmon and Iovita (see also [Reference DasguptaDas05]) prove the following formula:
$f$. In [Reference Bertolini, Darmon and IovitaBDI10] Bertolini, Darmon and Iovita (see also [Reference DasguptaDas05]) prove the following formula:
In particular, the automorphic ![]() $\mathcal {L}$-invariant is independent of the sign at infinity. They also prove a similar formula for Orton's
$\mathcal {L}$-invariant is independent of the sign at infinity. They also prove a similar formula for Orton's ![]() $\mathcal {L}$-invariant (cf. [Reference OrtonOrt04]) in higher weight. Moreover, if
$\mathcal {L}$-invariant (cf. [Reference OrtonOrt04]) in higher weight. Moreover, if ![]() $f$ admits a Jacquet–Langlands transfer
$f$ admits a Jacquet–Langlands transfer ![]() $\operatorname {JL}(f)$ to a definite quaternion group, which is split at
$\operatorname {JL}(f)$ to a definite quaternion group, which is split at ![]() $p$, they show the analogous formula
$p$, they show the analogous formula
for Teitelbaum's ![]() $\mathcal {L}$-invariant, thus proving that automorphic
$\mathcal {L}$-invariant, thus proving that automorphic ![]() $\mathcal {L}$-invariants are preserved under Jacquet–Langlands transfers. This result was extended to Jacquet–Langlands transfers to indefinite quaternion groups over the rationals, which are split at
$\mathcal {L}$-invariants are preserved under Jacquet–Langlands transfers. This result was extended to Jacquet–Langlands transfers to indefinite quaternion groups over the rationals, which are split at ![]() $p$, by Dasgupta and Greenberg [Reference Dasgupta and GreenbergDG12], Longo, Rotger and Vigni [Reference Longo, Rotger and VigniLRV12] and Seveso [Reference SevesoSev13].
$p$, by Dasgupta and Greenberg [Reference Dasgupta and GreenbergDG12], Longo, Rotger and Vigni [Reference Longo, Rotger and VigniLRV12] and Seveso [Reference SevesoSev13].
Over the last few years the construction of automorphic ![]() $\mathcal {L}$-invariants was generalized to various settings, e.g. to Hilbert modular cusp forms of parallel weight
$\mathcal {L}$-invariants was generalized to various settings, e.g. to Hilbert modular cusp forms of parallel weight ![]() $2$ by Spieß (see [Reference SpießSpi14]) and to Bianchi modular cusp forms of even weight by Barrera and Williams (see [Reference Barrera Salazar and WilliamsBW19]). These generalizations have been defined as automorphic
$2$ by Spieß (see [Reference SpießSpi14]) and to Bianchi modular cusp forms of even weight by Barrera and Williams (see [Reference Barrera Salazar and WilliamsBW19]). These generalizations have been defined as automorphic ![]() $\mathcal {L}$-invariants appear naturally in many context, from proving exceptional zero conjecture formulae to constructing and studying Stark–Heegner points.
$\mathcal {L}$-invariants appear naturally in many context, from proving exceptional zero conjecture formulae to constructing and studying Stark–Heegner points.
Most recently, the first named author defined automorphic ![]() $\mathcal {L}$-invariants for certain cuspidal automorphic representations of higher rank semi-simple groups over a number field
$\mathcal {L}$-invariants for certain cuspidal automorphic representations of higher rank semi-simple groups over a number field ![]() $F$, which are split at a fixed prime
$F$, which are split at a fixed prime ![]() $ {\mathfrak {p}}$ of
$ {\mathfrak {p}}$ of ![]() $F$ (see [Reference GehrmannGeh21]). The most crucial assumptions on the representation
$F$ (see [Reference GehrmannGeh21]). The most crucial assumptions on the representation ![]() $\pi$ are that it is cohomological with respect to the trivial coefficient system and that the local factor
$\pi$ are that it is cohomological with respect to the trivial coefficient system and that the local factor ![]() $\pi _ {\mathfrak {p}}$ of
$\pi _ {\mathfrak {p}}$ of ![]() $\pi$ at
$\pi$ at ![]() $ {\mathfrak {p}}$ is the Steinberg representation. Our main aim is to prove the analogue of equation (0.1) for these
$ {\mathfrak {p}}$ is the Steinberg representation. Our main aim is to prove the analogue of equation (0.1) for these ![]() $\mathcal {L}$-invariants. Previous works used explicit computations with cocycles and it seems unlikely that one can generalize these to higher rank groups; instead, we give a new, more conceptual approach, which is novel even in the already known cases.
$\mathcal {L}$-invariants. Previous works used explicit computations with cocycles and it seems unlikely that one can generalize these to higher rank groups; instead, we give a new, more conceptual approach, which is novel even in the already known cases.
In § 1 we recall the definition of automorphic ![]() $\mathcal {L}$-invariants. Just as in the case of modular forms these
$\mathcal {L}$-invariants. Just as in the case of modular forms these ![]() $\mathcal {L}$-invariants depend on a choice of sign character at infinity. They also depend on a choice of degree of cohomology, in which the representation occurs. For this introduction, we suppress it because we are mostly interested in the case that there is only one interesting degree. Given a simple root
$\mathcal {L}$-invariants depend on a choice of sign character at infinity. They also depend on a choice of degree of cohomology, in which the representation occurs. For this introduction, we suppress it because we are mostly interested in the case that there is only one interesting degree. Given a simple root ![]() $i$ of the group and a sign character
$i$ of the group and a sign character ![]() $\epsilon$ the space of
$\epsilon$ the space of ![]() $\mathcal {L}$-invariants
$\mathcal {L}$-invariants
is a subspace of codimension at least one. Here ![]() ${E}$ denotes a large enough
${E}$ denotes a large enough ![]() $p$-adic field. If strong multiplicity one holds, its codimension is exactly one. Whether a character of
$p$-adic field. If strong multiplicity one holds, its codimension is exactly one. Whether a character of ![]() $F_ {\mathfrak {p}}^{\ast }$ belongs to the space of
$F_ {\mathfrak {p}}^{\ast }$ belongs to the space of ![]() $\mathcal {L}$-invariants is decided by certain maps between cohomology groups of
$\mathcal {L}$-invariants is decided by certain maps between cohomology groups of ![]() $ {\mathfrak {p}}$-arithmetic subgroups with values in duals of (locally analytic) generalized Steinberg representations. These maps are induced by cup products with one-extensions of the smooth generalized Steinberg representation corresponding to the simple root
$ {\mathfrak {p}}$-arithmetic subgroups with values in duals of (locally analytic) generalized Steinberg representations. These maps are induced by cup products with one-extensions of the smooth generalized Steinberg representation corresponding to the simple root ![]() $i$ with the locally analytic Steinberg representations (see § 1.1 for a description of these extensions due to Ding, cf. [Reference DingDin19]).
$i$ with the locally analytic Steinberg representations (see § 1.1 for a description of these extensions due to Ding, cf. [Reference DingDin19]).
As a first step, in § 2.2 we show that one can replace generalized Steinberg representations by locally analytic principal series representations and the extension classes by infinitesimal deformations of these principal series. As a consequence, we prove an automorphic analogue of the Colmez–Greenberg–Stevens formula (see Proposition 2.4). Let us remind ourselves that the Colmez–Greenberg–Stevens formula (see, for example, Theorem 3.4 of [Reference DingDin19]) states that one can compute Fontaine–Mazur ![]() $\mathcal {L}$-invariants of Galois representations by deforming them in
$\mathcal {L}$-invariants of Galois representations by deforming them in ![]() $p$-adic families. Our analogue states that one can compute automorphic
$p$-adic families. Our analogue states that one can compute automorphic ![]() $\mathcal {L}$-invariants from the cohomology of
$\mathcal {L}$-invariants from the cohomology of ![]() $ {\mathfrak {p}}$-arithmetic groups with values in duals of big principal series representations, i.e. parabolic inductions of characters with values in units of affinoid algebras.
$ {\mathfrak {p}}$-arithmetic groups with values in duals of big principal series representations, i.e. parabolic inductions of characters with values in units of affinoid algebras.
Thus, we reduce the problem to producing classes in these big cohomology groups. Here is where we need to impose further restrictions. First, we assume that the group under consideration is adjoint. Under this assumption Kohlhaase and Schraen constructed a Koszul resolution of locally analytic principal series representations (cf. [Reference Kohlhaase and SchraenKS12]), which we recall in § 3.1. Using that resolution we can lift overconvergent cohomology classes which are common eigenvectors for all ![]() $U_ {\mathfrak {p}}$-operators to big cohomology classes. Second, in order to have a nice enough theory of families of overconvergent cohomology classes (in the spirit of [Reference Ash and StevensAS08]) we consider only groups whose Archimedean component fulfils the Harish-Chandra condition. This implies that the automorphic representation we study only shows up in the middle degree cohomology of the associated locally symmetric space. We further assume that the map from the eigenvariety to the weight space
$U_ {\mathfrak {p}}$-operators to big cohomology classes. Second, in order to have a nice enough theory of families of overconvergent cohomology classes (in the spirit of [Reference Ash and StevensAS08]) we consider only groups whose Archimedean component fulfils the Harish-Chandra condition. This implies that the automorphic representation we study only shows up in the middle degree cohomology of the associated locally symmetric space. We further assume that the map from the eigenvariety to the weight space ![]() $ {\mathcal {W}}$ is étale at the point corresponding to the automorphic representation
$ {\mathcal {W}}$ is étale at the point corresponding to the automorphic representation ![]() $\pi$. Étaleness is implied by a suitable strong multiplicity one assumption and, thus, holds for example for Hilbert modular forms. Under these hypotheses we can show that we can lift the cohomology class corresponding to
$\pi$. Étaleness is implied by a suitable strong multiplicity one assumption and, thus, holds for example for Hilbert modular forms. Under these hypotheses we can show that we can lift the cohomology class corresponding to ![]() $\pi$ to a big cohomology class valued in functions on an open affinoid neighbourhood of the trivial character in weight space (see Theorem 3.12). This allows us give the generalization of (0.1) in Theorem 3.16. In particular, we see that automorphic
$\pi$ to a big cohomology class valued in functions on an open affinoid neighbourhood of the trivial character in weight space (see Theorem 3.12). This allows us give the generalization of (0.1) in Theorem 3.16. In particular, we see that automorphic ![]() $\mathcal {L}$-invariants are codimension one subspaces under our étaleness assumption.
$\mathcal {L}$-invariants are codimension one subspaces under our étaleness assumption.
As a first application, in § 4.1 we prove a conjecture of Spieß (cf. [Reference SpießSpi14, Conjecture 6.4]): we show that the ![]() $\mathcal {L}$-invariants of Hilbert modular forms of parallel weight
$\mathcal {L}$-invariants of Hilbert modular forms of parallel weight ![]() $2$ are independent of the sign character used to define them. We further show that in this situation automorphic
$2$ are independent of the sign character used to define them. We further show that in this situation automorphic ![]() $\mathcal {L}$-invariants are invariant under Jacquet–Langlands transfers to quaternion groups which are split at
$\mathcal {L}$-invariants are invariant under Jacquet–Langlands transfers to quaternion groups which are split at ![]() $ {\mathfrak {p}}$. In fact, we show that all these
$ {\mathfrak {p}}$. In fact, we show that all these ![]() $\mathcal {L}$-invariants agree with the Fontaine–Mazur
$\mathcal {L}$-invariants agree with the Fontaine–Mazur ![]() $\mathcal {L}$-invariant of the associated Galois representation.Footnote 1 In particular, one can remove the assumptions in the main theorem of [Reference SpießSpi14] (see Theorem 6.10(b) there). Furthermore, the equality of automorphic and Fontaine–Mazur
$\mathcal {L}$-invariant of the associated Galois representation.Footnote 1 In particular, one can remove the assumptions in the main theorem of [Reference SpießSpi14] (see Theorem 6.10(b) there). Furthermore, the equality of automorphic and Fontaine–Mazur ![]() $\mathcal {L}$-invariants makes the construction of Stark–Heegner points for modular elliptic curves over totally real fields unconditional. Similarly, we prove the equality of automorphic and Fontaine–Mazur
$\mathcal {L}$-invariants makes the construction of Stark–Heegner points for modular elliptic curves over totally real fields unconditional. Similarly, we prove the equality of automorphic and Fontaine–Mazur ![]() $\mathcal {L}$-invariants for definite unitary groups under mild assumptions in § 4.2, i.e. we give an alternative proof of the main result of [Reference DingDin19] for our global situation.
$\mathcal {L}$-invariants for definite unitary groups under mild assumptions in § 4.2, i.e. we give an alternative proof of the main result of [Reference DingDin19] for our global situation.
We end the paper by considering the easiest case of a group that does not fulfil the Harish-Chandra condition, i.e. we study Bianchi modular forms. As we cannot deform the automorphic representation over the whole weight space, in general one cannot compute the ![]() $\mathcal {L}$-invariant completely in terms of derivatives of Hecke-eigenvalues. But at least in case the Bianchi forms is the base change of a modular form, we overcome this problem; we show that the
$\mathcal {L}$-invariant completely in terms of derivatives of Hecke-eigenvalues. But at least in case the Bianchi forms is the base change of a modular form, we overcome this problem; we show that the ![]() $\mathcal {L}$-invariants of the base change equal the
$\mathcal {L}$-invariants of the base change equal the ![]() $\mathcal {L}$-invariant of the modular form.
$\mathcal {L}$-invariant of the modular form.
The assumption that the coefficient system is trivial is not necessary for the arguments of this article. However, the construction of automorphic ![]() $\mathcal {L}$-invariants relies on the existence of a well-behaved lattice in the Steinberg representation, which is not known for twists of the Steinberg by an algebraic representation in general. In case the existence of such a lattice is known, e.g. if
$\mathcal {L}$-invariants relies on the existence of a well-behaved lattice in the Steinberg representation, which is not known for twists of the Steinberg by an algebraic representation in general. In case the existence of such a lattice is known, e.g. if ![]() $G$ is a form of
$G$ is a form of ![]() $\operatorname {PGL}_2$ by a result of Vignéras (see [Reference VignérasVig08]), one can easily generalize our results to arbitrary weights and non-critical slopes.
$\operatorname {PGL}_2$ by a result of Vignéras (see [Reference VignérasVig08]), one can easily generalize our results to arbitrary weights and non-critical slopes.
Notation
If ![]() $X$ and
$X$ and ![]() $Y$ are topological spaces, we write
$Y$ are topological spaces, we write ![]() $C(X,Y)$ for the set of continuous functions from
$C(X,Y)$ for the set of continuous functions from ![]() $X$ to
$X$ to ![]() $Y$. All rings are assumed to be commutative and unital. The group of invertible elements of a ring
$Y$. All rings are assumed to be commutative and unital. The group of invertible elements of a ring ![]() $R$ will be denoted by
$R$ will be denoted by ![]() $R^{\ast }$. If
$R^{\ast }$. If ![]() $M$ is an
$M$ is an ![]() $R$-module we denote the
$R$-module we denote the ![]() $q$th exterior power of
$q$th exterior power of ![]() $M$ by
$M$ by ![]() $\Lambda ^{q}_R M$. If
$\Lambda ^{q}_R M$. If ![]() $R$ is a ring and
$R$ is a ring and ![]() $G$ a group, we denote the group ring of
$G$ a group, we denote the group ring of ![]() $G$ over
$G$ over ![]() $R$ by
$R$ by ![]() $R[G]$. Given topological groups
$R[G]$. Given topological groups ![]() $H$ and
$H$ and ![]() $G$ we write
$G$ we write ![]() $\operatorname {Hom}^{\operatorname {ct}}(H,G)$ for the space of continuous homomorphism from
$\operatorname {Hom}^{\operatorname {ct}}(H,G)$ for the space of continuous homomorphism from ![]() $H$ to
$H$ to ![]() $G$. Let
$G$. Let ![]() $\chi \colon G\to R^{\ast }$ be a character. We write
$\chi \colon G\to R^{\ast }$ be a character. We write ![]() $R[\chi ]$ for the
$R[\chi ]$ for the ![]() $G$-representation, which underlying
$G$-representation, which underlying ![]() $R$-module is
$R$-module is ![]() $R$ itself and on which
$R$ itself and on which ![]() $G$ acts via the character
$G$ acts via the character ![]() $\chi$. The trivial character of
$\chi$. The trivial character of ![]() $G$ will be denoted by
$G$ will be denoted by ![]() ${{\mathbb 1}}_G$. Let
${{\mathbb 1}}_G$. Let ![]() $H$ be an open subgroup of a locally profinite group
$H$ be an open subgroup of a locally profinite group ![]() $G$ and
$G$ and ![]() $M$ an
$M$ an ![]() $R$-linear representation
$R$-linear representation ![]() $M$ of
$M$ of ![]() $H$. The compact induction
$H$. The compact induction ![]() $\operatorname {c-ind}^{G}_{H}M$ of
$\operatorname {c-ind}^{G}_{H}M$ of ![]() $M$ from
$M$ from ![]() $H$ to
$H$ to ![]() $G$ is the space of all functions
$G$ is the space of all functions ![]() $f\colon G\to M$ which have finite support modulo
$f\colon G\to M$ which have finite support modulo ![]() $H$ and satisfy
$H$ and satisfy ![]() $f(gh)=h^{-1}.f(g)$ for all
$f(gh)=h^{-1}.f(g)$ for all ![]() $h\in H,\ g\in G$.
$h\in H,\ g\in G$.
The setup
We fix an algebraic number field ![]() $F$. In addition, we fix a finite place
$F$. In addition, we fix a finite place ![]() $ {\mathfrak {p}}$ of
$ {\mathfrak {p}}$ of ![]() $F$ lying above the rational prime
$F$ lying above the rational prime ![]() $p$ and choose embeddings
$p$ and choose embeddings
If ![]() $v$ is a place of
$v$ is a place of ![]() $F$, we denote by
$F$, we denote by ![]() $F_{v}$ the completion of
$F_{v}$ the completion of ![]() $F$ at
$F$ at ![]() $v$. If
$v$. If ![]() $v$ is a finite place, we let
$v$ is a finite place, we let ![]() $\mathcal {O}_{v}$ denote the valuation ring of
$\mathcal {O}_{v}$ denote the valuation ring of ![]() $F_{v}$ and
$F_{v}$ and ![]() $\operatorname {ord}_{v}$ the additive valuation such that
$\operatorname {ord}_{v}$ the additive valuation such that ![]() $\operatorname {ord}_{v}(\varpi )=1$ for any local uniformizer
$\operatorname {ord}_{v}(\varpi )=1$ for any local uniformizer ![]() $\varpi \in \mathcal {O}_{v}$.
$\varpi \in \mathcal {O}_{v}$.
Let ![]() $ {\mathbb {A}}$ be the adele ring of
$ {\mathbb {A}}$ be the adele ring of ![]() $F$, i.e. the restricted product over all completions
$F$, i.e. the restricted product over all completions ![]() $F_{v}$ of
$F_{v}$ of ![]() $F$. We write
$F$. We write ![]() $ {\mathbb {A}}^{\infty }$ (respectively,
$ {\mathbb {A}}^{\infty }$ (respectively, ![]() $ {\mathbb {A}} {{}^{ {\mathfrak {p}},\infty }}$) for the restricted product over all completions of
$ {\mathbb {A}} {{}^{ {\mathfrak {p}},\infty }}$) for the restricted product over all completions of ![]() $F$ at finite places (respectively, finite places different from
$F$ at finite places (respectively, finite places different from ![]() $ {\mathfrak {p}}$). More generally, if
$ {\mathfrak {p}}$). More generally, if ![]() $S$ is a finite set of places of
$S$ is a finite set of places of ![]() $F$ we denote by
$F$ we denote by ![]() $ {\mathbb {A}}^{S}$ the restricted product of all completions
$ {\mathbb {A}}^{S}$ the restricted product of all completions ![]() $F_v$ with
$F_v$ with ![]() $v\notin S$.
$v\notin S$.
If ![]() $H$ is an algebraic group over
$H$ is an algebraic group over ![]() $F$ and
$F$ and ![]() $v$ is a place of
$v$ is a place of ![]() $F$, we write
$F$, we write ![]() $H_v=H(F_v)$. We put
$H_v=H(F_v)$. We put ![]() $H_\infty =\prod _{v\mid \infty }H_v$.
$H_\infty =\prod _{v\mid \infty }H_v$.
Throughout the article we fix a connected, adjoint, semi-simple algebraic group ![]() $G$ over
$G$ over ![]() $F$. We assume that the base change
$F$. We assume that the base change ![]() $G_{F_ {\mathfrak {p}}}$ of
$G_{F_ {\mathfrak {p}}}$ of ![]() $G$ to
$G$ to ![]() $F_ {\mathfrak {p}}$ is split. Let
$F_ {\mathfrak {p}}$ is split. Let ![]() $K_\infty \subseteq G_\infty$ denote a fixed maximal compact subgroup. The integers
$K_\infty \subseteq G_\infty$ denote a fixed maximal compact subgroup. The integers ![]() $\delta$ and
$\delta$ and ![]() $q$ are defined via
$q$ are defined via
and
Finally, we fix a cuspidal automorphic representation ![]() $\pi =\otimes _v \pi _v$ of
$\pi =\otimes _v \pi _v$ of ![]() $G( {\mathbb {A}})$ with the following properties:
$G( {\mathbb {A}})$ with the following properties:
(i)
 $\pi$ is cohomological with respect to the trivial coefficient system;
$\pi$ is cohomological with respect to the trivial coefficient system;(ii)
 $\pi$ is tempered at
$\pi$ is tempered at  $\infty$; and
$\infty$; and(iii)
 $\pi _ {\mathfrak {p}}$ is the (smooth) Steinberg representation
$\pi _ {\mathfrak {p}}$ is the (smooth) Steinberg representation  $\operatorname {St}^{\infty }_{G_{ {\mathfrak {p}}}}( {\mathbb {C}})$ of
$\operatorname {St}^{\infty }_{G_{ {\mathfrak {p}}}}( {\mathbb {C}})$ of  $G_ {\mathfrak {p}}$.
$G_ {\mathfrak {p}}$.
We denote by ![]() $ {\mathbb {Q}}_\pi \subseteq \overline { {\mathbb {Q}}}$ a fixed finite extension of
$ {\mathbb {Q}}_\pi \subseteq \overline { {\mathbb {Q}}}$ a fixed finite extension of ![]() $ {\mathbb {Q}}$ over which
$ {\mathbb {Q}}$ over which ![]() $\pi ^{\infty }$ has a model (see Theorem C of [Reference JanuszewskiJan18] for the existence of such an extension).
$\pi ^{\infty }$ has a model (see Theorem C of [Reference JanuszewskiJan18] for the existence of such an extension).
Hypothesis (SMO)
We assume that the following strong multiplicity one hypothesis on ![]() $\pi$ holds. If
$\pi$ holds. If ![]() $\pi ^{\prime }$ is an automorphic representation of
$\pi ^{\prime }$ is an automorphic representation of ![]() $G$ such that:
$G$ such that:
(i)
 $\pi _v^{\prime }\cong \pi _v$ for all finite places
$\pi _v^{\prime }\cong \pi _v$ for all finite places  $v\neq {\mathfrak {p}}$;
$v\neq {\mathfrak {p}}$;(ii)
 $\pi _ {\mathfrak {p}}^{\prime }$ has an Iwahori-invariant vector; and
$\pi _ {\mathfrak {p}}^{\prime }$ has an Iwahori-invariant vector; and(iii)
 $\pi ^{\prime }_\infty$ has non-vanishing
$\pi ^{\prime }_\infty$ has non-vanishing  $(\mathfrak {g},K_{\infty }^{\circ })$-cohomology;
$(\mathfrak {g},K_{\infty }^{\circ })$-cohomology;
then ![]() $\pi$ is cuspidal,
$\pi$ is cuspidal, ![]() $\pi ^{\prime }_ {\mathfrak {p}}\cong \pi _ {\mathfrak {p}}$ and
$\pi ^{\prime }_ {\mathfrak {p}}\cong \pi _ {\mathfrak {p}}$ and ![]() $\pi _\infty$ is tempered.
$\pi _\infty$ is tempered.
It is known that this holds for cuspidal representations of ![]() $\mathrm {GL}_n$ by work of Jacquet and Shalika [Reference Jacquet and ShalikaJS81b, Reference Jacquet and ShalikaJS81a] and Piateski-Shapiro [Reference Piatetski-ShapiroPia79] and thus, in particular, for representations of
$\mathrm {GL}_n$ by work of Jacquet and Shalika [Reference Jacquet and ShalikaJS81b, Reference Jacquet and ShalikaJS81a] and Piateski-Shapiro [Reference Piatetski-ShapiroPia79] and thus, in particular, for representations of ![]() $G=\mathrm {PGL}_n$.
$G=\mathrm {PGL}_n$.
For general groups strong multiplicity one fails, see, for example, [Reference Howe and Piatetski-ShapiroHP83]. Hence, it is harder to find explicit results about representations ![]() $\pi$ for which the hypothesis SMO holds, but nevertheless it is expected that SMO should hold in many cases; for example, for generic representation of
$\pi$ for which the hypothesis SMO holds, but nevertheless it is expected that SMO should hold in many cases; for example, for generic representation of ![]() $\mathrm {GSp}_4$ [Reference SoudrySou87]. The same strategy of [Reference SoudrySou87] could apply as long as we have an injective transfer from (a subclass of) representations of
$\mathrm {GSp}_4$ [Reference SoudrySou87]. The same strategy of [Reference SoudrySou87] could apply as long as we have an injective transfer from (a subclass of) representations of ![]() $G$ to representation of
$G$ to representation of ![]() $\mathrm {GL}_n$, e.g. tempered representations of unitary groups that at each prime are not endoscopic.
$\mathrm {GL}_n$, e.g. tempered representations of unitary groups that at each prime are not endoscopic.
1. Automorphic  $\mathcal {L}$-invariants
$\mathcal {L}$-invariants
In the following, we briefly sketch the construction of automorphic ![]() $\mathcal {L}$-invariants. For more details, see [Reference GehrmannGeh21].
$\mathcal {L}$-invariants. For more details, see [Reference GehrmannGeh21].
1.1 Extensions
In this section we recall the computation of certain ![]() $\operatorname {Ext}^{1}$-groups of (locally analytic) generalized Steinberg representations due to Ding (see [Reference DingDin19]). We fix a finite extension
$\operatorname {Ext}^{1}$-groups of (locally analytic) generalized Steinberg representations due to Ding (see [Reference DingDin19]). We fix a finite extension ![]() ${E}$ of
${E}$ of ![]() $ {\mathbb {Q}}_p$. If
$ {\mathbb {Q}}_p$. If ![]() $V$ and
$V$ and ![]() $W$ are admissible locally
$W$ are admissible locally ![]() $ {\mathbb {Q}}_p$-analytic
$ {\mathbb {Q}}_p$-analytic ![]() ${E}$-representations of
${E}$-representations of ![]() $G_ {\mathfrak {p}}$, we write
$G_ {\mathfrak {p}}$, we write ![]() $\operatorname {Ext}^{1}_{\operatorname {an}}(V,W)$ for the group of locally analytic extensions of
$\operatorname {Ext}^{1}_{\operatorname {an}}(V,W)$ for the group of locally analytic extensions of ![]() $V$ by
$V$ by ![]() $W$.
$W$.
Given an algebraic subgroup ![]() $H\subseteq G_{F_ {\mathfrak {p}}}$, we denote the group of
$H\subseteq G_{F_ {\mathfrak {p}}}$, we denote the group of ![]() $F_ {\mathfrak {p}}$-valued points of
$F_ {\mathfrak {p}}$-valued points of ![]() $H$ also by
$H$ also by ![]() $H$. We fix a Borel subgroup
$H$. We fix a Borel subgroup ![]() $B$ of the split group
$B$ of the split group ![]() $G_{F_ {\mathfrak {p}}}$ and a maximal split torus
$G_{F_ {\mathfrak {p}}}$ and a maximal split torus ![]() $T\subseteq B$ and denote by
$T\subseteq B$ and denote by ![]() $\Delta$ the associated basis of simple roots. For a subset
$\Delta$ the associated basis of simple roots. For a subset ![]() $I\subseteq \Delta$ we let
$I\subseteq \Delta$ we let ![]() $P_I\supseteq B$ be the corresponding parabolic containing
$P_I\supseteq B$ be the corresponding parabolic containing ![]() $B$.
$B$.
Suppose ![]() $M$ is a smooth representation of
$M$ is a smooth representation of ![]() $P_I$ over a ring
$P_I$ over a ring ![]() $R$; we define its smooth induction to
$R$; we define its smooth induction to ![]() $G_ {\mathfrak {p}}$ as
$G_ {\mathfrak {p}}$ as
The generalized ![]() $R$-valued (smooth) Steinberg representation associated with
$R$-valued (smooth) Steinberg representation associated with ![]() $I\subseteq \Delta$ is given by the quotient
$I\subseteq \Delta$ is given by the quotient
 \[ v^{\infty}_{P_I}(R)= i^{\infty}_{P_I}(R) \bigg/ \sum_{I\subset J\subset \Delta, I\neq J} i^{\infty}_{P_J}(R). \]
\[ v^{\infty}_{P_I}(R)= i^{\infty}_{P_I}(R) \bigg/ \sum_{I\subset J\subset \Delta, I\neq J} i^{\infty}_{P_J}(R). \]
Likewise, if ![]() $V$ is a locally
$V$ is a locally ![]() $ {\mathbb {Q}}_ {\mathfrak {p}}$-analytic
$ {\mathbb {Q}}_ {\mathfrak {p}}$-analytic ![]() ${E}$-representation of
${E}$-representation of ![]() $P_I$, we define its locally analytic induction to
$P_I$, we define its locally analytic induction to ![]() $G_ {\mathfrak {p}}$ as the space of functions
$G_ {\mathfrak {p}}$ as the space of functions
We define the locally analytic generalized Steinberg representation with respect to ![]() $I$ as the quotient
$I$ as the quotient
 \[ {\mathbb{V}}^{\operatorname{an}}_{P_I}({E})={\mathbb{I}}_{P_I}^{\operatorname{an}}({E})\bigg/\sum_{I\subset J\subset \Delta, I\neq J} {\mathbb{I}}^{\operatorname{an}}_{P_J}({E}). \]
\[ {\mathbb{V}}^{\operatorname{an}}_{P_I}({E})={\mathbb{I}}_{P_I}^{\operatorname{an}}({E})\bigg/\sum_{I\subset J\subset \Delta, I\neq J} {\mathbb{I}}^{\operatorname{an}}_{P_J}({E}). \]
We put ![]() $\operatorname {St}_{G_ {\mathfrak {p}}}^{\infty }(R)=v^{\infty }_B(R)$ and
$\operatorname {St}_{G_ {\mathfrak {p}}}^{\infty }(R)=v^{\infty }_B(R)$ and ![]() $\operatorname {St}_{G_ {\mathfrak {p}}}^{\operatorname {an}}({E})= {\mathbb {V}}^{\operatorname {an}}_B({E})$. Similarly, replacing locally analyticity with continuity we define the continuous Steinberg representation
$\operatorname {St}_{G_ {\mathfrak {p}}}^{\operatorname {an}}({E})= {\mathbb {V}}^{\operatorname {an}}_B({E})$. Similarly, replacing locally analyticity with continuity we define the continuous Steinberg representation ![]() $\operatorname {St}_{G_ {\mathfrak {p}}}^{\operatorname {ct}}({E})$ and, more generally,
$\operatorname {St}_{G_ {\mathfrak {p}}}^{\operatorname {ct}}({E})$ and, more generally, ![]() $ {\mathbb {V}}^{\operatorname {ct}}_{P_I}({E})$. It is easy to see that
$ {\mathbb {V}}^{\operatorname {ct}}_{P_I}({E})$. It is easy to see that ![]() $ {\mathbb {V}}^{\operatorname {ct}}_{P_I}({E})$ is the universal unitary completion of both
$ {\mathbb {V}}^{\operatorname {ct}}_{P_I}({E})$ is the universal unitary completion of both ![]() $v^{\infty }_{P_I}({E})$ and
$v^{\infty }_{P_I}({E})$ and ![]() $ {\mathbb {V}}^{\operatorname {an}}_{P_I}({E})$.
$ {\mathbb {V}}^{\operatorname {an}}_{P_I}({E})$.
Let ![]() $i\in \Delta$ be a simple root and
$i\in \Delta$ be a simple root and ![]() $\lambda \in \operatorname {Hom}^{\operatorname {ct}}(B,{E})$ a continuous homomorphism. Note that
$\lambda \in \operatorname {Hom}^{\operatorname {ct}}(B,{E})$ a continuous homomorphism. Note that ![]() $\lambda$ is automatically locally analytic and is trivial on the unipotent radical of
$\lambda$ is automatically locally analytic and is trivial on the unipotent radical of ![]() $B$. Thus, it can be identified with a character on
$B$. Thus, it can be identified with a character on ![]() $T$. We write
$T$. We write ![]() $\tau _\lambda$ for the two-dimensional representation of
$\tau _\lambda$ for the two-dimensional representation of ![]() $B$ given by
$B$ given by
By the exactness of the parabolic induction functor for locally analytic extensions (see [Reference KohlhaaseKoh11, Proposition 5.1 and Remark 5.4]) we have a short exact sequence of the form
We write
for the associated extension class. Further, we define the class
as the pullback of this extension along ![]() $i^{\infty }_{P_i}({E})\to {\mathbb {I}}^{\operatorname {an}}_{B}({E})$. Finally, taking pushforward along
$i^{\infty }_{P_i}({E})\to {\mathbb {I}}^{\operatorname {an}}_{B}({E})$. Finally, taking pushforward along ![]() $ {\mathbb {I}}_{B}^{\operatorname {an}}({E})\to \operatorname {St}_{G_ {\mathfrak {p}}}^{\operatorname {an}}({E})$ yields the extension class
$ {\mathbb {I}}_{B}^{\operatorname {an}}({E})\to \operatorname {St}_{G_ {\mathfrak {p}}}^{\operatorname {an}}({E})$ yields the extension class
By an easy calculation we see that the map
defines a homomorphism. The inclusion ![]() $B\hookrightarrow P_i$ induces an injection
$B\hookrightarrow P_i$ induces an injection
The quotient can be identified with the space ![]() $\operatorname {Hom}^{\operatorname {ct}}(F_ {\mathfrak {p}}^{\ast },{E})$ via the map
$\operatorname {Hom}^{\operatorname {ct}}(F_ {\mathfrak {p}}^{\ast },{E})$ via the map
Alternatively, let ![]() $i^{\vee }$ denote the coroot associated with
$i^{\vee }$ denote the coroot associated with ![]() $i$. Then, the kernel of the map
$i$. Then, the kernel of the map
is equal to ![]() $\operatorname {Hom}^{\operatorname {ct}}(P_i,{E})$ and, hence, the map induces an isomorphism
$\operatorname {Hom}^{\operatorname {ct}}(P_i,{E})$ and, hence, the map induces an isomorphism
which is the inverse of the isomorphism above up to multiplication by two.
Theorem 1.1 (Ding)
The following hold.
(i) The map
 $\operatorname {Hom}^{\operatorname {ct}}(B,{E})\to \operatorname {Ext}^{1}_{\operatorname {an}}(i^{\infty }_{P_i}({E}),\operatorname {St}_{G_ {\mathfrak {p}}}^{\operatorname {an}}({E}))$,
$\operatorname {Hom}^{\operatorname {ct}}(B,{E})\to \operatorname {Ext}^{1}_{\operatorname {an}}(i^{\infty }_{P_i}({E}),\operatorname {St}_{G_ {\mathfrak {p}}}^{\operatorname {an}}({E}))$,  $\lambda \mapsto \mathcal {E}^{\operatorname {an}}_{i}(\lambda )$ is surjective with kernel
$\lambda \mapsto \mathcal {E}^{\operatorname {an}}_{i}(\lambda )$ is surjective with kernel  $\operatorname {Hom}^{\operatorname {ct}}(P_i,{E})\subseteq \operatorname {Hom}^{\operatorname {ct}}(B,{E})$.
$\operatorname {Hom}^{\operatorname {ct}}(P_i,{E})\subseteq \operatorname {Hom}^{\operatorname {ct}}(B,{E})$.(ii) The canonical map
 $\operatorname {Ext}^{1}_{\operatorname {an}}(v^{\infty }_{P_i}({E}),\operatorname {St}_{G_ {\mathfrak {p}}}^{\operatorname {an}}({E}))\to \operatorname {Ext}^{1}_{\operatorname {an}}(i^{\infty }_{P_i}({E}),\operatorname {St}_{G_ {\mathfrak {p}}}^{\operatorname {an}}({E}))$ is an isomorphism.
$\operatorname {Ext}^{1}_{\operatorname {an}}(v^{\infty }_{P_i}({E}),\operatorname {St}_{G_ {\mathfrak {p}}}^{\operatorname {an}}({E}))\to \operatorname {Ext}^{1}_{\operatorname {an}}(i^{\infty }_{P_i}({E}),\operatorname {St}_{G_ {\mathfrak {p}}}^{\operatorname {an}}({E}))$ is an isomorphism.(iii) The induced map
 $\operatorname {Hom}^{\operatorname {ct}}(F_ {\mathfrak {p}}^{\ast },{E})\longrightarrow \operatorname {Ext}^{1}_{\operatorname {an}}(v^{\infty }_{P_i}({E}),\operatorname {St}_{G_ {\mathfrak {p}}}^{\operatorname {an}}({E}))$,
$\operatorname {Hom}^{\operatorname {ct}}(F_ {\mathfrak {p}}^{\ast },{E})\longrightarrow \operatorname {Ext}^{1}_{\operatorname {an}}(v^{\infty }_{P_i}({E}),\operatorname {St}_{G_ {\mathfrak {p}}}^{\operatorname {an}}({E}))$,  $\lambda \mapsto \mathcal {E}^{\operatorname {an}}_{i}(\lambda \circ i)$ is an isomorphism.
$\lambda \mapsto \mathcal {E}^{\operatorname {an}}_{i}(\lambda \circ i)$ is an isomorphism.
Proof. The third claim is a direct consequence of the first two. For the proof of the first two claims in the case ![]() $G=\operatorname {PGL}_n$, see § 2.2 of [Reference DingDin19]. The general case is proven in § 2.4 of [Reference GehrmannGeh21].
$G=\operatorname {PGL}_n$, see § 2.2 of [Reference DingDin19]. The general case is proven in § 2.4 of [Reference GehrmannGeh21].
1.2 Flawless lattices
We recall the notion of flawless smooth representations over a ring ![]() $R$.
$R$.
Definition 1.2 A smooth ![]() $R$-representation
$R$-representation ![]() $M$ of
$M$ of ![]() $G_ {\mathfrak {p}}$ is called flawless if:
$G_ {\mathfrak {p}}$ is called flawless if:
(i)
 $M$ is projective as an
$M$ is projective as an  $R$-module; and
$R$-module; and(ii) there exists a finite length exact resolution
of \[ 0\longrightarrow C_m\longrightarrow\cdots\longrightarrow C_0\longrightarrow M \longrightarrow 0 \]
\[ 0\longrightarrow C_m\longrightarrow\cdots\longrightarrow C_0\longrightarrow M \longrightarrow 0 \] $M$ by smooth
$M$ by smooth  $R$-representations
$R$-representations  $C_i$ of
$C_i$ of  $G_ {\mathfrak {p}}$, where each
$G_ {\mathfrak {p}}$, where each  $C_i$ is a finite direct sum of modules of the form
with
$C_i$ is a finite direct sum of modules of the form
with \[ \operatorname{c-ind}_{K_{\mathfrak{p}}}^{G_{\mathfrak{p}}}(L) \]
\[ \operatorname{c-ind}_{K_{\mathfrak{p}}}^{G_{\mathfrak{p}}}(L) \] $K_ {\mathfrak {p}}\subseteq G_ {\mathfrak {p}}$ a compact, open subgroup and
$K_ {\mathfrak {p}}\subseteq G_ {\mathfrak {p}}$ a compact, open subgroup and  $L$ a smooth representation of
$L$ a smooth representation of  $K_ {\mathfrak {p}}$ that is finitely generated projective over
$K_ {\mathfrak {p}}$ that is finitely generated projective over  $R$.
$R$.
The following is our main example.
Theorem 1.3 (Borel–Serre)
The Steinberg representation ![]() $\operatorname {St}_{G_ {\mathfrak {p}}}^{\infty }(R)$ is flawless for every ring
$\operatorname {St}_{G_ {\mathfrak {p}}}^{\infty }(R)$ is flawless for every ring ![]() $R$.
$R$.
Proof. It is enough to prove that ![]() $\operatorname {St}_{G_ {\mathfrak {p}}}^{\infty }( {\mathbb {Z}})$ is flawless. By [Reference Borel and SerreBS76, Theorem 5.6],
$\operatorname {St}_{G_ {\mathfrak {p}}}^{\infty }( {\mathbb {Z}})$ is flawless. By [Reference Borel and SerreBS76, Theorem 5.6], ![]() $\operatorname {St}_{G_ {\mathfrak {p}}}^{\infty }( {\mathbb {Z}})$ can be identified with the cohomology with compact supports of the Bruhat–Tits building of
$\operatorname {St}_{G_ {\mathfrak {p}}}^{\infty }( {\mathbb {Z}})$ can be identified with the cohomology with compact supports of the Bruhat–Tits building of ![]() $G_ {\mathfrak {p}}$. Thus, its simplicial complex gives a flawless resolution of
$G_ {\mathfrak {p}}$. Thus, its simplicial complex gives a flawless resolution of ![]() $\operatorname {St}_{G_ {\mathfrak {p}}}^{\infty }( {\mathbb {Z}})$.
$\operatorname {St}_{G_ {\mathfrak {p}}}^{\infty }( {\mathbb {Z}})$.
1.3 Cohomology of  $ {\mathfrak {p}}$-arithmetic groups
$ {\mathfrak {p}}$-arithmetic groups
Let ![]() $A$ be a
$A$ be a ![]() $ {\mathbb {Q}}_p$-affinoid algebra in the sense of Tate. Given a compact, open subgroup
$ {\mathbb {Q}}_p$-affinoid algebra in the sense of Tate. Given a compact, open subgroup ![]() $K^{{\mathfrak {p}}}\subseteq G( {\mathbb {A}} {{}^{ {\mathfrak {p}},\infty }})$, an
$K^{{\mathfrak {p}}}\subseteq G( {\mathbb {A}} {{}^{ {\mathfrak {p}},\infty }})$, an ![]() $A[G_ {\mathfrak {p}}]$-module
$A[G_ {\mathfrak {p}}]$-module ![]() $V$ and an
$V$ and an ![]() $A[G(F)]$-module
$A[G(F)]$-module ![]() $W$, which is free and of finite rank over
$W$, which is free and of finite rank over ![]() $A$, we define
$A$, we define ![]() $ {\mathcal {C}}_A(K^{ {\mathfrak {p}}},V;W)$ as the space of all
$ {\mathcal {C}}_A(K^{ {\mathfrak {p}}},V;W)$ as the space of all ![]() $A$-linear maps
$A$-linear maps ![]() $\Phi \colon G( {\mathbb {A}} {{}^{ {\mathfrak {p}},\infty }})/K^{{\mathfrak {p}}} \times V\to W$. The
$\Phi \colon G( {\mathbb {A}} {{}^{ {\mathfrak {p}},\infty }})/K^{{\mathfrak {p}}} \times V\to W$. The ![]() $A$-module
$A$-module ![]() $ {\mathcal {C}}_{E}(K^{{\mathfrak {p}}},V;W)$ carries a natural
$ {\mathcal {C}}_{E}(K^{{\mathfrak {p}}},V;W)$ carries a natural ![]() $G(F)$-action given by
$G(F)$-action given by
Suppose ![]() $V$ is a topological
$V$ is a topological ![]() $A$-module equipped with a continuous
$A$-module equipped with a continuous ![]() $A$-linear
$A$-linear ![]() $G_ {\mathfrak {p}}$-action we put
$G_ {\mathfrak {p}}$-action we put ![]() $ {\mathcal {C}}^{\operatorname {ct}}_A(K^{{\mathfrak {p}}},V;W)=C(G( {\mathbb {A}} {{}^{ {\mathfrak {p}},\infty }})/K^{ {\mathfrak {p}}},\operatorname {Hom}_{A}^{\operatorname {ct}}(V,W))$. Here
$ {\mathcal {C}}^{\operatorname {ct}}_A(K^{{\mathfrak {p}}},V;W)=C(G( {\mathbb {A}} {{}^{ {\mathfrak {p}},\infty }})/K^{ {\mathfrak {p}}},\operatorname {Hom}_{A}^{\operatorname {ct}}(V,W))$. Here ![]() $W$ is endowed with its canonical topology as a finitely generated free
$W$ is endowed with its canonical topology as a finitely generated free ![]() $A$-module.
$A$-module.
Let ![]() ${E}$ be a finite extension of
${E}$ be a finite extension of ![]() $ {\mathbb {Q}}_p$ with ring of integers
$ {\mathbb {Q}}_p$ with ring of integers ![]() $\mathcal {O}_{E}$. Suppose that
$\mathcal {O}_{E}$. Suppose that ![]() $V$ is a smooth
$V$ is a smooth ![]() ${E}$-representation of
${E}$-representation of ![]() $G_ {\mathfrak {p}}$ that admits a flawless
$G_ {\mathfrak {p}}$ that admits a flawless ![]() $G_ {\mathfrak {p}}$-stable
$G_ {\mathfrak {p}}$-stable ![]() $\mathcal {O}_{E}$-lattice
$\mathcal {O}_{E}$-lattice ![]() $M$. As
$M$. As ![]() $M$ is finitely generated as an
$M$ is finitely generated as an ![]() $\mathcal {O}_{E}[G_ {\mathfrak {p}}]$-module, the completion of
$\mathcal {O}_{E}[G_ {\mathfrak {p}}]$-module, the completion of ![]() $V$ with respect to
$V$ with respect to ![]() $M$ is the universal unitary completion
$M$ is the universal unitary completion ![]() $V^{\operatorname {un}}$ of
$V^{\operatorname {un}}$ of ![]() $V$. The following automatic continuity statement holds (see [Reference GehrmannGeh21, Proposition 3.11]).
$V$. The following automatic continuity statement holds (see [Reference GehrmannGeh21, Proposition 3.11]).
Proposition 1.4 Suppose that ![]() $V$ is a smooth
$V$ is a smooth ![]() ${E}$-representation of
${E}$-representation of ![]() $G_ {\mathfrak {p}}$ that admits a flawless
$G_ {\mathfrak {p}}$ that admits a flawless ![]() $G_ {\mathfrak {p}}$-stable
$G_ {\mathfrak {p}}$-stable ![]() $\mathcal {O}_{E}$-lattice
$\mathcal {O}_{E}$-lattice ![]() $M$. Then the canonical map
$M$. Then the canonical map
is an isomorphism for every character ![]() $\epsilon \colon \pi _0(G_\infty )\to \{\pm 1\}$, every compact, open subgroup
$\epsilon \colon \pi _0(G_\infty )\to \{\pm 1\}$, every compact, open subgroup ![]() $K^{{\mathfrak {p}}}\subseteq G( {\mathbb {A}} {{}^{ {\mathfrak {p}},\infty }})$ and every degree
$K^{{\mathfrak {p}}}\subseteq G( {\mathbb {A}} {{}^{ {\mathfrak {p}},\infty }})$ and every degree ![]() $d\geqslant 0$.
$d\geqslant 0$.
This proposition combined with Theorem 1.3 implies the following.
Corollary 1.5 The canonical map
is an isomorphism.
For a compact, open subset ![]() $K_ {\mathfrak {p}}\subseteq G_ {\mathfrak {p}}$ and a character
$K_ {\mathfrak {p}}\subseteq G_ {\mathfrak {p}}$ and a character ![]() $\epsilon \colon \pi _0(G_\infty ) \to \{\pm 1\}$ we put
$\epsilon \colon \pi _0(G_\infty ) \to \{\pm 1\}$ we put
If the level ![]() $K^{{\mathfrak {p}}}\times K_ {\mathfrak {p}}$ is neat, this group is naturally isomorphic to (the epsilon component of) the singular cohomology with coefficients in
$K^{{\mathfrak {p}}}\times K_ {\mathfrak {p}}$ is neat, this group is naturally isomorphic to (the epsilon component of) the singular cohomology with coefficients in ![]() $W$ of the locally symmetric space of level
$W$ of the locally symmetric space of level ![]() $K^{{\mathfrak {p}}}\times K_ {\mathfrak {p}}$ associated with
$K^{{\mathfrak {p}}}\times K_ {\mathfrak {p}}$ associated with ![]() $G$. More generally, let
$G$. More generally, let ![]() $V$ be a topological
$V$ be a topological ![]() $A$-module, which is locally convex as a
$A$-module, which is locally convex as a ![]() $ {\mathbb {Q}}_p$-vector space, with a continuous
$ {\mathbb {Q}}_p$-vector space, with a continuous ![]() $A$-linear
$A$-linear ![]() $K_ {\mathfrak {p}}$-action. We consider
$K_ {\mathfrak {p}}$-action. We consider ![]() $\operatorname {c-ind}_{K_ {\mathfrak {p}}}^{G_ {\mathfrak {p}}}V$ with the locally convex inductive limit topology. This is a continuous
$\operatorname {c-ind}_{K_ {\mathfrak {p}}}^{G_ {\mathfrak {p}}}V$ with the locally convex inductive limit topology. This is a continuous ![]() $A$-module with a continuous
$A$-module with a continuous ![]() $G_p$-action. We put
$G_p$-action. We put
Again, this space can be identified with the cohomology of the corresponding locally symmetric space with values in the sheaf associated with ![]() $\operatorname {Hom}_{A}^{\operatorname {ct}}(V,A)$.
$\operatorname {Hom}_{A}^{\operatorname {ct}}(V,A)$.
1.4 Automorphic  $\mathcal {L}$-invariants
$\mathcal {L}$-invariants
For the remainder of the article we fix a finite extension ![]() ${E}$ of
${E}$ of ![]() $ {\mathbb {Q}}_p$ that contains
$ {\mathbb {Q}}_p$ that contains ![]() $ {\mathbb {Q}}_\pi$ and a compact, open subgroup
$ {\mathbb {Q}}_\pi$ and a compact, open subgroup ![]() $K^{{\mathfrak {p}}}=\prod _{v\nmid {\mathfrak {p}} \infty }K_v\subseteq G( {\mathbb {A}} {{}^{ {\mathfrak {p}},\infty }})$ such that
$K^{{\mathfrak {p}}}=\prod _{v\nmid {\mathfrak {p}} \infty }K_v\subseteq G( {\mathbb {A}} {{}^{ {\mathfrak {p}},\infty }})$ such that ![]() $(\pi {{}^{ {\mathfrak {p}},\infty }})^{K^{{\mathfrak {p}}}}\neq 0$. We may assume that
$(\pi {{}^{ {\mathfrak {p}},\infty }})^{K^{{\mathfrak {p}}}}\neq 0$. We may assume that ![]() $K_v$ is hyperspecial for every finite place
$K_v$ is hyperspecial for every finite place ![]() $v$ such that
$v$ such that ![]() $\pi _v$ is spherical.
$\pi _v$ is spherical.
As ![]() $v_{P_I}^{\infty }({E})=v_I^{\infty }( {\mathbb {Z}})\otimes {E}$ we have a canonical isomorphism
$v_{P_I}^{\infty }({E})=v_I^{\infty }( {\mathbb {Z}})\otimes {E}$ we have a canonical isomorphism
for any ![]() ${E}$-vector space
${E}$-vector space ![]() $W$. Hence, we abbreviate this space by
$W$. Hence, we abbreviate this space by ![]() $ {\mathcal {C}}(K^{{\mathfrak {p}}},v^{\infty }_{P_I};W)$ (and similarly for
$ {\mathcal {C}}(K^{{\mathfrak {p}}},v^{\infty }_{P_I};W)$ (and similarly for ![]() $\operatorname {St}_{G_ {\mathfrak {p}}}^{\infty }$ in place of
$\operatorname {St}_{G_ {\mathfrak {p}}}^{\infty }$ in place of ![]() $v^{\infty }_{P_I}$).
$v^{\infty }_{P_I}$).
Let ![]() $I_ {\mathfrak {p}}\subseteq G_ {\mathfrak {p}}$ be an Iwahori subgroup. By Frobenius reciprocity the choice of an Iwahori-fixed vector yields a
$I_ {\mathfrak {p}}\subseteq G_ {\mathfrak {p}}$ be an Iwahori subgroup. By Frobenius reciprocity the choice of an Iwahori-fixed vector yields a ![]() $G_ {\mathfrak {p}}$-equivariant homomorphism
$G_ {\mathfrak {p}}$-equivariant homomorphism
which, in turn, induces a Hecke-equivariant map
Let
be the ![]() ${E}$-valued Hecke algebra of level
${E}$-valued Hecke algebra of level ![]() $K^{{\mathfrak {p}}}\times I_ {\mathfrak {p}}$. By abuse of notation, we denote the model of
$K^{{\mathfrak {p}}}\times I_ {\mathfrak {p}}$. By abuse of notation, we denote the model of ![]() $\pi ^{\infty }$ over
$\pi ^{\infty }$ over ![]() ${E}$ also by
${E}$ also by ![]() $\pi ^{\infty }$. If
$\pi ^{\infty }$. If ![]() $V$ is a
$V$ is a ![]() $\mathbb { {\mathbb {T}}}$-module, we put
$\mathbb { {\mathbb {T}}}$-module, we put
where we sum over all ![]() $\mathbb {T}$-homomorphisms
$\mathbb {T}$-homomorphisms ![]() $f\colon (\pi ^{\infty })^{K^{{\mathfrak {p}}}\times I_ {\mathfrak {p}}}\to V.$ Similarly, we define
$f\colon (\pi ^{\infty })^{K^{{\mathfrak {p}}}\times I_ {\mathfrak {p}}}\to V.$ Similarly, we define
to be the Hecke algebra away from ![]() $ {\mathfrak {p}}$ and, given a
$ {\mathfrak {p}}$ and, given a ![]() $ {\mathbb {T}}^{ {\mathfrak {p}}}$-module
$ {\mathbb {T}}^{ {\mathfrak {p}}}$-module ![]() $V$, we put
$V$, we put
where we sum over all ![]() $ {\mathbb {T}}^{ {\mathfrak {p}}}$-homomorphisms
$ {\mathbb {T}}^{ {\mathfrak {p}}}$-homomorphisms ![]() $f\colon (\pi {{}^{ {\mathfrak {p}},\infty }})^{K^{{\mathfrak {p}}}}\to V.$
$f\colon (\pi {{}^{ {\mathfrak {p}},\infty }})^{K^{{\mathfrak {p}}}}\to V.$
For the proof of the following proposition that crucially relies on the hypothesis (SMO) we refer to [Reference GehrmannGeh21, Proposition 3.6].
Proposition 1.6 The map ![]() $\operatorname {ev}^{(d)}$ induces an isomorphism
$\operatorname {ev}^{(d)}$ induces an isomorphism
on isotypic components. There exists an integer ![]() $m_\pi \geqslant 0$ such that
$m_\pi \geqslant 0$ such that
for each sign character ![]() $\epsilon$.
$\epsilon$.
By Corollary 1.5, we have a canonical isomorphism
Composing with the homomorphism coming from dualizing the continuous inclusion ![]() $\operatorname {St}_{G_ {\mathfrak {p}}}^{\operatorname {an}}\hookrightarrow \operatorname {St}_{G_ {\mathfrak {p}}}^{\operatorname {ct}}$ yields the map
$\operatorname {St}_{G_ {\mathfrak {p}}}^{\operatorname {an}}\hookrightarrow \operatorname {St}_{G_ {\mathfrak {p}}}^{\operatorname {ct}}$ yields the map
in cohomology. Thus, for every ![]() $i\in \Delta$ we get a well-defined cup-product pairing
$i\in \Delta$ we get a well-defined cup-product pairing
 \begin{align*} &\operatorname{H}^{d}(G(F),{\mathcal{C}}(K^{{\mathfrak {p}}},\operatorname{St}_{G_{\mathfrak{p}}}^{\infty};{E}(\epsilon))) \times \operatorname{Ext}^{1}_{\operatorname{an}}(v_{P_i}^{\infty}({E}),\operatorname{St}_{G_{\mathfrak{p}}}^{\operatorname{an}}({E}))\\ &\quad \longrightarrow \operatorname{H}^{d+1}(G(F),{\mathcal{C}}(K^{{\mathfrak {p}}},v^{\infty}_{P_i};{E}(\epsilon))), \end{align*}
\begin{align*} &\operatorname{H}^{d}(G(F),{\mathcal{C}}(K^{{\mathfrak {p}}},\operatorname{St}_{G_{\mathfrak{p}}}^{\infty};{E}(\epsilon))) \times \operatorname{Ext}^{1}_{\operatorname{an}}(v_{P_i}^{\infty}({E}),\operatorname{St}_{G_{\mathfrak{p}}}^{\operatorname{an}}({E}))\\ &\quad \longrightarrow \operatorname{H}^{d+1}(G(F),{\mathcal{C}}(K^{{\mathfrak {p}}},v^{\infty}_{P_i};{E}(\epsilon))), \end{align*}
which commutes with the action of the Hecke algebra ![]() $ {\mathbb {T}}^{ {\mathfrak {p}}}$. By Theorem 1.1 we have a canonical isomorphism
$ {\mathbb {T}}^{ {\mathfrak {p}}}$. By Theorem 1.1 we have a canonical isomorphism ![]() $\operatorname {Hom}^{\operatorname {ct}}(F_ {\mathfrak {p}}^{\ast },{E})\cong \operatorname {Ext}^{1}_{\operatorname {an}}(v^{\infty }_{P_i}({E}),\operatorname {St}_{G_ {\mathfrak {p}}}^{\operatorname {an}}({E}))$. Hence, taking cup product with the extension
$\operatorname {Hom}^{\operatorname {ct}}(F_ {\mathfrak {p}}^{\ast },{E})\cong \operatorname {Ext}^{1}_{\operatorname {an}}(v^{\infty }_{P_i}({E}),\operatorname {St}_{G_ {\mathfrak {p}}}^{\operatorname {an}}({E}))$. Hence, taking cup product with the extension ![]() $\mathcal {E}^{\operatorname {an}}_{i}(\lambda \circ i)$ associated with a homomorphism
$\mathcal {E}^{\operatorname {an}}_{i}(\lambda \circ i)$ associated with a homomorphism ![]() $\lambda \in \operatorname {Hom}^{\operatorname {ct}}(F_ {\mathfrak {p}}^{\ast },{E})$ in (1.4) yields a map
$\lambda \in \operatorname {Hom}^{\operatorname {ct}}(F_ {\mathfrak {p}}^{\ast },{E})$ in (1.4) yields a map
on ![]() $\pi {{}^{ {\mathfrak {p}},\infty }}$-isotypic parts.
$\pi {{}^{ {\mathfrak {p}},\infty }}$-isotypic parts.
Definition 1.7 Given a character ![]() $\epsilon \colon \pi _0(G_\infty ) \to \{\pm 1\}$, an integer
$\epsilon \colon \pi _0(G_\infty ) \to \{\pm 1\}$, an integer ![]() $d\in {\mathbb {Z}}$ with
$d\in {\mathbb {Z}}$ with ![]() $0\leqslant d\leqslant \delta$ and a root
$0\leqslant d\leqslant \delta$ and a root ![]() $i\in \Delta$ we define
$i\in \Delta$ we define
as the kernel of the map ![]() $\lambda \mapsto c^{(q+d)}_{i}(\lambda )^{\epsilon }$.
$\lambda \mapsto c^{(q+d)}_{i}(\lambda )^{\epsilon }$.
Alternatively, we can consider cup products with extensions associated with homomorphisms ![]() $\lambda \colon B \to {E}$ and define the
$\lambda \colon B \to {E}$ and define the ![]() $\mathcal {L}$-invariant as a subspace of
$\mathcal {L}$-invariant as a subspace of
This subspace is mapped to the ![]() $\mathcal {L}$-invariant defined above via the map (1.6) induced by the coroot
$\mathcal {L}$-invariant defined above via the map (1.6) induced by the coroot ![]() $i^{\vee }$ associated with
$i^{\vee }$ associated with ![]() $i$.
$i$.
Proposition 1.8 For all sign characters ![]() $\epsilon$, every degree
$\epsilon$, every degree ![]() $d\in [0,\delta ]\cap {\mathbb {Z}}$ and every root
$d\in [0,\delta ]\cap {\mathbb {Z}}$ and every root ![]() $i \in \Delta$ the
$i \in \Delta$ the ![]() $\mathcal {L}$-invariant
$\mathcal {L}$-invariant
is a subspace of codimension at least one, which does not contain the space of smooth homomorphisms.
Suppose ![]() $m_\pi =1$. Then, in the extremal cases
$m_\pi =1$. Then, in the extremal cases ![]() $d=0$ and
$d=0$ and ![]() $d=\delta$ the codimension is exactly one.
$d=\delta$ the codimension is exactly one.
Proof. This is Proposition 3.14 of [Reference GehrmannGeh21].
Remark 1.9 Let ![]() $\log _p\colon {E}^{\ast }\to {E}$ denote the branch of the
$\log _p\colon {E}^{\ast }\to {E}$ denote the branch of the ![]() $p$-adic logarithm such that
$p$-adic logarithm such that ![]() $\log _p(p)=0.$ Let us assume that
$\log _p(p)=0.$ Let us assume that ![]() ${E}$ contains the images of all embeddings
${E}$ contains the images of all embeddings ![]() $\sigma \colon F_ {\mathfrak {p}}\to \overline { {\mathbb {Q}}_p}$. We put
$\sigma \colon F_ {\mathfrak {p}}\to \overline { {\mathbb {Q}}_p}$. We put ![]() $\log _{p,\sigma }=\log _p \circ \sigma \colon F_ {\mathfrak {p}}^{\ast }\to {E}$. The set
$\log _{p,\sigma }=\log _p \circ \sigma \colon F_ {\mathfrak {p}}^{\ast }\to {E}$. The set
is a basis of ![]() $\operatorname {Hom}^{\operatorname {ct}}(F_ {\mathfrak {p}}^{\ast },{E})$. Suppose
$\operatorname {Hom}^{\operatorname {ct}}(F_ {\mathfrak {p}}^{\ast },{E})$. Suppose ![]() $\mathcal {L}\subseteq \operatorname {Hom}^{\operatorname {ct}}(F_ {\mathfrak {p}}^{\ast },{E})$ is a subspace of codimension one that does not contain
$\mathcal {L}\subseteq \operatorname {Hom}^{\operatorname {ct}}(F_ {\mathfrak {p}}^{\ast },{E})$ is a subspace of codimension one that does not contain ![]() $\operatorname {ord}_ {\mathfrak {p}}$. Then for each embedding
$\operatorname {ord}_ {\mathfrak {p}}$. Then for each embedding ![]() $\sigma$ there exists a unique element
$\sigma$ there exists a unique element ![]() $\mathcal {L}^{\sigma }\in {E}$ such that
$\mathcal {L}^{\sigma }\in {E}$ such that ![]() $\log _{p,\sigma }- \mathcal {L}^{\sigma }\operatorname {ord}_ {\mathfrak {p}} \in \mathcal {L}$ and these elements clearly form a basis of
$\log _{p,\sigma }- \mathcal {L}^{\sigma }\operatorname {ord}_ {\mathfrak {p}} \in \mathcal {L}$ and these elements clearly form a basis of ![]() $\mathcal {L}$.
$\mathcal {L}$.
2.  $\mathcal {L}$-invariants and big principal series
$\mathcal {L}$-invariants and big principal series
By the Colmez–Greenberg–Stevens formula (see [Reference DingDin19, Theorem 3.4]) one can calculate Fontaine–Mazur ![]() $\mathcal {L}$-invariants of certain local Galois representations by deforming them (or rather the attached
$\mathcal {L}$-invariants of certain local Galois representations by deforming them (or rather the attached ![]() $(\varphi,\Gamma )$-modules) in rigid analytic families. The goal of this section is to prove an automorphic version of that formula.
$(\varphi,\Gamma )$-modules) in rigid analytic families. The goal of this section is to prove an automorphic version of that formula.
This implies that ![]() $\mathcal {L}$-invariants can be related to the existence of cohomology classes with values in (duals of) families of principal series.
$\mathcal {L}$-invariants can be related to the existence of cohomology classes with values in (duals of) families of principal series.
2.1 Linear algebra over the dual numbers
Let ![]() $R$ be a ring and
$R$ be a ring and ![]() $R[\varepsilon ]=R[X]/X^{2}$ the ring of dual numbers over
$R[\varepsilon ]=R[X]/X^{2}$ the ring of dual numbers over ![]() $R$. Let
$R$. Let ![]() $M$ be an
$M$ be an ![]() $R[\varepsilon ]$-module. We define several maps on dual spaces associated with
$R[\varepsilon ]$-module. We define several maps on dual spaces associated with ![]() $M$. First, multiplication with
$M$. First, multiplication with ![]() $\varepsilon$ induces the map
$\varepsilon$ induces the map ![]() $\mu \colon M/\varepsilon M\to \varepsilon M\hookrightarrow M$. We denote by
$\mu \colon M/\varepsilon M\to \varepsilon M\hookrightarrow M$. We denote by
its ![]() $R$-dual. Second, reducing modulo
$R$-dual. Second, reducing modulo ![]() $\varepsilon$ yields the map
$\varepsilon$ yields the map
Finally, the map ![]() $\operatorname {add}\colon R[\varepsilon ]\to R, a+b\varepsilon \mapsto a+b$ induces the map
$\operatorname {add}\colon R[\varepsilon ]\to R, a+b\varepsilon \mapsto a+b$ induces the map
The following easy computation is left to the reader.
Lemma 2.1 The maps ![]() $\mu _\varepsilon ^{\ast }$,
$\mu _\varepsilon ^{\ast }$, ![]() $\operatorname {red}$ and
$\operatorname {red}$ and ![]() $\operatorname {add}$ are functorial in
$\operatorname {add}$ are functorial in ![]() $M$ and the following equality holds:
$M$ and the following equality holds: ![]() $\operatorname {red}=\mu _\varepsilon ^{\ast }\circ \operatorname {add}_\ast.$
$\operatorname {red}=\mu _\varepsilon ^{\ast }\circ \operatorname {add}_\ast.$
2.2 Infinitesimal deformations of principal series
Let ![]() $T\subseteq B\subset G_{F_ {\mathfrak {p}}}$ be the maximal torus respectively the Borel subgroup chosen in § 1.1. The map
$T\subseteq B\subset G_{F_ {\mathfrak {p}}}$ be the maximal torus respectively the Borel subgroup chosen in § 1.1. The map
defines an injective group homomorphism. Its image is the set of all continuous characters ![]() $\chi \colon B\to {E}[\varepsilon ]^{\ast }$ such that
$\chi \colon B\to {E}[\varepsilon ]^{\ast }$ such that ![]() $\chi \equiv 1 \bmod \varepsilon$. The underlying
$\chi \equiv 1 \bmod \varepsilon$. The underlying ![]() ${E}$-representation of
${E}$-representation of ![]() $\tau (\lambda )$ is the two-dimensional representation
$\tau (\lambda )$ is the two-dimensional representation ![]() $\tau _\lambda$ defined in (1.1). Thus, we can view
$\tau _\lambda$ defined in (1.1). Thus, we can view ![]() $ {\mathbb {I}}_{B}^{\operatorname {an}}(\tau _\lambda )= {\mathbb {I}}_{B}^{\operatorname {an}}(\tau (\lambda ))$ as an
$ {\mathbb {I}}_{B}^{\operatorname {an}}(\tau _\lambda )= {\mathbb {I}}_{B}^{\operatorname {an}}(\tau (\lambda ))$ as an ![]() ${E}[\varepsilon ]$-representation of
${E}[\varepsilon ]$-representation of ![]() $G_ {\mathfrak {p}}$. Reducing modulo
$G_ {\mathfrak {p}}$. Reducing modulo ![]() $\varepsilon$ induces the map
$\varepsilon$ induces the map
in cohomology.
Let ![]() $i^{\vee }$ be the coroot associated with
$i^{\vee }$ be the coroot associated with ![]() $i$. Given a character
$i$. Given a character ![]() $\lambda \colon B\to {E}$ we put
$\lambda \colon B\to {E}$ we put ![]() $\lambda _i=\lambda \circ i^{\vee }$.
$\lambda _i=\lambda \circ i^{\vee }$.
Lemma 2.2 Let ![]() $\lambda \colon B\to {E}$ be a continuous character. If the isotypic component
$\lambda \colon B\to {E}$ be a continuous character. If the isotypic component
is contained in the image of ![]() $\operatorname {red}_\lambda ^{q+d,\epsilon }$, then the homomorphism
$\operatorname {red}_\lambda ^{q+d,\epsilon }$, then the homomorphism ![]() $\lambda _i$ belongs to
$\lambda _i$ belongs to ![]() $\mathcal {L}_{i}^{(d)}(\pi, {\mathfrak {p}})^{\epsilon }.$
$\mathcal {L}_{i}^{(d)}(\pi, {\mathfrak {p}})^{\epsilon }.$
Proof. The inclusion ![]() $ {\mathbb {I}}_{B}^{\operatorname {an}}({E})\hookrightarrow {\mathbb {I}}_{B}^{\operatorname {an}}(\tau _\lambda )$ induces the map
$ {\mathbb {I}}_{B}^{\operatorname {an}}({E})\hookrightarrow {\mathbb {I}}_{B}^{\operatorname {an}}(\tau _\lambda )$ induces the map
in cohomology. Its image is the kernel of the cup product with the extension class ![]() $\widehat {\mathcal {E}}^{\operatorname {an}}(\lambda )$ defined in (1.2).
$\widehat {\mathcal {E}}^{\operatorname {an}}(\lambda )$ defined in (1.2).
Thus, by Lemma 2.1 our assumption implies that the ![]() $\pi$-isotypic component
$\pi$-isotypic component ![]() $\operatorname {H}^{q+d}(G(F), {\mathcal {C}}^{\operatorname {ct}}_{E}(K^{{\mathfrak {p}}}, {\mathbb {I}}_{B}^{\operatorname {an}}({E});{E}(\epsilon )))[\pi ^{ {\mathfrak {p}}}]$ is contained in the kernel of the cup product with
$\operatorname {H}^{q+d}(G(F), {\mathcal {C}}^{\operatorname {ct}}_{E}(K^{{\mathfrak {p}}}, {\mathbb {I}}_{B}^{\operatorname {an}}({E});{E}(\epsilon )))[\pi ^{ {\mathfrak {p}}}]$ is contained in the kernel of the cup product with ![]() $\widehat {\mathcal {E}}^{\operatorname {an}}(\lambda )$. We have the following commutative diagram.
$\widehat {\mathcal {E}}^{\operatorname {an}}(\lambda )$. We have the following commutative diagram.

The claim now follows from the first part of the next lemma and a simple diagram chase.
Lemma 2.3 Let ![]() $J\subseteq \Delta$ be a subset.
$J\subseteq \Delta$ be a subset.
(i) The canonical map
is injective for all \[ \operatorname{H}^{d}(G(F),{\mathcal{C}}_{E}(K^{{\mathfrak {p}}},v^{\infty}_{P_J}({E});{E}(\epsilon)))[\pi^{{\mathfrak{p}}}]\longrightarrow\operatorname{H}^{d}(G(F),{\mathcal{C}}_{E}(K^{{\mathfrak {p}}},i^{\infty}_{P_J}({E});{E}(\epsilon)))[\pi^{{\mathfrak{p}}}] \]
\[ \operatorname{H}^{d}(G(F),{\mathcal{C}}_{E}(K^{{\mathfrak {p}}},v^{\infty}_{P_J}({E});{E}(\epsilon)))[\pi^{{\mathfrak{p}}}]\longrightarrow\operatorname{H}^{d}(G(F),{\mathcal{C}}_{E}(K^{{\mathfrak {p}}},i^{\infty}_{P_J}({E});{E}(\epsilon)))[\pi^{{\mathfrak{p}}}] \] $d$.
$d$.(ii) It is an isomorphism in degree
 $d=q+|J|$.
$d=q+|J|$.
Proof. The Jordan–Hölder decomposition of ![]() $i^{\infty }_{P_J}({E})$ consists of all generalized Steinberg representations
$i^{\infty }_{P_J}({E})$ consists of all generalized Steinberg representations ![]() $v^{\infty }_{P_I}({E})$ with
$v^{\infty }_{P_I}({E})$ with ![]() $J\subseteq I$, each occurring with multiplicity one. Thus, the second claim follows from [Reference GehrmannGeh21, Proposition 3.9].
$J\subseteq I$, each occurring with multiplicity one. Thus, the second claim follows from [Reference GehrmannGeh21, Proposition 3.9].
Via the well-known resolution (see, for example, [Reference OrlikOrl05, Proposition 11])
 \[ 0 \to i^{\infty}_{P_\Delta}({E})\to \bigoplus_{\substack{I\subseteq J\subseteq \Delta\\ |\Delta\setminus I|=1}}i^{\infty}_{P_I}({E}) \to \cdots \to \bigoplus_{\substack{J\subseteq I\subseteq \Delta\\ |I\setminus J|=1}}i^{\infty}_{P_I}({E}) \to i^{\infty}_{P_J}({E}) \longrightarrow v^{\infty}_{P_J}({E}) \to 0 \]
\[ 0 \to i^{\infty}_{P_\Delta}({E})\to \bigoplus_{\substack{I\subseteq J\subseteq \Delta\\ |\Delta\setminus I|=1}}i^{\infty}_{P_I}({E}) \to \cdots \to \bigoplus_{\substack{J\subseteq I\subseteq \Delta\\ |I\setminus J|=1}}i^{\infty}_{P_I}({E}) \to i^{\infty}_{P_J}({E}) \longrightarrow v^{\infty}_{P_J}({E}) \to 0 \]
one can reduce the first claim to the following statement: Let ![]() $\mathcal {E}_{J,I}$ be any smooth extension of
$\mathcal {E}_{J,I}$ be any smooth extension of ![]() $v^{\infty }_{P_J}({E})$ by
$v^{\infty }_{P_J}({E})$ by ![]() $v^{\infty }_{P_I}({E})$, where
$v^{\infty }_{P_I}({E})$, where ![]() $J\subseteq I \subseteq \Delta$ with
$J\subseteq I \subseteq \Delta$ with ![]() $|I|=|J|+1$. Then the map
$|I|=|J|+1$. Then the map
is injective for all ![]() $d$. Equivalently, it is enough to show that the cup product
$d$. Equivalently, it is enough to show that the cup product
is the zero map for all ![]() $d$. Let
$d$. Let ![]() $\mathcal {E}_{I,J}$ be the unique up to scalar non-split smooth extension of
$\mathcal {E}_{I,J}$ be the unique up to scalar non-split smooth extension of ![]() $v^{\infty }_{P_I}({E})$ by
$v^{\infty }_{P_I}({E})$ by ![]() $v^{\infty }_{P_J}({E})$. By [Reference GehrmannGeh21, Corollary 3.8], the cup product
$v^{\infty }_{P_J}({E})$. By [Reference GehrmannGeh21, Corollary 3.8], the cup product
is an isomorphism. Therefore, it is enough to prove that taking the cup product with ![]() $\mathcal {E}_{J,I} \cup \mathcal {E}_{I,J}$ induces the zero map on
$\mathcal {E}_{J,I} \cup \mathcal {E}_{I,J}$ induces the zero map on ![]() $\operatorname {H}^{\bullet }(G(F), {\mathcal {C}}_{E}(K^{{\mathfrak {p}}},v^{\infty }_{P_I}({E});{E}(\epsilon )))[\pi ^{ {\mathfrak {p}}}]$. This is true because
$\operatorname {H}^{\bullet }(G(F), {\mathcal {C}}_{E}(K^{{\mathfrak {p}}},v^{\infty }_{P_I}({E});{E}(\epsilon )))[\pi ^{ {\mathfrak {p}}}]$. This is true because ![]() $\mathcal {E}_{J,I} \cup \mathcal {E}_{I,J}$ is a smooth
$\mathcal {E}_{J,I} \cup \mathcal {E}_{I,J}$ is a smooth ![]() $2$-extension of
$2$-extension of ![]() $v^{\infty }_{P_I}({E})$ by itself and the space of all such extensions is zero by [Reference OrlikOrl05, Theorem 1].
$v^{\infty }_{P_I}({E})$ by itself and the space of all such extensions is zero by [Reference OrlikOrl05, Theorem 1].
2.3 The automorphic Colmez–Greenberg–Stevens formula
Let ![]() $A$ be an
$A$ be an ![]() ${E}$-affinoid algebra and
${E}$-affinoid algebra and ![]() $\chi \colon B\to A^{\ast }$ a locally analytic character. The parabolic induction
$\chi \colon B\to A^{\ast }$ a locally analytic character. The parabolic induction ![]() $ {\mathbb {I}}_B^{\operatorname {an}}(\chi )$ is naturally an
$ {\mathbb {I}}_B^{\operatorname {an}}(\chi )$ is naturally an ![]() $A[G_ {\mathfrak {p}}]$-module. Given an ideal
$A[G_ {\mathfrak {p}}]$-module. Given an ideal ![]() $ {\mathfrak {m}}\subseteq A$ we let
$ {\mathfrak {m}}\subseteq A$ we let ![]() $\chi _ {\mathfrak {m}}\colon B\to (A/ {\mathfrak {m}})^{\ast }$,
$\chi _ {\mathfrak {m}}\colon B\to (A/ {\mathfrak {m}})^{\ast }$, ![]() $x\longmapsto \chi (x) \bmod {\mathfrak {m}}$ denote the reduction of
$x\longmapsto \chi (x) \bmod {\mathfrak {m}}$ denote the reduction of ![]() $\chi$ modulo
$\chi$ modulo ![]() $ {\mathfrak {m}}$. Similar to Proposition 2.2.1 of [Reference HansenHan17], one can prove that
$ {\mathfrak {m}}$. Similar to Proposition 2.2.1 of [Reference HansenHan17], one can prove that
Let ![]() $ {\mathfrak {m}}\in \operatorname {Spm} A$ be an
$ {\mathfrak {m}}\in \operatorname {Spm} A$ be an ![]() ${E}$-rational point such that
${E}$-rational point such that ![]() $\chi _ {\mathfrak {m}}={{\mathbb 1}}_{G {\mathfrak {p}}}$. Thus, the reduction map induces the maps
$\chi _ {\mathfrak {m}}={{\mathbb 1}}_{G {\mathfrak {p}}}$. Thus, the reduction map induces the maps
in cohomology.
Let ![]() $i^{\vee }$ be the coroot associated with
$i^{\vee }$ be the coroot associated with ![]() $i$. We put
$i$. We put ![]() $\chi _i=\chi \circ i^{\vee } \in \operatorname {Hom}(F_{ {\mathfrak {p}}}^{\ast },A)$. Suppose
$\chi _i=\chi \circ i^{\vee } \in \operatorname {Hom}(F_{ {\mathfrak {p}}}^{\ast },A)$. Suppose ![]() $v\colon \operatorname {Spec} {E}[\varepsilon ]\to \operatorname {Spm} A$ is an element of the tangent space of
$v\colon \operatorname {Spec} {E}[\varepsilon ]\to \operatorname {Spm} A$ is an element of the tangent space of ![]() $\operatorname {Spm} A$ at
$\operatorname {Spm} A$ at ![]() $ {\mathfrak {m}}$. The pullback
$ {\mathfrak {m}}$. The pullback ![]() $\chi _{i,v}$ of
$\chi _{i,v}$ of ![]() $\chi _i$ along
$\chi _i$ along ![]() $v$ is of the form
$v$ is of the form ![]() $\chi _{i,v}=1+ ({\partial }/{\partial v})\chi _{i}\cdot \varepsilon$ for a unique homomorphism
$\chi _{i,v}=1+ ({\partial }/{\partial v})\chi _{i}\cdot \varepsilon$ for a unique homomorphism ![]() $ ({\partial }/{\partial v})\chi _{i}\colon F_ {\mathfrak {p}}^{\ast }\to {E}.$
$ ({\partial }/{\partial v})\chi _{i}\colon F_ {\mathfrak {p}}^{\ast }\to {E}.$
Lemma 2.2 immediately implies the following.
Proposition 2.4 Suppose that the image of ![]() $\operatorname {red}_\chi ^{q+d,\epsilon }$ contains the
$\operatorname {red}_\chi ^{q+d,\epsilon }$ contains the ![]() $\pi {{}^{ {\mathfrak {p}},\infty }}$-isotypic component of
$\pi {{}^{ {\mathfrak {p}},\infty }}$-isotypic component of ![]() $\operatorname {H}^{q+d}(G(F), {\mathcal {C}}^{\operatorname {ct}}_{E}(K^{{\mathfrak {p}}}, {\mathbb {I}}_{B}^{\operatorname {an}}({E});{E}(\epsilon )))$. Then the homomorphism
$\operatorname {H}^{q+d}(G(F), {\mathcal {C}}^{\operatorname {ct}}_{E}(K^{{\mathfrak {p}}}, {\mathbb {I}}_{B}^{\operatorname {an}}({E});{E}(\epsilon )))$. Then the homomorphism ![]() $ ({\partial }/{\partial v})\chi _{i}$ belongs to
$ ({\partial }/{\partial v})\chi _{i}$ belongs to ![]() $\mathcal {L}_{i}^{(d)}(\pi, {\mathfrak {p}})^{\epsilon }$ for every element
$\mathcal {L}_{i}^{(d)}(\pi, {\mathfrak {p}})^{\epsilon }$ for every element ![]() $v$ of the tangent space of
$v$ of the tangent space of ![]() $\operatorname {Spm} A$ at
$\operatorname {Spm} A$ at ![]() $ {\mathfrak {m}}$.
$ {\mathfrak {m}}$.
3. Overconvergent cohomology
After giving a brief overview on Kohlhaase and Schraen's Koszul resolution of locally analytic principal series (see [Reference Kohlhaase and SchraenKS12]) we recall the control theorem relating overconvergent cohomology to classical cohomology as proven by Ash–Stevens, Urban and Hansen (see [Reference Ash and StevensAS08, Reference UrbanUrb11, Reference HansenHan17]). Combining the two results allows us to construct classes in the cohomology of (duals of) principal series. If ![]() $G_\infty$ fulfils the Harish-Chandra condition, i.e. if
$G_\infty$ fulfils the Harish-Chandra condition, i.e. if ![]() $\delta =0$, we can lift the construction to families of principal series. This implies our main theorem.
$\delta =0$, we can lift the construction to families of principal series. This implies our main theorem.
3.1 Koszul complexes
In [Reference Kohlhaase and SchraenKS12], Kohlhaase and Schraen construct a resolution of locally analytic principal series representations via a Koszul complex. We recall their construction in a slightly more general setup: instead of restricting to ![]() $p$-adic fields as coefficient rings we allow affinoid algebras. The proofs of [Reference Kohlhaase and SchraenKS12] carry over verbatim to this more general framework.
$p$-adic fields as coefficient rings we allow affinoid algebras. The proofs of [Reference Kohlhaase and SchraenKS12] carry over verbatim to this more general framework.
Let us fix some notation: we denote the Borel opposite of ![]() $B\subseteq {G_{F_ {\mathfrak {p}}}}$ by
$B\subseteq {G_{F_ {\mathfrak {p}}}}$ by ![]() $\bar {B}$. Let
$\bar {B}$. Let ![]() $\bar {N}\subseteq \bar {B}$ be its unipotent radical. The chosen torus
$\bar {N}\subseteq \bar {B}$ be its unipotent radical. The chosen torus ![]() $T\subseteq B\subseteq G_{F_ {\mathfrak {p}}}$ determines an apartment in the Bruhat–Tits building of
$T\subseteq B\subseteq G_{F_ {\mathfrak {p}}}$ determines an apartment in the Bruhat–Tits building of ![]() $G_ {\mathfrak {p}}$. We chose a chamber
$G_ {\mathfrak {p}}$. We chose a chamber ![]() $C$ of that apartment and a special vertex
$C$ of that apartment and a special vertex ![]() $v$ of
$v$ of ![]() $C$ as in § 3.5. of [Reference CartierCar79]. The stabilizer
$C$ as in § 3.5. of [Reference CartierCar79]. The stabilizer ![]() $G_{ {\mathfrak {p}},0}\subseteq G_ {\mathfrak {p}}$ of
$G_{ {\mathfrak {p}},0}\subseteq G_ {\mathfrak {p}}$ of ![]() $v$ is a maximal compact subgroup of
$v$ is a maximal compact subgroup of ![]() $G_ {\mathfrak {p}}$ and the stabilizer
$G_ {\mathfrak {p}}$ and the stabilizer ![]() $I_ {\mathfrak {p}}\subseteq G_{ {\mathfrak {p}},0}$ of
$I_ {\mathfrak {p}}\subseteq G_{ {\mathfrak {p}},0}$ of ![]() $C$ is an Iwahori subgroup. Let
$C$ is an Iwahori subgroup. Let ![]() $\mathfrak {G}_0$ be the Bruhat–Tits group scheme over
$\mathfrak {G}_0$ be the Bruhat–Tits group scheme over ![]() $\mathcal {O}_ {\mathfrak {p}}$ associated with
$\mathcal {O}_ {\mathfrak {p}}$ associated with ![]() $G_{ {\mathfrak {p}},0}$. We define
$G_{ {\mathfrak {p}},0}$. We define
The open normal subgroups ![]() $I_ {\mathfrak {p}}^{n}\subseteq I_ {\mathfrak {p}}$ form a system of neighbourhoods of the identity in
$I_ {\mathfrak {p}}^{n}\subseteq I_ {\mathfrak {p}}$ form a system of neighbourhoods of the identity in ![]() $I_ {\mathfrak {p}}$. The subgroup
$I_ {\mathfrak {p}}$. The subgroup ![]() $T_0=T\cap G_{ {\mathfrak {p}},0}$ is maximal compact subgroup of
$T_0=T\cap G_{ {\mathfrak {p}},0}$ is maximal compact subgroup of ![]() $T$.
$T$.
Let ![]() $X^{\ast }(T)$ (respectively,
$X^{\ast }(T)$ (respectively, ![]() $X_{\ast }(T)$) denote the group of
$X_{\ast }(T)$) denote the group of ![]() $F_ {\mathfrak {p}}$-rational characters (respectively, cocharacters) of
$F_ {\mathfrak {p}}$-rational characters (respectively, cocharacters) of ![]() $T$. The natural pairing
$T$. The natural pairing
is a perfect pairing. There is a natural isomorphism ![]() $T/T_0\cong X_{\ast }(T)$ characterized by
$T/T_0\cong X_{\ast }(T)$ characterized by
We denote by ![]() $\Phi ^{+}$ the set of positive roots with respect to
$\Phi ^{+}$ the set of positive roots with respect to ![]() $B$ and put
$B$ and put
Let ![]() $A$ be a
$A$ be a ![]() $ {\mathbb {Q}}_p$-affinoid algebra. Restricting to
$ {\mathbb {Q}}_p$-affinoid algebra. Restricting to ![]() $T_0$ gives a bijection between locally analytic characters
$T_0$ gives a bijection between locally analytic characters ![]() $\chi \colon B\cap I_ {\mathfrak {p}}\to A^{\ast }$ and locally analytic characters
$\chi \colon B\cap I_ {\mathfrak {p}}\to A^{\ast }$ and locally analytic characters ![]() $\chi \colon T_0\to A^{\ast }$. Given such a character
$\chi \colon T_0\to A^{\ast }$. Given such a character ![]() $\chi$ we write
$\chi$ we write
for the locally analytic induction of ![]() $\chi$ to
$\chi$ to ![]() $I_ {\mathfrak {p}}$. It is naturally an
$I_ {\mathfrak {p}}$. It is naturally an ![]() $A[I_ {\mathfrak {p}}]$-module. Restricting a function
$A[I_ {\mathfrak {p}}]$-module. Restricting a function ![]() $f\in {\mathcal {A}}_{\chi }$ to the intersection
$f\in {\mathcal {A}}_{\chi }$ to the intersection ![]() $I_ {\mathfrak {p}}\cap \bar {N}$ induces an isomorphism of
$I_ {\mathfrak {p}}\cap \bar {N}$ induces an isomorphism of ![]() $ {\mathcal {A}}_\chi$ with the space of all locally analytic functions from
$ {\mathcal {A}}_\chi$ with the space of all locally analytic functions from ![]() $I_ {\mathfrak {p}}\cap \bar {N}$ to
$I_ {\mathfrak {p}}\cap \bar {N}$ to ![]() $A$. There exists a minimal integer
$A$. There exists a minimal integer ![]() $n_\chi \geqslant 1$ such that
$n_\chi \geqslant 1$ such that ![]() $\chi$ restricted to
$\chi$ restricted to ![]() $B\cap I_ {\mathfrak {p}}^{n_\chi }$ is rigid analytic. For any
$B\cap I_ {\mathfrak {p}}^{n_\chi }$ is rigid analytic. For any ![]() $n\geqslant n_\chi$ we define the
$n\geqslant n_\chi$ we define the ![]() $A[I_ {\mathfrak {p}}]$-submodule
$A[I_ {\mathfrak {p}}]$-submodule
For later purposes, we define the dual spaces
By Frobenius reciprocity we can identify ![]() $\operatorname {End}_{A[ G_ {\mathfrak {p}}]}(\operatorname {c-ind}_{I_ {\mathfrak {p}}}^{G_ {\mathfrak {p}}} ( {\mathcal {A}}^{n}_{\chi }))$ with the space of all functions
$\operatorname {End}_{A[ G_ {\mathfrak {p}}]}(\operatorname {c-ind}_{I_ {\mathfrak {p}}}^{G_ {\mathfrak {p}}} ( {\mathcal {A}}^{n}_{\chi }))$ with the space of all functions ![]() $\Psi \colon G_ {\mathfrak {p}}\to \operatorname {End}_{A}( {\mathcal {A}}_{\chi }^{n})$ such that:
$\Psi \colon G_ {\mathfrak {p}}\to \operatorname {End}_{A}( {\mathcal {A}}_{\chi }^{n})$ such that:
(i)
 $\Psi$ is
$\Psi$ is  $I_ {\mathfrak {p}}$-biequivariant, i.e.
$I_ {\mathfrak {p}}$-biequivariant, i.e.  $\Psi (k_1 g k_2)=k_1 \Psi (g)k_2$ for all
$\Psi (k_1 g k_2)=k_1 \Psi (g)k_2$ for all  $k_1 ,k_2\in I_ {\mathfrak {p}}$,
$k_1 ,k_2\in I_ {\mathfrak {p}}$,  $g\in G_ {\mathfrak {p}}$; and
$g\in G_ {\mathfrak {p}}$; and(ii) for every
 $f\in {\mathcal {A}}_{\chi }^{n}$ the function
$f\in {\mathcal {A}}_{\chi }^{n}$ the function  $G_ {\mathfrak {p}}\to {\mathcal {A}}_{\chi }^{n}$,
$G_ {\mathfrak {p}}\to {\mathcal {A}}_{\chi }^{n}$,  $g\mapsto \Psi (g)(f)$ is compactly supported.
$g\mapsto \Psi (g)(f)$ is compactly supported.
Let ![]() $t$ be an element of
$t$ be an element of ![]() $T^{-}$ and
$T^{-}$ and ![]() $f\in {\mathcal {A}}_{\chi }^{n}$. The function
$f\in {\mathcal {A}}_{\chi }^{n}$. The function ![]() $I_ {\mathfrak {p}}\to A$,
$I_ {\mathfrak {p}}\to A$, ![]() $u\mapsto f(tut^{-1})$ defines an element of
$u\mapsto f(tut^{-1})$ defines an element of ![]() $ {\mathcal {A}}_{\chi }^{n}$.
$ {\mathcal {A}}_{\chi }^{n}$.
Lemma 3.1 For every element ![]() $t\in T^{-}$ there exists a unique
$t\in T^{-}$ there exists a unique ![]() $I_ {\mathfrak {p}}$-biequivariant function
$I_ {\mathfrak {p}}$-biequivariant function ![]() $\Psi _t\colon G_ {\mathfrak {p}} \to \operatorname {End}_A( {\mathcal {A}}_{\chi }^{n})$ such that:
$\Psi _t\colon G_ {\mathfrak {p}} \to \operatorname {End}_A( {\mathcal {A}}_{\chi }^{n})$ such that:
(i)
 $\operatorname {supp}(\Psi _t)= I_ {\mathfrak {p}} t^{-1} I_ {\mathfrak {p}}$; and
$\operatorname {supp}(\Psi _t)= I_ {\mathfrak {p}} t^{-1} I_ {\mathfrak {p}}$; and(ii)
 $\Psi _t(t^{-1})(f)(u)=f(tut^{-1})$ for any
$\Psi _t(t^{-1})(f)(u)=f(tut^{-1})$ for any  $f\in {\mathcal {A}}_{\chi }^{n}$ and
$f\in {\mathcal {A}}_{\chi }^{n}$ and  $u\in I_ {\mathfrak {p}}\cap \bar {N}$.
$u\in I_ {\mathfrak {p}}\cap \bar {N}$.
Proof. This is a minor generalization of [Reference Kohlhaase and SchraenKS12, Lemma 2.2].
For ![]() $t\in T^{-}$ we denote by
$t\in T^{-}$ we denote by ![]() $U_t$ the endomorphism of
$U_t$ the endomorphism of ![]() $\operatorname {c-ind}_{I_ {\mathfrak {p}}}^{G_ {\mathfrak {p}}} ( {\mathcal {A}}^{n}_{\chi })$ corresponding to
$\operatorname {c-ind}_{I_ {\mathfrak {p}}}^{G_ {\mathfrak {p}}} ( {\mathcal {A}}^{n}_{\chi })$ corresponding to ![]() $\Psi _t$. The following is a straightforward generalization of [Reference Kohlhaase and SchraenKS12, Lemma 2.3].
$\Psi _t$. The following is a straightforward generalization of [Reference Kohlhaase and SchraenKS12, Lemma 2.3].
Lemma 3.2 We have ![]() $U_t U_{\tilde {t}}= U_{t\tilde {t}}$ for all
$U_t U_{\tilde {t}}= U_{t\tilde {t}}$ for all ![]() $t,\tilde {t}\in T^{-}$.
$t,\tilde {t}\in T^{-}$.
Now let us fix a character ![]() $\chi \colon T\to A^{\ast }$ and let
$\chi \colon T\to A^{\ast }$ and let ![]() $\chi _0$ be its restriction to
$\chi _0$ be its restriction to ![]() $T_0$. Given an open subset
$T_0$. Given an open subset ![]() $C\subseteq G_ {\mathfrak {p}}$, which is stable under multiplication with
$C\subseteq G_ {\mathfrak {p}}$, which is stable under multiplication with ![]() $B$ from the left, we denote by
$B$ from the left, we denote by
the subset of all functions with support in ![]() $C$. Restricting functions to
$C$. Restricting functions to ![]() $I_ {\mathfrak {p}}$ gives an
$I_ {\mathfrak {p}}$ gives an ![]() $I_ {\mathfrak {p}}$-equivariant
$I_ {\mathfrak {p}}$-equivariant ![]() $A$-linear isomorphism
$A$-linear isomorphism
Thus, by Frobenius reciprocity its inverse induces a ![]() $G_ {\mathfrak {p}}$-equivariant
$G_ {\mathfrak {p}}$-equivariant ![]() $A$-linear map
$A$-linear map
for any integer ![]() $n\geqslant n_{\chi _0}$.
$n\geqslant n_{\chi _0}$.
As the group ![]() $G_{F_ {\mathfrak {p}}}$ is adjoint, there exist elements
$G_{F_ {\mathfrak {p}}}$ is adjoint, there exist elements ![]() $t_i\in T^{-}$,
$t_i\in T^{-}$, ![]() $i\in \Delta$, such that
$i\in \Delta$, such that
and
The element ![]() $t_i$ is uniquely determined by the value
$t_i$ is uniquely determined by the value ![]() $i(t_i)^{-1}\in F_ {\mathfrak {p}}^{\ast }$, which is a uniformizer. Every element
$i(t_i)^{-1}\in F_ {\mathfrak {p}}^{\ast }$, which is a uniformizer. Every element ![]() $t\in T$ can uniquely be written as
$t\in T$ can uniquely be written as ![]() $t=t_0\prod _{i\in \Delta }t_{i}^{n_i}$ with
$t=t_0\prod _{i\in \Delta }t_{i}^{n_i}$ with ![]() $t\in T_0$ and integers
$t\in T_0$ and integers ![]() $n_{i}\in {\mathbb {Z}}$. Let us fix a choice of
$n_{i}\in {\mathbb {Z}}$. Let us fix a choice of ![]() $t_i$,
$t_i$, ![]() $i\in \Delta$, and put
$i\in \Delta$, and put
Proposition 3.3 The ![]() $G_ {\mathfrak {p}}$-equivariant
$G_ {\mathfrak {p}}$-equivariant ![]() $A$-linear map
$A$-linear map ![]() $\operatorname {aug}_\chi$ is surjective with kernel
$\operatorname {aug}_\chi$ is surjective with kernel ![]() $\sum _{i\in \Delta }\operatorname {im}(y_i).$
$\sum _{i\in \Delta }\operatorname {im}(y_i).$
Proof. The same proof as for [Reference Kohlhaase and SchraenKS12, Proposition 2.4] works here.
By Lemma 3.1 the ![]() $G_ {\mathfrak {p}}$-representation
$G_ {\mathfrak {p}}$-representation ![]() $\operatorname {c-ind}_{I_ {\mathfrak {p}}}^{G_ {\mathfrak {p}}}( {\mathcal {A}}^{n}_{\chi _0})$ is a module over the polynomial algebra
$\operatorname {c-ind}_{I_ {\mathfrak {p}}}^{G_ {\mathfrak {p}}}( {\mathcal {A}}^{n}_{\chi _0})$ is a module over the polynomial algebra ![]() $A[X_i\mid i\in \Delta ]$, where
$A[X_i\mid i\in \Delta ]$, where ![]() $X_i$ acts through the operator
$X_i$ acts through the operator ![]() $T_i$. The Koszul complex of
$T_i$. The Koszul complex of ![]() $\operatorname {c-ind}_{I_ {\mathfrak {p}}}^{G_ {\mathfrak {p}}}( {\mathcal {A}}^{n}_{\chi _0})$ with respect to the endomorphisms
$\operatorname {c-ind}_{I_ {\mathfrak {p}}}^{G_ {\mathfrak {p}}}( {\mathcal {A}}^{n}_{\chi _0})$ with respect to the endomorphisms ![]() $(y_i)_{i\in \Delta }$ is the complex
$(y_i)_{i\in \Delta }$ is the complex ![]() $\Lambda ^{\bullet }_A(A^{\Delta }) \otimes \operatorname {c-ind}_{I_ {\mathfrak {p}}}^{G_ {\mathfrak {p}}}( {\mathcal {A}}_{\chi _0})$ with boundary maps
$\Lambda ^{\bullet }_A(A^{\Delta }) \otimes \operatorname {c-ind}_{I_ {\mathfrak {p}}}^{G_ {\mathfrak {p}}}( {\mathcal {A}}_{\chi _0})$ with boundary maps
 \begin{equation} d_k(e_{i_1}\wedge \cdots \wedge e_{i_k}\otimes f)=\sum_{l=1}^{k}(-1)^{l+1} e_{i_1}\wedge \cdots \wedge \widehat{e_{i_l}}\wedge \cdots \wedge e_{i_k}\otimes y_{i_l}(f). \end{equation}
\begin{equation} d_k(e_{i_1}\wedge \cdots \wedge e_{i_k}\otimes f)=\sum_{l=1}^{k}(-1)^{l+1} e_{i_1}\wedge \cdots \wedge \widehat{e_{i_l}}\wedge \cdots \wedge e_{i_k}\otimes y_{i_l}(f). \end{equation}The following is the main technical theorem of Kohlhaase–Schraen (cf. [Reference Kohlhaase and SchraenKS12, Theorem 2.5]) generalized to affinoid coefficient rings.
Theorem 3.4 (Kohlhaase–Schraen)
For any ![]() $n\geqslant n_{\chi _0}$ the augmented Koszul complex
$n\geqslant n_{\chi _0}$ the augmented Koszul complex
with boundary maps (3.2) and augmentation map (3.1) is exact.
Remark 3.5 All of the results above remain valid if one replaces ![]() $ {\mathcal {A}}_{\chi _0}^{n}$ by
$ {\mathcal {A}}_{\chi _0}^{n}$ by ![]() $ {\mathcal {A}}_{\chi _0}$.
$ {\mathcal {A}}_{\chi _0}$.
Example 3.6 Suppose ![]() $G_ {\mathfrak {p}}=\operatorname {PGL}_n(F_ {\mathfrak {p}})$,
$G_ {\mathfrak {p}}=\operatorname {PGL}_n(F_ {\mathfrak {p}})$, ![]() $T$ is the torus of diagonal matrices and
$T$ is the torus of diagonal matrices and ![]() $B$ is the Borel subgroup of upper triangular matrices. The simple roots of
$B$ is the Borel subgroup of upper triangular matrices. The simple roots of ![]() $T$ with respect to
$T$ with respect to ![]() $B$ are given by
$B$ are given by
for ![]() $1\leqslant i \leqslant d-1$. For each simple root
$1\leqslant i \leqslant d-1$. For each simple root ![]() $1\leqslant i \leqslant d-1$, we might choose for
$1\leqslant i \leqslant d-1$, we might choose for ![]() $t_i$ the image of the diagonal matrix
$t_i$ the image of the diagonal matrix
where ![]() $\pi$ is a uniformizer and exactly the first
$\pi$ is a uniformizer and exactly the first ![]() $i$ entries are equal to one. For the Iwahori subgroup
$i$ entries are equal to one. For the Iwahori subgroup ![]() $I_ {\mathfrak {p}}$, we may choose the image in
$I_ {\mathfrak {p}}$, we may choose the image in ![]() $G_ {\mathfrak {p}}$ of all matrices in
$G_ {\mathfrak {p}}$ of all matrices in ![]() $\operatorname {GL}_n(\mathcal {O}_ {\mathfrak {p}})$, which are upper triangular modulo
$\operatorname {GL}_n(\mathcal {O}_ {\mathfrak {p}})$, which are upper triangular modulo ![]() $ {\mathfrak {p}}$. Then
$ {\mathfrak {p}}$. Then ![]() $I_ {\mathfrak {p}}^{n}$ consists of all matrices in
$I_ {\mathfrak {p}}^{n}$ consists of all matrices in ![]() $I_ {\mathfrak {p}}$ which are congruent to the identity modulo
$I_ {\mathfrak {p}}$ which are congruent to the identity modulo ![]() $ {\mathfrak {p}}^{n}$.
$ {\mathfrak {p}}^{n}$.
There is also a smooth variant of the above result, which is probably well-known. As we could not find a reference in the literature, we give a proof of said variant in the following.
Let ![]() $\Omega$ be field of characteristic zero. With the same formula as before, we can define commuting Hecke operators
$\Omega$ be field of characteristic zero. With the same formula as before, we can define commuting Hecke operators ![]() $U_t\in \operatorname {End}_{G_ {\mathfrak {p}}}(\operatorname {c-ind}_{I_ {\mathfrak {p}}}^{G_ {\mathfrak {p}}}({E}))$ for
$U_t\in \operatorname {End}_{G_ {\mathfrak {p}}}(\operatorname {c-ind}_{I_ {\mathfrak {p}}}^{G_ {\mathfrak {p}}}({E}))$ for ![]() $t\in T^{-}$. Let
$t\in T^{-}$. Let ![]() ${{\mathbb 1}}\colon T_0\to \Omega ^{\times }$ denote the constant character on
${{\mathbb 1}}\colon T_0\to \Omega ^{\times }$ denote the constant character on ![]() $T_0$. In case
$T_0$. In case ![]() $\Omega ={E}$ we can identify
$\Omega ={E}$ we can identify ![]() ${E}$ with the subspace of constant functions in
${E}$ with the subspace of constant functions in ![]() $ {\mathcal {A}}^{n}_{{{\mathbb 1}}}$ and the induced embedding
$ {\mathcal {A}}^{n}_{{{\mathbb 1}}}$ and the induced embedding
is equivariant with respect to the operators ![]() $U_t$,
$U_t$, ![]() $t\in T^{-}$.
$t\in T^{-}$.
The operators ![]() $U_t\in \operatorname {End}_{G_ {\mathfrak {p}}}(\operatorname {c-ind}_{I_ {\mathfrak {p}}}^{G_ {\mathfrak {p}}}(\Omega ))$ are invertible. Moreover, by the Bernstein decomposition the map
$U_t\in \operatorname {End}_{G_ {\mathfrak {p}}}(\operatorname {c-ind}_{I_ {\mathfrak {p}}}^{G_ {\mathfrak {p}}}(\Omega ))$ are invertible. Moreover, by the Bernstein decomposition the map
is injective and ![]() $\operatorname {End}_{G_ {\mathfrak {p}}}(\operatorname {c-ind}_{I_ {\mathfrak {p}}}^{G_ {\mathfrak {p}}}(\Omega ))$ is a free module of finite rank (and, therefore, flat) over
$\operatorname {End}_{G_ {\mathfrak {p}}}(\operatorname {c-ind}_{I_ {\mathfrak {p}}}^{G_ {\mathfrak {p}}}(\Omega ))$ is a free module of finite rank (and, therefore, flat) over ![]() $\Omega [X_i^{\pm 1} | i\in \Delta ]$ (see, for example, [Reference ReederRee92] for more details). As
$\Omega [X_i^{\pm 1} | i\in \Delta ]$ (see, for example, [Reference ReederRee92] for more details). As ![]() $\operatorname {c-ind}_{I_ {\mathfrak {p}}}^{G_ {\mathfrak {p}}}(\Omega )$ is a flat module over its endomorphism algebra by a theorem of Borel (see [Reference BorelBor76, Theorem 4.10]), it is thus also flat as a
$\operatorname {c-ind}_{I_ {\mathfrak {p}}}^{G_ {\mathfrak {p}}}(\Omega )$ is a flat module over its endomorphism algebra by a theorem of Borel (see [Reference BorelBor76, Theorem 4.10]), it is thus also flat as a ![]() $\Omega [X_i^{\pm 1} | i\in \Delta ]$-module.
$\Omega [X_i^{\pm 1} | i\in \Delta ]$-module.
Therefore, for any choice of elements ![]() $a_i\in \Omega ^{\times }$ the Koszul complex
$a_i\in \Omega ^{\times }$ the Koszul complex
associated with the regular sequence ![]() $y_i=U_{t_i}-a_i$,
$y_i=U_{t_i}-a_i$, ![]() $i\in \Delta$, is a resolution of the
$i\in \Delta$, is a resolution of the ![]() $G_ {\mathfrak {p}}$-representation
$G_ {\mathfrak {p}}$-representation
Let ![]() $\chi _{\underline {a}}\colon T\to \Omega ^{\ast }$ be the unique smooth unramified character such that
$\chi _{\underline {a}}\colon T\to \Omega ^{\ast }$ be the unique smooth unramified character such that ![]() $\chi _{\underline {a}}(t_i)=a_i$. As before, we extend
$\chi _{\underline {a}}(t_i)=a_i$. As before, we extend ![]() $\chi _{\underline {a}}$ to a character of
$\chi _{\underline {a}}$ to a character of ![]() $B$. Let
$B$. Let ![]() $\phi \in i^{\infty }_B(\chi _{\underline {a}})$ be the unique element such that:
$\phi \in i^{\infty }_B(\chi _{\underline {a}})$ be the unique element such that:
(i)
 $\phi$ is invariant under
$\phi$ is invariant under  $I_ {\mathfrak {p}}$;
$I_ {\mathfrak {p}}$;(ii) the support of
 $\phi$ is
$\phi$ is  $BI_ {\mathfrak {p}}$; and
$BI_ {\mathfrak {p}}$; and(iii)
 $\phi (1)=1$.
$\phi (1)=1$.
Note that in case ![]() $\chi _{\underline {a}}={{\mathbb 1}}$ is the trivial character the image of
$\chi _{\underline {a}}={{\mathbb 1}}$ is the trivial character the image of ![]() $\phi$ under the quotient map
$\phi$ under the quotient map ![]() $i^{\infty }_B(\Omega )\twoheadrightarrow \operatorname {St}^{\infty }(\Omega )$ is non-zero and, thus, generates the space of Iwahori invariants of the Steinberg representation.
$i^{\infty }_B(\Omega )\twoheadrightarrow \operatorname {St}^{\infty }(\Omega )$ is non-zero and, thus, generates the space of Iwahori invariants of the Steinberg representation.
By Frobenius reciprocity ![]() $\phi$ induces a
$\phi$ induces a ![]() $G_ {\mathfrak {p}}$-equivariant homomorphism
$G_ {\mathfrak {p}}$-equivariant homomorphism
One can argue as in the proof of [Reference OllivierOll14, Proposition 4.4] that the map (3.4) induces an isomorphism
In conclusion, we see that the augmented Koszul complex
is exact.
3.2 Overconvergent cohomology
We show that the result from the previous section together with the theory of overconvergent cohomology allows us to construct cohomology classes with values in duals of locally analytic representations.
Before sticking to the case which is most relevant for our applications let us consider the general case: let ![]() $A$ be a
$A$ be a ![]() $ {\mathbb {Q}}_p$-affinoid algebra and
$ {\mathbb {Q}}_p$-affinoid algebra and ![]() $\chi \colon T\to A$ a locally analytic character. Denote by
$\chi \colon T\to A$ a locally analytic character. Denote by ![]() $\chi _0$ its restriction to
$\chi _0$ its restriction to ![]() $T_0$ and fix elements
$T_0$ and fix elements ![]() $t_i\in T^{-}$,
$t_i\in T^{-}$, ![]() $i\in \Delta$, as before. For
$i\in \Delta$, as before. For ![]() $n\geqslant n_{\chi _0}$ the continuous dual of the augmentation map (3.1) of the previous section yields the map
$n\geqslant n_{\chi _0}$ the continuous dual of the augmentation map (3.1) of the previous section yields the map
for every sign character ![]() $\epsilon$ and every integer
$\epsilon$ and every integer ![]() $d\geqslant 0$. We denote the operator induced by
$d\geqslant 0$. We denote the operator induced by ![]() $U_{t_i}$,
$U_{t_i}$, ![]() $i\in \Delta$, on the right-hand side also by
$i\in \Delta$, on the right-hand side also by ![]() $U_{t_i}$ and similar for
$U_{t_i}$ and similar for ![]() $U_{\tilde {t}}$. Then, Proposition 3.3 implies the following.
$U_{\tilde {t}}$. Then, Proposition 3.3 implies the following.
Corollary 3.7 We have
For the remainder of the section we study the case of the trivial character ![]() ${{\mathbb 1}}={{\mathbb 1}}_{T}\colon T\to {E}^{\ast }$ of
${{\mathbb 1}}={{\mathbb 1}}_{T}\colon T\to {E}^{\ast }$ of ![]() $T$ with values in the units of the
$T$ with values in the units of the ![]() $p$-adic field
$p$-adic field ![]() ${E}$. We denote its restriction to
${E}$. We denote its restriction to ![]() $T_0$ also by
$T_0$ also by ![]() ${{\mathbb 1}}$. Let
${{\mathbb 1}}$. Let ![]() $n\geqslant 1$ be any integer. The map (3.3) induces a homomorphism
$n\geqslant 1$ be any integer. The map (3.3) induces a homomorphism
in cohomology, that is, equivariant with respect to the commuting actions of the Hecke algebra ![]() $ {\mathbb {T}}^{ {\mathfrak {p}}}$ and the operators
$ {\mathbb {T}}^{ {\mathfrak {p}}}$ and the operators ![]() $U_t$,
$U_t$, ![]() $t \in T^{-}$.
$t \in T^{-}$.
In the following, we study the finite slope parts of the above cohomology groups (see, for example, [Reference HansenHan17, § 2.3], for definitions and notation).
Theorem 3.8 (Ash–Stevens, Urban and Hansen)
Let ![]() $\tilde {t}=\prod _{i\in \Delta }t_i.$
$\tilde {t}=\prod _{i\in \Delta }t_i.$
(i) The space
 $\operatorname {H}^{d}(X_{K^{{\mathfrak {p}}}\times I_ {\mathfrak {p}}}, {\mathcal {D}}^{n}_{{{\mathbb 1}}})^{\epsilon }$ admits a slope decomposition with respect to
$\operatorname {H}^{d}(X_{K^{{\mathfrak {p}}}\times I_ {\mathfrak {p}}}, {\mathcal {D}}^{n}_{{{\mathbb 1}}})^{\epsilon }$ admits a slope decomposition with respect to  $U_{\tilde {t}}$ and every rational number
$U_{\tilde {t}}$ and every rational number  $h$.
$h$.(ii) If
 $h$ is small enough with respect to
$h$ is small enough with respect to  $\tilde {t}$ and the trivial character
$\tilde {t}$ and the trivial character  ${{\mathbb 1}}$ (see, for example, the first formula on page 1690 of [Reference UrbanUrb11] or equation
${{\mathbb 1}}$ (see, for example, the first formula on page 1690 of [Reference UrbanUrb11] or equation  $(21)$ of [Reference Ash and StevensAS08]), then the map
is an isomorphism. In particular, this is an isomorphism for
$(21)$ of [Reference Ash and StevensAS08]), then the map
is an isomorphism. In particular, this is an isomorphism for \[ \operatorname{H}^{d}(X_{K^{{\mathfrak {p}}}\times I_{\mathfrak{p}}},{\mathcal{D}}^{n}_{{{\mathbb 1}}})^{\epsilon,\leqslant h} \longrightarrow \operatorname{H}^{d}(X_{K^{{\mathfrak {p}}}\times I_{\mathfrak{p}}},{E})^{\epsilon,\leqslant h}. \]
\[ \operatorname{H}^{d}(X_{K^{{\mathfrak {p}}}\times I_{\mathfrak{p}}},{\mathcal{D}}^{n}_{{{\mathbb 1}}})^{\epsilon,\leqslant h} \longrightarrow \operatorname{H}^{d}(X_{K^{{\mathfrak {p}}}\times I_{\mathfrak{p}}},{E})^{\epsilon,\leqslant h}. \] $h=0$.
$h=0$.
Proof. For the first claim see § 2.3 of [Reference HansenHan17] and for the second see [Reference HansenHan17, Theorem 3.2.5]. The third claim is [Reference UrbanUrb11, Proposition 4.3.10]. Note that in all cases the authors consider all primes lying above ![]() $p$ at once. The same proofs work in our partial
$p$ at once. The same proofs work in our partial ![]() $ {\mathfrak {p}}$-adic setup.
$ {\mathfrak {p}}$-adic setup.
Composing the dual of the augmentation map
with the map (3.6) yields the map
As the diagram

is commutative up to multiplication with a non-zero constant, which comes from the choice of a Iwahori-fixed vector in (1.7), so is the induced diagram in cohomology as follows.

Proposition 3.9 Let ![]() $a_i\in E^{\times }$,
$a_i\in E^{\times }$, ![]() $i\in \Delta$, be elements with
$i\in \Delta$, be elements with ![]() $p$-adic valuation equal to
$p$-adic valuation equal to ![]() $0$ and
$0$ and ![]() $\chi _{\underline {a}}\colon T\to E^{\times }$ the unique smooth unramified character such that
$\chi _{\underline {a}}\colon T\to E^{\times }$ the unique smooth unramified character such that ![]() $\chi _{\underline {a}}(t_i)=a_i$. The natural inclusion
$\chi _{\underline {a}}(t_i)=a_i$. The natural inclusion ![]() $i^{\infty }_{B}(\chi _{\underline {a}})\hookrightarrow {\mathbb {I}}^{\operatorname {an}}_{B}(\chi _{\underline {a}})$ induces an isomorphism
$i^{\infty }_{B}(\chi _{\underline {a}})\hookrightarrow {\mathbb {I}}^{\operatorname {an}}_{B}(\chi _{\underline {a}})$ induces an isomorphism
for all ![]() $d\geqslant 0$. In particular, the map (3.8) induces an isomorphism
$d\geqslant 0$. In particular, the map (3.8) induces an isomorphism
on ![]() $\pi$-isotypic components in degree
$\pi$-isotypic components in degree ![]() $q$.
$q$.
Proof. The second claim is a direct consequence of the first claim and Lemma 2.3.
Given an ![]() $I_ {\mathfrak {p}}$-representation
$I_ {\mathfrak {p}}$-representation ![]() $M$ we denote by
$M$ we denote by ![]() $\operatorname {Coind}_{I_ {\mathfrak {p}}}^{G_ {\mathfrak {p}}}M$ the coinduction of
$\operatorname {Coind}_{I_ {\mathfrak {p}}}^{G_ {\mathfrak {p}}}M$ the coinduction of ![]() $M$ to
$M$ to ![]() $G_ {\mathfrak {p}}$, i.e. the module of all functions
$G_ {\mathfrak {p}}$, i.e. the module of all functions ![]() $f\colon G_ {\mathfrak {p}}\to M$ such that
$f\colon G_ {\mathfrak {p}}\to M$ such that ![]() $f(kg)=kf(g)$ for all
$f(kg)=kf(g)$ for all ![]() $k\in I_ {\mathfrak {p}}$,
$k\in I_ {\mathfrak {p}}$, ![]() $g\in G_ {\mathfrak {p}}$. By taking continuous duals the Koszul complex of Theorem 3.4 with
$g\in G_ {\mathfrak {p}}$. By taking continuous duals the Koszul complex of Theorem 3.4 with ![]() $y_i=U_{t_i}-a_i$ yields a quasi-isomorphism
$y_i=U_{t_i}-a_i$ yields a quasi-isomorphism
of complexes. Note that taking continuous duals in this case is exact by the Hahn–Banach theorem. Similarly by the smooth Koszul resolution (3.5) we have a quasi-isomorphism
and the canonical diagram

is commutative.
From the associated spectral sequences for double complex, we deduce that it is enough to prove that the map of complexes
is a quasi-isomorphism for all ![]() $d\geqslant 0.$ The modules on the left-hand side admit a slope decomposition for
$d\geqslant 0.$ The modules on the left-hand side admit a slope decomposition for ![]() $U_{\tilde {t}}$ by Theorem 3.8(i), whereas the modules on the right-hand side admit a slope decomposition because they are finite-dimensional
$U_{\tilde {t}}$ by Theorem 3.8(i), whereas the modules on the right-hand side admit a slope decomposition because they are finite-dimensional ![]() ${E}$-vector spaces.
${E}$-vector spaces.
As the operators ![]() $y_i$ commute with
$y_i$ commute with ![]() $U_{\tilde {t}}$ they respect the slope decomposition on both sides (see [Reference UrbanUrb11, Lemma 2.3.2]). On the slope less than or equal to zero part the map (3.9) is even an isomorphism of complexes by Theorem 3.8(ii).
$U_{\tilde {t}}$ they respect the slope decomposition on both sides (see [Reference UrbanUrb11, Lemma 2.3.2]). On the slope less than or equal to zero part the map (3.9) is even an isomorphism of complexes by Theorem 3.8(ii).
Thus, we are reduced to proving that
is a quasi-isomorphism for all ![]() $d\geqslant 0$.
$d\geqslant 0$.
In fact, both sides are acyclic: standard properties of Koszul complexes imply that the operators ![]() $y_i$ act as multiplication by zero on the cohomology of the complexes. By the definition of a slope decomposition the operator
$y_i$ act as multiplication by zero on the cohomology of the complexes. By the definition of a slope decomposition the operator ![]() $U_{\tilde {t}}-\prod _{i\in \Delta } a_i$ acts via isomorphisms on both complexes and, thus, on their cohomology. However, because
$U_{\tilde {t}}-\prod _{i\in \Delta } a_i$ acts via isomorphisms on both complexes and, thus, on their cohomology. However, because ![]() $U_{\tilde {t}}-\prod _{i\in \Delta } a_i$ lies in the ideal generated by the operators
$U_{\tilde {t}}-\prod _{i\in \Delta } a_i$ lies in the ideal generated by the operators ![]() $y_i$, it also acts via multiplication by zero, which proves the claim.
$y_i$, it also acts via multiplication by zero, which proves the claim.
Remark 3.10 In order to keep the article short and avoid unnecessary notation, we decided to stick to the special case above. However, Proposition 3.9 also holds in a much more general situation, e.g. one can allow arbitrary coefficient systems and arbitrary non-critical principal series representations, given that the slope is small enough with respect to ![]() $\tilde {t}$.
$\tilde {t}$.
3.3 Overconvergent families
Let ![]() $ {\mathcal {W}}$ be the weight space of
$ {\mathcal {W}}$ be the weight space of ![]() $T$, i.e. it is the rigid space over
$T$, i.e. it is the rigid space over ![]() ${E}$ such that for every
${E}$ such that for every ![]() ${E}$-affinoid algebra
${E}$-affinoid algebra ![]() $A$ its
$A$ its ![]() $A$-points are given by
$A$-points are given by
It is smaller than the usual weight space as we only consider characters of the torus in ![]() $G_{F_ {\mathfrak {p}}}$. For any open affinoid
$G_{F_ {\mathfrak {p}}}$. For any open affinoid ![]() $\mathcal {U} \subset {\mathcal {W}}$ and we let
$\mathcal {U} \subset {\mathcal {W}}$ and we let ![]() $\chi _{\mathcal {U}}$ be the corresponding universal weight. As in § 3.1 we define the space of
$\chi _{\mathcal {U}}$ be the corresponding universal weight. As in § 3.1 we define the space of ![]() $n$-analytic functions and distributions
$n$-analytic functions and distributions ![]() $ {\mathcal {A}}_{\chi _{\mathcal {U}}}^{n}$ and
$ {\mathcal {A}}_{\chi _{\mathcal {U}}}^{n}$ and ![]() $ {\mathcal {D}}^{n}_{\chi _{\mathcal {U}}}$ for
$ {\mathcal {D}}^{n}_{\chi _{\mathcal {U}}}$ for ![]() $n\gg 0$.
$n\gg 0$.
We suppose now that the group ![]() $G_\infty$ has discrete series or, equivalently, that
$G_\infty$ has discrete series or, equivalently, that ![]() $\delta =0$ (see [Reference KnappKna01, Theorem 12.20] for the equivalence of these two properties). Thus, by Proposition 1.6, the representation
$\delta =0$ (see [Reference KnappKna01, Theorem 12.20] for the equivalence of these two properties). Thus, by Proposition 1.6, the representation ![]() $\pi ^{\infty }$ appears only in the middle degree cohomology
$\pi ^{\infty }$ appears only in the middle degree cohomology ![]() $\operatorname {H}^{q}(X_{K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}}, {E})$. Hence, we put
$\operatorname {H}^{q}(X_{K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}}, {E})$. Hence, we put ![]() $\mathcal {L}_{i}(\pi, {\mathfrak {p}})^{\epsilon }=\mathcal {L}_{i}^{(q)}(\pi, {\mathfrak {p}})^{\epsilon }$.
$\mathcal {L}_{i}(\pi, {\mathfrak {p}})^{\epsilon }=\mathcal {L}_{i}^{(q)}(\pi, {\mathfrak {p}})^{\epsilon }$.
Let ![]() $ {\mathbb {T}}_{\operatorname {sph}}^{ {\mathfrak {p}}}\subseteq {\mathbb {T}}^{ {\mathfrak {p}}}$ be the spherical Hecke algebra of level
$ {\mathbb {T}}_{\operatorname {sph}}^{ {\mathfrak {p}}}\subseteq {\mathbb {T}}^{ {\mathfrak {p}}}$ be the spherical Hecke algebra of level ![]() $K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}$ over
$K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}$ over ![]() ${E}$, i.e. the commutative Hecke algebra generated by all Hecke operators at finite places
${E}$, i.e. the commutative Hecke algebra generated by all Hecke operators at finite places ![]() $v$ such that
$v$ such that ![]() $K_v$ is hyperspecial. We define
$K_v$ is hyperspecial. We define ![]() $ {\mathbb {T}}_{\operatorname {sph}}$ to be the commutative algebra generated by
$ {\mathbb {T}}_{\operatorname {sph}}$ to be the commutative algebra generated by ![]() $ {\mathbb {T}}_{\operatorname {sph}}$ and all
$ {\mathbb {T}}_{\operatorname {sph}}$ and all ![]() $U_t$-operators for
$U_t$-operators for ![]() $t\in T^{-}$. Let
$t\in T^{-}$. Let ![]() $ {\mathfrak {m}}_\pi \subseteq {\mathbb {T}}_{\operatorname {sph}}$ (respectively,
$ {\mathfrak {m}}_\pi \subseteq {\mathbb {T}}_{\operatorname {sph}}$ (respectively, ![]() $ {\mathfrak {m}}_\pi ^{ {\mathfrak {p}}}\subseteq {\mathbb {T}}_{\operatorname {sph}}^{ {\mathfrak {p}}}$) the maximal ideal associated with
$ {\mathfrak {m}}_\pi ^{ {\mathfrak {p}}}\subseteq {\mathbb {T}}_{\operatorname {sph}}^{ {\mathfrak {p}}}$) the maximal ideal associated with ![]() $\pi$. We assume the following weak non-Eisenstein assumption on the maximal ideal
$\pi$. We assume the following weak non-Eisenstein assumption on the maximal ideal ![]() $ {\mathfrak {m}}_\pi$ throughout this section.
$ {\mathfrak {m}}_\pi$ throughout this section.
Hypothesis (NE)
We have
unless ![]() $d=q$.
$d=q$.
Example 3.11 If the group ![]() $G$ is definite, the hypothesis is automatically true. By strong multiplicity one and the Jacquet–Langlands correspondence, it is also true for inner forms of
$G$ is definite, the hypothesis is automatically true. By strong multiplicity one and the Jacquet–Langlands correspondence, it is also true for inner forms of ![]() $\operatorname {PGL}_2$ over totally real number fields.
$\operatorname {PGL}_2$ over totally real number fields.
Let ![]() $\mathcal {U}$ be an open affinoid of
$\mathcal {U}$ be an open affinoid of ![]() $ {\mathcal {W}}$ and define
$ {\mathcal {W}}$ and define ![]() $\mathcal {O}_{\mathcal {U},{{\mathbb 1}}}$ to be the rigid localization of
$\mathcal {O}_{\mathcal {U},{{\mathbb 1}}}$ to be the rigid localization of ![]() $\mathcal {O}_{ {\mathcal {W}}}(\mathcal {U})$ at the weight
$\mathcal {O}_{ {\mathcal {W}}}(\mathcal {U})$ at the weight ![]() ${{\mathbb 1}}$ (which is the cohomological weight of
${{\mathbb 1}}$ (which is the cohomological weight of ![]() $\pi$), i.e.
$\pi$), i.e.
The following theorem is instrumental in calculating ![]() $\mathcal {L}$-invariants.
$\mathcal {L}$-invariants.
Theorem 3.12 After localization at the ideal ![]() $ {\mathfrak {m}}_{\pi }$ of
$ {\mathfrak {m}}_{\pi }$ of ![]() $ {\mathbb {T}}_{\operatorname {sph}}$ and restricting to a small enough open affinoid
$ {\mathbb {T}}_{\operatorname {sph}}$ and restricting to a small enough open affinoid ![]() $\mathcal {U}$ containing
$\mathcal {U}$ containing ![]() ${{\mathbb 1}}$, the canonical reduction map
${{\mathbb 1}}$, the canonical reduction map
is surjective. Moreover, ![]() $\operatorname {H}^{q} (X_{K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}}, {\mathcal {D}}^{n}_{\chi _{\mathcal {U}}} )^{\epsilon }_{ {\mathfrak {m}}_\pi }$ is a free
$\operatorname {H}^{q} (X_{K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}}, {\mathcal {D}}^{n}_{\chi _{\mathcal {U}}} )^{\epsilon }_{ {\mathfrak {m}}_\pi }$ is a free ![]() $\mathcal {O}_{\mathcal {U},{{\mathbb 1}}}$-module of rank equal to the dimension of
$\mathcal {O}_{\mathcal {U},{{\mathbb 1}}}$-module of rank equal to the dimension of ![]() $\operatorname {H}^{q}(X_{K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}}, {E})^{\epsilon }_{ {\mathfrak {m}}_{\pi }}$.
$\operatorname {H}^{q}(X_{K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}}, {E})^{\epsilon }_{ {\mathfrak {m}}_{\pi }}$.
In addition, we have ![]() $\operatorname {H}^{d} (X_{K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}}, {\mathcal {D}}^{n}_{\chi _{\mathcal {U}}} )^{\epsilon }_{ {\mathfrak {m}}_{\pi }}=0$ for all
$\operatorname {H}^{d} (X_{K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}}, {\mathcal {D}}^{n}_{\chi _{\mathcal {U}}} )^{\epsilon }_{ {\mathfrak {m}}_{\pi }}=0$ for all ![]() $d \neq q$.
$d \neq q$.
Proof. The case of ![]() $\operatorname {PGL}_2$ over a totally real field is proven in detail in [Reference Barrera Salazar, Dimitrov and JorzaBDJ21, Theorem 2.14]. The main ingredient in their proof is the vanishing of the cohomology outside middle degree. Thus, the same proof works in our more general setup.
$\operatorname {PGL}_2$ over a totally real field is proven in detail in [Reference Barrera Salazar, Dimitrov and JorzaBDJ21, Theorem 2.14]. The main ingredient in their proof is the vanishing of the cohomology outside middle degree. Thus, the same proof works in our more general setup.
Definition 3.13 We say that ![]() $ {\mathfrak {m}}_\pi$ is
$ {\mathfrak {m}}_\pi$ is ![]() $ {\mathfrak {p}}$-étale (with respect to
$ {\mathfrak {p}}$-étale (with respect to ![]() $\epsilon$) if every Hecke operator
$\epsilon$) if every Hecke operator ![]() $h\in {\mathbb {T}}_{\operatorname {sph}}$ acts on
$h\in {\mathbb {T}}_{\operatorname {sph}}$ acts on ![]() $\operatorname {H}^{q} (X_{K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}}, {\mathcal {D}}^{n}_{\chi _{\mathcal {U}}} )^{\epsilon }_{ {\mathfrak {m}}_{\pi }}$ as multiplication by an element
$\operatorname {H}^{q} (X_{K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}}, {\mathcal {D}}^{n}_{\chi _{\mathcal {U}}} )^{\epsilon }_{ {\mathfrak {m}}_{\pi }}$ as multiplication by an element ![]() $\alpha _h\in \mathcal {O}_{\mathcal {U},{{\mathbb 1}}}^{\ast }.$
$\alpha _h\in \mathcal {O}_{\mathcal {U},{{\mathbb 1}}}^{\ast }.$
Theorem 3.12 immediately implies the following.
Corollary 3.14 Assume that ![]() $\dim _{E} \operatorname {H}^{q}(X_{K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}}, {E})^{\epsilon }_{ {\mathfrak {m}}_{\pi }}=1$. Then
$\dim _{E} \operatorname {H}^{q}(X_{K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}}, {E})^{\epsilon }_{ {\mathfrak {m}}_{\pi }}=1$. Then ![]() $ {\mathfrak {m}}_\pi$ is
$ {\mathfrak {m}}_\pi$ is ![]() $ {\mathfrak {p}}$-étale.
$ {\mathfrak {p}}$-étale.
Example 3.15 Suppose ![]() $G$ is an inner form of
$G$ is an inner form of ![]() $\operatorname {PGL}_2$ over a totally real number field. Then the above corollary together with strong multiplicity one implies that
$\operatorname {PGL}_2$ over a totally real number field. Then the above corollary together with strong multiplicity one implies that ![]() $ {\mathfrak {m}}_\pi$ is
$ {\mathfrak {m}}_\pi$ is ![]() $ {\mathfrak {p}}$-étale.
$ {\mathfrak {p}}$-étale.
Let ![]() $t_i\in T^{-}$,
$t_i\in T^{-}$, ![]() $i\in \Delta$, be a choice of elements as in § 3.1. Suppose
$i\in \Delta$, be a choice of elements as in § 3.1. Suppose ![]() $ {\mathfrak {m}}_\pi$ is
$ {\mathfrak {m}}_\pi$ is ![]() $ {\mathfrak {p}}$-étale (with respect to
$ {\mathfrak {p}}$-étale (with respect to ![]() $\epsilon$) with associated eigenvalues
$\epsilon$) with associated eigenvalues ![]() $\alpha _{U_{t_i}}\in \mathcal {O}_{\mathcal {U},{{\mathbb 1}}}^{\ast }$,
$\alpha _{U_{t_i}}\in \mathcal {O}_{\mathcal {U},{{\mathbb 1}}}^{\ast }$, ![]() $i \in \Delta$. By possibly shrinking
$i \in \Delta$. By possibly shrinking ![]() $\mathcal {U}$, we may assume that
$\mathcal {U}$, we may assume that ![]() $\alpha _{U_{t_i}}\in \mathcal {O}_{\mathcal {U}}^{\ast }$. Every element
$\alpha _{U_{t_i}}\in \mathcal {O}_{\mathcal {U}}^{\ast }$. Every element ![]() $t\in T$ can be written uniquely as a product
$t\in T$ can be written uniquely as a product ![]() $t=t_0 \prod _{i\in \Delta } t_i^{n_i}$ with
$t=t_0 \prod _{i\in \Delta } t_i^{n_i}$ with ![]() $t_0 \in T_0$,
$t_0 \in T_0$, ![]() $n_i\in {\mathbb {Z}}$. Hence, there exists a unique character
$n_i\in {\mathbb {Z}}$. Hence, there exists a unique character ![]() $\chi _\alpha \colon T\to \mathcal {O}_{\mathcal {U}}^{\ast }$ such that
$\chi _\alpha \colon T\to \mathcal {O}_{\mathcal {U}}^{\ast }$ such that
and
Theorem 3.16 Suppose that ![]() $ {\mathfrak {m}}_\pi$ is
$ {\mathfrak {m}}_\pi$ is ![]() $ {\mathfrak {p}}$-étale (with respect to
$ {\mathfrak {p}}$-étale (with respect to ![]() $\epsilon$) with associated character
$\epsilon$) with associated character ![]() $\chi _\alpha \colon T \to \mathcal {O}_{\mathcal {U}}^{\ast }$. Then for every tangent vector
$\chi _\alpha \colon T \to \mathcal {O}_{\mathcal {U}}^{\ast }$. Then for every tangent vector ![]() $v$ of
$v$ of ![]() $\mathcal {U}$ at
$\mathcal {U}$ at ![]() ${{\mathbb 1}}$ we have:
${{\mathbb 1}}$ we have:
where ![]() $\chi _{\alpha,i}$ denotes the composition
$\chi _{\alpha,i}$ denotes the composition ![]() $\chi _{\alpha }\circ i^{\vee }.$ Moreover, the subspace
$\chi _{\alpha }\circ i^{\vee }.$ Moreover, the subspace ![]() $\mathcal {L}_{i}(\pi, {\mathfrak {p}})^{\epsilon }\subseteq \operatorname {Hom}^{\operatorname {ct}}(F_ {\mathfrak {p}}^{\ast },{E})$ has codimension one.
$\mathcal {L}_{i}(\pi, {\mathfrak {p}})^{\epsilon }\subseteq \operatorname {Hom}^{\operatorname {ct}}(F_ {\mathfrak {p}}^{\ast },{E})$ has codimension one.
Proof. Let ![]() $ {\mathfrak {m}}_{{\mathbb 1}}\subseteq \mathcal {O}_{\mathcal {U}}$ be the maximal ideal corresponding to the trivial character. We put
$ {\mathfrak {m}}_{{\mathbb 1}}\subseteq \mathcal {O}_{\mathcal {U}}$ be the maximal ideal corresponding to the trivial character. We put ![]() $A=\mathcal {O}_{\mathcal {U}}/ {\mathfrak {m}}_{{{\mathbb 1}}}^{2}$ and
$A=\mathcal {O}_{\mathcal {U}}/ {\mathfrak {m}}_{{{\mathbb 1}}}^{2}$ and ![]() $\chi _0 = \chi _{\mathcal {U}} \bmod {\mathfrak {m}}_{{{\mathbb 1}}}^{2}$. Let us write
$\chi _0 = \chi _{\mathcal {U}} \bmod {\mathfrak {m}}_{{{\mathbb 1}}}^{2}$. Let us write ![]() $\widetilde {\chi }_\alpha = \chi _\alpha \bmod {\mathfrak {m}}_{{{\mathbb 1}}}^{2}\colon T \to A$. Using Theorem 3.12 and arguments with Koszul complexes as in the proof of Proposition 3.9 one shows that the image of the map
$\widetilde {\chi }_\alpha = \chi _\alpha \bmod {\mathfrak {m}}_{{{\mathbb 1}}}^{2}\colon T \to A$. Using Theorem 3.12 and arguments with Koszul complexes as in the proof of Proposition 3.9 one shows that the image of the map
is the intersection of the kernels of the homomorphisms ![]() $U_{t_i}-1$. Therefore, the first claim follows from Proposition 2.4.
$U_{t_i}-1$. Therefore, the first claim follows from Proposition 2.4.
We may assume that ![]() ${E}$ is large enough. We explain how to choose appropriate tangent vectors so that
${E}$ is large enough. We explain how to choose appropriate tangent vectors so that ![]() $\mathcal {L}_{i}(\pi, {\mathfrak {p}})^{\epsilon }$ contains elements of the form
$\mathcal {L}_{i}(\pi, {\mathfrak {p}})^{\epsilon }$ contains elements of the form ![]() $\log _{p,\sigma }-\mathcal {L}^{\sigma }\operatorname {ord}_ {\mathfrak {p}}$ for every embedding
$\log _{p,\sigma }-\mathcal {L}^{\sigma }\operatorname {ord}_ {\mathfrak {p}}$ for every embedding ![]() $\sigma \colon F_ {\mathfrak {p}} \to {E}$. This will show that the
$\sigma \colon F_ {\mathfrak {p}} \to {E}$. This will show that the ![]() $\mathcal {L}$-invariant has codimension at most one.
$\mathcal {L}$-invariant has codimension at most one.
Let ![]() ${E} \langle k_\sigma \rangle$ be the ring of power series in the
${E} \langle k_\sigma \rangle$ be the ring of power series in the ![]() $k_\sigma$ and let
$k_\sigma$ and let ![]() $\mathcal {O}_{ {\mathfrak {p}},1}^{\ast }$ denote the free part of
$\mathcal {O}_{ {\mathfrak {p}},1}^{\ast }$ denote the free part of ![]() $\mathcal {O}_{ {\mathfrak {p}}}^{\ast }$. By smoothness of the weight space, we can embed
$\mathcal {O}_{ {\mathfrak {p}}}^{\ast }$. By smoothness of the weight space, we can embed ![]() $\mathcal {O}_{\mathcal {U}}^{\ast }$ in
$\mathcal {O}_{\mathcal {U}}^{\ast }$ in ![]() ${E} \langle k_\sigma \rangle$ and the structural morphism of
${E} \langle k_\sigma \rangle$ and the structural morphism of ![]() ${E} [\kern-1pt[ \mathcal {O}_{ {\mathfrak {p}},1}^{\ast } ]\kern-1pt] $ into
${E} [\kern-1pt[ \mathcal {O}_{ {\mathfrak {p}},1}^{\ast } ]\kern-1pt] $ into ![]() $\mathcal {O}_{\mathcal {U}}^{\ast }$ can be described via the map
$\mathcal {O}_{\mathcal {U}}^{\ast }$ can be described via the map
We can, hence, identify ![]() $\chi _{\alpha,i}$ with a map from
$\chi _{\alpha,i}$ with a map from ![]() $F_{ {\mathfrak {p}}}^{\ast }$ to
$F_{ {\mathfrak {p}}}^{\ast }$ to ![]() $\mathcal {O}_{\mathcal {U}}^{\ast }$. For all
$\mathcal {O}_{\mathcal {U}}^{\ast }$. For all ![]() $n \in \mathbb {Z}$ and
$n \in \mathbb {Z}$ and ![]() $u \in \mathcal {O}_{ {\mathfrak {p}},1}^{\ast }$ we have
$u \in \mathcal {O}_{ {\mathfrak {p}},1}^{\ast }$ we have
Note that
where
 \[ \delta_{\sigma,\sigma'} = \begin{cases} 1 & \mbox{if}\ \sigma=\sigma' \\ 0 & \mbox{otherwise.}\end{cases} \]
\[ \delta_{\sigma,\sigma'} = \begin{cases} 1 & \mbox{if}\ \sigma=\sigma' \\ 0 & \mbox{otherwise.}\end{cases} \]
Take for ![]() $v$ the direction where only
$v$ the direction where only ![]() $k_{\sigma }$ varies, derive
$k_{\sigma }$ varies, derive ![]() $\chi _{\alpha,i}$ along
$\chi _{\alpha,i}$ along ![]() $v$, and evaluate at
$v$, and evaluate at ![]() $k_{\sigma '}=0$ for all
$k_{\sigma '}=0$ for all ![]() $\sigma '$ (corresponding to the weight
$\sigma '$ (corresponding to the weight ![]() ${{\mathbb 1}}$) to obtain
${{\mathbb 1}}$) to obtain
By the Steinberg hypothesis, ![]() $\alpha _{U_{t_i}}({{\mathbb 1}})$ is not vanishing and we are done.
$\alpha _{U_{t_i}}({{\mathbb 1}})$ is not vanishing and we are done.
By Proposition 1.8, the ![]() $\mathcal {L}$-invariant has codimension at least one and, hence, the second claim follows.
$\mathcal {L}$-invariant has codimension at least one and, hence, the second claim follows.
4. Applications
4.1 Hilbert modular forms
We want to study the case of inner forms of ![]() $\operatorname {PGL}_2$, which are split at
$\operatorname {PGL}_2$, which are split at ![]() $ {\mathfrak {p}}$, over a totally real number field
$ {\mathfrak {p}}$, over a totally real number field ![]() $F$ in detail. As there is only one simple root we drop it from the notation. If
$F$ in detail. As there is only one simple root we drop it from the notation. If ![]() $G$ is equal to
$G$ is equal to ![]() $\operatorname {PGL}_2$, one can attach
$\operatorname {PGL}_2$, one can attach ![]() $2^{[F: {\mathbb {Q}}]}$ a priori different
$2^{[F: {\mathbb {Q}}]}$ a priori different ![]() $\mathcal {L}$-invariants
$\mathcal {L}$-invariants ![]() $\mathcal {L}(\pi,p)^{\epsilon }$ to
$\mathcal {L}(\pi,p)^{\epsilon }$ to ![]() $\pi$; in this case, a conjecture of Spieß (cf. [Reference SpießSpi14, Conjecture 6.4]) states that the definition does not depend on
$\pi$; in this case, a conjecture of Spieß (cf. [Reference SpießSpi14, Conjecture 6.4]) states that the definition does not depend on ![]() $\epsilon$, i.e.
$\epsilon$, i.e.
for all choices of sign characters ![]() $\epsilon$ and
$\epsilon$ and ![]() $\epsilon '$. In the same paper, Remark 6.6(b), Spieß also states that ‘an interesting and difficult problem’ is to show that the
$\epsilon '$. In the same paper, Remark 6.6(b), Spieß also states that ‘an interesting and difficult problem’ is to show that the ![]() $\mathcal {L}$-invariant is invariant under Jacquet–Langlands transfers. In this section, thanks to Theorem 3.16, we settle both Spieß’ conjecture and his question.
$\mathcal {L}$-invariant is invariant under Jacquet–Langlands transfers. In this section, thanks to Theorem 3.16, we settle both Spieß’ conjecture and his question.
Moreover, let ![]() $\rho _{\pi }\colon \operatorname {Gal}(\overline { {\mathbb {Q}}}/F)\to \operatorname {GL}_2({E})$ be the Galois representation associated with
$\rho _{\pi }\colon \operatorname {Gal}(\overline { {\mathbb {Q}}}/F)\to \operatorname {GL}_2({E})$ be the Galois representation associated with ![]() $\pi$ (or rather associated with the Jacquet–Langlands transfer
$\pi$ (or rather associated with the Jacquet–Langlands transfer ![]() $\operatorname {JL}(\pi )$ of
$\operatorname {JL}(\pi )$ of ![]() $\pi$ to
$\pi$ to ![]() $\operatorname {PGL}_2$), which exists by work of Taylor (see [Reference TaylorTay89]). As
$\operatorname {PGL}_2$), which exists by work of Taylor (see [Reference TaylorTay89]). As ![]() $\pi$ is
$\pi$ is ![]() $ {\mathfrak {p}}$-ordinary, by Theorem 2 of [Reference WilesWil88] we know that the restriction
$ {\mathfrak {p}}$-ordinary, by Theorem 2 of [Reference WilesWil88] we know that the restriction ![]() $\rho _{\pi, {\mathfrak {p}}}\colon \operatorname {Gal}(\overline { {\mathbb {Q}}_p}/F_ {\mathfrak {p}})$ of
$\rho _{\pi, {\mathfrak {p}}}\colon \operatorname {Gal}(\overline { {\mathbb {Q}}_p}/F_ {\mathfrak {p}})$ of ![]() $\rho _{\pi }$ to a decomposition group at
$\rho _{\pi }$ to a decomposition group at ![]() $ {\mathfrak {p}}$ is ordinary. Moreover, because
$ {\mathfrak {p}}$ is ordinary. Moreover, because ![]() $\pi _ {\mathfrak {p}}$ is Steinberg, a result of Saito (see [Reference SaitoSai09]) implies that this restriction is a non-split extension of the trivial character by the cyclotomic character. Therefore, it gives a class
$\pi _ {\mathfrak {p}}$ is Steinberg, a result of Saito (see [Reference SaitoSai09]) implies that this restriction is a non-split extension of the trivial character by the cyclotomic character. Therefore, it gives a class ![]() $\langle \rho _{\pi, {\mathfrak {p}}}\rangle \in \operatorname {H}^{1}(\operatorname {Gal}(\overline { {\mathbb {Q}}_p}/F_ {\mathfrak {p}}),{E}(1))$, where
$\langle \rho _{\pi, {\mathfrak {p}}}\rangle \in \operatorname {H}^{1}(\operatorname {Gal}(\overline { {\mathbb {Q}}_p}/F_ {\mathfrak {p}}),{E}(1))$, where ![]() ${E}(1)$ denotes the Tate twist of
${E}(1)$ denotes the Tate twist of ![]() ${E}$. The Fontaine–Mazur
${E}$. The Fontaine–Mazur ![]() $\mathcal {L}$-invariant
$\mathcal {L}$-invariant ![]() $\mathcal {L}^{\operatorname {FM}}(\rho _{\pi, {\mathfrak {p}}})$ of
$\mathcal {L}^{\operatorname {FM}}(\rho _{\pi, {\mathfrak {p}}})$ of ![]() $\rho _{\pi, {\mathfrak {p}}}$ is the orthogonal complement of
$\rho _{\pi, {\mathfrak {p}}}$ is the orthogonal complement of ![]() $\langle \rho _{\pi, {\mathfrak {p}}}\rangle$ with respect to the local Tate pairing
$\langle \rho _{\pi, {\mathfrak {p}}}\rangle$ with respect to the local Tate pairing
By local class field theory we have a canonical isomorphism
and, thus, we consider ![]() $\mathcal {L}^{\operatorname {FM}}(\rho _{\pi, {\mathfrak {p}}})$ as a codimension-one subspace of
$\mathcal {L}^{\operatorname {FM}}(\rho _{\pi, {\mathfrak {p}}})$ as a codimension-one subspace of ![]() $\operatorname {Hom}^{\operatorname {ct}}(F_ {\mathfrak {p}}^{\ast },{E})$. We show that automorphic
$\operatorname {Hom}^{\operatorname {ct}}(F_ {\mathfrak {p}}^{\ast },{E})$. We show that automorphic ![]() $\mathcal {L}$-invariants equal the Fontaine–Mazur
$\mathcal {L}$-invariants equal the Fontaine–Mazur ![]() $\mathcal {L}$-invariant of the associated Galois representation.
$\mathcal {L}$-invariant of the associated Galois representation.
Theorem 4.1 Suppose ![]() $G$ is an inner form of
$G$ is an inner form of ![]() $\operatorname {PGL}_2$ over a totally real number field
$\operatorname {PGL}_2$ over a totally real number field ![]() $F$, which is split at the prime
$F$, which is split at the prime ![]() $ {\mathfrak {p}}$ of
$ {\mathfrak {p}}$ of ![]() $F$. Let
$F$. Let ![]() $\pi$ be a cuspidal automorphic representation of parallel weight
$\pi$ be a cuspidal automorphic representation of parallel weight ![]() $2$ of
$2$ of ![]() $G$ that is Steinberg at
$G$ that is Steinberg at ![]() $ {\mathfrak {p}}$.
$ {\mathfrak {p}}$.
(i) The automorphic
 $\mathcal {L}$-invariant of
$\mathcal {L}$-invariant of  $\pi$ is independent of
$\pi$ is independent of  $\epsilon$, i.e.
for all choices of
$\epsilon$, i.e.
for all choices of \[ \mathcal{L}(\pi,{\mathfrak{p}})^{\epsilon} = \mathcal{L}(\pi,{\mathfrak{p}})^{\epsilon'} \]
\[ \mathcal{L}(\pi,{\mathfrak{p}})^{\epsilon} = \mathcal{L}(\pi,{\mathfrak{p}})^{\epsilon'} \] $\epsilon$ and
$\epsilon$ and  $\epsilon '$. We therefore put
$\epsilon '$. We therefore put  $\mathcal {L}(\pi, {\mathfrak {p}})=\mathcal {L}(\pi, {\mathfrak {p}})^{\epsilon }$ for any choice of sign character
$\mathcal {L}(\pi, {\mathfrak {p}})=\mathcal {L}(\pi, {\mathfrak {p}})^{\epsilon }$ for any choice of sign character  $\epsilon$.
$\epsilon$.(ii) Let
 $\operatorname {JL}(\pi )$ be the Jacquet–Langlands transfer of
$\operatorname {JL}(\pi )$ be the Jacquet–Langlands transfer of  $\pi$ to
$\pi$ to  $\operatorname {PGL}_2$. The equality
holds.
$\operatorname {PGL}_2$. The equality
holds. \[ \mathcal{L}(\pi,{\mathfrak{p}}) = \mathcal{L}(\operatorname{JL}(\pi),{\mathfrak{p}}) \]
\[ \mathcal{L}(\pi,{\mathfrak{p}}) = \mathcal{L}(\operatorname{JL}(\pi),{\mathfrak{p}}) \](iii) Let
 $\rho _\pi$ the Galois representation associated with
$\rho _\pi$ the Galois representation associated with  $\pi$. Then
$\pi$. Then
 \[ \mathcal{L}(\pi,{\mathfrak{p}})=\mathcal{L}^{\operatorname{FM}}(\rho_{\pi,{\mathfrak{p}}}). \]
\[ \mathcal{L}(\pi,{\mathfrak{p}})=\mathcal{L}^{\operatorname{FM}}(\rho_{\pi,{\mathfrak{p}}}). \]
Proof. We actually prove that ![]() $\mathcal {L}(\pi, {\mathfrak {p}})^{\epsilon }=\mathcal {L}^{\operatorname {FM}}(\rho _{\pi, {\mathfrak {p}}})$ for every
$\mathcal {L}(\pi, {\mathfrak {p}})^{\epsilon }=\mathcal {L}^{\operatorname {FM}}(\rho _{\pi, {\mathfrak {p}}})$ for every ![]() $\epsilon$, which implies all other claims. As
$\epsilon$, which implies all other claims. As ![]() $ {\mathfrak {m}}_\pi$ is
$ {\mathfrak {m}}_\pi$ is ![]() $ {\mathfrak {p}}$-étale (with respect to
$ {\mathfrak {p}}$-étale (with respect to ![]() $\epsilon$) we can deform the Hecke eigenvalues of
$\epsilon$) we can deform the Hecke eigenvalues of ![]() $\pi$ to a family over an open affinoid subspace of weight space in the following sense: there exists an open affinoid
$\pi$ to a family over an open affinoid subspace of weight space in the following sense: there exists an open affinoid ![]() $\mathcal {U}\subseteq {\mathcal {W}}$ containing the trivial character such that the eigenvalue
$\mathcal {U}\subseteq {\mathcal {W}}$ containing the trivial character such that the eigenvalue ![]() $\alpha _h$ of each Hecke operator
$\alpha _h$ of each Hecke operator ![]() $h\in {\mathbb {T}}_{\operatorname {sph}}$ acting on
$h\in {\mathbb {T}}_{\operatorname {sph}}$ acting on ![]() $\operatorname {H}^{q} (X_{K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}}, {\mathcal {D}}^{n}_{\chi _{\mathcal {U}}} )^{\epsilon }$ is an element of
$\operatorname {H}^{q} (X_{K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}}, {\mathcal {D}}^{n}_{\chi _{\mathcal {U}}} )^{\epsilon }$ is an element of ![]() $\mathcal {O}_{ {\mathcal {W}}}(\mathcal {U})$. As explained in [Reference Barrera Salazar, Dimitrov and JorzaBDJ21, Theorem 2.14(ii)], we may shrink
$\mathcal {O}_{ {\mathcal {W}}}(\mathcal {U})$. As explained in [Reference Barrera Salazar, Dimitrov and JorzaBDJ21, Theorem 2.14(ii)], we may shrink ![]() $\mathcal {U}$ further such that the common eigenspace associated to the eigenvalues
$\mathcal {U}$ further such that the common eigenspace associated to the eigenvalues ![]() $\alpha _h$ is a free
$\alpha _h$ is a free ![]() $\mathcal {O}_{ {\mathcal {W}}}(\mathcal {U})$-submodule of
$\mathcal {O}_{ {\mathcal {W}}}(\mathcal {U})$-submodule of ![]() $\operatorname {H}^{q} (X_{K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}}, {\mathcal {D}}^{n}_{\chi _{\mathcal {U}}} )^{\epsilon }$ of rank equal to the dimension of
$\operatorname {H}^{q} (X_{K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}}, {\mathcal {D}}^{n}_{\chi _{\mathcal {U}}} )^{\epsilon }$ of rank equal to the dimension of ![]() $\operatorname {H}^{q}(X_{K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}}, {E})^{\epsilon }_{ {\mathfrak {m}}_{\pi }}$. By shrinking
$\operatorname {H}^{q}(X_{K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}}, {E})^{\epsilon }_{ {\mathfrak {m}}_{\pi }}$. By shrinking ![]() $\mathcal {U}$ even further we may assume that
$\mathcal {U}$ even further we may assume that ![]() $\alpha _{t_i}\in \mathcal {O}_{ {\mathcal {W}}}(\mathcal {U})^{\times }$ has absolute value one for each
$\alpha _{t_i}\in \mathcal {O}_{ {\mathcal {W}}}(\mathcal {U})^{\times }$ has absolute value one for each ![]() $i\in \Delta$. Then, by the classicality of small slope overconvergent eigenforms, the specialization of these eigenvalues at a classical point
$i\in \Delta$. Then, by the classicality of small slope overconvergent eigenforms, the specialization of these eigenvalues at a classical point ![]() $\lambda \in \mathcal {U}$ are the eigenvalues associated to a cuspidal representation
$\lambda \in \mathcal {U}$ are the eigenvalues associated to a cuspidal representation ![]() $\pi _\lambda$ of weight
$\pi _\lambda$ of weight ![]() $\lambda$.
$\lambda$.
Note that the Galois representation ![]() $\rho _{\pi }$ is irreducible, as the Hilbert modular form associated with
$\rho _{\pi }$ is irreducible, as the Hilbert modular form associated with ![]() $\pi$ is cuspidal. Thus, by standard arguments (see, for example, Theorem B of [Reference ChenevierChe14]) there exists (after possibly shrinking
$\pi$ is cuspidal. Thus, by standard arguments (see, for example, Theorem B of [Reference ChenevierChe14]) there exists (after possibly shrinking ![]() $\mathcal {U}$ again) a family of Galois representations
$\mathcal {U}$ again) a family of Galois representations ![]() $\rho _{\pi,\mathcal {U}}$ over
$\rho _{\pi,\mathcal {U}}$ over ![]() $\mathcal {U}$ passing through
$\mathcal {U}$ passing through ![]() $\rho _{\pi }$, i.e. the specialization of
$\rho _{\pi }$, i.e. the specialization of ![]() $\rho _{\pi,\mathcal {U}}$ at each classical point
$\rho _{\pi,\mathcal {U}}$ at each classical point ![]() $\lambda \in \mathcal {U}$ is isomorphic to the Galois representation attached to
$\lambda \in \mathcal {U}$ is isomorphic to the Galois representation attached to ![]() $\pi _\lambda$. It follows from the results of Saito (see Theorem 1 of [Reference SaitoSai09]) that for every classical point
$\pi _\lambda$. It follows from the results of Saito (see Theorem 1 of [Reference SaitoSai09]) that for every classical point ![]() $z\in \mathcal {U}$ the restriction of the Galois representation
$z\in \mathcal {U}$ the restriction of the Galois representation ![]() $\rho _{\pi,z}$ to a decomposition group is determined by the
$\rho _{\pi,z}$ to a decomposition group is determined by the ![]() $U_ {\mathfrak {p}}$-eigenvalue. Moreover, the Weil–Deligne module of
$U_ {\mathfrak {p}}$-eigenvalue. Moreover, the Weil–Deligne module of ![]() $\rho _{\pi }$ restricted at the decomposition group at
$\rho _{\pi }$ restricted at the decomposition group at ![]() $ {\mathfrak {p}}$ is the Weil–Deligne module associated with the Steinberg representation via the local Langlands correspondence. In particular, our representation (with the filtration induced by the ordinarity of the Galois representation) is non-critical special, as defined in § 3.1 of [Reference DingDin19]; indeed we know that the corresponding
$ {\mathfrak {p}}$ is the Weil–Deligne module associated with the Steinberg representation via the local Langlands correspondence. In particular, our representation (with the filtration induced by the ordinarity of the Galois representation) is non-critical special, as defined in § 3.1 of [Reference DingDin19]; indeed we know that the corresponding ![]() $(\varphi,\Gamma )$-module is an extension of special characters, so we just have to check whether the extensions are split or not. If one extension were split, then the Weil–Deligne representation would also be split, contradicting the fact the monodromy for the Steinberg is maximal.
$(\varphi,\Gamma )$-module is an extension of special characters, so we just have to check whether the extensions are split or not. If one extension were split, then the Weil–Deligne representation would also be split, contradicting the fact the monodromy for the Steinberg is maximal.
Comparing the Galois theoretic Colmez–Greenberg–Stevens formula (see [Reference DingDin19, Theorem 3.4]) with its automorphic counterpart of Theorem 3.16 yields the result.
Remark 4.2 (i) In the Hilbert modular form case, the constructions simplify substantially and, thus, one can check that our methods also work for higher weights assuming that the representation is non-critical.
(ii) One can prove the first two claims of Theorem 4.1 without passing to the Galois side. Namely, using methods as in § 5 of [Reference HansenHan17] one can show that the eigenvalue of the overconvergent ![]() $ {\mathfrak {p}}$-adic family passing through
$ {\mathfrak {p}}$-adic family passing through ![]() $\pi$ is independent of the sign character and stable under the Jacquet–Langlands transfer. Thus, by Theorem 3.16, we can conclude the argument.
$\pi$ is independent of the sign character and stable under the Jacquet–Langlands transfer. Thus, by Theorem 3.16, we can conclude the argument.
(iii) By definition, Fontaine–Mazur ![]() $\mathcal {L}$-invariants are stable under restricting the Galois representation to the absolute Galois group of finite extensions. Thus, we can deduce from Theorem 4.1 that automorphic
$\mathcal {L}$-invariants are stable under restricting the Galois representation to the absolute Galois group of finite extensions. Thus, we can deduce from Theorem 4.1 that automorphic ![]() $\mathcal {L}$-invariants of Hilbert modular forms are stable under abelian base change with respect to totally real extensions.
$\mathcal {L}$-invariants of Hilbert modular forms are stable under abelian base change with respect to totally real extensions.
(iv) In the case of modular elliptic curves over totally real fields of class number one the equality of automorphic and Fontaine–Mazur ![]() $\mathcal {L}$-invariants was conjectured by Greenberg (see [Reference GreenbergGre09, Conjecture 2]). Theorem 4.1 thus implies that the construction of Stark–Heegner points over totally real fields is unconditional (see [Reference Guitart, Masdeu and SengünGMS15] for a detailed discussion of Stark–Heegner points).
$\mathcal {L}$-invariants was conjectured by Greenberg (see [Reference GreenbergGre09, Conjecture 2]). Theorem 4.1 thus implies that the construction of Stark–Heegner points over totally real fields is unconditional (see [Reference Guitart, Masdeu and SengünGMS15] for a detailed discussion of Stark–Heegner points).
4.2 Unitary groups
Let ![]() $\tilde {F}$ be a CM field with totally real subfield
$\tilde {F}$ be a CM field with totally real subfield ![]() $F$. We assume that the prime
$F$. We assume that the prime ![]() $ {\mathfrak {p}}$ of
$ {\mathfrak {p}}$ of ![]() $F$ is split in
$F$ is split in ![]() $\tilde {F}$. Let
$\tilde {F}$. Let ![]() $U$ be the unitary group attached to a positive definite hermitian space over
$U$ be the unitary group attached to a positive definite hermitian space over ![]() $\tilde {F}$ and
$\tilde {F}$ and ![]() $G$ the associated adjoint group. By construction,
$G$ the associated adjoint group. By construction, ![]() $G_ {\mathfrak {p}}$ is isomorphic to
$G_ {\mathfrak {p}}$ is isomorphic to ![]() $\operatorname {PGL}_n(F_ {\mathfrak {p}})$. We can identify the simple roots with respect to the upper triangular Borel with the set
$\operatorname {PGL}_n(F_ {\mathfrak {p}})$. We can identify the simple roots with respect to the upper triangular Borel with the set ![]() $\{1,\ldots, n-1\}$. Let
$\{1,\ldots, n-1\}$. Let ![]() $\pi$ be an automorphic representation of
$\pi$ be an automorphic representation of ![]() $G$ such that
$G$ such that ![]() $\pi _\infty = {\mathbb {C}}$ and
$\pi _\infty = {\mathbb {C}}$ and ![]() $\pi _ {\mathfrak {p}}$ is the Steinberg representation of
$\pi _ {\mathfrak {p}}$ is the Steinberg representation of ![]() $\operatorname {PGL}_n(F_ {\mathfrak {p}})$. In this case the only sign character is the trivial character and, therefore, we drop it from the notation.
$\operatorname {PGL}_n(F_ {\mathfrak {p}})$. In this case the only sign character is the trivial character and, therefore, we drop it from the notation.
By Shin's appendix to [Reference GoldringGol14] the base change ![]() $\operatorname {BC}(\pi )$ of
$\operatorname {BC}(\pi )$ of ![]() $\pi$ to
$\pi$ to ![]() $\operatorname {PGL}_n$ over
$\operatorname {PGL}_n$ over ![]() $\tilde {F}$ exists and it is Steinberg at both primes of
$\tilde {F}$ exists and it is Steinberg at both primes of ![]() $\tilde {F}$ lying above
$\tilde {F}$ lying above ![]() $ {\mathfrak {p}}$. By the work of many people (see Theorem 2.1.1 of [Reference Barnet-Lamb, Gee, Geraghty and TaylorBGGT14] for a detailed discussion) we can attach a
$ {\mathfrak {p}}$. By the work of many people (see Theorem 2.1.1 of [Reference Barnet-Lamb, Gee, Geraghty and TaylorBGGT14] for a detailed discussion) we can attach a ![]() $p$-adic Galois representation
$p$-adic Galois representation
to ![]() $\operatorname {BC}(\pi )$. As we consider the trivial coefficient system the Steinberg representation is ordinary (cf. [Reference GeraghtyGer19, Lemma 5.6]). Therefore, as shown in [Reference ThorneTho15, Theorem 2.4], one deduces from the local–global compatibility theorem of Caraiani (see [Reference CaraianiCar14]) that the restriction
$\operatorname {BC}(\pi )$. As we consider the trivial coefficient system the Steinberg representation is ordinary (cf. [Reference GeraghtyGer19, Lemma 5.6]). Therefore, as shown in [Reference ThorneTho15, Theorem 2.4], one deduces from the local–global compatibility theorem of Caraiani (see [Reference CaraianiCar14]) that the restriction ![]() $\rho _{\pi, {\mathfrak {p}}}$ of
$\rho _{\pi, {\mathfrak {p}}}$ of ![]() $\rho _{\pi }$ to the decomposition group of a prime above
$\rho _{\pi }$ to the decomposition group of a prime above ![]() $ {\mathfrak {p}}$ can be brought in the following form: it is upper triangular and the
$ {\mathfrak {p}}$ can be brought in the following form: it is upper triangular and the ![]() $i$th diagonal entry is the
$i$th diagonal entry is the ![]() $(1-i)$-power of the cyclotomic character.
$(1-i)$-power of the cyclotomic character.
Therefore, we have ![]() $n-1$ canonical two-dimensional subquotients
$n-1$ canonical two-dimensional subquotients ![]() $\rho _{\pi, {\mathfrak {p}},i}$ which are extensions of
$\rho _{\pi, {\mathfrak {p}},i}$ which are extensions of ![]() ${E}(-n+i)$ by
${E}(-n+i)$ by ![]() ${E}(-n+i+1)$. We can consider the associated Fontaine–Mazur
${E}(-n+i+1)$. We can consider the associated Fontaine–Mazur ![]() $\mathcal {L}$-invariant
$\mathcal {L}$-invariant ![]() $\mathcal {L}^{\operatorname {FM}}_{i}(\rho _{\pi, {\mathfrak {p}}})=\mathcal {L}^{\operatorname {FM}}(\rho _{\pi,\pi,i}(n-i))$. Recall that the Weil–Deligne representation associated with the Steinberg has always maximal monodromy so the corresponding
$\mathcal {L}^{\operatorname {FM}}_{i}(\rho _{\pi, {\mathfrak {p}}})=\mathcal {L}^{\operatorname {FM}}(\rho _{\pi,\pi,i}(n-i))$. Recall that the Weil–Deligne representation associated with the Steinberg has always maximal monodromy so the corresponding ![]() $(\varphi,\Gamma )$-module is non-critical split à la Ding, see § 3.1 of [Reference DingDin19]. Replacing the local–global compatibility results of Saito by those of Caraiani (see [Reference CaraianiCar14]), we can apply Theorem 3.4 of [Reference DingDin19] to the
$(\varphi,\Gamma )$-module is non-critical split à la Ding, see § 3.1 of [Reference DingDin19]. Replacing the local–global compatibility results of Saito by those of Caraiani (see [Reference CaraianiCar14]), we can apply Theorem 3.4 of [Reference DingDin19] to the ![]() $(\varphi,\Gamma )$-module associated with the Galois representation
$(\varphi,\Gamma )$-module associated with the Galois representation ![]() $\rho _{\pi }$ and then the same proof as that of Theorem 4.1 yields the following result.
$\rho _{\pi }$ and then the same proof as that of Theorem 4.1 yields the following result.
Theorem 4.3 Let ![]() $F$ be a totally real number field and
$F$ be a totally real number field and ![]() $G$ the adjoint of a unitary group over
$G$ the adjoint of a unitary group over ![]() $F$ compact at infinity and split at
$F$ compact at infinity and split at ![]() $ {\mathfrak {p}}$. Let
$ {\mathfrak {p}}$. Let ![]() $\pi$ be an automorphic representation of
$\pi$ be an automorphic representation of ![]() $G$ such that
$G$ such that ![]() $\pi _\infty = {\mathbb {C}}$ and
$\pi _\infty = {\mathbb {C}}$ and ![]() $\pi _{ {\mathfrak {p}}}$ is Steinberg. Suppose
$\pi _{ {\mathfrak {p}}}$ is Steinberg. Suppose ![]() $\pi$ satisfies (SMO), that we can choose the tame level
$\pi$ satisfies (SMO), that we can choose the tame level ![]() $K^{ {\mathfrak {p}}}$ such that
$K^{ {\mathfrak {p}}}$ such that ![]() $ {\mathfrak {m}}_{\pi }$ is
$ {\mathfrak {m}}_{\pi }$ is ![]() $ {\mathfrak {p}}$-étale and that the Galois representation
$ {\mathfrak {p}}$-étale and that the Galois representation ![]() $\rho _{\pi }$ attached to
$\rho _{\pi }$ attached to ![]() $\pi$ is irreducible. Then we have
$\pi$ is irreducible. Then we have
for every ![]() $i=1,\ldots,n-1$.
$i=1,\ldots,n-1$.
Remark 4.4 Something can be said also when ![]() $F =\mathbb {Q}$ and
$F =\mathbb {Q}$ and ![]() $G=\operatorname {Sp}_{2g}$. In this case the Galois representations have been constructed by Scholze [Reference ScholzeSch15] but local–global compatibility is not known. Still, if one supposes that the
$G=\operatorname {Sp}_{2g}$. In this case the Galois representations have been constructed by Scholze [Reference ScholzeSch15] but local–global compatibility is not known. Still, if one supposes that the ![]() $2g+1$-dimensional Galois representation
$2g+1$-dimensional Galois representation ![]() $\operatorname {Std}(\rho _{\pi })$ associated with
$\operatorname {Std}(\rho _{\pi })$ associated with ![]() $\pi$ is semistable with maximal monodromy, then the Greenberg–Benois
$\pi$ is semistable with maximal monodromy, then the Greenberg–Benois ![]() $\mathcal {L}(\operatorname {Std}(\rho _{\pi }))$-invariant has been calculated in [Reference RossoRos15, Theorem 1.3].
$\mathcal {L}(\operatorname {Std}(\rho _{\pi }))$-invariant has been calculated in [Reference RossoRos15, Theorem 1.3].
In this case the root system of ![]() $\operatorname {Sp}_{2g}$ can be identified with the set
$\operatorname {Sp}_{2g}$ can be identified with the set ![]() $\{1,\ldots,g\}$ via the identification with the root system of
$\{1,\ldots,g\}$ via the identification with the root system of ![]() $\operatorname {GL}_g$, which is embedded in
$\operatorname {GL}_g$, which is embedded in ![]() $\operatorname {Sp}_{2g}$ by
$\operatorname {Sp}_{2g}$ by
and we see that the automorphic ![]() $\mathcal {L}$-invariant
$\mathcal {L}$-invariant ![]() $\mathcal {L}_{1}(\pi,p)$ coincides with that of [Reference RossoRos15].
$\mathcal {L}_{1}(\pi,p)$ coincides with that of [Reference RossoRos15].
The same calculation in § 4.2 of [Reference RossoRos15] gives us that ![]() $\mathcal {L}_{i}(\pi,p)$ is the Greenberg–Benois
$\mathcal {L}_{i}(\pi,p)$ is the Greenberg–Benois ![]() $\mathcal {L}$-invariant for
$\mathcal {L}$-invariant for ![]() $\operatorname {Std}(\rho _{\pi })(i-1)$. (This case has not been treated in [Reference RossoRos15] as the
$\operatorname {Std}(\rho _{\pi })(i-1)$. (This case has not been treated in [Reference RossoRos15] as the ![]() $L$-values are not Deligne-critical, but Benois’ definition applies also in this case, see formula (96) in [Reference BenoisBen21].)
$L$-values are not Deligne-critical, but Benois’ definition applies also in this case, see formula (96) in [Reference BenoisBen21].)
If ![]() $F_ {\mathfrak {p}} \neq {\mathbb {Q}}_p$, then the comparison is more subtle, as there is only just one Greenberg–Benois
$F_ {\mathfrak {p}} \neq {\mathbb {Q}}_p$, then the comparison is more subtle, as there is only just one Greenberg–Benois ![]() $\mathcal {L}$-invariant per
$\mathcal {L}$-invariant per ![]() $p$-adic place, and from the Galois side one needs to consider Galois invariant characters of
$p$-adic place, and from the Galois side one needs to consider Galois invariant characters of ![]() $F^{*}_ {\mathfrak {p}}$.
$F^{*}_ {\mathfrak {p}}$.
5. Beyond discrete series: the Bianchi case
When ![]() $G_\infty$ does not fulfil the Harish-Chandra condition, the representation
$G_\infty$ does not fulfil the Harish-Chandra condition, the representation ![]() $\pi$ contributes to several degrees of cohomology of the associated locally symmetric space and the techniques used in Theorem 3.12 break down.
$\pi$ contributes to several degrees of cohomology of the associated locally symmetric space and the techniques used in Theorem 3.12 break down.
There are two tools to tackle the problem: first, one can use Hansen's Tor-spectral sequence (see Theorem 3.3.1 of [Reference HansenHan17])
where ![]() $\mathcal {U}\subseteq {\mathcal {W}}$ is an open affinoid and
$\mathcal {U}\subseteq {\mathcal {W}}$ is an open affinoid and ![]() $\Sigma \subseteq \mathcal {U}$ is Zariski-closed, to analyse the overconvergent cohomology groups in question; second, one can use cases of Langlands functoriality in
$\Sigma \subseteq \mathcal {U}$ is Zariski-closed, to analyse the overconvergent cohomology groups in question; second, one can use cases of Langlands functoriality in ![]() $p$-adic families to reduce to groups, which fulfil the Harish-Chandra condition.
$p$-adic families to reduce to groups, which fulfil the Harish-Chandra condition.
In good situations it should be possible to calculate at least one of the ![]() $\mathcal {L}$-invariants
$\mathcal {L}$-invariants ![]() $\mathcal {L}^{(d)}_{i}(\pi, {\mathfrak {p}})$ for
$\mathcal {L}^{(d)}_{i}(\pi, {\mathfrak {p}})$ for ![]() $0 \leqslant d\leqslant \delta$, using Proposition 2.4. The main difficulty is that, in general, most classes do not lift to a big cohomology class as classes in
$0 \leqslant d\leqslant \delta$, using Proposition 2.4. The main difficulty is that, in general, most classes do not lift to a big cohomology class as classes in ![]() $\operatorname {H}^{q+1}$ give lifting obstructions. However, as soon as one can show that at least a class lifts to a family in
$\operatorname {H}^{q+1}$ give lifting obstructions. However, as soon as one can show that at least a class lifts to a family in ![]() $\operatorname {H}^{q+d}$ (combined with some results on the tangent directions in the eigenvariety) Proposition 2.4 lets us calculate
$\operatorname {H}^{q+d}$ (combined with some results on the tangent directions in the eigenvariety) Proposition 2.4 lets us calculate ![]() $\mathcal {L}^{(d)}_{i}(\pi, {\mathfrak {p}})$. If Venkatesh's conjecture (stating that the
$\mathcal {L}^{(d)}_{i}(\pi, {\mathfrak {p}})$. If Venkatesh's conjecture (stating that the ![]() $\pi$-isotypic component of the cohomology is generated by the minimal degree cohomology as a module over the derived Hecke algebra) holds, then these
$\pi$-isotypic component of the cohomology is generated by the minimal degree cohomology as a module over the derived Hecke algebra) holds, then these ![]() $\mathcal {L}$-invariants
$\mathcal {L}$-invariants ![]() $\mathcal {L}^{(d)}_{i}(\pi, {\mathfrak {p}})$, for varying
$\mathcal {L}^{(d)}_{i}(\pi, {\mathfrak {p}})$, for varying ![]() $d$, are essentially all the same by the main result of [Reference GehrmannGeh19a].
$d$, are essentially all the same by the main result of [Reference GehrmannGeh19a].
Using unpublished work of Hansen (see also [Reference Barrera Salazar and WilliamsBW21]) we study the case of Bianchi modular forms. We now fix ![]() $F$ to be a quadratic imaginary field where
$F$ to be a quadratic imaginary field where ![]() $p$ is unramified and
$p$ is unramified and ![]() $\pi$ a cuspidal representation of
$\pi$ a cuspidal representation of ![]() $\operatorname {PGL}_{2,F}$ of parallel weight
$\operatorname {PGL}_{2,F}$ of parallel weight ![]() $2$ such that
$2$ such that ![]() $\pi _ {\mathfrak {q}}$ is Steinberg for all primes
$\pi _ {\mathfrak {q}}$ is Steinberg for all primes ![]() $ {\mathfrak {q}}$ lying above
$ {\mathfrak {q}}$ lying above ![]() $p$. We put
$p$. We put ![]() $G=\operatorname {PGL}_{2,F}$ if
$G=\operatorname {PGL}_{2,F}$ if ![]() $p$ is inert and, if
$p$ is inert and, if ![]() $p$ is split, we define
$p$ is split, we define ![]() $G$ to be the Weil restriction
$G$ to be the Weil restriction ![]() $\operatorname {Res}_{F/ {\mathbb {Q}}}\operatorname {PGL}_{2,F}$. In the first case there is only one simple root and, thus, we drop it from the notation. In the second case, the simple roots can be identified with the two primes above
$\operatorname {Res}_{F/ {\mathbb {Q}}}\operatorname {PGL}_{2,F}$. In the first case there is only one simple root and, thus, we drop it from the notation. In the second case, the simple roots can be identified with the two primes above ![]() $ {\mathfrak {p}}$. In both cases, the only sign character is the trivial one and we shall drop it from the notation as well. (The following theorem indicates that in the case of a split prime the partial eigenvarieties we considered before may not be big enough. The case that
$ {\mathfrak {p}}$. In both cases, the only sign character is the trivial one and we shall drop it from the notation as well. (The following theorem indicates that in the case of a split prime the partial eigenvarieties we considered before may not be big enough. The case that ![]() $p$ is split and
$p$ is split and ![]() $\pi$ is only Steinberg at one of the primes above
$\pi$ is only Steinberg at one of the primes above ![]() $p$ could be handled similarly but one would have to introduce new notation. For the sake of brevity, we do not discuss it further.)
$p$ could be handled similarly but one would have to introduce new notation. For the sake of brevity, we do not discuss it further.)
We recall some result on the eigenvariety for Bianchi modular forms due to Hansen and Barrera–Williams (see [Reference Barrera Salazar and WilliamsBW21, Lemma 4.4] and the proof of Theorem 4.5).
Theorem 5.1 (Hansen, Barrera–Williams)
Let ![]() $\mathcal {U}\subseteq {\mathcal {W}}$ be an open affinoid neighbourhood of the trivial character.
$\mathcal {U}\subseteq {\mathcal {W}}$ be an open affinoid neighbourhood of the trivial character.
(i) The system of eigenvalues associated with
 $\pi$ appears in
$\pi$ appears in  $\operatorname {H}^{d}(X_{K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}}, {\mathcal {D}}_{\chi _{\mathcal {U}}})$ if and only if
$\operatorname {H}^{d}(X_{K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}}, {\mathcal {D}}_{\chi _{\mathcal {U}}})$ if and only if  $d=2$.
$d=2$.(ii) There is at least one curve
 $\mathcal {S} \subseteq \mathcal {U}$ passing through
$\mathcal {S} \subseteq \mathcal {U}$ passing through  ${{\mathbb 1}}$ such that
If such a curve
${{\mathbb 1}}$ such that
If such a curve \[ \operatorname{H}^{1}(X_{K^{{\mathfrak{p}}}\times I_{{\mathfrak{p}}}}, {\mathcal{D}}_{\chi_{\mathcal{S}}})_{{\mathfrak{m}}_{\pi}}\neq 0. \]
\[ \operatorname{H}^{1}(X_{K^{{\mathfrak{p}}}\times I_{{\mathfrak{p}}}}, {\mathcal{D}}_{\chi_{\mathcal{S}}})_{{\mathfrak{m}}_{\pi}}\neq 0. \] $\mathcal {S}$ is smooth at
$\mathcal {S}$ is smooth at  ${{\mathbb 1}}$, the space is free of rank one over
${{\mathbb 1}}$, the space is free of rank one over  $\mathcal {O}_{\mathcal {S}, {{\mathbb 1}}}$ and the canonical map
is surjective.
$\mathcal {O}_{\mathcal {S}, {{\mathbb 1}}}$ and the canonical map
is surjective. \[ \operatorname{H}^{1}(X_{K^{{\mathfrak{p}}}\times I_{{\mathfrak{p}}}}, {\mathcal{D}}_{\chi_{\mathcal{S}}})_{{\mathfrak{m}}_{\pi}}\longrightarrow \operatorname{H}^{1}(X_{K^{{\mathfrak{p}}}\times I_{{\mathfrak{p}}}}, {E})_{{\mathfrak{m}}_{\pi}} \]
\[ \operatorname{H}^{1}(X_{K^{{\mathfrak{p}}}\times I_{{\mathfrak{p}}}}, {\mathcal{D}}_{\chi_{\mathcal{S}}})_{{\mathfrak{m}}_{\pi}}\longrightarrow \operatorname{H}^{1}(X_{K^{{\mathfrak{p}}}\times I_{{\mathfrak{p}}}}, {E})_{{\mathfrak{m}}_{\pi}} \]
The following proposition completes the picture by taking into account the cohomology in degree two.
Proposition 5.2 For every curve ![]() $\mathcal {S}$ as in Theorem 5.1(ii) that is smooth at
$\mathcal {S}$ as in Theorem 5.1(ii) that is smooth at ![]() ${{\mathbb 1}}$ we have
${{\mathbb 1}}$ we have
More precisely, the space is free of rank one over ![]() $\mathcal {O}_{\mathcal {S}, {{\mathbb 1}}}$ and the canonical map
$\mathcal {O}_{\mathcal {S}, {{\mathbb 1}}}$ and the canonical map
is an isomorphism. Moreover, ![]() $\operatorname {H}^{2}(X_{K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}}, {\mathcal {D}}_{\chi _{\mathcal {S}}})_{ {\mathfrak {m}}_{\pi }}$ and
$\operatorname {H}^{2}(X_{K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}}, {\mathcal {D}}_{\chi _{\mathcal {S}}})_{ {\mathfrak {m}}_{\pi }}$ and ![]() $\operatorname {H}^{1}(X_{K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}}, {\mathcal {D}}_{\chi _{\mathcal {S}}})_{ {\mathfrak {m}}_{\pi }}$ are isomorphic as modules over the Hecke algebra.
$\operatorname {H}^{1}(X_{K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}}, {\mathcal {D}}_{\chi _{\mathcal {S}}})_{ {\mathfrak {m}}_{\pi }}$ are isomorphic as modules over the Hecke algebra.
Proof. Let ![]() $m$ be a generator of the maximal ideal of the localization. From the short exact sequence
$m$ be a generator of the maximal ideal of the localization. From the short exact sequence
we obtain a long exact sequence in cohomology
 \begin{align*} & \xrightarrow{\times m}\operatorname{H}^{1}(X_{K^{{\mathfrak{p}}}\times I_{{\mathfrak{p}}}}, {\mathcal{D}}_{\chi_{\mathcal{S}}})_{{\mathfrak{m}}_{\pi}} \longrightarrow \operatorname{H}^{1}(X_{K^{{\mathfrak{p}}}\times I_{{\mathfrak{p}}}}, {E})_{{\mathfrak{m}}_{\pi}} \xrightarrow{0} \operatorname{H}^{2}(X_{K^{{\mathfrak{p}}}\times I_{{\mathfrak{p}}}}, {\mathcal{D}}_{\chi_{\mathcal{S}}})_{{\mathfrak{m}}_{\pi}} \\ & \xrightarrow{\times m} \operatorname{H}^{2}(X_{K^{{\mathfrak{p}}}\times I_{{\mathfrak{p}}}}, {\mathcal{D}}_{\chi_{\mathcal{S}}})_{{\mathfrak{m}}_{\pi}} \longrightarrow \operatorname{H}^{2}(X_{K^{{\mathfrak{p}}}\times I_{{\mathfrak{p}}}}, {E})_{{\mathfrak{m}}_{\pi}} \longrightarrow 0. \end{align*}
\begin{align*} & \xrightarrow{\times m}\operatorname{H}^{1}(X_{K^{{\mathfrak{p}}}\times I_{{\mathfrak{p}}}}, {\mathcal{D}}_{\chi_{\mathcal{S}}})_{{\mathfrak{m}}_{\pi}} \longrightarrow \operatorname{H}^{1}(X_{K^{{\mathfrak{p}}}\times I_{{\mathfrak{p}}}}, {E})_{{\mathfrak{m}}_{\pi}} \xrightarrow{0} \operatorname{H}^{2}(X_{K^{{\mathfrak{p}}}\times I_{{\mathfrak{p}}}}, {\mathcal{D}}_{\chi_{\mathcal{S}}})_{{\mathfrak{m}}_{\pi}} \\ & \xrightarrow{\times m} \operatorname{H}^{2}(X_{K^{{\mathfrak{p}}}\times I_{{\mathfrak{p}}}}, {\mathcal{D}}_{\chi_{\mathcal{S}}})_{{\mathfrak{m}}_{\pi}} \longrightarrow \operatorname{H}^{2}(X_{K^{{\mathfrak{p}}}\times I_{{\mathfrak{p}}}}, {E})_{{\mathfrak{m}}_{\pi}} \longrightarrow 0. \end{align*}
Here the second map is the zero map as the first map is surjective by the second part of Theorem 5.1, and the last term is zero because the system of eigenvalues for ![]() $\pi$ does not appear in degrees greater by Theorem 5.1(i).
$\pi$ does not appear in degrees greater by Theorem 5.1(i).
We then get that multiplication by ![]() $m$ is injective on
$m$ is injective on ![]() $\operatorname {H}^{2}(X_{K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}}, {\mathcal {D}}_{\chi _{\mathcal {S}}})_{ {\mathfrak {m}}_{\pi }}$ and, therefore, the map
$\operatorname {H}^{2}(X_{K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}}, {\mathcal {D}}_{\chi _{\mathcal {S}}})_{ {\mathfrak {m}}_{\pi }}$ and, therefore, the map
is an isomorphism. By hypothesis, ![]() $\operatorname {H}^{2}(X_{K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}}, {E})_{ {\mathfrak {m}}_{\pi }}$ is one-dimensional. Therefore, the
$\operatorname {H}^{2}(X_{K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}}, {E})_{ {\mathfrak {m}}_{\pi }}$ is one-dimensional. Therefore, the ![]() $\mathcal {O}_{\mathcal {S}, {{\mathbb 1}}}$-module
$\mathcal {O}_{\mathcal {S}, {{\mathbb 1}}}$-module ![]() $\operatorname {H}^{2}(X_{K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}}, {\mathcal {D}}_{\chi _{\mathcal {S}}})_{ {\mathfrak {m}}_{\pi }}$ is cyclic by Nakayama's Lemma. If it were torsion, then multiplication by
$\operatorname {H}^{2}(X_{K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}}, {\mathcal {D}}_{\chi _{\mathcal {S}}})_{ {\mathfrak {m}}_{\pi }}$ is cyclic by Nakayama's Lemma. If it were torsion, then multiplication by ![]() $m$ would not be injective on it, which is a contradiction; so it is free.
$m$ would not be injective on it, which is a contradiction; so it is free.
Let ![]() $r$ be a generator of the ideal of
$r$ be a generator of the ideal of ![]() $\mathcal {O}_{\mathcal {U},{{\mathbb 1}}}$ corresponding to
$\mathcal {O}_{\mathcal {U},{{\mathbb 1}}}$ corresponding to ![]() $\mathcal {S}$. The modules
$\mathcal {S}$. The modules ![]() $\operatorname {H}^{1}(X_{K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}}, {\mathcal {D}}_{\chi _{\mathcal {S}}})_{ {\mathfrak {m}}_{\pi }}$ and
$\operatorname {H}^{1}(X_{K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}}, {\mathcal {D}}_{\chi _{\mathcal {S}}})_{ {\mathfrak {m}}_{\pi }}$ and ![]() $\operatorname {H}^{2}(X_{K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}}, {\mathcal {D}}_{\chi _{\mathcal {S}}})_{ {\mathfrak {m}}_{\pi }}$ are kernel and cokernel, respectively, of the multiplication by
$\operatorname {H}^{2}(X_{K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}}, {\mathcal {D}}_{\chi _{\mathcal {S}}})_{ {\mathfrak {m}}_{\pi }}$ are kernel and cokernel, respectively, of the multiplication by ![]() $r$ map on
$r$ map on ![]() $\operatorname {H}^{2}(X_{K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}}, {\mathcal {D}}_{\chi _{\mathcal {U}}})_{ {\mathfrak {m}}_\pi }$. Multiplication by the appropriate power of
$\operatorname {H}^{2}(X_{K^{ {\mathfrak {p}}}\times I_{ {\mathfrak {p}}}}, {\mathcal {D}}_{\chi _{\mathcal {U}}})_{ {\mathfrak {m}}_\pi }$. Multiplication by the appropriate power of ![]() $r$ yields the sought-after isomorphism.
$r$ yields the sought-after isomorphism.
We would like to apply Theorem 3.16 to conclude that ![]() $\mathcal {L}$-invariants are independent of the cohomological degree. There are, however, several problems. First, it is not clear whether one can find a curve
$\mathcal {L}$-invariants are independent of the cohomological degree. There are, however, several problems. First, it is not clear whether one can find a curve ![]() $\mathcal {S}$ as in the theorem that is smooth at
$\mathcal {S}$ as in the theorem that is smooth at ![]() ${{\mathbb 1}}$. Second, if one finds such a curve, the automorphic Colmez–Greenberg–Stevens formula in the inert case only produces one element in the intersection of
${{\mathbb 1}}$. Second, if one finds such a curve, the automorphic Colmez–Greenberg–Stevens formula in the inert case only produces one element in the intersection of ![]() $\mathcal {L}^{(0)}(f,p)$ and
$\mathcal {L}^{(0)}(f,p)$ and ![]() $\mathcal {L}^{(1)}(f,p)$. As these spaces are two-dimensional by Proposition 1.8 this gives us no new information. In the split case the situation is better: one can at least compute the
$\mathcal {L}^{(1)}(f,p)$. As these spaces are two-dimensional by Proposition 1.8 this gives us no new information. In the split case the situation is better: one can at least compute the ![]() $\mathcal {L}$-invariant of one of the primes lying above
$\mathcal {L}$-invariant of one of the primes lying above ![]() $p$ and, if the tangent space of
$p$ and, if the tangent space of ![]() $\mathcal {S}$ at
$\mathcal {S}$ at ![]() ${{\mathbb 1}}$ is generic enough, one can compute both.
${{\mathbb 1}}$ is generic enough, one can compute both.
Corollary 5.3 Let ![]() $F$ be an imaginary quadratic field unramified at
$F$ be an imaginary quadratic field unramified at ![]() $p$ and let
$p$ and let ![]() $\pi$ be a cuspidal Bianchi newform of parallel weight
$\pi$ be a cuspidal Bianchi newform of parallel weight ![]() $2$. Suppose that
$2$. Suppose that ![]() $p$ splits in
$p$ splits in ![]() $F$ as
$F$ as ![]() $p= {\mathfrak {p}} \overline { {\mathfrak {p}}}$ and
$p= {\mathfrak {p}} \overline { {\mathfrak {p}}}$ and ![]() $f$ is Steinberg at both,
$f$ is Steinberg at both, ![]() $ {\mathfrak {p}}$ and
$ {\mathfrak {p}}$ and ![]() $\overline { {\mathfrak {p}}}$. Then at least one of the equalities
$\overline { {\mathfrak {p}}}$. Then at least one of the equalities
or
holds.
Remark 5.4 It was shown in [Reference GehrmannGeh19a] that the theorem above would also follow from Venkatesh's conjectures on the action of derived Hecke algebras.
The situation simplifies substantially if ![]() $\pi$ is the base change of a modular form
$\pi$ is the base change of a modular form ![]() $f$.
$f$.
Theorem 5.5 Let ![]() $F$ be an imaginary quadratic field unramified at
$F$ be an imaginary quadratic field unramified at ![]() $p$. Let
$p$. Let ![]() $f$ be a newform of weight
$f$ be a newform of weight ![]() $2$ that is Steinberg at
$2$ that is Steinberg at ![]() $p$ and
$p$ and ![]() $\operatorname {BC}(f)$ its base change to
$\operatorname {BC}(f)$ its base change to ![]() $F$. The following hold.
$F$. The following hold.
(i) If
 $p= {\mathfrak {p}} \overline { {\mathfrak {p}}}$ is split in
$p= {\mathfrak {p}} \overline { {\mathfrak {p}}}$ is split in  $F$, then
$F$, then
 \[ \mathcal{L}^{(0)}(\operatorname{BC}(f),{\mathfrak{p}})=\mathcal{L}^{(1)}(\operatorname{BC}(f),{\mathfrak{p}})=\mathcal{L}^{(0)}(\operatorname{BC}(f),\overline{{\mathfrak{p}}})=\mathcal{L}^{(1)}(\operatorname{BC}(f),\overline{{\mathfrak{p}}})=\mathcal{L}(f,p). \]
\[ \mathcal{L}^{(0)}(\operatorname{BC}(f),{\mathfrak{p}})=\mathcal{L}^{(1)}(\operatorname{BC}(f),{\mathfrak{p}})=\mathcal{L}^{(0)}(\operatorname{BC}(f),\overline{{\mathfrak{p}}})=\mathcal{L}^{(1)}(\operatorname{BC}(f),\overline{{\mathfrak{p}}})=\mathcal{L}(f,p). \](ii) If
 $p$ is inert, we have
$p$ is inert, we have
 \[ \mathcal{L}^{(0)}(\operatorname{BC}(f),p)\cap \operatorname{Hom}^{\operatorname{ct}}({\mathbb{Q}}_p^{\ast},{E})=\mathcal{L}^{(1)}(\operatorname{BC}(f),p) \cap \operatorname{Hom}^{\operatorname{ct}}({\mathbb{Q}}_p^{\ast},{E})= \mathcal{L}(f,p). \]
\[ \mathcal{L}^{(0)}(\operatorname{BC}(f),p)\cap \operatorname{Hom}^{\operatorname{ct}}({\mathbb{Q}}_p^{\ast},{E})=\mathcal{L}^{(1)}(\operatorname{BC}(f),p) \cap \operatorname{Hom}^{\operatorname{ct}}({\mathbb{Q}}_p^{\ast},{E})= \mathcal{L}(f,p). \](iii) If
 $p$ is inert, we have
$p$ is inert, we have
 \[ \mathcal{L}^{(0)}(\operatorname{BC}(f),p)=\mathcal{L}^{(1)}(\operatorname{BC}(f),p). \]
\[ \mathcal{L}^{(0)}(\operatorname{BC}(f),p)=\mathcal{L}^{(1)}(\operatorname{BC}(f),p). \]
Proof. In § 5 of [Reference Barrera Salazar and WilliamsBW19] it is shown that one may take ![]() $\mathcal {S}\subseteq {\mathcal {W}}$ to be the parallel weight curve (see § 5 of [Reference Barrera Salazar and WilliamsBW19]), which is clearly smooth at
$\mathcal {S}\subseteq {\mathcal {W}}$ to be the parallel weight curve (see § 5 of [Reference Barrera Salazar and WilliamsBW19]), which is clearly smooth at ![]() ${{\mathbb 1}}$. Using
${{\mathbb 1}}$. Using ![]() $p$-adic Langlands functoriality as explained in [Reference Barrera Salazar and WilliamsBW19], the first two claims follow by applying Theorem 3.16 (respectively, its analogue in the Bianchi setting) for the modular form
$p$-adic Langlands functoriality as explained in [Reference Barrera Salazar and WilliamsBW19], the first two claims follow by applying Theorem 3.16 (respectively, its analogue in the Bianchi setting) for the modular form ![]() $f$ and its base change to
$f$ and its base change to ![]() $F$. The last claim is a consequence of the second claim and the Galois invariance of automorphic
$F$. The last claim is a consequence of the second claim and the Galois invariance of automorphic ![]() $\mathcal {L}$-invariants attached to base change representations (see Lemma 3.1 of [Reference GehrmannGeh19b]).
$\mathcal {L}$-invariants attached to base change representations (see Lemma 3.1 of [Reference GehrmannGeh19b]).
Remark 5.6 In the inert case the equality ![]() $\mathcal {L}^{(0)}(\operatorname {BC}(f),p)\cap \operatorname {Hom}^{\operatorname {ct}}( {\mathbb {Q}}_p^{\ast },{E})=\mathcal {L}(f,p)$ was proven in [Reference GehrmannGeh19b, Lemma 3.3], using Artin formalism for
$\mathcal {L}^{(0)}(\operatorname {BC}(f),p)\cap \operatorname {Hom}^{\operatorname {ct}}( {\mathbb {Q}}_p^{\ast },{E})=\mathcal {L}(f,p)$ was proven in [Reference GehrmannGeh19b, Lemma 3.3], using Artin formalism for ![]() $p$-adic
$p$-adic ![]() $L$-functions and the exceptional zero formula. An analogous result for higher weight forms was proven by Barrera-Salazar and Williams in [Reference Barrera Salazar and WilliamsBW19, Proposition 10.2].
$L$-functions and the exceptional zero formula. An analogous result for higher weight forms was proven by Barrera-Salazar and Williams in [Reference Barrera Salazar and WilliamsBW19, Proposition 10.2].
Our approach can be adapted to higher weights making the construction of Stark–Heegner cycles of [Reference Venkat and WilliamsVW21] unconditional in the base change case.