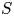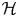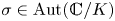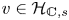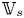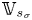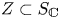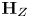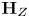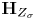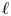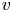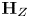1. Introduction
Let 
$f : X \to S$ be a smooth projectiveFootnote 1 morphism of 
$K$-varieties, with 
$S$ smooth and quasi-projective, and 
$K \subset \mathbb {C}$ a subfield. In this setting, the local system 
$\mathbb {V} = R^{2k} f^{\mathrm {an}}_{*} \mathbb {Q}(k)$ underlies a polarizable variation of Hodge structure, which has the property that the vector bundle 
$\mathbb {V} \otimes \mathcal {O}_{S^{\mathrm {an}}}$ admits a 
$K$-algebraic model 
$\mathcal {H} = R^{2k} f_{*} \Omega ^{\bullet }_{X/S}$, where 
$\Omega ^{\bullet }_{X/S}$ is the complex of relative differentials. Moreover, the underlying integral local system 
$\mathbb {V}_{\mathbb {Z}} \subset \mathbb {V}$ admits a comparison with the 
$\ell$-adic local system 
$\mathbb {V}_{\ell } = R^{2k} f^{\unicode{x00E9}\text{t}}_{*} \mathbb {Z}_{\ell }(k)$ on the étale site of 
$S_{\mathbb {C}}$. We recall that an 
$\ell$-adic local system is a lisse 
$\mathbb {Z}_{\ell }$-sheaf 
$\mathcal {F} = \{ \mathcal {F}_{i} \}_{i \geq 0}$, that is, a compatible projective system
\[ \cdots \to \mathcal{F}_{i+1} \to \mathcal{F}_{i} \to \mathcal{F}_{i-1} \to \cdots \to \mathcal{F}_{1} \to \mathcal{F}_{0} = 0 \]
of 
$\mathbb {Z} / \ell ^{i} \mathbb {Z}$-sheaves on the étale site of 
$S_{\mathbb {C}}$ such that each 
$\mathcal {F}_{i}$ is locally constant.
Notation For 
$s \in S(\mathbb {C})$, we denote by 
$c^{\mathrm {dR}}_{s} : \mathbb {V}_{\mathbb {C}, s} \xrightarrow {\sim } \mathcal {H}_{\mathbb {C}, s}$ and 
$c^{\ell }_{s} : \mathbb {V}_{\mathbb {Q}_{\ell }, s} \xrightarrow {\sim } \mathbb {V}_{\ell, \mathbb {Q}_{\ell }, s}$ the natural comparison isomorphisms.
The fact that 
$\mathcal {H}$ and 
$\mathbb {V}_{\ell }$ come from a morphism 
$f : X \to S$ of 
$K$-varieties means that, for each automorphism 
$\sigma \in \mathrm {Aut}(\mathbb {C}/K)$ and point 
$s \in S(\mathbb {C})$, there are isomorphisms 
$(-)_{\sigma } : \mathcal {H}_{\mathbb {C}, s} \xrightarrow {\sim } \mathcal {H}_{\mathbb {C}, s_{\sigma }}$ and 
$(-)_{\sigma } : \mathbb {V}_{\ell, \mathbb {Q}_{\ell }, s} \xrightarrow {\sim } \mathbb {V}_{\ell, \mathbb {Q}_{\ell }, s_{\sigma }}$ induced by conjugation. Combining these isomorphisms with the isomorphisms 
$c^{\mathrm {dR}}_{s}$ and 
$c^{\ell }_{s}$, we may consider several possible ways in which the rational structure of 
$\mathbb {V}$ may be preserved under conjugation.
Definition 1.1 Let 
$s \in S(\mathbb {C})$ be a point, 
$v \in \mathbb {V}_{s}$ be a vector, 
$W \subset \mathbb {V}_{s}$ a subspace, and 
$\sigma \in \mathrm {Aut}(\mathbb {C}/K)$. Then we say:
(i) that
$v$ has rational conjugates if $c_{s}^{\mathrm {dR}}(v)_{\sigma }$ (respectively, $c_{s}^{\ell }(v)_{\sigma }$ for all $\ell$) are rational vectors of $\mathbb {V}_{s_{\sigma }}$ (they lie in the image of $\mathbb {V}_{s_{\sigma }}$ under the comparison isomorphisms $c_{s_{\sigma }}^{\mathrm {dR}}$ and $c^{\ell }_{s_{\sigma }}$);(ii) that
$v$ has a canonical rational conjugate if there exists $v_{\sigma } \in \mathbb {V}_{s_{\sigma }}$ such that $c_{s}^{\mathrm {dR}}(v)_{\sigma } = c_{s_{\sigma }}^{\mathrm {dR}}(v_{\sigma })$ and $c_{s}^{\ell }(v)_{\sigma } = c_{s_{\sigma }}^{\ell }(v_{\sigma })$ for all $\ell$ (the vector $v_{\sigma }$ works for all comparison isomorphisms at once);(iii) that
$W$ has rational conjugates if each element of $W$ does;(iv) that
$W$ has a canonical rational conjugate if each element of $W$ does.
Remark 1.2 It is clear that if 
$w$ and 
$w'$ have (canonical) rational conjugates then so do 
$w + w'$ and 
$\lambda w$ for any 
$\lambda \in \mathbb {Q}$, so we lose nothing by considering subspaces with (canonical) rational conjugates.
In the case 
$K = \mathbb {Q}$, the property that a Hodge vector 
$v$ has rational conjugates is equivalent to the absolute Hodge conjecture for 
$v$ formulated in [Reference Charles and SchnellCS14].Footnote 2 The property that 
$v$ has a canonical rational conjugate is a priori stronger, and would follow for Hodge vectors from the Hodge conjecture in the geometric setting. These properties are expected to hold for Hodge vectors more generally in the motivic setting. Loosely speaking, we will say that a variation 
$\mathbb {V}$ is motivic if it is generated from the geometric situation by functorial constructions; we give a precise definition suitable for our purposes in § 2.1.
Our central technical result, from which new cases of the absolute Hodge conjecture will follow, gives a new way of deducing that a subspace 
$W \subset \mathbb {V}_{s}$ (or a subspace of the various tensor powers of 
$\mathbb {V}_{s}$) has rational conjugates by studying the monodromy of complex subvarieties 
$Z \subset S_{\mathbb {C}}$. To formulate the statement we introduce some notation.
Notation Given an 
$R$-module 
$V$, we let 
$V^{m,n} = (V^{*})^{\otimes m} \otimes V^{\otimes n}$, with the analogous definition for 
$R$-local systems 
$\mathbb {V}$.
Notation Given an 
$R$-module 
$V$, we let 
$\mathcal {T}(V) = \bigoplus _{m, n \geq 0} V^{n,m}$, with the analogous definition for 
$R$-local systems 
$\mathbb {V}$.
Notation Let 
$V$ be a vector space over 
$R$, and let 
$T \subset \mathcal {T}(V)$ be a vector subspace. We denote by 
$\mathbf {G}_{T} \subset \mathrm {Aut}(V)$ the 
$R$-algebraic subgroup defined by the property that it fixes each element of 
$T$.
Notation Let 
$Z \subset S_{\mathbb {C}}$ be an irreducible algebraic subvariety, and 
$\mathbb {V}$ be a local system. We denote by 
$\textbf {H}_{Z}$ the algebraic monodromy of 
$Z$, which is the identity component of the Zariski closure of the monodromy representation on 
$ {\mathbb {V}}\left| {_{Z^{\mathrm {nor}}}} \right.$, where 
$Z^{\mathrm {nor}} \to Z$ is the normalization of 
$Z$.
Remark 1.3 Given a subvariety 
$Z \subset S_{\mathbb {C}}$, we may regard 
$\textbf {H}_{Z}$ as an algebraic subgroup of 
$\mathrm {Aut}(\mathbb {V}_{s})$ for any point 
$s \in Z(\mathbb {C})$. We will use the notation 
$\textbf {H}_{Z}$ for each of these subgroups, even though the point 
$s$ may vary, as the context will leave no ambiguity about which algebraic group we mean.
Remark 1.4 It makes no difference if one considers a desingularization of 
$Z$ instead of its normalization to define algebraic monodromy, or instead considers the monodromy over an open subvariety 
$U \subset Z$ or an open subvariety 
$V \subset Z^{\mathrm {nor}}$. This can be checked by using the fact that normality implies that the map 
$\pi _{1}(V) \to \pi _{1}(Z^{\mathrm {nor}})$ is surjective for any such 
$V$.
Our main technical result is then as follows.
Definition 1.5 If 
$G \subset \mathrm {Aut}(\mathbb {V}_{s})$ is an algebraic group, and 
$W \subset \mathcal {T}(\mathbb {V}_{s})$ is a subspace, we will say that 
$G$ fixes 
$W$ as a 
$\mathbb {Q}$-subspace if for each 
$g \in G(\mathbb {C})$ we have 
$g W = W$.Footnote 3
Theorem 1.6 Let 
$\mathbb {V}$ be a motivic variation of Hodge structure on 
$S$, and let 
$s \in S(\mathbb {C})$. Suppose that 
$T \subset \mathcal {T}(\mathbb {V}_{s})$ is a subspace with canonical rational conjugates, that 
$Z \subset S_{\mathbb {C}}$ is a complex subvariety containing 
$s$ satisfying 
$\textbf {H}_{Z} \subset \mathbf {G}_{T}$, and that 
$W \subset \mathcal {T}(\mathbb {V}_{s})$ is a subspace containing 
$T$. Suppose that the normalizer 
$N$ of 
$\textbf {H}_{Z}$ inside 
$\mathbf {G}_{T}$ fixes 
$W$ as a 
$\mathbb {Q}$-subspace. Then 
$W$ has rational conjugates.
Remark 1.7 For a version of Theorem 1.6 which lets us conclude that 
$W$ has canonical rational conjugates, see Theorem 4.2.
The following corollary is then a simple application of Theorem 1.6.
Corollary 1.8 Suppose 
$\mathbb {V}$ is a motivic variation of Hodge structure on 
$S$, let 
$s \in S(\mathbb {C})$ and suppose that 
$Z \subset S_{\mathbb {C}}$ contains 
$s$. Then if the only non-trivial subspaces of 
$(m,n)$ tensors fixed by 
$\textbf {H}_{Z}$ are of the form 
$\mathbb {Q} w$ for some 
$w \in \mathbb {V}_{s}^{m,n}$, then the subspace 
$\mathbb {Q} w$ has rational conjugates.
Proof. We show in § 2.2 that any motivic variation admits a polarization 
$Q : \mathbb {V} \otimes \mathbb {V} \to \mathbb {Q}$ such that the class of 
$Q_{s}$ inside 
$\mathbb {V}^{2,0}_{s}$ has a canonical rational conjugate. Take 
$T$ to be the span of 
$Q_{s}$. From the fact that 
$N$ preserves 
$Q$ we learn that it acts on 
$w$ by 
$\pm 1$. Taking 
$W$ to be the span of 
$Q_{s}$ and 
$w$, we learn that 
$W$ has rational conjugates.
As we explain in § 5.1, a form of the argument in Corollary 1.8 appears in Voisin's paper [Reference VoisinVoi07]. There it is used to prove a ‘weakly absolute Hodge’ statement for Hodge classes coming from a family of 
$4$-folds for which neither the Hodge nor absolute Hodge conjecture is known. Our Theorem 1.6 gives the full absolute conjecture in this case; this is Theorem 1.14.
Let 
$\mathrm {Isom}(\mathbb {V}_{s}, \mathbb {V}_{s_{\sigma }})$ be the 
$\mathbb {Q}$-algebraic variety consisting of all isomorphisms between 
$\mathbb {V}_{s}$ and 
$\mathbb {V}_{s_{\sigma }}$. Our proof of Theorem 1.6 proceeds through the study of the 
$\mathbb {Q}$-subvariety
\[ \mathcal{I}_{T}(s, Z, \sigma) \subset \mathrm{Isom}(\mathbb{V}_{s}, \mathbb{V}_{s_{\sigma}}) , \]
defined by the property that 
$r \in \mathcal {I}_{T}(s, Z, \sigma )(\mathbb {C})$ if and only if 
$r \circ \textbf {H}_{Z, \mathbb {C}} \circ r^{-1} = \textbf {H}_{Z_{\sigma }, \mathbb {C}}$ and 
$r$ sends each 
$t \in T$ to its canonical rational conjugate 
$t_{\sigma } \in T_{\sigma }$. We observe that 
$\mathcal {I}_{T}(s, Z, \sigma )$ is a torsor under the normalizer 
$N$ of 
$\textbf {H}_{Z}$ inside 
$\mathbf {G}_{T}$. Theorem 1.6 follows immediately from the following two facts about 
$\mathcal {I}_{T}(s, Z, \sigma )$, established in § 3.
Proposition 1.9
(i) The map
induced by\[ r^{\mathrm{dR}}_{\sigma} : \mathbb{V}_{\mathbb{C}, s} \xrightarrow{c^{\mathrm{dR}}_{s}} \mathcal{H}_{\mathbb{C}, s} \xrightarrow{\sigma} \mathcal{H}_{\mathbb{C}, s_{\sigma}} \xrightarrow{(c^{\mathrm{dR}}_{s_{\sigma}})^{-1}} \mathbb{V}_{\mathbb{C}, s_{\sigma}} \]$\sigma$ is a $\mathbb {C}$-point of $\mathcal {I}_{T}(s, Z, \sigma )$.(ii) For each
$\ell$, the map
induced by\[ r^{\ell}_{\sigma} : \mathbb{V}_{\mathbb{Q}_{\ell}, s} \xrightarrow{c^{\ell}_{s}} \mathbb{V}_{\ell, \mathbb{Q}_{\ell}, s} \xrightarrow{\sigma} \mathbb{V}_{\ell, \mathbb{Q}_{\ell}, s_{\sigma}} \xrightarrow{(c^{\ell}_{s_{\sigma}})^{-1}} \mathbb{V}_{\mathbb{Q}_{\ell}, s_{\sigma}} \]$\sigma$ is a $\mathbb {Q}_{\ell }$-point of $\mathcal {I}_{T}(s, Z, \sigma )$.
Proof Proof of Theorem 1.6 (assuming Proposition 1.9)
We let 
$\mathcal {I} = \mathcal {I}_{T}(s, Z, \sigma )$ for ease of notation. That 
$\mathcal {I}$ is naturally a torsor under 
$N$ implies that the subspace 
$r(W)$ is independent of the choice of 
$r \in \mathcal {I}(\mathbb {C})$: any two choices 
$r$ and 
$r'$ are related by 
$r' = r n$ with 
$n \in N(\mathbb {C})$, and 
$N$ fixes 
$W$ by assumption. As 
$\mathcal {I}$ is a 
$\mathbb {Q}$-variety, it has a 
$\bar {\mathbb {Q}}$-point 
$r$, hence 
$W_{\sigma } := r(W)$ is defined over 
$\bar {\mathbb {Q}}$. If we can show that 
$W_{\sigma }$ is in fact a 
$\mathbb {Q}$-subspace of 
$\mathbb {V}_{s_{\sigma }}$, then the proof will be complete as Proposition 1.9 then implies both that 
$c^{\mathrm {dR}}_{s}(W)_{\sigma } = c^{\mathrm {dR}}_{s_{\sigma }}(W_{\sigma })$ and 
$c^{\ell }_{s}(W)_{\sigma } = c^{\ell }_{s_{\sigma }}(W_{\sigma })$ for each 
$\ell$.
By Proposition 1.9(ii) the variety 
$\mathcal {I}$ has 
$\mathbb {Q}_{\ell }$-points for every 
$\ell$, hence it follows that, under some choice of isomorphism 
$\mathbb {C} \cong \overline {\mathbb {Q}_{\ell }}$, every element of 
$W_{\sigma }$ is defined over 
$\mathbb {Q}_{\ell }$. The proof is completed by the following claim.
Claim 1.10 Let 
$v \in \mathbb {A}^{n}(\bar {\mathbb {Q}})$ be a 
$\bar {\mathbb {Q}}$-point in affine space, and suppose that for each 
$\ell$ there exists an isomorphism 
$\mathbb {C} \cong \overline {\mathbb {Q}_{\ell }}$ under which 
$v$ is identified with a 
$\mathbb {Q}_{\ell }$-point. Then 
$v$ is defined over 
$\mathbb {Q}$.
Proof. As 
$\mathbb {A}^{n} = (\mathbb {A}^{1})^{n}$, it suffices to consider the case 
$n = 1$. Let 
$f$ be the minimal polynomial of 
$v$. The statement is unchanged by replacing 
$v$ with 
$\lambda v$ for 
$\lambda \in \mathbb {Q}$, so we may assume that 
$v$ is integral and that 
$f$ is monic with integral coefficients. The hypothesis shows (using integrality) that 
$f$ has a root over 
$\mathbb {\mathbb {Z}}_{\ell }$ for every 
$\ell$, hence a root modulo 
$\ell$ for every 
$\ell$. As 
$f$ is irreducible, this implies that 
$f$ is linear by [Reference Cassels and FrölichCF67, p. 362, Ex. 6.2].
This completes the proof of the theorem.
Remark 1.11 We note that the proof of Theorem 1.6 in fact only requires Proposition 1.9(ii) for a set 
$\mathcal {S}$ of primes 
$\ell$ of asymptotic density one, since that is all that is required in the reference [Reference Cassels and FrölichCF67, p. 362, Ex. 6.2]. In that case the conclusion that 
$W$ has rational conjugates holds only in the de Rham case and for 
$\ell$-adic cohomology associated to primes 
$\ell$ belonging to 
$\mathcal {S}$.
Remark 1.12 The proof of Theorem 1.6 does not invoke the properties of the filtration 
$F^{\bullet }$ in any way, so it applies to motivic mixed variations as well. We focus exclusively on the pure case in this paper.
Theorem 1.6 lets us deduce the following result on the absolute Hodge conjecture, as we show in § 2.3.
Theorem 1.13 Let 
$\mathbb {V}$, 
$S$, 
$s$, 
$T$ and 
$Z$ be as in Theorem 1.6, and suppose that 
$W$ is a subspace of Hodge vectors. Then the 
$K$-absolute Hodge conjectureFootnote 4 holds for each element of 
$W$.
We give two applications of our results. The first is to resolve the absolute Hodge conjecture for classes coming from a family of 
$4$-folds considered by Voisin in her paper [Reference VoisinVoi07, Example 3.5]. More specifically, we show the following theorem.
Theorem 1.14 Let 
$f : X \to S$ be the family of degree six hypersurfaces in 
$\mathbb {P}^{5}$ stable under the involution 
$\iota (X_{0}, \ldots, X_{5}) = (-X_{0}, -X_{1}, X_{2}, \ldots, X_{5})$, let 
$\mathbb {V} = R^{4} f^{\mathrm {an}}_{*} \mathbb {Z}$ be the variation on middle cohomology, and let 
$\mathbb {V}_{-}$ be the subvariation obtained by taking anti-invariants under 
$\iota$ with algebraic Hodge bundle 
$\mathcal {H}_{-}$. Then there exists a dense non-empty Zariski open subset 
$U \subset F^{2} \mathcal {H}_{-}$ such that every Hodge class contained in 
$U(\mathbb {C})$ under the isomorphism 
$\mathbb {V}_{-} \otimes \mathcal {O}_{S^{\mathrm {an}}} \simeq \mathcal {H}_{-}^{\mathrm {an}}$ is absolute Hodge, except possibly for the 
$2$-adic cohomology.Footnote 5
Remark 1.15 We also show, as Voisin does, that 
$U(\mathbb {C})$ contains ‘many’ such Hodge classes, in the following strong sense: the locus of Hodge classes is topologically dense in the real subbundle of the quotient 
$F^{2} \mathcal {H}_{-}^{\mathrm {an}} / F^{3} \mathcal {H}_{-}^{\mathrm {an}}$ (the real structure coming from the Betti side), and has non-empty intersection with 
$U(\mathbb {C})$.
Our method of establishing Theorem 1.14 is similar to the argument employed in Voisin's paper to establish that such classes are ‘weakly absolute Hodge’. We are able to obtain a stronger conclusion due to the presence of 
$\ell$-adic input in our argument.
The involution 
$\iota$ in Theorem 1.14 acts trivially on the fibres of 
$\mathcal {H}^{4,0} = F^{4}$, where 
$F^{\bullet }$ is the filtration on 
$\mathcal {H} = \mathbb {V} \otimes \mathcal {O}_{S^{\mathrm {an}}}$, and the anti-invariant Hodge number 
$h^{1,3}_{-}$ is equal to 
$208$. In particular, the Hodge structures parametrized by 
$\mathbb {V}_{-}$ have Hodge level two, and the Hodge conjecture does not appear to be known for them. Moreover, there does not seem to be any way to realize the Hodge classes in the fibres of 
$\mathbb {V}_{-}$ as classes inside the cohomology of an abelian variety via an absolute Hodge correspondence, so the usual techniques for deducing absolute Hodge-type results do not seem to be applicable.
As a second application, we let 
$\mathbb {V}$ be a motivic variation on 
$S$, let 
$Z \subset S \times S$ be the algebraic locus of points 
$(x, y)$ such that 
$\mathbb {V}_{x} \cong \mathbb {V}_{y}$ as integral polarized Hodge structures, and let 
$Z_{0} \subset Z$ be an irreducible component containing the diagonal 
$\Delta \subset S \times S$. The variety 
$Z_{0}$ is a component of the Hodge locus for the variation 
$\mathbb {V} \boxtimes \mathbb {V}^{*}$ on 
$S \times S$ (see Definition 5.2). We call an isomorphism 
$\mathbb {V}_{x} \cong \mathbb {V}_{y}$ with 
$(x,y) \in Z_{0}$ generic if its class is Hodge at a generic point of 
$Z_{0}$. We have the following result.
Theorem 1.16 If 
$\mathbb {V}$ is a motivic variation of Hodge structure on the smooth 
$K$-variety 
$S$ such that 
$\textbf {H}_{S} = \mathrm {Aut}(\mathbb {V}_{s}, Q_{s})$ (monodromy is Zariski dense), then rational tensors fixed by 
$\textbf {H}_{Z_{0}}$ have rational conjugates, and hence generic isomorphisms between 
$\mathbb {V}_{x}$ and 
$\mathbb {V}_{y}$ are 
$K$-absolutely Hodge.
1.1 Structure of the paper
In § 2 we discuss motivic variations and the Hodge and absolute Hodge conjectures for such variations. We review some properties of motivic variations in § 2.1, and list all the properties that we will be needed for the remainder of the paper. The properties in § 2.1 relating to polarizations require further justification, so we carry out the necessary constructions in § 2.2. As mentioned, § 2.3 discusses the relationship between our notion of rational conjugates and the absolute Hodge conjecture.
In § 3 we prove Proposition 1.9. The proof of Proposition 1.9(i) is already implicit in the paper [Reference Klingler, Otwinowska and UrbanikKOU20], so we give a brief summary of the argument in § 3.1. To tackle the 
$\ell$-adic case in § 3.2 we reduce the necessary statement to a purely algebraic statement involving étale fundamental groups, after which the result follows by showing that 
$\sigma \in \mathrm {Aut}(\mathbb {C}/K)$ essentially conjugates the representation of 
$\pi _{1}^{\unicode{x00E9}\text{t}}(S_{\mathbb {C}}, s)$ on the fibre 
$\mathbb {V}_{\ell, s}$ to the representation of 
$\pi _{1}^{\unicode{x00E9}\text{t}}(S_{\mathbb {C}}, s_{\sigma })$ on the fibre 
$\mathbb {V}_{\ell, s_{\sigma }}$.
The same ideas that give Theorems 1.6 and 1.13 in fact give several other variants of Theorems 1.6 and 1.13, as we discuss in § 4. We then consider the example of Voisin in § 5.1, and the application to generic isomorphisms of Hodge structures in § 5.2.
2. Motivic variations
2.1 Properties of motivic variations
Our central example of a variation of Hodge structure of the type we will consider is the variation 
$\mathbb {V}$ obtained from a smooth, projective family 
$f : X \to S$ of 
$K$-varieties, with 
$S$ smooth, and with geometrically connected fibres. Let us briefly state some properties of such variations.
(i) The Hodge bundle
$\mathbb {V} \otimes \mathcal {O}_{S^{\mathrm {an}}}$ admits a canonical model as a $K$-algebraic vector bundle $\mathcal {H} = R^{2k} f_{*} \Omega ^{\bullet }_{X/S}$, where $\Omega ^{\bullet }_{X/S}$ is the complex of relative algebraic differentials.(ii) The filtration
$F^{\bullet }$ on $\mathcal {H}$ admits a canonical $K$-algebraic model, agreeing with the filtration in the analytic setting. This is obtained from the Hodge filtration $F^{p} \Omega ^{\bullet }_{X/S} = \Omega ^{\bullet \geq p}_{X/S}$ on the complex $\Omega ^{\bullet }_{X/S}$ and the Hodge-to-de Rham spectral sequence.(iii) The connection
$\nabla$ whose flat sections are given by $\mathbb {V}_{\mathbb {C}}$ is $K$-algebraic. This is due to Katz and Oda [Reference Katz and OdaKO68].(iv) The
$\mathbb {Q}$-local system $\mathbb {V}$ admits a canonical integral subsystem $\mathbb {V}_{\mathbb {Z}} \subset \mathbb {V}$, such that $\mathbb {V}_{\mathbb {Z}} \otimes \mathbb {Z}_{\ell }$ admits a comparison isomorphism with $\mathbb {V}_{\ell }^{\mathrm {an}}$, where $\mathbb {V}_{\ell }$ is an $\ell$-adic local system defined on the étale site of $S_{\mathbb {C}}$. This is the relative version of the comparison between Betti and étale cohomology.
The following additional properties relate to the polarization on 
$\mathbb {V}$, and will be established in the next section.
(v) The variation
$\mathbb {V}$ admits a polarization $Q : \mathbb {V} \otimes \mathbb {V} \to \mathbb {Q}$ which is $K$-algebraic, in the sense that we have a morphism $\mathcal {Q} : \mathcal {H} \otimes \mathcal {H} \to \mathcal {O}_{S}$ of $K$-algebraic vector bundles whose analytification is identified with $Q$ after applying the isomorphism $\mathbb {V} \otimes \mathcal {O}_{S^{\mathrm {an}}} \simeq \mathcal {H}^{\mathrm {an}}$.(vi) There exists a bilinear form
$Q_{\ell } : \mathbb {V}_{\ell } \otimes \mathbb {V}_{\ell } \to \mathbb {Z}_{\ell }$, compatible with the polarization $Q$ in (v).(vii) Let
$\sigma \in \mathrm {Aut}(\mathbb {C}/K)$, and denote by $\tau _{\sigma } : S_{\unicode{x00E9}\text{t}} \to S_{\unicode{x00E9}\text{t}}$ the induced automorphism of the étale site of $S_{\mathbb {C}}$. Then there exists a canonical isomorphism $\tau _{\sigma }^{*} \mathbb {V}_{\ell } \simeq \mathbb {V}_{\ell }$, compatible with the polarization $Q_{\ell }$ in (vi).
Properties (i)–(vii) are preserved under any sufficiently functorial construction; for instance, they are preserved under duals, direct sums and tensor products.
Definition 2.1 We say that 
$\mathbb {V}$ is motivic if properties (i), (ii), (iii) and (v) hold, and (iv), (vi) and (vii) hold for all primes 
$\ell$ outside of a finite subset 
$\mathcal {K} \subset \mathbb {Z}$.
We adopt the conventional understanding that in the theorems we prove the conclusions are shown to hold only for those primes not belonging to 
$\mathcal {K}$. If the set 
$\mathcal {K}$ is not specified, the theorem is understood to hold for any choice of 
$\mathcal {K}$.
We note the following elementary consequence of (v), (vi) and (vii) which will be useful later.
Lemma 2.2 For motivic variations, the 
$\sigma$-conjugate of the class 
$Q_{s} \in \mathbb {V}^{2,0}_{s}$ is rational for 
$\mathbb {V}^{2,0}_{s_{\sigma }}$ (and given by 
$Q_{s_{\sigma }}$) in both the de Rham and 
$\ell$-adic setting, where 
$\sigma \in\mathrm {Aut} (\mathbb {C}/K)$.
2.2 Construction of $K$-algebraic polarizations
The material in this section should be well known to experts, but we cannot find an appropriate reference.
We consider the geometric situation with 
$\mathbb {V} = R^{2k} f^{\mathrm {an}}_{*} \mathbb {Z}$, 
$\mathcal {H} = R^{2k} f_{*} \Omega ^{\bullet }_{X/S}$ and 
$\mathbb {V}_{\ell } = R^{2k} f^{\unicode{x00E9}\text{t}}_{*} \mathbb {Z}_{\ell }$, with 
$f$ as in the previous section. We will define the primitive cohomology subsystems 
$\mathbb {V}_{\mathrm {prim}} \subset \mathbb {V}$ and 
$\mathbb {V}_{\ell, \mathrm {prim}} \subset \mathbb {V}_{\ell }$, and vector subbundle 
$\mathcal {H}_{\mathrm {prim}} \subset \mathcal {H}$, as well as polarizations 
$Q, Q_{\ell }$ and 
$\mathcal {Q}$ on the primitive cohomology satisfying properties (v), (vi) and (vii). That properties (v), (vi) and (vii) hold for the original local systems and vector bundles follows from the usual procedure of obtaining a polarization on all of cohomology from a polarization on the primitive part.
In the case where 
$S = \mathrm {Spec} \hspace {0.15em} K$ is a point, our definition of 
$Q$ and 
$\mathcal {Q}$ essentially appears (among other places) in [Reference DeligneDel71]. Our goal is to generalize this to the relative setting, where we regard the scheme 
$X$ as an 
$S$-scheme via the map 
$f$. The first task is to define the relative Chern classes 
$c^{\mathrm {dR}}_{1, S}(\mathcal {L})$ and 
$c^{\unicode{x00E9}\text{t}}_{1, S}(\mathcal {L})$ of a line bundle 
$\mathcal {L}$ on 
$X$.
Lemma 2.3 Let 
$\mathcal {L}$ be a line bundle on 
$X$. Then there exists a (necessarily unique) global section 
$c^{\mathrm {dR}}_{1, S}(\mathcal {L})$ of 
$R^{2} f_{*} \Omega ^{\bullet }_{X/S}$ whose restriction to the fibre at 
$s \in S$ is the Chern class 
$c^{\mathrm {dR}}_{1}\big ( {\mathcal {L}}\left| {_{X_{s}}} \right.\big )$.Footnote 6
Proof. By [Sta20, Section 0FLE] we obtain a class 
$c_{1}^{\mathrm {dR}}(\mathcal {L}) \in H^{2}_{\mathrm {dR}}(X/S)$, where 
$H^{\bullet }_{\mathrm {dR}}(X/S)$ is the cohomology of the complex 
$R \Gamma \Omega ^{\bullet }_{X/S}$. Choose an injective resolution 
$\Omega ^{\bullet }_{X/S} \to \mathcal {I}^{\bullet }$. We may compute 
$R^{2} f_{*} \Omega ^{\bullet }_{X/S}$ as the cohomology sheaf of 
$f_{*} \mathcal {I}^{\bullet }$ in degree two. From the equality 
$\Gamma (S, f_{*} \mathcal {I}^{\bullet }) = \Gamma (X, \mathcal {I}^{\bullet })$ we therefore obtain a morphism 
$g : H^{2}_{\mathrm {dR}}(X/S) \to \Gamma (S, R^{2} f_{*} \Omega ^{\bullet }_{X/S})$, and we may define 
$c^{\mathrm {dR}}_{1, S}(\mathcal {L})$ as the image of 
$c_{1}^{\mathrm {dR}}(\mathcal {L})$ under 
$g$.
Let 
$s \in S$ be a point, and 
$r : \Gamma (S, R^{2} f_{*} \Omega ^{\bullet }_{X/S}) \to (R^{2} f_{*} \Omega ^{\bullet }_{X/S})_{s}$ be the restriction of a global section to the fibre at 
$s$. Let 
$b : (R^{2} f_{*} \Omega ^{\bullet }_{X/S})_{s} \to H^{2}_{\mathrm {dR}}(X_{s}/\kappa (s))$ be the canonical base-change morphism. As Chern classes are functorial, the map 
$h : H^{2}_{\mathrm {dR}}(X/S) \to H^{2}_{\mathrm {dR}}(X_{s}/\kappa (s))$ induced by the inclusion 
$\iota : X_{s} \hookrightarrow X$ sends 
$c^{\mathrm {dR}}_{1}(\mathcal {L})$ to 
$c^{\mathrm {dR}}_{1}\big ({\mathcal {L}}\left| {_{X_{s}} } \right.\big )$. It therefore suffices to check that 
$h = b \circ r \circ g$.
To make this verification, we recall the construction of the base-change map at the level of complexes, following [Sta20, Section 0735]. We may identify 
$\Omega ^{\bullet }_{X_{s}}$ with the pullback 
$\iota ^{*} \Omega ^{\bullet }_{X/S}$, and find an injective resolution 
$\iota ^{*} \Omega ^{\bullet }_{X/S} \to \mathcal {J}^{\bullet }$. We then obtain the commuting diagram
where the map 
$\beta$ is unique up to homotopy. The map 
$b$ (respectively, 
$h$) is constructed from 
$\beta$ by applying 
$f_{*}$ (respectively, 
$\Gamma$) and taking the induced map on cohomology. The required equality then follows from the fact that 
$(f \circ \iota )_{*} = \Gamma$.
Lemma 2.4 Let 
$\bar {K}$ be an algebraic closure of 
$K$ inside 
$\mathbb {C}$, and let 
$\mathcal {L}$ be a line bundle on 
$X_{\bar {K}}$. Then there exists a (necessarily unique) global section 
$c^{\unicode{x00E9}\text{t}}_{1, S_{\bar {K}}}(\mathcal {L})$ of 
$R^{2} f^{\unicode{x00E9}\text{t}}_{\bar {K}, *} \mathbb {Z}_{\ell }(1)$ whose restriction to the fibre at 
$s \in S(\bar {K})$ is the Chern class 
$c^{\unicode{x00E9}\text{t}}_{1}\big ({\mathcal {L}}\left| {_{X_{s}}} \right.\big )$.Footnote 7
Proof. We argue analogously to Lemma 2.3. For ease of notation, we assume 
$K = \bar {K}$ and so replace 
$X_{\bar {K}}$ by 
$X$ and 
$S_{\bar {K}}$ by 
$S$. By [Reference MilneMil80, VI, § 10] we obtain a class 
$c^{\unicode{x00E9}\text{t}}_{1}(\mathcal {L}) \in H^{2}_{\unicode{x00E9}\text{t}}(X, \mathbb {Z}_{\ell }(1))$. Choose an injective resolution 
$\mathbb {Z}_{\ell } \to \mathcal {I}^{\bullet }$.Footnote 8 Proceeding as before, we may compute 
$H^{2}_{\unicode{x00E9}\text{t}}(X, \mathbb {Z}_{\ell }(1))$ from the degree two cohomology of 
$\mathcal {I}^{\bullet }$, and 
$\mathbb {V}^{2}_{\ell }$ as the degree two cohomology sheaf of 
$f^{\unicode{x00E9}\text{t}}_{*} \mathcal {I}^{\bullet }$. From the equality 
$\Gamma (S, f^{\unicode{x00E9}\text{t}}_{*} \mathcal {I}^{\bullet }) = \Gamma (X, \mathcal {I}^{\bullet })$ we therefore obtain a map 
$g : H^{2}_{\unicode{x00E9}\text{t}}(X, \mathbb {Z}_{\ell }(1)) \to \Gamma (S, R^{2} f^{\unicode{x00E9}\text{t}}_{*} \mathbb {Z}_{\ell }(1))$, and define 
$c^{\unicode{x00E9}\text{t}}_{1, S}(\mathcal {L})$ as the image of 
$c^{\unicode{x00E9}\text{t}}_{1}(\mathcal {L})$ under 
$g$.
Letting 
$s \in S$ be a (geometric) point, one defines 
$r, b$ and 
$h$ analogously to Lemma 2.3, and similarly checks that 
$h = b \circ r \circ g$.
Definition 2.5 Let 
$f : X \to S$ be a smooth projective morphism of 
$K$-varieties, with 
$S$ smooth and fibres of dimension 
$n$. Let 
$\mathcal {H}^{2k} = R^{2k} f_{*} \Omega ^{\bullet }_{X/S}$, 
$\mathbb {V}^{2k}_{\ell } = R^{2k} f^{\unicode{x00E9}\text{t}}_{\bar {K}, *} \mathbb {Z}_{\ell }(k)$ and 
$\mathbb {V}^{2k} = R^{2k} f^{\mathrm {an}}_{*} \mathbb {Z}(k)$. Let 
$\mathcal {L}$ be a very ample bundle over 
$S$, and let 
$\omega ^{\mathrm {dR}} = c^{\mathrm {dR}}_{1, S}(\mathcal {L})$, 
$\omega ^{\unicode{x00E9}\text{t}} = c^{\unicode{x00E9}\text{t}}_{1, S_{\bar {K}}}(\mathcal {L}_{\bar {K}})$ and 
$\omega$ be the analytification of 
$\omega ^{\mathrm {dR}}$. We define:
(i) the operators
\begin{align*} L^{\mathrm{dR}} &: \mathcal{H}^{2k} \to \mathcal{H}^{2k+2} & \hspace{1em} \beta &\mapsto \beta \wedge \omega^{\mathrm{dR}}, \\ L^{\unicode{x00E9}\text{t}}_{\ell} &: \mathbb{V}^{2k}_{\ell} \to \mathbb{V}^{2k+2}_{\ell} & \hspace{1em} \beta &\mapsto \beta \wedge \omega^{\unicode{x00E9}\text{t}}, \\ L &: \mathbb{V}^{2k} \to \mathbb{V}^{2k+2} & \hspace{1em} \beta &\mapsto \beta \wedge \omega ; \end{align*}(ii) and the subbundle and subsystems
\begin{align*} \mathcal{H}^{2k}_{\mathrm{prim}} &= \mathrm{ker} \, L^{\mathrm{dR}, n-2k+1}, \\ \mathbb{V}^{2k}_{\ell, \mathrm{prim}} &= \mathrm{ker} \, L^{{\unicode{x00E9}\text{t}}, n-2k+1}_{\ell} ,\\ \mathbb{V}^{2k}_{\mathrm{prim}} &= \mathrm{ker} \, L^{n-2k+1} . \end{align*}
Now fix isomorphisms
\begin{align*} \xi^{\mathrm{dR}} &: R^{2n} f_{*} \Omega^{\bullet}_{X/S} \xrightarrow{\sim} \mathcal{O}_{S}, \\ \xi^{\unicode{x00E9}\text{t}}_{\ell} &: R^{2n} f^{\unicode{x00E9}\text{t}}_{*} \mathbb{Z}_{\ell}(n) \xrightarrow{\sim} \mathbb{Z}_{\ell}, \\ \xi &: R^{2n} f_{*} \mathbb{Z}(n) \xrightarrow{\sim} \mathbb{Z} , \end{align*}compatible with the comparisons coming from analytification; for instance, using the relative version of the trace isomorphism (see [Reference HartshorneHar75, Reference ConradCon]). We then further define
(i) the polarizations
\begin{align*} \mathcal{Q}^{2k} &: \mathcal{H}^{2k}_{\mathrm{prim}} \otimes \mathcal{H}^{2k}_{\mathrm{prim}} \to \mathcal{O}_{S} & \hspace{1em} \xi^{\mathrm{dR}} \circ [ (\alpha, \beta) &\mapsto \alpha \wedge \beta \wedge (\omega^{\mathrm{dR}})^{n-2k} ], \\ Q^{2k}_{\ell} &: \mathbb{V}^{2k}_{\ell, \mathrm{prim}} \otimes \mathbb{V}^{2k}_{\ell, \mathrm{prim}} \to \mathbb{Z}_{\ell} & \xi^{\unicode{x00E9}\text{t}}_{\ell} \circ [ (\alpha, \beta) &\mapsto \alpha \wedge \beta \wedge (\omega^{\unicode{x00E9}\text{t}})^{n-2k} ], \\ Q^{2k} &: \mathbb{V}^{2k}_{\mathrm{prim}} \otimes \mathbb{V}^{2k}_{\mathrm{prim}} \to \mathbb{Z} & \xi \circ [ (\alpha, \beta) &\mapsto \alpha \cup \beta \cup \omega^{n-2k} ] . \end{align*}
Proposition 2.6 The polarizations 
$\mathcal {Q}^{2k}, Q^{2k}_{\ell }$ and 
$Q^{2k}$ of Definition 2.5(iii) satisfy properties (v), (vi) and (vii) of § 2.1.
Proof. For properties (v) and (vi), this follows from the compatibility of the cup product with the comparison isomorphisms, as well as the compatibility of the maps 
$\xi ^{\mathrm {dR}}, \xi ^{\unicode{x00E9}\text{t}}_{\ell }$ and 
$\xi$. For property (vii) this follows from the compatibility of the cup product with conjugation by 
$\mathrm {Aut}(\mathbb {C}/K)$, as well as the fact that the section 
$\omega$ is defined over 
$K$.
2.3 The absolute Hodge conjecture
Let 
$Y$ be a smooth complex projective variety, and 
$k$ a non-negative integer. We define by 
$H^{2k}(Y)$ the intersection 
$H^{2k}(Y^{\mathrm {an}}, \mathbb {Q}(k)) \cap H^{k, k}(Y^{\mathrm {an}})$, where 
$H^{2k}(Y^{\mathrm {an}}, \mathbb {C}(k)) \cong \bigoplus _{p+q=2k} H^{p, q}(Y^{\mathrm {an}})$ is the Hodge decomposition. According to [Reference Charles and SchnellCS14], the absolute Hodge conjecture is as follows.
Conjecture 2.7 (Absolute Hodge)
Let 
$\sigma \in \mathrm {Aut}(\mathbb {C}/\mathbb {Q})$, and let 
$c^{\mathrm {dR}}_{Y} : H^{2k}(Y^{\mathrm {an}}, \mathbb {C}(k)) \xrightarrow {\sim } H^{2k}_{\mathrm {dR}}(Y/\mathbb {C})$ and 
$c^{\ell }_{Y} : H^{2k}(Y^{\mathrm {an}}, \mathbb {Q}_{\ell }(k)) \xrightarrow {\sim } H^{2k}_{\unicode{x00E9}\text{t}}(Y, \mathbb {Q}_{\ell }(k))$ be the comparison isomorphisms. Then:
(i) if
$v^{\mathrm {dR}} \in H^{2k}_{\mathrm {dR}}(Y/\mathbb {C})$ is the image of $v \in H^{2k}(Y)$ under $c^{\mathrm {dR}}_{Y}$ then $v^{\mathrm {dR}}_{\sigma } \in H^{2k}_{\mathrm {dR}}(Y_{\sigma }/\mathbb {C})$ is the image of some $v_{\sigma } \in H^{2k}(Y_{\sigma })$ under $c^{\mathrm {dR}}_{Y_{\sigma }}$;(ii) if
$v^{\ell } \in H^{2k}_{\unicode{x00E9}\text{t}}(Y, \mathbb {Q}_{\ell }(k))$ is the image of $v \in H^{2k}(Y)$ under $c^{\ell }_{Y}$ then $v^{\ell }_{\sigma } \in H^{2k}_{\unicode{x00E9}\text{t}}(Y_{\sigma }, \mathbb {Q}_{\ell }(k))$ is the image of some $v_{\sigma } \in H^{2k}(Y_{\sigma })$ under $c^{\ell }_{Y_{\sigma }}$.
Remark 2.8 Deligne in [Reference DeligneDel82a] requires the class 
$v_{\sigma }$ to be canonical, in the sense that it is the same for all comparison isomorphisms.
Remark 2.9 Conjecture 2.7 generalizes to all Hodge tensors in the obvious way.
Definition 2.10 More generally, we call the statement of Conjecture 2.7 with 
$\mathrm {Aut}(\mathbb {C}/\mathbb {Q})$ replaced by 
$\mathrm {Aut}(\mathbb {C}/K)$ the 
$K$-absolute Hodge conjecture.
Definition 2.11 By the (
$K$-)absolute Hodge conjecture for 
$v$, we mean the statement of Conjecture 2.7 for some fixed vector 
$v \in H^{2k}(Y)$.
Let us now deduce Theorem 1.13 from 1.6.
Proposition 2.12 In the situation of Theorem 1.6, if each element of 
$W$ is Hodge, then the 
$K$-absolute Hodge conjecture holds for each element of 
$W$.
Proof. What needs to be checked is that if 
$w_{\sigma }$ is a rational conjugate to 
$w \in W$, then 
$w_{\sigma }$ is automatically Hodge. We recall that a rational vector inside 
$\mathbb {V}_{s}$ is Hodge if and only if it lies inside 
$F^{0}$, where 
$F^{\bullet }$ is the Hodge filtration. As 
$F^{\bullet }$ is a filtration by 
$K$-algebraic bundles on 
$\mathcal {H}$, this shows the result in the de Rham case. In the 
$\ell$-adic case, we recall that because 
$\mathcal {I}_{T}(s,Z,\sigma )$ is a torsor under 
$N$, the subspace 
$W_{\sigma } := r(W)$ is independent of the point 
$r$ of 
$\mathcal {I}_{T}(s, Z, \sigma )$ chosen. Thus, taking 
$r = r^{\ell }_{\sigma }$, we see that the result holds 
$\ell$-adically as well.
3. Conjugation isomorphisms and monodromy
In this section we establish Proposition 1.9. The variety 
$\mathcal {I}_{T}(s, Z, \sigma ) \subset \mathrm {Isom}(\mathbb {V}_{s}, \mathbb {V}_{s_{\sigma }})$ is defined by the conditions 
$r \circ \textbf {H}_{Z} \circ r^{-1} = \textbf {H}_{Z_{\sigma }}$ and 
$r(t) = t_{\sigma }$ for each 
$t \in T$, where 
$r$ is a point of 
$\mathrm {Isom}(\mathbb {V}_{s}, \mathbb {V}_{s_{\sigma }})$ and the first equality is in the sense of 
$\mathbb {Q}$-subschemes. That 
$r^{\mathrm {dR}}_{\sigma }$ and 
$r^{\ell }_{\sigma }$ satisfy the second condition is just the assumption that each 
$t \in T$ has a canonical rational conjugate 
$t_{\sigma }$, so Proposition 1.9 reduces to the following statement.
Proposition 3.1 Fix 
$\sigma \in \mathrm {Aut}(\mathbb {C}/K)$. Then the following assertions hold.
(i) The map
induced by\[ r^{\mathrm{dR}}_{\sigma} : \mathbb{V}_{\mathbb{C}, s} \xrightarrow{c^{\mathrm{dR}}_{s}} \mathcal{H}_{\mathbb{C}, s} \xrightarrow{\sigma} \mathcal{H}_{\mathbb{C}, s_{\sigma}} \xrightarrow{(c^{\mathrm{dR}}_{s_{\sigma}})^{-1}} \mathbb{V}_{\mathbb{C}, s_{\sigma}} \]$\sigma$ satisfies the property that $r^{\mathrm {dR}}_{\sigma } \circ \textbf {H}_{Z, \mathbb {C}} \circ (r^{\mathrm {dR}}_{\sigma })^{-1} = \textbf {H}_{Z_{\sigma }, \mathbb {C}}$.(ii) For each
$\ell$, the map
induced by\[ r^{\ell}_{\sigma} : \mathbb{V}_{\mathbb{Q}_{\ell}, s} \xrightarrow{c^{\ell}_{s}} \mathbb{V}_{\ell, \mathbb{Q}_{\ell}, s} \xrightarrow{\sigma} \mathbb{V}_{\ell, \mathbb{Q}_{\ell}, s_{\sigma}} \xrightarrow{(c^{\ell}_{s_{\sigma}})^{-1}} \mathbb{V}_{\mathbb{Q}_{\ell}, s_{\sigma}} \]$\sigma$ satisfies the property that $r^{\ell }_{\sigma } \circ \textbf {H}_{Z, \mathbb {Q}_{\ell }} \circ (r^{\ell }_{\sigma })^{-1} = \textbf {H}_{Z_{\sigma }, \mathbb {Q}_{\ell }}$.
3.1 The de Rham case
The required statement is implicit in [Reference Klingler, Otwinowska and UrbanikKOU20, § 3]; we summarize the argument for expository purposes. Given a smooth complex algebraic variety 
$Y$, the Riemann–Hilbert correspondence gives an equivalence between the category 
$\mathrm {Loc}_{\mathbb {C}}(Y^{\mathrm {an}})$ of finite rank local systems on 
$Y^{\mathrm {an}}$ and the category 
$\mathrm {MIC}_{r}(Y)$ of algebraic modules with regular integrable connections on 
$Y$. Given an automorphism 
$\sigma$ of 
$\mathrm {Aut}(\mathbb {C}/K)$, we further obtain an equivalence of categories 
$\mathrm {MIC}_{r}(Y) \xrightarrow {\cdot \times _{\mathbb {C},\sigma } \mathbb {C}} \mathrm {MIC}_{r}(Y_{\sigma })$ by twisting via 
$\sigma$, where 
$Y_{\sigma } := Y \times _{\sigma, \mathbb {C}} \mathbb {C}$. By composing these equivalences one can associate to any local system 
$\mathcal {L} \in \mathrm {Loc}_{\mathbb {C}}(Y^{\mathrm {an}})$ a twisted local system 
$\mathcal {L}^{\sigma } \in \mathrm {Loc}_{\mathbb {C}}(Y_{\sigma }^{\mathrm {an}})$ obtained as the image of 
$\mathcal {L}$. In the special case where 
$Y$ is defined over 
$K \subset \mathbb {C}$ and 
$\mathcal {L}$ is obtained from an algebraic connection which is also defined over 
$K$, one can make the identification 
$\mathcal {L}^{\sigma } = \mathcal {L}$.
Turning now to the proof of Proposition 3.1, let us temporarily denote by 
$\mathbb {V}$ the associated complex local system, and fix a desingularization 
$\tilde {Z} \to Z$ with a lift 
$\tilde {s} \in \tilde {Z}$ of 
$s$; we note that 
$\tilde {Z}_{\sigma } \to Z_{\sigma }$ is a desingularization of 
$Z_{\sigma }$. Applying the above equivalence together with the 
$K$-algebraicity of the connection 
$\nabla$ defining 
$\mathbb {V}$, we obtain an equivalence
\[ \big\langle {\mathbb{V}}\left| {_{\tilde{Z}}} \right. \big\rangle^{\otimes} \simeq_{\tau} \big\langle {\mathbb{V}}\left| {_{\tilde{Z}_{\sigma}}} \right. \big\rangle^{\otimes} , \]
where the notation 
$\langle - \rangle ^{\otimes }$ denotes the neutral Tannakian category generated by the enclosed object (inside the appropriate category of local systems). If 
$\mathrm {Fib}_{\tilde {Z}, \tilde {s}}$ and 
$\mathrm {Fib}_{\tilde {Z}_{\sigma }, \tilde {s}_{\sigma }}$ are the obvious fibre functors, then the Tannakian groups associated to 
$\mathrm {Fib}_{\tilde {Z}, \tilde {s}}$ and 
$\mathrm {Fib}_{\tilde {Z}_{\sigma }, \tilde {s}_{\sigma }}$ have natural faithful representations on 
$\mathbb {V}_{s}$ and 
$\mathbb {V}_{s_{\sigma }}$, as follows from the fact that an automorphism of 
$\mathrm {Fib}_{\tilde {Z}, \tilde {s}}$ (respectively, an automorphism of 
$\mathrm {Fib}_{\tilde {Z}_{\sigma }, \tilde {s}_{\sigma }}$) is determined by its induced automorphism of 
$\mathbb {V}_{\tilde {s}}$ (respectively, 
$\mathbb {V}_{\tilde {s}_{\sigma }}$).
Under these representations, the Tannakian groups associated to 
$\mathrm {Fib}_{\tilde {Z}, \tilde {s}}$ and 
$\mathrm {Fib}_{\tilde {Z}_{\sigma }, \tilde {s}_{\sigma }}$ agree with the complex algebraic monodromy groups of 
$Z$ and 
$Z_{\sigma }$; here we use that by Remark 1.4, it makes no difference whether we use the normalization or a desingularization to define algebraic monodromy. It follows from the fact that 
$\tau$ is an equivalence that the induced map 
$r^{\mathrm {dR}}_{s} : \mathbb {V}_{\mathbb {C}, s} \xrightarrow {\sim } \mathbb {V}_{\mathbb {C}, s_{\sigma }}$ (the notation is in agreement with our previous definition of 
$r^{\mathrm {dR}}_{s}$) gives an isomorphism of representations, and hence conjugates the (complex) algebraic monodromy groups.
3.2 The $\ell$-adic case
We will reduce the problem to a statement about 
$\ell$-adic local systems and the étale fundamental group, which can then be solved entirely algebraically. We denote the normalization of an algebraic variety 
$Z$ by 
$Z^{n}$. If 
$Z$ is a subvariety of 
$S_{\mathbb {C}}$ and 
$s \in S(\mathbb {C})$ is a point lying in 
$Z(\mathbb {C})$, we will denote by 
$s^{n}$ a lift of 
$s$ to 
$Z^{n}$.
Definition 3.2 Let 
$\mathbb {V}_{\ell }$ be an 
$\ell$-adic local system on the complex algebraic variety 
$Z$. We define 
$\textbf {H}_{\ell, Z}$ to be the identity component of the Zariski closure of 
$\pi _{1}^{\unicode{x00E9}\text{t}}(Z^{n}, s^{n})$ inside 
$\mathrm {Aut}(\mathbb {V}_{\ell, s})_{\mathbb {Q}_{\ell }}$.
Lemma 3.3 Let 
$\mathbb {V}$ be a 
$\mathbb {Z}$-local system on 
$Z^{\mathrm {an}}$, let 
$\mathbb {V}_{\ell }$ be an 
$\ell$-adic local system on 
$Z$, and suppose that we have an isomorphism 
$\mathbb {V}^{\mathrm {an}}_{\ell } \simeq \mathbb {V} \otimes \mathbb {Z}_{\ell }$. Then the induced isomorphism on fibres identifies the groups 
$\textbf {H}_{Z, \mathbb {Q}_{\ell }}$ and 
$\textbf {H}_{\ell, Z}$.
Proof. Using the analytic (respectively, 
$\ell$-adic) equivalence between local systems and monodromy representations, and the canonical identification of 
$\pi _{1}^{\unicode{x00E9}\text{t}}(Z^{n}, s^{n})$ with the profinite completion 
$\widehat {\pi _{1}(Z^{n}, s^{n})}$, the statement amounts to the following claim: given the commuting diagram
the Zariski closures 
$M$ and 
$\hat {M}$ of the images 
$\mathrm {im} (\pi _{1}(Z^{n}, s^{n}))$ and 
$\mathrm {im} (\widehat {\pi _{1}(Z^{n}, s^{n})})$ inside 
$\mathrm {Aut}(\mathbb {V}_{\ell, s})_{\mathbb {Q}_{\ell }}$ coincide. We clearly have 
$M \subset \hat {M}$ from the inclusion 
$\mathrm {im} (\pi _{1}(Z^{n}, s^{n})) \subset \mathrm {im} (\widehat {\pi _{1}(Z^{n}, s^{n})})$, so it suffices to show the reverse inclusion.
It follows from the fact that a group is dense in its profinite completion that if 
$\pi _{1}(Z^{n}, s^{n}) \to F$ is a morphism to a finite group 
$F$, then the induced morphism 
$\widehat {\pi _{1}(Z^{n}, s^{n})} \to F$ has the same image. As a consequence, the image of 
$\widehat {\pi _{1}(Z^{n}, s^{n})}$ inside 
$\mathrm {Aut}(\mathbb {V}_{\ell, s}) \cong \varprojlim _{k} \mathrm {GL}(\mathbb {Z}/\ell ^{k} \mathbb {Z})$ consists of compatible sequences 
$(\alpha _{k})_{k \geq 1}$ where each 
$\alpha _{k}$ is a reduction modulo 
$\ell ^{k}$ of an element in 
$\mathrm {im} (\pi _{1}(Z^{n}, s^{n}))$. Letting 
$f$ be a polynomial function vanishing on 
$\mathrm {im} (\pi _{1}(Z^{n}, s^{n}))$ with coefficients in 
$\mathbb {Q}_{\ell }$, it now suffices to show that 
$f$ vanishes on such compatible sequences 
$(\alpha _{k})_{k \geq 1}$. Scaling if necessary, we may assume that 
$f$ has coefficients in 
$\mathbb {Z}_{\ell }$. But then 
$f(\alpha _{k}) = 0$ modulo 
$\ell ^{k}$ holds for all 
$k$, so the result follows.
Applying Lemma 3.3, the proof of Proposition 3.1(ii) is reduced to showing that the conjugation isomorphism 
$\mathbb {V}_{\ell, s} \xrightarrow {\sim } \mathbb {V}_{\ell, s_{\sigma }}$ sends the image of 
$\pi _{1}^{\unicode{x00E9}\text{t}}(Z^{n}, s^{n})$ inside 
$\mathrm {Aut}(\mathbb {V}_{\ell, s})$ to the image of 
$\pi _{1}^{\unicode{x00E9}\text{t}}(Z^{n}_{\sigma }, s^{n}_{\sigma })$ inside 
$\mathrm {Aut}(\mathbb {V}_{\ell, s_{\sigma }})$. Given a complex variety 
$X$ and an automorphism 
$\sigma \in \mathrm {Aut}(\mathbb {C}/K)$, we will denote by 
$\tau _{\sigma } : {\text F}\unicode{x00C9}{\text T}(X) \to {\text F}\unicode{x00C9}{\text T}(X_{\sigma })$ the categorical equivalence obtained by twisting coverings by 
$\sigma$, where 
${\text F}\unicode{x00C9}{\text T}(X)$ is the category of finite étale coverings of 
$X$. Applying the isomorphism 
$\mathbb {V}_{\ell } \simeq \tau _{\sigma }^{*} \mathbb {V}_{\ell }$, it suffices to show that there exist an isomorphism 
$j : \pi _{1}^{\unicode{x00E9}\text{t}}(S_{\mathbb {C}}, s) \xrightarrow {\sim } \pi _{1}^{\unicode{x00E9}\text{t}}(S_{\mathbb {C}}, s_{\sigma })$ sending 
$\mathrm {im}(\pi _{1}^{\unicode{x00E9}\text{t}}(Z^{n}, s^{n})) \subset \pi _{1}^{\unicode{x00E9}\text{t}}(S_{\mathbb {C}}, s)$ to 
$\mathrm {im}(\pi _{1}^{\unicode{x00E9}\text{t}}(Z^{n}_{\sigma }, s^{n}_{\sigma })) \subset \pi _{1}^{\unicode{x00E9}\text{t}}(S_{\mathbb {C}}, s_{\sigma })$ and a commuting diagram of the following form:
where the horizontal arrows are the natural representations and the vertical arrow on the right comes from the natural isomorphism 
$\mathbb {V}_{\ell, s} \simeq (\tau _{\sigma }^{*} \mathbb {V}_{\ell })_{s_{\sigma }}$ of étale stalks.
Conjugation isomorphisms
To describe the map 
$j$, we begin with a more general construction. For a complex variety 
$X$ with point 
$x$, denote by 
$\mathrm {Fib}_{X, x}$ the fibre functor of 
${\text F}\unicode{x00C9}{\text T}(X)$ at 
$x \in X$. Given 
$\alpha \in \pi _{1}^{\unicode{x00E9}\text{t}}(X, x)$, we may define an automorphism 
$\alpha _{\sigma }$ of 
$\mathrm {Fib}_{X_{\sigma }, x_{\sigma }}$ as follows: for each cover of 
$X_{\sigma }$, choose an isomorphic cover 
$X'_{\sigma } \to X_{\sigma }$ in the essential image of 
$\tau _{\sigma }$; this is the conjugate of a cover 
$X' \to X$ of 
$X$. Then define 
$\alpha _{\sigma }(x'_{\sigma }) = \alpha (x')_{\sigma }$. One checks that 
$\alpha _{\sigma }$ extends uniquely to a well-defined automorphism 
$\alpha _{\sigma }$ of 
$\mathrm {Fib}_{X_{\sigma }, s_{\sigma }}$, and that the map 
$\pi _{1}^{\unicode{x00E9}\text{t}}(X, x) \to \pi _{1}^{\unicode{x00E9}\text{t}}(X_{\sigma }, x_{\sigma })$ defined by 
$\alpha \mapsto \alpha _{\sigma }$ is a group homomorphism. We define the map 
$j$ to be the case with 
$X = S_{\mathbb {C}}$ and 
$x = s$, and the map 
$j_{Z^{n}}$ to be the case 
$X = Z^{n}$ and 
$x = s^{n}$.
Completing the proof
Let 
$i_{Z^{n}} : \pi _{1}^{\unicode{x00E9}\text{t}}(Z^{n}, s^{n}) \to \pi _{1}^{\unicode{x00E9}\text{t}}(S_{\mathbb {C}}, s)$ and 
$i_{Z^{n}_{\sigma }} : \pi _{1}^{\unicode{x00E9}\text{t}}(Z^{n}_{\sigma }, s^{n}) \to \pi _{1}^{\unicode{x00E9}\text{t}}(S_{\mathbb {C}}, s)$ be the natural maps. It now suffices check that 
$j \circ \iota _{Z^{n}} = \iota _{Z^{n}_{\sigma }} \circ j_{Z^{n}}$ and that diagram (1) commutes. In the first case, one immediately checks that if 
$\alpha \in \pi _{1}^{\unicode{x00E9}\text{t}}(S_{\mathbb {C}}, s)$ acts on fibres of 
$S' \to S_{\mathbb {C}}$ above 
$s$ by base-changing to a cover of 
$Z^{n}$ and acting via 
$\pi _{1}^{\unicode{x00E9}\text{t}}(Z^{n}, s^{n})$, then the same is true for 
$\alpha _{\sigma }$ with respect to 
$Z^{n}_{\sigma }$ and 
$\pi _{1}^{\unicode{x00E9}\text{t}}(Z^{n}_{\sigma }, s^{n}_{\sigma })$. In the second case, it is immediate from the explicit description of the isomorphism 
$t : \mathbb {V}_{\ell, s} \xrightarrow {\sim } (\tau _{\sigma }^{*} \mathbb {V}_{\ell })_{s_{\sigma }}$ that, together with the map 
$j$, the map 
$t$ gives a map of representations (i.e. acting by 
$\alpha$ then applying 
$t$ is the same as applying 
$t$ and then acting by 
$j(\alpha )$). But 
$t$ giving a map of representations is equivalent to the commutativity of (1).
4. Variants of the main theorem
Although our applications will use Theorems 1.6 and 1.13, we wish to briefly explain how Proposition 1.9 may be used to prove variants of Theorems 1.6 and 1.13 which may be of independent interest. Let us first generalize the notation 
$\mathcal {I}_{T}(s, Z, \sigma )$ established in the introduction.
Definition 4.1 Let 
$s \in S(\mathbb {C})$ be a point, 
$\{ Z_{i} \}_{i \in I}$ a collection of subvarieties of 
$S_{\mathbb {C}}$ containing 
$s$, 
$\sigma \in \mathrm {Aut}(\mathbb {C}/K)$ an automorphism, and 
$T \subset \mathcal {T}(\mathbb {V}_{s})$ a collection of tensors with canonical rational conjugates. Then we define
\[ \mathcal{I} = \mathcal{I}_{T}(s, \{ Z_{i} \}_{i \in I}, \sigma) \subset \mathrm{Isom}(\mathbb{V}_{s}, \mathbb{V}_{s_{\sigma}}) \]
by the property that 
$r \in \mathcal {I}(\mathbb {C})$ if and only if 
$r \circ \textbf {H}_{Z_{i}, \mathbb {C}} \circ r^{-1} = \textbf {H}_{\mathbb {Z}_{i, \sigma }, \mathbb {C}}$ for all 
$i$, and 
$r$ sends each 
$t \in T$ to its canonical rational conjugate 
$t_{\sigma } \in T_{\sigma }$.
We observe that the normalizer 
$N$ in the statement of Theorem 1.6 is equal to 
$\mathcal {I}_{T}(s, Z, \mathrm {id})$, so we may view 
$\mathcal {I}_{T}(s, \{ Z \}_{i \in I}, \mathrm {id})$ as its natural generalization. The following generalization of Theorem 1.6 is then immediate from Proposition 3.1.
Theorem 4.2 Let 
$\mathbb {V}$ be a motivic variation of Hodge structure on 
$S$, and let 
$s \in S(\mathbb {C})$. Suppose that 
$T \subset \mathcal {T}(\mathbb {V}_{s})$ is a subspace with canonical rational conjugates, that 
$Z_{i} \subset S_{\mathbb {C}}$ for 
$i \in I$ is a collection of complex subvarieties containing 
$s$, and that 
$W \subset \mathcal {T}(\mathbb {V}_{s})$ is a subspace containing 
$T$ such that either
(i)
$\mathcal {I}_{T}(s, \{ Z_{i} \}_{i \in I}, \mathrm {id})$ fixes $W$ as a $\mathbb {Q}$-subspace, or(ii)
$\mathcal {I}_{T}(s, \{ Z_{i} \}_{i \in I}, \mathrm {id})$ fixes $W$ pointwise.
Then
(i) each element
$w$ of $W$ has rational conjugates, or(ii) each element
$w$ of $W$ has a canonical rational conjugate,
in cases (i) and (ii), respectively.
Proof. As in the proof of Theorem 1.6, we obtain from Proposition 3.1 that 
$r^{\mathrm {dR}}_{\sigma }$ and 
$r^{\ell }_{\sigma }$ for all 
$\ell$ are points of 
$\mathcal {I} = \mathcal {I}_{T}(s, \{ Z_{i} \}_{i \in I}, \sigma )$. It follows as in Theorem 1.6 that the points of 
$W$ are defined over 
$\bar {\mathbb {Q}}$ and (under an appropriate isomorphism 
$\mathbb {C} \cong \overline {\mathbb {Q}_{\ell }}$) over 
$\overline {\mathbb {Q}}_{\ell }$ for every 
$\ell$. By Claim 1.10 we conclude in that 
$r(W_{\sigma })$ is a 
$\mathbb {Q}$-subspace, where 
$r \in \mathcal {I}(\mathbb {C})$. In case (ii) we additionally know that 
$r(w) = w_{\sigma }$ is independent of the choice of 
$r$, making the conjugates canonical.
Finally let us give a similar, but simpler argument which establishes cases of a kind of ‘
$\bar {\mathbb {Q}}$-absolute Hodge’ conjecture. We note that a ‘
$\bar {\mathbb {Q}}$-absolute Hodge’ conjecture may in fact be enough for certain applications of absolute Hodge to the algebraicity of periods. The following result requires no 
$\ell$-adic input.
Theorem 4.3 Let 
$\mathbb {V}$ be a variation of Hodge structure on 
$S$, suppose that 
$S$, 
$\nabla$ and 
$\mathcal {H}$ are defined over 
$K$, and choose 
$s \in S(\mathbb {C})$. Let 
$T \subset \mathcal {T}(\mathbb {V}_{\bar {\mathbb {Q}}, s})$ be a 
$\bar {\mathbb {Q}}$-subspace whose conjugate 
$r^{\mathrm {dR}}_{\sigma }(W)$ is defined over 
$\bar {\mathbb {Q}}$, let 
$Z_{i} \subset S_{\mathbb {C}}$ for 
$i \in I$ be a collection of complex subvarieties containing 
$s$, and suppose that 
$W \subset \mathcal {T}(\mathbb {V}_{\bar {\mathbb {Q}}, s})$ is a subspace containing 
$T$ such that the orbit of 
$[W]$ under 
$\mathcal {I} = \mathcal {I}_{T}(s, \{ Z_{i} \}_{i \in I}, \mathrm {id})$ inside the appropriate Grassmannian is finite.Footnote 9 Then 
$r^{\mathrm {dR}}_{\sigma }(W)$ is defined over 
$\bar {\mathbb {Q}}$.
Proof. The proof follows immediately, as Proposition 3.1 ensures that 
$r^{\mathrm {dR}}_{\sigma }$ lies inside 
$\mathcal {I}$ and the assumptions ensure that 
$r(W)$ is defined over 
$\bar {\mathbb {Q}}$ for any point 
$r$ of 
$\mathcal {I}$.
Finally, we note that there is an additional step involved in translating Theorems 4.2 and 4.3 to absolute Hodge statements (like Theorem 1.13), but this follows exactly as in § 2.3 and we leave it to the reader.
5. Applications to absolute Hodge
5.1 Voisin's example
In this section we prove Theorem 1.14, following an approach laid out by Voisin in § 3 of [Reference VoisinVoi07]. Let us first revisit the proof of our Corollary 1.8 in the context of Theorem 1.13.
We let 
$\mathbb {V}$ be a motivic variation on the smooth 
$K$-variety 
$S$, and 
$T \subset \mathcal {T}(\mathbb {V}_{s})$ be the 
$\mathbb {Q}$-span of the polarization 
$Q_{s}$; by Lemma 2.2 the subspace 
$T$ has canonical rational conjugates. Suppose that there exists a subvariety 
$Z \subset S_{\mathbb {C}}$ containing 
$s$ such that the only non-trivial subspace of 
$\mathbb {V}^{m,n}_{s}$ fixed by 
$\textbf {H}_{Z}$ is the line 
$\mathbb {Q} w$ spanned by the Hodge class 
$w \in \mathbb {V}^{m,n}_{s}$. Then if 
$n$ is a complex point of the normalizer of 
$\textbf {H}_{Z}$ inside 
$\mathbf {G}_{T}$, we have that 
$n w = \lambda w$ for some 
$\lambda \in \mathbb {C}$, and from the fact that 
$Q(n w, n w) = Q(w, w)$ we learn that 
$\lambda = \pm 1$. Theorem 1.13 therefore applies, and the tensor 
$w$ is absolutely Hodge.
A very similar argument is given by Voisin in her paper (see Remark 1.2 and Theorem 0.6(1) in [Reference VoisinVoi07]). The language used is slightly different: Voisin only considers Hodge vectors 
$v$ (the 
$(m, n) = (0, 1)$ case); the variety 
$Z$ is taken to be a special subvariety (irreducible component of the Hodge locus); and the condition that the fixed locus of 
$\textbf {H}_{Z}$ consist of exactly the line spanned by 
$w$ takes the form of the condition that the restricted variation 
${\mathbb {V}}\left| {_{Z}} \right.$ has 
$\mathbb {Q} w$ as its constant subvariation. Voisin also only obtains the weaker conclusion that the conjugate 
$v_{\sigma }$ is a 
$\bar {\mathbb {Q}}$-scalar multiple of a Hodge class; the essential difference, it seems to us, is the presence of 
$\ell$-adic input in our argument.
Given a variation of Hodge structure 
$\mathbb {V}$ of weight 
$n$ with Hodge bundle 
$\mathcal {H}$ and filtration 
$F^{\bullet }$, we define 
$\mathcal {H}^{p,q} = F^{p} / F^{p+1}$ for non-negative 
$(p, q)$ such that 
$p + q = n$. To study the example of Theorem 1.14, Voisin states a criterion [Reference VoisinVoi07, Theorem 3.1], whose proof gives the following proposition.
Proposition 5.1 (Voisin)
Let 
$\mathbb {V}$ be a polarizable variation of Hodge structure on the smooth complex variety 
$S$ of weight 
$2k$. Denote by 
$\overline {\nabla }^{p,q}$ the 
$\mathcal {O}_{S}$-linear map 
$\mathcal {H}^{p, q} \to \mathcal {H}^{p-1,q+1} \otimes \Omega ^{1}_{S}$ induced by the connection, let 
$\alpha \in \mathbb {V}_{s}$ be a Hodge class with Hodge locus 
$Z_{\alpha }$, and let 
$\lambda$ be its projection to 
$\mathcal {H}^{k,k}$. Suppose that:
(i) the map
$\mu _{\lambda } : T_{s} S \to \mathcal {H}^{k-1,k+1}_{s}$ defined by $\mu _{\lambda }(v) = \bar {\nabla }^{k,k}_{v}(\lambda )$ is surjective;(ii) for
$p > k$, $p+q = 2k$, the map $\mathcal {H}^{p,q}_{s} \to \mathcal {H}^{p-1,q+1}_{s} \otimes (T_{s} Z_{\alpha })^{*}$ obtained by restricting $\bar {\nabla }^{p,q}$ is injective;(iii) and the map
$\mathcal {H}^{k,k}_{s} \to \mathcal {H}^{k-1,k+1}_{s} \otimes (T_{s} Z_{\alpha })^{*}$ obtained by restricting $\bar {\nabla }^{k,k}$ has kernel equal to the span of $\lambda$.
Then the fixed locus in 
$\mathbb {V}_{s}$ of 
$\textbf {H}_{Z_{\alpha }}$ is exactly the line spanned by 
$\alpha$.
Proof. We briefly describe the argument appearing in [Reference VoisinVoi07], using [Reference VoisinVoi03] as a reference. We begin by giving a local analytic description of 
$Z_{\alpha }$ near 
$s$. Let us abusively think of 
$\alpha$ as a section of 
$\mathbb {V}(B)$ for a small analytic ball 
$B \subset S$ centred at 
$s$, and let 
$\beta$ be the induced section of 
$\mathcal {H} / F^{k} \mathcal {H}$. Locally on 
$B$, choose a decomposition 
$\mathcal {H} / F^{k} \mathcal {H} \simeq F^{k-1} \mathcal {H} / F^{k} \mathcal {H} \oplus \mathcal {F}$, where 
$\mathcal {F}$ is a holomorphic vector bundle. Let 
$\beta = \beta _{k-1} + \beta '$ be the corresponding decomposition of 
$\beta$. Then by [Reference VoisinVoi03, Lemma 5.15], the locus 
$B \cap Z_{\alpha }$ coincides on the level of analytic spaces with the locus in 
$B$ defined by the vanishing of 
$\beta _{k-1}$.
This local description has two consequences. First, we learn that the locus 
$Z_{\alpha } \cap B$ has codimension equal to at most the rank of 
$F^{k-1} \mathcal {H} / F^{k} \mathcal {H}$, which is the Hodge number 
$h^{k-1, k+1}$. Secondly, one argues as in [Reference VoisinVoi03, § 5.3.2] that the tangent space of 
$Z_{\alpha }$ at 
$s$ is the kernel of 
$\mu _{\lambda }$. The surjectivity of 
$\mu _{\lambda }$ then implies that this tangent space has codimension in 
$T_{s} S$ exactly equal to 
$h^{k-1,k+1}$, so it follows that from the upper bound that 
$Z_{\alpha }$ has codimension 
$h^{k-1,k+1}$ and is smooth at 
$s$.
Conditions (ii) and (iii) relate only to the variation on 
$Z_{\alpha }$, so, using Remark 1.4, it suffices to choose a smooth open subvariety 
$U \subset Z_{\alpha }$ containing 
$s$ and show that the identity component of the monodromy on 
${\mathbb {V}}\left| {_{U}} \right.$ fixes only the line spanned by 
$\alpha$. After replacing 
$U$ with a finite étale covering, any algebraic monodromy invariant vector in 
$\mathbb {V}_{s}$ is monodromy invariant, hence is induced by a global flat section 
$\gamma$ of 
$ {\mathbb {V}}\left| {_{U}} \right.$. By flatness we have 
$\bar {\nabla }^{p,q} \gamma ^{p,q} = 0$ for each 
$(p,q)$, and, applying (ii) and (iii) at 
$s$, we learn that 
$\gamma ^{p,q}_{s} = 0$ when 
$p > k$, and that 
$\gamma ^{k,k}_{s}$ is a scalar multiple of 
$\lambda$. Using Hodge symmetry to handle the case when 
$p < k$, we learn that 
$\gamma _{s}$ is a scalar multiple of 
$\alpha$.
Proof of Theorem 1.14 We observe that the variation 
$\mathbb {V}_{-}$ is motivic, with the implicit set 
$\mathcal {K} = \{ 2 \}$: it is obtained from the variation 
$\mathbb {V} = R^{4} f^{\mathrm {an}}_{*} \mathbb {Z}$ by taking the image under the relative idempotent correspondence 
$\frac {1}{2}(\mathrm {id} - \iota )$, and properties (i)–(vii) in § 2 are easily obtained from restriction under the assumption that 
$2$ is invertible. Checking as Voisin does in [Reference VoisinVoi07, Example 3.5], conditions (1), (2) and (3) of Proposition 5.1 hold for 
$\alpha$ a complex point belonging to a dense Zariski open subset 
$U \subset F^{2} \mathcal {H}^{4}_{-}$, where we regard the locus 
$Z_{\alpha }$ for a general 
$\alpha \in F^{2} \mathcal {H}^{4}_{-}(\mathbb {C})$ as the analytic germ at 
$s$ defined by the property that flat translates of 
$\alpha$ remain in 
$F^{2}$. The result then follows from Proposition 5.1, Theorem 1.13 (using Remark 1.11 to take into account the exception at 
$\ell = 2$) and the argument given at the start of this section.
Proof of Remark 1.15 From [Reference VoisinVoi07, Proposition 3.3] we know that the locus of Hodge classes is topologically dense in the underlying real subbundle of 
$\mathcal {H}^{2,2}_{-}$, so it suffices to exhibit a single Hodge class in 
$U(\mathbb {C})$. As Voisin points out in [Reference VoisinVoi07, Example 3.5], one can check this explicitly for Hodge classes belonging to the Hodge structure of the Fermat hypersurface.
5.2 Absolutely Hodge isomorphisms
In this section we study the question of when an isomorphism of Hodge structures between two fibres in a motivic family is absolute Hodge. Related questions are considered in [Reference VoisinVoi07, § 3].
Definition 5.2 Let 
$S_{1}$ and 
$S_{2}$ be algebraic varieties, and let 
$\mathbb {V}_{1}$ and 
$\mathbb {V}_{2}$ be variations of Hodge structure on 
$S_{1}$ and 
$S_{2}$, respectively. We define 
$\mathbb {V}_{1} \boxtimes \mathbb {V}_{2}$ to be the variation 
$p^{*}_{1} \mathbb {V}_{1} \otimes p^{*}_{2} \mathbb {V}_{2}$ on 
$S_{1} \times S_{2}$, where 
$p_{i} : S_{1} \times S_{2} \to S_{i}$ is the projection.
Suppose that 
$\mathbb {V}$ is an integral variation of Hodge structure on 
$S$, and let 
$Z \subset S \times S$ be the algebraic subvariety whose points are pairs 
$(x,y)$ such that 
$\mathbb {V}_{x}$ is isomorphic to 
$\mathbb {V}_{y}$ as an integral polarized Hodge structure. These isomorphisms are Hodge tensors of the variation 
$\mathbb {V} \boxtimes \mathbb {V}^{*}$. When a Torelli theorem is available, the locus 
$Z$ is simply equal to the diagonal 
$\Delta$, and its algebraic monodromy is easily determined to be equal to the image of 
$\textbf {H}_{S}$ under the diagonal action. In the general case, let 
$Z_{0}$ be an irreducible component of 
$Z$ containing the diagonal 
$\Delta \subset S \times S$. We determine 
$\textbf {H}_{Z_{0}}$ by reducing to the Torelli case using a recent result of Bakker, Brunebarbe and Tsimerman [Reference Bakker, Brunebarbe and TsimermanBBT18].
To show our main result we first prove some lemmas on algebraic monodromy.
Lemma 5.3 Let 
$f : S \to T$ be a proper, dominant morphism of irreducible complex algebraic varieties, and let 
$\mathbb {V}$ be a local system on 
$T$. Then for any point 
$s \in S$, the isomorphism 
$(f^{*} \mathbb {V})_{s} \xrightarrow {\sim } \mathbb {V}_{f(s)}$ induces an isomorphism between 
$\textbf {H}_{S}$ and 
$\textbf {H}_{T}$.
Proof. That 
$f : S \to T$ is proper means that it has a Stein factorization 
$f = g \circ h$, where 
$h : S \to V$ is proper with connected fibres and 
$g$ is finite. We are thus reduced to showing the theorem in two cases:
(i) when
$f$ additionally has connected fibres;(ii) and when
$f$ is additionally finite.
Let us first assume that both 
$S$ and 
$T$ are normal. If 
$X$ is a normal variety, then the fundamental group of any open subvariety 
$U$ surjects onto the fundamental group of 
$X$, so we may replace both 
$S$ and 
$T$ by Zariski open sets, restricting 
$f$ appropriately. In case (i) this lets us assume that 
$f$ is surjective and flat, and hence by [Sta20, Lemma 01UA] universally open. Kollár has shown in [Reference KollárKol19] that a universally open, surjective morphism of complex varieties with connected fibres satisfies the two-point path lifting property (see [Reference KollárKol19, Definition 30]), and therefore induces a surjection of fundamental groups, from which the result follows. In case (ii) we may assume that 
$f$ is étale, from which the result follows as the monodromy of 
$S$ will be finite index in the monodromy of 
$T$, and hence the Zariski closures will have the same identity component.
Working now in the general case, it follows from the definition of algebraic monodromy that the algebraic monodromy of a local system 
$\mathbb {V}$ on 
$X$ agrees with the algebraic monodromy of the restriction of 
$\mathbb {V}$ to the normal locus of 
$X$. The result then follows by restricting 
$f$.
Lemma 5.4 Let 
$\mathbb {V}$ be a polarizable integral variation of Hodge structure on the smooth complex algebraic variety 
$S$, and let 
$Z_{0}$ and 
$\Delta$ be as above. Then 
$\textbf {H}_{Z_{0}} = \textbf {H}_{\Delta }$.
Proof. The statement is unchanged under replacing 
$S$ with a finite étale cover, so we may assume that 
$S$ admits a log-smooth compactification 
$\bar {S}$ for which the monodromy around the normal crossing divisor 
$\bar {S} \setminus S$ is unipotent. Let 
$\varphi : S \to \Gamma \backslash D$ be the period map on 
$S$; here 
$D$ is the full period domain of polarized integral Hodge structures on a fixed lattice 
$V$, and 
$\Gamma = G(\mathbb {Z})$ where 
$G = \mathrm {Aut}(V, Q)$. Then 
$\Gamma \backslash D$ may be interpreted as the moduli space for polarized integral Hodge structures of the same type as the fibres of 
$\mathbb {V}$, and the map 
$\varphi$ sends 
$s$ to the isomorphism class of 
$\mathbb {V}_{s}$. Arguing as in [Reference Carlson, Peters and Müller-StachCPM03, Corollary 13.7.6], we may extend 
$S$ to a larger open subvariety 
$S' \subset \bar {S}$ and the map 
$\varphi$ to a 
$S'$ to reduce to the case where 
$\varphi$ is proper. Applying the main theorem of [Reference Bakker, Brunebarbe and TsimermanBBT18], we find that there exists a factorization 
$\varphi = \varphi ' \circ g$ where 
$g : S \to T$ is a dominant proper map of algebraic varieties and 
$\varphi ' : T \hookrightarrow \Gamma \backslash D$ is a closed embedding.
The variety 
$T$ admits a variation 
$\mathbb {V}'$ such that 
$\mathbb {V}$ may be identified with 
$g^{*} \mathbb {V}'$, and 
$\varphi '$ is the period map of 
$\mathbb {V}'$. The variety 
$Z$ is then the inverse image of the diagonal under the product morphism 
$g \times g : S \times S \to T \times T$. If 
$\Delta _{S} \subset S \times S$ and 
$\Delta _{T} \subset T \times T$ are the respective diagonals, the maps 
$Z_{0} \to \Delta _{T}$ and 
$\Delta _{S} \to \Delta _{T}$ are both dominant and proper, so the result follows by Lemma 5.3.
Let us note that it is a consequence of Deligne's Principle A (see [Reference DeligneDel82b, Theorem 3.8]) that if the tensor 
$Q_{s}$ has canonical rational conjugates, then so does every rational tensor fixed by 
$\mathrm {Aut}(\mathbb {V}_{s}, Q_{s})$. Theorem 1.16 now follows from the following more general result.
Theorem 5.5 If 
$\mathbb {V}$ is a motivic variation of Hodge structure on the smooth 
$K$-variety 
$S$ such that rational tensors fixed by 
$\textbf {H}_{S}$ have canonical rational conjugates and the points of the center 
$\mathcal {Z}(\textbf {H}_{S})$ are defined over 
$\mathbb {Q}$, then tensors fixed by 
$\textbf {H}_{Z_{0}}$ have rational conjugates, and generic isomorphisms between 
$\mathbb {V}_{x}$ and 
$\mathbb {V}_{y}$ are 
$K$-absolutely Hodge.
Proof. Let 
$T \subset \mathcal {T}(\mathbb {V}_{s})$ be the subspace of 
$\mathbb {Q}$-tensors fixed by 
$\textbf {H}_{S}$, and let 
$T^{*}$ be its dual. As the subspace 
$T$ (respectively, the subspace 
$T^{*}$) is fixed under algebraic monodromy, parallel transport gives a path-independent translate of 
$T$ (respectively, 
$T^{*}$) to any fibre of 
$\mathbb {V}$ (respectively, 
$\mathbb {V}^{*}$). It follows that we may unambiguously refer to the subspace 
$R = T \otimes T^{*}$ inside 
$\mathcal {T}(\mathbb {V}_{x} \otimes \mathbb {V}^{*}_{y})$ for any pair 
$(x, y)$. The fact that 
$T$ has canonical rational conjugates implies the same fact for 
$R$. We then have the following claim.
Claim 5.6 The groups 
$\mathbf {G}_{R}$ and 
$\mathbf {G}_{T} \times \mathbf {G}_{T^{*}}$ are equal as subgroups of 
$\mathrm {Aut}(\mathbb {V}_{x} \otimes \mathbb {V}^{*}_{y})$.
Proof. Let 
$U \subset \mathcal {T}(\mathbb {V}_{x} \otimes \mathbb {V}^{*}_{y})$ be the subspace of tensors fixed by 
$\mathbf {G}_{T} \times \mathbf {G}_{T^{*}}$. It suffices to show that 
$U = T \otimes T^{*}$. Let us first argue that the space 
$U$ is spanned by pure tensors; that is, it has a basis of the form 
$u \otimes u'$ where 
$u \in \mathcal {T}(\mathbb {V}_{x})$ and 
$u' \in \mathcal {T}(\mathbb {V}^{*}_{y})$. Indeed, suppose that 
$\mathbf {G}_{T} \times \mathbf {G}_{T^{*}}$ fixes 
$\sum _{k = 1}^{m} v_{k} \otimes v'_{k}$, where 
$\{ v_{k} \}_{k = 1}^{m}$ and 
$\{ v'_{k} \}_{k = 1}^{m}$ form linearly independent sets. Let 
$(g, g') \in \mathbf {G}_{T}(\mathbb {C}) \times \mathbf {G}_{T^{*}}(\mathbb {C})$ be a point. Then from the fact that 
$(g, 1)$ fixes 
$\sum _{k = 1}^{m} v_{k} \otimes v'_{k}$ we learn that 
$g$ fixes each 
$v_{k}$, and analogously we learn that 
$(1, g')$ fixes each 
$v'_{k}$. It follows that 
$(g, g')$ fixes each term in the sum.
We are reduced to arguing that any element of the form 
$v \otimes v'$ with 
$v \in \mathcal {T}(\mathbb {V}_{x})$ and 
$v' \in \mathcal {T}(\mathbb {V}^{*}_{y})$ fixed by 
$\mathbf {G}_{T} \times \mathbf {G}_{T^{*}}$ must satisfy 
$v \in T$ and 
$v' \in T^{*}$. But since 
$v \otimes v'$ is fixed by 
$\mathbf {G}_{T} \times \mathbf {G}_{T^{*}}$ it is in particular fixed by 
$\mathbf {G}_{T} \times \{ 1 \}$ and 
$\{ 1 \} \times \mathbf {G}_{T^{*}}$, so the result follows.
We may now complete the proof by computing the normalizer 
$N$ of 
$\textbf {H}_{Z_{0}}$ inside 
$\textbf {H}_{S} \times \textbf {H}_{S}$. It follows from Lemma 5.4 that 
$\textbf {H}_{Z_{0}}$ is the diagonal subgroup 
$D$ of 
$\textbf {H}_{S} \times \textbf {H}_{S}$. The normalizer 
$N$ of 
$D$ is the group generated by 
$D$ and the product of centers 
$\mathcal {Z}(\textbf {H}_{S}) \times \mathcal {Z}(\textbf {H}_{S})$. It follows that 
$N$ preserves the subspace 
$W$ of all rational tensors fixed by 
$\textbf {H}_{Z_{0}}$, and so the result follows by Theorems 1.6 and 1.13.
Acknowledgements
The author thanks Jacob Tsimerman for helpful discussions, and an anonymous referee for helping improve the exposition.
