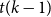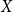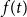1. Introduction
In 1965, Erdős and Pósa [Reference Erdős and Pósa6] showed that every graph
![]() $G$
either contains
$G$
either contains
![]() $k$
vertex-disjoint cycles or contains a set
$k$
vertex-disjoint cycles or contains a set
![]() $X$
of
$X$
of
![]() $\mathcal{O}(k \log k)$
vertices such that
$\mathcal{O}(k \log k)$
vertices such that
![]() $G-X$
has no cycles. The
$G-X$
has no cycles. The
![]() $\mathcal{O}(k \log k)$
bound on the size of
$\mathcal{O}(k \log k)$
bound on the size of
![]() $X$
is best possible up to a constant factor. Using their Grid Minor Theorem, Robertson and Seymour [Reference Robertson and Seymour9] proved the following generalisation: for every planar graph
$X$
is best possible up to a constant factor. Using their Grid Minor Theorem, Robertson and Seymour [Reference Robertson and Seymour9] proved the following generalisation: for every planar graph
![]() $H$
, there exists a function
$H$
, there exists a function
![]() $f_H(k)$
such that every graph
$f_H(k)$
such that every graph
![]() $G$
contains either
$G$
contains either
![]() $k$
vertex-disjoint subgraphs each having an
$k$
vertex-disjoint subgraphs each having an
![]() $H$
minor, or a set
$H$
minor, or a set
![]() $X$
of at most
$X$
of at most
![]() $f_H(k)$
vertices such that
$f_H(k)$
vertices such that
![]() $G-X$
has no
$G-X$
has no
![]() $H$
minor. For
$H$
minor. For
![]() $H=K_3$
, this corresponds to the setting of the Erdős–Pósa theorem.
$H=K_3$
, this corresponds to the setting of the Erdős–Pósa theorem.
The theorem of Robertson and Seymour is best possible in the sense that no such result holds when
![]() $H$
is not planar. The original upper bound of
$H$
is not planar. The original upper bound of
![]() $f_H(k)$
on the size of
$f_H(k)$
on the size of
![]() $X$
depends on bounds from the Grid Minor Theorem and is large as a result (though it is polynomial in
$X$
depends on bounds from the Grid Minor Theorem and is large as a result (though it is polynomial in
![]() $k$
if we use the polynomial version of the Grid Minor Theorem, see [Reference Chekuri and Chuzhoy4]). Chekuri and Chuzhoy [Reference Chekuri and Chuzhoy3] subsequently showed an improved upper bound of
$k$
if we use the polynomial version of the Grid Minor Theorem, see [Reference Chekuri and Chuzhoy4]). Chekuri and Chuzhoy [Reference Chekuri and Chuzhoy3] subsequently showed an improved upper bound of
![]() $\mathcal{O}_H(k \log ^c k)$
for a fixed planar graph
$\mathcal{O}_H(k \log ^c k)$
for a fixed planar graph
![]() $H$
, where
$H$
, where
![]() $c$
is some large but absolute constant. This was in turn improved to
$c$
is some large but absolute constant. This was in turn improved to
![]() $\mathcal{O}_H(k \log k)$
by Cames van Batenburg, Huynh, Joret, and Raymond [Reference Cames van Batenburg, Huynh, Joret and Raymond2], thus matching the original bound of Erdős and Pósa for cycles.
$\mathcal{O}_H(k \log k)$
by Cames van Batenburg, Huynh, Joret, and Raymond [Reference Cames van Batenburg, Huynh, Joret and Raymond2], thus matching the original bound of Erdős and Pósa for cycles.
An
![]() $\mathcal{O}_H(k \log k)$
bound is best possible when
$\mathcal{O}_H(k \log k)$
bound is best possible when
![]() $H$
contains a cycle. However, when
$H$
contains a cycle. However, when
![]() $H$
is a forest, it turns out that one can obtain a linear in
$H$
is a forest, it turns out that one can obtain a linear in
![]() $k$
bound on the size of
$k$
bound on the size of
![]() $X$
, as proved by Fiorini, Joret, and Wood [Reference Fiorini, Joret and Wood7]. Their proof gives an
$X$
, as proved by Fiorini, Joret, and Wood [Reference Fiorini, Joret and Wood7]. Their proof gives an
![]() $\mathcal{O}_H(k)$
bound with a non-explicit constant factor that grows very fast as a function of
$\mathcal{O}_H(k)$
bound with a non-explicit constant factor that grows very fast as a function of
![]() $|V(H)|$
. This is due to the use of MSO-based tools in the proof, among others. In this short note, we give a simple proof of their result with an optimal dependence on
$|V(H)|$
. This is due to the use of MSO-based tools in the proof, among others. In this short note, we give a simple proof of their result with an optimal dependence on
![]() $t$
and
$t$
and
![]() $k$
when
$k$
when
![]() $H$
is a tree.
$H$
is a tree.
Theorem 1.
Let
![]() $T$
be a tree on
$T$
be a tree on
![]() $t$
vertices. For every positive integer
$t$
vertices. For every positive integer
![]() $k$
and every graph
$k$
and every graph
![]() $G$
, either
$G$
, either
![]() $G$
contains
$G$
contains
![]() $k$
pairwise vertex-disjoint subgraphs each having a
$k$
pairwise vertex-disjoint subgraphs each having a
![]() $T$
minor, or there exists a set
$T$
minor, or there exists a set
![]() $X$
of at most
$X$
of at most
![]() $t(k-1)$
vertices of
$t(k-1)$
vertices of
![]() $G$
such that
$G$
such that
![]() $G-X$
has no
$G-X$
has no
![]() $T$
minor.
$T$
minor.
Observe that the bound on the size of
![]() $X$
in Theorem1 is tight: if
$X$
in Theorem1 is tight: if
![]() $G$
is a complete graph on
$G$
is a complete graph on
![]() $tk-1$
vertices, then
$tk-1$
vertices, then
![]() $G$
does not contain
$G$
does not contain
![]() $k$
pairwise vertex-disjoint subgraphs each having a
$k$
pairwise vertex-disjoint subgraphs each having a
![]() $T$
minor, and every set
$T$
minor, and every set
![]() $X$
of vertices such that
$X$
of vertices such that
![]() $G-X$
has no
$G-X$
has no
![]() $T$
minor has size at least
$T$
minor has size at least
![]() $|V(G)| - (t-1) = t(k-1)$
.
$|V(G)| - (t-1) = t(k-1)$
.
Theorem1 follows immediately from the following more general result for forests.
Theorem 2.
Let
![]() $F$
be a forest on
$F$
be a forest on
![]() $t$
vertices and let
$t$
vertices and let
![]() $t^{\prime}$
be the maximum number of vertices in a component of
$t^{\prime}$
be the maximum number of vertices in a component of
![]() $F$
. For every positive integer
$F$
. For every positive integer
![]() $k$
and every graph
$k$
and every graph
![]() $G$
, either
$G$
, either
![]() $G$
contains
$G$
contains
![]() $k$
pairwise vertex-disjoint subgraphs each having an
$k$
pairwise vertex-disjoint subgraphs each having an
![]() $F$
minor, or there exists a set
$F$
minor, or there exists a set
![]() $X$
of at most
$X$
of at most
![]() $tk-t^{\prime}$
vertices of
$tk-t^{\prime}$
vertices of
![]() $G$
such that
$G$
such that
![]() $G-X$
has no
$G-X$
has no
![]() $F$
minor.
$F$
minor.
Let us also point out the following corollary of Theorem1 (proved in the next section).
Corollary 3.
For all positive integers
![]() $p$
and
$p$
and
![]() $k$
, and for every graph
$k$
, and for every graph
![]() $G$
, either
$G$
, either
![]() $G$
contains
$G$
contains
![]() $k$
vertex-disjoint subgraphs each of pathwidth at least
$k$
vertex-disjoint subgraphs each of pathwidth at least
![]() $p$
, or
$p$
, or
![]() $G$
contains a set
$G$
contains a set
![]() $X$
of at most
$X$
of at most
![]() $2\cdot 3^{p+1}k$
vertices such that
$2\cdot 3^{p+1}k$
vertices such that
![]() $G-X$
has pathwidth strictly less than
$G-X$
has pathwidth strictly less than
![]() $p$
.
$p$
.
2. Proof
For a positive integer
![]() $k$
, we use the notation
$k$
, we use the notation
![]() $[k]\,:\!=\, \{1,\ldots, k\}$
, and when
$[k]\,:\!=\, \{1,\ldots, k\}$
, and when
![]() $k=0$
let
$k=0$
let
![]() $[k] \,:\!=\, \varnothing$
.
$[k] \,:\!=\, \varnothing$
.
Let
![]() $G$
be a graph. We denote by
$G$
be a graph. We denote by
![]() $V(G)$
and
$V(G)$
and
![]() $E(G)$
, the vertex set and edge set of
$E(G)$
, the vertex set and edge set of
![]() $G$
, respectively. Let
$G$
, respectively. Let
![]() $X\subseteq V(G)$
. Then
$X\subseteq V(G)$
. Then
![]() $G[X]$
denotes the subgraph of
$G[X]$
denotes the subgraph of
![]() $G$
induced by the vertices in
$G$
induced by the vertices in
![]() $X$
and
$X$
and
![]() $G-X=G[V(G)- X]$
. We define the boundary of
$G-X=G[V(G)- X]$
. We define the boundary of
![]() $X$
in
$X$
in
![]() $G$
to be
$G$
to be
![]() $\partial _G X \,:\!=\, \left\{v \in X \mid vw\in E(G),\, w\in V(G-X)\right\}$
. We omit the subscript
$\partial _G X \,:\!=\, \left\{v \in X \mid vw\in E(G),\, w\in V(G-X)\right\}$
. We omit the subscript
![]() $G$
when the graph
$G$
when the graph
![]() $G$
is clear from the context.
$G$
is clear from the context.
A path decomposition of
![]() $G$
is a sequence
$G$
is a sequence
![]() $(B_1, B_2, \dots, B_q)$
of vertex subsets of
$(B_1, B_2, \dots, B_q)$
of vertex subsets of
![]() $G$
called bags satisfying the following properties: (1) every vertex of
$G$
called bags satisfying the following properties: (1) every vertex of
![]() $G$
appears in a non-empty set of consecutive bags, and (2) for every edge
$G$
appears in a non-empty set of consecutive bags, and (2) for every edge
![]() $uv$
of
$uv$
of
![]() $G$
, there is a bag containing both
$G$
, there is a bag containing both
![]() $u$
and
$u$
and
![]() $v$
. The width of the path decomposition is the maximum size of a bag minus
$v$
. The width of the path decomposition is the maximum size of a bag minus
![]() $1$
. The pathwidth
$1$
. The pathwidth
![]() $\textit{pw}(G)$
of
$\textit{pw}(G)$
of
![]() $G$
is the minimum width of a path decomposition of
$G$
is the minimum width of a path decomposition of
![]() $G$
.
$G$
.
A graph
![]() $H$
is a minor of a graph
$H$
is a minor of a graph
![]() $G$
if
$G$
if
![]() $H$
can be obtained from a subgraph of
$H$
can be obtained from a subgraph of
![]() $G$
by contracting edges. Robertson and Seymour [Reference Robertson and Seymour8] proved that there exists a function
$G$
by contracting edges. Robertson and Seymour [Reference Robertson and Seymour8] proved that there exists a function
![]() $f\,:\,\mathbb{N}\to \mathbb{N}$
such that for every graph
$f\,:\,\mathbb{N}\to \mathbb{N}$
such that for every graph
![]() $G$
and every forest
$G$
and every forest
![]() $F$
on
$F$
on
![]() $t$
vertices, if
$t$
vertices, if
![]() $\textit{pw}(G)\geqslant f(t)$
then
$\textit{pw}(G)\geqslant f(t)$
then
![]() $G$
contains
$G$
contains
![]() $F$
as a minor. Bienstock, Robertson, Seymour, and Thomas [Reference Bienstock, Robertson, Seymour and Thomas1] later showed that one can take
$F$
as a minor. Bienstock, Robertson, Seymour, and Thomas [Reference Bienstock, Robertson, Seymour and Thomas1] later showed that one can take
![]() $f(t)=t-1$
, which is best possible. Diestel [Reference Diestel5] subsequently gave a short proof of this result. Our proof of Theorem2 builds on the following slightly stronger result, which appears implicitly in Diestel’s proof [Reference Diestel5].
$f(t)=t-1$
, which is best possible. Diestel [Reference Diestel5] subsequently gave a short proof of this result. Our proof of Theorem2 builds on the following slightly stronger result, which appears implicitly in Diestel’s proof [Reference Diestel5].
Lemma 4 ([Reference Diestel5]). Let
![]() $G$
be a graph, let
$G$
be a graph, let
![]() $t$
be a positive integer, and let
$t$
be a positive integer, and let
![]() $F$
be a forest on
$F$
be a forest on
![]() $t$
vertices. If
$t$
vertices. If
![]() $\textit{pw}(G)\geqslant t-1$
, then there exists
$\textit{pw}(G)\geqslant t-1$
, then there exists
![]() $Y\subseteq V(G)$
such that
$Y\subseteq V(G)$
such that
-
1.
 $G[Y]$
has a path decomposition
$G[Y]$
has a path decomposition
 $(B_1,\ldots, B_q)$
of width at most
$(B_1,\ldots, B_q)$
of width at most
 $t-1$
such that
$t-1$
such that
 $\partial Y\subseteq B_q$
, and
$\partial Y\subseteq B_q$
, and
-
2.
 $G[Y]$
contains
$G[Y]$
contains
 $F$
as a minor.
$F$
as a minor.
We now turn to the proof of Theorem2.
Proof of
Theorem 2
. We prove the following strengthening of Theorem2: Let
![]() $G$
be a graph, let
$G$
be a graph, let
![]() $c$
be a positive integer, let
$c$
be a positive integer, let
![]() $t_1\leqslant \cdots \leqslant t_c$
be non-negative integers, let
$t_1\leqslant \cdots \leqslant t_c$
be non-negative integers, let
![]() $T_1,\ldots, T_c$
be trees with
$T_1,\ldots, T_c$
be trees with
![]() $|V(T_i)|=t_i$
for every
$|V(T_i)|=t_i$
for every
![]() $i\in [c]$
, let
$i\in [c]$
, let
![]() $x_1,\ldots, x_c$
be non-negative integers, at least one of which is non-zero, and let
$x_1,\ldots, x_c$
be non-negative integers, at least one of which is non-zero, and let
![]() $I\,:\!=\, \{i\in [c]\mid x_i \geqslant 1\}$
. Then either
$I\,:\!=\, \{i\in [c]\mid x_i \geqslant 1\}$
. Then either
-
1.
 $G$
contains pairwise vertex-disjoint subgraphs
$G$
contains pairwise vertex-disjoint subgraphs
 $\{M_{i, j}\mid i\in [c],\, j\in [x_i]\}$
such that, for each
$\{M_{i, j}\mid i\in [c],\, j\in [x_i]\}$
such that, for each
 $i\in [c]$
and
$i\in [c]$
and
 $j\in [x_i]$
,
$j\in [x_i]$
,
 $M_{i,j}$
contains a
$M_{i,j}$
contains a
 $T_i$
minor, or
$T_i$
minor, or -
2. there exists
 $X\subseteq V(G)$
with
$X\subseteq V(G)$
with
 $|X|\leqslant \sum _{i\in I}x_it_i - t_{\max (I)}$
and
$|X|\leqslant \sum _{i\in I}x_it_i - t_{\max (I)}$
and
 $G-X$
does not contain
$G-X$
does not contain
 $T_i$
as a minor for some
$T_i$
as a minor for some
 $i\in I$
.
$i\in I$
.
We call the tuple
![]() $(G,c,T_1,\ldots, T_c,x_1,\ldots, x_c)$
an instance. Theorem2 follows by letting
$(G,c,T_1,\ldots, T_c,x_1,\ldots, x_c)$
an instance. Theorem2 follows by letting
![]() $T_1,\ldots, T_c$
be the components of the forest
$T_1,\ldots, T_c$
be the components of the forest
![]() $F$
and letting
$F$
and letting
![]() $x_1=x_2=\cdots =x_c=k$
.
$x_1=x_2=\cdots =x_c=k$
.
Roughly, the proof describes an inductive procedure that attempts to find a pairwise disjoint collection of models, where the number of models of each tree
![]() $T_i$
is
$T_i$
is
![]() $x_i$
. Induction is on the number
$x_i$
. Induction is on the number
![]() $\sum _{i\in [c]} x_i$
of models still missing from the collection. Failing to find one of the missing models at some step will establish (2).
$\sum _{i\in [c]} x_i$
of models still missing from the collection. Failing to find one of the missing models at some step will establish (2).
Let
![]() $(G,c,T_1,\ldots, T_c,x_1\ldots, x_c)$
be an instance, and let
$(G,c,T_1,\ldots, T_c,x_1\ldots, x_c)$
be an instance, and let
![]() $m\,:\!=\,\min (I)$
. Then
$m\,:\!=\,\min (I)$
. Then
![]() $T_m$
is a smallest tree among
$T_m$
is a smallest tree among
![]() $T_1,\ldots, T_c$
such that
$T_1,\ldots, T_c$
such that
![]() $x_m \geqslant 1$
, that is, such that we are still missing a model of
$x_m \geqslant 1$
, that is, such that we are still missing a model of
![]() $T_m$
. In the base case,
$T_m$
. In the base case,
![]() $\sum _{i\in [c]} x_i=x_{m}=1$
, and either
$\sum _{i\in [c]} x_i=x_{m}=1$
, and either
![]() $G$
has a
$G$
has a
![]() $T_{m}$
minor and the first outcome of the statement holds, or
$T_{m}$
minor and the first outcome of the statement holds, or
![]() $G$
has no such minor and the second outcome holds with
$G$
has no such minor and the second outcome holds with
![]() $X\,:\!=\,\varnothing$
, since
$X\,:\!=\,\varnothing$
, since
![]() $\sum _{i\in I} x_it_i -t_{\max (I)}= t_m - t_m = 0$
.
$\sum _{i\in I} x_it_i -t_{\max (I)}= t_m - t_m = 0$
.
For the inductive case, assume that
![]() $\sum _{i\in [c]} x_i \geqslant 2$
and that the statement holds for instances with smaller values of the sum. If, for every
$\sum _{i\in [c]} x_i \geqslant 2$
and that the statement holds for instances with smaller values of the sum. If, for every
![]() $i\in I$
,
$i\in I$
,
![]() $G$
has no
$G$
has no
![]() $T_i$
minor, then the second outcome of the statement holds with
$T_i$
minor, then the second outcome of the statement holds with
![]() $X\,:\!=\,\varnothing$
again. Thus, we may assume that
$X\,:\!=\,\varnothing$
again. Thus, we may assume that
![]() $G$
has a
$G$
has a
![]() $T_i$
minor for some
$T_i$
minor for some
![]() $i\in I$
.
$i\in I$
.
If
![]() $G$
has pathwidth at least
$G$
has pathwidth at least
![]() $t_{m}-1$
, apply Lemma4 with
$t_{m}-1$
, apply Lemma4 with
![]() $t=t_{m}$
and
$t=t_{m}$
and
![]() $F=T_{m}$
, and let
$F=T_{m}$
, and let
![]() $Y$
be the resulting subset of vertices of
$Y$
be the resulting subset of vertices of
![]() $G$
. If
$G$
. If
![]() $G$
has pathwidth less than
$G$
has pathwidth less than
![]() $t_{m}-1$
, simply let
$t_{m}-1$
, simply let
![]() $Y\,:\!=\,V(G)$
. In either case,
$Y\,:\!=\,V(G)$
. In either case,
![]() $G[Y]$
has pathwidth at most
$G[Y]$
has pathwidth at most
![]() $t_m-1$
and has a path decomposition
$t_m-1$
and has a path decomposition
![]() $(B_1, B_2, \dots, B_q)$
with
$(B_1, B_2, \dots, B_q)$
with
![]() $|B_\ell |\leqslant t_{m}$
for all
$|B_\ell |\leqslant t_{m}$
for all
![]() $\ell \in [q]$
, and such that
$\ell \in [q]$
, and such that
![]() $\partial _G Y \subseteq B_q$
. See Figure 1. Furthermore, observe that in both cases
$\partial _G Y \subseteq B_q$
. See Figure 1. Furthermore, observe that in both cases
![]() $G[Y]$
has a
$G[Y]$
has a
![]() $T_i$
minor for some
$T_i$
minor for some
![]() $i\in I$
, by our assumption on
$i\in I$
, by our assumption on
![]() $G$
.
$G$
.

Figure 1. The set
![]() $Y$
and the graph
$Y$
and the graph
![]() $G_\ell$
whose boundary in
$G_\ell$
whose boundary in
![]() $G$
is contained in
$G$
is contained in
![]() $B_\ell$
.
$B_\ell$
.
Let
![]() $\ell \in [q]$
be the smallest index such that
$\ell \in [q]$
be the smallest index such that
![]() $G_\ell \,:\!=\,G[B_1 \cup \cdots \cup B_\ell ]$
contains a
$G_\ell \,:\!=\,G[B_1 \cup \cdots \cup B_\ell ]$
contains a
![]() $T_{i}$
minor for some
$T_{i}$
minor for some
![]() $i\in I$
, and let
$i\in I$
, and let
![]() $i^{\prime}$
be an index in
$i^{\prime}$
be an index in
![]() $I$
such that
$I$
such that
Observe that
We claim that
To see this, suppose for a contradiction that
![]() $uv$
is such an edge, with
$uv$
is such an edge, with
![]() $u\in V(G_\ell )-B_\ell$
and
$u\in V(G_\ell )-B_\ell$
and
![]() $v\in V(G)-V(G_\ell )$
. First, note that
$v\in V(G)-V(G_\ell )$
. First, note that
![]() $u\in B_1 \cup \cdots \cup B_{\ell -1}$
. If
$u\in B_1 \cup \cdots \cup B_{\ell -1}$
. If
![]() $v\in Y$
, then
$v\in Y$
, then
![]() $u$
and
$u$
and
![]() $v$
appear together in some bag
$v$
appear together in some bag
![]() $B_j$
of the path decomposition
$B_j$
of the path decomposition
![]() $(B_1, B_2, \dots, B_q)$
of
$(B_1, B_2, \dots, B_q)$
of
![]() $G[Y]$
, and
$G[Y]$
, and
![]() $j \gt \ell$
since
$j \gt \ell$
since
![]() $v \notin B_1 \cup \cdots \cup B_\ell$
. However, since
$v \notin B_1 \cup \cdots \cup B_\ell$
. However, since
![]() $u\in B_1 \cup \cdots \cup B_{\ell -1}$
and
$u\in B_1 \cup \cdots \cup B_{\ell -1}$
and
![]() $u\in B_j$
, we conclude that
$u\in B_j$
, we conclude that
![]() $u$
belongs also to
$u$
belongs also to
![]() $B_\ell$
, a contradiction. If
$B_\ell$
, a contradiction. If
![]() $v\notin Y$
, then
$v\notin Y$
, then
![]() $u\in \partial Y$
, and thus
$u\in \partial Y$
, and thus
![]() $u\in B_q$
. Again, we deduce similarly that
$u\in B_q$
. Again, we deduce similarly that
![]() $u \in B_\ell$
, a contradiction. This completes the proof of (⋆⋆⋆).
$u \in B_\ell$
, a contradiction. This completes the proof of (⋆⋆⋆).
Let
![]() $G^{\prime}\,:\!=\,G - V(G_\ell )$
. Let
$G^{\prime}\,:\!=\,G - V(G_\ell )$
. Let
![]() $x^{\prime}_i \,:\!=\, x_i$
for each
$x^{\prime}_i \,:\!=\, x_i$
for each
![]() $i\in [c]-\{i^{\prime}\}$
and let
$i\in [c]-\{i^{\prime}\}$
and let
![]() $x^{\prime}_{i^{\prime}} \,:\!=\, x_{i^{\prime}}-1$
. Let
$x^{\prime}_{i^{\prime}} \,:\!=\, x_{i^{\prime}}-1$
. Let
![]() $I^{\prime}=\{i\in [c]\mid x^{\prime}_i\geqslant 1\}$
. Apply induction to the instance
$I^{\prime}=\{i\in [c]\mid x^{\prime}_i\geqslant 1\}$
. Apply induction to the instance
![]() $(G^{\prime},c,T_1,\ldots, T_c,x^{\prime}_1,\ldots, x^{\prime}_c)$
. If it results in a set of vertex-disjoint subgraphs
$(G^{\prime},c,T_1,\ldots, T_c,x^{\prime}_1,\ldots, x^{\prime}_c)$
. If it results in a set of vertex-disjoint subgraphs
![]() $\{M^{\prime}_{i,j}\mid i\in [c],\, j\in [x^{\prime}_i]\}$
, with
$\{M^{\prime}_{i,j}\mid i\in [c],\, j\in [x^{\prime}_i]\}$
, with
![]() $M^{\prime}_{i,j}$
containing a
$M^{\prime}_{i,j}$
containing a
![]() $T_i$
minor for each
$T_i$
minor for each
![]() $i\in [c]$
and
$i\in [c]$
and
![]() $j \in [x^{\prime}_i]$
, then we let
$j \in [x^{\prime}_i]$
, then we let
![]() $M_{i,j}\,:\!=\,M^{\prime}_{i,j}$
for each
$M_{i,j}\,:\!=\,M^{\prime}_{i,j}$
for each
![]() $i\in [c]$
and
$i\in [c]$
and
![]() $j \in [x^{\prime}_i]$
, and
$j \in [x^{\prime}_i]$
, and
![]() $M_{i^{\prime},x_{i^{\prime}}} \,:\!=\, G_\ell$
, which using (⋆) results in the desired collection of vertex-disjoint subgraphs. Otherwise, we obtain a set
$M_{i^{\prime},x_{i^{\prime}}} \,:\!=\, G_\ell$
, which using (⋆) results in the desired collection of vertex-disjoint subgraphs. Otherwise, we obtain a set
![]() $X^{\prime}$
of at most
$X^{\prime}$
of at most
![]() $\sum _{i\in I^{\prime}}x^{\prime}_it_i -t_{\max (I^{\prime})}$
vertices such that
$\sum _{i\in I^{\prime}}x^{\prime}_it_i -t_{\max (I^{\prime})}$
vertices such that
![]() $G^{\prime}-X^{\prime}$
does not contain
$G^{\prime}-X^{\prime}$
does not contain
![]() $T_a$
as a minor for some
$T_a$
as a minor for some
![]() $a\in I^{\prime}$
.
$a\in I^{\prime}$
.
Let
![]() $X\,:\!=\,X^{\prime}\cup B_\ell$
. Observe that
$X\,:\!=\,X^{\prime}\cup B_\ell$
. Observe that
 \begin{align*} |X| = |X^{\prime}|+|B_{\ell }| &\leqslant \sum _{i\in I^{\prime}}x^{\prime}_it_i - t_{\max (I^{\prime})} + t_{m} \leqslant \sum _{i\in I}x_it_i - (t_{\max (I^{\prime})} + t_{i^{\prime}} - t_{m})\\ &\leqslant \sum _{i\in I}x_it_i - t_{\max (I)}. \end{align*}
\begin{align*} |X| = |X^{\prime}|+|B_{\ell }| &\leqslant \sum _{i\in I^{\prime}}x^{\prime}_it_i - t_{\max (I^{\prime})} + t_{m} \leqslant \sum _{i\in I}x_it_i - (t_{\max (I^{\prime})} + t_{i^{\prime}} - t_{m})\\ &\leqslant \sum _{i\in I}x_it_i - t_{\max (I)}. \end{align*}
To see why the last inequality holds, there are two cases to consider: (i) if
![]() $\max (I^{\prime})=\max (I)$
, then the inequality follows immediately since
$\max (I^{\prime})=\max (I)$
, then the inequality follows immediately since
![]() $t_{i^{\prime}}\geqslant t_m$
. (ii) If
$t_{i^{\prime}}\geqslant t_m$
. (ii) If
![]() $\max (I^{\prime})\lt \max (I)$
, then
$\max (I^{\prime})\lt \max (I)$
, then
![]() $i^{\prime}=\max (I)$
and
$i^{\prime}=\max (I)$
and
![]() $\max (I^{\prime})\geqslant \min (I^{\prime})=m$
, so
$\max (I^{\prime})\geqslant \min (I^{\prime})=m$
, so
![]() $t_{\max (I^{\prime})}+t_{i^{\prime}}-t_m \geqslant t_{i^{\prime}}=t_{\max (I)}$
.
$t_{\max (I^{\prime})}+t_{i^{\prime}}-t_m \geqslant t_{i^{\prime}}=t_{\max (I)}$
.
Now, let us show that
![]() $G-X$
does not contain
$G-X$
does not contain
![]() $T_i$
as a minor, for some
$T_i$
as a minor, for some
![]() $i\in I$
. Let
$i\in I$
. Let
![]() $a\in I^{\prime}$
be such that
$a\in I^{\prime}$
be such that
![]() $G^{\prime}-X^{\prime}$
does not contain
$G^{\prime}-X^{\prime}$
does not contain
![]() $T_a$
as minor. We will show that we can take
$T_a$
as minor. We will show that we can take
![]() $i=a$
. To do so, it is enough to show that
$i=a$
. To do so, it is enough to show that
![]() $X$
meets every inclusion-wise minimal subgraph of
$X$
meets every inclusion-wise minimal subgraph of
![]() $G$
containing a
$G$
containing a
![]() $T_a$
minor. Let
$T_a$
minor. Let
![]() $M$
be such a subgraph of
$M$
be such a subgraph of
![]() $G$
. Note that
$G$
. Note that
![]() $M$
is connected, since
$M$
is connected, since
![]() $T_a$
is connected. Now, observe that by (⋆⋆⋆), either
$T_a$
is connected. Now, observe that by (⋆⋆⋆), either
![]() $M$
is contained in
$M$
is contained in
![]() $G^{\prime}$
, or
$G^{\prime}$
, or
![]() $M$
is contained in
$M$
is contained in
![]() $G_\ell -B_\ell$
, or
$G_\ell -B_\ell$
, or
![]() $M$
contains a vertex of
$M$
contains a vertex of
![]() $B_\ell$
. In the first case,
$B_\ell$
. In the first case,
![]() $M$
contains a vertex of
$M$
contains a vertex of
![]() $X^{\prime}\subseteq X$
, by the choice of
$X^{\prime}\subseteq X$
, by the choice of
![]() $a$
. The second case is ruled out by (⋆⋆). In the third case,
$a$
. The second case is ruled out by (⋆⋆). In the third case,
![]() $M$
contains a vertex of
$M$
contains a vertex of
![]() $B_\ell \subseteq X$
. Thus, we conclude that
$B_\ell \subseteq X$
. Thus, we conclude that
![]() $M$
contains a vertex of
$M$
contains a vertex of
![]() $X$
. This concludes the proof.
$X$
. This concludes the proof.
We may now turn to the proof of Corollary3. We will use the following lemma, which is a special case of a more general result of Robertson and Seymour [Statement (8.7) in [Reference Robertson and Seymour9]].
Lemma 5.
For every graph
![]() $G$
, for every path decomposition
$G$
, for every path decomposition
![]() $(B_1, B_2, \dots, B_q)$
of
$(B_1, B_2, \dots, B_q)$
of
![]() $G$
, for every family
$G$
, for every family
![]() $\mathcal{F}$
of connected subgraphs of
$\mathcal{F}$
of connected subgraphs of
![]() $G$
, for every positive integer
$G$
, for every positive integer
![]() $d$
, either:
$d$
, either:
-
1. there are
 $d$
pairwise vertex-disjoint subgraphs in
$d$
pairwise vertex-disjoint subgraphs in
 $\mathcal{F}$
, or
$\mathcal{F}$
, or
-
2. there is a set
 $X$
that is the union of at most
$X$
that is the union of at most
 $d-1$
bags of
$d-1$
bags of
 $(B_1, B_2, \dots, B_q)$
such that
$(B_1, B_2, \dots, B_q)$
such that
 $V(F) \cap X \neq \varnothing$
for every
$V(F) \cap X \neq \varnothing$
for every
 $F \in \mathcal{F}$
.
$F \in \mathcal{F}$
.
Proof of
Corollary 3
. It is known (and an easy exercise to show) that, for every positive integer
![]() $p$
, the complete ternary tree
$p$
, the complete ternary tree
![]() $T_p$
of height
$T_p$
of height
![]() $p$
has pathwidth
$p$
has pathwidth
![]() $p$
. First, apply Theorem1 on
$p$
. First, apply Theorem1 on
![]() $G$
with the tree
$G$
with the tree
![]() $T_p$
. If
$T_p$
. If
![]() $G$
contains
$G$
contains
![]() $k$
vertex-disjoint subgraphs each containing a
$k$
vertex-disjoint subgraphs each containing a
![]() $T_p$
minor, we are done. So we may assume that the theorem produces a set
$T_p$
minor, we are done. So we may assume that the theorem produces a set
![]() $X_1$
of at most
$X_1$
of at most
![]() $|V(T_p)|(k-1) \leqslant 3^{p+1}(k-1)$
vertices such that
$|V(T_p)|(k-1) \leqslant 3^{p+1}(k-1)$
vertices such that
![]() $G-X_1$
has no
$G-X_1$
has no
![]() $T_p$
minor.
$T_p$
minor.
By Lemma4,
![]() $G-X_1$
has a path decomposition
$G-X_1$
has a path decomposition
![]() $(B_1, B_2, \dots, B_q)$
of width strictly less than
$(B_1, B_2, \dots, B_q)$
of width strictly less than
![]() $3^{p+1}$
. It is easily checked that every inclusion-wise minimal subgraph of
$3^{p+1}$
. It is easily checked that every inclusion-wise minimal subgraph of
![]() $G-X_1$
with pathwidth at least
$G-X_1$
with pathwidth at least
![]() $p$
is connected. Apply Lemma5 on
$p$
is connected. Apply Lemma5 on
![]() $G-X_1$
with the path decomposition
$G-X_1$
with the path decomposition
![]() $(B_1, B_2, \dots, B_q)$
, with
$(B_1, B_2, \dots, B_q)$
, with
![]() $d=k$
, and with the family
$d=k$
, and with the family
![]() $\mathcal{F}$
of connected subgraphs of
$\mathcal{F}$
of connected subgraphs of
![]() $G-X_1$
with pathwidth at least
$G-X_1$
with pathwidth at least
![]() $p$
. If
$p$
. If
![]() $\mathcal{F}$
contains
$\mathcal{F}$
contains
![]() $k$
pairwise vertex-disjoint members, we are done. So we may assume that the lemma produces a set
$k$
pairwise vertex-disjoint members, we are done. So we may assume that the lemma produces a set
![]() $X_2$
of at most
$X_2$
of at most
![]() $3^{p+1}(k-1)$
vertices such that
$3^{p+1}(k-1)$
vertices such that
![]() $X_2$
hits every member of
$X_2$
hits every member of
![]() $\mathcal{F}$
. It follows that
$\mathcal{F}$
. It follows that
![]() $G-X_1-X_2$
has pathwidth strictly less than
$G-X_1-X_2$
has pathwidth strictly less than
![]() $p$
. Let
$p$
. Let
![]() $X\,:\!=\, X_1 \cup X_2$
. Since
$X\,:\!=\, X_1 \cup X_2$
. Since
![]() $|X| \leqslant 3^{p+1}(k-1) + 3^{p+1}(k-1) \leqslant 2\cdot 3^{p+1}k$
, the set
$|X| \leqslant 3^{p+1}(k-1) + 3^{p+1}(k-1) \leqslant 2\cdot 3^{p+1}k$
, the set
![]() $X$
has the desired properties.
$X$
has the desired properties.
Acknowledgements
This work was done during a visit of Gwenaël Joret and Piotr Micek to the University of Ottawa and Carleton University. The research stay was partially funded by a grant from the University of Ottawa.
Funding statement
G. Joret is supported by a PDR grant from the Belgian National Fund for Scientific Research (FNRS). V. Dujmović is supported by NSERC and a University of Ottawa Research Chair. P. Micek is supported by the National Science Center of Poland under grant UMO-2023/05/Y/ST6/00079 within the WEAVE-UNISONO program. P. Morin is supported by NSERC.