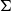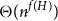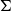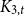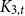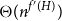1. Introduction
All graphs in this paper are undirected, finite, and simple, unless stated otherwise. Many classical theorems in extremal graph theory concern the maximum number of copies of a fixed graph H in an n-vertex graph in some class
![]() $\mathcal{G}$
. Here, a copy means a subgraph isomorphic to H. For example, Turán’s Theorem determines the maximum number of copies of
$\mathcal{G}$
. Here, a copy means a subgraph isomorphic to H. For example, Turán’s Theorem determines the maximum number of copies of
![]() $K_2$
(that is, edges) in an n-vertex
$K_2$
(that is, edges) in an n-vertex
![]() $K_t$
-free graph [Reference Turán67]. More generally, Zykov’s Theorem determines the maximum number of copies of a given complete graph
$K_t$
-free graph [Reference Turán67]. More generally, Zykov’s Theorem determines the maximum number of copies of a given complete graph
![]() $K_s$
in an n-vertex
$K_s$
in an n-vertex
![]() $K_t$
-free graph [Reference Zykov71]. The excluded graph need not be complete. The Erdős–Stone Theorem [Reference Erdős and Stone20] determines, for every non-bipartite graph X, the asymptotic maximum number of copies of
$K_t$
-free graph [Reference Zykov71]. The excluded graph need not be complete. The Erdős–Stone Theorem [Reference Erdős and Stone20] determines, for every non-bipartite graph X, the asymptotic maximum number of copies of
![]() $K_2$
in an n-vertex graph with no X-subgraph. Analogues of the Erdős–Stone Theorem for copies of
$K_2$
in an n-vertex graph with no X-subgraph. Analogues of the Erdős–Stone Theorem for copies of
![]() $K_s$
have recently been studied by [Reference Alon and Shikhelman4,Reference Alon and Shikhelman5]. See [Reference Alon, Kostochka and Shikhelman3,Reference Ergemlidze, Methuku, Salia and Győri21,Reference Gerbner, Keszegh, Palmer and Patkós24–Reference Gerbner and Palmer27,Reference Győri, Salia, Tompkins and Zamora34,Reference Luo49,Reference Ma and Qiu50,Reference Nešetřil and Ossona de Mendez55,Reference Timmons66] for recent related results.
$K_s$
have recently been studied by [Reference Alon and Shikhelman4,Reference Alon and Shikhelman5]. See [Reference Alon, Kostochka and Shikhelman3,Reference Ergemlidze, Methuku, Salia and Győri21,Reference Gerbner, Keszegh, Palmer and Patkós24–Reference Gerbner and Palmer27,Reference Győri, Salia, Tompkins and Zamora34,Reference Luo49,Reference Ma and Qiu50,Reference Nešetřil and Ossona de Mendez55,Reference Timmons66] for recent related results.
This paper studies similar questions when the class
![]() $\mathcal{G}$
consists of the graphs that embed
Footnote a
in a given surface
$\mathcal{G}$
consists of the graphs that embed
Footnote a
in a given surface
![]() $\Sigma$
(rather than being defined by an excluded subgraph). For graphs H and G, let C(H,G) be the number of copies of H in G. For a surface
$\Sigma$
(rather than being defined by an excluded subgraph). For graphs H and G, let C(H,G) be the number of copies of H in G. For a surface
![]() $\Sigma$
, let
$\Sigma$
, let
![]() $C(H,\Sigma,n)$
be the maximum of C(H,G), where the maximum is taken over all n-vertex graphs G that embeds in
$C(H,\Sigma,n)$
be the maximum of C(H,G), where the maximum is taken over all n-vertex graphs G that embeds in
![]() $\Sigma$
. This paper determines the asymptotic behaviour of
$\Sigma$
. This paper determines the asymptotic behaviour of
![]() $C(H,\Sigma,n)$
as
$C(H,\Sigma,n)$
as
![]() $n\rightarrow\infty$
for any fixed surface
$n\rightarrow\infty$
for any fixed surface
![]() $\Sigma$
and any fixed graph H. Before stating our theorem, we mention some related results that determine
$\Sigma$
and any fixed graph H. Before stating our theorem, we mention some related results that determine
![]() $C(H,\mathbb{S}_0,n)$
for specific planar graphs H where the surface is the sphere
$C(H,\mathbb{S}_0,n)$
for specific planar graphs H where the surface is the sphere
![]() $\mathbb{S}_0$
. Alon and Caro [Reference Alon and Caro2] determined
$\mathbb{S}_0$
. Alon and Caro [Reference Alon and Caro2] determined
![]() $C(H,\mathbb{S}_0,n)$
precisely if H is either a complete bipartite graph or a triangulation without non-facial triangles. Hakimi and Schmeichel [Reference Hakimi and Schmeichel35] studied
$C(H,\mathbb{S}_0,n)$
precisely if H is either a complete bipartite graph or a triangulation without non-facial triangles. Hakimi and Schmeichel [Reference Hakimi and Schmeichel35] studied
![]() $C(C_k,\mathbb{S}_0,n)$
where
$C(C_k,\mathbb{S}_0,n)$
where
![]() $C_k$
is the k-vertex cycle; they proved that
$C_k$
is the k-vertex cycle; they proved that
![]() $C(C_3,\mathbb{S}_0,n)=3n-8$
and
$C(C_3,\mathbb{S}_0,n)=3n-8$
and
![]() $C(C_4,\mathbb{S}_0,n)=\frac12(n^2+3n-22)$
. See [Reference Hakimi and Schmeichel36,Reference Harant, Horňák and Skupień37] for more results on
$C(C_4,\mathbb{S}_0,n)=\frac12(n^2+3n-22)$
. See [Reference Hakimi and Schmeichel36,Reference Harant, Horňák and Skupień37] for more results on
![]() $C(C_3,\mathbb{S}_0,n)$
and see [Reference Alameddine1] for more results on
$C(C_3,\mathbb{S}_0,n)$
and see [Reference Alameddine1] for more results on
![]() $C(C_4,\mathbb{S}_0,n)$
. Győri et al. [Reference Győri, Paulos, Salia, Tompkins and Zamora32] proved that
$C(C_4,\mathbb{S}_0,n)$
. Győri et al. [Reference Győri, Paulos, Salia, Tompkins and Zamora32] proved that
![]() $C(C_5,\mathbb{S}_0,n)=2n^2-10n+12$
(except for
$C(C_5,\mathbb{S}_0,n)=2n^2-10n+12$
(except for
![]() $n\in\{5,7\}$
). If
$n\in\{5,7\}$
). If
![]() $P_k$
is the k-vertex path, then
$P_k$
is the k-vertex path, then
![]() $C(P_4,\mathbb{S}_0,n)=7n^2-32n+27$
with finitely many exceptions [Reference Győri, Paulos, Salia, Tompkins and Zamora31] and
$C(P_4,\mathbb{S}_0,n)=7n^2-32n+27$
with finitely many exceptions [Reference Győri, Paulos, Salia, Tompkins and Zamora31] and
![]() $C(P_5,\mathbb{S}_0,n)=n^3+O(n^2)$
[Reference Ghosh, Györi, Martin, Paulos, Salia, Xiao and Zamora28]. Alon and Caro [Reference Alon and Caro2] and independently Wood [Reference Wood68] proved that
$C(P_5,\mathbb{S}_0,n)=n^3+O(n^2)$
[Reference Ghosh, Györi, Martin, Paulos, Salia, Xiao and Zamora28]. Alon and Caro [Reference Alon and Caro2] and independently Wood [Reference Wood68] proved that
![]() $C(K_4,\mathbb{S}_0,n)=n-3$
. More generally, Perles (see [Reference Alon and Caro2]) conjectured that if H is a fixed 3-connected planar graph, then
$C(K_4,\mathbb{S}_0,n)=n-3$
. More generally, Perles (see [Reference Alon and Caro2]) conjectured that if H is a fixed 3-connected planar graph, then
![]() $C(H,\mathbb{S}_0,n) = O(n)$
. Perles noted the converse: If H is planar, not 3-connected and
$C(H,\mathbb{S}_0,n) = O(n)$
. Perles noted the converse: If H is planar, not 3-connected and
![]() $|V(H)|\geqslant 4$
, then
$|V(H)|\geqslant 4$
, then
![]() $C(H,\mathbb{S}_0,n) \geqslant \Omega(n^2)$
. Perles’ conjecture was proved by Wormald [Reference Wormald70] and independently by Eppstein [Reference Eppstein18], who asked the following two open problems:
$C(H,\mathbb{S}_0,n) \geqslant \Omega(n^2)$
. Perles’ conjecture was proved by Wormald [Reference Wormald70] and independently by Eppstein [Reference Eppstein18], who asked the following two open problems:
-
Characterise the subgraphs occurring O(n) times in graphs of given genus.
-
Characterise the subgraphs occurring a number of times which is a nonlinear function of n.
This paper answers both these questions (and more).
We start with the following natural question: when is
![]() $C(H,\Sigma,n)$
bounded by a constant depending only on H and
$C(H,\Sigma,n)$
bounded by a constant depending only on H and
![]() $\Sigma$
(and independent of n)? We prove that H being 3-connected and non-planar is a sufficient condition. In fact, we prove a stronger result that completely answers the question. We need the following standard definitions. A k-separation of a graph H is a pair
$\Sigma$
(and independent of n)? We prove that H being 3-connected and non-planar is a sufficient condition. In fact, we prove a stronger result that completely answers the question. We need the following standard definitions. A k-separation of a graph H is a pair
![]() $(H_1, H_2)$
of edge-disjoint subgraphs of H such that
$(H_1, H_2)$
of edge-disjoint subgraphs of H such that
![]() $H_1 \cup H_2=H$
,
$H_1 \cup H_2=H$
,
![]() $V(H_1) \setminus V(H_2) \neq \emptyset$
,
$V(H_1) \setminus V(H_2) \neq \emptyset$
,
![]() $V(H_2) \setminus V(H_1) \neq \emptyset$
, and
$V(H_2) \setminus V(H_1) \neq \emptyset$
, and
![]() $|V(H_1 \cap H_2)|=k$
. A k’-separation for some
$|V(H_1 \cap H_2)|=k$
. A k’-separation for some
![]() $k'\leqslant k$
is called a
$k'\leqslant k$
is called a
![]() $(\leqslant k)$
-separation. If
$(\leqslant k)$
-separation. If
![]() $(H_1,H_2)$
is a separation of H with
$(H_1,H_2)$
is a separation of H with
![]() $X=V(H_1)\cap V(H_2)$
, then let
$X=V(H_1)\cap V(H_2)$
, then let
![]() $H_i^-$
and
$H_i^-$
and
![]() $H_i^+$
be the simple graphs obtained from
$H_i^+$
be the simple graphs obtained from
![]() $H_i$
by removing and adding all edges between vertices in X, respectively.
$H_i$
by removing and adding all edges between vertices in X, respectively.
A graph H is strongly non-planar if H is non-planar and for every
![]() $(\leqslant 2) $
separation
$(\leqslant 2) $
separation
![]() $(H_1, H_2)$
of H, both
$(H_1, H_2)$
of H, both
![]() $H_1^+$
and
$H_1^+$
and
![]() $H_2^+$
are non-planar. Note that every 3-connected non-planar graph is strongly non-planar. The following is our first contribution. It says that
$H_2^+$
are non-planar. Note that every 3-connected non-planar graph is strongly non-planar. The following is our first contribution. It says that
![]() $C(H,\Sigma,n)$
is bounded if and only if H is strongly non-planar.
$C(H,\Sigma,n)$
is bounded if and only if H is strongly non-planar.
Theorem 1.1 There exists a function
![]() $c_{1.1}(h, g)$
such that for every strongly non-planar graph H with h vertices and every surface
$c_{1.1}(h, g)$
such that for every strongly non-planar graph H with h vertices and every surface
![]() $\Sigma$
of Euler genus g,
$\Sigma$
of Euler genus g,
Conversely, for every graph H that is not strongly non-planar and for every surface
![]() $\Sigma$
in which H embeds, there is a constant
$\Sigma$
in which H embeds, there is a constant
![]() $c>0$
such that for all
$c>0$
such that for all
![]() $n\geqslant 4|V(H)|$
, there is an n-vertex graph that embeds in
$n\geqslant 4|V(H)|$
, there is an n-vertex graph that embeds in
![]() $\Sigma$
and contains at least cn copies of H; that is,
$\Sigma$
and contains at least cn copies of H; that is,
![]() $C(H,\Sigma,n)\geqslant cn$
.
$C(H,\Sigma,n)\geqslant cn$
.
There are two important observations about Theorem 1.1 First, the characterisation of graphs H does not depend on the surface
![]() $\Sigma$
. Indeed, the only dependence on
$\Sigma$
. Indeed, the only dependence on
![]() $\Sigma$
is in the constants. Second, Theorem 1.1 shows that
$\Sigma$
is in the constants. Second, Theorem 1.1 shows that
![]() $C(H,\Sigma,n)$
is either bounded or
$C(H,\Sigma,n)$
is either bounded or
![]() $\Omega(n)$
.
$\Omega(n)$
.
Theorem 1.1 is in fact a special case of the following more general theorem. The next definition is a key to describing our results. A flap in a graph H is a
![]() $(\leqslant 2)$
-separation (A,B) such that
$(\leqslant 2)$
-separation (A,B) such that
![]() $A^+$
is planar. Separations (A,B) and (C,D) of H are independent if
$A^+$
is planar. Separations (A,B) and (C,D) of H are independent if
![]() $E(A^-) \cap E(C^-) = \emptyset$
and
$E(A^-) \cap E(C^-) = \emptyset$
and
![]() $(V(A) \setminus V(B)) \cap (V(C) \setminus V(D))=\emptyset$
.
Footnote b
If H is planar and with no
$(V(A) \setminus V(B)) \cap (V(C) \setminus V(D))=\emptyset$
.
Footnote b
If H is planar and with no
![]() $(\leqslant 2)$
-separation, then the flap-number of H is defined to be 1. Otherwise, the flap-number of H is defined to be the maximum number of pairwise independent flaps in H. Let f(H) denote the flap-number of H.
$(\leqslant 2)$
-separation, then the flap-number of H is defined to be 1. Otherwise, the flap-number of H is defined to be the maximum number of pairwise independent flaps in H. Let f(H) denote the flap-number of H.
The following is our Theorem 1.2 theorem.
Theorem 1.2 For every graph H and every surface
![]() $\Sigma$
in which H embeds,
$\Sigma$
in which H embeds,
It is immediate from the definitions that
![]() $f(H)=0$
if and only if H is strongly non-planar. So Theorem 1.1 follows from the
$f(H)=0$
if and only if H is strongly non-planar. So Theorem 1.1 follows from the
![]() $f(H) \leqslant 1$
cases of Theorem 1.2.
$f(H) \leqslant 1$
cases of Theorem 1.2.
As an aside, note that Theorem 1.2 can be restated as follows: for every graph H and every surface
![]() $\Sigma$
in which H embeds,
$\Sigma$
in which H embeds,
The above limit is sometimes referred to as the asymptotic logarithmic density of H in
![]() $\Sigma$
. A related result of Nešetřil and Ossona de Mendez [Reference Nešetřil and Ossona de Mendez55] shows that for every infinite nowhere dense hereditary graph class
$\Sigma$
. A related result of Nešetřil and Ossona de Mendez [Reference Nešetřil and Ossona de Mendez55] shows that for every infinite nowhere dense hereditary graph class
![]() $\mathcal{G}$
and for every fixed graph H, the maximum, taken over all n-vertex graphs
$\mathcal{G}$
and for every fixed graph H, the maximum, taken over all n-vertex graphs
![]() $G\in\mathcal{G}$
, of the number of induced subgraphs of G isomorphic to H is
$G\in\mathcal{G}$
, of the number of induced subgraphs of G isomorphic to H is
![]() $\Omega( n^{\beta})$
and
$\Omega( n^{\beta})$
and
![]() $O( n^{\beta+o(1)})$
for some integer
$O( n^{\beta+o(1)})$
for some integer
![]() $\beta\leqslant f(H)$
. Our results (in the case that
$\beta\leqslant f(H)$
. Our results (in the case that
![]() $\mathcal{G}$
is the class of graphs embeddable in a fixed surface) imply this upper bound (since the number of induced copies of H in G is at most C(H,G)). Moreover, our bounds are often more precise since f(H) can be significantly less than
$\mathcal{G}$
is the class of graphs embeddable in a fixed surface) imply this upper bound (since the number of induced copies of H in G is at most C(H,G)). Moreover, our bounds are often more precise since f(H) can be significantly less than
![]() $\beta$
.
$\beta$
.
The lower bound in Theorem 1.2 is proved in Section 2. Section 3 introduces some tools from the literature that are used in the proof of the upper bound. Theorem 1.1 is proved in Section 4. The upper bound in Theorem 1.2 is then proved in Section 5. Section 6 presents more precise bounds on
![]() $C(H,\Sigma,n)$
when H is a complete graph
$C(H,\Sigma,n)$
when H is a complete graph
![]() $K_s$
. Section 7 considers the maximum number of copies of a graph H in an n-vertex graph in a given minor-closed class. Section 8 reinterprets our results in terms of homomorphism inequalities and presents some open problems that arise from this viewpoint.
$K_s$
. Section 7 considers the maximum number of copies of a graph H in an n-vertex graph in a given minor-closed class. Section 8 reinterprets our results in terms of homomorphism inequalities and presents some open problems that arise from this viewpoint.
Before continuing, to give the reader some more intuition about Theorem 1.2, we now asymptotically determine
![]() $C(T,\Sigma,n)$
for a tree T.
$C(T,\Sigma,n)$
for a tree T.
Corollary 1.3 For every fixed tree T, let
![]() $\beta(T)$
be the size of a maximum stable set in the subforest F of T induced by the vertices with degree at most 2. Then for every fixed surface
$\beta(T)$
be the size of a maximum stable set in the subforest F of T induced by the vertices with degree at most 2. Then for every fixed surface
![]() $\Sigma$
,
$\Sigma$
,
Proof. By Theorem 1.2, it suffices to show that
![]() $\beta(T)=f(T)$
.
$\beta(T)=f(T)$
.
Let
![]() $I=\{v_1,\dots,v_{\beta(T)}\}$
be a maximum stable set in F. Let
$I=\{v_1,\dots,v_{\beta(T)}\}$
be a maximum stable set in F. Let
![]() $x_i$
(and possibly
$x_i$
(and possibly
![]() $y_i$
) be the neighbours of
$y_i$
) be the neighbours of
![]() $v_i$
. Let
$v_i$
. Let
![]() $A_i\;:\!=\;T[\{v_i,x_i,y_i\}]$
and
$A_i\;:\!=\;T[\{v_i,x_i,y_i\}]$
and
![]() $B_i\;:\!=\;T-v_i$
. Then,
$B_i\;:\!=\;T-v_i$
. Then,
![]() $(A_i,B_i)$
is a flap of T. Since I is a stable set, for each
$(A_i,B_i)$
is a flap of T. Since I is a stable set, for each
![]() $v_i\in I$
neither
$v_i\in I$
neither
![]() $x_i$
nor
$x_i$
nor
![]() $y_i$
are in I, implying that
$y_i$
are in I, implying that
![]() $E(A_i^-)\cap E(A_j^-)=\emptyset$
for distinct
$E(A_i^-)\cap E(A_j^-)=\emptyset$
for distinct
![]() $i,j\in [\beta(T)]$
. Moreover,
$i,j\in [\beta(T)]$
. Moreover,
![]() $V(A_i) \setminus V(B_i)=\{v_i\}$
, so
$V(A_i) \setminus V(B_i)=\{v_i\}$
, so
![]() $(V(A_i) \setminus V(B_i)) \cap (V(A_j) \setminus V(B_j))=\emptyset$
for all distinct i,j. Hence,
$(V(A_i) \setminus V(B_i)) \cap (V(A_j) \setminus V(B_j))=\emptyset$
for all distinct i,j. Hence,
![]() $(A_1,B_1),\dots,(A_{\beta(T)},B_{\beta(T)})$
are pairwise independent flaps in T. Thus,
$(A_1,B_1),\dots,(A_{\beta(T)},B_{\beta(T)})$
are pairwise independent flaps in T. Thus,
![]() $\beta(T) \leqslant f(T)$
. Theorem 1.2 then implies that
$\beta(T) \leqslant f(T)$
. Theorem 1.2 then implies that
![]() $C(T,\Sigma,n) = \Omega( n^{\,\beta(T)} )$
. This lower bound is particularly easy to see when T is a tree. Let G be the graph obtained from T by replacing each vertex
$C(T,\Sigma,n) = \Omega( n^{\,\beta(T)} )$
. This lower bound is particularly easy to see when T is a tree. Let G be the graph obtained from T by replacing each vertex
![]() $v_i \in I$
by
$v_i \in I$
by
![]() $\lfloor{{\frac{n-|V(T)|}{\beta(T)}}}\rfloor$
vertices with the same neighbourhood as
$\lfloor{{\frac{n-|V(T)|}{\beta(T)}}}\rfloor$
vertices with the same neighbourhood as
![]() $v_i$
, as illustrated in Figure 1. Then, G is planar with at most n vertices and at least
$v_i$
, as illustrated in Figure 1. Then, G is planar with at most n vertices and at least
![]() $(\frac{n-|V(T)|}{\beta(T)})^{\beta(T)}$
copies of T. Thus,
$(\frac{n-|V(T)|}{\beta(T)})^{\beta(T)}$
copies of T. Thus,
![]() $C(T,\Sigma,n) \geqslant C(T,\mathbb{S}_0,n) = \Omega( n^{\beta(T)} )$
for fixed T.
$C(T,\Sigma,n) \geqslant C(T,\mathbb{S}_0,n) = \Omega( n^{\beta(T)} )$
for fixed T.

Figure 1. (a) A tree T with
![]() $\beta(T)=5$
. (b) A planar graph with
$\beta(T)=5$
. (b) A planar graph with
![]() $\Omega(n^5)$
copies of T.
$\Omega(n^5)$
copies of T.
For the converse, let
![]() $(A_1,B_1),\dots,(A_{f(T)},B_{f(T)})$
be pairwise independent flaps in T. Choose
$(A_1,B_1),\dots,(A_{f(T)},B_{f(T)})$
be pairwise independent flaps in T. Choose
![]() $(A_1,B_1),\dots,(A_{f(T)},B_{f(T)})$
to minimise
$(A_1,B_1),\dots,(A_{f(T)},B_{f(T)})$
to minimise
![]() $\sum_{i=1}^{f(T)} |V(A_i)|$
. A simple case-analysis shows that
$\sum_{i=1}^{f(T)} |V(A_i)|$
. A simple case-analysis shows that
![]() $|V(A_i)\setminus V(B_i)|=1$
, and if
$|V(A_i)\setminus V(B_i)|=1$
, and if
![]() $v_i$
is the vertex in
$v_i$
is the vertex in
![]() $V(A_i)\setminus V(B_i)$
, then
$V(A_i)\setminus V(B_i)$
, then
![]() $N(v_i)= V(A_i)\cap V(B_i)$
, implying
$N(v_i)= V(A_i)\cap V(B_i)$
, implying
![]() $v_i$
has degree 1 or 2 in T. Moreover,
$v_i$
has degree 1 or 2 in T. Moreover,
![]() $v_iv_j\not\in E(T)$
for distinct
$v_iv_j\not\in E(T)$
for distinct
![]() $i,j\in[f(T)]$
as otherwise
$i,j\in[f(T)]$
as otherwise
![]() $E(A_i^-)\cap E(A_j^-)\neq\emptyset$
. Hence,
$E(A_i^-)\cap E(A_j^-)\neq\emptyset$
. Hence,
![]() $\{v_1,\dots,v_{f(T)}\}$
is a stable set of vertices in T all with degree at most 2. Hence
$\{v_1,\dots,v_{f(T)}\}$
is a stable set of vertices in T all with degree at most 2. Hence
![]() $\beta(T)\geqslant f(T)$
.
$\beta(T)\geqslant f(T)$
.
2. Lower bound
Now we prove the lower bound in Theorem 1.2. Let H be an h-vertex graph with flap-number k. Let
![]() $\Sigma$
be a surface in which H embeds. Our goal is to show that
$\Sigma$
be a surface in which H embeds. Our goal is to show that
![]() $C(H,\Sigma,n) = \Omega( n^k )$
for all
$C(H,\Sigma,n) = \Omega( n^k )$
for all
![]() $n\geqslant 4|V(H)|$
. If
$n\geqslant 4|V(H)|$
. If
![]() $k=0$
, then there is nothing to prove. If H is planar and 3-connected, then we may take
$k=0$
, then there is nothing to prove. If H is planar and 3-connected, then we may take
![]() $\lfloor n/h \rfloor$
disjoint copies of H. Thus, we may assume that H has at least one flap. Let
$\lfloor n/h \rfloor$
disjoint copies of H. Thus, we may assume that H has at least one flap. Let
![]() $(A_1,B_1),\dots,(A_k,B_k)$
be pairwise independent flaps in H. If
$(A_1,B_1),\dots,(A_k,B_k)$
be pairwise independent flaps in H. If
![]() $(A_i,B_i)$
is a 1-separation, then let
$(A_i,B_i)$
is a 1-separation, then let
![]() $v_i$
be the vertex in
$v_i$
be the vertex in
![]() $A_i\cap B_i$
. If
$A_i\cap B_i$
. If
![]() $(A_i,B_i)$
is a 2-separation, then let
$(A_i,B_i)$
is a 2-separation, then let
![]() $v_i$
and
$v_i$
and
![]() $w_i$
be the two vertices in
$w_i$
be the two vertices in
![]() $A_i\cap B_i$
. Let H’ be obtained from H as follows: if
$A_i\cap B_i$
. Let H’ be obtained from H as follows: if
![]() $(A_i,B_i)$
is a 2-separation, then delete
$(A_i,B_i)$
is a 2-separation, then delete
![]() $A_i-V(B_i)$
from H, and add the edge
$A_i-V(B_i)$
from H, and add the edge
![]() $v_iw_i$
(if it does not already exist). Note that H’ is a minor of H, since we may assume that whenever
$v_iw_i$
(if it does not already exist). Note that H’ is a minor of H, since we may assume that whenever
![]() $(A_i,B_i)$
is a 2-separation, there is a
$(A_i,B_i)$
is a 2-separation, there is a
![]() $v_iw_i$
-path in
$v_iw_i$
-path in
![]() $A_i$
(otherwise
$A_i$
(otherwise
![]() $(A_i,B_i)$
can be replaced by a
$(A_i,B_i)$
can be replaced by a
![]() $(\leqslant 1)$
-separation). Since H embeds in
$(\leqslant 1)$
-separation). Since H embeds in
![]() $\Sigma$
, so does H’. By assumption,
$\Sigma$
, so does H’. By assumption,
![]() $A_i^+$
is planar for each i. Fix an embedding of
$A_i^+$
is planar for each i. Fix an embedding of
![]() $A_i^+$
with
$A_i^+$
with
![]() $v_i$
and
$v_i$
and
![]() $w_i$
(if it exists) on the outerface (which exists since
$w_i$
(if it exists) on the outerface (which exists since
![]() $v_iw_i$
is an edge of
$v_iw_i$
is an edge of
![]() $A_i^+$
in the case of a 2-separation). Let
$A_i^+$
in the case of a 2-separation). Let
![]() $q\;:\!=\; \lfloor{{ \frac{n}{|V(H)|}-1}}\rfloor$
and G be the graph obtained from an embedding of H’ in
$q\;:\!=\; \lfloor{{ \frac{n}{|V(H)|}-1}}\rfloor$
and G be the graph obtained from an embedding of H’ in
![]() $\Sigma$
by adding q disjoint copies of
$\Sigma$
by adding q disjoint copies of
![]() $A_i^+$
(if
$A_i^+$
(if
![]() $(A_i, B_i)$
is a 0-separation), pasting q copies of
$(A_i, B_i)$
is a 0-separation), pasting q copies of
![]() $A_i^+$
onto
$A_i^+$
onto
![]() $v_i$
(if
$v_i$
(if
![]() $(A_i,B_i)$
is a 1-separation), and pasting q copies of
$(A_i,B_i)$
is a 1-separation), and pasting q copies of
![]() $A_i^+$
onto
$A_i^+$
onto
![]() $v_iw_i$
(if
$v_iw_i$
(if
![]() $(A_i,B_i)$
is a 2-separation). These copies of
$(A_i,B_i)$
is a 2-separation). These copies of
![]() $A_i^+$
can be embedded into a face of H’, as illustrated in Figure 2.
$A_i^+$
can be embedded into a face of H’, as illustrated in Figure 2.

Figure 2. (a) A graph H with flap-number 2. (b) A graph with
![]() $\Omega(n^2)$
copies of H.
$\Omega(n^2)$
copies of H.
Since
![]() $(V(A_i)\setminus V(B_i)) \cap (V(A_j)\setminus V(B_j)) = \emptyset$
for distinct
$(V(A_i)\setminus V(B_i)) \cap (V(A_j)\setminus V(B_j)) = \emptyset$
for distinct
![]() $i,j\in[k]$
,
$i,j\in[k]$
,
By construction, G has at least
![]() $q^k \geqslant ( \frac{n}{|V(H)|}-2 )^k $
copies of H. Hence,
$q^k \geqslant ( \frac{n}{|V(H)|}-2 )^k $
copies of H. Hence,
![]() $C(H,\Sigma,n) = \Omega(n^k)$
.
$C(H,\Sigma,n) = \Omega(n^k)$
.
3. Tools
In Sections 3–5 of this paper, we work in the following setting. For graphs G and H, an image of H in G is an injection
![]() $\phi\;:\;V(H) \to V(G)$
such that
$\phi\;:\;V(H) \to V(G)$
such that
![]() $\phi(u)\phi(v) \in E(G)$
for all
$\phi(u)\phi(v) \in E(G)$
for all
![]() $uv \in E(H)$
. Let I(H,G) be the number of images of H in G, and let
$uv \in E(H)$
. Let I(H,G) be the number of images of H in G, and let
![]() $I(H,\Sigma,n)$
be the maximum of I(H,G) taken over all n-vertex graphs G that embed in
$I(H,\Sigma,n)$
be the maximum of I(H,G) taken over all n-vertex graphs G that embed in
![]() $\Sigma$
. If H is fixed, then C(H,G) and I(H,G) differ by a constant factor. In particular, if
$\Sigma$
. If H is fixed, then C(H,G) and I(H,G) differ by a constant factor. In particular, if
![]() $|V(H)|=h$
then
$|V(H)|=h$
then
So to prove our Theorem 1.2 theorems, it suffices to work with images rather than copies.
To prove the upper bound in Theorem 1.2, we need several tools from the literature. The first two were proved by Eppstein [Reference Eppstein18]. To state the first result we need the following definition. A collection
![]() $\mathcal{H}$
of images of H in G is coherent if for all images
$\mathcal{H}$
of images of H in G is coherent if for all images
![]() $\phi_1, \phi_2 \in \mathcal{H}$
and for all distinct vertices
$\phi_1, \phi_2 \in \mathcal{H}$
and for all distinct vertices
![]() $x,y\in V(H)$
, we have
$x,y\in V(H)$
, we have
![]() $\phi_1(x) \neq \phi_2(y)$
.
$\phi_1(x) \neq \phi_2(y)$
.
Lemma 3.1 ([18]) Let H be a graph with h vertices and G be a graph. Every collection of at least
![]() $c_{3.1}(h,t)\;:\!=\;h!^2 t^h$
images of H in G contains a coherent subcollection of size at least t.
$c_{3.1}(h,t)\;:\!=\;h!^2 t^h$
images of H in G contains a coherent subcollection of size at least t.
Theorem 3.2 ([18]) There exists a function
![]() $c_{3.2}(h,g)$
such that for every planar graph H with h vertices and no
$c_{3.2}(h,g)$
such that for every planar graph H with h vertices and no
![]() $(\leqslant 2)$
-separation, and every surface
$(\leqslant 2)$
-separation, and every surface
![]() $\Sigma$
of Euler genus g,
$\Sigma$
of Euler genus g,
The next key tool is the following result by Miller [Reference Miller52] and Archdeacon [Reference Archdeacon7].
Theorem 3.3 (Additivity of Euler genus [7,52]) For all graphs
![]() $G_1$
and
$G_1$
and
![]() $G_2$
, if
$G_2$
, if
![]() $|V(G_1)\cap V(G_2)|\leqslant 2$
then the Euler genus of
$|V(G_1)\cap V(G_2)|\leqslant 2$
then the Euler genus of
![]() $G_1\cup G_2$
is at least the Euler genus of
$G_1\cup G_2$
is at least the Euler genus of
![]() $G_1$
plus the Euler genus of
$G_1$
plus the Euler genus of
![]() $G_2$
.
$G_2$
.
We also use the following result of Erdős and Rado [Reference Erdős and Rado19]; see [Reference Alweiss, Lovett, Wu and Zhang6] for a recent quantitative improvement. A t-sunflower is a collection
![]() $\mathcal{S}$
of t sets for which there exists a set R such that
$\mathcal{S}$
of t sets for which there exists a set R such that
![]() $X\cap Y=R$
for all distinct
$X\cap Y=R$
for all distinct
![]() $X,Y\in\mathcal{S}$
. The set R is called the kernel of
$X,Y\in\mathcal{S}$
. The set R is called the kernel of
![]() $\mathcal{S}$
.
$\mathcal{S}$
.
Lemma 3.4 (Sunflower Lemma[19]) There exists a function
![]() $c_{3.4}(h,t)$
such that every collection of
$c_{3.4}(h,t)$
such that every collection of
![]() $c_{3.4}(h,t)$
many h-subsets of a set contains a t-sunflower.
$c_{3.4}(h,t)$
many h-subsets of a set contains a t-sunflower.
Finally, we mention some well-known corollaries of Euler’s Formula that we use implicitly. Every graph with
![]() $n\geqslant 3$
vertices and Euler genus g has at most
$n\geqslant 3$
vertices and Euler genus g has at most
![]() $3(n+g-2)$
edges. Moreover, for bipartite graphs the above bound is
$3(n+g-2)$
edges. Moreover, for bipartite graphs the above bound is
![]() $2(n+g-2)$
. For example, this implies that the complete bipartite graph
$2(n+g-2)$
. For example, this implies that the complete bipartite graph
![]() $K_{3,2g+3}$
has Euler genus greater than g.
$K_{3,2g+3}$
has Euler genus greater than g.
4. Strongly non-planar graphs
We begin by proving a quantitative version of the upper bound in Theorem 1.1 In fact, we will prove that Theorem 1.1 holds more generally for what we call ‘partially subdivided graphs’. A partially subdivided graph is a pair
![]() $(H, \mathcal P)$
, where H is a graph and
$(H, \mathcal P)$
, where H is a graph and
![]() $\mathcal P$
is a collection of internally disjoint paths in H such that the two ends of each path in
$\mathcal P$
is a collection of internally disjoint paths in H such that the two ends of each path in
![]() $\mathcal P$
are not adjacent in H, and every internal vertex of each path in
$\mathcal P$
are not adjacent in H, and every internal vertex of each path in
![]() $\mathcal P$
has degree 2 in H. Let
$\mathcal P$
has degree 2 in H. Let
![]() $H - \mathcal P$
be the graph obtained from H by deleting every internal vertex of each path in
$H - \mathcal P$
be the graph obtained from H by deleting every internal vertex of each path in
![]() $\mathcal P$
. Finally, let
$\mathcal P$
. Finally, let
![]() $H / \mathcal P$
be the minor of H obtained by contracting all but one edge from each path in
$H / \mathcal P$
be the minor of H obtained by contracting all but one edge from each path in
![]() $\mathcal P$
.
$\mathcal P$
.
Theorem 4.1 Let
![]() $c_{4.1}(h,g)\;:\!=\;c_{3.1}(h, c_{3.4}(h,2g+3))$
. Then for every partially subdivided graph
$c_{4.1}(h,g)\;:\!=\;c_{3.1}(h, c_{3.4}(h,2g+3))$
. Then for every partially subdivided graph
![]() $(H, \mathcal P)$
such that
$(H, \mathcal P)$
such that
![]() $H / \mathcal P$
is strongly non-planar and
$H / \mathcal P$
is strongly non-planar and
![]() $|V(H)|=h$
, for every surface
$|V(H)|=h$
, for every surface
![]() $\Sigma$
with Euler genus g, and for every graph G embedded in
$\Sigma$
with Euler genus g, and for every graph G embedded in
![]() $\Sigma$
, there are at most
$\Sigma$
, there are at most
![]() $c_{4.1}(h,g)$
images of
$c_{4.1}(h,g)$
images of
![]() $H - \mathcal P$
in G that extend to an image of H in G.
$H - \mathcal P$
in G that extend to an image of H in G.
Proof. Assume for the sake of contradiction that there is a collection
![]() $\mathcal{H}$
of more than
$\mathcal{H}$
of more than
![]() $c_{4.1}(h,g)$
images of H in G, such that all restrictions of these images to
$c_{4.1}(h,g)$
images of H in G, such that all restrictions of these images to
![]() $H - \mathcal P$
are distinct. By Lemma 3.1,
$H - \mathcal P$
are distinct. By Lemma 3.1,
![]() $\mathcal H$
contains a coherent subfamily
$\mathcal H$
contains a coherent subfamily
![]() $\mathcal H_0$
of size at least
$\mathcal H_0$
of size at least
![]() $c_{3.4}(h,2g+3)$
. Let
$c_{3.4}(h,2g+3)$
. Let
![]() $\mathcal V$
be the collection of vertex sets of the images of H in
$\mathcal V$
be the collection of vertex sets of the images of H in
![]() $\mathcal H_0$
. By coherence,
$\mathcal H_0$
. By coherence,
![]() $|\mathcal V|=|\mathcal H_0| \geqslant c_{3.4}(h,2g+3)$
.
$|\mathcal V|=|\mathcal H_0| \geqslant c_{3.4}(h,2g+3)$
.
By the Sunflower Lemma,
![]() $\mathcal V$
contains a
$\mathcal V$
contains a
![]() $(2g+3)$
-sunflower
$(2g+3)$
-sunflower
![]() $\mathcal{F}$
. (Abusing notations slightly, we equate sets in
$\mathcal{F}$
. (Abusing notations slightly, we equate sets in
![]() $\mathcal F$
with the corresponding images of H in
$\mathcal F$
with the corresponding images of H in
![]() $\mathcal H_0$
.) Let Z be the kernel of
$\mathcal H_0$
.) Let Z be the kernel of
![]() $\mathcal{F}$
. Thus,
$\mathcal{F}$
. Thus,
![]() $F \cap F'=Z$
for all
$F \cap F'=Z$
for all
![]() $F, F' \in \mathcal{F}$
. Let I be the set of internal vertices of all
$F, F' \in \mathcal{F}$
. Let I be the set of internal vertices of all
![]() $P \in \mathcal P$
. Since the restrictions of the images of H in
$P \in \mathcal P$
. Since the restrictions of the images of H in
![]() $\mathcal F$
to
$\mathcal F$
to
![]() $H - \mathcal P$
are all distinct, for each
$H - \mathcal P$
are all distinct, for each
![]() $F \in \mathcal F$
there exists a vertex
$F \in \mathcal F$
there exists a vertex
![]() $w_F \in F \setminus Z$
such that
$w_F \in F \setminus Z$
such that
![]() $w_F$
is the image of a vertex in
$w_F$
is the image of a vertex in
![]() $V(H) \setminus I$
. By coherence, we may assume that every
$V(H) \setminus I$
. By coherence, we may assume that every
![]() $w_F$
is the image of the same vertex of
$w_F$
is the image of the same vertex of
![]() $V(H) \setminus I$
. For each
$V(H) \setminus I$
. For each
![]() $F \in \mathcal F$
, let
$F \in \mathcal F$
, let
![]() $C_F$
be the component of
$C_F$
be the component of
![]() $F - Z$
that contains
$F - Z$
that contains
![]() $w_F$
and let
$w_F$
and let
![]() $N_F$
be the vertices of Z with at least one neighbour in
$N_F$
be the vertices of Z with at least one neighbour in
![]() $V(C_F)$
. By coherence,
$V(C_F)$
. By coherence,
![]() $N_F$
is the same for all
$N_F$
is the same for all
![]() $F \in \mathcal F$
. Therefore, we obtain a
$F \in \mathcal F$
. Therefore, we obtain a
![]() $K_{|N_F|, |\mathcal F|}$
minor in G by contracting each
$K_{|N_F|, |\mathcal F|}$
minor in G by contracting each
![]() $C_F$
to a vertex. Since
$C_F$
to a vertex. Since
![]() $|\mathcal F| = 2g+3$
and
$|\mathcal F| = 2g+3$
and
![]() $K_{3, 2g+3}$
does not embed in
$K_{3, 2g+3}$
does not embed in
![]() $\Sigma$
, we must have
$\Sigma$
, we must have
![]() $|N_F| \leqslant 2$
.
$|N_F| \leqslant 2$
.
For each
![]() $F \in \mathcal F$
, consider the pair of subgraphs
$F \in \mathcal F$
, consider the pair of subgraphs
![]() $(F_1, F_2)\;:\!=\;(F[Z], F[(V(F) \setminus Z) \cup N_F])$
of F. Since
$(F_1, F_2)\;:\!=\;(F[Z], F[(V(F) \setminus Z) \cup N_F])$
of F. Since
![]() $|N_F| \leqslant 2$
, either
$|N_F| \leqslant 2$
, either
![]() $(F_1, F_2)$
is a
$(F_1, F_2)$
is a
![]() $(\leqslant 2)$
-separation of F or
$(\leqslant 2)$
-separation of F or
![]() $F_2=F$
. For each
$F_2=F$
. For each
![]() $P \in \mathcal{P}$
choose
$P \in \mathcal{P}$
choose
![]() $e_P \in E(P)$
and let
$e_P \in E(P)$
and let
![]() $E_{\mathcal{P}}\;:\!=\;\bigcup_{P \in \mathcal{P}} E(P) \setminus \{e_P\}$
. For
$E_{\mathcal{P}}\;:\!=\;\bigcup_{P \in \mathcal{P}} E(P) \setminus \{e_P\}$
. For
![]() $i \in [2]$
, let
$i \in [2]$
, let
![]() $\Gamma_i\;:\!=\;F_i / (E(F_i) \cap E_{\mathcal{P}})$
. Since
$\Gamma_i\;:\!=\;F_i / (E(F_i) \cap E_{\mathcal{P}})$
. Since
![]() $w_F \in V(F_2) \setminus V(F_1)$
, it follows that either
$w_F \in V(F_2) \setminus V(F_1)$
, it follows that either
![]() $(\Gamma_1, \Gamma_2)$
is a
$(\Gamma_1, \Gamma_2)$
is a
![]() $(\leqslant 2)$
-separation of
$(\leqslant 2)$
-separation of
![]() $F / \mathcal P$
or
$F / \mathcal P$
or
![]() $\Gamma_2 \cong F / \mathcal P $
. Since
$\Gamma_2 \cong F / \mathcal P $
. Since
![]() $F / \mathcal P \cong H / \mathcal P$
and
$F / \mathcal P \cong H / \mathcal P$
and
![]() $H / \mathcal P$
is strongly non-planar, either
$H / \mathcal P$
is strongly non-planar, either
![]() $(\Gamma_2)^+$
is non-planar or
$(\Gamma_2)^+$
is non-planar or
![]() $\Gamma_2 = F / \mathcal P $
. In the first case,
$\Gamma_2 = F / \mathcal P $
. In the first case,
![]() $F_2^+$
is also non-planar since
$F_2^+$
is also non-planar since
![]() $\Gamma_2^+$
is a minor of
$\Gamma_2^+$
is a minor of
![]() $F_2^+$
. In the second case,
$F_2^+$
. In the second case,
![]() $F_2=F$
is also non-planar. Let
$F_2=F$
is also non-planar. Let
![]() $F_2'\;:\!=\;F_2^+$
if the first case holds, and
$F_2'\;:\!=\;F_2^+$
if the first case holds, and
![]() $F_2'=F$
if the second case holds. If
$F_2'=F$
if the second case holds. If
![]() $N_F\;:\!=\;\{x,y\}$
and
$N_F\;:\!=\;\{x,y\}$
and
![]() $xy \notin E(F)$
, let
$xy \notin E(F)$
, let
![]() $\Sigma'$
be obtained from
$\Sigma'$
be obtained from
![]() $\Sigma$
by adding a handle and using the handle to draw the edge xy, and let
$\Sigma$
by adding a handle and using the handle to draw the edge xy, and let
![]() $G'\;:\!=\;G \cup \{xy\}$
. Otherwise, let
$G'\;:\!=\;G \cup \{xy\}$
. Otherwise, let
![]() $\Sigma'\;:\!=\;\Sigma$
and
$\Sigma'\;:\!=\;\Sigma$
and
![]() $G'\;:\!=\;G$
. We conclude by noting that the family of subgraphs
$G'\;:\!=\;G$
. We conclude by noting that the family of subgraphs
![]() $\{F_2' \mid F \in \mathcal F\}$
of G’ contradicts the Additivity of Euler genus (Theorem 3.3), since they each have Euler genus at least 1, they pairwise intersect only in
$\{F_2' \mid F \in \mathcal F\}$
of G’ contradicts the Additivity of Euler genus (Theorem 3.3), since they each have Euler genus at least 1, they pairwise intersect only in
![]() $N_F$
, are drawn on a surface
$N_F$
, are drawn on a surface
![]() $\Sigma'$
of Euler genus at most
$\Sigma'$
of Euler genus at most
![]() $g+2$
, and
$g+2$
, and
![]() $|\mathcal F| = 2g+3 >g+2$
.
$|\mathcal F| = 2g+3 >g+2$
.
Note that if H is a strongly non-planar graph, then we recover Theorem 1.1 by applying Theorem 4.1 to the partially subdivided graph
![]() $(H, \emptyset)$
. We need the stronger statement in Theorem 4.1 for the proof of Theorem 5.9 to come.
$(H, \emptyset)$
. We need the stronger statement in Theorem 4.1 for the proof of Theorem 5.9 to come.
5. Proof of Theorem 1.2 theorem
The proof of our main theorem uses a variant of the SPQR tree, which we now introduce.
5.1 SPQRK trees
The SPQR tree of a 2-connected graph G is a tree that displays all the 2-separations of G. Since we need to consider graphs that are not necessarily 2-connected, we use a variant of the SPQR tree that we call the SPQRK tree.
Let G be a connected graph. The SPQRK tree
![]() $T_G$
of G is a tree, where each node
$T_G$
of G is a tree, where each node
![]() $a\in V(T_G)$
is associated with a multigraph
$a\in V(T_G)$
is associated with a multigraph
![]() $H_a$
which is a minor of G. Each vertex
$H_a$
which is a minor of G. Each vertex
![]() $x \in V(H_a)$
is a vertex of G, that is,
$x \in V(H_a)$
is a vertex of G, that is,
![]() $V(H_a) \subseteq V(G)$
. Each edge
$V(H_a) \subseteq V(G)$
. Each edge
![]() $e \in E(H_a)$
is classified either as a real or virtual edge. By the construction of an SPQRK tree, each edge
$e \in E(H_a)$
is classified either as a real or virtual edge. By the construction of an SPQRK tree, each edge
![]() $e\in E(G)$
appears in exactly one minor
$e\in E(G)$
appears in exactly one minor
![]() $H_a$
as a real edge, and each real edge
$H_a$
as a real edge, and each real edge
![]() $e\in E(H_a)$
is an edge of G. The SPQRK tree
$e\in E(H_a)$
is an edge of G. The SPQRK tree
![]() $T_G$
is defined recursively as follows.
$T_G$
is defined recursively as follows.
-
1. If G is 3-connected, then
 $T_G$
consists of a single R-node a with
$T_G$
consists of a single R-node a with
 $H_a \;:\!=\; G$
. All edges of
$H_a \;:\!=\; G$
. All edges of
 $H_a$
are real in this case.
$H_a$
are real in this case. -
2. If G is a cycle, then
 $T_G$
consists of a single S-node a with
$T_G$
consists of a single S-node a with
 $H_a \;:\!=\; G$
. Again, all edges of
$H_a \;:\!=\; G$
. Again, all edges of
 $H_a$
are real in this case.
$H_a$
are real in this case. -
3. If G is isomorphic to
 $K_1$
or
$K_1$
or
 $K_2$
, then
$K_2$
, then
 $T_G$
consists of a single K-node a with
$T_G$
consists of a single K-node a with
 $H_a \;:\!=\; G$
. Again, all edges of
$H_a \;:\!=\; G$
. Again, all edges of
 $H_a$
are real in this case.
$H_a$
are real in this case. -
4. If G is 2-connected and has a cutset
 $\{x,y\}$
such that the vertices x and y have degree at least 3, we construct
$\{x,y\}$
such that the vertices x and y have degree at least 3, we construct
 $T_G$
inductively as follows. Let
$T_G$
inductively as follows. Let
 $C_1,\dots, C_r$
(
$C_1,\dots, C_r$
(
 $r\geqslant 2$
) be the connected components of
$r\geqslant 2$
) be the connected components of
 $G - \{x,y\}$
. First add a P-node a to
$G - \{x,y\}$
. First add a P-node a to
 $T_G$
, for which
$T_G$
, for which
 $H_a$
is the graph with
$H_a$
is the graph with
 $V(H_a)\;:\!=\;\{x,y\}$
consisting of r parallel virtual edges and one additional real edge if xy is an edge of G.Next let
$V(H_a)\;:\!=\;\{x,y\}$
consisting of r parallel virtual edges and one additional real edge if xy is an edge of G.Next let
 $G_i$
be the graph
$G_i$
be the graph
 $G[V(C_i)\cup \{x,y\}]$
with the additional edge xy if it is not already there. Since we include the edge xy, each
$G[V(C_i)\cup \{x,y\}]$
with the additional edge xy if it is not already there. Since we include the edge xy, each
 $G_i$
is 2-connected and we can construct the corresponding SPQRK tree
$G_i$
is 2-connected and we can construct the corresponding SPQRK tree
 $T_{G_i}$
by induction. Let
$T_{G_i}$
by induction. Let
 $a_i$
be the (unique) node in
$a_i$
be the (unique) node in
 $T_{G_i}$
for which xy is a real edge in
$T_{G_i}$
for which xy is a real edge in
 $H_{a_i}$
. In order to construct
$H_{a_i}$
. In order to construct
 $T_G$
, we make xy a virtual edge in the node
$T_G$
, we make xy a virtual edge in the node
 $a_i$
and connect
$a_i$
and connect
 $a_i$
to a in
$a_i$
to a in
 $T_G$
.
$T_G$
. -
5. If G has a cut-vertex x and
 $C_1, \dots, C_s$
(
$C_1, \dots, C_s$
(
 $s\geqslant 2$
) are the connected components of
$s\geqslant 2$
) are the connected components of
 $G - x$
, then construct
$G - x$
, then construct
 $T_G$
inductively as follows. First, add a Q-node a to
$T_G$
inductively as follows. First, add a Q-node a to
 $T_G$
, for which
$T_G$
, for which
 $H_a$
is the graph consisting of the single vertex x. For each
$H_a$
is the graph consisting of the single vertex x. For each
 $i \in [s]$
, let
$i \in [s]$
, let
 $G_i \;:\!=\; G[V(C_i)\cup \{x\}]$
. Since
$G_i \;:\!=\; G[V(C_i)\cup \{x\}]$
. Since
 $G_i$
is connected, we can construct the corresponding SPQRK tree
$G_i$
is connected, we can construct the corresponding SPQRK tree
 $T_{G_i}$
by induction. If there is a unique node
$T_{G_i}$
by induction. If there is a unique node
 $b_i \in V(T_{G_i})$
such that
$b_i \in V(T_{G_i})$
such that
 $x \in V(H_{b_i})$
, then make a adjacent to
$x \in V(H_{b_i})$
, then make a adjacent to
 $b_i$
in
$b_i$
in
 $T_{G}$
. If x is in at least two nodes of
$T_{G}$
. If x is in at least two nodes of
 $V(T_{G_i})$
, then
$V(T_{G_i})$
, then
 $x \in V(C) \cap V(D)$
for some
$x \in V(C) \cap V(D)$
for some
 $(\leqslant 2)$
-separation (C,D) of
$(\leqslant 2)$
-separation (C,D) of
 $G_i$
. Since
$G_i$
. Since
 $G_i - x$
is connected, there must be a P-node
$G_i - x$
is connected, there must be a P-node
 $b_i$
in
$b_i$
in
 $T_{G_i}$
such that
$T_{G_i}$
such that
 $x \in V(H_{b_i})$
. Note that
$x \in V(H_{b_i})$
. Note that
 $b_i$
is not necessarily unique. Choose one such
$b_i$
is not necessarily unique. Choose one such
 $b_i$
and make a adjacent to
$b_i$
and make a adjacent to
 $b_i$
in
$b_i$
in
 $T_G$
.
$T_G$
.
As a side remark, note that the SPQRK tree
![]() $T_G$
of G is in fact not unique—there is some freedom in choosing
$T_G$
of G is in fact not unique—there is some freedom in choosing
![]() $b_i$
in the last point in the definition above—however, for our purposes we do not need uniqueness, we only need that
$b_i$
in the last point in the definition above—however, for our purposes we do not need uniqueness, we only need that
![]() $T_G$
displays all the
$T_G$
displays all the
![]() $(\leqslant 2)$
-separations of G.
$(\leqslant 2)$
-separations of G.
The next lemma is the crux of the proof. Let J and G be graphs and X and Y be cliques in J and G, respectively, with
![]() $|X|=|Y|$
. Let
$|X|=|Y|$
. Let
![]() $\phi\;:\;V(J) \to V(G)$
be an image of J in G. We say that
$\phi\;:\;V(J) \to V(G)$
be an image of J in G. We say that
![]() $\phi$
fixes X at Y if
$\phi$
fixes X at Y if
![]() $\phi(X)=Y$
. Let
$\phi(X)=Y$
. Let
![]() $(J', \mathcal P)$
be a partially subdivided graph such that
$(J', \mathcal P)$
be a partially subdivided graph such that
![]() $J=J'/ \mathcal P$
. We call
$J=J'/ \mathcal P$
. We call
![]() $uv \in E(J)$
a fake edge if u and v are the set of ends of some
$uv \in E(J)$
a fake edge if u and v are the set of ends of some
![]() $P \in \mathcal P$
. Otherwise, uv is a true edge.
$P \in \mathcal P$
. Otherwise, uv is a true edge.
Lemma 5.1 Let
![]() $c_{5.1}(j,g) \;:\!=\;12(g+1)c_{3.1}(j, c_{3.4}(j, 2g+3))$
. Let
$c_{5.1}(j,g) \;:\!=\;12(g+1)c_{3.1}(j, c_{3.4}(j, 2g+3))$
. Let
![]() $\Sigma$
be a surface of Euler genus g. Let
$\Sigma$
be a surface of Euler genus g. Let
![]() $(J', \mathcal P)$
be a connected, partially subdivided planar graph with
$(J', \mathcal P)$
be a connected, partially subdivided planar graph with
![]() $|V(J')|=j$
and let
$|V(J')|=j$
and let
![]() $J\;:\!=\;J'/ \mathcal P$
.
$J\;:\!=\;J'/ \mathcal P$
.
Let X be a clique in J such that:
-
1. there do not exist independent flaps (A,B) and (C,D) of J with
 $X \subseteq V(B \cap D)$
,
$X \subseteq V(B \cap D)$
, -
2.
 $|X| \in \{1,2\}$
, and if
$|X| \in \{1,2\}$
, and if
 $|X|=2$
, then X is a true edge,
$|X|=2$
, then X is a true edge, -
3. if
 $|X|=1$
and
$|X|=1$
and
 $J \cong P_3$
, then e is a true edge, where e is the unique edge of J not incident to X,
$J \cong P_3$
, then e is a true edge, where e is the unique edge of J not incident to X, -
4. if
 $|X|=1$
and
$|X|=1$
and
 $J \cong C_3$
, then e is a true edge, where e is the unique edge of J not incident to X,
$J \cong C_3$
, then e is a true edge, where e is the unique edge of J not incident to X, -
5. if
 $|X|=2$
and
$|X|=2$
and
 $J \cong C_4$
, then e is a true edge, where e is the unique edge of J not incident to a vertex of X,
$J \cong C_4$
, then e is a true edge, where e is the unique edge of J not incident to a vertex of X, -
6. if J is 3-connected, then all edges of J with neither end in X are true,
-
7. if (A,B) is a flap of J, with
 $X \subseteq V(B), |V(A \cap B)|=1$
, and
$X \subseteq V(B), |V(A \cap B)|=1$
, and
 $A \cong P_3$
, then e is a true edge, where e is the unique edge of A not incident to
$A \cong P_3$
, then e is a true edge, where e is the unique edge of A not incident to
 $V(A \cap B)$
,
$V(A \cap B)$
, -
8. if (A,B) is a flap of J, with
 $X \subseteq V(B), |V(A \cap B)|=1$
, and
$X \subseteq V(B), |V(A \cap B)|=1$
, and
 $A \cong C_3$
, then e is a true edge, where e is the unique edge of A not incident to
$A \cong C_3$
, then e is a true edge, where e is the unique edge of A not incident to
 $V(A \cap B)$
,
$V(A \cap B)$
, -
9. if (A,B) is a flap of J, with
 $X \subseteq V(B), |V(A \cap B)|=2$
, and
$X \subseteq V(B), |V(A \cap B)|=2$
, and
 $A^+ \cong C_3$
, then at least one e or f is a true edge, where e and f are the two edges of A with an end not on
$A^+ \cong C_3$
, then at least one e or f is a true edge, where e and f are the two edges of A with an end not on
 $V(A \cap B)$
.
$V(A \cap B)$
. -
10. if (A,B) is a flap of J, with
 $X \subseteq V(B), |V(A \cap B)|=2$
, and
$X \subseteq V(B), |V(A \cap B)|=2$
, and
 $A^+ \cong C_4$
, then e is a true edge, where e is the unique edge of A not incident to
$A^+ \cong C_4$
, then e is a true edge, where e is the unique edge of A not incident to
 $V(A \cap B)$
,
$V(A \cap B)$
, -
11. if (A,B) is a flap of J such that
 $A^+$
is 3-connected, then all edges of A with neither end in
$A^+$
is 3-connected, then all edges of A with neither end in
 $V(A \cap B)$
are true.
$V(A \cap B)$
are true.
Then for every n-vertex graph G embeddable in
![]() $\Sigma$
and every clique Y in G with
$\Sigma$
and every clique Y in G with
![]() $|Y|=|X|$
, there are at most
$|Y|=|X|$
, there are at most
![]() $c_{5.1}(j,g) n$
images of
$c_{5.1}(j,g) n$
images of
![]() $J' - \mathcal P$
in G with X fixed at Y that extend to an image of J’ in G.
$J' - \mathcal P$
in G with X fixed at Y that extend to an image of J’ in G.
Proof. Let G be an n-vertex graph embedded in a surface
![]() $\Sigma$
of Euler genus g and Y be a clique in G with
$\Sigma$
of Euler genus g and Y be a clique in G with
![]() $|Y|=|X|$
. We begin by proving the lemma when J is small. The lemma clearly holds if
$|Y|=|X|$
. We begin by proving the lemma when J is small. The lemma clearly holds if
![]() $|V(J)|=1$
or
$|V(J)|=1$
or
![]() $|V(J)|=2=|X|$
. If
$|V(J)|=2=|X|$
. If
![]() $|V(J)|=2$
and
$|V(J)|=2$
and
![]() $|X|$
=1, let y be the vertex of J not in X. Since there are at most
$|X|$
=1, let y be the vertex of J not in X. Since there are at most
![]() $n-1$
vertices of G to send y to, we are done. Similarly, we are done if
$n-1$
vertices of G to send y to, we are done. Similarly, we are done if
![]() $J \in \{P_3, C_3\}$
and
$J \in \{P_3, C_3\}$
and
![]() $|X|=2$
. If
$|X|=2$
. If
![]() $J \in \{P_3, C_3\}$
and
$J \in \{P_3, C_3\}$
and
![]() $|X|=1,$
let e be the unique edge of J not incident to X. Note that e exists in the case that
$|X|=1,$
let e be the unique edge of J not incident to X. Note that e exists in the case that
![]() $J \cong P_3$
, since the vertex in X cannot be the middle vertex of J by (1). By (3) and (4), e is a true edge, so there are at most
$J \cong P_3$
, since the vertex in X cannot be the middle vertex of J by (1). By (3) and (4), e is a true edge, so there are at most
![]() $|E(G)| \leqslant 3(g+1)n$
edges of G to send e to. Each edge gives at most two images of
$|E(G)| \leqslant 3(g+1)n$
edges of G to send e to. Each edge gives at most two images of
![]() $J' - \mathcal P$
with X fixed at Y in G, so there are at most
$J' - \mathcal P$
with X fixed at Y in G, so there are at most
![]() $6(g+1)n$
such images. Suppose that
$6(g+1)n$
such images. Suppose that
![]() $|V(J)|=4$
. Note that
$|V(J)|=4$
. Note that
![]() $J \not\cong P_4$
, by (1). If
$J \not\cong P_4$
, by (1). If
![]() $J \cong C_4$
, then
$J \cong C_4$
, then
![]() $|X| =2$
by (1). Let e be the unique edge of J not incident to a vertex of X. By (5), e is a true edge, so again there are at most
$|X| =2$
by (1). Let e be the unique edge of J not incident to a vertex of X. By (5), e is a true edge, so again there are at most
![]() $3(g+1)n$
edges of G to send e to. Each edge gives at most four images of
$3(g+1)n$
edges of G to send e to. Each edge gives at most four images of
![]() $J' - \mathcal P$
with X fixed at Y in G, so there are at most
$J' - \mathcal P$
with X fixed at Y in G, so there are at most
![]() $12(g+1)n$
such images.
$12(g+1)n$
such images.
In summary, by the above discussion we may assume that
![]() $|V(J)|\geqslant 4$
, and
$|V(J)|\geqslant 4$
, and
![]() $J \not\cong P_4, C_4$
in case
$J \not\cong P_4, C_4$
in case
![]() $|V(J)|=4$
.
$|V(J)|=4$
.
Let
![]() $T_J$
be the SPQRK tree of J. Suppose that
$T_J$
be the SPQRK tree of J. Suppose that
![]() $V(T_J)=\{a\}$
. If a is a K-node, then we are done since
$V(T_J)=\{a\}$
. If a is a K-node, then we are done since
![]() $|V(J)| \leqslant 2$
. If a is an S-node, then by (1),
$|V(J)| \leqslant 2$
. If a is an S-node, then by (1),
![]() $J\cong C_3$
or
$J\cong C_3$
or
![]() $J\cong C_4$
, so we are done. By the preceding remarks, we may assume that J is 3-connected, or
$J\cong C_4$
, so we are done. By the preceding remarks, we may assume that J is 3-connected, or
![]() $|V(J)| \geqslant 4$
and
$|V(J)| \geqslant 4$
and
![]() $|V(T_J)| \geqslant 2$
. A clique X’ of J is a true clique if
$|V(T_J)| \geqslant 2$
. A clique X’ of J is a true clique if
![]() $|X'|=1$
, or
$|X'|=1$
, or
![]() $|X'|=2$
and the edge of X’ is a true edge. If J is 3-connected, we have the following easy claim.
$|X'|=2$
and the edge of X’ is a true edge. If J is 3-connected, we have the following easy claim.
Claim 5.2 If J is 3-connected, then there exists a true clique X’ in J such that for all
![]() $w \in V(J) \setminus (X \cup X')$
, there are three internally disjoint paths in J from w to
$w \in V(J) \setminus (X \cup X')$
, there are three internally disjoint paths in J from w to
![]() $X \cup X'$
, whose ends in
$X \cup X'$
, whose ends in
![]() $X \cup X'$
are distinct.
$X \cup X'$
are distinct.
Proof. Since J is 3-connected, there is an edge X’ of J with neither end in X; otherwise, X is a cutset of J with
![]() $|X| \leqslant 2$
. By (6), X’ is a true edge. Since J is 3-connected, we are done by Menger’s theorem.
$|X| \leqslant 2$
. By (6), X’ is a true edge. Since J is 3-connected, we are done by Menger’s theorem.
We now suppose that
![]() $|V(J)| \geqslant 4$
and
$|V(J)| \geqslant 4$
and
![]() $|V(T_J)| \geqslant 2$
, and we prove that Claim Theorem 5.2 also holds in this case. Let W be the set of K-, S-, and R-nodes of
$|V(T_J)| \geqslant 2$
, and we prove that Claim Theorem 5.2 also holds in this case. Let W be the set of K-, S-, and R-nodes of
![]() $V(T_J)$
. Note that for each
$V(T_J)$
. Note that for each
![]() $a \in W$
,
$a \in W$
,
![]() $H_a$
is a subgraph of J. If U is a non-empty proper subset of W, we define
$H_a$
is a subgraph of J. If U is a non-empty proper subset of W, we define
![]() $H_U \;:\!=\; \bigcup_{a \in U} H_a$
,
$H_U \;:\!=\; \bigcup_{a \in U} H_a$
,
![]() $bd(U) \;:\!=\; V(H_U \cap H_{W \setminus U})$
,
$bd(U) \;:\!=\; V(H_U \cap H_{W \setminus U})$
,
![]() $\lambda(U) \;:\!=\;|bd(H_U)|$
, and
$\lambda(U) \;:\!=\;|bd(H_U)|$
, and
![]() $sep(U)\;:\!=\;(H_U, H_{W \setminus U})$
.
$sep(U)\;:\!=\;(H_U, H_{W \setminus U})$
.
Claim 5.3
![]() $T_J$
is a path and there is a leaf
$T_J$
is a path and there is a leaf
![]() $\ell$
of
$\ell$
of
![]() $T_J$
such that
$T_J$
such that
![]() $X \subseteq V(H_\ell)$
and
$X \subseteq V(H_\ell)$
and
![]() $X \setminus bd(\{\ell\}) \neq \emptyset$
.
$X \setminus bd(\{\ell\}) \neq \emptyset$
.
Proof. Since
![]() $|V(T_J)| \geqslant 2$
,
$|V(T_J)| \geqslant 2$
,
![]() $T_J$
has at least two leaves. For each leaf a of
$T_J$
has at least two leaves. For each leaf a of
![]() $T_J$
, there is a flap
$T_J$
, there is a flap
![]() $(C^a, D^a)$
such that
$(C^a, D^a)$
such that
![]() $V(C^a)=V(H_a)$
. Since
$V(C^a)=V(H_a)$
. Since
![]() $(C^a, D^a)$
and
$(C^a, D^a)$
and
![]() $(D^a, C^a)$
are independent flaps, exactly one of
$(D^a, C^a)$
are independent flaps, exactly one of
![]() $(V(C^a) \setminus V(D^a)) \cap X$
or
$(V(C^a) \setminus V(D^a)) \cap X$
or
![]() $(V(D^a) \setminus V(C^a)) \cap X$
is non-empty by (1). Thus,
$(V(D^a) \setminus V(C^a)) \cap X$
is non-empty by (1). Thus,
![]() $T_J$
has exactly two leaves and there is a leaf
$T_J$
has exactly two leaves and there is a leaf
![]() $\ell$
of
$\ell$
of
![]() $T_J$
such that
$T_J$
such that
![]() $X \subseteq V(H_\ell)$
and
$X \subseteq V(H_\ell)$
and
![]() $X \setminus bd(\{\ell\}) \neq \emptyset$
.
$X \setminus bd(\{\ell\}) \neq \emptyset$
.
Claim 5.4 Let r be the other leaf of
![]() $T_J$
. Then for all non-empty
$T_J$
. Then for all non-empty
![]() $U \subseteq W \setminus \{\ell, r\}$
such that U is not a single K-node,
$U \subseteq W \setminus \{\ell, r\}$
such that U is not a single K-node,
![]() $\lambda(U) \geqslant 3$
.
$\lambda(U) \geqslant 3$
.
Proof. Towards a contradiction, suppose that
![]() $\lambda(U) \leqslant 2$
for some non-empty
$\lambda(U) \leqslant 2$
for some non-empty
![]() $U \subseteq W \setminus \{\ell, r\}$
which is not a single K-node. Let
$U \subseteq W \setminus \{\ell, r\}$
which is not a single K-node. Let
![]() $(C^r, D^r)$
be the flap of J such that
$(C^r, D^r)$
be the flap of J such that
![]() $V(C^r)=V(H_r)$
. Since
$V(C^r)=V(H_r)$
. Since
![]() $X \subseteq V(H_\ell)$
,
$X \subseteq V(H_\ell)$
,
![]() $(C^r, D^r)$
and sep(U) are independent flaps of J which contradict (1).
$(C^r, D^r)$
and sep(U) are independent flaps of J which contradict (1).
Claim 5.5 Let
![]() $S\;:\!=\;\{s \in V(J) \setminus X \mid \deg_J(s) \leqslant 2\}$
. Then
$S\;:\!=\;\{s \in V(J) \setminus X \mid \deg_J(s) \leqslant 2\}$
. Then
![]() $|S| \leqslant 2$
,
$|S| \leqslant 2$
,
![]() $S \subseteq V(H_r)$
, and if
$S \subseteq V(H_r)$
, and if
![]() $|S|=2$
, then the two vertices in S are adjacent in J.
$|S|=2$
, then the two vertices in S are adjacent in J.
Proof. Since
![]() $|V(J)| \geqslant 4$
, for each
$|V(J)| \geqslant 4$
, for each
![]() $s \in S$
,
$s \in S$
,
![]() $(\delta(s), J - s)$
is a flap with
$(\delta(s), J - s)$
is a flap with
![]() $X \subseteq V(J - s)$
, where
$X \subseteq V(J - s)$
, where
![]() $\delta(s)$
is the subgraph of J induced by the edges incident to s. Thus, by (1), S is a clique in J, and therefore,
$\delta(s)$
is the subgraph of J induced by the edges incident to s. Thus, by (1), S is a clique in J, and therefore,
![]() $|S| \leqslant 3$
. Moreover,
$|S| \leqslant 3$
. Moreover,
![]() $|S|=3$
is impossible, since
$|S|=3$
is impossible, since
![]() $|V(J)| \geqslant 4$
and J is connected. Thus,
$|V(J)| \geqslant 4$
and J is connected. Thus,
![]() $|S| \leqslant 2$
. Since
$|S| \leqslant 2$
. Since
![]() $(A,B)=sep(\{r\})$
is a flap with
$(A,B)=sep(\{r\})$
is a flap with
![]() $X \subseteq V(B)$
, (1) also implies
$X \subseteq V(B)$
, (1) also implies
![]() $S \subseteq V(H_r)$
.
$S \subseteq V(H_r)$
.
Claim 5.6 J has at most two cut-vertices. Moreover, if J has two cut-vertices, then they are the vertex set of some K-node of
![]() $T_J$
.
$T_J$
.
Proof. Let c and d be distinct cut-vertices of J. Let
![]() $W_{cd} \subseteq W$
be the set of K-, S-, and R-nodes of
$W_{cd} \subseteq W$
be the set of K-, S-, and R-nodes of
![]() $V(T_J)$
strictly between the Q-nodes corresponding to c and d in
$V(T_J)$
strictly between the Q-nodes corresponding to c and d in
![]() $T_J$
. Note that
$T_J$
. Note that
![]() $sep(W_{cd})$
is a 2-separation of J, unless
$sep(W_{cd})$
is a 2-separation of J, unless
![]() $W_{cd}$
is just a single K-node. Moreover, if
$W_{cd}$
is just a single K-node. Moreover, if
![]() $W_{cd}$
is not a single K-node, then
$W_{cd}$
is not a single K-node, then
![]() $sep(\{r\})$
and
$sep(\{r\})$
and
![]() $sep(W_{cd})$
would contradict (1). It follows that J has at most two cut-vertices and that
$sep(W_{cd})$
would contradict (1). It follows that J has at most two cut-vertices and that
![]() $\{c,d\}$
is the vertex set of some K-node of
$\{c,d\}$
is the vertex set of some K-node of
![]() $T_J$
.
$T_J$
.
Claim 5.7 There exists a true clique X’ in J such that for all
![]() $w \in V(J) \setminus (X \cup X')$
, there are three internally disjoint paths in J from w to
$w \in V(J) \setminus (X \cup X')$
, there are three internally disjoint paths in J from w to
![]() $X \cup X'$
, whose ends in
$X \cup X'$
, whose ends in
![]() $X \cup X'$
are distinct.
$X \cup X'$
are distinct.
Proof. If r is an R-node, then all edges of
![]() $H_{r}^-$
are true by (11). In this case, we let X’ be any edge of
$H_{r}^-$
are true by (11). In this case, we let X’ be any edge of
![]() $H_{r}^-$
such that
$H_{r}^-$
such that
![]() $X' \cap bd(\{r\})=\emptyset$
. If r is an S-node, then by (1), either
$X' \cap bd(\{r\})=\emptyset$
. If r is an S-node, then by (1), either
![]() $H_r \cong C_3$
, or
$H_r \cong C_3$
, or
![]() $H_r \cong C_4$
and
$H_r \cong C_4$
and
![]() $|bd(\{r\})|=2$
. In either case, by (8), (9), and (10), we can choose X’ to be a true edge such that
$|bd(\{r\})|=2$
. In either case, by (8), (9), and (10), we can choose X’ to be a true edge such that
![]() $V(H_r) \setminus (X' \cup bd(\{r\})) = \emptyset$
. Lastly, suppose that r is a K-node. Then
$V(H_r) \setminus (X' \cup bd(\{r\})) = \emptyset$
. Lastly, suppose that r is a K-node. Then
![]() $H_r \cong K_2$
, say
$H_r \cong K_2$
, say
![]() $H_r$
consists of the edge uv with
$H_r$
consists of the edge uv with
![]() $v \in bd(\{r\})$
. If
$v \in bd(\{r\})$
. If
![]() $v \notin S$
, we let
$v \notin S$
, we let
![]() $X'\;:\!=\;\{u\}$
. If
$X'\;:\!=\;\{u\}$
. If
![]() $v \in S$
, we let
$v \in S$
, we let
![]() $X'\;:\!=\;\{u,v\}$
; note that uv is a true edge by (7) in this case.
$X'\;:\!=\;\{u,v\}$
; note that uv is a true edge by (7) in this case.
Suppose the claim is false for the above choice of X’ for some vertex
![]() $w \in V(J) \setminus (X \cup X')$
, and let
$w \in V(J) \setminus (X \cup X')$
, and let
![]() $X^+\;:\!=\;X \cup X'$
. Note that
$X^+\;:\!=\;X \cup X'$
. Note that
![]() $|X^+| \geqslant 3$
by our choice of X’, since if
$|X^+| \geqslant 3$
by our choice of X’, since if
![]() $|X|=1$
then J is 2-connected by (1). (Indeed, if J is not 2-connected then J has a flap (A,B) that is a 1-separation with
$|X|=1$
then J is 2-connected by (1). (Indeed, if J is not 2-connected then J has a flap (A,B) that is a 1-separation with
![]() $X \subseteq B$
, but then
$X \subseteq B$
, but then
![]() $(B, A \cup X)$
is also a flap, contradicting (1).) Thus, by Menger’s theorem, there is a
$(B, A \cup X)$
is also a flap, contradicting (1).) Thus, by Menger’s theorem, there is a
![]() $({\leqslant}\,2)$
-separation
$({\leqslant}\,2)$
-separation
![]() $(J_1,J_2)$
of J with
$(J_1,J_2)$
of J with
![]() $w \in V(J_1) \setminus V(J_2)$
and
$w \in V(J_1) \setminus V(J_2)$
and
![]() $X^+\;:\!=\;X \cup X' \subseteq V(J_2)$
.
$X^+\;:\!=\;X \cup X' \subseteq V(J_2)$
.
Let a be an S-node of
![]() $T_J$
. Observe that every 2-separation of the cycle
$T_J$
. Observe that every 2-separation of the cycle
![]() $H_a$
lifts to a 2-separation of J. We say that a 2-separation of J is rooted at a if it is a lift of a 2-separation of
$H_a$
lifts to a 2-separation of J. We say that a 2-separation of J is rooted at a if it is a lift of a 2-separation of
![]() $H_a$
. Since the SPQRK tree
$H_a$
. Since the SPQRK tree
![]() $T_J$
of J ‘displays’ all the
$T_J$
of J ‘displays’ all the
![]() $(\leqslant 2)$
-separations of J, every
$(\leqslant 2)$
-separations of J, every
![]() $(\leqslant 2)$
-separation (A,B) of J
$(\leqslant 2)$
-separation (A,B) of J
-
is equal to sep(U) for some
 $U \subseteq W$
, or
$U \subseteq W$
, or -
is rooted at some S-node a of
 $T_J$
, or
$T_J$
, or -
is obtained from a 1-separation (A’,B’) by adding an isolated vertex to A’ or B’ (which is thus in
 $A \cap B$
).
$A \cap B$
).
Suppose
![]() $(J_1, J_2)=sep(U)$
for some
$(J_1, J_2)=sep(U)$
for some
![]() $U \subseteq W$
. Since
$U \subseteq W$
. Since
![]() $X^+ \subseteq V(J_2)$
,
$X^+ \subseteq V(J_2)$
,
![]() $X \setminus bd(\{\ell\}) \neq \emptyset$
, and
$X \setminus bd(\{\ell\}) \neq \emptyset$
, and
![]() $X' \setminus bd(\{r\}) \neq \emptyset$
, we have
$X' \setminus bd(\{r\}) \neq \emptyset$
, we have
![]() $U \subseteq W \setminus \{\ell, r\}$
. This is a contradiction since
$U \subseteq W \setminus \{\ell, r\}$
. This is a contradiction since
![]() $\lambda(U) \geqslant 3$
by Claim Theorem 5.4. Similarly,
$\lambda(U) \geqslant 3$
by Claim Theorem 5.4. Similarly,
![]() $(J_1, J_2)$
cannot be rooted at an S-node, unless
$(J_1, J_2)$
cannot be rooted at an S-node, unless
![]() $\deg_J(x)=2$
for some
$\deg_J(x)=2$
for some
![]() $x \in V(J_1) \setminus V(J_2)$
. However, by Claim Theorem 5.5 and our choice of X’,
$x \in V(J_1) \setminus V(J_2)$
. However, by Claim Theorem 5.5 and our choice of X’,
![]() $\deg_J(x) \geqslant 3$
, for all
$\deg_J(x) \geqslant 3$
, for all
![]() $x \in V(J) \setminus X^+$
, so this is also impossible.
$x \in V(J) \setminus X^+$
, so this is also impossible.
Finally, suppose the third possibility holds for some 1-separation (A’,B’) of J. Observe that every 1-separation (A,B) of J has
![]() $X' \subseteq V(A)$
and
$X' \subseteq V(A)$
and
![]() $X \subseteq V(B)$
; or
$X \subseteq V(B)$
; or
![]() $X \subseteq V(A)$
and
$X \subseteq V(A)$
and
![]() $X' \subseteq V(B)$
. By swapping the order of (A’,B’), we may assume that
$X' \subseteq V(B)$
. By swapping the order of (A’,B’), we may assume that
![]() $X' \subseteq V(A')$
and
$X' \subseteq V(A')$
and
![]() $X \subseteq V(B')$
. Moreover,
$X \subseteq V(B')$
. Moreover,
![]() $(A',B' \cup \{a\}) \in \{(J_1, J_2), (J_2, J_1)\}$
for some
$(A',B' \cup \{a\}) \in \{(J_1, J_2), (J_2, J_1)\}$
for some
![]() $a \in V(A') \setminus V(B')$
; or
$a \in V(A') \setminus V(B')$
; or
![]() $(A' \cup \{b\}, B') \in \{(J_1, J_2), (J_2, J_1)\}$
for some
$(A' \cup \{b\}, B') \in \{(J_1, J_2), (J_2, J_1)\}$
for some
![]() $b \in V(B') \setminus V(A')$
. If
$b \in V(B') \setminus V(A')$
. If
![]() $(A' \cup \{b\}, B')=(J_1, J_2)$
, then (A’,B’) is a 1-separation of J such that
$(A' \cup \{b\}, B')=(J_1, J_2)$
, then (A’,B’) is a 1-separation of J such that
![]() $X \cup X' \subseteq V(B')$
. However, no such separation exists (by the proof that
$X \cup X' \subseteq V(B')$
. However, no such separation exists (by the proof that
![]() $(J_1, J_2) \neq sep(U)$
for all
$(J_1, J_2) \neq sep(U)$
for all
![]() $U \subseteq W$
). Similarly,
$U \subseteq W$
). Similarly,
![]() $(A',B' \cup \{a\})=(J_2, J_1)$
is impossible. If
$(A',B' \cup \{a\})=(J_2, J_1)$
is impossible. If
![]() $(A' \cup \{b\}, B')=(J_2, J_1)$
, then (A’,B’) and
$(A' \cup \{b\}, B')=(J_2, J_1)$
, then (A’,B’) and
![]() $(B', A' \cup \{b\})$
contradict (1). The reTheorem 1.2ing case is
$(B', A' \cup \{b\})$
contradict (1). The reTheorem 1.2ing case is
![]() $(A', B' \cup \{a\})=(J_1, J_2)$
. Let c be the unique vertex in
$(A', B' \cup \{a\})=(J_1, J_2)$
. Let c be the unique vertex in
![]() $V(A') \cap V(B')$
. Recall that by the choice of X’, if r is an R-node or an S-node, then
$V(A') \cap V(B')$
. Recall that by the choice of X’, if r is an R-node or an S-node, then
![]() $|X'|=2$
and
$|X'|=2$
and
![]() $c \notin X'$
. However, this contradicts
$c \notin X'$
. However, this contradicts
![]() $X' \subseteq V(J_2)$
. Thus, r is a K-node. Note that
$X' \subseteq V(J_2)$
. Thus, r is a K-node. Note that
![]() $(A',B')=sep(\{r\})$
is impossible, because
$(A',B')=sep(\{r\})$
is impossible, because
![]() $V(A') \setminus (V(B' \cup \{a\}))$
would be empty, and hence,
$V(A') \setminus (V(B' \cup \{a\}))$
would be empty, and hence,
![]() $(A',B' \cup \{a\})$
is not a 2-separation. Thus,
$(A',B' \cup \{a\})$
is not a 2-separation. Thus,
![]() $c \notin V(H_r)$
. Let v be the cut-vertex of J in
$c \notin V(H_r)$
. Let v be the cut-vertex of J in
![]() $V(H_r)$
. By Claim 5.6, c and v are adjacent and
$V(H_r)$
. By Claim 5.6, c and v are adjacent and
![]() $v \in S=\{s \in V(J) \setminus X \mid \deg_J(s) \leqslant 2\}$
. In this case, by our choice of X’, we have
$v \in S=\{s \in V(J) \setminus X \mid \deg_J(s) \leqslant 2\}$
. In this case, by our choice of X’, we have
![]() $|X'|=2$
and
$|X'|=2$
and
![]() $c \notin X'$
, so we again have a contradiction.
$c \notin X'$
, so we again have a contradiction.
Let X’ be the true clique of J given by Claim 5.2 or by Claim 5.7, depending whether J is 3-connected, or
![]() $|V(J)| \geqslant 4$
and
$|V(J)| \geqslant 4$
and
![]() $|V(T_J)| \geqslant 2$
. Suppose
$|V(T_J)| \geqslant 2$
. Suppose
![]() $|X'|=1$
. For each
$|X'|=1$
. For each
![]() $y \in V(G)$
, let
$y \in V(G)$
, let
![]() $c_y$
be the number of images of
$c_y$
be the number of images of
![]() $J' - \mathcal P$
in G, with X fixed at Y and X’ fixed at y, that extend to an image of J’ in G. Suppose
$J' - \mathcal P$
in G, with X fixed at Y and X’ fixed at y, that extend to an image of J’ in G. Suppose
![]() $|X'|=2$
. For each
$|X'|=2$
. For each
![]() $f \in E(G)$
, let
$f \in E(G)$
, let
![]() $c_f$
be the number of images of
$c_f$
be the number of images of
![]() $J' - \mathcal P$
in G, with X fixed at Y and X’ fixed at f, that extend to an image of J’ in G.
$J' - \mathcal P$
in G, with X fixed at Y and X’ fixed at f, that extend to an image of J’ in G.
We claim that if
![]() $|X'|=1$
then
$|X'|=1$
then
![]() $c_y \leqslant c_{3.1}(j, c_{3.4}(j, 2g+3))$
for all
$c_y \leqslant c_{3.1}(j, c_{3.4}(j, 2g+3))$
for all
![]() $y \in V(G)$
, if
$y \in V(G)$
, if
![]() $|X'|=2$
then
$|X'|=2$
then
![]() $c_f \leqslant c_{3.1}(j, c_{3.4}(j, 2g+3))$
for all
$c_f \leqslant c_{3.1}(j, c_{3.4}(j, 2g+3))$
for all
![]() $f \in E(G)$
. We will prove both inequalities simultaneously, since the proof is the same. Arguing by contradiction, suppose y or
$f \in E(G)$
. We will prove both inequalities simultaneously, since the proof is the same. Arguing by contradiction, suppose y or
![]() $f\;:\!=\;uv$
is a counterexample, and set
$f\;:\!=\;uv$
is a counterexample, and set
![]() $Y^+=Y \cup \{y\}$
if
$Y^+=Y \cup \{y\}$
if
![]() $|X'|=1$
and
$|X'|=1$
and
![]() $Y^+=Y \cup \{u,v\}$
if
$Y^+=Y \cup \{u,v\}$
if
![]() $|X'|=2$
. Then, there exists a collection
$|X'|=2$
. Then, there exists a collection
![]() $\mathcal J_1$
of more than
$\mathcal J_1$
of more than
![]() $c_{3.1}(j, c_{3.4}(j, 2g+3))$
images of J’ in G with X fixed at Y and X’ fixed at y (respectively, X’ fixed at f) such that the restrictions of these images to
$c_{3.1}(j, c_{3.4}(j, 2g+3))$
images of J’ in G with X fixed at Y and X’ fixed at y (respectively, X’ fixed at f) such that the restrictions of these images to
![]() $J' - \mathcal P$
are all distinct.
$J' - \mathcal P$
are all distinct.
By Lemma 3.1,
![]() $\mathcal J_1$
contains a coherent subfamily
$\mathcal J_1$
contains a coherent subfamily
![]() $\mathcal J_2$
of size at least
$\mathcal J_2$
of size at least
![]() $c_{3.4}(j, 2g+3)$
. Let
$c_{3.4}(j, 2g+3)$
. Let
![]() $\mathcal{V}$
be the collection of vertex sets of
$\mathcal{V}$
be the collection of vertex sets of
![]() $\mathcal J_2$
. Note that by coherence,
$\mathcal J_2$
. Note that by coherence,
![]() $|\mathcal V|=|\mathcal J_2| \geqslant c_{3.4}(j, 2g+3)$
. By Lemma 3.4,
$|\mathcal V|=|\mathcal J_2| \geqslant c_{3.4}(j, 2g+3)$
. By Lemma 3.4,
![]() $\mathcal{V}$
contains an s-sunflower
$\mathcal{V}$
contains an s-sunflower
![]() $\mathcal F$
, where
$\mathcal F$
, where
![]() $s \geqslant 2g+3$
. Let Z be the kernel of
$s \geqslant 2g+3$
. Let Z be the kernel of
![]() $\mathcal{F}$
. By construction,
$\mathcal{F}$
. By construction,
![]() $Y^+ \subseteq Z$
. Let I be the set of internal vertices of all
$Y^+ \subseteq Z$
. Let I be the set of internal vertices of all
![]() $P \in \mathcal P$
. Since the restrictions of each copy of J’ in
$P \in \mathcal P$
. Since the restrictions of each copy of J’ in
![]() $\mathcal F$
to
$\mathcal F$
to
![]() $J' - \mathcal P$
are all distinct, for all
$J' - \mathcal P$
are all distinct, for all
![]() $F \in \mathcal F$
there must be a vertex
$F \in \mathcal F$
there must be a vertex
![]() $w_F \in F \setminus Z$
such that
$w_F \in F \setminus Z$
such that
![]() $w_F$
is the image of a vertex in
$w_F$
is the image of a vertex in
![]() $V(J') \setminus I$
. By coherence, we may assume that each
$V(J') \setminus I$
. By coherence, we may assume that each
![]() $w_F$
corresponds to the same vertex in
$w_F$
corresponds to the same vertex in
![]() $V(J') \setminus I$
. By Claims 5.2 and 5.7, there are three internally disjoint paths from
$V(J') \setminus I$
. By Claims 5.2 and 5.7, there are three internally disjoint paths from
![]() $w_F$
to
$w_F$
to
![]() $Y^+$
in G[F] whose ends in
$Y^+$
in G[F] whose ends in
![]() $Y^+$
are distinct. For each
$Y^+$
are distinct. For each
![]() $F \in \mathcal {F}$
, let
$F \in \mathcal {F}$
, let
![]() $Z_F$
be the set consisting of the first vertices of Z on each of these three paths. By coherence, we may assume
$Z_F$
be the set consisting of the first vertices of Z on each of these three paths. By coherence, we may assume
![]() $Z_F$
is the same for all
$Z_F$
is the same for all
![]() $F \in \mathcal {F}$
. Thus, G contains a subdivision of
$F \in \mathcal {F}$
. Thus, G contains a subdivision of
![]() $K_{3, 2g+3}$
. However, this is impossible, since
$K_{3, 2g+3}$
. However, this is impossible, since
![]() $K_{3, 2g+3}$
does not embed in
$K_{3, 2g+3}$
does not embed in
![]() $\Sigma$
.
$\Sigma$
.
It follows that
![]() $c_y, c_f \leqslant c_{3.1}(j, c_{3.4}(j, 2g+3))$
for all
$c_y, c_f \leqslant c_{3.1}(j, c_{3.4}(j, 2g+3))$
for all
![]() $y \in V(G)$
and
$y \in V(G)$
and
![]() $f \in E(G)$
. The proof is complete by summing over all possible
$f \in E(G)$
. The proof is complete by summing over all possible
![]() $y \in V(G)$
if
$y \in V(G)$
if
![]() $|X'|=1$
, and summing over all possible
$|X'|=1$
, and summing over all possible
![]() $f \in E(G)$
if
$f \in E(G)$
if
![]() $|X'|=2$
.
$|X'|=2$
.
The final ingredient we need is the following ‘flap reduction’ lemma.
Lemma 5.8 Let H be a connected graph with flap-number
![]() $k \geqslant 1$
. Let A be a subgraph of H that is maximal (under the subgraph relation) subject to the following conditions:
$k \geqslant 1$
. Let A be a subgraph of H that is maximal (under the subgraph relation) subject to the following conditions:
-
A has no isolated vertices, and
-
there exists a flap (A,B) of H and a set
 $\mathcal F$
of k independent flaps in H with
$\mathcal F$
of k independent flaps in H with
 $(A,B) \in \mathcal F$
.
$(A,B) \in \mathcal F$
.
Then,
![]() $B^+$
has flap-number
$B^+$
has flap-number
![]() $k-1$
. Moreover, A is connected and
$k-1$
. Moreover, A is connected and
![]() $A^+$
does not contain independent flaps (C, D) and (C’,D’) such that
$A^+$
does not contain independent flaps (C, D) and (C’,D’) such that
![]() $V(A \cap B) \subseteq V(D \cap D')$
.
$V(A \cap B) \subseteq V(D \cap D')$
.
Proof. We first show that
![]() $B^+$
has flap-number at least
$B^+$
has flap-number at least
![]() $k-1$
. To see this, let
$k-1$
. To see this, let
![]() $\mathcal F$
be a set of k independent flaps in H such that
$\mathcal F$
be a set of k independent flaps in H such that
![]() $(A,B) \in \mathcal F$
. Every flap
$(A,B) \in \mathcal F$
. Every flap
![]() $(C,D) \in \mathcal F \setminus \{(A,B)\}$
corresponds to a flap (C, D’) in
$(C,D) \in \mathcal F \setminus \{(A,B)\}$
corresponds to a flap (C, D’) in
![]() $B^+$
, unless
$B^+$
, unless
![]() $k=2$
, H is planar, and
$k=2$
, H is planar, and
![]() $\mathcal F=\{(A,B), (B,A)\}$
. In either case,
$\mathcal F=\{(A,B), (B,A)\}$
. In either case,
![]() $B^+$
has flap-number at least
$B^+$
has flap-number at least
![]() $k-1$
.
$k-1$
.
We now prove the upper bound. Towards a contradiction, let
![]() $(C_1, D_1), \dots , (C_k, D_k)$
be independent flaps in
$(C_1, D_1), \dots , (C_k, D_k)$
be independent flaps in
![]() $B^+$
. Let
$B^+$
. Let
![]() $X\;:\!=\;V(A \cap B)$
. If
$X\;:\!=\;V(A \cap B)$
. If
![]() $X \subseteq V(S)$
for a subgraph S of
$X \subseteq V(S)$
for a subgraph S of
![]() $B^+$
, we let
$B^+$
, we let
![]() $S +_X A$
be the subgraph of H obtained by gluing A to S along X, and deleting the edge between the ends of X in
$S +_X A$
be the subgraph of H obtained by gluing A to S along X, and deleting the edge between the ends of X in
![]() $B^+$
if the edge does not exist in H. If X is contained in
$B^+$
if the edge does not exist in H. If X is contained in
![]() $V(D_\ell)$
for every
$V(D_\ell)$
for every
![]() $\ell \in [k]$
, then
$\ell \in [k]$
, then
![]() $(A,B),(C_1, D_1 +_X A ), \dots , (C_k, D_k +_X A)$
are
$(A,B),(C_1, D_1 +_X A ), \dots , (C_k, D_k +_X A)$
are
![]() $k+1$
pairwise independent flaps in H. Thus, X is not contained in
$k+1$
pairwise independent flaps in H. Thus, X is not contained in
![]() $V(D_\ell)$
for some
$V(D_\ell)$
for some
![]() $\ell \in [k]$
. By relabelling, we may assume
$\ell \in [k]$
. By relabelling, we may assume
![]() $\ell=1$
. Since
$\ell=1$
. Since
![]() $(V(C_1) \setminus V(D_1)) \cap X \neq \emptyset$
and
$(V(C_1) \setminus V(D_1)) \cap X \neq \emptyset$
and
![]() $(V(C_1) \setminus V(D_1)) \cap (V(C_i) \setminus V(D_i))=\emptyset$
for all
$(V(C_1) \setminus V(D_1)) \cap (V(C_i) \setminus V(D_i))=\emptyset$
for all
![]() $i > 1$
, we have
$i > 1$
, we have
![]() $X \subseteq V(D_i)$
for all
$X \subseteq V(D_i)$
for all
![]() $i>1$
. Then,
$i>1$
. Then,
![]() $(C_1 +_X A, D_1), (C_2, D_2 +_X A), \dots (C_k, D_k +_X A)$
are k independent flaps in H. Since A is a proper subgraph of
$(C_1 +_X A, D_1), (C_2, D_2 +_X A), \dots (C_k, D_k +_X A)$
are k independent flaps in H. Since A is a proper subgraph of
![]() $C_1 +_X A$
, this contradicts the maximality of A.
$C_1 +_X A$
, this contradicts the maximality of A.
Finally, we show that the last sentence of the lemma holds. Suppose that A is disconnected and
![]() $A_1, \dots, A_c$
are the connected components of A. Since H is connected,
$A_1, \dots, A_c$
are the connected components of A. Since H is connected,
![]() $A_i$
contains a vertex of
$A_i$
contains a vertex of
![]() $V(A \cap B)$
for all
$V(A \cap B)$
for all
![]() $i \in [c]$
. Thus,
$i \in [c]$
. Thus,
![]() $c=2$
and
$c=2$
and
![]() $A_1$
and
$A_1$
and
![]() $A_2$
each contain exactly one vertex of
$A_2$
each contain exactly one vertex of
![]() $V(A \cap B)$
. Since neither
$V(A \cap B)$
. Since neither
![]() $A_1$
nor
$A_1$
nor
![]() $A_2$
is an isolated vertex, there exist
$A_2$
is an isolated vertex, there exist
![]() $B_1$
and
$B_1$
and
![]() $B_2$
such that
$B_2$
such that
![]() $(A_1,B_1)$
and
$(A_1,B_1)$
and
![]() $(A_2,B_2)$
are independent flaps of H. Thus,
$(A_2,B_2)$
are independent flaps of H. Thus,
![]() $\mathcal F \setminus \{(A,B)\} \cup \{(A_1, B_1), (A_2, B_2)\}$
is a set of
$\mathcal F \setminus \{(A,B)\} \cup \{(A_1, B_1), (A_2, B_2)\}$
is a set of
![]() $k+1$
independent flaps of H, which contradicts that H has flap-number k. Similarly,
$k+1$
independent flaps of H, which contradicts that H has flap-number k. Similarly,
![]() $A^+$
does not contain independent flaps (C, D) and (C’,D’) such that
$A^+$
does not contain independent flaps (C, D) and (C’,D’) such that
![]() $V(A \cap B) \subseteq V(D \cap D')$
.
$V(A \cap B) \subseteq V(D \cap D')$
.
We call a subgraph A of H a half-flap if (A,B) is a flap of H for some B. Two half-flaps A and C are independent if there exist B and D such that (A,B) and (C,D) are independent flaps. We say that A is a full-half-flap if A satisfies the conditions of Lemma 5.8.
We stress that the condition that A is maximal is essential in the definition of a full-half-flap. To see this, let H be the
![]() $2 \times k$
grid, for k large. Note that even though H has many 2-separations, the flap-number of H is 2. Moreover, the only full-half-flaps of H are
$2 \times k$
grid, for k large. Note that even though H has many 2-separations, the flap-number of H is 2. Moreover, the only full-half-flaps of H are
![]() $H-y$
, where y is one of the four degree-2 vertices of H. In this case,
$H-y$
, where y is one of the four degree-2 vertices of H. In this case,
![]() $B^+ \cong K_3$
, which has flap-number 1. Reducing on any other flap of H yields a graph that still has flap-number 2.
$B^+ \cong K_3$
, which has flap-number 1. Reducing on any other flap of H yields a graph that still has flap-number 2.
We now complete the proof of the upper bound in Theorem 1.2.
Theorem 5.9 Let
![]() $c_{5.9}(h,g)\;:\!=\;6(g+1)c_{4.1}(h,g)c_{3.2}(h,g)c_{5.1}(h, g+2)^h.$
Then for every graph H with h vertices and every surface
$c_{5.9}(h,g)\;:\!=\;6(g+1)c_{4.1}(h,g)c_{3.2}(h,g)c_{5.1}(h, g+2)^h.$
Then for every graph H with h vertices and every surface
![]() $\Sigma$
of Euler genus g in which H embeds,
$\Sigma$
of Euler genus g in which H embeds,
Proof. Let
![]() $k\;:\!=\;f(H)$
. Since
$k\;:\!=\;f(H)$
. Since
![]() $c_{5.9}(h_1,g)\cdot c_{5.9}(h_2,g) \leqslant c_{5.9}(h,g)$
whenever
$c_{5.9}(h_1,g)\cdot c_{5.9}(h_2,g) \leqslant c_{5.9}(h,g)$
whenever
![]() $h_1+h_2=h$
, we may assume that H is connected by induction on
$h_1+h_2=h$
, we may assume that H is connected by induction on
![]() $|V(H)|$
. A reduction sequence of H is a sequence of graphs
$|V(H)|$
. A reduction sequence of H is a sequence of graphs
![]() $H_k, \dots, H_j$
for some
$H_k, \dots, H_j$
for some
![]() $j \leqslant k$
, where
$j \leqslant k$
, where
![]() $H_k\;:\!=\;H$
, and for all
$H_k\;:\!=\;H$
, and for all
![]() $i > j$
,
$i > j$
,
![]() $H_{i-1}\;:\!=\;B_i^+$
, where
$H_{i-1}\;:\!=\;B_i^+$
, where
![]() $(A_i, B_i)$
is a flap in
$(A_i, B_i)$
is a flap in
![]() $H_i$
satisfying the conditions of Lemma 5.8. By Lemma 5.8, every reduction sequence satisfies the following properties.
$H_i$
satisfying the conditions of Lemma 5.8. By Lemma 5.8, every reduction sequence satisfies the following properties.
Claim 5.10 Let
![]() $H_k, \dots, H_j$
be a reduction sequence of H, with corresponding flaps
$H_k, \dots, H_j$
be a reduction sequence of H, with corresponding flaps
![]() $(A_\ell, B_\ell)$
in
$(A_\ell, B_\ell)$
in
![]() $H_\ell$
. Then for all
$H_\ell$
. Then for all
![]() $\ell \in \{k, \dots, j+1\}$
,
$\ell \in \{k, \dots, j+1\}$
,
![]() $A_\ell$
is connected and
$A_\ell$
is connected and
![]() $A_\ell^+$
does not contain independent flaps (C, D) and (C’,D’) such that
$A_\ell^+$
does not contain independent flaps (C, D) and (C’,D’) such that
![]() $V(A_\ell) \cap V(B_\ell) \subseteq V(D) \cap V(D')$
. Moreover, for all
$V(A_\ell) \cap V(B_\ell) \subseteq V(D) \cap V(D')$
. Moreover, for all
![]() $\ell \in \{k, \dots, j\}$
,
$\ell \in \{k, \dots, j\}$
,
![]() $H_\ell$
has flap-number
$H_\ell$
has flap-number
![]() $\ell$
.
$\ell$
.
We now establish further properties of reduction sequences. Let
![]() $H_k, \dots, H_j$
be a reduction sequence of H, with corresponding flaps
$H_k, \dots, H_j$
be a reduction sequence of H, with corresponding flaps
![]() $(A_\ell, B_\ell)$
in
$(A_\ell, B_\ell)$
in
![]() $H_\ell$
. If
$H_\ell$
. If
![]() $V(A_\ell) \cap V(B_\ell)\;:\!=\;\{u,v\}$
and
$V(A_\ell) \cap V(B_\ell)\;:\!=\;\{u,v\}$
and
![]() $uv \notin E(H_\ell)$
, we declare uv to be a fake edge of
$uv \notin E(H_\ell)$
, we declare uv to be a fake edge of
![]() $H_{\ell-1}$
. An edge of
$H_{\ell-1}$
. An edge of
![]() $H_\ell$
is a fake edge if it is a fake edge of
$H_\ell$
is a fake edge if it is a fake edge of
![]() $H_{\ell'}$
for some
$H_{\ell'}$
for some
![]() $\ell' \geqslant \ell$
, and it is a true edge if it is not a fake edge.
$\ell' \geqslant \ell$
, and it is a true edge if it is not a fake edge.
Claim 5.11 Let
![]() $H_k, \dots, H_j$
be a reduction sequence of H, with corresponding flaps
$H_k, \dots, H_j$
be a reduction sequence of H, with corresponding flaps
![]() $(A_\ell, B_\ell)$
in
$(A_\ell, B_\ell)$
in
![]() $H_\ell$
. Then for all
$H_\ell$
. Then for all
![]() $\ell \in \{k, \dots, j\}$
, if (C,D) is a flap in
$\ell \in \{k, \dots, j\}$
, if (C,D) is a flap in
![]() $H_\ell$
such that
$H_\ell$
such that
![]() $C^+$
is 3-connected, then every edge of C with neither end in
$C^+$
is 3-connected, then every edge of C with neither end in
![]() $V(C \cap D)$
is true.
$V(C \cap D)$
is true.
Proof. Let (C,D) be a flap of
![]() $H_\ell$
that is a counterexample with
$H_\ell$
that is a counterexample with
![]() $|E(C)|-|V(D)|$
maximum. Let
$|E(C)|-|V(D)|$
maximum. Let
![]() $X\;:\!=\;V(C \cap D)$
. Note that, by the maximality of
$X\;:\!=\;V(C \cap D)$
. Note that, by the maximality of
![]() $|E(C)|-|V(D)|$
, if
$|E(C)|-|V(D)|$
, if
![]() $H_\ell$
contains an edge f whose ends are X, then
$H_\ell$
contains an edge f whose ends are X, then
![]() $f \in E(C)$
. We claim that each
$f \in E(C)$
. We claim that each
![]() $x \in X$
is incident to an edge of D. If not, then x must be an isolated vertex of D. But now,
$x \in X$
is incident to an edge of D. If not, then x must be an isolated vertex of D. But now,
![]() $(C, D-x)$
contradicts the maximality of
$(C, D-x)$
contradicts the maximality of
![]() $|E(C)|-|V(D)|$
. For all
$|E(C)|-|V(D)|$
. For all
![]() $i \in \{k, \dots, \ell+1\}$
set
$i \in \{k, \dots, \ell+1\}$
set
![]() $X_i\;:\!=\;V(A_i \cap B_i)$
. Let
$X_i\;:\!=\;V(A_i \cap B_i)$
. Let
![]() $\mathcal I$
be the set of indices
$\mathcal I$
be the set of indices
![]() $i \in \{k, \dots, \ell+1\}$
such that
$i \in \{k, \dots, \ell+1\}$
such that
![]() $X_i$
is the set of ends of a fake edge of
$X_i$
is the set of ends of a fake edge of
![]() $C^-$
. Let s be the smallest index in
$C^-$
. Let s be the smallest index in
![]() $\mathcal I$
, and let e be the corresponding fake edge. Since
$\mathcal I$
, and let e be the corresponding fake edge. Since
![]() $H_k, \dots, H_j$
is a reduction sequence, there is a collection
$H_k, \dots, H_j$
is a reduction sequence, there is a collection
![]() $\mathcal F_s$
of s independent flaps of
$\mathcal F_s$
of s independent flaps of
![]() $H_s$
such that
$H_s$
such that
![]() $(A_s, B_s) \in \mathcal F_s$
and
$(A_s, B_s) \in \mathcal F_s$
and
![]() $\sum_{(A',B') \in \mathcal F_s}|V(A')| +|E(A')|$
is minimum. Let (A,B) be an arbitrary flap in
$\sum_{(A',B') \in \mathcal F_s}|V(A')| +|E(A')|$
is minimum. Let (A,B) be an arbitrary flap in
![]() $\mathcal F_s \setminus \{(A_s, B_s)\}$
.
$\mathcal F_s \setminus \{(A_s, B_s)\}$
.
There are several cases to consider depending on how A and C interact.
Suppose that V(A) is a proper subset of V(C). Since
![]() $C^+$
is 3-connected and
$C^+$
is 3-connected and
![]() $V(C) \setminus V(A) \neq \emptyset$
, for some
$V(C) \setminus V(A) \neq \emptyset$
, for some
![]() $Y \in \{X_s, X\}$
, one vertex y of Y is in
$Y \in \{X_s, X\}$
, one vertex y of Y is in
![]() $V(A) \setminus V(B)$
and the other vertex of Y is in
$V(A) \setminus V(B)$
and the other vertex of Y is in
![]() $V(B) \setminus V(A)$
. Observe that
$V(B) \setminus V(A)$
. Observe that
![]() $V(A_s) \subseteq V(B)$
because
$V(A_s) \subseteq V(B)$
because
![]() $(A_s, B_s)$
and (A,B) are independent flaps of
$(A_s, B_s)$
and (A,B) are independent flaps of
![]() $H_s$
. In particular,
$H_s$
. In particular,
![]() $X_s \subseteq V(B)$
. By the minimality of
$X_s \subseteq V(B)$
. By the minimality of
![]() $\sum_{(A',B') \in \mathcal F_s}|V(A')| +|E(A')|$
, if
$\sum_{(A',B') \in \mathcal F_s}|V(A')| +|E(A')|$
, if
![]() $H_s$
contains an edge f whose ends are X, then
$H_s$
contains an edge f whose ends are X, then
![]() $f \in E(B)$
. Since V(A) is a proper subset of V(C) and each
$f \in E(B)$
. Since V(A) is a proper subset of V(C) and each
![]() $x \in X$
is incident to an edge of D, this implies
$x \in X$
is incident to an edge of D, this implies
![]() $X \subseteq V(B)$
. Therefore, for either choice of Y, we have
$X \subseteq V(B)$
. Therefore, for either choice of Y, we have
![]() $y \in V(B)$
. Thus,
$y \in V(B)$
. Thus,
![]() $y \in V(A \cap B)$
, which contradicts that
$y \in V(A \cap B)$
, which contradicts that
![]() $y \in V(A) \setminus V(B)$
.
$y \in V(A) \setminus V(B)$
.
Suppose that
![]() $V(A)=V(C)$
and
$V(A)=V(C)$
and
![]() $|X_s \cup X| \geqslant 3$
. Observe that
$|X_s \cup X| \geqslant 3$
. Observe that
![]() $X_s \cup X \subseteq V(A)$
. Since
$X_s \cup X \subseteq V(A)$
. Since
![]() $V(A_s) \subseteq V(B)$
,
$V(A_s) \subseteq V(B)$
,
![]() $X_s \subseteq V(B)$
. Moreover, since
$X_s \subseteq V(B)$
. Moreover, since
![]() $V(D) \subseteq V(B)$
,
$V(D) \subseteq V(B)$
,
![]() $X \subseteq V(B)$
. Therefore,
$X \subseteq V(B)$
. Therefore,
![]() $X_s \cup X \subseteq V(A \cap B)$
. Since
$X_s \cup X \subseteq V(A \cap B)$
. Since
![]() $|X_s \cup X| \geqslant 3$
, this implies that (A,B) is a
$|X_s \cup X| \geqslant 3$
, this implies that (A,B) is a
![]() $(\geqslant 3)$
-separation of
$(\geqslant 3)$
-separation of
![]() $H_s$
, which contradicts that (A,B) is a flap.
$H_s$
, which contradicts that (A,B) is a flap.
Suppose that
![]() $A \cap C=S$
, where S is a stable set and S contains a vertex
$A \cap C=S$
, where S is a stable set and S contains a vertex
![]() $x \notin X$
. If
$x \notin X$
. If
![]() $x \notin X_s$
, then x is an isolated vertex of A. If
$x \notin X_s$
, then x is an isolated vertex of A. If
![]() $x \in X_s$
, then since (A,B) and
$x \in X_s$
, then since (A,B) and
![]() $(A_s, B_s)$
are independent flaps,
$(A_s, B_s)$
are independent flaps,
![]() $V(A \cap A_s) \setminus X_s = \emptyset$
. Thus, x is an isolated vertex of A in this case as well. But now, replacing (A,B) by
$V(A \cap A_s) \setminus X_s = \emptyset$
. Thus, x is an isolated vertex of A in this case as well. But now, replacing (A,B) by
![]() $(A-x, B)$
contradicts the minimality of
$(A-x, B)$
contradicts the minimality of
![]() $\sum_{(A',B') \in \mathcal F_s}|V(A')| + |E(A')|$
.
$\sum_{(A',B') \in \mathcal F_s}|V(A')| + |E(A')|$
.
Suppose that
![]() $A \cap C$
consists of just a single edge xy. Since
$A \cap C$
consists of just a single edge xy. Since
![]() $C^+$
is 3-connected,
$C^+$
is 3-connected,
![]() $\deg_{C^+}(x) \geqslant 3$
and
$\deg_{C^+}(x) \geqslant 3$
and
![]() $\deg_{C^+}(y) \geqslant 3$
. For
$\deg_{C^+}(y) \geqslant 3$
. For
![]() $ z \in \{x,y\}$
, let d(z) be the number of
$ z \in \{x,y\}$
, let d(z) be the number of
![]() $Y \in \{X_s, X\} \setminus \{\{x,y\}\}$
such that
$Y \in \{X_s, X\} \setminus \{\{x,y\}\}$
such that
![]() $z \in Y$
. Observe that
$z \in Y$
. Observe that
![]() $\deg_{C^+}(z) \leqslant \deg_{A \cap C}(z) + \deg_{B \cap C} (z)+d(z)$
for both
$\deg_{C^+}(z) \leqslant \deg_{A \cap C}(z) + \deg_{B \cap C} (z)+d(z)$
for both
![]() $z \in \{x,y\}$
. Since
$z \in \{x,y\}$
. Since
![]() $\deg_{A \cap C}(z)=1$
for both
$\deg_{A \cap C}(z)=1$
for both
![]() $z \in \{x,y\}$
, this yields
$z \in \{x,y\}$
, this yields
![]() $\deg_{B \cap C}(z) \geqslant 2-d(z)$
for both
$\deg_{B \cap C}(z) \geqslant 2-d(z)$
for both
![]() $z \in \{x,y\}$
. If
$z \in \{x,y\}$
. If
![]() $\{x,y\} \subseteq X \cup X_s$
, then
$\{x,y\} \subseteq X \cup X_s$
, then
![]() $d(x) \leqslant 1 $
and
$d(x) \leqslant 1 $
and
![]() $d(y) \leqslant 1$
. Therefore,
$d(y) \leqslant 1$
. Therefore,
![]() $\deg_{B \cap C}(x) \geqslant 1$
and
$\deg_{B \cap C}(x) \geqslant 1$
and
![]() $\deg_{B \cap C}(y) \geqslant 1$
, which implies
$\deg_{B \cap C}(y) \geqslant 1$
, which implies
![]() $\{x,y\} \subseteq V(A \cap B)$
. But now,
$\{x,y\} \subseteq V(A \cap B)$
. But now,
![]() $(A -xy, B \cup \{xy\})$
is a
$(A -xy, B \cup \{xy\})$
is a
![]() $(\leqslant 2)$
-separation, which contradicts the minimality of
$(\leqslant 2)$
-separation, which contradicts the minimality of
![]() $\sum_{(A',B') \in \mathcal F_s}|V(A')| + |E(A')|$
. By symmetry, we may assume
$\sum_{(A',B') \in \mathcal F_s}|V(A')| + |E(A')|$
. By symmetry, we may assume
![]() $y \notin X_s \cup X$
. Thus,
$y \notin X_s \cup X$
. Thus,
![]() $d(y)=0$
, which gives
$d(y)=0$
, which gives
![]() $\deg_{B \cap C} (y) \geqslant 2$
. In particular,
$\deg_{B \cap C} (y) \geqslant 2$
. In particular,
![]() $y \in V(A \cap B)$
. Moreover, since
$y \in V(A \cap B)$
. Moreover, since
![]() $y \notin X_s \cup X$
, we have
$y \notin X_s \cup X$
, we have
![]() $y\in V(C) \setminus V(D)$
, and thus
$y\in V(C) \setminus V(D)$
, and thus
![]() $\deg_A(y)=\deg_{A \cap C}(y)=1$
. Observe that
$\deg_A(y)=\deg_{A \cap C}(y)=1$
. Observe that
![]() $|V(A - y) \cap V(B \cup \{xy\})| \leqslant 2$
because
$|V(A - y) \cap V(B \cup \{xy\})| \leqslant 2$
because
![]() $V(A - y) \cap V(B \cup \{xy\}) \subseteq (V(A \cap B) \setminus \{y\}) \cup \{x\}$
. Therefore,
$V(A - y) \cap V(B \cup \{xy\}) \subseteq (V(A \cap B) \setminus \{y\}) \cup \{x\}$
. Therefore,
![]() $(A -y, B \cup \{xy\})$
is a
$(A -y, B \cup \{xy\})$
is a
![]() $(\leqslant 2)$
-separation. But now
$(\leqslant 2)$
-separation. But now
![]() $A-y$
is a half-flap contained in A, which contradicts the minimality of
$A-y$
is a half-flap contained in A, which contradicts the minimality of
![]() $\sum_{(A',B') \in \mathcal F_s}|V(A')| + |E(A')|$
.
$\sum_{(A',B') \in \mathcal F_s}|V(A')| + |E(A')|$
.
Suppose that V(C) is a proper subset of V(A). Clearly,
![]() $X_s \subseteq V(A)$
. Also,
$X_s \subseteq V(A)$
. Also,
![]() $X_s \subseteq V(B)$
since (A,B) and
$X_s \subseteq V(B)$
since (A,B) and
![]() $(A_s, B_s)$
are independent flaps. Therefore,
$(A_s, B_s)$
are independent flaps. Therefore,
![]() $V(A \cap B)=X_s$
, since
$V(A \cap B)=X_s$
, since
![]() $|X_s|=2$
. Moreover,
$|X_s|=2$
. Moreover,
![]() $A \cap D$
contains at least one vertex not in X, since V(C) is a proper subset of V(A). If
$A \cap D$
contains at least one vertex not in X, since V(C) is a proper subset of V(A). If
![]() $A \cap D$
meets
$A \cap D$
meets
![]() $B \cap D$
at a vertex
$B \cap D$
at a vertex
![]() $x \notin X$
, then
$x \notin X$
, then
![]() $x \notin X_s$
and
$x \notin X_s$
and
![]() $x \in V(A \cap B)$
, which contradicts that
$x \in V(A \cap B)$
, which contradicts that
![]() $V(A \cap B)=X_s$
. Thus,
$V(A \cap B)=X_s$
. Thus,
![]() $V(A \cap D) \cap V(B \cap D) \subseteq X$
. It follows that
$V(A \cap D) \cap V(B \cap D) \subseteq X$
. It follows that
![]() $A \cap D$
is a half-flap, since
$A \cap D$
is a half-flap, since
![]() $|X| \leqslant 2$
. However, this contradicts the minimality of
$|X| \leqslant 2$
. However, this contradicts the minimality of
![]() $\sum_{(A',B') \in \mathcal F_s}|V(A')| +|E(A')|$
since
$\sum_{(A',B') \in \mathcal F_s}|V(A')| +|E(A')|$
since
![]() $|V(A \cap D)| < |V(A)|$
.
$|V(A \cap D)| < |V(A)|$
.
Suppose that
![]() $3 \leqslant |V(A \cap C)| < |V(C)|$
and
$3 \leqslant |V(A \cap C)| < |V(C)|$
and
![]() $V(A) \setminus V(C) \neq \emptyset$
. Since
$V(A) \setminus V(C) \neq \emptyset$
. Since
![]() $C^+$
is 3-connected, for some
$C^+$
is 3-connected, for some
![]() $Y \in \{X_s, X\}$
, one vertex y of Y is in
$Y \in \{X_s, X\}$
, one vertex y of Y is in
![]() $V(A) \setminus V(B)$
and the other vertex of Y is in
$V(A) \setminus V(B)$
and the other vertex of Y is in
![]() $V(B) \setminus V(A)$
. Since (A,B) and
$V(B) \setminus V(A)$
. Since (A,B) and
![]() $(A_s, B_s)$
are independent flaps, we have
$(A_s, B_s)$
are independent flaps, we have
![]() $A_s \subseteq B$
. Thus,
$A_s \subseteq B$
. Thus,
![]() $X_s \subseteq V(B)$
, and so
$X_s \subseteq V(B)$
, and so
![]() $Y=X$
. Let
$Y=X$
. Let
![]() $B^*$
be obtained from B by replacing
$B^*$
be obtained from B by replacing
![]() $A_s$
by an edge whose ends are
$A_s$
by an edge whose ends are
![]() $X_s$
, and adding the edge with ends X. Since
$X_s$
, and adding the edge with ends X. Since
![]() $C^+$
is 3-connected,
$C^+$
is 3-connected,
![]() $(C^+ \cap A, C^+ \cap B^*)$
is a
$(C^+ \cap A, C^+ \cap B^*)$
is a
![]() $(\geqslant 3)$
-separation of
$(\geqslant 3)$
-separation of
![]() $C^+$
. It follows that
$C^+$
. It follows that
![]() $A \cap C$
meets
$A \cap C$
meets
![]() $B \cap C$
in at least two vertices of
$B \cap C$
in at least two vertices of
![]() $V(C) \setminus X$
and thus exactly two since
$V(C) \setminus X$
and thus exactly two since
![]() $|V(A \cap B)| \leqslant 2$
. In particular,
$|V(A \cap B)| \leqslant 2$
. In particular,
![]() $V(A \cap B) \subseteq V(C) \setminus X$
, and hence
$V(A \cap B) \subseteq V(C) \setminus X$
, and hence
![]() $V(A \cap D) \cap V(B \cap D) = \emptyset$
. It follows that
$V(A \cap D) \cap V(B \cap D) = \emptyset$
. It follows that
![]() $A \cap D$
is a half-flap. However, this contradicts the minimality of
$A \cap D$
is a half-flap. However, this contradicts the minimality of
![]() $\sum_{(A',B') \in \mathcal F_s}|V(A')| +|E(A')|$
since
$\sum_{(A',B') \in \mathcal F_s}|V(A')| +|E(A')|$
since
![]() $|V(A \cap D)| < |V(A)|$
.
$|V(A \cap D)| < |V(A)|$
.
By the previous cases, there are only two cases left to consider for (A, B), namely (1)
![]() $V(A \cap C)\subseteq X$
and
$V(A \cap C)\subseteq X$
and
![]() $A \cap C$
has no edges, or (2)
$A \cap C$
has no edges, or (2)
![]() $V(A)=V(C)$
and
$V(A)=V(C)$
and
![]() $|X_s \cup X| \leqslant 2$
. Since (A,B) is an arbitrary flap of
$|X_s \cup X| \leqslant 2$
. Since (A,B) is an arbitrary flap of
![]() $\mathcal F_s \setminus \{(A_s, B_s)\}$
, we may assume that either
$\mathcal F_s \setminus \{(A_s, B_s)\}$
, we may assume that either
![]() $V(A' \cap C)\subseteq X$
and
$V(A' \cap C)\subseteq X$
and
![]() $A' \cap C$
has no edges for all
$A' \cap C$
has no edges for all
![]() $(A',B') \in \mathcal F_s \setminus \{(A_s, B_s)\}$
; or that
$(A',B') \in \mathcal F_s \setminus \{(A_s, B_s)\}$
; or that
![]() $V(A)=V(C)$
and
$V(A)=V(C)$
and
![]() $|X_s \cup X| \leqslant 2$
.
$|X_s \cup X| \leqslant 2$
.
Suppose that
![]() $V(A' \cap C)\subseteq X$
and
$V(A' \cap C)\subseteq X$
and
![]() $A' \cap C$
has no edges for all
$A' \cap C$
has no edges for all
![]() $(A',B') \in \mathcal F_s \setminus \{(A_s, B_s)\}$
. By replacing
$(A',B') \in \mathcal F_s \setminus \{(A_s, B_s)\}$
. By replacing
![]() $(A_s, B_s)$
by
$(A_s, B_s)$
by
![]() $(A_s +_{X_s} C, B_s -(V(C) \setminus X))$
in
$(A_s +_{X_s} C, B_s -(V(C) \setminus X))$
in
![]() $\mathcal F_s$
, we contradict that
$\mathcal F_s$
, we contradict that
![]() $A_s$
is a full-half-flap.
$A_s$
is a full-half-flap.
The last case is that
![]() $V(A)=V(C)$
and
$V(A)=V(C)$
and
![]() $|X_s \cup X| \leqslant 2$
. Since
$|X_s \cup X| \leqslant 2$
. Since
![]() $X_s$
is the set of ends of a fake edge of
$X_s$
is the set of ends of a fake edge of
![]() $C^-$
; this implies that
$C^-$
; this implies that
![]() $X_s \neq X$
. Thus, we must have
$X_s \neq X$
. Thus, we must have
![]() $|X|=1$
and
$|X|=1$
and
![]() $X \subseteq X_s$
. Let t be the smallest index in
$X \subseteq X_s$
. Let t be the smallest index in
![]() $\mathcal I$
larger than s, and let f be the corresponding fake edge. Note that t exists since
$\mathcal I$
larger than s, and let f be the corresponding fake edge. Note that t exists since
![]() $C^-$
contains a fake edge with neither end in X. Let
$C^-$
contains a fake edge with neither end in X. Let
![]() $\mathcal F_t$
be a collection of t independent flaps of
$\mathcal F_t$
be a collection of t independent flaps of
![]() $H_t$
such that
$H_t$
such that
![]() $(A_t, B_t) \in \mathcal F_t$
and
$(A_t, B_t) \in \mathcal F_t$
and
![]() $\sum_{(A',B') \in \mathcal F_t}|V(A')|+|E(A')|$
is minimum. Let
$\sum_{(A',B') \in \mathcal F_t}|V(A')|+|E(A')|$
is minimum. Let
![]() $(A^*,B^*)$
be an arbitrary flap in
$(A^*,B^*)$
be an arbitrary flap in
![]() $\mathcal F_t \setminus \{(A_t, B_t)\}$
. Let
$\mathcal F_t \setminus \{(A_t, B_t)\}$
. Let
![]() $A_s^* \subseteq H_t$
be obtained from
$A_s^* \subseteq H_t$
be obtained from
![]() $A_s$
by reversing all the flap reductions for all
$A_s$
by reversing all the flap reductions for all
![]() $j \in [s,t]$
. The reTheorem 1.2der of the proof is essentially the same as the previous cases with
$j \in [s,t]$
. The reTheorem 1.2der of the proof is essentially the same as the previous cases with
![]() $(A^*,B^*)$
taking the role of (A,B) and
$(A^*,B^*)$
taking the role of (A,B) and
![]() $\{X_s, X_t\}$
taking the role of
$\{X_s, X_t\}$
taking the role of
![]() $\{X_s, X\}$
. For completeness, we include all the details.
$\{X_s, X\}$
. For completeness, we include all the details.
Suppose that
![]() $V(A^*)$
is a proper subset of V(C). Since C is 3-connected, for some
$V(A^*)$
is a proper subset of V(C). Since C is 3-connected, for some
![]() $Y \in \{X_s, X_t\}$
,
$Y \in \{X_s, X_t\}$
,
![]() $V(A^*) \setminus V(B^*)$
contains one vertex y of Y and
$V(A^*) \setminus V(B^*)$
contains one vertex y of Y and
![]() $V(B^*) \setminus V(A^*)$
contains the other vertex of Y. By Lemma 5.8,
$V(B^*) \setminus V(A^*)$
contains the other vertex of Y. By Lemma 5.8,
![]() $A_s^*$
and
$A_s^*$
and
![]() $A_t$
are both connected. Since
$A_t$
are both connected. Since
![]() $V(A^*) \subseteq V(C)$
, this implies
$V(A^*) \subseteq V(C)$
, this implies
![]() $X_s \cup X_t \subseteq V(B^*)$
. Thus, for either choice of Y, we have
$X_s \cup X_t \subseteq V(B^*)$
. Thus, for either choice of Y, we have
![]() $y \in V(A^* \cap B^*)$
, which contradicts that
$y \in V(A^* \cap B^*)$
, which contradicts that
![]() $y \in V(A^*) \setminus V(B^*)$
.
$y \in V(A^*) \setminus V(B^*)$
.
Suppose that
![]() $V(A^*)=V(C)$
. Clearly,
$V(A^*)=V(C)$
. Clearly,
![]() $X_s \cup X_t \subseteq V(C)=V(A^*)$
. Since
$X_s \cup X_t \subseteq V(C)=V(A^*)$
. Since
![]() $A_s^*$
and
$A_s^*$
and
![]() $A_t$
are both connected by Lemma 5.8,
$A_t$
are both connected by Lemma 5.8,
![]() $X_s \cup X_t \subseteq V(B^*)$
. Therefore,
$X_s \cup X_t \subseteq V(B^*)$
. Therefore,
![]() $X_s \cup X_t \subseteq V(A^* \cap B^*)$
. Since
$X_s \cup X_t \subseteq V(A^* \cap B^*)$
. Since
![]() $|X_s \cup X_t| \geqslant 3$
, this implies that
$|X_s \cup X_t| \geqslant 3$
, this implies that
![]() $(A^*,B^*)$
is a
$(A^*,B^*)$
is a
![]() $(\geqslant 3)$
-separation of
$(\geqslant 3)$
-separation of
![]() $H_t$
, which contradicts that
$H_t$
, which contradicts that
![]() $(A^*,B^*)$
is a flap.
$(A^*,B^*)$
is a flap.
Suppose that
![]() $A^* \cap C=S$
, where S is a stable set and S contains a vertex
$A^* \cap C=S$
, where S is a stable set and S contains a vertex
![]() $x \notin X_s$
. If
$x \notin X_s$
. If
![]() $x \notin X_t$
, then x is an isolated vertex of A. If
$x \notin X_t$
, then x is an isolated vertex of A. If
![]() $x \in X_t$
, then since
$x \in X_t$
, then since
![]() $(A^*,B^*)$
and
$(A^*,B^*)$
and
![]() $(A_t, B_t)$
are independent flaps,
$(A_t, B_t)$
are independent flaps,
![]() $V(A^* \cap A_t) \setminus X_t = \emptyset$
. Thus, x is an isolated vertex of
$V(A^* \cap A_t) \setminus X_t = \emptyset$
. Thus, x is an isolated vertex of
![]() $A^*$
in this case as well. But now, replacing
$A^*$
in this case as well. But now, replacing
![]() $(A^*,B^*)$
by
$(A^*,B^*)$
by
![]() $(A^*-x, B^*)$
contradicts the minimality of
$(A^*-x, B^*)$
contradicts the minimality of
![]() $\sum_{(A',B') \in \mathcal F_t}|V(A')| + |E(A')|$
.
$\sum_{(A',B') \in \mathcal F_t}|V(A')| + |E(A')|$
.
Suppose that
![]() $A^* \cap C$
consists of just a single edge xy. Since C is 3-connected,
$A^* \cap C$
consists of just a single edge xy. Since C is 3-connected,
![]() $\deg_{C}(x) \geqslant 3$
and
$\deg_{C}(x) \geqslant 3$
and
![]() $\deg_{C}(y) \geqslant 3$
. For
$\deg_{C}(y) \geqslant 3$
. For
![]() $ z \in \{x,y\}$
, let d(z) be the number of
$ z \in \{x,y\}$
, let d(z) be the number of
![]() $Y \in \{X_s, X_t\} \setminus \{\{x,y\}\}$
such that
$Y \in \{X_s, X_t\} \setminus \{\{x,y\}\}$
such that
![]() $z \in Y$
. Observe that
$z \in Y$
. Observe that
![]() $\deg_{C}(z) \leqslant \deg_{A^* \cap C}(z) + \deg_{B^* \cap C} (z)+d(z)$
for both
$\deg_{C}(z) \leqslant \deg_{A^* \cap C}(z) + \deg_{B^* \cap C} (z)+d(z)$
for both
![]() $z \in \{x,y\}$
. Since
$z \in \{x,y\}$
. Since
![]() $\deg_{A^* \cap C}(z)=1$
for both
$\deg_{A^* \cap C}(z)=1$
for both
![]() $z \in \{x,y\}$
, this yields
$z \in \{x,y\}$
, this yields
![]() $\deg_{B^* \cap C}(z) \geqslant 2-d(z)$
for both
$\deg_{B^* \cap C}(z) \geqslant 2-d(z)$
for both
![]() $z \in \{x,y\}$
. If
$z \in \{x,y\}$
. If
![]() $\{x,y\} \subseteq X_s \cup X_t$
, then
$\{x,y\} \subseteq X_s \cup X_t$
, then
![]() $d(x) \leqslant 1 $
and
$d(x) \leqslant 1 $
and
![]() $d(y) \leqslant 1$
. Therefore,
$d(y) \leqslant 1$
. Therefore,
![]() $\deg_{B^* \cap C}(x) \geqslant 1$
and
$\deg_{B^* \cap C}(x) \geqslant 1$
and
![]() $\deg_{B^* \cap C}(y) \geqslant 1$
, which implies
$\deg_{B^* \cap C}(y) \geqslant 1$
, which implies
![]() $\{x,y\} \subseteq V(A^* \cap B^*)$
. But now,
$\{x,y\} \subseteq V(A^* \cap B^*)$
. But now,
![]() $(A^* -xy, B^* \cup \{xy\})$
is a
$(A^* -xy, B^* \cup \{xy\})$
is a
![]() $(\leqslant 2)$
-separation, which contradicts the minimality of
$(\leqslant 2)$
-separation, which contradicts the minimality of
![]() $\sum_{(A',B') \in \mathcal F_t}|V(A')| + |E(A')|$
. By symmetry, we may assume
$\sum_{(A',B') \in \mathcal F_t}|V(A')| + |E(A')|$
. By symmetry, we may assume
![]() $y \notin X_s \cup X_t$
. Thus,
$y \notin X_s \cup X_t$
. Thus,
![]() $d(y)=0$
, which gives
$d(y)=0$
, which gives
![]() $\deg_{B^* \cap C} (y) \geqslant 2$
. In particular,
$\deg_{B^* \cap C} (y) \geqslant 2$
. In particular,
![]() $y \in V(A^* \cap B^*)$
. Moreover, since
$y \in V(A^* \cap B^*)$
. Moreover, since
![]() $y \notin X_s \cup X_t$
, we have
$y \notin X_s \cup X_t$
, we have
![]() $y\in V(C) \setminus V(D)$
, and thus
$y\in V(C) \setminus V(D)$
, and thus
![]() $\deg_{A^*}(y)=\deg_{A^* \cap C}(y)=1$
. Observe that
$\deg_{A^*}(y)=\deg_{A^* \cap C}(y)=1$
. Observe that
![]() $|V(A^* - y) \cap V(B^* \cup \{xy\})| \leqslant 2$
because
$|V(A^* - y) \cap V(B^* \cup \{xy\})| \leqslant 2$
because
![]() $V(A^* - y) \cap V(B^* \cup \{xy\}) \subseteq (V(A^* \cap B^*) \setminus \{y\}) \cup \{x\}$
. Therefore,
$V(A^* - y) \cap V(B^* \cup \{xy\}) \subseteq (V(A^* \cap B^*) \setminus \{y\}) \cup \{x\}$
. Therefore,
![]() $(A^* -y, B^* \cup \{xy\})$
is a
$(A^* -y, B^* \cup \{xy\})$
is a
![]() $(\leqslant 2)$
-separation. But now
$(\leqslant 2)$
-separation. But now
![]() $A^*-y$
is a half-flap contained in
$A^*-y$
is a half-flap contained in
![]() $A^*$
, which contradicts the minimality of
$A^*$
, which contradicts the minimality of
![]() $\sum_{(A',B') \in \mathcal F_t}|V(A')| + |E(A')|$
.
$\sum_{(A',B') \in \mathcal F_t}|V(A')| + |E(A')|$
.
Suppose that V(C) is a proper subset of
![]() $V(A^*)$
. Clearly,
$V(A^*)$
. Clearly,
![]() $X_t \subseteq V(A^*)$
. Also,
$X_t \subseteq V(A^*)$
. Also,
![]() $X_t \subseteq V(B^*)$
since
$X_t \subseteq V(B^*)$
since
![]() $(A^*,B^*)$
and
$(A^*,B^*)$
and
![]() $(A_t, B_t)$
are independent flaps. Therefore,
$(A_t, B_t)$
are independent flaps. Therefore,
![]() $V(A^* \cap B^*)=X_t$
, since
$V(A^* \cap B^*)=X_t$
, since
![]() $|X_t|=2$
. Moreover,
$|X_t|=2$
. Moreover,
![]() $A^* \cap (D \cup A_s^*)$
contains at least one vertex not in
$A^* \cap (D \cup A_s^*)$
contains at least one vertex not in
![]() $X_t$
, since V(C) is a proper subset of
$X_t$
, since V(C) is a proper subset of
![]() $V(A^*)$
. If
$V(A^*)$
. If
![]() $A^* \cap (D \cup A_s^*)$
meets
$A^* \cap (D \cup A_s^*)$
meets
![]() $B^* \cap (D \cup A_s^*)$
at a vertex
$B^* \cap (D \cup A_s^*)$
at a vertex
![]() $x \notin X_s$
, then
$x \notin X_s$
, then
![]() $x \in V(A \cap B)$
, which contradicts that
$x \in V(A \cap B)$
, which contradicts that
![]() $V(A \cap B)=X_s$
. Thus,
$V(A \cap B)=X_s$
. Thus,
![]() $V(A^* \cap (D \cup A_s^*)) \cap V(B^* \cap (D \cup A_s^*)) \subseteq X_s$
. It follows that
$V(A^* \cap (D \cup A_s^*)) \cap V(B^* \cap (D \cup A_s^*)) \subseteq X_s$
. It follows that
![]() $A^* \cap (D \cup A_s^*)$
is a half-flap, since
$A^* \cap (D \cup A_s^*)$
is a half-flap, since
![]() $|X_s| \leqslant 2$
. However, this contradicts the minimality of
$|X_s| \leqslant 2$
. However, this contradicts the minimality of
![]() $\sum_{(A',B') \in \mathcal F_t}|V(A')| +|E(A')|$
since
$\sum_{(A',B') \in \mathcal F_t}|V(A')| +|E(A')|$
since
![]() $|V(A^* \cap (D \cup A_s^*))| < |V(A)|$
.
$|V(A^* \cap (D \cup A_s^*))| < |V(A)|$
.
Suppose that
![]() $3 \leqslant |V(A^* \cap C)| < |V(C)|$
and
$3 \leqslant |V(A^* \cap C)| < |V(C)|$
and
![]() $V(A^*) \setminus V(C) \neq \emptyset$
. Since C is 3-connected, for some
$V(A^*) \setminus V(C) \neq \emptyset$
. Since C is 3-connected, for some
![]() $Y \in \{X_s, X_t\}$
, one vertex y of Y is in
$Y \in \{X_s, X_t\}$
, one vertex y of Y is in
![]() $V(A^*) \setminus V(B^*)$
and the other vertex of Y is in
$V(A^*) \setminus V(B^*)$
and the other vertex of Y is in
![]() $V(B^*) \setminus V(A^*)$
. Since
$V(B^*) \setminus V(A^*)$
. Since
![]() $(A^*,B^*)$
and
$(A^*,B^*)$
and
![]() $(A_t, B_t)$
are independent flaps, we have
$(A_t, B_t)$
are independent flaps, we have
![]() $A_t \subseteq B^*$
. Thus,
$A_t \subseteq B^*$
. Thus,
![]() $X_t \subseteq V(B^*)$
, and so
$X_t \subseteq V(B^*)$
, and so
![]() $Y=X_s$
. Let
$Y=X_s$
. Let
![]() $\beta$
be obtained from
$\beta$
be obtained from
![]() $B^*$
by replacing
$B^*$
by replacing
![]() $A_t$
by an edge whose ends are
$A_t$
by an edge whose ends are
![]() $X_t$
and adding the edge with ends
$X_t$
and adding the edge with ends
![]() $X_s$
. Since C is 3-connected,
$X_s$
. Since C is 3-connected,
![]() $(C \cap A^*, C \cap \beta)$
is a
$(C \cap A^*, C \cap \beta)$
is a
![]() $(\geqslant 3)$
-separation of C. It follows that
$(\geqslant 3)$
-separation of C. It follows that
![]() $A \cap C$
meets
$A \cap C$
meets
![]() $B \cap C$
in at least two vertices of
$B \cap C$
in at least two vertices of
![]() $V(C) \setminus X$
, and thus exactly two since
$V(C) \setminus X$
, and thus exactly two since
![]() $|V(A \cap B)| \leqslant 2$
.
$|V(A \cap B)| \leqslant 2$
.
Thus,
![]() $A^* \cap C$
meets
$A^* \cap C$
meets
![]() $B^* \cap C$
in at least two vertices of
$B^* \cap C$
in at least two vertices of
![]() $V(C) \setminus X_s$
, and thus exactly two since
$V(C) \setminus X_s$
, and thus exactly two since
![]() $|V(A^* \cap B^*)| \leqslant 2$
. In particular,
$|V(A^* \cap B^*)| \leqslant 2$
. In particular,
![]() $V(A^* \cap B^*) \subseteq V(C) \setminus X_s$
, and hence
$V(A^* \cap B^*) \subseteq V(C) \setminus X_s$
, and hence
![]() $V(A^* \cap (D \cup A_s^*)) \cap V(B^* \cap (D \cup A_s^*)) = \emptyset$
. It follows that
$V(A^* \cap (D \cup A_s^*)) \cap V(B^* \cap (D \cup A_s^*)) = \emptyset$
. It follows that
![]() $A \cap (D \cup A_s^*)$
is a half-flap. However, this contradicts the minimality of
$A \cap (D \cup A_s^*)$
is a half-flap. However, this contradicts the minimality of
![]() $\sum_{(A',B') \in \mathcal F_s}|V(A')| +|E(A')|$
since
$\sum_{(A',B') \in \mathcal F_s}|V(A')| +|E(A')|$
since
![]() $|V(A \cap D)| < |V(A)|$
.
$|V(A \cap D)| < |V(A)|$
.
Since
![]() $(A^*,B^*)$
is an arbitrary flap of
$(A^*,B^*)$
is an arbitrary flap of
![]() $\mathcal F_t \setminus \{(A_t, B_t)\}$
, by the previous cases, we may assume
$\mathcal F_t \setminus \{(A_t, B_t)\}$
, by the previous cases, we may assume
![]() $V(A' \cap C)\subseteq X_s$
and
$V(A' \cap C)\subseteq X_s$
and
![]() $A' \cap C$
has no edges for all
$A' \cap C$
has no edges for all
![]() $(A',B') \in \mathcal F_t \setminus \{(A_t, B_t)\}$
. Therefore, by replacing
$(A',B') \in \mathcal F_t \setminus \{(A_t, B_t)\}$
. Therefore, by replacing
![]() $(A_t, B_t)$
by
$(A_t, B_t)$
by
![]() $(A_t +_{X_t} C, B_t -(V(C) \setminus X_t))$
in
$(A_t +_{X_t} C, B_t -(V(C) \setminus X_t))$
in
![]() $\mathcal F_t$
, we contradict that
$\mathcal F_t$
, we contradict that
![]() $A_t$
is a full-half-flap.
$A_t$
is a full-half-flap.
We will need to pick reduction sequences that satisfy a few additional properties. Let
![]() $H_k, \dots, H_j$
be a reduction sequence of H, with corresponding flaps
$H_k, \dots, H_j$
be a reduction sequence of H, with corresponding flaps
![]() $(A_\ell, B_\ell)$
in
$(A_\ell, B_\ell)$
in
![]() $H_\ell$
. We say that
$H_\ell$
. We say that
![]() $H_k, \dots, H_j$
is a good reduction sequence if for all
$H_k, \dots, H_j$
is a good reduction sequence if for all
![]() $\ell \in \{k, \dots, j\}$
,
$\ell \in \{k, \dots, j\}$
,
![]() $H_\ell$
is not a cycle, and for all
$H_\ell$
is not a cycle, and for all
![]() $\ell \in \{k, \dots, j+1\}$
$\ell \in \{k, \dots, j+1\}$
-
1. if
 $A_\ell \cong P_3$
and
$A_\ell \cong P_3$
and
 $V(A_\ell) \cap V(B_\ell)=\{x\}$
, then e is a true edge of
$V(A_\ell) \cap V(B_\ell)=\{x\}$
, then e is a true edge of
 $H_\ell$
, where e is the unique edge of
$H_\ell$
, where e is the unique edge of
 $A_\ell$
not incident to x,
$A_\ell$
not incident to x, -
2. if
 $A_\ell \cong C_3$
and
$A_\ell \cong C_3$
and
 $V(A_\ell) \cap V(B_\ell)=\{x\}$
, then e is a true edge of
$V(A_\ell) \cap V(B_\ell)=\{x\}$
, then e is a true edge of
 $H_\ell$
, where e is the unique edge of
$H_\ell$
, where e is the unique edge of
 $A_\ell$
not incident to x,
$A_\ell$
not incident to x, -
3. if
 $A_\ell \cong C_4$
and
$A_\ell \cong C_4$
and
 $V(A_\ell) \cap V(B_\ell)=\{x,y\}$
, then e is a true edge of
$V(A_\ell) \cap V(B_\ell)=\{x,y\}$
, then e is a true edge of
 $H_\ell$
, where e is the unique edge of
$H_\ell$
, where e is the unique edge of
 $A_\ell$
not incident to either x or y.
$A_\ell$
not incident to either x or y.
Note that, by Lemma 5.8, if
![]() $A_\ell \cong P_3$
and
$A_\ell \cong P_3$
and
![]() $V(A_\ell) \cap V(B_\ell)=\{x\}$
then x cannot be the centre of the
$V(A_\ell) \cap V(B_\ell)=\{x\}$
then x cannot be the centre of the
![]() $P_3$
, hence edge e is well-defined in case (1) above. Similarly, if
$P_3$
, hence edge e is well-defined in case (1) above. Similarly, if
![]() $A_\ell \cong C_4$
and
$A_\ell \cong C_4$
and
![]() $V(A_\ell) \cap V(B_\ell)=\{x,y\}$
, then x and y cannot be opposite vertices of the
$V(A_\ell) \cap V(B_\ell)=\{x,y\}$
, then x and y cannot be opposite vertices of the
![]() $C_4$
, and thus e is also well-defined in case (3).
$C_4$
, and thus e is also well-defined in case (3).
We now give conditions under which a good reduction sequence can be extended to a longer good reduction sequence. Let H’ be a graph where some edges are fake, and let
![]() $u, v \in V(H')$
. A u-culdesac of H’ is a cycle C of H’ such that
$u, v \in V(H')$
. A u-culdesac of H’ is a cycle C of H’ such that
![]() $u \in V(C), \deg_{H'}(u) \geqslant 3$
, and
$u \in V(C), \deg_{H'}(u) \geqslant 3$
, and
![]() $\deg_{H'}(w)=2$
for all
$\deg_{H'}(w)=2$
for all
![]() $w \in V(C) \setminus \{u\}$
. A u-alley of H’ is a path P of H’ such that u is an end of P,
$w \in V(C) \setminus \{u\}$
. A u-alley of H’ is a path P of H’ such that u is an end of P,
![]() $|V(P)| \geqslant 2, \deg_{H'}(u) \geqslant 3$
, and
$|V(P)| \geqslant 2, \deg_{H'}(u) \geqslant 3$
, and
![]() $\deg_P(w)=\deg_{H'}(w)$
for all
$\deg_P(w)=\deg_{H'}(w)$
for all
![]() $w \in V(P) \setminus \{u\}$
. A uv-path P in H’ is a uv-alley if
$w \in V(P) \setminus \{u\}$
. A uv-path P in H’ is a uv-alley if
![]() $|V(P)| \geqslant 3$
and
$|V(P)| \geqslant 3$
and
![]() $\deg_{H'}(u) \geqslant 3$
and
$\deg_{H'}(u) \geqslant 3$
and
![]() $\deg_{H'}(v) \geqslant 3$
and
$\deg_{H'}(v) \geqslant 3$
and
![]() $\deg_{H'}(w)=2$
for all
$\deg_{H'}(w)=2$
for all
![]() $w \in V(P) \setminus \{u,v\}$
.
$w \in V(P) \setminus \{u,v\}$
.
Claim 5.12. Let C be a u-culdesac of H’ with
![]() $|V(C)| \geqslant 4$
, and let
$|V(C)| \geqslant 4$
, and let
![]() $e\;:\!=\;uv$
be an edge of C incident to u. Let P and Q be the 3- and 4-vertex paths of C containing e and ending at u, respectively. If
$e\;:\!=\;uv$
be an edge of C incident to u. Let P and Q be the 3- and 4-vertex paths of C containing e and ending at u, respectively. If
![]() $|V(C)|$
is even, then P is a full-half flap of H’, and if
$|V(C)|$
is even, then P is a full-half flap of H’, and if
![]() $|V(C)|$
is odd, then Q is a full-half-flap.
$|V(C)|$
is odd, then Q is a full-half-flap.
Proof. Let
![]() $\mathcal F$
be a collection of f(H’) independent flaps in H’, and let
$\mathcal F$
be a collection of f(H’) independent flaps in H’, and let
![]() $\mathcal F'$
be the collection of flaps
$\mathcal F'$
be the collection of flaps
![]() $(F_1, F_1') \in \mathcal F$
such that
$(F_1, F_1') \in \mathcal F$
such that
![]() $E(F_1 \cap C) \neq \emptyset$
. Since C contains a set of
$E(F_1 \cap C) \neq \emptyset$
. Since C contains a set of
![]() $m\;:\!=\;\lfloor \frac{|V(C)|}{2} \rfloor$
independent half-flaps of H’, we must have
$m\;:\!=\;\lfloor \frac{|V(C)|}{2} \rfloor$
independent half-flaps of H’, we must have
![]() $|\mathcal F'| \geqslant m$
; otherwise,
$|\mathcal F'| \geqslant m$
; otherwise,
![]() $|\mathcal F|$
is not maximum. If
$|\mathcal F|$
is not maximum. If
![]() $\mathcal F'$
contains a flap
$\mathcal F'$
contains a flap
![]() $(F_1, F_1')$
such that
$(F_1, F_1')$
such that
![]() $F_1 \cap C=uv$
, then we replace
$F_1 \cap C=uv$
, then we replace
![]() $(F_1, F_1')$
by
$(F_1, F_1')$
by
![]() $(F_1 - v, F_1' \cup \{uv\})$
. Similarly, we may assume that
$(F_1 - v, F_1' \cup \{uv\})$
. Similarly, we may assume that
![]() $\mathcal F'$
does not contain a flap
$\mathcal F'$
does not contain a flap
![]() $(F_1, F_1')$
such that
$(F_1, F_1')$
such that
![]() $F_1 \cap C=tu$
, where t is the other neighbour of u in C. In particular,
$F_1 \cap C=tu$
, where t is the other neighbour of u in C. In particular,
![]() $|E(F_1 \cap C)| \geqslant 2$
for all
$|E(F_1 \cap C)| \geqslant 2$
for all
![]() $(F_1, F_1') \in \mathcal F'$
. This implies that
$(F_1, F_1') \in \mathcal F'$
. This implies that
![]() $|\mathcal F'| \leqslant m$
, and hence
$|\mathcal F'| \leqslant m$
, and hence
![]() $|\mathcal F'|=m$
. Observe that C contains a set
$|\mathcal F'|=m$
. Observe that C contains a set
![]() $\mathcal H$
of m independent half-flaps with
$\mathcal H$
of m independent half-flaps with
![]() $P \in \mathcal H$
if
$P \in \mathcal H$
if
![]() $|V(C)|$
is even, and
$|V(C)|$
is even, and
![]() $Q \in \mathcal H$
if
$Q \in \mathcal H$
if
![]() $|V(C)|$
is odd. It follows that P can be extended to a full-half-flap P’ if
$|V(C)|$
is odd. It follows that P can be extended to a full-half-flap P’ if
![]() $|V(C)|$
is even, and Q can be extended to a full-half-flap Q’ if
$|V(C)|$
is even, and Q can be extended to a full-half-flap Q’ if
![]() $|V(C)|$
is odd. Since every collection of f(H’) independent flaps of H’ must contain at least m flaps that use an edge of C, and
$|V(C)|$
is odd. Since every collection of f(H’) independent flaps of H’ must contain at least m flaps that use an edge of C, and
![]() $\bigcup_{F \in \mathcal H} F=C$
, it follows that
$\bigcup_{F \in \mathcal H} F=C$
, it follows that
![]() $C \cap P'=P$
. If P’ is not contained in C, then P’ contains two independent half-flaps, which is a contradiction. Thus,
$C \cap P'=P$
. If P’ is not contained in C, then P’ contains two independent half-flaps, which is a contradiction. Thus,
![]() $P'=P$
. The same argument gives
$P'=P$
. The same argument gives
![]() $Q'=Q$
.
$Q'=Q$
.
The same proof also establishes the following claim for uv-alleys.
Claim 5.13 Let P be a uv-alley of H’ with
![]() $|V(P)| \geqslant 5$
. If
$|V(P)| \geqslant 5$
. If
![]() $|V(P)|$
is even, let P’ be the 4-vertex subpath of P ending at u. If
$|V(P)|$
is even, let P’ be the 4-vertex subpath of P ending at u. If
![]() $|V(P)|$
is odd, let P’ be 3-vertex subpath of P ending at u. Then P’ is a full-half-flap of H’.
$|V(P)|$
is odd, let P’ be 3-vertex subpath of P ending at u. Then P’ is a full-half-flap of H’.
An edge e is at distance 2 from a vertex u if e is not incident to u and e is incident to an edge that is incident to u. A u-culdesac C is tame if C has a true edge at distance 2 from u. A uv-alley P is tame if P has a true edge at distance 2 from u or v. A u-alley P is tame if P has a true edge at distance 2 from u. Finally, we say that H’ is tame if for all
![]() $u,v \in V(H')$
all u-culdesacs, u-alleys, and uv-alleys of H’ are tame.
$u,v \in V(H')$
all u-culdesacs, u-alleys, and uv-alleys of H’ are tame.
Claim 5.14 Let
![]() $H_k, \dots, H_j$
be a good reduction sequence such that
$H_k, \dots, H_j$
be a good reduction sequence such that
![]() $j \geqslant 3$
and
$j \geqslant 3$
and
![]() $H_j$
is tame. Then
$H_j$
is tame. Then
![]() $H_k, \dots, H_j$
can be extended to a good reduction sequence
$H_k, \dots, H_j$
can be extended to a good reduction sequence
![]() $H_k, \dots, H_{j-1}$
such that
$H_k, \dots, H_{j-1}$
such that
![]() $H_{j-1}$
is tame.
$H_{j-1}$
is tame.
Proof. Suppose that
![]() $H_j$
contains a u-culdesac C with
$H_j$
contains a u-culdesac C with
![]() $|V(C)| \geqslant 4$
. Since
$|V(C)| \geqslant 4$
. Since
![]() $H_j$
is tame, C contains a true edge e at distance 2 from u. If
$H_j$
is tame, C contains a true edge e at distance 2 from u. If
![]() $|V(C)|$
is even (respectively, odd), let P be the 3-vertex (respectively, 4-vertex) path of C such that one end of P is u and
$|V(C)|$
is even (respectively, odd), let P be the 3-vertex (respectively, 4-vertex) path of C such that one end of P is u and
![]() $e \notin E(P)$
. By Claim 5.12, P is a full-half-flap of
$e \notin E(P)$
. By Claim 5.12, P is a full-half-flap of
![]() $H_j$
. Letting
$H_j$
. Letting
![]() $H_{j-1}$
be obtained from
$H_{j-1}$
be obtained from
![]() $H_j$
by applying Lemma 5.8 with
$H_j$
by applying Lemma 5.8 with
![]() $A=P$
, we have that
$A=P$
, we have that
![]() $H_\ell, \dots, H_{j-1}$
is a good reduction sequence and
$H_\ell, \dots, H_{j-1}$
is a good reduction sequence and
![]() $H_{j-1}$
is tame. Thus, we may assume that all culdesacs of
$H_{j-1}$
is tame. Thus, we may assume that all culdesacs of
![]() $H_j$
are triangles. By Claim 5.13, we may also assume that for all
$H_j$
are triangles. By Claim 5.13, we may also assume that for all
![]() $u,v \in V(H_j)$
, all uv-alleys of
$u,v \in V(H_j)$
, all uv-alleys of
![]() $H_j$
have at most four vertices.
$H_j$
have at most four vertices.
Let
![]() $(A_j, B_j)$
be a flap of
$(A_j, B_j)$
be a flap of
![]() $H_j$
such that
$H_j$
such that
![]() $A_j$
is a full-half-flap and let
$A_j$
is a full-half-flap and let
![]() $H_{j-1}=B_j^+$
. Suppose
$H_{j-1}=B_j^+$
. Suppose
![]() $H_{j-1}$
is a cycle. If
$H_{j-1}$
is a cycle. If
![]() $(A_j, B_j)$
is a 1-separation, then
$(A_j, B_j)$
is a 1-separation, then
![]() $H_{j-1} \cong C_3$
, since all culdesacs of
$H_{j-1} \cong C_3$
, since all culdesacs of
![]() $H_j$
are triangles. Since
$H_j$
are triangles. Since
![]() $f(C_3)=1$
, this contradicts
$f(C_3)=1$
, this contradicts
![]() $j \geqslant 3$
. If
$j \geqslant 3$
. If
![]() $(A_j, B_j)$
is a 2-separation, then
$(A_j, B_j)$
is a 2-separation, then
![]() $H_{j-1} \in \{C_3, C_4\}$
since all alleys of
$H_{j-1} \in \{C_3, C_4\}$
since all alleys of
![]() $H_j$
have at most four vertices. In either case,
$H_j$
have at most four vertices. In either case,
![]() $f(H_j)=2$
, which contradicts
$f(H_j)=2$
, which contradicts
![]() $j \geqslant 3$
. Thus,
$j \geqslant 3$
. Thus,
![]() $H_{j-1}$
is not a cycle.
$H_{j-1}$
is not a cycle.
Since
![]() $H_j$
is tame, it follows that
$H_j$
is tame, it follows that
![]() $H_k, \dots, H_{j-1}$
is a good reduction sequence. It only reTheorem 1.2s to show that
$H_k, \dots, H_{j-1}$
is a good reduction sequence. It only reTheorem 1.2s to show that
![]() $H_{j-1}$
is tame. Towards a contradiction, suppose
$H_{j-1}$
is tame. Towards a contradiction, suppose
![]() $H_{j-1}$
contains a u-culdesac C that is not tame. The cases in which
$H_{j-1}$
contains a u-culdesac C that is not tame. The cases in which
![]() $H_{j-1}$
contains a u-alley that is not tame, or a uv-alley that is not tame are similar and are omitted. We assume that
$H_{j-1}$
contains a u-alley that is not tame, or a uv-alley that is not tame are similar and are omitted. We assume that
![]() $(A_j,B_j)$
is a 2-separation (the case that
$(A_j,B_j)$
is a 2-separation (the case that
![]() $(A_j,B_j)$
is a 1-separation is easier and is omitted). Since
$(A_j,B_j)$
is a 1-separation is easier and is omitted). Since
![]() $H_j$
is tame, there must be an edge
$H_j$
is tame, there must be an edge
![]() $xy \in E(C)$
such that
$xy \in E(C)$
such that
![]() $V(A_j) \cap V(B_j)=\{x,y\}$
. Let
$V(A_j) \cap V(B_j)=\{x,y\}$
. Let
![]() $P_{xu}$
and
$P_{xu}$
and
![]() $P_{yu}$
be the x–u and y–u paths in C such that
$P_{yu}$
be the x–u and y–u paths in C such that
![]() $V(P_{xu}) \cap V(P_{yu})=\{u\}$
. Since all alleys of
$V(P_{xu}) \cap V(P_{yu})=\{u\}$
. Since all alleys of
![]() $H_j$
have at most four vertices,
$H_j$
have at most four vertices,
![]() $|V(P_{xu})|, |V(P_{yu})| \leqslant 4$
. Moreover, if
$|V(P_{xu})|, |V(P_{yu})| \leqslant 4$
. Moreover, if
![]() $|V(P_{xu})| \in \{2, 4\}$
, then adding the edge of
$|V(P_{xu})| \in \{2, 4\}$
, then adding the edge of
![]() $P_{xu}$
incident to x to
$P_{xu}$
incident to x to
![]() $A_j$
contradicts that
$A_j$
contradicts that
![]() $A_j$
is a full-half-flap. Thus,
$A_j$
is a full-half-flap. Thus,
![]() $|V(P_{xu})|, |V(P_{yu})| \in \{1, 3\}$
. In particular, this implies that C is not a triangle. For each fake edge
$|V(P_{xu})|, |V(P_{yu})| \in \{1, 3\}$
. In particular, this implies that C is not a triangle. For each fake edge
![]() $e \in E(C)$
let
$e \in E(C)$
let
![]() $\ell(e)$
be the smallest index such that
$\ell(e)$
be the smallest index such that
![]() $V(A_{\ell(e)}) \cap V(B_{\ell(e)})$
is equal to the set of ends of e. Among all fake edges of
$V(A_{\ell(e)}) \cap V(B_{\ell(e)})$
is equal to the set of ends of e. Among all fake edges of
![]() $C \setminus \{xy\}$
in
$C \setminus \{xy\}$
in
![]() $H_{j-1}$
, let f be such that
$H_{j-1}$
, let f be such that
![]() $\ell(f)$
is smallest. Since C is not a triangle, there are two edges of C at distance 2 from u (both of which are fake). Therefore, f exists. Let g be the unique edge of C such that
$\ell(f)$
is smallest. Since C is not a triangle, there are two edges of C at distance 2 from u (both of which are fake). Therefore, f exists. Let g be the unique edge of C such that
![]() $f \cup g$
is
$f \cup g$
is
![]() $P_{xu}$
or
$P_{xu}$
or
![]() $P_{yu}$
. Then adding g to
$P_{yu}$
. Then adding g to
![]() $A_{\ell(f)}$
contradicts that
$A_{\ell(f)}$
contradicts that
![]() $A_{\ell(f)}$
is a full-half flap.
$A_{\ell(f)}$
is a full-half flap.
In the case that H is non-planar, we do not need
![]() $j \geqslant 3$
in the statement of Claim 5.14.
$j \geqslant 3$
in the statement of Claim 5.14.
Claim 5.15 Let
![]() $H_k, \dots, H_j$
be a good reduction sequence of a non-planar graph such that
$H_k, \dots, H_j$
be a good reduction sequence of a non-planar graph such that
![]() $j \geqslant 1$
and
$j \geqslant 1$
and
![]() $H_j$
is tame. Then
$H_j$
is tame. Then
![]() $H_k, \dots, H_j$
can be extended to a good reduction sequence
$H_k, \dots, H_j$
can be extended to a good reduction sequence
![]() $H_k, \dots, H_{j-1}$
such that
$H_k, \dots, H_{j-1}$
such that
![]() $H_{j-1}$
is tame.
$H_{j-1}$
is tame.
Proof. The proof is identical to the proof of Claim 5.14, except for the second paragraph. Instead of using the assumption
![]() $j \geqslant 3$
, we directly observe that
$j \geqslant 3$
, we directly observe that
![]() $H_{j-1}$
cannot be a cycle because
$H_{j-1}$
cannot be a cycle because
![]() $H_{j-1}$
is non-planar. Note that if
$H_{j-1}$
is non-planar. Note that if
![]() $j=1$
, then
$j=1$
, then
![]() $H_1$
contains a flap since it is non-planar. Therefore,
$H_1$
contains a flap since it is non-planar. Therefore,
![]() $H_0$
exists.
$H_0$
exists.
The final ingredient we need is the existence of a certain collection of paths in H. Let
![]() $H_k, \dots, H_j$
be a reduction sequence of H with corresponding flaps
$H_k, \dots, H_j$
be a reduction sequence of H with corresponding flaps
![]() $(A_\ell, B_\ell)$
in
$(A_\ell, B_\ell)$
in
![]() $H_\ell$
, and for each
$H_\ell$
, and for each
![]() $\ell \in \{k, \dots, j\}$
let
$\ell \in \{k, \dots, j\}$
let
![]() $F_\ell$
be the set of fake edges of
$F_\ell$
be the set of fake edges of
![]() $H_\ell$
. For each fake edge e, we define a set of indices
$H_\ell$
. For each fake edge e, we define a set of indices
![]() $\mathcal I(e)$
recursively as follows. Let
$\mathcal I(e)$
recursively as follows. Let
![]() $\ell$
be the largest index such that e is a fake edge of
$\ell$
be the largest index such that e is a fake edge of
![]() $H_\ell$
and recursively define
$H_\ell$
and recursively define
![]() $\mathcal I(e)=\{\ell+1\} \cup \bigcup_{f \in F_{\ell+1} \cap E(A_{\ell+1})}\mathcal I(f)$
.
$\mathcal I(e)=\{\ell+1\} \cup \bigcup_{f \in F_{\ell+1} \cap E(A_{\ell+1})}\mathcal I(f)$
.
Claim 5.16 Let
![]() $H_k, \dots, H_j$
be a reduction sequence of H with corresponding flaps
$H_k, \dots, H_j$
be a reduction sequence of H with corresponding flaps
![]() $(A_\ell, B_\ell)$
in
$(A_\ell, B_\ell)$
in
![]() $H_\ell$
, and for each
$H_\ell$
, and for each
![]() $\ell \in \{k, \dots, j\}$
let
$\ell \in \{k, \dots, j\}$
let
![]() $F_\ell$
be the set of fake edges of
$F_\ell$
be the set of fake edges of
![]() $H_\ell$
. Then for all
$H_\ell$
. Then for all
![]() $\ell \in \{k, \dots, j\}$
, there is a collection of paths
$\ell \in \{k, \dots, j\}$
, there is a collection of paths
![]() $\mathcal P_{\ell}=\{P_f \mid f \in F_\ell\}$
in H such that for all
$\mathcal P_{\ell}=\{P_f \mid f \in F_\ell\}$
in H such that for all
![]() $f \in F_\ell$
,
$f \in F_\ell$
,
![]() $P_f$
has the same ends as f, and
$P_f$
has the same ends as f, and
![]() $P_f \subseteq \bigcup_{i \in \mathcal I(f)} A_i$
. Moreover, letting
$P_f \subseteq \bigcup_{i \in \mathcal I(f)} A_i$
. Moreover, letting
![]() $H_\ell'\;:\!=\;(H_{\ell} \setminus F_{\ell}) \cup \mathcal P_{\ell}$
, we have that
$H_\ell'\;:\!=\;(H_{\ell} \setminus F_{\ell}) \cup \mathcal P_{\ell}$
, we have that
![]() $(H_\ell', \mathcal P_{\ell})$
is a partially subdivided graph,
$(H_\ell', \mathcal P_{\ell})$
is a partially subdivided graph,
![]() $H_\ell'$
is a subgraph of H, and
$H_\ell'$
is a subgraph of H, and
![]() $H_\ell' / \mathcal P_\ell$
is isomorphic to
$H_\ell' / \mathcal P_\ell$
is isomorphic to
![]() $H_\ell$
.
$H_\ell$
.
Proof. We proceed by reverse induction. Since
![]() $H_k=H$
does not contain any fake edges, we may take
$H_k=H$
does not contain any fake edges, we may take
![]() $\mathcal P_k\;:\!=\;\emptyset$
. Suppose the claim is true for some
$\mathcal P_k\;:\!=\;\emptyset$
. Suppose the claim is true for some
![]() $\ell > j$
, and consider
$\ell > j$
, and consider
![]() $\ell-1$
. If
$\ell-1$
. If
![]() $|V(A_\ell) \cap V(B_\ell)|=2$
then let
$|V(A_\ell) \cap V(B_\ell)|=2$
then let
![]() $\{a,b\}\;:\!=\;V(A_\ell) \cap V(B_\ell)$
. We are done by induction if
$\{a,b\}\;:\!=\;V(A_\ell) \cap V(B_\ell)$
. We are done by induction if
![]() $|V(A_\ell) \cap V(B_\ell)| \leqslant 1$
or
$|V(A_\ell) \cap V(B_\ell)| \leqslant 1$
or
![]() $e\;:\!=\;ab$
is a true edge of
$e\;:\!=\;ab$
is a true edge of
![]() $H_{\ell-1}$
. Thus, we may assume that e is a fake edge of
$H_{\ell-1}$
. Thus, we may assume that e is a fake edge of
![]() $H_{\ell-1}$
. By the final part of Lemma 5.8, there is path
$H_{\ell-1}$
. By the final part of Lemma 5.8, there is path
![]() $P_{e}'$
in
$P_{e}'$
in
![]() $A_{\ell}$
between a and b. By induction, for each fake edge f in
$A_{\ell}$
between a and b. By induction, for each fake edge f in
![]() $P_{e}'$
, there is a path
$P_{e}'$
, there is a path
![]() $P_f' \subseteq \bigcup_{i \in \mathcal I(f)} A_i$
. Moreover, note that if
$P_f' \subseteq \bigcup_{i \in \mathcal I(f)} A_i$
. Moreover, note that if
![]() $f_1$
and
$f_1$
and
![]() $f_2$
are distinct fake edges of
$f_2$
are distinct fake edges of
![]() $H_{\ell-1}$
, then
$H_{\ell-1}$
, then
![]() $\mathcal{I}(f_1) \cap \mathcal I (f_2)=\emptyset$
. Therefore, replacing each fake edge f of
$\mathcal{I}(f_1) \cap \mathcal I (f_2)=\emptyset$
. Therefore, replacing each fake edge f of
![]() $P_{e}'$
with
$P_{e}'$
with
![]() $P_f'$
, we obtain a path
$P_f'$
, we obtain a path
![]() $P_{e}$
contained in
$P_{e}$
contained in
![]() $\bigcup_{i \in \mathcal I(e)} A_i$
. Every other fake edge e’ of
$\bigcup_{i \in \mathcal I(e)} A_i$
. Every other fake edge e’ of
![]() $H_{\ell-1}$
is a fake edge of
$H_{\ell-1}$
is a fake edge of
![]() $H_{\ell'}$
for some
$H_{\ell'}$
for some
![]() $\ell'> \ell$
. By induction, for each such fake edge e’, there is a path
$\ell'> \ell$
. By induction, for each such fake edge e’, there is a path
![]() $P_{e'}$
contained in
$P_{e'}$
contained in
![]() $\bigcup_{i \in \mathcal I(e')} A_i$
. Note that
$\bigcup_{i \in \mathcal I(e')} A_i$
. Note that
![]() $P_{f_1}$
and
$P_{f_1}$
and
![]() $P_{f_2}$
are internally disjoint for all distinct
$P_{f_2}$
are internally disjoint for all distinct
![]() $f_1, f_2 \in F_{\ell-1}$
, since
$f_1, f_2 \in F_{\ell-1}$
, since
![]() $\mathcal{I}(f_1) \cap \mathcal I (f_2)=\emptyset$
Thus,
$\mathcal{I}(f_1) \cap \mathcal I (f_2)=\emptyset$
Thus,
![]() $\mathcal P_{\ell-1}\;:\!=\;\{P_{f} \mid f \in F_{\ell-1}\}$
is the required set of paths.
$\mathcal P_{\ell-1}\;:\!=\;\{P_{f} \mid f \in F_{\ell-1}\}$
is the required set of paths.
We now prove the theorem in the case that H is non-planar.
Claim 5.17 Suppose H is an h-vertex, non-planar graph and
![]() $H_k, \dots, H_0$
is a good reduction sequence of H such that
$H_k, \dots, H_0$
is a good reduction sequence of H such that
![]() $H_\ell$
is tame for all
$H_\ell$
is tame for all
![]() $\ell \in \{k, \dots, 0\}$
. For each
$\ell \in \{k, \dots, 0\}$
. For each
![]() $\ell \in \{0, \dots, k\}$
, let
$\ell \in \{0, \dots, k\}$
, let
![]() $F_\ell$
be the set of fake edges of
$F_\ell$
be the set of fake edges of
![]() $H_\ell$
. Then for every n-vertex graph G embeddable in a surface of Euler genus g, and for all
$H_\ell$
. Then for every n-vertex graph G embeddable in a surface of Euler genus g, and for all
![]() $\ell \in \{0, \dots, k\}$
, there are at most
$\ell \in \{0, \dots, k\}$
, there are at most
![]() $c_{4.1}(h,g)c_{5.1}(h, g+2)^\ell \cdot n^\ell$
images of
$c_{4.1}(h,g)c_{5.1}(h, g+2)^\ell \cdot n^\ell$
images of
![]() $H_\ell \setminus F_\ell$
in G that extend to an image of H in G.
$H_\ell \setminus F_\ell$
in G that extend to an image of H in G.
Before proceeding with the proof, we quickly show that Claim 5.17 does indeed imply Theorem 5.9 when H is non-planar. First note that
![]() $H_k, \dots, H_0$
exist by Claim 5.15. Next, applying Claim 5.17 for
$H_k, \dots, H_0$
exist by Claim 5.15. Next, applying Claim 5.17 for
![]() $\ell=k$
, we get that there are at most
$\ell=k$
, we get that there are at most
![]() $c_{4.1}(h,g)c_{5.1}(h, g+2)^k \cdot n^k \leqslant c_{5.9}(h,g)n^k$
images of H in G.
$c_{4.1}(h,g)c_{5.1}(h, g+2)^k \cdot n^k \leqslant c_{5.9}(h,g)n^k$
images of H in G.
Proof. We proceed by induction on
![]() $\ell$
. When
$\ell$
. When
![]() $\ell=0$
, there are at most
$\ell=0$
, there are at most
![]() $c_{4.1}(h,g)$
images of
$c_{4.1}(h,g)$
images of
![]() $H_0 \setminus F_0$
in G that extend to an image of H in G, by Theorem 4.1. For the inductive step, suppose there are at most
$H_0 \setminus F_0$
in G that extend to an image of H in G, by Theorem 4.1. For the inductive step, suppose there are at most
![]() $c_{4.1}(h,g)c_{5.1}(h, g+2)^\ell \cdot n^\ell$
images of
$c_{4.1}(h,g)c_{5.1}(h, g+2)^\ell \cdot n^\ell$
images of
![]() $H_\ell \setminus F_\ell$
in G that extend to an image of H in G, and consider
$H_\ell \setminus F_\ell$
in G that extend to an image of H in G, and consider
![]() $\ell+1$
.
$\ell+1$
.
Let
![]() $\phi\;:\;V(H_\ell \setminus F_\ell) \to V(G)$
be a fixed copy of
$\phi\;:\;V(H_\ell \setminus F_\ell) \to V(G)$
be a fixed copy of
![]() $H_\ell \setminus F_\ell$
in G that extends to an image
$H_\ell \setminus F_\ell$
in G that extends to an image
![]() $\psi\;:\;V(H) \to V(G)$
of H in G. For every subgraph S of H, let
$\psi\;:\;V(H) \to V(G)$
of H in G. For every subgraph S of H, let
![]() $S^\psi$
be the subgraph of G obtained by restricting
$S^\psi$
be the subgraph of G obtained by restricting
![]() $\psi$
to S. Let
$\psi$
to S. Let
![]() $(A_{\ell+1}, B_{\ell+1})$
be the flap in
$(A_{\ell+1}, B_{\ell+1})$
be the flap in
![]() $H_{\ell+1}$
such that
$H_{\ell+1}$
such that
![]() $H_\ell=B_{\ell+1}^+$
, and let
$H_\ell=B_{\ell+1}^+$
, and let
![]() $F_{A_{\ell+1}}$
be the set of fake edges of
$F_{A_{\ell+1}}$
be the set of fake edges of
![]() $H_{\ell+1}$
contained in
$H_{\ell+1}$
contained in
![]() $E(A_{\ell+1})$
. By Claim 5.16, there is a collection of paths
$E(A_{\ell+1})$
. By Claim 5.16, there is a collection of paths
![]() $\mathcal P^\psi\;:\!=\;\{P_f^\psi \mid f \in F_{A_{\ell+1}}\}$
in
$\mathcal P^\psi\;:\!=\;\{P_f^\psi \mid f \in F_{A_{\ell+1}}\}$
in
![]() $H^\psi$
such that for all
$H^\psi$
such that for all
![]() $f \in F_{A_{\ell+1}}$
,
$f \in F_{A_{\ell+1}}$
,
![]() $P_f^\psi$
has the same ends as
$P_f^\psi$
has the same ends as
![]() $f^\psi$
and
$f^\psi$
and
![]() $((A_{\ell+1} \setminus F_{A_{\ell+1}})^\psi \cup \mathcal{P}^\psi, \mathcal {P}^\psi)$
is a partially subdivided subgraph of
$((A_{\ell+1} \setminus F_{A_{\ell+1}})^\psi \cup \mathcal{P}^\psi, \mathcal {P}^\psi)$
is a partially subdivided subgraph of
![]() $H^\psi$
.
$H^\psi$
.
Let
![]() $G_{\ell+1}$
be the minor of G obtained by contracting all but one edge from each path in
$G_{\ell+1}$
be the minor of G obtained by contracting all but one edge from each path in
![]() $\mathcal P^\psi$
. Since
$\mathcal P^\psi$
. Since
![]() $((A_{\ell+1} \setminus F_{A_{\ell+1}})^\psi \cup \mathcal P^\psi) / \mathcal P^\psi$
is isomorphic to
$((A_{\ell+1} \setminus F_{A_{\ell+1}})^\psi \cup \mathcal P^\psi) / \mathcal P^\psi$
is isomorphic to
![]() $A_{\ell+1}$
,
$A_{\ell+1}$
,
![]() $(A_{\ell+1} \setminus F_{A_{\ell+1}})^\psi \cup \mathcal P^\psi$
becomes an image of
$(A_{\ell+1} \setminus F_{A_{\ell+1}})^\psi \cup \mathcal P^\psi$
becomes an image of
![]() $A_{\ell+1}$
in
$A_{\ell+1}$
in
![]() $G_{\ell+1}$
.
$G_{\ell+1}$
.
Let
![]() $X\;:\!=\;V(A_{\ell+1}) \cap V(B_{\ell+1})$
and
$X\;:\!=\;V(A_{\ell+1}) \cap V(B_{\ell+1})$
and
![]() $Y\;:\!=\;\phi(X)$
. If
$Y\;:\!=\;\phi(X)$
. If
![]() $X\;:\!=\;\{a,b\}$
and ab is a fake edge of
$X\;:\!=\;\{a,b\}$
and ab is a fake edge of
![]() $H_{\ell+1}$
, then add a handle to
$H_{\ell+1}$
, then add a handle to
![]() $\Sigma$
and use the handle to draw an edge between the vertices in Y to obtain a graph
$\Sigma$
and use the handle to draw an edge between the vertices in Y to obtain a graph
![]() $G_{\ell+1}' \supset G_{\ell+1}$
embedded in a surface of Euler genus
$G_{\ell+1}' \supset G_{\ell+1}$
embedded in a surface of Euler genus
![]() $g+2$
. Otherwise, let
$g+2$
. Otherwise, let
![]() $G_{\ell+1}'\;:\!=\;G_{\ell+1}$
.
$G_{\ell+1}'\;:\!=\;G_{\ell+1}$
.
Note that by Claims 5.10, 5.11, goodness of the reduction sequence, and tameness of
![]() $H_{\ell+1}$
, the conditions of Lemma 5.1 are satisfied, with
$H_{\ell+1}$
, the conditions of Lemma 5.1 are satisfied, with
![]() $J=A_{\ell+1}^+$
. Therefore, by Lemma 5.1, there are at most
$J=A_{\ell+1}^+$
. Therefore, by Lemma 5.1, there are at most
![]() $c_{5.1}(|V(A_{\ell+1}^+)|, g+2)n$
images of
$c_{5.1}(|V(A_{\ell+1}^+)|, g+2)n$
images of
![]() $A_{\ell+1}^+$
with X rooted at Y in
$A_{\ell+1}^+$
with X rooted at Y in
![]() $G_{\ell+1}'$
. Hence, there are at most
$G_{\ell+1}'$
. Hence, there are at most
![]() $c_{5.1}(|V(A_1^+)|, g+2)n$
images of
$c_{5.1}(|V(A_1^+)|, g+2)n$
images of
![]() $H_{\ell+1} \setminus F_{\ell+1}$
in G that extend
$H_{\ell+1} \setminus F_{\ell+1}$
in G that extend
![]() $\phi$
and also extend to an image of H in G. By induction, there are at most
$\phi$
and also extend to an image of H in G. By induction, there are at most
![]() $c_{4.1}(h,g)c_{5.1}(h, g+2)^\ell \cdot n^\ell$
possibilities for
$c_{4.1}(h,g)c_{5.1}(h, g+2)^\ell \cdot n^\ell$
possibilities for
![]() $\phi$
, so there are at most
$\phi$
, so there are at most
images of
![]() $H_{\ell+1} \setminus F_{\ell+1}$
in G that extend to an image of H in G.
$H_{\ell+1} \setminus F_{\ell+1}$
in G that extend to an image of H in G.
The case when H is planar is similar, except that we must handle the case when H is a cycle separately, which we do now. We make a case distinction depending if the cycle has even or odd length.
Suppose
![]() $H \cong C_{2k}$
. Note that
$H \cong C_{2k}$
. Note that
![]() $f(C_{2k})=k$
. Let M be a perfect matching of
$f(C_{2k})=k$
. Let M be a perfect matching of
![]() $C_{2k}$
. For each copy
$C_{2k}$
. For each copy
![]() $\phi$
of
$\phi$
of
![]() $C_{2k}$
in G, let
$C_{2k}$
in G, let
![]() $\phi(M)$
be the subset of E(G) that
$\phi(M)$
be the subset of E(G) that
![]() $\phi$
maps M to. Since there are at most
$\phi$
maps M to. Since there are at most
![]() $\binom{|E(G)|}{k}$
choices for
$\binom{|E(G)|}{k}$
choices for
![]() $\phi(M)$
, and each such choice corresponds to at most
$\phi(M)$
, and each such choice corresponds to at most
![]() $2^k$
images of
$2^k$
images of
![]() $C_{2k}$
in G, there are at most
$C_{2k}$
in G, there are at most
![]() $2^k\binom{|E(G)|}{k} \leqslant c_{5.9}(2k,g)n^k$
images of
$2^k\binom{|E(G)|}{k} \leqslant c_{5.9}(2k,g)n^k$
images of
![]() $C_{2k}$
in G.
$C_{2k}$
in G.
Suppose
![]() $H \cong C_{2k+1}$
. Note that
$H \cong C_{2k+1}$
. Note that
![]() $f(C_{2k+1})=k$
. We prove by induction on
$f(C_{2k+1})=k$
. We prove by induction on
![]() $n=|V(G)|$
that there are at most
$n=|V(G)|$
that there are at most
![]() $6^k\binom{6(g+1)}{2}(g+1)^k \cdot n^k$
images of
$6^k\binom{6(g+1)}{2}(g+1)^k \cdot n^k$
images of
![]() $C_{2k+1}$
in G. For each vertex a of
$C_{2k+1}$
in G. For each vertex a of
![]() $C_{2k+1}$
let
$C_{2k+1}$
let
![]() $N_{C_{2k+1}}(a)$
be the two neighbours of a, and let
$N_{C_{2k+1}}(a)$
be the two neighbours of a, and let
![]() $M_a$
be the unique perfect matching of
$M_a$
be the unique perfect matching of
![]() $C_{2k+1}-(N_{C_{2k+1}}(a) \cup \{a\})$
. Since G is embedded in a surface of Euler genus g, G has a vertex x of degree at most
$C_{2k+1}-(N_{C_{2k+1}}(a) \cup \{a\})$
. Since G is embedded in a surface of Euler genus g, G has a vertex x of degree at most
![]() $6(g+1)$
. For each copy
$6(g+1)$
. For each copy
![]() $\phi$
of
$\phi$
of
![]() $C_{2k+1}$
in G containing x, there are at most
$C_{2k+1}$
in G containing x, there are at most
![]() $\binom{|E(G-x)|}{k-1}$
choices for
$\binom{|E(G-x)|}{k-1}$
choices for
![]() $\phi(M_x)$
. Since x has degree at most
$\phi(M_x)$
. Since x has degree at most
![]() $6(g+1)$
in G, there are at most
$6(g+1)$
in G, there are at most
![]() $\binom{6(g+1)}{2}$
choices for
$\binom{6(g+1)}{2}$
choices for
![]() $N_{C_{2k+1}}(x)$
. Each choice of
$N_{C_{2k+1}}(x)$
. Each choice of
![]() $M_x$
and
$M_x$
and
![]() $N_{C_{2k+1}}(x)$
yields at most
$N_{C_{2k+1}}(x)$
yields at most
![]() $2^k$
images of
$2^k$
images of
![]() $C_{2k+1}$
, so there are at most
$C_{2k+1}$
, so there are at most
![]() $2^k\binom{6(g+1)}{2} \binom{3(g+1)(n-1)}{k-1}$
images of
$2^k\binom{6(g+1)}{2} \binom{3(g+1)(n-1)}{k-1}$
images of
![]() $C_{2k+1}$
in G containing x. By induction, there are at most
$C_{2k+1}$
in G containing x. By induction, there are at most
![]() $6^k\binom{6(g+1)}{2}(g+1)^k \cdot (n-1)^k$
images of
$6^k\binom{6(g+1)}{2}(g+1)^k \cdot (n-1)^k$
images of
![]() $C_{2k+1}$
in
$C_{2k+1}$
in
![]() $G-x$
. Summing these two bounds, we conclude that there are at most
$G-x$
. Summing these two bounds, we conclude that there are at most
![]() $6^k\binom{6(g+1)}{2}(g+1)^k \cdot n^k$
images of
$6^k\binom{6(g+1)}{2}(g+1)^k \cdot n^k$
images of
![]() $C_{2k+1}$
in G. Note that
$C_{2k+1}$
in G. Note that
![]() $6^k\binom{6(g+1)}{2}(g+1)^k \leqslant c_{5.9}(2k+1, g)$
.
$6^k\binom{6(g+1)}{2}(g+1)^k \leqslant c_{5.9}(2k+1, g)$
.
If H is planar and
![]() $f(H)=1$
, then there are at most
$f(H)=1$
, then there are at most
![]() $c_{3.2}(h,g) n \leqslant c_{5.9}(h, g)n$
images of H in G. Therefore, the last remaining case is when H is planar,
$c_{3.2}(h,g) n \leqslant c_{5.9}(h, g)n$
images of H in G. Therefore, the last remaining case is when H is planar,
![]() $f(H) \geqslant 2$
, and H is not a cycle. This is handled by the following claim.
$f(H) \geqslant 2$
, and H is not a cycle. This is handled by the following claim.
Claim 5.18 Suppose H is an h-vertex planar graph,
![]() $f(H) \geqslant 2$
, and H is not a cycle. Let
$f(H) \geqslant 2$
, and H is not a cycle. Let
![]() $H_k, \dots, H_2$
be a good reduction sequence of H such that
$H_k, \dots, H_2$
be a good reduction sequence of H such that
![]() $H_\ell$
is tame for all
$H_\ell$
is tame for all
![]() $\ell \in \{k, \dots, 2\}$
Let
$\ell \in \{k, \dots, 2\}$
Let
![]() $H_1\;:\!=\;uv$
, where uv is a true edge of
$H_1\;:\!=\;uv$
, where uv is a true edge of
![]() $H_2$
such that there do not exist independent flaps (C, D) and (C’,D’) of
$H_2$
such that there do not exist independent flaps (C, D) and (C’,D’) of
![]() $H_2$
such that
$H_2$
such that
![]() $\{u,v\} \subseteq V(D \cap D')$
. For all
$\{u,v\} \subseteq V(D \cap D')$
. For all
![]() $\ell \in \{1, \dots, k\}$
, let
$\ell \in \{1, \dots, k\}$
, let
![]() $F_\ell$
be the set of fake edges of
$F_\ell$
be the set of fake edges of
![]() $H_\ell$
. Then for every n-vertex graph G embeddable in a surface of Euler genus g, and each
$H_\ell$
. Then for every n-vertex graph G embeddable in a surface of Euler genus g, and each
![]() $\ell \in \{1, \dots, k\}$
, there exist at most
$\ell \in \{1, \dots, k\}$
, there exist at most
![]() $6(g+1)c_{5.1}(h, g+2)^{\ell-1} \cdot n^\ell$
images of
$6(g+1)c_{5.1}(h, g+2)^{\ell-1} \cdot n^\ell$
images of
![]() $H_\ell \setminus F_\ell$
in G that extend to an image of H in G.
$H_\ell \setminus F_\ell$
in G that extend to an image of H in G.
Before proceeding with the proof, we note that
![]() $H_k, \dots, H_2$
exist by Claim 5.14. The true edge uv exists, by considering a leaf node of the SPQRK tree of
$H_k, \dots, H_2$
exist by Claim 5.14. The true edge uv exists, by considering a leaf node of the SPQRK tree of
![]() $H_2$
and using Claim 5.11 and the tameness of
$H_2$
and using Claim 5.11 and the tameness of
![]() $H_2$
. Again, Theorem 5.9 follows by taking
$H_2$
. Again, Theorem 5.9 follows by taking
![]() $\ell=k$
.
$\ell=k$
.
Proof. We proceed by induction on
![]() $\ell$
. For
$\ell$
. For
![]() $\ell=1$
,
$\ell=1$
,
![]() $H_1=uv$
is a true edge. Therefore, there are at most
$H_1=uv$
is a true edge. Therefore, there are at most
![]() $6(g+1)n$
images of
$6(g+1)n$
images of
![]() $H_1$
in G. For
$H_1$
in G. For
![]() $\ell=2$
, we apply Lemma 5.1, with
$\ell=2$
, we apply Lemma 5.1, with
![]() $J'=(H_2 \setminus F_2) \cup \mathcal P_2, \mathcal P= \mathcal P_2, J=H_2$
, and
$J'=(H_2 \setminus F_2) \cup \mathcal P_2, \mathcal P= \mathcal P_2, J=H_2$
, and
![]() $X=\{u,v\}$
, where
$X=\{u,v\}$
, where
![]() $\mathcal P_2$
is defined in Claim 5.16. Note that conditions (1) and (2) of Lemma 5.1 hold since uv is a true edge and there do not exist independent flaps (C, D) and (C’,D’) of
$\mathcal P_2$
is defined in Claim 5.16. Note that conditions (1) and (2) of Lemma 5.1 hold since uv is a true edge and there do not exist independent flaps (C, D) and (C’,D’) of
![]() $H_2$
such that
$H_2$
such that
![]() $\{u,v\} \subseteq V(D \cap D')$
. Conditions (3)–(6) hold vacuously. Conditions (7), (9), and (10) hold by goodness of the reduction sequence. Condition (8) holds since
$\{u,v\} \subseteq V(D \cap D')$
. Conditions (3)–(6) hold vacuously. Conditions (7), (9), and (10) hold by goodness of the reduction sequence. Condition (8) holds since
![]() $H_2$
is tame. Finally, (11) holds by Claim 5.11. Therefore, each of the at most
$H_2$
is tame. Finally, (11) holds by Claim 5.11. Therefore, each of the at most
![]() $6(g+1)n$
images of
$6(g+1)n$
images of
![]() $H_1$
in G extends to an image of J’ in at most
$H_1$
in G extends to an image of J’ in at most
![]() $c_{5.1}(h, g) n$
ways. Therefore, there are at most
$c_{5.1}(h, g) n$
ways. Therefore, there are at most
![]() $6(g+1)c_{5.1}(h, g)n^2 \leqslant 6(g+1)c_{5.1}(h, g+2) \cdot n^2$
images of
$6(g+1)c_{5.1}(h, g)n^2 \leqslant 6(g+1)c_{5.1}(h, g+2) \cdot n^2$
images of
![]() $H_2 \setminus F_2$
that extend to an image of H in G. For
$H_2 \setminus F_2$
that extend to an image of H in G. For
![]() $\ell \geqslant 3$
, the inductive step is exactly as in the non-planar case. Therefore, we conclude that for each
$\ell \geqslant 3$
, the inductive step is exactly as in the non-planar case. Therefore, we conclude that for each
![]() $\ell \in \{1, \dots, k\}$
there are at most
$\ell \in \{1, \dots, k\}$
there are at most
![]() $6(g+1)c_{5.1}(h, g+2)^{\ell-1} \cdot n^\ell$
images of
$6(g+1)c_{5.1}(h, g+2)^{\ell-1} \cdot n^\ell$
images of
![]() $H_\ell \setminus F_\ell$
in G that extend to an image of H in G.
$H_\ell \setminus F_\ell$
in G that extend to an image of H in G.
This completes the proof of Theorem 5.9.
6. Copies of complete graphs
This section studies the maximum number of copies of a given complete graph
![]() $K_s$
in an n-vertex graph that embeds in a given surface
$K_s$
in an n-vertex graph that embeds in a given surface
![]() $\Sigma$
. The flap-number of
$\Sigma$
. The flap-number of
![]() $K_s$
equals 1 if
$K_s$
equals 1 if
![]() $s\leqslant 4$
and equals 0 if
$s\leqslant 4$
and equals 0 if
![]() $s\geqslant 5$
. Thus, Theorem 1.2 implies that
$s\geqslant 5$
. Thus, Theorem 1.2 implies that
![]() $C(n,K_s,\Sigma)=\Theta(n)$
for
$C(n,K_s,\Sigma)=\Theta(n)$
for
![]() $s\leqslant 4$
and
$s\leqslant 4$
and
![]() $C(n,K_s,\Sigma)=\Theta(1)$
for
$C(n,K_s,\Sigma)=\Theta(1)$
for
![]() $s\geqslant 5$
. The bounds obtained in this section are much more precise than those given by Theorem 1.2. Our method follows that of Dujmović et al. [Reference Dujmović, Fijavž, Joret, Sulanke and Wood17], who characterised the n-vertex graphs that embed in a given surface
$s\geqslant 5$
. The bounds obtained in this section are much more precise than those given by Theorem 1.2. Our method follows that of Dujmović et al. [Reference Dujmović, Fijavž, Joret, Sulanke and Wood17], who characterised the n-vertex graphs that embed in a given surface
![]() $\Sigma$
and with the maximum number of complete subgraphs (in total), and then derived an upper bound on this maximum.
$\Sigma$
and with the maximum number of complete subgraphs (in total), and then derived an upper bound on this maximum.
A triangulation of a surface
![]() $\Sigma$
is an embedding of a graph in
$\Sigma$
is an embedding of a graph in
![]() $\Sigma$
in which each facial walk has three vertices and three edges with no repetitions. Let G be a triangulation of
$\Sigma$
in which each facial walk has three vertices and three edges with no repetitions. Let G be a triangulation of
![]() $\Sigma$
. An edge vw of G is reducible if vw is in exactly two triangles in G. And G is irreducible if no edge of G is reducible [Reference Barnette and Edelson8,Reference Barnette and Edelson9,Reference Cheng, Dey and Poon15,Reference Joret and Wood41–Reference Lawrencenko and Negami43,Reference Nakamoto and Ota54,Reference Sulanke63–Reference Sulanke65]. Barnette and Edelson [Reference Barnette and Edelson8,Reference Barnette and Edelson9] proved that each surface has a finite number of irreducible triangulations. For
$\Sigma$
. An edge vw of G is reducible if vw is in exactly two triangles in G. And G is irreducible if no edge of G is reducible [Reference Barnette and Edelson8,Reference Barnette and Edelson9,Reference Cheng, Dey and Poon15,Reference Joret and Wood41–Reference Lawrencenko and Negami43,Reference Nakamoto and Ota54,Reference Sulanke63–Reference Sulanke65]. Barnette and Edelson [Reference Barnette and Edelson8,Reference Barnette and Edelson9] proved that each surface has a finite number of irreducible triangulations. For
![]() $\mathbb{S}_h$
with
$\mathbb{S}_h$
with
![]() $h\leqslant 2$
and
$h\leqslant 2$
and
![]() $\mathbb{N}_c$
with
$\mathbb{N}_c$
with
![]() $c\leqslant 4,$
the list of all irreducible triangulations is known [Reference Lavrenchenko42,Reference Lawrencenko and Negami43,Reference Sulanke63,Reference Sulanke65]. In general, the best known upper bound on the number of vertices in an irreducible triangulation of a surface with Euler genus
$c\leqslant 4,$
the list of all irreducible triangulations is known [Reference Lavrenchenko42,Reference Lawrencenko and Negami43,Reference Sulanke63,Reference Sulanke65]. In general, the best known upper bound on the number of vertices in an irreducible triangulation of a surface with Euler genus
![]() $g\geqslant 1$
is
$g\geqslant 1$
is
![]() $13g-4$
, due to Joret and Wood [Reference Joret and Wood41].
$13g-4$
, due to Joret and Wood [Reference Joret and Wood41].
Let vw be a reducible edge of a triangulation G of
![]() $\Sigma$
. Let vwx and vwy be the two faces incident to vw in G. As illustrated in Figure 3, let
$\Sigma$
. Let vwx and vwy be the two faces incident to vw in G. As illustrated in Figure 3, let
![]() $G/vw$
be the graph obtained from G by contracting vw; that is, delete the edges vw,wy,wx, and identify v and w into v.
$G/vw$
be the graph obtained from G by contracting vw; that is, delete the edges vw,wy,wx, and identify v and w into v.
![]() $G/vw$
is a simple graph since x and y are the only common neighbours of v and w. Indeed,
$G/vw$
is a simple graph since x and y are the only common neighbours of v and w. Indeed,
![]() $G/vw$
is a triangulation of
$G/vw$
is a triangulation of
![]() $\Sigma$
. Conversely, we say that G is obtained from
$\Sigma$
. Conversely, we say that G is obtained from
![]() $G/vw$
by splitting the path xvy at v. If, in addition,
$G/vw$
by splitting the path xvy at v. If, in addition,
![]() $xy\in E(G)$
, then we say that G is obtained from
$xy\in E(G)$
, then we say that G is obtained from
![]() $G/vw$
by splitting the triangle xvy at v. Note that xvy need not be a face of
$G/vw$
by splitting the triangle xvy at v. Note that xvy need not be a face of
![]() $G/vw$
. In the case that xvy is a face, splitting xvy is equivalent to adding a new vertex adjacent to each of x,v,y.
$G/vw$
. In the case that xvy is a face, splitting xvy is equivalent to adding a new vertex adjacent to each of x,v,y.

Figure 3. Contracting a reducible edge.
6.1. Copies of triangles
In this section, we consider
![]() $C(K_3,\Sigma,n)$
and define the excess of a graph G to be
$C(K_3,\Sigma,n)$
and define the excess of a graph G to be
![]() $C(K_3,G)-3|V(G)|$
.
$C(K_3,G)-3|V(G)|$
.
Lemma 6.1 For each surface
![]() $\Sigma$
, every graph embeddable in
$\Sigma$
, every graph embeddable in
![]() $\Sigma$
with maximum excess is a triangulation of
$\Sigma$
with maximum excess is a triangulation of
![]() $\Sigma$
.
$\Sigma$
.
Proof. Let G be a graph embedded in
![]() $\Sigma$
that maximises the excess. We claim that G is a triangulation. Suppose on the contrary that F is a non-triangular facial walk in G.
$\Sigma$
that maximises the excess. We claim that G is a triangulation. Suppose on the contrary that F is a non-triangular facial walk in G.
Suppose that two vertices in F are not adjacent. Then, there are vertices v and w at distance 2 in the subgraph induced by F. Thus adding the edge vw ‘across’ the face increases the number of triangles and the excess. This contradicts the choice of G. Now assume that F induces a clique.
Suppose that F has at least four distinct vertices. Let G’ be the embedded graph obtained from G by adding one new vertex ‘inside’ the face adjacent to four distinct vertices of F. Thus G’ is embeddable in
![]() $\Sigma$
, has
$\Sigma$
, has
![]() $|V(G)|+1$
vertices, has at least
$|V(G)|+1$
vertices, has at least
![]() $C(K_3,G)+\binom{4}{2}=C(K_3,G)+6$
triangles, and thus has excess at least the excess of G plus 3. This contradicts the choice of G. Now assume that F has at most three distinct vertices.
$C(K_3,G)+\binom{4}{2}=C(K_3,G)+6$
triangles, and thus has excess at least the excess of G plus 3. This contradicts the choice of G. Now assume that F has at most three distinct vertices.
By Lemma 6.2 below,
![]() $F=(u,v,w,u,v,w)$
. Let G’ be the graph obtained from G by adding two new adjacent vertices p and q, where p is adjacent to the first u,v,w sequence in F, and q is adjacent to the second u,v,w sequence in F. So G’ is embeddable in
$F=(u,v,w,u,v,w)$
. Let G’ be the graph obtained from G by adding two new adjacent vertices p and q, where p is adjacent to the first u,v,w sequence in F, and q is adjacent to the second u,v,w sequence in F. So G’ is embeddable in
![]() $\Sigma$
and has
$\Sigma$
and has
![]() $|V(G)|+2$
vertices. If S is a non-empty subset of
$|V(G)|+2$
vertices. If S is a non-empty subset of
![]() $\{p,q\}$
and
$\{p,q\}$
and
![]() $T\subseteq \{u,v,w\}$
with
$T\subseteq \{u,v,w\}$
with
![]() $|S|+|T|=3$
, then
$|S|+|T|=3$
, then
![]() $S\cup T$
is a triangle of G’ but not of G. There are
$S\cup T$
is a triangle of G’ but not of G. There are
![]() $\binom{2}{1}\binom{3}{2}+\binom{2}{2}\binom{3}{1}=6+3=9$
such triangles. Thus,
$\binom{2}{1}\binom{3}{2}+\binom{2}{2}\binom{3}{1}=6+3=9$
such triangles. Thus,
![]() $C(K_3,G')\geqslant C(K_3,G)+9,$
and the excess of G’ is at least the excess of G plus 3, which contradicts the choice of G. Hence no face of G has repeated vertices, and G is a triangulation of
$C(K_3,G')\geqslant C(K_3,G)+9,$
and the excess of G’ is at least the excess of G plus 3, which contradicts the choice of G. Hence no face of G has repeated vertices, and G is a triangulation of
![]() $\Sigma$
.
$\Sigma$
.
Lemma 6.2 Let F be a facial walk in an embedded graph, such that F has exactly three distinct vertices that are pairwise adjacent. Then
![]() $F=(u,v,w)$
or
$F=(u,v,w)$
or
![]() $F=(u,v,w,u,v,w)$
.
$F=(u,v,w,u,v,w)$
.
Proof. Say u,v,w are three consecutive vertices in F. Then
![]() $u\neq v$
and
$u\neq v$
and
![]() $v\neq w$
(since there are no loops). And
$v\neq w$
(since there are no loops). And
![]() $u\neq w$
, since if
$u\neq w$
, since if
![]() $u=w$
then
$u=w$
then
![]() $\deg(v)=1$
(since there are no parallel edges), which is not possible since v is adjacent to the two other vertices in F. So any three consecutive vertices in F are pairwise distinct. If F has no repeated vertex, then F is the 3-cycle (u,v,w). Otherwise,
$\deg(v)=1$
(since there are no parallel edges), which is not possible since v is adjacent to the two other vertices in F. So any three consecutive vertices in F are pairwise distinct. If F has no repeated vertex, then F is the 3-cycle (u,v,w). Otherwise,
![]() $F=(u,v,w,u,\dots)$
. Again, since any three consecutive vertices in F are pairwise distinct,
$F=(u,v,w,u,\dots)$
. Again, since any three consecutive vertices in F are pairwise distinct,
![]() $F=(u,v,w,u,\dots)$
. Repeating this argument,
$F=(u,v,w,u,\dots)$
. Repeating this argument,
![]() $F=(u,v,w,u,v,w,\dots)$
. Each edge is traversed at most twice; see [53, Sections 3.2 and 3.3]. Thus
$F=(u,v,w,u,v,w,\dots)$
. Each edge is traversed at most twice; see [53, Sections 3.2 and 3.3]. Thus
![]() $F=(u,v,w,u,v,w)$
.
$F=(u,v,w,u,v,w)$
.
Theorem 6.3 Let
![]() $\phi$
be the maximum excess of an irreducible triangulation of
$\phi$
be the maximum excess of an irreducible triangulation of
![]() $\Sigma$
. Let X be the set of irreducible triangulations of
$\Sigma$
. Let X be the set of irreducible triangulations of
![]() $\Sigma$
with excess
$\Sigma$
with excess
![]() $\phi$
. Then the excess of every graph G embeddable in
$\phi$
. Then the excess of every graph G embeddable in
![]() $\Sigma$
is at most
$\Sigma$
is at most
![]() $\phi$
. Moreover, the excess of G equals
$\phi$
. Moreover, the excess of G equals
![]() $\phi$
if and only if G is obtained from some graph in X by repeatedly splitting triangles.
$\phi$
if and only if G is obtained from some graph in X by repeatedly splitting triangles.
Proof. We proceed by induction on
![]() $|V(G)|$
. By Lemma 6.1, we may assume that G is a triangulation of
$|V(G)|$
. By Lemma 6.1, we may assume that G is a triangulation of
![]() $\Sigma$
. If G is irreducible, then the claim follows from the definition of X and
$\Sigma$
. If G is irreducible, then the claim follows from the definition of X and
![]() $\phi$
. Otherwise, some edge vw of G is in exactly two triangles vwx and vwy. By induction, the excess of
$\phi$
. Otherwise, some edge vw of G is in exactly two triangles vwx and vwy. By induction, the excess of
![]() $G/vw$
is at most
$G/vw$
is at most
![]() $\phi$
. Moreover, the excess of
$\phi$
. Moreover, the excess of
![]() $G/vw$
equals
$G/vw$
equals
![]() $\phi$
if and only if G is obtained from some graph
$\phi$
if and only if G is obtained from some graph
![]() $H\in X$
by repeatedly splitting triangles.
$H\in X$
by repeatedly splitting triangles.
Observe that every triangle of G that is not in
![]() $G/vw$
is in
$G/vw$
is in
![]() $\{A\cup\{w\}\;:\;A\subseteq\{x,v,y\}, |A|=2\}$
. Thus,
$\{A\cup\{w\}\;:\;A\subseteq\{x,v,y\}, |A|=2\}$
. Thus,
![]() $C(K_3,G)\leqslant C(K_3,G/vw)+3$
. Moreover, equality holds if and only if xvy is a triangle. It follows from the definition of excess that the excess of G is at most
$C(K_3,G)\leqslant C(K_3,G/vw)+3$
. Moreover, equality holds if and only if xvy is a triangle. It follows from the definition of excess that the excess of G is at most
![]() $\phi$
. If the excess of G equals
$\phi$
. If the excess of G equals
![]() $\phi$
, then the excess of
$\phi$
, then the excess of
![]() $G/vw$
equals
$G/vw$
equals
![]() $\phi$
, and xvy is a triangle and G is obtained from H by repeatedly splitting triangles.
$\phi$
, and xvy is a triangle and G is obtained from H by repeatedly splitting triangles.
Conversely, if G is obtained from some
![]() $H\in X$
by repeatedly splitting triangles, then xvy is a triangle and
$H\in X$
by repeatedly splitting triangles, then xvy is a triangle and
![]() $G/vw$
is obtained from H by repeatedly splitting triangles. By induction, the excess of
$G/vw$
is obtained from H by repeatedly splitting triangles. By induction, the excess of
![]() $G/vw$
equals
$G/vw$
equals
![]() $\phi$
, implying the excess of G equals
$\phi$
, implying the excess of G equals
![]() $\phi$
.
$\phi$
.
In general, since every irreducible triangulation of a surface
![]() $\Sigma$
with Euler genus g has O(g) vertices [Reference Joret and Wood41,Reference Nakamoto and Ota54], Theorem 6.3 implies that
$\Sigma$
with Euler genus g has O(g) vertices [Reference Joret and Wood41,Reference Nakamoto and Ota54], Theorem 6.3 implies that
![]() $C(K_3,\Sigma,n)\leqslant 3n+O(g^3)$
. We now show that
$C(K_3,\Sigma,n)\leqslant 3n+O(g^3)$
. We now show that
![]() $C(K_3,\Sigma,n)=3n+\Theta(g^{3/2})$
.
$C(K_3,\Sigma,n)=3n+\Theta(g^{3/2})$
.
The following elementary fact will be useful. For integers
![]() $s\geqslant 2$
and
$s\geqslant 2$
and
![]() $m\geqslant 2$
,
$m\geqslant 2$
,
Theorem 6.4 For every surface
![]() $\Sigma$
of Euler genus g,
$\Sigma$
of Euler genus g,
where the lower bound holds for all
![]() $n\geqslant\sqrt{6g}$
and the upper bound holds for all n.
$n\geqslant\sqrt{6g}$
and the upper bound holds for all n.
Proof. First, we prove the lower bound. Because of the o(1) term, we may assume that
![]() $g\geqslant 4$
. Let
$g\geqslant 4$
. Let
![]() $p\;:\!=\;\lfloor{{\frac12 (7+\sqrt{24g+1})}}\rfloor$
. Note that
$p\;:\!=\;\lfloor{{\frac12 (7+\sqrt{24g+1})}}\rfloor$
. Note that
![]() $p\geqslant 8$
and
$p\geqslant 8$
and
![]() $p-\frac52>\sqrt{6g}$
. The Map Colour Theorem [Reference Ringel62] says that
$p-\frac52>\sqrt{6g}$
. The Map Colour Theorem [Reference Ringel62] says that
![]() $K_p$
embeds in
$K_p$
embeds in
![]() $\Sigma$
. To obtain a graph with n vertices embedded in
$\Sigma$
. To obtain a graph with n vertices embedded in
![]() $\Sigma,$
repeat the following step
$\Sigma,$
repeat the following step
![]() $n-p$
times: choose a face f and add a new vertex ‘inside’ f adjacent to all the vertices on the boundary of f. Each new vertex creates at least three new triangles. Thus,
$n-p$
times: choose a face f and add a new vertex ‘inside’ f adjacent to all the vertices on the boundary of f. Each new vertex creates at least three new triangles. Thus,
![]() $C(K_3,\Sigma,n)\geqslant 3(n-p) + \binom{p}{3}$
for
$C(K_3,\Sigma,n)\geqslant 3(n-p) + \binom{p}{3}$
for
![]() $n\geqslant p$
. Since
$n\geqslant p$
. Since
![]() $p\geqslant 8,$
we have
$p\geqslant 8,$
we have
![]() $\binom{p}{3} - 3p \geqslant \frac16(p-\frac52)^3 \geqslant \sqrt{6}g^{3/2}$
. Thus
$\binom{p}{3} - 3p \geqslant \frac16(p-\frac52)^3 \geqslant \sqrt{6}g^{3/2}$
. Thus
![]() $C(K_3,\Sigma,n)\geqslant 3n + \sqrt{6}g^{3/2}$
.
$C(K_3,\Sigma,n)\geqslant 3n + \sqrt{6}g^{3/2}$
.
To prove the upper bound, by Theorem 6.3, it suffices to consider an n-vertex irreducible triangulation G of
![]() $\Sigma$
. So
$\Sigma$
. So
![]() $n\leqslant 13g$
[Reference Joret and Wood41]. Let
$n\leqslant 13g$
[Reference Joret and Wood41]. Let
![]() $v_1,\dots,v_n$
be a vertex ordering of G, where
$v_1,\dots,v_n$
be a vertex ordering of G, where
![]() $v_i$
has minimum degree in
$v_i$
has minimum degree in
![]() $G_i\;:\!=\;G[\{v_1,\dots,v_i\}]$
. By Euler’s formula,
$G_i\;:\!=\;G[\{v_1,\dots,v_i\}]$
. By Euler’s formula,
![]() $i\cdot \deg_{G_i}(v_i) \leqslant 2|E(G_i)| \leqslant 6(i+g)$
, implying
$i\cdot \deg_{G_i}(v_i) \leqslant 2|E(G_i)| \leqslant 6(i+g)$
, implying
Let
![]() $m\;:\!=\;\lceil{{3\sqrt{g}}}\rceil$
. The number of triangles
$m\;:\!=\;\lceil{{3\sqrt{g}}}\rceil$
. The number of triangles
![]() $v_av_bv_i$
with
$v_av_bv_i$
with
![]() $a<b<i\leqslant m$
is at most
$a<b<i\leqslant m$
is at most
![]() $\binom{m}{3} \leqslant \binom{3\sqrt{g}+1}{3} \leqslant \frac{9}{2} g^{3/2}$
. Charge each triangle
$\binom{m}{3} \leqslant \binom{3\sqrt{g}+1}{3} \leqslant \frac{9}{2} g^{3/2}$
. Charge each triangle
![]() $v_av_bv_i$
with
$v_av_bv_i$
with
![]() $a<b<i$
and
$a<b<i$
and
![]() $i\geqslant m+1$
to vertex
$i\geqslant m+1$
to vertex
![]() $v_i$
. For
$v_i$
. For
![]() $m+1\leqslant i\leqslant n$
, the number of triangles charged to
$m+1\leqslant i\leqslant n$
, the number of triangles charged to
![]() $v_i$
is at most
$v_i$
is at most
Thus
 \begin{align*}C(K_3,G) & \leqslant\frac{9}{2}g^{3/2} + 18\sum_{i=m+1}^{n} \left(1+\frac{2g}{i}+\frac{g^2}{i^2} \right)\\& \leqslant \frac{9}{2}g^{3/2} + 18n + 36g(\ln(n)+1) + 18g^2 \sum_{i\geqslant m+1}\frac{1}{i^2}.\end{align*}
\begin{align*}C(K_3,G) & \leqslant\frac{9}{2}g^{3/2} + 18\sum_{i=m+1}^{n} \left(1+\frac{2g}{i}+\frac{g^2}{i^2} \right)\\& \leqslant \frac{9}{2}g^{3/2} + 18n + 36g(\ln(n)+1) + 18g^2 \sum_{i\geqslant m+1}\frac{1}{i^2}.\end{align*}
By (1) with
![]() $s=2$
,
$s=2$
,
Since
![]() $m\geqslant 3\sqrt{g}$
and
$m\geqslant 3\sqrt{g}$
and
![]() $n\leqslant 13g$
,
$n\leqslant 13g$
,
6.2 Copies of
 $K_4$
$K_4$
In this section, we consider the case
![]() $H=K_4$
and define the excess of a graph G to be
$H=K_4$
and define the excess of a graph G to be
![]() $C(K_4,G)-|V(G)|$
.
$C(K_4,G)-|V(G)|$
.
Lemma 6.5 For each surface
![]() $\Sigma$
, every graph embeddable in
$\Sigma$
, every graph embeddable in
![]() $\Sigma$
with maximum excess is a triangulation of
$\Sigma$
with maximum excess is a triangulation of
![]() $\Sigma$
.
$\Sigma$
.
Proof. Let G be a graph embedded in
![]() $\Sigma$
with maximum excess. We claim that G is a triangulation.
$\Sigma$
with maximum excess. We claim that G is a triangulation.
Suppose that some facial walk F contains non-adjacent vertices v and w. Let G’ be the graph obtained from G by adding the edge vw. Thus,
![]() $C(K_4,G')\geqslant C(K_4,G)$
. If two common neighbours of v and w are adjacent, then
$C(K_4,G')\geqslant C(K_4,G)$
. If two common neighbours of v and w are adjacent, then
![]() $C(K_4,G+vw)>C(K_4,G)$
, implying that the excess of
$C(K_4,G+vw)>C(K_4,G)$
, implying that the excess of
![]() $G+vw$
is greater than the excess of G, which contradicts the choice of G. Now assume that no two common neighbours of v and w are adjacent. Let
$G+vw$
is greater than the excess of G, which contradicts the choice of G. Now assume that no two common neighbours of v and w are adjacent. Let
![]() $G''\;:\!=\;G'/vw$
. Every
$G''\;:\!=\;G'/vw$
. Every
![]() $K_4$
subgraph in G’ is also in G”. Thus,
$K_4$
subgraph in G’ is also in G”. Thus,
![]() $C(K_4,G'')\geqslant C(K_4,G')\geqslant C(K_4,G)$
. Since
$C(K_4,G'')\geqslant C(K_4,G')\geqslant C(K_4,G)$
. Since
![]() $|V(G'')|<|V(G)|$
, the excess of G” is greater than the excess of G, which contradicts the choice of G. Now assume that every facial walk induces a clique in G.
$|V(G'')|<|V(G)|$
, the excess of G” is greater than the excess of G, which contradicts the choice of G. Now assume that every facial walk induces a clique in G.
Suppose that some facial walk F has at least four distinct vertices. Let G’ be the embedded graph obtained from G by adding one new vertex ‘inside’ the face adjacent to four distinct vertices of F. Thus, G’ is embeddable in
![]() $\Sigma$
, has
$\Sigma$
, has
![]() $|V(G)|+1$
vertices, has at least
$|V(G)|+1$
vertices, has at least
![]() $C(K_4,G)+\binom{4}{3}=C(K_4,G)+4$
triangles, and thus has excess at least the excess of G plus 3. This contradicts the choice of G. Now assume that every facial walk in G has at most three distinct vertices.
$C(K_4,G)+\binom{4}{3}=C(K_4,G)+4$
triangles, and thus has excess at least the excess of G plus 3. This contradicts the choice of G. Now assume that every facial walk in G has at most three distinct vertices.
Suppose that some facial walk F is not a triangle. By Lemma 6.2,
![]() $F=(u,v,w,u,v,w)$
. Let G’ be the graph obtained from G by adding two new adjacent vertices p and q, where p is adjacent to the first u,v,w sequence in F, and q is adjacent to the second u,v,w sequence in F. So G’ is embeddable in
$F=(u,v,w,u,v,w)$
. Let G’ be the graph obtained from G by adding two new adjacent vertices p and q, where p is adjacent to the first u,v,w sequence in F, and q is adjacent to the second u,v,w sequence in F. So G’ is embeddable in
![]() $\Sigma$
and has
$\Sigma$
and has
![]() $|V(G)|+2$
vertices. If S is a non-empty subset of
$|V(G)|+2$
vertices. If S is a non-empty subset of
![]() $\{p,q\}$
and
$\{p,q\}$
and
![]() $T\subseteq \{u,v,w\}$
with
$T\subseteq \{u,v,w\}$
with
![]() $|S|+|T|=4$
, then
$|S|+|T|=4$
, then
![]() $S\cup T$
induces a copy of
$S\cup T$
induces a copy of
![]() $K_4$
in G’ but not in G. There are
$K_4$
in G’ but not in G. There are
![]() $\binom{2}{2}\binom{3}{2}+\binom{2}{1}\binom{3}{3}=3+2=5$
such copies. Thus,
$\binom{2}{2}\binom{3}{2}+\binom{2}{1}\binom{3}{3}=3+2=5$
such copies. Thus,
![]() $C(K_4,G')\geqslant C(K_4,G)+5$
and the excess of G’ is at least the excess of G plus 3, which contradicts the choice of G. Therefore G is a triangulation of
$C(K_4,G')\geqslant C(K_4,G)+5$
and the excess of G’ is at least the excess of G plus 3, which contradicts the choice of G. Therefore G is a triangulation of
![]() $\Sigma$
.
$\Sigma$
.
Theorem 6.6 Let
![]() $\phi$
be the maximum excess of an irreducible triangulation of
$\phi$
be the maximum excess of an irreducible triangulation of
![]() $\Sigma$
. Let X be the set of irreducible triangulations of
$\Sigma$
. Let X be the set of irreducible triangulations of
![]() $\Sigma$
with excess
$\Sigma$
with excess
![]() $\phi$
. Then the excess of every graph G embeddable in
$\phi$
. Then the excess of every graph G embeddable in
![]() $\Sigma$
is at most
$\Sigma$
is at most
![]() $\phi$
. Moreover, the excess of G equals
$\phi$
. Moreover, the excess of G equals
![]() $\phi$
if and only if G is obtained from some graph in X by repeatedly splitting triangles.
$\phi$
if and only if G is obtained from some graph in X by repeatedly splitting triangles.
Proof. We proceed by induction on
![]() $|V(G)|$
. By Lemma 6.5, we may assume that G is a triangulation of
$|V(G)|$
. By Lemma 6.5, we may assume that G is a triangulation of
![]() $\Sigma$
. If G is irreducible, then the claim follows from the definition of X and
$\Sigma$
. If G is irreducible, then the claim follows from the definition of X and
![]() $\phi$
. Otherwise, some edge vw of G is in exactly two triangles vwx and vwy. By induction, the excess of
$\phi$
. Otherwise, some edge vw of G is in exactly two triangles vwx and vwy. By induction, the excess of
![]() $G/vw$
is at most
$G/vw$
is at most
![]() $\phi$
. Moreover, the excess of
$\phi$
. Moreover, the excess of
![]() $G/vw$
equals
$G/vw$
equals
![]() $\phi$
if and only if G is obtained from some graph
$\phi$
if and only if G is obtained from some graph
![]() $H\in X$
by repeatedly splitting triangles.
$H\in X$
by repeatedly splitting triangles.
Observe that every clique of G that is not in
![]() $G/vw$
is in
$G/vw$
is in
![]() $\{A\cup\{w\}\;:\;A\subseteq\{x,v,y\}\}$
. Thus
$\{A\cup\{w\}\;:\;A\subseteq\{x,v,y\}\}$
. Thus
![]() $C(K_4,G)\leqslant C(K_4,G/vw)+1$
. Moreover, equality holds if and only if xvy is a triangle. It follows from the definition of excess that the excess of G is at most
$C(K_4,G)\leqslant C(K_4,G/vw)+1$
. Moreover, equality holds if and only if xvy is a triangle. It follows from the definition of excess that the excess of G is at most
![]() $\phi$
. If the excess of G equals
$\phi$
. If the excess of G equals
![]() $\phi$
, then the excess of
$\phi$
, then the excess of
![]() $G/vw$
equals
$G/vw$
equals
![]() $\phi$
, and xvy is a triangle, and G is obtained from H by repeatedly splitting triangles.
$\phi$
, and xvy is a triangle, and G is obtained from H by repeatedly splitting triangles.
Conversely, if G is obtained from some
![]() $H\in X$
by repeatedly splitting triangles, then xvy is a triangle and
$H\in X$
by repeatedly splitting triangles, then xvy is a triangle and
![]() $G/vw$
is obtained from H by repeatedly splitting triangles. By induction, the excess of
$G/vw$
is obtained from H by repeatedly splitting triangles. By induction, the excess of
![]() $G/vw$
equals
$G/vw$
equals
![]() $\phi$
, implying the excess of G equals
$\phi$
, implying the excess of G equals
![]() $\phi$
.
$\phi$
.
Since every irreducible triangulation of a surface
![]() $\Sigma$
with Euler genus g has O(g) vertices [Reference Joret and Wood41,Reference Nakamoto and Ota54], Theorem 6.5 implies that
$\Sigma$
with Euler genus g has O(g) vertices [Reference Joret and Wood41,Reference Nakamoto and Ota54], Theorem 6.5 implies that
![]() $C(K_4,\Sigma,n)\leqslant n+O(g^4)$
. We now show that
$C(K_4,\Sigma,n)\leqslant n+O(g^4)$
. We now show that
![]() $C(K_4,\Sigma,n)=n+\Theta(g^{2})$
.
$C(K_4,\Sigma,n)=n+\Theta(g^{2})$
.
Theorem 6.7 For every surface
![]() $\Sigma$
of Euler genus g,
$\Sigma$
of Euler genus g,
where the lower bound holds for
![]() $g\geqslant 1$
and
$g\geqslant 1$
and
![]() $n\geqslant\sqrt{6g}$
, and the upper bound holds for all n.
$n\geqslant\sqrt{6g}$
, and the upper bound holds for all n.
Proof. First we prove the lower bound. If
![]() $\Sigma=\mathbb{N}_2$
then let
$\Sigma=\mathbb{N}_2$
then let
![]() $p\;:\!=\;6$
. Otherwise, let
$p\;:\!=\;6$
. Otherwise, let
![]() $p\;:\!=\;\lfloor{{\frac12 (7+\sqrt{24g+1})}}\rfloor$
. Since
$p\;:\!=\;\lfloor{{\frac12 (7+\sqrt{24g+1})}}\rfloor$
. Since
![]() $g\geqslant 1,$
we have
$g\geqslant 1,$
we have
![]() $p\geqslant 6$
. The Map Colour Theorem [Reference Ringel62] says that
$p\geqslant 6$
. The Map Colour Theorem [Reference Ringel62] says that
![]() $K_p$
embeds in
$K_p$
embeds in
![]() $\Sigma$
. To obtain a graph with n vertices embedded in
$\Sigma$
. To obtain a graph with n vertices embedded in
![]() $\Sigma,$
repeat the following step
$\Sigma,$
repeat the following step
![]() $n-p$
times: choose a face f and add a new vertex ‘inside’ f adjacent to all the vertices on the boundary of f. Each new vertex creates at least one new copy of
$n-p$
times: choose a face f and add a new vertex ‘inside’ f adjacent to all the vertices on the boundary of f. Each new vertex creates at least one new copy of
![]() $K_4$
(since the boundary of each face is always a clique on at least three vertices). Thus,
$K_4$
(since the boundary of each face is always a clique on at least three vertices). Thus,
![]() $C(K_4,\Sigma,n)\geqslant n-p + \binom{p}{4}$
for
$C(K_4,\Sigma,n)\geqslant n-p + \binom{p}{4}$
for
![]() $n\geqslant p$
. Since
$n\geqslant p$
. Since
![]() $\binom{p}{4}-p\geqslant \frac{1}{24}(p-\frac52)^4$
and
$\binom{p}{4}-p\geqslant \frac{1}{24}(p-\frac52)^4$
and
![]() $p-\frac52>\sqrt{6g,}$
we have
$p-\frac52>\sqrt{6g,}$
we have
![]() $C(K_4,\Sigma,n)\geqslant n + \frac{1}{24}(\sqrt{6g})^4=n + \frac32 g^2$
.
$C(K_4,\Sigma,n)\geqslant n + \frac{1}{24}(\sqrt{6g})^4=n + \frac32 g^2$
.
Now we prove the upper bound. The claim is trivial for
![]() $g=0$
, so now assume that
$g=0$
, so now assume that
![]() $g\geqslant 1$
. By Theorem 6.5, it suffices to consider an irreducible triangulation G. Joret and Wood [Reference Joret and Wood41] proved that
$g\geqslant 1$
. By Theorem 6.5, it suffices to consider an irreducible triangulation G. Joret and Wood [Reference Joret and Wood41] proved that
![]() $n\;:\!=\;|V(G)|\leqslant 13g$
. Let
$n\;:\!=\;|V(G)|\leqslant 13g$
. Let
![]() $v_1,\dots,v_n$
be a vertex ordering of G, where
$v_1,\dots,v_n$
be a vertex ordering of G, where
![]() $v_i$
has minimum degree in
$v_i$
has minimum degree in
![]() $G_i\;:\!=\;G[\{v_1,\dots,v_i\}]$
. By Euler’s formula,
$G_i\;:\!=\;G[\{v_1,\dots,v_i\}]$
. By Euler’s formula,
and
Define
![]() $m\;:\!=\;\lceil{{4\sqrt{g}}}\rceil$
. The number of copies
$m\;:\!=\;\lceil{{4\sqrt{g}}}\rceil$
. The number of copies
![]() $v_av_bv_cv_i$
with
$v_av_bv_cv_i$
with
![]() $a<b<c<i\leqslant m$
is at most
$a<b<c<i\leqslant m$
is at most
![]() $\binom{m}{4} \leqslant \binom{4\sqrt{g}+1}{4} \leqslant \frac{32}{3}g^2$
. Charge each copy
$\binom{m}{4} \leqslant \binom{4\sqrt{g}+1}{4} \leqslant \frac{32}{3}g^2$
. Charge each copy
![]() $v_av_bv_cv_i$
with
$v_av_bv_cv_i$
with
![]() $a<b<c<i$
and
$a<b<c<i$
and
![]() $i\geqslant m+1$
to vertex
$i\geqslant m+1$
to vertex
![]() $v_i$
. For
$v_i$
. For
![]() $m+1\leqslant i\leqslant n$
, the number of copies charged to
$m+1\leqslant i\leqslant n$
, the number of copies charged to
![]() $v_i$
is at most
$v_i$
is at most
In total,
By (1) with
![]() $s=2$
and
$s=2$
and
![]() $s=3$
,
$s=3$
,
Since
![]() $m\geqslant 4\sqrt{g}$
and
$m\geqslant 4\sqrt{g}$
and
![]() $n\leqslant 13g$
,
$n\leqslant 13g$
,
 \begin{align*}C(K_4,G)& \leqslant \frac{32}{3}g^2 +36 \left( \frac{g^2}{32} + \frac{3g^{3/2}}{4} + 3g( \ln (13g) + 1) + 13g \right)\\& = \frac{283}{24}g^2 + 27 g^{3/2} + 108 g( \ln (13g) + 1) + 468 g.\end{align*}
\begin{align*}C(K_4,G)& \leqslant \frac{32}{3}g^2 +36 \left( \frac{g^2}{32} + \frac{3g^{3/2}}{4} + 3g( \ln (13g) + 1) + 13g \right)\\& = \frac{283}{24}g^2 + 27 g^{3/2} + 108 g( \ln (13g) + 1) + 468 g.\end{align*}
6.3 General complete graph
Now consider the case when
![]() $H=K_s$
for some
$H=K_s$
for some
![]() $s\geqslant 5$
. Theorem 1.2 shows that
$s\geqslant 5$
. Theorem 1.2 shows that
![]() $C(K_s,\Sigma,n)$
is bounded for fixed s and
$C(K_s,\Sigma,n)$
is bounded for fixed s and
![]() $\Sigma$
. We now show how to determine
$\Sigma$
. We now show how to determine
![]() $C(K_s,\Sigma,n)$
more precisely.
$C(K_s,\Sigma,n)$
more precisely.
Theorem 6.8 For every integer
![]() $s\geqslant5$
and surface
$s\geqslant5$
and surface
![]() $\Sigma$
there is an irreducible triangulation G such that
$\Sigma$
there is an irreducible triangulation G such that
![]() $C(K_s,G)=\max_n C(K_s,\Sigma,n)$
.
$C(K_s,G)=\max_n C(K_s,\Sigma,n)$
.
Proof. Let
![]() $q\;:\!=\;\max_n C(K_s,\Sigma,n)$
. Let
$q\;:\!=\;\max_n C(K_s,\Sigma,n)$
. Let
![]() $G_0$
be a graph embedded in
$G_0$
be a graph embedded in
![]() $\Sigma$
with
$\Sigma$
with
![]() $C(K_s,G_0)=q$
. As described in the proof of Lemma 6.1, we can add edges and vertices to
$C(K_s,G_0)=q$
. As described in the proof of Lemma 6.1, we can add edges and vertices to
![]() $G_0$
to create a triangulation G of
$G_0$
to create a triangulation G of
![]() $\Sigma$
. Adding edges and vertices does not remove copies of
$\Sigma$
. Adding edges and vertices does not remove copies of
![]() $K_s$
. Thus,
$K_s$
. Thus,
![]() $C(K_s,G)=q$
. If G is irreducible, then we are done. Otherwise, some edge vw of G is in exactly two triangles vwx and vwy. Let
$C(K_s,G)=q$
. If G is irreducible, then we are done. Otherwise, some edge vw of G is in exactly two triangles vwx and vwy. Let
![]() $G'\;:\!=\;G/vw$
. Then, G’ is another triangulation of
$G'\;:\!=\;G/vw$
. Then, G’ is another triangulation of
![]() $\Sigma$
. Observe that every clique of G that is not in G’ is in
$\Sigma$
. Observe that every clique of G that is not in G’ is in
![]() $\{A\cup\{w\}\;:\;A\subseteq\{x,v,y\}\}$
. Each such clique has at most four vertices. Thus,
$\{A\cup\{w\}\;:\;A\subseteq\{x,v,y\}\}$
. Each such clique has at most four vertices. Thus,
![]() $C(K_s,G')=C(K_s,G)=q$
. Repeat this step to G’ until we obtain an irreducible triangulation G” with
$C(K_s,G')=C(K_s,G)=q$
. Repeat this step to G’ until we obtain an irreducible triangulation G” with
![]() $C(K_s,G'')=q$
.
$C(K_s,G'')=q$
.
We now prove a precise bound on
![]() $C(K_s,\Sigma,n)$
, making no effort to optimise the constant 300.
$C(K_s,\Sigma,n)$
, making no effort to optimise the constant 300.
Theorem 6.9 For every integer
![]() $s\geqslant 5$
and surface
$s\geqslant 5$
and surface
![]() $\Sigma$
of Euler genus g and for all n,
$\Sigma$
of Euler genus g and for all n,
 \begin{align*}\left(\frac{\sqrt{6 g}}{s}\right)^s\leqslant C(K_s,\Sigma,n) \leqslant \left(\frac{300 \sqrt{g} }{s}\right)^s,\end{align*}
\begin{align*}\left(\frac{\sqrt{6 g}}{s}\right)^s\leqslant C(K_s,\Sigma,n) \leqslant \left(\frac{300 \sqrt{g} }{s}\right)^s,\end{align*}
where the lower bound holds for all
![]() $n\geqslant\sqrt{6g}\geqslant s$
and the upper bound holds for all n.
$n\geqslant\sqrt{6g}\geqslant s$
and the upper bound holds for all n.
Proof. For the lower bound, it follows from the Map Colour Theorem [Reference Ringel62] that
![]() $K_p$
embeds in
$K_p$
embeds in
![]() $\Sigma$
where
$\Sigma$
where
![]() $p\;:\!=\;\lceil{{\sqrt{6g}}}\rceil$
. Thus, for
$p\;:\!=\;\lceil{{\sqrt{6g}}}\rceil$
. Thus, for
![]() $n\geqslant p\geqslant s$
,
$n\geqslant p\geqslant s$
,
 \begin{align*}C(K_s,\Sigma,n)\geqslant \binom{\sqrt{6g}}{s}\geqslant\left(\frac{\sqrt{6g}}{s}\right)^s.\end{align*}
\begin{align*}C(K_s,\Sigma,n)\geqslant \binom{\sqrt{6g}}{s}\geqslant\left(\frac{\sqrt{6g}}{s}\right)^s.\end{align*}
Now we prove the upper bound. The claim is trivial for
![]() $g=0$
, so assume that
$g=0$
, so assume that
![]() $g\geqslant 1$
. By Theorem 6.8, it suffices to consider an irreducible triangulation G of
$g\geqslant 1$
. By Theorem 6.8, it suffices to consider an irreducible triangulation G of
![]() $\Sigma$
. Joret and Wood [Reference Joret and Wood41] proved that
$\Sigma$
. Joret and Wood [Reference Joret and Wood41] proved that
![]() $n\;:\!=\;|V(G)|\leqslant 13g$
. Let
$n\;:\!=\;|V(G)|\leqslant 13g$
. Let
![]() $v_1,\dots,v_n$
be a vertex ordering of G, where
$v_1,\dots,v_n$
be a vertex ordering of G, where
![]() $v_i$
has minimum degree in
$v_i$
has minimum degree in
![]() $G_i\;:\!=\;G[\{v_1,\dots,v_i\}]$
. By Euler’s formula,
$G_i\;:\!=\;G[\{v_1,\dots,v_i\}]$
. By Euler’s formula,
Define
![]() $m\;:\!=\;\lceil{{\sqrt{g}}}\rceil$
. The number of copies of
$m\;:\!=\;\lceil{{\sqrt{g}}}\rceil$
. The number of copies of
![]() $K_s$
in
$K_s$
in
![]() $G[\{v_1,\dots,v_m\}]$
is at most
$G[\{v_1,\dots,v_m\}]$
is at most
Charge every other copy X of
![]() $K_s$
to the rightmost vertex in X (with respect to
$K_s$
to the rightmost vertex in X (with respect to
![]() $v_1,\dots,v_n$
). For
$v_1,\dots,v_n$
). For
![]() $m+1\leqslant i\leqslant n$
, the number of copies of
$m+1\leqslant i\leqslant n$
, the number of copies of
![]() $K_s$
charged to
$K_s$
charged to
![]() $v_i$
is at most
$v_i$
is at most
In total,
 \begin{equation*}C(K_s,G)\leqslant\left(\frac{2e}{s}\right)^s g^{s/2} +\left(\frac{84eg}{s-1}\right)^{s-1}\sum_{i\geqslant m+1}\frac{1}{i^{s-1}}.\end{equation*}
\begin{equation*}C(K_s,G)\leqslant\left(\frac{2e}{s}\right)^s g^{s/2} +\left(\frac{84eg}{s-1}\right)^{s-1}\sum_{i\geqslant m+1}\frac{1}{i^{s-1}}.\end{equation*}
By (1),
Since
![]() $m\geqslant\sqrt{g}$
,
$m\geqslant\sqrt{g}$
,
6.4 Computational results
For
![]() $\Sigma\in\{\mathbb{S}_0,\mathbb{S}_1, \mathbb{S}_2,\mathbb{N}_1, \mathbb{N}_2, \mathbb{N}_3,\mathbb{N}_4\}$
, we use Lemmas 6.1 and 6.5 and Theorem 6.8, the lists of all irreducible triangulations [Reference Lavrenchenko42,Reference Lawrencenko and Negami43,Reference Sulanke63,Reference Sulanke65], and an elementary computer program to count cliques to obtain the exact results for
$\Sigma\in\{\mathbb{S}_0,\mathbb{S}_1, \mathbb{S}_2,\mathbb{N}_1, \mathbb{N}_2, \mathbb{N}_3,\mathbb{N}_4\}$
, we use Lemmas 6.1 and 6.5 and Theorem 6.8, the lists of all irreducible triangulations [Reference Lavrenchenko42,Reference Lawrencenko and Negami43,Reference Sulanke63,Reference Sulanke65], and an elementary computer program to count cliques to obtain the exact results for
![]() $C(K_s,\Sigma,n)$
shown in Table 1.
$C(K_s,\Sigma,n)$
shown in Table 1.
Table 1. The maximum number of copies of
![]() $K_s$
in an n-vertex graph embeddable in surface
$K_s$
in an n-vertex graph embeddable in surface
![]() $\Sigma$
$\Sigma$

Let C(G) be the total number of complete subgraphs in a graph G; that is
![]() $C(G)=\sum_{s\geqslant 0}C(K_s,G)$
. For a surface
$C(G)=\sum_{s\geqslant 0}C(K_s,G)$
. For a surface
![]() $\Sigma$
, let
$\Sigma$
, let
![]() $C(\Sigma,n)$
be the maximum of C(G) taken over all n-vertex graphs G embeddable in
$C(\Sigma,n)$
be the maximum of C(G) taken over all n-vertex graphs G embeddable in
![]() $\Sigma$
. Dujmović et al. [Reference Dujmović, Fijavž, Joret, Sulanke and Wood17] proved that
$\Sigma$
. Dujmović et al. [Reference Dujmović, Fijavž, Joret, Sulanke and Wood17] proved that
![]() $C(\Sigma,n)-8n$
is bounded for fixed
$C(\Sigma,n)-8n$
is bounded for fixed
![]() $\Sigma$
, which is implied by Theorems 6.4, 6.7 and 6.9. The following conjectures have been verified for each of
$\Sigma$
, which is implied by Theorems 6.4, 6.7 and 6.9. The following conjectures have been verified for each of
![]() $\mathbb{S}_0$
,
$\mathbb{S}_0$
,
![]() $\mathbb{S}_1$
,
$\mathbb{S}_1$
,
![]() $\mathbb{S}_2$
,
$\mathbb{S}_2$
,
![]() $\mathbb{N}_1$
,
$\mathbb{N}_1$
,
![]() $\mathbb{N}_2$
,
$\mathbb{N}_2$
,
![]() $\mathbb{N}_3$
,
$\mathbb{N}_3$
,
![]() $\mathbb{N}_4$
.
$\mathbb{N}_4$
.
Conjecture 6.10 For every surface
![]() $\Sigma$
and integer n,
$\Sigma$
and integer n,
Conjecture 6.11 If
![]() $C(G)=C(\Sigma,n)$
for some n-vertex graph G embeddable in a surface
$C(G)=C(\Sigma,n)$
for some n-vertex graph G embeddable in a surface
![]() $\Sigma$
, then for
$\Sigma$
, then for
![]() $s\geqslant 0$
,
$s\geqslant 0$
,
Conversely, we conjecture that maximising the number of triangles is equivalent to maximising the total number of complete subgraphs. More precisely:
Conjecture 6.12 If
![]() $C(K_3,G)=C(K_3,\Sigma,n)$
for some n-vertex graph G embeddable in a surface
$C(K_3,G)=C(K_3,\Sigma,n)$
for some n-vertex graph G embeddable in a surface
![]() $\Sigma$
, then
$\Sigma$
, then
Note that
![]() $K_3$
cannot be replaced by some arbitrary complete graph in Conjecture 6.12. For example, every graph embeddable in
$K_3$
cannot be replaced by some arbitrary complete graph in Conjecture 6.12. For example, every graph embeddable in
![]() $\mathbb{N}_3$
contains at most one copy of
$\mathbb{N}_3$
contains at most one copy of
![]() $K_7$
, but there are irreducible triangulations G of
$K_7$
, but there are irreducible triangulations G of
![]() $\mathbb{N}_3$
that contain
$\mathbb{N}_3$
that contain
![]() $K_7$
and do not maximise the total number of cliques (that is,
$K_7$
and do not maximise the total number of cliques (that is,
![]() $C(G)<8|V(G)|+104$
). Similarly, every graph embeddable in
$C(G)<8|V(G)|+104$
). Similarly, every graph embeddable in
![]() $\mathbb{N}_4$
contains at most 8 copies of
$\mathbb{N}_4$
contains at most 8 copies of
![]() $K_7$
, but there are irreducible triangulations G of
$K_7$
, but there are irreducible triangulations G of
![]() $\mathbb{N}_4$
for which
$\mathbb{N}_4$
for which
![]() $C(K_7,G)=8$
and
$C(K_7,G)=8$
and
![]() $C(G)<8|V(G)|+216$
.
$C(G)<8|V(G)|+216$
.
7 Minor-closed classes
Consider the following natural open problem extending our results for graphs on surfaces: For graphs H and X and an integer n, what is the maximum number of copies of H in an n-vertex X-minor-free graph? This problem has been extensively studied when H and X are complete graphs [Reference Fomin22,Reference Fox and Wei23,Reference Lee and Oum44,Reference Norine, Seymour, Thomas and Wollan58,Reference Reed and Wood60,Reference Wood69]. Eppstein [Reference Eppstein18] proved the following result when X is a complete bipartite graph and H is highly connected.
Theorem 7.1 ([18)] Fix positive integers
![]() $s\leqslant t$
and a
$s\leqslant t$
and a
![]() $K_{s,t}$
-minor-free graph H with no
$K_{s,t}$
-minor-free graph H with no
![]() $(\leqslant s-1)$
-separation. Then every n-vertex
$(\leqslant s-1)$
-separation. Then every n-vertex
![]() $K_{s,t}$
-minor-free graph contains O(n) copies of H.
$K_{s,t}$
-minor-free graph contains O(n) copies of H.
What happens when H is not highly connected? We have the following lower bound. Fix positive integers
![]() $s\leqslant t$
and a
$s\leqslant t$
and a
![]() $K_{s,t}$
-minor-free graph H. If H has no
$K_{s,t}$
-minor-free graph H. If H has no
![]() $(\leqslant s-1)$
-separation, then let
$(\leqslant s-1)$
-separation, then let
![]() $k\;:\!=\;1$
; otherwise, let k be the maximum number of pairwise independent
$k\;:\!=\;1$
; otherwise, let k be the maximum number of pairwise independent
![]() $(\leqslant s-1)$
-separations in H. The construction in Section 2 generalises to give n-vertex
$(\leqslant s-1)$
-separations in H. The construction in Section 2 generalises to give n-vertex
![]() $K_{s,t}$
-minor-free graphs containing
$K_{s,t}$
-minor-free graphs containing
![]() $\Theta(n^k)$
copies of H.
$\Theta(n^k)$
copies of H.
The following question naturally arises:
Open Problem 7.2 Does every n-vertex
![]() $K_{s,t}$
-minor-free graph contain
$K_{s,t}$
-minor-free graph contain
![]() $O(n^k)$
copies of H?
$O(n^k)$
copies of H?
By Theorem 7.1, the answer is ‘yes’ if
![]() $k=1$
. The methods presented in this paper show the answer is ‘yes’ if
$k=1$
. The methods presented in this paper show the answer is ‘yes’ if
![]() $s\leqslant 3$
. We omit the proof, since it is essentially the same as for graphs embedded on a surface, except that in the
$s\leqslant 3$
. We omit the proof, since it is essentially the same as for graphs embedded on a surface, except that in the
![]() $k=1$
case we use Theorem 7.1 instead of the additivity of Euler genus (Theorem 3.3).
$k=1$
case we use Theorem 7.1 instead of the additivity of Euler genus (Theorem 3.3).
When H is a tree, this problem specialises as follows: Fix a tree T and positive integers
![]() $s\leqslant t$
. Let
$s\leqslant t$
. Let
![]() $\beta(T)$
be the size of the largest stable set of vertices in T, each with degree at most
$\beta(T)$
be the size of the largest stable set of vertices in T, each with degree at most
![]() $s-1$
. The construction in Corollary 1.3 generalises to give n-vertex
$s-1$
. The construction in Corollary 1.3 generalises to give n-vertex
![]() $K_{s,t}$
-minor-free graphs containing
$K_{s,t}$
-minor-free graphs containing
![]() $\Omega(n^{\beta(T)})$
copies of T.
$\Omega(n^{\beta(T)})$
copies of T.
Open Problem 7.3 Does every n-vertex
![]() $K_{s,t}$
-minor-free graph contain
$K_{s,t}$
-minor-free graph contain
![]() $O(n^{\beta(T)})$
copies of T?
$O(n^{\beta(T)})$
copies of T?
8. Homomorphism inequalities
This section reinterprets some of our results in terms of homomorphism inequalities and presents some open problems that arise from this viewpoint.
For two graphs H and G, a homomorphism from H to G is a function
![]() $\phi\;:\;V(H)\rightarrow V(G)$
that preserves adjacency; that is,
$\phi\;:\;V(H)\rightarrow V(G)$
that preserves adjacency; that is,
![]() $\phi(v)\phi(w)$
is an edge of G for each edge vw of H. Let
$\phi(v)\phi(w)$
is an edge of G for each edge vw of H. Let
![]() $\hom(H,G)$
be the number of homomorphisms from H to G. For example,
$\hom(H,G)$
be the number of homomorphisms from H to G. For example,
![]() $\hom(H,K_t)>0$
if and only if H is t-colourable. In the other direction,
$\hom(H,K_t)>0$
if and only if H is t-colourable. In the other direction,
![]() $\hom(K_1, G)$
is the number of vertices in G, and
$\hom(K_1, G)$
is the number of vertices in G, and
![]() $\hom(K_2, G)$
is twice the number of edges in G, and
$\hom(K_2, G)$
is twice the number of edges in G, and
![]() $\hom(K_3,G)$
is 6 times the number of triangles in G.
$\hom(K_3,G)$
is 6 times the number of triangles in G.
Homomorphism inequalities encode bounds on the number of copies of given graphs in a host graph. Much of extremal graph theory can be written in terms of homomorphism inequalities, and a beautiful theory has recently developed that greatly simplifies the task of proving such inequalities; see [Reference Lovász46].
Consider the following concrete example. [Reference Mantel51] proved that every n-vertex graph with more than
![]() $\frac{n^2}{4}$
edges has a triangle, which is tight for the complete bipartite graph
$\frac{n^2}{4}$
edges has a triangle, which is tight for the complete bipartite graph
![]() $K_{n/2,n/2}$
. [Reference Goodman29] strengthened Mantel’s Theorem by providing a lower bound of
$K_{n/2,n/2}$
. [Reference Goodman29] strengthened Mantel’s Theorem by providing a lower bound of
![]() $\frac{m}{3} ( \frac{4m}{n} - n )$
on the number of triangles in an n-vertex m-edge graph. Goodman’s Theorem can be rewritten as the following homomorphism inequality:
$\frac{m}{3} ( \frac{4m}{n} - n )$
on the number of triangles in an n-vertex m-edge graph. Goodman’s Theorem can be rewritten as the following homomorphism inequality:
In a celebrated application of the flag algebra method, Razborov [Reference Razborov59] generalised (2) by determining the minimum number of triangles in an n-vertex m-edge graph. The minimum number of copies of
![]() $K_r$
in an n-vertex m-edge graph (the natural extension of Turan’s Theorem) was a notoriously difficult question [Reference Lovász and Simonovits47,Reference Lovász and Simonovits48], recently solved for
$K_r$
in an n-vertex m-edge graph (the natural extension of Turan’s Theorem) was a notoriously difficult question [Reference Lovász and Simonovits47,Reference Lovász and Simonovits48], recently solved for
![]() $r=4$
by Nikiforov [Reference Nikiforov57] and in general by Reiher [Reference Reiher61]. All of these results can be written in terms of homomorphism inequalities.
$r=4$
by Nikiforov [Reference Nikiforov57] and in general by Reiher [Reference Reiher61]. All of these results can be written in terms of homomorphism inequalities.
The results of this paper can be written in terms of homomorphism counts, since I(H,G) equals the number of injective homomorphisms from H to G, which equals
![]() $\hom(H,G)$
if H is a complete graph.
$\hom(H,G)$
if H is a complete graph.
Here is another example of a homomorphism inequality for graphs on surfaces. Euler’s Formula implies
Footnote c
that the number of triangles in an n-vertex m-edge graph with Euler genus g is at least
![]() $2(m-2n+4-2g)$
. This result is an analogue of Goodman’s Theorem for graphs G of Euler genus g and can be written as the following homomorphism inequality:
$2(m-2n+4-2g)$
. This result is an analogue of Goodman’s Theorem for graphs G of Euler genus g and can be written as the following homomorphism inequality:
We consider it an interesting line of research to prove similar homomorphism inequalities in other minor-closed classes. The following open problems naturally arise.
-
Is there a method (akin to flag algebras [Reference Razborov59] or graph algebras [Reference Lovász46]) for systematically proving homomorphism inequalities in minor-closed classes?
-
Hatami and Norine [Reference Hatami and Norine39] proved that it is undecidable to test the validity of a linear homomorphism inequality. In which minor-closed classes is it decidable to test the validity of a linear homomorphism inequality?
These questions are open even for forests; see [Reference Bubeck, Edwards, Mania and Supko12–Reference Chan, Kráľ, Mohar and Wood14,Reference Czabarka, Székely and Wagner16] for related results.
Closely related to the study of graph homomorphisms is the theory of graph limits and graphons [Reference Lovász46]. While this theory focuses on dense graphs, a theory of graph limits for sparse graphs is emerging. For example, results are known for bounded degree graphs [Reference Borgs, Chayes, Kahn and Lovász11,Reference Hatami, Lovász and Szegedy38], planar graphs [Reference Benjamini and Schramm10,Reference Gurel-Gurevich and Nachmias30], and bounded tree-depth graphs [Reference Nešetřil and Ossona de Mendez56]. The above questions regarding graph homomorphisms parallel the theory of graph limits in sparse classes.
Acknowledgement
We would like to thank Kevin Hendrey for alerting us to an error in the proof of Theorem 1.2 in an earlier version of this paper. We also thank Casey Tompkins for pointing out reference [Reference Győri, Paulos, Salia, Tompkins and Zamora33]. Győri et al. [Reference Győri, Paulos, Salia, Tompkins and Zamora33] prove Corollary 1.3 in the case
![]() $\Sigma=\mathbb{S}_0$
and conjecture that
$\Sigma=\mathbb{S}_0$
and conjecture that
![]() $C(H,\Sigma_0,n)=\Theta(n^k)$
for some integer
$C(H,\Sigma_0,n)=\Theta(n^k)$
for some integer
![]() $k=k(H)$
, which is implied by Theorem 1.2. Finally, many thanks to the referee for several insightful comments.
$k=k(H)$
, which is implied by Theorem 1.2. Finally, many thanks to the referee for several insightful comments.
Postscript
Following the initial release of this paper, Open Problem 7.2 was answered in the negative by [Reference Liu45] and Open Problem 7.3 was answered in the affirmative by Huynh and Wood [Reference Huynh and Wood40].