Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-02-11T19:16:31.777Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability and Turán Numbers of a Class of Hypergraphs via Lagrangians

Part of: Graph theory

Published online by Cambridge University Press:  29 March 2017

AXEL BRANDT ,
DAVID IRWIN  and
TAO JIANG
AXEL BRANDT
Affiliation:
Department of Mathematics and Computer Science, Davidson College, Davidson, NC 28035, USA (e-mail: axbrandt@davidson.edu)
DAVID IRWIN
Affiliation:
Department of Mathematics, Ohio State University, Columbus, OH 43210, USA (e-mail: irwin.315@osu.edu)
TAO JIANG
Affiliation:
Department of Mathematics, Miami University, Oxford, OH 45056, USA (e-mail: jiangt@miamioh.edu)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

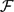Given a family of r-uniform hypergraphs ${\cal F}$ (or r-graphs for brevity), the Turán number ex(n,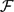${\cal F})$ of 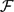${\cal F}$ is the maximum number of edges in an r-graph on n vertices that does not contain any member of 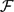${\cal F}$. A pair {u,v} is covered in a hypergraph G if some edge of G contains {u, v}. Given an r-graph F and a positive integer p ⩾ n(F), where n(F) denotes the number of vertices in F, let HFp denote the r-graph obtained as follows. Label the vertices of F as v1,. . .,vn(F). Add new vertices vn(F)+1,. . .,vp. For each pair of vertices vi, vj not covered in F, add a set Bi,j of r − 2 new vertices and the edge {vi, vj} ∪ Bi,j, where the Bi,j are pairwise disjoint over all such pairs {i, j}. We call HFp the expanded p-clique with an embedded F. For a relatively large family of F, we show that for all sufficiently large n, ex(n,HFp) = |Tr(n, p − 1)|, where Tr(n, p − 1) is the balanced complete (p − 1)-partite r-graph on n vertices. We also establish structural stability of near-extremal graphs. Our results generalize or strengthen several earlier results and provide a class of hypergraphs for which the Turán number is exactly determined (for large n).

MSC classification

Primary: 05C65: Hypergraphs
Secondary: 05C35: Extremal problems
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 26 , Issue 3 , May 2017 , pp. 367 - 405
Copyright
Copyright © Cambridge University Press 2017 

References

[1] Ajtai, M., Komlós, J., Simonovits, M. and Szemerédi, E. Unpublished. The solution of the Erdos-Sos conjecture for large trees, in preparation.Google Scholar
[2] Bollobás, B. (1974) Three-graphs without two triples whose symmetric difference is contained in a third. Discrete Math. 8 21–24.CrossRefGoogle Scholar
[3] Erdős, P. (1964) On extremal problems of graphs and generalized graphs. Israel J. Math. 2 183–190.CrossRefGoogle Scholar
[4] Erdős, P. (1965) A problem on independent r-tuples. Ann. Univ. Sci. Budapest 8 93–95.Google Scholar
[5] Erdős, P. and Simonovits, M. (1966) A limit theorem in graph theory. Studia. Sci. Math. Hungar. 1 51–57.Google Scholar
[6] Frankl, P. (2013) Improved bounds for Erdős' matching conjecture. J. Combin. Theory Ser. A 120 1068–1072.CrossRefGoogle Scholar
[7] Frankl, P. and Füredi, Z. (1983) A new generalization of the Erdős–Ko–Rado theorem. Combinatorica 3 341–349.CrossRefGoogle Scholar
[8] Frankl, P. and Füredi, Z. (1989) Extremal problems whose solutions are the blowups of the small Witt-designs. J. Combin. Theory Ser. A 52 129–147.CrossRefGoogle Scholar
[9] Füredi, Z., Pikhurko, O. and Simonovits, M. (2005) On triple systems with independent neighbourhoods. Combin. Probab. Comput. 14 795–813.CrossRefGoogle Scholar
[10] Hefetz, D. and Keevash, P. (2013) A hypergraph Turán theorem via Lagrangians of intersecting families. J. Combin. Theory Ser. A 120 2020–2038.CrossRefGoogle Scholar
[11] Jiang, T., Peng, Y. and Wu, B. Turán numbers of extensions of some sparse hypergraphs via Lagrangians, in preparation. arXiv:1609.08983 Google Scholar
[12] Katona, G. O. H. (1974) Extremal problems for hypergraphs. In Combinatorics (Hall, M. Jr and van Lint, J. H., eds), Vol. 16 of the NATO Advanced Study Institutes series, Springer pp. 215–244.Google Scholar
[13] Keevash, P. (2011) Hypergraph Turán Problems, Surveys in Combinatorics, Cambridge University Press, pp. 83–140.Google Scholar
[14] Keevash, P. and Mubayi, D. (2004) Stability theorems for cancellative hypergraphs. J. Combin. Theory Ser. B 92 163–175.CrossRefGoogle Scholar
[15] Mubayi, D. (2006) A hypergraph extension of Turán's theorem. J. Combin. Theory Ser. B 96 122–134.CrossRefGoogle Scholar
[16] Mubayi, D. and Pikhurko, O. (2007) A new generalization of Mantel's theorem to k-graphs. J. Combin. Theory Ser. B 97 669–678.CrossRefGoogle Scholar
[17] Motzkin, T. S. and Straus, E. G. (1965) Maxima for graphs and a new proof of a theorem of Turán. Canad. J. Math. 17 533–540.CrossRefGoogle Scholar
[18] Norin, S. and Yepremyan, L. (2017) Turán number of generalized triangles. J. Combin. Theory Ser. A 146 312–343.CrossRefGoogle Scholar
[19] Norin, S. and Yepremyan, L. Turán numbers of extensions, in preparation. arXiv:1510.04689 Google Scholar
[20] Pikhurko, O. (2008) An exact Turán result for the generalized triangle. Combinatorica 28 187–208.CrossRefGoogle Scholar
[21] Pikhurko, O. (2013) Exact computation of the hypergraph Turán function for expanded complete 2-graphs. J. Combin. Theory Ser. B 103 220–225.CrossRefGoogle Scholar
[22] Shearer, J. (1996) A new construction for cancellative families of sets. Electron. J. Combin. 3 R15.CrossRefGoogle Scholar
[23] Sidorenko, A. F. (1987) On the maximal number of edges in a homogeneous hypergraph that does not contain prohibited subgraphs. Mat. Zametki 41 433–455.Google Scholar
[24] Sidorenko, A. F. (1989) Asymptotic solution for a new class of forbidden r-graphs. Combinatorica 9 207–215.CrossRefGoogle Scholar
[25] Simonovits, M. (1968) A method for solving extremal problems in graph theory. In Theory of Graphs: Proc. Coll. Tihany, Hungary (Erdős, P. and Katona, G., eds), Academic Press, pp. 279–319.Google Scholar
[26] Yepremyan, L. (2016) PhD dissertation, McGill University.Google Scholar