Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-02-11T07:40:43.252Z Has data issue: false hasContentIssue false
  • English
  • Français

On Families of Subsets With a Forbidden Subposet

Published online by Cambridge University Press:  01 September 2009

JERROLD R. GRIGGS  and
LINYUAN LU
JERROLD R. GRIGGS
Affiliation:
Department of Mathematics, University of South Carolina, Columbia, SC 29208, USA (e-mail: griggs@math.sc.edu, lu@math.sc.edu)
LINYUAN LU
Affiliation:
Department of Mathematics, University of South Carolina, Columbia, SC 29208, USA (e-mail: griggs@math.sc.edu, lu@math.sc.edu)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

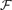Let ⊂ 2[n] be a family of subsets of {1, 2,. . ., n}. For any poset H, we say 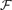is H-free if 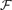does not contain any subposet isomorphic to H. Katona and others have investigated the behaviour of La(n, H), which denotes the maximum size of H-free families 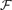⊂ 2[n]. Here we use a new approach, which is to apply methods from extremal graph theory and probability theory to identify new classes of posets H, for which La(n, H) can be determined asymptotically as n → ∞ for various posets H, including two-end-forks, up-down trees, and cycles C4k on two levels.

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 18 , Issue 5: New Directions in Algorithms, Combinatorics and Optimization , September 2009 , pp. 731 - 748
Copyright
Copyright © Cambridge University Press 2009

References

[1]Bukh, B. (2008) Set families with a forbidden poset. Preprint: arXiv:0803.3840.Google Scholar
[2]Carroll, T. and Katona, G. O. H. (2008) Bounds on maximal families of sets not containing three sets with A ∪ B ⊂ C, A ⊄ B. Order 25 229–236.CrossRefGoogle Scholar
[3]Chernoff, H. (1981) A note on an inequality involving the normal distribution. Ann. Probab. 9 533–535.CrossRefGoogle Scholar
[4]De Bonis, A. and Katona, G. O. H. (2007) Largest families without an r-fork. Order 24 181–191.CrossRefGoogle Scholar
[5]De Bonis, A., Katona, G. O. H. and Swanepoel, K. J. (2005) Largest family without A ∪ B ⊂ C ∩ D. J. Combin. Theory Ser. A 111 331–336.CrossRefGoogle Scholar
[6]Erdős, P. (1945) On a lemma of Littlewood and Offord. Bull. Amer. Math. Soc. 51 898–902.CrossRefGoogle Scholar
[7]Erdős, P. and Simonovits, M. (1966) A limit theorem in graph theory. Studia Sci. Math. Hungar. 1 51–57.Google Scholar
[8]Erdős, P. and Stone, A. H. (1946) On the structure of linear graphs. Bull. Amer. Math. Soc. 52 1087–1091.CrossRefGoogle Scholar
[9]Fortuin, C. M., Kasteleyn, P. N. and Ginibre, J. (1971) Correlation inequalities for some partially ordered sets. Comm. Math. Phys. 22 89–103.CrossRefGoogle Scholar
[10]Griggs, J. R. and Katona, G. O. H. (2008) No four subsets forming an N. J. Combin. Theory Ser. A 115 677–685.CrossRefGoogle Scholar
[11]Katona, G. O. H. (2008) Forbidden inclusion patterns in the families of subsets (introducing a method). In Horizons of Combinatorics, Vol. 17 of Bolyai Society Mathematical Studies, Bolyai Mathematical Society, Budapest, and Springer, pp. 119–140.CrossRefGoogle Scholar
[12]Sperner, E. (1928) Ein Satzüber Untermengen einer endlichen Menge. Math. Z. 27 544–548.CrossRefGoogle Scholar
[13]Thanh, H. T. (1998) An extremal problem with excluded subposets in the Boolean lattice. Order 15 51–57.CrossRefGoogle Scholar