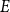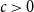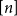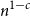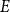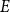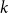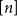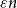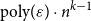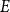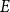1. Introduction
Turán-type questions are some of the most well-studied problems in combinatorics. They typically ask how ‘dense’ should an object be in order to guarantee that it contains a certain small substructure. In the setting of graphs, this question asks how many edges an
![]() $n$
-vertex graph should contain in order to force the appearance of some fixed graph
$n$
-vertex graph should contain in order to force the appearance of some fixed graph
![]() $H$
. For example, a central open problem in this area asks, given a bipartite graph
$H$
. For example, a central open problem in this area asks, given a bipartite graph
![]() $H$
, to determine the smallest
$H$
, to determine the smallest
![]() $T=T_{H}(\varepsilon )$
so that for every
$T=T_{H}(\varepsilon )$
so that for every
![]() $n\geq T$
every
$n\geq T$
every
![]() $n$
-vertex graph with
$n$
-vertex graph with
![]() $\varepsilon\!\left(\begin{smallmatrix}n\\ 2\end{smallmatrix}\right)$
edges contains a copy of
$\varepsilon\!\left(\begin{smallmatrix}n\\ 2\end{smallmatrix}\right)$
edges contains a copy of
![]() $H$
(see [Reference Bukh3] for recent progress). A closely related question which also attracted a lot of attention is the supersaturation problem, introduced by Erdős and Simonovits [Reference Erdős and Simonovits5] in the 80s. In the setting of Turán’s problem for bipartite
$H$
(see [Reference Bukh3] for recent progress). A closely related question which also attracted a lot of attention is the supersaturation problem, introduced by Erdős and Simonovits [Reference Erdős and Simonovits5] in the 80s. In the setting of Turán’s problem for bipartite
![]() $H$
, the supersaturation question asks to determine the largest
$H$
, the supersaturation question asks to determine the largest
![]() $T^*_{H}(\varepsilon )$
so that every
$T^*_{H}(\varepsilon )$
so that every
![]() $n$
-vertex graph with
$n$
-vertex graph with
![]() $\varepsilon\! \left(\begin{smallmatrix}n\\ 2\end{smallmatrix}\right)$
edges contains at least
$\varepsilon\! \left(\begin{smallmatrix}n\\ 2\end{smallmatrix}\right)$
edges contains at least
![]() $(T^*_{H}(\varepsilon )-o_n(1)) \cdot n^h$
labelled copies of
$(T^*_{H}(\varepsilon )-o_n(1)) \cdot n^h$
labelled copies of
![]() $H$
, where
$H$
, where
![]() $h=|V(H)|$
and
$h=|V(H)|$
and
![]() $o_n(1)$
denotes a quantity tending to
$o_n(1)$
denotes a quantity tending to
![]() $0$
as
$0$
as
![]() $n \rightarrow \infty$
. One of the central conjectures in this area, due to Sidorenko, suggests that
$n \rightarrow \infty$
. One of the central conjectures in this area, due to Sidorenko, suggests that
![]() $T^*_{H}(\varepsilon ) = \varepsilon ^{m}$
, where
$T^*_{H}(\varepsilon ) = \varepsilon ^{m}$
, where
![]() $m=|E(H)|$
(see [Reference Conlon, Kim, Lee and Lee4] for recent progress).
$m=|E(H)|$
(see [Reference Conlon, Kim, Lee and Lee4] for recent progress).
We now describe two problems in additive number theory, which are analogous to the graph problems described above. We say that a homogenous linear equation
![]() $\sum ^k_{i=1}a_ix_i=0$
is invariant if
$\sum ^k_{i=1}a_ix_i=0$
is invariant if
![]() $\sum _ia_i=0$
. All equations we consider here will be invariant and homogenous. Given a fixed linear equation
$\sum _ia_i=0$
. All equations we consider here will be invariant and homogenous. Given a fixed linear equation
![]() $E$
, the Turán problem for
$E$
, the Turán problem for
![]() $E$
asks to determine the smallest
$E$
asks to determine the smallest
![]() $R=R_{E}(\varepsilon )$
so that for every
$R=R_{E}(\varepsilon )$
so that for every
![]() $n\geq R$
, every
$n\geq R$
, every
![]() $S\subseteq [n]\,:\!=\,\{1,\ldots,n\}$
of size
$S\subseteq [n]\,:\!=\,\{1,\ldots,n\}$
of size
![]() $\varepsilon n$
contains a solution to
$\varepsilon n$
contains a solution to
![]() $E$
in distinct integers. For example, when
$E$
in distinct integers. For example, when
![]() $E$
is the equation
$E$
is the equation
![]() $a+b=2c$
we get the Erdős–Turán–Roth problem on sets avoiding
$a+b=2c$
we get the Erdős–Turán–Roth problem on sets avoiding
![]() $3$
-term arithmetic progressions (see [Reference Kelley and Meka7] for recent progress). Continuing the analogy with the previous paragraph, we can now ask to determine the largest
$3$
-term arithmetic progressions (see [Reference Kelley and Meka7] for recent progress). Continuing the analogy with the previous paragraph, we can now ask to determine the largest
![]() $R^*_{E}(\varepsilon )$
so that every
$R^*_{E}(\varepsilon )$
so that every
![]() $S \subseteq [n]$
of size
$S \subseteq [n]$
of size
![]() $\varepsilon n$
contains at least
$\varepsilon n$
contains at least
![]() $(R^*_{E}(\varepsilon )-o_n(1)) \cdot n^{k-1}$
solutions to
$(R^*_{E}(\varepsilon )-o_n(1)) \cdot n^{k-1}$
solutions to
![]() $E$
, where
$E$
, where
![]() $k$
is the number of variables in
$k$
is the number of variables in
![]() $E$
. We now turn to discuss two aspects which make the arithmetic problems more challenging than the graph problems.
$E$
. We now turn to discuss two aspects which make the arithmetic problems more challenging than the graph problems.
Let us say that
![]() $E$
is sparse if there is
$E$
is sparse if there is
![]() $C=C(H)$
so thatFootnote
1
$C=C(H)$
so thatFootnote
1
![]() $R_E(\varepsilon ) \leq \varepsilon ^{-C}$
. The first aspect which makes the arithmetic landscape more varied is that while in the case of graphs it is well known (and easy) that for every bipartite
$R_E(\varepsilon ) \leq \varepsilon ^{-C}$
. The first aspect which makes the arithmetic landscape more varied is that while in the case of graphs it is well known (and easy) that for every bipartite
![]() $H$
we have
$H$
we have
![]() $T_{H}(\varepsilon )=\text{poly}(1/\varepsilon )$
, this is no longer the case in the arithmetic setting. Indeed, while Sidon’s equation
$T_{H}(\varepsilon )=\text{poly}(1/\varepsilon )$
, this is no longer the case in the arithmetic setting. Indeed, while Sidon’s equation
![]() $a+b=c+d$
is sparse, a well-known construction of Behrend [Reference Behrend1] shows that
$a+b=c+d$
is sparse, a well-known construction of Behrend [Reference Behrend1] shows that
![]() $a+b=2c$
is not sparse.Footnote
2
The problem of determining which equations
$a+b=2c$
is not sparse.Footnote
2
The problem of determining which equations
![]() $E$
are sparse is a wide open problem due to Ruzsa, see Section
$E$
are sparse is a wide open problem due to Ruzsa, see Section
![]() $9$
in [Reference Ruzsa9].
$9$
in [Reference Ruzsa9].
Our main goal in this paper is to study another aspect which differentiates the arithmetic and graph-theoretic problems. While it is easy to translate a bound for
![]() $T_{H}(\varepsilon )$
into a bound for
$T_{H}(\varepsilon )$
into a bound for
![]() $T^*_{H}(\varepsilon )$
(in particular, establishing that
$T^*_{H}(\varepsilon )$
(in particular, establishing that
![]() $T^*_{H}(\varepsilon ) \geq \text{poly}(\varepsilon )$
for all bipartite
$T^*_{H}(\varepsilon ) \geq \text{poly}(\varepsilon )$
for all bipartite
![]() $H$
), it is not clear if one can analogously transform a bound for
$H$
), it is not clear if one can analogously transform a bound for
![]() $R_{E}(\varepsilon )$
into a bound for
$R_{E}(\varepsilon )$
into a bound for
![]() $R^*_{E}(\varepsilon )$
. The first reason is that while we can average over all subsets of vertices of graphs, we can only average over “structured” subsets of
$R^*_{E}(\varepsilon )$
. The first reason is that while we can average over all subsets of vertices of graphs, we can only average over “structured” subsets of
![]() $[n]$
. This makes is hard to establish a black-box reduction/transformation between
$[n]$
. This makes is hard to establish a black-box reduction/transformation between
![]() $R_{E}(\varepsilon )$
and
$R_{E}(\varepsilon )$
and
![]() $R^*_{E}(\varepsilon )$
. The second complication is that, as we mentioned above, we do not know which equations are sparse. This makes it hard to directly relate these two quantities. Following [Reference Girão, Hurley, Illingworth and Michel6], we say that
$R^*_{E}(\varepsilon )$
. The second complication is that, as we mentioned above, we do not know which equations are sparse. This makes it hard to directly relate these two quantities. Following [Reference Girão, Hurley, Illingworth and Michel6], we say that
![]() $E$
is abundant if
$E$
is abundant if
![]() $R^*_{E}(\varepsilon ) \geq \varepsilon ^C$
for some
$R^*_{E}(\varepsilon ) \geq \varepsilon ^C$
for some
![]() $C=C(E)$
. Clearly, if
$C=C(E)$
. Clearly, if
![]() $E$
is abundant then it is also sparse. Girão et al. [Reference Girão, Hurley, Illingworth and Michel6] asked if the converse also holds, that is, if one can transform a polynomial bound for
$E$
is abundant then it is also sparse. Girão et al. [Reference Girão, Hurley, Illingworth and Michel6] asked if the converse also holds, that is, if one can transform a polynomial bound for
![]() $R_{E}(\varepsilon )$
into a polynomial bound for
$R_{E}(\varepsilon )$
into a polynomial bound for
![]() $R^*_{E}(\varepsilon )$
. Our aim in this note is to prove the following.
$R^*_{E}(\varepsilon )$
. Our aim in this note is to prove the following.
Theorem 1.1.
If an invariant equation
![]() $E$
in four variables is sparse, then it is also abundant. More precisely, if
$E$
in four variables is sparse, then it is also abundant. More precisely, if
![]() $R_{E}(\varepsilon ) \leq \varepsilon ^{-C}$
then
$R_{E}(\varepsilon ) \leq \varepsilon ^{-C}$
then
![]() $R^*_{E}(\varepsilon ) \geq \frac 12\varepsilon ^{8C}$
for all small enough
$R^*_{E}(\varepsilon ) \geq \frac 12\varepsilon ^{8C}$
for all small enough
![]() $\varepsilon$
.
$\varepsilon$
.
Given the above discussion, it is natural to extend the problem raised in [Reference Girão, Hurley, Illingworth and Michel6] to all equations
![]() $E$
.
$E$
.
Problem 1.2.
Is it true that for every invariant equation
![]() $E$
there is
$E$
there is
![]() $c=c(E)$
, so that for all small enough
$c=c(E)$
, so that for all small enough
![]() $\varepsilon$
$\varepsilon$
It is interesting to note that Varnavides [Reference Varnavides11] (implicitly) gave a positive answer to Problem 1.2 when
![]() $E$
is the equation
$E$
is the equation
![]() $a+b=2c$
. In fact, essentially the same argument gives a positive answer to this problem for all
$a+b=2c$
. In fact, essentially the same argument gives a positive answer to this problem for all
![]() $E$
in three variables. Hence, Problem 1.2 can be considered as a generalisation of Varnavides’s theorem. Problem 1.2 was also implicitly studied previously in [Reference Bloom2,Reference Kosciuszko8]. In particular, Kosciuszko [Reference Kosciuszko8], extending earlier work of Schoen and Sisask [Reference Schoen and Sisask10], gave direct lower bounds for
$E$
in three variables. Hence, Problem 1.2 can be considered as a generalisation of Varnavides’s theorem. Problem 1.2 was also implicitly studied previously in [Reference Bloom2,Reference Kosciuszko8]. In particular, Kosciuszko [Reference Kosciuszko8], extending earlier work of Schoen and Sisask [Reference Schoen and Sisask10], gave direct lower bounds for
![]() $R^*_E$
which, thanks to [Reference Kelley and Meka7], are quasi-polynomially related to those of
$R^*_E$
which, thanks to [Reference Kelley and Meka7], are quasi-polynomially related to those of
![]() $R_E$
.
$R_E$
.
The proof of Theorem 1.1 is given in the next section. For the sake of completeness, and as a preparation for the proof of Theorem 1.1, we start the next section with a proof that Problem 1.2 holds for equations in three variables. We should point that a somewhat unusual aspect of the proof of Theorem 1.1 is that it uses a Behrend-type [Reference Behrend1] geometric argument in order to find solutions, rather than avoid them.
2. Proofs
In the first subsection below, we give a concise proof of Varnavides’s theorem, namely, of the fact that Problem 1.2 has a positive answer for equations with three variables. In the second subsection, we prove Theorem 1.1.
2.1 Proof of Varnavides’s theorem
Note that for every equation
![]() $E$
, there is a constant
$E$
, there is a constant
![]() $C$
such that for every prime
$C$
such that for every prime
![]() $p\geq Cn$
every solution of
$p\geq Cn$
every solution of
![]() $E$
with integers
$E$
with integers
![]() $x_i \in [n]$
over
$x_i \in [n]$
over
![]() $\mathbb{F}_p$
is also a solution over
$\mathbb{F}_p$
is also a solution over
![]() $\mathbb{R}$
. Since we can always find a prime
$\mathbb{R}$
. Since we can always find a prime
![]() $Cn \leq p \leq 2Cn$
, this means that we can assume that
$Cn \leq p \leq 2Cn$
, this means that we can assume that
![]() $n$
itself is primeFootnote
3
and count solutions over
$n$
itself is primeFootnote
3
and count solutions over
![]() $\mathbb{F}_n$
. So let
$\mathbb{F}_n$
. So let
![]() $S$
be a subset of
$S$
be a subset of
![]() $\mathbb{F}_n$
of size
$\mathbb{F}_n$
of size
![]() $\varepsilon n$
and let
$\varepsilon n$
and let
![]() $R=R_E(\varepsilon/2)$
. For
$R=R_E(\varepsilon/2)$
. For
![]() $b=(b_0,b_1) \in (\mathbb{F}_n)^2$
and
$b=(b_0,b_1) \in (\mathbb{F}_n)^2$
and
![]() $x \in [R]$
let
$x \in [R]$
let
![]() $f_{b}(x)=b_1x+b_0$
andFootnote
4
$f_{b}(x)=b_1x+b_0$
andFootnote
4
![]() $f_{b}([R])=\{x \in [R]\,{:}\, f_{b}(x) \in S\}$
. Pick
$f_{b}([R])=\{x \in [R]\,{:}\, f_{b}(x) \in S\}$
. Pick
![]() $b_0$
and
$b_0$
and
![]() $b_1$
uniformly at random from
$b_1$
uniformly at random from
![]() $\mathbb{F}_n$
and note that for any
$\mathbb{F}_n$
and note that for any
![]() $x \in [R]$
the integer
$x \in [R]$
the integer
![]() $f_{b}(x)$
is uniformly distributed in
$f_{b}(x)$
is uniformly distributed in
![]() $\mathbb{F}_n$
. Hence,
$\mathbb{F}_n$
. Hence,
It is also easy to see that for every
![]() $x \neq y$
the random variables
$x \neq y$
the random variables
![]() $f_b(x)$
and
$f_b(x)$
and
![]() $f_b(y)$
are pairwise independent. Hence,
$f_b(y)$
are pairwise independent. Hence,
Therefore, by Chebyshev’s Inequality we have
In other words, at least
![]() $n^2/2$
choices of
$n^2/2$
choices of
![]() $b$
are such that
$b$
are such that
![]() $|\,f_{b}([R])| \geq \frac{\varepsilon }{2}R$
. By our choice of
$|\,f_{b}([R])| \geq \frac{\varepsilon }{2}R$
. By our choice of
![]() $R$
, this means that
$R$
, this means that
![]() $f_{b}([R])$
contains three distinct integers
$f_{b}([R])$
contains three distinct integers
![]() $x_1,x_2,x_3$
which satisfy
$x_1,x_2,x_3$
which satisfy
![]() $E$
and such that
$E$
and such that
![]() $f_{b}(x_i) \in S$
. Note that if
$f_{b}(x_i) \in S$
. Note that if
![]() $x_1,x_2,x_3$
satisfy
$x_1,x_2,x_3$
satisfy
![]() $E$
, then so do
$E$
, then so do
![]() $f_{b}(x_1),f_{b}(x_2),f_{b}(x_3)$
. Let us denote the triple
$f_{b}(x_1),f_{b}(x_2),f_{b}(x_3)$
. Let us denote the triple
![]() $(f_{b}(x_1),f_{b}(x_2),f_{b}(x_3))$
by
$(f_{b}(x_1),f_{b}(x_2),f_{b}(x_3))$
by
![]() $s_{b}$
. We have thus obtained
$s_{b}$
. We have thus obtained
![]() $n^2/2$
solutions
$n^2/2$
solutions
![]() $s_b$
of
$s_b$
of
![]() $E$
in
$E$
in
![]() $S$
. To conclude the proof, we just need to estimate the number of times we have double counted each solution
$S$
. To conclude the proof, we just need to estimate the number of times we have double counted each solution
![]() $s_{b}$
. Observe that for every choice of
$s_{b}$
. Observe that for every choice of
![]() $s_{b}=\{s_1,s_2,s_3\}$
and distinct
$s_{b}=\{s_1,s_2,s_3\}$
and distinct
![]() $x_1,x_2,x_3 \in [R]$
, there is exactly one choice of
$x_1,x_2,x_3 \in [R]$
, there is exactly one choice of
![]() $b=(b_0,b_1) \in (\mathbb{F}_n)^2$
for which
$b=(b_0,b_1) \in (\mathbb{F}_n)^2$
for which
![]() $b_1x_i+b_0=s_i$
for every
$b_1x_i+b_0=s_i$
for every
![]() $1 \leq i \leq 3$
. Since
$1 \leq i \leq 3$
. Since
![]() $[R]$
contains at most
$[R]$
contains at most
![]() $R^2$
solutions of
$R^2$
solutions of
![]() $E$
this means that for every solution
$E$
this means that for every solution
![]() $s_1,s_2,s_3 \in S$
, there are at most
$s_1,s_2,s_3 \in S$
, there are at most
![]() $R^2$
choices of
$R^2$
choices of
![]() $b$
for which
$b$
for which
![]() $s_{b}=\{s_1,s_2,s_3\}$
. We conclude that
$s_{b}=\{s_1,s_2,s_3\}$
. We conclude that
![]() $S$
contains at least
$S$
contains at least
![]() $n^2/2R^2$
distinct solutions, thus completing the proof.
$n^2/2R^2$
distinct solutions, thus completing the proof.
2.2 Proof of Theorem 1.1
As in the proof above, we assume that
![]() $n$
is a prime and count the number of solutions of the equation
$n$
is a prime and count the number of solutions of the equation
![]() $E:\,\sum ^4_{i=1}a_ix_i=0$
over
$E:\,\sum ^4_{i=1}a_ix_i=0$
over
![]() $\mathbb{F}_n$
. Let
$\mathbb{F}_n$
. Let
![]() $S$
be a subset of
$S$
be a subset of
![]() $\mathbb{F}_n$
of size
$\mathbb{F}_n$
of size
![]() $\varepsilon n$
, and let
$\varepsilon n$
, and let
![]() $d$
and
$d$
and
![]() $t$
be integers to be chosen later and let
$t$
be integers to be chosen later and let
![]() $X$
be some subset of
$X$
be some subset of
![]() $[t]^d$
to be chosen later as well. For every
$[t]^d$
to be chosen later as well. For every
![]() $b=(b_0,\ldots,b_d)\in (\mathbb{F}_n)^{d+1}$
and
$b=(b_0,\ldots,b_d)\in (\mathbb{F}_n)^{d+1}$
and
![]() $x=(x_1,\ldots,x_d) \in X$
, we use
$x=(x_1,\ldots,x_d) \in X$
, we use
![]() $f_b(x)$
to denote
$f_b(x)$
to denote
![]() $b_0+\sum ^d_{i=1}b_ix_i$
and
$b_0+\sum ^d_{i=1}b_ix_i$
and
![]() $f_b(X)=\{x \in X\,{:}\,\, f_b(x) \in S\}$
. We call
$f_b(X)=\{x \in X\,{:}\,\, f_b(x) \in S\}$
. We call
![]() $b$
good if
$b$
good if
![]() $|\,f_b(X)| \geq \varepsilon |X|/2$
. We claim that at least half of all possible choices of
$|\,f_b(X)| \geq \varepsilon |X|/2$
. We claim that at least half of all possible choices of
![]() $b$
are good. To see this, pick
$b$
are good. To see this, pick
![]() $b=(b_0,\ldots,b_{d})$
uniformly at random from
$b=(b_0,\ldots,b_{d})$
uniformly at random from
![]() $(\mathbb{F}_n)^{d+1}$
, and note that for any
$(\mathbb{F}_n)^{d+1}$
, and note that for any
![]() $x \in X$
the integer
$x \in X$
the integer
![]() $f_b(x)$
is uniformly distributed in
$f_b(x)$
is uniformly distributed in
![]() $\mathbb{F}_n$
. Hence,
$\mathbb{F}_n$
. Hence,
It is also easy to see that for every
![]() $x \neq y \in X$
the random variables
$x \neq y \in X$
the random variables
![]() $f_b(x)$
and
$f_b(x)$
and
![]() $f_b(y)$
are pairwise independent. Hence,
$f_b(y)$
are pairwise independent. Hence,
Therefore, by Chebyshev’s Inequality we haveFootnote 5
implying that at least half of the
![]() $b$
’s are good. To finish the proof, we need to make sure that every such choice of a good
$b$
’s are good. To finish the proof, we need to make sure that every such choice of a good
![]() $b$
will “define” a solution
$b$
will “define” a solution
![]() $s_b$
in
$s_b$
in
![]() $S$
in a way that
$S$
in a way that
![]() $s_b$
will not be identical to too many other
$s_b$
will not be identical to too many other
![]() $s_{b'}$
. This will be achieved by a careful choice of
$s_{b'}$
. This will be achieved by a careful choice of
![]() $d$
,
$d$
,
![]() $t$
, and
$t$
, and
![]() $X$
.
$X$
.
We first choose
![]() $X$
to be the largest subset of
$X$
to be the largest subset of
![]() $[t]^d$
containing no three points on one line. We claim that
$[t]^d$
containing no three points on one line. We claim that
Indeed, for an integer
![]() $r$
let
$r$
let
![]() $B_r$
be the points
$B_r$
be the points
![]() $x \in [t]^d$
satisfying
$x \in [t]^d$
satisfying
![]() $\sum ^d_{i=1}x^2_i=r$
. Then every point of
$\sum ^d_{i=1}x^2_i=r$
. Then every point of
![]() $[t]^d$
lies on one such
$[t]^d$
lies on one such
![]() $B_r$
, where
$B_r$
, where
![]() $1 \leq r \leq dt^2$
. Hence, at least one such
$1 \leq r \leq dt^2$
. Hence, at least one such
![]() $B_r$
contains at least
$B_r$
contains at least
![]() $t^{d-2}/d$
of the points of
$t^{d-2}/d$
of the points of
![]() $[t]^d$
. Furthermore, since each set
$[t]^d$
. Furthermore, since each set
![]() $B_r$
is a subset of a sphere, it does not contain three points on one line.
$B_r$
is a subset of a sphere, it does not contain three points on one line.
We now turn to choose
![]() $t$
and
$t$
and
![]() $d$
. Let
$d$
. Let
![]() $C$
be such that
$C$
be such that
![]() $R_E(\varepsilon ) \leq (1/\varepsilon )^C$
. Set
$R_E(\varepsilon ) \leq (1/\varepsilon )^C$
. Set
![]() $a=\sum ^4_{i=1}|a_i|$
and pick
$a=\sum ^4_{i=1}|a_i|$
and pick
![]() $t$
and
$t$
and
![]() $d$
satisfying
$d$
satisfying
 \begin{equation} (1/\varepsilon )^{2C} \geq t^d \geq \left (\frac{2dt^2a^d}{\varepsilon }\right )^C\;. \end{equation}
\begin{equation} (1/\varepsilon )^{2C} \geq t^d \geq \left (\frac{2dt^2a^d}{\varepsilon }\right )^C\;. \end{equation}
Taking
![]() $t=2^{\sqrt{\log 1/\varepsilon }}$
and
$t=2^{\sqrt{\log 1/\varepsilon }}$
and
![]() $d=2C\sqrt{\log 1/\varepsilon }$
satisfiesFootnote
6
the above for all small enough
$d=2C\sqrt{\log 1/\varepsilon }$
satisfiesFootnote
6
the above for all small enough
![]() $\varepsilon$
. Note that by (3) and our choice of
$\varepsilon$
. Note that by (3) and our choice of
![]() $C$
, we have
$C$
, we have
![]() $R_E\left (\frac{\varepsilon }{2dt^2a^d}\right ) \leq t^d$
.
$R_E\left (\frac{\varepsilon }{2dt^2a^d}\right ) \leq t^d$
.
Let us call a collection of four vectors
![]() $x^1,x^2,x^3,x^4 \in X$
helpful if they are distinct, and they satisfy
$x^1,x^2,x^3,x^4 \in X$
helpful if they are distinct, and they satisfy
![]() $E$
in each coordinate, that is, for every
$E$
in each coordinate, that is, for every
![]() $1 \leq i \leq d$
we have
$1 \leq i \leq d$
we have
![]() $\sum ^4_{j=1}a_jx^j_i=0$
. We claim that for every good
$\sum ^4_{j=1}a_jx^j_i=0$
. We claim that for every good
![]() $r$
, there are useful
$r$
, there are useful
![]() $x^1,x^2,x^3,x^4 \in f_r(X)$
. To see this let
$x^1,x^2,x^3,x^4 \in f_r(X)$
. To see this let
![]() $M$
denote the integers
$M$
denote the integers
![]() $1,\ldots,(at)^d$
and note that (2) along with the fact that
$1,\ldots,(at)^d$
and note that (2) along with the fact that
![]() $r$
is good implies that
$r$
is good implies that
Now think of every
![]() $d$
-tuple
$d$
-tuple
![]() $x \in X$
as representing an integer
$x \in X$
as representing an integer
![]() $p(x) \in [M]$
written in base
$p(x) \in [M]$
written in base
![]() $at$
. So we can also think of
$at$
. So we can also think of
![]() $f_r(X)$
as a subset of
$f_r(X)$
as a subset of
![]() $[M]$
of density at least
$[M]$
of density at least
![]() $\varepsilon/2dt^2a^d$
. By (3), we have
$\varepsilon/2dt^2a^d$
. By (3), we have
implying that there are distinct
![]() $x^1,x^2,x^3,x^4 \in f_r(X)$
for which
$x^1,x^2,x^3,x^4 \in f_r(X)$
for which
![]() $\sum ^4_{j=1}a_j\cdot p(x^j)=0$
. But note that since the entries of
$\sum ^4_{j=1}a_j\cdot p(x^j)=0$
. But note that since the entries of
![]() $x^1,x^2,x^3,x^4$
are from
$x^1,x^2,x^3,x^4$
are from
![]() $[t]$
, there is no carry when evaluating
$[t]$
, there is no carry when evaluating
![]() $\sum ^4_{j=1}a_j\cdot p(x^j)$
in base
$\sum ^4_{j=1}a_j\cdot p(x^j)$
in base
![]() $at$
, implying that
$at$
, implying that
![]() $x^1,x^2,x^3,x^4$
satisfy
$x^1,x^2,x^3,x^4$
satisfy
![]() $E$
in each coordinate. Finally, the fact that
$E$
in each coordinate. Finally, the fact that
![]() $\sum _ja_j=0$
and that
$\sum _ja_j=0$
and that
![]() $x_i^1,x_i^2,x_i^3,x_i^4$
satisfy
$x_i^1,x_i^2,x_i^3,x_i^4$
satisfy
![]() $E$
for each
$E$
for each
![]() $1 \leq i \leq d$
allows us to deduce that
$1 \leq i \leq d$
allows us to deduce that
 \begin{equation*} \sum ^4_{j=1}a_j \cdot f_b(x^j)=\sum ^4_{j=1}a_j \cdot \left(b_0+\sum ^d_{i=1}b_ix^j_i\right)=\sum ^d_{i=1}b_i\cdot \left(\sum ^4_{j=1}a_jx^j_i\right)=0\;, \end{equation*}
\begin{equation*} \sum ^4_{j=1}a_j \cdot f_b(x^j)=\sum ^4_{j=1}a_j \cdot \left(b_0+\sum ^d_{i=1}b_ix^j_i\right)=\sum ^d_{i=1}b_i\cdot \left(\sum ^4_{j=1}a_jx^j_i\right)=0\;, \end{equation*}
which means that
![]() $f_b(x^1),f_b(x^2),f_b(x^3),f_b(x^4)$
forms a solution of
$f_b(x^1),f_b(x^2),f_b(x^3),f_b(x^4)$
forms a solution of
![]() $E$
. So for every good
$E$
. So for every good
![]() $b$
, let
$b$
, let
![]() $s_b$
be (some choice of)
$s_b$
be (some choice of)
![]() $f_b(x^1),f_b(x^2),f_b(x^3),f_b(x^4) \in S$
as defined above. We know from (1) that at least
$f_b(x^1),f_b(x^2),f_b(x^3),f_b(x^4) \in S$
as defined above. We know from (1) that at least
![]() $n^{d+1}/2$
of all choices of
$n^{d+1}/2$
of all choices of
![]() $b$
are good, so we have thus obtained
$b$
are good, so we have thus obtained
![]() $n^{d+1}/2$
solutions
$n^{d+1}/2$
solutions
![]() $s_b$
of
$s_b$
of
![]() $E$
in
$E$
in
![]() $S$
. To finish the proof, we need to bound the number of times we have counted the same solution in
$S$
. To finish the proof, we need to bound the number of times we have counted the same solution in
![]() $S$
, that is, the number of
$S$
, that is, the number of
![]() $b$
for which
$b$
for which
![]() $s_b$
can equal a certain
$s_b$
can equal a certain
![]() $4$
-tuple in
$4$
-tuple in
![]() $S$
satisfying
$S$
satisfying
![]() $E$
.
$E$
.
Fix
![]() $s=\{s_1,s_2,s_3,s_4\}$
and recall that
$s=\{s_1,s_2,s_3,s_4\}$
and recall that
![]() $s_{b}=s$
only if there is a helpful
$s_{b}=s$
only if there is a helpful
![]() $4$
-tuple
$4$
-tuple
![]() $x^1,x^2,x^3,x^4$
(as defined just before equation (4)) such that
$x^1,x^2,x^3,x^4$
(as defined just before equation (4)) such that
![]() $f_{b}(x^i)=s_i$
. We claim that for every helpful
$f_{b}(x^i)=s_i$
. We claim that for every helpful
![]() $4$
-tuple
$4$
-tuple
![]() $x^1,x^2,x^3,x^4$
, there are at most
$x^1,x^2,x^3,x^4$
, there are at most
![]() $n^{d-2}$
choices of
$n^{d-2}$
choices of
![]() $b=(b_0,\ldots,b_d)$
for which
$b=(b_0,\ldots,b_d)$
for which
![]() $s_b=s$
. Indeed recall that by our choice of
$s_b=s$
. Indeed recall that by our choice of
![]() $X$
the vectors
$X$
the vectors
![]() $x^1,x^2,x^3$
are distinct and do not lie on one line. Hence, they are affine independentFootnote
7
over
$x^1,x^2,x^3$
are distinct and do not lie on one line. Hence, they are affine independentFootnote
7
over
![]() $\mathbb{R}$
. But since the entries of
$\mathbb{R}$
. But since the entries of
![]() $x^i$
belong to
$x^i$
belong to
![]() $[t]$
and
$[t]$
and
![]() $t \leq 1/\varepsilon$
, we see that for large enough
$t \leq 1/\varepsilon$
, we see that for large enough
![]() $n$
the vectors
$n$
the vectors
![]() $x^1,x^2,x^3$
are also affine independent over
$x^1,x^2,x^3$
are also affine independent over
![]() $\mathbb{F}_n$
. This means that the system of three linear equations:
$\mathbb{F}_n$
. This means that the system of three linear equations:
 \begin{align*} b_0+b_1x^1_1+\ldots +b_dx^1_d=s_1 \\ b_0+b_1x^2_1+\ldots +b_dx^2_d=s_2 \\ b_0+b_1x^3_1+\ldots +b_dx^3_d=s_3 \end{align*}
\begin{align*} b_0+b_1x^1_1+\ldots +b_dx^1_d=s_1 \\ b_0+b_1x^2_1+\ldots +b_dx^2_d=s_2 \\ b_0+b_1x^3_1+\ldots +b_dx^3_d=s_3 \end{align*}
(in
![]() $d+1$
unknowns
$d+1$
unknowns
![]() $b_0,\ldots,b_d$
over
$b_0,\ldots,b_d$
over
![]() $\mathbb{F}_n$
) has only
$\mathbb{F}_n$
) has only
![]() $n^{d-2}$
solutions, implying the desired bound on the number of choices of
$n^{d-2}$
solutions, implying the desired bound on the number of choices of
![]() $b$
. Since
$b$
. Since
![]() $|X| \leq t^d \leq (1/\varepsilon )^{2C}$
by (3), we see that
$|X| \leq t^d \leq (1/\varepsilon )^{2C}$
by (3), we see that
![]() $X$
contains at most
$X$
contains at most
![]() $(1/\varepsilon )^{8C}$
helpful
$(1/\varepsilon )^{8C}$
helpful
![]() $4$
-tuples. Altogether this means that for every
$4$
-tuples. Altogether this means that for every
![]() $s_1,s_2,s_3,s_4 \in S$
satisfying
$s_1,s_2,s_3,s_4 \in S$
satisfying
![]() $E$
, there are at most
$E$
, there are at most
![]() $(1/\varepsilon )^{8C}n^{d-2}$
choices of
$(1/\varepsilon )^{8C}n^{d-2}$
choices of
![]() $b$
for which
$b$
for which
![]() $s_b=s$
. Since we have previously deduced that
$s_b=s$
. Since we have previously deduced that
![]() $S$
contains at least
$S$
contains at least
![]() $\frac 12n^{d+1}$
solutions
$\frac 12n^{d+1}$
solutions
![]() $s_b$
, we get that
$s_b$
, we get that
![]() $S$
contains at least
$S$
contains at least
![]() $\frac 12\varepsilon ^{8C}n^3$
distinct solutions, as needed.
$\frac 12\varepsilon ^{8C}n^3$
distinct solutions, as needed.
Acknowledgement
I would like to thank Yuval Wigderson and an anonymous referee for helpful comments and suggestions.