Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-02-11T16:33:34.725Z Has data issue: false hasContentIssue false
  • English
  • Français

Extremal problems for GCDs

Part of: Elementary number theory Sequences and sets

Published online by Cambridge University Press:  08 April 2021

Ben Green  and
Aled Walker
Ben Green
Affiliation:
Mathematical Institute, University of Oxford, Andrew Wiles Building, Radcliffe Observatory Quarter (550), Woodstock Road, Oxford, OX2 6GG, UK
Aled Walker*
Affiliation:
Trinity College, Trinity Street, Cambridge, CB2 1TQ, UK
*
*Corresponding author. Email: aw530@cam.ac.uk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that if 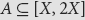$A \subseteq [X,\,2X]$ and 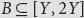$B \subseteq [Y,\,2Y]$ are sets of integers such that gcd (a, b) ⩾ D for at least δ|A||B| pairs (a, b) ε A × B then 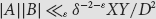$|A||B|{ \ll _{\rm{\varepsilon }}}{\delta ^{ - 2 - \varepsilon }}XY/{D^2}$ . This is a new result even when δ = 1. The proof uses ideas of Koukoulopoulos and Maynard and some additional combinatorial arguments.

MSC classification

Primary: 11A05: Multiplicative structure; Euclidean algorithm; greatest common divisors
Secondary: 11B75: Other combinatorial number theory
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 30 , Issue 6 , November 2021 , pp. 922 - 929
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Footnotes

The first-named author is supported by a Simons Investigator Award and is grateful to the Simons Foundation for their support. The second-named author is supported by a Postdoctoral Fellowship with the Centre de Recherches Mathématiques and by a Junior Research Fellowship from Trinity College Cambridge.

References

Koukoulopoulos, D. and Maynard, J. (2020) On the Duffin-Schaeffer conjecture. Ann. Math. 192(1) 251–307.CrossRefGoogle Scholar