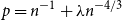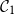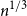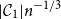1. Introduction
Consider the random digraph model D(n,p) where each of the
![]() $n(n-1)$
possible edges is included with probability p independently of all others. This is analogous to the Erdős–Renyi random graph G(n,p) in which each edge is again present with probability p independently of all others. McDiarmid [Reference McDiarmid15] showed that due to the similarity of the two models, it is often possible to couple G(n,p) and D(n,p) to compare the probabilities of certain properties.
$n(n-1)$
possible edges is included with probability p independently of all others. This is analogous to the Erdős–Renyi random graph G(n,p) in which each edge is again present with probability p independently of all others. McDiarmid [Reference McDiarmid15] showed that due to the similarity of the two models, it is often possible to couple G(n,p) and D(n,p) to compare the probabilities of certain properties.
In the random graph G(n,p) the component structure is well understood. In their seminal paper [Reference Erdős and Rényi4], Erdős and Rényi proved that for
![]() $p = c/n$
the largest component of G(n,p) has size
$p = c/n$
the largest component of G(n,p) has size
![]() $O(\log(n))$
if
$O(\log(n))$
if
![]() $c<1$
, is of order
$c<1$
, is of order
![]() $\Theta(n^{2/3})$
if
$\Theta(n^{2/3})$
if
![]() $c=1$
, and has linear size when
$c=1$
, and has linear size when
![]() $c>1$
. This threshold behaviour is known as the double jump. If we zoom in further around the critical point,
$c>1$
. This threshold behaviour is known as the double jump. If we zoom in further around the critical point,
![]() $p=1/n$
and consider
$p=1/n$
and consider
![]() $p = (1+\varepsilon(n))/n$
such that
$p = (1+\varepsilon(n))/n$
such that
![]() $\varepsilon(n) \to 0$
and
$\varepsilon(n) \to 0$
and
![]() $|\varepsilon(n)|^3 n \to \infty$
, Bollobás [Reference Bollobás3] proved the following theorem for
$|\varepsilon(n)|^3 n \to \infty$
, Bollobás [Reference Bollobás3] proved the following theorem for
![]() $|\varepsilon|>(2\log(n))^{1/2} n^{-1/3}$
,which was extended to the whole range described above by Łuczak [Reference Łuczak10].
$|\varepsilon|>(2\log(n))^{1/2} n^{-1/3}$
,which was extended to the whole range described above by Łuczak [Reference Łuczak10].
Theorem 1.1
([Reference Bollobás3, Reference Łuczak10]). Let
![]() $np=1+\varepsilon$
, such that
$np=1+\varepsilon$
, such that
![]() $\varepsilon = \varepsilon(n) \to 0$
but
$\varepsilon = \varepsilon(n) \to 0$
but
![]() $n|\varepsilon|^3 \to \infty$
, and
$n|\varepsilon|^3 \to \infty$
, and
![]() $k_0 = 2 \varepsilon^{-2} \log(n|\varepsilon|^3)$
.
$k_0 = 2 \varepsilon^{-2} \log(n|\varepsilon|^3)$
.
-
(i) If
 $n \varepsilon^3 \to -\infty$
then a.a.s. G(n,p) contains no component of size greater than
$n \varepsilon^3 \to -\infty$
then a.a.s. G(n,p) contains no component of size greater than
 $k_0$
.
$k_0$
. -
(ii) If
 $n \varepsilon^3 \to \infty$
then a.a.s. G(n,p) contains a unique component of size greater than
$n \varepsilon^3 \to \infty$
then a.a.s. G(n,p) contains a unique component of size greater than
 $k_0$
. This component has size
$k_0$
. This component has size
 $2\varepsilon n(1+o(1))$
.
$2\varepsilon n(1+o(1))$
.
Within the critical window itself, i.e.
![]() $p = n^{-1} + \lambda n^{-4/3}$
with
$p = n^{-1} + \lambda n^{-4/3}$
with
![]() $\lambda \in \mathbb{R}$
, the size of the largest component
$\lambda \in \mathbb{R}$
, the size of the largest component
![]() $\mathcal{C}_1$
is not tightly concentrated as it is for larger p. Instead, there exists a random variable
$\mathcal{C}_1$
is not tightly concentrated as it is for larger p. Instead, there exists a random variable
![]() $X_1 = X_1(\lambda)$
such that
$X_1 = X_1(\lambda)$
such that
![]() $|\mathcal{C}_1|n^{-2/3} \to X_1$
as
$|\mathcal{C}_1|n^{-2/3} \to X_1$
as
![]() $n \to \infty$
. Much is known about the distribution of
$n \to \infty$
. Much is known about the distribution of
![]() $X_1$
, in fact the vector
$X_1$
, in fact the vector
![]() $\mathbf{X} = (X_1,\ldots, X_k)$
of normalised sizes of the largest k components, i.e.
$\mathbf{X} = (X_1,\ldots, X_k)$
of normalised sizes of the largest k components, i.e.
![]() $X_i = |\mathcal{C}_i| n^{-2/3}$
converges to the vector of longest excursion lengths of an inhomogeneous reflected Brownian motion by a result of Aldous [Reference Aldous2]. In a more quantitative setting where one is more interested about behaviour for somewhat small n, Nachmias and Peres [Reference Nachmias and Peres16] proved the following (similar results may be found in [Reference Pittel19, Reference Scott and Sorkin21]).
$X_i = |\mathcal{C}_i| n^{-2/3}$
converges to the vector of longest excursion lengths of an inhomogeneous reflected Brownian motion by a result of Aldous [Reference Aldous2]. In a more quantitative setting where one is more interested about behaviour for somewhat small n, Nachmias and Peres [Reference Nachmias and Peres16] proved the following (similar results may be found in [Reference Pittel19, Reference Scott and Sorkin21]).
Theorem 1.2
([Reference Nachmias and Peres16]). Suppose
![]() $0<\delta<1/10$
,
$0<\delta<1/10$
,
![]() $A>8$
and n is sufficiently large with respect to
$A>8$
and n is sufficiently large with respect to
![]() $A, \delta$
. Then if
$A, \delta$
. Then if
![]() $\mathcal{C}_1$
is the largest component of
$\mathcal{C}_1$
is the largest component of
![]() $G(n,1/n)$
, we have
$G(n,1/n)$
, we have
-
(i)
 $\mathbb{P}(|\mathcal{C}_1| < \lfloor \delta n^{2/3} \rfloor) \leq 15 \delta^{3/5}$
.
$\mathbb{P}(|\mathcal{C}_1| < \lfloor \delta n^{2/3} \rfloor) \leq 15 \delta^{3/5}$
. -
(ii)
 $\mathbb{P}(|\mathcal{C}_1|>An^{2/3}) \leq \frac{4}{A} e^{-\frac{A^2(A-4)}{32}}$
.
$\mathbb{P}(|\mathcal{C}_1|>An^{2/3}) \leq \frac{4}{A} e^{-\frac{A^2(A-4)}{32}}$
.
Note we have only stated the version of their theorem with
![]() $p=n^{-1}$
for clarity but it holds for the whole critical window. Of course, there are a vast number of other interesting properties of
$p=n^{-1}$
for clarity but it holds for the whole critical window. Of course, there are a vast number of other interesting properties of
![]() $\mathcal{C}_1$
, see [Reference Addario-Berry, Broutin and Goldschmidt1, Reference Janson, Knuth, Łuczak and Pittel7, Reference Łuczak, Pittel and Wierman12] for a number of examples.
$\mathcal{C}_1$
, see [Reference Addario-Berry, Broutin and Goldschmidt1, Reference Janson, Knuth, Łuczak and Pittel7, Reference Łuczak, Pittel and Wierman12] for a number of examples.
In the setting of D(n,p), one finds that analogues of many of the above theorems still hold. When working with digraphs, we are interested in the strongly connected components which we will often call the components. Note that the weak component structure of D(n,p) is precisely the component structure of
![]() $G(n,2p-p^2)$
. For
$G(n,2p-p^2)$
. For
![]() $p = c/n$
, Karp [Reference Karp9] and Łuczak [Reference Łuczak11] independently showed that for
$p = c/n$
, Karp [Reference Karp9] and Łuczak [Reference Łuczak11] independently showed that for
![]() $c<1$
all components are of size O(1) and when
$c<1$
all components are of size O(1) and when
![]() $c>1$
, there is a unique complex component of linear order and every other component is of size O(1) (a component is complex if it has more edges than vertices). The range
$c>1$
, there is a unique complex component of linear order and every other component is of size O(1) (a component is complex if it has more edges than vertices). The range
![]() $p = (1+\varepsilon)/n$
was studied by Łuczak and Seierstad [Reference Łuczak and Seierstad13] who were able to show the following result which can be viewed as a version of Theorem 1.1 for D(n,p),
$p = (1+\varepsilon)/n$
was studied by Łuczak and Seierstad [Reference Łuczak and Seierstad13] who were able to show the following result which can be viewed as a version of Theorem 1.1 for D(n,p),
Theorem 1.3
([Reference Łuczak and Seierstad13]). Let
![]() $np=1+\varepsilon$
, such that
$np=1+\varepsilon$
, such that
![]() $\varepsilon = \varepsilon(n) \to 0$
.
$\varepsilon = \varepsilon(n) \to 0$
.
-
(i) If
 $n \varepsilon^3 \to -\infty$
then a.a.s. every component of D(n,p) is an isolated vertex or a cycle of length
$n \varepsilon^3 \to -\infty$
then a.a.s. every component of D(n,p) is an isolated vertex or a cycle of length
 $O(1/|\varepsilon|)$
.
$O(1/|\varepsilon|)$
. -
(ii) If
 $n \varepsilon^3 \to \infty$
then a.a.s. D(n,p) contains a unique complex component of size
$n \varepsilon^3 \to \infty$
then a.a.s. D(n,p) contains a unique complex component of size
 $4 \varepsilon^2 n (1+o(1))$
and every other component is an isolated vertex or a cycle of length
$4 \varepsilon^2 n (1+o(1))$
and every other component is an isolated vertex or a cycle of length
 $O(1/\varepsilon)$
.
$O(1/\varepsilon)$
.
As a corollary Łuczak and Seierstad obtain a number of weaker results inside the critical window regarding complex components. They showed that there are
![]() $O_p(1)$
complex components containing
$O_p(1)$
complex components containing
![]() $O_p(n^{1/3})$
vertices combined and that each has spread
$O_p(n^{1/3})$
vertices combined and that each has spread
![]() $\Omega_p(n^{1/3})$
(the spread of a complex digraph is the length of its shortest induced path).
$\Omega_p(n^{1/3})$
(the spread of a complex digraph is the length of its shortest induced path).
Our main result is to give bounds on the tail probabilities of
![]() $|\mathcal{C}_1|$
resembling those of Nachmias and Peres [Reference Nachmias and Peres16] for G(n,p).
$|\mathcal{C}_1|$
resembling those of Nachmias and Peres [Reference Nachmias and Peres16] for G(n,p).
Theorem 1.4
(Lower Bound). Let
![]() $0<\delta<1/800$
,
$0<\delta<1/800$
,
![]() $\lambda \in \mathbb{R}$
and
$\lambda \in \mathbb{R}$
and
![]() $n \in \mathbb{N}$
. Let
$n \in \mathbb{N}$
. Let
![]() $\mathcal{C}_1$
be the largest component of D(n,p) for
$\mathcal{C}_1$
be the largest component of D(n,p) for
![]() $p = n^{-1} + \lambda n^{-4/3}$
. Then if n is sufficiently large with respect to
$p = n^{-1} + \lambda n^{-4/3}$
. Then if n is sufficiently large with respect to
![]() $\delta, \lambda$
,
$\delta, \lambda$
,
provided that
![]() $\delta \leq \frac{(\log 2)^2}{4 |\lambda|^2}$
.
$\delta \leq \frac{(\log 2)^2}{4 |\lambda|^2}$
.
Note that the constants in the above theorem have been chosen for simplicity and it is possible to give an expression for (1) depending on both
![]() $\lambda$
and
$\lambda$
and
![]() $\delta$
which imposes no restriction on their relation to one another.
$\delta$
which imposes no restriction on their relation to one another.
Theorem 1.5
(Upper Bound). There exist constants,
![]() $\zeta, \eta >0$
such that for any
$\zeta, \eta >0$
such that for any
![]() $A>0, \lambda \in \mathbb{R}$
, let
$A>0, \lambda \in \mathbb{R}$
, let
![]() $\mathcal{C}_1$
be the largest component of D(n,p) for
$\mathcal{C}_1$
be the largest component of D(n,p) for
![]() $p = n^{-1} + \lambda n^{-4/3}$
. Then provided n is sufficiently large with respect to
$p = n^{-1} + \lambda n^{-4/3}$
. Then provided n is sufficiently large with respect to
![]() $A, \lambda$
,
$A, \lambda$
,
where
![]() $\lambda^+ = \max(\lambda, 0)$
.
$\lambda^+ = \max(\lambda, 0)$
.
A simple corollary of these bounds is that the largest component has size
![]() $\Theta(n^{1/3})$
. This follows by taking
$\Theta(n^{1/3})$
. This follows by taking
![]() $\delta = o(1)$
in Theorem 1.4 and
$\delta = o(1)$
in Theorem 1.4 and
![]() $A = \omega(1)$
in Theorem 1.5.
$A = \omega(1)$
in Theorem 1.5.
Corollary 1.6. Let
![]() $\mathcal{C}_1$
be the largest component of D(n,p) for
$\mathcal{C}_1$
be the largest component of D(n,p) for
![]() $p = n^{-1} + \lambda n^{-4/3}$
. Then,
$p = n^{-1} + \lambda n^{-4/3}$
. Then,
![]() $|\mathcal{C}_1| = \Theta_p(n^{1/3})$
.
$|\mathcal{C}_1| = \Theta_p(n^{1/3})$
.
Recently, some related results have been obtained by Goldschmidt and Stephenson [Reference Goldschmidt and Stephenson5] who showed a scaling limit for the sizes of all the strong components in the critical random digraph. This is analogous to the result of Aldous [Reference Aldous2] in G(n,p) and allows one to deduce that there is a limiting distribution for the random variable
![]() $n^{-1/3}|\mathcal{C}_1|$
. This distribution can be described in terms of the total edge length of a directed multigraph related to the Brownian continuum random tree. In principle versions of Theorems 1.4 and 1.5 can be deduced from the result of Goldschmidt and Stephenson, however their limit distribution is complex and difficult to extract precise information from. This author was only able to deduce that
$n^{-1/3}|\mathcal{C}_1|$
. This distribution can be described in terms of the total edge length of a directed multigraph related to the Brownian continuum random tree. In principle versions of Theorems 1.4 and 1.5 can be deduced from the result of Goldschmidt and Stephenson, however their limit distribution is complex and difficult to extract precise information from. This author was only able to deduce that
![]() $n^{-1/3}|\mathcal{C}_1|$
is tight using the results of Goldschmidt and Stephenson, whereas Theorems 1.4 and 1.5 give us much more explicit information about the tails of the random variable
$n^{-1/3}|\mathcal{C}_1|$
is tight using the results of Goldschmidt and Stephenson, whereas Theorems 1.4 and 1.5 give us much more explicit information about the tails of the random variable
![]() $n^{-1/3}|\mathcal{C}_1|$
.
$n^{-1/3}|\mathcal{C}_1|$
.
It should be noted that, in contrast to the undirected case, checking whether a set of W of vertices constitutes a strongly connected component of a digraph D requires much more than checking only those edges with at least one end in W. In particular, in order for W to be a strongly connected component, it must be strongly connected and there must be no directed path starting and ending in W which contains vertices that are not in W. This precludes us from using a number of methods which have often been used to study G(n,p). We therefore develop novel methods for counting the number of strongly connected components of D(n,p) based upon branching process arguments.
The remainder of this paper is organised as follows. In Section 2, we give a pair of bounds on the number of strongly connected digraphs which have a given excess and number of vertices. Sections 3 and 4 contain the proofs of Theorems 1.4 and 1.5, respectively, in the case that
![]() $p = n^{-1}$
. The proof of Theorem 1.4 in Section 3 is a relatively straightforward application of Janson’s inequality. The proof of Theorem 1.5 in Section 4 is much more involved. We use an exploration process to approximate the probability that a given subdigraph of D(n,p) is also a component. Using this we approximate the expected number of strongly connected components of size at least
$p = n^{-1}$
. The proof of Theorem 1.4 in Section 3 is a relatively straightforward application of Janson’s inequality. The proof of Theorem 1.5 in Section 4 is much more involved. We use an exploration process to approximate the probability that a given subdigraph of D(n,p) is also a component. Using this we approximate the expected number of strongly connected components of size at least
![]() $An^{1/3}$
and apply Markov’s inequality. The adaptations required to handle the critical window
$An^{1/3}$
and apply Markov’s inequality. The adaptations required to handle the critical window
![]() $p = n^{-1}+\lambda n^{-4/3}$
are presented in Section 5. We conclude the paper in Section 6 with some open questions and final remarks.
$p = n^{-1}+\lambda n^{-4/3}$
are presented in Section 5. We conclude the paper in Section 6 with some open questions and final remarks.
2. Enumeration of digraphs by size and excess
For both the upper and lower bounds on the size of the largest component, we need good bounds on the number of strongly connected digraphs with a given excess and number of vertices. Where the excess of a strongly connected digraph with v vertices and e edges is
![]() $e-v$
. Let Y(m,k) be the number of strongly connected digraphs with m vertices and excess k. The study of Y(m,k) was imitated by Wright [Reference Wright24] who obtained recurrences for the exact value of Y(m,k). However, these recurrences swiftly become intractable as k grows. This has since been extended to asymptotic formulae when
$e-v$
. Let Y(m,k) be the number of strongly connected digraphs with m vertices and excess k. The study of Y(m,k) was imitated by Wright [Reference Wright24] who obtained recurrences for the exact value of Y(m,k). However, these recurrences swiftly become intractable as k grows. This has since been extended to asymptotic formulae when
![]() $k = \omega(1)$
and
$k = \omega(1)$
and
![]() $O(m \log(m))$
[Reference Pérez-Giménez and Wormald18, Reference Pittel20]. Note that when
$O(m \log(m))$
[Reference Pérez-Giménez and Wormald18, Reference Pittel20]. Note that when
![]() $k = m\log(m) + \omega(m)$
, the fact
$k = m\log(m) + \omega(m)$
, the fact
![]() $Y(m,k) \sim \binom{m(m-1)}{m+k}$
is a simple corollary of a result of Palásti [Reference Palásti17]. In this section we give an universal bound on Y(m,k) (Lemma 2.1) as well as a stronger bound for small excess (Lemma 2.3).
$Y(m,k) \sim \binom{m(m-1)}{m+k}$
is a simple corollary of a result of Palásti [Reference Palásti17]. In this section we give an universal bound on Y(m,k) (Lemma 2.1) as well as a stronger bound for small excess (Lemma 2.3).
Lemma 2.1. For every
![]() $m, k \geq 1$
,
$m, k \geq 1$
,
Proof. We will prove this by considering ear decompositions of the strongly connected digraphs in question. An ear is a non-trivial directed path in which the end points may coincide (i.e. it may be a cycle with a marked start/end vertex). The internal vertices of an ear are those that are not end points. An ear decomposition of a digraph D is a sequence,
![]() $E_0, E_1, \ldots, E_k$
of ears such that:
$E_0, E_1, \ldots, E_k$
of ears such that:
-
•
 $E_0$
is a cycle.
$E_0$
is a cycle. -
• The end points of
 $E_i$
belong to
$E_i$
belong to
 $\bigcup_{j=0}^{i-1} E_j$
.
$\bigcup_{j=0}^{i-1} E_j$
. -
• The internal vertices of
 $E_i$
are disjoint from
$E_i$
are disjoint from
 $\bigcup_{j=0}^{i-1} E_j$
.
$\bigcup_{j=0}^{i-1} E_j$
. -
•
 $\bigcup_{i=0}^{k} E_i = D$
$\bigcup_{i=0}^{k} E_i = D$
We make use of the following fact.
Fact 2.2. A digraph D has an ear decomposition with
![]() $k+1$
ears if and only if D is strongly connected with excess k.
$k+1$
ears if and only if D is strongly connected with excess k.
Thus, we count strongly connected digraphs by a double counting of the number of possible ear decompositions. We produce an ear decomposition with m vertices and
![]() $k+1$
ears as follows. First, pick an ordering
$k+1$
ears as follows. First, pick an ordering
![]() $\pi$
of the vertices. Then insert k bars between the vertices such that the earliest the first bar may appear is after the second vertex in the order; multiple bars may be inserted between a pair of consecutive vertices. Finally, for each
$\pi$
of the vertices. Then insert k bars between the vertices such that the earliest the first bar may appear is after the second vertex in the order; multiple bars may be inserted between a pair of consecutive vertices. Finally, for each
![]() $i \in [k]$
, we choose an ordered pair of vertices
$i \in [k]$
, we choose an ordered pair of vertices
![]() $(u_i,v_i)$
which appear in the ordering before the ith bar.
$(u_i,v_i)$
which appear in the ordering before the ith bar.
This corresponds to a unique ear decomposition. The vertices in
![]() $\pi$
before the first bar are
$\pi$
before the first bar are
![]() $E_0$
with its end point being the first vertex. The internal vertices of
$E_0$
with its end point being the first vertex. The internal vertices of
![]() $E_i$
are the vertices of
$E_i$
are the vertices of
![]() $\pi$
between the ith and
$\pi$
between the ith and
![]() $i+1$
st bar. Furthermore,
$i+1$
st bar. Furthermore,
![]() $E_i$
has end points
$E_i$
has end points
![]() $u_i$
and
$u_i$
and
![]() $v_i$
and is directed from
$v_i$
and is directed from
![]() $u_i$
to
$u_i$
to
![]() $v_i$
. The orientation of every other edge follows the order
$v_i$
. The orientation of every other edge follows the order
![]() $\pi$
.
$\pi$
.
Hence, there are at most
ear decompositions. Note that each vertex of a strongly connected digraph is contained in a cycle. Therefore each vertex could be the end point of
![]() $E_0$
and hence at least m ear decompositions correspond to each strongly connected digraph. Hence the number of strongly connected digraphs of excess k may be bounded by
$E_0$
and hence at least m ear decompositions correspond to each strongly connected digraph. Hence the number of strongly connected digraphs of excess k may be bounded by
as claimed.
![]()
Lemma 2.3. There exists
![]() $C >0$
such that for
$C >0$
such that for
![]() $1 \leq k \leq \sqrt{m}/3$
and m sufficiently large we have,
$1 \leq k \leq \sqrt{m}/3$
and m sufficiently large we have,
The proof of the above lemma follows similar lines to the proof of Theorem 1.1 in [Reference Pérez-Giménez and Wormald18] to obtain a bound of a similar order. We then prove that this bound implies the above which is much easier to work with.
First we introduce some definitions and notation from [Reference Pérez-Giménez and Wormald18]. A random variable X has the zero-truncated Poisson distribution with parameter
![]() $\lambda>0$
denoted
$\lambda>0$
denoted
![]() $X \sim TP(\lambda)$
if it has probability mass function
$X \sim TP(\lambda)$
if it has probability mass function
 \begin{equation*}\mathbb{P}(X=i) =\begin{cases}\dfrac{\lambda^i}{i! (e^\lambda -1)} & \text{if } i \geq 1, \\0 & \text{if } i<1.\end{cases}\end{equation*}
\begin{equation*}\mathbb{P}(X=i) =\begin{cases}\dfrac{\lambda^i}{i! (e^\lambda -1)} & \text{if } i \geq 1, \\0 & \text{if } i<1.\end{cases}\end{equation*}
Let
![]() $\mathcal{D}$
be the collection of all degree sequences
$\mathcal{D}$
be the collection of all degree sequences
![]() $\mathbf{d} = (d_1^+, \ldots, d_m^+,d_1^-,\ldots,d_m^-)$
such that
$\mathbf{d} = (d_1^+, \ldots, d_m^+,d_1^-,\ldots,d_m^-)$
such that
![]() $d_i^+,d_i^- \geq 1$
for each
$d_i^+,d_i^- \geq 1$
for each
![]() $1 \leq i \leq m$
and furthermore,
$1 \leq i \leq m$
and furthermore,
A preheart is a digraph with minimum semi-degree at least 1 and no cycle components. The
![]() $\text{heart}$
of a preheart D is the multidigraph H(D) formed by suppressing all vertices of D which have in and out degree precisely 1.
$\text{heart}$
of a preheart D is the multidigraph H(D) formed by suppressing all vertices of D which have in and out degree precisely 1.
We define the preheart configuration model, a two stage variant of the configuration model for digraphs which always produces a preheart, as follows. For
![]() $\mathbf{d} \in \mathcal{D}$
, define
$\mathbf{d} \in \mathcal{D}$
, define
First we apply the configuration model to T to produce a heart H. That is, assign each vertex
![]() $i \in T$
$i \in T$
![]() $d_i^+$
out-stubs and
$d_i^+$
out-stubs and
![]() $d_i^-$
in-stubs and pick a uniformly random perfect matching between in- and out-stubs. Next, given a heart configuration H, we construct a preheart configuration Q by assigning
$d_i^-$
in-stubs and pick a uniformly random perfect matching between in- and out-stubs. Next, given a heart configuration H, we construct a preheart configuration Q by assigning
![]() $[m] \setminus T$
to E(H) such that the vertices assigned to each arc of H are given a linear order. Denote this assignment including the orderings by q. Then the preheart configuration model,
$[m] \setminus T$
to E(H) such that the vertices assigned to each arc of H are given a linear order. Denote this assignment including the orderings by q. Then the preheart configuration model,
![]() $\mathcal{Q}(\mathbf{d})$
is the probability space of random preheart configurations formed by choosing H and q uniformly at random. Note that each
$\mathcal{Q}(\mathbf{d})$
is the probability space of random preheart configurations formed by choosing H and q uniformly at random. Note that each
![]() $Q \in \mathcal{Q}(\mathbf{d})$
corresponds to a (multi)digraph with m vertices
$Q \in \mathcal{Q}(\mathbf{d})$
corresponds to a (multi)digraph with m vertices
![]() $m+k$
edges and degree sequence
$m+k$
edges and degree sequence
![]() $\mathbf{d}$
.
$\mathbf{d}$
.
As in the configuration model, each simple digraph with degree sequence
![]() $\mathbf{d}$
is produced in precisely
$\mathbf{d}$
is produced in precisely
![]() $\prod_{i=1}^m d_i^+! d_i^-!$
ways. So if we restrict to simple preheart configurations, the digraphs we generate in this way are uniformly distributed. Where in this case, simple means that there are no multiple edges or loops (however cycles of length 2 are allowed). We now count the number of preheart configurations. Let
$\prod_{i=1}^m d_i^+! d_i^-!$
ways. So if we restrict to simple preheart configurations, the digraphs we generate in this way are uniformly distributed. Where in this case, simple means that there are no multiple edges or loops (however cycles of length 2 are allowed). We now count the number of preheart configurations. Let
![]() $m' = m'(\mathbf{d}) = |T(\mathbf{d})|$
be the number of vertices of the heart. Then, we have the following
$m' = m'(\mathbf{d}) = |T(\mathbf{d})|$
be the number of vertices of the heart. Then, we have the following
Lemma 2.4. Let
![]() $\mathbf{d} \in \mathcal{D}$
, then there are
$\mathbf{d} \in \mathcal{D}$
, then there are
preheart configurations.
Proof. We first generate the heart, and as we are simply working with the configuration model for this part of the model, there are
![]() $(m'+k)!$
heart configurations. The assignment of vertices in
$(m'+k)!$
heart configurations. The assignment of vertices in
![]() $[m]\setminus T$
to the arcs of the heart H may be done one vertex at a time by subdividing any already present edge and maintaining orientation. In this way when we add the ith vertex in this stage, there are
$[m]\setminus T$
to the arcs of the heart H may be done one vertex at a time by subdividing any already present edge and maintaining orientation. In this way when we add the ith vertex in this stage, there are
![]() $m'+k+i-1$
choices for the edge we subdivide. We must add
$m'+k+i-1$
choices for the edge we subdivide. We must add
![]() $m-m'$
edges in this stage and so there are
$m-m'$
edges in this stage and so there are
 \begin{equation*} \prod_{i=1}^{m-m'} m'+k+i-1 = \frac{(m+k-1)!}{(m'+k-1)!} \end{equation*}
\begin{equation*} \prod_{i=1}^{m-m'} m'+k+i-1 = \frac{(m+k-1)!}{(m'+k-1)!} \end{equation*}
unique ways to create a preheart configuration from any given heart. Multiplying the number of heart configurations by the number of ways to create a preheart configuration from a given heart yields the desired result.
![]()
The next stage is to pick the degree sequence,
![]() $\mathbf{d} \in \mathcal{D}$
at random. We do this by choosing the degrees to be independent and identically distributed zero-truncated Poisson random variables with mean
$\mathbf{d} \in \mathcal{D}$
at random. We do this by choosing the degrees to be independent and identically distributed zero-truncated Poisson random variables with mean
![]() $\lambda>0$
. That is,
$\lambda>0$
. That is,
![]() $d_i^+ \sim TP(\lambda)$
and
$d_i^+ \sim TP(\lambda)$
and
![]() $d_i^- \sim TP(\lambda)$
such that the family
$d_i^- \sim TP(\lambda)$
such that the family
![]() $\{ d_i^+, d_i^- \ :\ i \in [m] \}$
is independent. Note that this may not give a degree sequence at all, or it may be the degree sequence of a digraph with the wrong number of edges. Thus we define the event
$\{ d_i^+, d_i^- \ :\ i \in [m] \}$
is independent. Note that this may not give a degree sequence at all, or it may be the degree sequence of a digraph with the wrong number of edges. Thus we define the event
![]() $\Sigma(\lambda)$
to be the event that
$\Sigma(\lambda)$
to be the event that
We shall now prove the following bound,
Lemma 2.5. For any
![]() $\lambda>0$
we have
$\lambda>0$
we have
Proof. Let
![]() $\mathbf{D}$
be the random degree sequence generated as above and
$\mathbf{D}$
be the random degree sequence generated as above and
![]() $\mathbf{d} \in \mathcal{D}$
, then
$\mathbf{d} \in \mathcal{D}$
, then
 \begin{equation} \mathbb{P}(\mathbf{D} =\mathbf{d}) = \prod_{i=1}^m \frac{\lambda^{d_i^+}}{d_i^+!(e^\lambda -1)}\frac{\lambda^{d_i^-}}{d_i^-!(e^\lambda -1)} = \frac{\lambda^{2(m+k)}}{(e^\lambda -1)^{2m}} \prod_{i=1}^m \frac{1}{d_i^+! d_i^-!}. \end{equation}
\begin{equation} \mathbb{P}(\mathbf{D} =\mathbf{d}) = \prod_{i=1}^m \frac{\lambda^{d_i^+}}{d_i^+!(e^\lambda -1)}\frac{\lambda^{d_i^-}}{d_i^-!(e^\lambda -1)} = \frac{\lambda^{2(m+k)}}{(e^\lambda -1)^{2m}} \prod_{i=1}^m \frac{1}{d_i^+! d_i^-!}. \end{equation}
By definition of
![]() $\Sigma(\lambda)$
, we have
$\Sigma(\lambda)$
, we have
as all of the above events are disjoint. Thus, we may rearrange (4) to deduce that
 \begin{equation} \sum_{\mathbf{d} \in \mathcal{D}} \prod_{i=1}^m \frac{1}{d_i^+! d_i^-!} = \frac{(e^\lambda-1)^{2m}}{\lambda^{2(m+k)}}\mathbb{P}(\Sigma(\lambda)).\end{equation}
\begin{equation} \sum_{\mathbf{d} \in \mathcal{D}} \prod_{i=1}^m \frac{1}{d_i^+! d_i^-!} = \frac{(e^\lambda-1)^{2m}}{\lambda^{2(m+k)}}\mathbb{P}(\Sigma(\lambda)).\end{equation}
Lemma 2.4 tells us that for a given degree sequence
![]() $\mathbf{d}$
, there are
$\mathbf{d}$
, there are
preheart configurations. As each simple digraph with degree sequence
![]() $\mathbf{d}$
comes from precisely
$\mathbf{d}$
comes from precisely
![]() $\prod_{i=1}^m d_i^+! d_i^-!$
configurations, and
$\prod_{i=1}^m d_i^+! d_i^-!$
configurations, and
![]() $m'(\mathbf{d}) \leq 2k$
as otherwise the excess would be larger than k, we can deduce that the total number of prehearts with m vertices and excess k is
$m'(\mathbf{d}) \leq 2k$
as otherwise the excess would be larger than k, we can deduce that the total number of prehearts with m vertices and excess k is
 \begin{equation}\sum_{\mathbf{d} \in \mathcal{D}} \frac{m'(\mathbf{d})+k}{m+k} (m+k)! \prod_{i=1}^m \frac{1}{d_i^+! d_i^-!} \leq \sum_{\mathbf{d} \in \mathcal{D}} (m+k)! \frac{3k}{m+k} \prod_{i=1}^m \frac{1}{d_i^+! d_i^-!}.\end{equation}
\begin{equation}\sum_{\mathbf{d} \in \mathcal{D}} \frac{m'(\mathbf{d})+k}{m+k} (m+k)! \prod_{i=1}^m \frac{1}{d_i^+! d_i^-!} \leq \sum_{\mathbf{d} \in \mathcal{D}} (m+k)! \frac{3k}{m+k} \prod_{i=1}^m \frac{1}{d_i^+! d_i^-!}.\end{equation}
Note that any strongly connected digraph is a preheart and so (6) is also an upper bound for Y(m,k). Finally, combining (5) and (6) yields the desired inequality.
![]()
It remains to prove that (3) can be bounded from above by (2). To this end, we prove the following upper bound on
![]() $\mathbb{P}(\Sigma(\lambda))$
.
$\mathbb{P}(\Sigma(\lambda))$
.
Lemma 2.6. For
![]() $\lambda <1$
,
$\lambda <1$
,
For the proof of this lemma, we will use the Berry–Esseen inequality for normal approximation (see, e.g. [23, Section XX.2].)
Lemma 2.7. Suppose
![]() $X_1,X_2,\ldots, X_n$
is a sequence of independent random variables from a common distribution with zero mean, unit variance and third absolute moment
$X_1,X_2,\ldots, X_n$
is a sequence of independent random variables from a common distribution with zero mean, unit variance and third absolute moment
![]() $\mathbb{E}|X|^3 = \gamma < \infty$
. Let
$\mathbb{E}|X|^3 = \gamma < \infty$
. Let
![]() $S_n = X_1+X_2+\ldots+X_n$
and let
$S_n = X_1+X_2+\ldots+X_n$
and let
![]() $G_n$
be the cumulative distribution function of
$G_n$
be the cumulative distribution function of
![]() $S_n/\sqrt{n}$
. Then for each n we have
$S_n/\sqrt{n}$
. Then for each n we have
where
![]() $\Phi$
is the cumulative distribution function of the standard Gaussian.
$\Phi$
is the cumulative distribution function of the standard Gaussian.
Here, the explicit constant
![]() $1/2$
in equation (7) was obtained by Tyurin [Reference Tyurin22].
$1/2$
in equation (7) was obtained by Tyurin [Reference Tyurin22].
Proof of Lemma 2.6. The in-degrees of the random degree sequence are chosen independently from a truncated Poisson distribution with parameter
![]() $\lambda$
. Thus, we want to apply Lemma 2.7 to the sum
$\lambda$
. Thus, we want to apply Lemma 2.7 to the sum
![]() $S_m = Y_1+Y_2+\ldots+Y_m$
where the
$S_m = Y_1+Y_2+\ldots+Y_m$
where the
![]() $Y_i$
are normalised truncated Poisson random variables. So all we must compute are the first three central moments of the truncated Poisson distribution. Let
$Y_i$
are normalised truncated Poisson random variables. So all we must compute are the first three central moments of the truncated Poisson distribution. Let
![]() $Y \sim TP(\lambda)$
, one can easily compute that
$Y \sim TP(\lambda)$
, one can easily compute that
![]() $\mathbb{E}(Y) = c_\lambda = \frac{\lambda e^\lambda}{e^\lambda - 1}$
and
$\mathbb{E}(Y) = c_\lambda = \frac{\lambda e^\lambda}{e^\lambda - 1}$
and
![]() $\textrm{Var}(Y) =\sigma_\lambda^2= c_\lambda(1+\lambda - c_\lambda)$
. Note that for
$\textrm{Var}(Y) =\sigma_\lambda^2= c_\lambda(1+\lambda - c_\lambda)$
. Note that for
![]() $\lambda <1$
we have
$\lambda <1$
we have
![]() $1< c_\lambda<2$
and so as Y only takes integer values which are at least 1,
$1< c_\lambda<2$
and so as Y only takes integer values which are at least 1,
![]() $\mathbb{E}|Y-\mathbb{E}(Y)|^3 = \mathbb{E}(Y-c_\lambda)^3 + 2(c_\lambda - 1)^3 \mathbb{P}(Y=1)$
. Computing this yields
$\mathbb{E}|Y-\mathbb{E}(Y)|^3 = \mathbb{E}(Y-c_\lambda)^3 + 2(c_\lambda - 1)^3 \mathbb{P}(Y=1)$
. Computing this yields
One can check that this is bounded above by
![]() $2\lambda$
for
$2\lambda$
for
![]() $\lambda<1$
.
$\lambda<1$
.
The normalised version of Y is
![]() $X = (Y - c_\lambda)/\sigma_\lambda$
. We have
$X = (Y - c_\lambda)/\sigma_\lambda$
. We have
For
![]() $\lambda<1$
one can check
$\lambda<1$
one can check
![]() $c_\lambda < 1+ 2\lambda/3$
, which allows us to deduce that
$c_\lambda < 1+ 2\lambda/3$
, which allows us to deduce that
![]() $\sigma_\lambda^2 > \lambda/3$
(also using
$\sigma_\lambda^2 > \lambda/3$
(also using
![]() $Y \geq 1$
). Hence,
$Y \geq 1$
). Hence,
![]() $\mathbb{E}|X|^3 \leq 6\sqrt{3} \lambda^{-1/2}$
. Substituting into Lemma 2.7 with
$\mathbb{E}|X|^3 \leq 6\sqrt{3} \lambda^{-1/2}$
. Substituting into Lemma 2.7 with
![]() $G_m$
the distribution of
$G_m$
the distribution of
![]() $S_m/\sqrt{m}$
,
$S_m/\sqrt{m}$
,
The probability that the sum of the in-degrees is
![]() $m+k$
is precisely
$m+k$
is precisely
Following an application of the triangle inequality, we see that this probability is bounded above by
As the event that the in-degrees sum to
![]() $m+k$
and the event that the out-degrees sum to
$m+k$
and the event that the out-degrees sum to
![]() $m+k$
are independent and identically distributed events, we may deduce the bound,
$m+k$
are independent and identically distributed events, we may deduce the bound,
Finally, we may prove Lemma 2.3.
![]()
Proof of Lemma 2.3. We choose
![]() $\lambda = 2k/m<1$
by assumption, then
$\lambda = 2k/m<1$
by assumption, then
![]() $\mathbb{P}(\Sigma(\lambda)) \leq 147/2k$
by Lemma 2.5. Combining this with Lemma 2.6 yields
$\mathbb{P}(\Sigma(\lambda)) \leq 147/2k$
by Lemma 2.5. Combining this with Lemma 2.6 yields
We use the inequality
![]() $e^x \leq 1+x+x^2/2+x^3/4$
which holds for all
$e^x \leq 1+x+x^2/2+x^3/4$
which holds for all
![]() $0 \leq x \leq 1$
to bound
$0 \leq x \leq 1$
to bound
![]() $(e^\lambda -1)/\lambda \leq 1 + \lambda/2 + \lambda^2/4$
. Thus,
$(e^\lambda -1)/\lambda \leq 1 + \lambda/2 + \lambda^2/4$
. Thus,
Then, we can use Stirling’s inequality,
![]() $e \sqrt{2k-1} (2k-1)^{2k-1} e^{-2k+1} \geq (2k-1)!$
, so that
$e \sqrt{2k-1} (2k-1)^{2k-1} e^{-2k+1} \geq (2k-1)!$
, so that
allowing us to rewrite the bound on Y(m,k) as
where we used
![]() $e^{k^2/m} \leq e^{1/3}$
. Thus proving the lemma with
$e^{k^2/m} \leq e^{1/3}$
. Thus proving the lemma with
![]() $C = 441e^3/2$
.
$C = 441e^3/2$
.
![]()
3. Proof of Theorem 1.4
In this section we prove a lower bound on component sizes in D(n,p). We give the proof for
![]() $p = 1/n$
for simplicity. The proof when
$p = 1/n$
for simplicity. The proof when
![]() $p = n^{-1} + \lambda n^{-4/3}$
is very similar, with more care taken in the approximation of terms involving
$p = n^{-1} + \lambda n^{-4/3}$
is very similar, with more care taken in the approximation of terms involving
![]() $(np)^m$
. See Section 5 for more details.
$(np)^m$
. See Section 5 for more details.
Theorem 3.1. Let
![]() $0<\delta<1/800$
, then the probability that
$0<\delta<1/800$
, then the probability that
![]() $D(n,1/n)$
has no component of size at least
$D(n,1/n)$
has no component of size at least
![]() $\delta n^{1/3}$
is at most
$\delta n^{1/3}$
is at most
![]() $2\delta^{1/2}$
.
$2\delta^{1/2}$
.
To prove this we will bound from above the probability that there is no cycle of length between
![]() $\delta n^{1/3}$
and
$\delta n^{1/3}$
and
![]() $\delta^{1/2}n^{1/3}$
. Let X be the random variable counting the number of cycles in
$\delta^{1/2}n^{1/3}$
. Let X be the random variable counting the number of cycles in
![]() $D(n,1/n)$
of length between
$D(n,1/n)$
of length between
![]() $\delta n^{1/3}$
and
$\delta n^{1/3}$
and
![]() $\delta^{1/2}n^{1/3}$
. Note that we may decompose X as a sum of dependent Bernoulli random variables, and thus we may apply Janson’s Inequality in the following form (see [Reference Janson, Łuczak and RuciŃski8, Theorem 2.18 (i)]).
$\delta^{1/2}n^{1/3}$
. Note that we may decompose X as a sum of dependent Bernoulli random variables, and thus we may apply Janson’s Inequality in the following form (see [Reference Janson, Łuczak and RuciŃski8, Theorem 2.18 (i)]).
Theorem 3.2. Let S be a set and
![]() $S_p \subseteq S$
chosen by including each element of S in
$S_p \subseteq S$
chosen by including each element of S in
![]() $S_p$
independently with probability p. Suppose that
$S_p$
independently with probability p. Suppose that
![]() $\mathcal{S}$
is a family of subsets of S and for
$\mathcal{S}$
is a family of subsets of S and for
![]() $A \in \mathcal{S}$
, we define
$A \in \mathcal{S}$
, we define
![]() $I_A$
to be the event
$I_A$
to be the event
![]() $\{ A \subseteq S_p \}$
. Let
$\{ A \subseteq S_p \}$
. Let
![]() $\mu = \mathbb{E}(X)$
and
$\mu = \mathbb{E}(X)$
and
Then,
To apply Theorem 3.2, we define S to be the set of edges of the complete digraph on n vertices. Let
![]() $A \in \mathcal{S}$
if and only if
$A \in \mathcal{S}$
if and only if
![]() $A \subseteq S$
is the set of edges of a cycle of length between
$A \subseteq S$
is the set of edges of a cycle of length between
![]() $\delta n^{1/3}$
and
$\delta n^{1/3}$
and
![]() $\delta^{1/2}n^{1/3}$
. Define X(m) to be the number cycles in
$\delta^{1/2}n^{1/3}$
. Define X(m) to be the number cycles in
![]() $D(n, 1/n)$
of length m. We start by approximating the first moment of X.
$D(n, 1/n)$
of length m. We start by approximating the first moment of X.
Lemma 3.3.
![]() $\mathbb{E}(X) \geq \log(1/\delta)/2$
$\mathbb{E}(X) \geq \log(1/\delta)/2$
Proof. Let
![]() $a = \delta n^{1/3}$
and
$a = \delta n^{1/3}$
and
![]() $b = \delta^{1/2}n^{1/3}$
. Then, we can write X as
$b = \delta^{1/2}n^{1/3}$
. Then, we can write X as
 \begin{equation*} X = \sum_{m=a}^b X(m). \end{equation*}
\begin{equation*} X = \sum_{m=a}^b X(m). \end{equation*}
Note that
So, we may bound the expectation of X as follows
 \begin{align*} \mathbb{E}(X) = \sum_{m=a}^b \mathbb{E}(X(m)) \geq \sum_{m=a}^b \frac{1}{m} \geq \int_a^b \frac{dx}{x} = \frac{\log(1/\delta)}{2}.\end{align*}
\begin{align*} \mathbb{E}(X) = \sum_{m=a}^b \mathbb{E}(X(m)) \geq \sum_{m=a}^b \frac{1}{m} \geq \int_a^b \frac{dx}{x} = \frac{\log(1/\delta)}{2}.\end{align*}
![]()
Let Z(m,k) be the random variable counting the number of strongly connected graphs with m vertices and excess k in
![]() $D(n,1/n)$
. Directly computing
$D(n,1/n)$
. Directly computing
![]() $\Delta$
is rather complicated so we will instead compute an upper bound on
$\Delta$
is rather complicated so we will instead compute an upper bound on
![]() $\Delta$
that is a linear combination of the first moments of the random variables Z(m,k) for
$\Delta$
that is a linear combination of the first moments of the random variables Z(m,k) for
![]() $m \geq a$
and
$m \geq a$
and
![]() $k \geq 1$
. To move from the computation of
$k \geq 1$
. To move from the computation of
![]() $\Delta$
to the first moments of Z(m,k) we use the following lemma,
$\Delta$
to the first moments of Z(m,k) we use the following lemma,
Lemma 3.4. Each strongly connected digraph D with excess k may be formed in at most
![]() $27^k$
ways as the union of a pair of directed cycles
$27^k$
ways as the union of a pair of directed cycles
![]() $C_1$
and
$C_1$
and
![]() $C_2$
.
$C_2$
.
Proof. Consider the heart H(D) of D. Recall that H(D) is the (multi)-digraph formed by suppressing the degree 2 vertices of D and retaining orientations. As D has excess k, H(D) has at most 2k vertices. Furthermore, the excess of H(D) is the same as the excess of D as we only remove vertices of degree 2. Thus H(D) has at most 3k edges.
Then, each edge of H(D) must be a subdigraph of either
![]() $C_1$
,
$C_1$
,
![]() $C_2$
or both. So there are
$C_2$
or both. So there are
![]() $3^{3k}=27^k$
choices for the pair
$3^{3k}=27^k$
choices for the pair
![]() $C_1, C_2$
as claimed.
$C_1, C_2$
as claimed.
![]()
We are now in a position to give a bound on
![]() $\Delta$
.
$\Delta$
.
Lemma 3.5.
![]() $\Delta \leq \log(2)$
for any
$\Delta \leq \log(2)$
for any
![]() $\delta \in (0, 1/800]$
$\delta \in (0, 1/800]$
Proof. Let
where
![]() $\overrightarrow{K_n}$
is the complete digraph on [n] and
$\overrightarrow{K_n}$
is the complete digraph on [n] and
![]() $\overrightarrow{C_k}$
is the directed cycle of length k. For
$\overrightarrow{C_k}$
is the directed cycle of length k. For
![]() $\alpha \in \Gamma(k)$
let
$\alpha \in \Gamma(k)$
let
![]() $I_\alpha$
be the indicator function of the event that all edges of
$I_\alpha$
be the indicator function of the event that all edges of
![]() $\alpha$
are present in a given realisation of
$\alpha$
are present in a given realisation of
![]() $D(n,1/n)$
. Also, define
$D(n,1/n)$
. Also, define
 \begin{equation*}\Gamma = \bigcup_{k=a}^b \Gamma(k).\end{equation*}
\begin{equation*}\Gamma = \bigcup_{k=a}^b \Gamma(k).\end{equation*}
Then, by definition,
Let
![]() $\Gamma_{\alpha}^{m,k}(t)$
be the set of
$\Gamma_{\alpha}^{m,k}(t)$
be the set of
![]() $\beta \in \Gamma(t)$
such that
$\beta \in \Gamma(t)$
such that
![]() $\alpha \cup \beta$
is a collection of
$\alpha \cup \beta$
is a collection of
![]() $m+k$
edges spanning m vertices. Then,
$m+k$
edges spanning m vertices. Then,
 \begin{align}\nonumber 2 \Delta &= \sum_{s=a}^b\sum_{t=a}^b \sum_{\alpha \in \Gamma(s)} \sum_{m=s}^{\infty} \sum_{k=1}^\infty \sum_{\beta \in \Gamma_{\alpha}^{m,k}(t)} p^{m+k} \\\nonumber & \leq \sum_{m=a}^{2b} \sum_{k=1}^{\infty} \sum_{s = a}^{m} \sum_{t= a}^m \sum_{\alpha \in \Gamma(s)} \sum_{\beta \in \Gamma_{\alpha}^{m,k}(t)} p^{m+k} \\ & \leq \sum_{m=a}^{2b} \sum_{k=1}^{\infty} 27^k \mathbb{E}(Z(m,k)),\end{align}
\begin{align}\nonumber 2 \Delta &= \sum_{s=a}^b\sum_{t=a}^b \sum_{\alpha \in \Gamma(s)} \sum_{m=s}^{\infty} \sum_{k=1}^\infty \sum_{\beta \in \Gamma_{\alpha}^{m,k}(t)} p^{m+k} \\\nonumber & \leq \sum_{m=a}^{2b} \sum_{k=1}^{\infty} \sum_{s = a}^{m} \sum_{t= a}^m \sum_{\alpha \in \Gamma(s)} \sum_{\beta \in \Gamma_{\alpha}^{m,k}(t)} p^{m+k} \\ & \leq \sum_{m=a}^{2b} \sum_{k=1}^{\infty} 27^k \mathbb{E}(Z(m,k)),\end{align}
where the last inequality follows from Lemma 3.4. Note that
by definition. We will use the following two bounds on Y(m,k) which follow immediately from Lemma 2.1.
-
• If
 $k \leq m$
, then
$k \leq m$
, then
 $Y(m,k) \leq \frac{2^k m^{3k} m!}{k! m}$
.
$Y(m,k) \leq \frac{2^k m^{3k} m!}{k! m}$
. -
• If
 $k > m$
, then
$k > m$
, then
 $Y(m,k) \leq \frac{(2e)^k m^{2k} m!}{m}$
.
$Y(m,k) \leq \frac{(2e)^k m^{2k} m!}{m}$
.
This allows us to split the sum in (10) based upon whether
![]() $k \leq m$
or
$k \leq m$
or
![]() $k>m$
to obtain
$k>m$
to obtain
 \begin{align} \nonumber 2\Delta & \leq \sum_{m=a}^{2b} \sum_{k=1}^{m} 27^k \binom{n}{m} \frac{2^k m^{3k} m!}{k! m} p^{m+k} + \sum_{m=a}^{2b} \sum_{k=m+1}^{\infty} 27^k \binom{n}{m} \frac{(2e)^k m^{2k} m!}{m} p^{m+k} \\ \nonumber & \leq \sum_{m=a}^{2 b} \frac{1}{m}\sum_{k=1}^{\infty} \frac{(54 p m^3)^k}{k!} + \sum_{m=a}^{2 b} \frac{1}{m} \sum_{k=m+1}^{\infty} (54e m^2 p)^k \\ & \leq \frac{\log(4/\delta)}{2}(e^{432 \delta^{3/2}}-1 +23328e^2\delta^2), \end{align}
\begin{align} \nonumber 2\Delta & \leq \sum_{m=a}^{2b} \sum_{k=1}^{m} 27^k \binom{n}{m} \frac{2^k m^{3k} m!}{k! m} p^{m+k} + \sum_{m=a}^{2b} \sum_{k=m+1}^{\infty} 27^k \binom{n}{m} \frac{(2e)^k m^{2k} m!}{m} p^{m+k} \\ \nonumber & \leq \sum_{m=a}^{2 b} \frac{1}{m}\sum_{k=1}^{\infty} \frac{(54 p m^3)^k}{k!} + \sum_{m=a}^{2 b} \frac{1}{m} \sum_{k=m+1}^{\infty} (54e m^2 p)^k \\ & \leq \frac{\log(4/\delta)}{2}(e^{432 \delta^{3/2}}-1 +23328e^2\delta^2), \end{align}
where the
![]() $23328e^2\delta^2$
term comes from noting
$23328e^2\delta^2$
term comes from noting
![]() $k \geq 2$
in the range
$k \geq 2$
in the range
![]() $k \geq m+1$
and that for
$k \geq m+1$
and that for
![]() $x\leq 1/2$
$x\leq 1/2$
 \begin{equation*}\sum_{k=2}^\infty x^k \leq 2x^2.\end{equation*}
\begin{equation*}\sum_{k=2}^\infty x^k \leq 2x^2.\end{equation*}
As (11) is increasing in
![]() $\delta$
, we simply need to check that the Lemma holds for
$\delta$
, we simply need to check that the Lemma holds for
![]() $\delta = 1/800$
which may be done numerically.
$\delta = 1/800$
which may be done numerically.
![]()
Finally, to prove Theorem 3.1. we substitute the values obtained for
![]() $\mu$
and
$\mu$
and
![]() $\Delta$
in Lemmas 3.3 and 3.5 respectively into Theorem 3.2. That is,
$\Delta$
in Lemmas 3.3 and 3.5 respectively into Theorem 3.2. That is,
So the probability there is no directed cycle of length at least
![]() $\delta n^{1/3}$
is at most
$\delta n^{1/3}$
is at most
![]() $2 \delta^{1/2}$
and, as cycles are strongly connected, this is also an upper bound on the probability there is no strongly connected component of size at least
$2 \delta^{1/2}$
and, as cycles are strongly connected, this is also an upper bound on the probability there is no strongly connected component of size at least
![]() $\delta n^{1/3}$
.
$\delta n^{1/3}$
.
4. Proof of Theorem 1.5
In this section we prove an upper bound on the component sizes in D(n,p). Again, we only consider the case when
![]() $p=1/n$
to simplify notation and calculations. The reader is referred to Section 5 for a sketch of the adaptations to extend the result to the full critical window. The following is a restatement of Theorem 1.5 for
$p=1/n$
to simplify notation and calculations. The reader is referred to Section 5 for a sketch of the adaptations to extend the result to the full critical window. The following is a restatement of Theorem 1.5 for
![]() $p=1/n$
.
$p=1/n$
.
Theorem 4.1. There exist constants
![]() $\zeta, \eta > 0$
such that for any
$\zeta, \eta > 0$
such that for any
![]() $A>0$
if n is sufficiently large with respect to A, then the probability that
$A>0$
if n is sufficiently large with respect to A, then the probability that
![]() $D(n,1/n)$
contains any component of size at least
$D(n,1/n)$
contains any component of size at least
![]() $An^{1/3}$
is at most
$An^{1/3}$
is at most
![]() $ \zeta e^{-\eta A^{3/2}}. $
$ \zeta e^{-\eta A^{3/2}}. $
We will use the first moment method to prove this theorem and calculate the expected number of large strongly connected components in
![]() $D(n,1/n)$
. Note that it is important to count components and not strongly connected subgraphs as the expected number of strongly connected subgraphs in
$D(n,1/n)$
. Note that it is important to count components and not strongly connected subgraphs as the expected number of strongly connected subgraphs in
![]() $D(n,1/n)$
blows up as
$D(n,1/n)$
blows up as
![]() $n \to \infty$
. Thus for each strongly connected subgraph, we will use an exploration process to determine whether or not it is a component.
$n \to \infty$
. Thus for each strongly connected subgraph, we will use an exploration process to determine whether or not it is a component.
The exploration process we use was initially developed by Martin-Löf [Reference Martin-Löf14] and Karp [Reference Karp9]. During this process, vertices will be in one of three classes: active, explored or unexplored. At time
![]() $t \in \mathbb{N}$
, we let
$t \in \mathbb{N}$
, we let
![]() $X_t$
be the number of active vertices,
$X_t$
be the number of active vertices,
![]() $A_t$
the set of active vertices,
$A_t$
the set of active vertices,
![]() $E_t$
the set of explored vertices and
$E_t$
the set of explored vertices and
![]() $U_t$
the set of unexplored vertices.
$U_t$
the set of unexplored vertices.
We will start from a set
![]() $A_0$
of vertices of size
$A_0$
of vertices of size
![]() $X_0$
and fix an ordering of the vertices, starting with
$X_0$
and fix an ordering of the vertices, starting with
![]() $A_0$
. For step
$A_0$
. For step
![]() $t \geq 1$
, if
$t \geq 1$
, if
![]() $X_{t-1}>0$
let
$X_{t-1}>0$
let
![]() $w_t$
be the first active vertex. Otherwise, let
$w_t$
be the first active vertex. Otherwise, let
![]() $w_t$
be the first unexplored vertex. Define
$w_t$
be the first unexplored vertex. Define
![]() $\eta_t$
to be the number of unexplored out-neighbours of
$\eta_t$
to be the number of unexplored out-neighbours of
![]() $w_t$
in
$w_t$
in
![]() $D(n,1/n)$
. Change the class of each of these vertices to active and set
$D(n,1/n)$
. Change the class of each of these vertices to active and set
![]() $w_t$
to explored. This means that
$w_t$
to explored. This means that
![]() $|E_t| = t$
and furthermore,
$|E_t| = t$
and furthermore,
![]() $|U_t| = n - X_t - t$
. Let
$|U_t| = n - X_t - t$
. Let
![]() $N_t = n - X_t - t - \unicode{x1D7D9}(X_t = 0)$
be the number of potential unexplored out-neighbours of
$N_t = n - X_t - t - \unicode{x1D7D9}(X_t = 0)$
be the number of potential unexplored out-neighbours of
![]() $w_{t+1}$
, i.e. the number of unexplored vertices which are not
$w_{t+1}$
, i.e. the number of unexplored vertices which are not
![]() $w_{t+1}$
. Then, given the history of the process,
$w_{t+1}$
. Then, given the history of the process,
![]() $\eta_t$
is distributed as a binomial random variable with parameters
$\eta_t$
is distributed as a binomial random variable with parameters
![]() $N_{t-1}$
and
$N_{t-1}$
and
![]() $1/n$
. Furthermore, the following recurrence relation holds.
$1/n$
. Furthermore, the following recurrence relation holds.
 \begin{equation} X_t = \begin{cases} X_{t-1} + \eta_t -1 & \text{if } X_{t-1} > 0, \\ \eta_t & \text{otherwise}. \end{cases}\end{equation}
\begin{equation} X_t = \begin{cases} X_{t-1} + \eta_t -1 & \text{if } X_{t-1} > 0, \\ \eta_t & \text{otherwise}. \end{cases}\end{equation}
Let
![]() $\tau_1 = \min\{t \geq 1 : X_t = 0\}$
. Note that this is a stopping time and at time
$\tau_1 = \min\{t \geq 1 : X_t = 0\}$
. Note that this is a stopping time and at time
![]() $\tau_1$
the set
$\tau_1$
the set
![]() $E_{\tau_1}$
of explored vertices is precisely the out-component of
$E_{\tau_1}$
of explored vertices is precisely the out-component of
![]() $A_0$
. If
$A_0$
. If
![]() $A_0$
spans a strongly connected subdigraph
$A_0$
spans a strongly connected subdigraph
![]() $D_0$
of
$D_0$
of
![]() $D(n,1/n)$
, then
$D(n,1/n)$
, then
![]() $D_0$
is a strongly connected component if and only if there are no edges from
$D_0$
is a strongly connected component if and only if there are no edges from
![]() $E_{\tau_1} \setminus A_0$
to
$E_{\tau_1} \setminus A_0$
to
![]() $A_0$
. The key idea will be to show that if
$A_0$
. The key idea will be to show that if
![]() $X_0$
is sufficiently large, then it is very unlikely for
$X_0$
is sufficiently large, then it is very unlikely for
![]() $\tau_1$
to be small, and consequently it is also very unlikely that there are no edges from
$\tau_1$
to be small, and consequently it is also very unlikely that there are no edges from
![]() $E_{\tau_1} \setminus A_0$
to
$E_{\tau_1} \setminus A_0$
to
![]() $A_0$
. This is encapsulated in the following lemma.
$A_0$
. This is encapsulated in the following lemma.
Lemma 4.2. Let
![]() $X_t$
be the exploration process defined above with starting set of vertices
$X_t$
be the exploration process defined above with starting set of vertices
![]() $A_0$
of size
$A_0$
of size
![]() $X_0=m$
. Suppose
$X_0=m$
. Suppose
![]() $0<c<\sqrt2$
is a fixed constant. Then,
$0<c<\sqrt2$
is a fixed constant. Then,
Proof. Define
![]() $\xi = c m^{1/2}n^{1/2}$
and consider the auxiliary process,
$\xi = c m^{1/2}n^{1/2}$
and consider the auxiliary process,
![]() $X_t'$
which we define recursively by
$X_t'$
which we define recursively by
where
![]() $W_t \sim \text{Bin}(n-t-10m,p)$
. Let
$W_t \sim \text{Bin}(n-t-10m,p)$
. Let
![]() $\tau_2$
be the stopping time,
$\tau_2$
be the stopping time,
We may couple the processes
![]() $(X_t, X_t')$
such that
$(X_t, X_t')$
such that
![]() $X_t'$
is stochastically dominated by
$X_t'$
is stochastically dominated by
![]() $X_t$
for
$X_t$
for
![]() $t < \tau_2$
. The coupling may be explicitly defined by setting
$t < \tau_2$
. The coupling may be explicitly defined by setting
![]() $\eta_t = W_t + W_t'$
with
$\eta_t = W_t + W_t'$
with
![]() $W_t' \sim \text{Bin}(10 m - X_{t-1},p)$
. Define another stopping time,
$W_t' \sim \text{Bin}(10 m - X_{t-1},p)$
. Define another stopping time,
![]() $\tau_1' = \min \{t \geq 1 : X_t' =0 \}$
. Consider the following events:
$\tau_1' = \min \{t \geq 1 : X_t' =0 \}$
. Consider the following events:
 \begin{align*}\mathcal{E}_1 & = \big\{ \tau_1 < c m^{1/2}n^{1/2} \big\}, \\
\mathcal{E}_2 & = \big\{ \tau_1' < c m^{1/2}n^{1/2} \big\}, \\
\mathcal{E}_3 & = \big\{ \tau_2 < c m^{1/2}n^{1/2} \big\}.\end{align*}
\begin{align*}\mathcal{E}_1 & = \big\{ \tau_1 < c m^{1/2}n^{1/2} \big\}, \\
\mathcal{E}_2 & = \big\{ \tau_1' < c m^{1/2}n^{1/2} \big\}, \\
\mathcal{E}_3 & = \big\{ \tau_2 < c m^{1/2}n^{1/2} \big\}.\end{align*}
And note that
![]() $\mathbb{P}(\mathcal{E}_1) \leq \mathbb{P}(\mathcal{E}_2) + \mathbb{P}(\mathcal{E}_3)$
by our choice of coupling and a union bound (as the coupling guarantees
$\mathbb{P}(\mathcal{E}_1) \leq \mathbb{P}(\mathcal{E}_2) + \mathbb{P}(\mathcal{E}_3)$
by our choice of coupling and a union bound (as the coupling guarantees
![]() $\mathcal{E}_1 \subseteq \mathcal{E}_2 \cup \mathcal{E}_3$
). Thus we only need to bound the probabilities of the simpler events
$\mathcal{E}_1 \subseteq \mathcal{E}_2 \cup \mathcal{E}_3$
). Thus we only need to bound the probabilities of the simpler events
![]() $\mathcal{E}_2$
and
$\mathcal{E}_2$
and
![]() $\mathcal{E}_3$
. We begin by considering
$\mathcal{E}_3$
. We begin by considering
![]() $\mathcal{E}_3$
. To bound its probability we consider the upper bound process
$\mathcal{E}_3$
. To bound its probability we consider the upper bound process
![]() $M_t$
defined by
$M_t$
defined by
where
![]() $B_t \sim \text{Bin}(n,1/n)$
. It is straightforward to couple
$B_t \sim \text{Bin}(n,1/n)$
. It is straightforward to couple
![]() $(X_t,M_t)$
such that
$(X_t,M_t)$
such that
![]() $M_t$
stochastically dominates
$M_t$
stochastically dominates
![]() $X_t$
. Furthermore,
$X_t$
. Furthermore,
![]() $M_t$
is a martingale. Hence,
$M_t$
is a martingale. Hence,
![]() $\mathbb{P}(\mathcal{E}_3) \leq \mathbb{P}(\tau_2' < c m^{1/2}n^{1/2})$
where
$\mathbb{P}(\mathcal{E}_3) \leq \mathbb{P}(\tau_2' < c m^{1/2}n^{1/2})$
where
![]() $\tau_2'$
is the stopping time,
$\tau_2'$
is the stopping time,
![]() $\tau_2' = \min\{t:M_t>10m\}$
. To bound the probability of
$\tau_2' = \min\{t:M_t>10m\}$
. To bound the probability of
![]() $\mathcal{E}_2$
consider the process
$\mathcal{E}_2$
consider the process
![]() $Y_t$
defined as
$Y_t$
defined as
![]() $Y_t = m - X_t'$
. One can check that
$Y_t = m - X_t'$
. One can check that
![]() $Y_t$
is a submartingale.
$Y_t$
is a submartingale.
As
![]() $x \mapsto e^{\alpha x}$
is a convex non-decreasing function for any
$x \mapsto e^{\alpha x}$
is a convex non-decreasing function for any
![]() $\alpha>0$
, we may apply Jensen’s inequality to deduce that
$\alpha>0$
, we may apply Jensen’s inequality to deduce that
![]() $Z_t^- = e^{\alpha Y_t}$
and
$Z_t^- = e^{\alpha Y_t}$
and
![]() $Z_t^+ = e^{\alpha M_t}$
are submartingales. Also,
$Z_t^+ = e^{\alpha M_t}$
are submartingales. Also,
![]() $Z_t^-,Z_t^+ >0$
for any
$Z_t^-,Z_t^+ >0$
for any
![]() $i \in \mathbb{N}$
. Starting with
$i \in \mathbb{N}$
. Starting with
![]() $Z_t^-$
, we may apply Doob’s maximal inequality [Reference Grimmett and Stirzaker6, Section 12.6] and deduce that
$Z_t^-$
, we may apply Doob’s maximal inequality [Reference Grimmett and Stirzaker6, Section 12.6] and deduce that
We may rewrite this by noting that
 \begin{equation*}Y_t = m - X_t' = t - \sum_{i=1}^t W_i = t - R_t,\end{equation*}
\begin{equation*}Y_t = m - X_t' = t - \sum_{i=1}^t W_i = t - R_t,\end{equation*}
where
![]() $R_t$
is binomially distributed and in particular
$R_t$
is binomially distributed and in particular
![]() $R_\xi \sim \text{Bin}(l\xi,p)$
for
$R_\xi \sim \text{Bin}(l\xi,p)$
for
Also, we choose x such that
![]() $x l \xi = \xi - m$
. Then (13) may be rewritten as
$x l \xi = \xi - m$
. Then (13) may be rewritten as
![]() $e^{-\alpha m} \mathbb{E}(Z_\xi^-) = e^{\alpha xl \xi} \mathbb{E}(e^{-\alpha R_\xi})$
. The next stage is to rearrange this into a form which resembles the usual Chernoff bounds (for
$e^{-\alpha m} \mathbb{E}(Z_\xi^-) = e^{\alpha xl \xi} \mathbb{E}(e^{-\alpha R_\xi})$
. The next stage is to rearrange this into a form which resembles the usual Chernoff bounds (for
![]() $x<p$
). So, let
$x<p$
). So, let
Then, we choose
![]() $\alpha^*$
to minimise f. Solving
$\alpha^*$
to minimise f. Solving
![]() $f'(\alpha)=0$
, we obtain the solution
$f'(\alpha)=0$
, we obtain the solution
Note
![]() $x<p$
so,
$x<p$
so,
![]() $e^{-\alpha^*}<1$
and
$e^{-\alpha^*}<1$
and
![]() $\alpha^*>0$
as desired. Thus,
$\alpha^*>0$
as desired. Thus,
 \begin{align*} f(\alpha^*) & = \bigg[\bigg( \frac{p(1-x)}{x(1-p)}\bigg)^{x} \bigg( x \frac{1-p}{1-x} + 1-p \bigg)\bigg]^{mt} \\& = \bigg[\bigg( x \frac{1-p}{1-x} + 1-p \bigg) \bigg( \frac{p}{x}\bigg)^x \bigg( \frac{1-p}{1-x} \bigg)^x \bigg]^{mt} \\& = \bigg[\bigg( \frac{p}{x}\bigg)^x \bigg( \frac{1-p}{1-x} \bigg)^{1-x} \bigg]^{mt}.\end{align*}
\begin{align*} f(\alpha^*) & = \bigg[\bigg( \frac{p(1-x)}{x(1-p)}\bigg)^{x} \bigg( x \frac{1-p}{1-x} + 1-p \bigg)\bigg]^{mt} \\& = \bigg[\bigg( x \frac{1-p}{1-x} + 1-p \bigg) \bigg( \frac{p}{x}\bigg)^x \bigg( \frac{1-p}{1-x} \bigg)^x \bigg]^{mt} \\& = \bigg[\bigg( \frac{p}{x}\bigg)^x \bigg( \frac{1-p}{1-x} \bigg)^{1-x} \bigg]^{mt}.\end{align*}
Which is the usual expression found in Chernoff bounds. As usual, we bound this by writing
and bound g, where
Computing the Taylor expansion of g we find that
![]() $g(p)=g'(p)=0$
. So, if
$g(p)=g'(p)=0$
. So, if
![]() $g''(x) \geq \beta$
for all x between p and
$g''(x) \geq \beta$
for all x between p and
![]() $p-h$
, then
$p-h$
, then
![]() $g(p-h) \geq \beta h^2/2$
. Furthermore,
$g(p-h) \geq \beta h^2/2$
. Furthermore,
As
![]() $0<x<p$
, we have
$0<x<p$
, we have
![]() $g''(x) \geq 1/x \geq 1/p$
. So, we deduce that
$g''(x) \geq 1/x \geq 1/p$
. So, we deduce that
![]() $g(x) \geq \delta^2 p/2$
where
$g(x) \geq \delta^2 p/2$
where
![]() $\delta = 1-x/p$
. All that remains is to compute
$\delta = 1-x/p$
. All that remains is to compute
![]() $\delta$
. As defined earlier, we have
$\delta$
. As defined earlier, we have
![]() $x l \xi = \xi - m$
which for convenience we will write as
$x l \xi = \xi - m$
which for convenience we will write as
Also, as
![]() $p=n^{-1}$
, and recalling the definition of
$p=n^{-1}$
, and recalling the definition of
![]() $l \xi$
from earlier,
$l \xi$
from earlier,
 \begin{align}\nonumber pl \xi & = c m^{1/2}n^{1/2} - \frac{c^2 m}{2} +O(m^{3/2} n^{-1/2}) \\ & = \xi\bigg(1 - \frac{cm^{1/2}}{2n^{1/2}} +O(m n^{-1}) \bigg). \end{align}
\begin{align}\nonumber pl \xi & = c m^{1/2}n^{1/2} - \frac{c^2 m}{2} +O(m^{3/2} n^{-1/2}) \\ & = \xi\bigg(1 - \frac{cm^{1/2}}{2n^{1/2}} +O(m n^{-1}) \bigg). \end{align}
We divide (14) by (15) and as the Taylor expansion of
![]() $1/(1-w)$
is
$1/(1-w)$
is
![]() $\sum_{i \geq 0} w^i$
,
$\sum_{i \geq 0} w^i$
,
 \begin{equation} \frac{x}{p} = \frac{1-\frac{m^{1/2}}{c n^{1/2}}}{1 - \frac{cm^{1/2}}{2n^{1/2}} +O(m n^{-1})} = 1 - \frac{m^{1/2}}{c n^{1/2}} + \frac{cm^{1/2}}{2n^{1/2}} +O(m n^{-1}).\end{equation}
\begin{equation} \frac{x}{p} = \frac{1-\frac{m^{1/2}}{c n^{1/2}}}{1 - \frac{cm^{1/2}}{2n^{1/2}} +O(m n^{-1})} = 1 - \frac{m^{1/2}}{c n^{1/2}} + \frac{cm^{1/2}}{2n^{1/2}} +O(m n^{-1}).\end{equation}
From which we may deduce
So,
We may proceed similarly for
![]() $Z_t^+$
, in particular we must still appeal to Doob’s maximal inequality as we seek a bound over the entire process. In this case we end up with a
$Z_t^+$
, in particular we must still appeal to Doob’s maximal inequality as we seek a bound over the entire process. In this case we end up with a
![]() $\text{Bin}(n \xi, p)$
distribution and are looking at the upper tail rather than the lower. We find
$\text{Bin}(n \xi, p)$
distribution and are looking at the upper tail rather than the lower. We find
![]() $p n \xi = \xi$
and
$p n \xi = \xi$
and
Thus,
Substituting into the analogous bound,
Observe that
![]() $\mathbb{P}(\mathcal{E}_2) \geq \mathbb{P}(\mathcal{E}_3)e^{O(m^2 n^{-1})}$
for
$\mathbb{P}(\mathcal{E}_2) \geq \mathbb{P}(\mathcal{E}_3)e^{O(m^2 n^{-1})}$
for
![]() $0<c<\sqrt{2(1+3\sqrt{6})}$
. Thus, in the range we are interested in, we may use
$0<c<\sqrt{2(1+3\sqrt{6})}$
. Thus, in the range we are interested in, we may use
![]() $2\mathbb{P}(\mathcal{E}_2)$
as an upper bound for
$2\mathbb{P}(\mathcal{E}_2)$
as an upper bound for
![]() $\mathbb{P}(\mathcal{E}_2)+\mathbb{P}(\mathcal{E}_3)$
and this proves the lemma.
$\mathbb{P}(\mathcal{E}_2)+\mathbb{P}(\mathcal{E}_3)$
and this proves the lemma.
![]()
We now compute the probability that any given strongly connected subgraph of
![]() $D(n,1/n)$
is a component. To do so, we use the simple observation that a strongly connected subgraph is a component if it is not contained in a larger strongly connected subgraph.
$D(n,1/n)$
is a component. To do so, we use the simple observation that a strongly connected subgraph is a component if it is not contained in a larger strongly connected subgraph.
Lemma 4.3. There exist
![]() $\beta, \gamma>0$
such that if H is any strongly connected subgraph of
$\beta, \gamma>0$
such that if H is any strongly connected subgraph of
![]() $D(n,1/n)$
with m vertices. Then the probability that H is a strongly connected component of
$D(n,1/n)$
with m vertices. Then the probability that H is a strongly connected component of
![]() $D(n,1/n)$
is at most
$D(n,1/n)$
is at most
![]() $\beta e^{-(1+\gamma)m^{3/2}n^{-1/2} +O(m^2 n^{-1})}$
.
$\beta e^{-(1+\gamma)m^{3/2}n^{-1/2} +O(m^2 n^{-1})}$
.
Proof. We compute the probability that H is a component of
![]() $D(n,1/n)$
by running the exploration process
$D(n,1/n)$
by running the exploration process
![]() $X_t$
starting from
$X_t$
starting from
![]() $A_0 = V(H)$
. So,
$A_0 = V(H)$
. So,
![]() $X_0 = m$
. Once the exploration process dies at time
$X_0 = m$
. Once the exploration process dies at time
![]() $\tau_1$
, any backward edge from
$\tau_1$
, any backward edge from
![]() $E_{\tau_1} \setminus A_0$
to
$E_{\tau_1} \setminus A_0$
to
![]() $A_0$
gives a strongly connected subgraph of
$A_0$
gives a strongly connected subgraph of
![]() $D(n,1/n)$
which contains H. Let
$D(n,1/n)$
which contains H. Let
![]() $Y_t$
be the random variable which counts the number of edges from
$Y_t$
be the random variable which counts the number of edges from
![]() $E_{\tau_1} \setminus A_0$
to
$E_{\tau_1} \setminus A_0$
to
![]() $A_0$
. Note that for
$A_0$
. Note that for
![]() $t \geq m$
,
$t \geq m$
,
![]() $Y_t \sim \text{Bin}(m(t-m),p)$
. Furthermore, H is a strongly connected component of
$Y_t \sim \text{Bin}(m(t-m),p)$
. Furthermore, H is a strongly connected component of
![]() $D(n,1/n)$
if and only if
$D(n,1/n)$
if and only if
![]() $Y_{\tau_1}=0$
.
$Y_{\tau_1}=0$
.
Let
![]() $\varepsilon>0$
and define the events
$\varepsilon>0$
and define the events
![]() $\mathcal{A}_i$
for
$\mathcal{A}_i$
for
![]() $i =1, \ldots, r$
(where
$i =1, \ldots, r$
(where
![]() $r \sim c/\varepsilon$
for some
$r \sim c/\varepsilon$
for some
![]() $c>1$
) to be
$c>1$
) to be
Clearly the family
![]() $\{ \mathcal{A}_i : i = 1, \ldots, r +1 \}$
forms a partition of the sample space. So, by the law of total probability,
$\{ \mathcal{A}_i : i = 1, \ldots, r +1 \}$
forms a partition of the sample space. So, by the law of total probability,
 \begin{equation} \mathbb{P}(Y_{\tau_1}=0) = \sum_{i=1}^{r+1} \mathbb{P}(Y_{\tau_1}=0 |\mathcal{A}_i) \mathbb{P}(\mathcal{A}_i).\end{equation}
\begin{equation} \mathbb{P}(Y_{\tau_1}=0) = \sum_{i=1}^{r+1} \mathbb{P}(Y_{\tau_1}=0 |\mathcal{A}_i) \mathbb{P}(\mathcal{A}_i).\end{equation}
By applying Lemma 4.2 when
![]() $1\leq i \leq r$
we find
$1\leq i \leq r$
we find
Note that
![]() $Y_{\tau_1}$
conditioned on
$Y_{\tau_1}$
conditioned on
![]() $\mathcal{A}_i$
stochastically dominates a
$\mathcal{A}_i$
stochastically dominates a
![]() $\text{Bin}(m((i-1) \varepsilon m^{1/2}n^{1/2} - m),p)$
distribution. Therefore,
$\text{Bin}(m((i-1) \varepsilon m^{1/2}n^{1/2} - m),p)$
distribution. Therefore,
Combining the above and substituting into (20) yields
for some
![]() $\gamma>0$
provided that
$\gamma>0$
provided that
![]() $\varepsilon$
is sufficiently small. The second term in (21) is a result of the fact
$\varepsilon$
is sufficiently small. The second term in (21) is a result of the fact
![]() $\mathbb{P}(A_{r+1}) \leq 1$
. This proves the lemma and if one wishes for explicit constants, taking
$\mathbb{P}(A_{r+1}) \leq 1$
. This proves the lemma and if one wishes for explicit constants, taking
![]() $\varepsilon = 0.025$
,
$\varepsilon = 0.025$
,
![]() $r= 45$
works and gives
$r= 45$
works and gives
![]() $\beta < 100 $
,
$\beta < 100 $
,
![]() $\gamma > 0.06 $
.
$\gamma > 0.06 $
.
![]()
The next stage in our proof is to show that a typical instance of
![]() $D(n,1/n)$
has no component of large excess and no exceptionally large components. This will allow us to use the bound from Lemma 2.3 to compute the expected number of large strongly connected components of
$D(n,1/n)$
has no component of large excess and no exceptionally large components. This will allow us to use the bound from Lemma 2.3 to compute the expected number of large strongly connected components of
![]() $D(n,1/n)$
. The first result in this direction is an immediate corollary of a result of Łuczak and Seierstad [Reference Łuczak and Seierstad13].
$D(n,1/n)$
. The first result in this direction is an immediate corollary of a result of Łuczak and Seierstad [Reference Łuczak and Seierstad13].
Lemma 4.4
([Reference Łuczak and Seierstad13]). The probability that
![]() $D(n,1/n)$
contains a strongly connected component of size at least
$D(n,1/n)$
contains a strongly connected component of size at least
![]() $n^{1/3} \log\log n$
is
$n^{1/3} \log\log n$
is
![]() $o_n(1)$
.
$o_n(1)$
.
The next lemma ensures that there are not too many cycles which enables us to prove that the total excess is relatively small.
Lemma 4.5. The probability that D(n,p) contains more than
![]() $n^{1/6}$
cycles of length bounded above by
$n^{1/6}$
cycles of length bounded above by
![]() $n^{1/3}\log\log(n)$
is
$n^{1/3}\log\log(n)$
is
![]() $o_n(1)$
.
$o_n(1)$
.
Proof. In this proof and subsequently we will use the convention that
![]() $\log^{(k)} x$
is the logarithm function composed with itself k times, while
$\log^{(k)} x$
is the logarithm function composed with itself k times, while
![]() $(\log x)^k$
is its kth power. We shall show that the expected number of cycles of length at most
$(\log x)^k$
is its kth power. We shall show that the expected number of cycles of length at most
![]() $n^{1/3} \log^{(2)}n$
is
$n^{1/3} \log^{(2)}n$
is
![]() $o(n^{1/6})$
at which point we may apply Markov’s inequality. So let C be the random variable which counts the number of cycles of length at most
$o(n^{1/6})$
at which point we may apply Markov’s inequality. So let C be the random variable which counts the number of cycles of length at most
![]() $n^{1/3} \log^{(2)} n$
in
$n^{1/3} \log^{(2)} n$
in
![]() $D(n,1/n)$
. We can calculate its expectation as
$D(n,1/n)$
. We can calculate its expectation as
 \begin{equation}\mathbb{E}(C) = \sum_{k=1}^{n^{1/3} \log^{(2)}n} \binom{n}{k} \frac{k!}{k} p^k \leq \sum_{k=1}^{n^{1/3} \log^{(2)}n} \frac{1}{k}.\end{equation}
\begin{equation}\mathbb{E}(C) = \sum_{k=1}^{n^{1/3} \log^{(2)}n} \binom{n}{k} \frac{k!}{k} p^k \leq \sum_{k=1}^{n^{1/3} \log^{(2)}n} \frac{1}{k}.\end{equation}
We use the upper bound on the kth harmonic number
![]() $H_k \leq \log k +1$
, which allows us to deduce that
$H_k \leq \log k +1$
, which allows us to deduce that
Thus the lemma follows by Markov’s inequality.
![]()
Corollary 4.6. The probability that
![]() $D(n,1/n)$
contains a component of excess at least
$D(n,1/n)$
contains a component of excess at least
![]() $n^{1/6}$
and size at most
$n^{1/6}$
and size at most
![]() $n^{1/3} \log\log n $
is
$n^{1/3} \log\log n $
is
![]() $o_n(1)$
.
$o_n(1)$
.
Proof. If D is any strongly connected digraph with m vertices and excess k, then note that it must have at least
![]() $k+1$
cycles of length at most m. This can be seen by considering the ear decomposition of D. The first ear must be a cycle, and each subsequent ear adds a path which must be contained in a cycle as D is strongly connected. So as we build the ear decomposition, each additional ear adds at least one cycle. As any ear decomposition of a strongly connected digraph of excess k has
$k+1$
cycles of length at most m. This can be seen by considering the ear decomposition of D. The first ear must be a cycle, and each subsequent ear adds a path which must be contained in a cycle as D is strongly connected. So as we build the ear decomposition, each additional ear adds at least one cycle. As any ear decomposition of a strongly connected digraph of excess k has
![]() $k+1$
ears, then D must have at least
$k+1$
ears, then D must have at least
![]() $k+1$
cycles.
$k+1$
cycles.
Thus, if D has k cycles, it must have excess at most
![]() $k-1$
. So applying Lemma 4.5 completes the proof.
$k-1$
. So applying Lemma 4.5 completes the proof.
![]()
Finally, we prove the main theorem of this section.
Proof of Theorem 4.1.
Let
![]() $\mathcal{C}_1$
be the largest strongly connected component of
$\mathcal{C}_1$
be the largest strongly connected component of
![]() $D(n,1/n)$
and
$D(n,1/n)$
and
![]() $L_1 =|\mathcal{C}_1|$
. We want to compute
$L_1 =|\mathcal{C}_1|$
. We want to compute
![]() $\mathbb{P}(L_1 \geq A n^{1/3})$
. Define the following three events:
$\mathbb{P}(L_1 \geq A n^{1/3})$
. Define the following three events:
 \begin{align*}\mathcal{E}_1 & = \{ L_1 \geq A n^{1/3} \}, \\\mathcal{E}_2 & = \{ A n^{1/3} \leq L_1 \leq n^{1/3} \log\log(n) \}, \\\mathcal{E}_3 & = \{ L_1 \geq n^{1/3} \log\log(n) \}.\end{align*}
\begin{align*}\mathcal{E}_1 & = \{ L_1 \geq A n^{1/3} \}, \\\mathcal{E}_2 & = \{ A n^{1/3} \leq L_1 \leq n^{1/3} \log\log(n) \}, \\\mathcal{E}_3 & = \{ L_1 \geq n^{1/3} \log\log(n) \}.\end{align*}
Clearly,
![]() $\mathcal{E}_1 \subseteq \mathcal{E}_2 \cup \mathcal{E}_3$
and by Lemma 4.4,
$\mathcal{E}_1 \subseteq \mathcal{E}_2 \cup \mathcal{E}_3$
and by Lemma 4.4,
![]() $\mathbb{P}(\mathcal{E}_3) = o_n(1)$
. If
$\mathbb{P}(\mathcal{E}_3) = o_n(1)$
. If
![]() $\mathcal{F}$
is the event that
$\mathcal{F}$
is the event that
![]() $\mathcal{C}_1$
has excess at least
$\mathcal{C}_1$
has excess at least
![]() $n^{1/6}$
then by Corollary 4.6,
$n^{1/6}$
then by Corollary 4.6,
![]() $\mathbb{P}(\mathcal{E}_2 \cap \mathcal{F}) = o_n(1)$
. All that remains is to give a bound on
$\mathbb{P}(\mathcal{E}_2 \cap \mathcal{F}) = o_n(1)$
. All that remains is to give a bound on
![]() $\mathbb{P}(\mathcal{E}_2 \cap \mathcal{F}^c)$
. To this end let N(A) be random variable which counts the number of strongly connected components of
$\mathbb{P}(\mathcal{E}_2 \cap \mathcal{F}^c)$
. To this end let N(A) be random variable which counts the number of strongly connected components of
![]() $D(n,1/n)$
which have size between
$D(n,1/n)$
which have size between
![]() $An^{1/3}$
and
$An^{1/3}$
and
![]() $n^{1/3}\log\log n$
and excess bounded above by
$n^{1/3}\log\log n$
and excess bounded above by
![]() $n^{1/6}$
. By Markov’s inequality, we may deduce that
$n^{1/6}$
. By Markov’s inequality, we may deduce that
![]() $\mathbb{P}(\mathcal{E}_2 \cap \mathcal{F}^c) \leq \mathbb{E}(N(A))$
. Computing the expectation of N(A),
$\mathbb{P}(\mathcal{E}_2 \cap \mathcal{F}^c) \leq \mathbb{E}(N(A))$
. Computing the expectation of N(A),
 \begin{equation} \mathbb{E}(N(A)) = \sum_{m=An^{1/3}}^{n^{1/3}\log^2(n)} \sum_{k=0}^{n^{1/6}} \binom{n}{m} p^{m+k} Y(m,k) \mathbb{P}(Y_{\tau_1}=0|X_0=m).\end{equation}
\begin{equation} \mathbb{E}(N(A)) = \sum_{m=An^{1/3}}^{n^{1/3}\log^2(n)} \sum_{k=0}^{n^{1/6}} \binom{n}{m} p^{m+k} Y(m,k) \mathbb{P}(Y_{\tau_1}=0|X_0=m).\end{equation}
In Lemma 4.3. we showed that
![]() $\mathbb{P}(Y_{\tau_1}=0|X_0=m) \leq \beta e^{-(1+\gamma)m^{3/2} n^{-1/2} +O(m^2 n^{-1})}$
. Also, using Lemma 2.3 we can check that
$\mathbb{P}(Y_{\tau_1}=0|X_0=m) \leq \beta e^{-(1+\gamma)m^{3/2} n^{-1/2} +O(m^2 n^{-1})}$
. Also, using Lemma 2.3 we can check that
 \begin{equation} \sum_{k=0}^{n^{1/6}} Y(m,k) p^k \leq (m-1)! + C(m-1)!(m^3 p)^{1/2} \sinh((m^3p)^{1/2}), \end{equation}
\begin{equation} \sum_{k=0}^{n^{1/6}} Y(m,k) p^k \leq (m-1)! + C(m-1)!(m^3 p)^{1/2} \sinh((m^3p)^{1/2}), \end{equation}
where the first term on the right-hand side of (26) comes from the directed cycles and C is the same constant as in Lemma 2.3. As
![]() $\sinh(x) \leq e^x$
we can bound (26) by
$\sinh(x) \leq e^x$
we can bound (26) by
 \begin{align*} \sum_{k=0}^{n^{1/6}} Y(m,k) p^k & \leq (m-1)! (1+C m^{3/2}n^{-1/2} e^{m^{3/2}n^{-1/2}}) \\ & \leq 2(m-1)! C m^{3/2}n^{-1/2} e^{m^{3/2}n^{-1/2}}.\end{align*}
\begin{align*} \sum_{k=0}^{n^{1/6}} Y(m,k) p^k & \leq (m-1)! (1+C m^{3/2}n^{-1/2} e^{m^{3/2}n^{-1/2}}) \\ & \leq 2(m-1)! C m^{3/2}n^{-1/2} e^{m^{3/2}n^{-1/2}}.\end{align*}
Combining these bounds and using
![]() $\binom{n}{m} \leq n^m/m!$
we deduce
$\binom{n}{m} \leq n^m/m!$
we deduce
 \begin{align}\nonumber \mathbb{E}(N(A)) & \leq \sum_{m=An^{1/3}}^{n^{1/3}\log^2(n)} \bigg(\frac{(np)^m}{m!}\bigg)\bigg(2(m-1)! C m^{3/2}n^{-1/2} e^{m^{3/2}n^{-1/2}}\bigg)\bigg(\beta e^{-(1+\gamma)m^{3/2} n^{-1/2} +O(m^2 n^{-1})}\bigg) \\[4pt]\nonumber & = \sum_{m=An^{1/3}}^{n^{1/3}\log^2(n)} \frac{2 \beta C m^{1/2}}{n^{1/2}} e^{-\gamma m^{3/2}n^{-1/2} + O(m^2n^{-1})} \\[4pt]& \leq \int_{m=An^{1/3}}^{n^{1/3}\log^2(n)+1} \frac{2 \beta C m^{1/2}}{n^{1/2}} e^{-\frac{\gamma}{2} m^{3/2}n^{-1/2}} dm, \end{align}
\begin{align}\nonumber \mathbb{E}(N(A)) & \leq \sum_{m=An^{1/3}}^{n^{1/3}\log^2(n)} \bigg(\frac{(np)^m}{m!}\bigg)\bigg(2(m-1)! C m^{3/2}n^{-1/2} e^{m^{3/2}n^{-1/2}}\bigg)\bigg(\beta e^{-(1+\gamma)m^{3/2} n^{-1/2} +O(m^2 n^{-1})}\bigg) \\[4pt]\nonumber & = \sum_{m=An^{1/3}}^{n^{1/3}\log^2(n)} \frac{2 \beta C m^{1/2}}{n^{1/2}} e^{-\gamma m^{3/2}n^{-1/2} + O(m^2n^{-1})} \\[4pt]& \leq \int_{m=An^{1/3}}^{n^{1/3}\log^2(n)+1} \frac{2 \beta C m^{1/2}}{n^{1/2}} e^{-\frac{\gamma}{2} m^{3/2}n^{-1/2}} dm, \end{align}
where (27) holds for all sufficiently large n. Now making the substitution
![]() $x = m n^{-1/3}$
we can remove the dependence of (27) on both m and n so that
$x = m n^{-1/3}$
we can remove the dependence of (27) on both m and n so that
 \begin{align}\nonumber \mathbb{E}(N(A))& \leq 2 \beta C \int_A^{\log^2(n) + n^{-1/3}} x^{1/2} e^{-\frac{\gamma}{2} x^{3/2}} dx \\[4pt]& \leq 2 \beta C \int_A^{\infty} x^{1/2} e^{-\frac{\gamma}{2} x^{3/2}} dx \nonumber\\[4pt]& = \frac{8 \beta C}{3 \gamma} \int_{\frac{\gamma A^{3/2}}{2}}^\infty e^{-t}dt = \frac{8 \beta C}{3 \gamma} e^{-\frac{\gamma A^{3/2}}{2}}. \end{align}
\begin{align}\nonumber \mathbb{E}(N(A))& \leq 2 \beta C \int_A^{\log^2(n) + n^{-1/3}} x^{1/2} e^{-\frac{\gamma}{2} x^{3/2}} dx \\[4pt]& \leq 2 \beta C \int_A^{\infty} x^{1/2} e^{-\frac{\gamma}{2} x^{3/2}} dx \nonumber\\[4pt]& = \frac{8 \beta C}{3 \gamma} \int_{\frac{\gamma A^{3/2}}{2}}^\infty e^{-t}dt = \frac{8 \beta C}{3 \gamma} e^{-\frac{\gamma A^{3/2}}{2}}. \end{align}
So, by Markov’s inequality
![]() $\mathbb{P}(\mathcal{E}_2 \cap \mathcal{F}^c) \leq \zeta e^{-\eta A^{3/2}}$
where
$\mathbb{P}(\mathcal{E}_2 \cap \mathcal{F}^c) \leq \zeta e^{-\eta A^{3/2}}$
where
![]() $\zeta$
and
$\zeta$
and
![]() $\eta$
are the corresponding constants found in (28). So,
$\eta$
are the corresponding constants found in (28). So,
Calculating
![]() $\zeta$
and
$\zeta$
and
![]() $\gamma$
using the values for
$\gamma$
using the values for
![]() $C, \beta$
and
$C, \beta$
and
![]() $\gamma$
in Lemmas 2.3 and 4.3 yields
$\gamma$
in Lemmas 2.3 and 4.3 yields
![]() $\zeta < 2 \times 10^7$
and
$\zeta < 2 \times 10^7$
and
![]() $\eta > 0.03$
.
$\eta > 0.03$
.
5. Adaptations for the critical window
In this section, we sketch the adaptations one must make to the proofs of Theorems 3.1. and 4.1. such that they hold in the whole critical window,
![]() $p = n^{-1} + \lambda n^{-4/3}$
where
$p = n^{-1} + \lambda n^{-4/3}$
where
![]() $\lambda \in \mathbb{R}$
.
$\lambda \in \mathbb{R}$
.
5.1. Lower bound
For Theorem 3.1, the adaptation is rather simple. We will still apply Janson’s inequality and so we only need to recompute
![]() $\mu$
and
$\mu$
and
![]() $\Delta$
. Furthermore, the only difference in these calculations comes from replacing the term
$\Delta$
. Furthermore, the only difference in these calculations comes from replacing the term
![]() $n^{-m-k}$
by
$n^{-m-k}$
by
![]() $p^{m+k}$
, and in fact the
$p^{m+k}$
, and in fact the
![]() $p^k$
in this turns out to make negligible changes. In this light, Lemma 3.3 changes to
$p^k$
in this turns out to make negligible changes. In this light, Lemma 3.3 changes to
Lemma 5.1.
 \begin{equation*} \mathbb{E}(X) \geq \begin{cases} -e^{\frac{\lambda \delta}{2}}\log(\delta)/2 & \text{if }\lambda \geq 0 \\[6pt] -e^{2 \delta^{1/2} \lambda} \log(\delta)/2 & \text{otherwise,} \end{cases}\end{equation*}
\begin{equation*} \mathbb{E}(X) \geq \begin{cases} -e^{\frac{\lambda \delta}{2}}\log(\delta)/2 & \text{if }\lambda \geq 0 \\[6pt] -e^{2 \delta^{1/2} \lambda} \log(\delta)/2 & \text{otherwise,} \end{cases}\end{equation*}
where the only difference in the proof is to bound
![]() $(1+\lambda n^{-1/3})^m$
by its lowest value depending on whether
$(1+\lambda n^{-1/3})^m$
by its lowest value depending on whether
![]() $\lambda \geq 0$
or
$\lambda \geq 0$
or
![]() $\lambda <0$
. We bound this via
$\lambda <0$
. We bound this via
 \begin{equation*} 1+x \geq \begin{cases} e^{\frac{x}{2}} & \text{if } 0 \leq x \leq 2 \\[6pt] e^{2x} & \text{if } -\dfrac{1}{2} \leq x \leq 0. \end{cases}\end{equation*}
\begin{equation*} 1+x \geq \begin{cases} e^{\frac{x}{2}} & \text{if } 0 \leq x \leq 2 \\[6pt] e^{2x} & \text{if } -\dfrac{1}{2} \leq x \leq 0. \end{cases}\end{equation*}
Furthermore, Lemma 3.5 changes to
Lemma 5.2. For all sufficiently large n and small enough
![]() $\delta$
,
$\delta$
,
 \begin{equation*}\Delta \leq \begin{cases} e^{2\delta^{1/2}\lambda} \log(2) & \text{if } \lambda \geq 0 \\[6pt] e^{\delta \lambda} \log(2) & \text{otherwise.} \end{cases}\end{equation*}
\begin{equation*}\Delta \leq \begin{cases} e^{2\delta^{1/2}\lambda} \log(2) & \text{if } \lambda \geq 0 \\[6pt] e^{\delta \lambda} \log(2) & \text{otherwise.} \end{cases}\end{equation*}
The proof again is almost identical with the only change being to approximate the
![]() $(np)^m$
term. This time we seek an upper bound so use the approximation
$(np)^m$
term. This time we seek an upper bound so use the approximation
![]() $1+x \leq e^x$
which is valid for any x. We still need to split depending upon the sign of
$1+x \leq e^x$
which is valid for any x. We still need to split depending upon the sign of
![]() $\lambda$
as for the above constants we upper bound
$\lambda$
as for the above constants we upper bound
![]() $(np)^m$
by its largest possible value over the range
$(np)^m$
by its largest possible value over the range
![]() $\delta n \leq m \leq 2 \delta^{1/2} n$
. Combining Lemmas 5.1 and 5.2 with the relevant constraints on
$\delta n \leq m \leq 2 \delta^{1/2} n$
. Combining Lemmas 5.1 and 5.2 with the relevant constraints on
![]() $\delta$
in relation to
$\delta$
in relation to
![]() $\lambda$
yields Theorem 1.4.
$\lambda$
yields Theorem 1.4.
5.2. Upper bound
There is no significant (i.e. of order
![]() $e^{\lambda A}$
) improvement which can be made with our current method of proof when
$e^{\lambda A}$
) improvement which can be made with our current method of proof when
![]() $\lambda <0$
. This is because the gains we make computing the expectation in the proof of Theorem 4.1 are cancelled out by losses in the branching process considerations of Lemma 4.2.
$\lambda <0$
. This is because the gains we make computing the expectation in the proof of Theorem 4.1 are cancelled out by losses in the branching process considerations of Lemma 4.2.
When
![]() $\lambda>0$
we cannot simply use our bound for
$\lambda>0$
we cannot simply use our bound for
![]() $p=n^{-1}$
and thus an adaptation is necessary. Note that by monotonicity in p, the results of Lemmas 4.2 and 4.3 remain true for
$p=n^{-1}$
and thus an adaptation is necessary. Note that by monotonicity in p, the results of Lemmas 4.2 and 4.3 remain true for
![]() $p = n^{-1} + \lambda n^{-4/3}$
with
$p = n^{-1} + \lambda n^{-4/3}$
with
![]() $\lambda>0$
. The next adaptation which must be made is in equation (23) where now, the expectation becomes
$\lambda>0$
. The next adaptation which must be made is in equation (23) where now, the expectation becomes
 \begin{equation*} \mathbb{E}(\mathcal{C}) \leq \sum_{k=1}^{n^{1/3} \log^{(2)} n} \frac{e^{k \lambda n^{-1/3}}}{k} \leq \sum_{k=1}^{n^{1/3} \log^{(2)} n} \frac{(\log n)^\lambda}{k} \leq 2 (\log n)^{\lambda+1} = o(n^{1/6}).\end{equation*}
\begin{equation*} \mathbb{E}(\mathcal{C}) \leq \sum_{k=1}^{n^{1/3} \log^{(2)} n} \frac{e^{k \lambda n^{-1/3}}}{k} \leq \sum_{k=1}^{n^{1/3} \log^{(2)} n} \frac{(\log n)^\lambda}{k} \leq 2 (\log n)^{\lambda+1} = o(n^{1/6}).\end{equation*}
Thus allowing us to deduce the result of Corollary 4.6 as before. Finally all that remains is to conclude the proof of Theorem 1.5. Ignoring lower order terms, the only difference to the proof compared to that of Theorem 4.1 is in the computation of
![]() $\mathbb{E}(N(A))$
where we must change the term
$\mathbb{E}(N(A))$
where we must change the term
![]() $(np)^m$
. Thus the integral in (27) becomes
$(np)^m$
. Thus the integral in (27) becomes
This is much more complex than before due to the extra term in the exponent. However we are still able to give a bound after making the obvious substitution
![]() $t = \frac{\gamma}{2} m^{3/2}n^{-1/2}- \lambda mn^{-1/3}$
, we obtain
$t = \frac{\gamma}{2} m^{3/2}n^{-1/2}- \lambda mn^{-1/3}$
, we obtain
 \begin{align}\nonumber \mathbb{E}(N(A)) & \leq \frac{8 \beta C}{3 \gamma} \int_{\frac{\gamma}{2}A^{3/2} - \lambda A}^{\infty} \frac{m^{1/2}n^{-1/2}}{m^{1/2}n^{-1/2} - \frac{4 \lambda n^{-1/3}}{3 \gamma}} e^{-t} dt \\[4pt]& \leq \frac{10 \beta C}{3 \gamma} \int_{\frac{\gamma}{2}A^{3/2} - \lambda A}^{\infty} e^{-t} dt = \frac{10 \beta C}{3 \gamma} e^{-\frac{\gamma}{2} A^{3/2} +\lambda A}, \end{align}
\begin{align}\nonumber \mathbb{E}(N(A)) & \leq \frac{8 \beta C}{3 \gamma} \int_{\frac{\gamma}{2}A^{3/2} - \lambda A}^{\infty} \frac{m^{1/2}n^{-1/2}}{m^{1/2}n^{-1/2} - \frac{4 \lambda n^{-1/3}}{3 \gamma}} e^{-t} dt \\[4pt]& \leq \frac{10 \beta C}{3 \gamma} \int_{\frac{\gamma}{2}A^{3/2} - \lambda A}^{\infty} e^{-t} dt = \frac{10 \beta C}{3 \gamma} e^{-\frac{\gamma}{2} A^{3/2} +\lambda A}, \end{align}
which is of the claimed form. Note the second inequality in (30) holds whenever A is sufficiently large compared to
![]() $\lambda$
.
$\lambda$
.
6. Concluding remarks
In this paper we have proven that inside the critical window,
![]() $p=n^{-1}+\lambda n^{-4/3}$
, the largest component of D(n,p) has size
$p=n^{-1}+\lambda n^{-4/3}$
, the largest component of D(n,p) has size
![]() $\Theta_p(n^{1/3})$
. Furthermore, we have given bounds on the tail probabilities of the distribution of the size of the largest component. Combining this result with previous work of Karp [Reference Karp9] and Łuczak [Reference Łuczak11] allows us to deduce that D(n,p) exhibits a ‘double-jump’ phenomenon at the point
$\Theta_p(n^{1/3})$
. Furthermore, we have given bounds on the tail probabilities of the distribution of the size of the largest component. Combining this result with previous work of Karp [Reference Karp9] and Łuczak [Reference Łuczak11] allows us to deduce that D(n,p) exhibits a ‘double-jump’ phenomenon at the point
![]() $p=n^{-1}$
. However, there are still a large number of open questions regarding the giant component in D(n,p). Recently, Goldschmidt and Stephenson [Reference Goldschmidt and Stephenson5] found a scaling limit for the sizes of all the strong components in the critical random digraph. This scaling limit is a little difficult to work with directly and so it would be interesting to know if there is a more explicit form for the size of the largest component. In G(n,p) such a result was given by Pittel [Reference Pittel19]
$p=n^{-1}$
. However, there are still a large number of open questions regarding the giant component in D(n,p). Recently, Goldschmidt and Stephenson [Reference Goldschmidt and Stephenson5] found a scaling limit for the sizes of all the strong components in the critical random digraph. This scaling limit is a little difficult to work with directly and so it would be interesting to know if there is a more explicit form for the size of the largest component. In G(n,p) such a result was given by Pittel [Reference Pittel19]
Question 1 Is there an explicit description of the limiting distribution of the largest component of D(n,p)?
Given the strong connection between G(n,p) and D(n,p), it seems likely that the limit distributions,
![]() $X^\lambda = n^{-2/3}|\mathcal{C}_1(G(n,p))|$
and
$X^\lambda = n^{-2/3}|\mathcal{C}_1(G(n,p))|$
and
![]() $Y^\lambda = n^{-1/3}|\mathcal{C}_1(D(n,p))|$
(where
$Y^\lambda = n^{-1/3}|\mathcal{C}_1(D(n,p))|$
(where
![]() $p=n^{-1} + \lambda n^{-4/3}$
) are closely related. For larger p, previous work [Reference Karp9, Reference Łuczak, Pittel and Wierman12] has found that the size of the giant strongly connected component in D(n,p) is related to the size of the square of the giant component in G(n,p). That is, if
$p=n^{-1} + \lambda n^{-4/3}$
) are closely related. For larger p, previous work [Reference Karp9, Reference Łuczak, Pittel and Wierman12] has found that the size of the giant strongly connected component in D(n,p) is related to the size of the square of the giant component in G(n,p). That is, if
![]() $|\mathcal{C}_1(G(n,p)| \sim \alpha(n) n$
, then
$|\mathcal{C}_1(G(n,p)| \sim \alpha(n) n$
, then
![]() $|\mathcal{C}_1(D(n,p)| \sim \alpha(n)^2 n$
. Note that the result found in Theorem 1.5 is consistent with this pattern as here we have an exponent of order
$|\mathcal{C}_1(D(n,p)| \sim \alpha(n)^2 n$
. Note that the result found in Theorem 1.5 is consistent with this pattern as here we have an exponent of order
![]() $A^{3/2}$
while for G(n,p) a similar result is true with exponent
$A^{3/2}$
while for G(n,p) a similar result is true with exponent
![]() $A^3$
implying that the probability we find a component of size
$A^3$
implying that the probability we find a component of size
![]() $Bn^{2/3}$
in G(n,p) is similar to the probability of finding a component of size
$Bn^{2/3}$
in G(n,p) is similar to the probability of finding a component of size
![]() $B^2 n^{1/3}$
in D(n,p) (assuming both bounds are close to tight). As such, we make the following conjecture to explain this pattern.
$B^2 n^{1/3}$
in D(n,p) (assuming both bounds are close to tight). As such, we make the following conjecture to explain this pattern.
Conjecture 6.1. If
![]() $X^\lambda$
and
$X^\lambda$
and
![]() $Y^\lambda$
are the distributions defined above and
$Y^\lambda$
are the distributions defined above and
![]() $X_1^\lambda, X_2^\lambda$
are independent copies of
$X_1^\lambda, X_2^\lambda$
are independent copies of
![]() $X^\lambda$
then,
$X^\lambda$
then,
![]() $Y^\lambda = X_1^\lambda X_2^\lambda$
.
$Y^\lambda = X_1^\lambda X_2^\lambda$
.
Finally, we consider the transitive closure of random digraphs. The transitive closure of a digraph D is cl(D) a digraph on the same vertex set as D and such that uv is an edge of cl(D) if and only if there is a directed path from u to v in D. Equivalently, cl(D) is the smallest digraph containing D such that the relation R defined by uRv if and only if uv is an edge is transitive. Karp [Reference Karp9] gave a linear time algorithm to compute the transitive closure of a digraph from the model D(n,p) provided that
![]() $p \leq (1-\varepsilon)n^{-1}$
or
$p \leq (1-\varepsilon)n^{-1}$
or
![]() $p \geq (1+\varepsilon)n^{-1}$
. For all other p this algorithm runs in time
$p \geq (1+\varepsilon)n^{-1}$
. For all other p this algorithm runs in time
![]() $O(f(n) (n \log n)^{4/3})$
where f(n) is any
$O(f(n) (n \log n)^{4/3})$
where f(n) is any
![]() $\omega(1)$
function. Now that we know more about the structure of D(n,p) for p close to
$\omega(1)$
function. Now that we know more about the structure of D(n,p) for p close to
![]() $n^{-1}$
, it may be possible to adapt Karp’s algorithm and obtain a better time complexity.
$n^{-1}$
, it may be possible to adapt Karp’s algorithm and obtain a better time complexity.
Question 2 Does there exist a linear time algorithm to compute the transitive closure of D(n,p) when
![]() $(1-\varepsilon)n^{-1} \leq p \leq (1 + \varepsilon)n^{-1}$
?
$(1-\varepsilon)n^{-1} \leq p \leq (1 + \varepsilon)n^{-1}$
?
Acknowledgements
The author would like to thank Guillem Perarnau for providing helpful feedback on a previous draft of this paper. The author was supported by the Spanish Ministerio de EconomÍa y Competitividad project MTM2017–82166–P and an FPI Predoctoral Fellowship from the Spanish Ministerio de EconomÍa y Competitividad with reference PRE2018–083621.