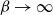1. Introduction
We consider a stochastic model, known in the literature as hard-core lattice gas model [Reference van den Berg and Steif10, Reference Gaunt and Fisher35], where particles have a non-negligible radius and therefore cannot overlap. Assuming a finite volume, the hard-core constraints are modelled with a finite undirected graph
![]() $\Lambda$
. More specifically, particles can reside on the sites of
$\Lambda$
. More specifically, particles can reside on the sites of
![]() $\Lambda$
and edges connect the pairs of sites in
$\Lambda$
and edges connect the pairs of sites in
![]() $\Lambda$
that cannot be occupied simultaneously. In other words, any hard-core configuration is an independent set of
$\Lambda$
that cannot be occupied simultaneously. In other words, any hard-core configuration is an independent set of
![]() $\Lambda$
. In this paper, we take
$\Lambda$
. In this paper, we take
![]() $\Lambda$
as a square grid graph with periodic boundary conditions. The resulting hard-core particle configurations are then those whose occupied sites have all the corresponding four neighbouring sites empty, see Figure 1 for an example of such configurations.
$\Lambda$
as a square grid graph with periodic boundary conditions. The resulting hard-core particle configurations are then those whose occupied sites have all the corresponding four neighbouring sites empty, see Figure 1 for an example of such configurations.

Figure 1. Example of a hard-core configuration on the
![]() $14\times 14$
square grid with periodic boundary conditions. On the left, the occupied sites in
$14\times 14$
square grid with periodic boundary conditions. On the left, the occupied sites in
![]() $V_{\mathbf{o}}$
(resp. in
$V_{\mathbf{o}}$
(resp. in
![]() $V_{\mathbf{e}}$
) are highlighted in black (resp. in red). On the right, we depict the same configuration using a different visual convention, in which we highlight the odd clusters that the configuration has by drawing only the empty sites in
$V_{\mathbf{e}}$
) are highlighted in black (resp. in red). On the right, we depict the same configuration using a different visual convention, in which we highlight the odd clusters that the configuration has by drawing only the empty sites in
![]() $V_{\mathbf{e}}$
(in white), the occupied sites in
$V_{\mathbf{e}}$
(in white), the occupied sites in
![]() $V_{\mathbf{o}}$
(in black), and a black line around each odd cluster representing its contour.
$V_{\mathbf{o}}$
(in black), and a black line around each odd cluster representing its contour.
This interacting particle system evolves according to a stochastic dynamics that is fully characterized by the Hamiltonian or energy function in (2.3) and is parametrized by the inverse temperature
![]() $\beta$
. In particular, the appearance and disappearance of particles are modelled via a Glauber-type update Markov chain
$\beta$
. In particular, the appearance and disappearance of particles are modelled via a Glauber-type update Markov chain
![]() $\{X_t\}_{t\in \mathbb {N}}$
with Metropolis transition probabilities induced by the Hamiltonian, see (2.4) later for more details. The stochastic process is reversible with respect to the corresponding Gibbs measure
$\{X_t\}_{t\in \mathbb {N}}$
with Metropolis transition probabilities induced by the Hamiltonian, see (2.4) later for more details. The stochastic process is reversible with respect to the corresponding Gibbs measure
![]() $\mu _\beta$
, cf. (2.2), which is then its equilibrium distribution. Specifically, for any independent set
$\mu _\beta$
, cf. (2.2), which is then its equilibrium distribution. Specifically, for any independent set
![]() $I$
on the graph
$I$
on the graph
![]() $\Lambda$
, the hard-core configuration with particles precisely on the vertices in
$\Lambda$
, the hard-core configuration with particles precisely on the vertices in
![]() $I$
has stationary probability proportional to
$I$
has stationary probability proportional to
![]() $e^{\beta |I|}$
. Taking
$e^{\beta |I|}$
. Taking
![]() $\beta =0$
, this process can thus be used to sample uniformly independent sets of
$\beta =0$
, this process can thus be used to sample uniformly independent sets of
![]() $\Lambda$
.
$\Lambda$
.
Considering a regime with large
![]() $\beta$
, on the other hand, the same Markov chain can also be seen as a randomized scheme with local updates to find maximum independent sets, which is an NP-hard problem [Reference Mossel, Weitz and Wormald45]. Indeed, in the low-temperature regime (i.e.,
$\beta$
, on the other hand, the same Markov chain can also be seen as a randomized scheme with local updates to find maximum independent sets, which is an NP-hard problem [Reference Mossel, Weitz and Wormald45]. Indeed, in the low-temperature regime (i.e.,
![]() $\beta \to \infty$
), the most likely states in view of
$\beta \to \infty$
), the most likely states in view of
![]() $\mu _\beta$
for this interacting particle system are those with a maximum number of particles. These configurations correspond to the maximum independent sets of
$\mu _\beta$
for this interacting particle system are those with a maximum number of particles. These configurations correspond to the maximum independent sets of
![]() $\Lambda$
and we will refer to them as stable states. On the square grid graph
$\Lambda$
and we will refer to them as stable states. On the square grid graph
![]() $\Lambda$
of even length, there are two such stable states, corresponding to the two chessboard-like patterns.
$\Lambda$
of even length, there are two such stable states, corresponding to the two chessboard-like patterns.
When
![]() $\beta$
grows large, however, it takes a very long time for the system to move from one stable state to the other, since such a transition involves visiting intermediate configurations that are very unlikely in terms of
$\beta$
grows large, however, it takes a very long time for the system to move from one stable state to the other, since such a transition involves visiting intermediate configurations that are very unlikely in terms of
![]() $\mu _\beta$
. Such transitions become thus rare events and, as a consequence, the stochastic process also takes a very long time to converge to stationarity, exhibiting so-called slow/torpid mixing [Reference Galvin31, Reference Zocca54]. It is natural to expect such slow mixing of hard-core dynamics for a large
$\mu _\beta$
. Such transitions become thus rare events and, as a consequence, the stochastic process also takes a very long time to converge to stationarity, exhibiting so-called slow/torpid mixing [Reference Galvin31, Reference Zocca54]. It is natural to expect such slow mixing of hard-core dynamics for a large
![]() $\beta$
, since fast mixing in this regime would imply that the NP-hard problem of finding maximum independent sets could be solved or approximated efficiently.
$\beta$
, since fast mixing in this regime would imply that the NP-hard problem of finding maximum independent sets could be solved or approximated efficiently.
Several papers [Reference Borgs, Chayes, Frieze, Kim, Tetali, Vigoda and Vu19, Reference Galvin31–Reference Galvin and Tetali33, Reference Greenberg and Randall36, Reference Kahn39, Reference Luby and Vigoda42, Reference Martinelli, Sinclair and Weitz44, Reference Randall53] studied the slow mixing of the hard-core model by identifying how the mixing times of the Glauber dynamics scale on other graphs, depending on the type of graph, the size, the boundary conditions or the maximum vertex degree. The common main idea behind this line of work has been to identify as precisely as possible the subset of configurations that constitutes a bottleneck for the dynamics to transition from one stable state to another. Some of these approaches also heavily rely on geometric features exhibited by the configurations in this bottleneck part of the state space, like the so-called fault lines in [Reference Randall53] and fat contours in [Reference Greenberg and Randall36].
In this paper, we look at a complementary aspect of the hard-core model in the low-temperature regime, focusing on the hitting times between its stable states and the “bottleneck configurations” visited along these trajectories. The asymptotic behaviour of the first hitting time between the maximum-occupancy configurations of this model in the low-temperature regime
![]() $\beta \to \infty$
has already been studied in [Reference Nardi, Zocca and Borst47]. Denoting by
$\beta \to \infty$
has already been studied in [Reference Nardi, Zocca and Borst47]. Denoting by
![]() $\tau _{\mathbf{o}}^{\mathbf{e}}$
the first hitting time of Markov chain
$\tau _{\mathbf{o}}^{\mathbf{e}}$
the first hitting time of Markov chain
![]() $\{X_t\}_{t\in \mathbb {N}}$
corresponding to hard-core dynamics on a grid graph
$\{X_t\}_{t\in \mathbb {N}}$
corresponding to hard-core dynamics on a grid graph
![]() $\Lambda$
, in [Reference Nardi, Zocca and Borst47] the authors showed that there exists a constant
$\Lambda$
, in [Reference Nardi, Zocca and Borst47] the authors showed that there exists a constant
![]() $\Gamma (\Lambda ) \gt 0$
such that for every
$\Gamma (\Lambda ) \gt 0$
such that for every
![]() $\epsilon \gt 0$
,
$\epsilon \gt 0$
,
and
In particular, the authors showed in the same article how this constant
![]() $\Gamma (\Lambda )$
, which characterizes the order of magnitude of the first hitting time between the two stable configurations, depends on the grid sizes and boundary conditions by means of an extension of the setting in [Reference Manzo, Nardi, Olivieri and Scoppola43].
$\Gamma (\Lambda )$
, which characterizes the order of magnitude of the first hitting time between the two stable configurations, depends on the grid sizes and boundary conditions by means of an extension of the setting in [Reference Manzo, Nardi, Olivieri and Scoppola43].
However, instead of directly using the general strategy proposed in [Reference Manzo, Nardi, Olivieri and Scoppola43], which allows to jointly derive the asymptotic behaviour of the transition time as
![]() $\beta \to \infty$
together with a characterization of the critical configurations, the authors of [Reference Nardi, Zocca and Borst47] adopted a novel combinatorial method to estimate the energy barrier between the two stable states of the model, which is disentangled with respect to the description of the critical configurations. Consequently, the geometrical description of the critical configurations had yet to be addressed.
$\beta \to \infty$
together with a characterization of the critical configurations, the authors of [Reference Nardi, Zocca and Borst47] adopted a novel combinatorial method to estimate the energy barrier between the two stable states of the model, which is disentangled with respect to the description of the critical configurations. Consequently, the geometrical description of the critical configurations had yet to be addressed.
The main motivation of this paper is to fill this knowledge gap. Indeed, the geometrical characterization of the critical configurations, also known as essential saddles, is a relevant goal both from a probabilistic and a physical point of view since it provides insightful details of the dynamical behaviour of the system. This represents a crucial point in describing the trajectories that the system follows with high probability during the transition from one stable state to the other. We remark that in several models analysed in the context of Freidlin-Wentzell Markov chains evolving under Glauber dynamics, the essential gate, i.e., the set of the critical configurations, was unique [Reference Apollonio, Jacquier, Nardi and Troiani1] but, in general, there may exist many minimal sets that are crossed with high probability during the phase transition, either distinct or overlapping (see e.g., [Reference Baldassarri and Nardi5, Reference Baldassarri and Nardi6] for this description in the case of the conservative Kawasaki dynamics). Interestingly, this is what happens also for our model despite evolving under the non-conservative Glauber dynamics. This peculiar feature relies on the hard-core constraints and on the intrinsic symmetry of the system due to the existence of two stable states. This is also the case of Glauber dynamics for the Ising and Potts models when there is no external magnetic field (see, e.g., [Reference Bet, Gallo and Nardi12]). In statistical physics, the study of such transition between stable states is usually referred to as tunnelling. When the particle system does not have an intrinsic symmetry or the symmetry of the system is broken, e.g., by an external magnetic field, the situation drastically changes. For interacting particle systems with a single stable state, the main object of investigation then becomes their metastability, i.e., the transition from the metastable state(s) to the stable one. Generally speaking, interacting particle systems that exhibit tunnelling behaviour have a much larger and complex set of essential saddles. This is precisely the case for the hard-core model on a square grid graph
![]() $\Lambda$
, with the additional complication that the only admissible configurations are its independent sets.
$\Lambda$
, with the additional complication that the only admissible configurations are its independent sets.
In order to geometrically characterize the critical configurations, we associate with each cluster of particles its contour, that is, a union of edges on the dual graph of
![]() $\Lambda$
. The equivalent representation of a configuration using its Peierls contour is a powerful tool that has been extensively used in the literature to study the phase transition of the hard-core model, identify sharper bounds for the critical temperature
$\Lambda$
. The equivalent representation of a configuration using its Peierls contour is a powerful tool that has been extensively used in the literature to study the phase transition of the hard-core model, identify sharper bounds for the critical temperature
![]() $\beta _c$
, and to obtain high-fugacity expansion of macroscopic quantities of the model; we refer the interested reader to, e.g., [Reference Blanca, Chen, Galvin, Randall and Tetali18, Reference Jauslin and Lebowitz38].
$\beta _c$
, and to obtain high-fugacity expansion of macroscopic quantities of the model; we refer the interested reader to, e.g., [Reference Blanca, Chen, Galvin, Randall and Tetali18, Reference Jauslin and Lebowitz38].
As part of our proof strategy, we provide some results regarding the model-dependent isoperimetric inequality for the hard-core model on grid graphs. In particular, we show that for a fixed area, the unique clusters that minimize the perimeter have a rhomboidal shape. However, the energy landscape is much more complex as the periodic boundary conditions give rise to other types of clusters with minimal perimeter for a given area, such as the configurations having a column containing a fixed number of particles.
We remark that our analysis yields a comprehensive geometrical description of the configurations in the bottleneck part of the state space, together with an overview of the exact structure of the bottleneck subset itself. However, pairing this analysis with precise counting arguments is beyond the scope of the present paper. Hence, we do not explore the energy-entropy trade-off of the hard-core model or shine more light on its phase transition.
In order to link geometrical properties of hard-core configurations with the properties of the stochastic process
![]() $\{X_t\}_{t\in \mathbb {N}}$
, in this paper we adopt the framework of the pathwise approach, introduced in the context of metastability by [Reference Cassandro, Galves, Olivieri and Vares24], later developed in [Reference Olivieri and Scoppola50, Reference Olivieri and Scoppola51], and summarized in the monograph [Reference Olivieri and Vares52]. A modern version of this approach can be found in [Reference Cirillo and Nardi26, Reference Cirillo, Nardi and Sohier27, Reference Manzo, Nardi, Olivieri and Scoppola43, Reference Nardi, Zocca and Borst47]. The pathwise approach has been widely adopted for studying the low-temperature behaviour of finite-volume models with single-spin-flip Glauber dynamics, e.g., [Reference Apollonio, Jacquier, Nardi and Troiani1, Reference Baldassarri, Gallo, Jacquier and Zocca2, Reference Bet, Gallo and Kim11–Reference Bet, Gallo and Nardi14, Reference Cirillo, Jacquier and Spitoni25, Reference Nardi and Zocca49, Reference Zocca55, Reference Zocca56], with Kawasaki dynamics, e.g., [Reference Baldassarri and Jacquier4–Reference Baldassarri and Nardi7, Reference den Hollander, Olivieri and Scoppola37, Reference Nardi, Olivieri and Scoppola46], and with parallel dynamics, e.g., [Reference Cirillo, Nardi and Spitoni28–Reference Cirillo, Jacquier and Spitoni30]. The more involved infinite-volume limit at low temperature was studied via this approach in [Reference Baldassarri, Gaudillière, den Hollander, Nardi, Olivieri and Scoppola3, Reference Gaudillière, den Hollander, Nardi, Olivieri and Scoppola34, Reference den Hollander, Olivieri and Scoppola37]. A different method to study the limiting behaviour of interacting particle systems is the so-called potential-theoretic approach, initiated in [Reference Bovier, Eckhoff, Gayrard and Klein22] and later summarized in the monograph [Reference Bovier and den Hollander23] (see, for instance, [Reference Bovier, den Hollander and Nardi20, Reference Bovier, den Hollander and Spitoni21, Reference Nardi and Spitoni48] for the application of this approach to specific models both in finite and infinite volume). Since these two approaches rely on different definitions of metastable states, they are not completely equivalent. The situation is particularly delicate for infinite-volume systems, irreversible systems, and degenerate systems, as discussed in [Reference Bet, Jacquier and Nardi15, Reference Cirillo and Nardi26, Reference Cirillo, Nardi and Sohier27]. More recent approaches are developed in [Reference Beltrán and Landim8, Reference Beltrán and Landim9, Reference Bianchi, Gaudillière and Milanesi16, Reference Bianchi and Gaudillière17, Reference Kim and Seo40, Reference Landim, Marcondes and Seo41].
$\{X_t\}_{t\in \mathbb {N}}$
, in this paper we adopt the framework of the pathwise approach, introduced in the context of metastability by [Reference Cassandro, Galves, Olivieri and Vares24], later developed in [Reference Olivieri and Scoppola50, Reference Olivieri and Scoppola51], and summarized in the monograph [Reference Olivieri and Vares52]. A modern version of this approach can be found in [Reference Cirillo and Nardi26, Reference Cirillo, Nardi and Sohier27, Reference Manzo, Nardi, Olivieri and Scoppola43, Reference Nardi, Zocca and Borst47]. The pathwise approach has been widely adopted for studying the low-temperature behaviour of finite-volume models with single-spin-flip Glauber dynamics, e.g., [Reference Apollonio, Jacquier, Nardi and Troiani1, Reference Baldassarri, Gallo, Jacquier and Zocca2, Reference Bet, Gallo and Kim11–Reference Bet, Gallo and Nardi14, Reference Cirillo, Jacquier and Spitoni25, Reference Nardi and Zocca49, Reference Zocca55, Reference Zocca56], with Kawasaki dynamics, e.g., [Reference Baldassarri and Jacquier4–Reference Baldassarri and Nardi7, Reference den Hollander, Olivieri and Scoppola37, Reference Nardi, Olivieri and Scoppola46], and with parallel dynamics, e.g., [Reference Cirillo, Nardi and Spitoni28–Reference Cirillo, Jacquier and Spitoni30]. The more involved infinite-volume limit at low temperature was studied via this approach in [Reference Baldassarri, Gaudillière, den Hollander, Nardi, Olivieri and Scoppola3, Reference Gaudillière, den Hollander, Nardi, Olivieri and Scoppola34, Reference den Hollander, Olivieri and Scoppola37]. A different method to study the limiting behaviour of interacting particle systems is the so-called potential-theoretic approach, initiated in [Reference Bovier, Eckhoff, Gayrard and Klein22] and later summarized in the monograph [Reference Bovier and den Hollander23] (see, for instance, [Reference Bovier, den Hollander and Nardi20, Reference Bovier, den Hollander and Spitoni21, Reference Nardi and Spitoni48] for the application of this approach to specific models both in finite and infinite volume). Since these two approaches rely on different definitions of metastable states, they are not completely equivalent. The situation is particularly delicate for infinite-volume systems, irreversible systems, and degenerate systems, as discussed in [Reference Bet, Jacquier and Nardi15, Reference Cirillo and Nardi26, Reference Cirillo, Nardi and Sohier27]. More recent approaches are developed in [Reference Beltrán and Landim8, Reference Beltrán and Landim9, Reference Bianchi, Gaudillière and Milanesi16, Reference Bianchi and Gaudillière17, Reference Kim and Seo40, Reference Landim, Marcondes and Seo41].
The paper is organized as follows. In section 2, we provide a detailed model description and state our main result regarding the geometric features of the critical configurations, Theorem 2.1. The rest of the paper is then devoted to the proof of this result. First, section 3 provides some preliminary definitions and auxiliary results, and then finally the proof of the main theorem is given in section 4. For the sake of clarity, the proofs of some auxiliary lemmas are deferred to a later section, namely section 5. Lastly, section 6 concludes the paper and discusses some future work.
2. Model description and main results
We consider the stochastic evolution of the hard-core model on finite two-dimensional square lattices. More precisely, given an integer
![]() $L \geq 2$
we consider the
$L \geq 2$
we consider the
![]() $L\times L$
square grid graph
$L\times L$
square grid graph
![]() $\Lambda =(V,E)$
with periodic boundary conditions, which we will refer to as
$\Lambda =(V,E)$
with periodic boundary conditions, which we will refer to as
![]() $L \times L$
toric grid graph. We denote by
$L \times L$
toric grid graph. We denote by
![]() $E$
the edge set of the grid graph
$E$
the edge set of the grid graph
![]() $\Lambda$
and by
$\Lambda$
and by
![]() $V$
the collection of its
$V$
the collection of its
![]() $N=L^2$
sites. We identify each site
$N=L^2$
sites. We identify each site
![]() $v \in \Lambda$
by its coordinates
$v \in \Lambda$
by its coordinates
![]() $(v_1, v_2)$
, that is, we take
$(v_1, v_2)$
, that is, we take
![]() $V\,:\!=\,\{0,\ldots, L-1\} \times \{0,\ldots, L-1\}$
as set of sites. In the rest of the paper, we will assume that
$V\,:\!=\,\{0,\ldots, L-1\} \times \{0,\ldots, L-1\}$
as set of sites. In the rest of the paper, we will assume that
![]() $L$
is an even integer, which guarantees that
$L$
is an even integer, which guarantees that
![]() $\Lambda$
is a bipartite graph, and that
$\Lambda$
is a bipartite graph, and that
![]() $L\geq 6$
, to avoid pathological trivial cases.
$L\geq 6$
, to avoid pathological trivial cases.
A particle configuration on
![]() $\Lambda$
is described by associating a variable
$\Lambda$
is described by associating a variable
![]() $\sigma (v)\in \{0,1\}$
with each site
$\sigma (v)\in \{0,1\}$
with each site
![]() $v \in \Lambda$
, indicating the absence (
$v \in \Lambda$
, indicating the absence (
![]() $0$
) or the presence (
$0$
) or the presence (
![]() $1$
) of a particle on that site. Let
$1$
) of a particle on that site. Let
![]() $\mathcal {X} \subset \{0,1\}^{N}$
be the collection of hard-core configurations on
$\mathcal {X} \subset \{0,1\}^{N}$
be the collection of hard-core configurations on
![]() $\Lambda$
, i.e.,
$\Lambda$
, i.e.,
i.e., the particle configurations on
![]() $\Lambda$
with no particles residing on neighbouring sites.
$\Lambda$
with no particles residing on neighbouring sites.
A site of
![]() $\Lambda$
is called even (respectively odd) if the sum of its two coordinates is even (respectively odd) and we denote by
$\Lambda$
is called even (respectively odd) if the sum of its two coordinates is even (respectively odd) and we denote by
![]() $V_{\mathbf{e}}$
and
$V_{\mathbf{e}}$
and
![]() $V_{\mathbf{o}}$
the collection of even sites and that of odd sites of
$V_{\mathbf{o}}$
the collection of even sites and that of odd sites of
![]() $\Lambda$
. Clearly
$\Lambda$
. Clearly
![]() $|V_{\mathbf{e}}| =|V_{\mathbf{o}}| = L^2/2$
. We denote by
$|V_{\mathbf{e}}| =|V_{\mathbf{o}}| = L^2/2$
. We denote by
![]() ${\mathbf{e}}$
(
${\mathbf{e}}$
(
![]() ${\mathbf{o}}$
, respectively) the particle configuration on
${\mathbf{o}}$
, respectively) the particle configuration on
![]() $\Lambda$
with particles at each site in
$\Lambda$
with particles at each site in
![]() $V_{\mathbf{e}}$
(
$V_{\mathbf{e}}$
(
![]() $V_{\mathbf{o}}$
, respectively), i.e.,
$V_{\mathbf{o}}$
, respectively), i.e.,
 \begin{equation*} {\mathbf{e}}(v) \,:\!=\, \begin{cases} 1 & \text { if } v \in V_{\mathbf{e}},\\[3pt] 0 & \text { if } v \in V_{\mathbf{o}}, \end{cases} \quad \text { and } \quad {\mathbf{o}}(v) \,:\!=\, \begin{cases} 0 & \text { if } v \in V_{\mathbf{e}},\\[3pt] 1 & \text { if } v \in V_{\mathbf{o}}. \end{cases} \end{equation*}
\begin{equation*} {\mathbf{e}}(v) \,:\!=\, \begin{cases} 1 & \text { if } v \in V_{\mathbf{e}},\\[3pt] 0 & \text { if } v \in V_{\mathbf{o}}, \end{cases} \quad \text { and } \quad {\mathbf{o}}(v) \,:\!=\, \begin{cases} 0 & \text { if } v \in V_{\mathbf{e}},\\[3pt] 1 & \text { if } v \in V_{\mathbf{o}}. \end{cases} \end{equation*}
Both
![]() ${\mathbf{e}}$
and
${\mathbf{e}}$
and
![]() ${\mathbf{o}}$
are hard-core configurations due to the assumption that
${\mathbf{o}}$
are hard-core configurations due to the assumption that
![]() $L$
is even.
$L$
is even.
Figure 1 shows an example of a hard-core configuration. Throughout the paper, all figures are drawn using the following conventions. They all depict hard-core configurations on a
![]() $14\times 14$
grid with periodic boundary conditions. The occupied (empty) sites in
$14\times 14$
grid with periodic boundary conditions. The occupied (empty) sites in
![]() $V_{\mathbf{e}}$
(
$V_{\mathbf{e}}$
(
![]() $V_{\mathbf{e}}$
, respectively) are shown in black (white), and we draw a black line around each odd cluster representing its contour. We tacitly assume that all the even (odd) sites outside the odd region are occupied (empty, respectively) but they are not displayed to avoid cluttering the figures. See subsection 3.1 for more precise definitions of odd clusters and odd regions.
$V_{\mathbf{e}}$
, respectively) are shown in black (white), and we draw a black line around each odd cluster representing its contour. We tacitly assume that all the even (odd) sites outside the odd region are occupied (empty, respectively) but they are not displayed to avoid cluttering the figures. See subsection 3.1 for more precise definitions of odd clusters and odd regions.
Consider the Gibbs measure on
![]() $\mathcal {X}$
given by
$\mathcal {X}$
given by
where
![]() $H$
is the Hamiltonian
$H$
is the Hamiltonian
![]() $H\,:\, \mathcal {X} \to \mathbb R$
that is taken to be proportional to the number of present particles, namely
$H\,:\, \mathcal {X} \to \mathbb R$
that is taken to be proportional to the number of present particles, namely
with
![]() $Z_{\beta, \Lambda }\,:\!=\,\sum _{\sigma \in \mathcal {X}} e^{-\beta H(\sigma )}$
being the normalizing constant. The two hard-core configurations on the
$Z_{\beta, \Lambda }\,:\!=\,\sum _{\sigma \in \mathcal {X}} e^{-\beta H(\sigma )}$
being the normalizing constant. The two hard-core configurations on the
![]() $L \times L$
toric grid graph
$L \times L$
toric grid graph
![]() $\Lambda$
introduced above have energy equal to
$\Lambda$
introduced above have energy equal to
which is the minimum value the Hamiltonian can take on
![]() $\mathcal {X}$
[Reference Nardi, Zocca and Borst47].
$\mathcal {X}$
[Reference Nardi, Zocca and Borst47].
We assume the interacting particle system described evolves according to stochastic Glauber-type dynamics described by a single-step update Markov chain
![]() $\{X_{t}^\beta \}_{t \in \mathbb {N}}$
on
$\{X_{t}^\beta \}_{t \in \mathbb {N}}$
on
![]() $\mathcal {X}$
with transition probabilities between any pair of configurations
$\mathcal {X}$
with transition probabilities between any pair of configurations
![]() $\sigma, \sigma ^{\prime} \in \mathcal {X}$
given by
$\sigma, \sigma ^{\prime} \in \mathcal {X}$
given by
 \begin{align} P_\beta (\sigma, \sigma ^{\prime})\,:\!=\, \begin{cases} q(\sigma, \sigma ^{\prime}) e^{-\beta [H(\sigma ^{\prime})-H(\sigma )]^+}, & \text { if } \sigma \neq \sigma ^{\prime},\\[3pt] 1-\sum _{\eta \neq \sigma } P_\beta (\sigma, \eta ), & \text { if } \sigma =\sigma ^{\prime}, \end{cases} \end{align}
\begin{align} P_\beta (\sigma, \sigma ^{\prime})\,:\!=\, \begin{cases} q(\sigma, \sigma ^{\prime}) e^{-\beta [H(\sigma ^{\prime})-H(\sigma )]^+}, & \text { if } \sigma \neq \sigma ^{\prime},\\[3pt] 1-\sum _{\eta \neq \sigma } P_\beta (\sigma, \eta ), & \text { if } \sigma =\sigma ^{\prime}, \end{cases} \end{align}
where
![]() $[{\cdot}]^+=\max \{\cdot, 0\}$
and
$[{\cdot}]^+=\max \{\cdot, 0\}$
and
![]() $q$
is the connectivity matrix that allows only single-step updates, i.e., for every
$q$
is the connectivity matrix that allows only single-step updates, i.e., for every
![]() $\sigma, \sigma ^{\prime} \in \mathcal {X}$
we set
$\sigma, \sigma ^{\prime} \in \mathcal {X}$
we set
 \begin{align} q(\sigma, \sigma ^{\prime})\,:\!=\, \begin{cases} \frac {1}{N}, & \text {if } \left |\{v \in V \,:\, \sigma (v)\neq \sigma ^{\prime}(v)\} \right |=1,\\[3pt] 0, & \text {if } \left |\{v \in V \,:\, \sigma (v)\neq \sigma ^{\prime}(v)\} \right |\gt 1.\\[3pt] 1 - \sum _{\eta \neq \sigma } q(\sigma, \eta ), & \text {if } \sigma =\sigma ^{\prime}. \end{cases} \end{align}
\begin{align} q(\sigma, \sigma ^{\prime})\,:\!=\, \begin{cases} \frac {1}{N}, & \text {if } \left |\{v \in V \,:\, \sigma (v)\neq \sigma ^{\prime}(v)\} \right |=1,\\[3pt] 0, & \text {if } \left |\{v \in V \,:\, \sigma (v)\neq \sigma ^{\prime}(v)\} \right |\gt 1.\\[3pt] 1 - \sum _{\eta \neq \sigma } q(\sigma, \eta ), & \text {if } \sigma =\sigma ^{\prime}. \end{cases} \end{align}
The resulting dynamics
![]() $P_\beta$
is reversible with respect to the Gibbs measure
$P_\beta$
is reversible with respect to the Gibbs measure
![]() $\mu _\beta$
given in (2.2). The triplet
$\mu _\beta$
given in (2.2). The triplet
![]() $(\mathcal {X}, H, q)$
is usually referred to as energy landscape and (2.4) as Metropolis transition probabilities.
$(\mathcal {X}, H, q)$
is usually referred to as energy landscape and (2.4) as Metropolis transition probabilities.
The connectivity matrix
![]() $q$
given in (2.5) is irreducible, i.e., for any pair of configurations
$q$
given in (2.5) is irreducible, i.e., for any pair of configurations
![]() $\sigma, \sigma ^{\prime}\in \mathcal {X}$
,
$\sigma, \sigma ^{\prime}\in \mathcal {X}$
,
![]() $\sigma \neq \sigma ^{\prime}$
, there exists a finite sequence
$\sigma \neq \sigma ^{\prime}$
, there exists a finite sequence
![]() $\omega$
of configurations
$\omega$
of configurations
![]() $\omega _1,\ldots, \omega _n \in \mathcal {X}$
such that
$\omega _1,\ldots, \omega _n \in \mathcal {X}$
such that
![]() $\omega _1=\sigma$
,
$\omega _1=\sigma$
,
![]() $\omega _n=\sigma ^{\prime}$
and
$\omega _n=\sigma ^{\prime}$
and
![]() $q(\omega _i,\omega _{i+1})\gt 0$
, for
$q(\omega _i,\omega _{i+1})\gt 0$
, for
![]() $i=1,\ldots, n-1$
. We will refer to such a sequence as a path from
$i=1,\ldots, n-1$
. We will refer to such a sequence as a path from
![]() $\sigma$
to
$\sigma$
to
![]() $\sigma ^{\prime}$
and denote it by
$\sigma ^{\prime}$
and denote it by
![]() $\omega : \sigma \to \sigma ^{\prime}$
. Given a path
$\omega : \sigma \to \sigma ^{\prime}$
. Given a path
![]() $\omega =(\omega _1,\ldots, \omega _n)$
, we define its height
$\omega =(\omega _1,\ldots, \omega _n)$
, we define its height
![]() $\Phi _\omega$
as
$\Phi _\omega$
as
The communication energy between two configurations
![]() $\sigma, \sigma ^{\prime} \in \mathcal {X}$
is the minimum value that has to be reached by the energy in every path
$\sigma, \sigma ^{\prime} \in \mathcal {X}$
is the minimum value that has to be reached by the energy in every path
![]() $\omega \,:\, \sigma \to \sigma ^{\prime}$
, i.e.,
$\omega \,:\, \sigma \to \sigma ^{\prime}$
, i.e.,
Let
![]() $\mathcal {X}^s \subset \mathcal {X}$
denote the set of global minima of the Hamiltonian
$\mathcal {X}^s \subset \mathcal {X}$
denote the set of global minima of the Hamiltonian
![]() $H$
on
$H$
on
![]() $\mathcal {X}$
, to which we will refer to as stable states.
$\mathcal {X}$
, to which we will refer to as stable states.
In [Reference Nardi, Zocca and Borst47] it has been proved that for the hard-core model on a finite
![]() $L \times L$
square grid graph the following statements hold:
$L \times L$
square grid graph the following statements hold:
-
(i) There are exactly two stable states
(2.8) \begin{align} \mathcal {X}^s =\{{\mathbf{e}},{\mathbf{o}}\}; \end{align}
\begin{align} \mathcal {X}^s =\{{\mathbf{e}},{\mathbf{o}}\}; \end{align}
-
(ii) The communication energy between the two stable states is equal to
(2.9) \begin{align} \Phi ({\mathbf{e}},{\mathbf{o}}) - H({\mathbf{e}})=L+1; \end{align}
\begin{align} \Phi ({\mathbf{e}},{\mathbf{o}}) - H({\mathbf{e}})=L+1; \end{align}
-
(iii) The corresponding energy landscape has no deep wells, i.e.,
(2.10) \begin{align} \max _{\sigma \in \mathcal {X}} [\Phi (\sigma, \{{\mathbf{e}},{\mathbf{o}}\}) - H(\sigma )] \leq L \lt \Phi ({\mathbf{e}},{\mathbf{o}}) - H({\mathbf{e}}). \end{align}
\begin{align} \max _{\sigma \in \mathcal {X}} [\Phi (\sigma, \{{\mathbf{e}},{\mathbf{o}}\}) - H(\sigma )] \leq L \lt \Phi ({\mathbf{e}},{\mathbf{o}}) - H({\mathbf{e}}). \end{align}
Together, these facts imply that the value of the constant appearing in the asymptotic statements (1.1) and (1.2) for the first hitting time
![]() $\tau _{\mathbf{o}}^{\mathbf{e}}$
is
$\tau _{\mathbf{o}}^{\mathbf{e}}$
is
![]() $\Gamma (\Lambda )$
$\Gamma (\Lambda )$
![]() $= L+1$
.
$= L+1$
.
2.1 Essential saddle characterization
Our results give insight into the way the transitions between
![]() ${\mathbf{e}}$
and
${\mathbf{e}}$
and
![]() ${\mathbf{o}}$
most likely occur in the low-temperature regime. This is usually described by identifying the optimal paths, saddles, and essential saddles that we define as follows.
${\mathbf{o}}$
most likely occur in the low-temperature regime. This is usually described by identifying the optimal paths, saddles, and essential saddles that we define as follows.
-
•
 $ \mathcal {S} ({\mathbf{e}}, {\mathbf{o}})$
is the communication level set between
$ \mathcal {S} ({\mathbf{e}}, {\mathbf{o}})$
is the communication level set between
 ${\mathbf{e}}$
and
${\mathbf{e}}$
and
 ${\mathbf{o}}$
defined bywhere
${\mathbf{o}}$
defined bywhere \begin{equation*} \mathcal {S} ({\mathbf{e}}, {\mathbf{o}}) \,:\!=\, \{ \sigma \in \mathcal {X} \,|\, \exists \, \omega \in ({\mathbf{e}} \to {\mathbf{o}})_{\mathrm {opt}}, \,:\, \sigma \in \omega \text { and } H(\sigma ) = \Phi _\omega = \Phi ({\mathbf{e}},{\mathbf{o}})\}, \end{equation*}
\begin{equation*} \mathcal {S} ({\mathbf{e}}, {\mathbf{o}}) \,:\!=\, \{ \sigma \in \mathcal {X} \,|\, \exists \, \omega \in ({\mathbf{e}} \to {\mathbf{o}})_{\mathrm {opt}}, \,:\, \sigma \in \omega \text { and } H(\sigma ) = \Phi _\omega = \Phi ({\mathbf{e}},{\mathbf{o}})\}, \end{equation*}
 $({\mathbf{e}} \to {\mathbf{o}})_{\mathrm {opt}}$
is the set of optimal paths from
$({\mathbf{e}} \to {\mathbf{o}})_{\mathrm {opt}}$
is the set of optimal paths from
 ${\mathbf{e}}$
to
${\mathbf{e}}$
to
 ${\mathbf{o}}$
realizing the minimax in
${\mathbf{o}}$
realizing the minimax in
 $\Phi ({\mathbf{e}}, {\mathbf{o}})$
, i.e.,
$\Phi ({\mathbf{e}}, {\mathbf{o}})$
, i.e., \begin{equation*} ({\mathbf{e}} \to {\mathbf{o}})_{\mathrm {opt}} \,:\!=\, \{ \omega \,:\, {\mathbf{e}} \to {\mathbf{o}} \,|\, \Phi _\omega = \Phi ({\mathbf{e}},{\mathbf{o}})\}. \end{equation*}
\begin{equation*} ({\mathbf{e}} \to {\mathbf{o}})_{\mathrm {opt}} \,:\!=\, \{ \omega \,:\, {\mathbf{e}} \to {\mathbf{o}} \,|\, \Phi _\omega = \Phi ({\mathbf{e}},{\mathbf{o}})\}. \end{equation*}
-
• The configurations in
 $\mathcal {S}({\mathbf{e}},{\mathbf{o}})$
are called saddles. Given an optimal path
$\mathcal {S}({\mathbf{e}},{\mathbf{o}})$
are called saddles. Given an optimal path
 $\omega \in ({\mathbf{e}} \to {\mathbf{o}})_{\mathrm {opt}}$
, we define the set of its saddles
$\omega \in ({\mathbf{e}} \to {\mathbf{o}})_{\mathrm {opt}}$
, we define the set of its saddles
 $S(\omega )$
as
$S(\omega )$
as
 $ S(\omega )\,:\!=\,\{ \sigma \in \omega \,|\, H(\sigma ) = \Phi _\omega = \Phi ({\mathbf{e}},{\mathbf{o}})\}.$
A saddle
$ S(\omega )\,:\!=\,\{ \sigma \in \omega \,|\, H(\sigma ) = \Phi _\omega = \Phi ({\mathbf{e}},{\mathbf{o}})\}.$
A saddle
 $\sigma \in \mathcal {S}({\mathbf{e}},{\mathbf{o}})$
is called essential if either
$\sigma \in \mathcal {S}({\mathbf{e}},{\mathbf{o}})$
is called essential if either-
(i)
 $\exists \, \omega \in ({\mathbf{e}} \to {\mathbf{o}})_{\mathrm {opt}}$
such that
$\exists \, \omega \in ({\mathbf{e}} \to {\mathbf{o}})_{\mathrm {opt}}$
such that
 $S(\omega ) = \{\sigma \}$
, or
$S(\omega ) = \{\sigma \}$
, or -
(ii)
 $\exists \, \omega \in ({\mathbf{e}} \to {\mathbf{o}})_{\mathrm {opt}}$
such that
$\exists \, \omega \in ({\mathbf{e}} \to {\mathbf{o}})_{\mathrm {opt}}$
such that
 $\sigma \in S(\omega )$
and
$\sigma \in S(\omega )$
and
 $S(\omega ^{\prime}) \not \subseteq S(\omega ) \setminus \{\sigma \} \quad \forall \, \omega ^{\prime} \in ({\mathbf{e}} \to {\mathbf{o}})_{\mathrm {opt}}$
.
$S(\omega ^{\prime}) \not \subseteq S(\omega ) \setminus \{\sigma \} \quad \forall \, \omega ^{\prime} \in ({\mathbf{e}} \to {\mathbf{o}})_{\mathrm {opt}}$
.
A saddle
 $\sigma \in \mathcal {S}({\mathbf{e}},{\mathbf{o}})$
that is not essential is called unessential saddle or dead-end, i.e., for any
$\sigma \in \mathcal {S}({\mathbf{e}},{\mathbf{o}})$
that is not essential is called unessential saddle or dead-end, i.e., for any
 $\omega \in ({\mathbf{e}} \to {\mathbf{o}})_{\mathrm {opt}}$
such that
$\omega \in ({\mathbf{e}} \to {\mathbf{o}})_{\mathrm {opt}}$
such that
 $\omega \cap \{\sigma \}\neq \emptyset$
we have that
$\omega \cap \{\sigma \}\neq \emptyset$
we have that
 $S(\omega )\setminus \{\sigma \}\neq \emptyset$
and there exists
$S(\omega )\setminus \{\sigma \}\neq \emptyset$
and there exists
 $\omega ^{\prime} \in ({\mathbf{e}} \to {\mathbf{o}})_{\mathrm {opt}}$
such that
$\omega ^{\prime} \in ({\mathbf{e}} \to {\mathbf{o}})_{\mathrm {opt}}$
such that
 $S(\omega ^{\prime})\subseteq S(\omega )\setminus \{\sigma \}$
.
$S(\omega ^{\prime})\subseteq S(\omega )\setminus \{\sigma \}$
. -
-
• The essential gate
 $\mathcal {G}({\mathbf{e}}, {\mathbf{o}})\subset \mathcal {X}$
is the collection of essential saddles for the transition
$\mathcal {G}({\mathbf{e}}, {\mathbf{o}})\subset \mathcal {X}$
is the collection of essential saddles for the transition
 ${\mathbf{e}} \to {\mathbf{o}}$
.
${\mathbf{e}} \to {\mathbf{o}}$
.
The aim of the present paper is to accurately identify the set
![]() $\mathcal {G}({\mathbf{e}},{\mathbf{o}})$
of essential saddles for the transition from
$\mathcal {G}({\mathbf{e}},{\mathbf{o}})$
of essential saddles for the transition from
![]() ${\mathbf{e}}$
to
${\mathbf{e}}$
to
![]() ${\mathbf{o}}$
for the Metropolis dynamics of the hard-core model on a
${\mathbf{o}}$
for the Metropolis dynamics of the hard-core model on a
![]() $L \times L$
grid with periodic boundary conditions.
$L \times L$
grid with periodic boundary conditions.

Figure 2. An example of a configuration in
![]() $\mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
(on the left) and one in
$\mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
(on the left) and one in
![]() $\mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
(on the right).
$\mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
(on the right).

Figure 3. An example of a configuration in
![]() $\mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
(on the left) and one in
$\mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
(on the left) and one in
![]() $\mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
(on the right).
$\mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
(on the right).

Figure 4. An example of a configuration in
![]() $\mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
(on the left) and one in
$\mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
(on the left) and one in
![]() $\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
(on the right).
$\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
(on the right).
The set
![]() $\mathcal {G}({\mathbf{e}},{\mathbf{o}})$
will be described as the union of six disjoint sets, each characterized by configurations with specific geometrical features. Although we refer the reader to section 4 for a precise definition of these sets (cf. Definitions 4.2–4.6), we provide here some intuitive descriptions of the geometrical features of the configurations in these sets. We denote by
$\mathcal {G}({\mathbf{e}},{\mathbf{o}})$
will be described as the union of six disjoint sets, each characterized by configurations with specific geometrical features. Although we refer the reader to section 4 for a precise definition of these sets (cf. Definitions 4.2–4.6), we provide here some intuitive descriptions of the geometrical features of the configurations in these sets. We denote by
-
•
 $\mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
,
$\mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
,
 $\mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
, and
$\mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
, and
 $\mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
the collections of configurations with a unique cluster of particles in odd sites of rhomboidal shape with exactly two adjacent even empty sites as in Figure 2 and Figure 3 (left). Roughly speaking,
$\mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
the collections of configurations with a unique cluster of particles in odd sites of rhomboidal shape with exactly two adjacent even empty sites as in Figure 2 and Figure 3 (left). Roughly speaking,
 $\mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
contains the configurations with
$\mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
contains the configurations with
 $(\frac {L}{2}-1)^2$
occupied odd particles and
$(\frac {L}{2}-1)^2$
occupied odd particles and
 $L^2+2$
empty even sites;
$L^2+2$
empty even sites;
 $\mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
(resp.
$\mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
(resp.
 $\mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
) contains the configurations obtained from
$\mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
) contains the configurations obtained from
 $\mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
(resp.
$\mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
(resp.
 $\mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
) by removing some occupied even sites attached to the rhombus and growing along one (resp. the longest) side by adding some particles in the nearest odd sites of the rhombus.
$\mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
) by removing some occupied even sites attached to the rhombus and growing along one (resp. the longest) side by adding some particles in the nearest odd sites of the rhombus.
-
•
 $\mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
,
$\mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
,
 $\mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
, and
$\mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
, and
 $\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
the collections of configurations with a unique cluster of particles at odd sites with at most two additional empty even sites as in Figure 3 (right) and in Figure 4. In particular,
$\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
the collections of configurations with a unique cluster of particles at odd sites with at most two additional empty even sites as in Figure 3 (right) and in Figure 4. In particular,
 $\mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
contains the configurations with
$\mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
contains the configurations with
 $\frac {L}{2}-1$
particles arranged in an odd column with two other empty even sites;
$\frac {L}{2}-1$
particles arranged in an odd column with two other empty even sites;
 $\mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
contains the configurations obtained from
$\mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
contains the configurations obtained from
 $\mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
such that there is at least one column or row with
$\mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
such that there is at least one column or row with
 $\frac {L}{2}$
particles arranged in odd sites.
$\frac {L}{2}$
particles arranged in odd sites.
 $\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
contains the configurations obtained from
$\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
contains the configurations obtained from
 $\mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
without having column or row with
$\mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
without having column or row with
 $\frac {L}{2}$
particles.
$\frac {L}{2}$
particles.
The following theorem characterizes the essential gate for the transition from
![]() ${\mathbf{e}}$
to
${\mathbf{e}}$
to
![]() ${\mathbf{o}}$
.
${\mathbf{o}}$
.
Theorem 2.1 (Essential saddles). Define the set
The essential saddles for the transition from
![]() ${\mathbf{e}}$
to
${\mathbf{e}}$
to
![]() ${\mathbf{o}}$
of the hard-core model on a
${\mathbf{o}}$
of the hard-core model on a
![]() $L \times L$
toric grid graph
$L \times L$
toric grid graph
![]() $\Lambda$
are all and only the configurations in
$\Lambda$
are all and only the configurations in
![]() $\mathcal C^*({\mathbf{e}},{\mathbf{o}})$
, i.e.,
$\mathcal C^*({\mathbf{e}},{\mathbf{o}})$
, i.e.,
Furthermore, the possible transitions at energy not higher than
![]() $-\frac {L^2}{2}+L+1$
among the six subsets that form
$-\frac {L^2}{2}+L+1$
among the six subsets that form
![]() $\mathcal C^*({\mathbf{e}},{\mathbf{o}})$
are as detailed in Figure 5.
$\mathcal C^*({\mathbf{e}},{\mathbf{o}})$
are as detailed in Figure 5.
3. Definitions and auxiliary results
The main goal of this section is to introduce the notion of odd clusters, which are the basis of the geometrical description of the configurations, and to inspect the relation between their shape and perimeter.

Figure 5. Schematic representation of the set of essential saddles, where we highlight with arrows between the set pairs that communicate at energy not higher than
![]() $-\frac {L^2}{2}+L+1$
and the initial cycles
$-\frac {L^2}{2}+L+1$
and the initial cycles
![]() $\mathcal {C}_{\mathbf{e}}$
and
$\mathcal {C}_{\mathbf{e}}$
and
![]() $\mathcal {C}_{\mathbf{o}}$
, see section 3. The vertical lines represent the partition of
$\mathcal {C}_{\mathbf{o}}$
, see section 3. The vertical lines represent the partition of
![]() $\mathcal {X}$
in manifolds, see (4.1).
$\mathcal {X}$
in manifolds, see (4.1).
In subsection 3.1 we define a geometrical representation of clusters associated with the occupied odd sites, and in subsection 3.2 we introduce the notion of rhombi, which turns out to be crucial in the description of the essential saddles. In subsection 3.3 we present two algorithms that, combined together, return a path whose last configuration has a rhomboidal shape and such that the energy along it never increases. We will use them to deduce that there exists a downhill path from the configurations without a rhomboidal cluster towards
![]() ${\mathbf{e}}$
or
${\mathbf{e}}$
or
![]() ${\mathbf{o}}$
.
${\mathbf{o}}$
.
Along the lines of [Reference Manzo, Nardi, Olivieri and Scoppola43, eq. (2.7)], we define
![]() $C_{\mathbf{e}}\,:\!=\,\{ \zeta \in \mathcal {X} \,|\, \Phi (\zeta, {\mathbf{e}}) \lt \Phi ({\mathbf{e}},{\mathbf{o}})\}$
to be the initial cycle of
$C_{\mathbf{e}}\,:\!=\,\{ \zeta \in \mathcal {X} \,|\, \Phi (\zeta, {\mathbf{e}}) \lt \Phi ({\mathbf{e}},{\mathbf{o}})\}$
to be the initial cycle of
![]() ${\mathbf{e}}$
, that is the maximal cycle that includes
${\mathbf{e}}$
, that is the maximal cycle that includes
![]() ${\mathbf{e}}$
but does not include
${\mathbf{e}}$
but does not include
![]() ${\mathbf{o}}$
, namely, it contains all the configurations that can be reached by
${\mathbf{o}}$
, namely, it contains all the configurations that can be reached by
![]() ${\mathbf{e}}$
by spending strictly less energy than the one needed for the transition between
${\mathbf{e}}$
by spending strictly less energy than the one needed for the transition between
![]() ${\mathbf{e}}$
and
${\mathbf{e}}$
and
![]() ${\mathbf{o}}$
, i.e., the communication height
${\mathbf{o}}$
, i.e., the communication height
![]() $\Phi ({\mathbf{e}},{\mathbf{o}})$
. The corresponding initial cycle of
$\Phi ({\mathbf{e}},{\mathbf{o}})$
. The corresponding initial cycle of
![]() ${\mathbf{o}}$
is defined analogously and is denoted by
${\mathbf{o}}$
is defined analogously and is denoted by
![]() $C_{\mathbf{o}}$
.
$C_{\mathbf{o}}$
.
Given a configuration
![]() $\sigma \in \mathcal {X}$
, denote by
$\sigma \in \mathcal {X}$
, denote by
![]() $\Delta H(\sigma )$
the energy difference with respect to either one of the stable states, i.e.,
$\Delta H(\sigma )$
the energy difference with respect to either one of the stable states, i.e.,
3.1 Odd clusters and regions
For any subset of sites
![]() $S \subseteq V$
we define the complement of
$S \subseteq V$
we define the complement of
![]() $S$
as
$S$
as
![]() $S^c\,:\!=\,V\setminus S$
, the external boundary
$S^c\,:\!=\,V\setminus S$
, the external boundary
![]() $\partial ^+ S$
as the subset of sites in
$\partial ^+ S$
as the subset of sites in
![]() $S^c$
that are adjacent to a site in
$S^c$
that are adjacent to a site in
![]() $S$
, i.e.,
$S$
, i.e.,
and
![]() $\nabla S$
as the subset of edges connecting the sites in
$\nabla S$
as the subset of edges connecting the sites in
![]() $S$
with those in
$S$
with those in
![]() $\partial ^+ S$
, i.e.,
$\partial ^+ S$
, i.e.,
A (connected) odd cluster
![]() $C \subseteq V$
is a subset of sites that satisfies both the following conditions:
$C \subseteq V$
is a subset of sites that satisfies both the following conditions:
-
1. If an odd site
 $v \in V_{\mathbf{e}}$
belongs to
$v \in V_{\mathbf{e}}$
belongs to
 $C$
, then so do the four neighbouring even sites, i.e.,
$C$
, then so do the four neighbouring even sites, i.e.,
 $\partial ^+ \{v\} \subset C$
;
$\partial ^+ \{v\} \subset C$
; -
2.
 $C \cap V_{\mathbf{e}}$
is connected as a sub-graph of the graph
$C \cap V_{\mathbf{e}}$
is connected as a sub-graph of the graph
 $(V_{\mathbf{e}}, E^*)$
, with
$(V_{\mathbf{e}}, E^*)$
, with
 $E^*\,:\!=\,\{(v,w) \in V_{\mathbf{e}} \times V_{\mathbf{e}} \,|\, d(v,w)=2\}$
, where
$E^*\,:\!=\,\{(v,w) \in V_{\mathbf{e}} \times V_{\mathbf{e}} \,|\, d(v,w)=2\}$
, where
 $d(\cdot, \cdot )$
denotes the usual graph distance on
$d(\cdot, \cdot )$
denotes the usual graph distance on
 $\Lambda$
.
$\Lambda$
.
We denote by
![]() $\mathrm {C}_{\mathbf{o}}(\Lambda )$
the collection of odd clusters in
$\mathrm {C}_{\mathbf{o}}(\Lambda )$
the collection of odd clusters in
![]() $\Lambda$
.
$\Lambda$
.
Consider the dual graph
![]() $\Lambda ^{\prime}=(V^{\prime},E^{\prime})$
of the graph
$\Lambda ^{\prime}=(V^{\prime},E^{\prime})$
of the graph
![]() $\Lambda$
, which is a discrete torus of the same size. Given an odd cluster
$\Lambda$
, which is a discrete torus of the same size. Given an odd cluster
![]() $C$
, consider the edge set
$C$
, consider the edge set
![]() $\nabla C$
that disconnects
$\nabla C$
that disconnects
![]() $C$
from its complement
$C$
from its complement
![]() $C^c$
. We associate with
$C^c$
. We associate with
![]() $\nabla C$
the edge set
$\nabla C$
the edge set
![]() $\gamma (C) \subset E^{\prime}$
on the dual graph
$\gamma (C) \subset E^{\prime}$
on the dual graph
![]() $\Lambda ^{\prime}$
which consists of all the edges of
$\Lambda ^{\prime}$
which consists of all the edges of
![]() $\Lambda ^{\prime}$
orthogonal to edges in
$\Lambda ^{\prime}$
orthogonal to edges in
![]() $\nabla C$
. Such a set, to which we refer as the contour of the cluster
$\nabla C$
. Such a set, to which we refer as the contour of the cluster
![]() $C$
, consists of one or more piecewise linear closed curves and, by construction,
$C$
, consists of one or more piecewise linear closed curves and, by construction,
![]() $|\gamma (C)|=|\nabla C|$
. Leveraging this fact, we define the perimeter
$|\gamma (C)|=|\nabla C|$
. Leveraging this fact, we define the perimeter
![]() $P(C)$
of the odd cluster
$P(C)$
of the odd cluster
![]() $C$
as the total length of the contour
$C$
as the total length of the contour
![]() $\gamma (C)$
, i.e.,
$\gamma (C)$
, i.e.,
As proved in [Reference Zocca, Borst, van Leeuwaarden and Nardi57], the perimeter of the odd cluster
![]() $C$
satisfies the following identity:
$C$
satisfies the following identity:
We call area of an odd cluster
![]() $C$
the number of odd occupied sites it comprises. We say that an odd cluster is degenerate if it has area 0 and non-degenerate otherwise.
$C$
the number of odd occupied sites it comprises. We say that an odd cluster is degenerate if it has area 0 and non-degenerate otherwise.
We introduce a mapping
![]() $\mathcal {O}\,:\, \mathcal {X} \to 2^V$
that associates to a given hard-core configuration
$\mathcal {O}\,:\, \mathcal {X} \to 2^V$
that associates to a given hard-core configuration
![]() $\sigma \in \mathcal {X}$
the subset
$\sigma \in \mathcal {X}$
the subset
![]() $\mathcal {O}(\sigma ) \subseteq V$
defined as
$\mathcal {O}(\sigma ) \subseteq V$
defined as
In other words,
![]() $\mathcal {O}(\sigma )$
is the subset comprising all occupied odd sites and even empty sites of the configuration
$\mathcal {O}(\sigma )$
is the subset comprising all occupied odd sites and even empty sites of the configuration
![]() $\sigma$
. It is immediate to check that
$\sigma$
. It is immediate to check that
![]() $\mathcal {O}$
is an injective mapping, and we will refer to the image
$\mathcal {O}$
is an injective mapping, and we will refer to the image
![]() $\mathcal {O}(\sigma )$
of a configuration
$\mathcal {O}(\sigma )$
of a configuration
![]() $\sigma$
as its odd region.
$\sigma$
as its odd region.
The odd region
![]() $\mathcal {O}(\sigma )$
of a configuration
$\mathcal {O}(\sigma )$
of a configuration
![]() $\sigma \in \mathcal {X}$
can be partitioned into its connected components, say
$\sigma \in \mathcal {X}$
can be partitioned into its connected components, say
![]() $C_1(\sigma ), \ldots, C_m(\sigma ) \in \mathrm {C}_{\mathbf{o}}(\Lambda )$
, for some
$C_1(\sigma ), \ldots, C_m(\sigma ) \in \mathrm {C}_{\mathbf{o}}(\Lambda )$
, for some
![]() $m \in \mathbb N$
, which are, by definition, odd clusters, that is,
$m \in \mathbb N$
, which are, by definition, odd clusters, that is,
Using the partition (3.5) of the odd region
![]() $\mathcal {O}(\sigma )$
into odd clusters, the definitions of contour and perimeter can be extended to the whole odd region in an obvious way, so that we can ultimately define the contour
$\mathcal {O}(\sigma )$
into odd clusters, the definitions of contour and perimeter can be extended to the whole odd region in an obvious way, so that we can ultimately define the contour
![]() $\gamma (\sigma )$
of a configuration
$\gamma (\sigma )$
of a configuration
![]() $\sigma \in \mathcal {X}$
as
$\sigma \in \mathcal {X}$
as
and its perimeter
![]() $P(\sigma )$
as
$P(\sigma )$
as
As shown in [Reference Zocca, Borst, van Leeuwaarden and Nardi57], starting from (3.3), a double counting argument yields the following identity that relates the perimeter
![]() $P(\sigma )$
of a hard-core configuration
$P(\sigma )$
of a hard-core configuration
![]() $ \sigma \in \mathcal {X}$
with its energy
$ \sigma \in \mathcal {X}$
with its energy
![]() $H(\sigma )$
(recall (3.1)-(3.2))
$H(\sigma )$
(recall (3.1)-(3.2))
Given a configuration
![]() $\sigma \in \mathcal {X}$
, we define the odd non-degenerate region
$\sigma \in \mathcal {X}$
, we define the odd non-degenerate region
![]() $\mathcal {O}^{nd}(\sigma )$
as a subset of
$\mathcal {O}^{nd}(\sigma )$
as a subset of
![]() $\mathcal {O}(\sigma )$
containing only odd non-degenerate clusters. See Figure 7 for an example of an odd region and an odd non-degenerate region.
$\mathcal {O}(\sigma )$
containing only odd non-degenerate clusters. See Figure 7 for an example of an odd region and an odd non-degenerate region.

Figure 6. Example of four different rhombi, namely
![]() $\mathcal {R}_{1,2}$
,
$\mathcal {R}_{1,2}$
,
![]() $\mathcal {R}_{4,2}$
,
$\mathcal {R}_{4,2}$
,
![]() $\mathcal {R}_{0,2}$
and
$\mathcal {R}_{0,2}$
and
![]() $\mathcal {R}_{1,0}$
(in clockwise order from the top-right corner).
$\mathcal {R}_{1,0}$
(in clockwise order from the top-right corner).
3.2 Odd rhombi
Given an odd site
![]() $\eta =(\eta _1,\eta _2) \in V_{\mathbf{o}}$
and two positive integers
$\eta =(\eta _1,\eta _2) \in V_{\mathbf{o}}$
and two positive integers
![]() $\ell _1,\ell _2\leq L$
, the odd rhombus
$\ell _1,\ell _2\leq L$
, the odd rhombus
![]() $\mathcal {R}_{\ell _1,\ell _2}(\eta )$
with reference site
$\mathcal {R}_{\ell _1,\ell _2}(\eta )$
with reference site
![]() $\eta$
and lengths
$\eta$
and lengths
![]() $\ell _1$
and
$\ell _1$
and
![]() $\ell _2$
is the odd cluster defined as
$\ell _2$
is the odd cluster defined as
where
![]() $S_{\ell _1,\ell _2}(\eta ) \subseteq V_{\mathbf{o}}$
is the subset of odd sites given by
$S_{\ell _1,\ell _2}(\eta ) \subseteq V_{\mathbf{o}}$
is the subset of odd sites given by
 \begin{align} S_{\ell _1,\ell _2}(\eta ) &\,:\!=\, \bigcup _{0 \leq k \leq \ell _1-1, \, 0 \leq j \leq \ell _2-1} \{ (\eta _1 + k + j, \eta _2 + k - j )\} \nonumber \\[3pt] &= \{ v=(v_1,v_2) \in V \,|\, \exists \, k \in [[0,\ell _1]], \, j \in [[0,\ell _2]] \,:\, v_1 = \eta _1 + k + j, \, v_2 = \eta _2 + k - j\}. \end{align}
\begin{align} S_{\ell _1,\ell _2}(\eta ) &\,:\!=\, \bigcup _{0 \leq k \leq \ell _1-1, \, 0 \leq j \leq \ell _2-1} \{ (\eta _1 + k + j, \eta _2 + k - j )\} \nonumber \\[3pt] &= \{ v=(v_1,v_2) \in V \,|\, \exists \, k \in [[0,\ell _1]], \, j \in [[0,\ell _2]] \,:\, v_1 = \eta _1 + k + j, \, v_2 = \eta _2 + k - j\}. \end{align}

Figure 7. Example of a configuration
![]() $\sigma$
, in which the contour of the non-degenerate (degenerate) odd clusters is highlighted in black (red, respectively). The contour
$\sigma$
, in which the contour of the non-degenerate (degenerate) odd clusters is highlighted in black (red, respectively). The contour
![]() $\gamma (\sigma )$
of the configuration
$\gamma (\sigma )$
of the configuration
![]() $\sigma$
is of the odd region
$\sigma$
is of the odd region
![]() $\mathcal {O}(\sigma )$
is the union of black lines (corresponding to
$\mathcal {O}(\sigma )$
is the union of black lines (corresponding to
![]() $\mathcal {O}^{nd}(\sigma )$
) and red lines.
$\mathcal {O}^{nd}(\sigma )$
) and red lines.

Figure 8. Example of a odd cluster
![]() $C$
(on the left) and its surrounding rhombus
$C$
(on the left) and its surrounding rhombus
![]() $\mathcal {R}(C)=\mathcal {R}_{8,5}$
in red (on the right). On the left, the red squares contain the antiknobs and the decreasing broken diagonals are highlighted with blue rectangles. On the right, we highlight the decreasing shorter (resp. complete) diagonals with blue (resp. green) rectangles.
$\mathcal {R}(C)=\mathcal {R}_{8,5}$
in red (on the right). On the left, the red squares contain the antiknobs and the decreasing broken diagonals are highlighted with blue rectangles. On the right, we highlight the decreasing shorter (resp. complete) diagonals with blue (resp. green) rectangles.
In the latter definition, the sums and subtractions of coordinates are taken modulo
![]() $L$
. In the case
$L$
. In the case
![]() $\ell _1\ell _2=0$
, we can take
$\ell _1\ell _2=0$
, we can take
![]() $\eta \in V_{\mathbf{e}}$
and define the degenerate rhombus
$\eta \in V_{\mathbf{e}}$
and define the degenerate rhombus
![]() $\mathcal {R}_{\ell _1,\ell _2}(\eta )$
as the odd cluster
$\mathcal {R}_{\ell _1,\ell _2}(\eta )$
as the odd cluster
 \begin{equation*} \mathcal {R}_{\ell _1,\ell _2}(\eta )= \begin{cases} \bigcup _{0 \leq j \leq \ell _2} \{ (\eta _1 + j, \eta _2 - j )\} &\hbox {if } \ell _1=0 \hbox { and } \ell _2\neq 0, \\[3pt] \bigcup _{0 \leq k \leq \ell _1} \{ (\eta _1 + k, \eta _2 - k )\} &\hbox {if } \ell _1\neq 0 \hbox { and } \ell _2=0, \\[3pt] (\eta _1,\eta _2) &\hbox {if } \ell _1=\ell _2=0. \end{cases} \end{equation*}
\begin{equation*} \mathcal {R}_{\ell _1,\ell _2}(\eta )= \begin{cases} \bigcup _{0 \leq j \leq \ell _2} \{ (\eta _1 + j, \eta _2 - j )\} &\hbox {if } \ell _1=0 \hbox { and } \ell _2\neq 0, \\[3pt] \bigcup _{0 \leq k \leq \ell _1} \{ (\eta _1 + k, \eta _2 - k )\} &\hbox {if } \ell _1\neq 0 \hbox { and } \ell _2=0, \\[3pt] (\eta _1,\eta _2) &\hbox {if } \ell _1=\ell _2=0. \end{cases} \end{equation*}
Note that, in this case,
![]() $\mathcal {R}_{\ell _1,\ell _2}(\eta )$
is a subset of even sites. The area of
$\mathcal {R}_{\ell _1,\ell _2}(\eta )$
is a subset of even sites. The area of
![]() $\mathcal {R}_{\ell _1,\ell _2}(\eta )$
is the cardinality of
$\mathcal {R}_{\ell _1,\ell _2}(\eta )$
is the cardinality of
![]() $S_{\ell _1,\ell _2}(\eta )$
in the non-degenerate case, whereas in the degenerate case it is equal to zero. Some examples of rhombi and degenerate rhombi are shown in Figure 6. We observe that the non-degenerate rhombus
$S_{\ell _1,\ell _2}(\eta )$
in the non-degenerate case, whereas in the degenerate case it is equal to zero. Some examples of rhombi and degenerate rhombi are shown in Figure 6. We observe that the non-degenerate rhombus
![]() $\mathcal {R}_{\ell _1,\ell _2}$
has
$\mathcal {R}_{\ell _1,\ell _2}$
has
![]() $\ell _1$
diagonals of length
$\ell _1$
diagonals of length
![]() $\ell _2$
and
$\ell _2$
and
![]() $\ell _2$
diagonals of length
$\ell _2$
diagonals of length
![]() $\ell _1$
in the opposite direction, which we will refer to as complete diagonals. We denote by
$\ell _1$
in the opposite direction, which we will refer to as complete diagonals. We denote by
![]() $\mathrm {R}_{\mathbf{o}}(\Lambda ) \subset \mathrm {C}_{\mathbf{o}}(\Lambda )$
the collection of all odd rhombi on
$\mathrm {R}_{\mathbf{o}}(\Lambda ) \subset \mathrm {C}_{\mathbf{o}}(\Lambda )$
the collection of all odd rhombi on
![]() $\Lambda$
including the degenerate ones. For every odd cluster
$\Lambda$
including the degenerate ones. For every odd cluster
![]() $C \in \mathrm {C}_{\mathbf{o}}(\Lambda )$
, we define the surrounding rhombus
$C \in \mathrm {C}_{\mathbf{o}}(\Lambda )$
, we define the surrounding rhombus
![]() $\mathcal {R}(C)$
as the minimal rhombus (by inclusion) in
$\mathcal {R}(C)$
as the minimal rhombus (by inclusion) in
![]() $\mathrm {R}_{\mathbf{o}}(\Lambda )$
such that
$\mathrm {R}_{\mathbf{o}}(\Lambda )$
such that
![]() $C \subseteq \mathcal {R}(C)$
; see Figure 8 for an example.
$C \subseteq \mathcal {R}(C)$
; see Figure 8 for an example.
Most of the results for odd rhombi that will be proved are translation-invariant, the reason why we will often refer to the rhombus
![]() $\mathcal {R}_{\ell _1,\ell _2}(\eta )$
simply as
$\mathcal {R}_{\ell _1,\ell _2}(\eta )$
simply as
![]() $\mathcal {R}_{\ell _1,\ell _2}$
, without explicitly specifying the reference site
$\mathcal {R}_{\ell _1,\ell _2}$
, without explicitly specifying the reference site
![]() $\eta$
. The next two lemmas, Lemmas3.1 and 3.2, concern the properties of rhombi on a square
$\eta$
. The next two lemmas, Lemmas3.1 and 3.2, concern the properties of rhombi on a square
![]() $L \times L$
grid with periodic boundary conditions. Their proofs, being involved but not particularly insightful, are deferred to Appendix A.
$L \times L$
grid with periodic boundary conditions. Their proofs, being involved but not particularly insightful, are deferred to Appendix A.
Lemma 3.1 (Set of sites winds around the torus). Given
![]() $\eta =(\eta _1,\eta _2)\in V_{\mathbf{o}}$
and two non-negative integers
$\eta =(\eta _1,\eta _2)\in V_{\mathbf{o}}$
and two non-negative integers
![]() $\ell _1,\ell _2\leq L$
such that
$\ell _1,\ell _2\leq L$
such that
![]() $\ell _1 \leq \ell _2$
and
$\ell _1 \leq \ell _2$
and
![]() $\ell _1\geq L/2$
, the following statements hold:
$\ell _1\geq L/2$
, the following statements hold:
-
(i) If
 $\ell _2\leq L-2$
, then
$\ell _2\leq L-2$
, then \begin{align*} \displaystyle \bigcup _{\substack {0\leq k\leq \ell _1 \\[3pt] \ell _2+1\leq j\leq L-1}}\{(\eta _1+k+j-1,\eta _2+k-j)\}\cup \bigcup _{\substack {\ell _1+1\leq k\leq L-1 \\[3pt] 0\leq j\leq \ell _2}} &\{(\eta _1+k+j-1,\eta _2+k-j)\} \\[3pt] &\subseteq \displaystyle \bigcup _{\substack {0\leq k\leq \ell _1 \\[3pt] 0\leq j\leq \ell _2}}\!\{(\eta _1 \!+\! k \!+\! j-1,\eta _2 \!+\! k-j)\}. \end{align*}
\begin{align*} \displaystyle \bigcup _{\substack {0\leq k\leq \ell _1 \\[3pt] \ell _2+1\leq j\leq L-1}}\{(\eta _1+k+j-1,\eta _2+k-j)\}\cup \bigcup _{\substack {\ell _1+1\leq k\leq L-1 \\[3pt] 0\leq j\leq \ell _2}} &\{(\eta _1+k+j-1,\eta _2+k-j)\} \\[3pt] &\subseteq \displaystyle \bigcup _{\substack {0\leq k\leq \ell _1 \\[3pt] 0\leq j\leq \ell _2}}\!\{(\eta _1 \!+\! k \!+\! j-1,\eta _2 \!+\! k-j)\}. \end{align*}
-
(ii) If
 $\ell _2=L-1$
, then(3.11)and
$\ell _2=L-1$
, then(3.11)and \begin{align} \displaystyle \bigcup _{\substack {\ell _1+1\leq k\leq L-1 \\[3pt] 0\leq j\leq L-1}}\{(\eta _1+k+j-1,\eta _2+k-j)\} \subseteq \displaystyle \bigcup _{\substack {0\leq k\leq \ell _1 \\[3pt] 0\leq j\leq L-1}}\{(\eta _1+k+j-1,\eta _2+k-j)\} \end{align}
(3.12)
\begin{align} \displaystyle \bigcup _{\substack {\ell _1+1\leq k\leq L-1 \\[3pt] 0\leq j\leq L-1}}\{(\eta _1+k+j-1,\eta _2+k-j)\} \subseteq \displaystyle \bigcup _{\substack {0\leq k\leq \ell _1 \\[3pt] 0\leq j\leq L-1}}\{(\eta _1+k+j-1,\eta _2+k-j)\} \end{align}
(3.12) \begin{align} \displaystyle \bigcup _{\substack {L/2\leq k\leq \ell _1-1 \\[3pt] 1\leq j\leq L-2}}\{(\eta _1+k+j,\eta _2+k-j)\} \subseteq \displaystyle \bigcup _{\substack {0\leq k\leq L/2-1 \\[3pt] 0\leq j\leq L-2}}\{(\eta _1+k+j,\eta _2+k-j)\}. \end{align}
\begin{align} \displaystyle \bigcup _{\substack {L/2\leq k\leq \ell _1-1 \\[3pt] 1\leq j\leq L-2}}\{(\eta _1+k+j,\eta _2+k-j)\} \subseteq \displaystyle \bigcup _{\substack {0\leq k\leq L/2-1 \\[3pt] 0\leq j\leq L-2}}\{(\eta _1+k+j,\eta _2+k-j)\}. \end{align}
For any subset of sites
![]() $A\subseteq V$
, we define the complement of
$A\subseteq V$
, we define the complement of
![]() $A$
as the complementary set of
$A$
as the complementary set of
![]() $A$
in
$A$
in
![]() $V$
, i.e., as
$V$
, i.e., as
![]() $V \setminus A$
.
$V \setminus A$
.
Lemma 3.2 (Properties of rhombi). Given
![]() $\eta \in V_{\mathbf{o}}$
and two non-negative integers
$\eta \in V_{\mathbf{o}}$
and two non-negative integers
![]() $\ell _1,\ell _2\leq L$
, the following statements hold:
$\ell _1,\ell _2\leq L$
, the following statements hold:
-
(i) If
 $\max \{\ell _1,\ell _2\}\leq L-2$
and
$\max \{\ell _1,\ell _2\}\leq L-2$
and
 $\min \{\ell _1,\ell _2\}\geq L/2$
, then the complement of the rhombus
$\min \{\ell _1,\ell _2\}\geq L/2$
, then the complement of the rhombus
 $\mathcal {R}_{\ell _1,\ell _2}(\eta )$
is a rhombus
$\mathcal {R}_{\ell _1,\ell _2}(\eta )$
is a rhombus
 $R_{L-\ell _1-1,L-\ell _2-1}(\hat \eta )$
for some
$R_{L-\ell _1-1,L-\ell _2-1}(\hat \eta )$
for some
 $\hat \eta \in V_{\mathbf{e}}$
.
$\hat \eta \in V_{\mathbf{e}}$
. -
(ii) If
 $\max \{\ell _1,\ell _2\}=L-1$
and
$\max \{\ell _1,\ell _2\}=L-1$
and
 $\min \{\ell _1,\ell _2\}\geq L/2$
, then the complement of the rhombus
$\min \{\ell _1,\ell _2\}\geq L/2$
, then the complement of the rhombus
 $\mathcal {R}_{\ell _1,\ell _2}(\eta )$
is the disjoint union of
$\mathcal {R}_{\ell _1,\ell _2}(\eta )$
is the disjoint union of
 $L-\min \{\ell _1,\ell _2\}$
odd sites.
$L-\min \{\ell _1,\ell _2\}$
odd sites. -
(iii) If
 $\max \{\ell _1,\ell _2\}= L$
and
$\max \{\ell _1,\ell _2\}= L$
and
 $\min \{\ell _1,\ell _2\}\lt L/2$
, then the rhombus
$\min \{\ell _1,\ell _2\}\lt L/2$
, then the rhombus
 $\mathcal {R}_{\ell _1,\ell _2}(\eta )$
contains
$\mathcal {R}_{\ell _1,\ell _2}(\eta )$
contains
 $L\, \ell _1$
odd sites and
$L\, \ell _1$
odd sites and
 $L(\ell _1+1)$
even sites.
$L(\ell _1+1)$
even sites. -
(iv) If
 $\max \{\ell _1,\ell _2\}= L$
and
$\max \{\ell _1,\ell _2\}= L$
and
 $\min \{\ell _1,\ell _2\}\geq L/2$
, then the rhombus
$\min \{\ell _1,\ell _2\}\geq L/2$
, then the rhombus
 $\mathcal {R}_{\ell _1,\ell _2}(\eta )$
coincides with
$\mathcal {R}_{\ell _1,\ell _2}(\eta )$
coincides with
 $V$
.
$V$
.
These two lemmas will now be used to prove the next proposition, which gives a formula for the perimeter of a rhombus
![]() $\mathcal {R}_{\ell _1,\ell _2}$
. To this end, we will use the fact that a rhombus
$\mathcal {R}_{\ell _1,\ell _2}$
. To this end, we will use the fact that a rhombus
![]() $\mathcal {R}_{\ell _1,\ell _2}$
and its complement in
$\mathcal {R}_{\ell _1,\ell _2}$
and its complement in
![]() $\Lambda$
have the same boundary for any
$\Lambda$
have the same boundary for any
![]() $0\leq \ell _1,\ell _2\leq L$
, and, in particular the same perimeter. In addition, we will say that a rhombus
$0\leq \ell _1,\ell _2\leq L$
, and, in particular the same perimeter. In addition, we will say that a rhombus
![]() $\mathcal {R}_{\ell _1,\ell _2}$
winds vertically (resp. horizontally) around the torus if there exists a set of
$\mathcal {R}_{\ell _1,\ell _2}$
winds vertically (resp. horizontally) around the torus if there exists a set of
![]() $\frac {L}{2}$
odd sites
$\frac {L}{2}$
odd sites
![]() $\eta _1,\ldots, \eta _{L/2}$
in
$\eta _1,\ldots, \eta _{L/2}$
in
![]() $\mathcal {R}_{\ell _1,\ell _2}$
all on the same column (resp. row). If the direction is not relevant, we will simply say that the rhombus winds around the torus.
$\mathcal {R}_{\ell _1,\ell _2}$
all on the same column (resp. row). If the direction is not relevant, we will simply say that the rhombus winds around the torus.
Proposition 3.3 (Formula for rhombus perimeter). Given a
![]() $L \times L$
toric grid graph
$L \times L$
toric grid graph
![]() $\Lambda$
and any sizes
$\Lambda$
and any sizes
![]() $0\leq \ell _1,\ell _2 \leq L$
, the perimeter of the rhombus
$0\leq \ell _1,\ell _2 \leq L$
, the perimeter of the rhombus
![]() $\mathcal {R}_{\ell _1,\ell _2}$
satisfies the following identity
$\mathcal {R}_{\ell _1,\ell _2}$
satisfies the following identity
 \begin{align} P (\mathcal {R}_{\ell _1,\ell _2}) = 4 \times \begin{cases} \ell _1 + \ell _2+1 & \text { if } \min \{\ell _1,\ell _2\} \lt L/2\ \text{and} \max \{\ell _1,\ell _2\} \lt L,\\[3pt] 2L-(\ell _1+\ell _2+1) & \text { if } \min \{\ell _1,\ell _2\} \geq L/2 \text { and } \max \{\ell _1,\ell _2\} \lt L,\\[3pt] L & \text { if } \min \{\ell _1,\ell _2 \} \lt L/2 \text { and } \max \{\ell _1,\ell _2\} =L, \\[3pt] 0 & \text { if } \min \{\ell _1,\ell _2 \} \geq L/2 \text { and } \max \{\ell _1,\ell _2\} =L. \end{cases} \end{align}
\begin{align} P (\mathcal {R}_{\ell _1,\ell _2}) = 4 \times \begin{cases} \ell _1 + \ell _2+1 & \text { if } \min \{\ell _1,\ell _2\} \lt L/2\ \text{and} \max \{\ell _1,\ell _2\} \lt L,\\[3pt] 2L-(\ell _1+\ell _2+1) & \text { if } \min \{\ell _1,\ell _2\} \geq L/2 \text { and } \max \{\ell _1,\ell _2\} \lt L,\\[3pt] L & \text { if } \min \{\ell _1,\ell _2 \} \lt L/2 \text { and } \max \{\ell _1,\ell _2\} =L, \\[3pt] 0 & \text { if } \min \{\ell _1,\ell _2 \} \geq L/2 \text { and } \max \{\ell _1,\ell _2\} =L. \end{cases} \end{align}
Proof. First of all, we identify which of the conditions in (3.13) imply that a rhombus winds around the torus. Consider the rhombus
![]() $\mathcal {R}_{\ell _1,\ell _2}(\eta )$
with
$\mathcal {R}_{\ell _1,\ell _2}(\eta )$
with
![]() $\eta =(\eta _1,\eta _2) \in V_{\mathbf{o}}$
. Let
$\eta =(\eta _1,\eta _2) \in V_{\mathbf{o}}$
. Let
![]() $\sigma =(\sigma _1,\sigma _2) \in S_{\ell _1,\ell _2}(\eta )$
be such that
$\sigma =(\sigma _1,\sigma _2) \in S_{\ell _1,\ell _2}(\eta )$
be such that
![]() $\sigma _2=\eta _2$
and
$\sigma _2=\eta _2$
and
![]() $d(\eta _1,\sigma _1)$
is the maximal distance along that horizontal axis. Similarly, let
$d(\eta _1,\sigma _1)$
is the maximal distance along that horizontal axis. Similarly, let
![]() $\xi =(\xi _1,\xi _2) \in S_{\ell _1,\ell _2}(\eta )$
be such that
$\xi =(\xi _1,\xi _2) \in S_{\ell _1,\ell _2}(\eta )$
be such that
![]() $d(\eta _2,\xi _2)$
is the maximal distance along the vertical axis. Recalling (3.10), since
$d(\eta _2,\xi _2)$
is the maximal distance along the vertical axis. Recalling (3.10), since
![]() $\sigma _2=\eta _2$
, we have
$\sigma _2=\eta _2$
, we have
![]() $k=j$
for any
$k=j$
for any
![]() $k,j=1,\ldots, \ell _{\min }-1$
, where
$k,j=1,\ldots, \ell _{\min }-1$
, where
![]() $\ell _{\min }=\min \{\ell _1,\ell _2\}$
. Thus, we obtain
$\ell _{\min }=\min \{\ell _1,\ell _2\}$
. Thus, we obtain
where the last equality follows from the fact that the maximal distance along the horizontal axis is precisely the distance between
![]() $\sigma _1$
and
$\sigma _1$
and
![]() $\eta _1$
. We note that if
$\eta _1$
. We note that if
![]() $d(\eta _1,\sigma _1) \lt L-2$
then the rhombus does not wind horizontally around the torus. Thus,
$d(\eta _1,\sigma _1) \lt L-2$
then the rhombus does not wind horizontally around the torus. Thus,
Now, consider the distance between
![]() $\eta _2$
and
$\eta _2$
and
![]() $\xi _2$
. Let
$\xi _2$
. Let
![]() $\ell _{\max }=\max \{\ell _1,\ell _2\}$
. In this case, if
$\ell _{\max }=\max \{\ell _1,\ell _2\}$
. In this case, if
![]() $d(\eta _2,\xi _2) \leq L-2$
then the rhombus does not wind vertically around the torus. Thus, we have
$d(\eta _2,\xi _2) \leq L-2$
then the rhombus does not wind vertically around the torus. Thus, we have
We conclude that if
![]() $\ell _{\min }\lt \frac {L}{2}$
and
$\ell _{\min }\lt \frac {L}{2}$
and
![]() $\ell _{\max }\lt L$
, then the rhombus does not wind around the torus and the perimeter is the length of its external boundary. In view of (3.3), the claim follows. Otherwise, there are three cases, which will be treated separately:
$\ell _{\max }\lt L$
, then the rhombus does not wind around the torus and the perimeter is the length of its external boundary. In view of (3.3), the claim follows. Otherwise, there are three cases, which will be treated separately:
-
(a)
 $\ell _{\min } \geq \frac {L}{2}$
and
$\ell _{\min } \geq \frac {L}{2}$
and
 $\ell _{\max } \leq L-2$
;
$\ell _{\max } \leq L-2$
; -
(b)
 $\ell _{\min } \geq \frac {L}{2}$
and
$\ell _{\min } \geq \frac {L}{2}$
and
 $\ell _{\max } \gt L-2$
;
$\ell _{\max } \gt L-2$
; -
(c)
 $\ell _{\min }\lt \frac {L}{2}$
and
$\ell _{\min }\lt \frac {L}{2}$
and
 $\ell _{\max }=L$
.
$\ell _{\max }=L$
.
-
(a) Consider the complement of the rhombus
 $\mathcal {R}_{\ell _1,\ell _2}(\eta )$
for some
$\mathcal {R}_{\ell _1,\ell _2}(\eta )$
for some
 $\eta$
. By virtue of Lemma 3.2(i), we know that its complement in
$\eta$
. By virtue of Lemma 3.2(i), we know that its complement in
 $V$
is a rhombus with side lengths
$V$
is a rhombus with side lengths
 $\tilde \ell _1=L-\ell _1-1$
and
$\tilde \ell _1=L-\ell _1-1$
and
 $\tilde \ell _2=L-\ell _1-1$
. We claim that this complementary rhombus does not wind around the torus. Using condition
$\tilde \ell _2=L-\ell _1-1$
. We claim that this complementary rhombus does not wind around the torus. Using condition
 $\ell _{\min } \geq \frac {L}{2}$
, we find that the maximal side length of the complementary rhombus is(3.17)that is,
$\ell _{\min } \geq \frac {L}{2}$
, we find that the maximal side length of the complementary rhombus is(3.17)that is, \begin{align} \max \{\tilde \ell _1, \tilde \ell _2\}=\max \{L-\ell _1-1,L-\ell _2-1\}=L-\ell _{\min }-1 \leq L-\frac {L}{2}-1 \lt L, \end{align}
\begin{align} \max \{\tilde \ell _1, \tilde \ell _2\}=\max \{L-\ell _1-1,L-\ell _2-1\}=L-\ell _{\min }-1 \leq L-\frac {L}{2}-1 \lt L, \end{align}
 $\max \{\tilde \ell _1, \tilde \ell _2\} \lt L$
. Moreover, the minimal side length is(3.18)that is,
$\max \{\tilde \ell _1, \tilde \ell _2\} \lt L$
. Moreover, the minimal side length is(3.18)that is, \begin{align} \min \{\tilde \ell _1, \tilde \ell _2\}=\min \{L-\ell _1-1,L-\ell _2-1\}=L-\ell _{\max }-1 \leq L-\ell _{\min }-1 \leq L-\frac {L}{2}-1, \end{align}
\begin{align} \min \{\tilde \ell _1, \tilde \ell _2\}=\min \{L-\ell _1-1,L-\ell _2-1\}=L-\ell _{\max }-1 \leq L-\ell _{\min }-1 \leq L-\frac {L}{2}-1, \end{align}
 $\min \{\tilde \ell _1, \tilde \ell _2\}\lt \frac {L}{2}$
. Since the perimeter of the rhombus
$\min \{\tilde \ell _1, \tilde \ell _2\}\lt \frac {L}{2}$
. Since the perimeter of the rhombus
 $R_{\ell _1,\ell _2}$
is the same as that of
$R_{\ell _1,\ell _2}$
is the same as that of
 $R_{L-\ell _1-1,L-\ell _2-1}$
, the claim follows from (3.3).
$R_{L-\ell _1-1,L-\ell _2-1}$
, the claim follows from (3.3).
We say that an odd cluster
![]() $C$
is monotone when its perimeter coincides with that of its surrounding rhombus
$C$
is monotone when its perimeter coincides with that of its surrounding rhombus
![]() $\mathcal {R}(C)$
if it does not wind around the torus, i.e.,
$\mathcal {R}(C)$
if it does not wind around the torus, i.e.,
![]() $P(C)=P(\mathcal {R}(C))$
. Otherwise, we say that an odd cluster
$P(C)=P(\mathcal {R}(C))$
. Otherwise, we say that an odd cluster
![]() $C$
is monotone when its perimeter coincides with that of a bridge, i.e.,
$C$
is monotone when its perimeter coincides with that of a bridge, i.e.,
![]() $P(C)=4L$
. Note that it immediately follows that a monotone odd cluster
$P(C)=4L$
. Note that it immediately follows that a monotone odd cluster
![]() $C$
has no holes, i.e., empty odd sites with the four even neighbouring sites belonging to
$C$
has no holes, i.e., empty odd sites with the four even neighbouring sites belonging to
![]() $C$
. An empty odd site
$C$
. An empty odd site
![]() $\eta \notin C$
is an antiknob for the cluster
$\eta \notin C$
is an antiknob for the cluster
![]() $C$
if it has at least three neighbouring even empty sites that belong to
$C$
if it has at least three neighbouring even empty sites that belong to
![]() $C$
. Figure 8 (left) highlights in red the antiknobs of a hard-core configuration.
$C$
. Figure 8 (left) highlights in red the antiknobs of a hard-core configuration.
Given an odd cluster
![]() $C\in C_{\mathbf{o}}(\Lambda )$
and an integer
$C\in C_{\mathbf{o}}(\Lambda )$
and an integer
![]() $k\geq 1$
, we say that
$k\geq 1$
, we say that
![]() $C$
displays an increasing (resp. decreasing) diagonal broken in
$C$
displays an increasing (resp. decreasing) diagonal broken in
![]() $k$
sites if there exist a sequence of sites
$k$
sites if there exist a sequence of sites
![]() $z_i=(x_i,y_i)\in V_{\mathbf{o}}\setminus C$
,
$z_i=(x_i,y_i)\in V_{\mathbf{o}}\setminus C$
,
![]() $i=1,\ldots, k$
, such that
$i=1,\ldots, k$
, such that
-
•
 $x_{i+1}=x_i+1$
and
$x_{i+1}=x_i+1$
and
 $y_{i+1}=y_i+1$
(resp.
$y_{i+1}=y_i+1$
(resp.
 $x_{i+1}=x_i+1$
and
$x_{i+1}=x_i+1$
and
 $y_{i+1}=y_i-1$
) for any
$y_{i+1}=y_i-1$
) for any
 $i=1,\ldots, k-1$
, and
$i=1,\ldots, k-1$
, and -
• the two odd sites
 $(x_1-1,y_1-1)$
and
$(x_1-1,y_1-1)$
and
 $(x_k+1,y_k+1)$
(resp.
$(x_k+1,y_k+1)$
(resp.
 $(x_1-1,y_1+1)$
and
$(x_1-1,y_1+1)$
and
 $(x_k+1,y_k-1)$
) belong to the cluster
$(x_k+1,y_k-1)$
) belong to the cluster
 $C$
.
$C$
.
By construction of a broken diagonal, the two sites
![]() $z_1$
and
$z_1$
and
![]() $z_k$
are always antiknobs. If it does not matter if an increasing or decreasing diagonal is broken, we simply say that a diagonal is broken. Broken diagonals are visualized in blue in Figure 8 (left). Given an odd cluster
$z_k$
are always antiknobs. If it does not matter if an increasing or decreasing diagonal is broken, we simply say that a diagonal is broken. Broken diagonals are visualized in blue in Figure 8 (left). Given an odd cluster
![]() $C\in C_{\mathbf{o}}(\Lambda )$
and an integer
$C\in C_{\mathbf{o}}(\Lambda )$
and an integer
![]() $k\geq 1$
, we say that
$k\geq 1$
, we say that
![]() $C$
displays an increasing (resp. decreasing) shorter diagonal lacking in
$C$
displays an increasing (resp. decreasing) shorter diagonal lacking in
![]() $k$
sites if there exist a sequence of sites
$k$
sites if there exist a sequence of sites
![]() $z_i=(x_i,y_i)\in (V_{\mathbf{o}}\cap \mathcal {R}(C))\setminus C$
,
$z_i=(x_i,y_i)\in (V_{\mathbf{o}}\cap \mathcal {R}(C))\setminus C$
,
![]() $i=1,\ldots, k$
, such that
$i=1,\ldots, k$
, such that
-
•
 $x_{i+1}=x_i+1$
and
$x_{i+1}=x_i+1$
and
 $y_{i+1}=y_i+1$
(resp.
$y_{i+1}=y_i+1$
(resp.
 $x_{i+1}=x_i+1$
and
$x_{i+1}=x_i+1$
and
 $y_{i+1}=y_i-1$
) for any
$y_{i+1}=y_i-1$
) for any
 $i=1,\ldots, k-1$
, and
$i=1,\ldots, k-1$
, and -
• the two odd sites
 $(x_1-1,y_1-1)$
and
$(x_1-1,y_1-1)$
and
 $(x_k+1,y_k+1)$
(resp.
$(x_k+1,y_k+1)$
(resp.
 $(x_1-1,y_1+1)$
and
$(x_1-1,y_1+1)$
and
 $(x_k+1,y_k-1)$
) do not belong to
$(x_k+1,y_k-1)$
) do not belong to
 $\mathcal {R}(C)$
.
$\mathcal {R}(C)$
.
Figure 8 (right) highlights the shorter diagonals in blue.
3.3 Expanding an odd cluster: the filling algorithms
We now describe an iterative procedure that builds a path
![]() $\omega$
in
$\omega$
in
![]() $\mathcal {X}$
from a configuration
$\mathcal {X}$
from a configuration
![]() $\sigma$
with a unique odd cluster to another configuration
$\sigma$
with a unique odd cluster to another configuration
![]() $\sigma ^{\prime}$
that (i) displays a rhombus, and (ii) whose energy
$\sigma ^{\prime}$
that (i) displays a rhombus, and (ii) whose energy
![]() $H(\sigma ^{\prime})$
is equal to or lower than
$H(\sigma ^{\prime})$
is equal to or lower than
![]() $H(\sigma )$
.
$H(\sigma )$
.
The path
![]() $\omega$
can be described as the concatenation of two paths, each obtained by means of a specific filling algorithm. The reason behind this name is that, along the generated paths, any incomplete diagonal in the odd cluster of the starting configuration is gradually filled by adding particles at odd sites until a rhombus is obtained.
$\omega$
can be described as the concatenation of two paths, each obtained by means of a specific filling algorithm. The reason behind this name is that, along the generated paths, any incomplete diagonal in the odd cluster of the starting configuration is gradually filled by adding particles at odd sites until a rhombus is obtained.
The two paths can be intuitively described as follows. The first path, denoted as
![]() $\tilde \omega$
, starts from a configuration with at least one broken diagonal and, by filling one by one all broken diagonals in lexicographic order, arrives at a configuration without broken diagonals. Each broken diagonal is progressively filled by removing a particle in the even site at distance
$\tilde \omega$
, starts from a configuration with at least one broken diagonal and, by filling one by one all broken diagonals in lexicographic order, arrives at a configuration without broken diagonals. Each broken diagonal is progressively filled by removing a particle in the even site at distance
![]() $1$
from an antiknob that lies on that diagonal and adding a particle in the odd site where the antiknob is. The antiknobs on the same diagonal are processed in lexicographic order. The second path, denoted as
$1$
from an antiknob that lies on that diagonal and adding a particle in the odd site where the antiknob is. The antiknobs on the same diagonal are processed in lexicographic order. The second path, denoted as
![]() $\bar \omega$
, starts from a configuration without broken diagonals (such as any ending configuration of the path
$\bar \omega$
, starts from a configuration without broken diagonals (such as any ending configuration of the path
![]() $\tilde \omega$
) and arrives at a configuration displaying an odd rhombus. The construction of this second path is similar to that of the first path, but in this case the particles are added in odd sites to fill all the shorter diagonals.
$\tilde \omega$
) and arrives at a configuration displaying an odd rhombus. The construction of this second path is similar to that of the first path, but in this case the particles are added in odd sites to fill all the shorter diagonals.
The filling algorithms that generate the two paths
![]() $\tilde \omega$
and
$\tilde \omega$
and
![]() $\bar \omega$
are designed so that the maximum energy along the resulting path
$\bar \omega$
are designed so that the maximum energy along the resulting path
![]() $\omega =\tilde \omega \cup \bar \omega$
, i.e.,
$\omega =\tilde \omega \cup \bar \omega$
, i.e.,
![]() $\Phi _{\omega }$
, is never larger than
$\Phi _{\omega }$
, is never larger than
![]() $H(\sigma )+1$
. More specifically, the perimeter of the odd cluster either decreases or does not change along
$H(\sigma )+1$
. More specifically, the perimeter of the odd cluster either decreases or does not change along
![]() $\tilde \omega$
, whereas it can increase and sequentially decrease by the same amount along
$\tilde \omega$
, whereas it can increase and sequentially decrease by the same amount along
![]() $\bar \omega$
. Proposition3.4, whose proof is postponed to subsection 5.1, specifies the requirement for the starting configuration and summarizes the properties of the path generated by the filling algorithm.
$\bar \omega$
. Proposition3.4, whose proof is postponed to subsection 5.1, specifies the requirement for the starting configuration and summarizes the properties of the path generated by the filling algorithm.
To formally define these two algorithms, we introduce the following notation. Given two configurations
![]() $\sigma, \sigma ^{\prime} \in \mathcal {X}$
and a subset of sites
$\sigma, \sigma ^{\prime} \in \mathcal {X}$
and a subset of sites
![]() $W \subset \Lambda$
, we write
$W \subset \Lambda$
, we write
![]() $\sigma _{|W} = \sigma ^{\prime}_{|W}$
if
$\sigma _{|W} = \sigma ^{\prime}_{|W}$
if
![]() $\sigma (v) = \sigma ^{\prime}(v)$
for every
$\sigma (v) = \sigma ^{\prime}(v)$
for every
![]() $v \in W$
. Given a configuration
$v \in W$
. Given a configuration
![]() $\sigma \in \mathcal {X}$
, we let
$\sigma \in \mathcal {X}$
, we let
-
•
 $\sigma ^{(v,0)}$
be the configuration
$\sigma ^{(v,0)}$
be the configuration
 $\sigma ^{\prime} \in \mathcal {X}$
such that
$\sigma ^{\prime} \in \mathcal {X}$
such that
 $\sigma ^{\prime}_{|V \setminus \{v\}} = \sigma _{|V \setminus \{v\}}$
and
$\sigma ^{\prime}_{|V \setminus \{v\}} = \sigma _{|V \setminus \{v\}}$
and
 $\sigma ^{\prime}(v)=0$
; and
$\sigma ^{\prime}(v)=0$
; and -
•
 $\sigma ^{(v,1)}$
be the configuration
$\sigma ^{(v,1)}$
be the configuration
 $\sigma ^{\prime}$
such that
$\sigma ^{\prime}$
such that
 $\sigma ^{\prime}_{|V \setminus \{v\}} = \sigma _{|V \setminus \{v\}}$
and
$\sigma ^{\prime}_{|V \setminus \{v\}} = \sigma _{|V \setminus \{v\}}$
and
 $\sigma ^{\prime}(v)=1$
.
$\sigma ^{\prime}(v)=1$
.
In general,
![]() $\sigma ^{(v,1)}$
may not be a hard-core configuration in
$\sigma ^{(v,1)}$
may not be a hard-core configuration in
![]() $\mathcal {X}$
, since
$\mathcal {X}$
, since
![]() $\sigma$
may already have a particle residing in one of the four neighbouring sites of
$\sigma$
may already have a particle residing in one of the four neighbouring sites of
![]() $v$
.
$v$
.
Algorithm 1 (resp. Algorithm 2) provide the detailed pseudocode for the filling algorithm that yields
![]() $ \tilde{\omega}$
(resp.
$ \tilde{\omega}$
(resp.
![]() $ \tilde{\omega}$
).
$ \tilde{\omega}$
).
Algorithm 1: Filling algorithm to build path
![]() $ \tilde{\omega}$
$ \tilde{\omega}$

Algorithm 2: Filling algorithm to build path
![]() $ \tilde{\omega}$
$ \tilde{\omega}$

Proposition 3.4 (Odd cluster expansion via filling algorithms). Let
![]() $\sigma, \sigma ^{\prime} \in \mathcal {X}$
be two hard-core configurations on
$\sigma, \sigma ^{\prime} \in \mathcal {X}$
be two hard-core configurations on
![]() $\Lambda$
,
$\Lambda$
,
![]() $\sigma \neq \sigma ^{\prime}$
, and
$\sigma \neq \sigma ^{\prime}$
, and
![]() $\mathcal {R}$
a rhombus such that
$\mathcal {R}$
a rhombus such that
-
(i) There exists a connected odd cluster
 $C \subseteq \mathcal {O}(\sigma )$
such that
$C \subseteq \mathcal {O}(\sigma )$
such that
 $\mathcal {R}(C) = \mathcal {R}$
;
$\mathcal {R}(C) = \mathcal {R}$
; -
(ii)
 $\sigma _{|\Lambda \setminus \mathcal {R}} = \sigma ^{\prime}_{| \Lambda \setminus \mathcal {R}}$
;
$\sigma _{|\Lambda \setminus \mathcal {R}} = \sigma ^{\prime}_{| \Lambda \setminus \mathcal {R}}$
; -
(iii)
 $\sigma ^{\prime}_{|\mathcal {R}} = {\mathbf{o}}_{|\mathcal {R}}$
.
$\sigma ^{\prime}_{|\mathcal {R}} = {\mathbf{o}}_{|\mathcal {R}}$
.
Then, there exists a path
![]() $\omega \,:\, \sigma \to \sigma ^{\prime}$
such that
$\omega \,:\, \sigma \to \sigma ^{\prime}$
such that
![]() $\Phi _\omega - H(\sigma ) \leq 1$
. In addition, if
$\Phi _\omega - H(\sigma ) \leq 1$
. In addition, if
![]() $C$
has at least one broken diagonal, then
$C$
has at least one broken diagonal, then
![]() $P(\sigma )\gt P(\sigma ^{\prime})$
, otherwise
$P(\sigma )\gt P(\sigma ^{\prime})$
, otherwise
![]() $P(\sigma )=P(\sigma ^{\prime})$
.
$P(\sigma )=P(\sigma ^{\prime})$
.
We note that conditions
![]() $(i),(ii)$
, and
$(i),(ii)$
, and
![]() $(iii)$
mean that there is a unique odd cluster in
$(iii)$
mean that there is a unique odd cluster in
![]() $\sigma$
different from a rhombus, i.e., there exists at least one broken or shorter diagonal.
$\sigma$
different from a rhombus, i.e., there exists at least one broken or shorter diagonal.
Thanks to Proposition3.4, we are able to characterize the configurations with minimal perimeter for a fixed number of occupied odd sites. This finding is formalized in the following two results, Proposition3.6 and Corollary3.7, whose proofs are deferred to subsection 5.1.
To state the precise results, we first introduce the notion of bars as follows. We define a vertical (resp. horizontal) bar
![]() $B$
of length
$B$
of length
![]() $k$
as the union of particles arranged in odd sites
$k$
as the union of particles arranged in odd sites
![]() $x_1,\ldots, x_k$
belonging to the same column (resp. row) such that
$x_1,\ldots, x_k$
belonging to the same column (resp. row) such that
![]() $d(x_i,x_{i+1})=2$
for any
$d(x_i,x_{i+1})=2$
for any
![]() $i=1,\ldots, k-1$
. In the case of
$i=1,\ldots, k-1$
. In the case of
![]() $k=1$
, we will refer to it as protuberance. If in the same column (resp. row) there are
$k=1$
, we will refer to it as protuberance. If in the same column (resp. row) there are
![]() $m$
disjoint vertical (resp. horizontal) bars, each of them of length
$m$
disjoint vertical (resp. horizontal) bars, each of them of length
![]() $k_i$
, we say that the total length of the bars is
$k_i$
, we say that the total length of the bars is
![]() $k=k_1+\ldots +k_m$
. Similarly, we can define a diagonal bar and note that it can correspond to a shorter or complete diagonal. If it does not matter whether the bar is vertical, horizontal, or diagonal, we simply refer to it as a bar. Finally, we will say that a bar
$k=k_1+\ldots +k_m$
. Similarly, we can define a diagonal bar and note that it can correspond to a shorter or complete diagonal. If it does not matter whether the bar is vertical, horizontal, or diagonal, we simply refer to it as a bar. Finally, we will say that a bar
![]() $B$
is attached to a cluster
$B$
is attached to a cluster
![]() $C$
when all the particles belonging to
$C$
when all the particles belonging to
![]() $B$
are at distance two from
$B$
are at distance two from
![]() $C$
. Note that in Figure 8 (right) the shorter diagonals of lengths three and one are diagonal bars. See Figure 8 (left) for examples of vertical bars.
$C$
. Note that in Figure 8 (right) the shorter diagonals of lengths three and one are diagonal bars. See Figure 8 (left) for examples of vertical bars.
Lemma 3.5. For any
![]() $n$
positive integer there exist two positive integers
$n$
positive integer there exist two positive integers
![]() $s$
and
$s$
and
![]() $k$
, with
$k$
, with
![]() $0\leq k\lt s$
, such that either (i)
$0\leq k\lt s$
, such that either (i)
![]() $n=s(s-1)+k$
or (ii)
$n=s(s-1)+k$
or (ii)
![]() $n=s^2+k$
.
$n=s^2+k$
.
Proof. See the first part of [Reference Cirillo and Nardi26, Lemma 6.17].
Proposition 3.6 (Perimeter-Minimal rhombi). Consider
![]() $n\leq L(L-2)$
and let
$n\leq L(L-2)$
and let
![]() $s,k$
be the unique integers as in Lemma 3.5. The set of odd clusters with area
$s,k$
be the unique integers as in Lemma 3.5. The set of odd clusters with area
![]() $n$
that have minimal perimeter contains either a rhombus
$n$
that have minimal perimeter contains either a rhombus
![]() $\mathcal {R}_{s,s-1}$
or
$\mathcal {R}_{s,s-1}$
or
![]() $\mathcal {R}_{s-1,s}$
with a bar of length
$\mathcal {R}_{s-1,s}$
with a bar of length
![]() $k$
attached to one of its longest sides if
$k$
attached to one of its longest sides if
![]() $n=s(s-1)+k$
and a rhombus
$n=s(s-1)+k$
and a rhombus
![]() $\mathcal {R}_{s,s}$
with a bar of length
$\mathcal {R}_{s,s}$
with a bar of length
![]() $k$
attached to one of its sides if
$k$
attached to one of its sides if
![]() $n=s^2+k$
.
$n=s^2+k$
.
Corollary 3.7 (Minimal perimeter). Consider
![]() $n\leq L(L-2)$
and let
$n\leq L(L-2)$
and let
![]() $s,k$
be the unique integers as in Lemma 3.5. The perimeter
$s,k$
be the unique integers as in Lemma 3.5. The perimeter
![]() $P$
of an odd cluster with area
$P$
of an odd cluster with area
![]() $n$
satisfies the following inequalities:
$n$
satisfies the following inequalities:
 \begin{equation*} \Bigl (\frac {P}{4}-1\Bigr )^2\geq \begin{cases} 4n &\hbox { if } s\lt L/2, \\[3pt] 2(L^2-2n) &\hbox { if } L/2\leq s\lt L. \end{cases} \end{equation*}
\begin{equation*} \Bigl (\frac {P}{4}-1\Bigr )^2\geq \begin{cases} 4n &\hbox { if } s\lt L/2, \\[3pt] 2(L^2-2n) &\hbox { if } L/2\leq s\lt L. \end{cases} \end{equation*}
In addition, for all
![]() $s\lt L$
we have that
$s\lt L$
we have that
and for
![]() $s\lt \frac {L}{2}$
the equality holds if and only if the odd cluster is the rhombus
$s\lt \frac {L}{2}$
the equality holds if and only if the odd cluster is the rhombus
![]() $\mathcal {R}_{s,s}$
.
$\mathcal {R}_{s,s}$
.
Lastly, in the next lemma, we derive an isoperimetric inequality assuming the total number of odd and even occupied sites is fixed. To this end, we first define the real area of a configuration
![]() $\sigma$
as
$\sigma$
as
where
![]() $o(\sigma )$
(resp.
$o(\sigma )$
(resp.
![]() $\tilde e(\sigma )$
) denotes the number of occupied odd (resp. empty even) sites of the configuration
$\tilde e(\sigma )$
) denotes the number of occupied odd (resp. empty even) sites of the configuration
![]() $\sigma$
.
$\sigma$
.
Lemma 3.8 (Perimeter-Minimal rhombi with fixed real area). Given
![]() $1\leq \ell \lt \frac {L}{2}$
, the unique odd cluster with real area
$1\leq \ell \lt \frac {L}{2}$
, the unique odd cluster with real area
![]() $\tilde n=2\ell ^2+2\ell +1$
and minimal perimeter is the rhombus
$\tilde n=2\ell ^2+2\ell +1$
and minimal perimeter is the rhombus
![]() $\mathcal {R}_{\ell, \ell }$
. In particular, for
$\mathcal {R}_{\ell, \ell }$
. In particular, for
![]() $\tilde n= \frac {L^2}{2}-L+1$
this rhombus is
$\tilde n= \frac {L^2}{2}-L+1$
this rhombus is
![]() $\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
.
$\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
.
We use this lemma to characterize the critical configurations with an odd cluster of rhomboidal shape that does not wind around the torus. Indeed, we identify the shape of protocritical configurations
![]() $\sigma$
with minimal perimeter and fixed real area
$\sigma$
with minimal perimeter and fixed real area
![]() $\frac {L^2}{2}-L+1$
such that
$\frac {L^2}{2}-L+1$
such that
![]() $\mathcal {R}(\mathcal {O}^{nd}(\sigma ))$
does not wind around the torus, and we show that if the trajectory visits another type of configuration with such a real area, then the corresponding path would not be optimal. The proof is given in subsection 5.1.
$\mathcal {R}(\mathcal {O}^{nd}(\sigma ))$
does not wind around the torus, and we show that if the trajectory visits another type of configuration with such a real area, then the corresponding path would not be optimal. The proof is given in subsection 5.1.
4. Essential saddles: proof of the main theorem
In this section, we first formally introduce in subsection 4.1 the six sets appearing in the statement of Theorem 2.1 and then prove the same theorem in subsection 4.2 by showing that the elements of those six sets are all essential saddles for the transition from
![]() ${\mathbf{e}}$
to
${\mathbf{e}}$
to
![]() ${\mathbf{o}}$
.
${\mathbf{o}}$
.
4.1 Preliminaries
We say that a configuration
![]() $\sigma \in \mathcal {X}$
has a odd (resp. even) vertical bridge if there exists a column in which the configuration
$\sigma \in \mathcal {X}$
has a odd (resp. even) vertical bridge if there exists a column in which the configuration
![]() $\sigma$
perfectly agrees with
$\sigma$
perfectly agrees with
![]() ${\mathbf{o}}$
(resp.
${\mathbf{o}}$
(resp.
![]() ${\mathbf{e}}$
). We define odd (resp. even) horizontal bridge in an analogous way and we say that a configuration
${\mathbf{e}}$
). We define odd (resp. even) horizontal bridge in an analogous way and we say that a configuration
![]() $\sigma \in \mathcal {X}$
has an odd (resp. even) cross if it has both vertical and horizontal odd (resp. even) bridges (see Figure 9). In addition, we say that a configuration displays an odd (resp. even) vertical
$\sigma \in \mathcal {X}$
has an odd (resp. even) cross if it has both vertical and horizontal odd (resp. even) bridges (see Figure 9). In addition, we say that a configuration displays an odd (resp. even) vertical
![]() $m$
-uple bridge, with
$m$
-uple bridge, with
![]() $m\geq 2$
, if there exist
$m\geq 2$
, if there exist
![]() $m$
contiguous columns in which the configuration perfectly agrees with
$m$
contiguous columns in which the configuration perfectly agrees with
![]() ${\mathbf{o}}$
(resp.
${\mathbf{o}}$
(resp.
![]() ${\mathbf{e}}$
). Similarly, we can define an odd (resp. even) vertical
${\mathbf{e}}$
). Similarly, we can define an odd (resp. even) vertical
![]() $m$
-uple bridge (see Figure 10). We refer to [Reference Nardi, Zocca and Borst47] for more details.
$m$
-uple bridge (see Figure 10). We refer to [Reference Nardi, Zocca and Borst47] for more details.

Figure 9. Examples of configurations displaying an odd horizontal bridge (on the left) and an odd cross (on the right).

Figure 10. Examples of configurations displaying an odd horizontal double (2-uple) bridge (on the left) and an odd vertical triple (3-uple) bridge (on the right).
The next lemma states that all configurations
![]() $\sigma \in \mathcal {X}$
with
$\sigma \in \mathcal {X}$
with
![]() $\Delta H(\sigma )\lt L$
must belong to one of the two initial cycles.
$\Delta H(\sigma )\lt L$
must belong to one of the two initial cycles.
Lemma 4.1 (Configurations with
![]() $\Delta H \lt L$
belong to one of the initial cycles). If a configuration
$\Delta H \lt L$
belong to one of the initial cycles). If a configuration
![]() $\sigma \in \mathcal {X}$
is such that
$\sigma \in \mathcal {X}$
is such that
![]() $\Delta H(\sigma ) \lt L$
, then there exists a path
$\Delta H(\sigma ) \lt L$
, then there exists a path
![]() $\omega \,:\, \sigma \to \{{\mathbf{e}},{\mathbf{o}}\}$
with
$\omega \,:\, \sigma \to \{{\mathbf{e}},{\mathbf{o}}\}$
with
![]() $\Phi _\omega \leq H(\sigma )+1$
. In particular, either
$\Phi _\omega \leq H(\sigma )+1$
. In particular, either
![]() $\sigma \in C_{\mathbf{e}}$
or
$\sigma \in C_{\mathbf{e}}$
or
![]() $\sigma \in C_{\mathbf{o}}$
.
$\sigma \in C_{\mathbf{o}}$
.
Proof. If
![]() $\Delta H(\sigma ) \lt L$
, then there exists both a horizontal and a vertical bridge. Due to the hard-core constraints, these
$\Delta H(\sigma ) \lt L$
, then there exists both a horizontal and a vertical bridge. Due to the hard-core constraints, these
![]() $L-1$
particles should all reside at sites of the same parity. Hence,
$L-1$
particles should all reside at sites of the same parity. Hence,
![]() $\sigma$
has either an even cross or an odd cross. Then, using the reduction algorithm introduced in [Reference Nardi, Zocca and Borst47], one can build a path to either
$\sigma$
has either an even cross or an odd cross. Then, using the reduction algorithm introduced in [Reference Nardi, Zocca and Borst47], one can build a path to either
![]() ${\mathbf{e}}$
or
${\mathbf{e}}$
or
![]() ${\mathbf{o}}$
, respectively, with the desired properties.
${\mathbf{o}}$
, respectively, with the desired properties.
Definition 4.2. A hard-core configuration
![]() $\sigma \in \mathcal {X}$
on the
$\sigma \in \mathcal {X}$
on the
![]() $L \times L$
toric grid graph
$L \times L$
toric grid graph
![]() $\Lambda$
belongs to
$\Lambda$
belongs to
![]() $\mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
if the following conditions hold:
$\mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
if the following conditions hold:
-
1. the odd region
 $\mathcal {O}(\sigma )$
contains only a non-degenerate cluster
$\mathcal {O}(\sigma )$
contains only a non-degenerate cluster
 $C$
and a degenerate rhombus
$C$
and a degenerate rhombus
 $D \in \{\mathcal {R}_{1,0}, \mathcal {R}_{0,1}\}$
at distance two from
$D \in \{\mathcal {R}_{1,0}, \mathcal {R}_{0,1}\}$
at distance two from
 $C$
;
$C$
; -
2. the cluster
 $C$
is monotone;
$C$
is monotone; -
3.
 $C$
is a rhombus
$C$
is a rhombus
 $\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
;
$\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
; -
4.
 $\sigma _{| \Lambda \setminus (C\cup D)} = {\mathbf{e}}_{| \Lambda \setminus (C \cup D)}$
.
$\sigma _{| \Lambda \setminus (C\cup D)} = {\mathbf{e}}_{| \Lambda \setminus (C \cup D)}$
.
See Figure 2 (left) for an example of configurations in
![]() $\mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
.
$\mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
.
Definition 4.3. A hard-core configuration
![]() $\sigma \in \mathcal {X}$
on the
$\sigma \in \mathcal {X}$
on the
![]() $L \times L$
toric grid graph
$L \times L$
toric grid graph
![]() $\Lambda$
belongs to
$\Lambda$
belongs to
![]() $\mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
(resp.
$\mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
(resp.
![]() $\mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
) if the following conditions hold:
$\mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
) if the following conditions hold:
-
1. the odd region
 $\mathcal {O}(\sigma )$
contains only a non-degenerate cluster
$\mathcal {O}(\sigma )$
contains only a non-degenerate cluster
 $C$
and a degenerate rhombus
$C$
and a degenerate rhombus
 $D=\mathcal {R}_{0,0}$
at distance one from an antiknob;
$D=\mathcal {R}_{0,0}$
at distance one from an antiknob; -
2. the cluster
 $C$
is monotone;
$C$
is monotone; -
3.
 $C$
is a rhombus
$C$
is a rhombus
 $\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
(resp.
$\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
(resp.
 $\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}}$
) with a single bar of length
$\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}}$
) with a single bar of length
 $k$
, for
$k$
, for
 $k=1,\ldots, \frac {L}{2}-1$
(resp.
$k=1,\ldots, \frac {L}{2}-1$
(resp.
 $k=1,\ldots, \frac {L}{2}-2$
), attached to one of its sides;
$k=1,\ldots, \frac {L}{2}-2$
), attached to one of its sides; -
4.
 $\sigma _{| \Lambda \setminus (C\cup D)} = {\mathbf{e}}_{| \Lambda \setminus (C \cup D)}$
.
$\sigma _{| \Lambda \setminus (C\cup D)} = {\mathbf{e}}_{| \Lambda \setminus (C \cup D)}$
.
See Figure 2 (right) and Figure 3 (left) for an example of configurations in
![]() $\mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
and
$\mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
and
![]() $\mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
, respectively. Note that for any
$\mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
, respectively. Note that for any
![]() $\sigma \in \mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
the surrounding rhombus
$\sigma \in \mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
the surrounding rhombus
![]() $R(\mathcal {O}(\sigma ))$
is
$R(\mathcal {O}(\sigma ))$
is
![]() $R_{\frac {L}{2}-1,\frac {L}{2}}$
, while for any
$R_{\frac {L}{2}-1,\frac {L}{2}}$
, while for any
![]() $\sigma \in \mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
the surrounding rhombus
$\sigma \in \mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
the surrounding rhombus
![]() $R(\mathcal {O}(\sigma ))$
is
$R(\mathcal {O}(\sigma ))$
is
![]() $R_{\frac {L}{2},\frac {L}{2}}$
.
$R_{\frac {L}{2},\frac {L}{2}}$
.
Definition 4.4. A hard-core configuration
![]() $\sigma \in \mathcal {X}$
on the
$\sigma \in \mathcal {X}$
on the
![]() $L \times L$
toric grid graph
$L \times L$
toric grid graph
![]() $\Lambda$
belongs to
$\Lambda$
belongs to
![]() $\mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
if the following conditions hold:
$\mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
if the following conditions hold:
-
1. the odd region
 $\mathcal {O}(\sigma )$
contains only a non-degenerate cluster
$\mathcal {O}(\sigma )$
contains only a non-degenerate cluster
 $C$
and a degenerate region
$C$
and a degenerate region
 $D$
consisting of two even sites at distance one from the same antiknob;
$D$
consisting of two even sites at distance one from the same antiknob; -
2. the cluster
 $C$
is monotone;
$C$
is monotone; -
3.
 $C$
is a single column or row of length
$C$
is a single column or row of length
 $\frac {L}{2}-1$
;
$\frac {L}{2}-1$
; -
4.
 $\sigma _{| \Lambda \setminus (C\cup D)} = {\mathbf{e}}_{| \Lambda \setminus (C \cup D)}$
.
$\sigma _{| \Lambda \setminus (C\cup D)} = {\mathbf{e}}_{| \Lambda \setminus (C \cup D)}$
.
Note that the unique possibilities are that (i)
![]() $D$
consists of two degenerate rhombi
$D$
consists of two degenerate rhombi
![]() $\mathcal {R}_{0,0}$
as in Figure 3 (right) or (ii)
$\mathcal {R}_{0,0}$
as in Figure 3 (right) or (ii)
![]() $D\in \{\mathcal {R}_{0,1},\mathcal {R}_{1,0}\}$
as in Figure 11 (left).
$D\in \{\mathcal {R}_{0,1},\mathcal {R}_{1,0}\}$
as in Figure 11 (left).

Figure 11. An example of a configuration in
![]() $\mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
that communicates with
$\mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
that communicates with
![]() $\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
and not with
$\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
and not with
![]() $\mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
(on the left) and an example of a configuration in
$\mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
(on the left) and an example of a configuration in
![]() $\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
(on the right).
$\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
(on the right).
Definition 4.5. A hard-core configuration
![]() $\sigma \in \mathcal {X}$
on the
$\sigma \in \mathcal {X}$
on the
![]() $L \times L$
toric grid graph
$L \times L$
toric grid graph
![]() $\Lambda$
belongs to
$\Lambda$
belongs to
![]() $\mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
if the following conditions hold:
$\mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
if the following conditions hold:
-
1. the odd region
 $\mathcal {O}(\sigma )$
contains only a non-degenerate cluster
$\mathcal {O}(\sigma )$
contains only a non-degenerate cluster
 $C$
and a degenerate rhombus
$C$
and a degenerate rhombus
 $D=\mathcal {R}_{0,0}$
at distance one from an antiknob;
$D=\mathcal {R}_{0,0}$
at distance one from an antiknob; -
2. the cluster
 $C$
is monotone;
$C$
is monotone; -
3.
 $C$
is composed either by:
$C$
is composed either by:-
• a odd
 $(L-3)$
-uple bridge, or
$(L-3)$
-uple bridge, or -
• an odd
 $m$
-uple bridge, with
$m$
-uple bridge, with
 $2\leq m \lt L-3$
, together with disjoint bars attached to either side of the
$2\leq m \lt L-3$
, together with disjoint bars attached to either side of the
 $m$
-uple bridge with total length
$m$
-uple bridge with total length
 $k$
, with
$k$
, with
 $k=0,\ldots, \frac {L}{2}-1$
, or
$k=0,\ldots, \frac {L}{2}-1$
, or -
• an odd bridge, together with disjoint bars attached to the bridge with total length
 $k$
, for
$k$
, for
 $k=0,\ldots, \frac {L}{2}-1$
, and
$k=0,\ldots, \frac {L}{2}-1$
, and
 $C$
does not contain
$C$
does not contain
 $\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}}$
;
$\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}}$
;
-
-
4.
 $\sigma _{| \Lambda \setminus (C\cup D)} = {\mathbf{e}}_{| \Lambda \setminus (C \cup D)}$
.
$\sigma _{| \Lambda \setminus (C\cup D)} = {\mathbf{e}}_{| \Lambda \setminus (C \cup D)}$
.
See Figure 4 (left) for an example of a configuration in
![]() $\mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
. Note that any configuration
$\mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
. Note that any configuration
![]() $\sigma \in \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
is such that
$\sigma \in \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
is such that
![]() $\mathcal {R}(\mathcal {O}(\sigma ))$
winds around the torus. Thus, the assumption that the non-degenerate cluster
$\mathcal {R}(\mathcal {O}(\sigma ))$
winds around the torus. Thus, the assumption that the non-degenerate cluster
![]() $C$
is monotone implies that in condition 3 not every choice of the bars is allowed. Indeed, in order for the cluster to be monotone, the bars on the right (resp. left) of the
$C$
is monotone implies that in condition 3 not every choice of the bars is allowed. Indeed, in order for the cluster to be monotone, the bars on the right (resp. left) of the
![]() $m$
-uple bridge can be adjacent only to a longer (resp. shorter) bar in lexicographic order. This implies that all bridges are in contiguous rows or columns. Furthermore, the length of a bar is inversely proportional to its distance from the nearest bar composing the bridge.
$m$
-uple bridge can be adjacent only to a longer (resp. shorter) bar in lexicographic order. This implies that all bridges are in contiguous rows or columns. Furthermore, the length of a bar is inversely proportional to its distance from the nearest bar composing the bridge.
Definition 4.6. A hard-core configuration
![]() $\sigma \in \mathcal {X}$
on the
$\sigma \in \mathcal {X}$
on the
![]() $L \times L$
toric grid graph
$L \times L$
toric grid graph
![]() $\Lambda$
belongs to
$\Lambda$
belongs to
![]() $\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
if the following conditions hold:
$\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
if the following conditions hold:
-
1. the odd region
 $\mathcal {O}(\sigma )$
contains only a non-degenerate cluster
$\mathcal {O}(\sigma )$
contains only a non-degenerate cluster
 $C$
and a degenerate rhombus
$C$
and a degenerate rhombus
 $D=\mathcal {R}_{0,0}$
at distance one from an antiknob;
$D=\mathcal {R}_{0,0}$
at distance one from an antiknob; -
2. the cluster
 $C$
is monotone and does not contain
$C$
is monotone and does not contain
 $\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
;
$\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
; -
3.
 $C$
is composed either by:
$C$
is composed either by:-
• one column (or row)
 $B$
with
$B$
with
 $\frac {L}{2}-1$
particles in odd sites or
$\frac {L}{2}-1$
particles in odd sites or -
• two neighbouring columns (or row)
 $B$
with
$B$
with
 $\frac {L}{2}-1$
particles in odd sites each;
$\frac {L}{2}-1$
particles in odd sites each;
In addition, in the other columns (or rows) there are
 $k$
particles arranged in odd sites, for
$k$
particles arranged in odd sites, for
 $k=0,\ldots, \frac {L}{2}-1-j$
, where
$k=0,\ldots, \frac {L}{2}-1-j$
, where
 $j$
is the distance from
$j$
is the distance from
 $B$
;
$B$
; -
-
4.
 $\mathcal {R}(C)$
is not contained in
$\mathcal {R}(C)$
is not contained in
 $\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
;
$\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
; -
5.
 $\sigma _{| \Lambda \setminus (C\cup D)} = {\mathbf{e}}_{| \Lambda \setminus (C \cup D)}$
.
$\sigma _{| \Lambda \setminus (C\cup D)} = {\mathbf{e}}_{| \Lambda \setminus (C \cup D)}$
.
See Figure 4 (right) and Figure 11 (right) for examples of configurations in
![]() $\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
.
$\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
.
Next, we provide several results investigating the main properties of the optimal paths connecting
![]() ${\mathbf{e}}$
to
${\mathbf{e}}$
to
![]() ${\mathbf{o}}$
. To this end, we introduce the following partition in manifolds of the state space
${\mathbf{o}}$
. To this end, we introduce the following partition in manifolds of the state space
![]() $\mathcal {X}$
: for every
$\mathcal {X}$
: for every
![]() $m=-\frac {L^2}{2},\ldots, \frac {L^2}{2}$
we define the manifold as the subset of configurations where the difference
$m=-\frac {L^2}{2},\ldots, \frac {L^2}{2}$
we define the manifold as the subset of configurations where the difference
![]() $m(\sigma )\,:\!=\,-e(\sigma )+o(\sigma )$
between odd and even occupied sites is equal to
$m(\sigma )\,:\!=\,-e(\sigma )+o(\sigma )$
between odd and even occupied sites is equal to
![]() $m \in \mathbb {N}$
, i.e.,
$m \in \mathbb {N}$
, i.e.,
where
![]() $e(\sigma )\,:\!=\,\sum _{v \in V_{\mathbf{e}}} \sigma (v)$
(resp.
$e(\sigma )\,:\!=\,\sum _{v \in V_{\mathbf{e}}} \sigma (v)$
(resp.
![]() $o(\sigma )\,:\!=\,\sum _{v \in V_{\mathbf{o}}} \sigma (v)$
) is the number of the even (resp. odd) occupied sites in
$o(\sigma )\,:\!=\,\sum _{v \in V_{\mathbf{o}}} \sigma (v)$
) is the number of the even (resp. odd) occupied sites in
![]() $\sigma$
.
$\sigma$
.
Lemma 4.7. For any hard-core configuration
![]() $\sigma \in \mathcal {X}$
, the following properties hold:
$\sigma \in \mathcal {X}$
, the following properties hold:
-
(a) The only configurations accessible from
 $\sigma$
with a single nontrivial step of the dynamics belong to
$\sigma$
with a single nontrivial step of the dynamics belong to
 $\mathcal {V}_{m(\sigma ) -1} \cup \mathcal {V}_{m(\sigma )+1}$
. In particular, any path from
$\mathcal {V}_{m(\sigma ) -1} \cup \mathcal {V}_{m(\sigma )+1}$
. In particular, any path from
 ${\mathbf{e}}$
to
${\mathbf{e}}$
to
 ${\mathbf{o}}$
must intersect each manifold
${\mathbf{o}}$
must intersect each manifold
 $\mathcal {V}_m$
at least once for every
$\mathcal {V}_m$
at least once for every
 $m=-\frac {L^2}{2},\ldots, \frac {L^2}{2}$
.
$m=-\frac {L^2}{2},\ldots, \frac {L^2}{2}$
. -
(b) The quantities
 $m(\sigma )$
and
$m(\sigma )$
and
 $\Delta H (\sigma )$
always have the same parity, i.e.,
$\Delta H (\sigma )$
always have the same parity, i.e.,
 $m(\sigma ) \equiv \Delta H (\sigma ) \pmod 2$
.
$m(\sigma ) \equiv \Delta H (\sigma ) \pmod 2$
.
The proof of (a) is immediate by noticing that at every step of the dynamics either
![]() $e(\sigma )$
or
$e(\sigma )$
or
![]() $o(\sigma )$
can change value and at most by
$o(\sigma )$
can change value and at most by
![]() $\pm 1$
and that of (b) follows from the fact that
$\pm 1$
and that of (b) follows from the fact that
![]() $\Delta H(\sigma )=-e(\sigma )-o(\sigma )+\frac {L^2}{2}$
and that
$\Delta H(\sigma )=-e(\sigma )-o(\sigma )+\frac {L^2}{2}$
and that
![]() $L$
is even.
$L$
is even.
A special role in our analysis will be played by the non-backtracking paths, i.e., those paths that visit each manifold exactly once. Lemmas4.8–4.10 below ensure the existence of a optimal path connecting
![]() ${\mathbf{e}}$
to
${\mathbf{e}}$
to
![]() ${\mathbf{o}}$
, which can be constructed as a suitable composition of the paths described below, and passing through the six sets that define
${\mathbf{o}}$
, which can be constructed as a suitable composition of the paths described below, and passing through the six sets that define
![]() $\mathcal {C}^*({\mathbf{e}},{\mathbf{o}})$
. The optimality of this path is guaranteed by the conditions on the height of each path described below. In addition, Lemma 4.11 below shows that some of the sets composing
$\mathcal {C}^*({\mathbf{e}},{\mathbf{o}})$
. The optimality of this path is guaranteed by the conditions on the height of each path described below. In addition, Lemma 4.11 below shows that some of the sets composing
![]() $\mathcal {C}^*({\mathbf{e}},{\mathbf{o}})$
do not communicate directly. Later, in subsection 4.2.2, combining these lemmas, we will show that the communication structure of these six sets at energy not higher than
$\mathcal {C}^*({\mathbf{e}},{\mathbf{o}})$
do not communicate directly. Later, in subsection 4.2.2, combining these lemmas, we will show that the communication structure of these six sets at energy not higher than
![]() $H({\mathbf{e}})+L+1$
is the one illustrated in Figure 5. The proof of these lemmas is deferred to subsection 5.2.
$H({\mathbf{e}})+L+1$
is the one illustrated in Figure 5. The proof of these lemmas is deferred to subsection 5.2.
Lemma 4.8. The following statements hold.
-
(i) For any configuration
 $\eta \in \mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
there exists a non-backtracking path
$\eta \in \mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
there exists a non-backtracking path
 $\omega \,:\,{\mathbf{e}}\rightarrow \eta$
such that
$\omega \,:\,{\mathbf{e}}\rightarrow \eta$
such that
 $\Phi _{\omega }-H({\mathbf{e}})=\Delta H(\eta )=L+1$
and
$\Phi _{\omega }-H({\mathbf{e}})=\Delta H(\eta )=L+1$
and
 $\arg \max _{\xi \in \omega }\Delta H(\xi )=\{\eta \}$
.
$\arg \max _{\xi \in \omega }\Delta H(\xi )=\{\eta \}$
. -
(ii) For any configuration
 $\eta \in \mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
there exists a non-backtracking path
$\eta \in \mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
there exists a non-backtracking path
 $\omega \,:\,{\mathbf{e}}\rightarrow \eta$
such that
$\omega \,:\,{\mathbf{e}}\rightarrow \eta$
such that
 $\Phi _{\omega }-H({\mathbf{e}})=\Delta H(\eta )=L+1$
and
$\Phi _{\omega }-H({\mathbf{e}})=\Delta H(\eta )=L+1$
and
 $\arg \max _{\xi \in \omega }\Delta H(\xi )=\{\eta \}$
.
$\arg \max _{\xi \in \omega }\Delta H(\xi )=\{\eta \}$
.
Lemma 4.9. The following statements hold.
-
(i) For any configuration
 $\eta \in \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
there exist a configuration
$\eta \in \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
there exist a configuration
 $\bar \eta \in \mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
and a non-backtracking path
$\bar \eta \in \mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
and a non-backtracking path
 $\omega \,:\,\bar \eta \rightarrow \eta$
such that
$\omega \,:\,\bar \eta \rightarrow \eta$
such that
 $\Phi _{\omega }-H({\mathbf{e}})=\Delta H(\eta )=L+1$
and
$\Phi _{\omega }-H({\mathbf{e}})=\Delta H(\eta )=L+1$
and
 $\arg \max _{\xi \in \omega } H(\xi )\subseteq \mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
.
$\arg \max _{\xi \in \omega } H(\xi )\subseteq \mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
. -
(ii) For any configuration
 $\eta \in \mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
there exist a configuration
$\eta \in \mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
there exist a configuration
 $\bar \eta \in \mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
, a configuration
$\bar \eta \in \mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
, a configuration
 $\tilde \eta \in \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
and two non-backtracking paths
$\tilde \eta \in \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
and two non-backtracking paths
 $\omega \,:\,\bar \eta \rightarrow \eta$
,
$\omega \,:\,\bar \eta \rightarrow \eta$
,
 $\omega ^{\prime}\,:\,\tilde \eta \rightarrow \eta$
such that
$\omega ^{\prime}\,:\,\tilde \eta \rightarrow \eta$
such that-
-
 $\Phi _{\omega }-H({\mathbf{e}})=L+1$
and
$\Phi _{\omega }-H({\mathbf{e}})=L+1$
and
 $\arg \max _{\xi \in \omega } H(\xi )\subseteq \mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
;
$\arg \max _{\xi \in \omega } H(\xi )\subseteq \mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
; -
-
 $\Phi _{\omega ^{\prime}}-H({\mathbf{e}})=L+1$
and
$\Phi _{\omega ^{\prime}}-H({\mathbf{e}})=L+1$
and
 $\arg \max _{\xi \in \omega ^{\prime}} H(\xi )\subseteq \mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
.
$\arg \max _{\xi \in \omega ^{\prime}} H(\xi )\subseteq \mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
.
-
-
(iii) For any configuration
 $\eta \in \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
there exist a configuration
$\eta \in \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
there exist a configuration
 $\bar \eta \in \mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
, a configuration
$\bar \eta \in \mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
, a configuration
 $\tilde \eta \in \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
and two non-backtracking paths
$\tilde \eta \in \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
and two non-backtracking paths
 $\omega \,:\,\bar \eta \rightarrow \eta$
,
$\omega \,:\,\bar \eta \rightarrow \eta$
,
 $\omega ^{\prime}\,:\,\tilde \eta \rightarrow \eta$
such that
$\omega ^{\prime}\,:\,\tilde \eta \rightarrow \eta$
such that-
-
 $\Phi _{\omega }-H({\mathbf{e}})=L+1$
and
$\Phi _{\omega }-H({\mathbf{e}})=L+1$
and
 $\arg \max _{\xi \in \omega } H(\xi )\subseteq \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
;
$\arg \max _{\xi \in \omega } H(\xi )\subseteq \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
; -
-
 $\Phi _{\omega ^{\prime}}-H({\mathbf{e}})=L+1$
and
$\Phi _{\omega ^{\prime}}-H({\mathbf{e}})=L+1$
and
 $\arg \max _{\xi \in \omega ^{\prime}} H(\xi )\subseteq \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
.
$\arg \max _{\xi \in \omega ^{\prime}} H(\xi )\subseteq \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
.
-
-
(iv) For any configuration
 $\eta \in \mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
there exist a configuration
$\eta \in \mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
there exist a configuration
 $\bar \eta \in \mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
, a configuration
$\bar \eta \in \mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
, a configuration
 $\tilde \eta \in \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
and two non-backtracking paths
$\tilde \eta \in \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
and two non-backtracking paths
 $\omega \,:\,\bar \eta \rightarrow \eta$
,
$\omega \,:\,\bar \eta \rightarrow \eta$
,
 $\omega ^{\prime}\,:\,\tilde \eta \rightarrow \eta$
such that
$\omega ^{\prime}\,:\,\tilde \eta \rightarrow \eta$
such that-
-
 $\Phi _{\omega }-H({\mathbf{e}})=L+1$
and
$\Phi _{\omega }-H({\mathbf{e}})=L+1$
and
 $\arg \max _{\xi \in \omega } H(\xi )\subseteq \mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
;
$\arg \max _{\xi \in \omega } H(\xi )\subseteq \mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
; -
-
 $\Phi _{\omega ^{\prime}}-H({\mathbf{e}})=L+1$
and
$\Phi _{\omega ^{\prime}}-H({\mathbf{e}})=L+1$
and
 $\arg \max _{\xi \in \omega ^{\prime}} H(\xi )\subseteq \mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
.
$\arg \max _{\xi \in \omega ^{\prime}} H(\xi )\subseteq \mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
.
-
Lemma 4.10. The following statements hold.
-
(i) For any configuration
 $\eta \in \mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
there exists a non-backtracking path
$\eta \in \mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
there exists a non-backtracking path
 $\omega \,:\,\eta \rightarrow {\mathbf{o}}$
such that
$\omega \,:\,\eta \rightarrow {\mathbf{o}}$
such that
 $\Phi _{\omega }-H({\mathbf{e}})=L+1$
and
$\Phi _{\omega }-H({\mathbf{e}})=L+1$
and
 $\arg \max _{\xi \in \omega } H(\xi )\subseteq \mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
.
$\arg \max _{\xi \in \omega } H(\xi )\subseteq \mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
. -
(ii) For any configuration
 $\eta \in \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
there exists a non-backtracking path
$\eta \in \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
there exists a non-backtracking path
 $\omega \,:\,\eta \rightarrow {\mathbf{o}}$
such that
$\omega \,:\,\eta \rightarrow {\mathbf{o}}$
such that
 $\Phi _{\omega }-H({\mathbf{e}})=L+1$
and
$\Phi _{\omega }-H({\mathbf{e}})=L+1$
and
 $\arg \max _{\xi \in \omega } H(\xi )\subseteq \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
.
$\arg \max _{\xi \in \omega } H(\xi )\subseteq \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
.
Lemma 4.11. The following statements hold.
-
(i) For any configurations
 $\eta \in \mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
and
$\eta \in \mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
and
 $\eta ^{\prime}\in \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
, there is no optimal path
$\eta ^{\prime}\in \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
, there is no optimal path
 $\omega \,:\,\eta \to \eta ^{\prime}$
such that
$\omega \,:\,\eta \to \eta ^{\prime}$
such that
 $\arg \max _{\xi \in \omega }\subseteq \mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
.
$\arg \max _{\xi \in \omega }\subseteq \mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
. -
(ii) For any configurations
 $\eta \in \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
and
$\eta \in \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
and
 $\eta ^{\prime}\in \mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
, there is no optimal path
$\eta ^{\prime}\in \mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
, there is no optimal path
 $\omega \,:\,\eta \to \eta ^{\prime}$
such that
$\omega \,:\,\eta \to \eta ^{\prime}$
such that
 $\arg \max _{\xi \in \omega }\subseteq \mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
.
$\arg \max _{\xi \in \omega }\subseteq \mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
. -
(iii) For any configurations
 $\eta \in \mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
and
$\eta \in \mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
and
 $\eta ^{\prime}\in \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
, there is no optimal path
$\eta ^{\prime}\in \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
, there is no optimal path
 $\omega \,:\,\eta \to \eta ^{\prime}$
such that
$\omega \,:\,\eta \to \eta ^{\prime}$
such that
 $\arg \max _{\xi \in \omega }\subseteq \mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
.
$\arg \max _{\xi \in \omega }\subseteq \mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
. -
(iv) For any configurations
 $\eta \in \mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
and
$\eta \in \mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
and
 $\eta ^{\prime}\in \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
, there is no optimal path
$\eta ^{\prime}\in \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
, there is no optimal path
 $\omega \,:\,\eta \to \eta ^{\prime}$
such that
$\omega \,:\,\eta \to \eta ^{\prime}$
such that
 $\arg \max _{\xi \in \omega }\subseteq \mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
.
$\arg \max _{\xi \in \omega }\subseteq \mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
.
4.2 Proof of Theorem 2.1
This section is entirely devoted to the proof of Theorem 2.1. More specifically, we prove that any essential saddle belongs to the set
![]() $\mathcal {C}^*({\mathbf{e}},{\mathbf{o}})$
in subsection 4.2.1, we describe how the transitions between essential gates can take place in subsection 4.2.2, and we prove that all the saddles in
$\mathcal {C}^*({\mathbf{e}},{\mathbf{o}})$
in subsection 4.2.1, we describe how the transitions between essential gates can take place in subsection 4.2.2, and we prove that all the saddles in
![]() $\mathcal {C}^*({\mathbf{e}},{\mathbf{o}})$
are essential in subsection 4.2.3.
$\mathcal {C}^*({\mathbf{e}},{\mathbf{o}})$
are essential in subsection 4.2.3.
4.2.1 Every essential saddle belongs to
 $\mathcal {C}^*({\mathbf{e}},{\mathbf{o}})$
$\mathcal {C}^*({\mathbf{e}},{\mathbf{o}})$
In this subsection, we will show that any essential saddle
![]() $\sigma$
belongs to the subset
$\sigma$
belongs to the subset
![]() $\mathcal {C}^*({\mathbf{e}},{\mathbf{o}})$
. This readily follows from Proposition4.12 below.
$\mathcal {C}^*({\mathbf{e}},{\mathbf{o}})$
. This readily follows from Proposition4.12 below.
Proposition 4.12. Let
![]() $\sigma$
be an essential saddle. Then, the following statements hold:
$\sigma$
be an essential saddle. Then, the following statements hold:
-
(i) If
 $\mathcal {R}(\mathcal {O}^{nd}(\sigma ))$
and
$\mathcal {R}(\mathcal {O}^{nd}(\sigma ))$
and
 $\mathcal {R}(\mathcal {O}(\sigma ))$
do not wind around the torus, then
$\mathcal {R}(\mathcal {O}(\sigma ))$
do not wind around the torus, then
 $\sigma \in \mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
.
$\sigma \in \mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
. -
(ii) If
 $\mathcal {R}(\mathcal {O}^{nd}(\sigma ))$
does not wind around the torus,
$\mathcal {R}(\mathcal {O}^{nd}(\sigma ))$
does not wind around the torus,
 $\mathcal {R}(\mathcal {O}(\sigma ))$
does, and
$\mathcal {R}(\mathcal {O}(\sigma ))$
does, and
 $\sigma$
belongs to
$\sigma$
belongs to
 $\omega \in ({\mathbf{e}}\to {\mathbf{o}})_{opt}$
that crosses the set
$\omega \in ({\mathbf{e}}\to {\mathbf{o}})_{opt}$
that crosses the set
 $\mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
, then
$\mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
, then
 $\sigma \in \mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
.
$\sigma \in \mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
. -
(iii) If
 $\mathcal {R}(\mathcal {O}^{nd}(\sigma ))$
does not wind around the torus,
$\mathcal {R}(\mathcal {O}^{nd}(\sigma ))$
does not wind around the torus,
 $\mathcal {R}(\mathcal {O}(\sigma ))$
does, and
$\mathcal {R}(\mathcal {O}(\sigma ))$
does, and
 $\sigma$
belongs to
$\sigma$
belongs to
 $\omega \in ({\mathbf{e}}\to {\mathbf{o}})_{opt}$
that does not cross the set
$\omega \in ({\mathbf{e}}\to {\mathbf{o}})_{opt}$
that does not cross the set
 $\mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
, then
$\mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
, then
 $\sigma \in \mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
.
$\sigma \in \mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
. -
(iv) If
 $\mathcal {R}(\mathcal {O}^{nd}(\sigma ))$
winds around the torus, then
$\mathcal {R}(\mathcal {O}^{nd}(\sigma ))$
winds around the torus, then
 $\sigma \in \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
.
$\sigma \in \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
.
We observe that these four cases (i)–(iv) listed in Proposition4.12 cover all possibilities and thus form a partition of the set
![]() $\mathcal {G}({\mathbf{e}},{\mathbf{o}})$
of essential saddles for the transitions
$\mathcal {G}({\mathbf{e}},{\mathbf{o}})$
of essential saddles for the transitions
![]() ${\mathbf{e}} \rightarrow {\mathbf{o}}$
.
${\mathbf{e}} \rightarrow {\mathbf{o}}$
.
Before presenting the proof, note that given a configuration
![]() $\sigma \in \mathcal {S}({\mathbf{e}},{\mathbf{o}})$
, if we know on which manifold
$\sigma \in \mathcal {S}({\mathbf{e}},{\mathbf{o}})$
, if we know on which manifold
![]() $\mathcal {V}_m$
it lies, then the quantities
$\mathcal {V}_m$
it lies, then the quantities
![]() $e(\sigma )$
and
$e(\sigma )$
and
![]() $o(\sigma )$
are uniquely determined and can be explicitly calculated as
$o(\sigma )$
are uniquely determined and can be explicitly calculated as
This readily follows from the fact that
![]() $\Delta H(\sigma ) = L+1=-e(\sigma )-o(\sigma )+\frac {L^2}{2}$
and
$\Delta H(\sigma ) = L+1=-e(\sigma )-o(\sigma )+\frac {L^2}{2}$
and
![]() $m=-e(\sigma )+o(\sigma )$
. Furthermore, since
$m=-e(\sigma )+o(\sigma )$
. Furthermore, since
![]() $\sigma \in \mathcal {S}({\mathbf{e}},{\mathbf{o}})$
,
$\sigma \in \mathcal {S}({\mathbf{e}},{\mathbf{o}})$
,
![]() $\Delta H(\sigma ) = L+1$
and
$\Delta H(\sigma ) = L+1$
and
![]() $m$
have to be odd integers by Lemma 4.7(b).
$m$
have to be odd integers by Lemma 4.7(b).
To prove Proposition4.12, we make use of an additional lemma (whose proof is deferred to subsection 5.3), which characterizes the intersection between any optimal path and a specific manifold, namely
![]() $\mathcal {V}_{m^*}$
with
$\mathcal {V}_{m^*}$
with
![]() $m^*\,:\!=\,3-L$
.
$m^*\,:\!=\,3-L$
.
Lemma 4.13 (Geometrical properties of the saddles on the manifold
![]() $\mathcal {V}_{m^*}$
). Any non-backtracking optimal path
$\mathcal {V}_{m^*}$
). Any non-backtracking optimal path
![]() $\omega \,:\, {\mathbf{e}} \to {\mathbf{o}}$
visits a configuration
$\omega \,:\, {\mathbf{e}} \to {\mathbf{o}}$
visits a configuration
![]() $\sigma \in \mathcal {V}_{m^*}$
that satisfy one of the following properties:
$\sigma \in \mathcal {V}_{m^*}$
that satisfy one of the following properties:
-
(i) If both
 $\mathcal {R}(\mathcal {O}^{nd}(\sigma ))$
and
$\mathcal {R}(\mathcal {O}^{nd}(\sigma ))$
and
 $\mathcal {R}(\mathcal {O}(\sigma ))$
do not wind around the torus, then
$\mathcal {R}(\mathcal {O}(\sigma ))$
do not wind around the torus, then
 $\sigma \in \mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
.
$\sigma \in \mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
. -
(ii) If
 $\mathcal {R}(\mathcal {O}^{nd}(\sigma ))$
does not wind around the torus but
$\mathcal {R}(\mathcal {O}^{nd}(\sigma ))$
does not wind around the torus but
 $\mathcal {R}(\mathcal {O}(\sigma ))$
does, then
$\mathcal {R}(\mathcal {O}(\sigma ))$
does, then
 $\sigma \in \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
.
$\sigma \in \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
. -
(iii) If both
 $\mathcal {R}(\mathcal {O}^{nd}(\sigma ))$
and
$\mathcal {R}(\mathcal {O}^{nd}(\sigma ))$
and
 $\mathcal {R}(\mathcal {O}(\sigma ))$
wind around the torus, then
$\mathcal {R}(\mathcal {O}(\sigma ))$
wind around the torus, then
 $\sigma \in \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
.
$\sigma \in \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
.
Proof of Proposition
4.12. Case (i). Let
![]() $\sigma$
be an essential saddle such that
$\sigma$
be an essential saddle such that
![]() $\mathcal {R}(\mathcal {O}^{nd}(\sigma ))$
and
$\mathcal {R}(\mathcal {O}^{nd}(\sigma ))$
and
![]() $\mathcal {R}(\mathcal {O}(\sigma ))$
do not wind around the torus. If
$\mathcal {R}(\mathcal {O}(\sigma ))$
do not wind around the torus. If
![]() $\sigma \in \mathcal {V}_{m^*}$
, by Lemma 4.13(i) we know that
$\sigma \in \mathcal {V}_{m^*}$
, by Lemma 4.13(i) we know that
![]() $\sigma \in \mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
. Otherwise, we assume that
$\sigma \in \mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
. Otherwise, we assume that
![]() $\sigma \notin \mathcal {V}_{m^*}$
. First, we observe that
$\sigma \notin \mathcal {V}_{m^*}$
. First, we observe that
![]() $\sigma \not \in \mathcal {V}_{m}$
with
$\sigma \not \in \mathcal {V}_{m}$
with
![]() $m\lt m^*$
, otherwise the saddle
$m\lt m^*$
, otherwise the saddle
![]() $\sigma$
is not essential. Indeed, every optimal path from
$\sigma$
is not essential. Indeed, every optimal path from
![]() ${\mathbf{e}}$
to
${\mathbf{e}}$
to
![]() ${\mathbf{o}}$
has to cross a configuration
${\mathbf{o}}$
has to cross a configuration
![]() $\bar \sigma \in \mathcal {V}_{m^*}$
in
$\bar \sigma \in \mathcal {V}_{m^*}$
in
![]() $\mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
due to Lemma 4.13(i). Thus, we can write a general optimal path
$\mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
due to Lemma 4.13(i). Thus, we can write a general optimal path
![]() $\omega =({\mathbf{e}},\omega _1,\ldots, \omega _k,\sigma, \ldots, \bar \sigma, \omega _{k+1},\ldots, \omega _{k+m},{\mathbf{o}})$
and define the path
$\omega =({\mathbf{e}},\omega _1,\ldots, \omega _k,\sigma, \ldots, \bar \sigma, \omega _{k+1},\ldots, \omega _{k+m},{\mathbf{o}})$
and define the path
![]() $\omega ^{\prime}=({\mathbf{e}},\tilde \omega _1,\ldots, \tilde \omega _n,\bar \sigma, \omega _{k+1},\ldots, \omega _{k+m},{\mathbf{o}})$
, where
$\omega ^{\prime}=({\mathbf{e}},\tilde \omega _1,\ldots, \tilde \omega _n,\bar \sigma, \omega _{k+1},\ldots, \omega _{k+m},{\mathbf{o}})$
, where
![]() $\arg \max _{\xi \in \{{\mathbf{e}},\tilde \omega _1,\ldots, \tilde \omega _n,\bar \sigma \}}H(\xi )=\{\bar \sigma \}$
. This path
$\arg \max _{\xi \in \{{\mathbf{e}},\tilde \omega _1,\ldots, \tilde \omega _n,\bar \sigma \}}H(\xi )=\{\bar \sigma \}$
. This path
![]() $\omega ^{\prime}$
exists thanks to Lemma 4.8(i). Thus, we are left to analyse the case
$\omega ^{\prime}$
exists thanks to Lemma 4.8(i). Thus, we are left to analyse the case
![]() $\sigma \in \mathcal {V}_{m}$
with
$\sigma \in \mathcal {V}_{m}$
with
![]() $m\gt m^*$
. We need to show that any essential saddle crossed afterward belongs to the set
$m\gt m^*$
. We need to show that any essential saddle crossed afterward belongs to the set
![]() $\mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
. Using again Lemma 4.13, the path
$\mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
. Using again Lemma 4.13, the path
![]() $\omega$
crosses a configuration
$\omega$
crosses a configuration
![]() $\sigma \in \mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
to reach
$\sigma \in \mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
to reach
![]() ${\mathbf{o}}$
. Starting from it, there is a unique possible move to lower the energy towards
${\mathbf{o}}$
. Starting from it, there is a unique possible move to lower the energy towards
![]() ${\mathbf{o}}$
along the path
${\mathbf{o}}$
along the path
![]() $\omega$
, that is adding a particle in the unique unblocked empty odd site. Afterward, the unique possible move is to remove a particle from an even site. If this site is at a distance greater than one from an antiknob, then there is no more allowed move. Otherwise, the resulting configuration belongs to the set
$\omega$
, that is adding a particle in the unique unblocked empty odd site. Afterward, the unique possible move is to remove a particle from an even site. If this site is at a distance greater than one from an antiknob, then there is no more allowed move. Otherwise, the resulting configuration belongs to the set
![]() $\mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
. By iterating this pair of moves until the shorter diagonal of the rhombus is completely filled, we find that all the saddles that are crossed belong to
$\mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
. By iterating this pair of moves until the shorter diagonal of the rhombus is completely filled, we find that all the saddles that are crossed belong to
![]() $\mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
. Moreover, from this point onward, it is only possible to remove a particle from an even site at distance one from the antiknob, obtaining a configuration in
$\mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
. Moreover, from this point onward, it is only possible to remove a particle from an even site at distance one from the antiknob, obtaining a configuration in
![]() $\mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})\cap \mathcal {V}_{1}$
.
$\mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})\cap \mathcal {V}_{1}$
.
Case (ii). By assumption, the path
![]() $\omega$
crosses the set
$\omega$
crosses the set
![]() $\mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
. Without loss of generality, we may consider
$\mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
. Without loss of generality, we may consider
![]() $\omega$
as a non-backtracking path. If this is not the case, we can apply the following argument to the last configuration visited by the path in the manifold
$\omega$
as a non-backtracking path. If this is not the case, we can apply the following argument to the last configuration visited by the path in the manifold
![]() $\mathcal {V}_{m^*}$
. In particular, in view of the properties of the path
$\mathcal {V}_{m^*}$
. In particular, in view of the properties of the path
![]() $\omega$
shown in case (i), we know that the last configuration crossed in
$\omega$
shown in case (i), we know that the last configuration crossed in
![]() $\mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
belongs to
$\mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
belongs to
![]() $\mathcal {V}_1$
and it is composed of a unique non-degenerate cluster
$\mathcal {V}_1$
and it is composed of a unique non-degenerate cluster
![]() $\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}}$
with a degenerate cluster
$\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}}$
with a degenerate cluster
![]() $\mathcal {R}_{0,0}$
at distance one from the antiknob. Starting from it, there is a unique possible move to lower the energy towards
$\mathcal {R}_{0,0}$
at distance one from the antiknob. Starting from it, there is a unique possible move to lower the energy towards
![]() ${\mathbf{o}}$
along the path
${\mathbf{o}}$
along the path
![]() $\omega$
, that is, adding a particle in the unique unblocked empty odd site. Afterward, the unique possible move is to remove a particle from an even site. The resulting configuration is in
$\omega$
, that is, adding a particle in the unique unblocked empty odd site. Afterward, the unique possible move is to remove a particle from an even site. The resulting configuration is in
![]() $\mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
. By iterating this pair of moves until the shorter diagonal of the rhombus is completely filled, we find that all the saddles that are crossed belong to
$\mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
. By iterating this pair of moves until the shorter diagonal of the rhombus is completely filled, we find that all the saddles that are crossed belong to
![]() $\mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
.
$\mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
.
Case (iii). As in case (ii), we assume that the path
![]() $\omega$
is non-backtracking. By assumption, the path
$\omega$
is non-backtracking. By assumption, the path
![]() $\omega$
does not cross the set
$\omega$
does not cross the set
![]() $\mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
, thus for Lemma 4.13(ii) the path crosses the set
$\mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
, thus for Lemma 4.13(ii) the path crosses the set
![]() $\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
, say in configuration
$\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
, say in configuration
![]() $\bar \eta$
. Let
$\bar \eta$
. Let
![]() $\mathcal {V}_{\bar m}$
the first manifold containing a configuration in
$\mathcal {V}_{\bar m}$
the first manifold containing a configuration in
![]() $\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
.
$\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
.
Consider first the case in which the saddle
![]() $\sigma$
is crossed by the path
$\sigma$
is crossed by the path
![]() $\omega$
on the manifolds
$\omega$
on the manifolds
![]() $\mathcal {V}_m$
, with
$\mathcal {V}_m$
, with
![]() $\bar m\leq m\lt m^*$
. Since
$\bar m\leq m\lt m^*$
. Since
![]() $\omega$
crosses the set
$\omega$
crosses the set
![]() $\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
, we will show that the saddle
$\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
, we will show that the saddle
![]() $\sigma$
belongs to the set
$\sigma$
belongs to the set
![]() $\mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
. To this end, we need to consider the time-reversal of the path
$\mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
. To this end, we need to consider the time-reversal of the path
![]() $\omega =({\mathbf{e}},\omega _1,\ldots, \omega _k,\bar \eta, \ldots, {\mathbf{o}})$
, where
$\omega =({\mathbf{e}},\omega _1,\ldots, \omega _k,\bar \eta, \ldots, {\mathbf{o}})$
, where
![]() $\bar \eta \in \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
. Starting from
$\bar \eta \in \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
. Starting from
![]() $\bar \eta$
, since
$\bar \eta$
, since
![]() $\Delta H(\bar \eta )=L+1$
, the energy of configuration
$\Delta H(\bar \eta )=L+1$
, the energy of configuration
![]() $\omega _k$
is less than that of
$\omega _k$
is less than that of
![]() $\bar \eta$
. Moreover, the unique possible move is to add a particle in the unique empty even site at distance one from an antiknob. Then, the unique possible move from
$\bar \eta$
. Moreover, the unique possible move is to add a particle in the unique empty even site at distance one from an antiknob. Then, the unique possible move from
![]() $\omega _k$
to
$\omega _k$
to
![]() $\omega _{k-1}$
is to remove a particle from an occupied odd site. The configuration
$\omega _{k-1}$
is to remove a particle from an occupied odd site. The configuration
![]() $\omega _{k-1}$
belongs to the set
$\omega _{k-1}$
belongs to the set
![]() $\mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
if it contains at least one bridge, otherwise, it belongs to the set
$\mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
if it contains at least one bridge, otherwise, it belongs to the set
![]() $\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
. By iterating this argument, we obtain the desired claim.
$\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
. By iterating this argument, we obtain the desired claim.
Consider now the case in which the saddle
![]() $\sigma$
is crossed by the path
$\sigma$
is crossed by the path
![]() $\omega$
on the manifolds
$\omega$
on the manifolds
![]() $\mathcal {V}_m$
, with
$\mathcal {V}_m$
, with
![]() $ m\gt m^*$
. Since
$ m\gt m^*$
. Since
![]() $\omega$
crosses the set
$\omega$
crosses the set
![]() $\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
, we will show that the saddle
$\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
, we will show that the saddle
![]() $\sigma$
belongs to the set
$\sigma$
belongs to the set
![]() $\mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
. Note that the unique admissible moves are the following: add a particle in the antiknob and then remove a particle from an even site at distance one from an antiknob. By iterating this couple of moves, we get that the resulting configuration belongs to the set
$\mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
. Note that the unique admissible moves are the following: add a particle in the antiknob and then remove a particle from an even site at distance one from an antiknob. By iterating this couple of moves, we get that the resulting configuration belongs to the set
![]() $\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
since
$\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
since
![]() $\mathcal {R}(\mathcal {O}^{nd}(\sigma ))$
does not wind around the torus.
$\mathcal {R}(\mathcal {O}^{nd}(\sigma ))$
does not wind around the torus.
It remains to consider the case
![]() $\sigma \in \mathcal {V}_m$
, with
$\sigma \in \mathcal {V}_m$
, with
![]() $m\lt \bar m$
. We will prove that any such
$m\lt \bar m$
. We will prove that any such
![]() $\sigma$
is not essential. Indeed, any non-backtracking optimal path that visits a configuration in
$\sigma$
is not essential. Indeed, any non-backtracking optimal path that visits a configuration in
![]() $\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
has crossed a configuration in
$\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
has crossed a configuration in
![]() $\mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
before, by using the same argument as in case (iii) of this proof for
$\mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
before, by using the same argument as in case (iii) of this proof for
![]() $\bar m\leq m\lt m^*$
. Thus, we can write
$\bar m\leq m\lt m^*$
. Thus, we can write
![]() $\omega =({\mathbf{e}},\omega _1,\ldots, \omega _k,\sigma, \ldots, \tilde \sigma, \ldots, \bar \sigma, \omega _{k+1},\ldots, \omega _{k+m},{\mathbf{o}})$
and define the path
$\omega =({\mathbf{e}},\omega _1,\ldots, \omega _k,\sigma, \ldots, \tilde \sigma, \ldots, \bar \sigma, \omega _{k+1},\ldots, \omega _{k+m},{\mathbf{o}})$
and define the path
![]() $\omega ^{\prime}=({\mathbf{e}},\omega _1^{\prime},\ldots, \omega _n^{\prime},\tilde \sigma, \ldots, \bar \sigma, \omega _{k+1},\ldots, \omega _{k+m},{\mathbf{o}})$
, where
$\omega ^{\prime}=({\mathbf{e}},\omega _1^{\prime},\ldots, \omega _n^{\prime},\tilde \sigma, \ldots, \bar \sigma, \omega _{k+1},\ldots, \omega _{k+m},{\mathbf{o}})$
, where
![]() $\tilde \sigma$
is a configuration in
$\tilde \sigma$
is a configuration in
![]() $\mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
,
$\mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
,
![]() $\bar \sigma \in \mathcal {V}_{\bar m}$
is a configuration in
$\bar \sigma \in \mathcal {V}_{\bar m}$
is a configuration in
![]() $\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
thanks to Lemma 4.13(ii) and
$\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
thanks to Lemma 4.13(ii) and
![]() $\arg \max _{\xi \in \{{\mathbf{e}},\omega _1^{\prime},\ldots, \omega _n^{\prime},\tilde \sigma \}}H(\xi )=\{\tilde \sigma \}$
. This path
$\arg \max _{\xi \in \{{\mathbf{e}},\omega _1^{\prime},\ldots, \omega _n^{\prime},\tilde \sigma \}}H(\xi )=\{\tilde \sigma \}$
. This path
![]() $\omega ^{\prime}$
exists thanks to Lemma 4.8(ii) and this concludes case (iii).
$\omega ^{\prime}$
exists thanks to Lemma 4.8(ii) and this concludes case (iii).
Case (iv). By Lemma 4.13(iii), we know that any optimal path
![]() $\omega \in ({\mathbf{e}}\rightarrow {\mathbf{o}})_{\mathrm {opt}}$
crosses the manifold
$\omega \in ({\mathbf{e}}\rightarrow {\mathbf{o}})_{\mathrm {opt}}$
crosses the manifold
![]() $\mathcal {V}_{m^*}$
in a configuration
$\mathcal {V}_{m^*}$
in a configuration
![]() $\bar \sigma$
belonging to the set
$\bar \sigma$
belonging to the set
![]() $\mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
.
$\mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
.
If the essential saddle
![]() $\sigma \in \mathcal {V}_{m^*}$
, then we deduce that
$\sigma \in \mathcal {V}_{m^*}$
, then we deduce that
![]() $\sigma \in \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
.
$\sigma \in \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
.
Suppose now that the saddle
![]() $\sigma$
belongs to the manifold
$\sigma$
belongs to the manifold
![]() $\mathcal {V}_m$
, with
$\mathcal {V}_m$
, with
![]() $m\gt m^*$
. Starting from such a saddle
$m\gt m^*$
. Starting from such a saddle
![]() $\bar \sigma$
, there is a unique possible move to lower the energy towards
$\bar \sigma$
, there is a unique possible move to lower the energy towards
![]() ${\mathbf{o}}$
along the path
${\mathbf{o}}$
along the path
![]() $\omega$
, that is, add a particle to the unique unblocked empty odd site. Afterward, the unique possible move is to remove a particle from an even site. If this site is at a distance greater than one from an antiknob, then there is no more possible move to reach
$\omega$
, that is, add a particle to the unique unblocked empty odd site. Afterward, the unique possible move is to remove a particle from an even site. If this site is at a distance greater than one from an antiknob, then there is no more possible move to reach
![]() ${\mathbf{o}}$
in such a way that the path
${\mathbf{o}}$
in such a way that the path
![]() $\omega$
is optimal. Otherwise, the resulting configuration belongs to the set
$\omega$
is optimal. Otherwise, the resulting configuration belongs to the set
![]() $\mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
. Indeed, by construction, we deduce that the resulting non-degenerate odd cluster is still monotone due to the properties of the bars attached to each bridge. By iterating this pair of moves until there is a row or a column that is not a bridge, we obtain that all the saddles that are crossed belong to
$\mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
. Indeed, by construction, we deduce that the resulting non-degenerate odd cluster is still monotone due to the properties of the bars attached to each bridge. By iterating this pair of moves until there is a row or a column that is not a bridge, we obtain that all the saddles that are crossed belong to
![]() $\mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
. Finally, from this point onward, it is only possible to remove a particle from an even site at distance one from the antiknob, obtaining the last configuration in
$\mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
. Finally, from this point onward, it is only possible to remove a particle from an even site at distance one from the antiknob, obtaining the last configuration in
![]() $\mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
. Afterward, the energy only decreases and therefore no more saddles are crossed.
$\mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
. Afterward, the energy only decreases and therefore no more saddles are crossed.
Suppose now that the saddle
![]() $\sigma$
belongs to the manifold
$\sigma$
belongs to the manifold
![]() $\mathcal {V}_m$
, with
$\mathcal {V}_m$
, with
![]() $m\lt m^*$
. Note that, starting from such
$m\lt m^*$
. Note that, starting from such
![]() $\bar \sigma \in \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
, the unique admissible moves to get
$\bar \sigma \in \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
, the unique admissible moves to get
![]() $\sigma$
are the following: add a particle to the unique empty even site at distance one from an antiknob and afterward remove a particle from an occupied odd site. By iterating this couple of moves, we get that the resulting configuration belongs to the set
$\sigma$
are the following: add a particle to the unique empty even site at distance one from an antiknob and afterward remove a particle from an occupied odd site. By iterating this couple of moves, we get that the resulting configuration belongs to the set
![]() $\mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
as long as
$\mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
as long as
![]() $\mathcal {R}(\mathcal {O}^{nd}(\sigma ))$
winds around the torus, otherwise the saddle
$\mathcal {R}(\mathcal {O}^{nd}(\sigma ))$
winds around the torus, otherwise the saddle
![]() $\sigma$
does not satisfy the properties in the statement.
$\sigma$
does not satisfy the properties in the statement.
4.2.2 Communications between essential gates
In this subsection, we show that the six subsets composing the set
![]() $\mathcal {C}^*({\mathbf{e}},{\mathbf{o}})$
communicate as illustrated in Figure 5. The next proposition makes it precise.
$\mathcal {C}^*({\mathbf{e}},{\mathbf{o}})$
communicate as illustrated in Figure 5. The next proposition makes it precise.
Proposition 4.14. Any non-backtracking optimal path
![]() $\omega \,:\,{\mathbf{e}}\to {\mathbf{o}}$
crosses the set
$\omega \,:\,{\mathbf{e}}\to {\mathbf{o}}$
crosses the set
![]() $\mathcal {C}^*({\mathbf{e}},{\mathbf{o}})$
in one of the following ways:
$\mathcal {C}^*({\mathbf{e}},{\mathbf{o}})$
in one of the following ways:
-
(i)
 $\omega$
passes first through
$\omega$
passes first through
 $\mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
, then through
$\mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
, then through
 $\mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
, and finally through
$\mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
, and finally through
 $\mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
;
$\mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
; -
(ii)
 $\omega$
passes first through
$\omega$
passes first through
 $\mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
, then through
$\mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
, then through
 $\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
and afterwards through
$\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
and afterwards through
 $\mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}}) \cup \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
. If
$\mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}}) \cup \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
. If
 $\omega$
passes
$\omega$
passes
 $\mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
, then it eventually has to visit
$\mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
, then it eventually has to visit
 $\mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
, otherwise it does not have to;
$\mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
, otherwise it does not have to; -
(iii)
 $\omega$
passes first through
$\omega$
passes first through
 $\mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
and then through
$\mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
and then through
 $\mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
.
$\mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
.
Proof. Consider a non-backtracking optimal path
![]() $\omega \,:\,{\mathbf{e}}\to {\mathbf{o}}$
. If
$\omega \,:\,{\mathbf{e}}\to {\mathbf{o}}$
. If
![]() $\omega$
visits at least one essential saddle, then we conclude using Proposition4.12. Thus, suppose that
$\omega$
visits at least one essential saddle, then we conclude using Proposition4.12. Thus, suppose that
![]() $\omega$
visits unessential saddles only, say
$\omega$
visits unessential saddles only, say
![]() $\sigma _1,\ldots, \sigma _n$
. By definition of unessential saddle, we know that there exists another optimal path
$\sigma _1,\ldots, \sigma _n$
. By definition of unessential saddle, we know that there exists another optimal path
![]() $\omega ^{\prime}\,:\,{\mathbf{e}}\to {\mathbf{o}}$
such that
$\omega ^{\prime}\,:\,{\mathbf{e}}\to {\mathbf{o}}$
such that
![]() $S(\omega ^{\prime})\subseteq \{\sigma _1,\ldots, \sigma _{n-1}\}$
, say
$S(\omega ^{\prime})\subseteq \{\sigma _1,\ldots, \sigma _{n-1}\}$
, say
![]() $S(\omega ^{\prime})\subseteq \{\sigma _1,\ldots, \sigma _m\}$
with
$S(\omega ^{\prime})\subseteq \{\sigma _1,\ldots, \sigma _m\}$
with
![]() $m\leq n-1$
. Iterating this argument, we deduce that there exists an optimal path
$m\leq n-1$
. Iterating this argument, we deduce that there exists an optimal path
![]() $\bar \omega \,:\,{\mathbf{e}}\to {\mathbf{o}}$
such that
$\bar \omega \,:\,{\mathbf{e}}\to {\mathbf{o}}$
such that
![]() $S(\bar \omega )=\{\sigma _1\}$
and this is a contradiction with the assumption that
$S(\bar \omega )=\{\sigma _1\}$
and this is a contradiction with the assumption that
![]() $\sigma _1$
is an unessential saddle. Thus, we conclude that any optimal path
$\sigma _1$
is an unessential saddle. Thus, we conclude that any optimal path
![]() $\omega \,:\,{\mathbf{e}}\to {\mathbf{o}}$
visits the set
$\omega \,:\,{\mathbf{e}}\to {\mathbf{o}}$
visits the set
![]() $\mathcal {C}^*({\mathbf{e}},{\mathbf{o}})$
. It remains to prove that the entrance in
$\mathcal {C}^*({\mathbf{e}},{\mathbf{o}})$
. It remains to prove that the entrance in
![]() $\mathcal {C}^*({\mathbf{e}},{\mathbf{o}})$
occurs in one of the ways described in (i)–(iii), which easily follows by combining Lemmas4.8–4.11.
$\mathcal {C}^*({\mathbf{e}},{\mathbf{o}})$
occurs in one of the ways described in (i)–(iii), which easily follows by combining Lemmas4.8–4.11.
4.2.3 All the saddles in
 $\mathcal {C}^*({\mathbf{e}},{\mathbf{o}})$
are essential
$\mathcal {C}^*({\mathbf{e}},{\mathbf{o}})$
are essential
In this first part of the proof, we will prove that every
![]() $\sigma \in \mathcal C^*({\mathbf{e}},{\mathbf{o}})$
is an essential saddle by constructing a non-backtracking optimal path
$\sigma \in \mathcal C^*({\mathbf{e}},{\mathbf{o}})$
is an essential saddle by constructing a non-backtracking optimal path
![]() $\omega \,:\, {\mathbf{e}} \to {\mathbf{o}}$
that visits
$\omega \,:\, {\mathbf{e}} \to {\mathbf{o}}$
that visits
![]() $\sigma$
.
$\sigma$
.
Leveraging the fact that
![]() $\sigma \in \mathcal C^*({\mathbf{e}},{\mathbf{o}})$
, we construct the desired non-backtracking path
$\sigma \in \mathcal C^*({\mathbf{e}},{\mathbf{o}})$
, we construct the desired non-backtracking path
![]() $\omega$
as a concatenation of two paths as follows. First, using a suitable concatenation of the paths described in Lemmas4.9–4.10, we can define a path
$\omega$
as a concatenation of two paths as follows. First, using a suitable concatenation of the paths described in Lemmas4.9–4.10, we can define a path
![]() $\omega _1$
that starts from the considered configuration
$\omega _1$
that starts from the considered configuration
![]() $\sigma$
to the initial cycle
$\sigma$
to the initial cycle
![]() $\mathcal {C}_{\mathbf{e}}$
. We then construct another path
$\mathcal {C}_{\mathbf{e}}$
. We then construct another path
![]() $\omega _2$
that goes from
$\omega _2$
that goes from
![]() $\sigma$
to the target cycle
$\sigma$
to the target cycle
![]() $\mathcal {C}_{\mathbf{o}}$
as a suitable concatenation of the paths described in Lemmas4.8–4.9. The desired non-backtracking path
$\mathcal {C}_{\mathbf{o}}$
as a suitable concatenation of the paths described in Lemmas4.8–4.9. The desired non-backtracking path
![]() $\omega$
is the time-reversal of
$\omega$
is the time-reversal of
![]() $\omega _1$
concatenated with
$\omega _1$
concatenated with
![]() $\omega _2$
and it is easy to show that it is also optimal.
$\omega _2$
and it is easy to show that it is also optimal.
Assume now by contradiction that
![]() $\sigma$
is not essential, which means that there must exist another optimal path
$\sigma$
is not essential, which means that there must exist another optimal path
![]() $\omega ^{\prime} \in ({\mathbf{e}} \to {\mathbf{o}})_{\textrm {opt}}$
such that
$\omega ^{\prime} \in ({\mathbf{e}} \to {\mathbf{o}})_{\textrm {opt}}$
such that
![]() $S(\omega ^{\prime}) \subset S(\omega ) \setminus \{ \sigma \}$
. Recall that by Lemma 4.7(a), such a path
$S(\omega ^{\prime}) \subset S(\omega ) \setminus \{ \sigma \}$
. Recall that by Lemma 4.7(a), such a path
![]() $\omega ^{\prime}$
that avoids
$\omega ^{\prime}$
that avoids
![]() $\sigma$
still needs to visit the manifold
$\sigma$
still needs to visit the manifold
![]() $\mathcal {V}_{m(\sigma )}$
where
$\mathcal {V}_{m(\sigma )}$
where
![]() $\sigma$
lives at least once. Let
$\sigma$
lives at least once. Let
![]() $\eta$
be any such configuration in
$\eta$
be any such configuration in
![]() $\mathcal {V}_{m(\sigma )}\cap \omega ^{\prime}$
. We claim that such a configuration
$\mathcal {V}_{m(\sigma )}\cap \omega ^{\prime}$
. We claim that such a configuration
![]() $\eta$
must satisfy
$\eta$
must satisfy
This claim readily follows from Lemma 4.7(b) in combination with the facts that
![]() $L$
is even and
$L$
is even and
![]() $\Delta H(\sigma ) = L+1$
by construction.
$\Delta H(\sigma ) = L+1$
by construction.
If
![]() $\Delta H(\eta ) \geq L+3$
, then
$\Delta H(\eta ) \geq L+3$
, then
![]() $\omega ^{\prime}$
is not an optimal path, since
$\omega ^{\prime}$
is not an optimal path, since
![]() $\Phi _{\omega ^{\prime}}- H({\mathbf{e}}) \geq L+3 \gt L+1 = \Phi ({\mathbf{e}},{\mathbf{o}})-H({\mathbf{e}})$
.
$\Phi _{\omega ^{\prime}}- H({\mathbf{e}}) \geq L+3 \gt L+1 = \Phi ({\mathbf{e}},{\mathbf{o}})-H({\mathbf{e}})$
.
On the other hand, if
![]() $\Delta H(\eta )\leq L-1$
, then from Lemma 4.1 it follows that
$\Delta H(\eta )\leq L-1$
, then from Lemma 4.1 it follows that
![]() $\eta$
belongs to one of the two initial cycles. Proposition4.14 ensures that every non-backtracking optimal path crosses
$\eta$
belongs to one of the two initial cycles. Proposition4.14 ensures that every non-backtracking optimal path crosses
![]() $\mathcal {C}^*({\mathbf{e}},{\mathbf{o}})$
in one of the three ways (i)–(iii) described therein, so that also the optimal path
$\mathcal {C}^*({\mathbf{e}},{\mathbf{o}})$
in one of the three ways (i)–(iii) described therein, so that also the optimal path
![]() $\omega ^{\prime}$
passing through
$\omega ^{\prime}$
passing through
![]() $\eta$
has to visit
$\eta$
has to visit
![]() $\mathcal {C}^*({\mathbf{e}},{\mathbf{o}})$
. Since, by assumption, the path
$\mathcal {C}^*({\mathbf{e}},{\mathbf{o}})$
. Since, by assumption, the path
![]() $\omega ^{\prime}$
has to avoid the saddle
$\omega ^{\prime}$
has to avoid the saddle
![]() $\sigma$
, we deduce that there exists another saddle
$\sigma$
, we deduce that there exists another saddle
![]() $\tilde \eta$
obtained starting from
$\tilde \eta$
obtained starting from
![]() $\eta$
that does not belong to
$\eta$
that does not belong to
![]() $\mathcal {V}_{m(\sigma )}$
. In particular, the two paths cross the set
$\mathcal {V}_{m(\sigma )}$
. In particular, the two paths cross the set
![]() $\mathcal {C}^*({\mathbf{e}},{\mathbf{o}})$
in three different ways according to Proposition4.14(i)–(iii). Thus, we deduce that
$\mathcal {C}^*({\mathbf{e}},{\mathbf{o}})$
in three different ways according to Proposition4.14(i)–(iii). Thus, we deduce that
![]() $S(\omega ^{\prime}) \not \subset S(\omega ) \setminus \{ \sigma \}$
.
$S(\omega ^{\prime}) \not \subset S(\omega ) \setminus \{ \sigma \}$
.
Thus, in view of the parity of
![]() $\Delta H(\eta )$
, we must have
$\Delta H(\eta )$
, we must have
![]() $\Delta H(\eta ) = L+1$
, but then
$\Delta H(\eta ) = L+1$
, but then
![]() $\eta$
is a saddle and, by construction, it did not belong to
$\eta$
is a saddle and, by construction, it did not belong to
![]() $S(\omega )$
and thus
$S(\omega )$
and thus
![]() $S(\omega ^{\prime}) \not \subset S(\omega ) \setminus \{ \sigma \}$
.
$S(\omega ^{\prime}) \not \subset S(\omega ) \setminus \{ \sigma \}$
.
5. Proof of auxiliary results
In this section, we give the proof of some auxiliary results stated in Sections 3–4.
5.1 Results on the perimeter of an odd region
Proof of Proposition
3.4
. The proof revolves around the simple idea that using the filling algorithms introduced in subsection 3.3 we can expand the odd cluster
![]() $C$
(i.e., progressively increase the number of the occupied odd sites in
$C$
(i.e., progressively increase the number of the occupied odd sites in
![]() $C$
) in such a way that
$C$
) in such a way that
![]() $\mathcal {R}$
remains the surrounding rhombus and the energy of all configurations along such a path never exceeds
$\mathcal {R}$
remains the surrounding rhombus and the energy of all configurations along such a path never exceeds
![]() $H(\sigma )+1$
. Since by assumption
$H(\sigma )+1$
. Since by assumption
![]() $\sigma \neq \sigma ^{\prime}$
, the odd cluster
$\sigma \neq \sigma ^{\prime}$
, the odd cluster
![]() $C$
cannot coincide with
$C$
cannot coincide with
![]() $\mathcal {R}$
, in view of conditions (i), (ii), and (iii). Thus,
$\mathcal {R}$
, in view of conditions (i), (ii), and (iii). Thus,
![]() $C$
contains at least a broken diagonal or a shorter diagonal than those of the surrounding rhombus.
$C$
contains at least a broken diagonal or a shorter diagonal than those of the surrounding rhombus.
We can define the desired path
![]() $\omega$
as the concatenation of the two paths returned by the filling algorithms
$\omega$
as the concatenation of the two paths returned by the filling algorithms
![]() $\tilde \omega$
and
$\tilde \omega$
and
![]() $\bar \omega$
. If
$\bar \omega$
. If
![]() $C$
has no broken diagonal, we take
$C$
has no broken diagonal, we take
![]() $\tilde \omega$
empty. If
$\tilde \omega$
empty. If
![]() $C$
has no shorter diagonal, then
$C$
has no shorter diagonal, then
![]() $C$
already has the shape of a rhombus, and therefore we take
$C$
already has the shape of a rhombus, and therefore we take
![]() $\bar \omega$
empty. By the definition of these two paths, the energy increases by one only if an even site has to be emptied, but all these moves are followed by the addition of a particle in an antiknob. Therefore, the energy along the path
$\bar \omega$
empty. By the definition of these two paths, the energy increases by one only if an even site has to be emptied, but all these moves are followed by the addition of a particle in an antiknob. Therefore, the energy along the path
![]() $\omega$
increases by at most one with respect to the starting configuration
$\omega$
increases by at most one with respect to the starting configuration
![]() $\sigma$
. This procedure ends when
$\sigma$
. This procedure ends when
![]() $C$
coincides with
$C$
coincides with
![]() $\mathcal {R}$
, which implies that the resulting configuration is
$\mathcal {R}$
, which implies that the resulting configuration is
![]() $\sigma ^{\prime}$
.
$\sigma ^{\prime}$
.
To conclude the proof, we need to show the properties claimed for the perimeter of
![]() $\sigma$
. If
$\sigma$
. If
![]() $C$
contains
$C$
contains
![]() $m\geq 1$
broken diagonals, we argue as follows. Since the cluster
$m\geq 1$
broken diagonals, we argue as follows. Since the cluster
![]() $C$
is connected, all the empty odd sites in which the diagonals are broken are antiknobs, i.e., they have
$C$
is connected, all the empty odd sites in which the diagonals are broken are antiknobs, i.e., they have
![]() $n \in \{3,4\}$
neighbouring even sites belonging to
$n \in \{3,4\}$
neighbouring even sites belonging to
![]() $C$
, see Figure 12. We distinguish the following two cases. If
$C$
, see Figure 12. We distinguish the following two cases. If
![]() $n=3$
, then we first need to remove a particle from the unique neighbouring occupied even site, like the site
$n=3$
, then we first need to remove a particle from the unique neighbouring occupied even site, like the site
![]() $v$
represented in Figure 12 on the left.
$v$
represented in Figure 12 on the left.

Figure 12. Example of a configuration
![]() $\sigma$
as in the statement of Proposition3.4 (on the left), where we highlight in red the site containing the target antiknob, and the configuration obtained from
$\sigma$
as in the statement of Proposition3.4 (on the left), where we highlight in red the site containing the target antiknob, and the configuration obtained from
![]() $\sigma$
by filling it after removing a particle from the even site
$\sigma$
by filling it after removing a particle from the even site
![]() $v$
(on the right), with highlighted in red the site containing the next target antiknob.
$v$
(on the right), with highlighted in red the site containing the next target antiknob.
After that move, when the particle is added in the antiknob, the perimeter does not change in view of (3.3), otherwise if
![]() $n=4$
then the perimeter decreases (see Figure 12 on the right). This also occurs when we add a particle in the target antiknobs except the last antiknob to obtain the complete diagonal, for which by construction, we have that the perimeter decreases by 4. By iterating this argument for every broken diagonal, we get
$n=4$
then the perimeter decreases (see Figure 12 on the right). This also occurs when we add a particle in the target antiknobs except the last antiknob to obtain the complete diagonal, for which by construction, we have that the perimeter decreases by 4. By iterating this argument for every broken diagonal, we get
If
![]() $C$
does not contain any broken diagonal, we argue as follows. By construction, we deduce that the first odd site we will fill, which is the nearest neighbour of the first shorter diagonal, has three neighbouring even sites belonging to
$C$
does not contain any broken diagonal, we argue as follows. By construction, we deduce that the first odd site we will fill, which is the nearest neighbour of the first shorter diagonal, has three neighbouring even sites belonging to
![]() $C$
. Thus, we need to remove a particle from the unique occupied neighbouring even site and then, when the first particle is added to the unique possible antiknob, the perimeter does not change thanks to (3.3). This also occurs when we iterate this argument.
$C$
. Thus, we need to remove a particle from the unique occupied neighbouring even site and then, when the first particle is added to the unique possible antiknob, the perimeter does not change thanks to (3.3). This also occurs when we iterate this argument.
Proof of Proposition
3.6
. Given any
![]() $n$
positive number, let
$n$
positive number, let
![]() $C$
be an odd cluster with area
$C$
be an odd cluster with area
![]() $n$
. If the cluster
$n$
. If the cluster
![]() $C$
is not connected, by (3.3) it directly follows that
$C$
is not connected, by (3.3) it directly follows that
![]() $C$
cannot minimize the perimeter of an odd cluster with
$C$
cannot minimize the perimeter of an odd cluster with
![]() $n$
particles. Indeed, when the cluster is not connected, the cardinality of
$n$
particles. Indeed, when the cluster is not connected, the cardinality of
![]() $C\cap V_{\mathbf{e}}$
decreases, while the cardinality of
$C\cap V_{\mathbf{e}}$
decreases, while the cardinality of
![]() $C\cap V_{\mathbf{o}}$
is fixed equal to
$C\cap V_{\mathbf{o}}$
is fixed equal to
![]() $n$
. Consider now a connected cluster
$n$
. Consider now a connected cluster
![]() $C$
. First, we will show that the minimal perimeter is that of the surrounding rhombus. To this end, we consider separately the following three cases:
$C$
. First, we will show that the minimal perimeter is that of the surrounding rhombus. To this end, we consider separately the following three cases:
-
1. There exists at least one broken diagonal. In this case, we have that
 $P(C)\gt P(\mathcal {R}(C))$
by applying Proposition3.4.
$P(C)\gt P(\mathcal {R}(C))$
by applying Proposition3.4. -
2. There is no broken diagonal, but there exists at least one shorter diagonal with respect to those of the surrounding rhombus. In this case, we have that
 $P(C)=P(\mathcal {R}(C))$
by applying Proposition3.4.
$P(C)=P(\mathcal {R}(C))$
by applying Proposition3.4. -
3. All diagonals have the same length as those of the surrounding rhombus, namely, all the diagonals are complete. In this case
 $C=\mathcal {R}(C)$
, so it is trivial that
$C=\mathcal {R}(C)$
, so it is trivial that
 $P(C)=P(\mathcal {R}(C))$
.
$P(C)=P(\mathcal {R}(C))$
.
Lastly, we need to show that the minimizing rhombus is either
![]() $\mathcal {R}_{s-1,s}$
or
$\mathcal {R}_{s-1,s}$
or
![]() $\mathcal {R}_{s,s-1}$
if
$\mathcal {R}_{s,s-1}$
if
![]() $n= s(s-1)+k$
and
$n= s(s-1)+k$
and
![]() $\mathcal {R}_{s,s}$
if
$\mathcal {R}_{s,s}$
if
![]() $n=s^2+k$
. We argue by induction over
$n=s^2+k$
. We argue by induction over
![]() $n$
. If
$n$
. If
![]() $n=1$
, then it is trivial that the rhombus
$n=1$
, then it is trivial that the rhombus
![]() $\mathcal {R}_{1,1}$
minimizes the perimeter and
$\mathcal {R}_{1,1}$
minimizes the perimeter and
![]() $n=1$
can be represented in the form
$n=1$
can be represented in the form
![]() $s(s-1)+k$
choosing
$s(s-1)+k$
choosing
![]() $s=1$
and
$s=1$
and
![]() $k=0$
. Suppose now
$k=0$
. Suppose now
![]() $n\gt 1$
and that the claim is true for any
$n\gt 1$
and that the claim is true for any
![]() $m\lt n$
. Suppose that
$m\lt n$
. Suppose that
![]() $n-1$
can be written as
$n-1$
can be written as
![]() $s(s-1)+k$
. In the other case, where
$s(s-1)+k$
. In the other case, where
![]() $n=s^2+k$
, we can argue in a similar way. If
$n=s^2+k$
, we can argue in a similar way. If
![]() $n-1=s(s-1)+k$
, with
$n-1=s(s-1)+k$
, with
![]() $0\leq k\leq s-2$
(resp.
$0\leq k\leq s-2$
(resp.
![]() $k=s-1$
), then either the rhombus
$k=s-1$
), then either the rhombus
![]() $\mathcal {R}_{s,s-1}$
or
$\mathcal {R}_{s,s-1}$
or
![]() $\mathcal {R}_{s-1,s}$
(resp. the rhombus
$\mathcal {R}_{s-1,s}$
(resp. the rhombus
![]() $\mathcal {R}_{s,s}$
) minimizes the perimeter of an odd cluster with
$\mathcal {R}_{s,s}$
) minimizes the perimeter of an odd cluster with
![]() $n$
particles. Indeed, in any other case, the surrounding rhombus could be either
$n$
particles. Indeed, in any other case, the surrounding rhombus could be either
![]() $\mathcal {R}_{s+1,s-1}$
or
$\mathcal {R}_{s+1,s-1}$
or
![]() $\mathcal {R}_{s-1,s+1}$
, which has a strictly greater perimeter in view of (3.13). Note that assumption
$\mathcal {R}_{s-1,s+1}$
, which has a strictly greater perimeter in view of (3.13). Note that assumption
![]() $n\leq L(L-2)$
is needed to avoid rhombi with a maximal side equal to
$n\leq L(L-2)$
is needed to avoid rhombi with a maximal side equal to
![]() $L$
, because in view of (3.13) we would lose the uniqueness of the minimizing configuration.
$L$
, because in view of (3.13) we would lose the uniqueness of the minimizing configuration.
Proof of Corollary
3.7
. We first consider the case in which the area
![]() $n$
is of the form
$n$
is of the form
![]() $n=s(s-1)+k$
. If
$n=s(s-1)+k$
. If
![]() $s\lt L/2$
, we have that the perimeter of the odd cluster is
$s\lt L/2$
, we have that the perimeter of the odd cluster is
![]() $P=4(2s+1)$
. Since the cluster is contained in a rhombus
$P=4(2s+1)$
. Since the cluster is contained in a rhombus
![]() $\mathcal {R}_{s,s}$
, we have that
$\mathcal {R}_{s,s}$
, we have that
![]() $n\leq s^2$
and, hence,
$n\leq s^2$
and, hence,
![]() $\bigl (\frac {P}{4}-1\bigr )^2\geq 4n$
. If
$\bigl (\frac {P}{4}-1\bigr )^2\geq 4n$
. If
![]() $L/2\leq s\lt L$
, then the perimeter of the odd cluster is
$L/2\leq s\lt L$
, then the perimeter of the odd cluster is
![]() $P=4(2L-2s-1)$
. Since the cluster is contained in a rhombus
$P=4(2L-2s-1)$
. Since the cluster is contained in a rhombus
![]() $\mathcal {R}_{s,s}$
and therefore the complement in
$\mathcal {R}_{s,s}$
and therefore the complement in
![]() $V$
is a rhombus
$V$
is a rhombus
![]() $\mathcal {R}_{L-s-1,L-s-1}$
, we have that
$\mathcal {R}_{L-s-1,L-s-1}$
, we have that
![]() $n\geq \frac {L^2}{2}-(L-s-1)^2$
. Hence
$n\geq \frac {L^2}{2}-(L-s-1)^2$
. Hence
Consider now the other case, when the area
![]() $n$
is of the form
$n$
is of the form
![]() $n=s^2+k$
. If
$n=s^2+k$
. If
![]() $s\lt L/2$
we have that the perimeter of the odd cluster is
$s\lt L/2$
we have that the perimeter of the odd cluster is
![]() $P=4(2s+2)$
. Since the cluster is contained in a rhombus either
$P=4(2s+2)$
. Since the cluster is contained in a rhombus either
![]() $\mathcal {R}_{s+1,s}$
or
$\mathcal {R}_{s+1,s}$
or
![]() $\mathcal {R}_{s,s+1}$
, we have that
$\mathcal {R}_{s,s+1}$
, we have that
![]() $n\leq s^2+s$
. Thus, it holds
$n\leq s^2+s$
. Thus, it holds
If
![]() $L/2\leq s\lt L$
, then the perimeter of the odd cluster is
$L/2\leq s\lt L$
, then the perimeter of the odd cluster is
![]() $P=4(2L-2s-2)$
. Since the cluster is contained in either a rhombus
$P=4(2L-2s-2)$
. Since the cluster is contained in either a rhombus
![]() $\mathcal {R}_{s+1,s}$
or
$\mathcal {R}_{s+1,s}$
or
![]() $\mathcal {R}_{s,s+1}$
and therefore the complement in
$\mathcal {R}_{s,s+1}$
and therefore the complement in
![]() $V$
is either a rhombus
$V$
is either a rhombus
![]() $\mathcal {R}_{L-s-2,L-s-1}$
or
$\mathcal {R}_{L-s-2,L-s-1}$
or
![]() $\mathcal {R}_{L-s-1,L-s-2}$
, we have that
$\mathcal {R}_{L-s-1,L-s-2}$
, we have that
![]() $n\geq \frac {L^2}{2}-(L-s-1)(L-s-2)$
. Hence,
$n\geq \frac {L^2}{2}-(L-s-1)(L-s-2)$
. Hence,
Using condition
![]() $n\leq L(L-2)$
, inequality (3.19) directly follows.
$n\leq L(L-2)$
, inequality (3.19) directly follows.
Proof of Lemma
3.8
. Let
![]() $\sigma$
be a configuration with real area
$\sigma$
be a configuration with real area
![]() $\tilde n=2\ell ^2+2\ell +1$
. First, we suppose that the set of odd clusters in
$\tilde n=2\ell ^2+2\ell +1$
. First, we suppose that the set of odd clusters in
![]() $\sigma$
is composed only of
$\sigma$
is composed only of
![]() $j \geq 2$
non-degenerate clusters. Each of them has area
$j \geq 2$
non-degenerate clusters. Each of them has area
![]() $n_i$
and perimeter
$n_i$
and perimeter
![]() $p_i$
for
$p_i$
for
![]() $i=1,\ldots, j$
. Suppose by contradiction that
$i=1,\ldots, j$
. Suppose by contradiction that
![]() $\sigma$
has minimal perimeter so that the area of the configuration
$\sigma$
has minimal perimeter so that the area of the configuration
![]() $\sigma$
is
$\sigma$
is
![]() $n_\sigma =\sum _{i=1}^j n_i$
and its perimeter is
$n_\sigma =\sum _{i=1}^j n_i$
and its perimeter is
![]() $p_\sigma = 4(2\sqrt {n_\sigma }+1)$
. By (3.19), we have
$p_\sigma = 4(2\sqrt {n_\sigma }+1)$
. By (3.19), we have
![]() $p_i \geq 4(2\sqrt {n_i}+1)$
for any
$p_i \geq 4(2\sqrt {n_i}+1)$
for any
![]() $i=1,\ldots, j$
. Then we obtain that
$i=1,\ldots, j$
. Then we obtain that
 \begin{align} p_{\sigma }=\sum _{i=1}^j p_i\geq \sum _{i=1}^j 4(2\sqrt {n_i}+1)\geq 8\sqrt {\sum _{i=1}^j n_i}+4j\geq 8\Bigg (\sqrt {\sum _{i=1}^j n_i}+1\Bigg )=4(2\sqrt {n_\sigma }+2), \end{align}
\begin{align} p_{\sigma }=\sum _{i=1}^j p_i\geq \sum _{i=1}^j 4(2\sqrt {n_i}+1)\geq 8\sqrt {\sum _{i=1}^j n_i}+4j\geq 8\Bigg (\sqrt {\sum _{i=1}^j n_i}+1\Bigg )=4(2\sqrt {n_\sigma }+2), \end{align}
that is a contradiction.
Second, we suppose that the set of odd clusters in
![]() $\sigma$
is composed of
$\sigma$
is composed of
![]() $k \geq 1$
degenerate clusters and of
$k \geq 1$
degenerate clusters and of
![]() $j \geq 1$
non-degenerate clusters. Each of these non-degenerate clusters has area
$j \geq 1$
non-degenerate clusters. Each of these non-degenerate clusters has area
![]() $n_i$
and perimeter
$n_i$
and perimeter
![]() $p_i$
for
$p_i$
for
![]() $i=1,\ldots, j$
, so that
$i=1,\ldots, j$
, so that
![]() $n_\sigma =\sum _{i=1}^j n_i$
. We denote by
$n_\sigma =\sum _{i=1}^j n_i$
. We denote by
![]() $\tilde p_i$
for
$\tilde p_i$
for
![]() $i=1,\ldots, k$
the perimeter of a degenerate cluster. Suppose by contradiction that
$i=1,\ldots, k$
the perimeter of a degenerate cluster. Suppose by contradiction that
![]() $\sigma$
has minimal perimeter. By (3.19), we have
$\sigma$
has minimal perimeter. By (3.19), we have
![]() $p_i \geq 4(2\sqrt {n_i}+1)$
for any
$p_i \geq 4(2\sqrt {n_i}+1)$
for any
![]() $i=1,\ldots, j$
and
$i=1,\ldots, j$
and
![]() $p_\sigma = 4(2\sqrt {n_\sigma }+1)$
. Thus, we obtain
$p_\sigma = 4(2\sqrt {n_\sigma }+1)$
. Thus, we obtain
 \begin{align} p_{\sigma } & = \sum _{i=1}^{j} p_i+\sum _{i=1}^{k} \tilde p_i \geq \sum _{i=1}^j 4(2\sqrt {n_i}+1)+4k\geq 8\sqrt {\sum _{i=1}^j n_i}+4j+4k\geq 8 \nonumber \\ & \quad \sqrt {\sum _{i=1}^j n_i}+4+4=4(2\sqrt {n_\sigma }+2), \end{align}
\begin{align} p_{\sigma } & = \sum _{i=1}^{j} p_i+\sum _{i=1}^{k} \tilde p_i \geq \sum _{i=1}^j 4(2\sqrt {n_i}+1)+4k\geq 8\sqrt {\sum _{i=1}^j n_i}+4j+4k\geq 8 \nonumber \\ & \quad \sqrt {\sum _{i=1}^j n_i}+4+4=4(2\sqrt {n_\sigma }+2), \end{align}
that is a contradiction. Thus, we obtain that
![]() $k=0$
and
$k=0$
and
![]() $j=1$
. Since the real area
$j=1$
. Since the real area
![]() $\tilde n$
of the configuration
$\tilde n$
of the configuration
![]() $\sigma$
is fixed, then also the area
$\sigma$
is fixed, then also the area
![]() $n_\sigma$
is fixed. Thus, given that
$n_\sigma$
is fixed. Thus, given that
![]() $\sigma$
contains only one non-degenerate cluster with minimal perimeter and with fixed area, by Corollary3.7 we obtain that the non-degenerate cluster is the rhombus
$\sigma$
contains only one non-degenerate cluster with minimal perimeter and with fixed area, by Corollary3.7 we obtain that the non-degenerate cluster is the rhombus
![]() $\mathcal {R}_{\ell, \ell }$
, which has precisely real area
$\mathcal {R}_{\ell, \ell }$
, which has precisely real area
![]() $\tilde n$
.
$\tilde n$
.
5.2 Results on optimal reference paths
Proof of Lemma
4.8
. We start by proving (i). The desired path
![]() $\omega =({\mathbf{e}},\omega _1,\ldots, \omega _{k(L)},\eta )$
is obtained as follows. Starting from
$\omega =({\mathbf{e}},\omega _1,\ldots, \omega _{k(L)},\eta )$
is obtained as follows. Starting from
![]() ${\mathbf{e}}$
, define the configuration
${\mathbf{e}}$
, define the configuration
![]() $\omega _1$
as that in which one particle is removed from an empty even site, say
$\omega _1$
as that in which one particle is removed from an empty even site, say
![]() $v_1\in V_{\mathbf{e}}$
. Similarly, we define
$v_1\in V_{\mathbf{e}}$
. Similarly, we define
![]() $\omega _2$
as the configuration in which a particle is removed from a site
$\omega _2$
as the configuration in which a particle is removed from a site
![]() $v_2\in V_{\mathbf{e}}$
such that
$v_2\in V_{\mathbf{e}}$
such that
![]() $d(v_1,v_2)=2$
. Similarly, by removing the particles in
$d(v_1,v_2)=2$
. Similarly, by removing the particles in
![]() $v_3,v_4\in V_{\mathbf{e}}$
in such a way
$v_3,v_4\in V_{\mathbf{e}}$
in such a way
![]() $d(v_i,v_j)=2$
for any
$d(v_i,v_j)=2$
for any
![]() $i,j=1,\ldots, 4$
and
$i,j=1,\ldots, 4$
and
![]() $i\neq j$
, we define the configurations
$i\neq j$
, we define the configurations
![]() $\omega _3$
and
$\omega _3$
and
![]() $\omega _4$
. Note that
$\omega _4$
. Note that
![]() $\Delta H(\omega _4)=4\lt L+1$
. Thus, we can define the configuration
$\Delta H(\omega _4)=4\lt L+1$
. Thus, we can define the configuration
![]() $\omega _5$
as that obtained from
$\omega _5$
as that obtained from
![]() $\omega _4$
by adding a particle to the unique unblocked odd site, i.e., the one at distance one from
$\omega _4$
by adding a particle to the unique unblocked odd site, i.e., the one at distance one from
![]() $v_i$
for any
$v_i$
for any
![]() $i=1,\ldots, 4$
. See Figure 13 on the left.
$i=1,\ldots, 4$
. See Figure 13 on the left.

Figure 13. Example of the configurations
![]() $\omega _5$
(on the left),
$\omega _5$
(on the left),
![]() $\omega _7$
(in the middle) and
$\omega _7$
(in the middle) and
![]() $\omega _{13}$
(on the right) visited by the path described in the proof of Lemma 4.8(i).
$\omega _{13}$
(on the right) visited by the path described in the proof of Lemma 4.8(i).
We obtain that
![]() $\Delta H(\omega _5)=3\lt L+1$
and
$\Delta H(\omega _5)=3\lt L+1$
and
![]() $\omega _5$
is composed of a unique non-degenerate odd cluster, which is
$\omega _5$
is composed of a unique non-degenerate odd cluster, which is
![]() $\mathcal {R}_{1,1}$
. To define the configuration
$\mathcal {R}_{1,1}$
. To define the configuration
![]() $\omega _6$
, we remove a particle from a site
$\omega _6$
, we remove a particle from a site
![]() $v_5\in V_{\mathbf{e}}$
such that
$v_5\in V_{\mathbf{e}}$
such that
![]() $d(v_i,v_5)=2$
for two indices
$d(v_i,v_5)=2$
for two indices
![]() $i=1,\ldots, 4$
. Similarly, we define
$i=1,\ldots, 4$
. Similarly, we define
![]() $\omega _7$
in such a way there is an empty odd site with all the neighbouring even sites that are empty, see Figure 13 in the middle. Note that
$\omega _7$
in such a way there is an empty odd site with all the neighbouring even sites that are empty, see Figure 13 in the middle. Note that
![]() $\Delta H(\omega _7)=5\lt L+1$
. Then, we define
$\Delta H(\omega _7)=5\lt L+1$
. Then, we define
![]() $\omega _8$
by adding a particle in the unique unblocked odd site, so that
$\omega _8$
by adding a particle in the unique unblocked odd site, so that
![]() $\Delta H(\omega _8)=4\lt L+1$
. Note that
$\Delta H(\omega _8)=4\lt L+1$
. Note that
![]() $\omega _8$
contains an odd cluster
$\omega _8$
contains an odd cluster
![]() $\mathcal {R}_{1,2}$
. By growing the odd cluster in a spiral fashion, emptying the even sites that are strictly necessary, note that the configuration
$\mathcal {R}_{1,2}$
. By growing the odd cluster in a spiral fashion, emptying the even sites that are strictly necessary, note that the configuration
![]() $\omega _{13}$
contains only the non-degenerate cluster
$\omega _{13}$
contains only the non-degenerate cluster
![]() $\mathcal {R}_{2,2}$
(see Figure 13 on the right). Then, our path visits all the configurations which have a unique non-degenerate odd cluster
$\mathcal {R}_{2,2}$
(see Figure 13 on the right). Then, our path visits all the configurations which have a unique non-degenerate odd cluster
![]() $C$
such that
$C$
such that
![]() $C=\mathcal {R}_{\ell, \ell }$
and
$C=\mathcal {R}_{\ell, \ell }$
and
![]() $C=\mathcal {R}_{\ell, \ell +1}$
for any
$C=\mathcal {R}_{\ell, \ell +1}$
for any
![]() $3\leq \ell \leq \frac {L}{2}-1$
up to the configuration
$3\leq \ell \leq \frac {L}{2}-1$
up to the configuration
![]() $\omega _{{k(L)}-1}$
, whose unique non-degenerate odd cluster is
$\omega _{{k(L)}-1}$
, whose unique non-degenerate odd cluster is
![]() $C=\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
. Then, the configuration
$C=\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
. Then, the configuration
![]() $\omega _{k(L)}$
is defined by removing a particle from an even site
$\omega _{k(L)}$
is defined by removing a particle from an even site
![]() $w$
at distance two from
$w$
at distance two from
![]() $C$
. Finally, the configuration
$C$
. Finally, the configuration
![]() $\eta$
is obtained by removing a particle from an even site at distance two from
$\eta$
is obtained by removing a particle from an even site at distance two from
![]() $C$
and from
$C$
and from
![]() $w$
. Since the procedure we defined is invariant by translation, given a fixed configuration
$w$
. Since the procedure we defined is invariant by translation, given a fixed configuration
![]() $\eta \in \mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
is possible to choose the position of the odd clusters in such a way the final configuration of the path we described coincides with the desired
$\eta \in \mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
is possible to choose the position of the odd clusters in such a way the final configuration of the path we described coincides with the desired
![]() $\eta$
. It remains to show that
$\eta$
. It remains to show that
![]() $\arg \max _{\xi \in \omega }H(\xi )=\{\eta \}$
. To this end, since
$\arg \max _{\xi \in \omega }H(\xi )=\{\eta \}$
. To this end, since
![]() $\Delta H(\eta )=L+1$
and therefore
$\Delta H(\eta )=L+1$
and therefore
![]() $\Delta H(\omega _{k(L)})=L$
and
$\Delta H(\omega _{k(L)})=L$
and
![]() $\Delta H(\omega _{{k(L)}-1})=L-1$
, we need only to show that
$\Delta H(\omega _{{k(L)}-1})=L-1$
, we need only to show that
First, we will show that
![]() $\Delta H(\eta )=3+2(\ell -1)$
by induction over the dimension
$\Delta H(\eta )=3+2(\ell -1)$
by induction over the dimension
![]() $\ell =1,\ldots, \frac {L}{2}-1$
of the rhombus
$\ell =1,\ldots, \frac {L}{2}-1$
of the rhombus
![]() $\mathcal {R}_{\ell, \ell }$
composing the unique odd cluster of the configurations
$\mathcal {R}_{\ell, \ell }$
composing the unique odd cluster of the configurations
![]() $\eta$
visited by
$\eta$
visited by
![]() $\omega$
. We have already proven the desired property in the case
$\omega$
. We have already proven the desired property in the case
![]() $\ell =1$
. Suppose now that the claim holds for
$\ell =1$
. Suppose now that the claim holds for
![]() $\ell$
, with
$\ell$
, with
![]() $1\leq \ell \leq \frac {L}{2}-2$
, thus we will prove that it holds also for
$1\leq \ell \leq \frac {L}{2}-2$
, thus we will prove that it holds also for
![]() $\ell +1$
. To reach the configuration displaying the rhombus
$\ell +1$
. To reach the configuration displaying the rhombus
![]() $\mathcal {R}_{\ell, \ell +1}$
starting from
$\mathcal {R}_{\ell, \ell +1}$
starting from
![]() $\mathcal {R}_{\ell, \ell }$
, we need first to remove particles from two even sites by increasing the energy by two. Then, we sequentially add a particle in an odd site and remove a particle in an even site until the length of the shorter diagonal is
$\mathcal {R}_{\ell, \ell }$
, we need first to remove particles from two even sites by increasing the energy by two. Then, we sequentially add a particle in an odd site and remove a particle in an even site until the length of the shorter diagonal is
![]() $\ell -1$
. Finally, the last move is the addition of a particle in an odd site without the need to remove any particle from an even site. Starting from
$\ell -1$
. Finally, the last move is the addition of a particle in an odd site without the need to remove any particle from an even site. Starting from
![]() $\mathcal {R}_{\ell, \ell +1}$
, to obtain
$\mathcal {R}_{\ell, \ell +1}$
, to obtain
![]() $\mathcal {R}_{\ell +1,\ell +1}$
we follow the same sequence of moves. Thus, for a configuration
$\mathcal {R}_{\ell +1,\ell +1}$
we follow the same sequence of moves. Thus, for a configuration
![]() $\eta$
containing as unique odd cluster a rhombus
$\eta$
containing as unique odd cluster a rhombus
![]() $\mathcal {R}_{\ell +1,\ell +1}$
we deduce that
$\mathcal {R}_{\ell +1,\ell +1}$
we deduce that
![]() $\Delta H(\eta )=3+2(\ell -1)+2$
, which proves our claim for
$\Delta H(\eta )=3+2(\ell -1)+2$
, which proves our claim for
![]() $\ell +1$
. Along the sequence of moves from
$\ell +1$
. Along the sequence of moves from
![]() $\mathcal {R}_{\ell, \ell }$
to
$\mathcal {R}_{\ell, \ell }$
to
![]() $\mathcal {R}_{\ell +1,\ell +1}$
, the energy is at most
$\mathcal {R}_{\ell +1,\ell +1}$
, the energy is at most
![]() $3+2(\ell -1)+3$
, which is strictly less than
$3+2(\ell -1)+3$
, which is strictly less than
![]() $L+1$
for
$L+1$
for
![]() $\ell \leq \frac {L}{2}-1$
. Note that we do not to consider the case
$\ell \leq \frac {L}{2}-1$
. Note that we do not to consider the case
![]() $\ell =\frac {L}{2}-2$
, indeed the path
$\ell =\frac {L}{2}-2$
, indeed the path
![]() $\omega$
stops before reaching the rhombus
$\omega$
stops before reaching the rhombus
![]() $\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}}$
. This concludes the proof of (i).
$\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}}$
. This concludes the proof of (i).
Now, we prove (ii). The desired path
![]() $\omega =({\mathbf{e}},\omega _1,\ldots, \omega _{k(L)},\eta )$
is obtained as follows. Starting from
$\omega =({\mathbf{e}},\omega _1,\ldots, \omega _{k(L)},\eta )$
is obtained as follows. Starting from
![]() ${\mathbf{e}}$
, define the configuration
${\mathbf{e}}$
, define the configuration
![]() $\omega _1$
as that in which one particle is removed from an empty even site, say
$\omega _1$
as that in which one particle is removed from an empty even site, say
![]() $v_1\in V_{\mathbf{e}}$
. Similarly, we define
$v_1\in V_{\mathbf{e}}$
. Similarly, we define
![]() $\omega _2$
as the configuration in which a particle is removed from a site
$\omega _2$
as the configuration in which a particle is removed from a site
![]() $v_2\in V_{\mathbf{e}}$
such that
$v_2\in V_{\mathbf{e}}$
such that
![]() $d(v_1,v_2)=2$
. Similarly, by removing particles in
$d(v_1,v_2)=2$
. Similarly, by removing particles in
![]() $v_3,v_4\in V_{\mathbf{e}}$
in such a way
$v_3,v_4\in V_{\mathbf{e}}$
in such a way
![]() $d(v_i,v_j)=2$
for any
$d(v_i,v_j)=2$
for any
![]() $i,j=1,\ldots, 4$
and
$i,j=1,\ldots, 4$
and
![]() $i\neq j$
, we define the configurations
$i\neq j$
, we define the configurations
![]() $\omega _3$
and
$\omega _3$
and
![]() $\omega _4$
. Note that
$\omega _4$
. Note that
![]() $\Delta H(\omega _4)=4\lt L+1$
. Thus, we can define the configuration
$\Delta H(\omega _4)=4\lt L+1$
. Thus, we can define the configuration
![]() $\omega _5$
as the one obtained from
$\omega _5$
as the one obtained from
![]() $\omega _4$
by adding a particle in the unique unblocked odd site, i.e., the one at distance one from
$\omega _4$
by adding a particle in the unique unblocked odd site, i.e., the one at distance one from
![]() $v_i$
for any
$v_i$
for any
![]() $i=1,\ldots, 4$
. We obtain that
$i=1,\ldots, 4$
. We obtain that
![]() $\Delta H(\omega _5)=3\lt L+1$
and
$\Delta H(\omega _5)=3\lt L+1$
and
![]() $\omega _5$
is composed of a unique non-degenerate odd cluster, which is
$\omega _5$
is composed of a unique non-degenerate odd cluster, which is
![]() $\mathcal {R}_{1,1}$
, see Figure 14 on the left.
$\mathcal {R}_{1,1}$
, see Figure 14 on the left.

Figure 14. Example of the configurations
![]() $\omega _5$
(on the left),
$\omega _5$
(on the left),
![]() $\omega _7$
(in the middle) and
$\omega _7$
(in the middle) and
![]() $\omega _{9}$
(on the right) visited by the path described in the proof of Lemma 4.8(ii).
$\omega _{9}$
(on the right) visited by the path described in the proof of Lemma 4.8(ii).
Next, we describe four steps that are used in the following iteration. The first step is to define the configuration
![]() $\omega _6$
by removing a particle from a site
$\omega _6$
by removing a particle from a site
![]() $v_5\in V_{\mathbf{e}}$
such that
$v_5\in V_{\mathbf{e}}$
such that
![]() $d(v_i,v_5)=2$
for two indices
$d(v_i,v_5)=2$
for two indices
![]() $i=1,\ldots, 4$
. The second step is to remove a particle from a site
$i=1,\ldots, 4$
. The second step is to remove a particle from a site
![]() $v_6\in V_{\mathbf{e}}$
in such a way there is an empty odd site with two neighbouring empty even sites and the other one is occupied. In this way, we obtain the configuration
$v_6\in V_{\mathbf{e}}$
in such a way there is an empty odd site with two neighbouring empty even sites and the other one is occupied. In this way, we obtain the configuration
![]() $\omega _7$
(see Figure 14 in the middle). The third step is to obtain the configuration
$\omega _7$
(see Figure 14 in the middle). The third step is to obtain the configuration
![]() $\omega _8$
by removing the particle in the site
$\omega _8$
by removing the particle in the site
![]() $v_7\in V_{\mathbf{e}}$
such that
$v_7\in V_{\mathbf{e}}$
such that
![]() $d(v_7,v_5)=d(v_7,v_6)=2$
. Note that
$d(v_7,v_5)=d(v_7,v_6)=2$
. Note that
![]() $\Delta H(\omega _8)=6\lt L+1$
. Then, the last step is to define
$\Delta H(\omega _8)=6\lt L+1$
. Then, the last step is to define
![]() $\omega _9$
by adding a particle in the unique unblocked odd site, so that
$\omega _9$
by adding a particle in the unique unblocked odd site, so that
![]() $\Delta H(\omega _9)=5\lt L+1$
and the energy cost of these four steps is
$\Delta H(\omega _9)=5\lt L+1$
and the energy cost of these four steps is
![]() $2$
. Note that
$2$
. Note that
![]() $\omega _9$
is composed of a non-degenerate odd cluster with two odd particles along either the same column or the same row, see Figure 14 on the right.
$\omega _9$
is composed of a non-degenerate odd cluster with two odd particles along either the same column or the same row, see Figure 14 on the right.
From this point on, we iterate these four steps for other
![]() $\frac {L}{2}-3$
times, until we obtain the configuration
$\frac {L}{2}-3$
times, until we obtain the configuration
![]() $\omega _{k(L)-1}$
in which either a column or a row contains
$\omega _{k(L)-1}$
in which either a column or a row contains
![]() $\frac {L}{2}-1$
odd particles. Note that
$\frac {L}{2}-1$
odd particles. Note that
![]() $\Delta H(\omega _{k(L)-1})=5+2(\frac {L}{2}-3)=L-1$
. Then, we repeat the first two steps described above and reach the configuration
$\Delta H(\omega _{k(L)-1})=5+2(\frac {L}{2}-3)=L-1$
. Then, we repeat the first two steps described above and reach the configuration
![]() $\eta \in \mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
with
$\eta \in \mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
with
![]() $\Delta H(\eta )=L+1$
. It is easy to check that
$\Delta H(\eta )=L+1$
. It is easy to check that
![]() $\arg \max _{\xi \in \omega }=\{\eta \}$
. Indeed, we get
$\arg \max _{\xi \in \omega }=\{\eta \}$
. Indeed, we get
 \begin{equation*} \begin{array}{lll} \Delta H (\omega _{i})&=\Delta H (\omega _{i-1})+1 \qquad &\text { if } 1\leq i\leq 4, \\[3pt] \Delta H (\omega _{2i-1})&=\Delta H (\omega _{2i})-1 \qquad &\text { if } 3\leq i \leq \frac {k(L)}{2}, \\[3pt] \Delta H (\omega _{2i})&=\Delta H (\omega _{2i-1})+3 \qquad &\text { if } 3\leq i \leq \frac {k(L)}{2}-1, \\[3pt] \Delta H (\omega _{k(L)})&=\Delta H (\omega _{k(L)-1})+2, \end{array} \end{equation*}
\begin{equation*} \begin{array}{lll} \Delta H (\omega _{i})&=\Delta H (\omega _{i-1})+1 \qquad &\text { if } 1\leq i\leq 4, \\[3pt] \Delta H (\omega _{2i-1})&=\Delta H (\omega _{2i})-1 \qquad &\text { if } 3\leq i \leq \frac {k(L)}{2}, \\[3pt] \Delta H (\omega _{2i})&=\Delta H (\omega _{2i-1})+3 \qquad &\text { if } 3\leq i \leq \frac {k(L)}{2}-1, \\[3pt] \Delta H (\omega _{k(L)})&=\Delta H (\omega _{k(L)-1})+2, \end{array} \end{equation*}
which concludes the proof of (ii).
Proof of Lemma
4.9
. We start by proving (i). Take the path described in Lemma 4.8(ii) until it visits for the first time a configuration in
![]() $\mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
as in Figure 11 on the left. Starting from such a configuration, add a particle in the unique unblocked odd site. Then, remove a particle from an even site at distance one from an antiknob, and finally add a particle in the unique unblocked odd site. Afterward, iterate the sequence of these two moves up to the target configuration
$\mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
as in Figure 11 on the left. Starting from such a configuration, add a particle in the unique unblocked odd site. Then, remove a particle from an even site at distance one from an antiknob, and finally add a particle in the unique unblocked odd site. Afterward, iterate the sequence of these two moves up to the target configuration
![]() $\eta \in \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
. By construction, the resulting path has the desired property.
$\eta \in \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
. By construction, the resulting path has the desired property.
Let us now focus on case (ii). Consider the path described in Lemma 4.8(i) until it visits for the first time a configuration in
![]() $\mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
. Starting from such a configuration, add a particle in the antiknob, obtaining a configuration
$\mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
. Starting from such a configuration, add a particle in the antiknob, obtaining a configuration
![]() $\eta ^{\prime}$
that displays a unique non-degenerate odd cluster, which is a rhombus
$\eta ^{\prime}$
that displays a unique non-degenerate odd cluster, which is a rhombus
![]() $\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
with a single protuberance. Starting from
$\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
with a single protuberance. Starting from
![]() $\eta ^{\prime}$
, consider the path returned filling algorithm
$\eta ^{\prime}$
, consider the path returned filling algorithm
![]() $\bar \omega$
up to the configuration
$\bar \omega$
up to the configuration
![]() $\eta \in \mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
. The described path has the desired property thanks to Proposition3.4.
$\eta \in \mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
. The described path has the desired property thanks to Proposition3.4.
Consider now the concatenation of the paths described in Lemma 4.8(ii) and Lemma 4.9(i) until it visits for the first time a configuration in
![]() $\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
. Starting from such a configuration, by iterating the pair of moves consisting of adding a particle to the unique unblocked odd site and removing a particle at distance one from an antiknob, it is possible to obtain a configuration with a unique non-degenerate cluster that contains
$\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
. Starting from such a configuration, by iterating the pair of moves consisting of adding a particle to the unique unblocked odd site and removing a particle at distance one from an antiknob, it is possible to obtain a configuration with a unique non-degenerate cluster that contains
![]() $\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
. By construction, this resulting configuration is in
$\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
. By construction, this resulting configuration is in
![]() $\mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
and it is possible to iterate this couple of moves up to
$\mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
and it is possible to iterate this couple of moves up to
![]() $\eta$
. By construction, the resulting path has the desired property.
$\eta$
. By construction, the resulting path has the desired property.
Consider now case (iii). Take the path described in Lemma 4.8(ii) until it visits for the first time the configuration in
![]() $\mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
as in Figure 3 on the right. Starting from such a configuration, add a particle in the unique unblocked odd site. Then, remove a particle from an even site at distance one from an antiknob, and finally add a particle in the unique unblocked odd site. This configuration is in
$\mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
as in Figure 3 on the right. Starting from such a configuration, add a particle in the unique unblocked odd site. Then, remove a particle from an even site at distance one from an antiknob, and finally add a particle in the unique unblocked odd site. This configuration is in
![]() $\mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
. Afterward, iterate the sequence of these two moves up to the target configuration
$\mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
. Afterward, iterate the sequence of these two moves up to the target configuration
![]() $\eta$
. By construction, the resulting path has the desired property.
$\eta$
. By construction, the resulting path has the desired property.
Consider now the concatenation of the paths described in Lemma 4.8(ii) and Lemma 4.9(i) until it visits for the first time a configuration in
![]() $\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
. Starting from such a configuration, with the same procedure described above, it is possible to reach the target configuration
$\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
. Starting from such a configuration, with the same procedure described above, it is possible to reach the target configuration
![]() $\eta \in \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
by visiting only saddles in
$\eta \in \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
by visiting only saddles in
![]() $\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
.
$\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
.
Let us now focus on case (iv). Consider the concatenation of the paths described in Lemma 4.8(i) and Lemma 4.9(ii) until it visits for the first time a configuration in
![]() $\mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
. Starting from such a configuration, add a particle in the antiknob, obtaining a configuration
$\mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
. Starting from such a configuration, add a particle in the antiknob, obtaining a configuration
![]() $\eta ^{\prime}$
. Note that
$\eta ^{\prime}$
. Note that
![]() $\eta ^{\prime}$
is composed of a unique non-degenerate odd cluster, which is a rhombus
$\eta ^{\prime}$
is composed of a unique non-degenerate odd cluster, which is a rhombus
![]() $\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
with a single protuberance. Starting from
$\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
with a single protuberance. Starting from
![]() $\eta ^{\prime}$
, consider the path returned by filling algorithm
$\eta ^{\prime}$
, consider the path returned by filling algorithm
![]() $\bar \omega$
up to the configuration
$\bar \omega$
up to the configuration
![]() $\eta \in \mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
. The described path has the desired property thanks to Proposition3.4.
$\eta \in \mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
. The described path has the desired property thanks to Proposition3.4.
Consider now the concatenation of the paths described in Lemma 4.8(ii) and Lemma 4.9(iii) until it visits for the first time a configuration in
![]() $\mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
. Starting from such a configuration, by iterating the pair of moves consisting of adding a particle in the unique unblocked odd site and removing a particle at distance one from an antiknob, it is possible to obtain a configuration with a unique non-degenerate cluster that contains
$\mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
. Starting from such a configuration, by iterating the pair of moves consisting of adding a particle in the unique unblocked odd site and removing a particle at distance one from an antiknob, it is possible to obtain a configuration with a unique non-degenerate cluster that contains
![]() $\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}}$
. By construction, this resulting configuration is in
$\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}}$
. By construction, this resulting configuration is in
![]() $\mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
and it is possible to iterate this couple of moves up to
$\mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
and it is possible to iterate this couple of moves up to
![]() $\eta$
. By construction, the resulting path has the desired property.
$\eta$
. By construction, the resulting path has the desired property.
Proof of Lemma
4.10
. We start by proving (i). Arguing as in the proof of Lemma 4.9(ii) we can show that there exists a path with the desired property that connects
![]() $\eta$
to
$\eta$
to
![]() $\bar \eta \in \mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
, where the unique non-degenerate cluster of
$\bar \eta \in \mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
, where the unique non-degenerate cluster of
![]() $\bar \eta$
is
$\bar \eta$
is
![]() $\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}}$
with attached a bar of length
$\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}}$
with attached a bar of length
![]() $\frac {L}{2}-2$
and there is a degenerate rhombus
$\frac {L}{2}-2$
and there is a degenerate rhombus
![]() $\mathcal {R}_{0,0}$
at distance one from an antiknob. Since the configuration displays two antiknobs, it is possible to sequentially add two particles in odd sites. Thus, by proceeding in this way the path reaches
$\mathcal {R}_{0,0}$
at distance one from an antiknob. Since the configuration displays two antiknobs, it is possible to sequentially add two particles in odd sites. Thus, by proceeding in this way the path reaches
![]() ${\mathbf{o}}$
without visiting any other saddle and so the described path has the desired property.
${\mathbf{o}}$
without visiting any other saddle and so the described path has the desired property.
Finally, consider case (ii). By arguing as in the proof of Lemma 4.9(iii)–(iv) we can show that there exists a path with the desired property that connects
![]() $\eta$
to
$\eta$
to
![]() $\bar \eta \in \mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
. If
$\bar \eta \in \mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})\cup \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
. If
![]() $\bar \eta \in \mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
, the claim follows by the previous argument. Otherwise, the configuration
$\bar \eta \in \mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
, the claim follows by the previous argument. Otherwise, the configuration
![]() $\bar \eta$
has two antiknobs after arguing as above. In either case, the described path has the desired property.
$\bar \eta$
has two antiknobs after arguing as above. In either case, the described path has the desired property.
Proof of Lemma
4.11. Consider first case (i). By construction, every non-backtracking optimal path from
![]() ${\mathbf{e}}$
to
${\mathbf{e}}$
to
![]() ${\mathbf{o}}$
that crosses a configuration in
${\mathbf{o}}$
that crosses a configuration in
![]() $\mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
has to visit a configuration in
$\mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
has to visit a configuration in
![]() $\mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
. Indeed, each move consists in adding a particle in an unblocked odd site or removing a particle from an even site. Thus, it remains to consider backtracking optimal paths only. In order to visit a saddle in
$\mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
. Indeed, each move consists in adding a particle in an unblocked odd site or removing a particle from an even site. Thus, it remains to consider backtracking optimal paths only. In order to visit a saddle in
![]() $\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
, a column (or row) with precisely
$\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
, a column (or row) with precisely
![]() $\frac {L}{2}-1$
particles arranged in odd sites needs to be created along these paths. To proceed, since we are considering backtracking optimal paths, the unique possibility is to visit a configuration in
$\frac {L}{2}-1$
particles arranged in odd sites needs to be created along these paths. To proceed, since we are considering backtracking optimal paths, the unique possibility is to visit a configuration in
![]() $\mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
before reaching
$\mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
before reaching
![]() $\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
. Thus, case (i) is concluded.
$\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
. Thus, case (i) is concluded.
Consider now case (ii). The claim follows after noting that every configuration in
![]() $\mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
contains one odd vertical (resp. horizontal) bridge
$\mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
contains one odd vertical (resp. horizontal) bridge
![]() $B$
, where the two neighbouring columns (resp. rows) to
$B$
, where the two neighbouring columns (resp. rows) to
![]() $B$
contains
$B$
contains
![]() $\frac {L}{2}-1$
odd particles each. Thus, all configurations in
$\frac {L}{2}-1$
odd particles each. Thus, all configurations in
![]() $\mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
differ from a configuration in
$\mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
differ from a configuration in
![]() $\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
in at least two odd sites. Then, suppose that
$\mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
in at least two odd sites. Then, suppose that
![]() $\eta \in \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
and
$\eta \in \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
and
![]() $\eta ^{\prime}\in \mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
such that they differ in only two odd sites. Starting from
$\eta ^{\prime}\in \mathcal {C}_{cr}({\mathbf{e}},{\mathbf{o}})$
such that they differ in only two odd sites. Starting from
![]() $\eta$
, if a bridge is created, then the resulting configuration is in
$\eta$
, if a bridge is created, then the resulting configuration is in
![]() $\mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
, while if the resulting configuration contains two neighbouring columns (or rows) with exactly
$\mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
, while if the resulting configuration contains two neighbouring columns (or rows) with exactly
![]() $\frac {L}{2}-1$
particles in odd sites, then it belongs to
$\frac {L}{2}-1$
particles in odd sites, then it belongs to
![]() $\mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
. If the two configurations differ in at least three sites, we argue as above.
$\mathcal {C}_{gr}({\mathbf{e}},{\mathbf{o}})$
. If the two configurations differ in at least three sites, we argue as above.
Consider now case (iii). The claim follows after arguing as in case (i) and noting that, in order to create a bridge, the path has to visit the set
![]() $\mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
. Lastly, in case (iv), the claim follows after arguing as in case (iii).
$\mathcal {C}_{sb}({\mathbf{e}},{\mathbf{o}})$
. Lastly, in case (iv), the claim follows after arguing as in case (iii).
5.3
Results on the saddles lying in the manifold
 $\mathcal {V}_{m^*}$
$\mathcal {V}_{m^*}$
Proof of Lemma 4.13 . We analyse separately the three cases.
Case (i). Suppose by contradiction that there exists a non-backtracking path
![]() $\omega ^{\prime}\in ({\mathbf{e}}\rightarrow {\mathbf{o}})_{\mathrm {opt}}$
that crosses
$\omega ^{\prime}\in ({\mathbf{e}}\rightarrow {\mathbf{o}})_{\mathrm {opt}}$
that crosses
![]() $\sigma \in \mathcal {V}_{m^*}\setminus \mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
such that
$\sigma \in \mathcal {V}_{m^*}\setminus \mathcal {C}_{ir}({\mathbf{e}},{\mathbf{o}})$
such that
![]() $R(\mathcal {O}^{nd}(\sigma ))$
and
$R(\mathcal {O}^{nd}(\sigma ))$
and
![]() $R(\mathcal {O}(\sigma ))$
do not wind around the torus. First, since
$R(\mathcal {O}(\sigma ))$
do not wind around the torus. First, since
![]() $\sigma \in \mathcal {V}_{m^*}$
and
$\sigma \in \mathcal {V}_{m^*}$
and
![]() $\Delta H(\sigma )\leq L+1$
, we get
$\Delta H(\sigma )\leq L+1$
, we get
 \begin{align} \begin{cases} e(\sigma )&\geq \frac {L^2}{4}-\frac {3}{2}, \\[3pt] o(\sigma )&\geq \frac {L^2}{4}-L+\frac {3}{2}. \end{cases} \end{align}
\begin{align} \begin{cases} e(\sigma )&\geq \frac {L^2}{4}-\frac {3}{2}, \\[3pt] o(\sigma )&\geq \frac {L^2}{4}-L+\frac {3}{2}. \end{cases} \end{align}
Since
![]() $o(\sigma )\gt 0$
for any
$o(\sigma )\gt 0$
for any
![]() $L$
, we deduce that
$L$
, we deduce that
![]() $\sigma$
cannot contain only degenerate clusters and therefore contains at least an odd non-degenerate cluster. Thus, one of the following cases occurs:
$\sigma$
cannot contain only degenerate clusters and therefore contains at least an odd non-degenerate cluster. Thus, one of the following cases occurs:
-
(1)
 $\mathcal {O}(\sigma )$
consists of at least two non-degenerate odd clusters;
$\mathcal {O}(\sigma )$
consists of at least two non-degenerate odd clusters; -
(2)
 $\mathcal {O}(\sigma )$
consists of a single non-degenerate odd cluster different from
$\mathcal {O}(\sigma )$
consists of a single non-degenerate odd cluster different from
 $\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
and possibly some degenerate clusters;
$\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
and possibly some degenerate clusters; -
(3)
 $\mathcal {O}(\sigma )$
consists of a single non-degenerate odd rhombus equal to
$\mathcal {O}(\sigma )$
consists of a single non-degenerate odd rhombus equal to
 $\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
and at least one degenerate odd cluster
$\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
and at least one degenerate odd cluster
 $\mathcal {R}_{0,0}$
at distance greater than one from the non-degenerate one.
$\mathcal {R}_{0,0}$
at distance greater than one from the non-degenerate one.
We consider the rhombus surrounding the odd non-degenerate region for all the above cases. Due to the isoperimetric inequality of Lemma 3.8, this rhombus
![]() $\mathcal {R}$
has a perimeter
$\mathcal {R}$
has a perimeter
![]() $P(\mathcal {R})$
greater than or equal to
$P(\mathcal {R})$
greater than or equal to
![]() $P(\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1})$
, i.e.,
$P(\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1})$
, i.e.,
![]() $P(\mathcal {R}) \geq 4(L-1)$
. In particular, for cases (1) and (2) we have
$P(\mathcal {R}) \geq 4(L-1)$
. In particular, for cases (1) and (2) we have
![]() $P(\mathcal {R}) \gt 4(L-1)$
since
$P(\mathcal {R}) \gt 4(L-1)$
since
![]() $\mathcal {O}(\sigma )\neq \mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
, and for case (3) we have
$\mathcal {O}(\sigma )\neq \mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
, and for case (3) we have
![]() $P(\mathcal {R})=4(L-1)$
. Let
$P(\mathcal {R})=4(L-1)$
. Let
![]() $P_i$
denote the perimeter of the
$P_i$
denote the perimeter of the
![]() $i$
-th cluster, with
$i$
-th cluster, with
![]() $i=1,\ldots, k$
. Note that
$i=1,\ldots, k$
. Note that
![]() $P(\sigma )=\sum _{i=1}^k P_i$
. We let
$P(\sigma )=\sum _{i=1}^k P_i$
. We let
![]() $k_d \geq 0$
(resp.
$k_d \geq 0$
(resp.
![]() $k_{nd} \geq 1$
) the number of degenerate clusters
$k_{nd} \geq 1$
) the number of degenerate clusters
![]() $\mathcal {R}_{0,0}$
(resp. non-degenerate clusters) such that the total number of clusters is
$\mathcal {R}_{0,0}$
(resp. non-degenerate clusters) such that the total number of clusters is
![]() $k=k_{d}+k_{nd} \geq 1$
.
$k=k_{d}+k_{nd} \geq 1$
.
Subcase (1). In this case
![]() $k_{nd}\geq 2$
, so that
$k_{nd}\geq 2$
, so that
![]() $k \geq 2$
. Denote by
$k \geq 2$
. Denote by
![]() $\tilde e_i$
(resp.
$\tilde e_i$
(resp.
![]() $o_i$
) the number of empty even sites (resp. occupied odd sites) of the
$o_i$
) the number of empty even sites (resp. occupied odd sites) of the
![]() $i$
-th cluster. Using (3.3), (3.7) and (3.8), we obtain
$i$
-th cluster. Using (3.3), (3.7) and (3.8), we obtain
 \begin{align} \begin{array}{ll} \Delta H(\sigma )&=\displaystyle \sum _{i=1}^{k} (\tilde e_i-o_i)=\sum _{i=1}^{k_d} \tilde e_i+\sum _{i=1}^{k_{nd}} (\tilde e_i-o_i) \geq \tilde e_{d}+ \left(\sum _{i=1}^{k_{nd}}\tilde e_i+2(k_{nd}-1)-\sum _{i=1}^{k_{nd}} o_i \right)\\[3pt] &=\tilde e_{d}+\left(\displaystyle \sum _{i=1}^{k_{nd}}\tilde e_i-\sum _{i=1}^{k_{nd}} o_i \right)+2(k_{nd}-1)\gt \tilde e_{d}+(L-1)+2(k_{nd}-1)\\[3pt] &\geq \tilde e_{d}+L+1, \end{array} \end{align}
\begin{align} \begin{array}{ll} \Delta H(\sigma )&=\displaystyle \sum _{i=1}^{k} (\tilde e_i-o_i)=\sum _{i=1}^{k_d} \tilde e_i+\sum _{i=1}^{k_{nd}} (\tilde e_i-o_i) \geq \tilde e_{d}+ \left(\sum _{i=1}^{k_{nd}}\tilde e_i+2(k_{nd}-1)-\sum _{i=1}^{k_{nd}} o_i \right)\\[3pt] &=\tilde e_{d}+\left(\displaystyle \sum _{i=1}^{k_{nd}}\tilde e_i-\sum _{i=1}^{k_{nd}} o_i \right)+2(k_{nd}-1)\gt \tilde e_{d}+(L-1)+2(k_{nd}-1)\\[3pt] &\geq \tilde e_{d}+L+1, \end{array} \end{align}
where
![]() $\tilde e_{d}=\sum _{i=1}^{k_{d}}\tilde e_i$
, the first inequality follows from the fact that the difference between the perimeter of two disjoint non-degenerate clusters and that of the cluster obtained by attaching the two is at least two, and the last inequality follows from the isoperimetric inequality applied to the cluster obtained by attaching the
$\tilde e_{d}=\sum _{i=1}^{k_{d}}\tilde e_i$
, the first inequality follows from the fact that the difference between the perimeter of two disjoint non-degenerate clusters and that of the cluster obtained by attaching the two is at least two, and the last inequality follows from the isoperimetric inequality applied to the cluster obtained by attaching the
![]() $k$
clusters forming
$k$
clusters forming
![]() $\sigma$
. Then, from inequalities (5.4) and
$\sigma$
. Then, from inequalities (5.4) and
![]() $\Delta H(\sigma )\leq L+1$
, it follows that
$\Delta H(\sigma )\leq L+1$
, it follows that
![]() $\tilde e_d\lt 0$
, which is a contradiction since
$\tilde e_d\lt 0$
, which is a contradiction since
![]() $\tilde e_d \geq 0$
.
$\tilde e_d \geq 0$
.
Subcase (2). The unique non-degenerate odd cluster of
![]() $\sigma$
has a shape different from a rhombus
$\sigma$
has a shape different from a rhombus
![]() $\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
by assumption. In this case
$\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
by assumption. In this case
![]() $k_{nd}=1$
and
$k_{nd}=1$
and
![]() $k_d\geq 0$
, so that
$k_d\geq 0$
, so that
![]() $k=k_d+1$
. Thus, we obtain
$k=k_d+1$
. Thus, we obtain
 \begin{align} \begin{array}{ll} \Delta H(\sigma )&=\displaystyle \sum _{i=1}^{k_d+1} (\tilde e_i-o_i)=\sum _{i=1}^{k_d} \tilde e_i+(\tilde e_{k_d+1}-o_{k_d+1})\gt \tilde e_{d}+L-1, \end{array} \end{align}
\begin{align} \begin{array}{ll} \Delta H(\sigma )&=\displaystyle \sum _{i=1}^{k_d+1} (\tilde e_i-o_i)=\sum _{i=1}^{k_d} \tilde e_i+(\tilde e_{k_d+1}-o_{k_d+1})\gt \tilde e_{d}+L-1, \end{array} \end{align}
where
![]() $\tilde e_{d}=\sum _{i=1}^{k_{d}}\tilde e_i$
, the first equality follows from the fact that
$\tilde e_{d}=\sum _{i=1}^{k_{d}}\tilde e_i$
, the first equality follows from the fact that
![]() $\sigma$
contains only one non-degenerate odd cluster, and the last inequality follows from the isoperimetric inequality applied to the non-degenerate cluster. Then by (5.5) and the fact that
$\sigma$
contains only one non-degenerate odd cluster, and the last inequality follows from the isoperimetric inequality applied to the non-degenerate cluster. Then by (5.5) and the fact that
![]() $\Delta H(\sigma )\leq L+1$
, we find
$\Delta H(\sigma )\leq L+1$
, we find
![]() $\tilde e_d \leq 1$
and so
$\tilde e_d \leq 1$
and so
![]() $k_d \leq 1$
.
$k_d \leq 1$
.
The configuration
![]() $\sigma$
thus falls in one of the following three subcases:
$\sigma$
thus falls in one of the following three subcases:
-
(2a) the only non-degenerate odd cluster of
 $\sigma$
is a rhombus
$\sigma$
is a rhombus
 $\mathcal {R}_{\ell _1,\ell _2} \neq \mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
;
$\mathcal {R}_{\ell _1,\ell _2} \neq \mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
; -
(2b) the non-degenerate odd cluster of
 $\sigma$
is a cluster with
$\sigma$
is a cluster with
 $m \geq 1$
empty odd sites corresponding to some broken diagonal and
$m \geq 1$
empty odd sites corresponding to some broken diagonal and
 $q=0$
shorter diagonals;
$q=0$
shorter diagonals; -
(2c) the non-degenerate odd cluster of
 $\sigma$
is a cluster with
$\sigma$
is a cluster with
 $m \geq 0$
empty odd sites corresponding to some broken diagonal and
$m \geq 0$
empty odd sites corresponding to some broken diagonal and
 $q \geq 1$
shorter diagonals.
$q \geq 1$
shorter diagonals.
We can ignore the case
![]() $m=0$
and
$m=0$
and
![]() $q=0$
as it corresponds to the rhombus
$q=0$
as it corresponds to the rhombus
![]() $\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
.
$\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
.
Subcase (2a). This case is not admissible since, if
![]() $R_{\ell _1,\ell _2} \neq R_{\frac {L}{2}-1,\frac {L}{2}-1}$
, we have
$R_{\ell _1,\ell _2} \neq R_{\frac {L}{2}-1,\frac {L}{2}-1}$
, we have
 \begin{align*} \begin{cases} \ell _1+\ell _2+1+k_d&=L+1, \\[3pt] \ell _1+\ell _2+1 &\gt L-1, \end{cases} \end{align*}
\begin{align*} \begin{cases} \ell _1+\ell _2+1+k_d&=L+1, \\[3pt] \ell _1+\ell _2+1 &\gt L-1, \end{cases} \end{align*}
and this implies
![]() $k_d\gt 2$
, which is in contradiction with the assumption
$k_d\gt 2$
, which is in contradiction with the assumption
![]() $k_d \leq 1$
.
$k_d \leq 1$
.
Subcase (2b). From the assumptions on
![]() $\sigma$
, it follows that
$\sigma$
, it follows that
 \begin{align} \begin{cases} \ell _1+\ell _2+1+k_d+m&=L+1, \\[3pt] \ell _1+\ell _2+1 &\gt L-1. \end{cases} \end{align}
\begin{align} \begin{cases} \ell _1+\ell _2+1+k_d+m&=L+1, \\[3pt] \ell _1+\ell _2+1 &\gt L-1. \end{cases} \end{align}
These give
![]() $k_d+m\lt 2$
, which, in view of the inequalities
$k_d+m\lt 2$
, which, in view of the inequalities
![]() $k_d \leq 1$
and
$k_d \leq 1$
and
![]() $m \geq 1$
, then imply that
$m \geq 1$
, then imply that
![]() $k_d=0$
and
$k_d=0$
and
![]() $m=1$
. Thus, we deduce that
$m=1$
. Thus, we deduce that
 \begin{align*} \begin{cases} o(\sigma )&=\ell _1\ell _2-1, \\[3pt] e(\sigma )&=(\ell _1+1)(\ell _2+1), \end{cases} \end{align*}
\begin{align*} \begin{cases} o(\sigma )&=\ell _1\ell _2-1, \\[3pt] e(\sigma )&=(\ell _1+1)(\ell _2+1), \end{cases} \end{align*}
so that
![]() $\ell _1+\ell _2=L-5$
since
$\ell _1+\ell _2=L-5$
since
![]() $\sigma \in \mathcal {V}_{m^*}$
, but this contradicts the condition
$\sigma \in \mathcal {V}_{m^*}$
, but this contradicts the condition
![]() $\ell _1+\ell _2+1+k_d+m=L+1$
in (5.6).
$\ell _1+\ell _2+1+k_d+m=L+1$
in (5.6).
Subcase (2c). From the assumptions on
![]() $\sigma$
, it follows that
$\sigma$
, it follows that
 \begin{align} \begin{cases} \ell _1+\ell _2+1+k_d+m&=L+1, \\[3pt] 2(\ell _1+\ell _2+1)-q & \gt 2(L-1). \end{cases} \end{align}
\begin{align} \begin{cases} \ell _1+\ell _2+1+k_d+m&=L+1, \\[3pt] 2(\ell _1+\ell _2+1)-q & \gt 2(L-1). \end{cases} \end{align}
This implies that
![]() $2(k_d+m)+q\leq 3$
, so we distinguish three subcases: (2c-I)
$2(k_d+m)+q\leq 3$
, so we distinguish three subcases: (2c-I)
![]() $k_d=m=0$
and
$k_d=m=0$
and
![]() $q \in \{1,2,3\}$
; (2c-II)
$q \in \{1,2,3\}$
; (2c-II)
![]() $k_d=1$
,
$k_d=1$
,
![]() $m=0$
and
$m=0$
and
![]() $q=1$
; and (2c-III)
$q=1$
; and (2c-III)
![]() $k_d=0$
,
$k_d=0$
,
![]() $m=1$
and
$m=1$
and
![]() $q=1$
. The other subcases are not possible in view of the conditions
$q=1$
. The other subcases are not possible in view of the conditions
![]() $k_d \leq 1$
,
$k_d \leq 1$
,
![]() $m \geq 0$
, and
$m \geq 0$
, and
![]() $q \geq 1$
.
$q \geq 1$
.
For subcase (2c-I),
![]() $k_d=m=0$
and
$k_d=m=0$
and
![]() $q \in \{1,2,3\}$
. Thus, by letting
$q \in \{1,2,3\}$
. Thus, by letting
![]() $s$
be the total number of empty sites needed to be filled in order for the shorter diagonals to become complete, we deduce that
$s$
be the total number of empty sites needed to be filled in order for the shorter diagonals to become complete, we deduce that
 \begin{align*} \begin{cases} o(\sigma )&=\ell _1\ell _2-s, \\[3pt] e(\sigma )&=(\ell _1+1)(\ell _2+1)-s, \end{cases} \end{align*}
\begin{align*} \begin{cases} o(\sigma )&=\ell _1\ell _2-s, \\[3pt] e(\sigma )&=(\ell _1+1)(\ell _2+1)-s, \end{cases} \end{align*}
so that
![]() $\ell _1+\ell _2=L-4$
since
$\ell _1+\ell _2=L-4$
since
![]() $\sigma \in \mathcal {V}_{m^*}$
, but this contradicts identity
$\sigma \in \mathcal {V}_{m^*}$
, but this contradicts identity
![]() $\ell _1+\ell _2+1+k_d+m=L+1$
in (5.7). The claims for (2c-II) and (2c-III) follow by arguing as in case (2c-I).
$\ell _1+\ell _2+1+k_d+m=L+1$
in (5.7). The claims for (2c-II) and (2c-III) follow by arguing as in case (2c-I).
Subcase (3). First, note that
![]() $k_d\leq 2$
, otherwise
$k_d\leq 2$
, otherwise
![]() $\Delta H(\sigma )\gt L+1$
and therefore the path
$\Delta H(\sigma )\gt L+1$
and therefore the path
![]() $\omega$
would not be optimal.
$\omega$
would not be optimal.
If
![]() $k_d=2$
, using the non-backtracking property of the path
$k_d=2$
, using the non-backtracking property of the path
![]() $\omega$
, it follows that there is no possible move to cross the next manifold towards
$\omega$
, it follows that there is no possible move to cross the next manifold towards
![]() ${\mathbf{o}}$
along an optimal path.
${\mathbf{o}}$
along an optimal path.
If
![]() $k_d=1$
, then
$k_d=1$
, then
![]() $\Delta H(\sigma )=L$
so that the energy along the path can increase by at most 1 to reach
$\Delta H(\sigma )=L$
so that the energy along the path can increase by at most 1 to reach
![]() ${\mathbf{o}}$
. The unique possible move is to remove a particle from an empty site, obtaining a configuration with
${\mathbf{o}}$
. The unique possible move is to remove a particle from an empty site, obtaining a configuration with
![]() $k_d=2$
. We can then prove the claim by arguing as in case
$k_d=2$
. We can then prove the claim by arguing as in case
![]() $k_d=2$
.
$k_d=2$
.
Case (ii). Suppose by contradiction that there exists a non-backtracking path
![]() $\omega ^{\prime}\in ({\mathbf{e}}\rightarrow {\mathbf{o}})_{\mathrm {opt}}$
that crosses that crosses
$\omega ^{\prime}\in ({\mathbf{e}}\rightarrow {\mathbf{o}})_{\mathrm {opt}}$
that crosses that crosses
![]() $\sigma \in \mathcal {V}_{m^*}\setminus \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
such that
$\sigma \in \mathcal {V}_{m^*}\setminus \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
such that
![]() $R(\mathcal {O}^{nd}(\sigma ))$
does not wind around the torus and
$R(\mathcal {O}^{nd}(\sigma ))$
does not wind around the torus and
![]() $R(\mathcal {O}(\sigma ))$
does. We observe that (5.3) holds for the configuration
$R(\mathcal {O}(\sigma ))$
does. We observe that (5.3) holds for the configuration
![]() $\sigma$
and, therefore, it contains at least one odd non-degenerate cluster and it cannot contain only degenerate clusters. Thus, we consider the following subcases:
$\sigma$
and, therefore, it contains at least one odd non-degenerate cluster and it cannot contain only degenerate clusters. Thus, we consider the following subcases:
-
(1)
 $\mathcal {O}(\sigma )$
consists of at least two non-degenerate odd clusters;
$\mathcal {O}(\sigma )$
consists of at least two non-degenerate odd clusters; -
(2)
 $\mathcal {O}(\sigma )$
consists of a single non-degenerate odd cluster different from
$\mathcal {O}(\sigma )$
consists of a single non-degenerate odd cluster different from
 $\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
and possibly some degenerate clusters;
$\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
and possibly some degenerate clusters; -
(3)
 $\mathcal {O}(\sigma )$
consists of a single non-degenerate odd rhombus equal to
$\mathcal {O}(\sigma )$
consists of a single non-degenerate odd rhombus equal to
 $\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
and at least one degenerate odd cluster
$\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
and at least one degenerate odd cluster
 $\mathcal {R}_{0,0}$
at distance greater than one from the non-degenerate one.
$\mathcal {R}_{0,0}$
at distance greater than one from the non-degenerate one.
Subcase (1). Suppose that
![]() $\sigma$
contains
$\sigma$
contains
![]() $k \geq 2$
non-degenerate clusters
$k \geq 2$
non-degenerate clusters
![]() $C_1(\sigma ),\ldots, C_k(\sigma )$
. By assumption, all the rhombi surrounding
$C_1(\sigma ),\ldots, C_k(\sigma )$
. By assumption, all the rhombi surrounding
![]() $C_i(\sigma )$
do not wind around the torus for any
$C_i(\sigma )$
do not wind around the torus for any
![]() $i=1,\ldots, k$
; thus, we can argue as in case (i-2c-II) above.
$i=1,\ldots, k$
; thus, we can argue as in case (i-2c-II) above.
Subcase (2). By arguing as in case (i-2) above, we deduce that this case is possible only when
![]() $\mathcal {R}(\mathcal {O}^{nd}(\sigma ))$
does not wind around the torus and
$\mathcal {R}(\mathcal {O}^{nd}(\sigma ))$
does not wind around the torus and
![]() $\mathcal {R}(\mathcal {O}(\sigma ))$
does, so that from (5.3) we deduce that there exists only one column or row with less than
$\mathcal {R}(\mathcal {O}(\sigma ))$
does, so that from (5.3) we deduce that there exists only one column or row with less than
![]() $L/2$
particles, but this contradicts the fact that
$L/2$
particles, but this contradicts the fact that
![]() $\sigma \notin \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
.
$\sigma \notin \mathcal {C}_{ib}({\mathbf{e}},{\mathbf{o}})$
.
Subcase (3). By arguing as in case (i-3) above, we deduce that this case is not possible.
Case (iii). Suppose by contradiction that there exists a non-backtracking path
![]() $\omega ^{\prime}\in ({\mathbf{e}}\rightarrow {\mathbf{o}})_{\mathrm {opt}}$
that crosses that crosses
$\omega ^{\prime}\in ({\mathbf{e}}\rightarrow {\mathbf{o}})_{\mathrm {opt}}$
that crosses that crosses
![]() $\sigma \in \mathcal {V}_{m^*}\setminus \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
such that both
$\sigma \in \mathcal {V}_{m^*}\setminus \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
such that both
![]() $R(\mathcal {O}^{nd}(\sigma ))$
and
$R(\mathcal {O}^{nd}(\sigma ))$
and
![]() $R(\mathcal {O}(\sigma ))$
wind around the torus. We observe that (5.3) holds for the configuration
$R(\mathcal {O}(\sigma ))$
wind around the torus. We observe that (5.3) holds for the configuration
![]() $\sigma$
, and therefore, it contains at least one odd non-degenerate cluster, and it cannot contain only degenerate clusters. Thus, we consider the following subcases:
$\sigma$
, and therefore, it contains at least one odd non-degenerate cluster, and it cannot contain only degenerate clusters. Thus, we consider the following subcases:
-
(1)
 $\mathcal {O}(\sigma )$
consists of at least two non-degenerate odd clusters;
$\mathcal {O}(\sigma )$
consists of at least two non-degenerate odd clusters; -
(2)
 $\mathcal {O}(\sigma )$
consists of a single non-degenerate odd cluster different from
$\mathcal {O}(\sigma )$
consists of a single non-degenerate odd cluster different from
 $\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
and possibly some degenerate clusters;
$\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
and possibly some degenerate clusters; -
(3)
 $\mathcal {O}(\sigma )$
consists of a single non-degenerate odd rhombus equal to
$\mathcal {O}(\sigma )$
consists of a single non-degenerate odd rhombus equal to
 $\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
and at least one degenerate odd cluster
$\mathcal {R}_{\frac {L}{2}-1,\frac {L}{2}-1}$
and at least one degenerate odd cluster
 $\mathcal {R}_{0,0}$
at distance greater than one from the non-degenerate one.
$\mathcal {R}_{0,0}$
at distance greater than one from the non-degenerate one.
Subcase (1). Suppose that
![]() $\sigma$
contains
$\sigma$
contains
![]() $k \geq 2$
non-degenerate clusters
$k \geq 2$
non-degenerate clusters
![]() $C_1(\sigma ),\ldots, C_k(\sigma )$
. If the rhombus surrounding
$C_1(\sigma ),\ldots, C_k(\sigma )$
. If the rhombus surrounding
![]() $C_i(\sigma )$
does not wind around the torus for any
$C_i(\sigma )$
does not wind around the torus for any
![]() $i=1,\ldots, k$
, we can argue as in case (i-1) above. Otherwise, suppose that there exists an index
$i=1,\ldots, k$
, we can argue as in case (i-1) above. Otherwise, suppose that there exists an index
![]() $i$
such that
$i$
such that
![]() $\mathcal {R}(C_i(\sigma ))$
winds around the torus. Thus, there exists at least one row or column that contains
$\mathcal {R}(C_i(\sigma ))$
winds around the torus. Thus, there exists at least one row or column that contains
![]() $\frac {L}{2}$
particles, say a column. Since
$\frac {L}{2}$
particles, say a column. Since
![]() $k\geq 2$
, this implies that there exists a row containing two odd particles that belong to
$k\geq 2$
, this implies that there exists a row containing two odd particles that belong to
![]() $C_i(\sigma )$
and another disjoint cluster. Thus, the energy difference contribution
$C_i(\sigma )$
and another disjoint cluster. Thus, the energy difference contribution
![]() $\Delta H$
along this row or column is at least two. In addition, all the other
$\Delta H$
along this row or column is at least two. In addition, all the other
![]() $L$
rows or columns composing
$L$
rows or columns composing
![]() $C_i(\sigma )$
have an energy contribution of at least one. Thus, the total contribution is
$C_i(\sigma )$
have an energy contribution of at least one. Thus, the total contribution is
![]() $\Delta H(\sigma )\gt 2+L-1=L+1$
, where the strict inequality follows from
$\Delta H(\sigma )\gt 2+L-1=L+1$
, where the strict inequality follows from
![]() $k\geq 2$
. This contradicts the assumption
$k\geq 2$
. This contradicts the assumption
![]() $\Delta H(\sigma )\leq L+1$
, and therefore, this case is not admissible.
$\Delta H(\sigma )\leq L+1$
, and therefore, this case is not admissible.
Subcase (2). By arguing as in case (i-2) above, we deduce that this case is possible only when both
![]() $\mathcal {R}(\mathcal {O}^{nd}(\sigma )$
and
$\mathcal {R}(\mathcal {O}^{nd}(\sigma )$
and
![]() $\mathcal {R}(\mathcal {O}(\sigma )$
wind around the torus, so that from (5.3) we deduce that there exists at least one column or row with strictly less than
$\mathcal {R}(\mathcal {O}(\sigma )$
wind around the torus, so that from (5.3) we deduce that there exists at least one column or row with strictly less than
![]() $L/2$
particles, but this contradicts the fact that
$L/2$
particles, but this contradicts the fact that
![]() $\sigma \notin \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
.
$\sigma \notin \mathcal {C}_{mb}({\mathbf{e}},{\mathbf{o}})$
.
Subcase (3). By arguing as in case (i-3) above, we deduce that this case is not possible.
6. Conclusions and future work
This work concludes the analysis of the low-temperature behaviour for the hard-core model on a square grid graph with periodic boundary conditions initiated by [Reference Nardi, Zocca and Borst47]. In that paper, this interacting particle system was shown to have two stable states, and the energy barrier between them was already identified. However, the argument carried out in that paper did not provide any geometrical insight into the trajectories followed by the process in the low-temperature limit and did not characterize the critical configurations, i.e., the states with the highest energy in these limiting trajectories. The goal of this paper was precisely to fill this gap. More precisely, we provide a geometrical description of all the essential saddles for this transition and highlight how these communicate with each other without exceeding the critical energy barrier
![]() $\Gamma (\Lambda )$
.
$\Gamma (\Lambda )$
.
The extension to other types of lattices naturally arises in this context. Indeed, in [Reference Zocca56], the authors investigate the same model on the triangular lattice, studying the asymptotic behaviour of the hitting times between stable states but without providing any information on the critical configurations. The type of analysis carried out in this paper could be useful to tackle that problem, even if it looks more challenging since there are three stable states and isoperimetric inequalities are probably harder to derive. This will be the focus of future work. Another possible direction could be the study of the asymptotic behaviour of the hard-core model on square grid graphs but with different boundary conditions or in the presence of some impurities. However, in this case, we expect the transition between two stable states to most likely occur by heterogeneous nucleation starting from the boundary, hence breaking the intrinsic symmetry and translation-invariance properties of the critical configurations. On the other hand, we expect that the techniques and machinery developed in this paper will also be useful in identifying critical configurations of other interacting particle systems on finite square lattices with similar blocking effects, e.g., the Widom-Rowlinson model [Reference Zocca55].
Acknowledgements
S.B and V.J. are grateful for the support of `Gruppo Nazionale per l’Analisi Matematica, la Probabilità e le loro Applicazioni’ (GNAMPA-INdAM). The authors are grateful to Francesca Nardi, Julien Sohier, Gianmarco Bet, and Tommaso Monni for useful and fruitful discussions at the early stage of this work.
A. Appendix A
Proof of Lemma
3.1
. We start by proving (i). Given
![]() $0\leq k_1^*\leq \ell _1$
and
$0\leq k_1^*\leq \ell _1$
and
![]() $\ell _2+1\leq j_1^*\leq L-1$
, we want to show that there exists
$\ell _2+1\leq j_1^*\leq L-1$
, we want to show that there exists
![]() $0\leq k_2^*\leq \ell _1$
and
$0\leq k_2^*\leq \ell _1$
and
![]() $0\leq j_2^*\leq \ell _2$
such that
$0\leq j_2^*\leq \ell _2$
such that
 \begin{align} \begin{cases} k_1^*+j_1^*=k_2^*+j_2^* &\, (\hbox {mod } L), \\[3pt] k_1^*-j_1^*=k_2^*-j_2^* &\, (\hbox {mod } L). \end{cases} \end{align}
\begin{align} \begin{cases} k_1^*+j_1^*=k_2^*+j_2^* &\, (\hbox {mod } L), \\[3pt] k_1^*-j_1^*=k_2^*-j_2^* &\, (\hbox {mod } L). \end{cases} \end{align}
The choice
![]() $j_2^*=j_1^*+L/2 \ \, (\hbox {mod } L)$
and
$j_2^*=j_1^*+L/2 \ \, (\hbox {mod } L)$
and
![]() $k_2^*=k_1^*+L/2 \ \, (\hbox {mod } L)$
implies the claim in (i), since the chosen indices
$k_2^*=k_1^*+L/2 \ \, (\hbox {mod } L)$
implies the claim in (i), since the chosen indices
![]() $j_2^*$
and
$j_2^*$
and
![]() $k_2^*$
satisfy (A.1) and they are modulo
$k_2^*$
satisfy (A.1) and they are modulo
![]() $L$
such that
$L$
such that
 \begin{equation*} \begin{cases} j_2^*\geq \ell _2+1+\frac {L}{2} \geq 1, \\[3pt] j_2^*\leq L-1+\frac {L}{2} \leq \ell _2-1, \\[3pt] k_2^*\geq \frac {L}{2}, \\[3pt] k_2^*\leq \ell _1+\frac {L}{2} \leq \frac {L}{2}-2\leq \ell _1-2. \end{cases} \end{equation*}
\begin{equation*} \begin{cases} j_2^*\geq \ell _2+1+\frac {L}{2} \geq 1, \\[3pt] j_2^*\leq L-1+\frac {L}{2} \leq \ell _2-1, \\[3pt] k_2^*\geq \frac {L}{2}, \\[3pt] k_2^*\leq \ell _1+\frac {L}{2} \leq \frac {L}{2}-2\leq \ell _1-2. \end{cases} \end{equation*}
By interchanging the role of
![]() $k_1^*$
and
$k_1^*$
and
![]() $k_2^*$
and arguing in the same way, the proof of (i) is concluded. The two inclusions stated in (ii) can be proved by arguing in an analogous way.
$k_2^*$
and arguing in the same way, the proof of (i) is concluded. The two inclusions stated in (ii) can be proved by arguing in an analogous way.
Proof of Lemma
3.2
. In this proof, all the sums will be tacitly assumed to be taken modulo
![]() $L$
. Denote
$L$
. Denote
![]() $\eta =(\eta _1,\eta _2) \in V_{\mathbf{o}}$
. We analyse each case separately.
$\eta =(\eta _1,\eta _2) \in V_{\mathbf{o}}$
. We analyse each case separately.
Case (i). Considering
![]() $S_{\ell _1,\ell _2}(\eta ) \subset V_{\mathbf{o}}$
and
$S_{\ell _1,\ell _2}(\eta ) \subset V_{\mathbf{o}}$
and
![]() $\partial ^+ S_{\ell _1,\ell _2}(\eta ) \subset V_{\mathbf{e}}$
, we observe that
$\partial ^+ S_{\ell _1,\ell _2}(\eta ) \subset V_{\mathbf{e}}$
, we observe that
 \begin{align} V \setminus \mathcal {R}_{\ell _1,\ell _2}(\eta ) & = V \setminus \{S_{\ell _1,\ell _2}(\eta ) \cup \partial ^+ S_{\ell _1,\ell _2}(\eta )\} \notag \\[3pt] & = \{ V_{\mathbf{o}} \cup V_{\mathbf{e}} \} \setminus \{S_{\ell _1,\ell _2}(\eta ) \cup \partial ^+S_{\ell _1,\ell _2}(\eta )\} \notag \\[3pt] & = \{V_{\mathbf{o}} \setminus \{S_{\ell _1,\ell _2}(\eta ) \cup \partial ^+S_{\ell _1,\ell _2}(\eta )\}\} \cup \{ V_{\mathbf{e}} \setminus \{S_{\ell _1,\ell _2}(\eta ) \cup \partial ^+S_{\ell _1,\ell _2}(\eta )\} \} \notag \\[3pt] & = \{V_{\mathbf{o}} \setminus S_{\ell _1,\ell _2}(\eta ) \} \cup \{ V_{\mathbf{e}} \setminus \partial ^+S_{\ell _1,\ell _2}(\eta )\}. \end{align}
\begin{align} V \setminus \mathcal {R}_{\ell _1,\ell _2}(\eta ) & = V \setminus \{S_{\ell _1,\ell _2}(\eta ) \cup \partial ^+ S_{\ell _1,\ell _2}(\eta )\} \notag \\[3pt] & = \{ V_{\mathbf{o}} \cup V_{\mathbf{e}} \} \setminus \{S_{\ell _1,\ell _2}(\eta ) \cup \partial ^+S_{\ell _1,\ell _2}(\eta )\} \notag \\[3pt] & = \{V_{\mathbf{o}} \setminus \{S_{\ell _1,\ell _2}(\eta ) \cup \partial ^+S_{\ell _1,\ell _2}(\eta )\}\} \cup \{ V_{\mathbf{e}} \setminus \{S_{\ell _1,\ell _2}(\eta ) \cup \partial ^+S_{\ell _1,\ell _2}(\eta )\} \} \notag \\[3pt] & = \{V_{\mathbf{o}} \setminus S_{\ell _1,\ell _2}(\eta ) \} \cup \{ V_{\mathbf{e}} \setminus \partial ^+S_{\ell _1,\ell _2}(\eta )\}. \end{align}
Thus, we want to show that the two subsets are equal to
![]() $S_{\hat {l}_1,\hat {l}_2}(\hat {\eta })$
and
$S_{\hat {l}_1,\hat {l}_2}(\hat {\eta })$
and
![]() $\partial ^+S_{\hat {l}_1,\hat {l}_2}(\hat {\eta })$
for some
$\partial ^+S_{\hat {l}_1,\hat {l}_2}(\hat {\eta })$
for some
![]() $0 \leq \hat {l}_1,\hat {l}_2 \leq L-1$
and
$0 \leq \hat {l}_1,\hat {l}_2 \leq L-1$
and
![]() $\hat {\eta } \in V_{\mathbf{e}}$
. In addition, we may write
$\hat {\eta } \in V_{\mathbf{e}}$
. In addition, we may write
and
 \begin{align} \partial ^+ S_{\ell _1,\ell _2}(\eta )= \bigcup _{\substack { 0 \leq k \leq \ell _1 \\[3pt] 0 \leq j \leq \ell _2} } \{ (\eta _1+k+j-1, \, \eta _2+k-j) \}. \end{align}
\begin{align} \partial ^+ S_{\ell _1,\ell _2}(\eta )= \bigcup _{\substack { 0 \leq k \leq \ell _1 \\[3pt] 0 \leq j \leq \ell _2} } \{ (\eta _1+k+j-1, \, \eta _2+k-j) \}. \end{align}
Thus, we have
 \begin{align} V_{\mathbf{e}} \setminus \partial ^+S_{\ell _1,\ell _2}(\eta ) & =\bigcup _{ 0 \leq k^{\prime},j^{\prime} \leq L-1 } \!\{(k^{\prime}+j^{\prime}+\eta _1-1,k^{\prime}-j^{\prime}+\eta _2)\} \setminus \bigcup _{\substack { 0 \leq k \leq \ell _1 \\[3pt] 0 \leq j \leq \ell _2} } \!\{ (\eta _1+k+j-1, \, \eta _2+k-j) \} \notag \\[3pt] &= \bigcup _{\substack { \ell _1+1 \leq \tilde k \leq L-1 \\[3pt] \ell _2+1 \leq \tilde j \leq L-1} } \{(\tilde k+ \tilde j + \eta _1-1, \tilde k - \tilde j + \eta _2) \} \notag \\[3pt] &= \bigcup _{\substack { 0 \leq \hat {k} \leq L-\ell _1-2 \\[3pt] 0 \leq \hat {j} \leq L-\ell _2-2} } \{(\hat {k}+\hat {j}+\ell _1+\ell _2+2+\eta _1-1, \hat {k}-\hat {j}+\ell _1-\ell _2+\eta _2\}, \end{align}
\begin{align} V_{\mathbf{e}} \setminus \partial ^+S_{\ell _1,\ell _2}(\eta ) & =\bigcup _{ 0 \leq k^{\prime},j^{\prime} \leq L-1 } \!\{(k^{\prime}+j^{\prime}+\eta _1-1,k^{\prime}-j^{\prime}+\eta _2)\} \setminus \bigcup _{\substack { 0 \leq k \leq \ell _1 \\[3pt] 0 \leq j \leq \ell _2} } \!\{ (\eta _1+k+j-1, \, \eta _2+k-j) \} \notag \\[3pt] &= \bigcup _{\substack { \ell _1+1 \leq \tilde k \leq L-1 \\[3pt] \ell _2+1 \leq \tilde j \leq L-1} } \{(\tilde k+ \tilde j + \eta _1-1, \tilde k - \tilde j + \eta _2) \} \notag \\[3pt] &= \bigcup _{\substack { 0 \leq \hat {k} \leq L-\ell _1-2 \\[3pt] 0 \leq \hat {j} \leq L-\ell _2-2} } \{(\hat {k}+\hat {j}+\ell _1+\ell _2+2+\eta _1-1, \hat {k}-\hat {j}+\ell _1-\ell _2+\eta _2\}, \end{align}
where at the second equality we used Lemma 3.1(i) and at the last equality we used the change of variables
![]() $\hat {k}=\tilde k -(\ell _1+1)$
and
$\hat {k}=\tilde k -(\ell _1+1)$
and
![]() $\hat {j}= \tilde j -(\ell _2+1)$
. Now, we consider
$\hat {j}= \tilde j -(\ell _2+1)$
. Now, we consider
![]() $\hat {\eta }=(\ell _1+\ell _2+1+\eta _1,\ell _1-\ell _2+\eta _2) \in V_{\mathbf{e}}$
and we obtain
$\hat {\eta }=(\ell _1+\ell _2+1+\eta _1,\ell _1-\ell _2+\eta _2) \in V_{\mathbf{e}}$
and we obtain
 \begin{align} V_{\mathbf{e}} \setminus \partial ^+S_{\ell _1,\ell _2}(\eta )= \bigcup _{\substack { 0 \leq \hat {k} \leq L-\ell _1-2 \\[3pt] 0 \leq \hat {j} \leq L-\ell _2-2} } \{(\hat {k}+\hat {j}+\hat {\eta }_1, \hat {k}-\hat {j}+\hat {\eta }_2) \} \end{align}
\begin{align} V_{\mathbf{e}} \setminus \partial ^+S_{\ell _1,\ell _2}(\eta )= \bigcup _{\substack { 0 \leq \hat {k} \leq L-\ell _1-2 \\[3pt] 0 \leq \hat {j} \leq L-\ell _2-2} } \{(\hat {k}+\hat {j}+\hat {\eta }_1, \hat {k}-\hat {j}+\hat {\eta }_2) \} \end{align}
Thus, we have
![]() $V_{\mathbf{e}} \setminus \partial ^+ S_{\ell _1,\ell _2}(\eta )= S_{L-\ell _1-1,L-\ell _2-1}(\hat {\eta })\subseteq V_{\mathbf{e}}$
. Arguing as above, we prove that
$V_{\mathbf{e}} \setminus \partial ^+ S_{\ell _1,\ell _2}(\eta )= S_{L-\ell _1-1,L-\ell _2-1}(\hat {\eta })\subseteq V_{\mathbf{e}}$
. Arguing as above, we prove that
![]() $V_{\mathbf{o}} \setminus S_{\ell _1,\ell _2}(\eta )= \partial ^+ S_{L-\ell _1-1,L-\ell _2-1}(\hat {\eta })\subseteq V_{\mathbf{o}}$
.
$V_{\mathbf{o}} \setminus S_{\ell _1,\ell _2}(\eta )= \partial ^+ S_{L-\ell _1-1,L-\ell _2-1}(\hat {\eta })\subseteq V_{\mathbf{o}}$
.
Case (ii). Without loss of generality we may assume
![]() $\ell _1=\min \{\ell _1,\ell _2\}$
. For
$\ell _1=\min \{\ell _1,\ell _2\}$
. For
![]() $\eta =(\eta _1,\eta _2)\in V_{\mathbf{e}}$
, by using (A.3) and (3.11), we have
$\eta =(\eta _1,\eta _2)\in V_{\mathbf{e}}$
, by using (A.3) and (3.11), we have
 \begin{align} \begin{array}{ll} V_{\mathbf{e}}&= \displaystyle \bigcup _{\substack {0\leq k \leq \ell _1 \\[3pt] 0\leq j \leq L-1}} \{(k+j+\eta _1,k-j+\eta _2)\} \cup \displaystyle \bigcup _{\substack {\ell _1+1\leq k \leq L-1 \\[3pt] 0\leq j \leq L-1}} \{(k+j+\eta _1,k-j+\eta _2)\} \\[3pt] &=\displaystyle \bigcup _{\substack {0\leq k \leq \ell _1 \\[3pt] 0\leq j \leq L-1}} \{(k+j+\eta _1,k-j+\eta _2)\} = \partial ^+ S_{\ell _1,L-1}(\eta ). \end{array} \end{align}
\begin{align} \begin{array}{ll} V_{\mathbf{e}}&= \displaystyle \bigcup _{\substack {0\leq k \leq \ell _1 \\[3pt] 0\leq j \leq L-1}} \{(k+j+\eta _1,k-j+\eta _2)\} \cup \displaystyle \bigcup _{\substack {\ell _1+1\leq k \leq L-1 \\[3pt] 0\leq j \leq L-1}} \{(k+j+\eta _1,k-j+\eta _2)\} \\[3pt] &=\displaystyle \bigcup _{\substack {0\leq k \leq \ell _1 \\[3pt] 0\leq j \leq L-1}} \{(k+j+\eta _1,k-j+\eta _2)\} = \partial ^+ S_{\ell _1,L-1}(\eta ). \end{array} \end{align}
Thus, it follows that all even sites belong to the rhombus
![]() $\mathcal {R}_{\ell _1,\ell _2}(\eta )$
. In addition, by using (3.12) we obtain
$\mathcal {R}_{\ell _1,\ell _2}(\eta )$
. In addition, by using (3.12) we obtain
 \begin{align} S_{\ell _1,L-1}(\eta ) &=\bigcup _{ \substack {0 \leq k\leq \ell _1-1 \\[3pt] 0\leq j \leq L-2} } \{(\eta _1+k^{\prime}+j^{\prime},\eta _2+k^{\prime}-j^{\prime})\} \notag \\[3pt] &=\bigcup _{ \substack {0 \leq k\leq \frac {L}{2}-1 \\[3pt] 0\leq j \leq L-2} } \{(\eta _1+k+j,\eta _2+k-j)\} \cup \bigcup _{\substack {\frac {L}{2} \leq k\leq \ell _1-1 \\[3pt] 0\leq j \leq L-2}} \{(\hat \eta _1+k+j,\hat \eta _2+k-j)\} \notag \\[3pt] &=\bigcup _{ \substack {0 \leq k\leq \frac {L}{2}-1 \\[3pt] 0\leq j \leq L-2} } \{(\eta _1+k+j,\eta _2+k-j)\} \cup \bigcup _{L/2 \leq k\leq \ell _1-1} \{(\hat \eta _1+k,\hat \eta _2+k)\}. \end{align}
\begin{align} S_{\ell _1,L-1}(\eta ) &=\bigcup _{ \substack {0 \leq k\leq \ell _1-1 \\[3pt] 0\leq j \leq L-2} } \{(\eta _1+k^{\prime}+j^{\prime},\eta _2+k^{\prime}-j^{\prime})\} \notag \\[3pt] &=\bigcup _{ \substack {0 \leq k\leq \frac {L}{2}-1 \\[3pt] 0\leq j \leq L-2} } \{(\eta _1+k+j,\eta _2+k-j)\} \cup \bigcup _{\substack {\frac {L}{2} \leq k\leq \ell _1-1 \\[3pt] 0\leq j \leq L-2}} \{(\hat \eta _1+k+j,\hat \eta _2+k-j)\} \notag \\[3pt] &=\bigcup _{ \substack {0 \leq k\leq \frac {L}{2}-1 \\[3pt] 0\leq j \leq L-2} } \{(\eta _1+k+j,\eta _2+k-j)\} \cup \bigcup _{L/2 \leq k\leq \ell _1-1} \{(\hat \eta _1+k,\hat \eta _2+k)\}. \end{align}
Thus, we deduce that the rhombus
![]() $\mathcal {R}_{\ell _1,L-1}(\eta )$
contains
$\mathcal {R}_{\ell _1,L-1}(\eta )$
contains
![]() $L^2/2-L+\ell _1$
odd sites, which implies that its complement in
$L^2/2-L+\ell _1$
odd sites, which implies that its complement in
![]() $V$
contains
$V$
contains
![]() $L-\ell _1$
odd sites.
$L-\ell _1$
odd sites.
Case (iii). Without loss of generality we may assume
![]() $\ell _1=\min \{\ell _1,\ell _2\}$
. In this case, after using the same argument we have shown above, for some
$\ell _1=\min \{\ell _1,\ell _2\}$
. In this case, after using the same argument we have shown above, for some
![]() $\hat \eta =(\hat \eta _1,\hat \eta _2)\in V_{\mathbf{o}}$
we obtain that
$\hat \eta =(\hat \eta _1,\hat \eta _2)\in V_{\mathbf{o}}$
we obtain that
 \begin{align} V_{\mathbf{o}}\setminus S_{\ell _1,L}(\eta )=\bigcup _{\substack {\ell _1\leq k\leq \frac {L}{2}-1 \\[3pt] 0\leq j\leq L-1}} \{(\hat \eta _1+k+j,\hat \eta _2+k-j)\} \end{align}
\begin{align} V_{\mathbf{o}}\setminus S_{\ell _1,L}(\eta )=\bigcup _{\substack {\ell _1\leq k\leq \frac {L}{2}-1 \\[3pt] 0\leq j\leq L-1}} \{(\hat \eta _1+k+j,\hat \eta _2+k-j)\} \end{align}
and
 \begin{align} V_{\mathbf{e}}\setminus \partial ^+ S_{\ell _1,L}(\eta )=\bigcup _{\substack {\ell _1+1\leq k\leq \frac {L}{2}-1 \\[3pt] 0\leq j\leq L-1}} \{(\hat \eta _1+k+j-1,\hat \eta _2+k-j)\}. \end{align}
\begin{align} V_{\mathbf{e}}\setminus \partial ^+ S_{\ell _1,L}(\eta )=\bigcup _{\substack {\ell _1+1\leq k\leq \frac {L}{2}-1 \\[3pt] 0\leq j\leq L-1}} \{(\hat \eta _1+k+j-1,\hat \eta _2+k-j)\}. \end{align}
This implies that the rhombus
![]() $\mathcal {R}_{\ell _1,L}(\eta )$
contains
$\mathcal {R}_{\ell _1,L}(\eta )$
contains
![]() $L\, \ell _1$
odd sites and
$L\, \ell _1$
odd sites and
![]() $L(\ell _1+1)$
even sites.
$L(\ell _1+1)$
even sites.
Case (iv). By arguing as above, we can show that the complement of the rhombus
![]() $\mathcal {R}_{\ell _1,\ell _2}(\eta )$
in
$\mathcal {R}_{\ell _1,\ell _2}(\eta )$
in
![]() $V$
has no even and odd sites and therefore
$V$
has no even and odd sites and therefore
![]() $\mathcal {R}_{\ell _1,\ell _2}\equiv V$
.
$\mathcal {R}_{\ell _1,\ell _2}\equiv V$
.