Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-02-07T01:54:32.805Z Has data issue: false hasContentIssue false
  • English
  • Français

The Compensation Approach for Walks With Small Steps in the Quarter Plane

Published online by Cambridge University Press:  11 January 2013

IVO J. B. F. ADAN ,
JOHAN S. H. van LEEUWAARDEN  and
KILIAN RASCHEL
IVO J. B. F. ADAN
Affiliation:
Department of Mathematics and Computer Science, Eindhoven University of Technology, PO Box 513, 5600 MB Eindhoven, The Netherlands (e-mail: i.j.b.f.adan@tue.nl, j.s.h.v.leeuwaarden@tue.nl)
JOHAN S. H. van LEEUWAARDEN
Affiliation:
Department of Mathematics and Computer Science, Eindhoven University of Technology, PO Box 513, 5600 MB Eindhoven, The Netherlands (e-mail: i.j.b.f.adan@tue.nl, j.s.h.v.leeuwaarden@tue.nl)
KILIAN RASCHEL
Affiliation:
CNRS and Université de Tours, Faculté des Sciences et Techniques, Parc de Grandmont, 37200 Tours, France (e-mail: kilian.raschel@lmpt.univ-tours.fr)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper is the first application of the compensation approach (a well-established theory in probability theory) to counting problems. We discuss how this method can be applied to a general class of walks in the quarter plane +2 with a step set that is a subset of

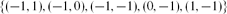\[ \{(-1,1),(-1,0),(-1,-1),(0,-1),(1,-1)\}\]
in the interior of +2. We derive an explicit expression for the generating function which turns out to be non-holonomic, and which can be used to obtain exact and asymptotic expressions for the counting numbers.

Keywords

Primary 05A15Secondary 05A16
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 22 , Issue 2 , March 2013 , pp. 161 - 183
Copyright
Copyright © Cambridge University Press 2013

References

[1]Adan, I. J. B. F. (1991) A compensation approach for queueing problems. PhD dissertation, Technische Universiteit Eindhoven.Google Scholar
[2]Adan, I. J. B. F., Boxma, O. J. and Resing, J. (2001) Queueing models with multiple waiting lines. Queueing Syst. 37 65–98.Google Scholar
[3]Adan, I. J. B. F., Wessels, J. and Zijm, W. H. M. (1990) Analysis of the symmetric shortest queue problem. Comm. Statist. Stochastic Models 6 691–713.Google Scholar
[4]Adan, I. J. B. F., Wessels, J. and Zijm, W. H. M. (1993) A compensation approach for two-dimensional Markov processes. Adv. Appl. Probab. 25 783–817.Google Scholar
[5]Bostan, A. and Kauers, M. (2009) Automatic classification of restricted lattice walks. In Proc. 21st International Conference on Formal Power Series and Algebraic Combinatorics, pp. 203–217.Google Scholar
[6]Bostan, A. and Kauers, M. (2010) The complete generating function for Gessel's walk is algebraic. Proc. Amer. Math. Soc. 432 3063–3078.Google Scholar
[7]Bousquet-Mélou, M. and Mishna, M. (2010) Walks with small steps in the quarter plane. Contemp. Math. 520 1–40.Google Scholar
[8]Fayolle, G., Iasnogorodski, R. and Malyshev, V. (1999) Random Walks in the Quarter-Plane, Springer.Google Scholar
[9]Fayolle, G. and Raschel, K. (2010) On the holonomy or algebraicity of generating functions counting lattice walks in the quarter-plane. Markov Process. Rel. Fields 16 485–496.Google Scholar
[10]Fayolle, G. and Raschel, K. (2012) Some exact asymptotics in the counting of walks in the quarter plane. In DMTCS Proc. AofA'12, pp. 109–124.Google Scholar
[11]Flajolet, P. and Sedgewick, R. (2009) Analytic Combinatorics. Cambridge University Press.Google Scholar
[12]Kurkova, I. and Malyshev, V. (1998) Martin boundary and elliptic curves. Markov Process. Rel. Fields 4 203–272.Google Scholar
[13]Kurkova, I. and Raschel, K. (2011) Explicit expression for the generating function counting Gessel's walk. Adv. Appl. Math. 47 414–433.Google Scholar
[14]Kurkova, I. and Raschel, K. (2012) On the functions counting walks with small steps in the quarter plane. Publ. Math. Inst. Hautes Études Sci. 116 69–114.Google Scholar
[15]Malyshev, V. (1971) Positive random walks and Galois theory. Uspehi Mat. Nauk 26 227–228.Google Scholar
[16]Melczer, S. and Mishna, M. (2012) Singularity analysis via the iterated kernel method. In preparation.Google Scholar
[17]Mishna, M. and Rechnitzer, A. (2009) Two non-holonomic lattice walks in the quarter plane. Theor. Comput. Sci. 410 3616–3630.Google Scholar
[18]Raschel, K. (2012) Counting walks in a quadrant: a unified approach via boundary value problems. J. Eur. Math. Soc. 14 749–777.Google Scholar
[19]Resing, J. and Rietman, R. (2004) The M/M/1 queue with gated random order of service. Statist. Neerlandica 58 97–110.Google Scholar
[20]Stanley, R. (1999) Enumerative Combinatorics, Vol. 2, Cambridge University Press.Google Scholar