Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-02-07T04:04:30.358Z Has data issue: false hasContentIssue false
  • English
  • Français

A Combinatorial Approach to a Model of Constrained Random Walkers

Part of: Limit theorems Combinatorics Markov processes

Published online by Cambridge University Press:  16 March 2015

T. ESPINASSE ,
N. GUILLOTIN-PLANTARD  and
P. NADEAU
T. ESPINASSE
Affiliation:
Institut Camille Jordan, CNRS UMR 5208, Université Lyon 1, 43 Boulevard du 11 novembre 1918, 69622 Villeurbanne, France (e-mail: Thibault.Espinasse@math.univ-lyon1.fr, nadine.guillotin@univ-lyon1.fr, philippe.nadeau@math.univ-lyon1.fr)
N. GUILLOTIN-PLANTARD
Affiliation:
Institut Camille Jordan, CNRS UMR 5208, Université Lyon 1, 43 Boulevard du 11 novembre 1918, 69622 Villeurbanne, France (e-mail: Thibault.Espinasse@math.univ-lyon1.fr, nadine.guillotin@univ-lyon1.fr, philippe.nadeau@math.univ-lyon1.fr)
P. NADEAU
Affiliation:
Institut Camille Jordan, CNRS UMR 5208, Université Lyon 1, 43 Boulevard du 11 novembre 1918, 69622 Villeurbanne, France (e-mail: Thibault.Espinasse@math.univ-lyon1.fr, nadine.guillotin@univ-lyon1.fr, philippe.nadeau@math.univ-lyon1.fr)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [1], the authors consider a random walk (Zn,1, . . ., Zn,K+1) ∈ 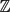${\mathbb{Z}}$K+1 with the constraint that each coordinate of the walk is at distance one from the following coordinate. A functional central limit theorem for the first coordinate is proved and the limit variance is explicited. In this paper, we study an extended version of this model by conditioning the extremal coordinates to be at some fixed distance at every time. We prove a functional central limit theorem for this random walk. Using combinatorial tools, we give a precise formula of the variance and compare it with that obtained in [1].

MSC classification

Primary: 60J10: Markov chains (discrete-time Markov processes on discrete state spaces)
Secondary: 60F05: Central limit and other weak theorems 05A19: Combinatorial identities, bijective combinatorics
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 25 , Issue 2 , March 2016 , pp. 222 - 235
Copyright
Copyright © Cambridge University Press 2015 

References

[1] Boissard, E., Cohen, S., Espinasse, T. and Norris, J. (2014) Diffusivity of a random walk on random walks. Random Struct. Alg., to appear. arXiv:1210.4745 Google Scholar
[2] Durrett, R. (1991) Probability: Theory and Examples, Wadsworth & Brooks/Cole.Google Scholar
[3] Gordin, M. I. (1969) The central limit theorem for stationary processes. Dokl. Akad. Nauk SSSR 188 739–741.Google Scholar
[4] Häggström, O. and Rosenthal, J. S. (2007) On variance conditions for Markov chain CLTs. Electron. Comm. Probab. 12 454–464.Google Scholar
[5] Lawler, G. and Limic, V. (2010) Random Walk: A Modern Introduction, Cambridge University Press.Google Scholar
[6] Spitzer, F. (1976) Principles of Random Walks, second edition, Springer.CrossRefGoogle Scholar