We establish sufficient conditions on the shape of a set $A$ included in the space $\mathcal{L}_{s}^{n}\left( X,Y \right)$ of the $n$-linear symmetric mappings between Banach spaces $X$ and $Y$ , to ensure the existence of a ${{C}^{n}}$-smooth mapping $f:X\to Y$, with bounded support, and such that ${{f}^{\left( n \right)}}\left( X \right)=A$, provided that $X$ admits a ${{C}^{n}}$-smooth bump with bounded $n$-th derivative and dens $\text{dens }X=\text{dens }{{\mathcal{L}}^{n}}\left( X,Y \right)$. For instance, when $X$ is infinite-dimensional, every bounded connected and open set $U$ containing the origin is the range of the $n$-th derivative of such amapping. The same holds true for the closure of $U$, provided that every point in the boundary of $U$ is the end point of a path within $U$. In the finite-dimensional case, more restrictive conditions are required. We also study the Fréchet smooth case for mappings from ${{\mathbb{R}}^{n}}$ to a separable infinite-dimensional Banach space and the Gâteaux smooth case for mappings defined on a separable infinite-dimensional Banach space and with values in a separable Banach space.

In this paper we study Hankel transforms and Hankel convolution operators on spaces of entire functions of finite order and their duals.

Consider $M$, a bounded domain in ${{\mathbb{R}}^{d}}$, which is a Riemanian manifold with piecewise smooth boundary and suppose that the billiard associated to the geodesic flow reflecting on the boundary according to the laws of geometric optics is ergodic. We prove that the boundary value of the eigen-functions of the Laplace operator with reasonable boundary conditions are asymptotically equidistributed in the boundary, extending previous results by Gérard and Leichtnam as well as Hassell and Zelditch, obtained under the additional assumption of the convexity of $M$.

We study the non-vanishing on the line $\operatorname{Re}\left( s \right)=1$ of the convolution series associated to two Dirichlet series in a certain class of Dirichlet series. The non-vanishing of various $L$-functions on the line $\operatorname{Re}\left( s \right)=1$ will be simple corollaries of our general theorems.

The main results deal with conditions for the validity of the weighted convolution inequality ${{\sum }_{n\in \mathbb{Z}}}|{{b}_{n}}\,{{\sum }_{k\in \mathbb{Z}}}{{a}_{n-{{k}^{x}}k}}{{|}^{p}}\,\le \,{{C}^{p\,}}\,{{\sum }_{k\in \mathbb{Z}}}\,{{\left| {{x}_{k}} \right|}^{p}}$ when $p\,\ge \,1$.

We give a new proof of former results by $\text{G}$. Zampieri and the author on extension of holomorphic functions from one side $\Omega$ of a real hypersurface $M$ of ${{\mathbb{C}}^{n}}$ in the presence of an analytic disc tangent to $M$, attached to $\bar{\Omega }$ but not to $M$. Our method enables us to weaken the regularity assumptions both for the hypersurface and the disc.

Let

$$\zeta \left( s,x \right)=\sum\limits_{n=0}^{\infty }{\frac{1}{{{\left( n+x \right)}^{s}}}}\left( s>1,x>0 \right)$$

be the Hurwitz zeta function and let

$$Q\left( x \right)=Q\left( x;\alpha ,\beta ;a,b \right)=\frac{{{\left( \zeta \left( \alpha ,x \right) \right)}^{a}}}{{{\left( \zeta \left( \beta ,x \right) \right)}^{{{b}'}}}}$$

where $\alpha ,\beta >1$ and $a,b>0$ are real numbers. We prove: (i) The function $Q$ is decreasing on $\left( 0,\infty \right)$ iff $\alpha a-\beta b\ge \max \left( a-b,0 \right)$. (ii) $Q$ is increasing on $\left( 0,\infty \right)$ iff $\alpha a-\beta b\le \min \left( a-b,0 \right)$. An application of part (i) reveals that for all $x>0$ the function $s\mapsto {{\left[ \left( s-1 \right)\zeta \left( s,x \right) \right]}^{1/\left( s-1 \right)}}$ is decreasing on $\left( 1,\infty \right)$. This settles a conjecture of Bastien and Rogalski.

Let $E$ be an elliptic curve defined over $\mathbb{Q}$, of conductor $N$ and without complex multiplication. For any positive integer $l$, let ${{\phi }_{1}}$ be the Galois representation associated to the $l$-division points of $E$. From a celebrated 1972 result of Serre we know that ${{\phi }_{1}}$ is surjective for any sufficiently large prime $l$. In this paper we find conditional and unconditional upper bounds in terms of $N$ for the primes $l$ for which ${{\phi }_{1}}$ is not surjective.

We show that several torsion free 3-manifold groups are not left-orderable. Our examples are groups of cyclic branched coverings of ${{S}^{3}}$ branched along links. The figure eight knot provides simple nontrivial examples. The groups arising in these examples are known as Fibonacci groups which we show not to be left-orderable. Many other examples of non-orderable groups are obtained by taking 3-fold branched covers of ${{S}^{3}}$ branched along various hyperbolic 2-bridge knots. The manifold obtained in such a way from the ${{5}_{2}}$ knot is of special interest as it is conjectured to be the hyperbolic 3-manifold with the smallest volume.

Let $\mathcal{M}$ be a type $\text{I}{{\text{I}}_{1}}$ von Neumann algebra, $\tau$ a trace in $\mathcal{M}$, and ${{L}^{2}}\left( \mathcal{M},\tau \right)$ the GNS Hilbert space of $\tau$. We regard the unitary group ${{U}_{\mathcal{M}}}$ as a subset of ${{L}^{2}}\left( \mathcal{M},\tau \right)$ and characterize the shortest smooth curves joining two fixed unitaries in the ${{L}^{2}}$ metric. As a consequence of this we obtain that ${{U}_{\mathcal{M}}}$, though a complete (metric) topological group, is not an embedded riemannian submanifold of ${{L}^{2}}\left( \mathcal{M},\tau \right)$

Let $G$ be a compact group.

Let $\sigma$ be a continuous involution of $G$. In this paper, we are concerned by the following functional equation

$$\int\limits_{G}{f\left( xty{{t}^{-1}} \right)dt}\,+\int\limits_{G}{f\left( xt\sigma \left( y \right){{t}^{-1}} \right)dt}=2g\left( x \right)h\left( y \right),\,\,\,x,y\in G,$$

where $f,g,h:G\mapsto \mathbb{C}$, to be determined, are complex continuous functions on $G$ such that $f$ is central. This equation generalizes d’Alembert's and Wilson's functional equations. We show that the solutions are expressed by means of characters of irreducible, continuous and unitary representations of the group $G$.

We study Calabi–Yau manifolds constructed as double coverings of ${{\mathbb{P}}^{3}}$ branched along an octic surface. We give a list of 87 examples corresponding to arrangements of eight planes defined over $\mathbb{Q}$. The Hodge numbers are computed for all examples. There are 10 rigid Calabi–Yau manifolds and 14 families with ${{h}^{1,2}}\,=\,1.$ The modularity conjecture is verified for all the rigid examples.

We prove that a Minkowski plane is Euclidean if and only if Busemann's or Glogovskij's definitions of angular bisectors coincide with a bisector defined by an angular measure in the sense of Brass. In addition, bisectors defined by the area measure coincide with bisectors defined by the circumference (arc length) measure if and only if the unit circle is an equiframed curve.

A continuumis said to be Suslinian if it does not contain uncountably many mutually exclusive nondegenerate subcontinua. We prove that Suslinian continua are perfectly normal and rim-metrizable. Locally connected Suslinian continua have weight atmost ${{\omega }_{1}}$ and under appropriate set-theoretic conditions are metrizable. Non-separable locally connected Suslinian continua are rim-finite on some open set.

Let $G$ be a finite group and $H$ be a subgroup. We say that $H$ is degree homogeneous if, for each $x\,\in \,\text{Irr}\left( G \right)$, all the irreducible constituents of the restriction ${{x}_{H}}$ have the same degree. Subgroups which are either normal or abelian are obvious examples of degree homogeneous subgroups. Following a question by E.M. Zhmud’, we investigate general properties of such subgroups. It appears unlikely that degree homogeneous subgroups can be characterized entirely by abstract group properties, but we providemixed criteria (involving both group structure and character properties) which are both necessary and sufficient. For example, $H$ is degree homogeneous in $G$ if and only if the derived subgroup ${H}'$ is normal in $G$ and, for every pair $\alpha $, $\beta $ of irreducible $G$-conjugate characters of ${H}'$, all irreducible constituents of ${{\alpha }^{H}}$ and ${{\beta }^{H}}$ have the same degree.

Maps preserving certain algebraic properties of elements are often studied in Functional Analysis and Linear Algebra. The goal of this paper is to discuss the relationships among these problems from the ring-theoretic point of view.

We find an infinite family of projective monomial curves all of which have $h$-vector with no negative values and are not Cohen–Macaulay.

Let $\mathcal{F}$ be an orthonormal basis for weight 2 cusp forms of level $N$. We show that various weighted averages of special values $L\left( f\otimes \text{ }\!\!\chi\!\!\text{ ,1} \right)$ over $f\in \mathcal{F}$ are equal to $4\text{ }\!\!\pi\!\!\text{ }c+O\left( {{N}^{-1+\in }} \right)$, where $c$ is an explicit nonzero constant. A previous result of Duke gives an error term of $O\left( {{N}^{-1/2}}\log N \right)$.

Let 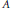$A$ be the inductive limit of a system

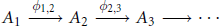$${{A}_{1\,}}\,\xrightarrow{{{\phi }_{1,\,2}}}\,{{A}_{2}}\,\xrightarrow{{{\phi }_{2,\,3}}}\,{{A}_{3}}\,\to \cdots $$

with 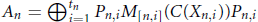${{A}_{n}}\,=\,\oplus _{i=1}^{{{t}_{n}}}\,{{P}_{n,\,i}}{{M}_{\left[ n,\,i \right]}}(C({{X}_{n,\,i}})){{P}_{n,\,i}}$, where ${{X}_{n,\,i}}$ is a finite simplicial complex, and ${{P}_{n,\,i}}$ is a projection in 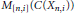${{M}_{[n,i]}}\,\left( C\left( {{X}_{n,i}} \right) \right)$. In this paper, we will prove that 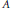$A$ can be written as another inductive limit

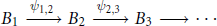$${{B}_{1}}\,\xrightarrow{{{\psi }_{1,\,2}}}\,{{B}_{2}}\,\xrightarrow{{{\psi }_{2,\,3}}}\,{{B}_{3}}\,\to \cdots $$

with ${{B}_{n}}\,=\,\oplus _{i=1}^{{{s}_{n}}}\,{{Q}_{n,i}}{{M}_{\left\{ n,\,i \right\}}}(C({{Y}_{n,\,i}})){{Q}_{n,\,i}}$, where ${{Y}_{n,\,i}}$ is a finite simplicial complex, and ${{Q}_{n,\,i}}$ is a projection in ${{M}_{\left\{ n,\,i \right\}}}(C({{Y}_{n,\,i}}))$, with the extra condition that all the maps 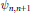${{\psi }_{n,n+1}}$ are injective. (The result is trivial if one allows the spaces ${{Y}_{n,\,i}}$ to be arbitrary compact metrizable spaces.) This result is important for the classification of simple 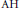$\text{AH}$ algebras. The special case that the spaces ${{X}_{n,\,i}}$ are graphs is due to the third author.

In this paper we consider multipliers on the real Hardy space ${{H}_{2\pi }}$. It is known that the Marcinkiewicz and the Hörmander–Mihlin conditions are sufficient for the corresponding trigonometric multiplier to be bounded on $L_{2\pi }^{p},1<p<\infty$. We show among others that the Hörmander– Mihlin condition extends to ${{H}_{2\pi }}$ but the Marcinkiewicz condition does not.